
김성래 서울대학교 공과대학 응용수학과를 졸업하고 한국과학기술원 선임연구원으로 재직 후 미국 일리노이 대학교에서 박사 학위를 받았다. 미국 워싱턴 대학교 방문교수, 한국 IBM 해외 파견교수 선정위원, 학술진홍재단 과제선정위원 현재 충남대학교 수학과 교수로 재직 중이다 . 저서로는 『미분적분학』, 연구 보고서 15 편, 연구 논문 10 편이 있다.
아르케 (arche, d p x !J) 는 ‘시초’ , ‘시작 이라는 어원적 의마를 가지며, 학술적으로는 ‘원리’ 를 의미합니다.
축차분석론 
 축차분석론
축차분석론
머리말 통계학에 있어서 축차분석론은 고정된 샘플수하에서 다루는 기존의 통계적 개념과 달리 자료에 따라 샘플수를 확률변수로 간주하는 여러 가지 통계적 이론과 방법을 다루는 것이다 . 축차분석 은 1947 년 Abraham Wald 의 저 서 Seq u enti al Anal y s i s 의 출간과 더불어 지금까지 학문 분야에서는 역사적으로 일천하지만 , 많은 통계학자들의 연구로 통계학의 모든 분야에서 괄목할 만한 발전을 이 루어 왔댜 이 책은 수학적으로는 측도이론, 확률론 및 기존의 통계적 여러 이론 에 익숙한 대학원 박사과정 이상울 대상으로 쓰여졌으며, 모두 6 장으로 이루어져 있다. 제 1 장은 축차분석의 개념과 필요한 이유, 더불어 간략 한 역사를 다루고 있다. 제 2 장은 이 분야의 개척자인 A. Wald 의 축차 확률비 검정과 검사특성곡선, 평균표본수 함수와 더불어 일반적인 축차 확률비 검정의 최적성과 상대효율성을 다룬다 . 제 3 장에서는 복합가설에 대한 축차 검정 문제를 다루고, 특히 불변 축차확률비 검정에 관한 여 러 이론에 대하여 논한다 . 제 4 장에서는 재생이론과 비선형 재생이론에 관하여 논하고, 이를 이용하여 축차확률비 검정에서 나타나는 문제를 다룬다. 제 5 장에서는 축차적 추정 문제에 대한 일반적인 개념과 이론에 대하여 살펴보고, 최근에 많이 연구되고 있는 축차적 점 추정과 신뢰집 합 추정문제를 다루며, 마지막으로 제 6 장에서는 축차적 베이즈 절차와 이를 이용한 응용을 다룬다.
앞에서 언급한 바와 같이 축차분석이 통계학 전 분야에 걸 쳐서 광범 위하게 연구되고 있는 관계로, 축차분석의 전 분야 를 다 루 지 못하고 주 요 분야만을 다루게 된 아쉬움과 함께, 전문용어에 대한 우리말 번역에 많은 조언이 있기를 기대한다 . 앞으로 많은 학자 들 이 이 분야에 대한 우수한 책을 집필하여 국내 연구가 활발하게 이루어지기 를 바란다 . 축 차분석의 역사에 관해서는 여러 가지 견해가 있겠지만, 이 책에서는 B. K. Ghosh 교수의 견해에 따른 것 임을 밝혀 둔다 . 이 책을 집필할 기회를 주신 재단법인 대우재단에 감사하며, 아울러 이 책의 출판을 맡아 준 도서출판 아르케에 감사한다. 마지막으로 저자 로 하여금 이 분야를 전공하도록 이끌어 준 Robert A. Wi jsm an 교수 에게 고마움을 표하며, 자료의 수집과 원고의 교정 작업을 도와 준 김 성균 박사에게 진심으로 감사한다. 1999 년 3 월 김성래
차례
머리말 5제1장 축차분석의 역사1.1 축차분석의 개념 91.2 축차분석의 동기 121.3 축차분석의 간략한 역사 18제2장 축차확률비 검정2.1 Wald의 축차확률비 검정 392.2 검사특성곡선과 평균표본수 함수 552.3 축차확률비 검정의 최적성과 상대효율 69제3장 축차 복합가설 검정3.1 하나의 매개모수에 대한 복합가설의 축차검정 773.2 Wald의 축차 복합가설 검정 903.3 불변 축차확률비 검정 98제4장 재생이론과 비선형 재생이론4.1 재생이론 1174.2 축차확률비 검정과 재생이론 1394.3 비선형 재생이론 147제5장 축차추정
5.1 축차추정의 일반적 이론 1615.2 축차적 점 추정 1695.3 축차적 신뢰집합 추정 186제6장 축차적 베이즈 절차6.1 베이즈 절차 2016.2 축차적 베이즈 절차 2076.3 축차적 베이즈 절차의 응용 225참고문헌·237찾아보기·261제 l 장 축차분석의 역사 축차분석의 개념을 기존의 통계적 개념과 비교하여 설명하고, 축차분 석이 탄생하게 되는 필연적인 동기에 관하여 논한다. 또한 축차분석의 역사를 B. K. Ghosh 의 분류에 따라 개념 도입기 , 탄생에서 유년시기, 청년시기부터 오늘날까지의 3 단계로 구분하여 살펴본다. 1.1 축차분석의 개념 통계적 추론의 목적은 전체를 나타내는 모집단(pop ula ti on) 의 특성을 모집단의 부분집합인 표본 (sam p le) 으로부터 이끌어 내는 데 있다 . 전통 적인 통계적 방법은 표본의 수가 일정한 모집단의 일부 구성원으로 이 루어진 표본을 분석하여, 그 자료가 나온 모집단의 특성에 관하여 추론 을 한다. 다시 말하면, 사전에 표본의 수를 고정하여 그 구성원을 결정 하고 이를 바탕으로 모집단에 관한 추론을 한다.
반면에 통계적 축차분석 (se q uen ti al anal y s i s) 은 전통적인 통계적 방 법과 달리 그 분석 대상인 표본에서 최종적인 표본의 수와 그 구성을 사전에 정하지 않고, 모집단으로부터 자료를 차례로 하나씩 혹은 그룹 별로 축차적으로 추출하여, 어느 단계에서 얻어진 축적된 자료의 정보 로부터 모집단에 관한 특성을 추론하는 통계적 방법이다. 다시 말하면, 일반적으로 확률적 실험이나 현상은 반드시 독립일 필 요가 없는 확률변수 또는 벡터들의 관측값 X1,X2, …를 산출한다 축 차분석은 관측값들의 최종적인 수를 미리 고정할 필요는 없지만, 자료 룰 이용할 수 있게 될 떄 어떤 지정된 방법에서 그 자료 자체에 의존할 수 있는 그런 자료를 분석하는 통계적 이론 및 방법과 관련이 있는 것 이다 따라서 이러한 축차분석은 크게 정지규칙 (s t o ppi ng rule 또는 sto p p ing tim e) 과 최종의사결정규칙(t ern 꼬 nal decis i o n rule) 으로 구성되 어 있다. 정지규칙은 모집단으로부터 자료를 어떻게 관측하고 언제 표본추출 을 중지하는가를 나타내는 것이다. 죽, 사전에 표본의 수가 고정되어 있 는 표본으로부터 추론을 하는 전통적인 통계적 방법과 달리, 표본의 수 가 주어지지 않고 표본의 수가 확률변수로서 축적된 자료들의 특성에 따라 표본의 수가 결정된다. 그리고 이 때의 표본추출은 그 추론에서 요구하는 정도에 의하여 미리 규정된 중지규칙에 따른다. 즉, 각각의 n 티에 대하여 실험을 (X1,X2, … ,X,,) 으로중지해야하는지 그렇 지 않으면 추가의 관측값 x .. +1 을 산출하면서 실험을 계속해야 하는가 를 지시하는 것이다. 이 때 n= 1, 2, … oo 에 대하여 정지규칙 N은 확 률변수로서, 사건 N= n 이 (X1 , X2, … , X,,) 에 의하여 생성되는 ¢ 대수 죽, a(X1 .X2, … ,Xn) 의 가측함수가 되는 확장된 확률변수이다.
일반적으로 N 은 0 을 포함하는 자연수이지만, 이 른 바 연속형 시간 모수 문제에서는 N 이 0 을 포함하는 자연수일 필요는 없다. 최종의사결정규칙은 표본추출의 각 단계에서 추론 문제에 관하여 어 떠한 행동을 취해야 할 것인가를 말하는 것으로, 전통적인 통계적 방법 에서 사용하는 추론 방법과 유사하다. 즉, 최종의사결정규칙 D 는 정지 규칙 N 하에서 잘 정의된 어떤 공간의 값을 갖는 a(X!, … ,XN) 의 가 측함수이댜 주어진 문제에 대하여, (N, D) 가 한 쌍 이상 존재할 수도 있다. 축 차분석은 어떤 경우에도 최적 (N, D) 또는 지정된 N 하에서 어떤 바 람직한 기준을 만족하는 최적 D 를 결정하는 것이다. 물론, 그 기준은 문제의 본질에 의해 암시된다. 만약 정지규칙이 어떤 m 에 대하여 1 의 확률로 N= m 이 라면, 그것 에 상응하는 절차를 고정 표본(fi xed-sam p le) 이라고 말한댜 그렇지 않으면 그 절차는 축차적 (s eq uen ti al) 이다. 대부분의 실험들은 시간적 또는 공간적인 순서로 관측값을 만든다는 점에서 본질적으로 축차적이다. 그러나 통계 문헌의 대부분은 고정표본 절차에 따라 그러한 자료를 분석하는 것과 관련이 있다. 이것에 대한 역사적인 이유는, 실험 과학자들 가운데 대부분은 그들의 실험 결과가 우연한 요인에 의해 영향을 받았을 수도 있는 것을 최초로 실현하게 되 었을 때도, 그들은 전체 자료를 수집한 후에만 통계학자들에게 조언을 구하였기 때문이댜
1.2 축치분석의 동기 축차분석의 현대 적 이 론 은 제 2 차 세계 대 전 중, 보다 효 율적 인 샘 플 링 검사 과정의 요구에 따라 미국과 영국에서 동 시에 그 존 재성이 확 인 되었댜 1947 년 A. Wald 가 축차 확률 비 검정 방법을 주내용으로 하여 축차분석의 기초적인 성질과 그 개념에 관한 내용을 담은 Se q u e n t ial Anal y s i s 란 책을 발간함으로써 학계에 축차분석이 처음으로 소개되었 다. 그러나 엄밀한 의미에서는 이미 오래 전부터 많은 문제 를 축차 적 인 개념을 이용하여 해결하였다. 단지 이 를 이용하고 있다는 것 자체 를 깨 닫지 못했을 뿐이다. 제 1 절에서 살펴본 바와 같이 축차분석은 그 개념상 혹은 방법 론 상 사용될 수밖에 없는 동기를 갖고 있으며 이를 요약하면 다음과 같다 . (a) 축차분석이 문제 해결의 본질인 경우 어떤 문제들은 고정표본 절차를 개념화조차 할 수 없다 . 예 를 들 어 산업의 공정관리에서 한 사람이 생산공정에서 일어난 변화 를 감지하기 위하여 일상적으로 1, 2, …의 순간에 XI, X 2, … 를 관측한다고 하자. 여기에서 X,, 은 그 공정에서 n 번째 순간에 생산된 어떤 품목의 표본 에서 나온 평균 측정값을 나타낸다. 공정이 관리상태에 있는 한, 그 관 측값들은 어떤 확률 법칙 lo 에 따라 서로 독립이고 동일하게 분포되어 있다고 가정한다 이와 반대로, 공정이 임의의 순간 N 에서 관리할 수 없게 되는 경우에 XN 의 확률 법칙은 /1 으로 바뀐댜 문제는 그 변화 가 일어나는 N 의 값을 결정하는 것이다. 이런 주제의 일종은 집중 치 료 중인 환자의 혈압 X( t)를 시간 t에 대하여 계속 감시할 때 일어난
다. 이 때 문제는 혈압의 갑작스런 변동을 분석하고 설명하는 방법이다. 분명히 두 예재에서 는 고정표본 분석을 생각할 수 없다. 더 나아가서는 고전적인 바서문제 (secre t ar y p roblem) 에서도 마찬가지이다. 여기서 관 측 자 는 어떤 특성에 따라 본질적으로 l( 최상), ••• , K( 최악)으로 순위가 정해지는 K 대상 들을 다루고 있지만 , 그들을 단지 시각적인 상호 비교 만으로 순위를 정할 수 있다. 그 대상들은 랜덤 순서로 도착하고 그들 중n에— 서l 선오행직 대하상 나들 만과이 비 교선하택여될 n수 번 째있 다도. 착관자측에자게는 순 위모 두x 기을각 되할었당던한 댜 문제는 관측자가 기각하지 않았을 때 최상의 것을 선택할 확률을 극 대화하 는 정지규칙을 설계하는 것이다. 이상의 예에서 살펴본 바와 같이 이런 종류의 문제는 재래의 통계적 방법으로는 개념화조차 할 수 없으며, 오로지 축차분석만이 문제 해결의 본질인 경우이다. (b) 축차분석만이 해를 구하는 유일한 경우 점 추정, 구간 추정 그리고 가설 검정에서 고정표본 절차가 개념화될 수는 있지만 해답을 주지 못하는 문제들이 있다. 예를 들면, 관측값들이 서로 독립이고 동일하며 P(X1=l)=p = l-P(X1=0) 인 베르누이 (Bernoull i) 변수라고 가정하고, p一 1 의 불편추정값을 구하려 한다. 그러 한 추정값은 어떤 m 2: l 에 대하여 고정된 자료 (X1, …, X,, , )을 고려 한다면 존재하지 않는댜 한편, X,,=1 인 최초의 n 으로 정의된 정지 규칙 N 은 그 자체가 p一 1 의 불편추정값이다. 이 정지규칙은 Haldane 의 역표본추출(i nverse samp ling ) 절차로 알려져 있다. 다음에, 관측값들이 미지의 평균 µ와 분산 군을 갖는 서로 독립이고 동일한 정규분포라고 가정하고, 주어진 길이 L 과 주어진 포함범위확률 r 를 갖는 µ에 대한 신뢰구간을 구하려 한다 . 이것이 소위 고정폭 신뢰구간(fi xed - wid t h
confi de nce int e r val) 문제이다. 그와 같은 신뢰구간은 어떤 m:?:1 에 대 하여 고정된 자료 (X1, ···, X,,, )을 고려한다면 존재하지 않는 데 반 댜하여 ,마 S지 t e막 i n으 의로 2 , 단관계측 값절들차이 (S t e구 i n'간s tw[ 0o—- s1ta/ 2g ,e p0 r+o1c/e2d]ur 상e)에 는서 해 서를로 마 독린립한 이고 동일한 균일 확률변수라고 가정하고, 제 1 종과 제 2 종의 오류확률들 울 0 으로 한 가설검정 H。 :Osl/3 대 H1:822/3 에 대하여 살펴보자. 그러면 이 경우에는 어떠한 고정표본 절차도 이것을 만족할 수 없다. 한편, 정지규칙 N 은 X,,s1/6 또는 X,,25/6 를 만족하는 가장 작은 정수 n 을, 결정규칙은 XNs1/6 이면 채택하고 XN:?:5/6 이면 기각하 는 축차분석은 희망했던 목표를 달성한다 . 물론, 어떠한 통계 절차도 바 라던 목표를 달성할 수 없는 상황이 있지만, 이상에서 살펴본 예제들은 축차분석만이 해를 구하는 유일한 방법이다. (c) 축차분석이 경제적인 경우 기존의 전통적인 통계적 분석 방법으로 해결할 수 있는 문제라 하더 라도 축차분석방법을 사용함으로써, 더 작은 표본수 혹은 더 작은 평균 표본수를 가지고 똑같은 추론 효과를 가져올 수 있다. 새로운 미사일을 개발한다거나 혹은 고가의 어떤 제품을 개발할 때는 그 효능을 통계적 으로 테스트한다. 새로운 미사일 개발을 예로 들면, 그 효능을 테스트하 는 전통적인 통계적 방법에서는 사전에 주어진 적당한 표본수에 의거 하여 미사일 발사 실험을 하고, 그 결과를 통계적인 방법으로 테스트한 다. 그러나 새로운 미사일의 성능 테스트에 대한 합격, 불합격의 결과는 통계적으로 처음 주어진 표본수보다 더 작은 표본의 수로도 같은 결과 롤 가져올 수 있다. 이 때 성능 테스트를 위하여 필요 이상의 미사일을 발사한 것이므로, 필요량 이외의 개수만큼 비용 손실을 가져오게 된다.
따라서 표본의 수가 작으면서도 어떤 추론 문제 를 원만히 해결할 수 있 다면 경제적인 측면에서 그만큼 이익이 될 것이다. 축차분석에 대한 근 본적인 매력은, 주어진 문제에 고정표본과 축차적 절차를 모두 적용할 수 있을 때, 축차적 절차가 가장 경제적이라는 데 있다. 축차분석은 실 험의 표본크기, 비용이나 기간을 감축함으로써 경제적인 이익을 가져오 게 한댜 구체적인 예로써 관측값들이 서로 독립이고 동일한 베르누이 확률변수라고 가정하고, 제 1 종의 오류확률을 a 이하로, 가설 H。 :P~ Po 대 H1:P > Po 를 검정하고 싶댜 그러면 최량(균일 최강력) 고정표본 절 차는 어떤 고정된 m 에 대하여 (X1, …, X') 을 관측하고, s,:;:::C 또 는 S111< C 에 따라서 Ho 를 기각 또는 채택하는 것이다. 여기에서 S,,=X1+ … +x,, _nPo 이고 c 는 (a, Po) 에 의해 결정된 상수이다. 한편, 어떤 n=l, …, m 에 대하여 s,,;;:::c+(m ― n)Po 이면 Ho 를 기 각하고 S,,< C ― (m ― n)(1_Po) 이면 Ho 를 채택하는 축차적 절차는, 같은 검정력을 보장하며 기껏 m 인 랜덤의 표본크기가 필요하다. 이것 이 소위 단축샘플링 (cu rt a il ed samp ling ) 절차이다. 더욱이, 약간의 검정 력 손실을 기꺼이 감수하더라도 높은 확률로 m 개의 관측값보다 더 빨 리 결정한다고 하는 더 큰 융통성을 발휘한다면, 어떤 n=n0, n 。 +1, …, M ― l 에 대하여 S,,>a 占이거나 sM;;::: b {M이면 Ho 를 기 각하고 단지 SM < b {M인 경우에만 채택하는 축차적 절차를 이용할 수 있다. 여기에서 no 과 M 은 미리 결정된 것이고 a 와 b 는 (a, n 。, M, Po) 에 의해 결정된댜 이것이 소위 반복유의성검정 (re pe a t ed sig nifica nce tes t) 이 댜 다음에 대 립 가설 이 H< : p;;:::p1 , P1 > Po 으로 바뀌 고, 제 2 종 오류확률이 기껏해야 /3라는 추가된 필요조건을 만족시켜야 한다고 가정하자. 그러면 최량 고정표본 절차의 m 과 c 는 모두
(a, /3, Po, P1) 에 의해 결정된댜 만약 그 때 P=Po 와 P1 에서 평균 표본크기를 극소화하는 절차를 찾는다면, 그 해답은 바로 축차확률비 검 정 ( sequ enti al pro babil it y rati o tes t) 이 다. 이 절 차는 어 떤 m~ l 에 대 하여 S,,~sn+b1 또는 S11~ sn+b2 에 따라 Ho 를 채택 또는 기각한 다. 여기에서 s 는 (Po, P1) 에 의해 결정되고, b1 과 b2 는 (a, /3, Po, P1) 에 의해 결정된댜 한편, 최대 평균표본크가를 극소화하는 절차를 구한다면, 그 해답은 Kief e r -Weis s ' 절차이댜 여기에서는 바로 앞 문제 의 b1 과 b2 도 1 t에 의존한댜 다른 기준에서, 어떤 형태의 축차적 절차가 어떤 결정을 내리기 위한 관측값들의 수를 감축하여 실험 비용을 절감한다는 것은 위의 예제 들 로부터 분명하다. 그 특징은 연속적인 관측값들 사이의 시간 간격이 크 거나 또는 품목 ·의 검사(죽, X 를 관측하는 것)가 그 품목에 해로운 결과 룰 가져올 때 더욱 더 중요하다. (d) 축차분석이 자연적이고 윤리적인 경우 통계적 추론에서 축차분석 방법을 자연스럽게 사용할 수밖에 없는 경우이다. 어떤 제약회사에서 새로운 약을 개발하여 그 효능을 테스트 하기 위하여 인체실험을 하거나, 병원에서 어떤 새로운 치료법을 개발 하여 그 치료법의 효능을 테스트하는 경우에는 사전에 표본을 추출하 여 실험하는 것이 현실적으로 어려울 뿐만 아니라, 아직 그 효능이 입 증되지 않았기 때문에 실험대상에 대한 실험결과의 부작용이 심각할 수도 있댜 따라서 이러한 경우에는 한 사람씩 차례로 약을 투여한다거 나 새로운 치료법을 실시하여 그 결과에 대한 정보를 축척하여 분석함 으로써 그 효능을 테스토할 수밖에 없으므로 자연스럽게 축차분석 기법
을 사용하게 된다. 또한 윤리적으로도 이런 방법을 사용할 수밖에 없다. (e) 축차분석이 고정표본 절차를 공고히 할 수 있는 경우 축차분석이 고정표본 절차 에 대한 추가의 정당성을 부여하는 문제들 이 있다 서로 독립이고 동일하며 미지의 평균 µ와 분산 1 을 갖는 정 규분포의 관측값들을 생각하자. 만약 고정표본 (X1 , ···, X,,, )을 추출 한다면, 표본평균 Y,1, 은 µ의 균일 최소 분산불편추정량이다. 축차적 배경에서 µ 를 불편 (unb i ased) 으로 추정하기 위하여 임의의 정지확률변 수 N과 N 에서의 불편추정량 T N 를 생각할 수 있다. 이 때 주어진 정수 m 에 대하여, (1) su p E/N):,;;m 의 조건에서 Varµ(T 사 또는 (2) sup Var ,』 ( T 사 :,;; m-1 의 조건에 서 Eµ (N) 또는 (3) m-2Eµ (N) +Va rµ (T 사 를 균일하게 극소화 하는 최적의 순서쌍 (N*, T\-) 를 찾는다고 가정하자. 각각의 세 문제에 대하여, 유일한 최적의 해는 N*=m 과 T*,,,= X,,, 이라는 사실이 증명된댜 이러한 결론은 분명히 비축차적 문헌에서 마주치는 것보다 훨씬 더 넓은 상황에서 고정표본 평균의 사용을 정당화한다. 정규성과 불편성의 가정을 생략하면, 유사 한 결론들은 임의의 모수에 대한 표준적인 최대우도추정량에( m-+OO 함 으로써) 점근적으로 적용된다. 유사한 특징이 가설 검정에 관한 Ney m an— Pe arson 보조정리에 대해서도 성립한다. 즉, N~m 과 제 1 종 의 오류확률이 a 이하인 모든 검정들 중에서 Ney m an-Pearson 검정은 검정력을 극대화한다. 따라서 축차분석은 때때로 기존의 어떤 통계적 방법이 최상인가를 보여 준다.
1.3 축차분석의 간략한 역사 제 2 절에서 살펴본 바와 같이 축차적 사고가 통계학자들의 시야를 넓 혀 준다는 것을 입증하였는데, 그 이유는 실험 과정 자체에 그들이 참 여하기 때문이다. 역사적으로 이러한 사고는 세 단계로 전개되었다 . 첫번째 단계는 17 세기 중반부터 1940 년대 중반까지 이어진 축차분석 에 관한 개념 정립시기이다. 어떤 고립된 문제에서 어떤 종류의 축차분 석에 대한 필요성에 눈을 뜬 시기였댜 이 때까지 체계적인 발전이 미 미한 것은 통계적 추론 그 자체가 아직 초기 단계였기 때문이므로 놀라 운 일은 아니 댜 Kolrno g orov 의 공리 와 Ne y man-Pearson 의 보조정 리 가 1933 년에 나왔댜 두 번째 단계는 Wald 에 의해 이끌어진 시기이댜 이 단계는 1940 년 대 중반 이후 1950 년까지 지속되었다. 이 기간에 Wald 와 그의 동시대 사람들은 축차분석을 통계적 추론의 진정한 부문으로 발전시켰다. 그 들은 주로 추정, 가설 검정 그리고 결정이론에서 모수적 문제에 관심 을 가졌댜 그 절차의 이론적 기초는, 비록 결과적인 절차의 성질들이 확률론의 점근적인 방법에 의해 연구되어야만 할지라도, 허용성 (ad miss ib i l ity), 충분성 (su ffi c i enc y), 불변성(i nv ari ance), 그리고 우도함수 (likel ih o od fu nc ti on) 의 개념에 근거를 두었다. 마지막 세 번째 단계는 지난 40 년 동안의 발전 시기이다. 오늘날 연 구 경향은 마아팅게일 (m arti n g ale) 과 재생이론 (renewal the ory ) 등의 더 복잡한 방법에 의해, 많은 분포의 가정을 생략하면서 초기의 절차들 을 어떻게 개선할 수 있는가 하는 문제를 지향하는 것 같다. 새로운 절
차는 바로 그 개념부터 대개 점근성 (as y m pt o ti cs) 에 의해 지배되고, 모 의 연구가 그들의 충분성을 확인하는 것으로 그 역할이 점차 증대되고 있댜 이상의 세 단계를 구체적으로 살펴보면 다음과 같다 . . (a) 개념 정립시기 (1657~1943) 축차분석의 기초는 Huy gh ens(1657), Bemoulli(1 713), Montm a rt (17 14), De Moiv r e(1711, 1756), Lag r ang e (1770~1773) 그리고 Lapl a ce (1774, 1812) 의 연구에서 찾을 수 있다. 그들은 모두 다음 문제의 변종 을 연구하였댜 그것은 당시 에 도박 시 간(D ura ti on of Pla y)으로 알려 져 있었으나 요즘은 혼히 도박사의 파산 문제 (Gambler's Ru in Problem) 문제라고 부른다. 두 경기자 A 와 B 는 a 와 b 의 초기값을 갖고 일련 의 게임을 한다( b 는 00 가 될 수도 있다). A 는 각 게임마다 이길 확 률이 p이고, 그 경우에는 B 로부터 1 의 값을 받으며, B 는 각 게임마 다 이길 확률이 1-P 이고, 그 경우에는 A 로부터 1 의 값을 받는다 (La p lace 는 1812 년 승자가 없을 수 있는 게임도 생각했다). 게임은 그 경기자들 중 어느 한 명이 파산하자마자 멈춘다. 문제는 n 번째 게임 에 파산할 확률 P, ,과, A 가 마침내 파산할 확률 Q(당연히, Q= P1+P2+ …)를 찾는 것이댜 이 문제는 확률론에서 확률보행과 통계적 추론에서 축차확률비 검정의 본질이다. 그러나 그 관계는 오랜 동안 주 목받지 못한 채 남아 있었다(B arnard 1944, 1988). 그 문제 의 해 에 관하 여 Q를 정확히 (Ghosh 1970) 또는 근사적으로 얻는 것은 가능하지만, 임의의 n 에 대한 P, i의 분석적인 결정은 오늘날까지도 굉장히 힘든 일 로 남아 있다.
Dodg e & Rom ig(l 929) 는 아마도 최초 로 축차적인 절 차 를 통계적인 문제에 적용하였을 것이다. 미지의 비율 p의 불량 품 을 포함한 품목 들 의 큰 로트 (Io t) 를 생각하자. 제조업자 는 p.::;:p。이면 그 로 토를 합격시 키고, 그렇지 않으면 불합격시키는 데 동의한다. 여기서 Po 는 지정된 작은 수이댜 Dod g e 와 Ro mig는, 2 회 샘플링계획 (double samp li n g p lan) 으로 알려진 다음의 검사 계획을 고안했다. 그 로트에서 n1 품목 의 초기 표본을 추출하고 이것에서 불량품의 개수 d1 을 센다. 그리고 d1~a 또는 d12b 에 따라서 그 로트를 합격시키거나 불합격시킨다. 여기에서 a 와 b 는 미리 정해진 두 정수이다 (O~a < b). 만약 a < d1 < b 이면 그 로트에서 두 번째 표본으로 n 2 개의 품목을 추 출 하고, 이 표본에서 불량품의 개수 d2 를 센다. 최종적으로 그 로트는 d i +d2~b 이거나 d1+d2> b 에 따라서 합격시키거나 불합격시킨다 . 그 절차는 분명히 H。 :p
단순한 형태로 , X 를 일정한 제품에 대한 어떤 종류의 확률적인 측정값 이라고 가정하자. X 가 평균 µ와 알려진 분산 군으로 정규분포되어 있다고 한댜 만약 생산 공정이 안정되어 있다면 , µ가 지정된 µ 。 주위 에 놓여 있을 것이라는 데 동의한다. 문제는 공정이 작동 중인 어느 순 간에 관리 할 수 없는가 를 조사하는 것이다. Shewha rt는 공정 이 정 말로 안정되어 있다면, 어느 생산 순간에서 표본으로 추출된 k 품목들의 평균 Y 가 99.7% 의 확률을 가지고, 관리 한계선 µ。 -3 이{如과 µ。 +3 이g; 사이에 놓여야만 한다고 주장했다 . 그러므로 그는 다음의 관리도를 제 안한다: l, 2, …의 순간에(말하자면, 1 시간마다) X1, X2, …를 관측 하고, 어떤 n 에 대해서도 又,,이 관리 한계선 밖으로 떨어지면 그 공 정을 멈춘댜 만약 공정이 멈추게 되면 당연히 전문가들이 고장 지점을 찾 아내 그 상태를 고치리라고 기대할 것이다 . 더 복잡한 문제에 대하여 Knudsen(l943) 은 수년에 컬쳐서 통계학자 둘 이 지녀 왔던 욕구를 만족시키는 축차적 절차를 제안했다. 미지의 분산을 갖는 정규분포의 평균에 대하여 유의수준 a (0.001::;; a:;;;0.05) 로 H。 :µ=µ。 대 H1:µ < µo 를 검정하고자 한다. 이 때 고정표본 (X1, …, Xm) 에 기초한 최단로 (sho rt - cu t) 검정은 T111=( Xm-µ 。)/ R111 < c111 이면 Ho 를 기각하는 것이다 여기서 文,,,과 R,,, 은 표본평균 과 표본범위이고, Cm 는 P(T111< c ml µ=µ。 )=a 를 만족하는 값이다. 그러나 이 검정의 p-값( p- value) 이 0.1% 와 5% 사이에 있을 때, 통계 학자들은 그 표본에 의해 마련된 증거가 Ho 에 또는 Ho 에 대립하여 아 주 결정적이지는 못하다는 것을 알 수 있다. 이 딜레마를 피하기 위하 여, Knudsen 은 고정표본 절차를 단순히 축차화했다. 즉 , X1 , X2 , … 를 하나씩 관측하고 T,,< a,1 또는 T,1 느 b,, 에 따라 Ho 를 기각하거나
채택한댜 여기서 수열 (a,,, b, 1 ) 은 P(T,,< a ,,I µ=µ。 )=0.001 과 P(T,, < b,,Iµ=µ 。 )=0.05 에 의하여 결정된다 . 그 절 차의 난점은, 비록 제 1 종의 오류확률이 0.001 과 0.0 5 사이에 놓여 있을 때에도, 그것을 근 사적으로라도 계산하는 방법이 없는 것 같고, 더욱이 최종 결 정에 이르 는 데 필요한 평균표본크기에 관한 의견도 없다는 것이다. 이러한 양상 은 축차적 t-검정과 반복유의성검정에 의하여 개정된다 . 통계적 추론과 실험계획법의 분야에서, Thomp s on( l93 3, 1935) 은 최 초로 축차적 요소를 도입하였다. 두 그룹, 처리 I 을 취하는 첫번째 그룹 과 처리 II 를 취하는 두 번째 그룹으로 나누어진 큰 모집단을 생각하자. P1 과 P2 는 처리 후에 일어나는 두 그룹에 대한 어떤 결정적인 사건의 미지의 발생 확률이라고 가정한다 . 문제는 P1-P 2 를 추정하는 것과 가 설 P1-Pi = O 를 검정하는 것이다 . Thom p son 은 이 두 집단에서 n1 과 n2 관측값의 예비표본을 추출할 것을 제안했다. 즉, g와 요가 P1 와 p 2 의 추정값들이라면, Q( P1, P2) 는 확률 P( Pi > 元)를 나타내고 (J= Q(Pi, ii;_)는 n1+n2 관측값들을 기초로 한 그것의 추정값이라 고 하자 (Thom pson 은 실제로 P1 과 P2 에 대한 적절한 사전 분포에서, Q 대신 사후확률 P(p l> p서를 생각했다). 0 과 1 사이의 증가함수 g( (J)를 선택하고, 두 번째 표본으로 첫번째 그룹에서 mg ( (J) 관측값들을, 그 리고 두 번째 그룹에서 m[l-g( (J)] 관측값들을 추출한다. 여기에서 m 은 두 번째 단계에서 표본으로 추출하도록 허용된 단위의 총수이다. 여기서의 생각은 소위 두 무장 강도 문제(t wo 一 anned band it pro blem) 와 관련이 있으며, 축차실험계획법의 기초를 형성한다. 충화 모집단에 서 전체 평균을 추정하는 것에 관한 Ne y man (l 943) 과 Sukhatm e (l935), 벵골 (Ben g al) 에서 황마 면적을 추정하는 것에 대한 Mahalanobis ( l940)
그리고 함수의 최대값을 추정하는 것에 대한 Ho t ell i n g (l941) 의 기본적 인 생각은 이것과 유사하다. 그들은 모두 주요 문제를 다루는 데 효과 적인 계획법을 세우기 위하여 예비표본을 추출할 것을 제안하였다. 이 시기의 미정리된 착상, 단편적인 노력 그리고 특별한 방법들은 축 차분석의 탄생을 위한 예비단계이자 축차분석의 개념 정립 단계였다. 축차분석은 그리고 두 번째 단계에서 Wald 와 그의 동시대 사람들에 의 해 구체화되었다. (b) 탄생과 유년시기 (1943~1950) 1942 년 6 월, 뉴욕의 컬럼비아 대학에 통계 연구 그룹이 세워졌다. 이 그룹은 W. A. Wal li s 가 지휘하였고, 그들의 목적은 당시 대규모로 이루 어지고 있던 실험에 대한 통계적 방법에 관하여 미국 국방성에 조언하 는 것 이 었다. 그룹의 구성 원 중에 는 K. ]. Arnold, C. Eis e nha rt, H. A. Freeman, M. A. Gir s h ick , H. Hote l lin g , F. Moste l ler, E. Paulson, L. J. Savag e , H. Solomon, A. Wald 그리 고 J. Wol fo w it z 가 있었고, 그들 은 모두 여 러 모로 축차분석 에 공헌했다. W alli s(1980) 에 따르면, 자신 과 F ri edman 은 1943 년 초에 다음 현상을 토론하였다. 고정표본 (X1, …, X,,1) 을 이용한 H。 : f=f。 대 H1: f=f1 의 검정에 대하여, Ney m an- P earson 이론은 A,,, 이 표본의 우도비라고 할 때, A111>c 이면 Ho 를 기각하는 최강력 검정이다. 어떤 문제에서는, 그 기각 기준이 음이 아닌 어떤 함수 ¢에 대하여 c' 로 바뀐다. 그런 경우에는 추가의 관측값 X,,+1, …, Xm 으로 Ho 를 기각하는 결 정이 바뀌지 않을 것이기 때문에, 어떤 n
적인 추측을 하게 하였다: X1, X2. …를 계속 관측하고 Ho 를 채택하 거나, Ho 를 기각하거나, 그렇지 않으면 축적된 자료에 의해 마련된 증 거에 의존하여 표본추출을 계속하는 절차를 아마 만들 수 있을 것이다. 그들은 직관적으로 새로운 절차의 검정력 손실은 평균표본크기의 감축 에 의해 충분히 보상될 수 있다고 주장했다. 그들은 실제적인 규칙을 정밀하게 만들어 가는 방법을 완전히 알지 못했기 때문에 Wol fo w it z 에 게 조언을 구했댜 그러나 Wol fo w it z 는 그러한 절차의 존재성에 회의적 인 태 도를 보였댜 그러 나 Wall i s 와 F ri edman 는 1943 년 4 월 초 Wald 에 게 자신들의 생각을 이야기했다. Wald 는 처음에는 별다른 관심을 보이 지 않다가, 이틀 후에 그들에게 전화하여 그들의 추측이 정말로 옳았음 을 인정하였다. 그 후의 모임에서, 그는 굉장히 단순한 새로운 절차의 규칙을 설명했다. 즉, n=l , 2, …에 대하여 A,,
올 처음으로 학계에 소개한 책이기도 한 Wald 의 Seq u enti al Analys is 는, 1947 년에 출간되었으며 이는 1945 년 그의 두 논문의 산물이다. 홍 미 있는 것은, 대부분의 경우 실제적인 참고 자료는 Wald 의 1945a 논 문에 거의 축어적으로 나타났는 데도, S t an fo rd 에서 S t eklov 를 거쳐 Tok y o 에 이르는 수백 명의 저자들이 Wald 의 책을 참조했다는 것이다. 그 동안 영국에서도 영국 군수성이 통계 품질관리를 위한 부대를 창 설했다 Barnard(l988) 가 회상한 바와 같이, 그는 1942 년 신병으로 모 집되었고, 그 부대의 다른 구성원으로는 F. J. Anscombe, P. Armitag e , J. P. Burman, R. L. Plackett 그리 고 C. M. S t ockman 이 있었다. 그들 역시 여러 모로 축차분석에 공헌했다. 축차검정에 있어서, 1944 년부터 시작된 Barnard 의 독립적인 연구는 두 가지 중요한 측면에서 Wald 의 전개와는 다르다. Barnard 는 관심을 베르누이와 포아송 (Po i sson) 모형 으로 한정했으며, 그의 분석 방법은 도박사의 파산 문제에 관한 La p lace 의 고전적 방식과 유사하였다 (Barnard l946). 얼마 후 영국 그 룹은 우연히 Wald 의 ‘기말 보고서를 입수할 수 있었다 (S t ockman 1944). 축차확률비 검정은 두 가지 두드러진 특징을 가지고 있다. 첫째, 축 차확률비 검정의 오류확률이 미리 정해진 값 ao 과 /3o 를 초과하지 않 게 하고 싶다면, Wald 는 a 。과 /3 o 가 상당히 작은 한, lo 과 f1 이 무엇 이든 상관없이, 경계치로 A= (l-/3。 )/a 。와 B= /3。 (l-a 。)을 선택하 면 목적을 달성할 수 있다는 것을 증명하였다. 둘째, 관측값들이 서로 독립이고 동일하게 분포되어 있다면, 축차확률비 검정은 오류확률이 기 껏해야 축차확률비 검정의 것과 같은 축차 또는 고정표본의 모든 검정 들 가운데 두 가지 평균표본크기 E(Nl/0) 과 E(Nl f!)을 극소화한다.
잘 알려진 이 최적 성질은 특별한 경우에 대해서는 Wald0945a) 가 증 명하였고, 일반적인 경우에 대해서는 Wald & Wolfo w i tz( 1948, 1950) 가, 그리고 부분적으로 Arrow, Blackwell & G i rsh i ck(1949) 이 증명하 였다(특별한 경우는 AN 이 1 의 확률로 경계선에 도달할 때 일어난다). 여러 가지 문제가 뒤이어 제기되었다. (1) 축차확률비 검정의 오류확 률과 평균표본크기의 정확한 값을 어떻게 구하는가? 이것은 어떤 특별 한 f에 대하여, Burman0946), Gir s hi ck (1946b), Wald(l947a 부록), P6lya 0 948), Samuelson(l948) 그리고 Walker(19_50) 에 의해 다루어졌 다. 그 과정에서, 이들은 La p lace(l812) 에 의해 제기된 오래 된 문제도 역시 해결하였다. (2) 축차확률비 검정의 기법을 실제적인 상황에 어떻 게 적용하는가? 이에 관해서는 J ohnson(l960) 과 J ackson(l961) 의 참고 문헌 목록은 수많은 예제들을 인용한다. (3) 축차확률비 검정을 lo 과 (또는) A 이 미지의 모수를 동반하는 경우에까지 확장할 수 있는가? Wald(l945a) 와 G ir s hi ck(1946a) 은 어떤 두 표본 문제로 확장하였다. Wald (l 945a) 와 Arrnit a g e(l947) 는 다른 경우에 대하여 똑같은 시도를 하였지만, 성공적인 결론은 나중에 나왔다. (4) 셋 또는 그 이상의 단순 가설 중 하나롤 식별하는 것에 대하여 축차확률비 검정과 유사한 절차 를 찾을 수 있는가? Sobel & Wald(1949) 그리고 Arm it a g e(1950) 는 이 방면에서 선구적인 연구를 해 냈다. 그들은 이러한 목적으로 둘 또는 그 이상의 축차확률비 검정의 채택역, 기각역 그리고 연속역들을 결합 시켰댜 가설 검정에서 축차분석의 성공은 여러 연구자들이 통계적 추정을 축차적 구성에서 고찰하도록 하였다. Haldane(1945) 과 S t e i n(1945) 은 점 또는 구간 추정에서 몇 가지 풀리지 않은 문제들이 축차적 절차에 의
해 풀릴 수 있다는 것을 보여 주었다. Gir s hic k , Moste l ler & Savag e (1946), Blackwell(1947) 그리고 Bara ki n(1949) 은 임의의 정지규칙에서 추정량의 불편성을 연구하였고, Wol fo w it z(1947) 는 Cramer-R ao 부등 식 (Cramer-Rao i ne q ua lity)을 축차적인 유사한 부등식으로 발전시켰으며 그리고 Lehmann & S t e i n (1 950) 은 완비성 개념을 축차 추정량에까지 확 장시켰다. 그러나 이러한 것은 최적 추정량을 찾기 위한 구체적인 방법에 이르지 못했다는 점에서 탐구상의 연구였댜 사실 Ste i n & Wald(l947), Anscombe 0947) 그리고 Wol fo w it z(l950) 의 결과는 일정한 공식에서 최적 신뢰구간 또는 점 추정량은 잘 알려진 고정표본의 대응 추정량이 될 수 있다는 것을 보이려는 경향이 있다. 그것은 이러한 경우에 있어 서, 그 정지규칙은 다루기 위한 어떤 대상도 주어지지 않고 결과적으로 는 고정표본 절 차가 정지할 때와 동시에 억지로 멈추게 한다는 것이다 (가설검정에서 그 ‘대상’ 들은 f0 과 f1 이 다) . 반편에 Wald(l950) 는 관측 값들이 [0-1/2, 0+1/2] 상에서 서로 독립이고 동일한 균일분포를 이 룰 때, 진정한 축차적 절차가 (2 차 손실하에서) 0 의 최적 추정량을 산출한 다는 것울 보였다. 이 때 계속되는 단계에서 표본범위는 대상 1 을 갖는다. 이 때 이미 Wald (l 947b) 는 Von Neumann-Morge nste r n 게임 이론 과 자신의 축차적 구성에서 나타난 통계적 결정이론을 종합하였다. 이 것은 1950 년 그의 유명한 책에서 더 상세히 설명되었다. 불행하게도, 그 결과는 주로 존재성과 완비성 정리들과 관련이 있는 매우 일반적인 것이라서 종종 통계적 관심이 있는 특별한 문제에 대한 해답을 마련하 지 못하였는데, 이것에 대한 예외가 축차확률비 검정의 이론이다. 그 동안, 축차분석은 확률론의 발전에도 영향을 주었다. 서로 독립 이고 동일하게 분포된 관측값들을 기초로 한 축차확률비 검정의 연속
역은 nzl 에 대하여 b < S,, < a 로서 표현할 수 있댜 여기에서 S,,= Z1+ … +z,, 이고 Z;= log { /1(X;)/fo ( X, )} 이댜 확률 론 가 들 은 곧 바로 축차확률비 검정은 확률보행, 검정력함수 P(S,,za I/ )는 경계선 울 넘어설 확률 S,, 一 nE(S1) 은 마아팅게일로 인지하였다. Wald(l944, 1947a) 자신의 연구 결과와 함께 이 것은 Kac( l9 45), Blackwe11(1946), Blackwell & Gir s hic k (l946) 그리고 Feller(l950) 가 확률보행, 재생이론, 그리고 마아팅게일에 더 많은 연구를 하도록 자극을 주었다. 여러 해가 지나고 많은 성과를 거둔 이후에도, Blackwell(l986) 은 여전히 자신이 축차확률비 검정에 관한 Wald(l945a) 방정식 E(ZN) = E(N)E(Z1) 을 임의의 정지규칙 N 으로 일반화했던 자신의 1946 년 논문에 관한 자부 심을 간직하고 있다. Abraham Wald 는 1950 년 12 월 13 일 비 행기 충돌 사고로 세상을 떠 났다. 그의 시대는 미래의 통계학자들에게 두 가지 유산을 남겼다 . 실제 적인 측면에서 축차분석의 출현은 실험 과학자들과 통계학자들이 어떠 한 방법으로 공동연구를 해야 하는가에 대한 인식을 바꾸어 놓았다. F i sher 와 다른 사람들은 이미 축차적 사고를 과학적 연구의 사전 계획 으로 도입하였다. 그러나 여전히 실험의 착수와 종결 사이에서 계속해 서 분석되지 않는 경우도 있다. 축차분석은 실제의 실험 과정에서 더 친밀한 공동연구를 하도록 하였다. 더욱이 과거와는 달리, 통계학자들 은 축적된 자료가 불충분할 때에도 어쩔 수 없이 최종 결정을 내리는 듯한 느낌을 더 이상 받지 않았다. 이론적인 측면에서는 Wald 와 동시 대 사람들은 통계학적인 연구가 어떻게 수행되어야만 하는가에 대한 개념을 바꾸어 놓았다. 그 당시의 통계분석은, 대부분 첫째가 직관적 통 찰이고 둘째가 수학적인 정확도를 의미했다. 바로 전 단락에서 언급한
연구 들 로 Wald 시대에 는 그 순서 가 바뀐 것만은 분명하다. Wald0944, 1945a, 19 5 0) 의 위험함수 (r i sk fun cti on ), 결정합수 (dec i s i on fun cti on ), 허용성 (a dmi ss i b il ity), 완비군 (com p le t e class ), 그 리고 최적성 (o pti ma lit y) 의 개 념은 매우 실제적인 생각이었고 여 전히 수학적 으 로 정확하 댜 그 의 일반적인 구성에 대한 끊임없는 추구와 수학적 해답을 구하려 는 엄격한 자세는, 그의 동시대 사람 들 과 후계자들에게 많은 영향을 주 었다 그가 동기를 부여하는 요인으로서 직관적 통찰을 싫어하지 않았 다는 것은 그의 1945b 논문 에 분명하게 나타나 있다 . (c) 청년기부터 성인가인 오늘날까지 (1951 ~) 축차분석은 그 탄생 이 후 지금까지 다방면에 걸쳐서 눈부신 발전을 거듭해 왔댜 축차분석에 관한 일부 주제들은 Bechhofe r , Kief e r & Sobel0968), Fu0968), Wasan0969), Ghosh(1970), Chow, Robbin s & Sie g m und(1971), Chemoff (1 972), Nevelson & Hasm ins ki i(1 973), Armi tag e 0975), Weth e rill ( 1971), Shir y a eev(1978), Govin d araju l u (1981 ), Sen(1981, 1985), Wooclroofe 0 982), Whit tle( 1982, 1983), White- head(1983), Sie g m und(1985) 그리고 Weth e rrill & Glasebrook(1986) 의 책에서 아주 집중적으로 취급되었다. 1940 년대 말에, 노스캐롤라이나 대학은 통계학계의 성지로 간주되었 댜 S. Monro 는 1948 년 가을, 그 곳에서 대학원 공부를 시 작했다. 몇 달 후에, 학과장 H. Ho t ell i n g은 Monro 에 게 박사 학위 연구를 위 한 어 떤 특별한 생각을 가지고 있는가를 물었다. Monro 는 다음 문제를 제안 했댜 그것은 그가 일찍이 전 동급생 A. H. Bowker 와 대화 도중에 떠 오른 것이다 . 만약 M(x) 가 알고 있는 함수이고 방정식 M(x)=a 는 유 일한 해 x= 0 를 갖는다면, O 를 결정하기 위한 Newt on 방법은 초기의
추측값 X1 으로 시작하여 n=1 , 2, …에 대하여 연속적인 근사값 x,,+1=x,,+a,,[a-M(x,,)] 에 의해 정확도를 높이면서 o 를 추정하는 것이다. 여기에서 a,,=1/M'(x , , )이고 M'(0) -=l=- 0 이댜 함수 M(x) 의 형태는 모르지만 x=x1, X2, ·에서 여전히 M(x) 의 확률값 Y1, Y2, …를 관측할 수 있을 때, O 를 통계적으로 어떻게 추정해야 하는가 (Monro 는 실제로 분포함수 M(x) 와 이것의 a- 분위수 0 에 대한 문제를 제기했다)? Ho t ell i n g은 그 문제는 본래 통계적인 것이 아니라는 반응을 보이면서, Monro 에게 다른 학부 교원들과 그 문제를 상의하도록 권했 다. 그래서 Monro 는 ]. Wolfo w i tz 그리고 D. ]. F i nne y에게 이야기를 꺼냈으나, 아무 성과도 없었다(당시에 Wol fo w it z 는 축차분석에 관한 권 위자였고, F i nne y는 Monro 가 축차화하려고 시도 중이던 프로빗 분석 (pro bit anal y s i s) 으로 잘 알려 져 있었다) . 1949 년 가을, Monro 는 결국 H. E. Robb i ns 에 게 자신의 생각을 이 야기 했다. Robb i ns 는 즉시 그것을 통계적 문제로 인지하였고, 그것을 풀기 위한 수학적 논법을 마련하였 댜 그 해답은 다음과 같다: Za,1=00 이고 La~, < oo( 예를 들면, a,,= n-1 )인 양수들의 수열을 선택하고, Newt on 방법에서 M(x,1) 을 Y,1 으로 대치하면서, 이러한 a,' 들을 사용한댜 이것이 Robbin s & Monro(l951) 의 확률 근사법 (s t ochas ti c app ro x ima ti on me t hod) 이댜 여 기에서 비록 어떠한 정지규칙도 그것에 의해 제안되지 않더라도, 결과 적인 x,, 은 확률적으로 0 에 수렴한다는 것을 보였다. 그 방법은 생물적 인 정 량에 있어 서 Di xon 과 Mood 의 상하향법 (up and down meth o d) 의 더 복잡한 해석이다. 일 년 후에, Kief e r & Wol fo w it z(l952) 는 Ho t e lli n g의 오래 된 문제를 해결하기 위하여 그것을 확장시켰다. 연속형 시간-모수 과정에 있어서 가설 검정과 모수의 추정에 대한 축차분석의 요소들은 Dvoretz k y, Kief e r & Wolfo w i tz( l953a, 1953b) 에
의해 도입되었다. 이 구성에서는 초기의 (X1 , …, X,,), n2l 을 확률 과정 {X(t) , t티 0} 으로 대치하고, f(x 1, t)는 X (t)의 분포를 나타낸 댜 첫번째 논문에서, 그 들 은 축차확률비 검정에 관한 Wald(1945a) 의 결과들은 그 과정이 동차이고 독립적인 증분을 가지고 있을 때 실행될 수 있다는 것을 보였다 . 두 번째 논문과 Ki e f er0957) 에서는 큰 f의 집 합에서 모수 O 를 추정하는 데 고정-표본 추정 절차가 최적이라는 것을 보여 주었댜 한편, T ry bula(1968) 는 같은 f의 집합에서 어떤 0 의 함 수들의 최소 분산불편추정에서 축차적 절차가 최적이 될 수 있다는 것을 보였다 예를 들면, 0 가 포아송 과정에서 단위 시간당 평균이라 고 가정하자. 그러면 O 를 추정하가 위해서 Dvoretz k y, Kief e r & Wol fo w it z0953b) 는 고정된 시간 t까지 그 과정을 관측할 필요가 있 고, O 를 x i/t로 추정하며 t가 상당히 클 때 사실상 그것은 어떤 다른 추정량이나 마찬가지라고 말하고 있다. 만약 µ=0-I 울 불편으로 추 정하고 싶다면, T rybula 는 k2l 에 대하여 추정량 Tk/k 들의 집합은 µ에 불편이라는 것을 보였다. 여기에서 Tk 는 X( t)가 k 와 같아지는 최초의 시간이댜 더욱이, Wol fo w it z(1947) 의 결과에 의하면, 어떤 다 른 정지시간 T 과 T 하에서의 어떤 불편추정량 µT 에 대하여 Eµ(Tk) Varµ(Tk)=µ-3 < Eµ(T) Varµ(µ 김이다. 통계적 추론에서 하나의 중요한 문제는, 결정을 하는 데 어떤 관측값 의 함수를 사용해야 하는가이다. Bahadur(1954) 는 충분성의 고전적인 Halmos-Savag e 개념을 축차분석적으로 확장시키고, (N, D) 를 세우 기 위해 단지 충분이고 추이적인 (su ffi c i en t and tran sit ive ) 함수들의 수 열만을 고려할 필요가 있다는 것을 보였다. 이것이 의미하는 것은 예를 들어, 만약 관측값들이 미지의 µ와 군을 갖는 서로 독립이고 동일하게 분포되어 있다면, 표본평균 文,,과 표본분산 초는 n2l 에 대하여 그러
한 수열을 형성하고, 따라서 (µ, a2 )과 관련한 어떤 문제들에 대하여 (N, D) 는 X1, …, X, ,이 관측된 후 단지 (X,,, s?, )만을 사용해야 한다는 것이다. Hall, Wi jsm an & Ghosh0965) 는 이 사실을 불변성 의 Hun t 一 S t e i n 개념과 결합시켜, 축차분석에서 여러 가지 광범위한 문제들을 충분이고 추이적인 수열로 다룰 수 있다는 것을 보였다. 바로 전의 예제에서 이 것이 의미하는 것은, 만약 결정이 관측값에서의 척도 변화에 의해 영향 을 받지 않아야 한다면, ?z::?:1 에 대하여 Y, J S,1 은 µ/
러한 결점들 은 Kiefer & Weis s (l957), Ande rs o n (196 0 J, Schwarz 0962), Kief e r & Sacks0963), Armi tag e , McPherso n & Rowe0969J, Robbin s (l970) 그리고 다 론 저자 들로 하여금 새 로운 축차적 절차믈 개 발 하게 하였다. 그 들은 모두 그 축차확률 비 검정이 가진 결점을 개선하 였다 대부 분 의 새로운 절차들 의 채택역과 연속역은, 축차확률 비 검정 의 것과 달 리, ‘곡선 모양의’ 경계선 에 의해 특징지 워진다 (즉, 축차확률 바 검정 의 A 와 B 는 이제 n 을 포함한다). 오류확 률 의 계산뿐만 아니라 실제로 그 경계선의 결정 은 Anderson0960), Woodroofe ( 1976) 그리고 Lai & Sie g m und(1 9 77, 1979) 가 발전시킨 점근성에 의해 매우 용이해 졌 다 그 후에 Berk0978), Lai( l 978), 그리고 Berk & Brown0978) 은 다양한 절차들 의 상대효율을 비교하는 기법을 발견하였다. 점 추정 분야에서, An s combe(l953) 는 어떤 문제에서는 축차적 절차가 고정표본 절차 만큼 효과적이라고 결론지음으로써, 당시의 결고뜹곱끝 요약 하였다. 더욱이 Anscombe(l952) 의 유명한 Anscombe 정리는 서로 독립 이고 동일한 분포를 갖는 관측값들을 기초로 한 임의의 정지확률변수 N 하에서, N 이 확률적으로 점점 커짐에 따라 µ=E(X1) 를 文 N 으로 일 관성 있게 추정할 수 있다는 것을 나타낸다 . 그럼에도 불구하고, Robbin s (1959) 는 미지의 a 를 갖는 정규 모집단의 µ를 추정하는 좋은 절차를 얻 기 위한 기발한 착상을 제안했다 . 2 차 손실에서 고정표본 (Xl , …, x,,) 을 기초로 한 µ의 미니맥스 추정값(minim ax esti m ato r ) 이 Y,n 이라 는 것은 잘 알려져 있다. 만약 a 가 알려져 있다면, 더 일반적인 위험 cm+E( 文 ,n ― µ)2 을 극소화하는 표본크기는 가장 작은 정수 m*2 a/ 됴일 것이댜 여기에서 c 는 관측할 때마다 소요되는 비용이댜 이러 한 사실에서 Robb i ns 는 a 가 미지수일 때, 위험 cE(N) +E(X,v - µ)2
를 극소화하기 위하여 다음 절차를 제안하게 되었다. n 。 ~3 관측값 들 로 시작하여, N* 를 가장 작은 수 n~ max[n0, S,,/Vc] 로 잡고, s,, 이 표본표준편차라고 할 때, 첫 N. 를 µ의 추정값으로 사용한다(R obb i ns 은 실제로 El X11’ -µI 를 생각했다). 그는 (N\ X N· )이 c-->O 일 때, (N\ 天 A’.) 과 (m\ 又 ,1 1 . )의 위험이 동일해진다는 의미에서 점근적 으로 최적이라는 것을 보였다 . S t arr(1966) 는 그 절차를 더 일반적인 위 험함수하에서 아주 철저하게 조사하였다. Bic k el & Yahav(1967) 는 베 이즈적 관점에서 유사한 절차를 개발하였다. 위와 유사한 생각은 Chow & Robb i ns (1 965) 가 고정폭 신뢰구간을 찾기 위해서 S t e i n 의 2 단계 절차를 일반화하는 데 사용하였다 . 관측값 들은 이제 정규분포일 필요가 없다. 만약 6 가 알려져 있고 m~4a 2 d2/ 간인 가장 작은 정수 m 개의 고정표본을 관측한다면, 구간 [ X,1 1 一 d/2, X,,,+d/2] 는 d--+0 일 때 확률 r 로 µ를 포함한댜 여기 에서 a 는 표준정규분포의 (1+-y )/2- 분위수이다. 따라서, 6 를 모를 때 Chow 와 Robb i ns 는 다음과 같이 제 안한댜 즉, X1 , X2 , … 를 하나씩 관측하고, N 은 n~4a2S~,/d2+4a2/n 간을 만족하는 가장 작은 정수 n 으로 잡고, 희망하던 µ에 대한 구간으로서 [XN-d/2, XN+d/2] 를 사용하면, (µ, d.) 가 무엇이 되더라도, d--+0 일 때 포함범위확률이 r 가 되고, 확률적으로 N/m--+1 이며 E(N)/m--+1 이라는 의미에서 그 구간 은 점근적으로 최적이라는 것을 증명하였다 (4a2/nd2 항은 X1 이 연속형 분포일 때 무시될 수 있다). 그러나 S t e i n 의 구간과는 달리, 임의의 d 에 대하여 [XN-d/2, XN+d/2] 의 포함범위확률이 실제 r 보다 작아질 수 있다는 데 주목해야 한다. W ij smann(1981) 은 지정된 N 하에서 신뢰
구간을 얻는 약간 다 른 문제로써 f3 - 프로텍션 문제 를 제기하였다. 즉, 참인 모수 µ에 대한 포함확률이 a 이고 오류모수 µ-a(µ) (a 는 실수 함수) 를 포함하는 확률이 f3 이하인 신뢰구간을 추정하는 것으로, 이것 을 f3-프로텍션이라 하였댜 일반적으로 비모수 추정에서 F 가 연속형이라는 것을 제외하고, f의 실제적인 형태 또는 그것의 분포함수 F 는 모른다고 가정한다. Savag e & Se t huraman(l966) 은, (Xl , …, x) 과 ( Yl , …, Y,, )은 n 칙의 표 본추출 단계에서, 각각 F 와 G 로부터 관측될 때 o ( > l) 가 지정되면 서, 검정 H。 : F= G 대 H1:F= G8 의 이표본 문제를 생각하였다 그들 은 불변 축차확률비 검정을 얻었고, 그것은 계속되는 단계에서 (X1,X2,···X,,, Yi, …, Y, ! )들 가운데 (Y1, …, Y,I) 들의 정렬된 순 위를 사용하면서 끝난다(여기에서 불변성은 관측값들의 연속이고 단조인 변환하에서 성립한다). 일찍이 W ils on, Rhodes & Braclle y(l 963) 는 유사 한 생각을 하여 축차검정을 개발하였지만 이는 Hall, Wi jsm ann & Ghosh(l965) 의 이점 (bene fit)을 살리지 못하는 덜 효과적인 것이다. 비 모수 문제들의 일반적인 어려움은, F 를 모르기 때문에 위치와 척도모 수들에 관한 ‘자연스란 가설들을 불변 축차확률비 검정으로 분석할 수 없다는 데 있다(예를 들면, 위의 가설 F= G 합트 매우 인위적이다). 더 유 망한 접근법은 S t rassen(1967) 이 이산형 시간을 갖는 마아팅게일에 대 한 Skorokhod- 매장 (Skorokhod-embed di n g) 문제를 확장시킴으로써 나 왔댜 그의 정리는 본질적으로 마아팅게일(예를 들면 경험분포함수, 순위 -순서 통계량, 둥)을 브라운 운동 과정으로 근사적으로 나타내고, 브라 운 운동 과정의 잘 알려진 성질들을 이용할 수 있다는 것을 보였다. 이 사실의 가장 빠른 응용들 중 일부는 Sen & Ghosh(l971, 1974) 에 의해 F(x) 가 F(x-0) 의 형태일 때, 0 에 대한 축차적 고정폭 신뢰
구간과 0= 0 。 대 0= 01 에 대한 축차검정을 개발하는 과정에서 이루 어졌다. 그들의 절차는 계속되는 단계에서 순위 _ 순서 통계량들의 수 열을 이용한다. 축차분석에서 가장 유용하면서도 소홀히 다루는 기법 들 중 하나는 Cherno ff( 1959) 의 실험 계획 법 (des ig n of ex p er i men t s) 이다. H。 : 0 혼 °2 대 H1: 81 < %를 검정한다고 하자. 여기에서 01 과 02 는 두 모집단 I 과 II 의 비교 가능한 두 모수들이다(예를 들면 비율, 평균, 분산). 언제 H。 를 채택할 것인지, Ho 를 기각할 것인지 또는 계속할 것인지를 지시할 뿐만 아니라 계속되는 각 단계에서 어느 모집단을 표본추출할 것인지 를 지시하는 절차를 마련하고자 한다. 직관적으로 만약 01 과 0 2 가, 6l 이 62 보다 훨씬 더 작으면서, 분산이 여과 석으로 알려진 두 모집단 의 평균들이라면, 상대적으로 더 자주 II 를 관측하려 할 것이다. Cherno ff는 관측할 때마다 소요되는 단위 비용 c, Kullback-Leib l er 정 보지수 그리고 01 과 02 의 최대우도추정값을 기초로 하여 이 문제에 대한 형식적인 정지규칙을 고안했다 (Kullback- Leib l er 정보지수는 하나 의 오류확률이 c----> O 일 때 0 으로 향하는 반면 다른 오류확률을 고정시켜 놓는 지수율로서 설명될 수 있다). Cherno ff는 01 과 02 가 유한히 많은 가능한 값들을 갖는다고 가정했고, Albe rt (l961) 는 이것을(무관심 영역 을 필요로 하면서) 무한히 많은 경우로 확장했으며, Kief e r & Sacks (1 963) 는 이 것을 Schwarz(l962) 의 결과와 통합하였다. 그들은 모두 Cherno ff의 기본적인 절차가 어떤 (01' 02) 값에 대하여 좋아지면 반 드시 어떤 다른 (01, t%)값에 대해서는 나빠질 수밖에 없는 다른 절차 들에 비해 점근적으로( c-o 일 때) 최적이라는 것을 보였다. 계획법의 특색은 Robbin s , Sim ons & S t arr(l967) 에 의해서 미지의 분산들을 갖 는 두 모집단의 평균에 관한 검정 01=02 에 대한 축차절차를 세우는
데에 도 도입 되었다 . 그 러나 그 들 절차는 앞서 기술된 Chow & Robbin s (196 5 ) 의 노 선을 따라 개발되었다. 축차 분석의 방법은 수많은 분야, 특히 산업의 공정관리와 임상 실험 을 동반하는 의학 연구에서 가장 두드러지게 이용되어 왔다 . 일부의 응 용은 그 들 이 새로운 문제와 방법을 발생시켰다는 점에서 결코 틀에 박 힌 것이 아니었다. Pa g e0954) 는 전통적인 Shewhart 관리도가 공정의 이상을 초기에 감지하 는 데에는 비효과적이라는 것을 가장 먼저 인식 한 사람 들 중 하나였다. 그는 이것을 개선하기 위하여 축차확률비 검정 에 기초한 이론을 이용하였고, 그 공정의 평균이 변화했는가를 점검하 기 위하여 n2l 순간에서 又 1+ …+ x, ,의 값들을 조사하는 누적합관 리 도 (CUSUM chart, cumulati ve sum ch art)를 고안하였다. 누적 합관리 도의 도표적 표현은 공정에 대하여 그것을 해석하는 전문관리자를 필 요 로 하지 않는다는 사실을 확실하게 말해 준다. 1 의 검정력을 갖는 Robb i ns(l970) 의 검정은 초기에 감지하는 유사한 목표를 가진다 (L ai 1977) ; 이 검정은 본질적으로 하한 경계선이 없는 축차확률비 검정이 댜 Arrnitag e (l 95 4, 1975) 는 의학 분야에서, 축차분석의 응용을 개척하 였다 수년간에 걸쳐서, 그는 임상 실험의 도덕적 요구와 특수한 제한 을 가설 검정과 추정에 대한 축차적 절차를 개발하는 데 교묘하게 반 영하였다. Ar mitag e , McPherson & Rowe (l 969) 는 반복유의성 검정을 고안하였댜 오늘날에 와서는 고속 컴퓨터의 출현과 소프트웨어의 개발로, 지금까 지 계산이 쉽지 않았던 복잡한 정지규칙에 따른 여러 문제들을 시뮬레 이션 기법 등을 사용하여 쉽게 해결할 수 있게 됨에 따라, 축차분석에 관한 연구가 활발히 진행되고 있다.
제 2 장 축차확률비 검정 1945 년 Wald 는 통계적 검정문제에서 고전적인 방법을 탈피한 새로 운 방법인 축차적 통계검정 방법을 제시하여 소개하고, 1947 년에 Seq u enti al Anal y s i s 라는 책을 발간하였댜 이 장에서는 Wald 의 축차 확률바 검정을 소개하고, 이에 따른 검사특성곡선과 평균표본수 함수를 다룬댜 또한 축차확률비 검정의 최적성을 다룬댜 2.1 Wald 의 축차확률비 검정 고전적인 통계적 검정 (h yp o t hes i s t es ti n g)은 무작위 표본 (random sam p le) 이 이루어진 후에 귀무가설 (null hy po th e sis ) H0 을 채택하거나, 대 립가설 (al t erna ti ve hy po th e sis ) H1 을 채택하게 된다. 이 때 두 가지 가설 중 하나를 선택하는 데 주저할 필요가 없는 강력한 통계적 자료가 있어서 선택이 용이할 때도 있지만, 하나의 가설을 채택하는 데 주저할 만한 통계적 자료가 주어질 때가 많다. 그러나 고전적인 통계적 검정은
두 가지 가설 중 하나 를 반드시 채택하게 한다. 축차적 검 정 (se q uen ti al hy po th e sis t es ti n g)은 주어 진 자 료 가 두 가 지 가설을 채택하는 데 있어서 유력한 증거를 제시하지 못할 때는 제 3 의 선택을 한댜 즉, 가설 선택을 미루고 계속해서 통계자료를 수집 보 완하여, 가설 선택에 있어서 강력한 증거자료를 확보할 때까지 통계자 료를 축적하여 선택하게 한다. 따라서 축차확률비 검정은 통계자료의 축척을 끝내는 정지규칙 (s t o ppi n g rule 또는 sto p ping ti me) 과 이 때 두 가설 중 하나를 선택하는 최종의사결정규칙(t e rmi nal decis i o n rule) 으 로 이루어진댜 (요, T )를 가측공간 (measurable s p ace) 이라고 할 때, 이 공간에서 정의되는 랜덤 샘플을 X i, X2, X3, …이라 하자. 이 때, K = ( X1 , X2 , … ) , X = ( X1 , Xz , … , X,1 ) 죠 = ( X1 , X2 , … ) , x = ( X1 , Xz , … , x,, ) 으로 표시한다. 통계적 가설 검정은 (2.1. 1 ) { Ho: 귀무가설, 점의 분포함수 P HI: 대립가설, K 의 분포함수 Q 라 하자. 이 때 P,, 과 Q,’을 각각 진의 분포함수가 P 와 Q일 때의 X 의 분포함수라고 하자. P,, 과 Q,,은 어떤 측도 µ,,에 대하여
(2.1. 2) P,1= Jp,I dµ11 , Q, 1= Jq,I d µ,, 으로 표시하고, P11 과 q, ) 은 밀도함수라고 한다. 정의 2.1.1 n 단계 x 의 확률비 또는 우도비(p robab il ity rati o( PR ) or lik e lih o od rati o) r,,(x) 은 다음과 같이 정의한다. r,, = p,, (x)/ q,, (x) 또한, n 단계에서의 확률비를 R, ,이라 하고 R,, = r,,(X) 으로 정의한다. 이 때 확률변수 { R,,: n = 1, 2,… } 를 우도비 수열 ( seq u ence of like li ho od rati o) 이 라고 한다. R,, 는 가측공간 (요, T) 에서 정의되고 다음과 같은 관계식을 만족 한댜I R,,dp = Q( A,,) , A,, = { w I X(w) eA.,} , A,,e R A,, 정의 2.1 .2 Wald 의 통계적 가설 검정 (2. 1. 1) 에 대한 축차확률비 검정은 다음과 같댜 적 당한 상수 A 와 B ( O < B < l < A < oo) 에 대하여 정 지규칙 N 을 (2.1 .3 ) N = inf{ n ~ 1 : R11 ::;; B 또는 R ~ A} 과 같이 정의하고, R11 ::;; B 인 경우에는 귀무가설 Ho 을, R ~ A 인 경 우에는 대립가설 H1 을 채택하는 최종의사결정규칙을 정한다. 또한, 상
수수열 {A,,} 과 {B,,} 에 대하여 정지규칙 N 을 (2.1. 4) N = inf{ n ~ l : R 군;. B,, 또 는 R,, > A,1} 으로 정의하고, 검정할 때에는 이것을 일반화한 축차확률비 검정(g en eraliz e d seq u enti al pro babil it y rati o tes t) 이 라 부른다 . 주 2.1.1 모든 n 에 대하여 B < R,, < A 일 때는 N=+oo 로 정의한댜 주 2.1 .2 일반화한 축차확률비 검정에서 B1 = B2 = … = B 110 -l = 0, A1 = A2 = … = A 110 -l = +co, B,,0= A110 = r, N = inf { n ~ l : R,, ~ B11 , R11 ~ A ,, } 으로 정의하면 표본 개수가 no 일 때의 고전적인 통계 검정과 일치한다. P(N =+oo ) = 0, 죽 P(N< +oo) = 1 이면 확률값 l 로, 축차적 통계 검정은 어떤 유한값 내에서 끝난다 . 따라서 다음은 어떤 경우에 P(N =+oo ) = 0 이 되는지 알아보자 . 정의 2.1.3 정지규칙 N 이 확률분포함수 P 에서 지수적으로 유계 (exp o nenti all y bounded) 하다는 것은 적당한 상수 c > O, O < p < l 에 대하여 (2.1. 5) P(N> n ) < cp , n = l, 2 , 3, … 롤 만족하는 경우이다.
다음 정리는 지수적으로 유계인 정지규칙 N 에 대한 성질을 나타낸 댜 정리 2.1.1 다음은 동치 관계를 나타낸다. (a) N 이 지수적으로 유계하다. (b) P(N < oo) = 1, P(N= n)< Ct p1 ', nEN, Ct >0, Pt E ( 0 , 1 ) (c) 상수 t。 ( > 0 ) 이 존재 하여 모든 t < t0 에 대 하여 Ee tN < 00 증명 (a) => (b): P(N = oo ) = ,l,i-.mo o P(N > n) < ,l,-i.mo o cp = 0 즉, P(N< oo) = 1 이다 또한 P(N= n) = P(N2 n) - P(N2 n+l) < cp 11-l = 信)p 11, n=2, 3, 4,··· n = 1 인 경우에는 적당한 상수 a> O 가 존재하여 P(N= 1) < ap 이 다 따라서 c1 '.'. max ( c/p , a) , Pi = P 라 하면 P( N = n ) < C1 p[' 이댜 (b) => (c): Ee1N= 훔합 ''P(N= n) < c1 혹(p 1 겅) t。 = -1nP1 > 0 라 하면, 모든 t< t 0 에 대하여 EetN < oo 이댜 (c) => (a) : Ee1N = 철 '[P(N> n-1) - P(N> n)] = e1 + (e1 -1) Lco e1P(N> n) < +oo 11=! 따라서 t< t0 에 대하여
철 'P(N > n) < += 이다. 그러므로 no 드 N 이 존재하여 .口..,_'-드---- n 2: n0, t < t0 에 대하여 e1P(N> n) < 1 이댜 즉, P(N> n) < (e-1 0 )” 이다. 그리고 n < n0 에 대해서는 p• = inf { p : p < l. P(N> n) < p} 이댜 따라서 p = max ( p*, e-,,) 라 하고 C = 1 로 두면 P(N> n) < p, n=l ,2, … , p< l 로서 증명은 끝난다 . D Wald 의 축차확률비 검정에서의 우도비 R,, 에 대하여 (2.1. 6) Lil = lnRII = 1n I i1 1 싶 I = 훔 ln[p (X ;)/q( X;)] = j효= I z j, Z; = 1n [p( X;) I q( X;) ] 라고 정의하면 Z1, Z2, …는 실수값을 갖는 랜덤 샘플이다. 또한 정의 2 . 1. 2 에서 (2.1. 7) a = InA , b = lnB 라 두면 (2. 1. 3) 에서 정의한 정지규칙은 (2.1. 8) N= inf{ n~ 1: L,, ;:: ;;; b 또는 L,, ::::: a}
로 정의되고, { L,,: n = l, 2, …} 는 확 률 보행 (random walk) 이 된다 . 이 때 정지규칙 N 에 대하여 다음과 같 은 보조정리 를 얻는다 . 보조정리 2.1 .2 P(Z = 0) = 1 이거나 N 은 지수적으로 유계하다. 증명 P(Z= 0) < 1 이라 가정하자 . 그리고 우선 P( I ZI ~ a-b) = q > 0 이라 가정하자. 그러면 P(N> n ) =P(b< L k kn) < (l —ql ) = (갑上) 如 이다. 따라서 N 은 지수적으로 유계하다 .D 보조정리 2 .1 .2 에 의하면 P(Z= 0) = 1 이 아니면 축차확률비 검정 은 유한의 표본수 내에서 확률값 l 로서 H。 또는 H1 을 채택하게 된다. 일반적으로 확률공간 (요, T) 에서 정의되는 확률변수를 X1,X2,… 이라 하자. 이 때 7,, 을 X 으로 나타나는 사건들에 의하여 생성되는 6- 대수라 하자 . 그러면 y;1 C y;2 C … 관계를 만족시킨다. 이 때 일 반적으로 정지규칙 N 은 다음과 같이 정의한다.
정의 2.1.4 N 이 {'Ji: n= l,2, …}에서 정의되 는 정지규칙이 되는 것은 {N> n }E' Ji11 , n=l, 2, …이 성립되는 경우이다. 그러면 {l'f=. n} = [ N: ::::: 미 _ [ N: ::::: ,z -l ] E 'Ji 11 . n = l , 2, ••• 이댜 일반적으로 U,, U2, …는 실수값을 갖는 확률변수로, U,, 은 T,1 가측 이라고 하고, N 는 임의의 정지규칙이라고 하자. 이에 UN = UN (w ) (w) 를 살펴보면 S11= [N= n], n= l, 2, …이라 하면 UN 은 S 에서는 UN= U(w) 로 정의한댜 N= +oo 를 고려하여 Uo o 를 T- 가측함수 라 하면, 다음의 보조정리 2. 1. 3 에 의하여 UN 이 확률변수가 되는데, 이 때 UN 을 정지확률변수 (s t o pp ed random var i able) 라 부른다 보조정리 2.1. 3 UN 은 (요, ? )에서 정의되는 확률변수이다 . 증명 임의의 상수 c 에 대하여 [ UN < c] = U00 [ N = n , U,, < c] U [ N = oo , Uo o < c] e 'Ji 11=! 로서 증명은 끝난다 .D {'Ji,,: n= l, 2, …}에 대하여 ?를 모든 ?11 을 포함하는 가장 작 은 a- 대수라 하고 N을 임의의 정지규칙이라 하자. 이 때 'Ji = 'Ji 00 로 표시하기도 한다. 정지규칙 N 에 대하여 'Ji N 을 다음과 같이 정의한다. 정의 2.1.5 모든 AE 'Ji 에 대하여
AE 'J,N ~ [N= n] n AE 'J,1 1, n= l, 2, … 로 정의한다 f N 이 6 _ 대수가 되는 것을 쉽게 보일 수 있다. (요, T) 에서 정의되는 분포함수 P 와 Q룰 생각하고, P, ,과 Q ,I 를 각각 P 와 Q의 7,, 에 국한하는 분포함수라고 하자. 그리고 어떤 가측 함수 µ,,에 대하여 P,1<µn , Q, 1<µ,1 , dP,1 = p,,d µ,1 , dQ ,1 = q,, dµ,, 이라 정의하자 . 그러면 우도비 R = q/p,,이 된다. 또한 Q ~P 라 하 면 모든 T,1 에 대하여 Q~p,,이 된다. µ = P , ·P11 = l, q = Rn 이라 하면 dQ = RdP 이 된댜 따라서 모든 AE 'Ji,,에 대하여 (2.1. 11 ) Q( A) = Ql l(A) = LR,,dP = LR11dP,, 이 되고 다음과 같은 정리를 얻는다. 정리 2.1.4 N 은 임의의 정지규칙이고, P 와 Q는 (요, T )에서 정의되 는 분포함수로, 모든 T,1 에 대하여 Q ~P 라 하자. 그러면 모든 Ae T,1 에 대하여 Q( A n [N< =]) = InAnrN[N<< =c o] lRNdP 이댜 증명 An [N= n] e 'Ji ,, , n = l , 2 , … 이므로 (2 . 1. 11) 에 의하여
Q( An[N< = ]) = ,110 t=0 1! Q ( An[N=n]) = /홍 I JI I n [ N = ) 1 1R , dP = I-P0~0 ·I Jf AAnn [f NN == 1n 1) lR•N• dP= Jf AAnn f[ NN - -c( oooo )l RN d P 이다 .D 따름정리 2.1.5 정리 2. 1. 4 의 가정이 만족할 때 정지규칙 N 에 대하여 Q( N< o o) = 1 이라 하자. 그러면 'JiI\에 대하여 Q ~ P 이면 ~ = R 파 [N < oo] 이댜 증명 만약 AE ']
다음 정리에서는 정지 우도비 R/\ ' 에 대한 기본 부등식을 얻는다. 정리 2.1.7 R1, R2, … 를 P 와 Q에서 정의되는 우도비라 하고, N 은 임의의 정지확률변수로서 P(N< = ) = 1 을 만족한다. 그러면 임의의 Os us vs= 에 대하여 (2.1. 12 ) uP(u ~ RN ~ v) ~ Q( u ~ RN~ v) ~ vP(u~RN~v) 이댜 증명 모든 nEN 에 대하여 Sil = [N=n]' T/1 =slln[u~RN ~ v] 라 하자 그러 면 [ u s RNs v] = 1U1o= o 1 [ N= n , usRNs v] = 1U1o= o I T,, 이 고 T;nTj = (/) , i=I=j 이댜 따라서 (2.1. 13 ) P[u:s ;;R N:s ;;v ] = I,I'0f=0; l/ C T11) = 홀00 L , , p ,,dµI l (2.1. 14 ) Q[ u:s ;;R N:s ;;v ] = I1효= I frT,, q ll dµll 이댜 그리고 u~R,,~v ¢,} u~—p ,1
이 되어 (2 .1.1 3) 과 (2 . 1.1 4) 에 의하여 증명된다 .D 정리 2. 1. 7 에서 P(u sRNs v) > 0 이면 u::;; PQ(( uu ~~R RNN~~ vv)) ~v 로 나타낼 수 있댜 만약 u=v=O 이면 Q( RN = O) = 0 이고, u=v-oo 이면 P(RN=+oo) = 0 이 된댜 .E..,E_ u=O, v > O 이면 Q( RN::=;:v) ::=;: v 이고, v-oo 이면 P(R 혼 u) <上u 이다 . 축차확률바 검 정 에 서 오류확률 (error p robab il ity)은 다음과 같이 정 의한다. 정의 2.1.6 통계적 검정에서 나타날 수 있는 제 1 종 및 제 2 종의 오류확 률은 다음과 같이 정의한다 . a = P(H0 기 각 I H。 ) = P(RN~A) : 제 1 종의 오류확률 B = P(H。 채 택 | H1) = P(RN~B) : 제 2 종의 오류확률 주어진 오류확률에 대하여 정의 2. 1. 2 에서 나온 상수 A 와 B 를 결정 해 보자. 정의 2. 1. 6 에서 정의한 오류확률들은 N < +00 이므로 다음과 같이 쓸 수 있다 (2.1 .1 5 ) 1-a= P(RN~B) , 1-/3 = Q (R 혼 A) 만약 P(RN.:::;;B)>O 이면 정리 2. 1. 7 에 의하여
 B
B
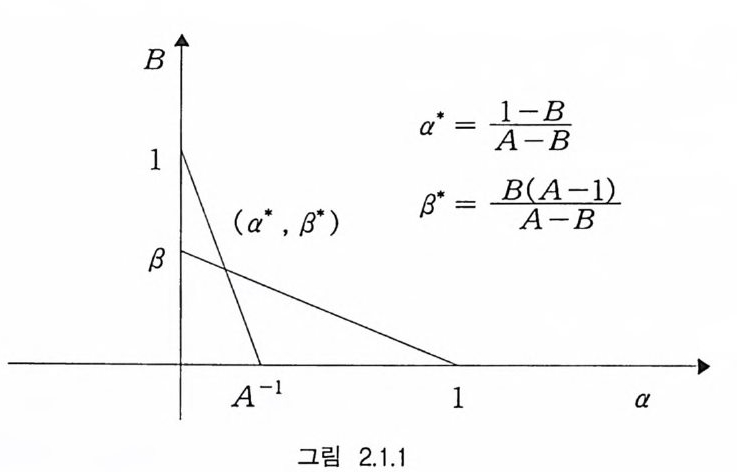
(2.1 .1 6) QP ((RR 혼 근 AA)) 컬_ AA , PQ(( RR 죠Ns BB)) 겹 B 이다. 따라서 (2. 1. 15) 와 (2. 1. 16) 에 의하여 (2.1. 17 ) 上a 책, 」l- La 익 B 를 얻는다 그림 2. 1. 1 은 주어진 경계치 A 와 B 에 대한 오류확률 a 와 B 의 가 능한 영역을 나타낸다 축차검정에서의 중요한 문제는 주어진 오류확률 a 와 B 에 대하여 정지경계치 A 와 B 를 어떻게 선택하는가이다 . 보수 적인 선택은 A=a-1, B= {J이댜 이 경우에 발생하는 제 1 종 및 제 2 종 오류확률 ao 와 fl o 은 a 。 ~A-1=a, fl,。 ~B= {J의 관계식을 만족시킨 다. 또한 정지경계치를 A'= 上二a 요 ,' ~B' = _l-요a- 로 잡으면 A~A', B~ ]3'이다. 이 경우의 오류확률을 a', g이라 하면 d+g < a+8 의
관계식을 만족하지만, 반 드 시 a'sa, (J三 8 일 필요는 없다. 이 때의 A 와 B 를 왈드의 정지경계치 (Wald's sto p p ing boundar y) 라고 한댜 예제 2.1. 1 X,~ Ber( 0 ) . H0 : 0=0.5 대 H1 : 0=0.6 이라 하면 X, = 1 인 경우에는 Z; = lnR(X;) = ln(0.6/0.5) = 0.182, X;=O 인 경우 에는 Z;= ln(0.4 / 0.5) =一 0.233 이다. 따라서 귀무가 설 Ho 에서는 P(Z; = 0.182) = 0.5, 대 립가설 H1 에서 는 P(Z; = 0.182) = 0.6 이 댜 만약 a 칙 0 . 01, /3착 ).05 에서 검정할 때 보수적인 선택은 A= (0.0 1) - 1=100,B=0.05 로써 a=lnA=4.61, b=lnB=-3.00 이 된 다. 한편 Wald 의 정지경계치들은 A'=0.95/0.01=95 . B'=0.05/ 99=0.051 로써 lnA'=4.55, lnB'=-2.99 이다. 이 경우에 lnR11= Li=II l Z•; =0.182S,•,• — 0.2 23(n-S11•• ), S1•1• = }i=II : l X, 이댜 따라서 InR,,~4.55 ¢=} S,'~ 11. 2 3+0.55n InR,,< 겔 .99 ¢=} S,,< —7.3 6 +0.55n 표 2.1.1 지수형분포족함수 분포함수 확률밀도함수 f(x , 0) C(0) D(0) 표준정규분포 石1e _ -(x -O J '/2 。 02/ 2 베르누이분포 ex( l-0 )1-x 1n —1— Oi _1n(1_O) 포아송분포 e-00-'/x ! ln0 。 지수분포 i 。 e -x/0 二。上 lnO
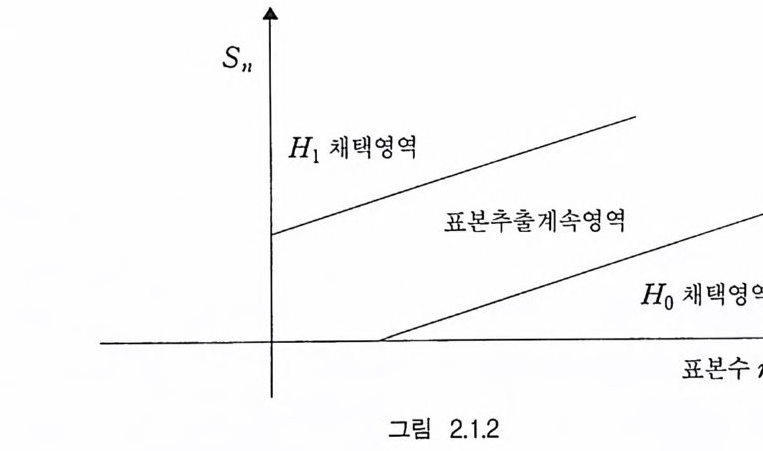
이 되어 정지규칙 N= i n f {n 티 : S,,:: :: ::ll.23+0.55n 또는 S,, 三一 7.36+0.55n} 이다 . 예제 2.1.2 X 가 표 2. 1. 1 과 같은 지수형분포족 (ex p onen ti al families of di s t r i bu ti ons) 을 갖는다고 할 때, 즉 확률밀도함수 f(x , 0) = h(x) exp (C(0)x-D(0)} 일 때의 축차검정 H0 : dP = f(x , 0 。 )µ(dx) 대 H1 : dQ = f(x , 01)µ(dx) 를 살펴보자. 그러면 Z; = In~ = [C(01)-C(0 。 )]X, 一 [D(01)-D(0 。)] 이댜 이 때 C(01)> C(0 。)라 하고 S,l= i2=’' Ix i라 하면 (2.1. 18 ) InR,,~a ¢'? s, 1 느 C( 01) a— C( 0 。) + n[CD(( O Ol)l )_ — CD(( O 0o 。) )] (2.1. 19 ) lnR11 집 台 SII< C(Ol)b- C(o 。) +, n[CD((O01l)) -―C D((00 。 )。 )] 이댜 따라서 정지규칙은 N= 펴{ n 칙 S 혼 C(OI):C(Oo) + n[雲 ::})] 또는 s,1< C(01) ―b C(0 。) + n[CD((OOII)) _―C D((00 。) 。 )] } 이며, 만약 정지규칙 N 에 대하여 lnRN2 a 이면 H1 을 채택하고 lnRNs b 이면 Ho 을 채택한댜 모든 k= 1, 2, …, n 에 대하여 b< lnRk < a 이면 표본을 계속적으로 축적한다. 이룰 그래프로 나타내
 s,,
s,,
면 그림 2 .1 . 2 와 같다. 지수형분포족에서는 E&= 싼幕이고 일반화된 중간값정리 (ge neralize d mean value the orem) 에 의 하여 E 。 .x i=C(~0*)= DC((0O1I)) ―- DC((00 。。)) 이드 o * 탁 0 。 , 81) 에 존재한댜 예를 들면 정규분포에서 는 E 。 .X;= e• = ..!!._。 ;°1 이고 , 베르누이분포에서는 01=l — 0 。라 하 면E 。 .X;= e• = 2-1 이댜 또한, X.:= S,,/n 이라 하면 식 (2 . 1. 18) 과 (2. 1. 19) 는 각각 다음과 같이 쓸 수 있다. (2.1. 20 ) 첫 ~E 。 .x i+ n[ C( 01)a - C( 0 。)] (2.1 .2 1 ) X:,s E 。 .X;+ n[ C( 01b) -C( 0 。)]
특히, 정규분포에서는 E0-X;= ¥ 이므로 c= a/[C(01)- C(o 。)]로 두면 H1 을 채택하는 정지영역은 Xn > 0 。 ;°1 +요n 이다 또한 0l = l ― 00 인 베르누이분포에서는 H1 채택영역은 Y,, >O.5 + 요n 이댜 2.2 검사특성곡선과 평균표본수 함수 이 절에서는 모수 0 에 따라 로트를 채택한 함수 죽, 검사특성함수 와 이를 이용하여 정지규칙변수 N 의 평균값 즉, 평균표본수 (avera g e samp le siz e 또는 averag e samp le number) 를 구한다 검사특성곡선 (o p era ti n g charact er i st i c curve) 은 통계검정에 있어서 단순가설 (s i m p le h yp o t hes i s) 일 때는 고려할 필요가 없지만 축차검정에 서 Ho:0= 0 。 대 H1:0= 01 가 예를 들어 가설검정 H'o:0~0 。 대 H':0 2: 01(01 > 02) 를 대표하는 것이라고 하면, 임의의 0 에 대한 검사 특성곡선을 살펴보는 것은 의의가 있다고 할 수 있다. 축차검정에서 검정력함수(p ower fu nc ti on) 는 (2.2.1 ) P 。 (Ho 기각)=P 。 (SN~a), SN= 훔 z j 로 표시하고, 이에 따라 검사특성곡선은 다음과 같이 정의한다.
정의 2.2.1 축차검정에서의 검사특성곡선 L(0) 는 (2.2.2 ) L(0) = l-P0(SN~a) = P 。 (SN~b) = p。 (Ho 채택) 으로 정의한다. 검사특성곡선을 구하기 전에 필요한 몇 가지 정리를 살펴보고자 한다. 보조정리 2.2.1 Z, Z1, Z2 , …는 확률 공간 (.Q, 'r ,P) 에서 정의되는 랜덤 샘플로서 t =/=0 인 t에 대하여 적률생성함수 rp(t) = Ee'z< +=이 다. N 은 정지규칙으로 P(N< = ) = 1 이면 (2.2.3) EA e IS.\. / ( ¢( t))싸 = l II 이다 . 여기에서 S11= iL= Z I ; 이댜 증명 분포함수 Q 를 (요, T) 에서 dQ = ;若 )dP 로 정의하자. 그러 면 Q <{:P 이 다 . P,, 울 ( Z1 , Z2 , … , z,1 ) 의 분포함수라고 하면 dQ ,1 = ( 짜e , ts).) dP,, 이다 . 따라서 Q,, ~ P ,,, n= l, 2, … 이다. 또한 R,, = dQ ,,/ dP,'= eIS /( p(t))”이고 P.(N < o o) = 1 이므로 따름정리 2. 1. 6 에 의하 여 증명된다 .D 식 (2 . 2.3) 을 왈드의 기본 항등식 (Wald's fun dermenta l i den tity)이라 부론다.
주 2.2.1 모든 nEN 에 대하여 EP[e,s.I ( rp (t))] = 1 이다. 그러나 일 반적으로 Ep f(X ) = 1 은 다음 예제와 같이 어떤 정지규칙 N 에서는 E 갑 (XN) -=I= 1 이댜 예제 2.2 .1 X1,X2, …는 랜덤 샘플로서 P(X;=O)=P(X;=2) =강이 댜 Y,, = (X1X2 … X,, )이라 정의하면 P(Y,,=O) =1-2- , P(Y,,=2)=2 크 1 이댜 따라서 EY,, = l(n = l, 2, 3, …)이댜 정지규칙 N 을 다음과 같이 정의하자. N= inf{ n~l : Y,, = O} 그러면 P(N< o o) = 1 이고 YN=O 이댜 따라서 E p YN=0 이댜 다음 정리는 자주 사용되는 젠센 부등식(J en?en's i ne q ual ity)으로, 증 명은 생략하고 기술만 한다. 정리 2.2 .2 X 는 확률변수로서 두 점 이상에서 정의되며, X 의 평균값 은 유한하댜 또한 /: R- ---> R 은 볼록함수 (s tri c t l y convex) 이댜 그러면 Ef (X) > /(EX) 이다 . 정리 2.2.3 Z 는 확률변수로 다음을 만족한다. (a) 기대값 EZ 가 존재하고 EZ= f-0 이다. (b) 어떤 양수 8 가 존재하여 P(ez< 1-8) > 0 이고 P(ez> 1 + 8) > 0 이댜
(c) 적률생성함수 q;(t) = E e 1z 가 모든 t에 대하여 존재한다. 그러면 EeloZ = l 인 t。 + o 가 유일하게 존재한댜 증명 t > O 에 대하여
특수한 경우를 제외하고는 일반적으로 만족한다. 첫째,모든 0 에 대하여 P 。 (Z > O) > O 이고 터 (Z < O) > 0 이댜 둘째,모든 0 에 대하여 적률생성함수 ¢o(t) = E 。 e t Z 가 0 을 포함하 는 개구간에 존재한다. 이상의 가정하에서는 보조정리 2. 1. 2 에 의하여 P(N< +oo)=l 이고 만약 Eo Z=I =0 이 면 정 리 2.2.3 에 의 하여 t0 = h( 0) =I= 0 인 t o 가 존재 하여 Ee e il(O lz= 1, 즉 터t o)= f; e1 0 2=1 이다. 따라서 Wald 의 기본 항등 식 (2 . 2 . 3) 에 의하여 (2.2.4 ) Eoe h(O)S.v = l 이댜 축차확률비 검정에서 정지경계치의 과표적 (overshoo t)을 무시하면 (2.2.5 ) P( SN= b ) = L( 0) , P(SN= a ) = l-L(0) 이다 식 (2.2.4) 에 의하여 (2.2 .6 ) Eo e h(O)S. v= e h(O)bL( 0) +e h(O)a( l-L ( 0)) 를 얻는댜 식 (2.2.6) 을 l 로 놓고 L(0) 에 대한 방정식을 풀면 L(0) 의 근사식 (2.2.7) L(0) 스 A A't(hO (O)_)B—' I1(O )
를 구할 수 있댜 여가에서 lnA=a, lnB=b 이다. 0=00 와 01 에서 의 검사특성곡선의 값을 구한 결과는 다음의 보조정리에서 기술한다 . 보조정리 2.2.4 단순가설 검정 Ho: 0=0 。 대 Hi : 0=01 에서 분포함 수 P 。 0 과 P 。 1 이 상호절대연속 (mu t uall y absolute l y conti nu ous, 기호로 는 Po 。 =P 。 1) 이면 h(0 。)=l, h(01)=— l 이 고, 이 때 L(0) 의 근사값 은
(2.2.8) L(0 。)= 1 걸 , L(01)=~一 _j 이다. 증명O ~ f o 。 (x) dµ(x) 이고 Pe。 =P 。 1 이라는 가정하에, 식 (2 . 2.8) 은 (2.2.9) p(J 。 (1) = fr/,.1 ,( xy ) / e1(x )dµ(x) = 1 이 된다. 따라서 h(0 。 )=1 이댜 또한 같은 방법에 의하여
(2.2.1 0 ) L( 02) =ah' (~ 02) -=b h' ( - 0 사! !a '— b 를 얻을 수 있다. 검사특성곡선 L(0) 의 정확한 식은 일반적으로 구할 수가 없지만, 식 (2.2.7) 은 훌륭한 근사식으로서 매우 유용하게 사용된다. Wald 는 L(0) 에 대한 상한과 하한값을 구하였는 데, 그것을 요약하면 다음과 같다 (Seq u enti al AnaTJ l(y 0s i)s =, plg 6 1r-1 b6 4 t 참E조 )。 .( e’i( O )Z I e’l( O)Z 나 ) o(0)= 1.t~ ·b t'> ~Er 。n (=e’ i (O)Z II e=’ i (O)Z-> 上 t ) 라 하면 L(0) 의 유계치는 첫째, L(0) > 0 인 경 우에는 (2.2 .1 1 ) ( A'I( 집 :)O-)1B'r(O)
이다. 식 (2.2 .1 3) 을 h(8) 대신 0 에 대하여 정리하면 (2.2.1 4 ) 0=[1-( 仁:;)’’] /[(訂 -( 仁:; )’'] 을 얻고 , 정지경계치 A 와 B 의 근사값을 식 (2. 1. 7) 에서 등식을 만족하 는 값 A= 上二a II,' ~B = 一1요-a- 라 하면 검사특성곡선 L(0) 의 근사값은 L( 0) 스[ (틀 )' I -l] / [ (군 )' I - (근 )’ ’] 를얻는다 예제 2.2 .2 xi~ i.i.d . N(0, 갑)일 때의 h(0)= 010+10- 。0一 。 20 이고 이 때의 검사특성곡선은 h(0) 를 식 (2.2.7) 에 대입하면 쉽게 구할 수 있 다 . 예제 2.2.3 확률과정 X (t)= b(t) + 0· t라 하고 b( t)는 브라운 운동 (Br own ian mo ti on) 을 한다고 하자 . 또한 Ho : 0 。 = -0.5 대 H1: 01 =0.5 이라 하자. 그러면 R( t)= exu) 이고 이 때의 검사특성곡선 L(0)=~:: 》노 이다. 이제 정지규칙 N 의 평균값에 대하여 살펴보자. 먼저 다음의 문제에 대하여 고찰하고자 한다 . 첫째, {X 戶 i = l, 2, …}는 모두 평균값 µ를 갖는 확률변수라고 하자. 그러면 s,1 = iz=” 1 x i이라 하면 ES,, = nµ 이다 N 이 어떤 정지
규칙이라 할 때 (2.2 .1 5 ) ESN = µEN 둘째, {X; : i = l, 2, …} 이 서로 독립이고 평균값이 0, 분산이 군 인 확률변수라 할 때 ES;, = ncl 이댜 이 경우에도 어떤 정지규칙 N 에 대하여 (2.2.16) Esi = cl-E N 이 성립하는가? 결론적으로 말하면 첫째 경우에는 어떤 조건에서는 식 (2 .2.1 5) 가 성 립한댜 식 (2 . 2 .1 5) 를 왈드의 첫번째 등식 (Wald's 1st e q ua ti on) 이라고 부르기도 한댜 둘째 경우에는 EN< +oo 이면 성립하며 식 (2 . 2 .1 6) 을 왈드의 두 번째 등식 (Wald's 2nd e q ua ti on) 이라 한다. 축차확률비 검정 에서 왈드의 첫번째 등식 (2. 1.1 5) 는 왈드의 기본 항등식 (2.2 . 3) 이 t에 대하여 미분가능하고, 기대값 부호 내에서 미분한 값과 같다고 하면 식 (2.2.3) 을 t에 대하여 미분하고 t = 0 에서 값을 구하면 (2.2 . 1 7 ) E{ iTt;〉告릅f }I . =o 1= 0 이다 이 때 rp( O) = 1, rp' (O) = µ를 이용하면 E(SN -Nµ) = 0 즉, 왈드의 첫번째 등식 (2.2 .1 5) 를 얻는다. 한편 EZ = 0 인 경우에는 식 (2 . 2.3) 을 연속 두 번 미분하고
N. L. Joh nson(Ann. l\tla th . Sta t i st ., 1959, 30, p l2 45- 1247) 은 왈드의 첫번째 등식에 관련하여 이를 일반화하였고, 이 를 요약하면 다음과 같 은 정리 를 얻는다. 정리 2.2.5 {X;: i = l, 2, …}는 실수값을 갖는 확률변수로서 같은 평 균값 µ롤 갖는다고 하자( X, 는 랜덤 샘플일 필요는 없다). 이 때 S = iL= Xl ; 로 두고 N 은 임의의 정지규칙이라 하여 다음의 세 가지 가정을 만족한다고 하자. (a) EIX11I < A< +oo , n = 1, 2, … (b) EN< +oo (c) 모든 ·n = l, 2, …에 대하여 사건 [N ::::::까는 X,, 에 독립이댜 그러면 ESN = µEN 이댜 주 2.2.2 {X 尸 i = l, 2 , … } 가 서 로 독립 이 면 가정 (c) 는 성 립 한댜 주 2.2 .3 X가 음이 아닌 정수값을 갖는 확률변수로서 그 기대값이 존 재하면 EX= L00 P(X~k) 이댜 k= I 증명 -口』'드- n = l . 2 . … 에 대 하여 Y,, = l [N 하]이라고 하자. 그러 면 가정 (c) 에 의하여 x,, 과 Y,, 은 서로 독립이댜 주 2.2.3 에 의하여 EN= I:l0=0f I EY ,, = E( l1f0= 0 1 Y,,) 이고, SN= Ifl= I x,,Y,, 이다. lti= 1 l x,.Y ,. < i2=,, |I Xi Y ,·1< iZ=00 l I X i Y J =U라 두자. 그러면 가정 (a) 에 의하여
EU::;;:AE( 홈CO 1 Y;)=AEN< +oo 이다 따라서 르베그 기O一 TOJ A o- l 수렴정 리 (Lebes g ue's domi na te d converge nce t heorem) 에 의하여 ESN = E( 홈oo IX,, Y,,) = E( 브 홈 IX; Y;) = :~군( 홈 I X; Y;) = ,l,i-.mo o iL=I I I E(X; Y;) 이댜 또한 가정 (c) 에 의하여 EXI.Yi = EXI • EYi이므로 ESN = L00 ( EX; • EY;) = µ L00 (EY;) = µE(N) i= l • • i= l 으로 증명된다 .D 주 2.2.4 {S11-nµ, 'Ji 11, n2l } 이 마아팅게일 (m arti n g ale) 일 때도 정리 2.2.5 가 성 립 한다. Wald 의 등식들 (2 .1.1 5) 와 (2 . 2 .1 6) 을 이용하여 정지규칙 N 의 평균값 에 대하여 살펴보자. 첫째, EoZ= f-0 인 0 에 대하여 식 (2.2 .1 5) 를 이용하면 (2.2.1 8 ) EoSN = EoZ • EoN 이고, 여기에서 EoSN 근사값을 시「(2.2.5) 를 이용하여 구하고 시「 (2.2.1 8 ) 에 대 입 하면 N 의 평 균값을 근사적 으로 (2.2.1 9 ) EoN 늑 무 0)+Ea(olZ- L(O))
를 얻는다. 둘째, E 。 , Z = 0 인 0 2 에 대해서는 왈드의 첫번째 등식 (2.2 .1 5) 에 대 입하면 Eo,S N = 0 • EN= 0 이라 E 。 2 N 의 값을 구할 수 없댜 그러나 식 (2.2.5) 를 이용하면 (2.2.20) E 。 , S N = bL( 0 김 + a( l —L( 02) ) = 0 이므로 L(0 사늑 a_a b 로 앞에서 구한 식 (2.2 .1 0) 을 구할 수 있다. 한편 E(J , Z = O 이므로 E(J , z2 = cl-이다 왈드의 두 번째 등식 (2.2 .1 6) 에 의 하여 (2.2.21) E 。 , si = Eo,Z 2 • Eo N 이고, 다시 식 (2.2.5) 를 이용하면 (2.2.22) E 。 2 s% 늑 b2L(0 사 + a2(1 - L(0)) 이다 . 이것을 식 (2 .2 .21) 에 대입하여 풀면 02 에서 N 의 평균값에 대한 근사값으로 (2.2.23) E 。 2 N= b2L( 02) +E a 。2 2 Z( l2 —L( 02)) 를 얻을 수 있으며, 식 (2.2 . 10) 에서 구한 L(02) 의 값과 E(},z 2 = Var(}2Z 를 이용하면 N 의 평균값에 대한 근사치로서
(2.2.24) E 。 , N 늑 一 ab I Var 。 2 Z 를 구할 수 있다 예제 2 . 2 .4 X,~Ber(O), H。 : 0=0o 대 H1 : 0=1-0 。 (0 。 E(O,1)) 이라 하면 E0Z = (20-l) d, d= ln(?, )이고, 예제 2.2 .l에서 구한 검사특성곡선 L(0) 를 식 (2.2.19) 에 대입하여 정리하면 (2.2.25) EoN 늑 bL( O) (二\ L( O)) , o =I= 0 . 5 이다 . 0 = 0.5 일 때는 EZ = 0 이고 EZ2 = d2 이므로 식 (2.2.23) 에 의하여 (2.2.2 6 ) EoN 누 -ab/d2 , 0 = 0.5 를 얻을 수 있댜 N 의 평균값에 대한 정확한 값을 계산하기는 일반적으로 불가능하다. 그것은 정지시각(정지규칙) N 에서 SN 의 값은 정지경계치 a 또는 b 를 초과함으로써 정확한 검사특성곡선의 값을 구할 수 없기 때문이다. 여 기에서 E0N 의 범위에 대하여 살펴보자. 우선 0o 와 01 에서 E0N 의 하 한값(l ower bound) 에 대하여 알아보자 . 젠센 부동식(정리 2.2.2) 에 의하여 임의의 볼록함수를 g (x) 라 하면 Jg(R N)dP = aL= H ,~dP+(1 - a)L= H u~ dP
느 ag ( JD= I I '~ dP) + (l - a) g( L =1 10 ~ dP) = a g(~;乙 A) ) +(l 一 a) g( P(~) 이다. 식 (2 . 1.1 5) 에 의하여 (2.2 .2 7) Jg( R N )dP 건 4 는) +(1-어 근) 이다. g(x ) = -lnx 라 하면 (2.2.2 8 ) f lnRNdP :S:: aIn 틀요 +(l ― a)ln 근 를 얻는다. 따라서 다음과 같은 정리를 얻는다 . 정리 2.2 .6 N 은 축차확률비 검정 Ho:0 = 0 。 대 H1:0 = 01 에서 정지 규칙이고, a 와 /3 (0< a, /3< l) 는 제 1 종 및 제 2 종의 오류확률이다. 만 약 N 에 대한 평균값이 0 = 00 와 01 에서 유한값을 갖는다고 가정하 면, N 의 평균값에 대한 하한치는 (2.2.29) 와 (2 . 2.30) 으로 표시한다. (2.2.2 9 ) E 。짜 [aln( 틀) + (1 _a)1n 근] / E 。 o z (2.2.30) E0,N 키 (1 一 /3) 1n 上군~ + /3I n 1 욘니 / E 。 IZ 여기에서 Z = ln(P 。, (X) IPo0( X )) 이 댜 증명 lnRN = %이고 SN = iZ=N l z i이다. 젠센 부등식에 의하여 E80Z
< O이 다. 따라서 왈드의 첫번째 등식 (2. 1.1 8) 을 이용하여 식 (2.2 .2 8) 을 다시 정리하면 식 (2.2 . 29) 를 얻는다 E0 , Z > 0 을 이용하여 유사한 방법 울 사용하면 식 (2.2.30) 을 구할 수 있다. 曰 0 = 00 와 01 이의의 일반적인 0 에 대한 N 의 기대값에 대한 상하 한값은 다음과 같다 (Se q uen ti al Analys is , pl7 0~172 참조) . s(0) = maxE 。 (Z-r IZ 一 r~O), r~O TJ( 0) = m i nE 。 (Z+r IZ+r~O), r~O 라두면, EoZ > O 인 경우에는 (2.2.31) L(O)(b + n(OE))o Z+ (l _L(O))a < E 십 <; L( O)b + (l 一E Lo(Z O ))(a + t( O)) 이고, EoZ < O 인 경우에는 (2.2.32) L( O)b + (l -EL e(ZO ))(a + t(O )) ~EoN 드 L( O)(b + n( OE))o Z+ (l -L( O))a 이댜 2,3 축차확률비 검정의 최적성과 상대효율 이 절에서는 축차확률비 검정이 모든 검정 방법 중에서 최적성을 갖
는다는 것에 대하여 논하고, 경쟁 가능한 검정 방법과의 효율성을 논 한다 모수공간 H= {Bo, 81} 인 경우에 귀무가설 Ho :8= 8 대 H1 : 8 = 81 에 대한 가설 검정에 대하여 살펴보자 . 이 때의 두 축차검 정 (se quen ti al t es t)을 S 와 S ' 라 하고, 각각의 경우 제 1 종 및 제 2 종 오 류확률을 각각 (a, /3)와 (d, g) (0< a, f3, ¢, g < 1) 라 하자. 정의 2.3.1 두 축차검정 S 와 S 가 같은 내구력 (s t ren gt h) 을 갖는다는 것은 a = a' , /3 = /3' 인 경우를 말한다. 만약 a< a ', {Js {3' 또는 asa', /3 < {3'인 경우에는 검정 S 가 3 보다 강하댜 또는 S 가 S 보다 약하다고 한댜 만약 a< a', B>g 또는 a> a ', /3 < /3'인 경우에는 두 검정 S 와 S' 를 비교할 수 없다고 한다. 주어진 같은 내구력 (a' /3)에 대하여 어떤 검정 방법이 더 바람직 한가는 검정시 소요되는 표본수의 평균값이 비교하는 다른 검정 방법 에서 나온 평균값에 비하여 적은 경우를 말한다. 다시 말하면 S 와 S' 를 두 개의 축차 검정이라 하고, (a, B) = (a' , g)일 때 E 。 0 (NIS) < Ee0( N I S') 이고 E 。, (NIS) sE 。 ,(NIS'), 또는 E8 。 (NIS) s Ee 。 (NI S') 이고 E 。 ,(NIS)
한댜 정의 2.3.2 내구력 (a , /3) 를 갖 는 검정에 대하여 0 = 0 。와 0 = 01 에서의 정 지규 칙 N 의 기대치 최소값은 다음과 같이 정의한다 (2.3 . 1) n 。 (a, /3) = i떤 {E 。 0 (NIS) : 내구력 S = (a, /3)} (2. 3. 2) n1(a, /3) = i평 {E0,(NIS) : 내 구 력 S = (a, /3)} 축 차확 률 비 검정에서 정지경계치 A 와 B 또는 a 와 b( a = lnA, b = lnB) 에 대하여 정 지 시각에 과표 적 하지 않을 경우, 죽 정지규칙 N 에서 정 확 히 RN = A 또는 RN=B(SN=a 또는 SN=b) 인 경우에 제 1 종 및 제 2 종의 오류확 률 은
a = P0 。 (S N = a) , /3 = P 。 ,(SN = b) 이다. 이 때의 정지규칙 N 의 기대치는 제 2 . 2 절에서 살펴본 근사값이 아닌 정 확 한 값으로 각각 (2. 3 .3 ) V 。 = Eo 。 (N / S) = [ aln 눅/j_ + (1 —a) ln 근 ] /E 。 O Z (2.3.4) v1 = Eo,(NIS) = [ (1一/3) 1n7 +/3 InT 令] /E 。 IZ 이고, 여기서 Z = lnPo,(X) I Po 。 (X) 이다. 따라서 정지경계치 A 와 B 에 대한 과표적이 없는 경우 축차확률비 검정은 정리 2 . 2.6 에 의하여 최 적성을 갖는다. 식 (2 . 3.3) 과 식 (2.3.4) 의 Vo 와 V1 은 식 (2.2.29) 와 식 (2.2.30) 의 오른쪽 값과 일치함을 알 수 있다. 일반적으로 축차확률비 검정이 최적성을 갖는다는 것은 다음 정리에서 기술한다 .정리 2.3.1 귀무가설 Ho : 0 = Bo 대 대립가 설 H : 0 = 81 에서 제 1 종 및 제 2 종의 오류확률을 각각 a, /3 (0 < a, /3< l) 라 하자. 이때 P{Ho 기각 |0 。 }~a, P{Ho 채택 101}~/ 3 이고, E 。 0 N < oo, E 。 I N < 00 인 모든 통계 검정(표본고정 검정 및 축차 검정) 중에서 제 1 종 및 제 2 종의 오류확률을 각각 a 와 /3로 갖는 축차확 률비 검정 S 가 최적성을 갖는다. 죽, Eo.(NIS) 와 Eo,(NIS) 가 최소 값을갖는댜 증명 정리의 증명에는 많은 개념들이 필요하므로 본 정리의 증명은 제 6 장의 축차적 베이즈 절차에서 다루고자 한다 . 仁] 축차확률비 검정의 최적성은 지금까지 정지경계치가 O < B< l
r1(S) = 麟나} : H1 이 참인 경우 로표시한댜 정리 2 . 3 .l에서 정지경계치에 대한 과표적이 없는 축차확률비 검정이 최적성을 가지므로 n0(a, /3)와 n1 (a , /3) 는 식 (2.3.3) 및 식 (2.3.4 ) 의 Vo 와 v1 과 일치하게 된댜 모든 검정 S 에서 r。 (S) s l, r1 (S) s l 이댜 만약 S 가 최적성을 가진다면 r。 (S) = r1(S) = 1 이 된다. 따라 入 1 r。 (S) 와 rI(S) 의 값이 클수록 더욱 바람직한 검정 방법이라 할 수 있다. 축차확률비 검정은 정지경계치에 대한 과표적이 없는 경우에는 r0 = r1 = 1 이다. 일반적으로 축차확률비 검정에서는 ro 와 r1 은 1 에 가까운 값을 갖는다. 그리고 01 이 0 。에 접근하면 ro 와 r1 은 l 에 접근 한댜 정리 2.3 .1에서 축차확률비 검정이 최적성을 갖는다고 하였으나, 일반 적으로 0 。와 01 이외의 값에서의 N 의 기대값에 대해서는 최소값을 갖 는다고 말할 수 없다. 다음에는 축차확률비 검정을 바탕으로 경쟁적인 검정, 특히 고전적인 고정 표본수를 갖는 검정 방법의 유효성을 살펴보고자 한다. 여기에서 는 정지경계치 (A , B) 에 대하여 편의상 B = A-1 인 경우의 축차확 률비 검정을 생각하고, 랜덤 샘플의 모집단이 정규분포와 베르누이분포 인 경우에 대하여 구체적으로 살펴보고자 한다. 정지경계치가 B = A-l 이므로 a = /3이고 또한 E(J . N = E (J ,N 이므 로, 0 = 0 。에서의 축차확률비 검정의 정지규칙 N 에 대한 기대치는 근
사적으로 (2.3.5) E 。 O N 늑 요E三 。 。 Z lna (2a-E1o 。 )Zl na ~ 이댜 {X;: i= l, 2, …}는 모집단 정규분포 N(µ, l) 에서의 랜덤 샘플 이라 하고, 통계적 가설 검정은 귀무가설 Ho : 0 = -0.5 대 대립가설 H1 : 0 = 0.5 라 하자. 그러면 Z = InP 。 ,(X) I P 。 0 (X) = X 이므로 E 。 . z= -0.5 이댜 따라서 축차확률비 검정의 정지규칙 N 에 대한 기 대치는 근사적으로 (2.3.6 ) E 。 0 N~ (2 -4a)ln 노a그 이다. 한편 제 1 종의 오류확률 a 를 갖는 고전적인 고정 표본수를 갖는 검정에서 표본수 m 은 (2.3.7) m 늑 4 갑, Za = P(Z~ 1 一 a) , Z~N(O , 1) 이다. 따라서 이 때의 축차확률비 검정과 고전적인 고정 표본수를 갖는 검정과의 상대효율성 r 은 근사적으로 (2.3 .8 ) r 늑 (2-4a4) 갑ln 上a 이다. 만약 새로운 검정 귀무가설 Ho : 0 。 = -0.5c 대 대립가설 Hi : 01 = 0.5C' C =I= 0 인 경우에도 식 (2.3.8) 의 상대 효율성 r 은 변
함이 없음울 쉽게 알 수 있다. 여러 가지 a 에 대한 %, m, E 。 0 N, r 의 값을 나타낸 것은 표 2.3.1 과 같댜 표 2 . 3 .1에서 보는 바와 같이 a :5: 0.2 에 대하여 축차확률비 검 정에 소요되는 정지규칙 N 의 기대치는, 고전적인 고정 표본수를 갖는 검정에서 소요되는 표본수에 비해 60% 이하임을 알 수 있으며, a 의 값이 적을수록 그 비율도 점점 적어진다는 것을 알 수 있다. a 가 O 에 접근하면 4 z/ ~ 8llna| 이고 (2 -4a)ln~ ~ 21lnal 가 됨을 쉽게 볼 수 있다. 따라서 a 가 0 에 접근하면 상대 효율성은 0.25 에 접근한다. 만약 0 。 = —0.5 c, 01 = 0.5c 가 아닌 경우의 가설 검정에서는 상 대효율성이 0.25 에 접근한다고 할 수 없다 . 일반적으로 0o 가 0 에 가까 표 2.3.1 a Za m E 내 .s (N) E-o.s(N)/m .20 .84 2.8 1.7 59% .10 1.28 6.6 3.5 54% .05 1.64 10.8 5.3 49% .02 5 1.96 15.4 6.9 45% .01 2.3 3 21. 6 9.0 42% .00 5 2.58 26.5 10.5 39% .001 3.09 38.2 13.8 36% .0001 3.72 55.3 18.4 33% .00001 4.27 72.8 23.0 32%
운 값일 때의 가설 검정에서는 고전적인 고정 표본수를 갖는 검정이 축 차확률바 검정보다 효율성이 좋을 수도 있다. 이 경우에는 Lorden 의 2- 축차확률비 검 정 (Lorden 2-SPRT) 방법 을 사용하면 효율성 이 더 높아 진다 . 다음에 는 예 제 2.2 .4에 서 와 같이 { X; : i = l , 2 , … } 는 모집 단이 베르누이( O) 에서의 랜덤 샘플이라 하고, 이 때 가설 검정은 귀무가설 Ho : 0 。 = 0.25 대 대립가설 H1 : 01 = 0.75(81 = 1-0 。 ) 라 하자. 그러면 0 。에 있어서 축차확률비 검정의 정지규칙 N 의 기대 값은 근사적으로 (2.3.9) E 。 。 ::::: (2_4a)l1nn3 l_a a 이다. 또한 고정 표본수를 갖는 고전적인 검정에서 소요 표본수 m 亡。 근사적으로 (2.3 .1 0 ) m 늑 3 갑 이다. 따라서 a 가 0 에 접근하면 그 상대 효율성은 ―Eo굽0N _. 一1國 늑 0.3 이다.
제 3 장 축차복합가설 검정 제 2 장에서는 귀무가설과 대립가설이 단순가설일 때를 다루었다. 이 장에서는 복합가설에 대한 축차검정을 한다. 복합가설은 첫째 장애모수 가 없을 때의 복합가설과 둘째 장애모수가 있을 때의 가설이 단순가설 또는 복합가설일 때를 의미한다. 따라서 제 1 절에서는 하나의 매개모수 에 대하여 H。 : 0< o 。 대 Hi : 0~ 01 형태의 복합가설에 대한 축차검 정을 다루고, 제 2 절에서는 복합가설에 대하여 가중치함수를 사용한 축 차검정을 다룬댜 마지막으로 제 3 절에서는 불변의 원리를 사용한 축차 검정을 다룬댜 3.1 하나의 매개모수에 대한 복합가설의 축차검정 이 절에서는 하나의 매개모수를 갖는 지수형분포족과 같은 분포의 모 수들에 대한 복합가설 H。 : 0< o0 대 H1: 0~ 01 ( 0 。< oI) 형태의 축 차검정 문제를 다룬다 . 이러한 형태의 축차검정에 대한 이론적인 배경
을 살펴보고, 그 예로써 하나의 매개모수 를 갖 는 지수형분포 족 분포에 대한 복합가설을 다루고자 한다. (Q,'Ji ,Po) 를 분포함수 Po 를 갖는 확률공간이라 하자. 이 때 모수 0 의 집합 O 를 모수공간이라 하고, 여기에서 O 는 실수의 부분집합이 댜 {X; : i= I,2,3, …}는 (요, T) 에서 정의되는 확률변수로서 분 포함수 Po 를 갖는다고 하자. 이 때 복합가설 (3.1. 1) Hi。: 0< o0 대 H1: 0~ 81 (0 。 < 81) 에 대한 축차검정을 하자. 제 2 장에서 정의한 바와 같이 L(0) 를 검사특성곡선, T(O) 를 검정력 함수라 하고 주어진 제 1 종 및 제 2 종 오류확률을 각각 a , (](0 < a, /3< 1) 라 할 때, 식 (3. 1. 1) 에 대한 검정은 (3.l.2) r( O) < a , v o조 0 。 , T( O) > 1 _ 8 , v o느 01 울 만족하여야 한다. 죽, 모든 0EHo 에 대하여 Ho 를 기각하는 오류확 률은 a 보다 작거나 같아야 하며, 모든 0EH1 에 대하여 Ho 을 채택하 는 오류확률은 8 보다 작거나 같아야 한다 . 복합가설 (3.1 . 1) 대신에 우선 단순가설 (3.1. 3) H。 : 0 = 0 。 대 H1: 0 = 01 울 생각하여 제 1 종 및 제 2 종의 오류확률 a, fJ에 대하여 ,r (0 。) = a, K 어 ) = 1- /1인 제 2 장에서의 Wald 의 축차확률비 검정을 실시하자.
이때 만약 (3. 1. 3) 에 대한 축차확률 비 검정 에서 검정력함수 7[( O) 가 0 에 대한 감소함수가 아니면 r( O) 는 식 (3. 1. 2) 를 만족한다. 따라서 복 합가설 (3. 1.1)에 대한 축차검정은 단순가설 (3. 1. 3) 에 대한 축차확률비 검정과 일치하게 된다. 죽, (3. 1.1)에 대한 축차검정은 Ho 를 대표하여 0 = 0o, H 를 대표하여 0 = 01 로 놓 고 축차확률비 검 정을 하면 된다. 이 절 에서는 어떠한 경 우에 검정력함수 T( O) 가 0 에 대한 감소함수가 아닌가에 대하여 살펴보고자 한다. 정의 3.1 .1 F 와 G 는 각각 실수값을 갖는 확률변수 X 와 Y 에 대한 분포함수라고 하자. 이 때 Y 가 X 에 대하여 확률적으로 크다 (s t ochas tica ll y large ) 또는 X 가 Y 보다 확률적 으로 작다 (s t ochas ti call y small) 는 것은 모든 xER 에 대하여 F(x)~G(x) 인 경우이다. 모든 분포함수 F(x) 에 대하여 F-1(p ) = inf { xE R: F(x) 느p}, 0< p깁 라 하자. 그러면 모든 xER 에 대하여 F(x)~G(x) 이면 F-l(p) :=;; c-I( p)이댜 또한 U 를 (0, 1) 에서 정의되는 일양분포 (un ifo rm dist r ib u ti on ) 라 하면 ( 기 호로는 U~ U( O , 1 ) ) F-1(U) ~ x , G-I(u) ~ Y 의 관계를 갖는다. 따라서 다음의 보조정리를 얻는다. 보조정리 3.1. 1 y가 X 에 대하여 확률적으로 크다. 그리고 깐 (x) 는 x 에 대하여 증가함수이다. 그러면 EW(X) ::;; E 1/f( Y) 이다.
증명 U~ U(O, 1) 이라 하자. 그리고 X 와 Y 에 대한 분포함수 를 각각 F 와 G 라 하자 . 그러면 lJf(X ) ~ lJf(F -1(U)) , lJf(Y ) ~ lJf( c- 1 (U)) 이고, 가정에 의하여 lJf(F -1 ( U) ) =,::; lJf( c-1 ( U) ) 이다. 따라서 E lJf(X ) = E lJf(F -1(U)) 냐lJf (c - 1(U)) = E lJf(Y ) 이다. 口 주 3.1.1 보조정리 3 .1.l에서 lJf(x ) 가 감소함수이면, El Jf(X ) ~ El Jf( Y) 이다. 따름정리 3.1. 2 Y 가 X 에 대하여 확률적으로 크면, 임의의 실수 a 에 대하여 P(X> a) =,;; P( Y> a) 이다 . 증명 보조정리 3. 1. 1 에서 7[J( x) = 1[ a < x < oo] 라 두면 lfl (x) 는 증가함수 이다.口 정의 3.1.2 {P8(x) : 0e e} 를 분포함수라 하자. 이 때 어떤 측도 µ에 대하여 밀도함수를 Po 라 하자. 즉 dP 。 (x) = Po(x)µ(dx) 이다. 밀도함 수군(family of densit ies ) { po(x ) : 0 e e} 가 단조우도비 성 질 (mono t one like lih o od rati o p ro p e rty)을 갖는다는 것은, 함수 T(x) 가 존재하여 모 든 81>0 。 (0o, 81E{:)) 에 대하여 PPoo0,((xx)) 가 T(x) 에 대한 증가함
수임을 의미한다. 정의 3. 1. 2 에서 F 와 G 는 각각 밀도함수 f (x) 와 g (x) 를 갖는 분포 함수라 하고, 이 때 묘f뇨(x 〉) 가 x 에 대한 증가함수이면 F(x) ~ G(x) 이댜 따라서 {Po(x) : 0E e} 가 x 에 대한 단조우도비성질을 갖는 밀 도함수군이라면 {Po(x) : OE e} 는 확률적 순서 (s t ochas ti cal or— der i n g)를 갖는댜 다음 정리들은 검정력함수 T(0) 의 단조성에 관한 것으로 복합가설 (3. 1. 1) 에 대한 축차적 검정 대신에 단순가설 (3. 1. 3) 에 대한 축차확률비 검정으로의 대체를 정당화한다 . 정리 3.1 .3 X,X1,X2,X3, …는 (요,'F .Po) 에서 정의되는 랜덤 샘 플로서 X 는 분포함수 Po 를 갖고, 측도 µ에 대하여 밀도함수 Po 를 갖 는다고 하자. 즉, dPo= Podµ 그리고 {Po(x) : OE G} 가 실수함수 T(x) 에 대한 단조우도비성질을 갖는다. 그러면 통계적 가설검정 (3 .1 .3) 에 대한 축차확률비 검정에서 검정력함수 T(O) 는 단조증가한다. 증명 우도비 R,, = iJJ1 1::::} 라 두자. 그리고 T(Xi) = Ti, T(X) = T 라 하자. 그러면 R,, 은 ( Ti , T2, …, T,, )에 대한 함수로서 각각 의 T서 대하여 증가한다. (3 . 1. 3) 에 대한 축차확률비 검정은 제 2 장에서 와 같이 정지경계치 (B, A) (B< l
이다. 이 때의 검정력함수 7[ (O) 는 1r(0) = p。 (R N ~A) 이댜 이제 T(X) 는 O 와 0' 에 대하여 각각의 분포함수 Fo 와 Fo 를 갖는다고 하자. 그러면 0> 0 에 대하여 F o (x)~F 1r (x) 이고 F01(x)~F 겅 (x) 이댜 이 때 U1, U2, …는 일양분포 (0, 1) 에서의 랜덤 샘플이라 하고, j=1,2, … 대하여 Tf =F e1(UJ , Tj (f =F;l(U] )라 놓자. 그러면 (T1 , T2, …)의 분포함수는 0 일 때는 ( Tf , Tf , …)이고, 0' 일 때는 ( Tf , Tf , … ) 이 며 모든 j = 1, 2 , … 에 대하여 T1 < Tlg 이 다. 우도비 R! = R,,( Tf , T~. … , T!), Rf , = R11( T( , Tf , … , T!.) 이 라 하자. 그러면 모든 n 에 대하여 단조우도비성질에 의하여 R~sRf , 이다. 임의의 n 에 대하여 [ Ns n , R! 2: A ] c [ Ns n , Rf , 2: A ] 이다. 따라서 [Rt 2:A ] c [R 念2: A] 이다 검정력함수 1r(0) = Po(RN>A) = P(R 麟 A)sP(R i2: A) = P( f( RN2 : A) = ;r( 0' ) 따라서 검정력함수 짜 0) 는 단조증가한다. 曰 정리 3 .1 .3 은 {X 戶 i= 1, 2, …}들이 서로 독립이고 동일한 분포를 갖지 않는 경우에 대하여 확장 가능하다. 이 때는 정지경계치 (B,A) 대신에 (B,I,A,,) (A,1 , B,, :상수들의 수열)를 채택하여 모든 0e e 에
대하여 정지규칙 N 이 P 。 (N < +(X)) = 1 인 경우에 성립한다. 예제 3.1.1 {p} (x) : 0E (9} 를 X 의 밀도함수군이라 하고, {서 (x) : OE 8} 는 실수함수 T(x) 에 대한 단조우도비성질을 갖는다고 하자. 그러면 T(X) 의 밀도함수 {사(t) : 0e e} 는 tE R 에 대한 단조우도 비성 질을 갖는댜 예로써 하나의 매개모수를 갖는 지수형분포족을 생각하 면 , 이 때 측도 µ에 대한 X 의 밀도함수는 짜= c(0)eOT(x) 이다. 여기 에서 X 는 벡 터 (vecto r ) 이 다( 즉, 일례로 x1.~ i.i.d. N(µ, 1) 일 때 T(X) = L” X;, X = ( X1 , X2 , •• • , X,, ) ) . 한편 T= T(X) 에 대한 i= l 밀도함수 PI 는 측도 v= µr - 1 에 대하여 pf(t) = c(O)eO t이다 . 따라 入1 o< o' 에 대하여 짜p}( (xx)) -= 고c(끄0) e ((! -0) T( x) 가 되어 T(x) 에 대하여 증가함수이고, 사사((tt)) = ~c(0) e c(f -(J ) 1 는 t에 대하여 증가함 수이다 . 이제 {X ; : i =1,2, 나들이 서로 독립이 아닌 경우에 대해서 고찰 하고자 한다 {X ;: i =1,2, …}는 실수값을 7六l -,亡._ 확률변수로 X = (X1 , X2, …, X, , ) 의 결합확률분포를 P,1. 。 (OEe) 라 하고, 모 든n 에 대하여 측도 µ, 1 이 존재하여 dP,l,0=p ,1 ,8 µ,1(dx) 라 하자. 그 리고 {P,,,0 : 0E 8} 는 T,, = T11(X1 , X2, … , X,1) 에 대하여 단조우도 비성질을 갖는다고 가정하고, 가설 검정 Ho: 0= 0 。 대H1:8= 01 ( 0 。 < 01) 에 대한 정지경계치로 (B,,, A,,)(B,,
은 상수들의 수열)을 갖는 일 반화된 축차확률비 검 정 (ge nerali ze d se- qu enti al pro babil it y rati o tes t) 이 라 하자. 이 때 우도바 는 R,,= PP,,,,,,o o, ,(( XX )) 이라 하고, 정지규칙 N 은 (3.1 .5 ) N= inf{ n~1 : R,,~B,, 또는 R,,~A,,} 이라 하자. 더불어 모든 0E $에 대하여 Po(N< 00) = l 이라 가정한 다. R,, 은 T,, 에 대하여 단조우도비성질을 가지므로 모든 n 에서 T,, 에 대한 증가함수이댜 따라서 구간 111, , 1112 , 111, ( 1 11, < 111, < 1,,.,) 이 존재하여 R,1 < B,, 台 T,I E I,I, B,,
t,,)이다 그러면 요p,, 은 (t!, t2, …, t, , )에 대하여 증가함수이다. 첫째, n= l 일 때는 명백히 Q1 ( Tr E 113 ) ~ Pr ( T1 E 113 ) (3.1. 7) Q1 ( Tr E lu ) s Pr ( Tr E lu ) 이다 n~2 에 대해서는 y11 - l = t- 1 = (t1 , tz, … , tn- 1 ) 이 주어졌을 때 의 T,, 의 조건부 확률밀도함수 (con diti onal pro babil ity densit y func - ti on) 는 p,,(t,Jt'l- 1) = p,,「::::〉 1) 이고, q,1 ( t , ,|t't-l ) = q,':::::>1 ) 이 다 . 따라서 (3.1. 8) Pq,,,,C( tt,,,,ll tt -- 11)) -= pq,,,,((tt)) . qp,,,, -_1 iC( tt-- 11 )) 이다 . 고정된 t -1 에 대하여 식 (3 . 1. 8) 은 t,,에 대하여 중가함수이다. 따라서 y11 - I = t- 1 이 주어졌을 때의 T, ,의 조건부 분포함수는 t,,에 대하여 단조우도비성질을 갖는다. 그러므로 (3.1. 9) Ql l (tll E 111, I T -1 = t- 1 ) ~ P11( T11 E l,,, l t11 -1 = t- 1 ) 이다 식 (3. 1. 9) 는 T-1 에 의한 모든 사건들에 대하여 성립하므로 (3.1. 10 ) Q, ,(T,,E/11, I N > n ― 1) 느 P,,(T,,EI,, 3 | N>n-l) 이 성립한다. 같은 이유로 [ T,,EI,,1] 에 대해서도
(3.1. 11 ) Q,,( T,, E /111 I N> n 키 ) :s:: P,,( T,, E /111 I N > n— 1) 이다. 따라서 다음과 같은 보조정리를 얻는다. 보조정리 3.1.4 모든 n 에 대하여 Q,, { N< 12 , TN E I,13 } > P,A N< n , TN E I,13 } (3.1. 12 ) Q,, { Ns n , TN E J,,.} s P,, { Ns n , TN E /111 } 이다. 층명 n=l 에 대하여 보조정리는 명백히 성립한다. 따라서 수학적 귀 납법을 사용하여 n22 에 대하여 증명하자. 편의상 R= H。 기각 台 TNE T,,3 A = H。 채택 ¢=> TNE T,,, 이라 하자. 그리고 주어진 n( 22) 에 대하여 (3 .1.1 2) 가 성립한다고 가 정하자. 이 때 Q{ N:;;; n , R} + Q{ N:;;; n , A} + Q( N> n) = 1 P{N:;;;n, R}+P{N:;;;n, A}+P(N>n) = 1 이므로 P(N>n) -+QQ( {N N>:;;n;n), =A }Q —{ NP:{;; N;n:,; ;R;n}, -AP}{ N:;;;n, R} 이다. 가정에서 주어진 n 에 대하여 Q{ N:;;;n, A}-P{N:;;;n, A} :=:;;o 이 성립P하(N므>로n )-Q ( N>n):=:;;Q { N:;;;n, R}— P{ N:;;;n, R}=i > O
이댜 따라서 Q( N$;n+l, R)-P(N$;n+l , R) = Q{ N$; n , R} + Q{ N= n + l, R} -P{N$; n , R} —P{ N= n + l, R} = 8+ Q( N> n ) Q{ N= n+l, R I N> n } —P( N> n )P{N= n+l, R I N> n } ~ 8 + [Q (N> n) —P( N> n )]P{N= n+l, R I N> n} 느 8[ l —P{ N= n+l, R I N> n }] ~ O 이다 따라서 Q( N~n+l, R)~P(N~n+l, R) 이댜 같은 방법으로 Q( N~n+l , A) ~ P(N~n+l , A) 임을 쉽게 보일 수 있으므로 증명은 끝난다 . 口 보조정리 3. 1. 4 를 이용하여 검정력함수 1r(0) 가 증가함수임을 다음 정리에서 보인댜 정리 3.1.5 n = l, 2, …에 대하여 X = (X1 , X2, … , X, , )은 T,1 = T,, (X1,X2, … ,X,,) 에 대한 단조우도비성질을 갖는다고 하자. 이 때 가 설 Ho: 0= 0 。 대 H1: 0= 01 에 대한 일반화된 축차확률비 검정을 (3. 1. 5) 와 같이 실시할 때, 모든 0E0 에 대하여 P(J ( N
7r( 0' ) = p(f {Ho 기 각 } = Q { R} = lim Q{ Ns n , R} ',.....O O ~ lim P{ Ns n , R} = P{ R} = P 。{ R} = 7r ( 0 ) ’,.....OO 이다. 口 지금까지 X= (X1,X2, … ,X,1) 이 단조우도비성질을 가질 때는 가설 (3. 1. 3) 에 대한 축차검정에서 검정력함수 T(O) 는 증가함수임을 보였댜 다음에는 단조우도비성질을 갖지는 않지만 확률적 순서를 갖는 경우에 대하여 살펴보자. {X1,X2, … ,X,,} 에 대한 n 단계에서의 확률 비를 {R,,: n=l, 2, …}이라 하고, 임의의 두 모수를 0 , 0' ( 0 < 0') 라하자 . 이때 {Ri = r;, i= 1,2, … ,n ― l} 이 주어졌을 때의 R 의 0 에서의 조건부 확률분포함수를 F(r,, I r-1) 이라 하고, O' 에서는 G(r,, I r' '-1) 이라 하자. 또 다음과 같은 확률적 순서를 갖는다고 가정 하자. (1) F( r,, I r-1) ~ G(r,, I r-1) , n=l,2,… (2) F( r,, I r-1 ) 와 G( r,, I r-1 ) 이 r1 ' r2, ···, r,I-1 에 대하여 감 소함수이다. 그러면 Ho: 0= 0 。 대 H1: 0= 01 에 대한 축차확률비 검정에서의 검정력함수 T(O) 는 정리 3. 1. 3 의 증명과 같이 증가함을 보일 수 있다. 또한 HoeHOn the monoto n ic ity of the OC of SPRT, 1970, MIS 41, 310 참조)은 다른 방법으로 증명하였다. 이제 하나의 매개모수를 갖는 지수형 분포족, 예를 들면 평균 0= (L), 분산 1 인 정규분포족, 파괴율 1 (L)|인 지수분포족, (J) = In0 인 포
아송분포족, (JJ = In 근广 인 베르누이분포족 등에 대하여 가설 Ho : (J) 三 (J)。 대H1 : (L} ~ (L)I ((L)。 < (L) 1) 에 대한 축차검정을 해 보자. 확률변수 Y1, Y2, …가 분포함수 {P 。 : WE e} 를 갖는다고 하면, 상 기의 분포족들은 단조우도비성질을 갖는다. 따라서 w = w0 와 (J) = w·i 에서의 R확,, 률= 비~d는P '~모, 든= enx 에p { 대((L)하 1여- ( L)。 )n —Y,, _ n[ lJf((L)1) 구((L)。)]} 이고, 이 때의 (l) = (l)。 대 (L)= (L) 1 에 대한 축차확률비 검정은 정지경계 치 (B, A) 에 대하여 N= inf {n~l:S,,~b 또는 S,,~a}, a=lnA , b=InB, s,, = ( (L)1 _ (L)。 ) n Y,-n[ lJf( (L)1 ) _ lJf( (L)。)] 이댜 또한 검정력함수 1r(w) = Pw{SN::::::a} 이고 7r((J )) 는 단조중가함 수이므로 , 짜(J)。 )=a' 7r((JJ 1 ) = 1- /3가 되는 정지경계치 A 와 B 를 제 2 장에서와 같이 정하면, 이 축차확률비 검정은 Ho : (L) 조 (L)。 대 Hl : (L)느 (L)1 에 대한 검정이다. 예제 3.1. 2 {X ; : i = 1 , 2 , ..• } 는 정규분포 N(0, 1) 에서 정의된 랜덤 샘플로 Ho: e:;:;;O 대 H1: 0~0 에 대한 축차검정을 하자. 이 때 어떤 c > O 을 선택하여 0=― C 와 0=c 에 대한 주어진 오류확률을 만족하 도록 하자. 예로써 c= 0.5 로 잡을 때 H'o: 0= -0.5 대 H '1: 0' =0.5 에 대한 축차검정을 실시하면 R11(X) =exp ( L” X;), 죽i= l R1(X) = exp ( X) 이다. 이 때 Ee,x=ex p(~)이고 제 2 장에서
정의한 h(O)=_2 0 (0+0) 이다. 따라서 검정력함수 7f (0) 는 0 수 0 에 대하여 짜 0) = ~ 이댜 0= 0 에서 검정력함수값 7f (0) 는 T(O) 의 연속성에 의하여 7f( 0 ) = lti m 7 f( 0) = 二a각— Lb 이고 , 이 때 a= InA, b= InB 이댜 특히 B= 숫 로 하면 Jf (0) 늑 1+\-20 이 고, 이 때의 7f( 0 ) = 0.5 이다. 3.2 Wald 의 축차 복합가설 검정 3.1 절에서는 장애모수가 없이 하나의 매개모수 를 갖는 분포족에 대한 복합가설 Ho: 0::,;;Bo 대 H1: 0~01(0 。 < o! )에 대하여 살펴보았다. 이 절에서는 장애모수가 존재하거나 장애모수가 없더라도 3 .1 절 에서 다룬 가설 이외의 복합가설에 대한 Wald 의 가중치함수 (we ig h t fu nc ti on) 를 이용한 축차검정을 다룬다. {Po(x) : 0E e} 를 확률변수 을X 의 o확 。 '률 8밀1 이도라함 수하라고, 하 자e. 。 모또수는공 간@1 은e 의 서로소(di sj o i n t)인 부분집합
적어도 2 점 이상의 원소를 갖는 집합이라 하자 . 이 때 다음의 복합가설 에 대하여 살펴보자. (3.2 .1 ) Ho : 0E e 。 대 H1 : 0E @1 o 。 또는 61 은 단순가설이 아니기 위해서 적어도 2 개 이상의 원소를 갖는다고 하자 . 가설 (3 . 2 .l)에 대한 검정에서 제 1 종의 오류확률은 o 。 내의 모수값에 따라 변하고, 제 2 종의 오류확률도 마찬가지로 61 내의모수값에 따라 변한다 . 이 때의 제 1 종 및 제 2 종의 오류확률을 각각 다 움과 같이 정의하자. a ( 0 ) = P 。 { H。 기 각 1 OE @。} (3.2.2) {3( 0) = P 。 {H 。 채 택 I 0E 81} (3.2 .1)에 대한 통계적 검정은 주어진 제 1 종 및 제 2 종의 오류확률 a, /3 (O
이 때 p;,와 q:,에 대한 새로운 가 설 검정은 다음과 같이 하자. (3.2 .6 ) Ho : P;, 대 H; : 야 , n = l, 2 , … 가설 (3.2.6) 은 단순가설검정으로 제 1 종 및 제 2 종의 오류확 률 을 각각 a, /3( 0< a , [3 < l) 를 갖는 축차확률비 검정을 하면 , 정지경계치 (B, A) (O
/3( 0 ) 의 81 에서의 최대값은 f] (B,A, g。 (0), g 1(0) )에 의하여 결정 된댜 주어진 정지경계치 ( B , A ) 에 대 하여 a ( B, A , g。 ( 0 ) , gi ( 0 )) 와 /3 (B,A, g。 (0), g l(0)) 의 값들이 적어지게 하는 g。 (o) 와 g1 (o) 가 가중치함수 중에서 바람직한 함수이다. 따라서 이 때의 a(B,A, g。 (o), g l(O) )와 /3 (B,A, g。 (O), g l(O)) 가 동시에 최소값을 갖는 가중치함수 g。 (O) 와 g l(0) 를 찾는 것은 가능할 수도 있다. 이러한 가중치함수 g。 (O) 와 g 1(0) 를 최적가중치함수라고 한다. 일반적으로 이러한 가중치함수를 실제로 찾기는 어렵다 . 그래서 때로는 a( B, A , g。 (0) , g1 ( 0)) 와 f]( B, A, g。 (0) , gl (0)) 가 동시에 최소 값을 갖는 가중치함수를 찾는 대신에 a(B, A, g。 (0) , g l(0)) 와 /3( B, A, g。 (0) , g 1(0)) 의 평균에 대해서 최소값을 갖게 하거나 미니 맥스 (m ini max) 해를 찾을 수도 있댜 어떠한 경우라도 일단 가중치함 수 g。 (O) 와 g 1(0) 가 찾아지면 o 。에서의 a(O) 의 최대값과 61 에서 의/3 (O) 의 최대값은 정지경계치 (B, A) 에 따라 결정되므로 지「
(3.2.3) 를 만족하는 정지경계치 (B,A) 를 구하면 된다. 예제 3.2.1 X는 확률변수로 P(X=l)=0, P(X=O)=l-0, OE (0, 1) 라 하자. 이 때 다음의 통계적 가설에 대하여 살펴보자. Ho: 8= 송 대 파 | o ―승 1 ~ 0 8: 주어진 양의 수 이 때 g가。 (중 0 치) ~함 수( :를 : 다:음:과! 같 ,이 두자.g 1 ( 0 ) = ( [旺。 _ _ 尸—2 l +I 8 그러면 주어진 총 표본수 n 에서 관측되는 수를 m 이라 하고 정지경계93
치 (B, A) 에 대하여 01= 강나라 하면, N= inf{ l~m~n : 2 -1 [ 0; (1- 01) -111 + 8;'-11 1( 1- 01)111] ~ B 또는 2'l - I[0 i (l ― 01)-111+0 「 ' (l_oI)' ]~ A} 이다. 최적가중치함수에 대하여 다음과 같은 정리를 얻는다. 정리 3.2.1 p ,1.o 를 X = (X1 , X2 , ... , X,,) 의 결합확률 밀도함수라 하 자 . 이 때 모수공간 0 에 대한 복합가설은 다음과 같다. Ho : 0E e 。 대 H1 : 0E 81 eo n 81 -=I= 0 , e; E e , i = o, 1 이 때 S1 를 81 의 경계값들의 집합이라 하자 . 그리고 Bo 와 81 에서 의 가중치함수는 각각 h 。 (0) , h1(0) 로서 JO o h 。 (0)d0= 1, lh1(0)d0= 1 을 만족한다고 하자. 그리고 확률비 R,l = JS: hI ( 0)P,l.o(X) d0 I J。 O h 。 ( 0)P,,, o(X ) d0 에 대한 축차확률비 검정은 다음의 3 가지 를 만족한다. (1) 제 1 종의 오류확률 a(0) 는 o 。에서 상수값을 갖는다. (2) 제 2 종의 오류확률 /3( 0 ) 는 S1 에 서 상수값을 갖는다. (3) 81 내부의 점(i n t e ri or p o i n t)에서의 /3 (0) 의 최대값은 S1 에서의 /3( 0) 의 상수값보다 크지 않다 . 그러면 이 때의 가중치함수 h 。 (0) 와 h1(0) 는 최적가중치함수이다.
증명 g。 (O) 와 g 1(0) 를 각각 eo 와 f} I 에서 정의되는 임의의 가중치 함수라고 하자. 이 때의 제 1 종 및 제 2 종의 오류확률을 각각 a·(e) 와 /3 *(O) 라 하자. 그러면 아주 좋은 근사값으로서 J。 0 a• (0) g。 (0)d0 늑 人」 J。 1 /3 *(0) g。 (0)d0 늑 탓 이다 이 때 B 와 A 는 정지경계치 (B,A) (O < B < l < A) 이댜 그 리고 max a*(O) > Al__BB OE 0 。 m0Ea0x1 /3* (0) 느 旦A 4_ 그B L 이다 가정 (1), (2), (3) 에 의하여 max a(O) = A1 —-BB OE 0 。 m0Ea0xl f3( O) = 쁜在밭 이므로 증명은 끝난다. 口 예제 3.2 .2 Xi , X2, … i.i.d . N(µ, 군)이고 모수공간은 8={0= (µ,
그러면 S1 = { (µ, 6) : 1q -1 = o} = { (µ, 6) : µ = µ。 土 68} 이 댜이때 Bo 와 81 에서의 가중치함수를 다음과 같이 정의하자 . 상수 c > O 에 대하여 h0c(O) = { : , 0 조 6 三 c 0, a> C hlc(o) = { 点 0 £ (1£ C , µ = µ。 ± 8 • (J 0 . 이외의 값 라 하자. 그러면 p;, II = hi h1c( <1)(古 )’'ex p(-감 훔 (x1 ―正 )d
3 가지 를 보일 수 있다. (1) Bo 에서는 a(µo ,
3.3 불변 축차확률비 검정 이 절에서는 벡터값을 갖는 모수 0 = (Ol, 02, ••• , 0 서를 매개로 하는 분포함수에 대하여 모수의 함수, 즉 어떤 실수값을 갖는 함수 ¢ 에 대하여, Ho : ¢(0)~ ¢。 대 H1 : ¢(0) 2: ¢1 과 같은 형태의 가설 에 대한 축차적 검정을 하고자 한다. 예로써 확률 X 가 정규분포(평균 µ, 분산 군)를 할 때, 모수 0 = (µ, 6) 에 대하여 ¢(0) = µ/a 에 대한 검정과 같은 것을 고찰하고자 한다. 이 때 우리는 랜덤 샘플 X1, X2, …로부터 모수 ¢(O) 에만 의존하는 확률변수의 수열 {T,,= T,,(X1, X2, … , X,,) :n = 1, 2, …}를 찾을 수 있으며, 이러한 수열은 서로 다른 것들이 많을지도 모른다 . 따라서 이런 많은 확률변수 의 수열에 대하여 그 영역을 제한함으로써, 쉽게 해결할 수 있다. 이런 방법의 하나로 이 절에서는 불변의 원리(pri nc ip le of inv aria n ce) 통계 량을 사용하여 축차검정을 하고자 한다. (Q , :F , p) 가 확률공간일 때 분포함수족을 P = {P8 : 0E 8} (e: 모수공간)라 하고, G 를 요에 대한 일대일 대응 변환군(t rans form ati on g rou p)이라 한댜 이 때 (요, G) 라 쓰고 G 는 요에서 작용 하는 변환군이라 부른다. 또한 G 를 모수공간 0 에 작용하는 변환군이 라 간주하고, (8, G) 라 쓴댜 이 때 다음과 같은 정의를 하자 . 정의 3.3.1 사건 A 가 변환군 G 에 대하여 불변이라는 것은 gA = {gw : wEA} =A, AE'}< , gE G 일 때이다.
정 의 3.3.2 { P 。 : 0E 0} 를 분포함수라 하고 G 는 모수공간 0 에 작용 하는 변환군일 때, 분포함수가 G 에 대하여 불변이라는 것은 Pg 0 (g A ) = Po (A ) , A e ']i , ge G, 0e e 일 때이다 . 따라서 분포함수와 변환군 G 에 대하여 다음과 같은 보조정리를 얻 는댜 보조정 리 3.3.1 X 의 분포함수를 {P0 : 0E 6} 라 하고 G 는 모수공간 0 및 확률공간 (요, 7) 에 작용하는 일대일 대응 변환군이라 하자 . 그러면 P co( g A ) = P0(A) , gE G, 0E6, AE'J i 일 필요충분조건은 gX 의 분포함수가 pg O 일 때이댜 증명 충분조건 : P(gX eA) = P(Xeg - 1 A) = P0(Xeg - 1A) = Pco( A ) 이므로 증명된댜 또한 필요조건: 임의의 AE Q에 대하여 P(gX eA)= P go (X EA) 이므로 P(XEg _ 1 A) = Pg 0 (A) 이다. 따라서 P(XeA) = Po (A ) = pgO( g A ) 이므로 증명된댜 口 가설 H0 : 0E60 대 HI : 0E0l, o 。 nol = o , o 。 Uol = 0 에 대 한 변환군 G 를 이용한 검정문제에 대하여 다음과 같이 정의한다. 정의 3.3.3 변환군 G 가 검정문제에 대하여 불변이라는 것은 다음의 3 가지를 만족하는 것이댜 (1) gA E'J i , \:/A 국 , ge G
(2) Pg O (g A ) = P 。 (A), \;/AE' .F. gE G, 0E8 (3) g e 。 = e 。 또는 ge l = 81 이 때 G 를 불변군 또는 불변변환군(i nvar i an t tra nsfo r mati on g rou p)이 라부른댜 요에서 정의되는 함수 f (x) 에 대한 변환군 G 에 대하여 다음과 같 이 정의한다. 정의 3.3.4 함수 f (x) 가 변환군 G 에 대하여 불변이라는 것은 f(gx ) = f( x) , \;/xE. Q, gE G 를 만족할 때이다. 특히, 정의 3.3 .4에서 I: 요- [o , 1] , 즉 검정함수(t es t f unc ti on) 일 때는 f (x) 를 불변검정함수(i nv ari an t tes t fu nc ti on) 라 부른다. 또한 정 의 3.3 .4에서 모든 WE 요에 대하여 Gw· = {gw : g eG} 를 G 에 대한 w 의 궤도 (orb it)라 부른다. 예제 3.3.1 요 = IR2, G 를 실수의 가산군으로 모든 g EG 에 대하여 (x1 , x2)-+ (x1 +g, x 십이라 하면, (X1 , X2) E 8 에 대한 궤도는 수평 직선이 된다. 정의 3.3 .4에서 어떤 함수 f (x) 가 불변이면 각 궤도에서 f (x) 의 값 이 상수임을 알 수 있다. 만약 불변함수 f (x) 가 다른 궤도에서 다른 상수값을 가지면 f (x) 를 변환군 G 에 대하여 최대불변함수 (ma xi mal inv a rian t fun c tion ) 라 하며 , 다음과 같이 정 의 한다.
정의 3.3.5 /(x) 가 G 에 대하여 최대불변함수라는 것은 (1) f(gx ) = /(x) , Vg E G, xEQ (2) /(x) = /(x' )이면 g EG 가 존재하여 x' = gx 일 때이다. 예제 3.3.2 예제 3.3.1 에서의 최대불변함수는 f( xl , X2) = X2 일 때이 댜 예제 3.3.3 요 = R2 , C 를 실수의 가산군으로 임의의 gE G 에 대하 여 (x1, Xz)-+ (x1 +g, Xz +g)로 정의하면 최대불변함수 f(x )= XI _X2 이다. 통계량에 대한 변환군 G 에 대하여 다음과 같은 주요한 정의를 얻는 댜 정 리 3.3.2 확률변수 X 는 분포함수 P0 , OE e 를 갖고, 이 때의 G 는 확률공간 및 모수공간에서 작용하는 변환군이라 하자. 이 때 통계량 TC. X) 를 변환군 G 에 대한 불변통계량이고, r = r(e) 는 6 에서의 변 환군 G 에 대한 최대불변이라 하자. 그러면 통계량 T(X) 의 분포는 모수 r(e) 에만 의존한다. 증명 T: (요, T)_,( lJT ,B) 라 하자. 그러면 보조정리 3.3 .l에 의하여 모든 gE G, 0EQ BEB 에 대하여 Pg 0 {TXEB} = P 。 {T( gX) eB} 이댜 또한 T 는 G 에 대하여 불변이므로, P 。{ T(g X)e B} = P 。 {TXeB} 이댜 따라서 T(X) 의 분포함수는 임의의 g EG 에 대하 여 o 와 g0 에서 같댜 죽 T(X) 의 분포함수는 모수공간 e 내의 각
궤도에서는 같다 . 따라서 r(0) 는 최대 불 변이므 로 T(X) 의 분포함수 는 r 을 통한 0 에만 의존한댜 曰 예제 3.3 . 4 X1 , X 2 ~ i.i.d . N(µ , J) 이고 G 는 예제 3. 3. 2 와 같 이 실수가산군으로, 확 률 공간에서는 (x i , Xz ) -+ (x 1 +g, Xz +g) , i/x1 , x2 , g EG 이고, 모수공간 8= {(µ, o): µER , o > O} 에서는 0 = (µ, Cl) -+(µ + g, Cl) 로 작 용하는 변환군이 라 하자. 그러 면 불 변 통 계 량 T(X)=X1-X 러고, 모수공간 e 에서의 최대불변함수는 r( 0)=o 이 다. 따라서 정리 3.3.2 에 의하여 T(X) = X1 -X z 의 분 포 함수는 평균 µ에는 관계없이 r(0) = o 에만 의존한댜 즉, X1-X2 ~ N (0, 21) 으로 /에만 의존한다 . 이제 검정문제에 대하여 살펴보자 . X1, X2 , …는 분포함수 P0 , 0E O를 갖는다고 하자 . 이 때 X = (X1 , X 2 , … , X,1) 은 모수 0 에 대한 정보를 모두 가지고 있댜 따라서 추론문제(i n f erence pro blem) 에서는 X 을 가지고 0 에 대한 정보를 얻게 된다 . 이 때 0 에 대한 정 보의 누출없이 그대로 간직하면서 자료의 절감을 가져오는 통계량 즉 충분통계량 (su ffici en t sta t i st i c) , T(X) 을 생각하게 된다 . 따라서 0 에 대한 추론은 일반적으로 충분통계량 T(X’' )으로 하게 된댜 이제 변환 군과 충분통계량에 대하여 살펴보고자 한다 . 확률변수 { U,, : n = 1. 2 , … } 를 확률변수 {X1 , X2 , … } 로부터 얻 은 불변통계량의 수열이라고 하자. 이 때 각 n 에 대하여 수열 { T,, : n = 1, 2 , … } 를 { Un : n = 1, 2 , … } 에 대 한 충분통계 량이 라 하
면’ {T: n = 1, 2, …}를 {X1 , X2 , … }에 대한 충분불변통계량 (suf fici e n t inv aria n t s t a ti s ti c) 의 수열이라 부른다. 불변통계량으로 충 분불변통계량을 구하기는 매우 힘 들 때가 많지만, 다음 예제 3.3.5 에서 보는 바와 같이 충분통계량으로 불변충분통계량을 얻기는 매우 용이하 다. 따라서 충분통계량으로 얻은 불변충분통계량이 불변통계량으로부터 얻은 충분불변통계량과 같은가에 대해서는 이 절의 마지막에서 다루고 자한다 . 예제 3.3.5 X1 , X2, …~ i.i.d. N(µ , 깁 G 는 양의 실수들의 곱셈 군으로 x- gx 이다. 그러면 불변통계량 수열 U,,=(sig nX 1, X2/X1, ••• , X,,/X1), (X1 = 0 은 제외)이다. 또한 이 때의 충분통계량 T,1=( 文, s2II), 立= 上n Fil x ,•,• S211•• = F효l (X,. _ X,,) 2' 즉 T,,= (文, S,,) 이댜 그러면 gE G 에 대하여 ( X,:, S)--+ (gX,:, gS n) , (g-4= 0) 이므로 G 는 TII 에 작용하는 변환군으로 이 때의 불변통계량은 { S11/X ,, : n = 2 , 3 , … } 이다 . 즉 불변충분통계량은 { S,,/X ,, : n = 2 , 3 , … } 이 다. 그러 나 불변통계 량 u,, :::: ( sig nX1 , X2 / X1 , …, X,,/X1) 에 대한 충분불변통계량을 구하기는 쉽지 않댜 고전적인 고정된 표본수 n 에 대하여 랜덤 샘플 (X1, X2, …, X,,) 로 검정하고자 하는 ¢(0) 에 대한 검정은 불변의 원리를 적용하면 불변 통계량 U, ,에 의존하고, 이 때 함수 ¢(0) 가 모수공간 0 에서 최대불변 이라 하면 정리 3 . 3.2 에 의 하여 U,, 는 ¢( O) 에 만 의 존한다. 따라서 ¢(0) 에 대한 u,1 을 근거로 한 검정은 u,1 에 대한 충분통계량 T,1 에
의하여 검정하게 된다 . 즉
이다. R 대 P 2 에 대한 축차검정 8 는 다음과 같 이 정의한다. X1=1 이면 R을 채택하고 , X1=2 이면 X 2 를 관 찰 하여 만약 X2 = l 이면 P 를 채택하고 , X2 = 2 이면 P 2 를 채택한댜 따라서 P,(P i 채택 |N=2, o)=1 , i=1, 2 이댜 8. 를 충분통계량 (T,, T 2 ) 에 근거한 축차검정이라 하자. 그러면 T1 은 상수이므로 N= l 일 때는 8. 는 X1 에 의존해서는 안 된다 . 따 라서 8. 는 Xl = l 또는 2 일 때 정지하는 확률과 계속할 확률은 각각 강이댜 P;{X1 = 1, N= 2lo 가 = } P;{ X 1=1, X2=1 N=2lo.}= 강 P;{ X1 = 1, N = 2 , X2 = 2l o. } = 강 이 므로 P;( P , 채 택 | N= 2 , o*) + 1 로서, Pi( P ,· 채 택 | N= 2 , o) = 1 이 므로 o· 로의 대체가 불가능하다. 정의 3.3.6 X1 , X2, … 는 확률변수이고 X = (X, , X2 , …, X,,) 이 라 할 때 확률변수의 수열 { T,, : n = l, 2 , … } 를 X, , X2 , … 에 대한 전이수열통계량(t rans iti ve seq u ence s t a ti s ti c) 이라는 것은 X’’ 과 T,,+I 이 T,, 이 주어졌을 때 조건부 독립 (con diti onal i nde p enden t)이다. 정 의 3.3.6 에 서 X’ 도누뇨 ( T,I , Y,,) 일 때 { T,, : n = l , 2 , … } 이
전이수열통계량이 되는 것은 T,, 이 주어졌을 때 (Y,,, T,,+1) 의 조건 부 분포가 T,, 이 주어졌을 때 Y,, 과 T,r+1 의 조건부 분포의 곱으로 나 타날 때이다. 예제 3.3 . 7 X1 , X2, … ~ i.i.d. N(µ , 1) , T,, = 훔 X; = n X,,라 하면 X 나~ ( T,, , x-1) 이다. 따라서 Y,, = X-1 이 라 하면 T,,+1 = T,,+X,,+1 이고 X,,+1 과 X - 1 는 서로 독립이므로 T,1 이 주어졌을 때 T,,+1 과 Y,, 은 조건부 독립이댜 따라서 {T,,: n=1, 2, …}는 전이 수열통계량이댜 일반적으로 (요, r, P) 를 분포함수 P 를 갖는 확률공간이라 하자. 이 때 {r;= i = 1, 2, …}를 61 대수(
또한 식 ( 3 .3.2 ) 는 일반 적 으로 i= 1, 2 에 대하여 f, 를 'ri 가측이고 적 분가능함수이면 (3.3.3) EUi /2 I ' J<3 ) = EU1 녀 ;- 3 ) • E (f:기 'J< 3) a.e. 로 쓸 수 있다 . 한편 { '}< ,, : n = l, 2 , … } 를 증가하는 6- 대 수의 수열이 라 하고, {六: n= l, 2, … }를 다른 6 - 대수의 수열로서 '}
예제 3.3.8 X1, X2, … ~ i.i.d. N(µ, /)이면 이 때의 충분통계량은 ( !i=I ;I I X;, iL=I I l XI ) = T,, 이 댜 이 때 Z; = X; , i = l , 2 , … 이 라 하면 T,,+1 = ( 홈I X;+Z,,+1 ' ,ti자 + z 노 ) 은 T,, 과 Z,,+1 만의 함수이 댜 따라서 정리 3.3.3 에 의하여 { T,,: n= l, 2, …}는 {X,,: n= l, 2, …} 에 대한 전이수열이다. 정리 3.3.4 주어 진 확률변수 X1 , X2 , … 에 대하여 모든 n = 1, 2 , … 에 대해 s,,, u,, 그리고 T,, 는 X = (X1 , X2 , … , X,1) 의 함수이댜 그리 고 T,, 는 S,, 의 함수이고 동시에 U,, 의 함수이다 . 또한 U, f上그 1 f' 이 라 하자. 만약 {S,,:n=l,2, …}이 {X,,:n=1 ,2 , ••• }에 대한 전이 수열이고 모든 n 에 대하여 T,, 이 주어졌을 때 S,, 과 U, ,이 조건부 독립이면, {T.,: n= 1, 2, …}는 {U,,: n= l, 2, …}에 대한 전이수 열이다. 증명 확률변수 X, Y, Z 에 대하여 만약 X 와 Y 가 Z 가 주어졌을 때 조건부 독립이면 (3.3.4 ) XI (Y,Z)~XI Z 와 필요충분조건이다. 따라서 만약 Z 가 Y 의 함수이면 식 (3.3.4) 와 (3.3.5) XI Y~XIZ 는 필요충분조건이다. 죽, 임의의 적분가능한 함수 f에 대하여
(3.3.6) E( f(X ) I Y) = E( f(X ) I Z) a.e. 이댜 그러므로 {T,,: n= 1, 2, …}이 {X,,: n= 1, 2, …}에 대하여 (3.3.7) EU( T,,+1 ) I X) = E( f( T,,+1 ) I T,,) a.e. 이면 {T :n =1,2, …}는 {X:n=1,2, …}에 대하여 전이수열이 다. 따라서 임의의 적분가능함수 f에 대하여 (3.3 .8 ) E( f( T11+1) I U) = E( f( T11+1) I T) a.e. 을 보이면 증명은 끝난다 . 그런데 가정에서 {S,,:n= l, 2, …}이 {X :n= 1,2, …}에 대하여 전이수열이므로 임의의 적분가능함수 g 에 대하여 E(g ( S,,+1) I X) = E(g ( S,,+1) I S,,) a.e. 이댜 이 때 g( S11+ 1 ) = /( T11+ 1 ) 이라 하면 (3.3.9) E( f( T,,+ i) I X) = E( f( T,,+1) I S11) = h(S11) a.e. 이고 T, ,이 주어졌을 때 S,, 과 U, ,이 조건부 독립이므로 (3.3 .1 0 ) E(h (S11) I U11) = E(h (S11) I T,,) a.e. 이므로 E( E (f( T,,+1) I X) I U,,) = E( f( T,,+1) I U,,) (3.3.1 1) = E( E( f( T,,+1) I X) I T,,) = E (f( T11+1) I T,,) a.e.
로서 증명된다. 曰 이제 검정문제에 대한 충분통계량과 전이수열에 대해서 살펴보면 다 음과같다. 정리 3.3.5 X1 , X2, … 는 확률변수라 하자 . 이 때 { T,, : n = 1 , 2 , … } 를 {X1,X2, …}에 대한 충분통계량이고 또한 전이수열이라 하자. 그러면 (X1, X2, …)를 기준으로 한 임의의 축차검정 8 는 {T,,: n= I , 2, …} 룰 기준으로 한 축차검정 a· 로 대체할 수 있으며, 이 때 8 와 8. 는 같은 검정 성과룰 갖는다. 증명 X1, X2, …는 분포함수 P 를 갖는다고 하자. 그리고 n= l, 2, … 에 대하여 T, ,은 X=(X,X2, … ,X,,) 에 의하여 생성되는 6- 대수 라 하자. 이 때 정지규칙 N 에 대하여
분포함수 P 에 대한 임의의 가 설 을 H라 하면 X1,X2,··· 룰 기준으 로 한 축차검정함수 8 는 ({a,’' f3 ,1} )에 의존한다. 마찬가지로 충분통계 량이고 전이수열인 { T,,: nE N} 에 대하여 T 信 I 는 T = (T1 , T2 , …, T,I) 에 의하여 생성되는 6- 대수라 하고, a~,' 까, 깝, 그리고 과를 앞에서와 같이 정의하고 a~, 는 T?, -가측함수라 하자. 그리고 축차검정 함수 8. 는 ({a!1' f3?,})에 의존한다고 하자. 그러면 임의의 분포함수 P 에 대하여, (3.3.1 2 ) Ep짜 짜 = Ep a 11 rp1 1 , n = l , 2 , … 임을 보이면 증명은 끝난다. 첫째로 (3.3 .1 3 ) Ep a ,, 짜 = EPa,,
다음에는 (3.3.1 4 ) E p a?, 짜 = E 迅式 , V12, P 임을 보이면 식 (3.3 .1 3) 에 의하여 (3.3 .1 2) 가 성 립한다. 식 (3 . 3 .1 4) 를 다 음과 같이 바꾸어 쓰자 . 즉, 식 (3 . 3 .1 4) 는 (3.3 .1 5 ) E 坪 ~,E( a~,I 묘) = E 坪 ~, E( a,,I 묘) , \/ n , p 이므로 모든 {짜 : n= l, 2, ···}에 대하여 (3.3.1 6 ) E(a~,I 합,) = E(a11l'J< ~,) . n = l, 2 , … 임을 보이면 된다. 짜 = E(a, ,l'Ji ?,)IE( /3 ,,I 묘) , n = l, 2 , … 라 두자. 그러면 n = l 일 때는 /31 = 1 이므로 a~ = E(ail 'Ji~) 이고 a~= 서이다. 따라서 E(a~| 럽) = E(a~| 짜) = a~ = E(a1I 짜) 로서 (3.3 .1 6) 이 성립한다. n=2 일 때는 /32 =1-a1, /3~ =1-a~, 때 =a 詞이므로 E( 때만) = a g E( 때만) = 麟鬪 E( 陶|만) a.e. 이다. 따라서 E( /3갭'J
이다. 따라서 E( 때만) = E[E( /3싸'J< ~V 깍 )1 만] = E( /3 2| 만) 이다 . 이와 같은 방법에 의하여 E( 武訂따) = E( /3 11l '1'~,)임을 모든 n 에 대하여 성립함을 보일 수 있다 . 따라서 (3.3 .1 6) 이 모든 n 에 대하여 성 립한댜曰 이제까지 정리 3 . 3.5 에 의하여 충분통계량이 전이수열이면 축차분석 에서 충분통계량을 근거로 한 축차검정을 할 수 있음을 살펴보았다. 다 음에는 앞에서 제기된 불변의 원리를 사용한 통계량에 대한 충분통계 량과 충분통계량에 대한 불변충분통계량이 같은 것인가에 대하여 살펴 보자 . (요,'f ,P) 를 확률공간이라 하고 G 를 불변변환군이라 하자. 또 한 'F s 를 충분통계량에 의하여 생성되는 T 의 부분체 (sub fi eld) 라 하고 'f1= {AE' f:g A = A, Vg e G} 라 두자. 그러면 함수 11 가 가측함 수이고 불변이라 함은 F[ 가 T 「가측함수일 때이다. 이 때 'JiS I= 'Ji sn 'f[라 하고 다음과 같은 가정을 하자. (3.3 .1 7 ) (1) g'f s = 'f s , V e G (3.3.1 8 ) (2) Is 가 'f s 가측함수이고 거의 불변 (almos t in v ari an t)이면 'f SI 가측함수 /SI 가 존재하여 Is= fs1 a.e. 이다. 그러면 다음과 같은 보조정리와 정리를 얻는다. 보조정리 3.3.6 앞의 가정에서는 임의로 주어진 T/ -가측함수 f1 에 대 하여 'Ji SI- 가측함수 fs 1 가 존재하여 EU1I'J is) = fs1 a.e. 이다.
증명 EU1I 'Ji s ) 를 Is 라 표현하자. 그러면 gE G 에 대하여 E(g 1 11' Jis ) = gE U1l'J is) a.e. 이므로 g/ 1= 11 이다 그 리고 Is = gfs a.e. 이므 로 Is 는 거의 불변함수이다. 따라서 가정 (2) 에 의하여 증 명된다 . 曰 정의 3.3.7 앞의 가정에서 'Ji S I 는 T[ 에 대한 충분부분체이다 . 증명 주어진 T[ 가측함수 fl 에 대하여 'Ji S I 가측함수 fs 1 가 존재하여 임의의 분포함수 P에 대하여 fs1 = E p(f기'Ji ;1) a.e. 임을 보이면 증 명된댜 그런데 Ep (/ 11'J is1 ) = Ep (E U1l'J is) l'J is1 ) = Ep (fs1l 'J is1 ) = fs1 a.e. 이므로 증명은 끝난다. 曰 정리 3.3 . 7 은 T 충분부분체 . y:; s 一 볼챌-> 'J, S I 와 y:;_:_ 볼 보 ➔ 'J, I _ 塗 L y:; S I 는 같음을 보이고 있다. 정리 3.3.8 앞의 가정에서 'f s 와 'f I 는 'f SI 가 주어졌을 때 조건부 독 립이다. 증명 보조정리 3.3.6 에서 EP(fI | TsI) = fsI a.e. 이고 정리 3.3.7 의 증명 과정에서 E(IJ l'J i s) = fs1 a.e. 이다. 'JiS IC 'JiS 이므로 E(/Ji'J is1 ) = E(I기 'Jis) a.e. 이다. 따라서 (3.3.5) 의 일반화에 의하여 중명된다. D 예제 3.3.9 X1 , X2 , …는 i.i.d. N(µ , 군) 일 때 µ룰 장애모수로 간주 하고 Ho : a2-~ ~ 대 H1 : / > 석 ( 해 < 석) 에 대 한 축차검 정을 하자.
이 때 변환군 G 를 가샨군으로 Xi - > x,.+ a, µ— > µ +a, 6-->6, aEI P. 이라 하자 그러면 X= (X,X 2 , … ,X,, )의 충분통계량은 (Y,s?I) 또는 S,1= (X,:. ~(X, _X,: )2) 이댜 이 때 G 에 대한 최대불변통계량 i= l 의 수열을 { U,, : n ~ 2 } 라 하면, U,, = (X2 -X1 , X3 -X1 , … , X,I _x1) 나그 ➔ u 이댜 또한, G 는 {S,, : n=2,3, ….}에 첫근•X.: +a, iL= (l X,- 文)?-- • iL= ( l X,- 굿간으로 작용한다. 따라서 앞의 정리에 의 하여 불변통계량 {U,,: n= 2, 3, …}에 대한 충분통계량은 {S,,: n = 2, 3, …}에 대한 불변통계량 T,l = i2=” ( l X, ―文간과 같다. 이 때 T, ,은 모수공간 0 에 대한 G 의 최대불변함수 균에 의존한다 또한 T, , 은 {U,,: n=2, 3, …}에 대한 전이수열이다 . 한편 7T 웅 의 분 포는 i, - 1 이며 단조우도·비성질을 가지므로, .Ho 대 H1 에 대한 축차검 정은 H 。:#=해 대 H1: 군=서에 대한 축차확률비 검정과 같다. 따라서 이 때의 축차확률비 검정은 정지경계치를 (B,A) 라 할 때 정 지규칙은 다음과 같댜 N= inf {n 켈 (n-3)ln 운나(〉길 )T,l? 또는 (n ― 3)1n 릅나(》갑 )T ::::: a}, a=lnA, b=lnB 예제 3.3.10 X1,X2, …는 i.i.d . N(µ, 군)일 때 r(0)=µ/a 라두고 Ho:r(B)sr 。 대 H1:r (0 )2r1 Cro
때 변환 G 는 X i一 cx, . , µ一 cµ, 6 一 C6, CE R +라 하자. 그러면 G 에 대한 X={X1,X2, … ,X,,} 의 불변수열 {U11:nEN} 는 ull= {sig nX 1,X2/X,, …, X)X1} 이고, 0 에 대한 최대불변은 r(0)=µ/
제 4 장 재생이론과 비선형 재생이론 이 장에서는 재생이론에 관한 여러 가지 성질을 살펴보고, 이를 이용 하여 제 2 장에서의 축차확률비 검정의 오류확률 및 정지규칙의 기대값 에 대한 점근적 성질에 대하여 알아본다. 또한 제 5 장에서의 축차분석의 추정을 위한 비선형 재생이론도 다룬다. 4.1 재생이론 지난 20 년 동안 재생이론과 비선형 (nonl i near) 일 때의 재생이론의 확 장은 축차분석에 매우 중요한 도구로 사용되어 왔다. 이 절에서는 재생 이론에 관한 일반적인 성질을 살펴보고자 한다. (요, 'Ji ' p)를 확률공간이라 하고 이 공간에서 정의되는 랜덤 샘플 을 X1, X2, …라 하자. 이 때 X i는 분포함수 F 를 갖고 평균을 µ, 분산을 /이라 하자. 또한 s 。 =0, S,,=Xi + X2+… +x,, (n 칙) 으로 하면 {S: n~O} 은 확률보행 (random walk) 이다. 예를 들어 어떤
전기제품의 특정 부품이 고장나면 죽시 새로운 동일 부품으로 교체하 여 고치는 것 또는 재생하는 것을 반복한다고 가정하자. 이때 만약 x,~o 이면 X 를 교체하는 i번째 부품의 수명으로 간주하고, s, ,은 n 번째 부품의 대체까지의 총수명으로 생각할 수 있을 것이다. 이러한 의 미에서 이것에 대한 이론을 재생이론이라 부르고, 수열 .{S: n~O} 을 재 생 과정 (renewal pro cess) 이 라 정 의 한댜 재생과정의 주요 연구대상 중 하나는 재생셈과정 (renewal counti ng pro cess) {N(t) : t ~O} 로 다음과 같이 정의한다. 정의 4.1. 1 N( t) = max{n: S,I:,;; t}를 재생셈과정이라 한다. N (t)를 시간 [0 , t]에 있어서의 재생하는 수로서 해석할 수도 있 으며 이것에 대해서 다음과 같은 정리를 얻는다. 정리 4.1.1 N( t)를 재생셈과정이라 하면 (1) P(N( t) < oo) = 1. Vt (2) E(N(t) ) r
s;; = 1, S,. = kL=” I Xk (k ~ l) 그리고 이 때 N(t) = max{n: 효~ t} 라 하면 Y;::; ;xk (k 티), 효 ~S,, (n~O), N(t) ~N( t) 이다 그리고 刃(t)는 모수(p arame t er) ([t ],P(X 칙))를 갖는 음이 항분포 (ne g a ti ve bin o mi al di s tri bu ti on) 를 하므로 N( t)에 대해서 정리 4 .1.1은 성립한댜 따라서 N(t)에 대해서도 성립하므로 증명된다. O 정리 4.1. 2 (재생셈과정의 강법칙 (S t ron g law for the counti ng pro cess)) N (t)를 재생셈과정이라 하고 µ>O 라 하면, t ->00 이면 (1) 幽t 一上µ a.s. (2) E( 亨 )r 니 °µ 7 , r > O 증명 Gut. A.(Sto p pe d Random Walks, 1987. p 54) 참조. 口 정의 4. 1. 1 을 일반화하여 J를 임의의 ( -oo , oo) 내의 부분구간 (sub int e r val) 이 라 하고 (4.1 .1) N(J ) = Zoo 1 [S.e./J 'I= O 이라 정의하면, N (J)는 구간 I 에 S,1 이 방문하는 횟수의 확률변수이 다. 또한 재생과정으로 생각하면 시간 구간 f에서 일어나는 재생의 수 로서 간주할 수도 있다. 이 때 구간 f에 방문하는 평균 횟수를 U( J) 라하면
(4.1. 2) U(J ) = EN(]) = 1L1co= ! P(S,, E j) 이고, 이 때 U 를 재생측도 (renewal measure) 라 부른댜 예제 4.1. 1 F 를 고장률(fai lure rate ) A( >0 ) 를 갖는 지수분포라 하면 s,, 은 확률밀도함수 /,,(x) = ¢N x-1e-.tr (x 칙 0 , n 칙 ) 를 갖는 다. 따라서 Jc (0, oo) 에 대한 재생측도 U( J)는 U( J) = I.lt0=J 0 ,l P (S11 e j) = .11t0 =J0 0O J I ,f,,(x )dx = 』 ,홍。f ,,(x)dx = 』 Adx = Aµ(]) 이고, 여기서 µ는 르베그 측도 (Lebes g ue measure) 이다. 이 제 X 를 음이 아닌 (non - ne g a ti ve) 값을 갖는 확률변수라 하고 J= [O, t], t 20 라 두면 재생측도 U 는 (4.1. 3) U( t) = U( J) = 홀。 P( S,' 질 ) = ,홍 1 P(N( t ) ~ n ) 이 댜 이 때 U( t ) 를 재 생 함수 (renewal fun cti on ) 라 한댜 만약 F0(x) = ( 0 (x < 0) 1 (x :::::: 0) F1(x) = F(x) F,,(x) = F• (n::::: :1 ) 죽, Fn 은 분포함수 F 자신의 n 번의 합성적 분포함수라 하자. 그러 면 재생함수 식 (4 . 1. 3) 은
(4.1 .4) U(t) = 1L1C= X) 1 F ,,(t) 이다 그리고 oo oo U(t) = F(t) + 1L1= 1 F 11•••+ -1( t ) = F( t) + 11L =_1 ( F*F)(t ) = F(t) + ( U*F)(t ) 즉’ (4.1. 5) U( t) = F( t) + l。' I U( t— s)dF(s) 로 표시되며 재생과정에 대한 적분식이라 한다. 정 의 4.1.2 확률변수 X 를 산술적 (arit hm eti c) 이 라 함은 어 떤 상수 d > O 에 대하여 P(XE {0, 士 d, 士 2d, …}) = l 이댜 X 의 분포함수를 F 라 할 때 F 를 산술적이라고도 한댜 그러면 모 든 S,l 은 d 의 배수에서만 양의 확률값을 갖는다. 따라서 이 경우의 재 생함수는 (4.1. 6) U(nd) = u 。 + U1 +… + u,I, Uk = i=0Z0 I . P (S; = kd) (k 착)) 이고 fk = P(X1 = kd) 으로 u11=f 11 + 홀。 U11-k fk 이다.
재생과정에서 다음과 같은 재생정리 (renewal t heorem) 를 얻으며 그 증명은 J. Lin d va1( 1 977), W. Feller(l971, Chap. 11) 또는 L. Breim an, (1968, Chap. 10) 에서 볼 수 있다 정리 4.1.3 (재생정리) 분포함수 F 는 평균 µ를 갖는다고 하자 . 그리 고 O < µ < oo 이면 모든 유한구간(fi n it e int e r val) J에 대하여 U( J) < o o 이댜 이 때 (1) F 가 비산술적 (non-a rit hme ti c) 이면 µ-IA(J ) (a->oo), A : 르베그 측도 (4.1. 7) lim U{a+J } = ( 。 (a->-oo) (2) F 가 산술적이면 Cl 一im土 0 0 U{a+J } = µ-1 • d • #{ k; k E J} 이댜 만약 g (x) 를 음이 아닌 함수로 H를 어떤 측도라 하면 g와 H 의 합성 (convolu ti on) g *H 는 다음과 같이 정의한다. (g *H )(x) = L。x g (x -y) H( dy ) , x e IR 따라서 다음과 같은 적분재생정리(i n t e g ral renewal t heorem) 를 얻는댜 정리 4.1.4 (적분재생정리) 분포함수 F 는 비산술적으로 F(O)=O 이고 함수 g( x )는 [0, 00 )에서 비증가 함수이며 르베그 적분 가능한 함수 라하면
(4.1. 8) lim ( g * U)(t) =>』 OO g dA , A: 르 베 그 측 도 卜 a :) 이댜 증명 G 를 G{(a,b]}=g ( a)— g( b), 0~a < b < oo 로정의된유한측도 라 하면 , g (x) 가 르베그 적분이 가능하므로 Jo C X)g (x)dx= Jo CX )X G(dx) 이다 또한 부분적분에 의하여 (g* U)(t )=g(t)U {[O, t]}+「。 U{ · [ t- x, t] }G(dx), t> O 이댜 재생측도 U 는 모든 x 칙 0 에 대하여 적당한 상수 CF 가 존재하 여 U{[ t -x, t]} ~CF (l +x) 이므로 lim g(t)U {[t -x , t] }=0 tCX) 이댜 한편 정리 4. 1. 3 의 재생정리에 의하여 모든 x> O 에 대하여 l/i-m•0 0 U{ [ t-x , t] } = µ-1x 이댜 따라서 t->CX) 이면 적분의 우월성 수 렴 정 리 (dom ina te d converge nce the orem) 에 의 하여 (g* U)( t)」 >』(X ) xG(dx) =; 』(X)g (x )dx 이다口 F 가 바산술적인 경우에 한하여 확률보행 {S,,: n20 }에 대한 첫 통 과시각(fir s t pa ssag e tim e) 과 잔여대기시간 (res i dual wa iting tim e) 에 대한 여러 가지 성질을 알아보고자 한다. 확률보행 {S : n 칙 0 }이 최초로 높이 a( 칙 0 )에 도달하는 시각을 ra 라 하면
(4.1. 9) r0 = inf { n~l : S,,> a }, a> O 로 나타내고, 모든 n 에 대하여 S,' ::::: a 이면 ra=+co 로 간주한다. 이 때 만약 F( O)=0 이면 ra 는 재생셈과정 N(a) 와는 (4.1. 10 ) ra=N(a)+l 의 관계식을 만족시킨다. a-+00 이면 ra-+00 임을 쉽게 알 수 있다. 만약 µ> 0 이면 대수의 강 법칙 (s tr on g law of large numbers) 에 의하여 모든 a 에 대하여 ra
정의하면 ra: .,; 감 w. p .l 이다 . 따라서 Ysb w. p .l 이므로 Era'< oo 이댜 그러므로 Era~ Era'< +oo 로서 증명된다. □
정리 4.1 .6 µ > 0 이고이므로 P {읍뀝; > z 尸 (J)( -z) = l-(J)( z) 曰 이제 잔여대기시간을 확률보행 {S,, : n20} 의 식 (4. 1. 9) 에서 경계 치 a(>O) 가 최초로 통과하는 시각에 경계치 a 를 초과하는 양으로 정 의하자. 그러면 {S11 : n 칙 0} 을 어떤 기구가 재생되는 총시간으로 생각 하면 초과하는 시간은 a 시각 이후의 다음 재생될 때까지의 잔여대기시 간을 의미하게 된다 . 따라서 이 때의 초과분을 잔여대기시간 또는 과표 적이라 부르며 다음과 같이 정의한다. (4.1. 11 ) Ra=Sr 。 -a, a> O 잔여대기시간 {R0: a>O} 에 대하여 살펴보기 전에 확률보행에서의 사닥다리 변수(l adder va ri able) 에 대하여 살펴 보고자 한다 . (4.1. 12 ) <11 = inf{n ~O : S,, >O } 라 두면 61 은 최초로 0 보다 클 때이다. 그리고 k~2 에 대하여 (4.1 .1 3 )
포 ( i.i.d. )를 이룬댜 따라서 {(J,,: k= l, 2, … } 는 i.i.d. 이고 , 식 (4. 1. 9) 에서 정의한 ra 는 {
변수에 대하여 증명하면 된다 이 때는 r=l 이고 Sr= X1 이댜 F,,(x) 를 S,, 의 분포함수라 하고 U 를 재생측도라 하면, 임의의 r~O 에 대 하여 P{Ra>r} = nL0=0I P{S,,_1 :;;; a, S,.> a+r} = P{X1 >a+r} + ,'l~=2? lOa P(X,. > a+r—s )dF,.-1(s) = l— F (a+r) + la。 [ (l-F (a+r—s )]U(ds) 이댜 한편 a 一CX)이면 모든 r~O 에 대하여 l-F(a+r) = 0 이고, 또 한 정리 4 .1.4에서 g(y) = l-F(r+y) (r>O) 라 하면 』 00 g(y) dy = i00( l -F (s))ds :;;; EX1 = µ a 이므로 a-oo 이면 정리 4 .1.4에 의하여 』 a (l -F(a+r-s))U(ds)-; 』(X)(l -F(r+ y ))dy = ; i(X)(l- F(y) ) dy 죽, P{R0> r} 一上µ iJr oo( l -F (y) ) dy 로서 증명된다. 口 예제 4.1. 2 c>O 에 대하여 1-F(x) = c exp (-f3x), x 칙 0, /3>0 라 하 자. 그러면 r~O 에 대하여 P{ra
= a(a)exp (-/3r) 따라서 r= 0 이면 a(a) = P(r < +(X))이고, 만약 µ〉 0 이면 r(,< +CX) w.p . l 이므로 P{R >r }=e-{Jr , 즉, R (1는 모든 a > O 에 대하여 고장 률 /3 를 갖는 지수분포가 되며 , 이 때 {Ra} 의 극한분포는 모든 a 에 대하여 같은 분포이다. 정리 4. 1. 7 에서 Ra 는 극한분포를 가지므로 (4.1. 16 ) Ra __!!__. R , a ---> (X) 라 하고, R 의 분포함수를 H, S, 의 분포함수를 F 라 하면 Ra 가 극한 분포 H, 즉, R 의 분포함수는 (4.1 .17 ) H(dr) = 志(l- F(r))dr 이댜 이제 {Ra} 의 적률에 대하여 살펴보자. 그러면 우선 다음의 보조정 리를 기술한댜 이의 증명은 W. Feller(Vol. II, pl5 0, Lemma 1) 를 참 고하기 바란다. 보조정리 4.1.8 임의의 a>O 에 대하여 F(O)=0 이면 Jo O O 갔 F(dx) = afn o0 0x0-1(1 - F(x)) dx 이댜 이 때 양변은 같이 수렴하가나 발산한다.
정리 4.1. 9 0 < µ < 00 이 고 p > O 에 대하여 E(X t)/)+ l < oo 이 면 {R~ , a 착) } 는 일양적 적분 가 능 (un ifo rml y i n t e g rabl e) 하다 . 즉, fn°00 1 ,1> -t sau> ~O P{R0 > r} d r < +oo 이다. 00 증명 P{R0 >r }= 11L= 1P {r0;; , :n, S,, > a+r} 이고 r a ;;,: n 이 면 s,, _1 ~a 이므로 .t P(R0 >r} ::;;; 11o=o !, P(S11_ 1: :;;;a, S11 >a +r}= J:0a 0(1 - F (a+r-y) )U(dy) , < 효 [l-F(a+ r - k-l)] U((k, k+l]} 그런데 모든 kE R 에 대하여 어떤 실 수 C 가 존 재하여 U{(k, k+l]} :-::;:c 이므로 (X) kL a [1- F(a+r-k- l )]U{(k, k+l ] } ~ CjL= O [ 1- F(r+j- 1 )] ~ C JrO-O 2( 1-F(y) )dy 이다 따라서 P(Ra > f) 조 CJ rO-O 2 ( 1 —F( y) )dy 이며 E(X+ )P + l < 00 이므로 보조정리 4. 1. 8 에 의하여 言 ERt = sa : 『 P 』 00 r- 1 P(R0 > r)dr~ Cp 』 00 r - 1 i:/ 1 -F(y) )dyd r < +oo 이다. 口
따름정리 4.1.10 0 < µ < 00 이고 P > O 에 대해 E(X t )+I < 00 이면 ES~+ I ER> >E Rp = (p+ 1)ESr 이댜 증명 Ra 보 R 이고 {R~: a 착)}은 일양으로 적분가능하므로 ER!- ER 이댜 ER = 』 OO 갑 H( dr:) = 志 』 OO r1'( l _ F( r))dr 이고, 보조정리 4. 1. 8 에 의하여 ERp = (p+ 1l )ESr 』 OO .;,+1P(r)dr= ~ESt+ 1 이다曰 따름정리 4.1. 11 0 < µ < = 이고 E(X+)2 < = 이면 ER= 屋ES~ =p
증명 F(O) = 0 이므로 r= 1, 즉 , S,=X1 이므 로 따 름 정리 4. 1. 11 에 의 하여 Er0= -; • (a+ 上:)이고 U{(0, a]} = Er 0 이므로 증명된 댜口 이제 X 의 분포와 Sr 의 분포와의 관계 를 알아보자. 식 (4. 1. 14) 에서 정의한 r 와 대비하여 첫 광의의 내리막 사닥다리 시각(fi rs t weak descend ing ladder epo ch) r 를 다음과 같이 정의한댜 r= inf {n 칙 : S, ' 직 0} 이 때 ¢를 F 에 대한 특성함수 (chara ct e ri s ti c fu nc ti on) 라 하면 ¢,(t) = Je itxF ( dx) 이 댜 또한 ( r, Sr) 에 대 한 결 합특성 함수(j o i n t characte r - ist ic fu nc ti on) 를 /3( s, t) 라 하면 (4.1 .1 8 ) /3( s, t) = 훔 s i = IIe it S ,. dP= J:
나타내는 정리를 얻는다. 보조정리 4.1. 13 f3+ r= 1 +sr 이다. 증명 P(s, t)와 r(s, t)를 s 에 대한 급수 (se ri es) 로 나타내면 oo oo 로 나타낼 수P (s있, 으t)며 =, kL=이 I sk때Pi • t)(B ,,• , +rr(,s,), (tt)) == k~J= _O ler i' . ItS .) d P 이다. 한편 r> n 칙에 대하여 X,1=S,1-S,I-I 는 S, i -I 와 {r>n-1} 에 대하여 독 립이므로J 心 1e'IS . dP= Jei IX ,' dP J ei IS . -Id P= ¢(t)r ,I-I(t) r> 1 1-l 이므로 n= l 에서 00 까지 합하여 정리하면 보조정리 결과를 얻는다. D 정리 4.1. 1 4 (스피처의 공식 (S pit zer's for mula)) (4.1. 21 ) _ln(l-8) = 흠》나 :e i lrF i dx) ' Fk = F 야 증명 보조정리 4. 1. 13 에 의하여 —1L-/ _3 = 1-1s ¢ 이므로 매우 작은 값 s 에 대하여 (4.1. 22 ) In 근 P + Inr= 1n1 노 = 훔 \sT 이다. 값= Eei tS ,= Jeit x F i d x) 이므로 고정된 s 에 대하여 k효=I Lks %k 는 유한측도(finit e measure) P= kf=: I ..k.1 skFk 에 대한 푸리에 변환
(Fouri er tra nsfo rm ) 이 고 , lnT ¾= 훔》감는 BS = k효= l 上k 짜에 대한 푸리에 변환이다 . 이 때, Bs {I } = Jr< o o, S, e/ srdP, I: 보렐 집합 (Bo rel set) 이 다. 그리고 sr> O a.s. 이므로 B.((-oo, O]) = 0 이댜 또한 lnr= 훔》 (1 ― r)k 는 측도 C 에 대한 푸리에 변환이고, 이 때 C((O, oo)) = 0 이댜 따라서 식 (4. 1. 22) 는 측도 Bs + C5= F5 에 대 한 푸리에 변환이고, 푸리에 변환은 측도에 의하여 유일하다. 또한 CS((0, oo)) = 0 이므로 임의의 Jc (0, oo) 에 대하여 Bs{I } = F5{ I} = 흡\ Skp •k { J} 이므로 증명된다. 仁] 정리 4.1.1 5 5(s, t) 에 대해서는 (4.1. 23 ) -ln ( l 一 겹) = kZ°=° l —1k s 汀 -O °O e itx F • k( dx) = 1n 'Y (4.1 . 24 ) (1-P) ( l-f]) = 1-s¢ 증명 식 (4. 1. 23) 은 r 와 T 의 정의에 의하여 정리 4 . 1. 14 에 의하여 쉽게 증명된다 . 한편 정리 4.1 .1 4 의 증명과정에 의해 -ln(l- 겹) = lnr 이다 . 따라서 보조정리 4 . 1. 13 에 의하여 식 (4. 1. 24) 는 증명된다. 口 정리 4.1.1 6 0<µ::,;;00 이면 (4.1. 25 ) Er= ~ = ex p{홈 1 싶 P(Sk 택)}< oo
증명 P{r
fl(a) = 喜 』 00 e - ar(1 —/: (r))dr = a 墓 』 OO(l-e-a')F(d 끼 = 므릅그 曰 또한, il(a) 와 Ra 의 극한분포 H 에 대한 평균은 다음과 같이 표현 된댜 보조정리 4.1. 18 모든 a> O 에 대하여 (4.1. 28 ) R(a) = +aµ. e-B(a) , B(a) = kf=; I 上k Ee-aSt 이고 VarX= rl- < oo 이면, Ra 의 극한확률변수 R 에 대한 기대값 (4.1. 29 ) ER= p= 교무2µ : 一 k효';;I 上k ES ;; 이다. 증명 f](l, ia) = Je-a s'dP= E(e-aS') 이 므로 정리 4. 1. 14 에 의하여 (4.1. 30 ) -lnE(l -e -as,) = 훔訂。~ e-axF*\dx) = 훔訂 fs,> o e -aS'd P 이고 Wald 의 첫번째 등식에 의하여 InESr = Inµ + InEr 이댜 따라서 정리 4 .1.1 6 에 의하여
(4.1. 31 ) InES, = Inµ + kL°=° I —1k P(S k~O) 이다. 또한 식(4 . 1. 26) 에 의하여 Inf l(a) = 一 Ina ― lnESr+ InE (1- e-a S.) 이므로 식 (4 .1 .30) 과 (4 . 1. 31) 에 의하여 1n fl(a) = -Inaµ —훔 *{ P(Sk~O) + fs,> o e-as,d P } = —In aµ-j ;l1 Je-a s:d P 로서 식 (4. 1. 28) 은 증명 된다. 또한 ER 의 값을 구하기 위하여 식 (4. 1. 24) 에서 s= 1 로 하고 t에 대 하여 두 번 연속 미분한 후 t =O 에서 값을 구한다. 이 때 /3(1, 0) = 1 이므로 (4.1 .3 2 ) -[ l 급(1, 0)] {3“ (1, t)| t=0 + 2 겹. (1, t)f(l, t)l t =O = -
「 00xF 야 (dx) = 검 ;1 7i ES; 이고 정리 4. 1. 16 의 증명과정에서 1- 귬(1, 0) = p( r= oo) = (Er)-1 이 므로 식 (4. 1. 32) 는 퍼 ES~+2ES 홈i 1ES i] = µ2 군 이댜 따라서 따름정리 4. 1. 11 과 왈드의 첫번째 동식에 의하여 식 (4 .1 .29) 는 증명 된댜 口
예제 4.1.3 X~ N(µ,e l-) o ,s ; -µ1 > 0e -이 oS면 , Sk ~ N(kµ, le) 이다. (Sk > 0) l (Sk < O) 이다 . 따라서 Ee -as: = P( Sk 택) + 』 coe- a.남 I e -강 ,; ( x -kµ) ' dx = (/)(-母) + exp {k( 강 a2-aµ)}(/)(y k( µ-a)) 여기에서 O 는 표준정규분포함수 (s t andard normal dist r i b u ti on ) 이 다 . 또한, ER 의 값을 구하기 위하여 ES-;; 을 구하면 ES; = _ J0_ .:. 멸1謀 e 꿉 (x-kµ) ' dx = yk
4.2 축차확률비 검정과 재생이론 제 2 장의 축차확률비 검정에서 검정력합수와 정지규칙의 기대값에 대 한 Wald 의 근 사값들은 우도비와 정지경계치와의 불일치를 고려하지 않 고, 단순히 정지시각에 확률변수 S, ,이 정지경계치를 갖는다고 가정하 여 구하였댜 이제 재생이론의 결과를 이용하여 이에 대한 좀더 정확한 결과를 가져올 수가 있다. 제 2 장에서와 같이 X,X1, X2, …는 i.i.d. 로서, 확률밀도함수는 가설 H, 하에서 p,.(i= 0, 1) 라 하고, 이 때 우도 비 Zi = lnP1(X i )/P 。 (X] )는 비산술적이라 가정하자. 그리고 S 。 = 0, S = j~=) 1 -I zi ( n 칙), 정지경계치를 (-b, a), a=lnA, b=-lnB>O (O a} 라 정의하자 . 이 때 E0Z= µ0, E1Z= µ1(µ 。 <0 , µI > O) 라 하고, µo 와 µI 을 각각 유한한 값이라 하자. 그러면 모든 nE N 에 대하여 가 설 H;(i= O, l) 하에서 분포함수 Po 와 R 은 7,1=6(X’I) 에서 서로 절대연속이다. 이제 (4.2.2) r0 = inf{ n~l : S11>a} 이라 하고, 이 때 잔여대기시간 (4.2.3) Ra = Sr - a 이라 하며, Ra 는 R1 으로 분포적 수렴 (conver g e in dis tri bu ti on) 을 한
다고 하자. 즉, (4.2.4 ) R0~R1. K1(dr)=P(R< r )(dr). r 착 0 이고 (4.2.5) rb= inf{ n~l : S11< -b}= inf{ n~l : -S11>b} (4.2.6) Rb = -Sr. - b, Rb ~ 腐 K 。 (dr) = P(R 。 < r) (dr) 이라 하자. 그리고 이 때 (4.2 .7 ) ri = J(。X )e -rK;(dr) , i = O, l 이라 하자. 그리고 제 1 종 및 제 2 종의 오류확률을 각각 a; (i=O , 1) 로서 a;= P;(H; 를 기각), i= 0, 1 이라 두자. 그러면 제 2 장에서 a 。::::: e-a' a1 :::::e -b 또는 a 。::::: el :一 e e 二 b b • a! :::::요:선:국µ 로서, 어느 경우에서도 만약 a, b-..oo 이면 a 。 e~1, a1eb-1 이다. 하지만 재생이론의 결과를 적용하면 다음과 같은 정리를 얻는다. 정리 4.2.1 만약 a, b-oo 이면 a 。 ea 一 YI( 기호로 a 。~ r1e-a), a1eb- ro 이다. 이 때 r;(i= O, l) 는 식 (4.2.7) 의 값이다. 증명 [SN>a] 에서는 N= Ta 이고 SN= Sr.= a+Ra 이다. 따라서
a 。 = P。 ( SN> a) = r.s ,.'.. >) an dP 。 이다. 정리 2. 1. 4 에 의하여 (4.2.8) a 。 = fs> o e-sd P1 = fs,\ > o e-s,,d P 1 = e-o fs.\ > o e-Rd P1 이다. 만약 a,b-oo 이면 P{SN > a}-1 이므로 식 (4.2.8) 은 수렴한다. 즉’ a 。강 -> l。 'e-rK1(dr) = r1 이댜 한편, a1eb->ro 도 비슷한 방법으로 쉽게 증명된다. 口 정리 4.2 .2 식 (4.2.7) 의 값 r;(i = O, l) 는 다음과 같댜 ro= 댜굽, rl= 士 , 4= exp { 홈 11 [Po(Sk>O) +P1(Sk 택)]} 이댜 증명 식 (4 . 1. 26) 에서 ili (1) = r1 이므로 식 (4. 1. 28) 에 의하여 r1 = 7i ex p{홈 I1E1e-s:} 이다. 그리고 E1 e-S: = P1 (S 리) + Is.>0 e-s.dP1= P1 (S 며) + P 。 (Sk > O) 이므로 r1 = 下넓 이댜 ro 에 대해서도 ro = fro(l) 이므로 쉽게 증 명된다 . 口
���ܭY� N �� �\� 0����� �X��� �L�X� Ȭ�|� �Ŕ��. Ȭ� 4.2.3 VarZ= if < oo t�t� a, b->oo |� L� �� (4.2 .1)
X� ��@�� �L�ܭY� N �� �\� 0����� �� o( EoN~ 0 (b+p0 )+l ) I� 01 E1N~ N (a+ pA� + o(l) �I t� L� P;( i=O, 1) �� �� (4.2.5) @� (4 . 2.7) ��� �X�� ����h�� K, X� ����.t ��Ʌ� 0���Ȭ� 4. 1.11 �� X�X��� }� �|� � ��<���\ �����\��. �f�� 4.2.1 X, X1 , X2, & � i.i .d. N(�, 1) |� L� �$��� � Ho : � = 0 i� H : � = 0 > 0 |� X�t� Z= 0 X �� o2 t���\� Z X� ���� �� {�Q����� Z~N( �� 82, 02) H1 ����� Z~N표 4.2.1 。 log L 1 Yo = YI Po = P1 = p( 0) .05 6.71359 .97 144 .02958 .10 5.3 5 650 .94348 .05959 .15 4.57477 .91 633 .09024 .20 4.02851 .89004 .12 160 .25 3.61133 .86 45 1 .15 443 .30 3.27578 .83972 .18 631 .50 2.37031 .74762 .32 385 .70 1.81 313 .66 589 .47 262 .90 1.42 570 .59344 .63 313 1.00 1.27 230 .56 037 .71794 1.40 .82 644 .44654 1.08 894 1.8 0 .54 640 .35743 1.51 362 각 8 의 값에 대하여 lnL1(8), ro=r1=r(0), Po=P i=p (8) 를 구한 결과는 표 4.2.1 과 같다. 표 4.2.1 에서 보는 바와 같이 0 의 값이 크면 이에 따라 오류확률 r i는 적어지고, p (8) 값은 커지고 있다. 이는 정리 4.2.3 에 의하여 N 의 기대치가 커지고 있음을 알 수 있다. 이제 하나의 매개모수를 갖는 지수형 분포족에 대하여 살펴보자. 즉, 분 포함수 Po (d x) = Po(x).1 ( dx) , 0E e, po(x ) = exp (0x-lJf (0 )) 로 깐는 협의의 볼록함수 (s tri c tly convex fu nc ti on) 라 하자. 그리고 이 때의 적률함수는 8 + tE 0 에 대하여 E0exp (tX ) = exp ( lJf(0 + t) - lJf(0 )) 이댜 따라서 EoX= 戶), Var8X= 맵 .(0)
이다. 적당한 변환에 의하여 분포함수 P 。 (x) 를 다음과 같이 쓸 수 있다. (4.2.9 ) P 。 (dx)=Po(x) Pi。 (dx) , 맵 (0) = 1/T( O)=0, 1/T .. (0) =1 이 다. 따라서 이 때 四( OI ) = 汀( 02 ) 인 o,에 대 한 가설 H1 : 0 = 01 대 H2 : 0 = 02 ( 0, < 0 < 02 ) 에 대 한 축차확률비 검 정 에 대 하여 재 생 이론을 적용하여 보자. 이제 4 = 02 -0 1 이라 두면 Z= In [Po , (X)/ p。 1(X)] = LIX 이다. 지금까지의 확률보행 S,1 = jZ= I zj 대신에 S,1 = 훔 x j라 하고 축차확률비 검정의 정지규칙에서 정지경계치 a 와 b 대 신 각각 L1a 와 4b 로 대체하면 각종 성질은 변함이 없다. 우선, 단측 축차확률비 검정 (one-s i ded SPRT) 에 대하여 생각하면 이 때의 정지규칙은 (4.2.1 0 ) N= inf { n2l : S112a} 이고, 모든 nE N 에 대하여 S,,< a 이면 N= +oo 이다. 이 때 P2(N
만약 0= 01 < 0 인 경 우에 는 n = 1. 2, …에 대하여 우도바 는 R,, = exp (L1S,, ) 이므로 P 。, (N< oo) = E 。 , {ex p (-L1S 사 : [N< oo] } = E 。,[ exp (-L1S 』 v)] = exp ( 一 L1a)E 。 , [ exp ( 一 4Ra)] 이다. 따라서 P1(N< o o) ~A-1 = e- tJ a 에 비교하여 좀더 나은 근사치 P 。 , (N < oo) 늑 exp ( -L1(a+p +)) 를 얻는다. 임의의 0 < 0 에 대해서는 . 四 0)= 敬 0* )인 0. 를 찾아서 L1(0)= o~ o 라 두면 식 (4 . 2 .1 1) 은 H1 : 0= 0 대 H2 : 0= e• 에 대한 단 측 축차확률비 검정으로 0l--->O, 02--->O\ 4--->L1(O) 로 대체하면 된다. 따라서 P0(N< oo ) 늑 exp {-L1( 0)(a+p +)} , 0 < 0 이댜 양측 축차확률바 검정(t wo-s i ded SPRT) 에서의 정지규칙은 식 (4.2.1 ) 과 같으며, 이 때 잔여대기시간 Ra 와 Rb 에 대한 정의와 극한분포에 대한 평균을 각각 P1 과 p。(정리 4.2.3 참조)라 하자. 만약 0= 0 이면 X는 대칭분포 (s y mme tri c di s tri bu ti on) 를 하므로 -Po = P1 이다. 또한 제 1 종 및 제 2 종 오류확률을 각각 a;(i = l, 2) 라 하고, 검정력함수의 01 과 02 에서의 값을 각각 /3;(i = 1, 2) 라 하면 (4.2.1 2 ) /31 = a1 , /32 = l -a 2
이댜 제 2 장의 식 (2.1. 16 ) 또는 (2 . 2.8) 로부터 주어진 정지경계치 (B, A) 에 대해 a1 과 a 2 에 대한 근사값은 (4.2.1 3 ) aI 나검 , a 2 늑땄넘 l, A=e0 , B=eb 이댜 이제 잔여대기시간을 고려하여 식 (4.2 .1 3) 에서 a 대신 LI(a+ P+), b 대신 LI(b+ p_)를 대입하여 정리하면 , 잔여대기시간을 고려한 좀더 정확한 근사값을 얻으며 그 결과는 다음과 같다 . (4.2.1 4 ) /31 늑 e 4(}+-;;5 L-J( eb+ p4 _(b) +p _ ) ' /32 늑 e_ eLJ( 4 a(+ap+ + p) f/),1 - -ee4 L(ib(b ++ pp _ _ )) ) 따라서 Po;{ S N= a+p +} 늑 /3;, Po;{ S N= b+p _} 늑 l ― 8; 이므로 왈드 의 첫번째 등식에 의하여 (4.2.1 5 ) E;N= 궁 X {(1-f];)( b+p _ ) + /3; (a+P+ )} , i= 1, 2 이고 /3;는 식 (4.2 .1 4) 의 값이다. 일반적인 0<0 에 대해서는 앞에서와 같이 lJf(e ·)= w(e) 인 0· > 0 을 구하여 4 대신 L1(0) = 0· -0, 01 대신 0, 02 대신 o* 룰 식 (4.2 .1 4) 와 (4.2 .1 5) 에 대입함으로써 얻을 수 있다. 또한, 0-+0 이면 식 (4.2 . 9) 의 ?P'(x ) 의 성질에 의하여 祠 = 강 02 +o(0) 이므로, 식 (2.2 . 24) 에서 a 대신 a+P+, b 대신 b+ p_를 대입하여 0=0 에서의 N 의 기대값에 대한 근사값은 (4.2.1 6 ) E0N 늑 -(a+p + )(b+p _)
를 얻을 수 있다. 또한 D. S i e g mund 는 r= inf { n~l : S,,:;;: Q}에 대해 P 。 2 다 < oo) = 표라 두고 식 (4.2.1 4 ) 대신에 (4.2.1 7 ) /31 늑 e 4(a}p : T- e4 p - ' /32 늑 e( lm:4(—ae+ ; p ♦ -) 임을 보였으며, 식 (4.2 .1 7) 를 식 (4.2 .1 5) 에 대입함으로써 N 에 대한 기 대값의 근사값을 구할 수 있다. 4.3 비선형 재생이론 제 4.1 절에서는 확률보행 {S11 : ne N } 이 경계치로서 상수값을 가질 때에 대하여 살펴보았다. 이 절에서는 주어진 상수값을 갖는 경계치에 대한 확률보행의 비선형함수 또는 확률보행에 대한 비선형경계치에 대 하여 알아보고자 한댜 즉, 예로써 Xi ~ i.i.d . 이며 평균 µ, 분산 8 이고, 이 때 g는 양의 값을 갖는 함수라 할 때 정지규칙이 (4.3.1 ) T = Ta = inf { n : n ~ l, n g( S,, ) ~ a } -tLE. 亡,_ (4.3.2) T= inf{ n~l : S11>en 가, re(O,l) 의 형태를 가질 때이다. 이런 경우에 대한 여러 이론을 비선형 재생이 론 (nonl i near renewal the ory ) 이 라 부른다. X, X1, X2, …는 i.i.d. 로 분포함수는 F, 평균 µ>0, s,, =
iL=” I X, 라 하고, 모든 n E N 에 대하여 'Ji II =
예제 4.3.1 x,. ~ i. i. d . I 평 균 µ, 분산 / < oo 라 하자. 이 때 nE N 에 대하여 Y,1= s,占,_ n6 µ =s; s,t= i2=n lX j 라 하면 { Y,, : nE N }은 확률적으로 일양연속이다. 편의상 µ = 0
극한분포로 정규분포를 갖는다. 그러나 어떤 정지규칙 N 에 대하여 정 규화된 정지확률변수 {S 짜는 일반적으로 극한분포를 갖지 않지만 정 지규칙 N 에 대한 어떤 조건하에서는 극한분포를 갖는다. 이것을 정리 한 것이 다음의 정리이며, 안스컴의 정리 (Anscombe's t heorem) 라 부 른다. 정리 4.3.1 {Y11:ne N} 은 확률적 일양연속인 확률변수의 수열이라 하 자. 또한 t a(a>O) 는 자연수 값을 갖는 확률변수로서 a-->oo 이면 t0/ a —L+ c (c>O) 이다. 이 때 Na = [ ac] 라 두고 a-->oo 이면 YIn_ YN“ 그一 。 이다. 만약 Yn ~ Y 이면 YIn 一뇨 Y 이댜 증명 { Y,, : nE N }은 확률적 일양연속이므로 ( c, 8) 는 식 (4.3 . 7) 을 만족하는 것이라 하자. 그리고 편의상 c= 1, 즉, a---->OO 일 때 t0/ a ~ I 이라 하자. 그러면 (4.3.1 1 ) P{I Y,. - YN. I > c} :s: P{lta -Nal > 유 } +\,,-?.I:i:tBN. I Y,,-y N . I > C} 이다. a-oo 이면 fa /Na _L., 1 이므로 식 (4.3 .1 1) 의 오른쪽 첫번째 항 은 0 으로 수렴한다. 또한 식 (4.3 .1 1) 의 오른쪽 두 번째 항은 가정에 의 하여 0 으로 수렴 한다. 따라서 Yta - YN0 _4 o 이다. 확률적으로 수렴
하면 분포적으로도 수렴하므 로 증명은 끝난다. □ 따름정리 4.3 .2 x,. ~ i.i.d. ' 평균 µ, 분산 cl < 00 이고, s;,= i:x; -nµ i= I 占 6 라 하자 . 만약 & (a > O) 가 자연수 값을 갖는 확률변수로, a - oo 일 때 t0/ a -----L+ c ( c> O) 이 면 s·/ n 와 SI찌n - 굶t;a µ 는 분포적으 로 표준정규분포로 수렴한다. 증명 예제 4.3.1 에서 {s;, : n~1} 는 확률적으로 일양연속이고 중심극 한정리에 의하여 분포적으로 정규분포에 수렴한다 . 따라서 정리 4.3 .1에 의하여 증명된다. 口 정의 4.3.2 확률변수들의 기쓰_여 '2. {~11 : ne N }이 느린변환 (slowl y chan gi n g)을 한다는 것은 (4.3.1 2 ) n-= 이면 -; max {l~,,I : k~n} --12.. 。 이고 (4.3 .1 3 ) {E,, : nE N } 이 확률적 일양연속 인 경우이다 . 정의 4.3.2 에 의하여 {~;, : neN} 과 {~;; : ne N } 이 느린변환을 하면 f,1 = e,. , + f ,‘1’ 도 느린변환을 함을 알 수 있다.
예제 4.3.2 Y, ~ i.i.d. 로써 EY;= V 이고 ~= _nl_ ,f.= I y,라 두자. 이 때 g는 양수값을 갖는 두 번 연속 미분가능(t w i ce conti nu ously differ enti ab le) 한 함수라 하자. 이 때 Z,, = ng ( Y;) 라 두고 S,,= n g (v)+n g ·(v)( 亢 _v), E , '나g ' (v,,)n( 亢 _v) 2 , v,,E( 亢, v) 라 두면, nE N 에 대하여 Z,, = S11 +t , ,이다. 이 때 X;= g(v) +g· ( v)( Yi _ v) 라 하면, { S,1 = 홈/ i } 은 평 균 µ = g( v) > 0 을 갖는 확 률보행이고, {t11 : neN} 은 느린변환을 한다 . 왜냐하면 문 = 강: (v,,) (立― v) -+ 0 w.p . l 이므로 식 (4.3 .1 2) 를 만족한다 . 또한, {½g .. (v,,) : neN} 과 {n(~-v)2 : neN} 은 확률적 일양연속임 울 쉽게 보일 수 있고 각각 확률적으로 유계이므로 , {t11 : ne N }은 확률적 일양연속이다. 따라서 {t11 : ne N }은 느린변환을 한다. 보조정리 4.3.3 neN 에 대하여 Z,,= S11+~, , 라 둘 때, 만약 {f,, : nE N }이 식 (4.3 .1 2) 를 만족하면, 식 (4 . 3.5) 에서 정의한 정지규칙 ta 는 모든 a> O 에 대하여 a--+oo 이면 P( t0 < oo) = 1 이고, 또한 a-1 ta 구 µ-1 이다. 죽, fa/ Na _~ 1 , Na = [ a/µ] 이다. 증명 대수의 강법칙과 가정에 의하여 ~n = ~n쓰 +요n L ~ µ이다. 따라서 부분열 (subs eq uence) {nk: ke N } 이 존재하여 —zn! !k!. . --->µ w.p .1 이댜 그러므로 P{t0 < 00} = 1 이다. 다음으로, 임의의 e>O 에 대하여
n 。 = a/µ 라 두고 n1 = n 。(l +c) 이라 하면 a = n1µ/(1 +c) 이므로 P{ta > n 。(1 +e)} = p( 門드 판 Zk< a) = P( ~:;;; Zk< 릅) 이댜 대수의 강법칙에 의하여 上n mk,;;a,,x Sk _~ µ 이고, 또한 {e,, : nE N }의 가정에 의하여 上n mk,;;a11 xzk ~ a 一 00 이면 P( ta > n 。(l +c) ) -o 이다. 마찬가지로 a->OO 이면 P(ta < n 。(1-€)) -o 임을 쉽게 보일 수 있으므로 증명된다. □ 보조정리 4.3 .4 보조정리 4.3.3 에서 만약 -;; ~,,-0 w.p . l. 이면 t0/ a->I w.p . l 이다. 다음은 확률보행의 경우 •a 에 대한 정리 4. 1. 6 과 같은 결과를 {t,, : nE N }에 대한 적당한 조건하에서 비선형 재생과정의 t a 에 대 해서도 얻을 수 있다 . 정리 4.3.5 분포함수 F 는 분산
증명 편의상 , ta 대신 t라 하자. 그러면 Z1 = a+R0 이므로 (4.3.1 4 ) 갑 (S, -µt) = 泣 (a 一µt) + 급 (R a _&) 이다. a--+00 이면 정리 4.3.2 에 의하여 f0 /(a/µ) ~ 1 이고, n--+00 이 면 ~ ~ N(O, l) 이다 . 그러므로 따름정리 4.3.2 에 의하여 W6 a--+00 이면 SI— µt 그 N(O, 1) 6 이다. 만약 a--+oo 일 때 w1 (RI _e) 一 4 0 이면 증명은 끝난다 . 첫째, 흙 그 0 이고 t/( a/µ) 구~ 1 이며, { 감;t 11 : nE N }은 확 률적 일양연속임을 쉽게 보일 수가 있으므로 정리 4 . 3 .l에 의하여 a--+OO 이면 r 눕tt 구 ➔ 0 이댜 둘째, O< R 츠 ZI _ zI-l = Z1+Et _ ft-I 이다. 따라서 0< {aR!aµ <.= {IaZ!I1µ +I {a&! µ —{&a -! µI 이고, a--+OO 이면 롭~ ~ o 와 :탑; 그나 0 은 앞에서 증명되 었다. 또한 줄= (a;µ) • 부이다. 가정에서 EX2
이면 0 으로 접근한다. 따라서 정리 4.3 .1에 의하여 a-oo 이면 w|XJ 二 0 이다 . D 정리 4.3 . 5 에서 {E,, : nE N } 이 느린변환을 한다는 가정 대신에 (a) {E,, : nE N } 는 {Xk : k~ n+l } 에 대하여 독립이고 (b) 古 max {ltk l : k~ n} ~ 0 (c) km ~ 죠ax lt ,.+ k-t ,.I ~ 0, c>O 인 경우에도 성립한다. 이 때, {Z,:=S,,+t ,, : nEN} 을 섭동확률보 행 (pe rt ur bed random walk) 이 라 부른다. 보조정리 4.3.6 {Z,, : nE N }이 섭동확률보행이면 임의의 c>O 에 대 하여 ,l,i-moo sau:2 :p1 P { a —c < Z., ~ a } = O 이댜 증명 z,1급 6nµ 구 N(O, 1) 이므로 쉽게 보일 수 있다. O 제 4.1 절에서 확률보행에서의 잔여대기시간 Ra= S,.-a 의 극한분포 H 는 정리 4. 1. 7 의 식 (4. 1. 4) 와 같이 주어졌다. 이제 비선형인 경우의 잔여대기시간 Ra = zI a -a 의 극한분포에 대해서는 다음의 정리로 기 술할 수 있다. 이에 관한 증명은 M. Woodroofe ( Nonli ne ar Renewal
Theory in Seq u enti al Analys is , p 43 ~45) 또는 D. Sie g m und(Seq u en- tial Analys is , pl9 1 ~194) 를 참고하길 바란다 . 정리 4.3 .7 {~11 : nE N }은 느린변환을 하고 X1 은 비산술적이면 식 (4.3 .4)에 정의된 정지규칙 L 에 대하여 l-i•m0 0 P{Z,. - a::;;;x } = H(x) 여기서 H(x) 는 식 (4. 1. 17) 에서 정의된 분포함수이다. 정리 4.3.8 {Z11 = S11 + ~11 : ne N } 이 섭동확률보행이고 X 의 분산 a2 < 00 이면 정리 4.3.5 에서 정희된 g와 Ra = zfa - a 에 대하여 a->oo 이면 ( t: , Ra ) ~ ( W, R) , W~ N( O, #尻 ) 이다. R의 분포함수는 식 (4. 1. 17) 에 주어진 H 이다. 또한 W와 R 는 확률적으로 서로 독립이다. 확률보행에서 정지규칙 ra 에 대한 기대값은 a--+oo 이면 Era= 上µ (a+ p)임을 따름정리 4 . 1. 11 에서 보였다 . 여기에서는 비선형인 경우에 식 (4 . 3.5) 에서 정의된 정지규칙 t a 에 대한 기대값에 대하여 알아보면 다음 정리와 따름정리로 기술된다. 정리 4.3.9 {Zn : ne N }은 섭동확률보행이고, X ; 의 분포함수 F 는 분산
(4.3 .1 5 ) L00 P(t,, 조 _nc) < CX) 'l= I 이다. 그러면 a-+OO 이면 Et 0/ a-->µ-1 이다. 증명 임의의 a 。 > O 와 식 (4.3 .1 5) 를 만족하는 c 에 대하여 e+S<µ 인 8 > 0 를 잡자. 그리고 d> µ -( le + 8) +' 」a- 。 이라 하자. 그러면 a > a 。에서 모든 자연수 n>[ad] 이면 a
a ~ a 。 } 는 일 양적 으로 적 분가능하다. 따라서 보조정 리 4.3.3 에서 a->OO 이면 t0 /a 一I!_, µ-I 이므로 Et a! a -> µ- I 이댜 보조정리 4.3.10 정리 4.3.9 의 가정하에서, 만약 a---->OO 일 때 E(Ra _g)2 =o(Na), Na=[ 미이면 a----+oo 인 경우 E (t a 一 Na) 도 µ-2 (4.3.20) nE N 에 대하여 사건 All 에서는 g,1 = g (4. 3.21 ) { maxl~11+ kl : nE N }은 일양 적 으로 적 분가능 k 도 n (4.3.22 ) c < µ 인 임의의 c > O 에 대하여 ?Lt0= 0 I P{~; 三 _nc}< o o (4.3. 2 3) g , 一느 g, f: 확률 변수 (4.3.24) 0 < 8 < 1 에 대하여 a->OO 인 경우 aP(ta : ; ;;Ba/µ)-o 정리 4.3 .1 0 {Z,, : ne N }는 섭동확률보행이고, X, 의 비산술적 분포 함수 F 는 분산 / < oo 를 갖는댜 또한 식 (4 . 3 .1 9) 에서 (4.3.24) 를 만족 하고 {~;, : ne N }은 느린변환을 한다고 가정하면 a 一 OO 인 경우 Et 0 = 上µ (a +p- E~) +o( l) 이 때, p는 따름정리 4 . 1. 11 에서 정의된 p = ES;/2ESr 이다. 증명은 M. Woodroofe 또는 D. S i e g mund 를 참조하길 바라며 이것과 관련하여 다음의 예제를 제시한다. 예제 4.3.3 Y;~ i.i.d. , EY;=v > 0 이고 ElYil a< o o, a>2 이며, 이 때 , nE N 에 대하여 Z,l = 강 n V,:이라 하자. nE N 에 대하여 Z,l= S 군f , l 이라 두고 , S,l= 강記 +nv(Y_v), E,l= 강 n (V,:-v )2 이라 하면 s,1 = 홈 IX i, X i =강 v 巨홍 (Y i _v) 으로, {Sn : neN}
은 평균 강 #을 갖는 확률변수 X, 에 대한 확률 보행이다 또한 식 (4 . 3 .1 9) 에서 (4.3.24) 에 대하여 살펴보면 All = 요, e:l = E,, 이라 두었 을 때 El Yil O < oo ( a> 2) 이므로 식 (4.3.21) 은 쉽게 보일 수 있으며 , 아울러 식 (4.3.23) 도 E,, 의 극한분포가 x2- 분포임을 보일 수 있다. 식 (4.3.24) 에 대해서는 Bk = {mII 石군기 이라 두면, 모든 a>O 에 대하여 P(Bk)sca-a/2 (c: 상수)임을 보일 수가 있어서 모든 가정을 다 만족함을 알 수 있다 .
제 5 장 축차추정 이 장에서는 축차추정 문제를 다룬다. 정지규칙하에서 통계량의 충분 성, 완비성 등의 개념과 축차추정과의 관계를 다루며, 아울러 불편추정 치에 대한 분산의 하한성을 살펴본다. 위험함수가 최소가 되도록 하는 축차적 점 추정 문제를 살펴보고, 신뢰폭이 일정한 축차적 신뢰구간 추 정과 B- 프로텍션을 갖는 축차적 신뢰집합 추정을 다룬다. 5.1 축차추정의 일반적 이론 표본수가 고정인 고전적인 통계적 추론에서는 채택영역 (acce pt ance re gi ons) 과 신뢰영역 (con fi dence re gi ons) 간에 아주 밀접한 연관이 있지 만, 표본수가 고정적이 아닌 축차적인 경우에는 이러한 유사함이 일반 적으로 성립하지 않는다. 따라서 이 절에서는 축차추정의 일반적인 이 론을 간단히 살펴보고자 한다. X1, X2, … 는 확률밀도함수 /(x; 0 ), 0 E e 를 갖는 랜덤 샘
플이라 하자 이 때 N을 닫힌 정지규칙 (closed sto p ping rnle) 이라 하 고 가측함수 o(X1 , X2 , … , X N ) 에 의하여 모수 o 를 추정하고자 한다 T,, = T(X1 , X2 , .. • X,,) 을 (X1 , X2 , … , X,,) 의 결합밀도함수 (joi n t densit y fu nc ti on) 에 대한 충분통계량이라 하자. 정의 5.1.1 충분통계량의 수열 (T1, T2, …)를 축차모델 (se q uen ti al model) 에서의 충분통계량이라 한다. 정리 5.1.1 만약 각각의 n 에 대하여 T,,= T(Xi, X2 , … ,X,1) 이 고 정된 샘플 X1, X2, … ,X,1 에 있어서 0 에 대한 충분통계량이면, 정 지규칙 N 에 대하여 (TN, N) 은 축차적인 경우 0 에 대한 충분통계 량이댜 증명 E 를 임 의 의 가측집 합 (measurable set) 이 라 하자. 그러 면 P(EIN=n, T,,= t) =P(E, N=nlT,,=t )/ P(N=nlT,,=t ) =P(EnE,,I T,,= t)/ P(E,,I T11= t), E,, = [N= n] 이다. EnE,,E T,1= o(X l, X2,… ,X,,) 이고 T,, 이 (X1, X2, … , X,,) 에 있어서 0 에 대한 충분통계량이므로 P(EnE,,I T,,= t)와 P(E,,I T,, = t)는 0 에 무관하다. 따라서 P(EI N= n. T,, = t)는 0 에 무 관하므로 (TN, N) 은 축차적인 경우에 8 에 대한 충분통계량이다. D {T사 이 확률변수 X1, X2,… 에 대한 충분통계량 수열이라 하자.
그러면 n 단계에서 축차확률 비 검정은 단순히 T, ,에 의 존합을 알고 있 다(제 2 장 참조). 이것은 축차추정 에 있어서도 실험이 n 단계에서 정지될 때 0 에 대한 추정은 T, ,에 의존한다고 생각하는 것은 일견 타당하게 여겨진다. 제 3 장에서 {T, , } 이 충분전이통계량이면 X = (X1, X2,… , X,1) 에 대한 축차검정은 {T, , }을 기준으로 한 축차검정과 같음을 살펴보았 댜 마찬가지로 X 에 의한 닫힌 축차절차 (closed seq u enti al pro cedure) 에서 는 n 단계에 있어서 X 에 의한 0 에 대한 추정은 {T,, }에 근거 한 추정과 밀접한 관계가 있다 다시 말하면 {T,,} 의 전이성은 X= (X1, X2 , …, X, 1 ) 을 포함하는 T,,+ l 에 관한 모든 정보량은 역시 T, 1(X ) 에 포함되어 있다. 따라서 Bahadur 는 만약 충분전이 수열 {T, 1 } 이 존재하면 X 에 근거한 닫힌 축차절차에서의 추정문제는 n 단 계에 있어서 {T,1} 에 근거한 절차와 동일함을 보였다 . 다음은 정지규칙 N 을 사용할 때 (TN, N) 에 대한 완비성을 살펴 보고자 한다. m 이 고정되어 있을 때 T,,, 을 0 에 대한 완비통계량이라 하자. 정의 5.1.2 { TN, N} 의 분포족이 완비성 (com p le t eness) 을 가진다 함 은 모든 e 와 n E N 에 대하여 Eeg ( TN, N) = 0 이면 g(t,,, n) = 0 a.e. 이다.
정의 5.1.3 { TN, N} 의 분포족이 유계완비성 (bounded comp le te n ess) 을 가진다 함은 모든 유계함수 g와 e, nEN 에 대하여 E0g (T N , N) = 0 이면 g(t,,, n) = 0 a.e. 이다 . {TN, N} 이 완비성을 갖기 위한 정지규칙 N 을 조사하는 것은 매 우 홍미로운 일이며, Lehmann & S t e i n(l950) 은 통계량 (TN, N) 의 완비성에 대한 일반조건을 특정한 분포에 대하여 구하였다. 즉 Lehmann 과 S t e i n 은 정 규분포 N( 0 , 1), 포아송 ( 0 ) ' 일 양분포 u( O, 0) 에 대하여 연구하였으며 N( 0 , 1) 과 포아송 ( o) 인 경우에는 111 만약 N=m 일 때 T,n= i2= lx i 이면 (TN, N) 은 완비Ill성 을 갖는다는 것을 보였다. 또한 이항분포 (o) 인 경우에는 T1 11 = iL= lX ; 이라 하고, s,Il 을 m 번째 관측값에서 정지할 때의 T,,, 의 값에 의한 집합이라 하 자. 그러면 (TN, N) 이 완비성을 갖는 필요충분조건은 집합 {S,} 가 서로 분리된 구간으로 각각 Si+ 1 > S i인 경우이댜 예로써 만약 주어진 상수 c 에 대하여 정지규칙 N 이 T111 > C 까지 샘플링을 계속하는 것이 라 하면 , 이 때 (TN, N) 은 완비성을 갖지 못한다 . 예제 5.1.1 (이항분포의 경우) P(X; = 1) = 0, P(X; = 0) = 1 - 0, 0E (0 , 1) 일 때 주어진 고정 된m 에 대하여 Tm= X1+X2+ … +x,,, 은 0 에 대한 충분통계량 이다. 이 때 {T,,,} 에만 의존하는 닫힌 정지규칙 N 을 생각하면 주어진 정지규칙에 대하여 각 점 (m, T,,I) 은 다음 중 하나이다.
(a) (m, T,,, )은 정지점 (b) (m , T,,, )은 샘플링을 계속하게 되는 점 (c) 불가능한 점 점 (N, T사 의 샘플공간은 모두 정지점으로 구성되어 있다. 여기에 서 샘플링을 계속하는 점들은 닫힌 정지규칙을 가지므로 충분통계량 (N, T 사예 의한 값이 아니댜 이제 0 에 대한 불편추정량 (unb i ased es ti ma t or) 을 구하는 문제를 생 각해 보자. 그러 면 X1 는 0 에 대한 불편추정 량이므로 Rao-Blackwell 정리를 적용하면, Y= E(X1 I N, TN) = P(X1 I N, T 사 는 0 에 대한 불편추정량이고 Var ( Y) ~ Var (X1) 임을 알 수 있다. 각 샘플 (X1, X2,… ,X,, )은 원점 O 를 출발점으로 하여 정지점 (n, T,,) 에서 끝나는 경로로 간주할 수 있댜 그러면 이러한 경로의 i 번째 단계는 만약 X i =0 이면 오른쪽에, 또한 X,=l 이면 위쪽에 있 게 된댜 각 경로는 점 (n, T,,) 에 도달하기 전에 정지점을 통과할 수 없일음경을로 는명 모백히두 알硏( 수1 —있다0). m -원1 점의 확O률 로을부 터갖 는정다지.점 (m, t)로 가는 단 이제 ;r(m , t)는 원점을 출발점으로 하여 정지점 (m, t)로 가는 모든 경로의 수라고 하고, 군 (m, t)는 점 (1, 1) 을 출발점으로 하여 정지점 (m, t)로 가는 모든 경로의 수라고 하자. 그러면
y( m, t) = P(X1 = 11 N= m, TN = t) P(X1 = 1, (N, TN ) = (m, t)) = °1 (1 P_( (oN ), '-1T N군) (=m ,( mt), t)) 01(1 — 0)111-11r(m, t) = 군 (m , t) / ;r(m , t) 즉’ Y= ;r*( N, TN) I ;r(N , TN) 이다. 예로써 정지규칙을 (a) 표본크기 m 으로 고정된 표본의 경우: ;r(m , t) = ( ? ), 군 (m, t) =( ??) 이므로 y = t/ m 이다. (b) C 개의 성공을 얻을 때까지 계속하는 정지규칙인 경우: 짜 m, c) = ( ';;~f ), 군 (m, c)=( 言) 이므로 y= ;-_ll 이다. (c) 정지점으로서 (1' 1) 을 갖는 정지규칙인 경우 : Y(m, t) = { 0l,, ((mm ,, tt)) ==I= ((11 ,, 11)) 따라서 Y=X1 이다. D 이제 일반적으로 정지규칙 N 에 대하여 주어진 모수에 대한 함수
g( 6 )에 대한 불편추정량 (N, T 사을 생각해 보자. 즉, E(T 사=g( e). 0 E /3 이면 고정된 표본에서의 불편추정량에 있어서 분산의 하한값(l ower bound) 에 대한 Cramer-Rao 의 부동식과 같은 것을 정지규칙 N 에서도 구할 수 있다. 정리 5.1.2 g( e ) = e + b( e ) . b( • ) 는 미분가능한 실수함수이고, TN=o(X1, X2, …, XN) 은 0 에 대한 추정량으로 E 。 (TN) = 0+ b( e )라 하자. 이 때 합과 적분기호 내에서 미분은 서로 교환가능 하다고 하자. 그러면 갑( o )가 E0 N· E 。(吉 1nf (X ; 6 ))2}-I(l + b,( o ))2 이댜 끈츠 ~5 □C~> 吉 -E 。(1)= 훔 L , [ 설 1 吉 In f (x;, 0)],u lf (x ,, 0)dx,=O 여기에서 E i는 (X1 , X2, … , X i)의 점으로 구성되는 정지점이다 . 따 라서 SN = 홈 1 --!--e lnf ( X; , 8) 라두면, f aa8 f(x , 8 )dx = O 이고 EoSN= 0 이다. 만약 E 。 [吉 lnf ( X, e ) ] < oo 일 때, E 。 ( TN) = 8 + b( 0 ) 를 미 분하면 E 。 ( TN • SN) = 1 + b'( 0 ) 조 6TA'( 0 )6SA’( 8 ) 이댜 한편 왈드의 두 번째 등식 (2.2.17) 에 의해
같( 0 ) = E0N· E 。 (--/e-ln /(X, e )f 이므로 증명된다 . 曰 정리 5. 1. 2 에 의하여 정지규칙 N 에 대한 Cramer - Rao 의 부등식은 다음 따름정리로 얻어진다. 따름정리 5.1 . 3 E 。 TN= g (0) 이고, g는 미분가능한 실수함수이면 Var ( TN) :::::: (g'( 0 ))미 (EoN· /( 0 )) 이다 . 여기에서 g ,(o)= 강~g (0) 이고 l(O)=Eo[ 겅~ lnf ( X, 0) 「 이다. 따름정리 5.1. 4 만약 E0N~n 。이고 E 。 TN= e 이면 갑( 0 ) ~ [noEo( 古 -ln/(X. O) ) 2]. -I 이다. 만약.fl= (01, 02,… , 0k) 인벡터일때 TN, j가 0 j에대한불 편추정량이면 [ Var(TN. i)]키 ~E()N· E[ 급汀 ln/(X, 0)] 2 임을 쉽게 보일 수가 있다. Tn 을 0 에 대한 주어진 불편추정량이라 하고, Vn 을 주어진 충분통 계 량이 라 하자. 이 때 어 떤 정 지규칙 N 에 대 하여 Rao-Blackwell 추정
량은 다음과 같이 정의하자. 새로운 추정량 U= U(N) 을 주어진 정지 규칙 N 과 V N 에 대한 조건부 기대값이라 하자. 즉 U(N) = E( TI N, V사 다시 말하면 N= n, V,,= V 일 때 U= U,,(V) U,,(V)=E(TIN=n, V,,= V)=E[T·lcN= 11 i l V11= V]·{E (1 [N= 1 1]I v,,= V)} - I 이댜 그러면 U 는 0 에 대한 불편추정량이고, 이 때 볼록손실함수 (convex loss fu n cti on) 에 대하여 T 보다 크지 않은 위 험 (ri sk) 을 갖는다. Wol fo w it z(l947a) 는 이항분포의 모수 0 에 대한 추정량에 대하여 {UN(V) }가 정지규칙 {N i}의 어떤 조건하에서 0 에 대한 일치추정량 (consis t e n t es tim a t or) 임을 보였다. 또한 L y ones(l969) 는 일반적인 경 우 어떤 조건하에서 U 가 0 의 일치추정량이 됨을 증명하였다. 한편 Berk(l969) 는 축차분석에 있어서, Rao-Blackwell 형태의 추정량은 정 지규칙 {Ni} 가 N,.-> oo a.s. 이고, N i가 c- 차수 (c-ordered) 일 때 강 일 치 추정 량 (s t ron g l y consis t e n t esti m ato r ) 이 됨 을 증명 하였다. 5.2 축차적 점 추정 X, X1, X2, … 는 평균 µ, 분산 군를 갖는 정규분포 N(µ, a2) 의 확률변수라 하고, 이 때 모수공간을 e = {(µ. a); µER. (J ER 가라 한다. 또한 표본평균과 표본분산을 각각 X::= i'=t I_ x; , s,,2= _n_j-_l_ i효= I (X;- X.: )2, n~2
이라하자. 분산 균이 미지일 때 평균모수 µ에 대한 점 추정을 하고자 한다. 이 때 손실함수(l oss f unc ti on) 는 모수 µ 대신 추정량 i를 선택함으로써 생기는 손실과 샘플링에 따른 비용으로 정의하자. 죽, 모든 n~2 에 대 하여 µ의 불편추정량 天;를 µ의 추정량으로 하고 샘플링하는 표본 개수당 비용을 c( > 0) 라 하면, 이 때의 손실함수 L,, 은 (5.2 .1 ) L,,(µ, X,,) = IX,, -µ 12P + c • n (p> 0 : 상수) 이댜 또한 평균손실함수인 위험함수(ri sk fun cti on ) R (J. c(n) 은 (5.2 .2 ) R( J. i n) = Eµ.( J( L ,,) = Kp
샘플링규칙 (se q uen ti al samp ling rule) 에서 최적임을 보일 수 있다 (Mukhapa dhy a y, 1982 참조). 또한 n. 는 文를 µ의 추정량으로 할 때 위 험 함수를 최 소화하는 데 소요되 는 최 적 고정 표본수 (o pti mal fixe d sarn- ple siz e ) 이 다. 만약 분산 /이 미지의 모수라면 위험함수 Ra.c(n) 을 모수 0 = (µ,
일반적으로 식 (5.2.6) 과 같이 규정되는 축차적 절차와 식 (5.2.3) 과 같이 가상적인 최적 고정표본절차와의 관계를 비교하기 위하여 다음과 같이 정의한다. 정의 5.2.1 R( 8 ) : 축차적 절차에서의 위험함수, 6 E e R(n.) : 가상적인 최적고정표본 n• 일 때 위험함수 라하면 (a) w(c) = R( 8) -R(n* )를 기회손실 (re g re t)이라 하고 (b) TJ( C) = 요R(요n• L) 를 위험효율(ri sk e ffi c i enc y)이라 한다. 보조정리 5.2.1 X1 , X2 , …는 i. i. d. N(µ, 하 이고 隋 = [ 설 l(X; -XH1)] / k(k+l)CJ , k 티 라두면 (a) W; ~ i. i. d. 갔 (b) Wi, 男,… . W, ,-1 과 文는 서로 독립이고 (c) i~=n _ I (X;-— X, :-) 2 = a2 i,Lr=~ 1I 昭 n 헉 2 이다. 증명 g가 (X1 + X2 + … +xk - kXk +1 ) 의 부호를 표시 한다고 하면, 모든 n~2 에 대하여 [e1{ w;. …. En-I~• fn/o(X ,,-µ)]
는 ( xl (J- µ ,• ... ,• x,, (J- µ )의 직교변환 (o rt ho g onal t rans fo rma ti on) 이 댜 따라서 보조정리는 증명된댜 曰 보조정리 5.2 .l에 의하여, 모든 n ~ 2 에 대하여 S,,2 = /h 仁구이고 (W , 男,… . w; ,-1) 은 Y; 과 서로 독립이므로, 식 (5.2.6) 에 정의된 정지규칙 T 에 대하여 사건 {T= n} 은 /W 仁 P 에 의하여 결정되기 때문에 x:;과 서로 독립이댜 따라서 Eµ.(1{ IX ::— µ안 | T= n} = K p念p n- p, n ~ 2 이고, 정지규칙 T 를 사용할 때의 축차적 절차에 따른 위험함수는 (5.2.7) Ra,c = Eµ,a[K p간y -P + cT] ,
n~ l,,+=1 l+ ... ~' n " n ~ 1 t� �, 11 NCX) t� t� 4,1 = l
Nlo t� � 0�|�� � 4.3 �X� D� �� ����t�`��� X�X��� Z"= S"+~"' n ��, S11= n-an( W,1 ) 1=~ 1� a(a+1 �)�_ )a 2+n( W,-1) 2[1 +-;L.11] 1+L.111 ~ I U" -1 < 1 W,I l | , Y, = l _ a(w , . 1) |� P�t�, { S" : n = 1. 2 , & } �� �� � 1 t� � ���� 2a2 x� U�`���� t� p�, {~" : n~l} �� �}�����X�D� h�D� � �|� � ��� �\� YI�� �� � l t�� ���� 2 a2 t��. \ո� n NCX)|� L� $��� �� U�`��<�\� 0 �� � ��X��,w�4� E, �� �� ��<�\� (aa+l)xi+ l lo �� �4�\�� 0�|�(�.25 .�8)�� ܭY� �� �� �X��� �L��� �@� �pȬ��|� �Ŕ��. �p�Ȭ� 5.2증명 확률 1 로서 요n —• O 이므로 보조정리 4.3 .4에 의하여 (a) 는 증명 된다 또한 정리 4.3.5 에 의하여 (b) 도 증명된다. {t(혼: m} 에서는 모든 a> O 에 대하여 식 (5 . 2.8) 에 대하여 규정되 는 정지규칙은 a - l t주 l 1. , • ~-a 이므로 이다. 한편 -口L-'드--- qsa u>> Op Oa 에 _ l ta 대 三하 m여 + s11u;,;',: 1p1 1s UNl, l'p _w _―尻,' _\Q a) 는 Marc inki ew i cz 一 Zy gm und 부등식 에 의 하여 적 분가능(i n t e g rable) 하므로 ( 뻥성 a-I ta r 도 적분가능하다. 따라서 (d) 도 증명된댜 (c) 에 대하여서는 임의의 O < c: < l 에서 ZCX> P( g,, < 一 nc ) 김 I p{ 홈 l w, > 1 + n:c —an } 11= · = 흡00 1P{x ,,2 > 1 ac-an} < I21o=o l (l+n%a 2n _ an)2 < +co 이므로 정리 4.3.9 의 증명과정의 식 (4.3.1 7 ), (4.3 .1 8) 과 유사하게 증명된 댜口 보조정리 5.2.3 a-> oo 이면 까&< 꿍 }~P{ ta= m-1}~Cm-I • a -(m-l)/ 2a 이고
c,1 = [ n • ( ?,l? ) ; 广 I占 情 + 1) n ~l 이댜 증명 G,, 를 x?, 의 분포함수라 하자. 그리고 C 드 [건 r( 꿍 + 1)rl n~ l 이라 하면 모든 x> O 에 대하여 G,1(x ) < c:IX 브2 이고, x ----> oo 이 면 모든 '~ 1 에 대하여 G,,(x) ~ c;, x 브2 이 다 . 따라서 a-> oo 이면 P {ta = m-l} = P{Z111-1 > a} = P{ (m -l)~ < (m-l)[ 끈;] I/a} ~c,1,_I a -(m-l)/2a 이다. n~ m-l 이고 a>O 이면 P {ta = n} ~ P{Z11 > a} ~ c,, • a -11l2a 이고 P {ta ~ n } = k. = L m” - 1 P {ta = k} 이댜 따라서 a-oo 이면 모든 n~m 에 대하여 2’’: P {ta = k} ~ Cm-I a -(m-l)/2a k=m-1 이댜 스틸링 공식 (S tirli n g 's fo rmula) 에 의하여 모든 k~l 에 대하여 ck ~ bkkk/2a 인 상수 b> 1 가 존재한다. 따라서 P{ n < ta < a314} 도 混\ b 년) k/2a ~ 효 +Ibka-k/Ba
이다. k= ~ 0101 +! bka - k /B a 는 n 이 충분히 크고 a - ► oo 이면 a - (m-1)/2u 보다 작은 크기의 차수 를 갖는다. 또한 kE (a31 4 , a/2] 에 대하여 a31 ,1 ::; ;; ta ::;: a/2 이면 Zk > a 이다 따라서 a 가 충분히 크다면 w;a < (k+l) / ah+1 < 1 이므로 e> O 가 존재하여 (5.2 .1 0 ) 까 a3/4 < ta 弓 } ~ p { W; -1 < 一 c , k E (a314 . 껑 ]} 머 mk,;;aa /x2 k I 男 -1· 1 > ca3/4 } 이댜 따라서 식 (5.2 .1 0) 의 마지 막 항은 a-+= 이면 a -(m - 1) / Z a 보다 작은 크기의 차수를 갖게 된다 . 口 보다.조 정t:리= Z5.2.a4 u\.1(- .0. a기l : ~m 1 )> 이 다l .+ 2a 이면 (t :)2 는 일양적으로 적분가능하 증명 Woodroofe 0982, Non line ar renewal the ory in seq u enti al anal- ys is , pl0 8) 참조. 口 정리(a ) 5.E2.5t a =만 a약 + mPa >- I a(+a2 +a 1에) +대 (하l。여 —, 1)a +-> oo(ol ) 일 때 (b) E(ta _ a)2 ~ 2a2a 이다. 여기에서 pa = 강 +a2 정 1 7i E(S;), s; 는 Sk= k-ak( 而
_1) 의 음수 부분이다. 증명 정리 4.3.10 에 의하여 (a) 는 증명되고, (b) 는 보조정리 5.2.2 의 (b) 와 보조정리 5.2.4 에 의하여 증명된다. 仁] 정의 5.2 .1에 정의된 기회손실 w(c) 는 w(c)=acE[ 기f )-uC l)], <1, c> O u : 실수함수로 u(x) = }x-P+x (x> O ) 로 쓸 수 있댜 따라서 요탕고 는 a 만의 함수로서 다음의 정리를 얻는 댜
정리 5.2.6 m> l + 2P 에 대하여 a- ► 00 이면 亨c 一그1 느+P ' w(c) 는 기회손실이다 증명 u'(l ) = 0 , u (x) = :습} 이므로 Tayl o r ex p ans i on 에 의하여 丑)- u( l) = 宁 (>)p+ 2(:- l)2 b 는 T/a 와 1 사이의 값, 죽, l b-11 < l a-1T-ll 를 만족하는 값 이댜 모든 a>O 에 대하여 T> 망 에서는 b~ 강 이다 따라서 f T> f a[L u(\ 王u )I -u( l) ]J dP= 宁~ .f, T > 껑 (1;)P+2 a-1(T-a)2dP이고, 정 리 5.2.5 에 의하여 a ― 心 0 이면 干 JT > : (-z-) 1,+ 2a - 1 ( T —a) 2 dP - 멸 2a2 = 占 이댜 따라서 a ―> 00 일 때 JT,; ; 4 -a [ u ( i )- u
n ( c) - ( 1 +1 , ( 2T) - 삼
한편 g(0 ) = aµ + b
(5.2.1 2 ) T= inf {n2k 。 -1 円泊 2 W,, }, n• = (~기 1/2 로 다시 쓸 수 있고, 다음의 정리 를 얻으며 증 명은 생략한다. 정 리 5.2 .1 0 0 = ( µ ,
이댜 또한 m> max{3, 1 ― b} 이고 A ― ~0 이면 E( a2 (N, b)) = a2 -( 2 + b)2 -i tzA -l/Z + o(A -t/2) 이다. 축차적 점 추정 문제에서 손실함수는 일반적으로 정방형 손실함수 (squ ared loss fu nc ti on) 와 비용함수로 이루어져 있다 . 이러한 손실함수 를 갖는 축차적 점 추정은 여러 분포에서 정규분포에서와 유사하게 연 구되어 있다. 예를 들면 X~ 지수함수 ( A )인 경우에는 Sta rr & Woodroo fe (1972) 와 Gardi ne r & Susarla(1984) 가 Y~ 음지수함수 (µ ' 11) 인 경우의 µ에 대한 축차적 추정은 Basu(1971) 와 Mukhop a d- h y ay(1 988) 가, 그리고 척도모수 (scale pa ramete r ) (J에 대해서는 Muk- hop a dhy a y & Ekwo(1987) 와 Ghosh & Mukho p adh y a y(1 989) 가 연구 하였댜 또한 X ~ U(O, 0) 에서 0 에 대해서는 Ghosh & Mukhop a d- h y a y (1975) 와 Mukhop a dhy a y ( 1983), 파레토분포 (Pare t o dis tri bu ti on) 에 대해서는 Ghosh & Wackerly( 1 986), Mukhop a dhy a y & Ekwo(1987), X~ 포아송 ( A )에 대해서는 Vardi (1 979), 이항분포 (b i no mi al dist r ibu - ti on) 와 음이항분포 (ne g a ti ve bin o m ial di s tri bu ti on) 인 경우에는 Robbin s & Sie g m und(1974), Wi lls on & Folks(1983) 등 여러 사람이 연구하였다. 일반적인 지수군에 대해서는 Tah ir (1994) 가 연구하였다. 정규분포군의 평 균둘의 일차결합에 대한 연구도 Mukhop a dhy a y (1 976, 1977), Ramkaran (1986), Mukhop a dhy a y & Lib e rman(1989) 등에 의하여 수행되어 왔다. 다변량 분포함수의 모수 추정에 대해서도 많은 연구가 이루어져 왔 댜 특히 다변량 정규분포 (mul ti v ari a t e normal dis tri bu ti on) 의 평균모 수벡터 (mean vecto r p arame t er) 에 대해서는 Ghosh et. al.( 19 76, 1987), Wodroofe ( 1977), Ghosh & Sen(1 9 83), Takada(1984), Ni ke ron(1987)
등이 연구하였으며 주요 결과 를 요약하면 다음과 같다. X1 , X2 , … ~ i.i.d. Np (J£, L) (p책) 일 때 亢 = ; 홈 1X;, S11 = 12 니 홈 l(X, - X,,) (X, - X,,)' ' n 캘 라 하자. 평균모수벡터 g의 추정량을 x::로 잡고 이 때의 손실함수 L,1 = (Y— _y )'A (X ::_ 띠 + en A : px p 양정 치 행 렬(p os iti ve defi nite matr i x ) 이라 하면 위험함수는 R( n, L , c) = EL,. = n- 1t r ( AL) + en 이고 R(n , c, L )를 최소화하는 n 의 값 n* = ( trA L!c) 1 1 2 이댜 Z 가 미지이므로 Z 의 추정량도 S 으로 하여 축차적 절차 를 정지규칙 (5.2.1 3 ) N= inf {nzk 。냐 2) : n 킨t rAS,,/c)1 1 2}, 싸 최초 시작 샘 플 수 라 하면 이 때의 위험함수 R( L , c) = tr( AL ) Elv1 + cEN 이다. 따라서 정의 5.2.1 에 의하여 정의되는 기회손실과 위험효율은 각각 w(c) =cE[ 草] TJ( c) = {E( N/ n*) + E( n*/N)}/2 이 되어 다음 2 개의 정리를 얻었다. 첫번째 정리는 Ghosh et. al. (19 76) 이 증명하였고, 두 번째 정리는 Woodroo f e (l 977) 이 최초로 증명하였 다. 그 증명과정은 정규분포와 유사하므로 생략한다.
정리 5.2.11 p ~2 이고 k 。 ~2 일 때 c - 0 이면 7] (C) - 1 이고 w(c)= o(c) 이다. 정리 5.2 .1 2 p 22 이고 k 。 21+2 p -l 일 때 c - o 이면 w(c) = ~tr[ (A~ )사 )사 + o(c) 이댜 또한 가우스-마코프 선형 회 귀 (Gauss-M arkoff line ar reg r essio n ) 모 델 (mode l) Y,. ~ x,·8 + E;, i = l, 2 , … x, ~ p x l 벡터, Ci ~ i.i.d. N(0,< r) B 는 px l 미지의 모수일 때 X'=(X1,X2,… , Xn), Y''= ( Yi , Y2 , …, Y,ly , 8 에 대한 추정량을 8,1 = 8( Y' I) 으로 하고 이 때 의 손실함수 L,1(8,1 , /3) = n-1(o,, -{J)' X'X( On -/3) + en 이 라 하자. 한편 /3의 추정 량으로서 t:. = ( X'X)-lxn• Y'' 라 하면 손실함수 R( n , /3, cJ ' C' 瓦) = E{L,.( P,,, /3} = n-1p cl-+ en 이 된댜 손실함수를 최소화하는 n 의 값은 n• = (pcl-/c ) 112 이고 여기 에서 /은 미지의 값이므로 군의 추정량도 s,,= ( Y'' -X '' (f;n: > •- (p Y ' ' -x n (f;:>
으로 하여 다음의 정지규칙을 규정한다. 이 정지규칙은 Mukhop a dhay (1974) 가 최초로 제안하였다. N= inf {n~ k 。( 나 +1) : n ~ (~) 1/2 } 이에 따른 손실함수 R( B, d2 ' C, PM) = E{Lt/ .. PN, /3} = P< rE (~1) + cEN 이며 다음의 정리를 얻는다 . 정리 5.2 .1 3 모든 P , /3 , 군 에 대하여 c-+O 이면 (a) i<(/3, 군, C, PM)IR(n•, /3, 군, C, 瓦:) -+ 1 (b) i<(/3, c?-, c, PM) - R(n•, /3, if' C, 瓦:) = O(c) (c) i<(/3, if, C, PM) = R(n•, /3• if' C, 瓦.) + 웅 + o(c) 이댜 증명 (a) 와 (b) 는 Mukho p adh y a y (l974) 가, (c) 는 F i ns t er(1983) 가 증명 하였고, N i ckerson (1 987) 은 최초의 시작 샘플수 ko 가 P+ l 이상이면 된다는 것을 보였으며 구체적인 증명은 생략한다. 曰 5.3 축차적 신뢰집합 추정 X= (X,,X2, …)는 모집단의 분포함수 F(x, 0), 0e e 를 갖고 서로 독립인 확률변수라 하자. 이 때 0 에 대한 축차적 신뢰집합 추정
의 개념은 다음과 같다 N 을 정지규칙을 나타내는 자연수의 값을 갖는 확률변수라 하고, 사건 {N= m} 은 X' = (X1, X2, …, X,,, )이 RI 의 부분집합인 E,, ,에 포함될 때라고 하자. 그리고 E1,E2, …는 서로 소인 집합이댜 이 때 만약 X'E E,,,, X1110 E E,,,· ( m' > m) 이면 xm· 의 R '에 대한 사영(p ro j ec ti on) 은 X' 과 일치하지 않는다 E,,,( m= l, 2, …)에 속하는 X '에 대하여 S(X111)={0Ee:xmEA(0)} 이라 하자. 그러면 정지규칙 N 에 대하여 scxN) = {BE e : xN E A(0) }는 실제 모수값을 포함한다고 한다 . 즉, S(XN) 을 축차적 추 정절차 (se q uen ti al esti m ati on p rocedure) 로부터의 신뢰집합이라 한다. 따라서 축차적 절차는 집합 E1, E2, … 내의 X 의 값으로 정의되는 집 합함수 (se t fun cti on ) S( X) 에 의하여 결정된다. 그러므로 축차적 신뢰 집합 추정을 위한 주요 문제는 집합 E1, E2, …와 함수 S(X) 에 대한 합리적인 선택이다. 일반적으로 다음의 2 가지 조건을 요구한다. 첫째, 축차적 절차에 의한 신뢰집합 S(XN) 은 기하학적인 관점에서 어떤 모양을 갖추어야 한댜 예를 들면, 모수공간(p arame t er s p ace) 이 1 차원 공간일 때는 S(XN) 에 대한 신뢰구간의 길이가 신뢰구간 중간점 에 대한 함수이거나, S(XN) 이 일정한 길이 (2d) 를 갖는 신뢰구간 또 는 신뢰구간의 길이에 대한 기대값이 최소가 되도록 한다. 따라서 이 조건은 실제로 통계적인 문제는 아니다. 둘째, 신뢰집합 S(XN) 는 다음의 부등식을 만족해야 한다. 죽, 주어 진 a E (Q , 1) 에 대하여
(5.3.1 ) P 。 {0 E S(XN ) I 0 } 느 1 -a, vo 이다 특히, 식 (5.3 .1)을 만족하는 신뢰집합 S(XN ) 을 신뢰수준 (con 一 fide nce level) 1-a 를 갖는 신뢰집합이라 한다. 이 조건은 순수한 통계 적인 문제로 신뢰집합 추정에서 필수적으로 요구되고 있다. 이제 X1,X2, …는 서로 독립이고 동일한 대칭인 분포함수 F(x— 0), 0E e 를 갖는 확률변수라 하자. 일반적으로 분포함수 F 는 미지 이고 단지 분포족 7 에 포함된다고 가정한다. 모수 0 에 대한 신뢰구간 을 In=I,,(X1,X2,···,X,,) 이라 하고, 이 때의 신뢰구간 폭을 L, 1 이 라 하자. 주어진 aE (0 , 1) 과 d> O 에 대하여 다음의 2 가지 조건을 만족하는 0 에 대한 신뢰구간 I,1 을 추정하자. (5.3.2) P8(8 E J,,) ~ 1-a 또는 lim Pe (B e I,,) 느 l-a ’,.....OO 그리고 (5.3 .3 ) L,,~2d T,, 을 8 에 대하여 전이동치(t ransla ti on e qu i v ari an t)이고 일치추정 량( cons i s t en t es tim a t or) 으로서 占 ( Tn _ o) --1£N ( O, 군( T, F)) 라 하자 . 그러면 주어진 값 l-a 에 대하여 (5.3.4 ) !~떤 p{I { Tn -n -l/2( J% 幻 0 < T,, + n -I/2( J% } = 1 -a Za 는 $(za) = 1-a, $(x) 는 표준정규분포함수이다. 길이가 2d 인 0 에 대한 가능한 신뢰구간을
(5.3.5 ) I,, = [ Tn - d' Tn + d] 이라 하자. 그러면 만약 분산 cl= cl(T, F) 가 주어진 값이라면 식 (5.3 . 4) 를 만족하는 표본수의 근사값 n 은 (5.3 .6 ) n= nd= d-2z;12< l-( T, F) 이 고 d-> O이 면 n -> oo 이 므로 lim P 。 ( O E I,, ) = l —a 이 다. 따라서 d---0 d 의 작은 값에 대하여 I,, 은 점근적으로 포함범위확률 (covera g e pro b-abil ity) 1 -a 를 갖고 유계의 신뢰폭 (bounded confi de nce w i d t h) 을 갖 는 신뢰구간이 된댜 그러나 분포함수 F 는 분산 cl(T,F) 가 미지이 므로 식 (5.3 . 6) 에서 분산 cl( T, F) 대신 /의 추정 량 S;, = S;, (Xl,X2, … ,X,1) 으로 대체하여 다음과 같은 정지규칙을 갖는 축차적 절 차 를 제시한다. (5.3 .7 ) Nd = inf { n ~ no : n ~ d2z;,12 책 }, n 。: 최초 시작 표본수 이 때의 신뢰구간은 (5.3 .8 ) IN, = [ TN, - d, TN, + d] 로 정의한다. 그러면 정지규칙 Nd 와 신뢰구간 IN d 에 대하여 다음의 정 리를 얻으며 증명은 생략한다. 정리 5.3.1 식 (5.3.7) 과 (5.3 . 8) 을 갖는 축차적 절차에 대하여 (a) 정지규칙 Nd 는 d 에 대하여 증가함수 (b) 모든 d> O 에 대하여 P(}(Nd < 00) = 1
(c) d--+ 0 이면 —N12d_d --> 1 a.s. (d) Jim ENd I nd = 1 (e) ldi-m-0 Po( O E INd ) = l —a d--0 이다. 위의 문제에서 T,, 울 M- 추정량 (M-es ti ma t or) 또는 R - 추정량 (R esti ma to r ) 등으로 하여 새로운 정지규칙을 정하여 해결할 수도 있다. 다음은 장애모수 (nu i sance p arame t er) 가 있을 때 평균모수 µ에 대한 포함확률 1_a 를 갖고 신뢰구간 폭이 2d 인 축차적 신뢰구간 추정문 제를 살펴보자 . 이 문제는 Chow & Robb i ns(l965) 가 최초로 연구하였 지만 실제로는 Ste i n ( l945, 1949) 의 아이디어 산물이다. X1,X2, …는 미지의 분포함수 Po, 0E e 를 갖는 서로 독립인 확 률변수이댜 단지 Po 는 분산 /이 유한하다고 가정한다. 亢= p$J x,•, • V,.1. = _nl_ ,f-;; -1 (• X;• — X, .:. )• 2 + _nl_ 이라 하고 {a,, }은 양의 값을 갖는 상수의 수열로서 n----+oo 이면 a11----+a 이고, 표준정규분포함수
보조정리 5.3.2 { Y,,} 는 확률 변수들의 수열로서 모든 n 에 대하여 Y,, ~ 0 a.s. 이고 lim Y,,= 1 a.s. 이다 . 그리고 {/(n) }은 양의 값 ’,-.OO 울 갖는 실수의 수열로서, n-->oo 이면 /(n)-->00 이고 f (n)/ f (n 一 1) -> 1 이 다. 임N 의= 의 N (n t 。 ) >= 0 i, nft {> n 0~ 에 n 。대 : 하 Y여, 조 1I ( n ) } 으로 정의하고, 모든 n 에 대하여 Y,. > 1f ( n) 이면 N(t) = +oo 라 한다 그러면 (a) 모든 t> 0 에 대하여 N(t) < oo a.s. 이고 N (t)는 증가함수 (b) lt-i-mc o N( t) = oo a.s. (c) lim EN( t) = oo a.s. EOO (d) E떤 7f (N ( t)) = 1 a.s. 이댜 또한 E( su11 p Y,,) < oo 이면 (e) lEi0m0 ~t E[ f( N( t)] = 1 이댜 증명 (a) t를 고정된 값이라 하고 n-oo 이면 1- /(n)-oo 이다. 확 률공간 .Q= {(JJ}에 대하여 n-oo 이면 Y,,( (JJ) -1 이므로 궁극적으로 Y,,((J J) ~ 1-/( n) 이다. 따라서 N((JJ ) < oo a.s. 이고 N( t)는 증가함 수라는 것은 명백하다. (b) 모든 n 에 대하여 Y,,((J J) > 0 이고 n-oo 이면 Yn@)-1 이므로,
U( (L)) = mt n Y1 1((L )) 라 두면 U( (L)) ~ 1f (N ((L ))) 이고 /(N((L ))) > t U( (L))이다. 따라서 t-=이면 f(N (t, (L)))- >= a.s. 이므로 N(t, (L))-= a.s. 아다. (c) N( t)는 증가함수이므로 (b) 와 단순수렴정리에 의하여 Iim EN(t) = E( Iim N(t) ) = += ,.....OO ,.....OO 이댜 (d) YN < 7 f (N) 이고 YN-1 > +f (N ― l) 이므로 YN < +/(N) < 갔폰 h YN-1 이다. 한편 t -+00 이면 N 一 00, N_l 一 00 이므로, YN-1, YN-1-I, f (N)/ f (N 키 )-1 이다. 따라서 1 ~ lim낸 i n f 上t /(N) ~ lim巳 。su p ~t f(N ) ~ l 이다. 그러므로 뿐남 /(N) = 1 a.s. 이댜 (e) Z= s~II p Y,, 이라 두면 EZ< oo 이다 . m( > n) 을 元問 ~ 2 를 만족하는 자연수라 하면 모든 N :::::: m 예 대하여 ·무 타 (N) f (N-l )/[/(N-l )t] ~ 2 Y回 ~ 2Z 이다. 그러므로 댜 l 에 대하여 i伊끄 < 2Z+/(1) +/(2) +… +/(m) 이다. 따라서 (d) 와 르베그 우월성 수렴정리 (Lebes q ue's dam- ina te d converge nce the orem) 에 의 해 증명 된다. 巳 정지규칙 (5.3.9) 를 갖는 축차적 절차에서 신뢰구간을
(5.3.1 0) IN = [)0 ;- d, y-;+ d] 라 하자. 그러면 다음의 정리 를 얻는다. 정리 5.3.3 식 (5.3.9) 의 정지규칙을 갖고 평균모수 µ에 대한 축차적 신 뢰구간 (se q uen ti al confi de nce i n t erval) 을 식 (5.3 .1 0) 이라 하면 (a) lEim0 a2~ / = 1 a.s. (b) li mP 。(µ E IN ) = l 一 a (~口 ]1그 처-, 일 치 성 (asym p tot i c consis t e n - d cy )) (c) ldi-m0 da2 2 E /N = l (점근적 효율성 (as y m pt o ti c eff ici e n cy )) 이댜 증명 Y,1= 뭍,f (n)= 무a,,, t=곱¢으로정의하면정지규칙 (5 . 3.9) 는 N= N(t) = inf{ n~ l : Y:,;;f ( n)It} 로 다시 쓸 수 있으므로 보조정리 5.3.2 에 의하여 (a) 는 증명된다. 또한 P 。 { µ e IN } = Po { I Y;-µ I 니 = Po{ 미 도-µ) 三 平!} 이다. 한편 중심극한정리에 의하여 五(6 ~ _rLN (O , l) 이고, (a) 에 의하여 t -oo 이면 N/t- 1 a.s. 이므로 N/t 1. 1 이다. 따라 入1 정리 4.3.1 에 의하여 표6~ _;l N(O , 1) 이고 교a6
- 나 a.s. , 즉, i6효 _ ► a 이므로 (b) 는 증명되고 (c) 는 보조정리 5.3.2 의 (e) 에 의하여 증명된다 . 曰 만약 µ4 = EX4 < = 이 면 ldi m P8{g :—{n; < x} =
적 (nonp arame t e ri c) 관점에서 연구하였다. 또한 Chan g (l992) 은 위치모수 (loc ati on pa ramete r ), Gij be ls & Veraverbeke(l989) 는 분위수(q uan ti le), Mar ti nsek(1993) 는 밀도함수, Gleser(l985) 와 Rahbar(l995) 는 회귀모수 (reg r essio n p arame t er) 에 대하여 연구하였다 그 밖에도 많은 사람이 여러 각도에서 연구하였으며, 다변량분포족에 대해서도 확장 연구되어 왔댜 한편 신뢰구간 폭 2d 를 갖는 축차적 신뢰구간 추정 문제와 약간 다 른 각도에서 다룬 축차적 신뢰집합 추정으로 W ij sman (l 981) 이 처음으 로 제기한 f3―프로텍션( (J-pro te c ti on ) 문제가 있다. 단편 신뢰구간 (one-sid e d confi de nce i n t erval) 에 대하여 모수 r= r(0) 를 포함하는 확률은 주어진 값 l _ a 보다 크고, 오류모수 r(O) _ 8(r(O) )를 포함 하는 확률은 주어 진 값 /J ( O< /J < l ) 보다 작은, 모수 r = r( 0 ) 에 대 한 신뢰구간을 구하는 문제이다. 즉 N을 어떤 정지규칙이라 하고 이 때의 Y=Y(O) 에 대한 신뢰구간을 IN=[LN(X1,X2,… ,XN),00) 라할때 (5.3.1 1 ) P 。 {r(0)E J N}=P 。 {LN:;;;r(0)}~l-a , 't/0 E( 9 이고 (5.3.1 2 ) P 。 {r(0) —o (r(0)) E J사 = P 。 {LN:;;; r(e ) - o(r(0)) } ::;; fl, V 0 E 6( o(x) > 0 은 어떤 주어진 함수) 를 만족하는 신뢰구간 IN 을 구하는 문제이다 X1,X2, …가 i.i.d . N(µ, 1) 일 때 r(0) = µ에 대한 B- 프로텍
션 문제 롤 실수함수 o(x ) ( > 0) 에 대하여 정 지규 칙 (5.3 .1 3) N = inf { n z n 。 : n 2 c2 [ o ( X,,) r2 } , C: 상 수二 豆: 표본 평균 이라 정의하고 이 때 단편의 축 차 적 신 뢰구 간을 (5.3.1 4 ) IN = [ 志 -p 8 ( 첫) , 00 ) , p E ( O, 1 ) 이라 정의한다. 그러면 다음의 정리 를 얻는다 . 정리 5.3.5 o(x) 는 양수값을 갖는 실수함수로 다음의 조건을 만 족 한다. (a) o(x) 는 연속함수로 x 一 _(X)이면 o( x )-o ,x--> (X)이면 o(x) ->00 (b) 모든 실수 µ와 x 에 대하여 I 8(x + µ) - 8(x) I < I x I (c) 어 떤 상수 b ( > 0 ) 에 대 하여 µ --> 士 00 이 면 흐預f;f- -1 로 I XI < b 에 일양적으로 성립한다. 그러면 주어진 O < a, /3, p < l 에 대하여 정지규칙 (5 . 3 . 13 ) 과 축 차적 신뢰구간 (5 . 3 .1 4) 로 주어진 축차적 절차에서 c 。 > 0 가 존재하여 모든 µ와 C > Co 에서는 pµ(µ E I사 느 l- a, Pµ(µ _ 8('µ ) E I 사 조 /3 이댜 증명 a(µ, c )=Pµ(µeIN), /3 (µ,c)=Pµ(µ - o(µ)E JN ) 이라 두면 a(µ , c) = Pµ{4 '> p o (µ + 玩) }, 玩 = Y;-µ /3(µ , c) = Pµ{Y ;, > o(µ ) - po (µ —4, ) }
이댜 o(x) 에 대한 조건 (b) 를 이용하면 /3(µ • C) ::;; Pµ{~ > 강(1 -p)o (µ — ~) } 임을 쉽게 보일 수 있다 . 이제 t = mi n {p, (1 一p )/2} 라 두면 a(µ , c) ~ Pµ{z ;; > to (µ + z;;) } {](µ , c) ~ Pµ { z;; > to (µ - °Z;;) } 이다 정지규칙 N 의 정의에 의하여 c-oo ( µ: 고정), µ-oo ( c: 고 정) 혹은 (c, -µ)-oo 이면 Nc-2[o(µ)]2-1 a.s, 임을 조건 (c) 를 이용하여 보일 수 있다. 따라서 a(µ , c) ~ Pµ{N112'z ;; > tc } 이댜 그런데 (c, -µ)-oo 이면 c2[o(µ)r2-oo 이므로 정리 4.3.1 에 의하여 a(µ , C)-o 이다. 따라서 cl > 0 과 µ1 이 존재하여 모든 c > c1 과 µ ~ µ I 에 대 하여 a ( µ , c) ~ mi n ( a , f]) 이 댜 한편 E: = mi n ( a , /3) 에 대 하여 a > O가 존재 하여 P{ Z,: < a , n= 1, 2, …} > 1- E:이므로 모든 정지규칙 N 에 대하여 P(z ;> a) < E:이다. 조건 (a) 에 의하여 µ2µ2 一 a 이면 o(µ)>a/ t를 만족하는 µ2 를 선택할 수 있다. 그러면 µ > µ2 이고 x> tmin { o(µ+x), 8(µ_x)} 이면 x > a 이다 . 따라서 µ 2 µ2 에 대하여 a(µ , c) ~ E:이다. 만약 距 ~ µI 이면 모든 µ와 c> C t에 대하여 a(µ , c) ~ E:이다. 만 약 µ,<µ2 이면 모든 µ1<µ<µ2 에 대하여 c2>0 가 존재하여 P(z ; > a) < E:임을 종명하자. 그러면 Co = mi n (C1 , C2) 로 잡으면 모
든 µ와 C > Co 에 대하여 a(µ, c) < E 이댜 z::-o a.s. 이므로 주어진 a 에 대하여 no 가 존재하여 P(S1) > l -E/2, S1 = { Z:: ~ a , n ~ n 。 } 이 댜 또한 S2 = { Z:: ~ b , n ~ n 。 } 라하면 P(S2) > 1-s/2 인 b 를 선택할 수 있댜 한편 조건 (a) 에 의하여 82 가 존재하여 -口i'-드- I X I < b 에 대하여 8(µ +x) ~ 82 이다. C2 = n 。 1/2 82 라 하면 사건 S2 에서는 c2[8(µ 土 ~)r2 ~ c202 = C% 。같이다. 따라서 만약 c~ c2 이면 S2 에서는 Nz n 。이댜 또한 c~ c2 이면 사건 s1ns2 에서는 z;~ a 이므로 P(S1nS2) > 1 一 c 이댜 따라서 a(µ , C) 에 대하여 증명이 완료되고 {J(µ' C) 에 대해서도 유사하게 증명된다. D 다음은 µ---> -00 일 때 포함범위확률과 /3-프로텍션 확률은 다음 따 름정리로 주어진다. 따름정리 5.3.6 µ--0 0 이면 표준정규분포함수
s,, = 土n-1 tI::;'1 ( X; - X,:)2 을 정의하고 이 때의 축차적 신뢰구간 IN = [ T,, 一 pd , oo ) , p E ( 0 , 1 ) 을 사용함으로써 /3-프로텍션 문제를 해결하였다. 아울러 | r I 一 OO 또는 I erI -oo 이면 告 _d_. N(O , l) 의 결과를 얻었댜 B - 프로텍션 문제에 대하여 많은 연구가 이루어졌는데 특히 Juh lin (1985) 은 지수분포( µ), Fakhre-Zake ri (l989) 는 모수벡터에 대하여 그리 고 Kim (l987, 1990, 1995) 은 장애모수가 있을 때 평균모수 µ에 대한 축차적 결과를 얻었댜 K i m 은 정지규칙 N= inf{ n ~ 2 ' n ~ c2s ,,2 I o'2-(克) } 를 제시하고 8 에 대한 약간의 제약조건하에서 E0X4 < oo 이면 E 。 (N/N0) 라, 下N-No 一d N(O , q) 여기에서 N0 = c2d2/o 'l-(µ), Z=(x-µ)/(5 q = EZ4 -1 +4[o(µ )r2[ 0' {µ )J2 d2 -4 [o(µ )r10· (µ )aEz~ 의 결과를 보였으며, 만약 µ--0 0 일 때 o(µ)-o 을 만족한다면 µ---+ -00 일 때 역시 EoN/N。 -1, 훑 _/4 N(O,1) 값 (0) = Var Z 임을 보였다.
제 6 장 축차적 베이즈 절차 제 1 절에서는 손실함수, 위험함수, 베이즈 위험 등 결정이론에 관한 개념을 다루고 고정된 표본에서 베이즈 추정을 다룬다 . 제 2 절에서는 축 차적 베이즈 절차 (se q uen ti al Bay e s p rocedure) 를 다루고, 제 3 절에서는 축차적 확률비의 최적성 등 축차적 베이즈 절차에 의한 응용을 다룬다. 6.1 베이즈 절차 (요, B ' p。)를 확률공간이라 하고 X~PoE{Po : 0 Ee}, e: 모수공간이라 하자 . 그리고 A 는 모든 원하는 해답의 형태를 포함하는 공간으로 작용공간 (ac ti on s p ace) 이라 한다. 예를 들면, 검정문제에서는 A = { H。 채택, Ho 기각}이 된댜 o( x) 는 X 에서 A 로 가는 함수로 정의하고 T = {o(x ) : o(x) E A }라 하자.
정의 6.1 .1 손실함수 L 은 e x A 에서 R 로 가 는 함수로 정의한다. 일반적으 로 손실함수는 오류 결정을 함으로써 생기는 손실, 샘플링에 따른 비용, 구조적인 비용, 인건비 등으로 이 루 어져 있으나 대개 구조적 인 비용과 인건비 등은 생략한다. 여기에서 는 일차적으로 오류 결정을 함으로써 생기는 손실만을 다루고 나중에 샘 플 링에 따른 비용을 추가 하여 다루고자 한다. 손실함수 L( e , o(X) )는 실제 모수 0 대신 o(X) 를 취함으로써 생기는 손실을 의미하며, 대부분의 경우에는 음의 값을 갖지 않는다. 정의 6.1 .2 R( 0, 8) = E0 L(0, B(X)) , 8E 'J 를 위험함수라 한다. 위험함수 R(o, 8) 는 0 의 함수로서 손실함수의 기대값, 죽, 평균손 실함수이댜 정의 6.1.3 모수공간 0 에서의 (J-대수를 B(e) 라 하고, ( e , B(e )) 에서 정의되는 확률분포함수를 7[( e ) 라 하면, 이 때 7[( e )를 사전분 포(pri or d i s tri bu ti on) 라 한다. 정의 6.1.4 R(n, S) = E (R(0, S)) = JR( 0, S)7 r(d 0 )를 베이즈 위 험 (Ba y es risk ) 이 라 한다. 보조정리 6.1. 1 만약 L(0, o) ~ k (k> -oo) 이면 모든 8 드 T 에 대하 여 베이즈 위험 R( 1r, o) ~ k 이다.
증명 R(7 [. 8) = fR( e , 8)7 r(d e ) 江 0 정의 6.1.5 주어진 사전분포 7[에 대하여 베이 즈 위험을 최소로 하는 8(X) 를 베이즈 추정치(B a y es es ti ma t or) 이라 하고 기호로 8 ;r라 한 댜즉 R(7[ , 8r ) 三 R(7 [, 8) , V8 E T 베이즈 추정치 8 ;r는 사전분포 硏세 따라 다르며 유일할 필요성도 없 댜 이제 베이즈 추정치 8” 를 구하는 절차를 생각해 보자. P 。 (dx) = p 。 µ(dx) 라 하면 R(1r, o) == JJJµ(dL x ()0 ,J oL ((x0),) Poo((xx))) µp。(d (xx))1 1rr((dd80)) 이므로 베이즈 위험 R(;r , o) 를 최소로 하는 8 ;r는 고정된 x 에 대하여 J L(0,a) p。 (x) ;r (d0 )를 최소로 하는 a 의 값이댜 정의 6.1 .6 주어진 X=x 에 대하여 p。 (x) 짜 de)/ fp(J (x) 7r( de)= 7rx(d0 )를 사후분포(p os t e ri or di s t r i bu ti on) 라 한다. 정의 6. 1. 6 에 의하여 베이즈 추정치는 손실함수 L(0, a) 의 사후분포 에 대한 기대치가 최소가 되는 a 의 값임을 알 수 있다. 일반적으로 베이즈 추정에서는 첫째 베이즈 위험의 최소값을 갖는가, 둘째 손실함수 L( • , 8( • ))가 B (e) x A 에 대하여 가측함수가 되
는가의 문제가 있으며, 이에 대해서는 Wald & Wol fo w it z(l950) 를 참 고하기 바란다. U 는 분포함수 7r( 0 ) 를 갖는 확률변수라 하고 X = x 가 주어 졌을 때 U 의 사후밀도함수를 ...l( eIx), 그리고 (X, U) 의 결합밀도함수를 h(x, 0 )라 하면 측도 µ(dx) 에 대하여 h(x, 0 ) = p。 (x)1r(d0 )이댜 그러면 다음의 보조정리를 얻으며 증명은 생략한다. 보조정리 6.1. 2 X = (X1 . X2 ... • . X,,) 일 때 T 를 0 에 대한 충분 통계량이라 하고 T 의 밀도함수를 g。 (t)라 하고, 또한 m( t)를 T 의 주변밀도함수 (mar gi nal densit y fu n cti on) 로서 m( t) > 0 이 라 하자. 만 약 인수분해정리(fa c t o ri za ti on t heorem) 가 성 립한다면 T(X ) = t가 주어졌을 때의 U의 사후밀도함수는 tl( e I t) = tl( e )g。 (t)/ m( t)로 주어지며 A( 8 )는 U 의 밀도함수이다. 예제 6.1. 1 X= (X1 , X2 , … , X11) , X,-~ i.i.d. N( 0 ,
예제 6.1.2 (a) 손실함수 L(0, a) = ( 0 - a) 2 이면 베이즈 추정치 oix ) = E{ U I X = x} = f 0 .-l( 0 I x)d0 이댜 (b) L(0, a) = Ie -a| 이면 8r(x) 는 사후분포함수의 중앙값 (me- di an) 이댜 즉, J_aOOA ( o | x)d0 = JaOOA( o | x) d0 를 만족하는 a 의 값이다. 1, la-0 I ~c (c) L(0, a) = ( 0 , I a - 0 I > c , c ( > 0) 는 주어 진 값 이라 하면 o l( (x) 는 길이가 2c 인 구간 I 에 대하여 AUE/I X= X) 를 최 대로 하는 구간 I 의 중간값(mi d- p o i n t) 이 다 . (d) H。 : O 드 e 。 대 H1 : e E e 1 , e 。 U e 1 = e , e 。 n e 1 = 0 인 검정문제에서 al . 는 H, 를 채택 (i= 0, 1) 하는 것이라 하고, 이 때 의 손실함수 L(0, ai) ={ °, OE6; (i= 0 , 1) l, 0 또 6; 이 라 한L댜( 8, U8~) -幻 L0 ) ~라· 8 ,하 면: : : 。 , 8 는 검 정 함수(t es t fun cti on ) 1-0, 0Ee1 이므로
R(0, o)=E 。 L(0, o)=( E( ]o (X), e E e 。 1-Eo o (X), 0 E B1 이다. 따라서 군에 대한 배이즈 위험 R(r, 8) = JOo E (] o( X) 点 d0 ) + f0 , (l - E 。 o(X))7 r(d 0 ) = JQ 따- ) JJ 0 。 p。 (x )7r(d e ) + Cl -o (x)) J0 ,P( ] (x )7r(d0 )]µ(dx ) 이므로 R(Jr , 0:) 를 최소가 되는 8 급는 8- —— ,. OL JJo 。 pp。。 ((xx) ) ;쩌r ( ddo0 )) <> fl。。 11 pp。 8 ((xx))Tn((dd00 )) o 。 . 임 의 의값JO o p。 (x) 点 do) = J。 1 p 8(x)r(d0 ) 임을 알 수 있다 . 이제 손실함수가 O 를 추정하는 데 발생하는 손실과 샘플링하는데 소 요되는 비용으로 이루어져 있다면, 죽, L(0, a, n) = L(0, a)+ c(n)(n 은 표본수)이라면 베이즈 추정치 8; 에 대한 베이즈 위험은 R(n, 젭, n) = E ;rE 。 {L(0, o(X) , n)} 이다 . 따라서 최적고정표본수는 R(n, o;, n) 을 최소로 하는 값이다. 예 제 6.1.3 X1 , X2 , …는 i . i . d . N( 0, d2) ' u~ N( µ , -?) ' ( d2 ' µ ' 근) : 주어진 값이고, 손실함수 L(0, a, n) = ( 0 -a)2 + c(n) 이라면 위험함수가 ( o -a )2 일 때 예제 6 .1.l과 6.1. 2 (a) 에 의하여 8~ = µII (X,,) 이고 이 때의 베이즈 위험은 p;' = ~규n 근 이다 따라서
(a) 샘 플 링에 소요되 는 비용 c( n) = nc 일 때 는 8' 에 대한 베이즈 위험 R(1r, 競 n) = / /규? + nc 이다 따라서 이 때의 최적표본수 (o pti mal samp le siz e ) n 은 n• =
B,, 은 X11= (X,, X2 , ·' · ,X,,) 에 의하여 생성되는 a - 대수로서 B,,CB,, + 1CB 라 하고 c(X) 은 B,, -가측이라 하며 c,,= c(X) 이 라 쓰고 n 에 대하여 증가함수라 한다 . 정지규칙은 a,, = a,,(X )이라 하고 이는 B -가측이라고 하자 . 그러면 축차적 절차는 (6.2.2)' . o= ( {a , d}) , {d,,} : 정지되었을 때의 결정규칙 죽, n 단계에서 X · =x 을 관측한 후 정지하고 a= d,,(x )을 결정함 울의미한댜 이 때의 8 에 대한 위험은 (6.2.3) R(8) = ILI0=0O Ea,J L ( U, d11(X)) + c(X)] (E 는 (U, X) 의 결합분포, 즉 Po(x)µ(dx) ,1 (d8) 에 대한 기대치를 의미한다.)로 정의한다. . 축차적 베이즈 추정은 R(o) 를 최소로 하는 o= ({a,,, d,,}) 를 구 하는것이댜 정리 6.2.1 L(. , .) ~o 이고 E[L(U, d,)]
이댜 증명 (a) 주어진 임의의 n 에 대하여 r=j: ;; EL(U, d) < oo 이라 하 자. 그리고 EL(U, d111') - •r 인 {d111' E 'J , m= l, 2, .•. } 를 잡자. d1 = d i ’라 하고 k= l, 2, ••• , m 一 l 에 대하여 Sk= {E[L(U, dk+ < I B] ~ E[L(u' dk) I B]} 이라 할 때 {dk = d/ls, + dk-115, : k = 2 , 3 , … , m} 로 하면 E[L( U, d111) I B ] ~ E(L( U, d111 一 1) I B) 이다. (b) (a) 에 의하여 임의의 d,IE T ,,에 대하여 E[L(U, d,,) I B ,,] 나 인 d,1' E 'J ,1 이 존재하므로 E[ L( U, d,,) I B ,,] 2 /11 a.s. 이댜 (c) 임의의 d,1 E 'J ,1 이면 d,, E 'J 11+ k (k 2 0) 이므로 (b) 에 의하여 l,,+k ~ E[L( U, d,,) I B n+k] a.s. 이댜 따라서 E( l,,+k I B ,,) ~ E{E[L( U, d/1 ) I B 11+ k] I B ,,} = E[L( U, dn) I B n] ~ l11 a.s. 曰 m = l, 2 , … 에 대하여 om = ( {a11} , {dllm} ) 이라 하면 식 (6.2.3) 에 의하여 R(8,,,) = n2o=o o Ea,,L( u, d,1., ) + ,12o= o O a ,,c,1
= I120= 0 O E {a,1E [L (U, d,,n,) I B ,,]} + IZl0=0 O E a,,c,, 이므로 정리 6.2.1 에 의하여 lFim OO R( am ) = 'Llo=o O_ E a11( l11 + cJ = ,Llo=o O_ a 11 W11 , W11 = l,, + c11 이다 따라서 ))Z0= 0 O E a,,W) ,의 값은 8 , ,, 에 의하여 추정할 수 있다. 정의 6.2.1 닫힌 정지규칙, 즉, P(N < +oo) = l 또는 1L1c =o 0 a,, = l 에서 oo 11L = 0_ E aw 을 모든 정지규칙 {a,, } 에서 최소로 하는 문제를 최적정지 문제 (o ptim al sto p ping p roblem) 라 한다 정의 6.2.2 자연수 k(~ o) 가 존재하여 N:::;; k a.s. , 즉, 1Z1 =k 0 a,l = 1 일 때 k- 절단된 절차 (k- t runca t ed p rocedure) 라 한다 . 이제 k- 절단된 절차에서 121k= 0 Ea,lw,, 울 최소로 하는 정지규칙 {a,1 } 을 찾아보고자 한다. Xk=Xk=(x1,Xz, … ,Xk) 일 때의 위험을 wk(xk) 라 하자 . 그리고 Vk-1 (xk-l ) = mi n { Wk-I (xk— 1 ) , E [ wk (Xk ) I xk-1 = xk-1 ]} 이라 정의하자. 그리고
* v==W=k.m l{ (6.2.4 ) . k杓 n {w “ W’ E (w11+ l I B 11)}, n = k-1, k-2 , …, O 요< ’ ’ .1 < n ’ V,, = w,1} , n=0,1, 2 ,… 이라 정의하고 정지규칙 {a~,} 은 a~, = ls , , 이라 정의한다 정리 6.2.2 k- 절단된 절차하에서 임의의 닫힌 정지규칙 {a,,} 에 대하 여 R= 'l~=k 0_ E a,,w,, ~ ,12=k: O _ E a~1w,, = R0 = v 。 이다. 증명 g( r) = 11±= _0 Ea,•,•v , ,• + E( l - 1±1 =0 a,,)vr (0 ~ r~ k) 이라 하자. 그러면 g( O ) = V 。이고 r:;::,,; 1 에 대하여 g( r) = IrlL=- 1O E a,,v,,+E( l-IrL1-=1 O a,,)vr 이댜 g0 ( r) = 1L1r= 0 . Ea~1•.•v 11 • + E( l - 1L1r= .0 a~,) Vr (0 ::s;; r ::s;; k) 이라두면 r< k 에 대해서는 g( r+1 ) == 111LZ1= =rr 00 _ E Ea a11,,•v-• v11,- -,• ++ EE[( l( l- - 1Z1 =1 rL1 0r=_ 0 a ,a,1)1v) r+• 1E (vr+1 I B r)] 이다. E(Vr+J I B 11) ;;::= V,. a.s. 이므로 r~l 에 대하여 g( r+l ) ~ g( r) 이댜 이제 s= ( 나。 S,,)c 라 하면
l —'r 합니I 。l., sS C 위위에에서서 이다. 따라서 (6.2.5) E[( l-,'j11;= ,00 a? ,)E(Vr+l I Br)] = fsE (Vr+l I Br) 한편 S 에서는 V; < W; (i ~ r) 이고, 특히 Vr = E(Vr+ l I B r) 이댜 따라서 식 (6.2.5) 는 E (l —'Li= O a~1)Vr 이므로 g0 (r + 1) = g0 (r) 이다. 또한, 모든 n 에 대하여 w, 오나),,이므로 k J R ~ 1~1=0 . Ea,,v,, = g( k) 이다 . R 드 I1Z= k O S. . w,, 이고 S,l 에서는 w,l = v,l 이므로 R 드 홀 0 JS ,'v, i= 홈。 a?,v,,= g 0(k)= g0 (O) 이다. 따라서 R ~ g( k) ~ g( 0 ) = v0 = g0 (k) 이다.曰 임의의 자연수 k 에 대하여 vk,k = wk v,,,k = mi n{ w,,, E(v11+1 ,k l B11)}, n < k 이라 정의하자. 그러면 최선의 k- 절단된 절차는 다음의 정지집합을 갖 는다.
(6.2.6) 511,1, = [ V;,k < W;, i < n, V,1.k = w,,], nsk 보조정리 6.2 .3 n = 0 , 1, 2 . …, k 에 대하여 V,1,k 는 k 에 따라 감소한다. 증명 _口_,_ 드'-- n~k 에 대하여 V11,k+ I ~ V11,k a.s. 임을 보여야 한다. 첫째, n= k 이면 vk. k + I = mi n { wk , E(vk+ l.k+I I B k) } ~ wk = vk .k a.s. 이므로 n=k 일 때도 성립한다. 만약 k-1, k— 2, …, m+l 에서 성립 한다면,즉 Vm+l,k+l ~ Vm+l .k a.s. 이라면 Vm,k+I = mi n{ w,,,, E(Vm+I .k+I I B,,.)} 조 mi n {w111, E(Vm+l,k I B ,,.) } = Vm,k a.s. 이므로 증명된다. 口 이제 V,1 = t떤 Vn . k 라 하자. 그러면 보조정리 6.2.4 에 의하여 k ― ► 00 일때 E(v,, +1.나 B ,,) L E(V11+I I B ,,) a.s. 이다. 그러므로 v,. = mi n {w,., E (V11+I I B ,,) } 이고 (6.2.7 ) S,, = { v; < w; , i < n , v,, = w,,}, n=0,1 ,2 ,… 이댜 따라서 다음의 보조정리를 얻으며 증명은 생략한다.
보조정리 6.2.4 식 (6.2 .6 ), (6 .2 .7 ) 에 정의된 S1 1.k, S , ,은 모 든 n = o, l, 2, …에 대하여 k 一 00 이면 1 s k 一 Is , , 이댜 임의의 8 에 대하여 k- 절단된 절차 하에서 8 를 8 k 라 하자 . 즉, k- 절 단된 절차하에서 정지규a칙? =은 I효 a,,, n = k a,,, n < k 0, n > k 으로 정의한댜 그러면 (6.2.8) k-1 oo k oo R(ok)= 1L1=E0 a,,--w -,-,+ E(1L1= ak ,,--)w k-- = 1L1= 0~ E a,-,w -,,+ E( 11L= k+I. a ,, )wk 이댜 정리 6.2.5 식 (6.2 . 3) 과 (6.2.8) 에 정의된 R(o) 와 R(o k ) 에 대하여 !11 s B a.s. 일 때 k 一 00 이면 R(ok)-- ► R(o) 이다. 증명 만약 n ::e: k 이면 cks c,, s w,, 이므로 wk = h+ cks B+ w,, 이 다. 따라서 k OO R(8k)= 1Z1= E0 a,,•w ,,• + E( 11Z= k+l a,,)wk :5: 1L1o= o 0 E a11 w11 + B • P( k < N < oo I 8) 이므로
1~1= ,,0 E a,,w,, s R(8 깁 s R(8)+B • P(k< N < o o I 8) 이다. k->oo 이면 효 Ea,,w, , - R(8) 이고 P(k < N < oo I 8) 때이 므로 증명된다 口 만약 c,, = cn (c > O) 이라면 R(o) ~ ckP(k < N < 00 I o) 이므로 R(8k) < (l + 꿉 )R(o) 가된댜 샘플링에 따른 비용함수에 대하여 다음의 보조정리를 얻으며 역수학 적 귀납법 (ma t hema ti cal ind ucti on of backwards) 을 사용하여 쉽게 증 명할수 있다 보조정리 6.2.6 모든 n = 0, 1, …, k 에 대하여 v,1.k 느 g a.s. 이 댜 보조정 리 6.2.7 식 (6.2.4 ) 에 정 의 된 S,, 에 대 하여 o0 = { ct~, } , 죽, s,, 에서 a~, = 1 a.s. 이면 2oo 짜 = l 이고, 임의의 2oo a,1 = 1 인 절차 Il=O I1= O 8 에 대하여 R(o) 2 R(o0) = v 。 이다 .
증명 정리 6.2.2, 보조정리 6.2.3 과 정리 6.2.4 를 이용하여 증명할 수 있 으며 구체적인 증명은 생략한다. 口 임의의 주어진 사전분 포함수 A 에 대하여 8A 를 베이 즈 추정치 라 하 자. 그러면 다음의 정리에 의하여 e = en 이면 베이 즈 추정치는 절단 된 베이즈 추정치의 극한 임을 알 수 있다. 정리 6.2.8 샘플링에 따른 비용함수 c,, = en ( c > 0), /11 ~ B a.s. 이 라 하고, 8 를 사전분포 A 에 따른 베이즈 추정치, 그리고 좌를 k- 절 단된 절차에서의 베이즈 추정치라 하면 k-> oo 일 때 A 에 일양적으로 R( 좌 )-R( ct)이다. 증명 임의의 k~O 에 대하여 R( ct )~R( 좌)이고 정리 6.2.5 에 의하여 R( 좌) 디 R( 성)(1 + 읍 ) 이므로 증명된다. 口 이제 Xi ~ i.i .d. 로써 주어진 0 에 대하여 분포 를 Pe(x)µ(dx) 라고 A = {A : A 는 사전 분포}, 샘플링 비용은 표본 단위당 1 죽 c,,= n 이라 하자. xn=x 이 주어졌을 때 U 의 조건부 분포 를 A x (d0) 라 하자. 그러면 Ax+ 1 (d0) = (Ax )x •• ' (d0) 임을 쉽게 알 수 있고, 임의의 d,IE T,, 에 대하여 E[L ( U, dn) I X = x] = f L(0 , d,,(x )))x( d0) 이다. 이제
l(,1 ) = m!n JL( 0, a)11(d0) 인 a 가 유일하게 존재한다고 가정하고 이 때의 a 를 a( tl)라 표시하자. 그리고 따, (x ) = a(tlx ) , d;, E 'J 11 이라 하자. 그러면 l,,(x) = i떤f L(0, a)A x •( d 0) = l(,-l x ) 이댜 따라서 l,l 는 A 와 x 의 함수로서 Ax 에만 의존한다. 이제, 이를 확률화하여 A,l=AX“ 이라 하고 l,1= l,I(X’l)= l(A,l) 이라 표시하자. 그러면 w,1 = l(A,I) + n 이 된댜 f는 A 에서 정의된 함수로 f (AX) 는 x 의 가측함수이고 적분가능한 함수라할 때 EA/( T.t l) = Ef (,1x ) = ff/(,1x )Po(x)µ(dx),1 ( d0) 라 정의하면 E[/(An+l) I X] = E, 1.f(T An) 이댜 정의 6.2.3 h 。 (A) = l(A) 를 0_ 절단된 절차하에서의 위험이라 한다. h/11) = mi n [ /(11) , .1 ;.E A hi- I ( T11) ], j = l, 2 , … 이라 정의하면 다음의 보조정리를 얻는다 보조정리 6.2.9 모든 n~ k 에 대하여 v,.,k= n+hk_,,(A,.), k= 0, 1, 2, …
증명 n=I, 일 때는 v k. k = wk = l, + !(11 시 = k + h 。 (ttk) 이 므로 성 립하고 I, — l, /, - 2 , … . m + l 일 때 성 립 한다고 가정 하면, 즉
Vm +I ,k= m+l +hk 키 )/-I(Am+I) 이라면 v,,,,k = mi n{ w,,,, E(v,,,+l. k I X') } = mi n {m + l(A ,,,) , E[m+l + hk 一 111- ] (Am+] ) I X']} = m + mi n { l(tl, ,,) , 1 +EA., h k-m-1 ( Tt l,,,) } = m +hk 一 m(Am) 이므로 성립한다. O h j는 j에 따라 감소함을 알 수 있고, 이 때 tim hj= h (X) 이라 표시하 r 국(X) 자. 그리 고 A ,1 = { A E A I h,, ( A ) = h 。 ( A ) } 라 하면 다음의 정 리 를 얻는다. 정리 6.2 .1 0 식 (6.2.6) 과 (6.2 . 7) 에 의하여 정의된 S, ,와 S,1.k 에 대하여 (a) S · k = { 11 로 A k-i , i < n , 11 ,, E /1 k_,, } (b) S,1 = { A i 또 A ~ ' i < n , A ,, E A 나 , A ,, L A C:0 이다. 증명 (b) 는 (a) 에서 k 一 CX) 일 때이므로 (a) 만 증명하면 된다. 보조정 리 6.2.9 에 의 하여s · k= {i +hk - i (A i) < i +h 。 (11;), i < n, n + hk-11 ( 11 ,, ) = n + h 。 ( A II ) } 이댜 따라서 hk- i( A i) < h 。( A ,.) 쓴 A ,E JIk -1 hk-i( A i ) = h 。 ( A i ) ¢cc> A i E JI k-I 이므로 증명된댜 曰 정리 6.2 .1 0 에 의하여 X, ~ i.i.d. 이고 표본 한 개당 샘플링하는 비 용이 1 일 때는 이중 수열 {S,r. 나는 수열 { A II } 으로 나타낼 수 있고, {S,,} 는 집합 A oo 으로 표시됨을 알 수 있다. 또한 정리 6.2 .1 0 의 (b) 에 의하여 hoo ( 11 ) < h 。 ( A ) O A 또 A OO hoo ( 11 ) = h 。 ( A ) 슈 A E A OO 가성립함도알수있다. 이제 p ( 11 ) = R ( 11 , 참 ) = mi n R ( 11 , o) , Pk( 11 ) = R( 11 , o; ) : k- 절단된 절차에서의 R( A , 8) 의 최소값 이라 정의하면 정리 6.2.2 에 의하여 Pk( A ) = Vo.k 이고 보조정리 6.2.7 에 의하여 p( A )=Vo 이다. k-oo 이면 hOO(A )=p(A )임을 알 수 있고 다음의 정리를 얻으며 증명은 생략한다. 정 리 6.2.1 1 (a) Pk ( A ) = mi n [ l ( A ) , l + E,1 Pk-1 ( T A ) ] (b) p (A)=mi n [/(A), l+E,1p ( TA)]
Po ( A ) = l( A ) 이므 로 정리 6.2. 1 1 (a) 에 의하여 P k 를 구 할 수 있으며 /l cx, = { A E 11 , p ( A ) = p。 ( A ) } 11 :;., = { A E 11 , p ( A ) < p。 ( A ) } 임을 알 수 있다 . 정리 6.2.12 A 는 주어진 사전분포라 하고 {a,, }은 양의 값을 갖는 상 수들의 수열이라 하면 (a) 만약 l( A ,1) < a,1 一 0 이면 베이즈 추정치 8A 는 절단되어 있다. (b) 만약 l( A ,,) = a,,. v n 이면 고정된 표본절차에 의한 베이즈 추 정치 참가 존재한다. 증명 (a) a, , -o 이므로 l( A ,, 。 ) < 1 인 n 。가 존재한다 . h, 의 정의에 의하 여 모든 n 에 대하여 h,,( A ,l 。 ) = l( A 110 ) 이다. 따라서 n = 0 , 1, 2 , … 에 대하여 A ,to E A n 이므로 A ,Io E A (X)이고 이는 N~ n 。 a.s. 이다. (b) 임의의 8 에 대하여 R( A , o) = L00 P(N = n l o) (n + a,,) 11 = 0 이므로 n+a,, 이 최소가 되는 n 의 값 no 를 잡고, 이 때 P{N= n 。} = l 이라 하면 R(..l , o) 는 최소가 되므로 증명된다. 曰 예 제 6.2.1 X; ~ i. i. d. N( 0 , 1 ) 이 고 U~ N(O , a2 ) ( 군 : 주어 진 값) 이 라 할 때 0 에 대한 베이즈 추정을 손실함수가 L(0, a, n) = (0-a)2 +n 일 때를 해 A보 x·자 ~. N 그( it러= I면 지 ( n + a-2 ) , 1/ ( n + a-2 ) ) n
임을 알 수 있고, d,,(x )을 J( 0-a)2 ,l x (d0) 를 최소로 하는 a 의 값이라 하면 d,,(x ) = i=iI:I . l x;/ (n 十 (J- 2 ) E 'J II 이며, 이 때 l(x) = ~n+
R( tl . 6) = 홀 。 f a,. ( x ){ ,l0 11 / J. ,,o .,( x ) + tl 1 ,t L(0 ; , d.,(x))P ... 0 ,( x ) }µ(dx) ( 01 = 1/4 ' 0 。 = 1/2 , 02 = 3/4 ) 이댜 주어진 X = x 에서 최상의 최종결정규칙 d11*(x) 은 2 따 기 (¼ ) L x;i~ (= ¾.l L )( 110 -;L, xa;) +P 1L1 .(o ¾, ( x , a)) =( ¾ ) Lx ; ( t )11 -L x, } 룰 a= 1/4 또는 3/4d ’’ 에 • (서 x ’ ’ )최 =소 로’, 4—하' ’ 는, a 의 X값>iw이X 다—2—2i . n 따 라 서 1_43F E n 임을 알 수 있다. X = x 이 주어졌을 때 최상의 최종결정규칙 d,,•(x) 에 대한 위험 R(A , 8)= 1.1= ~n0 J a11(x11){A0n+b,,(x)}P11,8 。 (x)µ(dx) b11 = 111 mi n {근: ’ 듯 }= 1112_113 11/2-I j;1x; -1 1/21 이다. 한편 bll :5: 서 (3/4) '2-0 이므로 8 는 절단된 절차(tru nca t ed p rocedure) 를 갖는댜 이제w ,,iL=(11 Tl X,,);== AT,o, 이n+라 A 두I자(t. )그n'/G2러 3면-I T.- , ,/2I' n=0, 1, 2, … 이고
v(T) = mi n{ w11(T11), E(v11+ 1 (T11 + Y) I X11)} = mi n { w11 ( T11 ) , E ( v11 + 1 ( T11 + Y) ) } , Y~ Ber( l/2) 이댜 k=3 이므로 V3 = W3 = 3 ,l O + ,l I (¾ ) m3/2; 3 -I T,- 3I2 I Wz = 2 ,l O + ,l I ¾ 3 -I T,- I I 이E 。다 ( .V 3 (X3 ) I X2 ) == 3E 。A V o3 +( T2A I+( ¾Y)f /2½{ 3 -I T,- 3/2I +3 -I T , 기 /21 } 이므로 w, -E 。 (v3 I X2) = { \。 A~,¾ A ', TT22 == 01 또는 2 그런데 _ A ° + ' l = A l (_n + 강 ) > O ( 7J E (O.l, 0•l25)) 이므로 T2 = l 이면 샘플링을 계속하고 T2 = 0 또는 2 이면 최종결정 울 한다. 즉, T2 = 0 이 면 0 = } 을 채 택하고 T2 = 2 이 면 0 = } 을 채택한다. 2..l O +¼ ..ll , T2 = 0 또는 2 V2 (X2 ) = ( 3 A °+ ' \ T2 = 1
w1= Ao+ 11 1(t f'23 _ I T 1- I /2 I = Ao + ] 이므로 E( V2 (X2 ) I X1 ) = ½A O + 尙 A I 임을 알 수 있다 . 따라서 W1 (X1 ) - E 。 ( Vz (X2 ) I X1 ) = 당 A o + 尙 A 1 > 0 이므로 Vl = 웅 A o+ 尙 A I 이고, w0=A1, v0=E0v1(X)= f A0+ 욥 A I 이므로 Wo-Vo= 社 A1- f A0 > 0 이다. 따라서 적어도 하나 이상의 샘 플 링이 필요함을 알 수 있다. 이 를 요약하면 n= l 이면 정지하지 않고 샘플링을 한다. n= 2 일 때는 T2 = 0 이면 정지하고 0= } 채택, T2 ~ 2 이면 정지하고 0= } 를 채택, T2 = 1 이면 샘플링을 계속한다 . 그리고 n=3 일 때는 x3=0 이고 T2=1 이면 0= }를 채택,
X3= 1 이고 T2 = 1 이면 0= } 를 채택한다. 따라서 이상의 축차적 베이즈 절차에서의 위험 v 。 == R(2(1 11 1 o, +참 t ) 1=1 1)1고1P= 3o 0 。 E(T[a2,=I 0w ,,또] 는 2)+ (311 ° + 강 111)Po 。 (T2 = 1) = ½A o + 尙 11 1 = Ev1 (X) 이고 정지점은 {(n, T,,): (2,0),(2,2),(3,1),(3,2)} 이며 샘플링 을 계속하는 점들은 {(n, T,,): (0,0),( 1, 0),( 1,1) ,(2,1) }임을 알수있다 6.3 축차적 베이즈 절차의 응용 먼저 m- 결정 문제를 다루어 보자. 즉0= {0l, 02, …, 0k} 이고 ,,l = (-11 , -12 , …, A 서이라 하며 A = {A E IRk: /\;~ O. 흡k A1= 나인 k ― 1 차원이라 하자. 그리고 A= {a1, a2, … ,am} 이라 하고 손실함수 L(0,a) 는 kxm 행렬 (!ii)이며 l;i = L(0; , a]) ~ o이 다. Wj = U1j , l2j, 0,lkj) ' j=l, 2, … ,m 이라하자 . 그러면사전분포 A 에 대하여 a j의 결정을 함으로써 생기는 평균손실은 Zi A,•. L ( Oi• , a•J .) =: iZ=k 1 Mb. = A • wj 죽, A 와 W j의 내적이댜 a j의 결정과 Wj는 1-1 대응이므로 A 대신
W= (w1 , W2, …, W,11) C Rk 로 대체하자. W,E1 EWA} 에라 정대의하하여자. 그l(러-1 )면 = ml 은ij n 오A 목• w함i,수 (c즉o’n cavl(eA f)u =n ctmi oin n ) {이A 고• w A: 에서 연속임을 알 수 있다. 보조정리 6.3 .1 W 는 R 떡 유한 부분집합이라 하고 WE W 에 대하여 T( w ) = {A E A : A • w E l(A ) } 라 정의하자. 그러면 (a) T(w) 는 오목이고 닫혀 있다. (b) W1, Wz E W 이고 w1 수 w2 이면 T(w1 )과 T(w 2 ) 는 공통의 처口
울 갖지 못한다. 증명 (a) 만 증명하고 (b) 의 증명은 생략하고자 한댜 f(A ) = l(A ) _A.w 라 놓으면 f는 A 에서 연속임을 쉽게 보일 수 있댜 따라서 T(w) = /-1({0} )이다. {0} 은 닫혀 있으므로 T(w) 도 닫혀 있다. A;e T(w) (i =1,2) 이고 A= i2=2 a l , . A,· (a i느 0,al+a2=l) 이라면 A • w= 훔마,. • w= 훔마(tl) = l(tl ) 이므로 A E T(w) 이다. D 이제 X;~ i.i.d . 이고 c,,= n 이라 할 때 m=k, 즉, k- 결정 문제 인 Hi : 0= Oi , a; 는 H 를 채택하는 결정(i=l, 2, … ,k) 문제룰 다루어 보자. 이 때 손실함수 L(0,a) 는 kx k 행렬 (lij) 이고 lii= O(i= l, 2, …, k) 이다. WE W 에 대하여 6 11(w) = A,, n T(w), 6oo( w) = iloo n T(w) 라 정의하자. 그러면 U T(w) = A 이므로 IU UD .11 (w) = 1111, UD .co (w) = iloo IU IU 이댜 따라서 최상의 k- 절단된 절차에서는 좌는 A,I E Ak-,1 가 되는 가 장 작은 n 에서 정지하고 만약 A,, E 6.k- 11(Wj ) 이면 H’ 를 채택한다. 그리고 절단된 절차가 아닌 경우에는, 鈴는 ,11 1 E A00 가 되는 가장 작 은 n 에서 정지하고, 만약 A E 6. 00(W, )이면 H’ 를 채택하게 된다. 구체적으로 k=2 인 경우 0={0l,0 김이고 A={a1,a 갑, 즉, Ho: 0= 01 대 0= 02 인 검정문제에 대하여 살펴보자 . n;;:,: 1 이라 가정하면 보조정리 6.3 .1에 의하여 6,,(w) 또는 Loo(W) 는 w 의 값 이 다르면 공통점울 갖지 못하므로, A,i = (서 , 서)에 대하여 8 는
 02
02
CJ < };, < C2 ( CJ < C 2 인 임의의 상 수) 이면 샘 플 링을 계속한다( 그 림 참 조) . 죽, 정지규 칙 N= inf{n ;'.;?:: 1 : };, ;'.; ?:: c2 또 는 서츠 아 이고, 만약 ANE 6 (X) (w,· ) 이면 O 를 채택한다 사 후 분포는 Ax (d0) = i}J= iI Po (xi ) }(d0) / f}JiPo (xi ) }(d0) 이므로 Po ,· '' 내 lPo , (x}), A=( 서 ,A 2 ), 어 +A 2 =l) 이라하면 A,l = (서 , 서) = Ii 8;;\, ’ i p0 L . A'. p A2 ,' 2T。2 이다. 따라서 [ CJ < 서 < c2] = [~ < ~ < I¾ ] = [di < 꾼 < d깁 = [꿉 d1 < 差 < 곱 d2 ] = [ B < R,, < A ] 이므로 R,, ~ A 또는 R,, < B 일 때까지 샘플링을 계속한다. 또한 { RR,,?< BA O台 A사,? ::; :c1: :~ :A ,.,:E: 스노 co ((wwl2)) 이이므므로로 HHI2 를를 채채택택 한댜 따라서 베이즈 절차 8 는 축차확률비 검정이다 . 한편 , 역으로 주 어진 축차확률비 검정이면 이것이 베이즈 절차인지에 대해서는 다음의 정리로 기술될 수 있다. 즉, Burkholder & W ij sman(1963) 은 정지 경계 치 (B,A) 에 대하여 B~l~A 를 만족하면 주어진 축차확률비 검정 은 베이즈 절차임을 보였고, 중명은 Burkholder & W ij sman(1963) 을
참조하길 바란다. 정리 6.3 .2 정지 경계치 (B,A) 를 갖는 주어진 축차확률비 검정을 상 이라 하자 . 그리고 사전분포 A=( 자 ,A2), A i E(0,1) 이라 하면 l1, lz > 0 가 존재하여 00 는 베이즈 절차 (A , A, l2) 이다. 여기에서 l1=L(01,a2), l2=L(02,a1) (/(0;,a;) =O) 이다 . 만약 좌는 A,I E ^k-n(wj ) 인 가장 작은 n 에서 정지하고 0, (j= 1 , 2) 를 채택하는 k- 절단된 축차적 베이즈 절차이면 좌는 정지 규칙 (B,1 , A,1) 을 갖는 일반화된 축차확률비 검정이 됨을 역시 보일 수있댜 다음은 정리 2.3 .1의 축차확률비 검정의 최적성을 살펴보자. 임의의 절차 8 에 대하여 a,·(8 ) = P8,( 오류의 결정 I o) (6.3 .1 ) Vi ( 8) = Eo,(N | 8) , N 은 정지규칙 이라 하고, 샘플링에 소요되는 비용은 표본 개수당 l 이라 하며, l;( i= 1, 2) 는 0 = 0 일 때 오류의 결정에서 발생하는 손실이라 하 고 사전분포 A= (자, A2) 라 하자. 그러면 (6.3.2) R(.-t , 0:)= tiAi[ l ;a;(o)+V;(o)] 이다.
정리 6.3.3 (축차확 률 비 검정의 최적성) X;~ i.i.d. 로써 밀도함수 P o 를 갖 는 다. 이 때80 는 정지경계치 (B, A) 를 갖는 H1: 0=01 대 H2 : e = e 2 의 검정문제에 대한 축차확률비 검 정 이라 하고, (B , A ) 는 l ~ B ~ A 를 만족한다. 또한 8 는 임의의 축차적 검정으로 식 (6 . 3 .1)에 정의된 a1·( 8 ) , V,(8) 에 대하 여 V;(o) < 00 이고 a,(8) < a , ( 성) (i= l, 2 )를 만족한다. 그러면 II;( 8) ~ II;( 8° ) (i = l, 2 ) 이 댜 증명 사전분포 A= (서, A2) 는 Ai E (0, 1) 인 임의의 분포라 하자 . 그러면 정리 6 . 3.2 에 의하여 !1 과 ! 2 가 존재하여 0 0 는 베이즈 절 차 (A , l1, l2) 이다 . 따라서 임의의 축차절차 8 에 대하여 R(11, t)느 R(,1 , 8° ) 이 댜 따라서 식 (6.3.2 ) 에 의 하여 22 Ai.u ,(8) + 4a,(8) ] > 22 A'[ v1(8°) + l,a,(8°) ] i= l i= I 또는 (6.3.3) iZ=2 Al i u ,•( 8) —v•, ( 8°)] 느 i2=2 Al i [ ai( 8°) —a,· (8 )] 이므로 가정에 의하여 식 (6 . 3 . 3) 의 오른쪽 항은 0 보다 작지 않다 . 이제 di= l/i(8 )-v,(8°) (i= l, 2) 이라 두면 서 d i+tl 2d220 이고 A= (서, A2) 는 임의의 양수이므로 di > O 로서 증명된다. D 정리 6.3.3 에서 적어도 하나 이상의 i에 대하여 ai( a) < ai( a0) 이면 적어도 하나 이상의 Vi ( 8) > ui( 8°) 가 됨을 알 수 있다.
이제 축차적 베이 즈 절차 가 축차적 검정 문제에 있어서 모든 축차 적 절차 에 대하여 정지규칙의 기대값을 최소로 하는 것임을 보이자. 죽 X, ~ i.i.d . 밀도함수를 p。 (x) 라 하자 . 이 때 I-11 : 0 = 0 1 대 I-12 : 0=0 2 의 검정문제에서 o 。 E(0I, 杓)일 때 E 。 0 (NI o) 를 최소로 하는 축차적 절차 8 는 축차적 베이즈 절차임을 다음 보조정리 에서 알 수 있다 보조정 리 6.3 .4 e = { e 1 , e o , e 사 에 대 한 사전분포 A = (자 , 110 , 112 ) (11i > 0) 이라 하고, L( o ,, a j)의 값은 8 。 또는 i=j일 때는 0, 그렇지 않을 경우에는 l 이라 하며, 샘플링에 소요되는 비용은 개수당 c( > 0) 로 0 = o 。에서만 발생한다고 하자. 또한 주어진 오류확률 ai E (0, 1) 에 대하여 모든 절차 8 는 a;(o) ~ a;, (i= 1, 2) 이다. 그러면 a;(o ' ) = a; , i= l, 2 를 만족하는 축차적 베이즈 절차 8 는 모 든 절차 중에서 E o 。 (N I o) 를 최소로 한다 . 증명 11(8) = Eo0( N I 8) 라 하자. 그러면 임의의 절차 8 에 대한 위험 R( 8, tl) = tl1a 1(8) +tl2a i 8 ) +tl0c v(8) 이고, 8 는 베이즈 절차이므로 R( A , 8A) < R(A , 8) 이댜 죽 tl0c [v(8) -v@)] 느 22 A'.[a i@ ) -a,·(8)] ~ o i= l 이므로 11(8) ~ 11(8A) 로서 증명된다 . 口
일반적인 경우로서 X,~ i.i.d. 로 밀도함수 p。 (x), 8 = ( 0o, 01, … , 0k} 라 하고 0 에 대한 사전분포는 ,1 = (,10 , 서, … ,Ak). ,10 > 0, 샘플링에 따른 비용은 개수당 c( > 0) 로 8 = 0 。에만 발생 한다고 하자. 즉, c( 0 ) = (c, 0, … , O), 손실함수는 L( 0 ,, aI.) 2 0 로서 모든 j= 1, 2 , … . k 에 대하여 L( 0 0, a) = L( 0 i• a) = 0 이 라 하자. 그리고 정지규칙은 닫힌 정지규칙 {a,,}, 즉 n2=00 O a,1 = l 이 라a2 , 하…고 ,, a 사최 의종 결값정을규 갖칙는을댜 {d여, ,기}' 에즉 서 ad,,, 는= d0, ,(=X 0) 이’를 라 채하 택고 하, 는 {것a1 을, 의미한다 . 그러면 임의의 절차 8 에 대한 위험 R(A, 8) = i2=k O AiR ( O i, 8) = 합k ,. 홈co 0 J[L( 0 ;, d,,(x)) + nc( 0 ;)]a11(x11)P11,;(x11)µ11(dx11) 접 0 Ja,,( x)[A0ncp ,,, 0(x) + it=k l1 A;L( 0 ;, d11(x11))]µ11(dx11) II 이다. 여기에서 P11,i ( x)= jD= .l Po ; (X j)이다. 이 제 i2=k l Ai L ( o ,. , d,,(x)) p ,I , i(x ) 를 최 소로 하는 d(x ) 을 구할 수 있으며 이를 d~, 라 하자. 그리고 (6.3.4 ) b,,(x'’) = i玄= l AiL ( O i, 짜 ,(x)) ~P ,1, 0(x) 이라 하자. 그러면 d~, 에 대한 위험은
(6.3 .5 ) R( A , o) = 홀 。 fa11 ( x11 ) [-1 ° n c + b,.(x)]p ,._0 ( x11)µ11 ( dx11) 이라 쓸 수 있으며 다음의 정 리 를 얻는다 . 정리 6.3.5 식 (6 . 3 .4)에 정의된 b,,(x )에 대하여 상수 수열 {b 세가 존 재하여 모든 x 에 대하여 b11( x11) :;;; b~,-o 을 만족한다면 축차적 베이 즈 절차 8 는 절단되어 있다. 증명 식 (6 . 3.5) 는 a,, = a,,(X) , b,, = b,,(X ) 이라 하면 다음과 같이 쓸수 있다 . 00 R(,1 , 8)= 1L1= 0A E 8 0a 11(11°nc+b11) 이제 5,1 = E( )0a 11b11 / E 。 0 a,, 이라 하면 5,1 < b 尸,이댜 따라서 R(A , o) = 홀。 (E 。 0 a11)(A0nc+ b,,) = 홈 0 /3, ,0°nc+ b,,) , /311 = E80 an 이다. 가정에서 b~ l -o 이므로 no 을 모든 n ~ n 。에서 b~ 1< A% 인 값으 로 잡자 . 그러면 n > n 。에서 8A 는 /3,1 = 0 이댜 따라서 n > n 。에서 Pe o 에 대하여 a11 = 0 a.s. 이다. 즉, 8A 는 no 에서 절단되어 있다. D 일반적인 축차적 베이즈 절차에서 샘플링에 대한 비용함수 c,1= c,I(x) 은 표본수 n 의 함수로 나타나고 0 에 무관하지만, 특수한 경우 에는 0 의 함수이기도 하다. 즉 c,1 = c,1(x , 0) 이다. 이 때는 c11(x 11 ) = f c11(x 11 , 0)11x ·( d0), w11 = l,,(xn ) + c11(x11)
t�|�X
00 R(A , o) �� = L Ea,,w,, ( E �� �������� X" �� �\� 0��X�) 11 = 0 |� h�<�\�h� ��tLj� �(��� �\� |���x� t�`�D� ȩ�X��� tհ�` �� ��� We i ss(1962) @� L ai (1973) �� X, ~ i.i.d . N(0 , l) |� L� H0 : 0 = -d � H1 : 0 = d ( d > 0 : �ȴ� �� �) X� ���8����� $�X�U�`�t� �� a, /3 (0 < a, /3�|� `� L� ���ܭ Y� N �� �X��� max E8N |� \͌�\� XՔ� ��8���| ���(�� ��tLj� 8 �(��� X�X��� tհ�X���. We i ss �� �L��� �@� ��(�� �(�� �� X���. e {= d, O, d }, tl = (��, tlo, tl2), 21l1+1l0=1, 111=112 ������� 0�x� D���@� \��� ���� c(B) = (0 , 1, 0) ����� ����h� ( 8 0 � =LL, a) ( 8i , a) = O , L ( 8; , a)i = l,i= f j ( i , j = l , 2 ) \� `�<�\�h� �� (6.3 .4)X� b,1(X") X� �D� l�X�t� b,,(X") = 111e-C11/2)d2-dl r.1 II T,1= 2xi i=l t�� ���t� b,, (X라 둔댜 따라서 w,,=11°n+b, ,이라 하고 축차적 베이즈 절차를 k= n 。에서 절단된 축차적 절차하에서 실행한댜 때로는 k= n 。의 값을 기AA° - el§ d· 2 > P( IXI < d), X~N(O,1) 를 한만편족 하La는 i( 1 9가73장) 는 작 은v :=k 로f i잡 (을v,, 수-1도1° n있),다 .v i;,= t (w,, -,1%)라 둠 으로써 We i ss 와 같은 결과를 얻었다.
참고문헌 Albert , A.(19 66). Fix e d siz e confi de nce ellip s oid s for lin e ar reg r essio n —— _(p1a9 r9a3m).e te rS se.q A u ennnt.i aMl aithn .t e Sr vtaa tl i st .e s3t7i m, 8a9ti4 o-n9 04b. ased on ge neralize d M-sta t i st ic s wi th piec ewi se -smooth inf l ue nce curves. Se qu enti al Anal. 12(2), 145— 16 7. —(196 1). The seq u enti al desig n of exp e ri m ents for infinitel y many sta t e s of natu r e. Ann. Math . Sta t i st . 32, 774-799. Alsmeye r , G. and Irle, A.(19 86). Asym p tot i c exp a nsio n s for the va rian ce of sto p p ing tim es in nonlin e ar renewal the ory . Sto c h.. Process Ap pl. 23, 235-258. Alvo, M. (1 978). Sequ enti al esti m ati on of a trun cati on pa ramete r . J. Amer. Sta t i st. Assoc, 73, 404-407. Anderson, T. W.(1960). A mod ifica ti on of the seq u enti al pro babil ity rati o tes t to reduce the samp le siz e . Ann. Math . Sta t i st . 31, 165-197. Anscombe, F. J.(19 49). The sta t i st i ca l analys is of ins ect counts based on the neg a ti ve bin o m ial dist r ibu ti on . Bio m etr ics 5, 165-173. (1949). Large samp le the ory of seq u enti al estim ati on . Bio m etr ika 36, 455-458. (19 52). Large samp le the ory of seq u enti al estim a tio n . Proc. Cambri dg e Phil o s. Soc. 48, 600-607.
0953). Seq u enti al esti m ati on . J. Roy . Sta t i st . Soc. B 15, 1-2 9. Aras, G.0988). Sequ enti al po in t esti m ati o n base d on U-sta t i st i cs . Sequ enti al Anal. 7(3), 203-226. Armi tag e , P.0950). Seq u enti al analys is wi th more tha n tw o alte r nati ve hy p o th eses and its relati on to disc ri m i na nt fun cti on analys is . J. Roy . Sta t i st . Soc. B 12, 137-144. (19 54). Seq u enti al tes ts in pro p h y la cti c and the rap e uti c tri a l s. Qu arl. J. Med. 23, 256-274. (1975). Seq u enti al Medic a l Tria l s. 2nd ed., Blackwell, Oxfo r d. Armitag e , P., McPherson, C. K. and Rowe, B. C.(19 69). Rep e ate d sig n if ica nce tes ts on accumulati ng data . J. Roy . Sta t i st . Soc. A 132, 235-244. Arrow, K. J., Blackwell, D. and Gi rs hir k, M. A.(1 949). Baye s and minim ax soluti on s of sequ enti al decis i o n pro blems. Econometr ica 17, 213-244. Bahadur, R. R.(19 54). Suff ici e n cy and sta t i st i ca l decis i o n fun cti on s. Ann. Math . Sta t i st . 25, 423-462. Baranldn, E. W.(1949). Locally best unbia s ed esti m ate s . Ann. Math . Sta tist . 20, 477-501 . Ba rtky , W.(1943). Multip le samp ling wi th consta n t pr obabil ity. Ann. Math . Sta t i st. 14, 363-377. Ba rtle tt , M. S.(1946). The large samp le the ory of seq u enti al tes ts . Proc. Cambri dg e Ph il. S oc, 42, 239-244. Basu, A P.( 1 971). On a seq u enti al rule for esti ma ti ng the locati on pa ramete r of an exp o nenti al dist r ibu ti on . Naval Res, Log ist . Q. 18, 329-337.
Basu , D.0 9 55 ). On sta t i st i cs ind epe ndent of a comp le te suff ici e n t sta t i st i c. Sa nkhy a 15, 377 -3 80. Be ch hofe r , R. E.(1960). A note on the lim i ting relati ve eff ici e n cy of the Wald seq u enti al pro babil it y rati o tes t . J. Amer. Sta tist . Assoc. 55, 660-663. Bechhofe r , R., Kief e r , ]., and Sobel, M.(1 9 68). Seq u enti al Jd enti nc ati on and Rankin g Procedures. Univ e r sit y of Chic a g o Press. Be rg e r, J. 0.( 1 9 80 ) . Sta t i st i ca l Decis i o n Theorem. Foundati on s, Concep ts and Meth o ds.( 2 nd Ed., 1985). Sp ring e r-Verlag , New York. Berk, R. H., Brown, L. D., a nd Cohen, A.0 981a). Prop e rt ies of Bay e s seq u enti al tes ts . Ann. Sta t i st . 9, 678- 68 2. Berk, R. H., Brown, L. D., and Cohen, A.(1 98lb). Bounded sto p p ing tim es for a class of seq u enti al Bay e s tes ts . Ann. Sta t i st . 9, 834 -845. Bhatt ac ha rya, P. K. and Mall ik, A.(1 973). Asym p tot i c norma lity of the sto p p ing tim es of some seq u enti al pro cedures. Ann. Sta t i st . 1, 1203-1211 . Bic k el, P. J. and Yahav, J. A.(19 67). Asym p tot i ca lly po in t w ise op tim al pr ocedures in seq u enti al analys is . Proc. Fif th Berkeley Sy m p . Math e mati ca l Sta t i st ic s and Probabil ity, vol. 1, 401-413(1. M. Lecam and J. Neym an, eds.), Un ive rsit y of Ca lifor n ia Press, Berkeley. Blackwell, D.( 19 46). On an equ ati on of Wald. Ann. Math . Sta t i st . 17, 84-87. —(194 7). Condit ion al exp e cta t i on and unbia s ed sequ enti al estim ati on . Ann. Math . Sta t i st . 18, 105-llO.
——(00 1999485863 )))... EAAx tree cnn oseni wov na e lr os tafh t e ia oo nrr e emnwe. w i tDhau l k Dteh ae Mvo irade mt h .B. l]Pa.,ac kc1w.5 ,]e .l 1l.4M 5a -St1th 5a . 0t i3. s , t. 3 1S5c-3i.2 01. , 40-53. Blom, G.0949). A ge neraliz a ti on of Wald's fun damenta l ide nti ty. Ann. Math . Sta t i st. 20, 439-444. Breakwell, J. and Chernoff , H .(1 964). Seq u enti al tes ts for the mean of a normal dist r ibu ti on II Oarge t). Ann. Math . Sta t i st . 35, 162-173. Breim an, L.(19 68). Probabil it y . Add iso n-Wesley, Read ing , MA. Burl Proc. Fourth Berkeley Sy m p . Math e mati ca l Sta tist i cs and Probabil it y , vol. 1, pp. 79- 91 , (J. Ney m an, ed.), Univ e rsit y of Calif orn ia Press, Berkeley. (1972). Seq u enti al Analys is add Op tim al Desig n. CBMS— N SF Reg ion al Conf. Ser. Ap pl. Math . SIAM, Phil a delph ia . Chernoff , H. and Petk a u, ].(1986). Numeric a l soluti on s to Bay e s sequ enti al decis i o n pro blems, SIAM J. Sci, Sta tist. Comp u t. 1, 46- 59 . Chow, Y. S., and Robbin s , H.(1963). On op tim al sto p p ing rules. Z, Wabrschein l ic h keit s— t he ori e 2, 33-49. (19 65). On the asy m p tot i c the ory of fixe d-wi dt h seq u enti al confi de nce int e r vals for the mean. Ann. Math . Sta t i st. 36, 457-462. Chow, Y. S. and Martin s ek, A. T( 19 82). Bounded reg re t of a seq u enti al pro cedure for esti m ati on of the mean. Ann. Sta tist . 10, 909-914. Chow, Y. S., Robbin s , H. and Sie g m und, D.(1 9 71). Great Exp e cta tion s : The Theory of Op tima l Sto p ping . Houg h to n Mi fflin, Bosto n . Chow, Y. S. Robbin s , H., and Teic h er, H.(1 9 65). Moments of randomly sto p p e d sums. Ann. Math . Sta t i st . 36, 789-799. Chow, Y. S., Hsiu n g , C. A. and Lai, T. L.(19 79). Exte n ded renewal the ory and moment converge nce in Anscombe's the orem. Ann. Prob. 7, 304-318. Chung , K. L.(1 974). A course in pr obabil it y the ory . Academ ic Press, New York. Cohen, A. and Samuel-Cahn, E.(19 82). Neeessa ry and su fficien t cond ition s for bounded sto p p ing tim e of seq u enti al Baye s tes ts in one pa ramete r exp o nenti al families . Se qu enti al Anal. 1, 89-99.
Cox, D. R.(19 52). Sequ enti al tes ts for comp o sit e hyp o th e se s. Proc. Camb. ——— P(1h9i6l. 3 )S. ocL. ar4g8e, 2s9a0m- 2p 9 l9e . seq u enti al tes ts for comp o sit e hy po th e ses. Sankhy a A 25, 5-12. Csenski, A.(19 80). On the converge nce rate of fixe d-wi dt h seq u enti al confi de nce int e r vals. Scand. Actu a ri al J. 2, 107-111. DeGroot, M. H.09 70). Op tim al Sta t i st i ca l Deci si o n s. McGraw-Hi ll, New York. DeMoiv r e, A.(17 11). De Mensura Sort is, seu, de Probabil itat a Eventu u m in Ludis a casu Fort ui t o Pendenti bu s. Phil , Trans. Roy , Soc. 27, —2( 11735-62)6.4 T. he Doctr i n e of Chances, Th ird Ed ition . Mi llar , London. Dix o n, W ]. and Mood, A M. (19 48). A meth o d for obta i n i n g and analyz in g sensit ivi t y data . J. Amer. Sta t i st . Assoc. 43, 109- 12 6. Dvoretz k y , A, Kief e r , J. and Wolfo w i tz, J.(1 953a, b). Sequ enti al decis i o n pro blems for pro cesses wi th conti nu ous tim e pa ramete r : Testi ng hyp o th e ses, Problems of esti m ati on . Ann. Math . Sta t i st. 24, 30, 254-264, 403-415. Eis e le, J. R.(19 90). An adap tive bia s ed coin desig n for the Behrens-Fis h er pro blem. Sequ enti al Anal. 9(4), 343-359. Eis e nberg, B. and Ghosh, B. K.(19 80). Cu rtaile d and ·un if orm ly most po werf ul seq u enti al tes ts . Ann. Sta t i st. 5(3 장) 8(1 장), 1123-1131. Eis e nberg, B., Ghosh, B. K. and Sim o ns, G.(1976). Prop e rt ies of ge neral ize d sequ enti al pro babil ity rati o tes ts . Ann. Sta t i st. 4, 237-251. Fakhre-Zakeri, 1.(1 989). Sequ enti al confi de nce sets wi th beta - pr o te c ti on
in multi - pa ramete r fam i lie s . Sequ enti al Anal. 8, 1-26. Fakhre-Z a keri , I. and S, Lee0992). Seq u enti al esti m ati on of the mean of a line ar pro cess. Sequ enti al Anal. 11(2), 181-197, Farrell, R. H.(1 964). As ym p tot i c behavio r of exp e cte d samp le siz e in cert ai n one-s id e d tes ts . Ann. Math . Sta t i st . 35, 36 구 2. (1966). Bounded leng th confi de nce int e r vals for the p- p o in t of a dis t r i b u ti on fun cti on . III. Ann. Math . Sta tist . 37, 586- 59 2. Feller, W.0950). An Intr o ducti on to Probabil ity Theory and Its Ap pli ca ti on s, vol. I . Wi le y, New York. (19 71 ). An Intr o ducti on to Probabil it y Theory and Its Ap plica ti on s, vol. II, 2nd ed., Wi le y, New York. Fergu son, T. S.( 19 67). Math e mati ca l Sta t i st i cs : A Deci si o n -Theoreti c Ap pro ach. Academ ic Press, New York. Fin s te r , M. ( 1983), A freq u enti st app ro ach to sequ enti al esti m ati on in the ge neral lin e ar model. J. Amer. S ta t i st . Assoc. 78, 403-407. (19 85). Esti m ati on in the ge neral line ar model when accuracy is spe cif ied befo r e data is collecte d . Ann. Sta t i st . 13, 663-675. Freeman, D. and Weis s , L.(1 964 ). Samp ling pla ns whic h app ro x ima te l y mini m ize the maxim um exp e cte d samp le siz e . J. Amer. Sta t i st . Assoc. 59, 67-88. Fushim i, M.(1 9 67). On the rate of converge nce cif asym p tot i ca lly opt im al Baye s tes ts . Rep. Sta t . Ap pl. Res. ]US E 14, 1-17. Geert se ma, J. C.(1970). Sequ enti al confi de nce int e r vals based on rank tes ts . Ann. Math . Sta t i st . 41, 1016-1026. 一(1 985). On the converge nce rate of the coverag e pr obabil ity of a seq u enti al confi de nce int e r val based on the sig n tes t. Sequ enti al
Analys i s 4, 199- 21 2. Gij be ls, I. and Veraverbe ke , N. (1 98 9) . Seq u enti al fixe d- w i dt h confi de nce int e r vals for qu anti les in the pre sence of censored, J. of. Sta t . pla nnin g and inf e r ence, 22, 213-22 2 Ghosh, B. K.(19 69). Mo ments of the dis t r ibu ti on of samp le siz e in a —S( 1P9R70T ) .. J.S eAqm u eenr.t i S alt a t Ti set. s tAs s soofc . S6t4a ,t i1 s5t i6 c0a- l1 5H75y . p o th e ses. Add iso n- —W( 19e8s7le).y , ORne adtihn e g , aMtt aasi ns m. ent of the Cramer-Rao bound in the sequ enti al case. Seq u enti al Anal. 6, 267-288. Ghosh, J. K.(19 60). On the monoto n ic i t y of the OC of a class of sequ enti al pro babil ity rati o tes ts . Calcutt a Sta t i st , Assoc. Bull. 9, —10 3996-11)4. 4.O n the op tima li ty of pro babil ity rati o tes ts in seq u enti al and multip le samp ling . Calcutt a Sta t i st . Assoc. Bull. 10, 73 선 2. Ghosh, M. and Mul
normal dis t r ibu ti on s. S, Af r. Sta t i st . J. 23, 251- 26 8. Ghosh, M. , M ukhop a dhy a y and N. Sen, P. K.(1 997). Seq u enti al Analys i s , Wi le y, New York. Ghosh, M. and Sen, P. K.(1 971). Seq u enti al confi de nce int e r val for the reg r essio n coeff icien t based on Kendall's tau . Calcutt a Sta tist . Assoc. Bull. 20, 23-36. (19 72). On bounded leng th confi de nce int e r val for the reg r essio n pa ramete r based on a class of rank sta t i st ic s . Sankhy a Ser. A 34, 33-5 2. (1973). On some sequ enti al sim ulta n eous confi de nce int e r vals pro cedures. Ann. Inst, Sta t i st . Math . 25, 65-75. (1983). On tw o-sta g e Jam es-Ste i n estim ato r s. Sequ enti al Anal. 2, 359-367. Ghosh, M. and Wackerly, D. D.0986). Fix e d-leng th int e r val estim a ti on of the locati on pa ramete r of a Pareto dist r ibu ti on . Cal. Sta tist . Assoc. Bui. 35, 67- 75 . Ghosh, M. , N ic k erson, D. M. and Sen, P. K.(1 987). Sequ enti al shr ink ag e esti m ati on . Ann. Sta t i st. 15, 817-829. Ghosh, M., Sin h a, B. K. and Mukhop a dhy ay , N.( 1 976). Multiv a riat e seq u enti al po in t estim ati on . J. Mult. Anal. 6, 281-294. Gir s h ick , M. A., Moste l ler, F. and Savag e, L. J.(1 946). Unbia s ed esti m ate s for cert ain bin o m ial samp ling pro blems wi th ap pli- catio n s. Ann. Math . Sta t i st. 17, 13-23. Gleser, L. J.(19 65). On the asym p tot i c the ory of fixe d-siz e sequ enti al confi de nce bounds for lin e ar reg r essio n pa ramete r s, Ann. Math . Sta tist . 36. 463-467 ; Correcti on , Ann. Math . Sta t i st. 37, 1053-105. 5.
Govin d araju l u, Z.0 9 87). The Seq u enti al Sta t i st i ca l Analys is , 2nd ed. Ameri ca n Scie n ces Press, Columbus, Ohio . Gut, A.(1 974). On the moments and limit dist r ibu ti on s of some firs t pa ssag e tim es. Ann. Prob. 2, 277-308. 一(1 988). Sto p p e d Random Walks. Sp ring e r-Verlag, New York. (19 89). Fir s t pa ssag e tim es in nonlin e ar renewal the ory . Technic a l Rep o rt, Univ e rsit y of Up ps ala, Sweden. Hag w ood, C. and Woodroofe , M.(1982). On the exp a nsio n for exp e cte d samp le siz e in non-lin e ar renewal the ory . Ann. Prob. 10, 844-848. Hall, W. J.(1 962). Some sequ enti al analog u es of Ste i n ' s tw o- st a g e tes t. ——— B(1i9o 8m 0e).t r Sikea q u4 e9n, t3i a6l7 -m37in8i.m um pro babil it y rati o tes ts . In Asym p tot i c Theory of Sta t i st i ca l Tests and Esti m ati on (in honor of Wassily Hoeff ding ), 325-350 (I. M. Chakrava rti, ed.) , Academ ic pre ss, New York. Hall, W. J., Wi jsm an, R. A. and Ghosh, J. K.(1 965). The relati on ship betw een suff ici e n cy and inv a rian ce wi th app lica ti on s in sequ enti al analys is . Ann. Math . Sta t i st. 36, 575-614. Hoeff ding , W.0960). Lower bounds for the exp e cte d samp le siz e and the averag e risk of a sequ enti al pro cedure. Ann. Math . Sta t i st. 31, 352-368. Huskova, M.(1 9 82). On bounded leng th seq u enti al confi de nce int e r val for pa ramete r in reg r essio n model based on ranks. In Nonp a rametr ic Sta t i st i ca l Infe r ence, vol. 1, 435-463 (B. V. Gnedenko, M. L. Puri , and I. Vin c ze, eds.), Coll. Math . Soc. Jan os Bolya i, 32, Nort h- Holland, Amste r dam.
Ibrag im ov, I. A. and Hasm i ns k ii , R. Z.(1 9 74). On seq u enti al estim a ti on . Theory Prob. Ap pl. 19, 233 一 244. lfram , A. F.( 19 66). On the samp le siz e of a class of seq u enti al pro babil it y rati o tes ts . Ann. Math . Sta t i st. 37, 425- 43 4. Irle, A.(19 84). Exte n ded op tim ality of sec[ u~ nti al pro babil ity rati o tes ts . Ann. Sta t i st. 12, 380-386. Irle, A. and Schmi tz, N.(1984). On the op tim ality of the SPRT for pro cesses wi th conti nu ous tim e pa ramete r . Math . Op e r. Sta tist. 15, 91-104. Isog a i, E and Uno, C.( 19 94). A note on seq u enti al esti m ati on of the normal va rian ce. Seq u enti al Anal. 13(3), 201- 2 06 Jam e s, W . and Ste i n , C.( 1 9 61 ). Estim a ti on wi th qu adrati c loss. Proc. Fourth Berkeley Sy m p . Math . Sta t i st, Probab., v ol. 1, pp. 361-~9. Joh nson, N. L.(19 59). A pro of of Wald's the orem on cumulati ve sums. Ann. Math . Sta t i st . 30, 1245 기 247. (19 61). Seq u enti al analys is : a survey . J. Roy . Sta t i st. Soc. A 124, 372-411 . Juh li n, K. D.( 1 985). Seq u enti al and non-seq u enti al con fide nce int e r vals wi th gu arante e d coverag e pro babil ity and beta - pr o te c ti on . Ph. D. diss ert at i on , Univ e rsit y of Illin o is at Urbana-Champ aign . Jur eckova, J.(1 979). Bounded 一 len gth seq u enti al con fide nce int e r vals for reg re ssio n and locati on pa ramete r s. Proc. 2nd Prag u e Conf. Asym p t. Sta t i st. , 239-250, Nort h- Holland, Amste r dam. —(198 5). Seq u enti al confi de nce int e r vals based on robust estim a ti on . In Se qu enti al Meth o ds in Sta tist i cs , Banach Cente r Public a ti on s 16, pp. 309-319.
Jur eckova, ]. and Sen, P. K.(1 98la). Invaria n ce pri n c ip le s for some sto c hasti c pro cesses relati ng to M- es ti m atD r s and the ir role in sequ enti al sta t i st i ca l inf e r ence. Sanld1Ya Ser. A 43, 190-210. _(198 1b). Sequ enti al pro cedures based on M-estim ato r s wi th dis- conti nu ous score fun cti on s. ]. Sta t i st . Plannin g Infe r ence 5, 253-266. Karunamuni, r.].0992). Emp irica l Bay es seq u enti al estim a ti on of the mean. Sequ enti al Anal. 11( 1), 37-5 3. Kemp , K. W.(1958). Formulae for calculati ng the ope rati ng characte r i st i c and the average samp le number of some seq u enti al tes ts . J, Roy . Sta tist . Soc. B 20, 379-386. Khan, R. A.(1 968). Sequ enti al esti ma ti on of the mean vecto r of a —m( 1u9l7t8iv) . a riOatn e ncoornmfi adle ndciset r isbeu qtui o en n. cSesa nkfohry a t3h0e , 3m31e-a3n3 4.v ecto r of a —m( 1u9l8t4iv) .a riOatn e ncourmmualla tdi vise t r ibsuu tmi o n .p r]o . cMeduulrtiev sa r.a nAdn alt.h e8 , 5S5P0R-5T5 8. wi th app li ca ti on s. J. Roy , Sta t i st . Soc. B 46, 79-85. Kiefe r , ]. and Weis s , L.(1 957). Some pro p e rt ies of ge neraliz e d sequ enti al pro babil ity rati o tes ts . Ann. Math . Sta t i st . 28, 57-74. Kim, S. L.(1 987). Se qu enti al confi de nce sets wi th beta - pr o te c ti on in the pre sence of nu isa nce pa ramete r s. Ph. D. diss ert at i on , Un iv. of Illino is at Urbana-Champ aign . (19 90). Se qu enti al confi de nce int e r vals for the mean wi th /3 -pro te c ti on in a cert ain pa ramete r spa ce. Jou rnal of the Korean Sta t. Soc iet y , 19(2), 113-121. —(199 5). Asym ptot i c pro p e rt ies of the sto p p ing tim es in a cert ain
seq u enti al pro cedure. Jou rnal of the Korean Sta t . Soc iet y , 24(2), 337- 34 7. Kuo, L. and Mukhop a dhy a y, N.0990a). Poin t esti m ati on of the large s t locati on of k neg a ti ve exp o nenti al po pu lati on s. Seq u enti al Anal. 9. (1990b). Multi— sta g e po in t and int e r val estim ati on of the large st mean of k normal po p u lati on s and the associa t e d second-order pro p e rtie s . Metr ika 37, 291-300. La i, T. L.(1 973). Op tim al sto p p ing and seq u enti al tes ts wh ich mini m ize the maxim u m exp e cte d samp le siz e . Ann. Sta t i st . 1, 659-673, (1975). Termi na ti on , moments and exp o nenti al boundedness of the sto p p ing rule for cert ain inv a rian t seq u enti al pro babil it y rati o tes ts . Ann. Sta t i st . 3, 581-598. (19 76). Asym p tot i c moments of random walks wi th app lica ti on s to ladder varia b les and renewal the ory . Ann. Prob. 4, 51-66. (19 81). Asym p tot i c op tima lity of inv a rian t sequ enti al pro babil ity rati o tes ts . Ann. Sta t i st . 9, 318-333. 一―― (1988b). Bounda ry crossin g pro blems for samp le means. Ann, —P( 1r9o8b8acb).. 1 O6,n 3B75a-y3e 9 s6 . seq u enti al tes ts . Sta t i st i ca l Deci si o n Theory and Relate d Top ics IV, vol. 9 (S. S. Gup ta and ]. 0. Berge r, eds.), pp. 131-143, Sp ring e r-V erlag, New York. La i, T. L. and Sie g m und, D.(1977, 1979). A nonli ne ar renewal theo ry wi th app lica ti on s to sequ enti al analys is I, II. Ann. Sta tist . 5, 7, 946-954, 60-76. La i, T. L. and Wi jsm an, R. A (1979). Fir st exit time of a random walk from the bounds /( n) 土 cg ( n) , wi th app lica ti on s. Ann, Prob. 7,
672-692. Lalley, S.0982). Non-Iin e nr renewal the ory for latt ice random walks. Se q. Anal. 1, 193-205. 0983). Rep e ate d like lih o od rati o tes ts for curved exp o nenti al fam i lie s . Zeit . Wahr. Geb. 62, 293-321 . 一―― (1984). Lim it the orems for firs t pa ssag e tim es in line ar and non-lin e ar renewal the ory . Adv. Ap pl. Prob. 16, 766- 80 3. ——Lehma(0 n 19n98,5 69E))... (1TT9ee8ss3tt)ii. nn ggT hSSettoaa rtt y ii ss tto i if aa zz p ll o HHin yyt pp eoos ttthh i eme ss aeestsi., o n2W . n id Wl e eyi ld, e . yN, W eNwi lee w yY, oYNrkoe. rwk. York. Lehmann, E. L. and Ste i n C.(1 9 50). Comp le te n ess in tne seq u enti al case. Ann. Math . Sta t i st . 21, 376-385. Lerche, H. R.(1 986a). The shape of Bay e s tes ts of po wer one. Ann, Sta tist, 14, 1030-1048. Lin n ik, Yu, V. and Romanovsky, I. V.(1972). Some new results in sequ enti al esti m ati on the ory . Proc. Six t h Berkeley Sy m p . Math . Sta tist . Probab., vol. 1, pp. 85-96. Lombard, F. and Swanepo el, J. W. H.(1978). On fini t e and inf i nite confi de nce se q따 ences. S. Afr . Sta t i st . J. 12, 1-24. (19 79). An asym p tot i c seq u enti al tes t based on confi de nce sequ ences. Commun. Sta t i st. -T heor. Meth . A 8(2) 107-116. Lorden, G.(1972). Lik e lih o od rati o tes ts for seq u enti al k-deci sio n pro blems. Ann. Math . Sta t i st. 43, 1412-1427. (1976). 2-SPRT's and the mod ified Kief e r -Weis s pro blem of —m( 1i9n8i0m).i zin S gt r uacn t u er xep eo cft e d s esq aum epn lte i als iz te e. s Ats n nm. iSntia mt ii szti. n g 4 , 2a8n1 -2e9x1p. e cte d
samp le siz e . Z. Wa hr sch. ve rw . Gebie t e 51, 291- 30 2. Ly on es, R. M. (1 9 69 ). The cons is t e n c y of cert ai n seq u enti al esti m a to r s. Ann. Math . Sta t i st . 40, 568-574. Mart ins e k , A. T. 09 82 ). Moments and error rate s of tw o-sid e d sto pping —r( 1u9le8s6.) .A nAn,s yPm ro pb t.o t1 i c0a, ll9y3 5 -f 9u4 l 1l y. eff icie n t fixe d~wi dt h confi de nce —i0n 9t 9e r3 v)a. l s Ffiox re da lowcia dtt ih o n cpoan rafim de entce re , p.brae npd risn t . for densit y fun cti on s. Sequ enti al Anal. 12(2), 169-177. Matt he s, T. K.(1 963). On the op tim ality of seq u enti al pro babil ity rati o tes ts . Ann. Math . Sta t i st . 34, 18-21. Meslem, A.(19 87). Asym p tot i c exp a nsio n s for fixe d wi dt h confi de nce int e r vals. J. Sta t i st . Plan. Inf. 17, 51- 65 . Montm o rt , P. R. de0714 ). Essai d'A nalys e sur !es ]eux de Hazards. Second Edit ion . J. Qu il lau , Pari s. Mukhop a dhy a y, N.(1 9 74). Seq u enti al esti m ati on of reg r essio n pa ramete r s —i( n1 9 G75a)u. sSse-qM u eanrtki aol f fe ssteim tu a p t. i oJn. Ionfd a. Slitna et ai srt . f uAn scstoi ocn. 1o2f , m39ea-n 43s . of three normal po pu lati on s. J. Arner. Sta t i st. Assoc. 71, 149-153. (1977). Remarks on sequ enti al esti m ati on of a line ar fun cti on of tw o means : the normal_c ase. Metr ika 24, 197- 20 1 . (19 81 ). Converge nce rate s of sequ enti al confi de nce int e r vals and tes ts for the mean of a U-sta tist i c. Commun. Sta t i st . Theor. M eth . A 10, 2231-2244. — (19 82). Op tim al sequ enti al esti m ati on pro cedures for the normal mean when the va rian ce is known. J. Sta t i st. Plan. Inf. 6, 131-134.
(19 87b). A note on esti m ati ng the rang e of a un iform dist r ibu ti on . —S0 9. 9A0f) r.: SSta ot mi set . J.p r2o 1p, e2 rt7 ie-3s 8 . of a tlr ree-sta g e pro cedure wi th app li ca ti on s in seq u enti al analys i s . Sankhy a A. Mukhop a dhy a y, N. and Ekwo, M. E.0 9 87a). A note on minim um risk po in t esti m ati on of the shape pa ramete r of a Pareto dist r ibu ti on . —C0 9a8l. 7 Sbt)a. t iS set .q u A esnstoi acl. eBsutii m., a3t6i ,o n 6 9p-r7o 8b. lems for the scale pa ramete r of a Pareto dist r ibu ti on . Scand. Act. J., 83- 10 3. Mukhop a dhy a y, N. and Lib e rman, S.(1989). Sequ enti al esti m ati on of a lin e ar fun cti on of mean vecto r s. Seq u enti al Anal. 8 , 381-395. Mukhop a dhy a y, N. and Vil< :, G.( 1 985). Asym p tot i c results for sto p p ing time s based on U-sta t i st i cs . Sequ enti al Anal. 4, 83-109. Nic k erson, D. M.0987a). Sequ enti al shri nk ag e estim ati on of the differ ence betw een tw o multiv a riat e normal means. Sequ enti al —A( 1n9a8l7, b6)., 3S25eq-3u 5 e0n.t i al shri nk ag e estim ati on of lin e ar reg r essio n pa ramete r s. Sequ enti al Anal. 6, 93-118. Pag e , E. S.(1954a). An impro vement to Wald's app ro xim ati on for some pro p erties of seq u enti al tes ts . J. Roy. Sta t i st. Soc. B 16, 136-139. Magh avacha ri, M.(1965). Op er ati ng characte r i st i c and exp e cte d samp le siz e off sequ enti al pro babil it y rati o tes t for the sim p le exp o nenti al dist r ibu ti on . Calcutt a Sta tist . Assoc. Bull. 14, 65-73. Rahbar, M. H. (19 95). Se qu enti al fixe d wi dt h confi de nce inter vals for reg re ssio n pa ramete r s from censored data wi th disc rete cova riat e . Se qu enti al Anal. 1 4(2), 143-156.
Ramkaran, Chatu r vedi, A. and Akbar, S. A.0 986). Seq u enti al estim ati on of a lin e ar fun cti on of k-normal means. J. Ind. Soc. ·Ag ric. Sta tist . 38, 395-402. Ray, S. N.0965). Bounds on the maxim um samp le siz e of a Baye s seq u enti al pro cedure. Ann. Math . Sta t i st . 36, 859-878. Robbin s , H.0959). Seq u enti al esti m ati on of the mean of a nonnal po pu lati on . Probabil it y and Sta t i st i cs (U . Grenander, ed.), Almq v is t and Wi ks ell, Sto c kholm, pp. 235-245. Robbin s , H. and Sie g m und, D. (1 970). Bounda ry crossin g pro babil ities for the Wi en er pr ocess and samp le sums. Ann. Math . Sta t i st , 41, 1410- 14 29. (1973). A class of sto p ping rules for tes ti ng pa rametr ic hy po th e ses. Proc. Six t h Berkeley Sy m p . Math . Sta t i st. and Prob. 4, 37-41, Univ . of Califo rn ia Press, Berkeley. (1974). The exp e cte d samp le siz e of some tes ts of po wer one. Ann. Sta t i st . 2, 415-436. Robbin s , H., Sim ons, G., and Sta r r, N.(1967). A seq u enti al analog u e of the Behrens-Fis h er pro blem. Ann. Math . Sta t i st . 38, 1384-1391. Rockafe ll ar, R. T.(1974). Conju g a te Duality and Op timiza ti on . CBMS-NSF Reg ion al Conf. Ser. Ap pl. Math . , No. 16, SIAM, Phil ad elph ia . Rohatg i, V. K. and O'Neill , R. T.(19 73). On sequ enti al esti ma ti on of the mean of a multin o rmal po p u lati on , Ann. Inst. Sta t i st. Math . 25, 321-325. Rootz e n, H, and Sim ons, G.(1977). On the exp o nenti al boundedness of sto p p ing tim es of inv a rian t SPRT's. Ann. Sta t i st . 5, 571-575.
Sacks, J.(19 65). A note on the seq u enti al t-tes t. Ann. Math . Sta t i st . 36, 1867-1869. Schwarz, G.(1962). Asy m p tot i c shape s of Bay e s seq u enti al tes ti ng reg ion s. Ann. Math . Sta t i st . 33, 224-236. _0981). Ap ply i ng asym p tot i c shap e s to nonexp o nenti al fam i lie s . Ann. Sta t i st. 9, 461-464. Sclove, S. L.(1 968). Imp ro ved esti m ato r s for coeff ici e n ts in lin e ar reg r essio n . J. Arner. Sta t i st . Assoc. 63, 596-606. Sen, P. K.(1 981). Seq u enti al Non-pa rametr i c s . Invaria n ce Prin c ip le s and Sta t i st i ca l In fere nce. Wi le y, New York. 0985). Theory and Ap plica ti on s of sequ enti al Nonp a rametr i c s . SIAL\1 , Ph ilad elph ia . Sen, P. K. and Ghosh, M.(1971). On bounded leng th seq u enti al confi de nce int e r vals based on one-samp le rank order sta t i st i cs . Ann. Math . Sta t i st. 42, 189-203. (1973). Asym p tot i c pro p e rt ies of some seq u enti al non-p a rametr ic estim ato r s in some multiv a riat e lin e ar models. In Multiv a riat e Analys i s , vol. 3, 299-316, (P. R. Krish na iah , ed. ), Academ ic Press, —N( 1e9w74 )Y. oOrkn. seq u enti al rank tes ts for locati on . Ann. Sta t i st , 2, 540-552. Serf ling , R. J. and Wackerly, D. D.(1976). Asym p tot i c the ory of seq u enti al fixe d-wi dt h confi de nce int e r val pro cedures. J. Arner. Sta tist. Assoc. 71, 949-955. Sh iryae v, A. N.(1978). Op tima l Sto p ping Rules. Sp ring e r-Verlag, New York.
Sie g m und, D.(1975). Error pro babil it i es and averag e samp le number of the sequ e nti al pro babil it y rati o tes t. ], Roy . Sta t i st . Soc. B, 37, 394-401. (1985). Seq u enti al Analys is . Tests and Confi de nce Inte r vals, Sp ri n g e r-Verlag , New York. —— _(1986). Bounda ry crossin g pro babil ities and sta t i st ic a l app lica ti on s. Ann. Sta t i st. 14, 361-404. Sim o ns, G.(1967a). Lower bounds for averag e samp le number of sequ enti al multih y p o th e sis tes ts . Ann. Math . Sta t i st. 38, 1343— 13 64. (1967b). A seq u enti al thr ee hy po th e sis tes t for dete r m ini n g the mean of a normal po pu lati on wi th known va rian ce. Ann. Math . Sta t i st . 38, 1365-1375. (1976), An im p ro ved sta t e m ent of opt im alit y for seq u enti al pro babil it y rati o tes ts . Ann. Sta t i st . 4, 1240-1243. (1980). Sequ e nti al esti m ato r s and the Cramer-Rao lower bound. J. Sta t i st. Plan. Inf. 4,67-74. Sin h a, B. K. and Mukhop a dhy a y, N.(1976). Sequ enti al esti m ati on of a biv a riat e normal mean vecto r . Sankhy a B 38, 219-230. Sp ro ule, R. N.(1969). A sequ enti al fixe d-wi dt h confi de nce int e r val for the mean of a U-sta t i st ic . Inst. Sta t i st . Mime o Ser. 636, Un iv. of Nort h Carolin a , Chape l Hill. (1985). Seq u enti al nonp a rametr ic fixe d-wi dt h confi de nce int e r vals for U-sta t i st i cs . Ann. Sta t i st. 13, 228-235. Sri va sta v a, M. S. (1967). On fixe d-wi dt h confi de nce bounds for regr e ssio n pa ramete r s and mean vecto r . J. Roy . Sta t i st. Soc. Ser.
—B0 9 2790,) .1 3O2n-1 4a0 .s eq u enti al analog u e of the Behrens -F is h er pro blem . J. Roy . Sta t i st. Soc., B , 32, 144-14 8. —— (19 71). On fixe d-wi dt h confi de nce bounds for reg re ss i o n par amete r s. Ann. Math . Sta t i st . 42, 1403-1411 . Sta r r, N.(1 9 66a). The per f or mance of a sequ enti al pro cedure for the fixe d- w id t h int e r val esti m ati on of the mean. Ann. Math . Sta t i st . 37, 36-50. (1966b). On the asym p tot i c eff ici e n cy of a seq u enti al pro cedure for esti m ati ng the mean, Ann. Math , Sta t i st. 37, 1173-1185. Sta rr , N. and Woodroofe , M.(1 9 69). Remarks on sequ enti al po in t estim ati on . Proc. Nat. Acad. Sci., USA 63, 285-288. (19 72). Furt he r remarks on sequ enti al estim a ti on : the exp o nenti al case. Ann. Math . Sta t i st . 43, 1147- 11 54. Ste i n , C.(1 9 45). A two -samp le tes t for a lin e ar hy po th e sis whose po we r —i(s 1 9 i4n6d )e. p e An dennott e o f otnh e cvuam riualna ctei v. e A nsnu.m Ms.a thA . nSnt. a t Mi sta. th1 .6 , S2t4a 3t -i s 2t5 . 8 . 1 7, —4( 19984-94)9.9 .S ome pro blems in seq u enti al esti m ati on . Econometr ica 17, 77-78. Ste i n , C. and Wald, A.(19 47). Sequ enti al confi de nce int e r vals for the mean of a normal dist r ibu ti on wi th known va rian ce. Ann. Math . Sta tist. 18, 427-433. Sto c kman, C. M. (19 44). A Meth o d of Obta ining an Ap pro x ima ti on for the Op e rati ng Characte rist i c of a Wald Sequ enti al Probabil ity Test Ap plied to a Bin o m ial Dist r ibu ti on . Bri t. Min. Supp ly Tech. Rep.
QC / R / 19 . Str a ssen, V.0967). Almost sure behavio r of sums of ind epe n dent random vari ab les and ma rting a les. Proc. 5th Berkeley Sy m p . II, 315-343, Univ . Calif. Press. Swanepo el, J. W. H. and Lombard, F.(1978). Fix e d wi dt h seq u enti al confi de nce int e r vals for the med ian of a dis t r ibu ti on . Commun. Sta t i st. -T heor. Meth . A 7, 829-835. Takada, Y.(1 984). Inad miss ib i l ity of a seq u enti al esti m ati on use of the mean of a multiv a ria t e normal dist r ibu ti on . Sequ enti al Anal. 3, 267-271. Tahir , M.0994). Sequ enti al esti m ati on of the mean of an exp o nenti al —f0 a9m9i5ly). inO nth r tehee satas gyem s _p. tJo. t io cf . r Segta rte . t p loa fn na i ngs e qanu den itni af el re pnroc ece. d 3u8r, e1 -f1o2r . esti m ati ng the mean of a normal dist r ibu ti on . J. of. Sta t. pla nnin g and inf e r ence. 48, 331-338. Uno, K. and Isog ai, E.( 1 994). A note on seq u enti al estim ati on of the normal mean. Sequ enti al Analys is 13(3), 201-206. Vardi, Y.(1 979). Asy m p tot ic op tim al seq u enti al estim a ti on : the Pois s on case. Ann. Sta tist. 7, 1040-1051. Wald, A.(1 943). Seq u enti al Analys is of Sta tist i ca l Data : Theory , Sta t i st. —R( 1e9s4. 4)G. r. ORne pc u7m5, uClaotliu vme bsiau m Usn ivo.f random va riab les. Ann. Math . —S( 1t9a 4t i5 sat) . . 15S, e2q8 u3 e-n2t9i a6l. tes ts of sta tist i ca l hyp othe ses. Ann. Math . Sta tist. 16, 117-186. ――一 0945b). Sequ enti al meth o d of samp ling for decid ing betw e en tw o
course s of acti on . J. Ame r. Sta t i st . As soc , 40, 277 - 30 6. (19 47a). Sequ enti al Ana ly s is . Wi le y , New York. __一 (1 947b) . Foundati on s of a ge ne ra l the ory of sequ enti al .de cis i o n fun cti on s. Econometr ica 15, 279- 31 3. (19 50). Sta t i st i ca l Decis i o n Functi on s. Wi le y, Ne w York. Wald, A. and Wolfo w i tz, ].(1948). Op tim um characte r of the seq u en t i al pro babil it y rati o tes t. Ann. Math . Sta t i st . 19, 326-339. 0950). Bay e s soluti on s of seq u enti al decis i o n pro blem s . Ann. Math . Sta t i st. 21, 82- 89 . Wallis , A. W.0980). The sta t i st i ca l research gro up . J. Amer. Sta t i st . Assoc. 75, 320— 33 4. Wang , Y. B.(1980). Seq u enti al esti m ati on of the mean of a multin o rmal po pu lati on . J. Amer. Sta t i st . Assoc. 75, 977- 98 3 . Weis s , L.(19 62). On seq u enti al tes ts whic h mini m i ze the maxim um exp e cte d samp le siz e . J. Amer. St at i st. Assoc. 57, 551-566. Weth e rill , G. B.(1977). Samp l in g Inspe cti on and Qu ality Contr o l. Chapm an and Hall, London. W血 ehead, ].(1983). The Desig n and Analys is of Seq u enti al Clin i c a l Tr ials . Ellis Horwood, Chic h este r . Whittle, P.0982, 1983). Op timi za ti on · Over Tim e, Volumes I, II. W ile y, New York. Wi jsm an, R. A.(19 67). General pro of of ter m ina ti on wi th pro babil it y one of inv ari an t sequ enti al pro babil it y rati o tes ts based on multiv a ri at e normal observati on s. Ann. Math . Sta t i st. 38, 8-24. (1979). Sto p p ing time of inv ari an t sequ enti al pro babil ity rati o tes ts . In Develop m ents in Sta t i st i cs , vol. 2, 235 전 14 (P. R.
K百 s hn a i a h , ed. ), Acade m i c Pres s, Ne w York ; 0983) Correcti on . De ve l . in Sta t i st ., vo l. 4, xiv . ( 198 1) . Confi de nc e set s base d on seq u enti al tes ts . Comm. Sta t i st . - T heor. M eth . A 10, 213 7- 214 7. _(198 2) . Se q u en t i al confi de n c e sets : esti m ati o n -ori en te d versus tes t- o rie n te d constr u cti on . In Sta t i st ic s Decis i o n Theory and Re la te d Top ics III, vol. 2, 435- 45 0 (S. S. Gup ta and ]. 0. Berge r, eds .), Academi c Press, New Yo rk. (19 83 ). Seq u enti al esti m ati on -and tes t- o r i en te d confi de nce int e r v als for µ/
—0 977). Second order app ro xim ati on s for seq u enti al po in t and —i( n19t e8 r 2v)a. l eNstoim nl ainti e oan r. Anrenn. eSwtaa lt i st .t h5e , o9ry8 4-9i9n5 . seq u enti al analys i s . CBMS-NSF Reg ion al Conf. Ser. Ap pl. Math . , No. 39, SIAM, —P0 h9i8l a7 d)e. l pCh o ina .f ide nce int e r vals wi th fixe d pro p o rt ion al accuracy. J, Sta tist . Plan. Inf. 15, 131-146. Woodroofe , M. and Keener, R.(1 987). Asym p tot i c exp a nsio n s in bounda ry crossin g pr oblems. Ann. Prob. 15, 102-114. Woodroofe , M. and Takahashi, H. 09 82). Asy m p tot i c exp a nsio n s for the error pr obabil ities of some rep e ate d sig n if ica nce tes ts . Ann. Sta tist . 10, 895-908. Zhang , C. H.0988). A nonli ne ar renewal the ory . Ann, Prob. 16, 793-825.
찾아보 71
기 가우스一마코프 선형회귀 (Gauss-Marko ff lin e ar reg re ssio n ) 185 가중치 함수 (we ig h t fun cti on ) 90 강일치추정 량 (s tr on g l y consis t e n t esti m ato r ) 169 거 의 불변 (almos t inv a rian t) 113 검사특성곡선 (o p era ti n g characte r i st i c curve) 55 검 정 력 함수(p ower fun cti on ) 55 검 정 의 성 과(p e rf ormance of tes t) 104 결정함수 (dec i s i on fun cti on ) 29 결합밀도함수(j o i n t densit y fun cti on ) 162 결합특성 함수(j o i n t characte r i st i c fun cti on ) 132 고장률(fai lure rate ) 120 고정폭 신뢰구간(fi xed-w i d t h confi de nce int e r val) 13 고정 표본(fi xed-sam p le) 11 과표적 (overshoot) 59 관리 도 (con trol cha rts) 20 궤 도 (orb it) 100 극한분포(limiti n g dist r ibu ti on ) 127 기회손실 (re g re t) 172 L 내구력 (s tr en gt h) 70 누적 합관리 도 (cumula ti ve sum cha rt) 37 느린변환 (slowl y chang ing ) 151
C 다회 샘플링계획 (mul tip le samp li n g pla n) 20 단조우도비 성 질 (mono t one like lih o od rati o pro p e rt y) 80 단축샘플링 (cur tai led samp li n g ) 절차 15 단측 축차확률비 검 정 (one-sid e d SPRT) 144 닫힌 정 지 규칙 (closed sto p ping rule) 162 닫힌 축차절차 (closed seq u enti al pro cedure) 163 대수의 강법칙 (s tr ong law of large numbers) 124 대 칭 분포 (s ymm e tri c dist r ibu ti on ) 145 도박사의 파산 문제 (Gambler's Ruin Problem) 19 두 무장 강도 문제(t wo - armed bandit pro blem) 22 근 Rao-Blackwell 정 리 (Ra o- B lackwell the orem) 165 라프라스 변환 (La p lace tra nsfo rm ati on ) 135 Lorden 의 2- 축차확률비 검정 (Lorden 2-S PRT ) 76 르베그 우월성 수렴정리 (Lebes g ue's dom ina te d converge nce the orem) 65, 192 □ 마아팅 게 일 (ma rti n g ale) 18, 65 모수(p arame t er) 119 모수공간(p arame t er spa ce) 187 무관심 영 역 (ind iffer ence reg ion ) 32 미니맥스 추정값(mini max esti m ato r ) 33 밀도함수군(fami l y of densit ies ) 80
닌 반복유의 성 검 정 (repe ate d sig nifica nce tes t) 15 베 이 즈 위 험 (Ba ye s risk ) 202 베 이 즈 추정 치 (Ba y e s esti m ato r ) 203 f3군프로텍션( /3-pro te c ti on ) 35, 195 변환군(t rans fo rma ti on gro up ) 98 보렐 집 합 (Borel set) 134 볼록손실함수 (convex loss fun cti on ) 169 분포적 수렴 (conver g e in dis t r ibu ti on ) 139 불변검 정 함수(i nvar i an t tes t fuc nti on ) 100 불변변환군(i nva ri an t tra nsfo rm atio n gr oup ) 100 불변의 원리(p r i nc ip le of inv a rian ce) 98 불변 축차확률비 검 정 (inv a rian t seq u enti al pro babil ity rati o tes t) 32, 98 불편추정 량 (unb i ased esti m ato r ) 165 브라운 운동(B rown i an moti on ) 62 비산술적 (non- arit hme tic) 122 비서문제 (secre tary pro blem) 13 비선형 재생이론 (non li near renewal the ory ) 147 人 사닥다리 변수(l adder va riab le) 126 사전분포(pri or dist r ibu ti on ) 202 사후분포(p os t e ri or dist r ibu ti on ) 203 상하향법 (up and down meth o d) 30 상호절대 연속 (mu t uall y absolute l y conti nu ous) 60 섭동확률보행(p e rt urbed random walk) 155 손실함수(l oss fun cti on ) 170
Skorokhod-매 장 (Skorokhod - embedd i n g) 35 S t e i n 의 2 단계 절차 (S t e i n's tw o- s ta g e pro cedure) 14 스틸링 공식 (S ti rl i n g 's for mula) 176 스피처의 공식 (S pit zer's form ula) 132, 133 c-차 수 (c-ordered) 169 a -대 수( a -al ge bra) 106 신뢰 영 역 (confi de nce reg ion s) 161 。 안스컴 의 정 리 (Anscombe's the orem) 150 R- 추정 량(R -es ti ma t or) 190 양정 치 행 렬(p os iti ve defi nite matr i x ) 184 역수학적 귀납법 (ma t hema ti cal ind ucti on of backwards) 215 역표본추출(i nverse samp ling ) 13 M- 추정 량 (M-es ti ma t or) 190 오류확률 (error pro babil ity) 50 완비성 (com p le t eness) 163 왈드의 기본 항등식 (Wald's fun dermenta l ide nti ty) 56 왈드의 두 번째 등식 (Wald's 2nd eq u ati on ) 63 왈드의 정지경계치 (Wald's sto p ping bounda ry) 52 왈드의 첫번째 등식 (Wald's 1st equ ati on ) 63 우도비 수열 (s 따 uence of like lih o od rati o) 41 우월성 수렴 정 리 (dom ina te d converge nce the orem) 123 위 험 (risk ) 169 위 험 함수(ri sk fun cti on ) 29, 170 위 험 효율(ri sk eff icien cy) 172 유계완비성 (bounded comp le te n ess) 164 유계의 신뢰폭 (bounded con fide nce wi dt h ) 189
유한측도(fi n it e measure) 133 유효성 (eff icie n cy) 72 음이 항분포 (ne g a ti ve bin o m ial dist r ibu ti on ) 119, 183 이 항분포 (b i no mi al dist r ibu ti on ) 183 2 회 샘플링계획 (double samp li n g pla n) 20 인수분해 정 리 (fac to r i za ti on the orem) 204 일 반화된 중간값정 리 (ge neral ize d mean value the orem) 54 일 반화된 축차확률비 검 정 (ge neraliz e d seq u enti al pro babil ity rati o tes t) 84 일양적 적분가능 (un ifo rml y int e g r a ble) 130 일 치 추정 량 (cons i s t en t esti m ato r ) 169 大 작용공간 (ac ti on spa ce) 201 잔여 대 기 시 간 (res i dual wa iting tim e) 123 장애모수 (nu i sance pa ramete r ) 190 재 귀 정 리 (recurrent the orem) 124 재생과정 (renewal pro cess) 118 재생셈과정 (renewal counti ng pro cess) 118 재생셈과정의 강법칙 (S tr ong law for the counti ng pro cess) 119 재 생 이 론 (renewal the ory) 18 재 생 정 리 (renewal the orem) 122 재 생측도 (renewal measure) 120 재 생 함수 (renewal fun cti on ) 120 적 분가능(i n t e g rable) 130, 175 적분재생정리(i n t e g ral renewal the orem) 122 전이 동치 (tran slati on equiva rian t) 188 전이 수열(tr ans iti ve seq u ence) 107 전 이 수열통계 량(tr ans iti ve seq u ence sta t i st i c) 105
절단된 절차(tru nca t ed pro cedure) 222 점 근적 위 험 효율 (as ympt o ti call y risk eff ici e n t) 180 점근적 일치성 (as y m pt o ti c consis t e n cy) 193 정방형 손실함수 (s quared loss fun cti on ) 183 정지규칙 (s t o ppi ng rule 또는 sto p ping tim e) 10, 40 젠 센 부등식 (Je nsen's ine q u ality ) 57 조건부 독립 (con diti onal ind epe ndent) 105 조건부 확률밀도함수 (con diti onal pro babil ity densit y fun cti on ) 85 주변밀도함수 (mar gi nal densit y fun cti on ) 204 중심 극한정 리 (centr a l limit the orem) 125 지수적으로 유계 (ex ponen ti all y bounded) 42 지수형분포족 (ex p onen ti al fam i lies of dist r ibu ti on ) 53 직교변환 (o rt ho g onal tra nsfo rm ati on ) 173 * 채 택 영 역 (accep tan ce reg ion s) 161 최 단로 (sho rt -cu t) 검 정 21 최 대불변함수 (m axim al inv a rian t fun cti on ) 100 최 적 고정 표본수 (o pti mal fixe d samp le siz e ) 171 최 적 성 검 정 (op tima l tes t) 70 최 적 정 지 문제 (op tima l sto p ping pro blem) 210 최 적 표본수 (o pti mal samp le siz e ) 207 최종결정함수(t e rmi nal decis i o n fun c tion ) 110 최종의사결정규칙(t e rmi nal deci si o n rule) 10, 40 축차모델 (se q uen ti al model) 162 축차분석 (seq u enti al analys is ) 10 축차적 검 정 (sequ enti al tes t) 40 축차적 베이즈 절차 (se q uen ti al Bay e s pro cedure) 201, 207
축차적 샘플링규칙 (se q uen ti al samp li n g rule) 170 축차적 신뢰구간 (se quen ti al confi de nce int e r val) 193 축차적 절차 (se q uen ti al pro cedure) 171 축차확률비 검 정 (seq u enti al pro babil it y rati o tes t) 16, 42 충분불변통계 량 (su ffi c i en t inv ari an t sta t i st i c) 103 충분통계 량 (su ffi c i en t sta t i st i c) 102 = 콜모고로프 부등식 (Kolmog o rov's ine qu ality ) 149 Cramer-Rao 부등식 (Cramer-Rao ine q u ali ty) 27 E 특성 함수 (charac t e ri s ti c fun cti on ) 132 立 편의 추정 량 (b i ased esti m ato r ) 182 평 균표본수 (avera g e samp le siz e 또는 averag e samp le number) 55 포함범 위 확률 (covera g e pro babil ity) 189 푸리 에 변환 (Four i er tra nsfo r mati on ) 133 E 하한값(l ower bound) 67, 167 합격 샘플링계획 (acce pt ance samp ling pla n) 20 합성 (convoluti on ) 122 확률 근사법 (s t ochas ti c app ro x ima ti on meth o d) 30
확률보행 (random walk) 45, 117 확률적 순서 (s t ochas ti c orderi ng ) 81 확률적으로 작다 (s t ochas ti call y small) 79 확률적으로 크다 (s t ochas ti call y large ) 79 확률적 일양연속 (u nifo rml y conti nu ous in pro babil it y ) 148
김성래 서울대 학교 공과대 학 응용수학과 를 졸업하고 한국과학기술원 선임연구원으로 재직 후 미국 일리노이 대학교에서 박사학위를 받았다. 미국 워싱턴 대학교 방문교수, 한국 IBM 해외파견 교수선정위원, 학술진홍재단 과제선정위원 현재 충남대학교 수학과 교수로 재직중이다. 저서로 『미분적분학』, 연구보고서 15 편, 연구논문 10 편이 있다. 축차분석론 대우학술총서 447 논저 1 판 1 쇄 펴냄 1999 년 7 월 20 일 지은이 김성래 펴낸이 이형진 펴낸곳 도서출판 아르케 출판등록 1999. 2. 25. 제 2-2759 호 서울특별시 중구 남대문로 5 가 526 대표전화 310-0 5 25, 팩시밀리 777-3 8 09 E-Ma il arche@dwf .o r .kr 값 15,000 원 ® 김성래, 1999 확률론 통계분석 KDC/413 Prin t e d in Seoul, Korea ISBN 89-8 8 791-26 -6 (94410) 89-8 8 791-0 0 -2 (세트)
대우학술총서 大宇財團은 1978 년에 설립된 이후 1980 년 재단 설립자인 金宇中 회장이 200 억 상당의 사재를추가로출연하면서 “韓國學 rR, 의 基礎分野 진홍에 사용해 줄 것”을 희망함에 따라 국내 연구가 부진한 끼초학문 분야의 진홍’ 을 목표로 각종 연구를 지원해 왔습니다. ‘大宇學術穀書 는 재단 학술사업의 결정체로서 1983 년 『문화사회학』을 시작으로 논저, 연구번역, 공동연구의 형태로 출간되어 왔습니다. 論著는 대학원급 수준의 고급 학술개요서’ 라고 정의되고 있는뱌 해당 분야에 대한 개설적 입문서 수준을 넘어서 그 분야에 대한 세계적 연구동향을 집약한硏究提要 B9 인 성격을 띠고 있으며 , 이를 통하여 학술용어 내지 이론적 표현을 정착시키는 역힐을 수행해 왔습니다. 硏究觀譯은 논저를 보완하는 성격을 갖는 것으로서 이 역시 전문연구서가 아닌 고급개요서에 대한 연구번역입니다. 특히 지난 98 년부터는 古典과 古典級 저작의 연구번역에 중점을 두고 있는 B}-. 학술용어 및 경합되는 학설 등을 역주로, 그리고 해당 저자 및 원저에 대한 학술적 평가는 해제의 형식으로 포함함으로써 원문에 대한 단순한 번역을 지양하고 있습니다. 또한 共同 硏究는 연관학문간 (Inte r di sc i plina ry ) 공동연구를 통해 점점 세분화 • 전문화되어가는 학계의 경향을 극복하고자 하는 재단의 기획의도를 반영한 것입니다. 아針 연구지원에서 연구결과의 출판에 이르기까지 모든 단계를 일관성 있게 지원한다는 학술사업 지원 방침에 따라 ‘대우학술총서’ 는 과제의 지정에서부터 연구계획서, 그리고 연구결과에 이르기까지 엄격한 심사와 평가를 거쳐 출판되고있습니다.
I 마i和」 I 의 대우학술총서 ] 422 한중관계사 I 김한규 423 한중관계사 11 김한규 424 두보와 이백 이 병주 425 한국의 전통민가 주남철 426 의학철학 울프 · 페데르센 · 로젠 베 르그/이호영 · 이종 찬 427 지구환경정치학 바이츠제커 /이필렬 428 기후학 r : 기후와 대기순환 오재호 429 기후학 1l : 변화하는 기 후 오재호 430 앙시앙 레짐 I 구베르/ 김주식 431 앙시앙 레짐 11 구베르/ 김주식 432 다양체의 미분위상수학 조용승 433 스페인 피카레스크 소설 김춘진 434 독일의 통일과 위기 코카/김학이 435 언어학파의 형성과 발달 암스테르담스카/ 임혜순 436 성간화학 덜리 · 월리엄스/민영기 437 생태학 매킨토시 /김지홍 438 웨이브렛의 기본이론과 통계에의 응용 김충락 의 439 고지자키학 궁:성 재·김광호 440 최소주의 이론의 이해 최기용 외 441 한국사회의 구조론적 이해 김일철 외 442 현대과학철학의 문제들 조인래 외 443 농업기상학 윤진일 444 한국의 초기국가 이종욱 445 고인류학 박선주 446 현대경제지리학 박삼옥 447 축차분석론 김성래 448 텍스트 이론 고영근 449 신뢰성분석 배도선·전영록 450 조선과 유구 하우봉 외 451 함수미분방정식론 하가식