

장건수 연세대학교 수학과와 동대학원을 졸업하고 미국 네브라스카 대학교에서 박사학위를 받았다. 이탈리아 국립과학연구소 방문연구원 . 네브라스카 대학교 방문교수. 일본 나고야 대학 객원교수 ,연세대학교 교무처장을 역임했으며 대한수학회 사업이사. 부회장 한국수학올림피아드 위원회 위원장. 교육부 교수자격 심사위원을 거쳐 현재는 대한수학회 회장. 교육두학술진 -홍 뷔뭔 _ 玉육적円 广 짐 -의 위원 , 연세대학교 수학과 교수로 재직중이다. 『 수치해석학』 『 파인만적분론 』 동의 저서와 「함수공간 작용소 해석적분」 외에 70 여편의 논문이 있다.
위너적분론 
 위너적분론
위너적분론
책 머리에 함수 공간에 서 가장 중요한 역 할을 하는 위 너 측도 (W ien er- measure) 의 기원은 브라운 운동 (Brown i an mo ti on) 에서 시작된 다. 1827 년 영 국의 식 물학자 브라운 (Robert Brown) 은 어 떤 한 종류의 꽃가루를 가지고 식물의 수정 과정을 연구하고 있었다. 그는 현미경을 통해서 물 속의 꽃가루를 관찰했을 때, 아주 작은 입자가 빠르게 전동 운동을 하는 것을 보았다. 매우 불규칙한 이 운동을 브라운 운동이 라고 부른다. 그 후 많은 과학자들이 이 이 상한 현상을 설명하려고 노력한 결과 이 운동에 관한 다음과 같 은 사실이 규명되었다. 첫째, 이 운동은 매우 불규칙하고 그 궤적은 접선을 갖지 않는 다. 둘째, 입자들의 운동은 서로 독립적이다. 셋째, 입자가 작을수록, 액체의 점도가 낮을수록, 온도가 높을 수록 운동은 더 활발하다. 넷째, 입자의 합성과 밀도는 운동에 영향을 미치지 않는다. 다섯째, 운동은 그치지 않고 끊임없이 계속된다. 이 운동의 원인에 대한 여러 가정이 많은 학자들에 의해서 제 시되었으나, 19 세기 후반에 와서야 그 원인아 규명되었다. 실제 로, 이 불규칙한 운동은 액체의 미분자와 그 속에 뜬 꽃가루 입 자들의 수없이 많은 충돌에 의해서 일어난다. 이와 같은 관찰 및 실험과는 독립적으로 아인슈타인 (Albe rt
E i ns t e i n) 은 브라운 운동을 이론적으로 연구하여 브라운 운동의 수학적 구조를 규명하였다. 그는 브라운 운동에 관한 첫 논문을 1905 년에 발표하였으며, 이 해는 아인슈타인의 유명한 상대성이 론이 발표된 해이기도 하다. 그 후 1908 년까지 그는 이 운동에 관해서 모두 5 편의 논문을 발표하였다.
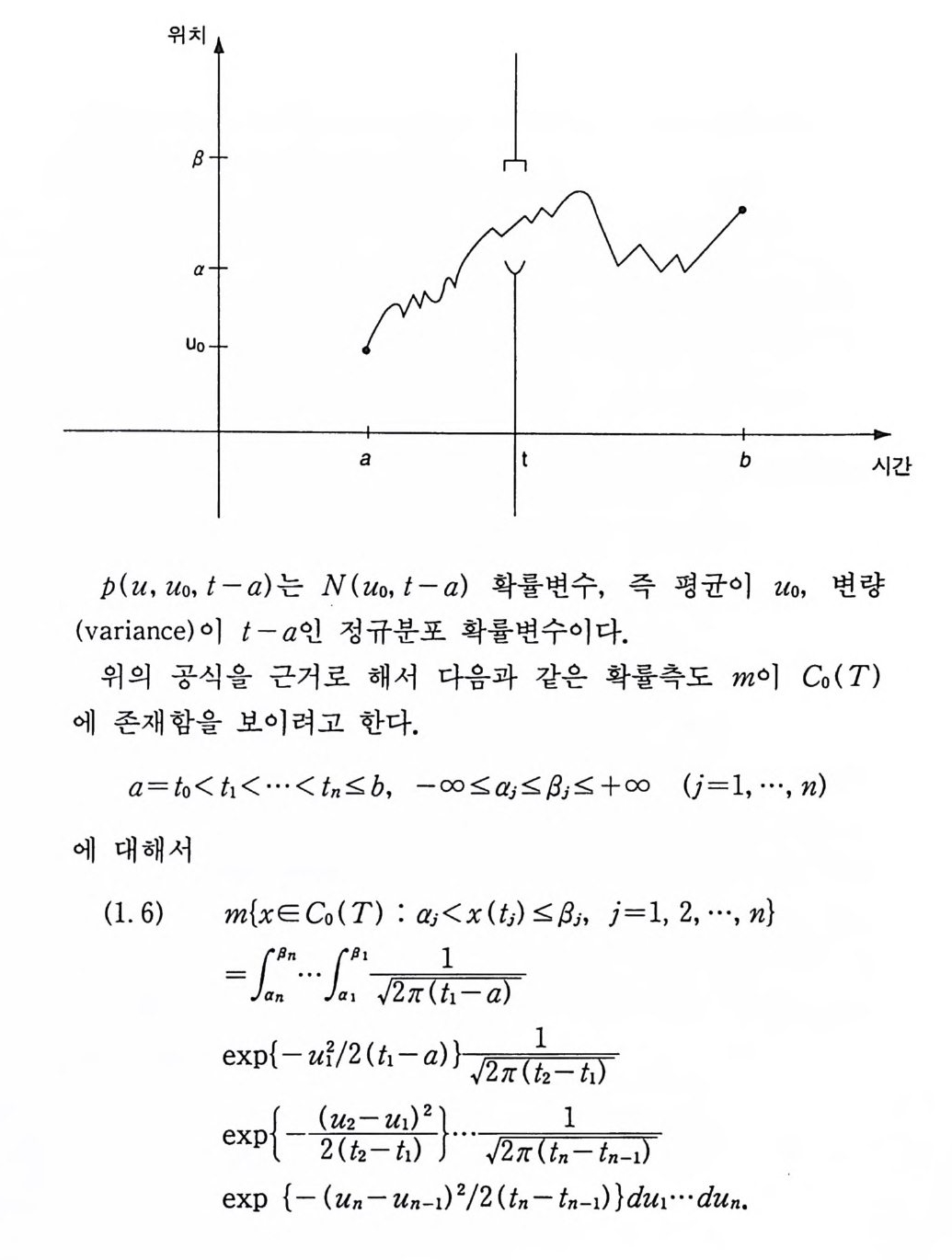
 시간이 0 일 때 원점에서 출발한 브라운 입자가 시간이 t일 때
시간이 0 일 때 원점에서 출발한 브라운 입자가 시간이 t일 때
1909 년 프랑스의 물리 학자 페 랭 (Je an Perrin ) 은 〈브라운 입 자의 궤적은 접선을 갖지 않는다〉는 사실을 관찰하고 바이에르스트라 스 (We i ers t rass) 의 〈모든 점에서 연속이고 어떤 점에서도 미분 가능하지 않는 곡선〉에 관해서 언급했다. 이 사실은 나중에 위너 정리 〈거의 모든 위너 곡선은 거의 모든 점에서 미분 가능하지 않다〉를 얻는 데 기여하게 된다. 페랭은 브라운 운동에 관한 연 구의 공로를 인정받아 1926 년에 노벨상을 받았다.
1923 년 위너 (Nobert W i ener) 는 아인슈타인과는 다론 방법으로 공식 (3) 을 얻었다. 그는 공식 (3) 을 얻기 위해서 중심 극한 정 리 (centr a l lim i t the orem) 와 비 교적 기 본적 인 물리 학 이 론을 사용 하였다. 브라운 운동에 대한 수학적 모델을 단순하게 만들기 위해서 브 라운 입자가 한 방향으로만 움직인다고 가정하자. 또한 공식 (3) 에서 확산 계수를 정규화하기 위해서 2D=l 로 놓고, 입방체 E 를 구간 [a, /3)로 택한다. 그러면 시간이 0 일 때, 원점에서 출 발한 브라운 입자가 시간이 t일 때 구간 [a, /3) 안에 있을 확률 울 P 라 하면, 공식 (3) 은
아인슈타인 공식 (3) 을 출발점으로 해서 얻은 공식 (5) 를 사용 하여 위너는 함수 공간에 측도를 도입하고(이 공간을 위너 측도 공간이 라고 한다) 르베 그 (Lebesgu e ) 적분 이 론과 같은 매 우 유 용한 위너 적분 이론을 개발했다. 위너 측도는 르베그 측도와 비슷한 성질을 가지지만 한 가지 공통되지 않는 중요한 성질은 평행 변환 불변성(t ransla ti on i nva ri an t)과 척도 변환 불변성 (scale i nvar i an t)이다. 르베그 측도 는 이 성질을 만족하지만 위너 측도는 이 성질을 만족하지 못한 다. 위너 적분은 후에 파인만 적분 연구에 없어서는 안될 결정적 인 역할을 하게 된다.
 (4) P=1Pa( 21r t)-七 ex p{군 /2 t }du
(4) P=1Pa( 21r t)-七 ex p{군 /2 t }du
이 책은 5 장으로 구성되었다. 제 1 장에서는 함수 공간에 위너 측도를 도입하고, 위너 적분 공식, 위너 곡선의 미분 불가능성, 척도 불변 가측성을 다루었다. 제 2 장에서는 팰리-위너-지그문드 (Paley -W ien er-Zy gm und) 적 분 을 정 의 하 고, 카 메 룬-마 틴 (Cameron-Marti n) 변환 정리, 푸리에-위너 (Fourie r -W iem er) 변 환 등 위너 적분의 변환 정리를 소개하였다. 제 3 장에서는 강한 극한 정리를 이용하여 확률 적분을 정의하고 브라운 운동 과정에 대한 확률 적분, 가우스 (Gauss) 과정에 대한 확률 적분, 위너 조 건 적분과 이 적분의 변환 정리를 다루었다. 제 4 장에서는 1960 년 예 (Ja mes Yeh) 가 정의한 예-위너 측도 공간에 관한 여러 가지 성질을 소개하였다. 두 변수 함수의 유계 변동과 변환 정리, 척 도 불변 가측성, 회전 변환, 위너 적분과 예-위너 적분 과의 관 계, 일반화된 역측도 정리, 푸리에-예-위너 변환 등이 4 장의 주 요 내용이다. 제 5 장에서는 예-위너 작용소 적분과 예 - 위너 조건 적분을 소개하고, 위너 적분 방정식의 존재 정리와 노이만 (Neuman) 급수, 예-위너 조건 적분의 변환 정리, 벡터 함수에 대한 예-위너 조건 적분 등을 다루었다. 이 책의 내용은 그 동안 이 분야에서 선구적인 역할을 해온 미 네 소타 대 학의 카메 룬 (Cameron) 교수와 스타빅 (St or vic k ) 교수, 네브라스카 대학의 존슨(J ohnson) 교수와 스코그 (Skou g) 교수, 마이애미 대학의 박철 교수, 캘리포니아 대학의 예 (Yeh) 교수 등과 필자의 연구 업적을 중심으로, 필자가 연세대학교 대학원에 서 강의한 내용을 바탕으로 했으며, 필자가 강의를 받았던 존슨 교수의 강의 노트도 많이 참조하였다. 매주 월요일에 열리고 있 는 연세대학교 수학과의 적분론 세미나는 이 책의 내용을 충실하 게 하는 데 많은 도움을 주었다. 이 책을 집필하는 동안 많은 분들의 도움울 받았다. 특히 필자
가 적분론을 전공할 수 있도록 이끌어 주고 격려와 조언을 해준 네브라스카 대학의 존슨 교수과 스코그 교수, 자료 제공과 연구 시설을 이용할 수 있도록 배려해 준 나고야 대학의 히다(飛田武 幸 ) 교수, 논저의 구상과 집필 과정에서 내용을 검토하고 자료를 보완하는 데 많은 도움을 준 적분론 세미나 팀 (건국대의 안재문, 한양대의 장주섭, 한남대의 류근식, 전북대의 박연희, 연세대의 유일, 대립대의 홍결표, 건양대의 최기성, 대전대의 김봉전, 대 헌대의 유승철 교수, 김정규, 고정원, 김영식, 임정아, 김선경, 김병수, 박정희 박사, 그리고 박사과정의 조동현, 송특섭, 임만 규 선생)에게 감사드린다. 끝으로 이 책을 집필할 수 있도록 기 회를 준 대우재단과 이 책의 출판을 맡아 준 민음사에 감사를 드 린다. 1998 년 7 월 장건수
차례
책머리에•5제1장 위너 측도와 위너 적분------------131 위너 측도공간•132 위너 적분•413 위너 적분의 미분 불가능성•564 척도불변 가측집합•665 회전변환•856 척도불변 가측함수•957 콜모고로프 정리•1018 위너 측도의 존재성:넬슨의 증명•1219 위너 측도가능한 집합의 확률계산•136제2장 위너 적분의 변환정리--------------1471 카메룬-마틴 변환정리•1472 팰리-위너-지그문드 적분•1663 위너 공간의 이동•1884 완비정규 직교집합•2055 푸리에-위너 변환•2266 위너 적분의 부등식과 극한정리•263제3장 확률적분과 위너 조건적분-------------269
1 강한 극한정리•2702 브라운 운동과정에 대한 확률적분•2843 가우스 과정에 대한 확률적분•2964 조건기대값•3095 위너 조건적분•3216 위너 조건적분의 변환정리•3407 위너 조건적분 공식•351제4장 예-위너 측도와 예-위너 적분------------3591 예-위너 측도공간•3592 예-위너 적분•3663 두변수함수의 유계변동과 변환정리•3714 척도불변 가측성•3855 회전변환•3986 두변수함수의 팰리-위너-지그문드 적분•4077 위너 적분과 예-위너 적분의 관계•4158 일반화된 역측도정리•4399 푸리에-예-위너 변환•446제5장 위너 작용소적분과 예-위너 조건적분----------------455
1 위너 작용소적분•4552 위너 적분방정식의 존재정리•4643 위너 적분방정식의 노이만 급수•4774 예-위너 조건적분•4875 예-위너 조건적분의 변환정리•4986 벡터 함수에 대한 예-위너 조건적분•504부록l 카라데오도리 확장•5212 변수변환정리•5273 적분공식•5284 리츠 볼록정리•5295 확률분포•5316 확률과정•538도움말•541참고문헌•545찾아보기•561제 1 장 위너 측도와 위너 적분 함수 공간에 측도를 도입한 위너 측도공간을 소개하고 위너 적 분을 르베그 적분으로 표시하는 위너 적분공식을 유도한다. 르베 그 측도와는 달리 척도불변성이 보장되지 않는 위너 측도에 대해 서 척도불변 가측집합과 척도불변 가측함수를 정의하고 위너 적 공간에서 회전변환에 관한 정리를 얻는다. 콜꾸,,쿠立의 정리를 사용해서 위너 측도의 가산가법 가능성을 증명하고 위너 측도의 존재성에 관한 넬슨의 증명을 소개한다. 1 위너 측도공간 함수 공간에 위너 측도를 도입하고 위너 측도와 르베그 (Lebesgu e) 측도 사이의 관계를 알아본다. 위너 측도가 르베그 측도와 같은 성질을 갖는다면 이상적인 측도가 되겠지만, 르베그 측도에 서 성 립 하는 평 행 변환불변 (tra nslati on inv aria n t) 이 위 너 측
도에서는 성립하지 않는다.
 정의 1.1 C[a, l 기를 구간 [a, b ] 에서 연속인 실가함수 (real
정의 1.1 C[a, l 기를 구간 [a, b ] 에서 연속인 실가함수 (real
주 바이 에 르스트라스의 근사정 리 (Weie r str a ss app r oxim ati on t heorem) 에 의해서 (C(T), I| 내)는 가분 바나하 공간 (se p arable Banach s p ace) 이다. Co(T) 는 C(T) 의 폐부분공간 (closed sub- s p ace) 이고, 또한 가분 바나하 공간이 된다. 정의 1.3 X가 위상공간일 때, X 의 모든 개부분집합 (o p en subse t)에 의해서 생성되는 6- 대수 1J (X) 를 X 의 보렐족 (Borel class) 또는 보렐 a- 대 수 (Borel a-alge bra) 라 한다. 보렐 a- 대 수 위에서의 측도를 보렐 측도 (Borel measure) 라 한다.
우리가 관심을 갖는 공간은 위너 공간이고, 이 공간의 보렐 6- 대수 13(C 。 (T)) 위에 다음 성질을 만족하는 측도를 도입하려 고한다. ® 0 보다 크거나 같은 측도이다. ® 가산가법 가능한 (count ab ly addit ive ) 측도이 다. ® 0 보다 크고 유한한 반경 을 갖는 모든 구 (sp h ere) 들의 측도 는 0 보다 크고 유한하다. 이와 같은 측도가 위너 공간에 도입된다면 , 이 측도는 실수에 서의 르베그 측도와 같은 성질을 갖는다. 다만, 르베그 측도와 공유할 수 없는 중요한 성질이 있다. 르베그 측도는 ® 평행변환불변이지만, 위너 측도는 이 성질을 만족하지 못한 다. 그러면, 르베그 측도와 같이 성질 ®~®를 만족하는 측도가 위너 공간에 존재할 수 있는가? 이 질문에 대한 대답은 부정적 이다. 정리 1.4 위너 공간의 보렐 (J-대수 .1J( Co(T)) 위에서 정의 되고, 성질 ®~®롤 만족하는 집합함수 (se t fu nc ti on) 는 존재하 지 않는다. 정리 1. 4 는 직접 증명할 수도 있으나 이 정리를 따름 정리로 얻을 수 있는 좀더 일반적인 정리를 소개하기로 한다.
 정의 1.s X를 바나하 공간, µ를 .13 (X) 에서의 측도라 하자.
정의 1.s X를 바나하 공간, µ를 .13 (X) 에서의 측도라 하자.
 +x)=O 이다.
+x)=O 이다.
 Cate g o ry the orem) 에 의 해 서 ,
Cate g o ry the orem) 에 의 해 서 ,
 (1. 3) f(x ) = 타 1( Ek) XE*(x), X 드 X
(1. 3) f(x ) = 타 1( Ek) XE*(x), X 드 X
위의 정리 1. 6 으로부터 다음 따름정리를 얻는다.
따름정리 1.7 J3 (C 。 (T)) 에서 정의된 측도 µ가 평행변환불변 이고 6- 유한이면 µ=0 이다.
주 위의 따름정리의 결과는 조건 ®에 모순되므로 정리 1. 4 가 성립한다.
 이제 위너 공간에 측도를 도입하기 위해서 서론에서 언급한 아
이제 위너 공간에 측도를 도입하기 위해서 서론에서 언급한 아
 위치
위치
 위a기치2 4 I /』
위a기치2 4 I /』
 정의 1-8 a
정의 1-8 a
 라고 하자. 그러면
라고 하자. 그러면
 (3) 카라데오도리 (Carath eodory) 확장에 의해서 !J에 의해서
(3) 카라데오도리 (Carath eodory) 확장에 의해서 !J에 의해서
 (t ;:t):S r} r) [ t _\ +근 ]2}
(t ;:t):S r} r) [ t _\ +근 ]2}
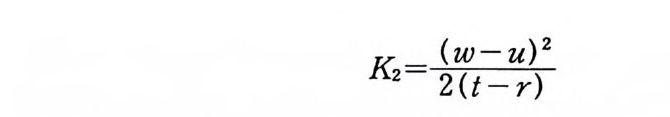 K2= 2(w(t —— u r))2
K2= 2(w(t —— u r))2
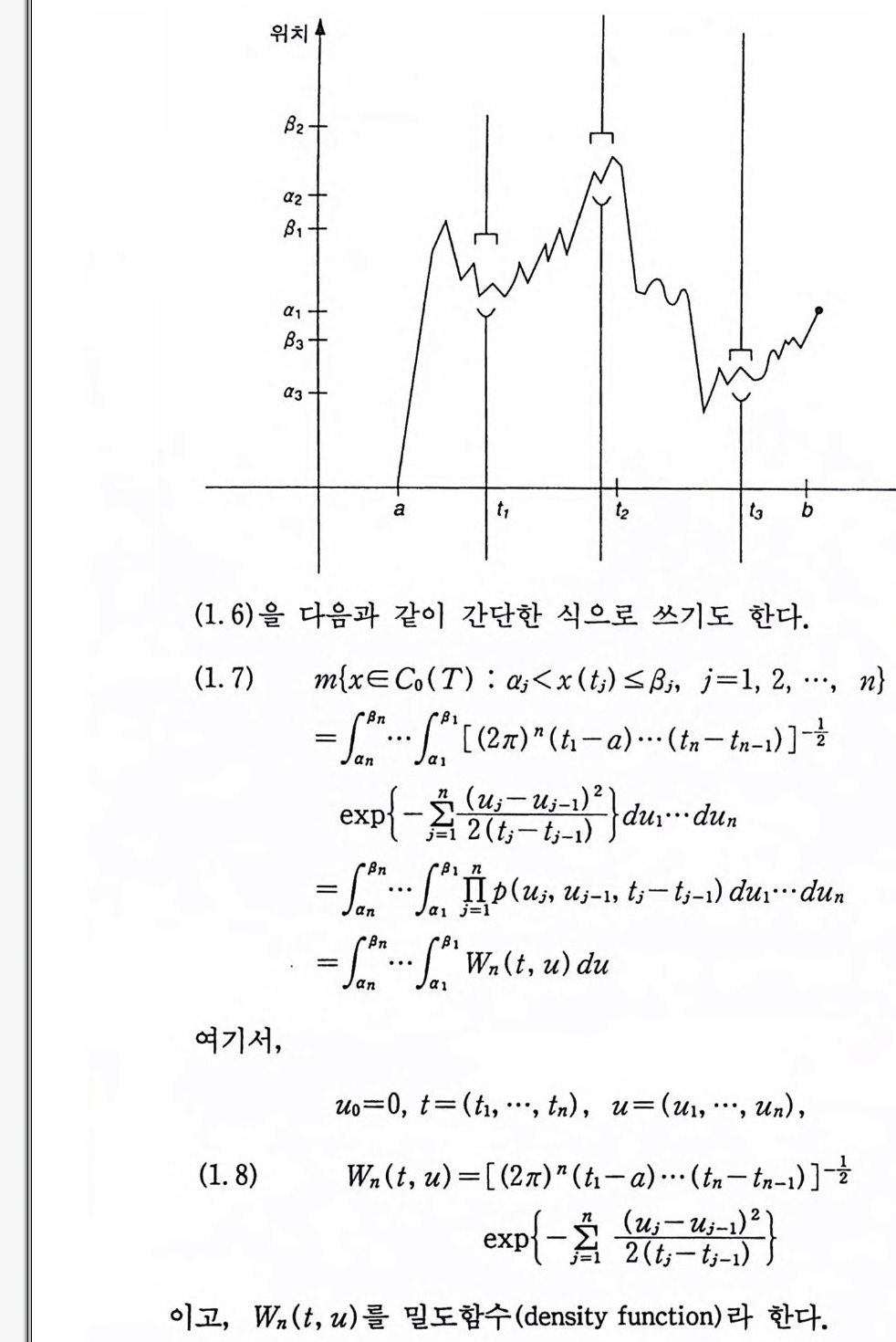
임은 쉽게 보일 수 있으므로 증명은 끝난다. m(/) 를 정의하는 식 (1. 6) 은 I 를 표시하는 식 (1. 9) 에 의해 서 결정된다. 식 (1. 9) 는 물론 tJ, aJ, 8i 에 의해서 결정되는데, I 를 표시하는 방법은 유일하지 않다. 식 (1. 9) 에 tj 이의의 다른 제한점 s 를 추가하고 s 에 대한 제한구간을 무한구간 (-oo, +oo] 으로 택하면 I 에 대한 또다론 표현을 얻을 수 있다. 이와 같이 무한제한구간을 택하면 제한점을 유한 개 추가해도 같은 I 를 나 타낸다. 예를 들면,
 (1.1 5) /={xEC。 (T) : a;
(1.1 5) /={xEC。 (T) : a;
정의 1.12 I 를 표시하는 식 중에서 무한제한구간이 없는 식을 I 의 최 소표시 (mi ni m al rep re senta t i on ) 라고 한다. 정리 1.2 m 은 f에서 잘 정의 (well de fi ned) 된다. 증명 1 의 최소표시 (1. 15) 에 제한점을 하나 추가했을 때, 두
 l��X� m �t� �L�D��tǐ�. �� (1. 15) @� (1. 16) ���
l��X� m �t� �L�D��tǐ�. �� (1. 15) @� (1. 16) ���
& Nexp{ �v _u t:_0 }dul & dukdvdu+ k 1 &dun(1. 18) X� <� � ��h�� 0 �� l���\� x�D� Ȳ (Fubini) � �� |� ȩ�t�� t� Ȅ�X� ��|� ������ v �� �t��
<�� Ĭ��\� �. ���t�, Ȭ� 1. 10 �� X�t�� t � Ȅ�@� (1. 6) X� ������ �D� ���. 0�|�� m (I )
� Ȅ�@� (1. 6) X� ������ �D� ���. 0�|�� m (I )
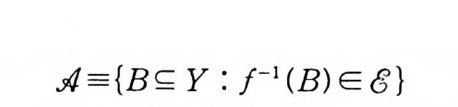 .:Jl ={B 드 Y : ;-1(B)E0}
.:Jl ={B 드 Y : ;-1(B)E0}
로 놓으면 4 는 Y 의 부분집합들의 한 6- 대수가 된다. (c) X, Y 가 위상공간이고 / : X-Y 가 연속이라 하자. 그러 면 /는 보렐 (Borel) 측도가능하다. 죽 모든 BE J3 (Y) 에 대해 서, /- I (B) E J3 (X) 이다.
정리 1.14 (a) m(C 。 (T))= 1. (b) I 든y, I* ¢ 이면 m(I) >O. (c) m 은 y 에 서 유한가법 가능 (fini t ely addit ive ) 하다. 증명 (a) Co(T)={xECo(T) : -co
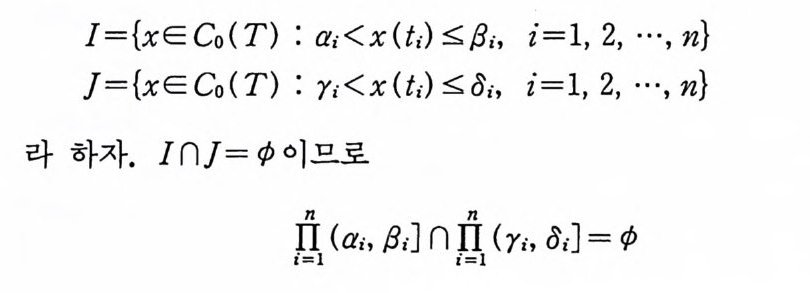 J= {xE Co( T) : ai < x (t,-) 조 /3i, i= l, 2, …, n}
J= {xE Co( T) : ai < x (t,-) 조 /3i, i= l, 2, …, n}
이다. 따라서,
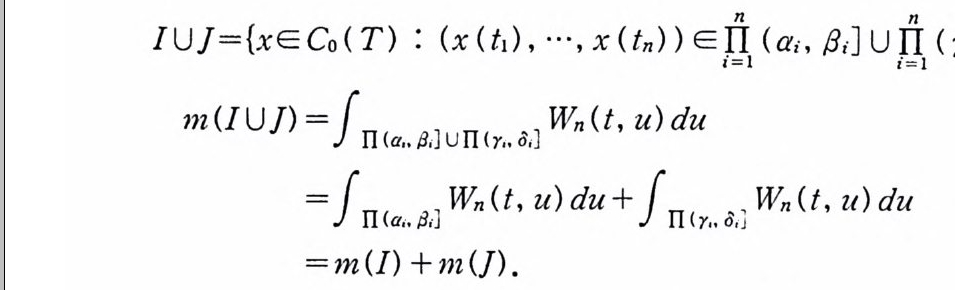 / U J = {x E Co ( T ) : ( x (t1) , … , x ( tn) ) 드 iI=nI I ( a /3J•• U iI=nI I ( Yi , 8 』 }
/ U J = {x E Co ( T ) : ( x (t1) , … , x ( tn) ) 드 iI=nI I ( a /3J•• U iI=nI I ( Yi , 8 』 }
다음 정리 1. 15 는 m 이 .!l에서 가산가법가능 (coun t abl y addi- ti ve) 함을 보여준다. 이 정리의 증명은 길고 복잡하므로 여기서 는 생략하기로 한다. 위너 공간을 확장한 예-위너 공간에서의 이 정 리 의 증명 은 Yeh [l] 을 참조. 7 절 에 서 는 콜모고로프 (Kolmog o rov) 의 정리를 사용해서 위너 측도 m 이 가산가법가능함을 간접적으 로 증명한다. 정리 1.15 (위너) 집합함수 m 은 .!l에서 가산가법가능하다.
 이 제 카라데오도리 (Carath e odory) 확장정 리 에 의 해 서 m 을 완
이 제 카라데오도리 (Carath e odory) 확장정 리 에 의 해 서 m 을 완
정 의 1. 16 ( C。 ( T) , .01, m) 을 위 너 측도공간 (W ien er measure s p ace) 이라 한다. 이때, m 을 위너 측도, .0 1 의 원소를 위너 측 도가능한 집 합 (W ien er measurable set) 이 라 한다. 실수 lR 의 보렐 6- 대수 J3 (R) 은 R 에서의 구간(i n t erval) 들에 의해서 생성된다. 다음 정리는, 위너 공간의 보렐 6- 대수 J3( Co (T)) 도 C 。 (T) 에서의 구간들의 집합 y에 의해서 생성됨을 보 여 준다. 이것이 §의 원소를 구간'’이라고 부르는 한 이유이기 도하다.
 정리 1.1 7 a(.1)=.13 (C 。 (T))
정리 1.1 7 a(.1)=.13 (C 。 (T))
개 구둘은 폐 구 (closed sp h ere) 들의 가산합이 다. 죽
 (1. 20) Sr(xo) ={xEC 。 (T) : llx-xoll< r}
(1. 20) Sr(xo) ={xEC 。 (T) : llx-xoll< r}
 임을 보이자. yf/= Ss(Yo) 이라고 하자. 그러면
임을 보이자. yf/= Ss(Yo) 이라고 하자. 그러면
주 ].18 정리 1. 17 에 의해서 위너 측도공간 (Co(T)'.J i.m ) 은 보렐 측도공간 (Co(T), J3 (C 。 (T)), m) 을 완비화해서 얻는 완비측도공간과 일치한다. 주 1.1 9 (1) 정리 1. 14(a) 에 의해서 위너 측도공간은 확률측 도공간 (pro babil ity measure spa c e) 이 된다. (2) AE 썩 m(A)=O이면, A 의 임의의 부분집합 E 에 대해 서 EE .0 1 이고 m(E) =O 이다. (3) .0 1 는 BUN 과 같은 형태의 집합들로 구성된다. 여기서, B 는 보렐 집합, NCNo, No 은 영보렐 집합 (null Borel se t)이다.
이제, 위너 측도공간의 보렐 집합과 르베그 측도공간의 보렐 집합 사이의 관계를 알아보자. a
 (1.2 4) ft (E)={xEC 。 (T) : (x( t,),… ,XUn))EE}
(1.2 4) ft (E)={xEC 。 (T) : (x( t,),… ,XUn))EE}
R 에 관한 다음 성질은 쉽게 얻을 수 있다. 증명은 각자에게 맡긴다. 정리 1-20 함수 R 는 연속이고, 따라서 보렐 측도가능하다.
 죽 모든 BE 1J (Rn) 에 대해서 ft (B)E 1J (Co(T) )이다.
죽 모든 BE 1J (Rn) 에 대해서 ft (B)E 1J (Co(T) )이다.
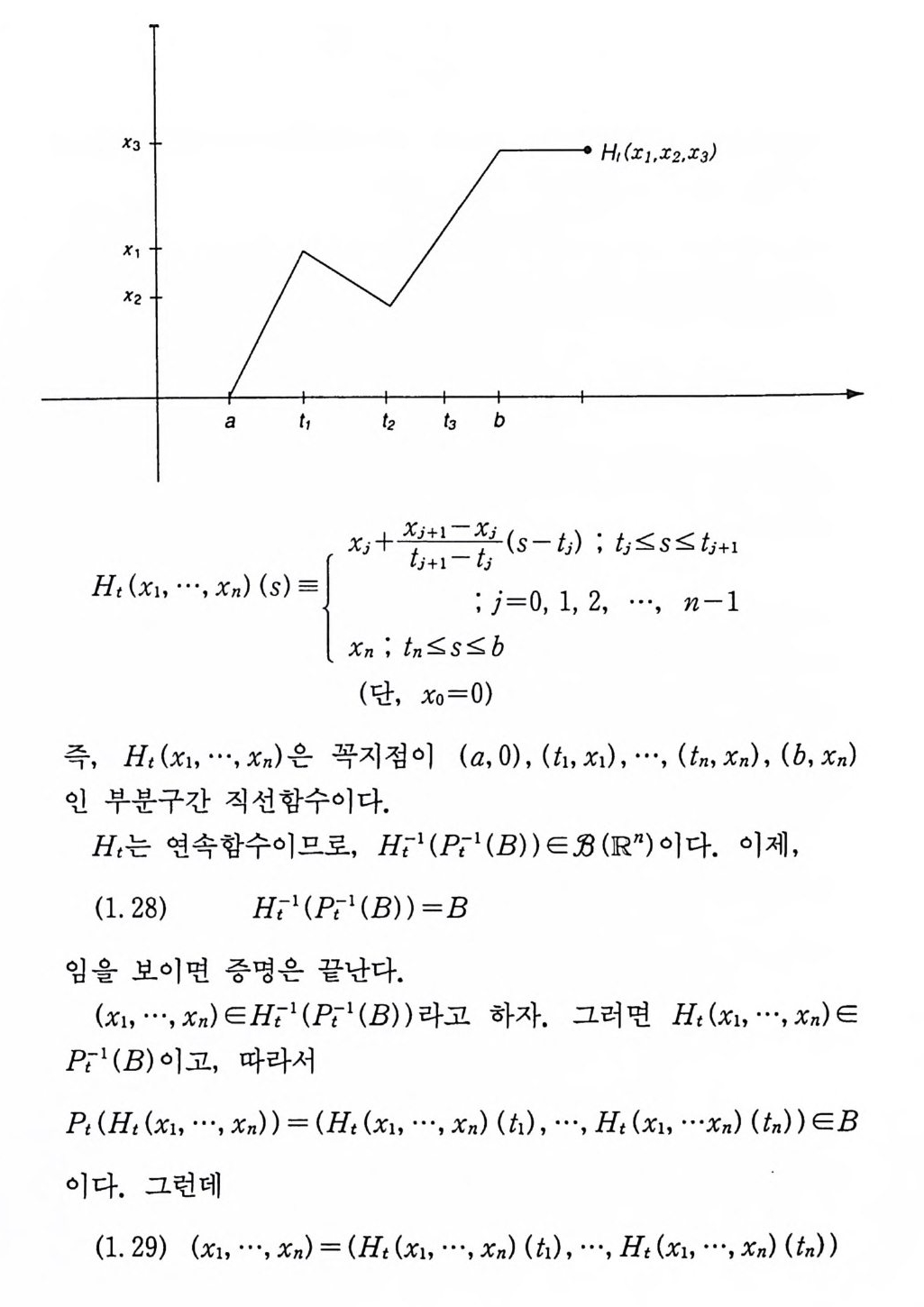 X3 H,(따 .I2,I 어
X3 H,(따 .I2,I 어
 이므로 (x1, … ,Xn)EB 이다.
이므로 (x1, … ,Xn)EB 이다.
임을 보이면 된다. 이것은 (1. 29) 에 의해서 바로 보일 수 있다. 정리 1. 20 과 정리 1. 21 의 결과를 다음 정리로 기술한다.
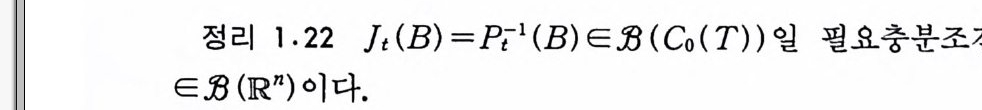 정리 1.22 ft (B)=P,1(B)E J3 (Co(T) )일 필요충분조건은 B
정리 1.22 ft (B)=P,1(B)E J3 (Co(T) )일 필요충분조건은 B
다음 공식은 위너 공간에서 보렐 측도를 르베그 적분으로 표시 하는 편리한 공식이다. 기호 1-23 ;f, (Rn) 을 Rn 에서 르베그 측도가능한 집합들의 6- 대수라 하고, A 를 ;f, (Rn) 에 서 르베그 측도라 하자.
 정리 1-24 BE13 (Rn) 이면,
정리 1-24 BE13 (Rn) 이면,
 로 정의하면, v 는 Z(Rn) 에서 측도가 된다. 또한,
로 정의하면, v 는 Z(Rn) 에서 측도가 된다. 또한,
면 ft (E) 는 위너 측도가능하고 그 측도는 르베그 적분으로 표시 할수 있다.
 정리 1.25 (1) Pt : Co(T) - ➔ Rn 는 .01 -;f, (R n) 측도가능한
정리 1.25 (1) Pt : Co(T) - ➔ Rn 는 .01 -;f, (R n) 측도가능한
 ft (E) = pt-I (E) = pt-I (B u N) = P,1 (B) u pt-I (N)
ft (E) = pt-I (E) = pt-I (B u N) = P,1 (B) u pt-I (N)
다음 결과는 정리 1. 25 의 역이다. 위너 공간이 완비가분 거리 공간이고 또한 확률공간이므로 위너 측도는 정규측도 (re gu lar measure) 이다. 이 정리의 증명에서는 정규측도의 개념이 중요한 역할을 한다.
 정리 1.26 E~Rn 이고 p ;-1(E) 가 위너 측도가능한 집합이면,
정리 1.26 E~Rn 이고 p ;-1(E) 가 위너 측도가능한 집합이면,
 (1. 42) sup A~sup B
(1. 42) sup A~sup B
 이다.
이다.
 (1. 56) v* (E 익 = u* (E 익
(1. 56) v* (E 익 = u* (E 익
이 다. (1. 56) 에 의 해 서 EC (따라서 E) 는 v- 측도가능한 집 합이 된다 (Cohn[l, Prop . 1. 55 』) 그런데 v- 측도가능한 집합들의 6_ 대수 와 르베그 측도가능한 집합들의 6_ 대수는 일치하므로 E 는 르베 그측도가능하다. 정리 1. 25 와 정리 1. 26 을 합해서 다음 정리로 기술한다.
 정리 1-27 E~Rn 일 때, ]1(E)=P,-1(E) 가 위너 측도가능할
정리 1-27 E~Rn 일 때, ]1(E)=P,-1(E) 가 위너 측도가능할
R 에서 보렐 집합이 아니면서 르베그 측도가능한 집합이 존재 한다는 사실을 이용해서, 위너 공간에서 보렐 집합이 아니면서 위너 측도가능한 집합이 존재함을 위의 정리로부터 증명할 수 있 다. 또한, 위너 측도가능하지 않는 집합이 위너 공간에 존재함을 보일 수 있다. 다음 따름정리를 보자.
 따름정리 l.28 ( i ) J3( Co(T)) ~.!01
따름정리 l.28 ( i ) J3( Co(T)) ~.!01
주 1.29 정리 1. 26 을 위너 공간에서 역측도정리라 한다. 예 위너 공간에서 역측도정리와 일반화된 역측도정리는 4 장에서 다 루기로 한다. 2 위 너 적 분 (Wi en er int e g r a l) 앞 절에서는 함수 공간에 측도를 도입하여 위너 측도 공간 (C 。 (T), 必 I, m) 을 만들었다. 위너 측도가능한 집합과 르베그 측 도 가능한 집합 사이의 관계를 조사하였고 위너 측도를 르베그 적분으로 표시하는 공식을 유도하였다. 위너 측도공간에서 정의 된 측도가능한 함수 F 의 위너 측도에 관한 적분을 F 의 위너 적 분이라하고
 (2. 1) loCo (( TT>) F(x) dm(x)
(2. 1) loCo (( TT>) F(x) dm(x)
로 표시한다. 이제 어떤 특정한 함수에 대해서 이 함수의 위너 적분을 르베 그 적분으로 표시하는 공식을 유도해 보기로 한다.
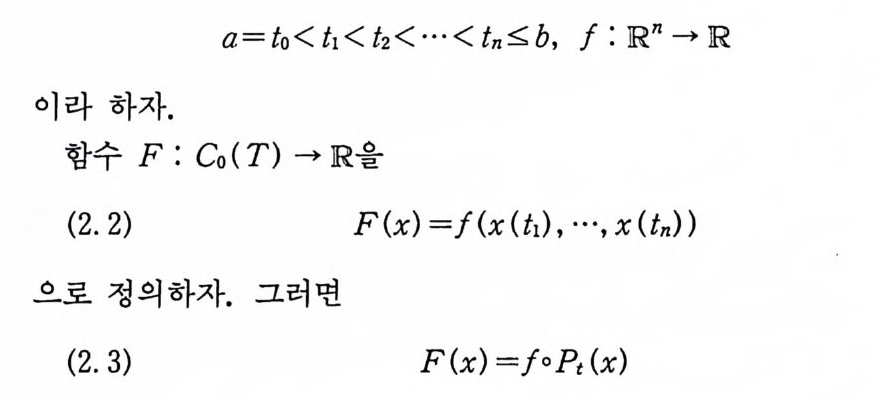 a=t o< ti< t2< …< tn:: :;;;b, I : Rn -R
a=t o< ti< t2< …< tn:: :;;;b, I : Rn -R
이다. 여기서 P, (x) 는 (1. 25) 로 주어진 함수이다. 정리 2.1 /가 르베그 측도가능할 필요충분조건은 F 가 위너 측도가능한 것이다. 이 경우에,
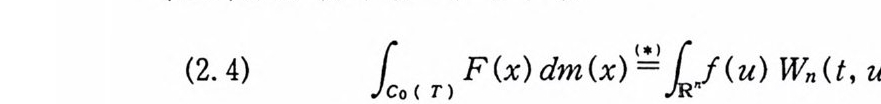 (2. 4) f F(x)dm(x) 날 k f (u) Wn( t, u)du
(2. 4) f F(x)dm(x) 날 k f (u) Wn( t, u)du
이다. 여기서 Wn( t, u) 는 (1. 8) 로 주어전 밀도함수이고, 등식 낱은 강한 의미의 등식을 뜻한다. 죽 (2.4) 의 어느 한 변이 존재 하면(무한대인 경우도 포함), 다른 변도 존재하고, 그 두 적분값 온같다. 증명 (I) f가 르베 그 측도가능하다고 하자. 정 리 1. 25 에 의 해 서 P t가 위너-르베그 측도가능하므로 (2.3) 에 의해서 F 는 위너 측도가능하다. 역으로 F 가 위너 측도가능하면 정리 1. 26 에 의해서 f는 르베 그측도가능하다. (2) 변수변환정리 (부록 정리 2.1) 에 의해서,
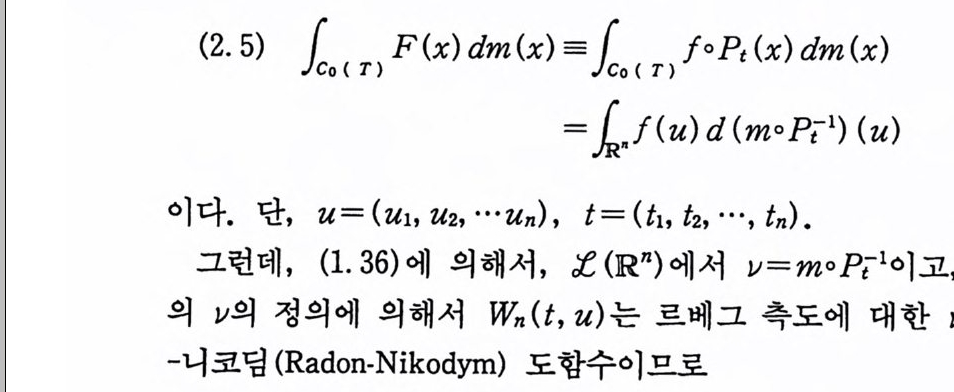 (2. 5) JcCo0 (< TT)l F (x) dm (x) 나JC o ( T) fO P t (x) dm (x)
(2. 5) JcCo0 (< TT)l F (x) dm (x) 나JC o ( T) fO P t (x) dm (x)
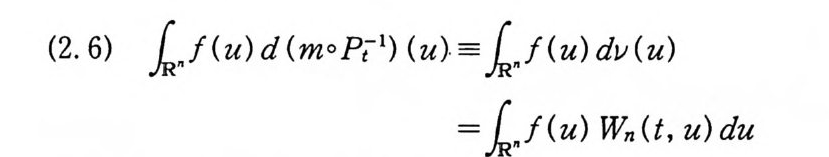 (2. 6) k J (u)d(m0P 기 (u).=kJ ( u)dv(u)
(2. 6) k J (u)d(m0P 기 (u).=kJ ( u)dv(u)
이다. (2. 5) 와 (2. 6) 에 의해서 (2. 4) 가 성립한다. 주 2.2 (1) 위너 측도가능한 모든 함수들에 대해서 공식 (2. 4) 를 적용할 수는 없으나, 우리가 관심을 갖는 많은 함수들의 경 우에 (2 . 4) 의 오른변 적분(따라서 왼변 적분)이 유한하다. (2) 공식 (2. 4) 는 무한차원인 위너 공간에서 적분을 유한차원 인 Rn 에서의 르베그 적분으로 전환한다. 이것은 일반적으로는 성립하지 않지만, 여기서는 함수 F 가 n 개의 제한점에서의 x 의 값에 만 의존하기 때문에 가능하다. 이제 정리 2.1 을 이용해서 특정한 함수들의 위너 적분을 계산 해 보자. 성질 2.3 a< t ~b 일 때 F(x)=x (t)로 놓자. 그러면 F 는 위 너 적분가능하고
 (2. 7) fcCo0 ,( TT>) F(x) dm(x) =O
(2. 7) fcCo0 ,( TT>) F(x) dm(x) =O
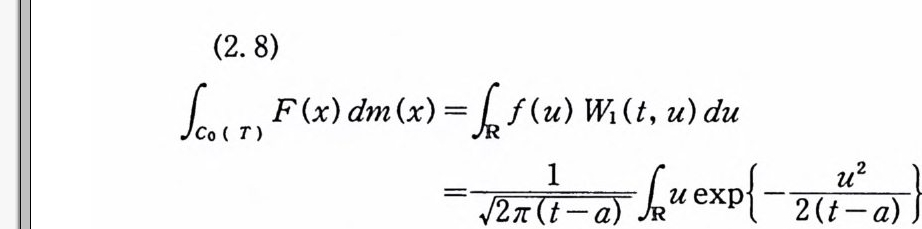 (2. 8)
(2. 8)
여기서, 마지막 적분의 피적분 함수는 기함수이므로 그 적분은 0 이 된다.
 성질 2 . .4 a< ti. t 2~b 일 때, F(x} =x( t 1)x( t 2) 로 놓자. 그러
성질 2 . .4 a< ti. t 2~b 일 때, F(x} =x( t 1)x( t 2) 로 놓자. 그러
이 적분을 계산하기 위해서 다음과 같이 변수변환을 하자.
 Vl= J2 (tuI _i a) , V. 2=_ J 2u(2 t 2- 가u1) •
Vl= J2 (tuI _i a) , V. 2=_ J 2u(2 t 2- 가u1) •
이 된다. 이것을 (2.10) 의 오른변에 적용하고, 푸비니 (Fubin i ) 정리를 사용해서 다음 식을 얻는다.
 (2. 11) loCo (( Tn) F (x) dm (x)
(2. 11) loCo (( Tn) F (x) dm (x)
 (2. 12) i v2ex p (-v2)dv= 우
(2. 12) i v2ex p (-v2)dv= 우
 이다.
이다.
조)이므로 연속확률과정이다. (1)은 성 질 2. 3, (2) 는 성 질 2. 6, (3) 은 성 질 2. 4 로부터 얻는다.
 X, y가 위상공간일 때, J3( X), J3( Y), J3( Xx Y) 를 각각
X, y가 위상공간일 때, J3( X), J3( Y), J3( Xx Y) 를 각각
증명 7r1 건 r2 를 각각 Xx Y 에서 X, y로의 사영사상(p ro j ec ti on map ) 이 라 하자. 그러 면 7r1, 7r2 는 연속함수이므로 보렐 측도가능 한 함수가 된다. EE.' B (X) , FE.' B ( Y) 라 하자. 그러 면
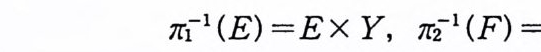 1r1-1 (E) = E x Y, 1r2-1 (F) = X x F
1r1-1 (E) = E x Y, 1r2-1 (F) = X x F
는 .'B (X X Y) 에 속한다. .'B (X) ® .'B ( y) 는 E X F 를 포함하는 가장 작은 (J-대수이므로 (2.18) 이 성립한다. 보조정 리 2 . 11 X, Y 가 제 2 가산 (second count ab le) 위 상공간이 라 하자. 그러면
 (2.1 9 ) J3 (X) ® J3 ( Y) =.13 (Xx Y)
(2.1 9 ) J3 (X) ® J3 ( Y) =.13 (Xx Y)
이다. 증명 { Ui, U2, U3, …}, { Vi, Vi, ••• }를 각각 X 와 Y 의 가산기 저 (counta b le base) 라 하자. 그러 면
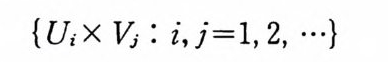 { U; x lt; : i, j= l, 2, …}
{ U; x lt; : i, j= l, 2, …}
는 XX Y 의 적위상(p roduc t t o p olo gy)의 기저 (base) 가 된다. 따 라서.
 (2.20) J3( Xx Y) =a{G : G 는 Xx Y 의 개부분집합}
(2.20) J3( Xx Y) =a{G : G 는 Xx Y 의 개부분집합}
가분거리공간은 제 2 가산 위상공간이므로 다음 정리를 얻는다.
 따름정리 2.12 X, Y 가 가분 (se p arable) 거리공간이면,
따름정리 2.12 X, Y 가 가분 (se p arable) 거리공간이면,
위의 결과를 이용해서 다음 위너 적분을 계산해 보자.
 성질 2.13 F:Co(T)- ► JR를
성질 2.13 F:Co(T)- ► JR를
위와 같은 방법으로 다음 두 적분도 계산할 수 있다. 증명은 각자에게 맡긴다.
 성 질 2 .14 F : C 。 ( T) 一 lR 을
성 질 2 .14 F : C 。 ( T) 一 lR 을
 xU2)-xU1) 로 정의하면, X~N(O, !2 기)이다.
xU2)-xU1) 로 정의하면, X~N(O, !2 기)이다.
 exp {_ 2( t 1만 a) _ 2(t2 V :h) }dvldv2
exp {_ 2( t 1만 a) _ 2(t2 V :h) }dvldv2
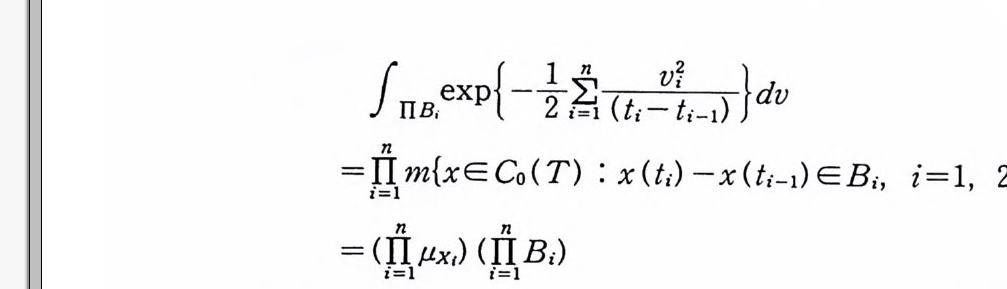 f IIB,ex p{―}훔 6}dv
f IIB,ex p{―}훔 6}dv
(2. 34) 의 두번째 등식은 X~N(0, t;-t i - I) 로부터 얻는다. (2. 33) 과 (2. 34) 에 의해서 (2. 32) 를 얻는다. 정리 2.16 으로부터 다음 정리를 얻는다.
 따름정리 2. 17 위너 과정 X (t, x) = x (t)은 브라운 운동과정
따름정리 2. 17 위너 과정 X (t, x) = x (t)은 브라운 운동과정
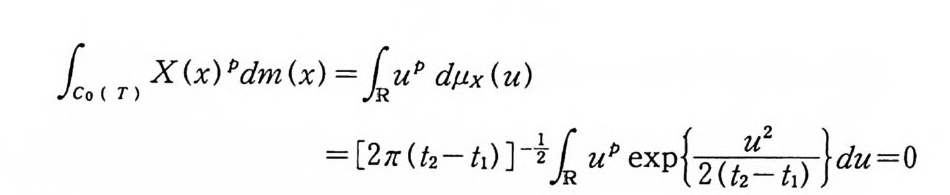 io ( T) X(x)Pdm(x) =l 값 dµx(u)
io ( T) X(x)Pdm(x) =l 값 dµx(u)
이다. 여기서, 처음 등식은 변수변환정리 (부록 정리 2.1 ), 두번 째 등식은 부록 정리 5.13 에 의해서 얻는다. 감은 방법으로 다음 식도 얻을 수 있다.
 1.< T> IX(x)IPdm(x) =fRlul Pdµx(x)
1.< T> IX(x)IPdm(x) =fRlul Pdµx(x)
증명 푸비니 정리와 성질 2.18 에 의해서, p가 기수이면,
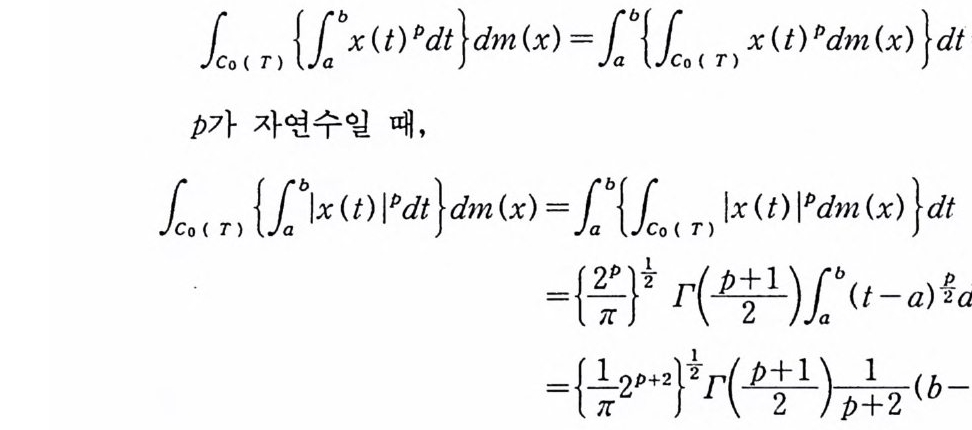 l.< n {lbx(t) P dt }d m(x) =lb{l.< n x( t)P dm(x)}dt =O .
l.< n {lbx(t) P dt }d m(x) =lb{l.< n x( t)P dm(x)}dt =O .
3 위너 곡선의 미분 불가능성 이 절에서는 〈거의 모든 (a. e.) 위너 곡선은 거의 모든 점에서 미분가능하지 않다〉는 사실을 증명하려고 한다. 이것은 1909 년 프랑스의 물리 학자 페 랭 (Je an Perrin ) 이 관찰한, 〈브라운 입 자의 궤적은 접선을 갖지 않는다〉는 사실로부터 예측된 바이지만 수학 적인 엄밀한 증명은 위너에 의해서 이루어졌다. 1872 년 바이에르스트라스 (We i ers t rass) 는 모든 접에서 연속이 고, 어떤 점에서도 미분가능하지 않은 함수 (Bar 虛 [l, p .195]) 를 발표하여 수학자들을 놀라게 했다. 그때까지는, 모든 연속 함수 들은 몇 개의 점만을 제의하고서는 모든 점에서 미분가능하다고 믿어 왔기 때문이다. 위너 곡선은, 바이에르스트라스의 예 이의 에도, 미분 불가능한 연속 곡선이 실재로 많이 존재한다는 사실 울 보여 주는 좋은 예이다.
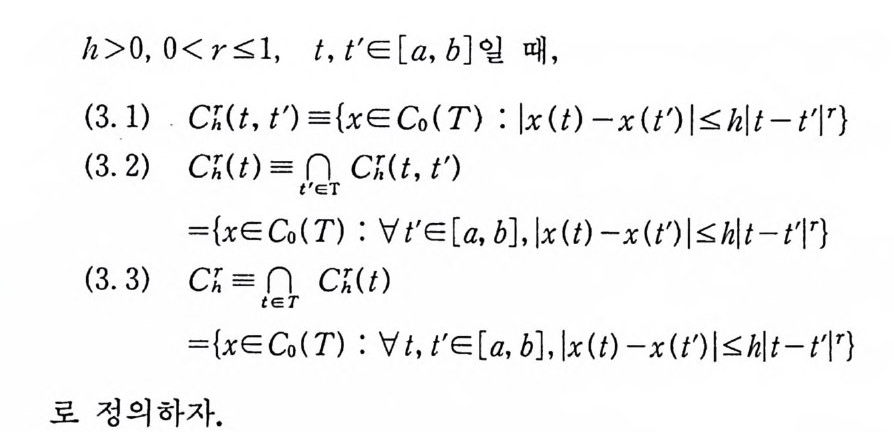 h>O,O
h>O,O
성질 3.1 CI(t , t'), CI (t), CI 는 Co(T) 는 폐부분집합이다. 따라서, 보렐 집합이다.
 증명 (xn) 을 ||Xn-X| 尸나) 되는 CJ :(t, t’)의 수열이라 하자. Xn
증명 (xn) 을 ||Xn-X| 尸나) 되는 CJ :(t, t’)의 수열이라 하자. Xn
성질 3.2 다음 부등식이 성립한다.
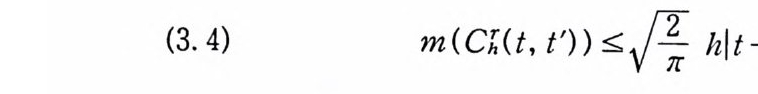 (3. 4) m(CJ :(t, t')) 김 An· hlt -t'lr-½
(3. 4) m(CJ :(t, t')) 김 An· hlt -t'lr-½
증명 a< t
 (3.5) E={(ui, u2)ER2 : lu, 一 u2I 집t|t―t'|가
(3.5) E={(ui, u2)ER2 : lu, 一 u2I 집t|t―t'|가
로 보낸다. 따라서
 (3. 9) m(CJ ;(t, t')) =吉 lex p{-룬 }ex p{부 }dv2dv1
(3. 9) m(CJ ;(t, t')) =吉 lex p{-룬 }ex p{부 }dv2dv1
 하면 r 차 횔더 연속 (Holder cont inu ous) 함수라 한다. 모든 t, t'
하면 r 차 횔더 연속 (Holder cont inu ous) 함수라 한다. 모든 t, t'
다음 성질은 횔더 연속인 위너 곡선들은 위너 공간에서 측도가 0 인 집합임을 보여 준다.
 성질 3.4 ½
성질 3.4 ½
 (3. 13) m(D1) =0
(3. 13) m(D1) =0
주 t =a( 또는 t = b) 인 경우는 우측(또는 좌측)도함수만을 생각 한다. 증명 이제,
 (3. 14) D 흡 hU0=0 I CJ .< t)
(3. 14) D 흡 hU0=0 I CJ .< t)
이제 이 절의 처음에 소개한 위너 곡선의 미분 불가능성에 대 한 정리를 증명해 보자. 정리 3.7( 위너) 거의 모든 (a.e.) 위너 곡선들의 미분가능한 점
둘의 집합은 르베그 측도 0 이다. 죽,
 (3.16) m{xECo(T) : ;l({tE T : x'( t)가 존재한다}) =O}=l
(3.16) m{xECo(T) : ;l({tE T : x'( t)가 존재한다}) =O}=l
이다. 이것은, a. e. x 에 대해서, F(x, t) =1 인 t들의 집합의 르 베그 측도는 0 임을 말한다. 즉 a.e.x 에 대해서, x' (t)가 존재하 는 t들의 집합의 르베그 측도는 0 이다. 따라서 (3 . 16) 이 성립한 다. 이제 F(x, t)가 측도가능함을 증명해 보자.
 (3. 21) G={ (x, t) E Co( T) x T : F(x, t) =1}
(3. 21) G={ (x, t) E Co( T) x T : F(x, t) =1}
 (3.26) m(Gn=o
(3.26) m(Gn=o
위의 정리로부터 유계변동에 대한 다음 정리를 얻는다. [a, b] 에서 유계변동인 함수들의 집합을 BV(T) 라 하자.
따름정리 3.8 유계변동 (boundedvar i a ti on) 인 위너 곡선들의 집합은 위너 측도 0 이다. 죽
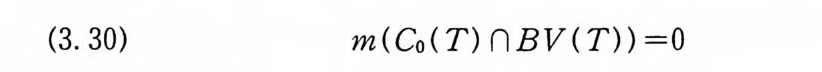 (3. 30) m(C 。 (T) nBV(T)) =O
(3. 30) m(C 。 (T) nBV(T)) =O
증명 x 가 [a, l 기에서 유계변동이면, 거의 모든 (a. e.) t에 대 해서 x' (t)가 존재한다. 즉,
 xt/ ={ xECo(T) : A({tE T : x' (t)가 존재한다}) =O}
xt/ ={ xECo(T) : A({tE T : x' (t)가 존재한다}) =O}
 다음 정리는 정리 3.7 과 같은 방법으로 증명할 수 있다.
다음 정리는 정리 3.7 과 같은 방법으로 증명할 수 있다.
(3. 31) m{xE Co( T) : ,1 (Z (x) ) =O}=l .
주 3.10 X 의 영집합 Z(x) 에 대해서 다음 사실이 성립한다
(Freedman[l]). 거의 모든 xECo(T) 에 대해서, Z(x) 는 완전집 합 (pe rfe c t set) 아 다. 즉, Z (x) 는 조밀 (dense) 한 폐 집 합이 다. 따 라서 Z(x) 는 셀 수 없는 집합이다 (uncoun t able set) . 그러나 Z (x) 의 르베그 측도는 0 이다. 4 척도불변 가측집합 위너 측도가 르베그 측도와 공유할 수 없는 중요한 성질 중의 하나가 평행변환 불변성이라는 것은 앞에서 논하였다. 여기서는 이들 측도가 공유할 수 없는 또 하나의 중요한 성질인 척도불변 성 (scale-in v aria n t) 에 대 해 서 논하기 로 하자. E 가 르베그 측도가능한 집합일 때, 모든 실수 a>O 에 대해서 aE 는 르베그 측도가능하고,
 (4. 1) ...l( aE) =a...l ( E)
(4. 1) ...l( aE) =a...l ( E)
인 것은 르베그 측도론에서 잘 알려진 사실이다. 그러나 위너 측 도는 이 성질을 만족하지 못한다(정리 4.18). 위너 공간에서의 척도불변성의 개념은 위너 측도 자체에서도 중요한 역할을 하지 만 파인만 적분에서는 필수적인 중요한 개념이다. 위너 공간에서 척도불변성에 관한 이론울 전개하는 데 ·필수적 인 정리가 있다. 이 정리는 위너 곡선의 이차변동(q uadra tic var i a ti on) 에 관한 것으로, 1940 년에 레비 (P. Le vy)에 의해서 얻 어졌다. 여기서는 이 정리의 특별한 경우로서, 1947 년에 카메룬 (R.H . Cameron) 과 마틴 (W.T. Martin ) 에 의 해 서 , 레 비 와는 독립 적으로 증명된 정리를 소개한다. 구간 [a, b] 의 분할 (pa rtit ion ) a = to < t1 < …< & = b 을 lf k 라고
 하자. xEC 。 (T) 에 대해서,
하자. xEC 。 (T) 에 대해서,
 다. 주어진 양의 정수 k 에 대해서, tj=j, j= O, 1, 2, …, k 로 놓
다. 주어진 양의 정수 k 에 대해서, tj=j, j= O, 1, 2, …, k 로 놓
 (4.9)
(4.9)
 (4. 11) En={xECo(T) : IS2n(x)-l|22-n/3}
(4. 11) En={xECo(T) : IS2n(x)-l|22-n/3}
임울 보이면 증명이 끝난다. 그런데 (4 . 13) 에 의해서, 모든 n 에 대해서,
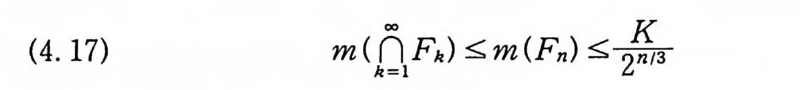 (4. 17) m (k[OJ=O 1l F k) ~ m (Fn) 소K尸
(4. 17) m (k[OJ=O 1l F k) ~ m (Fn) 소K尸
이므로 (4. 16) 이 성 립 한다. 주 4,2 (1) 따름정리 3. 8 을 정리 4 . 1 의 따름정리로서도 얻을 수 있다. 따라서, (2) 유계인 도함수를 갖는 위너 곡선들의 집합 도 위너 측도 0 이다. 물론 이 사실도 정리 4.1 을 이용해서 직접 증명할 수 있다. 다음은 1940 년에 레비 (P. Le vy)에 의해서 얻어진 정리를 소개 한다. 이 정리의 결과를 포함하는 보다 일반적인 정리(강한국한 정리)는 3 장에서 증명하기로 한다.
 정리 4.3 {Tk} 가 [a, b] 의 분할들의 수열이고, Jr1 CJ r2 C… , k
정리 4.3 {Tk} 가 [a, b] 의 분할들의 수열이고, Jr1 CJ r2 C… , k
여기서 최소상계는 [a, 싸의 모든 분할 7[ h 에 대해서 취한다. 정리 4.3 의 결과와는 대조적으로 다음 사실이 성립한다 (Freed man [1, p. 48] ) .
 a. e. xECo(T) 에 대해서, QV (X) =+(X)이다.
a. e. xECo(T) 에 대해서, QV (X) =+(X)이다.
 가능한 집합이다.
가능한 집합이다.
 (4. 24) ma=m0a-1
(4. 24) ma=m0a-1
 주 4-9 (1) (4. 27) 에 의해서, 보렐 측도 ma 는 C 려 1 집중되
주 4-9 (1) (4. 27) 에 의해서, 보렐 측도 ma 는 C 려 1 집중되
 되는 보렐 집합 B 와 ma- 영 집합 N 이 존재한다. ( i )에 의해
되는 보렐 집합 B 와 ma- 영 집합 N 이 존재한다. ( i )에 의해
 ( ii ) NE TJ 일 필요충분조건은, 모든 a>O 에 대해서, Nn Ca
( ii ) NE TJ 일 필요충분조건은, 모든 a>O 에 대해서, Nn Ca
 (4. 35) N=( UNa) UL
(4. 35) N=( UNa) UL
 주 4-14 ( i ) (4. 37) 은 서로 소인 집합들의 합집합이므로,
주 4-14 ( i ) (4. 37) 은 서로 소인 집합들의 합집합이므로,
[O, 1] 를 임의의 함수라 하자. 그러면 각 a>O 에 대해서, EaCCa, EaE .0 a 이고 ma(Ea) =/(a-1) 되는
 집합 Ea 가 존재한다.
집합 Ea 가 존재한다.
 따름정리 4.17 f : (O, CX)) --- ► [O, 1] 를 임의의 함수라 하자. 그
따름정리 4.17 f : (O, CX)) --- ► [O, 1] 를 임의의 함수라 하자. 그
이므로 aH 는 위너 영집합이다. 따라서 위너 측도가능하다.
 이제, G=a-1H(a>O, a -=l= l) 로 놓으면 G 는 위너 측도가능하
이제, G=a-1H(a>O, a -=l= l) 로 놓으면 G 는 위너 측도가능하
 증명 ( i ) T-1 은 연속함수이므로, B 가 보렐 집합이면 T- 1
증명 ( i ) T-1 은 연속함수이므로, B 가 보렐 집합이면 T- 1
 EE .0일 때, 이 두 분할들의 수열에 대한 정리 4.13 의 결과를
EE .0일 때, 이 두 분할들의 수열에 대한 정리 4.13 의 결과를
 도 척도불변 영집합임을 보일 수 있고
도 척도불변 영집합임을 보일 수 있고
 v = - U sin 0 + V cos 0
v = - U sin 0 + V cos 0
 xy (( tt) ) == X—(X t) ( ct)o ssi n( ) +8 +Y Y( t)( ts)i nc o (s) ()
xy (( tt) ) == X—(X t) ( ct)o ssi n( ) +8 +Y Y( t)( ts)i nc o (s) ()
 Jx ]={(X, Y)ECo(T) XCo(T) : aj < X({j) s f 3j,
Jx ]={(X, Y)ECo(T) XCo(T) : aj < X({j) s f 3j,
 사용하면 (5.7) 과 (5.9) 의 두 적분이 같음을 보일 수 있다.
사용하면 (5.7) 과 (5.9) 의 두 적분이 같음을 보일 수 있다.
 증명 따름정리 5. 4(2) 에 의해서 R 。(따라서 R i 1) 가 측도가능하
증명 따름정리 5. 4(2) 에 의해서 R 。(따라서 R i 1) 가 측도가능하
증명 ()를 다음과 같이 택한다.
 sin 0 = @p ' cos 0 = @q ·
sin 0 = @p ' cos 0 = @q ·
 (c) J (x + y) 는 (x , Y) 의 함수로서 mp X 11Z q 一 측도가능하다.
(c) J (x + y) 는 (x , Y) 의 함수로서 mp X 11Z q 一 측도가능하다.
 =loCo ,( TT )l mq ( E— x)d mp ( x)
=loCo ,( TT )l mq ( E— x)d mp ( x)
 (5. 17) mp (y + C,f ji2+q2) = 1
(5. 17) mp (y + C,f ji2+q2) = 1
다음은 척도불변 가측집합과 척도불변 영집합의 평행변환에 관 한 긍정적인 결과들이다.
 따름정리 5.14 EE.J , P>O 라 하자. 그러면, s-a. e. y에 대
따름정리 5.14 EE.J , P>O 라 하자. 그러면, s-a. e. y에 대
 증명 각 11>0 에 대해서, m.1 - a. e. y가 mp ( N+y ) =0 을 만족
증명 각 11>0 에 대해서, m.1 - a. e. y가 mp ( N+y ) =0 을 만족
 정의 6.l 척도불변 가측집합에서 정의된 함수 F 가, 다음 성
정의 6.l 척도불변 가측집합에서 정의된 함수 F 가, 다음 성
주 ~는 동치 관계이다• 여기서는 실가함수만을 취급하지만 복소수 값을 갖는 함수에 대해서도 같은 이론을 전개할 수 있다. 다음 세 정리는 각각 정리 4.11, 정리 5. 9 정리 4.15 에 의해서 얻는다.
 정리 6.2 .J (F) = 門 .0a (F)
정리 6.2 .J (F) = 門 .0a (F)
 정리 6.4 각 a>O 에 대해서,
정리 6.4 각 a>O 에 대해서,
 자. F-1(B)E .0임울 보이기 위해서, 각 a>O 에 대해서 F-1(B)
자. F-1(B)E .0임울 보이기 위해서, 각 a>O 에 대해서 F-1(B)
 (6. 5) lbF(anZ) dz -+ lbF(az) dz
(6. 5) lbF(anZ) dz -+ lbF(az) dz
주 6.8 (1) 위너 공간에서 척도변환에 관계된 문제점을, 보렐 집합이나 보렐 측도가능한 함수로 제한함으로써 해결할 수도 있 다. 그러나 이와 같이 제한한다고 해서 모든 문제점들이 극복되 는 것은 물론 아니다. (2) 함수 F 가 s-a. e. 에서 연속이 면 위너 공간에서도 (6. 5) 가
 성립한다. 즉, an-a 일 때,
성립한다. 즉, an-a 일 때,
다음 정리도 정리 5.9 를 사용해서 얻을 수 있다•
 고 정하리자 .6 .10r :F::: : G와 ) Gp 를, q척 >도O 가불 변임 의가로측 함주수어이전고 실s-수a.이e면. ,에 서 (m같,다x
고 정하리자 .6 .10r :F::: : G와 ) Gp 를, q척 >도O 가불 변임 의가로측 함주수어이전고 실s-수a.이e면. ,에 서 (m같,다x
롤 사용해서 함수공간 D(T) 에 측도를 도입하려고 한다. 집합함 수 (se t fun cti on ) µ를 幻에서 다음과 같이 정의하자.
 (7. 4) µ(/) =P{ 硏 E요 : aj< x(th o)
(7. 4) µ(/) =P{ 硏 E요 : aj< x(th o)
 가하는 순서일 필요는 없다)에 대해서, 집합함수 µ(ti, …, L) 을 ]Rn
가하는 순서일 필요는 없다)에 대해서, 집합함수 µ(ti, …, L) 을 ]Rn
 (1) µ(X) =1
(1) µ(X) =1
 00
00
그런데,
 µ(Kn) 김
µ(Kn) 김
 fl(I ), fiI), fiI)’ : {t1, …, t kI} 에서 수령
fl(I ), fiI), fiI)’ : {t1, …, t kI} 에서 수령
주 7.3 정리 7.2 의 증명에서 D(T) 를 C 。 (T) 로 대치하고 이 증명과정을 따라간다면 (Co(T), J3 (Co(T))) 에서 이 위너 측도 롤 얻을 수 있을까? 문제점들 중의 하나는 f가 Co(T) 에 속한 다는 보장이 없다는 것이다. 아인슈타인과 위너에 의해서 제시된 유한차원 보렐 측도에 대 해서 콜모T 쿠立 일관성 정리를 적용해서, (D(T), j)에 가산 가법 가능한 측도 w (a versio n of Wi en er pro cess) 를 얻 을 수 있 다. 이 과정을 설명하면 다음과 같다.
 a
a
 인 경우에는,
인 경우에는,
µ(tI, …, L) 가 일관성 조건 (7.7) 과 (7.8) 을 만족하는 것을 보일 수 있다. (지루하고 복잡하기는 하지만) 따라서 콜구 ,, 쿠 立 의 일관성 정리 (정리 7. 2) 에 의해서, (D(T), Y) 에 측도 w 를 도입할 수 있다. 확률측도공간 (D(T), Y, w) 는 위너보렐 측도공간 (Co(T), J3( Co(T)), m) 보다는 유용하지 않다. 그 이유 중의 하나는 공 간 D(T) 가 너무 큰 것에 비해서 6- 대수 Y 는 너무 작다. 7 에 속하지 않는 D(T) 의 부분집합들이 많이 있다. 예를 들면, 임의 의 단위 원소의 집 합 {x}, Co ( T) 동이 7 에 속하지 않는다. 이 것을 증명해 보기로 하자. S 드 R 일 때, S 에서 정의된 함수들의 집합 D(S) 의 적위상 (pro duct top o log y) 에 대 한 기 저 (basis ) 는 다음 집 합들로 구성 된 다.
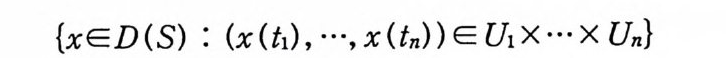 {xED (S) : (x (t,) , …, X Un) } E U1 X ••• X Un}
{xED (S) : (x (t,) , …, X Un) } E U1 X ••• X Un}
여기서 U; (i=l , 2, …, n) 는 R 의 개부분집합 (o p en subse t)이다. S 가 T 의 가산부분집 합 (counta b le subset) 일 때 ,
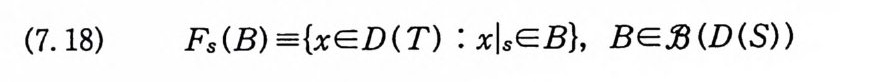 (7.18) Fs(B) ={xED(T) : xlsEB}, BEJ ) (D(S))
(7.18) Fs(B) ={xED(T) : xlsEB}, BEJ ) (D(S))
로놓자.
 보조정리 7.4 S 와 So 가 T 의 가산부분집합이고 sns 。=¢라
보조정리 7.4 S 와 So 가 T 의 가산부분집합이고 sns 。=¢라
 는 것 (closed) 은 보조정리 7. 4 를 이용해서 보일 수 있다. FSI
는 것 (closed) 은 보조정리 7. 4 를 이용해서 보일 수 있다. FSI
주 x 는 조밀집합 (dense set) T\S 에서 -1 이므로, x 가 연속이 라고 하면 x 는 T 에서도 -1 이 된다. 위와 같은 방법으로 다음 정리도 증명할 수 있다.
 따름정리 7,7 XoED(T) 일 때, {xo} 꾼 7 이다.
따름정리 7,7 XoED(T) 일 때, {xo} 꾼 7 이다.
 t���\� XoEFs(B) t��.
t���\� XoEFs(B) t��.
(P�� (Doob) Ȭ�) (X, 8, �� )U� `����t��, X a� X, �*(Xo )=1 t�|�
 주 정리 7.10 에서 Xo 는 8 에 속할 필요는 없다.
주 정리 7.10 에서 Xo 는 8 에 속할 필요는 없다.
 m (Kt (B) n C 。 ( T) ) =ls Wn (t, u) du.
m (Kt (B) n C 。 ( T) ) =ls Wn (t, u) du.
이제 정리 7.10( 두브 정리)을 (D(T), Y, w) 와 Co(T) 에 적용 해서, 확률측도공간 (Co(T), Co(T) nY, wo) 을 얻는다. 다음 정 리는, 이 측도공간과 위너보렐 측도공간이 일치함을 말한다.
 정리 7.12
정리 7.12
 증명
증명
정리 7.13 의 증명과 비슷한 방법으로 다음 정리도 증명할 수 있다.
 정리 7. 14 µ롤 (D(T), Y) 에서 임의의 확률측도라 하자. 그
정리 7. 14 µ롤 (D(T), Y) 에서 임의의 확률측도라 하자. 그
그러면, (C(T), 13(C(T)) )에 확률측도 µ가 존재해서, µ의 유한차원분포는 가정에서 주어진 µ(tl, … , t n) 이 된다. 이 정리의 증명은 생략한다(J ohnson[l]). 아인슈타인과 위너에
 의해서 제시된 유한차원분포(fi n i n t e dim ensio n al d i s t r i bu ti on) 가
의해서 제시된 유한차원분포(fi n i n t e dim ensio n al d i s t r i bu ti on) 가
위의 사실과 정리 7.16 에 의해서 (C(T), J3 (C(T)) )에 확률측 도 m 을 도입할 수 있다. m 이 C 。 (T) 에 집중되어 있는 것 (concen t ra t ed) 은 다음과 같이 보일 수 있다.
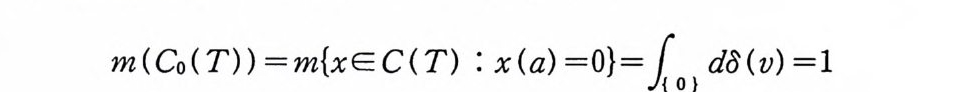 m(Co(T)) =m{xEC(T) : x(a) =O}=J 01 d o(v) =l
m(Co(T)) =m{xEC(T) : x(a) =O}=J 01 d o(v) =l
주 7.17 (7.24) 의 조건없이도 콜모고로프의 일관성 정리를 적 용해서 (D(T), Y) 에 측도를 도입했다. (C(T), :B (C(T))) 에 측도를 도입하는 데는 부등식 (7.24) 가 결정적인 역할울 한다. 다음 예 는 콜모고로프의 정 리 (정 리 7. 16) 를 만족하지 못하는 유한차원분포(보렐 측도)이다.
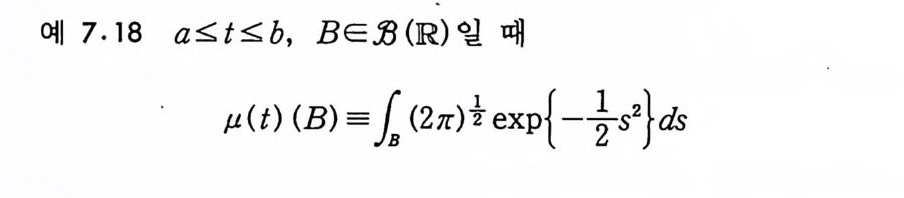 예 7-18 a 집 ~b, BE :B (lR) 일 때
예 7-18 a 집 ~b, BE :B (lR) 일 때
 \� �X�XՐ. �t;E [a, �,� i=l, 2, & , n �
\� �X�XՐ. �t;E [a, �,� i=l, 2, & , n �
, /30) �� ̹q�\��. ��췘�, �L� 1���@� �� :E (C(T) ���� ���� �� ���X��� J�LD��
 �����. 1��� 7.19 ��
�����. 1��� 7.19 ��
 n2°=° 2µ (Jn ) =— 14
n2°=° 2µ (Jn ) =— 14
주 7.20 x 가 연속이 아니면 (7. 28) 이 성립하지 않을 수도 있 다. 8 위너 측도의 존재성:넬슨의 즈o 며o [O, +(X)) 에서 정의되는 연속함수들의 공간 C[O, OO) 에 확률측 도를 도입하고, 이 측도가 위너 공간
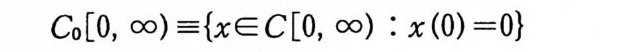 Co[O, oo) ={xE C[O, oo) : x (0) =0}
Co[O, oo) ={xE C[O, oo) : x (0) =0}
에 집중되어 있음 (concen t ra t ed) 을 보인다. R에 한 접을 추가해서 긴밀화한 (one po in t comp a cti fica ti on ) 집 합을 R 라 하자. 추가된 한 점을 00 로 표시하자.
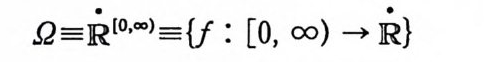 !J= R[O,. .) ={f : [O, oo) - JR}
!J= R[O,. .) ={f : [O, oo) - JR}
로 놓으면, 티코노프 (T ychono ff) 정리에 의해서 요는 긴밀한 (comp a ct) 집 합이 다. C( 요)를 요에서 정의된 연속인 실가함수들의 집합이라 하고,
 cf (요)를 다음 조건을 만족하는 함수 FEC( 요)들의 집합이라
cf (요)를 다음 조건을 만족하는 함수 FEC( 요)들의 집합이라
 그런데 Wa( t) - w (t) =oo 이므로
그런데 Wa( t) - w (t) =oo 이므로
(sup -n orm) 이 다. (8.1) 로 정의되는 함수 F 에 대해서, 함수 L 을
 (8. 6) L(F) =L(Ff) =iR.n f( u) Wn U, u) du
(8. 6) L(F) =L(Ff) =iR.n f( u) Wn U, u) du
이고 f와 f에 관계되는 (8. 6) 의 두 적분은, 채프만-콜모고로프 방정식(정리 1. 10) 에 의해서 같다. 따라서, 유한개의 점이 추가 되었을 때도 같은 결과를 얻는다. F 가 (8.1) 의 표현 이의에 다 음과 갇이 표시된다고 하자.
 (8. 7) F(w) =g(w (s1), …, w(sm)).
(8. 7) F(w) =g(w (s1), …, w(sm)).
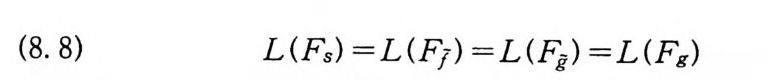 (8. 8) L(Fs) =L(F7) =L(Fg) =L(F8)
(8. 8) L(Fs) =L(F7) =L(Fg) =L(F8)
이다. (8 . 8) 의 첫번째 등식과 마지막 등식은 채프만-콜모고로프 방정식 (정리 1. 10) 에 의해서 얻는다.
 주 8,5 f 1=0 인 경우 (8. 6) 의 적분은 디락 측도(Di rac mea-
주 8,5 f 1=0 인 경우 (8. 6) 의 적분은 디락 측도(Di rac mea-
 =L(F) +L(G)
=L(F) +L(G)
다음 정리는 함수해석학에서 잘 알려진 정리이다. 정리 8.7 L 은 조밀 (dense) 부분집합 cf (요)로부터 C( 요)로 확 장 (ex t ens i on) 된다. L 의 확장은 유일하고, 연속, 선형이고 양 (po sit ive ) 이 다. 리 츠 (Rie s z) 의 표현정 리 (rep re senta t i on the orem) 에 의 해 서 다음 정리를 얻는다 (Roy den[l], Rudin [l]).
 정 리 8 . 8 다음 성 질을 만족하는 양의 정 규 보렐 측도 (po sit ive
정 리 8 . 8 다음 성 질을 만족하는 양의 정 규 보렐 측도 (po sit ive
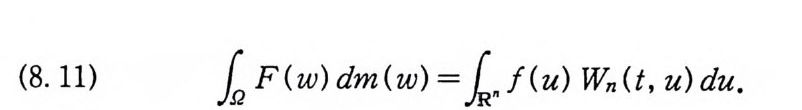 (8.11) kF (w)dm(w) ={./(u) Wn( t, u)du.
(8.11) kF (w)dm(w) ={./(u) Wn( t, u)du.
이제 J3(Q)에서 정의된 보렐 측도 m 이 Co[O, oo) 에 집중되어 있음 (concen t ra t e) 을 보이려고 한다.
 성질 a.10 c, o>O 일 때
성질 a.10 c, o>O 일 때
 lim %8) =O
lim %8) =O
 C={wEQ : lw(U-w( t n)|> 룹 j= l, 2, …, n— 1
C={wEQ : lw(U-w( t n)|> 룹 j= l, 2, …, n— 1
 c;===={(u;, Un) : luj - uni > 웅}
c;===={(u;, Un) : luj - uni > 웅}
 갤p(f, 8).
갤p(f, 8).
 m(G\0,o ) sm(G\C)
m(G\0,o ) sm(G\C)
이므로 (8. 21) 을 얻는다.
 보조정리 s.15 c>O, k 는 자연수이고, O
보조정리 s.15 c>O, k 는 자연수이고, O
이다.
 증명 Fc (k, c, o) 는 폐 집 합 (closed set) 이 므로
증명 Fc (k, c, o) 는 폐 집 합 (closed set) 이 므로
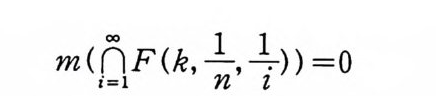 m(in°=° lF (k, —1n ,~lt )) =0
m(in°=° lF (k, —1n ,~lt )) =0
이다. 이것으로부터 (8. 23) 을 얻는다.
 정리 a.17 Co[O, CX))은 보렐 집합이고
정리 a.17 Co[O, CX))은 보렐 집합이고
서 배어 집합 (Ba i re se t)들의 6- 대수라 하자. 그러면, 물론 구간 I 는 배어 집합이다. 다음 정리는 6- 대수 J, 배어 (Ba ire )
 정리 8.18 :B o( 요 )=Y 됴있(요)
정리 8.18 :B o( 요 )=Y 됴있(요)
증명 참고문헌 (Nelson[l, Theorem 2.1 ] ) 참조. 주 8.19 넬슨 (Nelson) 은 또한 다음 집합들이 보렐 집합임을 보였다 (Nelson [니). (1) C(T). (2) 리 만 (Ri em ann) 적 분가능한 함수들의 집 합. (3) 계 단식 불연속점 Gump dis c onti nu it y) 만을 갖는 함수들의 집 합. 9 위너 측도가능한 집합의 확률계산 위너 공간에서 홍미 있는 몇 개의 위너 측도가능한 집합들의 위너 측도를 계산해 본다.
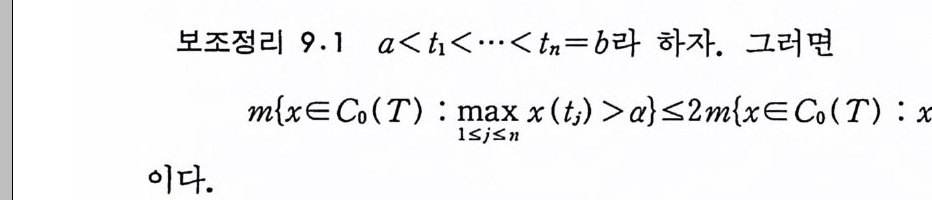 보조정리 9.1 a< t 1< … <&=b 라 하자. 그러면
보조정리 9.1 a< t 1< … <&=b 라 하자. 그러면
 증명 m{xEC 。 (T) : maxx( tj) >a }=m{x : x(b) >a}
증명 m{xEC 。 (T) : maxx( tj) >a }=m{x : x(b) >a}
 m{xEC 。 (T) : !떤?갑 x (t) >a} 갤 m{x : x(b) >a}
m{xEC 。 (T) : !떤?갑 x (t) >a} 갤 m{x : x(b) >a}
츠‘=, 며0
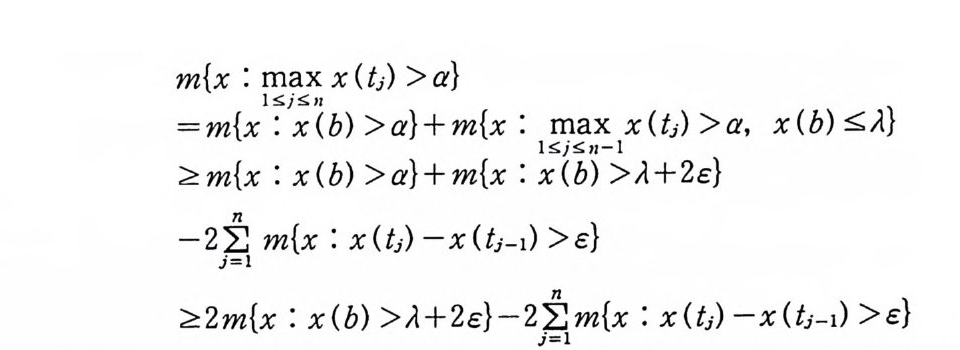 m=_2mm2{xg{{ :xx m )m S:: :{aj xxSx:x(1( 1 b b:x )) x ( >> t(Jtaaj )}}> ++_ amm}x ({{txxj- 1:: ) xI S>m(:jc bSa:} )1 1x - > I xA(+O2c >} a, x(b) :::;:A}
m=_2mm2{xg{{ :xx m )m S:: :{aj xxSx:x(1( 1 b b:x )) x ( >> t(Jtaaj )}}> ++_ amm}x ({{txxj- 1:: ) xI S>m(:jc bSa:} )1 1x - > I xA(+O2c >} a, x(b) :::;:A}
윗식의 첫번째 부등식을 보이기 위해서는 다음 부등식을 증명하 면 된다.
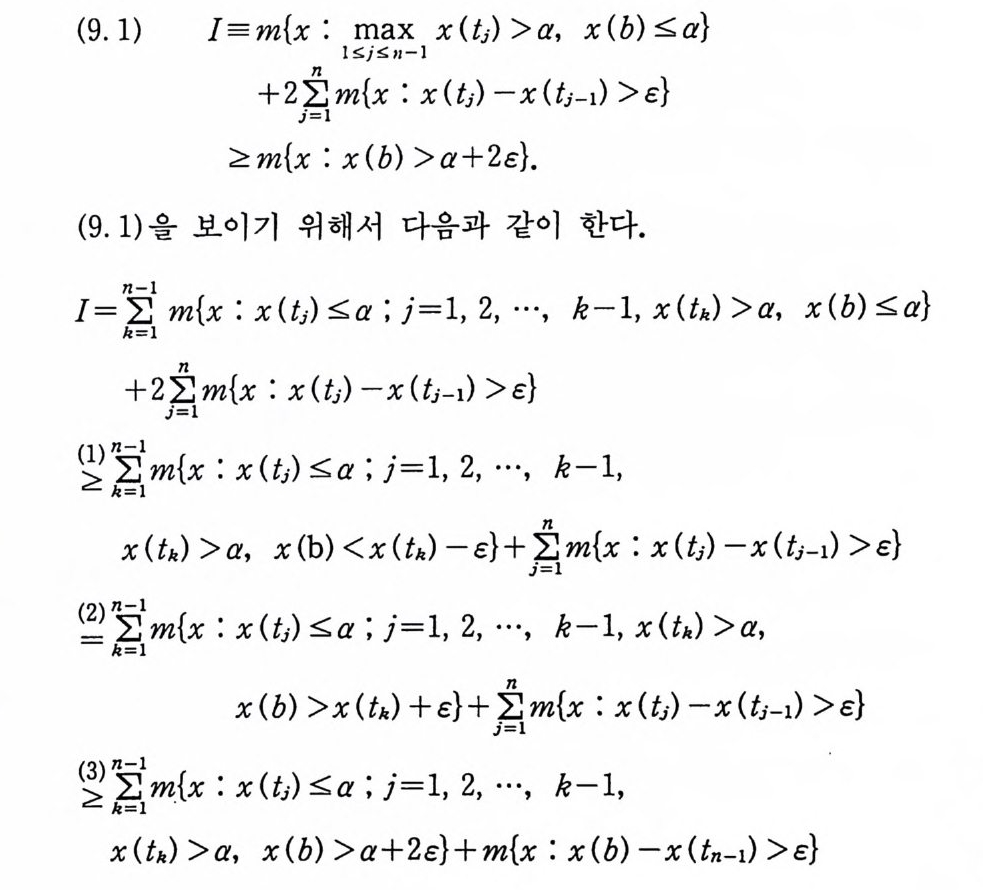 (9. 1) l=m{x : I Sm:jS a: 1x1- l x( tj) >a, x(b) ~a}
(9. 1) l=m{x : I Sm:jS a: 1x1- l x( tj) >a, x(b) ~a}
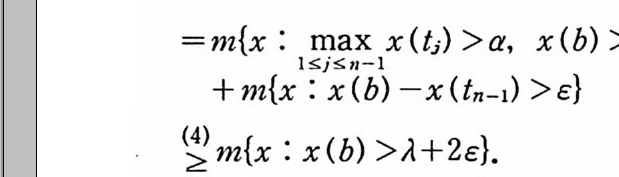 =m{x : max x( tJ >a, x(b) >J+ 2c }
=m{x : max x( tJ >a, x(b) >J+ 2c }
부등식 (1) 은 다음 집합의 포함관계로부터 얻는다.
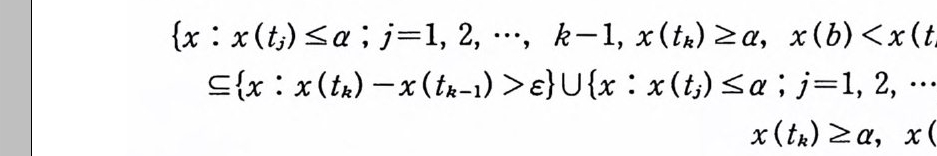 {x : X (tj) ~a ; j= l, 2, …, k-1, x(tk ) ::?:a, x(b)
{x : X (tj) ~a ; j= l, 2, …, k-1, x(tk ) ::?:a, x(b)
등식 (2) 는 다음과 같이 얻는다.
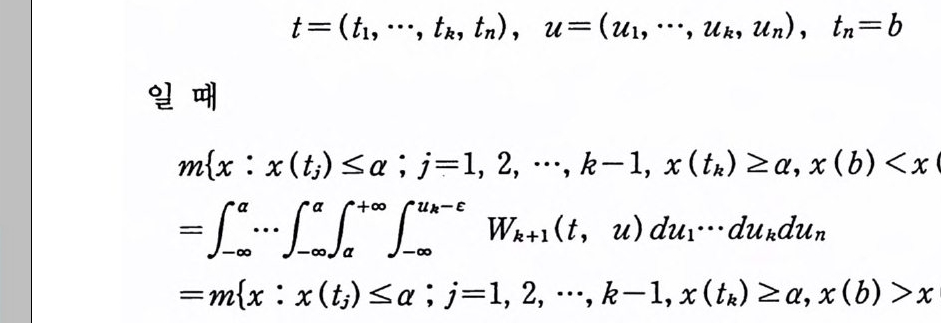 t= (h, …, [k, tn) , u=(u1, …, Uk, Un), ln=b
t= (h, …, [k, tn) , u=(u1, …, Uk, Un), ln=b
위의 마지막 등식이 성립하는 것은 다음 두 적분이 같기 때문이 다.
 1:•-£exp {-隣 n b二 ~ }dun=1~+£ exp {-넓 겁 ~}dun.
1:•-£exp {-隣 n b二 ~ }dun=1~+£ exp {-넓 겁 ~}dun.
부등식 (4) 는 다음 집합의 포함관계로부터 얻는다.
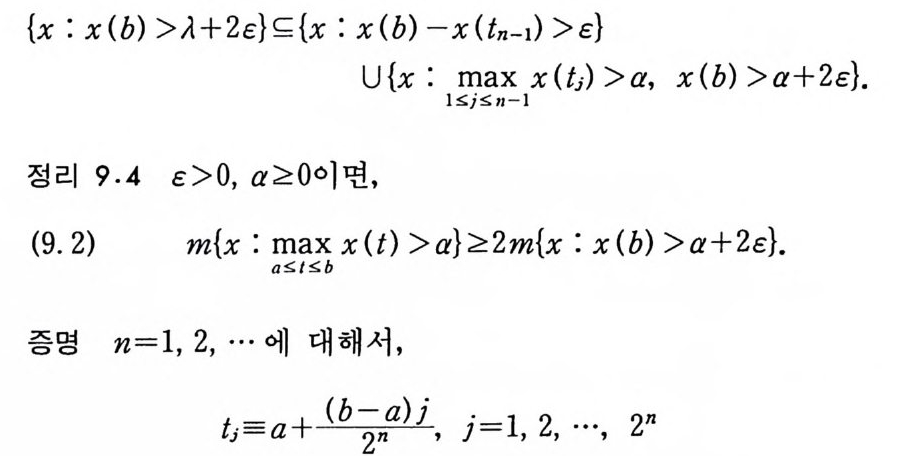 {x : x (b) >11 +2c} ~ {x : x (b) -x Un-1) > c}
{x : x (b) >11 +2c} ~ {x : x (b) -x Un-1) > c}
로 놓자. 그러면, 보조정리 9.3 에 의해서 다음 부등식을 얻는다. 모든 n 에 대해서,
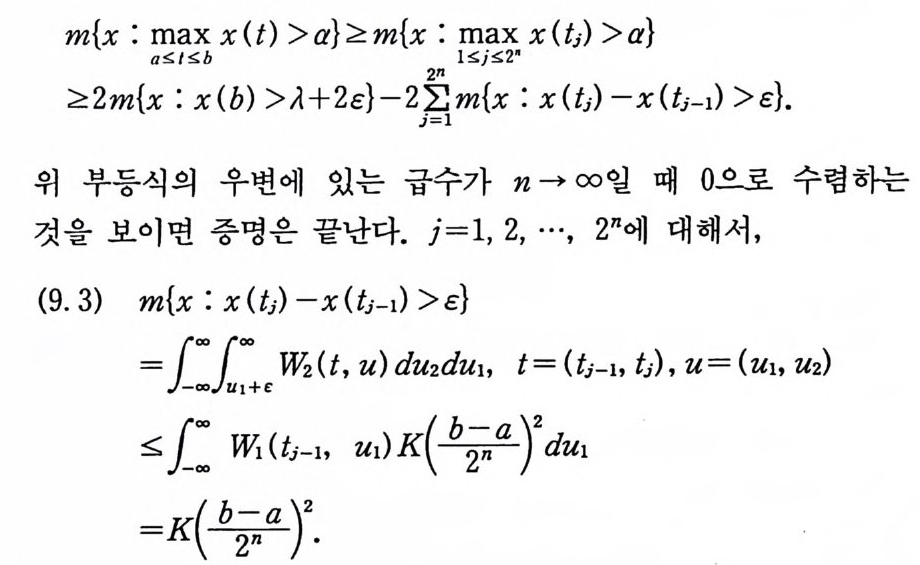 m{x : max x( t) >a}~m{x : max x( tj) >a}
m{x : max x( t) >a}~m{x : max x( tj) >a}
여기서, K 는 다음 부등식을 만족하는 상수이다.
 임의의 c>O 에 대해서,
임의의 c>O 에 대해서,
 = lci-mo• 2JJa +OO2 c W l ( b, Ul) dul
= lci-mo• 2JJa +OO2 c W l ( b, Ul) dul
 (9. 8) ,p (u)~{~ 二~ ex p{-~} : u~O
(9. 8) ,p (u)~{~ 二~ ex p{-~} : u~O
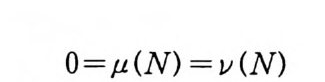 O=µ(N) =v(N)
O=µ(N) =v(N)
이므로 ))와 µ는 르베그 측도가능한 집합에서 같다.
 정리 9.7 / : R-> R 가 르베그 측도가능하면, /0 V(x) 는 위너
정리 9.7 / : R-> R 가 르베그 측도가능하면, /0 V(x) 는 위너
증명 V 는 보렐 측도가능한 함수이고, N 이 R 에서 영 보렐 집합이면 V-1(N) 은 C 。 (T) 에서 영집합이므로 V 는 위너-르베그 측도가능하다. 따라서 /0V 는 위너 측도가능하다. 변수변환정리 와 정리 9. 6 에 의해서 (9.11) 이 성립한다. 따름정리 9.8 A 가 르베그 측도가능한 집합이면,
 m{xEC 。 (T) : ma~ la ~ xb •x• (• t)• E A•• }' =fJ A n[O, oo) rp( u)du
m{xEC 。 (T) : ma~ la ~ xb •x• (• t)• E A•• }' =fJ A n[O, oo) rp( u)du
제 2 장 위너 적분의 변환정리 이 장에서는 위너 적분의 여러 가지 변환정리를 소개한다. 확 률적분의 일종인 팰리-위너-지그문드 (Pale y - W i ener-Z ygm und) 적 분을 정의하고 이 적분에 관련된 여러 가지 성질 및 팰리-위너 적분공식을 증명한다. 푸리에 변환의 개념과 유사한 푸리에-위너 (Fourie r -Wi en er) 변 환을 정 의 하고 프란세 렐 관계 (Plancherel's relati on ) 와 파시 발 (Parseval) 관계 가 성 립 하는 함수족을 조사한다. 1 카메룬-마틴 변환정리 함수
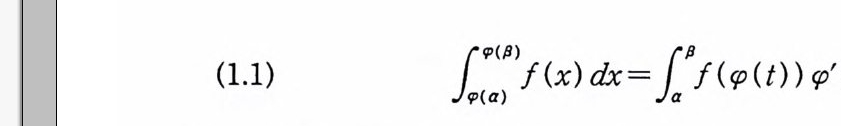 (1.1) 1;:;)1 (x) dx= lp1 (< p (t) )
(1.1) 1;:;)1 (x) dx= lp1 (< p (t) )
가 성립하는 것은 잘 알려진 사실이다. 이와 같은 변환정리가 위너 적분에서도 성립할 수 있을까? 이 질문에 대 한 처 음 정 리 가 카메 룬-마틴 (Cameron-Marti n) 변환정 리로서 위너 적분과 파인만 적분은 물론 확률적분 등에서 널리 유용하게 사용된다. 위너 측도공간에서 거의 모든 평행변환은 위 너 측도가능성울 보전하지 않지만 (1 장 따름정리 5.12) 다음에 소 개하는 카메룬-마틴의 변환정리는 어떤 특정한 평행변환에 대한 긍정적인 결과이다. 이 정리는 위너 적분과 파인만 적분에서는 물론이고 확률론에서도 많이 이용되는 유용한 정리이다.
 구간 T=[a, 짜에서 유계변동인 함수들의 집합을 BV(T) 라
구간 T=[a, 짜에서 유계변동인 함수들의 집합을 BV(T) 라
이 성립한다.
 주 Xo 든 Co(T) 이고 x6( t)=¢(t)이다. 따라서 (1. 3) 의 변환 L
주 Xo 든 Co(T) 이고 x6( t)=¢(t)이다. 따라서 (1. 3) 의 변환 L
이다.
 (1. 9) I =lnCo ,( TT)l F(Pny ) dm(y)
(1. 9) I =lnCo ,( TT)l F(Pny ) dm(y)
 n - oo 일 때, (1. 11) 과 (1. 12) 의 우변의 극한도 각각
n - oo 일 때, (1. 11) 과 (1. 12) 의 우변의 극한도 각각
 에 의해서 유계된다. (1) 의 경우 증명이 끝난다.
에 의해서 유계된다. (1) 의 경우 증명이 끝난다.
(b) F 가 유계이고 연속이면 (1.4)가 성립한다.
 증명 (a) fa b p(t )dx( t)는 x 의 함수로서 연속이므로 g (x) 는
증명 (a) fa b p(t )dx( t)는 x 의 함수로서 연속이므로 g (x) 는
 (1. 24) 1 。(7) F( y) dm(y) =fc0m F(y ) d (11°L- 1) (y)
(1. 24) 1 。(7) F( y) dm(y) =fc0m F(y ) d (11°L- 1) (y)
이다.
 증명 정리 1. 1 의 증명에서, L 이 .01 -.0 1 측도 가능하므로
증명 정리 1. 1 의 증명에서, L 이 .01 -.0 1 측도 가능하므로
 정리 1.5 Xo 가 정리 1. 1 에서 주어진 함수일 때, F(x) 가 위너
정리 1.5 Xo 가 정리 1. 1 에서 주어진 함수일 때, F(x) 가 위너
다음 정리는 따름정리 1. 2(a) 를 복소수까지 확장한 결과이다. 위너 측도공간에서의 복소수함수의 적분은 피적분함수를 실수부 와 허수부로 나누어서 정의한 적분의 복소수 합이다.
 정리 1.6 rp(t)E C(T) nBV(T) 라 하자. 모든 AEC 에 대해
정리 1.6 rp(t)E C(T) nBV(T) 라 하자. 모든 AEC 에 대해
온 위너 적분가능한 함수이다. 이제 (1. 30) 의 좌변이 A 의 함수로서 정함수임울 보이면, 유일 성 정 리 (uniq u eness the orem) (Rudin [l, p. 210]) 에 의해서 (1. 30) 이 성립한다. 이것을 보이기 위해서 모레라 (Morera) 정리 (Rudin [ !, p. 209] ) 를 사용한다. (1. 30) 의 좌변의 피적분함수는 정함수이다. lln -110 라 하고, 모든 n 에 대해서 |llnl~M 되는 M 을 택하자.
 그러면, uER 에 대해서,
그러면, uER 에 대해서,
는유계이고
 io( T) |exp { _Ai b¢( t )d x(t) } |dm(x)
io( T) |exp { _Ai b¢( t )d x(t) } |dm(x)
 (1.36) j I(f bp ( t)d x(t) ) dm(x)
(1.36) j I(f bp ( t)d x(t) ) dm(x)
부록 정리 4. 5 에 의해서 (1. 35) 를 얻는다. (1. 36) 은 부록 정리 4.7 로부터 얻는다. 주 정리 1. 7 은 카메룬-마틴 변환정리를 사용해서 얻을 수도 있다 (Cameron-Martin [ 이 ) . 다음은 위너 적분과 파인만 적분론에서 많이 사용되는 매우 유 용한 정리이다.
 정 리 l . 8 (팰 리 -위 너 정 리 : Paley- W i en er)
정 리 l . 8 (팰 리 -위 너 정 리 : Paley- W i en er)
 (1.3 8) [¢,(t)rpj(t)d t= {l: t=j
(1.3 8) [¢,(t)rpj(t)d t= {l: t=j
이고 정리 1. 7 에 의해서
 Y~N(O, ll cp||웅)
Y~N(O, ll cp||웅)
이므로 (1. 42) 가 성립한다. (1. 40) 은 부록정 리 4. 7 로부터 얻는다. 주 1.9 (1) 정리 1. 8 은 카메룬-마틴 변환정리를 사용해서도 얻을 수 있다 (Cameron and M~rtin [ 3]).
 (2) 이 절에서 다룬 함수 rpjE C(T) nBV(T) 를 rpiE L2(T)
(2) 이 절에서 다룬 함수 rpjE C(T) nBV(T) 를 rpiE L2(T)
로 정의하면, F 는 위너 적분가능하고, k 가 기수이면,
 !cCoo (c TT )) F(x) dm(x) =0.
!cCoo (c TT )) F(x) dm(x) =0.
카메룬-마틴의 변환에 관한 정리를 하나 더 소개하고 이 정리 의 결과를 이용해서, 비유계함수의 파인만 적분가능성 조사에 사 용되는 위너 적분을 계산한다.
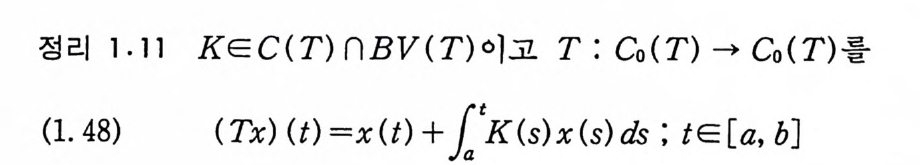 정리 1.11 KEC(T)nBV(T) 이고 T : Co(T)-Co(T) 를
정리 1.11 KEC(T)nBV(T) 이고 T : Co(T)-Co(T) 를
로 정의하자. (T 는 전단사(1 -1, onto ) 함수이고 T 와 T 기 는 연속이 다) 그러면, 다음 사실이 성립한다. (1) T 는 위너 측도가능하다.
 (2) AE. 십 1 이면,
(2) AE. 십 1 이면,
증명 Yeh [9, Theorem 34. 8] 참조.
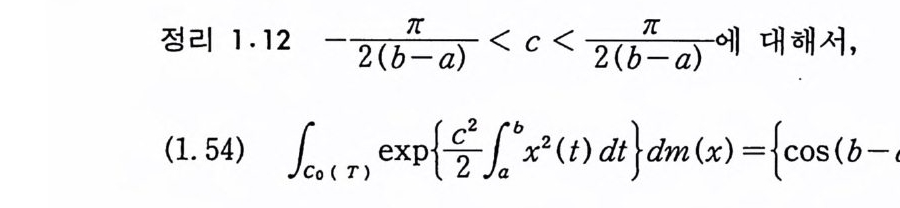 정리 1.l2 — 2(b7-[ a ) < c < 2(b7[— a) 에 대해서,
정리 1.l2 — 2(b7-[ a ) < c < 2(b7[— a) 에 대해서,
이다.
 증명 편의상 T=[O,1] 인 경우로 한정해서 증명하자.
증명 편의상 T=[O,1] 인 경우로 한정해서 증명하자.
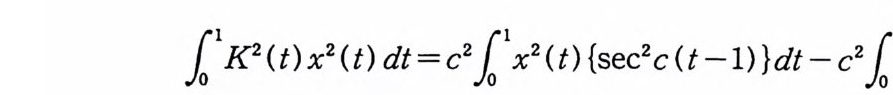 11K2( t)갔(t) d t =c211 갔(t) {sec2c (t-1 ) }d t -c2 /o 1 균(t) dt
11K2( t)갔(t) d t =c211 갔(t) {sec2c (t-1 ) }d t -c2 /o 1 균(t) dt
울 얻고, 이들 식을 (1. 56) 에 대입하면 (1. 54) 를 얻는다.
 주 1.1 3 (1) (1. 54) 의 좌변의 적분이 0 보다 크거나 갇기 때문
주 1.1 3 (1) (1. 54) 의 좌변의 적분이 0 보다 크거나 갇기 때문
정리 1. 12 보다 좀더 일반적인 위너 적분공식을 소개한다. 이 정 리 의 증명 은 Cameron-Marti n [ 2, Corollary 끽 참조.
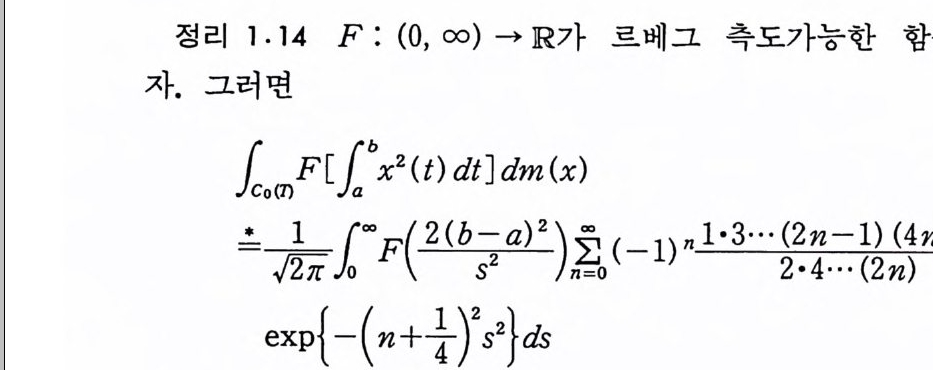 정리 1.14 F : (0, oo) 一 lR 가 르베그 측도가능한 함수라 하
정리 1.14 F : (0, oo) 一 lR 가 르베그 측도가능한 함수라 하
이 성립한다. 2 팰리-위너-지그문드 (P.W.Z.) 적분 함수 f가 〔 a ,이에서 유계변동이고, g가 연속함수일 때 리만
-스틸 체 스 (Ri em ann-St iel tje s ) 적 분
(2. 1) fbf (t ) dg (t) a 은 존재한다. 물론, /EL2(T) 인 경우 이 적분의 존재성은 보장 되지 않는다. 이 절에서는 L2(T) 에 속하는 함수들에 대한 팰리 - 위 너 -지 그문드 (Paley -W ien er-Z y gmu nd) 적 분을 (간단히 P. W. Z. 적분이라 쓴다) 정의하고 이 적분에 관한 여러 성질을 얻는다. I 가 유계변동인 경우 f의 리만-스틸체스 적분과 P. W . Z. 적분은 일치한다(정리 2.4). P. W. Z. 적분을 이용해서, 앞 절에서 소개 한 위너 적분의 변환정리를 확장한다. a, /3E L2(T) 일 때, a, /3의 내적 (inn er pro duct) (a, /3)은 (2. 2) (a, /3) =1ba (t) {J (t) dt a 로 정의한다. {ek} 가 L2(T) 에서 완비정규 직교집합 (com p let e orth o normal se t)이라 하자. 그러면, 각 aEL2(T) 에 대해서, C 翼, (2. 3) a= k~=I (a, ek) ek 이다. (2. 3) 의 수령은, 이 급수의 부분합이 L2(T) -노름에서 a 로 수령하는 것을 뜻한다. 다음의 파시발 등식 (Parseval ide nti ty) 도 성립한다. (2. 4) llall 는 ~oo . (a, ek)2 k=l 정의 2.1 e={ek} 가 L2(T) 에서 완비정규 칙교집합이고, ekE
C(T)nBV(T) 라 하자. aEL2(T), xEC 。 (T) 일 때, x 에 대 한 a 의 팰리-위너一지그문드 (P . W. Z.) 적분을 다음의 극한으로 정의한다.
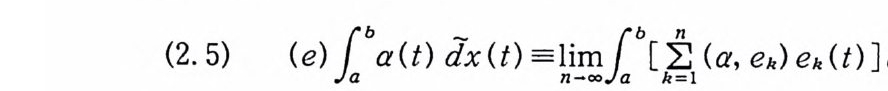 (2. 5) (e) lba a(t ) dx (t) =Lni-!o! o: .. l1a b [h'lJ= 1l ( a, eh) eh (t) ]d x (t) .
(2. 5) (e) lba a(t ) dx (t) =Lni-!o! o: .. l1a b [h'lJ= 1l ( a, eh) eh (t) ]d x (t) .
주 2.2 (2.5) 의 P. W. Z. 의 적분은 완비정규 직교집합 (e) 에 관계되므로 적분 앞에 (e) 를 표시했으나, 사실상, 이 적분은 (e) 와는 독립적이다(정리 2. 5). (2. 5) 의 P. W. Z. 적분은 a.e.xE c 。 (T) 에 대해서 존재한다(정리 2. 3 ).
 (2.6) Xk(x)=1bek( t)d x( t), k=l, 2, •••
(2.6) Xk(x)=1bek( t)d x( t), k=l, 2, •••
증명 {(a, ek)Xk} 의 0 이 아닌 원소들은 서로 독립이고,
 (2. 9) (a, ek)Xk~N(0, (a, ek)2)
(2. 9) (a, ek)Xk~N(0, (a, ek)2)
이다. 부록 정리 5.17( 콜모고로프 정리)에 의해서,
 (2. 10) k~0=0I ( a, ek ) 2 < co
(2. 10) k~0=0I ( a, ek ) 2 < co
임을 보이면 된다. 그런데 (2 . 10) 은 파시발 등식 (2. 4) 에 의해서 성립한다. 다음 정리는 aEBV(T) 인 경우, a 의 리만-스틸체스 적분과 P. W . Z. 적분이 m-a. e. x 에 대해서 같음을 보여 준다. 따라서, P. W. Z. 적분은 리만스틸체스 적분의 확장이다.
 정리 2-4 aEBV(T) 이고, e={ek} 가 정의 2.1 에서 주어전
정리 2-4 aEBV(T) 이고, e={ek} 가 정의 2.1 에서 주어전
 이므로
이므로
이므로 (2.11) 이 성립한다. 다음 정리는, P. W. Z. 적분을 어떤 특정한 완비정규 직교집합 울 가지고 정의했으나, 이 적분이 그 집합과는 본질적으로 독립 임을 보여준다.
 정리 2:5 e={ek} 가 정의 2.1 에서 주어진 집합이라 하고, c=
정리 2:5 e={ek} 가 정의 2.1 에서 주어진 집합이라 하고, c=
 이라 하자. 그러면 aEL2(T) 일 때, a. e. xEC 。 (T) 에 대해서,
이라 하자. 그러면 aEL2(T) 일 때, a. e. xEC 。 (T) 에 대해서,
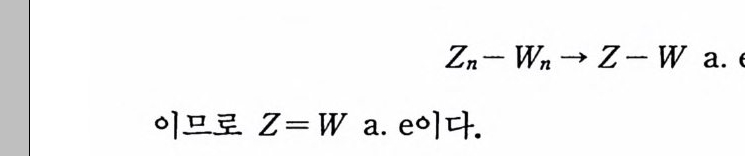 Zn - Wn - Z-W a. e.
Zn - Wn - Z-W a. e.
기호 2-6 P. W. Z. 적분이 완비정규집합과는 본질적으로는 무 관하므로 앞으로는 정의 2.1 에서 사용한 기호에서 (e) 를 생략하 고 쓰기로 한다. 죽, a 의 x 에 대한 P. W. Z. 적분을
 (2. 23) lba ba (t ) dx( t)
(2. 23) lba ba (t ) dx( t)
로 표시한다. P. W. Z. 적분도 리 만-스틸체 스 적분과 갇이 선형 성 (line arity ) 울 만족한다. 다음 정리는 P. W. Z. 적분의 선형성이다.
 정리 2-7 a, ai, a2EL2(T), c 가 임의의 상수라 하자.
정리 2-7 a, ai, a2EL2(T), c 가 임의의 상수라 하자.
(2. 26)
 fa b[aI (t) + a2 (t) ] Jx (t) =LJba aI (t) & (t) +Jf a ba2( t) 죠 (t)
fa b[aI (t) + a2 (t) ] Jx (t) =LJba aI (t) & (t) +Jf a ba2( t) 죠 (t)
증명 (1) 정의 2.1 과 리만-스틸체스 적분의 선형성으로부터 증명된다. (2) 와 (3) 정리 2.3 을 이용해서 (1)과 같은 방법으로 증명한 다. 주 2.8 정리 2. 7 (1)로부터 a 의 P. W. Z. 적분이 s-a. e. x 에 서 존재함을 알 수 있다. 따라서 정리 2. 3 에서 a. e. x 를 s-a. e. x 로 대치해도 된다. 같은 방법으로 정리 2.4 와 정리 2.5 도 s-a. e. X 에 대해서 성립한다.
 카메룬-마틴 번환정리의 확장
카메룬-마틴 번환정리의 확장
인 경우, 리만-스틸체스 적분을 P. W. Z. 적분으로 바꾸어 변환 공식 (1. 4) 를 얻는다. 따라서 이 정리는 카메룬-마틴 변환정리의 확장이다. 먼저 이 정리에 필요한 보조정리를 증명하자.
 보조정리 2.9 n=l, 2, … 에 대해서,
보조정리 2.9 n=l, 2, … 에 대해서,
 (2. 30) (Lx) (t) =x( t) +xo( t)
(2. 30) (Lx) (t) =x( t) +xo( t)
임을 다음 식에 의해서 보일 수 있다.
 lxo( t)- xo,n( t)1 =11a1 (rp ( s) —(f)n (s))dsl
lxo( t)- xo,n( t)1 =11a1 (rp ( s) —(f)n (s))dsl
 亡 io( T ) F(x+xo)ex p{―「ra p(t) dx( t)} dm(x)
亡 io( T ) F(x+xo)ex p{―「ra p(t) dx( t)} dm(x)
다음 정리는 따름정리 2.11 을 복소수로까지 확장한 결과이다. 정리 1. 6 의 증명에서와같이 해석적 연속의 방법을 이용해서 증명 하면 된다.
 정리 2-13 rp EL2(T) 라 하자. 모든 Aec 에 대해서,
정리 2-13 rp EL2(T) 라 하자. 모든 Aec 에 대해서,
 이다. / : R-R 가 르베그 측도가능한 함수이면,
이다. / : R-R 가 르베그 측도가능한 함수이면,
(3) 정리 2.16 롤 포함하는 일반적인 결과는 정리 2. 26 에서 다 룬다. (4) 정 리 2. 16 을 {(/J1 , …, rp n} 이 직교집 합 (or t ho g onal set) 인 경 우로 확장할 수 있다. 이 경우에 (2. 48) 은 다음과 같이 된다.
 (2.49) f Co ( T) f(.lfa b (•fJ 1 (t )Jx( t) ,….,lfa b ¢n(t )Jx( t) ) dm(x)
(2.49) f Co ( T) f(.lfa b (•fJ 1 (t )Jx( t) ,….,lfa b ¢n(t )Jx( t) ) dm(x)
이다. 따라서 다음 정리를 얻는다.
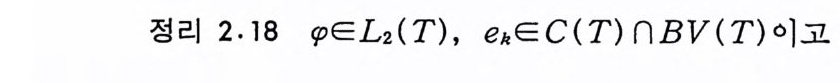 정리 2.18
정리 2.18
L2(T) 에서 완비정규 직교집합이라 하자. 그러면
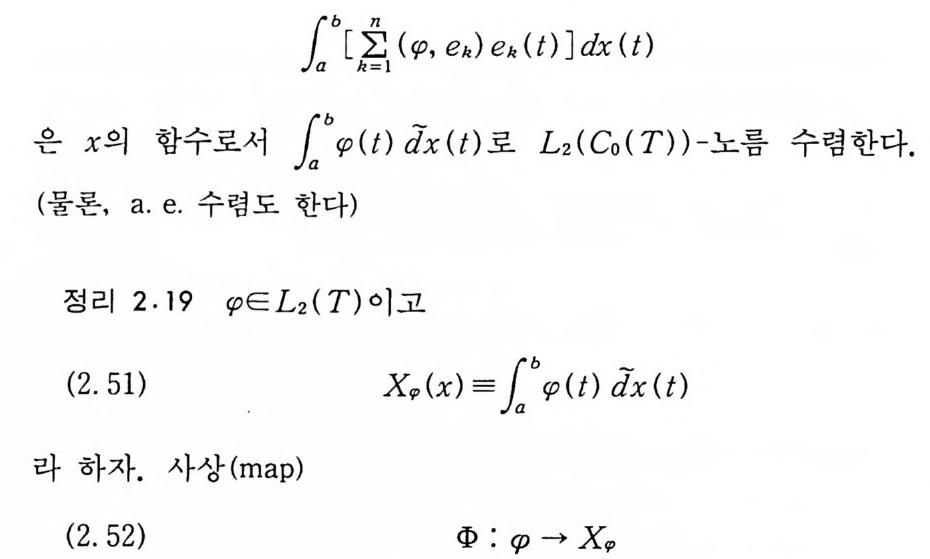 1b[£1 (
1b[£1 (
은 L2(T) 롤 L2(Co(T) )의 폐부분공간 위로 (on t o) 보내는 선형 거 리 보존 (line ar iso metr y ) 사상이 다. 증명 선형성 (li near ity)은 P. W. Z. 적분의 선형성으로부터 얻 는다. 거리보존성은 다음에 의해서 증명된다.
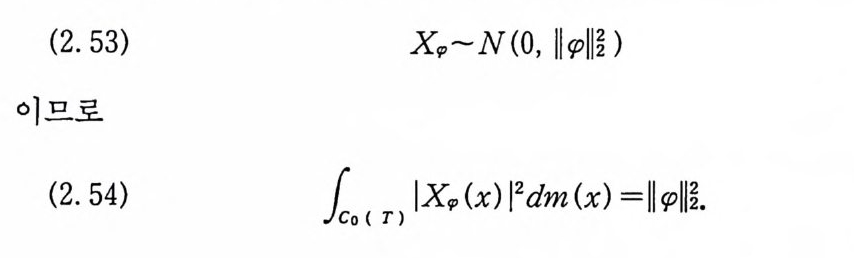 (2. 53) x,.,~N(o, 11 rp1 rn )
(2. 53) x,.,~N(o, 11 rp1 rn )
따름정리 2.20 (2. 52) 에서 정의된 사상 O 는 내적 (inn er pro d- uct) 를 보전한다. 죽,
 (2.55) (XOI, x김 = (
(2.55) (XOI, x김 = (
증명 힐베르트 공간(Hi lber t sp a ce) 에서 노름을 보전하는 사상 은 내적을 보전한다. 참고 힐베르트 공간에서 내적과 노름 사이에는 다음 관계가 성립한다.
 (2. 56) (h, k) =-¼-
(2. 56) (h, k) =-¼-
다음 두 적분은 존재하고 그 적분값은 같다.
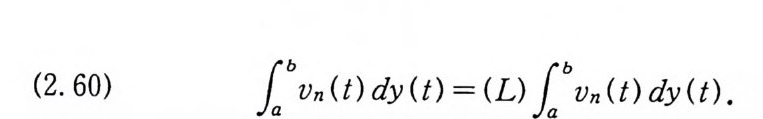 (2. 60) 1a \n (t) dy (t) = (L) 1a \n (t) dy (t) .
(2. 60) 1a \n (t) dy (t) = (L) 1a \n (t) dy (t) .
여 기 서 (2. 60) 의 우변 적 분은, 유계 변동 (bounded varia t i on ) 함 수 y에 의해서 만들어진 측도에 관한 르베그 적분이다.
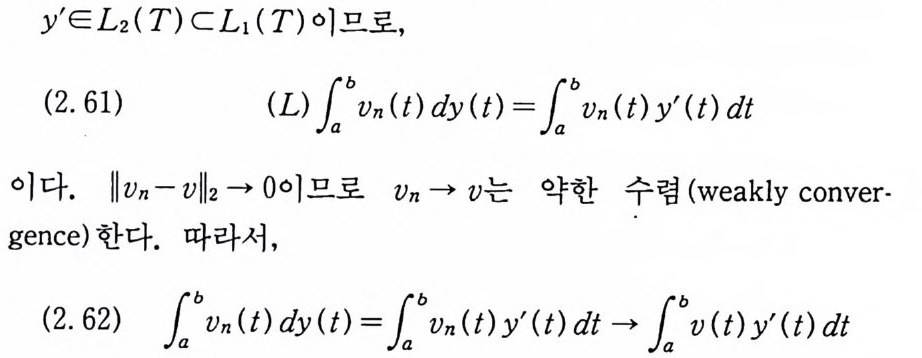 y'E L2( T) CL, ( T) 이므로,
y'E L2( T) CL, ( T) 이므로,
 이므로 (2. 57) 이 성립한다.
이므로 (2. 57) 이 성립한다.
 정리 2.22 µ를 J3 (L2(T)) 에서 정의되는 복소수 보렐 측도라
정리 2.22 µ를 J3 (L2(T)) 에서 정의되는 복소수 보렐 측도라
증명 P. W. Z. 적분의 정의에 의해서,
 (2.64) Lbv(t) &(t)=홀』\(t )en (t )d t lben (t )dx( t)
(2.64) Lbv(t) &(t)=홀』\(t )en (t )d t lben (t )dx( t)
따름정리 2.23 µ를 L2(T) 에서 복소수 보렐 측도라 하자. F 를
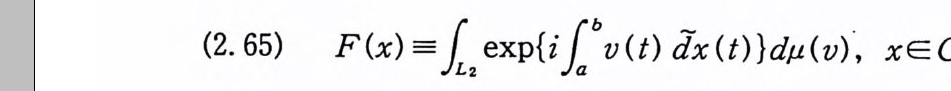 (2. 65) F(x) =12exp {i1b v( t) dx(t) }d µ(v), xECo(T)
(2. 65) F(x) =12exp {i1b v( t) dx(t) }d µ(v), xECo(T)
로 정의하면, s-a. e. x 에 대해서 F(x) 는 존재하고, 위너 적분 가능하다. G 를
 (2. 66) G(x) =12exp {i(
(2. 66) G(x) =12exp {i(
 이므로 P(x, w) 는 (x, w) 의 함수로서 보렐 측도 가능하다. 각 v
이므로 P(x, w) 는 (x, w) 의 함수로서 보렐 측도 가능하다. 각 v
의 관계는 다음의 P. W. Z. 적분의 부분적분공식에 의해서 설명 된다.
 정 리 2 . 24 (1) m X m-a. e. (x, w) E C 。 ( T) X Co ( T) 에 대 해
정 리 2 . 24 (1) m X m-a. e. (x, w) E C 。 ( T) X Co ( T) 에 대 해
의 공분산행 렬 (covari an ce matr i x ) 을 A 라 하고 A 는 non-
 s i n g ular(IAI*O) 라 하자. 그러면, /(u)exp {—}
s i n g ular(IAI*O) 라 하자. 그러면, /(u)exp {—}
 증명 R. Ewan [!, Theorem 2. 이 참조.
증명 R. Ewan [!, Theorem 2. 이 참조.
 그러면, /(u)ex p{―§창가이 Rn 에서 적분가능할 필요충분조
그러면, /(u)ex p{―§창가이 Rn 에서 적분가능할 필요충분조
증명 R. Ewan[l, Theorem 2. 사 참조. 3 위너 공간의 이동
 h 가 임의의 주어진 실수일 때 변환 Th : Co(T) - Co[a+h,
h 가 임의의 주어진 실수일 때 변환 Th : Co(T) - Co[a+h,
로 정 의 하자. 그러 면 Th 는 선형 거 리 보존 동형 (line ar iso metr i c
 iso morph is m ) 사상이 다. 또한 Th 는 바나하 대 수 Co ( T) 를 바나하
iso morph is m ) 사상이 다. 또한 Th 는 바나하 대 수 Co ( T) 를 바나하
 (2) Th 는 위너 측도가능한 함수이다.
(2) Th 는 위너 측도가능한 함수이다.
이므로 F 는 위너 측도가능하다. 식 (3. 4) 는 식 (3. 3) 과 변수변환정리로부터 얻는다. 위너 측도공간과 위너 적측도공간 사이의 변환에 관한 성질을 알아보기로 하자. 먼저 다음 두 정리를 소개한다• 성질 3 . 4 는 쉽 게 증명할 수 있으므로 증명은 생략한다.
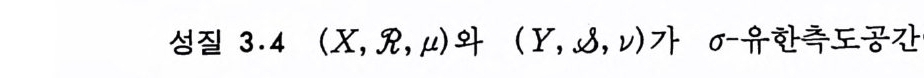 성질 3.4 (X: 나)와 (Y, .sJ, v) 가 a- 유한측도공간이라 하
성질 3.4 (X: 나)와 (Y, .sJ, v) 가 a- 유한측도공간이라 하
 자. F : X-Y 가 究-의 측도가능한 함수이고, 모든 u- 영집합
자. F : X-Y 가 究-의 측도가능한 함수이고, 모든 u- 영집합
증명 (3.5) 의 우변이 좌변에 포함되는 것만 증명하면 충분하 다. 먼저,
 (3. 6) Yi x~~ 究 X 의
(3. 6) Yi x~~ 究 X 의
이므로 (3. 7) 이 증명된다. 이제 H가 (3.5) 의 우변의 원소라 하자. 그러면 H 는 다음과 같이 표시된다.
 (3. 10) H=H1UN1,
(3. 10) H=H1UN1,
 oo __ oo
oo __ oo
 (2) H-1x= (x|m, x|T2— X( c))
(2) H-1x= (x|m, x|T2— X( c))
(3) H와 H-1 는 선형 (line ar) 이다.
 주 H(x|m, x1T2-x(c))(t) ={xx (( ct)) +: xa::l:r;: , t( :t:): ; :c- x (c) : c:::;: t:::;: b
주 H(x|m, x1T2-x(c))(t) ={xx (( ct)) +: xa::l:r;: , t( :t:): ; :c- x (c) : c:::;: t:::;: b
증명 (2) 는 (1)로부터 얻는다. (1)의 증명 : Co(T) 의 구간 [에 대해서 (3.18) 이 성립함을 보 이면 된다.
 a=to < t1< …< &=C< ln+I< …< ln+m=b
a=to < t1< …< &=C< ln+I< …< ln+m=b
 aj< y(c ) +z(tJ·) 三 /3; ; j= n+l, …, n+m}
aj< y(c ) +z(tJ·) 三 /3; ; j= n+l, …, n+m}
임을 보일 수 있다. 따라서 (3. 20) 과 (3. 22) 에 의해서 (3.18) 이 증명된다.
 따름정리 3.9 (1) N 이 Co(T) 에서 보렐 영집합이면 H-1N 은
따름정리 3.9 (1) N 이 Co(T) 에서 보렐 영집합이면 H-1N 은
증명 성질 3.4, 정리 3.8 로부터 증명된다.
 정리 3.10 H 가 (3.17) 로 주어전 변환이라 하자. F 가 Co(T)
정리 3.10 H 가 (3.17) 로 주어전 변환이라 하자. F 가 Co(T)
증명 따름정리 3.9 와 변수변환정리로부터 증명된다. 정리 3.11 G 가 Co(T1) 에서 위너 측도가능한 함수라 하자. 그러면,
 (3. 23) F(x) =G(xlr.) ; xE T
(3. 23) F(x) =G(xlr.) ; xE T
는 C 。 (T) 에서 위너 측도가능하고
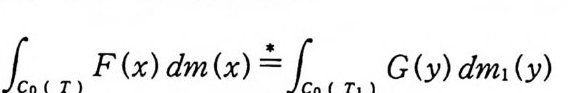 JCo ( T) F (x) dm (x) 汀./Co ( T1 ) G (y) dmI (y)
JCo ( T) F (x) dm (x) 汀./Co ( T1 ) G (y) dmI (y)
이다.
로 놓자. 그러면
 증명 (y ,z)ECo(T1)XCo(T2) 에 대해서,
증명 (y ,z)ECo(T1)XCo(T2) 에 대해서,
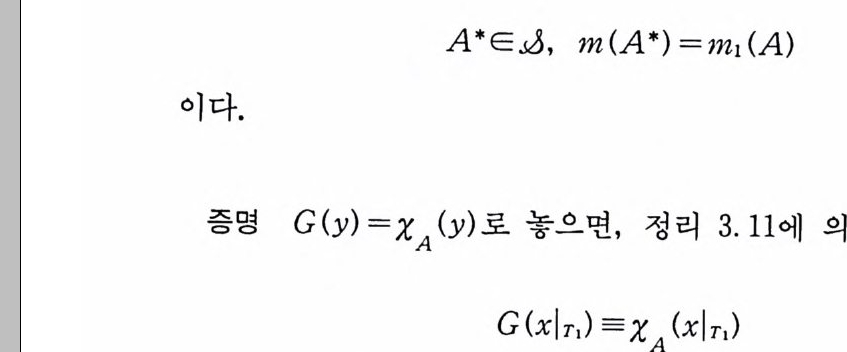 A*E. 0, m(A*) =m1(A)
A*E. 0, m(A*) =m1(A)
은 C 。 (T) 에서 측도가능하다. 그런데
 %(x1m) ={01 :: Xx|| T홉 로 AA
%(x1m) ={01 :: Xx|| T홉 로 AA
로 정의하자. 여기서 y*는 y를 T 로 확장한 함수이다. 그러면 G 는 Co(T1) 에서 위너 측도가능하고
 (3. 26) 1omF (x) dm (x) = 1o
(3. 26) 1omF (x) dm (x) = 1o
(3) Ta 는 x 의 함수로서 연속함수가 아니다. 성질 3.14 Ta 는 보렐 측도가능하다(따라서 확률변수이다).
 증명 {xE Co [O, oo) : Ta (x) :;;;: t}이 보렐 집 합임 을 보이 자.
증명 {xE Co [O, oo) : Ta (x) :;;;: t}이 보렐 집 합임 을 보이 자.
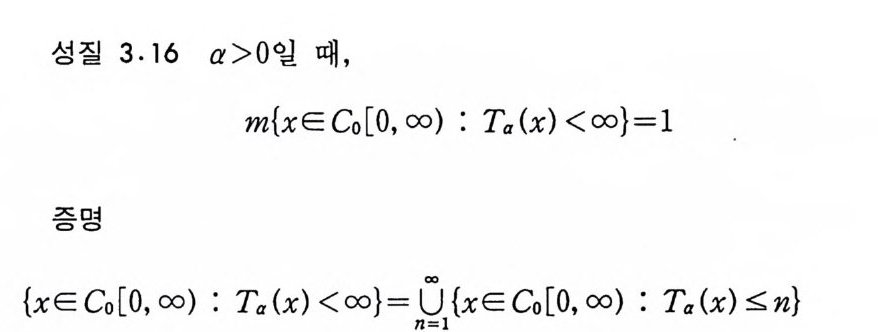 성질 3.16 a>O 일 때,
성질 3.16 a>O 일 때,
이고, 이 집합들은 중가수열이다. 따라서, 성질 3.15 에 의해서,
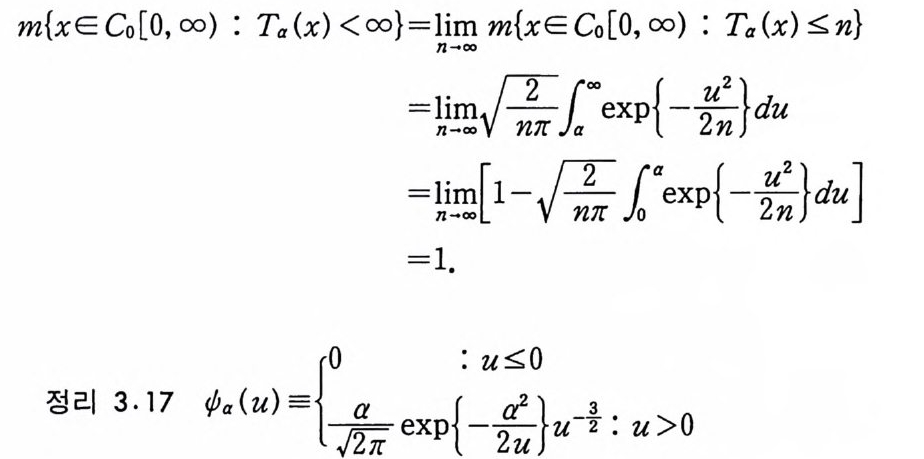 m{xE Co[O, oo) : Ta (x) < oo}=ln i-OmO m{xE Co[O, oo) : Ta(X) ~n}
m{xE Co[O, oo) : Ta (x) < oo}=ln i-OmO m{xE Co[O, oo) : Ta(X) ~n}
라고 하자. 그러면 moT감 는 르베그 측도에 대해서 절대연속 (absolute l y conti nu ous) 이고, 라돈-니코딤 (Radon-Ni ko dy m) 도함 수는 'P a(u) 이다.
 증명 O< t
증명 O< t
이다. 변수변환,
 u=a2t /v 2
u=a2t /v 2
에 의해서, (3.30) 의 우변 적분은 다음과 같이 된다.
 (3. 31) I= 昌 Io( - 柱)나 ex p{-:汀 a}du
(3. 31) I= 昌 Io( - 柱)나 ex p{-:汀 a}du
 m(Bi) =iCoo (I OO, , I1 l) xBBl,
m(Bi) =iCoo (I OO, , I1 l) xBBl,
 m (A1) ===!ciiCCCoooooo I[I[II OoOOttoo ,,,, ,• tttti11ttI ti---- 1]tt tt ooooX l]lIA A ,xX .(AAAAx, ,() < Tdxm)x d) ( mdxm) ( x()x )
m (A1) ===!ciiCCCoooooo I[I[II OoOOttoo ,,,, ,• tttti11ttI ti---- 1]tt tt ooooX l]lIA A ,xX .(AAAAx, ,() < Tdxm)x d) ( mdxm) ( x()x )
증명 보조정리 3.19 와 3.18, 식 (3.30) 과 (3.31) 에 의해서 다 음 식을 얻는다.
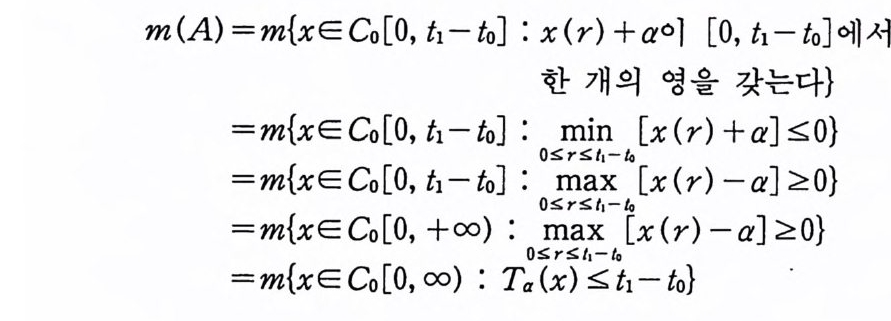 m(A) =m{xECo[O, ti_따 : x(r) +a 이 [O, t 1- t o] 에서 적어도
m(A) =m{xECo[O, ti_따 : x(r) +a 이 [O, t 1- t o] 에서 적어도
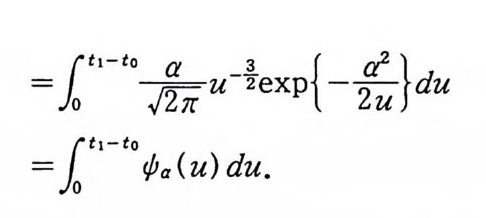 = 1 ti-t o½u- 홍 ex p{ -률 }du
= 1 ti-t o½u- 홍 ex p{ -률 }du
4 완비정규 직교집합 위너 적분과 파인만 적분론에서 유용하게 사용되는 위너 공간 에서의 완비정규 직교집합을 소개한다. 먼저, L2(R) 에서 정규직 교집합인 에르미트 (Herm it e) 함수를 정의하고 이것을 이용해서 L2(Co(T)) 에서 완비정규 직교집합을 찾아본다.
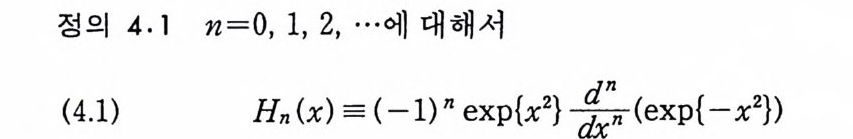 정의 4, 1 n=0, 1, 2, …에 대해서
정의 4, 1 n=0, 1, 2, …에 대해서
로 정 의 하자. Hn 은 n 차 에 르미트 (Hermi te) 다항식 이 라 한다. 간단한 에르미트 다항식의 예를 보면,
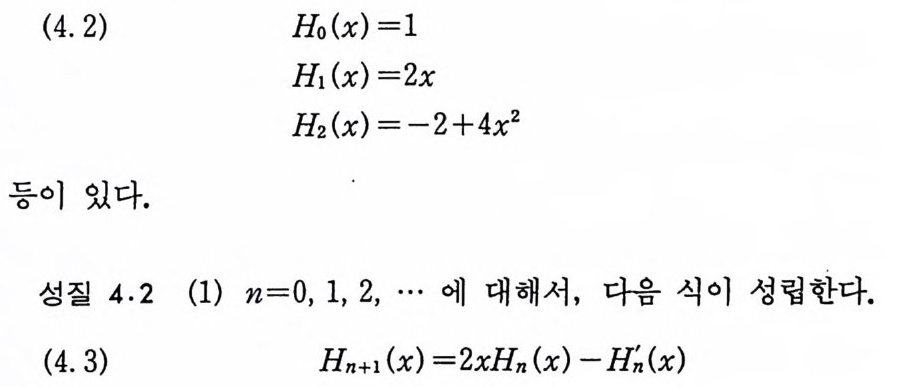 (4. 2) Ho(x) =l
(4. 2) Ho(x) =l
(2) Hn(x) 는 최고차 계수가 앙인 n 차 다항식이다.
 증명 (1) rp( x) =ex p {-x 악으로 놓으면, Hn( X ) 의 정의에 의해
증명 (1) rp( x) =ex p {-x 악으로 놓으면, Hn( X ) 의 정의에 의해
이다. (4. 5) 와 (4. 6) 의 양변을 비교해서 (4. 3) 을 얻는다. (2) 수학적 귀납법으로 증명한다.
 성질 4-3 (1) n 이 짝수이면, Hn(X) 의 모든 기수차 항의 계
성질 4-3 (1) n 이 짝수이면, Hn(X) 의 모든 기수차 항의 계
증명 식 (4.3) 과 수학적 귀납법으로 증명한다.
 정리 4-4 o::;;;n, m 일 때,
정리 4-4 o::;;;n, m 일 때,
계속해서 다음 식을 얻는다.
 I 루 (-1)nf_ :H m(x) rp< n>(x)dx : (식 (4. 4) 에 의해서)
I 루 (-1)nf_ :H m(x) rp< n>(x)dx : (식 (4. 4) 에 의해서)
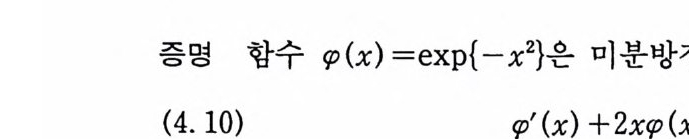 증명 함수 rp( x) =ex p{― x 악은 미분방정식
증명 함수 rp( x) =ex p{― x 악은 미분방정식
의 해가 된다. (4.10) 을 n 번 미분하고 식 (4. 4) 를 적용하여 (4. 9) 를 얻는다.
![]()
증명 식 (4. 3) 과 (4. 9) 를 비교해서 (1) 을 얻는다. (2) 는 식 (4. 9) 에서 얻는다. (1) 을 이용해서 수학적 귀납법으로 (3) 과 (4) 도 증명된다.
 성질 4-9 n=0, 1, 2, … 일 때, 함수 갔(따라서, n 차 다항식)은
성질 4-9 n=0, 1, 2, … 일 때, 함수 갔(따라서, n 차 다항식)은
증명 식 (4. 9) 와 수학적 귀납법을 사용해서 다음 식을 얻는 다.
 (4. 11) Hn+l (x) =zn+lxn+l + Pn (x)
(4. 11) Hn+l (x) =zn+lxn+l + Pn (x)
여기서 Pn(X) 는 차수가 n 보다 크지 않은 다항식이다. 수학적 귀 납법에 의해서 Pn(x) 는 차수가 n 보다 크지 않은 에르미트 다항 식들의 1 차 결합이므로 (4.11) 에 의해서 정리가 증명된다.
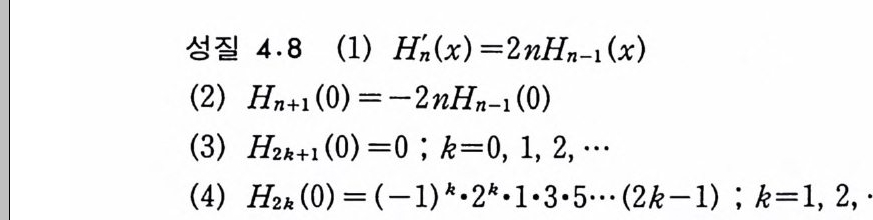 성질 4. 8 (1) H~(x) =ZnHn-1 (x)
성질 4. 8 (1) H~(x) =ZnHn-1 (x)
정리 4.10 {c/J n} 는 L2(R) 에서 완비정규 직교집합이다.
 증명 모든 n=O, 1, 2, …에 대해서,
증명 모든 n=O, 1, 2, …에 대해서,
F 는 C 의 모든 유계 개 (bounded op e n) 부분집 합에 서 해 석 적 (anal ytic)이므로, F 는 정함수 (en ti re f unc ti on) 임울 보일 수 있다 (모레라 (Morera) 정리 사용). 따라서, F(z) 는 다음과 같이 표시 된다.
 (4. 17) F(z) =홀回 ; zEC,
(4. 17) F(z) =홀回 ; zEC,
dament al subse t)이다. 즉, {'P n} 의 스팬 (s p an) 은 나 (lR) 에서 조밀 (dense) 하다. 증명 {'P n} 이 기본부분집합이 아니라고 하자. 그러면,
 M 마訂무 L p (lR)
M 마訂무 L p (lR)
다음 성질은 푸리에 변환에서 잘 알려진 사실이다.
 성질 4.13 (1) /(x) 와 /1 (x)=xf (x) 가 L1(R) 에 속하는 함수
성질 4.13 (1) /(x) 와 /1 (x)=xf (x) 가 L1(R) 에 속하는 함수
 성질 4.14 n=O, 1, 2, …에 대해서,
성질 4.14 n=O, 1, 2, …에 대해서,
(4. 26) 의 양변에 푸리에 변환을 취하고, 성질 4.13 을 이용하면 (4. 25) 를 얻는다. 정리 4.15 hn 은 푸리에 변환의 고유함수이고, 고유값은 (-i)n 이다. 즉,
 (4. 27) (jhn) (y) = (—i)n hn(y ),
(4. 27) (jhn) (y) = (—i)n hn(y ),
따라서, 'P n 도 푸리에 변환의 고유함수이고, 고유값은 (―l) n 이 다.
 증명 {hn} 과 {i nY(hn)} 은 동일한 순환관계 (recurrence rela-
증명 {hn} 과 {i nY(hn)} 은 동일한 순환관계 (recurrence rela-
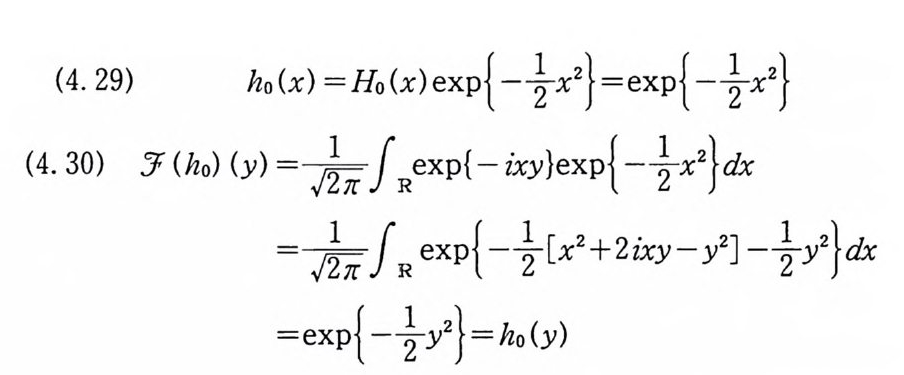 (4. 29) h 。 (x) =Ho(x)ex p {-½x2}=ex p{-:니
(4. 29) h 。 (x) =Ho(x)ex p {-½x2}=ex p{-:니
윗 식 의 적 분은 코시 (Cauchy ) 적분공식 을 사용해 서 계 산한다.
 정의 4.16 o::;;:m;(i= l, 2 , …, n) 가 정수이고 (x1, …, Xn) ERn 일
정의 4.16 o::;;:m;(i= l, 2 , …, n) 가 정수이고 (x1, …, Xn) ERn 일
로 정의하고, n 차 에르미트 함수라 한다. 정리 4.6 에 의해서 다음 성질을 얻는다. 성질 n 차 에르미트 함수들의 집합
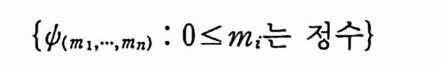 {¢(m1,··• ,m n) : o::;;m; 는 정수}
{¢(m1,··• ,m n) : o::;;m; 는 정수}
은 L2(Rn) 에서 정규직교집합이다. n 차 에르미트 함수들의 집합이 L p (lRn) 의 기본부분집합 (fun damenta l subset) 임 울 보이 기 위 해 서 먼저 다음 보조정 리 를 소개한다.
보조정리 4.17 다음과 같은 함수들의 집합
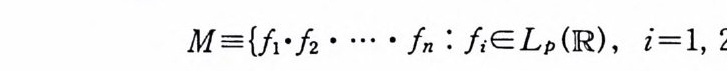 Af= {/1•/2 • … • In : fiE Lp (R) , i= l, 2, …, n}
Af= {/1•/2 • … • In : fiE Lp (R) , i= l, 2, …, n}
은 L p (Rn) 에서 기본부분집합이다. 증명 (1) ]R n 에서 컴팩트 지지집합 (com p ac t su pp or t)을 갖는 연속함수들의 집 합은 Lp (IRn) 에 서 조밀 (dense) 하다. (2) 따라서 다음과 같은 함수들의 집 합 S 가 Lp (!Rn ) 에 서 조밀 하다.
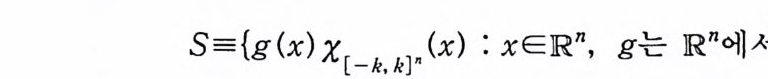 S={g ( x)X,[ — k, , k.],. (x) : xERn, g는 Rn 에서 연속}
S={g ( x)X,[ — k, , k.],. (x) : xERn, g는 Rn 에서 연속}
(3) 그러므로 S 에 속하는 각 함수들이 M 에 속하는 함수들의 유한일차결합(fi n it e line ar comb i na ti on) 에 의해서 근사 (a pp rox i mat e) 됨 을 보이 면 된다. 그런데 스톤-바이 에 르스트라스 (St on e-Weie r str a ss) 정 리 에 의 해 서 함수
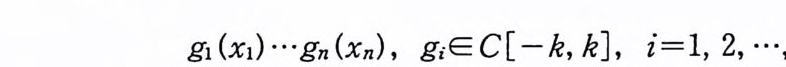 g1 @)… gn( Xn), giE C[-k,k], i= l,2,… , n
g1 @)… gn( Xn), giE C[-k,k], i= l,2,… , n
둘의 일차 결합들의 집합은 C([ ― k, 싸 n) 에서 최소상계노름 (sup -n orm) 에 대 해 서 조밀 (dense) 하므로 (3) 이 성 립 된다. 정리 4.l8 n 차 에르미트 함수들의 집합
 {仇 (mI, •••, m n) : 0 조 m i는 정수}
{仇 (mI, •••, m n) : 0 조 m i는 정수}
증명 보조정리 4.17 에 의해서 집합 M 의 각 원소들이 n 차 에 르미트 함수들의 유한일차결합에 의해서 근사됨을 보이면 된다. 1 차 에르미트 함수들의 집합은 L p (lR) 의 기본부분집합(따름정리 4.12) 이므로 Ij eL p (lR) 를 근사 (a pp rox i ma t e) 하는 함수 gj :
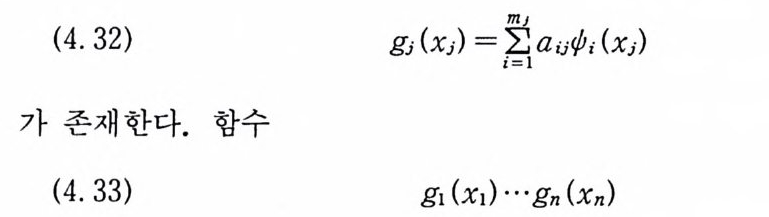 (4. 32) gJ (xJ ) = 2mj a,.j¢ I (xj )
(4. 32) gJ (xJ ) = 2mj a,.j¢ I (xj )
은 11 차 에르미트 함수들의 유한일차결합이므로 (4.33) 의 함수가 /1( x 1) …fn (Xn) 을 근사함을 보이면 된다. 이것은 다음 식에 의해 서 보일 수 있다.
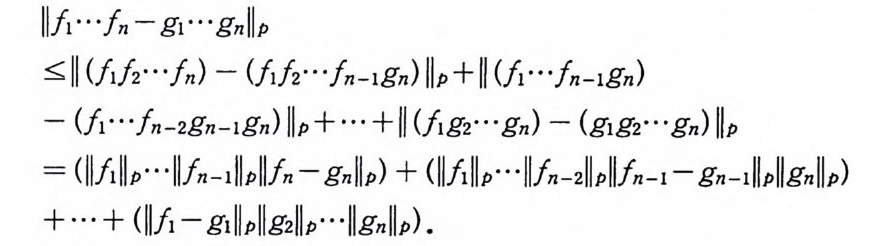 ll/1… fn- g1 ···g nl lP
ll/1… fn- g1 ···g nl lP
이제 L2(C。 (T)) 에서 완비정규 칙교집합을 정의하기 위해서, 정 의 4.1 과 정의 4. 5 에서 정의한 n 차 에르미트 다항식과 에르미트 함수 Hn(x), ,P n(x) 를 여기서는 다음과 같이 변형된 형태로 택해 서 사용하기로 한다.
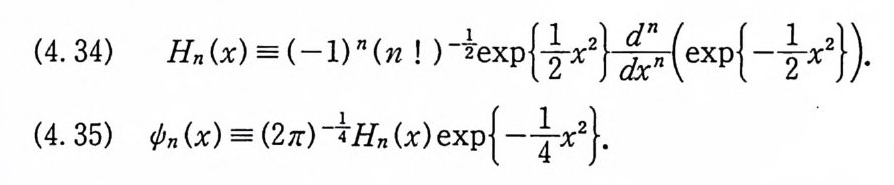 (4. 34) Hn (x) = ( —l) n ( n ! ) 당 ex p {½x2} 을 (ex p {-½x2}).
(4. 34) Hn (x) = ( —l) n ( n ! ) 당 ex p {½x2} 을 (ex p {-½x2}).
 {Pk} 를 L2(T) 에서 완비정규 직교집합이라 하자. k 가 자연수
{Pk} 를 L2(T) 에서 완비정규 직교집합이라 하자. k 가 자연수
증명 팰리-위너-지그문드 적분공식 (2.48) 을 사용해서 다음 식을 얻는다.
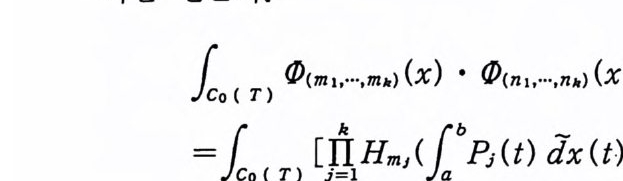 f 。 (m 】, ••• • m•> (x) •
f 。 (m 】, ••• • m•> (x) •
 [}Jh iHn , (「a Pi (t) dx (t) ) ] dm (x)
[}Jh iHn , (「a Pi (t) dx (t) ) ] dm (x)
를 F 의 푸리에 - 에르미트 계수라 한다.
 보조정리 4,21 J(u ), u=(u1, …, Un) 가 Rn 에서 르베그 측도
보조정리 4,21 J(u ), u=(u1, …, Un) 가 Rn 에서 르베그 측도
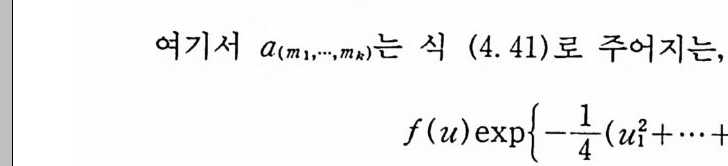 여기서 a(m1, ··• ,mk) 는 식 (4. 41) 로 주어지는,
여기서 a(m1, ··• ,mk) 는 식 (4. 41) 로 주어지는,
의 k- 차 에 르미 트 계 수 (Hermi te coef fici e n t) 이 다.
 증명 (4. 39) 에서는 (i)과 (ii) 두 가지 경우만 있다. 왜냐하
증명 (4. 39) 에서는 (i)과 (ii) 두 가지 경우만 있다. 왜냐하
보조정리 4·22 F 가 (4.38) 로 주어지는 함수라 하자. 그러면,
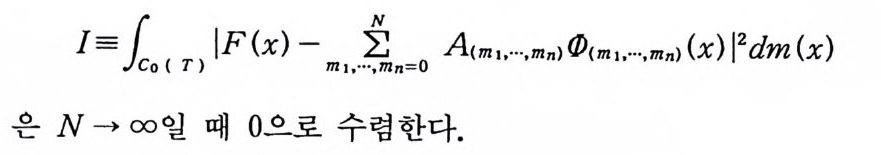 I=1.Coc ( TT)) I• F(x)-mm,1,,.··#• ,mm nn == OO Acm1,··•,m n)< P( m1,··• ,m n)(X)l2dm(x)
I=1.Coc ( TT)) I• F(x)-mm,1,,.··#• ,mm nn == OO Acm1,··•,m n)< P( m1,··• ,m n)(X)l2dm(x)
층명 위너 적분공식을 사용하면,
I= (21r 따 R |J(u ) —m .~. ..n ,m=n=OO Acm1,···, m n)Hm1 (u1) … Hmn(Un} 12 • ex p{ - ½흠 u~}du, u= (u1, ···, Un) = fR. I (2 1r) -n'4/ ( u ) ex p{-+훔 u;} —m1 .· t n=Oac m 1,··• ,m n)Jl [ (21r)-¾Hm1 (uJ ex p나러 ]l2du
이고, 윗식의 마지막 적분은, N-.oo 일 때, 0 으로 수령한다. 보조정리 4.23 F 가 (4.38) 로 주어지는 함수라 하자. 그러면 F 의 푸리에_에르미트 (Four i er-Herm it e) 급수
(4. 42) mo, · ·f·,m N=O A (m, , ···, m N) ~ (mo , ••·, mN) (x)
은 N---+ (X)일 때 F 로 L2(Co(T)) -노름 수령한다.
증명 N>n 일 때, m1 ,··2•N, m n=O 과 m,. ··Z·N, m N =O
에서 0 이 아닌 항들은 모두 갇으므로 보조정리 4 . 22 에 의해서 증 명된다. 처음 합 (sum) 에서 나타나는 모든 항들
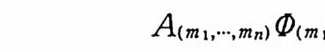 A(mI, ••• , mn) <1>( mI, ••• , mn) (x)
A(mI, ••• , mn) <1>( mI, ••• , mn) (x)
은 두번째 합에서도
![]() Acm 1,· · •, m n,O ,··, O )
Acm 1,· · •, m n,O ,··, O )
으로나타난다.
 어떤 j (n+l~ j ~N) 에 대해서 m j=I= 0 인 두번째 합에 있는 항
어떤 j (n+l~ j ~N) 에 대해서 m j=I= 0 인 두번째 합에 있는 항
이다. 정리 4-24 (4. 38) 로 주어지는 모든 함수들의 집합 (n 도 변함) 은 L2(Co(T)) 에서 조밀 (dense) 하다. 증명 단순함수 (sim p le fun cti on s) 들의 집 합은 L2 ( C 。 ( T) ) 에 서 조밀하므로, 위너 측도가능한 집합들의 특성함수 (charac t er i s tic fun cti on ) 를 (4. 38) 의 F 둘로 근사 (app ro xim ate ) 하면 된 다. 임 의 의 위너 측도가능한 집합 A 는 다음과 같이 표시된다 (Ro y den[l, Prop. 7, p. 294] )
 (4. 43) A=GUN
(4. 43) A=GUN
여기서 G 는 08- 집합이고 N 은 위너 영집합이다. 。「집 합은 0- 집 합들의 가산 교집 합 (counta b le int e r secti on )
 co
co
울 말하고, O - 집합은 구간(i n t erval) 들의 가산 합집합 (coun t able unio n )
 (4. 45) On= 빙co n ,
(4. 45) On= 빙co n ,
울 말한다. 식 (4. 44) 에서 {On} 은 감소수열로, (4. 45) 에서 아은 서로 소 (d i s j o i n t)인 구간들의 합으로 표시할 수 있다.
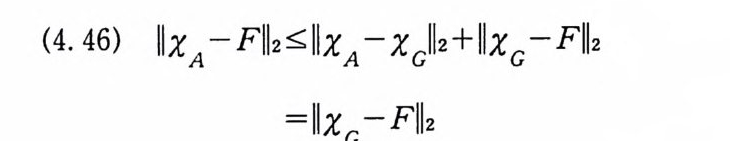 (4. 46) llxA-Fl| 조 |IxA-x)2+llxc-Fll2
(4. 46) llxA-Fl| 조 |IxA-x)2+llxc-Fll2
이고 우월수령정리 (domi na te d converge nce t heorem) 에 의해서, n -oo 일 때,
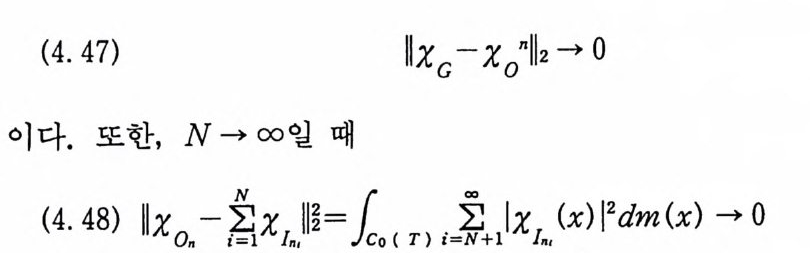 (4. 47) |IxG —x 。 n||2 一 。
(4. 47) |IxG —x 。 n||2 一 。
이 므로, (4. 46) , (4. 47) , (4. 48) 에 의 해 서 구간들의 특성 함수 xI (x) 를 F 둘로 근사하면 된다.
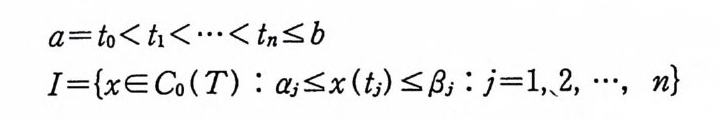 a=to < ti< …< tn ~b
a=to < ti< …< tn ~b
이라 하자. 그러면,
 (4. 49) XI (x) = jI= nl I x[ o . /J』 (x ( tj) )
(4. 49) XI (x) = jI= nl I x[ o . /J』 (x ( tj) )
로 놓고 gi를 완비정규 직교집합 {P1} 에 대해서 직교전개 (ort ho go nal exp a nsio n ) ,
 (4. 55) gj (t ) =~l0=0I b j,1 P1U)
(4. 55) gj (t ) =~l0=0I b j,1 P1U)
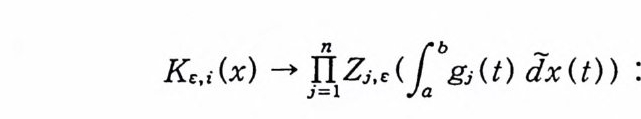 Kt: ,i( X) 기] n IZm( i/ b江 ) &(t)) : a. e. x
Kt: ,i( X) 기] n IZm( i/ b江 ) &(t)) : a. e. x
이다. 우월수령정리에 의해서, K t:,i (X) 는 C t: (X) 로 L2(Co(T)) -노름 수령한다. 그런데 Kt :,i (X) 는 (4. 38) 로 주어지는 함수들의 집합에 속하는 원소이므로 증명이 끝난다. 정리 4·25 {(/)(m1 ,·· • , mn)} 은 L2(C 。 (T)) 에서 완비정규 직교집합이 다.
 증명 {(/)(m 1 , · • , mn)} 이 L2(Co(T)) 의 기본부분집합(fu ndamen t al
증명 {(/)(m 1 , · • , mn)} 이 L2(Co(T)) 의 기본부분집합(fu ndamen t al
주 힐베르트 공간 L2(C 。 (T)) 에서 완비정규 직교집합을 얻었 으므로, 이와 관련된 힐베르트 공간의 모든 성질이 Co(T) 에서 도 성 립 한다. 푸리 에 급수 (Fourie r serie s ) 에 서 성 립 하는 성 질들이 푸리에-에르미트 급수에서도 성립하는가? 이 질문에 관한 여러 가지 성질들이 조사되었다. 다음에 소개하는 내용은 이와 같은 성질들 중의 하나이다. 정리 4· 26 F 가 다음 성질을 만족하는 함수라 하자.
 (1) FEL2(Co[O, 1])
(1) FEL2(Co[O, 1])
L2([0, 1]) 에서의 완비정규 직교집합을
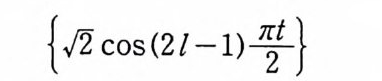 {-./2 cos(2l-1) 引
{-./2 cos(2l-1) 引
로 택하자. 그러면 Xo 에서 F 의 푸리에 - 에르미트 급수는 아벨 합 가능 (Abel summable) 하다. 즉,
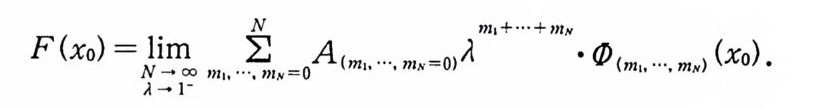 F(xo)=N,ll i-一 m 1° - ° 'I, •• •2N· 'N= oA (mI , .. ,nh=O)A m ,+ ·--+m , ·0(mI, ... ,mN)(xo).
F(xo)=N,ll i-一 m 1° - ° 'I, •• •2N· 'N= oA (mI , .. ,nh=O)A m ,+ ·--+m , ·0(mI, ... ,mN)(xo).
증명 참고문헌 (Cameron and Hatf iel d[2]) 참조.
 정의 4.27 (1) fP (m i ,··•,m n) 의 차수 (de gr ee) 를 m1+ … +mn 으로
정의 4.27 (1) fP (m i ,··•,m n) 의 차수 (de gr ee) 를 m1+ … +mn 으로
5 푸리에_위너 변환
 푸리에 변환과 유사한 푸리에-위너 변환을 정의하고, 푸리에
푸리에 변환과 유사한 푸리에-위너 변환을 정의하고, 푸리에
를 F(x) 의 푸리에 - 위너 변환이라고 한다. 주 5·2 푸리에 변환에서 사용하는 인수(fa c t or) ex p{i ux} 는 (5.1) 에는 나타나지 않는다. 왜냐하면 위너 적분의 정의에서 이 인수는 이미 사용되었기 때문이다. 푸리에-위너 변환 G( y)가 존재하고, 더욱이 다음 성질까지 만 족하는 함수 F(x) 들은 많이 있다.
 각각의 고정된 xEK 에 대해서, G( y一ix)가 y의 함수로서 Co(T)
각각의 고정된 xEK 에 대해서, G( y一ix)가 y의 함수로서 Co(T)
등이 있고 이 함수들을 (5) 에 적용하면 함수
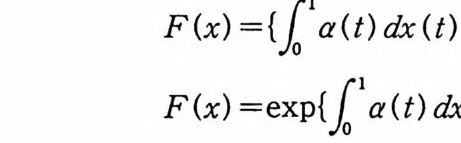 F(x) ={£1a( t) dx (t) }2
F(x) ={£1a( t) dx (t) }2
의 푸리에-위너 변환을 구할 수 있다. (1), (2), (3) 은 정의로부터 쉽게 얻을 수 있고 (5. 2) 를 만족하 는 것도 보일 수 있다. 여기서는 (4) 와 (5) 에 대한 계산만 한다. 먼저 (4) 의 경우를 보자. 이 경우 위너 적분공식과 푸비니 (Fubin i ) 정 리를 사용해 서 적 분을 계 산한다.
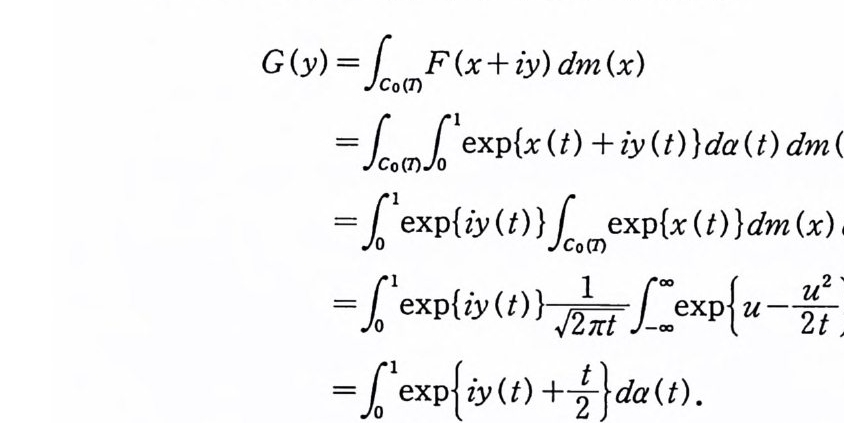 G (y) =fcCo0( nc nF(x+ iy) dm(x)
G (y) =fcCo0( nc nF(x+ iy) dm(x)
(5. 2) 의 역관계가 성립하는 것도 다음과 같이 보일 수 있다.
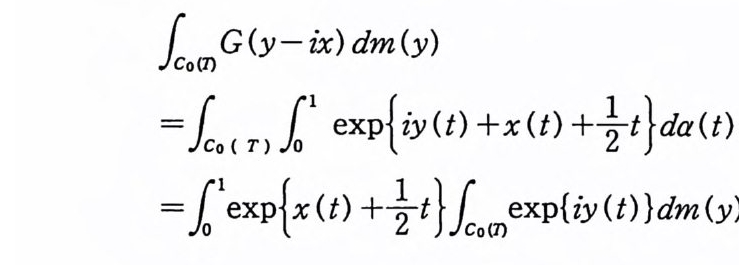 l=aCfomc( n0 G< n( y£-1ix e) xdpm { i(yy)( t) +x(t ) +송가 da (t )dm( y)
l=aCfomc( n0 G< n( y£-1ix e) xdpm { i(yy)( t) +x(t ) +송가 da (t )dm( y)
 =11exp { x(t) +½t} 志 1:ex p{i u- 망 }duda (t)
=11exp { x(t) +½t} 志 1:ex p{i u- 망 }duda (t)
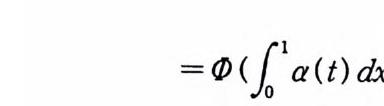 = 인 (f。 la( t) dx (t) ) .
= 인 (f。 la( t) dx (t) ) .
위의 마지막 두번째 등식은 코시 공식 (Cauchy 's fo rmula) 을 사 용해서 얻는다. 정의 5.4 (1) 함수 F 가 다음을 만족할 때 F 는 평균연속 (mean cont inu ous) 함수라 한다.
 x,xnEK 에 대해서, Xn 이 x 로 평균수령하면, 죽,
x,xnEK 에 대해서, Xn 이 x 로 평균수령하면, 죽,
울 만족하는 양의 상수 A,B 가 존재할 때, F 를 평균지수형 (mean exp o nenti al type ) 이 라 한다. 정의 5.5 Em 을 다음 세 조건을 만족하는 함수 F 들의 집합이 라하자. (1) F 는 평균연속이다. (2) F 는 평균지수형이다.
 (3) 모든 x, y EK 에 대해서, F(x+ tly)는 복소변수 A 의 함수
(3) 모든 x, y EK 에 대해서, F(x+ tly)는 복소변수 A 의 함수
이제 Em 에 속하는 함수 F(x) 들의 푸리에-위너 변환 G( y)가 존재하고 G 도 Em 에 속하고, G 의 푸리에-위너 변환은 F(-x) 임을 보이려고 한다. 보조정리 5.6 ~(z1, …, Zn) 이 완전함수이고, 지수형이라 하자. 죽,
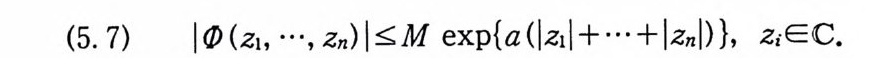 (5. 7) | 0 (zI, …, %) j ::;; M exp {a (lz,| + …+ |Zn|) }, ziE C•
(5. 7) | 0 (zI, …, %) j ::;; M exp {a (lz,| + …+ |Zn|) }, ziE C•
여기서, M, a 는 상수이다. 그러면, 함수
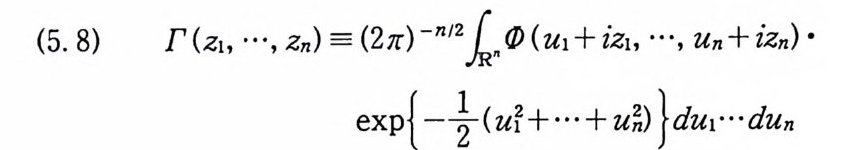 (5. 8) I'(z, , …, %) = (27 [) -nl2L
(5. 8) I'(z, , …, %) = (27 [) -nl2L
이 존재하고, I'는 완전함수이며 다음 역관계를 만족한다. 모든 (Zi, ···, Zn) ECn 에 대해서
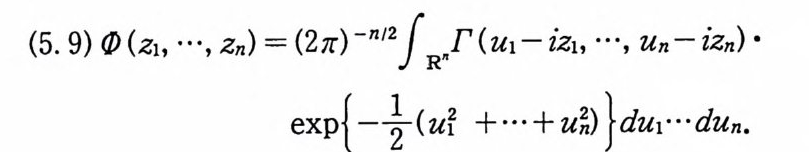 (5. 9)
(5. 9)
증명 (5. 7) 에 의해서 (5. 8) 이 존재하고 r 는 완전함수이고 지 수형이다. 실제로, (5.7) 에서와 같은 a 를 가진다. 역관계는 예 5.3 의 (5) 에서와 같이 코시 공식을 사용해서 얻는다.
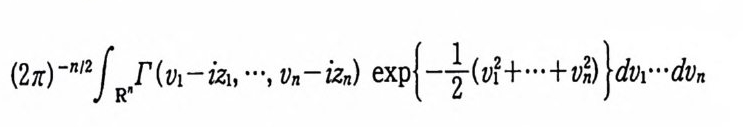 (2, rtn/Zf R. r(V 1 -iz 1, ... , Vn-iz n) ex p{단 (v f+…+짜 )}dV!'dVn
(2, rtn/Zf R. r(V 1 -iz 1, ... , Vn-iz n) ex p{단 (v f+…+짜 )}dV!'dVn
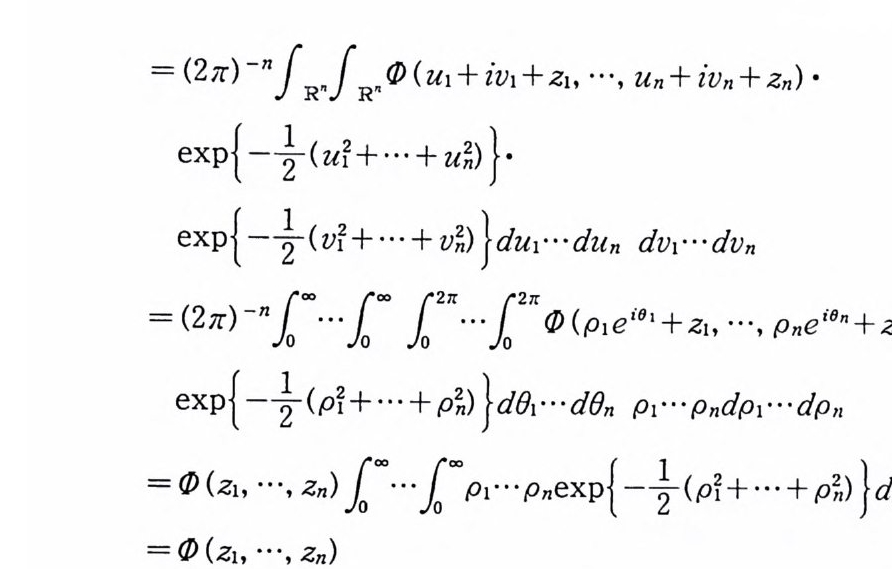 = (ZiC ) -nf R f R <1> ( u1 + iv1 + z1, …, Un + i v 규 리 •
= (ZiC ) -nf R f R <1> ( u1 + iv1 + z1, …, Un + i v 규 리 •
정리 5.7 (J)( z1, …, Zn) 이 완전함수이고 (5. 7) 을 만족하는 지 수형이라 하자.
 a;EC(T) nBV(T), i= l, 2, … n 이고, {a1, …, an} 이 정규직
a;EC(T) nBV(T), i= l, 2, … n 이고, {a1, …, an} 이 정규직
이다. 여기서, I'는 (5.8) 로 주어지는 지수형의 완전함수이다. 또한, G( y)의 푸리에-위너 변환은 F(-x) 이다. 증명 보조정리 5.6 과 팰리-위너 정리(정리 1. 8) 를 사용하면 (5.11) 을 얻을 수 있다. 식 (5. 9) 에 의해서 F(-x) 가 G( y)의
푸리에-위너 변환임을 보일 수 있다. 주 5.8 식 (5. 8) 에서 주어전 함수 r 에 대해서,
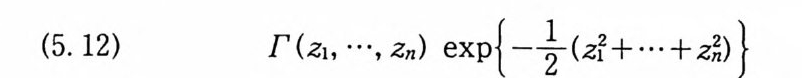 (5.12) I'(z1 , ···, Zn) ex p{단 (zl+ … +z~)}
(5.12) I'(z1 , ···, Zn) ex p{단 (zl+ … +z~)}
은 함수
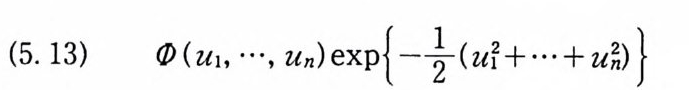 (5.13) (/)(u1, …, Un)exp {— ½(u?+… +u~)}
(5.13) (/)(u1, …, Un)exp {— ½(u?+… +u~)}
의 푸리에 변환이다. 이것은 식 (5.8) 에 변수변환을 적용해서 쉽 게 보일 수 있다. 정리 5. 7 을 {a1, …, an} 이 1 차 독립인 경우로 확장하자.
 정리 5.9 aJ( z,, …,%)이 완전함수이고, (5. 7) 을 만족하는 지
정리 5.9 aJ( z,, …,%)이 완전함수이고, (5. 7) 을 만족하는 지
증명 슈미트 (Erhard Schm i d t)의 정규직교화 방법 (Schmi dt ' s or t ho g ona li za ti on) 에 의해서, {a1, …, an} 을 정규직교화할 수 있 다. 죽,
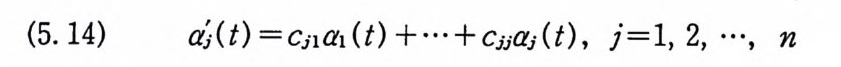 (5.14) a1U) =cjla 1 U) +… +Cjj aj ( t), j= l, 2, …, n
(5.14) a1U) =cjla 1 U) +… +Cjj aj ( t), j= l, 2, …, n
 을 만족하는 상수 Cjp (p= l, 2, …,j)가 }(n+ 갑)개 존재하고
을 만족하는 상수 Cjp (p= l, 2, …,j)가 }(n+ 갑)개 존재하고
이 때 Cu 와 du 는 다음 관계를 만족한다.
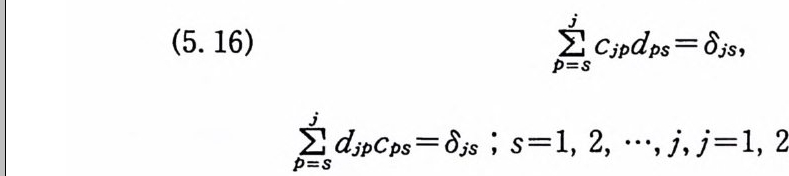 (5. 16) P~=j S Cjp d ps = Sis ,
(5. 16) P~=j S Cjp d ps = Sis ,
여기서 Oj s 는 크로네커델타 (Kronecker ' s delta ) 함수이다. 이 제 새로운 함수 0* 을 정의하자.
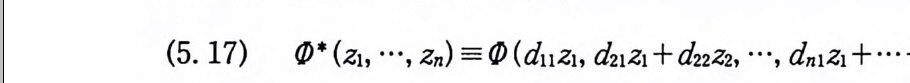 (5. 17) Q)* (z1, …, %) =Q ) (duz1, d21Z1 + d22Z2, …, dn1Z 1 + … + dnnZn)
(5. 17) Q)* (z1, …, %) =Q ) (duz1, d21Z1 + d22Z2, …, dn1Z 1 + … + dnnZn)
그러면 0* 는 지수형의 정함수이고
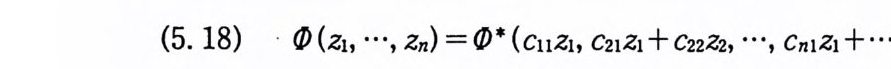 (5. 18) •
(5. 18) •
이다. 따라서 (5.10) 의 함수 F 를 다음과 같이 쓸 수 있다.
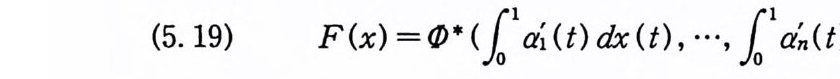 (5. 19) F(x) = (/)* (i 1 아 (t) dx (t) , …, f。 1 야(t) dx (t) )
(5. 19) F(x) = (/)* (i 1 아 (t) dx (t) , …, f。 1 야(t) dx (t) )
정리 5. 7 을 적용하면, F(x) 의 푸리에-위너 변환 G( y)는
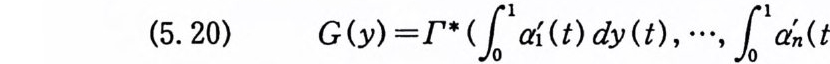 (5. 20) G (y) =I'* <[。1 a{ (t) dy (t) , …, i넒(t) dy (t))
(5. 20) G (y) =I'* <[。1 a{ (t) dy (t) , …, i넒(t) dy (t))
이 된다. 여기서 r* 는 (5. 22) 로 주어지는 지수형의 완전함수이 다. 이제, I'를
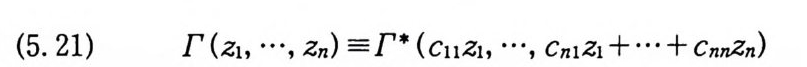 (5. 21) I' (z1, …, Zn) =I'* (C11Z1, …, Cn1Z1 + …+ CnnZn)
(5. 21) I' (z1, …, Zn) =I'* (C11Z1, …, Cn1Z1 + …+ CnnZn)
로 정의하면 (5.14) 와 (5. 20) 에 의해서, G( y)는 (5.11) 로 된다. 또한 G( y)의 푸리에 - 위너 변환은 F(_x) 가 된다. 정리 5 . 7 에 의해서,
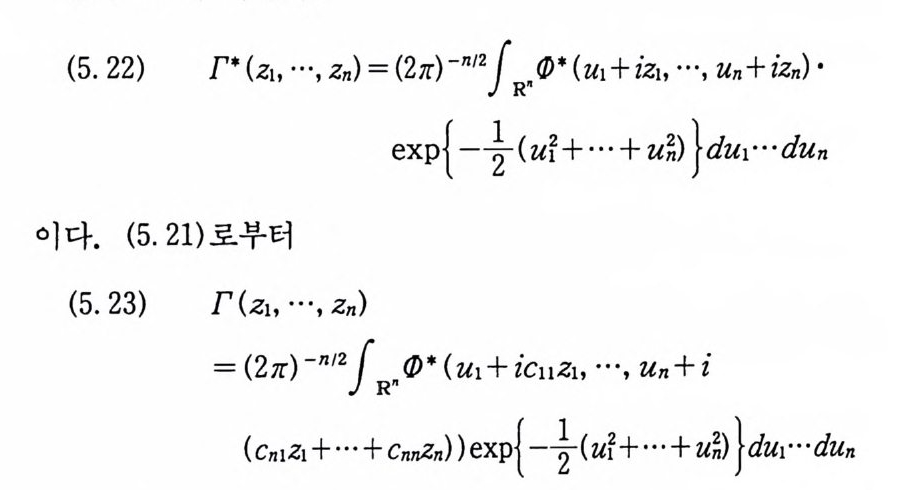 (5. 22) r· (z1, …, Zn) = (27! ) -n 1 2f RR' (J )* (U1 + iz1, …, Un+ izn ) •
(5. 22) r· (z1, …, Zn) = (27! ) -n 1 2f RR' (J )* (U1 + iz1, …, Un+ izn ) •
정리 5.l0 정리 5. 9 에서 주어전 함수 F(x) 와 G( y)는 다음의 프란세 렐 관계 (Plancherel's relati on ) 를 만족한다.
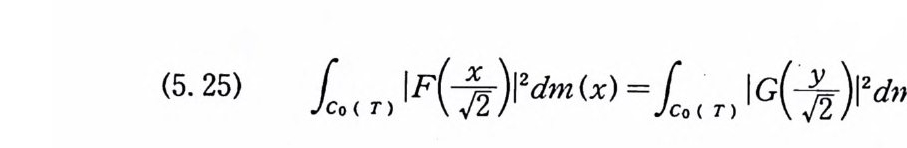 (5. 25} lo( T) IF( 令 )l2dm(x) =!co( T) IC( 令 )l2dm( y)
(5. 25} lo( T) IF( 令 )l2dm(x) =!co( T) IC( 令 )l2dm( y)
증명 (1) {a1( t), …, an (t)}가 정규직교집합인 경우 : (5.12) 의 함수는 (5.13) 의 함수의 푸리에 변환이므로 푸리에 변환의 프란 세렐 관계에 의해서 다음 식이 성립한다.
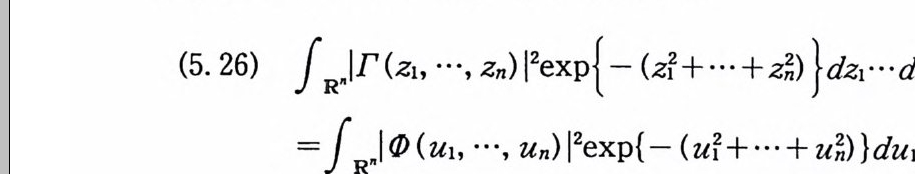 (5. 26) fR. II '(z i, ···, Zn) l2exp {-( 타 · 國) }dz1···d z n
(5. 26) fR. II '(z i, ···, Zn) l2exp {-( 타 · 國) }dz1···d z n
식 (5.10), 팰리 - 위너 정리 (정리 1. 8), 변수변환을 사용해서 다음 식을 얻는다.
 (5. 27) fc0 ( T ) IF( 言 ) l 2dm (x )
(5. 27) fc0 ( T ) IF( 言 ) l 2dm (x )
(5. 26) 에 의해서 (5. 27) 과 (5. 28) 의 우변이 같으므로 (5. 25) 가
성립한다. (2) {a1 (t ),a2U), … ,an( t)}가 1 차 독립인 경우:정리 5.9 의 증명 과정에서 보인 것과 같이, (5.10) 의 함수 F 를 (5.19) 로 표 시할 수 있다. 따라서 (1)의 경우에 의해서 증명된다. 정리 5.11 F1(x) 와 F2(x) 가 다음과 같이 정의되는 함수라 하 자. (5. 29)
 F; (x) = (j), (flaI ( t) dx (t) , …, l1an (t) dx (t) ) , (i=l , 2)
F; (x) = (j), (flaI ( t) dx (t) , …, l1an (t) dx (t) ) , (i=l , 2)
여기서 (j)i와 a1( t), a2( t), …, an (t)는 정리 5. 9 의 가정을 만족하 는 함수이다• G1(y ), Cn( y)를 각 F1(x), F2(x) 의 푸리에 - 위너 변환이라고 하면, 다음의 파시발 (Parseva l) 관계가 성립한다. (5. 30)
 io( T) F! (골)지-골 )dm(x) =io( T) G 信)이令 )dm( y).
io( T) F! (골)지-골 )dm(x) =io( T) G 信)이令 )dm( y).
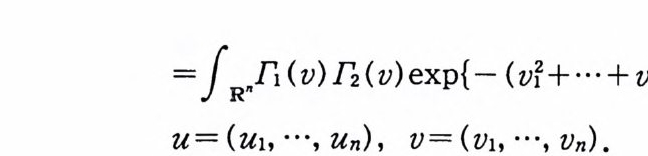 =fRR n (V) n (V) exp {— (vr+ … + v~) }dv,
=fRR n (V) n (V) exp {— (vr+ … + v~) }dv,
이제, 식 (5.10), 팰리-위너 정리(정리 1.8 ), 변수변환을 사용 하고 (5. 31) 의 등식을 적용해서 정리 5.10 과 같은 방법으로 (5. 30) 이 성립함을 보일 수 있다. (2) {a1< t), a2< t), …, an (t)}가 일차 독립인 경우 : (1) 의 결과 룰 이용해서 정리 5.10 의 증명과 같은 방법으로 한다. 보조정리 s. 12 Fn(X) 가 다음 두 조건을 만족하는 함수열이라 하자.
 (1) 푸리에-위너 적분방정식 : 모든 zEK 에 대해서
(1) 푸리에-위너 적분방정식 : 모든 zEK 에 대해서
이 면 F* 도 (5. 32) 를 만족한다.
주 식 (5. 1) 울 역 관계 (rec ipr ocal relati on )
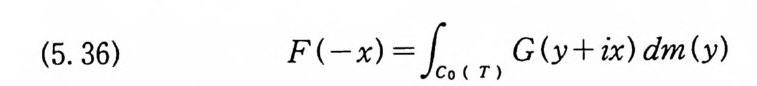 (5. 36) F( 一 x ) =10Co< ( rT I) G(y +ix)d m(y)
(5. 36) F( 一 x ) =10Co< ( rT I) G(y +ix)d m(y)
에 대입하면 적분방정식 (5 . 32) 를 자연스럽게 추측할 수 있다. 증명 p가 증가함수이고

 이 성립하므로, (5 . 34) 에 의해서 우월수령정리를 적용해서 다음
이 성립하므로, (5 . 34) 에 의해서 우월수령정리를 적용해서 다음
이고 이것은 (5.35) 에 의해서 F*(z) 와 같다. 따라서 (5 . 40) 에 의 해 서 F* 는 (5. 32) 를 만족한다. 위의 증명 방법을 적용하면 다음 정리도 증명할 수 있다.
 따름정리 5.13 보조정리 5.12 에서 조건 (5. 33) 과 (5. 34) 를 다
따름정리 5.13 보조정리 5.12 에서 조건 (5. 33) 과 (5. 34) 를 다
정리 5.14 Em 에 속하는 함수 F(x) 들의 푸리에-위너 변환 G( y) 는 존재하고 G 도 Em 에 속한다. 또한 G( y)의 푸리에_위너 변환 은 F(-x) 이다.
 증명 FEEm 이고 (5. 6) 을 만족한다고 하자. 함수
증명 FEEm 이고 (5. 6) 을 만족한다고 하자. 함수
(1) : Fn(x) 가 푸리에-위너 적분방정식 (5. 32) 를 만족한다. (2) : Fn(x) 가 조건 (5. 33) 을 만족한다(이때 針큰 (5. 42) 로 주 어진다). (3) : (5. 42) 로 주어 진 P 가 (5. 34) 를 만족한다. 단계 (1) : Fn 이 (5. 32) 를 만족하는 것을 보이기 위해서 함수 (f) n 을 다음과 같이 정의한다. 복소수 ZI, …, Zn 에 대해서,
 (5. 44) 0n(zI, …, %) =F(j~=n lZ j< pj).
(5. 44) 0n(zI, …, %) =F(j~=n lZ j< pj).
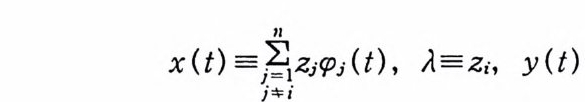 x(t) 三참j*”瑟 i (t), A=zI., y(t) =¢1·(t)
x(t) 三참j*”瑟 i (t), A=zI., y(t) =¢1·(t)
을 적용하면 된다. 따라서 하르독스 (Har t o g s) 의 정규화 정리 (regu la rit ythe orem) (Har t o g s 미)에 의해서 (/)n( 검,… ,Zn) 은 (zb …, %) 의 함수로서 완전함수이 다. (5. 44) 와 정 의 5. 5 의 (2) (식 (5. 6) )에 의해서 0 은 지수형이다. 죽
n =A ex p {B(~lzi l2) 까 j= I n ~A ex p {B~I~』 }. j= I 따라서 n 은 정 리 5. 9 에서 (/)에 주어진 조건을 만족한다. ai( t) =j1r pi( t) dt t 로놓으면, 부분적분법에 의해서, l1x (t) rpi (t) dt =l1ai ( t) dx (t) 이 된다. (주 : x(O) =aj( l) =0). 그러면 (5. 45) 를 (5. 46) Fn (X) 군 (f넒 (t) dx (t) , …, 11an (t) dx (t) ) 0 JO로 쓸 수 있다. 이제, Fn 이 정리 5. 9 에서 F 에 주어전 조건을 만족하는 것은 자명하다. 따라서 Fn(X) 는 정리 5.9 의 결과를 만 족하게 되므로, Fn(X) 의 푸리에-위너 변환 Gn(Y) 의 푸리에-위 너 변환은 Fn (-x) 가 된다. 죽 Fn 은 보조정 리 5. 12 의 조건 (5.
32) 를 만족한다. 단계 (2) : 식 (5. 43), 정의 5.5 의 조건 (2), 베셀 부등식 (Bessel i ne q ua lity)에 의해서 다음 식이 성립하므로 Fn 이 (5. 33) 울 만족한다.
(5.47)
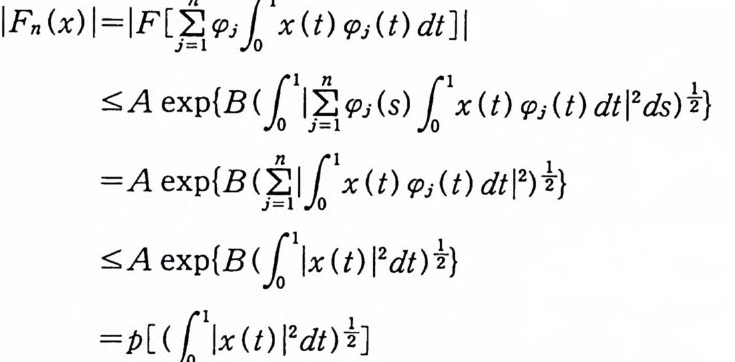 IFn (x) I =IF[it( f)j1 1x (t) ({Jj (t) dt] I
IFn (x) I =IF[it( f)j1 1x (t) ({Jj (t) dt] I
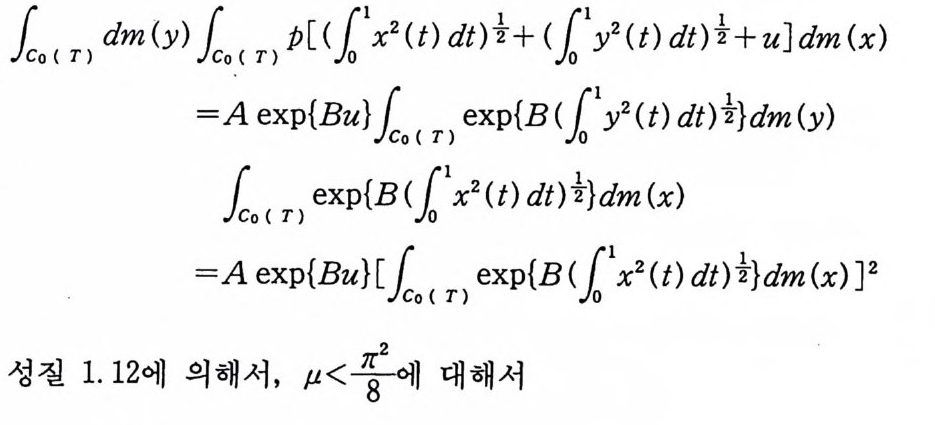 f Co ( T ) dm(y- ).JICo ( T ) p-[-( .1f0 1 갔(t )d t)송 +<1l y 2 (t )d t )½+u]dm(x)
f Co ( T ) dm(y- ).JICo ( T ) p-[-( .1f0 1 갔(t )d t)송 +<1l y 2 (t )d t )½+u]dm(x)
단계 (3) : p (u) 가 (5. 34) 를 만족하는 것을 다음과 같이 보일 수 있다. (5. 48)
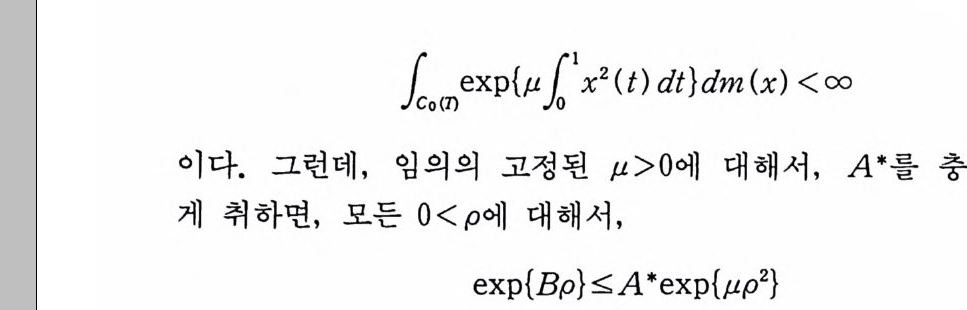 i o( 7) ex p{µi 1 균 (t) dt }d m (x) < oo
i o( 7) ex p{µi 1 균 (t) dt }d m (x) < oo
이 되므로 (5. 48) 의 우변은 유한하다. 이제, 단계 (1), (2), (3) 이 증명되었으므로 Fn 과 p는 보조정 리 5.12 의 모든 가정을 만족한다.
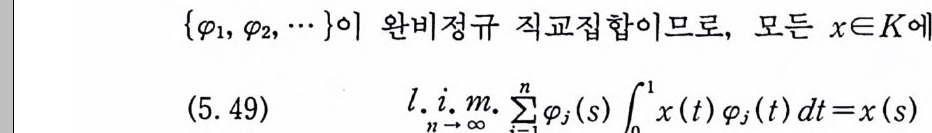 {¢l 내 '2, … }이 완비정규 직교집합이므로, 모든 xEK 에 대해서
{¢l 내 '2, … }이 완비정규 직교집합이므로, 모든 xEK 에 대해서
이다. 위의 극한의 수령은 평균수령 (L2- 노름 수령)을 뜻한다. (5. 49), (5. 43), 정의 5. 5 의 (1) 에 의해서, (5. 35) 가 성립한다(이때 F*=F 이다). 따라서 F 는 (5. 32) 를 만족한다. 죽 F(x) 의 푸리 에-위너 변환 G( y)의 푸리에-위너 변환은 F( ― x) 이다. 마지막으로, 만일
 G(y) =fcC.o (< Tr> ) F(x+ iy) dm(x)
G(y) =fcC.o (< Tr> ) F(x+ iy) dm(x)
 각각의 xEK 에 대해서, y군] y로 평균수령하면, 정의 5. 5 의
각각의 xEK 에 대해서, y군] y로 평균수령하면, 정의 5. 5 의
 + (i넛(t) dt )성 ]}dm(x)
+ (i넛(t) dt )성 ]}dm(x)
여기서 A 와 B 는 Em 의 정의에서 주어진 상수이고 A* 는 (5. 52) 에서 주어전 상수이다.
증명 (1) 은 (5. 46) 으로부터, (2) 는 (5. 47) 로부터 얻는다. (3) 은 (5. 51) 에 서 주어 진 방법 으로부터 얻는다. (식 (5. 51) 에 의 하면, (2) 를 만족하는 Em 의 함수들의 푸리에-위너 변환은 (3) 을 만족한 다. ) (4) 는 식 (5. 49) 다음에 기술한 내용에서 증명되었다• (4) 와 (5. 39), 그리고 G 와 Gn 은 각각 F 와 Fn 의 푸리에-위너 변환 이라는 사실로부터 (5) 를 얻는다.
 따름정리 5.16 (1) F(x) EEm 이고, G( y)가 F(x) 의 푸리에
따름정리 5.16 (1) F(x) EEm 이고, G( y)가 F(x) 의 푸리에
을 얻는다. 이제 보조정리 5.15 의 (2), (3), (4), (5) 와 우월수령정 리를 사용하면 (5. 53) 을 얻는다. 여기서, (5. 48) 의 우변적분의 피적분함수
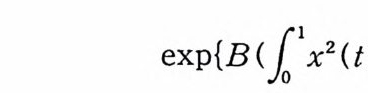 exp { B (「。 x 2 (t) dt) ½ }
exp { B (「。 x 2 (t) dt) ½ }
이 모든 실수 B 에 대해서 위너 적분가능하다는 사실을 사용했 다. (2) 따름정리 5 . 15 와 정리 5.11 을 사용해서 (1) 과 같은 방법으 로 증명한다. 푸리에-위너 번환의 접합 (Convolu ti on) 이제 푸리에-위너 변환의 접합 (convolu ti on) 을 정의하고 이에 관한 성질을 조사해 본다.
 정의 5.17 다음 식의 우변 적분이 존재할 때 그것울 함수 F1(x)
정의 5.17 다음 식의 우변 적분이 존재할 때 그것울 함수 F1(x)
먼저, 접합에 관한 정리를 소개하기 전에 지수형의 완전함수 (enti re fun cti on of exp o nent ial type ) 에 대 한 몇 가지 성 질을 알아 보자.
주 5•18 (/)1(z1,… , Zn), (/)2(z1, … ,Zn) 이 지수형의 완전함수이 면
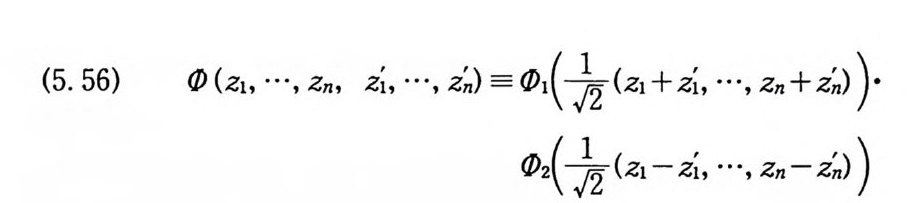 (5. 56) qJ (z1, …, Zn, z;, …, 라) = qJ1 (-¼(z1 +z;, …, Zn 표) )•
(5. 56) qJ (z1, …, Zn, z;, …, 라) = qJ1 (-¼(z1 +z;, …, Zn 표) )•
의 우변의 두 함수 q} I 과 02 는 따라서 0 도 (최, …, z~) 을 고정 했 을 때 (zI, … ,Zn) 의 함수로서 지수형의 완전함수이다 .(z1, … ,Zn) 을 고정했을 때도 같은 성질을 갖는다.
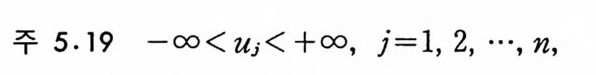 주 5.19 -oo< uj < +oo, j= I, 2, …, n,
주 5.19 -oo< uj < +oo, j= I, 2, …, n,
zED(D 는 복소평면의 한 영역)일 때, rp (u1, … ,Un,Z) 가 연속이 고, (u1, …, Un) 을 고정했을 때, z 의 함수로서 D 에서 해석적 (analyt ic) 이 라고 하자. 만일
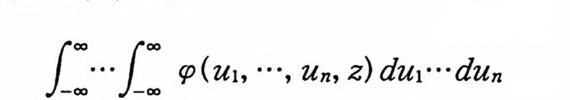 1: ... 1: rp( u1, …, Un, z) du1'''dun
1: ... 1: rp( u1, …, Un, z) du1'''dun
이 D 에 서 평 등수령 (unif or m converge n ce) 하면 이 적 분은 D 에 서 해석적이다. 주 s.20
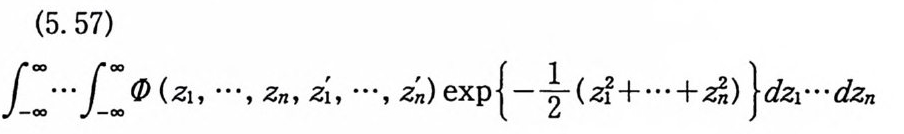 (5. 57)
(5. 57)
은 (z;, …,김의 함수로서 지수형의 완전함수이다.
 정리 5.21 F1(x),F2(x) 가 정리 5.9 의 가정을 만족한다고 하
정리 5.21 F1(x),F2(x) 가 정리 5.9 의 가정을 만족한다고 하
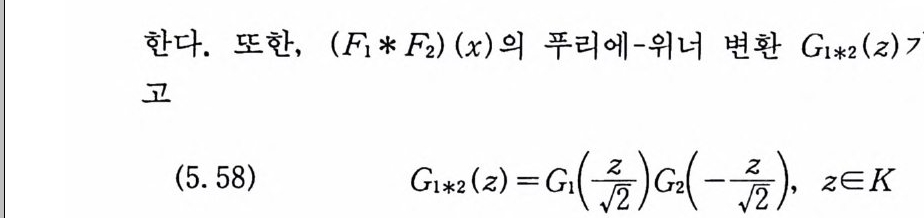 한다. 또한, (F1*F2) (x) 의 푸리에-위너 변환 G1 * 2(z) 가 존재하
한다. 또한, (F1*F2) (x) 의 푸리에-위너 변환 G1 * 2(z) 가 존재하
이다. 여기서 G1, Gi는 각각 R 과 F2 의 푸리에_위너 변환이다.
 증명 F;(x), i= l, 2 에 대해서
증명 F;(x), i= l, 2 에 대해서
여기서, O 는 (5.56) 에서 주어전 지수형의 완전함수 (z;, … ,z~ 이 고정되고, Z1 , ·••, Zn 의 함수로서) 이므로 (5. 60) 의 마지막 적분은 존
 재한다. 따라서 모든 x 든 K 에 대해서 (F,*F2) (x) 의 존재성이
재한다. 따라서 모든 x 든 K 에 대해서 (F,*F2) (x) 의 존재성이
 ·ex p{-杯 d+ vr+ …+ u 計 짜) }dudv.
·ex p{-杯 d+ vr+ …+ u 計 짜) }dudv.
 (5. 62) lim F;, n (x)=F;(x) : i= l, 2.
(5. 62) lim F;, n (x)=F;(x) : i= l, 2.
 (5. 66) l lJ ?kl2 구나 makx {IZII, …, I-Z p |-})2 구업 #- k2p= l |zk|2-c
(5. 66) l lJ ?kl2 구나 makx {IZII, …, I-Z p |-})2 구업 #- k2p= l |zk|2-c
이므로, (5. 55), (5.1), (5. 62) 와 우월수령정리에 의해서, 모든
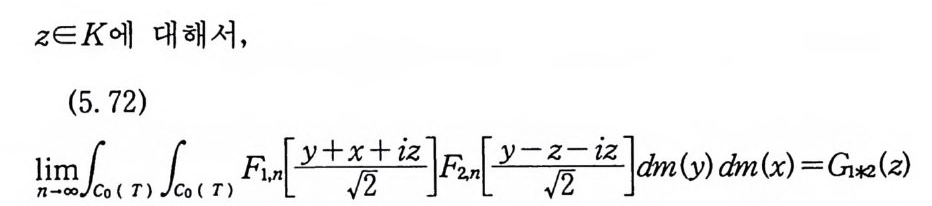 zEK 에 대해서,
zEK 에 대해서,
이다. (5. 65) 의 양변에 n- ➔ OO 일 때의 극한을 취하면, (5. 69), (5. 70), (5. 72) 에 의해서 정리가 증명된다. 다음 정리는 Em 에 속하는 함수에 대해서도 정리 5.21 의 결과 가 성립함을 말해 준다.
 정리 5- 23 F1 (x) , F2(x) EEm 일 때 F1, F2 의 접합 (Fi * F2) (x)
정리 5- 23 F1 (x) , F2(x) EEm 일 때 F1, F2 의 접합 (Fi * F2) (x)
이고, R , n(X) 는 보조정리 5. 22 의 조건(1)을 만족한다. n=l, 2, …에 대해서,
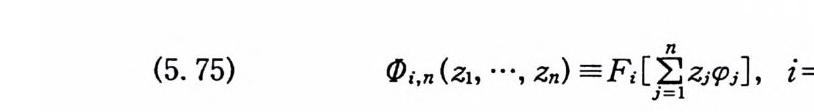 (5. 75)
(5. 75)
로 정의하자. (J)i ,n 이 지수형의 완전함수임을 보이기 위해서,
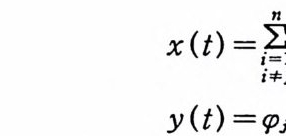 n
n
로 놓자. (5. 75) 로부터
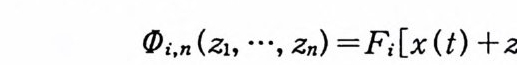 (/)i,n (z1, …, %) =F;[X (t) +Z;y (t) ]
(/)i,n (z1, …, %) =F;[X (t) +Z;y (t) ]
이고 Em 의 정의 (정의 5. 5(3) )에 의해서, (/)i ,n 은 변수 Zj 의 함수 로서 완전함수이다. 하르톡스 (Har t o g s) 의 정규화 정리 (reg ula rit y th eorem) 에 의해서, i ,n 은 (z1, …, %)의 함수로서 완전함수이 다. (5. 75) 와 Em 의 정의 (정의 5. 5(2)) 에 의해서
 I(/)i,n (z1, …, %) 回 eX p {BZ · ( f l|$ 碩j(t) l2dt )까
I(/)i,n (z1, …, %) 回 eX p {BZ · ( f l|$ 碩j(t) l2dt )까
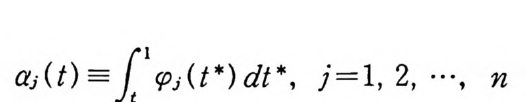 aj( t> =J1r p j(t*) dt* , j= l, 2, …, n
aj( t> =J1r p j(t*) dt* , j= l, 2, …, n
로 놓으면, 부분적분법에 의해서,
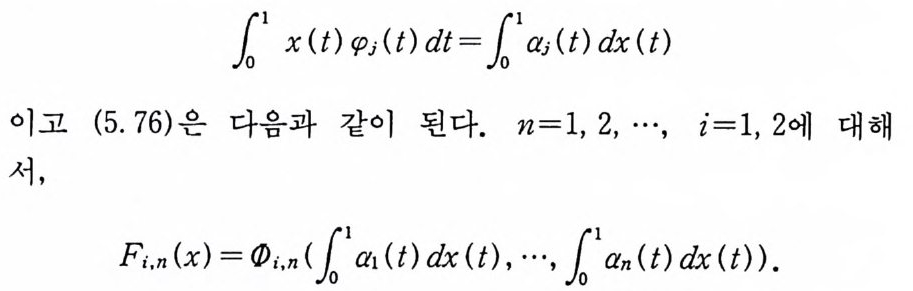 11 x (t} rpj (t) dt =l1aj ( t) dx (t)
11 x (t} rpj (t) dt =l1aj ( t) dx (t)
이제, F;,n(X) 가 정리 5. 9 의 조건을 만족하므로, F; ,n(X) 의 푸리 에 - 위너 변환이 존재한다. 또한 정리 5. 21 에 의해서, 접합 F1,n * F2,n (X ) 이 존재 하고 (5. 63) 을 만족한다. 따라서 보조정 리 5. 22 의 조건 (2) 가 만족된다. A.-, B, 가 F, (x) 에 대 해 서 식 (5.6) 을 만족하는 상수일 때 ,
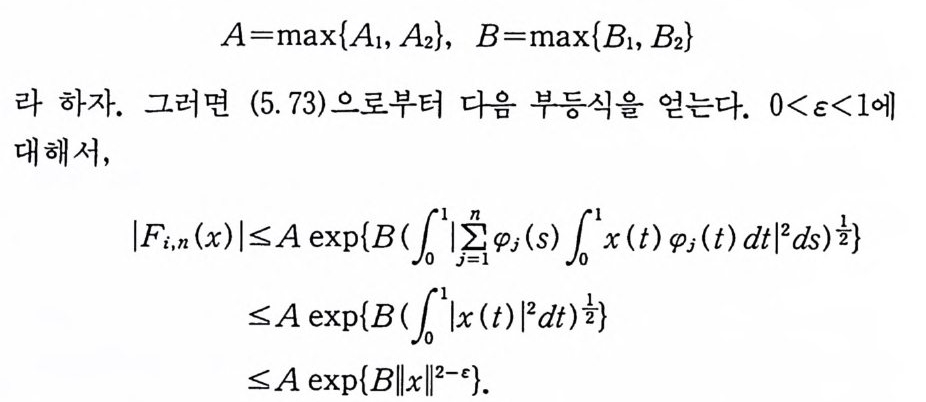 A=max{Ai, A 사, B=max{Bi, B2}
A=max{Ai, A 사, B=max{Bi, B2}
따라서, 보조정리 5.22 의 조건 (3) 이 만족되고 아 보조정리에 의해서 정리가 증명된다.
L2- 함수의 푸리에-위너 번환
 L2(Co(T)) 에 속하는 함수 F(x) 의 푸리에-위너 변환 G( y)를
L2(Co(T)) 에 속하는 함수 F(x) 의 푸리에-위너 변환 G( y)를
를 만족하는 것을 증명한다. (5. 53) 의 프란세렐 관계보다는 (5. 77) 의 관계를 얻기 위해서 정의 5.1 을 수정해서 푸리에-위너 변환을 다음과 같이 정의한다.
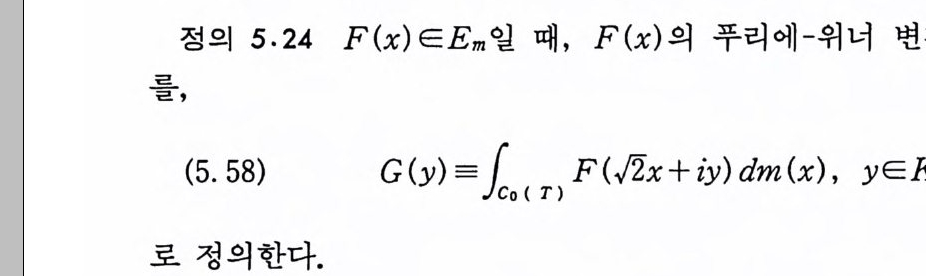 정의 5.24 F(x)EEm 일 때, F(x) 의 푸리에-위너 변환 G(y)
정의 5.24 F(x)EEm 일 때, F(x) 의 푸리에-위너 변환 G(y)
정의 5. 24 에 의하면, 정리 5.14, 따름정리 5.16 은 다음과 같이 된다. 정리 s.25 (1) Em 에 속하는 함수 F(x) 의 푸리에-위너 변환 G( y)는 존재하고, G( y)도 Em 에 속한다. 또한 G( y)의 푸리에 위너-변환은 F(-x) 이다.
 (2) F(x)EEm 이고 G( y)가 F(x) 의 푸리에-위너 변환이면,
(2) F(x)EEm 이고 G( y)가 F(x) 의 푸리에-위너 변환이면,
리에-위너 변환이면, 파시발 관계
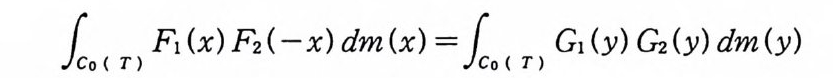 10 < T> F1 (x) F2(-x) dm (x) =10 < r> G1 (y) Gi(y) dm(y)
10 < T> F1 (x) F2(-x) dm (x) =10 < r> G1 (y) Gi(y) dm(y)
가 성립한다. L2- 함수의 푸리에 - 위너 변환을 다음과 같이 정의한다.
 정의 5.26 F(x)EL2(C 。 (T) )라 하자. 만일 F 로 L2- 노름 수
정의 5.26 F(x)EL2(C 。 (T) )라 하자. 만일 F 로 L2- 노름 수
가 존재한다. 따라서, G( y)는 Gn(Y) 들의 L2(Co(T) )에서의 평 균극한 (lim i t in the mean) 이 다. (5. 60) 이 잘 정 의 (well defi ne ) 되 는 것은 정리 5. 30 에서 보일 것이다. 주 5,28 (5. 77) 의 프란세렐 관계에 의해서,
 io( (5 .T 6) 2| G) n (y) —요 (y) J2 dm (y) = 1C0o <( TT)l IFn (x) -F m (x) J2 dm (x)
io( (5 .T 6) 2| G) n (y) —요 (y) J2 dm (y) = 1C0o <( TT)l IFn (x) -F m (x) J2 dm (x)
주 5-29 G( y)의 푸리에-위너 변환이 F( ― x) 임은 다음과 갇 이 보일 수 있다. (5.61) 에서 정의된 Gn(Y) 는 G( y)로 평균수령하므로, 정의 5. 26 에 의해서, G( y)의 푸리에-위너 변환 H(x) 는,
 H(x) =l. i.:..뿡 10( T) 요(/l,y+ix )dm( y)
H(x) =l. i.:..뿡 10( T) 요(/l,y+ix )dm( y)
정리 5-30 (5. 60) 의 G( y)는 Fn(X) 의는 독립적이다. 죽 Fn(X) 와 fn (X) 가 Em 에 속하고 F(x) 로 L2- 수령하는 수열이라 하고,
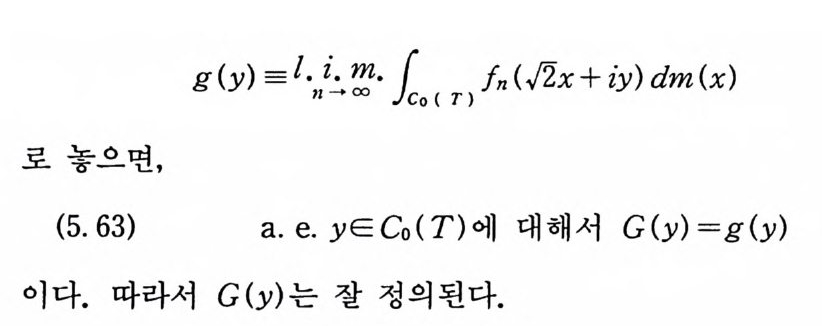 g (y) = !.남· lo ( T) In ( /2.x + iy) dm (x)
g (y) = !.남· lo ( T) In ( /2.x + iy) dm (x)
증명 Gn(Y) 가 (5. 61) 로 정의되고, gn (Y) 를
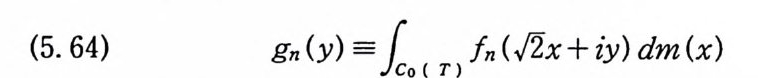 (5. 64) gn (y) =10 ( T ) fn( J2x + iy) dm (x)
(5. 64) gn (y) =10 ( T ) fn( J2x + iy) dm (x)
로 정의하자. 그러면 프란세렐 관계에 의해서, (5. 65)
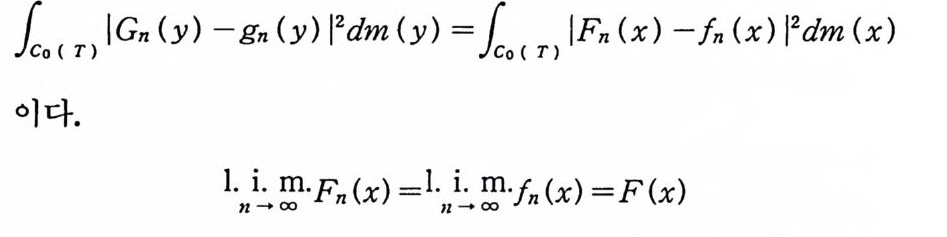 10 < T) IGn (y) -gn ( y) l2dm (y) =lo < T) IFn (x) -fn (x ) l2dm (x)
10 < T) IGn (y) -gn ( y) l2dm (y) =lo < T) IFn (x) -fn (x ) l2dm (x)
이므로 (5. 65) 의 우변의 극한 (n-+ oo 일 때)은 0 이다. 따라서 좌 변의 극한도 0 이다. 그런데,
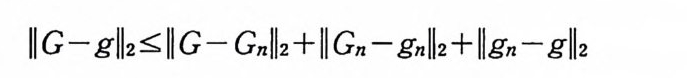 IIG ―g l| 조 IIG 一 Gnll2+IIGn- gn ll2+ll g n- g ll2
IIG ―g l| 조 IIG 一 Gnll2+IIGn- gn ll2+ll g n- g ll2
이므로 (5. 63) 이 성립한다. 이 제 , 푸리 에 -에 르미트 (Fourie r -Herim t e) 급수를 사용해 서 Em 이 L2(Co(T)) 에서 조밀 (dense) 하고, 따라서 L2(Co(T) )의 모든 함수들의 푸리에-위너 변환이 존재하고, 그것이 L2(Co(T)) 에 속함을보이려고 한다.
{a i(t)}가 L2(T) 에서 완비정규 직교집합이고 aj( l) =0, a;(t) 이 존재하고 유계변동이라 하자. n 차 에르미트 함수들의 집합 {qJ (m1, ·· ,mn)} 은 L2(Co(T)) 에서 완 비정규 직교집합이므로(정리 4. 25), 임의의 함수 F(x) EL2(C 。 (T) )는 푸리에-에르미트 급수 (4. 42) 의 평균수령 (L2- 노름 수령) 의 극한이다. 이제, n 차 에르미트 함수들이 Em 에 속하는 것을 보이면 Em 은 L2(Co(T)) 에서 조밀하다.
 'Pm ,i ( x) =Hm (-11x (t) 야(t) dt )
'Pm ,i ( x) =Hm (-11x (t) 야(t) dt )
도 Em 에 속한다. 따라서 Em 은 L2(Co(T)) 에서 조밀하다. 위의 결과를 다음 정리로 기술한다.
 정리 5-31 L2(C 。 (T) )에 속하는 임의의 함수 F(x) 의 푸리에
정리 5-31 L2(C 。 (T) )에 속하는 임의의 함수 F(x) 의 푸리에
6 위너 적분의 부등식과 극한정리
 위너 공간 Co(T) (여기서는, T= 〔 0,1]) 에 내적(i nnerp roduc t)을
위너 공간 Co(T) (여기서는, T= 〔 0,1]) 에 내적(i nnerp roduc t)을
또한, 임의의 실수 a 에 대해서
 (6. 4)
(6. 4)
이다. (6. 7) 을 Y( t)에 대해서 풀고 (6. 6) 의 결과를 적용하면 다음 식을 얻는다.
 (6. 8) £1x( t) y (t) dt =c, (y) £11dx (t) + c2(y ) £1 W (t) dx (t)
(6. 8) £1x( t) y (t) dt =c, (y) £11dx (t) + c2(y ) £1 W (t) dx (t)
 (6. 10) {Z (1) - y(1 ) }2~11 YII 드 2 Y(l) Z (l) + [ Y( 1) ]2
(6. 10) {Z (1) - y(1 ) }2~11 YII 드 2 Y(l) Z (l) + [ Y( 1) ]2
 되는 임의의 {y n}CCo(T) 에 대해서,
되는 임의의 {y n}CCo(T) 에 대해서,
증명 (6) (1. 14) 는 푸비 니 (Fubin i ) 정 리 와 정 리 1. 12 를 사용해 서 식 (6. 4) 로부터 얻는다. (2) (6. 15) 는 식 (6. 5) 로부터 얻는다.
제 3 장 확률적분과 위너 조건적분
 aEL2(T), xECo(T) 일 때 a 의 x 에 대한 팰리-위너-지그문
aEL2(T), xECo(T) 일 때 a 의 x 에 대한 팰리-위너-지그문
이다. 이 적분에서 위너 과정 X (t ,x) 를 브라운 운동 과정 B( t, w) 로 대치하면
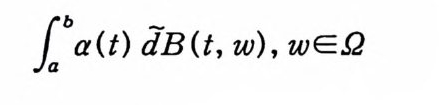 1ab a(t) dB(t, w), w 든요
1ab a(t) dB(t, w), w 든요
이 되고 이 적분을 확률적분이라 한다. 이 장에서는 브라운 운동과정에 대한 확률적분을 정의하고 이 것을 보다 일반적인 가우스 과정으로 확장한다. P. W. Z. 적분은 이 확률적분의 특별한 경우이다. 주어전 확률 벡터 X 에 대한 확 률변수 Y의 조건기대값울 정의하고, 이것을 이용해서 위너 조 건적분을 정의한다. 위너 조건적분에 대한 여러 가지 성질을 조 사하고, 칵-파인만 (Kac-Fe yn man) 공식을 유도한다. 또한 카메룬 -마틴 변환정리를 사용하여 위너 조건적분에 대한 변환정리를 증 명한다. 1 강한 극한정리 이 절에 서 는 레 비 (Lev y) 와 카메 룬-마틴 (Cameron-Marti n) 의 브 라운 운동과정에 대한 극한정리 (1 장 정리 4 . 1) 를 가우스 과정 (Gaussia n pro cess) 으로 확장한다. 이 확장된 정 리 (정 리 1. 4) 를 강 한 극한정 리 (str o ng lim i t the orem) 라 부론다.
 보조정리 1.1 I : (a, b) - R 가 (a, b) 에서 미분가능하고, 그
보조정리 1.1 I : (a, b) - R 가 (a, b) 에서 미분가능하고, 그
 증명 (1. 1) 을 보이기 위해서, [ao, 리 C(a,b) 라 하자. 그러
증명 (1. 1) 을 보이기 위해서, [ao, 리 C(a,b) 라 하자. 그러
 이다.
이다.
라고하자.
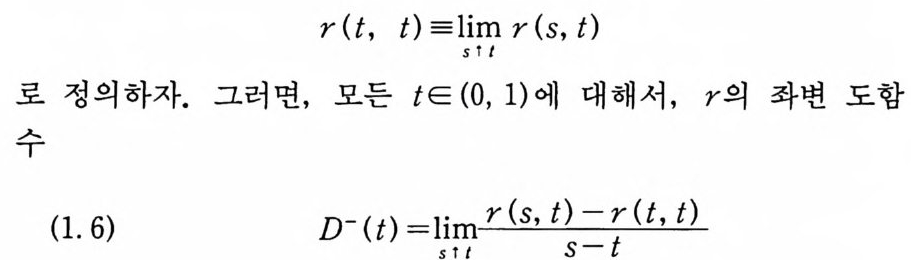 r (t, t) =lim r (s, t)
r (t, t) =lim r (s, t)
이 존재한다. 또한, D- 는 (0,1) 에서 유계이고 연속이며, 다음 식을 만족한다.
 (1. 7) n-(t ) =ls iT m I 싼8s -(s, t)
(1. 7) n-(t ) =ls iT m I 싼8s -(s, t)
에 대한 성질도 얻을 수 있다. 증명 고정된 tE (0, 1) 에 대해서
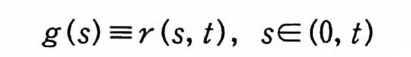 g( s) =r(s, t), sE (0, t)
g( s) =r(s, t), sE (0, t)
로 놓자. (0, t)에서 g이 유계이므로, 보조정리 1. 1 에 의해서,
극한 (1. 11) lsi mI O g ' (s) , lsi Im I g' (s) 이 존재 하고, 그 값은 유한하다. g'이 (0, t)에서 연속인 사실과 (1. 11) 에 의해서 g'은 (0, t)에 서 유계이다. 보조정리 1. 1 에 의해서,
 (1. 12) llsi 1m I g ' (s)-g' (s)I~B(t- s)
(1. 12) llsi 1m I g ' (s)-g' (s)I~B(t- s)
이다. 보조정리 1. 2 에 의해서, g의 좌변 도함수 D i(t)가 존재 하고
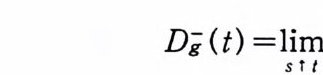 Di (t) =lsi mT I g ' (s) .
Di (t) =lsi mT I g ' (s) .
이다. g의 정의에 의해서 (1. 7) 을 얻고, (1. 12) 로부터 (1. 8) 을 얻는다.
 (1. 9) 를 증명하기 위해서, t', tE (0, 1), t'< t인 경우를 생
(1. 9) 를 증명하기 위해서, t', tE (0, 1), t'< t인 경우를 생
여기서 t* E (t', t). 위의 부등식에 극한 s i t’를 취하면, (1. 9) 롤 얻는다.
 정리 1.4 (강한 극한 정리) 확률공간 (요, J3, p)와 T= [0, 1 ]c
정리 1.4 (강한 극한 정리) 확률공간 (요, J3, p)와 T= [0, 1 ]c
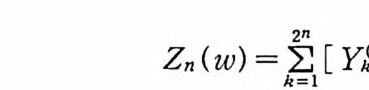 Zn(W) = k~2=I [ yin> (W)]2
Zn(W) = k~2=I [ yin> (W)]2
이다. {yJn> : k=l, 2, …, 2 가은 가우스 과정의 확률변수 {X( t, ·) : t ED} 들의 일차 결합들의 모임이므로 가우스 과정이다(부록정리 6.6). 따라서, 2n- 차원 확률 벡터
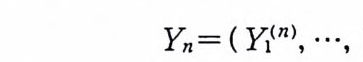 Yn= ( Yj
Yn= ( Yj
의 확률분포(p robab ility d i s t r i bu ti on) 는 평균 벡터가 0 이고 공분산 행렬이 Vn 인 2n- 차원 정규분포이다. 여기서,
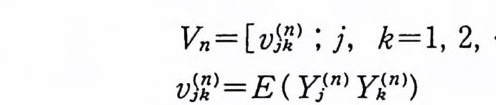 Vn= [vj;> ; j, k=l, 2, …, 2 가
Vn= [vj;> ; j, k=l, 2, …, 2 가
이 다. 또한 Zn 은 Yn 과 Y려 내 적 (inn er pro duct) 이 다. 죽,
 Zn= ( Yn, Yn)
Zn= ( Yn, Yn)
이 다. 체 비 세 프 (Cheby sh ev) 부등식 에 의 해 서
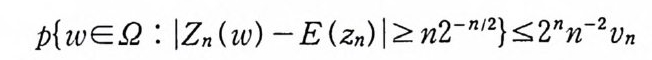 p {wE 요 : IZn(w)-E(zn)I :::2-: nz-n12} 갤 nn-2Vn
p {wE 요 : IZn(w)-E(zn)I :::2-: nz-n12} 갤 nn-2Vn
이 성립한다.
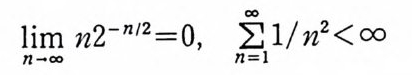 Ini-m00 nz-n12=0, n~o=o l l/n2
Ini-m00 nz-n12=0, n~o=o l l/n2
이므로, 만일 znvn(n=l, 2, …)이 유계인 것을 보이면, 부록정리 5.18 에 의해서,
 (1.1 8) t뻣 {Zn(w)-E(Zn)}=O : a. e. w 든요
(1.1 8) t뻣 {Zn(w)-E(Zn)}=O : a. e. w 든요
 =틀(꿈 着)-블(fn, 꿉)
=틀(꿈 着)-블(fn, 꿉)
이다. 따라서,
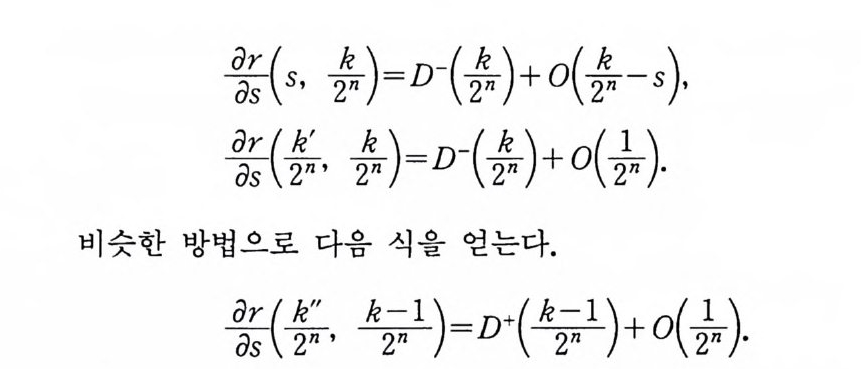 불 (s, 감 )=D 信)+ 0({n -s ),
불 (s, 감 )=D 信)+ 0({n -s ),
t E(0 , 1) 에 대해서, n-(t) , D+ (t)이 유계라는 사실로부터, 보조정리 1. 3 에 의해서 ,
 潭 ={D- 信)― D 伊군)}fn +o( (京 )2)=0 信)
潭 ={D- 信)― D 伊군)}fn +o( (京 )2)=0 信)
이다. (주 : D+(1) 은 정의되지 않는다).
 윗식과 식 (1.1 6), (1. 20) 에 의해서, k= 언에 대해서,
윗식과 식 (1.1 6), (1. 20) 에 의해서, k= 언에 대해서,
이 성립한다. (1. 21) 의 우변 적분은 이상(i m p ro p er) 리만 적분이 고, f가 (0,1) 에서 연속이고 유계(보조정리 1. 3) 이므로 그 적분 은 존재한다.
 (1. 18) 과 (1. 21) 에 의해서 m(t) =O 인 경우의 정리 1. 4 가 증명
(1. 18) 과 (1. 21) 에 의해서 m(t) =O 인 경우의 정리 1. 4 가 증명
 가우스 과정 X 에 대해서는 정리 1. 4 가 성립되므로,
가우스 과정 X 에 대해서는 정리 1. 4 가 성립되므로,
 따름정리 l.5 가우스 과정 X 가 정리 1. 4 의 가정을 만족하고 ,
따름정리 l.5 가우스 과정 X 가 정리 1. 4 의 가정을 만족하고 ,
따름정리 1.6 a( t)가 T=[O, 1] 에서 정의된 실가함수로서 T 에서 유계 도함수를 갖는다고 하자. b (t)는 단조증가함수로서 T 에서 유계 2 차 도함수를 갖는다고 하자. 일반화된 브라운 운동과정 (ge nerali ze d Brown ian moti on pro cess)
 X (t,w ), tE T, wE 요가 다음 조건을 만족한다고 하자. cE
X (t,w ), tE T, wE 요가 다음 조건을 만족한다고 하자. cE
 특히, a( t)= O,b( t)=t, tE T, c=O 인 브라운 운동과정
특히, a( t)= O,b( t)=t, tE T, c=O 인 브라운 운동과정
증명 부록 정리 6 . 8 에 의해서, 평균함수 m( t)와 공분산함수 r (s, t) 는 다음과 같이 주어 진다.
 m (t)= E(X( t, •))=a (t)一 a(O)+c, tE T
m (t)= E(X( t, •))=a (t)一 a(O)+c, tE T
이고, 정리 1. 4 에 의해서 (1. 26) 을 얻는다.
2 브라운 운동과정에 대한 확률적분 (요,:B,p)를 확률공간, X 를 이 확률공간에서 정의된 확률변수 라하자.
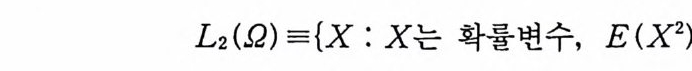 L2( 요) ={X : X 는 확률변수, E(X2) <00}
L2( 요) ={X : X 는 확률변수, E(X2) <00}
로 놓자. L2 (요) 에 서 내 적 (inn er pro duct) (X, Y) 를
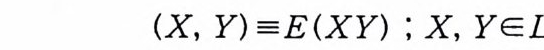 (X, Y) =E(XY) ; X, YEL2( 요)
(X, Y) =E(XY) ; X, YEL2( 요)
 로 정의하면 L2( 요)는 힐베르트 공간 (H il ber t spa c e) 이 된다. 실
로 정의하면 L2( 요)는 힐베르트 공간 (H il ber t spa c e) 이 된다. 실
 E (X2) = (X, X) = IIXll2
E (X2) = (X, X) = IIXll2
확률적분을 다음과 같이 정의하려고 한다. 먼저, S(T) 에서 L2( 요)로 가는 거리보존 선형변환(i some t r ic line ar tra nsfo r mat ion ) 으로서 확률적 분을 정 의 하고, 이 정 의 를 L2 (T) 로 확장한다. 이와 같은 변환의 존재성은 참고문헌 (Kre y sz ig [l] , p .139) 을 참조.
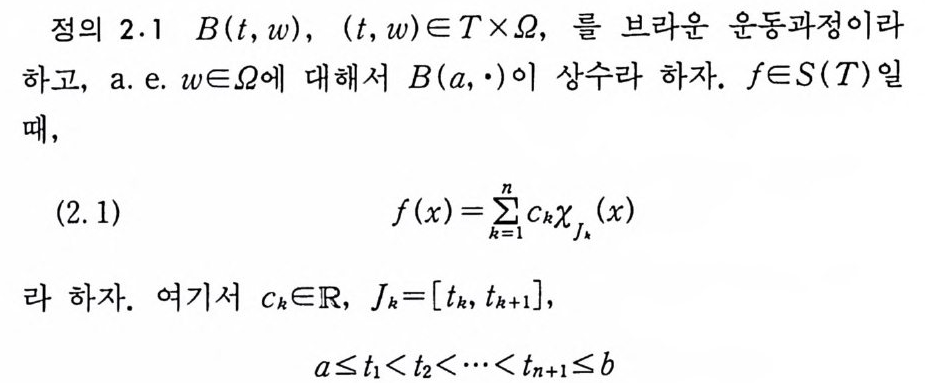 정의 2.1 B (t, w), (t, w)ETX Q , 룰 브라운 운동과정이라
정의 2.1 B (t, w), (t, w)ETX Q , 룰 브라운 운동과정이라
이다. 브라운 운동과정 B 에 대한 함수 f의 확률적분 J(f)는 다음과 같이 정의되는 확률변수이다.
 I(/) (w) = k~=n I ck{BUk+ I, w) -B( tk, w)}, w 든요.
I(/) (w) = k~=n I ck{BUk+ I, w) -B( tk, w)}, w 든요.
 (3) II I U) 112 = V [I U> J= 111112
(3) II I U) 112 = V [I U> J= 111112
(3) 은 (2) 의 특별한 경우이다. (4) {B( t, ·), tE T} 는 가우스 과정 (Gaussia n p rocess) 이므로 이 과정에 속하는 확률변수들의 임의의 일차 결합의 확률분포는 정규분포이다(부록정리 4.18). 따라서, 1(/) 의 확률분포도 정규 분포이다. (1)과 (3) 에 의해서,
 E (J(/)) =0
E (J(/)) =0
이다. 따라서, 만일 {fn } 이 L2(T) 에서 코시 (Cauchy ) 수열이면, {I (fn) } 은 L2 (요) 에 서 코시 수열 이 된다. L2 (Q) 는 완비 (com- p le t e) 이므로,
 (2. 2) L떤 IIIUn>-Xll=O
(2. 2) L떤 IIIUn>-Xll=O
정의 2.3 (2.2) 를 만족하는 X 를, 브라운 운동 B에 대한 f의 확률적분이라 하고, I (f)로 표시한다. 즉,
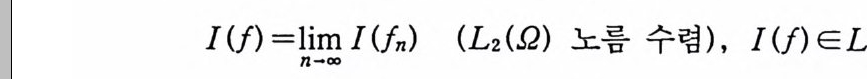 I( f) =lni-OmO IUn) (L2( 요) 노름 수령), I( f) EL2(Q ).
I( f) =lni-OmO IUn) (L2( 요) 노름 수령), I( f) EL2(Q ).
정리 2.4 I(/ )는 수열 {/n} 과는 독립적이다. 따라서 1(/) 는 잘 정의 (well de fi ne) 된다.
 증명 {gn }CS(T) 이고 lim ll gn - f ll=O 이라 하자. 그러면
증명 {gn }CS(T) 이고 lim ll gn - f ll=O 이라 하자. 그러면
증명 슈바르츠 (Schwarz) 부등식 에 의해서 ,
 I(X, Y)I:'.5: :I IXll·11YII,
I(X, Y)I:'.5: :I IXll·11YII,
 一 I( f)는 확률수령 (converge nce in pro babil ity) 이다. {JU n) : fn 든
一 I( f)는 확률수령 (converge nce in pro babil ity) 이다. {JU n) : fn 든
 M=f (b ) -I(a)
M=f (b ) -I(a)
이다. 증명 (1) /가 T 에서 단조증가함수인 경우,
로놓으면,
 Un : n=l, 2, … }cS(T)
Un : n=l, 2, … }cS(T)
 (2) /EBV(T) 인 경우,
(2) /EBV(T) 인 경우,
이므로 {fn } 은 L2(T) 에서 코시 수열이다. L2(T) 는 완비 (com p le t e) 이므로, In -I (노름 수령)되는 IEL2(T) 가 존재한
다. 정리 2. 6 의 (3) 과 (5) 에 의해서 12 一 00 일 때,
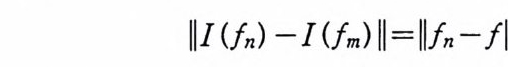 IIIUn)-IUm)ll=llfn — f|| 一 O
IIIUn)-IUm)ll=llfn — f|| 一 O
이다. 이것으로부터,
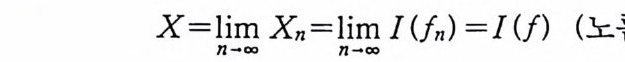 X=lni-OmO Xn=lni 一m O O IUn) =JU ) (노름 수령)
X=lni-OmO Xn=lni 一m O O IUn) =JU ) (노름 수령)
울 얻는다. 따라서, XEG 이고 G 는 폐집합이다. 힐베르트 공간 L2( 요)의 선형부분공간은 힐베르트 공간이므로, G 는 힐베르트 공간이다. 정리 2. 6 의 (2) 와 (5) 에 의해서 I 는 동형사상이 된 다.
 따름정 리 2 . 9 {I (fa) : aeA} 이 독립 (ind ep en dent) 일 필요충분
따름정 리 2 . 9 {I (fa) : aeA} 이 독립 (ind ep en dent) 일 필요충분
 주 다음 조건을 만족하는 {fa } 를 완비 (comp le te ) 하다고 한다.
주 다음 조건을 만족하는 {fa } 를 완비 (comp le te ) 하다고 한다.
증명 (1) 은 정리 2. 6 의 (2) 와 (3) 에 의해서 얻는다. (2) 는 따 름정리 2. 9 와 (1) 에 의해서 얻는다.
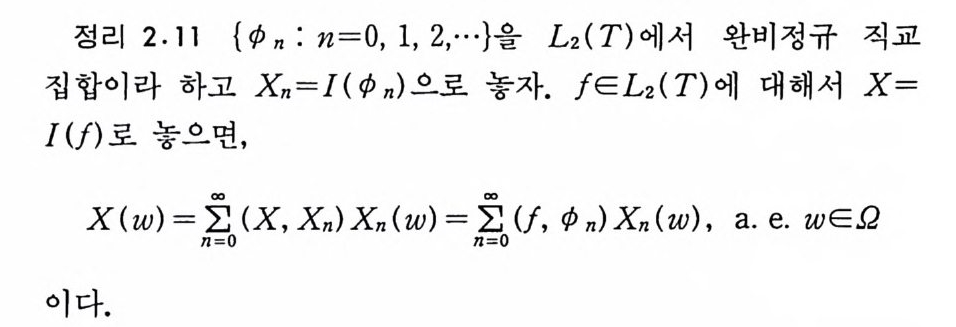 정리 2.11 {
정리 2.11 {
증명 따름정리 2. 9 와 2.10 에 의해서 {Xn} 은 독립이고 L2( 요) 에서 완비정규 직교집합이다. 따라서,
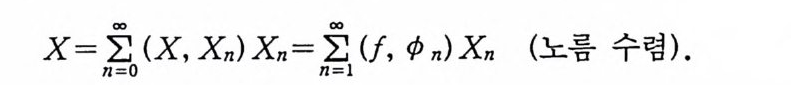 X= 1~10= 0 0 (X, Xn)Xn 죠n0= 0 l (/, ¢n)Xn (노름 수령).
X= 1~10= 0 0 (X, Xn)Xn 죠n0= 0 l (/, ¢n)Xn (노름 수령).
노름 수령 하면 확률수령 (converge nce in pro babil ity) 하고, 독립 인 확률변수들의 확률수령은 a. e. 점별수렴하므로(부록 정리 5. 19) 정리가 증명된다. 다음 정리는 확률적분과 팰리-위너-지그문드 적분 사이의 관계 를 말해 준다. 팰 리 -위 너 -지그문드 적분을 초보적 인 (pr oto t y pe ) 확률적분이라고 부르기도 한다.
 정리 2.12 확률공간 (요,:B,p)를 위너 측도공간, 브라운 운동
정리 2.12 확률공간 (요,:B,p)를 위너 측도공간, 브라운 운동
 B (t,x )=x(t ). 그러면 /EL2(T) 의 확률적분과 팰리_위너-지그
B (t,x )=x(t ). 그러면 /EL2(T) 의 확률적분과 팰리_위너-지그
3 가우스 과정에 대한 확률적분 이 절에서는 브라운 운동과정을 포함하는 어떤 가우스 과정에 대한 L2(T)- 함수들의 확률적분을 정의하고 그 성질을 조사한 다.
 (Q ,13, p)와 T=[O, 미에서 정의된 가우스 과정 X 가 다음 조
(Q ,13, p)와 T=[O, 미에서 정의된 가우스 과정 X 가 다음 조
 (3. 1) 평균함수 m(t) =O
(3. 1) 평균함수 m(t) =O
(3. 4) a2rIa t as 은 스 I U 스제서 a. e. 연속이다. 주 (3. 2) 와 (3. 3) 은 정리 1. 4( 강한 극한정리)에서 가정한 조건 이 다. (3. 2) 와 (3. 3) 을 만족하는 가우스 과정 을 박스터 (Baxte r ) 과정이라고 한다.
 C(T) 는 T 에서 정의된 연속함수들이 L2(T) 에서의 동치족들
C(T) 는 T 에서 정의된 연속함수들이 L2(T) 에서의 동치족들
보조정 리 3 . l 함수 r : T x T - ➔ R이 조건 (3. 2) , (3. 3) , (3. 4) 룰 만족하는 양의 정 부호 (po sit ive defi ni t e) 대 칭 함수 (sy mme tr i c fun cti on ) 라 하자.
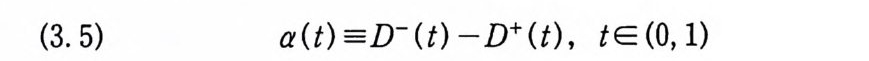 (3. 5) a(t) = D-(t) — D+( t), tE (0,1)
(3. 5) a(t) = D-(t) — D+( t), tE (0,1)
로 놓고 T 의 분할 (pa rti tion ) P,
 P : O=ao
P : O=ao
 + r (ak-1, a,-1) : l, k= 1, 2, …, q
+ r (ak-1, a,-1) : l, k= 1, 2, …, q
증명 a 는 (0,1) 에서 유계이고 연속이므로 다음 두 적분은 존 재하고 갇다.
 (3. 14) f0 l a(t) dt =.IfT a(t ) d).(t) .
(3. 14) f0 l a(t) dt =.IfT a(t ) d).(t) .
보조정리 1. 3 의 (1. 8), (1. 9) 를 적용해서 다음 식을 얻는다.
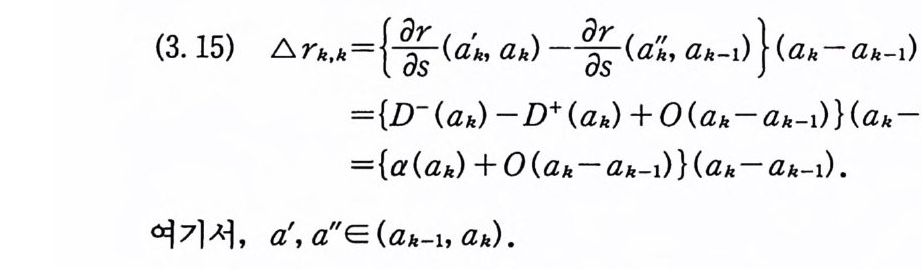 (3.15) D,. Yk,k={ 틀마, ak) ―틀 (a'/,, a,.-1 가 (ak_ak-1)
(3.15) D,. Yk,k={ 틀마, ak) ―틀 (a'/,, a,.-1 가 (ak_ak-1)
 리만 적분 「。 a (t )d t가 존재하므로, 각 c>O 에 대해서 다음을
리만 적분 「。 a (t )d t가 존재하므로, 각 c>O 에 대해서 다음을
 (3.19) IS1(P)- f亨틀 (s, t)d sdtl < c
(3.19) IS1(P)- f亨틀 (s, t)d sdtl < c
울 얻고, 이것을 이용해서 (3.12) 의 증명과 같은 방법으로 (3. 13) 을 얻는다. 정리 3.2 X가 (3.1), (3. 2), (3. 3), (3. 4) 를 만족하는 가우 스 과정이라 하자. p n 을 T 의 분할 :
 Q= an,O
Q= an,O
은 L2( 요)에서 코시 수열이다. 이 코시 수열이 L2( 요)에서 수령
하는 극한은 f에 의해서 결정되고, {P 가과 {a 가과는 독립적이다.
 증명 f가 T 에서 평등연속이므로, 주어진 c>O 에 대해서, 다
증명 f가 T 에서 평등연속이므로, 주어진 c>O 에 대해서, 다
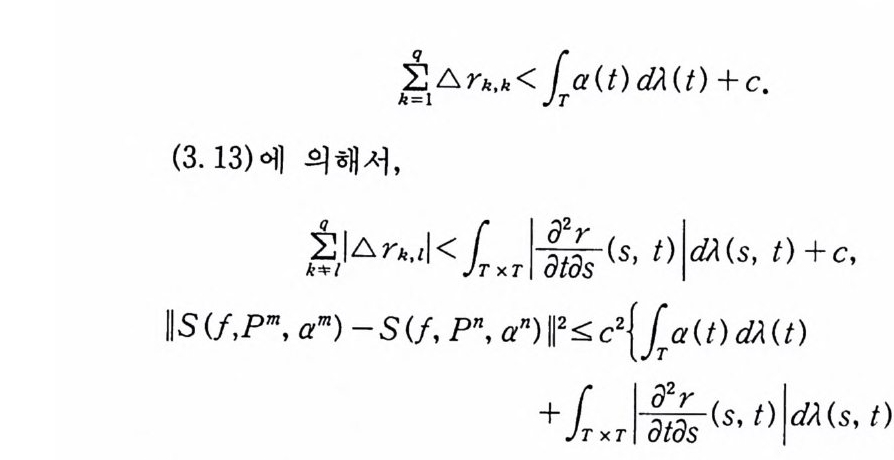 홉E rk,h< fTa(t) d), (t) + c.
홉E rk,h< fTa(t) d), (t) + c.
이것으로부터, {S (f,p n, 건)}은 L2( 요)에서 코시 수열이 된다. 이 코시 수열이 수령하는 극한이 {P 가, {a 가과 독립적임을 보이 기 위해서, {Q가 {(]가을 위와 같은 성질을 갖는 또 다른 수열이 라 하자. 수열 IP 사, I Q시, |P 기, I Q기, … 은 0 으로 수렴하므로, 수열 S (f, P1 , a1) , S (f, Q1 , (]1) , S (f, P2 , a2) , S (f, Q2 ' 합) , … 은 L2( 요)에서 코시 수열이 된다. 따라서, 이 코시 수열의 부분 수열 {S (f, pn ' 간) }과 {S (f, Q짝 pn) }은 L2@) 에 서 같은 국한으 로 수령한다.
 정의 3.3 /EC(T) 일 때, 가우스 과정 X 에 대한 f의 확률적
정의 3.3 /EC(T) 일 때, 가우스 과정 X 에 대한 f의 확률적
 정리 3-4 f,gE C2(T), a, bElR 일 때, 다음 사실이 성립한
정리 3-4 f,gE C2(T), a, bElR 일 때, 다음 사실이 성립한
이므로 (1) 이 성립한다. (2) 는 다음 식으로부터 얻는다.
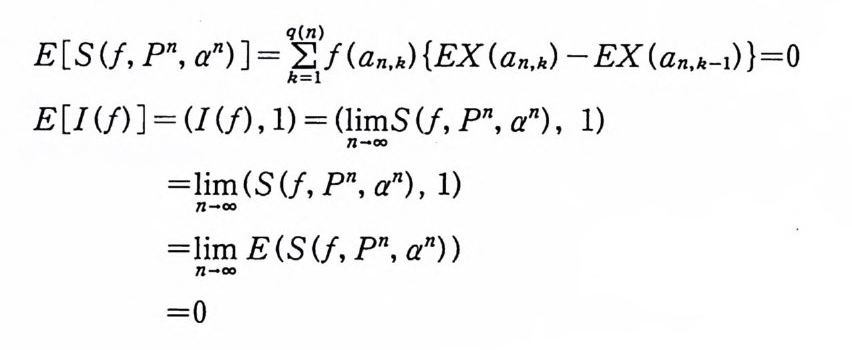 E[S( f, pn , an)] 홍f (an,k){EX(an,k) —EX (an,k-1)}=0
E[S( f, pn , an)] 홍f (an,k){EX(an,k) —EX (an,k-1)}=0
 (3. 20) (I (/) , J (g) ) = t뽀 (S (f, pn , an) , S (g, pn ' 간) ) .
(3. 20) (I (/) , J (g) ) = t뽀 (S (f, pn , an) , S (g, pn ' 간) ) .
(3) 을 증명하자.
는 르베그 적분으로 수령한다. 따라서,
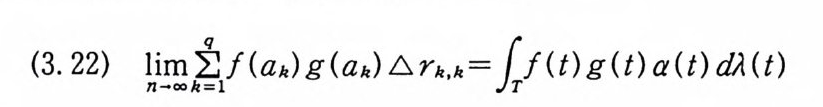 (3. 22) 1i~ £ /
(3. 22) 1i~ £ /
이다. 비슷한 방법으로, 다음 식을 얻는다.
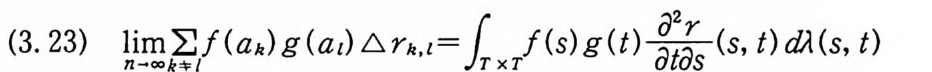 (3. 23) ~~k~/(ak)g ( a1) l:::,.r k.1=l x/(s)g (t)~ (s, t) &(s, t)
(3. 23) ~~k~/(ak)g ( a1) l:::,.r k.1=l x/(s)g (t)~ (s, t) &(s, t)
(3. 20), (3. 21), (3. 22), (3. 23) 에 의해서 (3) 이 성립한다. (4) 는 (3) 의 특별한 경우이다. (5) 와 (6) 은 정리 2. 6 의 (4) 와 (6) 과 같은 방법으로 증명한다.
 정리 3.5 X는 정리 3.2 에서 주어진 가우스 과정이라 하자.
정리 3.5 X는 정리 3.2 에서 주어진 가우스 과정이라 하자.
o] 다. 증명 T 에서, f가 유계변동 (bounded var i a ti on) 이고 X(·, w) 이 연속이므로 (3.24) 의 우변 적분은 모든 wE 요에 대해서 존재 한다. {S( f, pn , a 이}이 L2( 요)에서 J(f)로 수령하므로, 다음 식 울 만족하는 부분수열 {nk} 가 존재한다.
 (3. 25) 1떤 S( f, pn i., an) (w) =/(/) (w), a. e. wEQ
(3. 25) 1떤 S( f, pn i., an) (w) =/(/) (w), a. e. wEQ
이므로 (3. 24) 가 성립한다.
 보조정리 3.6 /EL2(T), fn EC(T) 이고
보조정리 3.6 /EL2(T), fn EC(T) 이고
이다. 따라서, {/n} 이 L2(T) 에서 코시 수열이라는 사실로부터, {I( fn )} 이 L2( 요)에서 코시 수열이 된다.
 g후 C(T), llg n — f|| 一 。
g후 C(T), llg n — f|| 一 。
 라 하자. 그러면, {/1,g 1 ,/2,g 2, …}은 C(T) 의 원소들의 수열이
라 하자. 그러면, {/1,g 1 ,/2,g 2, …}은 C(T) 의 원소들의 수열이
울 보이기 위해서 다음 식을 증명하면 된다.
 (3. 27)
(3. 27)
보조정리 3. 6 에서 정의한 A, B, 11-1 11 에 대해서,
 ln i -m..|. · .f1r 江) g-n ( t) a (t) cl).. (t) —./ITf (t) g (t) a ( t) d).. ( t) |
ln i -m..|. · .f1r 江) g-n ( t) a (t) cl).. (t) —./ITf (t) g (t) a ( t) d).. ( t) |
비슷한 방법으로 다음 식을 얻는다.
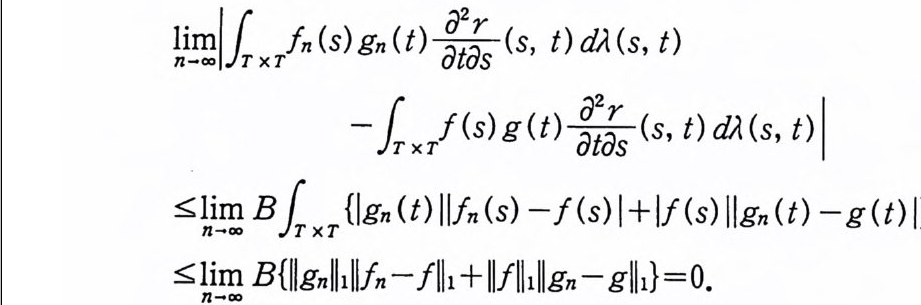 닌 lr x/n (s)g n (t)ftis(s , t) &(s, t)
닌 lr x/n (s)g n (t)ftis(s , t) &(s, t)
따라서 (3. 27) 이 성 립 하고, (3) 과 (4) 가 증명 된다. (5) 와 (6) 은 정리 2.6 의 (4) 와 (6) 의 증명과 같은 방법으로 얻는다.
4 조건기대값 이 절에서는 주어전 확률 벡터 X 에 대한 확률변수 Y 의 조건 기대값 (cond iti onal exp e ct at i on ) E( YIX) 를 정의하고, 함수 E (exp {i ( u , x) } Y) 의 역 푸리 에 변 환 (inv erse Fourie r -tr a nsfo r m) 으로 서 의 E ( YIX) 에 대 한 반전 공식 (inv ersio n for mula) 을 유도한다. (Q나'8, P) 를 확률공간, (S, Y) , ( T, '§ ) 를 측도가능공간이 라 하자.
 x : 요 -+ S, y : 요 -+ T
x : 요 -+ S, y : 요 -+ T
울 측도가능변 환 (measurable tra nsfo r mat ion ) 이 라 하고 X 에 의 해 서 결정되는 측도 Px 를,
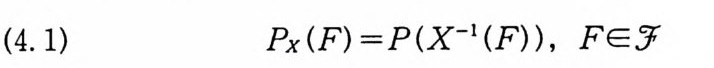 (4. 1) Px(F) =P(X-'(F)), F 겁
(4. 1) Px(F) =P(X-'(F)), F 겁
로 정 의 하자. Px 를 X 의 확률분포 (pro babil ity dis t r i b u t ion ) 라고 한다. Y 에 대해서도 같은 정의를 할 수 있다.
 정의 4.1 GE g라 하자. 주어전 X 에 대해서, Y 가 G 에 속
정의 4.1 GE g라 하자. 주어전 X 에 대해서, Y 가 G 에 속
 이 동치족을 대표하는 특정한 하나의 함수로 사용하기로 한다.
이 동치족을 대표하는 특정한 하나의 함수로 사용하기로 한다.
 /EL1(T, '§,P 사라 하자. 만일, P(YIX) 이 존재한다면, Px -a.
/EL1(T, '§,P 사라 하자. 만일, P(YIX) 이 존재한다면, Px -a.
한 함수로 확장하기 위해서는 보조정리 4.7( 조건기대값에 대한 단 조수령정리)을 사용한다. 증명은 각자에게 맡긴다. 보조정 리 4 . 7 단조수령 정 리 (monot on e converge nce the orem)
 ZnEL1( 요, 13,P), Zn(w) i Z。 (w) : p-a . e. wEQ
ZnEL1( 요, 13,P), Zn(w) i Z。 (w) : p-a . e. wEQ
이다. 여기서 느는 등식의 어느 한 적분이 존재하면 다른 적분도 존재하고, 두 적분이 같음을 뜻한다. 증명 (4.7) 의 처음 등식은 자명하다. 두번째 등식을 보이기 위해서 다음 경우를 생각하자.
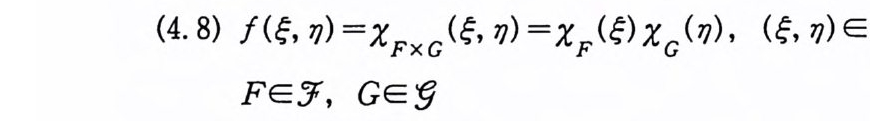 (4.8) f(f,TJ)= XFXG(f,T J) =XF(f) X G(TJ ), (f,TJ) ESXT,
(4.8) f(f,TJ)= XFXG(f,T J) =XF(f) X G(TJ ), (f,TJ) ESXT,
그러면 정의 4. 4 의 (1) 과 (2) 에 의해서, 그리고 (4. 2) 에 의해 서, 다음 식이 성립한다.
 fff(e, 7 J) dP( Y|X) (n, e) dPx (e)
fff(e, 7 J) dP( Y|X) (n, e) dPx (e)
따라서 (4. 7) 의 두번째 등식이 (4. 8) 의 경우에 성립한다. 이제, 푸비니 정리의 증명방법을 따르면, 임의의 측도가능함수 f에 대 해서도 (4.7) 의 등식이 성립하는 것을 보일 수 있다.
 성질 4.9 Z : .Q -+ ]R가 확률변수이고 E(|ZI) < oo 라 하자.
성질 4.9 Z : .Q -+ ]R가 확률변수이고 E(|ZI) < oo 라 하자.
이다.
증명 집합함수 O 를
 (I)( B)=fs z (w)dp ( w), B 겁
(I)( B)=fs z (w)dp ( w), B 겁
이다. 이제 (4.9) 를 증명하기 위해서 다음 식을 증명하면 된다.
 (4. 10) iDg-( X (w) ) d(!) (w) ~.1IS g ( e) E(ZIX)(e) dPx (e)
(4. 10) iDg-( X (w) ) d(!) (w) ~.1IS g ( e) E(ZIX)(e) dPx (e)
이므로 (4 . 10) 이 성립한다. 이 결과를 성질 4. 6 의 증명에서와 같 이 g가 S 에서 임의의 Y- 측도가능한 함수인 경우로 확장한다.
R 에서의 분포함수 F의 특성함수 rp가 르베그 적분가능하면, F 는 절대연속이고, 다음 식이 성립한다.
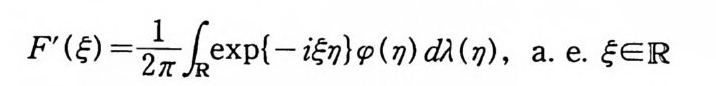 F'(~) =吉 lex p{-i~7J}rp(7J) dJ..(7}) , a. e. ~ER
F'(~) =吉 lex p{-i~7J}rp(7J) dJ..(7}) , a. e. ~ER
정 리 4 • 10 ( 레 비 -하 비 랜 드 반 전 정 리 : Levy -H avil an d inv ersio n the orem) µ를 (]Rn , J3(JR n)) 에서의 유한부호측도, ¢를 µ의 특성함수라 하자. 죽

증명 Chow and Teic h er[!, Theorem 1, p. 26 사참조. (4.11) 로부터 다음 정리를 얻는다. 정리 4.11 (]R n 나 8(lRn)) 에서의 유한측도 µ의 특성함수 ¢가 르베그 적분가능하다고 하자. 그러면, µ는 르베그 측도 A 에 대 해서 절대연속이고, 라돈-니코딤 (Radon-Ni ko dy m ) 도함수는 다 음과 같이 주어진다.
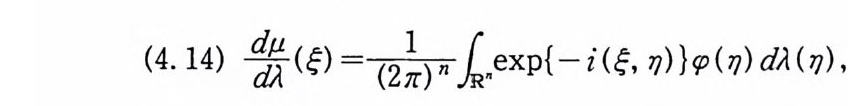 (4.14) 뿔正)= (2 노i .ex p{一i(~, 7J)}rp(7J) dtl( 7J), ~ElRn
(4.14) 뿔正)= (2 노i .ex p{一i(~, 7J)}rp(7J) dtl( 7J), ~ElRn
증명 (4.11) 의 우변의 피적분함수의 j번째 항은 T}j의 함수로 서 유계이고 연속함수이므로, 만일 rp가 Rn 에서 르베그 적분가능 하면, (4.11) 의 우변의 피적분함수도 Rn 에서 르베그 적분가능하 다. 따라서 (4.11) 은 다음과 같이 된다.
 (4. 15) 1 」1 굿 a,, b, (~J dµ (~)
(4. 15) 1 」1 굿 a,, b, (~J dµ (~)
하고, 따라서,
 (4. 16) (µ+,-l) (A6B) < E
(4. 16) (µ+,-l) (A6B) < E
각 B(k) 가 다음과 같이 주어진다고 하자.
 (4. 20) B(k) = g(k) 十 C(k)
(4. 20) B(k) = g(k) 十 C(k)
여기서,
 g (k) 드 Rn, c(k)= (-hik ), hlk)) X … X (-hhkl, hhkl) CRn.
g (k) 드 Rn, c(k)= (-hik ), hlk)) X … X (-hhkl, hhkl) CRn.
C(k) 가 개구간이라는 사실과 (4.13) 의 f aJ, bj 의 정의, 그리고 (4. 15) 로부터 다음 식 을 얻는다.
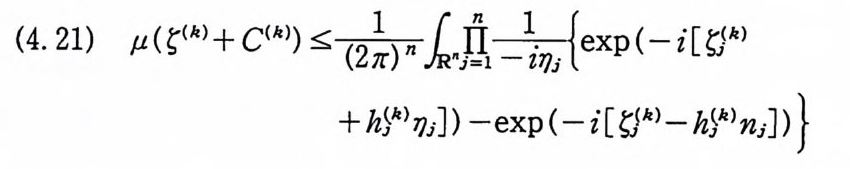 (4. 21) µ(s( k)+c
(4. 21) µ(s( k)+c
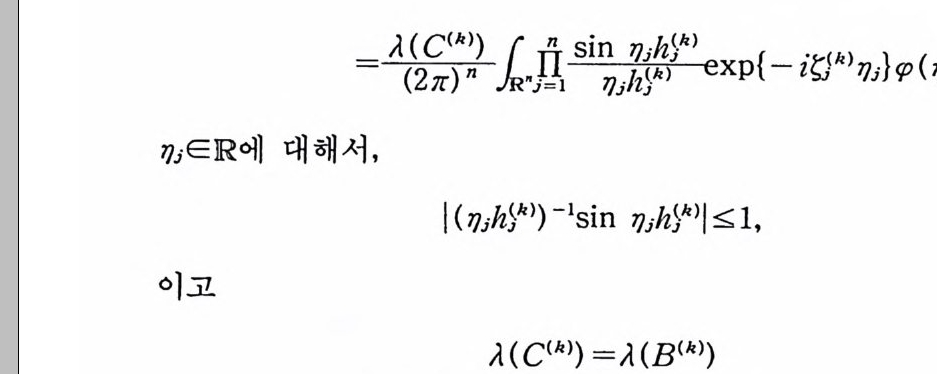 = A((2:? 鬪1 쁘昌信-e x p{― itJk) T Jj}
= A((2:? 鬪1 쁘昌信-e x p{― itJk) T Jj}
이므로, 다음 식이 성립한다.
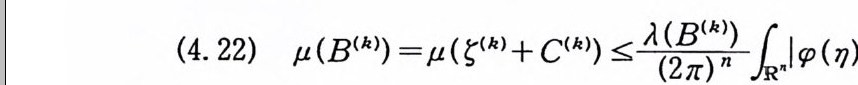 (4. 22) µ (B 이 = µ ( g(k) + c(k)) < A(멸 : L 」
(4. 22) µ (B 이 = µ ( g(k) + c(k)) < A(멸 : L 」
(4. 19) 와 (4. 22) 로부터
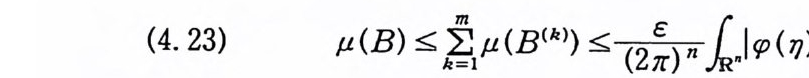 (4. 23) µ (B) 영mµ (B(k)) < (2:) n L 」 (f) ( n) | & ( 1J)
(4. 23) µ (B) 영mµ (B(k)) < (2:) n L 」 (f) ( n) | & ( 1J)
울 얻고, (4.23) 을 (4.17) 에 대입하면 다음 식을 얻는다.
 µ(A)
µ(A)
 (4. 24) f i; + c. 뿔~) dtt (~) =µ ( s+ C 사
(4. 24) f i; + c. 뿔~) dtt (~) =µ ( s+ C 사
을 얻고, 따라서 증명이 끝난다. 성질 4. 8 과 정리 4.11 로부터 다음 정리 (조건기대값에 대한 반전 정 리 (inv ersio n the orem) ) 를 얻는다.
 정리 4.12 Y 와 X를 각각 (Q ,11, p)에서 정의된 확률변수와,
정리 4.12 Y 와 X를 각각 (Q ,11, p)에서 정의된 확률변수와,
 (4.27) E( YIX) (~)껍『 (8) = (2 노 i.exp {— i(u , ~)}
(4.27) E( YIX) (~)껍『 (8) = (2 노 i.exp {— i(u , ~)}
로 정의하자. 성질 4. 8 의 (4. 7) 과 성질 4. 6 의 (4. 4) 를 f의 실수 부와 허수부에 적용해서 다음 식을 얻는다.
 (4. 28) 탸= i x.e px{pi ({iu (, uX, )e}) Y}k] T}d P ( YIX) ( 7}, e) dPx
(4. 28) 탸= i x.e px{pi ({iu (, uX, )e}) Y}k] T}d P ( YIX) ( 7}, e) dPx
와 음수부 (ne g a ti ve p ar t)에 적용해서 다음 식을 얻는다.
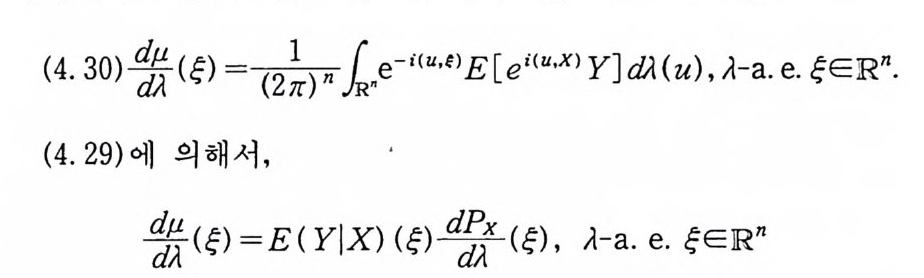 (4. 30) 뿔 5) = (2 노 i.e- i ( u , t ) E[ei( U,X) Y] cl}.( u), 11-a. e. eERn.
(4. 30) 뿔 5) = (2 노 i.e- i ( u , t ) E[ei( U,X) Y] cl}.( u), 11-a. e. eERn.
이 므로 (4. 27) 을 얻는다. 5 위너 조건적분 위너 측도가능한 함수 X 에 대한, 위너 적분가능한 함수 Y 의 조건 기 대 값, EW ( YI X) 를 위 너 조건 적 분 (condit ion al W ien er int e - gr als) 이라 한다. 위너 조건적분에 대한 푸리에 반전공식 (Fourie r inv ersio n fo rmula) 을 유도하고 위너 조건적분을 계산한다.
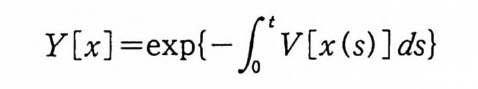 詞 =exp {-i。 tV[ x(s)] d s}
詞 =exp {-i。 tV[ x(s)] d s}
인 경우 EW(YIX) 에 대한 반전공식을 적용해서 칵-파인만 (Kac-F e y n man) 공식 을 유도한다.
 T=[O, t]이고, F 가 위너 적분가능한 함수일 때
T=[O, t]이고, F 가 위너 적분가능한 함수일 때
로놓자.
 정의 5.1 X, Z : Co( T) 一 lR 가 위너 측도가능한 함수이고 Z
정의 5.1 X, Z : Co( T) 一 lR 가 위너 측도가능한 함수이고 Z
는 위너 적분가능하다고 하자. Px 를 X 의 확률분포라 하자. 죽,
 Px (B) = m(X-' (B) ) , BE13 (R) .
Px (B) = m(X-' (B) ) , BE13 (R) .
주어전 X 에 대한 Z 의 위너 조건적분, EW(ZIX) 은 다음을 만족 하는 함수 船의 동치 족 (eq u iv a lent class) 이 다.
 (1)
(1)
주 라돈-니 코딤 (Radon-Ni ko dy m ) 정 리 에 의 해 서 함수 硏는 존 재하고 Px- 영집합을 제의하고는 유일하게 결정된다. EW(ZIX) 롤 함수 ¢의 동치족에 속하는 특정한 함수로도 사용할 것이다• 따라서,
 (5. 1) £_1 c Bl Z (x) dm (x) =fsE w (ZIX) (~) dPx (~) , B 걸 (R)
(5. 1) £_1 c Bl Z (x) dm (x) =fsE w (ZIX) (~) dPx (~) , B 걸 (R)
이다. 증명 성질 4.9 의 특별한 경우이다.
보조정리 5.3 f가 R 에서 구간적으로 르베그 적분 가능(l ocall y ;l-int e g rab le) 하다고 하자. 죽, f는 각 유계 구간 (bounded int e r -val) ICR 에서 르베그 적분가능하다. 그러면, a>O 에 대해서, 뻥 -&1. -a , Ha J / (x) d). (x) =/ (~) , tl-a . e. ~ER,
이다. 증명 참고문헌 Roy d en [1, 1 0. Theorem, p. 10 까 참조
 따름정리 5-4 X, Z 는 보조정리 5.2 에서 주어진 변환이고 Px
따름정리 5-4 X, Z 는 보조정리 5.2 에서 주어진 변환이고 Px
증명 Xe, 후 보조정리 5.2 의 g에 대응시켜서 다음 식을 얻는 다.
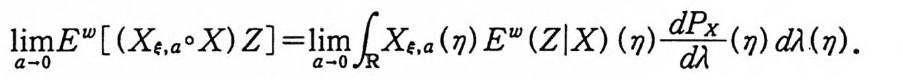 뻥 Ew[ (Xt, a 0X) Z] 켕 江 Xt ,a (TJ) Ew (ZIX) (TJ)필玉) 4 (n) .
뻥 Ew[ (Xt, a 0X) Z] 켕 江 Xt ,a (TJ) Ew (ZIX) (TJ)필玉) 4 (n) .
그러면, 보조정리 5.3 에 의해서 정리가 증명된다.
보조정리 5.5 X, Y : C 。 (T) 一 lR 를 위너 측도가능한 변환이 라 하고, Ew(IY I)
증명 이 정리는 확률공간이 (Co(T), .01, m) 인 경우의 정리 4. 12 의 식 (4. 28) 이 다.
 주 Px~ tl이면, Ew(eiu XY), uER 은 k 적분 가능한 함수 Ew
주 Px~ tl이면, Ew(eiu XY), uER 은 k 적분 가능한 함수 Ew
이 성립한다. 증명 참고문헌 Rees, Shah and St an oje v ic [!, Theorem 6.2.2, p .25 이 참조.
다음 정리는 이 절에서 소개하는 3 개의 푸리에 반전공식 중의 하나이다. 위너 조전적분의 (c,1) 형 반전공식이라 부른다.
 정리 5-7 X, Y : Co(T) 一 R 가 위너 측도 가능한 변환이고,
정리 5-7 X, Y : Co(T) 一 R 가 위너 측도 가능한 변환이고,
증명 보조정리 5 . 5 에 의해서 다음 식이 성립한다.
 (5. 3) Ew (eiu XY) =jeiu ( Ew ( YIX) (t) 필玉) d). (t) , uER
(5. 3) Ew (eiu XY) =jeiu ( Ew ( YIX) (t) 필玉) d). (t) , uER
다음 정리는 위너 조건적분의 레비 (Lev y)형 반전공식이다. 정리 5.8 X, Y 는 정리 5.7 에서 주어전 함수라 하자.
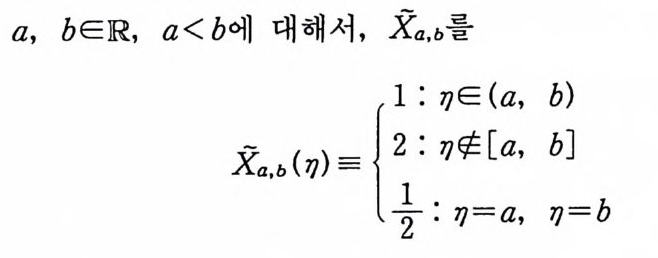 a, bElR, a
a, bElR, a
로 정의하자. 그러면, 다음 식이 성립한다.
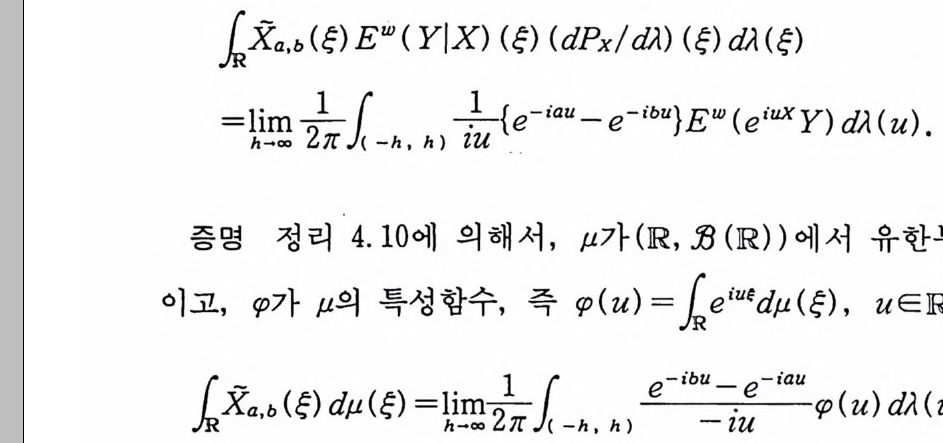 kXa,b (~) E 익 YIX) (~) (dP詞 ) (~) cf),. (~)
kXa,b (~) E 익 YIX) (~) (dP詞 ) (~) cf),. (~)
이다. 이 식과 식 (5. 3) 에 의해서 정리가 증명된다. 다음 정리는 이 절에서 마지막으로 소개하는 위너 조건적분의 반전공식이다. 정리 5-9 X, Y 는 정리 5.7 에서 주어전 변환이라 하고, Ew 〔 e i uX 幻가 u 의 함수로서 lR.에서 르베그 측도가능하다고 하자. 그러면, Ew(YIX) (dPx/dA) 이 존재하고 다음 식을 만족한다.
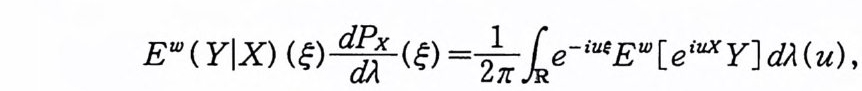 EW(YIX) (~)팔(~) =吉 le- i ueEw[e i판]d). (u), ~ER.
EW(YIX) (~)팔(~) =吉 le- i ueEw[e i판]d). (u), ~ER.
증명 정리 4.12 의 특별한 경우이다.
 T=[O, 시일 때, X를
T=[O, 시일 때, X를
로 정의하자. 이제, 주어전 X 에 대한 위너 적분가능한 함수 Z 의 위너 조건적분을 계산해 보기로 하자.
 예 5, 10 각 x 드 Co(T) 에 대해서, 구간 [0, t ]에서의 x 의 평균
예 5, 10 각 x 드 Co(T) 에 대해서, 구간 [0, t ]에서의 x 의 평균
식 (5.4) 에서 주어진 X 에 대한 Z 의 위너 조건적분을 계산한 다. 따름정리 5. 4 에 의해서, Ew(ZIX) (dPx/&) 이 존재하고 (5. 2) 를 만족한다. (5. 4) 와 (5. 5) 로 주어지는 x, z 인 경우에,
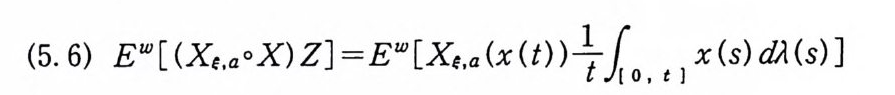 (5. 6) Ew[ (Xe,a 0 X) 幻 =Ew[Xe.a (x (t) )上t )J1 oo. • tt 1J x (s) &(s) ]
(5. 6) Ew[ (Xe,a 0 X) 幻 =Ew[Xe.a (x (t) )上t )J1 oo. • tt 1J x (s) &(s) ]
이다. (5.6) 의 우변의 두 적분의 순서를 바꾸기 위해서 다음과 같이 한다.
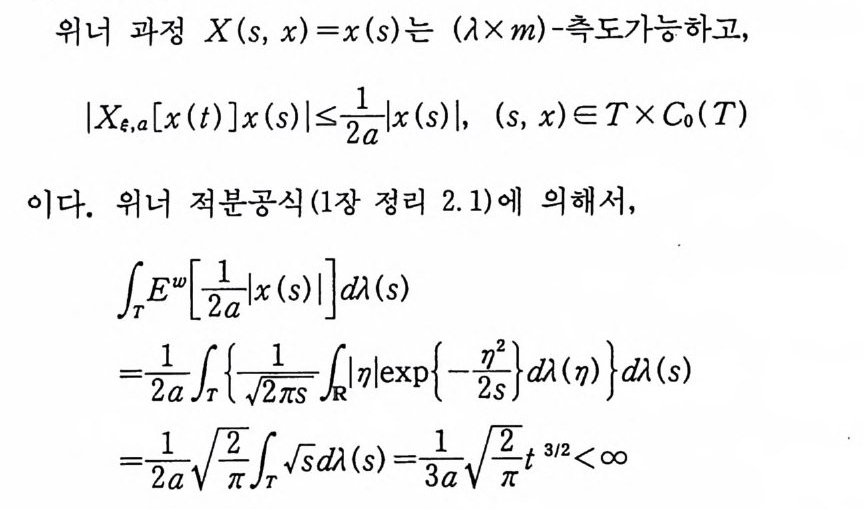 위너 과정 X(s, x)=x(s) 는 (Axm)- 측도가능하고,
위너 과정 X(s, x)=x(s) 는 (Axm)- 측도가능하고,
이다. 따라서 (5.6) 의 두 적분의 순서를 바꿀 수 있다. 1 장 정리 2.1 에 의해서,
 (5. 7) Ew [ (Xt, a 0 X) Z] =上tJ rT Ew [Xt, a [x (i) ] x (s) ] dA (s)
(5. 7) Ew [ (Xt, a 0 X) Z] =上tJ rT Ew [Xt, a [x (i) ] x (s) ] dA (s)
 = 詞 2at 2 {fTs d A(s)}{ j e-a.C+aI g ex p{망우 }&(s)}
= 詞 2at 2 {fTs d A(s)}{ j e-a.C+aI g ex p{망우 }&(s)}
일 때, X 에 대한 Z 의 위너 조건적분을 계산하자. 예 5.10 과 같은 방법으로 따름정리 5.4 를 사용해서 이 조건적 분을 계산한다.
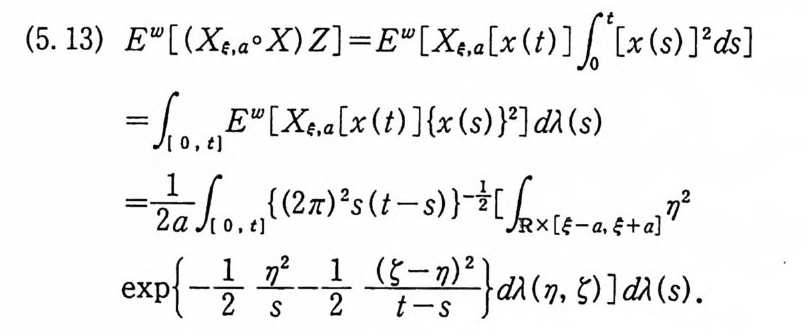 (5.13) E 기 (Xt ,a0X) 幻 =Ew[X나 x( t)〕ft [x(s) 〕 2ds]
(5.13) E 기 (Xt ,a0X) 幻 =Ew[X나 x( t)〕ft [x(s) 〕 2ds]
(5. 8) 에 의해서,
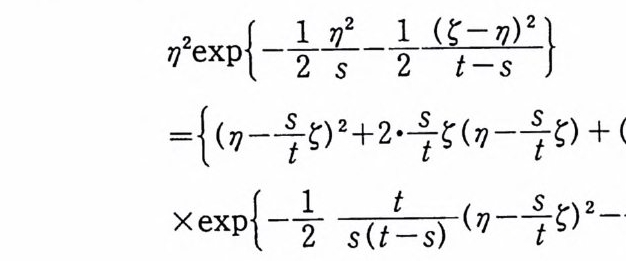 7J 2ex p{―只른-》 (gt—- ?2 }
7J 2ex p{―只른-》 (gt—- ?2 }
(5.13) 에서 d)..(7J, s) 에 대한 적분은, 먼저 d)..(7J)에 대해서 적 분하고, 식 (5. 9) 를 사용하면 다음과 갇이 된다.
 (5. 14)
(5. 14)
이므로 X 에 대한 Z 의 위너 조건적분은 다음과 같다.
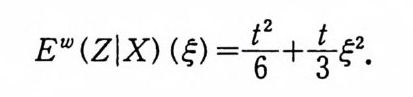 EW (ZIX) (E) =〔냉 8
EW (ZIX) (E) =〔냉 8
주 (5.1) 과 (5.15) 에 의해서,
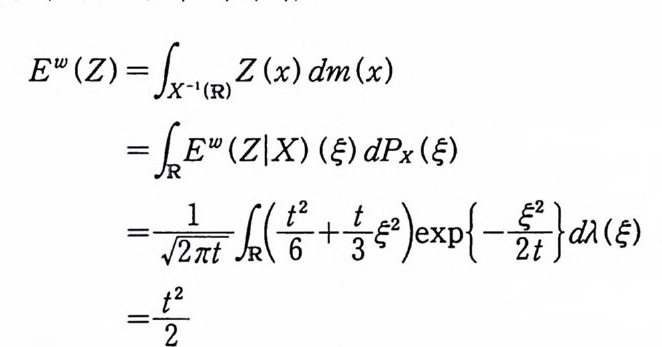 EW (Z) =Jx- 1(R) Z (x) dm(x)
EW (Z) =Jx- 1(R) Z (x) dm(x)
이다. 이것은 Ew(z) 를 직접 계산해서 얻은 결과 (1 장 성질 2. 13) 와 일치한다. 정리 5.l2 X와 Y 가 Co(T) 에서 다음과 같이 정의되는 함수 라하자.
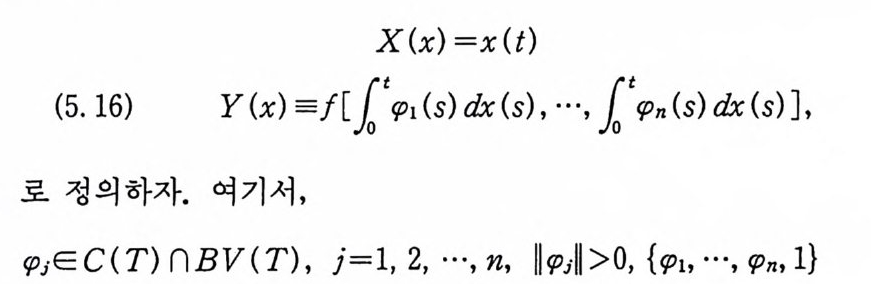 X(x) =x (t)
X(x) =x (t)
은 L2(T) 에서 정규집합이고, f는 Rn 에서 보렐 측도가능한 함 수로서 다음 조건을 만족한다.
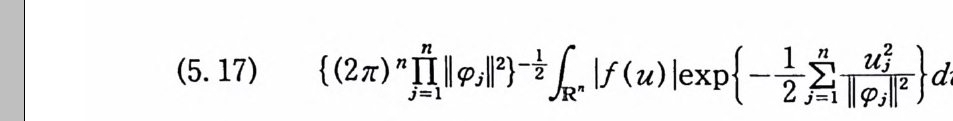 (5.17} {(21r}n }J』
(5.17} {(21r}n }J』
그러면, Y 는 위너 적분가능하고
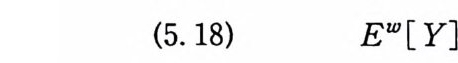 (5.18) Ew[ Y] =A.
(5.18) Ew[ Y] =A.
여기서 A 는 2 장 (2.49) 에서 주어진 Y 의 위너 적분값이다. 또한 EW(YIX) 가 존재하고 다음 식을 만족한다.
 (5.19} Ew ( YIX) (갑) =A, ~ElR .
(5.19} Ew ( YIX) (갑) =A, ~ElR .
 증명 (5. 18) 은 2 장 식 (1. 45) 이 다. (5. 19) 를 증명 하자.
증명 (5. 18) 은 2 장 식 (1. 45) 이 다. (5. 19) 를 증명 하자.
 Ew [eiu X Y] = Ew [exp{iu1 td x (s) }g [[
Ew [eiu X Y] = Ew [exp{iu1 td x (s) }g [[
따라서, E 〔 e i uXY] 는 u 의 함수로서 R 에서 르베그 적분가능하 다. 정 리 5. 9 에 의 해 서 , Ew ( YIX) (dPx/cO .) 이 존재 하고, 다음 식이 성립한다.
 EW( YIX) (~)뿔(g) =검 Le- i u'e-u2 t l2 d). (u)
EW( YIX) (~)뿔(g) =검 Le- i u'e-u2 t l2 d). (u)
로 놓자. 여기서 o~ v 는 다음 조건을 만족하는 연속함수이다.
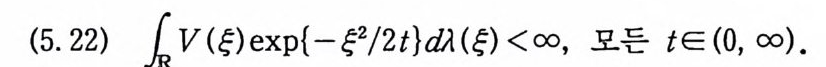 (5.22) lV(~)ex p{궁 /2 t}d). (E)< CX), 모든 tE (O, oo).
(5.22) lV(~)ex p{궁 /2 t}d). (E)< CX), 모든 tE (O, oo).
그러면 다음을 만족하는 EW( Yt lXt )가 존재한다.
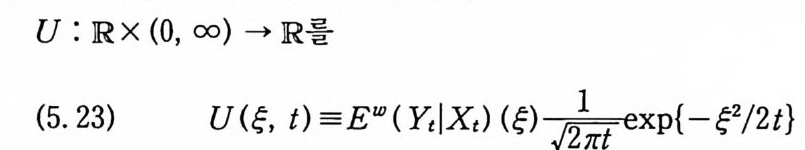 U : ]R X (0, oo) 一 R 를
U : ]R X (0, oo) 一 R 를
로 정의하면, U(s, t)는 다음 적분방정식을 만족한다.
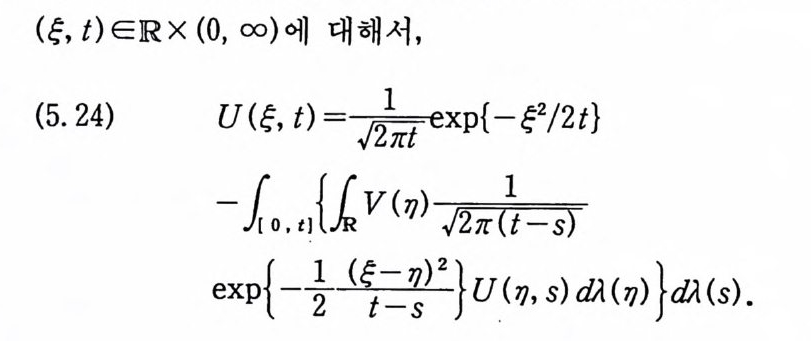 (t, t)E RX (0, CX))에 대해서,
(t, t)E RX (0, CX))에 대해서,
 주 V 가 lR 에서 연속이고, x 가 [O, t]에서 연속이므로, 1。 tv
주 V 가 lR 에서 연속이고, x 가 [O, t]에서 연속이므로, 1。 tv
로 정의하면, 示는 [O, oo) 에서 연속이다. 증명 정리 5.7 에 의해서, EW( Yt lXt )가 존재해서, (5.23) 에 의해서 정의된 U 가
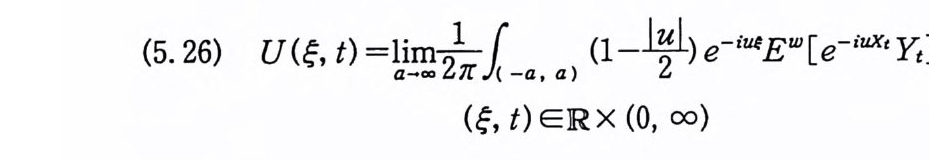 (5. 26) U(~, t) =1뽀 같 1-a, a) (1-부) e- 玉 [e- i uX1 Yt]cl). (u)'
(5. 26) U(~, t) =1뽀 같 1-a, a) (1-부) e- 玉 [e- i uX1 Yt]cl). (u)'
을 만족한다.
 훑 x p {-[sV[x (s) ]d s}= -exp{ -[sV[x (r) dr]} V(x(s) )
훑 x p {-[sV[x (s) ]d s}= -exp{ -[sV[x (r) dr]} V(x(s) )
01 므로,
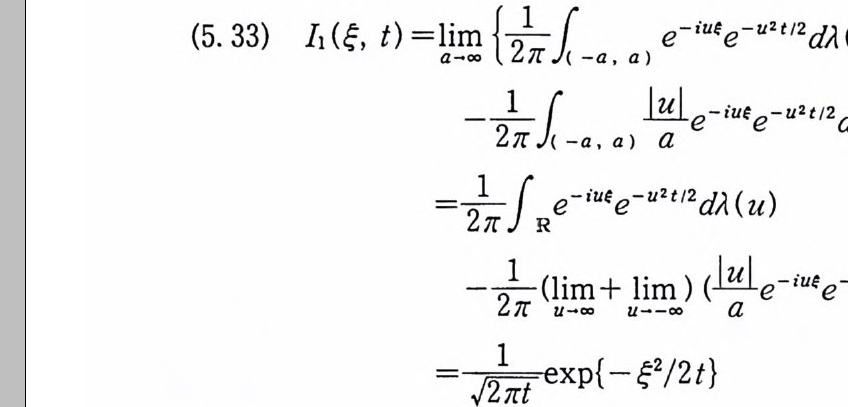 (5.33) /1(~, t)=타날 -a, a> e-iu te -u•112d11(u)
(5.33) /1(~, t)=타날 -a, a> e-iu te -u•112d11(u)
이다. (5.32) 에서 위너 적분과 르베그 적분의 순서를 바꾸기 위 해서, 다음과 같이 한다.
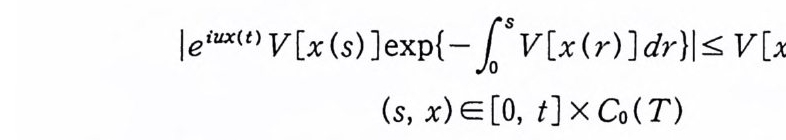 Ieiu x(t> V[x (s) ]e xp { -1sV [x (r) ]d r}l :s;; 四 (s) ],
Ieiu x(t> V[x (s) ]e xp { -1sV [x (r) ]d r}l :s;; 四 (s) ],
이고, 위너 적분공식 (1 장 정리 2 . 1) 과 (5. 20), (5. 25), 그리고 ¢ 가 [O, oo) 에서 연속이라는 사실에 의해서 다음 식을 얻는다.
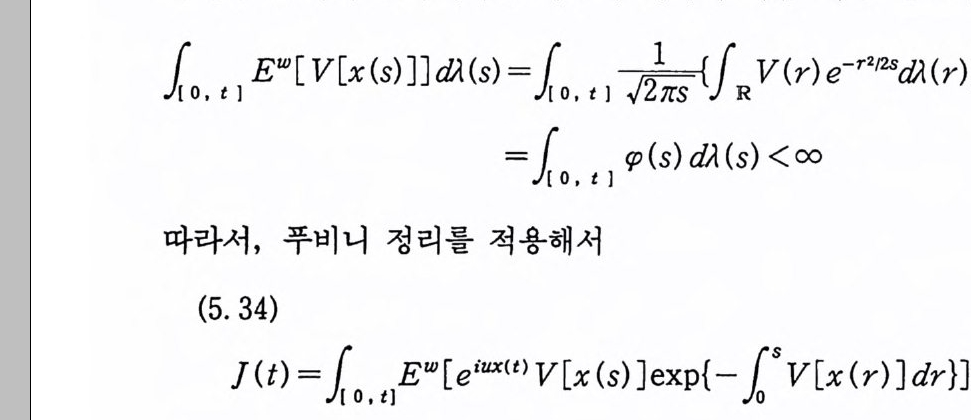 Jo . t l Ew [ V [x (s) ] ]d} . (s) = Jo , t 1 72 급f R V ( r) e-r2/2 Scl}. ( r) }cl}. (s)
Jo . t l Ew [ V [x (s) ] ]d} . (s) = Jo , t 1 72 급f R V ( r) e-r2/2 Scl}. ( r) }cl}. (s)
울 얻는다.
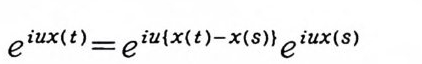 eiU X(t )= eiU {X(t ) -X(S) Ie iU X(S)
eiU X(t )= eiU {X(t ) -X(S) Ie iU X(S)
로놓자. 위너 적분공식(1장정리 2.1) 과 (5.20) 에 의해서
 (5. 35) Ew[eiu x(t ) -X(S)] = ex p{_(운)(t― s) }
(5. 35) Ew[eiu x(t ) -X(S)] = ex p{_(운)(t― s) }
보조정 리 5. 2 를 (5. 36) 의 위 너 적 분에 적 용하고, (5. 21) 과 (5. 23) 을 이용해서 다음 식을 얻는다.
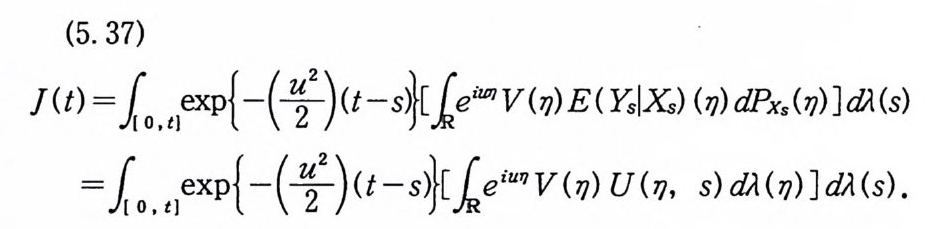 J(t()5 .= 37J)O , t ]ex p{-(운) (t -s)} 〔』강아(TJ) E ( YslXs) (TJ) dP.西) ] & (s)
J(t()5 .= 37J)O , t ]ex p{-(운) (t -s)} 〔』강아(TJ) E ( YslXs) (TJ) dP.西) ] & (s)
 (5. 37) 을 (5. 31) 에 대입해서 얻는 h 에 대한 식에서 세 적분
(5. 37) 을 (5. 31) 에 대입해서 얻는 h 에 대한 식에서 세 적분
(TJ, s, u) ElRX [0, t] X (— a, a) 에 대해서,
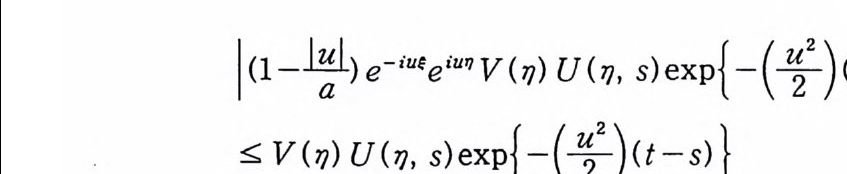 1(1 뿐) e-.-u~e.-u11 V ( r;) U ( r;, s) exp { _( 분) (t _ s) }1
1(1 뿐) e-.-u~e.-u11 V ( r;) U ( r;, s) exp { _( 분) (t _ s) }1
이다. 위너 적분공식 (1 장 정리 2.1) 과 (5.25) 에 의해서, 그리고 보조정 리 5. 2 와 (5. 23) 을 사용해 서 다음 식 을 얻는다.
 k V(r;) U(r;, s) d). (r;) =Ew[ V(x (s) ]e xp {_ iSV[ x (r) ]d r}]
k V(r;) U(r;, s) d). (r;) =Ew[ V(x (s) ]e xp {_ iSV[ x (r) ]d r}]
 a>O 에 대해서, (5. 38) 의 피적분함수는
a>O 에 대해서, (5. 38) 의 피적분함수는
울 만족한다. 초기조건 (5. 43) 을 갖는 마분방정식 (5. 41) 의 해는
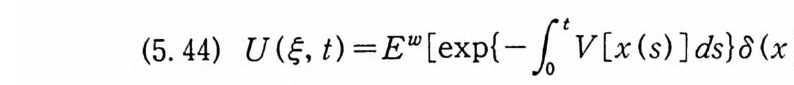 (5. 44) U(~. t) =Ew[exp { -1。 tV [x(s)] d s}o(x( t)군 )]
(5. 44) U(~. t) =Ew[exp { -1。 tV [x(s)] d s}o(x( t)군 )]
이고, 이것을 칵-파인만 (Kac - Fe y nman) 공식 이 라 한다 (Yeh [11]). (5. 23) 에서 정의한 U(f, t)는 (5. 24) 를 만족하고, 또한 U(f, t) 가 (5. 42) 를 만족하는 것은 자명하므로, 정리 5.13 은 칵-파인만 공식을 유도하는 또 다른 방법이다. 6 위너 조건적분의 변환정리 위너 조건적분에 대한 카메룬-마틴 (Cameron-Mar ti n) 변환정리 를 소개하고, 이 정리를 이용해서 위너 조건적분울 계산하는 예 룰 보기로 하자.
 (m보ea조su정ra리b le6 .s1p a c e() Q이, J라J ,하p자)를. 확z률 :공 요간 -, R (률S ,적Y) 분 를 가측능도한가 능확공률변간
(m보ea조su정ra리b le6 .s1p a c e() Q이, J라J ,하p자)를. 확z률 :공 요간 -, R (률S ,적Y) 분 를 가측능도한가 능확공률변간
그러면, 조건기대값 E(ZIX0T) 와 E(ZIX) 이 존재하고 다음 식이 성립한다.
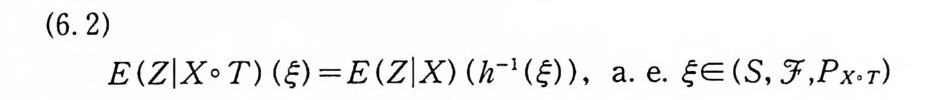 (6. 2)
(6. 2)
여기서, Px o T 는 식 (4.1) 에서와 같이 정의되는 X0T 의 확률 분포이다.
 증명 X0T : Q -S 는 측도 가능 변환이므로 조건 기대값
증명 X0T : Q -S 는 측도 가능 변환이므로 조건 기대값
이 성립한다. (6.1) 에 의해서, 다음 식을 만족하는 p-영집합 요 가 존재한다.
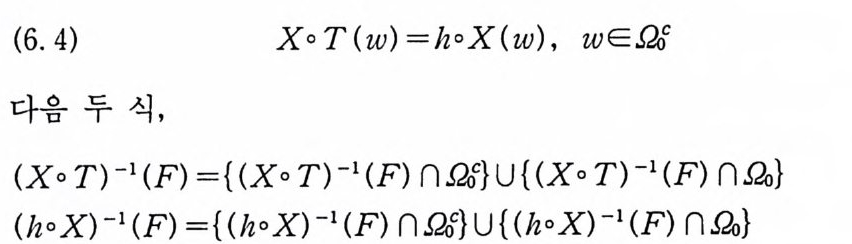 (6. 4) X0T(w) =h0X(w), w 캘
(6. 4) X0T(w) =h0X(w), w 캘
에서, 우변의 두번째 집합은 p-영집합이고, (6.4) 에 의해서 우 변의 첫째 집합은 같으므로,
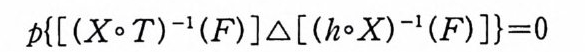 p{[( X 。 T) 크 (F)] 삭 (h0x)-1 (F) ]}= O
p{[( X 。 T) 크 (F)] 삭 (h0x)-1 (F) ]}= O
이다. 이것으로부터 다음 식을 얻는다.
 (6. 5) jx· T) -1 ( F)Z (w) dp ( w) =i,l0X ) - 1 ( F)Z (w) dp (tU)
(6. 5) jx· T) -1 ( F)Z (w) dp ( w) =i,l0X ) - 1 ( F)Z (w) dp (tU)
이다. 죽 확률공간 (S,Y,Px) 에서 h 의 확률분포와 확률공간 (요 ,13,P) 에서 h0X 의 확률분포가 같다. 따라서,
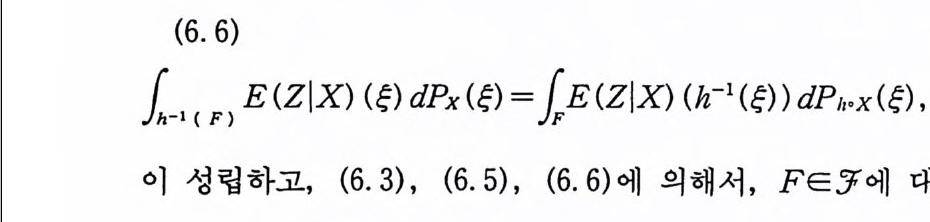 1_1(6 1. F 6l) E (ZIX) (~) dPx (~) =JF E (ZIX) (h 크 (~) ) dP1, , x (~) , F 급
1_1(6 1. F 6l) E (ZIX) (~) dPx (~) =JF E (ZIX) (h 크 (~) ) dP1, , x (~) , F 급
 (6. 7) 1E(ZIX0 T) (~) dPx -T ( ~) =1E(ZIX) (h-1 (~) ) dP,,.x ( ~)
(6. 7) 1E(ZIX0 T) (~) dPx -T ( ~) =1E(ZIX) (h-1 (~) ) dP,,.x ( ~)
 ==LL99 ij (=nt Z I C0i XT AA), j (( w T) (Jw ()w ))J d(µ w()w d)µ (w)
==LL99 ij (=nt Z I C0i XT AA), j (( w T) (Jw ()w ))J d(µ w()w d)µ (w)
(3) Z 가 임의의 측도 가능한 함수인 경우. 이 경 우에 는 Z 의 영 보다 큰 부분 (po sit ive pa rt) 과 영 보다 작은 부분 (ne g a ti ve p a rt)에 (2) 의 결과를 적용해서 (6 . 10) 을 얻는다.
 z 정: 요리 -6. I3R 를 (요적, 분13가, P능) 를한 확확률률변공수간,, x( S:, 요Y) - 를 s 를측 도측가도능가 능공변간,환
z 정: 요리 -6. I3R 를 (요적, 분13가, P능) 를한 확확률률변공수간,, x( S:, 요Y) - 를 s 를측 도측가도능가 능공변간,환
 1g(6( .e 1 ) 1E) (ZIX)
1g(6( .e 1 ) 1E) (ZIX)
 (6. 17) E[ (g0 X) Z] ~ isg (e ) E[ (Z0 T)J IX ] Uz -1 (e) ) dPx 0r ( e)
(6. 17) E[ (g0 X) Z] ~ isg (e ) E[ (Z0 T)J IX ] Uz -1 (e) ) dPx 0r ( e)
 (6.18) Ew( YIX) (e) =Ew[ Y(· +Xo)J IX ] (e— Xo ( t))
(6.18) Ew( YIX) (e) =Ew[ Y(· +Xo)J IX ] (e— Xo ( t))
이다. h 와 h - 1 는 보렐 측도가능한 변환이다. L 은 정리 6.3 의 조건 (2) 를 만족한다. 또한 카메룬-마틴 변환 정리 (2 장 따름정리 1. 4) 에 의해서, L 은 정리 6. 3 의 조건 (1) 도 만족한다.
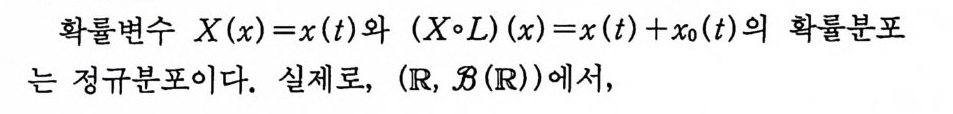 확률변수 X(x) =x( t)와 (X0L) (x) =x(t ) +xo (t)의 확률분포
확률변수 X(x) =x( t)와 (X0L) (x) =x(t ) +xo (t)의 확률분포
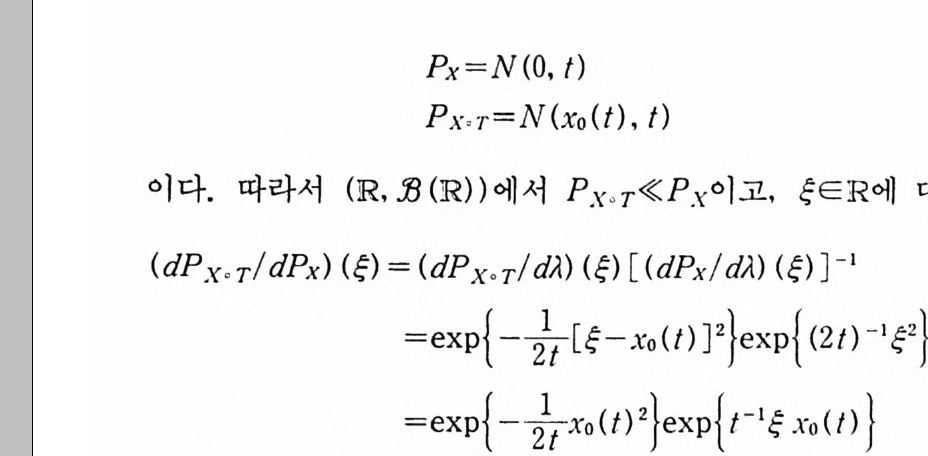 Px=N(O, t)
Px=N(O, t)
이 다. 이 식 과 (6. 12) 로부터 (6. 18) 을 얻는다.
 따름정리 6.5 X, Xo 가 정리 6.4 에서 주어진 함수이고, Z 를
따름정리 6.5 X, Xo 가 정리 6.4 에서 주어진 함수이고, Z 를
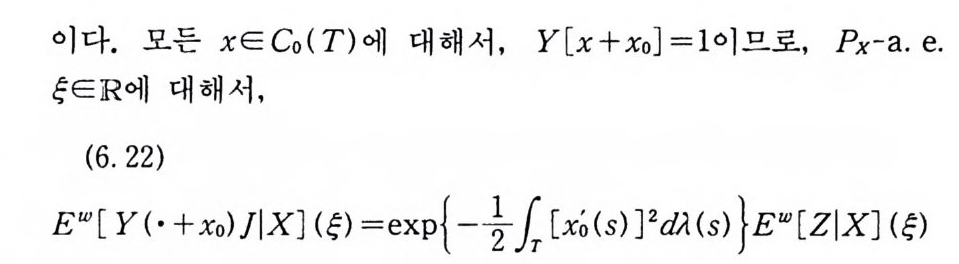 이다. 모든 xECo(T) 에 대해서' Y[x+x 。〕 =l 이므로, Px -a. e.
이다. 모든 xECo(T) 에 대해서' Y[x+x 。〕 =l 이므로, Px -a. e.
이 성립한다. 여기서 ](x) 는 (6 . 19) 에서 정의된 함수이다. Px 와 A 는 (lR , J3 (R) ) 에 서 동치 (eq u iv a lent) 이 므로 (6. 22) 는 11-a. e. ~ 에 대해서도 성립한다. 르베 그 영 집 합 (null set ) 은 평 행 변 환 (tra nslat ion ) 에 의 해 서 다시 르베그 영집합이 되므로, (6. 22) 의 양변에서 5 를 n-Xo( t)로 대 치하면 (6. 22) 는 11-a. e. r;에 대해서 성립한다. 이 식과 (6. 21) 을 (6.18) 에 대입해서 다음 식을 얻는다. 11-a. e. r; ElR 에 대해서,
 (6. 23) 1=Ew(ZIX) (TJ- xo< t)) exp {-½/r [x~(s)]2&(s)}
(6. 23) 1=Ew(ZIX) (TJ- xo< t)) exp {-½/r [x~(s)]2&(s)}
이 성립하고, Px 와 A 가 동치라는 사실로부터 (6. 20) 을 얻는다. 정리 6.4 를 사용해서 위너 조건적분을 계산하는 예를 보기로 하자.
 예 6.6 xECo(T) 에 대해서,
예 6.6 xECo(T) 에 대해서,
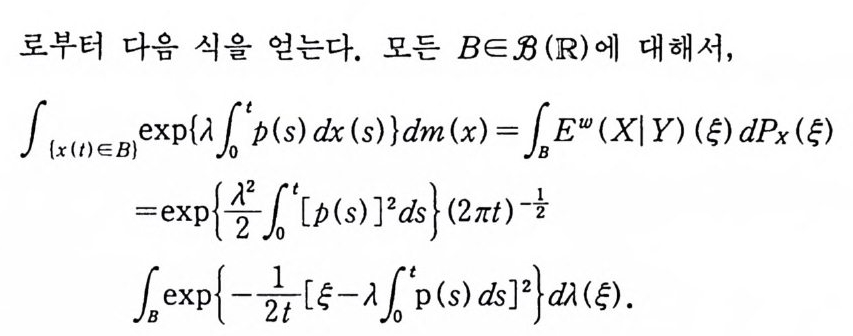 로부터 다음 식을 얻는다. 모든 BE g (lR) 에 대해서,
로부터 다음 식을 얻는다. 모든 BE g (lR) 에 대해서,
7 위너 조건적분 공식 이 절에서는 확률벡터 X 에 대한 위너 조건적분을 정의하고, 이에 관한 적분 공식을 유도한다.
 T=[O, 기라 하고, x : c 。 (T) - ► R 별 위너 측도가능한 함수
T=[O, 기라 하고, x : c 。 (T) - ► R 별 위너 측도가능한 함수
함수 軒의 동치족에 속하는 특정한 함수로도 사용할 것이다. 따 라서,
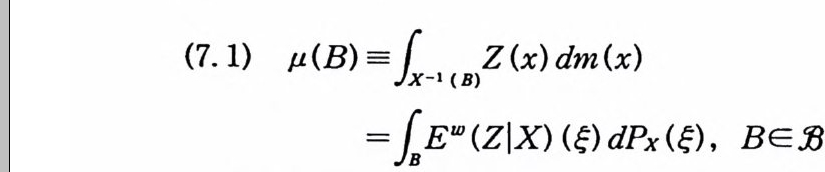 (7.1 ) µ(B)=fx _1
(7.1 ) µ(B)=fx _1
 이 성립한다.
이 성립한다.
 tj-l ~S~t j, j= l, 2, …, n, eo=O
tj-l ~S~t j, j= l, 2, …, n, eo=O
 따름정2. 1 7-2 {x(s) : sE T} 이 위너 과정이면,
따름정2. 1 7-2 {x(s) : sE T} 이 위너 과정이면,
이다. 따라서 (1) 의 경우가 증명된다. (2) 일반적인 경우는 측도론에서 사용하는 확장 방법에 의해서 증명할 수 있다.
 주 7·4 F 가 위너 적분가능하면, (7.8) 에 의해서
주 7·4 F 가 위너 적분가능하면, (7.8) 에 의해서
는 르베그 측도 가능한 함수이다(보렐 측도 가능할 필요는 없 다). 다음 예에서 이 관계를 보여준다. 예 7·5 G 를 R 에서 보렐 집합이 아닌 르베그 영집합이라 하 자. 그러면 함수
 f(E ) =x G (E)
f(E ) =x G (E)
는 보렐 측도가능하지는 않고, 르베그 측도가능한 함수이다.
 A={xECo(T) : x(t) E G}
A={xECo(T) : x(t) E G}
로 정의하면,
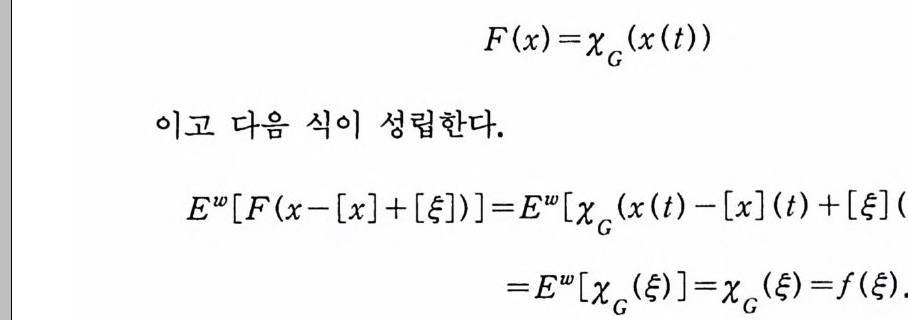 F(x) =Xc(x(t) )
F(x) =Xc(x(t) )
만일, f (E) 가 Rn 에서 르베그 측도가능하면, 보렐 측 도가능한 함수 f(~)가 존재해서
![]() /(~) =f(~). a. e. ~
/(~) =f(~). a. e. ~
울 만족한다. 또한 f(~)는 보렐 영집합을 제의하고는 유일하게 결정된다. 따라서 다음 정의는 타당성이 있다. 정의 7·6 F 가 위너 적분가능한 함수일 때, 함수
![]() E[F(x- 〔김 + [t])]
E[F(x- 〔김 + [t])]
를 다음과 같이 정의한다.
 (1) E(F(x- [지+[t])〕는 보렐 측도가능하다.
(1) E(F(x- [지+[t])〕는 보렐 측도가능하다.
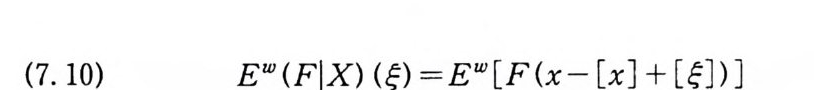 (7.10) EW(FIX) (e) =Ew[F(x— [지 + [인) 〕
(7.10) EW(FIX) (e) =Ew[F(x— [지 + [인) 〕
이다. (7. 9) 와 (7.10) 의 등식은, 양변의 보렐 측도가능한 함수이 고, 보렐 영집합을 제의하고는 같음을 뜻한다. 증명 주 7. 4 와 정의 7. 6 에 의해서 (7. 9) 는 자명하다. 만일 F
 가 보렐 측도가능하면, 푸비니 정리에 의해서, Ew 〔 F&_ 〔자
가 보렐 측도가능하면, 푸비니 정리에 의해서, Ew 〔 F&_ 〔자
정리 7. 7 을 이용하면 예 5.10 과 예 5.11 에서 계산한 위너 조건 적분을 쉽게 얻을 수 있다. 다음 예를 보자.
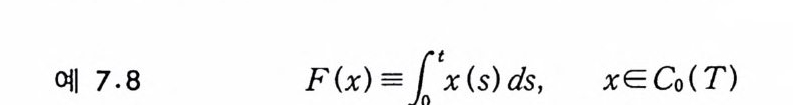 예 7-8 F(x) =i。t x (s ) ds, xE C 。 ( T)
예 7-8 F(x) =i。t x (s ) ds, xE C 。 ( T)
로 놓으면, (7.10) 에 의해서 다음 식이 성립한다.
 EW (FIX)
EW (FIX)
 예 7-9 F(x) =1t[ x(s)]2ds, xECo(T)
예 7-9 F(x) =1t[ x(s)]2ds, xECo(T)
제 4 장 예_위너 측도와 예-위너 적분 이 장에서는 예 - 위너 공간에 측도를 도입하여 예-위너 측도공 간을 만들고, 위너 측도공간의 성질들을 예-위너 측도공간으로 확장한다. 대부분의 성질들은 위너 공간의 성질들과 유사하고 그 증명 방법도 비슷하므로 몇몇 경우를 제의하고는 증명을 생략하 고 정리만 기술하기로 한다. 1 예_위너 측도공간 두 변수 함수들의 집합에 측도를 도입한 공간을 예-위너 측도 공간이라 한다. 예-위너 공간의 특별한 경우(한 변수를 고정한 경 우)가 위너 공간이므로 위너 공간에서 성립하는 성질들이 예-위 너 공간으로 확장될 수 있음을 쉽게 기대할 수 있다. 대부분의 성질들의 증명은 위너 공간의 경우와 유사하므로 생략하기로 한 다.
정의 1.1 사각형
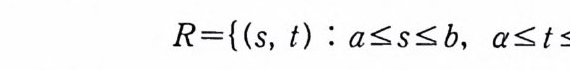 R={(s, t) : a 후::::: b, a 입:::::/3}
R={(s, t) : a 후::::: b, a 입:::::/3}
에서 정의된 모든 연속함수들의 집합을 C 〔 R 〕이라 하자· 집함
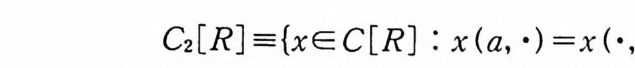 C2 〔 R 〕 ={xE 디 R 〕 : x( a, ·)=x ( ·, a )=아
C2 〔 R 〕 ={xE 디 R 〕 : x( a, ·)=x ( ·, a )=아
울 예 - 위너 공간 (Yeh-W i ener s p ace) 이라 한다.
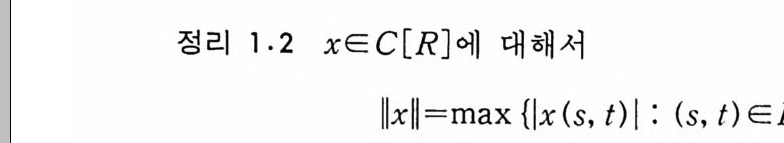 정리 1.2 xEC[R 〕에 대해서
정리 1.2 xEC[R 〕에 대해서
로 놓으면 |I • II 은 C[R] 에서 노름 (norm) 이 되고 (더 R ] , II • I|) 은 무한차원 바나하 공간이다. C2[R] 은 C[R 〕의 폐부분공간 (closed subs p ace) 이고, 따라서 C2[R] 도 무한차원 바나하 공간이다. 더욱이, (C2[ R ],I I • I|) 은 가분 (se p arable) 바나하 공간이다.
 정의 1.3 a=so
정의 1.3 a=so
이다. 점 (s;, tj) 를 I 의 제 한점 (restr i c t i on po in t ) , 구간 E 를 I 의 제 한
구간이라 한다. 정리 l-4 C2[R 〕의 모든 구간들의 모임 §는 준대수 (sem i alge bra) 이 다. 정의 l.5 ,9에 집합함수 m 을 다음과 감이 정의한다. (1. 1) 로 표시되는 I 에 대해서,
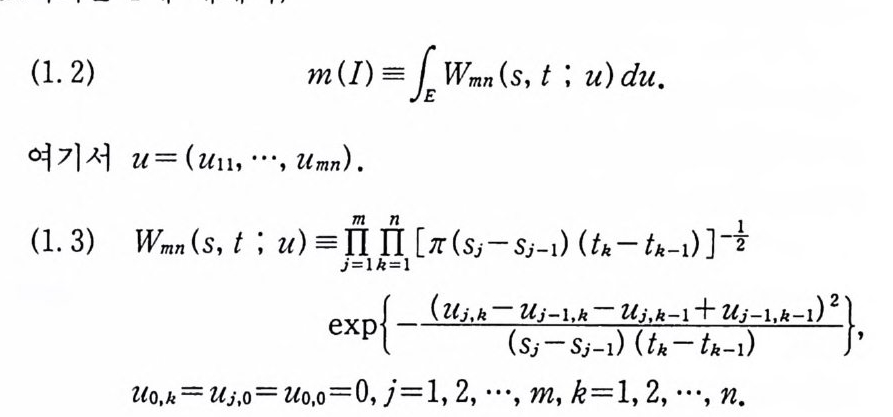 (1. 2) m (/) =1E Wmn (S, t : u) du.
(1. 2) m (/) =1E Wmn (S, t : u) du.
위너 측도의 경우와 같은 방법으로 m 에 대한 다음 성질을 증명 할수 있다.
 정리 1.5 (l) m 은 y에서 잘 정의된다.
정리 1.5 (l) m 은 y에서 잘 정의된다.
다음 정리는 위너 측도의 경우와 마찬가지로 그 증명이 간단하 지 않다. 증명은 Yeh 띠을 참조.
정 리 1 . 6 m 은 § 에 서 가산가법 가능 (counta b ly addit ive ) 하다. 따라서 m 은 y에서 측도가 된다. f에서 정의되는 측도 m 은 (J(f)에서 정의되는 측도 m 으로 확장된다. (부록 정리 1.1 0) 이 측도공간은 다시 완전측도공간 (C2[ R ], (J(f) , 玩)로 확장된다. 앞으로는 편의상 ;巳汀를 잎 b 굶를 m 으로 쓰기로 한다. 정의 l.7 완전측도공간 (C2[R], 잎 I, m) 을 예-위너 측도공 간이라 한다. 이때, m 을 예-위너 측도, 잎 1 의 원소를 예-위너 측도가능한 집 합 (Yeh-W ien er measurable set) 이 라 한다. 주 1.8 (1) 정리 1. 5(2) 에 의해서 예 - 위너 측도공간은 확률공 간이다.
 (2) AE 따 m(A)=O 이면, A 의 임의의 부분집합 E에 대해
(2) AE 따 m(A)=O 이면, A 의 임의의 부분집합 E에 대해
으로 정의하면,
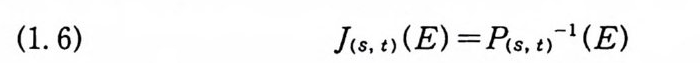 (1. 6) l
(1. 6) l
이고, Pcs, t)는 연속함수이다. 따라서 P(s, t)는 보렐 측도가능하 다. 모든 (s, t)와 모든 보렐 집합 BElRmn 에 대해서, J (s, t )(B) 들 의 모임을 었라고 하자. 그러면 었는 C2 〔 R 〕의 부분집합돌의 대 수 (al g ebra) 가 되고 다음 정리가 성립한다.
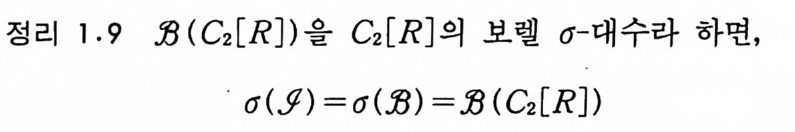 정리 1.9 :B (C2 〔 R]) 을 C2[R] 의 보렐 6- 대수라 하면,
정리 1.9 :B (C2 〔 R]) 을 C2[R] 의 보렐 6- 대수라 하면,
0] 다. 주 1 .10 (1) 정 리 1. 9 에 의해서, 예-위너 측도공간은 보렐 측 도공간을 완비화 (com p le t e) 해서 얻는 완비측도공간과 일치한다. (2) 잎 1 은 BUN 과 같은 형태의 집합들로 구성된다. 여기서, B 는 보렐 집합, N 은 보렐 영집합의 부분집합이다. 정리 1. 9 에 의해서, B 가 Rmn 에서 보렐 집합이면, J(s, t )(B) 는 C2[R] 에서 보렐 집합이 된다. 이 성질의 역을 증명하기 위해서 다음 보조정리가 필요하다.
 보조정리 1.11 주어전 실수 uu, Osi s m, Os j sn 에 대해서
보조정리 1.11 주어전 실수 uu, Osi s m, Os j sn 에 대해서
 되는 부분구간 직선(pi ecew i se li near) 함수 H(u) 가 존재한다. 또
되는 부분구간 직선(pi ecew i se li near) 함수 H(u) 가 존재한다. 또
정리 l• 12 Je s, t) (E) 가 C2[R 〕에서 보렐 집합일 필요충분조건 은 E 가 Rmn 에서 보렐 집합이다.
 증명 정리 1. 9 에 의해서 필요조건만 증명하면 된다.
증명 정리 1. 9 에 의해서 필요조건만 증명하면 된다.
이다. 이제 J (s, t )(E) 가 C2[R 〕에서 보렐 집합이라고 가정하자. 그러면 XE 는 두 보렐 함수의 합성함수이므로 보렐 함수가 된다. 따라서 E 는 Rmn 에서 보렐 집합이 된다.
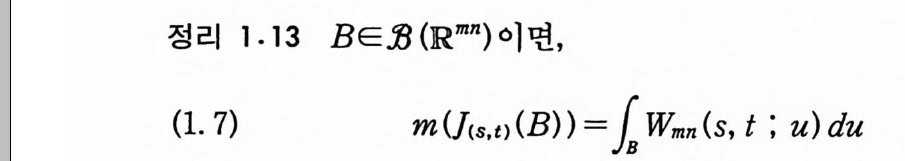 정리 1-13 BE J3 (Rmn) 이면,
정리 1-13 BE J3 (Rmn) 이면,
이다. 여기서 Wmn(S, f ; U) 는 (1. 3) 에서 주어전 밀도함수이다. 정리 1.14 (1) Pcs. t> : C2[R] -+ Rmn 은 예-위너 측도가능한 함
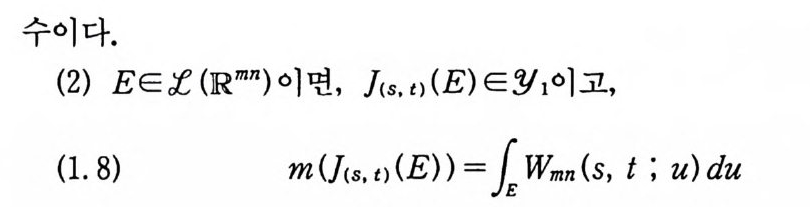 수이다.
수이다.
이다. 다음 정리는 정리 I. 14 의 역이다. 위너 측도공간에서 코호러 (F. Koehler) 가 증명 한 방법 을 모방해서 , 예-위 너 측도공간에서 의 이 정리를 스코그 (D. Skou g)가 증명하였다. (Skoug [ 2]). 그러 나, 이 증명 방법은 복잡하므로, 1 장 정리 I. 26 의 증명 방법을 따라서 증명하는 것이 보다 간단하다. 1 장 정리 1. 26 과 다음에 소개하는 정리 I. 15 를 포함하는 일반적인 역측도정리는 8 절에서 소개하기로 한다. 정리 1.15 E~ JR mn 이고, P (s!t )(E) 가 예-위너 측도가능한 집 합이면 E 는 1Rmn 에서 르베그 측도가능하다. 정리 1. 14 와 정리 1. 15 를 합해서 다음 정리로 기술한다.
 정리 1.16 E 드 lRmn 일 때, J(S, t )( E) =P(갑t )(E) 가 예-위너 측도
정리 1.16 E 드 lRmn 일 때, J(S, t )( E) =P(갑t )(E) 가 예-위너 측도
2 예-위너 적분 앞 절에서는 두 변수 함수 공간에 측도를 도입하여 예-위너 측 도공간 (C2[R], 잎 1, m) 을 만들었다. 예-위너 측도가능한 집합 과 르베그 측도가능한 집합 사이의 관계를 조사하였고 예-위너 측도를 르베그 적분으로 표시하는 공식을 얻었다. 이 절에서는 예-위너 적분을 르베그 적분으로 표시하는 공식을 소개하고 여러 가지 함수들의 예-위너 적분을 계산한다. 예-위너 측도공간에서 정의된 측도가능한 함수 F 의 예-위너 측도에 관한 적분을 F 의 예-위너 적분이라 하고
 (2. 1) E [F (x) ] = fcC22 1I RR II F (x) dm (x)
(2. 1) E [F (x) ] = fcC22 1I RR II F (x) dm (x)
이다. 여기서 P(s, t)는 (1. 5) 에서 정의된 함수이다. 정리 2.1 I 가 르베그 측도가능할 필요충분조건은 F 가 예-위 너 측도가능한 것이다. 이 경우에,
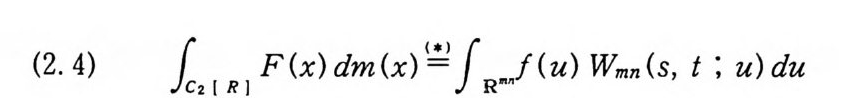 (2. 4) [21 R I F(x) dm(x) 밀f R ~ J (u) Wmn (s, t ; u) du
(2. 4) [21 R I F(x) dm(x) 밀f R ~ J (u) Wmn (s, t ; u) du
이다. 여기서 Wmn(S, t ; U) 는 (1. 3) 에서 주어전 밀도함수이고, 등식 낱은 강한 의미의 등식을 뜻한다. 즉, (2 . 4) 의 어느 한 변 이 존재하면(무한대인 경우도 포함), 다른 변도 존재하고, 그 두 적분값은 같다. 정리 2.2 (1) E 가 예-위너 측도 가능하면, -E 도 예_위너 측도가능하고 m(E)=m( ― E) 이다. (2) F(x) 가 예-위너 적분가능하면, F(_x) 도 예-위너 적분 가능하고 다음 식이 성립한다.
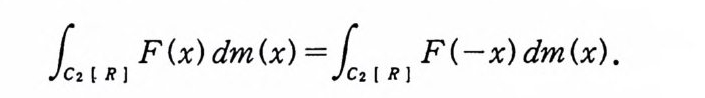 12C21 1 RR lI F(x) dm(x) =1C.21 [ RR IJ F(-x) dm(x).
12C21 1 RR lI F(x) dm(x) =1C.21 [ RR IJ F(-x) dm(x).
정리 2 . 1 의 적분 공식을 이용해서 여러 가지 함수들의 예-위너 적분을 계산해 보자. 예-위너 적분기호에서는 C2[R] 대신 간단 히 G로 쓰기로 한다.
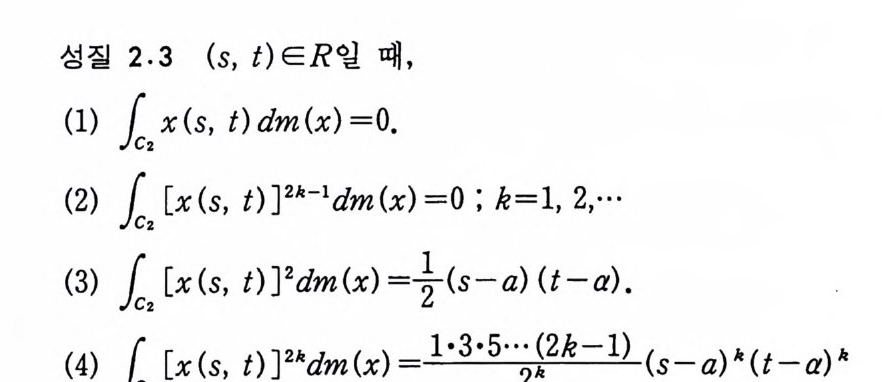 성질 2-3 (s, t) ER 일 때,
성질 2-3 (s, t) ER 일 때,
 ((65)) JJC2 [[.l「「a .11laPP [ [xx( s(s,, tt)) ]] 22dk dtdt d s s ]]d dmm( x(x)) = ½(b-a)2(/3 _ a)2.
((65)) JJC2 [[.l「「a .11laPP [ [xx( s(s,, tt)) ]] 22dk dtdt d s s ]]d dmm( x(x)) = ½(b-a)2(/3 _ a)2.
이다. 정리 2.1 과 적분공식 (부록 §3) 을 이용한다.
 성질 2-5 a=so
성질 2-5 a=so
 성질 2.a a=so
성질 2.a a=so
 (2) 1C2 [x ( s1, t1) ] 2x {s3, t3) x (s4, t4) dm (x)
(2) 1C2 [x ( s1, t1) ] 2x {s3, t3) x (s4, t4) dm (x)
3 두변수함수의 유계변동과 변환정리 두변수함수의 겨팰리 - 위너_지그문드 (Pale y -W i ener-Z ygm und) 적 분을 정의하는 데는 두변수함수에 대한 유계변동의 개념이 필요 하다. 이 개념은 한변수함수의 경우보다는 비교적 복잡하다. 여
러 가지 서로 다른 정의가 있으나 이 절에서는 세 개의 정의를 소개한다. 이 절에서 소개하는 대부분의 정리는 증명없이 기술한 다 (Skoug [4] 참조). 한변수함수의 경우에서 일단 두변수함수의 경우로 확장되면, 임의의 n 변수함수의 경우는 쉽게 확장된다. 어렵고 복잡한 과정은 항상 한변수에서 두변수의 경우로 확장하 는것이다. 두번수함수의 유계번동 (bounded varia t i on )
 정의 3.l( 아르젤라 (Arzela) 정의) (so, to) , (s1, t1) , …, (sn, t n) 이
정의 3.l( 아르젤라 (Arzela) 정의) (so, to) , (s1, t1) , …, (sn, t n) 이
정의 3.2( 하디-크라우스 (Hard y-Krause) 정의) 4 를 R의 분할 :
 a=so
a=so
라 하자. 두변수함수 /(s, t)가 다른 세 조건을 만족할 때 함수 f는 R 에서 유계변동이라 한다. (1) 모든 분할 4 에 대해서,
 (3. 4) i~=n l i~=mI If (s .-, tj) —J (s.-, tj-1 ) -J (s.--1, 0 +J (s.--1; tj-1 ) | :::;; k
(3. 4) i~=n l i~=mI If (s .-, tj) —J (s.-, tj-1 ) -J (s.--1, 0 +J (s.--1; tj-1 ) | :::;; k
하디 -크라우스 (Ha rdy -K rause) 의 정 의 에 의 한 유계 변동인 모든 함수들의 집 합을 H 라 하자.
 주 3.3 (i) /EH 이면, /는 R 에서 유계이고, 거의 모든 점
주 3.3 (i) /EH 이면, /는 R 에서 유계이고, 거의 모든 점
정의 3.4 (비탈리 (Vi tal i) 정의) 두변수함수 f가 정의 3. 2 의 조건 (1)을 만족할 때, f는 R 에서 유계변동이라 한다. 모든 분 할 4 에 대한 (3.4) 의 합들의 최소상계를 f의 전변동이라 하고 기호로는 Varv(/, R) 로 쓴다. 비탈리의 정의에 의한 유계변동인 모든 함수들의 집 합을 V 라 하자. 즉,
 (3. 5) V={/=Varv(/, R) <(X)}.
(3. 5) V={/=Varv(/, R) <(X)}.
정리 3.6 두변수함수의 유계변동에 대한 위의 세 가지 정의 사이에는 다음 관계가 성립한다.
 (1) H$V
(1) H$V
 g (s, t) ~j: sin (占) : :::.
g (s, t) ~j: sin (占) : :::.
그러면, 이 함수들에 대한 전변동은 다음과 같다.
Varv(/, R)=+co=VarA(g, R). VarA (/, R ) = l. Varv (g, R) =0 . 따라서, /EA— V, gE V-A 이다. 정리 3-7 /EA 일 필요충분조건은 /(s, t)=g(s , t)- h(s, t)
이다. 여기서 g와 h 는 R 에서 정의된 유계함수이고, 한변수함수 로서 단조증가함수이다. 즉, 각 sE[ a 싸에 대해서, g( s, ·), h(s, •)는 증가함수이다. 각 t E[a 나인에 대해서, g(·, t), h(·, t)는 증가함수이다. 정의 3.8 함수 /(s, t)가 다음 조건을 만족할 때 /는 R 에서 단조중가함수 (po sit ive ly monoto n e) 라 한다.
 a~s1
a~s1
이다. 여기서, g( s, t)와 h(s, t)는 R 에서 정의된 유계함수이고, R 에서 단조증가함수이다.
 정리 3-10 /EH 일 필요충분조건은
정리 3-10 /EH 일 필요충분조건은
이다. 여기서 g와 h 는 R 에서 정의된 유계함수이고, R 에서 단 조증가함수이다. 또한, g와 h 는 한변수함수로서 증가함수이다.
 정리 3.11 /EV 일 필요충분조건은 다음 식을 만족하는 fE
정리 3.11 /EV 일 필요충분조건은 다음 식을 만족하는 fE
여기서, g와 h 는 임의의 함수이다. 증명 Clarkson and Adams[ 끽 참조. 주 (1) 정리 3.11 에서 g와 h 는 르베그 측도가능할 조건도 요 구되지 않는 임의의 함수이다. (2) 집합 H 와 A 는 사칙연산에 대해서 닫혀 있다. V 는 곱셈 에 대해서 닫혀 있지 않다. 두번수함수의 절대연속 두변수함수의 절대연속에 대한 두 가지 정의를 소개한다. 정 의 3 . 12 (하디 -크라우스 (Hardy -K rause) 정 의 ) R 에 서 정 의
된 두변수함수 I(s, t)가 다음 두 조건을 만족할 때 f는 R 에서 절 대 연속 (absolute l y conti nu ous) 이 라 한다.
 (1) 주어전 c>O 에 대해서, 다음 식을 만족하는 O
(1) 주어전 c>O 에 대해서, 다음 식을 만족하는 O
이다. 여기서 R1, R2, …, Rn 은 서로 겹치지 않고, R에 포함되 는 임의의 사각형들이고, l 은 lR2 에서의 르베그 측도이다. (2) /(·, /3)와 /(b, •)는 각각 한변수함수로서 [a, b] 와 [a, /3 ] 에서 절대연속이다. 정의 3.13 (비탈리 (vit al i ) 정의) 함수 f(s , t)가 정의 3.12 의 조건 (1) 을 만족할 때 f는 R 에서 절대연속이라 한다. 정리 3.14 /(s, t)가 R 에서 절대연속(하디-크라우스) 일 필요 충분조건은
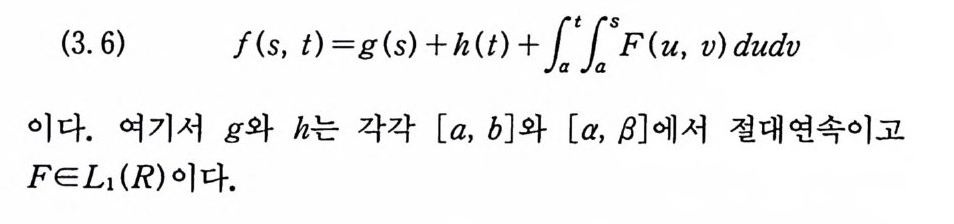 (3.6) /(s, t)=g( s)+h( t)+itisF( u, v)dudv
(3.6) /(s, t)=g( s)+h( t)+itisF( u, v)dudv
증명 Benkson and Gi lles pi e [ 1] 참조. 정리 3.15 f(s , t)가 R 에서 절대연속(비탈리)일 필요충분조건 은
 (3.7) /(s, t )=g (s)+h (t)+a「 J1 a5 F(u, v)d udv
(3.7) /(s, t )=g (s)+h (t)+a「 J1 a5 F(u, v)d udv
두번수함수의 리만-스틸체스 적분 다음은 두 변수 함수에 대한 리만-스틸체스 (R i eman-S ti el tj es) 적분을 소개한다. 보다 일반적인 n 변수함수에 대한 리만 - 스틸체 스 적분은 Yeh[ 끽를 참조.
 정의 3.17 P 를 사각형 R=[ a, 싸 x[a 』인의 분할 :
정의 3.17 P 를 사각형 R=[ a, 싸 x[a 』인의 분할 :
라 하자. 주어진 분할 P 에 대해서, 함수 g의 f에 대한 리만-스 틸체스 합 S(P, g, I) 을
 S(P : g, /) = k~n= l j~=m l g (~ h TJ,.) [/(sh t,.) -/(sj- 1 , t,.) 一f (s j, tk- 1)
S(P : g, /) = k~n= l j~=m l g (~ h TJ,.) [/(sh t,.) -/(sj- 1 , t,.) 一f (s j, tk- 1)
임의의 점이다.
 분할 P 의 노름 (norm) 11PII 은 mx n 개 의 부분 사각형 (sub-
분할 P 의 노름 (norm) 11PII 은 mx n 개 의 부분 사각형 (sub-
다음 정리는 두변수함수의 리만-스틸체스 적분에 대한 부분적 분 (int eg rat ion by pa rts ) 공식 이 다.
 정리 3.21 /EH 이고 g가 R 에서 연속이라 하자. 그러면 리
정리 3.21 /EH 이고 g가 R 에서 연속이라 하자. 그러면 리
 정리 3·23 장 /a:;'t t) 가 R의 각 점에서 존재하고, g와 :풀
정리 3·23 장 /a:;'t t) 가 R의 각 점에서 존재하고, g와 :풀
주 3,24 두변수함수에 대한 유계변동, 절대연속, 리만-스틸체 스 적분의 정의는 n 변수함수의 경우로 확장될 수 있다. 예를 들 면, 식 (3.4) 에 대응하는 세변수함수에 대한 식은 다음과 같이 쓸수 있다.
 R= [a, b] 지 a, /3]X [r, 하
R= [a, b] 지 a, /3]X [r, 하
다음 정리는 2 장 정리 1. 7 에 대응하는 예-위너 적분 공식이다.
 정리 3.25
정리 3.25
다음 정리는 2 장 정리 1. 8 에 대응하는 예-위너 적분의 팰리-위 너 정리이다.
 정리 3.26 (팰리-위너 정리)
정리 3.26 (팰리-위너 정리)
 여기서, u= (u1, u2, …, Un) 이다.
여기서, u= (u1, u2, …, Un) 이다.
카메룬-마틴 번환정리 다음 정리는 예-위너 적분에 대한 카메룬-마틴 변환정리이다. 이 정리의 증명은 Yeh 띠를 참조.
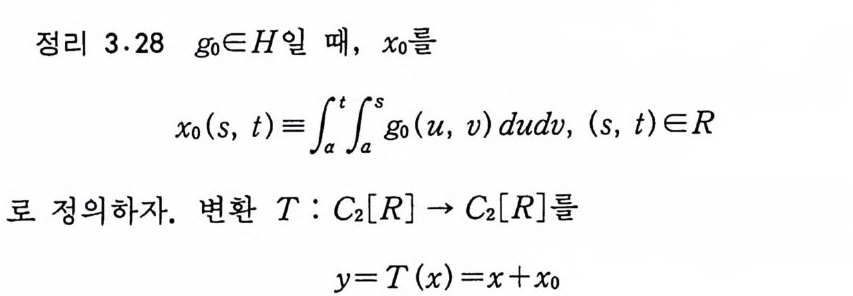 정리 3.28 go EH 일 때, Xo 를
정리 3.28 go EH 일 때, Xo 를
로 정의하면 다음 결과가 성립한다. (1) M 이 예-위너 측도가능한 집합이면,
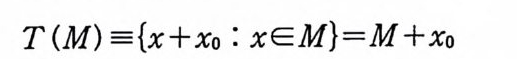 T(M) ={x+xo : x 캘 }=M+xo
T(M) ={x+xo : x 캘 }=M+xo
도 예-위너 측도가능하고,
 m(M+xo) =exp {-J: [go( s, t)]2d sdt} Lexp{ — 2J :god x}dm(x),
m(M+xo) =exp {-J: [go( s, t)]2d sdt} Lexp{ — 2J :god x}dm(x),
이다. 정리 3.28 로부터 다음 정리를 얻는다.
 정리 3.29 go EH 라 하자. 그러면, 임의의 복소수 A 에 대해서
정리 3.29 go EH 라 하자. 그러면, 임의의 복소수 A 에 대해서
4 척도불변 가측성 위 너 공 간 에 서 의 척 도 불 변 가 측 성 (scale-in v aria n t measur- ab ility)이 파인만 적분에서 기본이 되는 중요한 역할을 하는 것 과 마찬가지로, 예-위너 공간에서의 척도불변 가측성이 예-파인 만 적분에서 필수적인 중요한 개념이 된다. 먼저, 이 개념을 전 개하는 데 필요한 예-위너 곡면의 이차변동(q uadra tic varia t i on ) 에 관한 정리를 소개하기로 하자.
 g을 R= [a, b] 지 a, I 압에서의 분할(p ar titi on) :
g을 R= [a, b] 지 a, I 압에서의 분할(p ar titi on) :
이다. 또한 다음 관계가 성립한다.
 (4.3) C2[R] =(났° CA) U D.
(4.3) C2[R] =(났° CA) U D.
로 놓자. 그러면 {{pj ,k} 는 정규직교집합이고 각 (pj ,k 는 R 에서 유 계변동(하디-크라우스)이다. 또한 다음 식이 성립한다.
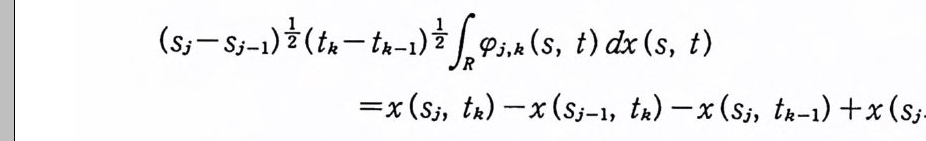 (sj- Sj- 1)½( tk- tk - 1)+1(f )j,k (S, t) dx (s, t)
(sj- Sj- 1)½( tk- tk - 1)+1(f )j,k (S, t) dx (s, t)
예-위너 적분에 대한 팰리-위너 정리(정리 3.26) 에 의해서 다음 식을 얻는다.
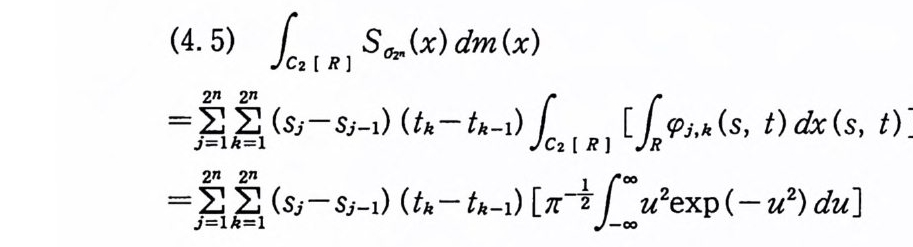 (4. 5) 1C22 [[ RR Jl s 어 (x) dm (x)
(4. 5) 1C22 [[ RR Jl s 어 (x) dm (x)
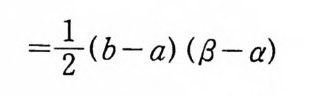 =전1 (b-a) (/3-a )
=전1 (b-a) (/3-a )
위와 같은 방법으로 다음 식도 얻을 수 있다.
로 놓자. 그러면, 고정된 n 에 대해서
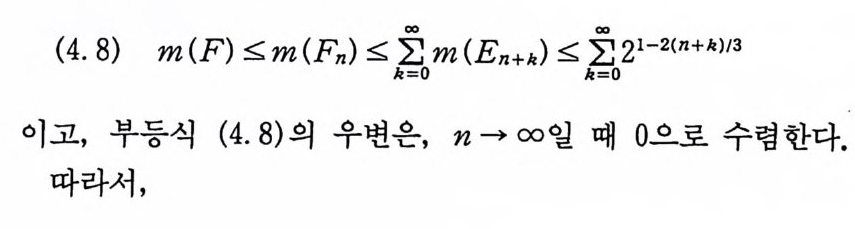 (4. 8) m (F) =,;: m (Fn) =,;: k~=coO m (En+k) =,;: k~=ooO 21-2
(4. 8) m (F) =,;: m (Fn) =,;: k~=coO m (En+k) =,;: k~=ooO 21-2
(4. 6) 121 R) [S 야 (x) ]2 dm(x) =[>(b — a )( /3-a )2] 1 2n 2n +—2 j~= I h~=I (S j -S J -I)2 (t h- f h-1) 민 식 (4. 5) 와 (4. 6) 에 의해서 다음 식을 얻는다. fC 2 ( I4 R. l7 )[ S(J ,, ( x)-½(b— a ) (/3— a)]2dm(x) = (b-a)2( 戶 )22-( 1+ 2n)0 따라서 S <1 l” (x) 는 C2[R 켜서 }(b— a ) (/3― a) 로 나수령한다• n=l, 2, …에 대해서, En={xE C2[R] : ISC n-( x) -f (b 一 a) (/3- a) I ~ ( b -a) (/3-a ) 2-0+2n13>} oo Fn= hU=nE h 00 F=nn=FI n
 m(F) =0.
m(F) =0.
이므로 정리가 증명된다. 따름정리 4·2 R 에서 유계변동(하디-크라우스)인 예-위너 곡 면들의 집합은 예-위너 측도 0 이다. 즉,
 m(C2[R] n H) =O.
m(C2[R] n H) =O.
증명 각 자연수 n 에 대해서, 다음 부등식이 성립한다•
 Varv (x, R) ~ ~짜 ~2n Ix (sh tk) -x (sj- 1, tk) —x (s h tk-1 ) +x (sj- 1, tk-1 ) I
Varv (x, R) ~ ~짜 ~2n Ix (sh tk) -x (sj- 1, tk) —x (s h tk-1 ) +x (sj- 1, tk-1 ) I
로놓으면
 (4. 9) m(Cf ) =l
(4. 9) m(Cf ) =l
이다. 증명 보조정리 4. I 의 증명에서 식 (4. 7) 을 얻는 방법에 의해 서 다음 식을 얻는다.
 lz I n1 {S<1 h l ll)( x) 검 (b ― a) ({3- a)}2dm(x) =t{(b— a ) (/3― a)/h(n)} 라
lz I n1 {S<1 h l ll)( x) 검 (b ― a) ({3- a)}2dm(x) =t{(b— a ) (/3― a)/h(n)} 라
이고, 위 부등식의 우변은 n- CX)일 때 0 으로 수렴한다. 따라 서,
 m(F) =0.
m(F) =0.
되는 척 도불변 가측집 합 N 을 척 도불변 영 집 합 (scale-in v aria n t null set) 이 라 한다. 척도불변 영집합을 제의한 Cz[R] 의 모든 점에서 성질 P 가 성
립할 때 P 는 s-a . e. 에서 성립한다고 한다. 척도불변 가측집합 둘의 모임을 잎, 척도불변 영집합들의 모임을 7J이라 하자.
 C2[R 〕의 보렐 집합 B 에 대해서, 집합함수 mA(11>O) 를
C2[R 〕의 보렐 집합 B 에 대해서, 집합함수 mA(11>O) 를
따라서, 잎는 6- 대수가 된다.
 정리 4·7 (1) E 드잎일 필요충분조건은, 각 J >O 에 대해서
정리 4·7 (1) E 드잎일 필요충분조건은, 각 J >O 에 대해서
이다. 여기서, EA 는 mr 측도 가능한 G 의 부분집합이고 L 은 CoUD 의 임의의 부분집합이다. 이 경우에,
 mA (E) = mA (EJ , 1t >O.
mA (E) = mA (EJ , 1t >O.
이다. 여기서, E1 은 예_위너 측도가능한 G 의 부분집합이고 L 은 ( U C;.) UDU Co 의 임의의 부분집합이다. 0<).*l (2) N 이 예-위너 영집합일 필요충분조건은
 N=N1UL
N=N1UL
이다. 여기서, N1CC1,N1 은 예-위너 영집합이고, L 은 ( O
 척도불변 가측집합의 간단한 예는 정리 1. 16 에서 주어전 집합
척도불변 가측집합의 간단한 예는 정리 1. 16 에서 주어전 집합
이고, E 가 르베그 측도가능하면 ,1 -IE 도 르베그 측도가능하기 때문이다.
 정리 4.l0 각 11>0 에 대해서, 다음 포함관계가 성립한다.
정리 4.l0 각 11>0 에 대해서, 다음 포함관계가 성립한다.
 증명 각 A>O 에 대해서, EACCA, EAE 잎.i, m. i( E.i ) =/(11 - 1) 되
증명 각 A>O 에 대해서, EACCA, EAE 잎.i, m. i( E.i ) =/(11 - 1) 되
가 원하는 집합이다. 왜냐하면, 정리 4.5 와 정리 4.8 에 의해서 다음 식이 성립하기 때문이다.
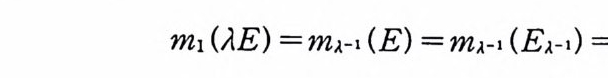 m1 (11E) = mA-1 (E) = mA-1 (EA-•) =/ (11) .
m1 (11E) = mA-1 (E) = mA-1 (EA-•) =/ (11) .
 보조정리 4.12 주어전 r 든〔 0, 1] 에 대해서 다음을 만족하는 집
보조정리 4.12 주어전 r 든〔 0, 1] 에 대해서 다음을 만족하는 집
 집합 CA, 尤착)와 D 는 R 의 분할둘의 수열 6m 에 의해서 결정된
집합 CA, 尤착)와 D 는 R 의 분할둘의 수열 6m 에 의해서 결정된
로 놓으면, 정리 4.3 에 의해서, 이제까지 G 와 D에 대해서 얻 은 결과와 대응되는 결과들을 C i'와 Dh 에 대해서도 얻는다. (주 : 잎 A, 刀 A, Y, 77, m .1는 분할들의 수열과는 독립적이다.) EE 잎일 때, 이 두 분할둘의 수열에 대한 정리 4.8 의 결과를 다음과 같이 표시하자.
 (4.12) E= (-1U >0E .1 ) UL= (.1U> 0E i' ) ULh.
(4.12) E= (-1U >0E .1 ) UL= (.1U> 0E i' ) ULh.
는 척도불변 영집합이다.
척도불번 가측함수
 C2[R] 의 한 척도불변 가측집합(보렐 집합 : mr 측 도가능한 집
C2[R] 의 한 척도불변 가측집합(보렐 집합 : mr 측 도가능한 집
정의 4.14 척도불변 가 측 집합에서 정의된 함수 F 가 다음 성 질을 만족할 때 F 는 척 도불변 가측함수 (scale inv aria n t measur-able fun cti on ) 라 한다.
 모든 J >O 에 대해서 F( 心)는 예 - 위너 측도가능한 함수이다 .
모든 J >O 에 대해서 F( 心)는 예 - 위너 측도가능한 함수이다 .
다음 세 정리는 각각 정리 4.6, 정리 5.8, 정리 4 . 10 에 의해서 얻는다.
 정 리 4 -15 'Y (F) = U 'YA (F) .
정 리 4 -15 'Y (F) = U 'YA (F) .
 정리 4.17 각 a>O 에 대해서
정리 4.17 각 a>O 에 대해서
이 ma- a . e 에서 정의되고 잎 a(F) 에 속하는 것이다.
 성질 4.19 a=so
성질 4.19 a=so
는 s-a. e. 에서 정의되는 척도불변 가측함수이다.
 정리 4-20 p >O 이고, F 가 척도불변 가측함수라 하자. 그러
정리 4-20 p >O 이고, F 가 척도불변 가측함수라 하자. 그러
5 회전변환 위너 공간에서의 회전변환 (ro t a ti on) 의 개념을 예-위너 공간으 로 확장하고 예-위너 공간의 평행변환에 관한 성질을 조사한다.
 정의 5. l Ro : C2[ R ] x C2[R] -+ C2[R] X C2[R 〕을 다음과 갈
정의 5. l Ro : C2[ R ] x C2[R] -+ C2[R] X C2[R 〕을 다음과 갈
이다. Re 는 전단사 (1-1, on t o) 이고 연속인 선형변환이다. 따라 서 보렐 집합을 보렐 집합으로 보낸다.
 보조정리 5-2 각 i= l, 2, …, n 에 대해서, (요i, u ..) 를 측도가
보조정리 5-2 각 i= l, 2, …, n 에 대해서, (요i, u ..) 를 측도가
증명 참고문헌 Bauer[l, Theorem 3.1. l] 참조.
 정리 5.3 C2[R] X C2[R 〕의 모든 보렐 집합 B 에 대해서 다음
정리 5.3 C2[R] X C2[R 〕의 모든 보렐 집합 B 에 대해서 다음
증명 보조정리 5.2 와 정리 2.1 그리고 다음 사실로부터 증명된 다.
 JJ (C2[ R ] X C2 僕]) =JJ (C2 園]) X J] (C2[ R ] )·
JJ (C2[ R ] X C2 僕]) =JJ (C2 園]) X J] (C2[ R ] )·
이다. 다음 정리는 따름정리 5.4 와 변수변환정리(부록 정리 2.1)I 그 리고 푸비니 정리에 의해서 얻는다. 예-위너 적분 기호에서는 C2[R] 대신 간단히 G 로 쓰기로 한다.
 정리 5·5 F 가 C2[R] x C2[R] 에서 정의된 실가함수라고 하
정리 5·5 F 가 C2[R] x C2[R] 에서 정의된 실가함수라고 하
 /c. xc. F(x, y) d(mx m) (x, y) ~1. xC2 F0Ro(x , y) d (m X m) (x, y).
/c. xc. F(x, y) d(mx m) (x, y) ~1. xC2 F0Ro(x , y) d (m X m) (x, y).
윗식의 첫번째 등식은 변수변환정리에 의해서 얻고, 두번째 등식 은 따름정리 5. 4 에 의해서 얻는다.
 정리 5.6 ¢가 C2 〔 R] oJ l 서 정의된 실가함수라 하자· 그러떤,
정리 5.6 ¢가 C2 〔 R] oJ l 서 정의된 실가함수라 하자· 그러떤,
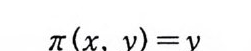 TC(X, y) =Y
TC(X, y) =Y
로 정의되는 사영함수(p ro j ec ti on ma p)라 하자. 그러면,
 ¢ (x sin 0+y cos0) = ¢ 0TC0R 。 (x, y)
¢ (x sin 0+y cos0) = ¢ 0TC0R 。 (x, y)
 =1. xc , (x sin 0+y cos0) d (m X m) (x, y) .
=1. xc , (x sin 0+y cos0) d (m X m) (x, y) .
 (3) f (x +y ) 는 mp X m q- 측 도가능한 (x, Y) 의 함수이 다.
(3) f (x +y ) 는 mp X m q- 측 도가능한 (x, Y) 의 함수이 다.
윗식의 첫째 등식은 정리 4.5 에 의해서, 두번째 등식은 변수변환 정리에 의해서 얻는다.
같은 방법으로 (3) 과 (4) 의 동치성과 이에 해당하는 적분방정 식을 얻는다. (1) 과 (4) 의 동치성과 이에 해당하는 적분방정식은 정리 5. 7 의 결과이다.
 정리 5.9 p, q가 양의 실수이고 AE 잎平巧균]라 하자. 그러
정리 5.9 p, q가 양의 실수이고 AE 잎平巧균]라 하자. 그러
증명 f를 A 의 특성 함수 (characte r is t i c fun cti on ) 로 택 하고, 정 리 5.8 과, 정리 2.2, 푸비니 정리를 사용해서 증명한다.
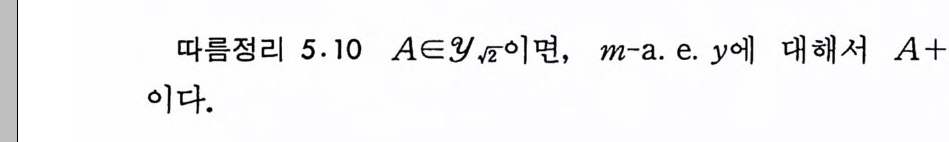 따름정리 5.10 AE 'Y.ff이면, m-a. e. y에 대해서 A+y E 'Y1
따름정리 5.10 AE 'Y.ff이면, m-a. e. y에 대해서 A+y E 'Y1
따름정리 s.11 p, q를 양의 실수라 하자. 변환
 Ty : (C2[R] 'Y q , mq ) - (C2[ R ],잎 P, mp )
Ty : (C2[R] 'Y q , mq ) - (C2[ R ],잎 P, mp )
이므로 정리가 증명된다. 따름정리 5.12 예-위너 공간에서, 거의 모든 평행변환(t ransla ti on) 은 측도가능성 (measurab ility)을 보전하지 않는다. 따름정리 5.13
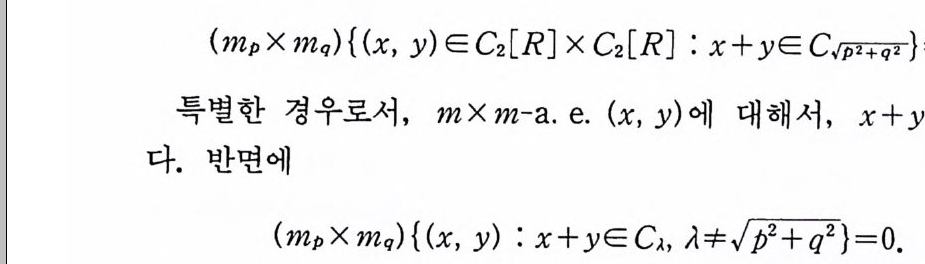 (mp X m q) {(x, y) E C2[R] x C2 灰〕 : x+y E C@ +
(mp X m q) {(x, y) E C2[R] x C2 灰〕 : x+y E C@ +
다음은 척도불변 가측집합과 척도불변 영집합에 대한 긍정적인 결과들이다.
 따름정리 5-14 AE 잎라 하자. p >O 일 때, s-a. e. y에 대해
따름정리 5-14 AE 잎라 하자. p >O 일 때, s-a. e. y에 대해
 증명 p >O 일 때, 각 1t > O 에 대해서, m.-a. e. y가 mp ( N+y )
증명 p >O 일 때, 각 1t > O 에 대해서, m.-a. e. y가 mp ( N+y )
6 두변수함수의 팰리-위너-지그문드 적분 한변수함수의 팰리_위너-지그문드 적분을 두변수함수의 경우로 확장한다. 두 변수 함수의 팰리-위너-지그문드 적분은, 물론 한 변수함수의 경우와 마찬가지로, 두 변수함수의 리만-스틸체스 적 분을 L2(R) 에 속하는 함수들의 적분으로 확장한 것이다. 이 적분에 관한 정리들의 증명은 한 변수의 경우와 비슷하므로 생략하기로 한다. 팰리-위너-지그문드 (P. W . Z.) 적분
 정의 6.1 e={ek} 가 L2(R) 에서 완비정규 직교집합이고 ekE
정의 6.1 e={ek} 가 L2(R) 에서 완비정규 직교집합이고 ekE
 긴다값 (f, ek) g (s, t) ] dx (s, t)
긴다값 (f, ek) g (s, t) ] dx (s, t)
 lf (s, t) dx (s, t) = l/ (s, t) dx (s, t) .
lf (s, t) dx (s, t) = l/ (s, t) dx (s, t) .
주 6.6 정리 6. 5 에 의해서 P. W. Z. 적분은 완비정규 직교집 합 (e) 와는 독립적이므로, 앞으로는 P. W . Z. 적분을 간단히,
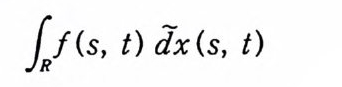 fRf (s, t )Jx( s, t)
fRf (s, t )Jx( s, t)
로 쓰기로 한다. 주 6.7 정리 6. 3 , 6. 4, 6. 5 에서 거의 모든 (a. e.) x 를 s-a. e. x 로 대치해도 된다.
 정리 6.8 /, g, hEL2(R) 이고, C 가 임의의 상수라 하자.
정리 6.8 /, g, hEL2(R) 이고, C 가 임의의 상수라 하자.
 (6. 2) igR (s, t) dx( t)와 iR h(s , t) dx(s, t)
(6. 2) igR (s, t) dx( t)와 iR h(s , t) dx(s, t)
로 정의하자. 그러면, 사상
 a>:g- +xg
a>:g- +xg
는 L2(R) 을 L2(C2[R] )의 폐부분공간 위로 (on t o) 보내는 선형 거 리 보존 (line ar iso metr y ) 사상이 다. 다음 정리는 두변수함수의 P. W. Z. 적분에 대한 부분적분법에 관한 공식 이 다. 증명 은 참고문헌 Joh nson and Skoug [3] 을 참 조.
 정리 6.11 (1) mxm-a. e. (/, g )EC2[R 〕 XC2[R] 에 대해서
정리 6.11 (1) mxm-a. e. (/, g )EC2[R 〕 XC2[R] 에 대해서
카메룬 마틴 번환정리의 확장 유계변동인 함수에 대한 카메룬-마틴 변환정리(정리 3.28) 를
 L2 (R) 에 속하는 함수의 경 우로 확장한다. fe L2 (R) 일 때 f의
L2 (R) 에 속하는 함수의 경 우로 확장한다. fe L2 (R) 일 때 f의
 너 측도가능하고, 다음 식 이 성 립 한다.
너 측도가능하고, 다음 식 이 성 립 한다.
정리 6.12 로부터 정리 6.13 을 얻고, 이것으로부터 정리 6.14 를
얻는다. 다음 증명은 정리 6.12 와는 독립적으로 정리 6.14 를 증 명할 수 있고, 이것으로부터 정리 6.13 울 증명할 수 있음을 보여 준다.
 증명 (정리 6.14) (1) e,.EC[ R ] n H 』i =l, 2, …이고' {e,. }는
증명 (정리 6.14) (1) e,.EC[ R ] n H 』i =l, 2, …이고' {e,. }는
이다. (참고문헌 Parzen[l, Theorem 4B]) (2) y가 정규분포이고 예-위너 측도 m 은 완전측도이므로 변 수변환정리에 의해서 증명된다.
 증명(정리 6.13) 11 가 실수인 경우는, 정리 6.14(2) 에 g( u)=
증명(정리 6.13) 11 가 실수인 경우는, 정리 6.14(2) 에 g( u)=
7 위너 적분과 예-위너 적분의 관계
 예-위너 적분을 위너 적분으로 표시하는 공식을 유도하고 위너
예-위너 적분을 위너 적분으로 표시하는 공식을 유도하고 위너
 (1) g(y) =X/Y) 인 경우.
(1) g(y) =X/Y) 인 경우.
이다• 반면에, (7. 2) 의 우변 적분은 다음과 같다.
 lo ( T) g(y) dm1 (y) =lo ( T) X/Y) dm(y) =1:m, .. 1,w,W m(S, v) dv.
lo ( T) g(y) dm1 (y) =lo ( T) X/Y) dm(y) =1:m, .. 1,w,W m(S, v) dv.
여기서 B 는 집합 A i ((2) 의 경우의 집합)들의 가산 교집합 (counta b le int e r secti on ) 이 다. A 들의 유한 교집 합 (fini t e int e r sec- ti on) 은 A 와 같은 형태의 집합이 되므로 이 경우에
 oo
oo
로 쓸 수 있다. 여기서 B 와 N 은 각각 (3) 과 (4) 의 경우의 집합 이다. XB 와 XN 을 (7 . 2) 에 적용해서 XE 에 대한 (7 . 2) 식을 얻는 다. (6) g (y) 가 단순함수 (sin p le fun cti on ) 인 경 우. g(y)는 (5) 의 경우의 함수들의 유한일차결합(fi n it e line ar combin a ti on ) 이 므로 (7. 2) 가 성 립 한다.
 (7) g(y)가 위너 측도가능한 함수이고, O~ g(y)인 경우.
(7) g(y)가 위너 측도가능한 함수이고, O~ g(y)인 경우.
여기서 g+, g-는 각각 g의 양의 부분(p os iti ve p ar t)과 음의 부 분 (neg a ti ve pa rt) 이 다. (7) 의 경우에 의해서 g+ , g -1 에 대해 (7. 2) 가 성립하므로 g(y) 에 대해서 (7. 2) 가 성립한다. 주 g(y)가 복소수 값을 갖는 경우는 g(y)를 실수부와 허수 부로 나누고 (8) 의 경우를 적용한다. 이제 정리 7.1 을 임의의 유한 개의 직선 위에서의 x 의 값에 관계되는 함수의 경우로 확장하자. 죽 다음과 같은 형태의 함수
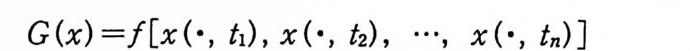 G(x)=/[X (•,! 1), X(•, !2), …, X(•, tn) ]
G(x)=/[X (•,! 1), X(•, !2), …, X(•, tn) ]
에 대한 예-위너 적분을 위너 적분으로 표시하는 공식을 유도한 n 다. XCo ( T) 를 n 개 위 너 공간들의 적 공간 (pr oduct spa ce) 이 라
하자. 즉
 n
n
 (1) g(y,, …, Yn) =X1(Y1, …, Yn) 인 경우.
(1) g(y,, …, Yn) =X1(Y1, …, Yn) 인 경우.
 < U j ,k-U j , k-1~ ✓ 三-r;;;__ W j , k~ +oo, k=l, …, n}.
< U j ,k-U j , k-1~ ✓ 三-r;;;__ W j , k~ +oo, k=l, …, n}.
 ==lfoCC oo ((( TTT ))l )汀'.')J.,IlCCo oo ((( TrT ))) JJgJ=:(- i1yX' 1I[,,, (…y , ,( sYj)n ,) d…m, 1Y(ny 1()s …J )d dmm11( y(y n, )). … dm 品)
==lfoCC oo ((( TTT ))l )汀'.')J.,IlCCo oo ((( TrT ))) JJgJ=:(- i1yX' 1I[,,, (…y , ,( sYj)n ,) d…m, 1Y(ny 1()s …J )d dmm11( y(y n, )). … dm 品)
(2) 일반적인 경우는 정리 7.1 의 증명과 같은 방법을 따른다.
 n
n
로 정의하자. 그러면 G 는 연속이고 전사함수 (on t o) 이다. 위의 기호를 사용하면 정리 7.2 는 다음과 같이 쓸 수 있다.
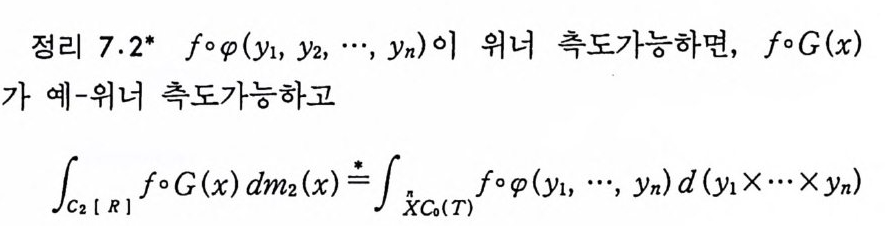 정리 7,2* /0q ;(y1, Y2, …, Yn) 이 위너 측도가능하면, /0G(x)
정리 7,2* /0q ;(y1, Y2, …, Yn) 이 위너 측도가능하면, /0G(x)
이 성립한다. .nX m 1 을 n 개 의 위 너 측도에 m 들의 적 측도 (pro duct measure) 라 하자.
n 따름정리 7.3 A 를 XCo(T) 의 임의의 부분집합이라 하자. 그 n 러면, cp -1A 가 Xm1_ 측도가능하면, G_IA 가 예-위너 측도가능하 고,
 (7. 10) Xn m1 (
(7. 10) Xn m1 (
다음 정리는 따름정리 7. 3 의 역이다. 이 정리로부터 정리 7.1 과 7.2 의 역(정리 7.5) 을 쉽게 얻을 수 있다. n 정리 7.4 A 를 XCo(T) 의 임의의 부분집합이라 하자. 만일 n c-1A 가 예-위너 측도가능하면 rp -lA 가 Xm1_ 측도가능하고 (7. 10) 이 성립한다. 증명 다음 식에서 첫번째 등식과 마지막 등식은 각각 예-위너 n 측도 m2 와 위너 적측도 Xm1°l 단단한 측도(tig h t measure) 라는 사실로부터 얻고, 세번째 등식은 따름정리 7.3 에 의해서 얻는다.
 m2(G-1A) =sup {m 2K : KcG-1A, K 는 C2[R] 에서 컴팩트 집합}
m2(G-1A) =sup {m 2K : KcG-1A, K 는 C2[R] 에서 컴팩트 집합}
이것으로부터,
 정리 7-5 /0G(x) 가 예위너 측도가능하면 /0r p(y1, …, Yn) 이
정리 7-5 /0G(x) 가 예위너 측도가능하면 /0r p(y1, …, Yn) 이
다음 정리는 위너 측도가능한 집합과 예-위너 측도가능한 집합 사이의 관계를 말해 준다.
 정리 7.6 a
정리 7.6 a
 증명 /(y )=XA( y)로 놓고 정리 7 . 1 과 정리 7.5 를 적용하면
증명 /(y )=XA( y)로 놓고 정리 7 . 1 과 정리 7.5 를 적용하면
정리 7-7 r, A, BA 가 정리 7.6 에서 주어졌다고 하자. 그러면 다음 사실이 성립한다.
 (1) r-a=2 일 때, BAE 잎 1~AE .0 1
(1) r-a=2 일 때, BAE 잎 1~AE .0 1
증명 (1) 정리 7. 6 의 특별한 경우이다. (2) G 를 위너 측도가능하지 않은 집합이라 하고,
 A= [ (r-a)/2] 상 (C1n G)
A= [ (r-a)/2] 상 (C1n G)
 로 놓자(주 : C1 은 1 장 (4. 20) 에서 주어진 집합이다). 그러면 A 는
로 놓자(주 : C1 은 1 장 (4. 20) 에서 주어진 집합이다). 그러면 A 는
정리 7-8 F(y1 , …, Yn) 이 Xn Co(T) 에서 위너 측도가능한 함수 이고, (cu), i, j= l, 2, …, n 를 직교행렬 (or t ho g onal ma t r i x) 이라 하자. 죽,
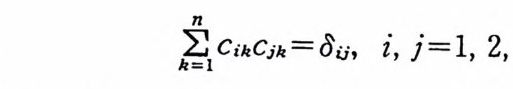 n
n
그러면, 변환
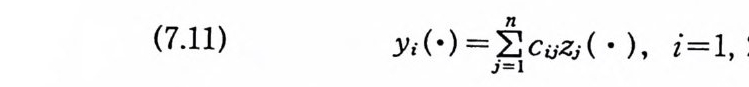 (7.11) y;(•) =~j=n cI uZ;( • ), i= l, 2, …, n
(7.11) y;(•) =~j=n cI uZ;( • ), i= l, 2, …, n
n 은 XCo(T) 를 그 자신으로 보내는 전사 (on t o) 함수이고, 측도보 전 (measure pre servin g ) 변환이 다. 이 경 우에 다음 등식 이 성 립 한 다.
 (7. 1=2) fC o !(c CT o) (…T) .!/…Cco. .((I C/TT ol) (FT<) Fjj= t(l Cy11j , Z j…, ,… Y, nj)t= dl mc 떠1 z(J y 1d) m…1 d( 작m 品 )·d m1( 길
(7. 1=2) fC o !(c CT o) (…T) .!/…Cco. .((I C/TT ol) (FT<) Fjj= t(l Cy11j , Z j…, ,… Y, nj)t= dl mc 떠1 z(J y 1d) m…1 d( 작m 品 )·d m1( 길
n 그러면, F 는 XCo(T) 에서 유계이고, 위너 측도가능하고 다음
 식을 얻는다.
식을 얻는다.
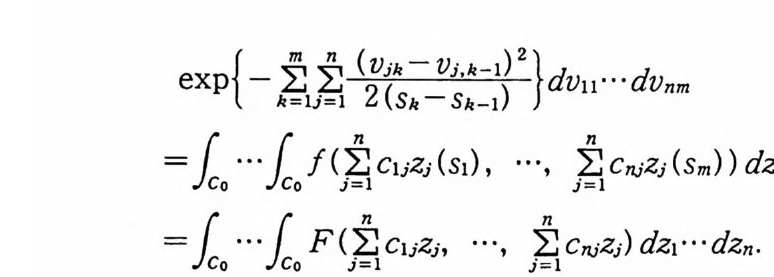 exp { 정흡 胃 ks :-V JS .:: 『 }d vu • •• d vnm
exp { 정흡 胃 ks :-V JS .:: 『 }d vu • •• d vnm
윗식에서, 각 적분의 피적분함수의 측도가능성은 /(u) 의 측도 가능성으로부터 얻고, /(u) 가 유계이므로 각 피적분함수는 적분 가능하다. 따라서 (1) 의 경 우 (7. 12) 가 성 립 한다 . f가 측도가능한 집합의 특성함수인 경우에 (7.12) 를 적용하 n 면, (7.11) 은 XCo(T) 를 그 자신으로 보내는 측도보전변환이 다.
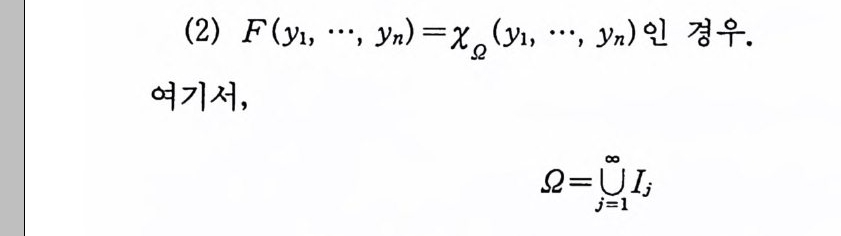 (2) F(y1 , …, Yn) =Xa(y1 , …, Yn) 인 경우.
(2) F(y1 , …, Yn) =Xa(y1 , …, Yn) 인 경우.
n 이고, Ij 는 XCo(T) 에서 서로 소인 구간이다. (정리 7.2 의 증명에 서 (1) 의 경우의 구간). 각 xI J 는 (1) 의 경우의 가정을 만족하므로, F 가
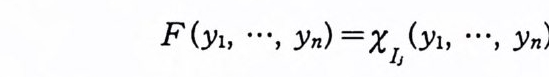 F(y1 , …, Yn) =X1J( y1, …, Yn)
F(y1 , …, Yn) =X1J( y1, …, Yn)
인 경우 정리가 성립한다. 요는 측도 가능한 집 합이고, x 를 (7. 12) 에 적용하고, (7. 12) [J
의 양변을 j에 대해서 합하면 x g에 대해서 (7 . 12) 가 성립한다.
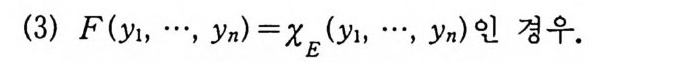 (3) F(y1 , …, Yn) =XE(y1 , …, Yn) 인 경우.
(3) F(y1 , …, Yn) =XE(y1 , …, Yn) 인 경우.
n 여기서 E 는 XCo(T) 에서 위너 측도가능한 집합이다. Q,가 (2) 에서 정의된 집합일 때, (2) 의 경우를 집합
Q =ni0=0 I Q ;
와 영집합 (null se t)의 경우로 확장해서 증명한다.
(4) 0 :5: F(x) 인 경우.
F(x) 가 단순함수인 경우는 (3) 에 의해서 증명된다. F(x) 가 단순함수가 아닌 경우에는, F(x) 를 단순함수들의 단조증가수열 의 극한으로 나타낼 수 있으므로 정리가 증명된다. (5) 일반적인 경우. F(x) 가 실가함수인 경우, F=F+-F- 로 표시하고 F+ 와 F- 에 (4) 의 경우를 적용하면 된다. F(x) 가 복소수함수인 경우에는 실수부와 허수부로 나누고, 위와 같은 요령으로 증명할 수 있다. 다음 정리는 두 수직선 위에서의 x 의 값에 관계되는 함수의 예-위너 적분을 위너 적분으로 나타내는 정리이다.
 정리 7,9 f(z , y)가 Co[a, l 기 x c。 〔 a 나인예서 정의된 함수이
정리 7,9 f(z , y)가 Co[a, l 기 x c。 〔 a 나인예서 정의된 함수이
 J[x (·, /3), x(b, 이는 C2[R] 에서 예-위너 측도가능하고 다음
J[x (·, /3), x(b, 이는 C2[R] 에서 예-위너 측도가능하고 다음
이제 2 장 정리 1. 8 을 적용하기 위해서 0A t)를 다음과 같이 놓
 자. j= l, 2, …, n 에 대해서,
자. j= l, 2, …, n 에 대해서,
(7.14) 에 (7.16) 의 값을 대입해서 다음 식을 얻는다.
 k=l, 2, …, n-l 에 대해서,
k=l, 2, …, n-l 에 대해서,
 위너 적분공식
위너 적분공식
 대해서
대해서
이므로, (1) 의 경우가 증명된다. 정리 7 . 1 의 증명에서 사용한 방 법에 따라서, 일반적인 경우로 확장해서 정리의 증명을 끝낸다.
 예 7.10 p드 L1 〔 a, b], qE L1[a, J기 일 때 함수
예 7.10 p드 L1 〔 a, b], qE L1[a, J기 일 때 함수
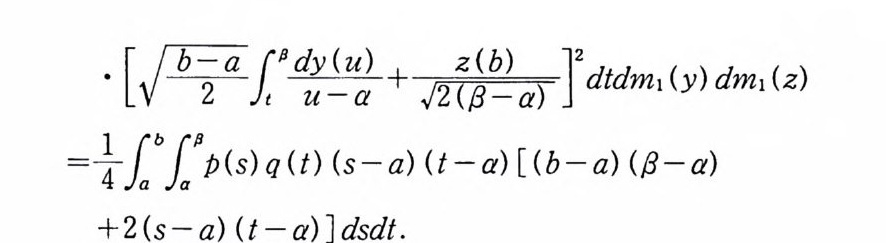 · [『尸[pd:모 + ~rdtdm 1 (y ) dm1(z)
· [『尸[pd:모 + ~rdtdm 1 (y ) dm1(z)
여기서, dm1( y)와 dm1(z) 는 각각 Co[a,b ]와 G 〔 a, t기에서의 위너 측도이다. 주어진 집합 위에서의 x 의 값에 관계되지 않는 함수의 예-위 너 적분을 위너 적분으로 표시하는 정리를 소개한다. a 를 [a, /3]의 분할 :
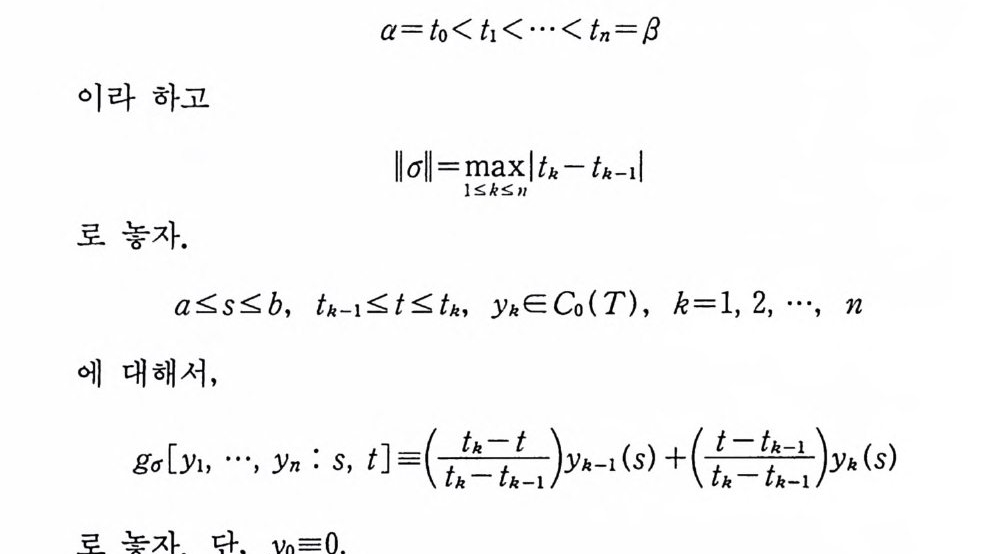 a= to< l1< …< ln=/3
a= to< l1< …< ln=/3
정리 7.11 F(x )가 G 〔 R] 에서 유계이고 연속이라 하자. 그러 면, 다음 식이 성립한다.
 M(l7im-. 1O .f1I C) o (/ cTC.2) 1I\ RR .1[lI CF o (( xT)) Fdmo2g 6(x °)r p=( yI, …, Yn)dm1(y 1) … d m1(y, z).
M(l7im-. 1O .f1I C) o (/ cTC.2) 1I\ RR .1[lI CF o (( xT)) Fdmo2g 6(x °)r p=( yI, …, Yn)dm1(y 1) … d m1(y, z).
이므로 f는 정리 7.2 의 가정을 만족한다. 따라서 다음 식을 얻 는다.
 fC 2 I R l f[x (•, h), …, x( 나)〕 dm2(x)=
fC 2 I R l f[x (•, h), …, x( 나)〕 dm2(x)=
이고, F 가 유계이므로 르베그 수령정리를 사용하면 (7.11) 을 얻 는다.
8 일반화된 역측도정리 이제까지 알려진 위너 공간과 예 - 위너 공간에서의 역측도정리 둘(1장 정리 1. 26, 정리 1.1 5, 정리 7. 4) 을 따름정리로서 얻을 수 있는 일반적인 역측도정리를 소개한다. 위상공간 X 의 보렐 6- 대수 J3 (X) 를 포함하는 6 대수 4 에서 정의된 확률측도 p가 다음 조건을 만족할 때 p는 단단한 측도
 (tigh t measure) 라 한다. 주어전 c>O 과 EE .A에 대해서
(tigh t measure) 라 한다. 주어전 c>O 과 EE .A에 대해서
되 는 컴 팩 트 (comp a ct) 집 합 K 가 존재 한다. 완비 가분 거 리 공간 (com p le t e sep a rable metr i c s p ace) 의 보렐 6- 대수에 서 정 의 된 확률측도는 단단한 측도이 다(부록 정 리 1.20 ) . S 와 T 를 위상공간, J3 (S) 와 J3 (T) 를 각각 S 와 T 의 보렐 6 - 대수라 하자. p를 J3 (S) 에서의 단단한 측도, v 를 J3 (T) 에서 의 측도라 하자. (S, g( S), 下)와, (T, 3(T), 了)를 각각 (S, J3 (S) , P) 와 ( T, J3 ( T) , II) 를 완비화 (com p le t e) 해서 얻 는 완비측도공간이라 하자. 下는 g (S) 에서 단단한 측도가 된다. J : s-T 가 연속함수라 하고, U={ECT : 1-1(E) 는 下-측도가능하다} 로 놓으면 U 는 6- 대수이다. 집합함수 µ를 U 에서, µE=p (J-1 (E)), EEU
로 정의하자. 그러면, JJ (T)UU 이고, (T,U, 짜는완비측도공간이 된다. 이제 µ 가 U 에서 단단한 측도임을 보이기 위해서, E 를 µ-측도가능한 집합이라 하자. 그러면, 각 자연수 n 에 대해서,
 Knc]-1(E), p(J-1 (E)\Kn) <上n
Knc]-1(E), p(J-1 (E)\Kn) <上n
되는 컴팩트 집합 K머 존재한다.
 n
n
 이다. 따라서 µ는 U 에서 단단한 측도이다.
이다. 따라서 µ는 U 에서 단단한 측도이다.
과 같은 가정에서, U=J 3( T) 이다.
가정 N 이 ii-영집합일 필요충분조건은 N 이 µ-영집합이다•
 증명 13(T) CU 는 쉽게 보일 수 있다• U~ 1J (T) 을 보이기
증명 13(T) CU 는 쉽게 보일 수 있다• U~ 1J (T) 을 보이기
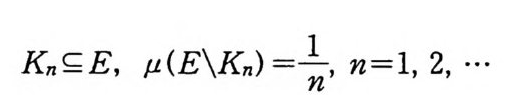 K 홉 E, µ(E\Kn) =—1n ' n=l, 2, …
K 홉 E, µ(E\Kn) =—1n ' n=l, 2, …
되는 컴팩트 집합 K 려 존재한다.
 00
00
이다. 증명 보조정리 8.1 에 의해서, N 이 µ-영집합이면 N 은 D- 영 집합임을 보이면 된다. 이제 다음과 같이 가정하자. N 은 µ-영 집합이지만 i-영집합은 아니다. 다음 두 가지 경우로 나누어서 생각하자. (1) N 이 P- 측도가능한 경우. (2) N 이 P- 측도가능하지 않은 경우. N 이 V- 측도가능하면,
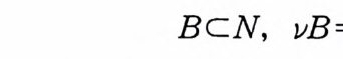 BcN, 11B= 까 V>O
BcN, 11B= 까 V>O
되는 보렐 집합 B 가 존재한다.
 µB=!a B g (t) av (t) >O
µB=!a B g (t) av (t) >O
되는 컴팩트 집합 Kn 이 존재한다.,
 oo
oo
일반화된 역측도정리 (정리 8.2) 를 이용해서 위너 공간과 예-위 너 공간에서의 역측도정리들을 따름정리로서 다음과 같이 증명할 수 있다.
 (1) 코호러 (Kochler) 정리 (1 장 정리 1. 26) 의 증명
(1) 코호러 (Kochler) 정리 (1 장 정리 1. 26) 의 증명
으로 정의하자. 이제, J -1(E) 가 위너 측도 가능하면, E 가 르베 그 측도 가능함을 보이자.
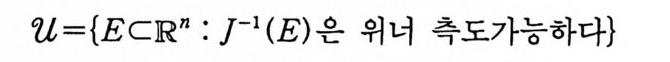 U={ECRn : ] - 1(E) 은 위너 측도가능하다}
U={ECRn : ] - 1(E) 은 위너 측도가능하다}
로 놓으면, Rn 에서 루베그 측도 가능한 집합들은 모두 U 에 포 함된다. EEU 에 대해서, 집합함수 µ를
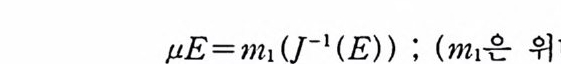 µE=m1U-1(E)) ; (m1 은 위너 측도)
µE=m1U-1(E)) ; (m1 은 위너 측도)
로 정의하자. 르베그 측도가능한 집합 E~lRn 는
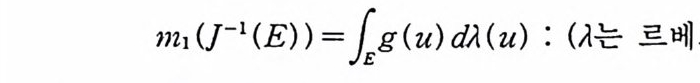 m1(/-1(E)) =lE g( u )d.A (u) : (;l는 르베그 측도)
m1(/-1(E)) =lE g( u )d.A (u) : (;l는 르베그 측도)
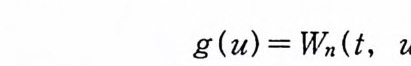 g( u) = WnU, u) >O
g( u) = WnU, u) >O
을 만족한다. 여기서,
이고 Wn(t, u) 는 1 장 식 (1. 8) 에서 주어진 밀도함수이다. 위너 측도는 의(위너 측도가능한 6- 대수)에서 단단한 측도이고 13(C 。 (T)) 드의이므로, (Rn,U,µ) 는 완비측도공간이고 µ는 단단한 측도이다. 따라서 정리 8.2 에 의해서, 1-1(E) 가 위너 측도 가능 하면 E 는 르베그 측도가능하다. (2) 정리 1.1 5 〔스코그 (Skou g) 정리〕의 증명
 a=so
a=so
이고 Wmn(s, t : U) 는 식 (1. 3) 에서 주어전 밀도함수이다. 이제 (1)의 경우와 같은 방법으로 증명하면 된다. (3) 정 리 7 .4의 증명 平와 G 를 각각 (7. 8) 과 (7. 9) 에서 정의된 함수라 하자. G-IA n 가 예-위너 측도가능하면, i:p -lA 가 XmI- 측도가능함을 보이자.
 J= i:p- 10 G
J= i:p- 10 G
 =Xm1(E) =1E1 dXm1
=Xm1(E) =1E1 dXm1
9 푸리에-예-위너 변환 2 장에서 취급한 푸리에 - 위너 변환과 유사한 푸리에 - 예_위너 (Fourie r -Yeh-W ien er) 변환을 정 의 하고 이 변환이 존재 하는 함수 들의 집합을 찾는다. 또한 이 집합에 속하는 함수들에 대해서 플 란세 렐 관계 (Plancherel's relati on ) 와 파시 발 관계 (Parseval' s rela- ti on) 가 성립함을 증명한다.
 R=[ a, b 〕지 a, /3]에서 정의되고, 복소수값을 갖는 연속함수
R=[ a, b 〕지 a, /3]에서 정의되고, 복소수값을 갖는 연속함수
이 존재할 때, G 를 F(x) 의 푸리에-예-위너 변환이라 한다.
 정의 9.2 /(z1, …, Zn) 이 Cn 에서 정의된 완전함수이고 (en ti re
정의 9.2 /(z1, …, Zn) 이 Cn 에서 정의된 완전함수이고 (en ti re
e1(s, t), …, en(s, t)이 일차 독립이고 R 에서 유계변동(하디 - 크라우스)일 때, 다음과 같은 형태의 함수 F 들의 집합을 E 라 하자.
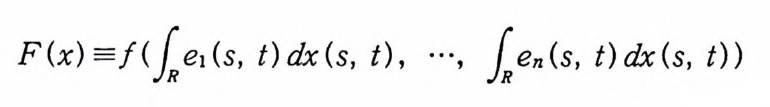 F(x)=/(leR1 (s, t)d x(s, t), …, len(s, t)d x(s, t))
F(x)=/(leR1 (s, t)d x(s, t), …, len(s, t)d x(s, t))
정리 9.3 J(z 1, …, %)이 Cn 에서 정의된 지수형의 완전함수 라 하자. {ek(S, f)}가 정규직교집합이고 R 에서 유계변동(하디 -크라우스)이라 하자. 그러면 함수
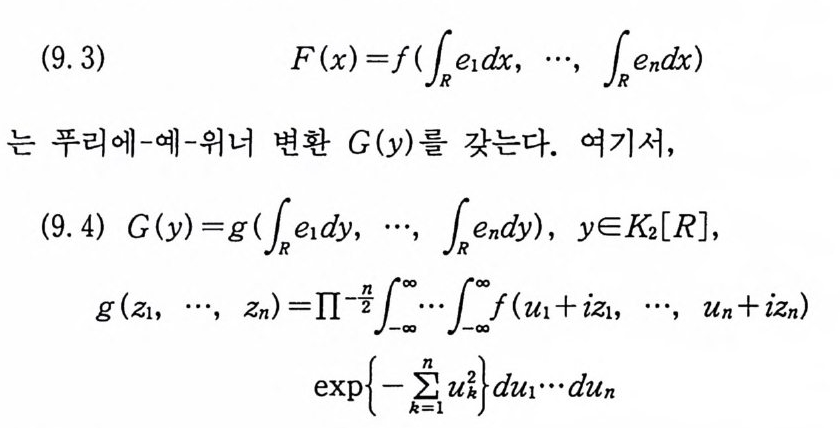 (9. 3) F(x) =f(L eIdx, …, lendx)
(9. 3) F(x) =f(L eIdx, …, lendx)
이다. 또한, G( y)의 푸리에-예-위너 변환은 F(-x) 이다. 증명 정리 6.15 에 의해서 다음 식을 얻는다.
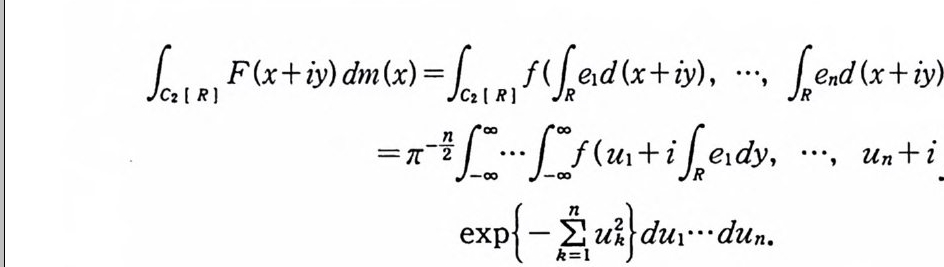 fc21 RI F(x+iy )d m(x) ={ 1 R1 /
fc21 RI F(x+iy )d m(x) ={ 1 R1 /
g( zI, …, Zn) 은 지수형의 완전함수이다 (2 장, 보조정리 5.6 과 주 5. 20 참조). 다음 식은 F(-x) 가 G( y)의 푸리에저]-위너 변환이 됨을 보 여준다.
 i1C222 I 1IR RRI l1겹 G ( 1y: +-- i-x1): d1m(u (1y+) i=t e1d( y+ix), Un+ iiR end( y + ix) )
i1C222 I 1IR RRI l1겹 G ( 1y: +-- i-x1): d1m(u (1y+) i=t e1d( y+ix), Un+ iiR end( y + ix) )
 은 함수
은 함수
따름정리 9.5 F(x) 와 G( y)가 정리 9. 3 에서 주어전 함수라 하면, 다음의 프란세렐 관계가 성립한다.
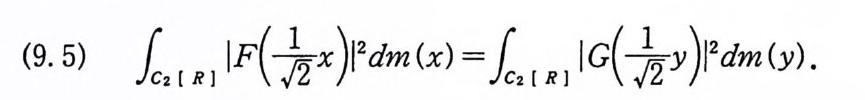 (9. 5) 12 [ R l IF( 뇽 )l2dm (x) = fc21 R J I C( 古y )l2dm (y) .
(9. 5) 12 [ R l IF( 뇽 )l2dm (x) = fc21 R J I C( 古y )l2dm (y) .
함수 F1(x) 와 F2(x) 가 다음과 같이 주어지고, G1( y)와 Gi(y)를 각각 R 과 R 의 푸리에-예-위너 변환이라 하자.
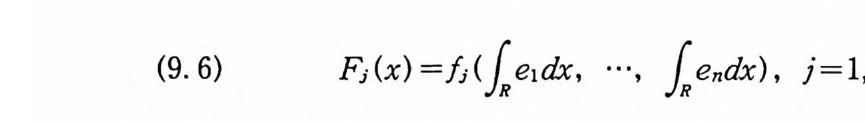 (9. 6) Fj ( x) =fj
(9. 6) Fj ( x) =fj
여기서, fj와 ek(s, t)는 정리 9. 3 의 가정을 만족하는 함수이다. 그러면 다음의 파시발 관계가 성립한다.
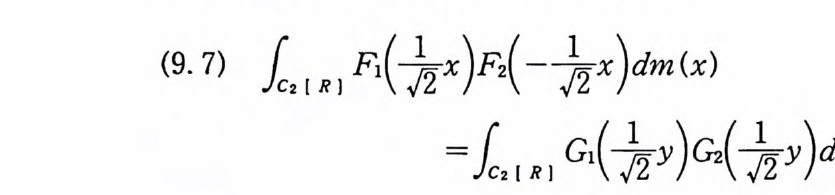 (9. 7) 1. I R I F1 心 )R( ―분 )dm (x)
(9. 7) 1. I R I F1 心 )R( ―분 )dm (x)
증명 푸리에 변환에 대한 플란세렐 관계를 따름정리 9.4 에 적 용해서 다음 식을 얻는다.
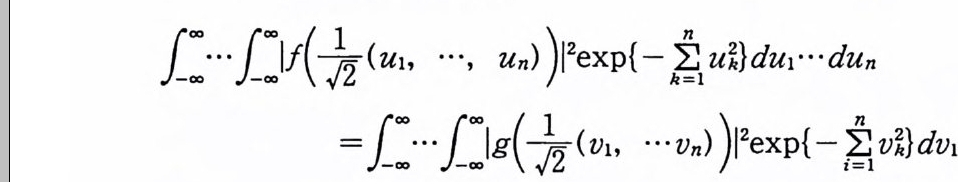 1:oo … 1:°1° 1( 건1 (uI, …, Un))12ex p{-홉n [ uUdu1···dun
1:oo … 1:°1° 1( 건1 (uI, …, Un))12ex p{-홉n [ uUdu1···dun
(9. 3), (9. 4), 정리 6.15 에 의해서 윗식은 (9. 5) 과 동치이다. 푸리에 변환에 대한 파시발 관계를 사용해서 (9. 7) 도 얻는다.
 정리 9.6 FEE 일 때, F(x) 의 푸리에-예-위너 변환 G( y)는
정리 9.6 FEE 일 때, F(x) 의 푸리에-예-위너 변환 G( y)는
증명 그램 수 F 미트 (Gram- Schmidt) 정규직교화 과정 (ort ho norm alization pro cess) 에 의 해 서 ,
 (9. 8) e1(s, t) = Cj 1 e1 (s, t) + …+ Cj jej (s, t) , j= l, 2, …, n
(9. 8) e1(s, t) = Cj 1 e1 (s, t) + …+ Cj jej (s, t) , j= l, 2, …, n
 n ; k=l, 2, …, j)가 존재한다.
n ; k=l, 2, …, j)가 존재한다.
로 정의하자. 그러면, (9. 8) 과 (9.12) 에 의해서, G( y)는 (9. 4) 로 표시되고, G( y)의 푸리에-예-위너 변환은 F(-x) 이다.
따름정리 9.7 (9.13) 의 함수 g( zI, …, Zn) 는 다음과 같이 주 어진다.
 g( z1, 리 =K- 장i OOOO … 1:1(duu,+ iz 1, j~=n I dn iu i + izn )
g( z1, 리 =K- 장i OOOO … 1:1(duu,+ iz 1, j~=n I dn iu i + izn )
몇 개의 함수들에 대한 푸리에-예-위너 변환의 예를 소개한다. a (s, t) 를 R 에 서 유계 변동 (하디 -크라우스) 이 라 하자.
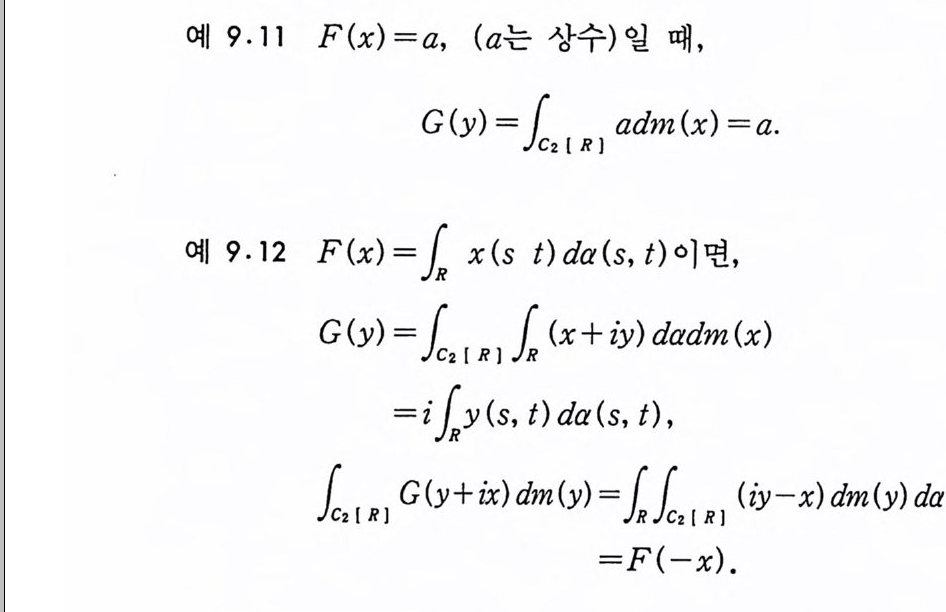 예 9-11 F(x) =a, (a 는 상수) 일 때,
예 9-11 F(x) =a, (a 는 상수) 일 때,
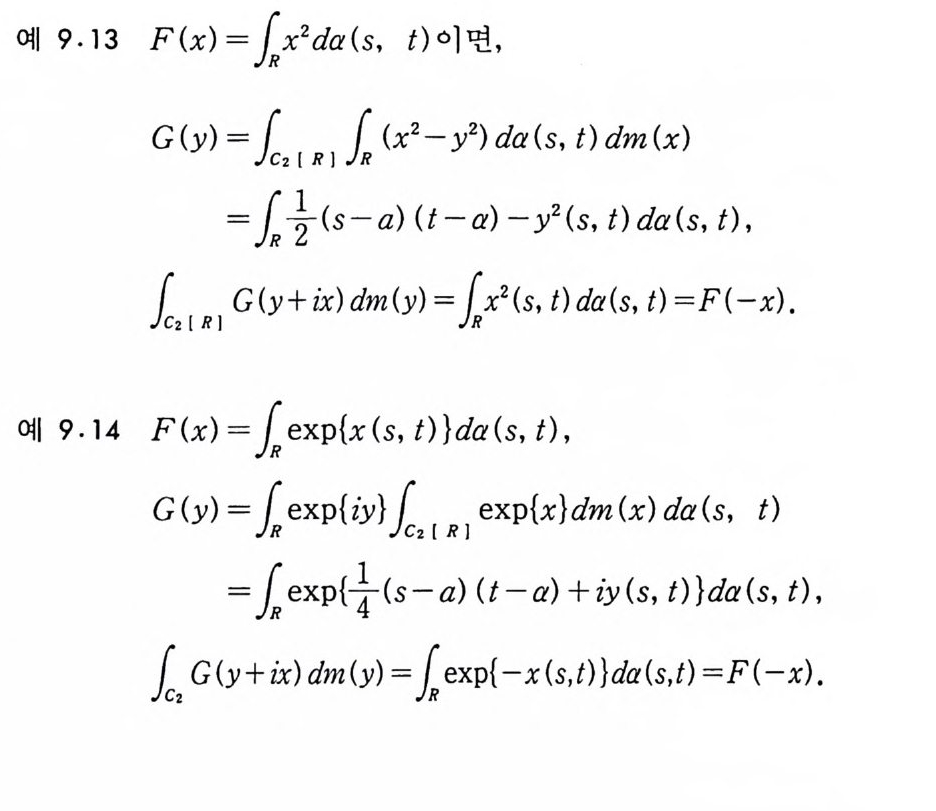 예 9.13 F(x) =i났 da(s, t)이면,
예 9.13 F(x) =i났 da(s, t)이면,
제 5 장 위너 작용소적분과 예-위너 조건적분 위너 작용소적분과 예-위너 조건적분을 정의하고, 이 적분의 존재성을 증명한다. 특히, 함수
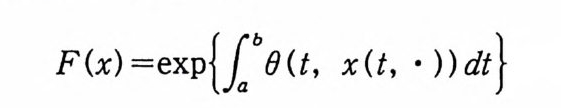 F (x) =exp { lab (] (t' X (t' • ) ) dt}
F (x) =exp { lab (] (t' X (t' • ) ) dt}
의 예-위너 작용소적분은 위너 적분방정식의 해가 되고, 이 해는 위너 적분들의 노이만 (Neumann) 급수로 표시된다. 위너 조건적분을 예-위너 조건적분으로 확장하고 이 적분의 존 재 성 을 증명 한다. 또한, 이 적분에 대 한 반전공식 (inv ersio n form ula) 과 변환공식 을 유도한다. 1 위너 작용소적분 ll>O 에 대해서 다음의 위너 적분을 생각해 보자.
여기서, F 는 C(T) 위에서 정의된 실수 값 (real valued) 또는 복소수 값을 갖는 함수이고 ¢:R 一 R( 또는 C) 는 a.e 에서 정 의된 함수이다. 만일 t/J EL2(R) 일 때, L(F)# 가 e 의 함수로서 L2(1R) 에 속한 다면, LF 는 힐베르트 공간 L2(R) 을 L2(IR) 로 보내는 작용소 (op e rato r ) 로 생 각할 수 있다. 이 작용소 IA (F) 를 위 너 작용소 적 분 (op e rato r -valued Wi en er int e g ral ) 이 라 한다.
 정의 1.1 tl >O 에 대해서, 식 (1. 1) 에서 주어진 lA(F) 가 L2
정의 1.1 tl >O 에 대해서, 식 (1. 1) 에서 주어진 lA(F) 가 L2
 F( y)가 유계이고, F( tl랑 x+ t)가 Co(T) XIR 에서 (x, t)의 함
F( y)가 유계이고, F( tl랑 x+ t)가 Co(T) XIR 에서 (x, t)의 함
![]() 보조정리 1.2 tl >O 이고 /(x) EL2(R) 일 때,
보조정리 1.2 tl >O 이고 /(x) EL2(R) 일 때,
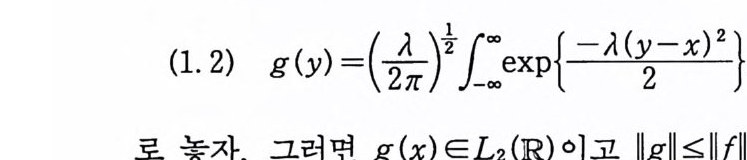 (1. 2) g(y) =(갑)t 1:ex p「 A (:— x)2 }f(x) dx
(1. 2) g(y) =(갑)t 1:ex p「 A (:— x)2 }f(x) dx
![]() 증명 ex p{―강(y -x)2}EL2(lR) n L1 (JR) 이므로
증명 ex p{―강(y -x)2}EL2(lR) n L1 (JR) 이므로
(1. 1) (/, (F) rp) (~) = loCo (( TT )l F (;l-상 X + ~)
(1. 2) 의 적분은 존재한다.
 lg( y) |由(습)½J :ex p{―강(y -x)2}II(x) ldx
lg( y) |由(습)½J :ex p{―강(y -x)2}II(x) ldx
위의 적분은 3 중적분으로 존재하고, 또한 반복적분으로도 존재 한다.
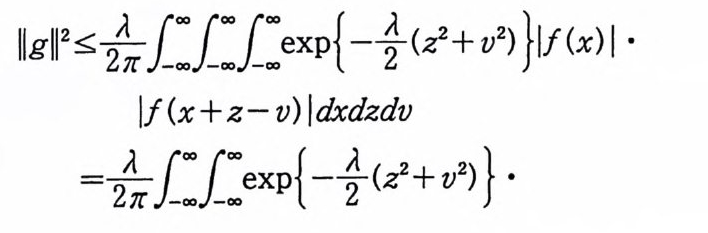 Il g露갑 :1:1:ex p{-강(강국 )}|I(x)I •
Il g露갑 :1:1:ex p{-강(강국 )}|I(x)I •
 [f-c. o. |f(x ) 11/(x+z— v) |dx 國'z dv .
[f-c. o. |f(x ) 11/(x+z— v) |dx 國'z dv .
변수변환,
 v=1t - zI u+e
v=1t - zI u+e
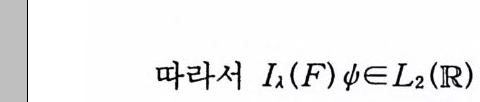 따라서 IA (F)
따라서 IA (F)
주 l·5 IA(FW 의 존재성과 이에 관한 성질은 여러 종류의 함 수 F 와 ¢의 경우에 얻어졌다. 특히, 함수
 F(x) =exp { lba 0 (s, x (s) ) 이, xE C 。 ( T)
F(x) =exp { lba 0 (s, x (s) ) 이, xE C 。 ( T)
J, (F) 를 예 _위 너 작 용 소 적 분 (op e rato r -valued Yeh-Wi en er int e - g ral) 이라 한다. F 가 C;[R] 에서 유계이고 연속이면 IA(F) 는, Co[a, /3]에서 유계이고 연속인 함수들의 집합을 그 자신으로 보내는 작용소이 다. 이제, 이 집합을 W(Co[a, /3])로 확장하려고 한다•
 보조정리 1.7 f(y ,z) 가 C 。〔 a, /3] XCo 〔 a, t기예서 보렐 측도 x
보조정리 1.7 f(y ,z) 가 C 。〔 a, /3] XCo 〔 a, t기예서 보렐 측도 x
들의 모임을 S 라 하자.
 T={AES : xA(x(c, ·), z) 는 C2[R] x Co[a, /3〕에서
T={AES : xA(x(c, ·), z) 는 C2[R] x Co[a, /3〕에서
인 경우 보조정리 1. 7 이 증명된다. (3) /(y ,z) 가 보렐 측도 x 보렐 측도에 대해서 단순함수 (sim p le fun cti on ) 인 경 우. f는 (2) 에서 정의된 특성함수들의 유한 일차결합이므로, 정리 가 증명된다. (4) Os / (y, z) 이 고 측도가능한 경 우, (5) / (y, z) 가 측도가능 한 경우, (6) I( y ,z) 가 복소수 값을 갖는 경우는 (3) 에서 (4), (4) 에서 (5), (5) 에서 (6) 으로 단계적으로 증명할 수 있다.
 주 ] .8 f( x, y)가 G [R ]x Co[a, /3]에서 보렐 측도 x 보렐 측
주 ] .8 f( x, y)가 G [R ]x Co[a, /3]에서 보렐 측도 x 보렐 측
다음 정리는 I. 1 (F) 의 존재정리이다. 여기서부터는 IA(F) 는
 정리 1.9 F 가 C;[R 〕에서 유계이고, 연속(최소상계 노름위상
정리 1.9 F 가 C;[R 〕에서 유계이고, 연속(최소상계 노름위상
(1. 3) 에서 주어전 예-위너 적분을 뜻한다.
 =/cC22 ,I RR Ii Q (x, Y) dm2 (x)
=/cC22 ,I RR Ii Q (x, Y) dm2 (x)
위 식의 마지막 등식은 1 장 따름정리 5.7 에 의해서 얻는다. 따라 서 J(y)는 보렐 측도가능하므로, 정리가 증명된다. 2 위너 적분방정식의 존재정리 위너 적분방정식의 해에 대한 존재정리를 증명한다. 이 적분 방정식의 해는 예-위너 적분으로 표시된다.
 xEC2 〔 R ]일 마 처긱 정의역울 (-o o, oo) X [a 나g]로 다음과
xEC2 〔 R ]일 마 처긱 정의역울 (-o o, oo) X [a 나g]로 다음과
 로 놓자. a=b 인 경우는 b 를 생략하고
로 놓자. a=b 인 경우는 b 를 생략하고
 f ({5 시)를 n p변수 ~j k 의 함수로서 유계이고 르베그 측도가능
f ({5 시)를 n p변수 ~j k 의 함수로서 유계이고 르베그 측도가능
 (2. 8) fc21 R1 F(x• )edxmp 2{(-xtj)* j m~= r+ 1I.t ~:'1I. ''!: 1(:s/j(- {~Su 노j- 1)다 (t),.- t,2.-1 ]2
(2. 8) fc21 R1 F(x• )edxmp 2{(-xtj)* j m~= r+ 1I.t ~:'1I. ''!: 1(:s/j(- {~Su 노j- 1)다 (t),.- t,2.-1 ]2
 /({y(s j, tk) }+{vjk })exp {— i= $m +lk$=I
/({y(s j, tk) }+{vjk })exp {— i= $m +lk$=I
 l= r1: 汀 ’’.P ! 1:1({W j k+ W~k})
l= r1: 汀 ’’.P ! 1:1({W j k+ W~k})
 분가능하고 (2. 3) 이 성 립 한다.
분가능하고 (2. 3) 이 성 립 한다.
로 가정할 수 있다. (3) 의 경우에 의해서, x QI (x) 에 대해서 정리가 성립한다. 이 함수에 극한을 취하면 F(x) 가 되므로 F(x) 에 대해서도 정리가 성립한다.
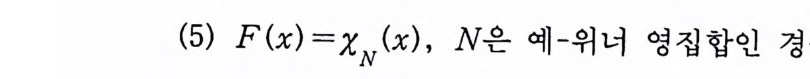 (5) F(x) =xN .. (x), N 은 예-위너 영집합인 경우.
(5) F(x) =xN .. (x), N 은 예-위너 영집합인 경우.
NcN흰 (4) 에서 정의된 집합 N1 이 존재한다. x NI (x) 에 대해 서 정리가 성립하고 식 (2.3) 에 F(x) 대신 X N.., (x) 을 대입하면 (2. 3) 의 양변은 0 이다.
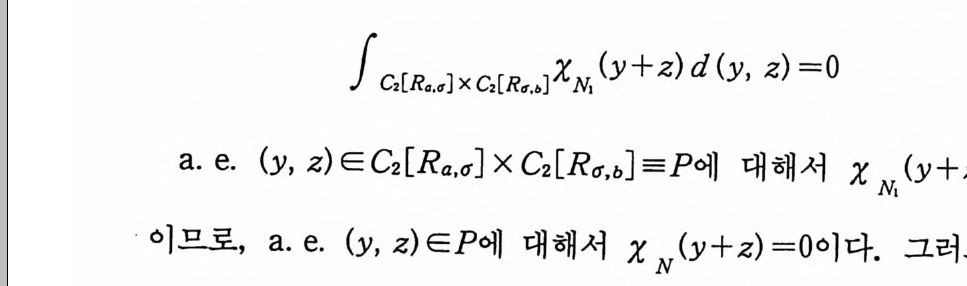 fC,[R .,]x C2 따.J XN, (y +z) d (y, z) =O
fC,[R .,]x C2 따.J XN, (y +z) d (y, z) =O
 X N ( y +z) 는 p에서 측도가능하고 (2. 3) 이 성립한다.
X N ( y +z) 는 p에서 측도가능하고 (2. 3) 이 성립한다.
되는 집합 S1 과 S2 가 존재한다. 여기서 S1 은 (4) 의 경우, S2 는 (5) 의 경우의 집합이다. 그러면, xs l (x) 와 xS 2 (x) 에 대해서 정리
 가 성립하고, 따라서 x5 ( x) =F(x) 에 대해서도 성립한다.
가 성립하고, 따라서 x5 ( x) =F(x) 에 대해서도 성립한다.
(7) F (x) 가 측도가능한 경 우. (6) 의 경우를 단순함수의 경우로 확장하고, 그 다음 영보다 큰 측도가능한 함수의 경우로, 그리고 일반적인 경우로 확장한다. 이제 F( y +z) 가 측도가능하다고 가정하고 정리의 역을 증명 하자.
 (8) F (y + z) = x, (y, z) , J는 C2 灰 a, <1] X C2 〔凡괴 에 서 구간인
(8) F (y + z) = x, (y, z) , J는 C2 灰 a, <1] X C2 〔凡괴 에 서 구간인
 / ({x (sj, tk) })
/ ({x (sj, tk) })
/({c;사)의 정의에 의해서, f는 Rn p에서 유계이고 측도가능한 함수이다.
 F (x) =f ({x (sj, tk) })
F (x) =f ({x (sj, tk) })
이므로 (1) 의 경우의 가정이 만족되고, F 는 x 의 함수로서 예-위 너 측도가능하다. 따라서 정 리가 성 립 한다. (2) ~ (7) 의 경우와 같은 방법을 함수 F( y +z) 에 적용해서 정 리의 증명을 끝낸다. 다음 정리는 위너 적분방정식의 해에 대한 존재정리이다. 이 방정식의 해는 예-위너 적분으로 표시된다.
 정리 2.2 0(s, y)가 [a, b] X Co[a, /3]에서 정의된 함수로서
정리 2.2 0(s, y)가 [a, b] X Co[a, /3]에서 정의된 함수로서
 (2.10) Fs(x)=exp {is b0( a,x(a, ·))d 사, xEC2[R]
(2.10) Fs(x)=exp {is b0( a,x(a, ·))d 사, xEC2[R]
증명 4 장 정리 7.1 과 Fs 와 ¢의 가정에 의해서, (2.11) 의 우 변 적분은 존재 한다. (2. 10) 으로부터 ,
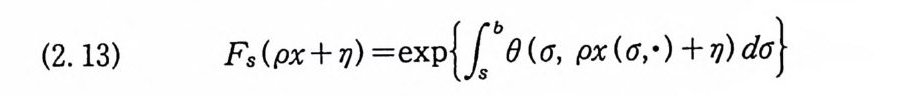 (2. 13) Fs (px + 7)) =exp { 1sb 0 (a, px (a,·) + 7)) d가
(2. 13) Fs (px + 7)) =exp { 1sb 0 (a, px (a,·) + 7)) d가
을 얻고, 변수 s 를 6 로 바꾸어서 (2.13) 을 미분하면,
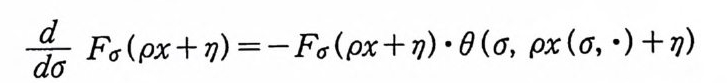 끓 F< 1(px +TJ ) =-F<1 (px +TJ ) ·0(a, px (a, ·)+7))
끓 F< 1(px +TJ ) =-F<1 (px +TJ ) ·0(a, px (a, ·)+7))
이다. 이 식을 s 에서 b 까지 적분하면 다음과 같이 된다.
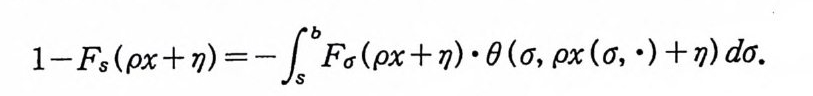 l-Fs (px + 7J) = —1sb F(f( px + 7)) • 0 (a, px (a, ·) + 7)) da.
l-Fs (px + 7J) = —1sb F(f( px + 7)) • 0 (a, px (a, ·) + 7)) da.
 이 식의 양변을 ,f;(px (b, ·) +刀)로 곱하고 C2[R 니 위에서 적분
이 식의 양변을 ,f;(px (b, ·) +刀)로 곱하고 C2[R 니 위에서 적분
식 (2.14) 의 좌변의 첫 적분은 4 장 정리 7.1 에 의해서 존재한다. #는 적분가능하고, 다른 피적분함수들은 유계이고 연속이므로 (2.14) 의 다론 적분들도 존재한다. (2.14) 의 마지막 적분은 적적 분 (pr oduct int e g ral ) 과 반복적 분으로서 , 두 경 우 다 존재 한다. 4 장 정리 7.1 과 푸비니 정리, 그리고 식 (2 . 11) 에 의해서 다음 식 울얻는다.
 (2.15) —lo [ a, /1]
(2.15) —lo [ a, /1]
이다.
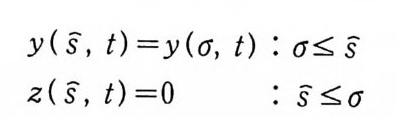 y ( s , t ) = y ( a, t ) : a ~ s
y ( s , t ) = y ( a, t ) : a ~ s
로 정의하면, 다음 식을 얻는다.
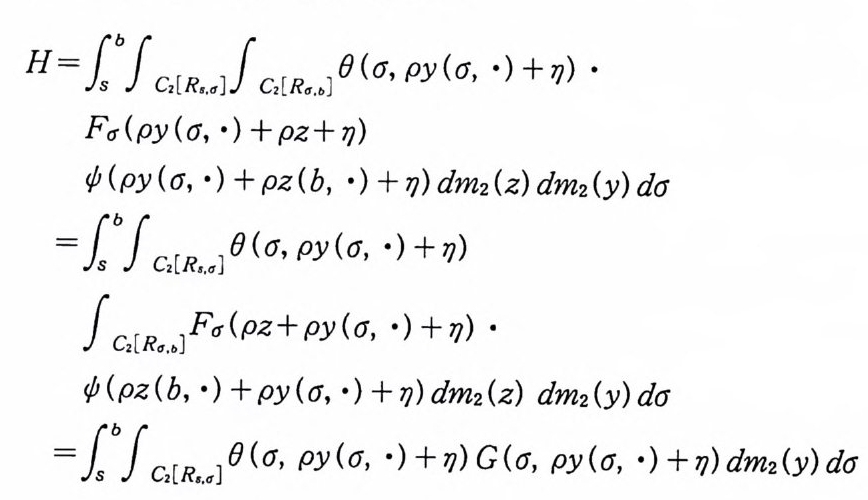 H=lbb !C,[ R ,, a] f C,[ R a , .] f J ( a,p y( a, ·) +TJ) •
H=lbb !C,[ R ,, a] f C,[ R a , .] f J ( a,p y( a, ·) +TJ) •
4 장 정리 7.1 에 의해서, 식 (2.15) 로 부터 식 (2 . 12) 를 얻고, 따라서 위너 적분방정식이 성립한다. 따름정리 2.3 식 (2.11) 에서 정의된 함수 G(s, TJ)는 다음 부 등식을 만족한다.
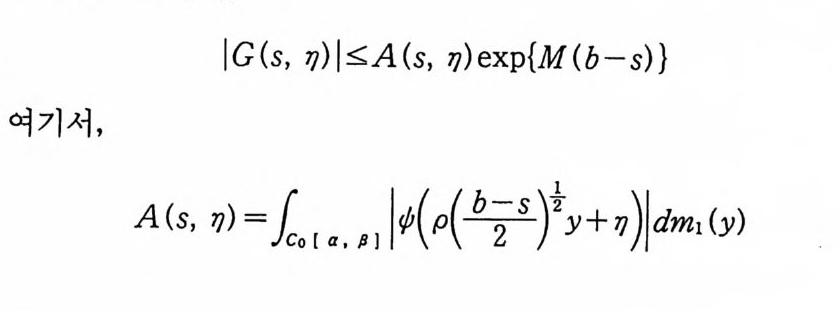 IG (s, TJ) i ~A (s, TJ) exp {M (b— s) }
IG (s, TJ) i ~A (s, TJ) exp {M (b— s) }
증명 4 장 정리 7.1 을 식 (2.11) 에 적용한다.
 따름정리 2-4 rp(
따름정리 2-4 rp(
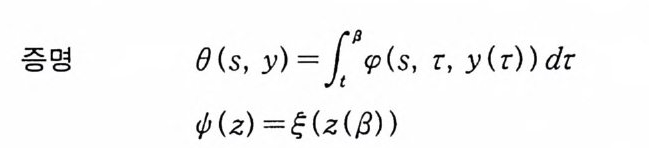 증명 0(s, y)=j/Jq;(s , r, y( r))dr
증명 0(s, y)=j/Jq;(s , r, y( r))dr
로 놓고 정리 2.2 를 적용한다. 3 위너 적분방정식의 노이만 급수
 위너적분 방정식 (2.12) 를 노이만 (Neumann) 급수 전개방법을
위너적분 방정식 (2.12) 를 노이만 (Neumann) 급수 전개방법을
 (3. 4) IG(s, 7J) l:::;;:B exp { M(b— a) }.
(3. 4) IG(s, 7J) l:::;;:B exp { M(b— a) }.
로 나타낼 수 있다. 여기서 G 는 유계이고 연속인 해이다. 함수 들의 급수 {Fn (s, TJ) }를 다음과 같이 정 의 하자.
 (3. 6) Fo= (/)
(3. 6) Fo= (/)
에 대해서 절대 (absolute l y) 수령하고 평 등 (unif or m) 수령한다. 따라서,
 TC (s, TJ) = [1o l a , /J I e( a, p(틀)상 w + TJ)
TC (s, TJ) = [1o l a , /J I e( a, p(틀)상 w + TJ)
이다. 따라서 G 는 (2.12) 의 유계, 연속인 해이고 (3. 4) 를 만족 한다. G 가 유일한 해가 되는 것도 쉽게 보일 수 있다. 정리 3.2 정리 3.1 의 가정에서, (2.12) 의 위너 적분방정식의 해 G 는 다음과 같이 예-위너 적분으로 표시된다.
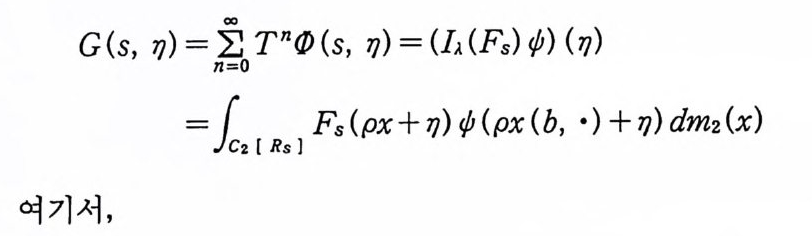 G (s, r;) = n~o=oO yn (/) (s, r;) = (IA ( F나 ) ( TJ)
G (s, r;) = n~o=oO yn (/) (s, r;) = (IA ( F나 ) ( TJ)
Fs (x) =exp { 1sb 0 (6, x (6, • ) ) d6}
이다. 증명 정리 2. 2 와 정리 3.1 로부터 얻는다.
 이제 위너 적분방정식 (2.12) 를 影가 유계가 아닌 보다 일반적
이제 위너 적분방정식 (2.12) 를 影가 유계가 아닌 보다 일반적
(s' 7J) 는 존재 하고, [a, l)] X Co[a, /3]에 서 보렐 x 보렐 측도가능하다. 함수
 (3. ll ) A(S, 7}) =lo, a, Pl l
(3. ll ) A(S, 7}) =lo, a, Pl l
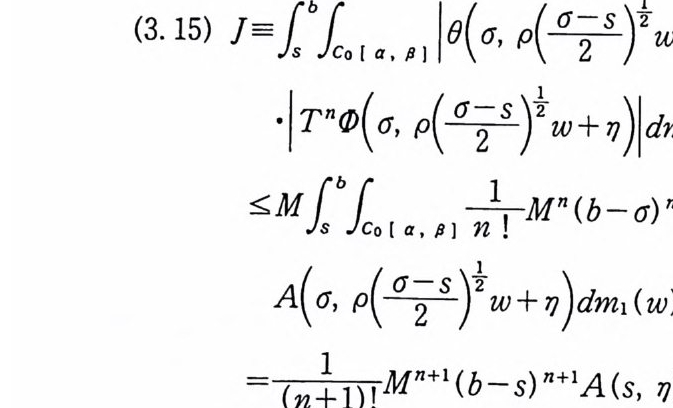 (3.15) ]=[101 a , Pl le((J, p( ?)½w+TJ ) I·
(3.15) ]=[101 a , Pl le((J, p( ?)½w+TJ ) I·
Tn fP EE 이고 1 의 피적분함수는 적분가능하므로 T(TnfP (s, 7})) 는 존재한다. 실제로 다음 부등식이 성립한다.
 Ir n+ IfP (s, 1J) |익~
Ir n+ IfP (s, 1J) |익~
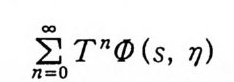 00
00
는 절대수렴하고, 다음 부등식이 성립한다.
 (3. 16) n~=00O I Tnq J (s, TJ) I~ n~°=°o ~ -n: 1:i! - M n (b-s) 입 (s, 7J)
(3. 16) n~=00O I Tnq J (s, TJ) I~ n~°=°o ~ -n: 1:i! - M n (b-s) 입 (s, 7J)
 (3. 18) G (s, 7J) = fJ (s, 7J) + [cl(o a,l ap . (P I T0( a,i pw (+합 1 J)) d방m w1 (+w 7)Jd) •a
(3. 18) G (s, 7J) = fJ (s, 7J) + [cl(o a,l ap . (P I T0( a,i pw (+합 1 J)) d방m w1 (+w 7)Jd) •a
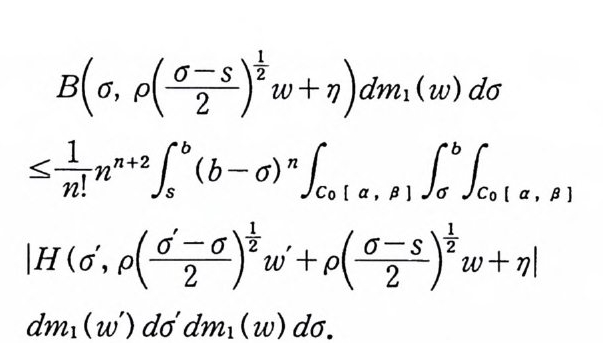 B(
B(
푸비니 정리와 1 장 따름정리 5.7 에 의해서 다음 부등식을 얻는 다.
 IH(s, 1J) |~~Mn+21\b-
IH(s, 1J) |~~Mn+21\b-
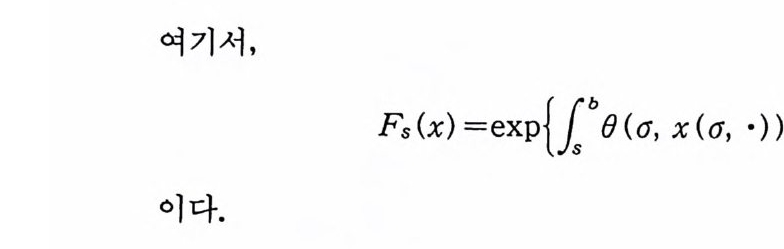 여기서,
여기서,
증명 이 정리는, 정리 2. 2, 정리 3. 3, 정리 3. 4, 따름정리 2. 3, 그리고 1 장 따름정리 5 . 7 에 의해서 증명된다.
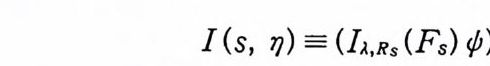 I (s, 까 = (hRs (Fs)
I (s, 까 = (hRs (Fs)
은 다음과 같이 보일 수 있다. 따름정리 2.3 에 의해서,
 II(s, 7J) |색 BA(s, 7}) =Blo I a, pl 1¢( p(틀기송y+ 7J) ldmi (y)
II(s, 7J) |색 BA(s, 7}) =Blo I a, pl 1¢( p(틀기송y+ 7J) ldmi (y)
3. 5 를 예-위너 적분을 계산하는 관점에서 기술한 것이다. 정리 3.6 정리 3.3 의 가정에서 다음 적분공식을 얻는다.
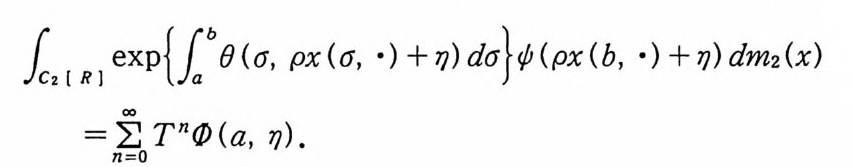 fcC22 1 I RRl J exp- {V 1ab 0 (
fcC22 1 I RRl J exp- {V 1ab 0 (
주 3.7 정리 3. 6 의 함수 Tn0(a, 7J)를 위너 적분과 르베그 적분들의 반복 적분으로 표시하는 공식과 그 증명 및 함수
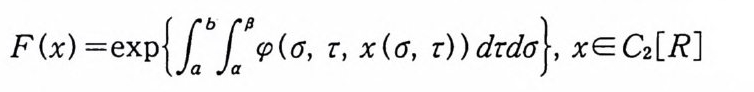 F(x) =exp { 1a bJ1 a /1c p(
F(x) =exp { 1a bJ1 a /1c p(
의 예 -위 너 적 분계 산은 참고문헌 Cameron and Sto r vic k [이 참조. 4 예-위너 조건적분 위너 조건적분의 개념을 예-위너 조건적분으로 확장하고 이 적 분의 존재 정 리 와 반전공식 (inv ersio n for mula) 을 유도한다.
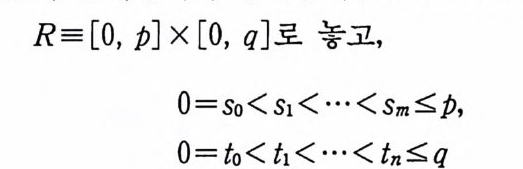 R=[O, 싸 x [0, q 〕로 놓고,
R=[O, 싸 x [0, q 〕로 놓고,
라 하자. 예-위너 공간 C2[R] 에 예-위너 측도를 도입할 때 사 용한 밀도함수 Wmn(S, t, u) (4 장 정의 1. 5 참조)를, 여기서는 정 규화 상수 (normali za ti on consta n t) 를 변형 해 서 다음과 같이 정 의 하기로 한다.
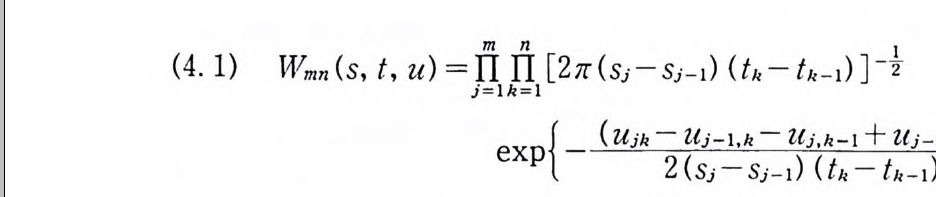 (4. 1) Wmn (s, t' u) =}'111 1 [27r (sj -Sj- 1 ) (tk — f k- 1 ) J-½
(4. 1) Wmn (s, t' u) =}'111 1 [27r (sj -Sj- 1 ) (tk — f k- 1 ) J-½
예-위너 측도공간이 위너 측도공간의 확장이라고 볼 때는, (4. 1) 의 밀도함수에 의해서 정의되는 예_위너 측도가 더 바람직한 정의이다. 그러나 이 두 정의에 근본적인 차이는 없고 예 - 위너 적분공식이나 적분방정식에서 정규화 상수만 다른 것이 그 차이 점이다. 예를 보면,
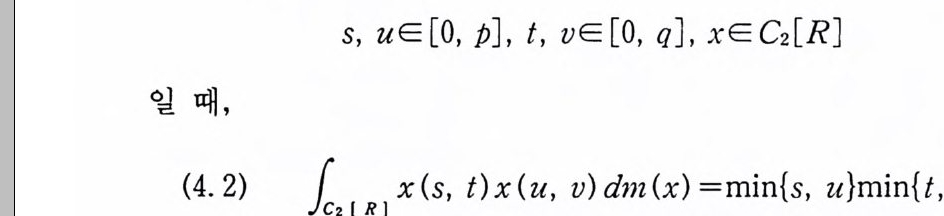 s, u 탁 O, pJ, t, v 드 [O, q\만 E C2[R]
s, u 탁 O, pJ, t, v 드 [O, q\만 E C2[R]
이다. 공식 (4. 2) 를 4 장 성질 2. 4 의 (1)과 비교하면 정규화 상수 만 다른 것을 알 수 있다. F(x) 가 예-위너 측도가능한 함수일 때 F 의 예-위너 적분을 기호,
 (4. 3) E(F) =E(F(x) ) =fc21 R1 F(x) dm(x)
(4. 3) E(F) =E(F(x) ) =fc21 R1 F(x) dm(x)
 서,
서,
을 만족한다. 따라서 (4. 5) 가 성립한다. 가정에 의해서, 모든 보렐 집합 B 에 대해서
 fsJ( u) dPx (u) =fsg( u) dPx (u)
fsJ( u) dPx (u) =fsg( u) dPx (u)
이므로, Y 는 르베그 X 예-위너 측도가능한 함수이다. 또한 Y 는 확률공간 (C2[R], 잎 I, m) 과 정의역 R 에서 정의되는 두 변수 가우스 과정 (Gaussia n pro cess) 이 다. 표본함수 (samp le fun cti on ) Y(·, X) 들의 공간은 표본공간 (sam p le sp a ce) C2[R 〕과 일치하고, 따라서 각 표본함수는 연속이다. 이 두 변수 가우스 과정 Y 를 예-위너 과정 또는 두 변수 위너 과정이라고 한다. 다음 정리(보조정리 4.5 부터 정리 4.10 까지)들은 위너 조건적분 에 대응하는 예-위너 조건적분에 대한 결과이다. 정리의 증명도 위너 조건적분의 방법과 같으므로 증명없이 기술하기로 한다.
 보조정리 4.5 X 와 Y 가 예-위너 측도가능한 함수이고 E(IYI)
보조정리 4.5 X 와 Y 가 예-위너 측도가능한 함수이고 E(IYI)
 E( YIX) (w) 쌉f4-1 - (w) =lai l一l )O. E[ (Jg1° X) Y].
E( YIX) (w) 쌉f4-1 - (w) =lai l一l )O. E[ (Jg1° X) Y].
 =lj 펑吉 1 - h, h 갑 (e- i au ― e- i bu)E(e i ux· Y)du.
=lj 펑吉 1 - h, h 갑 (e- i au ― e- i bu)E(e i ux· Y)du.
 ll gj『=f 函 (s, t)]2 ds dt
ll gj『=f 函 (s, t)]2 ds dt
를 얻는다. xI, …, X거 서로 독립임을 보이기 위해서 다음 사실을 증명하면 된다.
 임의의 상수 a1, … ,an 에 대해서,
임의의 상수 a1, … ,an 에 대해서,
이므로 (4. 9) 가 만족된다.
(2) 는 부록 정리 5.13 의 결과이다. 정리 4.12 X와 Y 가 C2[R] 에서 다음과 같이 정의된 함수라 하자.
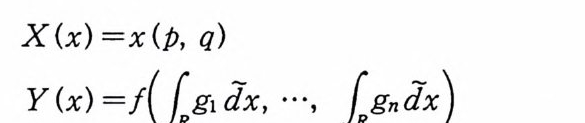 X(x) =x (p, q)
X(x) =x (p, q)
여기서, {g1, …, gn , l} 은 L2(R) 에서 직교집합이고, /는 Rn 에서 정의된 르베그 측도가능한 함수로서 다음 식을 만족한다고 하자.
 {(2 ;r)Jn] )gj ll2} 당•仁|J (u) i ex p{-1½ 얽n 파 /ll gj ll2}du<00
{(2 ;r)Jn] )gj ll2} 당•仁|J (u) i ex p{-1½ 얽n 파 /ll gj ll2}du<00
이다. 함수
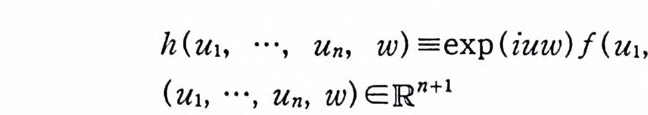 lt( UI, …, Un, w) =exp (iuw )f (u 1, …, Un) ,
lt( UI, …, Un, w) =exp (iuw )f (u 1, …, Un) ,
 롤 식 (4.8) 에 적용해서 다음 식을 얻는다.
롤 식 (4.8) 에 적용해서 다음 식을 얻는다.
정리 4.12 를 이용해서 예-위너 조건적분을 계산하는 예를 보기 로하자. 예 4-13 X 와 Y 가 C2[R 〕에서 다음과 같이 정의되는 함수라
하자.
 X (x) =x (p, q)
X (x) =x (p, q)
이다. 따라서,
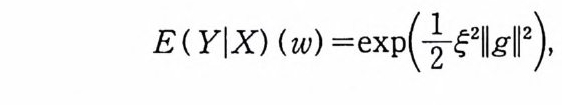 E( YIX) (w) =ex p(長||g ll2), w 슨 R.
E( YIX) (w) =ex p(長||g ll2), w 슨 R.
5 예-위너 조건적분의 변환정리 예-위너 조건적분의 변환정리를 증명하고, 이 정리를 이용해 서, 함수
 Y(x) =exp {J1 R g( s, t) dx(s, t)}, gE L2(R)
Y(x) =exp {J1 R g( s, t) dx(s, t)}, gE L2(R)
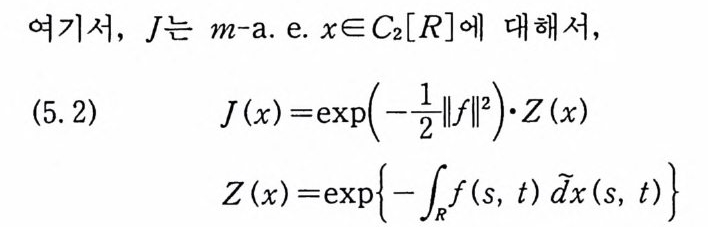 여기서, J는 m-a. e. x 든 댜 R] 에 대해서,
여기서, J는 m-a. e. x 든 댜 R] 에 대해서,
로 주어전다. 증명 C2[R] oJ]서의 변환 T 를
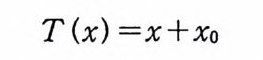 T(x) =x+xo
T(x) =x+xo
로 정의하자. 그러면 4 장 6.12 (1) 에 의해서 3 장 정리 6. 3 의 조 건 (1) 이 만족된다.
 이제, T 가 3 장 정리 6. 3 의 조건 (2) 를 만족하는 것을 보이
이제, T 가 3 장 정리 6. 3 의 조건 (2) 를 만족하는 것을 보이
 Px=N(O, pq)
Px=N(O, pq)
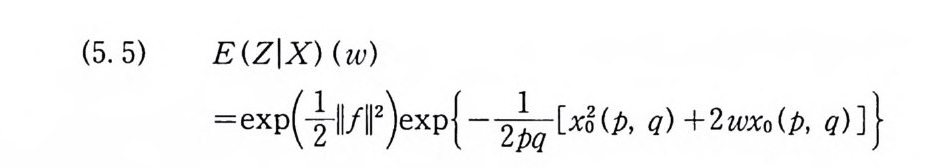 (5. 5) E (ZIX) (w)
(5. 5) E (ZIX) (w)
증명 4 장 정리 6.13 에 의해서 Z(x) 는 예-위너 적분가능하다. 따라서 E(ZIX) 는 존재한다.
 Y(x)=l, xEC2[R]
Y(x)=l, xEC2[R]
이다. (5. 8) 과 (5. 6) 을 식 (5.1) 에 대입해서 다음 식을 얻는다.
 J-a . e. uER 에 대해서,
J-a . e. uER 에 대해서,
 Y(x) =exp {—i /(s, t) dx ( s, t)}
Y(x) =exp {—i /(s, t) dx ( s, t)}
울 얻고, 이것은, A 가 실수인 경우에 4 장 정리 6.13 의 결과와 일치한다. 주 공식 (5.13) 과 4 장 정리 6.13 의 공식 (6. 5) 에서 }만큼 상 수가 다론 것은 예-위너 적분을 정의하는 밀도함수(식 (4.1) 과 4 장 식 (1. 3) )를 다르게 택했기 때문이다.
6 벡터 함수에 대한 예_위너 조건적분 벡터값을 갖는 함수에 대한 예-위너 조건적분의 여러 가지 성 질을 조사한다. 먼저, 예-위너 조건적분을 예-위너 적분으로 표 시하는 간단한 공식을 얻고, 이 공식을 이용해서 여러 가지 함수 의 예-위너 조건적분을 계산한다. 또한 예-위너조건 적분에 대한 일반화된 카메룬-마틴 (Cameron-Martin ) 의 변환정 리 를 유도한다.
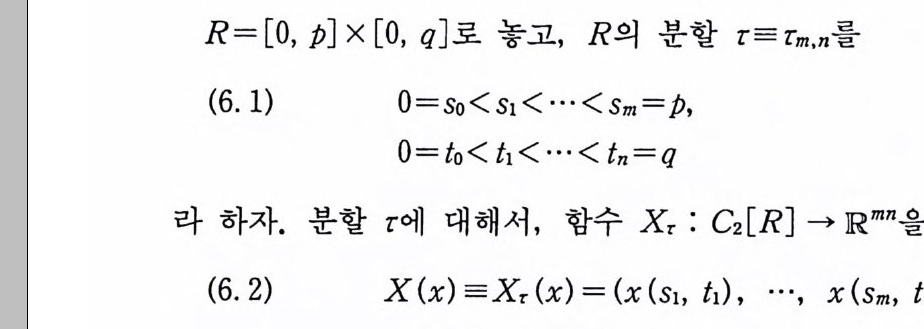 R=[O, p] X [O 나?〕로 놓고, R 의 분할 r=Tm,n 를
R=[O, p] X [O 나?〕로 놓고, R 의 분할 r=Tm,n 를
로 정의하자. (주 : 이 절에서 취급하는 함수 X 는 (6.2) 에서 정의된 함수만을 뜻한다)
 BERmn 가 보렐 집합일 때, 예-위너 적분가능한 함수 F(x) 에
BERmn 가 보렐 집합일 때, 예-위너 적분가능한 함수 F(x) 에
이다. 예-위너 조건적분 E(FIX) 는 E 의 함수로서 보렐 측도가 능하고 보렐 측도 -a. e. 에서 유일하게 결정된다.
 식 (6.1) 의 분할 r 에 대해서, 주어전 xEC2[R 〕에 대한 준다
식 (6.1) 의 분할 r 에 대해서, 주어전 xEC2[R 〕에 대한 준다
 4u f=&一ti -1, i-ti,j -l+ ti -1, j -l
4u f=&一ti -1, i-ti,j -l+ ti -1, j -l
이다. 각 R ij에서, [짜 (s, t)와 [t] (s, t)는 두 변수 함수로서 이 차 함수(q uadra tic fu nc ti on) 이고, 한 변수를 고정했을 때는, 다른 한 변수의 함수로서 선형 함수 (line ar fun cti on ) 이 다.
 정리 6.l {x(s, t) : (s, t )ER} 가 예-위너 과정이면, 확률과정
정리 6.l {x(s, t) : (s, t )ER} 가 예-위너 과정이면, 확률과정
 따름정리 6.2 확률 과정 {x(s,t )— [x](s,t) : (s, t )ER} 와
따름정리 6.2 확률 과정 {x(s,t )— [x](s,t) : (s, t )ER} 와
정리 6.3 F(x) 가 예-위너 적분가능한 함수라 하자. 그러면, IRmn 의 보렐 집합 B에 대해서,
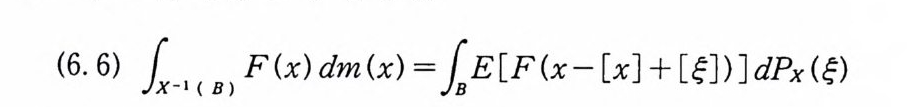 (6. 6) fx_, < B > F(x) dm(x) =iB E[F (x-[x ] + [인)〕 dPx(;)
(6. 6) fx_, < B > F(x) dm(x) =iB E[F (x-[x ] + [인)〕 dPx(;)
이 성립한다.
 증명 (1) F(x) =xM .. (x), M 이 예-위너 측도가능한 집합인 경
증명 (1) F(x) =xM .. (x), M 이 예-위너 측도가능한 집합인 경
(2) 일반적인 경우는 적분론에서 사용하는 방법에 따라서 (1) 의 경우롤 단계적으로 확장해서 증명한다.
주 6.4 식 (6. 3) 과 (6. 6) 에 의해서, 예-위너 적분가능한 함수 F 에 대해서,
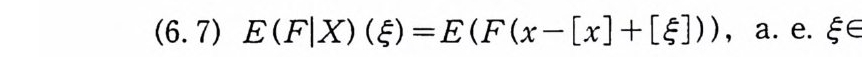 (6.7) E(FIX)(~)=E(F(x ―[짜+[언)), a. e. ~E]R m n
(6.7) E(FIX)(~)=E(F(x ―[짜+[언)), a. e. ~E]R m n
이 성립한다고 생각할는지도 모른다. 그러나 (6. 7) 의 좌변 함수 는 정의에 의해서 보렐 측도가능하고, 우변 함수는 르베그 측도 만 가능할 수도 있다. 다음 예를 보자. 예 6.5 A 를 Rmn 에서 보렐 집합이 아닌, 르베그 영집합이라 하자.
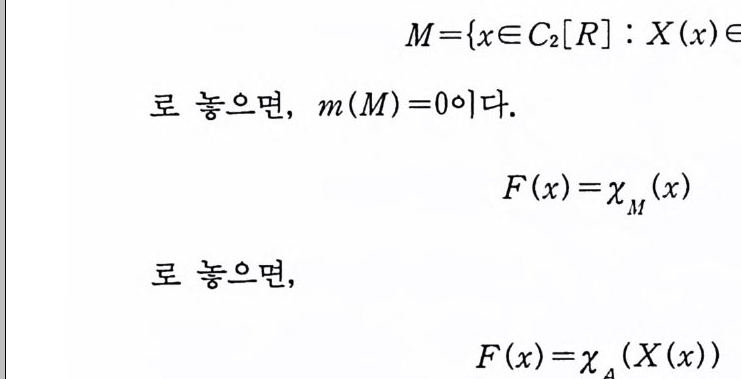 M={x 麟[ R 〕 : X(x) EA}
M={x 麟[ R 〕 : X(x) EA}
이고 다음 식이 성립한다.
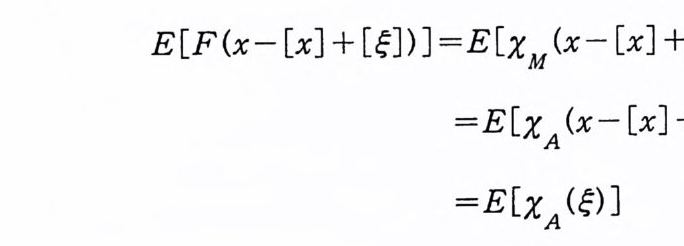 E 困 x_ [자 + [인)〕 =E[xM(x ― [x] + [언)]
E 困 x_ [자 + [인)〕 =E[xM(x ― [x] + [언)]
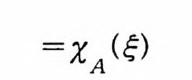 =x A (f)
=x A (f)
이 함수는 르베그 측도가능하지만, 보렐 측도가능하지는 않다. 그러나, f (E) 가 Rmn 에서 르베그 측도가능하면, 보렐 측도가능한 함수 1(E) 가 존재해서 보렐 측도 -a. e 에서 /(f)와 같다. 이와 같은 관접에서 다음을 정의하자.
 정의 6.6 F(x )가 G 〔 R] oJ]서 예-위너 적분가능한 함수일 때,
정의 6.6 F(x )가 G 〔 R] oJ]서 예-위너 적분가능한 함수일 때,
되는 함수로 정의한다. 이 정의로부터 다음 정리를 얻울 수 있다. 이 정리는 간단하지 만 매우 유용한 정리이다. 정리 6.7 F(x) 가 예-위너 적분 가능한 함수이면,
 (6. 8) E (F(x) IX) (~) 효〔 F(x- [x] + 〔인) ]
(6. 8) E (F(x) IX) (~) 효〔 F(x- [x] + 〔인) ]
이다. (6.8) 과 (6.9) 의 등식은, 양변이 E 의 함수로서 보렐 측도 가능하고, 보렐 측도 -a. e. 에서 같음을 뜻한다. 정리 6.7 을 이용해서 다음의 예-위너 조건적분을 계산해 보자.
 예 6.8 xEC2[R 〕에 대해서, 함수 F(x) 를
예 6.8 xEC2[R 〕에 대해서, 함수 F(x) 를
로 놓자. 그러면, (6.9) 에 의해서 다음 식을 얻는다.
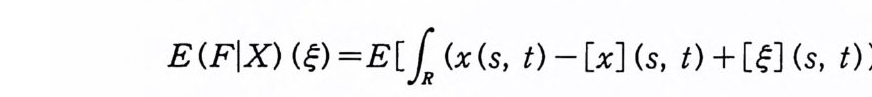 E (FIX) (t) =E[l (x (s, t) —[x] (s, t) + [친 (s, t) ) 2dsdt]
E (FIX) (t) =E[l (x (s, t) —[x] (s, t) + [친 (s, t) ) 2dsdt]
 =tR E[( x(s, t)— [x](s, t)) 2+([e](s, t)) 2
=tR E[( x(s, t)— [x](s, t)) 2+([e](s, t)) 2
을 이용해서 다음 식을 얻는다.
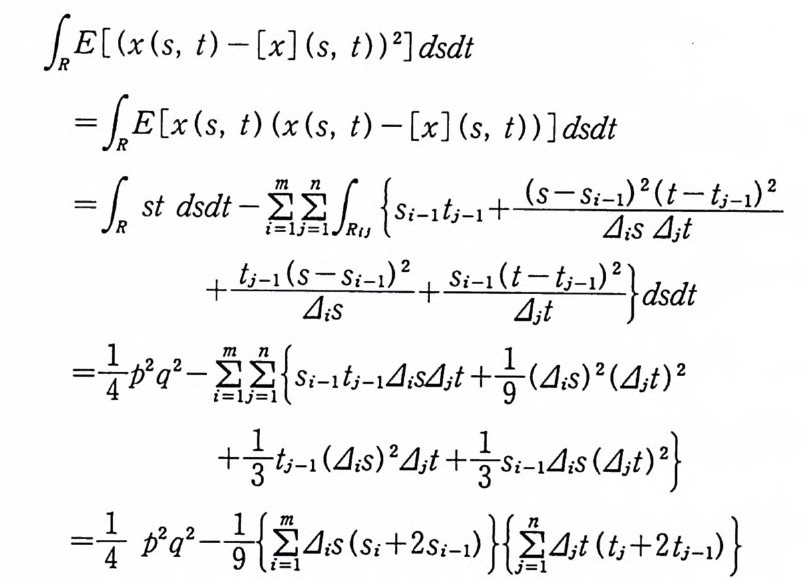 lRE [ (x (s, t) -[ x] (s, t) ) 2] dsdt
lRE [ (x (s, t) -[ x] (s, t) ) 2] dsdt
따라서 다음 공식이 성립한다.
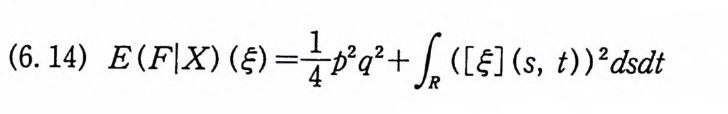 (6.14) E(FIX) (~) =+討+fR (〔리 (s, t)) 2dsdt
(6.14) E(FIX) (~) =+討+fR (〔리 (s, t)) 2dsdt
 _\{홈 4s(s1+2sI-I) }{접 4 t (tJ+ 2tJ - I) }.
_\{홈 4s(s1+2sI-I) }{접 4 t (tJ+ 2tJ - I) }.
이고 다음 극한울 얻는다.
 II~r ljl '一2 \ 0 E (FIXr) (Xr (y) ) =exp {iy (s, t) dsdt} .
II~r ljl '一2 \ 0 E (FIXr) (Xr (y) ) =exp {iy (s, t) dsdt} .
증명 (6. 16) 은 i의 정 의 로부터 얻고, (6. 17) 은 (6. 16) 으로부 터 얻는다. E 는 R 에서 유계변동 (bounded var i a ti on) 이고, [지는
 R에 서 절 대 연속 (absolute l y conti nu ous) 이 다. 또한,
R에 서 절 대 연속 (absolute l y conti nu ous) 이 다. 또한,
정리 6.13 함수 1 가 lRn 에서 정의되고 f 0H(x) 가 예-위너 적 분가능하면 다음 식이 성립한다.
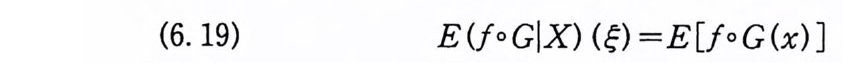 (6. 19) E (f0G IX) (~) =E[/0G(x)]
(6. 19) E (f0G IX) (~) =E[/0G(x)]
또한, 만일 {a1, …, ak} 가 R 에서 정의된 직교함수 (or t ho g onal fun cti on ) 들의 집 합이 고
 sp a n{a1, …, ak}=sp a n{g 1, …, g사
sp a n{a1, …, ak}=sp a n{g 1, …, g사
이라 하면, 다음을 만족하는 함수 g가 존재한다.
 (6. 20) /0 G (x) =g (l 국, …, lak dx)
(6. 20) /0 G (x) =g (l 국, …, lak dx)
이고, 이것으로부터 (6.19) 를 얻는다. (6. 20) 과 (6. 21) 은 쉽게 보일 수 있다.
 따름정리 6-14 h1, …, hNEL2(R) 이고
따름정리 6-14 h1, …, hNEL2(R) 이고
 J/ij(s, t)d sdt= O, j= l, ···, N
J/ij(s, t)d sdt= O, j= l, ···, N
라 하자. 그러면, /0H(x) 가 예-위너 적분가능한 함수이면 다음 식이 성립한다.
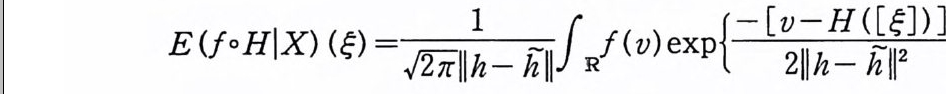 £(/oHIX) (~) =瓚||\ 갑 R/(v)ex p{~〕)〕 ~}dv.
£(/oHIX) (~) =瓚||\ 갑 R/(v)ex p{~〕)〕 ~}dv.
증명 정리 6. 7 과 (6.18) 에 의해서 다음 식을 얻는다.
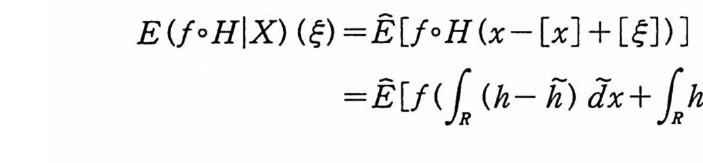 E(/0HIX) (~) =E[/0H(x— [ x] + [~]) ]
E(/0HIX) (~) =E[/0H(x— [ x] + [~]) ]
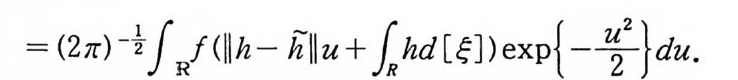 = (27r)- 汀 \/(llh 一 hllu+ i願티 )ex p{―운 }du.
= (27r)- 汀 \/(llh 一 hllu+ i願티 )ex p{―운 }du.
다음 정리는 예-위너 조건적분의 변환정리 (정리 5.1) 를 벡터값 울 갖는 함수의 경우로 확장한 것이다.
 정리 6.16 hEL2(R) 일 때, (s, t) ER 에 대해서,
정리 6.16 hEL2(R) 일 때, (s, t) ER 에 대해서,
이고, 4 장 정리 6.12 에 의해서,
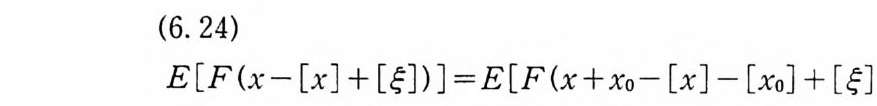 (띠6. 2 F4() x- [x] + [인) ]= E[F(x+xo_ [x] — [xo ] + [인 )] (x) ]
(띠6. 2 F4() x- [x] + [인) ]= E[F(x+xo_ [x] — [xo ] + [인 )] (x) ]
이다. (주 : J (x) 와 4 장 정리 6.12 의 공식에서 상수 방과 2 의 차이가 있는 것은 식 (4.1) 의 예-위너 측도의 밀도함수 Wmn 가 4 장(1. 3) 의 것과 다르기 때문이다). J (x) 를 다음과 같이 변형해서 표시하자.
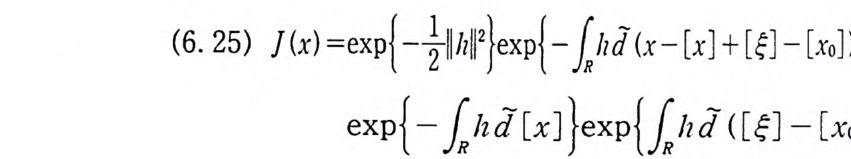 (6. 25) J (x) =ex p {-½lllzl l 2}ex p {-l 써 (x-[x ] + [~] - [ xo] ) }
(6. 25) J (x) =ex p {-½lllzl l 2}ex p {-l 써 (x-[x ] + [~] - [ xo] ) }
따름정리 6. 2 에 의해서, x— [x ] 와 長]는 R 위에서 서로 독립이 므로, (6. 24) 와 (6. 25) 로부터
 (6.26) E[F(x— [x ]+[e])]
(6.26) E[F(x— [x ]+[e])]
정리 6.12 롤 사용해서
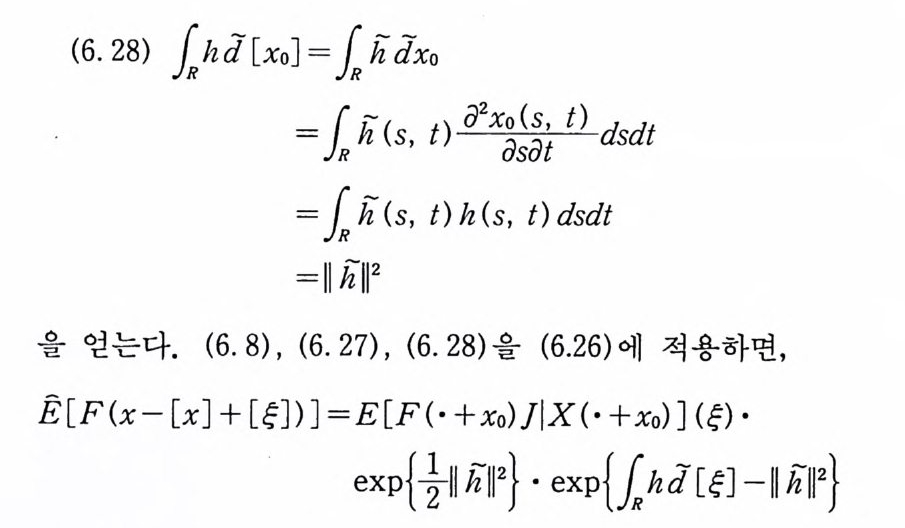 (6. 28) lhd[xo]= =Ll i iii(sd,x o t ) a2 일젊 t)_d sdt
(6. 28) lhd[xo]= =Ll i iii(sd,x o t ) a2 일젊 t)_d sdt
이 되고, 이 식과 (6. 23) 에 의해서 정리가 증명된다. R 의 분할 r 가 한점 (p, q)로 구성된 경우 다음 정리를 얻는 다. 이것은 정리 5.1 과 일치한다. 따름정리 6.17 F, h, xo 를 정리 6.16 에서 정의된 함수라 하자. 그러면, 다음 식이 성립한다.
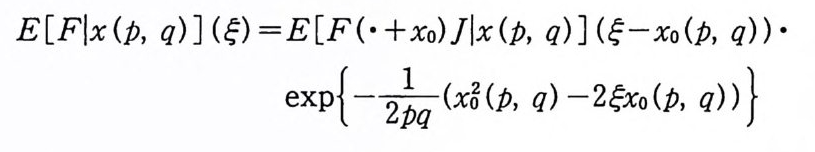 E[Flx(p, q )](~)=E 困 ·+xo) J lx( p, q)〕(~一 Xo( p, q))•
E[Flx(p, q )](~)=E 困 ·+xo) J lx( p, q)〕(~一 Xo( p, q))•
따름정리 6-18 h 와 Xo 를 정리 6.16 에서 정의한 함수라 하자. 그러면 다음 식이 성립한다.
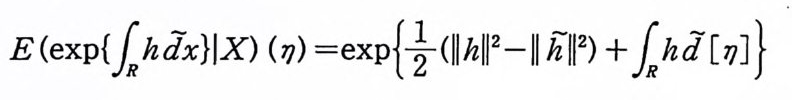 E(ex p {1 표 }|X) (7J) =ex p {½
E(ex p {1 표 }|X) (7J) =ex p {½
증명 정리 6.16 에서 F=l 로 놓고, 모든 (Si, lJ)든 r 에 대해서,
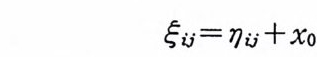 tu= TJ u +xo(Si, tJ
tu= TJ u +xo(Si, tJ
로 놓으면, 다음 식을 얻는다.
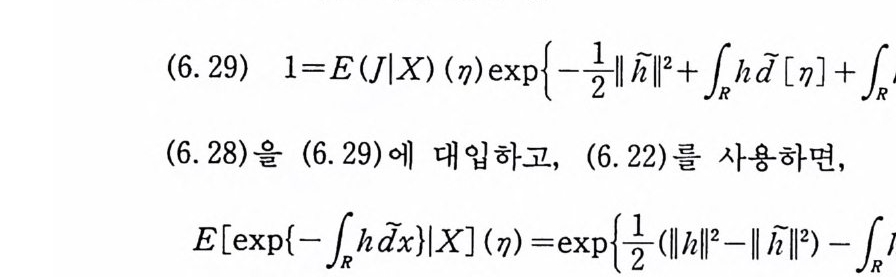 (6. 29) l=E(J IX ) (7}) exp { -{11 fill2 +lhd[TJ] +i1zJ [ xo ] }
(6. 29) l=E(J IX ) (7}) exp { -{11 fill2 +lhd[TJ] +i1zJ [ xo ] }
이 되고, 이 식에서 h(s, t)를 -h(s, t)로 대치하면 정리가 증 명된다. 주 따름정리 6.18 은 정리 6.15 의 특별한 경우이다.
-l:l 기로. 1 카라데 오도리 확장 (Carath e odory exte n sio n ) 정의 l.l 집합 X 의 부분집합들의 모임 7 가 다음 조건을 만 족하면 Y 를 대 수 (alge b ra) 라 한다.
 (1) A, BEY 이면, AUBEY 이다.
(1) A, BEY 이면, AUBEY 이다.
정의 1.2 집합 X 의 부분 집합들의 모임 (f)가 다음 조건을 만 족하면 幻룰 준-대 수 (semi -a lge bra) 라 한다.
 (1) A, B 켈이면 AnBE (f)이다.
(1) A, B 켈이면 AnBE (f)이다.
E 가 준대수일 때 서로 소인 (f)의 원소들의 모든 유한합들의 집합은 대수가 된다. 이 대수를 (f)에 의해서 생성되는 대수라고
정의 1.3 ®가 준대수이고, 집합함수 µ : 力一 [0, 0 0] 가 다음 조건을 만족할 때, µ룰 측도라 한다.
 (1) µ( ¢ ) =0
(1) µ( ¢ ) =0
이다. 준대수 力에서 정의된 측도는 的에 의해서 생성되는 대수에서 의 측도로 확장된다.
 정리 l.4 :I)가 준대수이고, 力에 의해서 생성되는 대수를 Y
정리 l.4 :I)가 준대수이고, 力에 의해서 생성되는 대수를 Y
한다.
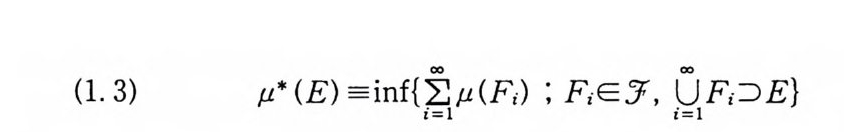 00 00
00 00
로 정의하자. µ*를 µ의 의측도 (ou t er measure) 라 한다.
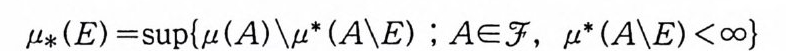 µ*(E)=sup { µ(A)\µ*(A\E) ; AEj , µ* (A\E) < oo}
µ*(E)=sup { µ(A)\µ*(A\E) ; AEj , µ* (A\E) < oo}
로 정 의 하자. µ*를 µ의 내 측도 (inn er measure) 라 한다.
 정리 l.6 µ가 대수 7 에서의 측도이고, µ (X) < oo 라 하자.
정리 l.6 µ가 대수 7 에서의 측도이고, µ (X) < oo 라 하자.
 (l.4) µ*A=µ*(AnE)+µ*(AnE 이
(l.4) µ*A=µ*(AnE)+µ*(AnE 이
정리 1.10 µ가 준대수 力에서의 측도라 하자. 그러면 µ는 6(®) 에서 정의되는 측도로 확장될 수 있다. µ가 대수 7 에서의 측도일 때, 정리 1. 9 에 의해서 a(Y) 로 확 장된 측도는 µ가 6 ―유한 (a- fi n it e) 일 때 유일하다. 다음은 이것 을 보장하는 일반적인 정리이다. 정리 1.11 µ가 대수 7 에서 (J-유한한 측도이고 µ1 과 µ2 가 다 음 조건을 만족하는 6(Y) 에서의 측도라 하자.
 모든 EEY 에 대해서, µ1(E)=µ2(E)=µ(E) 이다.
모든 EEY 에 대해서, µ1(E)=µ2(E)=µ(E) 이다.
정리 1.12 µ가 대수 7 에서의 6- 유한한 측도라 하자. 었*를
µ*-측도 가능한 집합들의 6- 대수라 하면 완비측도공간 (X, :B*, µ*)는 측도공간 (X, a(Y), µ*)를 완비화 (com p le t e) 해서 얻은 완비측도공간 (X, a(Y), /7)과 일치한다.
 정의 l.13 집합 X 의 부분집합들의 모임 瓜이 다음 조건을 만
정의 l.13 집합 X 의 부분집합들의 모임 瓜이 다음 조건을 만
모든 보렐 집 합이 µ-정 규집 합일 때 , µ를 정규측도 (re gu lar measure) 라 한다. 정리 1.16 X 가 거리공간이면, 모든 유한 보렐 측도는 정규측
도이다.
 따름정리 l.17 µ, 11 가 거리공간 X 에서 보렐 측도이고 모든
따름정리 l.17 µ, 11 가 거리공간 X 에서 보렐 측도이고 모든
정리 1.20 X가 완비가분 (com p le t e sep a rable) 거리공간이면, 보렐 6- 대수 J3 (X) 에서 정의되는 임의의 유한 보렐 측도는 단 단한 (tigh t) 측도이 다. 정리 1.21 X가 완비가분 거리공간이고, µ가 유한 보렐 측도 라 하자. 그러면 임의의 보렐 집합 E 에 대해서,
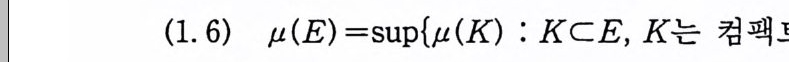 (1. 6) µ(E) =sup { µ(K) : KcE, K 는 컴팩트 집합}
(1. 6) µ(E) =sup { µ(K) : KcE, K 는 컴팩트 집합}
이다. X가 완비가분 거리공간이고, 측도공간 (X, :B( X), µ)를 완 비화 (com p le t e) 해서 얻는 완비측도공간을 (X, .sJ, µ.)라 하자. 그
 러면, 임의의 EE .0에 대해서
러면, 임의의 EE .0에 대해서
이므로 다음 정리를 얻는다. 정리 1.22 X 가 완비가분 거리공간이고, (X, .J, µ)가 (X, .'8 (X), µ)를 완비화해서 얻은 완비측도공간이라 하자. 그러면 임
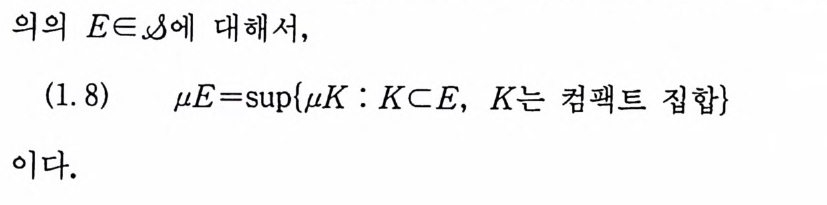 의의 EE .so에 대해서,
의의 EE .so에 대해서,
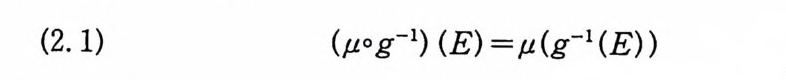 (2. 1) (µog -1 ) (E) = µ (g-1 (E) )
(2. 1) (µog -1 ) (E) = µ (g-1 (E) )
2 변수변환정리 (X, .A, µ_) 를 측도공간, ( Y, c) 를 측도가능공간이 라 하고 g : X-Y 를 4 ― c 측도 가능한 함수라 하자. 모든 EEc 에 대해 서 , 집 합함수 µo g -1 를
로 정의하자. 그러면 µo g -1 는 c 에서 측도가 된다. 이 측도를 µ 의 상측도 (im ag e measure) 라 한다.
실수 R 에 {_CX), + oo} 를 추가한 수집합을 확장된 실수계 (extended real number sy st em) 라 하고
 (2. 2) R=IRU{-oo, +oo}
(2. 2) R=IRU{-oo, +oo}
로 쓰기로 하자. 정리 2. l (X, .A, µ)를 측도공간, ( Y, c) 를 측도 가능 공간, g : X-+ Y 를 A-c 측도 가능한 함수, f : Y 一百 룰 e- 측 도 가 능한 함수라 하자. 그러면, f가 상측도 µo g -1 에 대해서 적분 가 능할 필요충분조건은 f o g가 µ-적분 가능한 것이다. 이 경우에, 다음 등식이 성립한다.
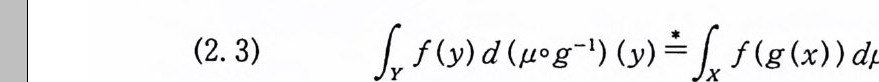 (2. 3) }:Y, f (y) d (µog -1 ) (y) ~ fx I (g (x ) ) dµ (x ) .
(2. 3) }:Y, f (y) d (µog -1 ) (y) ~ fx I (g (x ) ) dµ (x ) .
(2.3) 의 등식 느은 강한 의미의 등식을 표시한다. 죽, 등식의 어느 한 변이 정의되면(무한대인 경우도 포함) 다른 변도 정의되 고 두 적분값은 같다. 3 적분공식 다음 적분공식은 위너 적분과 파인만 적분 계산에서 자주 사용 되는 유용한 공식들이다.
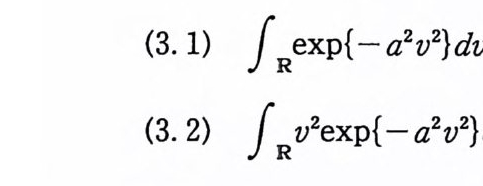 (3. 1) f RR ex p{군 #}dv= 됴a
(3. 1) f RR ex p{군 #}dv= 됴a
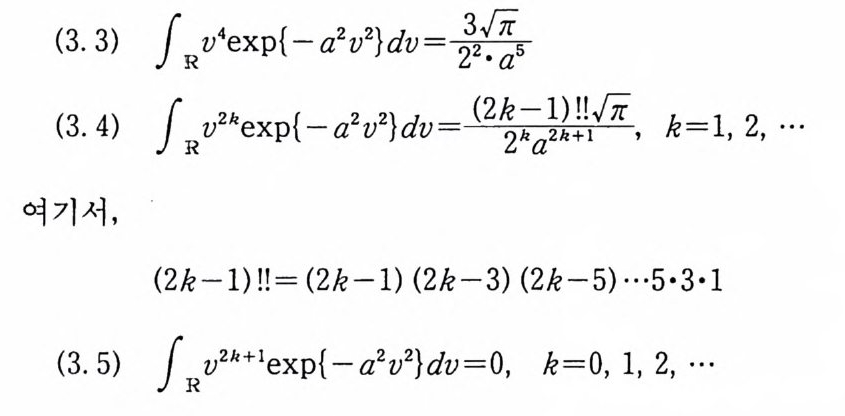 (3. 3) f R 군 ex p {-a2v2}dv= 喜: 5
(3. 3) f R 군 ex p {-a2v2}dv= 喜: 5
주 공식 (3.1) 은 극좌표로 변환하여 얻는다. 공식 (3. 2) 는 (3.1) 의 양변을 미분해서 얻는다. 또한 (3. 2) 의 양변을 미분해서 (3. 3) 을 얻는다. 공식 (3. 4) 는 귀납법을 사용해서 얻는다. (3. 5) 의 피적분함수는 기함수이므로 (3.5) 의 적분은 0 이 된다. p (v) 가 다항식일 때 공식 (3. 4) 와 (3. 5) 를 사용하면 다음 적 분을 계산할 수 있다.
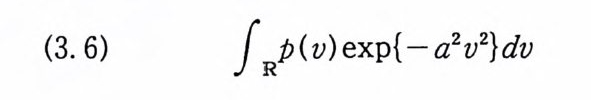 (3. 6) f RR p (v)ex p{一 a2v2}dv
(3. 6) f RR p (v)ex p{一 a2v2}dv
4 리 츠 볼록정 리 (Rie s z convexit y the orem) 정의 4.1 I 가 측도가능함수일 때, 다음 조건을 만족하는 함수 g를 f의 절단 (tru ncati on ) 이 라 한다.
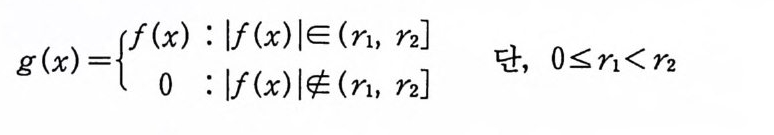 g( x) ={ I(x0 ) :: I1f/((xx )) I|$E. ((rrii,, rr22]] 단, O~ r1< r2
g( x) ={ I(x0 ) :: I1f/((xx )) I|$E. ((rrii,, rr22]] 단, O~ r1< r2
(M 」戶), (N, JV, II) 를 측도공간, D, E 을 각각 M 과 N 위 에서 정의된 측도 가능 함수들의 선형공간이라 하자. T : D -+ E 를 작용소라 하고 D 가 다음 조건을 만족한다고 하 자. (i) D 는 유한 측도를 갖는 집합 위에서 정의된 모든 특성함 수를 포함한다.
 (ii) /ED 이고 g가 f의 절단(t runca ti on) 이 면, g ED 이 다.
(ii) /ED 이고 g가 f의 절단(t runca ti on) 이 면, g ED 이 다.
T 를 (p, q)-형이라고 부론다. 위의 부등식이 성립하는 가장 작 은 k 를 T의 (p, q) -노름이 라 한다. 정리 4-2 (Rie s z convexit y the orem) i= O, 1 일 때 선형 작용소 T 가 (pi, qi) -형 이 고, (pi, q1- ) -노름 k i를 갖는다고 하자.
 0::;: t ::;;1 에 대해서,
0::;: t ::;;1 에 대해서,
5 확률분포 (.Q, J3, p)를 확률공간이라 하자. 요에서 정의된 측도 가능한 실가함수를 확률변수 (random var i able) 라 한다. 확률변수 X 의 기 대 값 (exp ec ta t i on ) (또는 평 균 (mean) ) E (X) 와 분산 (varia n ce) V(X) 를 각각
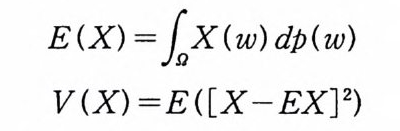 E(X) =!x(w}dp( w )
E(X) =!x(w}dp( w )
으로 정의한다. 정 의 5 . l 확률 공간 (lRn, J3 (lRn) , µ) 를 n 차원 확률공간이 라 하고, 확률측도 µ를 n_ 차원 확률분포 (pr obabil ity dis t r i b u ti on ) 라 한다. µ가 lRn 에서의 르베그 측도 A 에 대해서 절대연속이면, 라 돈-니코딤 도함수 dµ/d- 1를 µ의 밀도함수라 한다. 정의 5·2 X : (요, 13, p尸 (Rn, J3 (Rn) )가 측도 가능한 변환 (measurable tra nsfo r mati on ) 일 때 , X를 n 차원 확률벡 터 (random vecto r ) 라 한다. 집 합함수 µx :
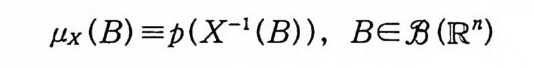 µx (B) =p( X-1 (B) ) , BEJ 3 (Rn)
µx (B) =p( X-1 (B) ) , BEJ 3 (Rn)
는 (!Rn , J3 (Rn)) 에서 확률측도이다. 이 µx 를 확률벡터 X 에 의 해서 결정되는 n 차원 확률분포라 한다. 물론, n=l 인 경우 X 는 확률변수이다. 정리 5.3 X가 n 차원 확률벡터이고, I:Rn 一 R 가 보렐 측도
가능한 함수이면, 변수변환정리에 의해서 다음 식을 얻는다.
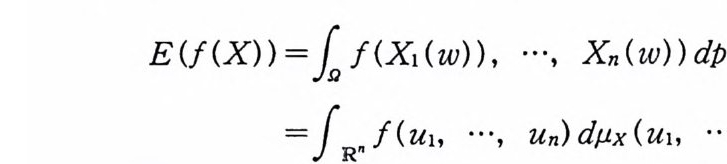 E( f(X ))=Lf ( Xi( w )), …, Xn(w))dp ( w)
E( f(X ))=Lf ( Xi( w )), …, Xn(w))dp ( w)
정의 5.4 µ룰 n 차원 확률분포라 하자. µ의 분포함수 F 는
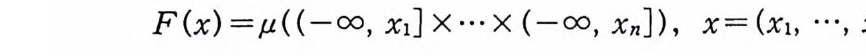 F(x) =µ((-oo, Xi] X ••• X (-oo, Xn]), x= (xi, ···, Xn) ElRn
F(x) =µ((-oo, Xi] X ••• X (-oo, Xn]), x= (xi, ···, Xn) ElRn
로 정의한다. n 차원 확률벡터 X 의 분포함수는 X 에 의해서 결정되는 n 차원 확률분포 µx 의 분포함수를 말한다. 정리 5.5 F 가 1 차원 확률분포의 분포함수라 하자. 그러면 F 는 다음 성질을 만족한다.
 (1) 단조 증가 : x< y이면 F(x) ~F(y) .
(1) 단조 증가 : x< y이면 F(x) ~F(y) .
정의 5.6 n 차원 확률분포 µ의 특성함수 ¢를 다음과 같이 정 의한다.
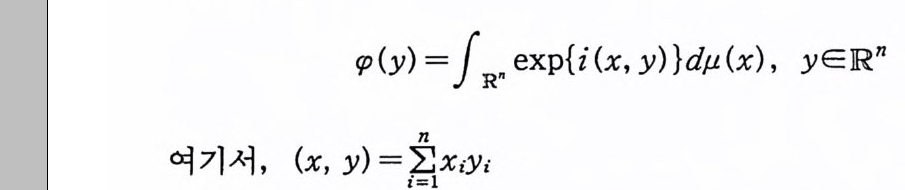 ({J (y) =jRR e xp {i (x, y) }dµ (x) , yE JRn
({J (y) =jRR e xp {i (x, y) }dµ (x) , yE JRn
n 차원 확률벡터 X=(X1, …, Xn) 의 특성함수 Y(x) (또는 푸 리에 변환)는 X 에 의해서 결정되는 n 차원 확률분포 µx 의 특성
함수를 말한다. 따라서,
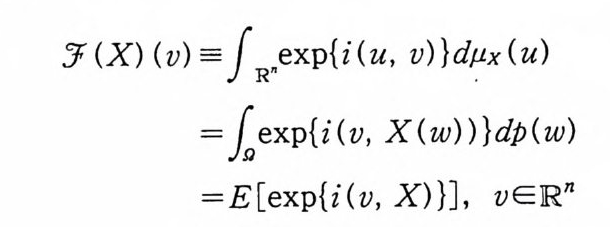 Y(X) (v) =fRR exp {i(u , v)}dµx(u)
Y(X) (v) =fRR exp {i(u , v)}dµx(u)
정의 5.7 n 차원 확률벡터 X=(X1, …, Xn) 의 평균 벡터 E (X) 와 공분산 행 렬 (covaria n ce matr i x ) V (X) 를 다음과 같이 정 의한다.
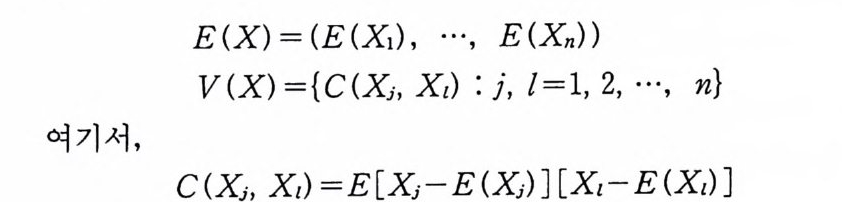 E(X) = (E(X1), …, E(Xn))
E(X) = (E(X1), …, E(Xn))
확률분포 µx 의 평균 벡터 E(µx) 와 공분산 행렬 V(µx) 를 각 각 X 의 평균 벡터와 공분산 행렬로 정의한다. 죽,
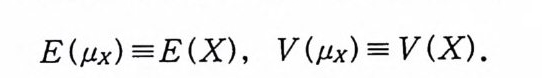 E(µx) =E(X), V(µx) = V(X).
E(µx) =E(X), V(µx) = V(X).
정의 5.8 확률변수 X1, …, x군 ] 다음 식을 만족할 때 서로 독립 (ind ep e ndent) 이 라 한다.
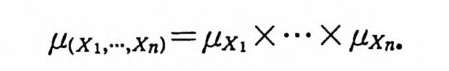 µ(X1,··•,Xn)=µxi X … X µxn.
µ(X1,··•,Xn)=µxi X … X µxn.
정리 5.9 X1, X2, …, X려 서로 독립인 확률변수이고 /1, …, In 이 보렐 측도 가능한 함수라 하자. 그러면,
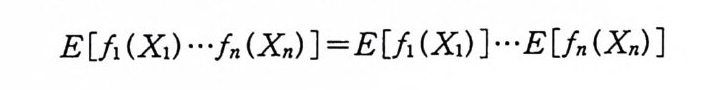 E[/1 (X1) …fn (X n) ]= E[/1 (X따 …E [fn ( Xn) ]
E[/1 (X1) …fn (X n) ]= E[/1 (X따 …E [fn ( Xn) ]
이다. 정 의 5 . 10 확률변수 X 의 확률분포 µx 가 식 (5. 1) 을 만족할 때, X를 매개변수 p, 궁을 갖는 정규분포 (normal d i s t r i bu ti on) 라 하고,
 X~N(p, cf)
X~N(p, cf)
로 표시한다.
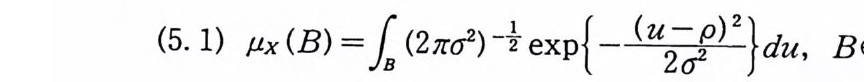 (5. 1 ) µx(B)=1B( 2 쿄) - 상ex p{- (u;#p) 2 }du, B 켈 (IR).
(5. 1 ) µx(B)=1B( 2 쿄) - 상ex p{- (u;#p) 2 }du, B 켈 (IR).
주 X~N(p, a2) 이면 다음 사실이 성립한다.
(1) E(X) =p, V(X) =a2 (2) j (X) (v) =f R(21ra2)- 상 ex p{i uv}ex p {-V}d~ =ex p{ip v ―강訂}. j= l, 2, …, n 일 때, xj~ N(pj , 여)이고, X1, … , Xn 이 서로 독 립이라 하자. X=(X1, …, Xn), v=(v1, …, Vn) 으로 놓으면, (5. 2) j (X) (v) =1exp {i (v1X1 + ... + VnXn) }dp =Jn99 e xp {iv1 X1}·exp {ivn Xn}dp =j (X1) (v1) …J (Xn) (vn) =ex p{ij=~n lp j v j-f1 jn~ 여 v;}.
정리 5.11 X,, …, Xn 이 서로 독립이고,
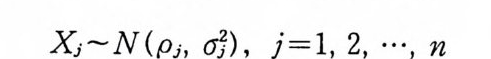 xj~ N(pj , 여), j= l, 2, …, n
xj~ N(pj , 여), j= l, 2, …, n
일 필요충분조건은 (5.2) 가 성립하는 것이다.
 정리 5.l2 X)~N(pj , 여), j= l, 2, …, n 이라 하자. X1, …, Xn
정리 5.l2 X)~N(pj , 여), j= l, 2, …, n 이라 하자. X1, …, Xn
정의 5, 14 n 차원 확률분포 µ가 다음 조건을 만족할 때, µ를 n 차원 정규분포라 한다. (1) µ는 르베그 측도 A 에 대해서 절대 연속이다. (2) 밀도함수는 다음과 같이 주어전다•
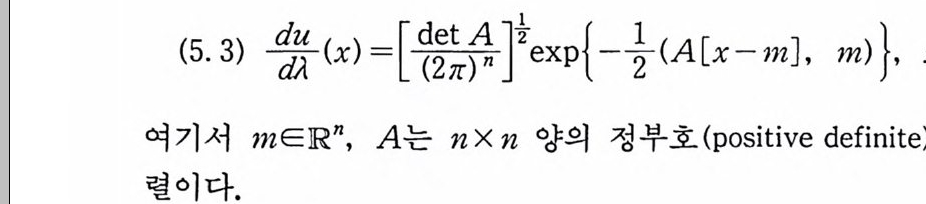 (5. 3) 뿔 (x) =[설냐 ]½ex p{」 -(A 닳 _m] , m)}, xERn.
(5. 3) 뿔 (x) =[설냐 ]½ex p{」 -(A 닳 _m] , m)}, xERn.
정리 5.15 n 차원 정규분포 µx 가 밀도함수 (5. 3) 을 가질 때 특성함수 Y(X) 는
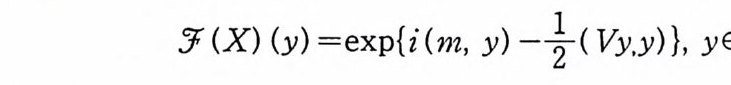 Y (X) (y) =exp {i(m , y) 켜-( Vy ,y)}, yE JRn
Y (X) (y) =exp {i(m , y) 켜-( Vy ,y)}, yE JRn
이다. µx 의 평균 벡터와 공분산 행렬은
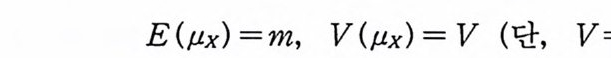 E(µx) =m, V(µx) = V (단, V=A-1)
E(µx) =m, V(µx) = V (단, V=A-1)
이다. 정리 5.16 확률벡터 X=(X1, …, Xn) 의 확률분포가 n 차원 정 규분포이고, 평균벡터가 O, 공분산 행렬이 V 라고 하자. 그러면, 임의의 nXn 대칭행렬 C 에 대해서,
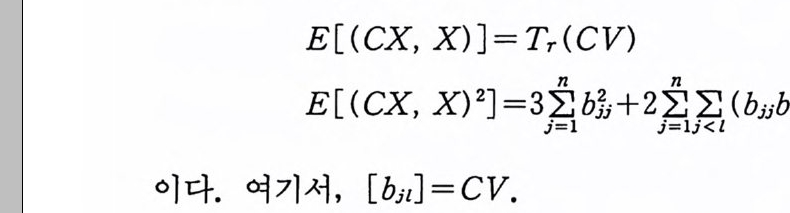 E[(CX, X)]= T r(CV)
E[(CX, X)]= T r(CV)
정 리 5 . 17 (콜모고로프 (Kolmog o rov) 정 리 ) {Yk} 가 서로 독립인 확률변수이고
 ~00 V( Yk)
~00 V( Yk)
은 a. s. (almost surely) 수령 한다. 정리 5-18 {Xn : n=O, 1, 2, 나울 확률벡터들의 수열이라 하 자. 만일
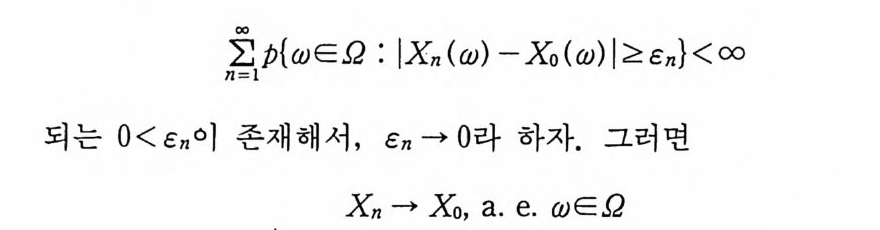 00
00
이다. 정리 5-19 {Xn} 이 서로 독립인 확률변수들의 수열아라 하자.
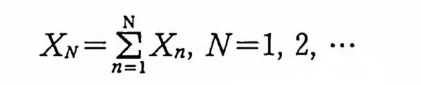 XN= n~=NI Xn, N=l, 2, …
XN= n~=NI Xn, N=l, 2, …
로 놓자. 다음 성질은 서로 동치이다. (1) XN 은 확률변수로 a. e. 수령 한다. (2) XN 은 확률변수로 확률수렴 (converge nce in pro babil ity) 한 다. (3) XN 의 확률분포는 1 차원 확률분포로 수령한다.
 정의 6.1 DCR 일 때 확률공간 (요, J3, p)에서 정의된 확률변
정의 6.1 DCR 일 때 확률공간 (요, J3, p)에서 정의된 확률변
6 확률 과정
정의 6.2 모든 표본함수 X(·, (/J)가 D 에서 연속일 때, 확률 과정 X를 연속이라 한다. a. e. (/J E Q에 대해서, X(·, (/J)가 연 속일 때, X를 거의 확실하게 (a. s. : almost surely) 연속이라 한 다. 정의 6.3 확률과정 X 가 다음을 만족할 때 브라운 운동과정 (Brownia n moti on pro cess) 이 라 한다.
 (1) 임의의 U1, t2, …, tn} CD, t 1< t 2< …
(1) 임의의 U1, t2, …, tn} CD, t 1< t 2< …
주 (1) 을 만족하는 확률과정 을 가산과정 (addit ive pro cess) 이 라 한다.
 정의 6.4 X 가 확률과정일 때, 모든 t ED 에 대해서
정의 6.4 X 가 확률과정일 때, 모든 t ED 에 대해서
주 공분산 함수 v 는 대 칭 (sy mm et ri c ) 이고 음이 아닌 정부호 (nonnega ti ve defi ni t e) 이 다. 즉,
 ((12)) {va (1s, , …t), =an v} (Ct,D s, )U , 1,s ,· ··t,E t D n},C lR 일 때, ggv ( aj, al) &&킥 0
((12)) {va (1s, , …t), =an v} (Ct,D s, )U , 1,s ,· ··t,E t D n},C lR 일 때, ggv ( aj, al) &&킥 0
정의 6.5 확률과정 X가 다음을 만족할 때 X를 가우스 과정 이라한다.
 임의의 유한부분집합 {a1, …, an}CD 에 대해서 n 차원 확률벡터
임의의 유한부분집합 {a1, …, an}CD 에 대해서 n 차원 확률벡터
정리 6.6 가우스 과정 X 는 다음 성질을 만족한다. (1) 가우스 과정의 임의의 부분집합은 가우스 과정이다. (2) 가우스 과정 X 에 속하는 확률변수들의 모든 일차 결합들 의 모임은 가우스 과정이다. (3) 가우스 과정에 속하는 확률변수들의 수열의 확률수령극한 (lim i t of converge nce in prq b abil ity) 들의 모임 은 가우스 과정 이 다. (4) X가 가우스 과정 일 필요충분조건은 X 에 속하는 확률변수
들의 모든 일차 결합의 확률분포가 정규분포이다.
 (5) 가우스 과정 {Xi, ···, Xn} 이 독립 일 필요 충분 조건은
(5) 가우스 과정 {Xi, ···, Xn} 이 독립 일 필요 충분 조건은
도움말 제 1 장 위너 측도와 위너적분 1. 참고문헌 : Bearman[!]. Cameron[4]. Hi da[ 때 Joh nson[!], Joh n- son and Skou g따, Gelfa n d and V i lenk i n[ 나, Yeh 〔吐 2. 정리 1. 4 의 직접 증명은 Joh nson[!] 참조. 3. 정 리 1. 6 의 증명 은 Gelfa n d and Vi len kin [L 정 리 4, ~대 5 이 참조 4. 정 리 1. 26 은 코흐러 (F. Koehler) 가 처 음 증명 했으나, 그 방법 이 복 잡하므로 여기서는 그라프 (S. Graf)의 증명 방법을 소개했다. 두 방법 모두 출판되지는 않았다. 5. 정의 1.1 6 : 위너 측도 공간을 위너 (W ien er) 자신은 처음에 미분공 간 (d iff eren ti al sp a ce) 이라고 하였다. 위너 과정의 가법성 (addit ive p ro p er ty)으로부터 이와 같은 이름을 붙인 것 같다(Hi da[2, Remark 2, p.5 0] ) 6. 정리 8.16 은 처음 위너가 증명하였다. 여기서는 넬슨 (Nelson) 의 증명 방법을 사용했다. 7. 회전변환 : 1952 년 베어만(J. Bearman) 은 평면에서의 회전변환의 개념을 확장하여 위너 적공간(p roduc t Wi en er s p ace) 에서 회전변환 에 관한 정리를 얻었다. 이 결과는 위너 공간에서 척도불변 가측성 (scale-in v aria n t measurabil ity) 을 연구하는 데 유용하게 사용되 었 다. 제 2 장 위너 적분의 번환정리 l. 참고문헌 : Cameron and Mar ti따 2, 3, 5, 7, 아, Ewan[ 니, Joh nson [l, 이 , Yeh[4, 5, 9]. 2. 정리 1. 8 은 Paley and W i ener 印 참조. 3. 정리 2 . 10 은 Cameron and Grave[!], Maru y oma[ 다, Sunouchi[ l ] 참조.
4. 정리 2. 21 의 조건을 만족하는 함수들의 힐베르트 (H i lber t) 공간에 서 정의되는 미분사상 (d iff eren ti a ti on ma p)과 적분사상(i n t e gr a ti on map : 미 분사상의 역 ) 에 관한 성 질은 Joh nson [이 참조. 5. 정리 2.24 는 정리 2 . 25 의 특수한 경우이다(정리 2 . 25 에서 g =l 인 경우) 6. 정 리 2. 25 는 정 리 2. 24 를 이용해서 존슨 • 스코그가 처음 증명 했다 (Jo hnson and Skoug [ 4]) 7. §5 에서는 Co 와 Cm 족 (class) 만 다루었다. 또 다른 족 (class) 에 관한 결과는 Cameron and Ma rti n 〔하 참조 8. 푸리 에 -에 르미 트 (Fourie r -Hermi te) 함수의 푸리 에 - 위 너 (Fourie r - Wi en er) 변환의 계산은 Cameron and Marti n[ 9] 참조. 9. 정리 6 . 1 은 예 (Yeh) 가 처음 증명했다 (Yeh[4]). 제 3 장 확률적분과 위너 조건적분 l. 참고문헌 : Baxte r [l], Breim an[l], Chang and Chang [ l], Chow and Teic h er[!], Park and Skoug [ 3], Park, Skoug and Smol- ow itz [ 1] , Rees, Shah and Sta n oje v i c [ 1] , Yeh [9, 10, 11, 12, 13] 2. 정 리 1. 4 (강한 극한 정 리 ) 를 박스터 (Baxte r ) 정 리 라고도 한다. (Baxte r [1]). 정리 1. 4 의 조건을 만족하는 가우스 과정 (Gaussia n pro cess) 을 박스터 과정 이 라고 한다. 3. 가우스 과정에 대한 확률적분은 예 (Yeh) 가 처음 정의하였다. (Yeh [1 끽). 4. 확률벡터에 대한 위너 조건적분의 개념은 장건수 • 장주섭이 처음 소개하였고 (Chan g and Chan g[다) 박철 • 스코그는 이 적분에 대한 유용한 공식을 개발했다. (Park and Skoug [3 ]). 5. 예 7.8 과 예 7.9 는 장건수 • 장주섭이 반전공식 (7 . 4) 를 사용해서 얻었으나 (Chan g and Chang [ l]), 그 계산 과정이 복잡하다. 여기서 소개한 방법은 박철 • :!::.구기가 얻은 결과이다. (Park and Skoug [3])
6. §5 에서 소개한 칵-파인만 (Kac-Fe y nman) 공식과 §6 에서 다룬 위너 조건적분에 대한 변환정리를 확장한 결과는 Park and Skou 깝 3] 참 조. 제 4 장 예-위너 측도와 예-위너 적분 1. 참 고 문 헌 : Cameron and St o rvic k [7] , Chan 파 1, 2] Chang and Ry u [l], Joh nson and Skoug [ 3], Skoug [ 2, 3, 4], Yeh[l, 2] 2. 예-위너 측도 공간은 예 (J. Yeh) 가 처음 소개하였다 (Yeh[l]). 3. 두 변수 함수의 유계변동에 관한 자세한 내용은 Skou 따 4], Berkson and G ill es pi e[ 니, Clarkson and Adam 해 1, 2], Hobson[l], Jef f er y [ l], Mac p ha i l[l] 을 참조. 4. 정리 3.21 : n 변수 함수의 리만-스틸체스 적분에 대한 부분적분의 공식 과 증명 은 Yeh[2] 참조. 5. 정리 7.1 과 7. 2 는 카메룬과 스타빅이 발견했고 (Cameron and Sto r vic k [7]), 정리 7.1 의 역과 정리 7. 6, 정리 7. 7 은 스코그가 증 명했다 (Skou g밍). 정리 7. 2 의 역인 정리 7. 4 와 7. 5( 역측도 정리) 는 장건수가 증명했다 (Chan g [l]). 장건수 • 유일은 정리 7. 4 의 증 명을 간단하게 하였다. (Chang and Yoo[l]} 6. 정리 7. 9 의 역이 성립하는지는 아직까지 알려지지 않았다. 7. 위너 공간과 예-위너 공간에서의 역측도 정리 (1 장 정리 1. 26, 4 장 정리 1.1 5, 정리 7.4) 들을따름정리로서 얻을수있는일반화된 역 측도 정리는 장전수 • 류근식이 증명하였다 (Chan g and Ry u [l]). 8. 푸리에-예-위너 변환은 김동연의 석사 논문에서 다루었다(Ki m 印). 9. 장건수는 위너 공간에서의 척도불변 가측성과 회전변환의 개념을 예-위너 공간으로 확장하였다 (Chan g [2]).
제 5 장 위너 작용소 적분과 예-위너 조건적분 1. 참고문헌 : Cameron and S t orv ic k 困, Chang and Ahn[l], Chung and Ahn[l], Park and Skoug [ 4]. 2. 위너 작용소 적분, 위너 적분방정식의 존재정리와 노이만 급수에 대한 결과는 카메룬 • 스타빅이 얻었다 (Cameron and Sto rvic k [ 8] ) 3. 정리 4 . 11 은 박철이 처음 증명했다 (Park[l 〕). 4. 예 - 위너 조건적분은 장건수, 정동명, 안재문, 장주섭 등이 계산하 였다. 계산 방법은 위너 조건적분 계산 방법을 그대로 두 변수의 경우로 확장하였으나, 계 산 과정은 매 우 복잡하다 (Chun g and Ahn [l] , Chang, Ahn and Chang [l] ) . 5. 예-위너 조건적분의 변환정리는 장건수 • 안재문이 증명했다 (Chan g and Ahn[l]). 6. 예-위너 조건적분을 계산하는 유용한 공식은 박철 • 스코그가 개발 했 다 (Park and Skoug [3, 5, 6] ) . 7. 벡터함수에 대한 예 - 위너 조건적분은 박철 • 스코그가 처음 계산했 다 (Park and Skoug [ 4]). 8. 예 - 위너 조건적분에 관한 최근 결과는 Park and Skoug [8 , 9, 10] 참조. 9. 예-위너 조건적분과 마팅게일 (mar ti n g ale) 수령정리의 개념을 사용 해서 예-위너 공간의 미분정리를 얻은 결과는 Chang , Park and Skoug [ l] 참조. 위너 공간의 미분정리에 관한 결과는 Park, Skoug and Smolowi tz [ l] 참조.
참고문헌 Adams, C. R. and Clarkson, J. A. 1. On defi ni t ion s of bounded varia t i on for fun cti on s of tw o varia b les, Trans. Amer. Math . Soc. 35(1933), 824-854. 2. Prop e rti es of fun cti on s f(x , y) of bounded varia t i on , Trans. Amer. Math . Soc. 36(1934), 711-730. Ahn, J. M. (안재문) , Jo hnson, G. W. and Skoug , D. L. 1. Functi on s in the Fresnel class of an abstr a ct Wi en er spa c e, ]. Korean Math . Soc. 28(1991), 245-265. Bartl e , R. l. The elements of real analys i s, Joh n Wi ley & Sons, New York, 1976. 2. Eleme n ts of int e g r a ti on , Joh n W ile y & Sons, New York, 1985. Bauer, N. l. Probabil it y the ory and elements of measure the ory , Holt Rin e hart and W ins to n , New York, 1972. Baxte r , G. 1. A str o ng lim i t the orem for Gaussia n pro cesses, Proc. Amer. Math . Soc. 7(1956), 522-527. Bearman, J. 1. Rota t i on s in the pro duct of tw o W ien er spa ces, Proc. Amer. Math ,
Soc. 3(1952), 129-137. Berkson, E. and Gil les pi e, T. A. 1. Absolute l y conti nu ous fun cti on s of tw o varia b les and well-bounded op e rato r s, ]. London Math . Soc. 30(1984), 305-321 . Breim an, L. l. Probabil it y , Addis o n-Wesley, Readin g , Mass, 1968. Cameron, R.H. 1. Some examp le s of Fourie r -W ien er tra nsfo r ms of analyt ic fun c- tion als, Duke Math . ]. 12(1945), 485-488. 2. The firs t varia t i on of an ind efi ni t e W ien er int e g r a l, Proc. Amer. Math . Soc. 2(1951), 914-924. 3. A Sim p s on's rule for the numeric a l evaluati on of W ien er's int e g ral s in fun cti on spa ce, Duke Math . ]. 18(1951), 111-130. 4. The tra nslati on pa th o log y of Wi en er spa ce, Duke Math . ] . 21(1954), 623-628. 5. A ge nerali ze d heat flow equ ati on and a corresp o ndin g Possio n form ula, Ann. of Math . 59(1954), 434-462. 6. A fam i ly of int e g ral s servin g to connect the Wi en er and Fey rn nan int e g ral s, ]. of Math . and Phys . 39(1960), 126-140. 7. The ILSTOW and Fey rn nan int e g ral s, ]. Analyse Math . 10(1962/ 1963), 287-361. Cameron, R.H. and Graves, R.E. 1. Addit ive fun cti on als on a spa ce of conti nu ous fun cti on s, Trans. Amer. Math . Soc. 70(1951), 160-176.
Cameron, R. H. and Hatf ield , C. 1. Summabil it y of ce rt a i n orth o g o nal develop m ents of non-lin e ar fun cti on als, Bu ll . Am er. Math . So c. 55(1 9 49), 130-145. 2. Summabil it y of certa i n serie s for unbounded non-li ne ar fun cti on als, Proc . Ame r. Math . Soc. 4(1 9 53), 375-387. Cameron, R. H. and Marti n, W. T. 1. An unsy m metr i c Fubin i the orem, Bull, A mer. Math . Soc. 47(1941), 121- 12 5. 2. W ien er measure of Hi lb ert neig h borhoods in the spa ce of real conti nu ous fun cti on s, ]. Math . an d Phys . 33(1 9 44), 195-209. 3. Transfo r mati on s of W ien er int e g r als under tra nslati on s, Ann. of Math . 45(1944), 386-396. 4. An exp re ssio n for the soluti on of a class of non-lin e ar int e g ral eq u ati on s, Ame r. ] . of Math . 66(1944), 281-298. 5. Fourie r -W ien er tra nsfo r ms of analyt ic fun cti on als, Duke Math . ]. 12(1 9 45), 489-507. 6. Evaluati on of vario u s Wi en er int e g ral s by use of certa i n Stu m - Lio u vil le dif fer enti al eq u ati on s, Bull. Amer. Math . Soc. 51(1945), 73 -89 . 7. Transfo r mati on s of W ien er int e g r als under a ge neral class of line ar tra nsfo r mati on s, Trans. Amer. M ath . Soc. 58(1945), 184- 21 9. 8. The behavio r of measure and measurabil ity under chang e of scale in W ien er spa c e, Bull. Amer. Math . Soc. 53(1947), 130-137. 9. Fourie r -W ien er tra nsfo r m of fun cti on als belong ing to 뇨 over the spa c e C, Duke Math . ]. 14(1 9 47), 99-107. 10. The orth o g o nal develop m ent of non-li ne ar fun cti on als in serie s of Fourie r -Hermi te fun cti on als, Ann. of Math . 48(1947), 385-392. 11. The tra nsfo r mati on s of W ien er int e g ral s by non-lin e ar tra nsfo r- mati on s, Trans. Amer. Math . Soc. 66(1 9 49). 253-283. 12. Non-l in e ar int e g ral eq u ati on s, Ann. of Math . 51(1 9 50). 629-642.
Cameron, R. H. and Shap iro , J. M 1. Non lin e ar int e g ral eq u ati on s, Ann. of Math . 62(1 9 55), 472-497. Cameron, R. H. and St o rvic k , D. A. 1. Analyt ic conti nu ati on for fun cti on s of several comp le x varia b les, Trans. Amer. Math . Soc. 125(1966), 7-1 2 . 2. An op e rato r -valued fun cti on spa ce int e g r al and a relate d int e g ra l eq u ati on , ]. Math . Mech. 18(1968), 517-552. 3. An int e g ral eq u ati on relate d to the Schrodin g e r eq u ati on wi th an ap plica ti on to int e g rat i on in fun cti on spa ce, Prob. in An aly s i s , Prin c eto n, (1970), 175-193. 4. An op e rato r -valued fun cti on spa ce int e g ral ap plied to int e g r als of fun cti on s of class Li, Proc. London Matlz . Soc. (3) 27(1973), 345- 36 0. 5. An op e rato r -valued fun cti on spa ce int e g ral ap plied to int e g ral s of fun cti on s of class L2, ]. Math . Anal. A p pl. 42(1973), 330-372 6. An op e rato r -valued fun cti on spa ce int e g ral ap pli e d to multip le int e g ral s of fun cti on s of class Li, Nago y a Math . ]. 51(1 9 73), 91-122. 7. Two relate d int e g ral s over spa ces of conti nu ous fun cti on s, Pacij i·c ]. of Math . 55(1974), 19-38. 8. An op e rato r -valued Yeh-Wi en er int e g ral and a W ien er int e g ral equ ati on , India n a Math . ]. 25(1976), 235-258. 9. Chang e of scale for mula for W ien er int e g ral , Supp le mento ai Rendic o nti de! Cir c olo Mate m ati co di Palermo, 17(1987), 105-115. 10. Relati on ship s betw een the W ien er int e g ral and the analyt ic Feyn - man int e g ral , Sup ple mento ai Rendic o nti del Cir c olo Mate m ati co di Palermo, 17(1 9 87), 117-133. Chang , J. S., (장주섭) Park, C. (박철) and Skoog , D. L. 1. Fundamenta l the orem of Yeh-W ien er calculus, Sto c hastic Analysi s
and Ap pl. 9(1991), 245-2 6 2 Chang , K. S. (장건수) I. Converse measurabil it y the orems for Yeh-W ien er spa ce, Pacif ic ] . Math . 97(1981), 59-63. 2. Scale-in v aria n t measurabil it y in Yeh-W ien er spa c e, ]. Korea n Math . Soc. 19(1 9 82), 61-67. 3. 『 파인만 적분론 』 (대우학술총서 98), 민음사, 1994. Chang , K. S. and Ahn, J. M. (장건수, 안재문) I. Converse measurabil it y the orem for Gaussia n pro cesses, ]. Korean Math . Soc. 19(1983), 87-95. 2. Translati on the orem for condit ion al Yeh-Wi en er int e g ral s, ]. Kore an Math . Soc. 20(1983), 163-172. Chang , K. S., Ahn, J. M. and Chang , J. S. (장건수, 안재문, 장주섭) 1. An evaluati on of the condit ion al Yeh-W ien er int e g ral , Pacif ic ] . Math . 124(1986), 107~117. Chang , K.S ., Ahn, J.M . and Chung , D.M. (장건수, 안재문, 정동명) 1. Rota t i on s and tra nslati on s in Yeh-W ien er sp ac e, ]. Korean Math . Soc. 18(1982), 181-188. Chang , K. S., Ahn, J. M., Kim , Y. S and Yoo, I. (장건수, 안재문, 김영식, 유일) 1. A chang e of scale for mula for Wi en er int e g ral s on the pro duct abstr a ct W ien er spa c es, ]. Korean Math . Soc. 33(1996), 269282 Chang , K. S. and Chang , J. S. (장건수, 장주섭 ) 1. Evaluati on of condit ion al Wi en er int e g ral s, Bull. Korean Math . Soc.
21(1984), 99-106. Chang , K. S. and Ry u, K. S. (장건수, 류근식 ) 1. A ge neraliz e d converse measurabil ity the orem, Proc. Amer. Math . Soc. 104(1988), 835-839. Chang , K. S. and Yoo, I (장건수, 유일) 1. A sim p le pro of of converse measurabil it y the orem for Yeh-W ien er spa ce, Bull. Korean Math . Soc. 23(1986), 35-37. Chow, Y. S. and Teic h er, H. 1. Probabil ity the ory , Sp r in g e r-Verlag, New York, 1978. Chung , D. M. (정동명) 1. Scale-in v aria n t measurabil ity in abstr a ct Wi en er spa ce, Pacif ic ] . Math . 130(1987), 27-40. Chung , D. M. and Ahn. J. M. (정동명, 안재문) 1. Condit ion al Yeh-Wi en er int e g ral s, ]. Korean Math . Soc. 20(1983), 209-221 . Chung , D. M. and Kang , S. J. (정 동명 , 강순자) 1. Condit ion al Wi en er int e g ral s and an int e g ral equ ati on , ]. Korean Math . Soc. 25~1988), 37-52. 2. Evaluati on for mulas for condit ion al abstr a ct Wi en er int e g ral s, Sto c hastic Analys i s and Ap pl. 7 (1989), 125-144. Clarkson, J. A. and Adams, C. R. 1. On defi ni t ion of bounded varia t i on for fun cti on of tw o varia b les, Trans. Amer. Math . Soc. 35(1933), 824-854.
2. Prop e rtie s of fun cti on s f(x , y) of bounded varia t i on , Trans. Amer. Math . Soc. 36(1 9 34), 711- 73 0. Cohn, Donald L. 1. Measure the ory , Bosto n , B i rkh 겼 user, 1980 Erdos, P and Kac, M. 1. On certa i n lim i t the orems of the the ory of pro babil ity, Bull. Amer. Math . Soc. 52(1 9 46), 292-302. Ewan, R. 1. The Cameron-Sto r vic k op e rato r -v a lued fun cti on spa ce int e g ral for a class of fini t e dim ensio n al fun cti on als, Ph. D. the sis , Univ . of Nebraska, 1972. Finl ay so n, H. C. 1. New app r oxim ati on s for W ien er int e g ral s wi th error esti m ate s , Canadia n ]. Math . 19(1967), 58-105 Freedman, D. 1. Brownia n moti on and Di ffusi o n , Holden-Day, San Franci sc o, 1971 . Gelfa n d, I. M. and Yag lo m, A. M. 1. Inte g rat i on in fun cti on spa ces and its ap plica ti on s in qu antu m ph y s ic s( in Russia n ), Us pe khi Mat. Nauk 11(1956), 77-144. Gelfa n d, I. M. and Ya Vi len k in, N. 1. Generalize d fun c tion s, Vol. 4, Ap pli ca ti on s of harmonic analy sis, Academi c pre ss, New York, 1964.
Gi h am, I. and Skorohod, A. l. Sto c hasti c Di ffere n ti al Eq ua ti on s, Erge bn is s e de r Matlz e in a ti l, u. ihr er Gren z ge bi e t e No. 72, Sp r in g e r-Verlag , Berin , 1972. Graves, R.E. 1. Addit ive fun cti on als on a sp a ce of conti nu ous fun cti on s II , Ann. of Math . 54(1951), 275-285. Gross, L. 1. Abstr a ct W ien er spa ce, Proc. 5th Berkeley Sy m p s. Math . Sta t . Prob. 2(1965), 31-42. Halmos, P. R. I. Measure Tlzeory , Van Nostr a nd, Prin c eto n , N. ]., 1 950. Harto g s , F. 1. Zur Theorie der analyt isc hen fun ckti on en mehrerer unabhang ige r veranderlic h en, Math e matis ch e Annalen 62(1906), 1-88. Hi da , T 1. On the unif or m conti nu it y of the W ien er pro cess wi th a multi di m en-sio n al pa ramete r , Na goy a Math . ]. 13(1958), 53-61 . 2. Brownia n Moti on , Sp r in g e r-Verlag, New York, 1980 Hobson, E. W. l. The Theory of Functi on s of a Real Vari ab le and the Theo r y of Fouri er Seri es, Vol. 1, Dover, New York, 1957. Hudson, W. N. 1. Volte r ra tra nsfo r mati on s of the W ien er measure on the sp a ce of
conti nu ous fun cti on s of tw o varia b les, Paci f ic ] . Math . 36(1971), 335 -34 9. Ito, K. 1. Multip le Wi en er int e g r a l, ]. Math . Soc. Jap a n , 3(1951), 157-169. 2. W ien er int e g r a l and Fey n man int e g r a l, Proc. 4th Berkeley Sym p . 12(1 9 61), 227- 23 8. Je ff er y, R. L. 1. Functi on s of bounded varia t i on and non-absolute l y converge n t int e g r a ls in tw o or more dim ensio n s, Duke Math . ] . 5(1 9 39), 753-774. Jo hnson, G. W. 1. Le ct u r e Note s on Wi en e r In te g r a l, Univ . of Nebraska, 1977. 2. An unsym m etr i c Fubin i the orem, Amer. Math . Month l y, 91(1984), 131-133. 3. The eq u iv a lence of tw o app r oaches to the Feyn ma n int e g ral , ]. Math . Phys . 23(1982), 2090-2096. Jo hnson, G. W. and Lap idu s, M. L. l. A noncommuta t i ve multip lica ti on of W ien er fun cti on als and Feyn - man's op e rati on al calculus, C.R . Acad. Sci. Paris , Ser. 1 Math . , 304(1987), 523-526. 2. Noncommuta t i ve op e rati on s on W ien er fun cti on als and Feyn ma n's op e rati on al calculus, ]. of Functi on al Analys i s 81(1988), 74-99. Jo hnson, G. W. and Skoug , D. L. 1. A fun cti on sp a ce int e g ral for a Banach spa ce of fun c tion als on Wi en er spa ce, Proc. Amer. Math . Soc. 43(1974), 141-148. 2. Scale-in v aria n t measurabil ity in Wi en er spa ce, Pacif ic ]. Math .
83(1979), 157-176. 3. A sto c hasti c int e g rat i on for mula for tw o-pa ramete r Wi en er x tw o- pa ramete r W ien er spa ce, SIAM ]. of Math . An a ly. 18(1987), 919 -932. 4. Note s on the Fey n man Inte g ral , II , ]. of Fu n cti on al Analys i s . 41(1981), 277-289. Kim , D. Y. (김동연) 1. A note on the Fourie r -Yeh-W ien er tra nsfo r m, M. S. the sis , Yonsei Univ . 1989. Kuelbs, J. D. 1. Measures on C(Y) when Y is a comp a ct metr i c spa ce, Pr oc . Ame r. Math . Soc. 18(1967), 248-254. 2. A Cameron-Martin tra nslati on the orem for a Gaussia n measure on C(Y), Proc. Amer. Math . Soc. 19(1968), 109-114. 3. Abstr a ct W ien er spa ces and ap plica ti on s to analys i s , Pacif ic ] . Math . 31(1969), 433-450. Kitag a wa. T. 1. Analys i s of varia n ce ap plied to fun cti on spa ces, Mem. Fae. Sci. Ky u shu Univ . Ser. A6(1 9 51), 41-53. Kuo, H.H. l. Gaussia n measures in Banach spa ces, Lectu r e Note s in Math . Vol. 463, Sp ri n g e r-Verlag, Berlin , 1975. Macp h ail , M. S. 1. Functi on s of bounded varia t i on in tw o varia b les, Duke Math . ]. 8(1941), 215-222.
Maruy o ma, G 1. Note s on W ien er int e g ral s, Kodai Math . Semi na r Re po rt s 3(1950), 41-44. Nelson, E. 1. Regu la r pro babil ity measures on fun cti on spa c e, Anal. of Math . 69(1959), 630-643. Paley, R. E. A. C. and Wi en er, N. 1. Fourie r -tr a nsfo r ms in the comp le x domain , Amer. Math . Soc. Colloq ui u m Pub. 19(1934). Paley, R. E. A. C, Wi en er, N. and Zy gm und, A. 1. Note s on random fun cti on s, Math . Zeit 37(1933), 647-668. Park, C. (박철) 1. A gen erali ze d Paley -W i en er-Z y gmu nd int e g ral and its a p plica ti on s, Proc. Amer. Math . Soc. 23(1 9 69), 388-400. 2. On Fredholm tra nsfo r mati on s in Yeh-Wi en er spa c e, Pacif ic ] . Math . 40(1972), 173-195. Park, C. (박철) and Skoog , D. L. I. W ien er int e g ral s over the sets bounded by secti on ally conti nu ous barrie r s, Pacif ic ] . Math . 66(1976), 523-534. 2. Dist r i b u ti on esti m ate s of Barri er -crossin g pro babil ities of the Yeh-W ien er pro cess, Pac ific ] . of Math . 78(1978), 455-466. 3. A sim p le for mula for condit ion al W ien er int e g ral s with ap plica - tion s, Pacif ic ] . of Math . 135(1988), 381-394. 4. Condit ion al Yeh-W ien er int e g ral s wi th vecto r -valued condit ion in g
fun cti on s, Proc. Amer. Math . Soc. 105(1989), 450- 46 1 . 5. A Kac-Feyn rnan int e g ral eq u ati on for condit ion al Wi en er int e g r als, ]. Inte g r a l Eq u ati on s Ap pl. 3(1991), 411-427. 6. Samp le pa th -v alued condit ion al Yeh-W ien er int e g r als and a W ien er int e g ral equ ati on , Proc. Amer. Math . Soc. 115(1992), 479-487. 7. An op e rato r -valued Yeh-W ien er int e g ral and a Kac-Fey n man Wi en er int e g ral eq u ati on , Proc. Amer. Math . Soc. 120(1 9 94), 929-942. 8. Condit ion al W ien er int e g r als, Pacif ic ] . Math . 167(1995), 293- 31 2. 9. Boundary- v alued condit ion al Yeh-W i en er int e g ral s and a Kac- Feyr una n W ien er int e g ral eq u ati on , ]. Korean Math . Soc. 33(1996), 763-775. 10. Grid - valued condit ion al Yeh-W ien er int e g ral s and a Kac-Fey n man W ien er int e g ral equ ati on , ]. Inte g r a l Eq ua ti on s and Ap pl. 8(1996), 213-230. Park, C., (박철) Skoug , D. L. and Smolowi tz, L. 1. Fundamenta l the orem of W ien er calculus, Int. ]. of Math . and Math . Sc ien ces, 13(1 9 90), 443-452. Parth asarath y , K. R. l. Intr o duc tion to Probabil ity and Measure, MacMi llan , London, 1977. Parzen, E. 1. Sto c hastic Process, Holden-Day, San Franc isc o, 1962. Rees, C. S., Shah, S. M. and St an oje v ic, C. V. I. Theory and Ap pli ca ti on of Fouri er Analys i s, Marcel Dekker, New York, 1981 .
Roy d en, H. L. l. Re al Analys i s, New York, Macmi llan , 1989. Rudin , W. 1. Real and Comp le x Analysi s, New York, Mc Graw Hi ll, 1966. Schil de r, M. 1. Asym t ot i c for mulas for Wi en er int e g ral s, Trans. A mer. Math . Soc. 125(1 9 66), 63-85. Sir a o, T. 1. On the unif or m conti nu it y of Wi en er spa c es, ] . Math . Soc. Jap a n 6(1954), 332-335. Skorokhod, A. V. 1. On a ge nerali za ti on of a sto c hasti c int e g ral , Theory Prob. Ap pl. 20(1975), 219-233. Skoug , D. L. 1. A ge nerali ze d ILSTOW and Fey n man int e g ral s, Pacif ic ] . of Math . 26(1 9 68), 171-192. 2. Converses to measurabil ity the orems for Yeh-Wi en er spa c e, Proc. Amer. M ath . Soc. 57(1 9 76), 304-310. 3. The chang e of scale for mula and tra nslati on pa th o log y in Yeh- Wi en er spa c e, Ri v. Mat. Univ . Parma, 3(1977), 78-87. 4. Feyn m an int e g ral s inv olvi ng qu adrati c po te n ti als , sto c hastic int e - grat i on for mulas, and bounded varia t i on for fun cti on s of several varia b les, Supp le mento al Rendic o nti del Cir c olo Mate m ati co di Palermo, Serie s II , No. 17 (1987), 331-347.
Sunouchi 1. Harmonic analys i s and W ien er int e g ra ls, Tohoku Math . ]. 3(1 9 51), 187-196. Truman, A. 1. The Feyn m an map s and the W ien er int e g ra l, ]. Math . Plzys . 19(1978), 1742-1750 : erratu m , 20, 1832-1833. Varberg, D. E. 1. On Gaussia n measures eq u iv a lent to Wi en er measure, Trans. Amer. Math . Soc. 113(1 9 64), 262-273. Wi en er, N. 1. Generali ze d harmonic analys i s , Ac ta Math . 55(1930), 117-258. Woodward, D. A. 1. A ge neral class of line ar tra nsfo r mati on s of W ien er int e g r als, Trans. Amer. Math . Soc. 100(1961), 459-480. Yeh, J. 1. Wi en er measure in a spa ce of fun cti on s of tw o varia b les, Trans. Amer. M ath . Soc. 95(1960), 433-450. 2. Cameron-Martin tra nslati on the orem in the W ien er spa ce of fun c- tion als of tw o varia b les, Trans. Amer. Math . Soc. 107(1963), 409-420. 3. Or tho g o nal develop m ent of fun cti on als and relate d the orems in the Wi en er spa ce of fun cti on s of tw o varia b les, Pacif ic ] . Math . 13(1963), 1427-1436. 4. Ineq u ali ties and a lim i t the orem for cert ai n Wi en er int e g ral s, Proc. Amer. Math . Soc. 16(1965), 915-918. 5. Convoluti on in Fourie r -Wi en er tra nsfo r m, Pacif ic ] . Math . 15(1965),
731-738. 6. Dif fer enti ab il it y of samp le fun cti on s in Gaussia n pro cesses, Proc. Amer. Math . Soc. 18(1967), 105-108, Correctu m , 19(1 9 68), 843. 7. Ap pr oxim ate evaluati on of a class of Wi en er int e g ra ls, Proc. Amer. Math . Soc. 23(1969), 513-517. 8. Mi ni m al coeff icien ts in Holder condit ion s in the Wi en er spa ce, Proc. Amer. Math . Soc. 25(1 9 70), 385-390. 9. Sto c hastic Processes and the Wi en er Inte g r a l, Marcel Dekker, New York, 1973. 10. Inversio n of condit ion al exp ec ta t i on s, Pacif ic ] . Math . 52(1974), 631 -640. 11. Inversio n of condit ion al Wi en er int e g ral , Pacif ic ] . Math . 59(1975), 623-638. 12. Sto c hasti c int e g r al of L2-fu n cti on s wi th respe ct to Gaussia n pro cesses, Tb'hoku Math . ]. 27(1975), 175-186. 13. Transfo r mati on of condit ion al Wi en er int e g ral s under tra nslati on and the Cameron-Martin tra nslati on the orem, Tb'hoku Math . ]. 30(1978), 505-515. Yeh, J. and Hudson, W. N. 1. Transfo r mati on of the ge neraliz e d W ien er measure under a class of line ar tra nsfo r mati on s, Tohoku Math . ]. 24(1972), 423-433. Yoo, I. (유일) 1. Convoluti on in Fourie r -Wi en er tra nsfo r m on abstr a ct Wi en er spa ce, Rocky Mount. Math . J 25(1995), 1577-1587. Yoo, I. (유일) and Skoug , D. L. 1. A chang e of scale for mula for W ien er int e g ral s on abstr a ct Wi en er spa c es, Int. J Math . and Math . Sci. 17(1994), 239-248.
2. A chang e of scale for mula for Wi en er int e g ra ls on abstr a ct W ien er spa ce, II., ]. Kore an Math . Soc. 31(1994), 115-129. Yoo, I. and Yoon, G. J. (유일, 윤국중) 1. Chang e of scale for mulas for Yeh-W ien er int e g ra ls, Comm. Kore an Math . Soc. 6(1991), 19-26.
찾아보기 가산가법 성 counta b le addit ivi t y 522 가산과정 addit ive pro cess 538 가산교집 합 counta b le int e r secti on 220 가산집 합 counta b le set 285 가산합집 합 counta b le unio n 2 21 가우스과정 Gaussia n pro cess 270, 539 강한국한정 리 str o ng lim i t the orem 270, 275 거리보존 선형변환i some t r i c lin e ar tra nsfo r mati on 285 공분산 행 렬 covaria n ce matr i x 186, 533 공분산함수 covaria n ce fun cti on 47, 275 구간 int e r val 21, 101, 360 그램 _슈미 트 Gram-Schmi dt 방법 264 그레 이 브 정 리 Graves the orem 22 5 기 본 부분집 합 fun damenta l subset 210 내 적 inn er pro duct 167, 263 내측도 inn er measure 425, 523 노이 만 급수 Neumann serie s 477 다각형 함수 po lyg o nal fun cti on 352 단단한 측도 tigh t measure 425, 439, 526 단조수령정 리 monoto n e converge nce the orem 152, 312 단조족 monoto n e class 5 2 5 단조중가 po sit ive ly monoto n e 함수 375 대수 alge bra 521 두변수 위너 과정 tw o pa ramete r W ien er pro cess 491 두브 정리 Doob the orem 113 디 락 측도 Dira c measure 109 레비-하비랜드 반전정리 Levy -H avi la nd inv ersio n the orem 315
리만-스틸체스 적분 Rie m ann- Sti el tje s int e g ra l 167, 378 리츠 볼록정 리 Rie s z convexit y the orem 529 리 프쉬 츠 조건 Lip sc hit z condit ion 67 밀도함수 densit y fun cti on 20, 531 모레 라 정 리 Morera's the orem 245 박스터 과정 Baxte r pro cess 297 보렐 6- 대 수 Borel a-alge bra 14 보렐족 Borel class 14 보렐 측도 Borel measure 14 부분구간 직선함수 piec ewi se lin e ar fun cti on 149, 364 부분구간 평 균 secti on al averag e 513 브라운 브리지 과정 Brownia n brid g e pro cess 353 브라운 운동과정 Brownia n moti on pro cess 54, 283, 538 사영 함수 pro je c ti on map 401 상측도 im ag e measure 73, 527 생성 spa n 16 서 로 독립 mutu a lly ind ep e ndent 潟 서로 절대 연속 mutu a lly absolute l y conti nu ous 35 순환관계 recurrence relati on 212 스코그 정 리 Skoug the orem 444 아벨합 가능 Abel summable 225 아벨합산 항등식 Abel summati on ide nti ty 151 약한 수령 weakly converge nce 78 에 르미 트 계 수 Hermi te c oeff icien t 21 s 에르미트 다항식 Herm ite po lyn o mi al 205 에르미트 함수 Hermi te f unc ti on 205, 207, 213
n- 평 행 선 정 리 n-pa rallel lin e s the orem 420 역 관계 reci pr ocal relati on 227, 239 역 푸리 에 변 환 inv erse Fourie r -tr a nsfo r m 209, 309 역측도 정 리 converse measurabil it y the orem 41, 365, 415 영집합 zero set 65 예 - 위 너 공간 Yeh- W ien er spa ce 360 예-위너 과정 Yeh-W ien er pro cess 491 예-위너 작용소 적분 op er ato r -valued Yeh-W ien er int e g ral 461 예 -위 너 적 분 Yeh-W ien er int e g ra l 366 예-위너 조건적분 condit ion al Yeh-W ien er int e g ral 490 예 - 위 너 측 도 가능한 집 합 Yeh- W i en er measurable set 362 예 -위 너 측 도공간 Yeh-W ien er measure spa ce 362 0- 집합 221 Os- 집합 220 완비정규 직교집합 com p le t e orth o normal set 167, 20s 완전함수 enti re fun cti on 227, 230, 447 의 측도 oute r measure 52 3 위 너 곡선 W ien er pa th 14 위 너 공간 W ien er spa ce 14 위 너 과정 W ien er pro cess 47 위 너 작용소 적 분 op e rato r -valued W ien er int e g ral 456 위 너 적 분 W ien er int e g ral 41 위너 적분공식 W ien er int e g ral for mula 179 위 너 적 분방정 식 W ien er int e g ral eq u ati on 464 위너 조건적분 condit ion al W ien er int e g ral 322 위너 조건적분의 레비형 반전공식 Levy type inv ersio n for mula 325 위 너 조건적 분의 반전공식 inv ersio n for mula 326 위너 조건적분의 변환정리 tra nslati on the orem 346 위 너 측도 W ien er measure 29 위 너 측도 가능한 집 합 W ien er measurable set 29
위너 측도공간 W i ener measure spa ce 23, 29 유계 변동 bounded varia t i on 371 유한차원 분포 fini t e dim ensio n al dis t r i b u ti on 103 이차 변동 qu adrati c varia t i on 71, 385 이 차 전 변동 qu adrati c tot a l varia t i on 71 일관성 조건 consis t e n cy condit ion 103 일반화된 브라운 운동과정 ge neraliz e d Brownia n moti on pro cess 282, 540 일 반화된 역 측도 정 리 ge neraliz e d converse measurabil ity the orem 441 절대 연속 absolute l y conti nu ous 376 접 합 convoluti on 93, 248 정 규분포 normal dis t r i b u ti on 534 정규 조건분포 reg ula r condit ion al dis t r i b u ti on 310 정규 직교화 방법 orth o normaliz a ti on 233 정규측도 regu la r measure 37, 525 정규화된 normali ze d n 차 에르미트 함수 207 정규화 정리 regu la rity the orem 242, 256 정 칙 non-sin g ula r 186 제 한구간 restr ict i on int e r val 21, 360 제한점 restr i c tion po in t 21, 360 조건 기대값 condit ion al exp e c tat i on 309, 310 조건 기대값에 대한 반전정리 inv ersio n the orem 319 조건확률 condit ion al pro babil it y 309 준다면체 함수 qu asi- po lyh edric fun cti on 505 준대수 sem i-a lge bra 21, 361, 521 준불변 qu asi- inv ari an t 15 지 수형 exp on enti al type 447 지수형의 완전함수 enti re fun cti on of exp o nenti al type 231, 248 채프만_콜꾸 ―구 쿠프 방정식 Chap m an-Kolmog o rov eq u ati on 23
척 도불변 가측집 합 scale-in v aria n t measurable set 72, 390 척 도불변 가측함수 scale-in v aria n t measurable fun ct ion 95, 396 척도불변 거의모든 scale-i n varia n t almost everyw here 73, 391 척 도불변 영 집 합 scale-i n v aria n t null set 72, 390 최소표시 mi ni m al repr e senta t i on 25 측 도 measure 5 2 2 측 도가능변환 measurable tra nsfo r mati on 309 카라테 오도리 확장정 리 Carath e odory exte n sio n the orem 28 카메 룬 - 마틴 변 환정 리 Cameron- M artin tra nslati on the orem 147, 173, 383 칵 _ 파인 만 공식 Kac-F e y n man for mula 340 코흐러 정 리 Kochler the orem 443 콜모고로프 일관성 정 리 Kolmog o rov consis t e n cy the orem 104 콜모고로프 정 리 Kolmog o rov the orem 101, 118, 536 특성 함수 characte r is t i c fun cti on 532 파시 발 관계 Parseval's r elati on 167, 247 팰리-위너 정리 Paley -W i en er the orem 160, 382 팰리-위너 - 지그문드 정리 Paley- W i en er-Zy gmu nd the orem 179 팰 리 - 위 너 -지 그문드 적 분 Paley -W i en er-Zy gmu nd int e g ral 166, 407 평 균극한 lim i t in the mean 259 평균수령 L2- 노름 수령 239, 259 평 균연속 mean conti nu ous 230 평균지수형 mean exp o nenti al type 230 평 균함수 mean fun cti on 47, 275 표본공간 samp le spa ce 538 표본함수 samp le fun cti on 538 푸리에-에르미트 계수 Fourie r -Hermi te coeff ici e n t 217 푸리에-에르미트 급수 Four i er-He rmit e seri es 219
푸리 에 -예 -위 너 변환 Fourie r -Yeh-W ien er tra nsfo r m 446 푸리에-위너 변환 Fourie r -W ien er tra nsfo r m 226, 258 푸리 에 -위 너 변 환의 집 합 convoluti on in Fourie r -W ien er tra nsfo r m 248 푸리에-위너 적분방정식 Fourie r -W ien er int e g ra l eq u ati on 238 플란세 렐 관계 Plancherel's r elati on 235, 247, 258 하르톡스 Ha rt o g s 의 정 규화 정 리 reg u larit y the orem 242 한 직선 정 리 one line the orem 41s 확률과정 sto c hasti c pro cess 538 확률 벡 터 random vecto r s 31 확률변수 random varia b le 531 확률분포 pro babil ity dis t r i b u ti on 489, 531 확률수령 converge nce in pr obabil ity 290 확률적분 sto chasti c int e g ral 2ss, 302, 307 확률측도공간 pr obabil it y measure sp a ce 31 회 전변환 rota t i on ss, 398 횔더 연속 Holder conti nu ous 60
장건수 연세대학교 수학과와 동대학원을 졸업 하고 미국 네브라스카 대학교에서 박사학위를 받았다 . 이탈리아 국립과학연구소 방문연구원. 네브라스카 대학교 방문교수, 일본 나고야 대학교 객원교수. 연세대학교 교무처장을 역임했으며 현재는 대한수학회 회장. 교육부 학술진홍위원 . 교육과정 심의위원. 연세대학교 수학과 교수로 재직중이다. r 수치해석학 』 『 파인만적분론 』 등의 저서와 『 복소함수론 』 r 공업수학 ,1 등의 역서 그리고 r 함수공간 작용소 해석적분』 외에 70 여편의 논문이 있다. 위너적분론 대우학술총서 자연과학 130 1 판 1 쇄 펴냄 1998 년 12 월 25 일 지은이 장건수 펴낸이 박맹호 펴낸곳 (주)민음사 출판등록 1966. 5. 19 제 16-4 90 호 서울특별시 강남구 신사동 506 대표전화 515-2000, 팩시밀리 515-2007 값 33,500 원 © 장건수 1998 해석학, 적분학 KDC/414.3 Printed in Seoul, Korea ISBN 89-374-3630-2 94410 89-374-3000-2 (세트)
대우학술총서사언과야 1
1 소립자와 게이지 상호작용 김진의 2 동력학특론 이병호 3 질소고정 송승달 4 상전이와 임계현상 김두철 5 촉매작용 진종식 6 뫼스바우어 분광학 옥항남 7 극미량원소의 영양 승정자 8 수소화붕소와 유기봉소 화합물 윤능민 9 항생물질의 전합성 강석구 10 국소적 형태의 Ati ya h-sin ge r 지표이론 지동표 11 Mucop ol y saccha rid es 의 생화학 및 생물리학 박준우 12 천체물리학 홍승수 13 프로스타글라딘 합성 김성각 14 천연물화학연구법 우원식 15 지방영양 김숙희 16 결정화유리 감병호 17 고분자에 의한 화학반응 조의환 18 과학혁명 김영식 19 한국지질론 장기홍 20 정보이론 한영열 21 원자핵반응론 정운혁 22 파괴역학 김상철 23 분자궤도 이론 이익춘 24 반응속도론 정경훈 25 미분위상수학 이현구 26 자기공명방법 조성호 27 플라스마 물리학과 핵융합 최덕인 28 천문관측과분석 이시우 29 석탄에너지변 환 기술 김상돈 30 해양미고생물학 백광호 31 편미분방정 식 론 김종식 32 대통일 이론 소광섭 33 금속전자계의 다체이론 김덕주 34 액정중합체 진정일 35 복합재료 권숙인 36 단백질 생합성 박인원 37 한국의 광물종 김수진 38 일반상대론 이철훈 39 레이저 광산란 분광학 김종진 40 복소다양체론 김상문 41 역학적 연구방법 김일순
42 핵구조물리학 만동필 43 후리에 해석과 의미분 작용소 김도한44 한국의 고생물 이 하영 45 질량분석학 김명수 46 급변론 박대현 47 생체에너지 주충노 48 리이만 기하학 박을룡 49 군표현론 박승안 50 비선형 편미분 방정식론 하기식 51 생체막 김형만 52 수리분류학 고철환 53 찰스 다윈 정용재 54 금속부식 박용수 55 양자광학 이상수 56 효소반응 속도론 서정현 57 화성암 성인론 아민성 58 확률론 구자홍 59 분자분광학 소현수 60 벡터속 이론 양재현 61 곤충신경 생리학 부경생 62 에너지띠 이론 모혜정 63 수학 기초론 김상문 64 신경과학 김승업 박찬옹 65 BCH 부호와 Reed- Solomon 부호 이만경 66 양자 전기역학 김영덕 67 군환론 박 재 걸 68 대수기하학 조영현 69 양자장이론 이 재 형 70 해양오염과 생태계 심재형 71 비기체 연소합성 ( SHS ) 여 철현 72 크로마토그래피 이대운 73 곤충의 사회행동 추종길 74 동위원소 지질학 김규한 75 X- 선 결정학 김양 77 통계역학 조순탁 78 고분자의 구조와 형태학 이석현 79 LC 에 의한 광학 이성질체의 분리 현명호 80 신경전달물질 서유헌 81 발생과 유전자 밭현 이양림 82 스테로이드 화학 김완주김득준 83 다체계론 엄정인 84 중 핵 반응론 김병택 85 비가역 열역학 이철수 86 등각장론 입체호 87 방사선생물학 남상열 88 석유지질학 이용일 89 베르누이 시행의 통계적 분석
배도 선김성 인 90 신경세포생리학 강만식 91 생리활성을 가진 C-P 화합물의 화학 김 용 준 강익중 92 생물유기화학 서정헌 93 조직배양 김승 업 94 유기전이금속화합물 조 남숙 외 95 실내환경 과학 김윤 신 96 유한요소법 정상권 97 대수적 위상수학 우무 하 김재 룡 98 파인만 적분론 장건수 99 응용 미생물학 박무영 100 리보플라빈 이 상선 101 노화 김숙희 김 화 영 102 애트릭스 격리분광학 정가 호 103 신경계 조직배양 김승 업 104 지구화학 김규한 105 은하계의 형성과 화학적 진화 이시우 외 107 액체의 미립화 아상 용 108 점토광물학 문희수 109 중국수학사 김용운 김 용 국 。 。 111 로렌츠 기하학 김 종 철 112 몬테카 를 로 방법의 물리학적 응용 김재삼 113 천체역학 최규홍 114 확 를 마분방정식 김재희 115 전자현미경의 원리와 응용 이정용 116 미세구조유체 흐름의 원리 양승만·박오옥 117 고분해능 분자분광학 이 상국 118 생명체의 신호전이 채쾌 의 119 고체추진제 노만균 120 군과 조화해석 계 승혁 121 인공 수정과 수정란 이식 임경순 의 122 인산이노시 를 정 성기 • 장영테 123 탄화수소의 산화반응 이 규 완 124 매듭톤 고기형 • 진교텍 125 빛의 양자이론 이해웅 126 양자유 체 'He 업정 인 127 Li e 군의 표현론 양 재현 128 작용소론 노재철 129 조화적분론 박진석