
김재삼 서울대학교 물리학과 졸업 캘리포니아 공과대학 이론물리학 박사 워싱턴 대학, 뉴욕 주립대에서 대통일 이론을, 존스홉킨스 대학에서 우주론을, 브리검영 대학에서 상전이 이론을, 캘리포니아 공대에서 병렬컴퓨터 등을 연구 현재 포항공과대학 물리 학과 교수 저서 『 파인만씨 농담도 정말 잘하시네요 』 『 전산물리학 』 Solvin g Problems on Concurrent Processors
몬테카를로 방법의 물리학적 응용 
 몬테카롤로 방법의 물리학적 으0 요O
몬테카롤로 방법의 물리학적 으0 요O
사랑하는 내 가족들  정현전, 김기범, 김소아에게 헌정함
정현전, 김기범, 김소아에게 헌정함
머리말 이 한권의 책이 나오기까지 우여곡절이 참 많았다. 해의에 나 가서 큰 도서관과 고장이 잘 나지 않는 컴퓨터가 있는 대학에 한 일년쯤 머무르면서 마음껏 파고둘면서 좀더 시간을 둘여 충실하 게 저술하고 싶었다. 하지만 착수한 지 벌써 6 년 이상이 흐르면 서 매년 방학 때마다 저술한다고 연구실에 틀어박혀 가족들의 발 울 묶고 다른 연구에도 몰두할 수가 없게 되어 더 이상 시간을 지체할 수가 없게 되어 주섬주섬 마무리짓게 되었다. 몬테카를로 방법과 컴퓨터는 원자핵 물리학자들의 필요에 의해 탄생되었다고 해도 과언이 아니다. 이차 대전중 맨해튼 사업에서 핵분열 과정을 모사하는 데에는 많은 수치계산이 필요했는데 수 십 명의 기능원들이 기계식 계산기를 가지고 전력을 다해 계산하 였다. 전쟁 후 전자식 계산기가 개발되자 맨 먼저 이것을 사용한 사람들은 바로 이들 원자핵 물리학자들이었다. 페르미는 이미 1930 년대에 무작위 표본추출에 의해 원자로에서 중성자의 운송을 기술하는 것이 효율적이라는 것을 간파하였고 이 방법을 사용하여 많은 실험 데이터를 기적처럼 예측해냈다. 하지만 페르미는 이 아이디어를 논문화시키지 않았다. 최초의 전 자식 계산기인 ENIAC 의 완성을 기념하는 학회에서 울람은 이 기계를 중성자 운송에 사용하는 방법을 구상하였고 폰노이만은 울람의 아이디어를 죽각적으로 수용하여 자신도 난수 생성 방법 에 지대한 관심을 가지며 많은 기여를 하였다.
몬테카를로 방법이 몇 가지 문제를 기적적으로 해결해 내는 것 울 보자 이 분야는 짧은 기간 내에 아주 활발해지게 되었다• 1949 년에는 첫번째 몬테카를로 학회가 로스앨러모스에서 개최되 기에 이르렀다. 주요 응용 분야는 방사선 운송과 통계역학 체계 였다. 초창기의 업적들은 Alder, Fernbach, Ro t enber g가 편집한 Meth o ds in Comp ut a t i on al Phys i c s , (Academi c, 1963) 에 잘 요약 되어 있다. 대학에서 전통적인 물리 교육을 받은 대부분의 학생들에게 확 률 개념은 생소하다고 본다. 따라서 1 장에서 3 장까지는 확률이론 의 기초 및 표본추출 방법들에 대해서 논의한다. 4 장에서는 기초 적 몬테카롤로 적분 방법을 논하고 5 장에서는 마르코프 과정에 대해서 그리고 6 장에서는 다차원 몬데카롤로 적분 방법에 대해서 논의한다. 요즈음은 물리연구 분야가 너무 세분화되어, 통계역학과 고에 너지물리학, 두 가지 주요 응용 분야를 모두 다 하는 사람들은 격자 게이지 이론가들밖에 없다. 어느 한 분야에 초점을 맞추면 독자층이 너무 엷어지게 되어 이 단행본의 초점을 어디에다 맞추 어야 할지에 대해서 많은 고심을 하다가 한 지붕 두 가족 개념을 생각하게 되었다. 응집물질 물리에 관심을 가전 사람은 7 장에서 아이성계의 모사 방법을 배운 다음, 8 장의 재규격화 이론과 임계 현상을 공부하면 될 것이다. 여기서 각자의 연구 분야로 들어가 는 것은 별로 어렵지 않다. 방사선 운송에 관심울 가전 사람은 6 장과 7 장을 건너뛰고 9 장에서 방사선 운송 모사 방법의 기초를 익힌 다음에 10 장에서 광자와 전자의 운송에 대해 공부하면 될 것이다. 여기서 독자는 상대론적 양자역학에 들어서게 되는데 옹 집물질 물리가 과잉 강조되고 있는 요즈음 대부분의 물리학도들 은 배우지도 않는 분야이지만 이 분야에 종사하는 적지 않은 사
람들은 받아들여야 할 주제이다. 중성자의 운송울 기술하려면 또 하나의 장을 열어야 하는데 그러기에는 너무 벅찼고 원자로의 문 제에서는 다른 공학적인 문제들도 비중을 많이 차지하므로 그냥 남겨두었다. 방대한 양의 지식을 모으는 데는 많은 저서들 , 평론들을 참조 할 수밖에 없는데 각 장마다 각각 다른 세트들을 참조해야 했다. 초기 에 는 고전적 인 교과서 로 평 이 나있는 Ha ITIIl} ersle y와 Handscomb 의 Monte Carlo Meth o ds (Meth u en 1964) 를 많이 참 조했는데 너무 간략하게 다루고 있는 부분이 많았다. Kalos 와 Wh it lock 의 Monte Carlo Meth o ds (Wi ley , 1986) 도 때 때 로 참조했 다. 해의에 나가 있는 지인들에게 부탁하여 힘들게 자료를 복사 받아도 거기에서 인용되는 다른 평론이나 연구 논문을 구할 수가 없는 경우가 많아서 애를 먹었다. 조카인 김승범 군이 영국에서 평론, 연구 논문들을 많이 보내주었는데 Me y er 가 편집한 Sy m p os iu m on Monte Carlo Meth o ds (Wi ley , 1956) 을 입 수 하 고 나서부터는 저술의 속도가 매우 빨라졌다. 2 장의 균일분포 난수에 관해서는 Knu th의 Ar t of Comp u te r Prog ra mmi ng , vol. 2 (Addis o n-Wesley, 1981) 을 많이 참조했다. 4 장, 5 장, 6 장, 7 장에 대해서는 참고문헌들을 많이 구할 수 있어 서 주제를 충분히 소화하여 내 나름대로 저술할 수 있었다. 8 장 을 쓰면서 임계현상에 관해 얼마만큼 논의해야 될지를 정하지 못 해 그때문에 지간이 많이 걸렸다. F i sher 의 평론, 김두철의 『 상 전이와 임계현상 』 (민음사, 1983) 이 많은 도움이 되었고 그밖에도 많은 문헌들을 참조했다. 9 장은 그럭저럭 넘어갔으나, 10 장에 와 서 또 한번 입자의 상호작용에 대해서 얼마만큼 논의해야 될 지 를 두고 많은 고심을 했다. 한 벌을 완전히 썼다가 또다시 크게 바꾸게 되었는데 전자의 상호작용에 대해서는 EGS4 매뉴얼을
많이 참조했다. 원래는 양자역학에의 응용과 격자 색깔역학에 대 해서도 논의하고 병렬 몬테카를로 알고리즘에 대해서도 심도 있 게 저술할 생각이었으나 주변 상황에 밀려 더이상 시간을 끌 수 없었다. 용어는 한국물리학회에서 1995 년에 편찬한 『 물리학 용어집』과 한국통계학회에서 편찬한 『 통계용어사전 』 (자유아카데미, 1987) 을 많이 참조했다. 주제가 연구에 직결되는 만큼, 참고문헌들을 되 도록 많이 인용하려고 하였다. 본 저술의 설명이 불충분할 경우 에 도움이 되리라고 본다. 하지만, 미비한 국내 도서자료에 주로 의존하다보니 빠뜨린 것들도 많았으리라고 생각되며 일부는 인명 밖에는 기재하지 못한 경우가 있었다. 의국인명은 잘 알려진 학 자들은 한글로 썼으나 덜 알려진 사람들은 원명으로 기재했다. 끝으로 삽화들을 그려준 내 학생들, 채윤상과 김정준에게 고마 움을 표한다. 특히 채윤상 군은 2 장의 표 2.5 난수 데스트롤 만 들었고 스펙트럼 데스트 코드도 썼으며 부록에 수록된 균일분포 난수 생성 루틴들을 수집하고 일부는 자신이 직접 썼다. 김정준 군은 7 장의 그림들을 그리기 위해 내가 짠 프로그램들을 디버깅 해 주었다. 몬테카를로 방법에 관해 저술할 것을 종용해 준 권숙일 교수에 게 감사를 드린다. 1 장과 2 장을 쓰면서 포항공대 수학과 이의용 교수의 도움을 많이 받았고 7 장과 8 장을 쓰면서 서울대학교의 이 구철, 김두철 교수의 도움을 받았다. 탈고 단계에서 지도와 편달 을 해준 부산대학교 홍낙형, 이남철 교수, 포항공대 전자과의 권 오대 교수에 게 고마움을 표한다. 1996 년 12 월 경 주 불국동에 서 김재삼
몬테카를로 방법의 물리학적 응용
차례 머리말 1 제1장 확률 이론의 기초 13 1.1 확률 변수와 분포 함수 13 1.2 기대값과 편차 16 1.3 상관관계 18 1.4 체바셰프의 부등식과 큰 수의 법칙 20 1.5 중심 극한 정리 21 참고문헌 24 제2장 확률 변수의 생성 25 2.1 균일 확률 변수의 생성 26 2.1.1 선형 합동적 방법 262.1.2 피보나치 수열 35 2.1.3 Tausworthe의 레지스터 자리이동 방법 37 2.1.4 빌려빼기 방법 38 2.1.5 난수열의 개선 방법 39 2.2 의사 난수의 확률론적 시험 41 2.2.1 카이평방 시험 42.2.2 콜모고로프-스미르노프 시험 442.2.3 경험적 시험들 46
2.2.4 스펙트럼 테스트 54 2.3 정해진 확률 분포에 의한 확률 변수의 생성 방법 612.3.1 역변환 방법 61 2.3.2 거절-허용 방법 63 2.3.3 합성 방법 68 참고문헌 73 제3장 대표적인 분포 함수들 75 3.1 이항분포 75 3.2 기하적 분포 76 3.3 푸아송 분포 78 3.4 감마 분포 80 3.5 지수적 분포 83 3.6 정규 분포一가우스 분포 85 3.7 코시-로렌츠 분포 92 3.8 베타 분포 93 3.9 와이블 분포 95 3.10 카이평방 분포 96 3.11 학생의 t-분포 97 참고문헌 98 제4장 몬테카를로 적분 99 4.1 서론 99 4.2 직설적 방법 101 4.3 편차 감소 기법 1054.3.1 중점적 방법 108
4.3.2 제어 함수 방법 112 4.3.3 단층적 방법 116 4.3.4 대조 방법 123 참고문헌 128 제5장 마르코프 과정과 응용 129 5.1 마르코프 과정 129 5.1.1 마르코프 사슬의 예 131 5.1.2 마르코프 사슬의 전이확률의 성질 134 5.1.3 배위의 성질-동등성, 주기성, 회귀성, 에르고드성 136 5.1.4 마르코프 사슬의 불변 분포 139 5.2 선형 방정식에의 응용 140 5.3 적분 방정식에의 응용 149 5.3.1 적분 변환 149 5.3.2 프레드홀름 제이종의 적분 방정식 151 5.3.3 예제들 154 5.3.4 실용적인 방법들 160 참고문헌 162 제6장 다차원 몬테카를로 적분 165 6.1 거절 방법 166 6.2 유동적 방법 168 6.2.1 유동적 단층 방법 169 6.2.2 유동적 중점 방법 1696.2.3 DIVONNE 알고리즘 174
6.2.4 순환적 단층 방법 177 6.2.5 다차원 적분 알고리즘들의 비교 181 6.3 중점적 방법과 마르코프 과정 184 6.4 메트로폴리스 방법 186 참고문헌 194 제7장 이차원 아이싱 모델 1957.1 서론 195 7.2 정확한 해석적인 해 200 7.3 몬테카를로 시뮬레이션 205 7.3.1 서론 205 7.3.2 중요 표본 추출—메트로폴리스 방법 206 7.3.3 경계 조건 210 7.3.4 초기 배위의 선택 214 7.3.5 초기 열적 완화 214 7.3.6 물리량의 측정 218 7.3.7 유한크기 분석 224 7.3.8 임계감속 230 참고문헌 232 제8장 재규격화 방정식과 임계현상 235 8.1 임계현상과 축척 법칙 235 8.2 카다노프의 구획 스핀 방법 241 8.3 란다우 이론 244 8.4 재규격화 군 방정식 2478.4.1 개요 247
8.4.2 일차원 아이싱 모델 250 8.4.3 재규격화 군 변환식의 계산 방법 253 8.5 재규격화 군 부동점과 임계지수 255 8.6 안정적 부동점과 상전이의 연속성 260 8.7 대칭성과 보편성 계보 262 8.8 몬테카를로 방법 263 8.8.1 Ma의 방법 263 8.8.2 Swendsen의 방법 268 8.8.3 임계점 찾기 272 8.8.4 문제점들 275 참고문헌 276 제9장 운송 현상의 모사방법들 279 9.1 서론 279 9.2 유사 방법 282 9.2.1 서론 282 9.2.2 유사 방법의 개요 283 9.2.3 생성원 287 9.2.4 반응점의 자유 경로의 추출 290 9.2.5 반응 후의 방향 292 9.2.6 입자의 소멸과 생성 294 9.2.7 물리량의 측정 294 9.3 비유사 방법 297 9.3.1 흡수 억제 방법 298 9.3.2 러시아 룰렛 3009.3.3 분열 방법 300
9.3.4 지수 변환 방법 301 9.3.5 강제 충돌 방법 302 9.4 볼츠만 운송 방정식 304 9.4.1 개요 304 9.4.2 몬테카를로 방법에 의한 해법 307 참고문헌 310 제10장 광자와 전자의 운송 313 10.1 서론 313 10.2 원자로부터의 산란에 관한 정확한 공식 315 10.3 원자의 형태 인자 318 10.4 광자의 상호작용 322 10.4.1 콤프턴 산란 322 10.4.2 광전 효과 330 10.4.3 쌍생성 334 10.5 전자의 상호작용 345 10.5.1 전자-전자의 산란 345 10.5.2 양전자-전자의 산란 347 10.5.3 쌍소멸 350 10.5.4 제동 복사 354 10.5.5 전자의 다중 산란 360 10.5.6 연속적 에너지 손실 365 참고문헌 366부록
A 균일분포 난수 생성자 371 A.1 난수 생성자 373 B 몬테카를로 적분 374 B.1 C 프로그램 376 B.2 FORTRAN 프로그램 379 찾아보기 385제 |장 확률 이론의 기초 1. 1 확률 변수와 분포 함수 주사위를 던졌을 때 나오는 수라든가 학생들의 시험 성적, 가 스 안의 분자의 순간 속도, 또는 가이거 계수기의 소리 또는 원 자로 내의 중성자의 수 같은 것들은 확률 변수의 예들이다. 확률 변수는 정해진 구간 내에서 값을 가지지만 똑같은 조건에서 여러 번 시도를 해도 구체적으로 어떠한 값이 나오게 될지를 사전에 미리 알 수 없다. 탄도체 문제에서 탄환의 낙하 지점은 바람의 영향을 무시하면 초기 조건에 의해 정확히 예측할 수 있지만 불 규칙적인 바람의 영향울 고려하면 확률적으로 밖에는 예측할 수 없다. 확률 변수의 값을 정확하게 예측할 수가 없기는 하지만 그 값 이 나오는 양상은 각각의 확률 변수에 대해 확정적으로 정의된 다. 확률 변수는 확률 밀도 함수 또는 확률 분포 함수에 의해 규 정된다. 확률 변수 X가 구간 (x, x+dx) 사아에 값을 가지게 될 확률을 다음과 같이 정의할 수 있다.
p(x ) dx=[x
의하여 표본추출을 할 경우 균일 분포 확률 변수를 [Px(x)=1] 변환하여 원하는 분포를 가지게끔 하는데 매우 유용하게 응용이 된다. 실제적인 상황에서는 확률 변수가 다차원 벡터, (XI, x2, …) 인 경우가 많다. 논의를 간단하게 하기 위하여 이차원인 경우에 국한시키기로 하자. 두 개의 확률 변수들 (X1, Xz) 의 동시 확률 밀도 함수(j o i n t pro babil it y densit y fu nc ti on) 를 식 (1. 1) 과 비슷하 게 정의할 수 있다. Px,.x.(xi, xz)dx1dx2=[x1
Y1 =/1 (x1, X2) , Y2=/2 (x1, X2) (1.1 1) 와 같이 주어진다고 하자. 또한 이 확률 변수들의 정의구간들 내 에서 x 의 y에 대한 J acob i an 이 존재한다면, 죽 j= 莘oy1 요oy2 (1.12) @oy1 호oy2 이 정칙 함수로서 정의된다면 그 역함수들이 존재할 것이므로 x1=F1(Yr , Y2), x2=F2(Y1, Y2) (1.13) 라고 표기하기로 하자. 그러면 이들 확률 변수들간의 기본 변환 법칙은 PY,, Y2 (yi, Y2) = I J IPx,,x2 (F1 (yi, Y2) , F2 (yi, Y2) ) (1.14) 에 의해 주어진다. 일차원의 경우처럼 주어전 p Y1,Y2 에 대해서 F;(yi , Y2) (i=l, 2) 들을 찾아내기는 매우 어려워 몇 가지 트-, 조-r- 한 경우를 제의하고는 역변환 방법을 적용하기는 어렵다. 1.2 기대값과 편차 밀도 함수 p (x) 를 가지는 확률 변수의 함수 f (x) 의 기대값 (exp ec ta t i on value) 은 구간 (a, b) 에서의 평균값으로서 다음과 같이 정의된다. E( f) =ia bf (x )p ( x) dx (1.15)
위 식의 특별한 경우로서 X 가 구간 (a, b) 에서 균일하게 분포 되어 있다고 하면 p(x ) =1/(b-a) 가 되어 기대값은 대수적 평 균값이 된다. E (/) = ~1°b / (x) dx (1.16) 함수 f (x) 의 분산 (var i ance) var(/) 또는 6었 근 다음과 같이 정의된다. var(/) =E([/— E ( f) ]2) =Ja b[f ( x) —EU ) ]2p (x ) dx (1.1 7) 분산의 평방근을 표준편차 (6f : sta n dard dev i a ti on) 라고 부른다. 함수 f (x) 의 비틀림 (Skewness) Skew(/) 와 뾰족도 (Ku rt os i s) Kur t{/)는 각각 다음과 같이 정의된다. Skew{/) =E([.f_ —:f(f) 『)=i b[ f (x) ;fE( f) ]3p ( x)dx (1.18) Kurt( f) =E([~) 『)내 =ib[f ( x) ;fE ( f) ]4p (x ) dx_3 (1.19) 기대값은 확률이 가장 큰 지점, 표준편차는 확률이 가장 큰 지 역의 폭, 비틀림은 기대값을 중심으로 한 확률 변수의 좌우 대칭 성, 뾰족도는 기대값 주위에 확률 변수가 몰려 있는 정도 등을 나타내 주어 확률 분포 함수가 무엇이든간에 상관없이 그 확률 변수에 대해, 다시 말하면 그 확률 분포에 대해서 어느 정도 윤 곽을 준다고 볼 수 있다. 그립 1. 1 을 참조하면 이들의 의미를 직 관적으로 이해하는데 도움이 될 것이다.
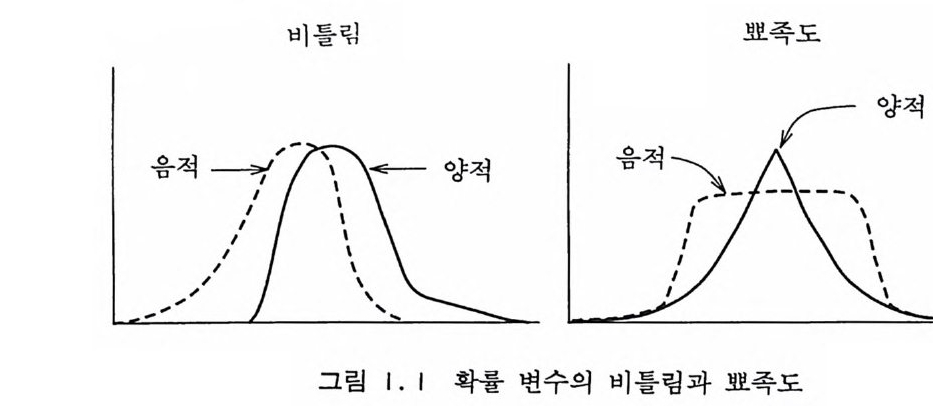 비 틀 링 뾰족도
비 틀 링 뾰족도
1.3 상관관계 우리는 종종 두 개의 확률 변수들 X 와 Y 가 서로 독립적인지 또는 그들 사이에 상관관계가 있는지에 대해 관심을 가지게 된 다. X 와 Y 의 평균값들을 각각 X 와 Y 라고 하면 상관관계를 측정하는 양으로서 공분산 (cova ri ance) 은 다음과 같이 정의된다. Cov(X, Y) =E([X-X][ Y-Y ]) (1. 20) =E(XY)-E(X)E(Y) X와 Y 가 독립적이면 E(XY)=E(X)E(Y) 이므로 Cov(X, Y)=O 이다. 하지만 그것의 역은 반드시는 성립하지 않아서 Cov (X, Y)=O 가 성립한다고 해도 X, y가 확률적으로 독립적이 라고 말할 수는 없다. 또한 상관 계수를 다음과 같이 정의한다. p= ✓ vaCro(vX()X ·,v aYr() Y) (1. 21 ) 이것은 언제나 士 1 사이에 놓이고 p =O 이면 X와 Y 가 서로 독
립적이고 p >O 이면 양적으로 상관되고 p
1.4 체비셰프의 부동식과 큰 수의 법칙 체비셰프 (Cheb y shev) 는 확률 변수의 평균값으로부터의 거 리가 임의의 작은 수 c 보다 크거나 같을 확률은 분산을 궁으로 나눈 것보다 작거나 같음울 증명했다. 확률 변수 X 의 평균값이 X 이 고 그 분산이 궁이라고 하면 임의의 작은 수 e 에 대해 다음과 갑은부등식 P[I X_Xl~c] 三군 /€2 (1. 24) 이 일반적으로 성립한다. 체비셰프의 부등식은 이보다 좀더 일반적인 부등식으로부터 유 도된다. X가 음이 아닌 확률 변수라고 하면 다음과 같은 부동식 P[X ~ c] ~ E (Xa) I€a (1. 25) 이 성립하는데 여기서 e 과 a 는 양의 실수아다. 많은 경우 우리는 어떤 사건이 일어날 확률이 1 에 얼마나 가깝 느냐 하는 데에 관심이 쏠리는데 큰 수의 법칙 (Law of Large Numbers) 은 이런 경우 중요한 의미를 가전다. 이 법칙은 두 가 지 형태가 있는데 그 첫번째는 체비셰프의 법칙이다. n 개의 상 호 독립적인 확률 변수 X1, X2, …, Xn 이 주어지고 그 기대값 둘이 Xi, X2, …, Xn 이며 그들의 분산들의 상한이 b2 이라고 하 자. 또한 그 기대값들의 대수적인 평균값을 x 라고 하자. 체비셰 프의 부등식 (1. 24) 를 여기에 적용하면 다음과 같은 부등식을 얻 을수있다. P[I ~ t X;-x l< c] 나 1-b2/(nc2) (1.2 6)
체비셰프에 의한 큰 수의 법칙이(이것을 큰 수의 약한 법칙이라 고도 부름) 의미하는 것을 말로 기술하면 n 을 충분히 크게 잡으 면 n 개의 상호 독립적인 확률 변수들의 기대값들의 대수적인 평 균값이 이돌 확률 변수들의 대수적인 평균값으로부터 C 보다 작 은 거리에 있을 확률을 1 에 원하는 만큼 가깝게 할 수 있다는 이 야기가 된다. 베르누이 (Bernou lli)는 큰 수의 법칙을 다른 형태로 기술했는데 이것은 체비셰프 법칙의 특수한 경우이다. 어떤 사건 E 가 일어 날 확률이 P 라고 하고 n 번의 독립적인 시도에서 사건 E 가 n1 번 만큼 일어났다고 하면 부등식 (1.24) 를 적용하여 P[I (n1/n)-p l
수 X들 을 측정한 결과 그 기대값들이 Xi, X2, …, Xn 과 같이 나 왔고, 이들의 분산들이 (Jf, 6 궁, …, 햐이라고 하자. 새로운 확률 변수 X를 X=X1+X2+ … +Xn 이라고 정의하고 또 하나의 확률 변수 Zn 을 Zn됴=~ (1. 28) 라고 정의하자. 그러면 Zn 은 근사적으로 정규 분포를 가지며 n - oo 인 국한에서 그 확률 분포 함수는 기대값이 0 이고 표준편차 가 1 인 정규 분포 함수가 된다. 따라서 Zn 이 두 개의 수 a 와 b 사이에 놓일 확률은 다음 식에 의해 주어진다. i뽀 P[a < Zn < b] ⇒ 言l 1fbbe xp ( —t2/ 2) dt (1. 29) 정리 |. . 2 동일한 분포 함수를 가지는 n 개의 독립적인 확률 변수들을 측 정한다고 하자. X 들의 공통적인 기대값을 x=E(Xi) , (i= l, …, n) 이라고 하고 또한 그들의 공통적인 분산을 a2=var(XJ , (i=l , …, n) 이라고 하자. 새로운 확률 변수 X를 X=~7=1 Xi 라고 정의하면 그것의 기대값은 E(X)=nx 이고 분산은 var(X) =na2 일 것이다. 또 하나의 확률변수 Zn 을 Zn=(X-nx)/Ina 라고 정의하면 Zn 은 근사적으로 정규 분포를 가지게 되고 n - oo 인 극한에서 그 확률 분포 함수는 기대값이 0 이고 표준편차 가 1 인 정규 분포 함수가 된다.
정 리 1. 2 를 P(X;=l) =P, P(X;=O) = (l-p) 와 같이 정의되 는 베 르누이 확률 변수에 대 해 서 적 용하면 DeMoiv r e-Lap la ce 정리를 얻는다. 죽 확률 변수 Zn=(X-np )I .fn iiCT-i;) 는 n ― ► CX)인 극한에서 정규 분포를 가진다. 식 (1. 29) 를 측정된 평균값 Yn=X/n 에 대한 밀도 함수로서 다시 써보면 迎p( Yn) \갈 ~ex p [-( :;言] (1.30 ) 이 된다. 따라서 n 이 커짐에 따라 확률 변수 Yn 은 기대값 x 에 아주 가까이 분포하게 되고 그 분산 또한 n 에 역비례해서 작아 질 것이다. 상기의 정리는 확률 변수 X 의 구체적인 성질에는 무관하므로 X 들이 각기 다른 어떠한 분포에 의한 확률 변수들이라고 할지 라도 상관없이 그들의 합은 n- ➔ oo 인 극한에서 정규 분포를 가 진다는 것을 의미한다. 따라서 중심 극한 정리의 적용 범위는 실 로 광범위하다. 중심 극한 정리는 몬테카를로 적분을 정당화시켜 주는 매우 유 용한 정리이다. 죽 측정 횟수 n 을 충분히 크게 취하면 원하는 기대값에 충분히 근접할 수 있으며 측정값의 편차는 l/{ ;에 비 례해서 줄어든다는 것을 의미한다. 다차원 적분에서 몬테카롤로 적분이 다론 어떠한 방법보다 더 정확한 답을 주는 원인은 근사 적분의 편차가 J下-에 반비례해서 줄어든다는 데에 있다.
참고문헌 [[12 ]J WW.. GF. eClleorc,h Irnantr ,o .S Pamropb lai nb g il it Ty eTchhneoiq ruy e sa, nd(W It isl eAy , p p1l9i 7c7 a )t i on s, (W iley , 1968) [ 3 ] A.N . Kolmog o rov, Foundati on s of Probabil it y , (Chelsea, 1956) [ 4 ] P. Revesz, The Laws of Large Numbers, (Academi c, 1968) [ 5 ]L. Snell, Intr o . Probabil it y , (McGraw-Hi ll, 1989) [ 6 ] T. Yamane, Elementa ry Samp lin g Theory , (Prenti ce -Hall, 1967) [ 汀 김재주, 조신섭, 김병천, 『 컴퓨터를 이용한 통계학 』 , (경문사, 1989)
제 2 장 확률 변수의 생성 2 장에서는 확률 밀도 함수 p (x) 가 주어졌을 때 이러한 확률 변수를 가지게끔 확률 변수의 값을 생성하는 방법을 논하고자 한 다. 가장 간단한 밀도 함수로서 균일 분포 함수 p(x )=1/(b ― a) 를 들 수 있겠는데 균일 확률 변수에 적절한 변환을 하면 다른 확률 분포를 가지는 확률 변수를 생성해 낼 수 있다• 따라 서 균일 분포 확률 변수의 생성은 모든 몬테카롤로 방법의 기본 이 된다. 미리 정해준 지시에 따라 정확하게 작동하는 컴퓨터로 균일 분 포 난수를 생성한다는 것은 앞뒤가 맞지 않는 것 같지만 주어전 알고리즘에 의해 결정론적으로 생성되는 일련의 수들이 마치 무 작위로 꺼내는 난수처럼 보이게 할 수 있다. 이렇게 해서 생성된 일련의 난수들을 여러 가지 통계적 방법에 의해서 테스트한 결과 가 우리가 난수를 사용하고자 하는 목적에 부합되면 될 것이다• 난수 생성에 있어서 좋은 지침은 1. 좋은 분포―무작위성, 균일성
2. 긴 주기 3. 재생 가능성 4. 계산의 효율성 등이다. 이 책에서 사용하는 난수들의 기호둘에 관한 약정을 말하면 그 리스 문자 E, g는 0 과 1 사이의 균일 분포 난수를 나타내고 S, T 는 정수들로 구성된 난수열을 뜻하고 X, y는 특정 분포에 의한 확률 변수이다. 2.1 균일 확률 변수의 생성 2. 1. 1 선형 합동적 방법 2.1. 1. 1 서론 논의를 간단하게 하기 위해 a=O, b=m 이라고 하고 이 구간 에서 정수만을 고려해 보자. Me t ro p o li s 와 von Neumann[l945] 이 몬테카를로 방법을 처음으로 개발했을 때 사용한 난수 생성 방법은 중앙 평방 방법으로서 수열의 현재 수를 제곱하여 생성된 수의 중간 부분을 꺼내서 사용하는 것이었다. 정밀한 난수의 데 스트 방법이 개발되면서 이 방법의 단점이 많이 드러나 더 이상 사용하지 않게 되었다. 난수를 만들어 내는 방법 중 가장 흔히 쓰이는 것으로 선형 합 동 적 방 법 (Lin e ar ConGruenti al meth o d) 이 있 다. 이 방 법 은 Lehme 다 1948] 가 처음 사용한 이래 거의 표준적으로 사용되어 왔 고 가장 좋은 방법으로 알려져 있다. 이 방법은 완전히 결정적인
과정에 의해 겉보기에 무작위하게 보이는 수를 생성해 내지만 이 렇게 해서 만들어지는 수들은 균일하게 분포되어 있고 통계적으 로 독립성이 있음을 증명할 수 있다. 기초적 합동 관계를 이용하는 것인데 어떤 정수 S i가 주어졌 울 때 이 수열의 다음 수는 아래 식에 의하여 얻어진다. S;+1 = (aS;+c) mod m (2.1) 위 에 서 a 는 승수 (multip lier ) , c 는 증분 (inc rement) , m 은 계 수 (modulus) 라고 부르며 이들은 모두 음이 아닌 정수들이다. N mod m 은 N 을 m 으로 나누고 난 나머지를 말한다. 예를 들어 보면 5 mod 3=2, 15 mod 10=5 등이 있다. 위의 방식으로 만들어지는 수열은 이상적인 경우에 m 번마다 반복될 것이다. 주목할 것은 a 와 c 를 어떻게 선택하느냐에 따라 수열 {SI . } 의 주기가 m 보다 작을 수 있다는 것이다. a=l, c=l 로 놓으면 S .. +1=S .. +l 이 되어 최대 주기 m 이 구현되지만 이렇 게 해서 생성되는 수열은 난수라고 보기에는 너무 규칙적이다. 또 하나의 예로서 a=3, c=l, m=l6 으로 놓고 S1=7 부터 시작 해 보면 [O~15] 사이의 수들 중에서 {7, 6, 3, 10, 15, 14, 11, 2} 만이 순서대로 구현되고 나머지 숫자들은 아예 빠지게 된다. 따라서 {a, c, m} 의 적철한 선택이 중요한 관건이 된다. 이에 관해서 많은 연구들이 되어 있는데 다음 절부터 몇 가지 선택된 세트들을 살펴보기로 한다. 2. 1. 1. 2 계수의 선택 m=W=2e 계수는 우선 최대 주기를 결정하기 때문에 사용하는 컴퓨터의 Word 크기만큼 잡는 것이 좋다. 예를 들어 32 비트 기계에서는
W=232 이 기계가 구별할 수 있는 가장 큰 정수이다. 그보다 더 큰 수들은 33 번째 비트부터는 잘리기 때문에 N mod W 만이 메 모리에 남게 되는 것이다. 계수를 기계의 Word 크기로 잡으면 좋은 또 하나의 이유는 식 (2.1) 의 대수 계산을 컴퓨터의 기초적 연산인 비트 이동에 의 해 아주 쉽게 할 수 있어서 난수를 생성하는 계산 시간이 단축된 다는 것이다. 몬테카롤로 시뮬레이션에서 난수를 생성하는 데에 들이는 시간이 전체 시간의 수십 퍼센트가 되는 것을 감안하면 이것은 상당히 큰 이점이다. 여기서 컴퓨터가 정수의 범람 (Over fl ow) 을 어떻게 처리하는지 롤 알아야 할 필요가 있다. 예를 둘어 8 비트 기계에서 28_1 과 46 을 더한다고 하자. 이 과정을 비트로 나타내 보면 28— 1= 11111111 + 46=00101110 1 의 여수를 취하는 기계 11010001 2 의 여수를 취하는 기계 11010010 와 갇이 범람을 처리하는 방법이 두 가지가 있다. 두 수의 합의 결과를 합해지는 두 수중 하나와 다시 합하면 1 의 여수 기계는 -1 죽 2e-1 이 되는 데에 반해 2 의 여수 기계는 0 이 되게끔 처 리한다. 컴퓨터의 제작 회사마다 위의 두 가지 중 어느 것을 랙 하는 규약이 다르므로 사용자 지침서를 읽어보고 확인을 해야 한 다. 요즈음 보편화된 몇 가지 CPU 들 (i80 486, MC68040, PDPll, MIPS R3000, PA-RISC, IBM 370, Cray - I, DEC 21064) 은 모두 2 의 여수를 취하는 기계들이다. rn=W 인 경우 식 (2.1) 의 연산이 어떻게 행해지는지 구체적으
로 살펴보자. 우선 CPU 에 레지스터 H, L 두 개가 있다고 가정 하면 이 과정에서 레지스터에는 프 1) H-a 2) L-(H x S,) 의 낮은 e 개의 비트 3) H - (Hx S,.) 의 높은 e 개의 비트 4) H <-( H, L) mod m 5) H <-( H+c) mod m 와 같은 순서로 숫자들이 저장된다. 2 의 여수 기계에서는 위의 과정들 1)~5) 가 자동적으로 수행된다. 따라서 연산 4)~5) 에서 mod m 을 별도로 하지 않아도 숫자들을 저장하는 과정에서 자동 으로 이루어지기 때문에 레지스터에 저장되어 있는 것을 그냥 읽 어내기만 하면 된다. m=W 土 1 m 이 W 이면 S i의 낮은 비트들이 높은 비트들보다 무작위한 정도가 훨씬 덜한 경향이 있다. 연산 과정이 조금 복잡하지만 m =W 士 l 로 취하면 이런 결점이 개선된다. m=W+l 로 취하고 c =O 으로 두고서 식 (2.1) 을 수행시키는 알고리즘은 고그工] 1) H<--X 2) (H, L) -Hxa 3) T <-L
4) H-H-T 5) H~O 이면 출력 67)) HH--HH++2 W —1 인데 5) 또는 7) 이후에 레지스터 H 에는 aX mod (W+l) 이 저장된다. 이 경우 c=O 으로 놓는 수가 많은데 그럴 경우 난수열 (2.1) 의 최대 주기는 소인수들을 승수로 하는 부분 난수열의 최대 주 기들의 최소공배수가 된다. 나중에 참고로 하기 위해서 몇 가지 m=W 더들을 소인수 분해해 보자.
표 2. I 계수 m= W 土 1 의 소인수 분해 2e-1 e 2e+1 7 • 31 • 151 15 32 • 11 • 331 3 • 5 • 17 • 257 16 65537 2147483647 31 3 • 715827883 3 • 5 • 17 • 257 • 65537 32 641 • 6700417 72 • 73 • 127 • 337 • 92737 • 649657 63 33 • 19 • 43 • 5419 • 77158673929 3 • 5 • 17 • 257 • 641 • 65537 • 6700417 64 274177 • 67280421310721
2. 1. 1. 3 승수의 선 택 앞 절에서 본 것처럼 계수를 결정하는 데에서는 선택의 여지가 많지 않다. 또한 증분은 난수열의 성질에 큰 영향을 끼치지 못한 다. 하지만 승수는 선택의 여지가 많을뿐더러 승수의 적절한 선 택은 최대 주기를 구현시켜 주고 난수열이 무작위하게 보이게끔 해준다. a=c=l 로 놓으면 최대 주기 m 이 구현되지만 이것을 난수라고 볼 수는 없다. 무작위성을 희생시키지 않으면서 난수열
의 주기를 늘리는 최적의 세트 (So, a, c, m) 을 간단히 선택하 게 해주는 긍정적인 수학 정리들은 존재하지 않는다. 하지만 다 음의 수학 정리들은 세트 (So, a, c, m) 이 주어졌을 때 그 수 열의 주기를 알아내는 데 유용하다. m 이 소수들의 곱이면 a=l 만이 최대 주기를 구현해 주는데 m 이 소수의 멱 (po wer) 이면 a 를 선택할 여지가 많다. 정리 2. I p가 소수이고 e 는 p e>2 를 만족하는 양의 정수라고 하자. 만 약 x=l mod p e 이고 x=I =-1 mod pe+ 1 이면 xP=I mod p e +1이고 Xp =I=-1 mod p e+z 이 다. 정리 2. 2 m=P f도 ·P f'와 같이 소인수 분해되고 P j가 소수라고 하면 선형 합동적 수열 (So, a, c, m) 의 주기는 다음의 선형 합동적 수열 들 각각의 주기 A j둘의 최소공배수이다. (S 。 mod PJ' , a mod PJ' , c mod PJ' , PJ ') (1 학잘) 정리 2. 3 l< a< p e 라고 하자(武근 소수). (aA— 1 )/(a— 1 ) =O mod p e 가 되게 하는 최소의 양의 정수를 A 라고 하면 A=Pe 일 필요충분조 건은 a=l mod P(P>2 인 경우) 또는 a=l mod 4(P=2 인 경우) 이 다. 위에서 열거한 정리 2.1, 2.2, 2.3 으로부터 다음의 정리를 유 도할수 있다.
정리 2. 4 식 (2.1) 의 수열이 최대 주기 m 을 가질 필요충분조건은 (,1= m) 1) C 가 m 의 약수가 아니고 2) m 의 모든 소인수 m 계 대해 b=a 一 1 이 m j의 배수이며 3) m 이 4 의 배수일 경우 b 도 4 의 배수라야 할 것 이다. e- 비트의 이전 컴퓨터에서 c=l 로 두고 승수를 적절한 k 에 대 해
a=2k+l , z:s;; k :s ;;e 로 취하면 정리 2.4 의 최대 주기 조건이 만족된다. 초창기에는 이 선택이 많이 장려되었지만 나중에 이 난수열의 무작위성이 충 분히 좋지 않다고 판명되었다. C 가 0 이면 계산시간이 조금 단축되기는 하지만 정리 2.4 로부 터 최대 주기 m 은 원천적으로 성취할 수 없다는 것을 금방 알 수 있다. 하지만 m 이 소수일 경우에는 (So, a) 를 잘 선택하면 주기를 (m-1) 까지 늘릴 수 있다. 정리 2. 5 C 가 0 이면 1) .-l =m 이 될 수 없고 2) S,=O 에 이르면 수열은 0 에서 머무르게 되며 3) (m/d) 와 (S;/d) 가 정수이면 Si 이후로 나오는 모든 수는 d 의배수이다. 4) 최대주기 ¢(m) 은 0 과 m 사이의 m의 약수가 아닌 정수들의 개 수이다. a 가 m 의 약수가 아닐 때 aA = l mod m 을 만족하는 최소의 정 수 A 를 a 의 m 에 대 한 계 수적 차수 (order) 라고 한다. m 의 가능 한 최대의 계수적 차수를 가지는 a 를 m 의 기본적 원소(p r i m iti ve element) 라고 부른다• m 의 최 대 차수를 ll (m) 이 라고 표기 하기로 하자. 계수가 다음과 같이 소인수 분해된다고 하면 m= 2 ep f'·· ·P 1 ' 식 (2.1) 의 난수열의 최대 주기는 계수 m 의 최대 차수와 같은데 tl (m) ={tl (2e) , tl (Pf ') , …, A( ptt) }의 최소공배수 로서 얻어지는데 여기서 각 인자들의 최대 차수들은 A (pe) =pe- 1( p— 1) (P*Ze) tl(2 e)=l (e= O, 1), 2(e=2), ze-2(e>2) 이다. 정리 2. 6 c=O 인 경우 가능한 최대 주기 11(m) 이 얻어질 승수 a 에 대한 조건들은 다음과 같다. 1) So 와 m 이 서로 소일 것 2) a 가 m 의 기본적 원소라야 할 것
2. 1. 1. 4 유명한 난수 생성자들 경험적으로 또는 위의 여러 가지 정리들을 사용하여 얻은 몇 가지 유명한 난수 생성자들의 (a, m) 을 목록화해 보기로 하자.
표 2. 2 유명한 선형 합동적 난수 생성자 a m c AB23C DEFGH10 8+1 0120L1e0hm0er0 0 3잉615 +4531195 92653 222233559 2 7l 8 8l 82 RRoAtNe n DbUer —g IB M/360 6196086097 =75 223312 — 1 MSUaRrsAagN li Da - -VIBAMX/ 360 J 517146562 49532825 85 222334127 — 1 IClM'DEScC u y e r
2.1 .1. 5 선형 합동적 난수 생성자의 무작위성 O m최o대d m주 을기 를( b가=a지—는 1 ) 선 형만 족합시동키적는 수최열소의의 효정능수 (P oL t e 로nc서 y) 은정 의bL된= 다. 효능은 무작위성의 척도로서 L>5 라야 충분히 무작위하다고 말할 수 있다. m= W 士 1 일 때는 큰 효능을 얻는 것이 불가능하 여 최대 주기를 포기하고 차라리 c=O 으로 두는 것이 낫다는 것 이 알려져 있다. 2. 1. 1. 6 선형 합동 방법의 일반화 선형 합동 방정식 (2.1) 을 한번 더 되풀이하여 Si +l= (aS;+ bS;-1+c) mod m (2 .2) 울 사용하여 생성되는 난수열은 2.2.4 절에서 논의하게 될 스펙트
럼 데스트에 나오는 초평면의 수를 더 많이 가진다. 2.1.2 피보나치 수열 Fib o nacci 수 열 Fib o nacci 수열은 원래 다음 식을 사용하여 생성되는 난수열 울뜻한다. S;+1= (S;+S;-1) mod m (2 . 3a) 또는 Green, Smi th, Klem[l95 이이 개선한 유사 -F i bonacc i 수열 은 S;+i= (S;+S;-k) mod m (k:::::16) (2.3b) 이다. 이 방법을 좀더 일반화시켜 현재의 난수를 만들기 위해서 전에 나왔던 두 개의 난수들을 합하거나, 빼거나, 또는 exor (exclusiv e or) 연산울 하여, 죽 S;= (S;-p (f) S;-q) mod m (2. 3c) 울 사용하여 난수를 생성하는 방법을 지연된 Fib o nacc i 방법이 라열의고 주한다기.는 e-(2 바P트— 1 )컴 (2퓨e터_1에) 까서지 P 와늘 어q날를 수적 절있히어 서선 택상하당면히 이길 어수 지고 실수에 직접적으로 적용되기 때문에 정수에서 실수로 환산 하는 번거로움이 덜어지는 이점이 있으나 무작위성에 관해서는 연산자 ®가 exor 이어서는 안 된다는 것말고는 찰 알려져 있지 않다. 원래의 Fib o nacci 수열 (2.3a) 는 2.2 절에서 논의할 여러 가지
데스트에서 별로 좋지 않은 결과가 나오고 특히 스펙트럼 시험에 서는 형편없는 결과가 나온다. M it chell - Moore 의 수열 이 방법 [Mi tch ell 등, 1958] 은 지연된 Fi bo nacci 수열의 특별 한 예로서 마법의 수(p =24, q =55) 를 선택한 것이다. si = (Si- 24+si- 5 5) mod m 냐 55) (2 . 4) 여기서 m 은 짝수라야 하고 수열 {So, …, S 나에서 전부가 짝수 만 아니면 된다. 평범하게 보이는 숫자들 24 와 55 는 아무렇게나 얻어전 것이 아니고 이 수열의 최저 비트의 주기가 (255 _ 1) 이 되게끔 해주는 수들이다. 이 수열의 주기는 ;l= 2f (255 _ 1) 으로서 f는 0 과 e 사이의 정수이다. 이 수열을 효과적으로 계산하는 알고리즘이 있는데 그것은 다 음과같다. E 1) T[l] +-S s ◄, T[2] +-S 53, …, T[55] +-S 。 2) j +-24, k +-55 3) Sn 을 생성할 차례에 와 있다면 현재 T[ j ]=Sn-24 이고 T[k]=Sn-SS 라야 할 것이다. T[k] +-( T[k] + T[j] ) mod 안을 출력 4) j와 k 를 1 씩 감소. 만일 j =O 이 면 j +-5 5 로 두고 혹은 k=O 이면 k +-55 5) 3) 으로 가서 반복
아 렇게 하면 S55, s56, …들이 순차적으로 얻어진다. 2.1. 3 Tauswor t he 의 례지스터 자리이동 방법 이 방법 은 Shif t-R eg ist e r Me t hod 라고 부르는데 Fib o nacci 수 열 (2.3) 에서 m=2 로 선택하여 비트롤 하나씩 생성하여 word 를 만드는 방법이다. 수열을 생성해 나감에 있어서 자리이동 (sh ift) 연산자 ®는 exor 를 사용하는 것이 상례이다. 이것은 원시 삼항식 (pr im i tive tri n o mi al ) xP+x q +l 에 근거를 두고 있다. 이러한 삼항식과 p개의 이진수들 Xo, X1, …, X p -1 이 주어졌다면 다음과 같은 재귀 관계식을 사용하여 아주 간단한 레 지스터 자리이동에 의해 수열을 생성해 낼 수 있다. X i= Xi- P ® x,.-q (2.5) 이렇게 생성된 이전 수열로부터 다음과 같은 b 개의 비트롤 가지 는 난수열을 만들 수 있다. i½,= Xjb X!+j b … X (b-l)+j b , j= O, 1, … (2 . 6) 이 수열의 최대 주기 (2P-1) 은 p가 소수인 동시에 (2P ― 1) 도 소 수일 경우 구현된다. 자리이동 방법을 구현하는 전자회로는 아주 쉽게 만들 수 있기 때문에 이 난수열은 아이싱 컴퓨터 같은 특수 용도 컴퓨터에 많 이 사용되었다. [Pearson 등, 1983 ; Hoog la nd 등, 1983] 하지만 레 지스터 자리이동 난수열의 성질들이 좋지 않다는 것이 판명되어 [Bhanot 동, 1986 ; Paris i 등, 1985] 그 개선이 필요하게 되었다. Lew i s 와 Pa y ne[l973] 은 레지스터 자리이동 방법을 일반화지켜 식 (2.6) 에 의해 생성된 숫자들 사이에 지연 관계를 두어 수열을
개선하였다. W;= Wi - P EB W.·- q, p>q (2 . 7) 이 수열의 초기화 단계에서 p개의 수가 필요한데 만일에 이들 p 개의 숫자들의 j-번째 비트가 영이면 그 다음에 나오는 숫자들 모두에서도 j-번째 비트가 영이 되기 때문에 조심해야 한다. 수 열 (2.7) 의 최대 주기도 (2P-1) 인데 레지스터 자리이동 난수열 (2.6) 에 비해서 많이 좋지는 않다. 2.1.4 빌려빼기 방법 Marsag li a , Narasim han, Zaman[199 아에 의해 고안된 빌려빼 기 방법 (Subtr a ct- w i th- Borrow) 의 난수 생 성 자는
S;= (S;- p 一 S, . - q― c) mod m (2 .8) 인데 여기서 c 는 S;- p― S i-q가 마이너스가 될 때는 c=l 로 정해 주고 반대일 경우는 c=O 으로 정해 준다. 그 주기 A 는 만일 (m q―硏 +1) 이 소수이고 m 을 소수 근으로 가지고 있다면 A=m q -m p가 된다. 싼 근방의 숫자들 중에서 m 을 선택하기로 하여 그들이 광범위하게 탐색하여 찾아낸 조합은 {m=232— 5 = 4294967291 , P=43, q =22} 이다. 따라서 주기는 A=232x43=21376 이 된다. 이 알고리즘을 좀더 구체적으로 설명하면 E 1) 임의의 난수열로부터 S1, S43 를 seed 값으로 채움, i <-44 2) t - S,-22— S i - ◄3 —c3) t ~ O 이 면 Si +--t , C +--O t < O 이 면 Si +--f + 4294967291 , C +--1 4) i +--i +l 로 놓고 2) 로 감 이다. 이 난수 생성자는 그 주기가 길기는 하지만 무작위성에 문제가 있다• 2.2 절에서 논의하게 될 여러 가지 시험 중에서 간격 테스 트 결과가 [Va tt ula i nen 등, 1993] 별로 좋지 않고 스펙트럼 시험 결과는 형편없다. L ti scher[1994] 는 Subtr a ct- w i th- Borrow 방법 에 의해 생성되는 수들 사이의 상관관계를 제거하기 위하여 수열 의 일부만 찰라서 사용하는 방법을 소개하였다. 2.1.5 난수열의 개선 방법 위에서 논의된 방법들에 의해서 얻는 난수열은 위에서 본 것처 럼 주기 또는 무작위성 면에서 만족스럽다고 할 수가 없다. 일차 적으로 얻어전 난수열을 제이의 독립적인 난수열을 사용하여 적 절히 범벅하여 주기도 늘리고 무작위성도 개선하여 훨씬 더 좋은 난수열을 얻어내는 방법이 개괄적으로 두 가지가 있다. 그 첫번째 범벅 방법 (Shu ffli n g)은 일차적으로 얻어전 난수열의 순서를 제이의 보조 난수열을 사용하여 무작위로 뒤바꿔 놓는다. 두번째인 비트 배합 방법은 두 개의 난수열을 동등하게 사용하여 Zi = Si ® Ti 에 의해 더욱 더 무작위한 새로운 난수열을 생성해 낸다. F i bonac ci의 방법은 배합 방법을 하나의 난수열에 대해 적용하는 특별한 경우라고 볼 수도 있다.
MacLaren- M arsag li a 범 벅 이 방법 [M acLaren 등, 1965] 은 무작위 성 을 상당히 개 선해 준 다. 독립적으로 얻어전 두 개의 난수열 {Sn} 과 {T사 이 주어졌을 때 배열 V[O], …, V[k-1] 을 {Sn} 으로부터 채운다. 巳 1) s 와 T를 생성한다 . 2) i= L kT;/m 」 이라고 놓는데 m 은 수열 {T서 울 생성할 때 사용 하는 계수이다 . (O~j ~ k) 3) V[ j]를 출력하고 V[ j]에는 S 를 저장해 둔다. 4) i <-i +I 로 놓고 1) 로 간다. 여기서 차례로 생성되는 SI 들은 일단 보조 배열 V에 잠정적 으로 보관된 다음 T, . 들을 사용하여 무작위하게 결정되는 순서대 로 뽑히게 되는 것이다. 이렇게 해서 생성되는 수열의 주기는 각 각의 수열들의 주기들의 최소공배수이므로 그 주기도 현저히 늘 어난다. Bays -Durham 방법 이 방법 [Ba y s 등, 197 이은 위의 알고리즘과 매우 유사하지만 난수열을 한 가지만 사용하기 때문에 효율적이고 간단하면서도 무작위한 난수열을 생성해 낸다. 여기서도 역시 보조 배열을 사 용하는데 위에서와 마찬가지로 V[O], …, V[k — 1] 을 {Sn} 으로 부터 채운다. 그런 다음 한 개의 보조 변수 T 를 sk 로 놓는다.
덴 1) j= L kT/m 」 이라고 놓는데 m 은 수열 {S 감을 생성할 때 사용 하는 계수이다. 2) T +--- V [j]로 놓고 T 를 출력하고 V[ j]에는 S 를 저장해 둔다. 이 방법에서는 난수열 자신을 이용하여 보조 배열에 저장되어 있는 숫자를 뽑아내는 순서를 결정하기 때문에 자칫하면 상관관 계가 발생하여 M-M 알고리즘보다 신뢰도가 떨어진다고 볼 수 있다. 2.2 의사 난수의 확률론적 시험 난수열의 무작위성을 개선하기에 앞서 그것을 정의하고 측정하 는 방법을 논하는 것이 순서이겠지만 편집의 편의상 그 개선 방 법을 먼저 앞 철에서 논하였다. 2.2 절에서 난수열의 무작위성을 시험하는 여러 방법들이 논의될 것이다. 선형 합동적 방법에 대 해서는 그 무작위성에 대해서 이론적으로 많이 연구되었지만 다 른 방법에 대해서는 그렇지가 못하여 보통 경험적 시험 방법을 사용하게 될 것이다. 난수의 생성 방법을 개선하려면 난수의 무작위성에 대한 철저 한 테스트 방법을 알아야 할 것이다. 여러 테스트 방법이 있는데 여기서는 그중 많이 알려진 것 몇 가지만을 논의하기로 하자. 어 떤 난수 생성 방법도 모든 데스트에서 합격 판정을 받기는 어렵 다. 난수열의 특성들 중 어떤 특성이 그 문제에 결정적인 역할을 할 때가 있는데 그 문제에 대해서는 그 특성의 테스트에 불합격
된 난수열을 사용해서는 안될 것이다. 보편적으로는 이들 중 대 여섯 가지의 데스트에서 합격 판정을 받으면 믿고 사용해도 될 것이다. 2.2.1 카이평방시험 카이 평 방 시 험 (Chi- S q u are Test) 은 확률의 가장 기 초적 인 이 론 에 근거를 둔 것으로서 대부분의 다른 시험 방법의 기반이 되고 있다. 여기서 사용되는 카이평방 확률 함수는 이미 19 세기에 확 립 되 어 [Pearson, 190 이 참고문헌 [A bramowi tz, . 1968] 에 목록화되 어 있다. 어떤 실험에서 k 가지의 다른 결과가 나올 확률이 각각 Ps(s= 1, …, k) 라고 하면 이 실험을 n 번 시행할 적에 결과 s 가 나오 는 횟수의 기대값은 nPs 이다. 실제 실험에서 s 가 나오는 횟수를 Xs 라고 하자. n 이 충분히 크면 X혼 nPs 가 성립할 것이다. 기대 값으로부터 벗어나는 정도를 측정하는 양으로서 카이평방 균이 있다. x 득 s$=l (Xs n_P ns Ps) 2 (2 . 9) =-¼tl ( 폰)― n 균이 어떤 값 x 보다 클 확률이 P(x2:::?:x) 라고 하면 이것은 n 이나 Ps 에 무관하게 확률론적으로 (l/, 군)에 의해서만 정의된 다. 여기서 l/는 자유도로서 위의 경우 Xs 의 합이 n 이라야 하기 때문에 이 실험의 자유도는 v=k-l 이라고 할 수 있다. 실제로 관측해서 얻는 양 균은 확률 변수로서 정규 분포를 가진다는 것이
표 2. 3 카이 평 방 확률 함수 L’ 5% 25% 50% 75% 95% 1 .00 393 .10 15 .45 49 1.3 2 3 3.8 4 1 3 0.3 5 18 1.213 2.3 6 6 4.108 7.815 5 1.1 4 55 2.6 7 5 4.3 5 1 6.6 2 6 11 .07 10 3.9 4 0 6.7 3 7 9.3 4 2 12.55 18. 31 2500 3140..7 865 4125..4 954 1499..3 334 5263.. 8333 3671 .. 4510
증명되어 있다. 카이평방 확률 함수 P(xI 1.1)는 단위 분산을 가지 고 정규 분포되어 있는 확률 변수에 대해서 자유도가 1)인 실험을 하여 여기서 측정된 균이 x 보다 작은 확률을 말한다. 따라서 P(x2~x) =P(x I 1.1) =r(1.1/ 2, x/2)/I'(1 .1/ 2) (2. 10 ) 이다. 카이평방 확률 함수를 몇 개의 1)와 퍼센트에 대해서 표 2.3 에 수록하였다. 위의 표에서 95 % 열의 1.1 =10 행에 18.31 이 있는데 이것은 독 립적 측정의 가짓수가 10 인 측정에서 측정 횟수가 충분히 클 때 x2 타 8.31 일 확률이 5 ' % 밖에 되지 않는다는 것을 의미한다. 이 실험에서 갔 218.31 일 확률이 그렇게 낮음에도 불구하고 이런 결 과가 얻어졌다면 그 ^실 험을 약간 의심스럽게 생각해야 할 것이 다. 일반적으로 25%~75% 이면 좋고 5%~10% 이면 의심스럽 고 그 이하는 받아들일 수가 없을 정도로 의심스러운 것이다. 측정 횟수 n 이 충분히 커야만 카이평방 데스트를 믿을 수 있 는데 일반적으로 모든 s 에 대해서 nPs25 정도이면 n 이 크다고 볼수있다. 난수의 균일 분포 데스트에서는 수직선의 구간 [O~(m ― 1)] 을
11 개의 부분구간으로 나누어 난수들이 각각의 구간에 떨어지는 숫자를 세어 본다. 균일 분포 난수는 각각의 구간에 떨어질 확률 이 모두 같기 때문에 Ps=l/11 일 것이다. 이렇게 하여 위에서 기 술한 카이평방 데스트를 적용해 보면 된다. 2.2.2 콜모고로프-스미르노프 시험 측정값들을 유한 수의 범주로 구분할 수 있울 때 확률 밀도를 사용하는 카이평방 테스트는 유용하다. 확률 변수가 연속적인 값 울 취할 때는 확률 분포를 사용하여 콜모고로프-스미르노프 시험 (Kolmog o rov-Smi rn ov Test) 을 하는 것 이 좋다. 확률 변수 X 의 분포를 고려해 보자. X 가 어떤 값 x 보다 작 을 확률이 분포 함수 P(x) 에 의해 주어진다면 P(x) = (X::;;:x) 일 확률 (2 .11) 이 성립한다. 예를 들어 0 과 1 사이에 균일 분포되어 있는 난수 에 대해서는 P(x) =x 이다. 따라서 X i
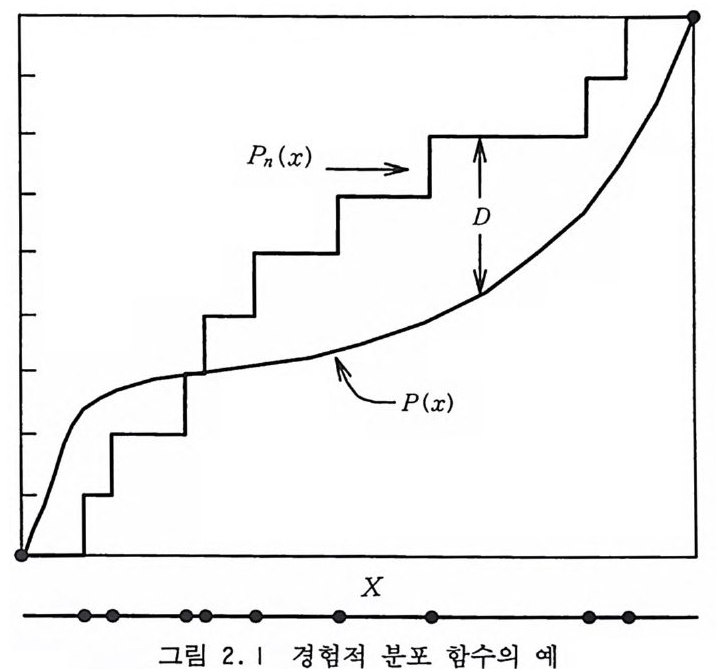 • • 그•림• 2. •I 경험•적 X 분 포• 함수의 예 • •
• • 그•림• 2. •I 경험•적 X 분 포• 함수의 예 • •
K;=m_E緊 OO[Pn(x) —P( x)] (2 .13a) K; ; = g홉緊」 P (x) -Pn (x) ] (2.13b) 측정 된 K춘 의 유의 성 (sig nifica nce) 은 확률 함수인 콜모고로프-스 미르노프 함수, QK s(x/.f n) =n폭 o 악z kS ::r (\k) (k— x) k(x+n-k)n-k-l (2.14) 를 통해 가늠할 수 있는데, 이것은 측정 횟수가 n 인 경우 QK s (x/.f n) = (K춘 ~ x/ .fn일 확률) (2 .15) 이라는 것을 뜻한다. 몇 개의 n 값과 퍼센트에 대해서 Q Ks(x/ .fn)의 값들을 표 2.4 에 수록하였다.
표 2. 4 콜모고로프-스미르노프 함수 12 5% 25 % 50% 75 % 95% 1 0.0500 0.2 5 00 0.5000 0. 75 00 0.9500 3 0.0 7 919 0.3 1 12 0. 51 47 0. 75 39 1.10 17 5 0.09471 0.3249 0.5245 0.7674 1.1392 10 0.1 1 47 0.3 2 97 0. 54 26 0.7 8 45 1.1658 20 0.1298 0.3 4 61 0.5547 0. 79 75 1.1 8 39 30 0.1351 0.3509 0.5605 0.8 0 36 1.1916
75 %의 열에서 n=5 의 행에 0.7674 가 있는 것은 K춘 가 0.7674 보다 작거나 같을 확률이 75 %라는 것을 의미한다. 난수의 데스트에서는 n 을 대략 100~1000 으로 잡고 난수열의 각기 다른 부분에서 KS 테스트를 하여, 예컨대 n=lOOO 인 경 우, 수열 K1to o (l), K森 00(2)' …, K1t o o(r) 울 얻어 보고 이들에 대해서 KS 데스트롤 또 한번 시행해 보면 난수의 국부적인 성질과 전체적인 성질 두 가지롤 다 파악할 수 있다. 두번째 KS 데스트에 대한 분포 함수는 n 이 클 경우 P(x) =l ― ex p(― 2 군) (2 .16 ) 와 거의 같다. 2. 2. 3 경험적 시험들 A. 균등 분포 테스트 (E q u i d i s t r i bu ti on tes t) 이 방법은 우리가 가장 먼저 생각할 수 있는 초보적인 방법으 로서 카이평방 데스트에서 논의된 방법을 사용하여 난수가 전구
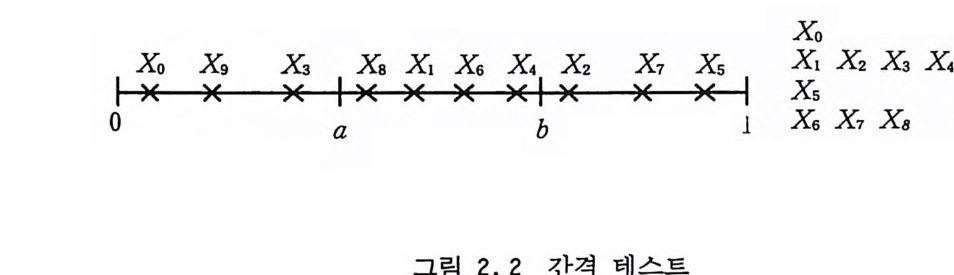
간에 골고루 분포되어 있는지를 데스트한다. N 개의 난수를 생성 하였다고 하면 이들이 나타나는 전구간을 d 개의 구간으로 균등 하게 나누어 각 구간에 몇 개씩 들어있는지를 헤아려 보고 이들 에 대해서 카이평방 데스트를 적용해 보는 것이다. 각 구간에 들 어 있어야 할 수는 N/d 이므로 아주 쉽게 데스트해 볼 수 있다. B. 순차성 테 스트 (Seri al tes t) 이차원 공간의 점 (x, Y) 의 좌표를 무작위하게 찍어 보고, X;=X;, y; =Xi+ l 이들이 모든 지역에 골고루 분포되는지를 점검해 봄으로써 난수 열에서 홀수 번째 수들과 짝수 번째 수들이 서로 독립적임을 테 스트해 보는 것이다. 이차원 바둑판의 각각의 네모 지역에 떨어 지는 점들의 수에 대해서 카이평방 데스트롤 적용하면 된다. x 방향으로 dx 개의 구간이 있고 y 방향으로 dy 개의 구간이 있다면 각각의 네모 지역에 떨어져야 할 점들의 수는 N/(dx•d y)일 것 이다. C. 간격 테 스트 (Gap tes t) 난수가 생성되는 전구간 중에서 부분구간 (a, b) 를 정해놓고 X가 이 구간에 처음으로 떨어질 때부터 시작해서 그 이후로 생 성되는 난수들 중 어느 하나 (X;+r) 가 다시 이 구간에 떨어질 때 까지의 간격 (r) 을 측정하는 방법이다. 수열 {x,., xi + 1, …, X;+r} 에서 길이 r 인 간격이 관측되었다면 a~Xi +r 요이 성립하 되 다른 숫자들은 구간 (a, b) 에 속하지 말아야 한다. 알고리즘 이 약간 복잡하고 그 결과를 해석하는 것도 단순하지 않기 때문 에 차근차근 살펴보자.
간격 r 은 확률 변수이고 구간 (a, b) 의 길이에 따라 그 영역 은 짧게는 1 에서부터 (전구간의 길이와 같게 잡으면 언제나 l 이 됨) 길게는 난수열의 주기에(최소 길이의 구간으로 잡울 경우) 이를 것 이다. 곧 이어서 설명하겠지만 간격을 적절히 택하면 r 의 관심 스런 영역은 l 에서부터 적절한 수 t에 이를 것이다. 무작위성의 척도로 사용할 수 있는 양은 r 의 분포이다. 죽 N개의 난수를 생성하는 과정에서 간격들이 어떠한 분포를 이루느냐 하는 것이 다. 각자의 간격이 나올 확률둘이 Po=P= (b-a)/( 전구간) (2 .17) P1=P(l-p) , P2=P(l-p) 2, …, Pt- 1=P(l-p) t-i, Pt = (l-p) t 이라는 것은 어렵지 않게 증명할 수 있다• 여기서 針큰 구간 (a, b) 에 떨어질 확률이고 (1- p)는 그 바깥에 떨어질 확률이다. 예 컨대 두번째 숫자가 구간 (a, b) 에 떨어질 확률은 첫번째에는 확률 (1 ―p)를 가지고 구간 바깥에 두번째는 확률 P 를 가지고 구간 내에 떨어져야 한다. 따라서 r 이 나오는 빈도 수를 측정하는 알고리즘이 필요한데 약술하면 다음과 같다.
 x。
x。
三1) i <-— I, s <-0, count [r] -o (Os rs t) 2) r -o 3) i -i+ I, asX.-sb 이면 5) 로 건너펌 4) r <-r +I, 3) 으로 되돌아감 5) r 타이면 count [t] <-count [t]+ 1 아니면 count [r] <-count [r]+1 6) s <-s+1 , s < N 이면 2) 로 되돌아감 이렇게 해서 얻어전 r 의 빈도 수 count [r] 에 대해서 위에서 주 어진 확률들을 가지고 카이평방 데스트를 적용한다. 여기서 N 과 t는 입력해 주어야 하는데 모든 r 에 대해서 count [r]~5 가 되도 록 택해 주는 것이 좋을 것이다. D. 포커 테 스트 (Poker tes t) 연속적 으로 나오는 다섯 개 의 숫자들, (X5j, X5j+ 1, …, x5 J +4) 을 포커 게임의 패와 비교해 보는 방법이다. 원래의 패와 비교하는 대신 좀더 간단하게 다섯 개의 숫자 중에서 서로 다른 숫자들의 가짓수에 따라 분류해 보자. 5 一모두 다름 4 - ➔ one pa ir 3 - ➔ tw o pa ir 또는 tri p le 2 - ➔ full house 또는 fou r card 1 - ➔ five card 일반적으로 각각의 카드가 0 에서 d— 1 사 이의 값을 취하고 k 개 의 카드에서 r 개의 다른 값들이 나올 확률은
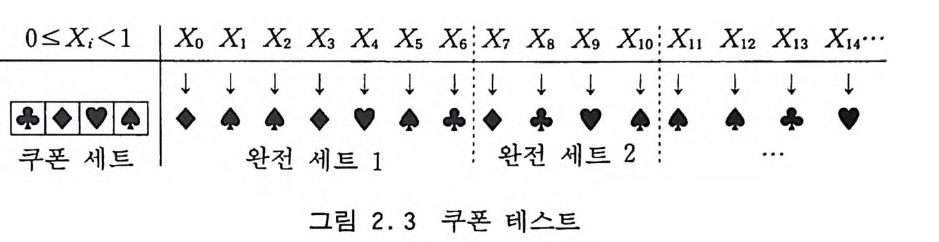
Pr= d(d-l) ·?id- r+1) { 나 (2 .18) 와 같이 얻어지는데 여기서 맨 뒤에 나오는 항은 S ti rl i n g의 수 이다. 포커 게임에서는 d=l3, k=5 이다. 수열에서 연속적으로 나오는 다섯 개의 숫자들의 패를 계속적으로 n 번 분류하여 관측 된 각 패의 출현 횟수 Nr 에 대해서 각각의 기대값 n 拓울 기준으 로 하여 카이평방 데스트롤 적용하는 것이 이 방법의 골자이다. E. 쿠폰 수집 가의 테 스트 (Coup o n Collec tor 's tes t) 이것은 난수열 (Xj+ 1, Xj + 2, …, Xj +r) 에 미리 정한 한 세트 의 정수들, [O~(d-1) ]이 모두 나올 때까지의 길이 r 을 측정해 보는 것이다. 이 알고리즘을 기술하면 다음과 같다. 下 12)) 초q <기-화r <: -j 0- , o—ccl,u rss [
 0
0
들의 수는 k= t -d+l 이 될 것이고 측정한 구간들의 수가 n 이 라면 각 항목이 나올 확률은 Pr= 뭉{ ;:11 }, d
해도 Au t아는 정확히 0 이 될 수는 없다. 대충 95 % 정도의 확 률을가지고 µn-2
가열들의 독립성이 보장된다. 숫자들이 r 번 증가한 다음에 r+l 번째에는 증가하지 말아야 하기 때문에 길이가 r 인 증가열이 나타날 확률은 Pr= 言1 _ (r+11 ) ! = (r+r1 ) ! (2 . 23) 이다. A=l/2, A=l/3, H=l/8, P4=1/30, Ps=l/144, A= 1/840 이기 때문에 t =6 이 상식적인 선택이 될 것이다. 이제 coun t [r] 을 세어보는 알고리즘은 다음과 같다. 巳 1) 초기화:j+-― 1;coun t [r]-o, lsrs6 2) r +-0 3) r-r+l, j+-j+l ; ~;<~m 이면 3) 으로 감 4) r ~ 6 이 면 count [6] 을 하나 증가 아니 면 count [ r] 을 하나 중가 5) j +-j+I ; j< n 一 1 이면 2) 로 감 H. 부분 수열 테스트 (Subse q uence tes t) 삼차원의 문제를 몬테카롤로 모사할 경우 우리는 흔히 세 개의 난수 X, Y, Z 를 한꺼번에 필요로 한다. 똑같은 난수열을 사용 할 경우 매 세번째 나오는 수들끼리 서로 상관관계가 있다면 바 람직하지 못할 것이다. 세 개의 부분수열들 ~o, 6, &, … ; 욘 I' &, 57, 令 ~5, ~8, … 에 대해서 지금까지 논의한 테스트들을 적용해 보면 좋을 것
표 2. 5 난수 생성자들의 시험 결과 난수 생성자 I. E G M-M SwB KS(K+ l 32. 43 32.41 28. 57 60.55 32. 84 KS(K_) 48.45 64.93 70. 39 35.54 61 .7 0 균등분포 86.02 70.31 42.39 39.38 46.92 순차성 100.0 57. 31 82.41 82. 75 53.89 간 격 52.55 41 .85 59. 62 81 .27 41 .41 포 커 100.0 59. 40 22. 39 49. 36 48. 15 쿠폰수집가 33.52 46.62 75.12 29.24 51.78
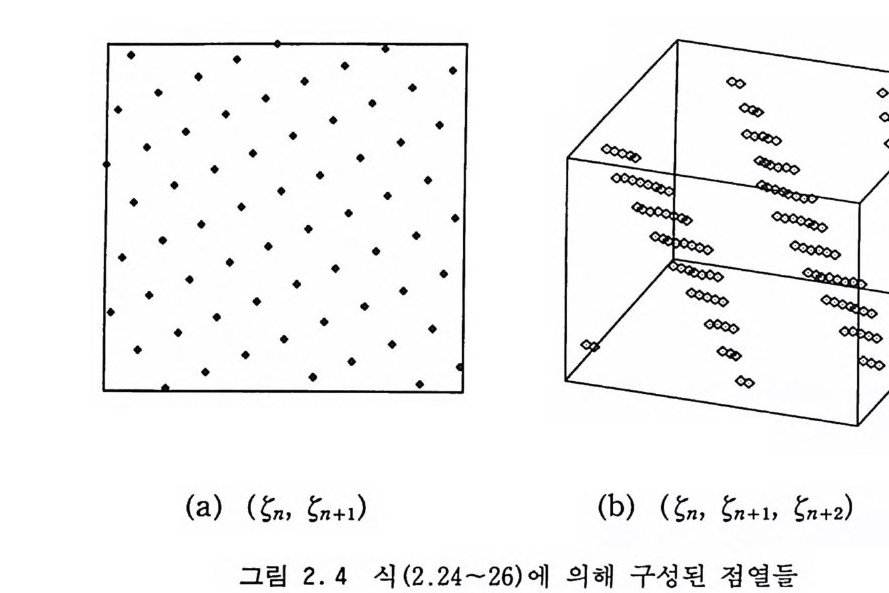
이다. I. 몇 가지 난수 생성자들의 시험 결과 경험적 시험 방법들을 사용하여 표 2.2 에 나오는 난수 생성자 둘을 시험한 결과로서 표 2.5 에 수록한다. 숫자들은 각각의 데스 트에서 카이분포의 퍼센트를 나타내는데 50% 근처일수록 좋다. 이 자료에 의하면 난수 생성자 E 와 SwB 가 비교적 괜찮아 보인 다. 2. 2. 4 스펙트럼 테스트 스펙트럼 테 스트 (Sp e ctr a l Test) 는 이론적 테 스트와 경 험 적 데 스트의 요소들을 모두 포함하는 매우 중요한 시험 방법으로서 좋 은 난수 생성자라면 반드시 이 시험에 합격해야 하고 나쁘다고 평이 나있는 난수 생성자들은 모두 이 시험에서 불합격된 바가 있다. 이 방법의 핵심적인 요소를 대략적으로 설명해 보면 난수열에 서 연속적으로 나오는 숫자들을 t개씩 묶어서 그들의 t-차원 공
간에서의 분포를 고려하는 것이다• 죽 주기 m 을 가지는 난수열 의 각 점에서 t-차원 벡터, {(gn, gn+ 1, …, sn+ t - 1)} 을 만들어 이것을 t-차원 공간의 점의 좌표로 취하고 이것을 m 번 반복하여 만들어지는 m 개의 다른 점들의 분포를 검토하는 것 이다. 논의를 간단히 하기 위하여 선형 합동적 수열 (Xo, a, c, m) 이 최대 주기 m 을 가진다고 가정하자. 그러면 위의 수열을 냐 (x, s(x), s(s(x)), …, st- l(x)) I o::;;x
 •• • • •• •• • • ••• • • •• •• • • • •• • • •• ••• • •• • • • •♦ ••• • • •• • • •• • •• • •• ♦ ••
•• • • •• •• • • ••• • • •• •• • • • •• • • •• ••• • •• • • • •♦ ••• • • •• • • •• • •• • •• ♦ ••
v 를 조정해 줄 때 어떤 현상이 일어나느냐 하는 것이다. 평행선 둘 또는 평행면들 사이의 최대 거리를 1/1.12 , 1/ 1/3 라고 하면 진짜 난수들을 가지고 찍은 점들은 1.1 2 ::::::1) 3 ::::::다룹 만족하는 데에 비해 의사 난수들을 가지고 찍은 점들 사이에는 l.l~l.1 2~ 1/ 3 이 성립한다 는것이다. 난수열을 가지고 만든 점들은 1/ I.It의 거리보다 더 가까워질 수 가 없기 때문에 I.It를 일반적으로 t-차원 정확도라고 부른다. 진 짜건 의사 난수건 t-차원 입방체에 m 개의 점들만 찍는다면 그 정확도는 I.I::::::짜ft를 넘지 못할 것이다. 컴퓨터에 의해 생성된 난수들은 마치 우리가 진짜 난수를 취해서 log 2 I.It개의 비트만 남 기고 나머지는 자른 것처럼 보인다. 고차원으로 갈수록 I.It가 줄 어들기 때문에 의사 난수의 정확도도 떨어지게 된다. 스펙트럼 시험은 2~t ~ 6 사이의 t에 대해서 I.It를 계산하는 것 인데 m 개의 난수 전체를 생성해서 그들이 이루는 평행면들 사이
의 최대 거리를 찾는 문제이기 때문에 그 계산량이 엄청나게 많 다. Knu t h[l981] 의 책에 복잡한 수학 이론을 사용하여 계산량을 크게 줄인 알고리즘이 소개되고 있는데 그것을 자세한 논의없이 기술해 보기로 하자. 이 알고리즘은 주어진 선형 합동 난수열, (a, c, m) 에 대해서, 그리고 몇 개의 저차원들, 2~ t ~T 에 대 해서 v,=m i n{ ✓ x f+…+xf I x1+ax2+… + a1-1x,=O mod m} (2.27) 을 찾아낸다. t 23 에 대해서는 tx t 행렬들 U, V 를 사용하는 데, 그것들의 행 벡터들을 U;= (u;1, …, Uit ), Vi= (V;i, Vi t) 라고 하면, 조건들 U;1+au;2+… +a1-1Ui t= 0 mod m, 1 철~t (2.28) ul• • Vj= 8i.im , 1 학, j집 (2.29) 울 만족한다. 또한 세 개의 한시적 t-차원 벡터들, X, Y, Z 도 사용한다. 알고리즘 전반에 걸쳐 r=at- i mod m 이고 s 는 지금 까지 찾은 녀의 상한값 중에서 가장 작은 것이다. 이제 Knu th의 알고리즘을 기술해 보자. 回 1) (초기 화) h +-a , h' +-m , P +-l, P' +-0 , r +-a , s +-1 + a2 이 라고 놓는다. 2) (Euclid 단계 ) q +-L h'/h 」 , u +-h'-qh , V +-p'-qp라고 놓는다. u2+v2
3) 區롤 계산) u -u-h, V-V- p라고 놓는다. u2+v2O 일 때 -롤 선택함. 4) (t를 증가) t= T 이면 알고리즘 종료. t <-t + l, r <-( ar) mod m 으로 놓고, 또한 Ut <-( -r, O, …, 0, 1) 로 놓은 다음, 1 후·
7) (j를 증가) j=t이면 戶― 1 로 놓고, 아니면 戶―j +l 로 증가 j-=I= k 이면 5) 로 돌아감 8) (탐색 준비) X <------ Y <-( 0, …, 0), k ,_ t로 놓고 또한 ZJ <-- L J[ (VJ. VJ )s/m 汀 」 , 1 학악 와 같이 놓는다. 9) (따를 전전) xh= 깊이면 11) 로 가고, 아니면 챠 <--xh+I, Y <--Y + uk 로 놓음. 10) (k 를 증가) k +--k + l 로 놓음. k:,;; t이면 Xk <--- zk, y <-- Y ― 2z.uk 로 놓고 10) 을 반복 아니면 s +--mi n( s, Y· Y) 로 놓음 11) (k 롤 감소) k +--k -l 로 놓음. k~l 이면 9) 로 가고, 아니면 V t =E 를 출력하고 4) 로 되돌아 감. 이렇게 해서 얻은 어느 의사 난수열의 정확도들이, l.lt 느 230l t, 2< t조 6 (2 . 30) 울 만족하면 그 난수열은 대부분의 응용 문제들에 대해서 충분히 무작위하다고 볼 수 있을 것이다. 좀더 정확하게는 t-차원 격자 에서 단위체적당 m 개의 점들이 뿌려져 있다면 lit의 이론적 상한 값은 I.It~ 'Ytm l/t (2 .31) rt = (4/3) 1,4, 21,5, 21,4, 23110, (6413) 1112, … 에 의해 주어진다[J. W.S . Cassels, 1959]. 또한 선택된 승수 a 가 어느 정도 좋으냐 하는 것은, 점열들이
(x1m-x2a— … _Xt a t - 1) 2+ 좌+ … +x ~:s ;; 1.1~ (2.32) 에 의해 정의되는 타원체 (ell ip so i d) 의 내부에 떨어져야 한다는 것 이다. 이 타원체의 체적을 계산해 보면 µ2= 교 /m, µ3= 下4 교 /m, µ4= t1 군마 /m µ5= 衍鴻 /m, /16내갑 /m (2 . 33) 을 얻는다. 만약에 2 부터 6 사이의 모든 t에 대해서 µ1 >O.l 이 성립한다면 그 승수는 시험에 합격했다고 말할 수 있고 µt느 1 이 성립한다면 장원급제라고 할 수 있겠다. 표 2.6 에 몇 가지 난수 생성자에 대한 스펙트럼 시험의 결과를 수록하였다. 세번째 행은 IBM 에서 RANDU 라는 라이브러리 함 수로서 10 년 이상 제공해 왔던 것으로 스펙트럼 시험에서는 논의 여지도 없이 불합격한 것을 알 수 있다. 네번째 행은 Marsag li a 의 것으로 VAX 에서 사용되어 오던 것인데 스펙트럼 시험에서 장원급제했다. 다섯번째 행의 생성자는 IMSL 에서 사용되는 것 으로 역시 탁월한 무작위성을 가지고 있다. 마지막 행은 64 비트
표 2. 6 몇 가지 선형 합동 난수 생성자의 스펙트럼 시험 결과 a m i72 J/3 1/4 ils µ2 µ3 µ4 µs 23 108+1 4.5 4.5 4.5 4.5 2· 군 5· 강 0.01 0. 34 71 128 3.2 2.3 1.0 1.0 2.0 3.8 0.6 1.3 65539 229 14. 5 3.4 3.4 3.4 3.14 e5 €4 e3 69069 232 16.0 10. 5 7.8 6.4 3.1 0 2.91 3.2 0 5.01 1664525 232 16.1 10. 6 8.0 6.0 3.61 3.45 4.6 6 1.31 Big nu m 2 31 .5 21 .3 16. 0 12. 7 1.50 3.68 4.5 2 4.02 주 : i7= log 2 11, c=l/1 0 , Big nu m=6364136223846793005
컴퓨터에서 사용할 수 있는 것으로서 역시 스펙트럼 속성이 탁월 하다. 스펙트럼 시험은 원래 Cove y ou 와 MacPherson[1967] 이 개발 한 것이지만 알고리좀 |A 2. 10I 에서처럼 행렬둘 U, V 를 사용하 는 것은 J anssens 와 Di e t er 가 제 안한 것 이 다. 2. 3 정해진 확률 분포에 의한 확률 변수의 생성 방법 2.3.1 역변환 방법 앞서 기술한 방법에 의해서 얻어전 균일 분포 확률 변수에 함 수적인 변환을 하면 방정식 (1. 6) 에 의하여 얻어지는 새로운 분 포함수를 가지는 확률 변수가 나온다. 방정식 (1. 4) 를 역으로 이 용하여 py(y)를 먼저 정하고 식 (1. 5) 를 적용하여 dx/dy 를 얻 은 다음 여기서 생기는 마분 방정식을 풀어서 변환 함수를 얻는 방법 을 역 변 환 방법 (Inverse Transfo r mati on Meth o d) 이 라고 한다. 이 방법은 역함수를 구해야 하기 때문에 실제적으로 적용하기에 는 비효율적이지만 많은 다른 방법의 기본이 된다. 간단한 예를 들어 이 방법을 설명해 보자. 균일 분포 확률 변 수의 변환 함수로서 y( x) =-ln(x) 를 취해 보면 방정식 (1. 4) 에 의해 PY( y )dy =Px(x)| 훑 |dy =e-Ydy (2.34) 가 되어 지수적 분포를 얻는다. 다시 말하면 균일 분포 확률 변 수 X 를 취하여 이것에 로그 변환을 가한 결과를 Y 라고 하면
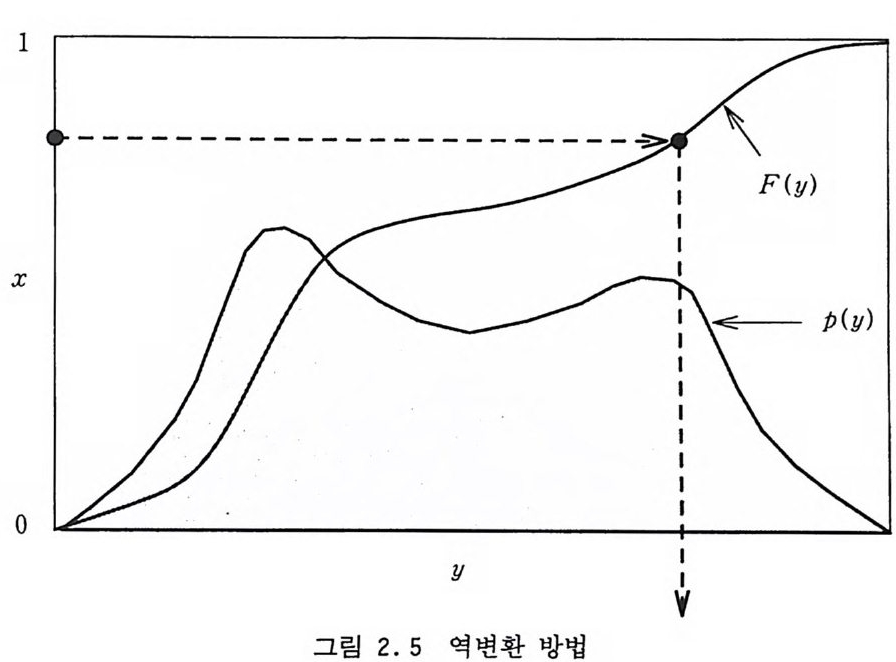
Y 는 확률 밀도 함수가 e- y인 확률 변수가 된다. 역으로 원하는 확률 밀도 함수 py(y )=e-Y 가 먼저 주어졌었다 면 미분 방정식 (2.34) 를 풀어서 변환함수 y( x) =一 ln(x) 를 얻 울 수도 있었을 것이다. 확률 밀도 함수 py(y) =f(y)가 임의로 주어졌을 경우에 어떻게 해야 하는지를 알기 위해 이 과정을 좀 더 자세히 고찰해 보자. 우리가 알고자 하는 것은 변환 함수 y (x) 인데 이것은 미분 방정식 (1. 5) 의 해를 구하면 될 것이다. Px(x) =l 일 때 이 식의 해는 x=1Yy J (t) dt = F(y) (2 . 35) 。 에 의해 주어진다. 이로부터 식 (2.35) 의 역을 취해서 y (x) = F-1 (x) (2 . 36) 를 구하면 찾고자 하는 변환함수 y (x) 를 얻을 수 있게 된다, 이 방법은 적분식 (2.35) 가 해석적인 해를 가지고 그것의 역함 수 (2.36) 이 쉽게 구해질 수 있다면 가장 효율적인 방법이 될 수 도 있겠지만 실제적으로는 그렇지 못한 경우가 대부분이고 특히 변수가 많을 경우에는 적용하기가 불가능하다. 역변환 방법에 의해서 표본추출하는 알고리즘을 상세히 설명하 면 巨 1) 적분 x= fo。 y/(t )dt =F( y)를 계산 2) y =F-1(x) 를 찾음 3) ~를 생성
 1
1
4) Y=F-1(~) 를 출력 이 방법의 기하학적인 의미를 알아두면 좀더 이해하기가 쉬울 것이다. 그립 2.5 에서 보면 식 (2.36) 을 풀어내는 것은 x 축에서 균일분포에 의해 한 점을 취해 x=F( y)인 y를 찾아 그것을 출 력하는 것과 같다. 2.3.2 거절-허용 방법 von Neumann[195 다의 거 절-허 용 방법 (Reje c ti on Me th od) 은 역변환 방법의 문제점들인 적분과 역함수를 필요로 하지 않기 때 문에 실용성이 있어서 널리 사용되고 있다. 역변환 방법에서 변
 A
A
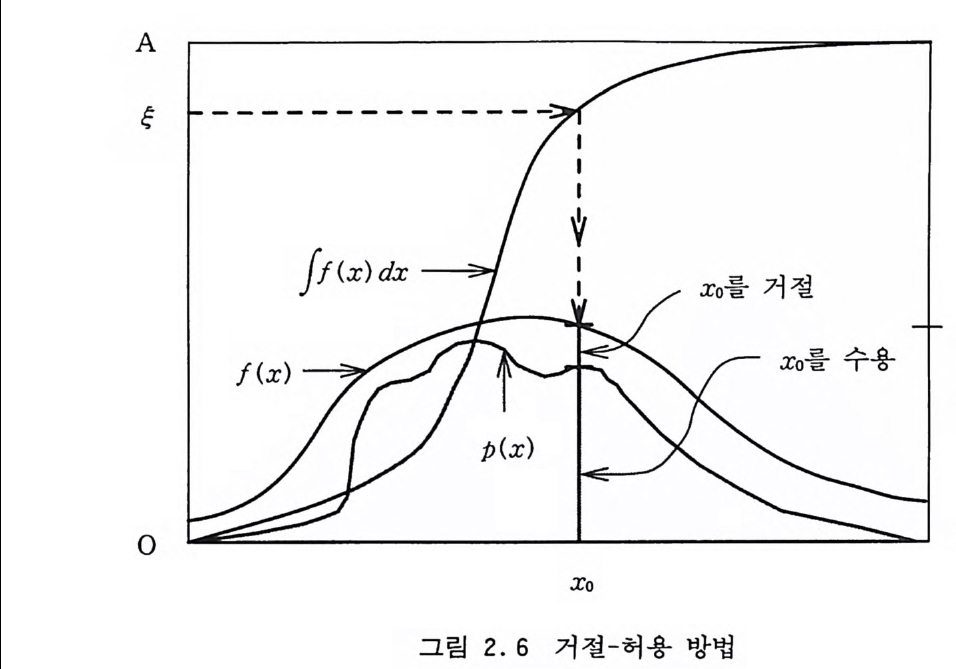
환 함수를 해석적으로 구해냈다 해도 그 계산 시간이 너무 많이 걸리면 효율이 나빠 실용적이지 못할 것이다. 앞으로 여러 예제 들에서 보겠지만 거절-허용 방법을 적절히 사용하면 아주 효율적 인 알고리즘들을 얻을 수 있다. 확률 밀도 함수 p (x) 에 의해 확률 변수를 취하는 과정은 기하 학적으로 쉽게 이해할 수 있다. (그립 2.6 을 참조) 곡선 p(x ) 밀 에 있는 면적 안에서만 균일하게 점을 취한다면 그 점이 구간 (x, x+dx) 에 있을 확률은 p(x)dx 에 비례하게 될 것이기 때문 에 우리가 원래 원했던 밀도 함수 p (x) 에 의해 확률 변수를 취 하는 것이 될 것이다. 또한 반대의 논리도 성립할 것이다. 거절-허용 방법은 곡선 p (x) 를 에워싸는 가상의 밀도 함수 f( x) 에 __가기교 함수라고 부름-의해 확률 변수 X 를 뽑아낸 다음,
(이것은 위에서 설명한 것처럼 곡선 f (x) 의 아래에 있는 면적에서 아 무 점이나 하나 고르는 것과 같음), 다시 그 점 /(X) 의 아래에서 임의로 점을 취하여 그것이 곡선 p (x) 의 아래에 떨어지면 받아 들이고 그렇지 않으면 버리는 방법이다. 이렇게 해서 취한 점들 은 곡선 p (x) 의 아래에 균일하게 분포될 것이다. 따라서 이 접 둘은 확률 밀도 함수 p (x) 에 의해 분포되는 확률 변수들이 될 것이다. 이 방법의 능률은 f (x) 가 p (x) 에 얼마나 근사한가, 그리고 f (x) 에 의한 역변환 방법아 얼마나 효율적인가에 달려 있다. 비 교 함수 f (x) 로서 좋은 대상은 우선 역변환 방법이 쉽게 적용될 수 있도록 해석적으로 적분 가능하고 그 적분 함수의 역함수를 쉽게 구할 수 있으면서 p (x) 에 근사한 함수라야 할 것이다. 거절 방법의 전체적인 효율 e 은 곡선 /(x) 아래의 면적 대 곡 선 p(x ) 아래의 면적 (=l) 의 비율에 반비례하는데 국부적으로는 p (x)//(x) 에 비례한다. 역변환 방법에서는 매번 시도할 때마다 확률 변수를 얻지만 거절 방법에서는 그렇지 못한데 성공하기 전 에 시도해야 하는 횟수는 l/e 이다. 좋은 비교 함수 f (x) 를 얻었다고 가정하고 거절-허용 방법을 좀더 구체적으로 설명해 보자. 곡선 f (x) 가 곡선 p (x) 를 에워 싸고 있으므로 그 적분은 1 보다 크다. 따라서 f (x) 에 의한 표본 추출을 하기 위해서는 모종의 규격화가 필요하다. /(x) 아래의 면적이 A 라고 하면 확률 밀도 함수 f (x)/A 에 의해 표본추출을 해야 할 것이다. 그것은 F( y )=l yt(t )d t가 해석적으로 계산 가 。 능하다고 하면 역변환 방법을 적용하여 구간 [O, A] 사이에서 균일 분포 함수에 의해 점 t를 취한 다음 F-1( t)롤 계산하여 X 롤 얻는 것과 갇다. 그런 다음 확률 p (X)//(X) 에 의해 거절
 1.5
1.5
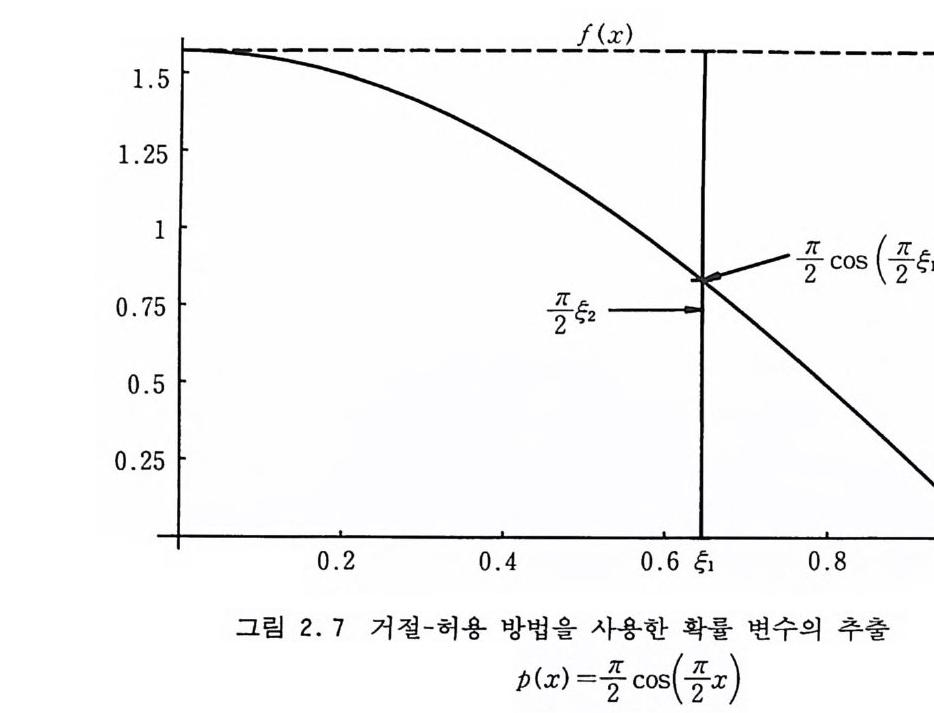
-허용 여부를 결정해야 하는데 그것은 간단한 과정으로서 구간 [O, J (X) ]에서 균일 분포 함수에 의해 점 Y 를 취하여 Y7} p (X) 보다 크면 버리고 아니면 취하는 것이다. 예로서 확률 밀도 함수 p(x ) =훔 cos( 令), osxsl (2 . 37) 를 고려해 보자. 비교 함수로서 f (x)= 공 취하면 확률 밀도 p (x) 에 의해 난수를 추출하는 거절 알고리즘은
匠 1) 令,g 2 를 생성 2) 꿍 E 조중 cos( 晉)이 면 g을 수용, 아니 면 폐 기 이다. 죽, 확률 밀도 f (x) 에 의해 임의의 . x- 점 令울 취하고 또 한 구간 [O, I( 令)]에서 균일 분포 난수를 취하여 이것이 p(~ 1) 보다 작으면 수용하고 아니면 폐기하는 것이다. (그립 2.7 을 참조) 위에서 든 예제에 대해 역변환 방법을 적용하기로 하면 균일 분포 난수 E 를 X=—27 [ asin ( ~) (2 .38) 에 의해 변환하여 원하는 난수를 얻어야 할 것이다. 예를 한 가지 더 들어보면 각도 0 가 구간 [O, 처에서 균일 분 포되어 있는 경우 sin 0 와 cos 0 를 생성해 내는 문제를 고려해 보자. von Neumann 의 거절-허용 알고리즘은 阿 1) 구간 [O, 1] 에서 두개의 균일 분포 난수 &과 令를 생성 2) 답+ff <1 이면 cos e= 祖暮 sin e= 뭉 을출력 3) 아니면 폐기하고 1) 로 감 이다.
구간 [O, 김에서 균일 분포 난수 O 를 생성하여 sin 0 와 cos 0 에 대입만 하면 될 간단한 문제를 왜 이렇게 복잡하게 계산하는 지 궁금해 할지 모르겠지만 컴퓨터가 sin 0 와 cos 0 를 계산하는 시간이 난수 계산보다 상당히 더 많이 걸리기 때문에 이 방법이 더 효율적이다. 길고도 긴 전산 모사에서는 난수들의 삼각함수를 수천만 번 계산해야 하는 경우 근소한 효율의 차이라도 전체 계 산 시간을 많이 절약해 줄 수 있을 것이다. 2.3.3 합성 방법 앞의 두 가지 방법은 밀도 함수가 복잡한 일반적인 경우에는 그대로 사용할 수가 없으나 여러 합성 방법 (Comp o sit ion Meth o d) 울 사용할 때 그 기본을 이룬다. 합성 방법의 간단한 예를 몇 가 지 들어보자. 확률 변수 X 려 분포 함수 Pi (x) 를 가지고 X2 는 분포 함수 P2(x) 를 가진다고 하자. 그러면 max(Xi, X2) 는 분포 함수 R(x)P2(x) 를 가지게 되고 mi n (Xi, X2) 는 분포 함수 A(x) +Pz(x)-A(x)Pz(x) 를 가지게 된다. 이 방법을 P(x) =x 인 균일 분포 확률 변수 x 에 적용해 보면 max(Xi, X2, …, Xn) 의 분포함수는 P(x) =xn 이다. 또한 이차원 확률 변수 (X, y)가 각기 독립적인 확률 변수 둘로 구성된다고 하자. 그러면 이들의 동시 확률 밀도 함수는
PxY(x, y) =Px(x)PY(y )=g( x)h(y) (2.39) 과 같이 쓸 수 있다. (X, y)의 합 Z=X+ Y, 곱 V=X· Y, 비율 W=X/Y 등도 확률 변수일 것이기 때문에 그들에 관한 밀도 함수들을 고려 할 수 있다. 먼저 Z 의 확률 밀도 함수는 Pz (z) =fg (t) h (z 一 t) dt (2 .40) 과 같이 두 밀도 함수들의 포갱 (convolu ti on) 에 의해 얻어전다. 예를들어 g (x) = µe-µ.x , h (y) = ve-vy ; O~ x, y < co (2 .41 ) 에 의해 (X, y)의 밀도 함수들이 주’ I . l.!기면 Z 의 밀도 함수는 Pz(z) =~l/—(µ e 산 -e- lJ Z) (2 .42a) 가 될 것이다. 단 µ=))일 경우에는 Pz (z) = µ2ze-µ.z (2 .42 b) 01 다. 또한 1. 1 절에서 논의한 이차원 확률 변수들의 변환 법칙 (1. 14) 를 적용하여 V 의P v(확v)률 = f밀g도(t )함 h 수信)를| +ld t (2 .43) 과 같이 얻을 수 있고 W 의 확률 밀도 함수는 Pw(w)=f g(tw) h(t) I t Idt (2 .44)
과 같이 얻는다. 확률 밀도 (2.41) 의 경우를 다시 한번 고려해 보 면 W=X/ Y 의 밀도 함수는 Pw(w)=~, o::;;;w
롤 고려해 보자. p (x) = 尹CO。 anxn, (2. 47) o::;;;x:,;;1 , an >O 위의 식을 적분하면 분포 함수가 oo P(x) = n~=O anxn+i; (n+1) (2 .48) 이 되므로 p (x) 의 분포를 가지는 X를 생성해 내기 위해 回 1) n 을 불연속적 밀도 함수 00 Pn= [an/(n+l)]/T, T= n~=O an/(n+l) 에 의해 선택한 다음 2) X 를 밀도 함수 9n (x) = (n+1) Xn 에 의해 추출하면 된다. Bu t cher 의 혼합 방법 합성 방법과 거절 방법을 결합하여 Bu t cher[l961] 는 다음과 같 은 혼합 방법을 고안해 냈다. 밀도 함수가 다음과 같이 분해된다 고하자. p (x) = n~=O. an fn ( x) gn (x) (2.49) 여기서 an>O 이고 fn 은 확률 밀도 함수이며 O~ g n~l 이 성립한다
고 하자. 이 식의 각 항을 조건부 확률로 간주하면 an 의 확률로 사건 n 이 일어나고 확률 fn (X) 가 일어나면 최종적으로 g n(X) 에 의해 X가 추출될 확률이 있다는 것이다. Bu t cher 에 의하면 p (x) 의 분포를 가지는 확률 변수 X를 생성해 내키 의해 匡 l) n 을 확률 p(n ) =an/~ an 에 의해 생성 2) X 를 밀도 함수 fn (X) 에 의해 생성 3) t를 생성하여 t:o;;:g n(x) 이면 X를 출력하고 그렇지 않으면 X를 폐기 하면 된다. 쓸데없이 복잡한 것처럼 보이는 이 방법이 실제로는 가장 유용한 방법이라는 것을 9 장의 방사선 운송에서 실감하게 될 것이다. 죽, 입자들의 산란 단면적 공식들이 너무 복잡하여 위의 식 (2.49) 와 같이 쓸 수밖에 없다. Marsa gli a 의 방 법 밀도 함수가 다음과 같이 분해된다고 하자. P(x) =~ Pn fn (x ) (2 . 50) 앞서 논의한 경우들의 특별한 경우로서 식 (2.46) 에서 H (t)= Pn 이거나 또는 식 (2.49) 에서 gn (x)=l 인 경우가 되는데 Marsa g li a[1961 비가 많이 연구했다. 정규 분포에 의해 확률 변 수를 뽑아내는 데에 활용하여 아주 효율적인 알고리즘을 개발할 수 있다. 3.6 절에서 이 알고리즘이 구체적으로 논의될 것이다.
참고문헌 [1 ] M. Abramowi tz and I.A. Ste g u n, Handbook of Math e mati ca l Functio n s, (Dover, 1968) [ 2 J I. Ang us, G. Fox, J. Ki m and D. Walker, Solvin g Problems on Concurrent Processors, vol. 2, (Prenti ce -H i ll, 1990) [ 3 J G. Bhanot, D. Duke and R. Salvador, ]. Sta t . Phys . 44 (1986) 985 [ 4 J C. Bays and S.D. Durham, ACM Trans. Math . Soft wa re 2 (19 76) 59 [ 5 J J.C. Butc h er, Comp ut e r J. 3 (1961) 251 [ 6 ] J.C. Butc h er and H. Messel, Nucl. Phys . 20 (1960) 15 [ 7 ] J.W . Butl e r, Sym p os iu m on Monte Carlo meth o ds ed. by H.A. Meye r, (Wi ley , 1956) 249 [8 ] J.W .S. Cassels, Intr o . the Geometr y of Numbers, (Sp r in g e r, 1959) 332 [ 이 R.R. Coveyo u and R.D . MacPherson, ]ACM 14 (1967) 100 〔 1 이 B.F. Green, J.E . K. Smi th, and L. Klem, ]ACM 6 (1959) 527 [11] A. Hoog la nd, J. Sp a a, B. Selman and A. Comp a g ne r, ]. Comp . Phys . 51 (1983) 250 [12] F. Jan ssens and U. Diet e r , 참고문헌 [13] [13] D.E. Knuth , The Ar t of Comp ut e r Prog ra mmi ng , vol. 2, (Addis o n-Wesley, 1981) 詞 D. H . Lehmer (1949) , see Proc. 2nd. Sy m p . on Large -Sacle Digital Calculati ng Machin e ry , (Harvard Univ . Press, 1951) 141 固 P.A. Lewi s and W.H. Payn e, ]ACM 20 (1973) 456 [16] M. LUscher, Comp . Phys . Comm. 79 (1994) 100 [1 기 M.d. MacLaren and G. Marsag lia, ]ACM 12 (1965) 83 ; CACM
11(1968) 759 [1 이 G. Marsag li a , Ann. Mat. Sta t. 32 (1961) 610 ; ibi d , 894 [19] G. Marsag li a , B. Narasim han, and A. Zaman, Comp . Phys . Comm. 60 (1990) 345 [2 이 N. Metr o p o li s, in Sym p os iu m on Monte Carlo Meth o ds, ed by H. A. Mey e r, (Wi le y, 1956) , pp. 29~36 [21] G.J. M i tch ell and D.P. Moore, unp u bli sh ed (1958) [2 끽 J. von Neumann, in Monte Carlo Meth o ds, ed by G.E . Forsyt he , H.H. Germond, A.S. Householder, NBS Ap p. Math , Serie s 12(1951) 36 [2 이 G. Paris i and F. Rap u ano, Phys . Lett . 157B (1985) 301 〔 2 사 R. Pearson, J.L. Ric h ardson and D. Toussain t , J. Comp . Phys . 51(1983) 241 [25 ]R .Y. Rubin s te i n , Sim ulati on and the Monte Carlo Meth o d, (Wi ley , 1981) [2 이 I. Vatt ul ain e n, K. Kankaala, J. Saarin e n, and T. Ala- Ni ss ila , Comp a rati ve Stu d y of some ps eudorandom number ge nerato r s, U. Helsin k i HU-TFT-93-22. [2 까 I. Vatt ul ain e n, New Tests of Random Numbers for Sim ulati on s in Phys i c a l Sys t e m s, (V. Helsin k i, Thesis , 1994)
제 3 장 대표적인 분포 함수들 3 장에서는 대표적인 분포 함수들을 소개하고 그 분포에 의해 확률 변수를 표본추출하는 방법들을 설명한다. 2 장에서 소개된 여러 표본추출 방법들의 좋은 적용 사례들이 될 것이다. 3.1 이항 분포 어떤 사건이 일어날 확률이 p이고 n 번 시도해서 그 사건이 m 번 일 어 날 확률은 이 항 분포 (Bi nomial Dist r i b u ti on ) 함수에 의 해 주어진다. B(n, m) m! (n~-mp!) m (l -p) n-m (3 .1) 예를 들면 가이거 계수기에 들어오는 입자가 감지될 확률이 p 이고 n 개의 입자가 계기에 둘어온다면 그 중에서 m 개가 감지될 확률은 위의 식에 의해 주어진다.
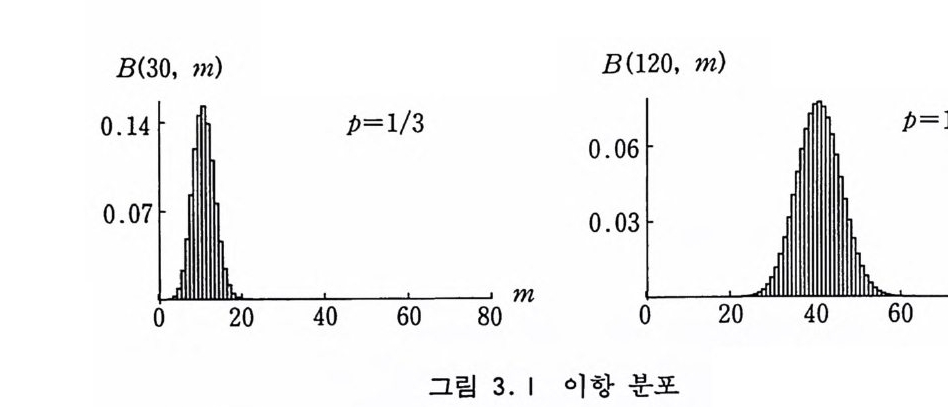 B(30, m) B(120, m)
B(30, m) B(120, m)
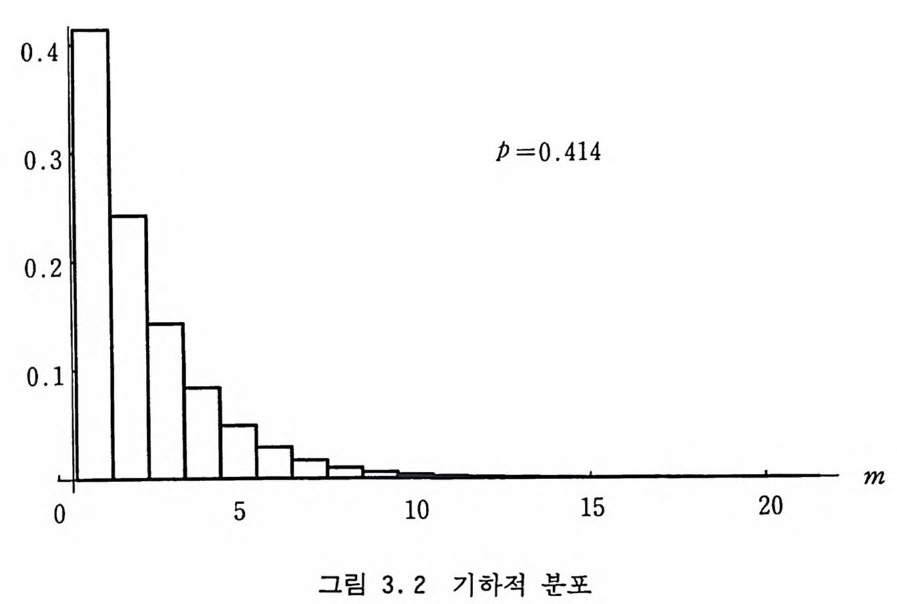
이항 분포에 의한 표본추출은 간단하게 n 개의 균일 분포 난수 둘 &, 令, …, ~n 을 생성하여 그 중에서 P 보다 작은 것들의 수 를 세어서 m 이라고 놓으면 된다. n 이 클 때에는 그 많은 수의 난수를 생성해 내는 작업에 시간이 많이 걸리기 때문에 좀더 효 율적인 방법이 필요하게 된다. 3.2 기하적 분포 어떤 사건이 확률 P 를 가지고 일어난다고 할 때 그 사건이 실 제로 일어날 때까지 시도하는 횟수 m 은 기하적 분포 (Geome t r ic Di s t r i bu ti on) 를 가진다. 죽, m 번 실패한 다음에 성공하는 것이 무 Pg (m) =p( l-p) m (3.2)
 0.4
0.4
라야한다. 이 분포는 3.5 절에 나오는 지수적 분포의 J =ln(l- p)인 경우 와 같다. 죽, 지수적 분포에 의해 추출된 확률 변수 X가 m 과 m+l 사이에 놓일 확률은 다음과 같다. P(m
 x뇨.. A `전 또 x| x | x | ••• 十―一> 시간 t
x뇨.. A `전 또 x| x | x | ••• 十―一> 시간 t
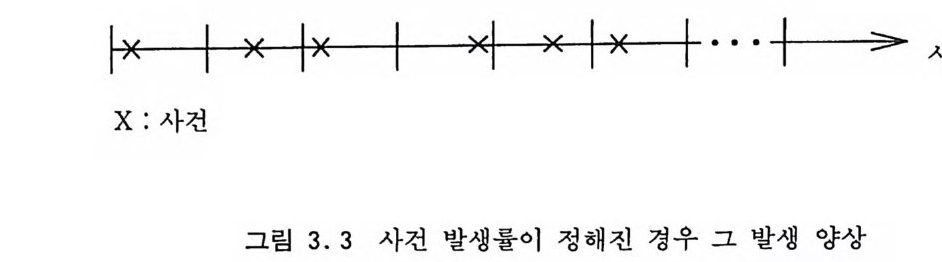
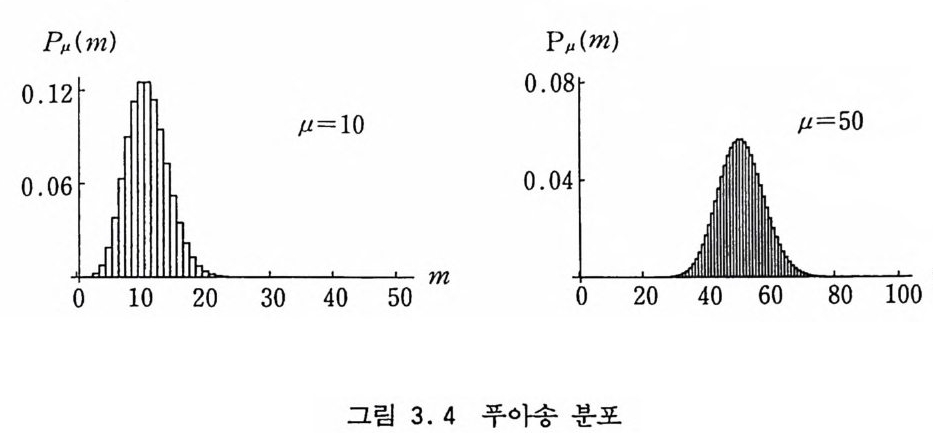
3.3 푸아송 분포 단위시간당 일어나는 사건들의 수 A 가 주어졌을 때 주어전 시 간 구간 4t 사이에 일어나는 사건들의 수가 m 일 확률은 µ= A4 t라고 놓으면 Pµ (m) =곱 e-µ, m=O, 1, … (3.5) 에 의해 주어진다. 그림 3.3 에서 방사성 물질이 알파 입자를 방출하는 시각을 ti, t2, …라고 하자. 평균적으로 일초 동안에 방출하는 알파 입자들 의 수가 A 라고 하면 시간축의 임의의 점에서부터 시작하여 4t 사이에 방출되는 입자들의 수는 상호 독립적이며 µ=;l L1 t인 푸아 송 분포 (Pois s on Dis t r i b u ti on ) 를 가질 것 이 다. 여기서 사건들 간의 시간 간격, 죽 사건이 일어난 직후로부터
 Pµ(m) Pµ(m)
Pµ(m) Pµ(m)
다음 사건까지 기다리는 시간, 8k 는 3.5 절에서 논의하게 될 평 균이 1/ J인 지수적 분포를 가지게 된다. 또한 to 로부터 k 번째 입 자가 방출될 때까지의 시간 h 는 3.4 절에서 논의하게 될 매개변 수들 (k, J)를 가지는 감마 분포를 가진다. 입자들이 일정한 율 로 방출되는 사건을 보는 관점에 따라 푸아송 분포, 지수적 분 포, 감마 분포를 얻게 되어 이들이 모두 서로 밀접한 관련이 있 음을 알 수 있다. 또한 µ가 크면 푸아송 분포가 종 모양의 정규 분포와 비슷한 모양을 가지게 되고 이러한 경향은 감마 분포나 이항분포에서도 마찬가지임을 볼 수 있는데 표본추출 알고리즘에 유용하게 사용할 수 있다. (그림 3.4 참조) 8 t를 계속적으로 추출하여 Z i 8 ti느 4 t일 때까지 일어난 사건들 의 수를 세어 m j라고 놓고 또 다시 이 과정을 반복하면 m j둘은 푸아송 분포를 가질 것이다. 가장 간단한 표본추출 방법은 평균 이 1/µ 인 지수적 분포를 가지는 수들을 역변환 방법에 의해 차 례차례 추출하여 더해가면서 —(ln g+… +ln ~n)/µ=-ln(~1 X ~2X …X ~n)/µ21
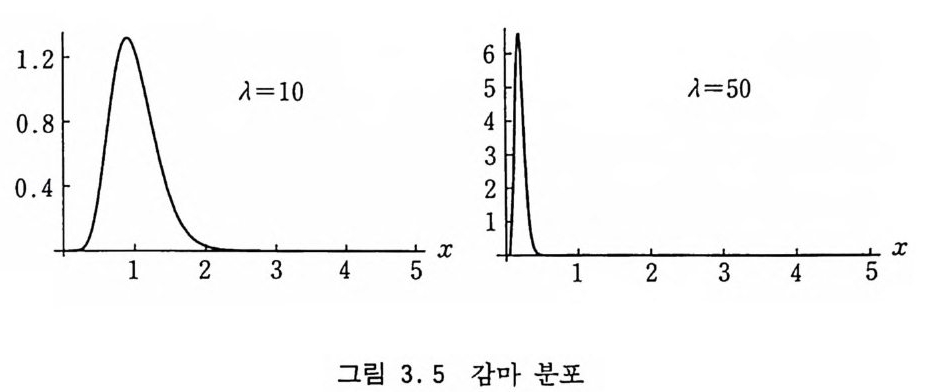
이 만족되면 m+--n ― 1 을 추출하는 방법이다. 이 방법을 더 간 단하게 할 수 있는데 균일 분포 난수들 令, 욘2 , ••• 을 차례차례 추출하면서 그들의 곱이 ~I X ~2X ••• X ~n S exp (—µ) (3 .6) 을 만족할 때까지 계속하여 m+--n-l 을 추출해 나가는 것이다. µ가 크면 부등식 (3.6) 을 만족할 때까지 난수들을 많이 생성 해야 하므로 이 방법은 효율이 떨어진다. Ahrens 와 Di et e r [1974] 의 알고리즘을 사용하면 대략 log µ번 만에 표본추출을 할 수 있다. m=L a:피라고 하면 ( a ::::::: 7/8 이 최적의 선택임) 다음과 갇 다. E l) m- 차의 감마 분포에 의해 확률 변수 X 를 추출 2) X<µ 이면 평균이 µ― X 인 푸아송 분포로부터 N을 식 (3.6) 을 사용하여 표본추출하여 m+N1 을 출력 3) X2µ 이면 이항 분포 B(m-l, µ/X) 에 의해 추출한 N1 을 출력 3.4 감마 분포 단위시간당 일어나는 사건들의 수가 A 일 때 n 번째 사건이 시 간 구간 (x, x+dx) 사이에 일어날 확률은 Pr (X ; n, 11) =~ exp ( —A X) (11x) n-I (3 . 7) 에 의해 주어진다. 감마 분포 (Gamma Di s t r i bu ti on) 에서 n=l 이면
 1·20·8·04 654321
1·20·8·04 654321
지수적 분포가 된다. 감마 분포의 특성이 있는데 X 의 확률 밀도 함수가 Pr(X ; n, A) 이고 Y 의 확률 밀도 함수가 拓 (x ; m, A) 라고 하면 X+Y 의 확률 밀도 함수는 Pr(X ; n+m, A) 라는 것이다. 이 성질로부터 n 개의 지수 분포 확률 변수의 합이 감마 분포를 가진다는 것을 어렵지 않게 증명할 수 있다. 이 성질을 이용하면 n 이 작을 때 유용한 알고리즘을 만들 수 있다. 죽 X1= _丁1 ln g1, xn= 分 ln tn 을 생성하여 합하면 되는데 X=i~=n 1 Xi = -+IA1n (s1···sn) (3.8) 이기 때문에 로그 계산을 한 번만 해도 된다. n 이 커지면 난수 를 많이 생성해 내야 하므로 이 방법은 효율성이 떨어지게 되고 또한 n 이 정수가 아니면 사용할 수가 없다. 거절 방법을 사용하 는 알고리즘 두 가지를 다음에 소개해 본다. O
던 1) p - e/ ( n + e) 2) gI, g2 를 생성 3) g l< p이면 x-tl'n , q -e-x 라고 두고 4) 아니면 X 크 _ln g2, q ― xn-1 로 둠 5) g3 를 생성 6) s3< q이면 X를 출력 아니면 2) 로 감 n 이 정수가 아니라도 n>l 인 경우에 언제나 사용할 수 있고 코시 분포를 비교 함수로 하여 거절 방법을 이용하는 Ahrens- Di e t er[I974] 의 알고리즘은 약간 복잡하지만 n>3 인 경우 아주 효율적이고 n 이 증가해도 효율이 0.56 정도로서 계산 시간이 거 의 일정하다. 五l) m+- n— 1 2) s 를 생성 3) t +-m + (1/tl) tan K(s-0.5) 4) 지수 분포로부터 Z 를 생성 5) —Z ~ln[l+A2(t- m)2]+m In(t/ m ) — (t-m ) 이면 X= t를 출력 6) 아니면 2) 로 감 식 (3.8) 에서 n 이 클 경우 X 가 많은 수의 합이므로 중심 극 한정리를 적용하면 정규 분포와 관련지을 수 있다. Y 가 평균이 l-l/(9n) 이고 표준편차가 1/ ./9n인 정규 분포 확률 변수라고 하면 X +--n Y3 은 감마 분포를 갖는다.
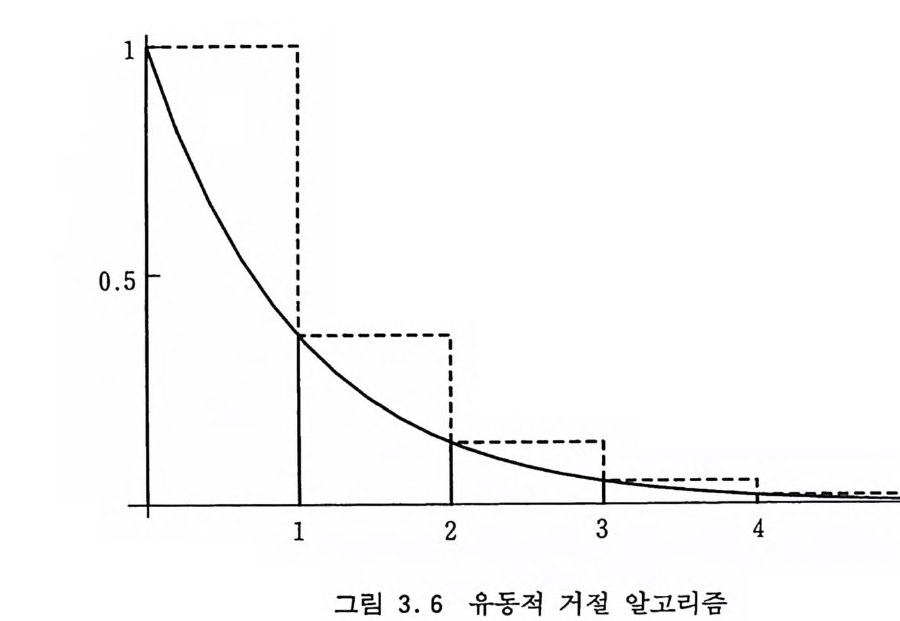
3.5 지수적 분포 평균이 µ=1/A 인 지수적 분포 (Ex p onen ti al D i s t r i bu ti on) 의 밀도 함수는 p(x ) =A exp (— AX) (3 .9) 과 같이 정의된다. 지수적 분포는 다른 분포들과 연관이 많이 되 어 정규 분포 다음으로 응용이 많이 되는 분포이기 때문에 표본 추출하는 알고리즘이 많이 개발되어 있다. 지수적 분포를 가지는 확률 변수는 기억상실적이라는 독특한 성질을 가지고 있다. x 가 어떤 계기의 수명이라고 하면 임의의 순간에서 볼 때에도 지수적 분포를 가지는 그 계기의 남은 수명 은 그 계기가 제작되어서 얼마나 많은 시간이 흘렀느냐에 상관없 이 똑같다. 매질과의 반응 단면적이 A 인 입자가 매질과 다음 반 응을 일으킬 때까지 가는 거리는 지수적 분포를 가진다. 또한 µ 초마다 알파 입자를 한 개씩 방출하는 물질이 입자를 하나씩 방 출하는 시간 간격도 평균이 µ인 지수적 분포를 가진다. 2.3 . 1 절에서 예로 든 역변환 방법에서는 로그 계산에 시간이 많이 걸리기 때문에 더 빠른 알고리즘이 요구된다. Forsy the [1972 〕의 거절-허용 방법을 적용하는 알고리즘은 巴 1) 배열에 r[k]=l-ex p(一 Ak) 를 저장 : k +-1 2) ~를 생성 3) ~> r[k] 이면 k +-k+1 로 놓고 2) 로 감 4) g를 생성 ; t +-A g로 놓음 5) &, g2, …를 t ~~N 일 때까지 차례로 생성
 1--------
1--------
6) N 이 짝수이면 2) 로 감 7) N 이 홀수이면 t를 출력 이다. 그림 3.6 에서 보다시피 이 알고리즘은 확률 분포 함수를 몇개의 구간으로 자르고 각 구간에서의 비교 함수를 그 구간의 시작점에서의 밀도 함수의 값으로 취한다. 확률이 가장 큰 원점 에서 가까운 구간부터 시도하여 거절되면 차례로 다음 구간을 시 도하는 식으로 추출한다. 가장 효율적인 알고리즘은 Marsag li a , Sib u y a , Ahrens[1975] 가 합성 방법을 사용하여 개발한 알고리즘으로서 계산 초기에 사용 하는 컴퓨터의 word 크기 w 에 따라 다음의 배열을 미리 계산해 야한다. Q[ k]=j~=k l L;/j! L=ln 2
수열의 상한 k 는 미리 정해져 있는 것이 아니고 합산울 계속해 가면서 Q[ k] >1 ― 21-W 일 때 중지하면 된다. 그런 다음 E 1) w- 비트의 균일 분포 난수 t= (. b1b2 … bw)2 를 생성 처음으로 0 이 되는 b J를 찾아 거기서부터 앞자리의 비트를 밀 어내고 t +--( . b;+I …如 )2 로 놓음 2) t
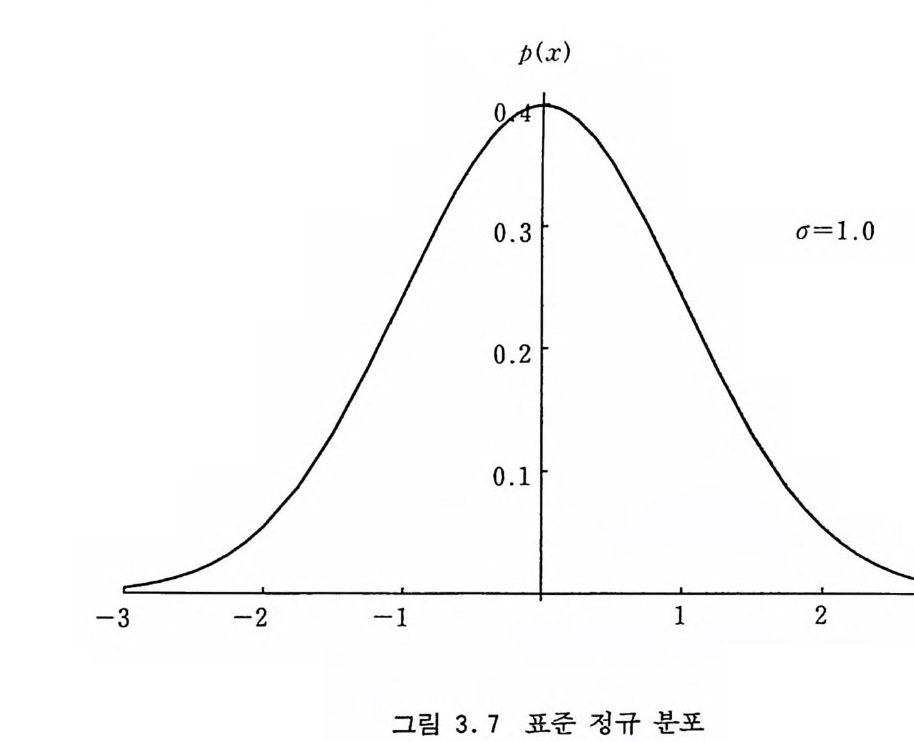 p( x)
p( x)
xo=O, 6=1 인 표준 정규 분포의 밀도 함수를 나타낸다. 극각 방법 교과서에 가장 흔히 나오는 알고리즘 [Box, Muller, Marsag lia, 1958 〕인데 E 1) Yi- 2~1-1, Yi- Uz-1 2) R-Yi2 + 합 3) R~l 이면 1) 로 감 4) 아니면 X1= Yi~瓦 X2=½ ✓ =汀澤-를 출력
 o . 9r /』1 6 fl7 f l8
o . 9r /』1 6 fl7 f l8
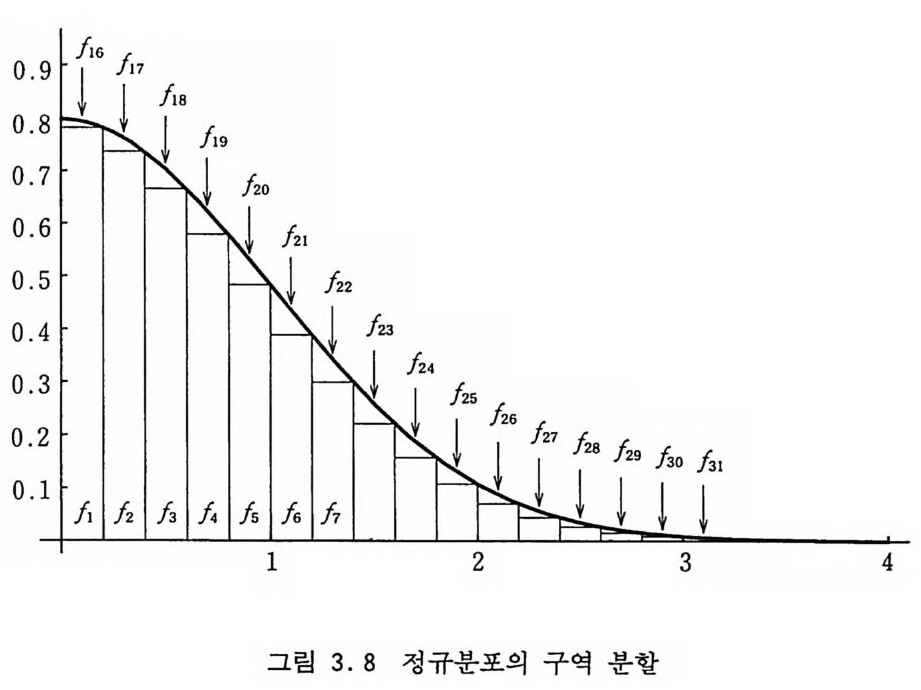
이렇게 생성되는 X 들은 정규 분포를 가진다. 이것은 R !S'.:: r 일 확률이 ― 2lnR !S'.:균일 확률, 죽 R~ex p(―군 /2) 과 같다는 점에 착안한 것이다. 이 방법은 간단하지만 효율은 별로 좋지 않다. 사각형-쐐기-꼬리 방법 개념적으로 분리-통치 방법인 혼합 방법을 [Marsa gli a, 1961] 이 용하면 일반적안 분포 함수에 대해서 아주 복잡하지만 굉장히 효 율적인 알고리즘을 개발할 수 있다. 우선 그립 3.8 을 보자. 그림에서 확률 밀도 함수 f (x) 가 31 개의 다른 확률 밀도 함수 fi(x) , …, /31 (x) 들의 합으로 표시 될 수 있음을 보여 주고 있 다. f (x) =Pd1 (x) + … +p31 f 31 (x) (3 .11)
여기서 /j (X) 는 각각이 확률 밀도 함수로서 IJ ( x) >0 이고 정의 구 간에서의 적분이 1 이다. 예를 들어 원점으로부터 첫번째 구간에 서는 f (x) =Pd1 (x) + Pl6f 1s (x) (3 .12) 인데 P1 과 P16 은 직사각형 부분과 쐐기 모양 부분의 면적들이다. 이것은 이 구간에서 f (x) 에 따라 난수를 추출할 때 직사각형에 서 추출될 확률이 P1 이고 쐐기에서 추출될 확률이 Pl6 임을 나타 내는 것이다. 곡선 f( x) 아래의 면적의 대부분을 차지하는 것들은 fi( x) 부 터 l1s(x) 까지의 직사각형들로서 정의구간 내에서 균일 분포 함 수이다. 이들이 차지하는 면적은 0 . 9183 으로서 J (x) 에 의한 난 수 추출에서 91 .83 %만큼은 균일 분포에 의해 난수를 추출하게 되어 이 알고리즘의 효율성의 근원이 된다. 나머지 중에서 7.9 %는 f1 6(x) 부터 /3。 (x) 까지의 쐐기들이 차지하고 30 밖의 꼬 리 부분이 차지하는 면적은 전체의 0.27 %에 불과하여 이 부분 에서의 난수 추출이 어렵다 하여도 그런 상황이 일어나는 빈도 수가 극히 드물어서 계산 시간에 별로 영향을 끼치지 못한다. /16(X) 부터 f3。 (x) 까지의 부분에 대해서는 거철 방법을 재치있게 적용하면 된다. 따라서 각 부분에서의 면적들 pj를 계산한 다음 확률 pj에 의 해 j를 선택한다. 우선 직사각형들의 면적을 계산해 보면 pj=\f (j/5) = {if; exp (-//50) , 1 亨 15 (3 .13) ]’가 직사각형 부분을 가리키면 난수 X 는 X=0.2 s+S (3 .14)
 b I`
b I`
 b
b
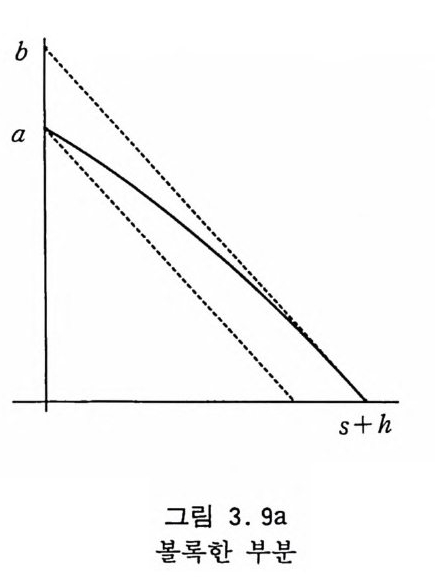
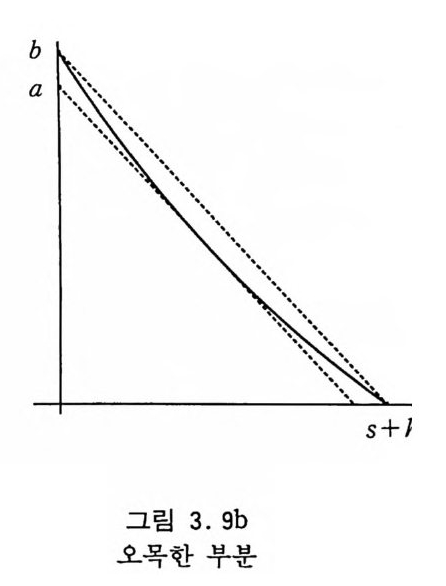
에 의해 얻는데 S 는 확률 pj에 의해 S=0.2 (j― 1) 가 된다. 약 92% 정도는 이렇게 간단히 추출된다. 쐐기 부분 f1 6(x) 부터 lao(x) 까지의 각각에서의 면적은 계산 초기에 수치적으로 계산해서 배열에 저장시켜 놓는다• 이들 부분 에서는 거절 방법을 기술적으로 사용하는데 단순한 비교 함수를 쓰지 않고 그림 3.9 에서처럼 곡선 부분을 두 개의 평행인 직선들 사이에 끼워 넣는다. x=l 이 변곡점이기 때문에 x
마지막으로 남은 꼬리 부분에 대해서는 거절 방법을 있는 그대 로 사용하는데 이 부분에서 표본추출을 하게 되는 빈도 수 비율 은 370 번에 한 번꼴이다. 이 알고리즘을 좀더 구체적으로 말하면 다음과 같다• 巨 1) 초기화 a) 각 구역의 면적들 p』를 수치적으로 계산하고 A=p1 , A=P1+P2, …, P3o=P1+… +p30 , P31=O.5 둘을 계산하여 메모리에 저장 b) a;, bj 롤 수치적으로 계산하여 n=a;/b;, Ej = l/b;, 2) sS 를j = 생0성.2.x (nj —― 1)g /를2 . 메sg모n 리 一에 ( g저의 장어 느 비트) 3) 이진 탐색 방법을 사용하여 Pj
표 3. I J P』 Pj+ 1 5 D ;+IS E ;+l5 sj 1 .07 82 .4602 .50 5 25. 00 0.2 2 .1519 .4627 .773 12. 50 o.4 3 .2185 .4664 .87 6 8. 33 0.6 4 .27 64 .47 09 .939 6.2 5 0.8 5 .3248 .47 57 .986 5. 00 1.0 6 .36 37 .48 04 .99 5 4.06 1.2 7 .39 36 .4848 .98 7 3.37 1.4 8 .4158 .48 85 .97 9 2.8 6 1.6 9 .43 16 .4916 .972 2.47 1.8 10 .4424 .49 40 .96 6 2.16 2.0 11 .44 95 .4958 .96 0 1.92 2.2 12 .45 40 .4970 .95 4 1.71 2.4 13 .4567 .49 78 .948 1.54 2.6 14 .4583 .4983 .942 1.40 2.8 15 .45 92 .4987 .93 6 1.27 3.0 16 .5000
6) aj) =새31로 이이면 두 개의 난수 g와 E 를 생성하여 X <--- ✓ 9-2ln s b) ~X 효이면 a) 로 되돌아감 c) 7) 로 감 7) s g n=l 이면 x -- x 여기서 g, 民는 [O, 1] 사이의 균일 분포 난수이다. 또한 이 알 고리즘에서 사용된 상수들 pj, Dj , Ej, Sj 들을 표 3.1 에 수록하 였다. 단계 2) 에서 n 룰 사용하는 것은 정규 분포 곡선의 반쪽이 차지하는 면적이 0.5 이기 때문인데 단계 7) 에서 음수도 표본추출 할 수 있도록 했다. Knu th는 단계 3) 의 이전 탐색 방법보다 더 효율적인 탐색 방법을 고안해 냈는데 여기서는 이해하기 쉬운 방
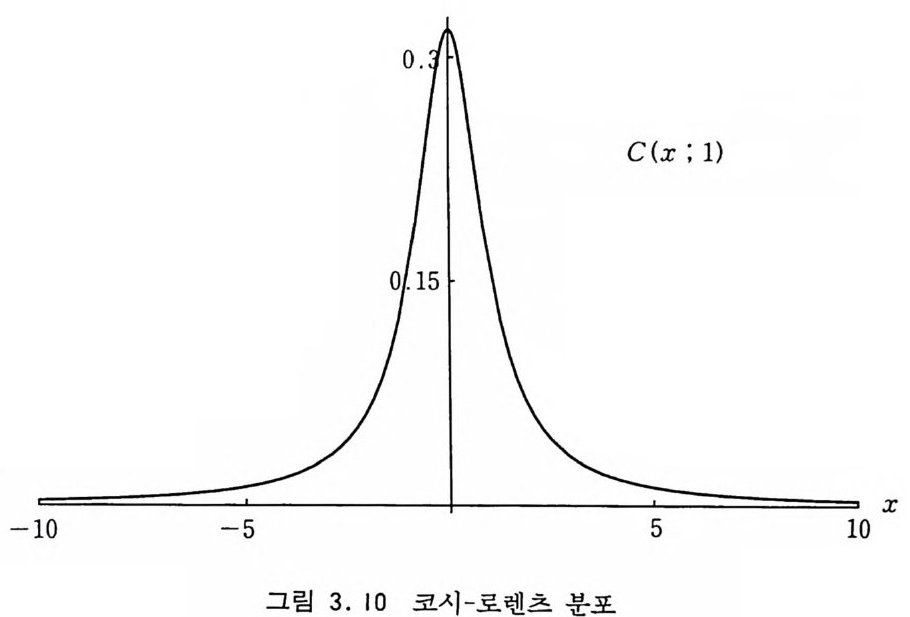
법을 채택했다. 3.7 코시-로렌츠· 분포 종 모양의 확률 밀도 함수 C(x ; a)=~습 ) (3 .15) 에 의 한 코시 -로렌츠 분포 (Cauchy -L orentz Dist r i b u ti on ) 를 종종 보게 된다. 푸아송 분포나 감마 분포에서 매개 변수가 크면 종 모양을 가지기 때문에 거절 방법을 사용할 때 이들 분포를 에워 싸는 비교 함수로서 코시-로렌츠 밀도 함수가 많이 사용된다. 또 한 정규분포를 가지는 두 개의 독립적인 확률 변수들의 비율이 코시-로렌츠 분포를 가진다는 것을 확률 기본 변환 법칙을 적용 해 보면 쉽게 알아낼 수 있다. 이 함수는 해석적으로 적분 가능하고 그것이 또한 쉽게 역변환 되므로 역변환 방법을 사용하여 표본추출하면 된다. 식 (3.15) 를 적분하면 F (x) =강+-¼ t an 詩) (3 .16) 울 얻고 F(x) 를 역변환하면 x =F-1 (y) = a t an[1r( y-강)] = - ~ (3 .17) 이 얻어진다.
 C (x ; 1)
C (x ; 1)
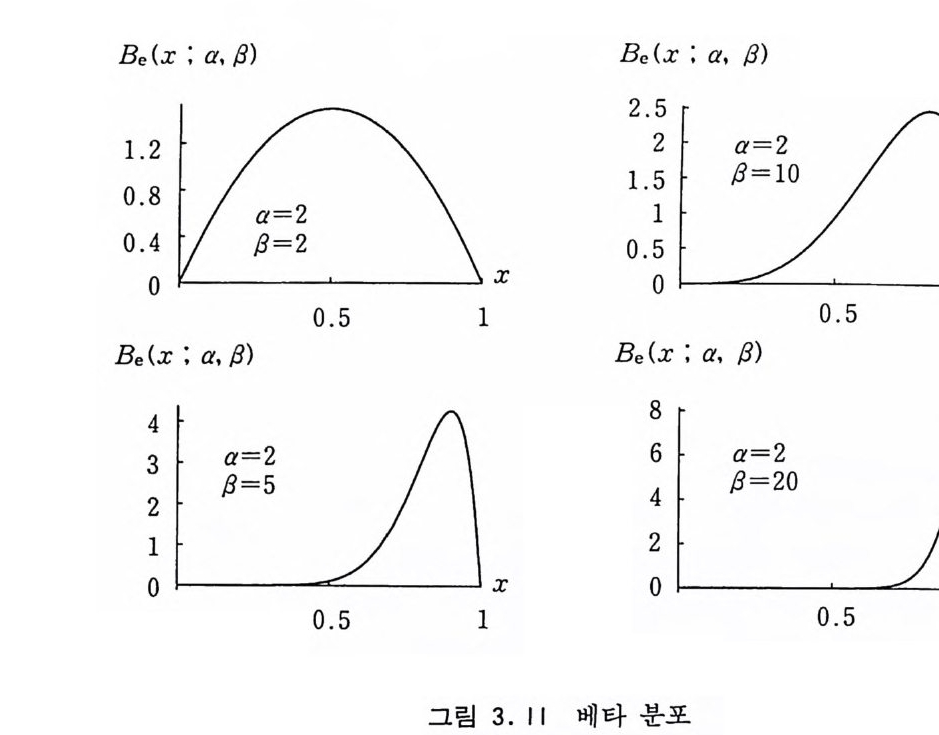
3.8 베타 분포 베 타 분포 (Bet a Dist r i b u ti on ) 의 밀도 함수는 Be(X ; a, f])= Cxa-1(l-x)P-1, C 나鬪 (3.18) 와 같이 정의된다. 그림 3.11 에서 보다시피 a 와 /3의 값에 따라 여러 모양을 가지기 때문에 거절 방법에서 비교 함수로 사용하면 좋을 것이다. 이 분포에 의한 표본추출은 차수가 a, /3인 두 개의 감마 분포 에 의해 난수들 Xi , X2 를 생성하여 X t-- X1/(X1+X2) 로 놓으면 된다. X 가 베타 분포를 가진다는 것은 확률 기본 변환 법칙으로 부터 쉽게 유도할 수 있다. a, /3가 정수일 경우에 사용할 수 있는 아주 간단한 알고리즘 은 (a+ /3― 1) 개의 균일 분포 난수들 &, &, ... ~a+ /J- 1 을 생 성한 다음 그중에서 /3번째로 큰 수를 선택하는 것이다. 이 방법
 Be· (X ; a, /3) aB==2 _2 X B01c..5o1(:x It ; a, _/38= )1 0 \ x
Be· (X ; a, /3) aB==2 _2 X B01c..5o1(:x It ; a, _/38= )1 0 \ x
은 (a+ /3 -1) 가 너무 크면 효율이 많이 떨어질 것이다. 효율은 별로 좋지 않지만 a, 8 의 임의 값에 대해서 사용할 수 있는 방법은 비교 함수로서 Be(X ; a, /3)의 극대값을 사용하는 거절 방법이다. 극대값은 xo=(a-1)/(a+ {3 -2) 에서 일어나는데 M=Be (Xo ; a, /3) 이라고놓고 回 1) &, &롤 생성 2) M終 [I' (a+ /3 )Ir(a)r( {3 )U f -1(1-~1)P-l 이면 綺 출력 아니면 1) 로 감
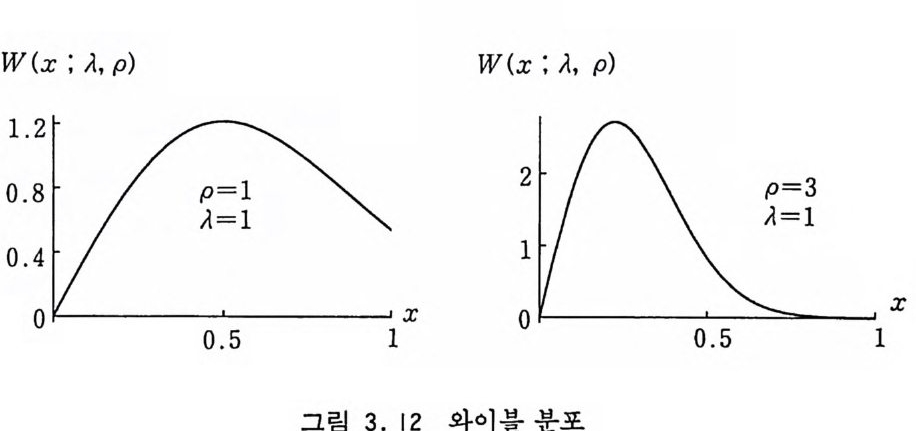
하면 된다. 지수적 확률 변수를 추출하는 데 사용했던 Forsyt he 알고리즘 巳〔工〕\ 적절히 사용하면 훨씬 효율적인 방법이 얻 어질 것이다. 3.9 와이불 분포 와이 불 분포 (Weib u ll Dist r i b u ti on ) 의 밀도 함수는 W(x ; A, p) = (Ap ) xP-1exp ( -AxP), x>O ; A, p킥 0 (3.19) 에 의해 주어진다. 그림 3 . 12 에서 보다시피 A, P 의 값에 따라 여러 모양을 가지는데 베타 분포와 다론 점은 그 꼬리가 길다는 것이다. 식 (3.19) 는 p =l 이면 지수 분포가 되고 p =2 이면 레일 리 (Ray le ig h ) 분포가 된다. 식 (3.19) 는 쉽게 적분되어 F(x) =1— e xp (— AXP) (3 .20)
 W(x;.- 1,p) W(x ; A, p)
W(x;.- 1,p) W(x ; A, p)
이 되고 이 식은 쉽게 역변환되어 x=F-1(y) =[-ln(l— y)/J]I IP (3 . 21) 이 얻어진다. 와이블 분포에 의한 표본추출은 다음과 같다. E 그三] 1) ~를 생성 2) X=(-In~/ ..-l )11P 를 출력 이 분포는 신뢰도 (Rel i ab i l ity) 문제에서 많이 사용된다. 지수 분 포는 고장률이 언제나 일정한 경우에 쓰이고, 감마 분포는 시간 이 흘러감에 따라 고장률이 일정해지는 경우에 쓰이는 데에 비해 와이불 분포는 고장률이 시간에 따라 증감할 수 있는 모든 경우 에 다 쓰인다. 3.10 카이평방 분포 감마 분포 (3.7) 에서 ...l=½, n= 『이라고 놓으면 자유도가 m 인 카이 평 방 분포 (Chi- S q u are Dist r i b u ti on ) 를 얻는다. Px2(x ; m)=~xm12-1e 구 /2, x>O (3 . 22) 정규 분포 PN(x ; 0, 1) 로부터 m 개의 수 X1, …, Xm 를 추출 하여 각각을 제곱하여 합한 수 X= }J1f'= 1Xl 는 자유도가 m 인 카 이평방 분포를 갖는다는 것은 찰 알려진 사실이다.
 Ps (X ; m)
Ps (X ; m)
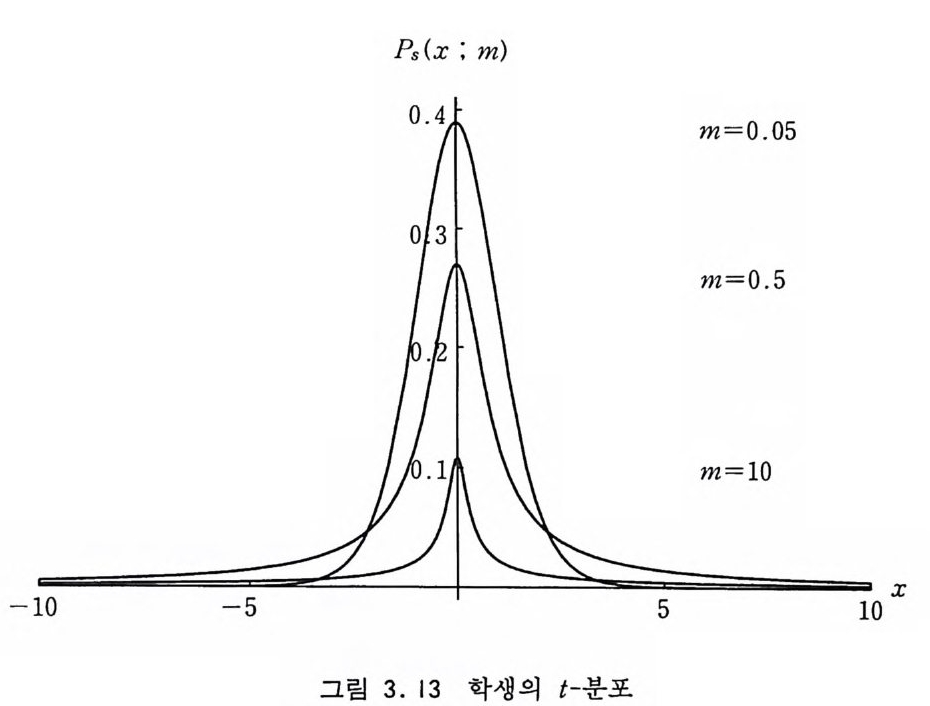
3. 11 학생의 t-분포 평균값이 0 이고 분산이 1 인 표준 정규 분포 PN(X ; 0, l) 로부 터 Z 를 추출하고 카이평방 분포 Pxz(x ; m) 으로부터 Y 를 추출 하여 다음과 같이 합성 해서 만드는, X= J z X는 자유도가 m 인 학생의 t-분포 (S t uden t 's t-Di s t r i bu ti on) 를 갖 는다.
Ps(X ; 11'l) = 店:::털 (1+ 릎 ) - < m +ll / 2, -oo
제 4 장 몬데카를로 적분 수치 적 분을 위 해 심 프슨 (Si m p so n) 의 공식 , 롬버 그 (Romberg) 적 분, 가우스 (Gauss) 적분 등 몇 가지 효율적인 방법이 오래전부터 개발되어 변수가 몇 개밖에 없는 경우 상당히 정확하게 적분 계 산울 할 수 있으나 변수의 수가 많아지게 되면 사실상 이런 방법 둘을 사용할 수가 없게 된다. 예를 들어 각 변수마다 적분 구간 을 10 개 로 잘라도 변수가 100 개 이 면 함수 계 산을 10100 번을 해 야 한다. 이것은 1 초에 함수 계산을 1010 번씩 할 수 있는 슈퍼 컴퓨 터로 317 년이 걸리는 계산량이어서 사실상 불가능하다. 4.1 서론 컴퓨터 속도의 제약으로 인해 함수 계산을 하는 점들의 수 N 울 고정시켜야 한다고 가정하자. 적분 영역이 d 차원 초입방체라 고 하고 각 차원의 구간을 똑같은 수만큼 자른다고 하면 각 차원 에서 취할 수 있는 간격의 수는 Nlld 에 비례하고 간격은 N-1/d 에
표 4. I 점의 수 N 에 따른 수치 적분의 부정확도 적분공식 1 차원 d 차원 사다리꼴 공식 N-2 N-2/d 심프슨의 공식 N-4 N-4/d 가우스공식 N-2m+ 1 N-(2m-l)ld 몬데카를로 N-112 N-112
비례할 것이다. 구체적으로 각 구적법에 의한 오차의 공식을 표 4.1 에 모아 놓았다. 각 구적법마다 간격의 길이에 따른 오차의 공식이 다르지만 대체적으로 N 의 어떤 차수에 역비례하여 오차 가 감소하는 경향은 공통적이다. 대략 d 가 10 이상일 경우 몬테 카롤로 방법이 다론 방법에 비해 압도적으로 정확하다는 것을 알 수 있다. 가장 초보적인 몬테카를로 방법은 주어진 구간 내의 임의 점에 서 함수 계산을 하여 그들의 평균을 취함으로써 적분의 근사값을 구하는 것이다. 임의 점의 수가 많아지면 정확도가 좋아지지만 수령의 속도가 N-112 에 비례하기 때문에 직설적 방법은 효율성에 문제가 있다. 하지만 균일 분포에 의한 확률 변수의 생성이 다른 분포에 의한 확률 변수의 생성의 시발점이 된 것과 마찬가지로 직설적 몬데카를로 적분은 효율이 별로 좋지는 않지만 다른 더 정교로운 몬테카를로 적분 방법의 바탕이 된다. N 을 너무 많이 늘리지 않고 몬테카를로 적분의 효율을 높이기 위해서는 실효 편 차를 줄이는 수밖에 없다. 이룰 위하여 여러 정교로운 방법들이 고안되었는데 이 장에서 몇 가지 잘 쓰이는 방법을 논의할 것이 다. 몬테카를로 적분 방법의 기본 개념을 쉽게 이해하기 위해 다음 과 갇은 1 차원 적분울 계산하는 방법을 고려해 보자.
I=1。1 g ( x)dx (4. 1) 임의의 구간 [a, b] 에서의 적분을 변수 변환 x-+a+(b-a) t에 의해 식 (4.1) 과 같은 형식으로 쓸 수 있기 때문에 식 (4.1) 은 일반성을 가지고 있다. I=1ab g (x)dx 一 (b-a)l1g [ a+(b-a)t] d t (4 .2) 적분 (4.1) 은 구간 [O, 1] 에서 g (x) 의 기대값이라고 볼 수 있는 데 그분산은 6 드 =£l。 [ g (X) 크 ]zdx=£1 g (x)2dx ― I2 (4.3) 에 의해 주어진다. 4.2 직설적 방법 적분 구간 [O, 1] 을 4x=1/N 간격으로 N 번 등분하여 i번째 x- 좌표를 X;라 고 하면 사각형 공식에 의하여 적분 I 를 근사적으 로 다음과 같이 쓸 수 있다. I~ Ni2=-O I g( xi) 4x=4x Ni고=-O I g( x,·) (4. 4) 만일 구간 [O, 1] 에서 균일 분포 함수에 의해 N 개의 임의 점을 뽑아내서 X, +1 >X,가 되게끔 분류했다고 가정하면, N 이 충분히 클경우, 4x i =X i +1-x 혼 1/N=Llx (4.5)
가 되어 I~ NiZ= - O1 g( xi) 4xi (4 . 6) ~ (1/N) Ni~=- O1 g( x;) =IN 과 같은 근사식을 얻을 수 있다. 이 식에서 g;=g (x,. ) 들도 확률변수로서 그 밀도함수는 1/ (dg/ d x) 로 주어진다. 확률 변수 gi둘의 합계인 IN 역시 매번 시도할 때 마다 값이 다르게 나오는 확률 변수이다. g들의 분산울 68=§ 접 값―(i철 사 (4 . 7) 라고하자. IN 이 많은 수의 확률 변수 g;둘의 합을 N 으로 나눈 평균값이 고 그 기대값이 I 에 의해 주어지기 때문에 중심 극한 정리 1. 2 에 의해 IN 이 기대값 I 로부터 €6사 g V 이내에 있을 확률은 聽 P[ ― c< 以腐 <+c]=* f」 Cex p(-f )d t (4 . 8) 와 감이 된다. 위 식으로부터 몬테카롤로 적분의 두 가지 중요한 특성을 알 수 있다. 첫째, 몬테카를로 적분의 규격화된 표준편차 6s~6 사 澤가 N 이 증가함에 따라 1/ /N에 비례해서 감소한다는 것이 다. 1/ /N에 의한 감소는 다른 1 차원 수치 적분 방법에 비해 아주 느린 것이지만 다차원의 경우 몬테카를로 방법은 여전히 l/ 澤 감소를 보이는 반면에 다른 방법들은 차원이 높아질수록 더 욱 더 느린 감소를 보인다. (표 4.1 참조) 둘째로는 6 g ~6N 가 작
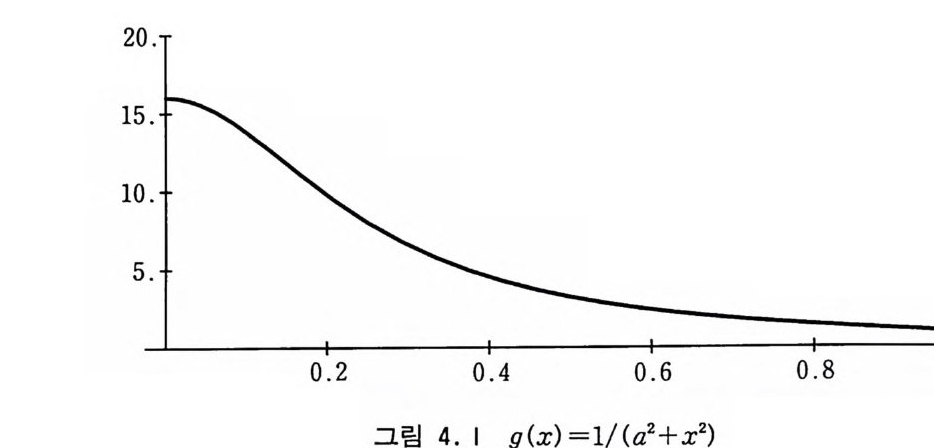
으면 작을수록 몬테카를로 적분의 편차도 이에 비례해서 작아진 다는 점이다. 따라서 N 을 고정시켜야 하는 상황에서 적분의 편 차를 줄일 수 있는 방법은 6 g를 줄이는 것이다. 기초 확률론에 의하면 확률 변수 gi가 평균값에 되도록 가까 이 있을수록 6 g가 작아진다. 다음 절부터 논의하는 편차 감소 기법둘의 대부분은 피적분 함수를 적절히 처리하여 변화가 적은 함수로 만든 다음 이것을 직설적으로 적분하는 전략을 사용하고 있다. 적분 방법이 복잡해짐에 따라 편차를 감소시키기 위해 별도의 계산울 해야 하는데 그 방법의 효율성이 문제가 된다. 두 가지 몬테카롤로 방법의 효율을 비교하는 방법은 난수를 생성하여 피 적분 함수 계산을 한 번 하는 데 걸리는 시간을 r 라고 하고 편 차를 군이라고 하면 방법 2 는 방법 1 에 비해서 T/1 2N=1r i~ar (4 . 9) 배만큼 효율적이라고 말할 수 있다. 간단한 예를 몇 가지 고려해 보자. 먼저 g( x) =~군’ a=0.25 (4 .10) 롤 보면 이것은 그림 4.1 과 같이 유연한 함수이다. 그 적분은 19=11kdx=~~5.30327 (4.11) 이고 이 적분의 분산은 ~= !o。 1g (x) 2dx-IJ~ 4 . 67235 (4.12)
 20.
20.
와 같이 쉽게 얻어진다. 이것의 몬테카롤로 적분 IN 은 N 이 클 경우 중심 극한 정리에 의해 정규 분포를 가지게 되어 그 기대값 I 로부터 6s=6g /gV 이내에 들어올 확률은 95% 이다. 실제로 표분추출 횟수를 N=100 으로 잡고 몬테카롤로 적분을 해보면 IN = 5 .l254l,
100 배 늘린 데에 대한 보답치고는 약소하지만 다차원 적분에서는 돋보이게 될 것이다. 몇 가지 굴곡이 심한 함수들에 관한 몬테카를로 적분 결과를 표 4.2 에 목록화하고 이 함수들을 그립 4.2 에 스케치하였다. 심 프슨의 방법에 의한 정확한 값이 먼저 제시되고 표본 횟수가 N =100, N=10000 인 순서로 제시했다. 이들 예제에서 g2 (x) 의 경 우를 제의하고는 N=lOOOO 에서는 몬테카를로 적분 값이 모두 표 준편차 이내에서 위치하는 것을 볼 수 있다. 4.3 편차 감소 기법 식 (4.3) 에서 볼 수 있듯이 피적분 함수가 적분 구간 내에서 많은 변화를 하면 분산 6; 가 커지는 반면 변화가 전혀 없는 상수 일 경우에는 편차가 전혀 없다. 따라서 피적분 함수의 모양에 따 라서 몬테카롤로 적분의 정확도가 달라져서 굴곡이 적은 함수는 표본추출을 적게 해도 적분의 비교적 정확한 추산이 얻어지는 데 에 비해 변화가 심한 함수는 표본추출 횟수를 늘려야만 적분의 정확도를 유지할 수 있는 것이다. 편차의 1/./N 감소 경향을 바꿀 수는 없으나 우리가 종종 피 적분 함수에 관해 가지게 되는 어느 정도의 정보를 유리한 방향 으로 이용하여 피적분 함수를 편차가 적은 함수로 변환하면 몬테 카를로 적분의 실효 편차를 줄여줄 수 있다.
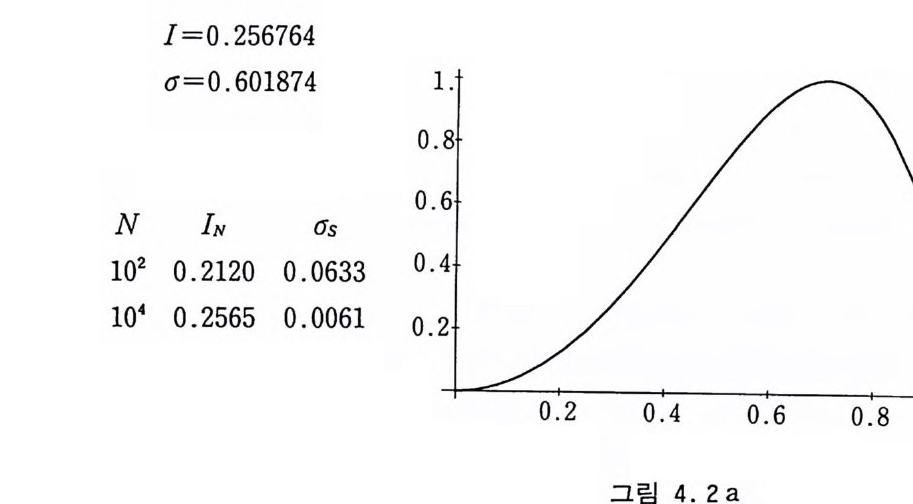
표 4. 2a 직설적 방법에 의한 몬테카 류 로 적분 9• (x) =sin ( n군 ) (4 .16 )
 l=0.2 5 6764
l=0.2 5 6764
92 (x) =sin (7rx) [1 +O .lsin ( l27rx) ] (4 .17)
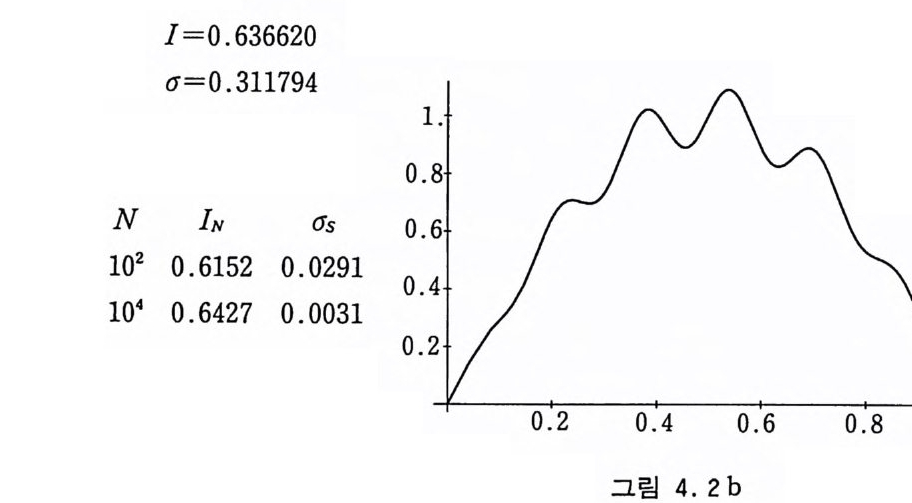 I=0.636620
I=0.636620
표 4. 2 b 직설적 방법에 의한 몬테카 를 로 적분 g3 (x) =exp [x sin (21rx) ][1 + 0 .1 sin (l21rx) ] (4 .18)
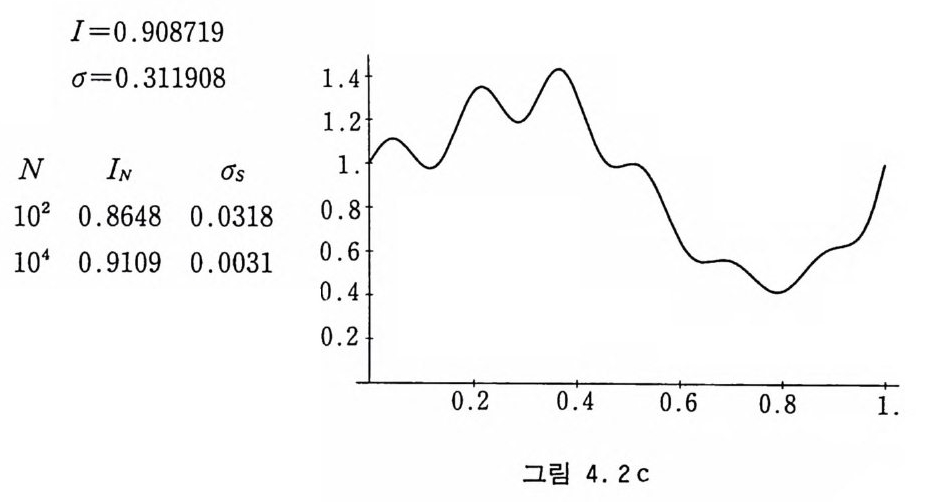 I=0.908719
I=0.908719
g4( X) =~+군 )|1{.l5+ 0+.s5i ne (x 4p1 r[xs)i n ( 12TX) (4 .19)
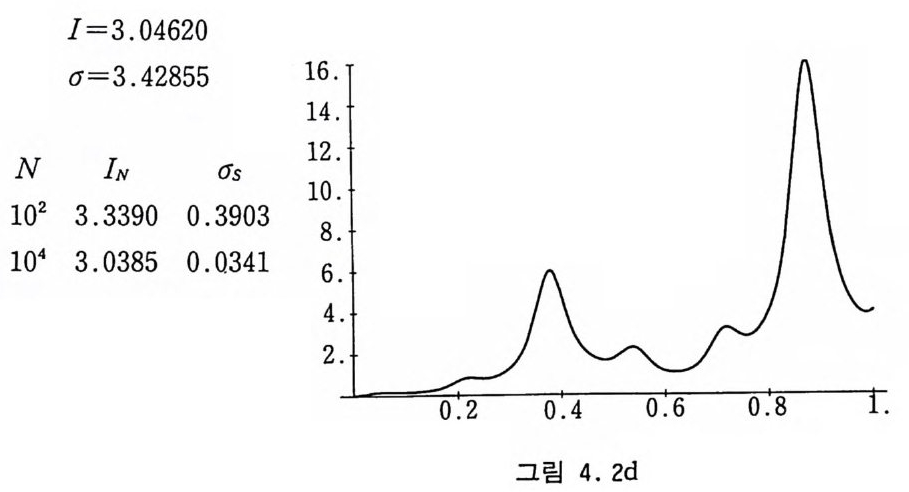 1=3.0 4 620
1=3.0 4 620
4. 3. 1 중점 적 방법 (Imp o rta n ce Samp ling ) 적분 구간 [O, 1] 에서 양이고 단위 규격화되어 있는 무게 함수 w(x) 가 정의된다고 하자. £。 1w(x)dx=l ; w(x) 책, o::;;;x::;;;1 (4.20) 앞 절에서의 적분 I 를 다르게 써보면 I=11$w(x)dx (4 . 21) 와 같이 쓸 수 있다. 여기서 x 에 다음과 같은 변수 변환을 해보 자. y (x) =£:。 xw (t) dt = F(x) (4. 22 ) 다시 말해저 뿔 =w(x) ; y( O)=O, y( l)=l (4 . 23) 이 되게끔 하는 것이다. 그러면 위의 적분은 I = 1ldy 길: --11((검 ) (4 . 24) 와 같이 된다. 앞 절에서 쓴 직설적 방법을 위의 식 (4.24) 에 적용하면 구간 [O, 1] 사이에서 균일 분포된 y에 관해 평균을 취하여 I 나N 上f;;'1 w $[x (瓜y;) ] (4 . 25)
과 같이 적분의 근사값을 구할 수 있다. 여기서 무게 함수 w(x) 를 피적분 함수 g (x) 와 같거나 모양이 아주 비슷한 함수로 취하면 g (x)/w(x) 는 아주 유연한 함수가 되어 위의 식 (4.25) 로부터 추산되는 적분의 분산은 0 이거나 아주 작을 것이다. 가장 적합하게 무게 함수를 w(x) =g (x)/1 로 취하면 식 (4.25) 에서 피적분 함수 g (x)/w(x) 가 상수가 되어 이것의 몬테카롤로 적분 의 편차는 0 이 된다. 문제는 적분 값을 구하기 전에는 I 를 알 수가 없다는 것이다. 따라서 무게 함수로서 g (x) 와 유사하면서 다루기 쉬운 함수를 택하는 것이 실용적인 방안이다. 균일 분포된 y들에 식 (4.22) 의 역변환을 적용하면 대응하는 X, 둘은 결과적으로 무게 함수 (dx/dy =l/w) 의 값이 큰 지역에 더 촘촘히 몰리게 된다. 따라서 식 (4.25) 에 의한 평균값 계산은 x 공간에서 w(x) 가 큰 지역에서 표본추출을 더 많이 하는 방식 으로 행해지는 것이다. 예로서 lu=1o1 g ( x) dx=ol \in( 1rx) dx=2/1r~0.63661977 (4.26) 룰 고려해 보자. Ig 의 편차 6 g는 a~= l1。 g (x) 2dx-I t국- (끝 )2 ~ o. 094715265 (4 . 27) 에 의해 주어진다. 무게 함수로서 포물선 함수인 w(x)=6x(l-x), 11w(x)dx=l (4.28) 。 롤 택해 보자. (그립 4.3 참조) 무게 함수를 사용하는 적분은
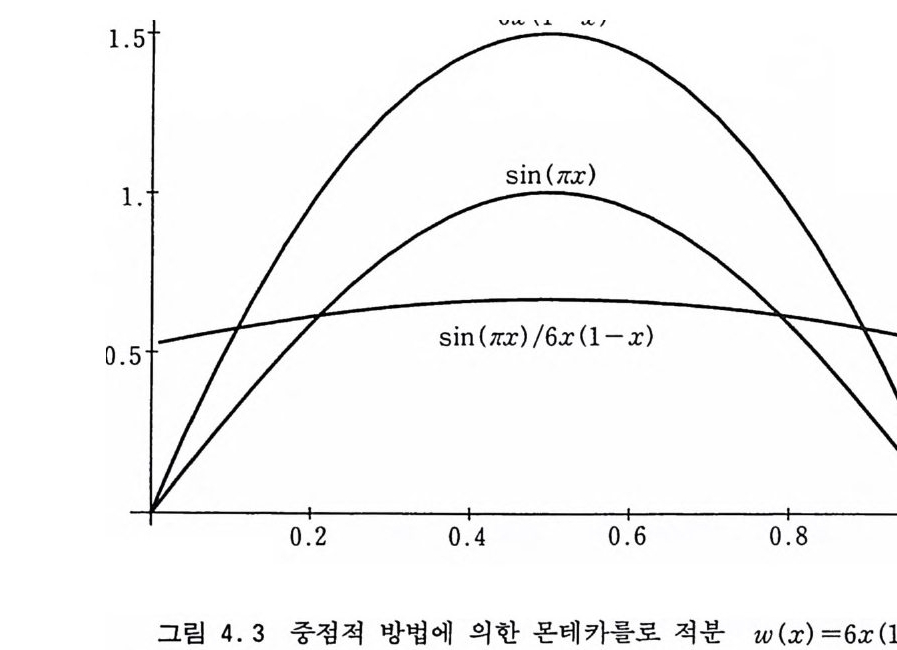 1.5
1.5
Ig /w[ 立t w(x)dx=11~맡 긴) w(x)dx (4 . 29) 와 같이 쓸 수 있다. Ig /w 에 대 한 편차 (JgJ w 는 6노 /w= 〔 雲)2 dx-IJ,w : :::::0 .0009908 (4 . 30) 로서 아보다 훨씬 작다. 실제로 계산하기 위해서는 무게 함수 w(x) 에 의해 난수를 생 성해야 하는 별도의 부담이 있다. 위의 무게 함수는 쉽게 부정적 분이 되고 3 차 방정식을 풀면 그 역함수도 명백하게 얻어진다. Y=F(x) =1x6x (l-x) dx=-2 군 +3x2 (4.31) 위 식은 O~ y ~l 에서 3 개의 실수 근을 가지는데 그 중 가운데에 있는 것은 O~x~l 사이에 존재한다. 그것은 cos r/> =l-2 y라고 하면 다음 식에 의해 주어진다.
x(y) =F-1 (y) =½+cos (『틀) (4.32) 중점적 방법의 알고리즘을 약술하면 巳 1) t를 생성 2) X;=F 一 1(EI) 를 계산 3) g (X;)/w(X;) 를 계산하여 적분값에 합산 4) i
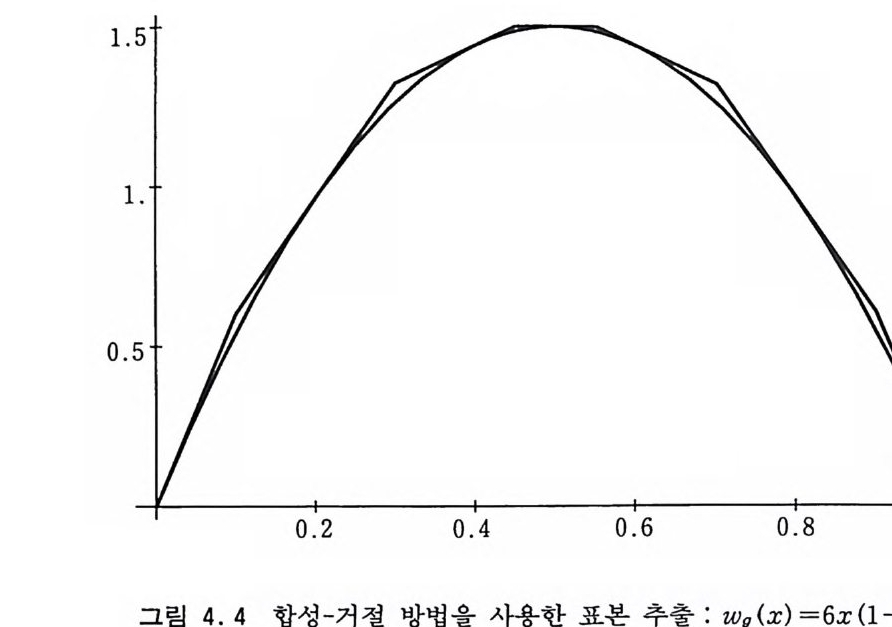 1.5
1.5
예를 들어 그림 4.4 와 같이 투박하지만 w g (x) 를 비교적 가까 이 에워싸는 비교 함수를 사용하면 식 (4.32) 를 사용하는 역변환 방법에 비해 계산 시간이 현저히 단축된다. 4.3.2 제어 함수 방법 중점적 방법에서는 피적분 함수를 비교 함수로 나누어서 적분 구간 내에서 큰 변화가 없이 1 근처에 머무르는 함수를 얻었다. 피적분 함수에서 비교 함수를 빼주어도 이와 비슷한 효과가 나타 난다. 그 결과로 나오는 함수는 적분 구간 내에서 큰 변화가 없 이 대략적으로 0 근처에 머무를 것이다. 중점적 방법에서는 비교 함수가 구간 내에서 0 에 너무 가까이 지나가지 않도록 조심해야 하지만 제어 함수법 (Contr o l Var i a t es) 에서는 그럴 필요가 없다. 좀더 구체적으로 말하자면
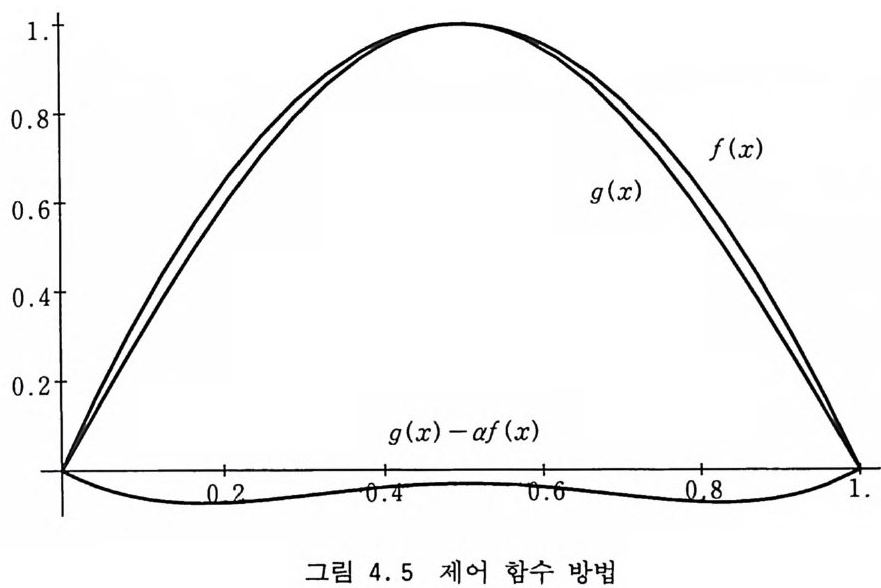 1.
1.
I=j[ g(x ) -af (x ) ]dx+aj t(x) dx (4.33) 를 직설적 방법으로 계산하는 것이다. 여기서 제어 함수 f (x) 는 우리가 잘 아는 함수라야 하고 특히 그 적분이 알려져 있어야 된 다. 이렇게 해서 얻은 적분의 분산은 여g -a f)=따 +a2
자. 제어함수로서 /(x) =l 국 (x 망 )2 (4. 35 ) 을 선택하면 fo1J (x) dx =출, 6}= 志 (4 . 36) 가 되고 g (x) 와의 상관 함수는 Cov(g, f) =[『 s i n(7Cx) -디 [1-4(x- 당 )2 ― 출 ]dx = 샘--검 와 같이 얻어져서 cto =~=l.03 06 279 (4 . 38) 에서 (J(g-af)가 최소값을 가지게 된다. 식 (4. 27 ), (4.36~38) 을 식 (4.34) 에 대입하면
6;=N1 얹N [g (xi) -a f (x,·) - 評 (4 . 40) 를 계산한다. 그런 다음 a 를 변화시켜 가며 6 璋를 a 의 함수로서 구하여 햐가 최소가 되게 하는 a 를 찾는다. 식 (4 . 40) 으로부터 석가 a 의 이차 함수임이 분명하므로 이 데이터들을 이차 함수 햐 =aa2+ ba+ c 에 근사적으로 맞춰 놓으면 ao= -b/2a 에 의해 곧바로 찾을 수 있다. 위의 예제에 이 방법을 적용해 보자. N=lO 으로 놓고 E와 6t 을 계산해 보면 a E 6h 0.8 +0 .1 0 32 0.0 7 096 0.9 +0.0 3 62 0.0 4 297 1.0 -0.0 3 08 0.0 1 866 11..12 —_。0 .. 1 0694788 00..0042931292 물 얻는다. 따라서 0 . 9
a IN 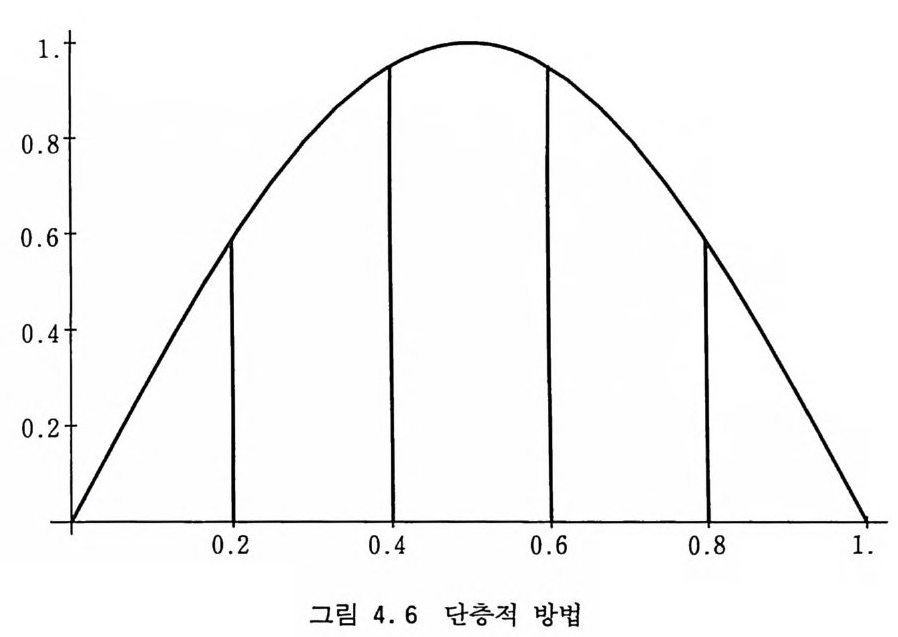 1.
1.
i2m= I ni= N 이 되고 IN 의 분산은 o1=if= l 요n-2i
는다. ni = N ~jS=iI6 Si J (J J (4 . 44) 이 경우 분산은 성 =\(2?=I S,6:)2 (4 . 45) 으로 된다. 중접적 방법에서는 피적분 함수의 값이 큰 지역에서 표본추출 횟수를 함수 값에 비례해서 늘리는 데 비해 단충 방법에서는 피 적분 함수의 표준편차가 큰 지역에서 그것에 비례해서 표본의 수 룰 늘리는 것이다. 죽 함수의 굴곡이 심한 부분에 중점을 둔다고 볼 수 있다. 앞 절에서 논의했듯이 함수가 상수인 경우에는 단 한번의 표본추출로도 정확한 적분값을 얻을 수 있는 것처럼 편차 룰 어떻게 줄이느냐가 중요한 것이다. 아에 대한 사전 지식이 없을 때는 단충적 방법을 효율적으로 적용할 수가 없지만 단순하게 구간을 균등하게 나누어서 사용하 기만 해도 편차가 줄어든다. 좀더 복잡하게는 시험적으로 적분 구간을 균등하게 나눈 다음 각 구간에서 표본추출하는 점들의 수 가 같게 하여 직설적 방법을 적용하여 I,· 와 6 i를 대충 구한 다음 여기서 얻은 정보를 이용하여 부분 구간의 길이 S j와 표본추출의 수 n i를 결정해 나가면 될 것이다. 이런 식으로 계속해서 반복 하면 꽤 정확한 적분을 구할 수 있을 것이다. 이 알고리즘을 요약하면
덴 1) 구간을 m 개로 쪼개고 표본 횟수 n; +-1 0 으로 놓음 2) 각 구간에서의 적분 I~? 와 편차 6 f를 계산 3) 식 (4.44) 에 의해 n, . 를 다시 결정 4) 각 구간에서의 적분 IA? 와 편차 6? 를 계산 4.3.1 절의 예제에서 적분 구간을 5 개로 균등하게 나누고 각 구 간에서 표본추출을 20 번씩 해서 몬테카롤로 적분 계산을 해보면 다음 결과를 얻는다. 지역 ni IA? aj 012230 4 0.06692804 0.15604239 20 0.15959858 0.09968640 20 0. 19 599672 0.01575188 20 0.15574693 0.11338144 20 0.05629645 0.18124163 위의 결과를 식 (4 . 44) 에 대입하여 n 를 재조정하고 전체 표본 추출 횟수를 10 배로 늘려서 계산울 다시 해보면 표 4.3 을 얻 는다.
표 4. 3 단충 방법에 의한 적분 m=5, N :::::: 10 。O 지역 n,. Ii? 6i 0122375 4 0. 06 031712 0.16563668 176 0. 15 801590 0.10376226 27 0. 19 639325 0. 01 576798 200 0.15842542 0.10282070 320 0.06247820 0.16700006 998 0.63562990 0.00352228
표본추출 횟수가 1000 번인 것에 비하면 이 결과는 별로 좋아 보이지 않는다. 전체 표본추출 횟수를 1000 번으로 고정하기 위하 여 적분 구간을 늘려서 10 개로 균등하게 나누고 각 구간에서 표 본추출을 10 번씩 해서 몬테카를로 적분 계산을 해보면 다음 결과 롤 얻는다. 지역 n,' IA:) 6i 。 10 0.0 1 904453 0.08980106 1 10 0.0 4 497753 0.0 6 059539 2 10 0.0 7 104252 0.07262192 3 10 0.0 8 852497 0.02811356 4 10 0.0 9 775960 0.01598755 5 10 0.09799615 0.01647627 6 10 0.08822887 0.04487869 7 10 0.06922916 0. 06 573917 8 10 0.04334922 0.0 8 049151 9 10 0.01536276 0.09947048 위의 결과를 식 (4.44) 에 대입하여 n,· 룰 재조정하고 전체 표본 추출 횟수를 10 배로 늘려서 계산을 다시 해보면 표 4.4 를 얻는 다. 똑같이 1000 개의 표본을 추출했는데 지역의 수를 5 구역에서 10 구역으로 늘린 결과는 표준편차가 절반으로 줄어든 것이다. 식 (4.42) 를 자세히 살펴보면 N 을 고정하고서 m 을 늘리면 s,· 가 줄 어드는 대신 n,· 도 똑같은 비례로 줄어들기 때문에 이들이 as 를 줄이는 데 직접적인 기여를 하지는 않는다는 것을 알 수 있다. 실인즉, 각 구간 내에서의 편차가 줄어든다는 것이 편차 감소의
표 4. 4 단충 방법에 의한 적분 m=lO, N ::::::1 000 지역 ni IA? 6i 0121536 450.6 01 754864992 0.0 8 639567 105 0.0 4 473993 0.07757450 126 0.06988188 0.06423929 48 0.08898924 0.0 3 637121 27 0.0 9 868415 0.01433090 28 0.0 9 840033 0. 01 319125 78 0.0 8 815689 0.04224892 114 0 . 07051168 0.06063378 140 0.0 4 624747 0.07627025 173 0.0 1 553533 0. 08 825484 995 0.6 3 661182 0.00179165
직접적인 원인이다. 여기서 문제는 구간을 얼마만큼 쪼개야 충분히 쪼겠느냐 하는 것이다. 극단적으로 위에서 m=lOOO 으로 두면 직설적 방법이 되 어 정확도가 떨어질 것이기 때문에 무작정 m 을 늘려나갈 수는 없다. 최적의 구간 수는 10~1000 사이의 어디에 있을 것이다. 경험적으로 볼 때 어느 구역에서든 몬데카를로 적분의 의미를 가 질 수 있도록 최소의 표본 수가 n,.= 5 ~10 정도면 좋을 것이다. 전체 표본 수 N=lOOO 을 대충 고정시키면서 지역의 수 m 을 변해가면서 위에서 똑같은 방법으로 적분한 결과를 표 4.5 에 나 타냈다. IN 에 관한한 m=lO 에서 가장 좋은 결과가 나왔는데 이것은 우 연일 뿐이다. 중요한 것은 그 추산의 표준편차이다. 표 4.5 를 살펴 보면 표준편차가 대략적으로 m 에 반비례해서 줄어드는 경향을 볼 수 있는데 m=34 에 이르러서는 반드시 그렇지 않음을 볼 수 있다. 따라서 우리는 m=20~25 에서의 결과를 가장 신뢰할 수
표 4. 5 단충 방법에 의한 적분 N ::::::1 000 N m IN 6s 998 568100.16 23 51662299002 5340 . 00 352228 956 0.6 3 628089 0.00306951 955 0.6 3 641423 0. 00 229249 995 0.6 3 661182 0.00179165 955 0.6 3 647415 0.00153342 952 0.6 3 658315 0.00116573 989 0,63633485 0. 00 091774 987 0. 63 637209 0. 00 075262 1004 0.63643583 0.00073723
있다고 판정을 내려야 할 것이다. 표 4 . 4 의 결과를 보면 단총 방법은 중점적 방법에 비해서 반대 의 전략을 사용하는 것처럼 보인다. 죽 함수 값이 작은 지역에서 표본추출 횟수를 늘리고 값이 큰 중앙 부분에서는 줄이는 것처럼 보인다.
표 4. 6a 단충 방법에 의한 식 (4.18)- ga (x) 의 적분 지역 nj JM> 6i 012430 4506.170668819 0. 03 6643 126 0. 10 94 93 0. 11 1671 83 0.1 2 8201 0.059137 88 0.1 3 4472 0.076985 162 0. 10 7922 0. 10 5012 166 0.089064 0 .10 8117 36 0.0 5 7225 0. 02 2321 67 0.0 4 9359 0. 04 8762 88 0.053380 0. 06 6485 140 0. 07 1859 0. 10 2924 996 0.907656 0.0 0 2357
표 4. 6b 단충 방법에 의한 식 (4.19)- g4 (X) 의 적분 지역 ni IA? 6I 01234 4506.0 71 048799 0.052430 9 0. 03 1435 0.1 3 9374 15 0 .092114 0.1 4 9730 141 0.385044 1.63 8475 93 0.2 4 4196 0.843090 36 0.188438 0.334922 47 0.149641 0. 55 9179 25 0.305845 0.229453 390 1.064028 4.1 5 9485 235 0.584351 2.278053 995 3.0 5 5572 0.033067
하지만 다른 함수에 단충 방법을 적용해 보면 반드시 그렇지는 않다는 것을 알 수 있다. 예를 들어 그림 4 . 2c 와 4.2d 에 보이는 변화가 심한 함수들에 단충 방법을 적용해 보면 표 4.6 을 얻는 다. 4.3.4 대조 방법 지금까지 논의된 어떤 방법보다 더 강력하게 편차를 줄여 주는 방법 이 대 조 방법 (Anti the ti c Varia t e s ) 이 다. 중점 적 방법 이 나 제 어 함수 방법에서는 최적의 중요 함수나 제어 함수를 찾기가 어렵고 단충 방법에서는 단충의 수를 늘리는 데에 한계가 있기 때문에 편차를 크게 줄이기가 어렵다. 하지만 대조 방법에서는 큰 어려 움이 없이 편차를 줄이는 조합을 찾아낼 수 있고 이것은 비슷한 종류의 함수이면 보편적으로 적용될 수 있어서 아주 실용적이다. 이 방법 역시 상관관계를 이용하는 것인데 제어 함수 방법이 양
의 상관관계를 이용한 것에 반하여 여기서는 음의 상관관계를 이 용하여 편차를 줄인다. I 를 두 가지 다른 방법으로, 예를 들어 l1N 과 I2N 을, 산출해 낸다고 하면 IN= U1N+I2N)/2 가 되고 IN 의 분산은 var [½u1N+l2N)]=t varU 1N) +tvar( /2N) +~ov(I IN, I2N) (4 . 46) 가 된다. 여기서 CovU1N, 12N) 가 음이 되게끔 하면 편차를 크 게 줄일 수 있을 것이다. 예를 들어 g (x) 의 적분, I=£1g ( x)dx (4 . 47) 。 롤 다르게 써서 1=½11[g( x) +g( l— x) ]dx (4 . 48) 로 놓을 수가 있다. g (x) 가 단조 증가 함수인 경우에 g (x) 와 g (l-x) 가 음의 상관관계를 가전다는 것을 증명하기는 어렵지 않다. 죽, flg ( x )g ( 1_x) dx 三 I2 (4 . 49) 。 여기서 주의해야 할 점은 식 (4.48) 의 몬데카롤로 적분에서 두 개의 적분에 사용하는 난수를 똑같은 수열에서 취해야 한다는 것 이다. 구간을 둘로 나누는 단충 방법을 적용해 보면
1= 下1 접N {ag (a ti) + (1-a)g [a + (1 급韓]} (4 . 50a) 이 되는데 s i =e, 로 놓으면 1=11 J 첩N {ag (as;) + (1— a) g [ a+ (1 급) gi]} =N1 꼽N 의 a g(&) (4.50b) 롤 얻는다. 또한 l ― e,. = &라고 놓으면 I =71v 얹n {ag (a?;,.) + (1-a) g( l-(1 -a) &]} 三下l 읽n .Jag ( ?;;) (4 . 50c) 롤 얻는다. g( x) =sin ( TCx), 0 :5:: x :5:: l 처럼 정의구간 내에서 증가-감소하는 함수에 대해서는 a=l/2 로 놓고 식 (4.50b) 를 사용하면 편차가 줄어들 것이다. 단조 함수에 대해서는 증가하는 항과 감소하는 항이 있는 식 (4 . 50c) 를 사용하면 편차가 감소될 것이다. 편차가 a 의 함수이므로 a 를 조정하여 최적의 a 를 선택할 수 있는데 다 음의 정리를 고려해 보자. 정리 4. I 다음과 같은 단충 방법을 고려해 보자. Um g(t)=占접g(~) (4 .51) g (x) 가 주기 1 을 가지는 주기 함수라고 하면 m-+oo 인 극한 에서 어떤 양의 수 k 에 대해 var {Umg ( s)}= eJ (e-km) (4 .52)
이 성립한다. 또한 비주기적 함수 g (x) 가 구간 (0, 1) 에서 연속적이고 그 도함수들이 연속적이면 식 (4 . 51) 의 편차를 점근적으로 전개할 수있다. var {Umg ( s) } = 흡。 (: :::;麟 (4 . 53) = 124mg 2 + 4 f7一20 2m4o44 2 + 쏴― 23042l404m+62 404 + 0 (m-6) 여기서 Bm 은 베르누이 수이고 4 三g( j )(1) ―g Ul(O) 이다. llo=O 을 얻기 위해서는 식 (4 . 50c) 를 이용하는데 x=O 과 x=l 에서 변환된 함수의 값이 같도록 하는 a 값을 취한다• g( a) = (1— a)g ( l) +ag( O) (4 . 54) 또한 il 1=0 을 얻기 위해서는 위의 식 (4.54) 와 함께 다음 식 울 사용하면 된다. '§ (x) =출 Y( 중) +높(톰) —½Y (x) , Y (x) = .!fag (x) (4 . 55) 4.3.1 절의 예제를 약간 수정하여 다시 대조 방법으로 계산해 보자• I=£1sin (두 )dx=~ (4 . 56a) 6 f=½-(층 )2= (0.307758)2 (4 . 56b) 식 (4.54) 를 만속하는 a 는
sin ( TCa/2) = (1-a) sin ( TC/2) + a sin (0) = 1-a (4 . 57) 로서 a~o.405388 이다. 식 (4.50c) 를 사용하여 N=lOOO 번 표본 추출하여 칙설적으로 계산한 몬테카를로 적분의 측정값은 IN = 0 . 63736828 이고 측정된 편차는
(Js = 0 . 00000469 이다. 계산량이 여섯배 정도 증가했을 뿐인데 표준편차는 5X 10-4 으로 줄어든 것이다. 죽, 여섯 배의 노력으로 표준편차를 2000 배만큼 줄인 것이다. 더하고 빼는 방법을 약간 수정했을 뿐 인데 몬테카롤로 적분이 이렇게까지 정확할 수 있다는 것은 실로 놀라운 일이다. 참고문헌 [1 ] P.J. Davis a nd P. Rabin o wi tz, Meth o ds of Numeri ca l Inte g r a ti on , (Academi c, 1984) [ 2 ] A.C . Genz and A.A. Mali k, ]. Comp u t. Ap pl. Math . 6 (1980) 295 [ 3 J S. Haber, S IAM Rev. 12 (1970) 481 [4 ]J .H . Halto n , SIAM Rev. 12 (1970) 1 [ 5 ]J .M . Hammersley and D.C. Handscomb, Monte Carlo Meth o ds, (Meth u en, 1964) [ 6 J F. Jam es, Rep. Prog. Phys . 43 (1980) , 1145 [ 7 ] M.H. Kalos and P.A. Whit lo ck, Monte Carlo Meth o ds, (W ile y, 1986) [ 이 N. Metr o p o lis and S. Ulam, ]. Amer. Sta t. Assoc. 44 (19 49) 335 [9 J R.Y . Rubin s te i n , Sim ulati on and the Monte Carlo Meth o d, (Wi ley , 1981) [10] Yu. A. Shreid e r, Monte Carlo Meth o d, (Perga mon, London, 1966) [11] A.H . Str o ud, Ap pro xim ate Calculati on of Mult iple Inte g r a ls, (Prenti ce -Hall, 1971)
제 5 장 마르코프 과정과 응용 마프코프 사슬은 그 응용 분야가 상당히 광범위하다. 5 장에서 는 선형 방정식과 적분 방정식에의 응용을 고찰하고 다음 장에서 는 다차원 공간에서 원하는 확률 분포에 의해 다차원 확률변수를 임의 추출하는 데 마르코프 사슬이 어떻게 응용되는지 논의할 것 이다. 5.1 마르코프 과정 마르코프 과정 (Markov Process) 에서는 미래의 상황을 결정하 는 데 있어서 과거는 완전히 무시한 채 현재의 상황만을 고려한 다. 그 일례로서 주정뱅이의 임의의 보행을 들 수 있다. 임의의 보행 자 (random walker) 가 다음에 뗄 발걸음은 지금까지 걸어온 발자취와는 전혀 상관없이 현재의 위치로부터 갈 수 있는 방향 중에서 아무데로나 향해지는 것이다. 임의의 보행자가 시발접을 출발하여 시간 단계 0 에서부터 시간
단계 11 까지의 사이에 (Xo 一 XI 一 … ---+ xn) 의 행로로 왔을 확률 울 P(Xo 一 XI 一… ---+xn) 이라고 하면 이것은 1 단계 전이 확률 (one-ste p tra nsit ion pro babil it y ) Pi j= P(x1=i- --+ X1+1=j ) =P(x1 ---+ X1+ 1 ) (5. 1 ) 들의 곱으로 나타낼 수 있다. P(xo - … _. Xn) =P(xo _. X1) P(x1 _. X2) …P (Xn-1 _. Xn) (5 .2) 위의 식 (5.2) 가 만족되는 점열을 마르코프 사슬 (Markov cha i n) 이라고 부른다. 마르코프 사슬은 초기 확률 Po 과 1 단계 전이 확률 pij에 의해 정의된다. 사슬에서 한 개의 고리는 자기 의 앞과 뒤의 고리하고만 연결되어 있기 때문에 마르코프 과정의 특성과 매우 유사하다. 위의 식에서 확률 변수 X t는 막연히 시간 단계 t에서의 임의 의 보행자의 위치를 지칭했는데, 좀더 구체적으로 말하면 시간 단계 t에서 확률적인 시도의 결과로 얻는 확률 변수의 값이다. 이것은 일차원에 국한되지 않고 일반적으로 다차원 공간에서 확 률 변수들의 집 합, 죽 배 위 (confi gur ati on ) 를 지 칭 한다. 따라서 X t는 어떤 단일 입자의 3 차원 공간에서의 위치를 나타낼 수도 있고 여러 입자들의 좌표 및 속도로 구성되는 입자계 전체의 배 위를 나타낼 수도 있다. 마르코프 사슬은 그 이론 자체가 다양하기 때문에 홍미롭다. 그보다 더 중요한 것은, 많은 수의 실제적인 현상들을 마르코프 사슬로 모형화할 수 있다는 것이다.
5.1.1 마르코프 사슬의 예 임의 보행 주정뱅이의 걸음을 좀더 구체적으로 보자. 시간 단계마다 좌측 이나 우측으로 한 걸음씩만 움직일 수 있다고 가정하고 약간 다 리를 절어 우측으로 갈 확률이 P 라고 하면 좌측으로 갇 확률은 (1-p)가 된다. P(x;= l) =p, P(x;=-l) =q= I-p (5.3) 시발점으로부터의 거리 | Sn l=I x1+x2+… +Xn l 은 마르코프 사 슬을 이루게 됨을 쉽게 알 수 있다• 단순 임의 보행 (Random Walk) 의 전이 확률은 다음과 같이 주어진다. Pi, i+ lp=i+I ~+Q =i + I l-Pi,i - 1, i> O (5.4) Po 」 = 1, P;,j = O for all oth e r cases Ehrenfe s t 사슬 A, B 두 개의 상자에 d 개의 공을 나누어 담았다고 하자. 1 에 서 d 사이의 정수를 무작위로 추출해서 그 번호를 가진 공을 현 재의 상자에서 꺼내어 다른 상자에 집어 넣는다고 하자. 이 과정 울 계속해서 되풀이하면서 그때마다 상자 A에 들어있는 공의 수, Xn 을 헤아려 본다면 Xn 은 배위 (1, …, d) 상에서 마르코 프 사슬을 이룬다. 그 전이 확률은
· #.t—j=jJ.1=t 1h 1 s 一 PIU J =예 1 t.+ (5 . 5) .o 。 er w.1 e 에 의해 주어진다. 도박사 사슬 (Gambler's Ruin Chain ) 도박사가 초기에 얼마간의 자금을 가지고 도박을 시작한다고 하자. 매번 도박할 때마다 돈을 1 원씩 거는데 돈을 딸 확률이 p 이고 잃을 확률은 q =l ― P 라고 하자. n 번째 도박을 할 때 도박 사가 가지고 있는 돈을 X군 ]라고 하면 Xn 은 마르코프 사슬을 이루는데 그 배위 공간은 음이 아닌 정수들이고 그 전이 확률은 i >O 일 때 Pt. J ={ : :.::.+-11 (5. 6) O, oth e rwi se 에 의해 주어전다. 자금이 0 으로 떨어지면 더 이상 도박을 할 수 가 없게 되기 때문에 Po,j 三 0 이다. Xn=O 인 배위를 흡수 배위 (absorbin g sta t e ) 라고 부른다. 이 사슬에서 관심을 가질 수 있는 것은 도박사가 돈을 완전히 다 잃어버릴 확률 또는 자금이 0 이 될 때까지 걸리는 시간일 것이다• 출생-사멸의 사술 유한 배위 집합 (1, …, d) 또는 무한 배위 집합 (1, 2, …) 상에서 정의되는 마르코프 사슬의 전이 확률이 다음과 갇이 주어
지는 경우 이것을 출생-사멸의 사슬 (B i r t h and Death Cha i n) 이라 고부른다. · q,.`’ ,J.=' .1=I 1=h1 P”) ll 이 pri: . J. j.i1 + w (5.7) . 0 。t er i se 여기서 qi, r,, p I 는 음이 아닌 수로서 확률 조건 qi+ ri+ pi=1 울 만족한다. 생사 (B i r t h and Dea t h) 라는 말을 붙이게 된 것은 이 과정을 이 용하여 생물의 증식 현상을 기술할 때 i---+ (i +l) 은 생명체의 탄 생을 의미하고 i ---+ (i -1) 은 생명체의 사멸을 의미한다고 볼 수 있기 때문이다. 대 기 사술 (Qu euin g Chain ) 슈퍼마켓 또는 은행에서 자기 차례를 기다리며 줄을 서는 현상 울 기술해 보자. 서비스를 받기 위해 기다리는 대기자들의 그룹 또는 이와 비슷한 것을 컴퓨터 용어로 보통 q ueue 라고 부른다. 논의를 간단하게 하기 위 하여 1 분마다 한 사람씩만을 도와준다 고 하자• n 분에 새로 도착하는 손님의 수를 ~n 이라고 하고 이것 의 확률 밀도 함수를 f라고 하자. 우리가 관심을 가지고자 하는 것은 n 분 후에 기다리고 있는 손님들의 수, Xn 이다. Xn+1={ XEnn+ —1 , l+~ n+I, XXnn>=OO 그러면 Xn, n 칙 0 은 그 배위 공간이 음이 아닌 정수들로 구성 되는 마르코프 사슬을 이루며 그 전이 확률은
PP ((Ox,, yy)) ==Jf ((yy)- x+l), x~l (5 . 8) 에 의해 주어진다. 가지 사슬 (Branchin g Chain ) 원자로 안에서의 중성자의 증식 또는 박테리아의 번식에 관해 서 생각해 보자. n 번째 세대에서 생성되는 입자들은 (n+l)- 세 대에 속하게 되는데 n 번째 세대에 속하는 입자들의 수를 Xn, n~O 이라고 하자. 이제 한 개의 입자의 번식률을 확률 밀도 함수가 /인 확률 변 수 E 라고 하자. 그러면 Xn, n 칙 0 은 그 배위 공간이 음이 아닌 정수들로 구성되고 그 전이 확률이 다음과 같이 정의되는 마르코 프 사슬을 이룬다. P(x, y) =P(&+… +~;r=y) (5 . 9) 여기서 &둘은 음이 아닌 정수들이고 그 밀도 함수가 1 인 서로 독립적인 확률 변수이다. 이 사슬에서 관심을 가질 수 있는 것은 한 개의 입자로부터 시 작해서 자손이 끊어지게 될 확률 p이다. 이것은 남자 자손의 수 만 헤아리는 족보에서 대가 끊어질 확률을 말한다. 5.1.2 마르코프 사슬의 전이 확률의 성질 이제 n- 단계 전이 확률, 죽 상태 i에서 n 단계 후에 상태 j로 전이할 확률 P fJ룰 고려해 보자. PIJ = P{Xn+m=j I Xm=i } (5 .10 )
Chap m an-Kolmog o rov 방정식은 이들 n- 단계 전이 확률들을 행렬 식의 곱으로서 연관지어 준다. p5 +m=~ Pf' ,,P f: J (5.11) k 따라서 n 단계 전이 확률을 1 단계 전이 확률로부터 쉽게 구할 수 있다. P[ J= (Pn) ij (5.12) 전이 행렬 pij의 구조에 따라 일부의 상태들이 응어리져서 전이 를 아무리 오래해도 그들 사이에서만 왔다갔다하게 될 수 있다. 이런 경우 그 사슬들은 분해 가능 (redu ci ble) 하다고 일컫는다. 이 에 반해 서 pij의 구조를 분해 불가능 (irr educ ibl e) 하도록 적 절히 선 택하면 임의의 보행자가 임의의 상태 i에서 출발했을 때 충분히 오랜 시간 후에는 다론 모든 상태에 도달할 수 있게 된다. 예를 들어 네 개의 상태가 있다고 하고 그들 사이의 전이 행렬 이 다음과 같이 주어진다고 하자. 이 전이 행렬에 (의해: :정 :의되는\ 마르\코프 사 슬에서는 상태 (51 에.1서3) 상태 3 으로 들어가는 확률이 1/4 인 반면에 3 에서 1 로는 가지 못 한다. 또한 상태 4 에서 상태 2 로 들어가는 확률이 1/3 인 반면에 2 에서 4 로는 가지 못한다. 따라서 상태 1 이나 4 에서 시작하여 3 이나 2 로 가면 2 하고 3 사이에서만 왕래할 뿐 다시는 거기서 빠 져나오지 못하게 된다. 죽 위의 전이 행렬은 분해 가능한 것이다.
또하나의 전이 행렬을 고려해 보자. 2/5 6/25 4/25 1/5 ([1:5 :< 1\ :1;1\\6) (5 .14 ) 위의 행렬식에 의해 정의되는 마르코프 사슬은 분해 불가능하여 임의의 상태로부터 출발해도 다른 모든 상태에 도달할 수 있다. 5.1.3 배위의 성질-동등성, 주기성, 순환성, 에르고드성 유한인 정수 n 에 대해 영이 아닌 전이 확률 P [J >O 이 존재할 경 우 상태 j는 상태 i로부터 접근 가능 (accessib l e) 하다고 말한 댜 두 개의 상태들 £, j가 서로 접근 가능할 경우 (n 이 반드시 갇울 필요는 없음) 이돌은 교류한다 (commun i ca t e) 고 말하고 기호 로는 £ <=>j와 같이 표기한다. 교류성은 일종의 동등성 (eq u iv a - lence) 으로서 다음과 같은 성질들이 있다. l) i ~ i 2) “-=; j이면 j ~ i이다. 3) i~j이고 }.~k 이면 i ~k 이다. 전이 행렬이 분해가능한 경우, 상태들은 서로 교류하지 않는 몇개의 동등성 부류 (e q u i valence class) 로 분류된다. 각 부류 내에 서는 상태둘이 서로 교류하지만 다른 부류끼리는 접근을 할 수 없다. 반면에 분해 불가능한 사슬에 속하는 상태들은 전체가 서 로 교류하고 단일의 동등성 부류에 속한다.
또한 어떤 상태로부터 시작해서 전이룰 오래 계속하다 보면 다 시 그 상태로 돌아오게 될 가능성이 있는데 그 주기를 고려해 보 자. 상태 i가 주기 d 를 가지는 필요충분조건은 어떤 n 이 d 의 정수 배가 아닐 때는 언제나 P 距 =0 이 성립하고 d 는 이런 성질 울 가지는 가장 큰 정수라는 것이다. d=l 이면 Pf l =O 을 만족하 고 d 의 정수 배가 아닌 n 이 존재하지 않으므로 분명히 비주기적 이라고 말할 수 있다. 같은 동등성 부류에 속하는 모든 상태들은 그 주기가 똑같음을 쉽게 증명할 수 있다. 임의의 보행자가 상태 i에서 출발하여 n 걸음만에 상태 j에 첫 발을 들여놓을 확률을 fl.r)라고 하자. (이것은 Pll 하고 다르다는 것 에 유의) 임의의 보행자가 i에서 출발하여 j롤 한 번이라도 거쳐 갈 확률 fij는 IiJ = ZCO fg) (5 .15) n=l 가 될 것이다. 또한 µi룰 다음과 같이 정의하면 µ,·= Zco nfi f) (5 .16) n=I 임의 보행자는 평균적으로 µi 걸음만에 원래의 상태 i로 돌아올 것 이 기 때 문에 µi를 평 균 순환 시 간 (mean recurrence tim e) 이 라고 일컫는다. /u =l 이면 x i에서 출발한 임의의 보행자는 유한한 시간 내에 다시 제자리에 돌아올 것이기 때문에 상태 i를 순환적 (recurrent) 이 라고 부른다. 상태 i가 순환적 일 필요충분조건은 ~;=l Pl} =oo 이다. 순환성 역시 동등성 부류에 속하는 성질이어서 어떤 상태가 순환적이면 이와 교류하는 다른 모든 상태들 역시 순환적 이다.
반면에 참시적 (t rans i en t)인 상태에 대해서는 fi ,< 1 이 성립한 다. 참시적인 상태는 유한 횟수만큼만 방문 가능하여 한 번 방문 하였더라도 다시는 그 배위에 돌아오지 못할 수 있다. 유한 수의 배위를 가지는 마르코프 사슬에서 모든 배위들이 잠시적이라면 충분한 시간 단계 후 어느 배위도 방문하지 못할 것이기 때문에 그들 중 적어도 하나의 배위는 순환적이라야 할 것이다. 예를 들어 흡수 배위는 그 정의에 의해 순환적이다. 또한 단순 임 의 보행 에서 ~~=I P~0 < oo 일 필요충분조건은 홀1 (4p (됴?) ) n < 00 (5 .17) 이다. 여기서 4 p (1_ p)는 莊½이면 1 보다 작기 때문에 단순 임 의 보행은 이 경우에는 잠시적이고 p=방인 경우에는 순환적 이다. 그러면 여기서 몇 가지 극한 정리를 살펴보자. 정리 5. I 상태 i와 j가 서로 교류하면 1) lni-m.. k~n= l —1n P/ j=µ1一j (5 .18) 2) 상태 j가 비주기적이면 ti~ PD=; ;이다. (5. 19 ) 3) 상태 J’가 주기 d 를 가지면 산모 Pg d= 〔이다. (5 . 20) 어떤 상태 i가 비주기적이고 유한인 평균 순환 시간을 가지고 서 영속적일 때 그 상태를 에르고드 (er g od i c) 하다고 정의한다.
에르고드한 원소들로만 구성된 마르코프 사슬 역시 에르고드하다 고 할 수 있다. 5.1.4 마르코프 사슬의 불변 분포 마프코프 사슬이 몬테카를로 시뮬레이션에서 중요한 이유는 불 변 분포 (inv ari an t dis t r i b u ti on ) 의 존재 때 문이 다. 임 의 의 비 평 형 상태에서 출발하여 마르코프 과정을 거쳐 연속적으로 전이룰 계 속시켜 나가면 충분히 오랜 시간 후에는 평형 상태인 불변 분포 에 도달하게 되는 것이다. 그러면 불변 분포란 무엇을 말하는 것 인가? 임의의 보행자가 상태 i에 있을 확률을 P i라고 하면 확률 분포 {pi}가 마르코프 사슬의 전이 행 렬 P ij의 불변 분포가 될 필 요충분조건온 四 1) 모든 i에 대해 pi> O 2) ~ p;= l I 3) P;=~’ PiP ij 이다. 위의 조건 3) 은 확률 분포 {pi}가 정적인 불변의 분포라는 것을 말하고 수학적으로는 {P i}가 piJ의 고유값이 1 인 고유상태임 울 의미한다. 정리 5. 2 분해 불가능하고 비주기적인 마르코프 사슬은 다음의 두 가지
경우 중 하나에 속한다. 1) 상태들 모두가 잠시적이고 이 사슬에 대한 불변 분포가 존 재하지 않는다. 이 경우에 모든 i, j에 대해 n-+OO 일 때 P[;-+0 가 됨 2) 모든 상태들이 순환적이어서 1r1=lim P[;>O n 一 OO 이 존재하고 {7rj, j= O, 1, 2, …}는 유일한 불변 분포이다. 불변 분포를 가지기 위해 어떤 마르코프 사슬과 전이 확률 PiJ 가 만족해야할 조건은 巳 1) 분해 불가능성 (irr educ ibl e) 2) 비 주기 성 (ap er io d ic ) 3) 에 르고드성 (ergo dic ) 이다. 이 경우 모든 k 에 대해 7rk>O 이고 오래이지만 유한인 시간 이 경과하면 초기 조건에 상관없이 최종 분포 {7rk} 에 점근한다. 5.2 선형 방정식에의 응용 몬테카를로 방법에 의해서도 선형 방정식을 풀 수 있지만 전통 적인 알고리즘들에 비해 정확도가 많이 떨어져 잘 사용하지는 않 는다. 하지만 미지 벡터의 특정 성분만을 구하거나 행렬의 차원
이 엄청나게 클 경우에는 이 방법은 매우 효율적이다. 선형 방정 식 을 위 해 개 발된 몬테 카롤로 방법 을 [von Neumann 등 ; Forsyt he 등, 195 이 적분 방정식에 적용해 보면 매우 효율적인 해법이 나 오게 된다. 행렬 A 와 벡터 f가 주어졌다고 하고 미지의 벡터 x 를 찾는 다 음의 선형 방정식을 고려해 보자. A·x=f (5 . 21) A 가 단위 행렬에 가까운 경우에 국한시켜서 고려하기로 하고 Jac obi 반복 방법 을 사용하여 x 를 구하는 과정 을 답습해 보자. 행렬 A 에서 단위 행렬 I 를 빼고 남은 부분을 -B 라고 하자. B=I-A (5 . 22) 그러면 위의 선형 방정식을 다음과 같이 쓸 수 있다. x=B·x+f (5 .23) 행렬 B 가 작아야 할 조건 II B II=m~i x j~=n l I bii I<1 (5 .24) 을 만족한다면 Jac obi 반복 방법을 적용할 수 있게 되어 위의 선형 방정식을 다음과 같은 순환 관계식에 의해 풀 수 있다• xCk +l l=B•xk+f (5 .25) 이 관계식을 k=O 까지 거슬러울라가면 x(k+1)= (I+B+B 나… +Bk-l+Bk) ·f = mI=k! O Bm,f (5 . 26) 을 얻게 되고 이것을 풀어 쓰면
x}k+1)=f j+ 2i1 bm f:.1 +it2 i2 b mb,.It 2 f , .2 + + I.I 2~2' •• ,.* bj; , b; 어 ' • b,.k-1 f,.k (5 . 27) 가된다. 식 (5.27) 에서 b ji가 전이 확률 행렬의 조건 ~n bj; =l, b ji느 0 (5 . 28) i= l 울 만족한다고 하자. 그러면 식 (5.27) 의 우변의 각 항들을 확률 적 과정과 연관지울 수 있다. 죽, n 개의 항아리가 있고 이들로 부터 n 가지 공을 꺼낼 수 있다고 하자. 또한 b j, · 가 j번째 항아리 에서 i번째 공을 꺼낼 확률이라고 하자. 그러면 두번째 항은 다 음과 같은 과정을 나타낸다고 볼 수 있다. j번째 항아리에서 꺼낸 공이 i 1 번 공이라면 i 1 번째 항아리에 가서 공을 또 꺼내는데 이것이 i 1 번 공이라면 이 과정에 점수 fi,점을 부 여한다. 따라서 2 i Ib ji I f ,.1 은 j번째 항아리에서 꺼낼 수 있는 모든 공에 대해서 시도하여 얻는 점수들의 합이라고 볼 수 있다. 일반적으로 b ji가 전이 확률 행렬일 수는 없으므로 bj .-와 f를 다음과 같이 정의해 보자. fi= t,•· Pi b· = Tj,· • p ji (5 . 29) 여기서 pi와 pji는 에르고딕 口}르코프 과정울 정의하는 확률둘 이다. 그러면 식 (5.27) 을 다음과 같이 다시 쓸 수 있다.
x?+l)= f;+I.I~ 으P沿뿐 f ,,PJ 1,+I.l2 i2 요 Pj노i , 으P뿌,.l i2 f ,. 2 PJi lPIIl2+ … + i, i~2··· i k 부 pj,.I幽 P무i n·2 .. Pb,k--1I I.k f PJ,.I P ,Ji2 ···P’嵐 -1 =fj+ 고2.l Tmf ilP jn + h2i 2 Tj il T ni2 fi 2P mPhi2 + ••• + n.l2~.··.· '. Tji , T, . 函·· T, . •-1 i.f.- .Pj i ,P,函 ··P.-.-1 i• (5 .30) 이 식의 구조는 중점적 방법에 의한 적분식 (4.21) 과 동일하다는 것을 볼 수 있다. I= f~(길 w(x)dx (4 . 21) 여기서는 x 를 무게 함수 w(x) 에 의해 임의 추출하고 적분 계산 울 위해 g( x) 대신 g (x)/w(x) 의 평균을 취하는 것이라고 보 면, (5.30) 에서는 지수 i를 전이 확률 Pj i에 의해 임의 추출하고 如 대신 b g/Pj 2 의 평균을 취한다고 볼 수 있다. 구체적으로 위 식의 해 벡터 x 와 임의의 벡터 h 와의 내적을 계산하는 문제를 고려해 보자.
Pio Pio i , P i, i2 ° • ·Pi• - 1 i k 가 될 것 이 다. 여기서 p 2 와 piJ는 임의로 정의 할 수 있는데, 예를 들어 I h; I pi三 (L!J=1 I hj I) pij (2?I= bI u| bIu |) (5 . 33) 와 같이 정의할 수도 있다. 식 (5.27) 에서 b ij가 클수록 기여도 가 높으므로 마르코프 사슬의 전이 확률을 (5.33) 과 같이 정의하 는 것은 바로 중점적 확률 추출 방법을 선택하는 것과 같다. 실제로 계산하는 과정에서 유용한 공식을 얻기 위하여, 이 사 슬에 관련해서 Wm Pbiioo ii, 1P b ii ,, ii22 °• •• •· bPimim - -1 ,i mim (5 . 34) = Tio iI Tin .2 … Tim -i im 을 정의하면, 이들은 순환 관계식 W m =WmP-i1m -1~i m ' Wo=l (5 . 35) 을 만족한다. 사슬과 관련해서 또 하나의 양 TJh (h) =Ph_ io m2k-: o Wm fim (5 . 36) = tio m2k= O Wmf 1.m 울 정의해 보자. 그러면 7/ k(h) 의 기대값은 다음과 같이 주어진다. <7J k (h) >=
따라서 〈 h·x
21 41 14 。 Pij = I 14 21 。 41 (5 . 41) 。 4I 2I 4I 13 。 。 32 그러면 —1 1 -1 。 Tv=I 01 11 1。 —11 (5 . 42) 요4 。 。 34 이 된다. X1 울 구하기 위하여 hT=(l, 0, 0, 0), p;=(l, 0, 0, 0) 이라 고 하자. 마르코프 사슬의 길이를 k=6 으로 놓고 h 에 대하여 〈T/ k(h) 〉를 추산하기 위하여 s=12 개의 경로들에 대한 평균을 구 해보자. i o 를 확률 P i에 의해 1~4 에서 무작위하게 추출하여 얻 고 Pu 에 의해 임의 보행을 하여 이어지는 지수들의 열, 죽 경로 룰 표 5.1 에 나타냈다. 마지막 열에는 이 경로를 따라갔을 때, 식 (5.36) 에 의해 얻는 접수를 기록했다. 따라서 niS ) (h) 의 평 균, 06=—1 12 S~l';2;;' l TJts> (h) :::::: 1. 0610 (5 . 43) 이 얻어진다.
표 5. I 마르코프 과정에 의한 지수들의 변천 행로 s lo 1I 12 l3 l4 ls 16 nis) ( h) 123141516117218211921101121211123111 221413113111 122432313113 24213213421 4224—312111.4.10 54 00 2040300 134l 24131 13 6.5000 3.0000 1.6 8 75 1.3 7 50 _1.1 7 19 一— 30 .. 07 05 0000 3.5000 _。2 ..32451080
마프코프 사슬의 길이 k 와 경로의 수 N 을 더 늘려 x 의 모든 성분에 대해 프로그램을 돌려본 결과를 표 5.2 에 수록했다. 상용적인 다른 행렬 알고리즘들은 일반적으로 (j (NJ )번의 연 산을 요하고 특별한 경우에 (j (NJ )번 또는 (j (Nd) 번만에 계 산할 수 있다. 하지만 식 (5 . 29) 와 (5.34) 를 보면 몬테카를로 방 법에서는 x 의 모든 성분을 모두 다 구할 경우에도 (j (NdxkxN)
표 5. 2 몬테카롤로 방법에 의한 식 (5 . 39) 의 해 k N X 1 X2 X3 X ◄ 6 110032 01..6051 0450 11..68050739 21..70353807 00..79777457 10 ◄ 0.9724 1.9330 1.9612 0.9704 102 1.31 11 2.0978 2.3 0 96 1.1506 12 103 1.0 9 20 2.0645 2.0575 1.0633 10~ 1.02 47 2.0 5 58 2.0162 1.0111
번만 계산하면 된다. 행렬의 차원 Nd 가 매우 커지떤 ( > 1000) 상 용적인 방법은 엄청난 양의 계산울 요구하지만 몬데카를로 방법 은 주어진 정확도를 유지하기 위하여 Nd 에 비례하는 양만큼만 더 계산해 주면 된다. 또 하나 주목할 만한 점은 선형 방정식을 푸는 다른 모든 방법 들은 부분적인 해만을 얻도록 하지 않는 데에 비해 마르코프 사 슬을 이용한 위의 방법에서는 미지의 벡터 x 의 특정 성분을 알 아내기 위하여 다른 성분을 몰라도 된다는 것이다. 이것은 Nd 가 매우 클 경우 중요한 이점으로 작용한다. 또한 h 와 f만 바꾸어 가면서 〈 h·x 〉 를 여러 번 계산해야 하는 경우에 똑같은 마르코프 사슬을 가지고 이들을 동시에 계산할 수 있다는 이점이 있다. Cur ti ss[195 이는 벡터 x 의 특정 성분만을 계산할 경우, 전통적 인 방법둘과 몬테카롤로 방법의 효율을 비교하였다. 그는 행렬 B 의 크기 (norm) II B II 에 따라서 그 효율들이 상대적으로 달라지 는 것을 간파했는데 || B ll<0.5 이고 1 % 정도의 정확도를 요구할 경우, Nd::::::150 부터, 그리고 10% 정도의 정확도가 필요하면 Nd ::::::20 에서부터 몬테카롤로 방법이 더 효율적이라는 결론을 얻 었다. 일반적으로 다른 반복적 행렬 알고리즘둘과 마찬가지로 식 (5.30) 에 의한 방법도 계수 행렬 A 가 단위행렬에 얼마나 가까운 지, 다시 말하면 조건 (5.24) 가 얼마나 만족되는지에 따라서 수 령 속도가 많이 달라진다. 이것은 마르코프 사슬의 길이 k 를 결 정하는 데에 참조해야 할 것이다. 하지만 주어전 k 에서 답의 편 차를 줄이기 위해서는 경로의 수 N 을 충분히 늘려야 한다. 실제로는 계산울 반복해 나가면서 계산된 x 를 식 (5.21) 의 좌 변에 대입해서 얻는 벡터와 식 (5 . 21) 의 우변과의 차이가 미리 설정한 정확도보다 작아지면 계산을 끝내도록 하는 것이 좋다.
5. 3 적분 방정식에의 응용 몬테 카를로 방법을 유용하게 적용할 수 있는 분야 중의 하나가 적분 방정식이다. 여기서도 5 . 2 절에서 논의한 것과 유사한 방법 울 적용하는데 전자의 경우보다는 다른 수치 해석법에 비해서 훨 씬 유리하다. Alber t [1956] 에 의해 개발된 적분 방정식의 몬테카 를로 해 법 은 특히 방사선 운송 현상의 시 뮬레 이 션 [Sp a nie r 등, 196 아에서 많이 사용되고 있다. 5.3.1 적분 변환 다음과 같은 적분 변환 f1 ( x) =~2]{ ]lJ{f ( (xx), = yf;]) {l J f( (xy,; ) Lyl)y l Jf (y) dy (5 . 44a) /2( x) =XYI 21J f (x) = jjX (x, y) J{ (y, z) 1/f (z) dy d z (5 . 44b) =ff~ 麟tt P(x, y) dyP (y, z)dz1J f( z) 죠YI 2g KP((xx,, YYii) ) PK ((yyi t,. , Z zj )j) P(x, yt.)4 yP (yi , zj )4z 伊 (zj ) 울 고려해 보자. 여기서 실제로 적분을 수치적으로 계산하려면 이산화된 합산으로 바꾸어 주어야 한다. 사다리꼴 공식을 사용하 여 적분 구간을 등간격으로 나눈다면 Yi, Zj 는 격자접들의 좌표 를 나타낸다. 따라서 위의 식을 좌표 공간에서의 행렬식으로 볼 수 있다. 죽, ]{(x;, Yj )라는 행렬에 印 (x t. )라는 벡터를 곱한 것이라고 볼
수 있다. 그러므로 5.2 절에서 개발한 방법들을 수정없이 그대로 사용할 수 있을 것이다. 행렬의 경우에는 임의 보행의 경로가 행 렬의 지수들로 구성되는 데 비하여 적분 방정식에서는 행렬의 지 수에 해당되는 것이 좌표이기 때문에 그 경로가 매 시간 단계에 서의 입자의 위치로 구성된다고 볼 수 있다. 죽, 좌표 공간이 바 로 배위 공간이다. 이 공간에서 두 개의 함수 h(x) 와 깐 (x) 의 내적을 직관적으 로 다음과 같이 정의할 수 있다.
의 기대값에 의해 추산할 수 있다. 여기서 Wm= WmP (Xm--I1, ~Xm)) ' Wo=l (5.49) 이다. 이 계산 과정의 실제 내용은 식 (5.44) 의 합산 부분을 확률 주 출 방법에 의해 추산하는 것이다. 식 (5.44b) 에서 마르코프 전 이 확률 P(x, y)를 커널의 절대값에 비례하도록, P(x, y) oc IK
로 구성되는 벡터로 대치하고, ]{(x, y) 대신 M X M 행렬로 대 치할 수 있다. 이 경우 선형 방정식울 푸는 전통적인 방법을 사 용하는 것이 훨씬 효율적이겠지만 몬테카를로 방법을 사용해야 하는 고차원 공간에서 미지 함수를 찾는 문제에서는 이런 방법이 너무 번거롭고 비효율적일 것이다. 몬테카를로 방법을 직접 적용하기 위하여 식 (5.52) 를 풀어서 써보면 다음과 같다. 1Jf( xo) =f(xo ) +fJC( xo, X1)f ( xi) dx1 (5 . 53a) +ffJC( xo, X1)]{(x1, x2)f (x 2) dx1dx2+ … =f(xo ) +f~ 깊 P(xo, xi ) dxd(x1) (5.53b) 내問::: 컵信,' :fP(xo, x1)dx1P(xi, xz )d xd(xz) +… 수치 계산에 적합한 몬데카를로 방법에 의한 해법은 5 . 2 절의 그것과 매우 유사하다. 5.2 절에서 정의한 것과 갇은 마르코프 사 슬에 의해 연결되는 임의의 경로 Xo-X i-… -Xk에 대해서 정의되는 양
Wm= ]P(((Xxoo,, Xxi1 ) )P](((xmi,, XX22)) …… P] (((XXmm--l,J , XXmm)) (5 . 56) 이다. 마르코프 사슬의 길이 m 은 식 (5 . 53) 에서 반복 항의 차수에 해당된다. 7Jf (xo) 를 추산하기 위해서는 여러 가지 길이의 사슬을 고려해야 하고 또한 주어전 차수의 반복항을 좀더 정확히 추산하 기 위하여 길이가 같은 여러 경로에 대해 평균을 취해야 한다. 따라서 7Jf (xo) 를 추산하기 위해서는 h(x) =p( x) =8(x-xo) 로 놓고 ok=—N1 s~=N 1 TJ1 Sl(h) ~
5.3.3 예제들 예를 들어 다음과 같은 적분 방정식을 고려해 보자. 예제 | 1Jf( x) =x+½1: (y- x) 1Jf(y) dy (5 . 60) ]{(x, y) =t1( y-x ) 이 적분 방정식의 해는 1Jf (x) =734 x +, 一14 (5 . 61) 이다. 마르코프 전이 확률 P(x, y)를 식 (5 . 33) 에서처럼 정의 하기 위하여 규격화 상수 C(x) 를 계산해 보면 2· C(x) =1:-11 J{ (x, y) I dy = 1:1 Y 一 x I dy (5. 62 ) =1;(x-y) dy + 1\y- x) dy =군 +1 이 얻어전다. 따라서 전이 확률 P(x, y)를 P(x, y)=\=부 n1 (5.63) 와 같이 정의할 수 있다. 그립 5.1 에 확률 밀도 함수 P(x, y)와 그 분포 함수 F(x, y) 롤 스케치했다. 여기서 주의해야 할 것은 x 는 매개 변수이고 y가
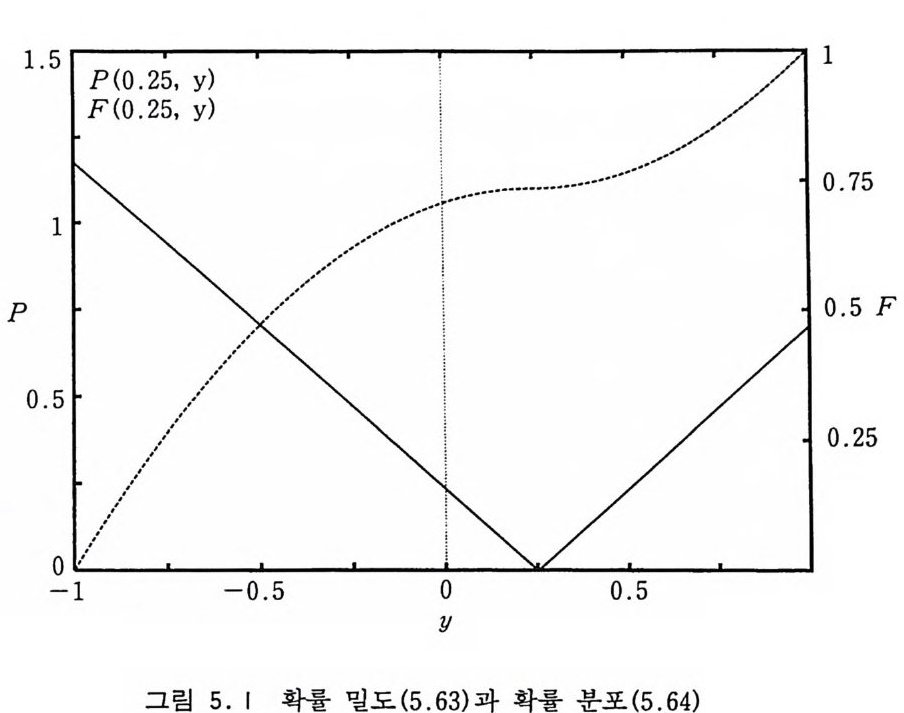 P1 0..55 l . FP((00..22.55.. ..,, · ' ‘ . .yy. ,. )),‘ . , ·•, •‘, x·, ,. . .. ,,,, ,,. ., .. - ·. . _ _ ..• ---.. ,il . ,. .............•••• --·· --·· .. .--?/ ' / / 00l0 ...7525 5 F
P1 0..55 l . FP((00..22.55.. ..,, · ' ‘ . .yy. ,. )),‘ . , ·•, •‘, x·, ,. . .. ,,,, ,,. ., .. - ·. . _ _ ..• ---.. ,il . ,. .............•••• --·· --·· .. .--?/ ' / / 00l0 ...7525 5 F
확률 변수라는 점이다. x 가 주어졌을 때 P(x, y)에 의해 y를 임의 추출하는 것은 어렵지 않게 할 수 있다. 누적 확률 분포 함수 F(x, y)를 얻기 위하여 P(x, t)를 t에 대해 적분하면 F(x, y) =1-~1 P(x; t) dt 三 七 +x y +x+½, y< x (5.64) 步 2 ― x y +x2+x+½, y갑 을 얻는다. 역변환 방법을 사용하기로 하면 그립 5.1 의 수직축의 구간 [O, 1] 에서 임의 접을 선택하여 그 점으로부터 수평선을 그 어 그것이 곡선 F(x, y)와 만나는 점의 수평축 좌표를 y로서 출력해야 한다. 식 (5.64) 에서 위의 식을 F1(x, y), 아래의 식
울 F2 (x, y) 라고 하고, 또한 Fe(x) =F(x, x) =(강 x2+x+½)/c(x) (5. 65 ) 라고 하자. 그러면 y를 확률 추출하기 위하여 균일 분포 난수 욘 를 생성하여 이것이 1. t
표 5. 3 마르코프 과정에 의한 적분 방정식 (5 . 60) 의 계산 k 250 500 1000 5000 10000 40000 8 0.5 9 21 0.6 1 18 0.6262 0.6 2 89 0.6276 0. 62 43 12 0.6 1 00 0. 62 95 0.6 2 25 0.6 2 42 0.6 2 62 0.6 2 42 16 0. 60 38 0.6175 0.6 1 52 0.6 2 90 0.6 2 91 0.6247 2204 00..6 644 6203 00..6 643 4048 00..6 6 22 1756 00.. 6 632 4662 00..6 6 22 9461 00..66 22 6401
예제 2 또 하나의 예로서 운송 방정식에서 자주 나오는 볼츠만 방정식 울 고려해 보자. lJf (x) = e:r + Af 1 e-( g구) 7Jf (y) dy (5 . 66) 。 }{(x, y) =i ex p[一 (y- x)] 이 적분 방정식의 해는 1Jf( x)=—l _e.Ar (5 . 67) 이다. 마르코프 전이 확률 P(x, y)를 정의하기 위하여 규격화 상수 C(x) 를 계산해 보면 C(x) =fo1J C ( x, y) dy = Af o。 1 exp [— (y- x) ]dy (5.68) =A (1-e- 1) ex=D (A) ex 이 얻어진다. 따라서 전이 확률 P(x, y)를 P(x, y)]=( (~x, =y) _W Ae-)Y (5 . 69) 와 같이 정의할 수 있다.
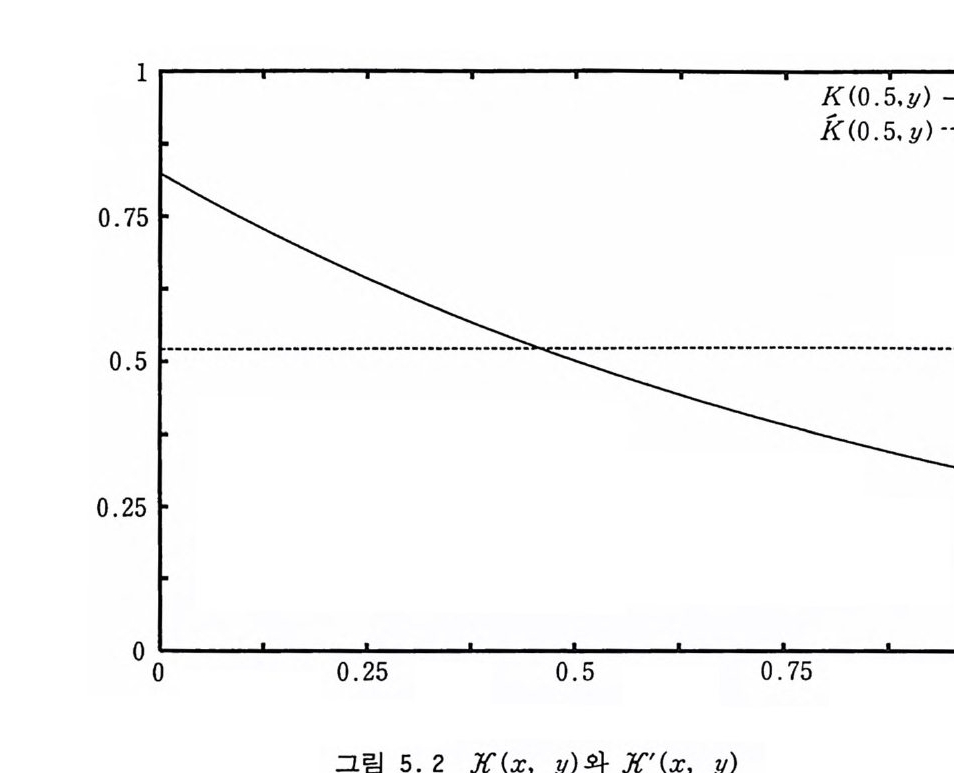 l kK ((O0 .. 55., yy )) -—-· ·-
l kK ((O0 .. 55., yy )) -—-· ·-
P(x, y)가 y만의 함수이기 때문에 임의 보행자는 현재의 위 치에 상관없이 다음 단계의 위치를 지수 분포에 의해 선택하게 된다. 또한 무게 함수에 의해 조정된 커널은, JC' (x, Y) =『昌 깊 =DU)ex (5 . 70) 가 되어 x 만의 함수가 된다 . 이것은 무게 함수를 가장 찰 선택 했을 때 피적분이 상수가 되는 것과 마찬가지이다. 주어전 x 에 서 JC( x, Y) 와 JC' (x, Y) 를 y의 함수로서 그려보면 그림 5 . 2 와 같다. 이제 P(x, y)에 의해 y를 확률 추출하기 위하여 누적 확률 분포 함수 F(x, y)를 계산해 보면
표 5. 4 마르코프 과정에 의한 적분 방정식 (5 . 66) 의 계산 k 250 500 1000 5000 10000 40000 8 4.2 4 48 4.2 2 66 4.2 1 72 4.2 1 75 4.2236 4.2 2 98 12 4.2 3 80 4.2339 4. 23 88 4.2 3 98 4.2385 4.2 3 44 16 4.2 7 31 4.2 1 45 4.2 1 09 4.2 1 75 4.2 2 82 4.2 3 51 2204 44..2 261 1899 44..22 23 8703 44..22 33 3115 44..22 34 0961 44..22446155 44..22334417
F(x, y )=1。 YP(x, t )d t =11(l-e 기 /D( ,1) (5 . 71) 울 얻는다. y를 추출하기 위하여 균일 분포 난수 E 를 취해서 이것을 F(x, y)와 같게 놓아 얻어지는 방정식의 근을 y의 표본으로 취 하면 될 것이다. 다시 말해서 ~=.-1 (1 —e-Y ) ID (.-1) (5 . 72) 을 y에 관해 풀어서 y - —ln[ l— (l -e 크) ~] (5 . 73) 울 취하면 된다. 이렇게 하여 계산한 결과를 표 5.4 에 수록했다. 여기서 tt= O.5, x=0.75 로 놓았다. 정확한 값, 1Jf( 0.75) =4.2340 과 비교해 보면 k=12 열의 값들이 바교적 괜찮은 것을 볼 수 있다.
5.3.4 실용적인 방법들 많은 경우에 커널 ]{(x, Y) 가 조건들 ]{(x, y) >O, yE :J) (5 . 74a) q (x) =1]{(x, y) dy < 1 (5 . 74b) 울 만족하는데 이런 경우에는 커널 자체를 전이 확률로서 사용할 수 있다. 이때 커널을 규격화시키지 않고, 그 대신 사슬이 종료 될 확률 r(x) =l ―q (x) 를 식 (5.55) 의 f (xm) 으로부터 나누어 주어도 된다. 죽, 식 (5.55) 대신 퍄 (h)= ph((Xx oo)) l$-;;o wmm fr((xX mm)) (5 . 75) 울 사용하는 것이다. 문제는 q (x) 를 계산하기 위해서 x 가 바뀔 때마다 식 (5.74b) 의 적분을 해야 하는데 이것은 매우 번거롭고 시간이 많이 걸리는 작업이다. 하지만 입자들의 운송에서는 흡수 확률 r(x) 를 물리적으로 쉽게 계산할 수 있어서 문제가 되지 않 는다. 적분 방정식 또한 적분 문제이므로 중요 표본추출 방법을 사용 할 수 있을 것이다. 적절한 전이 확률을 찾는 것이 관건인데 이 것을 위해 유용한 정리가 있다.
정리 5. 3 커널의 크기 ||JC II 를 II JC ll=m 훈x ll JC( x, y) I dy (5 . 76)라고 하고 적분 연산자 ](의 스펙트럼 반경 (sp e ctr a l rad i us) 을 p(]{) 크맷 II ]{n 111/ n (5 . 77) 와 같이 정의하자. 적분 방정식 (5.53) 에서 ]{(x, Y) 와 f (x) 가 음이 아닌 함수 라고 하고 p (]{)<1 이라고 하면, 전이 확률로서 P(x, y) = ]{ (x, y) 1Jf (y) (5 . 78) fJC (x, y) 1Jf (y) dy 을 사용하면 식 (5 . 55) 에 의해 정의되는 양의 기대값의 편차는 0 이다. 하지만 lJf(x ) 자체가 찾아야 할 미지의 함수이기 때문에 식 (5.78) 은 실용적이지 못하다. 실제로는 lJf (x) 와 비슷한 함수 J (x) 를 직관적으로 추측하여 다음과 같은 일련의 변환둘, Fo=1/(x) I(x ) dx (5 . 79a) 깐' (fx' )( x—) -1J f f( x()x I) I( xF;)。 /F。 ((55 .. 7799bc)) ]{ (x, y) - ]{ (x, y)I (x) /J (y) (5 . 79d) 을 하여 lJf'( x), f'( x), ]{'(x, Y) 를 식 (5.50) 에 대입하면 이 것이 원래의 식 (5.50) 과 항등적으로 갇다는 것을 증명할 수 있 다 [Kalos, 1986]. 이렇게 하여 y에 대해서 거의 변화가 없는 커 널, K'(x, y)를 얻게 되면 편차를 많이 줄일 수 있다•
참고문헌 [1 ] G.E . Albert, Sym p os iu m on Monte Carlo Meth o ds, ed by H.A. Mey er , (W ile y, 1956) , pp. 37-46 [ 2 ] J.A. Beekman, Soluti on s to ge neralize d Schroedin g e r equ ati on s via Feyn man in te g r als connecte d wi th Gaussia n Markov sto - chastic p ro cesses (Univ . Mi nn esota Thesis , 1963) [ 3 ] J.H . Curtis s , Sym p os iu m on Monte Carlo Meth o ds, ed by H. A. Meye r, (Wi ley, 1956) , pp.1 91-233 [ 나 R.E . Cutk o sky , ]. Res. Nat. Bur. Sta n d. 47 (19 51) 113 [ 5 ] S.E. Forsyt he and R.A . Leib l er, Math . Tabs. Ai ds Comp u t. 4(1950) 127 [ 訂 J.H . Halto n , SIAM Rev. 12 (1970) 1 [ 7 ]J .M . Hammersley and D.C. Handscomb, Monte Carlo Meth o ds, (Meth u en, 1964) [ 8 ]P .G. Hoel, S.C . Port a nd C.J . Sto n e, Intr o . to Sto c hasti c P rocesses, (Houg h to n Mi fflin, 1972) [ 이 M.H. Kalos, Nucl. Sci. Eng. 16 (1963) 227 [10] M.H. Kalos and P.A. Whit lo ck, Monte Carlo Meth o ds, (Wi ley , 1986) U다 S. Karlin and H.M. Tayl o r, A Fi rs t Course in Sto c hasti c P roces-ses, (Academi c, 1975) U 끽 N. Metr o p o li s, A.W . Rosenbluth , M.N. Rosenbluth , A.H . Teller, and E. Teller, ]. Chem. Phys . 21 (1953) 1087 [13] H.A. Mey e r, Sy m p os iu m on Monte Carlo Meth o ds, (Wi le y, 1956) [14] G.A. Mi kh ail o v, Optim i za ti on of Weig h te d Monte Carlo Meth o ds, tra ns. by K. Sabelfe ld , (Sp ri n g e r-Verlag, 1992) [15] E.S. Page , Proc. Camb. Phil. Soc. 50 (1954) 414 [1 이 S.M. Ross, Sto c hastic Processes, (Wi ley , 1983)
[l 기 R.Y . Rubin s te i n , Sim ulati on and the Monte Carlo Meth o d, (Wi le y, 1981) 頂〕 K.K. Sabelfe l d, Monte Carlo Meth o ds in Boundary Value Prob-lems, (Sp r in g e r-V erlag, 1991) [l 이 Yu. A. Shreid e r, Monte Carlo Meth o d, (Perga mon, 1966) [ 2 이 J. Sp a nie r , SIAM Rev. 4 (1962) 115 [2 디 J. Sp a nie r and E.M. Gelbard, Monte Carlo Pr inc ip le s and Neutr o n Transj )or t , (Addis o n-Wesley, 1969) [22] J. von Neumann and S. Ulam, 참고문헌 〔하 [23 ] 구자홍, 『 확률론 』 , (민음사, 1988)
제 6 장 다차원 몬데카를로 적분 다차원 적분에서 상용적인 수치 적분 알고리즘들이 사실상 실 용성이 없다는 것, 그리고 몬테카를로 적분이 특히 효율적이라는 것을 4 장에서 이미 언급했다. 하지만 4 장에서 논의한 대부분의 몬테카를로 적분 방식을 다차원 적분에 그대로 적용하기는 곤란 하다. 10~20 차원의 다차원 몬테카를로 적분에서는 가장 간단한 단충 방법이 실용적이기는 하지만 그 이상의 차원에서는 단충의 수가 너무 많아져서 사용할 수 없다. 또한 중점적 무게 함수를 단충화된 구간에서 유동적으로 찾아 나가면서 중점적 방법을 구 현하는 알고리즘도 개발되어 있으나 이 방법 역시 단충의 수에 제한이 있기 때문에 30 차원 이상까지 가기는 어렵다. 고차원 적 분에서 사용할 수 있는 방법은 마르코프 과정을 통해 중점적 방 법을 구현하는 메트로폴리스 방법이다. 이 방법은 전체 영역에서 단일 함수로 정의되는 중점 함수를 사용하기 때문에 차원의 수에 제약이 없다. 하지만 좋은 중점 함수의 존재를 전제로 하기 때문 에 이 방법 역시 제한된 적용 범위를 가지고 있다.
6.1 거절 방법 거절 방법을 다차원 확률 밀도 함수에 대해 직접적으로 적용해 보자. 이제 한 개의 확률 변수 대신 n- 차원 확률 벡터 X=(xi, …, Xn) 의 확률 밀도 함수 p(x 1, …, Xn) 을 고려해야 한다. 각 차원의 변수 X i둘이 유한인 구간 L1i = (ai: s;::X i :s;::b i) 내에서 정의 되고 이들이 전체적으로 밀도 함수 p (x) 의 정의 영역 ®롤 정의 한다고하자 幻 ={x,. e4} (6 .1) 또한 확률 밀도 함수의 상한값이 p( xI, …, Xn) ~M 과 같이 정 의된다고 하자. 그러면 일차원의 경우에 사용했던 거절 방법을 가장 초보적인 형태로 적용할 수 있다. 죽, 각각의 구간 4 에서 균일 분포 난수들 ~;, (i= l, …, n) 을 꺼내고 구간 (0, 1) 에서 또 하나의 난수 g를 꺼내어 g
도형의 체적을 구하는 적분을 고려해 보자. 죽, 적분 영역 ®가 다음과 같이 정의될 경우 죠 z:$'.;ex p(릅_fz )::;:;1 (6 . 3a) (x, y) E{e:$'.;ex p(-릅--fz)} (6.3b) 이 도형의 체적 V=ldx•dy •dz=las/XP( ―릅틀 )dxdy (6.4) 울 구하는 것이 문제이다. 여기서 base 는 c=ex p(_:;―『)에 의해 주어지는 타원의 내부 영역이다. 간단한 거절 알고리즘을 소개하면, 초기화 단계에서 그림 6.1 에서처럼 단면적이 정사각형이고 높이는 각각의 지역에서 피적분 함수의 극대값과 같은 기둥둘로서 에워싸고 기둥들 각각의 체적 울 v, 라고 두고 그 합을 w=~;V; 라고 한다. E 工工] 1) 확률 pi =v i /W 에 의해 i번째 기둥을 선택한다. 2) 기둥 내에서 임의로 점을 취하여 시도 횟수 n; 를 하나씩 증가시 키고 그것이 종의 내부에 떨어지면 적중 횟수 m i를 하나씩 증가 시킨다. 3) 이렇게 하여 충분히 많은 점들을 시도한 다음 전체 체적을 V= ~;V;• (m;/n;) 에 의해 얻는다.
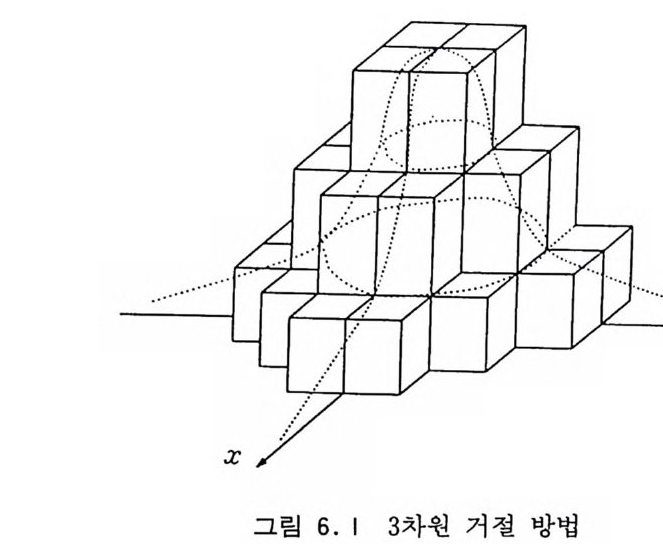 ....:
....:
6.2 유동적 방법 일차원 적분에서 효율적인 가우스 구적법은 겨우 이차원까지만 확대 적용할 수 있을 뿐이다. Genz 와 Ma li k[198 사은 가우스 구 적법을 일반화시켜 d~lO 에서 사용할 수 있는 유동적 알고리즘 (ADAPT) 을 개발하였다. 수치 적분에 관해서 광범위하게 다룬 단행본으로서 S t roud[l971] 와 Dav i s 와 Rab i now it z[198 사가 있으 나 몬테카를로 방법은 별로 다루고 있지 않다. d>lO 인 다차원 적분에서는 몬테카롤로 방법이 실용적인데 그 중에서도 단충 방법처럼 단순한 방법이 실용성이 있다. 따라서 다차원 적분을 위한 대부분의 알고리즘들은 유동적인 단충 방법 울 택하고 있다. 단층화하거나 하고 나서 적분하는 방법으로서 중점적 방법, 대조 방법 또는 편차들을 비교하는 방법들을 사용 하는 알고리즘들이 몇 가지 개발되어 있다.
6. 2. 1 유동적 단층 방법 (Adap tive Str a ti fica ti on ) SHEPPEY 알고리즘 가장 먼저 사용되기 시작한 것은 She pp e y의 알고리즘이다. 여 기서는 우선 d - 차원 직입방체인 적분 영역을 Nd 개의 균등한 구 역으로 나눈다. 각 구역마다 두 점에서 함수 계산을 하여 함수의 평균값을 구하는 데에 합산을 하는 한편, 각 구역에서의 편차를 구한다. 구역 편차들을 비교하여 다음 반복 단계에서 구역들의 크기를 유동적으로 재조정하는 데에 사용한다. 반복 단계마다 구 역들의 수를 일정하게 유지하면서 편차가 큰 지역은 줄여주고 작 은 지역은 늘려주어 궁극적으로 구역 편차들이 비슷한 값을 가지 도록 하는 것이다. 이 방법은 함수값의 대소는 따지지 않고 단충 화된 구역들에서 표본추출 횟수를 동일하게 취하기 때문에 함수 의 변화가 심한 구역에서 표본추출을 더 많이 하는 셈이다. 초기에 설정한 구역들의 크기를 재조정하지 않는 좀더 단순한 방법은 Haber[l97 이의 알고리즘이다. 여기서는 적분 영역을 Nd 개의 균등한 구역으로 나눈 다음, 각 구역 내에서 대조 방법을 적용하는 방식을 사용하고 있다. 6. 2. 2 유동적 중점 방법 (Adap tive Imp o rta n ce Samp ling ) VEGAS 알고리즘 소립자 물리 분야에서 많이 쓰이는 이 방법은 Le p a g e[198 이가 고안한 것으로서 원칙적으로 중점적 방법을 사용하는데 초기에 아무렇게나 설정한 무게 함수를 적분 계산을 하는 과정에서 반복 적으로 개선해 나간다. 이 알고리즘의 요지는 적절한 다차원 무게 함수를 찾을 수 있
고 그것이 분리 가능하다는 전제 하에서 w( x, y, z, …) =W x (X)W y (y)W z(Z)… (6.5) 울 찾는 것이다. 무게 함수의 인자들을 찾기 위해 Lep a g e [l978] 는 피적분 함수가 f( x, y, z, …)라고 하면 최적의 분리 가능한 무게 함수는 다음과 같이 주어진다는 것을 증명했다. Wx(x) ex: [/dy dz·· 『~] t (6.6) Le p a g e 의 알고리즘을 1 차원 적분에 대해서 설명해 보자. 초기 에 적분 영역을 N 개의 구간으로 균등하게 나누면 그 길이들은 모두 Llx ; =l/N 이 될 것이다. 시작 단계에서는 M 개의 점을 균 일 분포 함수에 의해 전체 적분 영역에서 추출하여 각 구간에 나 누어 준다. 그런 다음 각 구간을 (m ; +l) 개의 부분 구간으로 다 시 나누는데, 여기서 m i =K( fiL 1X i /후 E4xj) (6 . 7) 이고, K 는 임의로 설정해 주는 수이며 (K=lOO~1000), Ji= ~ J( x) xe 4 XI 이다. 죽 , 그 구간에서 함수값이 크면 그에 비례해서 부분 구간 의 수를 많이 잡아주는 것이다. 구간의 수를 다시 N 으로 복귀시키기 위하여 부분 구간들을 통 합해야 하는데 새로이 설정되는 각 구간에 소속되는 부분 구간들 의 수가 똑같도록 해준다. 이것은 실질적으로 구간의 길이 4xi 를 재조정하는 효과를 내는데, 그 결과 함수값이 큰 지역에서는 부분 구간들의 길이가 작아지고 그들로 구성되는 구간들의 길이
4x, · 도 동시에 작아지게 되는 것이다. 두번째 단계서부터는 각 구간에서 MIN 개의 점들을 균등하게 표본추출하는 데 함수값이 큰 구간에서는 4x, 가 작기 때문에 점들의 밀도 (M/N)/Llx ; 는 E 에 비례하게 된다. 이것은 각 구간에서의 값이 상수인 무게 함수에 의한 중요 표본추출인 것이다. 이 과정을 반복하여 m i= mh (i, j=l, …, N) 이 되어 더 이상 개선의 여지가 없으면 끝낸다. 반복 단계마다 적분값에 대한 추산을 얻게 되는데 이들을 종 합하기 위해서는 적적한 무게 인자를 곱하여 평균을 취해주어야 한다. t번째 단계에서 얻은 적분값과 분산을 Tt, 6? 이라고 하면, T1 = T1. lt /'|_햐互\ \,/I )F s 身8 (6·8(`6·`9 l ) 6T= 露꿉)당 에 의해 계산하면 된다. 적분의 신뢰도를 점검하기 위하여 확률 변수 L 의 카이평방을 계산하여, x2 ~ 무 (It _6 f T) 2 (6 .10) 이 반복 횟수보다 너무 크면 그 적분은 믿을 수가 없을 것이다. VEGAS 에서는 함수의 정의 영역이 d_ 차원 직입방체인 다차원 몬테카를로 적분을 위해 1 차원의 경우와 마찬가지로 /(x i)를 표 본추출하는 한편, 식 (6.6) 에 의해 무게 함수들을 반복적으로 개 선해 나간다. 연속적인 무게 함수를 모든 점에서 추산할 수는 없 기 때문에 일차원의 경우와 마찬가지로 각 좌표축에서의 정의 영 역을 N 개의 구간으로 나누어 w. r( x), W y(y), wz(z), …의 구
간 평균둘을 구하는 방식을 택하고 있다. 이렇게 하면 Nd - 개의 표본추출 대신 Nd- 개의 표본추출만 하게 된다. 식 (6.7) 에서 사 용하는 E를 계산하기 위하여, x 좌표에 대해서는 (E)2= XE24 X( Y2.'·· fW( x y, ( yy), …… ) (6 .11) 을 사용하고 다른 좌표에 대해서도 이와 비슷하게 하는 것이 1 차 원의 경우와 다를 뿐이다. 이 알고리즘에서는 무게 함수들을 별도로 계산하지 않고 구간 둘의 길이에 의해 무게 인자를 결정하고 초기에 설정한 구간들의 수는 변하지 않기 때문에 구간들의 상하한만 추적하면 될 것이 다. D 개의 좌표축을 각각 N 개의 구간들로 쪼캔다고 하면 구간 둘의 상하한들을 저장하기 위하여 배열들, XU[ D , NJ , XL[D, N 〕과 보조배열 M[D, N 〕올 미리 마련해 두고 적절히 초기화시 켜야 한다. 논의를 간단하게 하기 위하여 적분 영역이 d- 차원 직방체, 0 ::::::꾸::::::1, (j=l , …, d), 이라고 하자. E 1) 이미 식 (6.5) 형식으로 얻어전 무게 함수 w(t) ( x, y, z, …)에 의해 d 차원 공간의 점 x\t) = (xit) , yit), zit ), … )의 좌표롤 L 번 표본추출한다. 여기서 l=l, …, L 이고 t는 반복 단계 횟수를 뜻 한다. 죽, 한개의 점을 표본추출함에 있어서 x 좌표는 w it )(x) 에 의해, y좌표는 w t 0( y)에 의해, …, 표본추출하는 것인데 함수값 의 크기에 역비례해서 좌표축의 각 구간들의 길이가 정해져 있기 때문에, 이것은 동일 확률에 의해 구간을 선택한 다음 그 구간 내에서 균일 분포 함수에 의해 표본추출하는· 것과 같다. 2) 이들 L 개의 접들에서 계산한 피적분 함수의 값들, I(x~t))를 메
모리에 저장해 두고 적분값 I( t )=2 f = I f (x{ t ))/L 에 합산한다. 또 한 이것의 편차도 (5 2( t)=L上 li= I [f(x }t) ) -I(t) ]2 (6 .12) 에 의해 계산해 둔다. 3) 식 (6.11) 의 우변의 적분도 병행하여 각 좌표에 대해서 개선된 무게 함수 w(t+ 1)(x, y, z, …)를 얻는다. 죽 식 (6.7) 과 (6.11) 에 의해 w it +1)(x) 를 얻기 위해서는 E 를 (E)2= Z ie2 ' Zyl … WLt ) (yft)2 w( xz(t)t ) @) … (6 .13) 에 의해 계산하여 식 (6.7) 에 대입함으로써 m<).} 를 얻는다. 이렇 게 하여 모든 구간에 대해 무게 인자를 얻으면 m i들을 합한 다음 다시 구간의 수로 나누어 재분배함으로써 구간의 상하한울 다시 정하여 그 길이를 재조정한다. 이 과정을 모든 좌표축의 모든 구 간에 대해 반복한다. 4) 식 (6.8), (6. 9 ), (6.10) 에 의해 누적된 적분값, 편차 그리고 카이평방을 계산한다. 5) 이렇게 해서 누적된 적분값의 편차가 한계값보다 작으면 1)- 4) 를 반복하고 아니면 단계 4) 에서 얻은 결과들을 출력한다. 피적분 함수가 d 차원 공간의 몇 개 지역에서 지배적이라면 위 의 알고리즘은 이둘 지역에서의 무게 함수들을 급속하게 신장시 켜줄 것이다. 이런 경우에는 VEGAS 방법은 아주 효율적으로 정확도가 높은 적분값을 산출해 줄 것이다. 무게 함수가 분리 불 가능한 경우에는, 예를 둘어 피적분 함수가 다차원 직입방체의 대각선 방향의 지역에서 지배적일 때, 위의 알고리즘은 별로 효
과적이지 못하다. 일반적으로 VEGAS 방법은 피적분 함수가 1 차원인 곡선이나 혹은 수 차원의 초곡면 (h yp ersur fa ce) 에 몰려 있 는 경우에 취약하다. 6. 2. 3 DIVONNE 알고리즘 Fr i edman 과 Wr ig h t [198 니에 의해 개발된 DIVONNE 알고리 즘은 적분 영역을 반복적으로 쪼개가면서 각 부분 구역 내에서 피적분 함수의 변화가 정해진 값보다 작아질 때까지 반복한다. 죽, 함수의 값이 거의 변하지 않는 부분 구역들로 쪼개가는 것이 다. 함수값이 큰 지역을 찾기 위하여 VEGAS 는 표본추출에 의 존하는 반면, DIVONNE 는 함수가 거의 변하지 않는 구역을 찾 기 위하여 구역 내에서의 함수의 극대-극소점을 뉴턴 방법에 의 해 찾는다. DIVONNE 는 무게 함수가 분리 가능해 야 한다는 가 정을 하지 않기 때문에 VEGAS 가 취약한 피적분 함수들에 대해 서도 일반적으로 사용할 수 있다. 하지만 알고리즘이 복잡하기 때문에 분리 가능하거나 그와 비슷한 함수에 대해서는 그 효율이 VEGAS 에 비해서 떨어지는 편이다. 또한 VEGAS 는 단충화하는 과정에서도 적분 계산을 계속하지만 DIVONNE 는 단총화 작업 울 끝내어서 구역 내에서의 함수의 변화가 주어전 한계값 이하로 제한되면 그 다음에는 Korobov 〔없 roud, 1971] 의 유사 몬테카를로 방법에 의해 적분 계산을 한다. 일단 단총화 과정이 끝나면 이것 울 이용해 피적분 함수를 확률 밀도 함수로 하는 확률 벡터들을 표본추출할 수도 있다. DIVONNE 알고리즘에서는 적분 영역 R 을 단총화하는 세 가 지 전략을 세우고 있다. 첫째는 영역 R 내에서의 피적분 함수의 나쁜 정도를 나타내는 척도 s(R) 을 설정한다. 둘째는 s(R) 이
결정된 이후에 단총화하는 방법을 정하고 셋째는 새로이 생긴 부 분 구역들을 처리하고 단충화 과정을 끝내는 방법을 결정한다. 이것을 좀더 구체적으로 설명해 보자. DIVONNE 에서는 피적 분 함수의 확산 s(R) 을 다음과 같이 정의한다. s (R) =Llf ( R) ·vol (R) (6.14) 여기서 vol(R) 은 직입방체인 R 의 d 차원 체적으로서 vol (R) = IdI (x f一 x f) (6 .15 ) i= I 이고 Xu 와 XL 은 적분 영역을 정의하는 초입방체의 상한점과 하 한점의 좌표이며, 함수의 변화량 Llf (R) 은 Llf ( R) 투 max /(x) —m i n /(x) (6 .16) xER xER 와 같이 정의된다. 문제는 함수의 극대-국소집을 찾는 것인데 초기에 구역 내의 임의 점들에서 함수값을 계산해 보고 그 중에서 값이 가장 작은 점에서부터 시작하여 극소접을 찾아나간다. 이것은 함수의 정의 구역이 유한일 경우 유사 뉴턴 방법에 의해 어렵지 않게 찾을 수 있다. 이 방법에 대한 자세한 설명은 수치해석법 교과서들 또는 [F rie d man 등, 198 니로 미루기로 하자. 구역별로 함수의 확산이 얻어지면 전체 구역들 중에서 확산이 가장 큰 구역을 단총화하고 새로 생긴 구역들울 전체 구역의 목 록에 추가한다. 그 다음에는 새로 만들어진 전체 구역들 중에서 확산이 가장 큰 구역을 또 쪼개나간다. 문제의 구역을 두 개로 쪼개는 가장 좋은 방법은 적절한 등고 면을 택하여 尸 ax 를 포함하는 구역 Rmax 와 尸 In 을 포함하는 구역
Rmln 으츠료 가르는 것이다. 등고면의 값 T 로서는 (尸 ax —T) vol (Rmax) = ( T-F 'n) vol (Rmln) (6 .17) 와 같이 취하여 Rma x 와 Rmln 에서의 확산이 같아지도록 해주면 좋을 것이다. 하지만 고차원 공간에서 등고면을 찾는다는 것은 매우 힘들고 반복하기가 어려우므로 좌표 구간을 적절히 잘라서 Rmax 와 Rmln 이 또 다시 직입방체가 되도록 하는 것이 실용적이 다. DIVONNE 에서는 단충화하기 위하여 초기에 임의로 택했던 점들에서의 함수값들의 평균 T 를 계산한다. 그런 다음, (_rax +_ r1n ) /2 ~ T 이 면 JM =_rax , fm =_ri n 으로 놓고 아니면 JM =j m ln, f m= 尸 ax 로 놓는다. 다음에는 f M 에 대응하는 XM 을 포함하는 구역 RM 을 RM={x I xf -8 -;~x .. ~xr+a t}, 8-;, 8t~ O, i= l, d (6.18) 과 갇이 정의하는데, 여기서 8-;, 하는 J( xM+ 8te,. ) = f, J( xM-8-;e;) = J (6.19) 를 만족하도록 택해서 새로운 구역 RM 에서 함수의 변화량 Llf( RM) 이 대 략 반감하도록 한다. 이것을 재배열하면 8 f와 8 t에 관한 2d 개의 비선형 방정식, f( xM+Mei) -f(xM +8t e2 ) =O f (xM + 8!-1ed-1) —f (xM + 8!ed) =O f( xM+ 8;t ed ) 一f (xM-81-e1) =O
f(x M-81eI) —/(x M-02e2) =O I(xM-Dd-1ed-1/)( X—MI(x+ M Oi-e o1 d) e—dl)= =OO (6. 20 ) 룰 얻는다. 이것은 수치적으로 쉽게 풀 수 있는 방정식이다. 단충화 과정을 반복하여 S=[ 잡 s(R J 2] 송 (6 . 21) 이 주어전 한계보다 작아지면 끝낸다. 여기서 M 은 구역들의 수 이다. 궁극적으로 각 구역에서 여러 방법으로 적분을 하여 그 결과를 합산하게 되는데 이렇게 해서 얻은 적분의 편차는 (5= 2sN (6 . 22) 에 의해 추산하거나 구역 적분을 몬테카롤로 방법에 의해 얻었다 면 식 (6.8) 과 (6.9) 를 사용하여 추산할 수도 있다. 6. 2. 4 순환적 단층 방법 (Recursiv e Str a ti fied Samp ling ) She ppy의 알고리즘이나 Haber 의 알고리즘은 단충들의 수를 Nd 로 취하기 때문에 d 가 커지면 그 수가 폭발적으로 커진다. Press 와 Farrar 는 [199 아 최근에 이 Nd 폭발을 회피하는 알고리즘 울 고안해 냈다. 이들이 고안한 RSS 알고리즘은 초기에 전체 표 본추출 횟수를 정해 놓고 남아 있는 횟수의 일정한 퍼센트를 매 반복 단계에서 소화시켜 나간다. 반복 과정의 골자는 어느 구
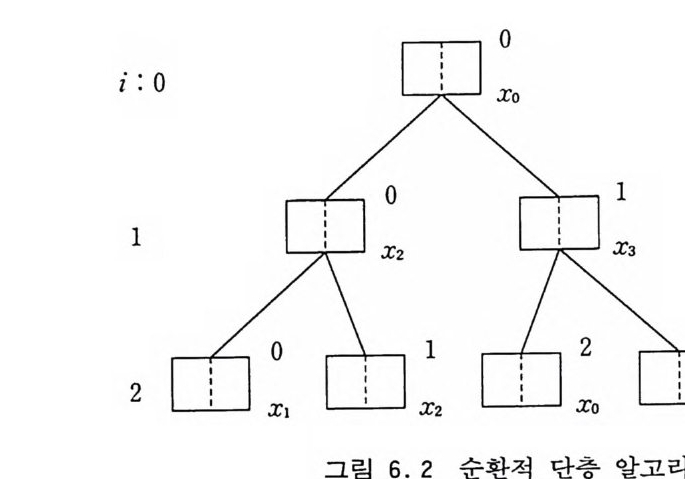 。
。
역에서 일정한 수만큼 함수 계산을 해보고 각 좌표축을 양분하여 생기는 두 개의 구역에서의 편차를 계산하여 다른 좌표축에 대한 그것과 비교하여 편차가 가장 큰 좌표축울 두 개로 잘라 다음 단 계의 구역으로 취하는 것이다. 그립 6.2 에 RSS 알고리즘을 스케치했는데 사각형들은 적분 구 역들을 나타낸다. i는 반복의 깊이를 말하고 사각형 오른쪽 위의 숫자는 주어전 깊이에서의 적분 구역 번호 j, 오른쪽 아래의 기 호는 다음 깊이에서 자르게 될 좌표축을 말한다. 그림에서 보다시피 반복 횟수가 증가함에 따라 구역의 수가 많 이 늘어나고 또한 데이터 저장을 위한 배열의 크기도 커진다. 하 지만 초기에 설정한 전체 표본추출 횟수를 많이 초과시킬 수 없 으므로 원하는 정확도를 정해 놓고 필요에 따라 표본추출 횟수를 늘릴 수는 없다. 이들은 실제적으로 C 언어의 순환적 함수의 기 능과 동적인 데이터 공간 운영 방식롤 사용하는 알고리즘을 개발 했다. 적분 영역이 대각점들의 좌표가 R={xa, X 나와 같이 주어지는
직입방체라고 하고 이 영역에서 함수 /(x) 의 적분을 구한다고 하자. 표본추출하는 횟수를 N 으로 고정시켜야 한다고 하고 RSS 알고리즘을 좀더 구체적으로 기술하면 巳 1) a=< i, j> 단 계에서 사용 가능한 표본추출 횟수가 Na 라고 하자. 또한 a- 구역의 직입방체를 고려한다고 하자. 그러면 직입방체의 전지역에 걸쳐 Ma=PN거 의 점을 무작위로 선택하여 함수 계산 울 하여 배열에 저장해 두고 그 구역에서의 기여를 Ia =—MV-a f -;A;~f'1 o f (xn) (6 .23) 울 계산한다. 여기서 Va 는 a- 구역의 d- 차원 체적을 말한다. Ia 의 분산은 6 는蓋섭 (/ (Xn) —Ia) 2 (6.24) 에 의해 주어진다. 식 (4.42) 참조. 2) s 번째 좌표축을 이등분하여 얻어지는 두 개의 영역, R i S) 와 Rhs)' Rhs)=[Xa+ 강 es • (Xb-xa)es, Xb]. (6.25a) Ri s> = [Xa, Xb ―송 es • (xb -Xa) es]. (6 . 25b) 각각에서 함수의 표준편차를 계산하여 이것을 어 s), 6hs) 라고 한 다. 이렇게 해서 각 좌표 구간을 쪼개서 만드는 두 개의 영역에 대해서 얻어지는 편차들의 합, 6(s)=aLS)+6hs) 을 비교하여 그중에 서 그 합이 가장 큰 좌표축을 선택한다. 이것을 t 번째 좌표축이
라고하자. 3) 두 영역 R it)와 Rh t)에 나머지 계산 횟수, (l- p )N 를 분배하는 데 각각의 횟수가 6lt), 6h t)에 비례하도록 한다. 4) 둘로 갈라진 각각의 영역에 대해서 1)-3) 의 과정을 반복하여 각 영역에서의 표본추출 횟수가 미리 정해둔 수 q보다 작아지면 반 복 과정을 중단하고 나머지 횟수만큼은 직설적 방법으로 표본추 출하거나 폐기한다. 이렇게 해서 여러 단계로부터 얻어지는 f (xn) 의 평균둘을 종 합해야 한다. 식 (6.23-24) 의 추산은 이미 무게화된 것이므로 i 번째 깊이의 단계들에 대해서는 4.3.3 절에서처럼 단순히 Im= L2-1 IJ, L=2i (6·(266·) 2 7) J= O 6f i}= LJ2 =一 O l 여 에 의해 평균과 분산을 얻는다. 여러 깊이에서 독립적으로 얻어 낸 추산으로부터 전체 평균을 얻기 위해서는 식 (6.10) 에 의해서 각각의 분산에 따라 적절히 무게화된 평균을 취해야 한다. 또한 전체 분산은 각각의 평균에 수반되는 분산들을 식 (6.11) 에 의해 계산해 주어야 한다. 이 알고리즘을 실제로 사용하는 데 있어서 1)-3) 단계를 매번 반복할 때마다 영역들의 수가 두 배씩 증가하기 때문에 단총화하 는 횟수를 10 회 이상 넘기기가 어려울 것이다. 이것은 또한 표본 추출 횟수를 어느 단계에서 소화하는 퍼센트 P 에도 의존한다. 전체 표본추출 횟수를 N=lOOOOO 으로 취하고 P 를 0.005~0.025 사이에서 변화시켜 줄 때 각각의 깊이의 단계들에서 소화하는 횟 수들, 죽 그림 6.2 의 사각형에서 소화되는 횟수들은 표 6.1 과 갇
표 6. I 순환적 단충 방법 의 표본추출 횟수 0.005 0.0 1 0 0.0 1 5 0.020 0.0 2 5 Ol24399 4569979 8 1499 1999 2500 497 990 1477 1960 2437 492 970 1433 1881 2315 482 931 1347 1731 2084 463 856 1185 1454 1667 426 719 901 988 1000 358 489 468 278 125 243 138 10 。。68 。 。 。 。
다. N 과 p의 값에 따라 평균값과 분산이 상당히 차이가 나므로 최적의 N, p를 실험적으로 찾는 것이 좋을 것이다. 6.2.5 다차원 적분 알고리즘들의 비교 지금까지 논의한 세 가지 몬테카를로 적분 알고리즘들과 NAG 에서 사용하는 Genz 와 Mal i k[l980] 의 ADAPT 알고리즘을 비교 하기 위하여 다음과 같은 적분들을 고려해 보자. /p= (¾Y11dPx exp [— 100 t (x: 법 2]= 1. 0 (6 .28) fp규(長 )P 』 1dPx{ex p[― 100 십(따단 )2] Kp = +101 edxPpx [— JnJ= 1:Ii 0 n0 x흠 戶( -1다=- 1½. )0 2]}=1. 0 (6.2(96,'、`’,`)`. 3(0.63 1 Hp =O.Ol11dPx~(xn-O.ln) 기 3
Qp=i1d Px cos 偉 Xn/n) (6 . 32) 다음 두 방정식들에서 S=~~=I Xn/n 이라고 하자. R p=출i 1dPx exp [ S sin (2nS) ][1 +O .1 sin (12nS) ] (6 . 33) S p=2요0 }!o1 du Px' [l. 5 +sin (4 값 S) ] (6. 34 ) 적분 Ip, Kp 의 피적분 함수는 분리 가능한 경우로서 VEGAS 에 유리하지만 나머지들은 그렇지 못하다. 또한 Ip, Hp 는 완만 한 산봉우리가 하나 있는 형태이고 fp는 두 개의 봉우리를 가지 는 완곡한 함수들인 반면 KP 는 xj = l 근방에서 절벽처럼 날카롭 게 증가하며 Qp는 적분 영역 내에서 완만하고 주기적이다. 또한 RP, S p는 4 장의 식들 (4.18), (4.19) 와 비슷한 함수들로서 굴곡 이 매우 심하다. 지금까지 논의한 방법들을 사용하여 위의 적분들을 계산한 결 과들을 표 6 . 2 에 수록했다. 여기서 허용 편차를 0.0010 으로 설정 하고 계산했는데 윗줄은 계산된 적분값과 편차를 0.0001 단위로 괄호안에 나타낸 것이다. 아랫줄은 이 결과들을 얻기 위해 함수 계산을 한 횟수이다. 표 6.2 에서 ADAPT 가 K6, H6, Q8 ] 대해서는 매우 효율적이 지만 Io J6, R6, S6 에 대해서는 효율이 크게 떨어지는 것을 볼 수 있다. 또한 예측했던 대로 VEGAS 는 I6, K6 에 대해서 효율 적인 반면에 k 에 대해서는 효율이 크게 떨어지고 있다. VEGAS 가 Hs, Q거 대해서 효율적인 것이 눈에 띄는데 이것은 이들 함수들이 완곡하기 때문이다. VEGAS 가 분리 불가능하고 굴곡이 심한 함수들인 Rs, Ss<>ll 대해서 비교적 좋은 성과를 보
표 6. 2 다차원 적분값들 피적분 VEGAS RSS ADAPT DIVONNE I6 1. 0 007 (13 ) 0 . 8778 (dl) 1. 0160 (09) 1. 0000 (02 ) 373248 2017986 1382729 1644541 ]6 1. 0017 (37) 0.8612(d2) 0 . 9982 (10) 0. 99 99(05) 2405700 2011542 2076473 890985 K6 1. 0011 (13) 0. 99 98(72) 1. 0000 (01) 1.00 04 (01) 69790 2005598 3517 477711 H6 0.5025(07) 0 .5011 (12) 0.5 0 17(06) 0.5021(01) 18304 404268 4107 233756 Q6 0.3 1 91(09) 0. 31 82(10) 0 .31 84 (00) 0 . 3184 (01) 18304 24498 3091 38476 R6 0.9636(06) 0 . 9640 (11) 0.9 6 30(el) 0. 96 44(01) 304512 801064 1999601 89733 s6 1. 18 37(05) 1. 18 57 (11) l.14 65 (e2) 1.1 824 (01) 1759488 2006760 1999721 128944 dl=407, d2=498, el=291. e2=8055
이는 반면에 ADAPT 가 효율적이지 못한 것은 주목할 만하다. 하지만 식 (6 . 33-34) 에서 ~~=I Xn/n 을 ~~=I Xn/ 답으로 바꾸면 ADAPT 가 아주 효율적임을 발견하게 된다. RSS 의 데스트에서 는 계 산 속도를 빨리 하기 위 하여 Press 와 Farrar 의 알고리 즘에 서 순환적 함수와 동적 데이터 운영을 사용하지 않았다. RSS 는 16, ]6 에서는 실패했고 K6 에서도 성능이 좋은 편은 아니지만 양 분된 구역의 표본 횟수를 조정하는 대신 구역의 크기를 조정한다 면 별 문제 가 없을 것 이 다. DIVONNE 는 K6, H6, Q5 o Jl 대 해 서 만 ADAPT 에 비해 효율이 떨어지고 다론 적분들에서는 가장 우 수하다는 점이 돋보인다. 하지만 DIVONNE 는 적분 영역을 단 층화해야 하기 때문에 10 차원 이상의 적분에서는 사용하기가 어 렵지만 3
사용할 수 있을 정도로 성능이 우수하다고 말할 수 있다. VEGAS 나 RSS 도 적분 영역을 단충화해야 하기 때문에 그 용도 는 중간 차원으로 제한된다. 6. 3 중점적 방법과 마르코프 과정 6.2 절에서 논의한 적분 방법들은 좌표 공간의 차원이 너무 크 지 않을 때 쉽게 사용할 수 있다는 장점이 있다. 하지만 d 가 너 무 커지면 이 방법들 역시 효과적이지 못하다. 통계역학적 물리 계처럼 d 가 압도적으로 큰 경우에 사용할 수 있는 유일한 방법 은 마르코프 과정을 이용한 중점적 방법이다. 5 장에서 논의한 마르코프 과정에 따라서 임의 보행을 충분히 오래하면 궁극적으로 주어진 전이 확률 행렬의 고유 상태인 어떤 불변 분포에 도달하게 되는데 역으로 우리가 원하는 분포에 도달 하게끔 어떤 전이 확률 행렬을 찾아내는 문제를 생각해 볼 수 있 다. 주어전 확률분포 p (x) 에 도달하기 위해 마르코프 과정의 전 이 확률 행렬 W(x;, x1) 가 지켜야 할 조건은 四 1) W(xi, x;) >O 이고 모든 X i 에 대해 L!; W(Xi, X;) =1 2) 임의의 쌍 (x i, X j)에 대해 어떤 유한인 정수 m 이 존재하여 Wm (Xi , X;) > Q 3) j=l, …, n 에 대해 L!iP ( xi) W(xi, x;) =p( x;) 이다. 조건 1) 은 주어전 x i에 대해 W(x;, Xj )가 확률 분포라야
한다는 것을 뜻하고 조건 2) 는 마르코프 과정이 에르고드성을 지 녀야 한다는 것을 말한다. 조건 3) 은 미리 정해전 불변 분포 P(x i)에로 수령해야 한다는 조건이다. p (x) 를 다차원 확률 변수 공간의 점 x 에서의 입자들의 밀도에 비유하면 논리의 전개에 도움이 된다. 좀더 간단하고 구체적으로 D 차원 확률 변수 공간이 각기 자기가 속해 있는 일차원에서만 움직이는 D 개의 입자들의 배위를 나타낸다고 보자. 그리고 그 배위들을 구별하기 위하여 각각의 배위에 번호를 매기기로 하자. 예컨대 X1={1, 0, —2 , —1, 3, …}와 같이 나타내는 것이다. 10 차원 유클리드 공간에서 각 차원에서의 적분 구간을 10 개씩으 로 쪼개서 근사시킨다면 10 개의 입자둘로 구성되는 이 계에서의 배위둘의 수는 1010 개가 될 것이다. 그러면 마르코프 과정의 매단계에서의 확률 밀도의 변화는 입 자들의 시간적 움직임이라고 해석할 수 있다• 죽, 단계 n 에서의 배위로부터 단계 n+l 에서 새로운 배위로의 전이는 시간 단계 n 에서 n+l 로의 시간 진화를 말하는 것이다. 입자들의 계가 배위 x i에 있을 확률은 시간적으로 다음과 같은 주방정 식 (Maste r equ ati on ) 의 지 배 를 받을 것 이 다. dp (:}, t) = —~ W(x;, xJ p(x ;, t) +~ W(xj, x;)p (x j, t) (6 . 35) 죽 x i에 있을 확률의 증가율은 다른 모든 X j로부터 x i로 옮겨울 확률에서 x i로부터 다른 모든 X j로 빠져나갈 확률을 뺀 것과 갇 다는 것이다. 충분히 오랜 시간이 경과해 불변의 확률 분포에 도 달했다면 모든 x i에서 dp ( x;, t) Id t =O 이 되어
~ W(x.-, xJ p( x.-, t) =~ W(xj, x.- ) p (x h t) (6.36) 와 갇은 등식이 성립해야 할 것이다. 죽 모든 x i 에서 X i 로 둘어 올 확률과 X i로부터 모든 x i로 나갈 확률이 같아질 것이다. 위의 N 개의 조건들은 N2 개의 전이 행렬 W(x,., X j )의 모든 원 소들을 확정적으로 결정할 만큼 많지 않기 때문에 어느 정도의 융통성이 있다. 이 융통성을 살려 식 (6.36) 보다 더 강한 세부적 균 형 (deta i l ed balance) 또 는 미 소 가 역 성 (mi cr oscop ic irr ever- s i b il ity)을 부여해도 무방하다. 죽, 임의의 쌍( i , j)에 대해 X i에 있다가 꾸로 갈 확률이 xi 에 있다가 X i로 갈 확률이 같도록 하는 것이다. W (x;, x; ) P (x;) = W (x;, x;) p (x;) (6 . 37) 조건 (6.37) 이 만족되면 조건 (6.36) 은 자동적으로 만족되므로 조건 (6.37) 은 조건 (6.36) 의 충분조건이 된다. 다음 절들에서 p (x) 를 불변 분포로 가지는 전이 확 률 행렬 W(x.-, 다룰 구하는 방법들을 논의할 것이다. 마르코프 과정을 충분히 오래 거쳐 불변 분포에 도달하면 그 이후로 표본추출되는 배위들은 확률 밀도 p (x) 에 의해 분포되기 때문에 중점적 표본 추출이라고 볼 수 있다• 따라서 이들 배위들로부터 얻는 적분값 의 분산은 상당히 적어지게 된다. 6. 4 메트로폴리스 방법 메 트로폴리 스 알고리 즘은 [Metr o p o lis 등, 1953 ; Bhanot, 1988] 전아 확률 W(xi, 다룰 다음과 같이 간단히 정의한다.
W (x;, xJ =A (x;, Xj ) • T (x .. , Xi ) (6 . 38) 여기서 T(x .. , X J)는 Xi , X J에 대해 대칭인 확률 밀도 행렬이다. 즉, 표본추출하기가 비교적 쉬운 임의의 확률 분포 T(xI, X j)에 의해 배위 x i로부터 배위 X J로의 이동을 제의한 다음, 따로의 이 동이 허용될 것인지 또는 거절되어 x i에 그대로 남을 것인지를 허용 확률 A(x .. , x j)에 의해 결정하는 것이다. A(xi, X j)는 우 리가 원하는 궁극적인 분포 p (x) 에 도달할 수 있도록 정의해 주 어야한다. 여기서 T(x;, X j)는 확률 밀도 함수이기 때문에 규격화 조건 jt T (xi, xJ =1, i= l, …, N (6 . 39) 울 만족해야 한다. 허용 확률 A(xi, x j)는 아래에서 구체화될 것 이지만 이것의 선택 여부에 따라 마르코프 과정의 불변 분포 p (x) 에로의 수령 여부가 결정된다. 세부적 균형 조건 (6.37) 은 A (xi, Xj ) • T (xi, xJ •p (xi) = A (xj, Xi ) • T (xh X i) • p (xJ (6.40) 이 될 것이다. 먼저 앞으로 자주 사용하게 될 양인 r (x;, xJ TT ((xx;j,, xXji ) ) •• p P ((xx;j)) 책 (6 . 41) 을 정의하자. 이 식에서 주목할 만한 점은 똑같은 성질을 가지는 양들의 비율이기 때문에 p (x) 의 규격화 조건과 무관하다는 것이 다. 통계역학적 물리계가 평형 상태에서 가지는 분포가
p(x ) oc fee- - P BX %: J )x (6.42) 인 것을 감안할 때, 분모의 적분을 수행하지 않아도 된다는 것을 의미하기 때문에 식 (6.42) 의 선택은 매우 효과적인 것이다. 이렇게 해서 정의된 전이 확률에 의해 연결되는 배위들의 열을 {X;, X2, …, Xn} 이라고 하고 확률 변수인 이들과 연관되는 확률 밀도 함수들의 열을 {P1(x), P2(x), …, Pn(X) }라고 하자. 메트 로폴리스 알고리즘의 목표는 A(x;, x j)를 적절히 선택하여, n 이 커짐에 따라 lim Pn (x) =P (x) (6 . 43) n 一 OO 가 되게 하는 것이다. A(x.-, x j)를 선택하는 방법은 여러 가지 가 있을 수 있다. 허용 확률 A(x;, X j)의 예로서 메트로폴리스 그룹이 원래 사 용했고 지금도 자주 사용되는 A (x;, xj ) =mi n [1, r (x;, xJ ] (6 . 44) 를 고려해 보자. 단계 n 에서 배위 아에 있다고 하고 확률 분포 T(xn, X~+l) 에 의해 X~+l 이 제의되었다고 하자. 만일 r(Xn, X~+1) >1 이 성립하면 위의 식 (6.44) 에 의하여 A(xn, X~+ 1 ) =1 이므로 이 제의는 허용이 되어 Xn+ l - X~+l 이 된다. 반대로 r (Xn, X~+1) < 1 이 라면 A (xn, X~+1) = r (xn, X~+l) 이 되 게 되 는 데, 식 (6.41) 에 의해 r (xn, 과 +1) TT (x(x;+n1, , 따X ; n+) 1 )· P•p((x x;n+)1 ) 킥 0 (6 . 45)
t��. r(Xn, X~+I) t� 0 t� D�Ȳ��\� X~+I D� 4�p�t� ������ J�� �թ� U�`� A(xn, X~+I) �� X�X���, �� (0, 1) ��t�X� |�� ���� ��� E � A �� �<�t�� ©X��� (X
n+I +--X~ + 1) , D� tȲ� � �0� \� X�n(+I +--X) n. ���� �X�\� �t� U�`� ��,� W(x ;, xj)=A(x;, xj)�T(x;, xj) � ȹt�T�� ���D� t��䲔� ��D� �Ʌ�XՔ� ��@� ��5��� J�.� 8���� � � pt��, �� x, ��� ��� \� �U�`t � X j��� x i\� � U �`�� ��D�|� �䲔� p�t�t� ̹q��䲔� ��D� �������. A(x;, xJ T(x;, xj)p(x;)=A(xj, X; ) T(j ,xx;)p(xJ (6.46) <�� rx;,( x �rJ(xj X ,; )=l x� ��@� �X���<�\���0� �Dž�X��. r(x;, xj )~1 x� ���ƀ�0� �����t�, t� �� �� A(x;, x J =1 t� �� ,r( xxj, ) ;.�),X ~ 1�� � |.�� t ����Lt�D0 8���A( xj ,x ; )=(xrj� �X� ��� � ���X�t�, ����@� LHS = T (x;, xJ p (x;) t� ��, �\� ����@� RHS = r (xj, x;) T (xj, X;) p (xj) T (x, ., xj) P (x, .) T (xj, Xi) P (xj) T (xj, X;) p (xj) = T점근하는지롤 좀더 구체적으로 살펴보자. 단계 n+1 에서의 확률 밀도 함수 Pn+I (x) 는 Pn+1 (x) = ~ A (y, x) T (y, x) Pn (y) 3 +Pn(x) ~[I-A(x, y) ]T(x, y) (6.47) 3 와 같이 쓸 수 있는데 첫번째 항은 다른 위치에 있는 입자들이 x 근방으로 옮겨울 확률둘의 합이고 두번째 항은 x 에 있는 입자 들이 다른 데로 빠져나가려다가 실패하여 그대로 남아 있을 확률 들을 합한 것이다. 이런 식으로 진화한 계가 궁극적인 평형 상태 Pn(x) =P(x) 에 도달했다고 가정하면 다음 시간 단계에서 Pn+1 (x) = ~ A (y, x) T (y, x) Pn (y) g +Pn (x) ~y [l-A (x, y) ] T (x, y) =Pn (x) ~yT (x, y) (세부적 균형 조건의 적용) =Pn (x) =P (x) (6 . 48) 임을 확인할 수 있다. 죽 p (x) 는 마르코프 과정의 불변 분포이 다. 다차원 함수의 적분을 위한 메트로폴리스 알고리즘을 좀더 구 체적으로 기술해 보자. 논의를 간단하게 하기 위하여 적분 영역이 각각의 좌표축에 대해서 0 에 1 까지 사이로 정의된다고 하자. E 1) 현재의 좌표점에서 피적분 함수 f (x) 의 값을 계산하여 이것을 Wo 라고 둔다. 2) 현재의 좌표점에서 새로운 점으로 옮겨가기 위하여 i번째 좌표
를 최대폭 8 이내에서 조금 변화시켜 본다. x[i] - x(i] + 8· (l— 2· ~) 새로운 x[ i]가 적분 영역의 밖으로 나가면 2) 를 재시도하여야 한 다. 여기서 E 는 (0, 1] 사이의 균일 분포 난수이다. 3) 새로운 좌표점에서 피적분 함수의 값을 계산하여 이것을 Wn 이 라고둔다. 4) (Wn/W 。 >1) 이면 새로운 좌표점을 받아들여 Wn 을 적분값에 합 산하고 현재의 좌표점을 새로운 좌표점으로 대치하고 1) 로 간 다. 5) 아니면 난수 g를 생성하여 (Wn/W 。>g)를 시험한다. ―부등식이 성립하면 새로운 좌표점을 받아들여 4) 에서와 같은 조치들을 취하고 1) 로 간다. -그렇지 못하면 거절하여 적분값에 대한 합산울 하지 않고 1) 로 간다. 이 알고리즘을 사용하여 다음의 몇 가지 함수들을 적분해 보 자. G1=( 芸 )P !o 1dPx( 접 리 ½ex p[― 100 흠 (x; ―½『] (6 .49 ) G2=0.1;:1dPx~古 결 :_o.1n) 기 3 (6 . 50) 이 두 함수들은 VEGAS 방법이 효율적일 것이고 ADAPT 도 저차원에서는 유용하므로 세 가지 방법들 모두를 이용하여 적분 한 결과는 표 6.3 과 같다. 표의 구성 방식은 표 6.2 에서와 같다. 표에서 공백으로 남아 있는 부분은 적분이 수령하지 못한 경우들 이다.
10 차원 이하에서는 ADAPT 가 확실히 우월성을 보이고 있고 VEGAS 도 무난한 편이다. RSS 는 G1 에 대해서 특별히 취약하다 는 것이 나타나는데 그것은 가우스 곡선의 중앙 고원으로 가지 못하고 그 절벽에서 왔다갔다 하기 때문이다. 양분법 대신 삼분 법을 사용하면 개선될 것이다. 메트로폴리스 방법은 G 에 대해서는 초강세를 보이는데 이것 은 볼츠만 분포에 강하다는 것을 의미하기 때문에 통계물리학에 는 아주 유용하다. 다른 방법들은 10 차원 이상으로 올려주기가 매우 힘들거나 불가능했는데 이 방법에서는 64 차원까지 올리는 데에도 별로 저항이 없었다. 새로운 점을 찾아감에 있어서 모든 좌표 축 방향으로 한 번씩 시도해 보기 때문에 확률 밀도 함수를 계산하는 횟수가 피적분 함수를 계산하는 횟수보다 공간의 차원 수만큼 더 많다. 표 6.3 에 수록한 횟수는 확률 밀도 함수에 대한 것이다. P 차원 공간에서 임의 보행의 걸음 폭을 얼마만큼 크게 잡느냐에 따라 거절률이 많이 차이가 나는데 표 6.3 의 데이터를 얻는 데에 실제적으로 사용한 것은 G 의 경우 &=0.06 이었다. 이때의 거절률은 대략 17 % 정도였다. G 의 경우에는 어떠한 & 의 값에 대해서도 수령하지 않았다. 메트로폴리스 방법에서는 확률 밀도 함수의 비례만을 사용해도 추출되는 확률 변수들이 규격화된 확률 분포에서 뽑아내는 것과 같 다. 이것은 매우 편리하지만 바로 그렇기 때문에 규격화 상수를 이 방법으로는 찾을 수 없고 다른 방법에 의해서 찾아야 한다. G 의 경우에는 적분 기호 앞의 인자가 바로 규격화 상수이므 로 실제 계산에서는 피적분에서 GfP > =exp [— 100 흠 (X i―½『] (6 . 51)
는 확률 밀도 함수로 사용하고 G(J ,I `l —— (` IpF터\ x 2'. ` \I—2` , '/ (6 . 52) 는 피적분 함수로서 사용했다. G 의 경우에는 피적분에서 분모를 확률 밀도 함수로 사용하고 분자인, rr~=I nX~-n 는 피적분 함수로서 사용했다. 그 규격화 상 수는 표 6.2 에서 H6 의 적분값에 의해 주어진다. 하지만 메트로 폴리스 방법이 G 에 대해서는 아예 수령조차 못하는 것을 볼 수 있다.
표 6. 3 메트로폴리스 방법과 다른 방법들의 비교 적분 p VEGAS RSS ADAPT METRO G1 6 1.23 54 (15 ) 1. 2340 (13 ) 1. 2357 (01) 470596 11999207 600000 G1 9 1. 5091 (41 ) 1.5667(09) 1. 5138 (01) 2883584 3048405 900000 G1 12 1. 7477 (01) 500000 G1 32 3.2 6 57(01) 3200000 G1 64 4.6001(01) 6400000 G2 6 1.1 3 16(03) 1.1 2 10 (66) 1.1 3 16(01 ) 352947 403902 50245 G2 9 0.2 4 54(02) 0.2379(98) 0.2450(01) 492075 1005488 775103 G2 12 0 . 0170 (31) 0 . 0365 (14 7) 989062 8994255
참고문헌 [ 口 G. Bhanot, Rep . Pr ag . Phys . 51 (19 88) 429 [ 2 ]P .J. Davis and P. Rabin o wi tz, Meth o ds of Nume ric a l Inte g r at i o n , (Academi c, 1984) [3 ] J.H . Frie d man and M.H. W righ t, DIVONNE 4: A Prog r am for Multip l e Inte g r ati o n and Adapt ive Jm p o rta .nc e Samp li n g , SLAC pu b. CGTM-193-REV (1981) [4 ]J .H . Frie d man and M. H . Wrig h t, ACM Trans. on Math . Soft wa re 70981) 76 [ 5 ] A.C . Genz and A.A. Malik , ]. Comp u t. A p pl. M ath . 6 (1980) 295 [ 6 ] S. Haber, SIAM Rev. 12 (1970) 481 [ 7 J N. Metr o p o li s, A.W . Rosenbluth , M.N. Rosenbluth , A.H. Teller, and E. Teller, ] . Chem. Phys . 21 (1953) 1087 [8 ]G . P. Lep a g e , ]. Comp . Phys . 27 (1978) 192 [ 9 ]G .P. Lep a g e , VEGAS: An Adapt ive Mult idim ensio n al Inte g r ati o n Prog ra m, Cornell Univ . pr ep r in t CLNS-80/447 (1980) [10] W.H. Press and G. R. Farrar, Comp . in Phys . 3 (1990) 191 [11] A.H. St ro ud, Ap pro xim ate Calculati on of Mult iple Inte g r als, (Prenti ce - H all, 1971)
제 7 장 이 차원 아이 성 모델 아이 싱 모델은 1920 년 에 렌츠 (Lenz) 에 의 해 발상된 이 래 1925 년에 아이싱이 [Is i n g, 192 이 일차원의 경우에 대해 풀었고 이차원 의 경 우는 그로부터 20 년 이 지 난 1944 년 에 온세 거 [Onsag e r, 1944] 에 의해 정확한 해석적인 해가 얻어졌다. 삼차원의 경우에 대해서는 아직도 해석적인 해가 얻어지지 않고 있으나 급수 전개 [Domb, 196 이 또는 몬테카롤로 방법에 의해 얻어진 근사적인 해 둘이 존재한다. 특히 이차원 아이성 모델은 새로운 계산 방법이 고안될 때마다 그 방법들의 정당성 여부를 점검하는 데 사용되어 왔다. 7.l 서론 이차원 공간에서 상상할 수 있는 가장 간단한 통계적 체계는 이차원 격자의 각 지점에서 정의되는 변수가 두 가지 값만을 가 지는 경우일 것이다. 이 체계를 이차원 아이싱 모델이라고 하는
데 간단하면서도 몇 가지 물리계 ―一?강자성체, 격자 기체 또는 쌍성 합금 등-에서 나타나는 상전이 현상을 보여주기 때문에 1900 년대 초부터 많은 연구가 되어 왔다. 이차원 격자 위에서 정 의할 수 있는 변수에 자유도를 좀더 추가하여 각 지점에서의 변 수가 q개 의 값을 가지 는 이 른바 포츠 모델을 [P ott s, 1 952 ; Wu, 198 끽 상상할 수 있다. 그보다 더 복잡한 모델은 변수가 단위 길 이를 가지는 벡터로서 그 방향이 연속적으로 변하는 XY 모델 (d=2) 또는 하이젠베르크 모델 (d=3) 이 있다. 이차원 아이싱 모델은 정확한 해가 알려져 있기 때문에, 급수 전개, 몬데카롤로 방법, 재규격화 방정식에 의한 분석 등 새로운 계산 방법이 고안될 때마다 그 방법들의 정당성 여부를 점검하는 데 사용되어 왔다. 이 모델에서 검증된 몬테카를로 방법은 해석 적인 해를 얻기가 불가능한 다른 어려운 문제를 푸는 데에 유용 한 도구가 될 것이다. 그런 연유로 이차원 아이싱 모델에 관해서 는 많은 평 론들 [Brush 1967 ; Baxte r , 1982] 이 나와 있고 또한 단 행본〔 McCo y and Wu, 1973] 조차 나와 있다. 이 계에서 배위는 Ns=NxXNy 개의 스핀들의 특정한 값들의 집합으로서, 예를 들어 다。 ={S(I,n=1, S(I,2)=-1, …}, (7 .la ) .0I ={S0,1)= -1, S0,2)=1, …}, (7 .lb ) 와 같다. 한 점을 제의한 모든 접들에서의 스핀들을 고정시키고 그 점의 스핀만을 변화시켜도 배위가 변하기 때문에 배위들의 전 체 수는 2Ns 이다. 스핀의 값이 두 가지만 있기 때문에 컴퓨터 연 산에서는 배위를 비트가 Ns 개인 이진법의 숫자 또는 길이가 Nx 인 Ny 개의 워드로 간주할 수 있고 그렇게 하면 메모리를 경제적
으로 사용할 수 있을뿐더 러 연산 속도를 크게 향상시 킬 수 있다. 이 방법은 컴퓨터 개발의 초창기에 제한된 메모리 용량과 연산 속도를 가진 컴퓨터를 사용하기 위해서 많이 채택되었다. 어떤 한 배위에 있는 가장 간단한 아이성 모델 계의 에너지는 다음과 같이 정의된다. J{J(의) = —]
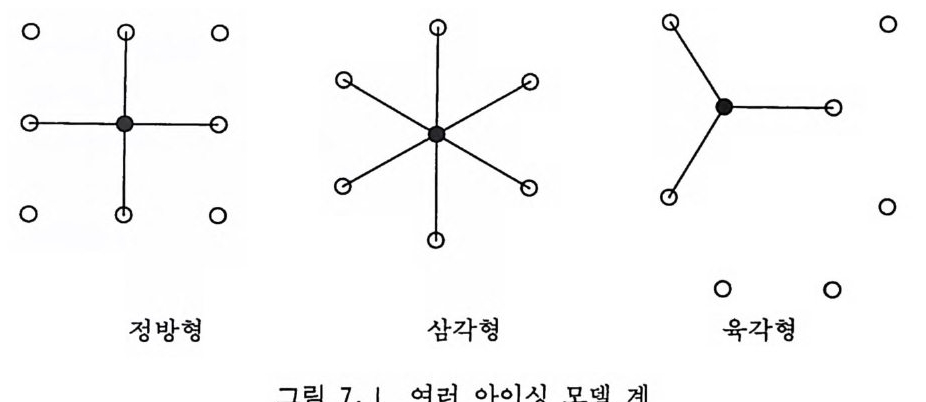 。 。 。
。 。 。
하는 두번째 항은 의부 자장과의 상호작용을 나타내는데 이로 인 해 의부 자장하에서 모든 스핀들이 자장의 방향으로 정렬하려는 경향을 띠게 될 것이다. 가장 간당한 아이싱 모델 계를 위에서 논의했는데 단위 격자의 모양새를 바꾸지 않고 좀더 복잡하게 모델을 짜기 위해서 최최근 접 이웃들과의 상호작용을 포함시킬 수도 있을 것이다. 이 정방 형 격자의 경우 이웃이 8 개가 될 것인데 최근접 이웃과의 결합상 수 ]와 최최근접 이웃과의 결합상수 K 는 일반적으로 다르게 잡 아 주어야 한다. 또한 정방형 격자 대신 다른 대칭상을 가지는 격자들을 고려해 볼 수 있는데 이러한 경우에도 아이싱 모델 계의 해밀토니안은 식 (7.2) 와 같은 형태인데 ~
로 무질서하게 늘어서 있지만 Tc 이하에서는 의부 자장을 걸어 주지 않아도 자발적으로 같은 방향으로 정렬한다는 것이다. 죽 상전이가 존재하는 것이다. 바로 이러한 상전이의 존재 때문에 이차원 아이싱 모델은 홍미 있는 물리계의 원시적인 모델계로 이 용되고 있는 것이다. 식 (7 . 2) 에 고차항들을 추가하거나 이차항의 계수 J를 상수로 두지 않고
울 얻을 수 있을 것이다. M= 건 W(.iJ ) m(.iJ ) =건 W(.iJ ) a~..JS a (7. 5) 내부 에너지 E 를 이와 마찬가지로 계산할 수 있는데 E=~ W( 의)%(.0) (7 . 6) 4 이다. 자기 감수율은 자장 변화에 대한 자기화의 변화율로서 x= 뿔=한 짜(.0) W( 必) _M2 (7 . 7) 으로서 이것은 자기화의 분산이기도 하다. 고정 자장에서의 비열 은
CB= 暮-=건 %나) w(.0 ) -E2 (7 .8) 으로서 이 역시 에너지의 분산이다. 7.2 정확한 해석적인 해 아이싱 계는 상상할 수 있는 가장 간단한 계이지만 수학적으로 는 어려운 문제여서 이차원 모델에 대한 해석적인 해가 나오기까 지는 아이싱아 강자성의 모델로 제시한 이후 20 년이 걸렸다. 이 차원 아이싱 계에 대한 상세한 논의는 참고 문헌 [Schul t z 등, 1964) 또는 McCo y와 Wu 의 단행본 [McCo y 등, 1973) 을 참조하기 바라고 여기서는 대충 설명하기로 하자. 일차원 아이싱 계에 대해서는 1925 년에 아이싱이 그 자유 에너지를 계산해 냄으로서 완전한 해를 구했다. 그는 자유도가 N 인 유한계에 대해 분배 함수 ZN(], B) 가 구해졌다고 가정하고 자 유도를 하나 늘린 계의 분배 함수 ZN+ 1 U, B) 를 계산하기 위해 이미 계산되어 있는 ZN(], B) 에 마지막으로 추가한 스핀이 기 여하는 항을 추가로 계산하는 회귀적 방법으로 무한계에 대한 자 유에너지롤 계산할 수 있었다. 죽, V(Si, S2) =exp [!S1S2+B(S1+S2)/2] (7.9) 이라고 하면 주기적 경계 조건을 부과할 경우 분배 함수를 zN= ~ V(S1 , S2) v
와 같이 유도해 낼 수 있게 된다. 전달 행렬을 대각화화면 j=,11 11> <1 1 +tt나 2>< 2 1 (7 .14) 의 형태로 쓸 수 있는데 여기서 고유값들은 111,2= e1 cosh B 土 (e21 sin h 2 B+ e-21) 112 (7 .15) 이다. 이 좌표계에서는 분배 함수 ZN 은 ZN =Af '+ Af N~-oo exp [ (In A1) N] (7 .16 ) 가 되고 스핀당 자유 에너지는 _kT 단위로 f (J, B) =ln [e1 cosh B + (e21 sin h 2 B + e-21) 112] (7 .17) 와 같이 얻어진다. 자기화는 자유 에너지를 자장 B 에 관해 미분 하여 m= ―aofi f_ =l閃 겅o.万-l1 =_ ✓ s i nshi2n Bh B+ e-4J (7.18) 와 같이 얻어지는데 B=O 이면 m=O 이 되어 유한인 온도에서는 (J< oo) 자발 자기화가 일어나지 않는 것을 알 수 있다. 이차원 무한 아이싱 계 (N:r , Ny -> oo) 에 대해서 온세거는 아 이싱의 전달 행렬 방법을 일반화함으로써 정확한 해석적인 해를 구했는데 B=O 일 때, K=csoisn hh2 2((Z2J~J ) ) :S:::1 K1=2 tan h2(2J ) -1 라고 하면 스핀당 자유 에너지를 kT 의 단위로
f= -ln(2 cosh 2J) —J7_r_J fon :J2- l-n - 1 + 工古2 詞 _d¢ (7.19) 와 같이 얻었다. 스핀당 내부 에너지는 자유 에너지를 8=1/kT 에 관해 미분함 으로써 얻을 수 있는데 u= 輩= —J coth (2]) [1+ 끔 K'K心 )] (7.20) 이다. 내부 에너지를 온도에 관해 미분하면 비열은 운=~(] coth 2]) 伊 (K)-E1(K) —¥ (f+K1K 1(K))] (7 . 21) 와 같이 얻어진다. 위의 식들에서 K1 과 E1 은 1 종과 2 종의 완전 타원 적분들이다. KI (K) =f,°r /2 ✓ (l ― &ds¢ i n 나) (7 . 22a) E1 (K) =1。 ,r/ Zd집 (1 —균 s i n2¢) (7 . 22b) K=l 에서 K1 은 대수적 특이성 (log a rit hm i c s i n gu lar ity)을 가지 게 되는데 이때의 f의 값 le 는 1=cos2h2(~2]c) (7 . 23) 의 근으로서 k= 송 ln(l+ ./2) :::::: 0.4406868 이다. k 가 상전이가 일어나는 임계점이라는 것은 다음의 논의에서 분명해질 것이다. 임계접 근방에서 비열 (7.21) 은 근사적으로
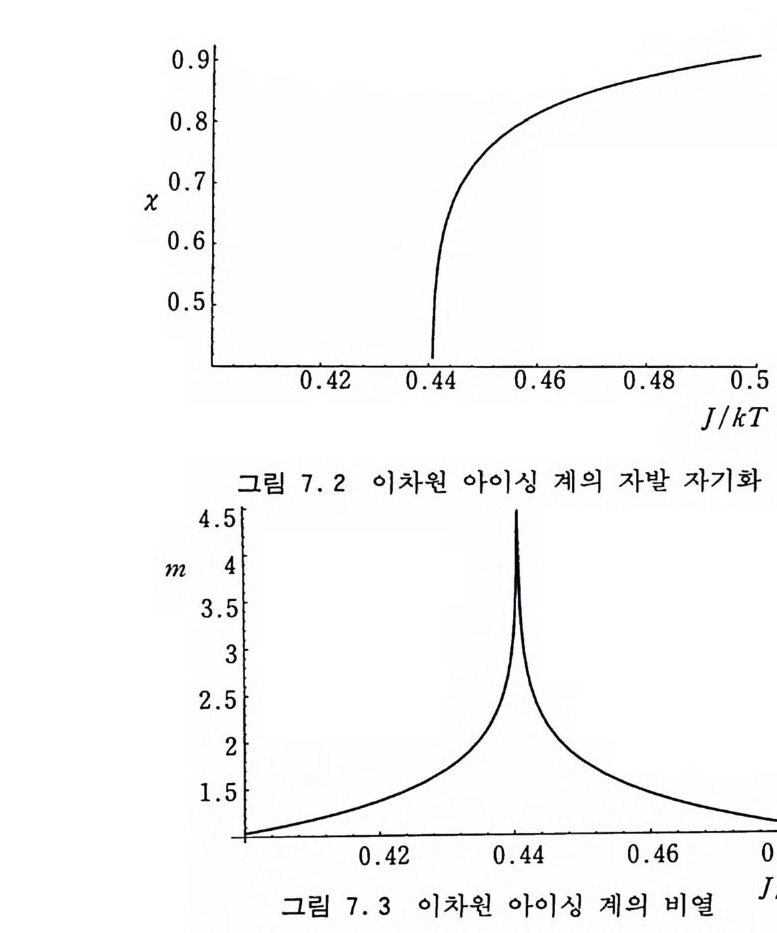 0908070605
0908070605
누~ ―;만 )2ln ! 1--f l+ const. (7 . 24) 와 같이 되어 임계지수 a=O 을 얻는다. 온세 거 는 [Onsage r, 1952 ; Yang , 1952] 는 자장이 0 이 아닐 경 우 에 대 해 서 도 해 를 구하여 자발 자기 화 (spo nta n eous magn e ti za - ti on) 를 계산하였는데
mo(T)= ―사탕하 (?ET)={[1 ― (116-tt aann hh24 ]]) 47] 118 f >Jc( 7.25) o J< lc 와 같이 주어진다. 이 식으로부터 임계지수 /3= 1/8 을 얻는다. McCo y와 Wu [McCoy 등, 1973] 는 자기 감수율을 계 산하여 x (O, T) =lBim-0 8m (『~ ex: I T-Tc I 구 /4 (7 . 26) 임계지수 r=7/4 을 얻었다. 자기화와 비열을 그림으로 표시해 보면 그림 7.2, 7.3 과 같다. 7. 3 몬테카를로 시뮬레이션 7. 3.1 서론 Fosd i ck[1963] 은 1960 년대 초에 메트로폴리스의 방법을 약간 수정하여 ILLIAC 컴퓨터롤 사용하여 아이싱 계에 적용시켜 봤 다. 당시의 컴퓨터는 원시적인 것이었기 때문에 충분한 양의 계 산을 하지 못했지만 비트 연산 방법을 사용하여 10X10 부터 최고 37X37 크기의 이차원 아이싱 격자계에 대해 몬데카를로 시뮬레 이션을 하여 질서맺음 변수를 측정했는데 그것은 정확한 값에 상 당히 근접한 값이었다. 이 논문에서는 메트로폴리스의 방법에 원 천적으로 내포되어 있는 주사-주사 간에서의 배위들의 통계적 비 독립성이 측정값의 표준편차에 얼마만큼 기여하는지 상세히 분석 되어 있다.
D. P. Landau[l976] 는 현대적 컴퓨터를 사용하여 여러 다론 크기의 아이싱 계에서 시뮬레이션한 결과를 서로 비교하여 F i sher 의 유한크기 축척 이론이 [Fis h er 등, 197 끽 유효함을 실증 해 보였다. 많은 사람들의 노력에 의해 이차원 아이싱 모델에 대 해서는 몬테카를로 방법에 의해서도 이미 상당히 정확한 결과들 이 얻어졌다〔 Blo t e 등, 1982 ; Hamer 등, 198 미. 삼차원 아이싱 모델은 아직 해석적인 해가 얻어지지는 않았지만 치밀하고 광범 위한 몬테카롤로 방법에 의해 임계온도와 임계지수가 얻어졌다 [Barber 등, 1985] . 이들은 몬테 카롤로 전용 컴 퓨터 를 제 작하여 최고 25 합 크기의 격자에 대해 아주 오랜 시간 계산울 하였다. 여기서 사용된 난수열이 아주 좋은 것은 아니어서 정확도에 약간 의 문제가 있기는 하였지만 전반적으로는 좋은 결과들을 얻었다. 이들의 결과들은 재규격화 군 방정석을 이용하여 얻은 결과둘 [Pawley 등, 198 사 하고 상충이 되지 않아서 순수 몬테카롤로 방 법이 유용하다는 것을 실증해 보였다. 1ox10 크기의 아이싱 계의 배위의 수는 무려 N=2! 。。:::::: 1.28X 1030 개나 되어 1 초에 l 한개씩 세어보기만 해도 4X1013 년이 걸릴 것이다. 수치 계산에서 이 모든 배위둘을 모두 다 고려한다는 것 은 거의 불가능하다. 하지만 최근에 각 에너지 준위에 대해 해석 적으로 이들 배위들을 분류하여 배위들의 수를 세어 보는 방법이 이구철 [Lee, 199 디에 의해서 개발되었다. 7.3.2 중요 표본추출―메트로폴리스 방법 어느 온도에서 평형 상태에 있는 통계역학적 계의 배위들은 배 위 공간의 아주 좁은 지역에 밀집되어 있다. 이 지역 밖에서는 배위들의 수가 급격히 감소하기 때문에 열역학적 양에 대한 그들
의 기여는 거의 무시할 만하다. 예를 들면 온도 T 에서 열적 평 형 상태를 이루고 있는 가스 분자들은 평균 속도 〈 V 〉 =具 T 万五 근방에 대부분이 몰려 있고 평균 속도보다 너무 높거나 낮은 지 역에서 발견될 확률은 아주 적다. 따라서 중요 표본추출 방법을 사용해서 임의의 배위 의가 나올 확률이 볼츠만 분포인 W 냐 )=ex p[一 B% (.0 )]/z 가 되게끔 할 수 있다면 확률이 큰 중요 지역으로부터 표본추출이 많이 될 것 이기 때문에 비교적 적은 양의 계산으로도 원하는 가관측량의 기 대값을 적은 편차 한도 내에서 얻을 수 있을 것이다. 식 (7.5)- (7.8) 을 보면 모든 가관측량의 기대값의 계산에서 무게 인자 w( 必)가 곱해져 있음을 알 수 있다. 아것은 식 (4.21) 과 (4 . 25) 에서 g=t) (.0) W 나)으로 두는 것과 같다. 따라서, 예를 들어, 자기화 M은 간단히 각 배위에서의 자기화 m( 의)의 평균 값으로서 얻을 수가 있다. M ::::::N1— a 2=N I 硏 4 서 (7. 27) 다차원 분포 함수에 대해서 사용할 수 있는 중요 표본추출 방 법은 6 장에서 논의한 메트로폴리스의 방법으로서 마르코프 과정 울 따라서 임의의 보행을 충분히 오래 계속하면 원하는 확률 분 포에 도달한다는 성질을 이용하는 것이다. 전이 확률(수학 분야 에서는 추이 확률이라고 함)울 적절히 정의하여 마르코프 과정의 불변 분포가 W( 必)가 되도록 하여 W( 必)에 의한 중요 표본추 출을 달성한다. a 위치의 스핀 Sa 를 뒤집어서 배위 .0 a 로부터 배위 .0 b 로의 전이를 시도한다고 하자. 마르코프 과정의 최종 정상 분포가 w( 必)가 되게끔 하기 위해 전이 확률 행렬을 6.4 절에서처럼
.0 a* .0 b 일 경우 다음과 같이 정의한다. T(.0 a - .0b ) =1 로 두 고, (1) W 냐 )
분해 보면 Lln(E) = -n(E) ~E. W(E, E') +~E· W(E', E) n(E') (7.30) 이 되는데 여기서 마르코프 전이 확률은 w(E, E') ={e-p(1 E -E) EE''<>EE 1f/(E ', E) ={ e -p(E -E) E'
의 보행돌이 서로 독립성을 가지는 것을 의미하고 임의 보행을 여러 대의 컴퓨터에 분산시켜 할 수 있다는 가능성을 시사해 준다. 허용 인자 r(.0 a , .0 b) 를 구체적으로 계산해 보면 r(.0 a , .0b )=exp [— 2Sa( JQ +B)] (7.31) Q =S(i+ 1.J) +s{E1.J) +S(,.J + 1)+ Sh.j- I) 가 나온다. Q는 5 가지 값 (0, 土 2, 士 4) 만을 가질 수 있고 Sa 는 (土 1) 두 가지 값만을 가질 수 있기 때문에 가능한 ?' (.0a , .0b ) 의 값은 10 가지밖에 되지 않는다. 컴퓨터 프로그램에서 시간이 많이 걸리는 지수 함수를 매번 계산하지 않고 이들을 미리 계산 하여 수표로 만들어 메모리에 기억시켜 놓고 필요할 때마다 끄집 어내서 쓰면 계산이 아주 빨라질 것이다. 7.3.3 경계 조건 컴퓨터의 기억 용량이 유한이고 연산 속도에도 제한이 있기 때 문에 주어전 컴퓨터를 가지고 너무 큰 부담이 없이 시뮬레이션 할 수 있는 적절한 격자의 크기가 정해질 것이다. 우리가 관심을 가지는 물리계의 크기가 충분히 작으면 유한크기 효과가 두드러 지게 나타날 것이기 때문에 경계면에서 아무런 조건도 부과하지 않는 자유 경계 조건을 택하는 것이 자연스러울 것이다. 실제적 으로는 〈작은〉 계라 할지라도 컴퓨터에 의해 시뮬레이션하기에는 너무 큰 경우가 대부분이어서 실제보다 작은 계를 다루게 되어 유한크기 효과가 훨씬 더 두드러지겠지만 여러 다른 크기의 계에 대해 시뮬레이션해 보고 얻은 결과들을 더 큰 계에 대해서 의삽 할 수 있을 것이다. 대부분의 경우에 우리는 격자의 간격에 비해서 거의 무한대로
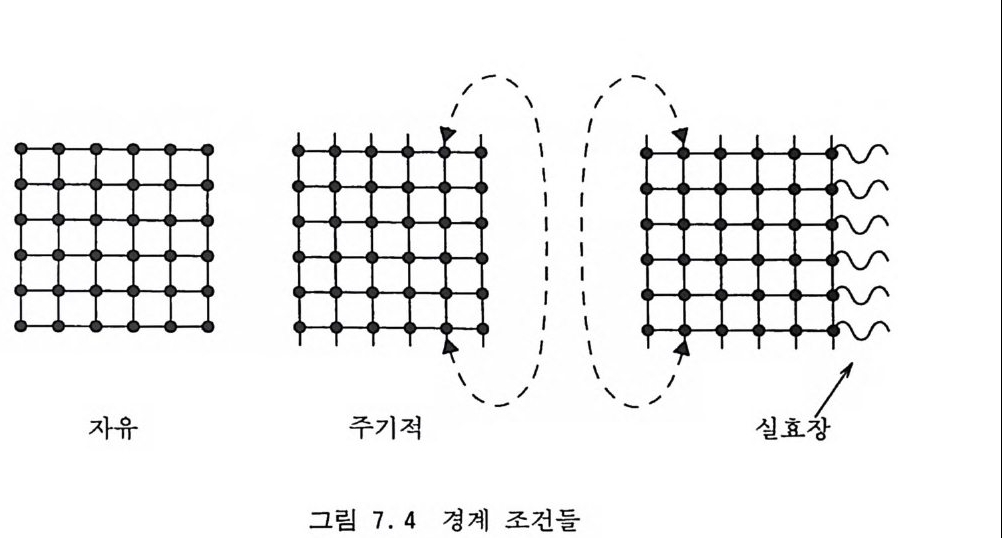 /-`\ \//I/\\ \\ //l
/-`\ \//I/\\ \\ //l
큰 물리계에 대해 관심을 가진다. 유한 격자에서 무한 격자의 특 성들을 뽑아낼 수 있도록 격자의 경계면에서 적절한 경계 조건을 부과할 필요가 있는데 관례적으로 사용되고 있는 것들은 주기적 또는 반주기적 경계 조건과 자체일관적 경계 조건들이다. 이로 인해 유한크기 효과가 아주 없어지는 것은 아니지만 경계면에서 아무런 조건도 붙이지 않는 자유 경계 조건보다는 무한계를 좀더 잘 나타내 줄 것이다. 주기적 경계 조건은 좌측 경계면에 있는 격자들의 이웃을 우측 경계면에 있는 격자들로 정해 주는 식으로 똑같은 유한 격자를 좌우 상하로 무한히 반복시켜 준다. 이렇게 해서 유한 격자들의 세포로 만들어지는 무한 격자에서는 아주 멀리 떨어져 있는 세포 들이 서로 보조를 맞추어 정확히 똑같은 세포 배위들을 유지해 나간다는 것을 뜻하기 때문에 다소 비현실적이기는 하지만 실제 적으로 무한계에 속해 있는 유한계의 상황은 국부적으로 이와 크 게 다르지는 않을 것이다. 크기가 N=N: r: XNy 인 격자에서 주기 적 경계 조건을 수식으로 표현해 보면
Sch+ N x , I) = Sch, I) = Sch, l + N y ) (7 . 32) 이다. 자체일관적 경계 조건은 경계면에 있는 격자들의 이웃이 존재 하는 것을 인정하지 않지만 있어야 할 이웃들과의 상호작용을 보 상하기 위 해 실효 표면 장 (ef fec ti ve surfa c e fiel d) 을 제 공해 준다. 이것은 실효 장의 크기를 결정하기 위해 일관성 조건을 붙인다. 해밀토니안 %에 균일 실효 표면장으로 인한 항을 추가하면 %=%o+µ%e ff2 Sa (7.33) bnd 이 되는데 의부 자장처럼 보이는 J{ ;e” 는 일관성 조건 <~ Sa> = < ~ s 갑 (7.34) Int bnd 울 부과함으로써 얻을 수 있다. 이것은 유한 격자가 이상적 무한 계에 포함되어 있다고 가정하면 유한 격자의 내부와 경계면에서 의 질서맺음 변수의 거시적 성질이 같아야 한다는 것을 뜻한다. 상기 두 가지 경계 조건들은 우리의 상식에 근거하여 적당히 고 안한 것들이기 때문에 무한계를 나타내는 데에는 한계점이 있게 마련이다. 연속적 상전이룰 하는 계에서 상관거리가 커지는 임계 온도 근방에서 그 한계점들이 드러나는데 주기적 경계 조건은 요 동들을 과잉 상관시키고 단파장 성분을 생략함으로써 임계점에서 의 질서맺음 변수, 임계온도 등의 값이 조금 차이가 나고 특이성 이 둔화된다. (그립 7.5 참조) 좀더 그럴싸해 보이는 자체일관적 경계 조건을 만족하는 유한계는 임계점 근방에서는 평균장 이론 처럼 되어 그 이론에 의해 나오는 틀린 임계지수를 예측한다. 또한 주기 비주기 상전이처럼 물리계가 주기성을 가지는 상태 에서 그것이 없는 상태로 가는 경우에는 주기적 경계 조건을 사용
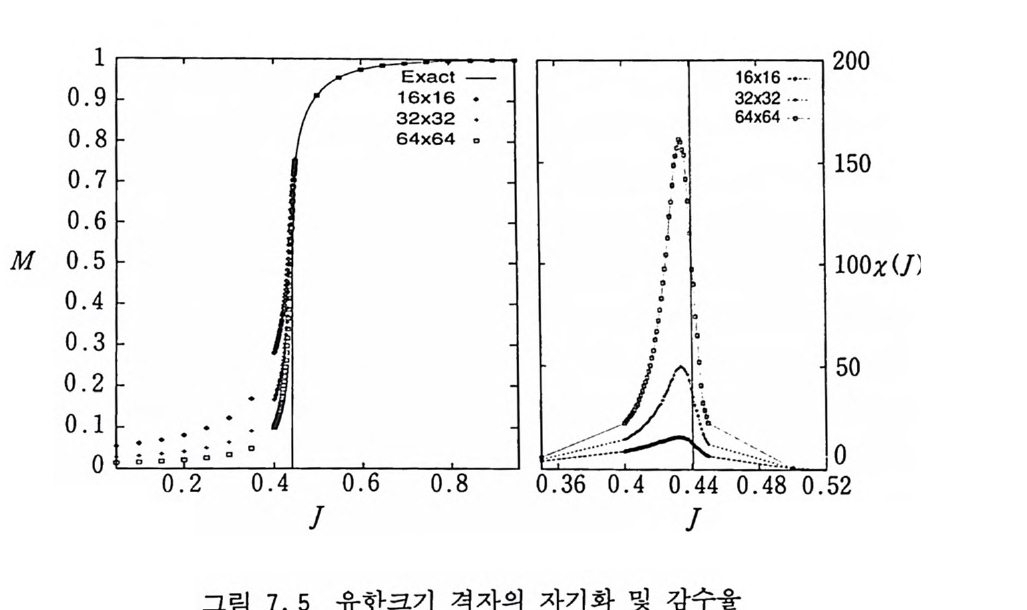 0.9 1 1E6xxa1c6t —• 16x32l6o6'·42.xi ..4is i. 20-0150
0.9 1 1E6xxa1c6t —• 16x32l6o6'·42.xi ..4is i. 20-0150
하는 것은 적절하지 못하다• 또한 반자성적 상전이를 나타내는 물리계에 주기적 경계 조건을 부과할 경우 어느 방향으로 격자들 의 수가 짝수가 아니면 경계면에서 스핀들의 〈정상적〉인 상호작 용을 인위적으로 교란시킬 것이므로 반주기적 경계 조건을 부과 시켜야 할 것이다. 하지만 임계온도에서 멀리 떨어진 영역에서 유한 격자계의 크 기가 상관 거리에 비해서 충분히 크면 무한계의 특성을 비교적 정확하게 알아낼 수 있다. 따라서 N 이 클수록 임계접 근방의 부 정확한 영역의 폭이 좁아질 것이다. 자체일관적 경계 조건은 다 른 경계 조건에 비해 계산 과정이 좀더 복잡하지만 N-oo 의 극 한에 좀더 빨리 수령한다는 장점이 있다. 죽 임계점 근방의 부정 확한 영역의 폭이 주기적 경계 조건에 비해 좁다. 좀더 자세한 논의는 7.3.7 절로 미루고 다음 주제로 넘어가자.
7.3.4 초기 배위의 선택 시뮬레이션을 맨 처음 시작할 때 배위를 초기화시켜야 하는데 스핀 변수들 전체가 하나의 값을 가지게 하거나 혹은 임의의 값 둘을 가지게 할 수도 있겠는데 어느 방법도 다른 방법에 비해 뚜 렷한 이점이 없을 것이다. 이것은 마르코프 과정을 오래 계속하 면 초기 상태에 무관하게 불변 분포에 도달할 수 있기 때문이다. 하지만 몬테카롤로 시뮬레이션을 하여 물리적 양을 산출해 내는 데 있어서 보통 물리계를 특징지우는 여러 매개 변수들을 변화시 켜 나가면서 여러 번 반복하게 된다. 대개 매개 변수를 조금씩 변화시켜 나가면서 매개 변수에 대한 변화율을 계산하기 때문에 이런 경우 바로 전의 최종 배위를 현재의 초기 배위로 택하면 좋 울것이다. 7.3.5 초기 열적 완화 임의로 선택한 초기 배위로부터 위에서 논의한 메트로폴리스 전이 확률에 의해 임의 보행을 계속하면 언젠가는 새로이 표본추 출하는 배위둘이 원하는 확률 분포 W(.0 ) =exp (-/3%(.0) )/z 에 의해 추출될 것이다. 마르코프 과정은 초기 상태로부터 열적 평형 상태로 완화시켜가는 과정이라고 볼 수 있다. 일단 불변 분 포에 도달한 것이 확인되면 식 (7.27) 을 사용하여 가관측량을 측 정하면 된다. 다음 절에서 좀더 자세히 논의하겠지만 불변 분포 에 아직 도달하지 않은 상태에서 가관측량을 계산하기 시작하면 통계적 편차가 커질 뿐이다. 문제는 계산 도중에 언제 불변 분포를 가지는 열적 평형 상태 에 도달했는지를 어떻게 아느냐 하는 것이다. 상식적으로 볼 때
비평형 상태에 있는 어떤 계가 열적 평형을 이루는 데까지 걸리 는 시간은 가장 멀리 떨어져 있는 입자들이 서로 정보를 교환하 는 데까지 걸리는 시간일 것이다. 이차원 아이싱 계에서 이 완화 시간은 주기적 경계 조건을 사용할 경우 귀퉁이와 중간에 있는 스핀둘이 정보를 주고받는 시간이다. 주사를 한 번 할 때마다 이 웃 스핀둘에게 정보가 전달되므로, 격자 전체를 한 번 주사하는 시간을 시간의 단위로 정하면, 완화 시간은 대략 Mo=(Nx/2)X (Ny /2) 주사가 될 것이다. 또한 주방정식으로부터 물리계의 완화 시간 r 를 알아낼 수 있다고 가정하면 열적 평형 상태에 도달할 때까지 걸리는 주사의 수 Mo 는 r ~ Mo 를 만족해야 할 것이다. 물론 이론적으로 또는 경험적으로 완화 시간을 추산할 수 있다 면 큰 도움이 된다. 몇 가지 완화 시간이 특별히 긴 예들을 고려 해 보자. 일차 상전이나 스핀 글라스처럼 에너지 장벽이 있는 경 우에는 평형 상태에 도달하려면 반응률이 아주 낮은 양자 터널링 을 거쳐야 하기 때문에 완화 시간 r 가 아주 길다. 또한 상관 거 리가 무한대로 발산하는 이차 상전이를 겪는 계에서 임계온도 근 처에 가까이 가면 계의 모든 입자들이 집단적인 성질을 갖게 되 어 완화하는 데 아주 건 시간이 걸린다. 또 하나의 아주 간 완화 의 예로서 N--+ oo 인 극한에서 감수율 x 가 아주 커지거나 무한대 로 발산하는 경 우이 다. van Hove 의 완화 이 론에 [van Hove, 1954] 의하면 비례 관계 r ex: X 가 성립하여 감수율이 커질수록 완화 시간이 길어진다. 이런 계들의 예로서 거의 연속적인 상전이를 겪는 계나 이차원 XY 모델 또는 이차원 하이젠베르크 모델들이 있다. 또 한가지 완화 시간을 길게 하는 조건은 어떤 가관측량이 보존되는 경우로서, 유체역학적 지연이라고도 하는데, 완화 시간 과 관계되는 가관측량의 푸리에 성분이 파장의 파수 k 의 제곱에 역비례하므로 k 가 작은 성분들은 아주 느린 완화를 하게 될 것
이다. 위에서 논의한 것처럼 상식적인 추측 또는 완화 이론에 의해 완화 시간을 추산할 수 있다면 좋겠지만 실제로는 몬테카를로 시 뮬레이션에서 어느 특정한 가관측량의 평균값을 수시로 계산해 보고 그것이 평형 상태의 값으로 완화되어 가는 경향을 보고서 M澤 결정하는 것이 관례이다. 아이성 모델의 경우처럼 연속 상 전이룰 하는 물리계에서는 다른 열역학적 양들보다 질서맺음 변 수가 완화하는 데 가장 긴 시간이 걸리는 것으로 알려져 있어서 질서맺음 변수의 완화 과정을 살펴보는 것이 상례이다. 그림 7.6 에 임계온도를 중심으로 세 가지 온도 영역에서 초기 배위의 전화 과정을 그렸다. 온도가 높은 ]
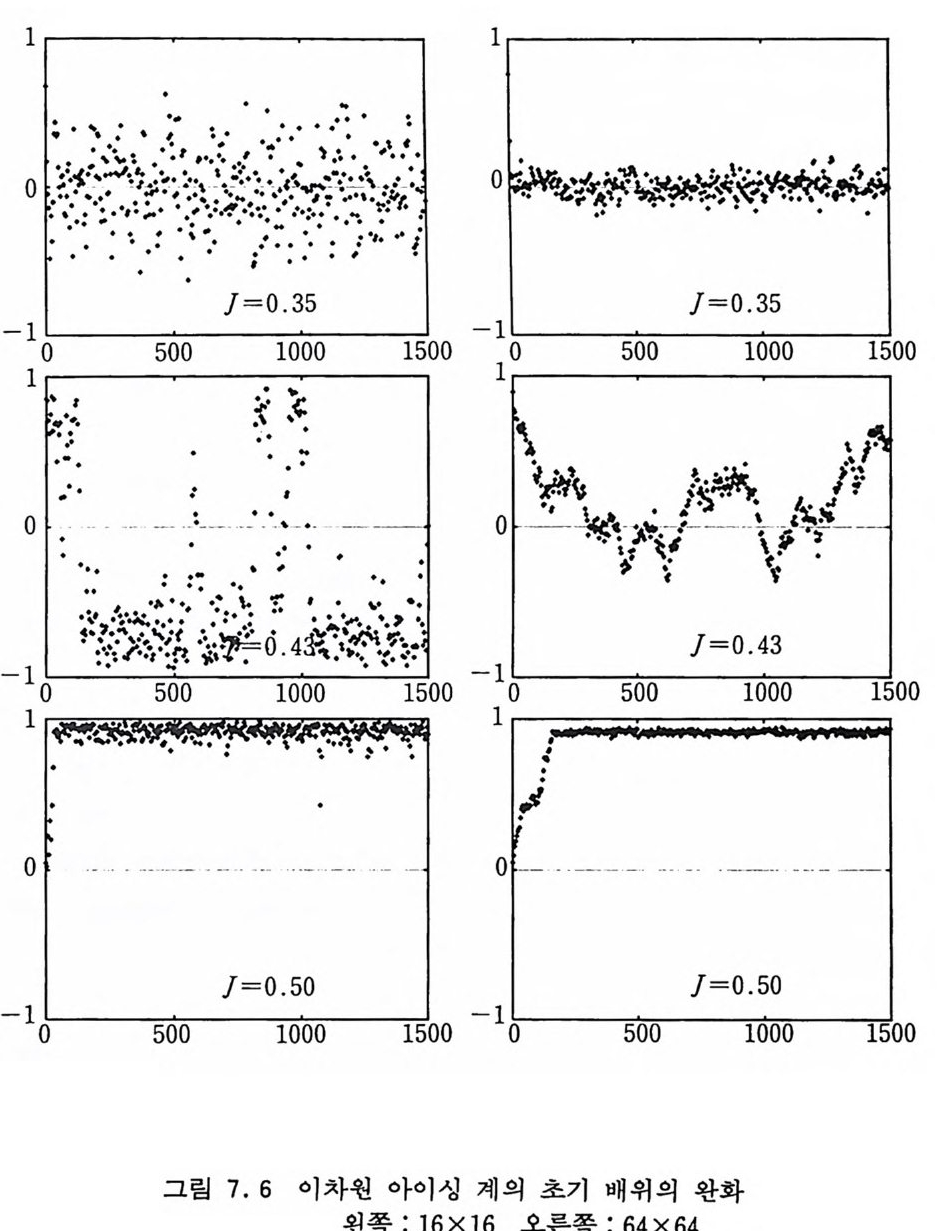 1 1
1 1
7.3.6 물리량의 측정 완화 시간을 사전에 알아내거나 혹은 경험적으로 확인하여 임 의의 초기 상태에서부터 시작하여 Mo 번만큼 마르코프 과정을 수 행한 다음에는 확률 W(.0 ) =ex p(-/3%(.0 ))/z 에 의해 표본추 출되는 배위들의 가관측량에 대한 기여들을 무게 함수를 별도로 곱하지 않고 단순 합산하여 그 대수적 평균값을 구함으로써 거시 적 기대값을 구하게 된다. 한데 메트로폴리스 방법에서 배위들의 표본추출은 새로운 배위 가 격자의 한 점에서만 변하기 때문에 인접해 있는 주사 단계에 서의 배위들이 통계적으로 완전한 독립성을 가지지 못한다. 따라 서 한번 가관측량을 추출한 다음에는 충분히 오랜 단계들을 거쳐 새로운 배위의 통계적 독립성이 인정되었을 때 다시 가관측량을 추출해야 한다. 그렇지 않으면 측정된 가관측량의 통계적 편차가 오히려 더 커질 것이다. 죽 측정 횟수를 무조건적으로 늘리는 것 이 반드시 현명하지는 않다는 것이다. 이 충분히 오랜 시간을 어떻게 정해 주느냐 하는 것은 자동 상 관 시간을 고려하면 알 수 있다. 이것은 초기 배위가 열적으로 완화하는 시간과 비슷할 것이지만 그보다는 훨씬 짧을 것이다. 우선 이상적으로 관측 시간이 무한대인 경우에는 관측량의 정확 한 기대값과 분산울 구할 수 있을 것이다. 62 가모 〈나접 (0 나)-〈 O 〉가 〉 (7. 35 ) 우리가 실험적으로 M 번의 측정에 의해 얻는 가관측량 〈 O 〉 M= i1右 참M O (.iot) (7 . 36)
들은 M--+ 00 인 극한에서 중심 극한 정리에 의해서 정규 분포를 가질 것이다. 이 정규 분포의 분산은 가관측량 O 와 전이 행렬에 따라서 차이를 보일 것이다. 일반적으로 〈 O 〉 M 의 분산은 o1,= <[> 훔 (0 나) ― 〈 O 〉 )『 〉 =万1 쿠M 〈 (0( 必t) -< O > ) 2> (7 . 37) +¥22 ~Mt ttM'~> t (< O ( .01 ) 0 (.0t') >— < O > 2) 와 같이 쓸 수 있는데 이 식의 우변의 첫번째 항은 가관측량 0 에만 의존한다. 마지막 항은 전이 행렬에도 의존하는데 분산이 마 르코프 사슬에서 배위들 간의 상관관계에 의존한다는 것을 말해 주고 있다. 마지막 항에서 괄호 안에 있는 각 항들이 양수이고 〈 02 〉 - 〈 O 〉 2 보다 적으며 t'―t가 늘어남에 따라 영으로 수령한다 는 것을 어렵지 않게 보일 수 있다. 따라서 위 식의 우변에 의해 주어지는 〈 O 〉 M 의 분산 6 記존 이상적인 경우의 분산 군=〈 02 〉 - 〈 O 〉 2 보다 언제나 더 크고 t'―t가 길어짐에 따라 a2/M 에 수령 한다. 따라서 몬테카를로 주사를 할 때마다 가관측량에 대한 측정을 하는 것은 측정 횟수 M을 늘려주지만 인접 주사들에서의 배위 돌 간의 상관관계로 인하여 분산을 그보다 더 많이 늘리기 때문 에 오히려 더 해롭다. 하지만 전체 주사 횟수를 고정해야 하는 경우 n= t'-t를 지나치게 길게 잡으면 측정 횟수 M을 줄이기 때문에 이 역시 현명하다고 볼 수는 없다. 최적의 n 을 결정하기 위해서는 주어전 전이 행렬에 의해 연결되는 배위들 간의 상관관 계에 대해 정량적인 척도가 필요하다. 가관측량 0 의 규격화된 완화 함수(또는 자동 상관 계수) po (t)
룰
Po (t)6&< -¾I( 1 + 2~) ( <0 2> _
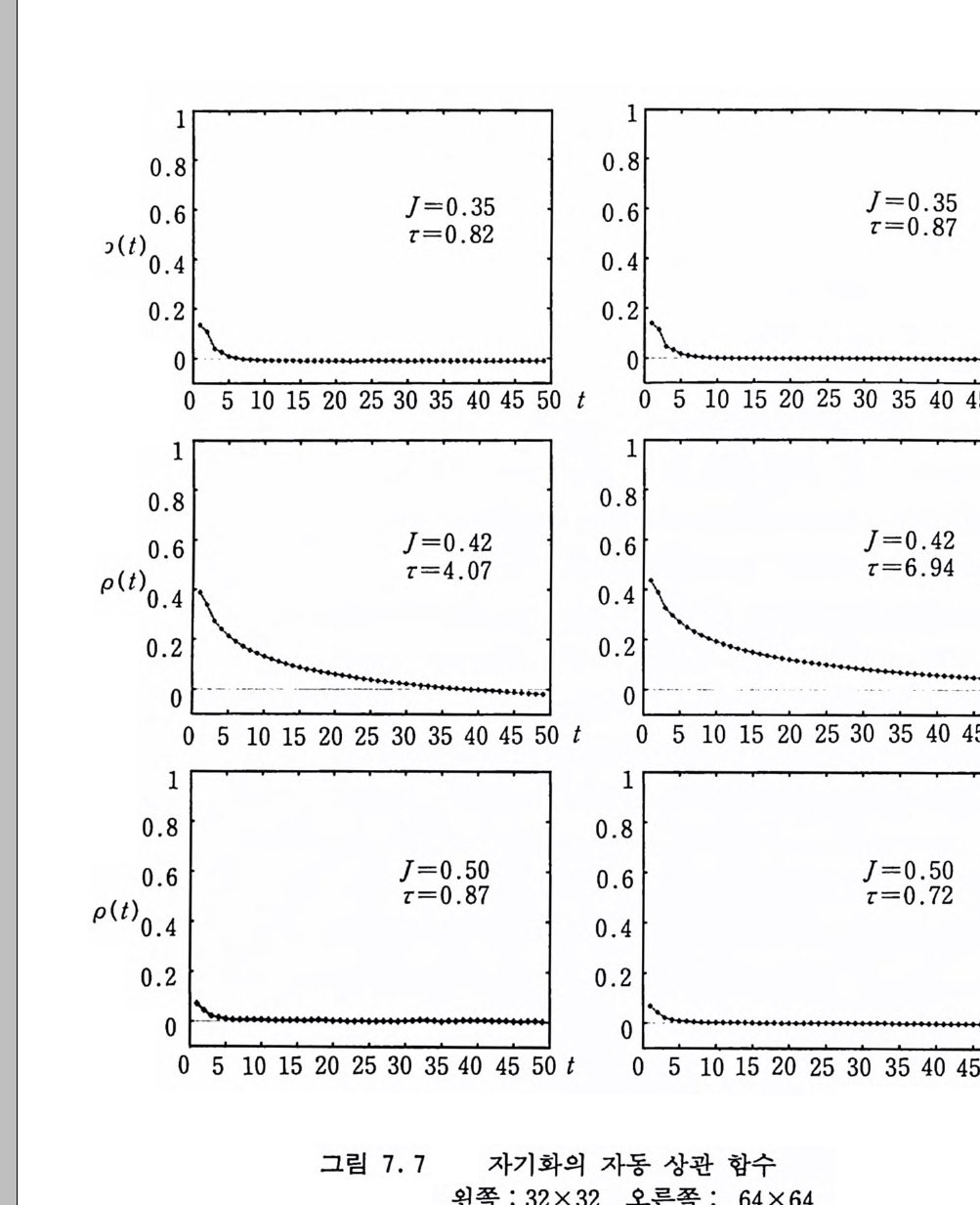 I00..86 I J~ 0.35 I 00..68I l ]=0.3 5
I00..86 I J~ 0.35 I 00..68I l ]=0.3 5
표 7. I 아이싱 격자의 자동 상관 시간 J 0. 35 0.40 0. 42 0. 44 0.50 16X 16 0. 70 1.33 1.66 1.67 0.69 32X 3 2 0. 82 2. 46 4.0 7 4.3 1 0.87 64X 6 4 0.87 3.1 4 6.94 7. 68 0. 72
수록하였다. ]=0.39~0.44 사이에서 완화 시간이 특별히 길지 만 그밖의 영역에서는 k :::::: 5 예서 이미 짜 k) <0.05 에 도달하고 있다. 아이싱 계의 시뮬레이션에서 직접적인 관측의 대상이 되는 양 둘은 내부 에너지 U, 자기화 M, 스핀-스핀 상관 함수 /(k)= 등이다. 또한 이들의 요동으로부터 비열 C, 자기화 감수 율 x 등을 산출할 수 있고 그들이 최대값을 가지는 온도를 〈임 계온도 〉 라고 정의할 수 있을 것이다. 또한 다음 절에서 논의하게 될 유한크기 분석을 통해 임계지수들을 추산할 수 있다. 지금까지 논의한 방법으로 64X64 크기의 이차원 격자에 대해 시뮬레이션한 결과의 일부를 그림 7.8 에 온도의 함수로서 나타냈 다. 여기서 자기화의 오차막대는 식 oM=[(
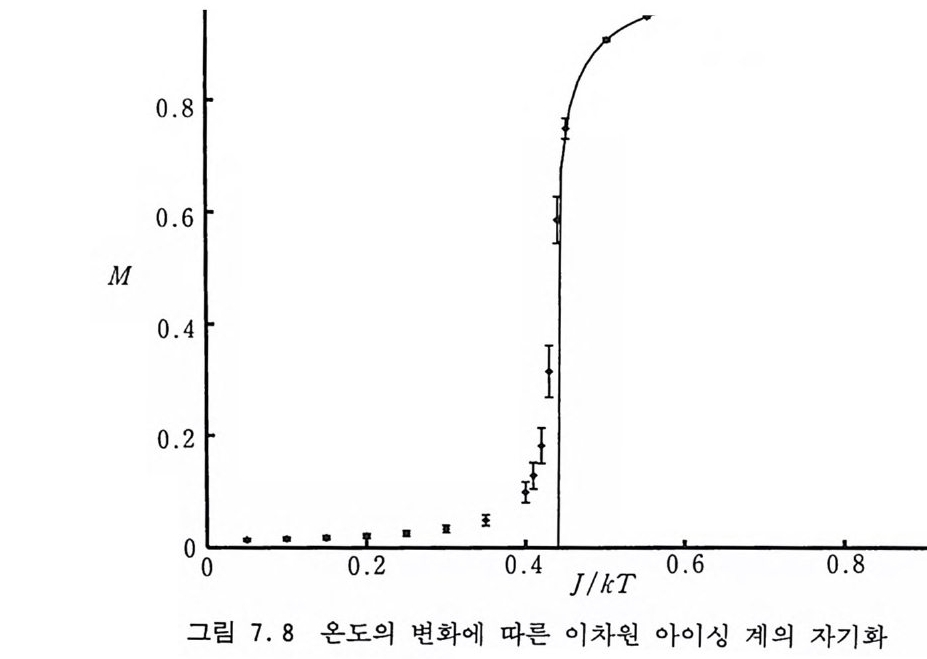 0.8
0.8
7. 3. 7 유한크기 분석 몬테카를로 시물레이션과 유한크기 문제접 크기가 유한인 계를 우리가 아무리 정확히 시뮬레이션해도 무 한계에서 일어나는 임계 현상을 볼 수는 없다• 그것은 임계점에 서 상관 거리가 무한대가 되어야 하는데 우리가 택할 수 있는 계 는 유한일 뿐이기 때문이다. 이것을 다르게 말하면 크기가 유한 인 피적분 함수를(볼츠만 함수) 유한인 위상공간에 대해서 아무 리 많이 적분해도 임계 현상의 특칭인 특이성을 얻어낼 수가 없 다는 것이다. 원칙적으로 유한인 이차원 아이싱 계에서는 상전이 가 존재하지 않고 어느 온도에서도 자기화가 영이다. 그렇다면 지금까지 논의한 것들은 모두 무의미하다는 것인가? 반드시 그렇 지 만은 않다. 그림 7 . 5 에 Ferd i nand 와 F i sher 가 [Fe rdin a nd 등, 1969] 아이싱 격자의 비열에 관해 계산한 결과가 나와있는데 유한계가 무한계의 성질을 어느 정도 가지고 있다는
것을 알 수 있다. 비열의 최대값이 계의 크기가 커점에 따라 점 점 커지는 것을 볼 수 있다. 그들은 이미 비열이 최대값을 가지 는 온도 Tm(L) 과 무한계의 임계온도 Tc 사이에 [T m(L)— T 』 /Tc~b/LA (7 .43) 인 관계가 있다는 것을 확인했다. 여기서 A=l/11 는 임계지수 이다. 유한크기의 아이싱 계는 높은 온도에서는 무질서한 상태에 있 지만 전이 온도보다 낮은 온도에서는 두 가지 정렬된 상태 중 하 나에 오랫 동안 머무르게 된다. 이것은 에너지가 극소 지점인 두 개의 정렬 상태 사이에 에너지 장벽이 존재하기 때문이다. 에르 고딕 시간 re 보다 충분히 오래 기다리면 한 가지 상태에서 다른 상태로 전이하는 것울 볼 수 있고 자기화는 영이라는 것을 확인 하게 되지만 낮은 온도일수록 E 가 길어서 사실상 초기 배위가 속해 있는 에르고드 분반을 떠나기가 어렵게 된다〔 B i nder 등, 1986]. 따라서 시뮬레이션 시간을 re 보다 훨씬 짧게 잡으면 마치 무한 계에서처럼 자발 자기화가 생겨난 것처럼 보인다. 이렇게 해서 얻은 측정 결과들은 물리계의 크기 L 과 사용된 경계 조건에 의 존하지만 L 을 무한대로 늘려주면 무한계의 그것들에 충분히 가 까워지리라는 것이 기대된다. 시뮬레이션 프로그램에 정렬 상태 들 간의 전이를 방지하는 장치를 하거나 자기화를 측정할 때 그 것의 절대값 또는 평균 평방근을 측정하면 무한계에서처럼 두 개 의 상태 사이에 무한히 높은 에너지 장벽을 설치하는 것과 같은 효과를 얻을 수 있을 것이다. 삼차원 계의 길이를 2 배 늘리면 부피는 23=8 배 늘어나고 계산 량도 이에 비례해서 늘어난다. 현재의 추세로 보면 컴퓨터의 연
산 속도를 두 배 늘리는 데 거의 일년 정도씩 걸린다. 현존하는 컴퓨터의 계산 속도는 우리가 시뮬레이션하고자 하는 물리계의 크기를 못따라가기 때문에 실질적으로 수 개월 이내에 시뮬레이 션이 가능한 계는 기껏해야 25 접〔 Ba illi e 등, 199 디 정도밖에 되지 않는다. 하지만 여러 가지 다른 크기의 격자들에 대해서 시뮬레 이션한 결과들을 유한크기 분석 방법을 사용하여 L-oo 인 국한 까지 의삽하면 무한계의 가관측량 또는 임계지수들을 추정해 낼 수 있다. 몬테카를로 시뮬레이션은 유한크기 축척 이론 (F i n it e-S i ze Scali ng Theor y)을 시험하고 실증하는 도구로서 사용되어 왔고 반대로 유한크기 축척 이론은 소규모의 계들에 대해 몬데카를로 시뮬레이션을 하여 얻은 결과들을 가지고 무한계의 그것들을 추 정할 수 있게 해중으로써 몬테카를로 방법을 아주 유용하게 해주 는 상보적인 관계를 유지해 왔다. 이 이론의 유효성이 계의 길이 L 이 충분히 길고 상관 거리가 충분히 짧은 임계점에서 멀리 떨어 진 영역에서 2, 3 차원의 아이싱 모델의 몬테카를로 시뮬레이션을 통해 입 증됨 으로써 [L andau,1 976 ; Barber 등, 1985] 좀더 복잡한 계에 대해서도 자신감을 가지고 연구해 볼 수 있게 된 것이다. 유한크기 축척 이론 F i sher 의 유한크기 축척 이 론은 [F i sher, 1971 ; Barber 등, 1972 ; Barber, 1983] 유한크기 의 물리 계 와 무한인 물리 계 의 가관 측량들 사이의 관계를 상관 거리와 유한계의 길이의 비례에 관한 급수로서 전개한다. 이것은 임계온도 근방에서는 물리계의 미세 한 거리에서 일어나는 상호작용들이 큰 의미를 가지지 못하고 무 한대로 발산하는 상관 거리보다 큰 거리에서 일어나는 현상들만 이 의미를 가전다는 소위 축척 가설에 (Scali ng Hy po th e sis ) 근거
룰 둔다. 무한계가 임계온도 근방에서 보이는 축척 법칙으로부터 열역학적 양의 특이 부분이 환원 온도의 지수법칙을 따른다는 것 울 유도할 수 있는데 이것은 다음 장에서 좀더 자세히 논의될 것 이다. 유한크기 축척 이론은 길이 축척의 변화에 따른 물리량들 의 변화를 분석하는 재규격화 방정식과도 밀접한 관련이 있다. 다음 장에서 논의되겠지만 축척 법칙은 재규격화 방정식의 당연 한 귀결로서 유도된다. 물리계의 기본적 길이의 단위로서 계의 크기 L, 상관거리 E, 격자 간격 a 등 세 가지가 있는데 L 과 e 를 a 의 단위로 표시하 기로 하면 사실상 두 가지가 된다. g::::::: L 일 때 유한크기 효과가 나타나는데 임계온도 근방에서 상관 거리가 은하 T— Tc 1-v (7. 44) 와 같이 변화하므로 | T— Tc 1-11 :::::: L 일 때 유한크기 효과가 나타 나게 된다. 이 이론에 의하면 온도 T 에서 길이 축척이 L 인 유 한계 의 자유 에 너 지 의 특이 한 (s i n gu lar) 부분은 다음과 같은 동차 식으로 표시할 수 있다. fsIn g ( L, T) =L-(2-a)/u5 (tL U) (7.4 5 ) 여기서 a 와 II 는 비열과 상관거리에 관한 임계지수들이고 t는 환 원 온도로서 t =(T ― Tc)/Tc 이다. 다시 말하면 자유 에너지는 온도와 계의 길이 축척에 따로따로 의존하지 않고 일반적으로 물 리계의 길이 축척과 상관 거리의 비율, L/~=L/r11 또는 tLl/ 11 의 조합에만 의존하는 것이다. 또한 축척 함수 Y 는 경계 조건에 의존하기는 하지만 물리계의 성분과 모양이 같으면 크기에 상관 없이 모든 크기의 계들에 두루 통용되는 보편적 단일 함수이다. 유한계의 전이온도 Tc(L) 을 그 계의 비열이 최대값을 가지는
온도라고 정의하면 유한계의 전이온도와 무한계의 임계온도 사이 의 차이는 다음과 같이 유한크기 축척 이론에 의해 L I ~ 만의 함 수로 표시된다. Tc-Tc(L) =L- 111 1 (1+ a L_,,+… ) (7.46) 여기서 유한크기의 물리계의 전이온도가 무한계의 임계온도로부 터 약간 이동되는 것을 확인할 수 있다. 유한크기 축척 이론의 기본 명제는 무한계의 가관측량 0 가 임 계점 근방에서 000 ( T) ~ CoorP, t - 。 (7 . 47) 와 같이 변화한다면 유한계의 그것은 OL ( T) ~LPl% ? (tL1 lu) (7 . 48) 와 같이 변한다는 것이다. 따라서 질서맺음 변수와 감수율 역시 M=L-P/J .J A1,(tL 1'J.J) (7 . 49) x = L7/ J.J 왓 ( tL llJ.J ) (7 . 50) 와 같이 나타낼 수 있다. 몬테카를로 시뮬레이션에서 유한크기 축척 효과를 확인하는 방 법은 여러 크기의 격자들에 대해서 시뮬레이션해서 얻은 결과들 을 log - log 도표에 그려 보는 것이다. 예를 들어 식 (7.49) 에 t-’를 곱하고 lo g를 취하면 ln (M戶 ) = 갤 ln ( tL1 111) + ln (j,(,) (7 . 51) 를 얻는다. 위의 식들이 맞는다면 x=ln( tL1 'v) , y =ln(M t기를 취하면 이 도표 상의 점둘은 In( 瓜)이 급격하게 변하지 않는 한 기울기가 -B 인 직선 상에 놓여야 할 것이다.
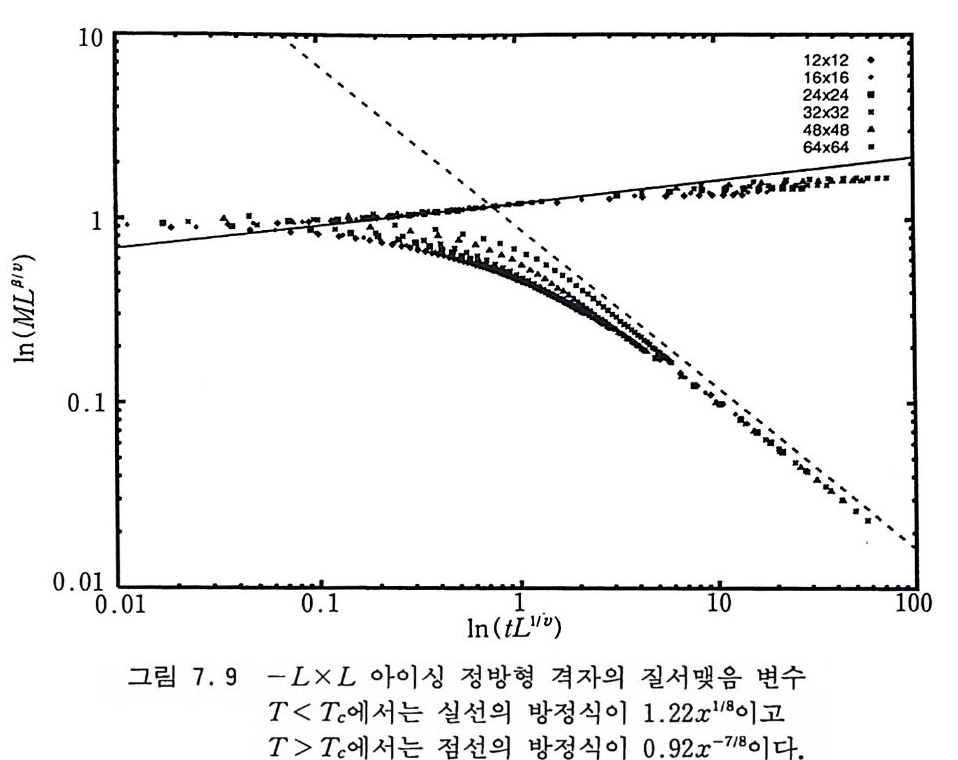 TH)ul1 0l `` ` `` `` ` `` ` ` ```一 `..` ` 、 `‘‘: .234611.244862,x;xxxxx:632114소442286; `.■••;••• 、
TH)ul1 0l `` ` `` `` ` `` ` ` ```一 `..` ` 、 `‘‘: .234611.244862,x;xxxxx:632114소442286; `.■••;••• 、
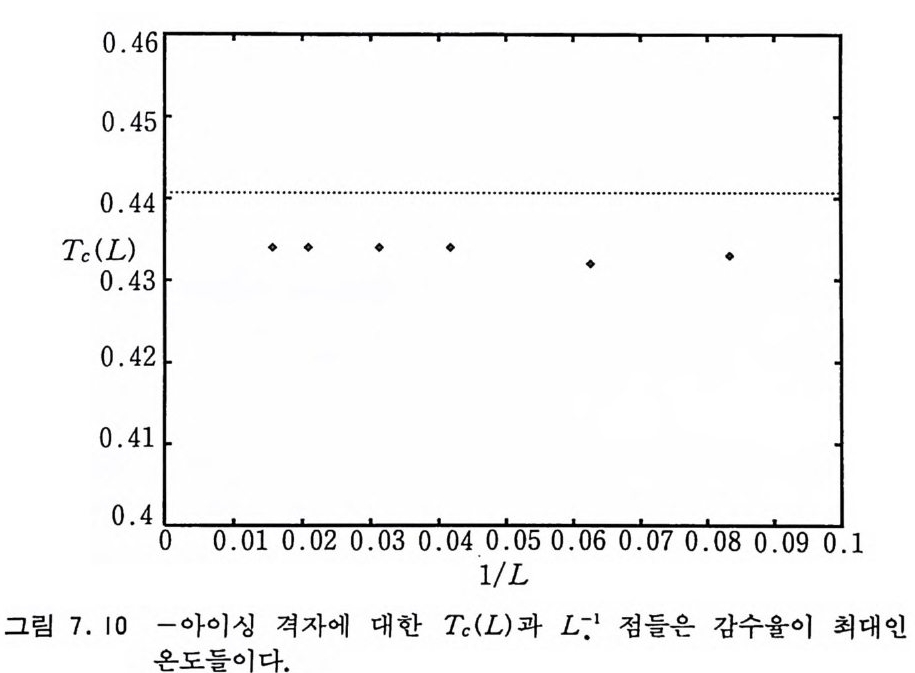 0.460.4 5
0.460.4 5
그립 7.9 와 7.10 에 앞에서 시뮬레이션했던 결과들을 새로운 방 법으로 제시했다. 64X64 격자에 대해서 J= {0.3, 0.35, 0. 40 0, 0.4 0 1 , …, 0.460, 0.5, 0,55, 0.6} 에서 시뮬레이션하면서 자기 화 M, M2, M 4, 내부에너지 U, U2 등을 측정하였는데 측정 횟수는 40,000 회였다. 여기서 주기적 경계 조전을 사용하였다. 이 격자에 포함되는 부분 격자들 {48X48, 32X32, 24X 2 4, 16X 16, 12X12} 에 대해서도 똑같은 세트의 관측량들을 측정하였다. 지금까지의 시뮬레이션 결과들을 종합하면 무한 이차원 아이성 계의 임계온도는 lc~0.4401 (7.52) 이고 임계지수들은 /3/ 11::;:::0.125 (7 . 53) r/11::;::: 1. 75 (7.54) 하는 결론을 얻게 된다. 7.3.8 임계감속 무한인 물리 계 의 본질적 완화 시 간 (Intr i n s ic Relaxati on Ti m e) r 는 임계접 근방에서 상관 거리의 지수 함수로서 r (X 꾼 (7 . 55) 와 같은 관계식을 가진다. 여기서 지수 z 를 동적 임계지수 (Dy na mi c Criti ca l Exp o nent) 라고 부른다, z 의 값은 l < z < 3 으로 서 물리계가 임계점 근처에 가까이 가면서 상관 거리가 무한대로 발산함에 따라 자동 상관 시간도 마찬가지로 발산하게 된다. 한편 상관 거리는 식 (7.44) 에 의해 환원 온도의 지수 함수로 나타낼 수
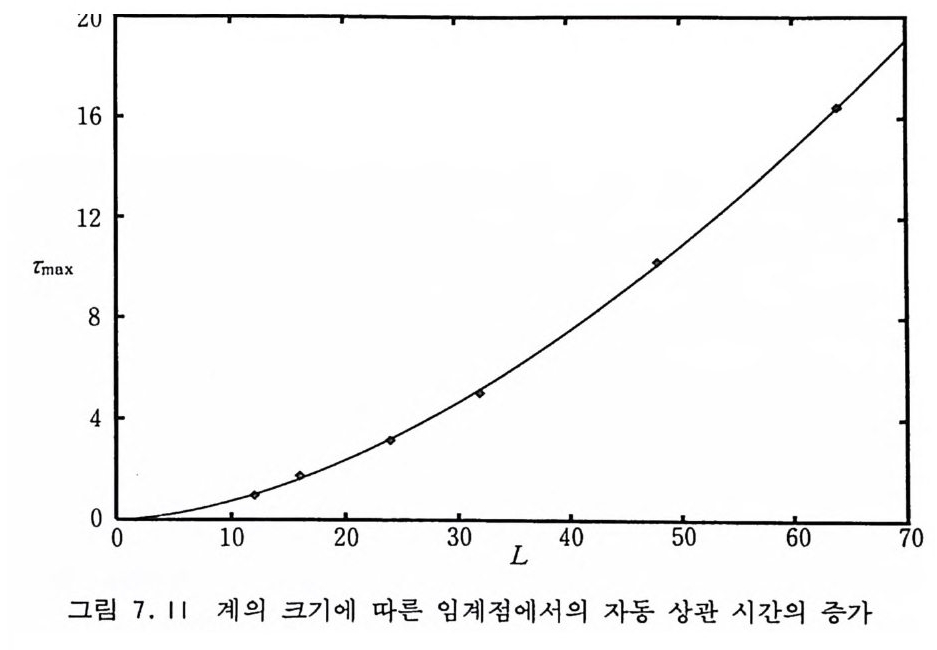 L,U
L,U
있으므로 임계온도 근방에서 완화 시간은 온도 T 와 꾼 ex ll- T/Tc l-vz (7 . 56) 와 같은 관계식을 가진다. 물론 유한계에서는 엄밀한 의미에서 특이성이 존재하지 않아 상관 거리가 발산하지 않으므로 극한적인 상황까지 가지는 않지 만 상관 거리가 격자의 크기보다 커지는 것은 사실이다. 상관 거 리가 격자의 크기와 바슷해질 때 특이성이 둔화되기 시작하여 유 한계의 완화 시간은 L 의 지수법칙 Tmax OC Lz ( T :::::: Tc) (7.57) 을 따르게 된다. 그립 7.11 에 앞에서 고려했던 아이싱 격자들의 자동 상관 시간을 나타냈는데 z~ l. 67 임을 알 수 있다. 위에서 논의했듯이 메트로폴리스의 방법을 적용하여 얻는 격자 배위들의 통계적 독립성을 얻기 위하여 자동 상관 시간보다 큰 n(>r) 번씩 주사룰 하고서 가관측량의 평균값의 계산에 대한 합
산을 한번씩 해나가는 것이다. 이런 경우, 예를 들어, 자기화의 편차는 자동 상관 시간이 0 인 경우에 비해, 식 (7.42) 에 의해 〈 (8M)2 〉 =꼬후n ( 〈 M2 〉 - 〈 I M I> 2) ex:: ~Lz+ nr / 1 1-d (7.58) 만큼이 더해진다. 따라서 주어진 정확도를 유지하기 위해 계산량 울 Lz +까 II :::::: L3 . 75 만큼 증가해 주어야 된다. 편차를 줄이기 위해 계의 크기를 늘린 결과 훨씬 더 많은 계산을 해야 하게 된 것이 다. 따라서 계산량의 상한이 제한되어 있다면 편차를 최소로 줄 이기 위하여 어느 크기의 격자에 대해 얼마나 많이 측정을 해야 할지롤 미리 추산해 봐야 할 것이지만 임계점 근방에서 사용할 수 있는 다른 좀더 효율적인 방법들도 있다. 임계감속 (Cr iti cal Slowdown) 의 근본적인 원인은 메트로폴리 스의 방법이 국부적이라는 데에 있다. 따라서 비국부적인 방법을 사용하면 임계감속의 문제를 어느 정도 해결할 수 있을 것이다. 비국부적인 알고리즘으로 현재 나와 있는 것들은 송이 알고리즘 [Swendsen 등, 1987 ; Wolff, 198 이 , Multig r id 알고리 즘 [Kandel 등, 1988] 등이 있다. 참고문헌 [ 니 G. Bhanot, Re p. Prog. Phys . 51 (1988) 429 [ 2 ] C. F. Bail lie and P. D. Coddin g ton , Phys . Rev. B43 (1991) 10617 [ 3 J M. N. Barber, Phase Transit ion s and Cr itica l Phenomenav. 8, ed. by C. Domb and M. S. Green (Wi ley , 1983) , 145 [ 4 J M.N. Barber. R.B . Pearson, and D. Toussain t , Phys . Rev.
B32 (1985)1 7 20 [訂 R.J. Baxte r , Ex a,c tly Solved Models in Sta tistica l Models, (Aca-demi c Press, 1982) [ 6 ] K. Bi nd er, P hase Transit ion s and Cr itica l Phen o mena v.5b, ed. by C. Domb and M. S. Green (W ile y , 1975) , 1 [ 汀 K. Bi nd er, Phys . Rev. Lett . 47 (1981) 693 [ 8 ]K. Bi nd er and A.P. Young, Rev. Mod. Phys . 58 (1986) 867 [ 9 ] H. W .J. Blote and M.P. Ni gh ti ng a le, Phys i c a 112A (19 82) 405 U 이 S.G . Brush, Re v. Mod. Phys . 39 (19 67) 883 [11] C. Domb, Adv. Phys . 9 (1960) 149 U 끽 C. Domb, in Phase Transit ion s and Cr itica l Phenomena, vol. 3 (Academi c Press, 1974) ed. by C. Domb and M.S. Green, 357 〔피 A. E. Ferdin a nd and M.E. Fis h er, Phys . Rev. 185 (19 69) 834 [14 ] A. M . Ferrenberg and D. P. Landau, Phys . Rev. B44 (1991) 5081 [15] M.E. Fis h er and M. N. Barber, Phys . Rev. Lett . 28 (1972) 1516 [16 ] L.D . Fosdic k , Meth o ds in Comp ut a tion al Phys i c s vol. 1, ed. B. Adler, (Academi c Press, 1963) , 245 U기 CJ . Hamer and M.N. Barber, ]. Phys . A14 (1981) 2009 [18] E. Isin g , Z. Phys . 31 (1925) 253 [l 이 D. Kandel, E . Domany, D. Ron, A. Brandt and E. Loh, Phys . Rev. Lett . 60 (19 88) 1591 〔 2 이 D.P. Landau, Phys . Rev. B14 (19 76) 255 [21] L.D . Landau and E.M. Lifsh it z, Sta tistica l Phys i c s , (Perga mon, 1980) [2 끽 KC. Lee, ]. Phys . A23 (1990) 2087 ; ]. Korean Phys . Soc. 24(1991) 32 [23 ]W . Lenz, Z. Phys . 21 (1920) 613 [24 ] N. Madras and A.D . Sokal, ]. Sta t. Phys . 50 (1988) 109 [25] B. McCoy and T.T. Wu, The Two-Di m ensio n al Isin g Model,
(Harvard Univ . Press, 1973) [26] N. Metr o p ol is, A.W . Rosenbluth , M.N. Rosenbluth , A.H . Teller, and E. Teller, ]. Chem. Phys . 21 0953) 1087 詞 H. Muller-Krumbhaar and K. Bin d er, ]. Sta t. Phys . 8 (1973) 1 [2 이 L. Onsage r, Phys . Rev. 65 (1944) 117 [副 L. Onsag e r, (unp u blis h ed, 1952) 〔 3 이 W. Op e chowski, Phys i c a 4 0937) 181 [3 나 G. Pawley, R.H . Swendsen, D.J. Wallace, and K.G . W ils on, Phys . Rev. B29 (1984) 4030 [3 끽 R.B . Pott s, Proc. Camb. Phil . Soc. 48 (1952) 106 [33 ]V . Priv m an, Fin i t e Siz e Scalin g and Numeri ca l Sim ulati on of Sta tistica l Sys t e m s, (World Sc ien ti fic, 1990) [3 사 T. Schultz , D. Matt is, and E. Lieb , Rev. Mod. Phys . 36 (1964) 856 [35 ]R .H . Swendsen and J.S. Wang, Phys . Rev. Le tt . 5 8 (1987) 86 [36] L. van Hove, Phys . Rev. 93 (1954) 1374 [3 까 L. van Hove, Phys i c a 21 (1955) 517 [3 인 F.Y. Wu, Rev. Mod. Phys . 54 (1982) 235 [3 이 U. Wolff, Phys . Rev. Lett . 62 (1989) 361 [4 이 C.N. Yang , Phys . Rev. 85 0952) 808
제 8 장 재규격화 방정식과 임계현상 재규격화 군 방정식 이론은 축척 법칙과 보편성을 좀더 만족스 럽게 설명해 줄 뿐만 아니라 임계지수를 계산하는 구체적인 방법 울 제시해 준다. 최근에 몬테카롤로 방법과 재규격화 군 이론을 사용한 계산에서 삼차원 아이싱 모델의 임계온도를 유효 숫자 6 자리까지 얻어냈다. 8. 1 임계현상과 축척 법칙 7 장에서 논의한 이차원 아이성 계에서처럼 많은 물질들은 높은 온도에서 무질서한 상태로 있다가 온도를 내려 주면 어떤 임계온 도 Tc 에서 상전이를 하게 된다. 예를 들어 물이 647.4 K, 218 a tm에서 액체성과 기체성을 동시에 가지게 된다든가 BaTiO a 결 정이 12o·c 에서 결정 구조가 0h 에서 Td 로 바뀌는 구조적 상전 이를 한다든가 강자성체가 임계온도에 이르면 자발적으로 자성을 띠게 된다든가 헬륨이 2K 에서 초액체성을 가지게 되고 금속이
초전도성을 가지는 등이다. 높은 온도에서는 열적 요동으로 인해 분자들이 인접 분자들 이 의에는 상관관계를 거의 가지지 못하고 무질서한 상태에 있다가 온도가 내려감에 따라 점점 멀리 떨어져 있는 분자들과도 상관관 계를 가지게 되고 임계온도에 이르게 되면 계 전체의 분자들이 획일화된 양상을 보이게 된다. 죽, 임계온도에 이르면 상관 거리 가 무한대에 이르게 되고 열역학적 변수들, 비열, 감수율 등이 무한대로 발산하는 특이성을 가지게 되는 임계현상이 일어나는 것이다. 우리는 7 장에서 질서맺음 변수인 자기화와 자기 감수율이 임계 접 근방에서 지수 법칙을 따르는 것을 관측했다. 임계온도 근방 에서 특이성을 가지는 열역학적 양둘이 일반적으로 지수 법칙을 따르는 것이 실험적으로 관측되는데 자성체의 지수 법칙둘을 열 거하면 다음과 같다. 액체계의 지수 법칙은 약간 다른데 자세한 것은 S t anle y [l971] 을 참조하기 바란다. C OC I T-Tc 1-a (8 .la ) M OC I T-Tc Ip (8 .lb ) x oc I T_T니 -T (8 .le ) H oc M8 (8 . Id) I' (R) oc R(2-d-T/ ) (8 .le) f; OC I T-Tc 「IJ (8 .lf ) 여기서 C 는 비열, M 는 자기화(질서맺음 변수), x 는 감수율, H 는 의부 자장(의부장), I' (R) 은 상관 함수, E 는 상관 거리, d 는 공간의 차원을 말한다. 이차원 아이싱 계는 그 구조가 사각형 격자이건 삼각형이건 또 는 육각형이건 상관없이 또 최근접 상호작용만 고려하건 최최근
접 상호작용도 포함하건 상관없이 그 임계지수들이 똑같다. 이것 은 물리계들의 일반적인 성질로서 물질들의 구조, 대칭성, 임계 온도가 다양하게 다르지만 임계온도 근방에서 이들 열역학적 양 둘이 변하는 양상은 거의 획일적이라는 것이 관측된다. 좀더 정 확히 말하자면가능한임계지수값들의조 ¢=(a, /3, y, a, 7J, JI) 는 몇 가지밖에 없고 모든 물질들이 그 중 하나의 조에 속한다. 이러한 성질을 보편성 (un i versal ity)아라고 부르고 어떤 ¢={¢;} 값을 취하는 물질들은 i번째 보편성 계보 (un i versal ity class) 에 속 한다고 말한다. 알려진 (모델)계의 임계지수들을 열거해 보면 표 8.1 과 같다. 이와 관련해서 또하나 주목할 만한 점은 이들 지수 중 두 개만 이 독립적이고 나머지는 이들의 함수로서 표현할 수 있다는 것이
표 8. I 몇 가지 (모델)계의 임계지수들 a B r 8 u n 아아성 모델 d=2 0 1/8 7/4 15 1 1/4 d=3 0. 11 0 0.3 2 5 1.24 1 4.82 0.630 0.031 하이젠베르크모델 —0 .115 0.365 1.3 86 4.80 0.705 0.033 2D Po tt s 모델 q= 3 1/3 1/9 13/9 14 5/6 4/15 q= 4 2/3 1/12 7/6 15 2/3 1/4 강자성체 -0.09 0.368 1.21 5 4.3 (CrBr3) 반강자성체 —0.1 4 0.3 2 1.37 0.70 (RbMnFJ)
다. 다시 말해서 이 여섯 개의 사이에 다음과 같은 4 개의 축척 법 칙 (scalin g law) 이 있음이 알려 졌다. a+2/3 + r=2 (Rushbrooke's law) 또는 (8 . 2a) r=/3 ( 8— 1) ((EWsi sdao mm 'asn lda wF)i s h er's law) (8. 2b ) r = (2-7J ) 11 (Fis h er's law) (8 . 2c) vd = 2-a (Jo sep h son's law) (8 . 2d) W i dom[l96 하, Domb 과 Hunte r [1965], Kadano ff [196 이 등은 위의 관계식들을 현상론적으로 설명했다. 위의 식들을 왜 축척 법칙이라고 부르는지는 W i dom 에 의해 제안된 다음의 논의를 통 해 알 수 있다. 7 장에서 간략하게 논의된 바이지만 임계온도 근 방에서는 요동이 심해져서 단거리에서 일어나는 상호작용들이 중 요성을 잃게 되고 길어진 상관 거리에서 일어나는 상호작용들이 압도하게 된다. 따라서 물리계가 획일적인 성질을 띠게 되어 상 관 거리만이 거리의 유일한 축척이 되고 나아가서는 모든 열역학 적 가관측량의 특이한 부분이 상관 거리만의 함수가 되는 것이 다. 특별히 상관 거리가 환원 온도 t =(T-Tc)!Tc 의 식 (8.1f) 에 의해 주어지는 지수 함수에 비례한다는 것을 받아들이기로 하 면 환원 온도가 상관 거리의 함수가 된다는 것은 상식적인 귀결 이다. 이것은 환원 온도에 의존하는 모든 물리량들이 상관거리와 관련이 된다는 것을 뜻한다. 논의를 간단하게 하기 위해서 자성의 예를 들면 임계점 근방에 서 자발적 자기화 M 은 실험적으로 환원 온도 t와 의부 자장 H 어 l 뺀 ~=em,[ 土 1+(B 信)}] (8.3)
과 같이 의존함이 관측된다. 여기서 B, D 는 물질의 구체적인 성질에 의존하는 상수들이고 4 와 f3는 임계지수들이다. 또한 + 부호는 t >O 안 지역을 — 부호는 t < O 인 지역에 적용된다. 특기 할 만한 점은 많은 물질들이 각기 다른 B 와 D 를 가지지만 4 와 f3는 같은 값을 가지게 되고 자기화와 의부 자장이 M/B I t I p와 DH/I t l .d의 조합으로만 나오며 그들 사이의 함수 형태가 그 물 질들 모두에 대해서 똑갇다는 것이다. 즉 자기화 M 은 자발적인 자기화 B I t I p에 의해 축척되고 의부 자장 H 는 I t l .d /D 에 의해 축척되어 궁극적으로 상관 거리의 지수 함수에 의해 축척된다는 것이다. 축척 법칙을 일반적으로 虐::::::”±(沼) (8 .4) 와 같이 쓸 수 있는데 이 식으로부터 (8 . 1) 식들의 지수 법칙들을 직접적으로 유도해 낼 수 있다. 예를 들어 감수율 x 는 t - 。+이고 H 一 0 인 극한에서 X oc ( 넓 )H=O=I t I /J(델杓 H=O=I t I/J-, l.,f(,~ (0) (8.5) 울 만족한다. 이것을 위의 식 (8.lc) 와 비교해 보면 4= f 3+ 7 (8 . 6) 를 얻게 된다. 또한 축척 함수 .A,f,(y)가 y-(X) 인 극한에서 지수 함수가 된다 고 가정하면, 죽 .Jt (y) 一 瓜 OO y A (8.7) 이라면 다음과 같은 식을 얻게 된다.
M 키 t I p.!U oo 庄/t 4A (8. 8) t 一 0 인 극한에서는 자기화 M 이 온도에는 무관하고 자장 H 만 의 함수가 될 것이기 때문에 B=A4 (8 . 9) 라야 할 수 있다. 식 (8.Id) 와 (8.8) 을 비교해 보면 o=l/ tl임을 확인할 수 있고 W i dom 의 축척 법칙을 간단히 유도할 수 있다. o=L1//3 = 1 + rl/3 (8 .10) 다른 지수 법칙들도 이와 비슷한 방식으로 유도해 낼 수 있다. 다시 말하면 지수 법칙들은 자기화와 의부 자장이 온도의 지수 함수들에 의해, 죽 상관 거리에 의해 축척되는 데에서 그 근원을 찾을 수 있다. 지수들 중 독립적인 것이 두 개라는 것은 자기화 M 과 의부 자장 H가 환원 온도에 각기 다르게 의존한다는 데에 그 근원이 있다. 축척 법칙을 분명히 확인하는 방법은 그림 8.1 에서처럼 실험 데 이터를 좌표축이 x=M/1 t IP 와 y= H/1 t l ,d와 같이 정의되는 공 간에서 그려보는 것이다. 그림은 Ho 와 L i s t er[l96 이가 작성한 CrBr3 의 위상 다이어그램이다. 이 실험 데이터들이 두 개의 축 척 함수들 죽 t >O 인 지역에서는 .Af, +(Y) 와 t
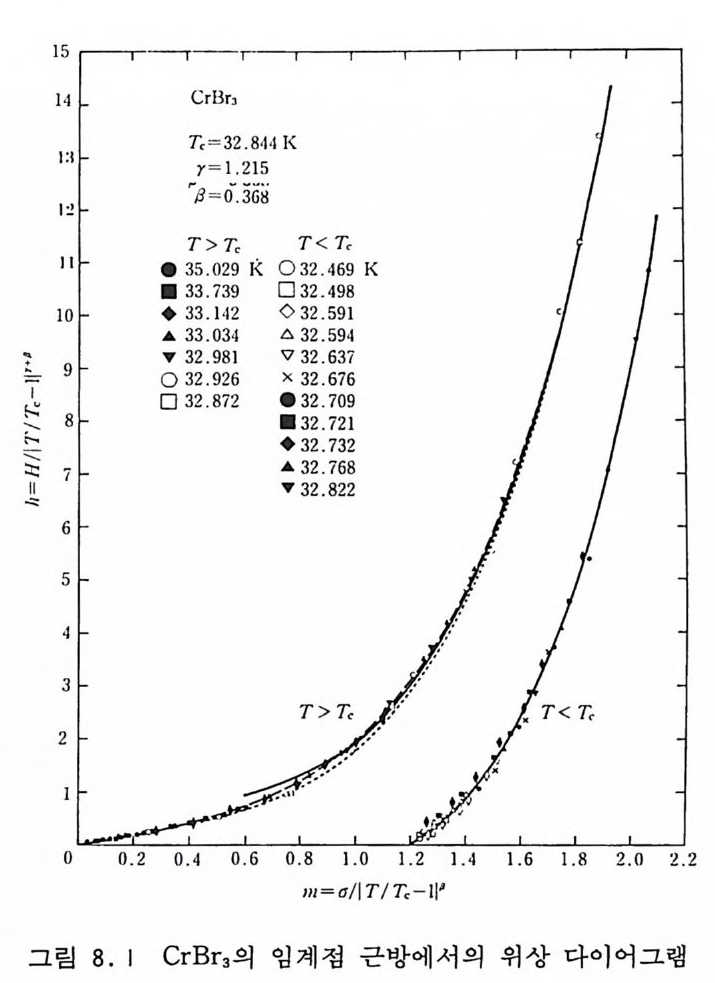 1154t I ' ---,-—
1154t I ' ---,-—
8. 2 카다노프의 구획 스핀 방법 앞 절에서의 논의는 자기화와 의부 자장 간의 관계식 (8.4) 에 근거를 두고 있지만 자유 에너지의 특이한 부분이 온도와 의부 자장에
fstn g ( T, H) ~ Aol t 12 군(/衍 (8 .11 ) 와 같이 의존한다고 가정하고 논의롤 전개해도 똑같은 결론을 얻 게 된다. 카다노프〔 Kadano ff, 1966] 의 논의 를 따라 자유 에 너 지 가 (8.11) 과 같은 형식이 되는 것을 보기로 하자. 그림 8 . 2 에서처럼 아이싱 격자를 변의 길이가 L 인 세포들로 나누어 보면 세포들 의 전체 수는 n=(N/L)2 일 것이고 각 세포 내에는 L 2 새의 스 핀둘이 포함될 것이다. 임계점에 아주 가까운 영역에서는 상관 거리 가 세포의 길이보다 훨씬 커서, 즉 E> L , 하나의 세포 내에 있
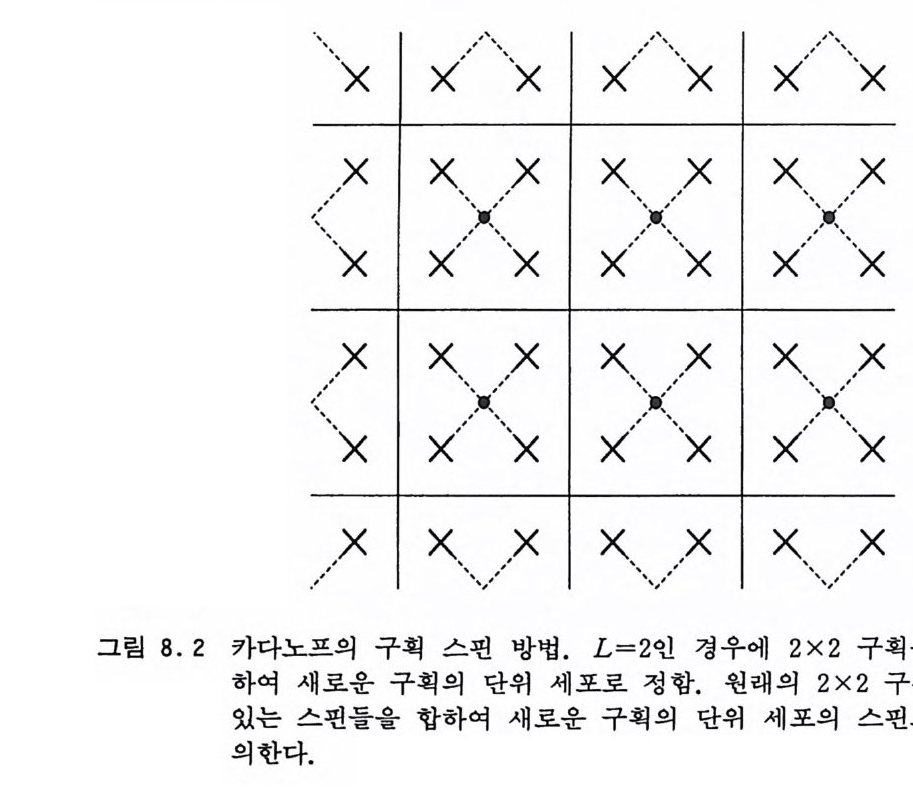 .` `X X , ,’ ^``\ X X’’ ’'\` ` X x,’’ ' \\ x
.` `X X , ,’ ^``\ X X’’ ’'\` ` X x,’’ ' \\ x
는 스핀들이 한 방향으로 정렬해 있을 확률이 매우 클 것이다. 그림 8.2 에서 보인 것처럼 이 세포들로 구성되는 새로운 격자를 정의하고 새 격자의 각 위치에서의 스핀을 세포 내의 미시적 스 핀 (s) 들의 합이라고 정의하자. 이렇게 해서 정의되는 거시적 스 핀 (S) 을 구획 스핀 (block sp in ) 이 라고 부르자. 임 계 점 근방에 있 기 때문에 구획스핀의 값은 L2 또는 -E 의 값을 가질 것이다. 거시적 격자의 스핀 단위를 L2 으로 취하면 아이싱 계의 미시 적 격자와 거시적 격자에서의 자유 에너지들이 임계점 근방에서 /macr 。 ({S}, ], H) = L2/m1cro ({s}, j, h) (8 .12) 과 같이 연관될 것이다. 매개 변수들 간에 비례 관계가 성립할 것이라고 가정하면, 죽 H=ho(L) h, J=j。 (L) j (8 .13) 이 성립한다고 가정하고 추가로 L 에만 의존하는 비례상수들이 축척의 지수 함수들이라고 가정하면, ho (L) = Lx, jo ( L) = LY (8 .14) 자유 에너지는 다음과 같은 동차식을 만족하게 될 것이다. f(L Yj , LXh) =L2f( j, h) (8 .15) 여기서 축척 L 을 L= j -1/Y 가 되게끔 선택하면 위의 식은 / (1, j-X /Yh) =j-21 Y j (j, h) (8.16) 이 되는데 j=t, h=H 입눌 ^0t -기하고
x/y= Ll, 2/y= 2-a (8 .17) 라고 인지하면 식 (8 . 11) 을 얻게 된다. 식 (8 . 11) 을 t 또는 H 에 관해 차례로 미분해 나가면 8 . 1 절에서 얻은 축척 법칙들 (8. 6, 8,9, 8 . 10) 을 얻는다. 이 논의에서 핵심적 요소는 식 (8,13-14) 로서 미시계와 거시계에서 매개 변수들이 길이 축척의 지수 함수에 의해 연관된다는 것이었다. 축척 법칙이라는 용어의 근원은 바로 여기에 있다. 8.3 란다우 이론 란다우 [Landau, 1937 ; Landau 등, 198 이는 상전이 현상을 설명 하기 위해 질서맺음 변수의 개념을 창출하고 자유 에너지를 통상 적 열역학 변수인 온도와 압력 이의에도 이 질서맺음 변수의 해 석적이고 대칭적인 함수로 표현할 수 있음을 논했다. 어떤 대칭 성을 가지는 물리계의 자유 에너지를 그 대칭성 변환에 대해서 벡터처럼 변환하는 질서맺음 변수 m 의 함수로서 급수 전개를 할 수 있다고 가정하고 g( m, T) =a( T) + b ( T) m2+ c( T) m4+d ( T) m6+ … (8.18) 과 같이 써보자. 또한 이차항의 계수를 온도의 함수로서 급수전 개하여 b(T) =b 。 (T ― Tc) 라고 하고, bo, c(T), d(T) >O 라고 하자. 그러면 임계온도 Tc 보다 높은 T>Tc 에서는 g( m, T) 가 m=O 에서 극소값을 가지게 되어 평형 상태에서 자기화가 0 이지만 T< Tc 에서는 그림 8.3 에서 보는 것처럼 m -=l= O 에서 극소값을
g g퍼……셜T…)의 …… .......... :
::::?:::그림 8. 3 란다우:온도에따른변화 : :가지게 된다. 따라서 자유 에너::지는 대칭성을 가지지만 평형 상 태 자체가 특정 방향을 선택함으··로써 대칭성이 자발적으로 깨지 는 현상이 일어나며 이 상태는 텐T>Tc 에서와는 다른 위상이다. 자발 자기화를 계산해 보면 mo= 土 [bo/2c ( Tc) ]112( Tc-T ) 112 (8 .19) 울 얻는다. 이것은 자발 자기화가 0 에서부터 연속적으로 증가하 는 이차 상전이에 해당한다. 또한 자기화 임계지수로서 /3=§이 얻어전다. 이 간단한 이론으로 연속적인 상전이 현상을 정성적으로 이해 할 수 있게 되었고 특히 대칭성의 변화를 정확히 예언할 수 있었 지만 란다우 이론은 출발부터 국부적 요동을 완전히 무시하고 있 기 때문에 미시적으로는 국부적 요동이 점접 확장되어 일어나는 장거리 상관 현상을 만족스럽게 설명할 수 없어서 임계지수를 틀 리게 예언하고 있다. 란다우 이론은 모든 물질들에 대해서 /3= 1/2 울 산출해 낸다는 의미에서 보편성을 정성적으로 설명해 주지 만 단 한가지의 보편성 계보밖엔 예보하지 못하고 있다. 하지만다음 절에서 논하게 될 재 규 격화 군 방정식 이론에 의해 분석할 물리계의 모형을 얻는 데에는 역시 란다우의 대칭성 이론에 근거 룰 두고 유도한 라그랑지안을 사용하게 된다. 공간 군 (s p ace gro up ) 대칭성을 가지는 결정들에서 연속적 상 전이가 일어나려면 이것을 유발하는 질서맺음 변수들이 우선 란 다우와 리 프쉬츠 (Li fsh it z) 의 군론적 규정 들을 만족해 야 한다. 첫 째 질서맺음 변수에 관해 3 차인 불변항들이 군론적으로 존재하지 않고 4 차항의 계수가 양수라야 하고 둘째로는 질서맺음 변수들의 반대칭적인 이차 결합 (m i m 广 -m j m t)이 대칭성 변환하에서 불변 인 항을 포함해서는 안 된다는 것이다. St o kes 등 [1987] 은 컴퓨 터를 사용하여 230 개의 공간 군들의 4000 여 개의 가능한 표현들 울 132 개의 영상으로 분류하였는데 그들 중 52 개밖에는 L-L 조 건을 만족시키지 못한다는 것을 알아냈다. 그들은 또한 이 수십 가지 가능한 라그랑지 안들을 분석 하여 모든 가능한 대 칭 성들의 변화를 목록화해냈다 [K i m 등, 1986]. 란다우 이론에 의해 연속 상전이가 일어나야 하는 계에서 종종 불연속 상전이가 일어나는 것이 관측되는데 이들 계에서는 임계 점 근방에서 요동이 너무 심하게 일어나서 불연속 상전이로 전환 된다는 주장들이 나오게 되었다. 이들의 라그랑지안은 재규격화 변환의 흐름에서 안정적 부동점을 가지지 않는다는 것이 확인되 었고 안정적 부동점의 존재는 연속 상전이에 대한 추가적인 조건 이 되었다. M i chel 과 Toledano[Mi ch el 등, 1985] 는 이 조건을 c- 전개 에 의 해 얻은 흐름공식 (flow equ ati on ) 에 근거 해 서 군론적 조건으로 변환시켜 연속 상전이가 일어나는 대칭성 계보를 군론 적으로 예측해 낼 수 있었다. Hatc h 등 [198 이은 6 차원과 8 차원의 질서맺음 변수들의 라그랑지안에 대해서 부동점들을 계산해 내어 그들의 예언을 c_ 전개의 범주 내에서 확인하였다. 하지만 그들
의 추측을 좀더 일반적으로 확인하려면 유효 범위가 더 넓은 몬 데카를로 재규격화 군 방법을 사용해야 할 것이다. 8. 4 재규격화 군 방정식 8.4.1 개요 축척 법칙과 보편성을 좀더 만족스럽게 설명해 줄 뿐만 아니라 임계지수를 계산하는 구체적인 방법을 제시해 주는 이론은 바로 재규격화 군 방정식 (Renormaliz a ti on Group Eq u ati on ) 이론이다. 재규격화 군 방정식은 원래 겔만 (Gell - Mann) 등 [1954] 이 양자장 론에서 일어나는 현상을 설명하기 위하여 고안했으나 통계역학에 서 널리 쓰이는 방법은 윌슨 (W i lson) [1971] 이 카다노프 [1971] 의 구획스핀 방법을 일반화시키고 수식화한 것이다. 임계현상을 직관적으로 고찰해 보면 임계온도에 가까워짐에 따 라 상관 거리가 격자간 거리에 비해 더 커짐에 따라 근접해 있는 원자들 간의 미시적인 상호작용들은 그 중요성을 잃고 대국적으 로 장거리에서 살아 남는 힘들만이 의미를 가지게 되는 것이 골 자이다. 따라서 단파장적인 성분을 미리 평균화시켜 버리고 남은 장파장적인 성분만을 고려하면 거시적 성질을 좀더 확연하게 볼 수 있을 것이다. 이 과정을 반복해 나가면 결국 계 전체에 걸쳐 유효한 성분만이 남게 될 것이다. 이 방법이 수학적으로 유용하려면 반복성이 있어야 되는데 그 것은 평균화 방법의 선택 여부에 달려 있다고 볼 수 있다. 죽, 평균화를 하기 전후에 해밀토니안의 모양새가 같아지도록 해주어 야 한다.
재규격화 군 변환의 과정을 세 단계로 쪼개서 볼 수 있는데 1) 단파장적인 성분의 평균화. 이것은 재규격화 변환의 첫번째 과정으로서 격자간 거리보다 짧은 파장을 가지는 성분들을 미 리 적분해 버리는 과정이다. 구획 스핀 방법에서는 한 구획 안 에 있는 스핀들의 평균값을 구하는 것이다. :2) 철단 매개 변수의 선택. 이것은 길이의 축척을 재조정하는 것을 말하는데 재규격화 과정을 반복할 수 있게 하기 위해 취 하는 과정으로서 새로운 격자간의 거리를 길이의 단위로 잡는 과정이다. (1) 단계에서 구획의 크기가 격자간 거리의 l 배였다 면 새로운 격자에서 격자간 거리는 la 이겠지만 이것을 a’ 으로 잡고 ’을 다시 떼어 버리는 것이다. :3) 질서맺음 변수의 재규격화. (1) 단계에서 평균화한 결과로 새로운 질서맺음 변수들에 대해서 정의되는 해밀토니안의 모양 새는 그전과 같지만 각 항들의 결합계수들이 변하게 된다. 반 복성을 위해 해밀토니안의 이차항 중 운동항의 계수가 원래의 것과 같도록 해주는 것이다. 그렇게 하기 위해서는 질서맺음 변수들의 크기를 재규격화해 주어야 한다. 좀더 구체적으로 설명해 보기 위해 계의 해밀토니안이 %'=2Ka 아(¢) (8 . 20) a 와 갇이 주어진다고 하자. 여기서 Oa(
sI = 1—ld 흡s ,. . (8 . 21) 와 같이 쓸 수 있는데, 여기서 l 은 변환의 축척이고 i는 변환 전 의 격자 위치를 뜻하며 I 는 변환 후, 죽 구획 스핀의 격자 위치 롤 나타낸다. 길이 축척의 재조정은 a'=la (8. 22) 룰 새로운 격자에서 단위 길이로 취하는 것을 말한다. 위의 두 과정을 거치고 남는 항들을 추려서 새로운 해밀토니안 울 만들면서 이차 운동항의 결합계수가 똑같도록 질서맺음 변수 룰 재규격화시키면 Je'=L! K;Oa(¢') +Ng ( K) (8 . 23) a 를 얻을 수 있다. 여기서 Oa 는 그전과 모양이 똑같은 불변 다항 식이고 '은 새로운 격자에서의 양둘을 뜻한다. 식 (8.23) 의 두번 째 항은 평균화 과정의 부산물로서 N 은 계 전체의 자유도이고 g는 질서맺음 변수 ¢에 무관한 함수이다. 자유도가 N 개인 물리계의 단위 자유 에너지는 분배 함수 Z=Tre- x 의 자연 대수로서 I=_ 1 Jln Z (8 .24 ) 에 의해 주어진다. 축척 l 의 재규격화 군 변환으로 인해 자유도 의 수가 l/ld 만큼 줄어들기 때문에 자유도당 자유 에너지는 f (K) =g (K) + 1-d1 (K') (8. 25) 과 같이 변환된다.
원래의 해밀토니안에 재규격화 군 변환을 적용하면 그 물리계 의 대칭성을 지키는 한도 내에서(죽 해밀토니안에 나오는 모든 항 둘이 질서맺음 변수에 대한 대칭성 군 변환에 대해서 불변아라는 조 건) 모든 가능한 상호작용이 나오게 된다. 죽 재규격화 군 변환 을 거치면 4 차항까지는 원래의 해밀토니안과 모양새가 비슷하지 만 고차의 상호작용들을 더 많이 가지는 해밀토니안이 나온다. 대칭성에 대해서는 8.6 절에서 좀더 자세하게 논의될 것이다. 이 변환을 계속하면 상호작용들의 계수들만 바뀌고 해밀토니안의 구 조는 더 이상 바뀌지 않는다. 재규격화 군 방정식을 수리적으로 나타내는 방법은 재규격화 군 변환에 의해 변환된 해밀토니안의 결합계수들을 원래의 결합 계수들의 함수로서 나타내는 것이다. K;= 究 aU){K}, a=l, 2, … (8 . 26) 따라서 재규격화 군 변환은 결합계수 공간에서 하나의 흐름을 정 의한다고 볼 수 있다. 축척 !1, !2 의 재규격화 군 변환을 연속 되 풀이하면 축척 /1 • /2 의 재규격화 군 변환을 한 결과와 같아야 하 므로, 죽 究 ( l2) {:R U1) {K}} = 究 ( l1 갑) {K} (8 . 27) 이라야 하므로 재규격화 군 변환은 결합성을 가져야 한다는 것을 알수 있다. 8.4.2 일차원 아이싱 모델 재규격화 군 변환 과정을 아이싱 모델을 예를 들어 좀더 구체 적으로 살펴보자. 먼저, 兎=/3%라고 하고, 분배 함수를 풀어서
써보면 ZN (K, h) =젊 e _ J겹/(. I,, { s,} ]={S;걷 1)ex p[N김 (Ks;S;+1 + hs;) ] (8.28) 와 같다. 논의를 간단하게 하기 위해 일차원 아이싱 계를 고려해 보자. 계의 자유도가 짝수라고 하고 /=2 로 취하여 홀수 자리와 짝수 자리의 스핀들을 한 쌍씩 묶어서 구획 스핀을 정의하고 그것을 S1 라고 표기하되 이것을 짝수 자리에 두기로 하자. (그림 8.4 참 조) 구획 스핀 S1 를 구성하는 원래 계의 스핀들을 s{라 고 하고 홀 수 자리의 스핀들에 대한 합산울 먼저 수행하고 짝수자리의 스 핀은 그냥 놔두기로 하자. 식 (8.28) 의 우변에서 짝수자리와 홀 수 자리 에 관한 합산울 구분하고 풀어 쓰면 다음과 같이 된다. 훑l} e- J7 f = • • ·s . 집 ••( … S2/ 潟 .. 근) (8 . 29) 예로서 1=3 인 경우에 s7 이 나오는 항들은 Ks7 (s6 + s8) + hs7 이 있을 뿐이다. 분배 함수에 대한 이 항들의 기여는 S7I=: 土 I exp [Ks1(ss+ss) +hs1]=2 cash [K(ss+ss) +h] (8 . 30)
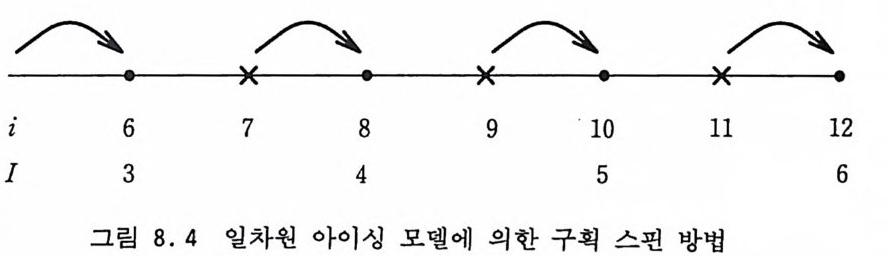 / • X/ • X/ • X/ •
/ • X/ • X/ • X/ •
이 다. S5S6 와 s8S9 으로 인 한 기 여 는 s5 와 s 9 에 대 한 합산에 서 고려 되기 때문에 식 (8 . 29) 에서 S7 과 인접한 짝수 자리 스핀들의 기 여에서 아직 남아 있는 부분은 의부 자장과의 결합 항들뿐이다. S6 와 s8 의 기여분 중 절반씩만 취하면 2e'5•+5 •> 1 2c osh[K (ss + sa) + h] =exp [2g + K' Ss Sa +½h' (s6 + s 8 기 (8 . 31) 울 얻게 된다. 이 식에서 결합계수들 (K, h) 에 관한 재규격화 변환식은 K'=T1 ln cosh (2K +c ho)s hc2ohs h (2K-h) (8 . 32) h'=h+] ln :::갑麟법 (8.33) g=--!8-- In [16 cosh (2K+ h) cosh (2K— h) cosh2h] (8 . 34)
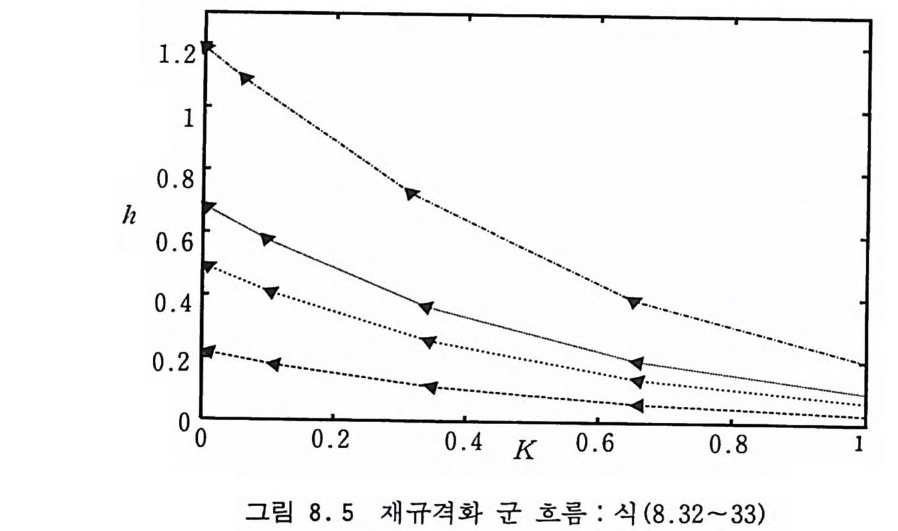 h 001...861 2 1 「, ``、 J r.` ` ` ` ·\ . ` 、· •.. .` ` 、 .`` `` * .`` ·` · ` ```` · ·-·-·- · - . .._ _ _
h 001...861 2 1 「, ``、 J r.` ` ` ` ·\ . ` 、· •.. .` ` 、 .`` `` * .`` ·` · ` ```` · ·-·-·- · - . .._ _ _
과 같다. (K, h) 의 흐름을 그림 8.5 에 나타냈다. 모든 홀수 자리의 스핀들에 대한 합산울 수행하면 재규격화된 볼츠만 밀도 함수를 exp [Ng (K, h) + K'~1s21s21-1 :2 + h'~1s21] =exp [Ng ( K, h) +K'~1S1S1+1+h'~1S1] (8. 35 ) 과 같이 얻는다. 재규격화 변환을 통해 결과적으로 ZN[K, h]=eNg ( K,hlZNn [K ', h'] (8 . 36) 울 얻은 셈이다. 이 식으로부터 스핀당 자유 에너지는 f[K , h]=g [ K, h]+f '[ K', h']//d ,.2 5) 과 같이 변환되는 것을 쉽게 확인할 수 있다. 8. 4. 3 재규격화 군 변환식의 계산 방법 이것을 좀더 일반화시켜서 eNg < K. > +xu c ,,.. (S,ll = (2St! ) II I p (s{, S1) eX
있다. (1) P(sf, S1)~O (2) P(sf, S1) 는 계의 대칭성을 보존해야 함 (3) ~
위에서 본 것처럼 재규격화 변환은 순전히 수학적인 조작에 불 과하기 때문에 어떤 흐름 상에 있는 해밀토니안들은 똑같은 물리 계를 기술하고 있다. 흐름 상의 각 점들은 재규격화 변환에 의해 같아질 수 있고 단지 다른 축척에서 보는 물리계들이라고 볼 수 있다. 하지만 일반적인 경우에는 변환식 (8 . 26) 은 유도하기도 힘 들거니와 비선형 방정식이기 때문에 그것을 풀어내기도 어렵다. 문제를 더 복잡하게 만든 것 같지만 재규격화 군 흐름이 정지되 는 부동점들의 존재와 그들이 임계점에 해당된다는 것으로부터 이 이론의 전가가 발휘된다. 재규격화 군 변환식을 유도하는 방법으로서 몇 가지가 시도되 었는데 위 에 서 논의 된 실공간에 서 의 직 접 적 인 방법 (Burkhardt 등, 1982) , Cumulant 근사 방법 (Ni em eij er 등, 1974 ; 1976) , 세 포 -송이 (Cell-Cluste r ) 근사 방법 (Ni em eij er 등, 1973) , c- 전개 방법 (Wi ls on, 1971 ; W ils on and Kog ut, 1974, Le Guil lou and Zin n -Ju s - tin, 1987) , 몬데 카를로 방법 (Ma, 1976 ; Swendsen, 1979) 등이 있 다. 8.5 재규격화 군 부동점과 임계지수 위에서 이미 논의한 바와 같이 재규격화 군 변환을 시도해 보 자마자 우리는 죽시 무한히 많은 결합계수들에 직면하게 되며 그 들 사이의 관계식을 완벽하게 이해한다는 것은 사실상 불가능할 것이다. 잘 알려진 방법들로서 c=4-d 에 관해 전개하는 방법과 1/n 에 (n : 질서맺음 변수들의 차원) 관해 전개해 나가는· 방법, 그 리고 몬테카를로 방법들이 있다. 이들 방법을 사용하여도 결합계 수들 모두를 추적해 나갈 수는 없어서 계산을 더 이상 지속하려
면 고차항들의 결합계수들은 어떤 이유에서 무시할 수 있다고 가 정해야 할 것이다. 이러한 가정이 타당한 지역이 있는데 그것은 부동점 근방이다. 물리계가 임계점으로부터 멀리 떨어져 있을 때는 재규격화 군 변환을 아무리 많이 되풀이해도 특별히 의미 있는 결과가 나오지 않는다. 재규격화 군 변환을 유용하게 하는 것은 바로 부동점 (fixe d po in t ) 과 이 점 으로 흐르는 임 계 흐름의 존재 이 다. 부동접 이란 재규격화 군 변환을 아무리 가해도 더 이상 결합계수들에 변화가 일어나지 않는 지점을 말한다. 죽 결합계수 공간에서 재 규격화 흐름이 정지되는 점이다. 일반적으로 축척이 [인 재규격화 군 변환을 가하면 상관 거리 가 t'=t /l 과 같이 변한다. 부동점에서는 결합계수들이 변하지 않기 때문에 t ' =t라야 한다. 위의 식과 일관성이 있으려면 상관
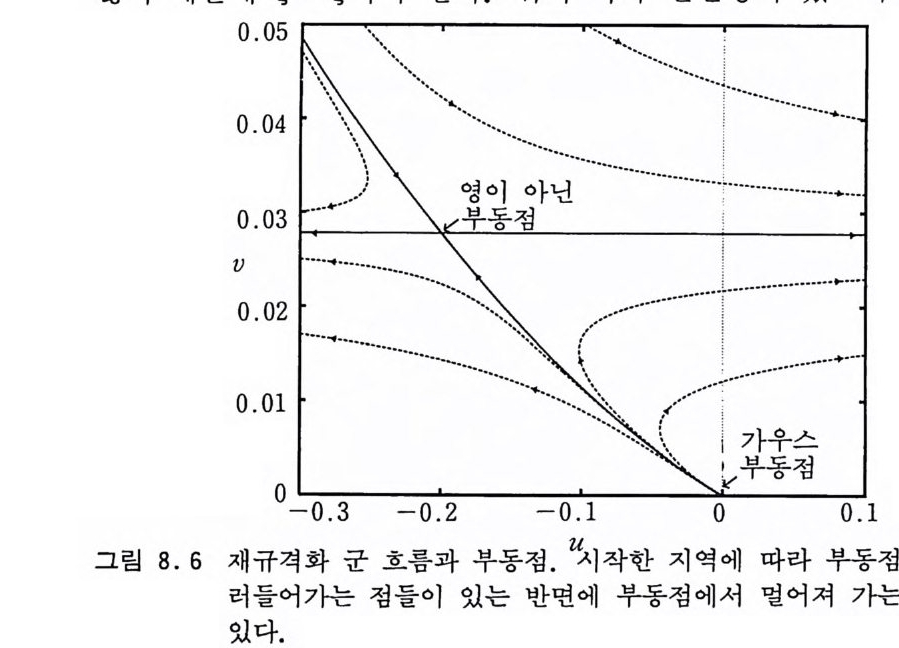 0000....0000 4352 .· - l \ \[ il``` ` i` .. 부영`f. i동이 f /0 점 \]尺 i ... . `[ ·-.. ... ... ·-i ... . . . . ...i. .. ··-..i가부. .· --- .i -. -. - . -.i- . - . -. -.-. ...► . -. .- -
0000....0000 4352 .· - l \ \[ il``` ` i` .. 부영`f. i동이 f /0 점 \]尺 i ... . `[ ·-.. ... ... ·-i ... . . . . ...i. .. ··-..i가부. .· --- .i -. -. - . -.i- . - . -. -.-. ...► . -. .- -
거리가 0 이거나 무한대가 되어야 하기 때문에 부동점은 바로 그 정의에 의하여 임계점이 된다. 재규격화 군 변환에 의해 연결되 는 점들이 사실상 똑같은 물리계를 나타낸다는 것은 이미 밝힌 바 있다. 특히 임계점에 연결되는 임계 흐름 상의 점에서 정의되 는 해밀토니안은 상관 거리가 무한대인 임계 해밀토니안을 기술 한다. 곧 이어서 설명하겠지만 임계 흐름은 결합계수 공간에서 t =O 인 곡면 상의 곡선이다• 재규격화 변환에 의해 상관 거리는 줄어들기만 하기 때문에 재규격화 흐름 곡선은 상관 거리가 무한 대인 임계곡면을 뚫고 다른 쪽으로 갈 수가 없으며 임계곡면 상 의 곡선들이 그 면의 밖으로 뛰쳐나갈 수도 없다. 임계지수들을 부동점의 성질에 의해 계산할 수 있고 축척 법칙 은 재규격화 변환의 형태로부터 자연스럽게 나오는 부산물이라는 것을 증명하기는 어렵지 않다. 또한 서로 다른 점들에서 출발한 해밀토니안들이 똑같은 부동점에 귀착하게 되면 그 부동점의 성 질에 의해 지배를 받는 똑같은 임계현상을 가전다는 결론을 얻을 수 있게 되어 보편성에 대한 정성적인 설명이 나오게 된다. 부동점 근방에서 재규격화 군 방정식을 선형화시키면 부동점에 서의 재규격화 군 변환 행렬의 고유값과 임계지수 사이의 관계식 울 얻을 수 있다. 축척 l 의 선형화된 재규격화 군 변환을 한번 적용시켜 보면 질서맺음 변수에 관해 2 차항의 결합계수인 환원 온도 t에 대한 변환식은 t(I)::::::究t (l) t (8 . 41) 가 되고 또 한번 변환을 시키면 식 (8.27) 에 의해 t (2) ::::::究 1(l) 究t (l) t ex: 兒t (/2) f (8.42) 가 된다. 따라서 우리는 재규격화 군 회귀 관계식
究t (l) 究t (l) =究t (/2) (8 . 43) 운 얻게 되는데 이 식을 만족시키려면 究t (l) 이 l 의 지수 함수라 야 할 것이다. 究t (l) = lAt (8 . 44) 온도의 함수인 상관 거리는 축척 l 의 재규격화 군 변환을 m 번 거치면 다음과 갇이 변환된다. g(t) ~l 구 (lAcm t) (8 . 45) 위의 식에서 m 을 [m= t-1 /At (8 . 46) 이 성립하도록 취해도t 무( t)방 ~하t- 므I IA로t E ( 우1) 리는 (8 . 47) 을 얻게 되고 v=l/At (8 . 48) 이라는 관계식을 쉽게 얻어낼 수 · 있다. 축척 법칙을 얻기 위해서 온도 이의에도 의부 자장 H 를 함께 고려해 볼 필요가 있다. 일반적으로 재규격화 군 방정식에 나오 는 무한히 많은 결합계수들을 동시에 고려해야 하겠지만 온도와 의부 자장 의의 다른 결합계수들에 관해서는 부동점에 이르렀다 고 가정해 보자. 부동점, (T*, H*) 근방에서 8T=T-T* 와 8H=H-H* 에 대해 선형화된 재규격화 군 회귀 관계식은 8T'= 8T( 情)* + 8H( 儒)* (8. 49a)
8H'=8T(~앞 )*+8H(~앎 )* (8.49b) 와 같이 써줄 수 있는데 여기서 식 (8.49) 를 행렬식으로 간주해 보자. 재규격화 방정식의 결합성 (8. 27 ) 때문에 행 렬 얹=a 究J 8K머 고유값들은 l 의 지수 함수라야 하는데 그들을 Al=lA\ A2=lA2 (8 . 50) 이라 하자. T 와 H 의 일차 결합으로서 이 고유값들을 가지는 고유 벡 터 들을 축척 장 (scalin g field ) 이 라고 부른다. 이 제 부동점 의 국부적 성질은 지수들 AI, A2 와 고유 벡터의 방향에 함축되게 되었다. 논의를 간단하게 하기 위하여 해밀토니안이 변환 H-- H 에 대해서 대칭성을 가지는 경우를 고려해 보자. 안은 oT 와 oH 에 관해 이미 대각 행렬이 되어 있울 것이므로 부동점 근방의 선형 화된 지역에서 8t (m )= lAIm8t, 8H(m)= lA2m8H (8 . 51) 가 될 것이다. 식 (8.25) 에서 함수 g (K) 는 단거리 요동을 평균화한 결과로 나온 것이기 때문에 임계점에서 정칙 함수일 것이다. 임계점 근 방의 선형화된 지역에서 자유 에너지의 특이한 부분에 대한 재규 격화 군 방정식은 fs ( t, h) ~ 1-dmf s ( l A' 만, lA2mH) (8. 52) 이 된다. 이것은 식 (8.15) 와 같은 동차식의 형태이므로 축척 법 칙은 재규격화 군 변환의 형태 (K두 (lA')mK,. ) 로부터 자연스럽게 나오는 귀결이다.
이 식은 m 의 임의값에 대해 성립해야 하므로 변환식아 선형화 지역을 벗어나지 않은 한도에서 lm = I f 1-l/A1 (8.53) 울 만족하도록 취하면 fs( t, h) ~I t ld!A 'fs( ITT ' TtF) (8.54) 이 된다. 이 식을 원래의 축척 공식 (8.11) 과 비교해 보면 임계 지수들과 재규격화 군 방정식의 고유값들 사이의 관계식 2 —a = d/A1 = d11 (8 . 55a) 4=A2/AI (8.55b) 을 얻게 되어 두번째 지수 A2 역시 임계지수와 관련이 있음이 밝 혀진다. 또한 축척 함수 Y 는 Y(y) =f(土1, y) (8 . 56) 로서 얻어진다. 8. 6 안정적 부동점과 상전이의 연속성 란다우 이론에 의해 연속적 상전이를 가져야 하는 물리계가 종 종 불연속적 상전이룰 보이는데, 이것은 임계점 근방에서 요동이 너무 심해진 탓으로 추측되고 있다. 부동점 근방에서 재규격화 군 흐름은 부동점에서 빨려들거나 밀려나게 되는데 이러한 국부 적 성질은 그 부동점이 지배하는 상전이의 연속성과 관련이 있다 는 것이 예측되고 있다.
그 계의 해밀토니안의 결합계수들을 지배하는 부동점의 국부적 안정성 여부에 따라서 불연속적 상전이를 하게 될 수도 있다는 것이다. 안정 행렬 맑의 고유값의 실수 부분이 양수이면 그에 대응하는 축척 장은 유관 (relevant) 하다고 하고 음수이 면 무관 (irr elevant) 하 다고 한다. 유관한 축척장은 재규격화 흐름을 따라갈 때 그 값이 증가하여 흐름이 부동점으로부터 멀어지게 된다. 무관한 축척장 은 그 반대의 효과를 가진다. 온도와 질서맺음 변수의 짝인 의부 장은 언제나 유관한 축척장들이고 임계곡면은 이들이 0 인 곡면이 다. 하지만 다른 결합계수들은 반드시 유관하지는 않은데 그들이 모두 무관할 경 우 그 부동점 을 안정 적 부동점 (sta b le fixe d po in t ) 이라고 한다. 안정적 부동점 근방에서는 임계곡면 상의 모든 흐 름들이 그 부동점에 빨려든다. 임계곡면 상에 이 부동점 주변의 특정된 지역 내부에서만 시작하면 이 접에 빨려들게 되는 경계면 이 존재 하는데 이 지 역 을 흡인 골짜기 (att ra cti on basin ) 라고 부른 다. 란다우 이론에 의해 연속적 상전이를 가지게 되어 있는 해밀 토니안의 결합계수들이 이 안정적 부동점의 홉인 골짜기에 있을 때에 한해서 비로소 2 차 상전이가 보장될 수 있으리라는 추측이 나왔다. 주어진 해밀토니안에 대해서 부동점은 여러 개 존재할 수 있지 만 그들 중 안정적 부동점이 반드시 존재하지는 않는다. 만일에 안정적 부동점이 존재한다면 그것은 유일한 점이라는 것을 M i ehe 耳 1984] 이 c- 전개의 범주 내에서 증명해 보였다. 그는 또 한 그의의 모든 다른 부동점들은 홉인 골짜기의 경계면 상에 놓 이게 됨을 증명해 보였다. (그립 8.7 참조) 이것은 230 개의 공간 군의 4 차원, 6 차원, 8 차원의 질서맺음 변수를 가지는 해밀토니안 들에 대해서 각각 Toledano 등 [1985] 그리고 Hatc h 등 [1986 〕의
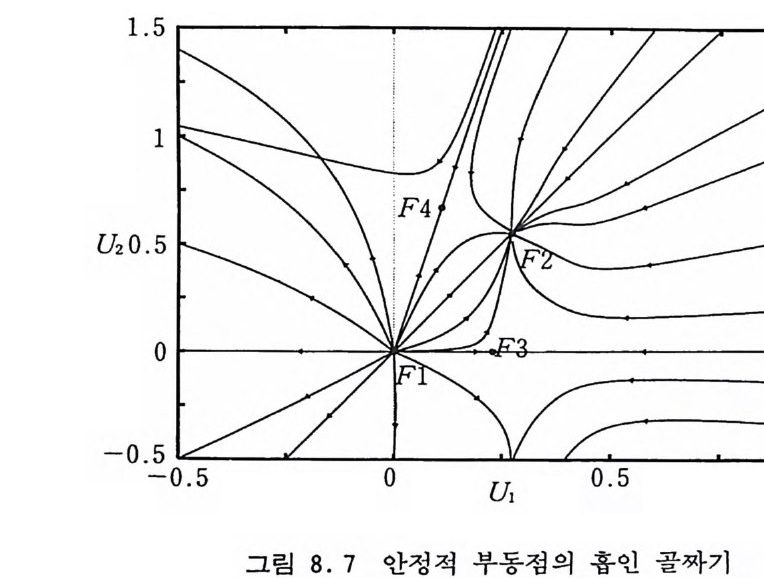 1.5
1.5
구체적인 계산에 의해 확인되었다. 또한 이들은 고체-고체 상전 이에서 있을 수 있는 모든 보편성 계보들을 분류하였다. 8.7 대칭성과 보편성 계보 무한 차원인 결합계수 공간에서 부동점들이 어디에 촌재하고 어느 지역에 있는 점들이 어느 부동점으로 흘러들어가는지를 만 족스럽게 알기는 힘들다. 우리가 확실히 알 수 있는 것은 부동점 에 접근하면 단거리 상호작용에 해당하는 대부분의 결합계수들이 0 이 되거나 그들 사이에 특별한 관계식이 성립하여 사실상 한 개 의 상호작용 항만이 남게 된다는 것이다. 이것은 해밀토니안의 대칭성이 다른 점에서보다 부동점에서는 좀더 커진다는 것을 의 미한다. 또한 부동점의 큰 대칭성은 많은 서로 다른 종속군 대칭 성들을 포함할 수 있기 때문에 이둘 사이에 체계적인 주종 관계
를찾을 수 있을 것이다. 구체적으로 어떤 해밀토니안들이 같은 보편성 계보에 드는지는 공간의 차원, 질서맺음 변수의 차원, 해밀토니안의 대칭성 등에 따라 체계적인 군론적인 고찰에서 해답을 얻을 수 있다• 일반적 으로 어느 대칭성의 군 변환 하에서는 불변인 4 차항들이 그것의 군-종속군(gr ou p -sub gr ou p) 고리 상의 너무 큰 종주군 변환 하에 서는 불변이 아닌 것이 된다. 주어진 해밀토니안의 보편성 계보 는 그것의 4 차 불변항까지의 구조를 보존하는 그 대칭성의 가장 큰 종주군 (sup e rgr ou p ) 을 대 칭 성 군으로 가지는 해 밀토니 안의 부 동점이 지배하는 보편성 계보라는 것을 M i chel 과 Toledano 가 [198 히 증명하고 보여주었다. 8.8 몬테카롤로 방법 8. 8.1 Ma 의 방법 Ma[1976] 는 몬테카를로 방법을 재규격화 군 변환에 이용하면 비교적 정확한 계산울 할 수 있다는 제안을 했다. 앞에서 보았듯 이 재규격화 군 방정식이 너무 복잡하여 이제까지 개발된 다른 방법들은 비현실적이고 특수한 상황을 제의하고는 재규격화 군 변환의 흐름을 정확히 추적하기에 별로 실용적이지 못하였다. 가 장 널리 알려진 c- 전개 방법은 공간 차원이 4 인 (d=4) 비현실적 인 경우에 가장 유효하며 3 차원 공간에서는 c 이 1 이기 때문에 그 유효성이 의심스러운 것이다. 한데 본질적으로 수치 실험을 통해 가관측량들을 〈측정〉해 나가는 몬테카를로 방법은 문제의 복잡성에 거의 무관하게 적용할 수 있어서 재규격화 군 방정식에
적용할 수 있다면 강력한 계산 도구가 될 것이다. 정확도 면에서 전통적으로 다른 방법에 비해서 떨어지는 몬테카를로 방법이 재 규격화 군 방정식에서는 더 정확할 수 있다는 것은 꽤 홍미로운 것이다. Ma 의 획기적인 발상은 주어진 크기의 물리계에 대해 몬테카 룰로 시뮬레이션을 수행하면서 가관측량에 대한 측정을 할 때마 다 그 특정 배위에 대해 구획 스핀 방법을 적용해 재규격화 군 변 환을 반복해 나가면 결합계수들의 재규격화 군 흐름을 직접적으 로 〈관측〉해 나갈 수 있다는 것이다. 따라서 고차항의 계수들이 재규격화 군 방정식에 끼어드는 것을 걱정해야 할 필요가 없어전 다. 재규격화 군 변환이 된 물리계들에 대하여 〈 관측 〉 된 결합계 수들 속에 이미 그들의 영향이 반영되어 있을 것이기 때문이다. 따라서 유한 개수의 결합계수들의 흐름을 조사하기 위해 무한히 많은 계수들을 고려해야 할 필요가 없이 관심의 대상이 되는 결 합계수들만 고려해도 된다. 죽 몬데카를로 방법을 수행해 나가는 노력은 문제의 난이도에 거의 상관없이 일정하다. 하지만 시뮬레 이션을 하는 물리계의 크기가 한정되어 있기 때문에 이러한 계의 해밀토니안은 본질적으로 유한 개수의 결합계수들만을 포함할 것 이지만 다른 방법으로 추적할 수 있는 것보다는 훨씬 더 많다. (수천 내지 수백만) 다시 아이성 모델을 예로 들어 Ma 의 방법을 구체적으로 살펴 보자. 지점 a 에서의 스핀을 6a 라고 하고 시간 구간 d t에 -야로 뒤집어질 확률을 다음과 같이 정의해 보자. Wa (aa) dt =I' exp ( —aa B 사 dt (8 . 57) 여기서 Ba 는 야가 느끼는 자장으로서 의부 자장과 이웃 스핀들 이 만들어내는 자장의 합이라고 볼 수 있다. 이것은 수식적으로
Ba=a(J~a (8 . 58) 과 같이 쓸 수 있다. 예를 들어 다음과 같이 정의되는 해밀토니 안을 고려해 보자. Jt=J
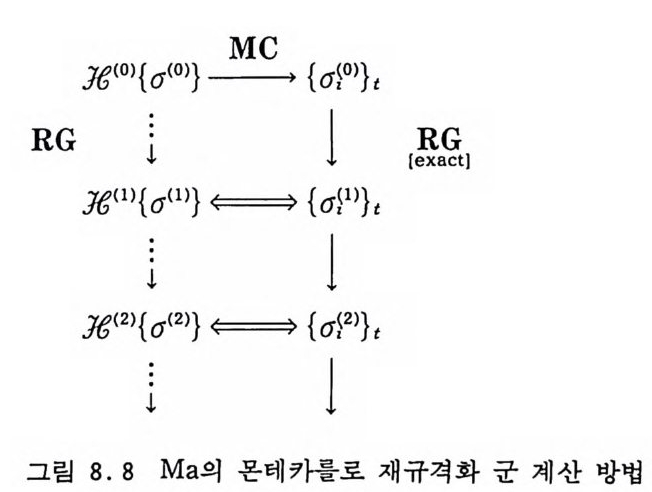 Je< O){(J (O )} 一MC {6}0l}t
Je< O){(J (O )} 一MC {6}0l}t
이것을 좀더 자세히 기술해 보면 E 1) 식 (8.57) 에 의해 배위들을 차례로 생성해 나간다. 2) 관측을 하는 배위마다 구획 스핀 방법으로 일련의 재규격화 변 환울한다. 6i0 ) - + 어 I) -+ 어 2) … 3) 각기 다론 축척에서 결합계수들을 측정한다. 비열 같은 전체적 인 양을 측정하는 대신 몇몇 이웃 스핀들이 어떻게 변화하는지를 관찰한다. 작은 탐침으로는 원래의 각자의 결합계수들을 관찰하 고 큰 탐침으로는 구획 스핀들의 실효 결합계수들 µ'=(I'', J', K', L', …)을 관찰한다. 결합계수들을 측정하기 위해서는 스핀이 주어진 환경 속에서 어 떻게 변화하는지를 관찰해 봐야 한다. 예를 들어 상호작용의 영 역이 최최근접 이웃이라면 어느 스핀의 이웃은 여덟 개가 있는 셈이다. 작은 검침으로는 3X3 스핀들을 측정하는데 스핀이 전복 될 때까지 +1 상태와 -1 상태에서 머무르는 시간들 r+ 와 r- 를 측정하는 것이다. 비율 r+/r-=ex p (2Ba) 로부터 J, K, L 에 관 한 방정식을 얻는다. 예를 들어, 그립 8.9a 에서처럼 여덟 개의 스핀 모두가 +1 인 :+.…++ ·· ··0 수@·::.:+. `. .~ .. · ..· +++:.:.,.. + .,_.:+.J. . ··. .. ...... ..· ... e(..:::一' F . b ... .) · ·· . 1 1+· :. :: :: ::· +.:::.F+· ..· · · ·+··.+~··$·.·: -). . ..-.+:+..….. . .. . 그림 8. 9 세 가지 스핀 배위에서의 국부적 해밀토니안
환경에서는 Ba=4 (J +K+L) 을 얻는다. 또한 그림 8 . 9b 에서는 Ba= ― 4] 를 얻고 그림 8.9c 에서는 Ba=4(K-L) 을 얻는다. 따 라서 이렇게 다른 환경 속에서 r + /r- 를 측정함으로써 ], K, L 에 관한 독립적인 방정식들을 얻을 수 있다. r 는 기하 평균 ( r+ T_) II2 에 의 해 주어 진다. 큰 검침으로는 구획 스핀둘의 결합계수들을 측정하는데 구획 스핀 하나가 2X 2 스핀들로 구성된다는 것을 제의하고는 작은 검 침으로 측정할 때와 같다. 구획 스핀은 다수결의 원칙에 의해 +l 또는 -l 로 정해주는데 네 개의 스핀의 합이 영이면 무작위 로 +1 또는 -l 의 값울 준다. 이렇게 하여 실효 결합계수들 µ' = (I'', ]', K', L', …)을 측정하는 것이다. Ma 의 방법에서는 국부적인 성질들을 보기 때문에 격자의 크 기라든가 경계 조건들은 문제가 되지 않는다. 단지 검침둘이 경 계면에서 떨어져 있으면 되고 재규격화 군 변환을 충분히 여러 번 할 수 있을 정도로만 원래의 격자가 크면 된다. 임계지수 )I는 행렬 8K;/8K려 (K1=], K2=K, &=L) 최대 고유값 AT=2llu 에 의해 얻어진다. 또한 임계지수 1)는 행렬 aM/ahj 의 (h1=h : 의부 자장, h2=3- 스핀 상호작용) 최대 고유값 AH= 22 - T/ /2 에 의해 얻어전다. 이들 행렬들은 큰 검침으로 측정하면서 구획스핀들의 평균값들로부터 계산할 수 있다. 예를 들어 곱(J '+K'+L') =강f 1n( 다 /r:..) (8.61) 와 같이 얻을 수 있다. 여기서 고려한 네 개의 결합계수들보다 더 많은 결합계수들의 흐름을 측정하려면 검침을 3X3 보다 더 크게 잡아야 한다. 따라 서 위에서 측정한 재규격화된 결합계수들은 이러한 절단으로 인
한 부적확성이 내재되어 있다. 또한 임계지수들을 구하기 위해서 는 부동점을 찾아서 그 근방에서 시뮬레이션을 해야 한다. 이러 한 것들은 Ma 의 방법의 결점으로 지적된다. 8. 8. 2 Swendsen 의 방법 Ma 의 방법이 결합계수들을 국부적으로 측정하는 데에 역점을 두었는 데에 비해 Swendsen[l97 이은 재규격화 군 방정식에 의해 연결되는 각기 다른 크기의 물리계들에서의 상관 함수들에 역점 을 두었다. Swendsen 의 방법에서는 부동점을 반드시 알아야 할 필요가 없고 부동점 해밀토니안의 상호작용들의 유효 영역이 짧 다면 절단 효과가 작으며 많은 결합계수들은 고려하지 않고 원래 의 해밀토니안에 있는 것들만 고려해도 되는 장점이 있어서 실제 계산에서는 Swendsen 의 방법을 주로 사용한다. Swendsen 의 몬테카를로 재규격화 군 방법에서는 원래의 해밀 토니안에 의거 몬데카롤로 시뮬레이션을 하면서 일정한 MC 시 간 간격으로 각각의 배위에서 어떤 상관함수들을 측정해 놓고 그 배위에서 구획 스핀 방법을 적용하여 재규격화 군 변환을 수행한 다. 그리고 이 새로운 격자에서 정의되는 상관 함수를 또 측정한 다. 그런 다음 새로운 격자에 대해서 다시 재규격화 변환을 반복 하고 상관 함수를 측정하는 식으로 계속적으로 충분히 많이 반복 한다. 그러고 나서 그 다음 배위로 넘어가서 또 이러한 과정을 반복하는 것이다. 몬데카롤로 과정을 충분히 오래 계속해 보면 우리는 여러 가지로 다른 축척에서의 많은 고차항들의 효과들이 절단되지 않은 꽤 정확한 상관 함수들을 얻게 될 것이다. 이렇게 해서 얻은 여러 다른 축척에서의 상관 함수들을 안정 행렬과 연관시켜 그 행렬의 고유값들로부터 유용한 물리량들, 죽
임계지수들을 추출해내는 것이 Swendsen 의 방법의 핵심 요소이 다. 이차원 아이싱 모델을 다시 예를 들어 Swendsen 의 방법의 기 본 틀을 설명해 보자. 식 (8.20) 에 의해 주어지는 해밀토니안에 대해 재규격화 변환을 가해 보면 원래 해밀토니안에 있지 않은 상호작용 항들을 생성해낼 것이다. 부동점의 아주 가까운 근방에서 재규격화 군 방정식이 근사적 으로 선형화될 것이라고 가정하면 식 (8 . 49) 를 일반화시킨 다음 과 같은 점근식을 얻을 수 있을 것이다. K~n+I) ― K느 2 TaW(Kjn )-K;) (8 .62) 여 기 서 안정 행 렬 (sta b il ity matr i x ) Tap = [cJK ~n+I) /cJK ?>]* (8.63) 는 부동점에서 계산된 값이다. 앞서 논의된 대로 임계지수들은 다음의 고유값 방정식으로부터 결정한다. ~p
~= I K 갤* |-u (8 . 66) 또한 홀수차항의 결합계수들에 대한 T싫 의 가장 큰 고유값을 A=lYo 라 하면 y o=(d+2- 刀 ) / 2 이다. 위의 식들이 유용하려면 도함수들 aK?+1l/aKt )이 완만하게 변화하는 지역, 즉 반드시 부동점 근처가 아니라도, 선형인 지역 에서만 계산하면 된다. 또한 임계지수들을 계산하기 위하여 안정 행렬의 고유값들만 알면 되므로 부동점을 꼭 알아야 할 필요는 없다. 하지만 임계온도를 근사적으로 찾은 다음, 그 온도에서 임 계흐름을 따라갈 필요가 있다. 안정 행렬의 원소들인 이 도함수들은 다음의 연환 법칙들로부 터 수치적으로 얻을 수 있다. 8< 80K 1}nn+)l )> = 2 a8K~Kni+n )I ) a0< 0K 1inn ++ 1l)) > (8 . 67) 위의 식에서 상호작용 항들의 결합계수들에 대한 도함수들은 몬 테카를로 방법에 의해 얻은 상관함수들과 다음과 같이 관련이 된 다. 떻; 1) 〉 =
尸 1) 메트로폴리스 또는 다른 방법으로 평형 상태의 배위들을 생산 2) 각 배위에 대해서 상관 함수들을 계산 3) 각 배위에 대해서 구획 스핀 방법을 적용하여 재규격화 변환을 시행 4) 재규격화된 계와 한 단계 전의 배위들에서의 상호작용 항들 사 이의 상관 함수들을 계산(식 (8.68) 의 우변의 첫번째 항) 5) 재규격화된 계의 현재 배위에 대해서 상관 함수들을 계산 6) 과정 3)-5) 를 계속 반복 7) 1) 로 가서 전화를 재개 이렇게 하여 식 (8.68-69) 의 우변둘이 얻어지면 상용적인 수치 계산법을 사용하여 식 (8. 67) 로부터 T싫 둘을 구할 수 있을 것이 다. 고차항들은 유효 영역이 짧아 부동점 근방에서는 그 효과들을 거의 무시할 수 있다는 것이 통상적으로 기대되는 바이다. 이러 한 근사가 적절한 것인지 적절하다면 어느 정도의 오차를 유발하 는지 사전에 확실히 알 수는 없다. 실험적으로 컴퓨터가 허용하 는 한 최대한으로 많은 상관 함수들을 계산해 보고 안정 행렬 T싫 의 a, (3가 높은 원소들을 계측해 봄으로써 근사적 절단을 추 인해 볼 수 있을 뿐이다. Swendsen 의 조잡한 계산 결과에 의하면 N=7 정도에서 이미 고차항들의 존재가 저차항들만 가지고 얻은 결과들에 거의 영향 을 끼 치 지 못하는 점 근성 이 나타난다. Swendsen 이 108 X 108 격 자에 대해서 축척 l=3 을 가지고 짝수차항을 세 개, 홀수차항을 한 개 포함하여 5 회의 주사마다 측정하여 6000 번 측정하여 얻은 결과를 표 8 . 2 에 나타낸다.
표 8. 2 Swendsen 의 몬테카 롤 로 재규격화 방법에 의한 계산 결과 RG 상호작용 Af L’ a’ Af 8 T/ 횟1수 개231수 222...888 550 258 111...000 644 847 ———000...00 1 992 478 7.7 0 5 13. 15 0.283 2 1 2.9 9 9 1.0 0 0 -0.0 0 1 7.8 2 8 14.75 0.2 5 4 2 3.0 2 5 0.9 9 2 0.015 3 3.0 2 1 0.994 0.0 1 3 3 1 2.9 2 6 1.023 -0.0 4 6 7.8 3 1 14.79 0.253 2 3.0 2 3 0.9 9 3 0.0 1 4 3 3.007 0.998 0.004 정확한값 3 1 。 7.845 15 0.25
여기서 사용된 짝수차의 상호작용들을 그림 8.10 에 나타낸다.
 ‘
‘
8.8.3 임계점 찾기 Swendsen 의 방법을 사용하면 임계지수들을 계산하기 위해서 부동점의 위치를 정확히 알아야 할 필요는 없지만 다른 방법에 의해서 얻은 결과들과 비교하기 위해서 한번 찾아보기로 하자.
윌슨의 쌍격자 시뮬레이션 방법은 [W il son, 198 이 원칙적으로는 유 한크기 효과를 제거하고 부동점을 찾아 줄 수 있으나 시뮬레이션 에서 발생하는 통계적 오차로 인해 그 효용도가 제한되어 실제로 는 부동점에서의 저차항들의 임계 결합계수들을 찾아내는 데에만 유용하다. 하지만 초대형 컴퓨터의 개발로 인해 격자의 크기를 늘리고 표본추출 횟수도 늘려 통계적 오차를 줄이면 그만큼 이 방법의 효용성도 증대될 것이다. 이 방법에서는 크기가 서로 다른 두 개의 격자들에 대해서 독 립적으로 몬테카롤로 시뮬레이션을 하는데 초기 결합계수들에 똑 같은 수치값을 준다. 큰 격자가 작은 격자보다 lm 배만큼 크다면 큰 격자에 대해서 재규격화 군 변환을 n 번 한 상태는 작은 격자 에 대해서 (n-m) 번 한 상태와 같아야 할 것이다. 특히 그들의 유한크기 효과도 같아야 할 것이다. 두 격자들이 임계흐름 상에 있다면
에 의해 계산해 낼 수 있다. 여기서 상관 함수의 결합계수에 대 한 도함수는 위의 식 (8.68) 에 의해 표현할 수 있다. 작은 격자 에 대해서도 이와 똑같은 식을 쓸 수 있는데 그들의 차이룰 써 보면 일련의 선형 방정식들 〈 o~n) 〉 L- 〈 o~n-m) 〉 s= 구( 富。))〉 L _ 8< ? :;)>s ) 8Kj0 ) (8.72) 을 얻는데 이 식들을 풀어 KJ O) 를 계산함으로써 부동점에서의 결 합계수들에 대 한 근사값을 K: = K~0' + 0K~0> (8 . 73) 에 의해 얻을 수 있다. 이러한 과정을 반복하면 임계 결합계수들을 찾아낼 수 있으나 고차항들의 상관함수들을 계산함에 있어서 통계적 오차가 8K 보 다 훨씬 더 커서 실제로는 저차항들의 임계 결합계수들을 찾아내 는 데에만 유용하다. Pawley 등 [198 산은 윌슨의 쌍격자 방법과 Swendsen 의 방법을 결합하여 삼차원 아이싱 모델에 대해서 방대한 시뮬레이션을 하 여 상당히 정확한 결과들을 얻었다. 또한 Bl6te 등 [1989] 은 특별 히 제 작된 Delft Isin g Sy st e m Processor (DISP) 를 사용하여 좀 더 많은 상호작용들을 포함하여 계산하였으며, 현재까지 삼차원 아이성 모델에서 가장 높은 차수까지 계산된 예는 AMT DAP 울 사용한 Bail lie 등〔 1990] 의 1283 이다. 그들은 메트로폴리스의 방 법과 Wol ff의 송이 알고리즘을 사용하여 임계감속의 문제를 극 복하여 통계적 오차를 크게 줄인 정교로운 시뮬레이션을 하여 N =40 정도까지 가야 점근성이 나타나는 것을 확인했다.
표 8. 3 삼차원 아이싱 모델에 대한 몬테카를로 계산 결과 Pawley 등 Blote 등 Bail lie 등 크기 643 643 1283 짝수차항 7 36 53 홀수차항 6 21 46 Kc 0.2 2 1654(6) 0.221652(6) 0 . 221651 (9) u 0.629(4) 0.6 2 9 (3) 0. 63 6(3) n 0. 03 1(5) 0 . 027 (5) 0.044(2)
8.8.4 문제점들 위에서 사용된 식들은 선형화된 지역에서 성립하는 근사식들이 기 때문에 모든 계산은 부동점 근방에서 적어도 임계흐름상에서 행해져야 한다. 하지만 임계흐름상에 있는 해밀토니안들에 대해 서는 상관 거리가 무한대이고 감수율 또한 무한대로 발산할 것이 기 때문에 완화 시간이 무한히 길어져 몬테카롤로 시뮬레이션의 효율이 영으로 떨어질 것이다. 실제로 시뮬레이션할 수 있는 계 의 크기는 유한이기 때문에 엄밀한 의미에서의 임계점이 존재하 지 않을 것이고 완화 시간 또한 길지만 유한일 것이다. 하지만 통계적 오차를 줄이기 위해 계의 크기를 늘리면 의사 임계점에서 의 완화 시간이 길어져 시뮬레이션을 오래오래 해야 하기 때문에 원하는 정도의 오차를 얻기 위해 드는 계산량은 Ld 보다 훨씬 빨 리 증가할 것이다. 또 하나의 문제점은 현존의 컴퓨터의 연산 속도와 기억 용량으 로 유한 시간 내에(수 개월 내지 수 년) 시뮬레이션 해볼 수 있는 물리계의 크기가 충분히 크지 못하다는 것이다. 예를 들어 길 이 축척이 128 격자 단위라 해도 재규격화 군 변환을 두세 번쯤 하고 나면 격자의 크기가 너무 작아져 버려 결합계수들의 개수가
현저하게 줄어들고 유한크기 효과가 심각한 영향을 끼치게 될 것 이다. 재규격화 군 변환의 시발점의 격자가 충분히 커서 재규격 화 군 변환을 십수 번 정도는 할 수 있어야 부동점에 충분히 접 근할 수 있을 것이고 재규격화 군 흐름의 종점이 되는 격자들의 크기 또한 어느 정도 이상은 되어야 할 것이다. 16X l 6 격자에서 몬데카를로 주사를 수억 번 한다고 해서 믿을 수 있는 데이터룰 얻는다고 확신할 수는 없을 것이다. 그러한 크기의 계에서 임계 감속의 문제를 해결하는 데에 효율적인 알고리즘을 개발한다 해 도 초강력하고 기억 용량이 거대한 초대형 컴퓨터가 필요하다는 것은 의심할 나위가 없다. 그러한 컴퓨터는 현존하는 기술로는 병렬형 컴퓨터 구조밖에 없다. 참고문헌 [1 ]C .F. Bail lie, J Mod. Phys . C (l990) 111 [ 2 ] C.F. Bail lie, K.N . Baris h , R. Gup ta and G. S. Pawley , Nucl. Phys . B (Proc. Sup pl.) 17 (19 90) 323 [ 이 H.W.J. Blote , A. Comp a g n er, J.H . Croockewi t, Y.T.J. C . Fonk, J.R. Herin g a , A. Hoog la nd, T.S. Smi t and A.L. van W illige n, Phys i c a 161A (1989) 1 [ 4 ] T.W . Burkhardt and J.M .]. v an Leeuwen, Real Sp ac e Renormal- iza ti on , (Sp r in g e r, 1982) [ 5 ] C. Domb and D.L. Hunte r , Proc. Phys . Soc. 86 (1965) 1147 [ 6 J M.E. Fis h er, Rep. Prog. Phys . 30 (1967) 615 [ 7 ] M.E. Fis h er, Rev. Mod. Phys . 46 (1974) 597 [ 8 J M . Gell-Mann and F.E. Low, Phys . Rev. 95 (1954) 1300 [ 이 N. Goldenfe ld , Lectu r es on Phase Transit ion s and the Renor-
maliza ti on Group, (Addis o n-Wesley , 1992) [10] F.J.W . Hahne, Cr itica l Phenomena, (Sp r in g e r, 1983) [11] D.M . Hatc h , H. T. Sto kes, J.S . Ki m , and J.W . Felix , Phys . Rev. B33 (1986) 6196 U 끽 D.M . Hatc h , H.T. Sto k es, J.S . Ki m , Phys . Rev. B35 (19 87) 388 [13] J.T . Ho and J.D . Litst e r , Phys . Rev. Lett . 22 (1969) 603 U 산 L.P. Kadanoff , Phys ic s 2 (19 66) 263 [15] L.P. Kadanoff , W. Gotz e , D. Hamblen, R. Hecht, E. Lewi s, V. V. Palcia u kas, M. Ray l, J. Swi ft, D. Aspn es, and J. Kane, Rev. Mod. Phys . 39 (19 67) 395 [16] L.P . Kadanoff , Proc of 1970 Varenna Summer School on Cr itica l Phenomena, ed. M .S. Green (Academi c, New York, 1971) [17] J.S . Ki m , H.T. St o kes, D.M. Hatc h , Phys . Rev. B33 (19 86) 1774 ; ibi d , 6210 [파 L.D . Landau and E.M . Lif sh it z, Sta t i stica l Phys i c s , (Perga mon, 1980) [1 이 J.C . Le Guil lou and J. Zin n -Ju s ti n, ]. Phys . Pari s 48 (1987) 19 [20 ] K.C. Lee, Phys . Rev. Lett . 69 (19 92) 9 [21] S.K . Ma, Phys . Rev. Lett . 37 (1976) 461 [22] L. Mi ch el, Phys . Rev. B29 (1984) 2777 [23] L. Mi ch el and J.C . Toledano, Phys . Rev. Lett . 54 (1985) 1832 [24] T.H. Ni em eij er and J.M .J. van Leeuwen, Phys . Rev. Lett . 31(1973) 1411 [25] T.H. Ni em eij er and J.M .J. van Leeuwen, Phys i c a 71 (19 74) 17 [26] T.H. Ni em eij er and J.M . J. van Leeuwen, Phase Transit ion s and Cr itica l Phenomena, vol. 6, ed. by C. Domb and M.S. Green (Academi c Press, 1976) , 425-505 [27] G. Pawley, R.H . Swendsen, D.J . Wallace, and K.G . W ilso n, Phys . Rev. B29 (1984) 4030
[2 이 P. Pfe u ty and G. Toulouse, Intr o . Renormaliza ti on Groups and Cr itica l Phenomena, (W ile y, 1977) [2 이 M. Plis c hke and B. Berge rsen, Eq ui l ib r i um Sta tistica l Phys ic s , (Prenti ce -Hall, 1989) [30] H.E. Sta n ley, Intr o . Phase Transit ion s and Cr itica l Phenomena, (Oxfo r d Un iv. Press, 1971) 詞 H.T. Sto kes, D.M. Hatc h , J.S. Kim , Acta . Cry st . A43 (19 87) 81 園 H.T. Sto kes and D.M. Hatc h , Isotr o p y Subg ro ups of the 230 Cry st a ll og ra p h ic Spa c e Groups , (World Sc ien ti fic, 1988) [33] R.H . Swendsen; Phys . Rev. Lett . 42 (1979) 859 [3 사 R.H . Swendsen, Phys . Rev. B20 (1979) 2080 [35 ]J .C. Toledano, L. Mi ch el, P. Toledano, and E. Brezin , Phys . Rev. Bll (19 85) 7171 [36] J.C . Toledano and P. Toledano, The Landau Theory of Phase Transit ion s, (World Sc ien ti fic, 1987) [3 기 B. Wi do m, ]. Chem. Phys . 43 (1965) 3898 [38] K.G . Wi lso n, Phys . Rev. B4 (19 71) 3174 ; ibi d . , 3184 〔 3 이 K.G . Wi lso n and J. Kog ut, Phys . Re p. 12C(1974) 76 [4 이 K.G . Wi lso n, Rev. Mod. Phys . 55 (19 83) 583 [4 디 J.M . Yeomans, Sta tistica l Mechanic s of Phase Transit ion s, (Clarendon, 1992) [4 이 김두철, 『 상전이와 임계현상 』 (민음사, 1983)
제 9 장 운송 현상의 모사 방법들 2 차 대전 후 원자로에 관한 연구가 활발하게 진행됨에 따라 핵 분열 과정을 전산 모사할 필요성이 절실히 제기되었다. 또한 군 사적인 목적에서 개발되어 온 전자계산기가 빛을 보게 되었다. 울람과 폰노이만은 새로이 발명된 전자계산기가 나오자마자 곧바 로 원자로 내에서 중성자의 운송을 모사하는 데에 적용하였다. 그들은 확률적인 운송 현상을 기술하기 위하여 몬테카롤로 방법 울 택했다. 몬테카를로 방법이 통계역학에 응용되게 된 것은 그 보다 수년 후의 일이었다. 9.1 서론 7, 8 장에서 고찰한 통계역학 문제들에서는 주어전 분포 함수 에 의해 다차원 적분을 하는 것이 목표였다. 고전적 통계역학에서 어떤 순간에 입자들의 위치와 속도는 거의 임의적으로 보이지만 입자들간의 역학 법칙이 주어지면 그들의 시간에 따른 경로를 분
자역학에 의해 확정적으로 추적할 수 있다. 이에 반해서 자연계 에는 본질적으로 확률적인 과정들이 있다. 원자로 안에서 중성자 들은 주변의 원자핵들에 의해서 흡수되기도 하고 그들과 충돌하 여 감속 또는 가속당하기도 하고 또는 핵붕괴를 유발하여 더 많 은 중성자들을 만들어 내기도 한다. 이러한 과정들은 본질적으로 확률적이기 때문에 뉴턴 역학에 의해 기술할 수가 없다. 또한 고 에너지의 입자가 물질을 뚫고 지나갈 때 여러 가지 반응을 일으 키는데 얼마만큼 가서 어떠한 반응을 일으켜 어떠한 입자들을 생 성해내고 그들이 어느 방향으로 어떠한 속도로 움직일지는 미리 알 수가 없다. 이 과정 역시 확률적으로밖에는 예측할 수가 없다. 운송 이론의 목표는 모체 물질의 성분과 형상이 주어지고 추적 하고자 하는 입자들의 생성원의 위치와 강도가 주어졌을 때 모체 내에서의 그 입자들의 분포, 죽 임의 점에서의 밀도와 속도 분 포, 또는 그들로부터 모체로 침전되는 에너지 분포를 알아내는 것이다. 역으로 천체물리학이나 의료물리학에서는 측정된 입자 분포로부터 입자둘의 생성원 또는 모체의 성질들을 알아내는 것 이 목표가 된다. 운송 이론은 단순히 호기심을 채워주는 경지를 지나서 방사선 치료 또는 원자로의 시뮬레이션과 같이 실험이나 실수가 허용되지 않는 경우에 필요불가결한 도구가 되었다. 초기에 많이 개발되었던 해석적인 방법은 중요한 개념들을 정 립하는 데 공헌했지만 복잡한 물리계에 적용하기에는 실용적이지 못했다. 페르미 (Fermi ), 메트로폴리스 (Me t ro p o li s), 울람 (Ulam), 폰노이 만 (von Neumann) 등이 2 차 대 전 도중에 폰노이 만 등이 발 명해 낸 디지털 컴퓨터를 사용하는 수치적 방법을 개발한 이래, 이 새로운 몬테카를로 모사 방법이 전적으로 사용되게 되었다. 컴퓨터의 발전과 더불어 또한 실험 장치들의 스케일이 커지고 정 교로워짐에 따라 운송 프로그램도 점점 더 복잡해지고 방대해지
게 되었다. 이러한 패키지들의 예를 들어 보면 전자와 감마선을 추적하기 위해 개발된 EGS4 는 소립자 가속기 실험에서뿐만이 아니고 병 원에서 방사선 치료에 널리 사용하는 패키지이고 GEANT3 는 광 범위한 에너지 영역에서 많은 수의 입자들을 추적할 수 있는 거 대한 패키지로서 CERN 의 대규모 소립자 실험들에서 사용하고 있다. 또한 MORSE 나 MCNP 와 같은 패키지는 입자들의 수가 아주 많은 원자로 내에서의 중성자와 감마선을 추적하는 프로그 램 으로서 핵 실 험 연구소들인 Oak Ri dg e 연구소, Los Alamos 연 구소, 또는 Lawrence Live rmore 연구소 등에 서 널 리 사용하고 있다. 이러한 패키지들은 입자들을 추적하는 것은 물론 추적에 필요한 각 입자들의 성질 및 모든 원소들과의 반응에 관한 데이 터 베이스를 포함하고 있고 사용자가 자신이 관심을 가지는 실험 장치 또는 체계의 물질 성분과 모양을 쉽게 정의할 수 있도록 정 교로운 그래픽 인터페이스를 내포하고 있다. 현재 사용되고 있는 몇 가지 패키지들을 표 9.1 에 목록화하였다.
표 9. I 운송 현상의 몬테카를로 전산 모사 패키지 이름 소장 기능 AEGIS FNAL 물질과의 전자기 작용 COG LLNL 차폐 문제를 위한 중성자-광자 운송 EGS4 SLAC 전자구광자의 운송 FLUKA CERN 중입자폭포 HADRIN CERN 중입자-핵 상호작용 HETC ORNL 물질과의 중입자 상호작용 MCNP LANL 중성자-광자의 운송 LAHET LANL HETC 와 MCNP 의 통합 코드 GEANT3 CERN 일반적 감지기 모사 코드 HERMES KFA 일반적 중성자 모사 코드
비교적 소수의 입자들을 추적하는 데에는 각 입자들의 경로를 일일이 추적하는 유사 방법을 사용해도 되지만 이 방법으로 많은 수의 입자들을 추적하기에는 곤란하다. 9.3 절에서 소개하게 될 여러 가지 비유사 방법들이 사용되기도 하지만 원자로 내에서의 중성자의 분포를 찾는 경우에서처럼 입자들의 숫자가 압도적으로 많은 경우에는 운송 방정식을 세우고 이것을 수치해석법 또는 중 요 표본추출과 같은 방법에 의해서 풀어나가야 한다. 9.2 유사 방법 9.2.1 서론 유사 방법 (Analog Me t hod) 에서는 입자가 매질 내에서 생성된 다음, 다른 데로 이동하고 거기에서 매질의 원자들과 충돌하여 경로를 바꾸어 또 이동하는 과정을 되풀이하다가, 소멸되거나 또 는 관심 지역에서 이탈할 때까지 입자의 역정 (life h i s t or y)을 실 제 물리 적 인 과정과 유사하게 모사한다. 말하자면 입자의 운송 과정을 컴퓨터로 모의 실험하는 것이다. 입자의 운송 과정 자체 가 예측 불허의 확률적인 것으므로 몬테카를로 방법을 사용하는 것은 당연하다고 하겠다. 입자의 수가 적어서 〈주어전 〉 환경 속 에서 입자가 운송되는 선형 운송 현상에서 유사 방법은 적절하게 사용될 수 있다. 많은 수의 경로를 추적하는 목적은 뭔가를 관측하고자 하는 데 에 있다. 예를 들어 입자 감지기에 들어오는 입자가 감지되는 효 율, 방사선 차폐물의 효능 또는 원자로 내부의 각 부위에서의 중 성자의 밀도나 열 발생률 등. 이것은 입자의 경로를 추적해 나가
는 도중에 필요한 물리적인 관측량에 대한 기여를 더해 나가고 충분히 많은 경로를 추적하여 관측된 값들의 평균 값울 구함으로 써 얻어전다. 이렇게 하여 얻는 관측량의 추정치에는 경로의 수에 역바례하 는 통계적인 오차가 따를 것이다. 이 l/N 오차를 줄이기 위해서 는 아주 많은 수의 경로를 추적해야 한다. 실제적인 문제에서 차 폐 문제처럼 영에 가까운 양을 측정해야 하는 경우에 추적해야 할 경로의 수는 천문학적으로 커지게 된다. 따라서 모종의 중요 표본추출 방법을 기용할 필요가 있다. 9 . 3 절에서 그런 방법들을 논의할 것이다. 통계역학적 체계의 성질을 알아내는 데 입자들의 운동을 일일 이 추적하지 않고 분포 함수를 다루었듯이 운송 현상의 문제에서 도 입자들의 분포 함수들에 대한 볼츠만의 운송 방정식을 세우고 이들의 시간적 진화를 찾아나가는 방법을 사용하는 것이 더 경제 적일 것이다. 여기에는 입자들의 반응에 관한 확률적인 요소가 이미 내재되어 있지만 분포 함수에 관한 확정적인 방정식인 운송 방정식을 적분 방정식으로 변환하면 4 장에서 논의한 마르코프 전 이 확률을 따르는 임의 보행에 의해 . 그 해를 구하게 되어 몬테카 롤로 방법을 또다시 사용해야 하는 경우가 종종 있다. 9.2.2 유사 방법의 개요 유사 방법의 예로서 광자가 주어전 물질을 투과하는 행로를 살 펴보자. 광자가 일으킬 수 있는 반응둘은 광전 효과, 전자_반전 자 쌍생성, 콤프턴 산란 들이다. 광전 효과는 광자가 원자 궤도 를 돌고 있는 전자에 흡수되어 원자계를 여기시킴으로써 외곽 전 자가 원자 궤도로부터 분리되는 현상이다. 전자-반전자 쌍생성은
에너지의 덩어리인 광자가 원자핵의 정전장의 영향 하에서 전자 와 반전자로 물질화되는 현상이다. 이 두 가지 반응에서 모두 광 자가 소멸되고 다른 입자들이 등장하는 데에 반해 콤프턴 산란은 광자와 전자 간의 산란 현상으로서 광자가 전자에 일단 흡수되었 다가 원래보다 낮은 에너지의 광자를 배출하고 그 에너지의 차이 만큼 전자의 운동 에너지가 증가하는 현상이다. 그림 9.1 에서 보이듯이 광자의 에너지에 따라 이 반웅들의 반 응률둘이 크게 변하는 것을 알 수 있다. lMeV 이하의 저에너 지에서는 쌍생성은 불가능하고 광전 효과가 콤프턴 산란에 비해 지배적이나 에너지가 높아감에 따라 급격히 감소하여 l MeV 근 방에서는 콤프턴 산란이 가장 높은 반응률을 보이고 더 높은 에 너지에서는 두 가지 효과가 다 미미해지고 쌍생성이 지배적으로 된다.
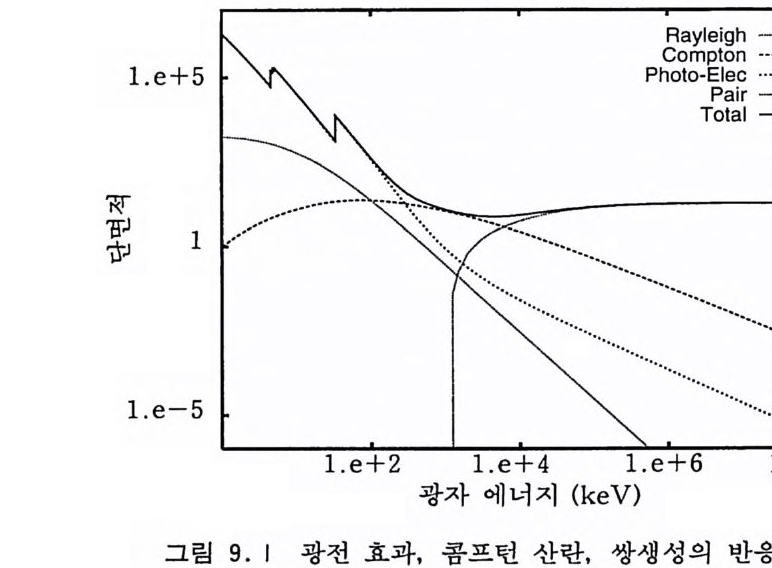 1.e +5 PhRoato y -T lEePo liaget a chirl •一——•••• ••
1.e +5 PhRoato y -T lEePo liaget a chirl •一——•••• ••
에너지 E 를 가지고 모체를 지나가는 광자는 이 세 가지 반응 돌 중 어느 것도 일으킬 수 있으나 실제로 그 광자가 물질을 어 느 거리만큼 투과해서 어느 반응을 일으킬지는 총 반응률 및 각 각의 반응률의 상대적인 비율에 따라 확률적으로 결정될 것이다. 입사 에너지 E 에서의 광전 효과, 콤프턴 산란, 쌍생성의 반응 단면적을 각각 6r, 6c, 6 p라고 하면 총 단면적은 6t = 67 + 6c + 6p 이 다. 매 질의 밀도를 p, 분자량을 M, 아보가드로 수를 Na 라고 하면 광자가 단위 길이의 매질을 통과하며 일으키는 반응들의 거 시적 단면적은 2 = 情%t (9 .1) 에 의해 주어진다. 2 의 단위는 (길이 )-1 안데 균일 매질에서 광 자의 평균 자유 경로는 간단하게 A=l/~ (9 . 2) 가된다 위치 x 에 있는 광자가 물질 속에서 dx 의 거리를 지나가는 동 안에 반응이 일어날 확률은 L! (x)dx 에 의해 주어진다. dx 를 지 나간 이후 광자가 반옹을 일으키지 않고 그대로 남아 있을 확률 U(x) 는 L! (x)dx 만큼 줄어들었을 것이기 때문에 U (x + dx) —U ( x) = —U (x) L! (x) dx (9 . 3) 가 될 것이다. 이 방정식울 풀어보면 U(O)=l 이라고 둘 때 U(x) =exp (-1:r:L ! (s) ds) (9 .4)
가 얻어져서 광자가 아무런 반응을 일으키지 않고 지나갈 확률은 거리가 증가함에 따라 지수적으로 감소한다. 균일 매질에서는 ~(x) 가 상수이므로 U(x)=exp (— x/A) (균일 매질) (9.5) 가 될 것이다. 반대로 위치 X 까지 가는 동안 광자가 반응을 일 으킬 확률은 1-U (x) ==1l—— ee xx pp ((-―x/「。A ~) (s) d(s)균 일 매질) (9.6) 이고 위치 x 에서 dx 만큼 가는 데 반응이 일어날 확률 밀도는 뺏P1- =ex p (-1:r~ (s) ds)~ (x) (9 . 7) =exp (— xi A) IA (균일 매질) 가 될 것이다. 광자가 반응을 일으키는 지점 Xo 를 찾기 위해 상기의 확률 분 포에 의해 표본추출을 할 필요가 있다. 분포 함수가 간단하기 때 문에 역변환 방법을 적용하는 것이 가장 간단하다. 분포 함수를 균일 분포 난수와 같다고 놓으면 1-U (x) =~'=1-~ (9. 8) 가되고 U(x) =~=ex p仁〔~ (s) ds) (9 .9) 가 된다. 따라서
_ln E= 「。 ~ (s) ds (9 .10 ) =x/A (균일 매질) 이 되어 균일 매질의 경우 Xo 는 쉽게 xo=-A ln ~ (9 .11) 와 같이 얻어진다. 이렇게 하여 반응 위치가 얻어지면 세 가지 반웅 중 하나를 택 일하는데 각각의 반응률에 비례해서 확률적으로 선택해야 할 것 이다. 선택이 광전 효과나 쌍생성일 경우에는 새로이 생기는 전 자를 추적하고 전자가 다시 매질과 반응하여 새로운 광자를 생성 해내면 또 광자를 추적하게 된다. 따라서 광자만을 추적한다는 것은 물리적으로 완벽하지 못하다. 9.2.3 생성원 생성된 입자를 기술하는 데에는 입자의 종류, 입자의 좌표 및 속도를 나타내 줄 필요가 있다. 이를 위해 세 개의 공간좌표와, r=(x, y, z), 에너지 E, 그리고 운동 방향을 나타내는 두 개 의 방향 여현, Q=(fix, Qy, fiz), IQ l=l, 도합 여섯 개의 매 개 변수가 필요하다. 입자의 생성원을 기술하는 데에는 상기의 6 차원 좌표공간에서 의 입자 생성의 확률 밀도 함수, S(r, ii, E) 를 정해주면 된다. 주어전 확률 함수에 의해 몬테카롤로 방법에 의해 표본추출하는 방법은 이미 3 장에서 논의하였다. 생성 밀도 함수가 복잡하면 이 과정에서 꽤 많은 시간을 소비할 수가 있다. 실제적으로는 물리 적으로 각 좌표들에 대해서 입자들의 생성 분포가 서로 독립적인
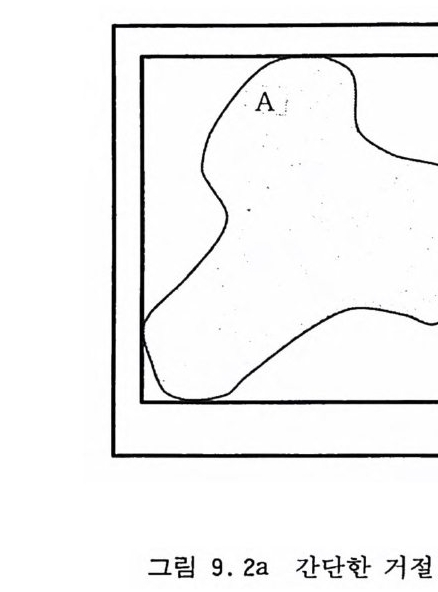 그림 9. 2a 간단한 거절 방법
그림 9. 2a 간단한 거절 방법
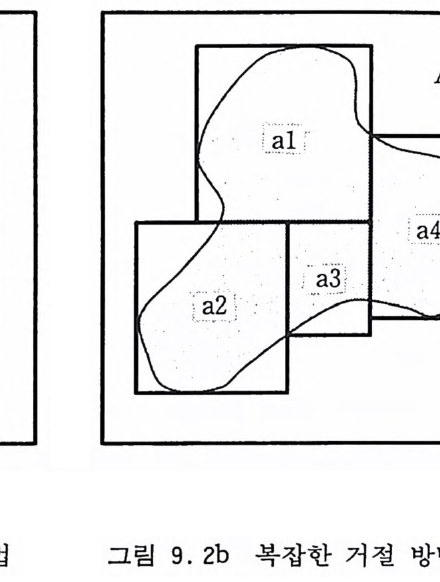 그림 9. 2b 복잡한 거절 방법
그림 9. 2b 복잡한 거절 방법
경우가 많은데, 이 경우에는 밀도 함수가 좀더 간단한 인자들의 곱으로 표시될 수 있어서 예상보다는 덜 복잡하다. S(r, Q, E)=s(r)·s(Q ) ·s(E) (9 .12) 분포 함수 s(r) 에 의한 표본추출에서 가장 문제가 되는 것은 입 자 생성원이 복잡한 모양을 가지고 있는 경우이다. 이런 경우 일 반적으로 적용할 수 있는 방법은 폰노이만의 거절 방법이다. 이 방법에서는 먼저 입자 생성 지역을 간단한 모양의 경계면으로 둘 러 싼다. 그립 9.2a 를 예를 들어 설명하면 생성 지역 A 를 직사 각형으로 둘러싼 다음 (x, y) 좌표가 직사각형 안에서만 균일 하게 표본추출되도록 한다. 이렇게 해서 선택된 점 (x, Y) 가 A 안에 떨어지면 수용하고 그렇지 않으면 버리는 방식으로 추출 해 나가면 수용된 점들은 지역 A 안에서 균일하게 분포될 것
이다. A 의 모양이 복잡하면 직사각형 하나를 가지고 둘러싸는 것이 비효율적일 것이기 때문에 3 장 3.6 절에서 정규 분포에 의한 표본 추출을 위해 사용했던 Marsa gli a 의 사각형-쐐기-꼬리 방법을 옹 용하여 작은 직사각형 여러 개를 모자이크로 만들어 에워싼다. 그림 9.2b 를 보자. 작은 직사각형들의 면적들의 합을 AR 이라고 하자. 우선 어느 직사각형을 선택하느냐를 결정해야 할 것이다. 한 점이 어느 직사각형에서 표본추출될 확률은 그 면적에 비례할 것이기 때문에 i번째 직사각형의 면적이 a i라면 확률 aJ A no Jl 의해 i 번째 직사각형을 선택한다. 그런 다음 점 (x, Y) 를 이 직사각형에서 선택하여 거절 방법을 적용하는 것이다. 이 방법은 간단하기 때문에 삼차원 공간에서 복잡한 모양의 생성 지역에 대 해서도 쉽게 적용할 수 있다. 많은 경우에 입자 생성 밀도가 동방성을 가지는데 이 경우에는 단순히 s( ii )=1/4 군]다. s( ii)가 각에 무관한 상수이므로 두 개의 각 (0, rp)를 구간 (0, 1[)와 (0, 21r) 에서 균일 추출해 내면 된다. 또 다른 많은 경우에 입자들이 빙의 형태로 관심 지역에 투입되는데 이런 경우에는 입사각을 고정시켜야 한다. 죽 s(ii ) = 8 (ii一ii o) . 입자 생성 밀도의 에너지 의존도는 매우 복잡다단한 것이 상례 이지만 특수한 상황에서는 입사 입자들이 균등 에너지롤 가지고 관심 지역에 들어울 수도 있다. 이런 경우에는 s(E)=8(E ― Eo) 가 된다. 입자들이 모체 내에서 반응을 일으켜 이차적인 입자들을 생성 해 내는 일반적인 경우에는 s(ii , E) 가 단순하지 않은 함수이고 인수분해되지 않는 경우가 대부분이다. 비교적 간단한 경우에는 역변환 방법에 의해 표본추출을 할 수 있겠지만 일반적으로는 거
절 방법 또는 혼합 방법을 사용해야 할 것이다. 9. 2. 4 반응점의 자유 경로의 추출 균등한 매질에서 입자의 반응률둘이 알려져 있는 경우에 반응 이 일어나는 지점까지의 자유 경로를 표본추출하는 방법은 식 (9.10) 에 요약되어 있다. 여기서는 입자가 매질의 성분이 다른 여러 지역을 통과할 때 자유 경로를 추출하는 방법에 대해서 논 의하기로 하자. 원칙은 식 (9 . 10) 을 일반화시키는 것이다. 즉, 자유 경로의 수 NA=1:~ (9 .13) 룰확률분포함수 F(N.1 ) =1— e xp (— N.1 ) (9 .14) 에 의해 표본추출하는 것이다. 논의를 간단하게 하기 위하여 각각 다론 매질로 구성되어 있는 n 개의 지역들이 그림 9.3 과 같이 평판 모양으로 되어 있고 각 지역 내에서는 매질이 균일하게 분포되어 있다고 하자. Xo 지점에 서 일어난 반응으로 인하여 입자가 이 지점으로부터 새로이 출발 한다고 하자. 그리고 입자의 운동 방향이 이 평판들에 대해서 수 직이라고 가정하고 그것을 x 방향이라고 하자. 또한 각각의 매질 에서 입자의 평균 자유 경로를 /\1, /\2, …, An 이라고 하자. 이 입자가 거쳐가는 경계면들의 x 좌표를 x1, X2, …, Xn 이라고 하 면 x 지점까지 진행하는 입자가 거쳐가는 자유 경로의 수는
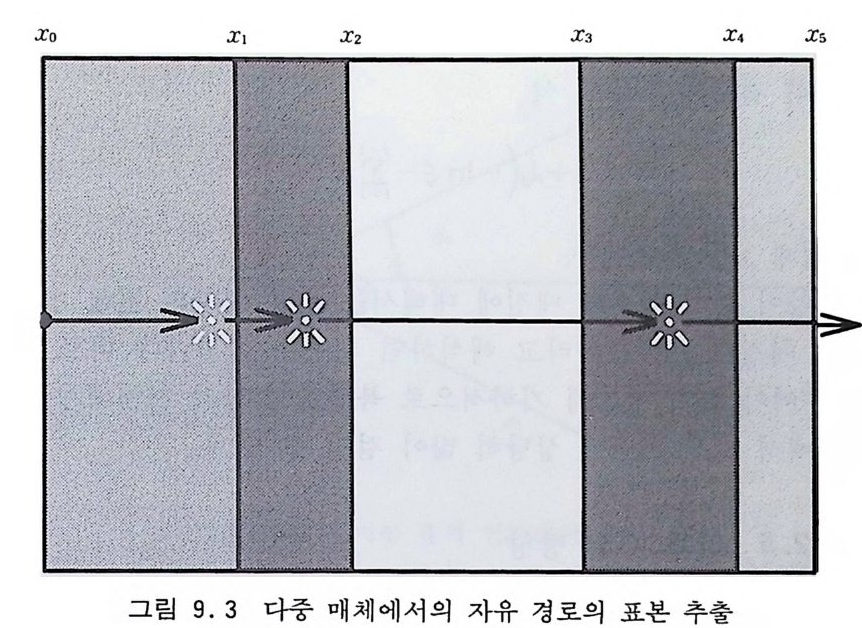 Xo XI X2 X3 X4 X5
Xo XI X2 X3 X4 X5
NA= 덩i= I x,·—A ,x· r l + x_AXj j - I (9 .15) 에 의해 간단히 나타낼 수 있다. 새로운 반응 지점을 찾는 방법 은 • NA= 一 In t에 의해 NA 를 표본 추출한 다음, • 식 (9.15) 를 풀어서 반웅 지점의 x 좌표를 구하는 것이다. 반응 지점의 x 좌표를 표본 추출하는 방법을 좀더 자세히 설명 하면 다음과 같다. 부호를 간단하게 하기 위하여 d;=X;-X i -1 이 라고 정의하자. 먼저 반응이 일어나는 지역 번호 j를 부등식 ji2=- 1l dI./Ai < —ln 5• < i2=j l dI./Ai (9 .16)
로부터 결정하고 다시 식 x=xj- 1 +11j( -ln ~-접 dJ A i) (9 .17) 에 의해 x 를 추출한다. 모양이 좀더 복잡한 매질에 대해서는 d; 를 입자의 진행 방향으 로의 매질의 두께둘이라고 해석하면 되는데 궤적마다 따로 계산 해 주어야 하기 때문에 기하적으로 복잡한 모양의 지역에서는 이 과정에서 계산 시간이 상당히 많이 걸릴 수 있다. 9.2.5 반응 후의 방향 입자들이 반응하여 이차적 입자들이 튀어나오는데 그들의 에너 지와 출사 각도는 미분 단면적에 의해 표본추출해야 한다. 이것 은 반응에 따라 각기 다르기 때문에 일반론을 펼 수가 없다. 여 기서는 운동학적인 면만 살펴보자. 입사 입자의 방향 여현이 (iix, iJY, Dz )이고 출사 입자의 입사 방향에 대한 각이 (O, ¢) 라면 실험실 좌표계에서의 출사 입자의 운동 방향(gg, gg, g;) 은, 다음 식들에 의해 구할 수 있다. igi~논== ((ssiinn 00II//33)) (( i-iyi isxi n s i ¢n — ¢ i—izi ii iz xi i CyO SC O¢S) ¢+) i+ix i iCyO SC O(Sj 0 g논 (sin 0 x /3) cos + iiz co s (j /3=g (9 .18) 입사 입자가 정지해 있는 표적 입자와 충돌하여 산란하는 경우 가 자주 나오게 되는데 여기서 그 운동학적 관계식들을 정립해 두는 것이 좋겠다. 4- 운동량 R 을 가전 입자가 정지 질량 m 을 가
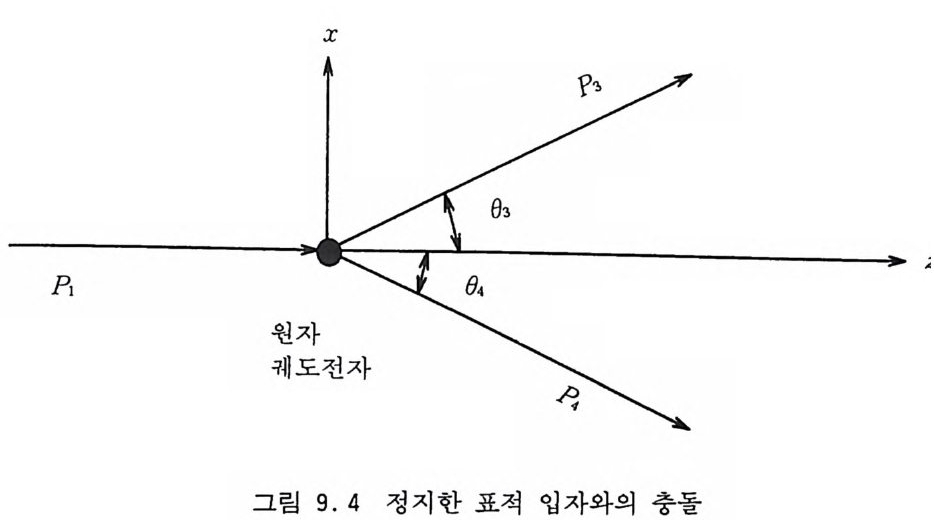 X
X
전 표적 입자와 충돌하여 4- 운동량 R 과 p4를 가전 입자들이 튀 어나온다고 가정하자. 논의를 간단하게 하기 위하여 그림 9 .4와 같이 좌표계를 설정해 보자. 이 좌표계에서 P,· 둘은 A = (E1, 0, 0, P1) (9 .19a) A= (m, 0, 0, 0) (9.19b) R= (E3, p3 s in 03, o, p3 C OS 03) (9 .19c) P4= (£4, -p4 s in 04, 0, p4 c os 04) (9 .19d) 와 같이 쓸 수 있다. 우리는 종종 E3 와 p 3 가 주어졌을 때 03 를 알기몰 원한다. 이것은 운동량 보존의 법칙과 관계식 Pl=m? 로 부터 cos 03= m~— m f — m2-m i 2+P 21P (3E 1 + m) £3— 2 E1m (9 . 20) 와 같이 얻을 수 있다. 또한 그립 9.4 의 대칭성을 이용하여 첨자 둘 3 과 4 를 교환함으로써 cos 04 에 관한 식도 얻는다.
9. 2. 6 입자의 소멸과 생성 입자가 매질에 흡수당하는 경우나 그 에너지가 미리 정해 놓은 기준값 이하로 떨어지는 경우 또는 입자가 관심 지역의 밖으로 이탈하는 경우에 그 입자는 소멸한 것으로 간주한다. 입자가 소 멸되면 현역 리스트에서 제거해야 한다. 입자가 매질과의 반응을 통해서 새로이 생성되는 경우에는 그 입자들의 종류, 위치, 속도 등울 현역 리스트에 추가하고 그들도 추적해야 한다. 그 많은 입 자들을 동시에 추적할 수는 없기 때문에 그 중 에너지가 가장 높 은 것 또는 가장 낮은 것 또는 무작위로 선택하는 방법이 있을 것이다. FORTRAN 언어처럼 프로그램 도중에 변수 메모리의 용량을 조절할 수 없는 경우에는 변수 행렬의 크기를 미리 크게 잡아두어야 하지만 C 언어처럼 프로그램 수행 도중에 메모리를 증가시킬 수 있는 경우에는 동적으로 메모리를 증감시켜가며 프 로그램을 수행시킬 수 있다. 비유사 방법에서는 필요에 따라서 적절한 무게 인자를 곱하여 소멸될 입자를 고의적으로 회생시키거나 존재하는 입자를 고의적 으로 제거하기도 한다. 자세한 설명은 9.3 절에서 논의하기로 한다. 9.2. 7 물리량의 측정 입자들의 운송을 추적함으로써 우리는 어떤 물리량을 측정하고 자 한다. 차폐 문제에서는 관심 지역을 빠져나가는 입자들의 퍼 센트가 문제가 된다. 입자 감지기의 설계 문제에서는 복잡한 모 양과 성분을 가지는 감지 장치계에 입자들아 입사하여 매질과 반 옹을 일으켜 어떠한 이차적인 입자들을 생성해 내고 정해진 경계 면을 얼마나 많은 입자들이 지나가면서 얼마나 많은 에너지롤 방
출하는지가 관심의 대상이 된다. 또한 암 환자에게 방사선을 두 사시키는 경우 환부에 방출되는 에너지량이 가장 큰 관심이지만 그밖의 부분에서는 정해전 양 미만의 에너지만 방출되어야 하는 것을 보장해야 한다. 원자로의 설계 문제는 아주 복잡한 것인데 그 중 문제가 되는 것은 핵분열 과정에서 나오는 중성자와 감마 선이 주변의 매체에 얼마나 많은 에너지를 방출하는가 하는 것이 며 중성자의 밀도가 임계값을 지나치지 않도록 하는 것이다. 일반적으로 우리가 측정하고자 하는 거의 모든 물리량들은 입 자들의 밀도 함수로부터 유도될 수 있는데 , 이 것은 좌표와 속도 의 6 차원 공간의 주어진 위치에서 발견되는 입자들의 수를 말한 다. 6 차원 공간의 점 (r, v) 근방의 체적소 d3rd3v 내에서 발견 되는 입자들의 수를 밀도함수에 의해 표현하면 n (x, y, Z ; Vx, Vy , Vz ; t) d3rd3v 이다. 밀도 함수 n 을 알면 공간의 주어진 점에서의 입자들의 밀 도, 흐름 또는 정해진 단면적을 지나가는 입자들의 수 등을 쉽게 산출해 낼 수 있다. 몬데카를로 방법에서는 입자가 탄생하면 그 행로를 추적하게 되는데 다음 반응 지점까지의 평균 자유 경로 개수, 반웅으로부 터 튀어나오는 입자들의 에너지와 출사 방향, 새로이 생성된 입 자들의 부수적 행로들을 끊임없이 추적한다. 생성원으로부터 탄 생한 이러한 임의의 주요행로를 N 개 추적한다고 하자. 그 과정 에서 가관측량 O 를 측정하게 되는데 유사 방법에서는
적으로는 행로의 수 N 을 많이 늘리면 중심 극한 정리에 의해 〈 O 〉 에 대한 충분히 정확한 기대값을 얻을 수 있다. O(h) 를 측정하기 위하여 행로를 따라 가관측량에 대한 기여, 죽 득접(t all y)을 어떻게 기록하는지롤 알아보자. 가장 간단하게 어느 체적소 V 를 아무 방향으로건 단위시간당 지나가는 입자들 의 수인 스칼라 선속 (scalar flux )
= —1- LN ! Cv ( h) (9 . 24) Nh= I 이 방법에서는 입자가 체적소 V 를 지나가면서 반응을 일으켜 야만 득점에 연결되므로 아주 비효율적이다. 스칼라 선속의 물리 적 정의에 의해 입자가 그 체적소를 지나가기만 하면 득점을 하 도록 할 수도 있다. 죽 입자들이 체적소 V 를 지나가는 평균 트 랙 길이를 〈 Lv 〉라고 하면 관계식 r/Jv =< L v> / V (9 . 25) 이 성립한다. 이 식을 사용하여도 V 가 적으면 지나가는 입자들
의 수가 워낙 적기 때문에 유사 방법은 역시 효율성이 떨어전다. 개별 입자들의 운송을 추적해서 6 차원 공간의 어느 체적소에서 의 밀도 함수를 계산해 내려면 수없이 많은 입자들을 추적해야 되고 그 계산 시간 또한 엄청나다. 예를 들어 10-6 정도의 차폐 효과롤 원한다면 한 개의 탈출 입자를 찾아내기 위해 백만 개의 입자들을 추적해야 한다. 9.3 비유사방법 9.2 절에서 논의한 유사 방법은 몬테카롤로 적분으로 말하자면 직설적 방법과 같아서 관측량의 편차를 줄이기 위해서는 엄청나 게 많은 입자 행로들을 추적해야 한다. 때에 따라서는 그 계산량 이 현실적으로 불가능하게 되어 중요 표본추출 방법과 같이 적은 노력으로도 편차를 줄일 수 있는 방법을 사용하지 않으면 안된 다. 대부분의 비유사 방법 (Non-Analog Me t hod) 에서는 입자 행 로를 인위적으로 조작하여 원하는 결과에 기여를 많이 하는 행로 둘을 되도록 살려내는 방식을 사용하고 있다. 다음에 논의할 몇 가지 방법들은 흔히 사용되는 편차 감소 기 법인데 이러한 방법들을 좀더 효과적으로 적용하려면 중요 사찰 지역에 대해 사전 정보가 필요하다. 이것은 문제의 해답을 알아 야만 가능한 것이 되어서 자가당착적이다. 비슷하지만 더 간단하 고 해석적으로 풀 수 있는 문제의 해답으로부터 유추하거나 경험 으로부터 얻은 직관에 의존하거나 또는 유사 방법에 의해 대충 중요 지역을 알아내고서 계산이 진행되어감에 따라 점차적으로 조정해 가면서 윤곽을 파악해 나가는 것이 실용적일 것이다. 비유사 방법은 입자의 행로에서 사건이 일어날 때 주로 적용된
다. 이제 몇 가지 방법들을 고려해 보기로 하자. 9.3.l 흡수 억제 방법 입자의 운송 과정에서 그 행로가 종료되는 경우는 세 가지가 있다. 1) 입자의 흡수 2) 관심 지역 이탈 3) 입자의 에너지 쇄전 유사 시뮬레이션에서는 위 조건들이 만족되면 그 입자의 행로 롤 더이상 추적하지 않고 폐기시킨다. 비유사 시뮬레이션에서는 효율을 증대시키기 위하여 몇 가지 인위적인 조작을 하게 된다. 사건 1) 이 일어날 경우 입자를 파기하는 대신 그 입자의 현재의 무게 인자에 현 지점에서의 회생 확률을 곱하여 새로운 무게 인 자로 취하고 그 입자를 살려내는 방법을 사용할 수 있다. 입자 운송 행로의 i번째 단계에서 입자의 무게 인자가 W려 고 그 지점 그 단계에서의 총 단면적을 6, 홉·수 단면적을 야라고 하자. (i -1) 번째 단계에서 무작위로 표본추출한 결과 흡수 반응 이 선택되었다고 하여도 이것을 제거하는 대신 무게 인자 wi= Wi - 1 (J- 6a (9 . 26) (J 룰 부여하면서 살려내고 비흡수 반응둘 중에서 하나의 반응을 그 들의 상대적인 반응률에 따라 무작위로 선택하는 것이다 . 유사 방법에서처럼 단순한 득점 방법을 사용하면 이러한 인위
적인 조작으로 말미암아 전혀 실제와 다르고 무의미한 측정값이 얻어질 것이다. 따라서 인위적인 조작에 대한 보상을 해주어야 하는데 i번째 지점에서 물리량울 측정할 경우 유사 방법에서의 측정량 야에 무게 인자 W를 곱해 주어야 한다. Ona= W.·O a (9 . 27) 사건 2) 가 일어나는 경우에도 이와 비슷한 무게 함수 조정 방 법을 적용시킬 수 있으나 입자를 살려내는 과정이 더 복잡하여 계산 시간이 많이 걸리므로 1) 의 경우에만 사용하는 것이 상례이 다. 위의 식 (9 . 26) 을 사용하기 위해서는 i =O 에서의 무게 인자를 정의해 주어야 하는데 보편적으로는 Wo=l 로 잡는 것이 타당할 것이다. 하지만 생성원의 분포 함수 S(r, E, ti)가 너무 복잡 하여 직접적인 표본추출을 하지 못하고 이와 유사하지만 다루기 가 쉬운 다른 함수 Se(r, E, tJ)를 사용하여 표본추출할 경우 초기의 무게 함수를 臨= SSe((rr,, EE,, g요)) (9 . 28) 로 잡아주어야 한다. 홉수 억 제 (Absorpt ion Sup pr essio n ) 방법 을 사용하면 입 자가 소 멸되지 않으므로 입자 행로당 계산 시간이 늘어나지만 그보다 훨 씬 더 편차를 줄여 주기 때문에 이 방법은 거의 모든 몬테카를로 운송 코드에서 채택하고 있다.
9.3.2 러시아 룰렛 러 시 아 룰렛 (Russia n Roulet te) 은 흡수 억 제 방법 의 반대 로서 입자 행로를 폐기하는 데에 관한 방침을 결정한다. 흡수 억제의 방법을 사용하면 무게 안자가 점점 감소하게 되는데 너무 감소하 여 미리 정해둔 하한값 Wm 보다 낮아질 경우 계산의 효율을 위 해 인위적으로 폐기해 줄 필요가 있다. 무조건 폐기해 버리면 비 록 작지만 측정량이 과소 평가될 우려가 있기 때문에 보상을 해 줄 필요가 있다. 무조건적인 폐기 대신에 회생 확률 p= W;/Wo 에 의해 살리면서 무게 인자롤 초기값 Wo 로 잡아주는 방법을 러 시아 룰렛이라고 부른다. 죽 아주 작은 확률에 의해 회생할 기회 룰 주면서 대부분의 경우에는 폐기하는 것이다. 하한값 Wm 을 중요 사찰 지역에서는 낮게 잡아 주고 그렇지 않은 지역에서는 높게 잡아 줌으로써 이 방법의 효율을 높일 수 있다. 이 방법은 제거해야 할 입자 행로를 살려낸다는 점에서 편차를 증가시키는 경향이 있으나 중요하지 않은 행로를 조기에 제거함 으로써 행로당 계산 시간 r 를 단축시키기 때문에 효율 1/(r 군)을 증가시켜 준다. 9.3.3 분열 방법 러시아 룰랫이 중요하지 않은 입자를 제거하는 데에 반해서 분 열 방법 (S plitti n g)은 중요한 입자를 증식시킨다. n- 대 -1 분열 방 법은 입자를 임의로 n 개로 늘리고 새로 생긴 n 개의 입자 각각에 무게 인자 W i n 을 준다. 이 방법은 원하는 결과에 많은 기여를 하는 중요한 입자 행로를 증식시키기 때문에 중요 표본추출 방법
의 일종이라고 볼 수 있어서 편차를 줄여 주지만 더 많은 입자 행로를 추적하게 하기 때문에 계산 시간을 증가시켜 준다. 하지 만 전체적인 효율성 l/(w2) 은 증가시켜 준다. 분열 방법은 입자들이 매질 깊숙이 침투하면서 거의 소멸되는 차폐 문제에서 편차를 줄이는 가장 효과적인 방법이다. 입자들이 지역간의 경계면을 지날 때 분열 방법을 적용시키는 것이 상례인 데 경계면을 지나와서 증식시켰을 때 새로 생긴 입자들의 수가 거의 일정하게 유지되도록 n 을 결정하는 것이 가장 좋은 결과를 내주는 것으로 알려져 있다. 9.3.4 지수 변환 방법 위의 세 가지 방법 이의에도 ' 여러 가지 인위적인 편차 감소 기 법들이 있지만 그 적용 범위가 제한되어 있다. 지수 변환 방법 (Exp o nenti al Transfo r mati on ) 은 침 투 문제 에 서 효율적 이 다. 침투 문제에서는 대부분의 입자들이 여행 도중에 폐기되어 버 리는데, 선호되는 방향으로의 여행 거리를 확대시키는 방법을 생 각해 보자. 가령 x 방향이 선호 방향이라고 하면 그 방향으로의 거시적 단면적을 인위적으로 적절히 줄여 줌으로써 입자가 x 방 향으로는 실제보다 저항을 덜 받으면서 진행하도록 할 수 있다. ~p=~ (l-p cos 0) (9 .29) 여기서 ()는 입자의 진행 방향과 x 축 사이의 각도이고 o:::;; p :::;;1 는 선호율을 나타낸다. 이렇게 반응률을 줄인 데에 대한 보상으로 입자의 무게 인자, Wp 를 늘려주어야 할 필요가 있다. 그것은 입 자가 지점 s 로부터 s+ds 까지 진행하는 동안에 반응을 일으킬 확률 ~ex p (-~s)ds 가 보존되어야 한다는 원칙을 적용하여
~exp ( 一 ~s) ds = Wi후p ex p ( —~ ps ) ds (9 . 30) 가 성립하게끔 Wp 를 택하면 된다. 이로부터 무게 인자를 Wp = ~1-sp c os0 0 ) (9 . 31) 과 같이 얻는디 입자가 경계면에 도달하면 다른 보상을 해야 한다. 그것은 경 계면에 도달할 확률을 보존시킴으로써 찾아낼 수 있다. exp ( -~s) = Wp exp (—~pS ) (9 . 32) 로부터 Wp = exp (-p~ s cos 0) (9 . 33) 룰얻는다. 한 가지 주목할 접은 이렇게 해서 얻는 측정값의 편차가 0~ Pm~l 에서 최소값을 가진다는 것이다. 하지만 Pm 은 사전에 미리 알 수가 없고 경험적으로 추정해야 한다. 9.3.5 강제 충돌 방법 관심 지역이 너무 비좁아 입자들이 충돌없이 통과해 버릴 확률 이 클 경우 지수 변환 방법과는 반대로 충돌간 여행 거리를 줄이 는 방법을 생각해 볼 수 있다. 강제 충돌 방법 (Forced Coll isio n ) 에서는 무게 인자 W를 가지고 이 지역에 들어오는 입자를 더 작 은 무게 인자를 가지는 두 개의 입자들로 분열시키는데, 하나는 그냥 지나갈 입자이고 다른 하나는 강제로 충돌을 하게 될 입자 이다. 각각의 무게 인자를 결정하는 데 참조할 것은 입자가 충
돌 없이 지나갈 확률은, 그 지역의 통과 거리를 R 이라고 하면, ex p (-~R) 이라는 사실이다. 통과하는 입자에게는 무게 인자, We = W exp (-~ R) (9 . 34) 롤 부여하고 충돌해야 할 입자에게는 무게 인자, We= W[l— e xp (—~ R)] (9 . 35) 를 부여하면 될 것이다. 통과하는 입자는 무게 인자 We 를 가지고 충돌 없이 그 지역을 빠져나오는데 새 지역에서 충돌 지점을 찾는 데에 있어서 계속 살아 남아 있을 확률이 exp (—~ R) 만큼 줄어들었다는 것을 감 안해 주어야 한다. 충돌하는 입자는 증폭된 확률 밀도 p(s ) lZ— eexx pp ((—- ~2 Rs)) ' 。후 sR (9 . 36) 에 의해 관심 지역 내에서 충돌 지점을 찾도록 해주어야 한다. 간단한 지수 분포에 의한 표본추출 방법은 2.3 절에서 논의한 바와 같이 균일 분포 난수 g를 뽑아서 s= -支 ln [l— s(l 一 e-IR) ] (9 .37) 에 대입하여 나오는 s 를 사용하면 된다. 일단 충돌이 일어나면 그 입자에는 무게 인자 We 를 새로 부여해 주어야 한다. 한 가지 주의할 것은 관심 지역이 작으면 We 도 작게 되는데 이보다 작은 Wm 을 가지고 러시아 룰렛 방법을 동시에 적용해서 는 안 된다는 것이다.
9. 4 볼츠만 운송 방정식 9.4.1 개요 운송되는 입자들의 수가 너무 많아서 그들 자신이 환경을 만드 는 데 기여하는 비선형 운송 현상에서는 어느 입자의 행로롤 끝 까지 추적하고 나서 또 다른 입자의 행로를 추적하는 유사 방 법이 부적절해질 것이다. 아런 경우에는 입자들의 미시적인 운 동 방정식을 직접 풀어가는 확정적인 방법을 사용해야 한다. 예 롤 들면 그것들이 만들어 내는 전자장이 무시할 수 없을 정도로 강하거나 그들 자신이 표적이 될 정도로 수가 많아지는 경우들이 다. 또한 운송 현상에 관한 정확한 결과를 원할 경우에는 입자의 위치와 속도의 함수인 입자 밀도 함수 또는 충돌 밀도 함수에 관 해 확정적인 운송 방정식을 설정하여 이것을 수치적으로 풀어나 간다. 확정적 운송 방정식을 푸는 비교적 정확한 방법들로서, 이 산적 좌표 방법 (Disc rete Ordin a te s Meth o d) , 구면 조화 함수 방 법 (Sp h eric a l Harmonic s Meth o d) , 유한 원소 방법 (Fin i t e Element Meth o d) , 적 분 운송 방법 (Inte g ral Transpo rt Meth o d) 등 여 러 가지가 있다. 이 방법들에 대한 자세한 설명은 Dudersta d t 등 [197 아울 참조하기 바란다. 입자 밀도 함수를 n(r, v, t)라고 하면 6 차원 위상공간에서 (r, v) 근방의 체적소, d3rd3v 내에서 발견되는 입자들의 수는 n(r, v, t) d3rd% 이다. 많은 경우에 속도 대신 에너지 E 와 운 동 방향 g를 사용한다. (r, E, iJ) 근방의 체적소, d3rdEdQ 내에서 발견되는 입자들의 수는 n(r, E, iJ )d3rdEd요 이다. 체적소 d3rd% 내의 입자들의 수의 변화율을
1) 생성원 또는 흡수원 2) 매체 또는 다른 입자와의 충돌 3) 체적소 의부로부터의 유입 또는 방출 에 의한 변화율둘의 합으로 써주면 볼츠만의 운송 방정식을 얻 는다. 寄8n =s(r, v, t) +8需n Ic o1-v·'1 r n(r, v, t) --!f; ·'1v n(r, v, t) (9 .38) 여기서 입자의 위치 변화는 세번째 항에만 기인하고 네번째 항은 가속으로 인한 속도 변화를 나타내는데 의부 전자장 하에서 대전 입자가 운동할 때 유효한 항이다. 두번째 항이 대부분의 물리를 내포하고 있는데 이 항으로 인해 입자의 속도가 바뀌거나 입자가 소멸되거나 또는 새로운 입자가 탄생될 수 있다. 이것을 미분 산란 단면적과 연관시키면 틀 |col = Jd3v 'v'~ (r, V' -+ v) n (r, v', t) -v ~ (r, v) n (r, v, t) (9 . 39) 와 같이 쓸 수 있다. 여기서 미분 산란 단면적, ~(r, V'-+ v) 를 속도에 관해 적분하면 거시적 산란 단면적, L! (r, v) =jd 3v ' L! (r, v' -+ v) (9 .40 ) 을 얻는다. 식 (9.40) 의 좌변은 식 (9.1) 의 우변과 같다는 점을 유의할 필요가 있다. 식 (9.38) 에서 입자의 속도 v 대신, 그 에너지 E 와 운동 방향
g를 사용하기로 하고 n 대신 각선속 (an gu lar flux ), (r, E, g)는 (r' E, ii) = ff! dE'd요 '~ (E' ---+ E, Q' - ➔ Q) cp (r, E', Q' )+s (9 . 44) 에 의해 정의된다. 또한 위의 식 (9 . 42) 에서 r 과 t 대신 r'=r ― Ri i와 t'=t— Ri v 를사용하면 》릅+g.짜=-孟 ¢(r', E, 요, t') (9 . 45) 가된다. 이제 식 (9.45) 의 양변에 적분 인자, exp [— 1R2 !t (r-R'ti, E)dR'] (9 . 46)
룰 곱해주고 R에 대해 적분을 하면 軒에 관해 다음과 같은 적분 방정식을 얻는다. 여기서 ~t는 총 단면적이다.
[fjfd E dQ'~꾼크 ?)_IP( r', E, Q')+ s(r', E, ii)] 또한 이 식의 해, rp( r, E, ii)로부터 어떤 가관측량을 계산하 고자 한다고 하자. 예를 들어, 7J (r, E) = 2!d ( r, E) /2! 1 (r, E) (9 . 50) 에 의해 정의되는, 감지기의 반응에 관심이 있다고 하자. I= 〈7J.¢ 〉 =ffd 3rdE dQ묘,’ 겁 ¢(r, E, Q) (9.51 ) 여기서 x=(r, E, iJ)라고 정의하면 위의 식둘이 다음과 같은 형식으로 되어 있는 것을 쉽게 볼 수 있다. ¢ (x) = fdx' ]{ (x', x) ¢ (x') + s (x) (9 . 52) H=j dx TJ (x) ¢ (x) (9 . 53) 5.3 . 4 절에서 원론적으로 논의했고 편차 감소 기법을 위해 9. 3 절에서도 논의한 홉수 억제 방법을 적용해 보기로 하자. 위상공 간의 접 x 에서의 흡수 확률을 r(x) 라고 정의하고 전이 확률 ]{(x', X) 를 다음과 갇이 몇 개의 인자들의 곱으로 써보자. ]{ (x', x) = [l-r ( x') ] p (x') K (x', x) (9 . 54) 여기서 [l-r(x') ]는 입자가 흡수되지 않고 산란될 확률이고 p (x) 는 보상 인자이며 K(X', X) 는 규격화된 전이 확률이다. K(x', x)fX=(x ',~ x) d x (9 . 55)
jJC (x', x) dx p( x') [1-Y(x') ] (9 . 56) 식 (5 . 55) 를 변형시켜 얻은 식 (5 . 75) 를 풀어서 다시 써보면 H= to fd x 。 ... dxn-1S(xo)(1-r(xo)]K(xo, X1) (9.57) …n( 1=O— Y( Xn-1)]K(Xn-1, Xn)Y(Xn)J (xo, …, Xn) 을 얻는다. 여기서 이 특정 행로에 대해서 주는 점수, Y(xo, Xn) 는 Y(xo, Xn) = 갑::} p( xo) …p( Xn-1) (9 .58) 에 의해 주어진다. 아것은 입자가 Xo 에 생겨서 x1 까지 간 다음, 거기서 또 충돌을 일으켜 X2 로 가고, 이런 과정을 반복하다가, 끝내는 n 번째 충돌에서 소멸되는 과정을 말한다. 위의 과정을 물리적으로 좀더 자세히 설명하면 유사 방법과 같 다는 것을 알 수 있다. 행로가 시작되기 위해서는 입자가 탄생해 야 하는데, 생성 확률 s(x)=s(r, E, iJ)에 의해 xo=(ro, Eo, no) 를 표본추출한다. 또한 새로 탄생한 입자에게 무게 인자 W =1 을 부여한다. 그런 다음 전이 확률 K(Xo, X) 에 의해 X1 을 표 본추출한다. 이것을 구체적으로 말하면, ~t(ro , Eo)ex p[一 r (ro, Eo, no, R)] 에 의해 R 을 표본추출하여 r1=ro+R iJ o 에 의 해 r1 을 계산한다. 이 시점에서 입자가 흡수될 수도 있는데 그 가능성을 배제하고, 이 행로의 점수와 입자의 무게 인자에 보상 인자, [1-r(x1)]=~s(ri, Eo)/~t( ri, Eo) 를 곱해 주기로 하고 무조건 산란만 시킨다. EI, g 1 은 산란 단면적으로부터 추출하는 데, E1 을,
fdQ ~ s4 7(Er~o s나 (r Ei, , Efoj)。 나J) (9 . 59) 에 의해 추출한 다음, 운동 방향 iJ 1 은, fd ~후 s(Eo (E -o 간E1러, ,Q 。 g-。 나QJ) ) (9.60) 에 의해 추출한다. 이런 방식으로 K(xI, x) 에 의해 X2 를 추출하 고, …, K(xn-I, x) 에 의해 Xn 을 추출한다. 이 과정을 계속하다 가, 입자의 무게 인자가 미리 설정한 하한값 이하로 떨어지거나, 입자가 관심 지역 밖으로 빠져나가면, 홉수 확률 짜 x) 에 의해 . Xn 을 표본추출하고 종료시 킨다. 참고문헌 [ 1 J B. Alder, Meth o ds in Comp ut a t i on al Phys ic s , (Academi c, 1963) [ 幻 J.F . Brie s meis t e r , MCNP: A General Monte Carlo Code for Neutr o n and Photo n Transp o rt : versio n 3A, LANL LA-7396-M (1986) [ 3 ] R. Brun, F. Bruy a nt, M. Mair e , A.C. McPherson and P. Zanarin i , GEANT3, CERN DD/EE/84-1 (1987) [ 4 ] S. Chandrasekhar, Rev. Mod. Phys . 15 (1943) 1 [ 5 ]S . Chandrasekhar, Radia tive Transfe r , (Dover, 1960) [ 타 J.J. Dudersta d t and W.R. Marti n, Transpo rt Theory , (W ile y, 1979) [ 7 ] M.B. Emmett , The 'MORSE' Monte Carlo Radia tion Transp o rt Code Sys t e m , ORNL-4972 (1975)
[ 8 ] E. Fermi , unp u bli sh ed (early 1930) [9 ]E . Inonil and P.F. Zweif el, Develop m ents in Transp o rt Theory (Academi c, 1967) [l 이 C. Jac oboni and P. Lug li , The Monte Carlo Meth o d for Semi - conducto r Devic e Sim ulati on , (Sp r in g e r, 1989) [11 ] H. Kahn, Ap pli ca ti on s of Monte Carlo, USAEC rep. AECU -3259 (RAND Corp. , 1954) U 끽 A.N . Kalin o vskii , N. V. Mokhov, and Yu.P. Ni ki t in, Passag e of Hi gh -Energy Part icle s thr oug h Matt er , (AIP, 1989) 園 E.E . Lewi s and W.F. Mi ller , Comp ut a t i on al Meth o ds of Neutr o n Transpo r t , (W ile y, 1984) 詞 I. Lux and L. Kobli ng e r, Monte Carlo Part icle Transp o rt Meth o ds: Neutr o n and Photo n Calculati on s, (CRC Press, 1991) [1 하 G.I. Marchuk and V. I. Lebedev, Numeri ca l Meth o ds in the Theory of Neutr o n Transp o rt , (Harwood, 1986) [16] N. Metr o p o lis, in Monte - Carlo Meth o ds and Ap pli ca ti on s in Neutr o nic s , Photo n ic s and Sta t i stica l Phys i c s , ed. by R. Alcouff e, R. Dautr a y, A. Forste r , G. Ledanois and B. Mercie r , (Sp r in g e r, 1985), pp.6 2-70 [l 기 H.A. Mey e r, Sy m p os iu m on Monte Carlo Meth o ds, (Wi le y, 1956) [18 ]W .R. Nelson, H. Hira y a ma and D.W.0. Rog e rs, The EGS4 Code Sys t e m , SLAC pu b. SLAC-265 (1985) [l 이 J. Sp a nie r and E.M . Gelbard, Monte Carlo Pr inc iple s and Neutr o n Transp o rt Problems, (Addis o n-Wesley, 1969)
제 10 장 광자와 전자의 운송 광자와 전자의 운송 현상은 저에너지 영역에서 광범위하게 옹 용되고 있다. 이들은 소립자이기 때문에 고에너지 영역에서도 그 둘의 운송은 복합 구조를 가지는 다른 입자들에 비해서 비교적 간단하다. 10 장에서는 이들의 운송을 어떻게 전산 모사하는지 자 세히 살펴본다. 10. 1 서론 9 장에서의 논의는 운송 현상을 기술하는 데에 필요한 좌표 및 환경 설정, 그리고 반응률이 주어졌을 때 원하는 확률 변수를 어 떻게 표본추출하는지와 같은, 운동학적이거나 방법론적인 것에 관해서였다. 운송 현상을 좀더 깊이 이해하기 위해서는 입자가 매질과 일으키는 반응들에 관한 단면적들이 필요하다. 매질을 두과하는 고에너지 입자들이 매질과 일으키는 반웅은 여러 가지가 있다. 이들에 관한 기본 물리 법칙들에 대해서는 핵
력이나 전자력처럼 잘 알려져 있는 것도 있으나 강작용처럼 아직 도 완벽하게 알려져 있지 않아 그것이 연구의 대상이 되는 수가 많다• 10 장에서는 가장 잘 알려진 전자기 작용을 하는 입자들에 한해서 논의하기로 하자. 광자와 전자는 소립자이기 때문에 그들 의 운송은 복합 구조를 가지는 다른 입자들에 비해서 비교적 간 단하다. 광자가 전자기력에 의해 매질과 일으키는 반응은 다양하다. 레 일 리 (Ray le ig h ) 산란, 광전 효과 (Photo e lectr i c eff ec t) , 콤프턴 (Comp ton ) 산란, 여러 가지 쌍생성들 (Pa i r creati on ), 전자-반전 자, 뮤언-반뮤언, 중간자-반중간자, 쿼크-반쿼크 등, 입사 에너 지의 크기에 따라 실로 많은 반응둘이 가능하다. 이들 중에서 콤 프턴 산란을 제의한 다른 반응들은 원자의 전하 분포에 민감하게 의존한다. 전자의 상호작용들은 궤도 전자로부터의 산란 (Moller 산란), 양전자로부터의 산란 (Bhabha 산란), 양전자와 결합해서 두 개 이 상의 광자를 방출하는 쌍소멸 (Pa i r annih i l a ti on ), 원자핵의 정전 장의 영향 하에서 일어나는 제동 복사 (Bremss t rahlun g), 원자핵 과의 탄성 충돌에서 에너지를 잃지 않고 방향만 바꾸는 다중 산 란 (Mu ltip le 산란) 등이 있다. 이들 상호작용들 중에서 제동 복사 를 제의한 나머지들은 원자의 전하 분포와는 거의 무관하여 그 산란 단면적을 계산하기 위해서 점입자들의 파인만 (Fe y nman) 진 폭만을 고려해도 된다. 광자와 중성자는 전기적으로 중성이기 때문에 다시 원자들과 상호작용을 할 때까지 직전한다. 하지만 전자는 원자핵과의 다중 산란에 의해서 끊임없이 방향을 바꾼다. 또한 의부 전자장이 존 재할 경우에도 전자는 영향을 받게 된다.
10.2 원자로부터의 산란에 관한 정확한 공식 입사 광자나 전자를 산란시키는 표적이 점 입자이면 그 산란 단면적을 파인만 진폭으로부터 쉽게 계산할 수 있다. 하지만 원 자 또는 원자핵처럼 단순하지 않은 내부 구조를 가지는 표적으로 부터의 산란은 상호작용하는 동안 표적을 구성하는 개개 입자들 의 상태에 관한 정보를 필요로 한다. 비상대론적 영역에서 광자 나 전자의 전하 분포로부터의 산란 단면적에 관해서 고급 양자역 학 교과서들〔 Landau 등 , 1965 ; Beth e 등, 1986 ; Loudon, 199 아에 자세한 설명들이 나와 있다. 하지만 광자는 본질적으로 상대론적 인 객체이고 전자도 입사 에너지가 수 MeV 를 초과하면 상대론 적으로 되기 때문에 이들을 양자장론에 의해서 다루어야 한다. [B j o rken 등, 1964 ; Cheng 등, 1984] Drell 과 Walecka[196 사는 Be t he 와 Re it ler[193 산의 결과를 일 반화시켜 경입자가 입사하여 질량, 스핀, 형태 인자와 최종 상태 가 임의적인 표적 입자로부터 산란하는 경우에 대해서 적용할 수 있는 공식을 유도했다. 광자의 벡터성과 전하 보존의 법칙으로부 터 유도된 그들의 공식은 한쪽 끝에는 경입자가 있고 다른 쪽 끝 에는 원자핵이 있어서 그들 각각의 전류 밀도들이 가상 광자에 의해서 연결되는 일반적인 전자기 반응에서 모두 유효하다. (그림 10. la , b 참조) 이 공식을 사용하면 표적 입자가 편극화되어 있지 않고 그 최종 상태를 측정하지 않는 경우, 표적 입자들의 전하 분포로 인한 영 향은 운동량 전달 q와 에너지 손실 4 에만 의존하는 두 개의 구 조함수들 Wi(q러 4) 와 昭(q 2, 4) 에 의해 완전히 결정된다. 입사 광자의 편극 벡터와 4- 운동량을 e 과 k, 출사 전자의 에너 지와 4- 운동량을 E 와 P, 출사 반전자의 에너지와 4- 운동량을
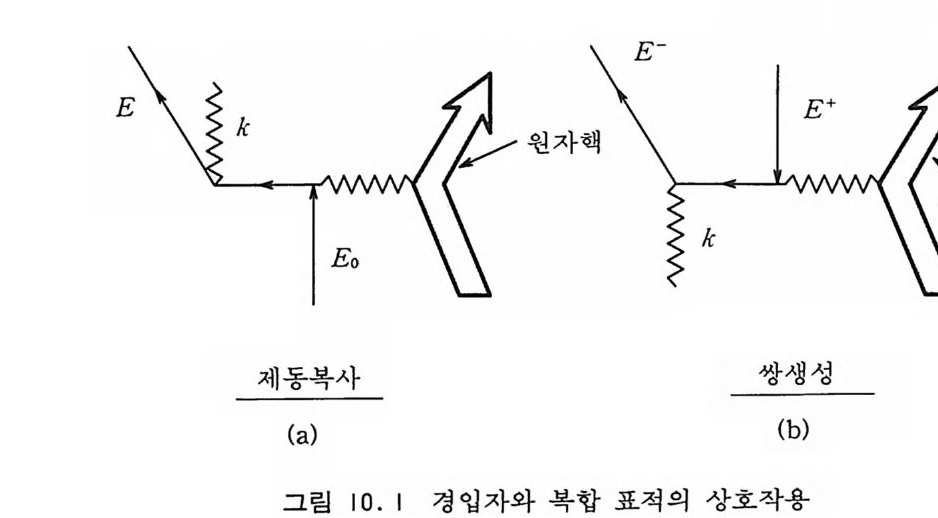 제동복사 쌍생성
제동복사 쌍생성
E+ 와 P+, 표적 원자의 질량과 초기 운동량을 m,., pi, 그리고 표 적 원자로의 4- 운동량 전달을 q라고 표시하면 미분 단면적은 da=e6~) 합충 ~7(LµWµ.,) (10.1) 와 같이 쓸 수 있다. 여기서 Lµ(p , P+, c, k) 는 전자의 여러 가지 가능한 진행자의 평균으로서 디락 (D i rac) 의 r- 행렬둘로 구 성되어 있다. 전류 밀도 ].µ(X) 마 (0) 의 표적 원자의 상태들에 대한 기대값들 의 합으로 정의되는 행렬 원소 Wµ., 에 관한 식에서, 구조 함수들 Wi(q라 L1) 와 J.½(q러 L1) 가 다음과 같이 간접적으로 정의된다. Wµv=L !
여기서 I P, 〉 는 운동량 P 를· 가지는 표적 원자의 초기 상태를 나 타내고 |f 〉 는 보존 법칙들을 만족하는 표적 원자의 임의의 충돌 후 상태를 말한다. W1 은 표적 입자의 자기 분포에 관해서, 그리 고 W2 는 주로 그 전하 분포에 관한 정보를 포함한다. 원자(핵)의 구조를 무시할 수 있느냐 없느냐는 입사 전자 또는 입사 광자로부터 표적 원자(핵)에로의 운동량 전달 t=―#이 원 자(핵)의 반경에 비해 얼마나 큰 가에 달려 있다. t - o 인 극한 에서는 표적 입자가 점 입자처럼 보일 것이지만 tR ~ t om(nucl)>1 이 되면 원자(핵)의 구조를 고려해야 한다. 우리가 10 장에서 고려하 고 있는 저에너지 (<2GeV) 광자의 경우 또는 입사 방향 근방으 로만의 산란의 경우에서는 원자핵의 구조를 무시할 수 있다. 식 (10.1) 을 양전자로 표적 입자의 최종 상태들에 관해 적분하 면 제동 복사의 출사 광자의 운동량에 대한 미분 산란 단면적을 다음과 같이 쓸 수 있다. d 야=:醫f뭉f空 x 성 (k+P++P f -P 一p ;)A(k, P+, Pf, p, p;) (10.3) 그림 10.la 와 10.lb 는 바깥에 붙어 있는 다리들의 위치만 다 롤 뿐이지 위상적으로는 사실상 동일하다. 따라서 제동 복사와 쌍생성은 그 산란 단면적들이 운동학적인 인자들만 서로 다르고 그 행렬 원소들의 형식은 같다. 구체적으로 말하면 제동 복사에 서의 출사 광자와 입사 전자가 쌍생성에서는 입자 광자와 출사 양전자로 바뀌기 때문에 kµ-- kµ, pµ-- pµ와 같이 대체하고 쌍생성에서는 반응 후에 생기는 전자-양전자가 양자장론적으로는 구별 불가능하기 때문에 제동 복사의 단면적에 위상 인자 (— 1) 울 별도로 곱해 주면 쌍생성의 단면적을 얻을 수 있다. 죽, 대체
공식 ― A( 一 k, P+, Pf, -P, P i)을 식 (10 . 3) 에 적용하여 쌍생 성에 관한 미분 산란 단면적을 다음과 같이 얻는다. da p=뜻登f空f맡 (10 . 4) x 성 (-k+P++ Pf+p-pi) (— l)A(-k, P+, Pf, -p, PJ 표적 입자와 양전자의 운동량들에 관해 적분하여도 제동 복사 와 쌍생성의 미분 산란 단면적들은 다음과 같이 연관이 된다. d요 dab d k =_ 一 (( dd요 a dpp \) 午: 검:. kp23E (10 . 5) 10. 3 원자의 형태 인자 원자의 형태 인자는 그 용도가 광범위하기 때문에 연구가 많이 되어 왔으나 계산이 용이하지 않기 때문에 산발적으로 다루어져 왔다. Do y le 과 Turner[I968] 는 구면 대칭성을 가지는 54 개의 원 자들에 대해서 상대론적인 Hartr e e-Fock 파동 함수를 사용하여 6MeV 이하의 저에너지 영역에서 형태 함수들을 계산하였다. Cromer 와 Waber 는 나머지 원소들에 대해서도 저에너지 영역에 서 형 태 인자들을 계 산하여 그 결과를 Inte r nati on al Tables for X-Ray Cr yst a l log ra ph y (v. W, 1984) 에 수록하였다. Hubbell 과 Overvo [1979] 는 이들 여러 문헌에 산재되어 있는 자료들을 종합 하고 고에너지 영역에서의 값들을 추가로 계산하여 q의 광범위 한 영역에서 (0 . 1keV< q
지만 형태 인자가 구조 함수들 W1 과 w2 와 어떻게 관련되는지 그리고 간단한 경우에 어떻게 계산할 수 있는지 살펴보기로 하 자. 우선 W1 과 W2 를 규격화시켜야 하는데, da (e + Z -+d요 e d' +E a ny thi n g ) 4~ {입 醫 (W 2+ 2 t an 멸 Wi) (10 . 6) 가 되게끔 하는 것이 관례이다. 원자의 형태 인자를 무시할 수 없는 영역은 운동량 전달이 작 은 영역으로서 q -0 인 극한에서는 완전 차폐된 중성의 입자처 럼 보인다. 반대로 q - CX)인 극한에서는 전자 구름이 사실상 존 재하지 않는 것이나 마찬가지로 입사 입자는 발가벗은 원자핵의 전하를 느끼게 된다. W1 은 (q2 /2m;) G1 에 비례하기 때문에, q가 작아서 형태 인자가 중요한 영역에서는, vfi <{ W2 이 되어 m 뢴· 고려해도 된다. W2 는 W2
또한 비탄성적 부분은 Wdnel(t ' 빠) =8(En-E 。_Q o) I ,~o f
F( t) = (l+a5t /4 )-2 (10 .14a) G 홍 1( t) =[1_F(t) ] 2 (10.14b) c~nel([) =1— | F( t) 12 (10 .14c) 와 같이 얻는데 여기서 ao= (ame)-I 은 보어 반경이다• 그림 10.2 에 몇 개 의 대 표적 인 원소들 ('H, 2He, 6C, 80, Na, 14Si , 29C u, 53I, B2Pb) 의 형태 인자들과 Z=53 인 Thomas-Fermi 원자의 형태 인자를 스케치했다.
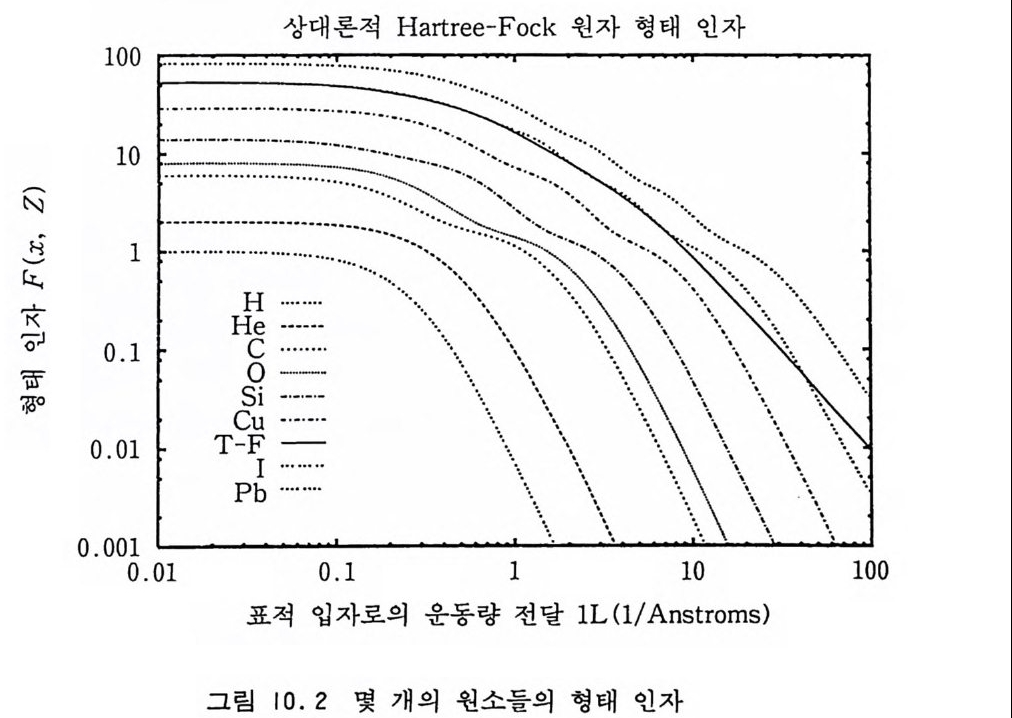 상대론적 Hart re e-Fock 원자 형태 인자
상대론적 Hart re e-Fock 원자 형태 인자
10. 4 광자의 상호작용 광자의 상호작용은 크게 세 가지로 구분할 수 있는데 그림 9.1 에 보이듯이 저에너지에서는 광전 효과가 지배적이고 고에너지에 서는 쌍생성이 지배적이지만 중간 에너지에서는 콤프턴 산란이 중요한 역할을 한다. 레일리 산란은 어느 에너지 영역에서도 지 배적이지 못하다. 저에너지 광자가 매질과 일으키는 상호작용에 관해서는 양자 전기 역학에 의해 거의 완벽하게 알려져 있다 [Re it ler 1954 ; Loudon 1990 ; Kalin o vskii 등, 1989] . 또한 산란 단면적 에 관해 방 대 한 데 이 터 도 NTIS [Saloman and Hubblell, 1986] 나 Brook- haven Lab [Ki ns ley, 1979] 또 는 Lawrence Li ve rmore Lab [Ple- chaty 등, 1978] 등에서 쉽게 구할 수 있다. 10. 4.1 콤프턴 산란 입사 광자가 정지 상태에 있는 자유 전자와 충돌하여 에너지의 일부를 전자에게 잃음으로써 산란되는 광자의 파장이 원래보다 길어지는 현상이 콤프턴 산란이다. Kle i n 과 N i sh i n 마 192 이가 최 초로 그 산란 단면적을 계산하였다. 입사 광자가 무극성일 때, 광자의 산란이 방위각에는 무관하므로 µ=cos 0 에서의 미분 산 란단면적을 훑 (a, µ) =21rr 근 )2( 꿉+f -1 + µ2) (10 .15) 과 갇이 나타낼 수 있는데, 여기서 a=k/mc2 은 입사 광자의 에 너지를 전자의 정지 질량의 단위로 잰 것이고 a'=k'/mc2 는 산
란광자의 에너지이다. re 는 전자의 고전적 반경이다 (re=e2/mc2 ::::::0 .2 8 A). 운동량 보존법칙을 사용하면 산란각 O 는 입사 광자의 에너지 a 와 산란 광자의 에너지 a ’ 에 의해 cos 0= (a+la) aaI '-a (10 .16) 와 같이 결정된다. 역으로 산란각 0 에 의해 a’ 를 표시할 수도 있다. a'= 1+ (1— ac os 0) a (10.17) cos 0 가 ― 1 과 +1 사이에서만 값을 가지기 때문에 산란 광자의 에너지의 최소값과 최대값은 dmI In= l+a2 a am’ ax=a 와 같이 얻어진다. 식 (10 . 15) 를 구간 [-1, 1] 에서 µ에 관해 적분하면 총 ` 산란 단면적을 얻는다. a=27r 머릉[ 2: 말!2- -In (1+2a)] +志 In (1+2a) —( 昌問 2} (10.18) 위의 식 (10.18) 은 비교적 간단하게 보이는 해석적인 식이지만 컴퓨터를 사용한 수치 계산에 있어서는 거의 비슷한 크기의 항들 이 서로 상쇄되어 유효숫자를 쉽게 잃어버릴 수 있고 또한 자연
대수 계산에 시간이 많이 걸린다. 이것을 빨리 계산하는 한 가지 방법은 이중 정확도에 의해 a 의 규칙적인 간격에서 6 를 미리 계 산하여 표로 만들어 둔 다음 원하는 a 값에서의 (5를 내삽시키는 것이다. 또 하나의 방법은 Has ti n g s[1955] 의 방식대로 식 (10.18) 을 유리식의 비율로 근사식으로 만들어 사용하는 방법이 다. 6=m2 7J3 +C1d 71/2 7+J 2 C+2d7J 2+n C+3 d3 (10.19) 여기서 매개 변수들은 다음 식들에 의해 주어진다. 7J = l + O. 222037a C1= 1.65 1035, C2= 9.340220, C3= —8 .325004 d1=12.501332, d2=— 1 4.200407, d3= l.69 9075 이제 산란각을 표본추출하기 위해서 확률 밀도 함수 p(µ)=la 一dd一µa 에 의해 µ룰 추출해야 한다. 식 (1 0.15) 가 겉으로 보기에는 간 단하지만 실제로는 µ의 복잡한 함수이다. 몇 개의 a 값에서 (da/dµ) 를 그림 10.3 에 스케치했다. 여기서 눈에 띄는 것은 a 값이 커짐에 따라 µ:::::::1 근방에서 곡선이 심하게 구부러지고 µ= 1 에서 (da/dµ) 가 최대값 4m 수를 취한다는 것이다• 거절 방법을 사용할 경우 적절한 거철 함수를 정해 주어야 하 는데 이것을 g(µ) =p (l) 로 취하면 간단하기는 하지만 곡선과의 사 이에 빈 공간이 많아 수용률이 매우 낮을 것이다. 간단한 거절 함 수를 찾을 수가 없을 때에는 3.6 철에서 논의한 사각형-쐐기-꼬리 의 방법을 응용하면 다소 복잡하기는 하지만 언제나 가장 효율적
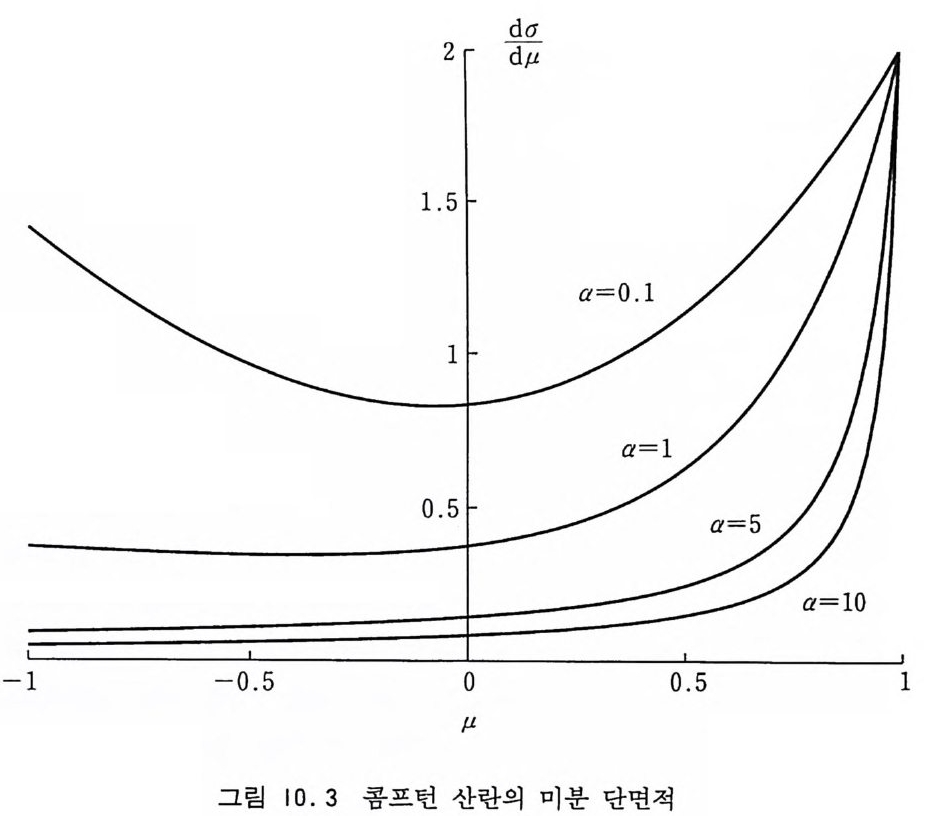 2 r ddµ6
2 r ddµ6
인 표본추출 방법을 얻는다. 하지만 a 의 값에 따라 확률 밀도 곡선의 모양이 변하기 때문에 매번 면적들을 계산해야 한다면 매 우 번거로운 일이다. 이런 경우에는 2.3.3 절에서 논의한 Bu t cher 의 합성 방법 을 사용하여 야 한다. Kahn[1954] 이 이 방법을 사용하여 개발한 알고리즘을 소개하 면 다음과 같다. Kle i n-N i sh i na 의 공식 (10.15) 에서 y =a/a’ 이 라고 두면 확률 밀도 함수는 p(y) =志 2(y -l+ 》군), l~y ~ (1+2a) (10 .15 ')
이 된다. 이제, 이 식을 두 개의 확률 밀도 함수들 P1(y ), P2(y ) 의 합으로 p(y) =¼P1(y) +志 P2( y), (10 .20 a) P1(y ) =¼,(y리), (10 .20 b) Pz(y ) = 孟2 2 (µ2+}) (10 . 20c) 과 같이 바꾸어 써준다. 여기서 KI, K초 jP i(y )dy =l 이 되게 끔 하는 규격화 상수들이다. 그런 다음, 확률 1r1=(1+2a)/ (9+2a) 를 가지고 PI, 또는 1r2=8/(9+2a) 를 가지고 P2 를 선택한 다. pi(y), P2(Y) 는 여전히 복잡한 함수들이기 때문에 이들과 비슷하면서도 간단한 비교 함수들에 의해 y를 일차적으로 표본추 출한 다음, 그것의 수용 여부를 pi(y), P2( y)에 의해 판가름하 는 전략을 세운다. (분포 -1) 이 선택되면 확률 밀도 함수 g1 (y ) =(1+2a)/2a y 2 에 의해 표본추출한 y를 PI( y)에 의해 수용 여부를 가린다. (분포 -2) 가 선택되면 정의구간 내에서 균일 분포 난수 y를 추출하여 P2(Y) 에 의해 수용 여부를 가린다. 입사 광자의 에너지가 낮을 때는 죽 a<3.5 일 때는, (분포 -2) 가 선택될 확률 이 더 크기 때문에 저에너지에서는 상당히 효율적일 것이다. Kahn 의 알고리즘을 요약하면 다음과 같다. 困 1) 세 개의 난수 &, 令 t3 를 추출하여 終 ;:나이면 y +-1+2a t2 로 놓고 2) 로 감
아니면 y +-1 2::a;2, µ +- 1 一 (y一 1)/a 라고 놓고 3) 으로 감 2) t 3~4( y -1- y -2 ) 이 성립하면 µ +-1 ― 2& 을 출력 아니면 1) 로 되돌아 감 3) t3~ (µ2+ y -1)/2 이 성립하면 µ룰 수용하여 출력 아니면 1) 로 되돌아 감 이 알고리즘의 표본 수용률은 a=2 에서 0 . 65 로서 수용할 만하 지만 에너지가 증가함에 따라 계속적으로 떨어져 a=20 에서는 0.34 정도가 되어 쓸모없게 된다. Kob li ng er[l975] 는 Bu t cher 와 Messel[1960] 의 혼합 방법을 이 용하여 azl+ /3에서 사용할 수 있는 직접적이고 효율적인 알 고리즘을 개발했다. 확률 밀도 p (x) 가 몇 개의 음이 아닌 항들 의 합으로 표시될 때, 죽 p(x ) = i~N= I cp; (x) (10.21) ¢i(x ) >O, i= l, 2, …, N 일 때, 이것은 언제나 식 (2.36) 또는 (2 . 37) 과 같은 형식으로 쓸 수 있다. 이런 경우, p (x) 에 따라 얻어지는 확률 변수 x 는 확률 p;=f¢;( x) dx 에 의해 i를 결정한 다음 확률 밀도 f1· ( x) = ¢i (x) /pi
에 의 해 표본추출하는 것 과 같다. 이 정 리 를 Klein - Ni sh in a 공 식에 적용하기 위해 식 (10.15) 를 다시 써보면 皇 =K(A+ 론+음+읍) (10 . 22) x=a/a', l~x~l+2a K= 굽 /a A=l/ 감, B=l ― 2(1+2a)/ 감, C= (1+2a)/a2, D=l 이 된다. 확률 밀도 p (x) = (J -Id( J/ dx 를 p (x) = L4!
P2 군 (1- 망 )In b, b=l+2a 와 같이 해석적인 형식이 얻어진다. 이제 각각의 ¢ , (x) 에 대해 역변환 방법을 쉽게 적용할 수 있 다. 죽 구간 [O, 1] *사이i:에 r 서rp ;(균t) 일dt = 분 t포 난수 g를 취한 다음 (10 . 25) 롤 x 에 관해 풀면 된다. 따라서 ¢1 에 대해서는 x=l+2as (10 . 26a) ¢2 에 대해서는 x=b' (10.26b) ¢3 에 대해서는 x= b/ (1+2at) (10.26c) ¢4 에 대해서는 x=l/n -cf (10.26d) 에 의해 확률 변수 x 를 구하면 된다. 다소 복잡하기는 하지만 a~l+ /3일 때는 Kahn 의 알고리즘 울 사용하고 a > l + {뭉게 서 는 Kobl i n g er 의 알고리즘을 사용하면 비교적 효율적인 방법이 얻어진다〔 Blom q u i s t 등, 1983]. 로소앨러 모스에서 개발하여 원자로 모사에 널리 쓰이고 있는 중성자-감마 운송 패키지인 MCNP 에서는 이 알고리즘을 채택하고 있다.
10.4.2 광전 효과 광전 효과는 광자가 원자에 흡수되어 소멸되고 이로 인해 들뜨 게된 원자로부터 전자가 튀어나오는 현상이다. 튀어나온 전자는 광자의 에너지에서 전자의 구속 에너지롤 빼준 만큼의 운동 에너 지를 가진다. 그림 9 . 1 에서 보이듯이 저에너지에서는 광자가 물 질과 가지는 가장 지배적인 반응이다. 광전 효과에 대한 상세한 설명과 입사 광자의 광범위한 에너지 영역에서 모든 원소들에 대해서 유용한 공식들 및 데이터가 Dav i dsson 과 Evans[l952] 의 평론에 나온다. 입사 광자의 세 개 의 에너지 영역에서 각기 다른 방법을 사용하여 산란 단면적을 얻는데 2 MeV 이상의 고에너지에서는 Hall [ l934] 의 공식이 유용 하다. Hulme 등 [1935] 은 구속 전자들에 대한 상대론적인 방정식 을 풀어서 광전 효과가 지배적인 중간 에너지 영역에서, 0.35 MeVsks2MeV, 정확한 산란 단면적 공식을 계산했다. 0.35 MeV 이하의 저에너지 영역에 대해서는 Sau t er[1931] 가 유도한 상대론적인 공식이 가장 정확하다. 최근에 나온 자료들로서 IsZslOO 사이의 원자들에 대해서 그리고 입사 광자 에너지의 IkeVskslOOMeV 영역에 걸쳐 S t orm 과 Israel[1970] 의 목록이 있고 또한 Sco fi eld[I97 외에 Hartr ee -Slate r 중심력 퍼텐셜을 사용하여 IsZsIOl 사이의 원 자들의 모든 원자 껍질들에 대해서 그리고 입사 광자 에너지의 1 keV 학후 .5MeV 영역에 걸쳐 상세하게 수치 계산한 결과들이 목록화되어 있다. 이들 자료들은 NIST 의 Cente r for Radia t i on Research 에 서 컴 파 일 하 였 는 데 [Saloman 등, 198 이 , BNL 의 NNDC(Nati on al Nuclear Data Cen t er) 의 컴퓨터를 통해 칙접 온 라인으로 얻을 수 있다. NNDC 데이터는 입사 광자 에너지의 1
keV 악 slOO GeV 영역에 걸쳐 lsZslOO 사이의 모든 원자들 에 대한 것이다. NNDC 데이터를 얻는 방법에 대한 자세한 설 명은 Chae 등 〔 199 이에 나와 있다. 수소 원자의 광전 효과에 대한 초보적인 설명은 Loudon[l990] 또는 Be t he 와 Jac kiw [l98 이 의 책 들에 나와 있는데 광전 효과 단 면적은 急= 2:;c 꿍 If 따 ex p(i k•r) €·vu ;d% 「 (10 .27) 에 의해 주어진다. 여기서 (1)와 e 은 입사 광자의 주파수와 편극 벡터이고 P f는 출사 전자의 운동량, u1· 와 U f는 표적 원자의 초 기와 말기의 상태 함수이다. 광자의 진행 방향을 z 축, 편국 벡터 e 이 x 축 방향으로 있다고 하고 출사 전자의 출사 각도를 (0,
표 10. I 식 (10.30) 의 계수들 “21 1l.. 56 2276a1481 XX 1100--99 ——25.. 6 ll8 O3bnXX 1l 00--1122 l4..1 07237C XXn 1l00--22 12p n 3 l.13 30 X l0-9 -2.1 7 7x 1 0- 12 2.0 1 3 X 10-2 3.5 4 一 9.12 X 10-11 。。 4
온라인 데 이 터 대 신 Sco fi eld 의 자료에 맞추어 K- 껍 질 광전 단면적 야에 대한 경험적인 식을 사용할 수도 있겠는데 頂 ubbell 등, 169K8 ~0]Z 5 n主~I aln + + c bnnZZ E~- Pn abta or mn (10.30) 이다. 여기서 입사 광자의 에너지 E 는 MeV 단위이고 매개 변 수들은 표 10.1 에 의해 주어진다. 야에 5/4 를 곱하면 총 단면적 이 얻어전다. 야의 간에 대한 비례성은 광전 효과의 일반적인 속성인데 원 자 번호가 큰 원소들에서는 광자의 에너지가 lMeV 근방에서도 광전 효과 단면적이 매우 커져 콤프턴 산란 단면적과도 비슷해지 는 것을 알 수 있다. 출사 전자의 출사 방향은 미분 단면적에 의해 표본추출해야 하 는데 식 (10.28) 은 ¢와 0 에 대한 인자들이 분리되어 있어서 편 리하다. ¢의 표본추출은 f(¢) ex: cos2 ¢ 에 의해 하면 된다. 0 의 표본추출은 f( 0) oc sin 2 0/[1— (vf / c)cos 0]4 (10 . 31) 에 의해 해야 되는데 sin 2 0 에 의해 표본추출한 O 를 거절 함수
g( 0) = (l— vf/ c)4/[l-(v f/ c)cos 0]4 (10. 32 ) 에 의해 수용 여부를 결정하면 될 것이다. 광전 효과 출사 전자의 각도에 따른 분포를 보기 위하여 그림 10 . 4 에 F(0) =sin 2 0/(l-{3 cos 0)4 (10 . 33) 를 스케치했다.
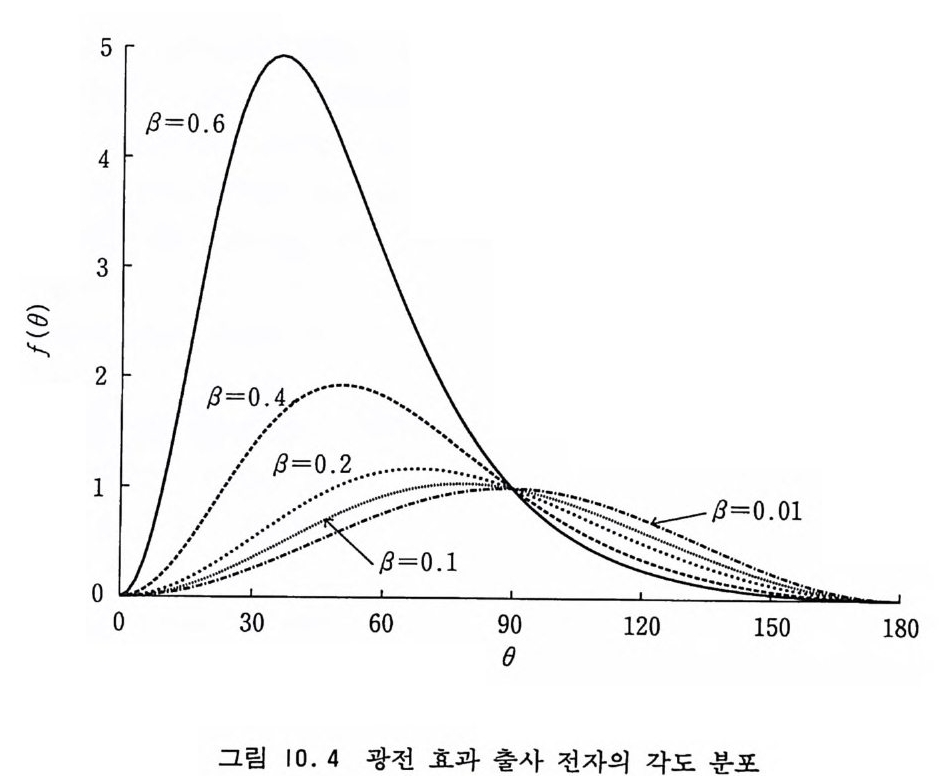 5
5
10. 4. 3 쌍생성 1933 년 에 Ni sh in a 와 Tomonag a [1933], Op pe nheim er 와 Plesset[ 1 933] 그리고 He it ler 와 Sau t er[l93 이에 의하여 쌍생성 전폭이 처음으로 계산되었다. 그 이듬해에 Be t he 와 Heit le r [1934] 가 보론 (Born) 근사법을 사용하여 쌍생성과 전자의 제동 복사 두가지 현상을 동일한 상대론적 방법으로 다루고 원자핵의 차폐로 인한 수정까지도 포함하는 공식을 계산하여 현재까지도 그 공식이 널리 통용되고 있다. 쌍생성에 관한 전통적인 평론은 Motz , Olsen, Koch[l96 이로서 상당히 체계적으로 다루어 고에너지의 상대론적인 영역에서 유용 한 단면적들의 근사 공식들과 도표들울 포함하고 있다. 하지만 저에너지 영역에서 유용한 공식은 도출해내지 못했다. SLAC 에 서 개발한 몬테카를로 패키지 EGS4 에서 사용하는 공식들은 이 평론에 나오는 공식들에 바탕을 두고 저에너지 영역과 비탄성 충 돌로 인한 효과를 보정하기 위하여 경험적인 인자들을 추가한 것 둘이다. Tsa i [l97 사의 평론에서는 Drell 과 Walecka[l96 사의 식 (10. 1) 을 사용하여 정확한 미분 단면적 공식들을 유도해 냈다. 그는 특 히 원자의 형태 인자를 비교적 완벽하게 다루었고 Motz 동 [1969 〕에서 무시한 전자 구름으로부터 쌍생성 효과를 포함했다. Tsa i의 공식은 완벽하지만 그 대신 너무 복잡하여 그것들을 사 용하여 컴퓨터에 의한 몬테카롤로 모사룰 하기에는 효율적이지 못하다. 그는 고에너지 좁은 생성각도 국한에서 유용한 공식을 유도하였는데 이것은 Motz 등의 공식에 전자 구름으로 인한 비 탄성항을 추가한 형태이다. 쌍생성에 관해 가장 최근에 나온 평론은 Hubbell 등〔 1980] 으
로서 입사 광자의 에너지 l MeV 부터 100GeV 까지의 영역에 걸 쳐 모든 원자들에 대해서 쌍생성은 물론이고 콤프턴 산란, 광전 효과, 레일리 산란을 포함하여 광범위하게 총 단면적을 소상하고 완벽하게 목록화하였다. 특히 다른 평론들에서 빠뜨린 저에너지 영역에서 유용한 공식들을 소개하였는데 총 단면적만 수록하고 있다. 미분 단면적은 나오지 않아서 운송을 모사하는 데에 부분 적인 도움이 될 뿐이다. 쌍생성에서는 광자가 전자 구름에 둘러싸인 원자핵 또는 궤도 전자들의 정전장과 반응하므로 그 산란 진폭을 계산하기 위해서 는 식 (10.1~2) 를 사용하여야 한다• 10. 4. 3.1 쌍생성 미분 단면적 식 (10.1) 을 반전자의 에너지와 산란각에 대해 적분을 시행하 고 지루한 대수 계산울 통해 식을 정리하여 얻는 전자의 에너지 와 산란각에 대한 미분 단면적을 좁은 쌍생성 각도 고에너지 극 한에서 m2/E 라 k·PIE 리 짜 /(k-E) 라 (k• p )/(k-E)2 에 관해서 전개하면 미분 단면적에 관한 Be t he-Re it ler 의 공식을 얻을 수 있다. [T sai, 1974] 蟲p =합(룹){ [ 2 강::)~) _1 2 {1: 군tl_] c.i (oo) +[합릅t 1 + 4l: \下 ] x [X— 2Z 2/c((aZ)2)]} (10.34) 여기서 x=E/k, l=E 냉 2/m 러 lm1n=[~ 問訂
이고, fc 는 쿨롱 보정항으로서 z=(aZ)2 라고 하면 le (z) =z n~c=o I [n (n2+z) ]-1 칙 . 202z-l. 0369 강 + 1. 0 08 강/ ( I + z) (10 . 35) 에 의해 주어지며, G (oo) = G 점 (oo) + G 評키 (oo) =Z2+Z (10 . 36) X=xel+xin e l (10 . 37) =f군 (1+ 1) 2 園(t) + Q nel(t )] 업 mInd t tm 1n' 아다. 따라서 원자의 형태 인자로 효과는 X 안에 모두 함축되어 있다. 이 식을 입체각에 관해 적분하면 운동량 p에 대한 미분 단면 적을 얻는다. 훌꾹ii codl[ 2x;;: fv-1-+~昌힌 j (X— 2 Z2/c) (10 . 38) 이 식 을 Be t he-Be it ler 의 공식 과 Wheeler-Lamb [193 이 의 공식 과 대조하기 위해 그들이 사용한 함수들 ¢I, ¢2 와 c/;1 , c/; 2 를 사용하 여 다음과 같은 형식으로도 쓸 수 있다. 출눅(붉검 x+l)[z2(
z2(¢ 2 - 방 ln z)=12l00- -dfwd t 00. 40 b) Z(¢< - lnZ )= 2 i OO (: ;nleI)2 dl (10 .40c) z(¢2-f ln z)=12 』 OO (i\In le;4 dl (10 .40d) 이다. 베데 (Be t he) 는 위의 식들의 우변에서 l 에 대한 적분을 하여 근 사식을 얻었다. EGS4 에서는 베데의 근사식에 Thomas-Fermi 원자의 형태 인자를 대입하여 ¢1, ¢2 를 계산하고 있다. 또한 Bu t cher 와 Messe 吐 196 이은 이렇게 해서 계산한 ¢I, ¢2 의 값들을 재현시키는 근사식들을 도출해냈다. 하지만 EGS4 에서는 #I, ¢2 룰 계산하지 않고 위의 식 (10.39) 에서 z 2 의 위치에 Z~(Z) 를 대입하여 추가함으로써 궤도 전자들로부터의 기여를 보완하고 있 다. Tsa i는 수소 원자에 대해 위의 식들 (10.40a~d) 를 해석적으 로 정확하게 계산하여 베데의 근사식과 비교하였는데 그 차이가 0~4% 에 불과하다는 것을 확인하였다. 그는 베데의 근사식에 Thomas-Fermi 원자들의 형태 인자를 대 입하여 Z 값이 큰 원자 들에 대해서 ¢1, 舊 #I, ¢'2 를 Z 와 p의 함수로서 계산하였다 . Tsa i는 Wheeler 와 Lamb 의 계산 결과와 대조해 보기 위하여 Z 와 p 대신 ¢1, ¢2 를 계산하는 데는 r=lOOmk/EE'Z113=2008/ (mZ113 ) (10 . 41a) 롤 사용하고 ,P1 , ,P2 를 계산하는 데는 e=lOOmk/EE'Z213 = 2008/(mZ213) (10 .41b)
를 사용하였다. 여기서 8=m2/[2kx(l-x) ]이고 E'=k ― E 이다. 그는 여러 가지 /, E 의 값에서 수치 적분을 하여 얻은 ¢I, ¢2 의 奭 ¢2 의 값들을 재현하는 근사식들을 설정했다.
사식을 손으로 유도한 다음 컴퓨터에 의한 수치 계산울 하는 것 이 현명하다. 쌍생성 총 단면적에 관해서는 원자물리학자들에 의해 많은 연 구가 행해져서 여러 에너지 영역에서 유효한 근사식들이 유도되 었다. 이에 대한 자세한 설명은 Hubbell 등 [198 이에 나온다. 또 한 이 참고문헌에는 Z=l 에서 100 까지의 모든 원소들과 l MeV 에서 100GeV 사이의 광범한 에너지 영역에서 쌍생성은 물론 광 자의 모든 상호작용에 대해서 총 단면적들이 수록되어 있다. 그림 10.5 에 몇 개의 대표적인 원소들 (6C, 1 ◄ s i, 29cu, e2 p b) 의 총 단면적들을 스케치했다.
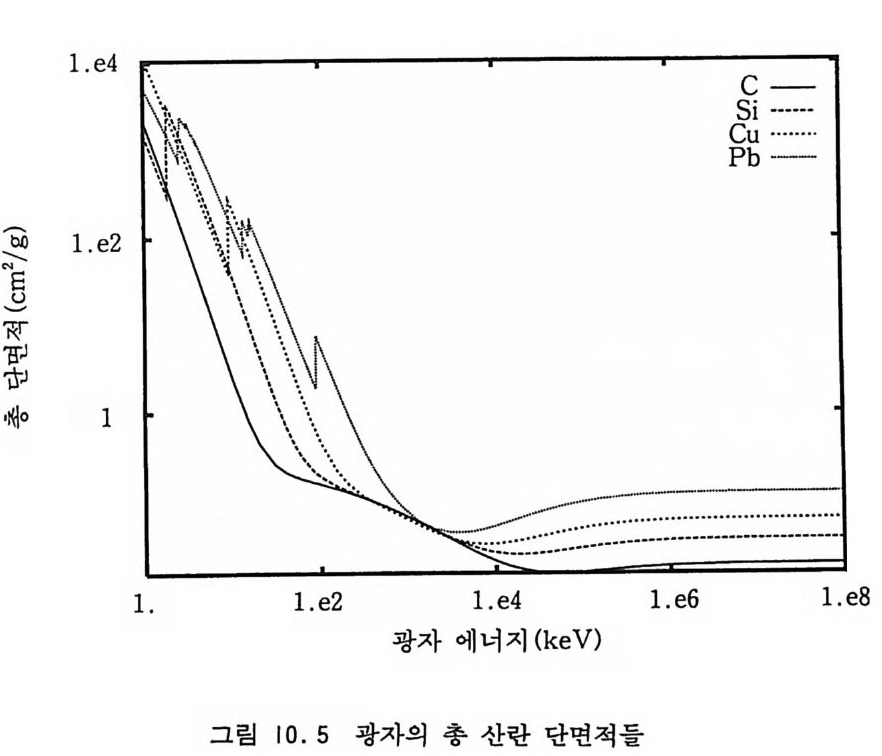 l·e41_\.. ·... e`2 CscuPib ―亡―
l·e41_\.. ·... e`2 CscuPib ―亡―
10.4.3.3 쌍생성 미분 단면적에 의한 표본추출 EGS4 에서는 쌍생성 미분 단면적의 공식으로 식 (1 0 . 39) 에서
식 (10.43) 의 대괄호 안에 있는 부분을 다음과 같이 써 보자. g( x ; k, Z) =~i2= I a;f; ( x)g ;( x) (10 . 44) 식 (10 . 43) 이 이미 이러한 형식으로 분해되어 있는 것처럼 보이 지만 두번째 인자, —fx (1 ― x) 가 음수이기 때문에 이대로는 적 합하지 않다. 하지만 대괄호 안의 식들은 언제나 양수이기 때문 에 항들을 재배열하면 식 (10 . 44) 의 형식으로 쓸 수 있다. 이제 /1(x) =3x 2 一 3x+ t3 (10.45a) 91 (x) =Z2(¢1 ―방 In Z ― 4/c)+z(¢1_ 훙 In z) (10.45b) a1=— 32 (10.45c) f2( x) =6x(l-x) (10. 45 d) g2 (x) 루 z2 信―강 In Z— 4/c)+z(¢2 ―흥 In z) (10 .45e) a 튼 T1 (10 . 45f ) 와 같이 정의하면 식 (10.43) 은 dq pp( xd p; k, Z) =-
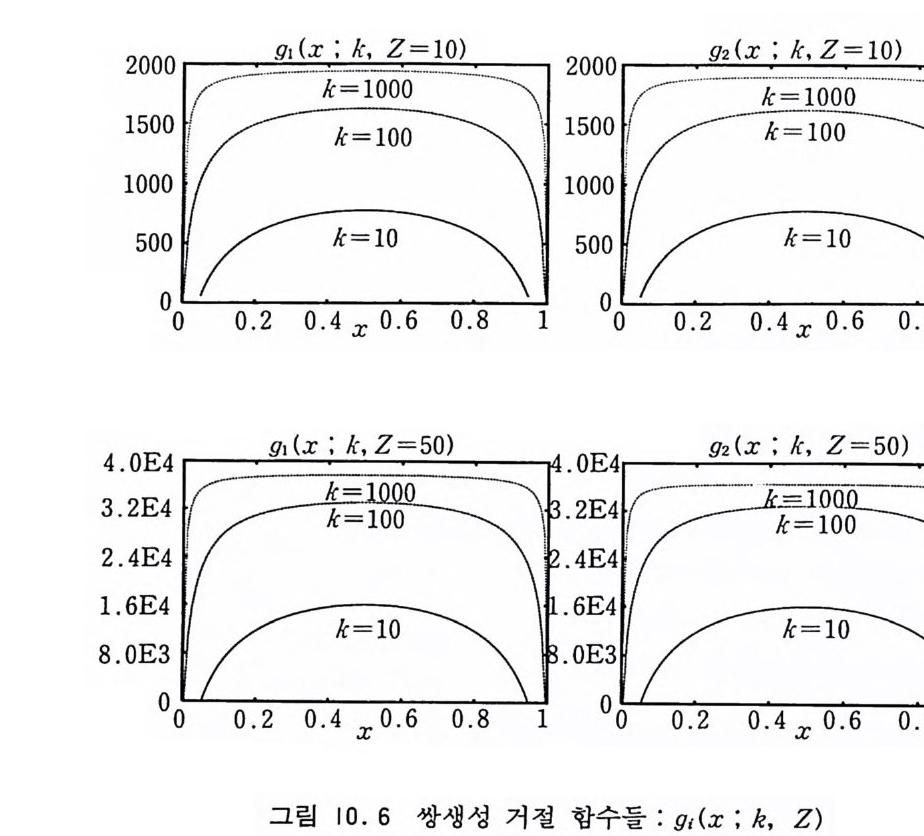 \\\o, 二三 Y1(x ; k:, Z=lO二 ) \| 1n2n:n:n 三g2 (x ; k, Z=lO) \
\\\o, 二三 Y1(x ; k:, Z=lO二 ) \| 1n2n:n:n 三g2 (x ; k, Z=lO) \
에 대해서 k=lO, 100, 1000 MeV 에서 이들 함수들울 그려보면 그립 10.6 과 같다. 또한 f1( x)g 1 (x ; k, Z) 와 /i(x )g 2 (x ; k, Z) 를 그립 10.7 에 나타냈다. 두 가지 분포 모두에서 Z 가 커지면 단면적이 매우 큰 것을 볼 수 있다. 또한 식 (10.46) 에서 l/k- 인자로 인해 k 가 작아지면 단면적이 커진다. (분포 -1) 에서는 /i (x) 와 gi(x ; k, Z) 가 서로 반대되는 성향을 가지기 때문에 출 사 전자와 양전자의 에너지가 o::;;; p ::;;;k/2 에 있는 k 。g 근방에 몰 리지만 k 가 작아지면 x=O 또는 x=l 근방의 아주 좁은 지역을
5.E 0o0 ( \ /014 .(2x ) 091.~ 4( x X \ ; 0k.,6 2Z .=5060.8 ) x1교~ E .5적~E~ o4· o,l 균 들일4을0하h..x28 (/게x 다/) 二시f~0g분kz. 4 =(포x Xa1 0;됨 i0 k에. ,을6 Z 곱 = 볼5해00. 8 )수\ ' 주 면있1 寧\ 寧
隣圈5 0。 8 1 ° 4.E4 ! \\k =1000 / 3.E 4 ~―一 / .4E 4 2.E 4 ti k=100 \f2. 2E4 .E 4 k=10 .1E4 그림 |0. 7 두 개의 쌍생성 분포함수들 : f,( x)g ,( x ; k, Z) 제의하고는 이돌의 에너지가 비다. (분포 -2) 에서는 출사 전자와 양전자의 에너지가 k/2 근방에 몰리는 경향이 있다. g , · (x) 들을 거절 함수로 사용하기 위해서는 그 값을 규격화시켜 두는 것이 편리하다. 그렇게 하기 위하여 이들을 그 최대값 g; (l/2 ; k, Z) 로 나누어 주고 최대값된다. g; (x ; k, Z) =g; (x ; k, Z) /g; (l/2 ; k, Z) (10 . 47) a,=aig i(l /2 ; k, Z) (10 . 48)g,-( x ; k, Z) = i~=2 l a'; f,-( x) g,-( x ; k, Z) (10 . 49) 확률 변수 x 의 이차 함수인 /1 (x) 와 /2(x) 에 의한 표본추출 방법에 대해서는 2 장에서 충분히 논의하였으므로 여기서는 자세 한 논의를 생략한다. 출사 전자의 방향은 원칙적으로 식 (10. 34 ) 에 의해서 표본추출해야 하지만 전방 방향으로 날카롭게 분포되 어 있으므로 입사 광자의 방향에 대해서 0=m/k 로 취해도 지장 이 없다. 광자의 운송을 실제로 전산 모사함에 있어서 입사 광자의 주어 전 에너지에 광전 효과, 콤프턴 산란, 쌍생성의 총 단면적들의 비율에 따라 세 가지 중 하나의 상호작용을 선택하는데, 만일에 쌍생성이 선택되면 먼 1) 식 (10.49) 에서 a i과 a2 의 비율에 따라 두 개의 분포들 중 하나 롤 선택한다. 2) /i (X) 에 따라 x 를 표본추출한다. 3) gi(X ; k, Z) 에 의해 수락 여부를 결정한다. 매질이 단일 원소로 구성되어 있으면 전체 식에 곱해지는 인자 둘은 p의 표본추출에서 전혀 상관이 없다. 매질이 복합 원소들 로 구성되어 있으면 좀더 복잡해지는데 더 자세한 논의는 EGS4 매뉴얼을 참조하기로 하고 여기서는 단일 원소 매질에 대해서만 논의를 국한시켰다.
10. 5 전자의 상호작용 전자가 물질 내에서 일으키는 반웅들은 복잡하다. 전자와 전자 사이의 Moller 산란, 양전자와 전자 사이의 Bhabha 산란 및 쌍 소멸 원자핵의 정전장 내에서 감속당하면서 광자를 방사하는 제 동 복사, 그리고 원자핵과 끊임없이 일으키는 충돌에 의해 표류 하는 다중 산란 등이다. 10. 5. l 전자-전자의 산란 두 전자의 질량 중심 좌표계에서 상대론적인 극한에서의 Moller 미분 산란 단면적은 훑=을(1¥+-b+o/) (10.50) 에 의해 주어진다. [B j orken 과 Drell, 1964, eq (7 . 84 )] 여기서 S= sin (0/2), c=cos(0/2) 이다. 위의 식을 표적 전자가 정지해 있 는 실험실 좌표계로 로렌츠 변환하고 출사 전자의 에너지 E 에 관한 미분 단면적으로 다시 쓰면 훑= /3『;。r [ C1 나(尸― C2) +召+,- c2)] (10 • s1) 와이고 ,같 이그 된속다.도 를여 기V 라서고 T하o=면E 。 /_3m= v 로 i 서e 이 다입.사 c전=자T의/T o운=동(E 에— 너m지) / To 로서 출사 전자의 운동 에너지의 To 에 대한 비율이며 c'= 1 ― e 이다. 또한 r=Eo/m 이라고 하면 C1=[ (r-l) /r]2, C2= (2r-1)/ 군
이다. 식 (1 0.51) 은 c 과 c' 에 대해서 대칭이므로 e 과 c' 의 상한이 1/2 울 넘지 못한다. 또한 식 (10 . 51) 의 발산을 방지하기 위해서 E 의 하한값 Ee 를 설정할 필요가 있다. 총 단면적을 얻기 위하여 미분 단면적 (10 . 51) 을 적분해야 하 는데 적분 영역을 ((Ec-m)/To=ccScSch=0 . 5) 로 취해야 한 다. ~ (cc, ch) oc (C1 (ch-cc) +;:-+>—¼-C2 ln 톱) (10 . 52) 여기서 주의할 것은 출사 전자의 에너지가 Ec 보다 적어서 c
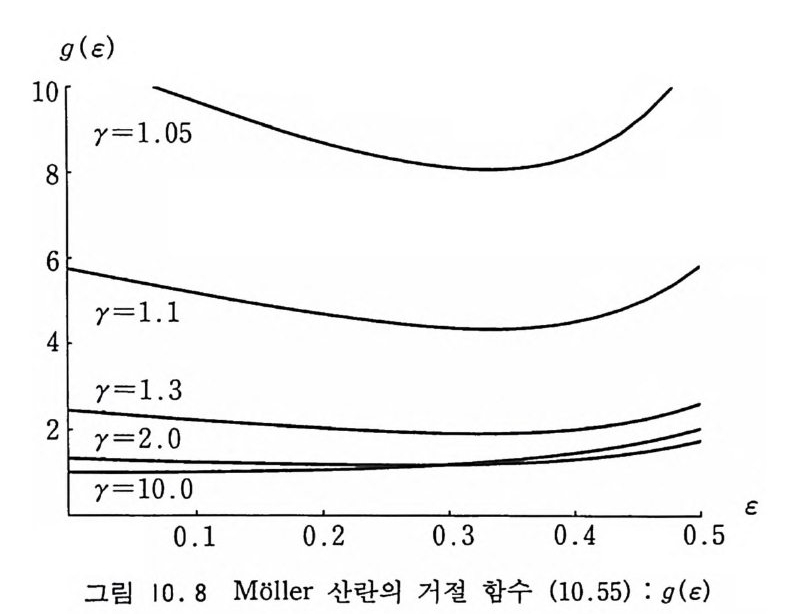 g( c)
g( c)
거절 함수인 g (E) 은 c=0.5 에서 최대값을 가지기 때문에 이것을 규격화시키기 위하여, g( E) 대신에 g( E) =g (E)/ g(Q .5) 을 사용 하면 될 것이다. 확률 밀도 f (E) 에 의한 c 의 표본추출은 역함수 방법에 의해 c= 1 一 ~(lc c- 2cc) (10 . 56) 로부터 손쉽게 구할 수 있다. I(c) 에 의해 추출한 e 을 g (c) 에 의해서 수락 여부를 결정하여 그것이 수락되면 e 을 출력한다. 주어전 e 에 대해서 전자의 출사각 O 는 식 (9.20) 에 의해 결정 된다. 10.5.2 양전자-전자의 산란 쌍생성에 의해 생성된 양전자가 그 짧은 생애에서 궤도 전자와
산란하는 현상이다. 두 입자의 질량 중심 좌표계에서 상대론적인 극한에서의 Bhabha 미분 산란 단면적은 훑=툴 (1:4C4 占팥+宁) (10 . 57) 에 의해 주어진다. 〔 B j erken 과 Drell, 1964, eq ( 7. 87 )] 위의 식을 표적 전자가 정지해 있는 실험실 좌표계로 로렌츠 변환하고 출사 전자의 에너지 E- 에 관한 미분 단면적으로 다시 쓰면 훑=-f[~(~三 )+B2+ c:(c: B4 홀)] (10 . 58) 과 같이 된다. 여기서 T+=E+-m 로서 입사 양전자의 운동 에 너지이고, 그 속도를 v 라고 하면 /3= v i e 이며, c= T- / T+= (E_ _ m)/T+ 로서 출사 전자의 운동 에너지의 입사 양전자의 운 동 에너지에 대한 비율이다. 또한 y =l/(r+l) 이라고 하면 B1=2 ―y리 B2= (1-2y ) (3+y 2 ), B3=2(1_y ) (1_2 y)러 B4= (1- 2y )3 이다• 양전자와 전자는 구별 가능이기 때문에 c 의 상한은 1 이 된다. 여기서도 (10.58) 의 발산울 방지하기 위하여 E- 의 하한값 Ee 를 설정할 필요가 있다. 총 단면적을 얻기 위하여 미분 단면적 (10 . 58) 을 적분해야 하 는데 적분 영역을 ((Ec-m)/T+=cc :s;;€::;;타 =l) 로 취해야 한 다. ~(cc, ch) 나》(土―土)― Bl ln 뭉 +B2(ch-cc)
며(석i_우 )_c 창(데노-,)J (10.59) 앞 절에서처럼 출사 전자의 에너지가 Ee 보다 작아서 E
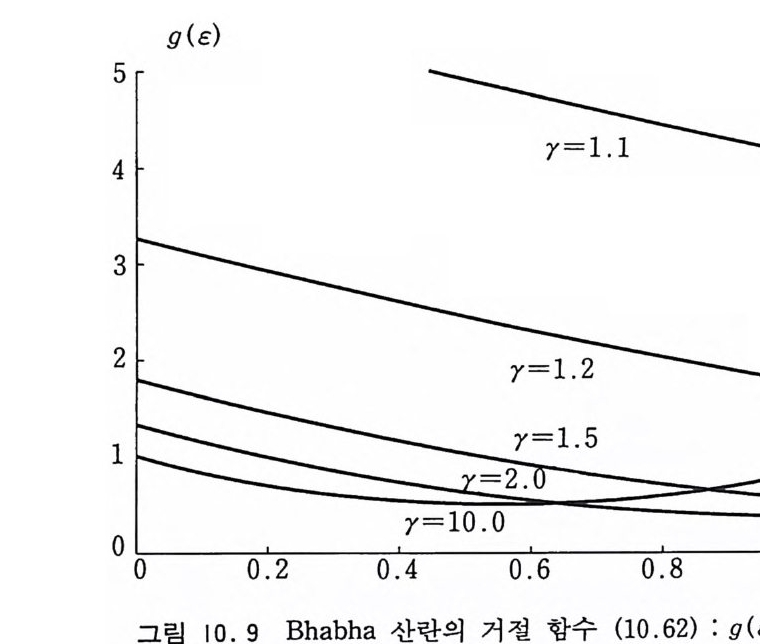 g( s)
g( s)
e= 1-~(€lc- ec) (10 . 63) 로부터 손쉽게 구할 수 있다. 주어전 c 에 대해서 전자의 출사각 O 는 식 (9.20) 에 의해 결정 된다. 10.5.3 쌍소멸 전자-양전자 쌍이 소멸하여 두 개 이상의 광자를 배출하는 현 상을 통틀어서 쌍소멸이라고 하는데 광자의 개수가 증가할 때마 다 단면적이 a::::-:1/137 만큼씩 줄어들기 때문에 사실상 두 개의 광자를 배출하는 현상만 고려해도 된다. 전자와 양전자가 부딪혀서 에너지와 스핀이 각각 (k, e),
(k', e’) 인 광자들로 쌍소멸하는 반응의 질량 중심 좌표계에서의 미분 단면적은 읊= 8p + (a;k:E) [운+f +2-4(e•e')2] (10.64) 에 의해 주어진다. [B j orken 과 Drell, 1964, eq ( 7.80)] 여기서 E+ 는 양전자의 에너지이고 p+는 양전자의 3- 운동량의 크기이다. 위의 식을 표적 전자가 정지해 있는 실험실 좌표계로 로렌츠 변환하고 광자둘의 스핀들을 평균화시켜서 출사 광자들 중 하나 의 에너지 k 에 관한 미분 단면적으로 다시 쓰면 훑 =S(k) +S(A— k) (10 .65 ) 가 된다. 여기서 r=E+!m 이라고 하고 A=r+l, T~=r-l C1=a2/AT~, C2=A+2r/A 라고하면 S(k) =Ci[ -1+ (C2-l/k)/k] (10.66) 이다. 두 개의 출사 광자들은 구별 불능이기 때문에 k 의 상한은 가 용 에너지(전자의 정지 질량 단위) A 의 절반인 A/2 이고 k 의 하 한은 출사 광자가 입사 양전자의 반대 방향으로 튀어나오는 cos 0= ― 1 에서의 값으로서 km1n=Al(A+P+Im) 이다. 쌍소멸의 총 단면적은 He it ler 의 공식에 의해 다음과 같이 주 어진다.
a(E+)= ¾i[군 :~ln (y+尸言)-問] (10.67) 식 (10.65) 에 의해서 표본추출하기 위해서 식 (2.46) 의 형식으 로 다시 쓰면 뿔= ,t;; 1n [ (1 一 cc) /cc]/(c) g (c) (10 . 68) 와 같이 쓸 수 있다. 여기서 c=k/A 이고 cc = km1n/A = l/ ( 汗 l + H 言) (10. 69 ) 이며 f(c ) ln [(1_ Cl c)/ Cc] —el , €cS€ScuS— A2 (10·(7100·、) 7 1 g( c) =l ― C+ 士 (2r_}) - .'I 이다. g(리울 몇 개의 r 값에 대해서 c 의 정의 영역에서 스케치해 보 면 그립 10.10 과 같다. g (c) 은 거절 함수이기 때문에 그 값이 0 보다 커야 한다. g (c) 이 0 보다 작을 수가 있는데 그림 10.10 에서 보듯이 r 의 값에 따라서는 상한값 (cu) 을 정해 주어야 할 필요가 있다. 또한 g (c) 은 c=l/A 에서 최대값을 가지는데 g( l/A) =1-2/A 저어서 1 보다 작다. 따라서 주어진 r 의 값에 대해서 식 (10.69) 에 의해 주어지는 cc 를 하한값으로 취하고 g(cu ) =O 을 만족하는 cu 를 찾아서 g (c) 의 값이 정의구간 (cc~€ ~cu) 에서 0 보다 크도록 해주어야 한다. g (c)=O 을 만족하는 cu 의 값을 r 의 함수로서 그립 10 .11 에 나타냈다. f (c) 에 의한 표본추출 역시 역함수 방법으로 할 수 있는데
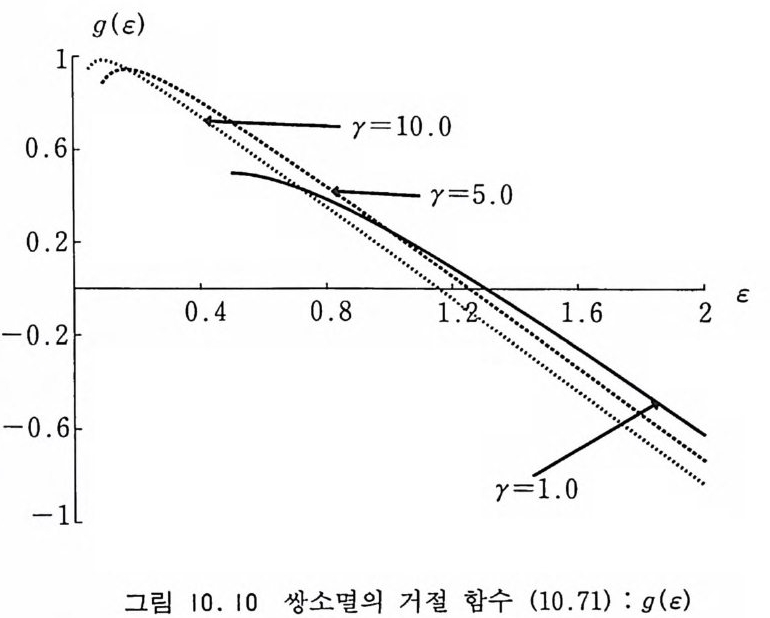 g( e)
g( e)
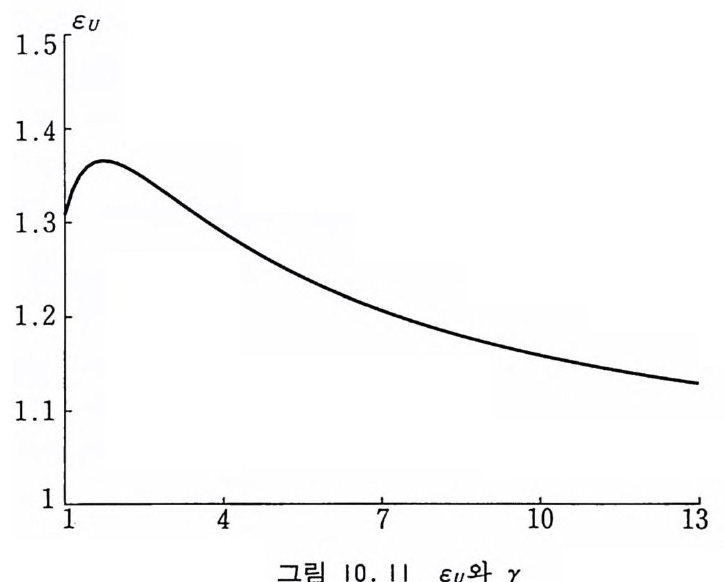 1.5 Eu
1.5 Eu
c= cc exp [~ In (1 —cc ) / cc] (10 . 72) 에 의해서 c 의 값을 얻을 수 있다. 그런 다음 g (E) 에 의해 수락 여부를 결정하고 c 이 수락되면 다른 광자에는 c'=l-E 을 부여하 면 된다. 또 한가지 언급해야 할 것은 양전자의 운동 에너지가 너무 작 아지면 식 (10.64) 가 발산하므로 p+의 하한값을 정해줄 필요가 있다. 이 경우 사실상 정지 상태에서 쌍소멸되는데 각각의 출사 광자에게 k=m 을 부여하고 그 방향은 서로 반대 방향으로 등방 적으로 분포되도록 해야 한다. 10.5.4 제동 복사 10. 5. 4.l 제동 복사의 미분 단면적 식 (10.5) 와 (10.34) 로부터 원자핵의 정전장 하에서 전자의 제 동 복사로부터 나오는 출사 광자의 운동량과 입체 산란각에 대한 미분 단면적울 다음과 같이 얻는다. 盆넒k 룹(를){[M,z+~」\》민 ]Gi(o o) (10. 73 ) +[2 (1만:f —4{ 갑* ]x[X ― 2Z2 fc ((aZ)2) J} 여기서 E 는 입사 전자의 에너지이고, 출사 광자의 에너지는 k, 그리고 출사각을 0k 라고 두면, y = k/E, l = E 냉t /m 러 lm1n= [ ::謨」 2 『 이다. G 와 X 는 식 (1 0.36~37) 에 의해 계산하는데 위에서 정 의 된 lm1n 을 사용해 야 한다.
또한 식 (10.5) 와 (10.39) 로부터 제동 복사의 출사 광자의 운 동량에 대한 미분 단면적을 다음과 갇이 얻는다. 言 =꾹胤§망y + y2) [ z2( ¢ 1- t In Z- 4 /c) +Z( 軒fi n z)] 내 (1 ―y) [Z2(¢1 玉) +Z( r/; 1 玉)]} (10 .7 4 ) 여기서 주목할 것은 쌍생성에서는 k 가 입사 광자의 에너지로서 초기 조건으로 주어졌고 E 는 출사 전자의 에너지로서 변수로 사 용되었는데 제동 복사에서는 E 가 입사 전자의 에너지, k 는 출사 광자의 에너지로서 그 역할이 반대로 되었다는 것이다. 하지만 두 가지 경우 모두 ¢1, 舊 r/;1, r/; 2 의 계산에서는 식 (10.41a ~b) 에 의해 정의되는 r, e 을 그대로 사용하여 식 (10.42a~d) 에 대입한다. 따라서 위의 식들의 우변의 중괄호 안의 원자 형태 인자와 관 련된 항들은 쌍생성의 경우와 똑같다. 하지만 그 앞에 곱해지는 y의 함수들은 이미 양의 수들이기 때문에 이미 식 (10.44) 의 형 식을 취하고 있다. 두번째 중괄호 안의 항은 (¢1 ― ¢2) 와 (r/;1 ―r/; 2) 를 포함하고 있어서 첫번째 중괄호 안의 항에 비해서 그 크 기가 매우 작다. 또한 전체 식에 곱해 주는 경험적인 인자, A' 는 쌍생성의 경우와는 별도로 얻어야 한다. 10.5.4.2 제동 복사의 총 단면적 Z=l 에서 100 까지의 모든 원소들에 대한 제동 복사의 총 단면 적들이 lMeV 에서 100GeV 사이의 광범위한 에너지 영역에 걸 쳐 Seltz e r 등 [1985] 에 자세하게 수록되어 있다. 그립 10.12 에 몇 개 의 대 표적 인 원소들 (6C, 80, 14Si, 29Cu, 53I, 82Pb) 의 제 동 복
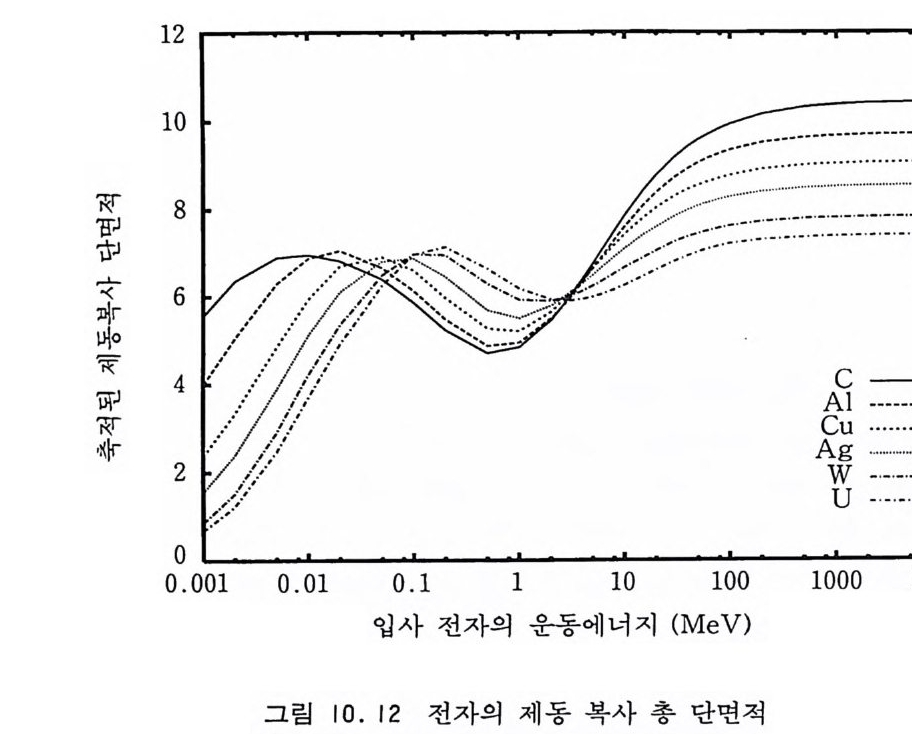 12
12
사 총 단면적들을 스케치했다. 10.5.4.3 제동 복사 미분 단면적에 의한 표본추출 출사 광자의 에너지를 너무 낮게 잡게 되면 식 (10.73) 이 발산 하기 때문에 하한값 kc 를 설정할 필요가 있다. kc 이하의 연성 제동 복사 광자들은 일일이 추적하지 않고 10.5 . 6 절에서 논의하 게 될 연속적 에너지 손실에 포함시키는 것이 효율적이다. 또한 k 의 상한값은 전자의 운동 에너지인 ku=E-m 으로서 주어진 다. 따라서 y =k/E 의 영역은 kc/E~ y ~ku/E 가 된다. 식 (10.73) 에 의해 표본추출하기 위해서 쌍생성의 경우처럼 혼 합 방법과 거절 방법을 병행해서 적용하기 위해서 식 (10.73) 을 다음과 같이 써보자.
g(y; E, Z)= i~=2 l aJ ; (y )g;(y) (10 . 75) 9/11 ((yy )) 三= Z (24 (¢2 1:4-t) (I방n Z- 강 -4y/ +c ) y + 2 )z (¢1-½In Z) ((1100 ..7 766ab)) a1= (Ll2-Ll1) (10 . 76c) 4= t1 (4 y c -2Y 접+ y 망 ), 42 = i l -(4 y u — 2y i+yt) /2 (Y) 三 (44 _2 4) (l- y ) (10.76d) gi(y ) =Z2(¢1-¢2) +Z(cf;1 - cf;2 ) (10 .76e) a2= 정1 다 ― 4) (10 . 76f) Lla=2Yc - Y~, L14= 2Yu - Yi g.(y ; E, Z) 와 g2 (y ; E, Z) 는 정의구간 (ye, Yu) 에서 양의 값을 가지며 y = y c 에서 최대값을 가진다. Z=lO, 50 에 대해서 E = lO, 100, 1000 MeV 에 서 이 들 함수들을 그려 보면 그림 10 .13 과 같다. 또한 Z=lO, 50 에 대해서 /1(y)gi(y ; E, Z) 와 /2(y) g2( y ; E, Z) 를 그림 10 . 14 에 나타냈다. (분포 - l) 에서는 /1(y ) 와 g1( Y ; E, Z) 의 증감이 서로 상충되어 말안장 모양의 곡선이 나온다. 이러한 변화는 입사 전자의 에너지가 높아질수록 더욱더 심해진다. (분포 - 2) 에서는 g2( y ; E, Z) 의 모양이 입사 전자의 에너지가 높아짐에 따라 오목한 모양에서 볼록하게 변하는 것이 눈에 뛸 정도로 심하다. (분포 -2) 는 (분포 - 1) 에 비해서 크기가 100 분지 1 정도로 작기 때문에 출사 광자는 사실상 (분포 -1) 에 의 해 표본추출된다고 볼 수 있다. g i (y)를 거절 함수로 사용하기 위해서 그 최대값 g; (Y c ; E,
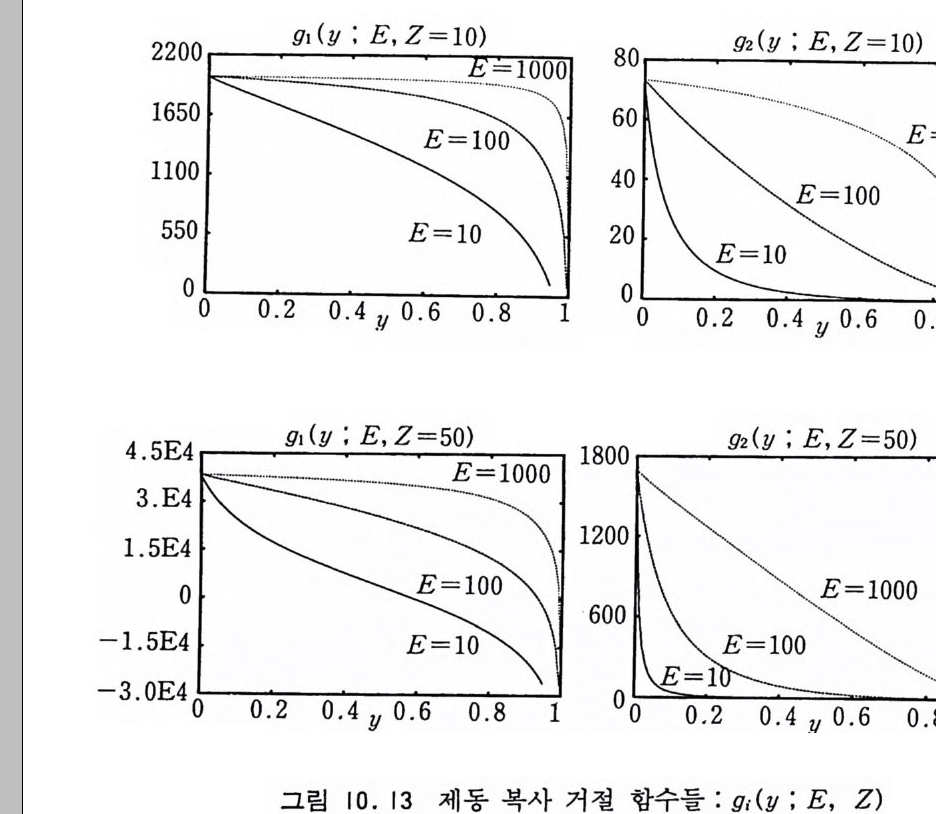 2200 g,(y ; E, Z=IOE) = l OOOj 80 gz( y : E, Z= l O)
2200 g,(y ; E, Z=IOE) = l OOOj 80 gz( y : E, Z= l O)
Z) 로 나누어 주어서 규격화시키고 최대값들은 a,에 곱해 주어야 한다. gi(y ; E, Z) =gi(y ; E, Z)/gi (Y c ; E, Z) (10 .77) a,=aig 1 ( Yc ; E, Z) (10 . 78) g(y ; E, Z) = ~2 a'J i(y) gi(Y ; E, Z) (10 . 79) i= l 전자의 여러 상호작용 중에서 제동 복사가 선택되면 출사 광자 의 에너지를 표본추출하는 알고리즘은
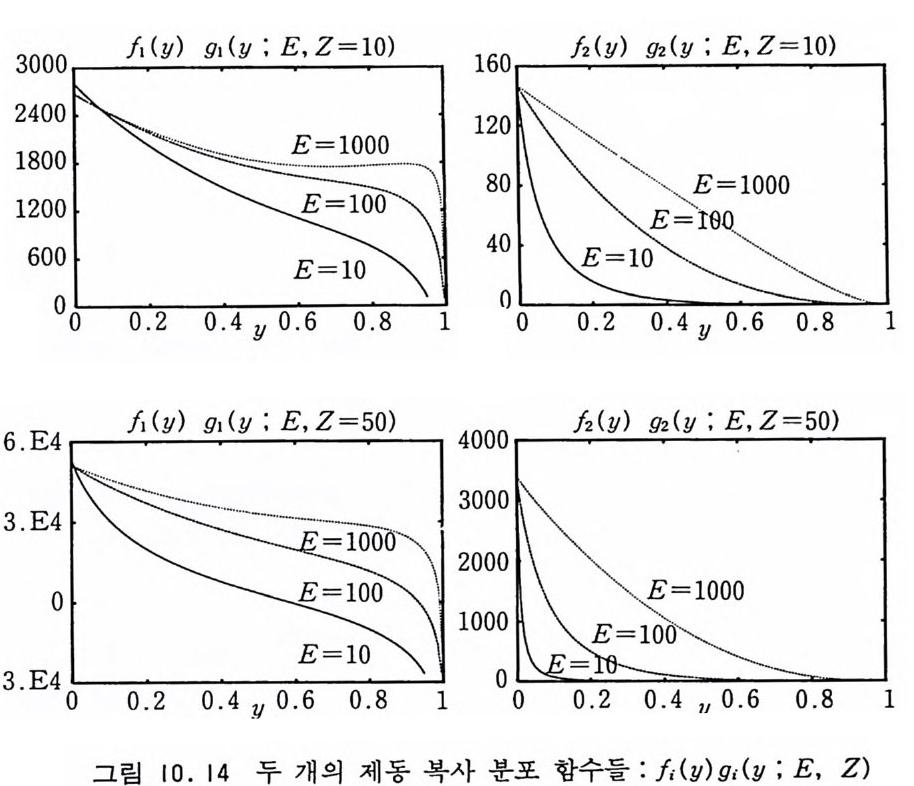 3000 I, (y) g, (y ; E, Z=lO) 160 fz( y ) gz (y : E, Z= l O)
3000 I, (y) g, (y ; E, Z=lO) 160 fz( y ) gz (y : E, Z= l O)
匠 1) 식 (10.79) 에서 a i와 a i의 비율에 따라 두 개의 분포들 중 하나 룰 선택한다. 2) /; (y~ 에 따라 y를 표본 추출한다. 3) g;(y ; E, Z) 에 의해 수락 여부를 결정한다. 출사 광자의 방향은 미분 산란 단면적 (10.73) 에 의해 표본추 출해야 하지만 전자의 방향 전환에 가장 큰 영향을 미치는 것은 다음 절에서 논의할 다중 산란이고 식 (10 .73 ) 에 의한 분포는 전
방 방향으로 날카롭게 분포되어 있기 때문에 광자가 입사 전자의 방향에 대해서 0=m/E 의 각도로 튀어나온다고 해도 지장이 없 다. 10.5.5 전자의 다중 산란 전하를 띤 전자는 매질을 뚫고 지나감에 따라 원자핵들과 탄성 충돌을 끊임없이 일으키게 된다. 이 과정은 주로 러더퍼드 산란 으로서 전자는 거의 에너지를 잃거나 얻지 않고 방향만 바꾸게 된다. 여기서 우리에게 관심의 대상이 되는 것은 전자가 두께 t 인 매질을 뚫고 지나왔을 때 누적된 산란각이 얼마냐 하는 것이 다. 다중 산란에 관해서 많은 연구가 진행되었는데 여기서는 Mo li ere [ l948] 와 Be t he[l95 인가 쓴 논문들을 참조하기로 하자. 10. 5. 5. 1 다중 산란에 관한 Mo li ere 의 이 론 Mo li ere 는 전자가 0 방향으로 튀어나갈 미분 산란 단면적에 대해서 다음과 같은 정확한 식을 설정했다. / ( 0, t) = 1 TJd TJ] o ( TJ0 ) X exp { —nt 1 a (x) xdx[l-]o ( TJx ) ]} (10 . 80) 여기서 6(x) 는 단일산란에서의 미분 산란 단면적이고 n 은 cm3 당 원자들의 숫자이며 lo 는 베셀 함수이다. x 가 충분히 커서 X>xo=XI(0 . 885aoz-113) 인 영역에서는 러더퍼드 산란처럼 a(x) 가 x-4 에 비 례 하여 감소하는 경 향이 있다. Mo li ere 는 6 (x) 에 서 이러한 인자를 따로 뽑아내어 ntC 1 (x) xdx =2x~xdxq (x) /X4 (10 . 81)
와 같이 나타냈는데 여기서 q (x) 는 실제 산란의 러더퍼드 산란 에 대한 비율을 나타낸다. 또한 Xe 는 x~=47rnte 4 Z (Z + 1) / (pv ) 2 (10 . 82) 와 같이 정의되는데 P 와 v 는 산란된 전자의 운동량과 속도이다. 위의 식의 두번째 인자에서 Z 대산 (Z+l) 을 사용함으로써 궤도 전자들로부터의 기여도 포함시키고 있다. 단일 산란에서 전자가 Xe 보다 더 큰 각도로 산란될 확률이 1 이 되기 때문에 Xe 를 단위 확률 각도 (unit pro babil ity ang le ) 라고 부른다. Mo li ere 는 또한 특성 차폐 각 (characte r is t i c screenin g ang le ) Xa 를 다음과 같이 정 의했다. —In Xa 玉 [1\ (x) dx/x +강 -In k] (10 .83) 베데는 x 에 대한 적분 영역을 세분화하여 각각의 영역에서 유 효한 근사식들을 사용함으로써 Mo li ere 의 식 (10.80) 을 좀더 간 단한 방법으로 유도했다. f ( 0) 0d0 = 11d111'yd y] o (11y ) ex 吐-¼y 2(- b + In -¼y2 )] (10 . 84) 여기서 b = In (xclXa) 도 l —2 C =l n (xc/x~) 2 (10 . 85) 인데 C=0.577 …는 Euler 의 상수이다. 또한 A=() / Xe 에 의해 정 의되는 A 는 ()의 단위확률 각도 Xc 에 대한 비율이다. 베데의 식 (10.84) 는 근사식이지만 산란각이 1 라디안에 비해 서 작은 영역에서는 매우 정확하다. 주목할 만한 점은 Molie r e 의 식 (10.80) 에서 유도된 베데의 공식은 매질과의 상호작용을
한 개의 매개변수 b 에 함축시키고 있다는 접이다• Mo li ere 는 Thomas-Fermi 퍼 텐셜을 사용하여 특성 차폐 각을 수치적으로 계산해 냈다. x 는 xHl .13+3 .76a2) , 검 =l.167x~ (10 .86) 여기서 a=Ze2/nv 이다. 이것을 위의 식둘 (10.82) 와 (10.85) 에 대입하면 eb= 효x;2= 66f3820 t A((1Z++31.)3Z4 百#I ) (10 . 87) 울 얻는다. 여기서 t의 단위는 g /cm2 이고 /3=v /c, 그리고 A 는 원자 질량 번호이다. 위의 식에서 A 가 z4 t 3 에 비례하고 a 는 작 은 수이기 때문에 마지막 인자는 사실상 Z 에 거의 무관하게 1 에 가까운 값을 가전다. 따라서 입사 전자의 에너지가 주어지면 매 개 변수 b 는 매질의 두께 t에만 의존하고 또한 산란각의 분포식 (1 0.84) 는 b 에만 의존하기 때문에 다중 산란에 의한 전자의 산 란은 매질의 원자 번호에는 거의 무관하고 두께 t에만 의존한다 는 결론을 얻게 된다. Mo li ere 는 식 (10 . 84) 를 계 산하기 위 하여 B— ln B=b (10 . 88) 에 의하여 매개 변수 B 를 정의하고 각변수 8 룰 f) = 0 I (xcB1'2) (10 . 89) 와 갇이 정의했다. Mo li ere 의 식 (10.84) 가 유효한 B의 영역은 보통 5 에서 20 사이인데 이제 식 (10.84) 를 l/B 에 관한 멱급수 로전개하면
/(0) 0d0=8d8[t< 0 >(8) +>I(I )(8)+ 畜 I(2)(8) +…] (10.90) 룰 얻는데 여기서 f(n ) ( 8) =占ia, z t du] 。 ( 8u) exp ( ― -¼-u2)[ }같 In( 뉴 2)r (10 . 91) 이고 8 - 00 인 극한에서 f(n )(8) oc 8-2n-2 이다. Be t he 는 f(O )(8), f(I )(8), f (2)(8) 의 값들을 o::;;;13::;;;10 영역에 대해서 계산하여 목 록화하였다. 1O. 5. 5. 2 Mol i ere 의 다중 산란 단면적에 의한 표본추출 식 (10.90) 에서 f(O )(8), f(1 )(8), f (2)(8) 가 8 의 정의구간의 일부에서 음수가 되기 때문에 식 (2.46) 처럼 분해하기 위해서는 인자들을 약간 조정해 줄 필요가 있다. 식 (10.90) 에 의한 8 를 표본추출하기 위해서 EGS4 에서처럼 다음과 같이 분해해 보자. 3 g(rJ ; E)=~ aJ ;(rJ)gi(rJ) (10 . 92) i= l a1=l— 2 /B (10.93a) /i(r3) =2 exp ( -r32) r3, r3E (O, oo) (10.93b) g1 루 1 (10 .93c) a2=l .8/ B (10 . 94a) /2(8) =1, r3E (O, 1) (10.94b) g2 (8) 門\ (2 f (O)(8) +j(1)( 8) +j(2) (8)/B) (10 .94c) a3=0.9/B (10 . 95a) /3( ,3) =28-3, r3E(1, oo) (10 .95b) g3 ( 8) 門쩡84 (2f (O ) ( 8) +j(1) ( 8) +j(2) ( 8) /B) (10. 95c)
첫번째 인자는 가우스 분포와 비슷한데 B 가 큰 경우 지배적이 다. 또한 세번째 인자는 단일 산란의 말미를 나타내며 두번째 인 자는 중간 부분에 대한 수정이라고 볼 수 있다. B<4 . 5 에서는 Mol i ere 의 공식의 정확도가 떨어지고 또한 B 가 2 보다 작을 경우 a1 이 음수가 되는데 EGS4 에서는 B=2 까지는 공식 (10.92) 를 그대로 사용하고 B=2 에서 B=O 까지의 구간에 서는 B= 2— 2In 2 b 로 놓음으로써 임의적으로 선형 내삽울 하고 있다.
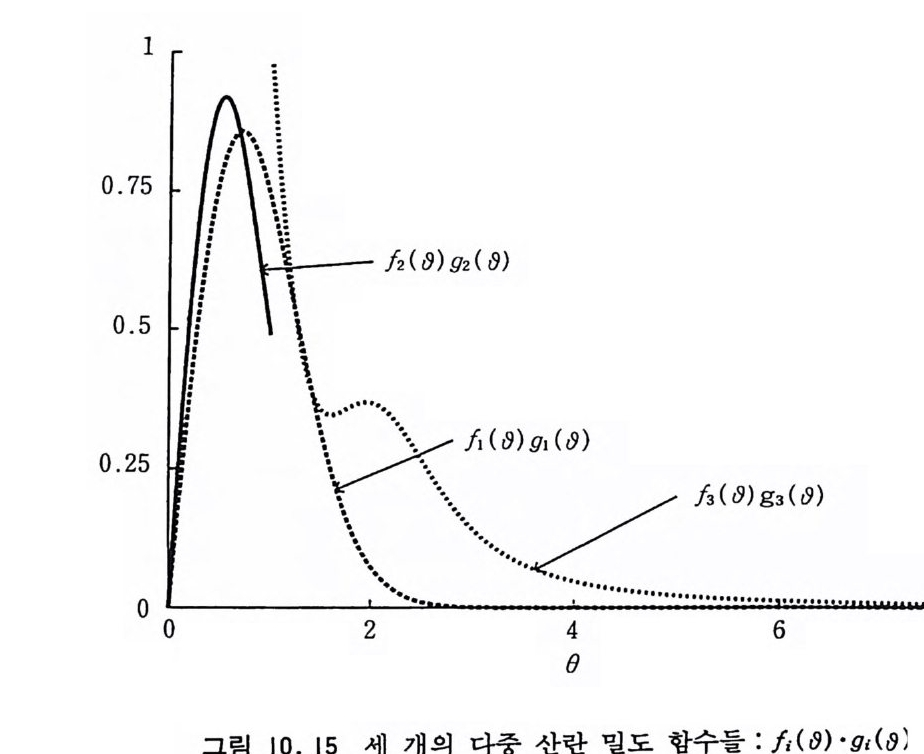 I
I
10.5.6 연속적 에너지 손실 앞 절에서 전자가 매질과 반응하여 하한 에너지 이하의 이차 입자들을 생성하는 경우에 대해서는 논의룰 미루어 왔다. 전자 또는 양전자는 매질을 지나면서 연성 제동 복사를 통해 저에너지 의 광자를 배출하거나 또는 궤도 전자들에게 미미한 에너지를 전 달함으로써 자신의 에너지롤 잃게 된다. 따라서 그 행로에서 끊 임없이 에너지를 잃는다. 단위거리당 평균 에너지 손실은 _(망 )T=-( 망 )bT_ ( 깥 )ae (10 .9 6 ) 와 같이 쓸 수 있다. 여기서 첫번째 항은 하한 에너지 이하에서 제동 복사의 산란 단면적에 광자의 에너지를 곱한 것을 적분하여 얻는 것과 같다. ―(망 )br=1Eck( 웅 )dk (10 .97) 식 (10.96) 에서 두번째 항은 Moller 또는 Bhabha 산란에 의 해 일어나는데 저에너지에서는 원자의 에너지 준위들을 고려해야 하기 때문에 상당히 복잡하다. 여 기서는 Ber g er 와 Sel t zer 의 〔 196 사 제 한적 정 지 력 (restr i c t e d sto p ping po wer) 에 관한 공식 을 사용하기로 하자. _F-((r운, L)la) e == f-1, [一합1 +nIn~ [亨 (r -+LFl)L玉l,]+ rLJ/) (-r8—] 4 ) (10.98) +[f+ (2r+1)In (1 ―군)〕 7 (10.99)
F+(r, il) =In(ril) ―구 [r+2 il―훙i] 2 y (10 .100) _ (4 ―½,1 3) y드 (長 픕 4 도長)y 3] r=y - 1 y= l/(y+ l) €max= 최대 에너지 전달량 =(r- 강, r/2-e- ) 4= 제한적 최대 에너지 전달량 =m i n(cc, €max ) l= 이온화 에너지 8= 밀도 효과 수정 여기서 매질이 여러 원자들로 구성이 되어 있는 경우에는 이온 화 에너지를 이들 구성 원자들에 대해 적절히 평균을 취한 값으 로 대치해야 한다. 또한 밀도 효과 수정 인자는 저에너지에서는 무시할 수 있는데 입사 입자의 에너지가 높아지면 고려해 주어야 한다. [Ste r nheim er, 1952] 참고문헌 [ 口 M.J. Berge r and S.M. Seltz e r, Tables of Energy Losses and Rang e s of Electr o ns and Posit ro ns, NASA rep. NASA-SP -3012(1964) [ 2 ] M. J. Berge r and S.M. Seltz e r, Sto p p ing Powers and Rang e s of Elect ro ns and Posit ro ns, USDC NBSIR 82-2550- A (1983) [ 이 S.M . Seltz e r and M. J. Berge r, Nucl. Instr . Meth . B12 (1985) 95 [ 4 ] H. A. Beth e , Phys . Rev. 89 (1953) 1256 [ 인 H.A. Beth e and W. Reit ler , Proc. R. Soc. A146 (1934) 83 [ 6 J H.A. Beth e and R. Jac kiw , Inte r media te Qu an tu m Mechanic s , 3
rd ed., (Benja m i n/ Cummi ng s, 1986) [ 7 J J.D . Bjo r ken and S.D . Drell, Relati vis t i c Qua ntu m Mechanic s , (McGraw-Hi ll, 1964) [ 8 ] RN. Blomq u is t and E.M. Gelbard, Nucl. Sci. Eng . 83 0983) 380 [ 9 ] H. Brys k and C.D . Zerby , Phys . Rev. 171 (1968) 292 U 이 J.C . Butc h er and H. Messel, Nucl. P hys . 20 (1960) 15 [11] J.C . Butc h er, Comp ut e r J. 3 (1961) 251 U 끽 Y.S. Chae and J.S . Ki m , Comp ut e r Sim ulati on of Radia tion Shie l d, RIST Rep. R94011 (1995) [13] T- P Cheng and L-F Li, Gaug e Theory of Elementa ry Part icle Phys i c s , (Clarendon, 1984) [14] D.T. Cromer and J.T . Waber, Inte r nati on al Tables for X-Ray Cr yst a l log ra ph y , v.I V , ed. by J.A . Ibers and W .C. Hami lt o n , (Int. Unio n of Crys ta l log rap h y , 1984) [1 하 C.M. David s son and RD. Evans, Rev. Mod. Phys . 24 (1952) 79 [16] P.A Doy le and P.S. Turner, Acta Cry st . A24 (1968) 390 [17] S.D. Drell and J.D . Walecka, Ann. Phys . 28 (1964) 18 U 이 J. Fis c her, Ann. Phys i k 8 (1931) 821 [19 ] H. Hall, Phys . Rev. 45 (1934) 620 ; Rev. Mod. Phys . 8 (19 36) 358 ; Phys . Rev. 84 (1951) 167 R 이 C.J. Hasti ng s, Ap pro xim atz 'on s for Digital Comp ut e r s, (Prin c eto n Univ . Press, 1955) [21] W. Reit ler and F. Saute r , Natu re 132 (1933) 892 〔 2 끽 W. Reit ler , Qua ntu m Theory of Radia tion , (Oxfo rd , 1954) 〔幻 J.H . Hubbell and I. Overbo ]. Phys . Chem. Ref Data 9 (1979) 69 [24 ]J .H . Hubbell, H. A. Gi m m, and I. Overbo , ]. Phys . Chem. Ref Data 9 (1980) 1023 [2 하 H.R. Hulme, McDoug a ll, Buckin g h am, and Fowler, Proc. Roy.
Soc. (London) 149A (19 35) 131 [2 이 H. Kahn, Ap pli ca ti on s of Monte Carlo, USAEC rep . AECU -3259 (RAND Corp. , 1954) 核깐 A.N . Kalin o vskii , N. V. Mokhov, and Yu.P . Ni ki t in, Passage of Hi gh -Energy Partic le s thr oug h Matt er , (AIP, 1989) [28 ]R . Ki ns ley, ENDF/B-V, BNL- N CS 17541 (1979) [2 이 0. Klein and Y. Ni sh in a , Z. fur Phys i k 52 (19 29) 853 [3 이 L. Koblin g e r, Nucl. Sci. Eng . 56 (1975) 218 [3 타 H.W. Koch and J.W . Motz , Rev. Mod. Phys . 31 (1959) 920 區〕 E.E. Lewi s and W.F. Mi ller, Comp ut a t i on al Meth o ds of Neutr o n Transpo r t , (Wi le y, 1984) [3 이 R. Loudon, Qu antu m Theory of Li gh t, 2nd ed., (Oxfo rd , 1990) [3 사 I. Lux and L. Koblin g e r, Monte Carlo Part icle Transp o rt Meth o ds: Neutr o n and Photo n Calculati on s, (CRC Press, 1991) [3 히 H. Messel and D.F . Crawf or d, Electr o n-Photo n Shower Di stri- buti on Functi on , (Perga mon, 1970) [3 이 G. Molie r e, Z. Natu r jors ch A2 (1947) 133 〔 3 기 J.W . Motz , H. A . Olsen, and H.W. Koch, Rev. Mod. Phys . 41 (19 69) 581 園〕 W.R. Nelson, H. Hi ra y a ma and D.W.0. Rog e rs, The EGS4 Code Sys te m , SLAC pu b. SLAC~265 (1985) [39 ] Y. Ni sh in a and S. Tomonag a , Proc. Phys - Math Soc Jap 15 (19 33) 298 [40] J.R . Op pe nheim er and M.S. Plesset, Phys . Rev. 44 (1933) 53 [41] E.F. Plechaty , D.E. Cullen, R.K. Howerto n , Tables and Graph s of Photo n -Inte r acti on Cross Secti on s fro m O. l ke V to 100 MeV, Nuclear-Data Libr ary LLL-50900 (1978) [4 끽 E.B . Saloman and J.H . Hubbell, X-ray At ten uati on Coeffi cien ts ( Tota l Cross Secti on s) : Comp ar i so n of the Ex pe ri me nta l Data Base wi th the Recommended Values of Henke and the Theoreti-
cal Values of Scofi eld for Energi es betw een O.l~100 keV, US NBSIR 86-3431 or NTIS PB87-102422, 1986 [43] F. Saute r , Ann. Phys i k ll (1931) 454 [4 사 J.H . Scofi eld , Theo r eti ca l Photo i o n iz a ti on Cross Secti on s fro m l to 1500 ke V, Lawrence Liv e rmore Lab. UCRL-51326 0973) [45] J. Sp a nie r and E.M . Gelbard, Monte Carlo Pr inc ip le s and Ne utr o n Transp o rt Problems, (Addis o n- W esley, 1969) [4 아 R.M . Ste r nheim er, Phys . Rev. 88 (1952) 851 [4 기 E. St o rm and H. I. Israel, At om i c Data and Nucl. D ata Tables 70970) 565 〔副 Y.S. Tsai, Rev. Mod. Phys . 46 0974) 815 [4 이 J.A. Wheeler and W .E. Lamb, Phys . Rev. 55 (1939) 858; ibi d , lOlE (1956) 1834
부록 A 균일분포 난수 생성자 여기서는 본문의 여러 프로그램들에서 사용한 균일 분포 난수 생성 자들의 코드를 수록한다. 4 장의 몬테카롤로 적분, 5 장의 마르코프 사 슬에 의한 선형 방정식의 해와 적분 방정식의 해, 6 장의 다차원 몬테 카를로 적분, 7 장의 아이싱 모델, 10 장의 입자 산란 단면적에 의한 표본추출 등에 서 두루 사용한 난수 생 성 자는 Ang us, Fox, Ki m , Walker 의 Solvin g Problems on Concurrent Processors, (Prenti ce -H all, 1990) 에서 사용된 것으로서 여기서는 간단히 C3P 라고 명한다. 이 난수 생성자의 계수는 MOD=231, 승수는 MULT=1103515245, 증분은 ADD=l2345 로서, 그 최대 주기는 231 이다. 본문의 표들을 작 성 하는 프로그램들에서는 초기 화 과정 에 서 seed 를 12345 로 주었다. 다른 난수 생성자들에 대해서는 본문 제 2 장에서 설명한 그대로 코 딩을 했다. 이 서브루틴둘은 C 와 FORTRAN 사용자들 모두가 사용 할 수 있도록 배려했다. 난수 생성자들을 사용하는 프로그램을 my c ode . c 또는 MYCODE . f라고 하자. 또한 난수 생 성 자들의 코드 롤 따로 ra :1 d.c 라고 명명하기로 하자. unix 운영체계에서는 다음과 같이 컴파일한다. cc -c my c ode . c cc -c rand.c cc -o.my c ode my co de . o rand . o -Im • • • 또는 f77 -c MYCODE . f cc -c rand. c f71 -o MYCODE MYCODE . o rand . o FORTRAN 프로그램에서는 서브루틴 이름의 맨 끝에 있는 underbar 를 삭제 하고 사용해 야 한다. 예를 들어 rn_c3p _ 대신 rn_c3~ 춘 사용 해야한다. 한편 VMS 운영체계에서는 다음과 갇이 컴파일한다. CC my c ode.c CC rand.c
LIN J ( my c ode , rand 또는 FOR MYCODE . fo r C'C rand . c LINK MYCODE , rand VMS 운영 체계에서는 C 와 FORTRAN 의 서브루틴 이름에 차이를 두지 않으므로 똑같은 이름을 사용해야 한다. A.l 난수 생성자 선형 합동 난수열, X;+1 = (MULT*X;+ADD) mod M (A . 1) 울 계산함에 있어서 계수를 M=232 로 취하면 32 비트의 프로세서에서 는 코드를 X=(MULT*X+ADD) 와 같이 써도 내부적으로는 mod M 을 취한 것과 마찬가지이다. 하지만 계수를 M=231 로 취할 때에는 32- 번째 비트인 사인 비트에 신경을 써야 한다. X 를 (unsig n ed lon g)으로 선언하면 modulus 연 산 %를 사용해야 한다. 한편 X 를 (l on g)으로 선언하면 32- 번째 비트 가 1 일 때 X 가 음수로 취급된다. 따라서 식 (A.1) 은 X = (MULT*X+ADD) (A . 2a) if (X < 0) X = XNASK (A . 2b) wi th N ASK = (Ox80000000) (A.2c) 와 갇이 32- 번째 비트만 영 이 아닌 수, NASK 와 exor 를 취 함으로써 구현해야 한다. 식 (A. 2a-c) 의 과정들을 한꺼번에 해내는 방법이 있 는데 그것은 X = (MULT*X+ADD)&MASK (A . 3a) wi th M ASK = (Ox7f ffffff) (A.3b) 와 같이 32- 번째 비트만 영인 수, MASK 와 and 를 취함으로써 구현 할수 있다.
#def ine MASK (unsig n ed long ) (Ox7f ffffff) #def ine TWOTD31 ((double)MASK+1.0) !*============================================== Thi s 1S a random number ge nerato r used in C3P ==============================================*! #def ine MULT (unsig n ed long ) ( 1103515245) #def ine ADD (unsig n ed long ) (12345) double rn_c3p _ (seed) unsig n ed long *seed; { *seed = (MULT*(*seed) + ADD)&MASK; } ret u rn ((double)(*seed)/TWOT031); #undef MULT #undef ADD !*============================================== The l'Ecuy e r's random number ge nerato r The adder is set to zero here. ==============================================*! #def ine MULT (unsig n ed long ) 742938285 double rn_ecu_(seed) unsig n ed long *seed; { *seed = (MULT*(*seed))1/. M ASK; ret u rn ((double)(*seed)/(double)MASK); } #undef MULT #undef TWOT031
#def ine TWOTD32 (double) 4294967296. !*============================================= The Marsag l i a 's random number ge nerato r =============================================*! #def ine MULT (unsig n ed long ) 69069 #def ine ADD (unsig n ed long ) 1 double rn_mar_(seed) unsig n ed long *seed; { *seed = (MULT*(*seed) + ADD); retu rn ((double)(*seed)/TWOTD32); } #undef ADD #undef MULT !*============================================== The IMS's random number ge nerato r The adder is set to zero here. =============================================*! #def ine MULT (unsig n ed long ) 1664525 double rn_i m s_(seed) unsig n ed long *seed; { *seed = MULT*(*seed); retu rn ((double)(*seed)/TWOT032); } #undef MULT
!*============================================== Thi s is a random number ge nerat o r by usin g th e Mi tch ell-Moore seq u ence whi c h is def ined by X_n = (X_{n-24} + X_{n-55}) mod m where m = r32, n >= 55 =============================================*! #def ine INIT 55 #def ine MULT (long ) 1103515245 #def ine ADD (long ) 12345 double rn_mm_(seed) unsig n ed long *seed; { st a t ic i n t fl ag, j, k; st a t ic u nsig n ed long Y[INIT] ; in t J. ; /* Ini tiali z i n g a qu eue wi th t h e C3P ge nerato r *I if (fla g == 0) { Y[ 이 = *seed; fo r (i=1 ; i< INIT; ++i) Y[i] = (MULT 아〔i -1] + ADD)&MASK; fl ag = 1; j = 23; } k = 54; I* ge nerati ng and savi n g a new random number *I *seed = Y[k] = Y[k] + Y[j] ;
I* set ting th e qu eue po i n t e rs to next ones *I iiff ((----kj ==== 00)) kj == 5544;; } ret u rn ((double)(*seed)/TWOTD32); #undef ADD #undef MULT #undef !NIT #undef TWOT032 !*============================================== Thi s is th e random number ge nerato r usi n g th e Subt r act- wi th-B orrow met h od. X_n = (X_{n-22} - X_{n-43} - c) mod m =w==h=e=r=e =r=n ==== r=3==2= =-== 5=,= =n= =>=== =4=3= =================*! #def ine RINDX 43 #def ine SINDX 22 #def ine MULT (unsig n ed long ) 69069 #def ine !NCR (unsig n ed long ) 1 #def ine ADD (unsig n ed long ) 4294967291 #def ine TWOT032_5 (double) 4294967291. double rn_swb_(seed) unsig n ed long *seed; { st a t ic i n t j, k, fl ag, carry; st a t ic u nsig n ed long Y 〔虹 NDX 〕 ; unsig n ed long sd;
I* Ini tiali z i n g a qu eue wi th r n_mar_ *I if (sfdla g= =*=s ee0)d ; { fo r(j= O; j< RINDX; ++j) { Ysd[ j]= M= UsLdT;* sd + !NCR; } kj == ROI;N DX -SINDX; } fcla argr y = = 1 0; I* checki n g if carry occurred *I if (*Y[s e旦e d> == YY 〔[k旦] + carry) { - y[피 - carry; }} elsc*cesaae rre{rr dyy === YO1 ;;[ j] Y[k] carry + ADD; I* saYv[ki ]n g =t h* es ereadn;d om number to th e qu eue *I I* miioffv i n(( ++g + +tkj h ==e== qRRu IeINNuDDeXX p)) o kji n t== e OOrs;; to next ones *I } retu rn (double)(*seed)/TWOT032_5;
#undef TWOT032_5 #undef ADD #undef INCR #undef MULT #undef SINDX #undef RINDX !*============================================== MacLaren-Marsag l ia 's shuf flin g pro cedure wi th t w o ge nerat o rs , ran1 () and ran2 () Not e : af ter callin g in _sf l _ 0 , use rn_sf l _ () =============================================*! #def ine KAY 100 unsi gn ed long seedx, seedy ; double V[KAY] , (*rd1) () , (*rd2) () ; voi d in _sf l _(ran1, ran2, seed1, seed2) unsi gn ed long *seed1, *seed2; double (*ran1) () , (*ran2) () ; { int j; I* set ting fu nct ion po i n t e rs and random seeds *I rd1 = ran1 ; rd2 = ran2; seedx = *seed1; seedy = *seed2; I* in i tiali z i n g a qu eue wi th r an! () *I fo r(j= O; j< KAY; ++j) V [j] = (*rd1)(&seedx) ; }
double rn_sf l _ () { in t J; double y, retv al; I* choosi n g a qu eue po i n t e r wi th r an2 () *I y = (*rd2)(&seedy ); j = (int ) fl oor(KAY*y ); I* retu rn V[j] in th e qu eue and savi n g a new random number ge nerate d by ran1 0 *I retv al = V[j] ; V[j] = (*rd i ) (&seedx); } retu rn (retv al) ;
부록 B 몬데카를로 적분 부록 A 에서 소개한 난수 생성자들의 사용법을 예시하기 위하여 4 장 4.3.1 절에서 논의한 중요 표본추출에 의한 몬테카를로 적분 프로그램 울 아래에 수록한다. 똑갇은 프로그램을 C 와 FORTRAN 두 가지 언 어로 코딩했다. B.l C 프로그램 #inc lude
pr i n t f( \n\tM C Int e g r ati on of Si n (Pi x)\n); pr i n t f(\t Inp u t in t e rval (Xlow,Xup p) => ); scanf( %lf%lf, &a,&b) ; pr i n t f(\t Inp u t Np o i n t s => ); scanf ( %d,&n); pr i n t f( \n\tM ont e Carlo st a rts .. . \n\n\n) ; seed = 762183; I* if yo u don't use shuf fli n g ge nerato r, *I seed1 = 12345; in _sf l _(rn_c3p _ ,rn_mars_,&seed,&seed1); I* remove th e li n es bet w een comment s *I dx = (b-a); fo r (i=O ,sam=O. ,hav=O. ;i
hav = dx*hav/(double)n; sam = dx*sam/(double)n; I* Comp u t ing Vari a nce *I fo r (i=O ,dh=O.;i < n;i+ +) { tm = 紅니 -hav; dh += tm *t m ; } sig m a = sq r t ( dx*dh/(double)n); I* Prin t ing out pu t *I pr i n t f (\tN= %5d Int e g r al=%11 . 8f ,n,hav) ; pr i n t f( Dh=%11.8f ,n,hav,sig m a); pr i n t f ( Si g_ S=%11 . 8f \ n , sig m a/sq r t ((double)n) ) ; pr i n t f(\t\tSi m p le MC:%11.Sf \ n,sam); } B . 2 FORTRAN 프로그램 PROGRAM IMP PARAMETER (PI=3.141592653589793,NMAX=10000) IMPLICIT DOUBLE PRECISION (A-H,0-Z) DOUBLE PRECISION W,RVAR,H(NMAX) DOUBLE PRECISION RN_SFL,RN_C3P,RN_MAR EXTERNAL RN_C3P,RN_MAR C WRITE(*,1000) READ (*,FMT=*) A, B WRITE(* , 1100) READ (*,FMT=*) n WRITE(*,1200) 1000 FORMAT(//16X, 'MC Int e g r at ion of Si n (Pi x) ' ,/ + 20X, ' Inp u t in t e rval (Xlow,Xup p) => ' )
1100 FORMAT(20X,' In p u t Np o i n t s => ') 1200 FORMAT(//16X , ' Mont e Carlo st a rts .. . ' //) ISEED = 7612183 C IF YOU DON't USE THE SHUFFLING GENERATOR, ISEED1 = 12345 CALL IN_SFL(RN_C3P,RN_MARS, IS EED,ISEED1) C REMOVE THE LINES BETWEEN COMMENTS DX = (B -A) SAM= 0. HAV= 0. DO 1X0A0R GI == A1 , + ND X * RN_SFL() CCC FOR OTHERXXAA RRGGGE N==E RAAA T++O RDDSXX, ** RRNN__ISMWSB ((!ISSEEEEDD)) c C DON'T FORGET TO DECLARE THEM C SIMPLE SSAAMM P=L INSGAM + SIN(PI * XARG) C IMPORTANCE SAMPLING HXA( RIG) == RSVINAR(P(XIA R*G X) ARG) / W(XARG) HAV = HAV + H(I) 100 CONTINUE HSAAMV == DDXX ** HSAAMV // NN
C C 미 PUTING VARIANCE DH = 0. DO 200 I = 1, N TM = H( I) - HAv DH = DH + TM*TM 200 CONTINUE SIGMA = DSQ R T(DX*DH/DBLE(N)) WRITE(*,1300)N,HAV,SIGMA,SIGMA/DSQ R T(DBLE(N)) WRITE(*,1400)SAM 1300 FORMAT(8X, 'N=' ,IS, ' Int e g ra l=' ,F11 .8 , ' Dh=' , +F11.8, ' Si g_ S=' ,F11.8) 1400 FORMAT ( 16X , ' Si m p le MC : ' , F11 . 8) STOP END C WEIGHT FUNCTION DOUBLE PRECISION FUNCTION W(X) DOUBLE PRECISION X C W = 6. * X * (1. -X) RETURN END C RANDOM VARIABLE DOUBLE PRECISION FUNCTION RVAR(Y) PARAMETER (PI=3.141592653589793) DOUBLE PRECISION Y, ANG C ANG = ACOS ( 1. - 2 . * Y) RVAR = COS(ANG/3. + 4.*PI/3.) + .5 RETURN END
찾아보기
-1 가관측량 220 가우스 분포 85 각선속 306 감수율 200, 205 감마 분포 80 강제 충돌 방법 for ced coll isio n 302 거시적 단면적 285, 301, 305 거절-허용 방법 re j ec ti on meth o d 63, 165, 288 결합계수 248, 265 결합성 250 경계조건 210 계 수 modulus 27 공분산 covar i ance 18 광자의 반응 284 광전효과 ph oto e lectr i c eff ec t 330 NNDC 데이 터 330 미분 단면적 331 총 단면적 332 출사각 표본추출 332 광학적 깊이 o ptic al thick ness 307 교류성 communic a te 136 구조함수 316, 319 구획 스핀 block spi n 242 균일분포 확률변수 25
균일분포 의사난수의 데스트 46 간격 테스트 47 균등분포 테스트 46 부분 수열 테스트 53 순차성 테스트 47 스펙트럼 테스트 54 증감 테스트 52 직렬 상관 테스트 51 쿠폰 수집가의 테스트 50 포커 테스트 49 기 대 값 exp e cta t i on value 16 기 하적 분포 ge ometr i c dis t r i b u ti on 76 L 내부 에너지 203 노이만 수열 151 c: 다수결의 원칙 254, 267 다차원 몬테 카롤로 적분 165, 181 단충적 방법 str at i fied samp li n g 116 대 조 방법 anti the ti c varia t e s 12 3 대칭성 계보 250, 260
동등성 eq u iv a lence 136 동등성 부류 e q u i valence class 136 동시 확률 밀도 함수j o i n t pro ba- bil it y densit y fun cti on 15 동적 임 계 지 수 230 득점 tal ly 296, 309 등거 리 수 coord i na ti on number 198 DIVONNE 알고리즘 174 三 란다우 이론 244 Landau-L ifsh it z 규정 246 러시아 룰렛 Russia n roulett e 300 레 지 스터 자리 이 동 방법 Tauswor- the shif t reg ist e r meth o d 3 7 □ 마르코프 과정 Markov pro cess 129, 184 마르코프 사슬 Markov chain 130 임의보행 사슬 131 Ehrenfe s t 사술 131 도박사 사슬g ambler's ruin chain 132
출생-사멸의 사슬 b i r t h and death chain 132 대기 사슬q ueu i n g chain 133 가지 사슬 branch i n g chain 134 MacLaren-Marsag l ia 범 벅 40 Marsa g li a 의 방법 72 메트로폴리스 알고리즘 186, 206 몬데 카롤로 적 분 99 직설적 방법 101 표준편차 102 알고리즘의 효율 103 중점적 방법 108 무게함수 108 제어함수 방법 112 분산 113 단충적 방법 116 분산 117 대조 방법 123 표준편차 126, 128 몬데카롤로 재규격화 군 방법 263 Ma 의 방법 263 Swendsen 의 방법 268 무게 함수 108 무관 irr elevant 261 무작위성 34 효능 po te n cy 34 물리량의 측정 218
미소 가역성 186 미분 산란 단면적 305, 316, 319 M it chell-Moore 의 수열 36 닌 배위 130, 196 배위의 성질 136 범 람 overfl ow 28 범 벅 shuff ling 방법 39 Bu t ler 의 방법 70 Bu t cher 의 혼합 방법 71, 327 Bay s- Durham 범 벅 40 VEGAS 알고리즘 169 베르누이 21 베타 분포 93 보상 인자 309 보편성 univ e rsali ty 237 보편성 계보 237, 245, 262 볼츠만 운송 방정 식 304, 307 부동점 fixe d poi n t 2 5 5 부정확도, 수치적분의 100 분배함수 199 분산 varia n ce 17, 110, 113, 117, 124, 219 분열 방법 sp litting 300 분해 가능 사슬 redu ci ble chain 135
분해 불가능 사슬i rredu ci ble chain 135 불변 분포i nvar i an t dis t r i b u ti on 139 비교 함수 64 비열 204 비 유사 방법 non-analog meth o d 297 비틀림 skewness 17 빌려 빼 기 방법 subtr a ct- w i th- bor- row meth o d 38 뾰족도 kur t os i s 17 人 사각형 - 쐐 기 -꼬리 방법 87, 289 사영 연산자p ro j ec ti on op e rato r 254 산란 커널 307 상관거 리 correlati on leng th 227, 230, 256 상관계 수 correlati on coeff icien t 18 선형 방정식 140 선 형 합동적 방법 line ar con- grue nti al meth o d 26 세부적 균형 de t a il ed balance 186 Shepp e y 알고리즘 169
순환적 recurrent 13 7 순환적 단충 방법 recursiv e str a ti fied samp ling 177 스칼라 선속 scala flux 296 S ti r li n g의 수 50 스펙트럼 반경, 적분 커널의 161 승수 mul tip l i er 27 쌍격자 방법 274 쌍생성p a i r creati on 316, 334 미분 단면적 335 Beth e -Reit le r 공식 337 EGS4 의 공식 337 Tsa i의 공식 338 총 단면적 338 Hubbell 데이터 335 표본추출 344 쌍소멸p a i r annih i l at i on 350 미분 단면적 351 총 단면적 352 표본추출 352 。 안정적 부동점 246, 261 안정 행렬 261, 269 양전자 - 전자의 산란 Bhabha scat- ter in g 347
미분 단면적 348 총 단면적 348 표본추출 349 에 르고드 ergo dic 138 n - 단계 전이확률 135 역 전 환 방법 inv erse tra nsfo r mati on meth o d 61 연속 상전이 246, 260 와이불 분포 95 완화 이론 215 완화 함수 219 완화시간(본질적) 230 운동량 전달 317 운동 전산모사 패키지 281 운송 현상t rans p or t ph enomenon 279 유관 relevant 261 유동적 단충 방법 adap tive str tifica ti on 169 유동적 중점 방법 adap tive im p o r- tan ce samp ling 169 유명 난수 생성자들 34 데스트 결과 54 유사 방법 analog meth o d 282 유한크기 효과 227 유한크기 축척 이 론fi n it e-s i ze scali ng the ory 226 의사 안정 상태 216
이 항분포 b i nom i al dis t r i b u ~·o n 75 일단계 전이 확률 one-s t e p tra nsi- tion pro babil ity 130 일차원 아이성 모델 250 임 계 감속 criti ca l slowdown 2 30 임계곡면 257 임계온도 198, 216, 227 임계점 203, 236, 257, 272 임계지수 204, 230, 236, 244, 255 임계현상 235 임계흐름 256 임의 보행자 random walker 129 입자 밀도 함수 295 입 자의 반웅후 방향 292 입자 방출 밀도 306 입자 생성 밀도 287, 309 입자의 소멸과 생성 294 입 자의 역 정 , 행 로 pa rtic l e's life his t o r y 282, 295, 309 . 즈 자기화 199, 202 자동 상관계 수 auto c orrelati on co-eff icien t 19 자동 상관시간 220 자발자기화 204 자유 에너지 202, 249
자체 일관적 경 계 조전 212 Jac obi 반복 방법 141 참시 적 tra nsie n t 138 재규격화 군 방정식 renormali za - tion gro up equ ati on 247, 2 50, 252 재규격화 군 흐름 250, 252 적분 방정식 149, 307 적분 변환 149 적분 커널 150 전달 행 렬 tra nsfe r matr i x 201 전이 온도 228 전 이 확률t rans iti on pro babil ity 134, 209, 309 전자의 다중산란 360 Mol i ere 의 이 론 360 Be t he 의 근사식 361 단위 확률 각도 361 특성 차폐각 361 표본추 출 363 전자의 연속적 에너지 손실 365 제한적 정지력 365 전 자-전 자의 산란 Moller scatt er - ing 345 미분 단면적 345 총 단면적 346 표본추출 346 접근 가능성 accessib l e 136
철단 매개 변수 248 정 규분포 normal dis t r i b u ti on 8 5 제 동복사 bremsstr a hlung 317, 3 54 미분 단면적 317, 354 표본추출 356-359 총 단면적 355 Seltz e r 데이터 355 제 어 함수 방법 contr o l varia t e s 112 조건부 확률 밀도 함수 cond iti onal pro babil it y densit y fun cti on 15 주기 137 주기적 경계 조건 211 주방정식 mas t er eq u ati on 185 중심 국한정 리 centr a l lim i t the orem 21, 204, 219, 221 중앙 평방 방법 26 중점적 방법, 중요 표본추출 im p o rta n ce samp li n g 108, 144, 151, 160, 184, 206 증분i ncremen t 27 지수 법칙 236 지수 변환 방법 301 지 수적 분포 exp o nenti al dis t r i b u - tion 83 직설적 방법 101 질서 맺음 변수 order pa ramete r 216, 228, 244
犬 Chap m an-Kolmog o rov 방정 식 135 체비셰프의 부동식 20 초기 배위 214 초기 열적 완화 214 최대 주기 30-33 최대 차수 33 축적 가설 226 축척 법칙 scal i n g law 238, 240, 259 축척장 259 축척 함수 227, 239, 260 =? 카이평방 분포 96 카이 평 방 시 험 Chi- S q u are tes t 42 카이평방 확률 함수 43 코시-로렌츠 분포 92 콜모고로프-스미 르노프 시 험 Kol-mog o rov-Smi rn ov tes t 44 콜모고로프-스미르노프 함수 45 콤프턴 산란 322 미분 산란 단면적 322 총 산란 단면적 323 산란각 322
Kahn 알고리 즘 326 Koblin g e r 알고리 즘 327 큰 수의 법 칙 law of large numbers 20 工 편 차 감소 기 법 varia n ce reducti on meth o d 105, 297 평 균 순환 시 간 mean recurrence tim e 137 평균 자유 경로 285, 290 평균 트랙 길이 296 평형 상태 216 포갬 convoluti on 69 표준편차 sta n dard devia t i on 17 Fredholm 제 이 종의 적 분 방정 식 151 푸아송 분포 78 Fib o nacci 수열 35
_-o Haber 알고리즘 169 학생 의 t-분포 stu d ent' s t-d is t r i b u - tion 97 합성 방법 comp o sit ion meth o d 68 확률 기본 변환 법칙 14, 69 확률 밀도 함수 pr obabil ity densit y fun cti on 14 확률 변수의 생성 방법 61 확률 변수 random varia b le 13 확률 분포 함수p robab ility dis t r i - buti on fun cti on 14, 75 환원 온도 reduced tem p e ratu r e 227, 238, 257 형 태 인 자fo rm fac to r 319 수소원자 320 Thomas-Fermi 원자 321 흡수 배위 138 흡수 억 제 absorpt ion sup pre ssio n 298, 309 흡수 확률 310 홉인 골짜기 att ra cti on basin 261
김재삼 서울대학교 물리학과 졸업 캘리포니아 공과대학 이론물리학 박사 워싱턴 대학, 뉴욕 주립대에서 대동일 이론을, 존스홉킨스 대학에서 우주론을, 브리검영 대학에서 상전이 이론을, 캘리포니아 공대에서 병렬컴퓨터 등을 연구 현재 포항공과대학 물리학과 교수 저서 『 파인만씨 농담도 정말 찰하시네요 』 『 전산물리학 』 Solvin g Problems on Concurrent Processors 몬테카롤로 방법의 물리학적 응용 대우학술총서 자연과학 112 1 판 1 쇄 찍음— 1997 년 2 월 15 일 1 판 1 쇄 펴냄 -1997 년 2 월 25 일 지은이—김재삼 펴낸이-朴孟浩 펴낸곳一(주)민음사 출판등록 1966. s. 19. 제 16-490 호 서울특별시 강남구 신사동 506 대표전화 515-2000, 팩시밀리 515-2007 값 22,000 원 © 김재삼, 1997 물리학, KDC/420.15 Prin t e d in Seoul, K orea ISBN 89-374-3612- 4 (94420) 89-374-3000-2 (세트)
1 대우학술총서(자연과학)
1 소립자와 게이지 상호작용 김진의 2 동력학특론 이병호 3 질소고정 송승달 4 상전이와 임계현상 김두칠 5 촉매작용 진종식 6 뫼스바우어 분광학 옥항남 7 극미량원소의 영양 승정자 8 수소화봉소와 유기봉소 화합물 윤능민 9 항생물질의 전합성 강석구 10 국소적 형태의 Ati ya h-sin ge r 지표이론 지동표 11 Mucop ol y sacchar id es 의 생화학 및 생물리학 박준우 12 천체물리학 홍승수 13 프로스타글라딘 합성 김성각 14 천연물화학연구법 우원식 15 지방영양 김숙희 16 결정화유리 김병호 17 고분자에 의한 화학반응 조의환 18 과학혁명 김영식 19 한국지질론 장가홍

43 후리에 해석과 의미분 작용소 김도한 44 한국의 고생물 이하영 45 질량분석학 김명수 46 급변론 박대현 47 생체에너지 주충노 48 리이만 기하학 박을룡 49 군표현론 박승안 50 비선형 편미분 방정식론 하기식 51 생체막 김형만 52 수리분류학 고철환 53 찰스 다윈 정용재 54 금속부식 박용수 55 양자광학 이상수 56 효소반응 속도론 서정현 57 화성암 성인론 이민성 58 확률론 구자홍 59 분자 분광학 소현수 60 벡터속 이론 양재현 61 곤충신경 생리학 부경생 62 에너지띠 이론 모혜정 63 수학 기초론 김상문

86 등각장론 임채호 87 방사선생물학 남상열 88 석유지질학 이용일 89 베르누이 시행의 통계적 분석 배도선 김성인 90 신경세포생리학 강만식 91 생리활성을 가진 C ― P 화합물의 화학 김용준 강익중 92 생물유기화학 서정헌 93 조직배양 김승업 94 유가전이금속화합물 조남숙 외 95 실내환경 과학 김윤신 96 유한요소법 정상권 97 대수적 위상수학 우무하 김재룡 98 파인만 적분론 장건수 99 응용 미생물학 박무영 100 리보플라빈 이상선 101 노화 김숙희 ’ 김화영 102 매트릭스 격리분광학 정기호 103 신경계 조직배양 김승업 104 지구화학 김규한 105 은하계의 형성과 화학적 진화
