조순탁
조순탁
서울대학교 문리과대학 물리학과 및 동대학원 졸업. 미국 미시건대학에서 이학박사 학위 받음. 서울대, 한양대, 서강대, 한국과학기술원 교수와 한국과학원 원장, 한국물리학회 회장 역임. 현재 한양대학교 대우교수, 대한민국 학술원 회원.
통계역학
통계역학
책 머리에 20 세기의 과학은 물질계가 여러 종류의 원자에 의하여 구성되고 있다는 원자론을 부동의 위치에 가져다 놓았다. 원자를 구성하고 있는 입자들이 비 교적 단순한 역학법칙에 의하여 지배되고 있디는· 데 의심할 여지가 없다. 그러나 우리의 경험에 나타나는 현상은 거의 모두가 막대한 수의 원자들에 의한 집단적 행위인데, 그것을 역학의 원리로 이해하려는 것이 통계역학의 과제가되어왔다. 통계역학은 Bol t zmann 의 생각에 출발점을 두고 있지만, 백 년이 넘는 역사를 갖고 있어서 이 학문의 큰 별이 되는 많은 학자가 있다. 이들이 여 러 가지 분야로 분화가 되도록 하였기 때문에 이제는 통계역학을 전공한다 고 자부하는 사람에게도 그 전모를 파악하는 것이 쉽지 않다. 더구나 전통 이 아직도 얕은 우리나라에서는 분화된 각 분야에 대하여 궁금증을 갖더라 도 그것을 쉽게 풀어보는 길이 제한되고 있다. 이 책은 그 궁금증을 다소라도 풀어주고 통계역학에 대한 넓은 시야를 갖는 데 도움이 되려는 생각에서 준비되었지만, 마치고 보니 그 목적에 어 느 정도까지 가까이 갔는지 의십이 간다. 처음부터 교과서로 생각하지는 않 았지만, 서술을 용이하게 하도록 노력하였기 때문에 내용을 간추리고, 연습 문제를 보충한다면 교재로 사용할 수도 있을 것으로 생각된다.
통계역학의 범위가 넓기 때문에 그 전체를 소개한다는 생각에서 벗어나 서 전통적인 분야인 역학법칙과 관계되는 면만을 선택하였다. 최근의 연구 경항이 Isin g 모형을 기점으로 하는 모형에 대한 이론이 중십이 되고 있다 고 할 수 있는데도, 이와 같은 모형이론은 완전히 할애되고 있다. 그 이유 중 하나는 그것에 대한 좋은 서적이 이 총서 안에 이미 포함되고 있기 때 문 0] 다. 전체를 3 부로 나누어, 제 1 부에는 이 학문의 출발에 초점을 맞추었고, 제 2 부는 평형상태에 있는 불완전유체, 제 3 부는 바평형상태를 다루고 있다. 이 책이 통계역학을 전공하거나, 인접한 분야에 있는 대학원생과 연구자에 게 도움이 되기를 바라면서 학계에 내보낸다. 1991 년 2 월 조순탁
통계역학
차례머리말 • 5제 1 부 통계적 고찰1 분자운동론1-1 기체압력에 대한 분자론적 해명 151-2 Maxwell의 속도분포함수 201-3 평균자유행로와 수송계수 241-4 Boltzmann 방정식 321 충돌단면적 322 Boltzmann 방정식의 유도 353 H 정리 384 일반적인 Boltzmann 방정식 415 거시법칙 • 유체역학적 방정식 422 Boltzmann 원리와 Gibbs의 ensemble2-1 Γ위상공간과 Liouville 정리 502-2 Boltzmann 의 원리 551 ergodic 역학계 552 Boltzmann의 구상 562-3 Gibbs 의 ensemble 611 microcanonical ensemble 612 canonical ensemble 693 grand canonical ensemble : Gibbs 분포 764 Gibbs 분포의 응용 81
3 이상기체의 양자통계3-1 동등입자의 이상기체에 대한 분배함수의 계산 : Darwin-Fowler 방법 841 동등입자의 양자론 842 Darwin-Fowler의 계산법 863 대분배함수와 열역학함수 913-2 양자효과에 대한 근사 951 Maxwell-Boltzmann 통계에 의한 근사 952 약하게 축퇴된 상태 1023-3 축되된 전자기체 1061 완전히 축되된 전자기체 1082 실온에서의 금속전자 1103-4 Bose-Einstein 통계의 응용 1141 Einstein 응축 1142 photon과 phonon 122제 2 부 불완전유체계4 불완전기체의 고전론4-1 서론 1334-2 Mayer의 방법 1381 선형 graph 이론의 요절 141
2 Mayer 의 정리 1433 열역학량의 계산 1474-3 응결현상의 설명 1521 Yang-Lee 의 이론 1522 수학적 모형의 하나 1563 입자분포함수 1574 입자분포함수의 정의 1585 열역학함수의 분포함수에 의한 표현 1606 상관함수의 근사계산 1655 양자유체에 대한 섭동이론5-1 서론 169제2양자화의 방법 1705-2 grand partition function의 섭동전개 1755-3 전개항의 graph 표시 1801 Bloch-De Dominicis의 정리 1802 Feynman graph 표시 1833 grand potential ⓗ의 계산규칙 1895-4 전자기체에 대한 예(I) 1945-5 온도 Green 함수 201Green 함수 G [u, u']의 성질 2025-6 Green 함수의 섭동전개 2091 상호작용표시 209
2 Green 함수의 Feynman graph 2133 self-energy 2195-7 전자기체에 대한 예 (II) 221제 3 부 비평형이론6 Brown 운동과 상관함수6-1 서론 2316-2 Markov 과정으로서의 Brown 운동 2351 Markow 과정 2352 Brown 운동의 기술 2406-3 Gauss 과정으로 본 Brown 운동 2441 Gauss 과정의 특칭 2442 Gauss 과정인 Langevin 방정식 2486-4 Langevin 방정식과 Fokker-Plauck 방정식의동등성과 path-integsal 방법 251 6-5 Wiener-Khintchine 정리아 요동-일산의 정리 2596-6 기억함수 방정식 2641 Mori의 표현 2662 Lee 의 전개식 2736-7 선형응답과 상관함수 2797 Boltzmann 방정식
7-1 Boltzmann 방정식과 제1원리 2881 BBGKY 방정식 2882 Boltzmann 방정식의 유도 2917-2 선형화된 Boltzmann 방정식의 유도 299소리의 전파 3067-3 Maxwell 분자의 기체 3111 Bobylev의 변환식 3122 moment 전개식 3217-4 수송계수의 도출 3261 Bhatnagar-Gross-Krooks 모형 3342 Maxwell 모형 3353 일반적인 경우 337참고문헌 • 341찾아보기 • 345
제 1 부통계적고찰
1 분자운동론 1-1 기체압력에 대한 분자론적 해명 기체를 빠른 속력으로 운동하고 있는 많은 분자들의 집합으로 생각하고, 분자들의 역학함수로 기체의 압력을 나타낼 수 있다는 착상을 갖게 되었다. New t on 의 운동방정식을 Ap一 /At = 一f 로터 쓰단면위,시 짧간은당 시변간화 가A t 힘사 이f- -에> 와 분 같자다의는 운 것동을량 나p一 타에낸 다나.타 기난체 변의화 분 A자p一 가 로 그부 용기의 벽에 충돌하여 운동량이 변화하는 데서 기체의 압력을 설명하려는 생각을 처음 한 사람은 D. Bernou lli (1738) 이다 .I)
이상기체의 압력을 구체적으로 역학적으로 구한 사람은 Kron ig( l856) 인데 ,2) 그는 한 변의 길이가 l 인 입방체의 용기 안에 완전탄성구로 생각할
1) D. Bernou lli의 저서 Hy drody nami ca 안에서 탄성유체의 성질과 운동의 항에 있음. 2) A. K Kron ig : Ann. Phy s @]9 9. 315(1856).
수 있는 분자가 N 개 들어 있다고 하였다. 분자들을 입방체의 변에 평행하 게 움직이는 같은 개수의 3 개의 군으로 분류할 수 있다고 하였으며, 그 속 력도 똑같이 u 로 하였다. 용기의 어떤 면에 충돌한 분자가 그 면에 디음으 로 충돌하게 된 시간이 2l/u 이므로 단위시간 안에는 u/ 임회의 충돌을 하 게 된다. 분자 한 개가 한 번 충돌에서 하는 운동량 변화 Ap 를 llp = (mu) - {m( -v)} = 2mv ( 1.1 ) 로 알 수(v /있 2어l)서 (2,m 단v) 위=시 간( 에+ ) ( mv2) 가 된다. 같은 군 안에는 분자가 (N/3) 개 있으므로, 단위시간에 벽면에서 일어나는 운동량의 변화, 즉 힘 F 가 F = 대) (+) (mu2) 이 된다.p 운= 동f량z 보=존 릅법칙 (에§ m의v하2)면 이 힘은 벽이 받는 힘과 같고, 압력 P 는 ( 1.2) 이 된다. 체적 V = [3 에 의하여 위의 식이 PV = 응 N ( 강 mv2) (1.3 ) 으로 쓰이게 되므로, 이상기체에 대한 실험식인 &yle -C h ales 법칙과 같게 하려면 l mol 기체에 대하여 우변이 RT 와 같다고 하면 된다. 여기서 R 은 8.31 J /mo l. K 인 기체상수]고 T 는 절대온도이며, N 은 Avog a dro 수 6. 02 x l()2 3 이다. 기체 안에 있는 분자를 입방체의 변에 따라서 움직이는 3 개의 군으로. 분 류하는 Kro nig의 방법보다 더 확실한 기초 위에 이론을 세우기 위하여 Claus i us 는전 기체분자가 평활한 강체면에 충돌하는 역학관계에 주목하였 다. 이 면의 면요소 da 에 분자들이 충돌하는 효과를 시간 t의 함수 f(t)로 3) R. Clausiu s : Ann. Phys 100. 353(1857) ; 영어번역이 Phil Ma g. vol 14, pp. 108(1857) 에 있음
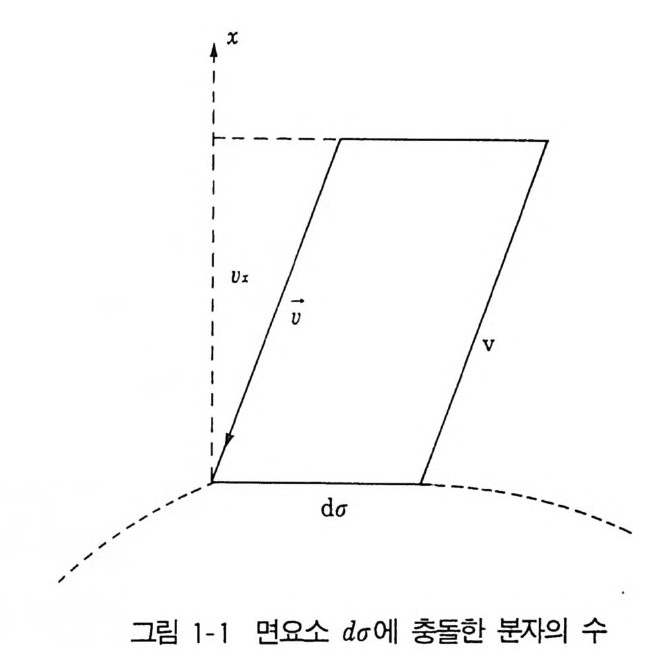
하면 f(t)가 나타낸 곡선은 막대한 수의 날카로운 돌기와 함몰울 갖게 될 것이다. 그러나 곡선 f(t)에 대한 시간평균을 평활한 곡선이 되게 취해주면, 그것이 측정 된 힘을 나타낼 것인데 이 힘을 Pd <1로 표현할 때, P 가 압력이 된다. 분자가 속력 u 로 d<1의 법선과 0 의 각을 이루면 그립 1-1 이 면요소 에 입사한 운동량의 변화는 2mv cos 0 가 된다• -V->. = (ux, Vy , Vz) 이고, d <1의 법선방향으로 x 축이 취해지면, 운동량의 변화는 2mvx, vx>O (1.4)
Ax_
아 된다. 면요소 da 에 대하여 단위시간내에 일어나는 모든 충돌을 생각하 -거 기 위하여는 da 를 밀면으로 하고 u 에 평행인 능선(길이 u) 을 갖는 기울 원어진통 안원에통 을들 어생 각있하는면 분되자고들, 이중때에 서一u . 는 속 도극 좌(-v표 , (一vv, +e,d u-< ➔p ）)• 로범 표위시에할 있 수는 있것다들. 은 단위시간내에 모두 면요소 d (J와 충돌하게 된다. 기체의 단위체적 안에 들어 있는 분자수, 죽 분자의 수밀도를 n 으로 하
단면 위d체a 적위 에안 에있 는있 고위 의속 도원가통 (안一v 에 , 는_v +ndvxv一d a ) 개범의위 에분 자있가는 들분어자 수있다를. q여,(一v 기· )서d 3 一v 로 하면 ,4) 당연히
4) d3 컵三 du ,d v~v,
n = .f 이 된다. 따라서 (1. 9) 는 P = 問 V 2 = 선 § ( 망 mv 2 ) = 웅 n 굽 (1.11 ) 이다. 여기서 운동에너지의 평균치— 하—는 Ck = z1m uz = 홍l m (u; + uy2 + u—i ) (1.ll a) 이고, PV = 了2 演~ =RT (1.1 2) 로하면 Ck = t내 )T= 출 kT (1.13 ) 이 된다. k 는 Boltz mann 상수이고 k = 下R - = ( 6~.02 ) X 1023 / mol = 1.3 8xl0-2 3J / K ( 1.14 ) 의 값을 갖는다. (1. 11) 은 Kron ig의 식 (1. 3) 과 비교할 때 운동에너지가 아니고 그 평균치가 절대온도 T 에 비례한다는 것을 보이고 있다. 이상기체의 내부에너지 U 는 U = Ni ; = 당 RT (1.1 4a) 이고, 따라서 비열은 C, = （景) , =f R,C p= (T 魯 )P =당 R+R =伊 (1.15 : 이다선 그리하여 비열비 y는 5) 열역학의 항등식 'Ill S=dU+ p dV 에서 C, = (T-멍『), . = (광令 ) V 이고 C ;, =( T-픔) p = （署)p+p(정 ) P 이다 . (署), = (%) . +(景 ) T 澤 )P 에서 g= （桐 +{p+ (景 ).} 풀 )p= 룹 ) , +R 이 된다 .
y = —ccp,, = 1.66 이다. (1. 13) 으로부터는 • ½mv2 = 웅 kT 에 의하여 제곱 • 평균 • 평방 속력 U r m s 이 Ur m s = 沿= 占m됴 ( 1.16 ) 로됨을알수 있다. 1- 2 Maxwell 의 속도분포함수 Bernoull i, Kro nig와 Claus i us 의 뒤를 이어서, 기체를 막대한 수의 분 자가 이루는 집합체라는 입장에서 Maxwell 은 더욱 정밀한 수학적 이론을 세웠다.° 그는 분자를 완전한 강체탄성구로 하고, 분자 사이에는 충돌하는 순면 간그에 만속 도힘 이-u 작=용 (하ux,고 u y 그, U z의) 는에 는여 러상 호가작지용 값이 을무 갖시게된 다된고다. 가 속정도하의였 다x. 성 기분 체가 평형상태에 있다면, 위치에 따른 어떠한 변화도 나타나지 않을 것이므 로 분자는 공간적으로 균등하게 분포되고 있다. 임의의 분자 하나를 취해보 이 (ux, ux+dux) 사의 값을 갖는 분자의 수를 통계적으로 7) 생각할 수 있다. 기체 안에 있는 전체 분자의 수에 대한 이 수의 비율은 확률이라고 할 수 있다. 그리하여 (ux, ux+dux) 에 속도의 x 성분이 있을 확률을 g (u .x )du .x로 한있+d다을-u면 ,)확 시률평이기형에 상g 태(있v 에 z 을)d v 있z확 가는률 기 된기 다체고에 서가 정방하향여성도이 좋없다다. 는그 리것하을여 알 속고도 있가으 므(v 로, uy 성분이 (vy, vy+ dVy ) 에 있을 확률은 g (vy )dv y이고, z 성분이 (uz, U z+duz) 에 --➔ - 6) J. C. Maxwell : Phil Mag. 19, 1 학 20, 21 (1 860). 7) 국세조사를 하기 위하여 통계국에서 어떤 나이 범위에 있는 장정이 몇 명인가 조사하는 것과 갇은 방법이다. Maxwe 底논 그의 이론이 통계적이라고 자랑하였다 .
g(u x) g(v y ) g(v z) dux dvy dvz 가된다. 기체 안에서 속도에 대한 방향성도 없어서 등방향적이라는 가정이 타당 하다면 속도가 (-u-> , -u-> +d一u ) 사이의 확률이 u = l一; I = J;f+v:＋파 만의 함수 G(u) 에 의하여 G(u) dux dvy dvz 로 쓰여져야 한다. 따라서 G ( 〈g+g+파) = g(v ,)g (u y }g(u ,) (1.17 ) 가성립하게 된다. 확률밀도라고 부를 수 있는 G(u) 와 g· (u,) 의 함수형을 구하기 위하여 (1. 17) 의 자연대수 (ln) 를 취하고 그것을 uX 로 미분한다 . 그 결과는 느u 요G(꾜u) -= gg'(( uu .z)) 인데, 이 식을 <1> (u) = 上u 忠G(u止) ' ¢'l'(\Vu xz)/ =- _ul_._ gg'((uu .x)) (1.18) 로하여
죽, ( 1. 18) 을 보면 dlndgv x ( v.) —2yu x ( 1.20 ) 이 되어, 결국 lng (v x) = c —yv ; 이 얻어진다. 다음에 e+0=a 로 하고 g(v .) = ae -,.: ( 1.21 ) 이 되는 것을 알 수 있다. 이 식에서 a 와 y 는 기체에 관한 어떤 상수가 될 것이므로 기체의 성질에서 구하게 된다 . 속도성분 (ux, ux+dux) 사이에 있을 확률이 g (ux)du x 이고 - CX)< uf< CX) 에서 I: OOg (u x)dux=1 ( 1.22 ) 이 요구된I다: O.g (그u x런)du데x = (a1. I 21\ ) e에 - w 의:d하ux여=a 틀) 1/2 = 1 로부터 a=( 밉 1/ 2 ( 1.23 ) 이 되는 것을 알 수 있다. 따라서 g (vx) 에 나타니는 미지의 상수는 y 하나 가 된다. Claus i us 의 이론에 의하면 (1.10 ), (l. lla) 와 (1. 13) 에서 송 nw; = 상 kT (1.24 ) 가 된다.> gT (1 uW: c ):d=u Ix 가: OO 뿡 (u파:c, g u :(c u+,d)udu :,c ）에 있을 확률이므로 (1.24 a) 이다.그런데
I言 -ux2 g (ux)dux = 뿔다 ) 1/2 「 OO Uz2 e - duz = 틀 信 )1 /2 갈 ( f 二 e-; v: d u,) = 틀 (; )1/2 갑 (: )1/2 = 信 (1.24 b) 이다. 따. 라서 꼬4y ~ -2¼ kT y =齊m (1.25 ) 를 알 수 있다. '/ 는 기체의 온도 T 와 분자의 질량 m 에 의히여 정해지고, 결국 g(v J =( 훑 ) 112 e 옮 (1.26 ) 이며, (1. 17) 에 의하여 G(v) = ( z 옮 ) 312 e - ~.;.바 .') =(蟲 ) 3/2 e 릅 (1.27 ) 이다. Claus i뼈 마一 )는 (1. 5) 와 (1. 8) 을 볼 때
P(v) = 4n:G (u) v2 = 4n( 감坊 ) 3/2 e 쭙 g ( 1.28 ) 이다.물론 [ 。~ P(u)du = 1 (1.28 a) 이고, P(u) 의 극대치를 이룬 U m 은 ~du= 0 에서 구할 수 있는데, (1. 28) 에 의하여 Um = (2kT/m)112 (1.28 b) 이다. Um 을 최빈속력이라고 한다. 속력 u 의 평균치를 확률 P(v)dv 에 의하 여구하면 v = f: v P(v)du = ( 巴 )1 /2 (1.29 ) 이다. 최빈속도 Um, 평균속력 V 와 (1. 16) 의 제곱 • 평균 • 평방 속력 Urm s 사 이에는 Um : V : Urms = 1 : 1.13 : 1.22 ( 1.30 ) 의 관계가있다. 1-3 평균자유행로와 수송계수 기체 안에서 어떤 한 개의 분자가 다른 분자와 충돌할 때까지, 자유롭게 날아갈 수 있는 거리의 평균치를 평균자유행로라고 정의하게 되는데 이와 같은 개념을 처음 생각한 사람은 Claus i us(1858) 이다 .8) 분자에 크기가 없 다고 한다면 평균자유행로 l 이 무한대의 값이 될 것이고, 유한한 크기의 l 8) R. Clausiu s : Ann. ph ys 105, 239(1 8 58).
값을 얻기 위하여는 분자를 강체구로 가정할 때 그 반경 r 이 유한한 크기 를 가져야 한다. 간단하게 생각하기 위해 대상으로 삼고 있는 분자의 속력 u 가 대단히 커서 기체의 다른 분지들이 모두 정지하고 있다는 근사가 가능 하다고 하자. 입사입자의 반경 n 과 충돌된 기체분자의 반경 r 2 의 합, 죽 rI + r 2 =S 를 유효 충돌단면적의 반경 또는 작용구의 반경이라고 하면, 입사 입자의 충돌을 점과 작용구의 충돌로 바꾸어놓을 수 있다. 단위시간 안에 작용구가 쓸고 지나간 체적은 단면 궁이고 높이가 u 인 원통이 된다. 단위 체적내에 있는 분자의 수, 죽 수밀도를 n 으로 할 때, 이 원통 안에 들어 있 는 분자의 총수는 입사입자가 단위시간내에 충돌하는 충돌수 V 와 같아질 것 0] 다. 즉, 11 = nrrs2u (1.31 ) 이 성립한다. 입사입자가 단위시간에 이동하는 거리가 u 가 되므로 평균자유 행로 l 을 l = 上v = n(nl s2) (1.32 ) 로 얻을 수 있다. 이 식을 얻는 과정에서 평균이라는 말이 막연하게 사용되 고 있으므로 참된 평균자유행로는 (1. 32) 의 l 과 어떤 계수만큼 다르게 될 수 있다고 생각하여야 할 것이다. 기체 안에서 분자의 수밀도 n 은 분자 하나가 평균적으로 차지하게 된 체 적 1/n 을 주게 된다. 이 체적이 입방체이고 그 한 변이 a 이면 a3=l/n 이고 (1. 32) 로부터 f = f ({-r (1.32 a) 를 얻게 된다. s=2X10-8cm 로취하고 0°C,1 기압에서의 a3= 겅尸 x10-18 cm3 를써서 a_s~ _- 강2x xl0 l-08-c6 mc m -= 160 0
울 얻으면 (1. 32a) 로부터 lIa = 104/ 3 6rr ~ 100 을알수 있다.그리하여 l : a : s ~104 : 102 : 6 이 된다. Claus i us 는 l : s 가 1000 : 1 정도라고 하여 분자의 크기 를 추 정한바 있다. 기체 안에서 분자 사이의 충돌이 불규칙적으로 91 일어난다고 하고, 한 입 자가 단위길이 안에서 하게 되는 충돌이 어떤 수 A 에 대하여 1/ }, 에 비례 한다면, dl 길이 안에서 충돌을 하는 확률은 dl/ ;_ 이 되며, 충 돌 하지 않는 확률은 l-dl/;. 이 된다. 지금 P (l)로서 길이 l 안에서 충 돌 이 일어나지 않 는 확률을 나타낸다고 하면, P(l+dl) 은 l 까지에도 충돌이 일어나지 않고, 또 계속하여 다음 dl 사이에도 충돌이 일어나지 않는 확률을 의미하게 되어 P(l + dl) = P(l) ( 1 — 뿐 ) (1.33 ) 의 관계가 성립한다. dl 이 미분소의 양이고 P(l+dl) = P( l) + 갑『 dl 로 쓸수있으므로 뺑= -P(l) } (1.33 a) 이고, P(O) = 1 을 고려하면 P(l) = e- l /;. ( 1.34 ) 울 얻게 된다. 따라서 충돌하지 않고 갈 수 있는 거리의 평균치 [은 T = J: z P(l) 뿐 = A (1.34 a) 이다. 이 식에서 P(l) 펫- 이 (l, l + dl) 사이 에 충돌하는 확률이 되는 데 9) random 하게.
주의하여야한다. 입사입자를 기체분자 중 하나로 할 때는 평균자유행로 (L32) 에 · 약간의 수정을 하면 된다는 것을 Maxwell 10) 이 지적하였다. (1. 31) 와 (1. 32) 의 속 력 u 대신에 충돌하는 2 분자의 상대속도 一g = V一t - V一2 ( 1.35 ) 의 크기 g = I 一g I 의 평균치를 (1. 27) 의 속도분포함수 G(v) 를 써서 g = .f d3- ;: Jd 3; ; G(u1) G( u2 ) I V--i > - u一 나 = ( 8kT ) 1/ 2= g ; ( 1.35 a) 틀 로 구한다. 여기서 F 는 ( 1.2 9) 에서 구한 속력의 평균치이다. 그리하여 충돌 수가 (1.31 ) 대신에 v = n1rs 정 = @ nrs2F ( 1.36 ) 로 된다. 한 분자는 단위시간에 평균적으로 F 의 거리를 날게 되는데 그 사 이에 v 번 충돌한다. 따라서 평균자유행로 l 은 l=J !_= u = 1 V ✓2n n: S 2 V - V 값 n n: s 2 ) (1.37 ) 가 된다• 이것은 (1. 32) 와 비교하면 11 h 계수만큼다를뿐이다.
10) J. C. Maxwell : Phil Mag. 19. 19, 20, 21( 18 60).
평균자유행로의 개념을 써서, 기체가 유체로서 행동하며 유속이 장소에 따라서 다른 경우 유체에 나타나는 점성을 처음으로 설명한 사람은 Maxwell(1860) 이다 .II ) 그는 분자가 유속에 의하여 갖게 되는 운동량이 평 균자유행로가 되는 거리를 다른 분자와 충돌을 하지 않고 그대로 수송되며, 단위시간에 수송된 운동량이 힘, 즉 점성으로 나타나는 마찰력이 된다고 하 여 점성계수를 구하였다. Maxwell 의 생각은 운동에너지의 수송과 관계된
11) J. C. Maxwell, ~l 기술한 논문인 Phil Ma g. 19, 20.
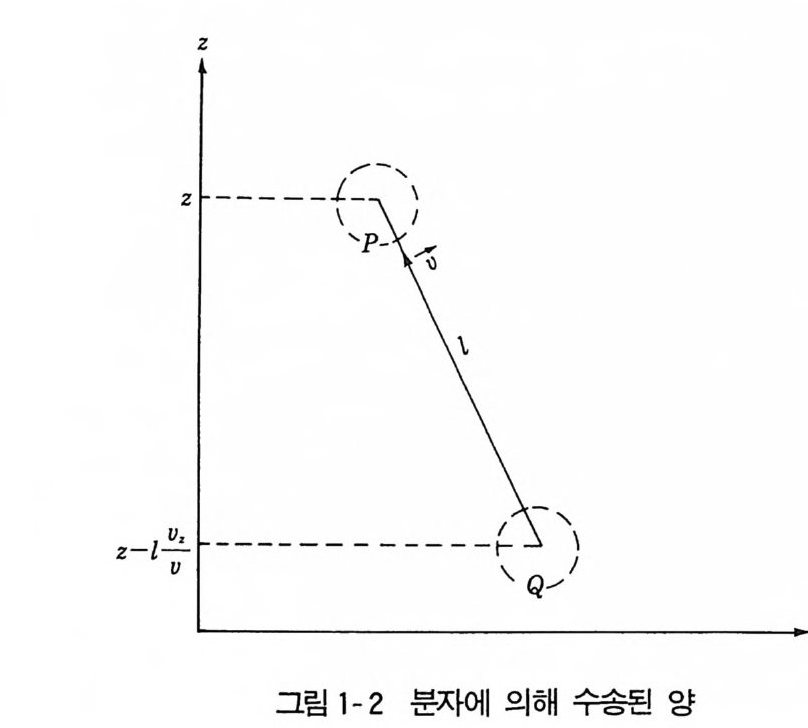
열전도에는 거의 같은 형식으로 성립하므로 디음에 약간의 일반성을 갖고 논할수있다. 수송될 유체의 양 A 가 xy 면상에서는 같고 z 축 방향으로만 변한다고 가 정속_하도여가 그( -림v , 1一v-2 처 +d럼u- 생) 각사한이다에. 있z 축는의 분 값자이의 z수 인는 P 점(1.에 2 7a그) 에값 이의 하z여 —
z
--> 수송된 유체적 성질 A 로서 유속 U (z) 의 성분이나 온도 T(z) 를 취하고 자 하는데 이들이 평균자유행로의 거리에서 하는 변화는 보통 아주 작다. 그리하여 작은 양에 대하여 전개하여 A A (z 키『) = A(z) —묘 匠 l 문+ …… (1.38 a) 로 쓸 수 있다. 이 전개를 (1. 38) 에 대입하고 (1. 27a) 에 의하여 짜 一u ) =nG(u) 를 고려하면 Q,1 = J[ A(z) - 요 뿔 러 -; z 값錢에량 관의계 없변으화므가로 힘 m이U一 되만 므 수로송 Q량A 으 는로 x 고 방려향한의 것유이속다에. 의하여 z 방향으로 작동하는 str e ss ten sor P ” 이며, 이것이 유체에 점성력으로 나타난다. 그 리하여 p' = 一경1 - nml, -u oUO,Cz z ) = —,I o U O,(z z) ( 1.40 a) 으로 쓰이게 되고, n 는 점성계수라고 불린다 . 따라서 n= 송 nmlu (1.40 b) 01 다. 평균자유행로 l 을 (1.32 ) 또는 (1. 37) 에 의하여 l => n:s2 로 하고,n 이=것_ 3을 ✓l 2(1_ . 4n0뿌sb2) 에 대입하면 (1.40 c) 이 된다. 기체의 압력 P = nkT와 비교하면 점성계수가 압력에는 무관하 고 일정하다는 결과가 된다. 처음에 이 결과는 실험사실과 모순된다고 생각 되었지만, 1875 년에 Kund t와 Waebur g에 의하여 1/60 기압의 압력까지 는 찰 성립되는 것이 증명되었다. 고압쪽에서는 이 이론이 잘 성립하지 않 는다는 것을 이해할 수 있다 . 그 이유는 위에서 생각한 기체에서 분자 사이 에 작용하는 힘, 죽 분자력이 무시되고 있기 때문이다. 분자력을 무시할 수 없는 기체에 대하여는 더욱 복잡한 이론이 요구되지만, 근사적으로 위의 이 론은 기체가 액체로 되기 전단계까지는 유효하게 사용된다. VCX : J T 이므로 기체에서 점성이 온도에 따라서 증가하지만 액체에서는 온도기- 올라감에 따 라서분 자점의성 이운 동갑에자너기지 감는소 그하 는평 균성치질가이 (있1.다 1.3) 에 의하여 Ek = 견3 _ kT 가 되는 것을 알고 있다. 열운동에서 분자가 병전하는 데 갖는 평균적 에너지가 바 로 이 값이 되고, 분자의 내부구조를 고려에 넣으면 열에너지 E 는
E = CT ( 1.41 ) 가 된다. 여기서 C 는 분자 1 개당의 비열(정적 비열)이 된다. 기체 안에서 z 방향으로 온도의 변화가 있고, T( z) 로 쓰일 때에, 수송되는 열량 Q는 (1. 39) 에서 A(z) 를 C T( z) 로 바꾸고 얻어지며 Q= -nl ¾3 c 낍 O gz L= -K 낍O~z (1.42 ) 가 되는 것을 알 수 있다. 윗 식에서 계수 K 는 열전도도로 불리워지고 있 는데 K = 갑1 nCl -u (1.42 a) 가된다. 점성계수 n 에 대한 (1. 40b) 와 열전도도 K 에 대한 (1. 42a) 를 비교하면 K17 = mC (1.43 ) 이다. 이 식의 우변에서 분자와 분모에 Avo g adro 수를 곱해보면 바로 lmol 에 대한 비열을 나타내고 있다는 것을 알 수 있다• 일반적으로 수송된 양을 계산하는 식 (1. 38) 에서 분자의 속도분포함수 o 유(u一 속) 가-U - 평>(r형_ )상 , 태온에도서 T (구一r)한 과 것입과자 밀같도다 고n( -r가) 정이하 있였다다.면 그기러체나는 장엄소격의한 의함미수에인 서 평형상태에 있지는 못한다. 그렇지만 이들이 장소에 따라서 서서히 변한 다면 국소적으로 평형상태에 대단히 가까운 상태에 있다고 생각할 수는 있 다-.-> 극한적으로 국소적인 평형상태를 가정하면 분자의 속도분포함수는 cp( 一r, u) 가 되며, cp (7.겁 = n(5 ( 2r 區 ) 파 • exp [三] (1.44 ) 로쓰인다. 사실 n(r) = .’ f
露) =志- [5
一 --> 속도이며 열속도로 불려지고 있다. 1-4 Bolt zm ann 방정 식 기체분자의 속도분포함수를 구하게 된 Maxwell 의 논문에 깊이 감명된 Bol t zmann 은 기체의 분자 사이에 상호작용이 있을 때에도 속도분포함수를 구할 수 있는 방법을 생각하였고, 더 니아가서 평형상태로부터 벗어난 기체 의 행위를 기술할 수 있는 Boltz m ann 방정식을 구할 수 있었다 .1 2 )
12) L. Boltz m ann : Sit zu n gsb eic h te Akad. W iss . Vi en na pa rt II , 66, 275 (18 72).
(1) 충돌단면적 하나의 표적입자에 막대한 수의 입사입자가 산란하는 현상은 충돌단면적 이라는 개념으로 기술할 때 더 편리하다. 질량이 m1 과 m 2 인 2 개의 입자에 대하여 그 위치와 속도 벡터를 -;:;, ~과 -;, 言로 할 때, 그들 입자 사이에 상호작용만 있고 의부의 힘이 작용하지 않는다면, 그들의 질량중심인 f = mm一In1 ++mm一22 r 2 (1.45 ) 는속도、 인 = mI~U1.+ m~2 U2 (1.45 a) m1+m2 로 등속오동을 하고, 상대위치인 一r =r1一 -r一2 (1.46 )
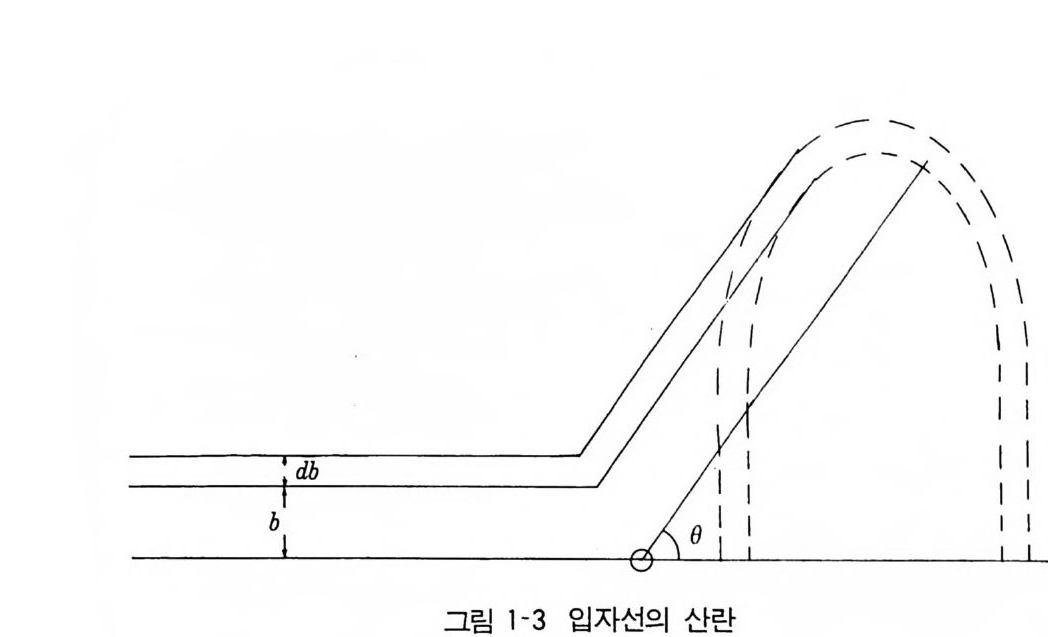
와상대속도인 -g = 一ul _ 一U2 ( 1.46 a) 의 시간적 변화는 환산질량인 m= m1m2 ( 1.47 ) m1+m2 을 갖는 하나의 입자가 고정된 중심에 대하여 하는 운동에서 알 수 있다. 상호작용m의 톱 p=o t e mn t- i afl= u(r )- 이V면 , u운( r동) 방정식이 (1.48 ) 가 된다. (1. 45a) 와 (1. 46a) 에 의하여 亡= V+ m1 m+ 2 m2 Z; ;= 7_ m1 m+ I m2 7 (1.49 ) 로 되는데, 충돌 후의 값을겁;; J와 V', -;로 하면 v' = v 이고, 또 충돌 전후에서 운동량과 운동에너지가 보존되므로 m1 -u; I+ m2 -u->; = m1 u규'1. +m2 u슈' 2 ( 1.50 ) 송祠 + 송 m 아 = 뇽 I 파 + 뇽 2U12 (1.50 a) 이 성립한다. 이들 식에 (1. 49) 를 대입하면 icl = 171 (1.51 ) 죽, 상대속도의 크기가 불변이라는 것을 알 수 있다. 따라서 충돌에 의하 여 상대속도는 그 방향만이 변할 뿐이다. 표적입자에 일정한 밀도 No 의 입자선속이 입사할 때, 충돌계수 b 의 값이 (b, b+db) 사이에 입사한 입자수는 8 t시간 사이에 N,, b = No2nbdbg{ Jt (1.52 ) 가 된다(그림 1-3 참조). 이들 입사입자는 충돌 후에 산란각 0 주위의 입체각 dQ = 2n sin 0 d0
/ /- -- -- ` \\\ \\
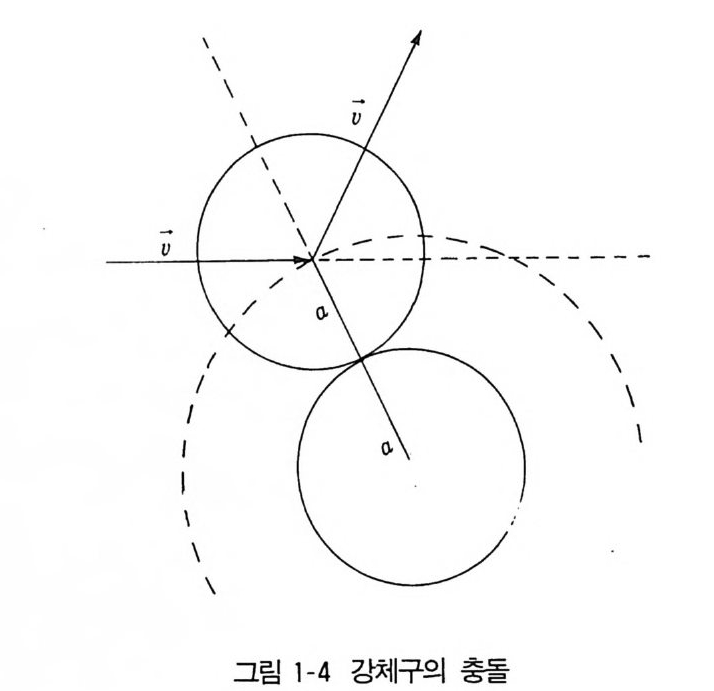
에 들어가게 된다. 따라서 N,, b를 N,, b = No 1(0, g)d Q g fJt (1.52 a) 로 쑬 수 있고, 계수 1(0, g)는I N , ,b > 어춘 고려하여 I(0, g) = | s i鬪 bd 。 (1.52 b) 로 정의된다. 1(0, g)에 의하여 d Q>追i 취하고 미분산란단면적 d<1 = 1(0, g) dn ( 1.52 c) 와산란단면적 q = Idu = fI(e, g ) dO (1.52 d) 가 정의된다. poten ti al u(r) 이 u(r) = { ~ rr~>22aa ( 1.5 3 ) 가되는강체구에서 b = 2acos 망 (1.53 a) 의 관계가있으므로
/(0,g ) = I ~ I = a?- ( 1.53 b) 이고 a = n(2a)2 ( 1.53 c) 이며, 소위 작용구의 기하학적 단면적과 같다(그림 1-4 참조) .
\\\
(2) Boltz m ann 방정식의 유도 평형상태에 대한 Maxwell 이론은 공간적으로 균등한 기체에 관한 것이 었는데, Bol t zmann 은 Maxwell 의 결과를 그와는 다른 시각에서 얻고자 하였다. 그리하여 Bol t zmann 이 처음에 생각한 기체는 공간적인 성질이 균 등하다고 가정되고 있다. 그러나 평형상태에는 도달하지 않고 있다면 분자 의 속도분포함수는 시간적으로 변하고 평형상태에 도달한 뒤에 시간적 변화 가없어질 것이다.
짧은 시간 t 사이에 속도가 (;;, ;; + d~) 에 있는 분자의 단위체적에 대한 통계적인 수 f(;;, t) d 3; ; 가 다른 (言, 言 + d言 ) 에 있는 모든 분자 와 충돌하여 감소되는 수를 I dn 으로 표시하면, (1. 52a) 를 볼 때 \dn = -rf(;, t)d 3 ~ .r.r~구 | 1(0, g) dQ f(言, t)d 3'u : ( 1.54 ) 로 표시되고 우변의 적분은 산란각에 대한 d Q과 속도 言에 대한 5 중적분 울의미한다. 시간 t 사이에 (vi, vi + dv i)와 (겅, 결 + d~) 의 분자들이 충돌하여 그 결과로 (i:, i: + d i:)의 분자가 생기는 수를 J dv 로 쓰면 여기도 (1. 52a) 에 의하여 Idv = T II`id3 v7 占 f(u ?, t) f(v 7, t) |v7 —v 7I 1(0 , g' )dQ ' (1.54 a) 가 된다. 역방향의 충돌에서 산란각이 (1. 54) 의 경우와 같고, 또 g = l一g I 와 g'= lg一 ' I 는 (1. 51) 에 의하여 g=g'이므로 (1. 54) 와 (1. 54a) 에서 1(0 , g)는 같다. 시각 t로부터 t시간 뒤의 (i:, °i: + di: ) 에 있는 분자수는 f(i:, t+ r) d3v--1> 인데{,( ~이, 것t+을 r) d30 := f(-;, t)d 30 : -J dn + jdv (1.54 b) 로 되는 것을 직관적으로 알 수 있다. t가 충분히 짧은 시간이므로 f(-:, t+-r) = {(-:, t) + .¥+ A군 (1.54 c) 로 전개하고 A71- 유한한 양이 된다고 할 수 있다. 그리하여 이 전개를 (1. 54b) 에 8대f(입 :,한 t ) 뒤에= 항다을 ~정리 하id고v -J d n} -A-r (1.54 d) 를 얻는다. (1.49 ), (1. 50) 과 (1. 50a) 에 의하여
d하 3 어一 ( va-;t,d 3tu)一 ; d=Q ' jj= dd3v3 -u-- ; iJ n d13(u一 e2 , d1Q- :--;:1 17i -~ I ( 1.54 e) 가 되는 것을 증명할 수 있으므로 1 31 (1. 54d) 에서 r-+O 인 극한을 취하여 {f~;, t) f(: t) —f(:, t) f(:, t)} ( 1.55 ) 을 얻을 수 있다• 단, 이 식에서 問, :와 u7, u7 사이에는 (1. 50) 과 (1. 50a) 의 관계가 있다.
13) d3 ui, a Uz d .n,=군피, d 따 d ,n의 증명을 (1. 50) 과 (1. 50a) 로 할 수 있다.
위의 식 (1. 55) 를 보면 f(_u ;, t) f(_u; t , t.)' = f,(,u- ; , t. )' f,(,u-; , t ) ( 1.56 ) 가 어떤 시각 t에서 성립하게 될 때 af (ua t司 = 0 (1.56 a) 이고, 그 이후에는 f (u一 , t)가 시간에 의존하지 않고 일정하게 된다. 또 2 분자가 충돌의 전후에서 운동량과 운동에너지가 보존되므로 m一V +l I+ mV-+2 = m－v수l + m국v2 홍l mu一f + 홍1 mu~一 = 홍1 mu궁; + 홍l mu;一2 (1.56 b) 이 성립한다는 조건하에서 (1. 56) 을 만족하는 함수형 t (u) 를 구하면 14) f(~) oc.A e 국 ' (1.56 c) 이 된다. 따라서 f (5) 가 갖는 물리적 의미를 생각하여 (1. 22)~( 1. 27) 에서 처럼 계산하여
14) f(굵) f(vi)=f(u,_) f(lJ?）의 해는 이 식의 h 을 취하여, 굶 =0 인 특수한 경우에 구하면 쉬운데, 그 해가 충분하다는 것을 알 수 있다.
高 = n( 급깁 3 / 2 e 틀 ( 1.57 ) 가되는것을 알수 있다• B(3o)l t zHm 정a리nn 은 분자의 속도분포함수 f(-v , t)가 시간 적으로 방정식 (1.55 ) 에 따라서 변하면 H( t)三 Id7 f(: t) {ln f(: t)가 } ( 1.58 ) 로 정의된 시간 t의 함수 H(t)가 삽dt s0 ( 1.58 a) 를 만족시킨다는 H 정리를 증명하였다. 위의 식에서 등호는 평형상태에 해당된다 . [증명뺀〕 식(1. 58=) 로IJ 정u 7의0된f ( :H( t)t )ln를 f시(:간, t )t 로 미분하면 이 되고, 이 식의 우변에 있는 적분에서 하 (一v i , t )lo t를 (1. 55) 에 의하 여 고쳐 쓰고, 펭 내 d:>d Q 1nf (:,t) t(u-I ,t ) f(u一2 , t ) —f(v一 i, t) {(v一2, t) }· l一v1-一v2 I 1(0, l一v 1 국(一 1 ). 25 I 9 ) 룰얻는다. 식 (1. 59) 의 우변에 있는 적분에서 -UI 과 一U2 는 적분변수이므로 이들을 IJ-2 와 -Ul 으로 고쳐 써볼 수 있다. 그리고 거기에 해당하여 u-11 는 一U 2’ 로, I一J2’는 一Ul’ 로 고치고 (1.59 ) 대신에
깽 = 규JJJ ( dv_3 z; , ;t d)_3f; (du 1,n t )1}n· /(一l-v; z; ,급 一나 ) 1(| I:(e t,) fI一(u u2 크:一 t ))I I ) (1.59 a) 를 얻는다. (1. 59) 와 (1. 59a) 의 적분을 비교하면 In f(;,t)가 1n /(;, t) 로 바꿔지고 있는 점을 제의하면 같다는 것을 알 수 있다. 따라서 (1. 59) 와 (1. 59a) 를 합하겨 2 로 나누고 펭 = ½HJ d 3 ;:d%걸 n ln f(:, t) f(;:, t)H
-Zn {f(:,t) /(;;,t)}]· [t(言t) f( Z t) —{(~t) t(Z:t) ] • ,;;―閃| I(O, j;1-u 2 I ) ( l.59 e) 이 되는 것을 알 수 있다. 여기서 ~ = f(v-~ , t) /(v-;, t), 17 = /(u一;, t) {(v一;, t ) 로 하면 (l. 59e) 의 적분은 피적분함수가 Iu一l _V一2 I I(0, |-u3l 국- ) 2 I ) 와 (ln ,_1n n)( t _n) 의 두 인자로 되어 있는데, 첫번째는 충돌단면적의 정의에 의하여 〉 0 이고, 두번째도 ’ , n 가 정의 실수이면 (ln ~-ln 17) (~ 一 n) 측 O ( 1.60 ) 이 된다. 따라서 (l. 59e) 에서 삽dt ~0 ( 1.61 ) 이 증명된다. 여기서 등호는 t = n, 죽 f(-v ;, t) f(v一 ;, t ) = {(v一i, t) f(v一 2, t ) 가 성립하는 경우이고 이것은 (1. 56) 에서 살펴본 평형상태에 해당된다• 평형상태에 대한 fc；)를 (1. 57) 에서 알고 있으므로 이것을 (1. 58) 의 H 의 표현에 대입하여 보자. H == jJ_ dd 3효0( 떠쇼 {,ln) fJ(컴 / 2—e 寄l } {lnn + 당 ln( 亞) - 릅 }-n = n 1n n- 청 n ln T+웅 nln( 益) 웅 n-n = 국 {NlnV + 방 NlnT-NlnN- 웅 Nln ( 益 ) 홉 N} . (1.62 ) 이것을 이상기체에 대한 entr o p y S 와 비교하면
_kH = }(s+s 。 ) (1.63 ) 이며, S o 는 상수항이다. 따라서 H 함수는 단위를 없게 한 en t ro py와 부호 를 반대로 갖는 양이다. ( 4 ) 일반적 인 Boltz m ann 방정 식 Boltz m ann 방정식은 처음에 기체가 공간적으로 균등한 상태에 있을 때 에, (2) 에서처럼 유도되었지만, 곧바로 공간적으로 균등하지 않은 일반적인 경우로 확장되었다. 기체의 상태가 공간적으로 균등하지 않으면, 속도분포함 d수 3• r 가 에 공있고간,좌 속표도에가도 (의一u1존, 一하u1 게 + 될d一u 1 것 )의이 다범 .위 시에간 있 t는에 서분 자장의소 통一r계 적주 위수의를 체 적 {(一 r, -ui , t) d3一r d3u一1 (1.64 ) 로 하는, 분포힘수 f(一n , -UI , t)가 만족시키는 방정식이 (1. 55) 를 확장하여 다음과 같이 된다고 Bol t zmann 은 제안하였다. 죽, 8f (7F 益 t) = s(n+c(r) (1.64 a) 이며, 여기서 S(f )는 분자들의 흐름에 의한 효과이고, C( f )는 분자들 사 이에 일어나는 충돌에 의한 효과라고 보았다. 이들 두 가지 효과가 서로 독립적이라고 생각한 데서 f(一r , -U->I , t)의 시간적 변화로 나타내는 식이 (1. 64a) 처럼 간단한 형이 될 수가 있다. 분자들 사이에 일어나고 있는 충돌을 무시하게 되면, 흐름만이 있을 것이 므(一r로, ,一V I 시) 점간의 t 에분 포(一r함, 一수VI 와 ) 으시로간 표 t 시+되 d는 t 에6서 차 원(一r의 + Edu一rc,l i-dv i 공 +간 인d-u1 )위접상의공 간분의포 함수가 같다고 할 수 있다. 그 이유는 위상공간에 나타나는 흐름이 t - t+ dt 사이에 (一r, 一VI )에서 (-r + d·r, 수v一i + d一u1 )으로 움직이기 때문이다. 그 러면 d-r국 = -u 1 dt 이고, 분자가 받은 가속도를 一a 로 할 때에 d一u1 = -a d 떠 관계가 성립하여야 한다. 따라서 f(-r , -u,, t) = f(-r + -u,d t , -u->, + -a니d t, t + dt) (1.65 )
아 된다• 무한소량 d t에 대하여 우변을 전개하고 1 차까지만 취하여 훌 = ―킵룹 二.를 三 S( f) ( 1.65 a) 를의 얻충게돌 에된서다 .같 은 장소 -r 에서의 속도 분포함수를 쓸 수 있다면, 이 충돌효과 분포함수 /(·r, 一v1 , t)의 -r 에 대한 의존이 비교적 완만하여, 두 분자 사이 의 표현은 (1. 55) 의 우변과 비슷하게 되어 C(t) = JJ d3:dn 1(0, :－더 ) . I-; 二| {f(r- :u::)} f(一r , 一u;, t) -f(一r , 一uI, t) f(r -, ➔ u-2, t)} (L66) 로 취할 수 있을 것이다. 이 식에서 모든 분포함수가 같은 공간좌표 一려송 갖 는다는 점에 주의할 필요가 있다. 흐름의 효과 S( f)를 (1. 65a) 로, 충돌의 효과 C({) 를 (1. 66) 으로 취하여 ( 1. 64) 를 다시 쓰면 아래와 같다. 죽 8f (76ut건 ) + 一ul • 8 f (7Our건 ) + a • 8 f(8芹u益l t) [[=d%7dQ I(O, |閃-디) 問 二사(~鬪 t) {0-,,-;;:, t) `` 一一 一一 —f(r , uJ, t) f(r , u2., t)} (1.67 ) 이 방정식은 f(一r ,- -v>i, t)를 변수 一r, 一VI 와 t의 함수로 구하는 미분 • 적분 방정식이며, 더구나 충돌효과의 적분은 비선형이어서 그 해를 구하기는 극 히 어려울 것이라고 짐작할 수 있다. (5) 거시법칙 : 유체역학적 방정식 보통 우리가 대상으로 잡은 기체 안에는 분자의 수가 막대 (N-1023) 하 므로 기체를 연속체로 보고 유체로 생각할 수 있다. 유체의 행위를 기술하 는 거시적이고 현상론적 법칙들이 방정식으로 표현되고 있다는 것은 잘 알 려지고 있다. Bol t zmann 은 이들 거시적 방정식들이 그의 방정식을 써서 2
분자충돌에서 보존되는 양의 평균치가 만족시키는 방정식들과 같다는 것을 밝혔다.따 - Ul ) + ua(-u2 ) = Wa(-u{) + ua(-u; ) (1.68 ) 2 분자충돌의 전후에서 보존되는 속도 一u 의 함수를 t/ta( -u ) 로 하면 이 되는데, 이들 함수는 u 記 = l u 沿 = mu,, tjJJ (7 } = mur, t/14 (7) = mvz U5( v ) = 問? _ (1.68 a) 이다. 지금 Ia 三 'fd3 u? c(f) 〈 a(u言 ( 1.69 ) 룰 정의하고, (1. 59a)~( l. 59 f)에서 사용한 수식운영을 다시 하면 Ia= 土[信言'f dQ g 1(0,g) (t ;/1’ 導) tp a—(V 1)+ t/J。 (_u 2 ) -u 。 (_u; ) -tjl(_u? ;, ) } = 0 ( 1.69 a) Iv一울ia, t=알), f0!수 이= f 나있(一r다온, .一v 것[ , 위이t에다)의.서 간g략 된= 기Iu一l 호가- 사U一2 용 | 이되고었,고 j 끝=으 1로, 2( 에1. 서68 ) 에~ =의 하f(여-r , 분포함수 f (一r-, ·v니, t) 에 의하여 거시적 양들을 정의하자. 처음에 n (7, t) 三 ]d3 ;f (7, ~ t) ( 1.70 ) 로 분자의 수밀도가 정의된다. 즉 n(一r , t)d 3一r 이 d3一r 체적 안에 들어 있는 분자의 평균적(통계적) 수이다. 보통 말하는 밀도 p는 질량밀도이고 p(-r , t) 三 mn(一r, t) (1.70 a)
이다. 또 一r 접 근방에서의 속도분포함수가 >(-r, tf)(一r는 , 一u, t) In(-r->, t) ( 1.70 b) --> 로 되는 것이 명백하다. 따라서 ua(v )의 속도분포에 대한 평균치 ,一 (r분 一 r의 간 자 , 단t가함) 을수 =받이 기 다은`J하 .d 기 가; 속t위/J도 cr:하 ( 言여-a t가이(7하 .있7의,어 t 논도)l 의 n그(에7다서, 지t는) 어-a려 운= 점0 로이 ( 1한있.7다1 는. )
로불려 쓸지 는수< u- 一-u>있 > 에다. =대 (하10.여 7 3 ) 이 U一 =
qi-r,➔ t) = n(-r; t) < 뿡 u2 u1> = J d V-뿡 u수 나(古?) ( 1.74 c) 로표현된다• 위에r./J1 서百 a= 정n1(,의 이r-,한 므t) 로거 + 시
이 된다.
로 정의되고, 대칭 ten sor 인데, strain te nsor 의 시간적 미분 을 의미한 다. (1. 74a) 에 의하면 평형상태에서 e = 방 kT (1.77 d) 가 되는 것을 알 수 있는데, 이것을 비평형상태에 대한 온도 T의 정의식으 로 하는 경우도 있다. (1. 77b) 는 열에너지의 시간적 변화가 s t ress 에 의한 일과 열류로 나타나게 된다는 내용이며, 열역학의 제 1 법 칙 을 유체에 적용한 경우가된다. 열역학의 제 2 법칙은 (3) 의 H 정리를 이용하여 얻 을 수 있다. 지금 (1. 58) 을 참조하고 entr o p y S 를 S 三 나기 d7 f(7, 7, t) {ln fc;.7 , t) - 1} (l.78) 로정의한다.그러면 생 == —-kkJ J idd3 7 3 기d i d%{S 룹 (/) ln+f C(/) } ln / ( 1.78 a) 를 (1. 6-4aI)I 에 감서자 얻: S게( f된 다) .1n f 가=속 도II 一da3 자= 70u 이 흥면 ln f 냐 ,[d3u u, ' 궁 (f ln f-f) = 0 • (1.78 b) 가 되는 것을 알 수 있다. 그 이유는 r, 변수에 대한 적분이 (f ln f-f)의 rj 경계치에 대한 값으로 정해지는데, 기체가 용기 안에 있거나, 유한한 공 간 안게 있다면 경계에서 f = 0 가 되기 때문이다.--; -:I 0 의 경우에도 vj 에 대한 적분에서 vi = 士CX)에 대하여 f = 0 이므로 같은 결과가 나온다. 그리하여 Boltz m ann 방정식의 흐름효과에 의해서는 S 의 변화가 없다는 것을알게 된다.
따라A 1 뿔 = -k J d~. ［國(/ ) ln/ (1.78 c) 이고, 여기서 一u 에 대한 적분은 (1. 59) 와 같다. 결국 뿔 = -k [d? 뿐l_ ~ 0 (1.78 d) 울 구하게 된다. 이 식은 열역학의 제 2 법칙을 나터내고 있다. 물론 등호는 · 평형상태에 해당된다.
2 Boltz m ann 원리와 G i bbs 의 조화 ensemble 2-1 r 위상공간과 Lio u vil le 정리 많은 입자들로 구성되고 있는 계를 입자 각각이 만족시켜야 하는 운동법 칙에 따라서 명확하게 기술하기 위하여 도입된 위상공간을 r 공간이라고 한 다. 어떤 순간에 N 개의 입자는 그들의 위치 vecto r --; (i = 1, 2, …… N) 와 운동량 vec tor p一; = m一u; (i = 1, 2, …… N) 의 수치 (-r ➔; ' -,.+;, … … 一rN , p-->I , …… p一이 에 의하여 그 역학적 상태 (mechan i cal st a t e) 가 p정 해 진다고 생각한다. 편리를 기하기 위하여 f = 3N, -r+· = (. x, y, z.) , -+ = (p,, Py, P,) 로 하고 (X1, yI, m, X2, …… z/I') 三 (q1, q2, …… q,) (p,1 , Pn_, P zi , P'2 … …P E.) = (p1, p2 , …… p,) 로 한다. 그리고 (q1, q2, …… q,, p,, …… p,)를 좌표축으로 하는 2f = 6N 차원의 Eucli d 공간을 생각하면 이것이 r 위상공간이 된다. r 공간의 한 점은 어떤 순간의 역학상태를 대표하고 있다 .15) 역학계에 H ami l t o ni an 이 존재하는 경우가 주로 우리의 대싱이 되는 데,
이 Ham i l t on i an 은 운동량으로 표시된 운동에너지와 위치에너지의 합을 나타내며 겨 H= 計읊 +w(1)]+, t< ; u(I;구 ) (2.1) 로 쓰인다. 여기서 u( I-;--; I )는 입자 i와 ]· 사 이에 작용하는 상호작용의 위치에너지이고, w(r一, ）는 입자 i가 의부력에 대한 위치에너지를 의미하는데 의부력으로는 용기의 벽을 나타내는 것만을 우리는 생각한다. 역학계로는 간단을 기하여 단원자 분자로 된 단일기체가 생각되고 있어서, 분자의 질량 은 모두 같은 m 이고, 또 분자를 질점으로 보고 있다• 분자 각각의 운동이 Hami lt o n ia n 운동방정식으로 기술되어 q. , 三층= 뿔 } i = 1, 2, ……, f (2.2) P· i = —dd pt i =- 一 _8a—Hq—, 가 성립한다. 이들 방정식은 시간 t가 독립변수인 1 계 미분연립방정식이며, i = 1, 2, …… , f 에 대하여 q;( t) , p ; (t)가 Qi( t = 0) 三 q1(O j p1( t = O) 三 p /0) 에 의하여 완전히 결정된다. 그리하여 t = 0 에서 r 공간의 한 접에 있던 역학상태가 시간에 따라서 이 공간에 곡선을 그리게 된다. 이와 같은 곡선은 자기 자신이나 다른 곡선과 교차할 수 없다 .1 6 ) 운동방정식 (2.2) 로부터 곧바로 알 수 있는 것은 o대q, =o。q 2-‘ 6H p ‘ -' 60=pp,, -Op02 ,Ho q , 이고, 두 식의 우변에 있는 미분의 순서가 교환가능하다고 생각하면 15) 한 개의 입자에 대하여 (;:; p)를 좌표축으로 하는 ~~ Euclid 공간이 µ 위상 공간이고 µ 공간의 한점은 입자의 상태를 나타낸다. µ7} molecul~ m 에, P} g터 터 해당되는 문자이다. 16) 떼 대한 어떤 역학상태에 대하여, (2. 2) 는 t+d t, 또 는 t _d 떠 상태가 유일하다 는것을나타내고있다.
—ooqq,, +—68pp,, =O (2.3) 이 성립하는데, 이 식의 중요성을 L i ouv ill e(1838) 은 강조하였다. r 공간의 한 점의 속도 V一 = (q\, …… q.I , p.I , …… p.,)에 대한 6 f 차원의 Ddi i vve,r Vg e 三nc eii =를 I (취o보하q.i 여 + 보6p.) i =O (2.4 ) 임을 (2.3) 에서 알 수 있다. N 이 대단히 큰 값이 되면 역학적 상태를 정 확하게 알 수 없기 때문에 r 공간의 한 점을 생각한다는 것은 그다지 의미 가 없다. 그보다는 역학적 상태를 확률적으로 정하는 것이 더욱 바람직스러 울 것이다. r 공간 안에 A 개의 점을 생각하고, 이 공간의 P 점 주위의 미분 체적을 du 로 하여 여기에 들어가는 점의 수를 (dA)P 로 하자. A 가 대단히 큰 값이 되면 점의 밀도를 생각할 수 있으므로 이것을 p (P) 로 하여 (dA)P = p( P) du (2.5) 의 관계를얻는다.물론 A= JPd r (2.5a) 이고, 이 적분은 r 공간의 모든 점에 대한 합이다. 점이 P 점 주위에 있을 확률 W( P） dE) 는 W(Pj drp) = 笠 = 프끈 dr p (2.5b) 이고, 따라서 확률밀도 D(P) 는 D(P) = 탱1.. (-2.5 c ) 가된다. r 공간에 우리가 생각한 A 개의 점은 그 수가 일정하게 남아 있어야 하 므로 점의 밀도에 대하여 연속방정식 웅+ Di v6 1 (p丙 = O (2.6)
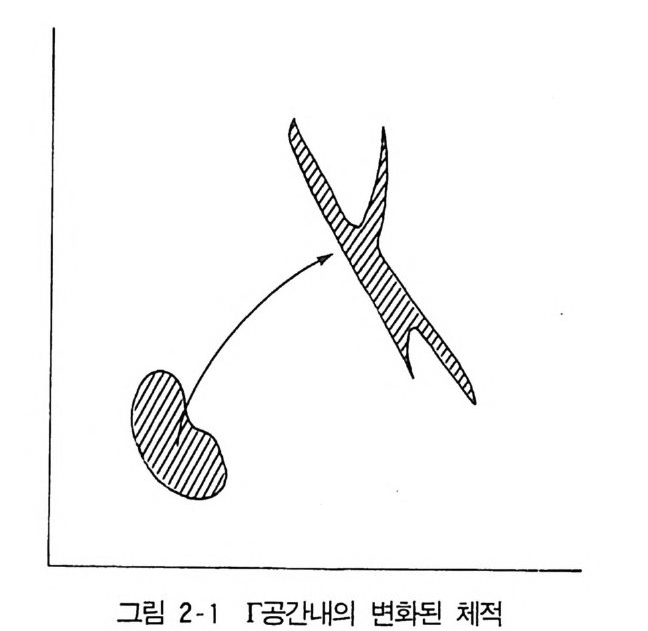그림 2-1 「공간내의 변화된 체적
이 성립한다. 점들의 흐름에 따라가면서 본 시간적 변화 웁 = 겁 + V· gra d61 = 꿉 + 접 (Qi* +Pi- /;; ) (2.6a) 를 취하면, (2.6) 에서 僧 = —p Di v6 1 V= 0 (2.6b) 가 된다. 즉, 한 점의 운동을 따라가면서 그 밀도가 시간적으로 어떻게 변 하는가를 보면 변화가 없다는 것을 알게 된다(그림 2-1 참조 ).1 1 > (2.6b) 를 17) 역학적 상태를 나타내는 접의 개수 dA를 일정한 값으로 하고 그 점의 운동을 따 라가보자. (2 . 6b) 에 의하여 P7} 불변하므로 (2.5) 에 의하여 dD} 시각적으로 불 변한다. t=어]서의 dr와 예의 그 값은 같다. 죽 dq1 (t) dq2 ( t) •••••• dp 1 (t) •••••• dp1 ( t) =dq 1( t= O ) …… dp1 (t =O) 가 성립한다 . 따라서 Jac obia n a(qa ,((tq= ,O (t)) ·…·· …… pp1,(( tt )= ) O ) ) =l 이된다.
뿔+섭(q 1:+ p I :) =O (2.6c) 로 쓰고, dI 와 P 를- (2.2) 로 고쳐 써주고 뿔걸(뿔:_뿔-t) ={H,p} (2.6d) 로 쓰기도 한다. 여기서 Po i sson 의 괄호기호 { ' }는 {A ,B} 三 i1= I (aq革1 책6p, —墓8p ‘ 革 aq), (2.6e) 로정의된다. 특히 {H, p} = 0 (2.6f) 이면 ..9a/?t --= 0 (2.6g ) 이고, r 공간의 모든 점에서 p가 변하지 않는다. 계의 역학적 상태가 r 공 간의 P 점 주위에 있을 확률이 (2.5c) 의 D(P) 로 주어지는데, D(P) 三 D(q1 , …… qr, p,, •••••• pr, t) (2.7) 이다. (2.6g ) 에서 8D(q, …… q f a,tp I, …… ~ = O (2.7a) 가 성립하는 조건은 (2.6 f)인데, 여기서 {H, D} = 0 이고, 그렇기 위하여 서는 D = D(H) (2.7b) 가성립하면 된다.
2-2 Bo lt zmann 의 원리 (1) ergo d ic 역학계 역학계의 상태를 어떤 순간 t = t o 에서 대표하는 r 공간의 점을 시간이 경과함에 따라서 한정없이 따라간다고 할 때, 역학계의 에너지가 일정한 값 E 가되는 H(q1 , …… q,, p1, …… p,) = E (2.8) 로 표현되는 r 공간내의 곡면의 모든 점을 통과한다고 가상해볼 수 있다. Bol t zmann18) 은 이와 같이 가상된 역학계의 부류를 er g od i쩌 ]19) 라고 하였 다.
18) L. Boltz m ann Stu d ie n iibe .r das Gleic h g wich t der lebend Kraf t ZUJisc hen 19) beepwye og ev t=e ne nmeragtry i,e l0l e8n0 Ps=unp katt e hn , Wi en Ber. 58(1 8 68), p. 517.
er g od i c 계에 대하여서는 역학상태의 대표점이 시간에 따라서 그리는 궤 도가 모두 같고, 다만 그 궤도상에서 출발점만 다르게 될 것이라는 것을 알 수 있다.¢( q따,p라)서 검 어펠떤 역~학함 수r를¢ (¢q(q(t, ),pp)(로t) )쓰 d고t q로써 QI , …… q r 를(2,. 9p) 로써 Pl, …… Pr 를 나타낸 것으로 하면, ¢(q(t), p(t))의 시간적 평균 는 t 1 과 k 를 어떻게 취하든지 언제나 같게 된다. 그 후 수학자들에 의하여 곡선으로 곡면의 모든 점을 통과시킬 수는 없 다는 것이 지적되어, 대표점은 (2.8) 의 곡면의 임의의 점의 임의의 근방을 통과할 때 er g od i c 하다고 한다(준 er g o di c 하다고 원래의 개념과 구별하기 도한다). 기체의 행위에 대하여 우리가 경험적으로 알고 있는 사실은, 고립되어 있 는 기체가 처음 열적 평형상태로부터 벗어나고 있으면, 이완시간으로 부르 는 어떤 시간이 지난 뒤에는 평형상태로 이행되고, 그 평형상태에서 영원히 머무르게 된다는 것이다. 이와 갇은 행위가 일반적으로 성립하는 가의 여부
를 Bol t zmann 의 문제라고 부르기도 한다. 모든 기체가 결국은 평형상태로 돌아가게 된다면, 장시간에 걸쳐서 그 기 체의 역학량에 대한 평균치를 구하는 것은 평형상태에 대하여 그 역학량의 평균치를 취한 것과 같을 것이다. 기체 model 이 er g od i c 이라는 가정하에 서 Bol t zmann 은 역학량 ¢(q, p) 의 시간적 평균을 계산하기 위하여 다음 과 같은 편법을 생각하였다. 죽, 기체 model 과 똑같은 성질을 갖는 무한개 의 model 의 집단을 취한다. 이 집단의 각 model 들은 서로 완전히 독립적 이며 r 공간의 곡면 (2.8) 위에 일정한 면밀도 u 로 분포할 것이다. 그러면 역학량 ¢(q, p)의 이 집단에 대한 평균을 ensemble 평균이라고 하고 <¢(q,p)> = ~Ju • ds (2.1 0 ) 로 정의한다. Bol t zmann 이 생각한 것은 (2.9) 와 (2.10) 에 대하여 ¢ (q, p) = <¢(q, p)> (2.1 1 ) 가 성립한다고 한 것이다. 시간평균과 ensemble 평균이 같다는 (2 .1 1) 의 증명을 하기 위하여 ensemble 평균 = ensemble 평균의 시간평균 = 시간평균의 ensemble 평균 = 시간평균 (2.l la ) 처럼 추리를 한다. 첫번째의 등식은 위상점의 분포가 시간적으로 불변하다 는 데서 나오고, 두번째의 등식은 평균하는 방법이 교환적이라는 내용이며, 세번째는 ensemble 의 모든 역학계에 대하여 시간평균이 모두 갇다는 ergo d ic 가설에 의한다 (er g o di c 가설에 의하면 위상점의 궤도가 유일하게 된다)． 그리하여 역으로 (2 .1 1) 이 성립한다는 것으로 역학계가 er g od i c 하 다고규정하기도한다. (2) Bol t zmann 의 구상 Bol t zmann 은 그의 생각을 구체적으로 밝히기 위하여 이상기체에 대한 이론을 전개하였다. 이상기체를 분자들 사이의 상호작용이 무시될 수 있는
역학계로 보면, 이 계를 r 위상공간의 한 점으로 대표할 수 있다는 것이 당 연하지만, 6 차원의 위상공간인 µ공간에 있는 N 개의 점으로도 나타낼 수도 있다. µ공간의 한 점이 분자 한 개의 위치 7과 운동량 7를 대표한다는 것 을 쉽게 알수있다. µ공간 안에 N 개의 위상점을 정확하게 표시하는 대신에 이들 점이 어떻 게 분포되는가를 보기 위하여 µ공간을 M 개의 세포 W1, Wz , ……, W M로 나누고 그들 세포 각각에 들어간 위상점의 수를 n1, nz , ……, n M 로 한다. 여기서 M 은 대단히 큰 수이지만, 세포의 크기 w , 는 n, 의 값이 충분히 큰 수가 되도록 취해야 한다. 이와 같은 조건이 만족되는 세포의 크기 w 를 〈물리적 의미에서의 무한소〉라는 표현으로 말하기도 한다• µ공간내의 세포 wI, W2 , ……, WM 안에 있는 분포 n1, n2 , ……, n M 에 의한 이상기체라는 역학계의 기술은 r 공간의 하나의 위상점에 의한 기술보 다는 정확하지 않다. 그러나 r 공간에서의 위상점의 어떤 분포에 대응될 것 이다• 사실 µ공간에 대한 위의 분포는 「공간의 영역 W= n1 ! n2 ! N…! ..• nM ! Wh 1..W n2 , …… w ,n\f. (2.1 2 ) 가 된디는 것을 증명할 수 있다. [증명] 각 세포 wI 안에서 n 1 개의 위상점이 움직일 때 µ공간의 분포는 그대 로 있지만 r 공간에서는 W1n , W2n , ··•• •• WMn, (2.12a) 인 체적을 차지하게 된다. 또 N 개의 분자를 ni, n2 , … … n , \ f의 군으로 분 할할수있는가능한수는 n1!n2! N…! … nM! (2.1 2 b) 이댜 따라서 (2 .1 2a) 와 (2 .1 2b) 의 곱이 r 공간에서의 체적 W 를 나터내게 된다분.할 (n1, n2 , ...... nM) ={ n, }에 대하여 당연히
.II iL= l n ; =N (2.1 3 ) 의 조건이 성립한다. 세포 w, 안에 분자가 있을 때의 에너지의 e 로 하면 (2 . 8) 의 에너지 관계는 LM Ci n; = E (2.14) i= l 로 표현된다. 에너지 c, 가 세포 wI 안에 들어 있는 n 개의 분자에 모두 갇 은 값이 되는 것은 역학계가 이상기체이고 분자 사이에 상호작용이 없기 때문이다. 또 세포 Wi 안의 장소에 따라서 에너지의 값이 약간 달라질 것이 라고 본다면 (2.14) 가 (2.8) 을 정확하게 나타낸 것이라고는 할 수 없다. 그 보다는 역학계의 에너지 값 E 도 정확하게 측 정할 수 없는 것이므로 (2.8) 대신에 E
!!J.l n W = ln(W+!!J .W ) - ln W = 一 E[(n 1 +An i) ln (n1+An,) _n, ln n』 + E AnI ln WI = L!! J.n , (-lnn ; -1+lnw , ) ―방 En, 춘 ) 2 + …… (2.1 7 b) 이 니온다. (2 .1 3) 과 (2 .1 4) 로부터는 E Ani = O (2.1 7 c) E & An, = O (2.1 7 d) 가 된다. 이들 조건에 La g ran g e 의 곱한 수인 (ln A+l) 과 _/3를 각각 곱하고 (2 .1 7b) 에 합한 다음 An 1 의 1 차항만 고려하고, /l ln W = 0 이 되는조건을보면 -ln ni + 1n A + 1n Wi - pei = 0 (2.1 7 e) 가 되는데, 이것이 W 의 극대치를 주는 {n,} 의 값 {,i,｝으로 Anwj j =e -P c. (2.1 7 f) 죽 (2 .1 6) 이나 (2 .1 6a) 를 주게 된다• 극대치를 갖는 W 를 而로 하면 (2 .1 7b) 로부터, (An I ) 2 까지 계산하여 타 釋센) = -杓효(풍 ) 2 = －풍 < (문 ) 2 > (2.18) 울얻게 된다.여기서 < ( 흡汀 2 > -i (:円 2 의 M 개의 세포에 대한 평균치를 의미한다. (2.18) 을 w+ AW 킥 Vex p ( －흥 <（멸 ) 2 >) (2.18a) 더로라써도보 면W N+ 가A대W단 의 히값 큰은 수대이단므히 로작 다<. ( 죽 ~ Wn으i 의 ) 2극 >대 가치아 주주변작의은 값 은값 이대 단되
히작다는것을알수있다. 특굴] WJ = W2 = … … = WM = W (2.1 9 ) 처럼 모든 세포의 크기를 갇게 잡으면 (2 .1 2) 로부터 w= n,!n2! N…! … nM! w N (2.1 9 a) 가 되는1n 것W을 = 알 In 수N ! 있+는 N데 1이n wW - 에 t 대 In하 n여; ! ;;-N ln N - Ln; l n(n;/ w) (2.1 9 b) 로 쓰인다. 기체가 공간적으로 균등하면 세포의 위치는 운동량 7 만의 함수 가 된다. W 로서 기체의 체적 V 에 대하여 Vdpx dp y dp , = Vd3 p로 취하 면, n 를 (p一 , p- ➔ +• d-p )- 사-이-의• 세-• 포라-고 하-여- n(--p ）를 쓰고 nj = n(一p ) = Vd3一p 찌(一p ) (2.1 9 c) 로 놓으N면 = GE) n ‘가 = 운V동 I량 d 공3간 의궁 분포함수이다. (2 .1 9c) 로부터 (2.1 9 d) 이며, (2.19b) 는 lnW 티 NlnN-V [ 갑-;if,r;) ln 먀따 (2.19e) 이다. 軒 G) 를 (1. 64) 의 t(7 ,-:, t)와 비교해보면 7 에 관계없이 같은 값 이고, 7 = -;Im 을 대입한 함수가 된다. 그리하여 (2 .1 9e) 는 상수항의 차 롤 무시할 때 (1. 78) 에 의하여 entr o p y S 와 S = kin W (2.20) 의 관계에있다. Bol t zmann 은 이상기체의 ent ro p y S 를 (2.20) 으로 정의하였는데, 이 식의 물리학 원리로서의 중요성을 강조하기 위하여 E i ns t e i n 은 Boltz - mann 원리라고 부르도록 제창하였다.
2-3 G i bbs 의 ensemble20l
20) J. W. Gibb s Elementa ry Prin c ip le in Sta t i tica l Mechanic s, Yale Un iv. , New Haven, 1902.
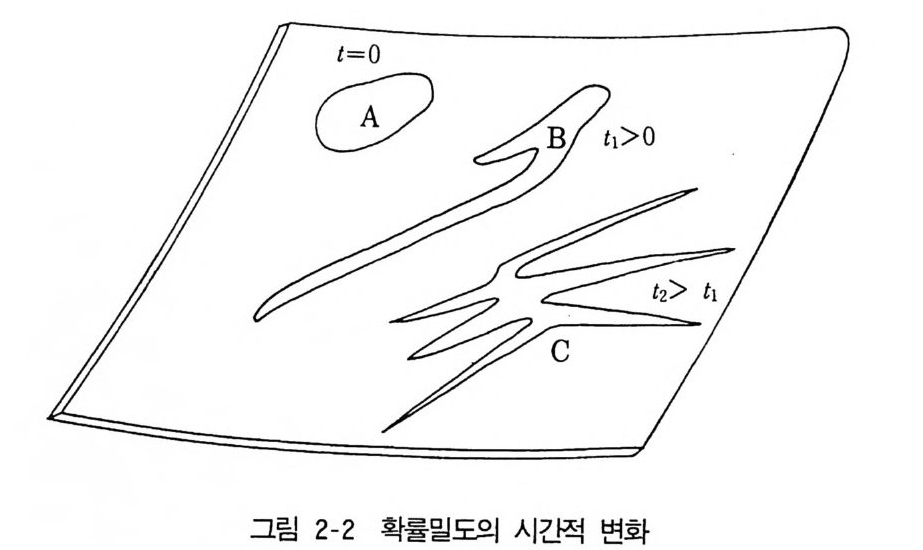
(1) micr ocanonic a l ensemble r 위상공간에서 L i ouv ill e 정리가 역학계에 대한 중요한 지식을 준다는 것 울 앞에서 2-1 의 내용으로 알고 있다. 특히 (2.7b) 에 의하면 위상점의 운동 울 따라가면서 확률밀도 D(q 1, …… Qr, P1, …… Pr, t)의 시간적 변화를 보면 그 값이 변하지 않는다. 그리하여 그립 2-2 에서 보이듯이 E :s;; H :s;; E
@t=O
+ fJE 사이의 energy shell 에 t =O 에서 영역 A 안에서만 일정한 값 a 이 고 다른 영역에서는 0 이 되는 확률밀도 D(q1 , …… qf, p1 , …… Pr, t= O) 는 ti >O 에서 영역 B 에서만 a 의 값을 가지며 t 2> t 1 에서는 영역 C 에서만 그 일정한 값 a 를 갖게 된다. 따라서 영역 A, B 와 C 는 모두 같은 체적을 갖는다. 여기서 디론 점을 찾는다면 영역 A 가 energy shell 의 한 부분에 모여 있는 데 대하여 영역 B 는 더 넓은 범위에 뻗쳐 있고 시간이 더욱 경
과된 뒤의 영역 C 는 B 보다도 더욱 넓은 범위를 차지하게 된 점이다. 즉, 시간 t가 증가함에 따라서 확률밀도 D 가 처음의 값 a 를 가지게 되는 영역 이 더욱 더 넓어져서 충분히 시간 t 가 크면 energy shell 의 모든 장소에 뻗쳐지게 된다. 그러나 D 의 값이 일정한 a 로 남아 있어야 하므로 D=a 인 부분과 D=O 인 부분이 밀접하게 인접하고 있다고 볼 수밖에 없다. 이러한 모양을 D 가 조잡한 관점에서 (coarse gra in e d sense) shell 에 균등하게 분포되었다고 한다. 조잡한 관점에서지만 energy shell 에서 확률밀도 D 가 균등하게 분포된 경우가 평형상태에 대응된다고 G i bbs 가 생각하였다. 대상 으로 하는 역학계와 거시적 조건이 같은 많은 역학계를 동시에 고려하고 이들이 ensemble 을 이루고 있다고 하면 ensemble 안의 역학계가 r공 간에 나타낸 위상점의 그 분포가 확률밀도 D 로 표현된다. 그리하여 G i bbs 는 평 형상태에 해당된 분포의 확률밀도가 E ~ H ~ E + {J E 인 energy shell 에 서 coarse gra in e d sense 로 균등한 값을 갖는다고 하여, 이것을 mi cr o-canonic a l ensembl 료 불렀다. coarse gra in e d sense 를 나타내기 위하여 r 공간을 일정한 크기의 세포 로 나누거서 모든 세포에 대하여 확률밀도 D 의 값이 같다고 하면, micr ocanon ica l ensemble 의 표현이 된다. 이것은 (2.1 9 ) 에서 Boltz m ann 이 µ공간을 세포 w 로 나누고 따라서 r 공간을 硏떠 크기를 갖는 세포로 나눈 것에 해당된다. 양자역학의 이론에 의하면 r 위싱공간을 h3 N의 크기 (h 는 Planck 싱수)의 세포로 나누면 각 세포가 하나의 양자상태를 나타낸다 는 것이 알려지고 있다• 따라서 이하에서는 r 위상공간 대신에 양자상태를 써서 이론을 전개시키도록 한다. 에너지가 (E, E+bE) 사이에 있는 모든 양자상태에 같은 확률로 역학계 가 나타난다고 하면, 그들 양자상태의 총수가 Q( E, bE) 로 표시될 때, 하나 의 양자상태에 존재할 확률은 1/Q( E, bE) 이다. 이 ensemble 에서 Gi bb s 는 entr o p y S 를, S = klnQ (2.21) 으로 정의하였다. 이와 같은 정의는 Bol t zmann 이 하였던 정의 (2.20) 을
그대로 계승한 것이라고도 볼 수 있다. G i bbs 는 바로 Bol t zmann 의 원리 를 기초에 두고 통계역학을 체계화시켰다• en t ro py와 밀접하게 관련된 거 시량은 온도가 되므로 디음에 이것을 역학량으로 구한다. ® 온도 평형상태는 원리적으로 열역학의 관계가 성립하는 상태를 의미한다고 하 고, 열역학계 중에서 거시적인 의부변수의 변화가 없어서 일을 하지 않는 경우를 생각한다. 두 개의 열역학계 사이에 에너지의 이동이, 일이 없는데 도 일어나면 그 에너지를 열이라고 한다. 열역학계 A 와 A ’ 가 각각 에너지 E 와 E ' 를 가지고 있을 때, 이 두 계를 접촉시키면 열로 에너지의 이동이 가능하다고 하자. 계 A 와 A ’ 를 합한 계를 에너지 Eo 인 Ao 로 하고 , Ao 는 의부와 에너지의 교환이 없는 고립된 상태에 있다고 하면 Eo = E + E' (2.22) 처럼 에너지는 보존된다. A 와 A' 사이에 에너지의 교환이 열로써 일어나고 결국 A o 가 열적으로 평형상태에 도달된다고 하자. 이 평형상태에 대한 상 태의 총수를 !lo (E o ) 로 한다. A 와 A’ 가 접촉되기 전에는 각각 평형상태에 있었다면, 그들의 상태수는 각각 Q (E) 와 Q ' (E' ）로 할 때 A 와 A ’ 를 합 한 계의 상태수는 (2.22) 에 의하여 Q( E) Q' (E ') = Q( E) Q '(E 。 -E ) (2.22a) 로 쓰인다. 그러므로 Ao=A+A’ 의 평형상태에 대하여 A 와 A’ 가 부분적 으로 평형상태에 있을 확률이 E 의 함수이고 P(E) = ~ Q( E) Q '(E 。 -E ) (2.22b) Q。 (E 。) 가 된다. P(E) 의 극대치는 A 와 A' 사이에 열이 이동하지 않는 Ao 의 열 적 평형상태에 해당될 것이다. 극대치의 조건은 dP(E) = 0, 또는 0= 祠l 麟dE = dlnPdE( E)
= 裂꼬 -뚜- fJifil- I E' = Eo - E (2.22c) 에서 나타난다. 이 식은 계 A 와 A ’ 의 각각에서 상태의 총수의 ln 을 에너 지로 미분한 양이 같다는 것을 나타내고 f)(E ) 三 d lnd QE( E) (2.22d) 룰 정의하면, 극대치에 해당된 E 의 값 祠에서 /J( E) = {J'(E ') ; E I = E 。 -E (2.22e) 이 된다. P(E) 가 계 A 에만 관계하고 A ’ 의 양이 나타나지 않는 데 주의할 만하다. 열역학에서 E 를 내부에너지 U 와 같다고 할 수 있으므로 (2.22d) 는 (2. 21) 에 의하여 B = 뚜譜요 = t(營 ) u = 꿉 (2.22f) 이 된다. 여기서 열역학적 관계식 (훑 ,-)V = 》이 사용되었는데 T 는 절 대온도를 나타낸다. 죽, 절대온도 T 가 (2.22 f)에 의하여 역학량으로 계산되 는것을알수있다. 또, 계에 들어온 에너지가 미소한 열 d Q이면, 계의 에너지는 U 에서 U+d Q로 되어 상태의 수가 증가하는 것을 d In Q( E) = In Q( E + dQ ) - In Q( E) ~~d Q=쌤 에서 볼 수 있는데, 열역학에서 보는 en tr o py의 정의 dS = 畢 (2.22g ) 를 얻게 된다. 이리하여 계의 entr op y S, 온도 T, 내부에너지 U 와, 명시는 하지 않았지만 체적 V 가 주어지게 되어 열역학적 관계식을 계산할 수 있 게 되었다.
® 이상기체에 대한 계산 분자가 질량 m 인 질점으로 생각된 이상기체의 Hami lt o nia n H 는 H= 같訂=김巨 f= 3N (2.23) 이다. 기체의 체적이 V 이고 E~H~E+ 하 E 의 조건이 있는 r 공간의 체적을 구하가 위하여 0 ~ H ~ E 의 체적 0 (E) 부터 구한다. ( E) = jv …… I 訂·…. d3r -- -:I… …[ 감；；；…… d3p - : 芬-양i ; =E =VN C 。 (2mE)3N /2 (2.23a) 울 다음과 같이 알 수 있다. 7 에 대한 적분은 체적 V 이고, i= l, …, N 이 되어 첫 인자 V N 이 나온다. 『에 대한적분은fil= 2mE 가 3N 차공 i= l 간에서의 반경 〈굽굽_인구를나타내므로( ✓ 굶굽 -) 3!,’ 인 입방체의 체적 에 구와 입장체의 체적비 Co 가 곱해져서 나온다. 여기서 C 。는 c 。 = 3Nr2n(3 견N 3/! 2N _) (2.23b) 가된다 . 2 1) energy shell E ~ H ~ E + l, E 의 체적 Ar 는 l, E 가 무한소량일 때 21) C 。의 계산 : J = I 二 ..... Je- <> I+· 나인 )d 사·…. dx, = (「ex, e －냐d.r） 2 = 7(/2 또극J 좌=표 S에( I : 의e하-,여, 1 -1 dr = 강 s, r ( f ) 이며C 。= 十 SI 이다.
Ar= 뺄 {)E = 擊 尸 (E) oE (2.23c) 이고 체적 h3N 의 세포의 개수, 죽 양자상태의 수 Q( E, oE) 는 Q( E, {)E) = 擊-
울 계산하는 데 (2.23b) 의 Co 의 값을 대입하고, 또 S ti r li n g의 공식 In N! ~ N In N-N 을 써서 간략하게 하면 S = Nk ln { (1『 )312 (ElN)312 V } + 방 Nk (2.26c) 롤 얻게 된다. (2.25 g)에서 E/N = f kT 로 하여 대 입하면 S = Nk {방 ln T+ ln V}+ const = C. 1n T + R ln V + const (2.26d) 가 되어 상수항을 무시한다면 열역학의 en t ro py와 같다고 할 수 있다. 그러나 en t ro py는 에너지 E 나 체적 V 처럼 지량반수 (ex t ens i ve qu an- tity)이고 S = Ns (v, T) (2.27) 처럼 표현되어야 하므로 (2.26c) 는 중대한 결함을 가지고 있다. 이것은 G i bbs 의 p aradox 로서 유명하며, 이미 G i bbs 에 의하여 Q( E, {JE ) 대신에 熹 Q( E, {JE ) = Q 。 (E, {J E) 로 하고 S = k ln Q。 (E, {JE ) (2.27a) 로 하면, S 가 (2.27) 의 관계를 만족시킨다고 밝혔지만, 그 해명에는 _E hre nfe s t의 공이 컸다 •22> (2.27a) 에 의하여 구해진 S 는 S = NkIn (u/A 3) + 웅 Nk (2.28) 이다. 여기서 V = VIN이 고 i은 열적 de Brog lie 파장으로. 불리며 ;. = ~(2mnkT ) 112 · (2.28a) 로 정의된 양이다. (2.28) 의 en t ro py표현은 Sackur-Te t rode 식이라고 알 려지고 있다 .23) 22) P. Ehren fes t & V. Trkal : Ann Phys i k 65(1921), 609. 23) 0. Sackur : Ann.d. ph ys . 36(1 9 11), 958, 40(1913) 67 ; H. Tetr o de ; Ann • d. Phys . 38(1912), 434.
(2) canonic a l ensemble ® 분배함수 에너지의 값이 크고, 따라서 양자상태의 수가 대단히 크다는 의미에서 큰 역학계이며, 또 열적 평형상태에 있고 작은 에너지의 출입에 대하여 열적평 형이 깨어지지 않는다고 볼 수 있는 계를 열원으로 부른·다. 열원 A’ 와 열 적 접촉을 하고 있는 역학계 A 가 에너지 E, 이 되는 하나의 양자상태 r 에 있을 확률을 생각해본다 . 24) A 와 A 를 합한 전체계 A o 가 에너지 (Eo, Eo + f JE ) 로 고립되고 있어서 그 평형상태가 앞에서 보았던 mi cr ocanon i- cal ensemble 로 기술되어 그 상태의 수가 !lo( Eo, fJ E) 로 표시된다. Ao 의 일부분이 되고 있는 A 가 양자상태 r 에 있어서 그 에너지가 Er 이면, A’ 의 에너지는 (Eo -E ,, E o -E,+ fJ E) 에 있고 그 상태의 수는 Q ' (E 。 -E r, 8 E) 가 된다. 따라서 A' +A , 즉 A o 가 이와 같은 조건에서 가지게 되는 상태 수가 1 X !l' ( E 。 _Er, 6E) 이다. 이 수는 !lo(E o, fJE ) 보디는 대단히 작을 것인데, 계 A 가 양자상태 r 에 있을 확률 R 이 Pr = 1 x QQ ' (。 (EE 。 a_ , EbrE ), 8E) (2.29) 가된다고할수있다.
24) 역학계 A 의 크기에는 제한이 없고, 분자 하나도 좋고 거시적인 역학계도 될 수 있다.
열원 A ’ 의 에너지 E' = Eo-E, 은 Er 에 비하여 대단히 크다. 즉, E' = E 。 -Er >> Er, 죽 E 。 >> Er (2.29a) 이 성립하므로 위의 R 을 E,/Eo 로 전개할 수 있다. (2.29) 에서 1n 을 취하 여 다음의 관계 1n P, = 1n Q '(E 。 -E 口 bE) -ln Q( Eo , bE) = 1n Q ' (E 。, bE) -~E ,. = IE 。E 『+ …… _ 1n Q。 (E o, bE) (2.29b)
을fJ E )얻 는게 그되것는데과, 관지계금없 계는 A상 만수에이 고주,목 한다0l면n Q1n n십' (E~o, fJE I) =一 flI n= O》o F(E 은0, E= Eo A’ 의 에너지가 Eo 일 때의 온도 T와 관계되고 E 。 ~ E ' 이므로 A ’ 의 온도 라고 할 수 있다. 또 A 와 A’ 가 열적 평형에 있으므로 이 T 가 A 의 온도 를나타낸다.
그리하여 (2.29b) 에서 무한소량이 되는 E,/Eo 전개의 1 차항까지만 취하 고 lnPr=a-f3 Er (2.29c) 로 쓸 수 있는데, 여기서 a = 1n n' (Eo, fJE ) 一 1n il o(E 。 ' fJE ) 이다. 따 라A 1 P, = C e-PE, ; (C = e 이 (2.29d) 이다. e - PE ’ 은 Boltz mann 인자로 불려진다. R 이 계 A 가 양자상태 r 에 있을 확률을 의미하므로 취할 수 있는 모든 양자상태에 대하여 합하면 1 = I: P, = C I:e-/ IE . (2.29e) r r 이고, 분배함수(partiti on function ) Z 를 Z 三 E e-' E , (2.30) 로정의하면 C = 1/Z (2.30a) 이고 (2.29d) 가 Pr = 上z e- /1E , (2.30b) 로표현된다. 계 A 가 에너지 op pJ-태 r 에 있을 확률 Pr 로부터 (E, E+bE) 사이에 있을 확률 W(E)oE 를 구할 수 있다. 죽,W(E)bE = ~ P, = ½e- f lE Q (E, bE) E< Er
虛 ) 2 = －普 = kT2 (景) , ' = kT2C , , (2.31d) 에 의하여 정적비열 C, ’ 와 관계된다. (2.31d) 로부터, (AE)2 20 에 의하여 열역학의 안정성조건 중 하나가 되는 C,’ ~ o (2.31e) 울알수가있다. 열역학에서 Helmhol tz 의 자유에너지 F 가 F=U-TS (2.32) 로 정의된다. 열역학의 제 1 법칙 dU = dQ - PdV 와 열과 en t ro py의 관계 (2.22 g)로부터 열역학의 항등식 dU = TdS -PdV (2.32a) 를 얻음으로써 (2.32) 에 의하여 S = - (aFIaT) (2.32b) 롤 알 수 있다 .25) 그러므로 (2.32) 는 F=U+ 지營) 。 (2.32c) 이고 U=F- 7\폼 ) u = 구: (2.32d) 이 된다. 내부에너지 U 에 대한 두 가지 표현 (2.31a) 와 (2.32d) 를 비교하 면 F = -kTln Z (2.32e) 25) dF = dU 一11J. S-SdT = 11J.S -PdV-11J .S -SdT = -SdT-PdV 로부터 다음을 알 수 있다. 죽, s= -(망) . , P= -（경 )T
롤 구하게 된다. 이 식에서 Z = e- F / k T (2.32f) 이고, (2.30b) 에 대하여 P, = exp ( F -E,) IkT (2.32g ) 울 알 수 있는데, 이 표현에는 열역학량 F 와 역학량 Er 이 동시에 나타나 고 있다. 분배함수 Z 를 계산하면 바로 (2.32e) 에 의하여 Helmholz 의 자 유에너지 F 를 알 수 있고 그것을 써서 entr o p y S 나 압력 P 를 s = -( 情 ) u = 草 情& (2.33) =k 1n Z+kT( l 털 ), (2.33a) p = -(aFJa V ), = kT( 법 z )T (2.33b) 를계산할수있다. 계가 양자상태 r 에 존재하는 확률 Pr 의 평균치를 구하면 (2.32 g)에 의 궁回 lnP, = L P,(l n P,) = L P,(F-E,) IkT r = (F— E) /kT= (F-U) /kT (2.34) 가 되어, (2.32) 의 정의에 의하여 S= -k 됴下 r= _kEPr1nPr (2.34a) 룰얻는다. 분배함수 Z 의 정의식 (2.30) 을 고쳐 쓰려면, 계의 에너지 고유상태 t/t r 은 연산자로 고쳐지는 Ha milt o n ian ft에 대하여 H wr(q I, …… q,) = E 『U r( q I, ……q,) (2.35) 롤만족시키고
Er =三 `[< ur: lf(qt Il, r…> … , qr) H wr (qJ, …… q,) hi=1 I dq, (2.35a) 이므로 Z = L
26) 연산자 0 의 'Ir은 임의의 직교완전계 |i >에 대하여 'lrO = 꾸 이다 .
양자상'Jr태 e로 -p서ff ~r I위e 상-f /공H d간r에 / h3 있N 는 체적 h 3N 인 세포 를 대응시키면 로 할 수 있다. 여기서 dr 는 r 공간의 미분체적이며, [,~I 1 dq j dp 를- 나타 내고, H ami l t o ni an 은 H(qI , …… qr, …… pI, …… p() 이다. 그러나 이상기 체에 대한 계산 (2.27) 에서 본 것과 같은 이유에서 z = N!1h3N Ie-/ IH d r (2.36) 가 분배함수에 대한 고전론적 근사로서 더 정확한 것이 된다 .'lJ) r 위상공간 의 한 점 r 주위의 작은 체적 Ar 안에 계가 있을 확률 P(r) Ar 는 (2. 30b) 에 P대(응r)하ll여r = +Z e -/ IH (r ) ~ N!h3N (2.36a) 가 되는 것이 당연할 것이다. ® 이상기체에 대한계산 이상기체의 Ha milt o n ian H 가
업) 입자의 동등성을 고려한 정확한 양자역학으로 분배함수 를 계산하고 그 고전역학 적 근사를 취하면 (2.36) 이 된다.
H=— 2ml ,E=N I 5? (2.37) 로 되어, 이것을 (2.36) 에 대입하면 z = N!1h 3N V1 … ··Ie - 타 森 ……忍 = 갑 h 3N vN [ 仁 읊 dp r N 요묘 . 깁汀꾹江 ) 2 = ½(i)N (2.37a) 이고, 여기서 열적 de Blog lie 파장 A 은 (2.28a) 에서 본 A=@h 01 다. 에너지Z =양 자Io: 상 …태 …의 E에~ 너 e -지.kT.로 .· L교 」'느 (;슨2:; (. n :2 +5 ¢b +)n. 를’ ) 사용하고 (2.30) 을 계산(하2.면38 ) /U, ~ I nz.= l 인데,여기서 ( = L。 e -.k .TL -,-m-1LL:'- n ' n,= I 을 계산하기 위하여 h2 Ik'IY .8 mL2) 이 대단히 작아서 합을 적분으로 근사 시키면 (= 국 [: e -zd x=L 군 이고, 따라서 z = [(]3N = VN (_Ji군균 ）二 (汀 (2.38a) 이 된다. 이 식은 싶「의 인자만큼 (2.37a) 와 다르다. 그러나 이미 micr o-canon ica l ensemble 의 계산에서 본 것처럼 (2.37a) 가 올바른 답을 줄 것 으로기대하게 된다. 분배함수 Z 로서 (2.37a) 의 표현을 사용하면 Helmhol t쩌 자유에너지
E 가 F == —-NkTk lTn Zln = ( -益kT l)n [ # 情) N ] (2.39) 로 쓰인다. 이 계산에는 S ti rl ing의 근사공식이 이용되었다. 자유에너지 F를 미분하여 다음과 같이 열역학함수들을 구하게 된다. 죽 P = —(a FIav) /I'.T = 감 N kT = nkT (2.4 0 ) 이며, n = N/V 이다. 또 s = -(aF/aT) v./I' = Nk ln ( >) + 망 Nk (2.4 0 a) 는 이미 구한 Sackur- 'Thtr ode 식이다. 내부에너지 U 는 U = k T1-若 lnZ = -kr1 --lf(F IkT) = 방 NkT (2.4 0 b) 이고, 화학 poten ti al µ는 µ 三 ( 藍) v.r = kTln().3/v) (2.4 0 c) 이 된다. (3) gra nd canonic a l ensemble : G i bbs 분포 계 A 가 열원이 되는 계 A’ 와 에너지를 열적으로 교환할 뿐 아니라 입 자도 교환하는 경우를 G i bbs 가 처음으로 고찰하였다. 이제 A ’는 열원과 입자원의 구실을 하게 되므로, 그 에너지와 입자수를 각각 E' 와 N' 로 하 면 계 A 에 대한 대응된 양 E 와 N 에 대하여 E ~ E' 와 N ~ N' (2.4 1 ) 이고 Eo=E+E' 와 No=N+N' (2.4 1 a)
의 Eo 와 N o 는 A 와 A’ 를 합한 전체계 A o 에 대한 양들이다. 계 A 와 A' 가 열적 평형과 입자교환에 대한 평형을 이루고 있는 경우에 계 A 에 입자 N 이 있고 그들이 양자상태 r 에 있다고 하자. A 의 상태수는 1 인데, 이것에 대한 A’ 의 상태수는 Q' (E 。 -E, (N), N。 -N) 이며, 전체계 Ao 의 상태수 는 Oo(Eo, N o ) 이다. 따라서 계 A 가 입자 N 을 가지고 그 입자들이 양자상 태 r 에 있을 확률 Pr(N) 은 P,(N) = 1 xn'( E ,-E, (N ), N 。 _N) (2.4 2 ) Q 。 (E 。 , N。 ) 이 된다. (2 .4 1) 의 조건에 의하여 P,(N) 을 작은 양으로 전개하면 In P,( N ) = In Q ' (E 。 _E , (N), N 。 -N) -In Q 。 (E o , N 서 -=~ ln Q ' (E 。 , NI E 。 ), (-Nln) 一 Q 。O ( Eln 。 , QN; (。 ) ,. N ' ) IN+… … NE'' == EN oo NE'' == EN oo (2.4 2 a) 가 되는데, 전개에서 첫째 항까지만 취하고, 전개계수에 대하여 fl=법?|=t(經)= k—1T —— 1—kT (2.4 2 b) NE'' == EN oo 과
a=~ 惡 | = +(蓋-） 나(―~) NE'' ==E Noo = -｝宁= —flµ (2.4 2 c) 가 되는 것을 알 수 있다 . 28 l (2 .4 2b) 에서 p는 열원과 입자원이 되는 계 28) 열역학의 항등식 dU = 'fli S 一 PdV + µdN에 서 묶 = (ifr)u,v 이 된다.A’ 에 전체의 에너지 Eo 와 입자수 No 가 있다고 할 때의 온도 T' 를 주는 데, 계 A 가 이것과 열적 평형에 있기 때문에 그 온도 T와 같다. 또 (2. 42c) 에 대하여도 µ ’ 는 계 A ’의 chemi ca l p o t en ti al 이지만 계 A 가 입자 교환에 대하여 A ’와 평형상태에 있으므로 A 의 chemi ca l po t en t ial µ과 µ' = µ의 관계가 성립한다. 그리하여 (2 .4 2a) 로부터 P,(N) = C1 e-P E,( N) -aN = C1 e - /I回 . (N) 때 (2.4 3 ) 을 알 수 있다. Boltz m ann 인자인 e-PE’ 에 대하여 e-p {EAN) - µ/I ' }는 Gi bb s 인자로불려지고있다. 확률 Pr(N) 의 계수 C1 은 모든 가능성이 일어날 순 있는 확률의 합이 1 이 된다는조건,죽 1 = IO: I:P,( N) = C1 IOO: (e11µ)/I ' L e-PE,( N) (2.4 3 a) N=O r N=O 에서 C1 = 1/J (2.4 3 b) 과 3 = NI=a::O (e/1µ )N Lr e- /1E .(N ) ( 2.4 4 ) 에서 구해진다. 여기에 (2 .4 4) 로 정의된 3 는 대분배함수(g rand pa rti tion fun ct ion ) 또는 Gib b s 의 합으로 불리고 있다. 확률 P,(N) 에 대한 (2 .4 3) 을 P,(N) = 上 e-' 요( N)+ '꼬 (2.4 5 ) 3 으로 하고, ent ro p y S 를 canon ica l ensemble 에서 (2.34a) 로 쓴 것처럼 S = -k 1n P ,(N) = -k NLo=o O L r P,(N) ln P,(N) (2.4 6 ) 으로정의하자.그러면 s = -k { -In 3 - PE + Pµ N }
=kln3+ 旦T -과T (2.4 6 a) 이고,여기서 U-TS-µN = -kT In J (2.4 6 b) 를 알수 있다. 이 식에서 F=U-TS 이고, 또 G i bbs 의 자유에너지 G 는 다음과 같이 G = µN, G = F + PV (2.4 7 ) 관계에 있다. 따라서 ® 三 U - 1S _ 函 = 一 PV (2.4 7 a) 로 새로운 열역학 p o t en ti al 을 정의하면 ® = _kT ln 3 = _PV (2.4 7 b) 이고, canonic a l ensemble 에서 분배함수 Z 에 대한 F = -kT ln Z 에 잘 대응된다. 열역학의 항등식을 써서 磯= dU -TdS - SdT-µ dN -Ndµ· = -PdV - SdT - 潟 (2.4 7 c) 를구하게 되어, P= _( 景)T,µ = k 7\場)T,µ (2.4 7 d) s = _( 홉) = (붉 (kTln 3))N,µ (2.4 7 e) N= _( 혼) = (孟 (kTln3))V,T = z( 끝 1n 이 = (體 )V,T (2.4 7 f)
의 관계를 얻는다. 여기 (2 .4 7 f)에서 z = e/ Iµ = eµ/ kT (2.4 8 ) 이며, 六근 absolut e ac ti v ity로 불린다. 대분배함수 3 에 대한 (2 .4 4) 를 z 를 써서 3 = L。 z' Z(N) (2.4 8 a) N=O 로 보기 좋게 쓸 수 있다. 여기 나온 Z(N) = Ee_f lE ( N) 는 입자의 수가 N인 계의 분배힘수이다. (2 .4 8a) 로부터 Z(N) = 京 릅 2 』 o ( 2.48b) 은 바로 알 수 있다. 죽 대분배함수 3 로부터 z 에 대한 미분만으로 분배함 수 Z(N) 을 구할 수 있다. 분배함수 Z(N) 을 (2.35b) 로 표현한 것처럼 3 = L모 ) I:
이 된다는 것도 canonic a l ensemble 의 경우와 비교하면 쉽게 알 수 있다. 여기서 대분배함수 3 는 (2 .4 8a) 와 같으나, 다만 분배함수 Z(N) 은 (2.36) 과같고,Z (N) = 詞 r e- /JH , d rN (2.50a) 으로 써서 입자수가 N 이라는 것을 강조하는 것이 더욱 좋을 것이다. (4) Gi b bs 분포의 응용 gra nd canonic a l ensemble 을 이용하는 예로서 두 가지만 고려한다. ® 이상기체에 대한 계산 이상기Z체(N에) =대 한½ 분 배(T함수3 rZ (N) 은 (2.37a) 에 이미 계산되어 있고 (2.51) 이다. 따라서 대분배함수 3 는 (2 .4 8a) 에 의하여 3 = Jo 떼 * (f)N = exp [1-] (2.52) 가된다. (2.4 7 f)에 의 하여 N = z-a- fz- -1 n J = 김섰 (2.52a) 이고, 따라서 입자수의 평균밀도 n 은 n=- 1u =- —NV = 섰z 이고, z = eµ/kT 로부터 µ = kTln nl 3 = kTln ( 춘) (2.52b) 인데, 이 chem ica l p o te n ti al 은 canon ica l ensemble 로 계산한 (2 .4 0c) 와 일 치된다. 압력 pYe (2 .4 7d) 에 의하여 p = kT( 맹)r.µ = kTT3 = nkT (2.52c) 이고 (2 .4 0) 과 일치한다. 압력에 대한 또 하나의 표현은 (2 .4 7b) 에 의하여
p = 伊 1n J = kT7 = nkT (2.52d) 가 되어 위와 같아진다. 그 이유는 3 에 대한 계산이 정확한 데 있다. 그리 하여 더 복잡한 계에서 3 를 근사계산하게 되면 이와 같이 압력에 대한 두 가지 표현이 어느 정도 일치되는가를 비교하여 근사의 좋고 나쁜 것을 정 할수도있을것이다. entr o p y S 도 (2 .4 7e) 에 의하여 S= 흙 (kTln 喜 =멜 (kTzT3) = k 差 +kT 骨불 +kTzV 若 (i) =웅N k 훑吉 =Nkln 나 )+½Nk (2.52e). 이며 Sackur 따itr ode 식을 다시 얻게 된다. 입자수의 평균 及가 열역학적 입자수를 나타낼 것이므로 계의 입자수가 N 이 되는 확률 W(N) 에 홍미롤 가지게 된다. 입자수 N 만이 문제가 되고 그들의 양자상태에는 무관하므로 W(N) = _l_ ? L e-{J E . (N ) 3 r(N ) = _3l_ ? Z(N) zN½( 紅 exp (내) =京~e ( N )N (2.53) 에 의하여 Pois s on 분포가 되는 것을 볼 수 있다. @ Lan gm u i r 의 등온흡착 앞에서 본 예의 이상기체는 분자가 질점이라고 생각되었기 때문에 일정 한 체적 V 에 들어가는 입자의 수 N 은 0 부터 OO 까지를 모두 다 취할 수
있었다. 현실적인 분자를 생각한다면 체적 V 안에 들어가는 분지수 N 은 N ~ Nmax 이고 Nma x 가 유한한 값이 된다. 이 경우 대분배함수 3 는 3 = -Nf 1.T U.1-x i ' Z(N) (2.54) N=O 이 되며 N '~ Nmax 에 대하여 Z(N' ) = 0 (2.54a) 이된다고할수있다• 기체가 들어 있는 용기의 벽에 기체분자를 흡착하는 장소가 있는 경우를 생각하자 . 이 장소 하나를 계로 하고 기체를 열원과 입자원으로 보며, 계에 는 분자가 하나만 흡착될 수 있고, 흡착된 분자의 에너지를 C 라고 하자. 그 러면 이 계에 gra nd canonic a l ensemble 을 적용할 때 대분배함수 3 는 3 = l+ze -/ lc (2.55) 가 된다. N=O 에 대하여 z N Z(N)=l 이고 N=l 이면 Z (l )=e-Pc 이고 zNZ (N) = ze 내 C 이다. N ;;:: 2 는 불가능하므로 Z(N) = 0 이다. 그리하여 홉 착점에 분자 하나가 흡착할 확률 W(l) 은 W (l) = ~1+ze-P • = -上,--- 8-1C +1 (2.55a) 이다. z 기체의 압력 p와 z 와의 관계 (2.52c) 를 쓰면 W (l) = ―요 ― (2.55b) p+p 。 이고, 여기서 f, p。 = e•/k T (2.55c) 가 된다. (2.55b) 는 Lan g mu i r 의 등온흡착식으로 알려지고 있다. 현실적으 로는 기체용기의 벽에 많은 수의 흡착점이 있지만 그들은 서로 독립적이므 로 각 흡착점에 대하여 (2.55b) 가 성립한다고 볼 수 있다.
3 이상기체의 양자통계 3-1 동동입자의 이상기체에 대한 분배함수의 계산 : Darw in- Fowler 방법 29)
29) C.G. Darw in & R.H . Fowler : Ph il. Mag 44(1922), 450, 823 : R.H .. Fow-ler, Sta tist ic a l Mechanic s . Cambrid g e Un iv( 1929).
(1) 동동입자의 양자론 전자, 양성자, 원자 등 물질을 구성하는 기본입자들은 같은 종류의 입자 들이 동등하여 서로 구별되지 않는다고 양자역학이 주장한다. 고전역학에 의하면 서로 구별이 안 되는 동등입자들도 시간 t =O 에서의 위치가 다르며, 시간에 따라서 그려지는 궤도가 서로 다르기 때문에 각 입자를 구별할 수 있다. 그러나 양자역학에서는 입자의 상태가 파동함수로 기술되고, 2 개의 입자가 충돌하면 그 뒤의 파동함수는 궤도처럼 구별이 되지 않는다. 따라서 동등입자들은 t =O 에는 그 위치에 의하여 구별할 수 있는 경우에도 곧 서 로 구별할 수 없는 상태가 된다. N 개의 동등입자로 된 역학계는 양자역학적인 상태를 나타내는 파동함수 ·
U(-rl, …… r一N ; t)에 대하여 |t/J 12 이 확률밀도를 나타내므로 동등입자를 나 타내는 조건이 l/J( _r1 , …… 一rj , …… 一rj, …… r一N :t) = 土 1/J( -r내;, …… 一rj , …… 一r, , •• …. 一rN ; t) (3.1 ) 널 로 주어진다. 위에서 (+) 기호이면 임의의 i번 입자와 j번 입자의 위치를 바꾸어도 파동함수가 불변하다는 것을 보이고, 대충성 파동함수를 의미한다. 여기에 대하여 (_）기호는 파동함수가 부호만 바꾸게 되어 확률밀도 Il/11 2 은 불변하지만 상태가 다르므로, 파동함수는 반대충성 파동함수라고 부른다. 양자역학은 자연계에서 2 종류의 입자군만이 존재할 수 있다고 주장하는데, 대충성 파동함수를 요구하는 입자를 Bose 입자, 반대충성 파동함수를 요구 히는 입자를 Fermi 입자라고 한다. 이상기체의 Hami lt o n ia n H = tI:i: —2:m:2 (3.2) N p i 는 분자 사이의 상호작용이 없으므로 분자 하나만 있을 때의 파동방정식 _ 8nh22m ~v 2? Ua(, r~ ) = C# 。 (~r) (3.3) 의 에너지 고유치 {다와 고유함수 {u2(7)}< >ll 의하여 그 고유치 E 와 파 동함수 U 가 표현된다. 즉 고유치는 E {n} = En& (3.3a) 로 되는데, 여기서 n a 는 에너지 %를 갖는 분자의 수이다. 분자의 총수가 N 이므로 N = [na (3.3b) 의 조건이 요구된다. 파동함수 針는 (3 .1)의 대충관계가 요구되지 않으면 ,Nu Uai (_ n) (3.3c)
로 되지만, 대충조건이 만족되려면 대충파동함수 U(+ )( --;, …… ；；)가 t/1(+)(~…… 7N ) = 志「 합 Uµ 立) (3.3d) 이고, 반E대 충(파r동:…함 …수 :U)( -=) (一r1값, …!… ~ r一 ( N- ) 는l ) P p~flai ( 7) ( 3.3e) 志= l1:u:a:1:: :(::컵:,:: :u::a:2:: (:r:,:): :…:::…::: :u::a:,\:·: :( :r:I:) ua1 (rN.) , ua2 (r/I,) … … ua.v (r/I.) (3.3f) 가 된다. (3.3d) 에 P 는 (7, …… 言)에 대한 치환(p ermu t a ti on) 을 의미 하고 가능한 모든 치환에 대하여 합을 취하고 있다. (3.3e) 도 기호 P의 의 미는 갇으나, P 가 우치환 (even p ermu t a ti on) 이면 ( -lV=l, 기치환 odd p ermu t a ti on 이면 ( -l)P = -1 을 의미한다. (3.3e) 와 (3.3 f)는 수 식의 다론 표현인데 (3.3 f)로부터 «i = «j가 되면 t/1(-) = 0 가 되고, 이 것은 Pa uli의 배타원리를 수식화한 것이 된다. Pau li의 배타원리는 하나의 양자상태 Urx(°?) 에는 입자가 없거나, 하나 들어갈 수 있는 두 가지 가능성을 의미하며 na = 0 또는 na = l (3.3g ) 만이 가능하다. 여기에 대하여 대충성 파동함수 (3.3d) 에는 n. . = 0, 1, 2, … … (3.3h) 의 모든 정의정수가 가능하게 된다. (2) Dar wi n-Fowler 의 계산법 동등입자의 이상기체에 대한 에너지 양자상태의 에너지가 (3.3a) 와 (3. 3b) 로 주어지고 있다. 따라서 그 분배힘수 Z(N) 은
Z(N) = I: e-/ IE r = I: 'e- / IE M = I: 'e - / 1~J.. (3.4 ) {n } (n } ~,=N [n ,=N 이다. 위에서 E' 는 [n~ = N 의 조건에서 정의정수 n1, n2, •…·에 대한 합을 의미한다. 여기서 ~a 三 e _{It. (3.4 a ) 로놓으면 Z(N) = E' rrg · (3.4 b ) hl 로 쓰인다. 《’를 z i로 고쳐주면 Z(N, z) = I:'n( z~J · = I' I:' n c (3.4 c ) h: h} 이며 [n . =N 의 조건이 제거된 합 Y(z) 는 Y(z) == …E싸… n+(zz 1:a-)1' z ' (N— 1) +z,vZ (N)+z1v+ 1Z (N+1)+ …… (3.5) 로 쓰일 것이다. 위에서 zNZ(N) 는 I:n, = N 인 조건에서의 합이고 z1v-1z (N-1) 은 I:na = N-1, zN+ 1z(N+1) 은 I:n. = N+l 에 대한 합이다. (3.5) 에서 z 를 복소수로 취하고 유수 (res i due) 에 대한 Cauch y의 정리 를 이용하Z(여N,) 분= 배갈함수 fZ( YN()z )을 z -N-1d z (3.6a) 에 의하여 구할 수 있다. 위에서 적분로는 z=O 주위의 폐곡선이다. F(z) = 1n Y(z) - (N+l) 1n z (3.6a) 로하면 Z(N) = 갈§e F(:)dz (3.6b)
이다. z 의 함수 F(z) 는 z = 0 에서 + OO (z = 0 에서 ln z = _ OO 이 다)이고 (3.6a) 에서 두번째 항이 우세한데 N 이 대단히 큰 수이므로 z = 0 에서 멀어지면 대단히 빨리 감소한다. z = l 에서 제 2 의 항이 0 이 되고, 그 앞에 제 1 항이 우세하게 되며, 그로부터는 단조롭게 증가한다. 따라서 정 의 실수축상의 점 Zo 에서 F' (z 。) = O (3.6c) 가 성립한다. ％에서 F( .zo )>O 이고 N 이 크면 F （히는 대단히 크다. 그리하여 z = Zo 주위에서 F(z) 를 전개하여 F(z) = F(z o) + 송 FH (Z o) (z-z 。 )나… … (3.6d) 로 생각한다. 복소수함수 F(z) 의 실수부가 실수축상의 점 Zo 에서 극소치를 가지므로 이 점을 통과하고 허수축에 평행한 선에서는 극대치를 갖는다 . 30 )
30) F(z)=u(x, y) + i u(x ,y）에서 Cauch y -R i eman 뼈 조건 꼬ax= = 호;fy• 7~iy= - -旦ay 이-1 성 0 립1 하-1 여I 효ax L2 +' 효ay~ 2 =0 이 성립한다.
죽 Zo 은 F(z) 의 안상점 (saddle p o i n t)이 된다. 적분 (3.6b) 에서 적분로를 z=O 를 중심으로 하고 반경 Zo 인 원을 취할 때 均 주위가 ste e p descen t한 길이 되고, 적분치는 均 근방에서만 고려하 면충분하다.따라서 z = z 。 + iy ; - y。 < Y < Yo (3.6e) 로취한다Z.(N그) 리=하 古여 eFk) I\ ex p { -½ F (z 。 )l}dy =eF(Z,) /~ (3.6f) 롤구할수있다. CD Bose-Ei ns te i n 통계와 Ferm i-D i ra c 통계
Bose 입자의 이상기체에 대하여는 (3.3b) 에 의하여 n; = 0, 1, 2, … … 인 모든 정의정수이고, Ferm i 입자의 이상기체에 대하여는 (3.3 g)에서 n; = 0 또는 n; = 1 의 두 가지 값만이 가능하므로 (3.5) 의 Y(z) 의 계산이 쉽게 된다. 죽 Bose 입자에 대하여는 Y(z) = EX> (z&)n, Ea : (z&)n' …… nn,= O n,= O == rrnI.x(= : O 1 (\z~ 」。 ) •• (3.7) 이 된다. 이 식의 첫번째 행은 (3.5) 에서 곱산과 합산의 순서를 바꾼 것이 고, 세번째 행은 lz ~ al
= ln Y(z 。 )-(N+l) ln z 。 ―½ In 2 n: F (z 。 ) (3.1 0 ) 인데, N 이 대단히 크므로, 이것에 대하여 1 이 무시되고, 또 In F(2o)~In N 도 무시될 수 있어서 (3 .1 0) 은 In Z(N) ~ In Y(z 。) -N ln Zo (3.1 0 a) 로 쓸 수 있다. Zo 를 결정하는 (3.6c) 는 (3.6a) 를 써서 0 = 뿔』 Zo = [円 ~-(N+ l)+t= io (3.1 1 ) 이 되는데 (3.9) 를 대입하고, N+l 을 N 으로 쓰면 E Zo'a =N (3.l la ) 1 士 Zo'a 이고, 여기에 Zo = e-a, ~; = e- /1 a 로하면 N = 꾸 e.+ /11 c i 士 1 (3.llb) 가된다. 양자상태 i에 있는 평균적 입자수를 국로 하고 n_i = e.+/1lc i 土 1 (3.l lc) 로 하면 (3.llb) 는 N= ~ii;- (3.l ld ) 가된다. 0뇽 PJ -태 i에 있을 평균적인 입자의 수 元가 (3 . llc) 로 되는 것을 Fer- mi 입자에 대하여는 Ferm i-D ria c 통계, Bose 입자에 대하여는 Bose- Ein s te i n 통계라고 부른다.
(3) 대분배함수와 열역학함수 열역학계의 여러 가지 열역학함수를 구하는 데는 분배함수 Z(N) 으로부터 출발하겨 (2.32e) 로 Helmholtz 자유에너지 F 를 구하고 (2.33a) 와 (2.32b) 로 entr o p y S 와 압력 P 를 구하여 그로부터 열역학적 관계식을 써서, 다른 함수를 구할 수 있다. 그러나 (2 .4 4) 와 (2 .4 8a) 로 주어지는 대분배함수 3 롤 구하고, (2 .4 7b) 로 열역학 po te n ti al ®를 얻은 다음에 (2.4 7 d, e, f)에 의하여 압력 P, entr o p y S 와 평균적 입자의 수 5 를 계산하여, 다음은 역 시 열역학적 관계식으로 다른 열역학함수를 구할 수도 있다. 동등입자의 이상기체에 대하여는 그 대분배함수가 쉽게 구해진다. 분배함 수 Z(N) 이 (3 .4)로 주어지므로 3 == ItX: (Ie: /eJ' ' -) /NJg Z.e( N/J ( 도)) µ .V= O N=O l•I =[ u~.= [Ne p( µ-%) ] % {n ) =U E [ e0(µ-%) ] % (3.1 2 ) 가 된다. 두번째 행은 Z(N) 에 (3 .4)를 대입하고 또 N=[n. 로 하여 바꿔 쓴 것이고, 세번째 행은 [n,=N 의 조건의 합을 하고, 다음에 N 을 伊十터 OO 까지 합한 결과가 조건 없이 n, 에 대한 모든 합을 취한 것과 같다는 것 울 나타내며, 네번째 항은 합과 곱의 순서를 바꾼 데서 얻어진다• Bose 입자에 대하여는 n.=O, 1, 2, ……이므로 e /J(µ-앙
z = eh , ~ .. = e-1 1' · 로 쓰고 (3.1 2 a, b) 를 J± = n [ 1 土 Z~,. ] 리 (3.1 2 c) 로 모아 쓸 수 있는데, (3.9) 와 비교하면 3± = y土 (z) (3. 1 2 d) 임을 알 수 있다 . 위의 부호는 Ferm i 입자, 아래 부호는 Bose 입자에 대 한계산결과이다. 열역학 po te n ti al ®는 (2 .4 7b) 에 의하여 -PV = ®-t = -kT 1n J土 = 土 kT ~ ln(l 土 z:2) (3.1 3 ) 이며, (2 .4 7 f)를 써서 N= -（롱) = z( 갑 In z 土 ) V,T = 혼 1 ;;;:a =I: e’(c.- 1µ) 士 1 (3.1 3 a) 룰 알 수 있다• 이것은 (3 .l lb) 와 근본적으로 같은 식이다. 기체 전체에 대한 gran d canonic a l ensemble 을 위와 같이 생각한 대 신, 분자 하나의 양자상태 u,, ( 7) 을 역학계로 하고, 이 계에 대한 gra nd canon ica l ensemble 을 생각할 수도 있다. Bose 입자이면 3d-) = nEa= O g (e~' '· )• = nI-o : 0 (z~J = 1-1z ~. . (3.14) 이고, Ferm i 입자에 대하여는
3..<+ > = n~=I O i'(e- /J_ t. ) . = mI= I: O ( z~J = 1+z~a (3.1 4 a) 이다. 또 이 양자상태에 n 개의 분자가 들어갈 확률 P ~ (n) 이 PJ n ) = 上 (ze - P c. ) (3.1 4 b) 3 이 되어, 평균된 입자의 수 元는 n,, == L-n~ o (P faa (·ln 니 ). =.1 n-3!3 - I: :n( ze- P'· )• (3.1 4 c) 이다. Bose 입자에 대하여는 (3 .1 4) 를 대입하고 瓦 )= e8 (C. - 1µ ) -1 (3.14d) 를 알 수 있고, Ferm i 입자에 대하여는 志)= eB(c. -lµ ) +1 (3.1 4 e) 울 구할 수 있다. ri «(±l 는 Ferm i-D i ra c 통계와 Bose-Ei ns te i n 통계로 부 른다고 이미 말한 바 있다. 다시 기체계에 대한 대분배함수 (3 .1 2c) 로 돌아가면, 압력 P 를 (3 .1 3) 에 의하여 P = 笠 1n3 土 = 序 {士 E 1n(1 士 z c;J} (3.1 5 ) av = 祖弓 ln (l국 e-,C.)} (3.1 5 a) 를 얻게 되는데, (3 .1 4d) 와 (3.14 f)에 의하여, n= 土 1 로 하면 e +/I(£,-µ) = _n1a _ n. = 1-nari n a (3.15b) 이고 t7 = -1 인 Bose-Ei ns te i n 통계에, t1 =+l 인 Ferm i-D i ra c 통계에 대응된다. (3 .1 5b) 로부터
1 + 11e/1 (µ -t.) = l l-n 瓦 을 알 수 있고, 따라서 (3 .1 5a) 를 P = 一 笠 n E 1n(1 —,1 元 ) (3.1 5 c) 로 고쳐 쓸 수 있다. 특히 元
s (B - E ) = S = ― k 혼 阮 ln 元 一 (1 + 元) In (1 + 元)} (3.1 6 b) 롤 알 수 있다. Ferm i-D ria c 통계에서는 n a 가 O 와 l 사이의 값이고, 따라 서 (1 ―元)는 1 과 0 사이의 값이 되는데, 이것을 입자가 비어 있는 구멍 (hole) 의 수를 나타낸다고 할 수 있다. 기체의 온도 T를 줄여가서 T-O 가되는 극한에서, Fermi -D ria c 통계 는 cz < 냐 모든 에너지 상태에 대하여 元 = 1 이고, · Ca > 타인 상태 에 대하여는元 = 0 이다. 따라서 T-0 에 대하여 S(F -D ) - 。 (3.1 6 c) 가 된다. 여기에 대하여 Bose-Ei ns te i n 통계에서는 T - 0 이면 기저상태 (gro und s t a t e) 에 모든 입자가 모이고 no - N, 元 - O(e: , =t= 0) 가 되 어 T-O 에 서 SIB- E > = -k{NlnN-(1 + N) 1n (1 + N)} =k(lnN+I+ 싶+……) 이고, S1B- E ) Nli ..m.. ::c N 一 。 (3.1 6 d) 가된다. 3-2 양자효과에 대한 근사 (1) Maxwell-Boltz m ann 통계에 의한 근사 동등입자로 구성되는 계의 파동함수에 대칭성이 요구된 데서 Bose-Ei- nste i n 또는 Ferm i-D i ra c 통계를 얻게 되었다. 양자역학으로 입자의 양자 상태가 결정되는 경우에도 파동함수의 대칭성이 무시된다면 어떤 결과가 나 타나는가를 알아볼 필요가 있다.
기체의 양자상태 R 이 입자 하나의 양자상태 E , 에 들어가는 입자의 수 n,· 에 의하여 R = (nI, n2, … …) (3.1 7 ) 로주어지고 N = Ln i, ER = [ni E , (3.17a) 의 조건이 만족된다. 기체의 분배함수 Z(N) 은 Z(N) = IR: e-PE, = n,.n E ,· · ··· ·g R (nI, n2, … … )e - /I 요 (3.17b) 표 j= N 이며, 여기서 gR (nb 杓, …… )는 R 상태의 축되도 (de g enerac y)를 의미하 고 gin n2, ……) = n,! nN2!! … … = ITN n!i ! (3.1 7 c) i= l 이다. 다항정리에 의하여 (x1 + X2 + …… )N = ....E' ;:. .... n 1! nN2!!… … [x1· ' x; … …] 2 i= N 이 성립하므로, (3 .1 7b) 와 (3.17c) 로부터 xi 一 e 내 연 로 하고 Z(N) = (e -p,, + e-Pc, + …… )N = (I: e-P 宁 = [Z(1)r (3.1 7 d) 이고, 여기서 Z(l) = I:e - Pt. (3.l 7e)
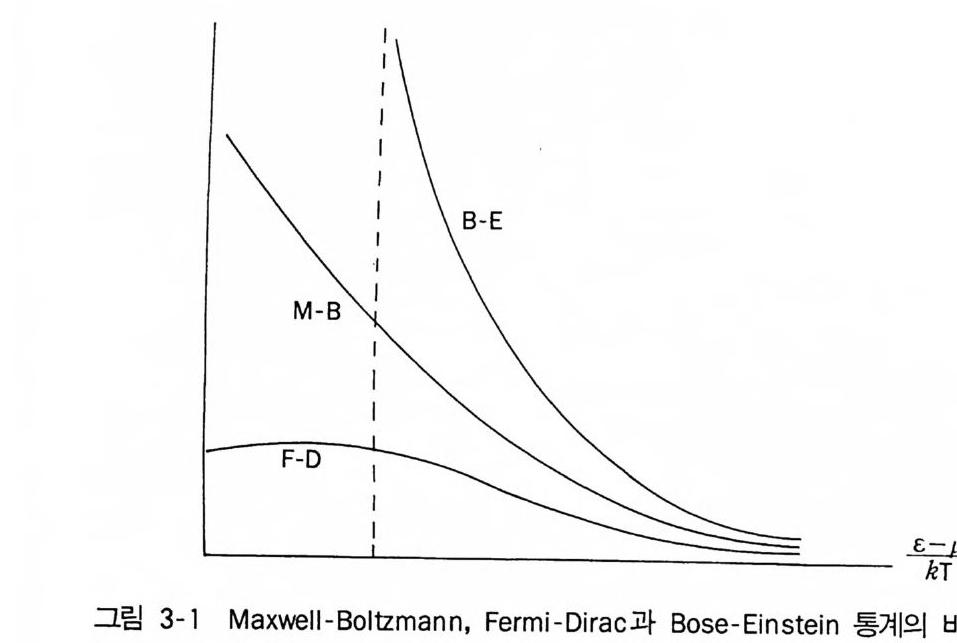
롤 얻을 수 있다. 따라서 대분배함수는 3 = LOO ~Z(N) = L여 [z Z(l))M N=O N=O = l-zZ1 (l) (3.18) 01 다. 입자 하나의 양자상태 s 에 들어가는 평균적인 입자의 수元는 n_, = I::Zn(, N e -)8 E. = I:뇨n,g R R( n(n1,i , nn22,, … … … … ) )eef- fJEn , C, ‘ = Z( 1N ) (- i8B 臨8c3 ) = -_B l_o&노 꼬 (3.19) 이다. Z元(N)= 으(로 -(3 .1 릅7d) 를~ 대)입하 =여 N- fuf (3.1 9 a) 도 알 수 있다 . 입자 하나만으로 구성된 계에서 양자상태 s 에 있을 확률이 e - /i 's IZ (l)이 될 것이므로, N 개의 입자로 된 기체에서 양자상태 s 에 있는 입자수가 (3.1 9 a) 처럼 된다. 이와 같은 것을 Maxwell-Boltz m an- n 통계라 부르고 있다. Fermi -D i ra c 통계와 Bose-Ei ns .te i n 통계에서 입자 하나의 양자상태 s 에 들어가는 입자의 평균수가 n = 士 1 (+1 은 F-D, -1 은 B-E) 에 대하 여 正= ep( e -1µ) +n (3.20) 인데,지금 ns ~ 1 (3.20a) 이면 l
M-8
가 되어야 하고 111I 가 무시될 수 있다. 따라서 ns =~ 샹 e-/JCS (3.20c) 가 되는데, 이것은 (3 .1 9a) 의 Maxwell-Bol t zmann 통계에 대한 분포와 비 슷하다.사실 e 도훑 (3.20d) 에 의하여 µ롤 구하면 (2 .4 0c) 의 결과를 쉽게 알 수 있다. n, 에 대한 근사 (3.20c) 에 의하여 Fi = I:n, = e/1µ I: e/1t s (3.20d) 가되어 pµ = ln N _ 1n (E e 내이 (3.20e) 를 얻는다. 그런데 (3 .1 0a) 와 (3 .1 2d) 에 의하여
ln Z(N ) =1 n 3 _ wp µ (3.21) 이고, (3 .1 2c) 에서 n = 士 1 이면 ln 3 = n 홉 ln [1 + ne/I (µ - c .l ] (3.21a) 인데, (3.20b) 에 의히여 e/i( ,I - Q < 1 (3.21b) 의 조전이 성립하여 ln J = 工a eB( µ-c. ) = E n 。 = N (3.21c) 로 고쳐 쓸 수 있다. 따라서 (3.21) 이 (3.20e) 에 의하여 ln z(N ) =N _ N8µ ==三 N-— ( INn- N N ln ! N{+ln 1—Nn 下[ )Z-( ll+ )n ] N~1n e(-El P c, }e _p 8,)N ((33(.3.22.222b2a))) =ln(Y) (3.22c) 를얻게 된다. Maxwell-Boltz m ann 통계에서 (3 .1 7d) 는 ZM. s( N) = [Z(l)r (3.23) 울 주고 있는데, 동등입자에 대한 파동함수의 대칭성에서 나온 결과는 (3. 22c) 로부Z터(N ) = 占 zMB(N) (3.24) 이 된다는 것을 알 수 있으므로, G i bbs 의 p aradox 에 대한 해명을 얻게된 다.
®근사의 조건 Ferm i -Dr i ac 과 Bose-Ei ns te i n 통계를 Maxwell-Bol t zmann 통계로 근 사시킬 수 있는 조건이 (3.20a) 로 주어지며, 따라서 (3.20b), 죽 e p(다 ) ~ 1 이 모든 에너지상태에서 성립한다. 기저상태의 에너지를 0 으로 하면 e- / 1µ = e-µ/ k T ~ 1 (3.25) 가요구된다. Maxwell-Bol t zmann 통계로 계산된 화학 po te n ti al µ가 (2 .4 0c) 로 주어 지며 µ = kT ln (J.3/ V) (3.25a) 이다. 여기서 열적 de Brog lie 파장 A 와 입자 하나에 배당된 체적 u 는 l = h/ V:굶굶 T, v= VIN (3.25b) 이다. (3.25a) 를 써서 (3.25) 의 조건을 보면 vi A3 ~ 1 (3.26) 가 된다. 죽 1 개의 입자가 차지할 수 있는 평균적 체적이 열적 de Brog li e 파장의 3 제곱으로 대표되는 입자의 유효 크기보다 대단히 크다면 동등입자 에 대한 파동함수의 대칭성이 분배함수를 N! 로 나눈 것으로 근사시킬 수 있다는 것을 알게 된 것이다. 입자 하나에 대한 양자상태를 고적역학으로 근사시키고 계산할 수 있는 조건이 v113 ~ i, 죽 VI > A3 (3.26a) 이고, 이와 같은 고전역학에 의한 근사에서 나타난 오차를 파동효과로 부르 기도 하는데 (3.26) 의 제한은 이것에 비하면 대단히 강하다.
실온, 1 기압의 He 기체에 대하여 u= -¾ 구 =｝『에서 P=1013250dy n/ cm2 , T=293°K , k= 1.38 X 10 - 1 6 er g /°K 를 대 입하고 u=4X l0 -20 cm 3 를 얻는데 , 2 = h/ 〈 급:교 R는 h = 6.63X10-v e rg. s ec,mH, = 4X1 .67 X 10 -2 4 g를 써 서 2 = 0.5 x l0cm - 별 구할 수 있다. 따라서 u/23 = ~(04.5x x 1 l00- -20 8 )3 = 32Xl04 ~ 1 이고 ( 3.2 6) 이 만족되고 있다. 여기에 비교하여 금속 안의 자유전자가 구성하는 전자기체에 대하여는 i = 40 x 10 _8 cm 이고, 전자 사이의 간격은 Ul/ 3 속 2 x 10- 8 cm 가 되어 (3. 26) 의 조 건이 성립하지 않는다. 그리하여 자유전지에 대하여는 Max-well-B o ltz mann 통계가 성립하지 않고 Ferm i-D i iac 통계를 사용하여야 하는이유를 알수 있다. Maxwell-Boltz mann 통계가 성립하도록 (3.26), 즉 V ~ A3 (3.27) 인 조전이 성립하는 영역을 고전적 영역이라고 부른다. 여기에 대하여 v < A3 (3.27a) 의 조건이 성립한 영역을 양자적 영역이라고 하고, 그와 같은 기체를 양자 기체라고한다.또 u = ,l3 에서 정해지는 온도 To, 죽 Ta = ( 소 )v-21 3 (3.27b) 로 하면, 양자기체는 그 온도가 T ~ To 인데, 이와 같은 기체는 축되기체 ( dege nerate d ga s ) 라고도 한다.
(2) 약하게 축퇴된 상태 Fermi -D ria c 통계나 Bose-E i ns te i n 통계를 만족시키는 기체의 종류와 는 관계없이 (3.27b) 로 정해지는 온도 To 에 대하여 T ::?: To (3.28) 이면, 기체의 성질이 고전적 영역과 많이 다르지는 않을 것으로 기대된다. 그러므로 고전적 기체에 대한 작은 보정을 구해보도록 한다. Ferm i입자의 대표로서 전자에 대하여 생각해본다. 전자 1 개의 위상공간 에서 공간좌표 (一r ,一 r +d_r )와 운동량좌표 (一p -, -p ➔ +d-p ) 사이에 있 는 위 상체적 d3-r— d3p一 에는 양자상태의 수가 sp in 상태까지 고려하여 2 • -h- h-강 7銅 (3.29) 이다. 따라서 기체의 체적이 V 일 때, 운동량의 크기 (p, P + dp ) 사이에 있는 양자상태의 수는 (3.29) 를 적분하여 2 • ~h1 V • 4np 2d p (3.29a) 가 된다. 에너지 £ = p 2 /2m 에 대하여 (£, £ + d£) 사이에 있는 양지상 태의 수 g(g )da은 (3.29a) 에서 p를 g으로 고치고 g(c )dc = 2 • V • 4rp 2dp h3 = ~h3 (Zm3 )1 1 2 g11 2d g (3.29b) 를얻게 된다. 여기서f.( z z) 의 - 함 rf수r if) n (Fz) 를f r, dx (3.30) 로 정의하면 편리하게 된다. 첫째로 f.-1 (2) = Z 읊 f.(z ) (3.30a)
의 관계f.를(z )쉽 =게 r알fn 수} 있J고~,d x또 x • -z 1 z
=*23N —k T ff35//22 (( zz )) (3.32a) = 방 NkT{1 + ( ~.. . 1- - ~)z + ……} (3.32b) 가된다. 입자의 수 N 과 체적 V 가 일정한 조건에서 (3.31) 을 T로 미분하고, (3.30a) 의 관계식을 사용하면 澤 )N,\ 1 = 웅+~ (3.33) 룰 얻을 수 있다. 따라서 (3.32a) 로부터 . C.== t（N웅k { 1) V += NO(kz){ } 『仁鬪 -｝仁鬪 } (3.34) 이 나온다. 기체의 압력 P 에 대하여는 PV=kTInJ = kT I: In(1 + ze-/Ic. ) a 로부E 1 PV 국= kT ff :: 。 d上E e:g /I c(gC)+ l1n g(l(c+ )zdec 기 ex: z =응 E (3.35) 를 얻는다. 위에서 두번째 행의 적분은 첫번째 행의 적분에 부분적분을 하 고, 적분된 항이 e = 0 와 8 = CX)에서 0 이 되는 데서 나온다. Helmhol t z 의 자유에너지 F 는 F = G - PV = Nµ - PV
== NN kkTT {(llnn zz _- 1言) } (3.35a) 이며, entr o p y S 는 S=¥=Nk{ 鬪鬪― lnz} = Nk( f-ln z) (3.35b) 로 얻어진다. R>s e 입자로는 spin 0 가 되는 입자, 특히 He 원자를 머리에 두고 계산한 다. 에너지 (t::, i:: + de) 사이의 양자상태의 수는 sp in 자유도가 없으므로 (3.29b) 대신에 g(£ )d£ = v · 4hr3p 2 dp = 擊 (Zm 3 )1 12 €11 2 de; (3.36) 를사용하여야한다. 이번에는 함수 g n(z) 를 gn( z) 三 rln) I 。~ Xn-1 上S dx (3.37) z 를 정의하면, z ~ 1 에 대하여 전개가 가능하고 g.( z) 三 rln) f。0 x•-1 곱 0:: (ze - •)1 dx
N = 드 五。 == JTT‘ `: eg f(!(El ’ -)c1 . )- ;- //lIµ _ \ - 1 dc . = ¾}V, g31i {z) (3.38 ) 이고, 에너지 E(=U )도 E=u=In 혼 = ½kr ( T3)gs 1 2( 2) (3.38a) 이다. 또 압력 P 에 대하여도 (3.35) 와 비슷한 계산으로 PV= 겅2 E— = ¾V)k kTg s, 2(2 ) (3.38b) 를 얻게FS 된=다 =.G -H~PelVm h==o lN t미µz 의-§ P 자V;유 = :에:N:너 鬪k지T -{F 와ln1 zne zn -}t r o p y 1S21 도2,) } (3.38c) gsg(Jz ,I(z (3.38d) 가 되어, 2 로 전개하면 임의의 근사석을 얻을 , 수 있다. 3-3 축퇴된 전자기체 1897 년에 J. J. Thomson 에 의하여 전자가 발견된 후, 금속회로 안에 존재하는 전류가 전자에 의한 것이라는 점에 의심을 가질 수가 없었다. 그 러나 금속서의 전자가 기체 안에서 분자가 하는 것처럼 운동하여 마치 전
자기체를 이루고 열적 평형상태에 있다는 생각을 P. Drude 가 발표한 뒤부 터 문제가나타났다. Drude 이론의 가장 큰 성공은 다음의 Wi ed emann-Franz 법칙이 유도 될 수 있디는 데 있다. 이 법칙은 열전도도 K 와 전기전도도 (J 사이의 관계 를
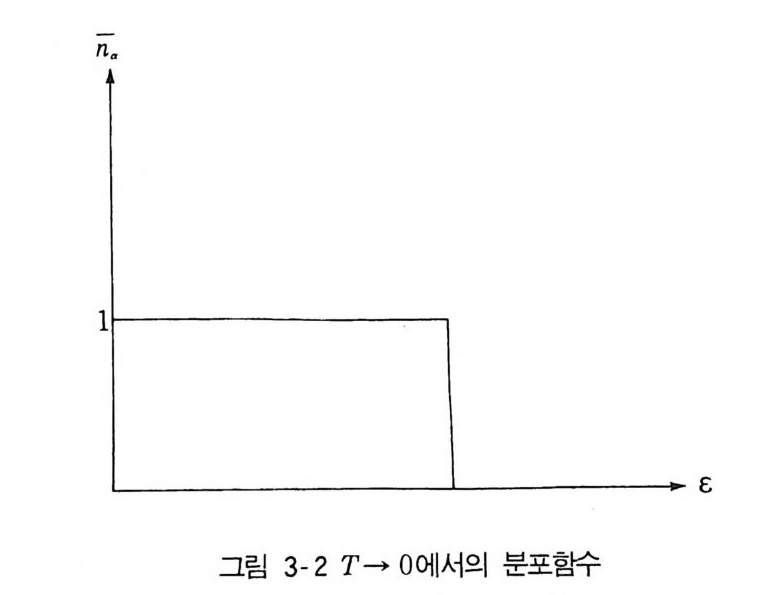
一K6 =3 一ke22 T (3.39) 로 주고 있다. Drud e-i근 전기 전도도를 6= em2l un (3.39a) 로 유도하였는데, 이 식에서 l 은 평균자유행로, e 는 전자의 전하, n 은 전자 의 수밀도이고, V 는 평균속력이다. 기체에서 열전도도는 단순한 이론에 의 굴}면 K = ½nlvc= tnlv kT (3.39b) 가 되므로 계수가 약간 다르게 되지만 (3.39) 가 타당하다고 할 수 있다. 열기전력, 전지기전력과 금속의 열전자방출 등의 많은 열전효과가 Drude 이론으로 정성적 설명이 가능하고 그들 효과 사이의 내적인 연결관계도 인 정될 수 있었다. 그러나 이 이론 또는 가설은 전자의 비열에 관한 한에서 실험치와 크게 다르게 나타났다. Durde 이론에 의한다면 열적 평형상태에 서 전자가 그 자유도에 평균적으로 (1/2) kT의 에너지를 가질 것이고키 따 라서 전자 lmol 에 대하여 비열이 (3/2) R = 3cal/mo l. de g가 될 것이 다. 실온에서 금속은 Dulon g -Pe tit의 법칙에 따라서 그 비열이 3R =_ 6 cal/mo l. de g가 되는 것이 실험사실이고, 전자의 비열을 그 값에 합한 웅 R + 3R = 9cal/mo l. de g가되지 않는다는것이 확실하다. 사실, 이 전자비열에 대한 곤란에 의하여 전자기체의 존재에 대한 Durd- 려 이론이 신뢰를 잃고 있었다. 그러나 192 8id에 Sommer fe ld31) 는 비열의 31) A. Sommerfe ld , Z. Phy s. 47, 1, 1928.곤란을 전자가 Fermi -D ria c 통계를 만족시킨다는 데서 해소시키고 Drude 이론에 새로운 생명을 주었다. (1) 완전히 축퇴된 전자기체 Ferm i-D ria c 통계에서 에너지 € a 인 양자상태에 있는 입자의 평균수는 (3.1 4 e), 즉 -na = e/J( c.-µ 1l + 1 로주어지_는na 데= ,r 'lpl0 = 갑EE Faa 이<<므 µµ로oo , T 一 0, 죽p一 OO 인 극한에서 (3.4 0 ) 가된다. 여기서 µ。 = µ(T~ 0) (3.4 0 a) 을 의미한다. Ta 가 (3 .4 0) 으로 주어질 때 기체는 완전히 축퇴되었다고 한 다. 완전히 축퇴된 상태에서는 µo 보다 작은 에너지를 갖는 궤도양자상태는 s pi n 상태까지 고려하여 입자가 2 개씩 채워져 있고, µo 보다 높은 에너지 상 태는모두비어 있다. 仰는 완전히 채워지거나, 아주 비워진 상태의 경계를 이루는 에너지의 값 이 되고, 흔히 Fer mi준위로 불려지며 EF 로 쓰이기도 한다. 죽 tF = µ。 = µ(T~ 0) (3.4 0 b) 이다. 이 에너지에 대한 운동량의 크기 PF 는 ~p~= €p=µo, PF=@ 급 (3.4 0 c) 가 된다. 완전히 축되된 상태에서, N 개의 전자로 구성된 전자기체에서 D-¥- 터 C p까지의 양자상태의 수가 N 과 같은 것이므로 N=2 *3- [v• 뜻갑] (3.4 1 )
n.
가 되는 것울 (3.29) 와 (3.29a) 에 의하여 알 수 있다. (3 .4 1) 에서 PF 를 구 굼}면 PF=h( 읊f )1 / 3 (3.4 1 a) 이 되고, 따라서 (3 .4 0c) 에 의하여 CF = 仰 = 읊 = 芸(志 흡 ) 2/3 = h 2 (83 n죠2m ) 2/ 3 (3.4 1 b) 를 얻게 된다. 이 식에서 Fer mi준위가 전자의 입자수밀도 n 의 2/3 제곱이 고, n 이 크면 €F 의 값도 커진다. Fer mi온도 TF 를 TF 三 T1 타 (3.4 1 c) 로 정의하여 쓰면 편리하다. 전자기체의 에너지 E(= u) 는 (3.29a) 에 의하여 U = E = j:끓i v 4np 2 dp
= 2 vh—J 툰습(3.4 2 ) =뿔(같꼽 ) 2/3 (3.4 2 a) = f Nµ 。 (3.4 2 b) 이고, 압력 P 는 (3.35) 에 의하여 PV = 송~ = 응 (Nµ 。 ) (3.4 3 ) 이고, 따라서 P = -g-내)µ。 (3.4 3 a) 이다. Helmholtz 자유에너지는 F = Nµ 。 -P V = Nµ 。 -응 學 = 웅 Nµ 。 (3.4 3 b) 인데, F = U - 霞에서 T 一 0 이고 F = U 가 되는 것이 당연하다. 동 (Cu) 에 대히여 계산하면 µ。 = 7 eV (3.4 4 ) P = 3.8 x 10 5 atm (3.4 4 a) 이고 따 =8X105K (3.4 4 b) 의 값이 된다. (2) 실온에서의 금속전자 元에 대하여, 에너지 e 의 함수 f (c) 을 f(e ) = e%-,µ1 + 1 (3.4 5 )
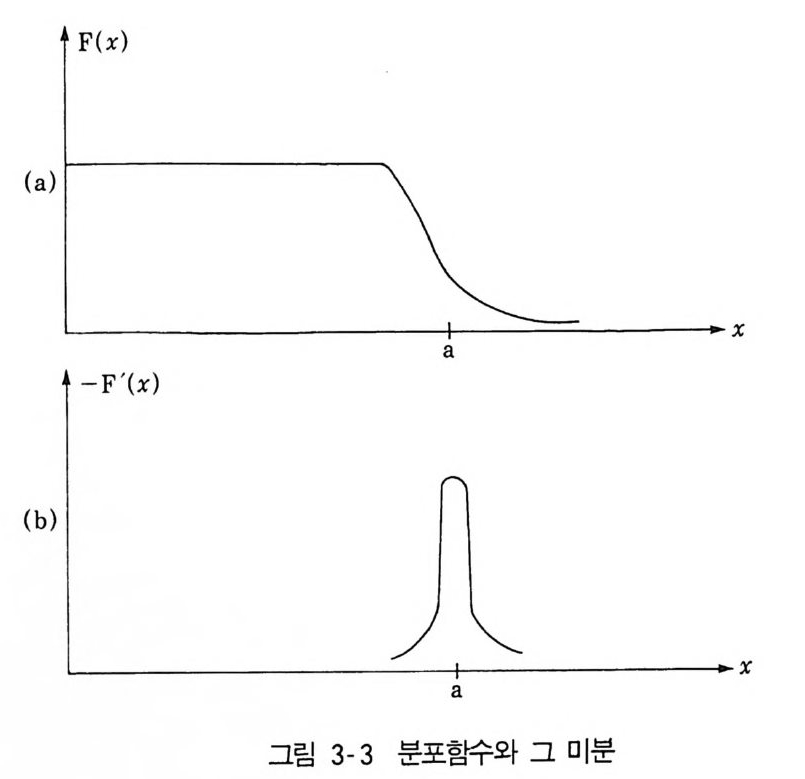F(x )
로 정의하고, X = pe;, a = pµ로 하여 F(x) = e•-a 1 + 1 (3.4 5 a) 로하면 _F(x) = (ex- ea , +-a 1)2 > O (3.45b) 이다. a ~ 1 에서 F(x) 와 _F' (x) 가 그립 3-3 에 보이고 있는데, 특히 -F' (x) = fJ( x - a) (3.4 5 c) 의 성질이 주목될 만하다. 지금적분 I 를 I 三 f:d x F(x) 뺨 (3.4 6 )
로 정의하고, 함수 q, (x) 는 비교적 원활한 함수를 의미하게 한다• 그러면 부분적분에 의히여 I = F(oo) q,(o o) -F(O)
= 三 I 。X e/1( c-] +1 cI/2 d c = 占 信) f~F ( x) dx (3.4 7 ) 인데, 뿔 = X11 2,
it 값의 0.4 % 정도가 되어 보통은 실험에서는 무시할 만하다. 3-4 Bose-Ei ns te i n 통계의 응용 ( 1 ) Ei ns te i n 응축 상호작용이 없는 Bose 입자의 기체는 특정한 천이온도에서 대단히 현저 한 효과를 나타낸다. 죽 그 온도보다 낮은 온도가 되면 기체를 이루고 있는 Bose 입자의 전체 수 N 의 상당한 부분이 기저상태에 모이게 되고, 첫번째 의 들뜬 상태를 포함하여 모두 들뜬 상태에서는 비교적 무시할 수 있을 정 도의 작은 수만이 모이게 된다. 이와 같은 기저상태에 대한 효과를 Ei ns te i n 응축이라고 한다. 기체의 온도가 10- 1 4 K 이면, 이와 같이 기저상 태에만 입자가 모이는 것은 놀랄 만한 사실이 되지 않는다고 말할 수 있다. 그 이유는 lcm3 의 체적에 들어 있는 He 기체에서 가장 에너지가 낮은 기 저상태와 다음으로 낮은 두번째 상태 사이의 에너지가 kB • (lQ- 1 4) = 2.4 8 X 10 선 erg. 정도이고 이 사실을 Boltz mann 인자로서 이해할 수 있기 때 문이다. 그러나 He 기체에서 Ei ns te i n 응축의 천이온도는 3K 정도의 높은 값이고, Bose-Ei ns te i n 통계에서 그 이유를 찾아야 한다. Bose-Ein s te i n 통계에서, 에너지 cx 인 양자상태에 있는 입자의 평균적 수下 a 가 -n. = e브 /fl'1 -1 (3.52) 이고, 기저상태 ex = 0 에서 ea = 0 이고 -no = e -.J/f1Ll' _ l (3.52a) 이다. 따라서 T 一 0 에서 no - N 이 되려면 µ/kT - 0 가 되어야 하고 liTm--- 0 no = N = TJ 귁im -e -;JI}.:(1..1 -'_1- ~ 1-(-f1 f )-1
= 一 kµT (3.52b) 가된다. 그리하여 µ = —kT /N (3.52c) 이고, N=1022 , T=lK 이면 µ =-1.4 X lQ -38er g를 얻게 된다. 또 z = e* ~ l + -k-&T = 1 - _Nl_ (3.52d) 울 알수도있다. 일반적으로 (3.52a) 에서 元 。 2 0 이므로 e-tr 2 1, 죽µ s O 이고 0 < z s 1 (3.53) 의 범위에 있다. 천이온도보다 낮은 온도에서 기저상태와 그것을 제의한 나머지 상태에 현저한 차이가 있으므로, 기저상태를 응축된 상으로 부르고, 그 의의 모든 상태를 합하여 정상의 상으로 부른다. 응축된 상에 있는 입자의 수를 N。 (T), 정상의 상에 있는 입자의 수를 Ne( T)로 하면 N = N 。(7) + N, (T ) (3.54) N。 (T) = n;。(T) = ―旦µ (3.54a) 이고 N. (T ) = I: 元(T) (3.54b) «FO 이다. 보통 상용되고 있는 Rie m ann 적분에서는 적분 영역의 유한개의 점 에 대한 피적분함수의 값이 적분치에 공헌하지 않으므로 Ne( 刀 를 (3.38) 의 적분과 같다고 놓을 수 있다. 죽 N, （刀 = I:g( c) e /I ( 』 _1 dc
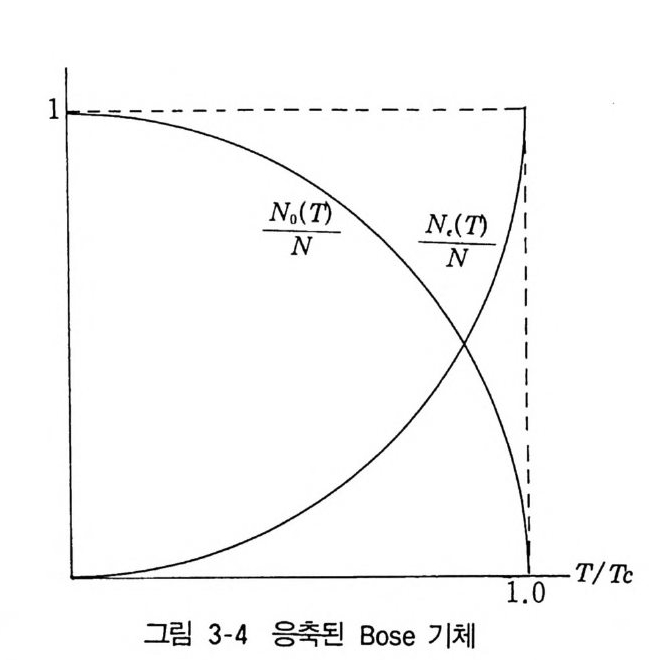
= ~V g312 ( z) (3.54c) 로할수있다. R i emann 의 { 향수가 ((n) = l~=~ l -l11 ' ; (3.55) 로정의되고,특히 n= 웅,t와：에대한값이 때) =2 ._61 2 …기 때) =1 .34 1 ……, 때) = 1.12 7 …… , (3.55a) 로 구해져 있다. (3.37a) 에 있는 g n(z) 의 전개식을 보면 gn( l) = ((n) (3.55b) 이고,특히 g31 2(l) = 때) =2 .612 …… (3.55c) 임을 알수 있다. T - O 이면 z - 1 이고, 또 z 의 함수인 g 3 /2 (z) 는 z = 1 에서 (3.55c) 로 주어전 값을 가지므로 z - 1 이 될 때 급격한 변화를 하지 않는다. 따 라서 (3.54c) 를 N.(T) 弓타(1) = T3 X (2.612… …) (3.56) 로 근사시켜도 좋다. 여기서 천이온도 TC 를 N = N.(T., ) = ±R(T-C-) X (2.612… ) (3.57) 로 정의하면, i(T) = hI .Jz;,_굶귬나] 의하여 T = 걸 [(~.612… …) f]2 /3 (3.57a)
1 _
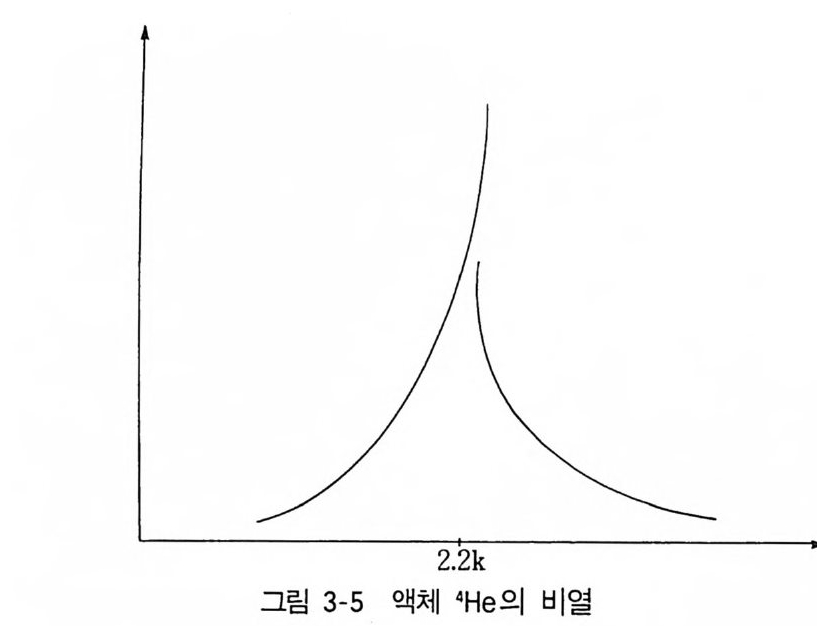
를 구할 수 있다. (3.56) 과 (3.57) 에 의하면 N. (T ) IN ;;-( f)31 2 (3.57b) TC 이고, 따라서 No(T> I N = l_ （꿈 )3/ 2 (3.57c) 이 된다(그립 3-4 참조). ® 액체 4H~ 초유체성 E i ns t e i n 응축으로 생각되는 상태변화가 액체 4H 터]서 천이온도 2.17K 에서 발견되었다(그림 3-5). (3.57a) 에서 4He 액체에 대한 N/V 과 m 의 값을대입T, 하=여3 .l얻K은 값은 (3.58) 이고, 실험치와 대단히 가깝다. 그리하여 액체 4He 에서 2.17K 이하로 온도 가 내려간다면 대부분의 원자가 기저상태에 모이게 된다고 믿어지고 있다.
T
계산치와 실험치가 완전히 일치되지 않은 이유로는 액체 4He 에 대하여는 원자 사이의 상호작용이 무시되는 이상기체로 볼 수 없고, 이에 대한 보정 이 필요하다는 데서 찾을 수 있다. 4He 기체는 원자 사이의 상호작용에 의 햐겨 1 기압에서 온도가 4.2K 이하로 내려가면 액화가 시작된다. 이 액화는 공간좌표에서 원자들을 한 가지 장소에 응집시키고 있다• 2 .1 7K 에서 일어 나고 있는 Ein s te i n 응축은 운동량공간의 원점 주위에 원자를 응집시키고 있어서, 액화에서의 응축과는 다르다. E i ns t e i n 응축은 Bose 입자의 특성이고 보통은 Fermi 입자에서는 가능 하지 않다. 그러나 2 개 한 쌍의 Ferm i 입자가 Bose 입자로 행위하는 Coo pe r 쌍을 이루는 경우가 있으며, 전자의 Coo p er 쌍으로 금속의 초전도 가 설명되고 있다. 또 3He 원자는 Ferm i 입자이지만 이것의 Coop e r 쌍은 3mK 이하에서 초유체의 특색을 나타내고 있다. 천이온도 이상에 있는 액체 4He 를 Hel 이라고 하고, 이하에 있는 액체 4He 를 Hell 라고 부른다 . Hel 은 정상적인 유체이지만, HeII 에는 정상유 체 성분과 에너지의 기저상태에 있는 초유체 성분이 혼합되어 있다고 생각 되고 있다. 초유체는 하나의 에너지양자 상태인 기저상태에만 존재하여 그
7
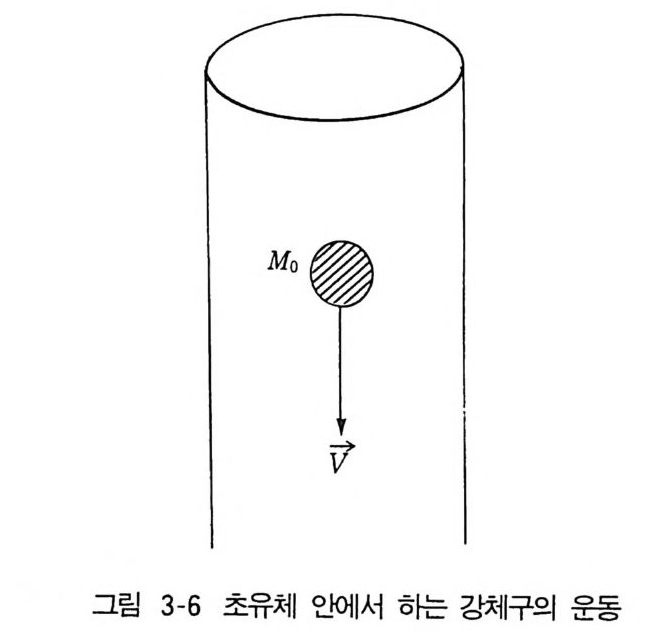
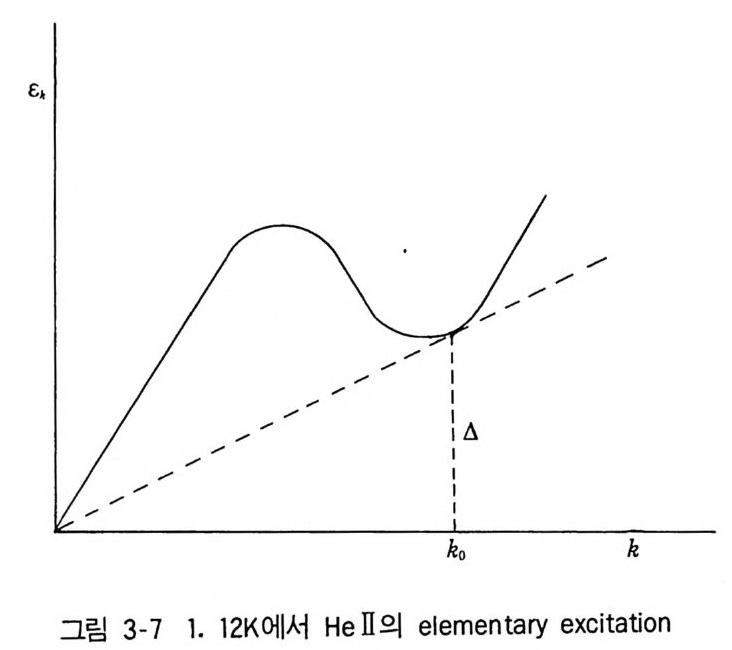
en t ro py는 0 이 된다. E i ns t e i n 응축을 하고 있는 No 개의 원자들에 의하여 구성되고 있는 초유체에는 들떠 있는 에너지 상태가 없다(들떠 있는 에너 지 상태는 모두 정상유체에 소속되고 있다)． 그리하여 초유체가 에너지를 가지려면, 그 질량중심이 실험실 좌표에 대하여 상대속도를 가질 때에 한하 게 된다. 이 유동에서 초유체 성분이 정상유체에 해당되는 들떠 있는 에너 지 상태로의 여기가 없는 한에서는 초유체를 구성하는 No 개의 원자는 어떠 한 점성저항도 받지 않고 흘러가게 될 것이다. 그와 같은 여기는 4He 원자 가 관의 벽면에 있는 불규칙한 돌기와 충돌하는 데서 일어날 수도 있는데, 그렇게 되면 4He 원자의 에너지와 운동량의 손실이 일어나고, 따라서 유동 은저항을받게 된다. 여기서 OK 의 액체 He 의 기둥이 정지하고 있다고 하고, 그 안에 질량 Mo 의 강체구 또는 중성자가 속도 一V 로 낙하一한 다고 생각하자(그림 3-6). 이 물체의 운동이 에너지 o 와 운동량 hk 인 elementa r y excit at i on3 2> 32) elementa ry exc itat i on : 기본이 되는 여기양자.
가울 만성들립하게며 된, 다여고기 가서정 -V하 는면 e(lhe m=e n갱ta ;r 로y 한ex다 c)it, a t i에 on너 을지 만보든존 에후서의 물체의 속 송 MoV 2 = 송 MoV ,z + £k (3.59) 도를 의미한다. 또 운동량 보존에서 M0V_ = M0一V' + h一k (3.59a) --> 가 성립하여야 한다—. —(3. 59) 와 (3.59a) 로부터 V' 를 소거하면 hV-;- : • ~k - 21M 。 h2 k2 = GA (3.59b) 가 나온다. 一k 가 V- c 에k +평 」행방― 향 h일 2 k 2 때에 V 의 최소치 VC 가 나타나고 V, = min ( ~2M 。 ) (3.59c) 울얻는다.따라서 MO 가충분히 큰물체를취하면 1 h 땅이 무시되어 2M 。 V, = min ( 읍) (3.59d) 를알게 된다. · 만일, elementa ry exc itati on 의 에너지 ek 가 질량 m인 자유입자와 갇아 入1 e:1 = ½ (hk)2 (3.60) 이면, k -+ 0 에 대하여 Ve = min ( 營) = O (3.60a) 가 되어 초유체에는 접성이 없다는 것을 설명할 수가 없다. 따라서 이상적 인 Bose 유체는 초유체가 되지 못한다 . elementa ry ex cit a ti on 이 4H e 액체 안에 생긴 압축파와 관련되는 long i- tud ina l p honon 이라면, 음속 u s 에 의하여 & = hw = huk (3.61)
&
가되는데, 이때 V, = min( hv,k / hk) = v, (3.61a) 를 얻게 된다. 그러나 실제로 측정된 Ve 의 값은 u S 보다는 상당히 작게 나 타난다 . 액체 He ll 에 나타난 elementa r y exc it a ti on 의 s p ec t rum 은 느린 중성 자의 비탄성충돌에서 실험적으로 구해지고 있는데 (그림 3-7) Ve = .1 /hk 。 ~ 5 X 103 cm s- 1 (3.62) 이며, ko 와 A 는 그립에서 볼 수 있다. ko 근방의 s p ec t rum 에 해당되는 q uas i-p ar ti cle 은 Laudau 가 ro t on 이라고 부른 것에 해당된다. 이 spe c- t rUI 諦 Bose 입자 사이의 상호작용으로 이론적 설명이 가능하다고 알려지 고있다.
( 2 ) ph oto n 과 ph onon 로,복® -E사 복에장사 은대장 한과전 기 파 p력h동 o장방to 정n E 식 통와 계 자 기력장 B 로 기술되지만 E 와 B 가 직교하므 --- - - - -+一 V 2 흉= .c.2 L호ofE (3.63) 만으로 전자기파의 성질을 결정할 수 있다. E-+ 에 대한 평면파는 了= Ae i(r . 7 - 어) (3.63a) 로 쓰이는데, 여기서 파수벡터 ·k一 와 각전동수 o 사이에는 k = lkl ' w = kc (3.63b) 의 관계가 있다. 전자기파가 한 변의 길이가 L 인 입방체 안에 있고, 또 주 기적인 경계조건을 만족한다고 하면 kx=k=꾼kzlg l nnY. =tg 0, 土 1, 土 2, …… 꾼꾼nn,y = = 00,, 士士 11,, 士士 22,, ………… (3.6 3 c) 가 성립한다. 따라서 (_k -, - k-> + d一k ) 사이의 파동의 수는 dnxdn.y d n, = (¼) dkx (秦) 미¼) dk, = ~ dkx dky dk, (3.63d) 이다. 따라서 파수 k 에 대하여 (k, k + dk) 사이의 파동의 수 g (k)dk 는 g(k )dk = ~ 4nk2dk (3.63e) 이고, 각전동수 (co, co + dco) 사이의 파동수 G'(co)dco 는 (3.63b) 에 의하여 G'(w)dw = (2:) 3 4r 信 )2 d( 7) = 갈: (J)2 d(J ) (3.63f)
--> 가 되는 것 을 알 수 있다. E 의 파동은 진행방향에 직각인 두 개의 편광방 향이 있으므로 (3.63 f)를 2 배 하고, 또 V = l 인 경우를 생각하면 (w, w + dw) 사이의 파동의 수 G(w)dw 가 G(w)dw = 국r'1c= 3 w2 dw (3.63g ) 로된다. 흑체복사에 대한 이론에는 관점을 달리하는 두 가지가 있다. 첫번째는 Planck (1 900) 에 의한 것인데, 복사를 양자화된 에너지가 n 2 hw2 인 당진동 의 집합으로 보고 있다 . 여기서 n , 는 0, 1, 2, ……인 정의정수이고 W a 는 z 번째의 당진동에 대한 각 전동수이다. 복사가 흑체하고 평형상태에 있으므 로 각진동수가 0 인 복사는 흑체를 이루고 있는 진동 중에서 각 전동수가 Q인 단전동과 에너지가 평균적으로 같게 된다• 단전동의 에너지는 canon i- cal ensemble 을 따르고 그 분배함수 za 는 Za = n[..=_ 0 e-/ In. hw . = ~1-e /I如. (3.64) 이고, 에너 지 의 평균치 료가 효 = ―읊 lnZ a = /도 1 (3.64a) 가 된다 . 따라서 각진동수가 (w, w+dw) 사이에 있는 복사의 에너지 u( w)dw 는 (3.64a) 와 (3.63 g)에 의하여 u(w)dw = ( ~ ) 言 w2d w =n一 h양 etv. /하k T -1 dw (3.65) 가 된다. 이 식이 바로 Planck의 복사공식이다. 복사를 두 번째의 관점에서 본 것은 Bose(1924) 와 Ei ns te i n ( 1924~ 1925) 이다. 이들은 복사를 서로 구별할 수 없는 동등한 광양자, 죽 ph ot on 의 기체라고 하였다. 각진동수 (I) a 인 pho t on 의 에너지는 h% 이고, 그 수가
na 이면, p ho t 、o n 기체의 에너지는 E {n } = [n a h(J )a (3.66) 가 된다. p ho t on 은 용기의 벽에 흡수되거나, 벽에서 발생하여 그 총수 E na 는 일정하지 않다. 따라서 p ho t on 의 chemi ca l p o t en ti al 은 0 가 된다. 그리하여 pho to n 기체의 분배함수 Z( p ho t on) 은 z 울 알 수 있다. X <{ 1 이면 복사의 장파장 영역이고 r(x) = x2 (3.68d) 으로 근사되는 Ra y le ig h (1 900) 와 J eans 의 공식을 얻게 되고, 또 x > l 인 단파장영역에서는 u(x) :::: x3e - • 인 W i en (1 896) 의 공식을 얻을 수 있다. 복사의 내부에너지 U 는 U/V = f 。~ u(x)dx = 뀝흙 [: :x 3만 \ =교15 -h上3c 3 T 4 (3.69) 로 구해진다. 공동의 벽에 뚫은 작은 구멍을 통하여 복사가 일산 (e ffu se) 하 면, 단위면적을 통하여 나가는 p ho t on 의 시간당 유량은 t내 )c=~T 4 = (JT 4 (3.69a) 이 되어, S t e fa n-Bol t zmann 의 상수 6 는 (1 = 6~0h 난 = 5.670 X 10 겁 w/m 2 K4 (3.69b) 01 다. p ho t on 기체의 분배함수 Z( p ho t on) 이 (3.67) 에 구해졌으므로 자유에너지 F 는 F = -kTln Z (ph oto n ) (3.70) 인데, (3.69) 와 비슷한 계산으로 F= -강 U (3.70a) 를 구할 수 있다. chem ica l po te n ti al µ가 0 이 되므로
G=Nµ=F+PV=0 로부터 PV= -F= ½U (3.70b) 를 알 수 있다. 또 entr o p y S 는 s= UT- F =百4 TU ex: VT3 (3.70c) 이고, 비열 CC 는 C, = T( 營) , . = 3S (3.70d) 01 다. ® 고체의 격자진동과 ph onon N 개의 원자로 구성된 결정체에서 원자의 위치좌표를 (xI, x2, …… x 3N ) 로 하고, 위치에너지가 최소가 되는 격자점의 좌표를 (x\o>, x~o ), …… x 器 )로 할 때 변위 ~i = X, _ 꾼 (i = 1, 2, .. …· 3N) (3.71) 에 의하여 운동에너지 K 는 K = 步릅 xf = 뇽며 ~f (3.71a) 으로 주어지고 위치에너지 O 는 (x1, …… x 3N ) 의 함수인데, 이것을 격자점 (x(O), …… 遠) 주위에서 전개하고 (1) = (1) ({x; }) = (1) ({xl0>}) + L( 쉽ax ~i ) oo (x;- x )o>) + 나 (¼axja x)j 0 j O (x;-x)0>) (xi- x}°>) + …… 로한다음, `(! a-x)i oj O = 0 를 고려하고, 또 2 차 이상의 고차항을 무시하면
= 。 + Ea ,, 값 , (3.71b) 롤얻는다. 단 。 = ({군 }) a,J = ½( ~ )。 로 하였다• 이 근사에서 결정체의 Ham ilt o n i an H 는 H = 。 + [ 計 me ~ + 도미 (3.72) 가 된다. 지금 정준좌표 (norma li zed coordin a te s ) q,을 t, = EB,,q , (3.72a) 로 취하여, Ham ilto nian H 를 H = 。 + [h, (3.7 2 b) h, = ½m (섬 + 아q,) (3.72c) 이 되게 할수 있다• 위에서 hr 은 1 차원 단전동의 H ami l t on i an 이고 양자화하면 그 에너지 cr 는
& = ( nr + 강 )hw,, n, = 0, I, 2 …… (3.73) 이다. 따라서 결정체의 에너지를 3N개 의 단전동의 에너지를 합하여 다음과 감이 얻을수있다.죽 E({n,}) = 。 + ? (nr + 랑 )h@ (3.73a) =E 。 + Enrhor N 이다. 이것은 상수 Eo 를 제의하면, 복사의 ph oto n 기체에 대한 에너지와 같다. 따라서 결정의 전동을 에너지가 h (J.) r 인 p honon 이 • nr 개씩 있는 ph onon 기체라고 생각하면 p ho t on 에서 얻은 식을 그대로 사용할 수 있 다. 죽 p honon 의 평균적인 수로서nr = e/Jh w1. _ 1 (3.74) 울 얻게 되고, 또 내부에너지 U 는 E 의 평균치로 보고 U=E 。 +Er e/Jh h w .( J )—r 1 (3.74a) 을 얻는다. 따라서 비열 C V 는 C, = 澤 ) . ~k i;:~ (3.74b) r (e-.r —1 )2 가된다. 복사의 경우와 다른 것은 각전동수 (J)의 분포를 쉽게 구할 수 없다는 점 이다. 그리하여 근사적으로 ((J), w + d(J )) 사이에 있는 진동의 수 g(w )d(J ) 룰 가정하게 된다. 잘 알려진 근사는 Ei ns te i n model 과 Deby e model 이 다. Ein s te i n model 은 g((J))d (J) = '8( (JJ _ (J) E)d(J J (3.75) 로하고있다.따라져 U = E 。 + 3N e/hIb w (‘J J- E l (3.75a) 이며, x = h (JJ E/kT로 하여 C = 3Nk E(x) (3.75b) 단 E(x) = (e갔'-강1 )2 (3.75c) X이다 ~. lX 에 ~서 는l 에 E서( x)E (=x) x 2= e -1x 이 이다고. c. = 3Nk 인 Dulon g -Pe tit의 값이고, Deby e model 은
g(w ) = { 言9N ° 2 (J) ~ WD 。 (J) > (J) D (3.76) 로 취하고 있다. 그러면 C, = 3NkD(x 사 (3.76a) 이고, 여기서 x 。=hw下o (3.76b) 이며 D(xD) = : `f : O (::::X)2 dx (3.76c) 이다. XD < l 이면 D(x 사 = 1 이고 C U 는 역시 Dulon g -Pe tit의 값이 된 다. 그러나 XD > l 이면 D(xD) = 강무XD (3.76d) 이고, % = h (J) D/k 에 대하여 C, =N k • 亨-(t r (3.76e) 이다. 이것이 유명한 T3 법칙이다.
제 2 부 불완전유체계
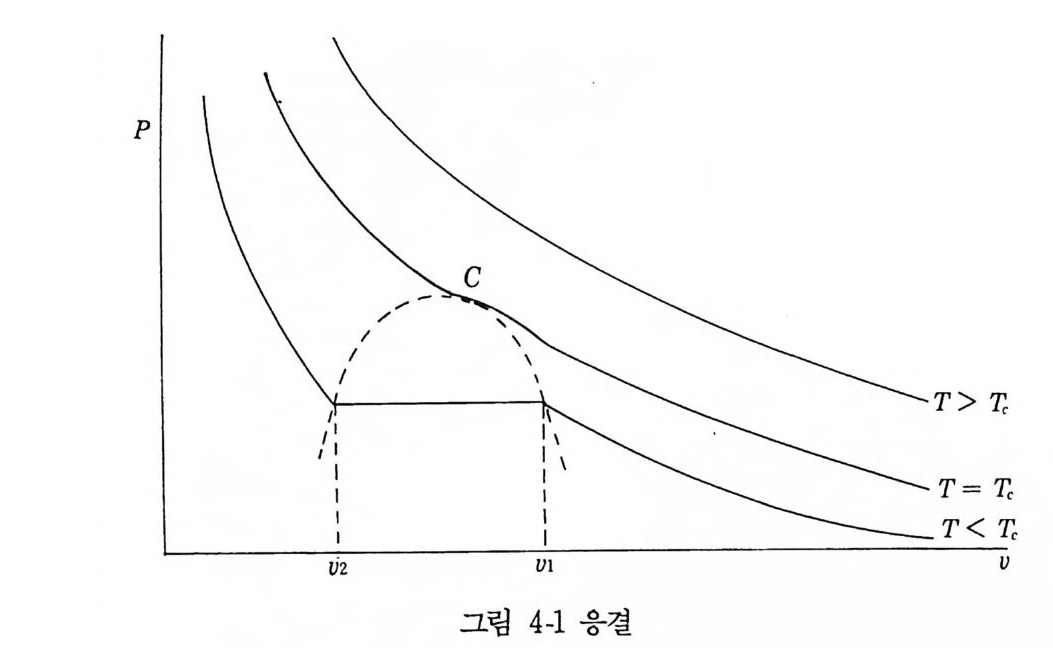
4 불완전기체의 고전론 4-1 서론 평형상태에 대한 통계역학은 그 일반론이 2 장에서 보았던 Gi b b~ en- semble 이혼]다. canonic a l ensemble 에서는 분배함수 Z(V, T, N) 를, 계 룰 이루고 있는 분자들 사아에 작용하는 상호작용 p o t en ti al 을 써서, 계산 할 수 있다면 계의 거시적인 양들을 모두 구할 수 있게 된다. 죽, 실험사실 과 비교하여 다음의 현상이 설명될 수 있다는 것을 의미한다. ® 일정한 온 도 T 에서 체적 V 가 N ,i ,(r1 은 분자력의 유효도달거리 )보다 대단히 크지 않으면 이상기체의 법칙에서 멀어진다. ® 응결현상 : 충분히 낮은 온도에서 ; 어이 떤경 우기에체 도등 온한곡계선밀은도 그」U- l 접 =선 이_V !il이 _에 밀이도르에도서록 불 압연축속되적면 변 응화결를이 한 다시.작 한u2다 <. u < u1 사이에서 계의 압력 P 는 일정한 값이고 증기 • 액체의 평형을 나타 내며, U2 부터는 액체싱이 시작한다. U2 에서 등온곡선은 그 접선이 명확한 불 연속적 변화를 하고 있다. U < U2 에서 등온곡선은 급하게 치솟아 울라가고, 액체의 압축률이 작다는 사실을 보이고 있다. ® 임계온도 TC 의 존재 : 모든 물질에서 옹결현상은 일정한 임계온도 TC 에 대하여 T < TC 가 성립한 경우
P
에만 일어난다. T 가 증가하여 TC 에 가까워지면 등온곡선의 수평부분이 짧 아지고 T = T,이면 임계점 C 에서 없어진다. T > TC 에 대하여는 등온곡선의 접선에 불연속이 나타나지 않아서 응결현 상이 일어나지 않는다(그림 4-1 참조). 위 웅결현상에 준하여 액체 • 고체 사이의 응고현상도 잘 알려지고 있는 실험사실이다. 액체의 v 를 더욱 작게 압축하면, 아마도 온도에는 관계하지 않고 물질이 고화하여, 고체 • 액체, 고체 • 기체의 상평형이 일어난다고 생 각되고 있다. 그러나 응고현상을 분배함수 Z(V, T, N) 에 의하여 해명할 수 있는 단계까지의 이론은 아직은 멀기 때문에 이 책에서는 생각하지 않 기로한다. van der Waals 의 이론 I ) : 기체와 액체의 성질을 이해하는 데 있어서 첫 번째의 큰 성공은 18731d 에 van der Waals 가 발표한 논문에서 볼 수 있 다. 1) J. D. v. d. Waals, Thesis , Leid e n , 1873
P
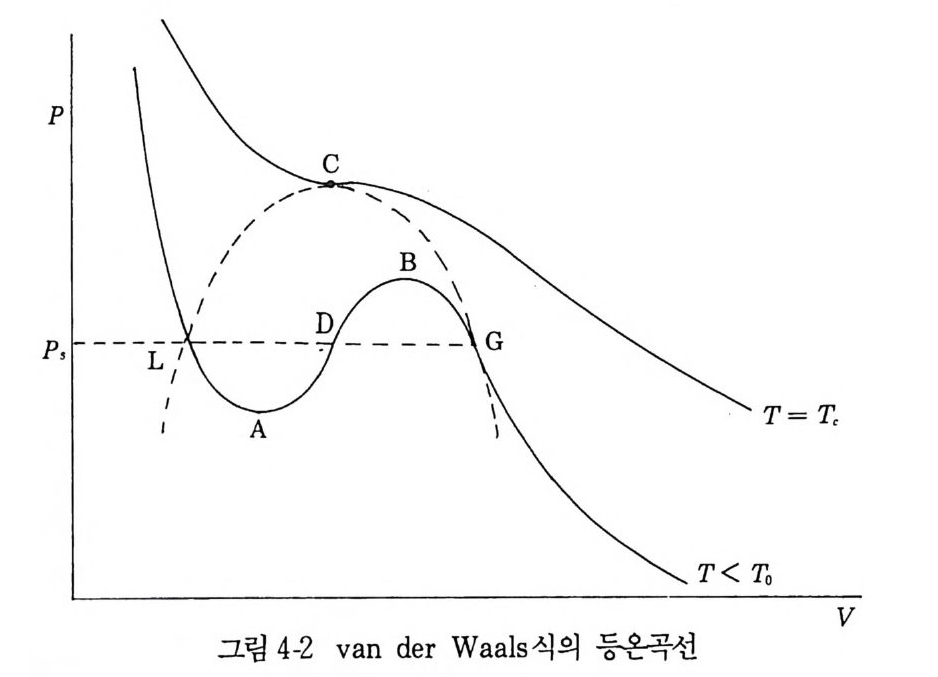
그는 분자력이 비교적 먼 거리에서는 인력으로, 아주 가까운 거리에서는 강 한 반발력이 된다고 생각하여 이상기체의 상태방정식을 수정하고 (P+ 슈 ) ( V -b) = NkT (4.1) 로 쓰이는 소위
의 등면적법칙을 빌려와야 한다. 곡선으로 싸여진 면적 GBD 가 LAD 와 같다는 것이 등면적법칙인데, 이것으로 포화증기압 P , 가 결정된다. T 의 값 이 커져서 T> T,이면, 2 개의 상으로 분리되지 않는데, T, 의 값은 임계점의 조건 (景 )C = 0. （景 ) C = 0 (4.2) 으로부터, V 와 Pc 하고 함께 구할 수 있다. 그들의 값은 Ve = 8b, Pc= 一27b2 ' Tc = 」Nk 후27b (4.2a) 이며, 분자력에 관계되는 상수 a 와 b 로 정해진다. 따라서 P, V 와 T를 P 。 VC 와 t를 단위로 하여 표현하면 분자력과 관계없이 모든 물질에서 성 립되는 상태방정식을 얻을 수 있다. 이것을 law of corresp o ndin g sta t e s 로 부르고 있다. 이 법칙이 불활성 기체에 대하여 찰 성립한다는 사실에서 이들 기체의 분자력 p o t en ti al 이 같은 형이고, 다만 거리와 에너지의 값을 조정하면 좋다는 것을 알 수 있다. 이 분자력 po te n ti al 중에서 대표적인
¢(r)
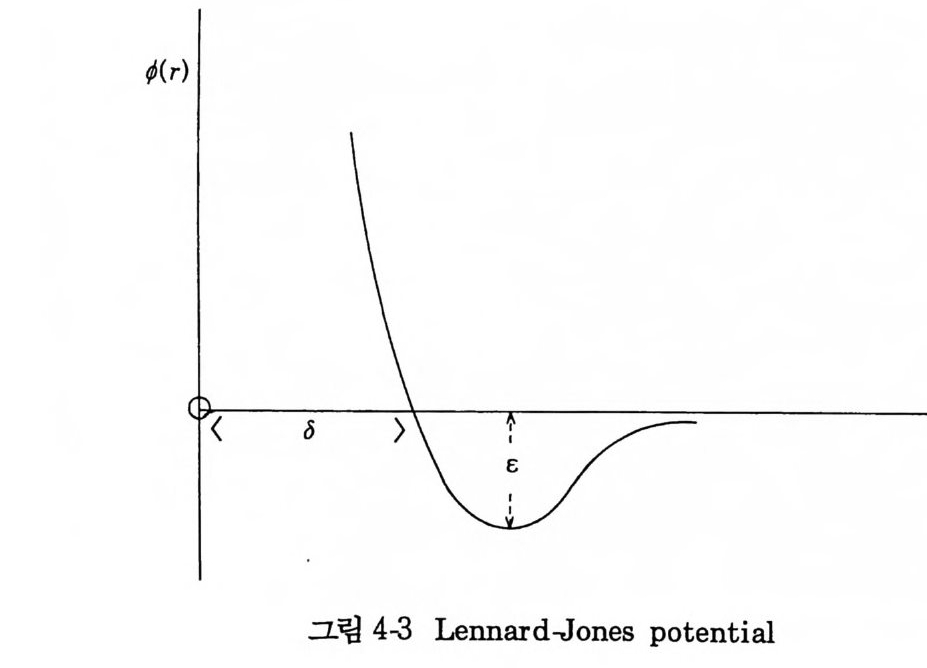
것이 (12 , 6) Lennard.J o nes po t en ti al ¢(r) 이고(그림 4-3) ¢(r) =4e[( 7)12 - ( 千『 ] (4.3) 으로 표현된다. 이 식에서 상수 (J와 상수 c 는 Vj N (J 3 과 kT/c 가 보편적 인 수가 될 것으로 기대된데, 실제로 Vj (2nNu3I 3 ) =1 .50 , —kET C = 1 .25 (4.3a) 가 된다고 알려지고 있다. 통계역학으로 직접 실험사실을 설명하기에 앞서서 van der Waals 상태 방정식을 비판적으로- 고려해보는 것이 바람직스럽다. 첫째로 중요하게 눈에 뜨이는 점은 포화중기압 E 를 결정하는 데에 Maxwell 의 등면적법칙을 빌 려 쓰고 있디는 것이다. Maxwell 의 이 법칙이 두 개의 상이 공존할 때 각 상의 chemi ca l po te n ti al µ가 그 값이 서로 같게 된다는 열역학의 법칙에 대한 한 가지 표현이라고 알려지고는 있지만, 완전한 통계역학의 이론이 되 려면 열역학의 도움 없이 사실이 설명되어야 하기 때문에 만족스럽지 못하 다고 할 수 있댜 또 분배함수 Z(V, T, N) 은 계가 열역학적 평형상태에 있는 경우를 계산한 것이므로 거기에서 불안전한 상태 또는 준안전상태가 나왔다면 논리적 모순이 된다. 그러므로 불안전상태를 포함하는 van der Waals 상태방정식에는, 통계역학적으로 이것이 도출되려면 허용할 수 없는 근사가 포함된 것이라고 생각하여야 한다. 1901 년에 Kammerli ng h On- nes 2 ) 는 벌써 van der Waals 상태방정식의 약점을 지적하고 상태방정식이 信 =1+ 썩 l+ 笠+…… (4.4 ) 로 기술되어야 한다는 소위 vir i a l 전개를 하고 실험 데이터를 정리하 였다. 위의 식에서 B( T)는 제 2 vir i a l 계수, C( T)는 제 3 vir i a l 계수 로부른다. 2) H. Kammerlin g h Onnes, • Proc. Kon. Ned. Akad. Wet. , Amste r da m. 4 (1902), 125.
vir i a l 전개는 기체가 이상기체로부터 멀어질 때 분자들 사이의 상호 작용효과가 분자의 2 쌍, 3 쌍,…… 등으로 나타난다고 암시하고 있는데, 이 사실을 확인시킨 이론은 1927 년에 UrselP) 이 시작하여 Ma y er4) 와 Ki - rkwood 와 Uhlenbeck 등에 의하여 완성되어갔다.
3) H. D. Ursell : Proc. Cambrid g e Ph ilo s. Soc. 23 ( 1927) 685 4) J. E. Maye r & M. G. May e r : Sta t is t ic a l Mechanic s (W iley , 1940)
4-2 Ma y er 의 방법 기체에 있어서 분자 상호간에 작용한 힘의 영향이 작다고 생각하여, 이것 울 이상기체의 분배함수에 대한 작은 보정으로 처음에 계산한 일은 Ursell 에 의한다. Ursell 이 착안한 것을 체계적으로 확장한 내용을- Ma y er 의 방 법이라고 할 수 있다. 이 방법에서는 분배함수 Z(V, T, N) 에 나타나는 분 자력 po te n ti al ~(11 . -미 )에 관계된 인자를 5 ¢(I -r--~+ k —T - 까--+ ).. . = l + fIJ (4.5) 가 되도록 In -미 의 함수 [ij = f(I n -미 )를 도입하고 있다. 그러면 Z(V,T ,N ) = N!1 A 3N fv… f V 詞 .. d 言 e 꿈i ¢( I ; 」 Nt A3N `仁 \f` vdi ... d댜 (1 + f,J) (4.6) 로 쓰인다. （이하에서 적분기호안의 d n-은 d 구하고 같은 의미를 갖는다) 위 에서 」A r 은 Ham i l t o ni an 의 운동량에 관계된 부분의 적분을 h 3 N 로나 누어서 얻어졌고 이상기체에 대하여 계산할 때 얻은 것과 같다. f (r) 의 함수형은 분자력 p o t en ti al 에 의하여 정해지지만 앞서 본 L-J 형에 대하여서는 대체로 그림 44 처럼 된다. r > ri이면 ¢ (r) ---+ 0 이고 따라서 f(r ) 一 0 이며, r< a 에서는 ¢ (r) ---+ oo 이 되며 f(r ) ---+-1 이다. 따라서
f(r ) -n- - ---- --- -- <6 > r -1 그립 4-4 f (r) 의 함수형
f, 1 에 대한 적분은 분자력이 도달하는 범위 r ~ r1 에 대하여서만 값을 가 지게 된다• 를 위양의가 본보배기 함위수하에여 대 우한선식 N( 4.=6) 의3 의피 적경분우함를수 예 로ktN<취ii (하l자 +. f 1즉q ), 가갖는형태
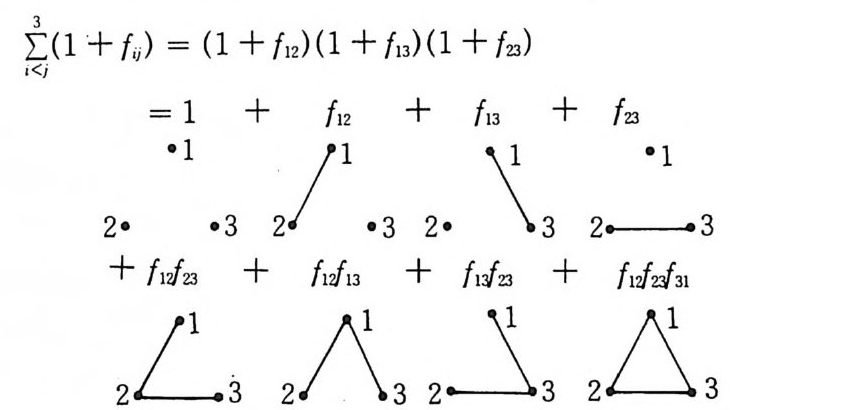[(1 + h) = (1 + {12 )( 1 + f13 )(l + f23)
자위의에 서위 치전 개규에된 대각하 항여이 점 시 i각를적 찍인었 고인,상 f을i j 를 줄 점수 i있와 도점록 j 하를 기연 결위하하여는, 선 분분 으로 나타내는 도형을 첨부하였다. N 이 증가한 데 따라서 전개식이 얼마나 더 복잡하게 되는가를 볼 수 있 도록 N = 4 의 경우도 그려본다. 4 점 중 2 점을 선택한 방법이 (!) =6 이
고 전개된 항의 수는 26 = 64 가 된다. 그리하여 도형 을 유형적으로 분류 하면 디음과 같다.
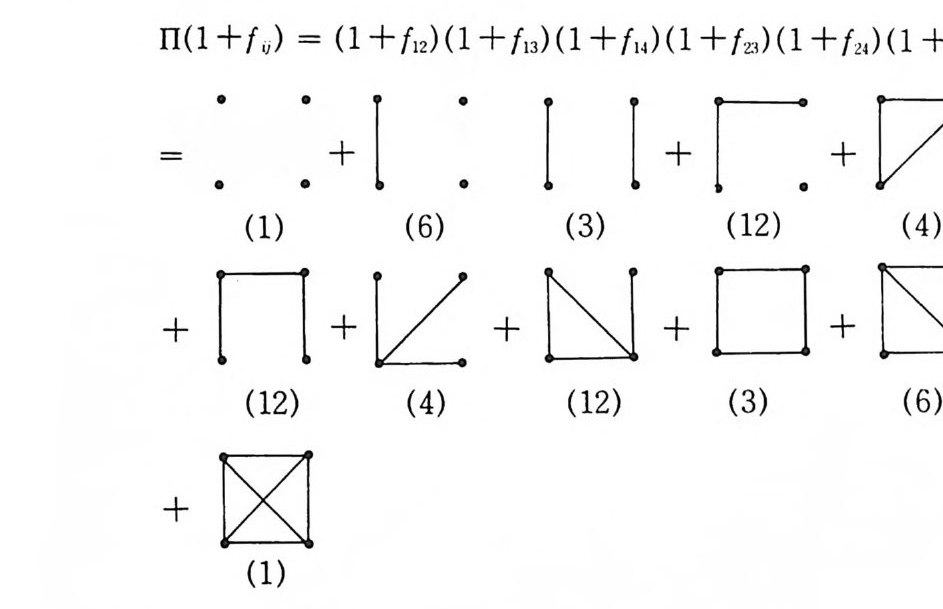n(1 +f,,) = (l +fl2) ( l +f13) ( 1 +fu)( 1 +fZi ) ( 1 +f24) (l +f 려 )
위에서 도형 밑에 적어놓은 수는 그 유형 안에 점 1, 2, 3, 4 에 대한 다 론 연결의 가능성을 의미하고 그들 수의 합이 647} 된다. 점과 그들을 연결하는 선분으로 그려진 도형을 선형 gr a p h 라 부르고 있 다. 그러면 tNi (1 + f,,)는 N 개의 점으로 된 모든 g ra p h 를 나타내며 그 수 N( N-I) i
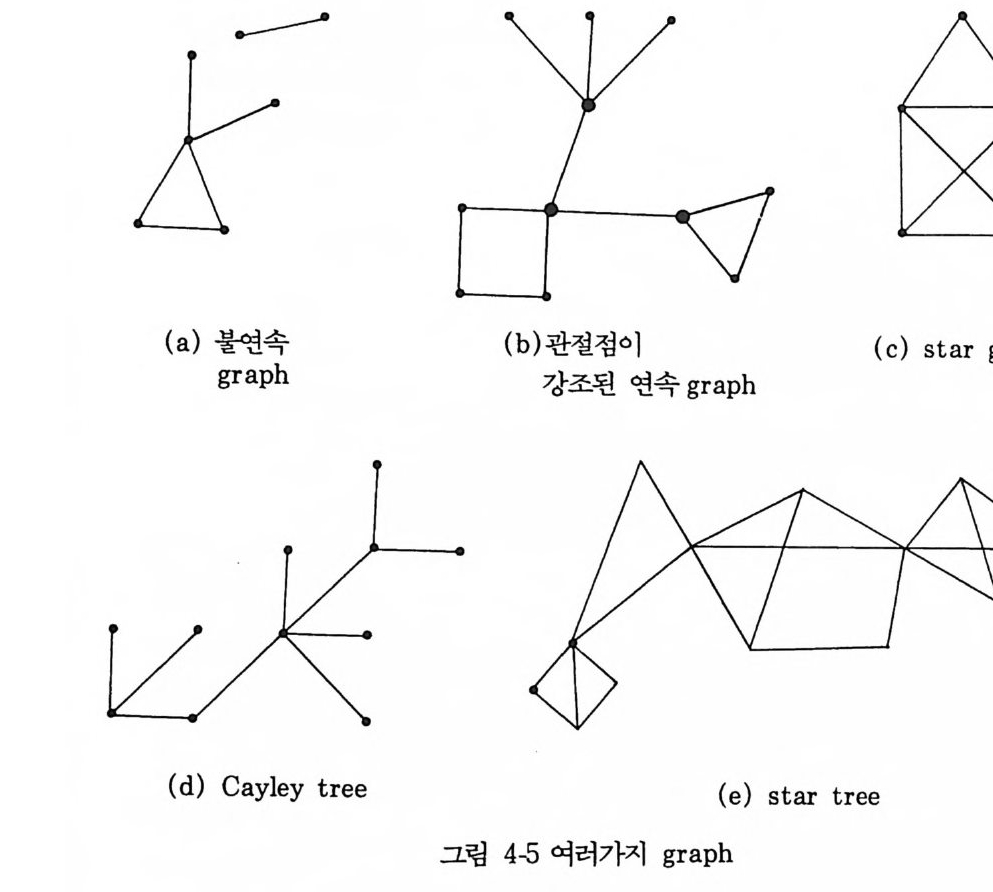
의 적분이 대응되며, 기타 경우도 위의 유추에 의하여 알 수 있다. 또 위상 학적으로 동등한 g ra p h 에 대한 적분이 같은 값이 되는 것은 명백하다. 분배함수 Z(V, T, N) 을 위와 같이 선형 g ra p h 로 전개하고 생각하면, 분자력이 단거리 까지에만 미치고, 그 도달거리 r1 보다도 멀어지면 f(r ) - 0 이고, 그 결과로 연결된 g ra p h 에 대한 적분은 체적 V 의 인자를 가지게 된다. Ursell 이 처음으로 한 계산은 N 점 gra ph 중 모든 점이 독립인 항 1 개와 2 점만이 연결되어 f가 하나만 있는 경우에 해당된다. 따라서 그 계 산에서는 Z(V,T ,N ) = ~ [VN + NVN -1 J /(접 dr+ …… ] 이 되어 이상기체에= 대~한분배 함[ l 수+ 픕깁 〔f개(접 d작 다은 보…정… ] (4.6a) 町 f(겹 d; 이 주어진다. f가 여러 개 나타나는 고차의 항을 체계적으로. 계산에 포함시 키려면 우선 선형 g ra p h 이론의 요점을 알아두는 것이 좋다. (1) 선형 g ra p h 이론의 요점 평면에 점을 찍어서 그린 도형의 모임이며, 두 개의 점 사이에는 직접 연 결하는 선분이 하나만 있거나 없으면 이것을 선형 gr a p h 라고 부른다• 선분 에 의하여 순차로 연결된 점들은 시발점과 종점을 생각할 수 있고, 연결된 선을 행로라고 한다• 시발점과 종점이 같은 행로는 회로가 된다. 임의로 취 한 두 점 사이에 행로가 있으면 연결 gr a p h 이며, 행로로 연결되지 않는 점 이 있는 불연결 gr a p h 도 있다. 연결 g ra p h 에는 관절점 (arti cu lati on p o i n t)이 있을 수 있는데, 이 점에서 그 연결 g ra p h 를 자르고 몇 개의 부 분 gr a p h 를 만들 수 있다. 관절점이 없는 연결 g ra p h 를 sta r g ra p h 라고 한다. 연결 gra p h 의 일반적인 형은 여러 개의 관절접에 sta r gra p h 가 붙 어 있는 sta r tre e !} 된다고 할 수 있다. 가장 간단한 sta r g ra p h 는 두
점과 그것을 연결한 선분인데 특히 이것들만으로 되어 있는 t ree 를 Cay le y t ree 라고 하는데 l 양 1] 기 말 Ca y le y 5) 에 의하여 자세하게 연구된 바있다.
5) A. Cay le y, Collecte d math e mati ca l pa p e rs; vol 3. p.2 42
‘一
gr a p h 가 물리학의 계산에서 응용되는 것은, 대체로 축차근사에 나타나는 수식의 항을 시각적으로. 보여주어서 편리하기 때문이다. 많은 경우에 점의 수 또는 점을 연결하는 선분의 수가 근사의 처수와 관계되고 있다. 이 축차 근사에는 주로 두 가지 문제가 나타난다. 죽 ® 조합의 문제와 ® 적분의
문제이다. 조합의 문제는 n 차의 근사에 나타나는 서로 다른 항의 수가 몇 개 있는가? 즉 n 점의 연결 gra p h 중에서 특정한 형을 갖는 것이 몇 개 있 는가 하는 것이 된다. 여기에 대하여 적분의 문제는 각 gr a ph 가 나타내는 가중적분 값을 어떻게 구하는가를 알아보는 것이 된다. 조합의 문제에서는 점에 번호가 붙어 있는 가부번 g ra p h 와 위상기하학 적으로 동등한 것을 한가지로 보는 자유 g ra p h 를 구별한다. 그리하여 하나 의 자유 g ra p h 에 관계되는 가부번 g ra p h 의 수가 몇 개가 되는가를 아는 데 홍미가 있게 된다. (2) Ma y er 의 정리 분배함수 Z(V, T, N) 를 전개하여 N 점 g ra p h 의 여러 가지 디른 형에 대한 적분으로 표현할때, 이미 (4.6a) 에서 처음 두 항을 본대로 각 grap h 는 서로 떨어져 있는 많은 개수의 연결 gr a p h 로 구성되고 있다. 각 연결 g ra p h 에 대한 적분을 모두 곱하면 하나의 N 점 g ra p h 의 적분이 되는데, Ma y er 는 그들 사이에 비교적 간단한 관계가 성립되는 것을 보았다. Ma y er 의 결과를 투시가 가능하도록 하기 위하여 일반적인 경우를 논하고, 그 특별한 예가 Ma y er 의 결과가 된다는 것을 본다 .6)
6) G. W: Ford & G. E. Uhlenbeck ; S t떠i es in sta tist ic a l mechanic s , vol I (1962) 안에 있는 논문
정리 : N 점에 관계된 양 F N 을 ' FN = (LG, . ) W(GN ) (4.7) 로 정의한다. 위의 정의식에 나타난 GN 은 N 점의 가부번 gra p h 중의 하 나이며, GN 에 대하여 합을 취한다는 것의 의미는 가능한 모든 N 점의 가부 번 gr a p h 를 모두 취하고 그것에 대하여 합한 것이다. 또 W(GN) 은 GN 의 하중 (we ig h t)이고, GRl 의하여 결정되는 양이며, 다음의 성질을 갖는다고 생각한다.죽,
CD W (G N ) 은 N 점에 번호를 붙인 방법에는 무관하고, 대응되는 자유 gr a p h 에 의하여 그 값이 정해진다. ® GA ’ 이 서로 떨어져 있는 몇 개의 연결 gra p h 로 구성되었고, 그 중에 서 [접의 연결 gr a p h 가 G 로 표시되면 W(G 사 = (nr,) w(Cl) (4.7a) 이 성립된다고 한다 위에서 W(C/ ）는 연결 gra ph C1 에 대한 하중을 의미 한다. 그리하여 (4-7a) 는 G N 에 대한 하중이 각 C 제 대한 하중의 곱이 된 다는 것을 나타내고 있다. 양 FN 에 대응하여 양 f1 을 f, = I: W(Ci) (4.7b) (C, ) 로 정의한다. 여기서 C1 은 [점의 가부번 연결 gra p h 중의 하나이고 합은 모든 G 의 가능한 g ra p h 에 대하여 취하고 있다. 다음 x 의 함수 F(x) 와 f (x) 를 F(x) = f己, FN N XN ! (4.8) f(x ) = :f1곱 (4.8 a ) 로정의하면 1 + F(x) = e((x) (4.9) 가 성립한다는 것이 정리의 내용이다. 이 정리는 다음의 보조정리를 증명하면 곧 증명된다. 보조정리 : 연결 grap h C p와 C q에 대하여 서로 다른 하중 W1(C q)와 W2(C q)를 취하고 양 Hp 와 G 롤 Hp = I(C:.)W 1 (C p) . (4.10) Gq = LWz(Cq ) (4.10a) (C,) 로 정의한다. N 점 gra ph 중에서 p점과 q점의 연결 g ra p h 만으로 된 것만
생각하면 P + q = N 인데, 위의 하중이 주어지면 N 점 g ra p h 의 하중 PN 은 PN = p+포 N 면割 Hp G q (4.10b) 가 된다. 따라서 (4.8) 과 (4.8a) 처럼 gen erati ng functi on 을 H(x) = pL,= ,, l Hp p—났! (4.1 1 ) G(x) = qfz=_ :i I G q 두q . (4.lla) P(x) = f 1P N 집 (4.l lb ) 으로정의하면 P(x) =H(x)G(x) (4.1 2 ) 가성립한다. 이 증명은 다음과 같이 간단하게 된다. 죽 P(x) = J; ,P N 곱 걸 [요 N VH p G q] 훑 = pI(=X :) l qI~=: I ―pH.广 pq G 「.q :x!'xq = H(x)G(x) 정리의 증명 : 연결 gr a ph 의 수가 m 개 있는 g ra p h 의 gen erati ng f unc ti on 을 Fm(x) 로 하면 F(x) = L。 Fm(x) (4.13) m~ l 가 된다. 그 이유는 연결 gr a p h 의 수에 따라서 g ra p h 의 종류가 분류되어 있기 때문이다. 다음에 보조정리에 의하면, Fm(x) = 갑 [f (x) ]m (4.1 3 a) 이 성립한다. m 개의 부분이 같은 하중을 갖는 연결 . gr a ph 의 집합이고, 따
라서 이 m7 사의 부분을 서로 바꾸어보아도 같은 결과가 되기 때문에 (4. 13a) 에서 1/m! 이 곱해지고 있다. 그리히여 1 + F(x) = 1 + i;l ,¾ r [/(x)]' = e (x)(4.1 3 b) 가 성립한다. 따라서 정리가 증명되었다. 분배함수 Z(V, T, N) 에 대한 (4.6) 에 정리를 적용하기 위하여 Z(V, T, N) = 熹 mw(GN ) (4.1 4 ) (G., ) 으로 하고, 여기서 하중 W(G , ) 을 W(GN ) = >. [ U …… JV d;:…… df n f,J (4.1 4 a) (G ,) 로 놓는다. 그러면 gra nd pa rti tion fun cti on J는 변수 z=e “ 인 gen er-- ati ng fu nc ti on 이라고 할 수 있어서 z= J 3 ( 로 하면 3(V, T, Z) = NI역:- 0 Z (V, T, N)z.v 걸훑(다…… .f . d ,:7…… d 덱fi j = exp {VX(V, T, ()} (4.1 5 ) 이고, 여기서 X(V, T, 0 = I크: bi(V , T)(' (4.16) I= ! 이고 b/(V,T ) = }介폴 j …… I 武 .. … d~c~ J ii (4.16a) 가 된다. 위에서 b,(V, T) 는 Ma y er 의 cluste r 적분이라고 하는데, C 은 l 점의 연결 grap h 중의 하나롤 나타내며 합은 가능한 모든 가능성에 대하여 취한다. 특히 l = 1 에 대하여는 bl = 1 (4.16b) 로한다.
(3) 열역학량의 계산 gra nd pa rti tion fun cti on 3(V, T, z) 가 (4 .1 5) 로 주어지므로 ' = 흡 )‘ 를 복소수로 보고 복소수 함수의 유수 (res i due) 의 정리에 의하여 23 N Z(V, T, N) = 갈기 昭 -N- i exp { VX(V, T, () } . (4.1 7 ) 로 되고, 여기서 적분로는 ( =0 를 둘러싸고 시계방향과 반대로 진행하는 폐곡선을 의미한다. 분자력에 대한 p o t en ti al 에 강체구에 해당되는 부분이 r s r 0 에 있다고 가정한다면, N ~ V/(4 짜 /3) 에 대하여 Z(V, T, N) = 0 이 될 것이므로, 3(V, T, z) 가 양의 값을 갖는 계수에 대한 z(=2 뜻)의 다항식이 된다. 따라서 (의 값을 양의 실수축에서 취한다면 X(V, T, ()는 단조롭게 증가하는 ( 의 함수이다• 그런데 , -N-1 은 ( 를 위와 같은 범위에서 취할 때 급격하게 감소하는 함수이다. 따라서 (4 .1 7) 의 피적분 함수는 N 과 V 를 대단히 크게 하고 N /V를 유한하게 취하는 극한, 즉 소위 〈열역학적 극한〉에서 ( 의 실수축에 취한 양의 값 Z o 에서 실수축으로는 극소치를, 허수 축에 평행한 적분로에서는 극대치를 갖는 소위 안상점이 된다. 따라서 (3. 6a~ f)와 같은 방법으로 계산하게 되는데, f(O = -l n ( + uX(Nu, T, () (4.17a) 로 하면 (4 .1 7) 이 열역학적 극한에서 A3 N Z(V, T, N) = 갈才 d( exp { Nf (O } {2nNef N / ((; :,z). 。 )} 1/2 (4.17b) 가 된다. z0 의 값은 f ' (z。 ) = O (4.1 7 c) 죽, (4 .1 7a) 에 의하여 ~1u = zo -a!aZ!o- X (Nu, T, z 。) (4.1 7 d) 에서 구해진다. cluste r 적분으로 전개된 X(V, T, C) 를 (4 .1 6) 에서 보면, l 의 값이 고정
되고 V 의 값이대단히 크게 될 때 b1(V, T)가 V 와 관계없는 값이 되는 것 울 알 수 있다. 사실 (4 .1 6a) 로 주어진 b1(V, T) 에 대한 적분은 L 에 의하 여 연결되고 있는 gr a p h 에 대한 것이므로 적분변수 7 울 고정시켜 본다면 피적분함수는 점 7 으로부터 l7 의 거리 (7 은 분자력의 도달거리)보다 먼 장소에서는 0 이 된다. 呼서bi ( T점) 7= 이½ 용J기 … 의 … 벽 I에d 서E …l閃 …보 다d;:; 충~(C, ) 분 ~C1히 f ij 먼 ,. 장소에 있다면 (4.1 8 ) 가 체적b V/( 와V ,관T계-y없 이j 일di 정 한詞 값이 된다. (4 .1 6a) 에서 (4.1 8 a) 의 관계가있으므로 柚 b1 (V, T) = 衍(刀 (4.1 8 b) 의 극한이 존재한다. 다음에 (4 .1 6) 을 (에 대한 급수로 볼 때 유한한 수령반경이 있다고 가정 한다.그러면 극한급수 NJ. j..I. oI l X(Nu, T, 0 =三 cEY0= l( -bTl, ( T( )) t (4.1 8 c) 가 유한한 수령반경을 가지게 된다. u 와 Zo 의 관계는 (4 .1 7d) 가 주고 있는데 u 一 OO이 면 z0-0 이다. 그러므로 u 를 충분히 크게 하여, %가 T(T, ()의 수령반경 안에 있도록 한다. 그러 면 (4.1 7 a, b) 에 의하여 Helmhol t z 의 자유에너지 F 가 F = —kT ln Z(V, T, N) = N[i/J ( v, T) + 0 ( 異杓 ] (4.19) U(u, T) = -kT{u~x (T, z 。) - ln@z。 )} (4.1 9 a) . 로 구해진다. 이 식에서 N 이 크면 F 가 N 에 비례하는 양, 죽 지량변수가 되는 것을 보여주고 있다 . u 와 Zo 의 관계 (4.17d) 에 (4 .1 8c) 를 고려하여
上u = z 。 -o!%- x( T, z 。 ) = [l=O3 l lb, (T )z'o (4.20) 처럼 전개한다.상태방정식 P = _(1f)T. N 은 (4 .1 9) 와 (4.19a) 에 의 궁回 P = 갤 1/1 Iau ) = kT { x'( T. z 。 ) +u-8 !%i- ~8 u _上% 브Ou , } = kT x (T, z, 。 ) (4.21) 가된다.즉 今 = Y(T, z 。 ) = l[= l bi (T) tc。 (4.22) 인 z0 에 대한 전개식을 얻은 것이다. (4.20) 과 (4.22) 를 Ma y er 의 방정식 이라고 하는데, P 와 u 의 관계식인 상태방정식을 보조변수 zo 를 써서 주고 있다고할수있다• chem ica l po te n ti al µ는 G i bbs 의 자유에너지 G 와 G = Nµ 로 주어지고, 또 G = F + PV 가 되어 F 에 대한 (4.19) 와 (4.1 9 a), P 에 대한 (4.21) 을 대입하여 µ = 1/!(u , T) + Pu = kT ln (A밉 (4.23) 를알수Z있o 다= .꿉따 E라 서= T3 (4.24) 의 관계를 알 수 있는데, 철대 acti vi t y z 에 대하여 Zo 를 ac ti v ity라고 부 른다• bl = 困 = 1 을 (4 .1 6b) 에서 알고 (4.20) 을 보면 u 가 대단히 크면 Zo ~_ l_u
이고 (Z4o. 2=2) 가-t- 이+ 상a기2 (체-t방-정r식 + 이 a 되3 다는 것) 3이 + 명…백…하 다. 그러므로 (4.2 5 ) 로전개하고 (4.20) 에 대입하여, ( +)에 대한각제곱항의 계수가갇 다고 하여 전개계수 Clz, a3, … … 등을 구하면 (4.25) 가 Zo = ―+ -(24ob iJz -(3 +o 函) •++ (48bb4 )f -(2 ;+;;)r ( ++ ) … 3 … (4.25a) 이 된다.t 이 군Zo 를 +(4B. 22 2信) 에 )대 2 +입B하 3 (면} P) 에3 + 대 …한… vi ri a l 전개 (4.26) 에서 B2 = -~ (4.26a) B3 = ( 4b [-2 f;; ) (4.26b) 울 얻게 된다. 여기서 분자력 po te n ti al ~(r) 을 써서 /(r) = [e 가(r) /k T-}] 로하여 B2 = -bz(T) = －비 료 /(r12) = 2nf 。~ dr 규 (1-e-d (r)/kT) • • (4.26c) B3 = -2b3+4bI = 버 I d~2 dri 3f 12 / 13 /23 = 론 I : dr1 니 。~ dr2 d 귬 I : d0 sin 0f (r ,) f r2) f(
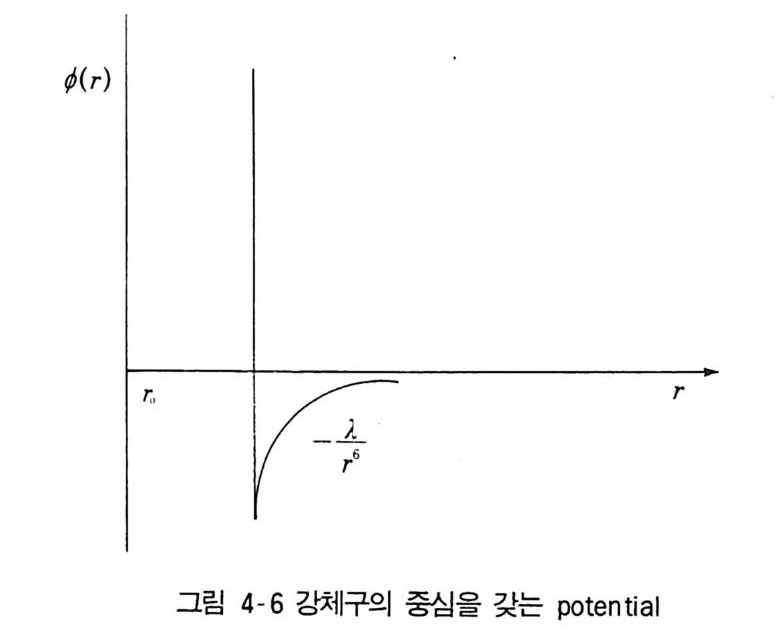¢(r)
vir i a l 계수 중에서 특히 B2 ( T)는 분자력에 대한 지식을 얻는 데서 가장 직접적인 바팅이 되고 있다. B 2 ( T)가 온도의 함수로 어떻게 되는가를 보기 위하여 분자력 po te n ti al ¢(r) 이 강체구를 나타내는 중심부분과 r - 예 비례 하는 인력으로 되는 경우(그림 4-6 참조)를 생각해보자. (4.26c) 의 지수함 수를 전개하고, 근사적으로 B2( T ) = b - 森 (4.27) b = 2n d/3 (4.27a) a = 2n-t / 3d (4.27b) 울 얻게 되는데, 이것은 van der Waals 방정식에서 알게 된 v i r i al 계수 kPT == +u-1+b 7- (으 b-u2f r ) + …… (4.28) 에 대응된다. B 2 ( 刀의 온도의존이 실측치와 정성적으로 비슷하다는 데서 분자력 p o t en ti al 이 그림 4-6 에 나타난 것과 비슷하다고 할 수 있다.
물론, B 2 ( 刀의 온도의존만으로는 po t en ti al ¢(r) 의 함수형이 유일적으로 결정되지 않는다. 그러므로 예를 들어서 (12 , 6) 의 Lennard-J o nes 형이 라고 가정해놓고 나타나게 된 계수를 정하고 있다. B 2 ( T)에서 구한 ¢(r) 이 B 3 ( T)도 잘 설명하는 데서 분자력에 대하여 어느 정도 확신을 가지게 된 다. 4-3 응결현상의 설명 기체를 이루고 있는 N 개의 분자 사이의 상호작용을· 체계적으로 고려에 넣고 (4.20) 과 (4.22) 에서 —lV = l고=a;I l b~/( T ) 걱 꿉=:幻T)타 를 구하고, P/kT를 1/v 의 함수로 나타내기 위하여 Zu 룰 매개변수로 보 았다. 그리하여 (4.26) 처럼 JV_ 이 충분히 작으면 vir i a l 전개가 얻어졌다. 기체가 액체로 응결된 현상을 설명하기 위하여 l/v 의 급수로 전개되는 P/kT 에 대하여 급수의 수령반경과 관계지으려는 노력이 May e r 등 7) 에 의 하여 시도되었지만 viri a l 계수의 일반적인 경우, 죽 임의의 l 에 대한 Bl (T)의 성질을 알 수 없어서 결정적인 결론이 나오지 않았다. 이때에 다음과 같은 새로운 생각에서 이 문제에 대한 가능한 설명이 얻어지고 있다.
7) J. E. May er & M. G. Maye r ; Sta t i st ic a l Mechanic s (Wi le y , 1940) 0J o1]서 볼 수있음.
(1) Yan g과 Lee 의 이론 8) gran d pa rti tion func ti on 3 를 나타낸 (4.1 5 ) 에서 (＝-fr =z 。 (4.29)
8) C. N. Yang & T. D. Lee ; Phys , Reu. 87 (1952) 404
인데, 여기 두번째 관계는 (4.24) 에서 볼 수 있다. 따라서 (4.15) 와 (4.1 6 ) 을
3(V, T, z 。 ) = NLo=oO (A3 Zo) N Z(V, T, N) = exp {V X(V, T, z 。 )} (4.30) X(V, T, z 。 ) = ta b, (V, T)z'0 (4.30a) l~ l 로 쓸 수 있다 . 이들 식은 어떤 V 의 유한한 값에 대하여도 성립한다. 분자력 po te n ti al ¢(r) 의 중심부가 반경 r o 인 강체구로 되어 있다면 N = V/(2r。 ) 3 (4.3 1 ) 로정해지는 N 이 있고 N > N 이면 Z(V, T, N) = 0 (4.31a) 이다. 따라서 (4.30) 에서 3(V, T, ~ 。 )는 z 0 에 대하여 N 차의 다항식이 된 다. 이 다항식의 0 점을 z,( i = l, 2, …… 丙)로 하면 3(V, T, z 。 ) =E( 군) (4.32) 가 성립한다. 따라서 (4.30) 의 두번째 식에서 X(V, T, z:。)을 구하여 X(V, T, z 。) = tit 1n ( 1-> (4.33) 를 얻게 된다. Zo 에 대한 다항식이 된 · 3(V, T, 킹에서 각의 계수는 J3N Z (V, T, N) > 0 이다 . 따라서 z‘ 의 어떤 것도 Zo 축의 (+）축에는 있을 수 없다. 그리하여 유한한 V 의 값에 대하여 X(V, T, z。 )는 실수축에서 z0의 해석함수가된다. 이제 V 一CX)로 하는 극한을 생각하자. 물론 N 一®이고 u = VIN 가 주어전 값이 되는 열역학적 극한을 생각한 것이다. (4.33) 은 정전기학에서 전하 」-이 z , 에 있는 2 차원문제의 정전f o t en ti a1 과같은형을 나타내 고있다 .V 가증가하는데 따라서 전하 v- 은감소하지만,전하의 수인 N 는 증가해간다. v 一 CX)의 극한에서 전하는 그림 4-7 에서처럼 양의 실수축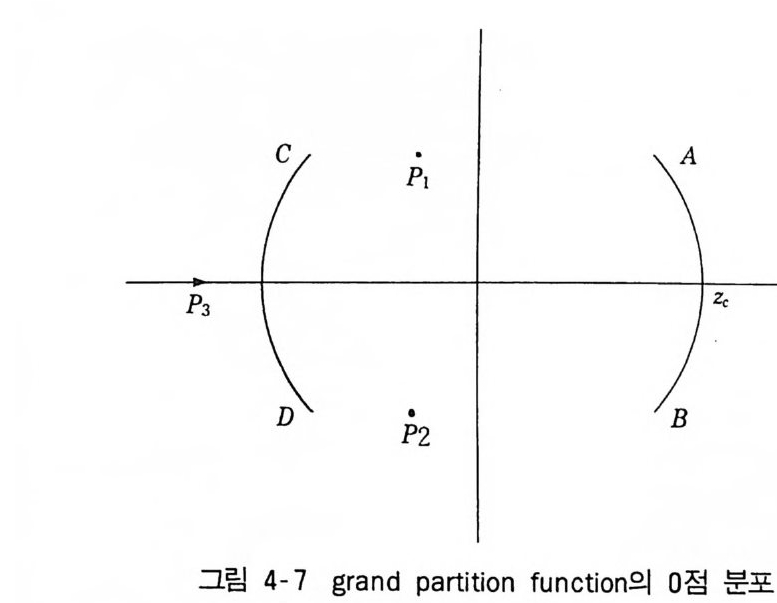
c .P A
에 교차되는 단일충 AB 를 만들게 된다고 생각해보자.물론 CD 와 같은 다 른 단일충이 있거나 PI, P2, P 3와 같은 고립된 극이 있어도 문제될 것은 없 다. V 一 OO 의 극한에서 결정되는 함수 x~ (T, z。 ) = lvi-m i r X(V, T, Zo) (4.34) 는 Zo 가 작으면 기체상에 해당하고 (4 .1 8c) 에서 (를 z o 로 바꾼 식이 된다. 그러나 충 A~ 의부 (zo = 但 1 반대쪽)에서는 다른 해석함수의 분지 (bran- ch) 를 이루게 된다. 정전기학에서 단일전하층의 양쪽에서 p o t en ti al 이 연 속이지만, 그 일차 미분인 전기장이 불연속적으로 변한 것이 잘 알려지고 있다. V 가 1―크1UP t 지 f= =만z 。~X 유 (aT한-x ,( 하0zTZ 。, o면) z 。 ) Ma y er 의 방정식 ((44..3365))
는, x(T, z 。 )가 (4 .1 8c) 에서 ( = zr}i: - 하는 전개식으로 되거나, 그렇게는 되지 않거나 관계없이 성립되는 것을 (4.1 7 d), (4.1 9 ), (4 .1 9a) 와 (4.21) 에서 .쉽 게 알 수 있다. 그런데 충 AB 의 양쪽에서 T(T, Z 。)는 연속적이지 만 ox( 8T%, z 。) 는불연속이면 꿉규를 \로그릴 때 응결곡선과비슷한그 림을 얻게 된다(그림 4. 8a, b, c 참조, 이 그림에서 점선으로 나타낸 곡선 은 V 가 유한할 때에 해당된다). Yan g -Lee 의 생각은 응결현상에 대한 완전한 이론이라고 할 수는 없고
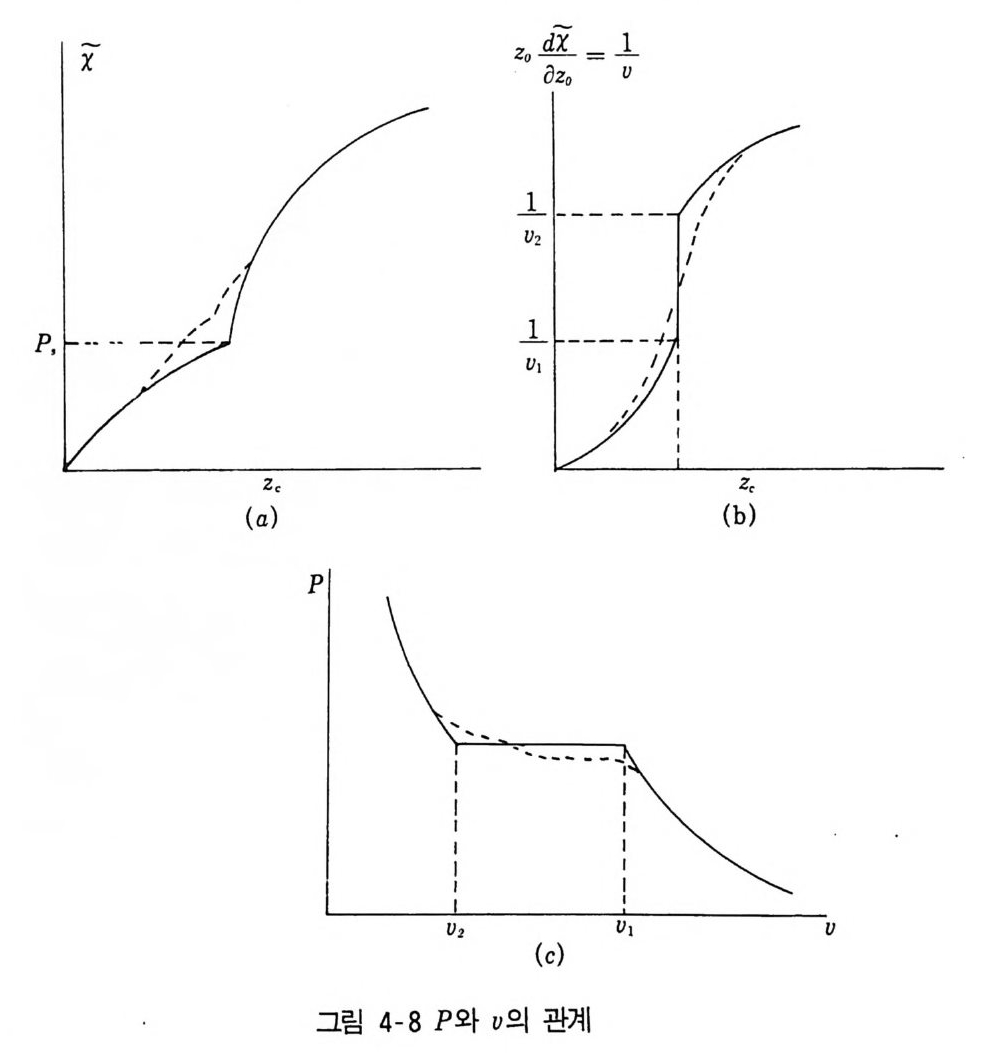~x z 。da一zXo =―1u
수학적 가능성을 보인 것이라고 보아야 할 것이다. Y(T, Z 。 )에 대한 (4. 18c) 의 전개급수가 0 이 아닌 수령반경을 가지고 z 。 = 0 에 가까운· 영역인 립충한 A BT 의 (T ,내 z부。 )에의서 해 기석체함상수을를 나결타정낸하다는고 데 하서더 도라움도이 충되 A지B 의못 하바고깥,쪽 실에제서적 성으 로는 충 AB 를 결정하는 방법도 없다. 그리하여 대표적인 상변화현상의 하 나인 응결현상에 대한 결정적인 이론이 앞으로 개발되는 것이 기대될 뿐이 다.
(2) 수학적 모형의 하나 9)
9) G. W. Ford ; Thesis , Un iv. of Mi ch i ga n (19 54)
체적 V 안에 들어갈 수 있는 입자의 최대수 N 이 V 에 비례하는 것을 (4.31) 에서 볼 수 있으므로 gra nd pa rti tion fu nc ti on 을 V 차의 다항식으 로생각하여 3(V, z 。) = (1 + z 。 )V ~ll--zz; 。; (4.37) 로 취해본다. 이 다항식은 2V 차이고 0 점은 모두 z。 = 0 을 중심으로 하는 반경 1 의 원 위에 있다. 특히 z 。 = ― 1 에는 0 점이 V 중으로 겹쳐 있지만 양의 실수축에는 0 점이 없다. V 一 OO 의 극한울 취하면 zo<1 인 경우와 z0>1 인 경우에 서로 다른 해 석함수가되고 { 1n( 1 + z。 ) ; zo < 1 T(z 。) = 1n(l +z。 ) +1n z。 ; z0 > 1 (4.38) 가 된다.-1u = zo<:1Z o 에— aa서%x- =Ma y1 e+.r zo % 방 정식은 (4.38a) 와 kPT = X- = ln(l + z 。) (4.38b) 이고 Zo = 了뉴, 2
욥 = ln ( 占 ) = -ln ( 1 —+ ) =}＋岭+t·i+…… (4.38c) 의 vir i a l 전개가 가능하다• 이에 대하여 z 。 > 1 이면 一1V =Z- ov 8o~.-xz·-o-- = 11 ++ 2Zz 。 。 (4.38d) 이고 욥 = X= ln( l + z 。 ) + 1n z 。 = 1n z 。( 1 + z 。) (4.38e) 이다. 따라서 (4.38d) 로부터 Zo = Tu=-z1v (4.38f) z1
~(T)는 그 자체가 l 개 입자에 관계되는 다중적분이고 l = 1, 2, 3 정도의 작은 수이면 비교적 쉽게 계산할 수 있지만 l=5 이싱이면 전산기에 의한 수치계산도 벌써 쉬운 일이 아니다. 그러므로 열역학적 함수를 직접 분배함 수 Z(V, T, N) 이거나 3(V, T, z) 를 통하지 않고 근사계산할 수 있다면 편리할 것이다. 이와 같은 목적에 적합한 함수가 입자분포함수이다. (1) 입자분포함수의 정의 N 개 입자에 대한 r^, 위 상공간 안에 있는 작은 체적 A 凡 안에 입자계가 존재할 확률은 canonic a l ensemble 에서 P(HN ) LlrN = 上Z N e~- P H, ~N!h3,\ ' (4.4 0 ) 이 된다. 위에서 HA ’ 은 N 개 입자계의 Ham i l t o ni an 이고 Z N 은 분배함수이 다. 또 gran d canonic a l ensemble 에서는 P(HN )L lrN = 묘主3 - e-OH., N~!hl.` ’ (4.4 1 ) 이 되는것을알고있다. j 번째 입자의 위치 芹가 (7, 7 +d7) 사이에 있다면 <5(--;:; - 7) d~의 값이 1 이 되고, 그렇지 않으면 0 이 된다. 따라서 {iZ =N l b(r-I —一 r) }d3—r 은 (7, 7 + d7) 인 체적소 안에 들어 있는 입자의 수가 된다. 그리하여 입자밀도 nl~) 이 n1-(r ) 三 LA’ ~一(ri - -r>) (4.4 2 ) j= 1 로 정의된다. 입자밀도의 ensemble 평균 111( 접 三
= < 1i= 1 1 t=1 b(7- 겁 b( ；；구 )> (4.4 3 a) (j# l ) 이 정의되고, 일반적으로 값 7 군……-;(I - l l ) = < n1(i r7 : ……~ (1- 1)> =
비슷한國 방겁법으 로== 모上2Q 입A' 자`f 분 e 포홉함 ( r, －f수 문 는e(i -=j 교 #l 1lt=) , ::C : : . ,o ) 詞(;; - \-(겅i- -{J-(~- ;구,)) 1正=i~ l ,d3r , =臨QN~ Je 홉 ( r7 7. :-- ;:, ii~= 3 d 3- ; (4.4 4 c) 로 구할 수 있고, 일반적으로 國广…••:-;(1 - 1 )) = ~ 訂 e - ~ ; - , -;. , . : 건 In d3 r ; (4.4 4 d) 가 되는 것을 알 수 있다. gran d canon ica l ensemble 을 사용한 계산도 비 슷하게 된다. N 개의 입자계가 유체를 이루고 있으면 1 개 입자분포함수는 (4.44) 처럼 入評 n=Nv 과_, 같-1고 ~, 2n _개,, A입l 자-1 분~ 포.,... .함;.1 수~ nz, (r-, r7' \) ,는_, IIr- --r t' I 가 크면 n2 이 된다. 따라 A1 귬?, 7) = n2 g( l7 -71) (4.4 5 ) 로 놓고 g (l7-71) 를 상관함수라고 한다. (2) 열역학함수의 분포함수에 의한 표현 canon ica l ensemble 에서 분배함수 ZN 은 (4 .4 4b) 에 정의된 위치분배함 수 Q N 을쓰면 ZN=1 ~QN (4.4 6 ) 단
A,=h ~ (4.4 6 a)로된다. 입자계 전체의 에너지에 대한 평균치가 내부에너지 U 인데 U=E= ―검 ~Z N =k'r ( ~)N.v = ½NkT+c l> (4.4 7 ) 이고, 여기서 q> = kTz (~t.. v = -(7/3~ )N,V (4.4 7 a) 이다. (4 .4 4b) 에 정의된 Q N 을 대입하면 5 = 같 I……[ e- 8 0 7r,7 `)
= kT( 01o nv Q /1.' ),\ T (4.4 8 ) 이 되는데, 이것을 계산하기 위하여 체적이 Vl / 3 의 길이룰 한 변으로 하는 입방체라고 생각하는 것이 편리하다. 그러면 (4 .4 4b) 에서 Q,_ . = J; ' ' …… 'r :··· e -/ 10 (z, y : x ` y` \\ dx, dy , dz, (4.4 8 a) 로쓰고적분변수를 X1 = vl/3 자 , y, = vl/3 y ,', Zt = vl/3 더 (4.4 8 b) 로 고치면Q,N =Q ,\ V , 이 N J; …· ·· I:e 효 (x ' , . ) : . i , •• x: .) ' ,.\ \ d;: d y, ' dz‘’ (4.48c) 로 된다. 위에서 $(x ;, y;, z;, …… x’ ', y :\, z.\' ) 는 ( x1 ,Yi, Z1, …… XN, YN, Z N ) 에 (4 .4 8b) 를 대입한 것이고 O(xI, yI, z1… …X N , YN , ZN) = 흡 ¢(r,J) 에 대하여 ¢(x;, y;, z; …… x ~, Y ~, z~) = 묘 (Vl /3 r'I/ ) (4.4 8 d) i
,If r1·-2 漏(8r 1r1 22 ) n2( ,: :, ;:;) d 3 芹 d 3 r7 (4.4 8 f) 를 유도P할 = 수 n k있T다-.t 따 n라2 서 [ 뿐(f4 .-4 8)g 이 ( r) 4nr2 dr (4.4 8 g) 로 고쳐지게 된다. 이 식의 우변에 있는 첫번째 항은 이상기체에 대한 값이 고 두번째 항이 분자력의 영향을 나타내고 있는데 상관함수 g (r) 이 중요한 역할을한다. 또 하나의 중요한 열역학함수가 되는 ent ro p y S 를 입자분포함수로 표시 하는 방법은 약간 복집하다. S 를 분배함수 Z N 으로 나타내면 s = -( 關 ) V A = ( 8 ( kT;> ZA ') \, N = —kP F— kP 읊 In Zs (4.49) 인데 내 꿉 ln ZA = N fh3\ f e: p H ,건 d3i : d37 : 이고, r 위상공간의 확률밀도 P(p一 1, 一r I, …… p一,\' , 一r N ) 이 P(p_ I, _ rl> ’ …… p_A ,_ rA> ) = Mhl 3'\' eZ -PNH ` (4.4 9 a) 로 되므S로 = ( 4k.4 9J)( 는— PF + PH,\ ,) P(-p I, -rl’ ··…. -pA , -r N)• l·1-d -3 p- , d-3 r-, .(4.4 9 b) 로 쓰인다. (4 .4 9a) 로부터 1n p~,:, …… 元-;:) = -ln (N! h3N ) -pH ,\ ,-1 n ZN = 一 1n (N! h3N ) -pH N + p F (4.4 9 c) 를 알 수 있으므로 (4 .4 9b) 를
s = —k J P ln P IT d 3閃 d3; : :-k ln(N! h3N ) (4.4 9 d) 로쓸수있다. 입자계의 Ham ilt o n ia n H .v이 HN =H0+< I) 의 형이며 Ho 는 운동량만의 힘수이고 O 는 위치좌표만의 함수이다. 새로운 Ha milt o n ia n HNU) 를 HN(l) =:= H0 + A
뺨 = k/3 尸근 計 n d 3: 訂 =댜 k/3 k[/3 三] `i A¢ - ({r12:玩 }元 (,尸 ~ f r7- :) l) d 3- ;:; d3; : ; (4.50c) 가 된다. 위의 식의 두번째는 운동량에 대한 적분으로 위치좌표공관에 대한 확률로 바꾼 것이고, 세번째는 (4 .4 7b) 를 구하는 것과 같은 방법에 의한 것이다. Jc = 0 가 이상기체에 대응하는 것이 명백하여 S(0) = side o l gos 로 놓으면 (4.50c) 를 A 에 대하여 적분하고 S = Sid e alg os 十 -if J: d }. JJ J c¢ (r12) 훑 n2(7, :A) d 37 강 r 2 = sid,o l gn s + 뿔2 I。~ dr 4 러 (r) [ 。 d}, [ 玉g (r, }l) ] (4.51) 을 얻을 수 있다. 위에서 g( r, ｝노 )는 분자력 p o t en ti al 이 A¢(r) 이 되는 상 관함수를 의미한다. 그리하여 0 ~ Jc ~ 1 인 모든 A 에 대하여 g(r , Jc)이 알려지면 그 적분된 효과로서 en t ro py가 얻어지는 것을 보게 된다. (3) 상관함수의 근사계산 열역학함수 중에서 가장 중요한 내부에너지 u, 압력 P 와 entr o p y 87} 상관함수 g (r) 에 의하여 어떻게 표현되는가를 보았는데, 다른 열역학함수에 대하여도 비슷한 계산이 가능하다. 그러나 2 입자 분포함수 또는 상관함수를 분자력에 대하여 구체적으로 계산하려면, 분배함수에 대하여 g ra p h를 써서 전개하여 계산하던 것과 마찬가지 계산을 하여야 하므로 이 방법이 더 유 리하다고 생각할 이유가 없다• 입자분포함수가 더 편리한 이유는 그들 서이 에 성립하는 관계식이 있어서, 그것을 근거로 하여 근사계산을 하는 방법이 발견되기 때문이다. 그와 같은 관계식을 여러 가지 방법으로 찾을 수 있으
나, 아래에 하나의 예로서 가장 알기 쉬운 Born-G ree n -Y von 적분방정식 을보려고한다. canonic a l ensemble 에서 데자분포함수가 (4 .4 3b) 에 다음과 같이 주어 지고있다.죽 元 儒 …… 芹 = (NN-!l) ! 걸 Je -p < 1 >
처럼 깨끗한 형이 된다. 식 (4.5 3 ) 은 l=l, 2, … … 에서 모두 성립하는 소위 계층방정식 (hier achy e q ua ti ons) 이며 Born - Green - Yvon 의 계 충적 분방정식으로 알려 지고 있다. 특 히 l = 1 과 l = 2 를 따로 써보면 1 8 J亨 元(r;:~ d3F 7 - 一p ＝Or1 긴 n 元 = 元 __f1 一0 r1 ln 元 (r 1 ,r 2 ) = 8r一1 + 元 (r1, r2) ((44..5533ba)) l 6 海 (r1 2 ) ·I 8¢ :: ) it3(r1 , r2, r 3) d% 이다. 유체계에서 짜이 장소에 관계없는 상수가 되므로 (4.53a) 의 좌변은 0 이다. 우변에서 元 (-;::' --;:: ) = n 2g (r 1 2 ) 이고:에 대한 우함수인데 a¢8(rr1 1 2) 은 기함수가 된다. 따라서 그들의 곱에 대한 적분은 당연히 0 이다. 결국 (4 .5 3a) 로부터는 새로운 지식을 얻을 수가 없다. (4.53b) 에서 n_2-( r➔ 1, - r 2 ) 를 구하려면 元 (7, :' : ）에 대하여 알아야 하고, (4.53) 에서도 元룰 구하는 데도 元 +1 의 지식이 필 요하다. 계층방정식의 정확한 해는 입자계 전체에 대 한 완전한 지식이 요구되고 있다. 그리하여 근사해를 구하려면 계층의 어떤 단계 를 절단할 수밖에 없다• 대표적인 방법이 K i rkwood 의 중첩근사 (su p e rp o sit ion ap pr ox im ati on ) 인데 n一3 ( 一r I, 一r2, 一r 3 ) 一 斤2 7,n 검 . n 2
g (r) 의 함수형을 구하는 노력이 계속되고 있다. 상관함수 g (r) 의 함수형을 구하기 위하여, 다른 근사방법을 써서 구한 적 분방정식에는 다음과 같은 것이 찰 알려지고 있다. CD Deby e- Hi ick el 방정식 1n g( r) = 틀) _ nJ {g( l7-y l) -1} {3¢(y) d3y ® Ki rk wood-Salsburg 방정식 g(r )ePl(r) -1 = n J{g( 17-y l) — 1} (eM li· ) - 1) d3y @ Percus-Y evic k 방정식 e 郞)g (r)- 1 = n J{g (17 -y I) - 1} {1- er.J1> · > }g (y)d 3y @ CHNC(Convaluti on -Hy pe rnett ed Chain ) 방정식 1n g(r ) + {3¢ (r) = ~.\ {g『 - 了 |) —1} ~(y) —1 - In g(y) - P¢(y )} d3y 위에서 Deby e -Hi ick el 방정식은 전해질용액에서 이온 서이의 상관함수 를 구하는 데 쓰이고, 나머지 세 가지는 액체에 대한 근사식으로 얻어졌다. 전산기에 의하여 많은 수치계산이 이미 수행되었지만 아직도 만족스러운 결 과를 얻었다고 할 수는 없다.
5 양자유체에 대한 섭동이론 ' 5-1 서론 입자계의 온도를 낮게 하여 OK 가까이 하거나, 입자밀도가 충분히 커져 서 입자의 열적 de Brog lie 파장이 입자 사이의 평균거리와 비교하여 비슷 하거나, 크게 되면 계의 열역학적 성질을 계산하는 데 Ferm i-D i ra c 또는 Bose-Ei ns te i n 통계 , 즉 양지통계가 중요하게 된다. 우리논 이미 決}에서 입지들 사이에 상호작용이 없는 이상적인 계에서 그와 같은 경향을 보았다. 이상적 인 Fermi 입자계와 Bose 입자계는 높은 온도에서는 비슷하게 열역 학적 성질을 나타내지만, 아주 낮은 온도에서는 판이한 성질을 나타내는 것 울보았다. 이 장은 3 장의 내용을 보충한다는 입장에서 입자들 사이에 약한 상호작 용이 있는 축퇴된 양자유체에 대하여 고찰하려고 한다. 상호작용이 약하다 고 가정하여 양자역학의 섭동이론이 어떻게 적용되어 전개되는가를· 보게 된 다. 이상적인 입자계에 대한 3 장의 결과가 0 차 근사, 죽 근사의 첫 항이 되도록 gra nd pa rti tion f unc ti on 을 계산한다. 입자계의 양자상태를 입자 수로 표시하는 방법을 발전시킨 것이 제 2 양자화방법이 되므로 처음에 제 2
양자화방법을 보도록 한다. (1) 제 2 양자화의 방법 많은 수의 입자로 구성된 계에 대한 양자상태를 표시하는 방법 중에 입 자수 표시가 있다. 그것은 단일입자의 양자상태 r 에 있는 입자의 수를 연산 자 8 『로 한 것이다. 입자들 사이의 상호작용이 없는 이상적인 계에 대하여 계의 Hami lt o nia n 연산자 Ho 가 H^ 。 =Ecrnr^ (5.1 ) r 로 되며, 여기서 g은 양자상태 r 에 있는 입자의 에너지이고 파수 I呼 r 에 대 病 (이하 h= 검-이다) &=—h2 방m (5. la) 이다. 또 입자의 총수도 gra nd canonic a l ensemble 에서는 일정한 값이 아 니고 연산자 N 로 표시되며 N^ = En^r (5.l b) 이 된다. 연산자 요 r 의 고유치는 Ferm i 계에서는 0 과 1 이고, Bose 입자계 에서는 0, 1, 2, … … 인 정의정수이다. 연산자 8r 의 고유치를 nr 로 할 때 그 ket 양자상태 I nr> 에 대하여 생성 연산자 따와 소멸연산자 ar 를 서로 Herm ite con j u g a t e 하다고 하며 다음 과같이 정의한다. 처음에 Bose-Ei ns te i n 통계에 대하여 ar I nr > = 占 | 凡 —1 > (5.2) a: I nr> = 占구~ l n,. + l > (5.2a) 로정의한a;다 a., I그 n러, >면 = a;+ ,J;, In,-1 > = \jn, a,.+ I n, - l >
= n, I n, > (5.2b) 와 a, a; I n, > = ( n, + 1 ) I n, >( 5.2c) 울 알 수 있다. (5.2b) 에서 n^, = a+, a r (5.2d) 이고, (a5r. 2ab;) 와- 따(5. 2ac,) 에= 서1 (5.2e) 울 알 수 있다. 이 표시에서 양자상태 r 과 s 는 서로 독립적이 되는 것이 명백하여 a, a: _ 따 ar = 6rs a,a, _ a5a ,=O a? a: _ a+, a: = O (5.2f) 의 교환관계가 존재하게 된다. 다음, Ferm i-D i ra c 통계에 대하여서는 교환관계를 (5.2f) 대신에 ar a; + a +, ar = & ara, + asa r=O a; a; + 야 a; = 0 (5.3) 을 주면 된다. 그러면 a? ar(l —a? a) == aa?; aarr —_ aa} ?( a1r a—} aar : ar)ar = a; a? ar ar = 0 (5.3a) 가 된다. 그 이유는 (5.3) 의 두번째와 세번째 식에서 ar ar = 0, a;: a;:-= 0 이기 때문이다. (5.3a) 는 8r(l - 8r) = O 로 쓰이고, 이 식은 年 r 의 고유치가 0 과 1 이라는 것을 밝혀주고 있다. 그리고
a, I O> = o (5.3b) a; I l> = O (5.3c) 는 입자가 없는 상태 r 에서 입자를 소멸시킬 수는 없고, 입자가 하나 있는 상태 r 에 입자를 생성할 수 없기 때문에 요구된다. 또 a, I l> = I O> (5.3d) a; I O> = I l> (5.3e) 가되어야한다. 생성연산자 a; 와 소멸연산자 ar 에 붙어 있는 양자수 떠 파수 vecto r 다 sp in (J를 나타낸다고 하여 r 三 (k, (J）로 놓고, 이들에 의하여 장 (fi eld) ¢의t ( 7연 )산 자== ¢守 . (g7) 꾸 와¥ ¢a; a r +r( 7ee) -I' 를k.\ x 8 c s. (5.4 ) ¢,(7) 로정의해보자. Ferm ¢i-,D(7ir)a¢ c }통(?계)의 + 경 ¢우;, (?(5).¢3), (에7 )의 하=여 v1 5'r(/ a,a+ : +I a;+士 ar)\ e'ik> • -z-I—k x 磁 6 . s · = 令 Ee ; （감) ds. =函드컵 ·8 , , . (5.5) 롤 알 수 있다. Bose-E i ns tei n 의 경우는 (5.2 f)가 이용되어야 하기 때문에 (5.5) 의 첫번째 식과 두번째 식의 (+) 기호가 (-) 기호로 바꾸어져야 하 는 것을 알 수 있다. 그리하여 장의 연산자에 대한 교환관계식이 다음과 같 게 된다.죽 寧)詞) 士 ¢;-(f)¢,(°t) = fJ(°t구) • & ¢,(다, . (f) 士 ¢,.( 7 )¢,(°t ) = 0 ¢;(°t)¢ ;:(7) 土 ¢;:(7)¢;(° t) = 0 (5.6)
이며, (+）기호는 Ferm i-D i ra c 통계에, ( —) 기호는 Bose-Ei ns te i n 동계 에 대하여 성립한다. 또 f杯값(김 dx = 杓 EIar+ e- \, a,e7 k :& , dx一 ` = kEJ .6 . a:o a m && = I: a 춘3 a k.s =I: n;;' (5.7) 이며, 앞에서 본 N 는 서 =¥H + （갑 , (5.7a) 가 된다. Ham i l t on i an 의 운동에너지 부분인 H가 (5 .1)과 같으려면 g。 = 디 # ,+ (x) ( ―溫 - V 2 )¢ S (검 d7 (5.8) 이 H되l 어=야 방한 다E.. I상 ¢호:작（검용 禪을 )나타 u내(는7 _H7a)m¢ i Cl t(o ? n )ia 翼n 부 분)d 言 H 이 (5.8a) 뚜 될 것으로 짐작된다. 그것은 ¢ ; . (7 ' )¢..(?) 와 ¢;(7)¢C(7) 가 각각 x킹 에 있는 sp in (J＇인 입자의 밀도와 7 에 있는 sp in CJ인 입자의 밀도를 나타내기 때문이다• H 연산자와 N 연산자에 대한 동시적 인 고유상태를 | ,jJE. N > 로 쓰면 <'PE , N I 'PE , N> = 1 (5.9) H^ I 'E, N> = E I 'E. N> (5.9a) N^ I 'PE .N> = N I 'PE . N> (5.9b) 이 성립한다. 간단하게 쓰기 위하여 ¢(i) 三 ¢(?i) 로할때
10) 증명은 조순탁 저 『 통계물리학 』 이나 Huan g의 Sta t is t ic a l Mechanic s 등 교과서 에 많이 나와있다.
Ha milt o n ian (5.8) 과 (5.8a) 는 (5 .4)를 대입하면 ~ o = 賈뿔 )a 『+ ar (5.11 ) H1 == 前강 t.E. < r凉s I ~u II ru's I' t>,a I-:; ) 따 a :a. ,a :a,, ,, a k.• · a k.. ((55..llllaa')) k , .k ,.k쇼 , . G,c ’ rsr3 가되는데(,m 訂여 I 기v서 |E ,t) 三 버 e-ik, . -, --ik -_ , · v ( ?• — ?•) ei-k, · ,- + ;- i.-. ,· d? d£ (5.llb) 룰의미한다. 특히 u(x) = V1 ~qv (q) ei一q ·-x (5.llc) 처럼 Fou rier 전개가 되면 E, E |u1 E, 閃) = 8( 閃 + E, 閃 + 閃) v(~ —閃 ) (5.l ld ) 의 관계가fk1 있_ 다_fk.3 따= 라=f서q fq 죽fk l= =fk3 + fqfq kf4 fk 2 kf2 fk4 I
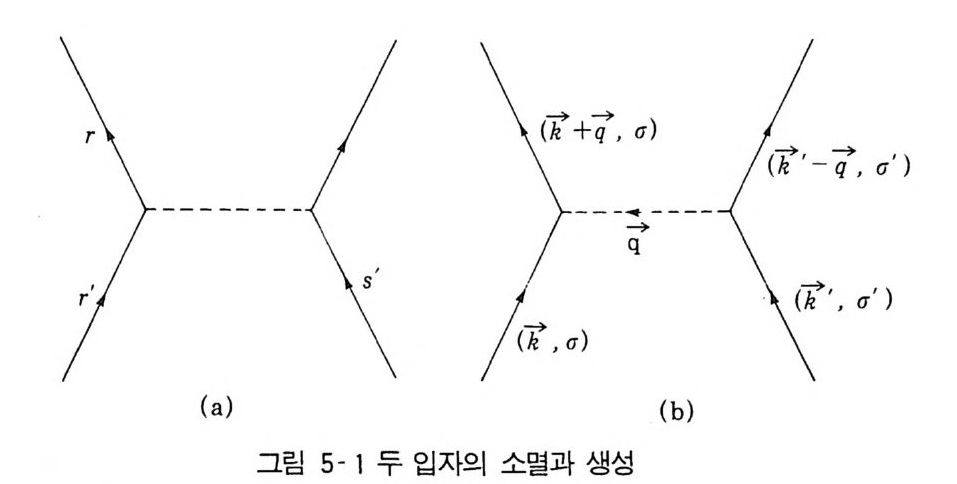r’ s’ If \\ c+ ~一 qf’ 6 `'` , (_k> ( ,7k - ,_ q , ,(J ' ( )j ' )
로 하고, 다시 閃 -J !, ~ - i7로 바꿔 쓰면 (5.lla) 는 (-k +- -qH ^, l (=J• ） 初와- 1 ( ·k- IqE, k,k — v-(q一q ,) a(J노 I ) 인 소입 자 . 가a급 생 C£성£. 되는 것을 나타낸다. 이(5 .과lle정) 처럼 쓰이게 된다. 이것은 (k, (J）와 (-;;7, (J I ) 로 표시된 입자가 소멸되고 에서 두 입자 사이에 작용하는 p o t en ti al 이 7 의 운동량을 (~. (J') 입자 로부터 (k, (J) 입자에 전달하고 있는 것을 볼 수 있다. 이 과정을 그림으 로 나타내면 그립 5-1 처럼 된다. 5-2 gra nd pa rti tion fu nc ti on 의 섭동전개 입자 사이에 상호작용력이 없는 이상기체에 대하여 양자통계를 논한 羽} 에서 gra nd pa rti tion f unc ti on 을 기초로 두고 계산하는 것이 가장 자연 스럽다고 느껴졌다• gran d pa rti tion fun cti on J는 3 = Loo (ePµ )N Z (N) (5.12) J= O 이며 , N개 입자계의 pa rti tion fun cti on Z(N) 은 Z(N) = I: e-pc . = I:
Z(N) = Tr e -PH/1<. /\., (5.1 2 b) 로 쓸 수 있다. (5.9), (5.9a, b) 에서 본 고유상태 | U E, ^ ' ＞을 쓰면 (5. 12b) 가 Z(N) E
로 되어 편리한 꼴이 된다. 또 입자 사이에 상호작용이 있으면 (5 .1 3) 이 3 = Tr e 대 (^~ +H^ , ) (5.1 6 ) 로 되고, H 가 작을 때는 섭동전개가 가능하다는 것을 알 수 있다. 섭동전개를 하기 위하여 e 내 (^2 + H^ , ) = e-~ U(/3 ) (5.1 7 ) 로놓으면 U(O) = U(/3 =0 ) = 1 (5.1 7 a) 이고 3 = 'Ir e - 타‘ U( {J) = Jo' Ir ( ~U({J) ) 의 관계가성= 립J한o <다U?(] {J )식> 은。 3 o 가이상기체에 대한값이고,으-—.- 가(5이.1 8상 ) 기체계에서의 확률을나타낸다. 따라서 o 는 U( p)의 이3‘상’ 기체계 에서 계산한 평균치를 나타낸 것이다. U( {J)를 (5.17) 에서 구하기 위하여 p로 미분하면 _ H 。 e -P:. U( /3） + e-o;뿡 尸 = ― (n 高) e- p(모 , ) (5.1 9 ) 을 얻는데, 이 식이 (5 .1 7) 에 의하여 간단화되어 e- 普尸 = -H1 e-p( ;+t:) = -JI I e-/.,'U (/3) (5.1 9 a) 가된다. 이것을 뺀 = -H, (P) U(/3 ) (5.19b) 로 쓰고 새로운 연산자 H^l ( {J)를
HI\1 (f3 ) 三 epI. \ H1 e-p I\, (5.1 9 c) 로 정의한다. (5 .1 9b) 를 g에 대하여 적분하고 (5 .1 7a) 의 조건을 쓰면 U(/3 ) = 1 - _f 。: H1(u) U(u) du (5.20) 를얻게 된다. U(P) 에 대한 적분방정식 (5.20) 의 해를 축차근사법으로 형식적이기는 하지만 구할 수 있다. 축차로 U( p)로서 (5.20) 의 우변을 대입하면 결국 U(P) = 1 + 포。 니 。 dul 'Iuo' du2 …… I:• _, d u n H (ul) …… ~(uJ (5.21) 을 얻게 된다. 위의 적분을 대칭적인 형으로 고치려면 u 를 시간변수로 보 고 D y sPo[n H의, ( uP! ） 기江호)를〕 도=입 [하[면1( u 가l ) <능 하I(u다 2.) P 기ul 호>는 u2 H1(uz) H 1(u1) Uz > u1 (5.22) 로정의f된: 다du .1 따J라: d서u 2 P[ 瓦 (u 筑 (u 2 )] += ff: : fd du : u1 2f f: '。 d, u d 2u lH 江1(u1)H )H11((uu21) ) = 2 p du1 f。u, d% H^I (ul)H^I (u2) (5.22a) 이고, 일J반:d 적u1으 f로: d u2 ……, I: dun P[ g [(ul) …·요 (u.) J = n! J: du1 f:• du2 …… I:I dun [#1( 마·…요 (un) 〕 (5.22b)
이 된다. 따라서 (5.21) 을 U(/3 ) = 1 + fi 덩 L [:'d u1… … :r : du. 祠 (u l ) …… H1(u.) 〕 (5.23) 으로고쳐서 쓸수 있다. 3 o와 3 에 대한 gra nd p o t en ti al 을 ® o 와 ® 로 하면 3o = e 내® • , 3 = e-lt !!> (5.24) 이고, (2 .4 7c) 에 의하여 d@= -P dV -S dT —N dµ (5.24a) 이며, d@ o 은 이상기체에 대한 같은 관계식을 준다. (5 .1 8) 은 e - P<( 만 ~ ) == l 〈 +U( /nt3) l〉 덩。 _ t_ f:d u1 …… f:d u.
。 (5.25) ` 로 풀어서 쓰인다. H1 로 (5 .l la) 를 대입하면 결국 생성연산자 ar 과 소멸연 산자 a;에 의한 표현을 다음과 같이 알 수 있다. 죽 e 대 x( ®`[O: … = … l` [ +。: d un:1= l… 도 n … ! ( 2dVu). n< P댜[ai= 『? I (
a 『+ (/3） 三 eP^. 따 e-p ^, (5.25b) 로정의된다. 5-3 전개항의 gra p h 표시 II)
11) 아베류소, 『통계역학 』 (동경대학) .
gra nd pa rti tion f unc ti on 을 섭동전개한 식의 하나가 (5.25a) 인데, 그 전개항에는 생성연산자 a;(u) 와 소멸연산자 ar(u) 의 여러 개를 곱한 항을 이상기체의 상태에서 평균을 취한 값이 나타나 있다. 양자장론에서 Wi ck 의 정리로 알려지고 있는 관계를 통계역학의 이론에 적합하도록 수정한 것 을 Bloch-De Do mini c i s 의 정리라고 하는데 그 내용은 다음과 같다. ( 1 ) Bloch-De Domi nici s 의 정 리 이 정리는 Ferm i-D i ra c 통계 및 Bose-Ei ns te i n 통계에서 모두 성립하 고, 그 증명도 비슷하게 할 수 있으므로 이하에는 Ferm i-D i ra c 통계에 대 해서만 증명하기로 한다. 지금 A 를 a 또는 a + 를 나타낸다고 하고, 2n 개의 A‘(i = l, 2,… …, 2n) 사이에 Ai Ai + Ai Ai = Cii (5.26) 의 교환관계가 성립한다고 한다. 단, 여기서 c ij는 연산자가 아니고 보통의 수를 의미한다. 그러면 평균치에 대하여 o + …… + c12n
가 성립되는 것을 교환관계 (5.26) 에서 알 수 있다. 위에서 맨 앞에 있었던 Al 이 가장 뒤로 옮겨졌고, C 상 = 2,… …, 2n) 를 계수로 갖는 2n-1 개의 평균치가 나타나고 있다. 또 (5.25b) 에서 (이하에서 간단하게 구 o 를 규 。 로 한다. ) ar(p ) = em ar e- m = ar e- k. a 지) = ep-;, ,,. a 『+ e-p :i, . = 따 e- p, (5.27) 이 나오며 1 2) , 여기서 er = cr-µ 가 (5 .1 5a) 에서 정의되고 있다. A 를 ar 또는 따와 같은 성질의 연산자로 보는데, 평균치 。 = Tr(A2 … …Tr eA-2Pn ·A 1 e- P. .) (5.28) 롤 의미한다. 여기서 (5.27) 에 의하여 a,e-, n , = e - 陀 (e “ are-” ) = e- m ar(p ) = e- m are-k 떠 e - 陀니 = e- m (e” 따 e- P ') = e-p. a;({J ) = e-p , a 『+ e 뱌 이다. 따라서 7}-( A2 ….. . A2n Ai e- ~ .) = 1r (A2 …… A2 n e- p_ . A1) e±P •- = 7}-( A1 & …… A2n e/1'.1 .) e~/Jt . (5.28a) 12) a,(P) = a,e-P•, 의 증명 뷜 = em(%. ,- a,~)e_, ,,_ 이.:i!., ~,-a,念 = 홈 e‘(a,+a,g -a4,+a,) = 홈 e,(a,+ a, a,+a,+a4,- 다) = -e ,a,이다. 죽혹信 = -e,a (p) 이고 a,(O) = a 러므로 a+ (P) = a.e -f k. 이다. 비슷하게 a:(p) = -a;e+ fk 도증명된다.
가 성립한다. 그러므로 (5.28) 에서 o e 土,' · (5.28b) 이 나온다. 이 관계식을 쓰면 (5.26a) 의 우변에 있는 가장 뒤의 항이 좌변 에 옮겨지고 (1 + e 士 /It. ) o = C12 0 + ... … + 0 = ; ( -1)6(P)
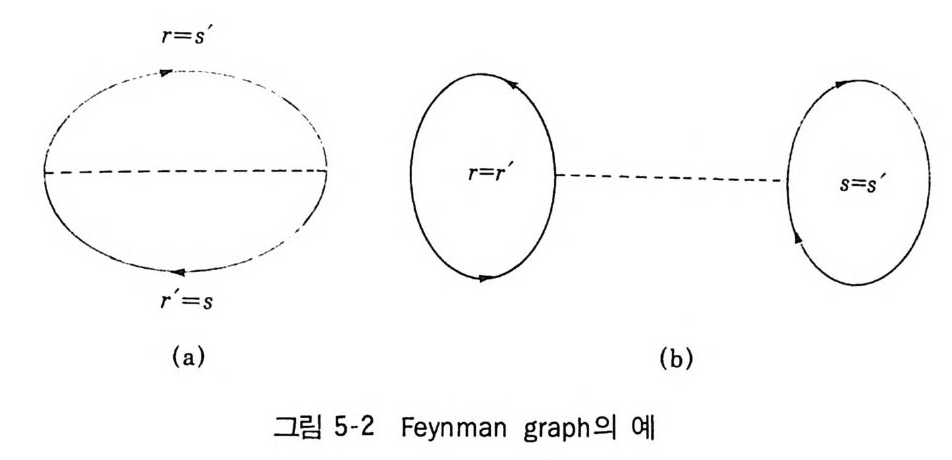r=s ,
0 + o d u (5.31) 로 쓰여진다. (5.27) 에 의하여 a;(u) a:(u) a,.(u) a,(u) = (e+ ... a,)(e+.,. a ,) (e-u,. a,-)(e- ... a ,) (5.31a) 로 쓸 수 있고, 따라서 (5.30a) 를 써서
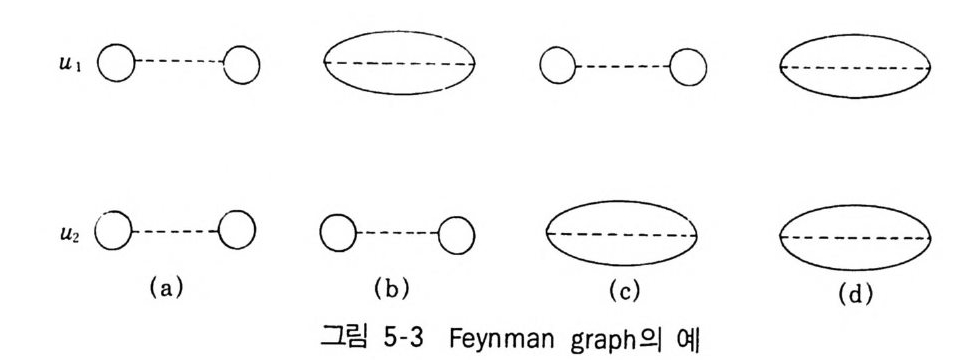u, o------o 二-〉 0----- - 0 二
a,+ ( u2) a,. ( u2) a,. ( u 2 ) 〉 。 (5.34) 이다. 여기에는 UI 과 u2 두 개의 시간이 나타나므로 여기에 대한 Fey nm an g rap h 는 시간이 밀에서 위로 진행한다고 약속하여 그리고 있다. 그러면 I2 에 나타니는 g ra ph 에는 그림 5-3 처럼 연결되지 않은 것과 그립 54 처럼 연결된 g ra p h 이 두 가지 종류가 있다. 연결되지 않은 gra ph 중 그림 5-3(a) 는 틀 (I:
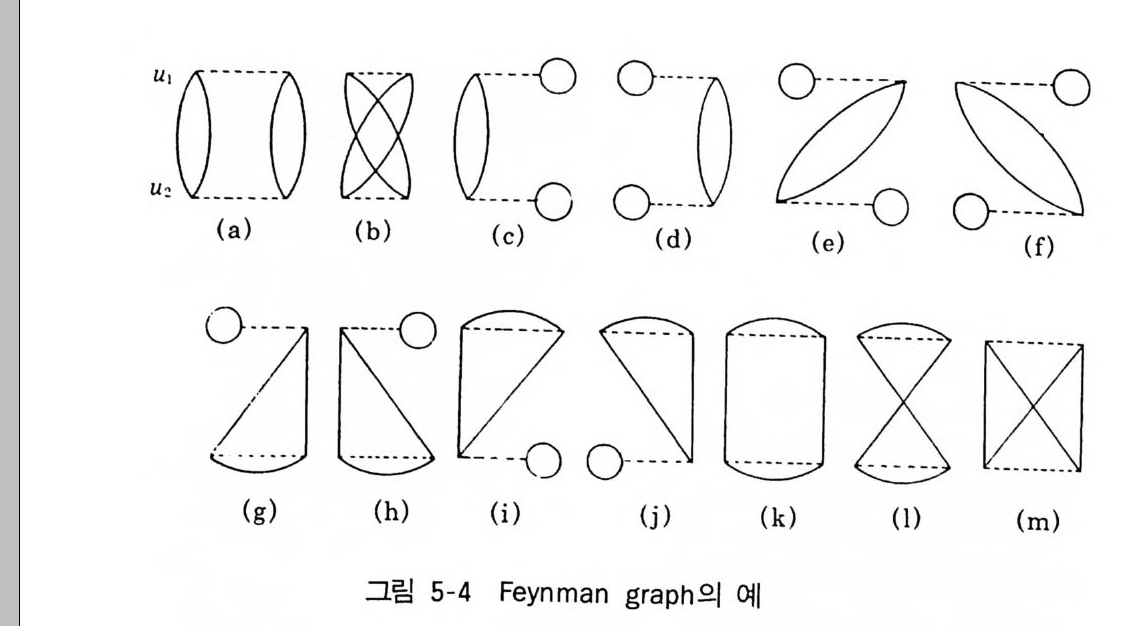uuo (a)° >0二 。。( d)O /-0 0\
여 얻은 gr a ph 와 같다. 따라서 (5.25a) 의 ln 을 취하고 다음의 식을 얻는 다.즉 -p(@ -@o) = fn=.I ~n! (2V)n L IT oL du1 …… d un (5.35) 이며, 여기서 < 〉 oL 은 연결된 gra ph (li nk ed clus t er) 만을 취하는 것을 의 미한다. 2 차의 연결된 grap h 중에서 그립 5 -4의 (g)를 더 자세히 살펴보자• 그 립 5-5 처럼 기호를 주고, Ul> ％로 하면 이 그림에 해당되는 수식이 2!(;V)2 m@q I u Ipr > • f:du1 f :1du 2 〈따 (1) 여(1) a,(1) aP(l) a:(2) a~(2) a,(2) a i 2) 〉。 (5.36) 로 쓰인다. 단, 위에서 시간 u, 롤 i로 생략하여 쓰고 있다.
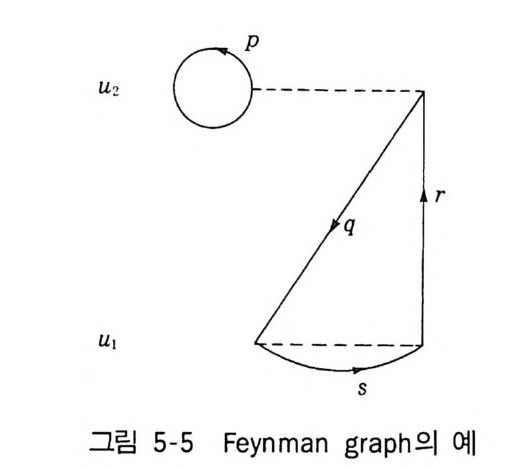p
…… a,( 2 ) a.(2) 〉 o 를 (5.30) 으로 전개하면 0 이 되지 않고, 남는 항은 〈 a;(l)ap (l) 〉。 〈 야 (l)a q (2) 〉 。 0 판타는 것을 쉽게 알수 있다. 그리하여 (5.35) 의 전개식의 일반항인 n 차 항에 대하여 시간을 u1 > u2 > …… > un 으로 놓으면, (5.30) 의 정리에 의하여
변화가 없다. 그러므로 위에서 a + (k) 를 가장 앞자리로 가져가면 (-）부호 가 된다. 따라서 con t rac ti on 하여
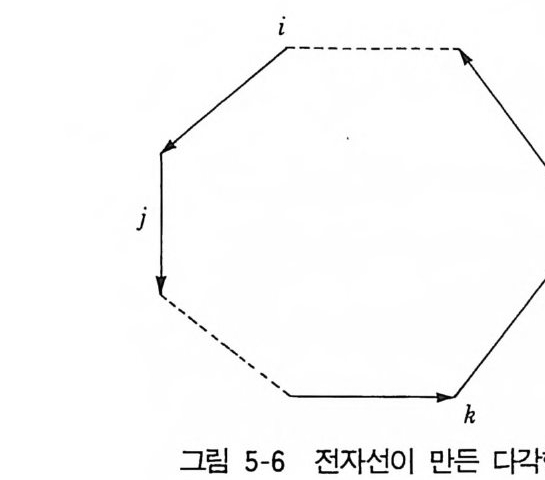J. 1
또 (5.37) 의 우변과 (5.37a) 를 비교하자. a 의 시간 u1 가 a + 의 시간 u, 보다 크다면
위에서 ® 의 조건을 u 와 u ’ 의 함수 g, [ u, u' ] = -
의 범위에서 정의된 함수 g, [u ] —fr( + ) e -u c. u > o g [ u ] = { tE ) e -u c. u < o (5.4 1 ) 를 생각하면, 이것이 주기 2 /J의 주기함수가 된 것을 다음과 같이 증명할 수있다. [증명 ] -/J < u < 0 이면 O < u + {J < {J인데, (5 .4 1) 에 의하여 g, [ u + /3 ] = - /,i+) e -( u + p), = - 1+e -e'e -.P •. e '· = - /,(- ) e -u,. = 一 g, [ u ] (5.4 1 a) 이다• u 의 범위를 -p ::;; u ::;; p의 의부까지 확장하고, 거기에서도 (5. 41a) 의 관계가 성립한다고 하면 g, [ u + 2p ] = - g, [ u + p ] = g, [ u ] (5.4 1 b) 이며 gr [u ]가 주기 2 p의 주기함수가 된다. g, [u ]가 주기 2 p의 주기함수이므로 -p ::;;u ::;; fJ의 구역 안에서 Fourie r 급수로 다음과 같이 전개할 수 있다. 즉 g,[ u ]= 1f꾸i區) e - 다 (5.4 2 ) 로하면 Q n = 碧- , n = O, 土 1, ± 2 … … (5.4 2 a) 이고, (g5,.(4 i1w a0 )) 에 =의 하송여 I f J가 g, [ u ] e•w. , . du = 송 (1 -eiM ) f;,[ u ] e,w., .d u
0 : (n ; 짝수) = { ”·° n l— e, ; ( n ; 홀수 1 3) ) (5.4 2 b)
13) n 이 훌천면 n = 2l + 1, l = 0, 土 1, 土 2,-· …·로 쓸 수 있다. (5 .4 2a) 에 의하겨 (J)2 1+1 = 요텁끄프 이고 i(iw.) = 굵i w21+1) = -/~+>f。' e-(e . - ' 戶, J udu =r 무lW-,2L 1土+ 1-e도, l.W 21+11 - e,
가 된다. n 이 홀수인 경우에만 값이 나타나게 되므로 n = 2l + 1 로 하 여 Q I = Q 2 / + I 를, Q,로 고쳐 쓰고 0l = 꿉 (2/ + 1) (5.4 2 c) 을 정의하여 (5 .4 2) 에서 g, [ u, u ' ] = 1/3- 亡, L Q- u,v . l_ u - ue·r) (5.4 2 d) 을 얻게 된다. 특히 u = u' 이면 g, [u, u + 0 ] = 1/3- L, ~LQ , _ eer -i,v , · O (5.4 2 e) 로한다. ®에 대한 전개식 (5.39) 에 나타나는 적분 J: IT g, [ u, u ' ] du1· •• … du. 에 (5.42d) 를 대입하고, 하나의 적분변수에 대해서만 주목하면 그림 5-7 에 대응하여, (5 .4 2c) 의 관계가 있으므로 Je=x p [f_i (:1 )e(x ,,p + [ i((1)l,1 +- (l12)/ , - - [3, ,)-u ][ 4d)u tu ] d u = /Jb (l1 + l2, [3 + [4) (5.4 3 ) 가 성립한다. 이것은 당연히
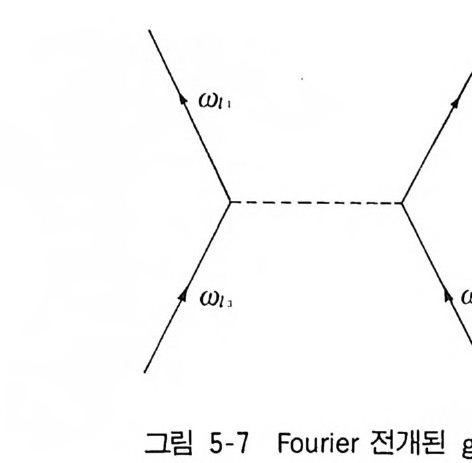(JJ1 , a)l:
W1, + W 1, = W1, + W1, (5.4 3 a) 롤 의미하고, 각 전자선에 Q,인 ener gy가 붙어 있다고 한다면 energy 보 존을나타낸다. 전개식의 n 차 항에는 점선이 n 개 있다. 따라서 Ul’… …, un 의 mn 변수에 대한 적분에서 (5 .4 3) 에서 보인 것과 같이 p의 n 곱이 나온다. (5 .4 2d) 에 있는 gr [u, 正 ]의 Fourie r 급수 전개에는 p - 1 의 인자가 있고, n 차의 항에 는 전자선이 2n 개 나타난다. 따라서 결국 연결된 Fey ru nan 도형에 p-· 이 인자로서 존재하게 된다. @-® o = ®/에서 ®/의 전개식 (5.39) 에서 n 차 항을 계산하는 규칙을 다음과 같이 정리할 수 있다. ® n 차의 연결된 Fey nma n g ra p h 의 가능한 모든 것을 그린다. ® 각 gr a p h 에 노{3n !· • 上(2{끄3 V )i i':〈1 r1s i I u I r·1 s \ > (5.4 4 ) 를 대응시킨다. 여기서 n1 은 전자선으로 된 폐다각형의 개수를 의미한다. @ r, l 로 규정되는 전자선에는 g~r ( t.( J)1) iw 1,- e, (5.4 4 a)
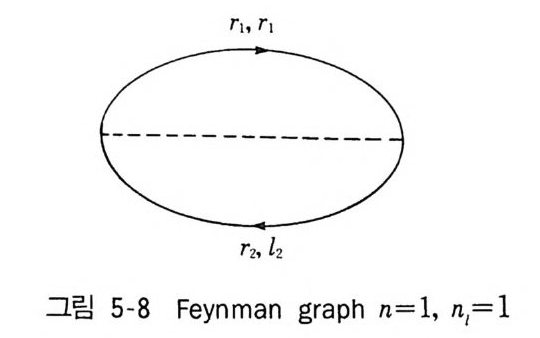n, rI
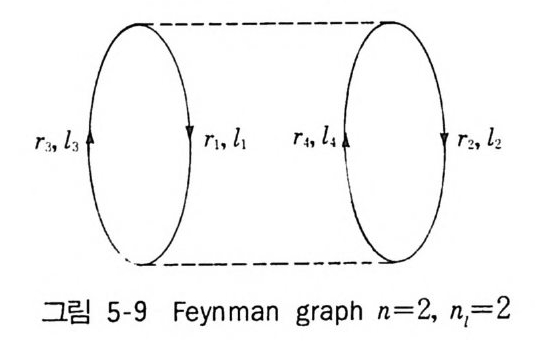그림 5-9 Fey nm an gra p h n=2, n,= 2
울대응시킨다. @ energy 보존 아 , + 아 . = 아 , + 아 . , 죽 li + l2 = /3 + /4 (5.4 4 b) 를고려하여야한다. ® 모든 r, s 와 l 에 대하여 합을 취한다. 위의 계산 규칙의 예를 간단한 경우 두 가지에서 알아보고자 한다. n = 1, n, = 1 인 Feyn man grap h 그립 5 -8은 당 肅王
三 듦 E
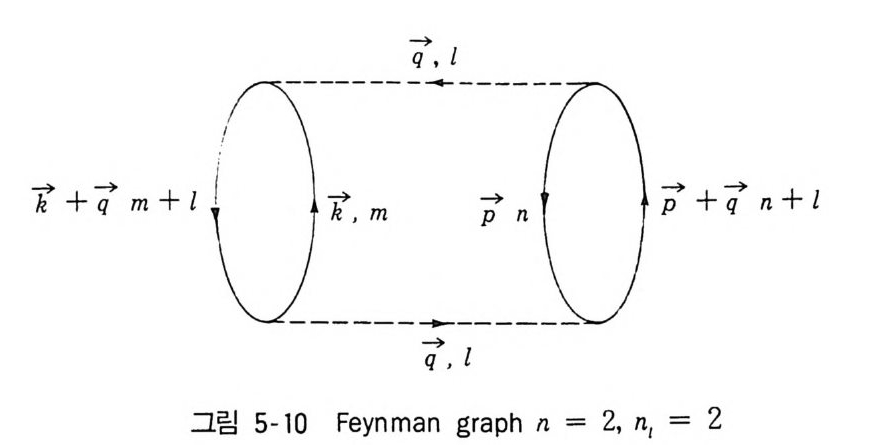fq’ l
또 일반식 (5 .4 5a) 에 있는 lJ(l1 + lz, l J + l 4 ) 와 (5 .4 6) 의 8(7 + k? 閃 + 閃)의 효과는 이미 그림 5-1() oll 포함되고 있다. 그리하여 (5 .4 5a) 에 해당되는식이 E2 三 멸 듦 : v2( q) 풀 [ { (i(J)m _e)(:(J)m + 1- e k+ q ) } • { (L(J )n _ep) (:(J)~ } ] (5.4 6 b) 으로쓰인다. 위의 식에서 l, q의 함수 H , (7) 를 n,(김 三 곱훑 (l (J) m-e k ) （노 ,-e ttq) (5.4 7 ) 로 정의하면, (5 .4 6b) 가 E2 = 一 22;!p 곱 V2( q ) rrf (汀 (5.4 8 ) 가 되는 것을 알 수 있다. rrI(7) 는 분극 부분(p olar i za ti on p ar t)으로 불 려지기도한다•
섭동전개의 2 차 근사에 나타나는 E 2 는 (5 .4 8) 이고, 이 식에서 v(q ) = 門이드로 ~n t (q)가 q = 0 에서 유한하다면 E 가 OO 의 값이 된다. 그러나 합의 순서를 바꾸는 재규격화 (renorma li za ti on) 에 의하여, 유한 한 값을 얻게 될 것이라는 기대를 가지고 소위 rin g 근사를 해보자. rin g 근사는 전개식의 각 차수의 항에 있는 Fey n man gra p h 중에서 그 림 5-11 과 같은 r i n g형만을 취하여 계산하는 것이고, 가장 큰 공헌을 하는 gr a p h 만을 취해보는 것이다. n = 2 에 대한 r i n g형 g ra p h 는 그림 5-12 에 있는 두 가지가 있는데, 이들은 위상학적으로 같고, 따라서 그것들에서 나온 값도 같 다. 그리하여 (5 .4 8) 을맡 2 배하 :여 곱 (q) nf ( q) (5.4 9 ) 롤얻는다.
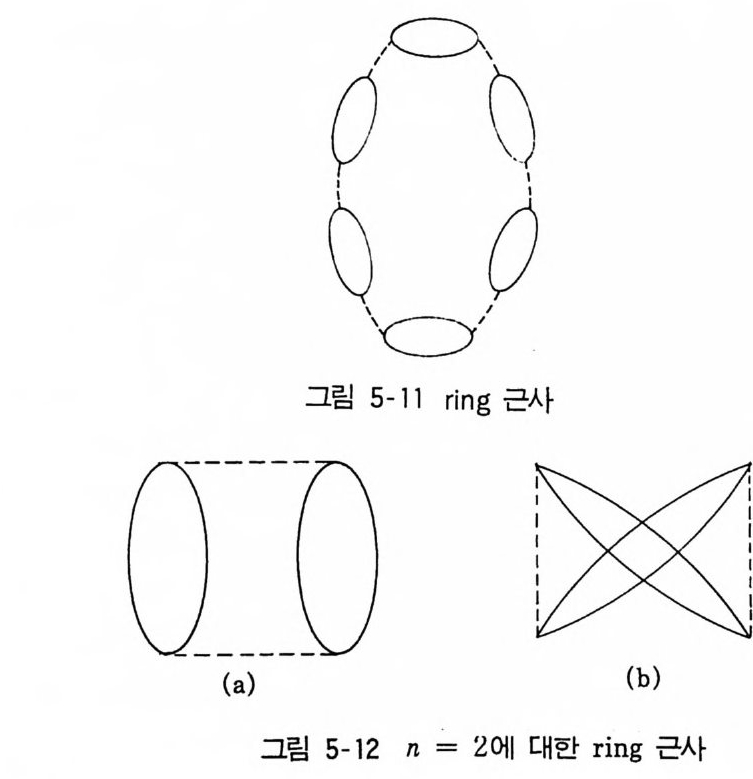'Y〈广I 二二\\\ o/
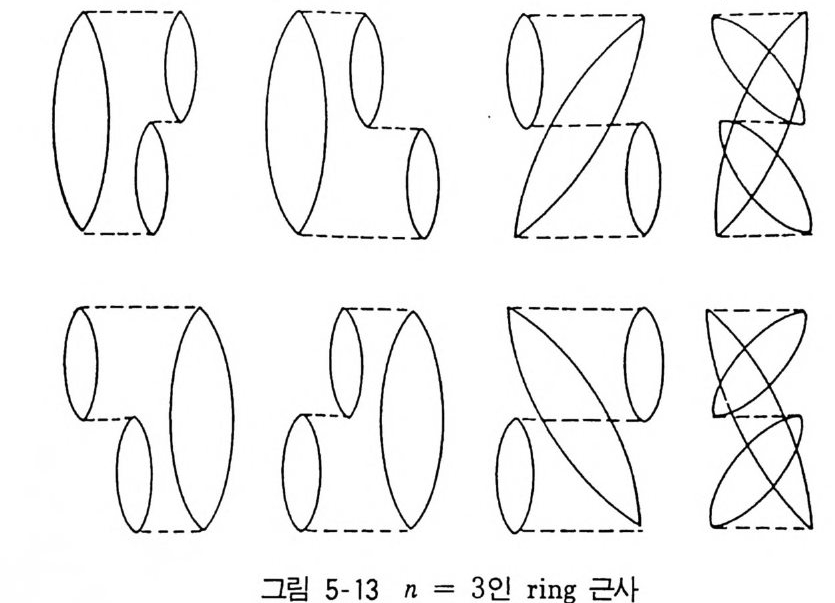그림 5-13 n = 3 인 rin g 근사
1 • …………………… • 1'
n = 3 에 대한 rin g gr a p h 는 그립 5-13 에 있는 8 개인데, 그들은 위상 학적으로모두갇다. 일반적인 n 에 대한 rin g g ra p h 의 수를 그림 5 - 14 를 써서 알 수 있다. 점 l 에서 l’ 에는 선을 그을 수 없고, 나머지 2(n - 1) 개의 점은 선울 그 을 수 있다. 다음 1 에서 점 i에 선이 그어졌다면 점 i'부터는 1, 1', i 와 i를 제의하는 2(n - 2) 개의 점에만 선을 그을 수 있다. 이와 같은 방법을 되풀이하면, 결국 2(n -1 ) 2(n -2 ) ·… .. 2(n -n + 1) = 2211- 1 (n - 1) ! (5.4 9 a)
개의 다른 도형이 가능하지만 이들이 모두 위상학적으로는 같다. 따라서 n 차 항에 있는 rin g 근사는 (5 .4 4) 에서 n , =n 이며 계수는 ( 一p nl)! (n2+1p( v -)l )nn 2n_ I (n-1) ! = 2n(/3 -( P1V) ) (5.49b) 이고, 여기에 하나의 g ra p h 에 대한 적분치가 곱해전다. rin g gra p h 는 {n I(1)} 를 주는데 HI(7) 의 정의에 있는 인자 (/J V) - 1 이 (5 .4 9b) 의 ({JV )-• 울 흡수하고, 결국 rin g 근사에서 얻은 값이 틀: W (q) {n (컨 }n (5.4 9 c) 이 된다. 中서 ®_ ®o=@Y 를 rin g 근사로 계산하여 {@-® 바 = {@}R =西1 E[- 了V2n f + 了v3n ―f v44n : +……] = 삶 홉 [ ln {l + v(q ) II 衍} -v (q ) II,(q ) ] (5.50) 를 얻는다. 따라서 I11(7) 를 계산할 수 있으면 {@}@)。 }R 의 값을 알 수 있 게 된다. I11(-q-> )에 대한 정의식 (5 .4 7) 에서 直) = -옮곱 (i(JJ m +1l一 ek+q - i(JJ~) • [ eHq - e. +1 i (1)m -i(1)m+ I ] (5.51) 로고쳐 써보면 (5 .4 2c) 에 정의된 o 의 값에 의하여 Wm-Wm+l = >(- 2l) 이고, m 에는 관계없다. 복소수 z 에 대한 임의의 함수 a(z) 에 대하여
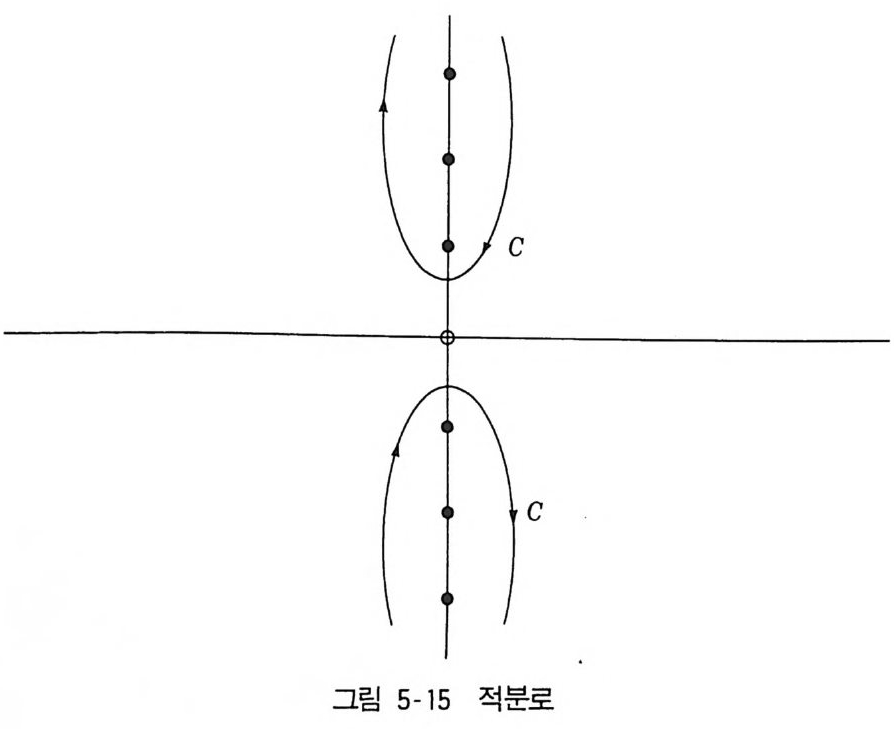C .
}혼 a (i wm) = 겁 广炳 dz (5.52) 가 적분로 C 를 그립 5-15 처럼 취하면 성립한다 .14)
14) (eP •+l) -lo ] z=(2m+l)ni/ P =iw ,.(m =O, 士 1, 士와·…)에서 1 차의 국을 가 지며 그 유수가 규 rlo] 다.
따라서 (5.51) 을 n,(1) = -요V 7E (eHq - e. 1- 2l ni I {3 ) 갑 ] C( z -le 난q -*) ep2 d: 1 (5.53) 로 쓸 수 있는데, 적분로 C 는 그림 5-16 처럼 고칠 수 있다. 그러면 z 의 실 수수因 z=eH q와 z=e. 에 있는 유수만 계산하면 된다. 그리하여
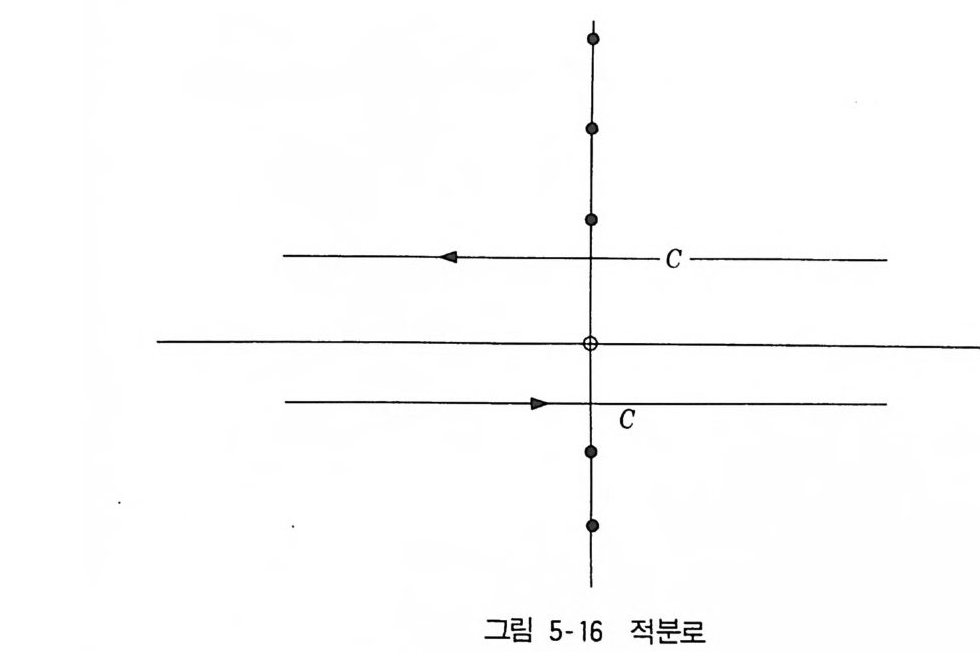c
頭) = -윤픈 ek+q -fk;: 二 ft ni I /3 (5.54) 이고, 여기서 f. = l/(e{J,, + 1) (5.54a) 는 전자의 Ferm i 분포함수가 된다. III(7) 가 실함수가 된다는 것을 알 수 있으므로 15) 頭) = 上V ;E (e(.f+k+qq - e-. )2h) +(e k( Z-l n ek/+[3q )) 2 (5.54b) 로쓸수도있다. 15) -J-+i +-i-i+ = -k구 로 바꾸건 n,(-q-+ ) = -v2 ~k. ek.+q - efk&.+ q + - f2kl• 7t i/p 가 되며 {Il,(-q-+ )}*=Il,(-q구 )이다•
5-5 온도 Green 함수 자유입자에 대하여 (5 .3 8) 로 정의된 함수 g, [u, u' ］는 그 성질이 (5. 4 1) ~(5 .4 2e) 에서 고찰되었고, 그것이 계산하는 데에 대단히 편리하다는 것 을 알수있었다• 상호작용을 하는 입자계에 대하여 이 함수를 더 확장하고 온도 Green 함수 1 6) 를 정의한다. Hami lt o n ia n H = H0 + H 1 에 대하여 ~^ =H^ -µN ^ (5.55) 로 하고, 구I\ 에 대한 Heis e nberg 표시를 A,(u) = e'°^ a, e- ^~ (5.55a) A;(u) = e'^° a; e 국^ (5.ffiij 로하고, 비슷한 관계인 a(u) = eu /\2 a e- u/ \ ‘ , ar+(u) = eu\^’ a r+ e 국 ^l 와구별하여 쓰고있다.
16) T. Mats u bara. Prog. Theor. Phy s. 14 (1955), 351
온도 Green 함수는 Wi ck 기호 T 를 써서 G, [u, u' ] = —
(1) Green 함수 G, [u, u ' ] 의 성질 규^ 의 고유상태와 고유치를 ~^ I ex' > = E' I ex' > (5.58) 로 표시하고, u'>u 일 때 G, [u, u' ］를 그 고유상태와 고유치로 나타낸다. 그러면 Gr [ u, u' ] = T [ ep( 0?^) e“ ar+ e~ ^’ eu^’ ar e-l^’ ] = E. e 뼈 - E ' ) e- (£'- £ 1(u-u.) < a 'I a 『+ | a? @ | ar | a' > a,a (5.59) 이고, u>u ' 일 때는 G, [ u, u' ] = ~-eP <®-E' ) e -(E' -E 1(u- u ) a,a (5.59a) 이다. 따라서 다음 성질을 곧 알 수 있다. ® Gr 은 u-u' 만의 함수이다. 따라서 G, [ u, u ' ] = G, [ u - u ' ] 로쓸수 있다. @ G, [ u + p ] = -G, [ u ] rn [증명 ] -p < u < 0 이면 O < u +/3 < /3이고 (5.59a) 의 관계에서 G,[u+{ J] __ __ fcE., e강P (( @®-EE' ) ) ee (-E (E· -E' - 1E ( 1uu+ _ _ E e0(O-E1 e(E· -E 1 —-G , '[ u ] 17) 위에서 Ferm i 통계에 대하여 논하고 있지만 Bose 통계이면 G,[u + /J] =G,[u] 이다. 이다. 위에서 제3열은 합의 기호 a’ 와 a’를 서로 교환한 것이다. 성질 ®에 의하여 G, [ u + 2p ] = -G, [ u + p ] = G, [ u ] 가 성립하여 —p :,;; u :,;; p에서 Gr[u]는 주기함수가 된다. 따라서 FourieGr ,급 [ u수 의] = 전t개 가꾸 가G,능(i(하J)다，).e 기죽아 (5.60) 이고 w, = (2l + l)n/p (5.6Qa)IB) 이며 祐iw) = J: G, [ u ] e’따du (5.60b) 가된다.
18) Bose 통계에서는 (J)1 = 갑터다.
(i ) G ,(z) 에 대한 Lehmann 전개 Green 향수의 Fourier 계수 G,(iw1)를 계산하는 식 (5.60b)에 G, [u ] 로서 (5.59a)를 대입하여 a,( iw,) = -「aE.a ep(@E)
G, (z ) = f . 丘广E .)(~ (ix' I a, I ix')
19) 占 I 二 p,((l))d( l) == .L.E.... e e, <’ (® ® - -E1E 1〈 〈cx I 'X 'I ia a 『+ 『+ ||aa? 字 〈(X ，， l |aar |『+ a | 'a 〉 ' 〉 (e ~( E '- £1+1) + e 야 ) -E1@l a? I a?<( X, ,|a , l cx')] = 1}-e 琦-, ) ( a,a ? + a;a,) = 1
spe c tr a l int e n sit y p ,(w) 를 상호작용이 없는 자유입자의 계에서 보기 위하여 I ex' > = I n1, n2, ……, n,, … … > | a' > - I n1, n2, … …, n,-l, …… > (5.65)
로하고 E' = [ n, e,, E' —E ,, = er (5.65a) 로쓰면 pr( o) = 2TCE e pi@드 h, ( i ' · + 1) b((J ) - e,) = 2TC t(e µ`'+ 1) b(Q - er) = 2TC b(o - e,) (5.6 5 b) 이=다 .e1 1•·. n+1 , 의 1 - 에평서균 치위가의 F식e이rm 나i-온D 다i r.a c 따분라포서함 수 L 이며,f, = ~/<•.- µ) + 1 G, (z ) = 古 f:,_~ dw=~ (5.65c) 이다. 자유입자에 대하여 (5 .4 2b) 와 (5 .4 2c) 에서 ~g ,（也) = u. u/1_ e, (5.65d) 을 알고 있으므로 ~g ,(z) = z-1e , (5.65e) 이고 (5.65c) 의 Gr(z) 와 같다. ( ii ) se lf -ener gy의 정의 Ar(u) 에 대한 정의 (5.55a) 에서 8A8Au u) = e~^ （구^ ar -a r 구^) e_u ?^ = [ ~ (u), A,(u) ]20> (5.66) 20) [A, B] = AB -BA
울 알수 있다. 여기서 ~u) = e 따,iI\ e-JI \' = -;jI;\ 01 지만 ~I\( u) = L e 『 Ar+(u) Ar(u) r + 步 I:(r s I u I r' s') A;(u) A: ( u) A, (u) A,(u) (5.67) 를 (5.66) 에 대입하고, 교환관계식을 이용하면 aA~,(u) = -e,A,(u) - fr:
로 놓고, self ener gy에 관계된 I:, [ u, u ］를 정의한다. 이 묘 (u, u' ]와 합을 나타내는 E 를 혼동하지 않도록 주의한다. 그러면 (5.69) 가 ac=, [~ -u,J u:' L ] [+u ,ub(u ]G—,u ['u ) ,+u ' e],dGu, [ u ,u' ] (5.71) 로 된다.G , 이 [ u,식 u의' ] Fo=u ri+e r ~변 환G을,(i w보 ,) 기 e -위i w , <하 •-여•·,) G, [u, u' ]가 (5.60()5 에.7서1a ) 로 전개되므로, L, [u, u' ]도 드『 [ u, u ' ] = } 홉 E r( t @) e -Io,( u - u . I (5.71b) 로 전개된다고 한다. 그러면 r: L r[u,uII]Gr[uII'uI ]duII = 信 혼(i o,) 5( 血)) e-i w , (u - u ' ) (5.71c) 이고, (5.71) 에서 } 무 [ i(J)/- e, - f,(i(J)/) ] 5『 (i(J)/) e-iw , (u -u' ) = fJ( u - u' ) (5.72) 이다.따라서 Gr(i(J )1) - i(l) / -e,-1 ~I : ,(幽) (5.73) 이 된다. z 공간에 해석접촉하여 G,(z) = z-er-1E r(z) (5.74)
을처럼 얻 는(5다 . 7.4 ) 자에유서입 G~자, (에z) 의대 하p여o l e, (5죽.6 5c) 는 z = e , 이 z 공간의 p ole 이 된 것 z - [,(z) - e, = 0 (5.74a) 의해 z=E,-µ 에서 E,ol q uas i-p ar ti cle 의 에너지가 될 것이다. ( iii) gra nd po te n ti al @봐 Green 함수의 관계 U I > U 이면, (5.70) 의 좌변에서 A ; (u' ) 를 가장 앞으 로 가져가 는 데 (-1) 인자가 나오므로 } ,E. < r s I v I r' s' > 三 [ p。 Lr[U,U 11 ]G r [U11,U 1 ]du11 나 무 (fr 區) 효(터 ) e-, u.(u -u ') (5.75) 를 얻는다. 두번째에서 세번째로 넘어가는 관계는 (5.71c) 에서 주어지고 있 다. H ami l t oni an을 pa ramete r }에 의하여 ~I\ ,l) = 익I\ + AHI \ I (5.76) 로하면 e - ,® 이 = T e-m i. ) (5.76a) 이고, i에 의한 미분으로 -{3 e 규 ®Ul d?l) = 뀝 'Ir(e -tn H, ) 에서 id―®互0―) = 〈潟^〉 (5.76b)
이다. 따라서 @ '== [® I d)(lA t = 1<)A H-,> ® ().=O) (5.76c) 으로 상호작용의 효과가 gra nd po te n ti al 에 나타나는 것을 계산할 수 있 다. 여기서 (5.67) 을 보면 #1 (u ) = 赤 두
e-~ 三 e-, ~. U({J ) (5.7 9 ) 로 U( {J)를 정하면 (5.1 7 ) ~ (5.23) 에 의하여 U({J ) = 1 + t 년 .[ 。' p [ H1(Ul… … H,(u ) ] du1… … du n (5.79a) 이고 i^il (u) = e^-:1 !, H1 e-u ^~ (5.79b) 이다. 이U (결p과) =를 PP e기xp 호 [에 - J의 하:H 여1 (u)du ] (5.79c) 로 기술하는데, 여기서 D y son 의 P 기호는 P [ H1(u1) H1(u) ] = { :H11~(~u12)) H旦1 ,((uu 2 )) ;; uu2l >> uu12 를의미하였다. P 기호에 대비하여 W i ck 의 T 기호는 (5.38) 에 정의되고 있는데, a, a+ 등의 연산자를 시간의 순서로 정리하는 점에서 P 기호와 같은 구실을 하지 만, 이들 연산자를 기수번 치환하면 (-), 짝수번 치환하면 (+）를 붙이도 록 하는 점에서는 다르다. HI 가 a, a + 의 우수개의 곱으로 되는 항으로 구 성되면, 시간 순서에 따른 H 려 교환에는 a, a + 의 짝수번 치환이 되므로, H/o!l 대한 P 기호와 T 기호는 같은 결과를 준다. 따라서 (5.79c) 대신에 U(/3 ) = Texp [ J: 瓦 (u) du ] (5.79d) 로쓸수도있다. gran d pa rti tion func ti on 3 에 (5.79) 의 관계를 쓰고, 3 = 'Ir e -,r., = 3o .11:.L.31oJ .J.f}) (5.80) = 3 。〈 U( /3)〉。 (5.80a)
= JbT exp [ —.r : H l(u)du ] 〉。 (5.80b) 로 할 수 있다. 여기서 Jo= 'Ir e -p , (5.80c) 이고, < 〉 o 는 상호작용이 없는 이상기체계 Ho 에 대하여 취한 평균치를 의 미한다. 상호작용표시는 (5.79) 와 그 역연산자에 대한 군 = e - 라 u({J) , e; = u -1( {J ) e..; , (5.81) 에서, (5.55a) 를 고쳐서 A,(u) = e' a, e- ' = u -1 (u) e 따 a, e 국 ' U(u) = u -1 (u) a,(u) U(u) (5.82) 를 얻는 것이다. 여기서 ar(u) 는 5-2 절에서 많이 이용한 ar( u ) = eu :I l\!, a r e- u ,I \, (5.82a) 이다. 마찬가지 방법으로- A; (u) = u -1 (u) a 『+ (u) U(u) (5.82b) 도얻는다. 여기서 U(u, u' ) 三 U(u) u -1 (u' ) (5.83) 로하면U (u, u' ) = Texp [ -f u面 (u)du ] (5.83a) 이 된다 • 2 1) 21) 卑 = -H1(u)U(u, u') 이고 U(u', u') = U(u')U -1( u') = 1 이다. 뻔·서 (5.20) 대신에 U(u, u') = 1 -f : . H1(u1)U(u 1, u' 따이며, 여기서 (5.83a) 가나온다.
이와 같이 준비를 마치고, Green 함수를 상호작용 표 시로 고쳐 본 다. 우선 u>u ' 로 하면 G, [u, u' ] = _< T A, (u )A 『+ (u ' )> = _< A , (u )A ; ( u' )> = 上3 'Ir e- ~A ,(u) A 『+ (u ' ) = ~ 'Ir [ e- ,; U(/3 ) u- 1( U)a,( u ) J o (U( /3）〉 。 U(u) U -1( u ' ) a; ( u' )U(u' ) ] (5.84) 인데, 위에서 (5.80a) 에 의하여 3 가 고쳐서 쓰여지고 있다. 위의 식의 분자 에 있는 인자는 'Ir [ e- ~ U({J, u) a,(u) U(u, u') a ; (u' ) U(u' , 0) ] = 'Ir e d-u~1 }T • [a e ;x( pu {' -) Jex :ppH ^ ,{( u-1J_) d:·u H1 /}a( u, (1u))d ue 』xp { - J :. H 1(.u 1) (5.8 4 a) 가 된다. 죽 처음 각 exp 앞에 있었던 T 기호를 전체에 대한 T 기호로 대 체한 것이다 . T 기호 아래에 있는 지수함수가 서로 가환하고, 또 a,(u) 와 a-; (u) 와도 가환한다. 그러므로 교환 가능한 두 연산자 A 와 B 에서 eA • 한 = eA +B 이 성립하므로 (5.84a) 를 'Ir =e_ p3; _^o· T < T[ e[x epx p{ -qJ: H:H 1 1(u(u11)d)duu11}} aa,,((uu)) aa; 『+( (uu' ' )) 〉 。] (5.84b) 로쓸수 있다. 결국 (5.84) 가
G, [u, u' ] = -T [
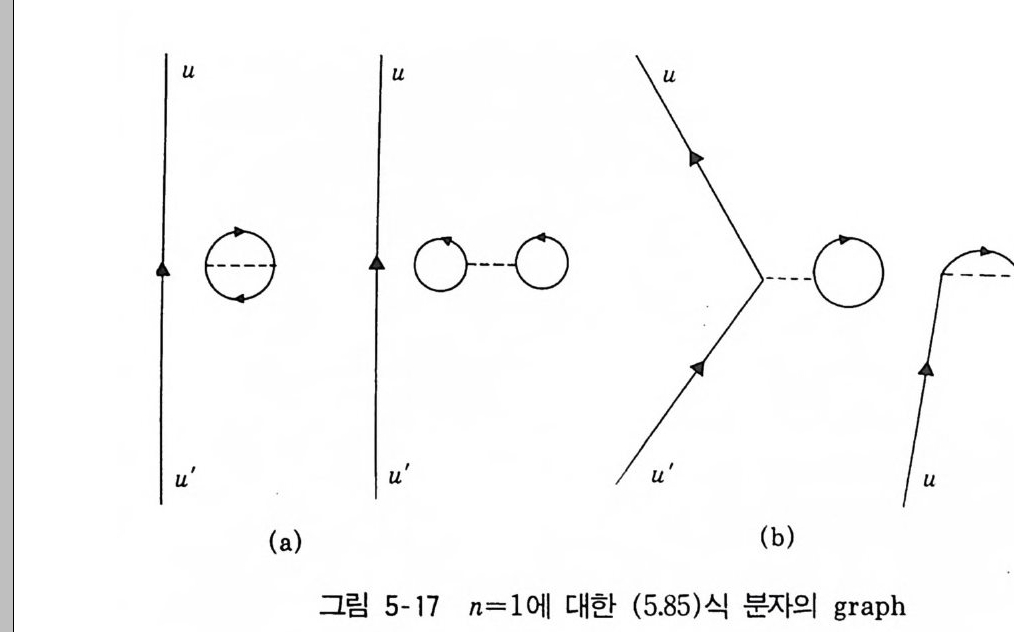u u u, u’
항] a,(u)a;{u') 〉 0 을 생각하면 역시(의선을 포함하는 연결된 도형의 기여) x( 외선이 없는 도형의 기여)로 되어, 결국 (5.86b) _
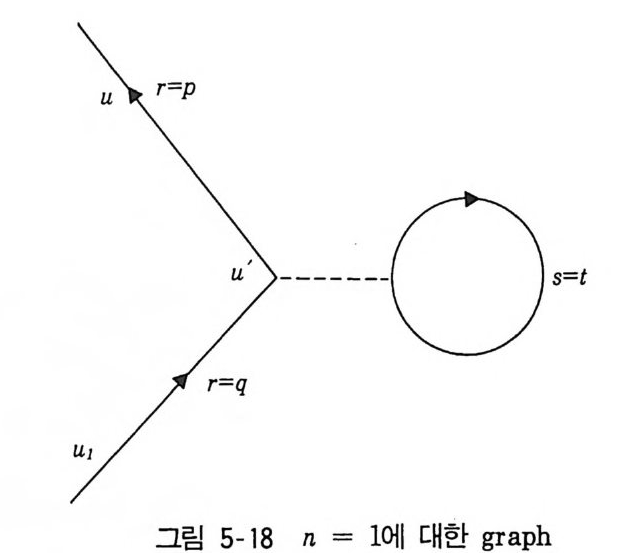u ~ r=p
이다. gr [ u, u' fl Fourie r 전개 (5 .4 2d) 와 (5.4 2 e) gr [ u, u' ] = _pl EI eL.W -1l W, -(u - ue' )r gr [ u, u + 0] = —P1 7.E.--, i. w ee 1-iw-, O e , . 롤 대입—하2V고p 2U l, EJ .에,,.
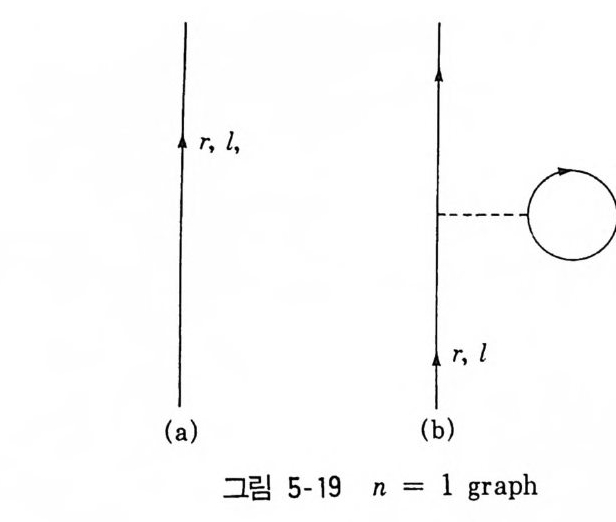r, l,
G,[u, u'] = } 밑 Gr( i wI) e 키 u ·, (u - u ' ) (5.89) 로 할 때, 그림 5-H 싸서 G,( i cv1) 에 기여하는 항이 ~G ,(iw 1 ) = (iwI 1_ er) + [土 E
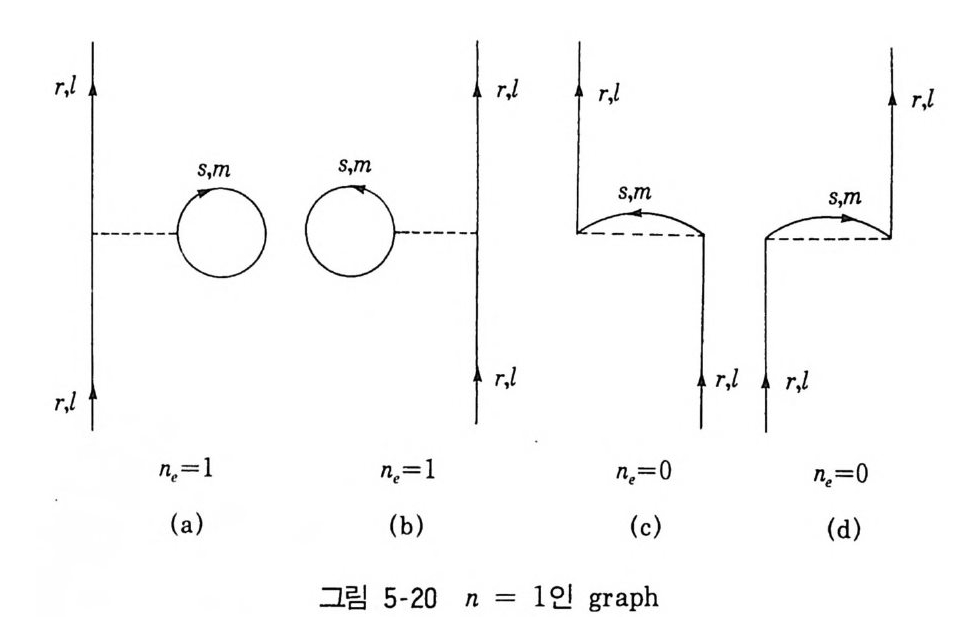r,I -6 6----r,l r,l r,l
元(i w) = (iw1 - e,)- 1 (5.90a) 을 대응시킨다. 단, 같은 시간을 연결하는 전자선에는 (iw, - e)-1 e i w,. 를 대웅시킨다. (iv) 에너지 보존법칙 W1, + W1, = W1 , + w,, (ll + l2 = [3 + ZJ (5.90b) 를고려한다. ( V ) 의선의 (r, l) 은 일정한 값이지만 그 밖의 전자선 (r', l' ）에 대하여 는 가능한 모든 값에 대하여 합을 취한다. 위의 계산규칙의 예로서 n = 1 차 항에 대하여 알아본다. 가능한 Fey n - man 도형은 그림 5-2 떠 네 가지가 된다. 그림 5-20 의 (a) 와 (b) 는 n, = 1 이며, 특히 (a) 는 그림 5 - 19(b - ）와 같 다.따라서
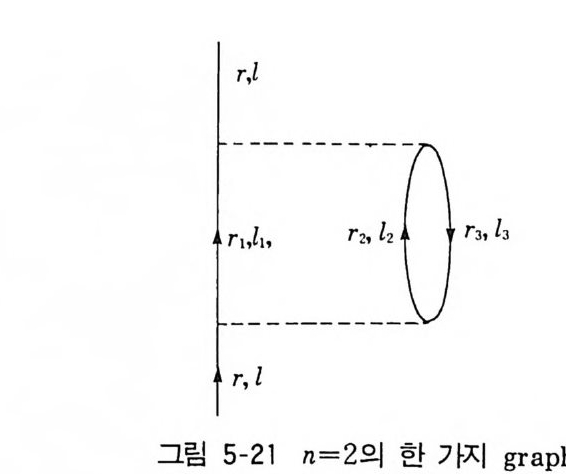r,l
(a) 에서 노2OV (i(w ―I 1_ ) 나e) 2 E&m - L W m1— ;:€ iw. · O 이다. 이에 대하여 (c) 와 (d) 는 nI = 0 이므로 (c) 에서 멜仁円露〈 rslvlsr 〉 ~eiw .·O (d) 에서 노2p v (i(w_ t l_)° 1er)2 E.. m < s rl v l rs> i wm L_ _e, eiw .• O 이고, 전—체적으로.는 —2p1v < r s (li wv Il1_ s err>) 2— E·,m< s[ r< rl s v l l vr ls >r ]s> i w+ m 1<- s re , l ev 畑 •l• 。s r> 이다. 이 값은
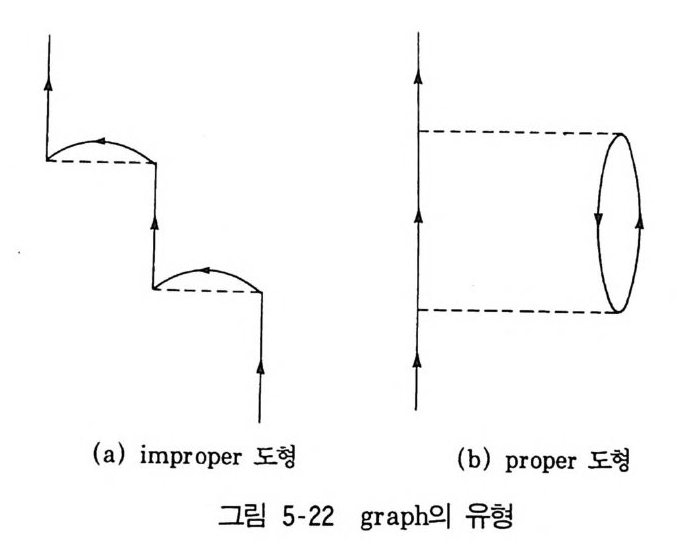(a) im p ro p er 도형 (b) pro pe r 도형
n = 2 차 항에 나타나는 Fey n man 도형 그림 5-21 을 보면 n1 = 1 이고 그기여가 댑 r , J , 노 ,
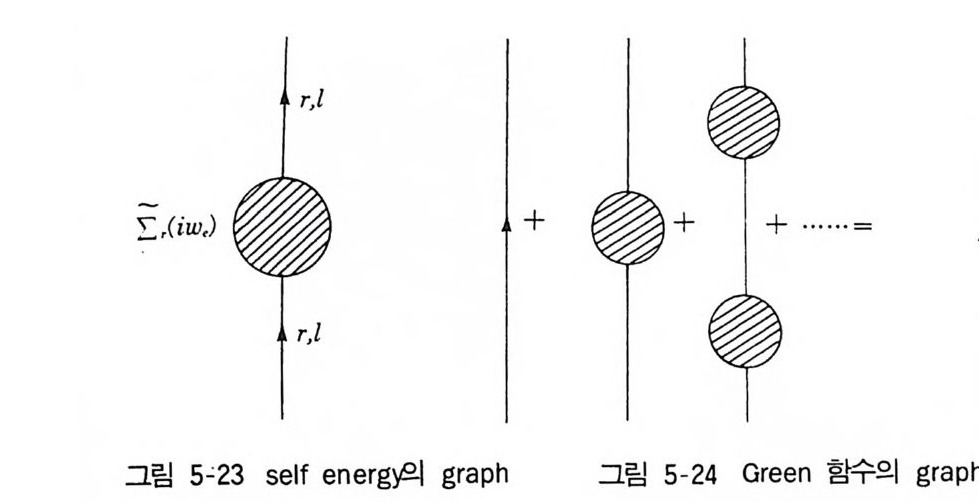드-_, (i w,) +
(iwI _1 er) 2 ~E (iw I ) (5.91) 로된다. se lf-e ner gy가 전자선의 각 부분에 존재할 수 있으므로 그림 5-24 의 합 이 Green 함수가 된다고 할 수 있다. 죽 G,(iw 1 ) = g,(iwJ +g;( i w, ) ~ 드( i w,) + …… = gA iw I ) [1 -g A iw 1I ) 巴 r( 터] = g?(iwI ) -1 :r(iw I) = iwI — er _1 fr( i w I) (5.92) 이 된다. (5.92) 의 마지막 식은 se lf-e ner gy의 정의식에서 나온 (5.73) 과 같다. 이것은 pro pe r g ra p h 의 모든 기여가 se lf-e ner gy에 해당된다고 보 는 입장의 타당성을 의미한 것이다. 상호작용을 포함한 입자의 행위를 q uas i-p ar ti cle 의 행위라고 하는데 그 림 5-24 에서 II 는 이 q uas i-p ar ti cle 의 Green 함수이다. 그 에너지 Er은 z _ er _ Er(z) = O 와 z = Er _ µ (5.93) 에서 구할수있다.
5-7 전자기체에 대한 예 ( II ) 계산의 예로 중성인 전자기체에 대하여 그 sel f-e ner gy를 가장 낮은 차수 의 근사에서 구해본다. 중성인 전자기체는 (+）전하가 배경에 균일한 분포를 하고 그 안에서 전 자가 가V체 '2를u ( - r~구 )- 성 = 하 고— 4•있r c다 e2. . [ b 그 (-7리' ) 하-여 1전 / V자 ] 사이의 유효한 상호작용 p(o 5 t.9e 4 n )- tial 이 Coulomb 형 인 u(-;: r = 으r 과 다르고 를 만족시켜야 한다• 따라서 u(_r > ) = V1 ~ v(_q . ) e 며:+ . ,-- (5.94a) 로 Foubr(ie7 r ) 전=개 t하 여~보 면e ’; , 一 (5.94b) 이기 때v문(q에 ) = { ?' 一q 수 0 4 군 一 0, q = 0 (5.95)
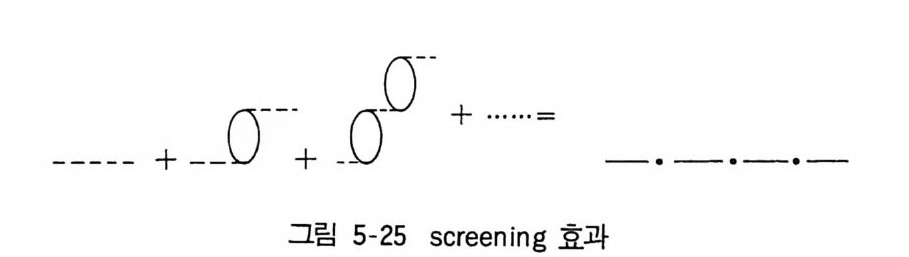-----+ -_0-\O-0-- + … …=
가 된다. 전자기체가 중성이라는 조건으로 (5.95) 에서 q = 0 에 대하여 v (q) = 0 가 요구된 것이다• 상호작용이 screen ing 효과를 받게 되고, 그립 5-25 처럼 된다. 이 합을 그림에 -· -· -으로 그리고 Ul( Q)로 표시하면 (5 .4 7) 을 볼 때
u1(q ) = v(q ) —vz ( q ) IT1( q ) + v3( q ) n 2 (q ) …… = v(q ) I (l + v(q ) ll,(q ) ) (5.96) 로쓰여진다. 자(q) = 1 + v(q ) ll1(q ) (5.97)
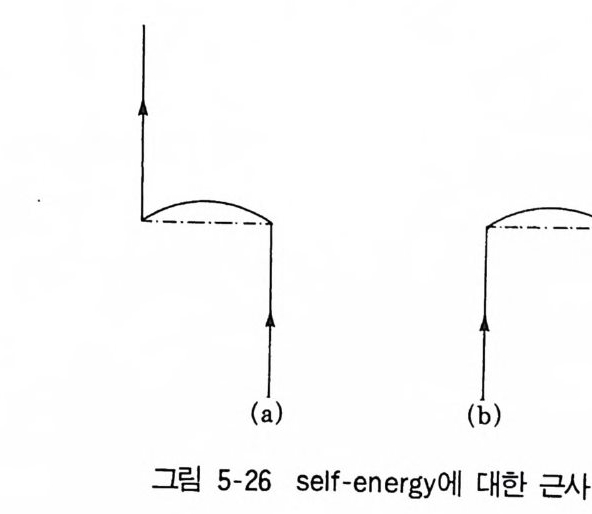(a} (b)
로 하고, l 을 생략하여 (5.96) 을 u(-q )• = v(.-q- -+ )• /X• (.-q- -+ ) (5.97a) 로 써보면 X(q )가 유전율의 의미를 갖는 것을 알 수 있다. gr a전 p자 h 는의 그se립 lf -e5 n-e2r0 g 에y 를나 오근사는적 으4 개로.인 데구 하그려 중고 (할a) 와때, (가b) 장는 차(5수.95가) 의낮 7은 =0 에 해당되어 값이 0 이 된다. 그리하여 (c) 와 (d) 만을 고려하면 된다. 상호작용을 …… 대신에 —._._ 로 바꾸면 그림 5-26 처럼 된다. 이 gr a p h 에 대한 se lf -ener gy는 ~E k(iw l) = _—plv EII,q un一(q ) e(Lx.Wp l(-L nW _l -n e• 古 0 3)
= —_{3lV _ 드 고Xn(요i ) e(xiwp I( -in w _I -n e •F 0J ) (5.98) 이다 . 여기서 짜q) ;::' X 。 (q) (5.98a) 로 놓고 (5.98) 의 합 밖으로 내면, 그 나머지 합이 (5 .4 2e) 에 의하여 도/3 ;;-' e(xi pw1 (- n 도-e ~다 = gr- -; ( -0) = f~-; (5.98b) 를 얻는데 f; :.; 는 전자에 대한 분포함수를 의미한다. 또 상수 q T 를 도입하여 교Xo( q =) q2닳 + q ~ (5.99) 로쓰면 q~ = 4ne2mk~ / nh2 (5.99a) 가 되는료 (것i을 wI )뒤 =에 一설 명(:하r고: \있f 으d므: q로2f : 1 q; (5.1 0 0) 로고쳐쓸수있다. x 討)의 계산 : nI(7) 에 대한 한 가지 표시가 (5.54) 에 福) = ―上V 고 e 古;_店 e_r_f 2 rl ri/f 3 로 주어지고 있는데, l=O 이면 아주 간단하게 되어 福) = 옮::二;-+ = _¾V rI' :e_ 나q A_ _ek (5.101) 가 된다. 여기서 두번째 식을 얻는 데는 fk + q 를 포함한 항에 대하여 Y:+ 1
--Y!로 하고 다시 7 一 T 로 하면 된다. 또 F1er m방 i향 온을도 z보 축다으 충로분 잡히은 낮 극은좌 표온도를에 취서하 여fk 는 계단함수로 생각할 수 있다. rr 。(q) = 틀 `f :· k2d k 「- l 2k qtd 나 = 릅니 :' kln|~l dk = ~ [州 k ~ —( 방 ) 2 } 1n l~I + ~:- ] (5.1 0 2) 로계산된다. 여기서 x = q/2 kF (5.1 0 2a) 로하면 FII( 。x(q)) == 1( m+k ¥F/ 2rr2h 21 ) n F|( x}) ~ I ((5 5..11 00 22bc)) 으로 쓰인다. 이 F(x) 는 전자기체에 관한 문제에 자주 나타나고 Kohn 의 함수로알려지고있다. 특굴1 X ~ l, 죽 q ~ 2kF (5.1 0 2d) 이면 F(x) = F(O) = 2 (5.1 0 2e) 로근사되어 I1 。(q) = (mk/n2h2) (5.103) 이고, 따라서
X(-q )· = l +. v(-q )· n 。 (·-q ) = 1 + q:J/ q2 (5.1 0 3a) q: J = 4e2m k;/ h2 (5.1 0 3b) 가니온다. u(q ) = 갑4+rreq2 i (5.1 0 4) 의 역 ¢Fo(7u)r ie r =변 환—r에 e서 얻어전 p o t en ti al 은 (5.104a) e2- -q ~ 이다• 이 효과는 'lho mas-F e rm i 의 screeni ng 효과라고 한다• 고체 안에서 전자는 서로 @ulornb 상호작용을 하지만, 격자진동과도 상 호작용을 한다 . 격자의 변형으로 주위의 장이 변하여 그 영향이 전자에 미 치게 된 것이다. 격자진동의 양자가 p honon 이므로 이와 같은 새로운 상호 작용을 전자 - p honon 상호작용이라고 부른다• p honon 은[ bE-;,i nbs 깁te i n=- B o bs(e_q 통, 계q - 에) 따르고, 그 파수 \ect.or q에 대한(5 .소1 0멸 5,) 생성연산자 b;, b 군 는 [b-l , bf] = [b 건 b-;-] = 0 의 교환관계를 만족시킨다. 자유 ph ono~ Ha milt o n ian H^ p 는, ph onon 한 개의 energy h s q로 H^p = 꾸 hs q(硏 b;-+ 방) (5.106) 처럼 쓰인다. 전자나 p honon 의 상호작용은 그 Ha miltonian H^t p가 ^H =s 4V Eq A四 여학터b-;+ b~김 (5.1 0 7)
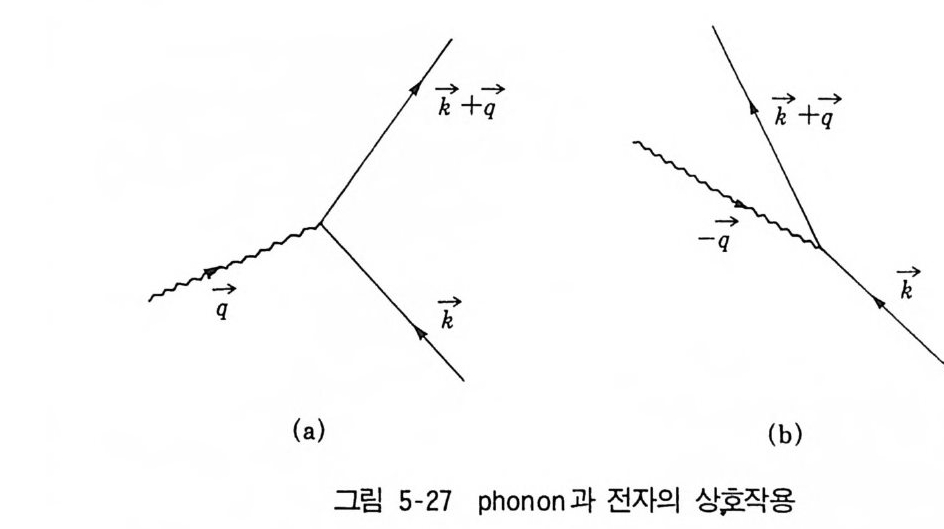-k3 +q一
로 쓰이고 상호작용을 특칭지어준 A q는 A-1 = A; (5.1 0 7a) 를 만족시킨다. 이 상호작용을 Fey ru nan g ra p h 로 표시할 때 p hono 퍼출 WWW 으로 표시하여 그림 5-27 과 갇게 한다. 전자-p honon 계 전체의 H ami l t o ni an 을 H^ =H^t +H^p +H^t p (5.1 0 8) 로 생각한다. He 는 (5 .1 5) 에 나온 자유전자의 Ha mi l t on i an 이고, Hp 는 (5. 106), Ht p는 (5.107) 인데, 전자 사이의 Coulomb 상호작용은 편의상 여기 서는무시되고있다. He + HP가 비섭동항 Ho 이고, He p는 섭동 HI 로 하면, 전자기체에 대한 관계가 비슷한 형으로 성립한다. 다만 · 전자 사이의 상호작용 대신에 p honon 의 Green 함수가 들어온다 .• 예로서 전자의 Green 함수에 대한 2 차의 섭동항을 보기로 하자(1차항은 0 이 된다). fP;+ = bt+ b 녹 (5.1 0 9) 로 하면 (5.87b) 의 G,[u, u1 의 疾}항은 HI = H,p 로 하고
정 ,i: 〈 詞) H1(2) a,(u) a-:-(u') > o L du1 du2 = 당1 .r : du1 du2 LA q A-: 〈 T忍 1) ap (l) ¢(1) a 꿉 .{2) a,(2) • H,_2 ) 야 (u) 어 (u') 〉 O l 〉 (5.1 1 0) 이다. 이 식 중에서 u>u1>u 2 >u ’ 의 경우는 전자기체에 대한 것과 비슷한 계산에서fv -f:dg u p1 [duu1,2 u Eq.2p ] •I Ag-.k 1[ u2 z〈, u鶴 ' A] b 나 (k, - 心P)+:qg ) •[u, 미 (S.lll) 인데 그립 5-28(a) 에 해당된다. 그림 5.28(b) 에 대한 계산도 똑같이 나온 다. 자유 p honon 에 대한 Green 함수를 전자에 대한 방법과 비슷하게 구하 면
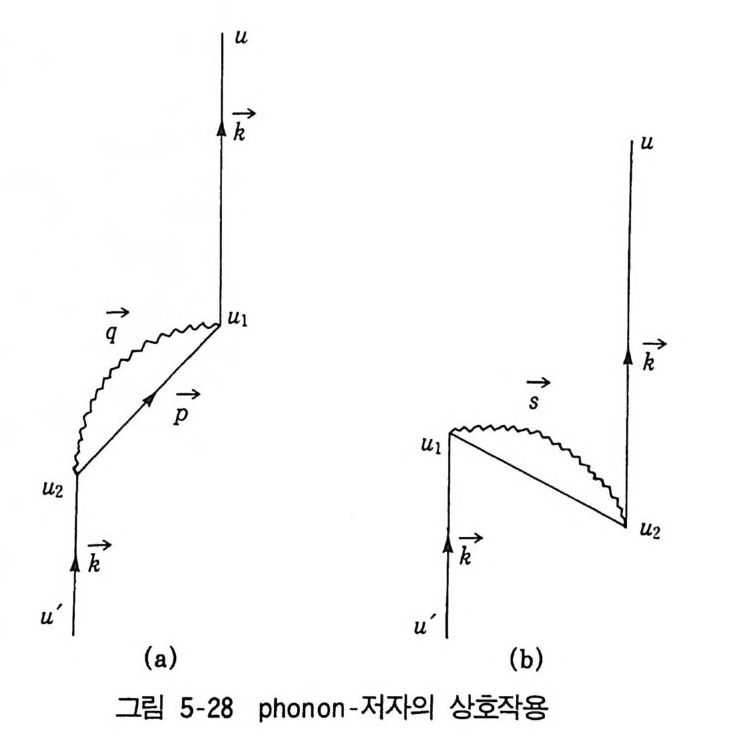u
D;(u, u1 = IA 낸 2
제 3 부 비평형이론
6 Brown 운동과 상관함수 6-1 서론 물 위에 떠 있는 꽃가루의 입자는 아주 불규칙적이고 좌충우돌적인 운동 울 하여, 마치 그 운동이 미세한 생물체에 의한 것처럼 느끼게 한다. 이 현 상은 1827 년 Robert Brown 에 의하여 발견되었으므로 Brown 운동이라고 부르고 있다. 처음에는 Brown 운동을 생명체와 관련시켜서 연구가 진행되 었으나, 곧 물에 떠 있는 어떠한 작은 입자들, 죽 유리, 광석, 이집트의 스 핑크스에서 떼어낸 돌가루에 대하여도 같은 현상이 나타나는 것이 알려져서 생명체와의 관련은 배제되었다 . Brown 운동에 대한 수수께끼는, 그 뒤에도 쉽게 풀리지는 않았는데, 1905 년 E i ns t e i n! ）에 의하여 열의 분자운동론에 입각한 해명이 성공적으로 이루어졌다. 거의 같은 시기에 Smoluchowsk i2)에 의한 비슷한 이론도 있 었다. 1) A. Ein s te i n ; Ann. Phys . (L eip z ig ) 17, 549, 1905. 2) M. von Smoluchowski ; Ann. Phy s. (L eip z ig ) 21, 756, 1906.
E i ns t e i n 이론은 자연현상을 통계적 모형으로 이해하는 방법의 시초를 이 루고 있다고도 할 수 있으며 그것은 다음과 같다. 1 차원인 x 축에 국한하고, 전체가 n 개의 입자이며 이들이 액체 위에 떠 있다고 한다. 각 입자가 x 축상의 위치를 A 만큼 변했다고 한다면, 이 A 의 값은 입자마다 그 크기와 부호가 다르게 될 것이다. 그러므로 A 에 대한 확 률밀도 ¢(A) 가 존재하고, (A, A + dA) 사이의 입자수 dn 이 dn = 짜 (A)dA (6.1 ) 로주어전다. 당연히 「 ¢(!::.)di::. = 1 (6.2) 이 성립하지만, ¢(A) 가 l t::. 1 의 작은 값에 대하여서만, 0 과 다론 값을 가지 며, ¢(A) = ¢( _A) (6.3) 의 대칭관계가 있다고 생각할 수 있다. 여기서, f(x , t)로서 시각 t에서 x 접의 입자밀도를 나타내게 하면, (x, X +dx) 사이에 있는 입자수에 대하여 f(x , t + r)dx = dxf :X ' f(x + 11, t)¢ (11)dl1 (6.4 ) 가 성립한다고 할 수 있다 . 시간 /(tx,가 t 충+분 r히) =작 아f(서x , t) + r ¥ (6.4 a ) 로 할 수 있고, 또 IAI 가 충분히 작아서 f(x + 11, t) = f(x , t) + 11 뺏군 + 슝 A 2 뿡 (6.4 b ) 로 쓰인다면, (6 .4)가 f(x , t) + 覽J.L · -r = f(x , t) 「0 ¢(A)dA + 覽止·
「x A¢(A)dA + 紅 冒 ,「x 안¢(Li )d Li (6.4 c ) 로 된다• 이 식의 우변에 나온 적분에 (6.2) 와 (6.3) 의 관계를 쓰고, 또 D 三 江 %(A)dA (6.5) 를 정의하면 (6 .4 c) 에서 '[ >xA ¢ (A)dA = 0 이고 뵤8t = D _f8xl2 드 (6.6) 를 얻는다. 이 식은 확산방정식안데, 그 한 가지의 해가 f(x, t) = J n e _이z ·/ 4 DI (6.7) 로 되는 것을 직접 대입하여 알 수 있다. 이 해는 t = 0 에서 n 개 입자 모 두가 X = 0 에 있다고 할 때 확산하여 시각 t에서 x 접에 있는 입자밀도를 나타내고있다. (6.7) 의 해에 의하여 시각 t에 대한 x2 의 평균치 7 을 x2 = 니-: x2/( x , t)d x (6.7a) 로구하면 J=墨 (6.7b) 가 된다. 이 관계는 실험에 의한 측정치와 비교해볼 수 있는데 잘 일치되고 있다. E i ns tei n 의 이론이 발표된 뒤에 (6.7b) 의 관계식을 얻을 수 있는 더 간단 한 방법이 있다고 La ng e vi n3) 이 주장하였다. 평형상태에 대한 통계역학에서 1 차원에 한정하면, 에너지 등분칙에 의하여 입자의 운동 에너지의 평균치가 야 mu2) = ½kT (6.8) 3) P. Lang ev in ; Com ptes Rendues 146, 530, 1908.
이다. 위에서 평균치를 나타내기 위하여 < 〉 가 사용되었고, k 는 Boltz mann 싫나이다. 유체 안에 질량 m 인 입자가 운동하면, 작용하는 힘을 두 가지로 나누어 서저 항생력각이할 있수는 데있,다 .유 체®역 유학체에의서 점6성;m에; 겅의}하 로여 속주어도진 4겁 도. 에 여 기대서하 여입 자생를기 구는 로 볼 때 a 는 지름이고, n 는 점성계수이다 . ® 질량 m 인 Brown 입자가 유체의 분자와 계속적으로 충돌하는 데서 나타나는” 요동력 X 가 있다. 즉, Brown 입자와 유체의 분자 사이의 상호작용을 저항력과 요동력으로 나누· 어서 생각할 수 있다는 것이다. 요동력 X 에 대하여 직관적으로알 수 있는 성질은 (+）와 (-）의 값이 모두 같은 확률로 나타날 것이라는 것이고, 따라서
탭 = 걸 +Cex p( - 면) (6.1 1 ) 이고, 여기서 C 는 임의의 적분상수이다. (6.11) 의 우변에 있는 두번째 항 은 Lan g ev i n 이 추정한 바에 의하면 10-8 s ec 후에는 무시될 만큼 작아진다. 따라서 (6 .1 1) 에서 C = 0 로 하고, 다시 t로 적분하여 〈갔〉 _
PJ x1 , t1 ; x2, t2 ; …… : xn, t)d xl… … dx = Pr{ x1 < x(t) < x1 + dx1 : … … ; xn < x(tn ) < xn+dxn} (6.1 3 a) 로 쓸 때 그 의미가 명백하다. n 개의 시각 ti, ……, t n 에 대한 확률밀도 P.(x1, t1 : x2, t2 : … … ; xn, tn) 과 (n-1) 개 시각에 대한 Pn-1(x2, t2 ; …… ; xn, tn) 사이에는 Pn-1(x2, t2 ; …… ; xn, tn) = Jd xlPn(xi, ti ; Xz, t2 ; … … ; xn, tn) (6.13b) 의 관계가 있고, 비슷한 여러 가지 관계식도 생각할 수 있다 . 시각에 대하여 ti > t2 > … … tn-l > tn 으로 하고 조건부 확률밀도 P(x1, t1 I Xz, t2 ; … ; xn, tn) —P nP(x.I-,1 t(l x :2 , xt 22, ;t 2… ; …… …; x n; , xt.n,) t.()6 .1 4 ) 울정의할수있다. 조건부 확률밀도 (6 .1 4) 가 (xl, t I) 과 (x2, t 2 ) 에만 관계하고 t3, ……, t n 에 대한 x3, ……, xn 에는 관계하지 않는 특별한 확률과정이 Markov 과정이 라고 이름 붙여지고 있다. 죽 Markov 과정에서는 ti > t 2 에서 P(x1, t1 I x2' t2 : …… : x., t) = P(x1, t1I x2, t) (6.1 5 ) 이다. P(x1, t1 I x2, t 2) 는 천이확률(t rans iti on p robab i b ity)의 밀도라고 하는데, e 一 0 에서 t1 = t + E 이고 t2 = t이면 lcim P(x1, t + 6 I x2, t) = [)(x1 一 찌 (6.1 5 a) 가되어야한다. Markov 과정에서는 (6 .1 4) 와 (6 .1 5) 에서
P.(x1, t 1 ; x2, t 2 ; … … ; x., t.) = P(x1, t 1 I x2, t 2) … … P(x• .1 , t . .1 I x., t ) P1( x ., t ) (6.1 5 b) 이 성립한다. 그러므로 (6 .1 3b) 와 (6 .1 5b) 에 의하여 P1(x1, t1) = Jdx2 P/ x 1, t1 ; x2, t2) = Jdx2 P(x1, t 1 l x2, t 2) P1( x 2, t ) ( 6.1 6 ) 가 성립한다. 또 P/ x 1, t 1 ; x:i, t) = fdx2 P3( x l' t1 : x2, t 2 : x3, t ) 인데, ( P6 (.1x 5l b' )t 1에 I x의3, 하t )여P 1( x 3, t ) = fdx2 P (xl' t1 I x2, t ) ,. P (x2, t 2 I x3, t ) P1(x3, t1) 로되므로 P(x,, t, l x3, t ) = Jdx2 P(x1, t1 l x2, t ) P(x2, t 2 l x3, t) (6.1 7 ) 도 성립한다. (6 .1 7) 은 Chap m an-Kolomog o rov 방정식으로 알려지고 있 다. (6 .1 6) 에서 t1 = t + r, t2 = t로 하고 작은 T 에 대하여 전개해본다. 즉
P1(x1, t + 1:) = Jdx2 P(x1, t + , I x2, t ) P1(x2, t ) 를 T 에 대하여 전개하여 1 차까지만 취하고, (6 .1 5a) 의 관계를 쓰면 P1(x1, t) + ~ · -r = Jd x2 { I 뽀 P(x1, t + , I x2, t ) +~,」, : 1: }P1(x2,t)= Jdxj o (x1 -X2) + W(xi, X2 ; [) 아 P1(X2 , t ) 이고, 결국 하러 ('x1P, t) = Jd x.2 W (x1 X2 : t) P1(X2 , t ) (6. 18) 이 나온다. 여기서 시간당 천이확률 W(x1, x2 : t)는 W(x1 X2, ; t) _ aP(xi, 6( t' I X2, t ) I ,= t (6.1 8 a) 로정의된다. 특히 W(x1, x2 ; t) 三 T(x1 , x2 ; t) —b( x1 -x) J dx_' T(x ', Xi ; t) (6.18b) 이면 (6 .1 8) 이 6PI(8xtI , t) = [ dx2{ T (x1, x2 ; t)P 1(x2, t) •' - T(x2, x1 ; t)P 1(x1, t)} (6.1 9 ) 의 형으로 쓰이게 되는데, 이 식은 Mas t er 방정식으로 알려지고 있다• 단위시간에 대한 천이확률인 T(x,, x2 ; t)는 많은 경우에 I x1 -x2 I 가 커 지면 급속하게 감소되는 함수가 된다. 이와 같은 경우에는 T(x1, x2 ; t) 三 T(x2, t ; x1-x) = T(x2, t ; ~) = T(xl-e, t ; ~) (6.1 9 a) 로 놓고, (6.19) 를 8PI(axtI , t ) = Id 訂T (x1 궁, t ; ')P1(-x1 국, t)} _ P1(x, t)Id ( 궁 )T(x, t, -0 (6.1 9 b) 로 쓰는데, t롤 생략하여 쓰고 T(x1-, : ,)P1(x1 국) = T(x1-11 ; 紅 )P1(x1-11)111=,
= T (xl’ 칸 )P(x l ) - a{ T(x 냐8x )1P 1(x1) } : + _2l!_ 疏 (x 나ax f) R(xl)} <2 + …… (6.1 9 c) 의 전개를 (6.1 9 b) 우변의 첫 항에 대입하면 8P I(8xt l , t ) = +- ½—8 8x 1- f{;e:t1 ( X{1) 亨P1( )XPi ,l (tx)I}, t)} + …… (6.20) 을 얻는다. 여기서 忍) = ’[國 T(x1 ; ~) n = 1, 2, …… (6.20a) 이며, 확률함수 T(x1 ; ;)에 대한 momen t들이다. 특굴 l IX.{ x1 ) = 0 n ~ 3 이면 (6.20) 은 aP1(8xt1 , t) +, —axa1 {1X1(X1)P1(X1 , t)} + 썬릅亨 )P1(X 1,t)} = 0 (6.2Gb) 로 되는데, 이 식은 Fokker0-Planck5) 방정식으로 알려지고 있다. (6 .1 7) 과 (6 .1 6) 을 비교하면 천이확률밀도 P(x1, t1 I x3, t 3) 가 Pl(xl, tl) 과 같은 형의 방정식을 만족시키고 있다는 것을 알 수 있다. 따라서 P(x1, t1 I X3, t 3 ) 에 대한 Chap m an-Kolomog or ov 방정식도 (6 .1 9) 인 Maste r 방정 식과 (6.20a) 인 Fokker-Planck 방정식으로 고쳐 쓸 수 있다. 4) A. D. Fokker ; Ann. Phy s. (Leip zig) 43, 310, 1915. 5) M. Planck ; Sitz u ng sb er. Preuss. Akad. Wi ss . Phy s. Math . KL 325, 1917.
(2) Brown 운동의 기술 많은 Brown 입자들을 동시에 고찰하더라도 그들 사이에는 상호작용이 없다고 생각하므로 실제로는 한 개의 입자가 매체를 이루는 유체와 갖는 관계만이 중요하다. 많은 Brown 입자의 통계적인 행위를 보기 위하여 입자밀도 n(r, t)의 변화를 조사해볼 수 있다. 간단을 기하기 위하여 문제를 1 차원에 한정하면 입자밀도는 n(x, t)이다. 입자밀도가 균일하지 않으면 확산과정으로 균일하 게 되기 위하여 확산류 j/x , t)가 생기는데, 실험적으로 알려진 F i ck 의 법 칙에 의하면 jix,t) = -D 返8x ( 6.2 1 ) 이고, 여기서 D 는 확산계수이다. 연속방정식이 延at = ••• -고ax -E (x, t) (6.22) 이므로, 위의 두 식으로부터 ~at= D 쵸ax2 (6.23) 가 나오는데, 이 식은 확산방정식이다. Brown 입자의 운동이 Markov 과정이라 생각하고, (6 .1 6) 에 해당된 n(x, t) = Jd x0 P(x, t I Xo , t。) n(x 야%) (6.24) 에서 천이확률밀도 P(x, t I x 。, t。)가 만족시킨 식을 (6.23) 에서 구할 수 있 다.죽 aP(x, t~ I X 냐) = D 굽장 -P(x, t I x 나) (6.24a) 가된다. 따라J..1 lim P(x, t I Xo , t。) = D(x - Xo) (6.24b) t-1.
의 초기 조건하에서 (6.24a) 의 해를 구하면 P(x, t I xo, t 。 ) = V4nD(1t - t J exp { 4(Dx(- tx-ot) 。2 ) } (6.24c) 이 된다. (6.24) 에서 n(x 。 , t 。 ) = nb(x 。 ) (6.24d) 이고, t 。 = O 에서 모든 입자가 X = 0 에 있었다면 n(x, t) = ~ exp { -갑2 타 (6.24e) 이고, E i ns t e i n 의 (6.7) 과 같아진다. 중력 등 일정한 의력 K 가 Brown 입자에 작용하면, 유체의 점성에 의한 저항력이 속도 u 에 비례하여 _au 이므로 K = a% 로 정해지는 종속도 % 가있고 jK = nu 。 = n_ Ka_ (6.25) 인 입자류가 확산류 L 에 합쳐진다. 따라서 전체의 입자류 j는 i = iK +id = 폰 ~n - D 젤 (6.26) 이고, 입자밀도가 만족시키는 식이 邑 = －훑(f n(x, t)) +D 후ax2 (6.27) 이고 Fokker-P l anck 방정식이 된다. Brown 입자의 변위뿐만 아니고, 그 속도도 Markov 과정을 한다고 가 정하자. 시간의 원점에는 관계없고, 시간차만이 필요한 문제에서는 P(u 。, t。 | u, t) = P(u 。 | u, s) (6.28) s= t-t。 (6.28a) 로 하고, Chapm an-Kolomog o rov 식 (6.1 7 ) P(u 。, t。 I u, t) = JP (u 。, t。 I Vi, t1) du1P(u1, t1 I u, t) (6.28b)
를P(v 。 I v, s + r) J: P(u 。 I u, s)P (u1 I u, r)dv1 (6.29) 으로쓴다. 여기서 s=t 1 -t0, r = t -t1, t _ t 。 = s +·. (6.29a) 인데 (6.29) 를 Smoluchowski 방정식이라고 부르기도 한다. (6.29) 에서 T 가 작다고 하고, 그 때 P(ul I ul’ T) 는 u1 이 u 와 크게 다르 지 않을 때만 0 가 아니므로 u1 = u _ < 로 하여 (6.29) 를 P (u 。 1 u, s) + 8P(v 。8 sI u, s) T = .f 크:-a a:: P(u 。 I v - ,, s) P(u - , I u, -r) d' (6.29b) 로 쓰고, 이 식의 우변을 전개한다. 즉 P(v 。 | u 국, s) P(v-e I v, r) = [ P(u 。 I u_n, s) P(u— n I u + e —n, t)] n=t = [ fo 는 ~f ufu; ; {P(u 。 I u, s) P(u I u+ ＇서}] n=¢ = 효 눅 {P(u 。 I u, s) P(u I u + ,, 이} (6.29c) 를대입하M여. =as +I : =' d ~n:=I t 노 P(n v! 「 v +· 요 8~u,n - r {) M.P(v 。 I v, s)} 8P(u 。 I u, s) (6.29d) n = l, 2,… … (6.29e) 을얻는다.
특굴l Ml = -y v, M2 = 巴 \ Mn = O n ~ 3 (6.29f) 이면 (6.29d) 로부터 Fokker-Planck 방정식 붕= y 훑 (uP) + y 폰 · 릅 (6.3 0 ) 가 나온다. 뒤에서 Lange v in 방정식과 (6.29 f)와 (6.30) 의 관계에 대하여 더 자세하게 논하게 될 것이다. 위의 식은 초기 조건 lim P(v I v 。 ; s) = b(u - Vo) (6.31) ,...。 에 대하여 다음의 해를 가지게 된다. P(u|u 。 ;s) {~}112e xp { 2mk(Tv ( _1V —oee-- ;2 ';·)' )2 } (6.32) 이 해를 广 ?ro 에서 보면 뻔 P(u I u 。 ; s) = (갑 )1 /2 ex p (-齋) (6.32a) 이고, Maxwell 분포가 되는 것을 알 수 있다. [(6.30) 의 해〕 P(v I v 。 ; s) = P(v, s) 로 놓고 dP(v, s) = 一aOP~S ~d,vs +,' —aaP~v du 와 (6.30)a— 에s 서— — 우 I변 의+ 두 Iv번 째폰 항을 죽 무y시 한= 식 _ a8Ps _ y u 一a8Pu ~BP ~P ~P ~ - 에 대응d시P 키=고 적A.y분P 인자= lI(.u— ,8 ss ) 를_ 곱l y하u — 여8 u 8~P 6-P 와비교한다. 그러면
ds = ,i(u , s), du = -,l(u, s)yu , dP = A)'P 가된다.一dd us따 라=-서 -)'Urv,, —aa.Ps = yP~ 이므로 적분하여 u = ue 구 , p- = qe;• 를 얻는다. 다음에는 q롤 u 와 s 의 함수로 보는 소위 상수변화법을 써서 2afs.: -= y 3m!- e2 ;•, 효8u2 - 롤 얻는다. 또 e-2;~ ds = d0 로 하여, 이 식을 返ao = y 上m 호au2 로 고치면 확산방정식 (6.23) 과 같은 꼴이 되어 (6.24c) 와 비슷한 해를 알 수 있다. 변수를 각각 원래로 되돌리면 (6.32) 를 얻는다. 6-3 Gauss 과정으로 본 Brown 운동 확률이론기나 통계이론에서는 Gauss 분포가 특히 중요성을 갖는다. 그 이유는 수학적으로 단순하다는 점에 있고, 또 중앙극한정리가 성립할 수 있 도록 많은 요인이 결합하겨서 현상이 나타난다는 점에 있다. (1) Gauss 과정의 특칭 확률분포를 알고자 할 때, 그 특성함수 (charac t er i s ti c fu nc ti on) 는 매 우 편리한 수단이 된다. 임의의 확률밀도 f (x) 가 있고 (x, x+dx) 사이에 있을 확률기 {(x)dx 가 되는데, 그 특성함수 짜:)는 禪 = f :'° dx ei(x f(x ) (6.33)
/(x) = 1;: J: d~e- '1' 값) (6.33a) 로 정의되며, /(x) 의 Fourie r 변환이다• f (x) T에 대= 한I \n 차 다의 (xm)odmx en t가 (6.34) 로 정의되奭므)로 ,= j(6 .\33 )d 은xf (x ) 戶n= 。 草n. =n =t 。 n亨 . r (6.35) 으로 된다. 따라서 momen t가 특정함수에 의하여 X = t [〔禪 ] {=0 (6.36) 로 주어진댜 또 n = 0, I, 2,… … 에 대한 모든 momen t를 알 수 있으면 (6.35) 에 의하여 특성함수가 알려지므로, (6.33a) 에 의하여 확률밀도 f(x ) 도구할수있다. 특성함수 o( 《)에 대하여 그 cumulant 함수 W(:) 가 짜~) = exp i/1(<), t/J(~) = 1n
등이 된다. 확률이 Gauss 분포이고 f(x ) = ~ exp {— 뇨걸부 ::_ } (6.39) 이면,그 특성힘수가 禪 = exp (im~ 一 훙2t ) (6.4 0 ) 이고, ciu/Jr( neu) la=nt i함m 수e 는- t e2 ( 6.4 1 ) 이다.따라서
으로 쓰고, a ” 를 요소로 하는 matr i x A 를 이용한다. 그러면 f( x ) = C exp { - t ( x —m ) r A ( x -m ) } ( 6.4 3 ) 이고 r l_ I z.1. '_ . I 전 = ( ~I' ~ …… , ~ ) _\J‘F 울 써서, 특성함수가 ½ cp(~ ) = exp {i m 껏 — e (A 一 I)~} (6.4 4 ) 로 된다 여기서 A - I 은 A 의 역 ma t r i x 이다 . cumulant 함수는 鬪 = im T~ - ½e(A-1)~ (6.4 5 ) 이고, 따라서
죽 Z( t)가 Gauss 과정을 하는 양이고, 그 선형변환 Y(t) = J: C(t, t' ) Z(t' ) dt' (6.51) 룰 생각하면 Y( t)도 Gauss 과정이 되는 것을 증명할 수 있다• [증<명Y] ( t위) >의 = (6j. :51C ) (의t, t평' ) 균 <을Z ( t취' 하) > 면 d t ' (6'.5 la) 이고 , 2 <차Y 의(t I )c Yum(tu2l ) a>
u(t) - u(t 。 ) e- ; (I - I ) = .[ I' , e - ; ( 1 가 ) ~m R (t' ) dt' (6. 5 3a) 로 쓰이게 되는데, 이 식은 (6.51) 과 같은 형태를 가지고 있다. 따라서 R (t)가 Gauss 과정을 하므로 u(t) -u( t 。 )e 내재 도 Gauss 과정을 하게 된다. -츠,
Fokker.P la nck 방정식 ( 6 .30) 이 (6. 3 1) 의 초기조건에서 갖는 해 (6.32) 와 비 교하면 완전히 일치되고 있다. 사실,6 .Lu( atn) g e=v i nu (방t 정+r식) (-6. 5u2(at)) 에;;서- - t y가u r 충+분 히 上m작 은I, , 값이R(면t' ) d t' (6.56) 1+ r 로할수있는데 lI,,ii-m一m oo —上1Tr <<•.A 1 vu ((•t r)) • >2•> = == -l+l,i,iy-m-m ovo ; 上 上rr <{fy'(: 2+ E- , yd vt\r- I +드_: + m¼' dt; ~ < `:iIR+ ',•+ ( ,t ;
에서 f(t)가 Gauss 과정을 밟는다고 가정한다. 죽
이고, Gauss 과정은 f(t)와 관련되어 있다. 이제 f(t)의 ensemble 에 대한 평균을 취해본다• x 의 임의의 함수 F(x) 에 연산자 K(x, t)를 연산하고 ensemble 평균을 취하면
( :니+t. i dt 1, 1 . r :d,t dIt 2I < K,1, d(tx2 <, Kt , () xK,(txI ,) Kt2() gx ,( xt,2 ) t >)(>g ( x,t) > 1+t.1 = 짠 f :+t.1··d t 1 J:+t.1 dt2 2 2fJ (t, 一 t2) ;'- ,,n 훑 ;(1- ,,l n 걸 e',n (g( x, t) > = Lit • 2 e-,n~ e,o (g( x, t)> (6.64b) 로 한다. 고차의 항은 K(x, t)의 기수개의 곱이면 0 이고, 2n 개의 곱이면 (A t)에 비례한다. 따라서 At 一 0 인 limit에서 ~ = ,le -\>e' n ( g( x, t)> (6.65) 가만족된다. p(x , t)를 f(t)의 ensemble 에서 취한 평균을 P(x, t)로 하면 P(x, t) =
A 一폰 예 해당한다• 이 경우 (6.68) 은 革-&-11- = 걸- (xP) + ~m 효8x2 (6.68a) 이고, 바로 Fokker-Planck 방정식이 된다. Fokker-Planck 방정식을 약간 일반화한 것으로 생각되는 (6.68) 을 墨~ = —H ( 갑 ,x ; t) P(x,t) (6.69) 로쓰고, H( 갑 ,X ; t) = ―{亨 + A(x) 훑-＋틀} (6.69a) 로 하면, 양자역학의 Schrodin g e r 방정식과 많이 닮은 꼴이라는 것을 알게 된다. 그리하여 Schrodin g e r 방정식에서 개발된 수학적 기법을 이용할 수 있다. 그 중 한 가지인 pa th - in t e g r al 방법을 다음에 설명해보자• 위에 (6.69) 의 Green 함수를 G(x, t ; x 。, t。)로 하면, 그 정의식이 P(x, t) = JG(x , t ; 모 )P(x0, t 0)dx 。 ; t >t 。 (6.70) 이고, G(x, t ; x 。, t。)는 aG(x, t~。) + H ( 검 , x ; t) G(x, t ; Xo, t0) = 0 ; t > t。 (6.70a) 를 만족시키며, 초기조건인 lim G(x, t。 + t ; Xo, t。) = b(x - x 。) (6.7Gb) t- 0 도 만족시켜야 한다 .6) 그러므로 (6.70a) 와 (6.70b) 에서 6) P. Ramond : Fie ld the ory , A Modem prim er: Add iso n Wesley, 1989
G(x, t 。 + At : x0, t 。 ) ::: cli-+m o G(x, t0+ £ : x0, t 。 ) =_ Ab(tx H _ ( X감o) — 리At H c~(-T + 검o o G( x리, to+ £fl (;x x 0-, t 。x )o ) + 0(,1 t)2 = [ 1 _ A t H( 검 X, t 。 ) ] 广 〔 e’I( x - x ) = [ : 뿔 [1 - !J.tH ( il, x ; t 。 ) ] e 'I(x-x) (6.71 ) 롤 유도할 수 있다. 위에서 세번째 식은 D(x - X 。 )를 [\ 겅 〔 e ＇ I (x . x ) 로 고쳐 쓴것이고,네번째 식은 H( 걸 ; 'X ; t)에 있는 ：广 연산이 ei/( x - x , ) 에 작용하면 il e '/(x_ x , ) 가 되 기 때 문이 다. 다음에 A t를 미분소량으로 취하면 1 - ~t H(il , x ; t 。 ) = e 깁 H(, l . ,, t..l (6.71a) 로 되어,G (x(,6 .t 。7 1+) 을 fi t ; Xo, t 。) = 仁 맵- e -/ J,J H(I/ ,x :I n) e '/(x _ L) == ] i :: --eeA +I 占(I/ i _ H( 브I/,x -:I H) (]i / , , : 1 , ) j (6.71b) 로고쳐쓸수있다.위에서 x=~ (x-Axt o ) 로하였는데,그이유는 A t가 미분소량이므로 조건 (6.70b) 에 의하여 x 는 xo 와 미한소량만큼 다른 값이 될 때만 Green 함수의 값이 ()ol 아니기 때문이다. 양자역학과의 관계를 보기 쉽게 하기 위하여 (6.71b) 에서 i l을 운동량을 나타내는G(px,로 t。고 +쳐 A t쓰 :고 x0 , t) == II' ..f：: 農틀-마 (e ”X[p ~ ,-H X( . p,), x, r) ) (6.71c)
처럼 쓸 수도 있다. 위에서 H( p, x, t)를 Ha mi l t on i an 으로 보면 L(x, x, t)는 바로 La g ran gi an 이 된다. 간단한예로서 H(p, x, t) = K (1)p 一 갑 K(2)p 2 (6.72) 로 하며,G (xK, ( t＂ 과+ /K),t (2:) 를X o,x t 만) 의= r함:수j:,c가 -고農- 한 e 다A '.Pi - K( ' 6p .냐71 Kc) ' p 의 1 첫적분에 의하여 = `같 [' -\ dp e 색 당 [ /(' /p' + (x·-K'’ )p l = _L `[ ‘~ dp e 야 K ' ’ ' Ip. ＋도 풍 l p l 2ni I -j:xc = 上 `I 'x dp e쏭 K : p+ 子 l ' e- 풍 K' 눅 2ri ·iz =1 효아도; e －다函소工 ' ) (6.72a) 을 얻을 수 있다. 위의 마지막 식은, ―i OO 에서 i OO 로 가는 적분로로 _OO 에서 OO 로 가는 적분로로 바꿀 수 있다는 관계에서 얻어진다. • A t가 미분소량일 때 위에서 Green 함수 G(x, t + At ; x 。, t)를 구하였 다. t와 to 가 유한한 차이룰 가질 때 G(x, t ; x 。 , t。)를 구하기 위하여는 (6. 70) 을 다시 보기로 한다. t + 2M, t 사이에는 G(x,t + M ; x 。,t)의 지식을 이용하여P (x(,6 .t7 0+) 에2/서l t ) = jG(x, t + 2M : x o, t)P (xo, t )dx 。 (6.73) 와
P( Xo, t + 2M) = JG(x o, t + 2A t : xi, t + At) P(xi, t + At) d x1 (6.73a)P(X1, t + !::.t) = JG(x 1, t + lit ; x0, t )P (x0, t )dx 。 (6.73b) 에서 P(x, t + 21:: .t) = JG(x , t + 2/i t ; x 1, t + !it)d x1 jG(xi, t + lit ; Xo, t )P (x0, t )dx 。 (6.73c) 가 성립하고, P(x 。, t)는 임의로 취할 수 있다. 따라서 (6.73) 과 (6.73c) 를 비교하여 G(x, t + 2/::. t ; x o, t) = .fG (x, t + 2/::. t ; xi, t + !::.t) G(x.,t + /::.t ; Xo, t ) d x1 (6.74) 울 알 수 있다. 마찬가지로 t와 t o 의 차이가 유한한 값이면, 그 사이를 At 의 간격으로 N 등분하여 (6.74) 와 같은 관계를 얻게 되는데 At一 0, M 一 OO 로하여 G(x, t ; xo, t。) = 터…···J dxM-1 …… dx, G(x, t ; XM -h tM -1 ) …… G(xi, t1 ; X o,t。) (6.74a) 울 구하G게( x,된 t다 ;. x 나(6).7 1c=) 를 f 위 D에( x대) 입f 하D여(p ) exp {f:. d s L(x(s), ;(s)::~} (6.74b) 로 표시하고 있는데, 그 의미는 (6.74a) 로 나타낸다. 위와 같은 적분을 p a t h-i n t e gr al 이라고 부른다. 특히 H( p, x, t)가 (6.72) 로 주어지면 p에 대한 적분이 쉽게 이루어져서 G(x, t ; x 나) = f D(x) exp { -f:. _Ll님툴모 dt} (6.75) 가 된다. 이 적분형에서 most pro bable pa tb 7 } .i: = Km . (6.75a)
으로 주어지고, x. -K(I l = f(t)에서 f(t)가 fl uc t ua ti n g하는 함수이면 f(t)가 Gauss 분포를 하고 있다는 것을 알 수 있다. 위에서 독립변수가 x 하나인 경우에 대하여 논하였지만, x 가 (x1, x2, …, xn) 을 나타내는 vec t or 로 하면 N 개의 변수가 있는 경우 쉽게 확장할 수 있다. 6~5 Wi en er-Khin tc h in e 정리와 요동-일산 정리 값이 확률적으로 주어진 변수 y가 확률량인데, 이것이 다른 변수 t의 함 수이면 y(t)를 확률함수 (random fu nc ti on) 라고 한다. 이 확률함수가 정상 (s t a ti onar y)이라는 것은, 어떤 평균 〈 〉 에 대하여 (y(t)〉가 t에 관계없는 값이고, (y(t)y(t + s) 〉 =K(s) 가 t에는 관계하지 않고, s 만의 함수가 되는 것을 의미한다. Wi en er-Khin t c hin e 정리는 정상적인 확률함수에 대하여 성립한다. 위에 나온 상관함수 K(s) 의 Fourie r 적분을 K(s) = 仁 J(Q) e‘' d(J ) (6.76) 로쓰면 K(O) = (y(t)y(t)> = 仁X J( w)d(J) (6.76a) 이 되는데, J((JJ）는 spe c tr a l dens ity로 불려진다. (6.76) 의 역 Fourie r 변환이 J( w) = 버 :00 K(s) e-i ~·• ds • (6.77) 아며, spectral den sity J (w) 가 상관함수 K(s) 의 Fourie r 변환으로 얻어지 는 것을 보인다. (6.76) 과 (6.77) 은 상관함수와 그 spe c tr a l densit y 사이 의 관계를 나타낸 것이고 위에 말한 정리의 내용이다. 특히 y(t)가 실수함 수이면, K(s) 가 실수이고, 또 상관힘수가 정상적이므로.
K(s) = (y(t)y(t + s)> = (y(t - s)y( t)> = (y(t)y(t - s)> = K( —s ) (6.78) 가 된다. 위에서 두번째 식은 t에 관계하지 않는다는 조건에서 t 대신에 t -s 를 대입하여 얻은 것이다. (6.78) 은 K(s) 가 s 의 우함수가 됨을 보인 다. 따라서 (6.77) 을 써서 J* (r o) = J( ro) (6.78a) J( -ro) = J(r o) (6.7 8 b) 울알수있다. 상관함수와 그 spe c tr a l densit y 시이의 관계를 Lange v in 방정식에 이 용하려고 한다. 이 방정식은 (6.52a) 에 뿔 = -yu + ¾-R(t) ; y = !- (6.79) 로 하였다. 지금 Fourie r 적분으로 u(t) = J:크 a 3 : u((J )) e'wl d(J ) (6.80) u((J )) =' 같 「' u(t) e_ , 아 dt (6.80a) 로 표시하R며(t), =또 I요二 동 r하(o는) e힘1에 d o대 하여도 (6.81) r(w) = 버 :.,, R(t) e- i떠 dt (6.81a) 처럼 표시한다. 그러면 u(t' )와 u( t)의 상관함수 K, (t -t' ) = 사이의 관계를 계산할 수 있다. 죽 奭) = 버 :00 K.(s) e-;..,, ds = 古 j:。
로하면 = ( 六 ) 2 I \ d t' ] \ d t e -IW 1 기 W. ,- 〈 v( t ')v( t)〉 -나 ) [\ dt' e-I( o + w) / 나) I: ,, dt ` e-i w (t- t') K. (t -t' ) -나 ) I ::Lo dt' e-i( w +w' )t 같 j :' ds e 기 w · , K.(s) = o(w + w' ) J,( w ' ) (6.83) 처럼, (6.84) 에 대하여도 그 sp e ctr a l densit y J R( 이룰 JR ((J )) = 六 I :z KR(s) e 가 w, ds (6.84a) 로 하면, (6.81a) 에 정의된 r(w) 도 (6.83) 과 비슷한 계산울 하여
=~(~)(~)
인데, 이 경우 (6.89) 의 적분이 쉽게 계산되고 K. (s ) = : 「 OO do o 』 규 e''' = 교m 2y e-; , (6.91) 이 얻어진다• 평형상태에 대한 에너지등분법칙이 성립하면 1 차원 운동에서 K(O) =
x(t) = f I。 v(t' )dt' (6.93) 로주어지므로 〈갔(t)〉 = .f~ dt' J:dt
dAd(t t ) = -y A (t) + R(t) (6.96) 로 확장할 수 있고, 여기서 R( t)는
하게 표현할 수 있다는 것을 밝혔고, 그 식을 응용하기 위하여 Lee81 등이 체계적인 연구를 하였다.
8) Lee, M. H. : Phys . Rev. B26 2547, 1982.
(1) Mor i의 표현 역학변수 A 가 좌표 qi(t)와 운동량 p i (t)만의 함수이고 시간변수 t를 양 으로 포함하지 않는다고 하면, 시간 t에 대한 A 의 값 A( t)가 Hami l- ton ian H 에 의하여, 고전역학에서 썬 = {A(t) , H} (6.98) 로 기술된다. 여기서 {F, G~ 곤 역학량 F 와 G 에 대한 Pois s on 괄호식 9 ) 이 다. 또 양자역학적으로는 (이하 h = 겁;이다) · 雙 = 군 [A (t) , H ] (6.98a) 이고, [F, G ]는 FG ― GF를 의미한다. 위의 두 식은 모두 갇은 형 雙 = iL A(t) (6.99) 로 쓰이고LF, 다= 만+ 연{산F , 자H } L 의 의(고미전를역 학고)전 역학과 양자역학에서 각각 (6.99a) LF = _t[F, H] (양자역학) (6.99b) 로 해석하면 L 이 Hermi tian 연산자가 된다.
9) Pois s on 괄호식 ; {F,G} = ri: (8q회, 迷0p j 一 깊0p 1 j 료oqi, ) 를의미한다.
이하의 논의는 (6.99) 에 대한 형식적 연산만을 하게 되므로 역학의 종류 에 관계없이 성립된다. (6.99) 에 대한 형식적인 해는 A(t) = 싼 A(O) (6.1 0 0)
로 얻어진다. 여기서 A(O) 는 t = 0 인 좌표 qj(t = 0) 와 P,(t = 0) 에 대 한 역학함수를 의미한다. 이하에는 편의상 A(O) 三 A (6.1 0 0a) 로한다.그러면 ( ¥)1=0 三 A( 0) = iL A (6.1 0 0b) ( 贊)‘ = O 三 A( n)( O) = (iL) nA (6.100c) 로쓸수있다. 다음, 연산자 ¢U 에 대한 Lap la ce 변환을 보면 £ • e'u 三 I\ d r e- e'Lf = s] LL (6.1 0 1) 이 되는데, 임의의 연산자 A 와 B 에 대하여 성립되는 항등식 + - if = +(B -A) if 에 A = s - i L 과 B = s - iQ L 로 놓고 s-1 iL = s— LQ1 L + s-1 IT: (iL - iQL ) ~ 울 얻는다e'u. =이 ei식Qu 을 + LI:ap d lar cee i L <,역 국)변 i환(l하 -여 Q) L eiQ L , (6.101a) 。 를 알 수 있다. 위에서 Q는 임의의 새로운 연산자이다. 역학함수 F 와 G 에 대한 내적 (inn er p roduc t)을 적당하게 정의하고 (F, G) 로 쓴다 .10) 지금 pr oje c ti on op e rato r P10) 를 P(O)F = 鬪 A (6.1 0 2)
로 정의하면 P O): = P (O) 이고 Q(O ) 三 1 —P ( O )’ Q(0 ) 2 = Q(O ) p Q(O )L = L( l) (6.1 0 4) 로하고, A( I) 三 A( l)( O ) = iQ( 01L A = iV 1>A (6.1 0 4a) A(ll(t) = eiL ' , Aoi (6.1 0 4b) 로 고쳐A 쓰( I)면( t ) (+6 . 1I 03。 bd)T 의 e IL (우I- 변r) i이P (0 )L A( I)( t ) (6.1 0 5) 이고, 여기서 iP (O ) LA( I)( T) = (A.{:?;))k)) A -— (iLA , A( I)h ) A (A,A) = _ {( i P (O) LA,A 王))+(iQ (0) LA, A ° ( 이) A (A,A) (6.1 0 5a) 인데 Am(r) = eiL ', Am ( O) = eiQ L'iQ 0 LA = eiQ ' L, i Q< o>2 LA = Q(O ) e'Q ' “L r iQ( 0) LA = Q(O )A(I)(r) (6.1 0 5b) 에 의하여 (iP(O ) LA,A(I )) = 0 이고 (iQ< 0> LA, A<0(r) ) = (Am(O), Am(r) ) (6.105c) 이댜 따라서 기 억함수 (memory fun cti on ) 을 ?(I) ( r) = (A(I)(( O A),, AA()I )(r) ) • (6.106) 로 정의하A(면I),(t ) (6- .1 0f5o) d가r y(I )(r)A(t _ r) 로 쓰인다. 따라서 (6 .1 03) 에 의하여
뺏 = -[ ' y(I )(r) A(t —-r) + A 01(t) (6.1 0 7) 를 알게 된다. 이 식을 (6.96) 과 비교하면 Alll (t) 가 R(t) 에 해당하고 y(I) (T) =y 8( t)이면 두 식이 일치하게 된다. y II)(r) 는 (6 .1 06) 에서 보인 것처럼 (6.97e) 에 대응하여 요동하는 양 A (I) ( t)로 기술된다. A(I ) ( t)는 (6 .1 05b) 에 의하여 (A, A (1)(T) ) = (P(O )A , Q( 0)A(”(T) ) = O (6.1 0 7a) 0l 다. A(t) , y< ll( t)와 A(1)( t)의 Lap la ce t rans fo rm 을 a(s) = 「~ d t e_., A(t) = £ • A(t) (6.1 0 8) rm(s) = £, • ')'(I)(t) , am(s) = £ • A111(t) (6.1 0 8a) 로 하면, (6 .1 07) 의 Lap la ce t rans fo rm 이 sa(s) - A(t= O) = -r 0>(s)a(s) + a0>(s) (6.1 0 8b) 가되어 a(s) = ~s + r(l) ( s) (A + a0>(s)) (6.109) 를 알 수 있다. (a(s), A) 는 상관함수 (A(t) , A(O)) 의 Lap la ce tra ns- fo rm 인데 (6 .1 09) 에서 (a(s), A) = ~(A, A) (6.1 0 9a) 가 된다. 그 이유는 (6.107a) 에서 보인 (am(s), A) = 0 의 관계가 있기 때문이다. 또 (6.106) 과 (6 .1 08a) 에서 r(1)(s) = (A((I)A, a,(AI))( s)) (6.1 0 9b)
도명백하다. A (I) ( t)는 (6 .1 04b) 에서 알 수 있듯이 꼬dt = iL( “A(I)(t) (6.1 1 0) 를 만족시키고 그 형이 (6.99) 와 같다. 따라서 A( t)에 대하여 하던 방법을 되풀이하巴여 뿐 = -J~d r y(:lf( r)A01(t- r) + A( 21 (t) (6.111) 를 얻을 수 있다. 여기서 pro j ec t ion op e rat o r P( F 三 (A(Aoi, ),A F()ll ) A(I) (6.l lla ) 으로정의되고 Q(l) = 1 —p( l) (6. lllb ) Q(I )L (I) = L(2 ) (6.lllc) A(2) = A(2) ( t= O) = iL( 2) A(I) (6. llld ) A(2)(t) = e'L(2 )'A(2) (6. llle ) y(2 )(r) = (A((A2)0, A\ (A2)( l()r)) ) (6. lll f) °]다. (6 .1 11) 의 Lap la ce t rans fo rm 으로부터 a(I )( s) = s + r1( 2 )( s) (A( + a(2) ( s) ) (6.112) 를 얻는데, 여기서 am(s) = £ • A( l)(t), a<2>(s) = £ • A<2>(t) r(2)( s) = £ y(2 )(t ) (6.l12a) 이다. 또 (6 .1 09a) 에 해당된 식으로 (a(I)(s), A(I)) = s( A+(I )r,( 2A)((Is))) (6.1 1 3) 울 얻는데, (6 .1 09b) 를 보면 (A, A) 로 나누고
r(I)(s) = (A( I)s, +A 이 r (2/) ( (sA) , A) (6.114) 를알게 된다. 마찬가지 계산을 되풀이하여 일반적으로 王 = -.f ; dT y(n +1)(T) A(n)(t — r) + A(n+ ll(t ) (6.115) 를 알 수 있다. 여기서 pr oje c ti on op e rato r p < • ) 이 P 가? = (A(n), F) A(n) (A(n) , A(n) ) 이 정의되고 Qh ) = l - P(n) (6.115a) Q(n )L(n) = L(n+ l) (6.1 1 5b) A(n+l) = A(n+ l)(t=Q} =iL(n +l)A(n) (6.115c) A(n+l>(t) = eiL (n+l )1A (+l) (6.1 1 5d) '/(n+ll(t) = ~(Ah), A(n)) (6.1 1 5e) 를 의미한다. n = 0 이면 A(O) 三 A 로 볼 때 (6 .1 07) 이 되고, n = l 이면 (6 .1 11) 이다. 따라서 n = 2, 3, …… 에 대한 식도 명백하게 알 수 있다. Lapl a ce t rans fo rm 을 (6.115) 에 취하여 (a(n)(s), A(n)) _ s + r(1n+ 1)(s) (A(n) , A(n)) (6.1 1 6) 울구하면 rh)(s) = (A(n), As( n+)) / r((nA+(1n)-( s1 )), A(n-I)) (6.117) 울 보게 된다. 그리하여 (6 .1 09a) 를 다음과 같이 연분수 (con ti nued frac - ti on) 로 써볼 수 있다. 죽
(a((As,) ,A A) ) -= s + r10 1( s) 1 s+ (A S, T+ wr(2( >A( s), A) s + s + ((AA(1( 2) ), , A A1m( 2)) ) / / ((AA(1 A), )A (1) ) (6.1 1 8) s+… … 이 된다. (2) Le 려 전개식 11)
11) Lee, M .. H . Phy s. Rev. 826, 2547 (19 82), Phy s. Rev. Letl 49, 1092, 1982. 김재화, 고려대학교 박사논문 (1986).
처음에 (6 .1 15c) 로 정의된 A ( n ) 에 대하여 (A(O ) = A 이다) (Av> , AU >) = (A 따 Av >) bi k (6.1 1 9) 를증명한다. [증명 ] (A
임의의 F 에 대하여 P (l)P (01 F = 0 가 성립하므로 P (l)P (01 = 0 로 볼 수 있 다. (AIO>, A(J) ) = (A, iQ< 2)£(2 )A (2)) = (A, iQ1 2)Q ll lQ ( O)£Al2)) = (A, {(1 - P (2)) (1 一 P (I)) (1 - P (O)) }iL A (2 )) _ (A, iLA (2)) _ (A, P (2)i LA (2) ) - (A, P(I)iL A(2 )) (A, P(0)iL A (2)) —(A , iLA (2)) —o —0 - (A, iLA 12l) = 0 룰 p.2)P (I)P(O) = O, p.2)P (I) = O, P (2lp .0) = 0, P(I) P (0) = O 와 (A, A<2l) = 0 에서 (A, P(2)iL A (2)) = 0 이고 (A, A0>) = 0 에서 (A, P (I)iL A (2) ) = 0 가 되기 때문에 알 수 있다. 다음 (A(O), A 이 = 0 가 i = l, 2, ……, k-l 이 성립한다고 가정하 고 (A(O), AU)) = 0 을 증명한다. (A(O), AU)) = (A, iQU -I)L(k_ “A (k- I)) 一— ((AA ,, i{Q(1U -_nQ (pk -t2H)… > ) …(1 Q ( _O )LpAt1(kt-I2)))) …… (1 - P (O)) } iLA U-I)) -= ((AA,, iiLLAA U.(-kI>I))) -— 0( A -, i…LA …< H->(A) ,= P(0O) iL A U- I)) 롤 Ph)PU) = 0( 푸j) 이고 또 (A, P(i) iL A(H)) = ~ (A, Ah)) 로 되는 데서, (A(O), A 이 = O 를 써서 0 이 되는 항이 계산되었다. 이렇게 하여 i = l, 2, ……에 대하여 (A(O), A{I)) = O 가증명된다. A(” 과 A 맷i = 2, 3, ……)의 구성되는 관계가 A(O) 와 A(I)(i = l, 2,… …)와 같으므로 위에서 같은 방법으로 (A<1> , A( j)) = 0 j = 2, 3,… …
이 증명된다. 또 A (i)와 A<,+n l = 1, 2,… …에 대하여도 마찬가지로 (Ah ', Ali+ /)) = 0 l = 1, 2,… … 이 증명되어, 결국 (6 .1 19) 가 증명된다. A'') 의 직교관계를 쓰면 iLA vl = AU+ Il - 1).1 • AH> j = 0, 1, 2,… … (6.1 2 0) 이고, 여기서 A ) = ((AA lU, -) l,) AA O(j기))) ) J = 1, 2,… … (6.1 2 0a) l:!,.o = 0 (6.1 2 0b) 도증명된다. [증명 ] A( = iL( “A = iQ( O) L A = (l _ P(O))i LA = iLA —P (O)i LA 인데 p
p(O )i L A = (—A((,(AA Ai (L,I,)AA ,A ()AI) )( )I) ) AA 一_ A((iLAIAA ,A , A) (l)) A 가되어 iLA m = A(2) - A1A 를구하게 된다. iLA UI = AU+ll AJ A V - ” 가 j = 0, 1, 2, …… k-1 까지 성립한다고 가정하여 iLA (k ) = A(HI) - !i kA(k 내를 증명해보자. Alk+I) = iV Hl )A W = iQW LWA! k) = iQW Q < H) …… Q!O ) iLA W = (1- PW (1-P
A(t) = `.L ~。 0 !X,(t) Al•·) (6.1 2 1) A(t = O) = A 이므로 (A, A(O' ) = a 。 (O)(A(O), A(0') 에서 a 。 (O) = 1 (6.1 2 1a) 이고, 마찬가지 이유로 ix,( O) = 0 V ~ 1 (6.1 2 1b) 01 다. A( t)의 시간적 변화가 (6.99) 로 주어지고 썽 = iLA (t) (6.1 2 2) 인데, 여기에 (6 .1 21) 의 전개식을 대입하면 픕OO da&V( t ) A(,) = J工; 0 tX , (t ) iL Ah ·l = E'=xO ap (t){ A(v+ 1 ) _ A, A (v- I)} r=O 이 된다. 위에서 두번째 식은 (6 .1 20) 을 이용한 결과이다. {A 매의 직교성 에 의하여 dr:t.d, .(t t) = a.·- I( t) - A`'+1 a 다!(t) (6.1 2 3) 을 알 수 있다. a V ( t)의 Lap la ce t rans fo rm 을 a:( s) 로 쓰면, (6 .1 23) 의 변 환이 (6 .1 21a) 와 (6.121b) 에 의하여, V = 0 에서 s;-0(s) - 1 = -!).1;-1(s) (6.1 2 3a) 이고, v # 0 에서 si ,(s ) = ;--,_1(s) -li,+1 ;~- ,+1 (s) (6.123b) 가 된다. 그리하여 (6 .1 23a) 에서 a~ 。 (s) = s+A11— 값i i;— ((ss—) ) (6.1 2 4)
과 (6.1 2 3b) 에서 瓦~ -. (1 s(. )s ) = s+Av+ 一11 —'aa `;—'.+ ( sI —( )s ) (6.1 2 4a) 울 구하고, %(s) 에 대한 연분수 표현인 a겁 s) s+ s+ s1+A AIA 3 ·2 · · … (6.1 2 5) 를 알 수 있다. a 。(t) = (A(t) , A) / (A, A) 에서 그 Lap la ce tra ns-fo r m 이 ;-0(s) =(a(s), A) / (A, A) 이고, 또 fl.,= (AM , Ai• ·>) I (A< •·- 1> , A h - I ) ) 이 므로 (6 .1 25) 는 (6 .1 18) 과 일치된다. A( t)의 전개식 (6.121) 에 대응하여 A ( I)( t)의 전개식을 A(l) (t ) = LO {J,.( t) AM (6.126) .~1 으로하면 /31 (0) = 1, 8I'( O ) = O V ~ 2 (6.1 2 6a) 이다. (6 .1 21) 과 (6 .1 26) 의 Lap la ce t rans fo rm 을 a(s) = I。; a, (s )A( ,) (6.1 2 7) ,=O a(I)( s ) = E。 困 (s) A(v) (6.1 2 7a) m=I 으로 쓰고, 이것을 (6 .1 09) 로 나타나 있는 a(s) = s + rl (l) ( s) (A+a(I) (s)) (6.1 2 8) 에 대입하고, {A 매의 직교성을 이용하여 a--,a(。 s( ) s ) == ss + + } r(1I <) l)((s s )) K(s) v~l (6(6.1. 12 299a)) 을구한다.따라서
/3 `'(s ) = —rax 。, — (( ss )) (6.1 3 0) 가 되어, A( t)의 전개계수로 A(I)( t)의 전개계수가 결정되는 것을 보게 된 다. 6-7 선형응답과 상관함수 Brown 운동의 이론을 통하여 지금까지 역학량 사이의 상관함수가 중요 한 물리적 의미를 가지게 되는 것을 볼 수 있었다. 그러므로 다음에 평형통 계역학의 체계 안에서 요동하는 양과 상관함수가 어떠한 역학의 관계를 만 족시키는가를 보려고 한다. (1) 선형응답의 이론 역학량의 A(q, P) 의 시간적 변화가 —aaAt = iLA (6.1 3 1) 로 쓰이는 연산자 i L 이 Ham ilt o n ian H 에 대하여 고전역학에서는 Pois s on 기호로 iLA = -{H, A} (6.1 3 1a) 이고, 양iL자A 역 학= 에t서는[H 교 ,A환 자] 기호로 (6.1 3 1b) 가 되는 것을 이미 알고 있다. 확률밀도p는 뿔 = 一i L p (6.1 3 2) 를 만족시키고 (6 .1 31) 과 비교하여 우변의 부호가 반대이다. Ha milt o n ian H 가
H = H0 + )J-/I (6.1 3 3) 으로 쓰이고, 여기서 A 는 작은 양을 나타내주는 p arame t er 라고 한다. 그 러면 L = L 。 + J..LI (6.1 3 3a) 이고, (6.132) 가 웅 = -(i L 。 + liL 1 )p (6.1 3 4) 가된다 여기서 aa p。t = -i L 。p。 = O (6.134a) 를 만족시킨 Po 가 알려졌다고 하고 P = Po + lp, (6.134b) 이 된다고 하자. 그러면 A 의 일차까지만 생각하는 근사에서, p 1 은 굼0p― I = -iLop , -i L, p。 (6.134c) 가만족시킬 것이다. 지금 P1(t) = e 기I.o r e(t) (6.1 3 5) 로 놓으면 (6.134c) 로부터 뿡 = _e-i Ld (iL1 p o) (6.135a) 이 나온다. 따라서 t = -00 에 대하여 p(t = -oo) = p。 (6.1 3 5b) 을요구하면 p1( t = _m) = O, 죽 e(t = -oo) = 0 (6.135c) 가되어
副 = I’잡 dr e-; t.,, ( -iL1p 0) 울얻으므로 PI(t) = .[ \ dT e - I 나 - r)( -iLIP o) (6.1 3 6) 을알수있다. 여기까지는 수식의 유도에 형식적인 관계만 사용하였으므로, 고전역학이 나 양자역학에서 똑갇이 성립한다. 역학이 다를 때도 대부분의 계산은 비슷 한 결과를 주게 되는데, 양자역학이 보다 더 간단하므로 이하에는 양자역학 으로 계산하고 h-+O 인 극한에서 고전역학의 결과를 알 수 있도록 한다. 확률밀도 p가 양자역학에서는 확률밀도행렬이고 Tr p = I, Tr Po = 1 (6.1 3 7) 인데, 여기서 pa rti tion fun cti on 2c 가 Z 。 = Tre 갸 H . (6~1 3 7a) 이고, Pop 。를 =평 형—z상 태e 에 대한 확률밀도 (6.1 3 7b) 1 갸 H . 라고 한다. 따라서 (6 .1 34b) 에 의히여 Tr p.(t) = 0 (6.1 3 7c) 을알수있다. 역학량 B 에 대하여 o = Tr Po B (6.1 3 8) 로 하고 B - 〈 B 〉 0 의 p(t)에 대한 평균치를 A8 〈 B 〉로 하면 A6< B > = Tr [ (p0 + ,l.p.) (B - 〈 B 〉。) ] = ,l. Tr [p1( B - 〈 B 〉。) ] = ,l. Tr P1B (6.1 3 8a) 이다. P1( t)가 (6 .1 36) 으로 주어져서
8< B > = Tr p 1B = TrBp 1 = J1-_· ,어,, d-r Tr [ B e- ,1.. .,(, - , ) ( —iL1 p o) ] (6.1 3 9) 이 유도된다. 이 식은 (6 .1 31b) 에서 iL1 Po = T; [ H i, p。 ] (6.1 3 9a) 이고, 또 임의의 역학량 G(q, P) 에 대하여 e -IL.,{ I -r) G=e -tH.,(t-r ) Get H.,{I- T) (6.1 3 9b) 가 성립하는 것을 알고 있으므로 Tr [ B e -i L 。 (1 -r )(- i LIPo) )= 『 Tr [ B e- t H,( I - r) ] (H1p o - p沮\) e댄 ( 1 - t) (6.1 3 9c) 이 나온다. 이 식 안에서 Tr [ B e -tHo(I - r) HIPo e 卞 H , (I-r) ] = = \,''-(X) &
로된다. 실제적인 문제에서 HI 은 자화 갑'(7, t)와 자기장 s(7, t)에 의하여 HI = -f d7M(7, t) 函 7, t) 으로 되기도 하고, 전기장 E(7, t)와, 전기편극 PC:, t)에 의하여 _HP I( _r= , t-) f d= 7I ::P eC, 1_r, ' , t)o (江_r ,— tr) ,) 등이 되어, 일반적으로 HI = -J d7 A(7, t) -;(7, t) (6.141) 로 쓰인다• (6 .1 40) 에 H 에 대한 (6 .1 41) 을 대입하고, B 가 A;( i = l, 2, 3) 중하나fJ라< A고i( 하-;:면:t) > = J'--r-d r f d7 2i XiiC :, t ; 7, r)F/7, r) (6.1 4 2) 이고 여기서 응답함수 xijc :, t : 7, ,)는 x;,C : , t : 7, ,) = <*[ A i ( 7, t) ; Ai( 7, r) ] 〉。 = 〈값 [A;(7, t — r) ; A/°7 , 0) ] 〉。 (6.1 4 3) 로정의된다. (2) 상관함수와 응답함수 상관함수는 역학량 Ai t, t)와 AI( 7 , O) 에 대하여 s)7, 7, t) =
= S)7, 7, ~t - ih/ 3 ) (6.1 4 5) 의 관계가 성립하는 것을 증명할 수 있다. [증명 ] sij( 7, 7, t) =
0) 와의 관계를 얻을 수 있다 . 즉 2hX,j (7 , t ; 7, 0) = <[ A,( 7 , t), Ai( 7, 0) ] 〉。 =
= 군 -t Tr e- PH , {A/7,o) A,(7 , t) 一 A/° 7, t) A/7, O)} = t <[ Ai( 7, t), {Ai( 7, 0) ] 〉。 = 2Xii (7 , 7, t) 이 새로운 상관함수가 양자역학이 사용될 때 더 편리하다는 사실이 알려 지고있다.
7 Bolt zm ann 방정식 평형상태와 그것에 아주 가까운· 역학계에 대한 통계역학은 앞에서 알게 된 바와 같이 잘 정리된 이론체계를 갖추고 있다. 여기에 대하여 바평형상 태에 있는 계를 잘 기술하고 또 계산아 가능하여 실용성을 갖추고 있는 이 론은 장차의 연구에 기대하여야 할 것 같다. 다만 100 여 년 전에 기체의 분자가 하는 행위를 기술하기 위하여 제안된 Boltz m ann 방정식은 통계역 학의 역사에 특출한 위치에 있을 뿐만 아니라 그 실용성도 높이 평가될 만 하다. 이 방정식은 비선형인 미분 • 적분 방정식이며 비평형상태를 기술하는 이론의 원형을 이루고 있다고 생각할 수도 있으므로, 이 식을 통계역학의 일반적인 이론체계로부터 도출하는 것은 중요한 의미를 갖게 될 것이다. 또 이 방정식에 입각하여 실제의 문제를 해명히는· 방법도 공부하는 것이 필요 할것이다. 이 장은 보통 기체에 대하여 고찰하고, 양자효과가 중요한 전자기체는 도 의시하고 있기 때문에 제 1 원리는 고전역학이 되고 있다.
7-1 Boltz mann 방정식과 제 1 원리 (1) BBGKY 방정식 한 같가은장 종일류반의적 인입 자방 정N식 개은가 L체i적o u vVil le안 식에이 다있.는 i 역번 학입계자를의 통좌계표적를으 1로, 기운동술 량p一‘ 로하고 XI 三 (--r>j, p一,) 로 대표시키면 x1, x2, ……, xA ’ 으로 된 6N 차원의 Euclid 공간이 r 우]싱공 간이다. r 공간에 정의된 확률밀도함수는 시각 t에서 pN( xl, Xz , ……, XN ; t) 三 pA,( _ r I, p一I , -r2 , 一p2, …… , 一r -pA ' ; t) 인데, 이 밀도함수가 만족시킨 Lio u vil le 방정식이 (2.6c) 에 도출되어 있다. 이 식은 Oapt N = —iLN P N (7.1 ) 로 고쳐 쓰이는데, 여기서 (6.99a) 에 정의된 연산자 i L 에 해당하여 iLj i' = {F , HN } ( 7.l a) 으로 정의한다. Po i sson 의 괄호식 {A, B} 가 {A, B} 三 i폰:i , (oqj교 op책j _op革j o`qj (7.lb) 이며, (x1, Y1, z1, Xz, ……, z깁 = (q1, qz, q3, ……, q 3N) 으로 대응시키고 있다. ' HN 은 N개 입자의 H ami l t o ni an 이고 HN = t-fk-김 u( 『 一 머) (7.l c) 를의미한다.따=라 꼽서N p-下i 8言p N - ~ eiiP N (7.l d) iLN p N = {pN' H 갔
이 되는데, 이 식에서 u(-\r~ 一- -r> I ) 三 u ,, 로 하여 o,1 三 +—a aur , ,1· ·—aap= : +I _aaur ,j ,· . —aap 一 , (7.le) 로 정의되었다. p(x 1, xi, … …, XN ; t)가 「공간에 정의된 확률밀도이므로 k) x 1, x 2, …… , xi... ; t)d x1… … d x;V = 1 (7.2) 이다. s•~e cif ic dis t r i b u ti on fun cti on p1( x1 , x2, … …, x1 : t)는 p1( x 1, x ~, …… , x, : t) = J dx,+ 1… … d.% P1\, ( x1 , …… , x.v : t) (7.3) 로 정한다. 같은 종류의 입자만으로 된 계에 대하여는 pA.( x1, X2, ……, x.~· : t = 0) 가 Xl, ……, X V 의 대충함수로 취하게 되는데, (7: 1) 과 (7. ld) 에 의하여 P.v (x 1, x2, ……, x,\ ; t)가 x1, … …, x , , · 의 대충함수가 되는 것을 알 수 있다. 따라서 gen eric dis t r i b u ti on fun cti on //xi' ... , x, ; t)를 h(x/, … … ,xl ; t) = (NN —! l) TP 1( X 1, …… ,X1 ; t) (7.4 ) 로 정의하여 사용하는 것이 편리하다. 특히 /1(x1 : t) = N p1( x1 ; t) (7.4 a ) f/x 1, x2 : t) = N(N - 1) p/x 1, x2 ; t) (7.4 b ) 가 뒤에 중요하게 될 것이다. 배치공간, 즉 (~, ……,:,) 공간에서 함수의 크기를 바슷하게 하기 위하 여 志 FI(xI, ……, x, ; t) = p,(x 1, ……, X1 ; t) (7.5) 로 F1(x1, … …, x, ; t)를 도입하면 (7 .4)로 f,(x I, …… , x, ; t) = (NN 국!) ! v1t F,( x1, …… ,x1 : t) (7.6) 으로 쓰인다. 열역학적 극한이라고 말하고 있는 N-co, v-co 이지만
n=vN = 了l ; 유한한값 을 취하면, 유한한 l 값에 대하여 (NN-!l )! 上v' ⇒ N(N— 1 )…V I… (N-l) - n’ 가되어 /,(x1’ ……, x, ; t) = n' F1 (x 1’ ……, x, ; t) (7.6a) 를알수있다. (7 .l d) 로 주어진 iLN p ,\ 울 (7 .1)의 우변에 대입하고, x,+1 • ……, % 에 대한 적분을 하면 (7.5) 에 의하여 0FI(xh …a …t , x, ; t) + iL, F, = V' J … r dx1+ 1 ···dxN ( 검수! 다 :1 홉)〈 I JN + IgJ O,I ) PN = V'(N 국) i니s:I dx1+ 1 0;1 +1 Jd x 回. dxN pN ( x,, …, XN ; t) = 망 f dx1 +1 ~ 0i/ F1+ 1( x1, …, X1+ 1 ; t) (7.7) 를 구하게 된다 i L, 은 ` (7. ld) 에 나온 i L N 에서 N-l 인 경우이고, l~N 에 대하여 i LN 을 i L, 과 기타 부분으로 나누어볼 때 우변 첫번째 식의 적분 안 이에는p N 면 있0 에 이는 7고대괄 변 한호또수 적안의 i분~의 : 적 은l 식분면 mp이이 N목 a된 의r0:다 이 P. NX t도된+ l(다 77,. ….l변 e,) 수 그에X에N 리 하보대에여인 한 대 0적 하ij 뭍의분여 치0 표ij 현P가대N에 충 O 에이이의 다고하대.여 한 영 E『적i, 분몰j>0치덴,Jl 'T°ll 대 한 적분치가 같기 때문에 (N-l) Jd X1+ 1 ~i< I 0il Pt+ l 이 되는데, P1+ 1 = 꿈 F,+1 로하여 세번째 식을얻게 된다. (7.7) 의 열역학적 극한울 취하면 言aF, + iL, F, = n J dx,+1 li:s;:I 0a F,+1 (l = 1, 2, … … ) (7.7a)
이고 l=l, 2, …… 에서 성립한다. l=l, 2 에 대하여 (7.6a) 의 f1 에 대한 식 울쓰면 言하 1 + iL1 /1 = Jd x2 012/2 (7.7b) Ta/2t + iL 2 / 2 = Jd x3 (012 + 023 ) /3 (7.7c) 이 된다. (7.7), (7.7a) 는 Born, Bog ol i ub ov, Green, K i rkwood 와 Yvon 이 각기 독자적으로 구하였기 때문에 BBGKY 방정식이라고 한다. 이들 방정식은 계층방정식이고 그 내용은 (7 .1)의 Li ou vil le 방정식과 다를 것이 없다. 다만 (7.7b) 는 iL1 /1 = 흥 · 吉 /1 (7.7d) 으로 된다는 것을 생각하면 Boltz mann 방정식과 유사하다고 할 수도 있다 . (2) Boltz mann 방정식의 유도 한 개의 입지에 대한 gen eric dis t r i b u ti on fun cti on /1(x1 ; f)가 만족시 키는 방정식 (7.7b) 는 2 개 입자에 대한 함수 f/x 1, x2 ; t)와 관련되어 있 고 또 f/x1 , x2 : t)는 (7.7c) 에 의하여 {3( X I ' X2, X3 ; t)와 관련되어 있다. 여기서 (7.7c) 의 k 를 포함하는 우변적분을 3 개의 입자들 서이에 일어나고 있는 상호작용(이하에는 간단히 충돌과정이라고 한다)을 나타낸 것이라고 볼 때에, Boltz mann 방정식과의 대응에서 이 적분이 무시되어야 한다. 그 이유는 Boltz mann 방정식이 2 개 입자 사이의 충돌만 고려하고, 3 개 입자 이상의 충돌효과가 무시되고 있기 때문이다. Boltz万( md-af nl+)nc o 굶방I一I·=정 식 [ 8 ➔rf1 d=%- 2 -d( -Q福 'I ) uc-oll2 -u- l.| I-(,O-,I' u-2-u-l |) 8/1 ' p~ 8/1 (7.8) VI(7, u구 ; t) t(t, 훔 ; t) — /1~, -:; t) /1~, 霜; t)} (7.8a)
에서 그 충돌효과를 나타내는 항이 (a ,r l) col , 인데, 충돌 전의 속도 閃, 閃와 釋 후의 속도 근, v7 사이에는 2 개 입자충돌의 역학법칙, 즉, 운동량 보 존법칙과 운동 에너지 보존법칙이 성립하고 있다. 특히 주목하여야 할 점은 충돌과정에서 L 대신에 업 H f 1 의 곱이 나타나 있고 또 f 1 은 모두 같은 공간 좌표 7 에서 고려되고 있다는 표현이다. BBGKY 방정식 중 (7.7b) 가 Boltz mann 방정식 (7.8) 과 깊이 관련될 것이라고 생각할 때, (7.7b) 가 제 1 원리로부터 직접 도출된 것이므로- (7.8) 을 (7.7b) 의 근사식으로 생각하게 된다. 죽, (7.7c) 대신에 a하t 2 + iL 2 f2 = 0 (7.9) 울 만족시키는 L 에 의하여 .f dx2 01 2 ! 흔 (福) 때 (7.9a) 울 어떤 타당성을 갖는 가정을 하고 유도할 수 있을 것이다 . /2(x1, x2 ; t)가 만족시키는 식이 (7.9) 라고 하면, 그 형식적인 해로 /2(x 1 , x2 ; t) = exp ( -iL}) /2( x l' x2 ; O) (7.10) 울구할수있다. 이 식은 f2(x 1, x2 ; t) = exp ( —iL2 s ) exp (-iLi t — s))/2(x 1, x2 ; 0) = exp ( -i L ,p냐 (x1, x2 ; t-s ) (7.1 0 a) 로 고쳐서 쓸 수도 있다. 임의의 역학함수 A(x1, x2) 에 대하여 exp (-iL2s ) A(x1, x) = A(e-,L ,, x,,e 기 L,s X 2 ) (7.11) 가 성립하는 것이 잘 알려지고 있다. 그리하여 (7.10a) 를 f2(x J, x2 ; t) = h(e 랴 Xi, e-iL , s X 2 ; t- s) (7.1 2 ) 로 고쳐 쓰고, 그 의미하는 바를 생각해볼 수 있다. 우 4i
x:2 '( -s) = e-, 1.,, . x , i= 1,2 로 놓으면 (7 .l a) 의 정의식에 의하여 dx\2>~( - s) = -iL 2 e 기 X, = -iL2 꾼 (-s) = {H2 , x )2 > ( -s)} = -{x)2> ( -s), H2 } (7.1 3 ) 로 되는데, 여기서 H 2 는 업서 입자에 대한 Ha mi l t on i an 이다. 그러므로 x 언 ( -s) 는 s = 0 에서 x,(i = l, 2) 에 있는 입자의 s 시간 전 위상점을 나타낸 다.특히 는, s =r{ 2 )0( 에 —서-s) 7=, 7e- •인 L. ' r一공1: 간 위치rff에 ( -있s)는 =입 자e-의'. i ,. 7sz 시, 간 전의 위치가(7 .된1 3다 a.) Jdx20 1J /x 1, Xz ; t)에서 01 2 는 (7.le) 의 표현에 의하여, 분자력 po te nti - a분l 이u 가| 단一r 2거 --r리-> 』 <반 발r 。 력의을 나범타위내에고서그만도값달을갖거게리 가된 다%. 이 면그 리一r2 하에여 대 한s 가적충 • 분히 큰값이면 홉( 一 s) - ;:p,( -s) I ~ r 。 (7.1 3 b) 이 된댜 평형상태에서 입자 사이의 거리가 충분히 클 때 2 입자 분포함수 가 1 입자 분포함수의 곱으로 표현되는 것을 알고 있기 때문에, 비평형상태 에 대하여도 이 성질이 유지된다고 가정해볼 수 있다• 이와 같은 가정하에 서는 s 가 충분히 크다고 하면, (7 .1 2) 를 fz{x i, x2 ; t) = /2(x\2l ( -s), xf l ( -s) : t - s) ;;; fi(x\ 2 , ( -s) : t - s) /1 (xJ2 J( -s) : t - s) (7.1 4 ) . 로할수있다.죽 fz{x i, Xz ; t) = l~im a c exp {一i L§} f 2(x J, x2 ; t— s} = lSi mX, exp {-iL-z S } [{.(x1 ; t一 s) /1(X2 ; t— s)] (7.1 4 a)
가 된다. 이 식은 (7 .1 1) 의 관계를 다시 이용하여 (7 .1 4) 에서 x 만 ( —s), X ( 창 (-s) 로 하는 대신에 ex p{-i L 2 s} 를 밖에서 x1 과 x 2 에 연산하도록 하고 있다. 이고우,리 1-는 r+2 --(r+7J . .1 4
S2 0 ,2) = lim exp {-iL 2s } (7.1 6 b) S X) 를 도입하고 (7 .1 6) 을 /2( x 1, x 2, t) = S/ l , 2) S/1) S1( 2 ) /1(x1 ; t) /1(x2 : t) (7.1 6 c) 로쓰면 Jdx2 01d2( X 1 , X2 ; t) = .rd ~ d閃 012 sz< 1 , 2) s1(1) s1 (2) /1 (x1 ; t) /1( x2 ; t) (7.17) 를얻는다. 간략하게 쓰기 위하여, 새 연산자 U(i) = S( l, 2) S/i) (7.1 8 ) 롤 도입하는 것이 편리하다. U( i)는 입자 i를 s 시간 자유롭게 운동시킨 뒤 다른 하나의 입자와 상호작용하는 조건에서 역으로 s 시간 운동시켜 처음 위상에 나타난 변화를 준다. 그리하여 (7 .1 7) 의 좌변적분 안에서 /2(x 1, x2 ; t) = /1(U( l) x1 ; t) /1(U(2) x2 ; t) (7.1 8 a) 01 댜 Sl( i)는 (7 .1 4d) 에 의하여 USl(( i서i) ) -閃p( ,7 = .=1 8 閃)S -에 2 ( • •l 의, 2하- )· 여 -p I (7(.71 .19 9a )) 이고, 따라
이다.그러므로 f1(U= (fi)/ U X;( ;i )-tr )~ , S/•1 , 2-·) -p; ; t) = f1(U ( i)7, U(i) 閃 ; t)= f1(一r I, S2( 1 , 2) 一p, ; t) + 8fl (-r ‘,S2( 。l 7 ,2 )p , ,t) | 一r, = 一rI . (U(i) 1 --;::) + …… (7.20) 처럼 공간좌표에 대한 전개가 가능한 경우를, 기체가 공간적으로 비교적 균 일하다면 생각할 수 있다. 우리는 이 전개의 첫항만을 생각하여 Boltz m an- n 의 충f돌2(적x I분, x과2 ; 비t) 교=하려fJ 고O ) (x한I,다 x.2 ;이 t) 근사를 = /1V--1➔, S2( • 1 , •2) -i 1 : t) /1 V--1➔, S2( • 1 , •2) -P ~ : t) = II d問 d~ f潤, i ; t) f1(-; ::, ~ ; t)- ’ 'A(i, ~ : S2( 1 , 2) 閃 : S2( 1 , 2) 閃 : t) (7.21) A(7 국 ; S2(1, 2) 閃 , S/1, 2) Pz) = ~(閃 — S2 (1 , 2) 閃) 짜(閃 — S2( 1 , 2) 閃) · (7.21a) 로 하면,'C[d (x二 (27 .°1국1 72 )f 2:대(閃 x )I신, x에2= ; tj;)j S 2=詞(1 , ` d2閃 \)d ,-npoI1' 1 閃2, dS A n-2; J( ( i,t1) _, I, (C r2--(;p·); 閃: -pnI~국 ) : t ):· 閃) (7.22a) 一 --> _-> ·一 (7.22) 를얻는다. 다음어] S2( 1, 2)p一; = P一; ; i = 1, 2 (7.23) 로 하면 閃(i = 1, 2) 가 I~--;:l
H2 = 같(pf + m+ u(r12 ) = 亡 (Ff + p;) (7.23a) 의 관계가 성립한다. 그리하여 {H2 ’ 0( 閃 — 丙 )O(: _ 丙)} = O (7.23b) 즉
(f · 흙 + 홉 •> _ 。 1 2 )· 函硏 —同 )福(i - ~) = 0 (7.23c) 이다. 이 식에서 01 2 ()( 閃 — 同) 8(? _ 丙) 가(7. 2나3a온)다 =문. ]-;P-i서-: ( - （i 명= 『 백l, 하출2겨)•+ 가,-호 g8-r_72.1 == > --으r82므 r- 교 _8(昴 -― r閃1 만 = 으—土로고 同 )6―공 컴 (간 I[ J+좌(i표는 -에i ~=의2),존 되_는는i 것 =이l) = 土 (戶 —P t) • 훑 8(? - 同) [J(-;;: - ~) . (7.23d) ^- 로하였다. 그리하여 (7.22a) 는 C( 江?：1i )=H 函 d7( p 2 ; p I) *8(7 - 丙)· 8(-n->2 - 一P2 ) (7.24) 가된다. 여기서 7 = 上m (閃 - 閃) (7.24a) 는 입자 2 의 입자 l 에 대한 상대속도인데, 7의 방향에 7의 z 축을 잡고 원통좌표 (b, z) 로서 硏를 표시하여 (7.24) 를 C(7, 閃 ;閃) = I 函g JJz nb db dz 훑 tJ(-;;: - 丙) 8(i - ~) (7.24b)로 고쳐 쓰게 된다. 이 적분 안에서 J: 'dz 훑 8( 閃 _ 丙) 8( 閃 _ E) = 8(_n31 -P-I )6(-n- ►2 - P---2► ), | z• =c c 켓- ( ,-n+ 1 -P-1) 8(-n2 —P一 2 )1 z =-Z (7.24c) 에서 z -P축ri 이 ·I!2, = =c상c a::대 == 속p 도-p;i ;의i 방= 향l 이, 므2 로 ((77..2244de)) 는 2 입자가 충돌한 후의 값이고 는 충돌하기 전의 값에 해당된다. 그리고 이 충돌에서 충돌단면적이 2nb db = 1(0, g) dQ (7.24f) 에 의하여 입체각 d Q과 관계된다. 따라서 (7.24b) 는 C=( n一Jl’ 議 一I'/2 g: p一 jII )( 0, g )d Q {b( 戶-p7 ) b(:- p겅 _ b(7 子) b( 간閃)} (7.24g ) 가 된다. 그러므로 (7.22) 에 의하여 Idx2 °12 f2 (x I, x2 ; t) 네 玩 d~ 忍 閃;t) {(~국:t)· b•〔( I 子dp~~) g IIr_ J y(,60~ ,( g7),- 閃 d·)Q- {b, b(~閃 (,l'f- · 1- -Ep -)--r f1 r ) = H 玩 dQ g 1(0, g) 詞 p-,: ; t)· f룬, ~ ; t) - /(~, 閃 ; t) f E 국 ;(t)} (7.25) 이고, 본질적으로 (7.8a) 에 나온 Bol t zmann 의 충돌적분과 일치된다. 이상으로 BBGKY 방정식으로부터 Boltz m ann 방정식을 근사적으로 유 도하는 데는, 첫째로 2 입자의 분포함수 /2(x1, X2 ; t)가 평형상태에서처럼 r21= 同구 l 이 충분히 클 때 1 입자 분포함수 f1(x , ; t)의 곱으로 표현된다고
가정하는 것이 중요하고, 두번째로는 계가 공간적으로 비교적 균일하다는 조건이 필요하다는 것을 보았다. Boltzmann 방정식을 BBGKY 방정식을 써서 체계적으로 확장하여 3체 충돌 이상의 효과까지도 고려하려면121 (7.7a)에서 n(실제로는 nf5°l 됨 )을 작은 전개변수로 보고 전개하여 축차적으로 구할 수 있다. 이때에 F1(x1, … …, x1 ; t)는 제 0차의 근사에서 F1(x; : t) i = l, 2, …… l의 곱으로 (7. 18a)처럼 표현되어야 하고, 그 시간적 변화가 Fl을 통해서만 이루어전다고 한다. E의 시각적 변화를 나타내는 방정식의 형태는 言8F1 = A(x1 I F1( ; t)) (7.26) 이고, 이것이 Boltzmann 방정식의 확장된 형이 된다.
12) N. N. Bogolinbov : Studies in statistical physics(North Holland 1962) vol. 1의 논문
A(x 1 I F1( : t) ) = 10 n1 A1(x1 I F1( : t) ) (7.26a) 로전개할때 AA1。((Xx11 II FF11)) == J만一md x 복z8 0r1➔I2 FF11 (U(l) X1 ; t) F1(U(2) X2 ; t) ((77..2266bc)) 가 되도록 하여야 한다. (7.26b)는 l=l에 대한 (7.7a)에서 알 수 있고, (7.26c)는 (7.17)에 해당되는 식이다. 7-2 선형화된 Boltzmann 방정식 Boltzmann 방정식을 제 1원리로부터 합당하다고 생각되는 가정을 하여 도출할 수 있다고 알게 되었으므로, 그 방정식에 대한 응용에 더욱 홍미를 가지게 된다. 시간 t 에서 공간좌표 (-r ,- r -+d-r )과 속도공간 (-u -, ➔u -+-du- ) 에 있는 통계적인 입자의 수가 {(7, ~ ; t) d7 d~로 되는 소위 분포함수 f(一r , 一u ; t)가 만족한 Boltzmann 방정식
훑 +了 룹 = [ [ d閃 dQ g I(g, O) {/'['1 - ff) ( 7.27) 은 적분 • 미분방정식이고 적분부분은 비선형이다. 위의 기호에서 f1 = f( _r ,_ u+1 ; t), f' = f(_r + , u- ; t), f'1 三 f(7 , u7; t)를 의미하고 업사 입자 사 이의 충돌 (-:, ~) 一 (u一 , 言)에서 (-:, V:)이 충돌 전의 속도이고, -:, 7;)가 충돌 후의 속도를 나타내고 있다. 방정식 (7.27) 을 체계적으로 살펴보게 되려면 제한된 조전, 즉 f(7 , 7 ; t)가 평f형。 (상7,태 t의) 분=포 n함( 수亞 ) 3/ 2 e 틀 (7.28) 으로부터 많이는 벗어나지 않아서 fc:, 7 ; t) = f。 (7, t) [1 + h(7, 7 ; t)] (7.28a) 로 쓸 수 있고 h 에 대한 2 차 이상의 항은 무시될 수 있다고 가정하여야 한다. 그러면 (7.27) 의 소위 충돌적분항이 C(h) = JJ 瓦 dD. g I(g, 0) ~。 f0J h ' + h'1 —h —hJ (7.29) 이 된다. 여기서 hi, h', h'I 의 의미는 f에 대한 경우와 같다. 위의 적분이 도출되는 데는 운동에너지 보존에 의하여 f。 101 = f。'f o; (7.29a) 가 된다는 관계가 사용되고 있다. C(h) 를 전형적인 적분방정식과 관계짓기 위하여 C(h) = J du: KJ ,/, U:) _h (閃 ) - K。 (7) h(:) (7.30) 로 고쳐K 쓸。 (~ 수) _=있 다 H. 여dU 기: d서~ Kg 。IC(g；,) 는0 ) (_f7o. 2 /091) 에서 곧바로 알 수_ 있고(7 .30a) 이며, KI(7, 閃)는 h ' 의 u수 와 h ' I 의 u? 를 새롭게 적분변수閃으로 고쳐가 논방법으로얻어지는데
l o K( l붉(-;, 죠V:) ~=I c2o 다t 杓。 fo1 {f;1-(Vg :-1 1• J: , (Le ~) -s mi I nu -L4 ' , 21· CO l 망 · + I( |一J一, n - e) } -SIl(n 『7 -디, 0)] sin 0 d0 (7.30b) smz 가 된다. 여기에 나온 함수 I 。 (x) 는 0 차의 Bessel 함수에서 허수의 변수를 가갖 는명 백J 。하 (i고 x), 이 -다u. • - u-(,l7 .=30 bu) u에l 서co s대 ¢칭로관 계하면 , 또 K// ( 7, ~) = Kl (~. 7 ) (7.30c) Kl(V- ' -V-+ I) = K/V, ~, cos ¢) (7.30d) 가 성립되는데, 이 성질을 등방성 (i so t ro pi c) 이 있다고 한다. KI(u一 , -ul ) 과 K l (-;) 에서 · K(7, 閃) = Kl(~, ~) - K。 (7 나 (7 — ~) (7.30e) 푸 정하면, K(7, ~) = K(~, 7 ) 인 대칭관계가 성립하고 (7.30) 이 C(h) = J K(7, 閃) h(~) d~ (7.31 ) 으로쓰인다. 수식의 수학적 내용을 명백하게 하는 데는 모든 양을 di mens i on 이 없는 양으로 고쳐놓으면 편하다. 이하에서 속도에 대하여 7 = （옮 )' I , 7 (7.31a) 로하:iL, (7.29) 에서 _l_ C(h) 에 해당된 Jh = r_3/2 [ f;Z e-c, '[ dQ F(u, 0) [h (c了 + h( 二 一 h(7) - h(~)] (7.31b) 은 충돌단면적 6 에 관계된 양으로
uF (u=, 0() 옮= — )61 .1 1u2g I (u, 0) ((77..3311cd)) 처럼 표시하였다. r-3 / 2 e 국 을 하중으로 갖는 scalar 적 (X,
—o (-c->I ) —
)] = 걸 \ f H d7d 言 d Q F(u, 0)e -, 궁 [X(~) + X(7) -X( s) _ x(7 )] • [cp(군) + cp( 7) —Q (s) _ 富)] (7.33) 위_에+서 _ 세번째 7 적분_은+ 7 와:울 교환하는 데서 얻어졌고, 다섯번째 적분 은 (c , cI) 과 (c,. , C ' ! ）를 교환하여도 좋디는 데서 얻어졌다. 이와 비슷한 계산을 1 장의 끝에서 H 정리를 증명하는 데서 한 바 있다. (7.33) 은 (X, J
® 서로 다른 고유치에 속하는 고유함수는 서로 직교한다. 그 이유는 JI/I; = A,'P , ' JI/I, = 사 ’ I ' A1 # AJ 이면
(1/J, ' JI/I) = ,1.1( 1/ J j ' I/ii ) = (JU 1’ u ,) = A 炫, u l ) 에서 (j.l _ A,) (UI ' ul ) = O 가 i. ＇ -1:- Al 에서 직교함을 의미한다. 같은 고유치에 속하는 고유함수들에 대하 여는 서로 직교하는 고유함수를 구성할 수 있다. 그러므로 모든 고유함수를 직교하게 만들 수 있다. 이들을 규격화되게 하면 (U,~ w, ) = 8,J (7.34c) 라고할수있다 . ® 연산자 J는 scalar 연산자이다 . 그 의미는 h(-c-> )의 변환과 J h 의 변 환이 같다는 것인데 Jh = J ds 雲, 각 詞) (7.35) 으로 쓰면, (7.. 30d) 에서 _c · • 一c·1 = c c1 cos X 의 X 로 -Li ;, 각 = L(c, c1, cos X) (7.35a) 로쓰인다.따라서 L(c, c1, cos X) = lt=cc l G,(c, c1) P,(cos X) (7.3 6 ) 로 Lege n dre 다항식 P,(cos X) 로 전개된다. 7 의 각 (O,h(C :) = Rrl(cI) Y,m(Ol’ 이 (7.37a) 이면 Jh = Fr1 ( c) Y,J 0, ({)) (7.37b) 가 된다. 특히 Rrl(c) YIm( 0 , o) 가 고유함수이면, 고유치 ;L rl 에 의하여 F,,(c) = Jr1 RJ c) (7.37c) 로 쓰인다. 고유치 Arl 은 m 에는 관계하지 않고, l 의 값에 대하여 (2l + 1) 개의 축퇴도를 갖는다. r 은 7 의 각에는 관계하지 않지만 고유치를 규정하 는 데 필요한 또 하나의 계수이다 . 적분 J h 에 대한 적분핵 L( 7, 건)이 L( 7, s) = e- c; I: ;,j 1/1,(7）안,（적) (7.38) 으로 전개될 수 있다는 것이 (7.35) 로 자명하게 된다. 고유함수계의 완전성 에서 후 t/; , (c 露這 e-c ' = b(7_? i) (7.39) 도성립한다. h(-r ,一 뿡c , t=) 가J 공h ,간 적으r로 = 균 t일(n 하a여) ( h~(7 ,) t )1/로2 되면 (7.27) 이 (7.4 0 ) 후i 간략화된다. 그러므로 고유함수 Urlm(7) 로 h(7, t)를 전개하여 h(-c➔ , r). = E- arlm.( T). Urlm-(-c ) (7.4 0 a) 로 하면 전개계수 a,1m(r) 가 ddr ar1m(r) = A.,1 ar1m(r) (7.4 0 b) 를 만족할 것이므로, a,1m(r) 가 ar1m(r) = ar1m(O) e 샤 = ar1m(O) e -|Ll(nc) （꾼) ' t (7.4 0 c)
처럼 감쇠하는 것을 알 수 있다. 다만 고유치가 0 인 계수는 불변하여 lim h(c, t ) = a 。 + a 。 , C, + a()y Cy + a 。 z cz + a 。 1C 2 (4.4 0 d) 1-X 가남게 된다 . (1) 소리의 전파 선형화된 Boltz m ann 방정식은 기체 안에서 전파하는 음파를 아주 잘 해명하여준다. 기체는 많은 분자가 집합하여 이루게 된 다입자계인데 그 안 에서 일어나고 있는 파동은 소위 collecti ve mo ti on 을 나타내는 것이므로 입자의 단독운동과 집단운동 사이의 관계를 볼 수 있디는 점에서 홍미가 있다. 방정식 (7 . 27) 을 간단하게 고쳐서 쓰기 위하여 (7.3la)-, (7.31b) 를 고려 에 넣으면 (沿 1)1/ 2 뿔 묘 · 뿔 = n( 1Jh (7.4 1 ) 로 되는데, 음파를 각진동수 o 와 파수 T 의 섭동인 h(7, 7, t) = h .,, . (7 ) e’(r . 7 河 ) (7.4 2 ) 에 주목한다. 그러면 h ., (7) 는 [급(듦 )1 12 w + ik ·-;!]h.,, . = n(J Jh u,k (7.4 2 a) 를만족한다. 양자역학의 섭동이론을 형식적으로 적용하여 (7 .4 2a) 의 해를 구하기 위 굴回 E = -i( 듦 )1/2 읍 (7.42b) e = -i. nku (7.4 2 c) 로 놓고,J hw (.7 l .+4 2a )e 를 c, 一khw . l방 =향 으Eh로w,k z 축에 취하여 (7.4 3 ) 로 쓴다. 그러면 J + e c, 가 Ham ilt on i an 에 해당되고, J가 섭동 없는
Ham i l t on i an 에 해당된다 . 기체분자의 산란단면적 6~10- 1j c m2 , n~1019 cm -3 로 하.JI, l,OOOHz 의 음파를 생 각하면, k~ ½cm- 1 이 고 上na ~ 1019 1 x/ 51 0- is ~ ―50 」00_0 이므로, (7 .4 2c) 에서 l i: l<{ l 이다. h 야 를 c 으로 전개하여 hw ,k = h ~~ + e h 일 + c2 h 엷 + … … (7.4 3 a) E = c E( + c2 E( 2) + …… (7.4 3 b) 울 (7 .4 3) 에 대입한다. (7 .4 3b) 에 E (O ) = O 로 취한 이유는- 음파는 k = 0 에 대하여는 w = 0 가 되기 때문이다. 대입하여 얻은 식에서 c 의 계수가 같다고하여 J h~l = 0 (7.4 4 ) J h 앓 = (E( II _ Cz ) h$ (7.4 4 a) J h 엷 = (E11> - c,) h 덟 + E( 2) 福 (7.4 4 b) 등을구하게 된다. 소위 0 차 근사인 (7 .4 4) 의 해를 구할 때, z 축에 대칭이 되도록 하면 고 유치 0 에 속하는 고유함수로 1, c , 와 판만을 생각하면 된다. 고유치 0 에 속 하는 직교, 규격화된 고유함수
J u:,) = A, UI(') ( 7.4 7 ) 된다고한다. h$ 를 h :Oi 에 직교하도록취하여 hI(』 = 1.,E.i,# 0 a:2) u!’) (7.4 7 a) 로 하고, (7 .4 4a) 에 대입한다. 그러면 E A, a: 미 l/J)'> = (E0> -c,) ( a~11
의 세 가지 해가 있다. 위에서 값이 결정되지 않는 a 냉 a 넹 a 망 를 편의상 1 로놓았다. 음파가 (7 .4 2) 로 표현되고, T가 z 축 방향이어서 h(7, 7, t) = [h~ 0l + e h$ + …… ] ej(k z -wl ) (7.4 9 ) 로부터 음파의 위성속도 % 가 이.x., (V7o . 4 2=b ) 를k(1 ) 보면, E (1) = ( 울) 1/2 에 대 해서 (7.4 9 a) (1) = l. (/ ZkmpT \) 11 2 n(J E = i( 루) 1/2 nc [e E (1) + e2 E (2) + …… ] = i( 몬) 11 2 n(J ( ＿갑) E ( + …… = （亨 )1 /2 어 ) 1 /2 + …… (7.4 9 b) 를 (7 .4 2c) 로 c 의 값을 대입하고 알 수 있다. 여기서 Boltz m ann 상수를 kB 로 하여 파수 k 와 구별하였다. 이 근사에서 u 。 = 뿡 = (§구 )1 /2 (7.4 9 c) 을알게 된다.여기에 대하여 E m = -（울 )1 /2 는 z 축의 (-）방향으로 진행하는 파동이고, 그 위싱속도의 크기는 (7 .4 9c) 와 같다. 또 하나의 E (I ) 의 값 E( = O 는 음파에 해당되지 못하며, 더 높은 차원의 근사를 하여 열E전(도I) 에 = 관信계5)된 \다 1/는2 의 것 경을우 알에 수h 갭 있 룰다.구 하기 위하여는, (7 .4 8) 에 硏를 scalar pr oduct 하여 a:·) = ( 1/J/• >|,A c, ,| ( {)1 ) (7.50) 을얻으므로
h,( ~ = Ij.: 2 ( l/1 :미 , C|, 시<{J 1 ) 社 ) (7.50a) 이다. 이것을 (7 .4 4b) 에 대입하고 E( 2) 을 구하면 E(2) = 7Y:-: I ( l/1'. '11, 2c. ,1 < fJ1 ) 12 (7.50b) 을 알 수 있다 .h( i 와 E (2) 를 계산하기 위하여는,고유치 A, 와 고유함수 U 민 의 지식이 필요하다는 것을 보았는데, 실제적으로 그들을 구하기는 대단 히 어렵다. 그러므로 (7.4 7 a) 대신에 e-c 2 을 하중으로 하고
= 켓(： 적) + e- [1 + 27• C: + t(c 2 —출 ) (cf 」-) ] (7.52) 이고, 이것을 Jh = JL (7, ;) h(;) d; ` 에 대입하면, (7 .4 1) 이 `)1 /2 뿔 + c 뿡 + ~ah_ = (~) j dc1e 굽 [1 + 2c • c1 + 웅( c2 —방 ) ( Ci _ 방) ] h(cI) (7.52a) 으로 쓰인다. 이 근사는 Kac 에 의하여 제안되었고 음파의 전파를 정성적으 로 알아보는 데 많은 도움을 주고 있다. 7-3 Maxwell 분자의 기체 대체로 Boltz m ann 방정식은 수학적으로 매우 어렵다고 알려지고 있으 며, 그 선형화된 충돌연산자의 고유치와 고유함수도 구체적으로 알 수 있는 예가 거의 없다고 할 수 있다. 다만 분자 사이의 상호작용 p o t en ti al 이 득 수하여 시간당 충돌수에 대한 표현이 충돌계수 b 로 g • 2nb db == ga-· . l((0g) , d0Q) dQ (7.53) 처럼, 산란각 0 만의 함수가 되고, 상대속도 g에는 관계없게 될 때는 그 방 정식이 대단히 단순화된다. 상호작용 po te n ti al ¢(r) 이 ¢(r) = a r-• (7.54) 로 주어지면, 산란각 0 가
0 = r _ 2 j 。U [1 군 -;군 ) ] ! /2 (7.54a) 처럼 구해진다. 위에서 b 는 충돌계수이고, u o 는 피적분함수의 분모가 갖는 0 점 중최소한값이다. 이 식으로부터 0 가 4mabg-2 n 에 의하여 결정되는 것을 알 수 있다• 따라서 0 의 함수 l(0) 로 ~mg2 = l(0) (7.54b) 로놓으면 2ng b db = Zn g문) (폰 ) 군 \) 「 -; - i (0) dl(0) (7.54c) 으로 계산된다. 그리하여 n = 4 면 충돌수가 산란각 0 만의 함수가 된다. p o t en ti al 이 ¢(r) = ar- • 인 반발력이 분자 사이에 작용한다고 생각되는 기체에 대하여 Maxwell 이 점성, 열전도 등 소위 수송현상을 주로 연구하 였다는 데서 이와 같은 기체가 Maxwell 모형이라고 불려지고 있다. ( 1 ) Bob y lev 의 변환식 13)
13) A. V. Boby le v : Sov. Phys i cs Dokl. 20 (19 76) 820 M. H. Ernst : Phys i c s Rep o rt (North Holland 1981)
공간적으로 균일한 Maxwell 모형의 기체에 대한 Boltz m ann 방정식을 국L = [信 d6 a(i · ;) (f' f\ 一 ff1) (7.55) 척료 쓸 수 있다. 위•에• 서 g^ 는 상대속도 7 방향의 단위 벡터이고 e^ 는 산란 방향의 단위 벡터이다. 그리하여 c^ · e^ = cos (Jo l 고 de^ = sin 0 d0 d
f(7 , t) = n I (:s3 e;--:¢(T , t) (7.56a) 를 취하고, Bob y lev 는 (7.55) 의 Fourie r 변환을 다음과 같이 구할 수 있 었다.죽 뺏 = nIdeAa (i .마 ( 쌍 (k나 ), t) r/J( 쌍(i一:), t) -¢ 0:, t) ¢(0)} (7.57) 여기서 k 는 了방향의 단위벡터이며 (7 . 56) 에서 명백한 것처럼 ¢(0) = 1 (7.57a) 이다. 그리하여 충돌단면적과 관계된 µ,x, = nJ d ; a(k • ;) (7.57b) 를 정의하면 (7.57) 이 뺏 +^ µo o ¢(k, t) = n.f d -;a(k • ;)} [ ¢情(i +eA ) , t)· ¢( f(k- e), t) ] (7.57c) 으로 쓰인다. (7.5 7 ) 또는 (7.57c) 는 2 중적분에 대한 방정식이고, 또중적분 에 대한 (7 . 55) 와 비교하면 대단히 단순화된 것임을 알 수 있다. [Boby le v 식의 증명〕 Fourie r 변환 (7.56) 을 하여 (7.55) 로부터 n 뺑 = _f dfu(-u- e -) 기f(~u `l ) f` } du: d;
11 = HJ瓦 d; a(; • ;) 군 다 (7) /(~) (7.58a) ••••• 을 고쳐서 쓰는 데 약간 어려운 접이 있다. 두 입자가 하는 충돌의 역학에서 질량중심의 속도 V: m = ½(v+t) = 강(古?!）와상대속도 7 =7-閃 」수 = u구 _u? 에 대하여 7= 7c.m+> :7 = v,,m + >7 = 방 (7+ 汀 + 》끓 7i = V:.m - >-;, 一V1 = V_>, .m -t1g 구 (7.58b) 가성립하고 _>_ /\ __ /\ du du1 de = du' du'1 dg (7.58c) 도 증명된다 .l4) 따라서 (7.58a) 의 적분에서 적분변수를 一u ―, >u), e＾ 에서 구u' , 국u;, g로바I꾸l 고== [[IIII 孟記 詞d訂 d d; ; exe(x;( ;• •; ;)) e군 가(?) ft((u0 ): ')f ( u l) -;;. 十건적 1 rt !'\ rt ~ (7.58d) 를 구한다. 마지막 식을 얻는 데에 (7.58c) 와 (7.58b) 가 사용되고 있다. (7.58) 의 L 는 그대로 두되, ―v➔ = 71 (u― ➔ + I ~v1\) +I ?1 ”로 바꿔서 쓰면 (7.58) 이n 뺑止 = II d갑 V: e-if -(다 ;) f (7) f(閃 )B(T, 7) (7.58e) B(fe , g) = J d;ex( 戶 ){e -성.- k ./\ - e 令, k➔/.\ } (7.58/) 으로된다. 그런데 14) d-u-+ d-u-1+ dAe = d-V-+c . m d-g-+ deA = ~--m+ g2 dg dg/\ de/\ d-u-+' d-u-+; = d--V+ ~ d-g-+ ' dgA = d--v+; , m g2 dg de^ dg^
B(_k , -g ) = B(一g ' , -k수 ) (7.58g ) 가 증명되어 1 5 ) B(一k ' ' -g->) = [dea(l. e){e 令 kg ~·; 一 e - 송 이 (7.58h) 으로 고쳐 쓸 수 있다 이 B(k, ;)를 (7 .5 8c) 에 대입하고 喜『+言=) t +(k ½+ 1 k· ~()k7e+) 홍 (k - ke)u l 1,7 /\ 一 =拉+霜+ 망(g _8 )閃 『n(神;~+ (-k7, ;t))= + f½&- a;.( 戶-;=) 홍Hkd ,(u 댜- +,다 - V(1,) 집 +I f (전k;; ),( u- - -V 1) = 一k •一 V 롤 고려하면 (7.58c) 로부터 {`e 숭 ( :k(?-3:` 一 e;7.1 =n2` [ 타 (戶)’댜 (k+;))¢ 情戶)) -¢ (파 (0)] (7.58i) 을 알 수 있다. 따라서 (7.57) 이 증명된다. 평형상태의 속도분포 f, q (겹 = n ( 2nmks T ) 3/2' 15) B( k,;) = B(g), k) ) 의 증명 ^e -g^ = _g>로 하면 g^ • ^e = l _ 웅r-2 ; (O g 도 2) 인데, 8 를 고정하면 d; = d7 이다. (7 .5 8d) 로부터 B( 言) == e[ d令e- •- · --1: (J 1d e - ex운 ( )1 {一 e t운-一; + 一);[I e숭 - U.^ .一e: )- ， 당，，- 나-· 一1 ] = e 令•一 · 一• A(kg )
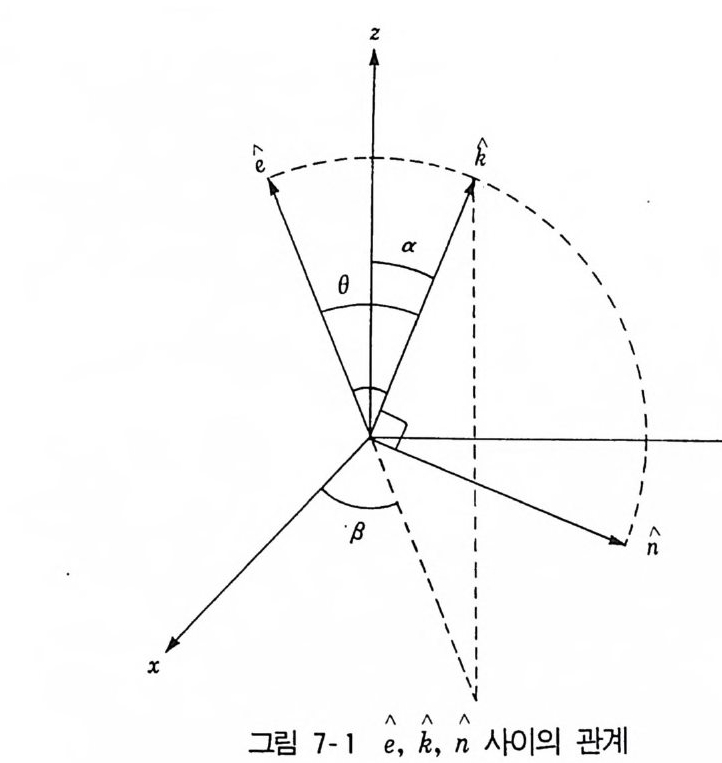z
에 대응한 ¢」 (T) 는 (7 .5 6) 에 의하여 ¢디 (k) = e -(몫 )k ' (7.59) 이다. 여기서 Boltz m ann 상수를 %로 하여 파수 k 와 혼동되는 것을 피하 였다. (7.57) 에서 ¢(T, t) = ¢여 (k) [1 + e/\J h(k)] (7.60) 로 놓고 h(k) 에 대하여 1 차까지만 취히여 Ah(k) = n J d;,a( 食 • ;){h( 성尸 다)) + h(½
h(k) 에 대한 (7.61) 은 선형인 적분방정식이고, A 는 고유치에 해당된다. 이 방정식k^ 의 + 고 e^유 =치 와2c o고s 유망함, 수를 구하기lk^ —위하e^l여 ,= (k2 s •. ln; ) 2오= cos e 로 하면 (7.62) 이다. 지금 새로운 단위 벡터 n^ 을 ; = cos 0k + sin 0 요 (7.62a) 이 되도록 취하면 요는 t에 직교하고 &라 £가 만든 평면성에 있다. 따라서 I\ k, = sin a cos p, k/\1 = sin a. sin p, k^ z = cos a. (7.62b) 로 k 의 방향을 정해주면 n/\, = cos rx cos /3 cos
ILTL, i i = si. n 홍0 cos 0: 十, cos 20 si. n o: cos
ku+ 1 P,( c os a) (7.64) 이고,그 고유치가 A r 』 = n 仁 n sin 0 d0 a(cos0) { cos2r +/ ( 망) P, ( co~ 망) +'' sin 2r +/ ( 망) P, ( sin 망) -1 - b,.ob ,.o } (7.54a) 로된다. Fouie r 역변환식 (7.56a) 와 h (h）에 대한 (7.60) 을 보면, 고유함수 (7. 64) 에 대응하는 속도분포함수가 霞) [l + e' l/1,J(,!)] 가 되며f,。 ( ,!u)rl./1I,( , 7I)( 7가) 충=돌 n연J 산자~ (7 e. 이31,b)q 의 ( k고) k유2r함 +1 수P 1가(c o된s 다a). 죽 (7.65) 이며, 여기서 묘 (u) 에 대한 규격화는 고려되지 않고 있다. k = t가 (7.62b) 로 주어졌으므로, 7 에 대하여는 u, = u sin a cos b, uy = u sin a sin b, u, = u cos a (7.65a) 로할때 _k-> • 一v· = kv {co s (X cos a + sin tX sin a cos(/3 一 b )} = kv cos @) (7.65b) 로된다.그리하여 e'r. -: = e i lwco, 도 f (2l + 1) i'j,(kv ) P,(cos @)) (7.65c) l= O 와 P,(cos ®) 에 대한 합의 정의 P,(cos @)) = 2l 問 효, Y1m((X , p) Y't ,( a, b) (7.65d) 룰사용하면
fo( - -: ) i/J,. /--: ) ~ I(v) P,(cos a) (7.66) 이고 I(v) = j[ 。~ k2dk ¢,. k2r+i ~ 1: kv ) = [ 。~ dk k 파 /+ 2 e- （몽 )k :二J, + 송 (kv) (7.66a) ` 이다. Bessel 함수에 대한 적분공식에서 I(u) = C [( 급 )1 /2 U 「 을얻을수Jt슨있r는(r 방데( 방 ,++이r +l식 l+에+ n서n) )s =古 l (+2 -방二 , v )l n= (-f;r r /2 V 로(쓰7.6고6b ) IJ은 r(rs( +s + r +n +n +l) 1) ( 군n! )n = r! e - 오2 도(一:(y7.6 6c) 단
ap = >( r —(ps) 十 !i (ls l+_p -)-- ! (7.66d) 의 관계가성립되는것을이용한다.수반 La q uerre 의 다항식 L:s)(x) 와 Son ine 다항식 S(;(x) 는 같은 함수이며, 그 전개식이 L:s)(x) = S!r)(x) = 홀 j ! (r ( jt검+ j ) ! ( _x)} (7.66e) 이므로 .16) I(v) ~ e 죽 S 다 ( 后 )u1 (7.66f) 16) S 떳 (x) = L 딩 (x) = 1 S 잇 (x) = L'!' (x) = -x + k + 1 ff-t (x) = L 덩 (x) = 소2 -( k + 2)x + (k+2)2 ( k+1)울 알 수 있다. 결국 고유함수 U,,I C；)는 u,, 1(-u-> ) = N,1 로 ( 二)2 v1 P,(cos a) (7.67) 이다. (7.37a) 에서 알 수 있는 것처럼 ur,I mC :) = Nr1m s:; ( 릅) uI YIm(a, b) (7.67a) 가 Maxwell 분자에 대한 충돌연산자의 일반적인 고유함수가 된다. (2) moment 전개식 확률밀도 P(x) 에 대하여, 그 특성함수
- -u:;,P ,+t· )· ·+l P,n> V은 ~r, +·속··+ 도r ,) 臨7- n에 대 한 확률(7밀 .69도) 이다. 그리하여 (7.56) 은 3 차원에서 (7.68) 에 해당된다. 따라서 ¢(k, t)는 특성함수이고, (7.68b) 에 해당되어 로 momen t가 정의된다. Maxwell 분자에 대한 Boltz m ann 방정식 (7. 55) 는 많이 단순화된 꼴이지만,비선형인 적분방정식이기 때문에 그대로 풀
쑨 없다 그러나 특 성힘수 ¢(T , t)가 (7.5 7 ) 의 Boby le v 방정식을 만족 시키고 있기 때문에, 이 식에서 moment 사이에 성립하는 방정식을 구하여 간접적으로 해를 구해볼 수 있다. 평형상태처럼 속도공간에서 f(u一 , t)가 등방성을 갖는다면, /(7, t) /n ⇒ P(u, t)이고 문제가 대단히 간단하게 된다. 그러므로 처음에 이 경우를 생각해보자• ¢(k, t) = J ;· 一 e' lvcosO P(u, t) = s: = 。 (( 2_sl +)’ (1k )2 )! ’ 下U (7.70) 이 되는데서 y = k2, ~
A. = µoo ( 1 + b.o) —µ n0 —µn n (7.72b) 이다. (7.72) 의 우변에는 M, (l< n) 만이 나타나고 있으므로, Ml(t) , M2 (t), ……를 축차로 정확하게 구할 수 있다• 속도공간에 등방성이 없는 경우는 수식이 복집하게 되지만 그 방법은 위 와 크게 다르지는 않다 . T와 (7.62e) 의 7선 了등을 7 로 대표하고 ¢(1,t) = 1 一 iq 꾸q . M; _ 喜q 2 E Q : &M ? + …… (7.73) 후i 전개한다. 여기서 治 는 7 방향의 단위 벡터이고 ;’는 그 a 성분을 의 미한다. (7.62e) 에서 了는 산( ~ + t) = 망 [(l + cos e)t + sin 0 ~] 了 = §(t _ 8) = 망 [(l + cose)t -si n 0 ~] 을 (7.57c) 와 동등한 呼 + µoo ¢(k, t) = n j 恥(岭)｛詞+t)¢花,t)} 에 대입하고 k 의 계수를 비교한다. (7.74) n = l, 즉 k 의 계수에서 一i ~ k. [aTM?i + µoo Mi ] = —in` [ de^ a(k^ e^) 다. .+仁] M1 을 얻는데, (7.62e) 에서 l+. + L. = ka 가되어, 이 식에서 뿔 + µ라i = nJ d eix ( k • ;/\)M i = J1oo M1 (7.75) 울 (7.57b) 의 µ 00 의 정의를 써서 얻는다. 죽 쁘at =O
따라 A1 M1(t) = M:(O) = const (7.75a) 이다. M f=
(n, 令) = 占 j : fix 令 dq> (7.76e) 를의미한다. 따라서 (7.62c) 에 의하여 7짜 = ( cos2r t. cos2/ 3 + sin 2 / 3) / 2 g= (cos2a sin 2 p + cos 내) /2 T짜 = sin 2 a /2 (7.76f) n^ , .n^• p = -sin 2 r x sin / 3 cos f3I 2 n^ X n^ 1 = —s i. n ct. cos ct. cos {J/2 n^y n^ 2 = -sin a cosa sin p /2 이 됨을고려하고 k. = sin a cos p, k, = sin a sin p , t z = cos a. 의 a, p에 정당한 값을 대입한다. 그러면, a = /3 = 0 일 때 견aMf + µ00M? = A(2) M 7 + B(2) M : 止 + 쩡B(―2) [ 隋 — M~M t + 碩 _ 聞 M f] (7.76g ) 을얻고 a= 李 /3＝땅이면 —8M~ 꿍 , a=f7 t, /3＝ 0 이면 0M8t ? 에 대한비슷 한식을얻는다. a= 훙 /3＝t이면 T8M/?, a=f , f3 = 0 이면 二8 碩 T_' a = Tr 섀 = 망이면了8M T 꿍 에대한식을얻는다.이들식에서중요한 관계는 M2=M? ＋昭 +M'{ 로할때 쁘at = 0, 죽 M2(t) = M2(0) = const (7.76h)
이다. 이 석은 운동에너지 보존을 나타낸 것이다. Mt = cons t인 (7.75a) 와 M2 (t ) = cons t에 의하여 (7.76 g)와 그것에 대응되는 식으로부터 Mf (t ) = [ Mf (O ) - 강 M2 (0 ) ] e 용 u •+ t M2 (0 ) (7.76i) 롤 구할 수 있다• 또 여기에 대응한 M? (t ) = M? (O ) e -용 B '“ 1 (7.76j ) 도알수있다 . n = 3, 죽 k 3 의 계수 관계에 대하여도 갇은 방법으로 계산할 수 있다. 그중중요한관계는 Mj = M ju + M j»' + Mj 끄 (7.77) 에 대하여 성립한 Mj (t) = Mj (O ) e- B ', (7.77a) 01 다. 더 높은 처수의 momen t에 대한 식도 원리적으로 같은 방법으로 구할수 있을 것이다. 그러나 수식이 대단히 복잡하게 되어 일반적인 관계식을 구할 수 있을까는 의심이 간다. 또 계가 공간적으로 균등하지 않은 경우도 ¢(T, t) 대신에 ¢(7, T, t)로 하면 더 복잡하지만 이와 비슷한 관계식을 얻을 수있다. 7-4 수송계수의 도출 평형상태로부터 벗어나 있는 기체에 대하여 물리적으로 의미있는 양을 정의하기는 쉽지가 않다. 그러나 평형상태로부터 벗어나고 있는 정도가 비 교적 작고, 벗어나게 되는 원인이 기체가 공간적으로- 균일하지 않을 때는 점성과 열전도의 현상이 물리적 측정의 대상으로 나타난다. Boltz mann 방정식이 제안된 뒤 바로 점성계수와 열전도도 등의 수송계수를 도출하려는
시도가 있었으나, 체계적인 방법은 H i lber t 1” 가 제시하였고 Enskog 18> 등이 실행하였다. 이와같이 계산된 수송계수를 실험의 측정치와 비교한 데서 Boltz m ann 방정식에 대한 신뢰도가 깊어 갔다 . 1 9 )
17) D. Hi ll bert ; Ma th. Ann. 72, 562 (1912) 18) D. Enskog ; Thesis , Up ps ala Univ . (19 17) 19) J. Ferzig e r & H. Kap e r ; Ma the mati ca l the ory of tran spo rt pro cesses in gas es ; North Holland (1972)
Boltz m ann 방정식 紙草J0t . L + --:. 료0F = C(/) (7.78) 에서 충돌효과를 나타내는 적분 C( f)는 C(/) ={ fc[f: , d77, dt)Q fIc(O:,, 근問, ―t)7 1- ) fc1-:;,: -7--:, 1 t ) fr, 7, t)} (7.78a) 인데, 이 식을 써서 장소 7 에서 거시적인 물리량들인 입자밀도 n(7, t), 유체속도 U_ (-r·, t.) 와- 온 . 도 T(·-r ·, t)의 시간적 변화를 구하기 위하여, 이들 과 fc:, 7, t) 사이의 관계식 n(--r> , t) = Jd --; /(7, --:, t) (7.79) 一U (.r , t) = n(Fl, t) 'f d_u +一u f(_r> , 一u , t) (7.79a) T( 7, t) = 칭2 T1 n(r1, t) Jd 7퉁 (:―따(二) (7.79b) 가성립한다고한다. 贊할때 1, 芹뿡 -v 2 이 보존하기 때문에 충돌적분 (7.78a) 에 의한공 헌이 없어지고,
교0교t + -0%r n(-;, t) 硏?, t) = 0 (7.80) n(1, t)m (뿔+fl-~) = -틀: (7.80a) 와 웅 nk (呼요 + 『． 뿔) = —i,fj P jj D ii _ 广총 (7.80b) 가 성립되는 것을 제 1 장의 끝부분에서 보았다. 여기에 나타난 PJ -7-➔, t). = mJr d--+;( .u i - U). (.u ; - U). t(:- 7-- ➔ , --+;, t) (7.80c) 는 str e ss ten sor 이고 DJ 7, t) = >(:+ 뿔 ) (7.80d) 의 sqtr,aF in, tte) n sor= 의 I시d u간(u적, _변 화U이) 며붕 (1_ 汀)3/(7.~t) (7.80e) 는 열류를 나타내는 vecto r 량이다. 기체의 비균등성의 정도가 작아서 0 차의 근사에서 기체가 국소평형상태 에 있다고 하여, 그 상태를 f。t, 7, t) = nt , t) ( 潟芹 7, t) ) !/2 exp {_ m(u一국 ,?}) t)) 2 } (7.81) 로 나타낼 수 있다고 하자. 그러면 (7.80c) 에서 F 갱 = n(--r> , t) kT (-r , t) 8IJ = P(--r> , t) 8 (7.81a) 이고, 기체의 압력을 나타낸다. 또 q써) = O (7.81b)
이고 열류가 없다는 것을 알 수 있다. 그리하여 (7.80a) 는 이 근사에서 nm( 필+「을) = -: (7.81c) 인 Euler 의 유체방정식이고, (7.80b) 는 (뿔 +v. 률) = -응 T(E:-) (7.81d) 이다. 이 식은 (7.80 澄· 이용하여 나 + fJ. 훑) (n r-312 ) = 0 (7.8le) 으로 고쳐 쓸 수 있는데, 유체의 단열변화를 보이고 있다. 기체가 전체적으로는 평형상태로부터 많이 벗어나고 있다 하더라도, 국소 적으로는 (7.81) 로 표시된 국소평형상태에 아주 가까운 상태에 있고 f(-r- >, -u- , t) = f。 (-r-',> u-·, t ) (1 + c; h(-r', -u·, t)] (7.82) 로 표시된다고 하자. 여기서 작은 양을 나타내는 pa ramete r ,는 비균등성 척도라고 부르며, 국소평형으로부터 t(7 , -:, t)가 벗어나는 이유를 공간적 인 비균등성에 있다고생각한것이다.따라서 시간적 변화 훑-도 ,1- 로 하며,공간적 변화 고ar 一‘ 도 'a요r, —로고쳐 놓고생각할수있다. 그러면 (7.78) 이 8 의 1 차까지에서 《(꿉 + 7 紀 f。(言--:, t) 二 c( f。 (1 + ~h)) (7.82a) 인데 C( f。(1 + 'h)) = C( fi。) + (7, 7, t) J(h ) + 0( 꾼) (7.82b) 이고 C( f。) = O (7.82c) 가 성립한다. 따라서 (7.82a) 로부터
i(: + v弓 홍 ) = J( h) (7. 83 ) 를구하게 된다. 여기서 J( h) = [[ d-u l d-Q I-(O• , I·-u _ -u 』 ) |-u _ 一UI I f。 (-r ➔ , -u l, t) 福`， 군, t) + h 룬, 訂, t) —h (7, -C:, t) —h { J,q, t)} (7.83a) 01 다. f。 (7, -:, t)는 (7.81) 에 보인 것처럼 n, fl와 뗀} 통해서만 t와 7 의 함 수이다. 그리하여 (7.83) 의 좌변을 범함수미분으로 i(홍 +7 찰) = [ ~\ （블+『틀+: 룹 ) ] 미말( 。: -T· 6:' +u〈 ·多)] 니 멀\（뿔+fl.뿔 +7 률)] (7.83b) 로 하고 20 ) 登의 1 차에서 (7.80), (7.80a) 와 (7.80b) 로 얻게 되는 (7.80), (7. 81c), (7.81d) 를 대입한다. 그 결과는 i(룹 +7 을) = I ( 言 정) u, a;:IT + 骨t (U;Ui - 송 u 2 <> J Dii (7.83c) 가된다. 위에 쓰인 20) 기호 [%~' ~骨]의 의미는 a7}x 의 함수인 경우 검 = AE 忠 A(a(x) ＋있길 )-A(a(x)) 이고 [붕총] =［감빵 dx
-U = -V - _U (7.83d) 는 소위 입자의 열운동 속도이다. 결국, (7.83) 이 J( h) =+ 訂혼 붉齋 (u , -u, 당-) t u ju~ 2 o,) D,j (7.84) 로 되고, 선형인 적분방정식을 나타내고 있다. 그리하여 그 해는 J(ijJ)= 0 의 일반1/해J (— u· ) = C 1 + IJ; C2i U, + c3 _U > 2 (7.84a) 1= 1 과 J( A;) = (景2 _ 응) u 1 (7.84b) J( Bk l) = 룹 ( U, U1 - ½U2 {Jk l) (7.84c) 의 특수해 Ai( - ;), B k! (-;)에 의하여 h = 1I=: l A,(~ ~8r, + [LI B 五) D kl + 1/J(-;) (7.84d) 처럼 구해전다. J (h) 는 (7.31b) 의 연산자 J에 의하여 J( h) = J • h 가 되고, 또 연산자 J는 등방성을 가지고 있으므로 Ai( - ;) = A(u) u, t u2 <>t ,) . ((77..8844ef)) B (U: ) = B(u)(u k u, —
로 쓰_+인 댜 여-+기_서 A(u), _B (u) 는 u = 1U : 1 만의 함수이다. n(r', t), U (r', t)와 T(r- , t)를 정해주는 식 (7.79), (7.79a) 와 (7.79b) 에 (7.82) 와 (7.84d) 를 대입하면 c1 = 0, c2i = 0, c3 = 0 (7.85)로하고 ·[dJ {0 A(u) u2 = 0 (7.85a) 를 요구하면 된다. A(u) 에 대한 조건 (7.85a) 만 고려한다면 h = I: A, (訂 Oa lnri T + ET.i B u (訂 Du (7.85b) 로할수있다. str e ss ten sor (7.80c) 의 0 차 근사가 압력을 나타내는 것을 (7.81a) 에 보았는데, 그 1 차 근사는 P/『 == mm \I 五d一u· Lf0uh,uu ,A EB (u ) ( uk ul _ § u: 8kI ) Dk I =(m U •尸~ U1 다— (강u , uu,2 D u- ) tDk l U2 () , ,) tk,l B(u ) = 뿡 ［타 [bk,l (uku, - ½u빌) B(u) (u고 1 - 송 u 벌) ] sij (7.86) 로 쓰이며, 새로운 stra in ten sor S , 늠 D ii 에 의하여 siJ = D,J - 강(? DII) & (7.86a) 로 정의된다. (7.84c) 를 다시 사용하고 Pi t = 町 du fo ~ B 니 (Bkl) sij 로 쓸 수도 있고, 새로운 기호를 (7.33) 에 해당하여 [F, G] 三 'f f。 G J( F) £ = (G, J • F) (7.86b) 룰 정의하면 [F, F] ~ 0 이고 (7.86b')
Pt1 1 = 草 E[ B k/ , B 』 S (7.86c) 로 간결한 형이 되게 할수도 있다. 점성계수 n 가 p~l l = -217 s,, (7.86d) 로 정의되기 때문에 n = -罰 t, [Bk/ , BfJ ] (7.86e) 가나온다. 열류는 (7.80e) 로 정의되고, 그 0 차 근사는 (7.81b) 에서 0 이 됨을 보았 다. 1 차 근사는 硏 == ['I 타盆f u뿔 h u u, I 뿔 U2 Eu2 AI (u ) a 18nrI T = 뿡 ,[ 孟f 。 A(u) u4 81 nT (7.87) 8r I 이다. 그런데 A(u) 가 (7.85a) 의 조건을 만족시키므로 위의 식에서 A(u)u4 대신에 A(u) {ui - 롭다 = 亨꾸 A(u) u. (景 -웅 ) Uk 를 대입q하:l) 여 =도 炤값이 j변d7하/지o ~ 않 A는(u댜) u따 . (라 景서 _ ½)uk = 43F Lk [A., A 』 6 Olnr, T (7.87a) 로 쓰인다. 위에서 (7.84b) 와 (7.86b) 의 기호가 사용되고 있다. 열전도도 K 는 q)ll = --K 8OrTi (7.87b) 로정의되므로
K = _麟 [AhA 』 (7.87c) 를알게 된다. (1) Bhatn a ga r -G r oss-Krooks 모형 2 1)
21) Bhatn a ga r -G r oss-Krooks ; Phy s. Reu. 94, 511 (19 54)
일반적으로. 충돌적분을 나타내는 (7.78) 의 우변이 수학적으로 복잡한 구 조를 가지므로, 그것을 단순화시켜 생각한 근사가 이용되기도 한다. 그 대 표적인 것이 평균자유시간을 생각하는 물리적인 모형이며 B-G - K에 의하여 제안된 것이다. 평균자유시간의 역수인 소위 충돌빈도 v 를 써서 충돌적분 C(f )를 C(f) ~v ( f。 - f) (7.88) 로하고있다.그러면 J( h) = —vh (7.88a) 이고 (7.84b) 와 (7.84c) 에 의히여 A, (一u ) = ―}(齋 _ 망 )u, (7.88b) B/C:) = ―十 붉 ( u,. u / _ 강 u2 fl.1 ) (7.88c) 이다. 또 (7.86b) 에서 [F, G] = _v ·[ d7 f。 GF (7.88d) 이다. 따라서 열전도도 K 는 (7.87c) 에 의하여 K = 강¥ v'f d -:fo { -} (齋 —웅 )나 = 요2 (\ m¼ ) )~V (7.89) 이고, 점성계수 n 는 (7.86e) 에 의하여
I'/ = 層 ~(-v) .f d, J기-冒告 (U , U1 一 ½u 기 } 2 꼬V (7.89a) 으로계산된다 충돌단v 면~적 4u 를 쓰=면 n평a균( 亨자유행 )1로 /2 l 과 평균속력에 의하여 (7.90) 이다. 따라서 n = 四a \ 그2kT )1 /2 =(무Jh, (7.90a) K = 〕나 )n = 웅巳 (옮 )1 /2 (7.90b) 으로쓸수도있다• (2) Maxwell 모형 Maxwell 분자의 기체에 대하여는 J( W = AI UI (7.91) 의 적분방정식에 대한 고유치와 고유함수가 (7.64a) 와 (7.67a) 에 주어지고 있다. 그러므로 점성계수 (7.86e) 와 열전도도 (7.87c) 가 쉽게 계산된다. 고 유치 7} A,., = n2rr j sin 0 d0 rx.( cos 0) [ cos 2r+/ ( 망) P, ( cos 망) + sin2 r+/ 틀) Pi ( s i n 운) — 1 — fJr, o tJ 1. 。] (7.91a) 이고, 이 적분 안에서 a(O) = {g I(g, 0)}/n
이며 ,m 은 -l~m~l 인 정수이고, 고유치 Ar. 1이 2l + 1 중으로 축퇴되고 있다. 특히 고유치 A l 」에 대한 고유함수 III 낸 一 c2) c Y1m (0 ,
n= (22crm I kA 刀'0. 21 / I 2 (7.96a) 으로 하면, (7.90b) 와 (7.90a) 가 비슷하게 된다. (3) 일반적인 경우 열전도도의 일반식 (7.87c) K = －강 [元 저 (7.97) 울 계산하기 위하여 -A (•u) •= •A(•u) -u -와 비-슷 한- 형-을· 갖•-는 -a· = a(,u ), -u+ 롤
詞 -;] = [-;, 지 (7.98) 룰 만족l되a,도 -록;] 취三하 [면; , m (7.98a) 가 만족된다 . Zl)22) (7.86b' ）에서 o :;;; [-a니 ► —-A+, -a+- A--] = :[-a+, -a-]- [-A- , -a -]- [:-a+ , -A-]+ [-A-, -A+ ] = -[A--., -a-] + [-A-, -A + 제 서 [1, 저 ~ [1,-;] = [:, 1] = 「'검
Sonin e 함수의 직교성 울 이용言하`[ 여。)~ e -- a• =S(·-u' .P a')((xu를)) -S전;':..개 q ' ( 한 x=다) .x-' d즉(x 晶= ~) 1/2 i a;n) sjt)2 (bcp2.q) 7 (7(.71.0909)) p= O 의 전개에서 -A (-u-> )에 대한 조건 (7.58a) 가 a(u) 에도 성립되도록 하면 Jd t ff구 ,J = J/ o a(u) u2 du != 0 (7.1 0 0a) 가 요구되어, (7.100) 에서
a 깝 ) = O (7.1 0 0b) 로취한다. 7(7) 에 대한 전개 (7 .1 00) 을 대입하여 s. = [- a', -a',] = n 商75 - k, qq.=;- f.ll pp :.=r ;II A q r aq(n ) a/l (7.1 0 1) 으로하면, 여기서 Aq ' = n :2T [S j}詞) c'; S i ; 詞)?] (7.1 0 1a) 이다.또 [ 一a' , -A ] = [ _A , 一a'] = .[ d: f。 7 J(;) = .I du f。(I: a( i s 隔 (亭) ( 齋 -f) u = [ d7 k(E a(? S( 정/ 2 (c2)7) (S1Y12 (c2) 7) = ,.n T1a5 I(n) (7.1 0 2) 이 되어, 조건 (7.98) 이 w. = 籠망溫 Na;n)a;n _ 부 a:n) = O (7.102a) 01 다. (7.101) 의 S.를 (7.102a) 의 조건에서 극대화시키는 데는 La g ran g e 의 미 정계수 ±방8a법;n.)을 [ s쓴 .다 +. 즉~,. w미 』정 계= 수O :a 에p 의=하 여1, 2, …, n (7.103) 으로한다.그결과는 2 • 籠 k (l + ,.) Eq Apq a;r) _ e· 분 & = O (7.1 0 3a) 이다. 미정계수 ea 를 구하기 위하여 a(? 을 곱하고 p에 대하여 합하고 (7. 102a) 와 비교하면
~. = -2 를 얻는다. 따라서 (7 .1 03a) 는 Eq A pq a .() = 김()p , 1 : p = l,2,… … ,n (7.1 0 4) 이고, 여기서 a? 을 구할 수 있다. 그러나 (7.101) 과 비교하면 [C:, -;] = 州 아 ) (7.1 0 5) 을 알 수 있으므로 a
다. n = 1 이면 ,, = ―뚜副 = _志 (7.1 0 8) 이고, n = 2 이면 n= 」〔副= _(1+ 尸 HlHlO I一 H IHO OI HIO ) (7.1 0 8a) 01 다. N 을 (7.101a) 에서, H pq를 (7 .1 07b) 에서 구하는 것도 쉽지는 않지만, 필 요하면 수치계산울 하면 되기 때문에 임의의 근사에서 K 와 n 를 계산하는 방법을 알게 되었다고 할 수 있다•
참고문헌 동계역학의 역사적 발전과 관계된 문헌 1. Brush, S. G. : Ki ne ti c the ory I , II , Perga mon pr ess ( 1966) 2. Boltz mann, L. : Lectu r es on gas the ory , Un iv. of Cali for nia pr ess (19 64) 3. Gi bb s, J. W. : Elementa r y pr in c ip le s in sta t i st ic a l mechanic s , Dover (1956) 4. Ei ns te i n , A : Investig a ti on s on the the ory of the Brownia n moti on , Dover (19 56) 5. Ehren fes t, P & Ehrenfe s t, T. : The concep tion al fou ndati on s of the sta t i sti ca l app ro ach in mechanic s , Corne! Un iv. pre ss (19 59) 6. Tolman R. C. : The pr in c ip le s of sta t i sti ca l mechanic s , Oxfo r d Univ . pr ess (19 38) 7. Cohen, E. G. D. & Th irr in g , W. ed. The Boltzm ann equ a ti on , Sp r in g er -Verlag (19 73) 대표걱인 교과서 8. Ki ttel, C. : Elementa r y sta t i st ic a l ph ys i c s , Jo hn Wi le y & Sons (1958) 9. Ki ttel, C. & Kroemer, H. : Thermal Phys ic s , W. H. Freeman & Co (19 80) 10. Reif , F. : Sta t i st i ca l and the rmal Phys ic s , McGraw-Hi ll(1 965) 11. Sommerfe ld , A. : Thermodyn ami cs and sta t i sti ca l mechanic s , Academ ic pr ess (19 56) 12. te r Haar, D. : Elements of sta t i st ic a l mechanic s , Ri ne hart & Wi n- sto n (1961) 13. Fowler, R. H. & Gug ge nheim E. A. Sta s ti st ic a l the rmodyn ami cs , Cambrid g e Un iv. pr ess (19 39, 1965) 14. Maye r, J. E. & May e r M. G. : Sta tist i ca l mechanic s, Jo hn Wi ley & Sons (19 40)
15. Landau, L. D. & Li fsh itz, E. M. : Sta t i st ic a l ph ys ic s , Perga mon (19 58, 1980) 16. Huang , K. : Sta t i sti c a l mechanic s , Jo hn Wi le y & Sons (19 63) 17. Kubo, R. : Sta t i sti c a l mechanic s , W ile y ( 1965) 18. Reic h }, L. E. : A modern course in sta t i st i ca l ph ys ic s , Edward Arnold (1980) 19. 조순탁 : 통계물리학, 교학연구사 (19 83) 전문적 연구의 전단계 문헌 고전적 유체의 평형상태 19. Hi ll T. L. : Sta tist i ca l mechanic s , McGraw-Hi ll (19 56) 20. Uhlenbeck G. E. & Ford G. W. : Stu d ie s in sta t i sti c a l mechanic s vol. l(J. de Boer & G. E. Uhlenbeck ed.) North - Holland (1962) 21. Fris h H. L. & Lebowi tz, J. L. : The equ i l ibr iu m the ory of classic a l flui d s , W. A. Benj a mi n Inc. (19 64 ) 양자적 유체의 평형상태 22. Abe, R. 통계역학 (일본어) 동경대학출판부 (1967) 23. Mi lls, R. ; Prop_ aga to r s for many pa rtic le sys t e m s, Gordon & Breach (19 69) 24. Fett er, A. & Walecka J. D. ; Qu antu m the ory of many pa rtic le syst e m s, McGraw-Hi ll (19 71 ) 25. Neg el e J. W. & Qr land, H. : Qu antu m many pa rtic le syst e m s. Addis o n-Wesldy (19 88) Brown 운동과 상관함수 26. Wax, N. ed. ; Selecte d pa p e rs on nois e and sto c hasti c pro cesses, Dover (1954) 27. Forste r , D. ; Hy dr odyn a mi c fluc tu a ti on s, Broken sym metr y and corre-lati on fun cti on s. W. A. Benja min (1975) 28. Boon , J. P. & Yip , S. ; Molecular hyd rody n ami cs , McGraw-Hi ll (19 80)
29. Berne, B. J. & Pecora, R. : Dy n ami c lig h t scatt er in g , Jo hn Wi le y & Sons ( 1976) Boltz mann 방정식 30. Chap m an, S. & Cowl ing T. G. : Math e mati ca l the ory of non-unif orm gas es. Cambrid g e Un iv. pr ess (19 52) 31 . Hirs h feld er J. 0., Curti s, C. F. & Bi rd , R. B. : Molecular the ory of ga ses and liq u id s , W ile y (19 54) 32. Uhlenbeck, G. E. & Ford, G. W. : Lectu r es in sta tist i ca l mechanic s , Americ a n math emati ca l socie t y ( 1963) 33. Wu, Ta-Y ou : Ki ne ti c equ ati on s of ga ses and pla smas, Addis o n- Wesley ( 1966) 34. Bog o liu b ov, N. N. : Stu d ie s in sta t i st i ca l mechanic s vol. I .(de Boer & Uhlenbeck ed) North Holland ( 1962) 35. Ferzig e r J. H. & Kap e r H. G. : Ma the ma tica l the ory of tra nspo rt pr ocesses in ga ses. North -Holland (19 72) 36. Resib o is , P. & de Leener M., Classic a l kin e ti c the ory of flu id s , Jo hn W ile y & Sons ( 1977)
찾 0 卜보 71
거 Gauss 과정 244 r 위상공간 50 거시법칙 42 q uas i-p ar ti cl 려 에너지 208 국소적인 평형상태 31 gran d canon ica l ensemble 76 grap h 표시 180 기억함수 269 기체 model 56 기체상수 16 기하학적 단면적 35 Gi bb s 분포 76, 81 G i bb 려 ensemble 50, 61 G i bbs 의 자유에너지 79 G i bbs 의 par adox 68 L 내부에너지 64 내부에너지 (이상기체 ) 19 C: D y so 팩 P 기호 178 Dar wi n-Fowler 의 계산방법 86
대분배함수 78, 91 Dulong -P eti t 법칙 128, 129 Deby e m odel 128 Deby e- Huckel 방정식 168 Drude 이론 107 2 La g ran g려 곱한 수 59 Lan gmui r 의 등온흡착 82 Lan g ev i n 의 방정식 235 law of corresp o ndin g sta t e s 136 Ra y le ig h -J eans 의 공식 125 Lennard..J o nes po te n ti al 137 Lehmann 전개 203 roto n 121 Liou vil le 52 Lio u vil l~ 방정식 54 rin g gra ph 197 rin g 근사 196 口 Maxwell 20, 27 Maxwell 모형의 기체 312 • Maxwell-Boltz m ann 통계 97 Maxwell 의 동면적 법칙 136
Markov 과정 236 Maste r 방정식 238 mi cr ocanonic a l ensemble 61 Ma y er 의 방법 138 Ma y er 의 정리 143 µ 공간 57 µ 공간의 세포 57 Mor i의 표현 266 moment 전개식 321 미분산란 단면적 34 1::1 Bhatn ag ar -Gross -Knooks 모형 334 백색 spe c tr u m 262 Bernoull i 15 Born-Green-Yoon 적분방정식 116 Boltz mann 방정식 32 Boltz m ann 방정식의 유도 291 Boltz m ann 상수 19 Boltz m ann 원리 50, 52 Bol t zmann 의 구상 56 Boltz m ann 인자 70 Boy le -Chales 법칙 16 Bob y lev의 변환식 312 Bose-Ei ns te i n 통계 88 Bose 입자 85 본질적 시간미분 (subs t an ti al time deriv a ti ne ) 46 Brown 운동 231 Bloch-De Dom ci n i c i s 의 정리 180
분배함수(p ar titi on fun dti on ) 70 분포함수 159 BBBGKY 방정식 288 viri a l 계수 137 viri a l 전개 137 비열비 20 人 Sackur-Te t rode 의 entr o p y 표시식 68, 76, 82 산란단면적 34 상관함수( 정상상태 ) 283 상관함수(평형상태) 160 생성연산자 170 선형 grap h 140 선형응답의 이론 279 선형화된 Boltz m ann 방정식 299 self -€n ergy 205 소리의 전파 306 소멸연산자 170 속도분포함수 20 수밀도 17, 43, 81 수송계수 326 수송량 28 screen ing 효과 221 sta r gra p h 141 sta r tre e 141 sti rl i n g의 공식 68 Ste f a n -Boltz m ann 상수 125 str a in ten sor 47, 328 str e ss ten sor 30, 328
spe c tr a l densit y 261 sp ec tr a l int e n sit y 204 spe c if ic dis t r i b u ti on Functi on 289 시간적 평균 55 CHNC 방정식 168 。 Ei ns te i n model (고체의 ) 128 Ei ns te i n 응축 114 Ein s te i n 이론 (Brown 운동의 ) 232 acti vity 149 압력 73 absolute acti vi t y 80 Waeberg 30 Yan g과 Le 려 이론 152 H 정리 38 Ehren fes t 68 에너지 밀도함수 71 ergo d ic 역학계 55 energy shell 58, 61, 65 entr o p y (이상기체의 ) 40, 48 entr o p y 62, 67, 73, 78 ensemble 평균 56 Enskog 327 연분수 272 연속방정식 46 열적 de Brog lie 파장 68 연결된(li nked) grap h 186 열속도 32, 45
열전도도 31, 333, 335, 336, 339 Euler 형의 방정식 47 온도 63, 67 온도 Green 함수 201 요동 • 일산 정리 263, 265 Wi ed emann-Franz 법칙 107 W i en 의 공식 125 Wi en er-Khin t c h in e 정리 259 W i ck 의 정리 180 W i ck 의 T 기호 210 유체역학 방정식 47 유체역학적 방정식 42 응결현상 133 응답함수 283 입자분포함수 158 임계온도 133 im p ro p e r grap h 219 x: 작용구 25 장의 연산자 172 재규격화 (renormal i za ti on) 196 점성계수 30, 333, 335, 336, 339 점성력 30 gen erati ng fun cti on 145 gen eric dist r i b u ti on fun cti on 289 제곱 • 평균 • 평방 속력 Urma 20 제 2 양자화의 방법 170 조잡한관점 (coarse gra in e d sense) 62
준 ergo d ic 계 55 중첩근사 167 지량변수 68 犬 Chap m an-Kolomog o rap h 방정식 237 천이확률(t rans iti on pr obabil it y ) 236 최빈속력 24 축되기체 101 축되된 전자기체 106 충돌연산자 301 구' canonic a l ensemble 69 Kammerlin g h- Onnes 식 137 curnnlant 245 K i rkwood 의 중첩근사 167 Ki rk wood-S a lsburg 방정 식 168 Cayl e y tre e 142 Kohn 의 함수 224 coasse gra in e d sense ( 조잡한 관점) 62 contr a cti on 182, 188 collecti ve moti on 306 Coop e r 쌍 118 Kundt 30 Clausiu s 16, 24 cluste r 적분 146 cluste r 전개 157
Kronig 15 E Thomas -Fer mi의 screenin g 효과 225 특성함수 (charac t er i s ti c fun c tion ) 244 工 pa th -in t e g r a l 방법 251, 255 Feyn ma n grap h 184 Percus-Yevic k 방정식 168 Ferm i-D i ra c 통계 88 Ferm i 온도 109 Ferm i 입자 85 Ferm i 준위 108 평균속력 24 평균자유행로 24 Photo n 기체 127 Pois s on 분포 82 Phato n 통계 122 Fokker-Planck 방정식 239 pra pe r gra ph 210 궁 van der Waals 이론 134 화학 po te n ti al 76, 77, 81 He I , He II 118 Helmhol t떠 자유에너지 72 Hi lbe rt 327
조순탁
대우학술총서 자연과학 1 소립자와 게이지 상호작 용 김진의 46 금변론 박 대 현 2 동력학특론 이병호 47 생체에너지 주충노 3 질소고정 송승달 48 리이만 기하학 박을용 4 상전이와 임계현상 김두철 49 君表現論 박승안 5 촉매작용 진종식 50 비선형편미분 방정식론 하기식 6 외스바우어 分 光學 옥힝남 51 생체막 김형안 7 극마량원소의 영 양 승정자 52 수리분류학 고철 환 8 수소화붕소와 유 기 붕 소 윤능민 53 찰스 다윈 정용재 9 항생물질의 全 合 成 강석구 54 금속부식 박용수 10 국소적 형태의 At iya hs in g er 55 양 자광학 이상수 지표이론 지동표 56 효소반응속도론 서 정현 11111324 생M프天천화u체然로c학스o물物및p타리化 o 글학學 l생y라硏 물s홍딘究a리승c 合法c수학h 成 a우r박 원i김준 d식e성우 s각 의 65559708 확분화백 자률성터 분암속론 광성이구론학인자 론홍양소 재현이현 수민 성 111756 脂結고防晶분자化營에유養리 의김 숙한김회병 화호학 반응 조의환 666231 수에곤학너충지 신기 경초띠 론이생 론리김 학 상모 문세부 정경 생 18 과학혁명 김영식 64 신 경 과학 김승 업 박찬옹 19 한국지질론 장기홍 65 SBaClHm 부on호 부와호 R 이ee만d영- 20 정보이론 한영열 66 양자 전가 역학 김영덕 21 원자핵반응론 정운혁 67 군환론 박 재 걸 22 파괴역학 김상철 68 대수기하학 조 영 현 23 분자궤도 이론 이악춘 69 양자 장이론 이 재 형
