 민동필
민동필  민동필
민동필
저자는 서울대학교 문리과대학 울키학과를 졸업했으며, 불란서 翁 (Orsay) 대학에서 이학박사 및 국가박사 학위를 취득했다. 불란서 Sacla y기초과학연구소 연구관을 역임하고, 서독뮌헨대학물리학과를 거쳐, 현재 서울대학교 자연과학대학 물리학과 교수로 재직중이다. Sph e roid a l Sky rm i on 둥 다수의 논문이있다.


책 머리에
이 책은 1981, 1982 년 그리고 1984 년 서울대학교 물리학과 학부 4 학 년 및 대학원 석 • 박사과정 원자핵 물리학 시간에 강의한 내용 중 구조 론 부 분 을 기초로 작성되었다. 이 책 은 독자가 양자역학을 이미 친숙히 일고 있다는 전제하에 씌어 졌 으나, 원자 핵 물리학 자체에 대한 독자의 지식을 요구하고 있지는 않 다. 교육적인 입장에서 이 책을 1,2 부로 구분하였고, 제 1 부는 원자핵 구조 론 의 뿌리를 이루는 여러 거시적 기초 개념을 중심으로, 제 2 부는 미시적인 이해 및 계산 방법울 중심으로 구성하였다. 그러나 막상 실 재 연구를 위한 거의 모든 계산은 복잡한 컴퓨터 계산을 통해 실험 결 과치와 비교 가능해진다. 이러한 계산과정 및 세부사항은 그 중요성에 도 불구하고 책에 싣기에 매우 비효과적이라고 생각되어 삭제하였고 단 지 실 제 핵 구조의 이해를 위한 물리적 개념 설명의 명확성을 살리려고. 많 은 모델을 엮어서 설명했다. 이 모델들윤 통 해 독자는 핵 내부의 전 반적인 현상에 대한 구조핵물리학의 연구 동향을 이해하게 되리라 기대 한다. 사실상 핵물리학을 모델로만 펼쳐나간다는 것이 얼마나 위험한가 하 는 것은 핵물리학을 전공하는 사람들은 모두 이해할 것이다. 이는 핵 내부 현상의 복합성으로 인해 기인된 필연적인 것이기는 하지만, 서로 다른 모델의 상호 차이점 또는 연계성, 통합가능성 및 실제 실험치와의 엄밀한 비교가 수반되지 않는한, 이론 모델은 하나의 〈모델〉일 뿐, 〈물 리〉가 되지 못하는 경우가 많기 때문이다.따라서 이 책의 약점을 보완하기 위해 독자 자신이 본문에 주어진 실험 데이타 이외의 실제 실험치와도 자세히 비교하여 보기 바란다.
한편 최근 QCD(Quantum Chromodynamics)가 출현한 이래, Quark와 Gluon 둘로 핵 내부 현상 자체를 선명하거나, 극한 상황에서 이들 자유도의 역할을 탐구하는 많은 연구가 급격히 증가하고 있다. 하지만 이 분야의 소개는 이 책에서 취급하지 않았다. 이는 이를 취급하기에 많은 분량의 지면을 할애해야만 할 것으로 사료되기 때문이다.이 책이 나오기까지 후원과 지지 를 다해 준 대우재단에 감사하며, 교정 및 내용에 대한 의견을 말해 준 박병윤, 김도원 및 권경훈 제씨에게 감사한다. 이들의 도움이 없었으면 이 책은 아직 나오지 못했을 것이다. 나에게 언제나 새 힘을 준 철희, 정현 아내에게, 그리고 두 부모님들께 이 책을 바친다.안양에서핵구조물리학·차례
책머리에 5제 1 부 기초 핵물리학제 1 장 핵구조물리학의 개요 131 핵물리학의 역사 132 단위 및 핵의 기초적 성질 173 핵계의 대칭성과 불변치 30제 2 장 독립입자 핵각모델 461 소개 462 중심장의 일반적인 성질 및 단진자 포텐셜 483 핵각의 스펙트럼 514 핵각 모델의 응용 555 핵의 변형 63제 3 장 핵의 단체회전 731 회전좌표계와 팽이 파동함수 742 손으로 돌리는 회전 모델 813 회전에 대한 통합 모델 93제 2 부 미시적 핵물리학제 4 장 제2양자화 방법과 핵상태 1051 한 개의 입자로 구성된 계 1052 동일한 N개의 페르미온들의 반대칭 상태 1073 하나 또는 여러 물체에 관한 대칭 연산자 111
4 생성연산자와 소멸연산자를 사용한 반대칭 상대의 표현 1135 생성연산자와 소멸연산자를 사용한 연산자 둘 의 표현 1156 단일입자 상태의 선형 변환 1207 입자와 구멍 1238 준-스핀 방법을 사용한 입자-구멍 변환 1249 두 종류의 페르미온들로 구성된 계 12810 하전스핀 130제 5 장 시간배열곱 (T-곱), 정상곱, 축약과 Wick의 정리 1331 페르미 바다 1332 정상곱 1343 인수 또는 시간에 의존하는 생성 또는 소멸연산자 1354 T-곱(시간 배열 곱 ) 1365 생성연산자와 소멸연산자의 축약 1376 Wick 의 정리 1387 l > 에 대한 평균값의 계산 1408 인수 가 없는 연산자의 경우 1409 Wick의 정리 확장 141제 6 장 하트리―포크 이론 1421 밀도행렬 1432 하트리-포크 방정식 1453 해밀토니안의 대칭성과 관계된 범함수 E〔p〕의 불변성 1484 하트리-포크 해밀토니안의 대칭성과 대칭성 파손 1515 하트리-포크 궤도 1576 하트리-포크 궤도의 에너지 1587 궤도 에너지의 실험적인 결정 1618 밀도행렬의 변분에 대한 하트리-포크 상태의 안정 조건 1739 정적인 외부장에서의 선형 반응 17810 보기 : 밀도에 의존하고 도달거리가 0인 힘 18011 갈릴레이 변환과 병진운동에 의한 가짜 상태 18312 하트리-포크 계산에 사용되는 유효력 187
제 7 장 핵의 쌍짓기 1951 소개 1952 초전도의 간단한 모형 1973 BCS 파동함수 2034 BCS 방정식 2075 BCS 표현에서의 핵 해밀토니안 2166 독립적인 준-입자 근사에서 들뜸스펙트럼의 기술 2177 BCS 방정식의 역전-쌍짓기의 유효력 2228 BCS 방정식의 역전방법의 수렴결정에의 응용 2259 BCS 모형의 타당성에 대한 현상론적 시험 226제 8 장 Feynman 그림식과 섭동이론 2291 해밀토니안의 구분과 Dyson 전개 2292 진화연산자의 진공기대치 2313 Feynman의 그림식 2344 Feynman의 진공그림식 2395 연결된 뭉치정리 2446 에너지로 표기하는 Feynman 그림식 2477 핵질의 교환력 2498 밀도에 의존하는 유효핵력과 유효질량 255찾아보기 259제 1 부  기초핵물리학
기초핵물리학
제 1 장 핵구조물리학의 개요1 핵물리학의 역사1) 1955년 이전1866년 Becquerel에 의해 방사선 알파입자가 발견되면서부터 시작되었다고 볼 수 있는 핵물리학은 현재에 이르기까지 핵의 성질을 규명하려는 노력 속에서 계속되어 왔다. 그러나, 아직도 핵의 모든 성질이 파헤쳐졌다고 여기기에는 매우 먼 상태이며, 이러한 핵에 대한 지식을 확장시키기 위해 점점 정확한 측정을 가능하게 하는 가속기들이 세계 각곳에서 건설되고 있다.실지로 핵의 동력학적인 성질은 아주 풍부하며, 중력을 제외한 핵력, 전자기력 , 약력 등에 의해 지배되고 있다. 이로 인해 핵은 마치 서로 상반된 성질들을 함께 보유하고 있는 물질처럼 이해되곤 했다. 즉 핵의 주된 구성 입자인 양성자와 중성자가 독립적으로 움직이는 듯한 성격이 있는가 하면, 이들 구성 입자가 서로 얽혀 있는 듯한 성격도 있어 소위 집단운동(collective motion)을 하고 있기도 하다. 또한 양자법칙에 의해 지배되는 미시적 물질인 핵은, 고전역학적인 해석이 불가능한 포논 (phonon)의 생성 및 거대한 공명(giant resonance), 핵질의 초전도 상태 등으로밖에는 설명될 수 없는 많은 성질들을 나타내고 있다. 이러한 현상들을 이해하는 데에는 핵의 구성 인자들, 즉 소립자들의 개별적인 성질들을 알아야 하며, 뿐만 아니라 이들이 핵을 구성함에 있어서 가지는 역할을 알아야 할 것이다. 또 우리는 이들이 어떻게 핵이라는 집단
속에서 운동하고 있으며, 이 운동이 실험적으로 측정할 수 있는 물리량에 어떻게 나타나는가를 계산할 수 있어야 할 것이다.다른 한편, 우리는 먼저 〈우리가 한 집합체를 이해했다〉라는 말을 과연 언제 할 수 있는지를 명확히 규정해야 할 것이다. 물몬 모든 구성 인자를 이해하고 이들이 일으킬 수 있는 모든 가능한 현상을 이해하면 이 말을 할 수 있겠지만, Schrodinger 방정식을 다체계에 대해 완전히 푼다는 것은 비상대론적인 경우라 할지라도 가능하지 않을 뿐 만 아니라 이는 우리의 흥미의 대상도 아니다. 왜냐하면 비록 Schrodinger 방정식을 다 풀었다 해도 그 해가 다른 집합체에 대한 우리의 간단한 물리적 예측에 도움을 주지 못할 정도로 복잡하다면, 우리는 이 집합체를 이해했다고 할 수 없기 때문이다. 다시 말하면, 우리가 이해했다는 말은 그로 인해 다른 현상이나 다른 대상의 특성도 예측할 수 있을 때에야 비로소 할 수 있으며, 이러한 점진적인 예측은 각각의 구성 인자가 어떻게 집단의 영향을 받으며 운동하고 있는가를 이해함으로써 비로소 가능하게 된다. 즉 구성 인자의 독립적인 운동을 이해하는 것도 중요하지만, 집합체 속에서의 운동을 이해하는 것이 다체 핵물리학의 주된 목표인 것이다. 이러한 목표에 도달하기 위한 노력은 지금도 활발히 진행되고 있다. 우리는 역사적으로 이 노력에 대한 발자취를 더듬어 봄으로써 우리의 핵에 대한 이해의 발전 과정을 알 수 있을 것이다. 1935 년 보어 (N. Bohr) 는 중성 자가 원자핵 속에 포획 (cap tur e) 되 는 것을 발견한 페 르미 (E. Fermi : 1934) 의 결 과를 이 용하여 , 핵 반응에 서 의 복합핵 (comp ou nd nucleus) 모델 을 발표했 다. 이 에 반해 2 차대 전 칙 후 M.G. Ma y er 와 J. Je 函 en 은 독립적으로 핵각 (nuclear shell) 모델을 밀 표하여 (1947), 핵을 이루고 있는 핵자 (nucleon) 들은 강력한 핵력 에 의 하여 집합적으로 엉겨 있기보다는 원자들 속의 전자들처럼 어떤 포텐 셜 (po te n ti al) 에 의 해 서 생 긴 독립 된 고유상태 속에 들어 있는 것 같다는 주장을 발표했다. 특히 이러한 포텐셜을 단진자 (s i m p le harmonic oscil l- ato r ) 포텐셜로 가정하고 원자내의 전자들의 경우보다 훨씬 큰 스핀-궤 도 상호 결 합력 (sp in-o rbit coup li n g int e r acti on ) 을 도입 하여 핵 성 의 주 기성을 설명할 수 있었다 (1963 년 노벨상 수상). 이상의 두 모델이 취하고 있는 물리적 근본방상은 상반된 듯하지만 오늘날 :::z.에 대한 이유는 찰 설명되어 있다. 또한 실험적으로도 핵에는
이러한 두 성격이 공존하고 있는 것이 측정되곤 하였다. 특히 복합핵 모델이 핵반응에서 핵자들의 상호응집의 정도를 중요시한 것과 감이, 핵의 구조를 설명함에 있어 , 핵 속의 핵자들이 액체 속에서의 분자들의 성 질 융 가진 다는 물방울 (liqu id drop) 모델 이 1952 년 에 A. Bohr 와 B. Mo tt eIson 에 의해 발표되었다. 그로부터 2 년 후인 1954 년 실험적으로 이 예측이 맞다는 사실이 판명되고부터 (1975 년 노벨상 수상), 물방울 모델과 핵각 모델의 통합이 시도되었다. 이는 실제 핵이란 우리가 일상 생완에서 접촉하는 기체, 액체 또는 고체의 어느 한 성격만을 소유한 집합체가 아니며, 이들의 성질을 모두 가질 수 있음을 명백하게 보여주 는 것이라 하겠다. 그 이후 핵의 성격 규명을 위한 노력은 집합체적인 성격과 핵자들의 독립적 성격의 공존 또는 상호 관계를 하나의 테두리 속에서 이해하려는 방향으로 시도되었으며, 이는 다체 핵물리학의 기원 이 되 었 다. 이 시 도물 가리 켜 미 시 적 핵 구조 이 론 (mi cro scop ic the ory of nuclear str u ctu r e) 이 라고 일 컫 는다. 2) 1955 년 이후 미시적 핵구조 이론의 형성, 죽 핵의 미세 구조에 대한 연구는 높은 에너지물- 갖는 포물체들의 사용이 실험적으로 가능하게 되면서부터 시 작 되었다고 할 수 있다. 특히 핵의 반지름에 해당하는 거리보다 훨씬 짧 은 파장을 갖는 고에너지 포물체 를 실험실에서 가속할 수 있게 되면 서 핵 내부의 성격이 알려지게 되었고, 다체핵 (중수소, a- 입자 등 가벼 운 핵둘의 이온)들을 가속하여 충돌 반응을 일으키고 두 핵 사이에 한 개 또는 몇 개의 핵 자가 교환되는 핵반응을 동해 핵자가 핵내에서 가지 는 상태를- 관찰하면서 미시적 핵구조 이론의 연구가 시작되었다. 또한 중간자 (meson)-n, K 또는 경 입 자 (l e pt on)- 전자, µ 등 새 로운 핵 탐지 입자 물 사용하여 핵의 성질들에 대한 정보를 얻게 되었다. 지난 약 25 년간의 핵물리학에서의 대표적인 발전 또는 발견을 몇 개 들어보면 다음과 같다. i) 거 대 한 2 중국자 공명 현상 (gian t dip o le resonance, 약자로 GDR) : 1954 년 실험적으로 발견되어 1956 년 D.H. W ilki nson 에 의해 설명된 현상으로 핵내의 중성자 전체와 양성자 전 체 가 함께 상대진동하는 것을 가리킨다. 이러한 동력학적인 운동방식 (mode) 은 미시적 핵구조 이론에 서 의 표현 에 따르면 입 자-구멍 (pa rtic le - ho le) 들뜸상태 라고 하며 이 는
제 5 장에서 다부어질 것이다. ii) 핵의 크기와 형태 : 수백 MeV 의 에너지를 가지는 전자를 핵에 충 돌시켜 핵의 크기와 형태에 대하여 알게 되었다 (Ho f s t ad t er 는 1957 년 이 실험을 행하여 1961 년에 노벨상을 받았다). iii) 핵 질 속에 서 의 초전 도 현 상 : 1962 년 , A. Bohr 와 B. Mott el son 에 의해 규명된 현상으로 실제 핵내에서는 이러한 현상은 약화되어 일 종의 근사적 현상으로 나타난다. 이는 핵에서도 마치 절대 영도에서의 초전도 금속과 같이, 바닥상태에서 둘뜸상태로의 전이에서 에너지의 최 소값이 무시할 수 없을 정도로 크다는 사실을 두고 명명되었다. 이는 제 6 장에서 다루게 될 것이다. iv) 이성 원자핵 (i somer) 의 발견 : 1965 년, 한 핵 에 여 러 다른 형 대가 존재하는 것이 발견되었다. 죽 에너지의 증감이 없이도 핵은 서로 다른 형태를 가질 수 있는데, 이것은 핵이 분열하는 경우 분열 도중에 아령 처 럼 늘어난 상태로 오래 머물 수 있음을 말해 주고 있다 (1957). v) 유사상태 (analog sta t e ) 의 발견 : 핵 력 은 작용되 는 소립 자들의 전하 와 무관하다는 것에서부터 유발된 유사상태가 1967 년에 발견되었고 핵 과 핵의 충돌에서 형성되는 미세구조 (1972) 및 매우 큰 스핀상태의 붕 안정성 (1977) 등이 실험적으로 관측되었으나 이론적인 규명을 필요 로 하는 것도 있다. 또 중입자(b ar y on) 중 특히 무거운 .A, 2 등의 핵내 존재의 가능성도 밝혀졌다 (1978: CERN). 이러한, 핵성에 대한 재로운 발견들의 대부분을 설명하는 데에 단 한 가지의 가정만을 사용하려는 시도가 바로 미시적 핵구조 이론이다. 이 가정은 낮은 에너지를 가지고 있는 핵의 성질을 중입자 특히 핵자들 상 호간의 2 체력 (two -body fo rce) 만을 현상학적으로 도입하여 모두 선명 하자는 것이다. 이러한 목표는 어느 정도 달성되었다고 여겨지지만 아 직도 모두들 설명할 수는 없으며 이는 오히려 당연하다 할 것이다. 다음 절에서는 다체 핵물리학을 정량적으로 논하는 데에 있어 필요한 기초적 개념들을 공부하기로 한다.
2 단위 및 핵의 기초적 성질 1) 단위 a) 거리 핵물리학에서 상용되는 거리의 단위는 페르미 (f erm i)이다. 1 fer mi (fro ) =10-13cm 예 물 들면 , z 중간자의 반지 음 ~0. 7 fer mi 핵 력 의 작용 거 리 ~1. 4 fer mi 해내에서의 두 핵자 사이의 거리~1. 7f er mi 핵 의 반지름 ~2 내지 7 fer mi 1 barn=10-21cm 두 100 fm 2 b) 에너지 에너지 를 표 시하는 단위는 MeV(mi llion electr on Vol t)이다. 1 MeV=l. 6 x 10-13J ou le 예 물들 면 전자의 질 량 m,C2=0. 511 MeV x 중간자의 질 량 m~C2=139. 6 MeV 양성 자의 질 량 mp C 2=938. 2 MeV 중성 자의 질 량 mnC2=939. 5 MeV 안정된 핵 속에 있는 마지막 핵자의 분리 에너지 ~8MeV 이다. c) 시간 핵력의 작용 시간을 기준으로 하여 핵물리학에서 상용되는 시 간의 단위는 lfm /c, 죽 갑 -.10-23 초이며 이에 대한 특별한 명칭은 없다. 핵력의 작용 시 간이란 예를 들면 핵력에 의해 하나의 강입자 (harclron) 가 붕괴할 때의 반수명 (half l if e) 의 시간 정도를 가리킨다. 또한 다음의 두 양은 실질적 계산을 하는 대에 자주 사용되므로 이를 암기해 둘 필요가 있다. tzc =197 MeV •f er mi e2 1 hc 137
2) 핵의 크기 및 밀도 핵의 크기를 측정하는 실험으로는 전자를 이용하는 산란 방법이 가 장 보편적이다. 물론 전자는 주로 핵 내의 양성자와 쿨몽힘 으로 작용하 기 때문에 핵내의 양성자의 분포물 측정하는 데에 사용되지만 중성자와 양성자의 차이도 역시 쿨롱힘의 차이이므로 핵 전체의 크기 및 밀도에 대한 정보 탐지에 전자가 이용되는 것이다. 에 너 지 가 E 인 전자의 드 브로이 (de Brog li e) 파장울 계 산하면 x 러유 =197/E( f m) (1. 1) 이다. 죽 약 lfm 정 도의 크기 를 갖는 물체의 성격을 규정하기 위해서 는 독수 상대론의 지배를 받는 200MeV 정도의 에너지 물 가 진 전자가 필요하게 된다. 그러나 이러한 전자산란 실험에서는 전자가 매우 높은 각운동량 (ang ula r momentu m ) 을 갖게 되 고, 핵 속의 핵 자들의 각운동 량 또한 중핵의 경우 약 10h 정도까지 미치기 때문에 산란 현상을 단 순 한 공식으로 기술하기는 어렵다. 즉 매우 많은 부분파들이 함께 충돌에 가담하게 되기 때문이다. 따라서 이들 부분과로써 자세한 핵 의 정보를 얻기는 어려우므로 핵의 전체적인 성격, 죽 전체 핵자들의 공간적인 분 포 정도를 탐지하여 왔으며, 이러한 탐지로부터 우리가 현재 알고 있는 정보는 다음과 같다. 양성자의 수 (Z) 가 적은 (Z/137~1) 핵에 대해서는 충돌 단면적 (cross secti on ) 이 다음과 갇이 표시 된 다. u (0) =(JM ot t (0) [F ( q) ]2 (1. 2) (JM ot t (0) = (충 )2 COS1 (1. 3) s i n4_2 一 여기에서 E 는 질량중심계에서의 에너지이다. 그리고 F( q)는 형태인 자(fo rm fa c t or) 라 불리며 다음과 같이 표시되는 물리량이다. F(q) =切fd 3r ~.-;p,, (r) =붕 f:p,, (r) sin (qr ) rdr (1. 4)
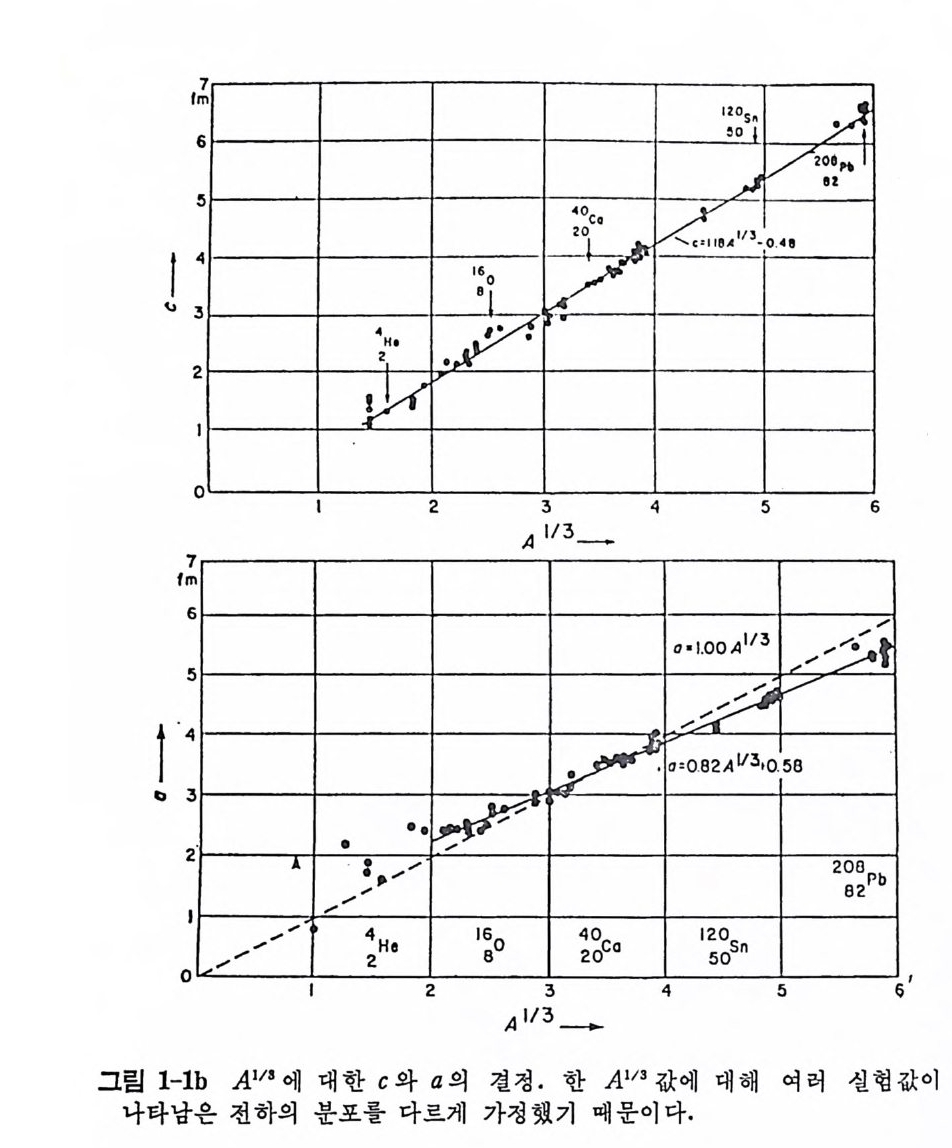
이때 q는 q=f2cE- s .i n 경0- , 죽 운동량의 변화값이고, P ,, (r) 은 양성자분 포함수이다. 죽 형태 인자의 푸리에변환이 이 분포함수이다. 실험적으 로 측정한 충돌 단면적 o(O) 로부터 형태 인자몰 유도해내고 아것의 푸 리에 빈환을 동해 양성자의 분포함수 p ,.(r) 을 유출하는 것은 이론적으 로는 가능하지만, 일반적으로 실험을 동해 F( q)는 모든 q(운동량 변화 값)에 대하여 값을 가지고 있어야 푸리에변환을 할 수 있으며 그러기 위해서는 전자의 가속 에너지가 커야 하기 때문에 사실상 이러한 방법 은 쓰이지 않고 있다. 역으로 분포함수 p ,(r) 을 가정하고 이 값으로 F ( q )픕 구한 다음 u(O) 의 실험치와 바교하는 것이 널리 쓰이는 방법이 다. 이러기 위해서 p (r) 울 가정하려면 핵내에 대한 정보가 필요하게 된 다. 우선 거시적 p (r) 을 두 개의 매개상수몰 이용한 패르미 분포함 수의 형태로 가정해 보자. p( r)l=+ex~ p〔 (r 一 c) !이 (1. 5) 실험치와 비교하여 얻어진 매개상수 a 와 c 는 대개 다음의 값을 가진 다(그림 1-1 참조). c~l. 10 A1t 3f m (1. 6) a~O. 53f m p Al2 。 C r 그림 1-la
 ’7 m
’7 m
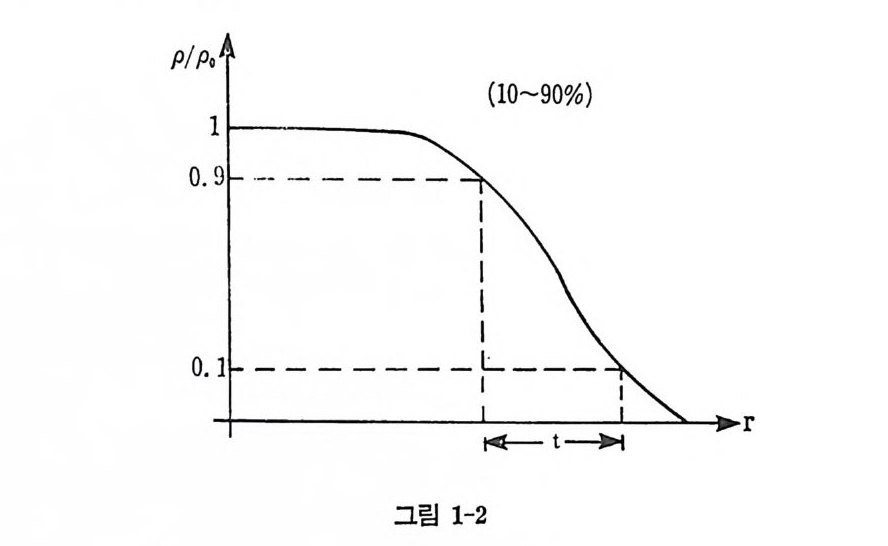
페르미 분포에서 c 값은 밀도가 중심에서 갖는 값의 절반 정도로줄어 든 곳의 반지 름 (half densit y rad ius ) 이 고 표면 확산도 (surfa c e dif fus en-ess) a 는 표면 두께 (su rfac e thick ness) t 와 다음과 같은 관계 가 있 다. t= 4.40a (1. 7) 이 t는 밀도가 중심 부분에 비해 10% 인 곳과 90% 인 곳과의 거리이
다(그립 1-2 참조).
 PIP 。
PIP 。
양성자들 사이의 정전기적 힘은 핵력에 비해 거의 무시될 수 있으므 로 핵내의 핵자들의 분포는 주로 핵자간의 핵력에 의해 조정될 것이다. 따라서 우리는 핵내의 양성자의 분포와 중성자의 분포가 거의 비슷하리 라고 추측할 수 있다. 단지 중핵에서의 정전기적 힘의 역할은 무시할 수 없으나 이 힘에 의한 양성자들의 부풀음 현상과 쿨롱힘의 장벽 효과 로 인하여 양성자 분포와 중성자 분포는 거의 비슷해진다. 그렇지만 쿨 몽 에너지 문제는 아직도 완전히 해결되지 않고 있다. 핵내의 핵자들의 분포가 페르미 분포로 어느 정도 설명될 수 있다는 사실로부터 핵자가 핵 속에서 느끼는 포텐셜 또한 거의 페르미 분포의 형태를 가질 것이라는 추측을 할 수 있다. 이는 마치 어떤 용기에 물을 담았을 때, 밀도의 분포가 용기의 모양을 하게 됨과 같다. 따라서 핵자 들 사이의 핵력에 대한 구체적인 형태에서 얻은 결과를 논하기 앞서 이 러한 평군 포텐셜을 가정하고 이에 대한 결과를 살펴보는 일도 홍미로 을 것 이 다. 페 르미 분포의 형 태 를 가진 포텐설 을 우리 는 Woods-Saxon 포텐셜이라고 한다. V(r) l+ex p〔 i( r-c)/ 이 (1. 8) 여기에서 대략
V 。욱 _50MeV (1. 9) 이다. 네모우물 (s q uare-well) 포텐셜이 이러한 평군 포텐설과 거의 같은 헝 태이므르 이를 써서 대강의 핵자밀도를 계산해보면, 핵내의 평균 핵자 밀도 (averag e nuclear densit y) 는 다음과 같다. po =A~ f:::0 . 17nucleons/fm 3 (1. 10) _3J rC3 이 p o 가 핵의 크기와 거의 무관하게 상수로 되는 현상응 우리는 핵자 포화현 상 (nuclear satu r ati on ) 이 라고 인 컫 는다. 이 러 한 포화 선 상은 또한 핵 의 전체 결 합에 너 지 (tot a l bin d in g energy ) 가 대 개 핵 자수 A 에 비 례 하는 것에서도 볼 수 있는 현상이다. 다시 말하면 핵의 크기가 커져도 핵의 밀도는 커지지 않고 부피만 커지는 헌상이다. 이는 핵이 마치 일 반 액체와 같지 않겠는가 하는 의혹을 일으키며, 물방울 모형을 낳게 했다. 하지만 우리는 이 모형을 다움과 같은 각도에서 고려해야 할 것 이다. 즉 일반 액체의 기준 구성단위인 분자들은 상호간의 분자력이 안 정된 국소값을 가지는 거리에 있는 반면 핵자들은 그렇지 않다. 핵자 사이 의 평 균 거 리 는 약 2~2. 2 fm 임 에 비 해 핵 력 의 극소값은 대 강 0. 7 fm 에 있기 때문이다. 이러한 차이의 제일 중요한 원인은 핵자들이 페 르미 동계 (Fermi sta t i st i cs ) 를 만족하는 페 르미 온이 기 때 문이 며 , 따라서 핵자는 다른 핵자에 너무 가까이 접근할 수 없게 된다. 이러한 현상을 일 컬 어 파울리 의 배 타 상호관계 (Pauli Exclusio n Correlati on ) 라고 한다. 이를 간단히 살펴보기로 하자• 3) 페르미 기체 모델파 파울리의 배타 상호관계 핵자들이 페르미온이라는 사실만을 중점적으로 다루기 위해서 평균 핵 포텐셜아 완전히 평평한, 죽 포텐설이 없는 경우물 생각하기로 하자. :::z.. 리고 핵자 상호간의 작용력 또한 없다고 하자. 이때 각 핵자의 파동함 수 국)은 :::z. 핵자의 운동량 p=tz k 에 의존하게 된다. 冠 m, (;, f) = 毒 -ex p (ik • r ) x ... (f) (1. 11)
여기에서 우리는 부피 규격 화 ( volume norma l i z a ti on) 를 취했으며 (Q 는 부 피), Xm‘( f)는 핵자 의 규격화된 스핀 (f는 스핀 공간 좌표) 고유 함 수이다. 즉 〈 Xm,IXm, ' 〉 =8 m,,m ,’( 단일 핵자의 경우만을 고려한다). 이러한 핵자들로 이 우 어 진 계의 전체 파동함수는 파울리 배타 원리 (Pauli exclusio n pr in c ip le ) 를 만족하는 반대 칭 화된 (ant i-s y m metr i z e d) 파동 함 수여야 한다. 상호 작용력이 없는 지금의 경우 이 파동함수는 소 위 Slat er 행 렬 식 (det er mi na nt) 의 형 태 로 만들어 진 다. 죽 A 개 의 핵 자들 로 이 루 어 진 계의 바닥상대 를 표시하는 전체 파동함수 中는
유도 과정은 다음과 같다. 우선 식 (1.14) 중 o(r-r1) 항 하나만 생 각하면 (志) 2dxr •• dXII {r pu , ( (지 [rp., (x2) rpu , (x,) …rpVA (a) -rp u , (x2) < pv , (xs) …r pv , (x,.) + … ( (A-) ! 째 항) J -rp v , (x1) [cp,,, ( x 2) rpv , (Xs) • • ·rpl 回 -… ] + rpu , (x1) 〔안 (x2) cp,,, (지 •• ·rp,,, (x,.) -… ] +…… }*8(?-7l) {…} (1.16) =-¾i-(A -1) ! 昆 |rp~ Cr) 12}= 숫g』rp ~(r) 12 여기서
핵 내의 핵자에 대해서는 하전스핀 (iso spi n) 양자수에 의해 두 배의 축퇴가 형성된다 . 죽 중성자와 양성자가 같은 준위에 둘어갈 수 있어서 밀도도 두 배가 된다. 죽 2 妹 p o= 경 이 고 식 (1. 10) 을 이 용하면 kF~1. 36 fm -1 이 다. 한편 두 핵자의 상호 작용을 알기 위한 2 체 밀도 연산자(t wo pa rtic le densit y op e rato r ) 는 다음과 같이 정 의 된다. 죽 하나의 핵 자가 공간위 치 r 에 있고 다른 하나가 7 에 있을 가능성을 축정 하기 위한 밀도 연산자는 p( ?, r') =I : o (戶구 1) 0 (?' 구.) (1. 20) 1*• 이다. 이 연산자의 기대치를 계산하여 보자. 먼저와 같이 식 (1. 20) 중 에서 o(r 군) X8(7I_r2) 항만을 고찰하자. 〈中= |8 J(trr-Jrd1x)1 o d(Xr2' •- •• rd 2xA) {| [#rp>v, ( xi) rpv , (石) _ Pu, (i) Pu, (石) ] X [ (rpv , (Xs) 짠 &) …'f'•• (XA) ) 와 이 것의 순서 가 바뀐 항들의 합] _ [rpu1 (X1)
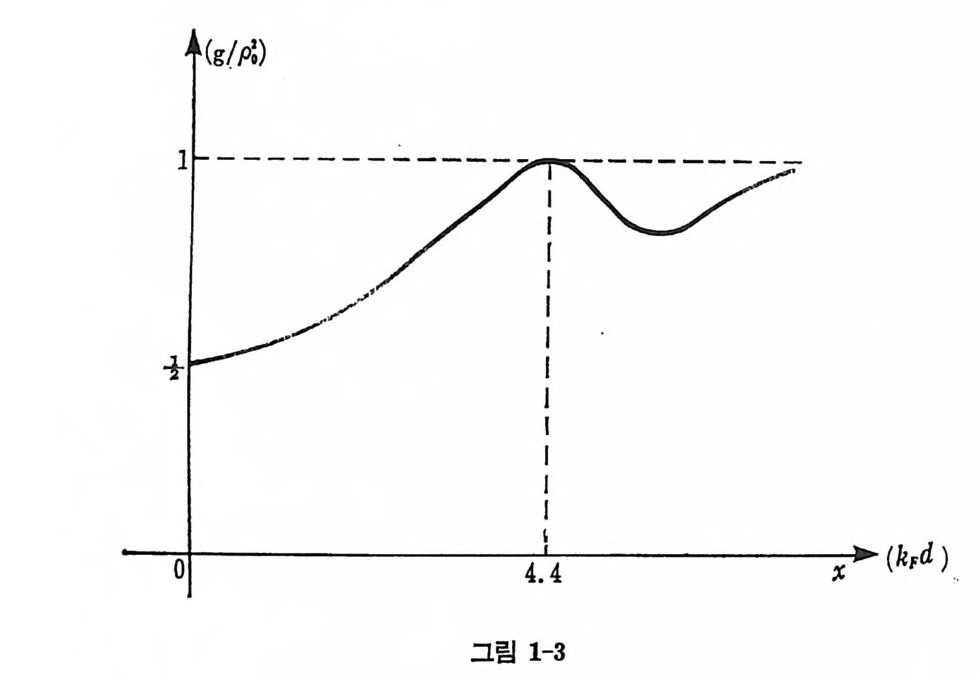
이다. 식 (1. 22) 물 유도하면서 m,,= 士당입을 이용하였다. 한편 식 (1. 20) 의 관계와 적분을 통하여 2 체 밀도 상관함수(t wo par tic le densit y correlati on fun cti on ) g 를 얻 을 수 있 다. g(r , r') =<,trlp ( r ,r ') I t〉 =P~[1 一당 -c2(k 시?구 I)] c (x) =울(무 -cos x) (1. 23) 따라서 밀 도 상관함수는 그립 1-3 과 같은 모양을 갖는다. 이 밀도 상관 함수를 보면 한 핵자와 다른 한 핵자와의 거리 d 가 약 d:::::0 에서부터 d~3. 2 fm (kFd~4. 4) 인 장소에 이를 메까지 점차로 밀도가 커지게 됨을 볼 수 있다 (d=O 에 서는 다른 스핀 양자수의 입자가 있을 확률 로 인해 g/p~은 1/2 이 됨).
 (g/p!)
(g/p!)
따라서 아무 작용력이 없는 입자들이라고 해도 파울리 배타 원리로부터 핵자들의 접근은 어려워지게 된다.
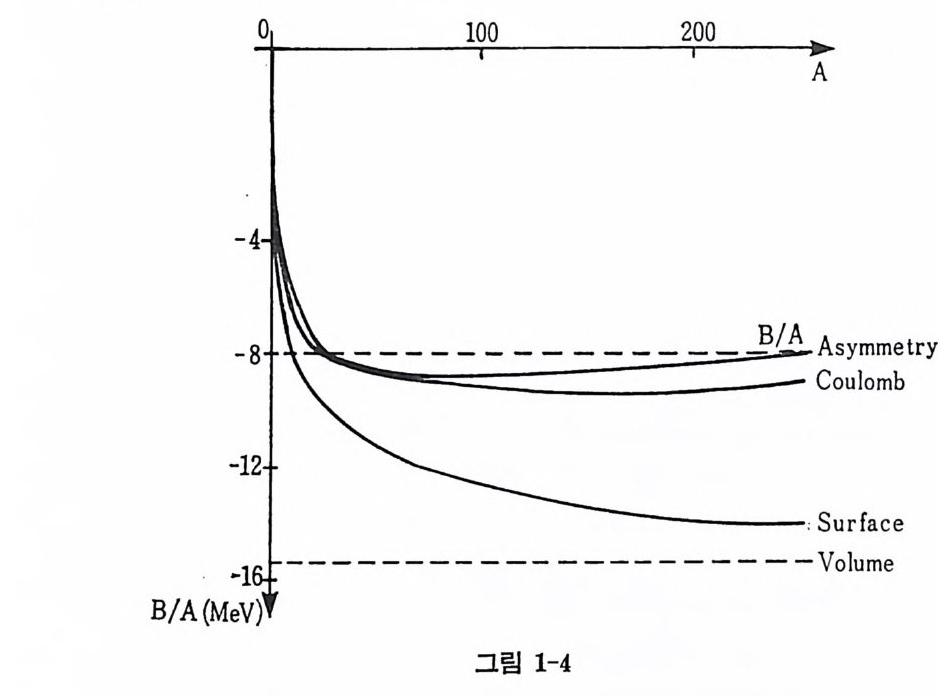
이러한 페르미 기체 모델로부터 또한 이 기체계의 전체 운동에너지물 구해 보기로 하자. A 72 〈 T〉=〈,fr|홉孟 I ,tr〉 =5上 2끄m A~23MeV•A (1. 24) 죽 핵질의 밀도가 주어지면 핵자들의 평균 운동 에너지 〈 T 〉 /A 가 정 해지며 전체 에너지 〈 E 〉는 핵자수 A 에 비례한다. 이러한 결과는 실험 적으로도 큰 차이 없이 잘 맞고 있다. 4) \Yeis z acker 결합에 너지 공식과 포화현상 바닥상태에 있는 핵의 전체 에너지 E 로부터 결합에너지 (bin d in g energy ) B 를 다음과 갑이 정 의 한다. E=Nmnc2 + Zmp c2 -B (1. 25) 여기서 11tn C2=939. 55 MeV m,c2=938. 26 MeV N은 전체 중성자 갯수, Z 는 전체 양성자 갯수이다. 핵은 주로 인력인 핵력으로 집합상태를 이루고 있기 때문에 식 (1.2 5) 에서 B 는 언제나 양수이다. We i szacker 는 이 결합에너지를 몇 개의 매개상수를 이용하여 공식화했다. B=bvo 1A + b,u,1A213 + 뭡드 (N-AZ) 2 + 운 꿈꾼 bvol 브 -15. 68 MeV b,ym ~50 MeV b,ur1~l8. 56 MeV Re 브 1. 24 A1/3 (1. 26) 쌍짓 기 효과 (pa ir in g eff ec t) 를 포함하려 면 b,A (N, Z) A-31,, A(N, Z) =[ -1o ;; 짝짝수수--짝홀수수 1 ; 홀수-홍수 를 식 (1.26) 에 삽입하게 된다. b,=34MeV
각항의 크기는 그림 1-4 에서 볼 수 있다• 핵질이란 N=Z 이며 N 과 Z 가 모두 무한대의 수를 갖되 일정한 밀도를 유지하는 (0 ➔ oo, 그러나 p는 유한한 값) 계를 말한다. 이러한 계에서는 Z 가 무한대가 되면서 정전기력 역시 무한대로 커지기 때문에 정전기력은 무시하여 생각해야 한다. 또한 일정한 핵자밀도를 유지하기 위해서는 부피 0 가 무한대가 되어야 하기 메문에 식 (1.26) 의 두번째 항안, 핵의 표면의 크기에 관 계하는 에너지 항은 계산할 수 없다. 실제 핵의 성질을 살펴보는 데에 는 핵질 (nuclear matt er ) 이론이 미 흡함 이 있다고 하겠으나 그립 1-4 에 서 보는 바와 같이 표면의 크기에 비례하는 항은 부피에 비례하는 항에 비해 작으므로 이 이론은 핵성의 중요한 부분을 포함하고 있다고 볼 수 있다.
 。 100 200 A
。 100 200 A
특히 여기서 핵력을 무시하면 페르미 기체 모델과 같이 되겠으나 이 런 경우 결합에너지식 (1.2 6) 중 부피에 비례하는 첫 항에 대한 값과 비교하기 위해서는 핵자 전체는 식 (1.26) 과 식 (1.24) 로부터 평균 결 합 포텐셜에너지 소A끄 ~ (-16-23)MeV=-39 MeV (1. 27)
룰 가져야 할 것이다. 즉 실제 핵 자들이 핵내에서 느끼는 평균 포텐 셜 에너지는 거 의 일정해야 한다. 이것은 핵의 포화현상의 단말을 나타내 주고 있다. 만일 핵자와 핵 자 사이의 인력의 작 용 범위가 매우 넓고 (oo), 그 크기가 Vo 로 일정하다고 하면 핵내의 핵 자들의 전체 에너지는 -V° A(A2 - 1) (1. 28) 이므로 뀝 Lcc( A -1) (1. 29) 일 것 이 다 . 따라서 핵 자 - 핵 자 사이의 핵력 은 주어진 일정한 수 No 개의 핵 자 들과만 작용하 여야, 뀝 ccN0= 상수 (1. 30) 가 되어 포화 현상을 설 명 할 수 있다. 핵 내 의 핵 자들 사이 에 작 용하는 핵 력 중 단거 리 힘 (short- r ang e for ce) 과 파울 리 배 타 원 리 및 불확 정 성 원 리 (uncerta i n t y pr in c ip le ) 모두가 이러 한 포화현 상을 일으키게 된 다. 즉 두 핵자가 d( f m) 라는 거리 속에 위치 할 때 불확 정성 원리에 의 해 생 기는 운동에너지는 T~ mhd2 2 ~누a40 〔 MeV 〕 (1. 31) 이다. 이것과 비교할 만한 두 핵자 사이의 포텐셜에너지 형태는 단순하 지는 않다. 찰 알려진 r- 중간자 교환 포텐셜 (one pion exchang e pa te - n ti al) 은 두 핵자가 어느 정도 떨어져 있으면 찰 맞지만, 좀더 가까이 붙어 있는 경우에는 r- 중간자보다 더 무거운 p-중간자 교환 및 Q-중간 자 교환에 의한 포텐셜이 주효하다고 알려져 있다. 정 상적 인 이 해 를 위 해 유가와 (Yukav.: a) 포텐셜을 생 각하자. V(d)=-V 。e下 가 T d (1. 32) Vo~50MeV
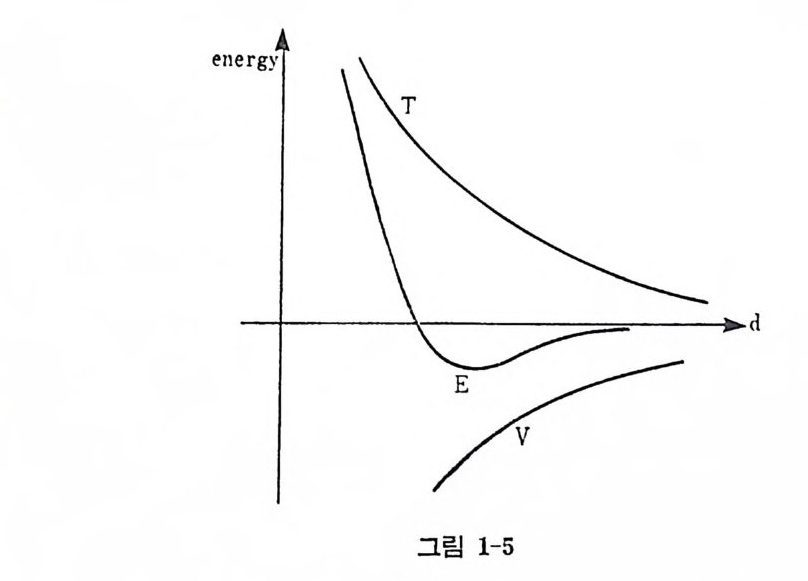
µ~0. 7f m -1 두 핵자의 전체 에너지 E 는 약간의 극소치 를- 가지게 된다(그립 1-5 참조).
 energy
energy
실재 로 -중간자의 역 할이 라고 알려 져 있는 단단한 심 (hard core) 을 감안하면 핵자간의 거리 를 약 0.54f m 이내로 접근시키기 위해서는 무 한의 에너지가 필요함을 알 수 있다. 그렇더라도 d~2.4 f m 정 도에서 전체 에너지는 극소값을 갖게 되며 약 3f m 이상 떨어져 있는 핵 자에 대해서는 포텐설이 작용하지 않게 된다. 3 핵계의 대칭성과 불변치 1) 일반적인 성질 실험적으로 측정되는 보존치는 이론적인 해밀토니안 H 에 부여되거나 내재되어 있는 대칭성 또는 불변치와 상호 관계 물 가진다. 죽 H 자체 가 가지고 있는 성질이 핵의 파동함수나 스펙트럼에 대한 연구에 중요 한 정보를 제공하는 셈이다. 따라서 계의 운동학적인 성질을 따지기 전 에 H 에 대한 정보는 스펙트럼의 분류나 선 택 규칙 (selecti on rule) 을 이용한 스펙트럼상의 예 측 을 가능하게 한다.
그러나 이러한 대칭성 (s y mme t r i es) 이나 불변치 (i nvar i an t s) 들은 관측 에 의해 측 정되므로 결국 실험적인 겅밀도와 깊은 관련이 있다. 또한 핵자둘의 운동을 지매하고 있는 핵력, 전자기력, 약력들은 같은 대칭 법칙을 만족시키지는 못하는 까닭에, 전체 핵의 대칭성이란 가장 지배 적인 성질의 대칭성에 대한 것을 주로 연구하게 되고 비대칭적 요소는 섭 동 (pe rtu r bati on ) 으로 취 급하게 된 다. 해 밀 토니 안 H 가 변 환군 (tra nsfo r mati on grou p ) 0 와 교환 관계 (com- muta t i on relati on ship ) 를 만족시 칸 다면, 죽 〔 H, 이 =O (1. 33) 이면 우리는 H 와 0 에 대해 공통된 고유함수를 만들 수가 있다(그러나 언제나 H 의 고유 함 수와 0 의 고유함수가 같은 것은 아니다). H, frn, .=En,f rn, • 0 少 n, a=C. 中' • (1. 34) 어떤 연산자가 이 군(g rou p)의 요소로만 표시되는 함수라면 이 연산 자의 고유함수 또한 하나의 i/r n, .로 표시되며, 이 연산자의 고유치는 계 의 운동항 량 (consta n t of moti on ) 인 것 이 다. 그러나 i/r n,a 의 결합으로 표시되는 상태함수 ,fr= a,fr n, a + b,fr n, ~ (1. 35) 는 H 에 대해서는 고유함수이지만 0 에 대해서는 그렇지 않다. 우리는 이런 경우물 시간 역전(ti me reversal) 대칭성의 경우에 볼 수 있다. 먼저 핵에 대해서 언제나 만족되는 몇 가지 보존 법칙을 들어보자. i) 에너지는 보존된다(그러므로 H 는 Herm iti an 이어야 한다). ii) 전체 운동량은 보존된다. 죽 위치 이동에 대해 H 는 불변이다. iii) 전체 각운동량이 보존된다. 죽 회전 이동에 대해 H 가 불변이다. iv) 이 의에도 핵자의 수가 불변임과 전체 전하가 불변임도 찰 알려 져 있다. 따라서 모든 핵의 상태는 위에서 든 다섯 개의 보존치에 해당되는 양자 수들로 구분될 수 있다. 한편 핵계에 대해 근사적으로 만족되고 있는 보존 법칙들을 좀더 자 세히 조사해 보자.
(1) 반전성 보존 한 점 0 에 대한 점대칭에 해당하는 반전 연산자 So 는 다음의 성질을 갖는다. sss 。。。 ?rpSS S t t t == = s-- r:P 스: :위핀 운 치 동 량 St= l (1. 36) 따라서 s 。中 (?, k) =中 (구, 1Ik) = 士中 (?, 1m) (1. 37) 이다. 핵력이나 전자기력은 反轉性(p ar ity)을 보존하지만 약력은 보존하지 못한다 (이 론 : Lee 와 Yang , 1956/ 실 험 : Wu, 1958) . 그러 나 약력 은 핵 력에 비해 10-6 정도로 작으므로 핵내에서는 이 보존법칙이 거의 유지된 다고 볼 수 있다. (2) 하전스핀 (iso sp in) 보존성 〈전 하대 칭 (charge s ym me t r y)과 전 하무관성 (charge ind ep e ndence)> 중성자와 중성자 (n-n) 사이의 핵력과 양성자와 양성자(p-p) 사이의 핵력의 크기가 거의 같다는 사실은 거울핵 (mi rr or nucle i)의 전체 질량 의 차이 곧 에너지의 차이가 정전기력 효과를 배제했을 경우 lOOKeV 보다 작은 것으로부터 추측할 수 있다. 이러한 대칭적 사실을 전하대칭 이라고 한다. 이러한 대칭성은 전하의 교환에 대한 대칭성의 일부분을 가리킨다. 죽 p-p나 n -n의 핵력 크기와 n -p의 핵력의 크기도 같을 수 있다. 두 전하의 교환에 대해 대칭인 파동함수는 (p-p) : ,fr= x, (l) x, (2) (n- n) : ,fr=X n (1) Xn (2) (n-p) a 처=* (x, (1) Xn (2) + Xp (2) Xn (1) ) (1. 38) 이 며 반대 칭 (anti sy m metr i c ) 인 파동함수는 (n-p) I : 논 슈 (X1 (1) Xn (2) -x, (2) Xn (1) ) (1. 39)
이다. PP 나 nn,n p 3 에서의 핵력이 갇다고 할 수 있다면 이러한 성질을 우리는 전하무관성이라고 한다. 따라서 이럴 때 pp: 11,1>=IT,Mr> nn : 11, -1) np, : 11, 0) nP1 : 10,O> 와 갇이 하 전 스핀 양자수 (T: tot a l iso spi n, Mr: p ro j ec ti on) 를 이용하여 상대함수 룹 기술 할 수 있게 된다. 따라서 두 핵자 사이의 작용력은 T 값에 의존하며 Mr 에 대해서는 축 퇴 (de g enera t e) 되어 있다. 그러므로, 해밀토니안 H 가 전하무관성을 갖 기 위해서는 頂,杓 =O (1. 40) 즉 H 는 하전스핀(i sos pi n) 공간에서의 희전에 대해 불변이어야 한다. 따라서 두 핵자의 가장 보편적인 H 의 형태는 H=a+,;;(1) 구 (2) (1. 41) (-;.(1) 과 -;(2) 는 각 핵자의 하전스핀 연산자) 이고 계가 A 개의 핵자로 되어 있다면 전체 해밀토니안은 H=a+b ~A r➔( t) · r➔( ;) (1. 42) i>j 로 표시되어야 한다• 따 즉 전체 하전은 언제나 보존됨에 비해 T 는 보존되지 않을 수 있 다. 이는 다음 세 가지 연유로부터 보존되지 않는다; 첫째, 전자기력에 의해 둘째, 중성자와 양성자의 질량 차이로 세째, 핵력 자체의 원인으로(군-중간자와 元°-중간자의 질량의 차이가 약 4MeV 만큼 존재하는데, 이들의 교환에 의한 핵력도 이 영향을 받게 된다. 그러나 이는 근본적으로 전자기력에 의하여 나타나는 현상이다) 이처 럼 비보존의 경우를 특별히 취급하고 싶은 때를 제외하고는 비보 존의 영향은 일반적으로 무시되는데, 그 이유는 하전스핀이라는 개념을 사용하면 많은 계산을 쉽게 할 수 있기 때문이다.
(3) 시간 역전 대칭성 시간 역전(ti me reversal) 에 대한 대칭성에는 어떤 보존치가 부여되지 는 않지만 이 대칭성은 실험적 결과들을 이해하는 데 중요한 역할을 한 다. 시간을 역전시키는 연산자 K 는 다음 성질을 갖는다. KKp짜 K += 7= -p Kl 距=-; (1. 43) 따라서 만일 계가 스핀이 없는 입자로 되어 있다면 H 는 t ➔ -t 에 대 해 불변 이 고 그 고유함수가 ,tr (ri, r2, …?A ) 일 때 K,t r (紅 YA) =中* (?I, r2, …D (1. 44) 이다. 그리고 中*도 역시 고유함수이다. 스핀이 있는 경우에 이 연산자 는 모든 수를 그 수의 복소공액으로 변화시킴과 동시에 스핀의 방향도 바꾸게 된다(in• ➔ -m.). 이때 편의상 위상(p hase) 에 대한 변화를 주기 로한다. 죽 Kljm )=(-)i+ lj, -m> (1. 45) 이다. 스핀 1/2 인 N 개의 페르미 입자를 예로 들면 K,J r (r1, …, rN, tnS ,, …m s.) = (-) 타 '''꾼 (;J, …, YN, -nzs1, …- ms 眞) (1. 46) 이 된다. 이 연 산자 K 는 반-유니 터 리 (anti -u nit ar y) 연 산자이 다 ; K(C1,J r1 +C2,J r2) =Cf K i r1+ Ct K ,J r2 · (1. 47) 이 연산자는 전체 각운동량 연산자 I-*~ 와 다음과 같은 관계를 갖는다 (➔l= L➔ + S➔) . :. KK-l[+KI-K+== O-l (1. 48) 죽 H 와 7 의 고유상태는 K 에 대한 운동 항량을 갖지 못하게 된다(식
(1. 35) 참조 ) . 핵물리학에 있어시 시간 역전의 대칭성에 대한 실험적 자료가 많지는 않지만 해밀토니안 H 중에 이 대칭성을 위반하는 부분과 위반하지 않는 부분의 비가 약 1/12.5 보다 작다는 것이 일반적 결론이다. 2) 핵자용니자 (측 두 핵자) 상호 작응에 대한 응옹 (1) 2 체 포텐셜의 일반적 형태 앞질에서 언급한 대칭성과 불변치에 대한 응용의 한 예로 핵자-핵자 사이의 상호작용에 대해 생각해 보기로 하자. 먼저 이 상호작용이 포텐 선 예 의해 표시될 수 있다고 가정하면 두 핵자 사이의 포텐셜 V12 는 위 기-, --+--+ ➔➔ ➔➔ 치 (r,, r2), 운동량(p I, p2 ) 및 스핀 ((Jb (J2 )' 하전스핀 (TI, m) 에 대한 과 울리 행 렬 의 함수로 나타낼 수 있다. 이 포텐셜이 다음 조건들을 만족 한다고 하자. i) Hermi tian 일 것 (에 너 지 보존) ii) 두 입자의 교환에 대해 대칭일 것(하전스핀을사용하였을경우두 핵자는 구별이 불가능한 등일 입자이다) iii) 상대위치 (;12=;1_;2) 및 상대운동량 (7n=11_12) 만의 함수일 것 (위치 변환에 대해 불변) iv) 상대위치의 크기 1;l21 만의 함수일 것(반전성 보존 또는 p 31 의 ii) 와 iii)의 종합적인 이유에서) v) 전체 각운동량(I)의 공간에서 스칼라일 것(전체 각운동량 보존) l=L+S L- =/1-수 +/2 S➔ =(➔J , +(-J 2 여기에서 ➔h 는 i 입자의 궤도 각운동량을 나타낸다. vi) 하전스핀 공간에서 scalar 일 것 (전하무관성) vii) p와 다] 대한 짝수차 함수일 것(시간 역전 대칭성) 따라서 포텐셜의 간단한 형태를 우리는 일반적으로 다음과 같이 쓸 수 있다• V12= (S12®L12) CO>- c-1 2 (1. 49) 여기에서
T12=A+B -➔r- 1 · 다➔ (1. 50) 이고 S12 는 값 과 값 의 함수로 스핀 공간에 작용하며 L12 는 ;., ;2, Pi 및 P2 둘의 함수로 좌표 공간 및 각운동량 공간에 작용한다• (S12® L12)CO ) 는 이 두 함수가 스핀과 각운동량 공간에서 스 칼 라이도록 구성되는 것 을 나타낸다. 특히 값과 ;2 로부터 S12 몰 스칼라 형태로 만드는 경우 이 를 중심 력 (centr a l for ce) , 벡 터 형 태 굵 +;2 로 만드는 경 우 스핀구 1] 도 력 (spi n- orbit for ce), 텐서 형태 (;1X 값 ) ( 2 ) 로 만드는 경우 텐서 력 이라 부른다. 실험적인 결과들을 분석하는 데에는 이 들 모두 를 합하여 사용 하고 있고, 이들에 대한 매개 변수를 조정하여 이 론 치와 실험치문 비교 한다. ® 중십력 S12=C+Du-1 ·一(l 2 L12=f c( l-r1 -r一2 I) V12= (S12 X L12) ' !'12 (1. 51) 이때 /.(r12) 를 중심력의 지름 형태인자라고 부른다 . ® 스핀궤도력 S12=(..l .1 + (..l.2 = S... L12= (r➔1 -➔r 2.) I\ (. p- ➔ 1-p-➔ 2 )/1 , (r12) =L'f1s (r12) :. V12=➔S · L-*f i, (rd-r 12 (1. 52) ➔ -, ➔ -, © 텐서력 T12= 3( (l rr 업(l 2·m) _麟 V12=/r (Y12) T12•12 (1. 53) 이상의 형태는 모두 E,P 및 f .s 에 대해 선형인 형태들이다. 이 의 에도 E 또는 (E. 점 2 동 2 차에 비례하는 형태들도 생각할 수 · 있으나 핵물리에서 이들 2 차 형태들은 중요한 역할을 하지 않기 때문에 생략 한다. (2) 중심력에 대한 상용적 형태 및 매개함수 중심력의 표현에 사용되는 매개상수둘의 정의는 일정치 않다. 이 중 한 형태를 먼저 살펴보자. Vc (l, 2) = V 。 (r) + V., (r) -u1. ·➔u2 + V--, (. r ). i➔1➔• -r2 + V--u, (•r ). l-l1 ➔• fl➔2T 1 •➔ -r 2 (1. 54)
여기에서 r=Ir-1-r-2| 이 고 V 。 (r), Vu(r), V,(r) 및 Vu,(r) 은 r 만의 함수 로 표시된 지름 형태 인자 들 이다. 이 포텐 셜 은 다음과 같 은 교환력 (exchang e forc e) 을 나타내 는 연 산자 룹 이용하여 다시 적을 수 있다. Pc=\(1+:I.? (1. 55) P'=i -(1+ r1·r2) (1. 56) 죽
pul S =l, Ms)=IS=l, Ms> pu lS =O, 0)=-1S=O, 0) prl T =l, Mr)=I T=l, Mr> P'I T =O, O>=-I T =O, 0) 하전스핀까지 합 치먼 두 개의 동일한 핵자는 페르미 통계를 만족하므 로 prp u p r lSTMsMr>=-IS TMsMr> (1. 57) 이다. 이기서 P 『은 위치교환 연산자이다. P',fr ( ➔r1 , ➔r2 ) =,fr (r2, Y1) 따라서 언제나 Pr=-FPr (1. 58) 이 며 Vc(l ,2) 는 다음의 형태로 쓸 수 있다. Vc(l, 2) = W(r) +M(r)P 『 +B(r)P-H(r) P' (1. 59) 이 때 W(r) , M(r) , B (r) 및 H(r) 을 각각 Wi gn er 력 , Majo r ana 력 , Barlett e 력 , Heis e nberg 력 이 라고 하며 이 들은 모두 Vo, V11, Vn V.(Tr 의 함 수이다. 핵 속에 있지 않은 자유스러운 두 핵자의 실험 결과와 직접 연관이 되는 형태를 갖는 포텐설로 Vc(l,2) 를 표기하기도 한다. 죽 두 핵자가 전체 스핀 (또는 하전스핀)의 단일항 상태 (sin g l e t s t a t e) 와 삼중항 상태 (tri p le t sta t e ) 에 있을 두 경 우를 각각 분리 하여 고찰하기 위 한 사영 연 산자 (pro je c ti on ope r ato r ) 를 이 용하는 방법 이 다.-,, _ . P ~ = 포4仁 (1. 60) Pr=4一 ~-* (1. 61) 하전스핀의 경우에도 감은 형태 를 갖는다. 이들 연산자의 성격은 다 음과 같다. Pg lS =l, Ms>=IS=I, Ms> Pg lS =O, 0)=0 !P f lS =O, 0)=1S=O, 0) Pf l S=l, Ms ) =O 따라서 Ve(1, 2) =11V(r) P ,: P f +3 1 V(r) P gP f + 마 1 (r)P 低 + 33 V (r) P gP 5 (1. 62) 이며, 이때 예를 들어 마 l (r) 은 두 핵 자의 충돌 에서 스핀 및 하전스핀 의 다른 두 채널 (channel) 에 대한 형 태인자 들 이다. (3) 스핀-궤도력에 대한 형태 및 매개변수 연산자 l-s 의 상태함수 15=0,µ , =0> 에 대한 고유치는 0 이다. 따 라서 스핀궤도력에 대한 일반적인 형태 를 다음과 같이 쓸 수 있다. VLS= (+ VLs (r) P 炳 + -VLs ( r) P 的) E. 5 (1. 63) (4) 텐서력의 형태와 성격 텐서 연산자(식 (1.63)) 의 |S=O,O> 에 대한 고유치도 역시 0 이므로 텐서력에 대한 일반적인 형태도 식 (1.63) 처럼 다음과 같이 쓸 수 있다. Vr= (+VrP[P [+ -VrP[J> r) T12 (1. 64) Tu 는 식 (1. 53) 에서 정의되었다. 텐서력의 성격은 T12 로부터 다움과 갇이 고찰될 수 있다. i) 단일항 상태에 대한 고유치는 0 이다. s=O=➔(l 1+ ➔(l2 이 므로 ➔(l 1= -(➔l 2= C➔ 라 하면 (;. 刀) 2=A2 이 어 서
:. T12-=3~(➔a + · .r, a ) 2 2,= -::-- 3+3=0 (1. 65) 따라서 단일 항 상태에서 핵릭은 오직 중심력뿐이다• 이든 좌표 공간 파동함수가 ;: 의 원접에서부터 등방형인 경우 T,2 에 대한 기대치 또한 0 임을 말해준다 : <,fr I T 12 | 中〉 =0 (1. 66) 증명 〈,fr lx y|中〉=귬 =0= 됴=됴 굿 2 구=궁 2 = f ... 〈류〉=停〉=等〉=+ :. <( ;(I).?;(2):t) >=+ ;(I).;(2) :. ;r.n; =U-c-+ l) • 0➔( 2) -U➔c1)➔ 'C2 ) =O (증명 끝) (1. 67) ii) 좌표 공간에서 헝테 인자 fr (r) 가 음 의 함 수인 경우 가장 안정된 상 태는 두 핵 자의 스핀 방향이 서로 평행이며 두 핵자의 스핀이 같은 방 향 으로 나열되어 있을 때이다. 이 를 알기 위해 각각의 경우를 생각해 보기로 하자. .• S=1’ ^_ 2M=3_1’ s l=2 (ms1=ms2= 1 /2) .:.f ._ f f TI 1 T12=0-1=-1 T: 1S2=:=l,- 3M+ s1==O- 2 (mTis 1,=2-=m0s+,1==11/2 ) f iii) T12 에 대한 운동 항량 다는 반전성 So, 전체 각운동량 l, z 축에의 두사 각운동량 [z 및 전 체 스핀운동량 동과 다음과 같은 교환 관계를 갖는다. [T12, So]=O
[T12, I 汀 =O [T12, I 』 =O [T 12,S 汀=O (1. 68) 따라서 T12 에 대한 고유상태는 반전성 z= 士 1, F=(L냐 +5)2, Iz 및 하전스핀 T, Ts 등의 양자수에 의 해 분리 됩 수 있다. 그러나 T12 는 E 및 5 의 z 축에의 두사 각운동량 요와는 교환 관계 를 갖지 않는다. [T12, L 인 =\=O [T 12,S 』 =\=O (1. 69) 특별히 요와는 직접 교환 관계는 성립하지 않지만 양자수 S 는 좋 은 양자수가 됨을 다음과 같이 알 수 있다. 증명 두 핵자의 고유상태를 다음과 같이 S 에 대한 고유함수로 전개 하자. II, Iz, 1l, T, Tz>=S =~O ,l asll, lz, 1l, T, Tz ; S) (1. 70) 이 상태함수는 두 핵자의 상호 교환에 대하여 반대칭이어야 한다. 따라 서 전개항 개개에 대해 (-) 웅 (I- :: )+S+T= -l (1. 71) 이어야 한다. 만일 X 와 T 가 정해지면 S 값은 다음과 같이 단일하게 결 정되어야 하는 것이다. S=O : 쉽 -(1- 元) +T 가 홍수인 경우 S=l : 갑 -(1 급) +T 가 짝수인 경우 따라서 식 (1. 70) 에서의 전개는 오직 하나의 항만 존재하게 된다(증명 끝). 식 (1. 69) 로부터 T12 에 대한 고유함수(식 (1. 70) 의 좌항)를 L 에 대 한 고유함수만으로 전개할 수 있음을 알 수 있다.
II, Iz, 元 , S, T, Ta> =f, ai• ll , lz, 元 , S, E, T, T3> ;1. 72; 그러나 텐서 릭 에 작 용가능한 상태인 S=l 을 예로 들면 E=1 급一 E=[II +l l-1 이고, 元=土 1{+ : L’ 가 짝수일 때 - :L’ 가 홀수일 때 로 구분 된다. 따라서 T12 가 존 재 하는 중성 자_양성 자계 (예 를 들면 중성 자와 양성 자 의 충돌 에서 나 타날 수 있는 상태 또는 중수소에서의 상태)를 궤도 각 운동량 의 고유상태 로 표 시 하면 표 1. 1 과 같다. 여 기 에 서 aL 들 은 T12 를 포함하는 Schordin g er 방정 식 의 해 로 결정 될 것 이다 (주 의; 중수소에 대한 해밀토니안 중에 중성자구양성자 사이의 상 호 작용력 이 중심 력 과 텐서력의 합이라고 하자• 이 계의 전체 스핀상태 는 S=O 인 경우와 S=l 인 경우로 구분되지만 S=O 인 단일항 상태에서 는 T1 2 =0 임 을 알 았다. 이것이 의미하는 바는 S=O 인 상태에서는 핵력 은 중 심 력 이며, 따라서 이때에는 궤도각운동량 L 도 좋은 양자수이어서 5= 0 인 상태에서는 단일 L 값을 갖는 에너지 고유상태를 만들게 됨을 의미한다• 표 1.1 에서는 삼중항 상태만을 표시하였다)•
 표 1.1 중수소의 3 중항 상태
표 1.1 중수소의 3 중항 상태
이 절에서 우리는 대칭성 및 불변치가 어떻게 핵물리에서 사용되는지
그 기초적인 입장에서 두 핵자의 계를 예로 들어 고찰하였다. 이와 갇 은 대칭성 및 불변치들은 다체 핵물리학의 모든 시도에 가장 엄지한 새 약을 주게 된다. 다시 말하면 이러한 대칭성은 우리가 다무고자 하는 핵의 상내함수에 대한 이론적 고찰이 정확한지운 판별하는 방법으로도 쓰이고, 한편 문 제에 대한 사전 칭보를 제공하기도 한다. 3) 핵의 전자기적 성격 및 변형 자연 속에는 두 개의 중성자, 또는 두 개의 양성자로 형성된, 안정하 게 속박된 계는 존재하지 않고 다만 중성자와 양성자 한 개씩으로 이 ·; f 어 진 계 (중수소, deute r on) 만이 두 핵 자계 로서 존재 한다. 또한 두 해 자 계야말로 다체계 중에서 가장 간단한 계이다. 이 계에 대한 실험적 결 과를 요약해 보면 다음과 같다. i) 결합에너 지 B0=-2. 2245 MeV ii) 전체 각운동량 l=l iii) 전체 하전스핀 T=O iv) 자기 쌍극자 모멘 트 (mag n eti c dip o le moment) µD=O. 8574 µ (µ=efz / 2 Mp c ; 핵 마그네 돈) v) 전기 사중국자 모멘 트 (electr i c qua drup ol e moment) Qu =2. 738 mi lliba rns vi) 중수소는 바닥상태 이 의 의 둘뜸상태 를 갖지 않는다. 전기 사중국자 모멘트를 보면 중수소는 약간 pro late 형 태 로 변형 된 밀 도분포를 가지고 있음을 알 수 있고 따라서 궤도 각운동량이 영인 고유 함수로만 나타낼 수는 없다. 그러나 만일 핵자간의 상호 작용력이 중심 력뿐이라면 바닥상태는 L=O 인 상태뿐일 것이므로 표 1.1 에서 보는 바 와 같이 텐서력이 존재해야만 이 사실은 설명될 수 있을 것이다. 또한 S=O 안 단일항 상태는 존재할 수 없음을 먼저 밝혀 보자. 전체 스핀 S 는태 는좋 은분 광양표자기수법 에이 므의로,하 면만 일1P 1S 인= O상 인태 일상 태것에이 다.중 수따소라가서 있M다면L=,— 그1, 0 상,1 의 세 상태는 에너지 축퇴상태둘이고, 이 세 상태에 있을 확률은 갈아 야 한다. 이렇게 된 경우에는 중수소는 구대칭 밀도 분포를 갖게 되겠 지만, 실험 결과는 약간의 p rola t e 모양이어서 S=O 인 상태의 가능성은 없다. 따라서 S=l 인 상태만이 가능하며, 이때 표 1.1 에서 간단한 두
가지 가능성 을 살펴 보면 다움과 같다• /=1 일 매 {a(3(Sl) +/3( 3Dl), 仁 =+1 3Pl , JC =-1 또한 元 =-1 의 경우도, ap l 상대는 L=l 이고 z 축에의 투사 각운동 량이 M 1. =-l,O,1 인 상태들이 축퇴되어 있으므로 핵자의 평균 분포는 구대칭이 되어 역시 변형된 중수소의 고유함수가 될 수 없다(또는 식 (1. 17) 에서부터 S=l, T=O 을 대입하고 보면 元는 +1 이어야 합을 알 수 있다). 혼합개 수 a 와 f3 문 계 산하기 위 해 서 는 일 반적 으로 Schrodin g e r 방정 식웅 풀어야 하겠으나, 여기서는 자기 쌍극자 모멘트의 실험 결과를 사 용하여 보기 로 하겠다. 중수소의 파동함수는 n=+l안 경우만이 가능하며, 이는 ,Jr= a,Jr o + /3,fr2, (1. 73) 여기서 ,fro= IL =O, S=l ) ,fr2= IL=2, S=l) ,Jr= II,M> (1. 74) 이며, 이매에 a2+ {3 2=1 이다. l 웅 질량중심에 대한 각 핵자의 궤도 각운동량이라 하면, ➔lp = ln=l -lp.+ ➔ln =L-•=-2令l (1. 75) 이다 (E 은 핵자들의 상대적 궤도 각운동량아나 이제 문제에서 E 은 진 량중심점에 대한 전체 각운동량과 갇다)• 자기 쌍국자 모멘트 연산자 》는 중수소의 경우 다음과 같다(여기서 µN 는 핵 mag n eto n 이 다) • µ➔ =µTN (g,,➔ l ,+2g ., -s, ,+2g, .s ➔n ) (1. 76) 따라서 측정 된 자기 쌍극자 모멘트는
µ=
A. de Shalit and H. Feshbach, Theoreti ca l Nuclear Phy si c s , Vol. I , Joh n Wi le y & Sons, Inc., 1974, N.Y., Chic h este r , Bris b ane, Toronto . M.A. Presto n and P.K . Bhaduri, Str n ctu r e of the N11cleus, Addis o n-Wesley Pub. Co., 1975, London, Armste r dam, Onta r io , Toky o. J.M . Blatt and V.F. Weis s kop f, Theoreti ca l Nuclear Phys i c s , Joh n Wi le y & Sons, Inc., 1966, N.Y., London, Sy dn ey.
제 2 장 독립입자 핵각 모 델 ] 소개 실 험 적 으로 알려 진 마법 수 (mag ic number) 들 , 죽 2, 8, 20, 28, 50, 82, 126, … ••• 또는 스핀 반전성 및 여러 핵 상태의 성격들은 원자물리에서 사용되는 각 (shell) 모델과 같은 특성을 핵자들에게 부여함으로써 간단 하게 설명할 수 있다. 1949 년 Ma y er 와 J ensen 에 의해 설립된 이 핵 각 모델은 다음 세 가지 가정을 내포하고 있다. i) 각 핵자는 다른 핵자들과 무관하게 움직이며 그 핵자의 위치좌 표 ;‘의 함수로 표시되는 중심장 V(;,) 가 존재한다. 포텐ii) 셜원 f자(-물r ,. ,)리-l,· 의 ➔s 가 경 우존보재한다다 훨(씬이 로큰써 ( 3각~ 5핵Me자V의) 스스핀핀- 방궤향도에 상 대호한 결 합핵 을의- 상태의 축퇴는 벗겨지게 된다). iii) 일명 쌍짓기 (p a i r i n g)라고 불려지는 현상이 존재한다. 이 현상은 한 양성자는 다른 한 양성자와 한 중성자는 다른 한 중성자와 결합하여 하나의 두 핵자 부분계를 이루되 이 계의 전체 각운동량은 0 이 되도 록 형성되는 것을 가리킨다(한 중성자와 다른 한 양성자 사이의 결합은 가 정하지 않는다). 이 쌍짓기에 대한 가정은 핵각 모델과 직접 관련이 있 는 것은 아니며, 실험적인 사실을 설명하기 위해 첨부된 가정이다. 이 핵각 모델의 가정은 핵 구조 물 이해하는 데에 하나의 중요한 변화 를 일으켰다. 이것은 언뜻 보기에는 그때까지 우리가 이해하고 있던 핵 력의 성격과 모순되는 것처럼 느껴졌었다. 그 당시까지 알려진 바로는
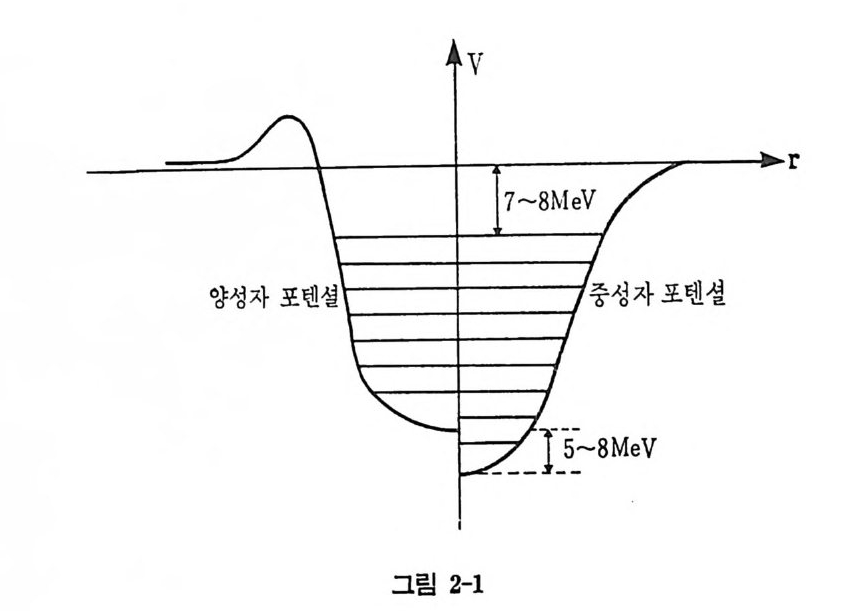
핵력은 매우 강하고 그 작용 범위는 핵의 크기에 비해 짧은 것이었다. 이러한 모순성의 일부는 이미 파울러 배타 원리를 이용하여 앞장에서 설명되었다. 모순이라고 생각되는 다른 면은 다음 장에서 취급하기로 하고 우선은 이 핵각 모델의 주요 내용을 살펴보기로 하자. 이미 앞장에서 언급한 것과 같이 핵자들의 분포 형태로 추정된 Woods-Saxon 포텐셜 외에 양성자들을 위한 포텐셜 수정은 대략 다음과 같다. 핵내 양성자들의 분포가 반경 R 내에서 균일하다고 가정하면 쿨롱 포텐 설은 다음과 같이 주어진다. {Vc(r) 홀 (3 玉), ZR Vc (r) =—Zre— 2 , r~R 이때 쿨롱 반경 R 을 R= l. 2AI/S 으로 보면 핵의 중심 부분과 껍질 부분과의 차이는 약 Ze2/2R 이고 이는 우라늄의 경우 대강 9MeV 정도 이다. 한편 칼슘의 경우는 약 3.5MeV 이며 변화는 정도도 작으므로 이 에 대해 보정된 포텐셜을 보면 그림 2-1 과 같다. 한편 바닥상태에 있는 핵의 경우 핵자들이 차지하고 있는 핵의 상태에서 정의되는 페르마 준
 v
v
위는 약 -7~-8MeV 정도로 속박되어 있고(결합에너지 참조), 포텐 설의 껍질 부분 (r~R) 에서는 파동함수가 적게 분포되어 있어서 사실상 중성자나 양성자들이 보는 포텐셜의 모양은 바슷하다고 할 수 있다. 중 성자계와 양성자계가 평행을 이루고 있는 자연계의 핵들을 보면 양성자 나 중성자의 페르미 준위는 안정된 핵에서는 거의 비숫할 것이다. 2 중심장의 일반적인 성질 및 단진자 포텐셜 핵자의 스핀과 하전스핀을 무시하면 독립적인 핵자의 상태 ¢。(;)는 Schrodin g e r 방정 식 을 만족한다 (m 은 핵 자의 질 량이 며 , 질 량중심 의 효 과는 무시하였다). [-읊 V 나 V(r)]«(r) =E««(r) (2. 1) V(,. )이 구대칭이므로 ¢«(1:) (a=n,l,m) 을 다음과 같이 놓으면 ni . (r) =A¥Y,. (0, ¢,) (2. 2) 지름 파동함수 Un i (r)=U 는 _읊 U+{~+V(r)-e}U=O (2.3) 을 만족하며 경계 조건들 u➔ 0, r ➔ 0 u➔ 0, r ➔ 00 및 규격화 조건 I
읊 l (l』 !L +V(rr)-e=O(= 읊 問? ) (2.5) ii) 따라 서 r>rr 인 곳에서 는 {겁: l(lr+21) + V(r)-e} 의 값이 양수 이 며 , 경 계 조건을 참작하면 U( r) 은 단순 감소하 는 함 수여 야 한다. 그 러므로, r-> CX)일때 V(r) 이 0 으로 되는 경우는 U(r) _냐가 /L, r ➔ OO (2. 6) 이며 여기서 특성길 이 L 은 L 텍 沒1詞 (2. 7) 로 주어지는 값이다. iii) 궤도 각운동량 l 이 정해진 경 우, 에너지 c 는 마디수 n 이 커질수 목 커지 며, iv) 마디수 11 이 정해진 경우 c 은 l 이 커질수록 커진다. 중심장의 한 예로 단진자 포텐셜을 생각해 보자. 이 포텐 셜은 핵각 모 델 에 서 중요한 역 할 을 해 왔 다. 이 는 파동함수들이 우선 \Voods-Saxon 형 포텐설과 비슷한 형태를 하며 계산상 간단히 해를 얻을 수 있기 때 문이다. 보편적인 양자역학 책에서 찾 아 볼 수 있는, 이 포텐셜에 대한 결과들을 알아보자. 단진자의 해밀토니안은 다음과 같다 . h(r)=_ 言fi2 한 ~. +. 1J극lW 2 },2 (2. 8) 애너지 스펙트럼은 동일 간격으르 배열된다. EN= (N+3/2)tzw , N= O, 1, 2, …... (2. 9) 반전성 亢는 JC= +l ; N 이 짝수인 경우 JC= -1 ; N 이 홍수인 경우 (2.10) 이며 N 이 주어진 각 (shell) 은 궤도 각운동량 l 에 대해 축퇴되어 있고, l 의 값은 다음과 같다 (N 이 주어진 각에 들어갈 수 있는 핵자수는
(N+ l) (N+ 2) 이 다· 표 (2. 1) 참조) . 1-N, N-2, N-4, ···, 1 또는 0 (2.11) 따라서 반전성 元는 x=(-1)1 로도 주어진다. 핵자의 상태는 ket IN,I,m> 으로 표시하기보다는 일반적으로 원자문 리에서와 같이 |n,l,m> 으로 많이 쓴다. 여기에서 11 은 주양자수라고 하며 11= N-12 +2 (2. 12) 로 주어지고, 이 숫자는 지름 파동함수의 마디수에 해당한다 (r ―> C0 에시 의 마디는 포함되어 있으나, r=O 에서의 마디는 포함되어 있지 않다 ) . 표 2.1 에 위의 결과를 정리하여 보았다. 표 2.1 I l {o p1 2d 3f 4g h5 6I 7j N(tr) I 1r{+ + + + 6 (+) 4s 3d 으 li 5 (-) 으 으 lh 4 (+) 3s 2d 뇨 3 (-) 요 」 2 (+) 2s ld 1 (-) .JP.... O(+) 1h ls |三 I 지름 파동함수는 다음과 갈이 표시된다. 亨국 /2Cn,e-( 아 /2 (ar) 1 L;?『 ((ar) 이 (2. 13) 여기에서 a= {국고이다. (2.14) 규격화 상수 Cn, 은
cn t=솔[ :;;:;2_-1}\\ ]1/2 (2.15) 이 며 , Lag ue rre 다항식 L~~V2(z) 의 처음 몇 개의 값을 보면 아래와 같 다. L~+ 1 1' ( z) =1 LL~~++ 1 11122 ((zz)) ==브 +2 {드 ~ -(z22 1+ 5) (2/+ 5) z2 + z'} (2.16) 매개상수 a(sc a le cons t an t)는 n,l 에 의해 결정된 궤도 반지름의 제 곱 의 평균과 연 길 된다.
대해 우선 조금 큰 r 에 대한 분포 뮬 많 이 갖도 록 지몽 파동함수를 번화 시키기 시 작할 것이다. 따라서 핵자들은 핵 의 표먼 부근에 좀더 많 이 분포되며 이로써 핵의 평균장은 표면 부분 이 더욱 깊어지게 된다. 그러 므로 한 핵자의 평균에너지는 단진자의 경우보다 낮아지게 된다. 반면 에 핵의 중심 부분에 있는 핵자들은 더욱 적어지게 되고 이러한 핵자 (예를 들면 l=O,1) 들이 느끼는 평균장은 더욱 얕은 것처럼 될 것이어 서, 이들의 평균에너지는 단진자의 경우에서보다 높아지게 된다. 이로 써 포텐셜이 공간에 국한되어 있는 경우 핵자상대의 에너지는 마치 -CF(c>O) 의 부수적인 항을 원형 탄진자 포텐 설 에 넣어준 것과 비 슷 하게 된다. 따라서 고유함수는 단전자의 경우와 같지만 , 그 에너지는 EN,i= E.v - Cl(l+ l) (c)O) (2.18) 로 변한다. 2) 스핀-궤도 결합항 이제까지 포텐셜은 핵자의 위치만의 함수였다. 핵자가 가진 스핀이 망이므로 그 해는 j =l 士 1/2 (j 는 전체 스핀 각운동량) 에 대 해 축퇴 되 어 있다. Ma y er 와 J ensen 은 j= l+l/2 상태가 j =l-1/2 인 상태보다 더욱 핵에 속박되어 있다고 가정함으로써 핵의 마법수들을 선명할 수 있었다. 죽, 해밀토니안 속에 스핀-궤도 결합항을 V,1=-Af (r )s·l (A> 0) (2. 19) 로 넣고 이때 스핀구1 ] 도 결합 형태 인자 f(r ) 및 A 를 조정하여 측정 량에 맞출 수 있었다. 이러한 결합항 (2.19) 는 원자물리에서와 같이 (Thomas-Fermi 스핀-궤 도 결 합이 라고 부름) f (r)= 쁜 (2. 20) 로 취하기도 한다. 그 이유는 평균장 V(r) 부분이 비교적 평평한데 퀘 도 각운동량은 이렇게 평평한 곳에서는 의미를 잃게 되고 그 의미가 가 장 부각되는 지역은 역시 표면 부근이기 때문이다. 이 표면 부근에서 쁩-은 국대화되어 의미가 커진다. 이렇게 설정된 형태와 실제 실험치를 비교하여, V .i올 보다 간단하게
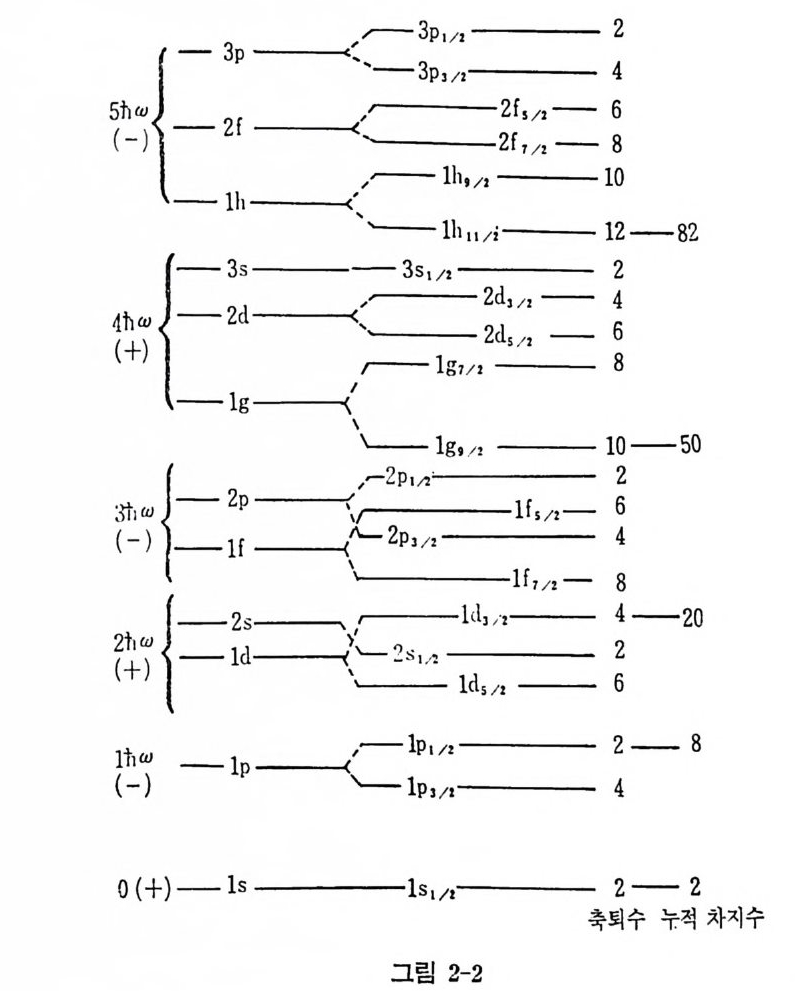
vsL=-A f.?로 놓더라도 충분하 다는 것이 알려져 있다. 단 A 는 핵 의 크기, 즉 N 에 따라(식 (2.17) 참조) 약간씩 변화한다. vs[ 은 F, J.2 및 j=와의 교환조건을 만족시키기 때문에 고유상태는 J nlj m> 으로 표시할 수 있고 그 고유치를 보면
 王\广\二二一二 一『크一
王\广\二二一二 一『크一
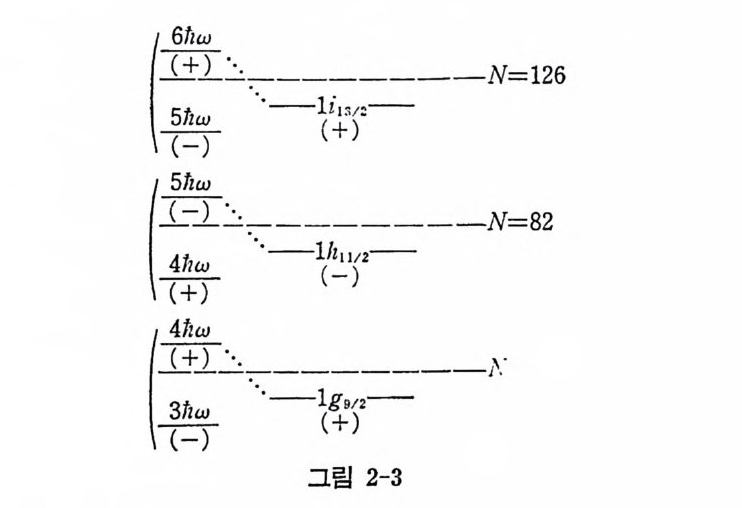
차가 나타난다. AEa=A— 2 (2!+ 1) (2. 22) tl2 이 격차는 실험적으로 경핵의 경 우 6MeV, 남의 경우 3MeV 그 이 상의 무거운 핵에 대해서는 1 MeV 보다 작은 값을 갖는 것이 알려져 있다. 해밀토니안 h(r) =弓릅+ 亨노 -Cl2_A51 (2. 23) 에 대한 에너지 준위는 그립 (2-2) 와 같다. 이 그립에서 우리는 다음과 같은 점들을 알게 된다. i) 마법 수 50, 82 및 126 의 출현은 N=4, 5, 6 인 준위 들에 있는 lmax, j mu 인 상태가 N=3,4,5 인, 에너지가 낮은 준위 들 사이로 심하게 번하 여 내려감으로써 나타날 수 있다. 그러므로 핵자수 N 이 50,82,126 인 준위 에 는 속칭 비 정 상 반전 (anomalous par it y) 상태 가 나타난다 (그 립 2-3 참조) .
 /皇告(무툴1퉁豊 •1·.1 .. · ··· 1. .. _...._.一. / - 1 _― _1( 1(_ 그l(썬一산+림_ .h _ gI) 1)2 2— / —因)_――二―― 1—-一_ '[ 구그 —= 126 =82
/皇告(무툴1퉁豊 •1·.1 .. · ··· 1. .. _...._.一. / - 1 _― _1( 1(_ 그l(썬一산+림_ .h _ gI) 1)2 2— / —因)_――二―― 1—-一_ '[ 구그 —= 126 =82
이러한 준위의 변화도 실험적으로 규명되었다. ii) I2 항과 7.-;'5J - 사이의 경쟁 효과로 핵 상태가 에너지 준위를 바꾸 기도 한다. 예를 들면 1 ds/2 와 2 S112 및 1f 5/2 와 2p 3/2 등이다.
4 핵각 모델의 응용 1) 입자상태와 구멍상태 핵각 모 델에서는 핵 자 들 로 이루어진 핵의 전체 상태를 나타내는 파동 함 수는 이미 제 1 장에서 언급한 것과 같이 파울리 배타 원리가 적용되 어 반대 칭화된 Slate r 행렬식으로 표시할 수 있다. 죽 각 핵자가 독립적 인 운 동윤 하 는 핵 각 모델에서 이 핵자 각각의 고유상태 를 . (x) 루 'P nl j .. &r-r , Xu, x,) =
• 이 강에서는 하 전 스 핀 양성 자 T 는 실제로 사용하지 않겠다 . 따라서 양성자와 중성자는 완전히 다 론 인 자로 간주 된 다 .
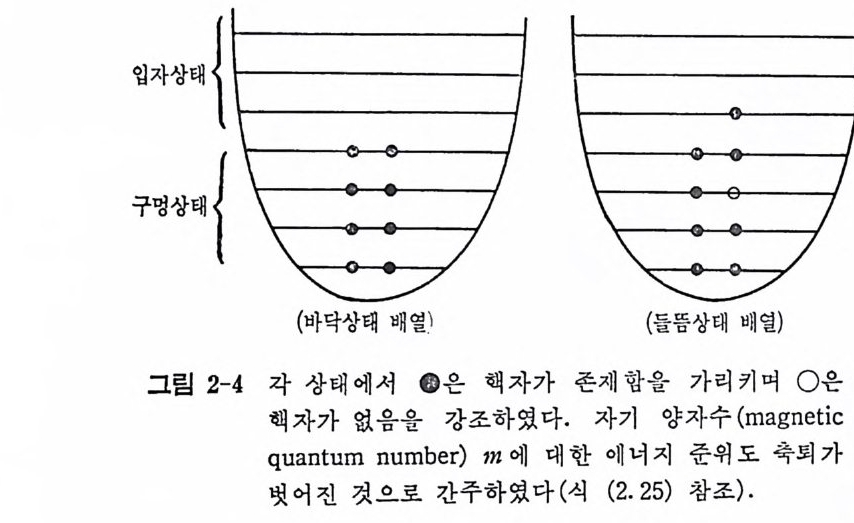
체의 상태를 나타내는 것이며 상징적으로 1l= {aI' 야, … a 사 (2. 31) 으로 쓸 수 있다. 따라서 a i를 어 떻게 취했느냐에 따라 핵 전체가 바 댜 상태인지 둘뜸상대인지를 구분할 수 있다. 죽 En 의 값 이 국소치가 되기 위 해 서 는 식 (2. 29) 으로부터 모든 a; (i= l, 2, … A) 가 그림 2-2 에 표시 된 에너지 준위 중 가장 낮은 에너지 준위에서부터 A 번째 준위까지에(히 전스핀은 무시한다) 해당하는 A 개의 상태 들로 이 루 어져야 할 것이다. 이 러 한 핵 자들의 배 열 은 바닥상태 배 열 (gro und sta t e confi gu rati on ) 이 라 한다(식 (2.28) 과 (2.29) 에서 n=O 으로 표기된다). 한편 A 개의 핵 자에 대한 이러한 배열 이의의 배열은 그 배열이 내포하고 있는 에너지 의 크기가 부등식 Eo
 ,41`
,41`
그립 2-4 에서 보는 바와 같이 어떤 j상태도 (2 j +l) 만큼의 축퇴가 있으며 이 축퇴수에 해당하는 단일 핵자들로만 모두 메워진 핵각을 가 리켜 닫힌 핵각 (closed shell) 이라고 부른다. 이러한 닫힌핵각의 전체 각 운동량은 0 이다. 증명 닫힌 핵각에 대한 파동함수는(양자수 짜인 일정한 한 껍질에
대하여) 1 Icpj ,_ j (l) φ j_j(2) cpj,_ j (3)'cpj,_ j(2j+l) ψ cs=j걷 느누묶누I ~j ,-J+ I(I) CPj,- J+I (2) cpj ,j+1 (3)'cpj,_ j+I(2j+l) φ J,+ j(l) cpJ ,+j (2) cpj ,j(3 ) 'cpj,j ( 2j+l) /파늑 {[cpj , -1( 1)C Pj,- J + I ( 2). C Pj ,j(2 j+ 1) J -[ cpj,l+ 1 ( 1) CPl,- j (2 ) 'CPj,j ( 2j+ 1 )] + ...} (2.31) 로 주어진다. 전채 각운동량 연산자 j 는 각 핵자의 각운동량 연산자들 7의 맥터합이다. J= 첩 1 7 (i) (2.32)
따라서 Jr= L,j ,, (i) (2.33)J소 = L,j± ( i) (2.34) U±=jy± 센 y) 이다. JI : ψ«= L, η1ψ«= {-j + (-j + 1 )+ ...+j } ψ«=0 (2.35) 이 므로 Jrψ ‘ «=0 이 고 ψ j , _j+1 (I) cpj,_ j (2) '''CPj,_ j (2 j +1 ) i+( 1) ψ« 에 CPj,- j +2 ( 1) 와, -1+1 (2)'' 'CPj,- } +I( 2j+ 1 ) CPM(1) cpj ,j_1( 2) '''cpj, j_1 (2j+1) o cpj ,j(2 ) '''cpj, j(2 j+1) =CPj,- j+ 1( 1)C Pj,- J +I (2 )'' 'CPj ,j(2 j+ 1 ) +CPj,- j+ 1( 1). ...··c pj,-1 + 1( t).. ....cpj ,j(2 j+1 )+ . ..... +CPj,- 1 + 2( 1)C Pj.- j+2 ( 3). .....+ CPj,- j +2 ( 1).. .. ..cp j,- j +2 ( x)·· +.. .... 다른 i+(t) 를 계산해 보연 같은 종류의항들이 부호만 바뀌게 나타나게됨을 쉽게 발견하게 되어 이어서 한 준위에 두 개의 입자가 들어간 형태 이 다. 결 국 ]마 r,.=0 이 됨 을 알 수 있 다. 마찬가지 로 ]서 r,.=0 이 다 . 즉
J士,fr ,.=O (2. 36) 이다• 죽 i/rcs 는 ]=0, M;=O 인 상태 이 다 (증명 끝) . (2. 37) 따라서 닫힌 핵각만으로 구성된 핵의 전체 각운동량은 핵자 상호간의 작용력이 무시된 독립입자 핵각 모델에서는 0 이다. ** 또한 이 핵각의 반전성온 +이다.
만일 닫힌 핵각들에 속한 핵자 의에 한 개의 핵자가 핵에 존재한다면 (예물 들면 170) 이 핵자를 가리켜 원자가 입자 (Valence p ar ti cle) 라 하
 d 감 ,/ ~5.05-½+ fLI p|广
d 감 ,/ ~5.05-½+ fLI p|广
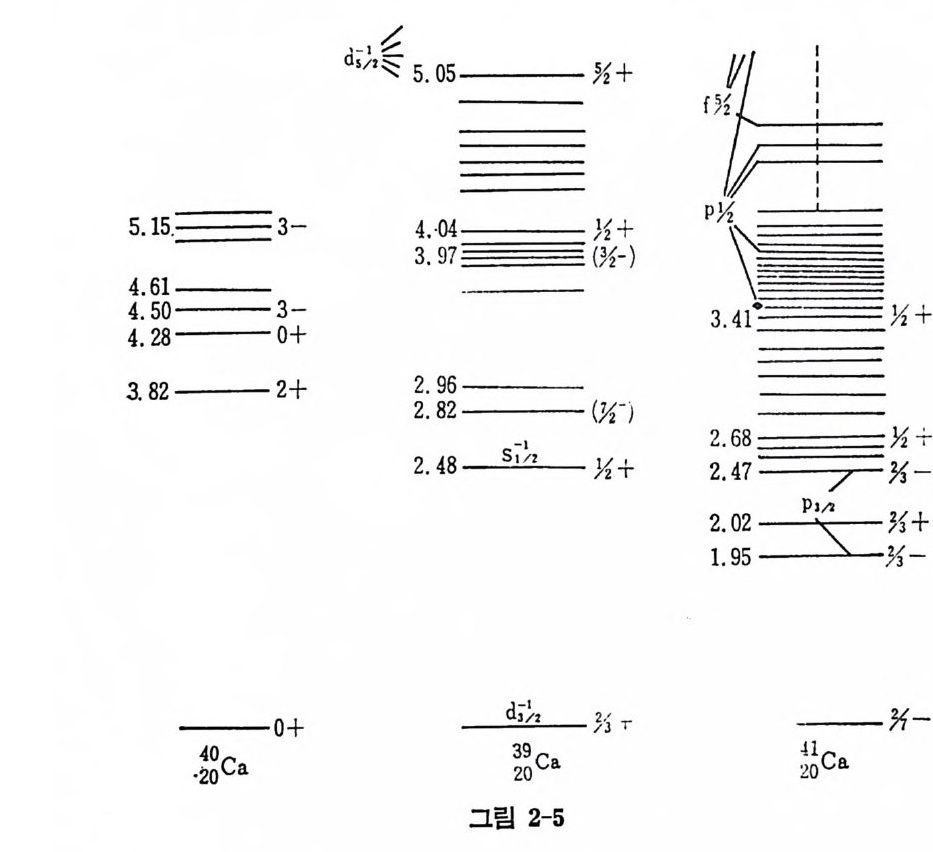
고 아러한 핵의 전체 각운동량은 곧 이 입자가 취하고 있는 각운동량이 된다. 이 핵의 반전성 역시 이 핵자가 가지는 반전성으로 대표될 것이 다. 반면에 한 핵에서 모든 핵각이 한 핵각을 제외하고는 모두 닫한핵각 이며 이 예의적인 한 핵각도 한 개의 핵자만 더 합한다면 닫힌핵각이 된다고 할 때(예를 들면 ISO), 이러한 핵의 전체 각운동량이나 반전성은 한 핵 자가 들어 갈 수 있는 구멍 상태 (hole sta t e ) 의 그것들과 같아질 것 이 다. 이 러 한 구멍 상태 몰 원자가 구멍 (valence hole) 이 라 한다. 원자가 입자가 가질 수 있는 모든 핵자상태를 통칭해서 입자상태 (pa rti cl e s t a t e) 라 하고 원자가 구멍이 가질 수 있는 모든 상태를 구멍 상태 라 한다 (그림 2-4 참조) • 원자가 입자나 원자가 구멍상태가 가장 명확하게 나타나는 경우를 그 림 2-5 에서 설명하였다. 이 그림에서 보면 이들 분광학 (s pec t rosco py) 실험 결과들은 그림 2-2 의 에너지 준위와 거의 일치하고 있으나, 핵각 모델이 보여주는 반전상 과 다른 값을 갖는 에너지 준위가 존재하거나 (s9ca 의 에너지가 2.48 MeV 인 준위) 또는 하나의 전체 각운동량을 갖는 에너지 준위가 복수 로 나타난다는 점이 색다르다 하겠다 (“Ca 에서 1.95 및 2.47MeV 인 준 위둘). 이러한 내용은 좀더 정확한 모델이 필요함을 말해 주고 있다(변 형핵 모델 동 참조). 2) May er 와 Jen sen 의 경 험 적 가설 핵이 두 개 이상의 원자가 입자 또는 원자가 구멍둘을 가지고 있는 경우는 제 5 장에서 자세히 취급하겠으나 핵이 갖는 스핀, 반전성 및 자 기 쌍극자 모멘트, 전기 사중국자 모멘트의 양에 대해서는 Ma y er 와 J ensen 이 다음 가설을 사용하여 어느 정도까지 설명하였다. 아 가설은, 핵력이 쌍짓기 (pa ir in g ) 영향이라는 미시적인 원인에서 유발된다고현재 알려져 있으며 각운동량 j를 갖는 상태에 있는 두 핵자는 각운동량의 합이 0 일 경우에 인력이 국대화된다는 내용이다. 이러한 성질은핵력이 아주 근거리에서만 작용한다는 데에 기인한다. 이를 설명하기 전에 우 선 May er 와 Jen sen 의 경 험 적 가설 을 들어 보면 다음과 같다. i) 모든 짝수-짝수 (양성 자수 및 중성 자수가 각각 짝수) 인 핵의 바닥 상태는 l=O 및 반전성 K=+l 이다.
ii) 따라서 짝수-홀수 (양성 자수 또는 중성 자수 중 하나만이 짝 수) 인 핵의 전체 각운동 량 및 반전성은 짝 이 없는 한 핵 자가 점하 는 상태 (그 립 2-2) 의 값을 갖는다. 많은 경우 의 짝 수- 홍수 인 핵은 이러한 가선 을 따르고 있다. 이러한 쌍짓기의 영향에 대한 자세한 이론은 제 7 장에서 다루기로 하 고 여기서는 단지 간단한 물리적 이유만을 설명하고자 한 다. (1) 두 핵자에 대한 반대칭 화 a) j 一 j 결합형 (cou p li n g scheme) 두 핵자가 각운동량이 j 인 핵각 중 m1 과 1112 인 상태에 있다고 하자. 이 두 개의 핵자들이 이 루는 전체 각운동 량 상태 는 Clebsch-Gordan 계 수를 이 용하여 ljjIM > =표 L,t ;'나] |Hm1m2) (2. 38) 로 표시되며 하l™ 전스r> 핀= 부훑분 mr2은[, 'r: ,};,2 ' 디 I+ - ½-mr,mr, ) (2. 39) 이다. 따라서 두 핵자의 전체 상태함수는 |jj [M 隨 |TMr> (2.40) 로 표시되며 이 상태함수는 두 핵자의 교환에 대해 반대칭이 되어야만 한다. Clebsch-Gordon 계 수의 성 질 [;!’나]= (-1)21-1[~2 나] (2. 41) 을 이용하면 (-) 2J- I (-) l-T=-1 (2. 42) 이어야 하며 2j 는 언제나 홀수이므로 l+T 가 홀수 (2. 43) 이어야 한다. b) l-s 결합형 한편 두 핵자의 각운동량 상태는 식 (2. 38) 과 다른 형
으로 만 들- 수 있다. 즉 I LMi S Ms > 겁 l叫 나 11 , 》』 [~s: ;~麟』 | l, l, mlllr2> 11/ 2, 1/2, ms., ms, ) (2. 44) 따라서 반대칭화는 (_) 21-L (—) 1-S (-) l-T = -1 (2. 45) 뭉 요구 한다 . 2l 은 언제나 짝수이므로 L+S+T 는 홀 수 (2. 46) 이어야 한 다. (2) 파동 합 수의 겹 침 과 잔류 상호작용 두 스핀 궁J I 과 수巨 사이의 각도는 반고전적 (sem i -class i cal) 으로 -7 군 cos✓ i0=~~i 2+l) = I(I+21 ✓)] ~\ (jl+ +1)E(E1+1) ) (2. 47) 이므로 같은 상태 U1= i 2= i)의 경우 cos 0= l(l+12)j ( -j2+j1( ) j +1 ) (2. 47) ' 로서, 전체 각운동량 I 에 따라 다음과 같은 각을 가진다. l=O; cos0=-1 l=2j; cos0=_ j+j _l (2. 48) 따라서 I 가 짝수이고 j) l/2 인 경우에는 I=O 만이 두 각운동량 ]\= h= j가 반대 방향으로 나란할 수 있고, I 가 홀수인 경우에는j가 충분 히 크면 ()5/2), I=2 j에서 두 각운동량은 거의 나란히 배열되었다고 볼 수 있다. 식 (2. 43) 으로부터 우리 는 i) 두 핵자가 모두 중성자이거나 모두 양성자일 경우 l=O 에서만 두 각운동량의 방향이 (반대 방향으로) 나란할 수 있으며 (j=l/2 인 경 우 제
외) ii) 두 핵자가 한 개의 중성자와 한 개의 양성자로 되었다면 i ) 과 건 이 서로(반대 방향으로) 나란한 각운동량 배열뿐 아니 라 , l=2j ( j ) 5 /2) 에서와 같이(같은 방향으로 거의) 나란한 경우도 생각한 수 있다 . 두 각운동량의 방향이 거의 나란한 배열이란 과연 무엇인가 융 생각해 보기로 하자. 각운동량에서 스핀의 기여도 를- 무시 할 때 핵자의 파동협 수가 갖는 공간상의 분포 죽 Y t m(0, ¢) 의 노양은 m=l 인 경우 를 한 예 로 살펴보면 <0 ¢ I Im >= Yu (0, ¢) = (sin 0 ) 21c;19 (2. '19 ) 로서, 그립 2-6 과 같다. 두 각운동량이 방 향 만 다르게 나란히 매열 되 어 있다 하는 것은 두 핵자의 공간분포가 완전히 겹쳐 있되 희전방향민 반대로 되어 있음을 가리킨다. 죽 두 핵자는 Il,I>IIl-I>2 (2. 50) 라는 상태에 있게 된다. 일반적인 경우 (m=\=l) 에도 우리는 Ilm>l|l-m>2 (2. 50) ' 인 상태에 있는 두 핵자가 서로 같은 공간분포를 갖게 되는 것웅 안 수 있다. 아렇게 되어 있는 상태를 우리는 〈두 핵자가 서로 시간 역 전 싱 태에 있다〉고 말한다(식 (2.45) 참조). 이러한 논리로 보면 두 핵자의 각운동량이 l=2j 로 합쳐지는 ii)의 경우도 역시 두 핵자의 파동합수기 거의 겹쳐 있다고 말할 수 있다. 이제까지 우리는 독립입자 핵각 모델에서는 핵자 상호간에 미치는 힘 이 없는 것처럼 취급하여 왔다. 업밀하게 말하던 핵자 상호간의 힘은 존재하기는 하지만, 이는 핵자 전체에 대한 평균 포텐셜을 형성하는 대
 그림 2··5
그림 2··5
에만 사용된 셈 이다. 만일 이런 평균 포텐셜 의에도 핵자 상호간의 힘 이 존재한다면 (이것을 우리는 〈잔류 상호 작용〉이라고 부른다). 대개 덩 균 포낸 셜 을 형 성 하는 데 에 는 원 거 리 작용력 (lon g rang e int e r ac tion ) 이 기 여 하고, 근거 리 작용력 (short rang e int e r acti on ) 은 기 여 하지 못한 다(이는 제 4 장에서 자세히 언급하겠다). 근거리작용의 역할을 보기 위 해서 델타인러울 생각해 보자. 이 힘의 경우 두 핵자의 파동함수가 겹 쳐 있웅 메 두 핵자는 가장 큰 힘을 받게 될 것이다. 죽 두 핵자는 이 라한 잔류 상호 작용에 의하여 두 각운동량의 방향이 나란해지며, ii) 의 경 우에 서 는 같은 방향으로 나란해 지 기 도 할 것 이 다. May e r-Je n sen 의 가선은 결과적으로 핵내에 이러한 짧은 거리의 작용릭이 있음을 시 사하고 있다고 해석할 수 있다. 이러한 잔류 상호작용은 사실상 각각의 핵자의 운동이 독립적이라는 가정하에 세워진 독립 핵각 모델의 붕괴를 조래한다. 그러나 잔 뮤 상호작용의 역할이 핵을 변형시키는 데 있다고 보아 변형된 핵 평군 포텐셜을 사용하여 핵각 모델을 확장시킨 Ni ls son 모델은 미시적 모델을 연구하거나 많은 실험적 사실을 분석하는 데에 큰 공헌을 했다. 5 핵 의 변 형 (defo r mati on ) 한 핵이 닫한 핵각 의에 몇 개의 원자가 핵자들로 되어 있다고 하면 이러한 핵자들의 분포는 둥근 공모양은 아닐 것이다. 따라서 이제까지 처럼 핵자들의 분포로 평군 포텐셜을 잡는다면, 마땅히 핵의 평군 포텐 설도 변형된 형태로 잡아야 할 것이다. 사실상 구형 단진자 모델에서 핵자의 준위는 자기 양자수 m 에 대해 축퇴되어 있으므로, 만일 찬류 상호 작용이 없으면 한 개의 원자가 핵자를 가지는 핵의 경우 모든 m 상대에 같은 확률로 존재할 수 있어서 구형의 핵자분포를 계속 유지할 것이다. 그러나 찬류 상호 작용의 존재로 말이암아 구형분포는 깨어지 게 된다. 또한 앞질에서 언급한 바와 같은 찬류 상호작용의 영향은 변 형된 평군포텐셜을 사용하여 좀더 작게 만들 수 있을 것이다. 그러나 평균 포텐셜을 변형된 모양으로 잡음으로써 우리는 새로운 현 상을 설명하지 않을 수 없게 되었다. 즉 전체 핵의 파동함수는 공간회 전에 대한 불변성을 잃게 되고, 회전불변성으로 인한 핵자상태의 양자 수 죽 궤도 각운동량 양자수가 좋은 양자수가 되지 못하게 된다.
다론 한편 이렇게 변형된 평균포벤설을 사용하여 기술되는 핵이 들 뜨 게 되면 핵은 두 가지 다론 둘뚱상대를 가질 수 있다. 하나는 핵자가 입자-구멍상태 를 만들어 둘뜸스펙트럼융 만드는 것으로 원형 단전자 모 델에서 보는 것과 같은 과정이며 다른 하나는 핵자둘의 잔류 상호작용 에 의해 전체 핵자가 움직이는 과정이다. 전자의 경우를 〈 고유입자 둘 뜸과정 (int r i n s ic (pa rtic le ) excit at i on mechanis m ) >이 라고 하며 후자를 〈단체 둘뜸과정 (collecti ve excit at i on mechanis m ) 〉이 라고 한다. 득히 고 유 들뜸과정으로 설명할 수 없는 핵의 스펙트럼을 분석해 보면, 핵의 변형은 대체로 타원체 (ell ip so i d) 로서 하나의 회전 대칭축을 가짐이 밝혀 진다(이의의 복잡한 형태에 대한 것은 이 책의 정도에서 벗어나므로 언 급하지 않겠다). 1) 변형된 단진자 모델 타원체 모양을 갖는 평균포텐설로 변형된 단전자 (N i lsson) 포텐설을 사용하면 해밀토니안은 lt= - 言ti2 -v2• +. 了1 叫야 (x2 +y2) + w: 민 (2. 51) 이 된 다. 죽 이 포텐 셜 의 등포 텐 셜 선 (eq u ip o te n ti al lin e ) 은 (갔+土y) 22 + (¾z2 -)2 =상수 (2. 52) 이며, 전체 에너지가 주어진 계에서 핵자밀도의 분포는 평균적으로 가 능한 극대 등포텐실선에 분포될 것이다. 핵자 분포의 포화 현상으로부 터 이 변형된 핵의 부피는 같은 핵자수를 갖는 구형 핵의 부피와 같을 것이므로 x,u ,::= Q。3 (2. 53) 이어야 하며 여기에서 구형핵에 해당하는 Wo 는 nwo~40A-113MeV 이다. 따라서 우리 는 하나의 변형 매 개 상수 (defo r mati on pa ramete r ) o를 이 용하여 h=- 읊 -V 나亨나 (x2 균) +e~262 가 (2. 54)
로 적을 수 있고, 이 값이 작은 경우, 즉 작게 변형된 경우, (e6~l+o) 임을 이용하여 h= -읊 -V 나 구 r 나 亨i 8 (# +y 2- 2 균) (2. 55) 을 얻는다. x2 +y2 -2z2= -4 J%따 (0, ¢) (2. 56) 를 대입하면 다음과 같이 쓸 수 있다. l t=-읊 -v2+ 구 r2+ v6(r, 0, ¢) (2. 57) 이때 V 。 (r, 0, ¢) = -om w 硏Pf Y2, o (0, ¢) (2. 58) 이다. 6>0 인 경우 핵의 형태는 cig a r 모양(p rola t e), o<0 이면 빈대떡 모 양 (oblate ) 이 다. 원형 단진자 모델에서와 같이 스핀-궤도 결합항 및 공간 국한성에 대 한 명령을 식 (2.57) 에 첩가시키면 h N =lz 。+ v6+ vsl (2. 57)' hvsot== -- A一2Izm2? JV• 2-C+' 7 ―21 n2 i r2 ] (2. 58) ' 이 되고 이를 Nil s son 해밀토니안이라 한다. (1) 식 (2. 51) 의 해 식 (2.51) 의 해밀토니안, Il 은 z 축의 회전에 대해 불변이다. 따라서 [h,l』 =0 이며 고유함수 中는 I, ,fr a 」 =Ah ,fr aA (2. 59) 이다 (A 는 분자물리학에서의 표기 방식인데, N il sson 이 이것을 사용하
였기에 그대로 따르기로 한다). a 는 A 의의 모든 양자수물 가리킨다. 단진자 포텐셜에서와 거의 마찬가지로 식 (2.57) 의 고유상태도 A 를 제 외하면 다음과 같은 양자수를 갖는다. N=n 댜 ?ty + 11r NL=11r+11_. (2. 60) 또는 N=nr+ny + n,,, n,,,=N-nr-ny (2. 60) I N 과 n,. 가 주어지면, 이 고유상태는 A 의 士값에 대하여 축퇴되어 있는 데, 이는 z 축상에서 운동하고 있는 입자는 궤도 각운동량의 z 축에 대 한 성분 A 에 영향을 줄 수 없기 때문이다. 양자수 |Al 는 다음의 값을 가질 수 있다. IAl =NL, NL-2, NL--1, …, 1 또는 0 (2. 61) 문 이 를 원 기 등 (cy li n d ric a l) 좌표계 를 사용하여 중명 하시 오• 핵자의 스핀도 좋은 양자수이므로 K=A 土―21 (2. 62) 도 또한 좋은 양자수이다. 해밀토니안 h 는 반전성을 보존하므로 고유 함수의 반전성은 ;c= (土 l)N (2. 63) 이 된다. 따라서, N i lsson 의 고유함수는 K: ,r郞 n~, A] (2. 64) 로 표기하고 이를 〈점근 양자수 (as y m pt o ti c qu antu m number) 〉라고 부 른다. (2) 식 (2. 57) ’ 에 대 한 고유함수와 에 너 지 준위 ho, /2, l,, 및 s 려 는 서 로 교환가능한 연 산자들이 다. 따라서 이 들은 상태 벡텨 INIA~> 를 이루며, 이 상태벡터는 다음과 같이 정의된다.
ho l Nl A ~ ) =hwa(N + 引 I N/AI ; > l21 NlA fi > =fz2l ( l + l) I N/ AI :, ) lclNlAI :) = hAIN lA f,) (2. 65) sc I NLA f, > =hf , I NlA f, > 목히 2 는 연산자 s 군의 고유치로 분자물리학에서 사용하는 표기법에 따 랐 다 (I:= 土 1/2) . 한 편 ]2, 72, le 및 Sc 중 어 느 것도 hN 과는 교환가능성 을 갖지 않는다. 단지 j .,=l.+s., 는 [/zN , 1 』 =O (2. 66) 이어서, 상태백터 |aNK> 를 만 들 수 있다. hN l aNK) =SaN Kl aNK) j』 aNK) =Kfz l a lNK> (2. 67) hN 의 에너지 준 위 를 구하기 위하여 |aNK> 를 |NA~> 로 전개하자 . laNK>=IAZZ X 쩝f lNIA~> (2. 68) K 가 정해진 경우 K=A+~ =A 土 1/2 (2. 69) 으로부터 A 와 2 는 A+=K+l/2, E=-1/2 또는 A-= K-1/2, :E= +l/2 만이 가능하므로 laNK>=Ll Xf: :f |N lA+, _1/2> + Ll Xf:( ~ IN IA- , + 1/2 ) (2. 70) 임을 알 수 있다. 표기를 간단히 하기 위하여 앞으로 상태벡터에서 2
는 적지 않겠냐 에너지 li N 의 기대치 8. NK 는 l'~A-‘ ’ < NIAdlzN I N/'A;>x~셉 ~=Oa N K X~, 싼 (2. 7 1) 이다. 여기에서는 상태벡터의 칙교성을 이용하였다; < NlA1 IN 'l'A; > =ON N'0 11' 0A ,,f, ' (2. 72) a) 변형이 작은국한의 경우 (I Vi l
• 현 표기업에서 m=k 이다.
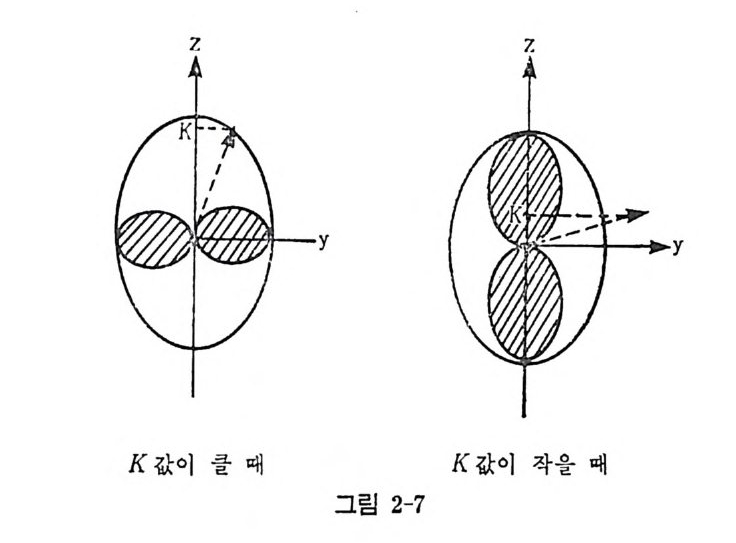
i) pro late 의 경우 (o)O), K 가 클수록 핵자의 궤도는 그림 2 구 에서 보는 바와 같이 x- y평면에 집중되어 있다. 따라서 이 입자는 마치 좁은 공간에서 움직이는 것과 같은 영향을 받아 에너지 준위가 높아질 것이다.
 z z
z z
반대로 K 값이 작으면 핵자의 궤도는 z 축 주위에 집중되어 포텐셜의 범위가 커지므로 에너지 준위는 낮아진다. ii) obla t e 의 경우에도 쉽게 설명될 수 있다(각자가 해볼 것). 식 (2,76) 에서 보는 바와 같이 K 값에 대한 구형 탄진자 모델에서의 축되는 단지 土 K 에 대한 축퇴로 축소되는 것을 알 수 있다. 다시 말하 면 V 。 (o«l) 의 형태로 변형된 핵의 에너지 준위는 거의 좋은 양자수 N,l, j ,K 를 가지며 士 K 에 대해서만 축퇴되어 있다. b) 중간 크기의 변형 (|Vd~IK,d) 이 경우 섭동 원리에 의한 식 (2.70) 은 이미 성립하지 않는다. 식 (2.67) 에서부터 Ii N 의 |NlAi > 위에서의 비 대 각 행 렬 요소 (non-d iag o nal matr i x element) 들이 어 떻 게 생 기 는지 를 알아보자. vs t의 -;.1 항은 5 • I=s 占 lz+ T1 (l+s_ +I_s+) (2. 78) • 이므로, INIA,> 와 INIA;) 사이에 4=A i土 1 (동시 에 ~;=~.+1) (2. 79)
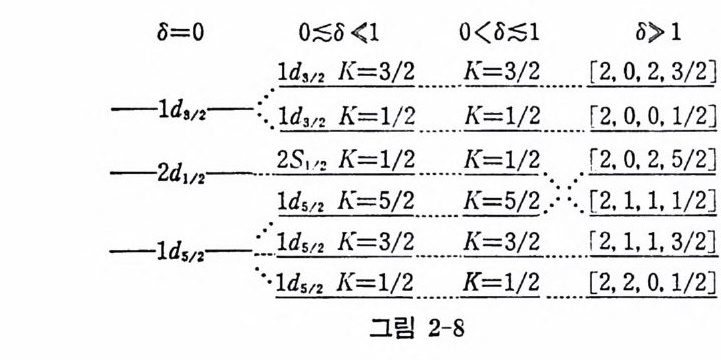
인 관계가 있으면 행렬 요소가 존재함을 알 수 있다. 따라서 한 에너지 준위는 이들의 복합체이다. 한편 V. 는 N'=N, N 土 2 l'=l, I 土 2 (2. 80) 사이의 행렬 요소를 만든다. 문 위의 사실을 증명하시오. 따라서 V6~Vs,1 인 경우 좋 은 양자수라고는 K 하나뿐이다. c) I V41> I V,. il인 경우 이 경우에는 오히려 점근 양자 수 로 표시된 INn,.AK> 가 좋은 기준 상태벡터로 사용될 수 있다. 이 절의 마지막으로 어 떻 게 6 가 작은 경우의 양자 수 [N , l,j, K ] 가 국 한인 경우의 양자수 〔 K,nr,A,K 〕로 변해가는가 을 N =2 의 경우 를 예로 들어 살펴보기로 하자(그림 2-8 참조).
 ——_-1d12oSd=5/O/d22 _— 1_: 1: ..:. ·: l2l1 dd Sd2 sso3,1n/:, :222s - o KKKK · <====·1531 l ~////22 2 2 .· · ..·.·.··..··..· . ·.· ·..· ·o 또 -KK~K -< -=== o-무53-l::'//s/ -2221- ' •.. .. .·.. .. •..... •.. ·.. . .• . . 「「[ 「 2222 ,, ,, 100l ,,,o. 1120>,,,, 31511 ////2222 ]]]]
——_-1d12oSd=5/O/d22 _— 1_: 1: ..:. ·: l2l1 dd Sd2 sso3,1n/:, :222s - o KKKK · <====·1531 l ~////22 2 2 .· · ..·.·.··..··..· . ·.· ·..· ·o 또 -KK~K -< -=== o-무53-l::'//s/ -2221- ' •.. .. .·.. .. •..... •.. ·.. . .• . . 「「[ 「 2222 ,, ,, 100l ,,,o. 1120>,,,, 31511 ////2222 ]]]]
o=O 일 때 의 K 에 대 한 축되 는 6* O 이 되 면 점 차 벗 겨 진 다. 8 가 어 지간히 커지면 K 하나만이 좋은 양자수이며, 이때 한 에너지 (고유상대, 예를 들어 I 中 K=3/2>) 는 사실상 |lda12, K=3/2> 와 |lds1 2 , K=3/2> 의 결합으로 된다. 좀더 변형이 커지면 z 축 자유도에 대한 에너지는 x,y 축의 그것에 대해 작아지게 되어 다음 식이 성립한다. tz oe-5
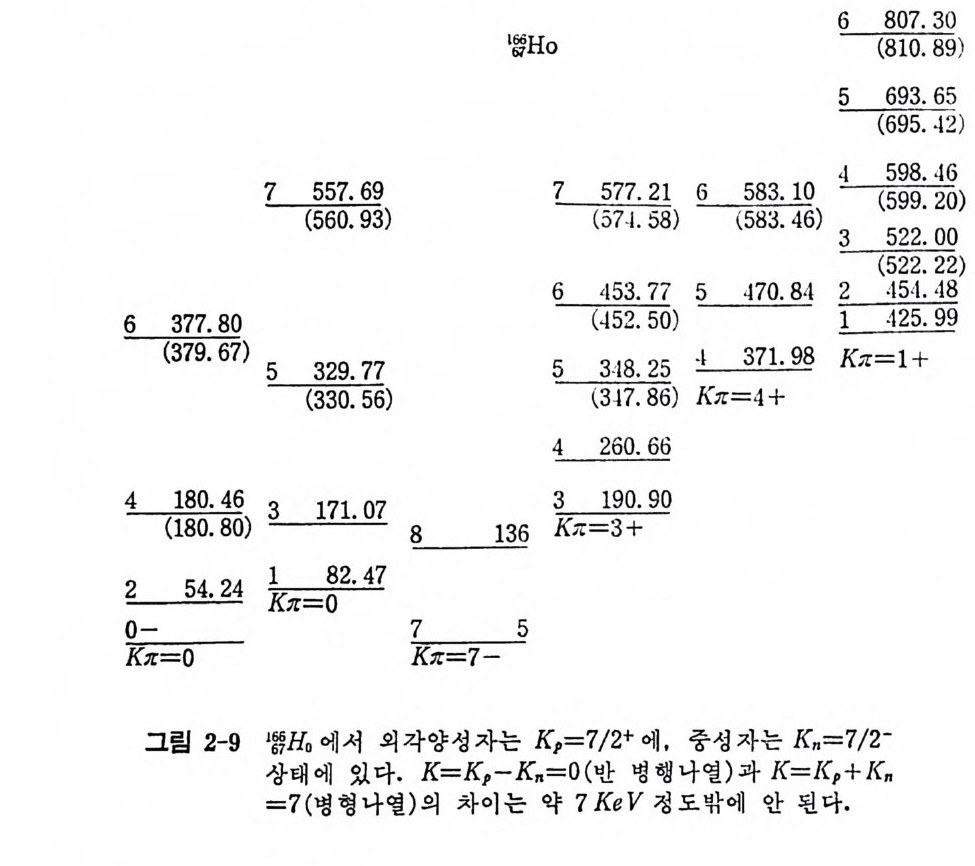
K=3/2 인 경우는 x- y평면상에 적어도 한 개의 각운동량이 존재해야 하므로 1L=N_1 인 경우가 가장 낮은 에너지준위를 갖게 된다. 2) Nil s son 모델과 실험치와의 비교 구형 단전자 모델과 마찬가지로 N i lsson 모델의 모든 실험적인 고찰을 위해서는 핵자의 에너지 준위의 바닥에서부터 점차로 핵자들을(하나의 양성자 또는 중성자) 주어진 핵자수에 맞추어 채워감으로써 핵을 형성 하게 하여야 한다. 이러기 위해서는 핵의 변형도 8 및 w,A,C 를 미리 결정하여야 할 것이다• 이들은 실험 결과나 다음과 같은 논리에서 비교 하여 얻을 수 있다. 양성자 및 중성자의 수가 짝수인 핵의 바닥상태에 서는 그 해밀토니안과 아울러 핵의 상태함수도 시간 역전에 대해 대칭 성을 가진다. 왜냐하면 항상 o/ aNK 와 o/ a,N,-K 는 같은 에너지 준위를 갖 기 때문이다• 죽 짝수-짝수이며 변형된 핵은 바닥상태에서 모든 K 값이 O 아다. K= 'I=A; 1 K,=0 (2. 81) 한편 타원체의 대칭성을 가진 핵은 바닥상태뿐 아니라 들뜸상태의 모 든 고유함수가 갖는 반전성이 +1 이기 때문에 각 회전에너지 스펙트럼 의 각운동량(이는 다음 장에서 새로이 언급하겠다) 또한 l=0, 2, 4, 6… … (2. 82) 의 배 열 을 갖게 된 다. 이 를 〈바 닥 회 전 띠 (grou nd rota t i on al band) 〉라고 한다. 만일 한 핵자의 입자 들뜬 상태 (pa rtic le excit ed s t a t e) 가 일어나 면 이에 대해서는 반전성의 제한 조건이 없기 때문에 I=K, K+ l, K+2, …… (2. 83) 에 해당하는 회전띠를 보유하게 된다(들뜬 회전띠라고 함). 따라서 실 험적으로 알 수 있는 에너지 스펙트럼의 감마전이에서 /가 구해지며 그 바닥 회전띠 및 들뜬회전띠로부터 대강의 8 값을 구할 수 있다. 한편 홀수-홀수인 핵에 대해서는 K+=K,+Kn( 병행나열) 및 K-=IK,-Knl (반병행나열)에 해당하는 두 준위가 거의 같다. 이 두 나열의 경쟁을 Gallagl :er -Moskowski 효과라 한다. 간단한 경 우들을 그림 2-9 에 서 찾
아볼 수 있다• 그러나 각 회전띠의 가장 낮은 준위는 핵자의 에너지 준 위를 가지고 설명되지만, 그 이외의 스펙트럼상에 나타난 준위의 규명 은 다음 장에서 언급하는 회전모델로써 가능하다.
 6 807.30
6 807.30
제 3 장 핵의 단체회전 럭바공처럼 타원체꼴로 찌그러진 강체에 대해서는 타원체의 대칭축 방향을 정해 주는 오일러 (Euler) 각을 회전을 기술하는 변수로 정할 수 있다. 핵이 강체는 아니라 할지라도 정상상태로서 그 모양을 유지하고 있다면 이 핵의 회전은 양자화되어 에너지 스펙트럼에 그 흔적을 나타 내게 될 것이다. 핵이 단체회전하고 있다 함은 핵을 형성하는 개개 핵 자가 비록 똑같은 위상을 가지고 희전하고 있지는 않더라도 거의 비슷 한 위상으로 회전에 참가하고 있다는 것을 말한다. 따라서 우리는 주어 진 각속도를 가지고 회전하는 회전좌표계 속에서 개개의 핵자들이 정상 상태를 형성하고 있는 것으로 핵의 회전을 기술할 수 있다. 이 기술방 식을 〈크랭킹 (crankin g ) 모델〉이라고 하며, 〈손으로 돌리는 회전 모델〉 이라고도 한다. 그런데 비록 비슷한 위상을 가지고 회전에 참가하고 있 다고는 하지만, 주어진 회전좌표계의 각속도처럼 의부에서 정해준 양이 아닌 자발적인 단체회전 각운동량이 정의되어야 할 것이다. 따라서 핵 의 회전을 기술하기 위해서는 〈손으로 돌리는 희전 모델〉과 아울러 핵 자들의 고유운동과 단체운동을 결합시킨 〈동합 모델〉이 필요하다. 다시 말하면 〈손으로 돌리는 희전 모델〉에서 회전 각속도는 하나의 상수이며 핵 자의 고유운동에 서 고유 파동함수가 가지 는 시 간의 존성 은 각속도와 연결되어 있다. 반면에 〈동합 모델〉에서 고유 파동함수와 단체회전은 동력학적으로 결속되어 있기 때문에 오일러각은 마치 〈집단 자유도〉와 같은 역할을 하게 된다. 우리는 이 장에서 회전이라는 집단운동을 기술
하는 모델들을 연구하기 위하여 먼저 첫째 절에서 희전좌표계와 〈팽 이 파동함수〉를, 그리고 다음 절에서 〈손으로 돌리는 모델〉을 살펴보겠다. 죽 단체회전하고 있는 핵을 팽이로 보아 그 회전운동에 대한 단체 파동 함수를 구하고, 이렇게 회전하는 가운데에서의 핵자 자신의 운동울 중 점적으로 살펴보기로 한다. 마지막 절에서는 위의 두 모델을 결합한 동 합 회전 모델 또는 팽이-입자 모델이라 불리는 Bohr 와 Mo tt elson 의 모델을 소개하기로 하겠다. l 회전좌표계와 팽이 파동함수 1) 오일러각과 고유좌표계 변형된 핵의 모양으로 인하여 공간에서의 방향이 정해지는데, 이 방 향을 기준으로 해서 직교 단위벡터 e 。 (a=l,2,3) 를 정하자. 이풀 〈 고유 좌표계〉 또는 〈물체에 고정되어 있는 좌표계〉라 한다. &·gb =8ab, & x gb= eobc6c (3. 1) 여기에서 eabc 는 반대칭화된 텐서 (€123=l=-E21s …)이다. 한편 실험실 좌표계에서의 기본 벡터 ?,j,£를 다음과 같이 회전시키면 고유좌표 계의 단위벡터 &를( :얻:)을= (수一 :l있o다::. : ;:: [ )(:l0::! \\::) . (-~::: :;: : [) ( i ) (3. 2) 여기에서
의 회전으로 정의하기로 하자. 즉 &= 2 R i。 (w) e. (3. 4) 。 이다. 여기에서 &는 ?,j ,E 를 나타낸다. 아 식을 다시 쓰면 e.=I : (R-1) ;。 (w) e, (3. 4) ' 이 된다. 한편 실험실좌표계에서 성분 &.V 를 가지는 벡터 V=(V,, Vj, V i)는 R(w) 라는 회전에 의하여 성분 g vI 를 가지는 벡터 V1=(V,'., v ;, v;) 가 되며 , 이들 사이에는 다음과 같은 관계가 성립한다.* V,'= 2I Ri j@ ) Vj (3. 5)
* 이 표기 는 Bohr & Mot tels on 의 표기 와 갇다.
갇은 원리로 양자역학에서 R(w) 는 상대벡터 Iv> 를 R(w) IV> 로 변화 시킨다;
참죠), 이때의 회전 연산자 R.(d
= < [교 • 「=+(-뭉 훑 +s i n ,Jr훑 + cot e cos ,Jr옳-) I2 로·f국( 言 훑+ cos ,Jr훑 -cot e s i n ,Jr嗣 I3 루 &·I;-= ―11_ a_a 中 (3.17) 이들 1;,1;,1; 은 〈고유(좌표계) 각운동량 연산자〉라고 부른다. 위의 두 식에서 정의된 I 및 I’ 은 다음과 같은 성질울 가진다. [Ii, I 』 = 1. • eij& k (3.18) u;, I~] = -i Eabc 1; (3.19) F=2 I;E =2 IJ i (3. 20) 。 [I/, I』 =O (3. 21) 이것들로부터 F,Ij 및 L 은 서로 교환가능이므로, 공통된 고유상대함 수 i l,K,M> 을 얻을 수 있음을 알 수 있다. I21IKM)=l(I + l) IIKM) I;IIKM> = K! IKM) Ir llKM> =MI IKM) (3. 22) 단, -I::;::K::;::I, -[직起 I 이고 I 는 자연수 또는 자연수의 반이 될 수 있 다 (Messia h , 양자역 학 13 장 참조) . 식 (3. 22) 를 유도하기 위 해 서 는 다음과 같은 〈울림 (내림)연산자 〉 가 필요하다. I±=I 士il v l~=I;±il (3. 23) 이둘은 I土 II KM> = ✓ (I 土 M) (I± M+ 1)i I, K, M 士 1 > I 全 |I KM> = ✓ (I 干 M) (I 土 K+Ifl l, K 士 1, M> (3. 24) 와 같이 작용한다. 한편 고유함수 IIKM> 은 완전 칙교-규격화된 상태 집합을 이룬다.
이 들 고유함수를 〈대 칭 팽 이 파동 함 수 (sy m metr i c top wave fun cti on ) > 라 하는데 이는 이들이 대칭팽이 해밀토니안 H=A J탸 (Aa-A1)I? (3. 26) 에 대한 고유함수이기 때문이다. 이 해밀토니안은 회전자 해밀토니안 (Roto r Ham il t on i an) 이라고도 한다. 해밀토니안을 생각하기 전에 먼저 팽이 파동함수의 성질을 알아보기로 하자. 우선식 (3.23) 의 정의가식 (3 . 24) 를이끌었는데, 이 후자로부터 I~ 의 K 에 대한 역할은 마치 I :i:(순서가 바뀌었음에 유의 할 것)의 M 에 대한 역할과 같은 것임을 알수 있다. 이로부터 I 는 I;’ 과, Iy 는 _E 과, L 는 I; 과 같은 역할을, 다른 양자수인 M 과 K 에 하고 있음을 알 수 있다. 따라서 일반적인 구면 조화함수 (s p her i cal harmonic s ) Y1 .. 의 성 질에 의하여, 고유좌표계에서의 각 축에 대한 z 만큼의 회전은 다음과 같은 결과를 준다. R.I(x) |IKM>=e-I·aI , 'I I KM>= (-)-tI|I , _K, M> R.., (元) | IKM) =e-'1 1· II KM> = ( 키 l+K | I, _ K, M> R.,(x) IIKM> =e-d •' II KM)=e-ix K IJ , K, M> (3. 27) 다움에는 이러한 파동함수의 오일러각에 대한 두사형 태, <
=ew dt,, M . ( 0) e;M',i, (3. 30) 이다. 윗 식 의 Wi gn er 함수는 Bohr & Mott els on 의 책 에 서 정 의 된 것 과 같다. 한편 식 (3. 29) 의 함수는 K 의 고유함수이 므로 식 (3. 17) 에 서 정 의 된 K 과 식 (3. 30) 을 이 용하면 M'=K (3. 31) 가 됨을 알 수 있다. 따라서 식 (3.29) 의 합은 단 하나의 항만을 가지 게 되어
(고전적 강 체 는 .Y .=M< X t +X: >의 관계가 있 다) Hrur 의 고유함수는 상태 |!KM > 을 대 각 선화 합 으로써 얻어 진 다. 이때 없어지지 않는 행렬요소들은 다움과 같다.
Ek=AJ (J+ l) + (Aa-A1)K2 (3. 44) 이므로 주어진 I 에 대해 이 갱 이의 에너지는 K=O 에서 가장 낮은 값을 가진다. 이것은 고유 각운동량이 관성능률이 가장 큰 방향으로 정렬 (alig n ment) 되 어 있음을 가리 킨 다• ii) K= -1 인 경 우 (oblat e 팽 이 ) 51)52=53, A1
있다(주의 : 이 전에서 Q는 오일러각이 아니고 각속도임). R1 (w) =exp (iw ]if) (3. 48) 여기에서 ]1 은 &축 방향으로의 전체 각운동량 연산자로서 각 핵자에 작용한다. Schrodin g e r 방정 식 은 H(t) l 'lfl'>=i영 -|w> (3. 49) 이므로, 회전계에서의 파동함수 를 1 1/1''>라 하면 l'lfl'' > =e•wJ ,, l 'lfl' > (3. 50) 로서 이 파동함수는 (H 나야) |1f!' ')=1 . 불|1/J'') (3. 51) 울 만족한다. 여기에서 H'=e’ 나 I l He-Ia J l’ (3. 52) 이고, 이는 회전계에서의 해밀토니안이 된다. 이 H’ 은 만일 H가 회전 에 대해 불변인 경우에는 H'=H (회전불변인 경우) (3. 53) 가 된다. 식 (3.49) 에서 명시한 H 의 시간에 대한 함수관계는 핵 전체 의 회전을 고려한 것이다. 만약 H 가 식 (3.53) 을 만족한다고 하면 사 실상 핵자들의 회전에 의한 시간의존성을 없앨 수 있게 된다. 이러한 경우에 관련된 실제적인 문제는 다음 절에서 자세히 언급하기로 하고, 식 (3.51) 의 좌변을 회전좌표계에서의 해밀토니안 H~=H'-nw]1 =H'-liw ]; (3. 54) 으로 놓고 이에 대해 고찰하기로 하자. 윗식에서는 Ji =e i hI J。 e-‘UJ ,‘ =]1 (3. 55)
임을 이용하여 회전좌표계에서의 각운동량 연산 자물 정의하였다. 이 H: 은 회전계에서 각 핵자의 고유 자유도에 작용하는 연산자인데, 전체 핵 의 회전이 상수인 Q에 의해 규정되었으므로 H > 은 시간에 직접적으로 의존하지는 않게 된다. 따라서 회전계에서의 Schri:id in g e r 방정식은 H 니 W'>=E』 '1/1') (3. 56) 으로서 정상상태 방정식이 된다. 여기서 E” 는 회전계에서 정의된 H냐 의 고유치이지만 핵의 에너지라고 할 수는 없다. 이 핵의 에너지는 E==< < WP l eIH-iUl J 'Il’/ J H') 'eiu J l' | w> =<'1/J''IH 'l'I/J ') =Ew+ fz w < 'I/ J''I J;l' I/J '') (3. 57) 이 될 것이다. 따라서 핵의 바닥상태에 해당하는 1w> g는 E ~ 몰 최소값 으로 만드는 l 'I/J''>라고 말할 수는 없으며, E 를 최소값으로 만드는 것 곳이에어서야 는한 다〔 .H' ,이];때] =0회 이전기좌 표때계문에에서 고 정유의치된라 할전 체수 각있운음동)량까의지 도기고대려치되 •(어 이 야 한다. 식 (3. 54) 의 w]1 항을 일 반적 으로 Corio l is 항 (또는 힘 ) 이 라고 하지 만 사실은 원심력도 포함되어 있음을 알 수 있다. 이를 확인하기 위해 스 핀이 없는 하나의 고전적 입자가 희전좌표계내에 있을 경우를 생각하 자. 이때 고전적 해밀토니안은 다음과 같다. l t ' =읊 -+U(; ) 구 (rxp ) (3. 58) 해밀토니안 운동방:v정_=식 — dd으,t: 로 =_ 부 터oalzp一 ., =_ --mp- -:x+. .. r: 운=-a촉r 국 x; __뽀 ar- (3.59) 이 되므로, 이 입자에 미치는 힘은 F=m 음.... =웅一 --m;xv
=P..... xw一 -mw一 x v- , -—aa u—; = (mv~ _11--1- ➔W X.. r~) , .x. Q➔ -11lW➔ XV➔ _aa_u; = -2 m (w... x v➔ ) 크 /1 Q... X (Q➔ X r-, ) _ —aa-ur¥ - (3. 60) 으로 된다. 윗식의 마지막 우변의 첫항 은 Cor i ol i s 힘, 그 다음이 원심 력 마지막 항은 포텐셜에 의한 힘인 것을 알 수 있다. 2) Ing lis 관성능률 식 (3. 54) 에 서 의 Corio l is 항은 Q 가 작을 매 H' 에 대 해 섭 동으로 생 각할 수 있다. H’ 의 고유함수의 완전 칙교 규 격화 집단은 쉽개 알 수 있다고 가정한다: I1 fl'':::: I rHp。 >IIQ+ , I>; =CnE l (;J) InQ > ,> (3. 61) +` =|o 。> +h 표 앗費?Q.L l q; n> (3. 62) 우리는 =0 일 때 핵이 바닥상태 (11=0) 에 있었다고 가정하겠다. 여 기에서 l 'lfl''>은 1 차 섭동 (ocw) 까지만 생각했다. 따라서 에너지는 식 (3. 57) 로부터 E::=:'. << q'l[; l'o'I I HH'' Il q'l;f。l '>'> + I: I Cn l2 (E,, -E ~) r.'1'0 =E~ + 1z2 硏 z'구j l < onE l; k _ EI (J;) 。 > | 2 (3. 63) 가 되며, 식 (3.63) 을 얻기 위하여 조건
E:::::::E 計上2 1 Q 2 (3. 65) 의 형태를 가지므로, 관성능 률 ..f1 을 다음과 같이 정의할 수 있다 (Ing li s) . /a=2tl2 ~ 2 | <@nIEk~|- 요E 。 지 2 (3. 66) 아 릅c Ing li s 관성능률이라 부른다. 이 식은 각운동량 A의 기대치를 계 산하여 비교 함으로써 다시 얻응 수 있다•
매우 작은 경우에 적용되나 식 (3.57) 에서의 전체 에너지는 임 의의 Q에 대하여 적용된다. 하지만 식 (3.57) 의 E : U 를 구하려면 ]1 이 가지는 각 핵자 상태간의 연결이 모두 고려되어야 한다. 따라서 매우 큰 행렬식옹 풀어야 한다. 이론적으로 비교적 쉽게 완전한 해답을 구할 수 있는 경 우 중의 하나는 희전하는 단진자 모형이다. 단진자 포텐설 자체가 1 축 주위를 각속도 Q로 회전하며, 이 포텐셜 속에는 A 개의 독립핵자(상호 간의 험이 없음)가 들어 있다. 이 경우 해밀토니안 H~ 은 Hlt=' =2—piIm=A : 2 l h +( ,' t)-_ 2l m ( 따져 +M+wM) J.=iI=A ;I j. (i) (3. 71) 라놓으면 H,'~ = H'—Q J, (3. 72) 이다. 핵자의 스핀을 무시하면 lH1 눅w ==h i-~=A lf zJ wz~ ((ir) X -p(-+i ) 는 1 표기 하지 않 았음) (3. 73) 이 된다. 이러한 독립 핵자들의 고유상태는 일반적안 단진자 문제에서의 〈내림 및 울림〉 연산자로 표시할 수 있다. 죽 &=( 소 )1/ 2 ( C.+C:) p.=+ (mw.li/ 2 ) 112 (C. -C:) (3. 74) 皇 =h 홉, 2,3w.(c:c. + 송) 一 inS (Ct Cs -C2C;) 一 itzD (Ct Ct -C 2Cs) (3. 75) S=~ D=“‘2 (w'32w— sQ) 21 12 (3. 76)
[c. ,Ct ] =oah (3. 77) 이다. 식 (3 . 75) 에서 보는 바와 감이 Ct C; 및 C2C, 의 역할은 단진자 고유 상 태들 가운데 전체 양자수가 N 인 상태와 N 土 2 인 상태의 결합을 나타 낸 다. 따라서 D 를 무시한다 함은 이러한 결합을 무시함을 의미하며 (Bo hr & Mott el son 참조) , 이 는 Q 2~3 일 때 실 질 적 으로 가능해 진 다. 이는 단진자 포텐셜이 1 축에 대한 희전에 거의 대칭일 경우를 나타낸 다. 그러나 이러한 경우는 앞절에서 언급한 것과 같이 허구상태를 나타 내게 되어 실질적인 단체회전의 의미는 없어진다. 그러나 AN=2 의 전 이는 단진자의 에너지 고유치 사이에 많은 간격이 있음을 의미한다. AE. = e(N +2) -e(N) ::::2 flW o ::::2. 4Q A - 11 3( MeV) (3. 78) 즉 D 에 비례하는 항은 식 (3.75 ) 의 다른 항들에 비하여 매우 작은 전이도 를 가지게 되므로 무시 할 수도 있 다 하겠다• 그러나 앞장에서 보 인 바와 같 이 타원체로 변 형 된 핵에서는 고유상태들의 축퇴가 없어지면 서 A N = 土 2 인 상태들도, 핵이 많이 변형된 경우에는 서로 교차할 수 있 다. 따라서 보다 일반적인 경우를 고찰하기 위하여 우리는 일반적인 해 를 모색 하기로 한다(자세한 내용은 본장의 참고문헌 [2] 를 참조하기 바 람 ). 식 (3. 75) 를 보면 단진자의 1 축에 대한 고유상태둘은 1 축 주위 로의 의 전에 의하여 영향을 받지 않는다 . 따라서 2 축과 3 축에 대한 울 림 및 내림 연산자를 조정함으로써 ll 노 울 대각화시키고자 한다. ak= b=~2, 3 (Ut Cb + V[Ct ), (k=2, 3) (3. 79) 이 문제는 정상좌표계를 찾는 문제와 같다. 우리는 따를 〈정상내림 연산자 〉 라 하고, 이것의 수반 연산자 따를 〈정상울림 연산자〉라 하겠 다. 한편 이 연 산자들이 h~ 을 대 각화한다면 우리 는 ll; 을 다음과 같이 쓸수있다. h~=hw1 (Ct C1 + ½) + tz n2(a 표 + 방) + h03(a t a 곱 송) (3. 80) 식 (3. 75) 와 식 (3. 80) 을 같게 놓음으로써 U, V 및 Qi 를 알 수 있다.
이 식을 푸는 과정을 보다 명확히 하기 위하여 다움과 같은 수학적 방 법을 도입하자. 우선 정상 울림 및 내림 연산자는 회전 단진자 포텐셜 내에 있는 정상상태를 만드는 연산자로서 보존 (boson) 입자의 관계식을 유지한다. [야 ,a 깁 =8n (3. 81) 한편 식 (3.81) 은 다음과 같이 쓸 수 있다. [h' ' a 디 =h0.a; (3. 82) 식 (3. 75) 와 (3. 79) 를 (3. 82) 에 넣 음으로씨 MXk=0k1/ x k (3. 83) 를 얻는다. 여기에서 X 뇨 (U•, V5 = (U?, u;, v;, v;) M=(;* AB*), 1/=(二) A=( -i£SI)2 wtS 3 )r, B=(\i °D 낍0 (3. 84) 이다. 고유치 문제는 de t (M-11 요) =O (3. 85) 을 푸는 것이고, 그 해는 야= };”i + (S2_D2) +웅 (3. 86) 여= ¥+ cs2-D 힙 ―웅 (3. 87) a=[(wl-wD2-4(D2-S2) (따+}) +8 파 (S2+D2) 〕 1/2 이다. 식 (3.86) 과 (3.87) 에서의 土웅-항은 03 가 02 보다 작도록 만들며, 이는 3 축으로의 포텐셜의 모양을 더 길쭉하게 만든다. 각 핵자에 대한 에너지 고유상태를 위와 같이 구했다 하더라도 핵자 둘이 어떻게 고유상태 속에 배열되는지는 정해져 있지 않다. 다시 말하
면 식 (3.80) 에서 부 터 i번째 핵자의 }l ~ 에 대한 고유치 (에너지는 아님) 는
e~ (i) =fzw 1 (n1 (i) + 방) + h 파 (t) + 방) + t10 3(n3 (t) + 송) (3. 89) 이고, 여기에서 no( i)는 i번째 핵자가 들어가 있는 에너지 고유상태의 a 축 에 대한 양자수이다. 따라서 회전 단진자의 고유상태에 대한 양자수 (n1( i), n2(i) , n3 (i))가 주어져야만 e~ 룰 구할 수 있게 된다. 그러므로 자 각 의 e~ 이 가 장 작은 상태를 핵자의 바닥상태라고 정하여 (이것을 단 열 (ad ia b ati c) 배 열 이 라 함) e~ 이 작은 상태 부터 핵 자들이 들어 가도록 한 다. A 개의 핵 자가 이러한 배열로 들어가 있다고 하면 이때 전체 핵의 HU . , 에 대한 고유치 죽 희전계내에서의 핵자의 전체 에너지는 E;1 = h (2lI + 2202+ 2 요 3) (3. 90) 이 다 . 여기에서 2a 는 핵 자로 채워진 상태 (페르미 바다)의 a 축에 대한 양자수의 합으로서 도 a= ~F ( n.(tJ +송) (3. 91) 이 된다. 4) 회전으로 인한 변형과 바닥상태 조건 회전하고 있는 핵의 바닥상태에 해당하는 핵의 모양이 어떠한지를 결 정하는 데에 지금까지 앞절에서 풀어온 과정을 재움미해 불 필요가 있 다. 우선 회 전이 없는 경우를 생각하자. H~ 은 =0 인 경우 H 가 되어, 바닥상태의 에너지는 식 (3.90) 으로부터 E .. =o=n(~1W1+~2W2+~3W3) (3. 92) 임을 알 수 있다. 이제까지 우리는 “It W2,Ws 를 주어진 상수로 보아 왔 지만 사실 포텐셜의 모양을 결정하는 이 상수들도 결국은 핵자들에 의 해 형성되는 것이다. 따라서 핵자 사이의 힘을 무시하고 평균 포텐셜 속에서의 운동만을 기술하는 현재의 모델에서는 새로운 이론적 가설에 의 하여 이 값들이 주어 져 야 한다. Bohr 와 Mott els on 은 다음과 같은 가 설을 이용하였다.L1W1=I :2w 2=I :sw3 (3. 93) 이 가설은 핵자들의 분포가 포텐셜의 모양과 일치한다는 것이다. 죽 단진자 포텐셜에서의 핵자들의 좌표의 평균치는
식 (3. 58) 에 단진자 포텐셜을 넣으면 h^ . . =11- mv ;+T1 m[wf Xf + (야곱 )x~+ (따군 )X깁 (3.100) 임을 알 수 있다(식 (3. 59) 에서의 v 는 사실상 회전계내에서 측정한 v' 이다). 죽 -내 ;'=꿉-걸 x? (3.101) 이며 조건
라 변하게 된다. 죽 자체부합 조건을 만족시키기 위해서는 핵의 포텐셜 이 변형되어야만 하는 것이다. 식 (3.86)~(3.88) 로부터 (wJ -w D2=I6w1-8w2(OH. OD + (Oi -O D2~0 (3.106) 이어서 w2 은 w2<(~)2 .. w2>(¥ 아 (3.107) 의 범위를 가진다• 다시 말하면 이 범위믈 벗어난 u 에 대해서는 자체 부합 조건을 만족하면서 핵이 변형할 수는 없으며, 결국 핵자둘의 내부 배열인 노가 변해야 할 것이다. 이러한 한계 각속도 Q c 는(주의 : w> °2;°3 인 경우는 고려하지 않겠음) w:-:;::wc = 요2 -0 3 (3. 108) 이고 이 값에 {.JJ가 이르면({.J)={.JJ, ) 2=3= Q2 .,+ Q 3 (3. 109) 이 되어 핵은 회전축 주위로 회전대칭성이 있는 빈대떡 모양이 된다. 앞절에서 언급한 바와 같이 이러한 회전대칭성이 생기면 단체회전이 허 구상태가 되어 버린다. 식 (3. 104) 로부터 핵 의 사중국자 모멘트를 구할 수 있 다. Q2 =(2X5 — X f -X ~> (3. 110) 또한 이 핵의 각운동량은 일반적으로 h
하면
l=R+J (3. 115) 여 기 서 f는 전체 각운동량, R은 단체 각운동량, J는 핵 자 둘 의 각 운동 량이다(앞절에서의 표기와 갇음). 이 식에서의 단체 각운동량 E 는 제 2 절에서 ”로 표시되었던 양과 다음과 같은 관계를 맺는다. w= 뿐 (3. 116) 다시 말해서, R 은 핵의 고유좌표계서 회전시키는 데에 해당하는 각운 동량이다. 따라서 단체회전에 대한 HroI 는 Hrot =a= 1 ±2J~ a (3. 117) 이다. 팽이 문제에서처 럼 I 와 M(=l) 은 운동상수이며, 괭이가 고유좌 표축 3 에 대해 희전대칭성이 없는 한 k 는 운동상수가 될 수 없다. 대 부분의 실험적 결과로는 핵이 대강 3 축에 대한 회전대칭성을 가졌다고 간주될 수 있기 때문에 우리도 이룰 가정하겠다. f-1= f -2= f - (3. 118) 인 럭 비 공 모양 (pro late ) 의 핵 을 가정 한다. 따라서 Hrot 는 다음과 같이 쓸수있다. Hrol= 四h2 { I.2.. -I 는]i) + vh2 , u3-J, ) 2 걸~ Cl+f -+ LJ+ ) + 옵] 2 (3.119) 윗식의 멘 나중 항은 사실상 H i m 에 들어갇 성격의 항이며, 그 앞항아 바로 Cor i ol i s 항에 대옹되는 항이다(실제로는 ]i에 대한 것이 추가되어 야 함. T.J = I3L + 당- (l+f -+ L] 김 참조) . 이 항을 Corio l is 항 또는 〈팽 이-입자 결합항 (Ro t or-Par ti cle Coup li n g ; RPC) 〉이라 부른다. 이 항을 무시하고 각 핵자 운동의 함수인 관성능률을 고정시켜 만든 모델을 〈단 열 모델 (adia b ati c model) 〉이 라 한다. 1) 단열 모델 이 모델에서의 해밀토니안은
H •d= Hrol + H in tr , (3. 120) Hro1= 四h2 (F-I i -B ) + 21/3 (k-k) 라 (3.121) H i n1r=Hi n t +玄fl]2 2 (3.122) 으로서, 회전상태를 나타내기 위한 좋은 양자수는 I, M=J, ,, K=I,, 0=]3 등이다. 따라서 이러한 상태에 대한 고유함수는 팽이의 그것(식 (3. 32) )과 핵자에 대한 파동함수, 예를 들면 단전자 모델에 대한 Slate r 행렬식의 결합으로 표시될 수 있을 것이다. 죽 W1 tf K.o= J템計 D i ,K(w)~n(w; q) (3.123) 가 된다. 여기에서 w 는 다시 오일러각이고, q는 핵자들의 고유 자유도를 나타 내며, ~o(w; q)는 회전 대칭축이 3 축인 핵자들의 운동을 나타내는 고 유 파동함수이다. 한편 Hra 에 대한 에너지는 다음과 같다. Era t=옵 [l(l+l)-K2-0 汀+긋~ (K-0)2 (3.124) 2) 파동함수의 대칭성 회전 대칭 축을 가진 핵이라 하면, 고유좌표의 설정 방법은 단일하지 않다. 다시 말하면, 파동함수들은 다음의 두 가지 변환에 대하여 불변 이어야 할 것이다. i) 고유좌표계물 회전 대칭축 주위로 8 만큼 희진시켜도 아무것도 변 하지 말아야 한다. 이러한 좌표계의 회전에 대해 팽이 파동함수는 D~K(
임을 알게 된다. ii) p rola t e 로 변형된 경우이므로 제 2 축 주위로 X 만큼 고유좌표계를 희전시켜도 아무런 변화가 없어야 한다. 따라서(식 (3.27) 참조) D if K(
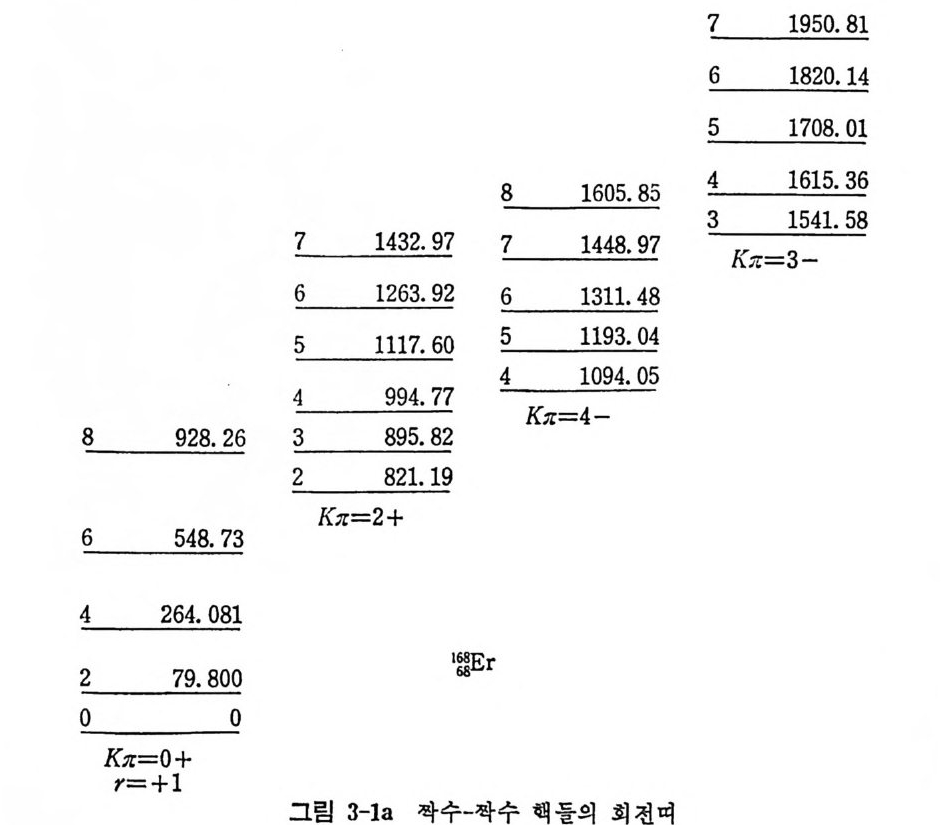
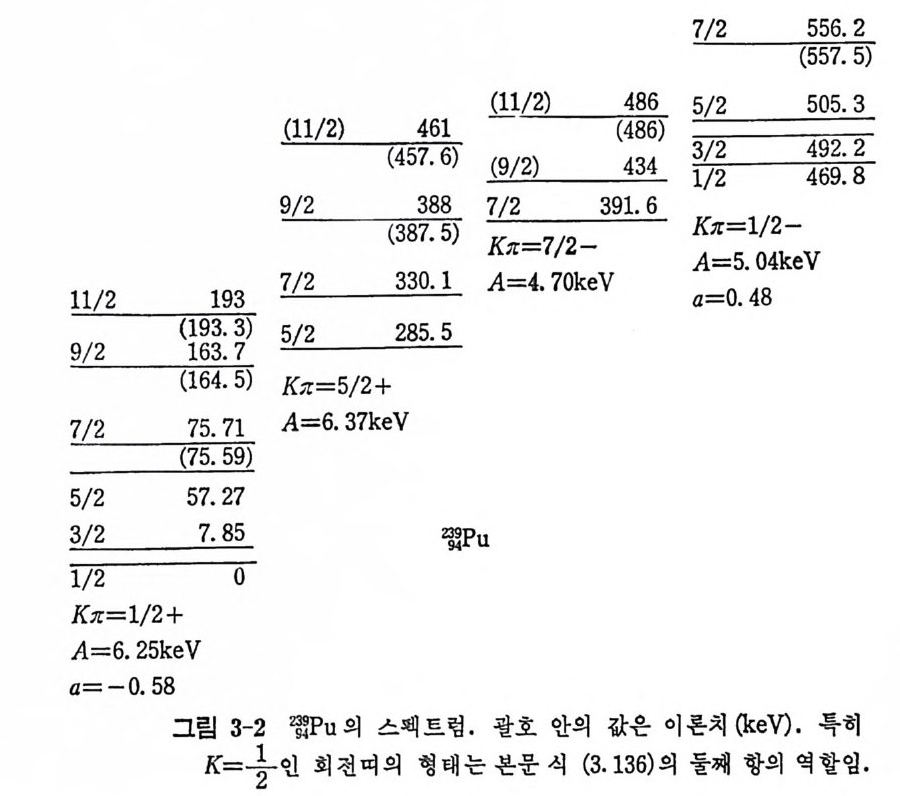
보자. 일반적으로 K=O 인 상태에서는(식 (2.4 5) 참조) (J)。= ( 一 ) 'o 。 =r tP。 이 므로 sig n atu r e r 은 r= 士 1 (3.133) 의 값을 가진 다. 따라서 상태 함수 (3. 130) 으로부터 K=O 인 경우; l=O,2,4 (r=+l 일 때) l=l, 3, 5 (r=-l 일 때) 임을 알 수 있다. 이는 핵 이 p rola t e 형 이기 위한 필요조건이다(그림 3-1 참조) . 한편 짝수―짝수인 핵 은 r=l 인 상태 만을 가지 지 만 홍수-홀수인 핵은 r=-1 인 상태도 가질 수 있다.
 7 1950.81
7 1950.81
 6 80.3 07詞9)8 5 539.6 654 )29.{6 4986 45.函29.0 3 500.22 2T52{)2 2 4684. 4 1259.9 4=K +1!7: eV51. 6 =k9AB 583.=-eV IA:leVl ;S
6 80.3 07詞9)8 5 539.6 654 )29.{6 4986 45.函29.0 3 500.22 2T52{)2 2 4684. 4 1259.9 4=K +1!7: eV51. 6 =k9AB 583.=-eV IA:leVl ;S
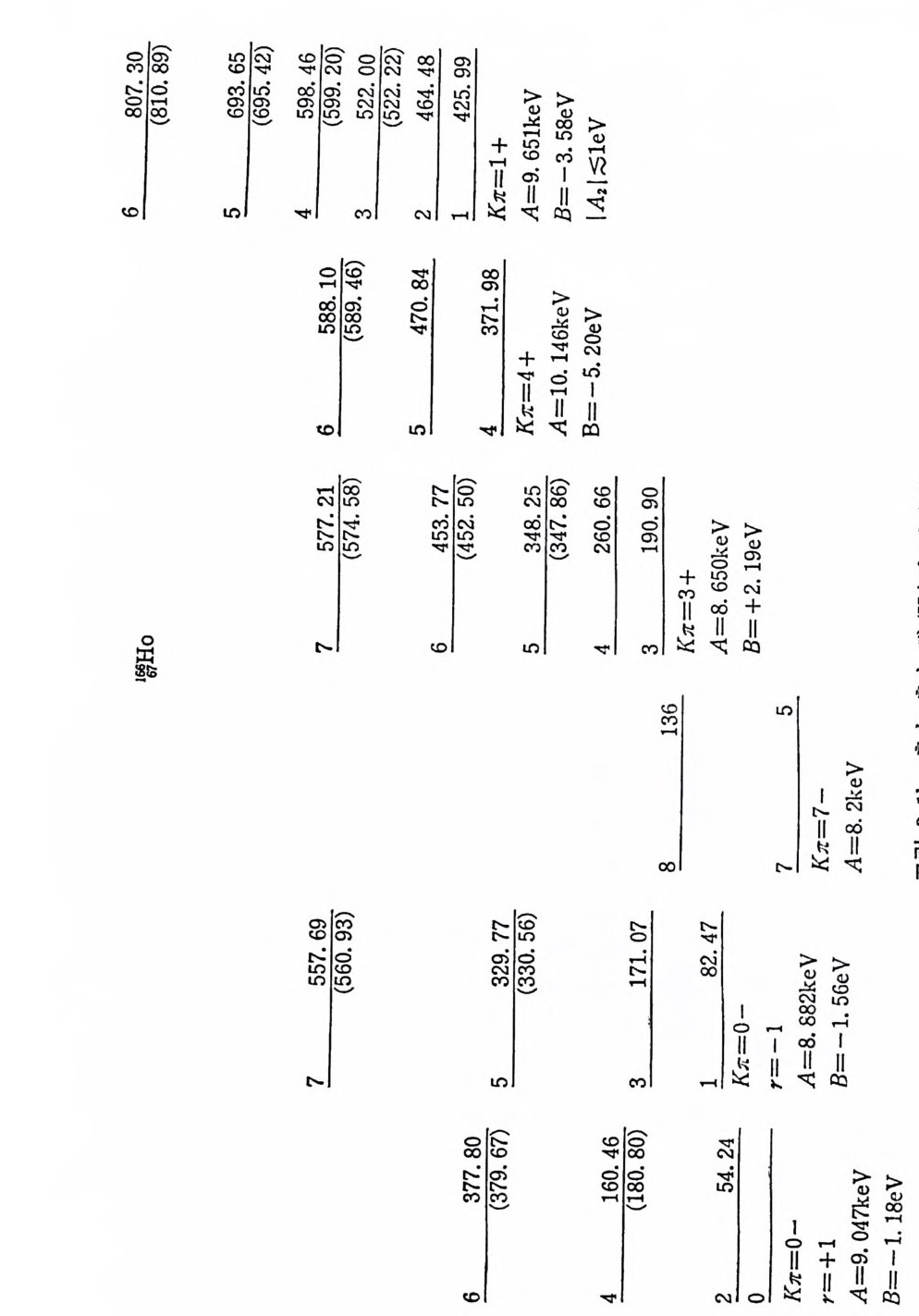
4) 희 전띠 의 혼합 (band mi xi n g ) 괭이케자 결 합항은 K= 」2- 인 회전띠에 대해서만은 Hro t의1 행렬 요소 중 대각선 요 소 에도 영향을 미친다. 즉 RPC 결합항은 K= -t인 경우에 는 무시 될 수 없다. 우선 a=-
 7/2 556.2
7/2 556.2
E:: Ot( I) =옵-〔[(I +1) +oK, ~a(- )나 (l+ 송)〕 (3. 136) 이 된 다. a 를 〈배 결 합상수 (decoup li n g consta n t) >라 하는데 그 이 유는 단열 (ad i aba ti c) 모델이 마치 모든 핵자가 핵의 평균 포텐션에 구속되어 함께 돌고 있는 것처럼 묘사한 데에 반해 이 RPC 항은 이 구속을 깨뜨 리고 있는 것으로 해석될 수도 있기 때문이다. 한편 강한 결속 모델도 성공적으로 실험치를 맞추기는 하지만 완전히 잘 맞는다고 할 수는 없 다. 죽 스펙트럼 l(l+l) 형태가 아주 찰 지켜진다고 할 수 없다. 따라 서 무시되었던 RPC 항이 가지는 다른 역할을 생각해 볼 수 있다. 이 항은 aK= 土 1 인 두 개의 서로 다른 띠둘을 연결시키고 있다. K 와 (K+1) 띠를 생각 해 보자. 섭 동 원 리 에 의 하여 (Br il lou in - W ign er 전 개 ) 섭 동 후의 에 너 지 는
 Exp t. Theory
Exp t. Theory
E=E 。+ g 》:감 n (3.137) 가 된다. 여기서 Eo 는 섭동울 고려하기 이전의 에너지이다. 또한 vno= -玄 h,2 -< IK+ l, MI LJ + ll, K, M> =-A, 간(l +l)-K(K+l), (3.138) AK =경jft2-
 제 2 부
제 2 부
제 4 장 제 2 양자화 방법과 핵상태 이 장에서 우리는 N 개의 입자들로 구성된 계의 상태와 연산자를 기 술하는 방법인 재 2 양자 화방 법 을 공부하려 한다. 이 표현법은 계의 동 력학적 기술에 있어 근사법 을 발전시켜 나아가기에 편리하다는 사실이 밝혀질 것이다. 한 개의 입자로 구성된 계 한 개의 입자로 구성된 계에 있어서 양자역학에서 말하는 상태와 표 현을 먼저 공부하기로 하자. 1) 스핀이 없는 입자 입자는 |a>, IP> , … … 1 >와 같은 상태의 완전한 집합으로써 표현 될 수 있다. 여기에서 |a>, IP>, …… 1 >는 뒤에서 명시하게 될 해밀 토니안 h 와 감은 가관측량의 고유벡터들이다. lzla>=eala> (4.1) 고유벡터 la> 는 완전한 집합을 이룬다. Ia: la>
이 식 을 (4. 7) 식 에 집 어 닝 고 식 (4. 4) 몰 이 용합 으로써 다음 식 을 얻 는 다. [-읊귬 2 + U( r )] rp자) =e. 군) (4.1 0) 윗식은 Schodin g e r 방정식의 일반적인 형 태이다. 2핵) 자스 등핀은파 좌하표전 스r 핀이을외 에가 진스 핀입 자(J 와 하전스핀 T 를 가지고 있다. 스핀 의 두영은 주 어진 축운 따 라 土겅려 두 값을 가질 수 있고, 하전스핀 은 핵자가 중성자 인 가 혹은 양성자인가에 따라 土+의 값들을 가진다. 해자 등 의 스핀과 하전스핀의 좌표를 고려하기 위하여 우리는 상태 1; > 을 상 대 I r (J T > 로 대치해야 한다. 식 (4.4) 는 다음과 같이 된다.
반대칭이어야 한다. ,fr (X1X2… X .1.) 이 N 개 의 입 자둘의 반대 칭 파동함수라 하자• ,fr (Xi , X2, …, X.v ) = -,fr (X2, Xi, …, x.I') = … 우리는 ,fr(m ,.T2, … ,m) 을 완전하기는 하지만, 반드시 직교규격화되어 있을 필요는 없는 단일입자 상태 들 로 전개할 수 있다. ,fr(x .,X2, ···,x.v) = a,~p . . .. , w
de t{<떠 |a>
동일하다. 죽 슬레 이 터 행 렬식 (4. 14) 는 상태 |a /3 ···w> 의 좌표공간 {xI,x2, … ,xA . } 에서의 한 표현이라고 생각해도 된다. <따, X2, ···, X,\' la/3 · ·· w> =det {
aIP:·· · w l aP .. ·w> < aP …이 =N! (4. 24) 닫 힘 관계식 안의 계승 N! 은 상태들 lap . .. >와 |X1X2 … XN> 의 집합 이 지나치게 많기 때문에 나타난다. 죽 페르미 입자들의 동일성 때문이 라고 할 수 있다. 실제로 부호 를 생각하지 않으면, laP·· ·w > 또는 lx1X2 ··· XN> 상태 이후에 첨자 물 치환하는 과정에서 N! 개의 동일한 상 태 들 이 나타난다. 자주 쓰이지는 않지만 이러한 이유로 단일입자 상태들 {a} 의 사전식 배열을 사용하는 것이 편 할 때가 있다. 사전식 배열을 잘 나타내기 위 하여 우리는 단일입자 상태들을 정돈되고 완전한 순서로 다음과 같이 적겠다. a
V=+~12 v~(Jx ,, 찌 (4. 29) 여 기 에 서 u (x‘, xj) =u (xJ, 지 이 다. 좌표 따 는 i 번 째 입 자의 위 치 ;‘ 와 스핀 (1‘ 그리 고 하전스핀 T 서문 동시 에 나타낸 다는 사실을 상기 하자. 우 리는 또한 다체 연산자도 다루게 된다. 예를 들어 3 체 연산자 V(x;,x;, 띠가 핵자들 사이의 유효 포텐셜올 나타낼 수도 있다. 3 체 포텐셜은 좌표 g 와 xj 그리 고 Xi 간의 치 환에 대 하여 대 칭 이 어 야 한다. 따라서 대 칭 3 체 연산자는 다음과 같이 적을 수 있다. v3= 강. ,.*2 j *k v (\ xi, xJ, xk) (4. 30) 연산자 (4.28), (4.29) 와 (4.30) 은 X- 표현으로 표시되었는데, 이 표현 에서는 연산자들이 대각선화되어 있다. 그러므로 일체 연산자 (4.28) 에 대하여 <자 ·xN| Tl4···xk> =i2=N l
4 생성연산자와 소멸연산자를사용한반대칭상태의 표현 반대칭상태 |a f3 ···w> 는 진공이라 불리는 상태 10> 와 생성 연산자 야 로부터 만들어질 수 있다. 진공에 1,2, … ,N 개의 생성연산자를 적용함 으로써 우리는 1,2, … ,N 개의 입자상태를 만들어낸다. 10> 〈진공〉 a:IO> 〈단일입자상태〉 a; 야 10> <2 입 자상태〉 a; 야 ... a!IO> 〈 N 입자상태〉 (4. 33) 진공과 1, 2, …개 의 입 자상태 의 집 합을 포함하는 공간을 우리 는 Fock- 공간 (Fock s p ace) 이라 부른다. 이 공간에서 상태 a t a; … a!IO> 는 반대 칭상태 |a g… a> 를 나타낼 수 있다는 사실을 보이기로 하자. la/3 …Q> =a; 야 ··a:l0> (4. 34) 그러기 위해서는 생성 연산자들이 반교환성을 가져야 한다. a; 야 +a t a t=〔야, a;J + =O (4. 35) 한편 Fock 공간 (4. 34) 에 대 한 쌍대 공간 (dual spa c e) 을 만들 수 있다. 진공의 수반상태 (ad j o i n t)는 <01 로 나타내기로 한다. Fock 공간에서 bra
연산자 야와 a, 가 반교환성을 따라야 한다. a 。야 +a t a.=[a., at] +=
따 라서 [中 (지 , 中+ (石) ]+ =O (X1 -X 2) (4. 45) 이다. 상태 IX1%2···XN> 은 Fock 공간에서 다음과 같이 표현될 수 있다. I X1X2···XN> =中+ (功) ++ (x2) …++ (XN) 10),
따라서, 위와 같이 ,;+(x) [_」忘 -52 寸 (x) 〕 -홍 中(.'\,.i)와 왼쪽으로 교환합 으로써 다음과 같은 결과를 얻는다.
여기에서 v(x,x’) 는 x 와 X’ 의 함수로서, 미분항을 포함하지 않고, 또한 장 연산자와 교환가능하다고 가정하자. 반교환성의 규칙을 적용하여 우 신 다음 식을 얻을 수 있다. N <지 .. 미,fr +(x) ,Jr (x) = ~ o(x- 지 <자 .. 미 (4. 57 ) l=l 또한 다음 관계식에 유의하자. ,Jr+ (x) ,Jr+ (x') i/r (x/ ) ,fr (x) =,Jr+ (x) ,fr (x) ,y+ (x’) ,[J-( x') -o (x-x’ ) v-+ (x) ,fr (x) (4. 58) 식 (4.58) 의 좌측에 <자 ··X 사을 곱하고 식 (4.57) 을 이용하면 다음 식 을 얻는다. < 사 • • xK I ,fr+ (x) ,fr+ (x') ,fr (x') ,fr (x) =<자·미 c,t 1 rt o(x 타)-,t o(x-x')o(x- 지] (4. 59) 식 (4. 59) 과 식 (4. 56) 을 이 용하면 다음과 같은 식 이 나타난다. <사 ··X N I V= <자 •• 미 [방흡1 V(x, 다] (4. 60) 마라서 식 (4.56) 과 식 (4.32) 가 증명되었다. 장 연산자들을 식 (4.41) 을 사용하여 전개하면 다음의 결과를 얻는다. V=— 12_ a~p rd (ap I V I ro) a:at a6a , (4. 61) 윗식에서 (ap I V I ro) =Idx1dX2 tp詞) tp} (x:) V (Xi , X2) 군) 'f'6( x2) (4. 62) 이다. 행 렬 (4. 62) 의 요소는 〈반대 칭 화 (ant isy m met rize d) 되 지 않은 행 렬 요 소〉라 불리운다. 우리는 대부분의 경우에 다음과 같이 정의된 반대칭화 된 행렬요소를 사용한다. <떄 lvlro>=
반대칭화된 행렬 요소를 사용하면 V 는 다음과 같이 된다. v=4+ ·p~rd.
v=+fd x1d x2dx3dx,,tr + (x1) ,fr따) (X1X2 IV I X3X,) 中(지中 (x3) =-t1- dx 1dx2dx3dx,,tr + (x1) 맡 (x2)
과 같다. 라그랑지안은 상대론적으로 불변인 운동 방정식을 기술하는 데에 매 우 적합하다. 6 단일입자 상태의 선형 변환 단일입자상태의 완전한 기저 I ;i>의 유니터리 (unit ar y) 변환웅 생각 하자. 이 변환은 유니터리 연산자 e· 』 (』=』+)로써 나타낼 수 있다. Ci , /IA)= ~ <µle'.I| A> Iµ> (4. 74) µ a! 와 a. 는 각각 페르미온을 상대 |A> 에 생성시키고 소멸시키는 연산 자라 하자. b! 와 bA 는 각각 페르미온을 변화된 상대 e 나 |A> 에 생성시 키고 소멸시키는 연산자라 하자. 식 (4. 74) 에 의하여 b!= ~
a: b,= ~µ <..:lle -j~ • lµ )a, (4. 75) /I 변 환 (4. 75) 는 정준 (canon ica l) 변황이 라 불리 는데 , 그것 은 이 변 환이 반 교환 관계물 보존하기 때문이다. [b., b 』+= [a. ,a 』 +=0, [b., b;]+=[ % 야 ]+=
우선 다음 항동식을 알아두자. eBe-=B+ 〔 A,B 狂강 [A, [A,B]] + 갑_ [A ,[ A, [A, B]]] + ... (4. 79) S 와 야의 교환자물 계산하자. [S, a !]= ~ a
행렬 J. ,=
|B'>=a EHP (/J2E F F . 占}) |0> === aaa HEEnIElFFF (((a11;+++ rr 2G~er2FFe FCC cr ,ra.aaa 아.;))a . I )|A0야>) | 0> =exp {lFa~F 요아따 | A> (4. 92) 식 (4. 91) 과 식 (4. 92) 를 결 합 하면 마지막으로 다음 결과 를 얻는다. IB>=
• D.J . Thouless, The Qu antu m Mechanic s of Many -B ody Sy st e m s, Academ ic Press, 1961 .
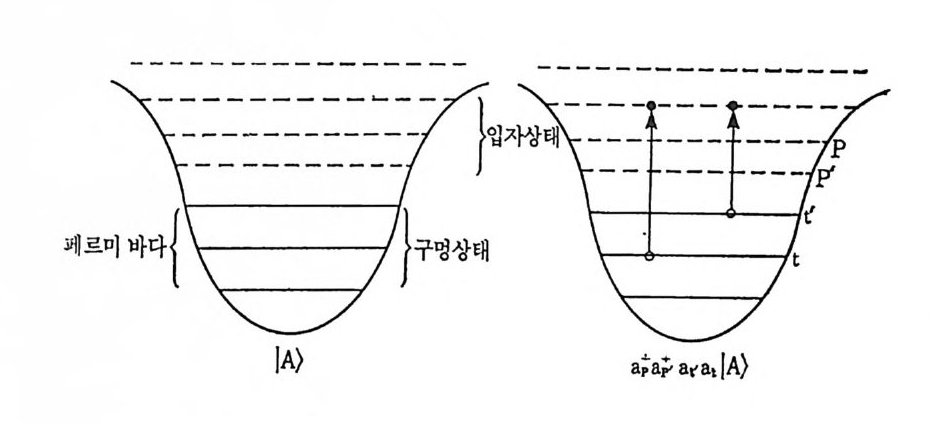
7 입자와 구멍 . 계 수 Cra 의 값이 작을 때에는, 지수함수 (4.93) 을 전개하여 술레이터 행렬 식 |B> 를 숭례이터 행렬 식 IA> 의 함수로 나타낼 수 있다. 문제 룹 간단히 하기 위하여 다음과 같 이 행렬식 IB> 를 미리 규격화시키자.
 二二::::二_/ k
二二::::二_/ k
I
개의 성분을 가지는 두 스피너 (4. 102) 와 (4. 103) 으로 다시 묶 어 놓았 다. 그런데, 우리는 y축울 중심으로 亢만큼 둘 렀을 때 스피너 I t >가 스 피너 I i>로 변환된다는 사실을 알고 있으므로, 다움과 갇 이 쓸 수 있 다. Gal =e-•r.S ya at e '-T S, ba i = e_ ,XS yb a t eIrS y (4. 104) 그러므로, 유니터리 연산자 C 를 다음과 같이 정의하자. C=e- i -~ s y =ex p{-중흡。 @a ; _a 따)} (4. 105) E F 변환식 (4. 104) 를 다시 쓰면 다음과 같 다. aa=CatC - 1, -at= C aaC-1, -a.=CatC - 1, at =C aaC-1. (4. 106) 역 관계식은 한 축을 중심으로 21r 만큼 돌 렸을 때 1/2 스피너에 _1 의 계수가 곱해진다는 사실로부터 얻을 수 있다. 연산자 C 는 a a: F일 때 연산자 at ,aa 와 교환된다. 따라서 다 음 의 번 환을 고려하면 : b;=Ca;c -1= {ad, a 탁 따, a~F, b.=Ca.C-1= e:..,• a호~F, (4. 107) 모든 a 에 대하여 b 』o 。 >=0 임을 알 수 있다. 우리는 I <.P。>를 연산자 b 」의 진공이라 부른다 . 연산자 C 는 페르미 바다 안의 상태의 생성 연산자를 소멸 연산자로, 그리고 또한 그 역으 로 변환시키는데, 우리는 이것을 입자 _ 구멍 변환 연산자라 부른다. 페르 미 바다 안의 상태의 갯수를 N 이라 할 때, 연산자들을 묶는 방법은 (N/2) ! 이나 되므로 연산자 C 믈 정의하는 방법은 식 (4.105) 로 유일하 게 주어지는 것은 아니다. 핵뭉리학에서는 I <.P。>가 닫힌 껍질들로 구성된 술례이터 행렬식으로
주어지는 경우가 많다. 다시 말해서 페르미 바다가 각운동량 j와 2 축 에 대한 두영 ji를 가지는 궤도 laj m> 둘로 구성되어 있고, 또한 |o 。> 는 주어진 a 와 j에 대한 2j +1 개의 궤도 |a j m> 둘을 모두 포함하는 경우가 많다. 이 경우에는 페르미 바다 안의 상태둘을 |a j m> 과 (-)i-.. laj -m> 의 쌍으로 묶고 l a>。>을 다음과 같이 쓰는 것이 편리 하다. 幽 >= Il { ( 一 ) ;-.. a ;J .. a:j- m } 10 ) (4.109) a,mJ> EO P 준-스핀 연산자의 성분은 이 경우에 다음과 같이 된다. S+=.1 _2_ _ a,J2 E F 2m (-)j -ma;j ,a 노 S-=+a -5蠶 (키j -naa j- .. a.J .. Sr= 송 (R- Q), Q= 2 Q.J (4.110) a,J E F 여기에서 N 은 입자 갯수 연산자이고, n. j=j+l/ 2 이다. 이렇게 연산자물 쌍으로 묶는 독특한 방법을 사용하면, 세 연산자 S+,S- ,오가 스칼라가 된다는 잇점이 있다• 다시 말해 그것들이 전체 각운동량 ]와 교환된다. 우리는 l q)。>를 아래와 같이 적을 수 있다. I (J)。> =古 (S+) °| 0> (4.111) 진공 10> 의 각운동량은 0 이고 (-]+I O>=O), S+ 는 J➔ 와 교환되기 때문에 I a>。>의 각운동량도 또한 0 이다(J Io 。 >=0). 따라서, 닫힌 껍질의 각운 동량은 0 이다. 식 (4.106) 은 다음과 같이 쑬 수 있다(식 (1. 45) 와 비 교하고, 식 (6.47) 이하의 설명을 참고하기 바람). (-) i-.. a .J- .. =C at1 ., c -1 (4.112) 상태 |a j m>=a:J m|0> 이 각운동량 j와 2 축에 대한 성분 m 을 지니므 로, 연산자 야j .. 는 계수가 j이고 성분이 m 인 텐서이다. 입자-구멍 변 환 연 산자 C=e 어:r S’ 가 각운동량 연 산자와 교환되 므로, 식 (4. 112) 는 연 산자 (-)J -aa J-”이 회전에 대하여 마치 연산자야j m 처럼 변환되고, 따 라서 (-)j -na. J-•도 역시 계수가 j이고 성분이 m 인 텐서라는 사실을 보여 준다.
9 두 종류의 페르미온들로 구성된 계 원자핵은 중성자와 양성자로 구성되어 있는데, 중성자와 양성자는 서 로 다른 입자이므로 파울리의 원리가 적용되지 않는다. 따라서 우리는 중성자와 양성자를 핵자라는 한 입자의 직교하는 두 상태로 생각할 수 있다. 역으로, 어떤 축에 대한 스핀의 두영이 +1/2 인 중성자는 그 축에 대 하여 스핀이 -1/2 인 중성자와는 다른 입자이므로 파울리의 원리가 적 용되지 않고, 따라서 스핀이 반대인 중성자들에 대해서는 파동함수를 반대칭화할 필요가 없다. 일반적으로 입자는 양자수들(예 : 위치 ;;, 스핀 6 등)로써 칭의되는 데, 입자는 그 양자수가 나가내는 상태에서 발견된다. 우리는 직교하는 상태에 있는 두 동일입자를 서로 다른 입자로 생각할 수도 있고, 거꾸 로 서로 다른 입자를 동일한 한 입자의 칙교하는 두 상태로 생각할 수 도 있다. 먼저의 경우에는 파울리의 원리가 적용되지 않고, 나중 경우 에는 적용된다. 명백히 모순인 것처럼 보이지만 이 두 가지 기술법은 동일한 것이다.* 야와 b; 는 각각 양성자와 중성자를 상태 |a>=lru> 에 생성시키는 연산자라 하고, |0> 는 aa 의 진공이며 동시에 ba 의 진공이라 하자. a 』 0>=b 』 0)=0 (4.113) 파울리의 원리는 중성자와 양성자에 따로따로 적용되므로 연산자 a. 와 ba 는 다음의 교환법칙들을 만족시킨다. 〔따' a;]+ =0, [aa ,야 ]+=% [aa, apJ + =O, [b;, bp ]+ =0, [ba ,b pJ + =Oap, [ba, bpJ + =O (4. 114) 그러나 파울리의 원리가 연산자 aa 와 ba 사이의 교환법칙을 규정하지는 않는다. 우리는 임의로 이 연산자들이 교환성을 가지거나 또는 반교환 성을 가지도록 할 수 있다. [a+ ,b +] 土 =0, [a, b]±=O. (4.115) • Messia h , Qu antu m Mechanic s Vol. 2, Dunod, Paris.
상태 a… o 에 있는 양성 자들과 상태 8···e 에 있는 중성 자들로 만들어 진 다음의 상태를 생각하자. la···w, o… e > =a;… a !b;t… bt lO) (4.116) 교환법 칙 (4. 114) 와 (4. 115) , 그리 고 식 (4. 113) 을 사용하여 우리 는 식 (4.116) 과 같은 형태로 주어지는 상태들의 스칼라곱이 식 (4.115) 의 부 호를 +로 선택하든지 또는 -로 선택하든지 동일하게 다음과 같이 주 어진다는 것을 보일 수 있다.
10 하전스핀 중성자 (In>=1 -r- =1/2> )와 양성자 (IP>=l -r- =-1/2> )의 두 상태는 하전스핀 공간이라 불리우는 2 차원 벡터 공간에서 서로 수직한 벡터라 고 생각할 수 있다. 두 상대 |-r- =1/2> 와 |-r- =-1/2> 물 기저로 백하면 중성자와 양성자는 1/2 스피너로 표시된다. 중성자=(:\\)=(:)· 양성지=(:_ 二)=(:) (4. 121) 이 공간에서 연산자들은 세 개의 파울리 행렬 로씨 표현된다. 러~ ~), T2=(~ ~i), Ts=(~ -~) (4.122) 이 행렬들은 하전스핀 공간의 벡터 연산자, 죽 하전스핀 연산자의 세 성 분을 나타낸다. t=一21 -T (4. l23) 우리는 하전스핀 연산자의 세 성분 t I, t 2, t s 의 교환법칙이 각운동량의 경우와 같다는 것을 쉽게 보일 수 있다. tjtj-tjt‘=ieij, . th (4. 123') 식 (4. 121) 과 식 (4. 122) 를 이 용하면 중성 자상대 와 양성 자상태 는 하 전스핀이 1/2 이고 두영이 士 1/2 인 상태라는 것을 알 수 있다. t2 ln>=f In ) t2 IP>= flP> t sln> =웅 |n> t 3I p>=-방 IP> (4.124)
여러 개의 핵자들 로 구성된 계에 대해서는 전체 하전스핀 연산자를 칭 의한다. T➔ =~A t7 (i) (4.125) i= l 상태 (4. 120) 은 T3 의 고유상태 이 다. Tsla… ' 6… e>=¥ 1a… u , 8… E) (4. 12 6) 여기에서 N 은 중성자의 갯수이고 Z 는양성자의 갯수이다. 상태 (4.120) 은 일반적으로 子 2 의 고유상태가 아니다. 하전스핀 연산자의 세 성분은 제 2 양자 화된 표현을 사용하여 다음과 같이 표시된다. T+=2 b;a a , T3= 묘 (b!b.-a!a 。), L=f a!b . (4.127) 윗 식에서 {a} 는 하전스핀 이외의 모든 양자수들의 집합을 나타낸다. 두 핵자로 구성된 계물 생각 해 보자. 중성자 두 개로 구성된 상태 b;;b t lO> 는 전체 하전스핀 T 가 1 이고 그 두영 Ts 는 +1 이다. 두 개 의 양성자로 구성된 상태 야야 10> 의 전체 하전스핀 T 는 1 이고 두영 Ts 는 -1 이다• 중성자와 양성자가 각각 한 개씩 있는 상태 b; 야 10> 는 전체 하전스핀 T 가 O 이고두영 Ts 가 0 인 상태와, T=l 이고 T3=O 인 상태의 혼합상태이다. b;;b t l o>= laf3 , T=l, Ts=l> abt; 야a t 1 100>) == flat/3, IaT /3=, lT, =TOs,= -T1s=>O > +;hla /3, T=l, Ts=O> 상태 IT=O, Ts=O> 와 IT=l, T,=0> 은 각각 다음과 같이 주어진다. laf3, T=O, Ts= O>=f .t(bt a t - a tb t ) IO> la/3, T=l, T,=O>= -;n (b tat +a; 妹) IO> (4.129) 양성자들 사이에만 작용하는 쿨롱력을 제의하면, 핵력은 2% 정도의 한계 에 서 전하 무관성 (charge ind ep en dence) 원 리 를 따른다. 이 원 리 에
의하면 두 양성자, 두 중성자, 식 (4.129) 에서 하전스핀 T=l 인 상태 의 중성자와 양성자 사이에 작용하는 핵력은 모두 같다. 그러나 하전스 핀 T=O 인 상태의 중성자와 양성자 사이의 핵력은 다르다. 이러한 사 실들로부터 우리는 핵력이 하전스핀 공간에서 스칼라라는 것을, 즉 핵력 이 전체 하전스핀 연산자 (4.125) 의 세 성분과 교환된다는 것을 추론할 수 있다. 핵력은 다음과 같이 표시할 수 있다. V+W!➔1 ·!➔2 (4. 130) 여기에서 V 와 w 는 두 핵자의 하전스핀을 재의한 좌표들(위치와 스핀) c의2 =함93수8.이 2 6다M. eV중) 성과 자거의 의 질같 량으 (M므n로 c 2운=9동39 . 에5 5너M 지e V연) 은 산 자양도성 자또의한 진— 강— ( oM. 1p % 정도 내외에서- 하전스핀 공간에서 스칼라이다. 그러므로 쿨롱력 을 무시하면 핵의 해밀토니안은 하전스핀의 세 성분과 교환되고, 따라 서 핵의 상태는 T2 와 T3 의 고유상태인 것이다(핵의 상태가 각운동량 ]2 와 ]=의 고유상태인 것과 마찬가지이다). 우리는 하전스핀을 물리적으로 해석할 수 있다. 어떤 상태의 전체 하 전스핀 T 는 핵자들의 좌표들간의 치환에 대한 그 상태의 대칭성을 결 정한다.* 핵자가 두 개인 간단한 경우에, 두 핵자간의 좌표치환에 대하 여 하전스핀 T=l 인 상태는 반대칭이고 T=O 인 상태는 대칭이다. 식 (4. 128) 과 식 (4. 129) 에 의 하여 , la/3, T=l, T,>=-1/3 a , T=l, Ts> l af3 , T=O, Ta > = I /3a , T=O, Ta > (4. 131)
• Bohr and Mott els on, Nuclear Str u ctu r e, Vol.1, Benja m i n, 1969, p. 104.
* 참고문현 페르미온, 또는 보존의 생성 연산자와 소멸 연산자의 선형 변환에 관한 상세 한 내 용은 다음 문헌을 참조하라 : R. Bali an and E. Br~zin , Nouvo Cim ento 64B (1969) 37. C. Bloch and A. Messia h , N11cl. Phys . 39 (1962) 95. 입 x1 --구멍 변환의 보다 상세 한 설명 과, 다른 유도식 은 다음을 참조하라 : Bohr and Mott els on, Nuclear Str u ctu r e, Vol. 1. W. A. Benja m i n (1969) , New York and Amste r dam, pp. 367-77. J.S . Bell, Nuclear Phy s ic s 12 (1959) 117.
제 5 장 시간배열곱 (T- 곱), 정상곱, 축약과 W i ck 정리 상태와 연산자 를 제 2 양자 화 하여 기술하는 방법을 익혔으므로, 이제 W i ck 의 정리 윤 제시 함 으로써 우리의 수학적 도구를 확장시키기로 하 자. W i ck 의 정리는 주로 슬레이터 행렬식에 대하여, 또는 진공에 대하 여 연산자들의 곱의 평균값을 계산하는 데 사용된다 . l 페르미 바다 h( x ) 는 단일입자의 변수 x=(r, (l,'C)에 작용하는 해밀토니안이라 하 고, |a> 는 고유치 %에 해당하는 고유상태라 하자. hla>=e.la> (5.1) 해밀토니안 h 는 Fock 공간에서 대칭 일체 연산자 Ho 를 규정하는데, Ho 는 |a>- 표현을 사용하면 다음과 같이 주어진다. Ha = I; e.ata . (5. 2) a Ho 의 고유상태는 슬레이터 행렬식으로 주어진다. | (J)。> =a; 야 · •·a! I O> (5. 3) 여기에서 |0> 은 식 (4.38) 의 진공이다. 우리는 앞으로 상태둘 |a> 가 직교규격화된 기저를 이룬다고 가정하겠다 :
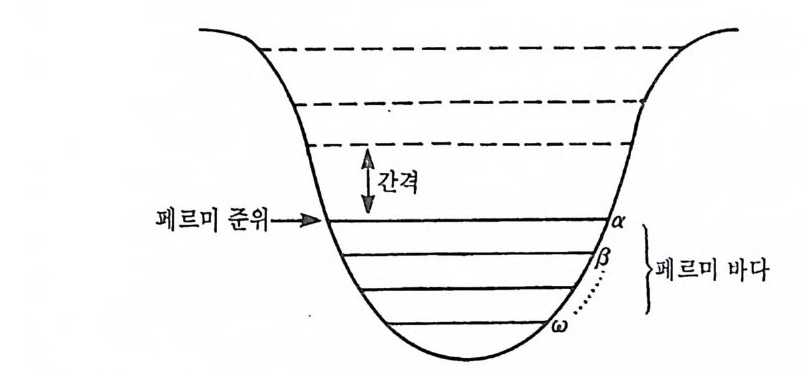
[Ha, a 디 =c. 야, [H o,a 』 = -e .a. (5. 4) 그리하여, Ho|o 。 >=€0I <1>。>, €0= ~ e. (5. 5) aEF 가된다. 식 (5.5) 안의 합 훑F 은 슬레이터 행렬식 (5. 3) 을 구성하는 N개의 상태 a,p , …f) 에 한정되어 있다. 이 N 개의 상태들의 집합을 우리는 페르미 바다라 부른다. 페르미 바다에 나타나는 채워진 궤도둘의 에너지 ea 는 빈 궤도들의 에너지보다 훨씬 낮은 경우가 매우 많다. 이 경우에 에너지 간격이 빈 궤도와 채워진 궤도를 갈라 놓는다. 우리는 가장 높 이 채워진 궤도의 에너지를 페르미 준위라 부른다.
 !간격
!간격
I
정의 연산자 U, V,… X, Y,Z 들이 다음과 감 은 방법으로 곱해졌을 때, 곱 UV·•·XYZ 를 정상배열이라 부른다. 즉 연산자들이 재배열되어 <@oI V=O 이 되 는 V 에 속하는 야 (.-:l~ F) 와 a, (.-:l~ F) 는 왼쪽으로, Ul tp。 > =0 이 되 는 U 에 속하는 a, (.-:l~ F) 와 야 (.-:lE F) 는 오른쪽으로 모인 형 태를 말한다 : 연산자들의 이러한 곱에는 재배열하는 등안 연산자가 짝 수 번, 또는 홍수 번 치환되었는가에 따라 + 또는 ―의 부호가 곱해진 다. 앞으로는 곱의 정 상배 열 을 간단히 정상곱이 라 부르기 로 한다. 예 a, f3는 페르미 바다에 나타나는 두 개의 궤도이고, ;i,µ는 페르 미 바다 밖에 있는 두 개의 궤도라 하자. 그러면, N[a!ata µ a,]= -a!apa µa; N 因 a 』 =a 詞 N[aµa! 〕 =-a 瓦 N[a;a;a.a,]= a!a;a.a6 N[a; 야 a,a 』 =a,aµ 야야 (ct, {3E F; A, µ~F) 와 같이 된다. U I (I)。 > =0 이 되는 모든 u- 연산자는 <(I)。 I V=O 이 되는 모든 연산자 와 마 찬가지로 자기들끼리 반교 환 되므로, 정상곱을 정의할 때 U- 연산 자의 순서와 V- 연산자의 순서는 생각할 필요 가 없다. 정 상곱은 주어진 상태 I
aj (8) =epH o aj e- 81/o al (/3) =ePH o ale-PHo (5. 8) 상태 |A> 가 ]1 물 대각선화시키는 경우에는 (식 5.1) aj (.B) = e p‘ 마 aA (/3) =e- p .Aa 』 (5. 8') 가된다. 식 (5. 8) 은 항등식 (4. 79) 에 A=f3 H o 와 B=a1 또는 a; 를 대 입 하고, 교환식 (5.4) 를 고려하여 얻을 수 있다. 양자역 학 에서는 시간 t 에 의 존 하는 연산자가 자주 등장하는데, 이 경우에 f3는 it 죽 허 수이다. 몽계 역학에서는 섭동되지 않은 분배함수 e-H o/ kT 가 많이 사용되는데, 이 경 우 T 는 온도를 나타내고 B 는 l/kT 로서 실수이다. 또한 온도가 O이 아닌 비평형계의 시간에 대한 변화를 연구 할 때에는 복소수 /3도 생각한 다. 마지막으로, 8 가 실수인 경우 연산자 硏@)는 a(/3)의 에르미트 공 액이 아니라는 사실을 지적하자. 반면 다음의 관계식이 성립 한 다• [a ({ 3) ]+ =a+( -/3) , 〔硏 (/3) ]+=a (-/3) (5. 9) 4 T- 곱(시간 배열곱) U, V… , X, Y,Z 가 인수에 의존하는 생성 연산자 a+({3 ) 또는 소멸 연 산자 a (/3) 등이 라 하자. 정의 우리는 연산자 U, V,•··,X, Y,Z 의 인수 들 이 작아지는 순서로 왼 쪽에서 오른쪽으로 배열되었을 때 이 연산자들의 곱 UV···YZ 를 T - 곱 (시 간배 열 곱 : Tim e-orderi ng Product) 이 라 부른다. 이 곱에 는 재 배 열 하는 동안 연산자가 짝수 번, 또는 홀수 번 치환되었는가에 따라 + 또 는 -의 부호가 곱해진다. 만약 둘 이상의 연산자들이 동일한 인수를 가지면 그것들이 나타나는 순서대로 적는다. 예 p8> B2>BI T[a+ (f31 ) a+ ({32 ) a (鈴 a+ (f3s ) ] = -a+ (/3s ) a+ (鈴 a (鈴 a+ ({31 ) , T[a+ (/31 ) a (鈴 a+ (/32 ) a+ (/3s ) ]= -a + (Pa ) a (鈴 a+ (鈴 a+ ({31 ) , T[a (/31 ) a+ (/31 ) ] =a (/31 ) 갑 (/31 )
5 생성연산자와 소멸연산자의 축약 정의 두 연산자 U 와 V 의 축약 (Con t rac ti on) 은 그것들의 T- 곰과 정 상곱의 차와 같다. 「_기 UV= T[UV] - N[UV] (5.10) 이 차는 0 이거나 반교환자이다. 따라서 이 차는 항상 어떤 수이지 연산 자가 아니다. 반교환되는 두 연산자의 축약은 0 이다. 또한 〈두 연산자 U 와 V의 축약은 I~ 。>에 대한 두 연산자의 T- 곱의 평균값과 동일하다〉. U,一V = <( 1)。 I T[ UVJ I (1)。 > (5. 11) 정상곱과 마찬가지로 축약은 주어진 상태 l (1)。>에 대해서만 정의된다• 일단 |(1)。>가 주어지면 우리는 식 (5. 8' )와 식 (5. 6) 을 이용하여 식 (5.10) 으로부터 축약을 계산할 수 있다. 따라서 다음과 같이 된다. aI j ({31 ) 야l (鈴 =a1A (/Ji) al µ (鈴 =0, al f ({Ji) a1µ ({32 ) = oiµe'i@랴), ;i, µEF 이 고 8l 느 82 인 경 우 =-8 냐 4 p l- p 9, A,µ 순 F 이고 Bl
Pi= l, ti=O , .ii순 F 일 때 Pi= O, tA =l, .ilE F 일 메 (5. 14) 정상곱 내부의 축 약 : 정상곱 내부에 축약이 있을 때에는 축약을 밖으로 꺼내고 두 연산자 믈 인접시키는 치환의 횟수가 짝수인지 홀 수인지에 따라 + 또는 -의 부호를 붙인다. I I 广기 예 N[UVX 四 =UYN[VX] N[UI VXl Y]= -U 「X N[VY] 6 W i ck 의 정리 宜 UVW … Y幻 =N[UVW … YZ] +N[ ur一 v w.. . y幻 +N[UI vwI . .. Y Z] + ... +N[U「VW ·r·· Y幻 + ... (5. 15) T- 곱은 정상곱에 축약이 한 개 있는 정상곱을 모두 더하고, 축 약이 두 개 있는 정상곱을 모두 더하고, 이런 방법으로 계속해서 완전히 축 약된 항까지 더한 것과 같다. 증명 비크 (\V i ck) 의 정리를 수학적 귀납법으로 증명하겠다. 두 개의 연산자를 곱한 경우는 정의 (5.10) 에 의하여 자명하다. 이 정리가 연산자를 n 개 곱한 경우에 맞는다고 가정하자. 연산자 A 의 첨자 /3가 가장 작은 값일 때 n+l 개의 연산자의 T- 곱 UV···A···YZ 를 생각하자. 그러면, T[UV···YZAJ = T[UV… Y Z]A (5.16) 가 된다. 만약 A 가 소멸 연산자 a i (A~F) 이거나생성 연산자야(,1든 F) 라면, 그것과 다른 모든 연산자와의 축약은 0 이 다. U「A ==UTA[U— AU]A- N=O[U A] 식 (5.15) 의 양변의 우측에 A 를 곱하자. 식 (5 . 16) 을 이용하여 A 를 T- 곱의 내부에, 그리고 모든 정상곱의 내부에 집어넣을 수 있다. A 와
다른 모든 연산자와의 축약은 0 이므로 이것을 식 (5.15) 의 우번에 더 하면 n+1 개의 연산자의 곱에 대해서도 정리가 성립함을 알 수 있다. 이번에는 A 가 생성 연산자 야(ilE:\: F) 또는 소멸 연산자 a i(及든 F) 라 고 가정하자. 연산자 UV … YZ 의 정상곱은 다음과 같이 쓸 수 있다. N[ UV… Y 幻 =S1 U' V/… Y 'Z' (5. 17) 여기에서 U 사”… YIz’ 는 연산자 UV••·YZ 를 정상형태로 다시 쓴 것이 고, 이 과정에서 행해진 치환의 횟수가 짝수인지 홀수인지에 따라 요은 土 1 의 값을- 가진다. 윗식의 양변 우 측 에 A 를 곱하자. N[ UV… Y Z] A=S1 U1 V/… Y 'Z'A (5. 18) 계속해서 A 를 다 른 모든 연산자와 교환하자. U'V'•·· Y'Z'A=-U'V/… Y'AZ'+ U'V'•·· Y'[Z', A] + =U'V'···AY'Z 냐 U'V/… [Y ',A J +Z '+ U'V'···Y'[Z', AJ + = (-) AU'V'··· Y'Z'+ U'V'… Y 'Z~ + U' V' …Y I 'Z'AI + …+ UI ' V'… Y 'Z'AI (5. 19) 윗식에서 1l 은 연산자 U, V, … Y,Z 의 갯수이다. 식 (5.19) 의 끝부분에 서 우리는 A 와 다 몬 연산자와의 반교환자가 축약과 같다는 사실을 이 용했다. U「--A, =T[ 厚〕 _ N[UA 匡 UA+AU=[ U, AJ + 식 (5.19) 의 결과물 식 (5.18) 에 대입하면 다음과 같이 된다. N[UV·•· YZJ A = (-) S1AU1V/… Y 'Z'+S,U'V/ … Z껴 + •• • + S1 UI ' V/… Y 'Z'AI (5. 20) 식 (5. 20) 의 우변 중 첫째항은 N[UV••·YZA 〕와 같다. 다른 항들의 합은 다음과 같다. N[UV… Y Z「서 +N[UV·· •I Y Z 서I + …+ N[UI V… Y ZAI ] 따라서 다음의 결과를 얻는다.
N[UV••· YZ]A=N[UV··· YZA J +N[UV··· YZ「A J +· ·· + N[UI V… YZAI ] 마찬가지로 N[Ur 一 V. • • YZ]A 와 같은 항도 계산 할 수 있고, 결국 비크 의 정 리 는 n + l 개 의 연 산자의 곱 UV• •• YZA 에 대 하여 성 립 한다. 그러므로, 이 정리가 n 개의 연산자의 곱에 대하여 성립하면 n+1 개 의 곱에 대해서도 성립하고, 앞서 두 개의 곱에 대해서도 성립하였으므 로, 비크의 정리는 모든 경우에 성립한다는 것이 증명되었다(증명끝). 7 l q; o> 에 대한 평균값의 계산 연산자의 정상곱의 1 (J)。>에 대한 평균값은 모두 0 이므로 연산자의 T- 곱의 평균값은 모든 축약의 합계와 동일하다. 예 문 둡면 다음과 같다. <(J)。 | T[UVXYJ l
U「국V =UV-N[UVJ (인수가 없는 연산자) (5. 23) 따라서 비크의 정리 (5.15) 는 다음과 같이 쓸 수 있다. UV … XYZ=N+[NUV[ •u「 -•v- 1· ..X. xY,幻 ,y 幻 ++N […U 「V … XYZ]+ … (5. 24) (인수가 없는 연산자) 인수가 없는 연산자들의 곱의 |o 。>예 대한 평균값은 축약의 모든 형태 룹 합함으로써 얻을 수 있다. 인수가 없는 두 연산자의 |o 。>에 축약은 l q)。>에 대한 두 연산자의 기대치와 갇다. 이 결과 를 이용하여, 식 (4.34) 에서와 같이 생성 연산자를 사용하여 만든 반대칭 상태들의 스칼라곱이 행렬식 (4.21) 과 똑같다는 사실울 증 명해 보자. < a'P='…
제 6 장 하트리-포크 이론 하트리 -포크 (Ha rtr e e-Fock) 이 론은 어 떤 계 의 동력 학을 독립 입 자 들 의 운동으로 접근시키는 방법이다. 핵물리학에서 이 이 론 이 적용되는 경우 는 구형 또는 변형된 핵의 평형 형태의 계산, 전하와 물질 분포, 의부 장내에 있는 핵의 편광과 변형, 핵분열의 장벽, 핵 자의 분리에너지 등 매우 많다. 시간에 의존하는 하트리-포크 이론으로는 진동과 집합적인 운동의 계산을 할 수 있고, 또한 이 이론은 무거운 이온 사이의 반응에 적용되기 시작했다. * 원자 물리에서는 중심을 향하고 정적인 쿨롱장이 전자 둘 에 영향을 미 치는 주된 요소이다. 핵물리에서는 독립입자들의 운동이라는 근사가 선 험적으로 인정되는 것은 아니다. 이 근사의 타당성이 보장되는 것은, 상호작용하고 있는 핵자가 자기 궤도에서 다른 핵자가 점유하고 있는 인접 궤도로 전이하지 못한다고 하는 파울리 원리에 의해서이다. ** 하트리-포크 이론은 핵의 집합적인 거시적 성질(크기, 평균 포텐션, 표면의 진동)과 개개의 핵자의 운동에 기인하는 미시적 성질을 동시에, 그리고 자체 부합성 (se lf -cons i s t en t)있게 설명하는 하나의 가능한 동일 모형이다. 하트리-포크 해밀토니안의 대칭성은 우리가 이 장에서 다루고 뒷장에 서도 여러 번 다시 다룰 중요한 문제이다. 하트리-포크 해밀트니안에 의하여 강하게 깨진 대칭성 (예 : 변형된 핵에 있어 공간의 회전에 대한 * P. Bonche et al Phy. Rev. C 13, 1226 (1976) . .. L.C. Gomes et al. Ann. Phy s. (N.Y) 3, 241(1958).
불변성 의 깨침)은 실험적으로 관측되는 집합적인 운동(변형된 핵의 회 전띠)을 만들어 낸다. 한편 하트리-포크 해밀토니안에 의하여 약하게 깨어진 대칭성 (예 : 쿨롱력 이 없을 경우 중성자가 과다한 핵에서 하전스 핀 공간에서의 회전에 대한 불변성)은 어려움을 야기시키며, 특별한 주 의를 요한다. 텐서항과 근접 척력은 핵자-핵자 상호작용을 하트리-포크 계산에 직접 이용할 수 없게도 한다. 이 때문에 우리는 유효 상호작용 올 이용해야 한다. 현재 가장 많이 사용되고 있는 유효 상호작용은 상호작용하는 위치 부근의 핵자 밀도에도 의존한다. 우리는 하트리-포크 이론을 힘이 밀도 행렬에 의존하는 보다 일반적인 경우에서 체계화했다 . 밀도 의존성의 효과를 보여주는 예는 제 6 장 10 절에 제시하겠다. 이 장에서 우리는 정적인 하트리-포크 장이론만을 다루기로 한다. l 밀도행렬 하트리-포크이론은 밀도행렬을 도입하면 용이하게 기술할 수 있다. i,j,…가 완전하고 직교규격화된 단일 입자의 기저라 하고, I ,Jr>는 임 의의 상태라 하자. 상태 I ,Jr>의 단일물체 밀도행렬은 다음 식에 의하 여 정의된다.
1 ,tr >=a; 어 ··a!IO)=_II a!IO) (6. 4) ..lE F 기저 를 a, {3,…로 잡으면 밀도행렬은 다움과 같다. p.,= <, fr I apa . I ,fr >= o.p ; a, {JE F =O ; (6. 5) 따라서 p 2= p를 만족한다. 이 행렬 관계식은 다른 모든 칙교규격화된 기저에 대해서도 마찬가지로 성립한다. 그 이유는 직교규격화된 기저들 은 유니터리 변환에 의하여 서로 연결되기 때문이다. 충분조건 : 밀도행렬은 에르미트형이므로 대각선화될 수 있다. 硏ij C j =n.Cr (pI a>=n.Ia>) (6. 6) p2=p 라면 짜 =na 이 고, 따라서 na=O 또는 1 이 다. Trp = I; na=N 이 므. a 로 N 개의 고유치는 1 이고 나머지 고유치는 모두 0 이다. 궤도 bt= .E era t를 사용하여 술레이터 행 렬 식 l0> 를 만들자. I~>= II bt lO ) aEF 페르미 바다 F 는 고유치 n.=1 에 해당하는 N 개의 상태 a 로 구성되어 있냐 따라서 우리는 상태 I ,fr> 를 |({)>의 입자-구멍 둘 뜸상태들로 전 개할 수 있다(식 4.97 을 보라). I v > = <(j ) | 中 > [1 + ~ph x,-ha;• ah +! s~!: h P',hh'a ;a ;ah,a h + •. . J I ({) > 윗식에서 P 와 h 는 각각 페르미 바다 밖과 안의 궤도를 나타낸다(증명 끝). 밀도행렬 p는 단일입자 상태 공간에 작용하는 연산자 p로 생각할 수 있다. p,;=
마지막으로, 상태 I ,fr>가 술례이터 행렬식일 때 밀도행렬은 아래의 연산자로 나타낼 수 있다는 사실에 유의하자. p= _I:_ I A> < A I (슬레이터 행렬식에 대하여) (6. 9) AEF 위의 합은 술례이터 행렬식 |中>를 구성하는 페르미 바다 안의 상태에만 국한된다. 따라서 연산자 p는 페르미 바다내로 두영하는 연산자이다. 2 하트리-포크 방정식 하트리-포크 근사법은 계의 상태를 슬래이터 행렬식으로 근사시키는 것이다. I qy >= IT a; I o> (6.10) AE l·· 술 레이터 행렬식 (6.10 ) 을 결정하기 위하여 우리는 리츠 (R it z) 의 변분 원리를 상기하자. 이 원리에 따르면 I ,fr>가 계의 해밀토니안 H 의 고 유상태일 때 에너지 <中 IHI 中>는 I ,fr>의 미소 번분에 대하여 멈춤상 태 (s t a ti onar y)이다. 2 체 상호작용이 있을 때에는 H 의 고유상태가 술 례이터 행 렬 식으로 기술될 수 없다. 그러므로 우리는 술레아터 행렬식 의 에너지를 국소화함으로써 바닥상태에 접근하려고 한다. 해밀토니안 은 다음과 같다(식 4. 53 참조). H= Li,j
식 (6. 13) 과 식 (6. 14) 물 이 용하면 식 (6. 12) 는 다음과 같이 쓸 수 있 다• E[p] = Tr (tp) + 붑 Tr (J( (p) p+@ p) (6. 15) 핵력은 텐서항과 근집 척력을 포함하고 있다. 이 항은 두 물체 사이 에 상관관계를 주는데, 술례 이터 행렬식으로 파동함수를 근사시키는 경 우에 그 상관관계는 정확하게 기술 될 수 없다. 그러므 로 , 우 리는 유효 럭을 정의하겠는데, 이것은 핵 자들의 패르 미 바다 밖으로의 가상적인 둘뜹 (ex cit a ti on) 을 고려하는 것으로서, |,fr>와 H 가 각각 계의 정확한 파동함수와 해밀토니 안이 라면, <0|Hc ff |0> :::::::<,tr lHl ,tr>가 되도독 하 는 것이다. 하트리-포크 계산에서 이용되는 유효력은 핵 자 들 이 상호작 용하는 영역의 핵자밀도에 의존하는 경우가 많다. 예 몰 들 면, 다음은 밀도에 의존하는 상호작용이다. -v ... v(p) = v1Cr1-r2) +v2Cr1-r2)n( 입~) (6.16) 여기에서 n(; )은 위치 ; 에서의 핵자밀도로서 다음과 같이 주어진다. n(;)= 설 <;(Jr- l p lr (J T> =실 정 <;(Jr-li > p,1 에 적용할 수 없다. 이 경우에는 차라리 식 (6.12) 에서 정의된 E[ p]를 밀도행렬 p의 범함수로생각하는것이 편하다. 우리는이 범함수가p2=p 인 조건 하에서 p의 변분이 변분 원리를 따른다고 가정하겠다. p를 결정하기로 하자. 변분식은 다음과 같다. -8{p8J iE &] +Ik:i A u(p2 -p)1 1}=0 (6.18) 조건 p 2= p를 고려하여 라그랑지 매개변수 Au 을 윗식에 도입하였다. 하트리-포크 해밀토니안을 다음과 같이 정의하자.
것들은 유효력이 밀도에 의존하기 때문에 생긴다. 실제로 밀도행렬의 변분을 취할 때 그것은 에너지 변분에 기여하는 유효력 v( p)에 해당한다. 3 해밀토니안의 대칭성과 관계된 범함수 E[ p〕의 불변성 유니터리 (또는 반유니터리) 연산자 U 에 의하여 나타내어지는 변환을 생각하자. uu+=U+U=I 이 변환에서 슬레 이터 행 렬식 I~> 는 다음과 갇이 된다. |i>=U I~> 식 (4.81) 에 의해서 생성 연산자와 소멸 연산자는 다음과 같이 변환 된다. Uat U -1=~
따]=~ij p ji+2+ i~jhI- (i jlv( p) lkl)p. ; p ij (6. 25) 운동 에너지항은 다음과 감 이 적을 수 있다. Ii;j
u-lV(p) U 국fd ;1d;2u-11 ;1;2> [v1 (r 1 -;2) +v2 (;1-;2) <익巴 |Up U-11 업” 기 <;1r2Iu 국fd r1dr 晶 +a, ;:2 + a>[ V1( ;l-;2)+ v2(;1_ 入) < -업 거r2 +alp| 1·1;r2 五 >]<;1 표, r2+a1 국fd r1d?21 r1r2> [V1 (r1 국) +v 晶 국) < 업 ’Ll p l 업 ~>]<1: 러 =v (p) (6. 31') 가 된다. 식 (6.31’) 의 세째줄에서는 적분 변수 를 치환하였다 : ;1 ➔ ;1 +a니, 기Y2 ➔ r., 2+a여. 조건 (6.28), 죽 에너지가 병진운동에 대하여 불 변이라는 조건은 상 호작용 v( p)가 병진운동에 대하여 불변이라는 조건 u-1v(p) U=v( p)와 같지 않다는 사실에 주의하기 바란다. 핵의 해밀토니안에는 다음과 같은 대칭성들이 있다. i) 반전성 ; 핵 자 사이 의 강한 상호작용보다 10-6 배 나 작은 약한 상호 작용의 효과를 무시하는 경우 ii) 시간 역전 iii) 회 전 iv) 공간에서의 병진 운동 v) 시 간에서의 병진 운동 vi) 하전스핀 공간의 z 축에 대한 회전(전하 보존) vii) 하전스핀 공간에서의 회전(쿨롱력과, 양성자와 중성자의 질량차, 그리고 핵력의 전하 비의존성의 파괴 등을 무시하는 경우) vii i) 핵자 수의 보존 . ix) 연산자 U=e-Im:.;;h , R= 〉盆;i로 표시되는 갈릴레이 변환은 (6.3 2) 운동량 연산자를 다u음-IP과-I U같=이P- I- 변11환1시; 킨 다. (6. 33)
이 변환은 계의 대칭성은 아니지만, 상호작용은 변화시키지 않고 운동 에너지만을 변화시키는 매우 간단한 것이다. u-1TU= ‘:=^z : l —2m1 (p一 ‘- mv➔ )2=T-V➔ ·P-;t +. —A 2 - mv2 (6. 34) 따라서 갈릴레이 변환 T=Up U -1 에 대하여 범함수 E 〔p〕는 다옴 조건울 만족해야 한다.E 印 =E[ pJ -v-, ·~if p計소2 ,nv2 (6. 35) 4 하트리-포크 해밀토니안의 대칭성과 대칭성 파손 식 (6.24) 의 의미로서의 해밀토니안의 대칭성에 해당하는 변환 (6.22) 룹 |(J)>에 작용하자. 하트리-포크 해밀토니안이 다음 변환을 따른다는 것을 보이자. u-11z[ P] U =h 印 (해밀토니안의 대칭성) (6. 36) 식 (6.21') 로부터 이 관계를 증명할 수 있다. 祠=t+훑 @I V(p) I(J) > I: 〔?〕=t+훑 @I V(p) I(J) > lp=p (6. 37) 모든 참수 f(p) 에 대 하여 :白 p=p=~?) 가 성 립 한다. 다음과 같이 놓자. f(p) = <~I V(p) I~>= 十 곱
가된다. 변 환 이 해밀토니안의 대 칭성에 해 당하면 식 (6.28) 을 적용하여 다음 과 같은 결과를 얻는다. h[p ]=t+- dia;p - <@ I V(p) I@> (6. 40) 또한 u-1t U =t 이 므로 u-11z[pJ U =t+ u- 1 훑 -U<¢1 V(p) 1¢) (6. 41) 가된다. 관계식 [겅》, p ]=1 의 왼 쪽 에 U 를 곱하고 오 른쪽 에 u-1 를 곱하면 훑 =U훑 u-1 입을 보일 수 있다. 그렇게 해서 식 (6.42) 은 다음과 같이 된다. u-1h[ pJ U= t+훑 <¢I V(p) 1¢>=1印 (6. 42) 따라서 식 (6.36) 이 증명된 것이다. 식 (6.36) 이 보여주는 것은 연산자 U 로 표시되는 변 환 이 하트리- 포 크 해밀토니안의 대칭성이라는 것은 아니다. 그렇게 되려면 U 가 하 트 리-포크 해밀토니안과 교환가능해야 한다. 다시 말해 다음 식이 만 족 되 어야 한다. u-1h[ 짜 U=h 印 (하트리-포크 해밀토니안의 대칭성) (6.43) 식 (6.36) 과 (6.43) 에 의하면, 해밀토니안의 대칭성이 또한 하트리 포크 해밀토니안의 대칭성이기 위해서는 h 印 =h 印 (6. 44) 이어야 한다. 일반적으로 조건 (6.44) 는 p=p일 때에만 만족된다. 죽 p= Up U - 1 =p (6. 45) 일 때에만 만족된다. 식 (6.9) 는 p가 페르미 바다 위로의 두영 연산자라는 것을 보여준다.
그 러 므로, 조건 (6.45) 는 다음과 같이 표현될 수 있다 : 연산자 U 가 페 르 미 바다를 변화시 키 지 않는다면, 다시 말해 U 가 페 르미 바다의 각각 의 궤도를 페르미 바다 안에 있는 궤도들의 선형결합으로 변환시킨다면 p는 U 와 교환된다. UIA)= ~ <µI Ul;i> µEF 따라서 다음 정리가 성립한다. 정리 U 가 식 (6.24) 에서와 같은 의미로서 해밀토니안의 대칭성을 나 타내는 유니터리 (또는 반유니터리) 연산자라고 하자. U 가 페르미 바다 문 번화시키지 않는다면, U 는 하트리-포크 해밀토니안과 교환가능하 다. 즉 U 는 하트리-포크 해밀토니안의 대칭성을 나타낸다. 이 절과 앞질에서 얻어진 결과, 특히 식 (6.24), (6.36) 과 하트리-포 크 해밀토니안에 관한 정리는 하트리-포크 방정식 (6.20) 과는 무관하다. 따라서 하트리-포크 방정식의 해이거나, 또는 아니거나 모든 술례이터 행렬식 1(J )>, 또는 모든 밀도행렬 p에 대하여 위의 결과가 적용된다. 우리는 제 6 장 5 철에서 하트리-포크 방정식은 먼저 |(J)> 또는 p에 대 하여 첫번째 근사를 예측한 후에 반복 방법을 사용하여 풀 수 있다는 것을 알게 될 것이다. 따라서 페르미 바다가 변환 U 에 대하여 불변인 지 아닌지를 결정하고, 하트리-포크 해밀토니안의 대칭성을 결정하는 것은 바로 I(J)> 또는 p의 첫번째 선택이다. 이 대칭성은 이후의 모든 반복 과정에서 계속 보존된다. 제 6 장 3 절의 끝에서 언급된 해밀토니안의 대칭성을생각해 보자. 어 떤 조건하에서 그것이 또한 하트리-포크 해밀토니안의 대칭성이 될 수 있는지 살펴보자. 연산자 U 가 나타내는 변환이 하트리-포크 해밀토니안의 대칭성이기 위해서는 연산자 U 가 변화시키지 않는 패르미 바다를 만들면 된다. 그 러기 위하여 페르미 바다 안의 궤도 A 를 상태 lnlj m 'l>를 기저로 하여 전개하자. l.-1 >= ~ C:lj., ,. lnljm - r> (6. 46) n1j ' r a) 반전성 식 (6.46) 의 전개항들을 l 이 짝수인(또는 홀수인) 것들로 제한하면 각각의 궤도는 주어진 반전성 (p ar ty)을 가지며, 반전성 연산
자는 각각의 궤도를 자기 자신으로 변환시키므로 페르미 바다룰 변화시 키지 않는다. b) 시간 역전 시간 역전 연산자 K 는 궤도 (6.46) 을 다음과 같이 번 환시킨다. Klil >= ~ C1,J. . r(-)1+1-lnlj- mr) (6. 47) •ljm r 단, K2=-l, Kl ;!) =\= I; !> 이 다. 따라서 하트리-포크 해 밀 토니안이 시간 역전연산자와 교 환 되기 위해 서는 핵자의 수가 짝수라야 한다. 대부분의 계산에 있 어 하 트리-포 크 해밀토니안은 하전스핀의 세 번째 성분 T., 와 교환된다. 이 경우에 시 간 역전에 대한 /t의 대칭성은 짝수-짝수인 핵에 있어서만 성립한다. 식 (6.46) 의 전개를 (-)'+;-.. = +1 또는 -1 인 상태로 재한하고, 계수 c~lj m':' 를 실 수만으로 덱 하면 1; i± :> 는 확실 히 직 교한다. * 참고 : 위 에 서 정 의 된 시 간 역 전 연 산자와 식 (1. 45) 및 (3. 129) 에 서 사용된 시간 역전 연산자의 정의는 독립입자의 궤도 파 동 함 수를 선 택하는 두 가지 서로 다른 선택 방법이 있기 때문에 달 리 표현 되었다. 산란문제나 짝짓기문제 등에서는 시간 역전 불변성을 다 루 기 위해 일 반적으로 제 1 장 및 제 3 장에서의 방법을 이용하는데, 이는 핵 자의 파 동함수를 i) ifri•= L.. , (l~2 m ,m-mt ljm) R(r)i' Y ,,m, Xm -m, 로 표시하는 방법이고, 핵의 핵각 모델을 다루는 사람 들 에 의해서 흔히 사용되는 것은 제 6 장에서와 같이 ii) ,frj.= Im: U+2m ,m-mdj m )R(r) Yi ... , X .. -.. , 로 표시하는 방법이다. 한편 시간 역전은 스핀의 방향을 y-축에 대해서 -X 또는 +x 만큼 둘리고, 전체 파동함수에 대해 복소 공액을 취함으로써 이루어지기 때 문에, 干 X 에 따라 (-)/土 m 의 위상 변화가 있을 수 있다. -X 로 돌리는 경우는 KY1.= Y~= (-) Yi, -.= (-) 1e':c i,y1..
이고, KX=e’,7S y x m= (-) }+mx_ .. 이어서, K中 j .. = (-)J +n 中j- .. 국j.. ((i)의 경우) 임을 알 수 있다. 식 (6.47) 에서는 (ii)의 경우를 +元만큼 돌린 경우를 시간 역전으로 취하고 있다. c) 회전 하트리-포크 해밀토니안이 각운동량의 성분 ]z 와 교환되 면, 그 해밀토니안은 축대칭성이 있다고 한다. [h, ]』 =O (축대 칭성) (6. 48) 식 (6.46) 의 전개를 주어진 111A 에 대한 상태에 국한시키기만 한다면 이 대칭성은 항상 실현시킬 수 있다. I. :l, ml >= I: c~lj, I nljm l-r > (6. 49) olj r 사실상 이 궤도들은 고유치 11h 에 해당하는 L 의 고유상태들이고, 따라 서 ]z 는 패르마 바다름 변화시키지 않는다. 하트리-포크 해밀토니안의 축대칭성이 항상 실현될 수 있다는 사실이 그 해가 핵의 평형상태를 나타낸다는 것을 의미하는 것은 아니다. 실제 로 이 해의 에너지는 안정하기는 해도 반드시 최소일 필요는 없다. 최 소가 되기 위한 조건은 제 6 장 8 절에서 밝혀질 것이다. 마지막으로, 만약 그 해가 최소라고 해도 다른 대칭성을 나타내며 에너지가 더욱 낮 은 최소에 해당하는 또 다른 해의 가능성을 배제할 수 없다는 사실을 지적하자. 이러한 점들은 우리가 고려하는 모든 대칭성에 적용된다. 하트리-포크 해밀토니안이 각운동량 ]의 세 성분과 교환될 때, 그 해 밀토니안은 구대칭성을 가지고 있다고 한다. [h,]]= O (구대칭성) (6. 50) 이 대칭성을 주기 위하여 궤도의 전개를 다음과 같이 제한하기로 하 자. l il, j., m. >= I: C 십 r I nlj,m ,-r ) (6. 51) nlr
연산자 ]±=J죠七i]y 를 이 궤도에 작용시키면, I 나 ..:l, ii, m i >= (j곤 mA) 1/2 (j』 士 m i + 1) 112 I ..:l, jJ, m i 士 1 ) (6. 52) 이 된다. 그러므로, 연산자 ]土가 패르미 바다를 변화시키지 않으려면, 각각의 j』에 대하여 다른 111A 값을 가지는 2 ji +l 개의 궤도가 모두 페르미 바다 안에 있거나 모두 밖에 있어야 한다. 그러기 위해서는 핵이 닫힌 껍질 을 형성하는 데 필요한 수의 핵자들을 가져야만 된다. 제 4 장 8 절 에서 우리는 이 경우의 상태 I({) 。>의 운동량이 0 이라는 사실을 안았다. d) 병진 운등 유한하고 묶여 있는 핵에서 페르미 바다는 연산자 (6. 29) 에 의한 병진 운동에 대하여 결코 불변이 아니다. 이것을 증명하기 위하여는, p가 병진 운동에 대하여 불변이려면 물질의 밀도가 전 공간 에 균일하게 분포되어야 한다는 사실을 이해하는 것으로 충분하다. c) 시간병진운등 시간병진운동은 다음 연산자에 의해서 실행된다. u=e-iH I/h (6. 53) 명백히 U 는 해밀토니안과 교환되고, 따라서 다음과 같이 정의된 밀도 행렬 p (t) =e'1 t•p e 一i H t / h (6. 54) 에 대한 범함수 E[ p(t)〕는 t 에 의존하지 않아야 한다 : 움파(t )]=O (6. 55) 식 (6. 55) 는 다음과 같이 된다. 표ij aPj르 i 쁘dt =0 또는 식 (6. 19) 를 고려 하면, 2ij Itij Pj i =O (6. 56) 이 된다. 이 식은 시간에 의존하는 하트리-포크 이론 (TDHF) 에서도 성립하며, 이때 에너지는 보존된다.
f) 하전스핀의 z- 축에 대한 회전 각각의 궤 도가 끄 의 고유상태 로시 페 르미 바다 를 변화시키지 않으려면 전개식 (6.46) 을 다음과 같이 제한하 기만 하면 된다. IA , T 』 >= nIlj;m C 麟 | nljm rA ) (6. 57) 중성자와 양성자의 궤도는 항상 섞이지 않고 있다. g) 하전스핀 공간에서의 회 전 우선 쿨롱력 이 없 다고 하자. 이 경 우에 하전스핀 공간에서의 회전은 해밀토니안의 대칭성이다. 그럼에도 불구 하고 하트리-포크 해밀토니안은 N=Z 인 경우, 즉 중성자 수와 양성자 수가 갇은 경우를 제의하고는, 하전스핀의 세 성분과 교환되지 않는다. [h, T]=f' O . 중성자가 남아 돌 기 시작하면 연산자 T-=Yr- i T:, 는 남아도 는 중성자 룹 양성자로 변환시켜 빈 궤도에 채워넣는다(제 7 절을 보라). 그러 므로, 하트리 -포크 해 밀 토니 안은 중성 자가 남아돌기 시 작하면 하전 스핀 공간에서의 회전에 대한 불변성을 항상 깨뜨린다. 이것은 쿨롱력 이 없을 때에도 마찬가지아다. 이 대칭성의 파손에 의한 결과들은 아직 자세히 분석되지 않았다• 갇 릴레이 변환에 대해서는 제 11 절을 보라. 5 하트리-포크 궤도 식 (6.19) 와 식 (6.20) 과 감은 하트리-포크 방정식을 푸는 방법은 보 봉 하트리一포크 해밀토니안을 대각선화하는 것이다. ~ h,je j=e .Cf (h I .:l > =e. I .:l > ) (6. 58) j 이렇게 얻어진 고유상태 |..:i )=~C?l i>는 하트리-포크 궤도라 불리우 고, 고유치 eA 는 하트리-포크 궤도의 에너지이다 . h 가 에르미트형이므로 하트리-포크 궤도들은 단일입자상태의 직교규 격화된 완전한 기저를 이룬다. N 개의 하트리-포크 궤도들을 사용하여 다움의 슬레이터 행렬식과 갇은 페르미 바다룰 만들면; I~>= II (a ;;가 0 >, (6. 59) ,lE F 하트리-포크 궤도를 기저로 사용했을 때 다음과 갇이 됨을 알 수 있다.
h 』 µ=e A 8Aµ, pAµ = <0|a ; a 』(f)> =%, AE F =0, 그밖의 경 우 (6. 60) 이 기저에서 h 와 p는 대각선화되어 있고, 따라 서 그 둘 은 교 찬 가 능하 며, 그 결과 하트리-포크 방정식 (6.20) 이 만 족 된다. 결국 우리는 에너 지 E[ 짜를 안정시키는 상태 |o 。>와 밀도행 렬 p 룹 찾 은 것 이다. 그러 나, 실제로는 h 가 식 (6.21) 에서와 같 이 p에 의 존 하므로, 미리 밀 도 행 렬 p 를 알고 있지 않으면 고유치 문 재 (6.58) 을 풍 수 없다. 따라서 다음과 같은 반복 방법으로 이 를 해결해야 한다. i) 단진자 또는 우드-색슨 포텐 셜 의 궤도 둥 을 대 하여 궤도 IA > 의 첫 번째 근사를 추 축 한다• 그것은 결국 계수 C t의 첫 번 째 집합 을 추 축 하는 것이다. ii) 페르미 바다를 만들기 위하여 N 개의 궤도(일반적으로 가장 낮 은 궤도)를 선덱하고, 다음과 같이 밀도행렬을 계산한다. p 1 ; = 훑p
이자. 幽>가 N 개의 입자로 구성된 핵 (일반적으로 짝수그짝수 핵)의 하트 리_포크 해라 하자. 페르미 바다 밖의 궤도 a 에 한 개의 핵을 첨가한 상태 a t l
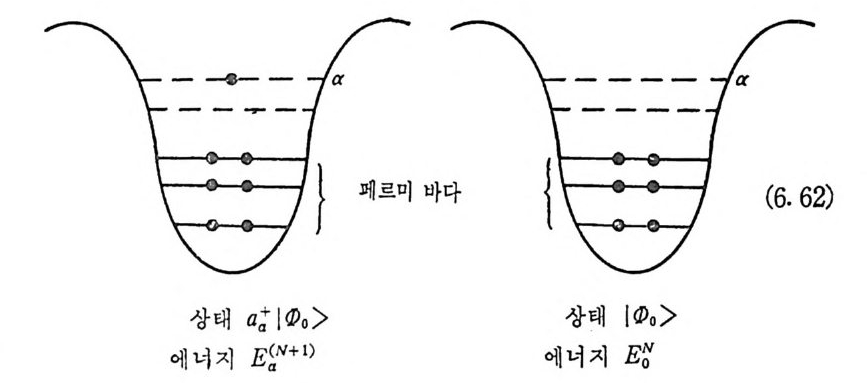 페르미 바다
페르미 바다
이 상태의 에너지 E;!+l) 을 계산하자. E ';!+ll = <( j)。 | a.H 따 I( [)。 > (6. 63) 상태 야 1o 。>는 숟례 이터 행렬식이다. 따라서 그것은 p (N) 이 상태 I Q。> 의 밀 도행 렬 일 때 밀 도행 렬 p(N +ll =p'·V > + p(로 나타낼 수 있 다. p
궤도 불 기저로 하는 하트리-포크 해밀토니안의 행렬요소로서 대각선화 되어 있다. 따라서 (6 . 60) 에 의 하 여 다음과 같은 식이 얻어진다. 훑 I p= p(N ) =eA% (6. 67) 한편 p>? != 82µ6 A a 이므로 식 (6. 7) 은 다음과 감이 된다. e.=E~'-+I) - Et > (a~ F ) (6. 68) 이 식에 의하면 궤도 a 의 에너지는 한 입자가 우물 가장자리 로부터 궤 도 a 에 붙 잡 혔을 때 얻는 에너지와 같다. 따라서 이 에너지 는 이 궤도 에 있는 입 자의 분리 에 너 지 (sepa r ati on energy ) 와 크기 는 갑고 부호가 반대이다. 페르미 바다 안의 궤도 8 에 있는 입자 한 개 를 제거한 상태 a , | Q。> 를 생각하자.
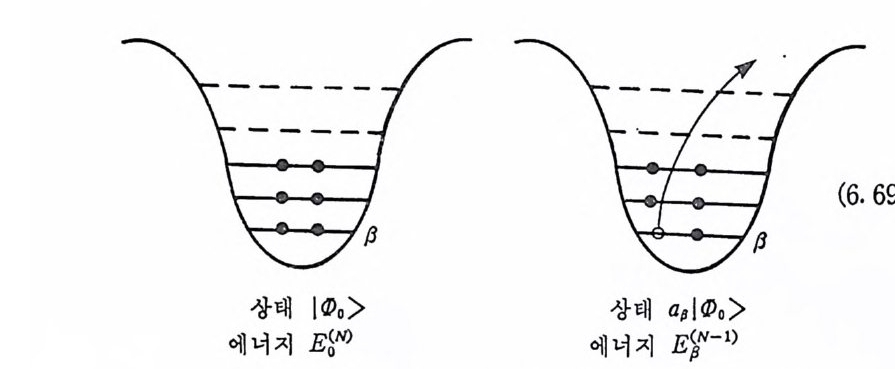 에너상지태 Elq~;,N0 > > 에너상태지 aE,>|N0 -01 >)
에너상지태 Elq~;,N0 > > 에너상태지 aE,>|N0 -01 >)
상태 a,|o 。>의 에너지 El f- 를 계산하자. 이 상태는 밀도행 렬로 표현 할수 있다. p(N - 1)= 2 1A>
윗식에서 e , 는 궤도 f3의 하트리-포크 에너지이다. 따라서 다음과 같이 쓸 수 있다. e,= EiN ) - EkN- (8 드 F) (6. 72) 이 식에 의하면 궤도 8 의 하트리-포크 에너지는 궤도 8 에 있는 핵자의 분리 에너지에 음(-)의 부호를 붙인 값이다. 하트리-포크 궤도의 에너지는 핵자의 분리 에 너지와 갇으므로, 다음 결에 제시 될 바와 같 이, 실험적으로 결정될 수 있다. 이 결과에 이르기 까지 취한 근사 를 다시 생각해 보자. i) p ( a) 와 p( p )가 p ( N ) 에 비하여 작다고 가정했으므로 범함수를 1 차까지 전개 할 수 있었다. 밀 도에 의존하지 않는 힘에 대해서는 전개식이 1 차 에서 멈 춘 다는 사 실을 쉽게 증명할 수 있다. ii) 핵 자 를 첨 가하거나 제 거할 때 밀도행렬과 그에 의존하는 하트리 포크 장 은 변화 된다• 그러 면 모든 핵 자의 에너지와 파동함수가 변하게 된다. 추 가 핵 자 ( 또는 구멍 ) 에 의한 핵 의 편국이라고 불리우는 이 효과 는, 우리가 N- 입자 핵 의 궤도를 사용하여 (N 土 1) -입자 핵의 파동함수 룹 만 들 었기 때문에 무시되었다. 7 궤도 에너지의 실험적인 결정 닫 힌 껍 질 핵에 대하여 핵자 이동 반웅을 조사하여, 중성자와 양성자 의 궤도에너지를 결정할 수 있다. 예로서 抵 g Ca28 의 경우를 제시하겠는 데, 양성자와 중성자는 주 껍 질 ls,l p와 2s,1d 을 차지하고, 나머지 8 개 의 중성자는 궤도 l f 7/2 를 차지한다 .
 .-- -.--\ .-.•.:• : : : :···---- - --- - I : :::::二二. :::::
.-- -.--\ .-.•.:• : : : :···---- - --- - I : :::::二二. :::::
하트리-포크 계산에 의하여 얻어진 슬레이터 행립식 I@ 。>가 기본상 태 앞 ;ea28 을 나타낸다고 하자. 이 상태의 스핀-반전성은 0+ 아다. 또한 상태 |(j)。>의 하전스핀 To=(N-Z)/2=4 이고 두영 T,.=(N-Z)/2=4 라 하자. 중성자와 양성자가 같은 포텐셜 속에 있으면 이것이 사실이라 는 것울 증명하자. 우리는 쿨롱력이 존재하더라도 인재나 이 조건을 실 현할 수 있다. A 가 평균 포텐셜 우물 속의 궤도라 하자. 하전스핀 연 산자의 세 성분은 다음과 같다. T,,= 망 홈 (b!b1-a!ai) T+= I; b1a1, T_= I; a!b 』 (6. 74) A A 위에서 b+ 와 a+ 는 각각 중성자와 양성자의 생성 연산자이다. 그립 (6.73) 과 같이 채웠을 때 술레이터 행렬식 |(J)。>는 바로 T,, 의 고유벡 터이다. T,, l
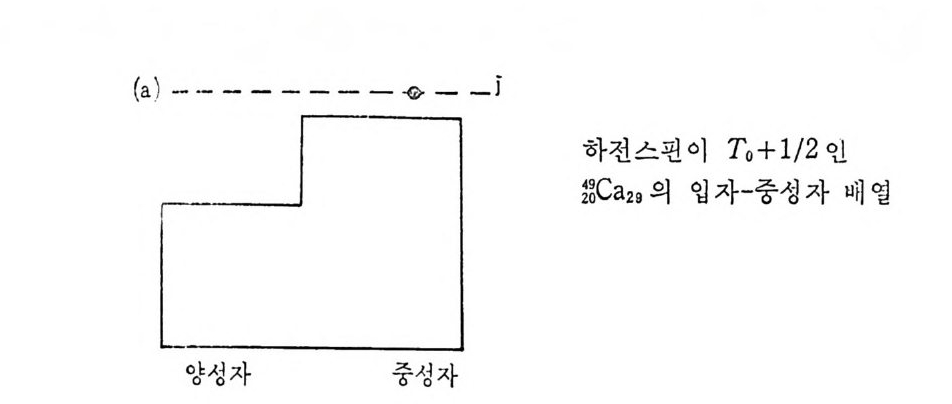 (a) -- -- ----- -G-一 _j
(a) -- -- ----- -G-一 _j
bi I n ) = ~ (C •J I Aj T o + 1/2 ) < .-1jT o + 1/2 I b 기 (})。 > (6. 76) A 입 자一 중성자 궤도의 에너지는 식 (6.68) 에 의하여 주어진다. et = <(J )o l b i-l切 |
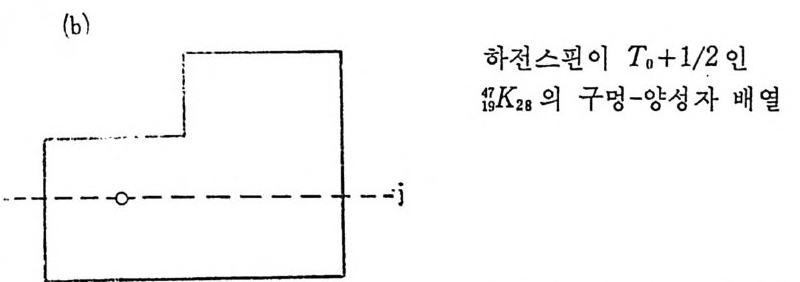 (b)
(b)
하는 t ~K2a 의 배열 이 o 。>이 얻어진다. 따라서 이 배열은 하전스핀이 Ta+l/2 이고 '7K 의 상태 lµ i Ta+l/2> 의 완전한 집 합으로 전개 할 수 있다. aJ Io 。>=I; (K)lµi To+l/2) <µi To+l/21a i l a>。> (6. 78) µ 구멍-양성자 궤도의 에너지는 식 (6.72) 에 의하여 주어진다. eJ> = <( J)。 I H | (J)。 >- <( J)。 l a 간 la j I (J)。 > = <(J)。 |HI (J)。> -~(K) I <µj T 。 + 1/21 aj I ( [J。> 12E? To+1/2 ) (6. 79) JI 여기에서 Ef •To+l/2) 는 '1K 의 상태 lµ j~。 +1/2> 의 에 너지이고, I< µ }T o +1/2la j l([) 。> 12 은 이 상태의 분광학적 인자이 다. I([) 。>가 슬러 ] 이 디 행 렬식이면 분광학적 인자는 합의 규칙을 다른다 . l=<([)ola} 이 o 。>=I; CKll <µi To+l/21a j l([) 。> |2, (jEF ) (6. 79') µ 중성 자가 아직 차지 않은 궤 도 j 에 양성 자를 한 개 첨 가한 ;fSc 28 의 배열 아 |o 。>을 생각하자. 이 배열의 하전스핀의 두영 Tz=T。 -1/2 이 고 T+a jia>。 >=b}|o 。 >=\=0 이다• 따라서 배열 아 |o 。>는 하전스 핀 이 T 。 -1/2 인 상태와 To+l/2 인 상태의 혼합이다. 우리는 이것을 ;i SC 2s 의 상태 IA j T 。士 1/2> 의 완전한 집합으로 전개할 수 있다.
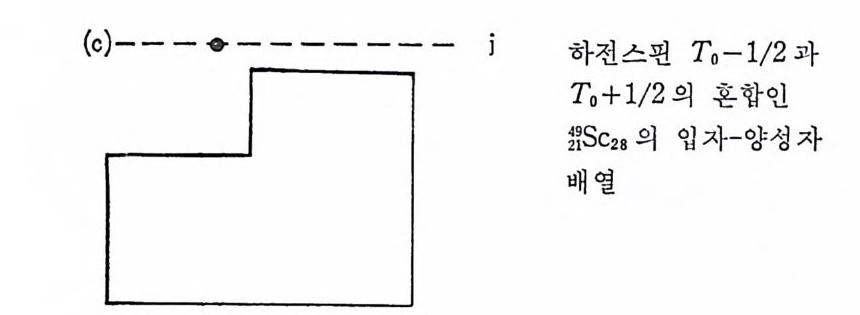 (c)--一 •------ -j 하전스핀 T 。 -1/2 과
(c)--一 •------ -j 하전스핀 T 。 -1/2 과
a;-l tb。> =E‘A1 1Sc) { IA j T。 -1/2)
eJJ = ~ (Sc ) {I <.i !J T 。 _ 1/21 aj l (J)。 > j 2£SJ , To-1/2) +-
전스핀이 To-1/2 인 “Sc 의 배열 a 기(J)。>을 얻는내, 이것은 “Ca 의 유 사 상대가 아니다. 따라서 이 배열은 “Sc 의 상대 l ..1j T。 -1/2> 로 선개 된다.
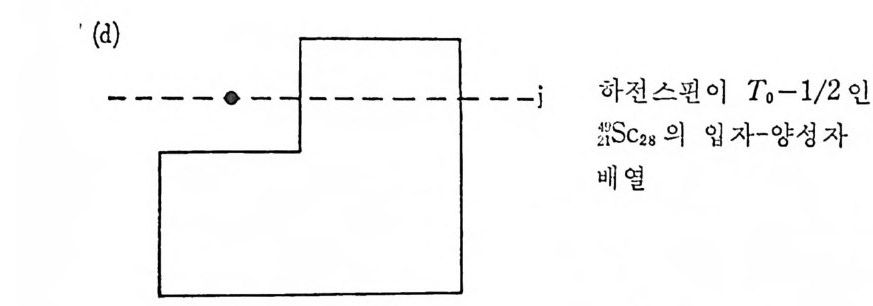 , (d)
, (d)
a; I (J)。> =.z:::c Sc> I ttj T 。 -1/2)
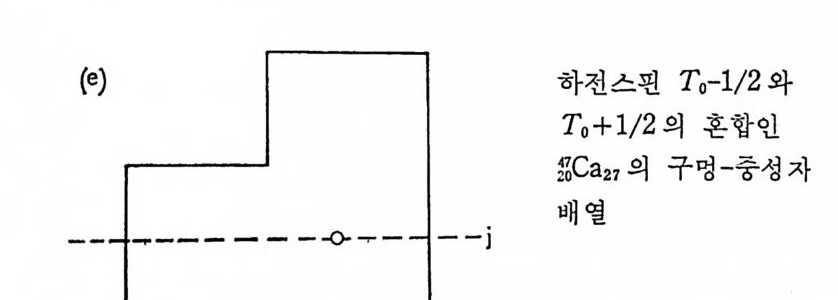 (e) 하전스핀 T。 -1/2 와
(e) 하전스핀 T。 -1/2 와
b j l (J)。> =핥 'C• > { !µjT o-1/2) <µi To -l / 21b i l(/) 。> + 1µj To + 1/2> <µjT0 + 1/2 IbJ I( /)。>} (6. 86) 구멍-중성자 궤도의 에너지 (6.72) 는 다 음과 같다. e5> = <( J)。 IH I( J)。 > 一 ~ (C• > { I <µ i To -l/21 bi l (f)。 > | 2£f• To-1/2)} + I <µi Ta+l/21b i l(/) 。> 12Ef ·r, +1 1 2> } (6. 87) 분광학적 인자는 합의 규칙을 따른다. 1= <@。 lb ; b 』(/) 。> =I;
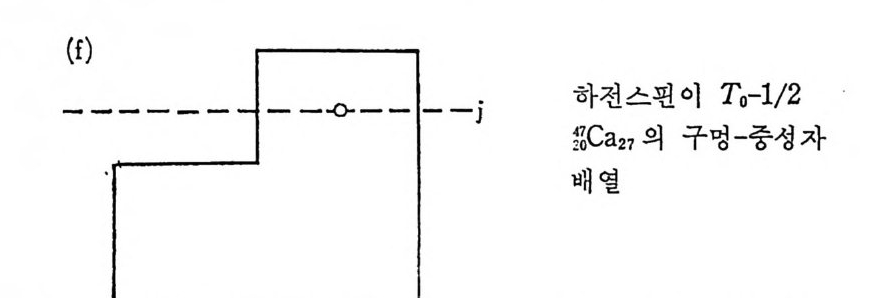 (£)
(£)
마지막으로 양성자가 차 있지 않 은 궤도의 중성 자 를 제거하면 하전 스핀이 To-1/2 이고 섭 K28 의 스펙트럼과 유사하지 않 은 g Ca27 의 배영 b j l (J)。>을 얻는다. 이 배열은 하전스 핀 이 T 。 -1 / 2 인 “Ca 의 상대로시 전개된다. bj l (J)。> =2(., c,> I µJ T 。 一 1/ 2 > <µj T 。― 1/2lbj I (J)。> (6. 89) 이 궤도의 에너지 (6.72) 는 다음 식에 의하여 주어진다. e},=< (J)。 |HIo 。>- <(J)。 |b 간 lb j l ([J 。 > =<({)。 IHl (J)。 >-~(/I Ca ) I
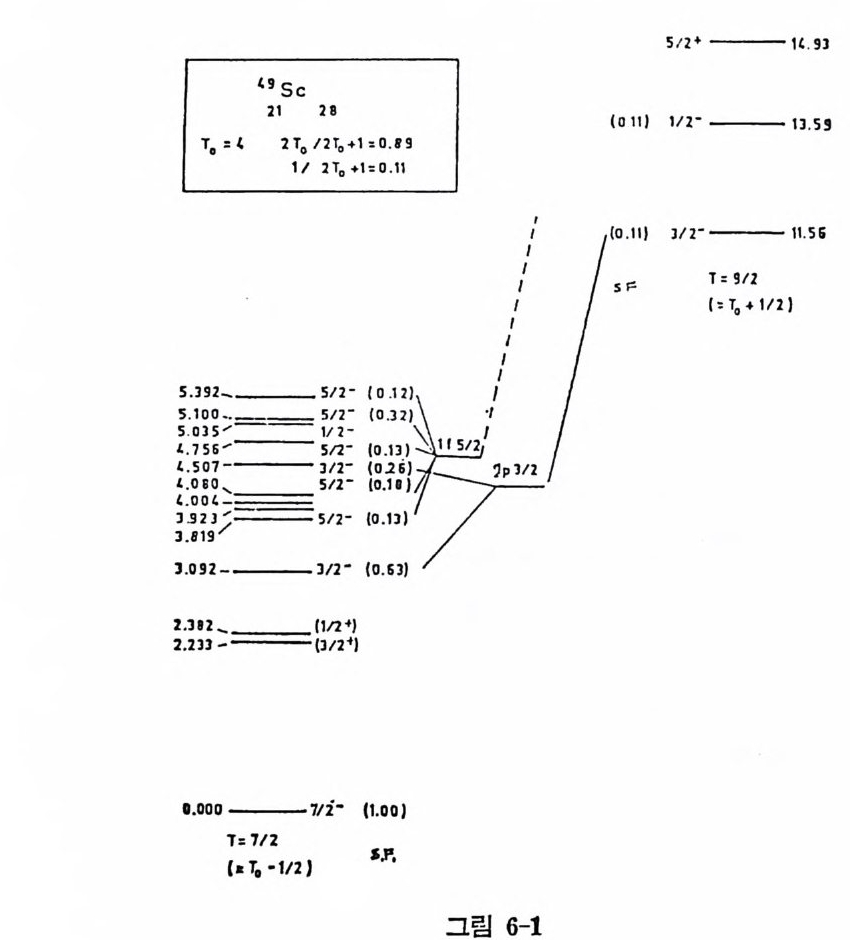 51 2 +-1(.9 )
51 2 +-1(.9 )
또한 합 의 규칙 은 다 음과 같 다. l= <
자료들은 기본상태(그립 6-2) 가 2s 감배열이고, 0.36M eV 의 재 1 등적문 상 태 3/2+ 는 1d 값 에 해당한다는 것을 시사한다• 우리는 분광학적 인자에 대해서는 아무런 정보도 가지고 있지 않으며, 다만 1 이라고 추측했을 뿐이다.
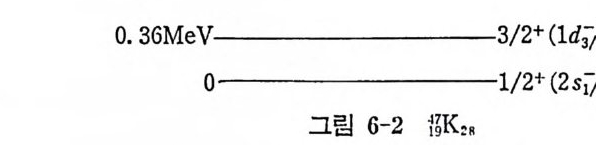 。• 36MeV 3/2+(ld 값)
。• 36MeV 3/2+(ld 값)
식 (6.79) 와 (6.91) 의 값들로부터 다음과 같이 양성자 궤도의 에너지를 구할 수 있다. e g旋 / 2 = -15. 26MeV e}:~12 = -15. 62iv ie V 앞서 인용된 Nuclear Data Sheets 에 따르면 “Ca 의 스펙 트럼 은 다음 과 같다.
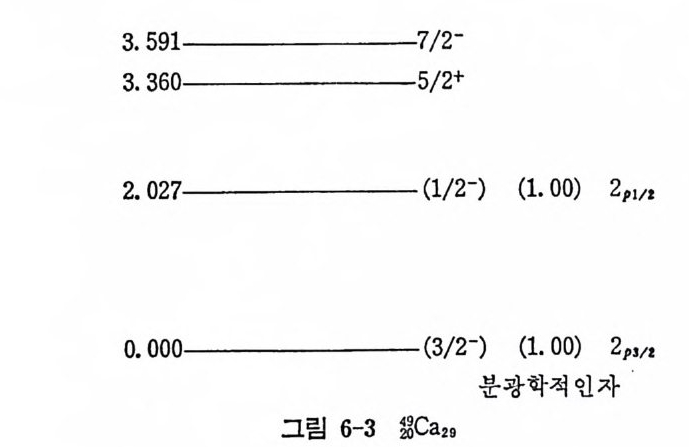 3.591 7/2-
3.591 7/2-
'8Ca (d, p) '8Ca 의 반응으로부터 페 르미 바다 밖의 중성 자 궤 도를 결 정 할 수 있다. * 실험에 의하면 처음 두 상태 3/2- 와 1/2- 의 분광학적 인 자는 1 이 다 (그립 3) . 이 돌은 “Sc 의 3/2-(1 1. 56MeV) 와 1;2-(1 3. 59 MeV) 상태의 유사 상태들이다(그림 6-1), 식 (6. 77) 과 (6. 91) 의 값들 로부터 다음과 같이 중성자 궤도의 에너지를 얻을 수 있다. • CBoelnottr e ., IDnoter er .n bCuoscnhj. ePt r Roapp e ar p toi e r st , NNuuccl.l . SPtah t ye ss ., MAol2n0t(r 1e 9a6l(8l9) 694)0 1;2 58B) og a ards et Roy ,
e\;~12 = -5 . 14MeV e~;(12= -3 . 12MeV 반응 48Ca( p ,d)41Ca 으로부터는 구멍-중성자 궤도를 결정할 수 있다 (그림 6-4).
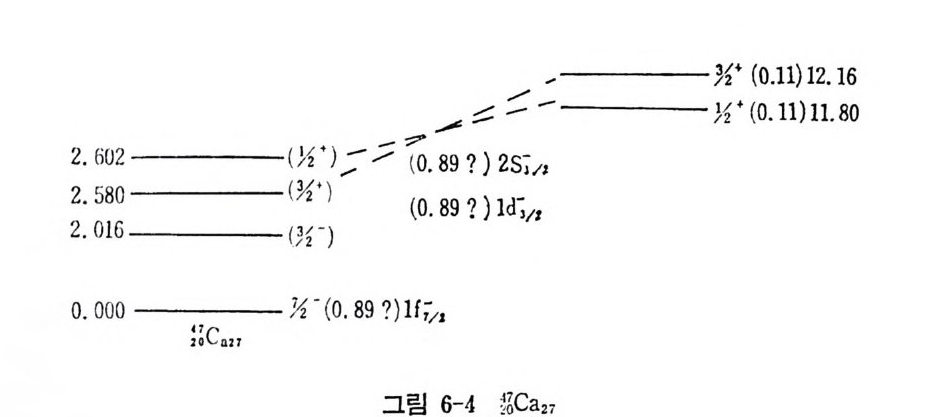 / %' (0.11) 12. 16
/ %' (0.11) 12. 16
Nuclear Data Sheet s 에 서 인 용된 분광학적 안 자의 자료는 아직 도 부 정확한 것 이므로 우리는 식 (6.86) 의 구멍-중성자 배열의 바닥상태와 2. 580i\1 e V 의 3/ 양 상태 , 그리 고 2. 602MeV 의 1/ 양 상태 를 순수한 상태 로 선정하고 이 상태들의 분광학적 요소몰 식 (6.88) 에 따라 2To/(2T 。 +l)=0.89 로 규격화했다. Ca 에서 47K 의 T。 +1/2 상태의 유사상대들의 위치는 결정하지 않 았다(그림 6-2). 하전스핀이 9/2 인 47Ca 의 이 상태둘은 유사 상태들의 축퇴를 제거하 는 쿨롱 에너지물 고려함으로써 계산할 수 있다. 쿨롱력이 주어진 상태 의 파동함수를 많이 변화시키지 않는 한(즉 섭동의 제 1 차까지), 47K 와 \ca 의 유사상태 |A,j, To+l/2> 의 에너지 차이는 쿨롱 에너지의 차 AUC 와 같다. A Uc=ESJ· To+ l/2) (HCa) -ESJ· To + l/2) (미 7K) 그런데, 쿨롱에너지는 경험 법칙에 따르면 N 과 Z에 대하여 충분히 규 칙적으로 변화한다.
U혼 ~ Rc'.::'.l. 25A113 따라서 우리 는 이 법 칙 을 사용하여 “Sc 와 “Ca 의 유사상대 3/ 2 -와 1 / 2~ 를 갈라놓는 차이 11Uc 를 A=49 인 계에 대해 연역해 보자(그립 6-1 과 6-3). .dU c=E[1t- 112 ('9Sc) -E[J ;-_ 1 12 ( 49Ca) =7. 08MeV llUc=E [J간 ('9Sc) -E[;t-11 2 ( 49Ca) =7. 08MeV A=47 인 계에 대해서는 다음과 갇다. A.U c=Ei, To+112(47Ca) -£1,To +l /2(47K) =6. 48MeV 이로부터 47Ca 의 To+l/2 상대의 들뜸 에너지 를 구할 수 있다. E5 판 (“Ca) -E 。 (47Ca) = 11. 80MeV E 접t 112 (47Ca) -E 。 (41Ca) = 12. 16MeV 따라서 식 (6.87) 을 이용하여 중성자 궤도 ld3 12 와 2S1/2 의 에너지를 구 할 수 있다. ef;~ 1 2= -13. 57MeV e~:/ 12= -13. 55MeV 마지막으로 “Ca 의 바닥상태의 분광학적 인자가 1 일 때, 구멍-중성
 -3.12… ………………… 2P11z
-3.12… ………………… 2P11z
자 궤도 !112 의 에너 지는 다음과 같다. e1½12=E 。 (48Ca) -E 。 (47Ca) = -9. 94MeV 이렇게 계산된 중성자와 양성자 궤도는 그립 5 에 나타나 있다. 섬 Ca2s 에서 중성자 궤도의 에너지는 양성자의 에너지에 매우 근접해 있다는 것을 불 수 있다. 이것은 서로 상쇄하는 두 효과에 기인한다. 죽, 쿨롱에너지는 양성자 궤도의 에너지를 다시 윤려주고, 같은 종류의 핵자 사이의 상호작용보다 더욱 강하게 잡아당기는 중성자-양성자 상호 작용은 중성자 궤도의 에너지에 비하여 양성자 궤도의 에너지를 낮추어 준다. 토론 궤도의 에너지를 실험적으로 얻기 위하여 전개된 이 모든 노력에 도 불구하고, 얻어진 자료는 아직도 단편적인 것에 불과하다. 궤도에너 지의 결정 역시 많은 계산을 필요로 한다. 보다 깊은 궤도 (l p 3;2, lP112, 1s11 2) 는 반응 (p, 2p) ' 또는 (e, e'p) 에 의 하여 탐색 될 수 있 다. 우리는 우리의 분석에 대하여 다음과 감은 반론을 제기할 수 있다 : 어째서 술레이터 행렬식 I <1>。>가 “Ca 의 바닥상태를 나타낸다고 가정하 고, 배열 a t l (J)。> 또는 이(J)。>가 홀수핵의 여러 상태로 갈라진다고 가정 했는가? 닫힌 껍질 핵은 인접한 짝수_홀수핵보다 안정하다는 사실이 이 가정울 어느 정도 정당화하지만, 우리는 짝수-짝수 핵도 역시 여러 배열의 혼합으로서 숟례이터 행렬식 1 (J)。>가 여러 상태로 갈라지는 배 열일 가능성을 생각할 수도 있다. 실제로 단일입자 그린 함수 수식화 체계에서는 이 효과를 고려할 수 있다. 그때에는 특히 분광학적 인자에 대한 합의 규칙아 수정된다. 8 밀도행렬의 변분에 대한 하트리-포크 상태의 안정 조건 하트리-포크 방정식은 에너지 E 〔 P 〕가 밀도행렬 P 의 미소 변분에 관 하여 정상적이라고 하는 변분 문제 (6.18) 로부터 유도되었다. 어떤 조 건하에서 E 〔p〕가 최소인지몰 살펴보자• p C0) 가 슬레이터 행렬식 |(J)。>의 밀도행렬이라 하자. 에르미트형이고 p 2= p와 Tr p =Tr p(O) =N 을 만족하는 다른 모든 밀도행렬 p는 에르미 트형 연산자 S(Su=SJ :)를 사용하여 다음과 같이 쓸 수 있다.
p= c;sp co > e - i s = p
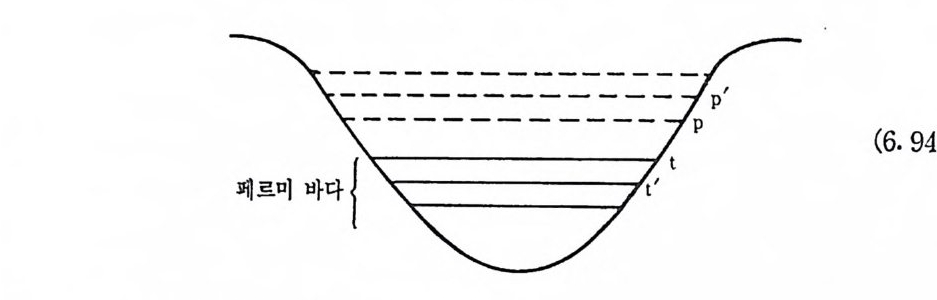 --_ -二- _-_-__二二_-_-_-:.;; p'
--_ -二- _-_-__二二_-_-_-:.;; p'
이 표현에서는 다음 관계가 성립한다. p8! = &:'. p잡k = p芹=p芹 =O (6. 95) 식 (6. 93) 으로부터 p CI) 과 p ( 2 ) 의 행 렬 요소 물 계 산하면 다음과 같 이 된다. ppPiWii~ === i- IS:‘,I ,s: , ,ss,,,,sp,;=p距,' • == I ’: _ - piiI1 Sl:P1 쌉,P 쌉 pi~p\ l}l= pi ~,= 0 p?=강[f, Spp ' Sp, ,- ~ S;,,' S11,] p;?=송먹 % Sp'p - ~ Su, S,,p] (6. 96) 에너지 E[ p]를 p(O ) 부근에서 S 에 관한 제 2 차까지 전개하자.
E[ p ]=E[ p <0) 〕+芬 p l} 틀 I p' ''+휴 P; }틀|p (0’ + 宁 읊 P:}l pi}) ap? J2: PkL Ip< , , (6. 97) p (O) 가 하트리-포크 방정식의 한 해인 경우를 생각하자. 이 경우에 h8=aE/a p ulP'm 는 표현 (6.94) 에서 대각선화되어 있다• h1°},,=epo pp', h)~i =e 1011,, lz1°1=h)~=0 (6. 98) 또한 식 (6.96) 을 고려하여 전개식 (6.97) 을 S 에 관한 제 2 차까지 쓰 면 다음과E [같p]이 = E된 〔다갑. 0 ) 〕 + ~p, (e,-e,) p ~1, 자} + +2 {~jkI. P W V ,j, ttPW (6. 99) 식 (6. 99) 에 서 첨 자의 쌍 (i1) 와 (kl) 은 각각 (pt) 이 거 나 (tp) 이 고, v,j, ‘ 1 은 다음과 같아 정의되었다. 露 v‘j, u= aPji aP u =
B,,•,p • 1 • =V,1,1•p •= ~02E o2E A t,,p •,•=on,011,(e, 급) +v pt ,r= 瓦志言 B;1,p' , '=v,p,P ' I'= 6p po12 6Ep p 'I ' (6.103) 이다. 행렬 A 는 에르미트형이고 행렬 B 는 대칭형이다 : A=A+, B=B 식 (6.99) 는 다음과 갇이 쓸 수 있다. 따] =E[p' O)] + -½-< V *, MV) (6. 101 ) 식 (6.104) 는 하트리-포크 해 p(O ) 부근에서 에너지가 어떻게 번화하는 지를 보여준다. 해 p (O) 에서 에너지는 정적이므로 변분은 분명히 제 2 차 이다. 다음의 안정 조건은 행렬 M 의 모든 고유치가 양수이어야만 실현 될 수 있다. E 印 >E 〔 P@ 〕 (6. 105) 변환 (6.92) 가 하트리-포크 해밀토니안에 의하여 깨어진 해밀토니안 의 연속적 대칭성인 경우를 생각하자. 연속적인 변환은 a 가 연속적인 실변수일 때 연산자 U= i •S 로 나타낼 수 있다. 예 를 들면, Z- 축 주위 로 각 a 만큼 회전시키는 연산자는 e- i a J.이다. 따라서 이 연속적인 번 환에 대하여, p=iaSp 'O) e-ia S=p (O) + p(I) + …. . . (6. 106) 이고, 여기에서 p(l)=ia[ S, p'0 '] (6.106') 이다. h 印를 a 의 제 1 차 항까지 계산하자. h 印 =h[ p co> +pm ]=h[p'o )] + -u4 v.1,klpW (6. 107) 한편, [h[p< O >J ,p
l 心] =e i • S 展p (O) J e- i •S 이고, p= eia s p CO )e-ia S 이므로, 떠p], p ]=e•• S u 心 (0) 〕, p(O )] e -ia s=O 이다. 전개식 (6.106) 과 (6.107) 을 식 [h 〔사'p〕 =0 에 넣으면, a 에 대한 제 1 차까지 다음과 같은 식 이 나온다. 情〔p( 0) 〕, p
9 정적인 외부장에서의 선형 반응 계물 정적인 의부장 -AF 속에 놓자• 여기에서 F 는 에르미트형의 일 체 연산자이다. F=Lij F;ja ta j (6, 111) 이 경우에 범함수는 다음과 같이 된다. E 印 =2,j
이 것 은 다시 h(0)P(I) -p (I )h(O) + h(I)P(O) -p(O )'l(I) =O (6. 115) 이 된다. 이 식 의 1l(I) 에 (6. 114) 에 의 하여 정 의 된 값들을 집 어 넣고, 상태 (pt) 와 (tp) 사이 의 행 렬 요소 를 취 하면, p (0) 와 fl (O) 가 대 각선화된 표현에 서 다음과 같은 식이 얻어진다. (;* ! * ) (;t~) =;i (;j (6.116) 윗식 의 행렬 A 와 B 는 식 (6.103) 에 의하여 정의되었다. 따라서, 밀도 행란 의 변화는 섭동의 크기 A 에 비례하고, 에르미트형의 행렬 (6.102) 의 역으로 주어진다. (;;~)=A(;* ! *)-1(;,) (6.117) 교란된 계는 다음과 같은 연산자 F 의 평균치를 얻는다.
111 -i (F) = +(F i,~ Fp~ ) ( ;* 1 『 (;:;) 이다. 하트리-포크 해밀토니안이 연속적인 대칭성을 깬 때 행렬 M’ 은 특이하고, 따라서 우리는 식 (6.117) 을 분명히 해 야 한다. 에르미 트형 의 행렬 M 은 그것의 고유벡터를 기저로 사용하여 전 개할 수 있다. Map =~. W~e.Wp * (6. 121) 식 (6.121) 에서 첨자 a 와 f3는 배열 (pt)와 (tp) 를 나타낸다. w~ 를 0 인 고유치 e,=0 과 관련된 고유벡 터 라 하면 식 (6. 116) 은 다움과 같 이 쑬수 있다. 2 2 Wg enW 『p 상 =AF. (6. 122) n* S ,1 따라서 식 (6. 117) 은 다음과 같이 된 다. p~n =A I; W 난 -W p* F~ (6.123) n* s Cn 이 식은 p(I)이 가짜 고유벡터를 제거한 행렬을 사용하여 계산되어야 합 을 나타낸다. 이것은 곧 식 (6.117), (6.118), (6.119) 가 행렬 M 이 아 닌, 다음과 같은 행렬의 역을 취함으로싸 계산될 수 있다는 것을 듯 한 다. Map = 2 W;en w;* (6. 124) n*S 10 보기 : 밀도에 의존하고 도달거리가 0 인 힘 매우 단순한 힘을 생각하자. ..., ..., v (p) =o (r1-r2) [a+bn (r1)] (6.125) 여기에서 n(; )은 다음과 같이 적을 수 있는 핵의 밀도 (6.17) 이다. n(r) = IOT: A_EI:F
n,, ,., .•, r , (-r,) = ~- < r-' (J T | A> < A | 니r (J1 단 > (6. 127) A 드 F 포텐셜에너지는 힘 (6.125) 물 사용하여 다음과 같이 쓸 수 있다. <¢1 V(p) 1¢)=_1 2__ A,~µ EFJ (A µlv(p) IAµ) -(Aµlv(p) lµA)] (6. 12 8) 힘 (6.125) 를 대입하여 이 식을 계산하면 다음과 같다. <¢1 V( p) 1¢>= 宁J파망) 〔 a+b 玉)〕 _占 곱; Jd; I n u,r 1, u2 讓) 円 a+ bn (;) ] (6. 129) ,272 시간 역전과 하 전 스핀의 세째 성분 m 가 페르미 바다를 변화시키지 않는 다고 가정 하자. 이 경 우에 혼합밀 도 (6. 127) 은 스핀과 하전스핀 공 간에 서 대 각선 화되 어 있으므로, 다음과 같이 나타낼 수 있다. n11 gt m- r), g =2 r2n (P여r• .)( - r=) 8+. 。 In g 2. 8 r(I-rr) , n r (➔r) (6.130) 식 (6.130) 에서 첨자 r=n 또는 P 는 중성자 또는 양성자의 밀도를 구 분한 다. 따라서 식 (6.129) 의 포텐셜 에너지는 다음과 같이 적을 수 있다. <
=o( ;구)&& 8<08|n Vr((fr)) 1E> (6.132) 다음 식은 쉽게 증명된다. 8 < ➔r8I ?(1l,.' -, ,r '( I; p) I ➔r a'C' > =%8~8 냐 (; _ ;) o( ;냐) (6. 133) ➔ U,(r) 이 국소적인 하트리-포크 포텐셜이라 하자. U사 ) = ana, ( :r:).: -< ([) | V (p) I( [) > (6. 134) 식 (6.131) 을 사용하여 미분 (6.134) 를 계산할 수 있다. 그 길과는 다음과 같은 형태이다. 隨국따) 〔 a+ 강타)J_물 [n,( r )-11 자 )]2 +Tr[np ( r) _,2n(r)] [a+ bn(1·)] (6.135) 식 (6.135) 에서, 중성자의 포텐셜에 대하여 Tr=+l 이고 양성자의 도 텐셜에 대하여는 'C',, =-1 이다. 핵에 중성자가 남을 메에는 n,(r)=\=n.(i '.) 이므로 양성자의 하트리-포크 포텐셜은 쿨롱력이 없을 때에라도 중성자 의 포텐셜과 다르다. 이것이 바로 깨어진 대칭성의 예아다 : 연산자 e-1 갑 Ty 로 표현되는 전 하 대칭성이 문제이다. 전하 대칭성은 중성자를 양성자로 바꾸고, 따라 서 n,(; )을 n 자)로 변환시킨다. 식 (6.131) 울 보면, 이 변 환 에 대하여 에너지가 불변이지만, 하트리-포크 포텐셜 (6.135) 는 그렇지 않다. 하트리-포크 포텐셜의 재배열항은 다움과 같다. U자 )=<이 a,~l (l)>=푼西) 감 -[n p (r) _1ln (r) ]2 (6.136) 유효 상호작용 (6.125) 가 합 n,(r) +nn(; )에만 의존하기 때문에 재배 열 포텐셜은 중성자와 양성자에 대하여 같다. 재배열 포텐셜은 득히 핵 중심의 밀도가 높은 영역에서 영향을 미친다. 이것의 크기를 계산해 보 기로하자.
핵질이 E/A=-16~1eV 이고, llF=l .36 fm ~1 에 해당하는 밀도 를 가지 도 록 a 와 b 의 값 을 택 하면 a= -9 84MeV, b=2187MeV (6. 137) 이 된다. 핵 의 중심 에 서 핵 자의 밀 도는 n (r) ~o. 17 핵 자/f m3 이 고 11, (;) -n ,, (r) <( 11 2 (;) 이다. 따라서 식 (6.136) 에 의하여 핵의 중심에서는 재 배열항이 척력을 주 고, 우 물 의 바닥을 24MeV 만큼 높인다는 사실을 알 수 있다. 식 (6. 135) 에 따르면 핵 의 중심 에 서 우물의 깊 이 는 -54. 36MeV 이 다 (제 8 장 8 절 을 보자) .
 u (~')
u (~')
11 갈 릴 레이 변환과 병진운동에 의한 가짜상태 유니터리 연산자에 의하여 나타내어지는 갈릴레이 변환 (6.32) 를 생 각하자. U=exp (~;l;.R ), E=*g r ‘ (6.139) 이 변환에서 i입자의 운동량 연산자 7i는 다음과 같이 된다. u-1.p.. .. ;U =-p ;- mv- 亨 (6.140) 우리는 재 3 전에서 p와 E[ p]가 각각 계의 밀도행렬과 에너지라면,
갈릴레이 변환은 p를 p =Up U-1 로, 그리고 에너지 E 〔짜를 E 印 =E[ p ]-v • <(,/)IP'ri,j q.....) ,> +. —A2 m__ v:--2 (6.141) 로 식변 (화6.시14킴1)울 은 보<았0다|P.--|+ 0>=\=0 인 슬레이 터 행렬식 10> 는 하트리-포크. 방정식의 해가 될 수 없음올 보여준다. 왜냐하면 이 경우에는 술례이너 행렬식의 에너지가 보다 낮아지도독 하는 속도 i를 항상 잦울 수 있기 때문이다 . 실제로
101) 에 의하여 정의된 벡 터와 같은 역 할 을 한다. 식 (6.104) 와 (6.102) 에 따라 우리는 다음과 같이 에너지를 전개할 수 있다. E 印 =E 印 + 嘉- (X:, 一 짜) (;」 * ) (_ ;j (6. 145) 이 식과 식 (6.142) 를 비교하면, 행렬 (;* !*)의 다움과 같은 독득한 성질을 얻을 수 있다. 뿐= cx:,-x,~) (;* !*)( _ 1j (6.146) 이재 연산자 U 로 표현되는 병진운동 (6.29) 를 생각하자. U=ex p『 Ph. ; ), P= 訂 (6.147) 입자의 위치벡터 ;r 를 U-l;‘U=;‘_a 로 바꾸는 이러한 변환은 해밀토 니안의 대칭성이고, 그 결과 p =Up U-1 에 대하여 E 印 =E 印 (6.148) 가 된다. 크기가 작고 X- 축에 평행한 a 를 택하자. p =Up U-1 를 식 (6.92) 에서 처럼 a 의 멱으로 전개하면, U=exp (i S) =ex p[뿜 홉1 p:r (i) ] 이므로, s=+h if=A: ,I p,, (i) (6.149) 이다. 벡터 P 를 다음과 같이 정의하자. P=( 之)=(雲Z 雲 ) (6.150) 제 8 절의 끝부분에서 본 바와 같이, 벡터 P 는 행렬 (BA* AB* )의 고유벡
터이며 고유치는 0 이다. (;* !* )(_~j=o (6. 151) 이 식을 식 (6.146) 과 결합하자. 식 (6.144) 와 (6.150) 에 의하여 정의된 벡터 X 와 P 는 교환법칙, [Rz, P 』=itz (6. 152) 움 따르는 한 쌍의 연산자, Rr=.. AL ‘$=I .t·i P.,= iI=A ; l P.,(i) (6. 153) 로써 만들어졌다는 점에서 서로 관련되어 있다. 상태 1([) >에 대하여 교환자 (6.152) 의 평균값을 취하면, :”E { 해밀토니안 H=H-』 ,211 (6. 156) 올 사용하게 된다. H 도 역시 일체 연산자와 2 체 연산자의 합이라는 것은 쉽게 증명할 수 있다. fi =(l 군) 홈 0|tu > ata j 나 젊 Ik l> a t a;a,a 을 (6.157) 해밀토니안 H 룹 사용할 경우에는 병진운동 (6.147) 과 마찬가지로 갈 릴 레 이 번 환 (6. 139) 도 해 밀 토니 안의 대 칭 성 이 다. 이 경 우 두 변환 (6.139) 와 (6.147) 에 대하여 다음 식이 성립한다(해밀토니안 H로 계산 된 모든 양 들 에는 기호 ^룰 침 가하겠다). E[p] = E[pJ, p= Up U -1 (6.158) 따라서, 행 렬목 〔; * ! . )온 고유치가 0 인 두 개의 선형독립인 고유벡 터몰 가진다. (!*1 *)(_~:)=o, (t* !* )(_;j=o (6.159) 12 하트리 -포크 계 산에 사용되 는 유효력 전체 견합 에너지, 질량 분포 등 핵의 전체적인 성질의 계산 결과를 보면, 자유로운 핵자-핵자 충돌 실험의 자료를 고려한 2 체력을 사용하 는 것은 만족스러운 일치를 얻기 힘들다는 것을 알 수 있다. 핵 안에서 의 상대적인 운동에너지의 크기 정도인 0 부터 300MeV 까지의 실험 결 과의 현상을 설명하기 위해서는 힘 안에 근접 (r J ohns t on 포텐선과 같이, 실질적이고 완전한 포텐셜에 바 하여 간단하면 서도 관축된 결합 에너지와 밀도를 고려하여 근접 척력항이 작도목 매 개변수를 선택하여 2 체력들을 사용한 덕분이다. 이러한 힘들은 특 히 50MeV 이상의 중간에너지 영역에서, 자유로운 핵자-핵자 상호작용을 근사시켜 기술할 뿐이다. 이러한 관점에서 그런 힘들을 유효력이라고 한 다. 그것들의 도입은 부분적으로는 핵질 (nuclear matt er ) 안에 있는 두 핵자 사이의 상호작용과 자유로운 두 핵의 충돌 사이의 상호작용간에 존 재하는 불확실성에 의하여 정당화된다(제 8 장 참조)• 가장 유용한 포텐셜 네 가지를 소개하려 하는데, 그 중 Volkov 포텐 설과 Green 포텐셜은 매우 간단한 것으로서 가벼운 핵에 국한된 및몇 의 자료만을 설 명 할 수 있고, 보다 복잡한 Sky rm e 력 과 Gog n y 력 은 주기 율표에 나타나는 많은 핵둘의 성질을 하트리-포크 근사 를 사용하여 성 공적으로 설명한다. 1) Volkov 력 Volkov 포텐셜은 세르베형의 교 환 연산자가 있는 중심포텐셜이다. V(r) =f(r) (0. 4+0. 6p 『) (6.160) 포화현상을 설명하는 핵의 근접 척력의 효과는 형태인자 f (r) 을 사용하 여 얻을 수 있는데, 이것은 가우스형의 평균거리 인력과 가우스형의 근 집 척력을 합한 것이다. 즉, f(r ) = -v.e-<•/µ,)'+ V2e-<•lµz)' (6. 161) 이며, 여기에서 Vi = V2=60MeV µ1=1 . 8fm (평 균거 리 ) µ2=1 . Olf m ( 근접 거 리 ) 이다. 이 값들은 i) s 파 상태의 자유로운 핵자-핵자 단일항과 삼중항의 유효 거리와 확산 거리, ii) 가벼운 핵, 4He, 160, … 등의 결합 에너지 와 질량 밀도를 동시에 얻을 수 있도목 해준다. 2) Green 력 Green 포텐셜은 두 핵자의 상대 운동량 7의 제곱에 의존하는 힘이다.
이 포텐셜은 운동 에너지가 큰 만큼 더욱 척력이 커짐으로써 근접 척력 의 효과를 나타낸다. 에르미트형이 되도록 하기 위하여 속도에 의존하 는 항을 연산자 1=+L- ;a-r 에 대하여 대칭으로 만둔었다 • v= 깁屈) + 같g; (;) +g, (;) -f] (6. 162) 합은 핵자-핵자 단일항 상태와 삼중항 상태의 네 경우에 대하여 계산하 고, 항태인자둘은 가우스형의 함수로 주어진다 . f; (;) =A;c-(-;/µ,) ' g沿 =B,e 홉/ A i )2 (6. 163) 계산을 s 파에 한정시키면, 매개 변수들의 가능한 값들은 다음과 같다 (A. 와 B i는 단위가 없다).
 I i= (S=O, T=l) I i= (S=l, T=O)
I i= (S=O, T=l) I i= (S=l, T=O)
이 값들로써 Green 력은 핵질의 결합 에너지와 밀도를 선명한다(무거운 핵에 한하여). 3) Sk y rme 력 Sk y rme 력은 주기율표의 많은 핵에 대하여 실행한 많은 하트리-포크 계산에서 큰 성공을 거둔, 매우 유용한 것이었다. 이것은 Green 포텐셜 과 마찬가지로 두 핵자의 상대 운동량 p➔' = - ;ht - V.... ,(~r 은- 상., 대., 좌_, 표- r➔1 -r➔2 이다)의 2 차항을 포함하는데, 이번에는 에르미트형을 보존하는 가능 한 모든 2 차의 불변 량들의 항까지 포함하고 있다. 포화현상을 보장하기 위하여 새로운 항을 도입하는데, 그것은 상호작용하고 있는 두 핵자의 질량중심에서 계산된 밀도 p (R)= p(.i당노)에 비례하는항이다. 이 항 의 도입은 높은 밀도에서 파울리 원리에 의한 근접 척력의 효과가 강해
진다는 고찰에 기인한다. Sky rm e 력의 모든 형 대 인자는 상대좌표 k 국 ’.1 一 /:2 의 델타함수 0(;) 이 되어 계산이 쉬워진다. 힘의 매개민수들은 전통칙으로 to, t I, t 2, t 3, X 와 Wo 로 표시한다. V 의 모양은 V=V.+VP+VP (6. 164a) 이고, 여기에서 Vc 는 중심포텐셜로서, V.= t。 (1 + XPu) o( .r., ) (6. 164b) 이며, v, 는 속도에 의존하는 힘으로 V,=- 才t [.v...; o(r..)., +.o ( l, ➔· ).v... 汀+t...묘. (➔r )V...,. +i W( (-+J 규(.J... 2) • (V.... xo(r➔) V- ) (6. 164c) 이다(우번의 마지막 항은 스핀-궤도 5·E 형이다). VP 는 밀도에 의존하 는 힘 (처력)이며 VP= 웅 (l+Pu) p(P;高) (6.164d) 가 된다. 질량과 밀도를 매우 잘 일치시키는 매개 변수의 세 집합을 약 자 S I, SII,Sm 로 표시하여 적으면 다음과 같다.
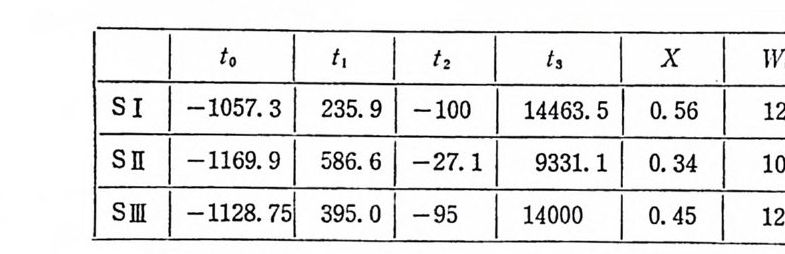 SSSI ITIII IIII ---111101t562。 879... 9735 11II 352f9831556 ... 609 1III ---21t97025 0. 1 IIII 1149430t4s036 031 . . 15 IIII oo0..X. 345 546 IIII 11w1022.500
SSSI ITIII IIII ---111101t562。 879... 9735 11II 352f9831556 ... 609 1III ---21t97025 0. 1 IIII 1149430t4s036 031 . . 15 IIII oo0..X. 345 546 IIII 11w1022.500
to는 MeV-fm 3 으로, ti, t2 와 Wo 는 MeV·fm 5 으로, 그리 고 h 는 MeV· f m6 으로 표시되었으며, X 는 단위가 없다. 4) Go g n y력 Sk y rme 력과 마찬가지로 Go g n y릭은 실험 자료와 매우 잘 일치하는 결과를 보여준다. Go gny력은 근접 척력의 역할을 흉내내기 위해 핵자
간의 상대 속도의 제곱항까지만을 가지고 전개하지 는 않으므로, 큰 값 을 얻을 수 있다. Gog n y 력에는 세 항이 있는데, 그것 들은 중 심포텐셜, 스핀때도 포텐셜, 그리고 Sk y rme 력에서와 같 이 밀도에 의존하는 포 텐셜이다. V= Vc + V,. + V, (6.165a) 중심 포텐셜 은 Volkov 력과 같이 두 가우스형 힘의 중첩 인데, 그 중 근 접력은 근거리에서의 척력 효과 를 부분적으로 흉내낸 척력이다. 이 두 힘의 교환혼합은 Volkov 력과는 달리 완전하다. V.=, ~~1, 2 . ( W, + M,P' + B,P u -H,P ' ) e- <,/ 正) (6.165b) 스핀때도력은 Sky rm e 력과 동일하다. V,.= i W o (a-1 +a-,2 ) • (v一 x o( 기r)- v ) (6.165c) 밀도에 의존하는 힘 : Vp= A[ p( R) ]•(1 + Xr) o (r) (6.165d) 은 Sk y rme 력과 비슷한데, 매개변수 a 와 교환 혼합 X 가 첨가된 점만 이 다르다. 좋은 결과를 주는 Gog n y 력의 매개변수의 집합은 다음과 같다.
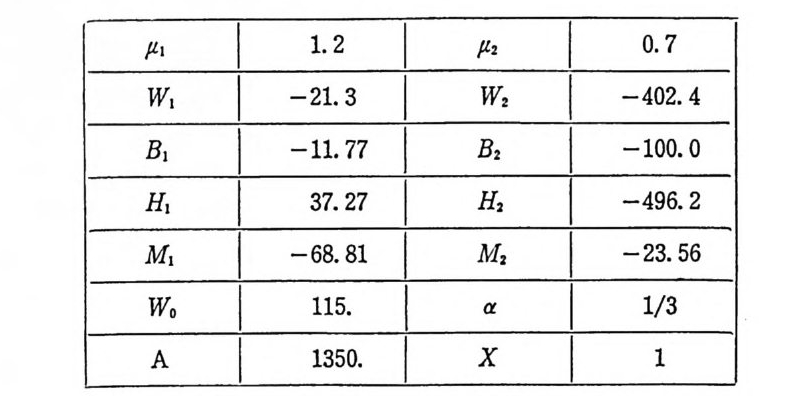 µHMBWAl1 I11 IIIIIII ---62113187.131 ...2.5 37820 717. III|II| µBXHMW2222 2 IIII|II ----4142o00931.2067. ... 5 6042
µHMBWAl1 I11 IIIIIII ---62113187.131 ...2.5 37820 717. III|II| µBXHMW2222 2 IIII|II ----4142o00931.2067. ... 5 6042
µ‘는 f m 로; w 나 ,B,,H, 와 M‘ 는 MeV 로; Wo 는 MeV• f m2 으로; A 는 MeV• f m' 으로 표시되었으며, a 와 X 는 단위가 없다.
5) 결합에 너지와 핵의 반지름 Sk y rme 력의 여섯 개의 매개변수를 사용하여 주기율표의 원소 중에서 매우 많은 수의 핵의 질량을 5MeV 정도의 오차 한계로 맞출 수 있고, 또한 전자 충돌실험 등으로 측정된 2 차 평균 반지 름을 O.l fm 이내로 맞출 수 있다. sm 의 매개변수를 사용하여 계산된 결과는 다음 표에 나 타나 있다.
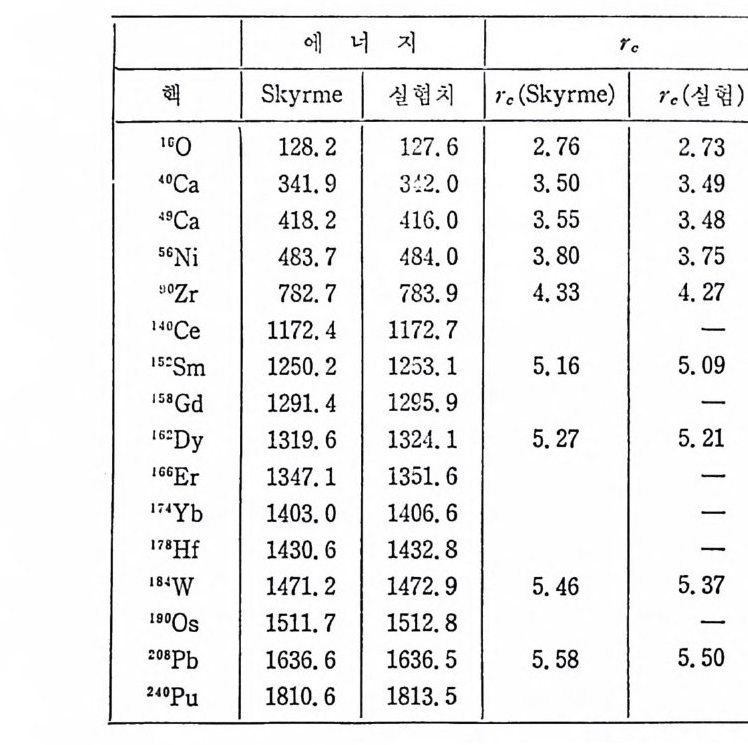 어1 L1 又] re
어1 L1 又] re
나트륨 동위핵 (l9N a 에서 “Na 까지)의 질량의 실험치와 Sky rm e 력을 사용한 이론적 결과의 차이를 비교해 보면, 안정성 계곡으로부터 매우 멀리 떨어진 불안정한 동위핵에까지도 매우 찰 맞는다. 점선으로 표시 된 두 곡선은 매개 변수를 약간씩 달리 잡아 계산한 값들을 나타낸다. 6) 초중핵의 예측* 결합에너지가 크게 증가하는 것은 구형 핵 껍질이 닫히는 것과 관련 • W.D. Mey e r and W.J. Swi at e c ki, Nucl. Phy s. 81, 1 (1966) .
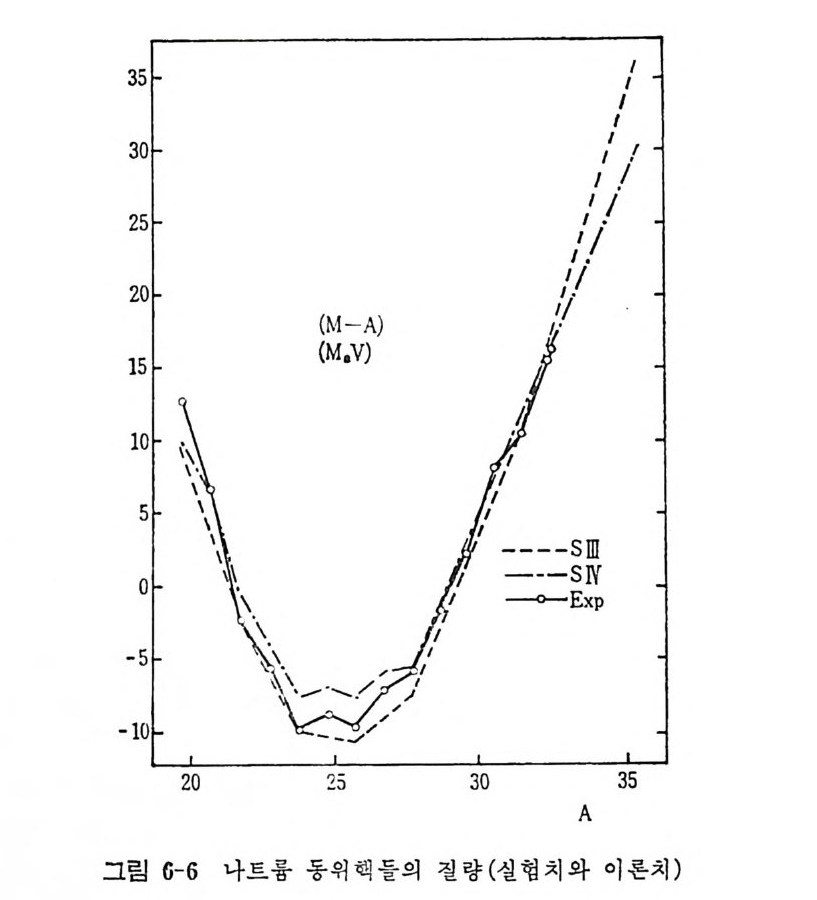 II,
II,
되어 있다. 이러한 사실은 우리로 하여금 A=298 인 초중핵의 존재를 담색하도 록 한다. 초중핵은 양성자나 중성자의 방출에 대해서는 안정하 지만 /3± 방사, a 방출, 또는 핵 분열 동에 대해서는 불안정하다. 이 핵들 의 안정성은 쿨롱력을 차단시킬 수 있을 정도로 강한, 닫힌 껍질의 결 합에너지의 증가에 기인한다. 이미 알려진 핵들의 기술에 성공한 하트 리-포크 방법은, 구형의 해가 채워진 입자상태와 빈 입자상태 사이에 큰 간격을 주는, 죽 닫힌 껍질을 시사하는 그러한 N( 중성자 수)과 Z (양성자 수)를 찾아 보도록 해 준다. Sky rm e 력 을 사용하여 얻 어 진 몇 몇 의 292
114, 126, 138 인 경 우이 며 , 독히 Z=114 이 고 N=184 인 경 우에 그 효과 가 크게 나타난다.
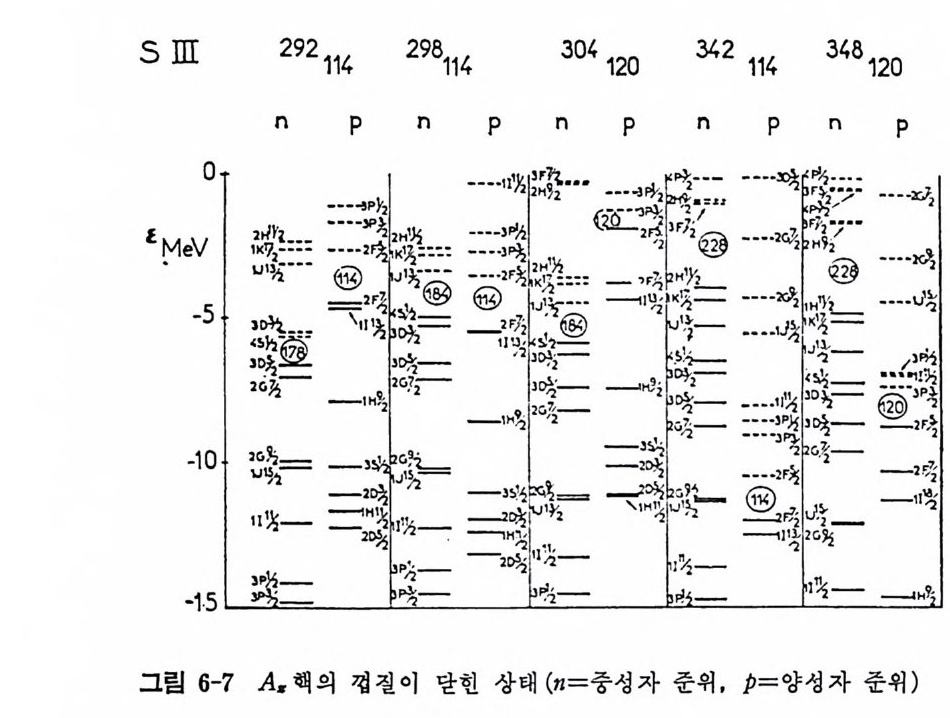 SIII 292 114 298 114 304 1·-20- 342 1.1 .4 . 348 120
SIII 292 114 298 114 304 1·-20- 342 1.1 .4 . 348 120
* 참고문헌 D.J. Thouless, Nuc/. Phys . 21 (1960) 225 와 Nucl. Phy s. 22 (1961) 78. 하트리-포크 이론을 핵에 적용한 예는 매우 많다. 다음 문헌을 참조하라 : D. Vauth e rin and D. M. Brin k , Phy s. Rev. C5 (1972) 626. D. Vauth e rin , Phy s. Rev. C7 (1973) 296. H. Flocard, P. Qu enti n, A.K . Kerman and D. Vaut he ri n, N11cl. Phys . A203 (1973)433. 최근의 옹용에 대한 재고는 다음 책에서 찾을 수 있다 : Nuclear Self-C onsis t e n t Fie l ds~, (Ed. Rip k a et Pomeuf) North - Holland, 1975. 첫 번째 응용은 Kelson and Levin s on, Phys . Rev. 134 (1964) 에 서 이 다. 쉬 운 설 명 온 G. Rip k a, Advances in Nuclear Phys i c s , Vol. 1 (1968) , Plenum Press 에 나 와 있다.
제 7 장 핵의 쌍짓기 1 소개 양성자에 대해서 또는 중성자에 대해서 단 하나의 열린 부껍질 (subshell) 을 가지고 있는 핵둘은 핵 의 평균장에 의해서 둘뜬 입자 또는 구멍모우 드의 기술이나, 액체방울의 집합적인 진동 또는 회전모우드의 기술에서 벗어나는 특이한 행동을 한다. 이 행동의 메카니즘은 사실상 절대 0 도 에서 나타나는 몇몇 금속의 초전도성 또는 몇몇 액체의 초유동성의 그 것과 흡사하다. 초전도핵들은 다음과 같다. a) 니 켈, 주석 , 납의 동위 핵 (iso to p e ) : 양성 자 껍 질 은 각각 Z=28, 50, 85 에서 닫혀 있고, 중성자는 각각 N>28, N>82, N<126 으로 열려 있다. b) 중성 자가 닫힌 동중성 자핵 (iso to n e) : N=28 인 ”Sc, 50Ti, 51V, 52C r, 53M, “Fe, 55C0 등, N=50 인 86Kr, 87Rb, 88Sr, 89Y, 90Zr, SINb, •2M o, asTc 등, N=82 인 Ba 에 서 Sm 까지 의 희 토류. 이 핵둘은 모두 구형이다. 이런 경우 하트리-포크 근사의 가능한 상 태들은 강하게 축퇴되어 있다; 열린 부껍질의 빈 입자상태에 핵자들을 분배할 수 있는 방법의 수는 매우 많다. 이 축퇴는 껍질모형의 찬류상 호작용에 의하여 깨진다. 실제로 이 핵둘의 스펙트럼은 다음과 같은 득 징을 가지고 있다: i) 하트리-포크 근사에서, 에너지가 축퇴된 서로 다른 가능한 상태의 밀도는 열린 껍질들 안의 동일한 핵자수 N 에 따라 급격히 증가하지만
관측된 첫번째 들뜸상대의 밀도는 N 이 증가해 도 그대로 있다 . 상 대일 도는 짝수-짝수 핵 의 경 우에 매 우 작고, 홀 수-짝수 또는 짝수 ― 홀 수 넥 의 경우에는 보다 크다. ii) 짝수-짝수(짝수 N) 핵에서, 첫 번째 들뜸상 태는 기저 상태 의 에 너 지 보다 2A 의 에너지만큼 높이 있는데, 이 값은 열린 껍질 속 의 핵 자 수 N 에 비교적 무관하다. 이 에너지준위 사이의 간격은 N 이 홍수 인 핵에서는 사라진다. iii) 짝수-짝수 핵의 기저상태의 스핀은 항상 1=0 이다. 게다가 에너 지 스펙트럼은 독특한 구조를 나타낸다 : 2A 의 에너지에서 겨우 및?! 의 상태들 (2+, 4+, …)이 관측된다; 약 4A 정도의 에너지 이상에서는 상대 밀도가 매우 빨리 증가한다. iv) 기저상태의 에너지는 핵자수 N 의 선 형함 수이지, 핵 자- 핵 자의 안 결 가짓수와 같이 N 의 제곱에 비례하지 않는 다. 실험적으로, 메아어와 옌센의 결 합법 칙은 그 결과 의 일부분을 핵 자 핵자 쌍짓기효과 탓으로 돌린다 : 같 은 껍질 j 에 있는 동일한 두 핵 자 는 그들의 운동량이 0 일 때 가장 강하게 상 호작용한다. Schif fer 의 곡선 ', 은 핵자들의 상호작용에 있어서 개개 혁 자의 파동함수의 겹침의 중요성 울 보여준다. 두 핵자가 동일할 때에 파울리원리가 허용하는 궤도의 최 대 겹침상태는 반정렬 (1 =0) 상태일 대 일어난다. 이것이 핵 의 쌍짓기 이다. 이 문제로 들어가기 위해 멘 먼저 부껍질 j에서 간단한 쌍짓기힘으로 상호작용하는 N 개의 핵자계를 생각하자. 이 힘은 각 핵의 각운동량이 반정렬하도록 하는 핵자 사이의 힘을 제외한 다른 모든 상호작용을 :.r 시한다. 이 모형은 준-스핀의 간결한 방법으로 정확히 풀 수 있다. 이 방법으로는 앞에서 간단히 제시했던 초전도핵의 분광학적 성질의 대부 분을 정상적으로 이해할 수 있다. 특히 그것은 핵자 계에서 중요한 새 로운 양자수 시니오리티 (Senio r ity ) 수를 도입한다. 이 양자수는 해들을 각운동량이 반정렬되지 않은 핵자 수의 함수로, 에너지가 층가하는 순 서로 분류할 수 있도록 해준다. 따라서 짝수-짝수인 초전도핵의 기저상 태는, 열린 주껍질의 모든 핵이 쌍으로 반정렬된 시니오리티 0 의 상대 이다. 실제적인 협의 일반적인 경우와 열린 주껍질의 다른 부껍질 ji,j2,j s• ·· • J.P . Sch iffer , Ann. Phy s. (N.Y.) 66(197 1). 798.
예 분 포되 어 있는 ( 준 축 퇴된 ) 핵 자계에 대 해 서 쌍 짓기의 효과를 정확 히 다 루는 것 은 불가능하 다. 관련된 고유치문 제 는, 하트리_포크 근사의 축 퇴된 상 대의 수 를 고려하 면 , 한 차원 높은 문제일 것 이다. 그 렇 지만 이 문재 는 초 전 도 계 의 이 론 에 서 빌 어 온, 변 분형의 유사 한 체 계로 써 대체 됭 수 있다 . 그 것 은 바딘, 쿠 퍼 , 슈리퍼의 방법 (보다 간략하게는 BC5 방법 ) 또는 , 형 태 는 다 르 지 만 등등 한, 하트리 -보골리 우보프의 방법 이 다. 이 방법은 변분공간을 모 든 슬 례이터 행렬 식 IF1), IF2 > …의 공간으로 확장하는 것 인 데 , 상 태 IF i > 에 서 상태 l j m > 예 한 핵자가 차 있으면, 상 태 l j -m > 도 또 한 차 있 도 록 한다. 이 번분을 간단히 하기 위하여 BC S 방 법 에서는 핵 자수 N 은 보존하지 않고 그 평균값만을 보존하는 목별 한 시행 합 수 룹 이용 한 다. B CS 방 법 은 결 국 기 저 상태 물 새로운 기저상태인 |BCS> 와 생 성에 매 우 큰 에너지 를 요 하는 준구입자 로써 근사시 켜 기술한다• 채운 정도에 비 교적 무관한 이 큰 에너지는 첫 째 들 뜸 상태의 작고 불변인 밀도를 설 명한 다. 실험과 비 교했을 때, 초전 도핵의 스핀과 자기모멘트, 전자기적 전 이 등의 성질둘을 설 명 함에 있어, 준 -입자의 묘사는 매우 성공적이다. 핵 의 해 밀 토니안 H 를- 표현하 기 위해 하트리一포크의 방법과 함께 기 저상태 |BCS > 를 이용하 겠 다. 이 방법은 또다시 완전한 해밀토니안을 준 -입 자 배 열의 표현기저 를 정 의하는 단체 해밀토니안 Hacs 와 이 준입 자 들 사 이 의 찬류상호작용인 2 체 연 산자 Vec s 로 나눌 수 있도록 한다. 이 잔유상 호작용을 여하히 찰 다루느냐 하는 것이 이론을 세우는데 중 요 한 관전 이다. 2 초전도의 간단한 모형 (1) 쌍짓기 힘 열린 주 껍 질 속의 동일한 입자로 구성된 핵자계의 분광학적 특칭에 나 타나게 해주는 메카니즘을 이해하기 위하여 우리는 멘먼저 양자수 (nl;) 인 한 껍질속의 입자만을 생각하자. 개개의 상태는 각운동량 j의 두영 m j =국, -j+l, 나에 대하여 축퇴되어 있다 . 이 계를 (JY ' 으로 쓰기로 하자. 동일 한 껍질 i 속의 두 핵자 사아의 상호작용은 파울리원리에 의하여 T=l 이고 ]=파수인 상태에 한정된다 . 실험치에서 볼 수 있듯이 이 상
호작용은 ]=0 인 경우에 복히 효과가 있다. 이 효과의 요점울 고려하는 간단한 험인 짝짓기 힘을 도입하자. 그것은 다음의 행렬요소로 정의된 다: <( j)2J M I V 사 (j)2J M > =-G( 요근 )o,o (7.1) 여기에서 G 는 차원이 에너지와 같 고 G>0 인 결합상수이다. 이 힘은 ]=0 상태의 에너지를 내려주고 다른 모든 상태 (]=\=O) 를 에너지 2 험 에 축되된 상태로 놓아 둔다 .
 2£j ..... . .. .. .. .. . ]=\=O 2£j l AE= 요尸]*O
2£j ..... . .. .. .. .. . ]=\=O 2£j l AE= 요尸]*O
식 (7.1) 의 인자 (2j +1) 은 ]=0 의 에너지 준위가 낮아지는 정도가 j =O 에서 보다 큰 j에서 더욱 중요해침을 시사하고 있다• 포크공간에서 양성자 및 중성자로 꽉 채워져 있는 핵심을 나타내는 하트리-포크의 기준상태를 IF> 로 표시하자. 껍질 j에 있는, JM 으로 결합된, 두 핵자를 그래프와 벡터로 표현하면 다음과 같다.
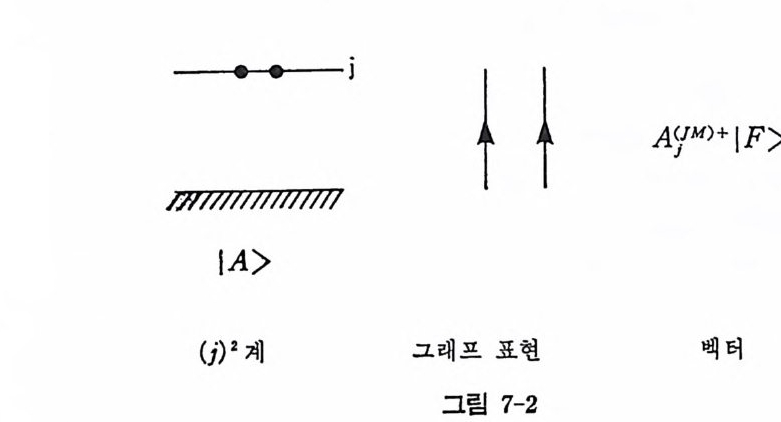 • • t 1
• • t 1
여기에서 A f M ) += 」 집~ M~m ~]a;,' a;.,,_,. (7. 2) 이며, 인자 1/ ✓ 2은 규격 화 상수이다; Clebsch Gordan 계수의 성질을 이용하여 다음을 쉽게 보일 수 있다.
는 상태쌍 (|jm> , |j -m>) 에 다음과 같은 스핀연산자 5(m) 을 대응시 킨다 : 다음 두 경우에는 스핀 1/ 2 인 계의 고유치 물 가지고 S,.(m)=+1/2, (ljm ), lj -m> )이 모두 찬 경우 sz(m)=-1/2, (|jm> , |j -m> )이 모두 빈 경우 세번째 경우에는 스핀 0 인 계의 고유치문 가진다; S,,(m)=0, (ljm ), lj -m> )중 한 상태만 찬 경우 포크 표현에서, 이 세번째 성분 S,.(m) 은 다움과 같이 쓸 수 있다. sz (m) = T1 (a;ma + a;_ m aj -m -1) (7. 7) 계 속하여 각운동량의 교환관계 식 을 만족하는 연산자 S+ (m) 과 노 (m) 을 정의하자. [S,, (m) , S+ (m) J= S+ (m) , [S,, (m) , s_ (m) J= -S _ (m) , [S+ (m) , s_ (m) ]= 2S,, (m) (7. 8) 은
S+(m) = (-1)i- aJm a 1-m, s_ (m) = (-1) j- naj -..a j n (7. 9) 이면 만족된다. 이것들은 각각 한 쌍의 핵자를 상태쌍 (lim> , l j -m> )에 생성시키 거나 소멸시킨다. 계의 전체 준-스핀연산자를 도입하자. S一 = mI>;d S-.* (m), (7.10a) S,,= mI>;O S,,(m), (7.10b) S+= mI>;O S+ (m) , (7.10c) S-= m2>O S-(m) (7.10d) 그러면 쌍짓기 힘 (7.6) 을 다음과 같이 쓸 수 있다. VA=-GS+S- (7.11) 또한 관계식 S+S-=S2-S;+S 으로부터 (j )N 계의 에너지를 바로 얻을수 있다. 에너지의 고유치 E(S,Sr)=-G(S2-S;-Sr) 는 전체 준-스핀 5 와 5 의 두 영 Sr 로 분류될 수 있다. S., 는 식 (7.7) 과 (7.10b) 에 의하여 입 자수 N 에 관련된 상수이다. S 론방 (N- 요근) (7.12) 결과적 으로, 스펙트럼은 전체 준-스핀 S 에만 의존한다. S 가 취하는 값은 다 음과 같다. Smi a S: S S :Sm ,., Smi n =S r, Smax= 2j+2 1 마 지막 값은 식 (7.10a) 의 모든 준-스핀 S(m) 이 정렬되어 있을 때에 해당한 다. 결국 E(S) =-c{s2-+(N- 요분 )2+ 李 (N- 브근)} (7.13) 이 된다. 가장 많 이 구속된 상태는 준-스핀이 최대 즉 S=Saux 인 상태이다. 준 스핀 S 대신에 우리는 S 에 직결된 다른 양자수 죽 Senio r ity 양자수 V 풀 이용한다. V=-2S+— 7_ (7. 14) 2j+ l 식 (7. 13) 은 다음과 갇이 된다. E(V) =-G~{(2j+ 1) -N-V+2} (7.15) 3) 쌍짓기 스펙트럼에 관한 토론 N 개의 쌍이 있는 경우의 토론에 국한시키기로 한다. 기저상태는 S=Smu 또는 V=O에 해당한다. 죽 모든 핵자들이 상태쌍 (1j m > |j-m >) 에 쌍을 지 어 있다. I± 가 단체 연산자들의 합 j±( 1) + j土 (2) +… ... j ±(N) 일 때,
l~lf> = O, J+ If> =I-If > =0 이고, 따라서 전체 각운동량 I 는 0 이다(소개의 성질 iii). 들뜸상태는, 에너지가 커지는 순으로, 전체 준-스핀이 다음과 같은 경우이다. S=Smu— 1, Sm .. -2, …… 또는 Senio r ity 가 V=2,4,6… … 인 상태이다. 죽 2 개 (V=2), 4 개 (V=4) 등의 핵자만이 쌍을 짓지 않 은 상태이다. 식 (7.15) 에 의하여 V
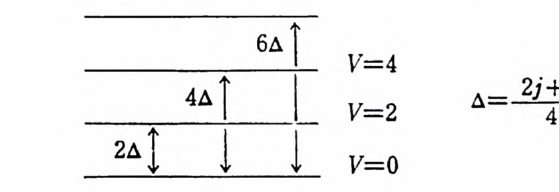 6AI V= 4
6AI V= 4
각각의 V( =t= O) 에 대하여 모든 핵자들의 각운동량의 가능한 결합은 매우 많지만, (j )N 계에서 껍질모형의 상태의 축퇴는 쌍짓기힘 때문에 많은 경우가 제거된다. 다시 말해서 상태밀도가 작다(소개의 성질 i). 기저상태와 첫번째 들뜬 상태 V=2 사이의 에너지 간격은 다음과 같 다. E(V=2)-E(V=O)~~G=2A, N< 2 j+ 1 (7.16) 이 것은 두 핵자의 ]=0, T=l 상태 쌍짓기 에너 지 에 해 당한다. 2A 의 에너지와 다른 스펙트럼 E(V+2) -E(V) =G( 쁘른-f) (7.17) 온 핵자수 N 에 무관하다. 정확한 해 (7.15) 의 한 독성온 핵자수 N 의 함수로 기저상태 (V=O) 의 에너지가 특별하게 변화하는 것이다. 그것은 N 의 제곱으로 변화하
지 않고(만약 에너지가 두 물체의 연결 방법수 N(N-l)/2 에 비례한다 면 N 요] 비례할 것이다) 선형으로 변화한다 (N < 2i +l). E(V=O)~_ (2j ; l) G 쑨 (7.18) 기저상태는 N/2 개의 쌍이 있는 상태로서, 각각의 쌍은 - 2j+2 1 G 의 결 합에너지를 전체 에너지에 기여한다. 이것은 준-독립적인 쌍의 상태 이다(소개의 성질 iv) . 3 BCS 파동함수 핵의 쌍짓기에 관한 앞의 간단한 취급에서 실제의 경우에 비해 두 가 지를 제한해야 했다 : 유일하게 부껍질 j만울 고려하고 간단한 힘을 이 용했다. 지금부터 이 제약들을 제거하기로 한다. 열린 부껍질 ]\,i2· .. 에 분포되어 있고, 껍질모형의 2 체력 V 로써 상호 작용하는 동일한 N- 핵자계를 생각하자. 앞의 간단한 모형에 따르면, 기저상태의 합당한 근사는 모든 핵자들 이 각 운동량이 반정렬하도록 쌍으로 결합되어 있는 파동함수이어야 할 것이다. 원리상으르 이 근사해는, 상태 (j m) 과 (j -m) 이 동시에 차 있 는 슬 레이터 행렬식 |F1), IF2> …에만 국한된 힐버트 공간에서 핵 해 밀토니안의 고유치 문제를 해결함으로써 얻을 수 있다. 이렇게 되면 핵 문제는 또다시 너무 큰 차원의 문제로 된다. 그 렇 지만 핵자-핵자 상호작용의 쌍짓기효과는 특별한 시행함수 즉 바 던, 쿠퍼, 슈리퍼의 파동함수에 변분원리를 적용하여 간단히 다룰 수 있다. 우리는 이 절에서 멘먼저 BCS 변분파동함수의 모양과 성질을 논의하 기로하자. 상태쌍 (lim >, li- m > I) 에 한 쌍의 핵자를 생성시키는 연산자 P},. 올 도입하자. Pl'= (-)j-•a; 'a;_,. (7.18) 이 식 에 도입 된 상수는 전체 각운동량 ]=0 일 때 Clebsch-Gordan 의
결합상수에 해당한다(식 (7.5)). 쌍생성 연산자 p ;m 과 A;n,( 식 7.2) 는 서로 다르다. 전 자는 사실상 ]=0 으로 결합된 쌍을 생성하고 , 우 자는 각각 명시된 상태를 차지하는, 결합되지 않은 쌍을 생성한다. 표기물 간단히 하기 위 하여 다음과 같이 쓰자. p:=pjm (7. 19a ) lr>=Um>, a:= a;m (7. 19b) lr>=U-m>, a:=a 노 (7. 19c) 각각의 상태쌍 (Ir>, Ir>) 에 파동함수 中 r= (ur+v 本) 10> (7. 20) 를 대옹시키자. 여기에서 IO> 은 입자의 절대진공 이다. 여기에서 따온 두 상태 (Ir>, Ir> )가 찰 확삼진폭 이고, u, 은 그것이 빌 확률진폭이다. 물돈 다음 조건이 성립된다. v;+u;=l (7. 21) 함수 中,은 정해진 핵자수를 가지고 있지 않다. 이 함수에는 입자수 가 0 인 성분과 입자수가 2 인 성분이 있다. 입자수가 1 인 성분은 없다. 바딘, 쿠퍼, 슈리퍼의 파동함수는 파동합수 (7.20) 을 임의의 핵자수 N=0, 2, 4, … 00 에 대 하여 일 반화한다. I BCS > = I} ,fr,= 1: (u 『 + v,P: ) I o> (7. 22) 여기에서 무한곱은 모든 가능한 r=(n,l, j ,m1)0) 을 취한다. 유한개 의 입자수를 가지는 상태에 대한 성분은 다음과 같다.
(a) 이것은 독립된 쌍 의 함수이다. 다시 말 해 쌍생성자들온 a+ 의 반 교 환관계 에 의 해 교환된다. [p: , P :]= 0 (7. 24a) 배타원리는 명백히 만족된다. (p:) 210) =0 (7. 24b) (b) 이 상태는 조건 (7. 21) 에 의하여 1 로 규격화되 어 있다.
bj .. =Uj aj .. - (-)j-마아- .. , (7. 29a) 생성연산자(에르미트 공액)이다. b}. . =Uj a j,. . - (-)i-.. V ja J- ... (7. 29b) 우리는 진폭 U 와 V 가 회전에 대하여 불변인 에르미트형 해밀 토 니안 의 해라고 가칭했다 . 따라서 그것들은 각각의 각운동량에 의존하지 않 는 실수로 택할 수 있다. 표기를 간단히 하기 위해 다음과 감이 놓자. br=bj . . , b,=bi- .. (7. 30a) 5r= (一)i -v i (7. 30b) 따라서 변환 (7.29a) 와 (7.29b) 는 보다 간략하게 쓸 수 있다. b,=11,a , -v,a: (7. 29a) b:=u,a: - v,a, (7. 29b) (e) 기준상태 IBCS> 의 준-입자는 페르미온이다. 실제로 정의 (7.29) 는 반교환관계를 준다. [b, ,b tJ + = (u; + 파) 8rs= 8' [b, ,b 』 +=0, 〔競 b :J +=O. 선형변환 (7.29) 는 반교환관계를 보존한다. 이 성질 때문에 아 변환은 정준변환이라 불리운다. (f) 상태 |BCS> 의 준-입자의 성질은 그것의 파동함수를 계산함으로 써 나타난다. b: IB CS ) ==bat: ( sun*,r +( uv,,P+:v ), psI*T: r ) (1us0 +) VsPn 10 > (7. 31) 준-입자 상태는 핵자가 홀수개인 상태이다. 이 상태가 상태 IBCS> 와 다른 점은 식 (7.31) 의 무한곱에 상태쌍 (Ir>, Ir> )가 빠져 있고 한 핵자가 (확률 1 로) 상태 Ir> 에 있는 것이다. 마찬가지로 두 준-스핀 상태
a;b ; I BCS >= a:a: '*IT' ·' (u, + v,p ;) 10 ) (7. 32) 가 상태 |BCS> 와 다른 점은 두 상태쌍 (Ir>, Ir>) 와 (Is>, Is>) 가 없고 두 핵자가 (확률 1 로) 상태 Ir> 과 |s> 에 있는 것이다. 기저상태의 도입은 그 진공으로부터 준-입자를 생성하는데 큰 에너지 가 요구될 때에만 소용이 있다. 이 경우에 계의 첫번째 들뜸상태는 새 진공으로부터 생성된 적은 수의 준-입자로써 근사적으로 기술될 수 있 다. 우리는 이것이 실제로 (7.31) 과 (7.32) 의 들뜸상태의 경우라는 것 을 알 수 있다. 왜냐하면 무한곱에서 빠진 쌍 (Ir>, Ir>) 와 (Is>, Is>) 의 결합에너지가 없어지기 때문이다. 4 BCS 방정식 1) 변분문제 문제를 간단히 하기 위하여 하트리-포크 문제가 닫힌 2 중껍질의 어 떤 계에 대하여 풀렀다고 가정하자. 우리는 이 결과를 오직 독립된 입 자들의 파동함수의 완전한 기저를 얻기 위하여 사용한다. 따라서 핵의 완전한 해밀토니안을 원래의 형태로 써 보자. H= L (e, -V,) a:a, + 上4 r.Ls, 1,u
신, 식 (7.27) 의 핵자수 연산자 』 / 울 도입함으로써 평균값 N 을 보존 하는, 보다 덜 구속적인 방법에 만족한다면,
Eac,= < BCS I H-.-1 .A/ I BCS > =E 。 -.-1 N (7. 38) 연 산자 %’ 는 a:a, 형 의 항들을 포함한다. 식 (7. 33) 과 (7. 27) 로부터 , T- .-1』 / = g ( £,-V, 국 )a:a,. %' 는 또한 (J: a:a,at 형 의 상호작용항을 포함한다. t=--44 -rIs I:u
한되지 않았다는 점을 제외하고는 바로 하트리-포크 입자에너지와 같 은 형태이다. 이번에는 모든 입자상태 s 로 확장되었는데, 이 무한합의 각 각의 항은 점유확률 파에 비례한다. 마찬가지로 에너지 간격 Ar 울 도입하자. Ar=- 令 ~ (-)1,-.. , +i,-.. ,
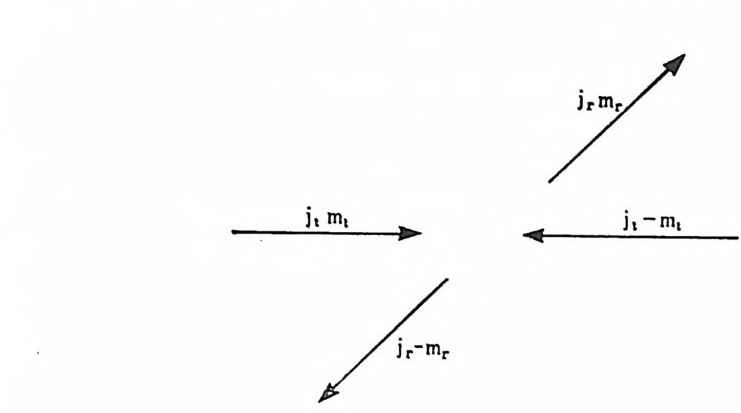 /
/
이렇게 정의하면 식 (7.39) 의 BCS 에너지는 다음과같은형태로된다. E11cs= ~ {(e,-A-+ 임
진폭 tlr 과 t ’ 『사이의 관계식d vr (7l.l r21=) -으—로U r부 ’터 , d vr 또한 간격 As 의 v, 에 대한 의존성 (식 (7.41) )으로부터 : As= - 강 (-) 1,-m,·1, -m , u .v,(u 『 - 운) 운 얻는다. 식 (7.42) 로부터 시작해서, 필요할 때에는 첨자를 r ➔ s, s ➔ r 또는 r->t, t ➔ r 로 바꾸고, Ar 속의 행렬요소의 대칭성을 이용해서 계산하면, —aav, EB Cs=2 (er-A) v 广 -A, u;v_, 짜 =O 또는 2 (e,-A) u,v,-t:;. , (u;-v~) =0 (7. 43) 을 얻는다. 식 (7.40) 과 (7.41) 에 따르면 자기에너지 g와 간격 A, 은 우리가 찾 는 진폭 v,,v,, ••• 의 함수이므로, 위의 조건 (7.42) 은 새로이 자체부합성 문제로 된다. BCS 방정식은 식 (7.21) 을 이용하여, 수치적인 해를 구하기 쉽고 해 석에 편한 다음과 같은 형태로 쓸 수 있다. 2u,v,= ✓ (E,-AA,) 2+A: ’ (7. 44a) t 4: -짜= ✓ (&e-,A-)A2 +A: ’ (7. 44b) 짜=방 (1+ 詞됴\), (7. 44c) V 국 (1- ✓ (e,E_:::)A2 + A: ) • (7. 44d ) 이 식에, 식 (7.35) 의 평균값 N 의 보존조건에서 나오는 A 에 대한 조건을 첨가해야 한다.
2 ~ 짜= 홈 난 _ E.『 n)=N (7. 45) BCS 방정 식 (7. 44) 와 (7. 45) 는, 다음과 같은 방법 으로 반복에 의 하여 풀 수 있는, 비대수계를 이룬다. i) 초기시행치 V,,V 어 •• 룰 선택한다. ii) 사용하는 하트리 -포크 기 저 에 대 한 상호작용의 행 렬 요소를 알아서 식 (7.40) 과 (7.41) 의 정의에 의하여 E.,와 Ar 을 계산한다. iii) E.,와 Ar 의 값을 가지고 식 (7.45) 를 풀면 파라미터 A 가 결정된 다. iv) 과정 ii)와 iii)에 의하여 결정된 e. ,,A,,A· 를 식 (7.44) 에 넣어 u v‘’ …의 값을 새로이 구한다. 이 새로운 값들을 가지고 과정 ii)부터 반 복한다. 반복은 과정 v i)에서 얻어진 값 따 ,vs, …이 계산에 이용된 값 v~,v;,··· 과 같아질 때까지 계속한다. 하트리-포크 방정식에 대하여 언급한 수령에 관한 여러가지 주들은 마찬가지로 타당하다. v 霞 •• 의 초기시행치에 해당하는 처음 에너지에 가장 가까운 국값으로 수령 한다. 초기 값을 다르게 잡은 집 합들을 이 용 하여 에너지를 구함으로써, 그 국값이 정말로 최소값인지를 확인해 불 필요가 있다. 4) BCS 해에 대한 토론 식 (7.44) 와 (7.45) 의 해 중에서 항상 가능한 것은 다음과 같은 자명 한해이다. A,=0, u,v,=0, (임 의 의 r 에 대 하여 ) (7. 46) 이 경우, 식 (7. 44c) 와 (7. 44d) 에 의하여, 짜 =l, u;=O, e.조김 일 때 , u;=O, 짜 =1, E.r >A 일 때• 로된다. 정의 (7.40), (7.41), (7.42) 를 생각하면 자명한 해는 하트리-포크 해에 해당한다는 것을 쉽게 알 수 있다. 아래 그립과 같이 E.조김인 모 든 준위는 확률 1 로 점유되어 있고, E.;키인 다른 준위는 비어 있다.
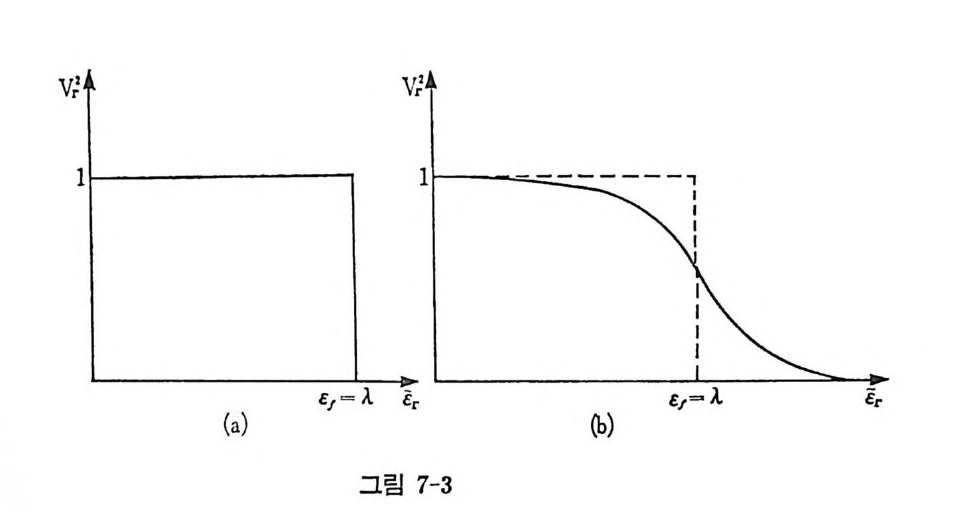 v;• v;
v;• v;
에너지의 차원을 가진 파라미터 A 는 이 경우에 페르미에너지이다• 쌍짓기 상호작용이 강하면 다음과 같은 다른 해가 존재한다. A,=;=O (7. 47) 식 (7.44d) 에서 점유확률 파의 형태는 핵자의 페르미분포가 급격히 변화하지 않는다는 것을 보여 준다. 그러나 짜 ➔ 1, £. A 일 때, 로 되고 & A 일 때에는 점유확률이 그림 (b) 와 같은 모양으로 된다. 쌍짓기 상호작용은 페르미준위 A 의 아래 상태에 있는 입자들을 그 위에 있는 상태로 확산시킨다. g이 A 근처인 입자들만이 이 확산의 영 향웅 크게 받는다. 이 확산의 세기는 준위 A 부근의 점유확률 짜의 변 화에 의하여 측정된다는 점에 주목하자. 쁘aE., - LI ,_,==키l ~- 上2A, 페 르미 준위 부근의 확산은 식 (7. 41) 의 A, 안의 쌍짓 기 상호작용이 강 할수록 크다. 일반적인 경우에 BCS 방정식의 타당성을 논의하는 것은, 그 식이 복 잡하기 때문에, 실험과 비교하는 것 이외에는 어려운 일이다.
그러나 우리가 논의 할 수 있는 간단한 경우는 식 ( 7.1 ) 과 같은 간단 한 쌍짓기 힘 VA 로 써 상호작용하고 있고 부껍질 ]· 안에만 N 개의 입자 가 있 는 경우이다. 우리는 이 문제의 정 확한 해를 안다. N쌍에 대하여, 기 저상태 의 전 체 에 너 지 는 Senio r ity V=O 일 때 식 (7. 15) 로써 주어 진 다. E. xac t=―운 N {(2 j +1)- N +2} (7. 48) 상태쌍 (1j m >, 1 j -m > )의 점유확률 파 은 모두 같다. v2= 2jN+ l (7. 49) 이 것은 조건 (7. 45) 를 찰 만족한다. 2 ~ 짜 =2 훑「 tol= N 정확한 진폭 (7.49) 는 BCS 방정식 (7. 4 4d) 와 같 은데, 이 것 은 자기에 너지와 e=~Gv2 =-~G (7. 50) 에너지간격 (G>O) A=+ (2j+ l) Gu i · =+G ✓ ~ (7. 51) 을 계산하여 이 결과를 v2 에 관한 식 (7.44d) 에 넣어서 증명할 수 있다. 식 (7.51) 의 에너지간격 A 는껍질이 시작할때, 즉 N=O 일 때와껍 질이 끝날 때, 죽 N=2j+ l 일 때에 0 이다. A 는 껍질의 중간 죽 N= (2j + l)/2 에서 가장 크다. (2j + I)G Amax= 8 이 변화는 아래 그림에 나와 있다. 페르미면의 확산은 껍질의 중간에서 최대이다. 자기에너지는 식 (7.5) 과 같이 쌍의 수 N/2 에 비례한다. BCS 근사에서의 기저에너지는, 식 (7.42) 로부터
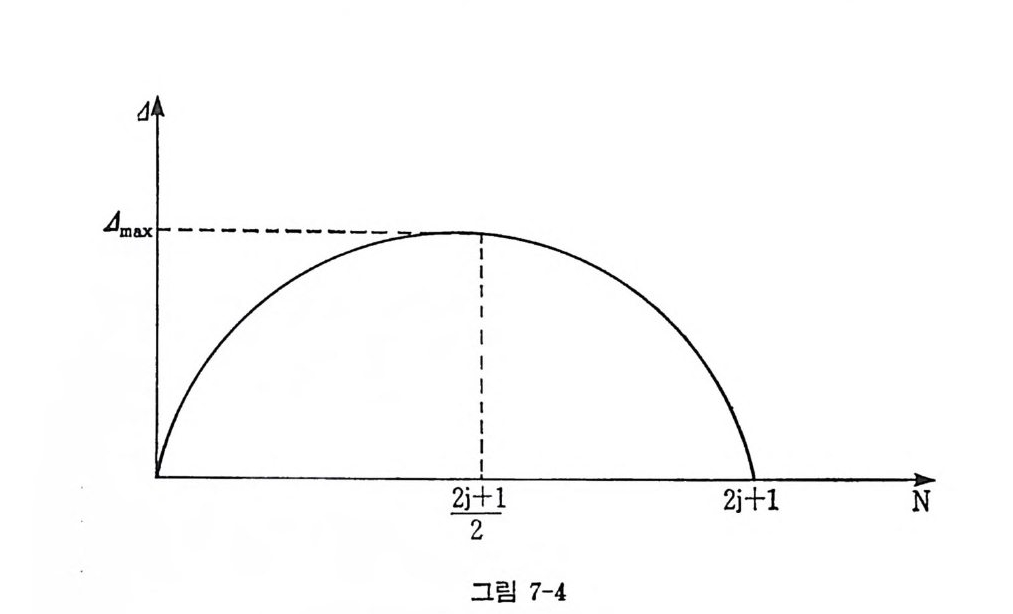 d
d
E~=Encs+ .-1 N=- 운싸 (2 j +l)-N+ 귈紀 이 된다. 이것을 식 (7.48) 의 정확한 에너지와 비교하면, BCS 근사의 상대오차는 다음과 같은 정도임을 알 수 있다. oE=Em~el 仁• 2j2+ l 이것은 상태 j의 축퇴가 클수록 작다. 에너지가 비슷한, 죽 E.j,,E.j,,E.1 , •• 인 몇몇의 부껍질이 열린 실제적인 경우에 축퇴는 다음과 같다. O= ~ (2j, + 1) (7. 52) i 여기에서 합은 입자들이 확산할 수 있는 페르미준위 부근의 모든 부 껍질에 대하여 취한다. 가능한 상태수는 이 부껍질의 에너지간격에 비 하여 상호작용이 강할수록 많다. 결국, 각각의 부껍질의 축퇴는 작다 하더라도 쌍짓기 행렬요소가 크면 기저상태의 BCS 근사는 좋다.
5 BCS 표현에서의 핵 해밀토니안 식 (7.37) 의 변분원리로부터 나온 상태 |BCS> 를 기준상태로 잡아 식 (7. 33) 의 완전 한 해 밀 토니 안을 표현하자. 연산자 %'=H-A ✓ V 에 W i ck 의 정리를 적용하자. 완전히 축약된 항은 상태 IBCS> 에 대한 %'의 평균값을 준다. 그것 은 제 4-(2) 절에서 계산되었다. 식 (7.39) 의 에너지 Eecs=E '; -AN 이 그것이다. 완전히 축약되지 않은 항은 기준상태 |BCS> 의 준-입자 생성연산자 와 소멸연산자 합,f r … 동으로 표시되어야 한다. 그러기 위해서는 정의 식 (7. 29a) 와 (7. 29b) 의 역 을 취 하자. (.Ir= 14rbr + Drb,+ (7. 53a) a: =u .b : + v,b, (7. 53b) 제 2 차의 정상곱을 포함하는 항은 운동에너지항과 한번 축약된 상호작 용항으로부터 나온다. : a;a, : = : (u,b; + ii,b,) (u,b , + ii,b,) : =u;b;b,-毋 b ; b, + u,v, (b;b; + b,b,) , 계 산이 완료되 면 b+, b, … 에 2 차인 항이 두개 나오는데 이 것을 각각 H11 과 H20 로 표기 하자. H11= I: {(e,-A) (u ; - 파) +2Ar1lrvr}b:br, H20= I: {2 (e, -A) u 『 v , -~ . (u;- v ~)} (b:bt + b,b,) (7. 55) 파라미터 t lr,vr, …의 값은 변분원리로부터 정해졌다. 식 (7.43) 에 의 하여 H2o=O (7. 56) 이 된다. 식 (7.56) 은 초전도를 다루는 출발점으로 생각할 수도 있을 것이다. 시행함수 IBCS> 에 턴분원리를 적용하는 대신 우리는 정준변환 (7.29a) 와 (7. 29b) 를 정의하여 이 변환의 계수 v,, v,··· 로 하여 금 H 속의 b:b,스
와 b,b, 같은 2 차항들을 없애버리도독 할 수 있을 것이다. 이것이 하트 리-보골리우보프의 정준변환 방법이다. 마지막으로, 상호작용에서 축약되지 않은 정상곱 Vscs=- 1;r f'.
이 근사법의 정당성은 기저에너지 E~ 과 준입자에너지 E, 의 정의에 내포된 평균장과 쌍짓기의 효과의 중요성에 근거한다. 실제로 그것이 그러한지는 실험과 비교해 보아야 한다. 우리는 첫째, 들뜸상태가 동일한 핵자배열로써 기술되는 핵에 국한 해서 논의하겠다. 이중으로 마법인 핵심을 가지고 있고, 중성자에 대해 서이건(니첼, 주석, 납의 동위핵), 양성자에 대해서이건 (N=20,50,80 동중성자핵) 부껍질이 다 차지 않은 핵둘이 그것이다. 이 근사에 있어서 짝수-짝수핵의 기저상태의 파동함수는 IBCs > 로 근 사된다. 이 파동함수를 결정하는 변분문제는 또한 식 (7.59) 와 같 이 이 기저상태의 기초들뜸에너지 Er 을 결정하여 둘뜸상태 문재도 해전한다. 준입자 생성연산자는, 식 (7.31) 에서 보는 것과 같이, 입자수의 반전 성을 바꾸므로 다 차지 않은 부껍질 속의 동일한 핵자수 N 이 울 수인 핵과 짝수인 핵을 나누어 생각해야 한다. a) N 이 홀수인 핵의 들뜸상태 N+ l 이 짝수일 메 식 (7. 35) 와 (7. 37) 의 해인 상태 |BCS> 로부터 출발하자. 하나의 준입자상태는 식 (7.31) 에서 이미 계산되었다. b:IBCS>=a: II (u,+v,p: ) IO> (7. 61) ‘수 r 이것은 껍질모형에서 정의된 첨자 r 인 상태를 제의한 모든 입자들의 쌍이 지워진 상태이다. 이 상태의 입자수의 평균은 홀수이다. 우한곱 (7. 61) 은 쌍 s::\=r 을 포함하지 않으므로, BCS 근사에 서 N 이 홀수인 핵 의 기처상태를 계산하기 위해서는 수정된 시행파동함수 (7.61) 에 변분 원리를 새로 적용해야 한다. 그렇게 하면 진폭 v,, v,··· 에 대하여 식 (7.44), (7.45) 와 유사한 식이 얻어진다. 유일한 차이는 상태 r 이 식 (7.40), (7.41) 의 모든 합에서 제의된다는 것이다. 가능한 각각의 상대 의 축되 Q(식 (7.52) 를 보라)가 커질수록 상태 r 을 제의하는 것이 변 분식의 해에 영향을 덜 미치게 된다. 따라서 우리는 N 이 홀수인 핵의 상태를 식 (7.61) 의 준-입자상태로 기술하겠는데, 여기에서 기저상태 |BCS> 는 상태 r 을 포함시키거나 포 함시키지 않거나 하여 얻은 핵자수 N-1 인 핵의 기저상태의 근사이다. 그 상태의 에너지는, 식 (7. 60) 에 따라,
이 된다. 홀수핵의 스펙트럼 AEr,AEs, …는 이 핵의 기저상태에 대한 것이지 상태 |BCS> 의 기저에너지 Eo 에 대한 것이 아니다. ~E,=E,-E1 (7. 63) 여기에서 EI 는 가장 낮은 준-입자에너지 (7.59) 이다. 그것은 페르미 준위 A 에 가장 가까운 자기 에 너 지 E.1 이 다. E.1 ~A 라 놓으면 식 (7. 59) 는 다음과 같 이 된다. E1=Et -1 +t. . (7. 64) 이 식으로부터, 스펙트럼은 4Er= ✓ (g- A) 2+A:-A (7. 65) 이 된다. 식 (7.41) 과 같이 모든 입자상태에 대한 무한합으로 정의된 에너지간 격 A,A” …온 서로 차이가 크지 않다. g이 A 에 가까우면, 첫번째 둘 뜸상태에 대한 최소에너지 간격 AE, 은 작을 것이다. 죽 홀수핵의 애너 지간격은 크지 않다(소개의 성질 iii). 부껍질이 찬 정도의 함수로서 준입자준위의 에너지가 행동하는 형태 는 아래와 같이 요약할 수 있다. N 이 증가할 때 £조업안 한 (e,-i!) 2
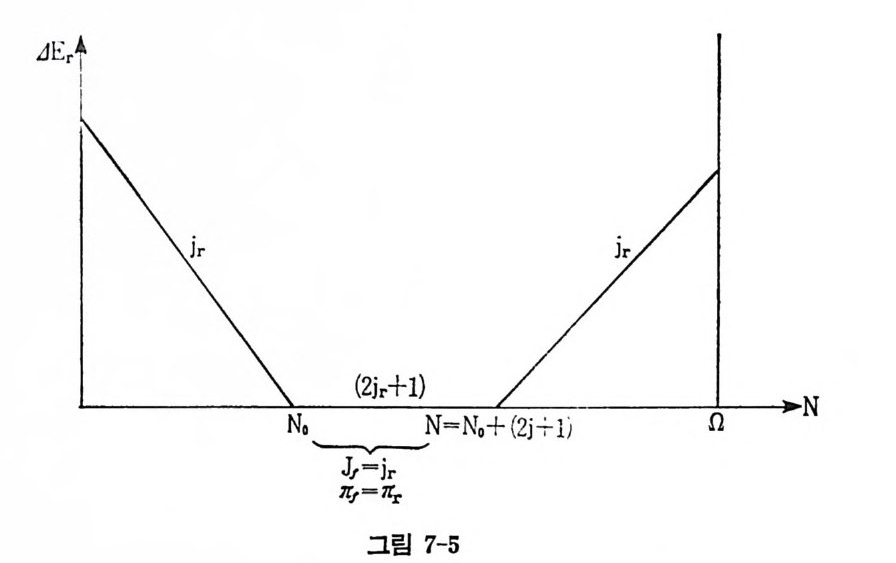 4 Er 1凰P
4 Er 1凰P
은 감소한다 . 그것은 부껍질 ].J I lr 이 찼을 때 No 에서 0 이다. 부껍질 jr 이 차기만 하면 그것은 증가한다. N。 ~ N ~No+(2 j ,+1) 인 홀 수핵에시 는, 준입 자 파동합수의 성 질 (7. 61) 에 의 하여 기 저 상태 가 양자수 J,=j『' rr,=rr, 올 가진다. 홀수핵둘의 둘뜸스펙트럼은 연속된 열린 부껍질 ji,j2,j 3, ••• 가 찬 정 도의 함수로서 아래와 갇은 모양이다. 기저상태의 스핀은 차례로 ]\,j2, js· ·· 이다. 주껍질의 중앙에서, 둘뜸스 펙 트럼은 껍질모형스 펙 트럼에 대 하여 많이 역전되어 있고, 매우 복잡한 상황을 보여준다.
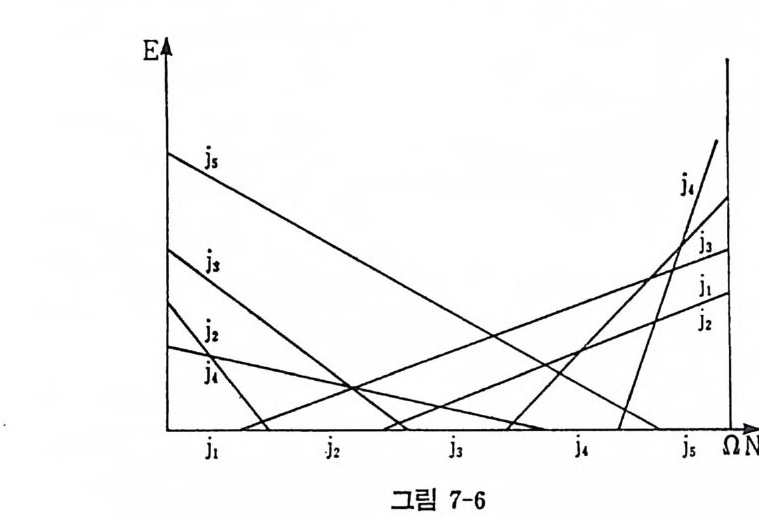 E
E
납과 주석에 대해 독립 준입자모형으로 계산한 결과와 실험결과 를 비 교한 것이 다음 그립에 나와 있다. 관측된 스핀과 반전성이 찰 재현되어 있다. 실험결과와 보다 정량적 으로 비교했을 때, 일반적으로 첫째 둘뜸상태의 에너지는 그 값이 매우 찰 맞는다. 그러나 이 비교는 이 모형의 타당성의 징후정도밖에는 되지 않는다. 왜냐하면 계산의 파라미터가 많기 때문이다• 실제로는 2 체력 과 더불어, 조정할 수 있는 파라미터로서 자기에너지 g은 도입하는 경 우가 많다. 이러한 불확실성을 없애기 위하여 우리는
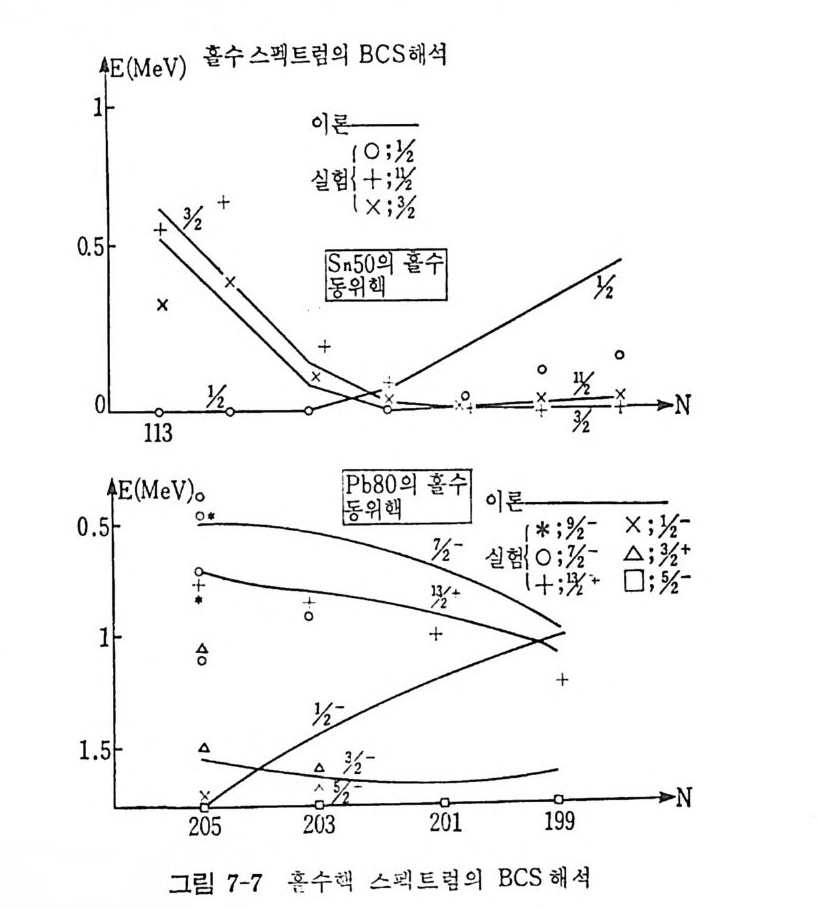 E(MeV) 홀수스펙트럽의 BCS 해석
E(MeV) 홀수스펙트럽의 BCS 해석
b:bt l BCS ) =a:a: '=IT :r , s (u, + v,N) 10 ) , (7. 66) 에너지가 E,.=(BCSIb,b.Hab:b:IBCS>=E~-2+E 사 ·E, (7. 67) 이어야 한다. 앞서와 마찬가지로 에너지 Er,Es, … 의 정의에 들어가는 진폭 vI, ••• 를 얻기 위해서는 상태 r 과 s 를 제의한 시행함수 (7.66) 으 로 변분문제를 풀어야 한다. 실제로 우리는 이것들을 제의하지 않고, N 핵자의 기저상태 해인 IBCS> 를 가지고 스펙트럼을 계산한다. 가장 낮은 에너지의 두 준입자상태는 e£ 값, &~A 인 경우에 해당한 다. 이제 그것들은 기저상태 Eo 로부터 다음과 같은 최소에너지만큼 떨 어져 있다.
Ef -2 ~Ef 으로 놓았을 때 , AE .. ~E 서 -£,~2A (7. 68) 이것이 초전도간격(에너지 도약)이다. A,~A.=A 라고 가정했다. 우 리는 다시 소개의 성질 ii) 를 얻었다. 다음 여기상태는 네 개의 준입자상태로서 b:b:bt bt II (u .. + v. . P!) I O> =a:a:a ta t “”*I Tr s tu ( u., + v.,P !) I O> 최 소에 너 지 가 £r~A, £s~A, £1~A, £E 라 인 경 우 AE,sI 꾼 ~ 4 A 이다 . 이 둘뜸상태는 두 준입자 둘전 유 상대 보다 최소한 두 매의 에너지 물 필요로 한다(소개의 성질 ii). A 의 근사치는 실험적인 질량차로 써 주 어진다 1:!..B =-BN-1+B.v (7. 69) 여기에서 B N 은 기저상태가 에너지 E1(7.64) 안 두 준입자상태에 해당하 는 N 이 홀수인 핵의 결합에너지이고 B.v = E,=Et·- 1 + ..:i, B .v -1 는 인접한 짝수핵의 결합에너지이다• BN-1=Er: -l 결국 A=AB 실험적으로 측정된 양 2A 는 Z=50 에서 2MeV 정도이고, A 가 중가함 에 따라 감소하여 납의 동위핵에서 0.8MeV 정도가 된다. 이것은 정 확 히 각각의 영역에 있는 짝수핵 스펙트럼의 간격이다. 7 BCS 방정식의 역전-쌍짓기의 유효력 BCS 방정식을 수치적으로 풀기 위해서 우선 다음과 갇이 중심을 향하 는, 특별한 형태의 2 체력을 선택하기로 한다.
V(r) = Vof (r / µ ) (13P+a33P) (7. 70) 여기에서 V o 는 깊이이고, µ는 도 달 거리이다. 우리가 다루는 것은 중성 자 또는 양성자의 동일입자계이므로, 이 형태는 두 두영자 2s +1 ,2r+1p 가 나 타 내듯이 하전 스핀 T=l 인 핵 자- 핵 자상태에 작용하는 힘만을 포 함한 다. 보동 이 두 항에 대하여 공통된 형태인자 f (r/µ) 를 택하고, 그 들 의 혼합계수 로서 a 룹 사용하는 것으로 충분하다. 펑 균장 의 변분문제 를 푸는 것을 피하기 위해, 계수 Vo,µ,a 의에 식 (7. 4 0 ) 의 하트리-포크 에너지 &이 조정 가능한 파라미터로 취급되는 경 우 가 많 다. 이 렇 게 조정 가능한 파 라미터를 많이 사용하면 실험과 일 치시키는 것은 쉬 운 일이다. 그러나 이렇게 하는 것은 이 방법의 타당 성 을 보이 는 방법으로는 적 절 하지 못하다. 이 이 론의 모호함은 대부분의 조정 가능한 과라미터를 제거하는, BCS 방정식의 반전 방법으로 써 없앨 수 있다. 이 방법으로는 독립된 준입자 의 가 정과 N 이 홀수인 핵 에서 관측된 핵준위가 얼마나 찰 일치하는지 를 바로 알 수 있 다. 이것을 하기 위하 여 우리는 문 제를 시작할 때 주어졌던 식 (7.69) 의 실 험 적인 질량차 AB 와 이 핵 둘의 실험적인 에너지 E, 을 이용한다. 준 입자의 에너지 E, 은 다음과 같 이 결정된다. E1~aB E,~E, -aB… 이 값들을 사용하여 다움과 같은 행렬을 만 들 자. Mr1=.1 4.. . (-) J,- m,+ j ,-..」 丘 WEI | ti> (7. 71) 여기에서 V 는 위의 상호작용 (7.70) 에 Vo=l 울 대입한 것이다. 벡터 Cir > , Ir> )의 위상은 Mr t가 실수이고 양인 행렬이 되도록 선 택된다 . 식 (7.44a) 와 같은 형태의 BCS 방정식 t‘『 V t=21 -EA一r, (7. 72) 을 Ar 의 정의식 (7.41) 에 대입하면 다음과 같이 된다. Ar=- 뇨4 2, (-)E,.'+j, -m,
그리하여 우리는 초전도 간격에 대하여 실수이고 비대칭인 고유치문제 를 얻는다. 기上o Ar= 2, MrIA, (7. 74) 이 수식체계에서 자유로운 파라미터는 혼합계수 a 와 힘의 도달거리 µ뿐이다. 깊이 Vo 는 식 (7.74) 의 고유치이고 Ar 은 그에 해당하는 고 유벡터의 성분이다. 물리적으로 받아들일 수 있는 해는 모든 초전도 간격이 양인 것뿐이 다. Ar>O, 임의의 r 에 대하여 Frobe ni us 의 정리에 따르면 양의 실수인 행렬 M’ 의 고유백터 중에는 항상 모든 성분이 양인 고유벡터가 유일하게 존재한다. 그것은 가장 큰 양의 고유치 -1/VoCVo
의 깊이 Vo 와 간격 Ar, 확률 파와 자기에너지 £r 을 얻었다 . 그립 9 와 10 은 이 방법에 기초한 몇 가지 토론을 제시한다. 이것을 분석해 보면 쌍짓기 효과는 파라미터 a 에 그다지 민감하지 않은데, 가 장 좋은 값은 a=-0.4 정 도이다. 도달거리 1. 7 f m 인 가우스형의 형태인자를 사용했을 때, 식 (7.73) 의 행렬 M 을 만들기 위하여 사용된 실험적인 스펙트럼은, 조사된 핵의 영 역에서, 깊이 Vo 에 대강 -25MeV 와 -38MeV 사이의 값-응 준다. 8 BCS 방정식의 역전 방법의 수렵결정에의 응용 1) 유효력의 수렴에 관한 고찰 식 (7.74) 에 나오는 고유치 Vo 는 행렬 M 의 차원 즉 BCS 방정식에 사용되는 상태 |r> 의 갯수 D 의 함수이다. 원리적으로 이 값은 D 가 충분히 크면 상수가 되 어 야 한다. 123Sn 과 2osp b 에 서 Vo 를 D 의 함수로 나타내는 아래의 결과에서 실제로 그러한 것을 불 수 있다. 표현공간은 ls112 에 서 1j1 5/ 2 까지 모든 부껍 질 이 포함될 때 까지 페 르미 준위 A 의 부 껍질들을 쌍방에서 차례로 첨 가함으로써 확장된다. 두 곡선은 페르미준 위의 가장 인접한 두 주껍질이 고려되면서부터 거의 일정해진다. 이렇
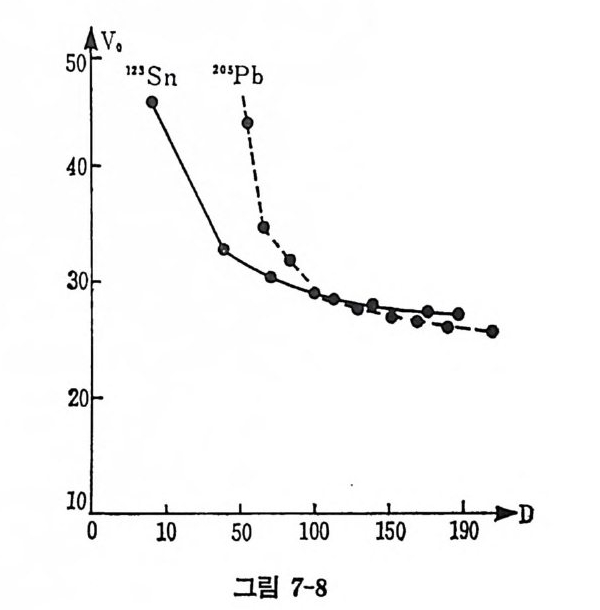 so· v, msn 2Pb
so· v, msn 2Pb
게 얻어진 힘 Vo 의 크기는 125Sn 과 2os p b 에서 같다 (a=-0. 4 일 때, V;;:::::-2 7.M e V) . 2) 간격 A 『파 진폭 V, 의 수렴에 관한 고찰 식 (7.7 4 ) 의 해에 나온 Ar, g r, v r 에 대하여 마찬가지로 이야기 할 수 있다. 차 원이 D 인 배위공간이 페르미준위의 인접한 두 주 껍 질을 포합 하기만 하면 수렴이 보장된다.
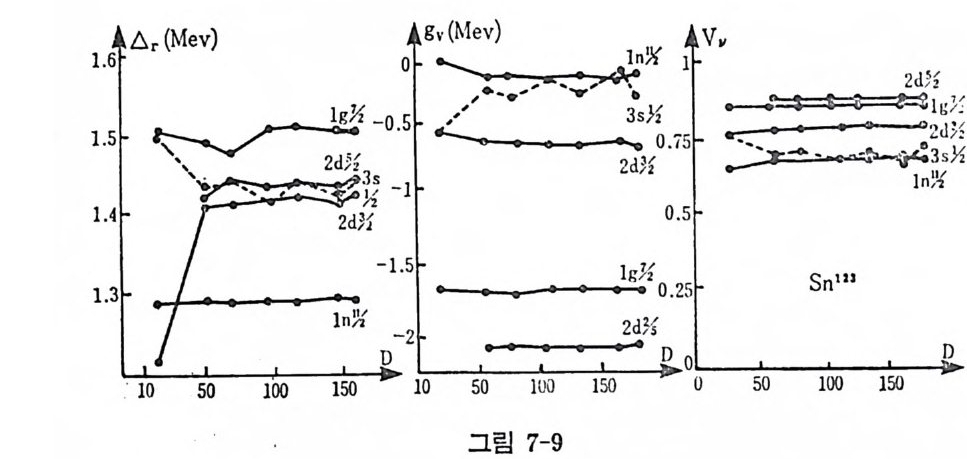 1.4 Ar (Mev) ,끈7- 0:t 二Ig v( Mev) : : 7o.s lv 二 :
1.4 Ar (Mev) ,끈7- 0:t 二Ig v( Mev) : : 7o.s lv 二 :
9 BCS 모형의 타당성에 대한 현상론적 시험 N 이 홀수인 핵에 대한 BCS 모형의 타당성은 BCS 방정식의 반전방법 의 결과로부터, 조정 가능한 파라미터의 모호성이 없이 , 평가될 수 있 다. 예 를 들어, 식 (7.74) 와 같이 관측된 스펙트럼으로부터 단순한 방 법으로 구한 깊이 V 는 주어진 핵의 영역 안에서 N 에 대하여 상수인 양이 어 야 할 것이 다. 아래 그립 은 세 값의 혼합과라미 터 a(a=O, -0. 4, -0.1) 에 대한 Vo 의 값을 보여준다. 식 (7.70) 에 주어진 힘의 형태인 자는 가우스형으로서 도달거리가 1. 7 f m 이다. 결과는 파 라미터 a 에 그 다지 의존하지 않는다. 각각의 영역에서, 에너지의 실험치로부터 만 들 어진 행렬 M 의 고유치는 평균값 부근에서 lMeV 이내로 변화함으로써, BCS 모형과 분석된 스펙트럼의 일치를 나타낸다. 마찬가지 방법으로, BCS 방정식의 반전에 의하여 주어지는 자기에너 지 cr 로부터 계산된 하트리-포크 에너지는, 정의에 의하여, 주어진 영
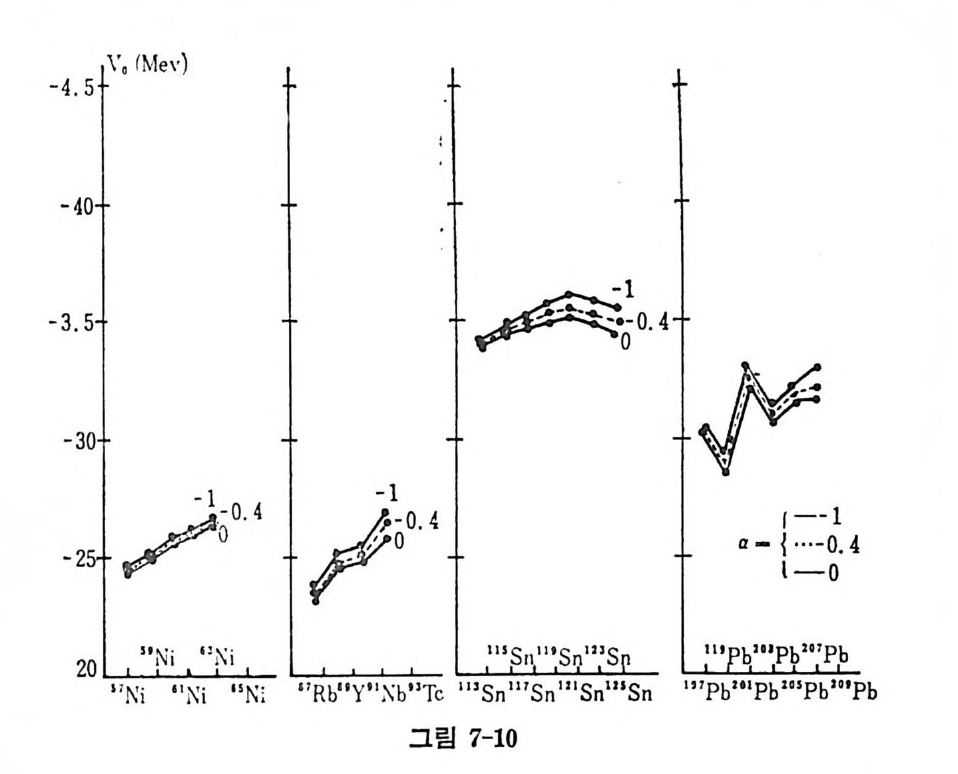 -4. 5 _\', /M e)
-4. 5 _\', /M e)
역에서 N 에 대하여 상수인 양이어야 한다. 하트리-포크 에너지는 다음 과 같이 주어진다. e,-A=g ,-bA
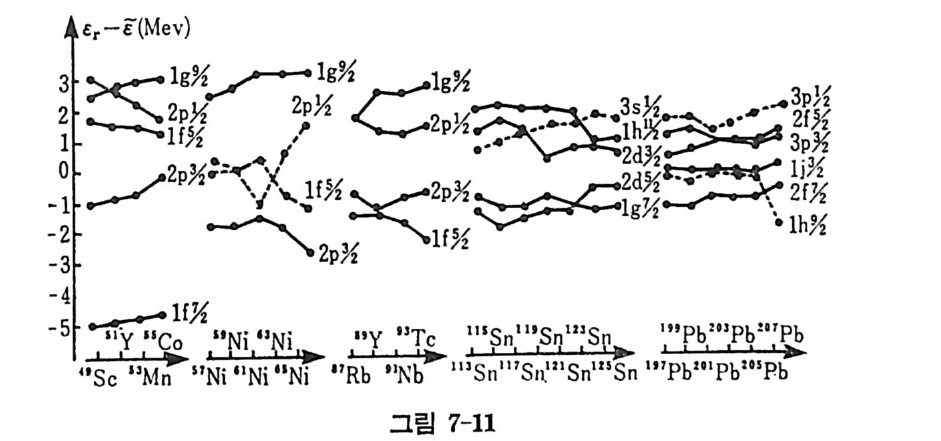 4tr - E(Mev)
4tr - E(Mev)
여 기 에 서 g, 는 식 (7. 75) 와 (7. 77) 의 BCS 방정 식 의 반 전 에 의 하여 스펙트럼의 실험치로부터 구해진다. 합은 각각 선택된 하트리-포크 기 저상태 IF> 의 빈 상태와 채워진 상태에 대하여 취한다• 아래 그립에 의하면 e, 은, 조사된 서로 다른 영역들에서, 평균값 부근에서 (행렬요소 가 N 에 관하여 규칙적으로 변하는 것을 고려하여) 0.25MeV 이내로 번 화하여 거의 상수이다.
제 8 장 Fe y nman 그림식과 섭동이론 섭동전개를 그립으로 표시하고 있는 Fe y mnan 의 그립식은 전개항 하 나하나에 대한 고찰에서뿐만 아니라 전개항들의 부분적인 합을 계산하 는 데 있어서도 매우 강력한 계산 수단이다. 그림식으로의 표현방법은 매우 다양한데 이 장에서는 시간에 의존하는 섭동전개에 대해 그 기본 을 익히기로 한다. 한편 핵물리학에서의 응용 가운데 비교적 간단한 예 둘을 공부함으로써 좀더 높은 수준에서의 응용에 대한 기초로 삼고자 한다. 다음 참고서적 및 논문은 이 장의 내용을 이해하기 위해서나 좀 더 다양한 응용을 위해서 필요할 것이다. C. Bloch, wDi ag r a m Exp an sio n s in, Stu d ie s in Sta t i sti ca l Mechanic s , Vol m, par t A, Eds. de Boer and Uhlenbeck, Nort h Holland, 1965. N. H. March, W.H. Young and S. Samp an th a r, The Many- B ody Problems in Qu antu m Mechanic s , Cambri dg e Univ e rsit y Press , London, 1967. R.D . Matt uc k, A Gtt ide to Feyn m an Di ag ra ms in the Many- B ody Problem, P. NozMi~ cr eG, raLwe -HPrio llb lIenmc.e , aN eNw- cYoroprsk , , D1u9n79o d(,2 nPd aErids, . ) 1. 963. 1 해밀토니안의 구분과 D y son 전개 N 입자계의 해밀토니안 H 는 이체 상호작용까지만을 포함시켜 H= f읊- ++ 곱 v( 따, xj) (8.1 ) ('*J)
로 씌어진다. 그러나 입자등이 평 군장 u(x) 죽 하나의 포멘설 안에서 거의 독립적인 운동운 하고 있는 경우에 해밀토니안의 독립입자 부분을 따로 메어내어 HH=o=H,to+1 {V 읊 표 (x 가 ; 독립입자 해밀토니안 ((88.. 23)) V=+21 i.수E} v(x1 心)- 터LN U(.이 잔류작용 (8. 4) 로 표시하는 것이 좀더 실제적이라 하겠다. 윗식에서는 핵자들의 직접 적 상호작용 중에서 평균장을 동해서 이루어지는 작용을 삭감시킵으로 써, 평균장 속에서의 입자들의 상호작용, 죽 잔류작용만을 독립입자 해 밀토니안의 〈섭동항〉처럼 표시하였다. 식 (8.3) 과 (8.4) 에서 사용된 평균장 u(x) 를 어떻게 구하는가 하는 문제는 이미 하트리-포크이론에서 그 한 예를 본 셈이다. 죽 e. 를 a- 궤도의 에너지준위라고 했을때 독립핵자 해밀토니안은 Ho= I; e.a:a. (8. 5) a 로 표시됨을 보았다. 이때 무시되었던 잔류작용은 사실상 〈정상곱〉 항 이었다. 독자는 이 :a+a+aa: 항이 무시된 이유가 Sla t er 행렬식을 사용하 였기 때문에 자연스럽게 영이었다는 사실을 기억할 것이다. 그러나 일 반적인 N 입자계의 파동함수라면 그 항이 영일 이유는 전혀 없음을 알 아야 한다. 식 (8. 4) 가 표시 하는 찬류작용은 이 항을 섭 동으로 취 급할 수 있도록 만들었다고 보아야 할것이다. 앞으로 우리는 포텐셜을 그 자 체가 찬류작용인 것처럼 취급하겠다. 만일 포텐셜이 매우 커서 섭동항 으로서의 자격이 없다면, 우리는 식 (8.4) 가 의미하는 것처럼 평군장의 역할을 감안한 후에 새로운 포텐셜을 정의하고 이를 섭동항으로 취급하 고자한다. 상호작용묘사 (Inte r acti on Pic t u re) 에 서 진화 연 산자는 다음 식 을 만 족한다 (h=l). 볼 U( t) =V(t) U(t) (V(t) =e0Ve-11H•) (8. 6)
이 식을 만 족하 는 형 식 적 인 형 태의 해는 U(t) =eH •e -u (8. 7) 로서 초기조건으로 U(O)=I 를 만족해야 한다. 이제부터 {)=it 로 치환하여 사용하기로 한다. /31 >/3 2 라는 기호는 t,>t 2 로 이해하도록 하자. 식 (8. 6) 의 해 는 u(/3 ) =1-f' v(f3 1 ) U(g ,)d f3 1 。 =l- J:。 V( /3 1)d /3 1+ J :d/ 3『' d/3 2 V(/31 ) V( 鈴 U(/32 )d/3 1 d/3 2 =1+ 흡oo I (-마·….Jd f3 r••d#n 陽) V(/32 ) .. ·V(/3. ) (8. 8) (g> #l>g 2 •• • >O) 이 된다. T- 곱(시조배열 연산자 ;5 장 참조)을 사용하고 또한 V(#) 가 네 개의 생성 또는 소 멸 연산자로 구성되어 있어 V(# i)와 V (/3j)의 위 치 를 교 환 해도 전체 부호가 불변임을 상기해 보면 다음 관계식은 쉽게 이해된다. 죽 V(/31 ) V(/32 ) …V (/3 .) =T[V(/ 31 ) V( /32 ) ... V( /3n )] = T[ V (/32 ) V (/31 ) ... V (/3니 (8. 9) 이댜 이 식을 이용하면 식 (8.8) 은 U(/3) =1+ 홀 딩E Jd g 1 •••d f3 n TW (/31 ) 陽) …V ({3 .)] (8.10) 이 된다. 이곳에서 적분영역은 모두 0 에서 /3까지이다. 파이 나오는 것 에 유의 하자. 식 (8. 10) 을 Dy so n 전개 라고 한다. 2 진화연산자의 진공기대치 독립핵자 해밀토니안 Ho 의 기저 고유상태를 슬레이터 행렬식 Io 。> 로 표시하자.
Ho 10n> =cn |(J)n > (8.11) 기저상태에 대한 에너지 고유치는 Eo= -
需}1 nlnRR (( tt)) II ==ii e o+ ~홈 (-iEn) (J1)。< E
따 (B) =epH ,a;c-8H, ag (8) =epH , aae-8H, (8. 21) 이다. 한편 (p ulvlvµ) 는 반대칭화가 되어 있지 않 은 행렬요소이다. 식 (8.19) 중에 ( ~o l T[ V ({31 ) V ({32 ) …V ({3n ) ]| (J)。 > <( J)。 =I 賞 a~/J ra d ; . 12({_ 3 1( ) aa{3; l ( v{3 l1 r )o a6) (a{3'-f~J1 ' )r 'da ,r (.{132_ 1 ) (aa;' ({{33' 2| ) v a l; r,' (o{3 '2) ) …ad’ ({32 ) a,, ({32 ) …]| ( J)。 > (8. 22) 로서 제 5 장에서의 비크정리에 의해 기대치 <(J)。卜 ··I (J)。>는 완전한 축 약항들로만 표시된다. 죽 <(J)。 I 宜야 ({31 ) 야 ({31 ) a6 ({31 ) Gr ({31 ) a;, ({32 ) 아 ({32 ) a6 ({32 ) ar ({32 ) …]I( J)。 > =at (鈴 야 (/31 ) a6 ({31 ) a~ ({31 ) a.;, ({3기 a;, ({32 ) ad' ({32 ) a,, ({32 ) …… … I +…... 一 I ' 1 | (8. 23) 이다(+이하는 다른 방법 에 의한 완 전 축약항들). 윗식에서의 축약의 값은 식 (5.12’) 에서 계산되었다. 위에서 보는 바 와 같이 모든 축약 방식들을 모두 식으로 표시하기는 매우 복잡한데 이 를 간단히 그립으로 구분 표시하는 방법이 Fe y nman 그립식이다. 3 Fey n man 의 그림 식 (기 초 규약) 1) 상태 Fock 공간에서의 한 벡터는 입자로 메워져 있는 상태들을 수직선으로 표시하고 그 상태에 대한 첨자 부호를 표시함으로써 다음과 같이 표시 할 수 있다(우선 시간에 대한 표기는 생략한다). (1 : 야 ··•a:;1 > aI If3 …”| 벡터 그림표현 그러나 입자들이 많을 경우에 위와 같은 방법은 많은 선들을 일일이
표시하게 되어 복잡하므로, 우리는 〈 기저상대 〉 또는 〈새진공(상태)〉를 정의하기로 한다. 이는 다음처럼 표시된다. l
= \=0 ( rEF) (8. 24) 한편 I© 。>를 진공처럼 갖는 연산자 br 를 정의할 수 있다. 만일 소멸 연산자 룹 br= {a아r,, 단단 rrEE:tFF :: ((입구 자멍 소소멸멸)) (8. 25) 로 정의하고, 생성 연산자를 b;= {dar;,, 단단 rr E로:tF : ((입구 자멍생생성 성) ) (8. 26) 으로 정의하면 IIP 。>는 b7 에 대해 진공임을 알 수 있다. b 』 o 。 >=O (어떤 r 에 대해서) (8.27) 이러한 br(b; )를 준_입자소멸 (생성) 연산자라고 한다(제 4 장 참조). 준 입자 연산자를 정의하기 위해서는 기저상태 I ([J o> 가 먼저 주어져야 한 다는 사실에 주목하기 바란다. 앞으로 구멍상태 즉 |([J o> 에 포함된 상태를 소문자 알파벳 a,b,… ,z 등으로 표시하고 입자상태는 대문자 알파벳 A,B, … ,Z 등으로 표시하겠 다. 구멍 및 입자상태로 구분하지 않은 상태들은 그리스문자 a, {3 ,···,w 로 표기하기로 하자. {a}=(a,b, ···, z ), 만일 aEF {a} = (A, B, …, Z) , 만일 a~F (8. 28) 지금껏 생략했던 시간의 흐름을 표시하자. 수직의 위쪽 방향을 시간 의 흐름 방향으로 잡겠다. 이러면 준_입자의 생성 및 소명연산자의 그 림표기는 다음 도표에 주어진 바와 같다.
 따 g러 ^|t|·. . A· 입 b+r+<、Ar. ® i생Il@AA 성~ .·. a구~o ba a 멍+ 'F(AL nB. 'R`._ .0 ~성j •), a .-·-. cu”、b_a AK}(( .I A소衍 f衍 ~ ·명 A · 구~c b 멍+a.' ·.L' 節 소aBl ~멸 I ( ( 8· 책
따 g러 ^|t|·. . A· 입 b+r+<、Ar. ® i생Il@AA 성~ .·. a구~o ba a 멍+ 'F(AL nB. 'R`._ .0 ~성j •), a .-·-. cu”、b_a AK}(( .I A소衍 f衍 ~ ·명 A · 구~c b 멍+a.' ·.L' 節 소aBl ~멸 I ( ( 8· 책
. ai (8) 야 (P) a. (P) ab (P) I (j)。 > = …l•I … A •lf … B •+1… a •+| …b C 8 벡터 그림표현 임을 알 수 있다. 2) 연산자 Fock 공간에서의 연산자를 그 림 으로 표시해 보자. 므a로) 일다체음 과연 산같자은 일네체 개 연의 산그자림는표 e현(/을3 ) =갖 r~는.µ 다 (.r1 0Iµ)a t({3 )a µ ( /3)로 표시되
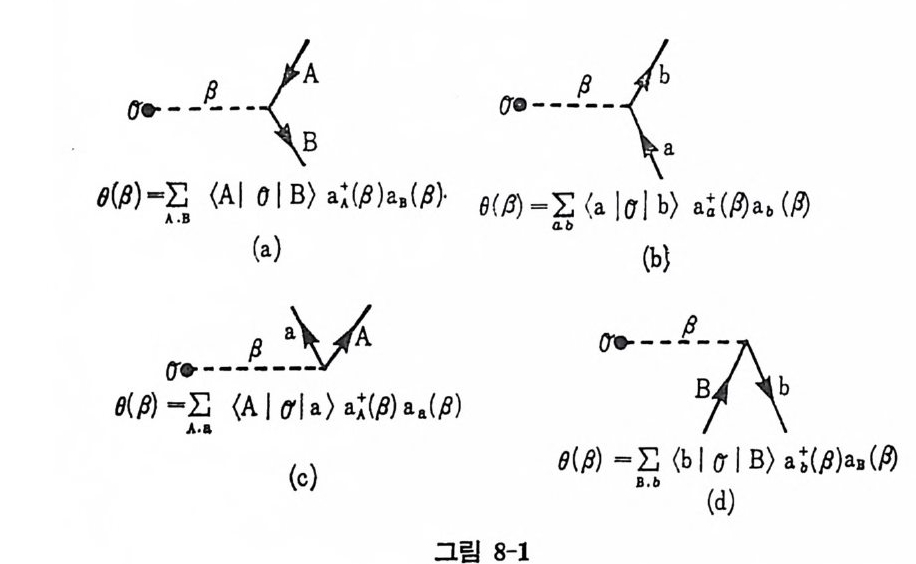 g --8,- - n> 。 --i B -
g --8,- - n> 。 --i B -
b) 이체 연산자 이체 연산자는 V(/3 )= aI{J :r d +2 (a/31 v\ro) at (/ 3) a;(f3 ) a6 (f3 )ar( f3 ) 로 표시되므로 a, /3 ,r,o 의 상태 구분에 따라 16 개로 서로 달리 표시된다. 이 중에서 네 개만 그려 보자.
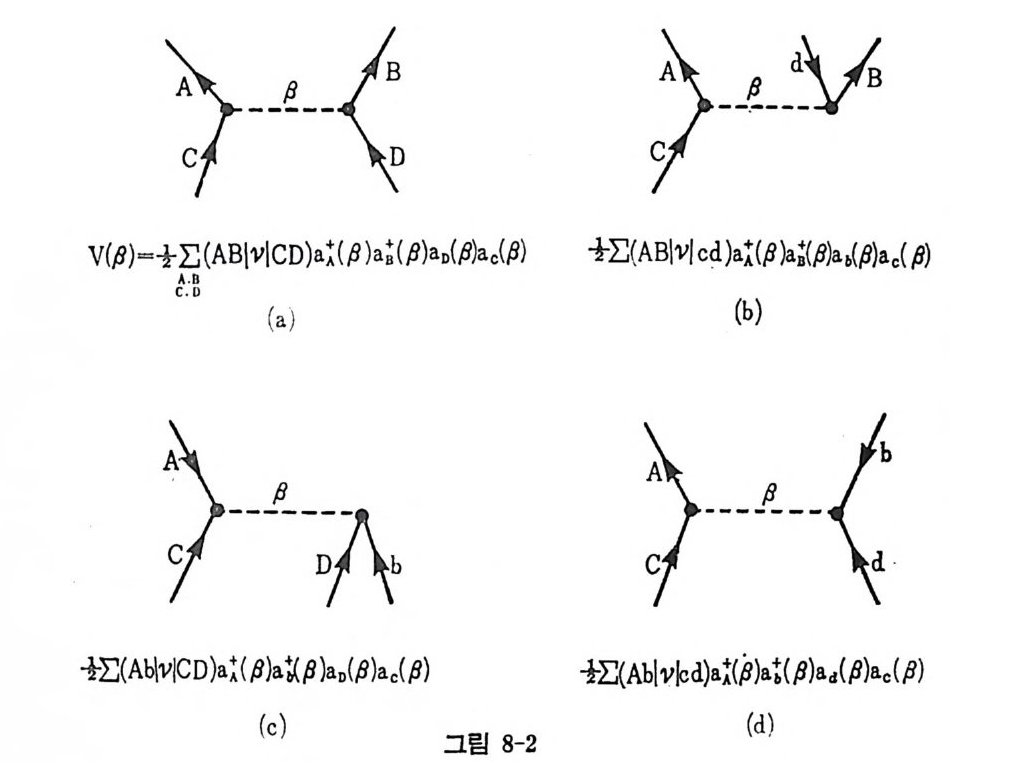 --R-- 入-.o --
--R-- 入-.o --
독자는 윗그림들이 오른쪽 부분만을 모두 변화시킨 형태임에 주목하 였을 것이다. 왼쪽 부분 (A 와 C 로 표시된 부분)을 변화시킴으로써 나 머지 12‘ 개의 그립도 쉽게 얻을 수 있다. 윗그립에서 A 와 C 를 한쪽 꼭지점 (ver t ex) 에 표시하는 이유는 이 두 상태가 행렬요소 (ABlvlCD) 에서 같은 좌표공간에 묶여 있기 때문이다. 윗그림들에서 그리고 앞으로도 계속 접선 부분은 상호 작용을 표시하고 있음에 유의 하기 바란다 . • ... …• =방( , Ivi, ) x… … • = ( 101 ) (8. 30)
c) 축약 일반적인 축약 (Con t rac ti on) 의 값은 식 (5.12’) 에 집약적으 로 표시되었다. 이를 다시 써 보자. aI ! (f31 ) al, (/32 ) =oJ. {0 (f31 -/32 ) tc 0 ({)2-/3 1 )p ,} exp (eJ ( /31 -/)2) ) aI , (f32 ) a!I (f31 ) = -% {0 (8l-B2) t』 _o (f32 -/31 )PA} exp (eJ ( p1 - /32) ) = -aI ! Cft1) alj C ft2) (5. 12') 식 (5.12’) 에 표시된 축약을 하나의 일반적인 형태로 표시하기 위해 〈일체 전파 연산자〉를 정의하자. g,, (/3i -8j) =aI 。 (鈴 a;I (/3j) (8. 31) 식 (5, 12’) 와 식 (8. 31) 으로부터 g. (/J려,) =exp (e 。 (fi‘ 尹) ) • [-; ((aa~EFF 이이고고 g¢,j>> Bgj, 일일때때)) 。 (그밖의 경우) (8. 32) 로 집약하여 적을 수 있다. 단 f3‘=f3j인 경우는 특별한 조심이 필요하다. g. (0) = { 드l 야1 (B) =p. (8. 32') -야
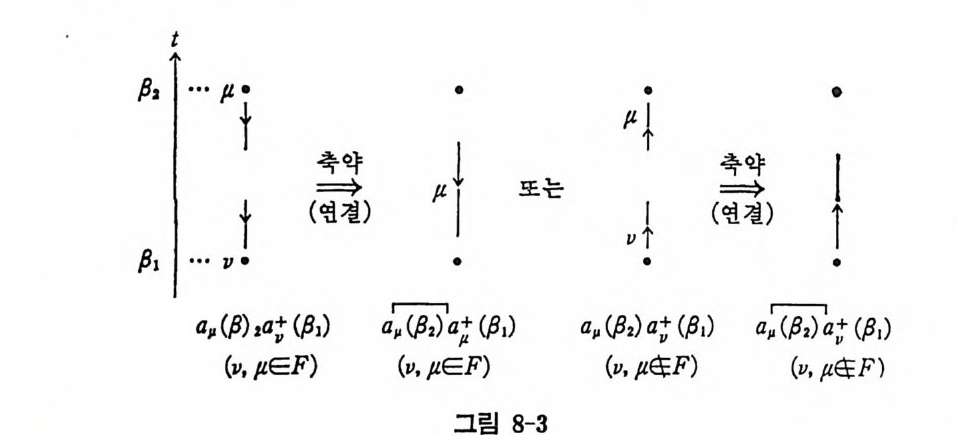 p/J,I 1 t| ·…· · µtt . (=연=결>) 기l•• 또는 µu+i•• (一연결) l••
p/J,I 1 t| ·…· · µtt . (=연=결>) 기l•• 또는 µu+i•• (一연결) l••
식 (8. 32) 및 (8. 32’) 에 나타난 표현은 이 미 축약된 형 태로서, a~(/32 ) 와 따(/3 1) 를 그림 규약 (8 .29 ) 에 맞추어 그리면 다음 두 가지로 표시된 다. /3l >/3 2 인 경우도 같은 방법으로 표시된다. 즉 /31 과 /3 2 의 순서에 대 해 특별히 명시하지 않고 축약을 일체 전파 연산자로 표시하기로 하자. /3, j« =g. (/3, 강) (8. 33) f3j 이 값의 구체적인 표현은 식 (8.32) 및 (8.32’) 를 이용하면 된다. 4 Fe y nman 의 진공그림식 전정에서 세운 기초적 규약을 가지고 식 (8.19) 중 몇 개의 n=l,2 에 대해 그립식을 만들어 보자. a) a=l 의 경우 식 (8.19) 중 n=l 인 항은 -J:od / 3 I aa f{JrT d 上2 (a/3 | V I ro) << Po I T[ 야 (/31 ) ap ( /31 ) a6 (/31 ) a, (/3)) ]| o 。 > =- J。, d /3 l a 麟 (a/3 | v l ro) (야 (/31 ) ap ( /31 ) a6 (/3)) a 』 (/3)) = -J:od-,/ -3 ·1 a 다P ,4 + 2 따 ( a(//33 1l ) v 야 l r 8(/3) 1 () a-6) ( /23 (1g ) a. ,( O(/)3 g1 ), ) ( O) 6m8,6-g ‘ (0) g, (0) 6.g ,r) =-/3a ,bL( Em___ + 2( (ablvlab)-(a blvl (ba))
 a
a
윗 그립식은 사실상 이체 연산자의 그림표현 식 (8.30) 으로부터 유도 할수 있다
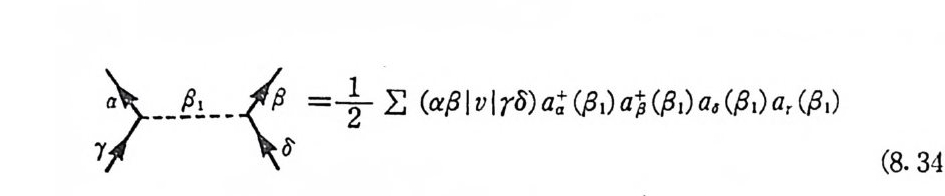 >_8i - <국 I: (aPlvlrS)a: 潤)禪)홀)
>_8i - <국 I: (aPlvlrS)a: 潤)禪)홀)
에서 a 와 r 를 축약시키거나, a 와 6 를 축약시킴으로서 식 (8.33) 을 얻 을 수 있다. 이때 시간에 대한 적분과 n=l 즉 점선아 하나 있기 때문 에 발생하는 음수 부호에만 주의하면 된다. 한 그립식의 부호(+ 또는 -)는 다음과 같은 규칙을 따 른 다. 그립식 이 상호작용을 11 개 가지고 있고 둥그라미를 11C 개 가 지 고 있으 면( 식 (8.33) 의 첫째 그립식은 1le=2, 둘 째 그립식은 ?le=l 이다), 전재부 호 는 (-) +“ ” (8. 35) 이다. b) 11=2 의 경우 이 경우에는 식 (8. 34) 와 같은 그립식 을 두 개 그려 놓고 그림의 가지들을 연결시 컴 으로 싸 모든 그립식 둘 을 구 할 수 있다. 그 방법은 상호작용(점선)과 상태 (실선)의 교차 꼭지점 (ver t ex) 에서부 터 나가는 가지에 대해서 처 음 에는 4 개의 들어오는 가지가 있고, 한번 연결(축약)된 이후에는 3 개, 그 다음 2 개, 다음에는 1 개가 생겨 4!= 24 개의 방법이 있다. 서로 다른 방 법으로 형성된 그립식 을 모두 모아 보면 그림 8-4 와 같다. 그림 8-4 중 몇 개 의 예 를 들어 보자. 그림 식 (1.1) 은 식 (8.33) 에서부터 곧바로 구할 수 있다. 그립 식 (1. 1) =룬( f ~)2 (8. 36) 설
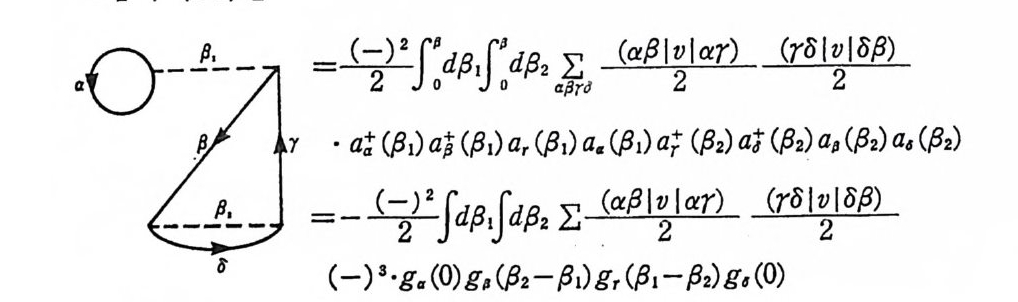 =._仰JfI+d- 8 lg(@ |t J dg rg od_2g}R a A2 0 2 2국ra d셔r@g SBS ,|)vv`|g.a2Jla ) 82@ +Ia仰dARCrd ,C (|8D2vIr. l v i@|F &S2 8A衍 ( G) s8 8 (| R 2F ))
=._仰JfI+d- 8 lg(@ |t J dg rg od_2g}R a A2 0 2 2국ra d셔r@g SBS ,|)vv`|g.a2Jla ) 82@ +Ia仰dARCrd ,C (|8D2vIr. l v i@|F &S2 8A衍 ( G) s8 8 (| R 2F ))
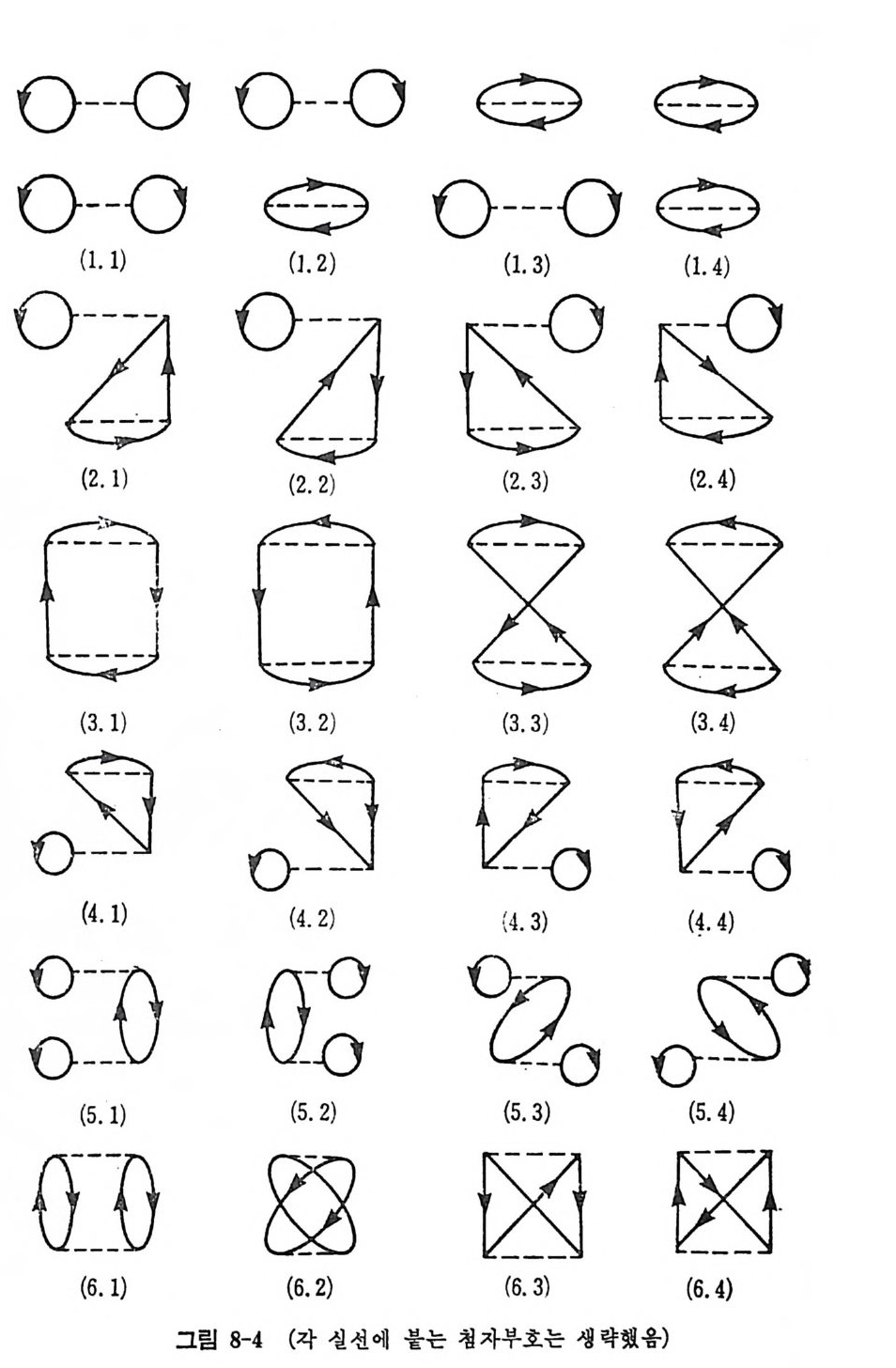 0---0 0--0 죽 죽
0---0 0--0 죽 죽
이 며 , /31 과 /32 의 적 분에 관여 하는 부분만을 쓰고 식 (8. 32) 를 이 용하 면 I:df31 f : d82 g, (B2 따) gr @ l -f32) =J:0 d f3 JJ :0 d /3 2 [0 (/32 쟁) p, -O ( 8l 活) t,][0 (/31 沿) P, -O (B2_8l) tJe xp { (f31 _ g2) (e,_er) } = -J:0 d f3 JJ :0 d f32 { 0 (/32 뎃 ) p,t, + 0 (/31 -/32 ) t,p,} exp { (/31 - P 2) (e, -e,) } (8. 38) 이 된다. 치환 x= 요許, y= 8l-B2 에 의해 J :d fJJ: d 합(/J 1- /J 2) =J:dy (fJ-y)f(y) +f~,dY (fJ +y)f(y) (8. 39) 를 얻고, 독히 8 ➔ 00 인 국한에서의 값만을 구해 보면 (P ➔ OO 국한값의 중요성은 이 다음 절에서 취급하겠음) 그림 (2.1) 上二댕峰 )2 (acIv|a?:::bIpI b c) (8. 40) D 이 다. 식 (8. 35) 의 부호규칙 이 찰 맞고 있음을 유의 하고, 식 (8. 36) 에 서 구한 그립식 (1.1) 과 비교하면 8 에 대한 의존도가 다른점을 유의하 기 바란다(입자상태 D 는 r 에서 유출되었음). 그립식 (1.1)~(1.4) 처럼 그림 부분이 연결되어 있지 않은 그립식 ~을 〈연결되 지 않은 그립 식 (unlin k ed dia g ram ) 〉이 라 하고, 그림 식 (2. 1) (6.4) 들과 같이 연결된 그립식을 〈연결된 그림식 (link ed d i a g ram) 〉이라 고 한다. 이들은 8 에 의존하는 승률이 다르다. 식 (8.40) 에 나타난 행렬요소 (aclvlaD) 를 독립입자상태 'P a(x) 로 풀 어 쓰면 (ac l v l aD) =fd x ijd x 갑 (x 國 (石) t) (X1 -X2) ,Pa (X1) tpD (X2) (8. 41)
이다. 여기서 a,C 가 구멍상태 죽 페르미 바다 내부상태이고 D 가 입자 상태 즉 페르미 바다 외부상태이기 때문에, ~o 가 입자-구멍 상태의 구 분이 명확한 계의 파동함수라면, 이 행렬요소의 값은 에너지 (또는 운동 량) 보존법칙에 의해 영이다. 즉 m 에서는 에너지가 보존되나 X2 에서 보존되지 않아 전체값은 영이 된다• 이 책에서 다루지는 않겠지만 한 계가 온도에 의존하는 경우 독립입자상태는 부분적으로 구멍상태이고 부분적으로 입자상태가 될 수 있다. 이러한 경우는 위의 행렬요소도 값 을 갖게 된다. 결국 에너지보존법칙을 적용할 수 있는 경우, 한 그립식 은 결코 다음과 같은 그립 부분을 포함할 수 없다. 이들의 값은 영이다.
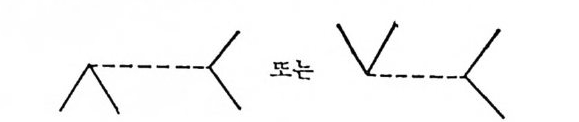 六---〈 또는 V_---<
六---〈 또는 V_---<
따라서 그립 8-4 가운데, 에너지가 보존되는 경우라면, 영이 아닌 그 립식은 그림식 (1.1) 에서 (1. 4), 및 그림식 (6.1) 에서 (6.4) 까지 여덟 개의 그림식이다. 그림식 ( 6.1) 의 값은
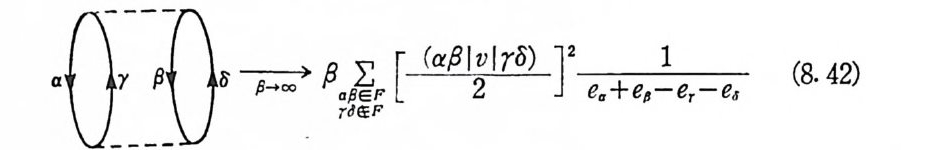 f3::f [ (af 3 1 ;W) e.+c,2er-e6 (8. 42)
f3::f [ (af 3 1 ;W) e.+c,2er-e6 (8. 42)
이 된다. 핵자간의 상호작용에 대한 일반성 (제 1 장)을 참고하면 그림식 (6.2) 도 그림식 (6.1) 과 같은 값을 갖는 것을 보일 수 있다. 한편 그립 식 (6. 3) 및 (6. 4) 는 같은 값,
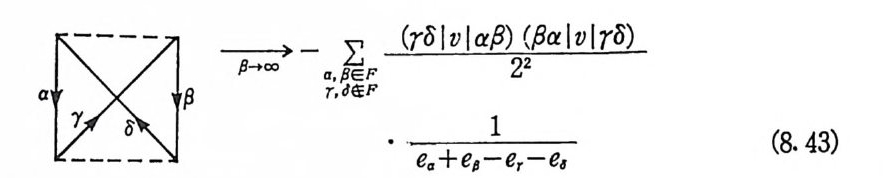 戶 一l qr J準EfT F F· .e 1T 2 (8. 43)
戶 一l qr J準EfT F F· .e 1T 2 (8. 43)
이 된다. 식 (8. 43) 은 식 (8. 42) 에 대 해 하나의 교환항을 갖고 있다 . 한편 식 (8.43) 에서도 규약 (8.35) 가 들어 맞고 있음도 주목할 만하다(그립식 (6.3) 및 (6.4) 는 하나의 실선 동그라미가 있다). c) 시간적분을 하기 이전의 Fey n man 그립식의 규약 위 에서 열거 한 예들
옹 동해 Fe y nman 그림식을 시간 직분을 하기 전에 수식표현으로 바꾸 는 네 필요한 일반적인 규약웅 정리해 보면 다음과 갇다. i) 그림에 첨 자 부호를 부친다(경우에 따라서 첨자 부호가 없이 정의 된 그림식 표현이 있다. 이 책에서는 사용하지 않겠지만 이럴 때에는 대칭인자를 생각하여야 한다). ii) 1 체 상호>작용을-x 표°시 =하 (는a|V 1꼭f 3지) 점에 대해서는 와 같이 표현한다. iii) 이체 상호작용을 표시하는 꼭지정에 대해서는 ><8 국 (a f3 IvIr8) 로 표현한다. iv) 축약을 나타내 는 선 은 식 (8. 82) , (8. 32’) 을 이 용하여 (8. 33) 으로 표현한다. -P、 ---凰 ia- pii= & 偉 .. gJ. ) v) n 이 상호작용(접선)의 갯수이고, nC 가 실선 동그라미의 갯수이면 다음 계수를 곱한다. (-) +ne n! vi) 모든 시간 첨자에 대해 적분하고, 일체상태를 나타내는 첨자 부 호들의 합을 구한다. 단 (3一~ 인 국한값을 구할 때에는 적분 후의 값 을 구하는 간편한 방법이 있다. 이는 6 철에서 다루겠다. 5 연결된 뭉치 정리 연결된 그립식으로 된 덩어리물 연결된 뭉치라고 한다. 따라서 그립
(8.4) 중에 그림식 (1 .1 )~(1 .4 ) 까지는 두 개의 뭉치로 되어 있고 나머 지는 한 개의 뭉치로 되어 있다고 할 수 있다. 하나의 그림식이 및 개 의 뭉치로 되어 있느냐에 따라서 그림식의 계의 부피, Q 에 대한 의존 도가 달라진 다. 연 결 된 뭉치 정 리 (Lin k ed Cluste r Theorem) 를 공부하 기 전에 뭉치의 O 에 대한 의존도룹 간단히 일별해 보자. 굉장히 콘 계를 생각해 보자. 이 계의 해밀토니안을 운동에너지항과 퍼텐셜 항으로 구분하여 후자를 섭동항으로 취급하자. 전절에서 계산된 행렬 요소를 계산하기 위한 독립입자 파동함 수는 다름 아닌 평면파 파동 합 수이다 . 즉
표시된 O 의 의존도 를 —감nu안, 하o면 v,, -( u1 한' - 그 VI)립 = 식0의l’’ 요의 존 도는 (8. 39) 1 이어서 뭉치의 수 µt에만 의존하게 된다. 죽 그립 (8. 4 ) 중에 그림 식 (1.1)~(1. 4) 들은 n2 에 비례하고, 그립식 (6.1) ~ (6. 4) 들 은 Q I 에 비 례한다. 여기서 우리는 O 의 같은 차에 비례하는 항 둘 만을 합하게 되 는 이유를 알 수 있다. 죽 한 뭉치로 된 것들을 합한다는 것 은 이 들 이 n1 에 비례하기 때문이다. 한편 그림식 (6.1)~(6.4) 까 지의 값은식 (8.19) 중 11=3 에서 나오는 두 뭉치로 된 그립식의 성분 과 상쇄되어지 지만 이 는 증명을 생략한다. 이제부터 연결된 뭉치 정리 를 고 찰 해 보자. 식 ( 8.18 ) 에서 U (l ) 의 전 공기대치가 기저 상태에너지에 기여하는 양 상 은 log 속에서 이 루 어 침을 알았다. 이곳에서 증명은 생 략 하고 * 그 의미만 을 고 찰하겠 다• 연결된 뭉치 정리는 다음과 같다. <( J)o I U (/3) I (J)o > = exp <( J)。 I U (/3) I (JJ。 >L (8. 40) 여기서 <(J)o IU(/3) I (J)。>는 연결된 뭉치로만 이루어진 그립식들이다. 즉, 에너지보존을 생각할 때 <(J)o Iu(/3) I (J)。 >L= 0 - 0 • 0 • 0 : :0홍江 장 ~• -- - - (8. 41) 따라서 식 (8. 18) 을 그립 식 으로 표현하면 Eo=e 。一諒(d< (J)。 I U(/3) I (J)。 >L) l fJ ➔ 00 =eo- 읊〈 O- _ -O 〈己广汀 - - ----)I {J ➔ oo cs.42) 이 된다. 전절에서 8 ➔ 00 인 경우만을 고려했던 이유는 식 (8.51) 에 나 타나 있다. • MN.eH c. h Manairc cs h,, WCa.mHb. rYi dogu e n gU , nSiv. . S aPmrep sasn , t1h 9 a6r7, , pT. h1 1e6 1. \{ a ny -B ody Problem in Qu ant u m
6 에너지로 표기하는 Fey n man 그림식 본장 제 4 절에서 언급된 규약 득히 v i)항을 계산하는 것은 복참하다. 하지만 제 5 전에서 천명된 8 ➔ 00 인 국한만이 에너지에 기여하므로 vi) 항에서의 시간적분을 규약화시키는 하나의 방법이 있다. 시간적분을 실질적으로 계산하는 데에는 언제나 다음과 같은 적분형 태가 나타난다. [ ({3) =『。 Jd f 3 1 • • ·df3 .. g. ({3‘ 강) g話 -/31) • • • (8. 43) 이 적분은 일체 그린함수 g의 변수가 전체 시간을 일률적으로 이동시 킹에 대해 불변이므로 적분구간을 -f3 /2< f3g
식 (8. 48) 의 지수들을 모아 보면, \>
=P 훑 4[ 방 (aPlvlro) 『ff仁 望广 1 1 1 ea-i( s r+s6-s,) • e,-is, • er-is r 1 e8-1S8 =Bap: F [+
한편 밀도의 행렬요소는
이식에 서 I … >는 반대칭화가 되어있다. 따라서 < ka,, k'a' ,' =l v l( kkak,', l v 私 ( 'ra)' ,|' 江 >) ]W _ M8 。q' 모 -(kk'lv(r) I 鬪 [Wo 짜 8T f _M 〕 (8. 63) 으로 계산되며 좌표공간에 대한 행렬요소는 일반적으로 : 鬪 lvl 麟) , ___ _ 〈一 =--b-Id ;IId;2 e- 효:)도i(;.;;따 .r; E k4 =8r 국,詞(-frµ)~나 (白 )2 (8. 64) 이 되고, 스핀과 하전스핀의 합을 취하면 <:> 국 (4W-M) -~ (kk'lv(r) lkk') •.’ * ’'E F 급 (W-4M) ~ (k, k'lv(r) |江) k’.* ’'E F =
k ➔ = kf I l2kf 2 ’ Kf = kf I + f7l 2 (8. 68) 축 F1 과 12 가 페르미 공내에 있어야 하므로 아래 그립에서와 같 이 K/2 는 적분 구간 v 속에 있게 된다.
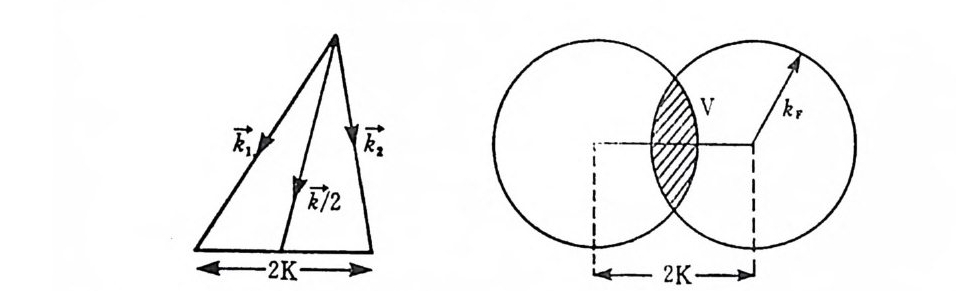 빼 2K .. 노― 2 K 一_J
빼 2K .. 노― 2 K 一_J
부피 v 물 kF 와 k 로 표시하면 u = 브3 (2k}+k3-3kk}) (8. 69) 으로. I(kF, µ) =-kfdk ~ ·8f. d(f ) =급平J :'(2 1f,.. +k 3 -3kk } ) ~dk =습 [2k 造 (6 /fF 군) + 문 (µ2 + l2k}) log (1 + 뿔-) -16/f F µ t an-1( 은)] (8. 70) 가된다. 따라서 핵자당 평균에너지는 운 31정 ~ +(4W-M) 경告 -_(W-4M) 읍贊묘) (8. 71) 이다. 이를 k, 에 대한 함수로 그리면 그림 (8.5) 와 같다. 한편 실험적으로 핵은 소위 포화현상이 있다(제 1 장 참조). 이는 웃 I., a:l.3 &rm-•= -16MeV, 겁; (운) Ik ,=l , J6 fm ·•= O (8. 72)
로 표시되며, 이 두 조건으로부터 W 와 M 의 크기를 구할 수 있다. 4W-M=21. 66MeV, W-4M=282MeV (8. 73)
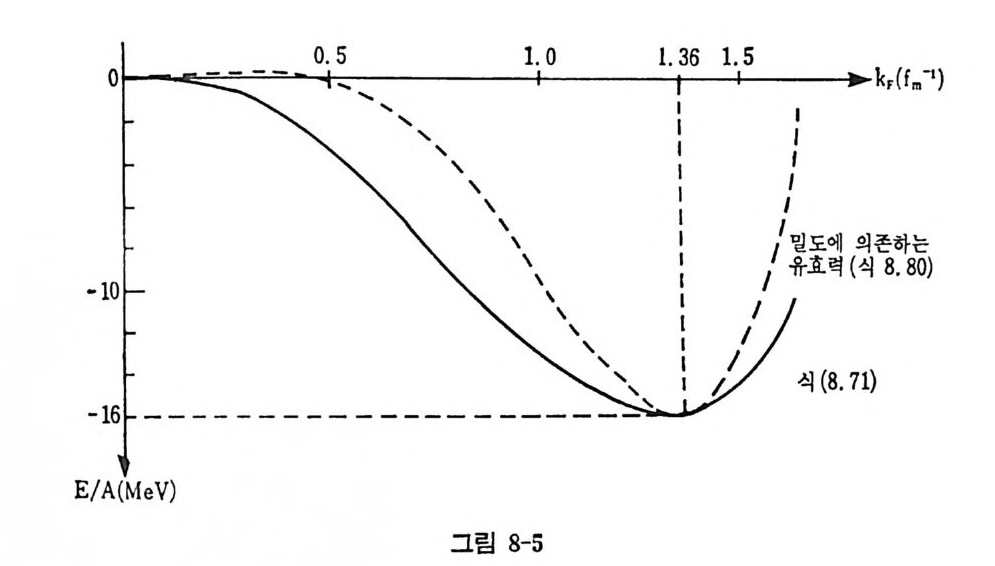 。 望 ` .... ``` \ 1. 0 1.3 6 1.5 kr(f m- 1)
。 望 ` .... ``` \ 1. 0 1.3 6 1.5 kr(f m- 1)
핵질내 핵자당 평균에너지, (식 (8.71), 뿐만 아니라 특정한 1&m·> 상태에 있었던 핵자의 에너지 변화도 개별적으로 구할 수 있다. 죽 핵 자간의 작용력이 들어음에 따라 핵질내의 핵자밀도도 변하게 되며, 한 궤도, |짜, 에의 에너지 준위는 식 (6.19) 에서와 같이 e•= 8ogE E (8. 74) 로 계산된다. 여기서 Pm=
이며, UD (k) =~= (4 W-M) ➔~ (k, k' l v (r) l kk') ➔ 眞 ' EF =(4W-M) 오2 따보 ,2 (8, 77) 이고 Us(k)=aR~C1 1=' -(W-4M)一 •'~ E F (k,k'lv(r) I 質) =-(W -4M)*2L 군'µE Jk k,'Edk,kun’ , ―µ2 ―+ 」(k -k')2 =-(W -4M)따¼ L (1--/kF f; tan- 1 써 µ+ k 궁-t an-1 kF-k _ k2_4::F-µ2 log (kF-~k)2+µ2) (8. 78) 이다. 식 (8.73) 을 이용하여 u.=uDCk)+uECk) 및 e,. 를 그려보면 그립
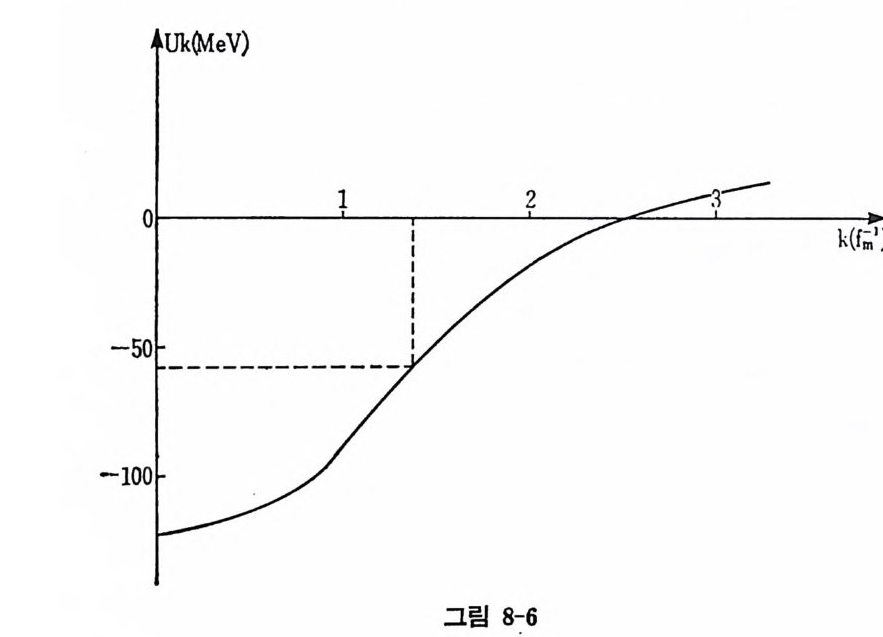 Uk(M e V)
Uk(M e V)
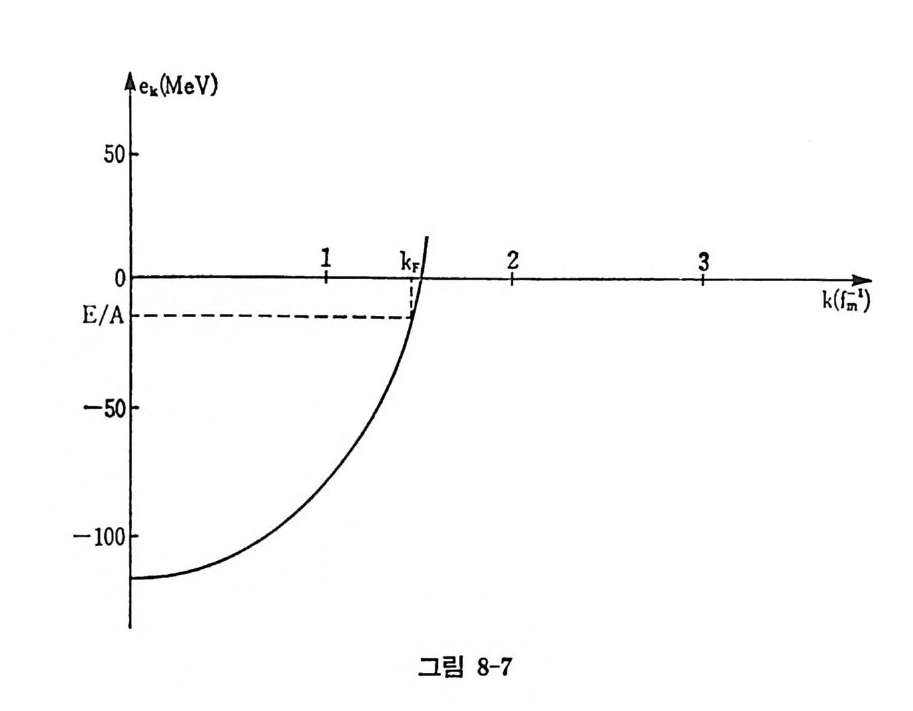 ek(M e V)
ek(M e V)
8-6 및 그립 8-7 과 같다. 그립 8-6 에서 보면 k ➔ 0 인 국한점에서 핵자는 -118MeV 나 되는 깊 은 포텐셜 우물 속에 있다. 탄성 충돌 실험결과는 실제로 핵의 평균장 깊이는 약 50MeV 로 알려졌다. 결과적으로 포텐셜 (8.58) 은 실제 핵에 적용하기는 부적당하다는 것이 밝혀진 셈이다. 8 밀도에 의존하는 유효핵력과 유효질량 전절에서 취급한 교환력이 실제 핵의 성질을 이해하는 데는 부적합하 지만 제 6 장에서 언급된 유효핵력들이 가지고 있는 성질을 파악하는 데 에는 교육적인 도움이 되었다. 유효핵력 중 Sk y rme 력에는 핵밀도에 의존하는 항들에 있었는데 이러한 항의 역할을 공부하기로 하자. 제 6 장에서의 모든 유효력은 하트리-포크 계산을 통해 실제 실험데이 타와 비교하기 위해 매개상수들이 도입되었다. 따라서 컴퓨터를 사용한 수치계산을 통하여여만 하기 때문에 간단한 특성을 알기에 역시 부적합 하다 하겠다. 이러한 난정을 피하고 간단한 성질을 파악하기 위해 핵질
모델 을 이 용하기 로 한다. 다음의 포 텐 셜 을 생 각 하 자 ( 식 (6. 134 ) 참조 ) . v=o(r수) [a +bn] (8. 79) 이미 제 6 장에 서 자세한 설명을 했으므로 이 포 벤설을 이용 한 핵 자의 평균 에너지가 다음과 같음은 다시 유도하지 않겠다. -AE= -_ 31t0z2 m fr i.. +', —38n -[ a +bnJ (8. 80) 포화조건 (8. 72) 를 이 용하면 상 수 a, b 는 다음과 같 다. a= -984M e V, b=2187MeV (8. 81) 한 궤도에서의 핵자의 에너지는 e /rh= 양言 + 丁3n r[ a. +3bTn J =r~2i2mk 2- 54. 3 5MeV (8. 82) 이며, 이 속에는 재정돈 함 〈뿔〉=뿐: (8. 83) 이 아미 포함되어 있다. 이 결과를 그립으로 표시하여 전결에서 취급 된 교환력이 있는 경우와 비교하였다(그림 8-3~8-5 참조). 다시 한 번 말 하거니와 이 재정돈항 때문에 중앙 (k ➔ O) 에서의 포텐셜은 약 54M e V 로 거의 실험치에 비교할 만하다. 식 (8. 76) 및 (8.82) 에서 핵내의 한 핵자가 갖는 궤도에너지 불 알 때 이들의 일반적인 표현 eIr=— 12zm2—k2 +UIr (8. 84) 은 한 핵자가 갖는 포텐셜이 k 에 의존함을 알 수 있다. 이런 경우 유 효질량 m* 를 다음과 갇이 정의한다. _ooe h;k _ =-_ mh* 2 (kk ) =_- -hm2+k _,' a—ouk~ (8.85) 윗식을 다시 쓰면
m*(k) 1+ 그fl2mk 으ak (8. 86) 이다. 이러한 유효질 량 은 실험 측정가능치이며, 실제 실험치는 1n*~m 이 다. 전절에서의 포텐셜을 사용하면 식 (8. 77), (8. 78) 로부터 m*~ 0.43m 입을 쉽게 계산할 수 있고, 식 (8.82) 에서는 m*=m 임을 알 수 있어 밀도에 의존하는 유효력이 매우 실제와 가까움을 알 수 있다. 한편 핵질에서의 압축 률 은 다음과 같이 정의된다. K=k} _E_(핥 It,=1.36 fm -, (8. 87) 이룹 이용하면 전정에서의 유효핵력을 사용한 결과는 K=115MeV (8. 88) 이고, 밀도에 의존하는 유효력의 경우 K=380MeV (8. 89) 인데, 핵의 흉극 (mono p ole) 거대 공명실험 결과로 예측하기는 실제 핵 에서는 K~210MeV 정도로 알려져 있다. 이 압축률은 핵내에서의 일반 음속을 계산하는 데 사용된다. V,=J ~• VF (8. 90) 이러한 음속보다 더 빨리 핵에 입사하는 입자가 있을 경우 이 핵내에 는 shock wave 가 발생하게 될 것이다. 현재 이 현상을 연구하기에 충 분한 가속장치들이 각국에 많이 있어 이들에 대한 연구도 활발히 진행 중이다.
찾 0~ 보J I
〈 기〉 Gallag h er-Moskowski 효과 71 갈 릴 레이 변환 183~ 강입 자 (hadron) 17 강한 전 속 모델 (str o ng -c oup ling model) JOO 거 대 한 이 중국자 공명 (gian t dip o le res on ance: GDR) 13, 15 거 -응 해 (m i rr or nuclei) 32 경 합에 너 지 (bi n d in g energy ) 27 경 입 자 (lep ton ) 15 Gog n y 력 190 고 유 각운동 량 (int r i n s ic ang u lar moment um ) 75 고유입 자 들뜸과정 (int r i n s ic - pa rti cl e excit at i on mechanis m ) 64 고유좌표계 (int r i n s ic coordin a te ) 74 공간밀도 연산자 (s p a ti al densit y op er ato r ) 23 관성능 융 79~ Ing li s 관성 능률~ 84~ 교환 관계 (commuta t i on relati on ship ) 31 교환력 (exchang e for ce) 37 교환 연 산자 (exchang e op e rato r ) 250 구멍 상태 (hole sta t e ) 55~ 규격 화 (normaliz a ti on ) 23 곡지 점 (verte x ) 237
단열 (adia b ati c) 모델 94~ 단열 (adiJ b a: ic ) 배 열 89 단일입자 상태 (si n g le pa rti cl e sta t e ) l5 단일항 상 태 (si n g le t sta t e ) 37 단진자 모 델 48 변형된 --64 회전하는 -8 .5 단체 둘뜸과정 (collecti ve excit at i on mechanis m ) 64 단체 회 전 (collecti ve rota t i on ) 73~ 닫한 핵 각 (closed shell) .56 닫험 관계 (closure relati on ) 107, no 대 칭 성 (sy m metr y ) 30, 148~ 대칭 1 체 연산자 III 대칭 2 체 연산자 III, II2 대 칭 팽 이 (sy m metr i c roto r ) 과동함수 78 동위 핵 (iso t op e) 19.5 동중성 자핵 (iso to n e) 19.5 둘뜸 상태 (excit ed sta t e ) .56 등포텐셜 선 (eq u ip o te n ti al lin e ) 64 <2 > 라그랑지 안 밀도 119 Lag ra ng e -pa ramete r 방법 208 Lag u erre 다항식 51 <口 > 마법 수 (mag ic number) 46, 54 Majo r ana 력 37 물방울 모델 (liqu id drop model) 15 밀 도행 렬 (densit y matr i x ) 143~ 〈 닌 ) 바닥상태 (gr ound sta te ) 56 Weis z acker 결 합에 너 지 27ff
Barlett e 력 37 반교환성 (anti -c ommuta b il i ty ) r 13 반대 칭 (anti -s ym metr y ) 32, 108 반대 칭 화된 행 렬 요소 (anti sy m metr i z e d matr i x element) 117 반-유니 터 리 (anti -u nit ar y) 연 산자 34 反純性, pa rity 32, 153~ 배 결 합 상수 (decoup ling consta n t) 100 변분파동함수 (varia t i on al wave fun cti on ) 203 BCS 번분파동함수 203 변형 (defo r mati on ) 63 변 형 매 개 상수 (defo r mati on pa ramete r ) 64 변 환군 (tra nsfo r mati on gr oup ) 31 복합핵 (comp o und nucleus) I-1- Volkov 력 I88 분광학적 인자 (sp e ctr o scop ic fac to r ) I63 불확정 성 원 리 (uncerta i n t y pr in c ip le ) 29 Brill ou in - W ign er 전개 IOO 비 국소적 연 산자 (non-local op e rato r ) II6 Wi gne r 력 37 Wi gn er 함수 79 Wi gn er-Eckart 정 리 167 비대칭 매개변수 (as y mme t r y pa ramete r ) 80 BCS 방법 I97 비 정 상 반전상태 (anomalous pa rit y sta t e ) 54 Wi ck 의 정 리 138~
상 전 이 (ph ase tra nsit ion ) 233 상대 일 도 (densit y of sta t e ) 196 상호작용 묘사 (int e r acti on pict u r e) 230 생 성 연 산자 (creati on op e rato r ) r 13 선텍 규칙 (selecti on rule) 30 섭 동 (pe rtu rbati on ) 30 소 멸 연 산자 (annih i l a ti on op e rato r ) II3 수반상태 (adjo int sta t e ) u3 Sky rm e 력 255 스핀 - 궤도력 (sp in- o rbit for ce) 36, 38 스핀-궤도 상호 결 합력 (spi n -orbit coup l in g in te r acti on ) 14, 38 술래 이 터 행 렬식 (Slate r Dete r mi na nt) I03 시 간 역 전 (tim e reversal) 154~ 시 간 역 전 불변 성 (tim e reversal inv aria n ce) 154~ 시 간 역 전상태 (tim e reversal sta t e ) . 62 sig n atu re 97 senio rit y 수 201 Schrodin g e r 묘사 I40 쌍대 공간 (dual sp a ce) r13 쌍생 성 연 산자 (pa ir creati on op e rato r) 204 쌍짓기 (pa ir i n g ) 195~
운동의 항량 (cons t an t of moti on ) 31 원 자가 구멍 (valence hole) 59 원 자가 입 자 (valence pa rti cl e) 58 유가와 (Yukawa) 포텐선 250 유니 터 리 (unit ar y) 변환 I20 유사 상태 (Analog Sta t e ) 16, 165 유효력 (eff ec ti ve for ce) 187~ 이 성 원자핵 (iso mer) 16 2 체 민도 상관함수(t wo pa rti cl e den- sit y corr elati on fun cti on ) 13, 26 2 채 민도 연산자( t wo - p ar ti cle densit y op e rato r ) 25 2 체 연산자 111 1 체 연산자 111 1 체 전과 연산자 (one-bod y pr op a g a to r ) 238 입 자-구멍 둔뜸 상태 (pa rti cl e-hole excit ed sta t e ) 85 입자 -구멍 t신 환 124~ 입자-구멍 변환 연산자 126 입 자상태 (pa rti cl e sta t e ) 55, 59
정상곱 (normal pr oduct) 134 깅 준빈 환 (canonic a l tra nsfo r mati on ) 120, 206 j-i 결합형 60 준-스핀 (qu asi- s pi n) 199~ 준-입자(q uas i-p ar ti cle) 205 준입자 소멸 (생성) 연산자 235 중입자 (bar y on) 16 지공 형태 인자 (rad i al for m fac to r ) 36 진공 (vacuum) 상태 II3 집 단 운동 (collecti ve moti on ) 13 〈大〉 초전도 간격 (에너지 도약) 222 초전도성 (sup e r-conducti vi t y) 195 초중핵 (sup e r-heavy nucleus) 192 축약 (contr a cti on ) I37 충둡 단면적 (scatt er in g cross secti on ) I8 • 〈더〉 Corio l is 항 83, 94 크랭 킹 (crankin g ) 모델 81~
r - 중간자 교환 포텐셜 (one pion exchang e po te n ti al, OPEP) 29 Fey n man 그립 식 229~ 팽 이 -입 자 결 합항 (roto r-pa rtic l e coup li n g ter m: RPC) 94 팽이-임자 모델 : 동합 모델을 보라 팽이 파동함수 75~ 페르미면 214 페 르미 바다 I2I, I33~ 평 균 핵 자밀 도 (averag e nuclear densit y) 22 포물체 (pro je c ti le) 15 포크 공간 (Fock spa c e) n3 표면 확산도 (surfa c e dif fus eness) 20 〈굴〉 하전스핀 (iso sp in) 32~ 하전스핀 연산자 33, I3I
하트 리 -보골리 우보프 (Hartr e e- Bog o liu b ov) 방법 197 하트리 -포크 (Hartr e e- F ock) 이 론 142~ 핵 각 모델 (nuclear shell model) 14,46~ 핵 자 포화 현 상 (nuclear satu rati on ) 22 핵 질 (nuclear matt er ) 28, 허 구 (spu rio u s) 상태 85 형 태 인 자 (for m fac to r ) 18 지 름 형 태 인 자 (radia l for m fac t or ) 36 훈극 거 대 진동 (monop o le gian t resonance) 257 희 귀 정 (tur nin g po in t ) 48 희 전며 (rota t i on al band) 96 회 전띠 의 혼합 (band mi xi n g ) 99
민동필 서웅대학교 뭉리학과 졸업 프랑스 파리대학에서 이학박사 및 국가박사 학위 취득 프랑스 Sacla y기초과학연구소 연구관 서독 뮌헨대학 뭉리학과 교수 현재는 서울대학 뭉리학과 교수 논문으로는 Sp h eroid a l Sky rm i on 외 다수
 i J
i J
핵구조물리학 대우학술총서 • 자연과학 42 적은 날 1987 년 6 월 . 1 일 펴낸날 1987 년 6 월 . 15 일 겨은이 민동필 펴낸이 朴孟浩 펴낸곳 民音社 출 판동 목 1966, 5. 19 제 1-142 호 우편대체계좌번호 010041-3·1 - 523282 110 시웅시 종로구 관철동 44-1 734-2000, 735-8524 (영 업 부) 734-6 1 10 • 4234( 편집부) *파본은 바꾸어 드립니다 . 값: 5,300 원
대우학술총서 • 자연과학 I 소립자와 게이지상호작용 金鎭義著 / 값 3, 600 원 2 動力學特論 和想 J 값 5, 400 원 3 질소고정 宋承達著 / 값 2,800 원 4 相轉移와 臨界現 象 김두철 著 / 값 2, 800 원 5 觸媒作用 陳宗植 著 / 값 2, 800 원 6 뫼스바우어分光學 玉恒南著 / 값 2,800 원 7 극미량원소의 영양 昇正子著 / 값 6,500 원 8 水素化峴 素와 有機視素化合物 尹能民 著 / 값 5, 000 원 9 抗生物質의 全合成 姜錫久 著 / 값 9, 000 원 10 국소적 형태의 A tiy ah - S i ng er 지표이론 지동표著 / 값 2,800 원 11 Muco p ol y sacchar i des 의 生化學및生物理學 박쫑공 / 값 3 , 800 원 12 ASTROPHYSICS( 天體物理學) 洪承樹著 / 값 4 ,700 원 13 프로스타글란딘 합성 金登표 著 / 값 3 , 600 원 14 천연물화학연구법 禹源植 著 / 값 7, 000 원 15 脂防營養 金 ·淑 喜 著 / 값 6, 300 원 16 結晶化유리 金炳 患 著 / ~4. 500 원 17 高分子의 化學反應 趙義 煥 著 / 값 4 ,000 원 18 과학혁명 金永植著 / 값 4,200 원 19 韓國地質論 登基弘 著 / 값 4, 000 원 20 정보이론 한영열 著 / 값4,5 00 원 :21 原子 核反應論 鄭雲赫著 / 값 8,500 원 ”23 四擊圈O I 른頓뼈뺄3, - 28 碑퍼파꾼 l m 교 刃석탠庫杯 변환가술싶謙훌값때 警庫 n 32 ”. . 1 t .r I \ 따' 따’ 깝핵頭'• 다警• 庫, ~ * 』 3, 뷔. ”庄警偉 l %련.ffl ’ 틀t 37 헌국의鑛嶋를 ..~ 1.IQl t; 311 일반상대른亭衝警/it '-000 월 刃 繼因명신확“麟書/i!S. 000 휩 40 복소湘성聽!”文書偉 7. 鵬원 41 역혁적 연구탈법 鼻警沿때 42 핵 , 도를리확텐躍警 / 값s.繼뭔 43-' 석파의 01 분적용소걷璋警 f · 값s. 800 룹 44 한華古生嶋尹홀 / 〈조 4, 질량분석학김硏署/ 값 800 원 쏘 굽변른毗圈 署沮s. OOO 원