김종진
김종진
저자는 서울대학교 문리과 대학 물리학과를 졸업하고 미국 캘리포니아 (싼타 바바라) 대학교에서 물리학 박사학위를 받았다. 영국 슈트라쓰 클랴가드 대학교 물리화학 연구실 연구원을 거쳐 현재 한국 과학기술원 물리학과교수로있다. ro-H… 0 Raman Bands in KDP Mel .t s」 , 「 Commen t s on Surfa c e Carbon Peaks in S ERS」 등 58 편의 논문을발표하였다.
레이처 광산란분광학 
레이처 광산란분광학
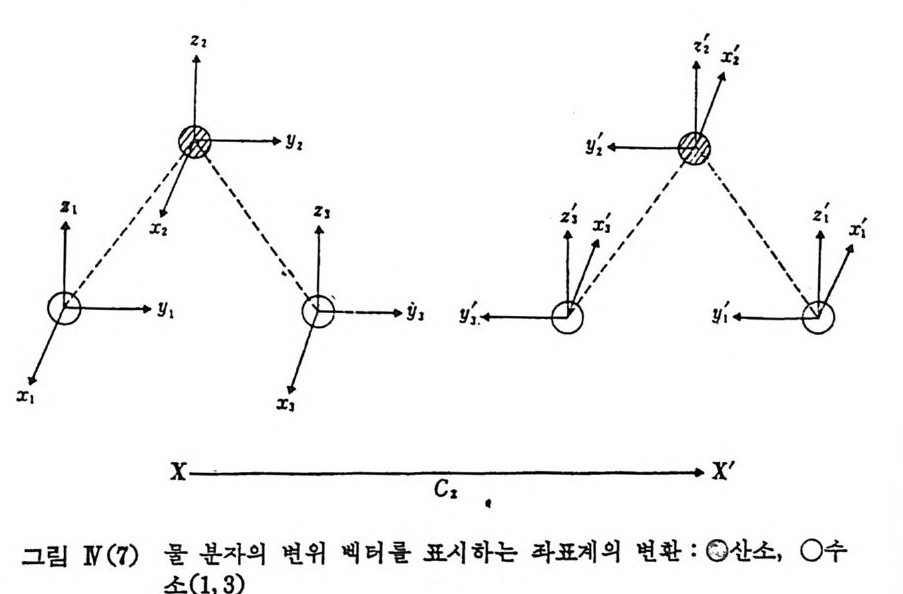
머리말 이 책자는 본인이 한국 과학원에서 대학원 강의로 계속해 오던 고체 분광학, 광산란과 입계현상, 군론의 응용, 이들 세 교과목의 내용을 한 데 묶어 간추려 놓은 것이다. 광산란 현상은 레일레이, 브릴루엥, 라만에 의하여 물리학의 한 중요 한 분야를 이 루기 시 작한 지 이 순이 넘 는 (Ra y le ig h 1899, Brill ou in 1922, Raman 1928) 건 연문에 서 , 그동안 특히 레 이 저 의 출현 이 후, 수 많은 연구 결과가 쌓여 광산란에 대한 책 및 해설 논문들이 수없이 출 판된 상태에 있지만 오히려 우리 국내 학생들에게는 그만큼 어더서부터 시작해야 될지 더 갇피룬 못 잡게 만드는 실정이 되고 있다. 광산란은 이제 고전 분광학의 법주를 넘어서 액체에서의 분자 운동, 고체 내 의 들뜸 양자 (elemen t a ry exc itat i on s) 및 그들 사이 의 상호작용 에 관한 연구 죽 물성론에도 큰 기여를 하고 있다. 강의를 통한 학생들과의 오랜 접촉이 책의 내용 • 구성에 큰 영향을 주 었31.. 또 제한된 지면 수 및 시간도 많은 영향을 주었다. 첫째, 분광학 분야 일반올 소개하고 그 가운데에 광산란 분야의 좌표 를 찾아보았으며 둘째, 간단한 광산란 문제를 고전 전자기학의 입장에 서 이해시키고 이와 함께 물성론적 입장에서 양자역학, 동계역학적 취급 을소개하였다. 제血장에서 광산란 실험실에 필요한 실험기구, 득히 라만 산란 실험 의 실험장치에 대하여 상술하였으며 제 N, V 장에서 기체, 액체, 고체에 서의 광산란 실험의 간단한 문제 예를 골라서 충실히 설명하는 과정에
서 광산란 연구가 물리학의 어떤 문제와 관련이 있는지 이해시키려고 노력하였다. 끝으로 제 W 장에서 현재 이 분야의 연구 • 관심이 세계적으로 어떤 문 제들에 집중이 되고 있는지 몇 가지 골라서 설명 소개하였다. 이 책의 출판을 계기로 해서 앞으로 국내에서도 훌륭한 후베, 후진들 에 의해서 좀더 전문적 분야로 세분된 광산란 관계 전공서적이 줄을 이 어주었으면 하는 소망이며 인내로 지켜보아 준 대우재단과 민음사에 감 사드린다. 1986 년 8 월 홍능에서 김종전
레이저 광산란 분광학·차례
머리말 5제Ⅰ장 서론 13Ⅰ-1 빛과 분광학 13Ⅰ-2 분광학적 광산란 15Ⅰ-3 광산란 연구의 현황 19참고문헌 20제Ⅱ장 전자파 산란 21Ⅱ-1 고전 전자기 학적 고찰 22Ⅱ-1.1 산란 단면적 22 Ⅱ-1.2 유전체 구형 입자 25 Ⅱ-1.3 완전도체의 구형 입자 26 Ⅱ-1.4 광학적 회절 27 Ⅱ-1.5 부분파와 위상 변이 30Ⅱ-2 원자 및 분자적 속성 33Ⅱ-2.1 로렌츠 단전자 모델 33 Ⅱ-2.2 원자 및 분자들에 의한 광산란 35 Ⅱ-2.3 푸른 하늘의 기원 36Ⅱ-3 양자역 학적 고찰 39Ⅱ-3.1 광량자 39 Ⅱ-3.2 파동의 간섭성 (coherence)과 광자의 상관성(correlations) 42 Ⅱ-3.3 원자 및 분자의 양자 역학적 에너지 준위 45 Ⅱ-3.4 흡수, 형광 및 산란 50참고문헌 54제Ⅲ장 광산란 스펙트럼의 측정 55
Ⅲ-1 레일레이 산란 56Ⅲ-1.1 단일 모드 레이처의 필요성 56 Ⅲ-1.2 스펙트럼 분해기 56 Ⅲ-1.3 상관함수 측정기 61Ⅲ-2 브릴루엥 산란 65Ⅲ-2.1 실험장치 65 Ⅲ-2.2 파아브리-메로 간섭계 67 Ⅲ-2.3 산란각에 따른 변화 70Ⅲ-3 라만 산란 73Ⅲ-3.1 실험설비 73 Ⅲ-3.2 레이저 광원 74 Ⅲ-3.3 이중 회절발 분광기 76 Ⅲ-3.4 스펙트럼 신호처리 77 Ⅲ-3.5 몇 가지 광학 소자들 86Ⅲ-4 레이저 및 광전 증배관 92Ⅲ-4.1 레이저 92 Ⅲ-4.2 광전 증배관 96참고문헌 101제Ⅳ장 기체와 액체의 광산란 분광학 103Ⅳ-1 기체 103Ⅳ-1.1 회전운동 에너지 준위 103 Ⅳ-1.2 회전준위 스펙트럼 105 Ⅳ-1.3 분자의 진동운동 109 Ⅳ-1.4 대칭성과 군론 114 Ⅳ-1.5 선택률 122 Ⅳ-1.6 분자진동 라만 스펙트럼 123Ⅳ-2 액체 125Ⅳ-2.1 액체에서의 분자운동 125 Ⅳ-2.2 요동과 상관성 129 Ⅳ-2.3 협동운동과 유체역학적 모드 133Ⅳ-3 스펙트럼의 분석 134Ⅳ-3.1 비편광 광산란과 분자들의 상호작용 134 Ⅳ-3.2 분자 전동 라만 스팩트럼과 분자의 방향각 운동 143Ⅳ-4 임계점 산란백광 147
Ⅳ-4.1 임계점 147 Ⅳ-4.2 광산란의 요동이론-Ornstein-Zernike 이론 149 Ⅳ-4.3 모드-모드 상호결합 152참고문헌 156제Ⅴ장 고체에서의 광산란 분광학 159Ⅴ-1 격자 운동과 광산란 159Ⅴ-1.1 음파성 포논과 광파성 포논 159 Ⅴ-1.2 브릴루엥 산란 165 Ⅴ-1.3 라만 산란 168 Ⅴ-1.4 편극률텐서 172 Ⅴ-1.5 결정의 대칭성과 라만텐서 177 Ⅴ-1.6 L.O. 포논과 T.O. 포논 182 Ⅴ-1.7 Second Order 스펙트럼 186Ⅴ-2 기타의 다른 기본 여기파 187Ⅴ-2.1 폴라리톤 라만 산란 187 Ⅴ-2.2 플라스몬 라만 산란 190 Ⅴ-2.3 매그논과 라만 산란 196 Ⅴ-2.4 엑씨톤과 라만 산란 201Ⅴ-3 불순물 및 결함 205Ⅴ-3.1 상자성 중심자, 결정 전장, 전자 준위 라만 스팩트럼 205 Ⅴ-3.2 반도체의 donor 및 acceptor들에 의한 라만 산란 206 Ⅴ-3.3 국재형 모드와 공명형 모드 208 Ⅴ-3.4 색소 중심자 21O참고문헌 212제Ⅵ장 특수 논제 215Ⅵ-1 공명성 라만 산란 215Ⅵ-1.1 가변주파수 염료레이저 215 Ⅵ-1.2 공명성 라만 산란 217Ⅵ-2 표면-증강 라만 산란 220Ⅵ-2.1 실험적 관측 사실 220 Ⅵ-2.2 이론적 고찰 221
Ⅵ-3 soft-mode 라만 분광학 224Ⅵ-3.1 soft-mode 이론 224 Ⅵ-3.2 central mode 228 Ⅵ-3.3 couple 된 모드의 라만 스펙트럼 229Ⅵ-4 비선형 산란문제 235Ⅵ-4.1 비선형 광학 감응계수 235 Ⅵ- 4.2 하이퍼-라만 산란 및 유도 라만 산란 238 Ⅵ-4.3 카스 간섭성 라만 산란 240 Ⅵ-4.4 라이크스 스펙트럼 243참고문헌 245색인 247제 I 장 서론 광산란 분광학 분야는 레이처의 출현과 함께 물성론 연구에 새로운많 은 기여를 해오고 있다. 본 서론의 장에서는 빛의 물리적 의미를 재고해 보고 이와 관련된 분 광학의 발전 상황에 대한 몇 가지 정보, 광산란 연구의 분광학적 위치, 이에 대한 연구의 발전 과정을 간단히 소개하고자 한다• I -1 빛과 분광학 빛을 비추어 우리들 얻굴의 생김새를 눈으로 들여다분 수 있듯이 자 연에 대한 대부분의 과학적 정보, 크게는 태양계, 은하계, 우주 공간, 작게는 분자, 원자, 원자핵, 핵자, 또 그 핵자 속에는무엇이 어떠한상 대로 들어 있느냐에 대한 정보도 빛(태디오 전자과, 적의선, 가시광, 자의 선, X- 선, r- 선 등 모든 과장의 전자파를 포함한)을 통해 서 얻고 있다. 1900 년 12 월 Max Planck 에 의해서 빛의 에너지가 양자화되어 있다 논 사실, 죽 전동수 o 의 빛은 오칙 ho 의 정수배 값 e=nhw 로 주어지 논 에너지 값만을 가질 수 있다는 사실이 소개되었고 뒤이어서 1913 년 에는 Nie l s Bohr 가 수소 원자의 에너지도 양자화되어 e=-Rh/ 군으로 주어지는 죽 n=l,2,3, …의 정수에 대웅하는 값들만 가질 수 있다는 사 실을 밝히게 되었다.
분광학은 바로 이 빛을 동해서 원자분자의 양자역학적 구조와 물질의 여러 가능한 상태(기체, 액체, 고체, 플라스마)에서의 양자역학 및 몽 계역학적 정보를 보다 더 정밀하계 찾아내려고 연구하는 학문이다. 제 일 간단한 원자, 분자계에 대한 분광학을 예로 들면, 가령 수소 원자에 대한 양자역학적 정보라 함은 과연 수소 원자에서 Bohr 의 이론대로 에 너지 값이 오칙 n 값에만 의존하고 있는가에 대한 실험 연구를 들 수 있다. 죽 수소 원자의 고전적 스펙트럼인 라이만 계열 (Ly man ser i es) 의 자 의선 영역 스펙트럼 선들은 Bohr 이론의 n=2,3,4, …에 해당한 에너지 준위 에 서 n= 1 의 기 처 상태 로, 발머 계 열 (Balmer ser i es) 의 가시 광 영 역 스펙트럼 선들은 n=3,4,5,··· 의 상태에서 n=2 의 상대로, 파센 계 열 (Paschen ser i es) 의 적의선 영 역 스펙트럼 선들은 n=4, 5, 6, … 의 상 태에서 n=3 의 상태로 천이할 때에 방출되는 스펙트럼 선들로 그 배열 간격이 보어 이론에 적중하고 있음을 보였었다• 그러나 수소 원자의 분광학이 고도로 발전됨에 따라서 사실 같은 n=2 의 2s 상대와 2P 상태의 에너지가 서로 완전히 같지 않고 2s 상태가 2P 상태보다 미소한 차이 (~109Hz) 이지만 높은 에너지를 갖고 있음이 밝혀졌고 이 Lamb 변이의 관측은 바로 전자기장의 양자화에 기인하고 있는, 한 미소한 그렇지만 기본 원리면에서 아주 중대한 효과를 제시해 준 이것와이 다같.이 가령 수소 원자에서 보면 n 와 n— 1 상 태 사이의 정확한 에 너지 간격을 구하는 데에 목적을 두고 있는 주파수(또는 파장) 영역 분 광학(fr e q uenc y domain s pe c t rosco py)이 한 주류를 이 루고 있 으며 여 기 서는 각 에너지 준위 n 의 초미세 구조에 대한 연구를비롯하여 n 이 아 주 커지면 n 준위와 n-1 준위와의 에너지 간격 L1en::::::'.2Rh/n3 가 Dop pl er 퍼집의 선폭보다 작온 값이 되어 실험적으로 새로운 기술이 요구되고 이 러 한 높은 n 값의 상태 (hig h Ry d berg s t a t es) 에 대 한 연구가 최 근에 많온 전전율 보이고 있다. 또 하나 다론 주류를 이 루고 있는 시 간 영 역 분광학(ti me domain s p ec t rosco py)에 서 는 가령 수소 원자가 2P 상태 에 올라가서 자발 형 광 복사의 과정에 따라 다시 1S 상태로 내려올 때까지 얼마나 오랫동안 머 물러 있는가, 즉 각 고유상태의 평군 수명을 축정하는 실험을 포함 한다.
예를 둔어 수소 원자를 보면 2p -- 1s 천이에 대한 평군 수명이 ~1.6 x 10-9 초, 4/-+3d 천이는 ~7.3 x 10- s 초, 6h-+5 g천이에 대한 6h 준 위 의 평 군 수명 이 ~6. 1 X 10-7 초에 달하고 있 다. 이와 같이 원자에서는 스펙트럼의 중요한 영역이 가시광 및 자의선에 해당하고 이둔 천이에 대한 평군 수명이 ~10-9 초가 되고 있다. 이제 분자를 살펴보면 모든 내부 에너지가 원자에서처럼 전자에만 주 어지지 않고 휠싼 크고 무거운 원자핵들에게도 진동운동 (v i bra ti onal moti on ), 회 전운동 (ro t a ti onal mo ti on) 의 내 부 에 너 지 가 주어 진다. 이들 전동운동의 고유 전동수, 따라서 고유상태 사이의 에너지 간격 은 원자핵의 질량에, 회전운동은 분자 전체의 질량에 관계되어 일반적으 로 분자의 크기와 질량이 커질수록 그 분자의 전동 에너지 및 회전 에 너지 준위들 사이의 간격이 작아지고 이에 따라서 분자의 전자 준위 스 펙 트럼 (electr o nic s p ec t ra) 온 대 체 로 원자에 서 와 같이 가시 광 및 자의 선 영 역 에 속하고 있 지 만 전동 준위 스펙 트럼 (vib r ati on al s p ec t ra) 은 적 의 선 영 역 , 회 전 준위 스펙 트럼 (rota t i on al s p ec t ra) 은 원적 의 선 내 지 마이 크로 전자과 영역에 속하고 있다. I-2 분광학적 광산란 이제 거시적 물질을 생각하면 내부 에너지의 일부가 이 거시적 물질 전체 또는 일부가 하나의 분자처 럼 행 동하는 자유도 (de g rees of free dom) 에 주어질 수 있고 이때 이 거시적 분자의 전체 질량에 관계되는 에너 지 준위 사이의 간격은 무한히 작아지고 결국 실온에서의 열 에너지 (the rmal energy fl uc t ua ti on) 보다 적 어 질 경 우 완전히 고전 역 학의 연 속적 에너지를 갖는다고 볼 수 있다. 이러한 경우 열 에너지에 의해서 위 • 아래로 근접해 있는 연속적 고유 상대 들 사이 의 위 • 아래 천이 는 소위 열적 요동(th ennal fl uc t ua ti on) 이 라는 개념으로 전환되고 또한 이 거시적 물질 내의 원자 또는 분자는 한 높은 에너지를 갖는 고유상태로부터, 연속적으로 주어전 고유상태를 가지는 거시분자 즉 물질 전체와의 에너지 교환율 거쳐 결국 가장 낮은 에너지의 상태로 천이해 가는 열적 이완(t hennal relaxa ti on) 의 현상을 나타내고 있다. 앞에서 언급한 바와 같이 원자와 분자에서 전자의 에너지(바닥상태의
에너지를 0 으로 기준하여)는 가시광 내지 자의선 정도의 에너지로서, 적외선 에너지 정도인 분자의 진동운동, 마이크로 전자과 에너지 정도 인 분자의 회전운동보다 훨씬 높은 에너지가 되며, 각각의 경우에 따타 다르지만, 이들 에너지의 절반을 운동 에너지로 가정하여 각각의 고유 상태에 관여하는 전자, 원자(핵), 분자의 운등속도를 구해 보면 각각의 고유상태에 연관된 운동체의 질량이 커질수록 속도가 느려지고 있음을 볼수있다. 마찬가지로 물질울 하나의 거시적 분자로 생각할 때에 이 분자의 전 체 질량 또는 일부 질량이 관련되는 고유상태에 해당하는 다체 문제 목 유의 상대 운동은 원자 또는 작은 분자에 비해서 지극히 느린 운동상태 도 포함할 것이 예상된다. 이와 같이 고유상태 사이의 에너지 차이가 적외선 또는 마이크로 전 자파 영역을 벗어나는 경우 광원(lig h t source) 자체를 구하기 힘들기 대 문에 우리가 원자 및 분자 분광학에서 사용하고 있는 흡수또는형광복 사에 의 한 실험 방법 의 져 용이 힘 들게 되 며 시 간영 역 분광학(ti me domain s p ec t rosco py)의 실험 도 마찬가지 광원 문제 로 광펄스(lig h t pu lse) 여 기 (exci tat i on ) 방법 의 적 용이 불가능해 진 다. 그러나 빛과 원자, 분자, 물질 사이의 상호작용에는 흡수, 형광복사 이의에 산란 현상이 있다. 이 산란 작용은 흡수와 복사에 바해서는 무시할 정도로 약한 상호작 용이지만 흡수와 복사가 전혀 없는 경우에 오히려 매우 약하지만 항상 존재하는 산탄광을 관측, 분석함으로써 물질상태에 대한 중요한 미시 적 정보를 얻을 수 있다. 가시광 영역에서 전혀 흡수가 없는 두명한 물질에 전동수 (J)。 강도 1。 의 가시광선이 들어가면 대부분이 기하광학적 광로에 따라 직전해 나가 지만 극히 적은 일부의 빛 (~10-8 1o) 은 기하광학적 진로에서 벗어난 다 론 방향 가령 90° 칙각 방향에서도 산란광으로 관측이 된다. 이 산란광은 바로 물질 내에서의 요동(fl uc t ua ti on) 에 기인하고 있으 며 입 사광의 전동수 (J)。 와 같은 진동수의 빛으로서 다만 선폭이 넓 어 전 것으로 볼 수 있는 산란광을 레일레이 산란 (Ra y le ig h scatt er i ng ), 음속 의 파동운동에 의 한 도풀러 변이 정 도로 전동수가 변이 (sh ift)되 어 나오 논 산탄광을 브릴루엥 산란 (Br ill ou i n scatt er in g ), 분자 운동의 여 러 가지 에너지 준위에 해당하는 전동수의 변이 (sh ift)를 가지는 산란광울 라만
산란 (Raman sca tt er i n g)에 의 한 산란광이 라고 한다. 이 와 같이 물질 내 에 서 의 여 러 가지 이 완 현상 (relaxa ti ons) 및 요동 현 상(fl uc t ua ti ons) 을 고려하는 분자론적 측면에서 빛의 산란 현상을 다루 고 이로부터 물성론의 중요한 정보를 얻는 분광학적 광산란의 연구 분 야가 정의되며, 다론 한편으로는 물질의 내부 자유도(i n t ernal deg re es of fr e e dom) 를 완전히 무시하는 측면에서 보면 빛과 물질 사이의 미시적 상 호작용에 의한 분광학적 광산란은 일단 무시해 버릴 수 있는 섭동 효 과의 하나에 지나지 않고 대신 전자기 또는 광학적 산란이 문제가된다· 여기서는 여러 형체의 물체에 의한 전자파의 회철 현상, 죽 회절각의 함수로 회 철광의 강도(i n t ens ity) 및 편광도 (de p olar i za ti on ra ti o) 를 축 정하는 실험이 중요시되며 가령 미립자들에 대한 이러한 광산란 실험 결과로부터 이들 미립자의 크기, 유전상수, 기하학적 형체 등 거시적이 고 평균적인 성질에 대한 유용한 정보를 얻을 수 있다. 이와 같이 광산란 분야는 미시적 내부상태와 분자론적 성질이 중요시 되는 레일레이, 브릴루엥, 라만 산란의 분광학으로서의 광산란과 거시 적 형체와 전자기적 성질이 좌우하는 회절광학 분야의 광산란으로 대 벌할 수 있고 찰 알려진 미이 산란 (M i e scatt er in g ), 틴달 산란 (T y ndall scatt er in g ) 등이 후자에 속하고 있 다. 이 제 일 반적 으로 분자와 빛 사이 의 광산란 상호작용을 가장 간단한 수 준의 수식 전개를써서 이해하여 브기로하자. 가시광에 해당하는 ~1015 Hz 의 전자파가 분자에 와 닿으면 분자의 무거운 핵과 아주 가벼운 전 자듄이 서로 반대 방향의 힘을 동시에 받게 되지만 주로 전자들의 강제 운동에 의해서 전자과 재복사가 일어나게 된다. 의부에서 E=E 。 ex p(-i w 。t)의 전기장이 분자에 작용하면 결국 전자 들만이 ~1015Hz 에 달하는 Wo 전동수로 움칙일 수 있게 되고 분자 내 에 전기 쌍극 모멘트가 이러한 전동수로 전동운동하고 있다고 볼 수 있 다. 즉, p =aE=aE 。 ex p(-i(J.)。t) 여기서 분자의 전기 편극몰 a 는 사실 분자를 구성하는 원자핵들의 상 호위치에 따라 그 값아 달라지는 양으로서 분자 자체가 고유 전동수로 내 부 진동운동을 한다는 사실을 고려하면
a=a 묘(織)。Q n+ …… Q n= Q갭 exp (—i9n t ) 로 쓸 수 있 다. 여 기 서 Qn 은 분자의 고유전동 정 격 모드 (normal mode) 를 나타내는 좌표이다. 따라서 실수 부분만을 고려 하여 p= aE ={a 。땅(훑-)。Q n° cosQ nt} E 。 cosw 。t =aoE 。 cosw 。t+ 읽훑-) Qn° E 。 [cos(w 。 +Dn) t -cos(w 。-Q)t] 。 를 얻을 수 있다. 이러한 진동운동 상태에 있는 쌍극자는 바로 전자과 발생원 죽 재복 사의 원체가 되는 것이다. 쌍극자의 가속운동에 의한 전자과 발생은 E, o:: d2p /d t2 로 주어지므로 재복사 전자파의 진동수에 는 Wo 분만 아니 라 (L)。土Q n 이 포함되 어 있음을 알 수 있다. 입사과와 같은 전동수로 재복사하는 경우에 해당하는 산란 광울 레일레일 산란광이타 하고 입사과와 다른 진동수로 산란되어 나오 논 빛을 라만 산란광이라고 부른다. 여기서 오 죽 분자의 전동운동은 고체가 되면 포논(p honon) 이 되어 나타난다. 이 포논은 다시 광과성 포논 (o ptical p honon) 과 음파성 (acousti c) 포 논으로 분류가 되 고 9n 이 광과성 포논의 진동수에 해 당할 때 에 Raman 산란, 음과성 포논에 해 당할 때 에 Brill ou in 산란이 라고 부른다. 액 체에 대해서도 이러한 개념을 일반화시켜 볼 수 있으나, 즉 광과성 포 논은 분자의 전동 모드들로 축되되고 음파성 포논온 음향파동 (sound wave) 모드들로 축되되는 것으로 해석할 수도 있겠지만 상당한 무리가 따르게 된다. 오히려 실험 측면에서 보면 분자 하나하나의 재복사를 고려하는 것 보다는 거시적인 쳐도로 들여다보는 것이 훨싼 바람직한 결과를 줄 수 있다. 액체에서 지금 입사과 광선이 N 개의 분자(또는 원자)들과 상호작용
하면서 지나간다고 할 때에
및 고체의 산란광이 브릴루엥 스펙트럼의 성분 이외에 더욱 복잡한 구 조의 스팩트럼 소위 타만 스펙트럼을 나타내고 있음을 확인하였다. 이로부터 많은 사람들의 연구가 광산란에 집중되었으나 곧 실험적인 난관으로 적외선 흡수 스펙트럼 이상의 벌다른 아무런 새로운 것을 줄 수 없다는 인상이 질어져 갔고 이로 인해서 기초 학문적 물리학자들의 관심 보다 분자들의 대 칭 성 • 구조를 규명 하는 한 수단으로서 화학자들의 관심을 끌고 있었다. 그러나 1964 년에 레이처(l aser) 광원이 광산란 실 험에 적용되면서부터 다시 본격적인 광산란 연구에 세계적으로 불이 붙 었고 매 2 년마다 계속되어 오는 라만 분광학 국제회의 제 10 차 회의가 1986 년 9 월 미국 오레곤대학교에서 열리게 되었다. 타만 분광학은 새로운 떤이 계속 개발, 확장되어 위 오레곤대 회의에 서는 논문 발표 주제가 생물 • 의학적 응용, 초미세 시료에 대한 연구, 액체에서의 다체론 효과, 비선형 현상, 표면 및 계면충 분자의 산란 증 강, 상전이 문제, 공명 산란 등 11 개 분야로 나뉘어져 진행되고 있다. 라만 분광학은 이 밖에도 다론 여러 국제 회의들, 록히 강 유전체 국 제회의, 포논 물리학 국제회의, 반도체 물리학 국제회의, 양자 전자공 학 국제회의 등에서도 계속 중요한 한 분야를 차지하고 있다. 참고문헌 1. Raman Sp ec tr o scop y(L i ne ar and Nonlin e ar), edit ed by Jea n Lascombe and Pham V. Huong , Joh n-W iley & Sons (Chic h este r , New York, 1982). Proceedin g s of the 9th Int' l Conj. on Raman Sp e ctr o scop y, Toky o ( 8 월 27 일~ 9 월 1 일, 1984). 2. NLewi~ h Yt oSrkc,a tt1 e9r6 i9n )g . S고p 체ec tr 물a 리of 학 S o분li d야s, 광ed산. b란y G연.B구. 의W r제ig h1 t 회( S p국 r i제n g 회 e r -의V er발la표g, 논문집 으로서 Brill ou in 과 Raman 의 회 고록이 수록되 어 있 다. 3. 아태의 책둘도 모두 제 1 장에서 광산란의 역사적 개요문 소개하고 있다. Ben. Chu, Laser Li gh t Scatt er in g , Academi c Press (New York, 1974). B. Berne and R. Pecora, Dy n ami c Lig ht Scatt er in g , Joh n Wi le y & Sons (New York, 1976). W. Hay es and R. Loudon, Scatt er in g of Lig h t by Crys t a l s, Joh n Wi le y & Sons (New York, 1978). 4. 제 10 차 Raman Spe c tr o scop y 국제 회 의 가 1986 년 8 월 31 일부터 9 월 5 일 까지 미국 오레곤대학교에서 열리며 발표논문집이 발간된다.
제 1I 장 전자파 산란 우리는 이미 원자물리 또는 핵물리 교과목에서 자유전자 및 양성자 (pro to n ) 입자에 의한 X- 선 또는 7 선의 산란 현상에 대해서 배운 바 있다. 즉 하전 입자가 X-선, 또는 7 선의 전기장 속에서 갖게 되는 가속도 를 구하여, 하전 입자의 가속운동에 의한 전자과 복사울의 공식에 대 입함으로써 소위 Thomson 산란 단면적을 얻었고 이때에 광선의 에너지 가 커지면 광량자(p ho t on) 가 가지는 운동량을 무시할 수 없게 되고 따 타서 하전 입 자의 되 뒤 김 (recoil ) 에 너 지 를 고려 에 넣 어 야 하고 이 때 에 산 란광의 에너지 죽 전등수에 변이 (sh ift)가 생기는 Comp ton 산란의 결과 를 얻었었다. 그러나 전자와 양성자가 단순한 정전하 입자가 아니고 내부 자유도로 서 스핀을 가지고 또 양성자(p ro t on) 의 유한한 크기 (~O.8x10-13cm) 등 을 고려에 넣기 시작하면 산란 단면적의 계산온 더욱 복잡해지고 어려 워지기 마련이다. 마찬가지로 파아란 하늘, 붉게 물든 저녁 노을의 산란 현상을 이해하 논 데에 공기 분자들의 상제한 양자역학쳐 내부구조를 고려해야 되는 것은 아니다. 죽 공기 분자들이 반드시 산소, 질소가 아니었더라도 하 늘은 여전히 파아랗게 보일 것이며 이것온 바로 원자 또는 분자의 정성 적 모델_＿모든 원자 또는 분자에 공통되는 평균적 모델에 입각하여 빛 의 산란을 계산한 결과도 파아란 하늘을 설명할 수 있다는 뜻이 된다.
빛의 산란을 동해서 무엇을 어느 정도 알아내고 싶은가에 따라서 우리 는 빛을 산란시키는 물질의 일반적 성질만을 취합, 또는 미시적 성질의 어떤 일부 아니면 전부를 계산에서 완전히 무시해 버릴 수 있게 된다. 본 제 Il 장에서는 우선 전자기학과 고전 광학에서 익힌 전자파 산란 문계둘을 요약하고 이들 결과로부터 이해할 수 있는 몇 가지 광산란 문 제를 소개하고 다론 한편으로 원자 및 분자와 빛의 상호작용에 대한 양 자역학적 고찰로부터 같은 광산란의 문제를 미시적 관정에서 살펴보기 로한다. Il -I 고전 전자기 학적 고찰 ]I-1 .1 산란 단면적 전자파 산란 현상온 산란체에 의한 2 차적 재복사 현상으로 분 수 있 냐 죽 산란체는 복사의 원체 (source) 로 취급되고 우리논 입의의 원체 집합에 대한 파동 방정식의 해를 구하면 산란 문제를 이해할 수 있게 되 논것이다. 벡터 포텐셜 A 와 스켈라 포텐셜 O 는 로렌츠 게이지에서, 죽 /7· A +7 1i ftorI >= O (Gauss 단위) /7 •A+µE i3 군 =O (MKS 단위) 의 조건에서 다음과 같은 맥스웰 파동 방정식을 만족시킨다. F20- 송옮 a>= -477: p 172A--[ 1z T안t2 A=-47 元 J (Gauss 단위) F2 止-µe 장한 a>=p/e 172A-µei tz A=-µJ (MKS 단위) a2 여기서 p는 전하밀도, J는 전류밀도를 나타낸다• 위 방정 식 의 해 는 Oackson, 1975)
( X, t) =) d3X' )dl' G( X, t ; X', t')p( X', t') =))d3X ' dt '~’ ―t'깊＼감’ !lf2.__p( X', t') =)d3X 'p( X', t— | X-X' II c)I IX -X' I 가 되고 특히 p( X', t') = p (X')e 마이’ J(X ', t') =J (X')e- i아’ 로 주어질 때 ( X) =)d3 X'p (X’) 下ei il적Z -Z TII 의 해를 얻는다. 위에서 k= (J)／ C 이다. 산란에 관련된 실제 문제에서 IX-X'l~r-r•X’+ 이-므f-로 ei k I~X-X~’1 1 =:+e'E((I-Ix 1,• ••• , Ir ♦ X…’… )c os{)') 가 되고 ==::eUre-iA X 1co1e1 ==:eil r( l-ikX' cosO' + ……) 여기서 r=IXI, X'=IX'I, r=X/IXI, O' 은 X’ 이 X 즉 탸 이루는 각을 나타내고 있다. 따타서 丁ei：.ld X：-X：1 ：I ： Te•ir 〔 1+(+- i k)r•X'+ ……〕 가 되어 다음과 갇온 해를 얻는다. ~(X) =우 ~d3 X'p (X’)+ 우(f-i k)Sd3 X'p (X')r·X'+ …… 굳~ Q+우(+-i k) ;-.p+…… ( JI .1)
여기서 Q는 전체 하전량울, P =5d3X'p( X')X' 는 전기 쌍극 모멘트 (ele ct r ic dip o le momen t)를 나타내 고 있 다. 마찬가지로 A (X) 국무 5d3X' J (X') ++무 (十_ ik) x5d3X'J( X')r·X' +…… 를 얻고, 부분 적분과 연속 방정식에 의해서 다시 51 J( X')d3X'=-5X'(l7'·J) d3X' = 크: w5X' p (X')d3X' = —iw P 가되고, ..c.L ( r·X')J =+2C [(i'•·X ')J+ (i'• J) X'] +-2bc- (X ' x J) X i' 이 되는 것에 주목하면 A(X)= -i kP 뚜+i k( f- xm)(1- 습)우-+ ...... ( II . 2) 가 됨을 알 수 있다. 위에서 m=5d8X 'M = 갛 5a8X'(X' x J( X')) 온 자기 쌍극 모멘트 (m ag ne ti c dip o le momen t)를 나타내 고 있 다• 위의 A(X) 로부터 B=rxA, E=i ii v'XB 를 구할 수 있으며 우리의 관십은 복사파 영역 (r -t oo) 에 있으므로
EB==kk22((rr xx PP )) 一xe rirA r— r+. k,_2- (h kr 2x. (. mr ),x x.m.r )• 一一erir l r eik r eik r 가 됨을 알 수 있다. 이러한 쌍극자 모멘트 근사에서 산란광 전자파는 E, =k2erih ~ [(k x P) x k-k x mJ B,=kx E , ( II . 3) 가 됨을 알 수 있다. 여기서 k 는 산탄광의 전행 방향의 단위 벡터를 나타내며 관측 방향, 즉, t 벡터와 같다. 따라서 입사광이 E 。 = 8 。 E 。 ex p(i k 。 · X) Bo=k 。 x E 。 로 주어질 때에 편광 벡터 e, 파등 벡터 k 의 산란과로 산란되는 확물 즉 미분 산란 단면적 꿉~ -(k,e;k 냐)는 아래와 같이 주어진다. 듦r습2 습 l eI e。 ··EEos/I22 =옹 le•P+(kx e )•m'2 (II.4) 위의 산란 단면적의 공식을 몇 가지 경우에 적용시켜 보기로 한다. Il -1. 2 유전체 구형 입자 입사광의 파장 A 에 비해서 휠싼 작은 반경 a 의 유전체 구에 의한 광산란 단면적을 구하여 그 특성을 살펴브기로 한다. A»a 의 조건에서는 입사광 전자파에 의해서 군일 전장에 의한 쌍극 모멘트 P 가 유전체 구형 입자 안에 유도된다고 볼 수 있다. 즉, 구의 유전상수를 E 이라 하면
P=( 룹) a3Eo 가 되고(J ackson, 1975) µ=1 인 경우 m=O 가 되므로 식 (II.4) 에 의해서 옮 =k'aol 릅 l2( 다 )2 의 산란 단면적 을 갖는다. 산란각 0 가 주어질 때 e 은 산란평면 위에 놓이는 경우와 산란평면에 수칙인 두 경우로 나누어지며 각각 분리시켜 계산하면, (웅 )Il= 무 I 母 I2cos 댕 (옮)J.=뿐틀 |2 (1I.5) 로 주어지며 따라서 입사광이 자연 편광 상태일 때에 산란광의 모든 펀 광 상태를 고려한 전체 산란 단면적은 옮=뿐|당「(1 +cos28) 죽 8=90° 에서 극소치를 갖게 되고 (J) 4 과 강에 비례함을 주목할 수 있다. II-1.3 완전 도체의 구형 입자 J ~a 의 경우 위에서와 마찬가지로 군일 전장 및 군일 자장 안에 반경 a 의 완전 도체 구가 놓여 있다고 볼 수 있다. 이때에 도체 구 안에는 P=a3E0, m=- .21 a3B 。 로 주어지는 쌍극 모멘트들이 유도된다. 따라서 식 (II.4) 에 의해서 옮 (k, e;ko, e 。 )=k 냥 |e•e 。담 (kxe)•(k 。 Xeo) 12 를 얻을 수 있고 자연 편광 상태의 입사광에 대해서 산란광의 편광 e 가 산란평면에 평행, 또는 수직인 두 경우를 생각하면 각각
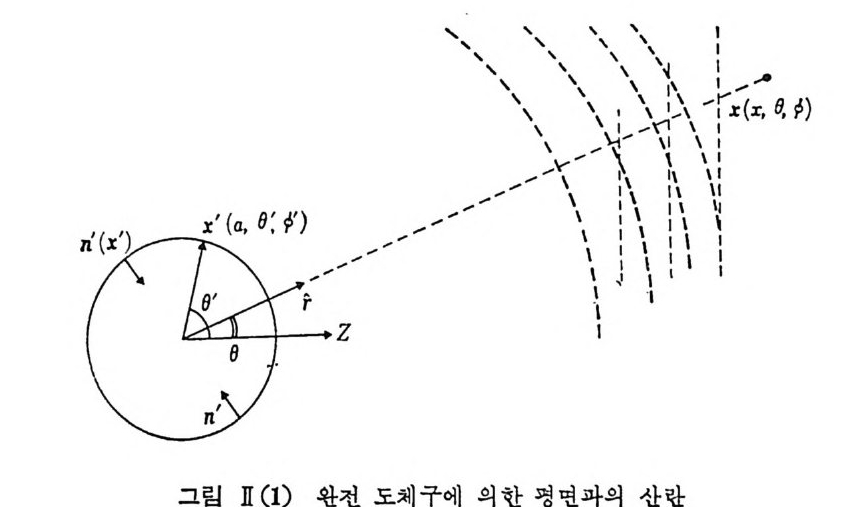
(器) |I = 亨 -I cos f)단 |2 馮)J.=부나- 방 cos f)「 (II.6) 의 결과를 얻게 된다. 위의 두 편광 상태를 모두 고려에 넣으면 전체 산란 단면적 듦 =k4 러울 (1 +cos2(}) _ cos(} } 를 얻을 수 있다. 앞에서 본 유전체 구와 비교할 때 도체 구의 경우, (}=oo 즉 전방 산 란보다도 (}= 180° 의 후방 산란이 훨씬 강하게 나타남을 볼 수 있 다. II -1. 4 광학적 호 1 절 산란체의 크기가 이제 입사광의 과장에 비해서 휠싼 큰 경우 죽 단 파장 근사 (ka ~ l) 의 영 역 에 서 는 광학적 회 철 현상이 나타나고 이 때 에 전 자파 산란온 완전히 회절 문제로 해석하여 회 철에 관한 Ki rc hoff 적 분식 cp( X) = 志 )dS' 유~ n' • 터 (X') +ik r cp( X')] ( II . 7) 울 이 용하여 산란 문제 를 풀 수 있 다(J ackson, 1975) . 다음 그립 II (1)에서와 같이 반경 a 의 완전 반사체 구형 입자에 의 한 산란을 생각해 보자. 지금 Z 축 방향으로 진행하논 평면과의 산란을 생각하면 복사과 영 역 (radia t i on zone) 에 서 전체 파동함수 ¢ 는 cp= eia z+< p, 로 놓을 수 있으며, 완전 반사의 조건에서 cp( a)=O 를 만족시켜야 됨을 알 수 있다. 한편 식 (II.7) 에서
:r’ (a , o:n .r/ ’ ,/ z/ / ’ ’ / ```/ \ \'``/、`, //,`\,\\ Y `.\1\ / /1'IIIIY\'\'、I\' 、\\\\\\/ \ ` 'VII `나\,`_\ II_III Ii 1/ 1\ / \\1\ \1 1/II`II rx`1,1 I1II`I'도 I 1Io1 1_, , `_I1 '' .II
17'e 따 = z' 훑- eil• ' =i kz'e 따 17' rp (X')= i kz' rp (X’) 이 므로 석 (I.7) 은 rp( X) = 꼽 rds ' -fi싶 Tn'•(z'+r)e i h' 가 되고 우리가 관십을 갖고 있는 복사파 영역에서는 IXl~ I X'I , IX-X'l-+ o o 따타서 IX-X'l~IXl-r·X' 로 쓸 수 있으므로 'Pr ad ：：：：：：유 sdS'e-ll(r ,Z'-z')n' • (z ' + r) (]I.8 ) 울얻는다. 한편 그림 Il (1)에서 z'=acos8'
X'=-an' nI . gI = -c os()’ X'•r= -a n'•r=a[cos 8cos()'+sin ( ) sin ( )' cos(¢ 군)〕 가되므로 ¢ rad ::::::: ~eil r JdS'e -ila Cco10co,01+. ino sln91co,c~-~/)-cos9'l x {— cos 8' —co s8cos8'-sin 8 sin 8 'cos(¢ 군’)} 를얻는다. 여기서 0=T 즉 후방 산란의 경우 ¢rad(0=T)-o 이 됨을 알 수 있고 8=0 의 전방 산란이 매우 강하게 나타날 것이 예상된다. 따라서 O~ l 죽 전방 산란에 가까운 경우를 생각해 보면 ¢r: :::: Tei5k ~1I d(cos0')5 。2 x d¢'cos0' X (1+cos8)eila cos6'Cl-co,O) e-ila sin ~ •ln6'cosC~--') 이 된다• 이 결과는 대칭성 때문에 ¢에 무관해야 되고 따라서 ¢=0 으 로 놓고 8 一 0 즉 cose:::::1, sin () :::::() 의 극한울 취 하면,
Ir/ ii'
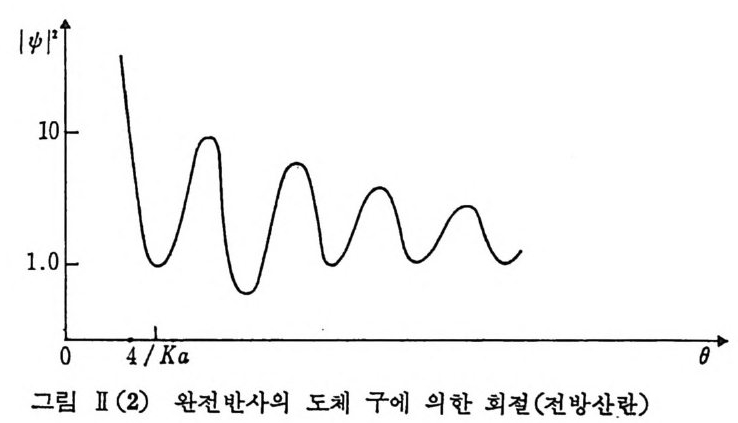
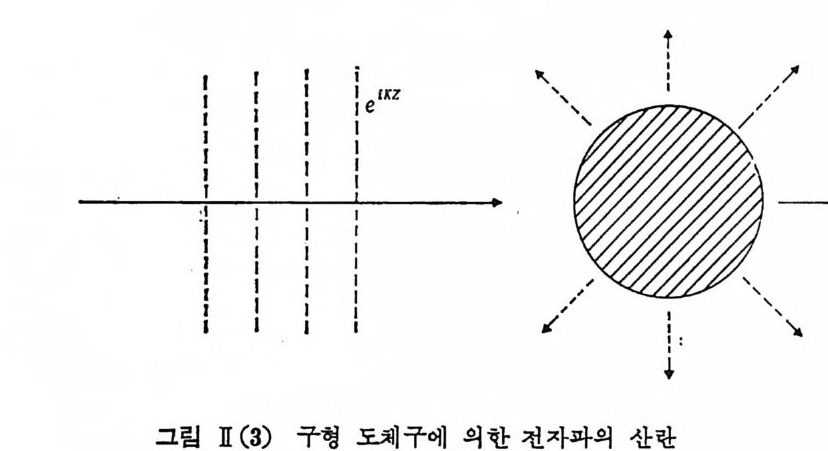
= 2 ~(e)ik r2 X ]1 (XI) 〕。k a6 = 멸 ;O) ' {}~ 1 를얻는다. 위 에 서 X' =ka (j sin ( j’ 이 다. 위 함수는 그립 II(2) 에서 보는 바와 같이 회철 무늬를 나타내고 있다. ]1 -1. 5 부분파와 위상 변이 끝으로 구형 산란체에 적용되는 좀더 일반적인 해법에 대해서, 즉 산란광은 주어전 경계 조건에서 파동 방정식의 산란체로부터 멀리 떨어 전 곳에서의 해를 구하여 얻을 수 있다는 일반적 개념에서 출발하는 한 해법에 대해서 겁토하고자 한다. 아래 그림 ]1（ 3) 에서와 같이 지금 산란체를 역시 r=a 의 완전 도체 구로 가정하면 도체 구면 표면에서 만족해야 되는 경계 조건은 n•B=O, nxE=O 로 쑬 수 있다.
t
또한 전자과 전자장의 성 분을 구좌표 성 분으로 나누면 (E,, Ee, E9 및 Br, B,, B1), 이 중에 E, 또는 B, 성 분은 다음의 스칼라 파동 방정 식 을 만족시키게 된다.
(I12 + k 힙 cp = O ( II -9) B. 성분이 만족시키는 경계 조건 B.(r=a)= O 에 주목하여 cp =B. 로 택하면 이로부터 E=rX f7 c p B=-+vxE 룹 구할 수 있다. 파동 방정식의 해 ¢논 입사 파동 c/J o 와 산란 과동 #s 의 중첩으로 cp=c/Jo +c /J, 와 같이 놓을 수 있으며 경계 조건의 계면이 구면임에 주목하여
(/;s::::::1:T 꾸 (2[+I) i 1(em•-I) 萩eik r , (- i) 1+1P, ( cos(} ） =e~irk , Il: (2/+I) sin o z ei4 , P1(cos(}) (I I-12) 를얻는다. 한편 B,(r=a) =O 의 경 계 조건에 서 e2i6 •h/ll(ka) +h,'2'(ka) =O 즉, e2i6 l= -hl(2 ) (k a)/Itl( I) (ka) 이 주어지고 따라서 sin o , ei6• = 一211 (e2i6 , 一 1) =吉〔― ~-1] =ij,(k a)/h1m(ka) ( II -13) 가 된다. 위의 식은 ka<{ I , 즉, 장과장 극한의 근사에서 sin o , ei6• = -( 2l+ I()k !a!) 2(12+1l -l)T! :::::: & ( Il -14) 이 됨을 알 수 있고 l=O 에 해당하는 소위 S 과 위상 변이 (S wave ph ase shif t) o0 가 아래와 같이 주어진다. 8o=_ka ( Il -15) 다론 한편으로 ka~ I, 즉 단과장 극한의 근사에 서 는 sin o z e'6•=s i n( 문 l-ka) 깡 GI/2-ka) 따라서 &＝군 -ka 를 얻는다. 이때에는 최소한 l=::ka 까지의 모든 부분과(p ar ti al · wave) 의 위상 변이 &울 고려해 주어야 하며 아래와 같 온 결과를 얻게 된다. 즉, ka ~ l 에서는 ¢=e—-ri i a ~rk; -a . (2/+1)(_;1)1 sin k(r-a) P,(cos8) ( II-16)
가된다. 이때에는 。：：：：：： 0 즉 전방 산란의 경우 수령하지 않고 발산되므로 실제 로 쓰기가 어려워진나 가령 J =lOm의 래디오 전자과의 지구에 의한 산란을 위 공식 (II-16) 에 의해 계산하려면 k=21r/J, a ：：：：：： 6000km 이므로 무려 ka ：：：：：： 3.6X1067 사의 항을 계산해 야 된다는 어려움이 따르게 됨을 알 수 있다. II -2 원자 및 분자적 속성 II -2.1 로렌츠 단진자 모델 (Loren t z Oscil lat o r Model) 모든 원자 또는 분자에 공동되는 정성적인 문제를 논할 때 가장 적합 한 모델로써 N 개의 원자 또는 분자를 질량 m, 전하 q를 가전 N 개의 감쇠 전동자 (dam p ed harmonic osc ill a t or) 들로 보는 로렌츠 단전자 모 델이 찰 알려져 있다. 이들 전동자들이 의부 전자과에 의해서 다음의 운동 방정식에 따라서 강제전동을 하게 된다. m(X+ I' X + w / X)= q E 。 exp (-iwt) ( Il -17) 이 방정식의 해는 X= mq( EOo 。 e2x_p0 ( 드 크i O w [t)' ） ( Il -18) 로 주어지며 가령 N 개 중에 fo N 개만이 고유 진동수 OJ o 를 가질 때 이 들 f0 N 개의 단전자들 즉 원자 또는 분자들에 의한 편극(p olar i za ti on) P 가 아래와 같이 주어진다. P= foN Vq X = lo N # E 。 ex p(크야) Vm( 썩 —0 )2 —1 .O JI') 따라서 편극률 (susce pti b ility) x(w) 는 P(w)=Eo x(w)E(w) 로부터 x(w) €。 vm(O/oO2l y__ qo2 2 _ i피I') ( II-19) 가 됩올 알 수 있다.
이들 N 개의 전동자들이 다시 고유 전동수 (J)j, 감쇠 계수 I'i 룬 갖는 각각 N/;7 서의 서로 다론 전동자듄의 합으로 구성되어 있다면 이들 N 개의 원자들에 의한 xC (J)）는 x(o)= €N。 111# V iZ=I (I)i2 _ (If),2 _ i-(—I) I'i ( II -20) 로 쓸 수 있으며 여 기 서 fi 는 2fi =1 CI I -21) i= I 울 만족시키고 있다. 한편 x((I) ) =X'((I) )) + ix ((I) ) =(n+ fr)드 1 ( lI -22) 로부터 X(w)=2n JC가 주어지며 위의 로렌츠 단전자 모델에서 x C(J) ) = 뷜笠 (Wo2 _ (J)김：포 (J)2I ' 2 ~_€ 。I oo 。N m#V (Wo-w)I '포/(4I ' /2)2 , (I'도) ( Il -23) 가 됩올 알 수 있다. Z 축 방향으로 빛이 입사하는 경우 l(z)= li。 exp ( -az) 로 정의되는 홉수 계수 a 는 a(ai) =2 ai K/C 로 주어지므로 n=1 을 가정하면 a(ai) ~ ai x(ai) / c =Co 處vmc (Oo-o)I2'/+4( I' /2) 2 ( ]l-2 4) 즉 로렌츠 단전자로 이루어전 기체의 홉수계수는 (I)＝(I) o 에서 극대치를 가지 며 선폭이 4(I )=I' 로 주어 지 는 소위 로렌츠형 선 모양(li ne shape )
을 나타낸다. ]1 -2.2 원자 및 분자들에 의한 광산란 원자 또는 분자들에 의한 빛의 산란은 이를 원자 내의 전자들을, 핵 을 중심으로 단전자 운동을 하는 질량 m, 전하 -e 의 하전 입자들로 보고 계산할 수 있다. 광파의 전기장에 의한 이들전자들의 가속운동은 복사 감쇠 (radia t i on damp ing 또는 radia t i ve reac ti on) 를 고려 해 서 소위 Abraham-Lorentz 운동 방정 식 을 만족시 키 며 다음과 같이 쓸 수 있 다 (Jac kson, 1975) . X.. +I 'aX. + wo2X= -구 me E 。 e-t., 1 +-.…x ( 1I-25) 이 방정X식=의 -해—m는 血 o2 _02- i o I' ( 1I-26) e eo Eo e-i .. t 로 쓸 수 있으며, 여기서 I'= I'd + （근 )2 I' r • I가',속=(도J) 。％x 는, 전복하사 -감e쇠 의 상하수전 ( ra입d 자i a t에i v e 의de한ca y복 c사on과s t a전n t기)이장 다 .E 따온 Erad = -7e -f1- Cr x (rxX•• )Jre i ( JI- 27) 로 주어지므로 위의 단전자 원자(또는 분자)가 발생하는 복사파의 전기 장은, & E방ra향d'으e,로=— m편c광2 된(J )。 2성_분 (J) 을2_ i(보J)면I' ,— r ClI-28) e 맙 E 。 e-iGJ ( l-rlc) €。 .eS 가 되고, 따라서 이들 단전자 원자들에 의한산란의 미분단면적 dq / d!J 논 아레와 같이 주어진다. 四dq L,‘1=
=（울 )2le 샤 012 (c (J)。 2_ (J) :42+ (J) 2r2 ) ( II ~29) 이 제 (J)< (J)o 의 경 우를 보면 옮 I.,,c , = (골 )21 e, •e 。 I 2( 근) ( II -30) CV~CVo 의 경우를 보면 옮 L,;'= （울 )\e 챠 o|2 1+ 노 ( Il -31) 가 됨을 알 수 있으며, (J)＝(J) o 에서는 공명 현상이 일어나고 소위 공명 형광 또는 공명 산란이타고 불리는 경우가 된다. 이제 이러한 원자 또는 분자들이 대기에서처럼 ~6X1023 분자 /22.4L 정도로 밀집해 있고 도 모든 원자들이 고정되어 있지 않고 제멋대로 무 질서한 운동을 하고 있을 때 이들 모든 원자들에 의한 전체 산란은 N 개의 모든 원자들에 대한 합을 포함하여 옮=윤 /t [e,•P,+(kxe,)•m,]e xp (iq• X,)「 (II-32) 의 형태로 쑬 수 있으며 이것은 분자적 속성에 관계 없이 구했던 식 (II- 4) 로부터 칙접 구할 수 있음을 알 수 있다. 여기서 PI,ml 은 각각 l 번째 원자 또는 분자에 유기된 전기 및 자기 쌍극자 모멘트를 나타내고, q는 산란각 (sca tt er i n g wave) 벡터 k ― k 。 를 나타낸다. Il-2.3 푸른 하늘의 기원 우리 는 업 청 난 수의 합이 포함된 석 ( II -32) 보다도 Born 근사에 해 당 하는 다음의 근사적 해법을 생각할 수 있다. 죽 어떤 매질이 군일하고 등방적인 상태로부터 어떤 섭동 효과에 의 해서 아주 미소하게 벗어나 있을 때, 여기에 의부 전자기 장을 가하여 그 반웅올 보면 D(X) = [E+ oE(X)JE (X) B(X)=[µ+oµ(X)JH (X)
와 같온 선형 반웅의 관계 식을 생각할 수 있다. 제 1 차 근사로 D 국 E ::::::: 紅c X ） D 。 (X) B— µ H:: ::::: 모µ악 L B 。 (X) ( II -33) 와 갇이 표시하고 우선 oµ(X) 를 무시할 때 맥스웰 방정식으로부터 다 음과 같은 파동 방정식을 얻게 된다. (/72 + k 2)D=-VX £ 7 X (~D 。 (X)) ( II -34) 여기서 D 。 (X) 는 섭동을 완전히 무시할 때, 죽 (/7 2 + k2)D 。 (X) =O 울 만족하고 있다. 식 ( JI -34) 의 일반 해 는 D(X) =D 。 + 같 -)d3X' ~17' x17' x (브尹나。) ( JI -35) 로 주어지며, 산란과 접근영역의 해를 -: ear D-+D 。 +I?P 와 같이 표시할 때 7= 옵) d3X'e 군 ·x' [lex 목 프찌 xk ( lI-36) 가 되고, 입사 과가 평면 과일 때에 죽 D 。 (X)=eoDoe j.t， .x 률 가정하면 이러한 상태의 매질에 의해서 다음과 같온 산란이 나타남을분수있다. 옮 = le,•71211n 。 P 켜옵j d3Xe i q •Z~e 。·세 ( 1I-37)
위에서 q=k 。 -k 이다. 이제 대기중의 공기 분자들에 의한 광산란에 위의 결과를 적용하연, 분자의 편극문을 a, 각 분자의 위치를 x .. 으로 표시할 때 oE(X)=4ii :I: a o(X-X. . ) ' 로 주어지고 이로부터 쁘dQ =--k,4. I,a-I,2 I,e-,.• e-u 。 ,1 2II I-;',.e • 9•z.Iz cn -38) 올 얻을 수 있다. 한편 E=1+4 김 Va 이고 분자들이 제멋대로 분포되어 있으므로 i7= N17m =詞k4 IE-l i 2N 의 결과를 얻고 여기에 IE-112= I (n+l)(n-1) 12 =:::4l n-1 J2 울 대입하여 (J：：：2：k：4 홍 'n-112 ( 1I -39) 울얻을수있다. 위에서, 산란각 0 에 대하여 J
따라서 대양 광선이 산란되어 오는 방향에서 브면 과장이 짧은 파랑 색의 빛이 가장 강하게 나오고, 태양 광선이 루과되어 오는방향에서 보 떤 과장이 긴 빨강색의 빛이 가장 많이 보일 것이 예상된다. 태양에서 멀리 벗어난 하늘이 파랗게 보이고 아침에 떠오르는해와처 녁에 지논 해를 칙접 바라 보면 빨갛게 보이는 것이 바로위의 레일레이 산란에 기인하고 있음을 알 수 있다. 만일 레일레이 산란이 빛의 과장 i의 4 승, ).4 에 비례하는 산탄 탄면 적이었다면 우리논 빨간 하늘, 과랑색의 태양올 보고 있을 것이다. 그리고 만일 대기가 없는 전공의 하늘이라면 하늘은 항상 까맣고 눈 부신 백색의 태양만이 있을 것으로 예상된다. n-3 양자역학적 고찰 lI-3.1 광량자 빛에 대해서 우리는 너무나 찰 고전적인 개념에 익숙해져 있고 실지 로 우리 일상 생활에서의 빛에 대한 인식 • 경험은 모두가 고전 물리에 따르고 있 다. 그러 나 빛 의 본질은 양자역 학적 개 념 인 광량자(p ho t on) 의 집합으로 분 수 있다. 광량자는 질량아 없고(실험적으로 현재 알려진 상한선 값은 mr<4X l0-48 gm 이 다), 전공중에 서 C=299, 792, 456. 2 土1. 1 m/sec 의 속도를 가 지며 이 속도는 광량자의 에너지에 관계없이 모두 일정한 값을 갖는다. 전자과의 전기장 E 에 대한 과동 방정식 172E_- 1f rit()2z E =O 에서 공전— 상자에 대한 경계조건을 만족시키는 해는 io)2t2E =-m2E 즉 조화 단전자의 운동 방정식을 만족시킨다. 이러한 관계를 양자역학적으로 확장시키면 상0 Eo l E(X, t) l2 d3X= (
의 관계 식 에 이 르며 E(X, t) =E 。 (X)e 규” 에 서 Eo 의 층가 또는 감소, 즉 공전 상자 내에 전자장 에너지가 증가 또는 감소하는 것을 〈 1l 〉 의 증 가 또는 감소로 표시할 수 있음을 알 수 있다. n 이 가령 3 에서 4 로 증가하면 광량자가 한 개 생성 (crea t e) 된다고 하고 3 에 서 2 로 감소하게 되 는 경 우 광량자가 한 개 소멸 (annih i l at e ) 된다고 표현하고 있다. 따라서 n 은 광상자 (cav ity)의 복사장 에 너 지 (field ener gy)가 양자화 되어 있음을 나타내며 여기상태의 에너지 양자수 또는 광량자 수를 가 리키고 있다. 이 러 한 개 념 은 광상자의 열적 여 기 (the rmal excit at i on ) 즉 열과 복 사 Cth e rmal rad i a ti on) 에 그대로 적용이 되며, 온도 T 에서 전동수 o 의 광량자가 n 개 여기되어 있을 확률, 즉 광상자가 양자수 n 의 여기 상 태에 있을 확률을 P 이타 하면 Pn 2ne exxpp ( (- E-E/kJa k BTT) ) exp (-{3n h w ) 홈 ex p(-f3 nho) =ex p(-/3떠!(I)） [l-exp( -{31iw )] ( Il -40) 로 주어지며, 온도 T 에서 n 값의 기대치 〈 n 〉은
n군w c33 enIdkwB T-1 ( II-42) 가 되 며 이것 은 Planck 의 유명 한 흑체 복사 (black body radia t i on ) 법 칙이다. 이제 빛에 대한 고전 전자기적 개념과 광량자 개념을 몇 가지 보기를 들어 비교해 보자. 가령 IOOW 백열 전등에서 1m 떨어전 접에서의 평군 전기장의 제기 와 광량자의 속밀도(fl ux) 를 구해 보면 첫 째 4,.R2S=100 Jo ule/sec 에서 R=Im, S= f oc/E 。 /2, fo =l07/4;.c2 룹 대입하면 I E 。'：：：：：：： O.SV / cm 를 얻게 되며, 가시광의 전동수를 평군 (J)::::::: 3 X l01 5 Hz 로 댁하면 광자(p ho t on) 의 에너지는 加(J)：：：：：：： 3x10-19 J oule 이 되 고 1m 거리에서 매초 1cm 2 당 흘러 나가는 광자의 수 즉 광자 속밀 도는 4,r; X 00100~ Jou: le:/s:e:c :1015 ph oto n s/cm2•sec 에 달하고 있다. 마찬가지 로 가령 108 Hz 의 래 디 오 전자과의 100 watt 출력 의 등방성 FM 안데나를 생각해 보자. 이 송신 안데나로부터 100km 떨어진 곳 에서의 IE 。 I 를 구해 보면 역시 4 김끈 CEalE 。 12=100wa tt의 관계식에서 IE 。|：：：：： SµV/cm 의 아주 미약한 신호가 된다. 이때 같은 R=IOOkm 지 점 에 서 이 FM ph oto n 의 속밀도는 ~1012 ph oto n s/cm2•sec 가 됨 을 알 수있다. 이 108Hz 의 진동수를 가전 FM 전자파의 과장은 /4 =3m 에 해당하고 R=lOOkm 지접에서 ,
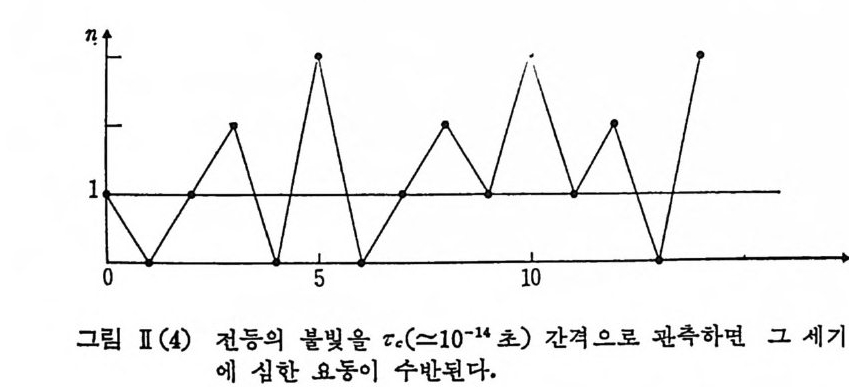
n(.t): :::::6 . 6 X 10- t o J야！ e ：：：：：： 4 X 109 eV=4 GeV 에 달하고 있다. 1I -3. 2 파동의 간섭 성 (coherence) 과 광자의 상관성 (correlati on s) 이 제 다시 광상자 (cav ity) 문제 로 돌아가서 광량자 수의 열적 요동 4n 을 구해 보면 (L1n)2= 1: (n— < 11 > )2 p =〈군〉-(〈 n 〉 )2 =(
n.
위 그립에서 따논 백열 전등의 필라멘트 내에서 자유 전자들과 전동 운동을 하는 필라멘트 금속의 원자들 사이의 평균 충돌시간 정도의 크기 를 갖고 있다. 이러한 강도 요동은 그 빛의 간섭성 상태와 연결됨을 뒤에 볼수있으 며 우선 실험적으로 두 개의 바늘 구멍(또는 슬릿)에 의한 Youn g실험 의 간섭 무늬가 바로 빛의 간섭성 (coherence) 에 대한 정보를 어떻게 제 공하고 있는지 살펴보기로 한다. 입의의 지점 X 에서의 간섭무늬를 결정하는 빛의 전폭의 합성, 따라 서 강도는 두 바늘 구멍 각각에 서 기 여 하는 강도 l1(X), l2(X) 이 의 에
J~(X )m=, x+ /(eX) mi nx p(-I' IS1-S 나 / c ) ( II -48) 로 주어전다. 여기서 1: =-IS1-S2l/c 로써 X 에서 두 바늘 구멍 zI,z2 에 이로는 거리의 차이가 커질수록 간섭 무늬의 선명도가 지수함수적으로 감소하 게 됨을 알 수 있다. 두 바늘 구멍에서 나오는 빛이 간섭무늬를 형성하여 보여줄 때 이들 빛은 서로 ‘coheren t'하다고 말하고 이들 간섭성의 정도을 나타내는 제 1 차 간섭도 함수 g( I)(rb h;r2, t 2) 三g l/1) 는 바로 위에서 본 두 광원 사 이의 상관도 함수를 써서 다음과 같이 정의하고 있다. g1z 'l ) = J<|| E〈 E(r *b ( rh 냐) | 2)XE (| Er (냐r2), k〉 )1 I 2> ( lI -49) 간섭성이 전혀 없는 비간섭성 빛에 대해서는 g1 2'l) = O, 진폭과 위상 이 고정된 단일 과장의 고전 전자기에서 취급하는 빛은 g 12m=1 의 값 울 가지며 강도 요동을 가지지 않는다. 사실 빛의 강도 요등은 제 2 차 간섭 성 (second order coherence) 에 관련되 어 있 다• 즉, <(l(X,t1 ) -l) (l(X. t2 )-l)> =
수 분포를 가지는 경우륜 생각하연
=z (올 +'Yc F(r,)) A• =Ei= I 炭 ,0 ( II -57) 즉, 중심 력 장 근사 (cen t ral field a pp rox i ma ti on) 를 써 서 단독 전자 ( one elec t ron) 의 문제 로 근사시 킬 수 있 으며 이 때 多，전 의 해 는 ¢nlm(ri, Oi, ¢ i)= RnI(ri)Y lm(0,, ¢i) ( II -58) 가 됨이 찰 알려쳐 있다. 이때의 에너지 고유치는 Wnrm=W(n,!), 즉 11, ［만의 함수가 된다. 이와 같은 근사에서는원자의 에너지 준위가 n 과 [이 증가하는 순서로 높아지 고 수소 원 자에 서 부터 차례 로 내 부 전자각 (shell) 을 채 워 나가는 원자 구조가 예상된다. 사실 원자 번호 1 번인 수소부터 시 작해서 원자 번호 18 번 Argo n 까 지는 11=1,2,3 의 순서로 전자각을 차례로 채워나가고 있다. 그러나 19 번 K(p'. >ta ssiu m ) 원자부터 는 이 러 한 근사식 의 결과에 따라 에 너 지 준위 가 채 워 지 지 않고 소위 불완성 내 부각(i ncom p le t e inn er shell) 을 가지 게 된다. 죽, 1 s2 2 s2 2# 3 S2 3 삼 3 d0 4 51 에서처럼 3P 전자각에 6 개의 전자가 채워진 다음 나머지 19 번째 전자 가 3d 준위가 아니고 4S 준위로 들어가게 된다. 이것은 바로 좀더 자 세히 계산하면 4S 상태가 3d 상태보다 에너지가 낮다는 것을 의미하 논것이다. 이 제 스핀-궤 도 (s pi n-orb it) 상호작용을 무시 하고 소위 Russell-Saunders 결합을 적용하면 원자의 에너지 준위가 L= :E l; 과 S= :E(1i의 값으로 표시가 된다. 가령 각운동량 k,l2 률 가지는두전자에 대한에너지 준위를 생각할때 S=0,1 L=l1+l2, l1+l2-l, ……, ll1-l2I 의 각각에 대응하는 준위들을 생각할 수 있다. 이 중에서 최저 에너지 를 갖는 준위 죽 바닥 상태를 찾는 문제가 중요하며 이것은 다음의 Hund 법칙에 의하여 쉽게 결정할 수 있다.
Hund 법칙은 주어전 전자 배열 (elec t ron con fig ura ti on) 에 대하여 바 닥 상태는 Pauli 법칙이 허용하는 한 S 가 최대, L 도 가능한 최대값을 갖는다는 법칙으로서 다전자 원자의 바닥 상태를 결정해 준다. 예를 들어 Cr+++ 이온은 그 전자 배열이 1 S2 2 s2 2 # 3 s2 3 삼 3 d3 로 주어지며 3P 전자각까지는 모든 전자가 서로 짝을 이루면서 완전히 차 있는 S=O, 1:, =0 의 Argo n 원자의 전자각 구조에 해당하고 따라서 보통 (Ar)3 d3 로 표시 하고 있 다. 이때 바닥 상태는 Hund 법칙에 의해서 S= i + i + i =3/2 L=2+l+0=3 으로 주어지며 2S+I (L) ( Il . 59) 의 표기에 따라 4F 의 상태가 됨을 알 수 있다. 위에서 l1=l2=l3=2 를 택 하여 L=6 의 바닥 상태가 될 수 없는 것은 Pauli 법칙에 위배되기 때문이다. 만일 스핀-궤 도 (s pi n-orb it) 상호작용을 고려 해 야 되 는 경 우에 는 ~ILS=AL•S= LAnl li.• 81 k Anzl•s=::::µ•B =µ· E2xmpc =그2m느c. f( r) rxp = -2dm!:-c:: -·I (r) l =-~f(r)s•l ( Il . 60) 위에서 B 와 E 의 상대론적 변환, E 가 중십력장, µB= 급등 -s 등을 고려했음에 주목할 수 있다. 또한
도-蜀눅 @ll f( r)In t 〉 움 실제로 이온의 기처상태에 대해서 계산해 보면, 전자각이 철반 이상 차 있을 때에는 -<
됨을 뜻하고 있다. 이제 핵의 spi n I 을 고려하면 원자의 각운동량 F 는 F= J +l 로 합 성되고 핵의 자기 모멘트 µ1 와 전자의 J에 대웅하는 자기장 HJ 사이 의 상호작용으로 볼 수 있는 소위 초미세 구조 (h yp er fi ne s t ruc t ure) 의 갈립이 생간다. 즉 KN'~ -µ1 H, cos(/, ]) ~AN 〔 F(F 나 1)-J( /+ 1)-]( ]+ l)] ( II . 63) 를 얻을 수 있다. 이상 원자 또는 분자에서 전자의 에너지에 기여하는주요항들을살펴 보면 炭。 ~105 cm 가 忠길 .s~102-103 cm 가 %'s.s~1 cm 가 ,Pf'B ~0.1-1 cm-I, 忠 N'~0.1-10-3 cm-1 가 됨이 찰 알려져 있다. 분자에서 전자의 에너지 준위를 나타낼 때에는 2s +1 Aco, ( II . 64) 의 기호를 쓰고 있다. 가령 NO 분자를 예르 들면 N 원자와 0 원자를 잇는 축에 대해서 NO 분자의 모든 전자들의 궤도 및 스핀 각운동량을 양자화시킬 수 있고 각각 A 와 2 의 기호를 써서 표시하고 있다. 죽 A 는 원자에서의 ML 에 2 는 Ms 에 대응한다고 볼 수 있으며 A=O, I, 2, ……, L Z=S, S-I, ……, -S 의 값을 취하게 되고 이들의 합성 결과를 9 로 표시한다. 따라서 Q= A+Z =A+S, A+S-I, ……, .A -S 가 되고 A=O,I,2,3,… .. . 에 대응하는 상태를 Z,II,LI,(!>,······ 로 표시하 고있다. NO 분자의 바닥 상태가 믹로 표시될 때 우리논 S=½' A=I, 2= -i2 의 상태임을 곧 알 수 있다.
이상 원자 및 분자에서 전자들이 갖는 에너지 준위에 대한 분광학적 용어를 설명했으며 분자의 전등 양자 상태, 회전 양자 상대에 대해서는 계 W 장의 라만 분광학에서 따로 취급하기로 한다. JI- 3.4 흡수, 형광 및 산란 시 간 의 촌 섭 동 이 론의 제 1 차 근사, 즉 Fermi 황금물 (Golden Rule) 에 의하면 wdo = 틍- |
=-m上 V /2(J) 무V ;-;
동론에 의한 기여를 생각할 수 있다. 즉 (k, e) 의 광량자가 들어 와서 (k', e•' ）의 광 량자로 산란되 어 나갈 때에
위 에 서 ro= 4:\2 :: ::: 2. 82 x 10-13cm 로써 전자의 고전 반경 을 나타 낸다. 」tr士/, l{L~,-, p-].J =- ±in( XP-PX)=l
참고문현 1. JD . Jac kson, Classic a l Elctr o dy n ami cs , 2nd ed., Joh n Wi le y & Sons (New York, 1975). 2. L.D . Landau and E.M . Lif sh it z, Electr o dy1 1 ami cs of Conti nu ous Media (Translate d from the Russia n by Sy k es and Bell), Perga mon Press (Oxfo r d, New York, 1960), Chap . XIV. 3. J.J. Sakurai, Advanced Qu antu m Mechanic s , Addis o n-Wesley (Re ad in g , Massachusett s. 1967), Chap. 2. 4, H.A. Beth e , Inte r media t e Qu antu m Mechanic s , W.A . Benja m i n (New s. YRo.r kL, o1u9d6o4n), , TPhaert q Iu. antu m the ory of lig h t, Clarendon Press (Oxfo r d, 19 73). 6. 이 상수, Ii'파동 광학』, 교학연구사(서 울, 1983). 7. 송회성, Ii'양자역학』, 교학연구사(서울, 1984).
제 冊 장 광산란 스펙트럼의 측정 타만 산란의 초기에는 태양 광선 또는 수은등 광원에 필터를 써서 단 색광을 만들고 또 프리즘 분광기, 사전 필름에 의한 기록등으로실험을 수행하는 데에 큰 어려움이 따르게 되었었다. 이것은 광산란의 단면적이 ~10-8 정도로, 아주 강한 광원이 아니면 산란광은 너무 약해서 도처히 측정 불가능하게 되고, 가령 햇빛 또는수 은등 광원에서 필터와 분광기를 사용하여 중심 파장이 soooA 이고 선 폭이 10A 이내의 단색광을 만들 때, 그 강도가 얼마나 약해질 것인지 계산해 보면 그 어려움을 알 수 있다. 여기에 감도가 떨어전 사진 필름의 경우 산란광의 분산 스 펙 트럼을 기록하기 위해서는 하루 종일, 때에 따라서는 며칠 동안 계속, 분광기 에 진동·충격이 가지 않도록주의하면서 격리되고밀페된암실을찰유 지시켜야 되는 어려움이 따르게 됨을 가히 짐작할 수 있을 것이다. 이 기간에 광원의 전원 공급이 고장난다거나, 햇빛의 경우 계속 날씨가 호 리면 실험이 도중에 중단될 수도 있을 것이다. 오늘날 우리 들은 레 이 처 , 이 중 격 자 분광기 (double grat i ng monochro-mete r ), 광전 증배 관(p ho t omul tip l i er tub e), 광자 계 수 장치 (ph oto n counti ng sy st e m ) 등을 써서 얼마나 편리한 실험을 하고 있는지 명십해 야 할 것이다. 본 장에서는 레일레이, 브릴루엥 산란의 스펙트럼을 구하는 데에 쓰 이는 실험 장치 및 방법을 간단히 소개하고 라만 스펙트럼을 구하는 실
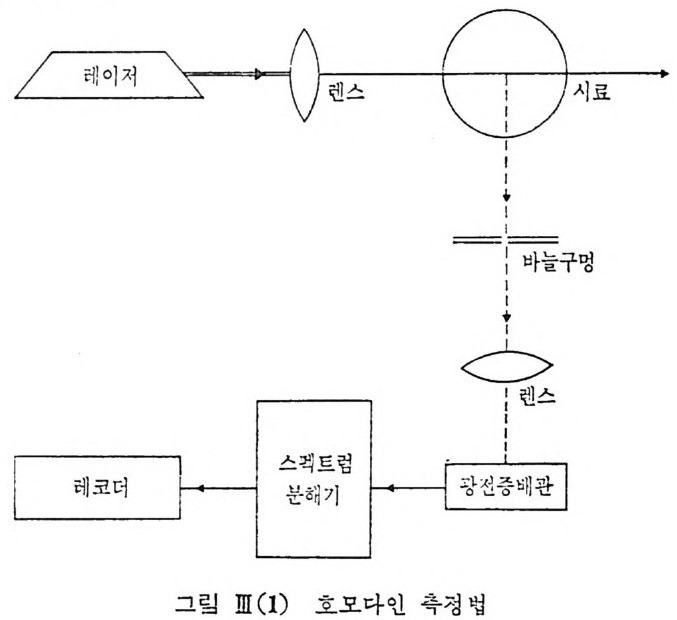
현에 대해서는 비교적 상세히 설명하고자 한다. III-1 레일레이 산란 m-1. 1 단일 모드 레이저의 필요성 레이저는 분명히 단색 광원 중에 가장 뛰어난 광원이다. 그러나 보통 레이저희사에서 칙접 구매할 수 있고 그 중에 찰 알려진 Argo n 이온 레 이 처 에 서 나오는 단색 광 광선을 보면 그 선폭이 무려 5 GHz(~o. 15 cm-1) 에 달하고 He-Ne 레 이 처 의 선폭도 1. 5 GHz(~O. 05 cm-1 : ) 에 이 르 고있다. ’ 물론 이것은 보통 아크등과 필터를 써서 얻 을 수 있는 단색 광 원 에 비 하면 업 청 난 것 이 다. 죽 4880 A 에 서 생 각하면 그 선폭이 o. 0357 A 이 된다. 그러나 고체에서 브릴루엥 산란광의 주과수 변이 4WB 는 보통 3~10 GHz(0.1~O.3cm-1) 정도이고 그 선폭은 보통 ~700MHz 정도가 되므 로 브릴루엥 산란과 레일레이 산란의 스펙트럼을 같이 관축하려면 레이 처의 선폭을최소한 ~70MHz 이하로 줄여야 하고 따라서 다중 모드 레 이처를 단일 모드 레이처 (sin g le mode laser) 로 개조시켜 작동시켜 야 된 다. 레이저에 대해서는 ][-4 철에서 설명하기로 한다. ][-1. 2 스펙트럼 분해기 Fabry -P erot 간섭계를써서 스펙트럽을 분석할 대 우리는 10MHz 이상 의 분해도를 얻기는 실제로 거의 불가능하다. 그러나 레일레이 산란과 관련하여 우리는 대로는 ~10 에 이르는 분해능 (w / o (J)）이 요구될 때 가 있다. 이 경 우에 는 스펙 트럼 분해 기 (spe c tr u m analyz er) 를 쓰는 소위 광과 맥놀이 분광범 (ligh t beati ng 또는 opt ica l mi xi n g s p ec t rosco py)에 의촌 하고있다. 여 기 에 는 소위 동질 합성 분광법 (homody n e s p ec t rosco py)과 혼성 분 광법 (hete r ody n e s p ec t rosco py)의 두 가지 가 있 다• 호모다인 측정에서는 산란광을 광전 증배관과 같은 비선형 소자를 통 하여 서로 혼합시켜 이때에 나오는 광전 전류를 전자계기인 스펙트럼 분해기가 Four i er 성분으로 분해시키고 여기서 얻는 전압 스펙트럼은
✓下 7詞 5계 해 당하 고 이 신 호 를 제 꼽하여 얻 는 Pt ((JJ) 즉 광전 전류의 출력 스 펙 트럼 은 전류 간 자 신 상관함수 ( curr e n t auto c o r r el a ti on fun c- tio n ) 스 팩 트 럼 〈 i(t) i( t + t) 〉 의 푸리에 변환에 해당된다. 이 것 은 바르 Wo ~5 x l014 H z 룬 중심 으로 한 광 과 ( o pti cal wave) 스펙 트럼 을 %~ O Hz 중 심 의 광 전 전류 (elec t r i cal current) 스 펙 트럼 으르 옮 겨 놓은 것 에 해 당함을 알 수 있 다. 아 레 의 그 림 IlI (I ) 에 호 모다인 측정 법 (ho mody n e de t ec ti on) 의 설계 도 를 보여 주고 있 다.
二렌 스 二시료
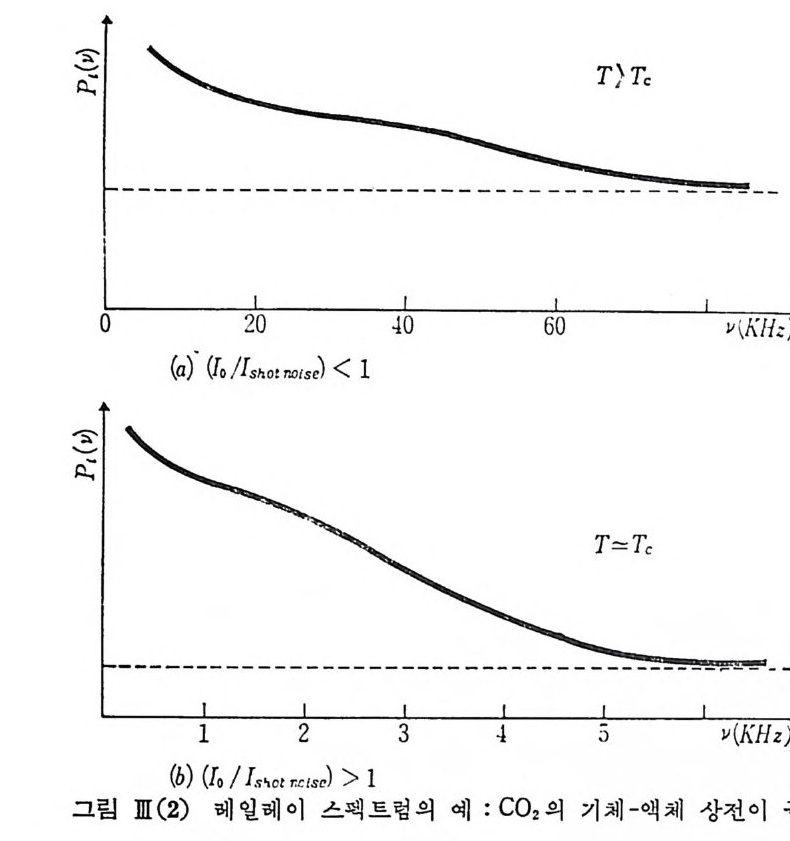
레코더 (r e corder) 에 얻어지는 레일레일 산란 스펙트럼의 전형적인 모 양이 그림 I[ (2) 에 나타나 있 다. 그림 mc 2) 에 서 보는 바와 같이 신호대 난발잡음 (s ig nal to shot nois e ) 의 비가 스펙트럽의 양상에 큰 영향을 끼치고 있음을볼 수 있다. 레이 처의 퍼침각을 줄이고 초점거리가 짧은 렌스를 써서 유효 산란 부피를 적게 하면 신호대 잡음비믈 증가시킬 수 있다. 헤테로다인 측정법에서는 산탄광 신호와 따로 주어지는 기준신호를 서로 결합시키고 있다. 내 부 전등자 신호 (local oscil la to r s ig nal) 로 볼리 우는 이 기 준 신호는 보통 산탄통 (cell) 을 그대 로 무과해 나오는 레 이저 광선을 광선 분할기
(n)rd
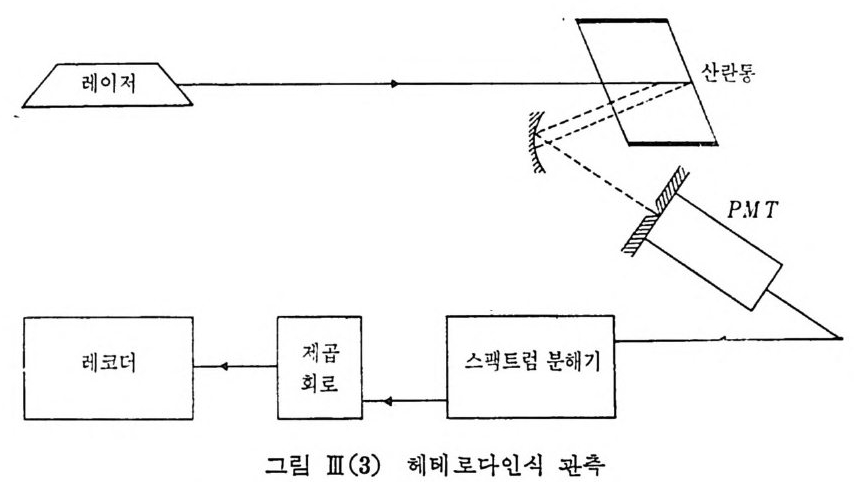
를 써서 그 일부를 광전관에 산란광 신호와 같이 들어가도록 하는 방 법 이 있고 또 아예 산란통 (cell) 안에 반사울이 큰 것빛 석 영 또는 데 폴론(t e fl on) 조각을 집 어 넣고 이 로부터 반사되 는 신호를 이 용 할 수도 있다. 또는 아래 그림과 같이 산란통의 벽을 이용할 수도 있다• 가장 간단한 한 예로 전동수가 각각 (J)。’(J)，인 두 광선이 서로 중첩되 어 광전 중배관의 음극 표면에 나란히 들어와 닿는경우를생각해 보자. Eo=eoE 。 cos (J)。 ! E, = e,E, cos (J)s t (J) o::::: (J),이고 모두 가시광 영역의 전동수라 할 때에 광전전류 i는 i= CIEo+E,l2 =C{ 송 E 。 2 (1 +cos 2 (J)。t) +½합 (1 +cos 2 (J),t)
/ t三 몽
+E0E,[c o s(w 0 +w ,)t+ cos(w0-w,)t] } (IlI.1) 로 주어진다. 그러나 광전 증배관의 감웅 시간이 유한하기 때문에 죽 주파수 감웅의 며폭 (band w i d t h) 이 제한되어 있기 때문에 실제로는 떠 폭 밖의 신호들은 평군되어 i =c{-.:£ 。~ +E0E, cos( (J)。_(J),)t} (1[.2 ) 의 결과를 얻게 된다. 위에서 가령 (L)。를 레이저의 한 모드를 나타내는 주파수라 하면 위의 식은 레이처의 각 모드에 적용이 되므로 단일 모드 레이처의 필요성이 없어지고 훨씬 강한 다중 모드 레이저를 그대로 레일레이 산란에 쓸 수 있게 되는 것이다. 이제 두 개의 광선 대신에 단일 광선만을 생각하면 ii((wt ))= =K K[Ef -O,0O(0 dt)t J e2 i 1 [E, (t)J 2 (][. 3) oo 가 되 고 푸리 에 변환의 중복정 리 (convoluti on t heorem) 를 적 용하면 i((/)) =I깁 oo E,((/)’) E,((/)- (/)’)d (/)’ (][. 4) -c x:' 를 얻는다. 그러나 우리가 알 수 있는 것은 전자장의 스펙트럽 E,((/))
가 아니고 산란광의 po wer 스팩트럽 S(w) 에 해당하므로 이것을 고려 하여 i2( (J. )) = af 0-0Oo Oo S( (J.) ’ )S((J.) 一 (J.)’ )d(J. )’ ( llI . 5) 로 고쳐 쑬 수 있고, 다시 중복 정리에 의해서 i 2( (J.))＝사 00 [S(t)J 2 ei., 1dt ( Ilf . 6) -OO 를 얻을 수 있다. 산란광의 po wer 스팩트럼 이 선폭이 2 I' 인 르렌츠 선 모양(li ne shap e ) 울 갖는다고 가정할 때 S(q, w) =const. (0S_ 2(J.)。r ) 2+r2 이의 푸리에 역변환 S(q, t)= const. e 구 1 t I 울 식 (]I. 6) 에 대 입하면 i2( q, w) =const. f0•0• } OO -2r 111 ei' 1 dt =const. Cw, 국)。4I )' 2 +(2 I' )2 (血. 7) 을얻는다. 따라서 스펙트럼 분해기에 나타나는 광전 전류 i(t)에 의한 전압 신호 스펙 트럽 %(q, (I)）는 r(q, (J ))= const. 1/ ((J) s_ 』: 2+4 I' 2 (m. 8) 가된다. (]따[. 라8)서 로 부스터펙 트럼 분해기에서 얻는 스팩트럽의 반폭을 4v1’ 라 하면 식 4, m=7C ~r (][.9)
의 관계석을 얻을 수 있다. m-1. 3 상관함수 측정기 위에서 광전 증배관의 출력 신호를 스펙트럼 분해기 대신에 소위 상 관함수 측정기 (d igit al corr e la t or) 에 연결하면 우리는 광전 전류의 자기 자신 상관함수를 얻게 되고 이 함수의 지수 함수적 감쇠 시간으로 주 어지는 상관도 시간은 스펙트럼 분해기를 써서 얻는 선폭 2r 의 역수 에 해당한다. 스펙트럼 분해기는 보통 전체 스펙트럼을 동시에 보지 않고 여러 주 파수 구간으로 나누어 한 순간에 한 구간씩 측정 (sam p l i n g)하면서 전체 영 역 울 주사 (swee pi n g)해 가는 반면에 dig ital correlato r 는 항상 모든 순간에 스펙트럼 전체에 대해서 자료처리 (sam p l i n g)를 하게 되므로 월 씬 효율이 높은 것으로 알려져 있다. 또 한편 신호 계수가 매우 낮을 때 광전 증배관 출력을 연속선호로 브는 적 분형 측정 (analog de t ec ti on) 에 서 는 신호대 잡음비 가 매 우 작아지 므로 특히 신호가 매 우 약할 때 에 는 진법 형 (dig ital ) 즉 광자수 계 축상관 함수를 측정하는 것이 훨 씬 유리해진다. 여 기 서 전법 형 (d igit al) 이 라 함은 측정 기 입 력 (correlato r i n p u t)이 캐 파시 터 형 적 분회 로 (ca p ac iti ve int e g r ato r ) 등을 쓰는 적 분형 입 력 (analog i npu t)이 아니 고 광자수 계 축 자료처 리 회 로(p ho t on-coun ti n g samp ling un it)를 쓰는 전법 형 입 력 (dig ital i n pu t)을 가지 고 있 다는 접 이 다. 흔히 상용으로 나오는 analog correlato r 와 dig ital correlato r 를 써 서 각각 상관함수를 구했을 때 이들의 정확성을 비교해 보면 광자수 계축 의 경우, 競 n( i T) n(iT +-.) = Cn(-r) 로 주어지는 상관함수의 이탈도 (var i ance) 가 fr var(n(O)n(i-) ) 궁(〈 n2〉 2_ 〈 n 〉•)
=tJ C2 한+한) 따라서 상대 이 탈도 (rela ti ve var i ance) 는 va
와 바교해 보면 mT» 1 즉 계수울이 높을 때에는 상대 이탈도가 analog correlato r 쪽이 dig ital 쪽보다 2 배, mT li( t) 三 를 정의하면 C (t)=
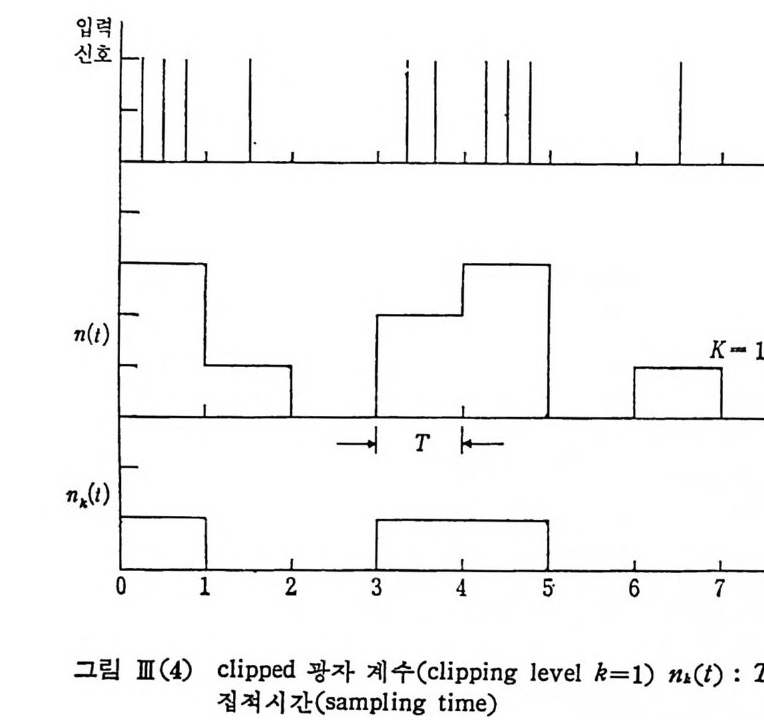
m(t) = {1o ;; n11((t t)) ~> kk cnr. 11) 이때에 k 를 제분 준위 (cl ippi n g level) 라고 부르며 실제 계측수 n(t) 와 n1( t)의 관계 를 그림 III (4) 에 표시 하였 다. 따라서 n(O)n( t)의 곱셈 을 n( t)에 0 또는 1 로 곱하는 간단한 셈 으로 환원시 켜 처 음의 multib i t 곱셈 을 sin g le bit 작동 즉 게 이 트 회 로 ( g a t e) 를 써서 n1=0 또는 n1=l 에 따라서 n( t)를 비치 등록회로 (s t ora g e reg ist e r ) 로 보내거나 안 보내는 간단한 작동으로 바뀌어 상관함수 측정기의 전 자 회로가 아주 간소화되는 것이다.
입력
그러나 입력 신호의 통계 분포가 가우스 분포를 이루지 않을 때에는 clip ping 보다도 scalin g 을 적 용시 켜 야 됨 이 알려 져 있 다. 죽 〈 n 。''' (O) n( t)〉로 표시 되 는 scali ng 된 자기 자신 상관함수를 축 정 합으로써 빛 의 강도의 자기 자신 상관합수(i n t ens ity -au t ocorrela ti on f unc ti on) 를 구할 수 있 다.
여기서 n''>( t, T) 는 다음 관계 석을 만족하는 약분된 (scaled) 광자 계 수, 즉 n (t ,T)=n''> (t ,T)s+r 로서 r~s-1 은 scal i n g시키고 난나머지, s 는 scalin g 상수이 다. 또 짜')(t, T) 는 scaled counts n''>(t, T) 를 다시 제분준위 k 에서 제분 시 킨 광자계 수 (cl ipp ed-a t -k counts of scaled-by - s p ho t ocoun t s) 이 다. 이상을 그립으로 표시 하면 아래와 같다.
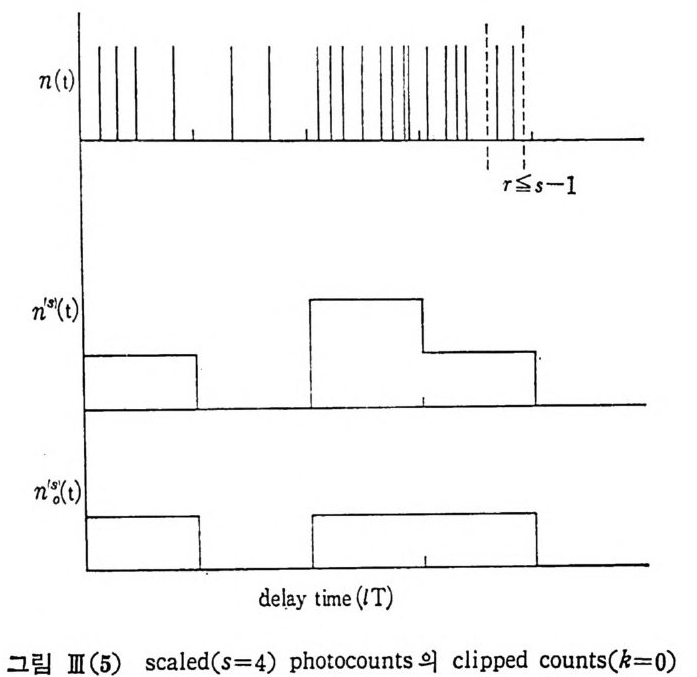n(t )
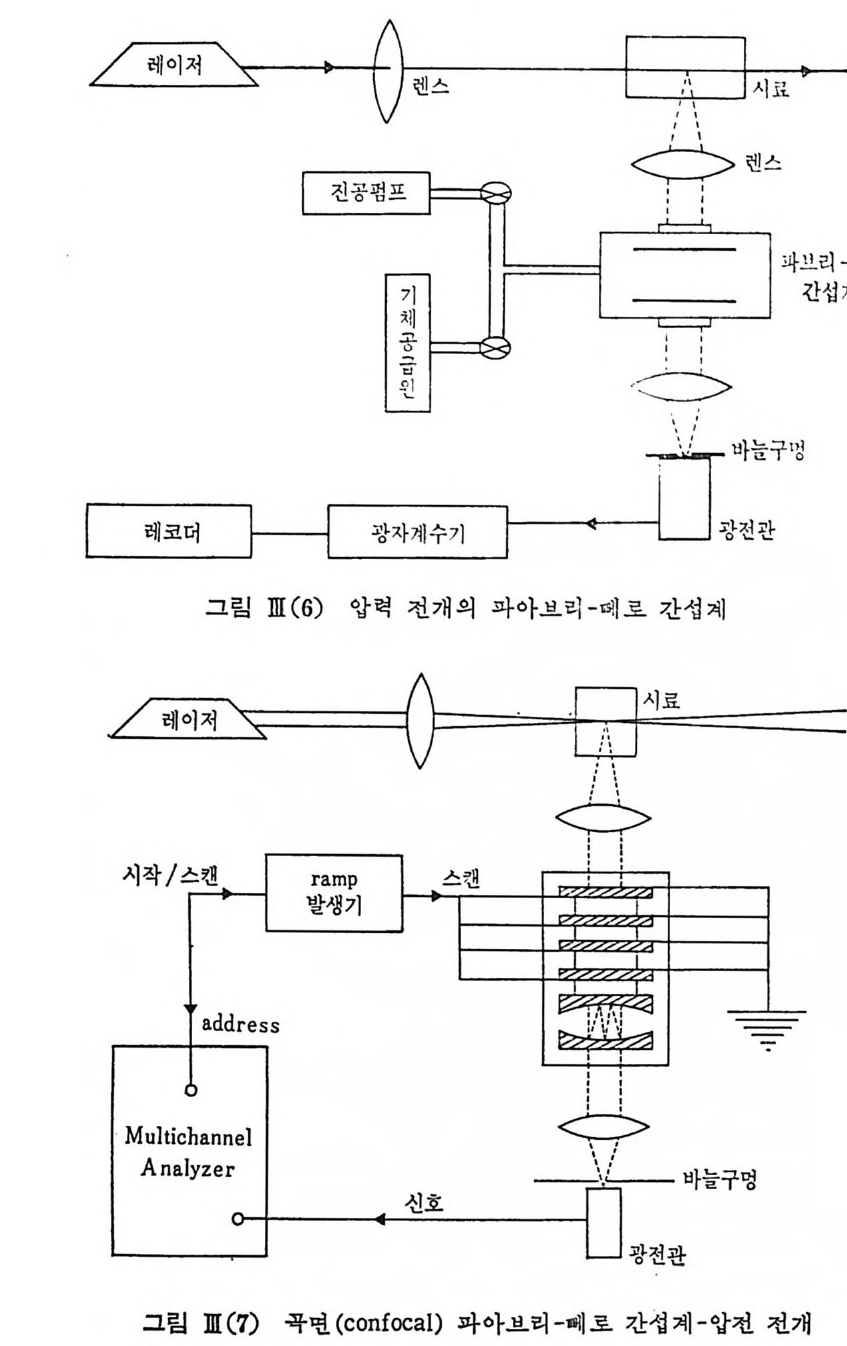
1II-2 브릴루엥 산란 Ill-2. I 실험 장치 대 략 10GHz(o. 3cm-1) 이하에서 나타나는 브릴루엥 (Brill ou in ) 산란 의 스팩 트럼 은 단일 모드 레 이 처 와 Fabry- P erot 간섭 계 가 필수적 이 다. Fabry -P erot 간섭 계 는 아래 그립 에 서 와 같이 압력 전개 (pr essure scannin g , 그립 m( 6)) 또는 압전 전개 (piez oelectr ic scannin g , 그립 m( 7) ）의 방 법을 이용하여 사용하고 있다.
렌스 <=’’, , '' ’스' ” .lI ’. II '’’ > 렌시스료
과아브리-데로 간섭계를 루과해 나오는 광의 강도는간섭계의 두거울 표면의 반사울, 두 거울 사이의 거리 t, 거울면의 법선과 이루는 두과 각 (}, 두과광의 파장에 따라 달라진다. 지금 과장이 i b22 인 두과광에 대해서 생각하면 각각 다음 식으로 주 어 지 는 (}b (}2 의 방향에 서 두과광 ih i2 의 강도가 극대 값을 갖는다. —2;r 2t cos{) 트1> 1=2 11: m1 -2? r.—1. 2l cos02 三1> 2=2 r. m2 (lII.15) ?.2 즉 두과광 i I,22 의 두과각이 40=OI_o2 만큼 차이가 생기고 있다. 이때 초접거리가 J인 렌스로 두과광을 스크린에 모으면 J 1,A2 에 대웅 하는 원 둘레 무늬가 생기고 이들 사이에 f4 0 의 간격이 주어진다. 이제 스크린 대신에 바늘구멍을 놓고 그 뒤에 광전 증배관을 대어 놓 으면 }.h }.2 의 두과광이 각각 fJ1 = 0, fJ2 = 0 가 되 는 순간에 바늘구멍 을 통 과하게 될 것이다. 따라서 (Ill.15) 에서 두 거울 사이의 거리 t를 압전 전개 방법을 써서 가령 최소 간격에서 최대 간격으로 접차 중가시켜 갈 때에 바늘구멍과 광전관을 통해 파장이 작은 쪽에서 큰 쪽으로 전체 스펙트럼을 차례로 통과시 키 는 scannin g 이 가능함을 알 수 있 다. 마찬가지 로 t 는 고정 시 켜 놓고 간섭계 즉 두 거울 사이의 광로를 굴절물의 변화에 의해서 증 가 또는 감소시킬 수도 있다. 파아브리-데로 간섭계를 우선 전공 펌프에 연결시키고 그 안에 argo n 기체 또는 공기 자체를 서서히 주입시킴으르 써 기체의 밀도 즉 굴철률을 일정한 울로 변화시켜 가면서 전체 스펙 트럼을 차례로 조사하는 압력 전개가 가능하다. 이때 굴절률의 변화는 가령 공기를 전공에서 대기압까지 변화시킬 때 n= l. 000000 에서 n= 1. 000200 까지 매우 적은 변화이지만 실제로 대부분의 실험에서 충분한 값이 되고 있다. m-2.2 파아브리-뻬로 간섭계 파아브리-대로 (Fab ry -Pero t) 간섭계는 매우 높온 반사울(之 98%) 을 갖는 두 거울을 서로 완전 평행을 유지시키도록 장치해 놓은 광학 기구 이다. 이 간섭계의 특성을 결정짓는 FSR(fr ee spe c tr a l rang e ), fine sse, 분해
능은 다음과 같이 정의되고 있다. 보통 광산란의 실험에서와 같이 간섭계의 거울면에 수칙하게 임사하 논 빛을 생각할 대 이 간섭계를 루과할 수 있는 빛의 파장 2 는 다음과 갇이 제한되어 있다. m—2 A =t cnr. 16) 여기서 m 은 정수, t는 두 거울면 사이의 거리이다. 이 식에서 보면 주어전 t값에 대해서 m 번째 차수에 대응하는 .<=.
로 주어지며 IT=2+ lo 에 해당하는 ()’, 즉 8' 을 구하면 s i n2 f-三~ = (검 )2 에 서 o'=(l— R )/ ✓ R (][.19) 울얻는다. o=2 r. m 일 때 IT=lo 가 되므로 8' 는 루과한 스펙트럼 선의 반폭에 해 당된다. 지금 k,A2(=21+6A) 에 대한 ¢니 62 의 차이가 위의 스펙트럼 선 반폭 보다 적을 때에는 도처히 A1,A2 를 따로 식벌할 수 없는 상태가 된다. 따라서 최소한 ¢I_¢2 츠 261' 를 만족시켜야 하며 석 (][.18) 과 (]I .19) 를 대입하여 T8A = 言) 71-R ( III. 20) 의 결과물 얻을 수 있다. }./8i 를 분해능 (resolv i n g p ower) 이 라고 부른다. 실제로 간섭계의 거울면은 완전한 반사 도는 완전한 평면을 가전 이 상적인 거울이 아니며 따라서 모돈 스펙트럼 선은필연적으로유한한선 폭을 가지 게 된다. 이 선폭이 바로 8i 에 해 당하고 이 62 와 FSR(L12) 사이의 비 F= 윤=멸 cm. 21) 를 반사능 (re fl ec ti v ity) fine sse 라고 정 의 하며 이 것 은 간섭 무늬 (fring e ) 의 선명도를 나타내는 쳐도가 된다. 가령 R=O.70 에 대해서는 F=8.3 인 데 바하여 R=O.95 가 되면 F= 6 1. 2 로 증가함을 분 수 있다. 한편 분해능을 Q라 하면 Q=-j}; : =mF* (][. 22) 로 유효 fine sse F* 를 정의한다. 여기서 m 은 간섭무늬의 차수를 나타
내고 있다. 가령 Q= l07, F*=25 에 대해서 m=4Xl05 이 되는데 이것은 식 (][. 15) 에서 보면 t= IOcm, A=SOOOA 에 대한 간섭무늬계(fri n g e rin g s y s t em) 의 한 중앙에 나타나는 (0=0) 무늬의 차수에 해당하고 있다. 거 꾸로 생 각하면 보통 scannin g 의 경 우 바늘구멍 을 무늬 계 의 한 중앙에 맞추어 놓으므로 m=4Xl05 에 해당하고 만일 F * =25 의 파아브리며 ll 로 간섭계를 쓰고 있다면 이때 분해능은 Q =l07 에 탈하고 있다는 뜻이 된다. 위의 F* 는 간섭계 거울면의 거칠기를· 포함하는 실제로 설협상 문제가 되는 모든 불완전성을 포함하고 있어 식 (][. 21) 의 반사능 fine sse F 보다 훨씬 적은 값이 된다. 血 -2.3 산란각에 따른 변화 브릴루엥 산란은 음과에 의 한 빛 의 간섭 성 반사 (coheren t re fl ec ti on) 로 생각할 수 있다. 이 때 반사할 때 에 옴칙 이 는 반사면의 속도, 죽 음속에 상당한 Dop ple r 번이가 생기는 것으로 해석할 수 있다.
Ci' .h/ A, I
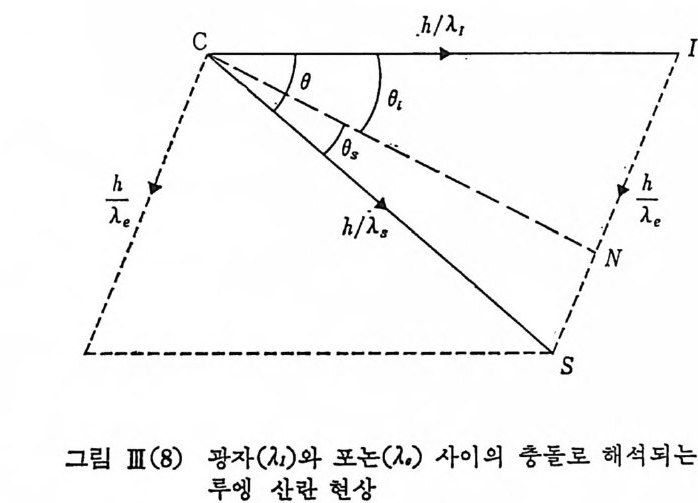
다론 한편으로, 비 단성 산란의 관접 에 서 그립 ]l[ （ 8) 에 서 와 같이 광자와 포논의 개념을 써서 브릴루엥 산란 현상을 나타낼 수 있다.
여기서 운동량 보존 법칙을 생각하면 입사 광자의 파수 벡터 CI, 산 란 광자의 과수 벡터 cs, 포논의 과수 벡터 IS 가 모두 같은 평면에 놓이고 다음 관계식을 만족시키는 것을 알 수 있다. 소위 산란각 과수 백터 IS 를 기준으로 하여 이에 평행 및 수직 성분으로 나누어서 생각 하면 尤h __ 言h ―ni sin f i ;= yh n S sin (}3 Th ni COS f)j = 一hJn.― , cos (}, (][• 23) . 다시 정리하면 n, sin (}i + n, sin (}, = }./}.. n; cos (}i- n, cos (},=O (1[. 23) 또 각각 제곱한 다음에 서로 합하여 nj2 + 11,2-2 ni n, cos(I)i + 0s) = A2/A.2 을 얻고 그림 ll! (8) 에서 8,+8,=8 이므로 工A- = J nj2 +ns2-2 ni ”s C05I) cnr. 24) 를 얻는다. 여기서 k 는 전공에서의 빛의 과장, n,,n, 는 입사 및 산탄광에 대한 굴절물을 나타내고 있다. 한편 에너지 브존법칙에 의해서 h )),=h ))i 士 h )). (IlI. 25) 즉 4)) ＝ ))s_ ））i=土)) ． (IlI . 26) 로 브릴루엥 산란에서의 주파수 변이가 주어진다. 따라서 식 (][. 24) 와 식 (][. 26) 으로부터 ))=c /2, )Je =oJ k 이므로 —Luiv = 士, —uc—. J ni2 +nS2_2 ni n, cos f} (][. 27) 의 결과를 얻는다. 이제 입사각과 산란각이 정해질 때 죽 0 가 정해질 때 일반적으로, 복
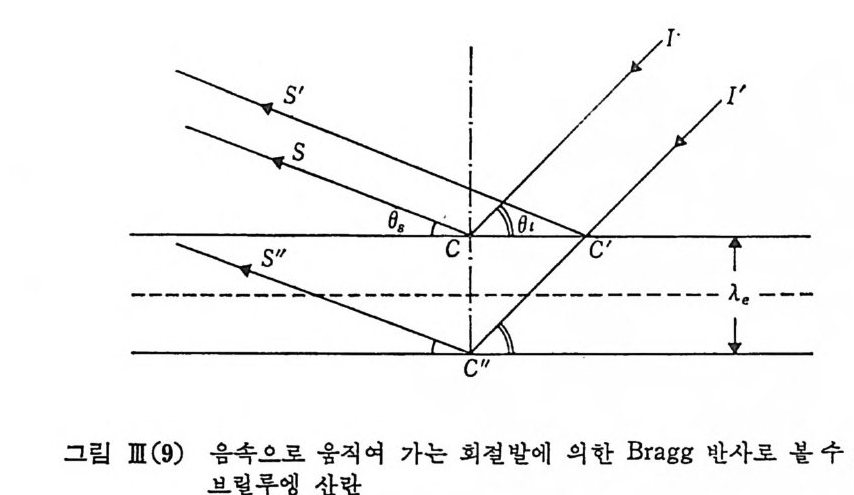
굴철 또는 등방성 매 질 에 서 도 광학적 활성 (op tica l acti vi t y) 이 있 는 경 우 를 포함해서, 11 i와 113 는 각각 두 편광 상대에 따라서 서로 다른 두 개 의 값을 가질 수 있다. 한편 11 i ,11s 가 정해지면 식 (III.23) 에 의해서 포논의 파장 및 파수 벡터 즉 그림 ][(8) 의 CN 하 결정된다. 그러나 파장과 파수 벡터가 정해전 경우에도 그의 편극 상태에 따라서 속도가 서로 다른 세 가지 포논을 생각할 수 있다. 따라서 4 ））의 값으로 식 (][ . 27) 에서 2X4X 3=24 개의 서로 다론 값이 주어질 수 있음을 알 수 있다. 즉 경우에 따라서는 브릴루엥 산란 스펙트럼에 12 쌍의 선들이 관측뭘 수 있음을 볼 수 있다. 또 한편으로는 아래 그림에서와 같이 탄성파가 음속으로 진행해 가면 서 2. 의 주기로 밀도의 소밀을 가져오므로 바로 2c 의 선 간격을 가전 회절발 표면이 웅칙여가고 입사광이 이 회절발에 의해서 일정한 방향으 로 회절되어 나가는 것으로 해석할 수도 있다.
I
그립에서 CS 방향으로 회철되어 가는 광과들이 전체적으로 산란광에 기여하기 위해서는 CC 방향으로 진행하는 음파에 의해서 생성되는 모 든 희철면들이 기여하는 광파들이 서로 위상이 합치되어야 한다. 즉, 그립 m(9) 에서 같은 회걸면의 C 와 C’ 에 대해서 보면 ni cos ();=ns cos ()s,
서로 인접해 있는 두 회철면, 즉 C 와 C'’ 에 대해서 보면 (ni sin 0i+ ns sin 0s)2e=mA 를 만족시켜야 한다. 적용이하들여 관 계구식했은던 관바계로식 광 자cn-r.포 2논3)의 과 같개은념 에결 과입가각 해됨서을 알운 동수량 있 다보.촌 법칙을 따라서 브릴루엔 산란은 u. 로 진행하는 Bragg 반사면에 의해서 주어 진 특정 방향으로 그 방향의 속도성분에 해당하는 도플러 변이를 수반 하는 Bragg 반사 현상으로 볼 수 있 다. 복굴 절 현상이 없는 즉 단일 굴절률의 특성을 가전 결정체에서는 一4)i) i =士~C ✓ 2n2-2 군 cos() =士으C느 2 n sin 8/2 (][. 28) 즉, 오칙 3 쌍의 브릴루앵 성 분이 가능하고, f)一 0 에 접 근할 때 L1v -+ 0 가 됨을 알 수 있다. m-3 라만 산란 血 -3.1 실험설비 라만 산란 스팩트럼을 구하는 실험 장치에는 강한레이저, 분광기, 광 전자 증배관이 팔수적이고 광전관의 출력 신호를 처리하여 레코더에 기 록하는 과정의 전자 회로는 일반적으로 신호가 매우 강할 때에는 가장 편리한 방법인 직류식 측정법, 죽 광전관 출력을 직접 피코(pi co) 전류 계로 받아 적분형 도표 기록기에 기록하는 방법과, 신호가 약할 때에는 광신호 단락기와 위상공액 증폭기를 쓰는 교류식 측정법 또는 펄스 중 폭기를 쓰는 펄스 계수방법으로 대벌할 수 있으며 소위 sin g le -ph oto n counti ng 온 신호가 매 우 약한 경 우 흔히 체 택 되 는 pu lse counti ng 의 한 극한에 해당한다. 이들 설비에 대한 신호 검출능과 신호 대 잡음비에 대해서 살펴보자. 광전 증배관의 출력 신호는 크기가 다양한 전하 펄스들로 구성되어 있고 이것은 피코 전류계를 써서 순간적인 양국 전류를 직접 여러가지 시간 상수 ?를 선택 측정하는 방식으로 기록할 수 있으며 또는 펄스를
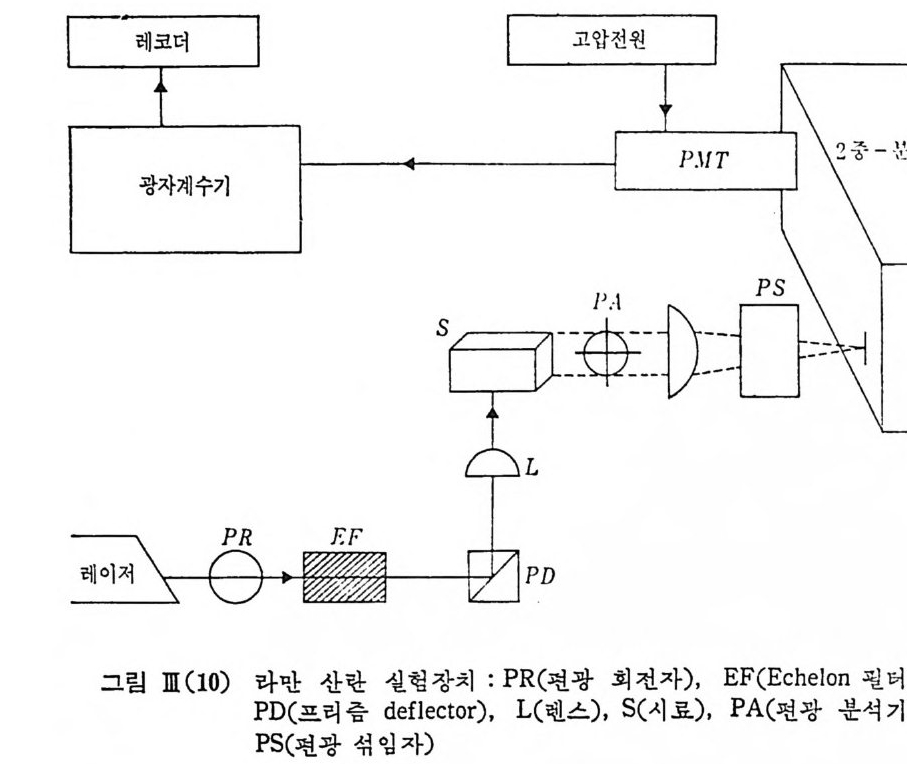
rate me t er 로 계수 축정하고 rate me t er 의 출력울 임의의 시 간상수 T 를 선택 기목할 수 있다• 아래에 거의 표준화된 라만 산란 실험의 장치를 보이고 각 부문벌로 차례차례 설명하고자 한다.
레코더 고압전원
JII-3 . 2 레이저 광원 라만 산란 실험의 광원으로 가장 이상적인 것은 단일 과장이고 세기 가 강한 광원으로써 레이처가 가장 훌륭한 광원으로 쓰이고 있다. 그러나 실제 레이처는단일 과장의 례이저선 밖에도레이처 풀라스마의 형광성 바닥선호와 플라스마 선스펙트럼의 일부가 레이처 공명관의 후 방 반사경에 의해서 레이처와 같이 시료에 도달하게 된다. 물론 이들 자발 복사에 의한 바닥 신호는 유도 복사에 의한 레이처 광선의 강 도에 비해서 무시할 정도로 작지만 만일 시료 표면이 거칠어 난반사 를 무시할 수 없는 경우에는 레이처 선에 의한 타만 산란광과 풀라스마
형광의 시료 표면 에 의 한 직 접 반사에 의해서 들어온 입력 신호들이 거 의 같은 제기로 나타날 수 있다. 따라서 보통 풀라스마 바닥신호를 제거시키기 위해 레이처 광선을 시료에 전입시키기 전에 둘침형태의 두과 곡선을 가지는 레이저용 고급 간섭 필터를 거치게 하고 있다• 타만 산란의 실험에 가 장 널리 쓰이는 레이저로는 Ar+(argo n 이온) 레이처, Kr+( k ryp ton 이온) 레이처 및 He-Ne 레이처가 있다. Ar+ 레 이 저 의 가장 강한 선은 초록빛 의 5145A, 파란빛 의 4880A, Kr+ 레 이 저 의 가장 강한 선은 초록빛 의 5208 A, 5309 A, 노란빛 의 5682 A, 빨강빛의 6471 A, He-Ne 레이처로부터는 6328A 선을 이용할 수 있다. 보통 파장 2 의 4 승에 반비 례 하는 산란 단면적 때 문에 4880 A. 선과 51 45A 선이 가장 많이 쓰이지만 스펙트럼의 분해능이 문제가 될 때에는 장과장일수록 유리하기 때문에 5682A . 또는 6471A 의 레이처선을 선택 하계 된다. 이 득룰이 큰 Ar+/ K r+ 레 이 저 에 있어 서 는 편광도의 완전도 (ex ti nc ti on ra ti o) 가 50~100 정 도이 고 He-Ne 또는 He-Cd 레 이 처 의 선편광 완전도 는 500 이상의 값을 갖게 되어 편광 관계를 보는 실험에 있어서는 He-Ne 레이처가 훨씬 우수함을 알 수 있다. 또 보통 라만 산란 실험에서, 레이저 광선을 아래 그림에서와 같이 렌스를 써서 시료에 집속시켜 쓰고 있으며 이 경우에도 세기가 문제가 되면 짧은 파장의 4880A , 514 5 A 선이 유리하고 편광도 문제가 중요
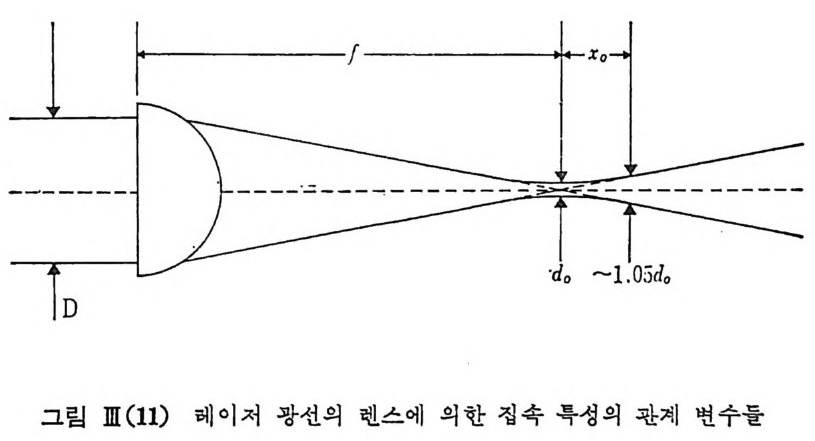그립 따 (11) 레이처 광선의 렌스에 의한 집속 목성의 관계 변수들
한 경우에는 건 과장의 6328A 선이 유리함을 볼 수 있다. 즉, 위 그림에서 보는 바와 같이 집속된 집접의 크기 do 는 do= 밥 ?.f/D ( Irr -29) 로 주어지며 레이처의 파장 2 에 비례하고 Xo= 곱- d 范 oc). ( IT-30) 로 주어지는 집속된 평행 선속의 길이 X 나요 A 에 비례하므로여러 파장 의 레이저 선들이 주어져 있을 때 신호의 세기, 편광도 관계 및 분해능 문제와 관련하여 선덱이 달라질 수 있다. fil-3 . 3 이 중 회절발 분광기 (Double gr ati ng spe ctr o mete r ) 이상적으로 델타 함수의 분포를 가전 단색광 신호가 분광기의 입구 s lit을 동하여 들어가 회철발과 거울에 의해 출구 slit 위치에 집속되어 나오는 신호를 기록할 때 이 기록된 신호는 입사광의 델타 함수 그대로
...
-
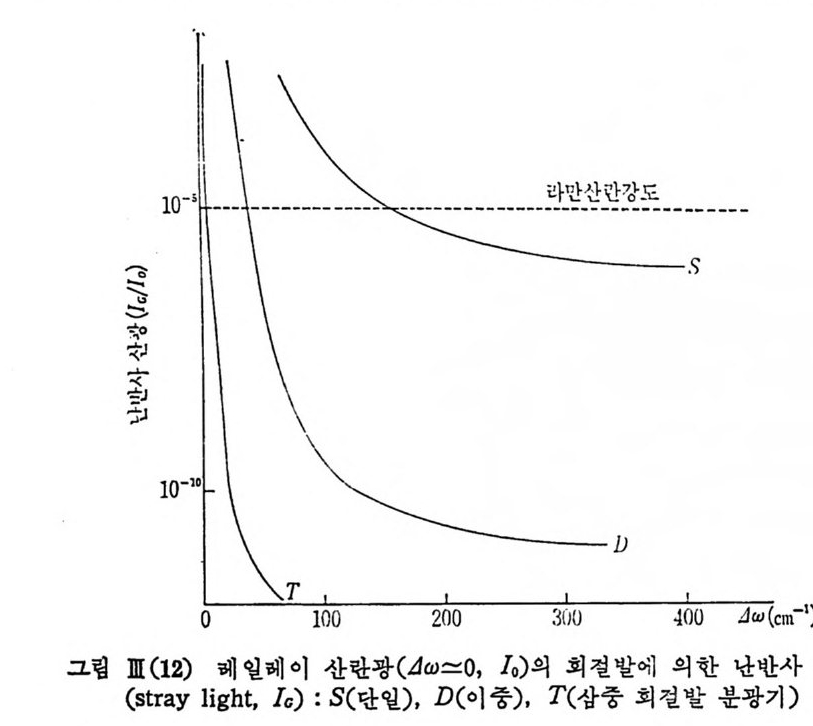
가 아니고 그 입사 광의 파장에 서 극대치를 가지고 유한한 폭 을 가지고 있는 광원처럼 기록 되기 마련이다. 이것은 sl it의 유한한 폭, 분광기 내부 광학 부품 즉 거 울, 회절발, 내부 벽 표면에서 의 난반사에 의한 소위 난산 광 등에 의해서 사실 그립 l[ (1 2) 에서 브는 바와 같이 어느 수준의 약한 빛을 기록하느냐 에 따라 가령 ~300 cm-1 밖에 까지도 델타 함수의 단색 입사 광에 의해서 순전히 분광기의 독성 때문에 신호가 나오는 것 으로 기록된다. 이 난산광의 영향은 단일, 이중, 삼중분광기로갈수록크 게 감소되고 있음을 그림에서 볼 수 있으며 단일 회철발의
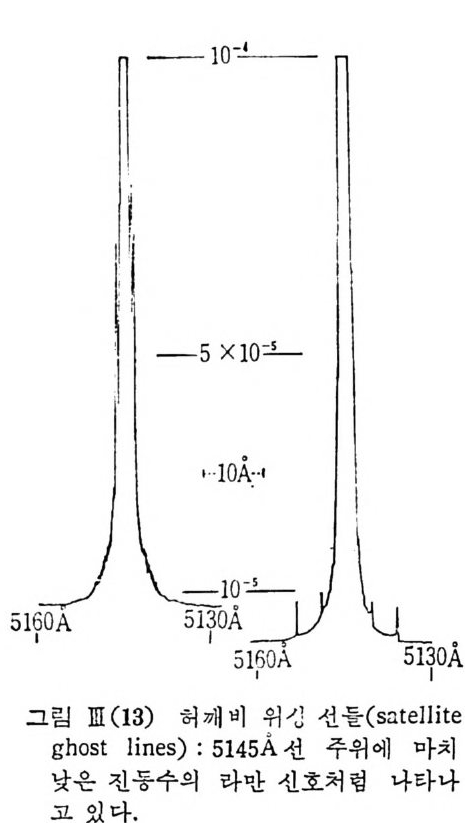
분광기로썬 100cm-1 이하의 낮은 전동수 라만 스젝트럼을 얻는 것이 거 의 불가능하게 됨을 알 수 있다. 최근의 고급 회철발들에는 옛날 회절발에서 문제가 되었던 Rowland 및 Ly m an gh ost 들은 거 의 나타나지 않지 만 소위 ‘sate l lite gh ost' , 'wal- kin g gh ost' 또는 ‘gr ass gh ost' 들이 아직 도 다이 어 몬드의 줄질 (ru li n g) 에 의해서 만들어진 회철발에는 계속 문제로 남아 있다. 그러나 최근의 홀로그래퍼형 회절발에서는 희철발의 난산광도 훨씬 적어지고 g hos t도 거의 나타나지 않는 반면, 입사광의 편광상태에 따라 서 효율이 변화하는 문제가 따르고 있다. m-a.4 스펙트럼 산호처라 분광기 에 서 나오는 광신호를 광전관으로 받아서 이 광전관의 출력 을 기록하여 스펙트럼을 얻는다. 이때에 측정 장치의 S/N( 신호 대 잡음
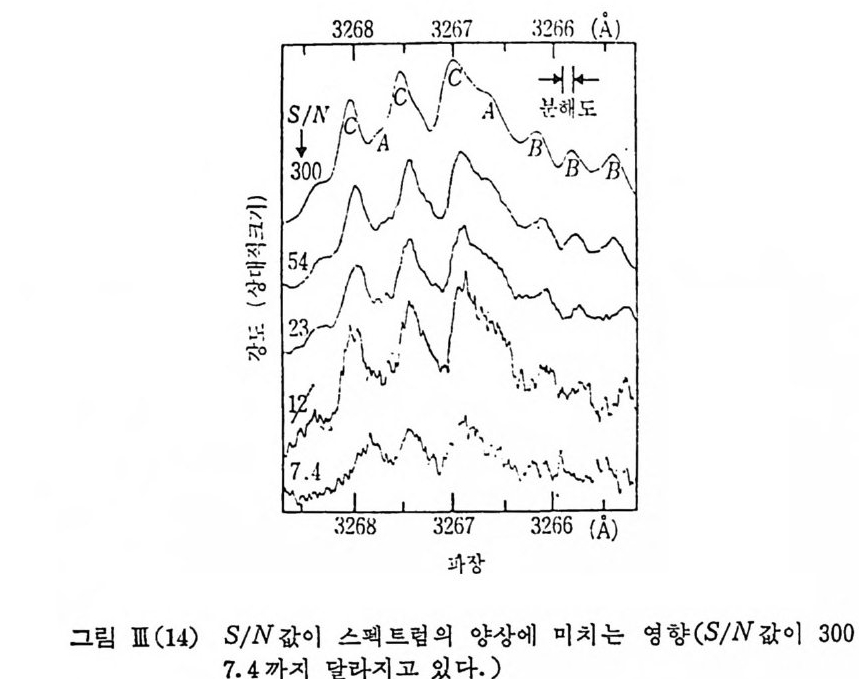
비)값에 따라서 기록된 스 펙 트 럼 의 질에 많 은 차 이 가 날 수 있다. S/N 값 이의에도 스펙트럼 전체 를 얻는 데에 걸리는 시간 및 분 해 도 등의 문제와 결부시켜 스 펙 트럼의 기록방법을 선 덱하게 된다. 우선 아 래 그림에서 S/N 값에 따라 기 록된 스펙트럼이 어 떻 게 나타나 보이는 가 바교해 분 수 있다.
326 8 326 7 326(i (k )
위의 예에서 보는 바와 같이 스펙트럼의 전체 길이 W, 필요한 파 장 분해도를 42, 전체 기록에 소요되는 시간을 T 라 하면 S/N 을 증 가시키기 위해 광전관을 포함하는 측정 장치의 시간 상수 ?를 길게 잡 올수록 좋지 만 감웅이 너 무 늦으면 분광기 의 scannin g 속도를 따라가지 못하여 신호의 크기가 많이 감소되어 역효과를 가쳐올 수 있다. 위의 경 우 우리가 분해도를 42 로 택했다는 사실은 우리가 기록하는 스펙트럼 에서 가장 예리한 신호선의 폭이 42 가 될 것이타는 예상에 근거하는 것이며 만일 감웅이 너무 늦어 s ig nal 의 강도가 2% 이상 감소되어 나 타나선 아니 된다고 할 때 이 4A 의 폭을 가지 는 스펙트럼 선을 scannin g 하는 데 소요되는 시간 A t는 다음 식의 A t보다 커야 됨을 알 수 있다.
e 내 / '=O. 02 :::: e-• 따라서 4t= 4 r 로 주어 진다. 한편 scannin g 속도를 42 의 단위로 표시하면 W/ L1?.T 가 되고 바로 이 scannin g 속도가 위의 4A/ 4t ( 4 t= 4 r) 보다 빨라선 안 되므로 L1A T/W;;:: 4r 와 같이 주어진 조건에서 T 의 최대 허용치가 결정된다. 한 예 를 들면 15 분 (~1000 초) 동안에 250 L1A 를 2% 이 하의 변형 (d i s t or ti on) 올 보장하는 t 는 위 의 식 에 서 T:::::1000 초, W::::: 250 L1A 를 대입하면 仁：：：：： 1 초의 값을 얻게 된다. 직류형 측정이 매우 편리하고 간단한 방법이 되겠으나 ohmi c 또는 빛의 룹생에 의한 부동 (dr ift) 문제, 또 칙류 증폭기 자체의 불안정성 등 으로 최근에는 벌로 쓰이지 않고 있으며 그 감지도는 아래의 위상 공액 증폭기 (loc kin am plifi er) 몰 쓰는 경 우와 같은 정 도이 다. 위상 공액 증폭기는 좁은 벤드 폭, 위상 차별(p hase-sens iti ve) 증폭 기에 처주과 통과 RC 필터를 결합시칸 것아다. 입력 단자에 선호가 걸리면 기준 전동수 le 를 중십으로 일정한 벤드 폭 B1 가 선택이 되고 이들 IC 중십의 신호를 진동수 0 울 중십으로 한 같은 벤드 폭의 신호로 전환시킨다. 이 직류 신호가 증폭되어 저주과 통과 필터를 동과하게 되는 것이다. 이러한 증폭기에 대한 S/N 은 S/N= 2 ,/ V2B,; v;2Bf 로 주어지며 여기서 V 는 입력 전압 신호의 rms 값이고, VN 은 입력 전압 잡음의 rms 값, Bs 는 입력 회로의 벤드 폭을 나타내고 있다. B, 는 광전관 회로의 시간 정수로 결정이 되며 죽, 부하 처항을 RL, 광전관 내의 내부 전기 용량과 증폭기에 연결시키는 전선의 전기 용량 울 합쳐서 C 라 하면 B,=I/RLC 로 주어전다. 또 V=RdAM, vN~RL[2e(µIA+µ'ld)B,]112 로 주어지며 여기서 h 는 직류 신호 전류, h 는 암전류, M~I 은 광신호 단속기 의 단속 유형 에 관계 되 는 교류 형 태 상수 (ac form fa c t or) 이 다. µ, µ’ 은
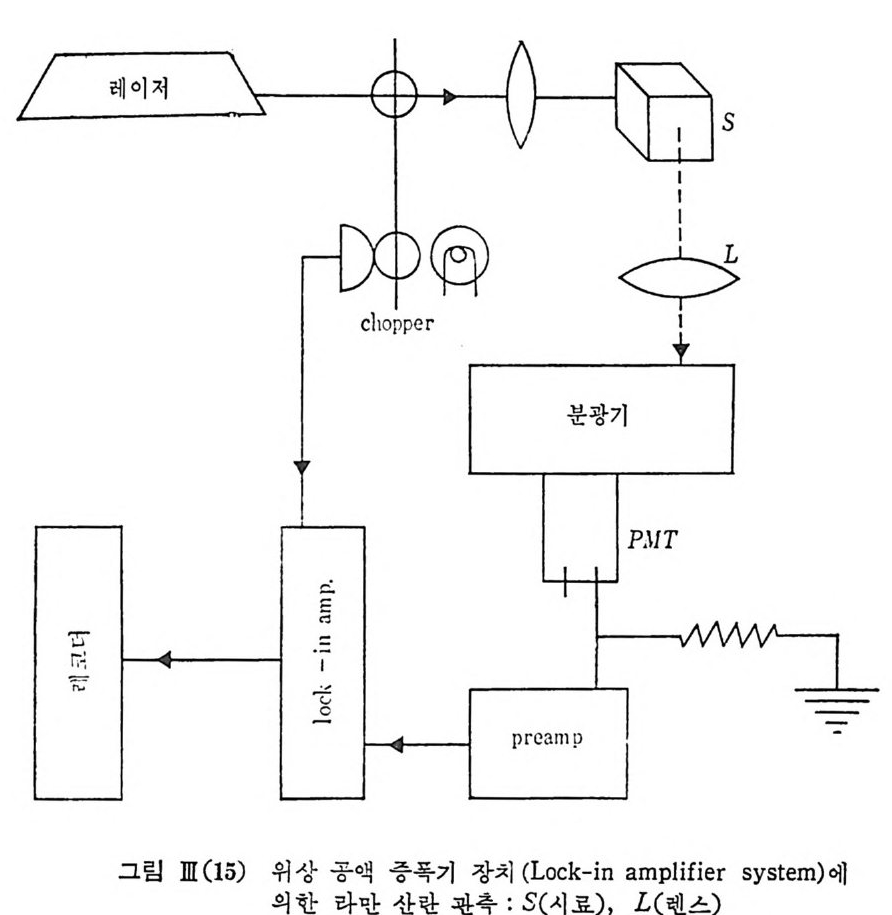
dy n ode 집선 (cha i n) 에 의한 신호 전류와 암전류에 대한 광전관의 이득 울 나타내고 있다. 따라서 µ:::::# 울 가정 하면 S/N:::::[2 IA2/e µ B, (]A+Id)]1 / 2 의 결과를 얻게 됨을 알 수 있다. 가령 ld=2.3X10-10A, 1A=6.O X 10-11A 로써 라만 산란광에 의한 신 호 전류가 암전류보다 훨씬 져온 경우를 예로 들면 Rt = 106D, µ= 1 06, B,=O. Ic p s 의 값을취할 때 S=GIARL 이므로 (G 는 증폭기의 이득 물 , G 쿠 X 104), S/N칙 0 의 값을 얻는다. 이것은 가령 출력의 rms 신호가 S=3.l V 였다면 rms 잡음이 N= o.075V, 즉 s ilt을 열고 닫을 때 위상 공액 증폭기의 출력의 rms 전압 올 나타내 고 있으며 만일 잡음이 가우스 분포를 하고 있 다면 pe ak to pea k 잡음 전압은 0.38V 에 이르게 된다. IA=6. 0XI0-11A 는 광전 음극에서의 광전 전류가 6X10-17A 죽 370 electr o ns/sec 에 해 당된다. EMI 9558 A 광전관의 6328 A 에 대 한 광전 음극 감도 O.024A/W 의 값을 취하면 위의 IA 값온 라만 산란광 2.SX 10-1 s w 의 입사광에 대응하고 있다. 이것은 또 6328A 의 광자수로 계 산하면 ~6400 ph oto n s/sec 의 광속에 해 당하고 있 다. S/N= I 즉 축정 가능한 최 소의 신호 강도를 구해 보면 IAmi n ::::::1. 4X 10-12A 가 되고 이것은 바로 EMI 9558A 광전관과 위상 공액 측정법을 쓰면 광전 음극에 서 9 electr o ns/sec 의 광전자를 방출시 킬 수 있 는 광신호 즉 ~175 ph oto n s/sec 또는 5. 7 X 10-11W 의 세 기 를 가전 라만 광신호이 면 겨우 축정 가능하게 됨을 알 수 있다. 이상의 결과는 Bf 대신에 칙류 중폭기의 벤드 폭울 대치하면 모두 칙류 측정법의 경우에 적용이 되고 따라서 직류 측정법의 경우에도 거 의 같은 감도를 예상할 수 있다. 아래에 위상공액 증폭기를 쓰고 있는 라만산란 스펙트럼의 관측방법 울 보이고 있다.
레이저 s
이제 펄스 증폭기와 펄스 판벌기를 사용하는 펄스 계수 측정법 (pu lse counti ng sys t e m ) 에 서 의 S/N 을 살펴 보기 로 한다. 이들 펄스 계수법은 핵물리 및 X 선 관측실형에서 먼처 개발되었던 기술로서 문제논 라만 산란에서 신호가 매우 약한 접이었다. 로에여 기만서들는어 광지 전는관 전의류 음 펄극스으 로하부나터하 나시를작 하d는ig i ta광l 전또자는에 an의a해log서 방양법 극에 회의 해서 축적시키는 기술이 요구된다. 이들 펄스들의 크기는 아주 크기가 적은 암전류 펄스에서부터 광전 관 내 의 찬류 개 스의 이 온화를 수반하는 Cerenkov 방사선에 의 한 굉 장 히 큰 펄스에 이 르기 까지 모든 크기 를 포함하는 Pois s on 분포를 이 루
고 있다. 직류형 측정에서는 이 모든 크기의 펄스들에 의한 양극 전류를 피코 전류계를 써서 계속 측정 • 기목하는 것이며 펄스 계수에서는 펄스들 울 모두 증폭시킨 다음 단일 구간 펄스 전폭 분석기로 보내어 아주 작 온 크기 의 암전류 펄스둘과 아주 큰 Cerenkov 펄스들을 골라 버 리 고 죽 하한 준위 E 와 상한 준위 E+LlE 사이의 신호 펄스들만 골라서 규격 화시 킨 다음 (1 µsec, 30 V 펄스) scalar 또는 선형 계 수율 계 기 로 펄스-계수 죽 일정한 울로 적분하여 결정되는 de 준위에 비례하는 출 력 (0~1V, O.5~80sec 시간정수)을 얻게 되고 기록기에 기록, 스펙 트럼을 얻게 된다. 이 경우 신호 계수 S 는 S=(n-nd) z-가 되고, 여기서 t는 계수율 계 기의 시간정수, n 은 신호와 암전류를 포함한 전체 계수율, 1ld 는 암전 류 계수율이다. 광전관 출력의 잡음은 광전자의 방출물의 통계성 요동에 기인하고 있 으며 광자 속밀도가 아주 적은 경우 이것은 입사 광속의 광자수 요동에 관계 되 고 Pois s on 분포를 가정 하면 이 요동의 rms 값 즉 신호 계 측수 의 표준 편차 N 은 평군 계축수의 제곱근 값으로 주어진다. 따라서, N= 서 r S/N= (n-n,1 )i-/ ,j荒 =n,-r/ ,/(n,+na)-c 가 되 고 S/N=l 을 대입하여 광자 신호 하한치 n,m i n 을 얻는다. n,mln=l /2-c [ l+ ,/ 1+4 nd'C ] 광전관을 냉각시키고 1250V 에서 동작시킬 때 삭제 준위를 0.15V 로 하면 n,1 =:::40cts / sec 정도가 되고, -r =lOsec 를 택하면 위의 식에서 다 음 결과를 얻는다. n,mln =::: 2 CtS / SeC 이 것 은 JA mln=n,mln , e µ =:: 3. 2 X 10-13A 에 해 당하고, 따라서 광전음극에 서 2elec tr ons/sec 의 광전자 방출은 타만 산란광의 제기로 1.3X10-17 W 죽 40 ph oto n s/sec 에 해 당되 는 것 이 다. 이 펄스 계축에서의 유효 암전류는
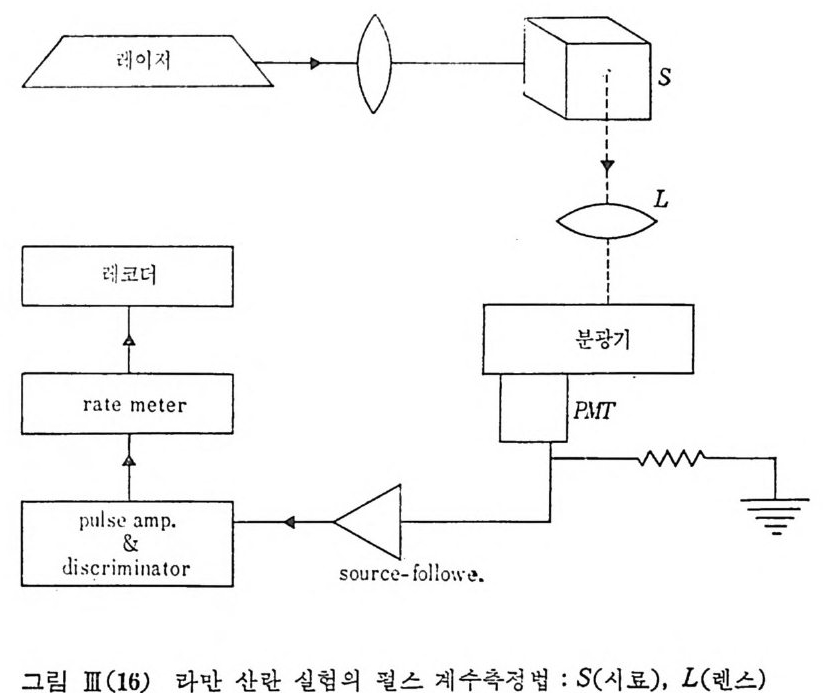
Id/ : :::: nd eµ ::::: 40X l. 6X l0 잡 X lO 댓 =6. 4x 10-12A 로써 앞에서 논한 위상 공액 측 정법에서의 Id 보다 휠싼 줄어들고 있음 을 볼 수 있다 . 아래 그 립 은 펄스 계수 축정법이 타만 산란의 실험에 쓰일 때의 윤 곽 도 형을 나타내고 있 다 .
대이지 \ \ ~ I I 二 s
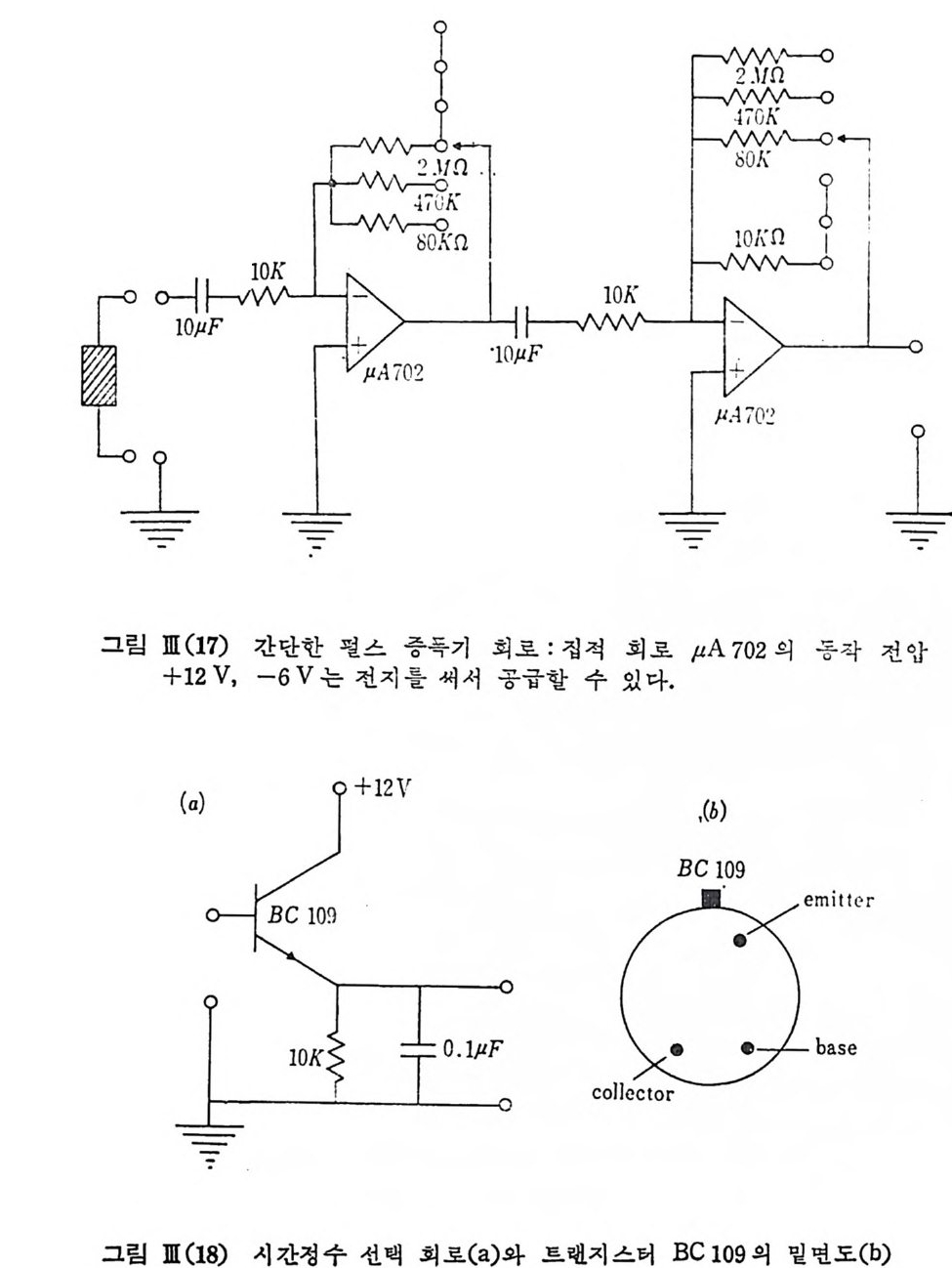
아래에 직접 제작하여 쓸 수 있는 값 싼 펄스 중폭기의 한 성공적인 회 로를 소개한다. 전문 메이커의 상품은 여러가지 조건하에서도 사용할 수 있는 다용성 컴퓨터 처리를 위한 중계자(i n t erface) 등 고급화되고 편리한 반면에 $10, 000 이상의 값이 나가고 있다. 실험실에 rate me t er 가 있으면 위 회로의 펄스 출력을 그대로 rate me t er 로 받아서 레코더에 기록시킬 수 있고 만일 rate me t er 가 없으 면 아래와 같은 시간정수 출력 회로를 연결 값싼 대치를 할 수 있다.
[
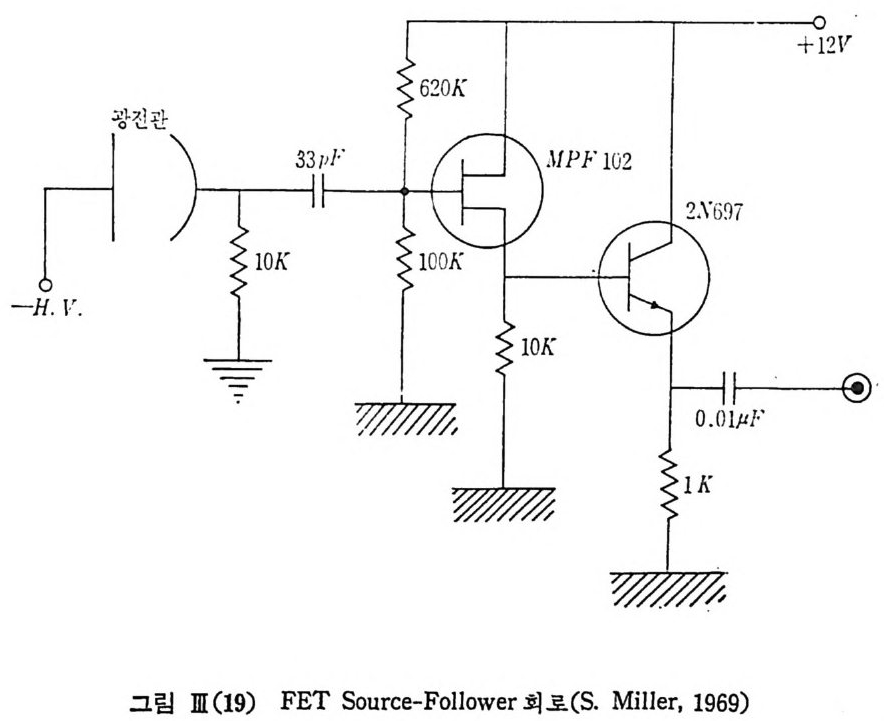
신호가 지극히 약한 경우, 광자 1 개가 광전 음극에서 광전자를 발 생시킬 확 률은 1 보다 적다는 사실을 고려해야 된다. 소위 개별 광자 계 수 (s i n g le ph oto n coun ti n g)의 기 숟은 바로 광전관에 들어 오는 광신호 광자 한 개 한 캐륭 계축해내려는 통계를 고려하는 축정 방법이며 브 통 광자 계수기로 불리는 측정 장치는 일단 광전 음극에서 발생된 광 전자들 하나 하나를 계축하는 데 목적을 두고 있다. 일반적으르 잡음 펄스들은 이들 단일 광전자에 기인하는 펄스들보다 아주 크거나, 아주 작거나 하므로 단일 광전자 펄스 전폭 스펙트럼을 조사하여 적 당한 삭제 준위 를 정 하 면 신호 대 잡음바 S /N 이 크게 증가 될 수 있다. 광전관의 이득룰이 통계적 성질을 가지고 있기 대문에 암전류 펄스의 펄스 전폭 스팩트럼과 신호 펄스의 펄스 전폭 스펙트럼이 일부 서로 중첩되어 있으므로 걷국은 S/N=1 이 되는 신호 강도의 하한값이 존재 하고 또 신호가 너무 강한 경우에도 매우 과론 광전관을 사용하더라
。
도 양전극 펄스 폭이 ~10 nsec 죽 팔스간 분해능 시 간이 ~10 11sec 정 도이므로 만일 ~10 ph oto ns/sec 이상의 강한 신호는 소위 펄 스 누적 (pu lse pile u p)이 생기고 광자 계수 계기률 사용할 수 없게 되는 것 이 다. 또 광전관 자체의 문제 의에도 펄 스 판별기의 밴드 폭 제약 죽 불 감 시간 문제로 역시 108Hz 이상의 계수울은 힘들게 된다. 광자 계수 축정기도 처령한 값으로 제작할 수 있는 회로가 브고 되어 있으며 (S.A. M iller , 1968) 광자 계수기를 사용할 때 광전관에 역부하 가 걸릴 우려 가 있으므로 FET source-fo l lower(ca th o de foll ower, im p c'.d ance t rans fo rmer) 를 광전관에 바 짝 연결시 켜 쓰면 50 요 동축 cable 울 상당 히 길게 연결시켜도 아무런 문제가 생기지 않는다. 또 설령 광자 계수 기를 광전관에 바짝 연결시킬 수 없는 경우에도 source- fo llower 를 쓰 떤 광전관의 부하 저항울 광자계수기의 입력 im p e da nce (1 K0) 에 구애 받지 않고 크게 증가시킬 수 있고 따라서 출력 펄스가 커지고 펄스 판 벌기의 작동이 용이하게 되는 이접이 있다. m-3.5 몇 가지 광학 소자들 광선의 편광 상태는 서로 수칙인 두 선편광 상태의 중첩으로 표시할 수있다. 중첩되는 두 선편광, 죽 수직 선편광성분과수평 선편광 성분 사이에 위상 차 (re t arda ti on) 가 O 또는 J./ 2 가 되 면 합성 파는 선편광을 나타내 고, 위상차가 J./ 4 또는 3 J./4 가 되 면 합성 과는 각각 오른손 나사방향의 원편광, 왼손 나사방향의 원편광을 나타내게 되고, 만일 두 성분이 전 폭이 서로 다르고 임의의 위상차 42 를 가질 때에는 타원 편광을 가지게 된다. 타만 산란 실험에서 종종 레이처 광속을 시료에 입사시키기 전에 광 속 분리소자 또는 광선 조향소자를 거치고 있다. 이때 레이처 광선의 편광상태에 따라 큰 차이가 날 수 있다는 사실울 예를 들어 보이기로 한다. 광속 분리 소자 유리판에 입사각 45° 로 6328 A.의 He-Ne 레이처를 입 사시킬 때 S 편광상태(입사 평면에 수칙인 편광)에서는 25% 가 두과하고 P 편광상태(입사 평면에 평행인 편광)에서는 57% 가 두과하게 된다. 따 라서 90° 각 반사광은 각각 S 편광이 75%, P 편광이 43% 에 이르고 있 다. 따라서 입사광의 편광상태, 더 일반적으로 S/P 편광의 구성비에 따
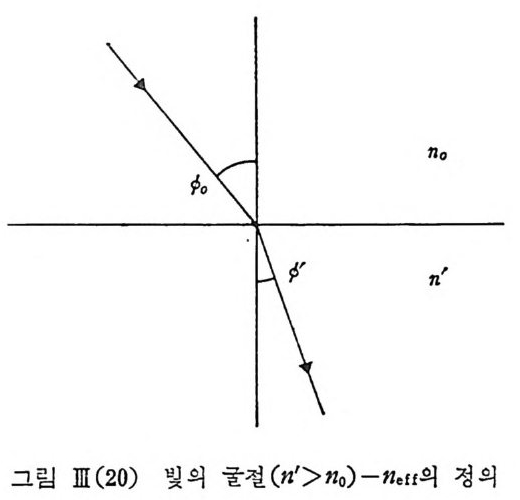
라 무과광의 캉도에 상당한 차이 가 예상된다. 수칙으로 입사하는 광속에 대해서는 편광상태에 관계없이 다음의 Fresnel 공식에 의해서 반 사계수 r 이 주어진다. r= nno 。 ++ nn I' 만일 아래 그림에서와 같이 입사각이 9o, 굴철각이 ¢’이타고 하면 복굴 절 현상에서와 같이 다음의 유효 굴절률 ne ff를 정의하여 각각의 편광 상태 에 대 한 반사계 수를 Fresnel 공식 으로부터 구할 수 있 다. 즉, 11scI1=11 COs ¢ (S 편광) 1lpc l{ = l1/ C 0S (? (P 편광) 110sin 90= n'sin ?'
n 。
한 예로 공기 (no=l) 에서 굴철룰 n'=1.52 인 유리로 ¢0=45° 각으로 입사할 때 반사울을 구해 보면 1. 52 sin ¢' = 1. Os in 45° 로부터 ¢'~27.72°, 따라서 S 편광 성분에 대해서 n0,c11= l. Oc os 45° =0. 707 n'e11 = l. 52 cos 27. 72° = 1. 34
1's =oo.. ~7700 77= --i-11 ..- 33440 .31 Rs=rs2=0. 0961, 즉 9. 61% 가 반사하계 됨을 예상할 수 있고, P 편광 성분에 대해서는 110, cu = 1. 0/c o s 45° = 1. 4142 n',u= 1. 52/ co s 27. 72° = 1. 717 rp = -0. 0967, Rp = O. 00935, 죽 0.935% 가 반사됨을 볼 수 있다. 위의 경우 우리가 이미 알고 있는 Bre,vste r 입사각 9 o=56.66° 에 대 해서 계산해 보면 1. 52 sin ¢'= 1. 0 sin 56. 66° 에 서 '=33. 33° 를 얻고 P 편광이 면 no,eu=1 . 0/cos 56. 66° =1. 819 n'eu= 1. 52/cos 33. 33° = 1. 819 따라서 Yp = O, 즉 RP=O 의 예상된 결과를 얻는다. 일반적으로 두명한 매질 사이의 경계면에서는 0<¢o < ¢B 의 경우 반사 를 거의 무시할 수 있고, ¢o>¢B 에서부터 반사가 급격히 증가 o=90° 즉 밀깔림(gr az i n g) 입사에서는 100% 에 이르게 된다. 상한 기편대 알할루 수미 늄없,지 은만등 편으광로상금태속에피 따막른의 차증이착가을 ,시P o<키4면5° 에반서사 울거은의 9나0%타 나이·
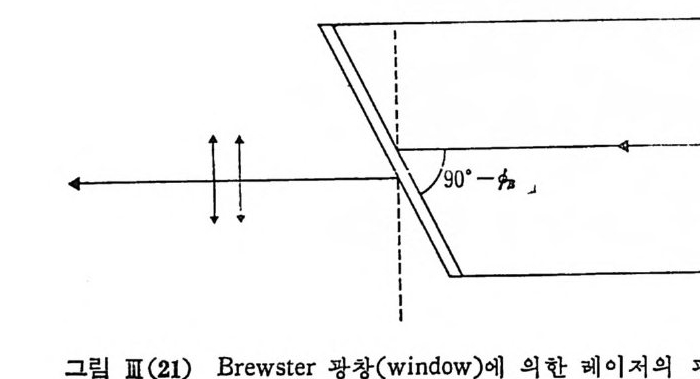그립 m(2 1) Brewste r 광창 (w i ndow) 에 의 한 레 이 처 의 편광
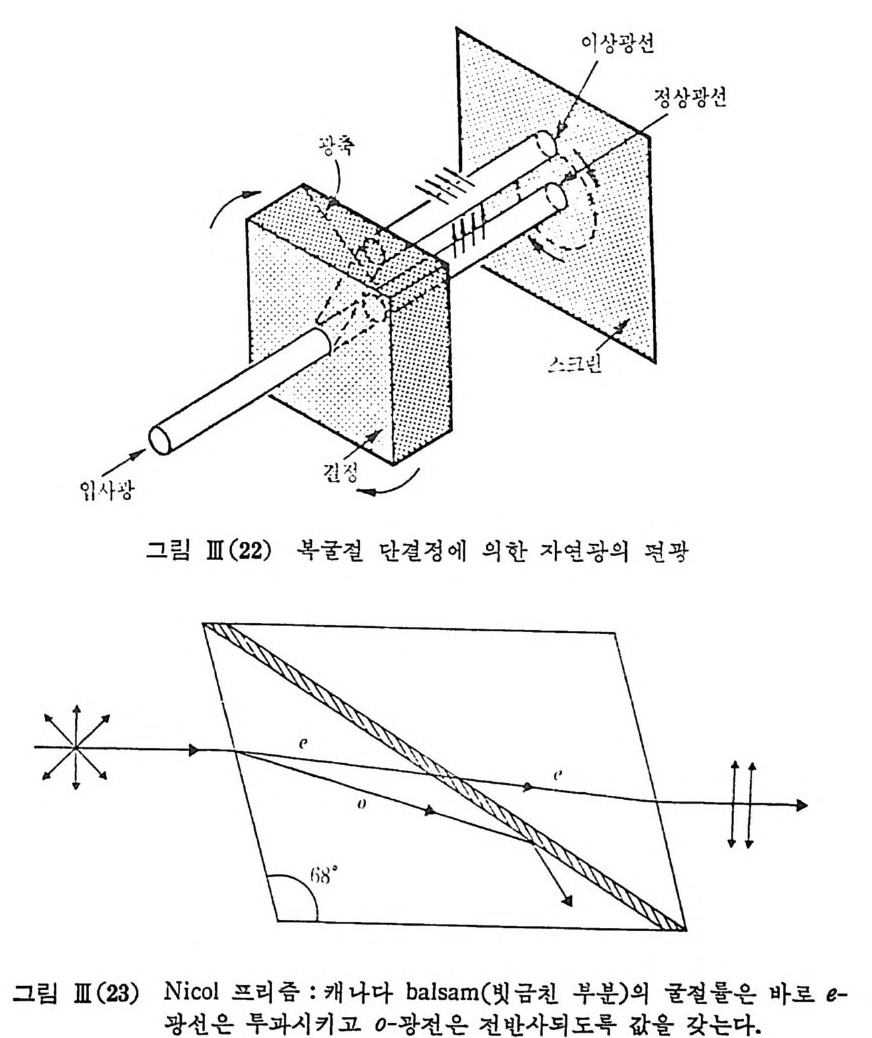
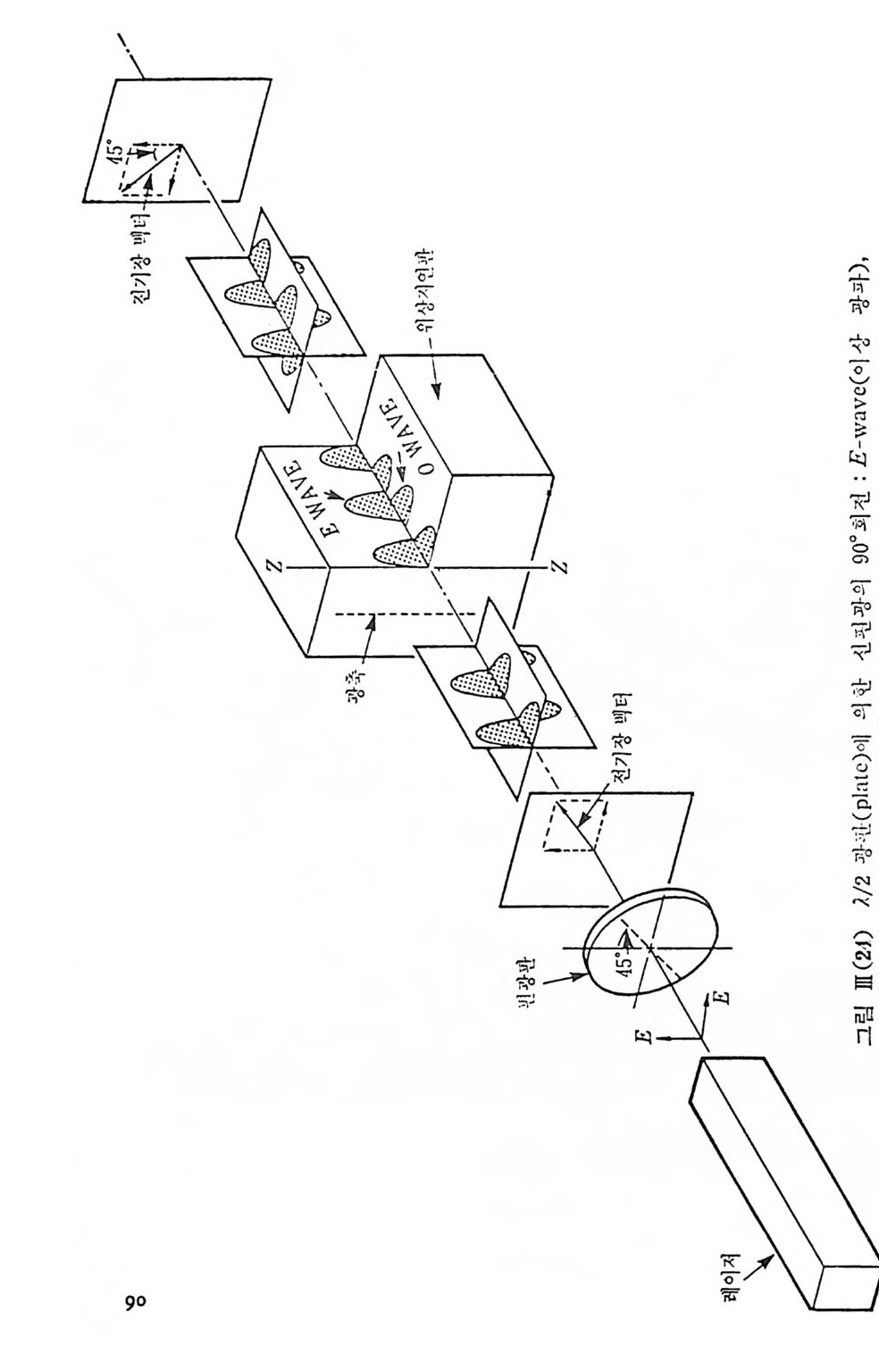
지c큰t r i 차c않 고 이c,oa가 ti거 n생 g의간) 의다1 .0경0 %우이 에는러 달한반는 1사 0반°율 사의이 율 상을이편 광가되상 질면태 에수펀 광있다상 는른대 유 에차전 이체따를 라펴 이반막용사 (d하울 i el여에e 레이처광의 편광상태룹 조정할 수 있다. 첫 째 앞의 그림 1II (21) 에 서 와 같이 소위 Brewste r 각 wi nd ow 를 사용 레이처 광속을 선편광시키고 있다. 타내석 고영 또있으는며 방 해아 레석 (c그al림c it eII)I (단22)결 에 정서 은와 소같위이 복광굴축철이 (b입 i r사e fr광i n에 g en평ce행) 을 조 는나
입 사/ 강
\
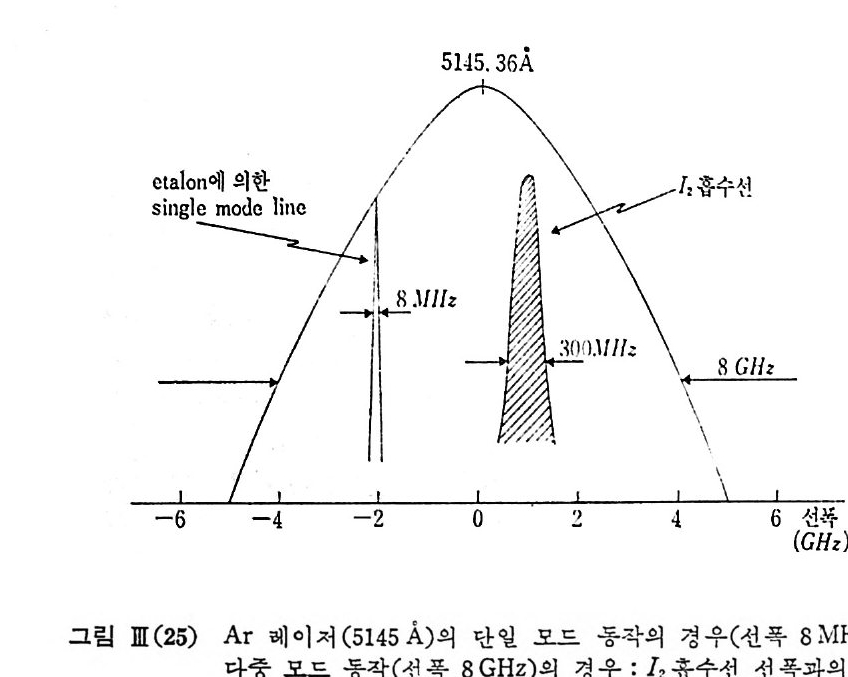
수칙한 방향이 아니면 편광상태에 따라 굴철각이 달라져 소위 정상 광 선 (ord i nar y ra y)과 이 상 광선 (ex t raord i nar y ra y)의 두 갈래 로 나누어 진다. 이러한 복굴절 결정은 그림 血 (22) 와 같이 Nic o l 프리즘을 만들어 편 광소자로 사용할 수 있 다. 이둔 복굴절 단결정을 적당한 두께로 찰라서 소위 위상지연판 (re t ar dati on p la t e) 을 만들고 그림 冊 (22) 에 서 와 같이 1/4 과장 광판 0 / 4 pla te ) 은 S,P 광파 사이에 )J 4 의 위상지연이 생기게 자른 것이며 이 A/4 광판에 광축과 45° 각을 갖는 펀극의 선편광 광속이 통과할 때 원편광이 되 어 나온다. 마찬가지 로 1/2 과장 광판 0 / 2 p la t e) 은 선편광의 펼광 방 향을 90° 회전시키게 된다. 쓰이는 용도에 따라서 A/4 광판은 간혹 편 광 혼합소자, A/2 광판은 편광 회전소자라고 불린다. 고분자 생체 분자 등 분자량이 매우 큰 분자들은 매우 전동수가 낮은 분자운동을 포함하고 있 다. 사신 50cm-1 이하의 타만 스펙트럼은 아주 두명한 단결정이 아니면 얻기가 매우 어려 워치 는데 이것은 주로 난반사 산란광이 너무 강하게 들 어오기 대둔이다. 이제 소위 Iodin e 필터와 5145.36A 의 단일 모드 알곤 레이처를사용 하여 3cm-1 이내의 라만 스펙트럼을 얻는 방법을 기술하고자 한다• Iodin e 층기의 1od i ne 분자는 X 냉g+ 전자 준위 바닥상태의 전동 준위 바닥상태 (v=O), 회전 준위 여기상태 (/=12) 로부터 B3II 。＋ 전자 준위 여기상태의 v=43, l=ll 의 진동-회전 결합상태에로의 천이에 해당하 는 5145. 42 A( 19 , 429. 27 cm-1) 의 흡수선을 가지고 있다. 이 0-43 P (12 ) 흡수선은 0-43R( 14 ) 흡수선과 일치하고 있으며 이 흡수선 죽 회 전 준위 선폭이 불과 250~300 MHz(~O. 01 cm-1) 밖에 되 지 않으므로 아래 그림에서와 같이 레일레이 산란광 및 기하 광학적 반사광을 완전 히 흡수 제 거 시 키 려 면 알곤 레 이 처 를 sin g le mode 로 동작시 키 는 것 아 펄 요하다. 5145A 의 알곤 레이저의 선폭은 보통 8GHz 에 달하고 이 안에 모드 사이 간격이 ~100MHz 가 되는 60~80 여 개의 종축 모드들이 서로 무 작위하게 공전하고 있다. 이 레이처 공전기 안에 모드 사이 간격이 8~9 GHz 에 달하는 e t alon 을 집어 넣으면 어느 한 순간에는 오칙 한 개의 단일 모드가 공전하게 된다.
5145. 36A.
이 단일 모드의 선폭은 8 MHz 정 도르써 300 MHz 의 선폭을 갖는 Iodin e 흡수선에 완전히 일치시키면 완전한 흡수, 차단시킬 수 있는 것 이다. 12 증기압은 cell 의 온도를 50~90°C 에 유지시컬 때 레일레이 산탄광 이 2500 배까지 감소되는 최적치가 유지되고 그 이상에서는 오히려 라 만 산란광이 흡수되 기 도 한다. ][-4 레이처 및 광전 증배관 lII-4.1 레이저 레이저란 우리가 이미 마이크로 전과 이하의 전동수를 가지는 전자과 에 대해서는 반도체 소자 또는 LC 회로를 써서 단일 진동수 발진기 및 동조 증폭기를 제작하여 쓰고 있듯이 이러한 증폭기 및 발전기를 광과 의 전동수를 갖는 전자과에 대해서 실현시킨 것이다. 이것은 오칙 원자 및 분자 자체를 전자과 발전의 소자로 쑬 때에 가
능하고 소위 유도복사 (s ti mula t ed em i ss i on) 에 의해서 광학적 공전기 얀 의 모든 원자(또는 분자)들이 위상을 맞추어 발생하는 광과 전동수의 전자파에 해당하는 것이다. 원자 또는 분자가 기체 상태에서 빛을 발생시킬 때 이 빛은 유한한 선 폭을 가지 고 있 다. 소위 균일 선폭퍼 침 (homog e neous broaden i n g)을 가 져오는 원자의 여기상태의 유한한 수명, 원자들 사이의 충돌 죽 압력퍼 집 (pre ssure broaden i n g)과 이보다 훨씬 큰 불군일 선폭퍼침 (inh omo· ge neous broaden i n g)을 가져오는 도플러 퍼짐을 고려해야 된다. 맥스웰 분포를 가지는 기체의 경우 도플러 퍼침은 가우스 선폭 모양 울 가쳐온다. g(））)=느 ✓ lW /2r&T e-llC2(M-’'l2k. m ,, l-'o 이때의 반폭 4VD 는 4VD=2% 凡봅 In2 로 주어지며 He-Ne 레이처의 Ne 이 T=300°K 에서 6328A 의 빛을 내 는 경우 」）） D ：：：：：：1. 5 X l09Hz 가 된다. 이 4 )J D 의 선폭 안에 레이저 공전기의 정격 모드가, 가령 공전관 길이 가 Im 일 때, c/2 뇨 150MHz 의 간격으로 들어가게 된다. 이 중에 문턱 세기 이상으로 펌핑되는 모드들만이 레이처 공전을 하 계 되며 모드 사이의 간격을 5 ））군이라 하면 N=L1 찌 6 ）） n 개의 종축 모드가 등시에 공전할 수 있다. 이들 종축 모드 하나하나의 선폭은 레이저 공전기의 성능인자(q ua lity fa c t or) 를 Q라 하면 4 (J)＝(J)。/Q로 쑬 수 있으며 Q= P (표幻표)/r. h(LI Q c) 로 주어진다. 여기서 P 는 레이저 출력, N 广 Al 은 상태밀도 반전, 49c 논 공전기의 공전 폭으로써 공전기의 fine sse F 와 49e=6v. . /F 의 관계를 갖는다.
저 출력 (P= l mW) He-Ne 레 이 처 (wo=4. 73 X 1014 1-I z) 에 대 해 서 생 각하 떤 공전관 길이 l= 100 cm, 공전기 손실 a= O . 01/ m (~1% pe r p a ss) 의 값에 대해서 49 c = 2:c = 읊듄 '.'.::'. 5X 105 Hz, 따타서 4 (1)＝。 。 ！ Q ::::: 10-3 Hz 의 단일 모드에 대 한 선폭값을 얻는다 . 이 값은 이론적으로 가능한 한 극한치에 불과하고 실제로논 공진 관 길이의 열 및 음전동 요동에 의해서 4(1 ):2:1 03Hz 이상으로 관측 되고 있다. 공전관 길이의 미소 변화를 dl 이라 하면 이에 대한 공명 전 동 수 ))n 의 변이 4)) .. 는 4))m = - 롯눕 dl 로 주어침을 알 수 있다. 레 이 처 광속의 모드 구조를 보면 TEMp q ( m) 모드가 모두 가능하지 만 공 유초접 공전관 (con fo cal resonato r cav ity)의 경 우 가령 R1=R2 = IOO cm 의 공전관 거울을 사용할 때 플라스마도관의 내심 적경을 2mm 이내로 줄이 면 TEMoo 모드만 나타나게 할 수 있 다. 이 TEl\ lfooc m) 모드는 강 도 분포가 다음의 가우스 함수로 표시 되 며 1=I。 exp ( -2 r2/r 。 2) 여기서 Yo 는 보동 광속의 광점 반경으로 정의되고 있으며 r::;;;ro 안에 레 이처 출력의 86.5% 가 포함되고 있다. 타'CJ: 산란의 실험에서 가장 많이 사용되고 있는 Ar+ 이온 레이저 를 중심으로 레이처에 대한 현재 상황을 개략하기로 한다. 이 레이저는 보통 lm 의 공전관 길이를 가지고 있으며 가령 4880A 의 레이처 광선을 스펙트럼 분해기로 분석해 보면 이 안에 40 여 개의 종축 모드（ m ：：：：： 106) 가 동시에 나타나고 있으며 전체 선폭이 ~8GHz 에 달하고 있음을 볼 수 있다. 이 다중 모드 레이처의 모드 하나하나는 이론적으로 ~10-3Hz 의 선 폭으로 좁힐 수 있지만 실제 상용으로 만들어지는 에탈몽을 레이처 공 전기 안에 집어넣어 얻어지는 단일 모드 레이처의 출력은 ~3MHz 이 하의 선폭을 유지하기란 지극히 어려운 일이다• 이것온 공전관의 열팽창, 냉각수의 유속, 의부전동, 음파공명 등에 기인하논 공진관 거울의 미소 전동에 의해서 MHz 단위의 떨림(jitt er) 이 생기기 때문이다.
보몽 다중 모드 레이처에서는 모드들 사이에 서로 독립적으로 무작위 하게 공전하고 있지만 소위 mode - lock i n g을 시켜 모든 모드가 서로 위 상을 맞추어 공전하도록 개조하면 이때 출력은 T=인／ C ：：：：： 7nsec 의 간 격으로 4 t：：：：： 2 。 0 p s e c 의 펄스 폭올 가지는 펄스 형대의 츨럭이 나오개 된다 . 도 출력 거울 대신에 소위 cavit y dum p er 로 블리는 음향 광학적 d e fl ec t or 을 부치면 펄스 사이의 간격 즉 빈도수 를 조절할 수 있고 펄스 폭은 ~15nsec 가 되는 펄스 형태 출력을 얻을 수 있다. cavit y dump e r 와 mode- lo cker 를 함께 사용하면 펄스 빈도수를 단일 펄스에서부터 수 MHz 에 이르기까지 조절할 수 있고펄스폭이 O.5nsec 가 되는 펄스 레이처를 만들 수 있다. mode-lock i n g시킨 Ar+ 이온 레이처로 염료 레이저를 소위 등위 펌핑 을 시키면 12nsec 의 간격으로 ~3 p sec 의 펄스 폭을 가지는 레이저 펄 스 을 얻을 수 있다. 이 등위 펌핑은 염료 레이처의 공전관 길이를 조정 하여 염료 례이처의 모드 사이 간격이 Ar 레아처의 mode-locker 전동 수의 정 수 배가 되도록 하면 염료 분자가 가지는 매우 큰 유도 복사 단 면적에 기인하여 레이저 펄스 자체가 이득률에 큰 영향을 미치고 일종 의 ga in swi tch in g 의 현상으로 순간적 인 (~3 ps ec) 염 료 레 이 처 펄스가 되 어 나온다. 여 기 에 또 cavit y dump ing 의 sys te m 을 추가시 키 면 소위 sy n chronously- pu mp e d mode-locked, cavit y-d ump e d dy e laser 를 얻고 이것은 펄스 폭은 ~15p se c 정도이지만 펄스 작동률은 단일 발사 동작 에서부터 4MHz 까지 임의로 선택하여 등작시킬 수 있게 된다. 이제 선폭이 1MHz 이내에 달하고 ~수 W 정도의 고출력을 넬 수 있 논 단일 전동수 동조가변 레이처인 소위 Ri ng Dy e Laser 에 대해서 알 아보기로 한다• 우선 보통의 단일 파장 영로 레이처는 Ar+ 이온 레이저의 펌핑 광속 이 정상파 염료 레이저 공전관에 들어가 염료 용액 순환계의 영로 유속 에 브루스터 각으로 입 사하여 공전관 안의 가변 에 탈롱, tun in g wedg e 등에 의해서 선폭이 ~30GHz 에서부터 ~15MHz 까지 되고 펌굉 입력 IW 에 대해서 ~30mW 출력을 내고 있다. 이 정상파 형식의 작동에서는 용액의 이득 체적 전체가 레이처 발전 에 참여하지 못하고 따라서 단일 전동수 발전에 대한 효율이 낮은 편이 며 또 펌핑 입력을 너무 증가시키면 선덱한 모드가 node 를 나타내는 곳
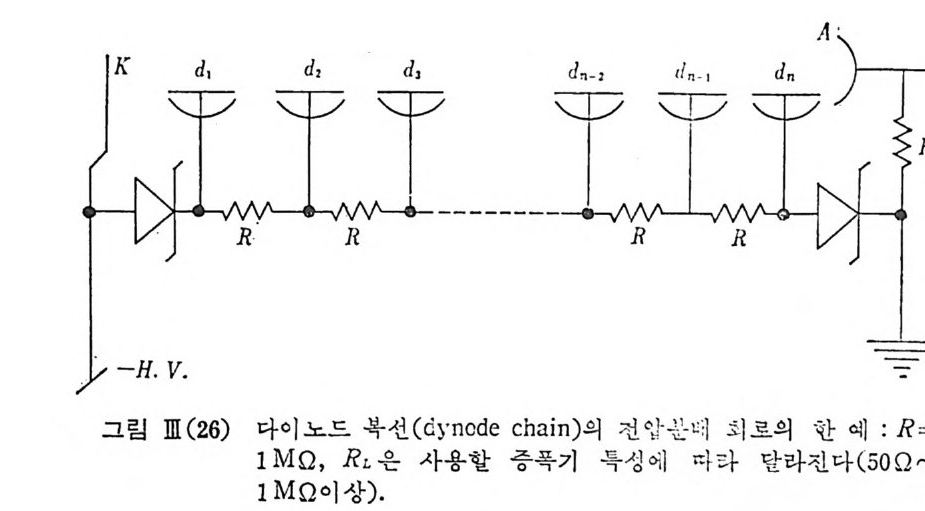
에 바로 인접한 모드가 an ti node 를 형성하며 발진 문턱에 도달하게 된 다. 환형 레이저는 바로 이러한 문재룹 해결하고 있으며 한쪽 방향으로 만 진행하는, 진행과 여기가 진행되는 레이저이다. 이때 이득 체적 안에 node 또는 an ti node 의 무늬가 형성 되지 않고 진 행과에 의하여 연속적으로 염료내 이득이 증가되어 정상과 레이저보다 도 보통 ~15 배의 출력을 기대할 수 있다. 이 진행과의 rin g las e r 에서 는 펌핑 에너지 밀도에 거의 제한이 없고 군일형 선 퍼침을 가지기 때 문에 퍼이네쓰가 높은(～손실이 콤) 에탈롱을 쓰지 않고서도 손실이 제 일 적은 오칙 몇 개의 cavit y 모드만이 발전하게 된다. 여기에 mi cr o- pro cessor contr o l 에 의 해 서 움직 이 는 기 준 간섭 계 (FSR = SOO KHz ) 을 포함하는 주과수 안정 장치 를 부치 면 mode-hop ping 을 방지 할 수 있 고 떨림에 의한 선폭이 O.5MHz(l. 6 x 1 0-5cm-1) 이하가 되논 단일 전동수· 고출력 ·고안정성 례이처를 얻게 된다. 이 진행파 레이처는 rin g cavit y 안에 한쪽 방향으로만 레이처 발진이 가능하계 해주는 과러데이 회전 원리의 광과 정류기를 포함하고 있다. 이 원환 레이처를 mode-lock i n g시킨 Ar+ 이온 레이처로 동조성 펌핑 울 시켜 0.6~1.5 p sec 의 레이저 펄스를 얻을 수도 있다. 이 밖에 Nd : YAG 펄스 레이처, CO2 레이저 등 득히 반도체에 대한 라만 산란 연구 에 쓰이고 있는 다론 레이처들도 많이 있다. llI-4. 2 광전 중배관 광전 증배 관 (PMT) 은 광전 음극, 다이 노드 복선 중배 회 로, 양국으 로 구성되어 있으며 스팩트럼의 영 역 (자의선, 가시광, 적외선), 강도, 시간적 번화 양상에 따라 PMT 의 선택과 사용 방법이 탈라진다. 금속 도는 반도체 에 서 광전자의 방출은 方h―e =E1c+
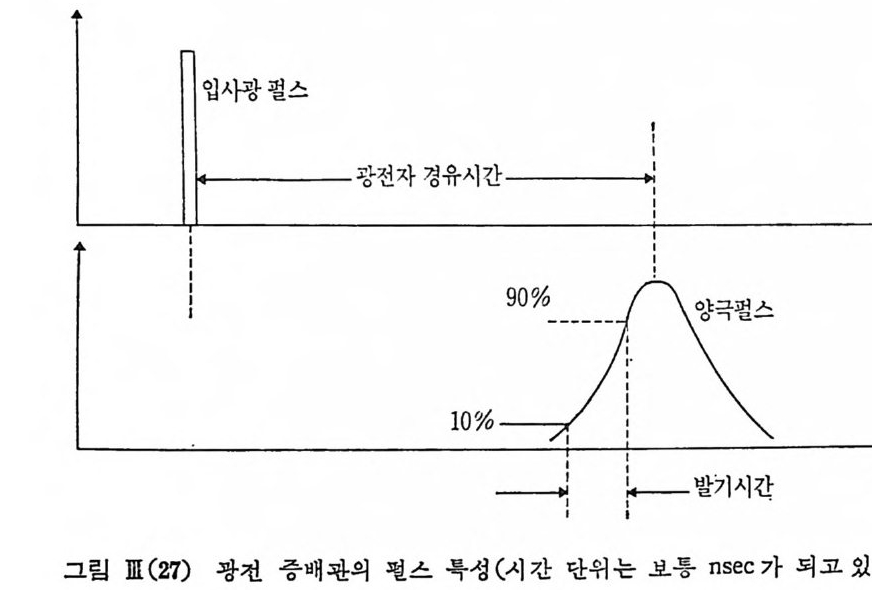
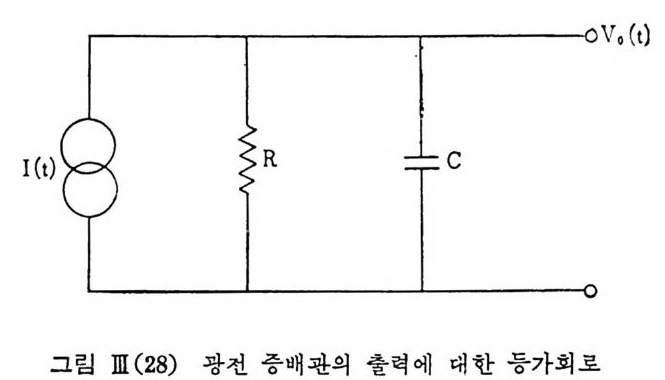
극의 종류에 따라서 달라침 을 보았으며 , S-20 으로 표시 되 는 spe c tr a l respo nse 윤 갖는 광전음극은 가시 광 영 역 에 서 가장 효율이 좋고 CsNa2 KSb 등 소위 bia l kali 광전음극이 이 에 속하며 S-1 으로 표시되는 분광 감지도는 7800A~lµm 의 적의선 영역에서도 효울이 좋은 광전음극을 나타내 고 Ag O Cs 광전음극이 이 에 속하고 있 다. 이 광전음극에서 방출되는 광전자들은 차례로 다이노드 표면에 가속 되어 입사하고 이때 소위 이차 방출 과정에 의해서 다이노드 표면으르 부터 많은 전자들이 방출되고 계속해서 다이노드 복선을 차례로 거쳐 건국 양극에는 광전자 한 개당 105~109 개의 전자들이 전하 펄스 형태 로 집속된다. 다이노드의 이차 방출 인자 6 는 6=AVa 르 주어진다. 여기서 A 는 다이노드 형태, 물질 종류 (SbCs, BeCu 등)에 관계된 상수, a=0.7~ 0.8 이 된다. 전체 n 개의 다이노드 복선에 의한 PMT 전체의 이득 G 는 PMT 의 음극과 양국 사이의 전압을 VC 라 하던 G= (A V 잉 = {A( 불行汀 n=k VCcn 이 되고 n=9~12 에 대해서 G 는 VC6~VclO 의 전압 종속 관계를 갖는 다. 따라서 PMT 에 사용되는 고압 전원은 안정도가 아주 높은 것을선 E석 해야 됨을 알 수 있다. PMT 의 다이노드사이에 일정한 전압을 공급 하는 데에 아태와 같은 전압 분배 회르를 사용하고 있다. 특히 음전극 (K) 과 첫 번째 다이 노드 (d i) 사아 에 걸리 는 전압은 일정 한 값으로 고정시켜 놓기 위해서 찌너 다이노드를 사용하고 있으며 또 멘 군번의 다이 노드 (d) 와 양전국 사이 에 도 찌 너 다이 노드를 쓰면 양전극 펄스에 의한 전압 변등 즉 이득 변동을 막을 수 있으며 양전국 전류가 분배 복선 회로에 흐르는 전류의 ~5% ｀ 이상이 되면, 죽 빛의 강도가어 느 정도 이상이 되면 감도가 선형관계에서 벗어나는것을 막을수있다. 광전음극에 광펄스 (~6 함수)가 들어올 때 양전극에 생기는 전류 펄 스를 보면 아래 그림에서와 같이 광전자가 다이노드 복선을 거쳐 양전 극에 이 르는 데 에 유한한 시 간 (elec t ron tra nsit ti me) 이 걸 리 고 또 유한 한 폭을 가전 펄스가 됨을 알 수 있다. 이 전하 펄스가 저항 R 을 통해 흘러갈 대 또는 캐퍼시터 C 를 충전 시킬 때 이에 해당하는 Uo(t) 즉 전압 신호를 기록함으로써 PMT 의 광 신호 입력을 축정하게 되는 것이다.
K dI dl dn
R 을 사용하여 u 。(t)를 측정 할 때 전 류형 작등 ( curren t mode op e ra- tion ), C 를 사용하여 Uo( t)를 측정할 대 전압형 작등 (vol t a g e mode op e- rati on ) 이 라고 부른다. 따라서 우리는 PMT 를 다음과 같온 전류 발생원 l(t ) , 출력 처항 R 및 C 로 구성된 등가회로로 취급할 수 있다. 다이노드 복선을 포함하는 PMT 의 출력 처항은 실제로 무한대 값에 달하므로 R 온 양전극의 부
입사광펄스
V,(t )
하 처항 RL 로 완전히 결정되며 C 는 a.c. cou p l i n g이 아니면 무시할 수 있 다. 지 금 입 력 신호, 따라서 l (t)가 다음과 같이 지 수함수적 감쇠 (시간 정수 T, ）를 가지는 신호라고 하면 l(t) = Aexp ( 크/'C,) 위의 회로에 의해서 Vo(l) ＝훑 [ex p(-t/r: ,)-ex p(크/乙)〕 의 결과를 얻을 수 있다. 여기서 •c=RC 이다. A 는 PMT 의 이득 G, 광전 음극에서 방출된 전자수 N, 전자의 하전량을 e 라 하면 A=NeG 로 놓을 수 있으며, N=lOO, G=106, -.,=Snsec 가 되는 경우를 한 예 로 들면 乙 =RC 값에 따라 여러가지 형태의 u 。(t)를 얻게 됨을 볼 수 있다. 아래 그림에서 보는 바와 같이 •c <{ ?;', 를 만족하는 RC 를 택할 때에 만 Uo( t)가 입력 신호 l (t)를 변형시키지 않고 원형 그대로 나타넬 수 있음을볼수있다. 가령 C=lOp F , R
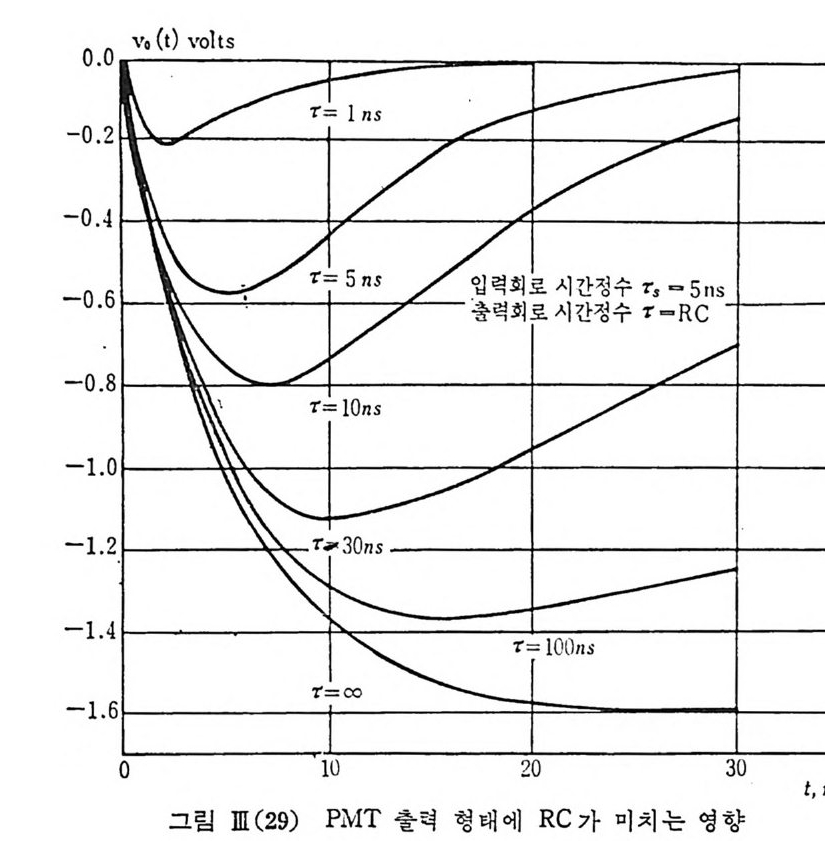-0.2
제가된다. PMT 에 빛이 전혀 들어가지 않을 때에도 광전음극 자체 또는다이노 드에서의 열이온 방출, 우주 방사선 및 전자들에 기인한 광전관의 찬류 기체의 이온화 등에 의해서 암전류 죽 암전류 펄스가 나타나며 이것은 약한 신호를 측정하는 경우 S/N 값에 큰 영향을 미치고 있다. 암전류 논 온도 T에 지수함수적인 관계를 나타내므로 PMT 를 냉각시키면 암 전류를 급격히 줄일 수 있지만 이때에 광전자 방출의 효율 즉 양자 효 울도 상당히 떨어지므로 PMT 에 따라 최적 온도가 주어져 있지만 일 반적으로 계수율이 상당히 높을 때에는 오히려 PMT 를 냉각시킬 때 S록/ N암 값전이류 가떨 어줄질어 들수지도 만 있 b다i.a l ldSi - 1광 전광음전극음은극 은— 1一0 °1c8 0정°C 도 까면지 암냉전각류시 킬계 수수 가 벌문제 되지 않음이 알려져 있다.
참고문현 1. Ben. Chu, Laser Ligh t Scatt er in g , Academi c Press (New York, 1974) Chap. IV, V, VI. 2. H. Cummi ns and H. Swi nn ey, Lig h t Beati ng Sp e ctr o scop y, in Prog r . Op t. 8. (E. Wolf, ed.), North - H olland (Amste r dam, 1970), p.1 33. 3. C.J. Oliv e r, Correlati on Techniq u es, in Photo n Correlati on s and Lig h t Beati ng Sp e ctr o scop y (H. Cummi ns and E. Pik e , eds.) , Plenum Press (N ew York, 1974), p. 151 . 4. A. Nu ssbaum and R. Phil li p s , Conte m p o rary Op tics for Sc ien ti sts and Eng ine ers, Prenti c e -Hall(Eng le wood Clif fs, 1976), Chap. 7, 8. 5. D.M . Munroe, Semi na r Note s on Recoverin g Sig n als from Nois e and Me asu rement Problems in Low Level Radia t i on , EG&G Prin c et o n Ap pli e d Resea r ch (GIN S CO-Seoul, 1980). 6. J. Rolfe and S. Moore, Ap pl. Op t. 9 . 63(1 9 70). PM tub e 의 효율적 안 사 용에 대한 실험 논문. 7. R. Alfa n o and N. Ockman, ]. Op t. Soc. Am. 58. 90(1968). 약한 신호 의 축정 에 관련 여 러 가지 amp li fi er sys te m 에 대 한 실험 적 고찰 울 기 술한 논문 8. S.A. Mi lle r, Rev. Sc i. Instr u ments 39. 1923(1 9 68). 분광학 실험 에 쓰이 논 ph oto n counti ng sys te m 의 값싼 제 작 • 회 로. S.A. Mi ller, Raman Newslett er No. 7. 1(1969). 위의 ph ot o n count e r 와 관련 ph oto m ultip lier 에 loadin g 시 키 지 않도록 FET source foll ower 를 사용하는 예를 기술하고 있음. 7. Eric Hass, Polariz a ti on and Lasers (Laser Technic a l Bulleti n No.7), Sp ec tr a Phy s ic s (M o unta i n Vie w , 1975). 8. D.O . Landon and A.J. Mi tteld orf , The SPEX Sp e aker XVII-No.I, Sp e x Industr i e s (Metu c hen, N.J. , 1972), p.1. dif frac ti on gra ti ng 의 문제정 들 울 갈 지적하고 있다. 9. D.O . Landon and P. Reed, The SPEX Sp ea ker XVII-No. 2. Spe x Industr i e s (Metu c hen, N.J. , 1972), p. 4. monochromato r 의 str a y lig h t 에 대 한 논의 와 3 rd monochromat o r 의 웅용에 대 한 선명 서 . 10. G. Hib l er, J. Lip pe rt and W.L. Peti co las, The SPEX Sp e aker XVI- No.I. Sp e x Industr i e s Inc. (Metu c hen, N.J. , 1971), p.1 0. iod in e filter 의 사용에 대한 상제한 설명서. 11. EMI Cata l og u e(POO 1/E 79) Photo m ult ipliers (I979). Hamamats u Cata l og ( SC 1-4-1) Photo m ultip li e r Tubes(1981). 12. Coherent Technic a l Note , CR-699 Rin g Lasers(1982).
제 W 장 기체와 액체의 광산란 분광학 기 체 상태 에 서 는 분자들기 병 전(t ransla ti ona l), 회 전 (ro t a ti onal), 전등 (v i bra ti onal) 의 모든 운동상태를 가질 수 있지만 액체상대에서는 분자 의 희전 주기가 분자들 사이의 충돌시간에 비해서 너무 느리기 때문에 완전한 회전운동이 거의 불가능하게 된다. 우리들은 여기 제 1\ I 장에서 광산란 분광학이 기체 및 액체 속에서 분 자들이 어떻게 운동하고 있는가에 대한 중요한 정보를 제공하고 있음을 살펴보기로 한다. N-1 기체 w-1.1 회전운동 에너지 준위 분자의 회전운동을 기술하는 데 기본이 되는 양으르서 입의의 회전축 에 대한 관성능몰이 아태와 같이 정의되고 있다. l=Im,r;2 여기서 r; 는 i번째 원자에서 회전축에 내린 수칙선의 길이, m, 는 이 i번째 원자의 질량을 나타낸다. 분자의 질량중심 으로부터 모든 방향으로 1/ ./T 의 값울 도시 하면 일 반적으로 타원체를 형성하며 이 관성 타원체는 소위 분자의 관성 주축 이라고 불리논 서로 수칙한 세 축을 갖는다.
이 세 주축에 대한 관성능률을 각각 1.,lb,le 라고 하면 이 분자의 회 전 운동에너지 ER 은 ER= 孟L.2 +, 盆Lb2 +, 孟Lc2 (l\'. l) 가 되고 여기서 La=l~wa, Lb=lbWb Lc=lcWc 는 각운동량을 나타낸다. 가령 CH4, CC14 와 같은 구대칭성을 가지는 분자에 대해서는 la= k=L=I 가 되고 이들 분자를 소위 ‘sph eric a l t o p'형의 분자라고 부 돈다. 선형 분자는 fa= O, Jb = Jc 에 해당하며 Lb2+Lc2=L .I. 2 를 정의하면 ER=L,.2/21& ( l\' . 2) 로 주어진다. 관성 타원체가 회전 타원체인 소위 ‘sym metr i c top ' 유형의 분자들은 la=lb
되도]고 고체에서도 일정한 평형 방위각울 중십으로 하는 l i bra ti on 으로 축퇴되어 분자의 회전 에너지 준위를 따로 고려한다는 것이 무의미해 진다. 기체에서 온도가 T일 때 분자들의 실제 에너지 분포는 N,ccg e xp (-E J /ksT) 의 볼쯔만 분포에 따르고 선형 비대칭 분자의 경우에는 축 되계수가 g= 2]+1 이므로 N=:E NJ cc :E (2 J+l) e 설 C J+l) B/ i 1T ocf 3 3 (2 ]+ l)e 설 ( J+l) B/kaT dj 。 oc!OOe-hBX /k.T dx 。 ock aT/hB (N.5) 따라서 갚_＝룹 (2]+1) e-hJ ( J+l)B llaT (N.6) 가 되고 可d (N1/N)=O 로부터 ]ma+½= 沿 TI2Bh (N.7) 를 얻을 수 있다. 이로부터 온도 T 에서 가장 많이 정유되는 에너지 준위 ]max 에 대하 여 £
하고 있다. 실제 분자들을 강체 회전자로 가정하면 파동함수 少는 ¢=✓— 21r r c•M ¢ (I\T• 9) 가 되고 만일 이 회전자의 쌍극자 모멘트가 회전축에 수칙한 성분을 가 지고 있을 때 이 쌍극자 모멘트 µ와 마이크로 파의 전기장 사이에 다 음과 같은 상호작용을 생각할 수 있다. 즉
『。 ·산란 스펙트럼을 살펴보기르 한다. 원자 또는 분자가 의부 전기장 e 속에 놓여 있을 때 이돌 원자(또는 분자)에 유기되는 쌍극자 모멘트는 µj=균 e (l\r.1 2) 로 주어지며 µ나고 e 와 같은 진동수로 전동하게 되고 이들 쌍극자의 전 동은 바로 산란광의 원체 (source) 가 되 는 것 이 다. 광과 전동수를 가진 전기장에 의한 µ i 에 관계된 식 (IV.12) 의 a 는 주 로 전자둘의 변위 에 기 인하는 전자 편국물 (elec t ron i c p olar i zab i l ity)을 나타내고 있다. a 값아 분자의 여러가지 측 방향에 따라 서로 다를 때 편극률이 비 등방성이타고 말하며 이때에는 µi가 e 에 평행한 방향으로 주어지지 않 고 따라서 산란광의 편광 성분이 입사광의 편광 성분과 다른 평면에 놓 여지게 된다. 1/ ✓ a.의 값을 모든 방향에 따라서 도시 하여 얻게 되 는 표면온 편국 몰 타원체몰 이루며 주축을 x', y ',z' 축으로 표시하면 d=-1} (a:c1 :c1 +ay1 y1 +az1z1) (N.13) 로 평군치를 정의할 수 있다. 이 편극률 타원체는 분자의 희전운동과 함께 분자와 같이 그 방위각 이 같이 변동하게 되므로 비등방성 분자에 대해서는 주어전 공간 좌표 계에서 관측할 때 바로 회전 주기의 간격으로 편국물의 변화가 생기게 되는 것이다. 그러나 등방성 분자에 대해서는 편극물 타원체가 구면임으로 방위각 에 따른 편극물의 변화가 없고 따라서 회전 준위 라만효과가 나타나지 않는다. 영구 쌍극자 모멘트가 없는 벤진 분자에서는 마이크로 전자과 흡수가 나타날 수 없고 그 회전 준위 스펙트럼은 오칙 라만 산란에 의해서 얻 어질 수 있다. 즉 벤진은 대칭 팽이형의 분자로서 팽이축 (z 축) 주위의 회전은 편극물에 아무런 변화를 가져오지 않지만 여기에 수직인 x, y축 주위의 회전은 분명히 편극률에 변화를 가쳐온다. 따라서 회전 준위 천 이의 라만 산란에 의해서 K 값은 변하지 않고 J값의 변화만 있을 분 이다. 한편 x, y축 주위의 회전에서 180° 회전은 영구모멘트가없으므로
편극물 타원체를 완전히 같은 상태로 가쳐가는, 즉 360° 회전운동이 한 주기가 아니고 두 주기에 해당함을 알 수 있다. 따라서 벤전 유형의 분자들에 대해서는 L1]= 土 2 의 선택물이 적용되 고 전체적으로 L1K=O Ll]=O, 土 1, 士 2 ( l\'. 14) 의 선택물이 주어진다. 벤진을 강체 대칭 팽이로 보면 회전 준위 라만 진동수 4 )J는 4I= 士 1 에 대하여 h.d v =EU+l, K)-E(], K) =h(2 B]+2 B), ]=O, 1, …… h..dd v] ==土h (24 에 B ]대+하6여 B ), ]= l, 2, …… 로 주어지는 일련의 선 스팩트럼을 예상할 수 있다. 라만 스펙트럼의 선 간격, 가령 .dj=士 2 에 대웅하는 4B 값을 측정 하면 I너 를 구할 수 있고 이로부터 C-C 결합 길이, C-H 결합 길이 등 울 계산할 수 있다. 죽 lh=3 { T2c-c me+ (rc-c+rc-H)2ma } 를 이용하여 C6H6 와 C6D6 각각에 대해서 1&0= (14 7. 59 土 O. 04) X 10-40 gc m2 ; C6H6 f&0 = (17 8. 45 土 O. 09) X 10-•0 gcm 2 ; C 晶 를 얻고 이로부터 rr00cc--Hc== 11.. 309874 土 土 oO.. 000016 AA. 의 결과를 얻게 된다.
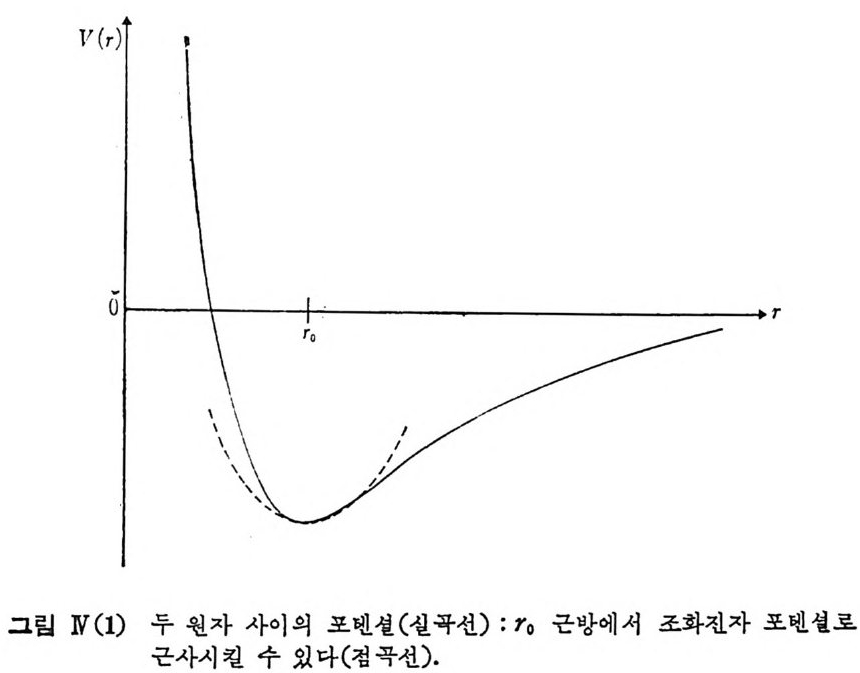
W-1. 3 분자의 진동운동 분자물 구성하고 있는 원자들 사이에 작용하는 포텐셜은 일반적으로 아래의 그림 W(1) 에서 실선으로 표시된 함수형으르 볼 수 있다.
V(r)
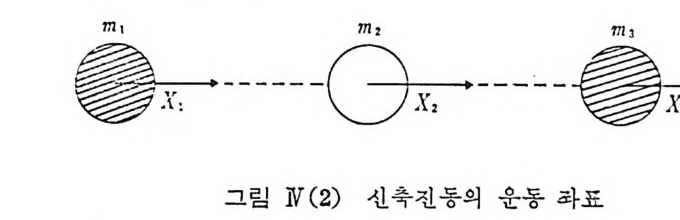
위의 실선 곡선에 근사한 함수형으로 찰 알려진 포텐셜로서 V(x)=D( l-e-a) 2 ：：：：：：： Da2 갔 (ax~l) (N.15) 로 주어지는 Morse 포텐선 함수가 있으며 x=O(r=r 。) 근방 (ax 띠)에 서는 점선으로 표시한 조화전자 함수가 됨을 알 수 있다. 비 교적 단순한 분자의 한 예 로서 제 원자들로 구성 된 선형 분자 (CO2, CS2 등)의 신축 전동에 대해서 자세히 계산해 보기로 한다. 세 원자의 평형 위치로부터의 변위를 각각 따 ,x2,x3 로 나타내면 X1-X2, x2_X3 는 두 원자 사이의 결합 길이의 변화에 해당하고따라서 전체 포 텐셜 에너지를 조화 함수 근사에서 2 V=F12 (X1-Xz)2+F2s (xz-Xa)2
틀------\-----广
로 쑬 수 있다. 원자 #1 과 #3 이 같은 원자일 때 그 화학 결합이 같을 것이므로 F12=F23 로 놓고 각 원자에 작용하는 힘을 구하면 /A2 == --——OO a8XX1 2 VV ==F -(Fx1(-x2i-X x22 타) ) A =-—8xa3 V=F(x2-Xs) (N.16) 가 되고 각 원자에 대한 New t on 의 운동 방정식은 아래와 같이 쓸 수 있다. ---서=11 =1 -qI= - 서— 4 Fq 1 + ✓—µ 2 Fq 2 -+✓ µ1=2 ii2= 서i- 1 Fq i-2 서i- 2 Fq 2 + 서i- s Fq 3 一✓i µI 3 j.. 3= 서,i-;, .F,q 2 -서, l-3 Fq 3 (N. 17) 위에서 µl=µ3, µi= 1/mi , qj= Xj / 야五이 다• 방정식 (N.17) 의 일반해로서 qi = A; cos(D t + ¢) (N. 18) 를 위의 식들에 대입하면 (µ1F-D2)A1-. ,/µ詞 FA2=0 -.,/µ;ji; FA1+(2µ2F-D2)A2-.. /AA FAs=O -.,/µ;ji; FA2+(µ1 F-fJ2 )As=O (N, 19)
로 주어지는 소위 영년 방정식을 얻는다. 여기서 A 값이 0 이 아닌 물 리적 해가 촌재하려면 Q 2 은 다음의 영년 행렬식을 0 으로 만드는 고유 치가 되어야 한다. µ_ 1야F-詞Q 2 F _2 µ✓2 ~F— FQ2 _ 싸— µ1µ2 F I =O (N. 20) I _ ✓ µ1µ2 F µ1F-Q 2 이를 펼치면 (Q드µ, F) g2 [Q드 (µ1+2µ2)F J =O 를 얻고 이로부터 D/=µ1F, D2=0, D/=(µ1+2 µ2)F 의 세 근을 구할 수 있다. 위의 Q I,92,93 는 세 원자가 같은 위상(i n ph ase, ¢)으로 전동하는소 위 정격 모드 전동의 전동수를 나타내며 Q k 의 정격 모드에 대한 각 원 자의 전동 전폭 Au 는 위의 영년 방정식 (N.19) 에 Q.._값을 대입하여 얻을 수 있다. 이 결과를 표로 만들면 아래와 같다.
표 N(A) 각 정 격 모드 (k) 에서의 원자들(i)이 갖는 변위
여기에 균등 분배 정리를 적용시켜 각 정격 모드가 가지는 에너지가 같도록 전폭 A i le 를 규격화시키면 위의 상대적인 진폭울 철대적으로 결 정지율 수 있다. 죽
Au2+A212+As12=1A1/+A222+As/= l AJ + A232+A332=1 의 규격화 조건에 따르면 아래 표와 갇은 결과를 얻을 수 있다.
표 N(B) CO2 형 분자의 신축모드 고유 뻑터
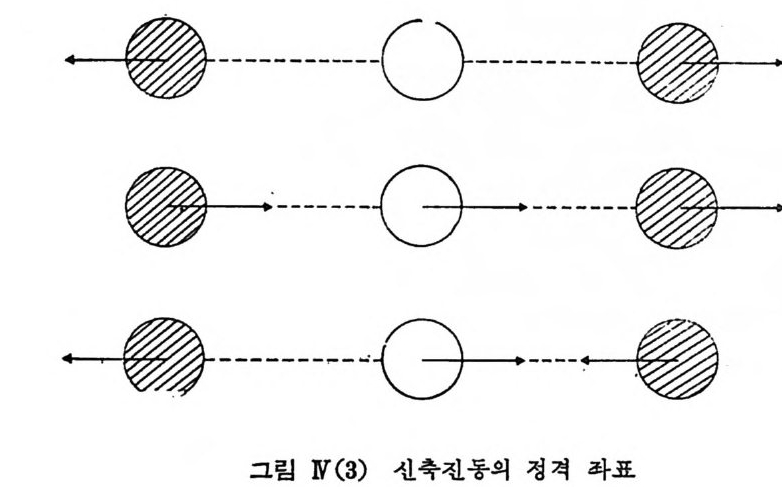
위 표에서 !J2 =0 모드을 보면 A12= ../----;;;J( µl+2µ2) = ]／감( 』胃孟 1 ) = ../m1/(m,+m2+ 炳) = Jm I/(ml+m2 + ?n_3) 가 되고 q;= 사n': x 집을 고려하면 세 원자 모두가 똑같이 웅칙이는 병 전 운동에 해당함을 알 수 있다. 마찬가지로 91,93 에 대해서 각 원자의 변위를 구하여 그림으로 나타 내면 아래와 같다.
--------------0--------- 《-를 °1
우리가 위에서 구한 운동 방정식의 해 q a. 로부터 다음과 같은 새로운 해를 구성할 수 있다. 즉
Q.=~ ✓ 갑 :k2 q, (N. 21 ) 는 운동 방정식의 해가 되며 정격 좌표를 나타내고 있다. 그립 N(3) 에서 가령 Q k 의 정격 좌표에서 1. －번째 원자에 대한 화살 표 길이는 바로 위의 A i k/ J덥경구강] 비례하고 있으며 실제로 식 (N.21) 에 표 N(B) 의 값윤 대입하면 QI =1* (qi-q3) Q2 = 準 +12µ2 ( ✓ 詞 qi+ 玩 q2+ ✓ 云 q8 ) 1 _ _ _ Q3 = ✓ 2(µ1 + 2µ2) (서 l1 qi -2 서 12 q 2+ ✓ µ1 q 3) (N.22) 르 정격 좌표가 주어진다. 이들 정격 좌표는 rk: D>.2 Qk 2=2 V (N. 23) 를 만족시 키 며 I: (Ai h2 / I: Ak2) = 1 이 므로 E Qk 2=E qi2 k i 2 Qk 2=E qi2 (N.24) k i 가 되고 따라서 2 T=:E Q12 (N.25) k 임을 알 수 있다. 식 (N.23) 과 (N.25) 로부터 분자의 진동운동에 대한 해밀토니언 %는 정격 좌표를 써서 표시할 때JfP =T+ 앗r = -2¼ 1:E (Qi2 + fJ 112 합) (N. 26) 로 주어침을 알 수 있다. 따라서 ~¢=E¢ 의 슈뢰딩거 방정식에 cp= ¢v(Q 1 ) v(Q 2 )·… < pv (Q s N-s) E=Ev( l) +Ev(2)-••· .. +Ev(3N-6) (N. 27) 를 가정하여 풀어보면 (－을 옳캬!2 12 Q 12) v(Q 1 )=Ev(k) 9v(Q 1 ), k=l, 2, ……, 3N-6 (N. 28) 와 같이 각 정격 좌표에 대해서 독립적으로 단위 질량을 가전 조화 단 진자 형태의 슈뢰덩거 방정식이 됨을 알 수 있다. 따라서 이미 찰 알려진 조화 진자의 결과로부터 분자 전체로서의 전동에너지 E 는 E= 問 (刀 k+ 송 )h9& (N.29) 로 쑬 수 있다. N-1.4 대칭성과 군론 위에서와 같이 분자에 대해서 전동에너지 해밀토니언을 구하고 운동 방정식을 풀어 그 해로써 정격 모드를 구하는 것은 분자가 커질수록 영 년 행렬식의 차원이 커지고 이에 따라 컵퓨터에 의촌하는 긴 계산을 요 하게 된다. 이러한 경우 분자가 대칭성을 가질 때 이 분자의 해밀토니언과 호환 (commu t e) 하는 대칭성 연산자의 고유 벡터를 구함으로써 훨씬 문제를 간단히 해결할 수 있다. 물(H 2 이 분자를 예 로 둘떤 아래 그립 에 서 보는 바와 같이 180° (2 1t:/2 )
회 전축 (C2), 두 개 의 반사거 울 면 ((Jv , (J v' ）을 대 칭 요소로 가지 고 있 으 며 이 들 대 칭 요소들의 집 합은 C2v 로 표기 되 는 한 겁 군(p o i n t g rou p)을 형성하고 있다.
c, c; 그립 N(4) 물 분자가 가지는 대칭요소
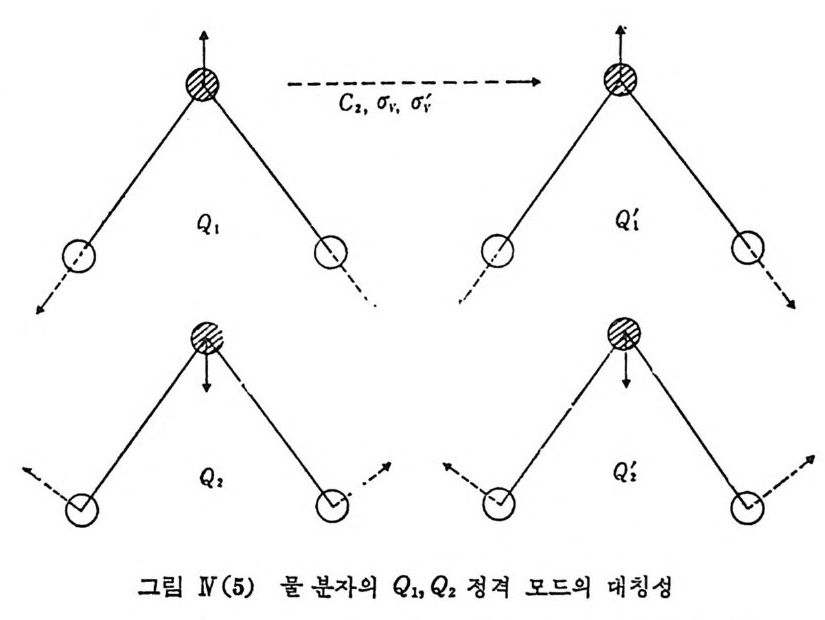
물 분자의 정격 모드에 대해서 각 대칭성 연산자 작용의 효과를 보면 우선 그림 N(5) 에 표시된 두 정격 모드 Q I, Q 2 는 C2v 의 모든 대칭 요소 (E,C2, (1 v, (1 v') 들에 대하여 전혀 달라지지 않고 똑같은· 상태를 유지하 게 됨을 알 수 있다.
---c-,, -Cf,- •• 어- -----
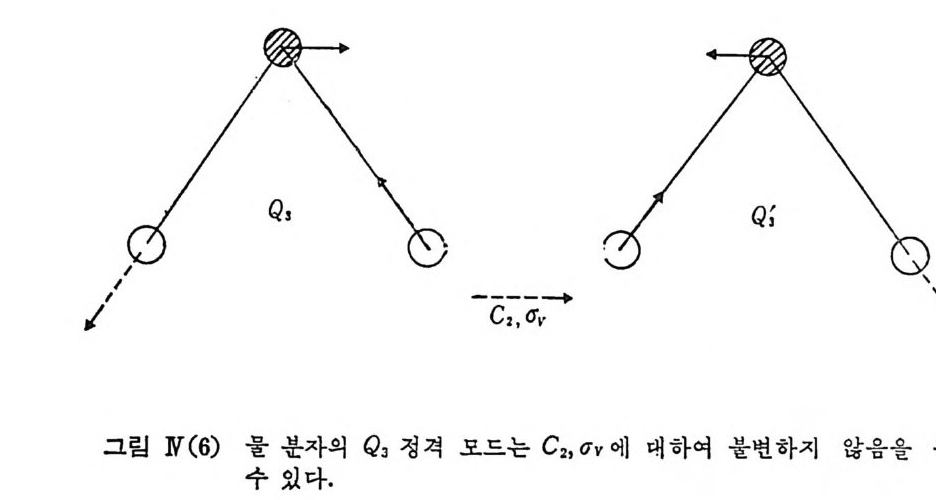
반면에 나머지 Q3 정격 모드에 대해서는 아래 그림에서 보는 바와 갇 이 대칭성 연산자 아와 C2 에 의해서 화살표 방향이 각각 반대 방향으 로 달라침을 볼 수 있다.
Q;
따라서 Q3 모드에 대 하여 EQ 3 =Q '3 =Q 3 , C&3=Q 3 '= -Q3 , 6VQ 3 =Q 3 '= -Q3 , 6v'Q 3 =Q 3 '=Q 3 (N. 30) 르 쓸 수 있으며 이대 Q 3 는 C2v 군의 한 표현식 (B2) 의 기조함수 를 이 루고 있다고 말한다. 특히 이 경우에서와 같이 기조함수가 하나인 1 차원 표현식의 경우 에는 표현식이 바로 특성치가 됩울 알 수 있다. 즉 Q s 를 기조함수로 하는, C2v 군의 B2 표현식의 목성치는 위의 식 (N.30) 으로부터 X(E) = 1, X(C2) = -1, X(q v ) = -1, X(q v ') = 1 이 됨을 알 수 있다. C2v 군은. 4 개의 기 악: 표.현식을 가지며 이들 표.현식의 복성치 표를 보면 표 N(C) 와 같다. 이 표는 또한 Q a 가 B2 표현식에, Q I 과 Q 2 는 A1 표현식에 속하고있음을 나타내고 있다. 이와 같이 분자의 정격 모
드는 분자가 속해 있는 대칭군의 기약 표현식 죽 대청성 s p ec i es 로 분 류할 수 있다. 이것을 C2v 대칭성을 갖는 물 분자에서는 I'oD= 2A9 B2 로 나타내고 있다.
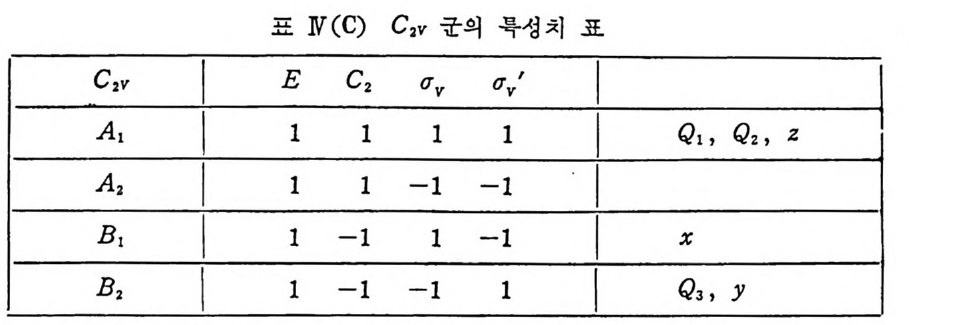표 N(C) C2v 군의 목성치 표
그러나 군론 웅용의 본래 목적은 분자의 정격 좌표 자체를 미리 알기 전에 정격 모드들이 어떤 대칭성 s p e ci es 에 속하고 있는지를 알아내는 데에 있다. 가장 일반적인 방법을 역시 물 분자에 져용해 보기로 한다. 우선 아래 그립 에 서 와 같이 문 분자의 각 원자에 (xI, yi, z I) 의 좌표축 을 정해 주면 이 좌표계가 각각대칭성 연산작용에 의하여 어떻게 변환 되는가륜 살펴본다.
z’ 'tl;''
가령 물 분자에 C2 대칭성 연산작용을 가하여 얻어지는 좌표 변환의 견과를 아래와 같이 표시할 때 C2X=I '(C 2)X=X' (IV.31) 여 기 서 X= (xI, yI, zI, x2, y2, z2, x3, ys, z3) X'=(-x3, -y3, z3, -x2, -y2, z2, -XI, - yI, zl) 이 고 I' (C2) 는 대칭성 연산 작용의 결과 X 를 X’ 으로 변환시키는 행렬식을 나타내며 C2 의 표현식 이 라고 부른다. 이 표현 행 렬식 I' (C2) 를 구체적 으로 써 보면 아래 와 같다. 죽 X' =I' (C2)X 를 행 렬식 으로 써 보면
_Xs 0 0 000000000001000001000001000100001 00o10000o0 0001000 00X0I00 0000 000 0
가 되고 여기서 행렬식 I' (C2) 의 특성치 x(C2), 츠기 ’ 대각선 성분의 합은 x(C2)=0+0+0-1-1+1+O+O+O=-1 이 됨을 알 수 있다. 이 행렬 표현식의 특성치를 결정하는 대각선 성분 울살펴 보면: 대칭성 연산 작용(위에서 C2) 의 결과 변환되지 않고 그대로 남아 있 논 좌표는 +1, 자리는 바뀌지 않고 방향만 변환되는 좌표는 -1, 자리가 다른 원자의 위치로 바뀌는 원자의 좌표에 대해서는 0 이 됨 울볼 수 있다. 가령 동본 연산자(i den tity ope r ati on ) E 에 의 해 서 는 위 의 H20 에 서 9
개의 모든 좌표가 그대로 제자리에 남게 되므로 죽 EX=X'=X 이므로 x(E)=9 가 되고, (j V 는 두 수소 원자들의 자 리를 서로 바꾸어 주고 산소 원자에 대해서는 Qv X2=X21=X2, (jvY 2=Y/ =Y2 u 군 2=Z/=Z2 와 같은 좌표 변환을 중으로 결국 x((jv )=l, (Jv ’ 은~ 모든 원자에 대해서 z, y좌표는 그대로 남겨두고 x 좌표를 모두 -X 로, 즉 z'=z, y'=y, x'=-x 의 좌표 변환을 해주므로 x((J v') =3+3-3=3 이 됨을 알 수 있다. 이와 같이 물 분자에 대해서 전체 자유도, 9 개의 좌표를 bas i s 로 택 하는 소위 전체 표현식 (tot a l rep re senta t i on ) I'aN 의 목성 치 를 모든 대 칭성 연산자에 대하여 구한 결과를 정리해 보면 아래와 같다.
표 N(D)
위의 I' 3N 은 다시 C2v 의 특성치 표 N(C) 를 참조하여 l'3N =3 A1 E8 2 B1 EB 3 B2 (N. 33) 로 약분됨을 보일 수 있다. 그러나 이들 9 개의 자유도 중에는 병전과 회전이 함께 포함되어 있 으며 이들을 제의한 나머지 3 개가 우리가 구하는 전동 모드가 되는 것 이다. 우선 병전 모드의 정격 좌표는 X, Y,Z 이며 이들의 대칭성 변환을 보 면 EX=X, C2X=-X 등으로부터 x(E)=l, x(C2)=-l, x((Jv )=l, x((Jv ') = -1 가 됨 을 알 수 있 고. 따라서 x- 방향의 병 전운동을 나타내 는 모드 Tx 는 B1 표현식에, 마찬가지로 T y는 B2, Tz 는 A1 에 속하게 됨을 알수 있다. 죽 전체 병전운동의 표현식은 I'tra n=A1 EB B1 EB B2 (N. 34) 로써 이 미 표 W(C) 에서 본 바와 같다. 마찬가지로 회전 운동에 해당하는 정격 모드의 대칭성 변환올 보면 우선 분자의 질량 중십을 지나는 제 회전축에 대한 회전 운동을 나타
내는 그립 N(8) 에서 대칭성 연산자 C2 에 의해서 각 원자의 변위 벡터 가 어떻게 변환해 가는지를 볼 수 있다.
。• I I / I , I I I@Rxr ,' ' \ \ \ \ ’o• Ii \ I ,一’ ,I I @R\r \ 、 \ \ \c{II I o• ’I ’ , , ’ ’ ’ 急Rz ` ` ` ` ``、 ` bX
위 그림에서 C2Rx=Rx'=-Rx, C2RY=Ry 1 =-Ry, C2Rz=Rz '= Rz 로 변환되는 것을 볼 수 있고, 따라서 XR 蠶 (C2)=-l, XR,(C2)s:: ::- l, XR.(C2)=l 임을 알 수 있다. 마찬가지로 다른 대칭성 연산자에 대하여 실제 그립을 그려보면 XR 蠶 ((Jv )=-1, XR 蠶((J v')=l 을 얻을 수있고다타서 R,, 를기조함수로 택하는 C2v 의 표현식은 바로 B2 기약 표현식이며, 마찬가지로 R :1는 BI, Rz 논 A2 표현식에 속하게 됨을 알 수 있다. 죽 x- 축, y-축, Z- 축을 회전축으로 하는 세 회전 운동온 결국 I'rot = A2 E9 B 흡 B2 (W. 35) 로 약분되는 정격 모드로 볼 수 있다. 따라서 전체 표현식에서 병전 표
현식 I'tran 와 회전 표현식 I' ro t율 제의시키면 r .. ib =I 'sN -I' tran -I'rot =2A1© B2 (N. 36) 의 결과를 얻게 되고 이로부터 물 분자는 2 개의 A1 ~,1동 모드와 1 개 의 B2 진동 모드를 가지고 있음을 알 수 있다. 분자의 운동을표시할 때 이와 같이 칙교 좌표 성분의 좌표를 직접 쓰 지 않고 분자의 화학결합의 결합 길이와 결합각의 변화를 나타내는 소 위 내재좌표(i n t ernal c o ord i na t es) 를 선택하면 좀더 간편한 해석이 가능 해진다. 결합손 신축에는 두 개의 0-H 결합과 관련된 결합손 길이의 신장을 생각할 수 있고 이들 두 OH 결합손의 신축성 운동은 E 와 6v’ 에 대 해 서 는 불변이고 C 2 와 6V 에 대해서는두 OH 결합손의 신축운동이 서로 자리 바꿈을 가지게 된다. 따라서 x(E)=2, x(qv ')=2, x(C2)=0, x((lv ) =O 의 결과를 얻고 이러한 목성치를 갖는 표현석을 I' (r1,r2) 라 하면 I'(ri , r 2)=A, EB B2 로 약분됨을 알 수 있다. 여기서 rI,r2 는 두 OH 결합손의 신축을 나타 내는 좌표를 bas i s 로 택하고 있음을 표시하고 있다. 한편 乙 HOH 결합각의 변화(증가 또는 감소)는 하나의 좌표로 나타 넬수 있으며 이 결합각의 변화는 모든 대칭성 연산 작용에 대해서 불 변이므로 x 。 (E) =x0(C2) =xo( qv ) =x 。(q v') = l 즉 I'(8) =A1 °J울 바로 알 수 있다. 이상의 결과로부터 A1 표현식에 결합손 신축 모드 하나와 변각 모드 (bendin g mode) 가 같이 속해 있고 따라서 이들 두 모드들 사이에는 서 로 상호작용이 가능하다고 예상되며, 나머지 다른 하나의 선축 모드는 B2 표현식에 속하므로 AI- 모드와는 서로 상호작용이 있을 수 없고, 결 합각과 전혀 무관한 순수한 결합손 신축의 정격 모드입을 알 수 있다.
1V-1.5 선택률 선택룰을 결정하는 행렬 요소의 일반적인 형태는 ('P.l,Ci'), ,7f7'少 k( J)) =j ¢k'( J I) 念 ’¢kG)dT (N. 37) 로 주어진다. 위에서 cp.1t C i)는 대칭성 연산자 R 을 포함하는 한 군의 j번째 기약 표 현식을 형성하는 기조함수들 중 k 번째 함수를 나타내고 있으며 다음 관계식을 만족한다. R ¢kCi )= E ¢£’(i)I'G )(R)i’ k (N. 38) k’ 한편 기조 함수들 사이에는 다음과 같은 칙교성 정리가 주어져 있다. (¢k(j) , ¢k'(i1 ) ) = 6ii ' 8H'Z1 옳'!!. 야전), ¢I(i) ) (N. 39) 식 (l\T .37) 에서 炭'’이 I'7.’로 주어지는 표현석에 속한다떤 K''Pk ( j) 는 I' K’ 와 I'(J)의 dir e ct pro duct I':r' ® re;) 로 주어 지 는 표현식 에 속하 게 되며 따라서 식 (IV.39) 에 의하여 아래와 같온 결론을 내릴 수 있다. 죽, (¢1,'J'), JJi'컸 %G)) 가 O 이 아니 기 위해 서 는 I'(J I) 이 I':r-'®I''J)에 속 해야한다는 결론이다. 이 것 은 다시 말해 서 I''i') ® I':r' ® I''J)의 dir e ct pro duct 가 반드시 A1 (또는 I'1) 표현식 을 포함해 야 된다는 뜻이 다. 이와 같은 결론은 사실 행렬요소 적분값아 괴적분 함수의 고유 변환 즉 괴적분함수가대칭성 연산 작용에 대하여 불변이어야 된다는 사실에 기인하고 있다. 따라서 cpJ, l( j l) 允겁 bA( J)가 모든 대칭성 연산 작용 R 에 대하여 불변이 되려면 이 함수는 scalar 표현식에 속해야 됨을 알 수 있다. 이상에서 언급한 내용을 종합하면 rCJ ' ® rr' ® rG) = L a,r, (N. 40) ’
에서 S=l 죽 a1i =O 일 때에만 條y)念'¢(i )dr 수 0 의 결과를 얻게 된다. 이와 같이 군론의 웅용은 모든고유상태를 대칭성으로분류해 줄분만 아니라 이들 고유 상태들 사이의 의부 섭동 쵸 '/?I 에 의한 천이의 가능성 여부를 결정짓는 선택룹을 유도해 주고 있다. 다음 철에서 위의 일반적인 선택률이 전동준위 라만 산란 천이에 어 떻게 적용이 되는지를 알아보기로 한다. N-1. 6 분자진동 라만 스펙트럼 우리는 앞에서(제 l\ l -1.2 철) 영구 쌍극자 모멘트를 가지고 있지 않 논 분자들의 회전 운동 스팩트럼은 적의선(또는 mi cr owave) 흡수로 는 불가능하고 라만 산란에 의해서만 얻을 수 있다는 라만 분광학의 한 장접을 지적한 바 있다. 여기서는 이제 분자들의 진동 운동 스펙트럽을 얻는 데 라만 산란이 어떠한 이접을 가지고 있는지 살펴본다. 타만 효과의 근본 원인은 분자의 전자 분국를 a 가 분자의 전동운동 에 의하여 변조되는 사실에 있다. 지금 전동수 9 근의 정격 모드 Q에 의한 a 의 변조량을 아태와 갈이 근사시키면 a=a 프 (oa/o Q.)。 Q1 (N. 41) 외부에서 E=2E0cosw t의 전기장을 수반하는 빛에 의하여 아래와 같 이 단전동 쌍극자 모멘트가 유도된다. µ1=aE =2{ 갑+（경합)。업 cosD1 t }E 。 cos 叫 =2 a0E 。 cosw t +E 。(훑-)。아 [cos(w+D .. )t+c os(w-Q .It)t] (N. 42) 따라서 위의 µ‘에 의해서 (l), (l)+9 k, (l)－ 9k 의 전동수를 갖는 전자과
복사가 나오게 됨을 알 수 있다. 이 때 (I)土Q k 의 진동수를 갖는 복사광이 바로 라만 산란에 해 당하고 일반적으로 a0~ (oa/oQ ) oQ , 죽 전동 운동에 의한 편극물의 변화가 매 우 작으므로 타만 산란이 레일레이 산란보다 훨씬 약한 산란임을 알 수 식있 다(N.. 42) 에서 ( $ )。 =0 이떤 정격 모드 Q8 ] 의해서는 타만 산 란이 있울 수 없다. 간단한 분자들 가령 2 원자 분자와 같은 경우에는 대칭성 논의에 의해서 (oa/0 Q 1)0 가 0 이 될 것인지 아닌지를 쉽게 알아 낼 수 있으나 분자가 커지고 복잡해지면 식 (N.40) 의 군론적 선댁율을 적용하지 않을 수 없다• 식 (N.42) 를 보면 양자 역학적 천이의 행렬 요소에 듈어오는 연산자 %'은 a 에 대웅할 것임을 알 수 있다. 따라서 ¢G) 에서 cp'i') 상태로 분자전등 라만 천이가 허용되기 위해 서는 최소한 다음 중 하나가 I' 1( 또는 Ai ) 기약 표현식을 포합해야 된다. I'(少(i’))®I' (axx) 합(cjJCil) I'(¢C J l ))®I '(ax y )®I'(¢(j)) I' (¢C i I))® I' (axz) ® I'(少(j)) I'(¢C i l) )®I '(ay y )®I'(¢C i )) I'(¢ (jl) )®I '(ay z ) ®I'(¢C i )) I'(少(i l)) ®I'(az z) ®I'(¢C i ) ) (N. 43) 한편 µxi = auE,,, µ/=a,,,Ex, µz: '=au 요 등의 관계식에서 µx i는 x 처럼, E 도 x 처럼, µ,'는 Y, µ,/는 z 처럼, 대칭성 연산 작용에 대하여 변환되는 것에 주목하면 axx 는 갔, a y x 는 xy, au 는 xz 처럼 대칭성 변 환을 하게 됨을 알 수 있다. 이제 C2v 의 대칭성을 보유하는 분자들, 가령 H20 분자에 대해서 위 의 선택물을 져용해 보면, 표 N (C) 로부터 xy 죽 a,,, 는 A2, a,z 는 B2, au 는 BI, x2 온 A1 에 속하게 됨을 알 수 있다. 만일 ¢(I) 가 영접전동 준위 죽 기처상태라 하면 이는 A1 에 속하게 되 므로, 少 (II) 도 A1 대칭성의 정격 전동이 되려면 a~' a,,, azr 를 선택해 야 한다.
즉
I'(¢(J)) ® I'(ax x) ® I'(¢(JI) ) 를 보면 A1 ® A 홉 A1=A1 이 되며 선대문을 만족시키고 있다. 少(J I) 이 만일 A2 대칭성의 정격 전동일 경우에는 I'(少(J ) ) ® I'(ax ,) ® I'(¢C i I )) =A1 ® A2 ® A2=A1 이 되므로 '를 선택해야 되며, 少 C i I) 이 B1 또는 B2 대칭성의 정격 모 드가 되려면 이 경우에는 I'(少(J)) ® I'(ax x) ® I'(#C J I) ) I'(cpu i ® I'(a, ,) ® I'(少(J I)) 가 각각 A1 표현식을 포함하게 되므로 B1 및 B2 정격 모드도 각각 a' a yz 에 의해서 라만 활성, 죽 라만 산란으로 관축할 수 있음을 볼 수 있다. N-2 액체 N-2.1 액체에서의 분자운동 액체 속에서 한 원자들 생각할 때 이 원자는 다른원자들과수없이 많 온 충돌을 하게 된다. 그러나 충돌시간보다 훨씬 건 시간 간격으로 관 찰할 때 이 원자는 소위 브라운운동 방정식으로 주어지는 느린 속도를 가지고 운동하는 것처럼 보인다. 이 러 한 충돌에 의 한 무작위 힘 (random forc e) F' (t)를 고려 한 m 꿈 V=-CV+F'(t) (N. 44) 의 방정식을 Lan g ev i n 방정식이라 부르며 이 방정식의 해로써 V( t)= V(O)e-w•+J :t dt' e -W -1')' .. F'(t') (I\T• 45) 。 여기서 무작위성 힘 F'(t)의 통계역학적 성질이 주어쳐야 한다. 초기 속도 V(O) 가 맥스웰 분포를 따르고,의 결과를 얻을 수 있다. 즉 액체 속에서의 분자의 운동은 l~ n z/( 척도에서는 완전히 자유 입 자처럼 웅칙이고 l ~ m~ 의 쳐도에서 브떤 확산으로 볼 수 있음을 알 수 있다. 이제 아무런 가정이 없이 N 개의 입자 전체에 대한 운동 방정식을 보면 컨dI ' = {I', K} = i!l'I' (N. 49) 여기서 I'는 N 개 입자계의 한 상태를 나타내는 위상 공간의 6N 차 원 벡 터 에 해 당하며 , 즉 I'= (q파 12 ……q 3N, pi, P2, •…·· PsN) 이 고 요’은 소 위 Lio u vil le 연산자로서 따섭(뚱읊-뚱당~) (N. 50) 로 정의되며 따라서 {I',%'}는 포아송 괄호를 나타내고 있다. 식 (N.49) 의 해는 I'i = eiS t'i I'。 (N. 51 ) 로 쑬 수 있으며 마찬가지로 이 역학적 다체계의 상태의 함수로 주어지 는 한 역 학적 물리 량을 A=A( I')라고 하면 왕- = {A, K} =i.?A (N. 52) 로 주어지고 이 방정식의 해로서 형식상 A(I', t) =e 따 A(I', O) (N. 53) 로 쓸 수 있다. 따라서 A 의 시간져 상관함수 CA( t)는 C(t) = =)dI'p 0( I' )A *(I') ei~ 1A(I' ) (N. 54) 로 쑬 수 있음을 알 수 있다.
위 에 서 Po( I')는 앙성l-블 평 군에 필요한 평 형 상태 앙쌍볼 분포함수 이다. {e 내 r, Jf }=O, 따라서 iS!'p。(I' )=O 이므로 식 (l\' .54) 는 다음과 같아 쑬수있다. jdI' .;p; A*(I' ) 군' .;p; A(I') = (e;.Y• A, A*) =(A(t), A*) (I\'. 55) 즉, 시간적 상관함수는 양자역학에서의 스켈라 내적에 대응하고 또 이것은 e·오 1 의 ¢,1= ✓ i; A 에서의 기대치로 해석할 수 있다. 위의 스켈라 내적으로부터 사영 연산자를 정의할 수 있고 이를 이용 하여 식 (l\ r.s2) 의 Lio u vil le 방정식을 다음과 같이 고쳐 쑬 수 있다. 쑨 =iQA ( t)-tdr: K (r:) A ( t-r:)+ F(t ) (N. 56) 위의 일반화된 Lang e vin 방정식은 미시적인 관접에서 얻어진 것으르 현상론적인 제약을 받지 않으며 위에서 Q= (.? A, A*)/(A, A*) K(-.)=(F(-.), F*(O))/(A, A*) F(-.)=eiO S !T Q i.? A 여기서 P+ Q =l 의 사영 연산자 P 는 P= -h,강:f- A (IV. 57) 로 주어진다. 위에서 기억 함수 K(r) 가 무작위 힘 F(r) 의 자체내 상관함수개 비례 함을 알 수 있으며 이 를 제 2 요동-소산(fl uc t ua ti on-d i ss ip a ti on) 정 리 라 고 부르기도 한다. 위의 일반성 Lang e vin 방정식 (N. 56) 에 A* 로 스켈라 내적을 취하 떤 C( t )=(A( t ),A*(O) ）에 관한 다음의 기여함수 방정식을 얻을 수 있다. 웁- C( t) = iDC (t) -tt d-.K(-.)C(f- -.) (N. 58)
즉 상관함수에 무작위 힘 이 K( t')를 통하여 간접 적 으로 영 향을 미 치게 됨을 알 수 있다. N-2. 2 요동과 상관성 (Flucta t i on s and Correlati on s) 평형상대에서 벗어난 계가 어떻게 결국 평형상태로 들아오고, 이미 평형상태에 있는 계는 또 어떻게 계속 평형상태를유지하게 되는가에 대 한 근본 문제를 어떻게 해결하고 있는지 알아보기로 한다. 한 열역학적 계가 평형상태로부터 요동에 의해서 다론 한 상태로 옮 겨갈 때, 이때 각각의 엔트로피 값을 So,S 라 하면 L1S=S-S 。 =ks lnD1-ka ln Q 。 (N. 59) 가 되고 여기서 Q o 와 Qf는 요동을 전후하여 그 계의 주어전 온도에서 가능한 서로 다른 모든 상태 수에 해당된다. 요동이 일어날 확물은 p oc9,/ Q。 =ex p (L1S/ka) (N. 60) 로 주어지며, 이제 주어전 계의 한 부분을 계 #1 이라 하고, 나머지 계 ~2 의 요동을 전혀 무시할 수 있을 때 dE2=-dE1 , dV2=-dV i L1S= L1S1 + L1S2 =4Sl+ 4E2+P2 4V2 T2 =4S1_ 4E 급 -TP 4V1 (N. 61) 로 쑬 수 있으므로 식 (IV.60) 온 poc exp {-(L IE1-TAS 다 -PA Vi)/k B T} 가 되고 AE 를 S 와 V 의 함수로 보고 테일러 전개시키고 첨자를 무시 하면 pcc exp {-(LI TLIS-LI PLI V)/2 kB T} (N.62) 를 얻을 수 있다.
이것은 다시 열역학적 관계식을 져용하여 다음과 같은 식으로 쓸 수 있다. poc exp {-읊 ~ (L1T)2-~ (L1V)2} (N.63) 따라서 4T 와 4V 는 서로 독립적으로 주어지며 가우스 분포를 나타내 게 됨을 알 수 있다. 이로부터 에너지 E 가 정해쳐 있을 때 다음 결과를 얻을 수 있다. 따=뭉’ 따 =kBTrTV, (ATAV)=O (I\T. 64) 여기서 rT 는 등온 압축물이다. 이제 AT 와 AV 대신에 AS 와 4P 를 독립 변수로택하면 아래와 같은 결과를얻고 p ocex p{方 k( J S)2_ 훑(J P)2} (N. 65) 이로부터 (?s) 2= ksC,, (刃Y) 2= ks T/r, V, ws.JP)= O (N. 66) 의 결과를 얻을 수 있다. (AV)2 로부터 입자 한 개당의 체적 u, 죽 입자 밀도 n 에 대한 요 동을구하면 눕=〈平 = (言 =ksTrrV/N2 (TnY= (五 TIu4 =ksT rr N2/ va (N. 67) 가된다. 만일 계 (#1) 의 V 가 정해쳐 있고 N 이 요동하는 경우를 생각하면 g짜 =V2(万 于
=knTrTN2/ V (N.68) 의 결과를얻는다. 이러한 열역학적 요동이 광산란에 어떻게 관련되어 있는지 다음 제 ]\ ! -4 철에서 살펴보기로 한다. 액체 또는 기체에서의 분자의 운동에 대한 기본적인 가정으로서 임의 의 한 분자에 대해서는 주어전 공간 V의 임의 지접 r 에 가 있을 확물 이 모두 같다는 것이다• 그러나 두 분자를 동시에 생각하면 두 분자의 상대 적 위치 r2-r1 의 값온 두 분자 사이의 상호작용 때문에 그 실재할 확물이 서로 다르게 나타나기 마련이다. 즉 두분자의 어느 한 순간에 있어서의 상대적 위치에는 일정한 상 관성이 따르.고 있다. 이 상관성을 함수적으로 정의하기 위해서는 다음 몇 가지 함수를 먼 처 정의할 필요가 있다. 확물 밀도에 상당한 N- 입자 분포함수 FN(m,r2 …… ,m) 은 Jrv FN(T1 , T2, … … TH) d3r1d3r2 •••••• d3rN=l (N. 69) 을 만족시 키 고 이 로부터 소위 단일 입 자 분포함수 F1(r1) 이 아래 와 같이 정의된다. F1(r1)=N) v Fu (r i, r2, ...... , rN)d3r2d 3 r3 …… d3rN V 三 n(r1) (N. 70) 이것은 )vV n(r1)d3r 1 =N (N. 71) 이 되므로 n(r1) 즉 F1(r1) 온 m 에서의 입자밀도를 나타내고 있음을 알 수 있다. 마찬가지 로 두 개 입 자 분포함수 R(rI, r2) 는 Fz (r i, r2)=N(N-I) )vV A(ri, r 2, ••• … rN)d3r3d 묘·… •• d3rN =n2g ( r) (N. 72) 로 정의되고 있으며 여 기 서 r=r2-r1, n=n(r1) 이 다.
위의 g (r)d3r 은 r=O 에 한 입자가 있고 이로부터 r 만큼 떨어전 지 검 주위의 체적소 d3r 안에 다론 한개의 입자가 촌재할 확률을 나타내 며 이 g (r) 을 입 자쌍 분포함수라고 부른다. 입자 사이의 상호작용을 · 완전히 무시할 때 g( r)=I 이 되므로 C(r) =g(r ) -1 (l\r. 7 3) 온 상호작용에 의해서 주어진 상관성의 크기의 한 쳐도로 생각할 수 있으며 이 C(r) 을 입 자쌍 상관함수라고 부른다. 이계 유체 속에 한 부분 VA 를 생각하고 이 VA 안에 존재하는 입자 수 NA 를 생r각하 면 =1+n Jv. C(r)d3r (I\'. 7 4) 짜_ NT 의 결과를 얻을 수 있으며, 액체에서 밀도의 평군자승 요동이 상관함 수와 밀접한 관련을 가지고 있음을 알 수있다. 한편 식 (N.68) 에서 [XN)2/ N=ksT Tr n 을 얻고 이를 식 (N. 74) 에 대입하면 5C(r)d3r=½?t {nksTrx-l} (1\7 . 75) 를얻는다. 액체에서는 nksTrx< {l 가 되므로 5 C(r)d3r :::::-n上 (I\'. 7 6) 이것은 입자들이 서로 관동할 수 없다는 사실, 죽 g( lr|->u)=O 또 논 C(lr|-(J) =-1 이 됨을 시사하고 있다. 한편 r=O 를 포함시켜 정 의하면, 상관성이 없는 기체에서도 g( r) = I-{o(r) (N. 77) 와 같이 8- 함수로 주어지는 r- 의촌도를 첨가시켜야 된다. 다음 철 (N-3) 에서 우리는 광산란 실험을 통해서 위의 입자쌍 상관함 수를 어떻게 구할 수 있는지 알아보기로 한다.
W-2.3 협동운동과 유체역학적 모드 우리는 이미 무작위 힘에 의한 단일 입자들의 브라운운동을 살펴보았 고 또 열적 요동이 상관성과 어떻게 관계되어 있는지를 보았다. 지금 A(t) =) V 西 a(r,t) 로 정의되는 a 가 다음의 연속 방정식을 만족시킬 때 i3[ -a+ p •Ja= ua (N. 78) 여기서 Ja 는 V 의 표면을 통해 나가는 A 의 유속 밀도, (1 a 는 V 의 내부에 촌재하는 A 의 내부 생성원을 나타내고 있다. 만일 A 가 전체 질량 또논 에너지와 같이 보촌량일 때에는 cra=O 가 되고, 평형상태에서 자발적 열적 요동을 갖는 열역학적 계를 생각하면 a(r,t) = + oa(r,t) Ja (r,l) =
요동이 q -+O 에서는 무한히 건 수명, 즉 r(q- + O)->0 0 가 됨을 알 수 있다 . 이 와 같이 q-+ O 에 서 '{:->00 가 되 는 요.동을 유체 역 학적 모드 (h y d ro dy n ami c mode 또는 hy d rody n ami c fl uc t ua ti on) 이 타고 부르며 확산성 모드만일와 전a 가과 성보 촌모량드이로 아구닐분 되때어에진는다 .6 (J a (q, t)=l=-0 , 따라서 q-+ O 에서―衍a一 oa(q, t)=1=-o , 즉 -c(q)의 값이 q-+ O 에서 유한한 값을 가지게 된다. 단원자 액체의 경우, 서로 독립적인 요동을 가지는 5 개의 열역 학 적 변수량에 대한 유체역학적 운동방정식을 풀면, 횡편극 전단과 모드 에 해당하는 두 개의 확산성 유체역학적 모드와 세 개의 종편극 유체역학 적 모드가 존재하며 이중 하나는 확산성 열확산 모드, 나머지 두 모드 는 전과성 파동 모드를 이루고 있다. 레일레이 산란은 바로 위의 종편극 열확산 모드에 상당한 유체역학적 요동에 기 인하고 있으며 벤드 폭은 바로 열 확산도(t hermal dif fus iv i t y) DT< >11 비례하여 4 야 =DT q 2 로 주어지며 브릴루엥 산란은 전파성 음과 에 상당한 종편극 유체역학적 요동에 기인하고 있다 . 이때 주과수 변이 는 土Q(q)＝土 c. q, 벤드 폭은 4 야=I'q 2 로 주어침으로 이러한 광산란 실험을 동해서 단열 음속 Cs 및 음과 감쇠 계수 r, 열확산도 DT 등의 수송 계수를 측정할 수 있다. N-3 스펙트럼의 분석 N-3. 1 비편광 광산란과 분자들의 상호작용 액체 속의 분자들에 의한 광산란의 계산에서 우선 이들 분자의 유효 편극물 a 가 요구된다. 지금 고립된 또는 자유 원자의 편극률을 ao 라 하면 이들 원자 (또는 분자)들이 N 개가 함께 모여 서로 상호작용을 하게 되는 경우에는 그 립 N(9) 에서 보는 바와 같이 의부에서 전장 Eo 가 작용할 때에 원자 #1 에 유기되는 쌍극자 모멘트 P1 은 P1=aoEo 로 주어지지 않고 PI =aoE(r1) 로 주어진다. 여기서 E(r1) 은 원자 #1 이 있는 위치에서의 유효 전장을 나타내며 주위의 모든 다론 원자들도 동시에 쌍극자 모멘 트를 가지게 되므로 이들 쌍극자에 의한 전장을 고려해 주어야 한다.
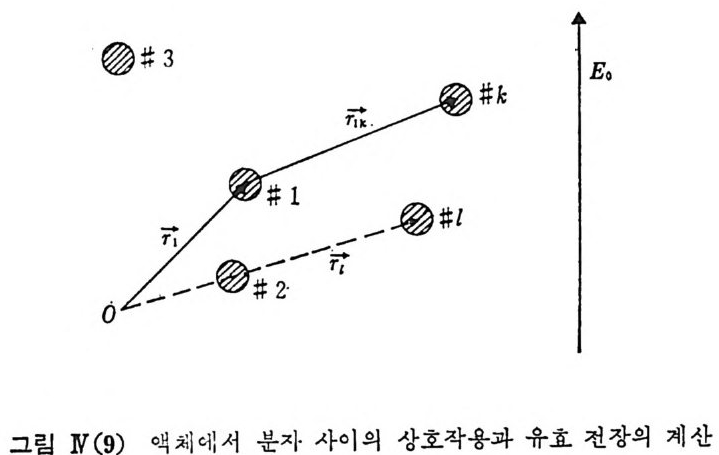@#3 E,
원자 #k 가 m 에 미치는 전장을 E1(T1) 으로 표시하면 E.1i( r1) 3 f 11~ Y무11aP3 k)-Pk (IV. 80) 여 기 서 ?n=ru/rIk 이 다. P .1i =a0E(r,.) 이 므로 E(r1)==EEo~++a IN: 。 E2Nk (r13) %(%·E검(m ))--E(… k=2 1< =2 =E 。 +a 。1 2N= 2 (3 ?냐 f1 따1-i } •E(r.) (l\l8 1) 로 쓸 수 있다. C 三 3??_I 로 놓으면 E(r1)=E 。 +a 。 JI.=N :2 r1.-3 G1k·E(ri.) (N;82) 마찬가지로 E(r 1t )=E 。 +a 。 i: E.. k ru-3 Gu·E(r1) (N. 83)
로 쓸 수 있으므로 식 (N. 84) 을 식 (N. 82) 에 대 입 하여 E(r1)=E 。 +a 。k L. . I Y11-3Gu·E 。 +a 。 2 kE. . I IE h r11-s ru-3 G11·G1,•E(r,) =(I+a。 kE. . I ru-3 Cn+a 。 2 kE. . I lE .. k rIk-3 Xru-s C11•G11+ …… )·E 。 (N. 84) 따라서 P1=aoE(r1) =(a 。 l+a 。2 kI,;.I r11-3 C11+a 。 3 kE. . I IE • rIk-3 rkl-3Cn·Cu+ …… )•E 。 =aE 。 (IV. 85) 에서, 액체 속에 있는 원자가 가지는 유효 펀극물 a 는 dip o le ind uced dip o le(DID) 상호작용의 근사에서 아래와 같이 주어진다. a=a 。 I+a 。 2 kL,.I Y11o~3 G11o+O( 파)…… (N. 86) 이제 한 분자에 집중해 보면 가령 분자 #1 이 평군적으로 오칙 다른 한 개의 분자 (#2) 와 서로 가까이 있고 나머지 분자들과는 서로 멀리 떨어쳐 있다고 할 때 석 (N. 86) 에서 a12=a 。 I+a 。 2 r12-3 li 12+a 。 3 Y12-3 Y21-3 G,2 G21+… … =a 。 [+a 。 2 r2 C+a 。 3 r-6 C·C+… … (N. 87) 가된다. 이 경우 그림 N (lO) 에서와 같이 z 축 방향으로 의부 전장이 주어지 면 임의의 분자 쌍 (#1, :lf 2) 에 대하여 P12= ii 12•E 。 즉 P: c= (ii u)uE 。 =〔왕 (G)+ 완 (G):cA (C)Az +……〕 E 。 , P,= 〔왕 (G) 국 왕 (G) y A(G)Az+ ……〕 Eo , P.,,= 〔 a 。+ 왕 (G) 국왕 (G),.A(C)Az+ ……〕 E 。 (N. 88)
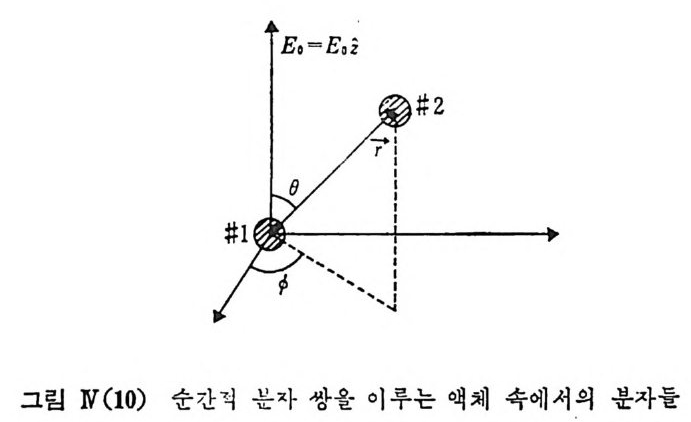E,=E,i
가 주어진다. 위에서 (G) 。 ,=3 f a?,-6 야 (N. 89) 또 그림 N (lO) 으로부터 ’翼 = sin { ) cos¢ f7 =sin { ) sin ¢ f:i= cos{) 가 되고, (N. 90) (G)aiC G )i, = 〔 c.c 〕야 =(3 faf i -O ai) ( 3 fifp- Oip ) =9 ?a?Af A ?,-3 ?af A 6A,-3 fA ?, 6a+8aA8 =3 faf p + Oap (N. 91) 여기서 1'Af A = 1'111 ',, + fyfy + fzY z = (X1i + Y1l+z122)/r1i = l (N.92) 의 합공식을 져용하고 있다. 식 (N. 88), (N. 89), (N. 90), (N. 91) 식으로부터 P,,= 〔왕 (3 fi z)+ 완 (3 로)+ ......〕 E 。
= (왕+완나 ... …) (3 cos() sin ( ) cos¢) Ea , P1= (왕+뮤 +…… )(3cos() sin ( ) sin ¢ ) £0, P,. = 〔 a 。+ 왕 (3 cos2() - l) + 왕 (3 cos2() + 1) + ……]E 。 (N. 93) 을얻는다. 만일 분자 쌍(:ff 1, :tf 2) 의 축 r12 가 의부 전장 Eo 에 대해서 평행 또 논 수칙하게 같은 확률로 나타난다면, 즉 r12 가 Eo 에 평행인 분자 쌍 의 수가 Eo 에 수칙인 분자 쌍의 수와 같은 수로 존재한다면 분자(또는 원자) 한 개당 평군 편극물 E 는 a=½(2a,.+ 파) (N. 94) 가된다. 위에서 a.._ 는 Eo 에 수칙인 (f)=:)분자 쌍, a0 은 Eo 에 평행인(()= 0) 분자 쌍의 편국률에 해 당된다 . 이때 이들 가상 분자 쌍의 이방성 O 를 다음과 같이 정의하고 있다. /3 =a,_ 죠 ... (N. 95) 식 (N.93) 으로부터 균 , 과 죠 ... 을 구하면 8=0 에 대웅하는 au 은 P'(8=0)=P~(8=0)=0 , Pz(8=0)= (a 。 +2 왕 +4 왕-+…… )E 。 에서 ao=a 。 +2a 7。2 +4a~ 。 3 +…… (N. 96) 로주어지고, 0= ；에 대웅하는 a .L은 P(o= 문) =P.,(o= 중) =o ,
Pz(0= 공) = (a 。 -완 - + 왕 + …… )E 。 에서 a ... =a 。 -a7 。z +, ~a 。 3 + …… (N. 97) 가 되고 따라서 죠 12=a 。 + 2a7 。 3 (IV. 98) 즉, 등방성인 부분과 /3= a0-a.1. =3 왕 +3 완 (lV. 99) 로 주어지는 비등방성인 부분으로 나눌 수 있다. 여기서 주목해야 할 것은 au 는 물론 a J.도 모두 Pz 에 대해서 정의 되어 있다. 이제 이렇게 분자들 사이에 짝을 지어 상호작용하는액체에 의해서 산 란되는 산란광의 스펙트럼을 조사해 보기로 한다. 첫째, 분자 하나하나는 모두구 대칭성을 가지고 있으며 ii o=a 。 I 로서 분자의 내재적 비등방성 /3 o 는 0 이라고 가정하고 둘째 , 임 의 의 두 분자를 생 각할 때 이 들은 쌍을 이 루는 상태 (0 一 0) 또 는 쌍을 이루지 않은 상태 (0 … 0) 의 어느 한 상태에 존재한다고 가정 하며 셋째, 위의 두 분자에 대한 공유 쌍결합 상태에서는 /3={3*, 무결합 독럽상태에서는 {3＝ 0 이라고 가정하면 이들 분자 쌍의 총 수효를 N 이라고 할 때 산란광의 스펙트럼은 아래 와 같이 주어지는 편극물(비편광 스펙트럼의 경우에는 비등방성 {3)의 자체상관함수 C,( t)의 푸리에 변환으로 주어진다. C~(t) =N< {3( 0){3 (t)P z( co s (N.100) 여 기 서 cp(t)는 r12Co) 와 ru( t)가 이 루는 각도를 나타내 며 cosc f;(t) = r12(0) •r12( t)이 다.
지금 분자들 사이의 충돌에 의해서 f3 (t) = + N< L1 ( 3( 0)L1 f 3(t) Pi (co s¢(t) )> (N. 101) 로 쑬 수 있으며 특히 4 f3(t)가 P2(co 와(t))보다 훨씬 빨리 이완도]는 경우에는 !。집 (3 (O) t.1(3(t)〉/〈 (4 /3 )2 〉 dt 니。~ 2 〈 P i( cos rp(t))〉 +N여 (3 (O) .J(3(t)〉 (N.102) 로 근사시킬 수 있다. 이제 두 원자가 충돌에 의해 분자 쌍을 이루게 될 확물을 PB 라고 하 떤 〈(3〉 =PB (3*로 쑬 수 있고 N< 8 >2 < P z (co scp ( t))>= NPs2(3 *. ( N . 103) 를 얻게 되며, 또 PB( t)를 t= O 에서 분자 쌍을 이루는 두 원자가 l=t 에서도 분자 쌍을 이루게 될 확몰이타 하면 가 됨을 안 수 있다• 한편 Ps(O) = I, Ps(oo) =Ps, ![민＠忠 (0) L1~(t) >- o 가 되는 조건으로부터 Ps (t) = (l —P B)f( t) + PB (N.105) 의 형태로 쓸 수 있고 이때 <4 8(O)48(t) >=fi*' Ps(l -P s)/(t) (N.106) 를 얻는다. 여기서 f(t)는 다음의 경계조건을 만족시키는 함수이다. /(0)=1, /(oo)=O (N.107) 따라서 식 (N.103) 과 식 (N.106) 을 식 (N.102) 에 대입시키면 C,(t) = N{3 * '[Ps(l -P s)f(t )+ Pa2F(t) ] (N.108) 를 얻을 수 있다. 위 에 서 F (t) = tc, tc 는 충돌 시 간) Tdt C, (t)내 (t-+ O) C,( t)는 다음과 갇온 함수꼴이 된다. C,(t ) =e 가 /T+~(I) (1\7. 110) 단, ¢(t)는 다음 조건을 만족시 켜 야 한다. ¢(t) =const. (t)> t.) 歷옮 ¢(l) = l/-r (N.111 ) 이러한 함수 (t)는 아래와 같이 주어지며 그림 N(ll,a) 에서 보는 바 와갇다. (t)=훑 ::::::: t/r( 1-t/ tC+ … …), (t갚 c) cw.112) 따라서 이를 식 (N.110) 에 대입하여
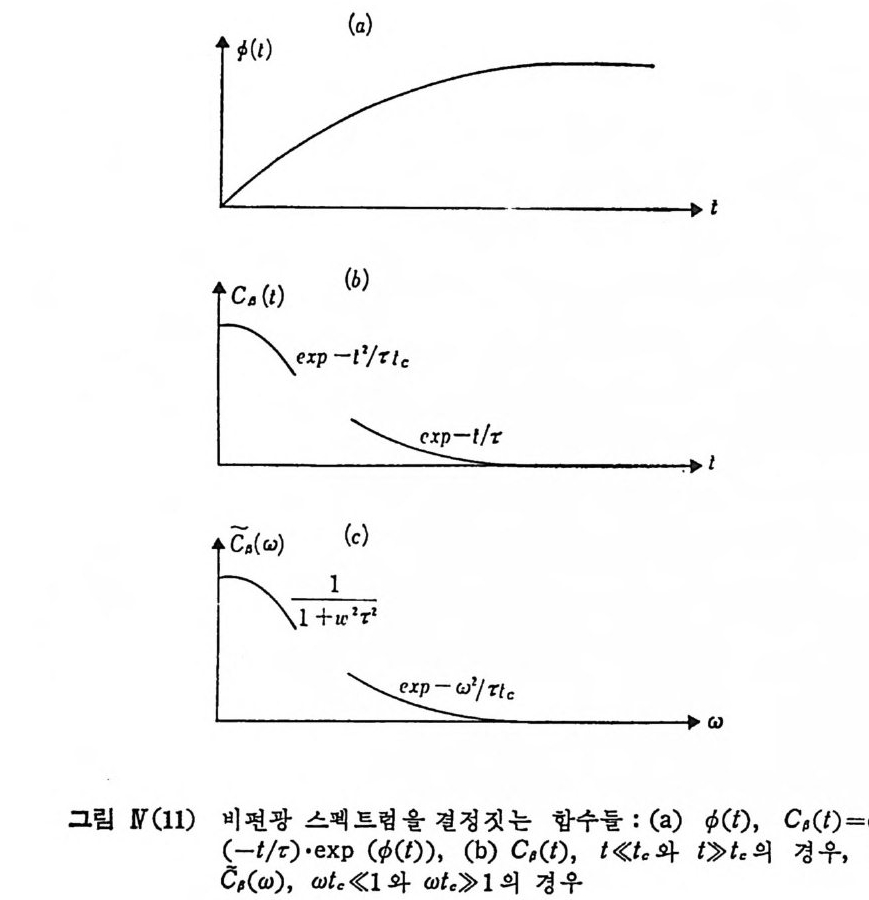(a)
Cp (t) = e 가 /'ex p(¾) = exp (-t;-.- (1 -* )) = exp (-끔½ t-) (N.113) 의 결과를 얻게 된다. 이것온 t> te 에 서 C,(t) = e 가 /T t 깊 c 에 서 는 C~(t) ==: e-12,T,, 가 됨을 알 수 있다. 따라서 이의 푸리에 변환, 즉 스펙트럼을 살펴보면 (l)幻/t c 영 역 에 서 는 (1+ w2-c 2 )-1 (l)> 1/tc 에 서 는 exp ( -w2/-c l e) 형태로 주어질 것이 예상되고 있다. 이상을 그림으로 나타내면 그림 N(11) 과 같음을 볼 수 있다. N-3. 2 분자진동 라만 스펙트럼과 분자의 방향각 운동 이제 액체에서 분자들이 가지는 준회전운동에 관한 정보를 타만 산 란 스펙트럼으로부터 어떻게 얻을 수 있는가 알아본다. 분자가 전동운동을 할 때 편극물 aab 가 정 격 좌표 rt(t)에 의 해 서 연 조되고 있으며 이때 aab(f) =a0ab(f) + L a•ab( t)q•(t) (N.114) u 와 같이 전개시킬 수 있다. 여 기 서 a 남(t) = oaa&/oq • I q•= O 이 다. 산탄광의 강도 la&( (J)）는 이 aab( t)의 상관함수 0ab( t)의 푸리 에 변환 으로서 다Ia음b(과w) =같 이r- .... d 주t 어 tl>진a b다(t) .e -io, t (N.115) .. 여 기 서 ~ah(t) = I: 〈 a 님(t) a•ah(O) 〉이 며 , l, m 은 분자들을 나타내 는 ·‘
첨자이다. 이제 분자들의 운동에서 진동-회전 상호작용을 무시하면 〈 a 님(t) a'ab(O)> = ( N . 117) u 를 얻는다. 따라서 방향회전 운동이 설령 분자들 사이에 상호 관련되어 있다 하더라도 라만 산란에서는 이에 기인하는 간섭효과가 전혀 나타 나지 않고 결국 식 (N.117) 에서 보는 바와 같이 단일입자 레일레이 산 란, 단체협동 레일레이 산란, 단일입자 라만 산란으로 나타나게 됨을 알수있다. 위의
{3 ab 로부터 아래와 같은 텐서 성분을 정의하면, 忠 uo= 沿乃 § uz z 釣=}(휴 u xx_ 忠) /3° ±2 나 ({3도요)국 u (N.119) 이들 분자 좌표계에서의 성분과 실험실 좌표계에 대한성분이 다음식 으로 연결된다. (3n •(Q ) = roL2= - 2 D CZ)n,.( Q ) (3 .. (0) (N.120) 여 기 서 Q( a, {3, f)는 분자 좌표계 와 실험 실 좌표계 사이 의 Euler 회 전 각을 나타내 며 D (2)(Q)는 Wi gn er 의 회 전축 변환 행 렬을, {3 .. (0) 는 분자 좌표계에시 표시한 /3 텐서의 성분을 나타내고 있다. Y 축 방향으로 레이처광이 입사하고 X 축 방향에서 라만 산탄광을관 축할 때, 산란 평면 즉 위의 xy 평면에 평행한 편광을 H, 수칙한 편광 올 V 라 하면, 입사광 레이처와 산탄광의 편광상태를 V 또는 H로 선 택 함으로써 ( VV), ( VH), (H V), (HH) 의 네 가지 편광 라만 스펙 트럼을 얻을 수 있다. 가령 (VH) 스펙트럼온 {3 YZ( Q)에 의해서 결정되며 f3~ z (요) = 托 斜 (SJ) +/3~I (요)] =i 2m, [D { 갑 ( S2)+D 닷 .. (Q) ](3~ (0) (N. 121) 이므로 방향각 회전운동이 기여하는 광산란 성분을 보면 IfJ( o)-J oo dt e-I \/3& (t)/3 &(9) 〉에서
P( 」Q,t)라 하면 〈綜 (요') 0& (g)> 구 .尹 JfaQ d(L1.Q ) P(LI.Q , t)〔霜 (요') +D 낫; . (요')][ D; 섭 (g)十 D 累 n (Q)](J~ (O) (J요 (0) (N.123) 로 쓸 수 있다. 만일 P(LJQ , t)를 다음과 같이 전개 시 키 고 P(Ag , t)국간 II i 團)f 1kII( t) D~ (Q') = ~ D 업 (g) D1; 1; , (4.Q ) (N. 124) 의 관계식을 이용하면 아태와 같은 결과를 얻게 된다. = C 卓隣 (0) 閃 (t -) (I\7. 125) 즉, 타만 산란이 검지할 수 있는 것은 상관함수의 l=2 성분이며 lml=O, 1,2 의 각 성분은 분자의 여러 대칭축에 대한 굴러넘기(t um· bli ng ) 또는 방향회 전 (reorie n ta t i on ) 의 목성 을 대 표하고 있 다. 다론 한편으로 분자의 대칭축 U 가 주어지면 /3 ab 의 정의식 (N.118) 로부터
fm( 2)(t) oc exp (-t/Tm (2)) (N.127) 로 주어지고 여기서 .. '(2 ) 는 다 (2) = 6Di +?군 1( D u -D~) (N. 128) 로써 회전각 확산텐서에 관련되어 있다. 실제 실험적으로 분자전동 라만 벤드로부터 방향각 회전운둥에 의한 기여 를 구하려면 식 (N.115), (N.117) 에서 브는 바와 같이 내재적 전 동준위 이완에 기인하는 성분을 분리시켜야 하며 따라서 회전운동성 폭 넓 힘 이 내재적 전동벤드 폭보다 커 야 하며 따라서 타만 산란에서 연구 할 수 있 는 방향각 회 전운동의 시 간 영 역 온 10-11~10-13 sec 정 도로 국 한 되어 있다. N-4 임계점 산란백광 N-4.1 임계점 어떤 물질이 기체, 액체, 고체르 갈라져 촌재하는 것은우리 지구상의 목 수한 물리적 조건 때문에 나타나는 한 우연이타고 볼 수 있다. 가령 우리가 대기압이 수백 기압이 되는 다론 천체에 혹시 살고 있다면 아마 많은 물질이 기체 상태를 보이지 않고 액체와 고체로만 촌재하게 될 것 이다. 마찬가지로 꿇는 점의 온도가 마치 액체가 기체 상태로 변하는 어떤 철대적 의미의 온도로 생각하는 것은 우리 지구상의 한 우연일 분이다. 엄밀히 이야기하면 뚜껑이 없는 그릇에 담겨 있는 고체 또는 액체는 열역학적으로 평형상태에 있는 것이 아니다. 우리는 평형상태를 취급하기 위해서 항상 전공상태의 원통 속에 물질 을 집어넣고 자유로 웅칙일 수 있는 피스톤으로 막아 놓은 경우를 생각 하면 주어 전 온도와 압력 에 따라서 증발, 승화 또는 웅축이 가능하고 적당한 비울의 기체, 액체, 고체의 새로운 평형상태가 항상 가능하게 된다. 이러한 평형상태에서만이 액체와 기체가 구별되어 공촌할 수 있는, 다시 말해서 이 원통 속에 그 경계 충면이 뚜렷이 나타날 수 있는, 온
도가 압력에 따라 어떻게 변하는가의 철대적 의미를 찾을 수 있다. 물울 예로 들면, 가령 이 원통 속에 20°c 실온에서 공기를 다 뽑아내 고 물을 1/3 정도 채웠다고 하자. 그러면 물의 포화 증기압이 약 0.023 기 압이 되 고 밀도가 O. 998 gm/ cm3 인 물(액 체 )과 밀도가 1. 85 X 10-5g m / cm3 인 수증기(기체)로 분리되어 나타난다. 이때에 피스톤의 위치를 고 정시키고 계속 가열하면 수증기의 밀도가 증가하고 압력이 증가하게 된다. 계 속 가열하여 온도가 100°c 에 다다르면 증기 압은 1 기 압에 이 르지 만 이 경우 공기중에서와 같이 눈으로 보이는 꿇는 현상온 보이지 않고 사실 다몬 온도와 아무런 차이를 나타내 보이지 않는다. 또계속해서 가 열하여 온도가 3so0c 가 되 면 증기 압이 163 기 압으로 증가했을 분 역 시 기 체 (밀도가 O. 114 gm/ cm3 로 증가)와 액 체 (밀도가 O. 575 gm/ cm 3 로 감 소) 사이의 경계층은 계속 남아 있게 된다. 이 제 더 가열시 켜 온도가 Tc=374. 15°C 가 되 면 압력 이 Pc=218. 3 기압, 밀도가 Pc=O.32 g m/cm3 에 이르고 액체와 기체의 구벌이 완전히 없어지고 소위 단순 유체가 된다. Tc 이상의 온도에서는 유체 전체가 압력에 따라서 밀도가 아주 커지 거나 또는 아주 적어지거나 하지만 액체와 기체로 분리되어 나타나지 않는다. 즉 Tc 는 액체가 존재할 수 있는 절대적인 상한 온도이다. 다시 이 밀폐된 원동의 초기 상태를 생각하고 이제 온도를 내리기 시 작하면 o.01°c 에서 얼음(고체)이 생기기 시작하고 온도를 더 내리면 완 전히 얼음과 수증기(기체)만이 촌재하고 액체 상태가 없어진다. 이와 같이 액체 상태가 존재할 수 있는 철대적인 하한 온도를 삼중점 이라 하고 만일 온도을 정확히 이 삼중점에 고정시키면 고체, 액체, 기 체의 제 상태가 평형상태에서 공촌하게 된다. 이와 같이 한 열역학적 상태가 사라지는 온도를 바로 임계접 온도 (criti ca l p o i n t)라고 하며 아래 와 같이 상전이 와 관련하여 많은 예 를 들 수 있다. 즉, 기체―액체에서 밀도가 다론 두 유체의 공촌 평형상태, 부분적으로 혼합 가능한 액체에서 배합 성분비가 다른 두 액체의 공 존평형상태, 강자성체의 자발적 자화 편극,
반자성체 및 bin a ry 합금에서의 장거리 질서 정열, 초전도체에서의 에너지 분격 (ga p) , 액체 헬리움에서의 초유체 밀도, 강유전체에서의 자발 분극, 등 많온 예에서 임계점이 나타나고 있다. N-4. 2 광산란의 요등이론 -Orns t e in -Zern i ke 이론 레일레이 광산란 이론은 기체에 대해서 매우 성공적이지만 액체와 고 체에 적용할 때에는 실제 관측치보다 훨씬 큰 값을 주고 있다. 이것은 분자들에 의한 산탄 광과의 상쇄적인 간섭 효과에 기인하고 있으며 이 간섭 효과를 제대로 고려하면 그 결과는, 이들 액체와 고체 를 마치 완전한 연속 매질로 볼 대에 열져 요동에 의해서 국소적 불균 일성, 즉 밀도 또는 성분벌 농도의 요동이 내재하게 되고, 실제 관측 되는 산탄광의 강도가 바로 이들 밀도, 성분 농도의 평군제곱 요동에 비례하게 됨을 알 수 있다. 위의 평군제곱 요동은 등온 압축물 또는 삼부압의 농도 의존성 등, 거시적 물리량으로 연결되고 다라서 매질의 상제한 분자구조에 관계 없 이 광산란의 강도를 계산할 수 있다. 우리는 이미 N-2.2 절에서 요동과 상관함수 사이에 어떤 관계가 있 논지를 보았다. 분자 수의 요동 oN 은 밀도 요동 6 p에 의해서 oN=J v d3r op( r) (N. 129) V 와 같이 주어지므로
한편 전자기학적 광산란 이론에서(JI -2.3 철) l(q, (J)) 다心 )2-¾- f .. dt e 기 O t
l(q- > O) = (ea • e,)2 (룹): Vp 2 ks TrT (N. 137) 의 결과를 얻을 수 있다. 위에서 q -->O 가 아닌 경우에도 가시광 영역에서는 g (R) 이 단거리 영 역 일 때 에 는 그 영 역 내 에 서 e•q• R-->1 이 되 므로 e• q•Rg (R) ：：：：：g (R) 로 가정 할수있다. 그러나 임계점 근방에서는 g (R) 이 장거리 함수가 되고 따라서 e•q• R 을 무시할 수 없으므로 산란광 강도가 q, 죽 산란각에 크게 의촌한다. 또 한편 임계정에 접근함에 따라 TT 가 급격히 증가하므로 광산란도 급격 히 증가하여 소위 〈 임 계 정 산란 백광 (cr iti cal op alescence) 〉이 라는 현 상을 가져오게 된다. 요동을 푸리에 전개해서 보면 과장 A 또는 과수 q =2 1r /A 의 요동 성분파를 생각할 수 있고, 가령 파장이 Ao 인 입사광은 산란각 0 가 정해지면 2A sin ( 0/2) = Ao 또는 q=4A一 。77 : sin ( 0/2) (N.138) 의 Brag g 조건을 만족시키는 요동과에 의해서 산란되는 것으로 해석할 수 있다. 이상 논의한 결과는 Ein s te i n 이론으로 알려쳐 있으며 이것은 요동의 과장 A 가 g (R) 의 유효 영려에 비해서 훨씬 길다고 가정한 것이며 따 라서 이 Ein s te i n 공식 은 임 계 영 역 에 서 는 q-> O(A ..... oo) 죽 0 ..... 0 의 전방 산란에 대해서만 성립할 것이 예측된다. 0#0 의 임계접 광산란에 대한 이론은 Orns t e i n 과 Zern i ke 에 의해서 시도되었고 그 결과는 l(q) = l0Ap 2k s T Tr/ (1 + 강/q e2) (N.139) 로 쑬 수 있으며 여기서 q c 는 g (R) 의 상관도 거리의 역수에 해당된다. 이 Ornste i n - Zernik e 이 론은 자유에 너 지 의 요동을 밀도 요동 및 기 울 기 항으로 테일러 전개시킬 수 있다는 가정에 입각하고 있으며 따라서 열역학적 함수의 데일러 전개가 촌재한다는 원칙의 고전 이론에 속하며 임계접에 아주 근접할 때에는 오차가 있을 것으로 예상된다. 식 (N.139) 에서 감의 함수로 lo/l( q)의 그래프를 그리면 직선이 되고
이 칙선의 기울기는 % 따라서 상관도 거리 f에 관계된다. 이대의 ：는 분자 상호작용 거리 정도의, 따라서 산란계의 물질 특성 에 관계되는, 단거리 상관도 거리이다. T-. Tc 에 서 rT-> OO 가 되 고 동시 에 qc 一 0 이 므로, 산란광 ](q)는 q- -o 죽 전방 산란에서 대우 강해짐을 알 수 있고 이것은 Tc 에서 멀리 벗 어 난 영역의 Ein s te i n 공식에서 균일하게 산란도]는 결과와 큰 대조를 이 루고있다. 임 계 영 역 에 서 Ornste i n - Zemi ke 이 론을 엄 밀히 겁 정 하는 것 은 q-> O 에서의 실험 결과를 요하며 이때에 나타나는 다중 산란의 효과에 대한 보정 등의 어려움으로 아칙 확실한 증거는 없으나 Is i n g모델의 계에 대 한 자세한 계산에 의하면 f의 발산이 rT 의 임계 발산 과 다론 덕 수 ( ex p onen t)를 가져 야 됨 이 알려 쳐 있 다. N-4. 3 모드-모드 상호결합 Van Hove 시공간 상관함수 g (r, t)는 한 입자가 t =O 에 r=O 에서 관측이 되었을 때 (r, t)에서 입자가 발견될 확물을 나타낸다. 그리고 앞 철에서 산란광의 스팩트럼 ],(q,也)가 아 g (r, t)의 푸리에 변환에 비 례함을 보았다. 이 g (r, t)를 액체에 대해서 계산하는 것온 무척 어려운 일이며 오히 려 광산란 실험을 동해서 g( r, t)= const. jj /,(q, (l)) e 규(야 -a·•) dq d(J) (N.140) 의 푸리에 변환으로부터 실험적으로 구할 수 있다. 그러나 액체에 대한 g (r, t)의 근사적 해는 유체역학 방정식들을 아용 하여 구할 수 있다. 좀더 구체적으로 r 과 t가 충분히 큰 거시적 영역에 대해서는 g( r,t) 를 밀도요동 자체상관 합수로 대치시킬 수 있으며 이 밀도요동 자체상 관함수의 시간 의촌성, 즉 평형겁울 중심으로 한 요동의 운동을 유체역 학 방정식을 써서 구할 수 있다. 즉 1 밀도 요동의 감쇠를 선형화시킨 유체역학 방정석들로부터 기술할 수있으며 2 유체 가 열역 학적 으로 평 형 상태 에 있 다는, 즉 Navie r -Sto k es 방정 식과 에너지 관계식의 압력 P 와 엔트로피 S 를 열역학적 관계식을
써서 밀도 P 와 온도 T 로 대치시킬 수 있다는 가정과 3 분자들 사이 의 방향각 상관성 을 무시 , 즉 Navie r -Sto k es 방정 석 의 횡축 속도를 무시할 수 있다는 가정에서 선형화시킨 연속 방정석, Navie r -Sto k es 방정 식 및 에 너 지 방정 식 으로부터 p(q, t)를 구하견 아래와p( q, 칼 t이) = p주(어q진) {다 ¥. exp (r T q2 t/p Cp ) ...I- 운p ex p曰｝r;따따 (난―권)） 만 /2 기 cos Q。(q)t} (N. 141) 한편 g ( r,l) 는 (r, t)의 입자가 (r=O, t =O) 의 입자와 갇울 때의 g,( r , t ) 와 (r, t)의 입 자가 (0, 0) 의 입 자와 다른 경 우의 gir, t )로 나 누어 g( r, t) =g,( r, t) +g a (r, t) (N. 142) 르 쑬 수 있고, 밀도가 아주 적은 경우 입자들이 서로 독립적으로 확산 운동을 할 대 에 는 gd (r, t)--- +0 가 된다. 브라운운동윤 하는 입자들에 대해서는 g,( r, t)::::( 471D t )3/2e-Cr-'' (N.143) 로 주어지고 있다. 그러나 임계 영역에서는 이와 같은 선형화시킨 고전 유체역학의 적용 이 성립할 수 없음이 찰 알려쳐 있다. 이 임계 영역과 관련하여 p (x)- 〈p〉를 질서도 변수라 하면 g( k) = )d3x e-· 뇨 <(p( x)- < p>)(p (O ) -〈 p〉)〉를 정 의 할 때 에 p(x ) =令 곤 pke ih (N.144) 즉, p (x) 를 유체역학적 모드의 중첩으로 생각할 수 있으며 P1· 는 k 성 분 모드의 전폭을 나타내고 있다. 위에서
g(O ) =~d3x< (p( x)-
)(p ( O)-
)> 이고, 따라서 T->Tc 에서 g(O ), 죽 l, (k->O) 가 발산한다는 것은 p( x) 자체는 밀도-제한된 유한정 양이므로, (p (x)- 〈p 〉 )와 (p (O)- 〈 p 〉 )가 x 가 매우 큰 모든 영역에 걸쳐서 같은 부호 죽 같은 방향을 가지게 된다 는 뜻이 된다. 즉 요동이 장거리 상관 관계를 갖기 때문인 것으로 생각 할수있다. 식 (N. 140) 에 Ornste i n - Zernik e 이 론의 I,(q) , 식 (IV. 139) 를 대 입 하 떤 q-> O 따라서 r 一 00 의 경우에 g (r) ：：：1： ：下-e―- ~7,r ( l\' . 145) 를 얻을 수 있다. 여 기 서 l 은 l2q c2 =( 3/p rT 로 주어 지 며 Ornste i n - Zernik e 도적 (plo t) 의 기울기를 결정하는 매개 변수이다. 그러 나 T-> Tc 에 서 Ornste i n - Zemi ke 도적 , 즉 I。 /l( q)대 감 이 칙 선이 안 되고 q 2 一 0 에서 아래로 굽어지는 경향의 실험 결과들이 보고되어 있 으며, 2 차원의 경우에는 또 g( r) IT~Tc =:::Inr, 죽 r 이 커질수록 상관도 가 증가하는 모순을 내 포하고 있다• 상관함수의 실제 계산은 요동의 과수 q가 q C 보다 훨씬 적은, 죽 2=2 1r:/q가 상관도 거리 E 보다 훨씬 큰, 소위 유체역학적 극한 (q« q c, 2>E) 에서만 계산되고 있음을 지적한 바 있다. 그러나 T->Tc 의 임계 영역에서는 qc~ ( TTCTC )p --+0 이므로 q<{q c 의 가정이 흔들리계 됨을 알 수 있다. 그러 나 90° 산란각의 광산란에 서 ( T-_ Tc)/ Tc~ 10-5 까지 는 q <{qc 가 됨이 알려져 있으며 따라서 Tc 에 상당히 가까운 영역인 (T-Tc)!Tc~ 10~8 에서도 유체역학적 근사의 결과를 충분히 적용해 볼 수 있다. q=문 s i n 승 0 이므로 산란각 O 를 적게 택하면 유체역학 이론에 의 한 실험 결과 해석을 Tc 에 더 가까이 접근하여 적용할수 있으며 열중 성 자 산란에 서 는 1 。 :::::: 1 A 에 닫하므로 유채 역 학의 적 용 가농 영 역 이 Tc
에서 비교적 멀리 떨어지게 될 것이 예상되고 있다. 유체역학의 결과를 종합하면 1 레일레이 성분의 선폭 I' R 이 I'R~ 」pC느 p # (N. 146) 로 주어지고, KT 는 열전도도이다. 2 브릴루앵 성분의 선폭 I' B 는 전단류 접성도 ?, 내적 접성도 ’가 Tc 에 서 유한하면 같이 유한하고, 이 들이 발산 또는 /.T 가 Cv 보다 더 강한 발산을 가지 면 I'8 가 발산하게 된다. 3 브릴루엥 쌍선의 위치는 (t) B*= 土 Us q로 주어지며 맙 =(oP/o p )s =土이므로 7s 가 T-.Tc 에서 발산하면 W8->0 가 됨을 알 수 있』 .sP 4 Landau-Placzek 비 가 T-> Tc 에 서 발산한다. 즉 Tli 따m (I 사 2h)~ —CC!v : _=.!.rIs._ ->00 의 결과를 예측해 주고 있다. 이러한 유체역학적 이론이 찰 맞지 않는 영역의 실험 결과를 성공적 으로 선명 해 주는 한 이 론으로서 mode-mode coup ling 의 이 론이 발전 되고 있다. 죽 임계접에서논 이들 선형 근사의 유체역학 방정식에 비선형 항들을 추가로 고려해 주어야 하고 이로써 음파, 열전달 모드, 접성 모드 등 서로 다론 모드들 사이에 아래 그림과 같이 상호작용을 하게 되고 서로 사이에 바선형적으로 상호결합이 일어날 수 있음을 가정하고 있다. 가령 레일레이 선 폭을 결정하는 열전도도 KT 에 아래 그립 (c) 에 기인 하는 기여를 보면 !CT ,~~( 덩 C )-2/3 (N.147) 또 그림 (d) 가 나타내 는 상호작용을 고려 하면 !CT ,S~( TTCTc )° (N.148)
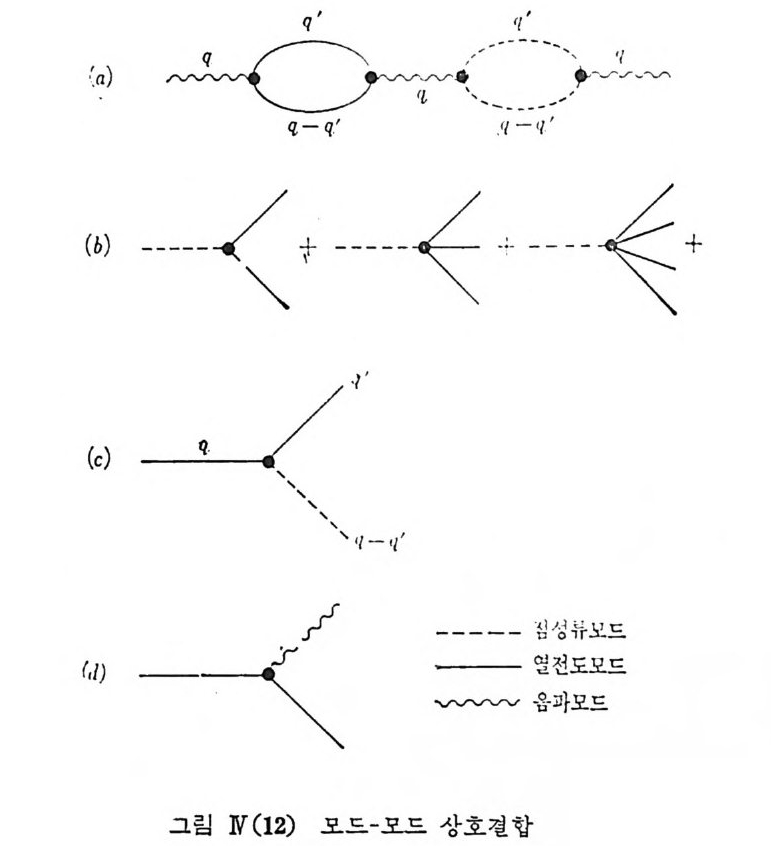('.ba)) --一-〈--二<드q+q-· q• -' `\<\\\.(
가 수어진다. 따라서 열전도도는 발산하고 있으며 그 떠수는 2/3 정도 가 될 것울 예측할 수 있으며 이것은 Sw i nne y와 Cumrn i ns (l 968) 의 CO2 에 대한 I' R/ 강 대 T-Tc 의 관계를 Jog -Jo g 쳐도로 도시했을 때 나 타나는 기울기가 주는 실험 결과와 일치하고 있다. 참고문헌 1. J.A. Pryd e, The Liq u id Sta t e , Hutc h in s on Univ e rsit y Lib r ary( London, 1966). 2. N.H. March and M.P. Tosi, At om i c Dy n ami cs in Liq u id s , MacMi llan Press(L on don, 1976).
3. J.C . Brand and J.C . Sp e akman, Mole c ula r St ru ctu re, Edward Arnold (London, 1960). 4. M. Ti nk ham, Group The o ry and Qu antu m Mechmz ics , McGrawH ill (Ncw York, 1964). s. E. Lif sh it z and L. Pit ae vskii , St at i sti ca l Phys ic s 3rd ed., Part l(Landau and Lif sh it z Course of Theor. Phy s. Vol. 5 ), Perga mon Press(Oxfo rd , 19 80), Chap s. XII(Fluctu a ti on s) & XIV(Phase Transit ion s and Crit ica l Phe-nomena). 6. E. Lif sh i t z and L. Pit ae vskii , St at i sti ca l Phys . Part 2(Landau and Lif s h it z Course Vo!.9), Perga mon Press(Oxfo r d, 198 0 ), Chap . IX(Hy d rod- yn am i c Fluctu a ti on s). 7. R.K . Path r ia , St at i sti ca l Mechanic s , Perga mon Press(Oxfo r d, 1972), Chap . 13( F luctu a ti on s). 8. 조 순탁, 『 동계 물리 학』, 교학 연구사(서 울, 1983), ;:,] II 부 4 장(상 변 이 ) 및 재 l11 부(비평형 상대의 동계역학). 9. H. E. Sta n ley, Intr o d11cti on to Phase Trasit ion s and Crit ica l Phenom- ena, Oxfo r d Univ . Press(London, 1971), Chap s. 7(0rnste i n - Zernik e Theory ) & 15 (Mode-mode coup li n g ap pro xim ati on ). IO. R.D. Mounta i n , Genraliz e d Hy d rody n ami cs , in Adv. in Molecular Re la xati on Processes 9, 225(1 9 76). 11. C.J. Montr o se, Graduate Lectu re Note s (Vi tre ous Sta t e Laborato r y, Cath o lic Univ e rsit y of Americ a , 1979). 12. K. Kawasaki, Mode Coup ling and Crit ica l Dy na mi cs , in Phase Tran-sit ion s and Criti ca l Phenomena, ed. by C. Domb and M.S. Green, Aca- demi c Press(London, 1976), Chap. 4.
제 V 장 고체에서의 광산란 분광학 기체 또는 액체에 비해서 고체의 밀도가 크다는 사실을 고려할 때 그 만큼 산란광의 원체인 원자 또는 분자의 수가 증가함으로써 고체가 기 체 또는 액체보다 더 강하게 빛을 산란시키리라고 생각하기 쉽다. 그러 나 우리는 이미 단결정의 고체에 대한 X- 선 산란에 대해서 찰 알고 있 다. 즉 Bragg 산란조건에 맞는 특정된 산란각 방향으로는 사실 N2 에 비례하는 산란광이 예측되지만 그 밖에 다른 방향으로는 거의 0 에 가 까운 산란광이 예측됨을 알고 있다. 또한 기체, 액체에서는 분자 하나 하나의 여러 운동이 직접 라만 산란에 기여하고 있지만 고체에서는 이 들 원자 또는 분자의 운동이 p honon 을 형성하고 있다. 또 어떤 결정 체에서는 전자들의 운동 및 스핀의 운동이 서로 사이에 상호 연관되어 각각 pla smon, spi n wave 등을 이 루고 있 다. 본 장에 서 는 이 와 같이 고 체에서 새로 형성되는 포논, 플라스몬, 스핀파동 둥의 여러 가능한 양 자 역학적 상태에 대해서 간략하게 설명하고 이들과 관련된 라만 산란 에 대해서 기술하고자 한다. V-1 격자 운동과 광산란 V-1. 1 음파성 포논과 광파성 포논 고체 속의 원자의 운동은 이 원자에 다론 모든 원자둘이 작용하고 있 는 힘에 의해서 결정된다.
두 원자 사이에 작용하는 힘은 인력과 쳐력으로 나눌 수 있으며 정성 적으로 볼 때 두 원자 사이의 상호작용에 의한 위치 에너지 U 는두 원 자 사이의 거리 r 에 대해서 아레 그림과 갇이 주어전다.
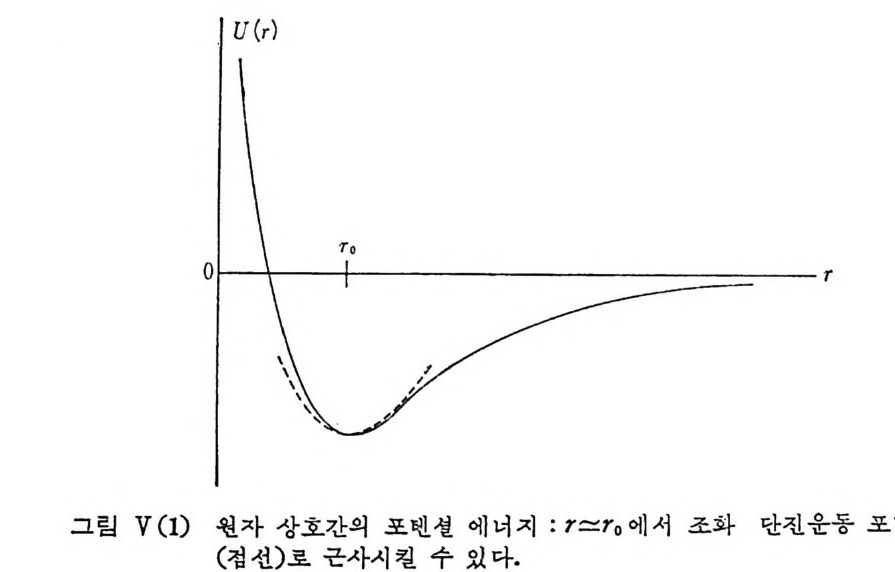U(r)
위 그립에서 보는 바와 같은 U(r) 을 모든 r 에 걸쳐서 하나의 해석함 수로 정확히 표현할 수는 없지만 r 。 즉 두 원자 사이의 거리가 평형 거 리에 매우 가까울 때에는 위 그림에서 접선 곡선 죽 찰 알려진 조화 단 진자의 위치 에너지 곡선으로 훌륭히 근사시킬 수 있음을 볼 수 있다. 죽 U(r)=½k(r-r 접으로 근사시킬 수 있으며 이것은 N 개의 원자로 구성된 일차원 격자에 대해서 다음과 같이 일반화시킬 수 있다. 죽N 개의 모든원자에 대해서 펑형위치로부터 벗어난미소변위를각 각 Ui , U2, ••••••UN 이 타 하면 전체 위 치 에 너 지 V(ui, u ……, UN) 는 V= Vo +-½-沼 곱읊 l 。 UI UU+… ••• 와 같이 테일러 전개가 가능하고 여기서 최근접 원자 사이의 상호작용 만을 고려 하면 (l' =［土 1), V=Vo+ 강무 (급磁j 0u1U1+1+ 귈읊 IOUlu1
+¾a2vI 。 U1U1-1) 가 되고 병전이동 대칭성울 고려할 때 n 번째 원자에 대한 운동 방정식 으로 mi in =-O~3t l n v =aL(lln+i - Un) +aL(lln-1-ttn ) 을 얻게 된다. 여 기서 aL= ai『』~ lo 은 원자의 종변위 (lon g itud in a l dis p l a cement) 에 대한 복원력 힘상수를 나타내고 있다. 위의 운동 방정식을 만족시키는 해로서 X- 방향으로 진행하는 파동을 생각하면 ttn( t) =A exp i(w t + kx) 를 가정하여 위의 운동 방정식에 대입하면 w=/~/s i n 두 1 (V.1) 의 결과를 얻는다. 여기서 a 는 우리가 고려한 일차원 격자에서 원자 사 이의 거리 죽 격자 상수를 나타내며 우리가 가정한 해 t L( t)는 실제로 x=na 에서만 물리적 의미를 갖고 있다. 식 (V. 1) 을 그림 으로 나타내 면 (/) 가 k 의 주기 함수(주기 , 2 r. /a) 로 서 한 (/)값에 대해서 k,=k'+l 풍, l=O, 土 I, 土 2, …... 로 주어지논 모든 k 값이 가능하게 됩울 알 수 있다. 그러나 우리의 원 래 문제가 연속체가 아니고 x=na 에만 원자가 있는 불연속체이며 따라 서 k=k' 의 파동과· k=k, 의 파동은 실제 원자의 운동만을 고려 할 때 동등한 해라고 볼 수 있다. 따라서 k 값을 -드a ::;k <프a 의 법 위 로 제 한하여 소위 Brill ou in zone 을 정 의 하.ii. 있 다.
&
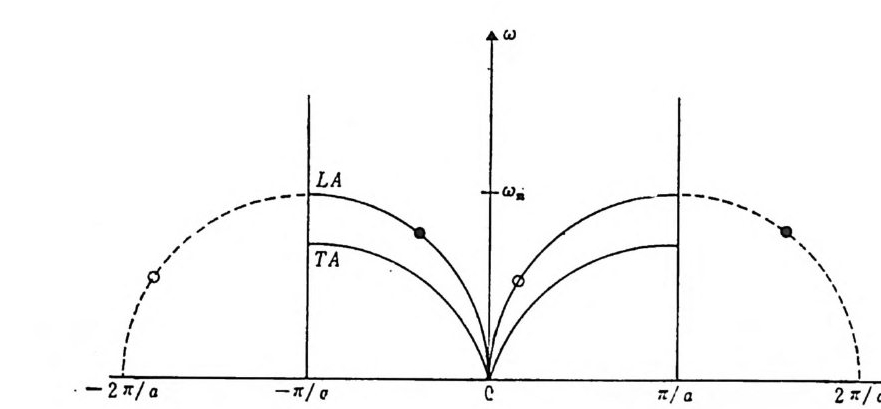그립 V (2) Brill ou in zone 안의 물리 적 해 (실선, 아론 J E 죠万 5 위에서 @> ✓ 4a讚 의 해를생각해 보면 s i n2 감r- >1 에서 k= ¾+ir 즉 cosh(ra/2)=w/ ✓ 4a!in 가 되어 w> ✓ 4a/m 일 때에 감쇠계수 r 가 급격히 증가함을 볼 수 있다. 한편 파동의 위상 속도 V 는 v= 으k 니고m a sikn ak /a2/ 2 (V.2) 로 주어지며 k-+O 의 극한을 생각하면 v= 산교 Tm a 가 되고 이것은 연 속체의 란성파에 대한 결과 C= ,/T/p와 비교할 때, 선질량 밀도 p= m/a, 강성물 J. =aLa 에 대웅함을 알 수 있다. k ＝타 a ::::: 108 cm-1 에 서 의 (J)m ax 울 구해 보면 (J)=v k 에 식 (V. 2) 로부터 v=c sin ( t./ 2 )/(t./ 2 ) ::::: 105 cm/sec 의 값울 대 입 하여 (J)m ::::: 1013 rad/sec 죽 원 적의선 영역에 속함을 알 수 있다. Un 이 파의 진행 방향과 같은 방향, 죽 X- 방향의 변위를 나타넬 대 위 의 해 는 종파(l on git ud i nal wave) 를 나타내 고 y-방향의 변위 에 대 해 서 도 같은 형태의 운동 방정식 my n= ar(Yn+l+Yn-i- 2Yn) (V.3)
울 풀어 서 그립 V (2) 의 횡 파(t ransverse wave) 에 해 당하는 해 를 얻을 수 있다. 같은 1 차원에 서 크기 가 2 a 인 기 본 칸(p r i m iti ve cell) 안에 질량이 서로 다론 두 원자가 있을 때에는 아태와 같은 운동 방정식을 생각할 수 있다.
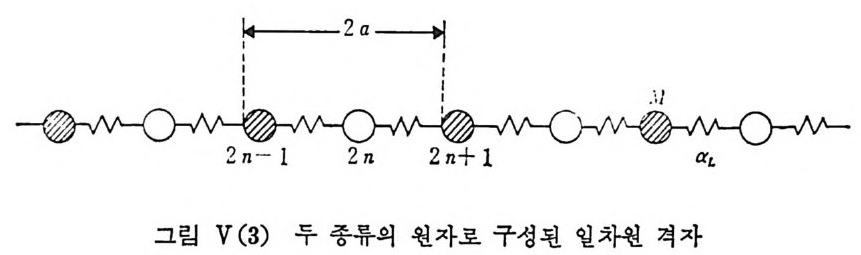~2a ――어
M% ＝야 (U2•+I+U2n-1-2 U2n) lnZlzn+l=aL(U2n+2+U2n-2 U2n+1) (V. 4) 여기에, tt(.x, t) =A ei(w l +b ) 즉, U2n(t) =A1 eiC w t + 2nla) U2n+I(t) =A2 eiC w t+ (2n+l )h ) (V.5) 형태의 해를 대입하면 Al ((J)2 M-2 야 )+2 A2 a cos ka=O 2 A, a cos ka+A2 ((J)2 m_2 aL)=O (V.6) 를 얻고 이로부터 硏 =a 먀 도 (µ-2-4 복醫訂 /2, —µl -_m= l- 1+,l v 1l cv.7) 로 주어지는 분산 관계석을 얻을 수 있다. k--+O 에서 갑 =2 adµ , w-2= 급눔 . k2a2 (V. 8a)
k= 드2_a 에서 W+2=2adm, 같 =2aL/M. CV. Sb) 로 각각 분리되며 이때 (I)+ 가지를 광과성 포논, (I)- 가지를 음과성 포 논 가지라고부른다. k->O 에서 (I)- 가지의 해는 Ai !A 2=l 즉 두 원자 (m,M) 가 모두 같은 방향, 같은 진폭으로 움칙 이 는 경 우가 되 고, (I)+ 가지 의 해 는 A, / A 尸 -m/M 죽질량 1n 의 원자와질량 M 의 원자가 서로 반대 방향으로, 질량에 반바례하는 진폭으로 움칙이는 것을 나타내고 있다. 단원자 격자의 경우에서와 같이 이 경우에도 원자들이 파동운동의 전 파방향에 수칙 으로 진동하는 횡 파(t ransv P. rse wave) 가 되 논 해 를 생 각 할 수 있으며 최근접 이웃 원자 이상의 장거리 상호작용을 포함시키면 실제 분산 곡선에 서 보는 바와 같이 k= 士;r /a 에 서 (I) 가 반드시 극대 가 되지 않을 수도 있다. 이상에서와 같이 위치 에너지에 원자의 변위에 대해서 2 차 항들만이 기 여 하는 조화 진동 근사에 서 S 개 의 원자를 포함하는 unit cell N 개 로 구성되는 3 차원 결정 격자로 확장시켜 생각하면 모두 3SN 개의 서로 연계된 운동 방정식이 성립됨을 알 수 있다. 그러나 이 결정 격자는 병전 대칭성을 가지고 있으며 따라서 Bloch 정리에 의해서 이들 운동방정식의 해는 Ux(f ) = Ux( 옹 ) exp iq• l (V. 9) 를 만족시켜야 된다. 여기서 U: c(l ,S) 는 unit celll 의 원자 S 의 변위 U 의 x- 방향 성 분을 나타내 고 U:c ( O, S) 는 기 준 unit cell (l =O) 의 대 웅 된 원자 cs) 의 X- 성분 변위를 나타내고 있다. 위의 관계식을 쓰면 3SN 개의 서로 연립된 운동 방정식이, 서로 다른 q값에 대웅하는 N 개의 독 립된 조들로 분리되고 각 조에는 3S 개의 운동 방정식들이 서로연립되 어 남아 있게 된다. 따라서 q값이 주어지면 이들 3S 개의 연립 방정식 만 풀면 되고 이로부터 3S 개의 고유치 죽 진동수가 구해지며, 또 각 진동수 값을 식 (V.6) 와 같은 영년 방정식에 대입하여 unit cell 내의 S 개 원자들의 각 성 분 변위 를 포함하는 고유 벡 터 (죽 normal mode) 를 구 할 수 있다.
한 주어전 방향에 대해서 N 개의 q값이 가능하고, 이들 q값의 각각 에 대하여 3S 개의 연립 운동 방정석을 풀어 (1.)(q)를 구하여 아래 그립 에서 보.는 바와 같은 3S 개의 분산 곡선을 얻는다.
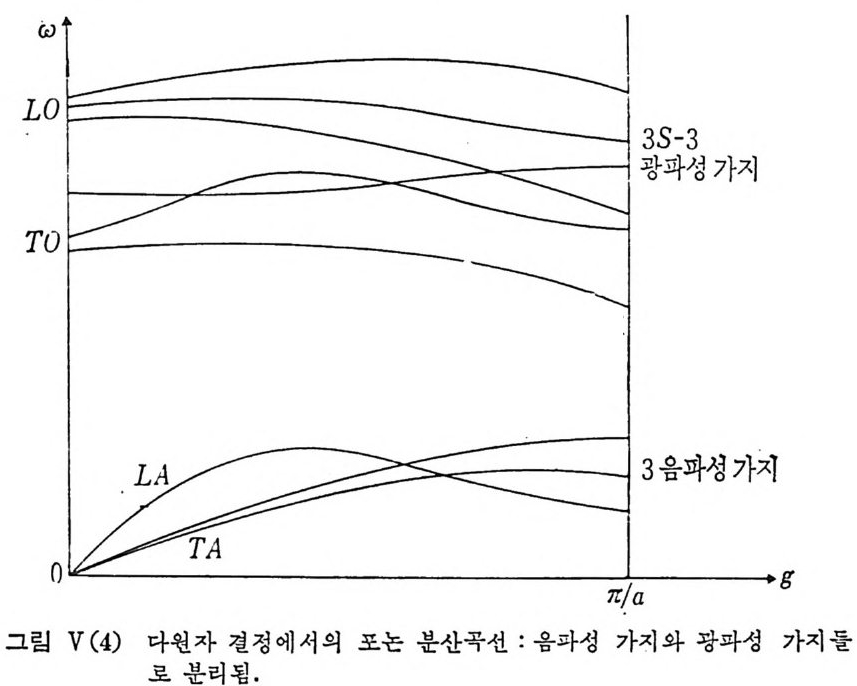LO
V-1. 2 브릴루엥 산란 임의의 겨자전동 (q,(JJ）에 의해서 결정체의 유전상수 c 이 다음과 같 이 변한다고 볼 수 있다. E(r, t)= Eo+ .E,., E0,., exp i(q• r-(J) .t) =Eo+OE(r, f) (V.10) 여기에 평면 광과 E(r, t )=E 。 ex pi (k 。 .r- (I)。t)가 진행해 갈 때 편극 요동 oP(r, t) =oEE/4;,; 가 생기고 이것이 바로 산탄광 Es(r, t)의 발 원이 된다고 볼 수 있다. 따라서 Es(r, t)는 다음과 같이 주어진다. Es(r, t)oc _gL,: _0 , E q ,., exp i (ks•r-( (I)。±(I)q)t))v ,ex p i (ko 士q -ks)•r'dV'
~ .,t. ,. E0, ai ex pi (ks•r-( (JJ o 土(JJ．)t )o(k 。士q -ks) (V.11) 따라서 주어진 입사파 (ko,Wo) 에 대해서 모든 3SN 개의 격자 진등이 광산란에 전부 기여하지 않고, 입의의 산란각 0 에 대하여 q= lk 。 -ksl =2 k 。 sin ½ 0 (V. 12) 로 주어지는 일정한 q값의 정격 모드 즉 3S 개만이 기여하게 됨을 알수있다. 이것은 포논 개념으로 보면 에너지와 운동량 보촌의 결과이며 h0s=l iw o 士 llW q ks=ko 土 q (V.13) 와 갇이 위에서와 갇온 결과를 얻을 수 있다. 여기서 주목할 것은 결정체 해밀토니언이 모든 병전이동이 아니고 번호가능 (d i scre t e) 한 격자 벡터에 국한되어 병전이동 대칭성을 만족 시 키 므로 Umklapp 현상도 가능하지 만 실제 광산란에 서 는 거 의 문제 가 되지 않는다. 정 광도의산 란과에장 을기 여갖 하게는 되 포 며논 온Br ilql o~u. iJ2n , kz o。 nsien 의 .2l , 크{) 기$ 1: 05 =cm 1-018 로cm서- 1 즉에 광비 과하여장 무시할 수 있는 q 값 즉 q -+0 의 zone 중십에 아주 가까운 모드들이다. 이 중에 브릴루엥 산란은 음파성 모드들에 의한 산란이 며 q-+ 0 의 음 파성 전동은 unit cell 안의 모든 원자들이 갇은 위상으로 진동하는, 다 라서 최소한 unit cell 수백 개 정도의 거리에 걸쳐 원자들의 변위가 균일한 모드들이므로 탄성물체에서의 탄성과 파동으로 근사시킬 수 있다. 따라서 음과성 포논에 의 한 광산란 현상을 음과에 의 한 Bragg 반사 현상으로 취급할 수 있게 되며 아래 그림 V(5) 에서 브래그 반사의 조 건을구해 보면 꿈 =2 A s i n( 송 7C 국) =2A sin 0 /2 (V.14)
도플러 변이는 (J) s= (J)。 ±( 2 v/ 음)(J)。 s i n 拉 =(J)。 土 2 v n k 。 sin ½ (} (V.15) 가 됨을 알 수 있다.
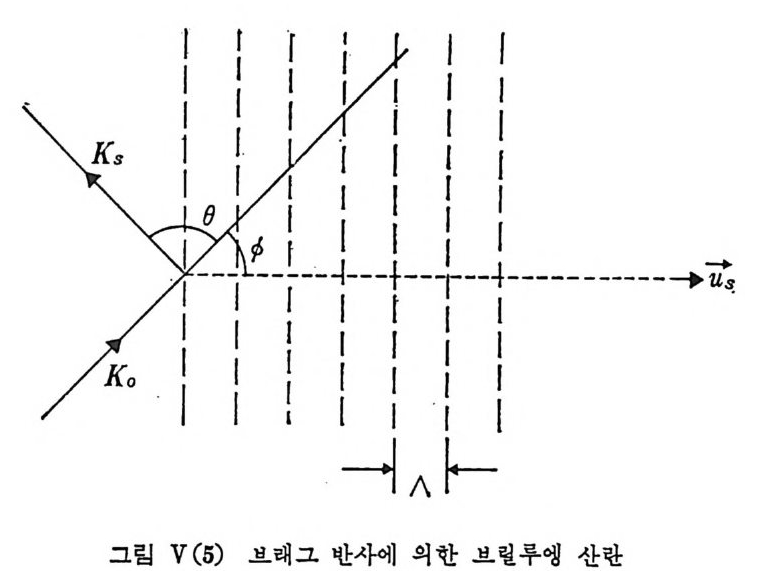- -➔fu s.
따라서 위의 두 식으로부터 (J)s = (J)。土 v k 。 lo/A =(J)o 土 V 뚜=(J) o 土 v q (V.16) 를 얻을 수 있다. 한편 음파성 모드의 분산곡선을 보면 q -+0 에서 W q =V q가 되므로 4 (I) B=0s_ (I)。=土% ==士土 24 vin.kAn 。~o s iv~n s-. ·J2i·n. · { —} 21- 0 (V.17)
로 주어지고 따라서 브릴루엥 주파수 변이는 후방 산란({) ..... r) 에서 재일 크고 전방 산란({) ..... 0) 에서는 0 이 됨을 알 수 있다. 많은 결정에 대해서 v/c:::: :::: 1 。 _5 에 달하므로 4 야 I :::::::: 1~3cm 기 정도가 된다. 좀더 미시적으로 보면 장과장의 음파성 포논에 의해서 국소적 왜형 (s t ra i n) 이 생기고 이 왜형 eu 죽 탄성 변형이 아래와 같이 주어지는 가시광 주과수 영역의 유전율텐서 c 의 변화를 가쳐온다. 8€µa = -E cm Ppm ij cU, eiJ (V. 18) P,IT 여기서 P p c,u 는 Pockels 광란성 계수이고, 또 여기서 6cµ’ 의 시간 변 화가 eiJ 죽 음파성 포논의 전동수 (J)q에 따르게 됨을 볼 수 있다. 한 가지 주의할 점은 q =O 의 음파성 모드는 사실 결정 전체가 그 대로 움칙여 가는 병전 운동에 해당하므로 업밀하게 따지면 유전상수의 아무런 변화도 가져올 수 없다. 따라서 q -0 이지만 q * 0 의 사실 때문에 브릴루엥 산란이 가능하 게 되는 것이다. 브릴루엥 산란에서는 라만 산란과 달리 한 결정에 대 해서도 산란텐서가 q의 방향에 따라 달라진다. 가령 진행 방향 q와 편극 U 가 주어전 한 음파성 노드에 의한 브럴 루엥 산란을 실제 계산하려면 변위 벡터 u 에 대한 운동 방정식을 풀 어서 그 해로부터 이 음과성 모드에 의한 e i 1 를 구하는 계산이 요구 된다. V-1.3 라만 산란 의 부에 서 E 。 cos (J)。t 의 전장을 가전 광과가 편극물 a 의 분자들로 구 성된 계에 입사하면 분자들에 유도되는 쌍극자 모멘트 P( t)는 P(t) = a(t) Eo cos w 。t 로 주어진다. 여기서 a (t)의 시간 변화는 분자의 회전, 전동 및 분자 사이의 충돌 등에 기인하고 있다. a( t)를 푸리 에 전개 하면 a(t) = I; iin c os(Qn t + 8n) CV. 19) ” 에서 죠「울 n 번째 정격 모드(Q n) 에 관련된 라만텐서라고 볼 수 있다.
P(t) = I: (a E 。 )cos( Q n t + ()n) COS (J)。t =}2 }n2 (a E 。) {cos[( Q급 Wo) t + fJ』 + COS[(Q n -Wo)t + fJ』 } (V. 20) 에 서 P (t)는 바로 (J)。, (J)。±Q n 에 해 당하는 복사의 발원 이 되 고 있 다. 이제 라만 산란의 스펙트럼 분포밀도를 계산하기 위하여 이둘 발원 에 의해서 방출되는 복사 전자장을 E(r,t) , H(r, t)라 하면 분명히 유 한한 시간 T에 한하여 E(r, t)= Er(r, t) 수 O H(r, t)三/l T(r, t) =O !ti
이므로 Sr(r) = 紅 :. . dw {E(r, w) x ii(r, - w)} (V. 23) 를얻는다. 한편, ET(r, (J))= 点仁 d t ET(r, t)e ;.,, 료 (r, (I)) = 去 仁 dt HT(r, t)ei ., C 에서 iicr, - (J))= H*(r, (J)）가 되므로 ST(r) = 으4 !J .0.. dw {E(r, w) x if* (r, (J)) +C.C. } (V. 24) 를 얻게 된다. 이제 r 만큼 떨어진 거리에서 면적소 dA 를 동해 나가는 복사과 출력을 dl(r) 라 하면 dl(r) =ST • dA 로 주어진다. 한편 J (k,w)=- i wP(k,w) 에 의한 복사 전자장은 ECr,w)=-무 (J(k ,o)Xf )X f eiE €a) r =-上 c (P(o) rX f ) Xt eik r, ii(r, w )=-노 C P((Jr) ) ~ eik •r (V. 25) 로 주어지므로 E(r,w)xi i(r, - w)=( 음)우 {[(P(w)xt )x rJ X [P(-w) Xr]}
= 上f: ..Cl. . 됴 릅 {rlP(w)X f- 1 가 CV. 26) 따라서 dl(r) = 上4 -1E!: ...J.i _ O.O. d(I ) k(I) | P(w) x k l2 r • dA/r2 = +촨 :d (I) k (I) |P( (I)） xkl2dD 따라서 옮=十쓴仁 dwkw j P(w)xkl2 三J__:.., ]o(w)dw 로부터 스펙트럽 분포밀도 ]o(w) 가 아래와 같이 얻어진다. ]o(w)= -4! --€~ k wlP(w) xkj2 (V. 27) 한편 Wi en er-Khin t c h in e 정 리 에 의 해 서 IP (w) x k l2 == -土½2 군z- 1i- - ...... .. < = -fr-t: dt P ... (t)•P _.(t+ r) =令 L:d tJ_：다 :d a,' P,.(a,) • P_.(a,' ) e-i .. t e-w(t+ r) =土2Tj J_ .길. j _.. .. da ,'P ,.(a,) • P_.(a,' ) L:dt e-. . +.,,,, e-;.,,, = 11: J_: 다 .... da ,' P,.(a, ) •P,.(a,' ) e-;.,,, 뿡
= 寸 -OoOo d(J) P ... ((J)) ·P ... C-(J) ) eiw r (V . 29) 가 되고 이것의 역푸리에 변환에서 김 E~( (J)） ·P~. .. (-(J)) =,.1 ¥ ... ((J)) | 2 = 吉條 e- i 〈 P ... (t)• P ... (t+ r)> 즉, IP~((JJ) P= 습깁: &
e -iG IT& (V. 31) 의 결과를 얻게 된다. 이로부터 산란광의 스펙트럼이 편국요동의 상관함수의 푸리에 변환 으로 주어지고 있음을 볼 수 있다. 우리는 다음 철에서 편극요동이 편극물 요등과 어떻게 연관되는지 알아보기로한다. V-1. 4 편극률텐서 이제 광산란 상호작용을 양자역학적으로 보면 결국 K=Ko-P(t) • E(t) 에 대한 해를 구하는 문제가 된다. 위에서 E(t)= e+ e1 ... t+ e-e -i '‘ Kolm〉 =당 .. |m〉 를 가정하고 我써(t)=iti경「a# '(t)로 놓을 때에 ¢.(t)= lm> e-•t/ a + {¢.+ eiGJ o t +¢. . -e -;.,,1} e-,r. ~ (V. 32)
을 대입시키면 災써(t)= ［我。 -P• (e ... eiU ot + e-e-'Uo t ) H Im> e-;a-. ''• + (¢. . + ei• •ot + ¢. . -e - iw ot ) e- ;;,. ''} =? -!f .P. lm· (> ee+ -,eg1. t' 'I ''+ ＋e -念e。-(,r./,0>' n) 나 lm ?i w> o te +-,¢g ... -tIe A 다+ O…o t )…e- ; '’. CV . 33) 또 ih 홉 ¢ .. (t)＝마-수 Im> e -ir .II . +
=In: 앙
로 쓸 수 있다. 여기서 蟲 I)( (J)。 )=2” { 〈 m I力P 』 (n 〉〈( n |JPb|)l 〉 ~++
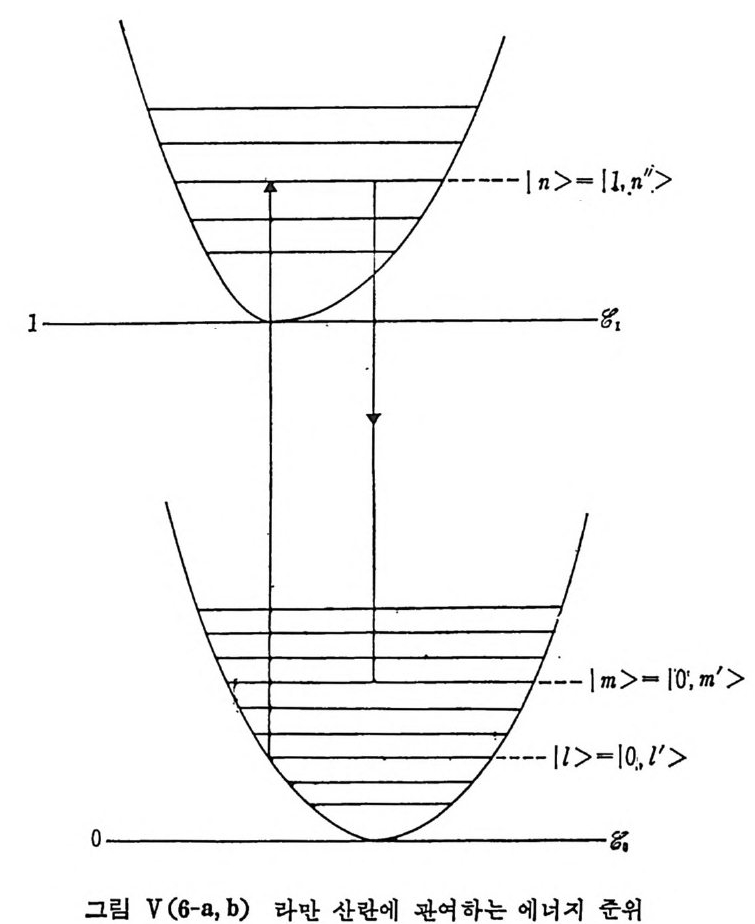-----1 n>= 11,.n '<>
이 제 소위 Placzek 근사에 따라 라만텐서 를 계 산해 본다. 위의 그림에서 |l 〉 =|0,!' 〉과 |m 〉 =|O,m' 〉온 전자에너지 상태가 모 두 기처 상태이고 전동에너지 상대는 각각 !',m' 의 여기 상태에 있음 을 나타내고 |n 〉 =I1,12 〉온 전자에너지 상태가 여기 상태(1), 전동에 너지 상태도 n” 의 한 여기 상태에 있음을 나타내고 있다. 이때 Placzek 근사로첫째 (J)n l= (당 n- 8' 1)/ fl =@+C%_Co- 타 )/h :::::::(e1-eo)/tz =(J)10 둘째 (J)1 0~(J )o 를 가정 하면 a 땅=〈 mlaabll 〉 = = = E.. 2I p .{(a<•I) ．살) ... e i (C1 ■ 1+41o)I +(7xc. . o•e-).a. e i(야 ,-.,o) t} {(였야)． e+),. e1<.,.,+ CJo )Ct + T) + (7xc1 ■ > -e-) .a. ei( .,,.-.,o>C t+ T)} =휴 홈 P,. {(었 GI) .e+), .(aCl> •e-),. el<.,p -o.)T + (겼 ( m i) .e-) 上(였 (lm) .e+) ... e1(.,,.o)T} (V. 44) 를 얻게 된다. 이 제 6 가, 즉 입 사광이 b- 축 방향으로 편광되 고, 산란광 즉 P .1.7 ]-a - 축 방향으로 편광된 경우를 고려하면 a g ll a&m) eg e b-e iC .,,.-o.” +a( 감 ac ~: ' eb-eb+ e;c ., ,.+.,o)r} =L L p' { 동으로 하여금 편극물 타원체가 변형된다는 것을 뜻하며 그 변형 양상 이 바로 관계된 격자 전동의 대칭성에 의해 결정된다. 광과 편국물텐서의 가장 일반적인 변형은 세 주축 방향의 신장 또는 수축과 제 축 주위의 회전의 결합으로 표시할 수 있으며 이것은 다음과 같은 방정식으로 나타넬 수 있다. (A+E x:x: )X 댜 (B+ 1: 11) y 2+(C+Ezz)z2+ 1: ,,,xy +E1zYZ+EuZX=1 (V. 46) 여 기 서 Exx, E' c' c' E' €~ 가 바로 편극물텐서 타원체 의 변형 을 가 쳐오는 텐서성분이 된다. 먼처 tot a l ly sy m metr i c vib r ati on 과 관련 된 위 의 텐서 성 분율 생 각해 보면 이러한 진동운동은 타원체의 대칭성을 그대로 유지해 주고 있으므 로 세 주축의 방향이 그대로 불변이고 다라서 Ex,=E,z=Ezx=O 가 되어 야 함을 알 수 있다. 오칙 가능한 변형은 전체 타원체가 균등하게 그대로 닮은 꼴을 유지 하면서 팽창 • 수축하는 것을 생각할 수 있고 이것은 입방체 결정에서 €xx=E yy =Ezz*0 을 뜻하고, 단일축 결정에서는 Eu=En*Ezz, orth o rhom- bic cry st a l 에 서 는 cxx 수 c 수 €zz 가 될 것 이 예 상된다. 이제 비대칭 진동 모드 중에서 한 예를 듣어, 가령 어떤 전동 운동 상태에서 unit cell 내의 원자 배열 구조 죽 전동 모드가 (Jy 거울면 (xz 평면)에 대한 반사에 대해서 대칭이고 z 축 주위의 180° 회전에 대해 서 반대칭인 대칭성을 보이는 경우를 생각해 보면 이 전동 모드의 모 든 변위 벡터는 분명히 c y평면 (xz 평면)에 국한되어 있고 z 축이 반대칭 축이 되어야 하므로 Z- 축의 x-z 평면에서의 운동은 회전운동이 된다. 죽 이러한 전동 모드에 의해서 편극물 타원체는 y축을 회전축으로 만 순히 회전하게 되며 이 경우 E :x::x: =E77=Ezz =O 가 되고 또 이때 희전에 의 해서 y축 방향으로는 아무런 변화가 생기지 않으므로 Ex1=E1z=O 가 되 어야한다• 마찬가지로 z 축 회전축에 대해서 반대칭이고 y축 회전축에 대해서 대칭인 전동 모드를 생각하면 y축이 대칭축이므로 z 축이 우선 xz 평 면에서 머물러 있어야 하고 또 z 축 자신이 반대칭축이 되어야 하므 로 z 축의 xz 평면상의 운동은 희전운동으로 국한된다. 이러한 전동 모 드는 또 당연히 x 축에 대해서도 반대칭입을 알 수 있다. 따라서 위
의 세 경우에 각각 해당하는 대 칭 성을 가지는 전동 모드 전부가 오직 도 성분만 0 이 아닌 값을 갖게 됨을 알 수 있다. 이제 z 축에 대해서 반대칭이고 (J,:거울 반사면(y z 평면)에 대해서 대 칭인 전동 모드를 보면 c y z*O 이고 다른 나머지 성분들은 모두 0 이 될 것이 분명하다. 만일 z 축에 대해서 반대칭이라는 조건만 보면 이것은 바로 (Jz 거울 떤 반사에 대해서 반대칭인 경우와 같고 이러한 대칭성을 갖는 전동 모 드는 ( x z 수 0, c yz 수 0 가 되고 나머지 성분들온 모두 0 이 되는 편국을 미 분텐 서 를 나타넬 것이 예상된다. 따라서 유일한 대칭축 (z 축)을 가 지는 monocl i n i c 구조의 결 정에서 반대칭 격자 진동을 생각하면 모두 도 =En =E zz =O 및 €x y = 0 가 됨을 알 수 있다. 다 음으로 축되 전등 모드를 살펴보면 이들 전동 모드는 대칭주축 주 위의 회전에 의해서 서로 사이에 치환되는 것이 목칭이며 따라서 이 주 축을 z 축으로 택하면 이들 진동 모드는 x 축과 y축상의 병진운동 또는 x 축과 y축 주위의 회전 운 동으로 구성되어 있다고 볼 수 있다. 따 라서 이들 축되 모드에 대한 라만텐서를 결정할 때에는 가령 x 축 또 는 y 축 주위의 회전 운동이 동시에 여기된 것에 해당하는 전동 모드 로 생각하여야 한다. 이러한 전동 모드는 이들 두 축에 수직한 yz 및 xz 평면 내에 국한되어 있어야 하며, 따라서 가령 OX 축 방향으로 전 장이 걸릴 때에는 y z 평면상의 성분은 쌍극자 모멘트 유도에 전혀 기 여할 수 없으며 오칙 xz 평면상의 성분에 의해서 2 축 방향으로 전등 쌍극자 모멘트가 생길 수 있는 것이다. 따라서 cxx=€xy = O, €x 쵸 ~o 가 됨을 알 수 있고, 전장을 Y 축 방향으로 걷 대에는 전동 운동의 xz 평 면상의 성분은 전혀 무관하고 yz 평면상의 성분에 의하여 역시 z 축 방 향으로 전동 쌍극자 모멘트가 유도될 수 있 다. 따라서 €xy =g= O, € z 룬 : O 를 알 수 있고, 전장이 z 축으로 주어질 대에는 xz 평면 및 yz 평면상의 전동 변위에 의해서 각각 x 축 및 y축 방향으로 쌍극자 모 멘트의 요동이 생기며 이때 축되에 의해서 Exz=E ” 가 됨을 알 수 있다. 족, 이와 같은 축되 전동 모드에 대해서 전체적으로 E,,,,=E11=Ezz=O, Ex,=O, E , z=Ezx-:/=O 의 결과를 얻게 된다. 마찬가지로 병전운동형 축되 진동 모드를 생각하면, 죽 x 축과 y축상의 동등한 병전운동형의 전동 모드가 동시에 여기되는 그러한 형태의 축되 전동 모드를 생각하면 이 러한 전등 운동은 분명히 xy 평면상에 국한되어 있다. 이러한 진동 모
드에 대해서는 앞에서 논의한 바와 같이 c x x=-E “ 수 0, G.Y =g = E===o 로 주어지는 편극물 타원체의 변형이 가능하고 축되 조건에 따라 cxx= € 죽 OX 축 방향으로 전장이 주어지면 x 축과 y축 방향의 변화가 완 전히 같은 결과를 주게 됨을 알 수 있다. 이상과 같이 기하학적 대칭성울 라만텐서의 결정에 칙관적으로 도 입하는 예를 보였지만 군론의 수학을 적용하여 체계적으로 타만텐서의 구조를 여러 대칭군에 따라 각각 분류 결정할 수 있다. 이제 고체 내에서의 라만산란 단면저에 대한 계산 내용을 보면 포논에 대해 , 아래 그림에서와 같이 상호 작용 이전의 초기상태 Inj, 0 ; o,0 〉 와
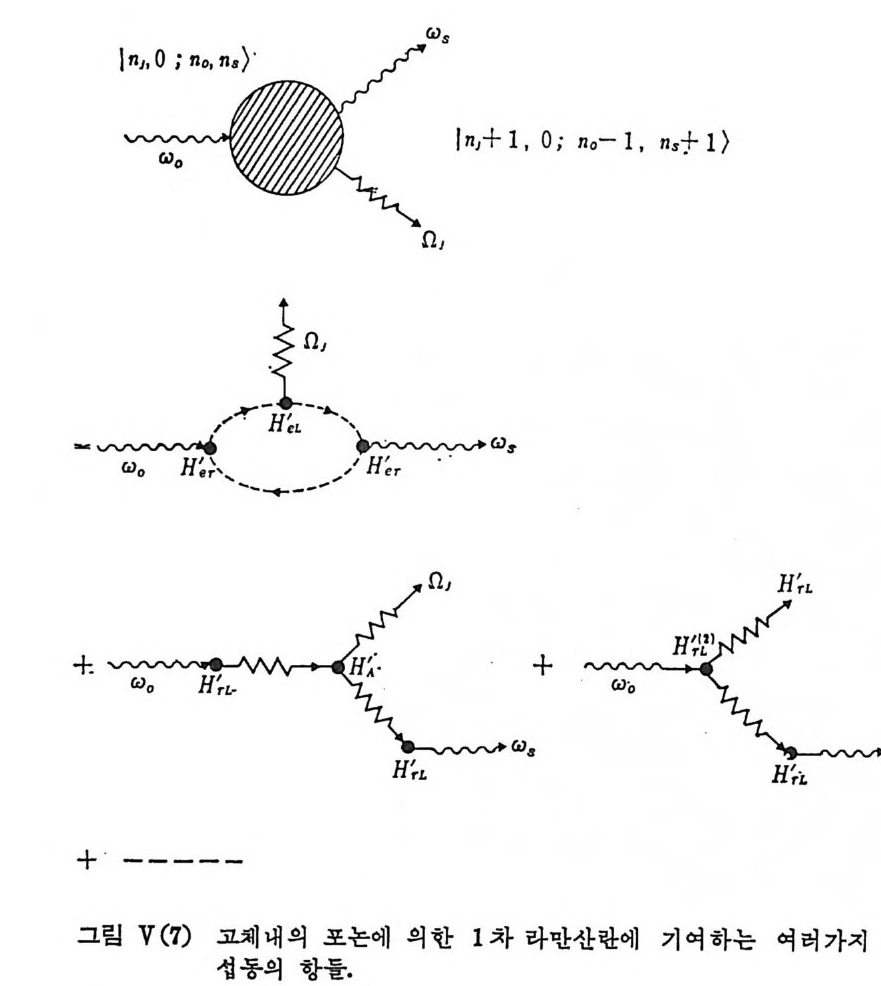Cus
상호작용 이후의 종말장태 |n;+ 1 , O ; n 。 -1, 1 〉 를 비교해 보면 nj- -- +ni + 1 즉 포는(Qj, qj)이 하나 생 성 되 고, (t)。 의 입 사광 광자 하나가 소멸 (n 。---+ n 。 -1), (t)，의 산란광 광자 하나가 생성 (0---+1) 되었음을 나타내고 있으며 이 대 에 상호작용에 관여 하는 전자의 상태 는 I o 〉 에 서 들뜬상태 (exc ited s t a t e) 로 갔다가 다시 바닥상태 IO 〉 로 되돌아감을 (0---+0) 알 수 있다. 드 그림에서 H',L 은 전자와 격자 운동 즉 포는, H'., 은전자와광자, H',L 과 H'rL(2) 은 각각 광자와 포는 사이 의 1 차 및 2 차 상호작용을, HA’ 는 포논과 포논 사이의 비조화 상호작용을 나타내고 있다. 위 그립에서 전자가 중간 상태에서 참여하고 있는첫번째 섭동항이 대 부분의 고체 결정에서 가장 중요한 기여를 하고 있으며, HIcr 와 H'cL 에 관여하는 중간 상태를 분석해 보면
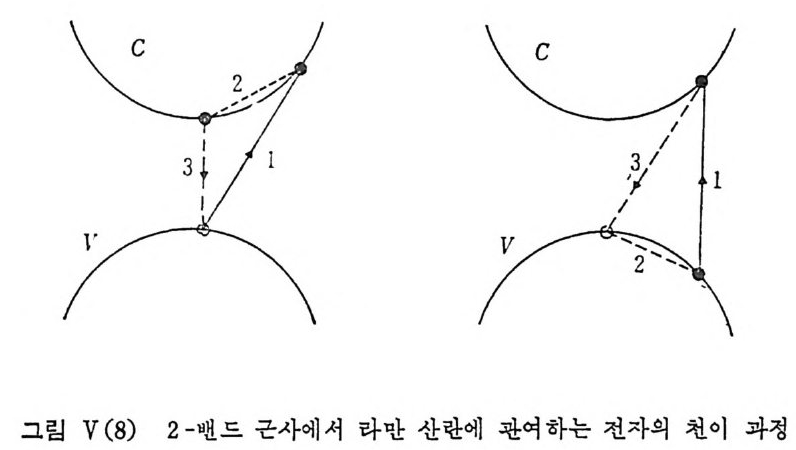\2广 c I 3I/ I' I I '鼻 l
위 그림 에 서 와 같이 2 -벤드 근사(t wo-band a pp rox i ma ti on) 에 서 〈 alH'.,= p •e 。 IO 〉, , 〈 OIH'.,= p •e,1 (3〉의 차례로 3 차 섭동 론의 계산이 요구됨을 알 수 있다. 즉, 그림 V (7) 의 첫 번째 도해 (d i a g ram) 에 의 한 기 여 는 아태 와 같이 주어지는 라만텐서로 쑬 수 있다. R10,,(q ) =杓 aE, P {
x <(3|H ,‘L |a>< a lp • e,I O >/ ( Wop + wo)(wao+w,)} 여기서 H'cL 은 <(3, ~1cLl a>= L pa X(q) +Up a J (q)+ F1pa +A1pa 와 같이 나누어 계 산할 수 있 으며 L,a 는 변형 포텐셜 (defo r mati on po te n ti al ) , x( q)는 포논 Q;(q)에 의 한 원자 사이 의 변위 , y(q)는 포논 Qj(q)가 초래하는 탄성변위의 기울기를 나타내며, 따라서 처음 두 항은 이 들 포논 Q;(q)에 의 한 뒤 돌림 변형 장 (s t ra i n fi eld) 과 전자 사이 의 상호 작용을 나타내고 F t a 는 9I( q)의 포논이 수반하는 전장 E1( q)와 전자 사 이 의 상호작용을, A,a 는 역 시 Q;(q) 포논에 기 인하는 횡 과 전장(t rans verse electr i c fi eld) 에 의 한 운동량 교환칙 용 (momen t um i n t erac ti on) 을 지칭하고 있다. 이러한계산결과즉위의 |R\,12 에 비례하는라만산란효율을구하 떤 다이어몬드 단결정의 경우 ~10-·cm-1 Q-넥 1 달하는 값이 되고 있다. V-1. 6 L.O. 포논과 T.O. 포논 입방체 대칭성을 가지는 결정에서 보면 포논의 파수 벡터 q에 대하 여 편극 벡 터 E가 q 에 평 행 한 종 모드와 f 가 q 에 수칙 한 두 개 의 횡 모드가 촌재한다. 이들 종 모드와 횡 모드가 각각 라만 산란에 어떻게 다론 기여름 하개 되는지를 검토해 보기로 한다. L.O• 모드와 T.0. 모드가 분리되는 극성 포논에 대해서 라만 산란 단 면적이 아래와 같이 주어진다. 젊 ;o, oc | e,i a ’I:hq h e 。j 「 (V. 47) 위에서 a iJ는 유전감수율의 미분값 (der i va ti ve), 죽 Eo 경 :TX ii를 나 타내며, E 는 극성 포논 W 에 의해서 형성되는 편극의 단위 벡터, q는 극성 포논의 파수 백터 i,j ,h 는 모두 x,y, z 성분을 지칭하는 첨자를 나 타내고 있다. Td(43m) 대칭성의 입방체 결정에 대해서 a{ J한 가 표 V (A) 에서와 같이 주어지므로
표 V(A) a 텐서
임의의 산란각 0 의 라만 산란 실험, 그림 V(9) 에 대해서 식 (V. 47) 을 적용해 브면
T9
종파모드는 | e, i(q Xa iJ e 다-q za ii단 )e 。J I 2 =I (c+os( O三 O ,;n O )) [S(l n ~ ½fo) ] o0( a\!a Ic) o。 )s 2 1—2 。 。 =I (cos8 O sin 8 ) [(.c\ 。 ) + ( as:½ °) ] 2
= 1( a sin e cos ½e+ a cos e sin ½e ) 12 = IaI 2s in 2 (e + 송 이 =__= l a_( l2 0Cs Si.n o2( O요2 lI o宁o.\msSom/.Sns a I1 0so—c—lslo_.le— 2\` 11o _)。 aooO . m -2|끄\궁/1za0l l. mo1l2 a200꾹 /2 aO1 I_ 2c' r s- s'2 a2.0\ 0.1\+ n0a\c ) .0—o2_S Os 0a .I—12 /) \0O_o 0 0,,\ _0_/4|\‘ _2( (0l|a V V`'0__. 0. 1\. a a44)\982/) 00)o ) l 0 o0 /\ 0_ _ 1 00 횡과모드는 eJ.. . ( q raI~J Ey +qxsd . c -ql ~~oa cc ~r Exoc q0)o3 |1yas ))oeOO,..| 2o2O la-o_ a OR2o o ou/n ' 1\ / '1\ 이것을 그림으로 표시하면 아래와 같다 . 아래 그림에서 보는 바와 같이 T.O. 모드는 전방 산란(fJ =O) 에서, L.O . 모드는 후방 산란 (8=180°) 에서 아주 강하게 나타남을 알 수 있 고, 8= 9 0° 죽 칙각 방향의 산란 실험에서 우리논 T.O. 모드와 L.O . 모 드를 동시에 관측할 수 있게 됨을 볼 수 있다. 이제 비슷한 문제로 단일축 결정의 경우를 생각하면 주 대칭축을 z 축 으로 택할 때 격자 진동의 모드 편극이 z 축에 평행할 때를 ))II , 수 직할 때를 ))J. 로 표시하면 아래 표 -V(B) 에서 보는 바와 같이 결정축 x, y ,z 축 방향으로 진행하는 격자 진동에 대하여 여러 경우 를 생각할 수있다. 만일 q 가 z 축에 대해서 일반각 f)”의 각을 이루는 때에는 이방성을
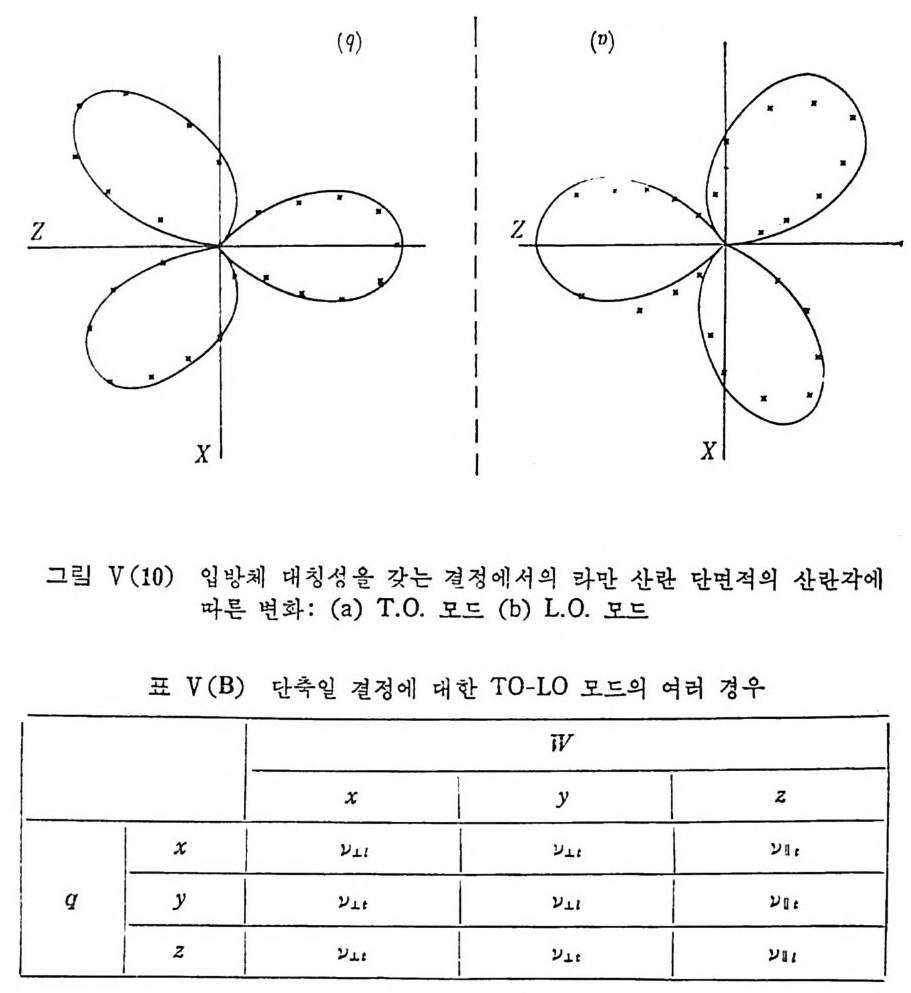(q) ( 미
가져오는 단거리 힘이 TO-LO 분리를 가져오는 장거리 정전력보다 훨 씬 큰 경우 편국이 서로 혼합되어 다음과 같이 q의 방향에 따라 진동 수 o 가 O t와 0l 사이에서 여러가지 값을 가지게 된다. 죽, xz 평면상에서는 (I)2 =(I )2 u, sin 2 ()''+(I )2 u1 cos2()'’ (V. 50)
xy 평면에 대해서는 w2=w2.L t COS2(}''+w2.L z sin 2 (}'’ (V. 51 ) 의 결과를 얻게 된다. 반대로 단거리 힘이 LO-TO 분리의 항보다 휠싼 적은 경우에는 xz 평면의 포논에 대해서 wi2 = w2 u1 sin 2 {}'' +(l)2J .I COS2{}'’ (V. 52) 마찬가지로 종파 모드에 대해서도 (J)l2 =(J )2 u z cos28 +(J) .. ,2 sin 2 8 ( V . 53) 로 주어지며 이와 같이 포는 진동수가 q와 z 축 사이의 각 0'’ 에 따라 서 (J)o 와 (J).L 사이에서 달라지게 됨을 알 수 있다. V-1. 7 Second Order 스펙트럼 제 2 차 라만 산란온 두 개의 포는이 참여하는 산란 현상이다. 이중에 2- 포논 생성 과정의 라만 산란을 고려하면, 에너지 및 운동량 보존 법칙에 따라 {).,q+Q,,,q,= Wo— m' q+q '=l( 。 _K' (V. 54) 훌 만족시켜야 된다. 여기서 s,s’ 은 포논의 가지 기호이다• 따라서 q가 제 1 차 산란에서처럼 반드시 적은 값 (:::::O) 이 되어야 할 필요가 없으며 브릴루엥 구역 전체의 모든 값을 다 가질 수 있게 되는 것이다. 빛, 즉 레이처의 과수 벡터는 브릴루엥 구역 전체를 생각하면 그 크기가 0 에 가까운 매우 적은 값이므로 q+q ':::::O 를 가정할 수 있 으며 Q,,q+Q,,,-q=<.V。 _o'=4 <.V CV. 55) 의 결과를 얻는다. 따라서 라만 주과수 변이 4(J ) 에 해 당하는 산탄광 강도 는 결국 두 진동수의 합이 4 (J)가 되는 포논쌍의 총 갯수에 비례하며 이 것온, 모든 가지에 대해서 Qq=Q국이므로, 4 (J):=Q의 함수로 볼 때에 p,,,,(fJ)= 'LpI Lg o(Q -Q,,q-Q,,,q)
로 쓸 수 있고 소위 결합상태 밀도 또는 포논쌍 상태 밀도라고 부 론다. 이 함수는 사실 거시적인 결정체 시료를 생각할 때 9 의 연속함수가 되며 따라서 제 1 차 산란에 서 선스팩트럼이 되는 것과 달리 제 2 차 스 펙트럼은 연속 스펙트럼이 됨을 알 수 있다. 이러한 결합상태 밀도에서도 /7q(Q,,q+Q,,,q )=O 에서 van Hove 특이 정 이 나타나며 이 것은 /7q Q,,q = O, /7q Q,,q=Q 즉. s 및 s' 가지 가 모두 임 계접을 갖는 q에서 특이접이 생기고, 또 s,s’ 가지가 크기가 같고 방 향이 반대인 기울기를 갖게 되는 q에서도 특이접을 갖게 되므로 p,,,(Q) 가 단일 포논상태 밀도브다 칠,l(J. 복잡한 van Hove 득이접을 가질 것 이 예상된다. 일반적으로 제 2 차 스펙트럼은 /7qQ,,q=Q의 임계접들이 대부분 zone 경계면에 촌재하므로 이들 zone 경계면 포논들의 결합에 해당하는 9 에서 정봉이 나타나고 다론 특이접들은 주로 급한 칼날을 형성해 주고. 있다. 이 밖에 다중 산란에 의한 제 2 차 선 스펙트럼, 죽 q =O 의 포논 Q I 에 의한 계 1 차 산란의 광자가 결정을 빠쳐 나오기 전에 다시 q= O 의 다른 포논 92 에 의하며 다시 1 차 산란되어 나오는 경우 라만 주과 수 변이 4o 는 4o=9 급-Q 2 가 된다. 이것은 결정의 크기에 비례할 것 이 예상되며 또 결정의 비조화성에 기인하는 배전동 291 및 결합 벤드 Q 1± Q 2 에 의한 제 1 차 라만 스펙트럼은 원칙적으로 본성 제 2 차 스펙 트럼과는 구벌되어야 한다. V-2 기 타의 다론 기 본 여 기 파 (O t her Elementa ry Exci- tat i on s) V-2.1 폴라리톤 (Polar it on) 라만 산란 격자 전동 중에 결정이 전체적으로 편국을 갖도록 하는 변위의 모드 가 가능하고 이 정격 모드에 의한 격자 편국을 유효 전하 Zs 를 써서 다음과 같이 표시할 수 있다. P= 衍 ZsWs~s (V. 56)
여기서 es 는 정격 모드 S 가 기여하는 편국의 방향을 나타내는 단 위 펙터이다. 의부에서 전장 E 가 주어질 때 이 정격 모드에 대한 운동 방정식은 Ws+I 'sW s+Q s 2 Ws=Zsfs • E (V. 57) 로 쓸 수 있다. 여기서 Q s 는 I's=O , E=O 일 대의 격자 전동이 갖는 진동수이다. 그러나 극성 전동은 그 자체에 의해서 거시적 전장이 생기 므로 위의 E 를 의부 전장 대신에 모드 자체에 의한 내부 전장으로 보 면(단, 종 모드에 한함) 모드 전동수가 9 s 와 스스로 달라침을 알 수 있다. 한편 진동과(q ,9) 의 전기장은 맥스웰 방정식에 의해서 c2q (q• E)+(c2q2 -n2)E=4 김 22 p (V. 58) 즉, 아래와 같은 관계식을 만족하고 있다. -c2q (q• E)+(c2q 2 -E Q2 )E=O CV. 59) 여기서 E=l+4nx, P;=X;;E; 이며 x 죽 €은 석 (V.56) 과 (V.57) 로 부터 구할 수 있다. 식 (V.59) 에서 E 를 소거하고 c ~ Q / q률 가정하면 아래와 같은 결과 를 얻을 수 있다. €x 합+€y섭 +€z 합 =U CV. 60) 한편, 결정이 입방체 대칭성을 가질 때에는 모든 q에 대해서 식 (V. 59) 로부터 다음 관계식을 얻게 된다. E (c2q2 - E Q2 ) =O (V. 61) 이들 결과에서 첫째 E=O 를 만족하는, q에 무관한 종 모드 전등수를 얻고, 다른 두 해는 횡 모드들로서 Tc2qz 2 =E(Q) =Eoo TH((((//..)i)2f --QQ22 )) (V. 62) t 로 주어진다.
이돌 해 를 그 립 으로 그리면 아래와 같 이 포논과 광자가 완 전 히 결합 된 소위 폴라리톤 여기과의 분산곡선을 얻게 된다•
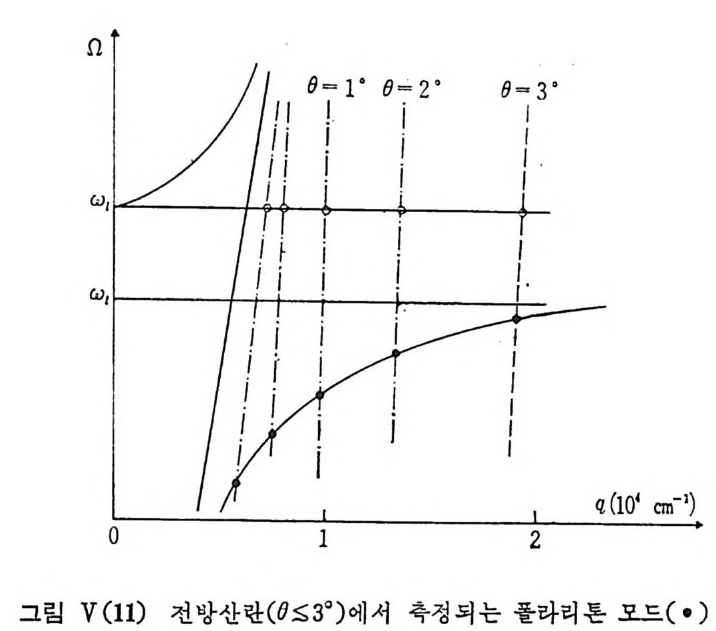wn, II. l.i.Il’ a u.’iI- il · 8- iI-i= 2 · 。= II'I‘3I ·
석 (V.62) 에서 Q > 야의 경우에는 요Q= 五乙 (V. 63) 즉, 매질 속에서의 광과를 나타내며, 또 q :}> 104cm-1(8 :}> 3°) 가 되면 이 둘 폴라리돈 결합 모드는 본래의 격자전동과 전자파 사이의 폴라리톤 결합이 없어지고 완전히 독립된 전자과와 원래의 횡파 포논 (J)t로 분리 되어 있음을 볼 수 있다 . . 풀라리돈의 위쪽 가지는 q =O 에서 종과 포논과 서로 만나고 있으며 이로 인해 바로 3 중 축되가 생기고 있는 것이다. 위 그림에서 산란각이 30 이내의 거의 전방 산란의 실험에서만 폴라리 돈의 분산이 관측될 수 있음을 알 수 있다. 위 그림에서 O 로 표시한 산란각 곡선은 다음 식을 만족시키는 곡선둘이다. 즉, 그립 V (1 2) 에서 q =K 。 -Ks
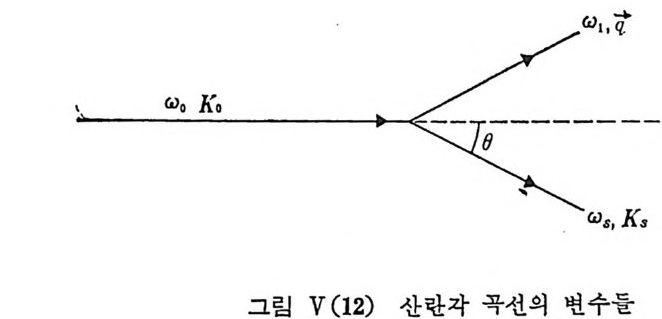씩 7
q 2=K。 2+Ks2-2 KoKs cos 8 Ko=W 。 ”0/c, Ks=Wsns/C (V. 64) 의 산란각 곡선 방정식을 얻을 수 있다. 가령 입방체 대칭성을 가지는 결정에서 no=ns 로 놓으면 훑 = 터 + 4(1-출 ) sin 2 f (V. 65) 가 얻어지고 여기서 8=1°,3° 에 대한 (J),q곡선을 구하여 그립 V(ll) 에 함께 표시 하였 다(-·-·-). 이 러 한 그림 으로부터 우리 논 산란각에 따 라서 풀라리톤의 어떤 모드가 실제 관축에 나타나고 있는지 식텔할 수 있다. V-2. 2 풀라스몬 (Plasmon) 라만 산란 금속 또는 반도체의 전도대에 속해 있는전자들에 대해서는 전자들 사 이의 상호작용을 나타내는 위치에너지 U 가 운동에너지 K 보다 훨씬 적 고 이 러 한 상태 의 전자들은 풀라스마(p lasma) 를 이 문다. 전도대의 자유전자에 대해서 보면 저온 영역에서 운타음 /h (l) P=( 우(잡)미터 ~1 (V.66) 가 되 고 &T> 加)p 의 고온 영 역 에 서 는 전자들이 Fermi -D i ra c 분포가 아니 고 Maxwell-Bo!tz m ann 분포를 따르게 되 고 운군 운 /&T=::: （子(봅 )118/ksT) ~1 (V. 67)
를 만족시켜야 한다. 이러한 조건은 처온에서 축되전자 기체를 이룰 때에는 물론, €::::::1 0 의 반도체에 대해서 전자 밀도가 10“Icm3 이하로 되면 상온에서도 성 립하게 된다. 이들 전자 풀라스마에서 전하밀도 종전동이 가능하고 이들 여기과의 양자불 풀라스몬으로 정의하고 있으며 아래와 갈은 분산 관계식을 가지 게 된다. 갑(q)=(L)/+ +쁩 ~ q2 (V. 68) 여기서 0 p2 =47r : 了n굶e2 r 이며 이들 전하밀도 파동 q가 지니는 쿨롱 포 텐션 에너지 U( q)는 U(q) = 47! V p //€ q2 (V. 69) 로 주어진다. 따라서 q가 커질수록 상호작용 에너지가 적어지고 결국 독립적인 단일입자 거동윤 보일 것이 예상된다. 이들 단일입자가 광산란으로 얻을 수 있는 에너지 加)는 w=w 。 -Ws= 읊 {(k+ q)2 -k 가 =옵- {+qz+ k•q } (V. 70) 로 수어지고 여기서 o 의 최대치는 Wmox(q ) = ~부-(꼴- q2 +kP q) (V. 71) w 의 최소치 Wm i n 은 Wmi n (q ) = 곱 (꼴-q 2-kF q) (V. 72) 로 주어침을 알 수 있냐 이들 결과를 모두 한 그래프에 나타내면 아래의 그립 V (13) 과 같다. 아래 그림에서 보면 qqc 에 서는 단일입자 여기상태가 됨을 볼 수 있다.
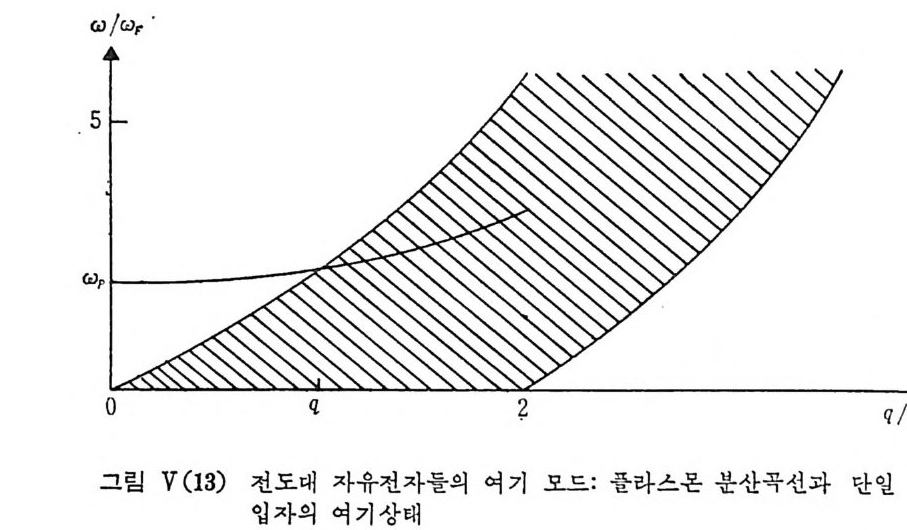o /야 ’
위에서 q c 는 (옵-(+q巨福 ))2= (1)：국쁩엄 즉 q c:::::: 프n尸kF또 CV. 73) 로 주어진다. 이 결과는플라스마에시 차페된 쿨롱 포텐셜, 즉 으€ _r ex p(-q ,r) 에서 주 어 지 는 처 온의 축되 풀라스마에 대 한 Fermi -T homas 차페 파수 벡 터 qsl' T =n~kp (JJp (V. 74) 또는 고온의 비 축되 풀라스마에 대 한 Deby e 차페 과수니 터 qsD = 효1 -1,mk *T (JJp (V. 75) 의 결과와 일치하고 있으며 모두 집체적 효과가 주요하게 나타나는 여°
역을 규정하고 있다. 이러한풀라스마 여기상태는금속의 경우 h 야 ~ 10eV 로서 주로 X- 선 산란 또는 전자선 에너지 손실 실험으로만 실제 연구가 가능하지만 반도 차 의 경우는 불순물 청입농도에 따라 f-l w p가 적의선 에너지 구간의 여러 값을갖게되어 광산란실험을동해 많은연구가수행되고있으며, 반도체의 경우 벤드 간 천이에 의한 흡수문제가 따르기 때문에 가시광 레이처보다도 적의선의 Nd : YAG 레이저가 많이 쓰이고 있다. 이제 플라스마에 의한 광산란 단면적을 계산하려면 念갑습— (P . －운재+당·홍운 =炭。- me* c E_ P~ i· A. ,+ 2me2* · c 2 ZA,2 (V. 76) 로 주어지는 해밀토니언에서 P·A 항의 2 차 섭동 계산과 A2 항의 1 차 섭등 계산에 의한 산란 행렬요소.에의 기여를 고려해야 한다. 고전적 풀라스마에 대해서는 P·A 항의 기여를 무시할 수있고 A2 항 만이 주요한 기여를 하게 되지만 결정체 내에서의 플라스마에 대해서는 P•A 항의 벤드간 행렬요소가 유한한 값을 가지며 특히 입사광의 주과 수가 에너지 벤드 간격에 접근할 때에는 이들 벤드간 행렬요소의 기여 가 커지고 스핀 밀도 도는 에너지 밀도의 요동에 기인하는 광산란울 기 대할 수 있다· 먼처 A2 항에 의 한 광산란, 죽 빛 이 (Ko, (J)。）에 서 (Ks, (J) s) 로 산란 되는 경우를 보면 _2m으*c―2 Zi Ai 2 = ”(J뜨)。(J亡) s 그m누*c-2 Ii :(e o•es)exp (iq• r;) 가 되고, 따라서 훑= (급 )2 군 (표 )z S(q,( J.}) (V. 77) 를 얻게 된다. 여 기 서 구조과악 인자 S(q, m:) 는 S(q, m) = ½211 : JJ_ ... .. dt exp imt (p/t)p_iO) > (V. 78) 를 나타내며 pg는
Pe =) p( r)e-iq • r dSr =) l;.l o(r-r;)e-iq• r d5r =~i e-iq • r, (V. 79) 로서 전자밀도 연산자의 푸리에 변환에 해당된다. 즉, 풀라스마에서의 주된 광산란은 전자밀도 요등(또는 전하밀도 파 동)에 기인하고 있음을 볼 수 있다. 한편 전하밀도 p(q)와 전기 장 E 사이 에 iqE =4 r.e p(q) 의 관계가 있으므로 S(q, (I))=
€(Cu, 0) = f~ ( 1-編 ) 츠기’ -Im E(cv1, 0) =- 즈TE으;: (아 -cvr)/ 2토7[r: i/ 2)2 을 적용할 수 있고 이때 풀타스마 진동수 (J)p를 중십으로 선폭이 7 인 로 렌 츠 밴드형의 풀라스몬 선이 관측될 것으로 예상된다. 그러나 실제로 플라스몬과 광과성 종편국 포논과의 결합 작용 대문에 ✓ n 에 비례하는 (n, 자유 운반자 죽 전자 밀도) (Vp에 극봉이 생기지 않고 이 들 결합 모드의 전등수((J)＋ 와 (J)＿)에 해 당하는 극봉들이 관측되 고 있다. 이 것 은 E(cv, 0) 에 플라스몬((J)p)과 광과성 중편극 포는 (CVL) 이 동시 에 기여하는 경우의 «(I), 0) = EOO (1 + 야 ?:2;2 (:I) ;o I' _ (I)2 :P:(I) 7 ) (V. 82) 으로부터 «(!J ,O)=O 의 해를 구하면 r= I'：：：：：：：。의 근사에서 같 = i2 (갈+갑)土 {（검 +W p 2 )2 -4 Wp 2 Wr2} 112 (V. 83) 로 주어침을 알 수 있다. 또한 고체 내의 전자 플라스마는 군집 모드 이의에 단일입자 모드를 가지 므로 산란 과수벡 터 q 의 값을 차페 파수벡 터 (qsD 또는 qsP T, 식 (V.74) 와 (V.75) 를 참조할 것)보다 크게 택하면 단일입자 에너지 스 팩 트럼을 관측할 수 있다. 이대 유전 상수 E(w, q)의 허수 부분 E(w, q)는 아래와 같이 주어 치며 E( (I),q)=블臼 (nk_nk+ q) 8((I )- 옵(行 +k• q)) 고온에서의 m 를 대입하면
E((I), q) = 麟~ (-i5;-r)1'2 exp (- m*w2/2kuTq 2) 를 얻을 수 있다. 따라서 고체 내의 전자 플라스마에 의한 단일입자 산란의 단면적은 d% = 합 (/)s (%8s)2 ( (/)c2 )2 dQ d(/)s C4111* 2(/) 。 (/)c2 _ (/)。 2 xN(~)1'2 e xp ( -W) 로 주어지며 전자들의 백스웰 속도분포에 의한 도플러 선폭확대의 벤 드형이 됨을 알 수 있다. 실제로 이들 단일입자 광산란은 전도 대 (conduc ti on band) 가 완전한 k2 에 비례하는 포물선 형태가 아니고 가령 k4 항을 포함하는 형태가 될 때에는 (P·A)2 즉 #의 에너지 밀도 요동에 기인하는 항을 포함하여 이것은 전자들 사이의 상호작용, 즉 유전울 차페에 벌로 영향을 받지 않고 따라서 q<{q s 에서도 관측될 수 있다. 또 다른 단일입자 광산란으로 처온에서 중요하게 나타나논 스핀 밀 도 요동에 기 인하는 부분은 e 。 .es=O, 즉 eo.l _e s 의 경 우에 도 가능하게 되며 이때에도 유전율 차페의 영향이 거의 무시되고 있다. V-2. 3 매그논(l\ la g non) 과 라만 산란 매그논온 스팬들의 방향각 요동의 결합작용으로 나타나는 스판과의 양 자를 나타내고 있다. 이들 원자들의 스핀 운동을 다음의 교환 상호 작 용에서부터 고려해 보면 당.f =-2 Z ]iiSj . si i j .. i =--¼2 :Ei µ1•B, (V. 84) 로 쓸 수 있고 여기서 원자의 자기 쌍극자 모멘트 µt는 µ;=rflS ;, 분자력장 B i는 B,= 吉g ]uS J (V. 85)
가 되고 최근접 이웃 사이의 상호작용만을 고려하면 B;= 룹 (S i -I+S i+t), 따라서, 弓운=µi X B i (V. 86) =2]S;X (S;_1+Si+ 1) 의 운동방정식을 얻을 수 있다. 아제 원자의 스핀이 분자력장 방향으로 거의 정열이 되어 있다고 가 정하면 Si = Sz+ a ; (V. 87) 6i 는 X-)' 평 면상의 미 소한 성 분이 된다. 식 (V. 86) 으로부터 6 의 1 차항들만 고려하면 弓우 =2 ]S,x (
加)：：：：：： 2 ]S:a 양 (V. 91) 아 됨을 알 수 있고 이들 관계식은 바로 강자성 계의 스핀파동 에너지 죽 전동수와 과수 사이의 관계가 음파성 포논의 분산 관계와 다룹을 브 여주고 있다. 또한 이방성 에너지와 의부 자장을 고려하면 위에서처럼 k=O 매그 논의 에너지가 0 이 아니고 마이크로 파 또는 원적의선 정도의 유한한 값울 가지게 된다. 매그논 진동수는 일반적으로 포논 전동수보다 훨씬 낮아서 강자성 또는 f err i ma g ne ti c 계에서는 이들 자기적 여기 스펙트럼에 대한 연구는 주로 브릴루엥 산란에 의촌하고 있다. 그러나 반자성 계의 매그논 전동수는 라만 산란에 의해서 관측될 수 있는 충분히 큰 값을 가지고 있으며 따라서 대부분의 매그논 라만 산란 은 반자성 결정체에 국한되어 있다. 자성체 결정의 유전 감수율텐서 x 는 입방체 대칭성을 갖는 결정에 대해서 x.,(M) = I :;Mz -iG:Z -11::,,y (V. 92) -iGM :1 iG M,, Xo 로 주어지며 여기서 G 는 Xu(M ) =x0u+ （編 x ii)。 MI =x%+i G MI (V. 93) 를 나타낸다. 이러한 자성체 결정의 전기 편극 P 는 P=Eo xE=Eo xoE+i E 。 GMxE 가 됨을 알 수 있고 자기적 광산란은 바로 M 의 열적 요동, 4Mi =M I -〈 M,〉에 기인하고 있다. 즉 4M 은 광산란의 복사원 Ps 와 Ms 에 각각 다음과 같은 기여를 하 게 되며 L1Ps= i E 。 4MX E 。
L1111s = i r L1M x B 。 /(J)。 (V. 94) 따라서 전기 쌍극자 죽 L1Ps 에 의 한 광산란은 홀 ocw 。 ws3 G2 (esXe 。), (esXe 。)j <4 Mi 4 MJ > (V. 95) 자기 쌍극자 즉 L1Ms 에 의 한 광산란은 ddQ2 dq ( J) s cc 言(t)s 3군 (b^s x b 。); (bsXb 。); <4 Mi 4 MI> (V. 96) 따라서 자기적 광산란에서도 가시광 영역에서는 전기 쌍극자에 의한 광산란이 휠싼 크게 기여하게 됨을 알 수 있다. 이제 우리의 관십사인 복사출력 스팩트럼을 구하기 위해서 炅=一 VM;B; 의 일반적인 해밀토니언을 고려하면 M i 一
울 얻을 수 있다. 요등-소산 정 리 에 따라서 〈 tl MLIM *〉 는 위 의 반웅 함 수 0 의 허 수 부 분과 연결되고 마침내 아래와 같은 결과를 얻을 수 있다. ( 갈; Os ) J. oc 군:대 w r<1 l L > ! (es 따 ) 『 (n( w) + 1) x l / 다 (0 i I_o) 나 (1/-.2)2 , ( 孟2 ;0s )II oc (1)。Q s3 G 下 x.I, 1 ( ＆亭)平 x (n(w) + l) 二條 广 전자를 횡 축 ( J_) 산란 단면적 , 후자를 종축( ,)' ) 산란 단면적 이 라 부 르며 아들의 온도 함수를 Xn(Mw=)N 타：µ：： 。： ,8 ：/： k VBTkIsh(T (I)— Tc ) 에 주목하여 그래프로 그려 보면 아래와 같다.
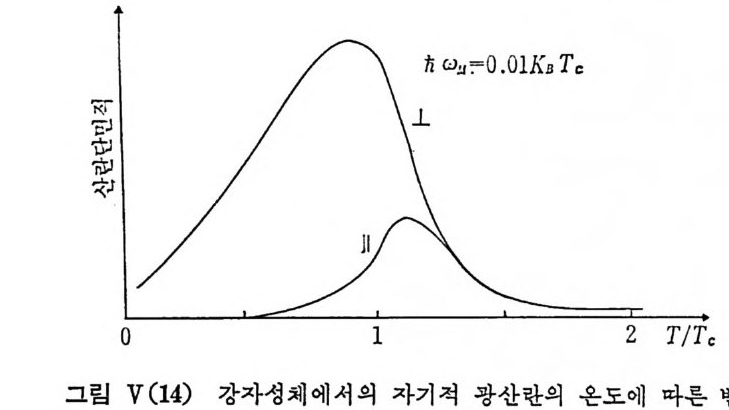ti (;):.1: =0.Ol Ka Tc
위 그림에서 보는 바와 같이 종축 산란의 경우 Tc 에 접근할 때 입계 성 산란이 나타나게 됨을 볼 수 있다. 거시적인 자기 요동온 사실 미시적 이론의 q= O 모드에 해당하는 여 기과이며 광산란에 관여하는 여기파는 q：：：：：：。로 가정할 수 있음은 이미 포는 광산란에서 논의한 바 있다.
v-2. 4 엑씨톤 (Exc it on) 과 라만 산란 엑씨톤은 전자의 기처상태와 여기상태 사이에 에너지 분격이 존재 하는 비금속 고체 죽 반도체, 이온결정, 희토류 원자결정, 분자결정 등 에서 나타나는 전자와 정공 사이의 상호결합에 기인하는 기본 여기파 이다. 주로 분자결 정 에 서 보는 Frenkel excit on 은 원자 또는 분자의 여 기 상태가 한 격접에서 다론 격점으로 움칙여 가는 즉병진운동의 자유도를 가지는 여 기 상태 에 해 당하고 대 부분의 반도체 에 서 나타나는 Wannie r exc it on 은 에 너 지 벤드 이 론의 전자와 정 공 사이 에 쿨롱 상호작용에 의하여 자유전자-자유정공의 연속상태 아래에 일련의 속박상태가 형 성되고 이러한 여기상태는 병전운동 이의에 상대좌표의 운등을 포함 하여 No 개의 전자-정공 쌍에 대하여 No2 개의 상태를 고려에 넣어야 한다. 브통 유전울 차페가 큰 경우 유효질량 근사가 가능하고 이때 전자 정공의 결합 쌍에 대한 슈뢰딩거 방정식은 수소 원자에 대한 슈뢰딩거 방정식과 유사한 결과를 얻게 된다. 그러나 항상 국재 상태는 전자 포 논 상호작용에 의해 격자에 결합되므로, 즉, 국소적 격자변형이 생기 고 엑씨돈의 결합 에너지에 이러한 격자 변형의 기여를 고려에 넣어야 한다. 바로 이러한 결합에 의해서 엑씨튼 흡수 또는 엑씨돈 복사 과정 과 관련하여 이와 동시에 항상 포는 방출이 수반하게 되며 따라서 엑씨 돈 스펙트럼의 위성 스펙트럼 선들이 나타나는데 이를 엑씨돈 스펙트럼 선의 ph onon rep lica 라고 부른다. 만일 엑씨돈-광자 사이의 상호작용 H'. ，이 매우 커서 섭동이론적 취급이 부적당할 때에는 H. ,,+Hrad+H' ．「울 칙접 대각선화시켜야 하고 이 때 의 고유상태 를 exc iton po larito n 이 라 부른다. 이 엑씨 톤 폴라리 돈 의 전파 양상을 지배하는 분산곡선은 아래와 같으며 그림에 표시된 바 와 같이 엑씨돈 폴라리톤이 초기상태 I 에서 종말상태 (I /~N') 로 천이하는 과정에서 음과성 포논의 방출 또는 흡수가 관련되므로 이러한 공명 브릴루엥 산란 실험에 의하여 엑씨돈 폴라리톤의 분산 곡선을 구 할수있다. Cu20 결정은 엑씨튼 라만 산란이 제일 많이 연구되어 있는 결정의 하 나로서 6000A 근처에서부터, 포논-보조 쌍극자 여기에 기인, 제일 낮
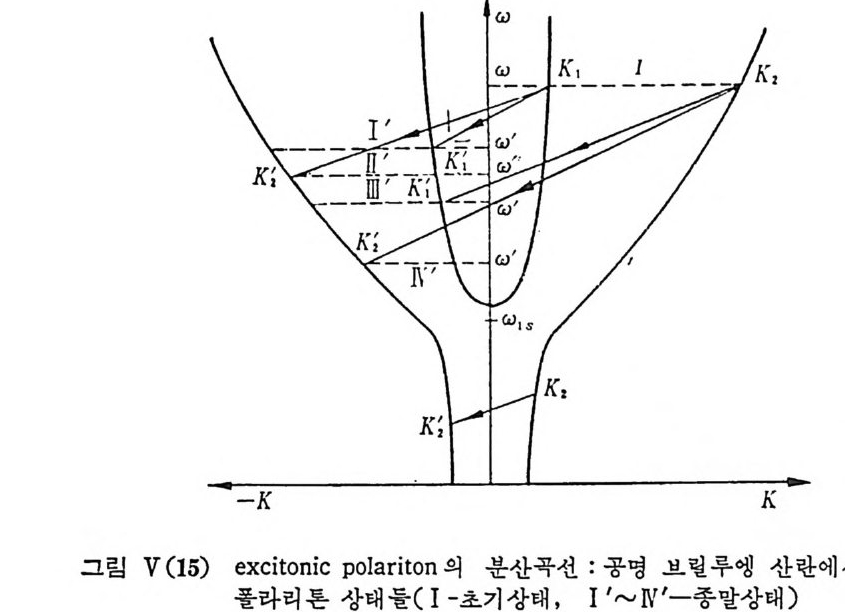-K K
온 에너지의 Is ye llow 엑씨톤 상태로의 천이 흡수가 시작되어 5800 A ~5300 A 사이 에 는 ye llow 엑 씨 돈 및 gree n 엑 씨 돈의 2P, 3P, 4P 에 너 지 준위로 쌍극자 천이를 함으로써 생기는 격리형 흡수선 스팩트럼이 나타난다. 보통 입사 레이처의 진동수 (J) L 을 흡수벤드 하단에 조준시키면 (E,/11, ~ 16470 cm-1 > (J), ,~16400 cm-1) 우선 다중포논 라만 산란이 굉 장히 강하게 나타납을 볼 수 있다. 이것은 다음의 2- 단계 과정으로 해 석할 수 있다. 즉, 加(J) L 의 입사 광자가 가령 I'12 대 칭성의 포논 加(J) 12( q) 의 방출을 수반하는 ls 엑씨돈 1I (J) 1,( q)를 생성시키고 이어서 이 엑씨론 이 제 2 의 포는 加(J)’(q)를 방출시키면서 복사성 천이로 산란광 광자 n(J), 가 주어지는 과정으로 볼 수 있다. 따라서 'llwL =h(I) 1 ,(q ) +h(I) I2 (_ q) (V. 97) 加(I) ,=h (I) 1,( q )-h (I)’(_q) (V. 98) 를 만족시 키 는 I'12® (I)’의 2 개 -포논 라만 산란을 생 각할 때 그 산란 단 면적은
Rrn0.,' :::: an,(OL) rrad((V I ) r.? 의 형태가 됨을 알 수 있다. 여기서 ar.,( 야,)은 포논(I' 12) －보조 Is ex· citon 여기에 기인하는 흡수계수로서 아트 w0,,+w12 에서부터 기여가 커 지 고 바로 이 WL 값에 서 w' =I'12, I'2s, I '1s, I '2 에 해 당하는 라만 산란이 크게 증강되어 나타나게 된다. 위의 식 (V. 97~98) 로부터 타만 산란에 기여하는 포논과 엑씨돈의 과수 백터 q가 입사 례이처의 광자 에너지 加仰,에 따라서 결정됨을 알 수있다. 따라서 I'12 포논이 분산성이 쿨 때에는 위의 식 (V.97~98) 로부터 wL-w,=w,z( q) +w '(-q) 즉 라만 천이 전동수가 입사 레이저의 진동수 야.에 따라 달라질 수 있 음을 보이고 있다. 그러 나 2 I'12 와 I' 12 승 I' 25 에 해 당하는 라만 산란의 주과수 변이 가 (J)L 의 변조에 무관한 일정한 값으로 관측되었고 이로부터 I'12- 및 I' 25- 포논은 거의 분산이 없다는 것을 알 수 있다. 분산이 상당히 큰 음파성 종 포논을 포함하는 엑씨돈 라만 산란을 보생면 성, 되 즉고 이입 사n(J )1 레 s(q이 )처 엑 씨h ( J돈) L 이에 L의A해 서포 논포 .,는,,(J) A(I q' 1'2 ）와를 생엑 성씨 시돈 키 加면(J)서 1s ( qtz()J)가1 s (q-q')로 산란된 다음, 여 기 서 다시 I'12 포 논을 수반하는 복사성 천이 로서의 공명 산란울 고려하면 R2me»m(q’ ) ((JJL , (JJs =(J JL -2(JJ 1 2_(J JA ) ::::::a( 야) rralI'1 2) rA(q, q') r;l 와 같은 산란단면적이 주어지고, 여기서 rA( q,q')은 Is 엑씨돈과 (L)A (q ') 포논 사이의 산란계수를 나 타내며, 이로부터 R2., .. +.,A 가 극대가 되는 정봉 주과수를 구하면 2 (J)1 2+2 vq= =:2 (J)1 2+2 v ./m {(J)L _(J )1 ,(0)...::.(J )12 } /力 가 됨을 알 수있다. 여기서 m 은 엑씨돈의 유효질량, V 는 종파포논의 음속을 나타내고 있다.
위석으로부터 (!)L 에 따라서 3 개군 E는 (2W12 승 WA) 라만 산란의 변이 주파수의 변화를 측정함으로써 포논 WA 의 분산, 따라서 엑씨돈의 분 산 곡선을 구할 수 있음을 알 수 있다• 이상 WL 을 흡수벤드하단에 조준시켰을대의 공명성 타단산란을보 았으며 만일 야.올 Cu20 의 노랑 또는 초목 엑씨돈 준위에 조준시킬 대 에는 제일 강하게 나타나는 모드가 오히려 적의선 흡수 가능한I'포논 인데 이 것 은 엑 씨 톤-포논 상호작용으로서 Frohlic h 상호작용이 가장 중요하게 작용하는 대문인 것으로 해석된다.
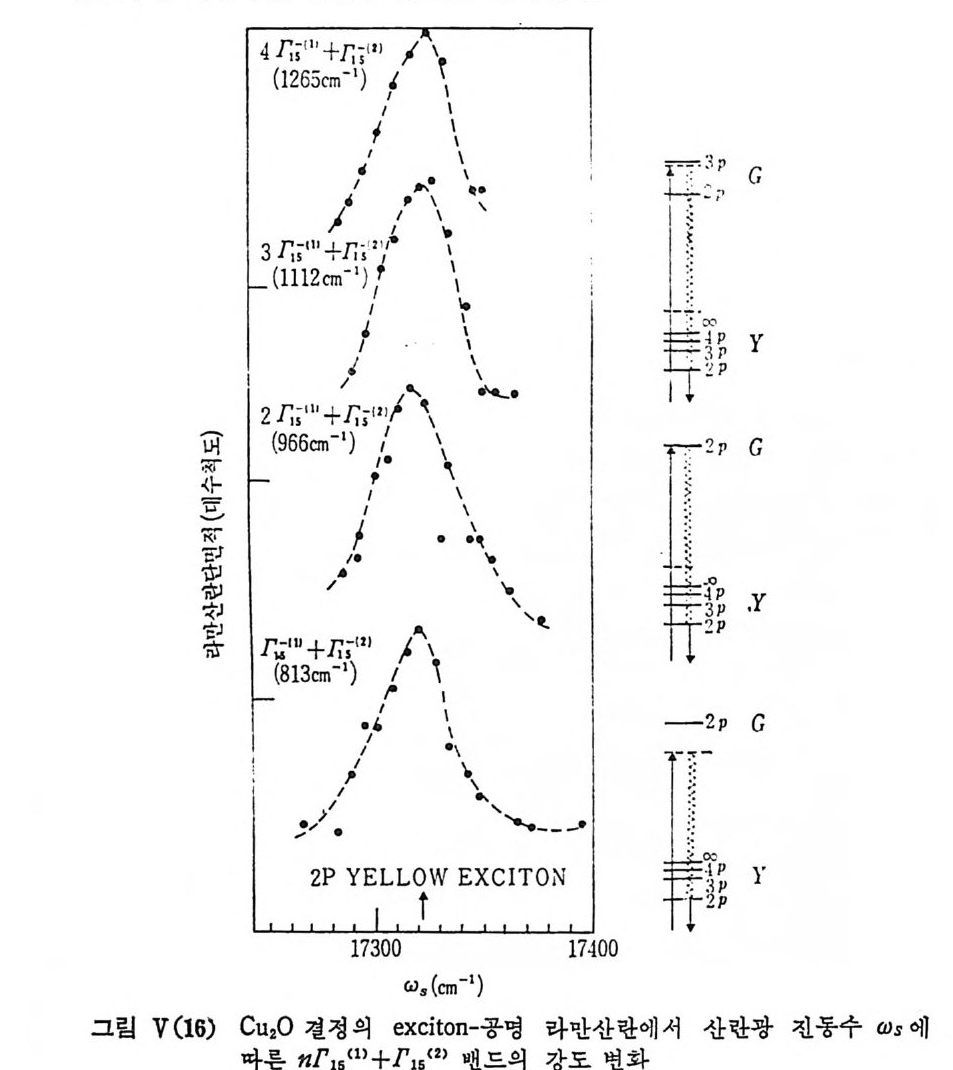4_,\12氐 6{ h +cR fT'_m)3r/JI ,2I37',/, I111I?+'‘R,l22'c*·.m'/7Ic2P,+/ m/ , '
또 이대에는 엑씨돈 상대와 관련 되어 수많은 공명성 중간 상 태가 주 어지기 때문에 산란 훈). 灰 W s 에 대한 다중 공명 죽 다중포논 에 의 한 라 만 산란이 매우 강 하 게 나타날 수 있다. 가 령 따 \ 5( I ) 5 I' 1 5(2) (I1= 1 , 2, 3, 4) 의 다중포논 라만 산란을 보면 모 두 Ws 가 2P ye ll ow 엑씨돈 준위에 공명을 이루게 되는 그러한 야에 대해서 공 명 증 강율 갖게 되어 상당히 강한 다중포논 스펙트 럼 을 얻을 수 있다. 즉 , 야 .을 gr ee n 엑씨톤의 한 에너지 준위에 조준 시 키면 가 능 한 모 든 다중포는 방출 과정을 거쳐 (I) 5 를 결정하는 종말상 태 가 바로 ye llo w 엑씨톤의 2P 준위가 될 대 라만 산란이 중강되어 강하게 나타 난 다. 엑 씨 돈 풀 라리 톤의 분 산 곡 선과 관련해 서 최 근에 소위 abc 든제 (addi- tion al bou n da ry condit ion s) 가 큰 관심 의 대 상이 되 고 있 다. 엑 씨 돈 풀 라리 본 의 분산곡선은 그립 V (l 5) 에 서 보는 바와 같이 포 논 풀라 리본에서 와 달 리 아래쭉 가지가 k 에 대하여 포물선형 함수 관 계군 보 이고 있으며 이로 인 해 서 입사광 (I)。에 의해서 위쪽 가지와 아 래 쪽 가지 의 서 로 k 값이 다론, 즉, 굴절몰 n(n=c2k 키(I)。 2) 을 가지는 두 개의 풀 라리돈파가 등시에 생성되고 결국 경계면에서 입사과, 반사파, 두 개의 루과과에 대한 전폭과 위상을 결정하려면 통상의 맥스웰 방정 식에서 주어지는 경계조건만으론 부족하고 또 다른 경계조건이 더 주어 겨야 됨을 알 수 있다. 광산란의 입장에서 볼 때에 이것온 두 개의 서 로 다른 입사광에 대한 산란에 해당하고 따라서 간섭에 의한 복잡한 스 액 트 럼 이 예상된다. 이러한 산란 스펙트럼, 득히 ex cit on- 공명 브릴루엥 산란 실험의 결과 는 abc 문 결정짓는 데에 큰 공헌을 할 수 있다. V-3 불순물 및 결함 V-3.1 상자성 층십자, 결정 전장, 전자 준위 라만 스펙트럼 천이족 금속 및 희토류족 이온들온 결정 내에서 자기 모멘트룬 가지는 소위 상자성 중심 자(p arama gn e tic cen t er) 들로서 이 들은 라만 산란으로 연구할 수 있는 낮온 에너지의 전자 에너지 준위들을 가지고 있다. 특히 4/n 의 전자 궤도 배열을 가지는 희토류족 이온들의 홍미 있는 전자상태는 l•s 결합작용으로 주어지는 여러 J 값에 대웅하는 다중체
구조문 갖는 상태들르 이들은 다시 결정 전장 에 의 해 서 수 백 cm-1 겅 도로 Sta r k 세분이 된다. 이들 상태는 전기 쌍극자 천 이 가 금지되어 원적의선 흡수 스펙트럼에 의한 연구가 거의 불가능한 경우로서 타 만 산란의 연구가 가장 적합한 한 예를 이루고 있다. 자유이온의 경우에는 4f n 전자들에 대한 에너지 준위들의 다중도 및 대칭성온 l=3 에 해당하 는 회전군의 표현식들로 주어지고 이들 자유이온의 상태는 결정 속에서 결정 내부장의 영향으로 자리군 (s it e g rou p)의 불가분 표현식에 속하는 상태들로 각각 분리되고 있다. 만일 우리가 고려하는 이온이 홀수 개의 전자를 가지면 이때에는 단 순군이 아니고 소위 2 중 군의 대칭성을 가지며 모든 표현식이 최소한 2 차원 이상이 되고 이것은 Kramers 축되도가 계속 촌재하게 됨 을 나타내 고있다. 만일 이들 이온들의 첨업농도가 충분히 작아서 서로 멀리 떨어쳐 있 고 이들 불순물 이온둘 사이의 상호작용을 완전히 무시할 수 있다면 모. 든 이온들이 계각기 독립적으로 광산란에 기여하게 되고 따라서 전체 산란 단면적은 각 이온들에 의한 개벌적인 기여의 단순한 합이 될 것 이다. 또 기본 칸(p r i m iti ve cell) 에 이러한 이온이 접유할 수 있는 대칭 자 리가 오칙 한 개분인 경우에는 결정체 전체로서의 선택물 및 산란광의 대칭성 문제가 바로 단일 이온에 대한 자리 대칭성을 고려한 해석의 결 과와 같게 된다 . 그러나 기본 단위 칸이 첨입되는 이온에 대해서 여러 대칭 자리를 가지고 있는 경우에는 합을 취할 때 자리군의 대칭 축들에 대한 여러 가능한 방향을 모두 고려해 주어야 한다. 따라서 이들 상자성 중심자들에 대한 타만 산란 연구는 에너지 준위 의 위치는 물론, 이들 에너지 준위들의 대칭성 및 자리 대칭성에 대한 많은 정보를 제공할 수 있다. 이둘 희토류 이온들이 결정 격자의 모든 자리를 점유하는 한 극한을 생각해 보면 이온들 사이의 상호작용이 강해지고 그 결과 이온의 전자 여기상대가 결정체 전체로 전파되고 이에 따라서 격자의 공간군에 대웅 하는 대칭성을 고려해야 되는 엑씨론 상태를 형성하게 된다. V-3. 2 반도체의 donor 및 accep tor 들에 의한 라만 산란 불순물의 전자 준위 라만 산란의 또 다른 한 예로서 반도체의 donor
또는 accep tor 불순물의 전자 준위 들 시 기의 천 이에 기인하는 라만 산 란을 들 수 있다. Ge 또는 Si 전정에서와 같이 전도대 하단이 브릴루엥 구역 중심에 있 치 않을 때에는 donor 상태에 대한 파동함수는 l/f(x ) = ~ c. cp( x) Q.1;( x) k-kc 로 표시할 수 있다. 여기서 kc 는 모든 상등한 전도대 하단에 대응하 논 k 벡터를 나타내고 Q k 는 각각의 kc 에 대한 Bloch 파동함수, ¢(x) 는 수소 원자 해 밀토니 언에 대 한 과동함수를 나타내 고 있 다. 즉 shallow donor 상태 는 전도대 하단의 Bloch 파동함수들로 구성 된 파동 집 속으로 볼수 있다. 이들 donor 준위는 그 자리 대칭성 이 Td 일 때에, 가령 Si 결정의 donor 불순물울 예로 들면, 공간 대칭성에 의한 축되로서, 기처상태인 lS 상 태가 6- 중 축되름 가지게 되고 따라서 6 개의 에너지 바닥골이 나타 난다. IS 상태의 이온화 에너지는 ~O. I eV 정도이고 이 1S 상태에서의 바 닥골대] 도 갈라침 (I'i, I'~, r3) 은 ~ lO meV 정 도이 다. kc 에서 hoE 각 간접 벤드간격을 가지는 2- 벤드 모델의 근사 계산에 따르면 11S 〉 에서 |2S> 사이의 라만 산란 단면적은 거의 무시되고 상 접 적 분이 큰 11 S> 종속상태 사이 의 천이 , 주로 1 S(I' 1) - > 1 S(I' ,)
\\\\\\\\\\\\\\\\<>\\\\\\\\\\\\\\\\\
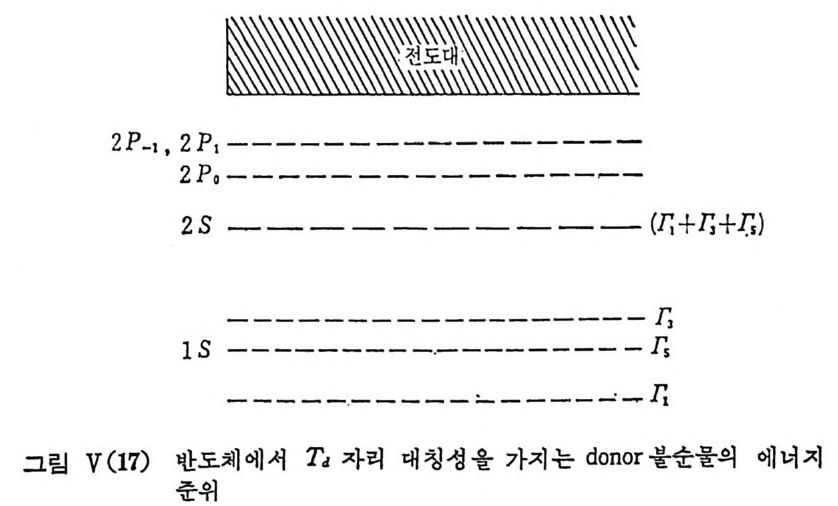천이가 제일 크게 기여하고 있다. Si : P 에서 I. 065µm 의 Nd : YAG 레이처를 써서 라만 스펙트럼을 조사해 보면 전동 모드 (37.9meV, 64. S meV) 이 의 에 이 보다 훨씬 낮은 전동수에 서 (13 . I meV) 전자들 상 태에 기인하는 타만 벤드가 관측되고 있다. donor 농도를 증가시키면 소위 금속-절연체 상전이 (Mo tt천이)가 가 능하고 이 때 에 는 가령 Si : P 에 서 불순물의 농도가 nc:::::3 X l018/ c m3 에 이르면, 위의 라만 벤드가 갑자기 심한 폭넓힘을 나타내며 소위 바닥 골 사이 요동에 기인하는 연속체 바닥신호가 생기게 된다. 마찬가지로 GaP : Zn 등 accep tor 불순물을 포함하는 경우에도 이들 accep tor 준위 사이 의 전자 천이 에 기 인하는 라만 산란을 볼 수 있 다. Ps,2 가전자 벤드에 대 한 accep tor 준위 를 보면 4 중 축되 를 갖는 기 처 상태 I' B 는 ~128meV 정도의 결합 에너지를 가지며 이로부터 ~33.7 meV 멀 어진 제 1 여기상태는 따 정군의 I' 7 표현식에 속하는 Kramers 2 중쌍이 다. 이 I'8-+ I '7 천 이 에 기 인하는 ~33. 7 meV 의 타만 벤드가 GaP 의 LO 및 TO 포논에 해 당하는 라만 벤드와 함께 나타나고 있 다. 단일축 웅력을 가하여 Td 대칭성을 깨드리면 I'8 기 저상태가 두 개의 Kramers 2 중쌍으로 갈라지 고 이 들 2 중쌍 사이 의 천이 에 대 응하는 라만 벤드가 관측된다. V-3. 3 국재형 모드와 공명형 모드 KCl 과 같은 이온 결정 속에 수소를 흡수시키면 H 저온으로 격자 음 이온(여기선 Cl- 이온)을 치환해 들어간다. 이때 H 지온은 질량이 매우 작기 때문에 보통 포논 전동수의 2~3 배나 되는 높은 전동수의 국재형 진동 모드를 형성한다. 죽 이들 모드 논 전동 여기운동이 결함 이온에 국한되어 있고 보통 예리한 선 스펙트 럼을 나타낸다. 이들 국재 진동자의 에너지 준위들은 다음의 비조화 전동자에 대한 해로 주어전다. 죽, H 지온의 자리 대칭성을 Td 라 하면 K=Ar2+Bxy z+C1( 났+y4 +z4)+C z( x2y 2+ y낫 +z2x2) 로 주어지고 자리 대칭성이 반전을 포함하면, 가령 Oh 에서는, 두번째 항이 제의된다.
이들 에너지 준위들은 Td( 또는 O.) 겁군의 불가분 표현식에 각각 속 하게 되고 선택물에 따라서 아래 그립에서 보는 바와 갈이 여러 가능한 타만 천이를 관측할 수 있다.
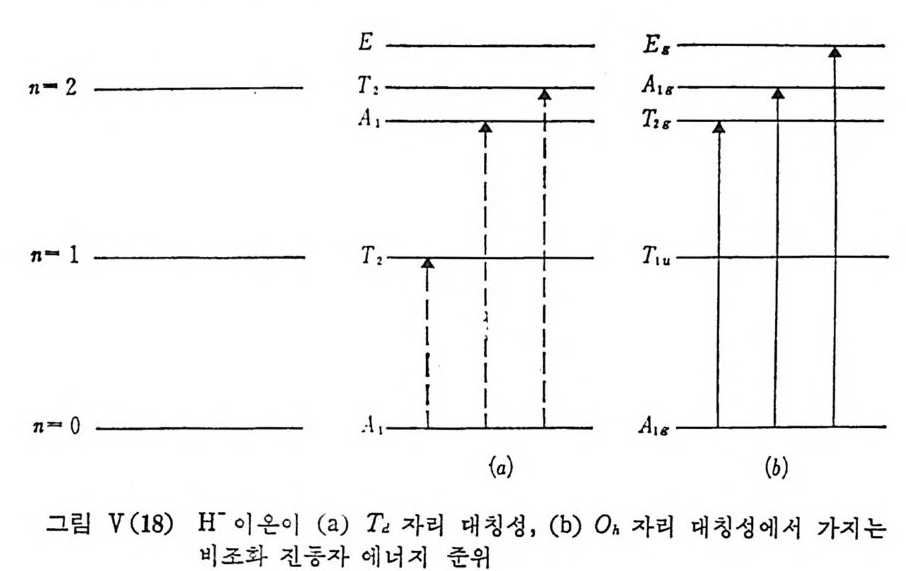n-2 AE.I T f AmEmI.I `
한편 단순 이온 결정에서 두 이온의 질량차이가 큰 경우 가령 NaBr, Nal, KBr, KI 등의 결 정 온 음과성 분지 와 광과성 분지 사이 에 상당히 큰 갭울 가지고 있으며 이 안 에 H-이 온의 국재형 모드가 갭 모드로 촌재하게 되며 예리한 선 스 팩 트럼을 제공한다. 단위 칸 안에 두 개 의 원 자문 포함하는 이 들 alkali halid e s 결정 은 OJ, 입 방체 대 칭 성 을 가지 고 있 으며 오칙 하나분인 rests t r a hl 흡수의 강 한 흡수벤드를 나타내고 있 다 . 그러나 여기에 접 결함을 첨가시키면 광학적 불활성이었던 포논 모드 들이 병전이동 대칭성에 관련되는 선택를의 제약을 받지 않기 때문에 흡수 스펙트럼에 새로운 기여를 하게 되고 또 포논벤드 영역 밖에 새 로운 모드에 의한 흡수 스펙트럽이 나타날 수 있다. 이러한 결함-유도된 흡수 덴드는 일반적으로 격자의 포논 상태밀도 와 관계되어 매우 폭넓은 벤드가 된다. 그러나 공명형 모드 또는 준국재 모드로 볼리우는 바교적 예리한 홉 수벤드가 나타날 수 있으며 이것은 결함 모드가 포논 벤드 안에 들어 오더라도 그 근처에 격자 전등의 상태밀도가 아주 적거나 격자이온과의
국소적 교합 정수가 메우 적은 목일한 겅우에 해당 된다• 이 들 공명 형 모드는 아주 강한 rests t r a hl 흡 수 대 문 에 광과성 포논벤 드 내에서는 관측하기 힘둔고 보통 음파성 포는 벤드 내에서 관측되고 있다. 이러한 포논벤드 영역 밖의 소위 국재형 모드듄은, 갭 모드를 포함, 보통 매우 예리한 벤드로 나타나며 이것은 오직 바조화 항에 의해서 격 자 포논과의 간접 상호작용을 동한 섭 동감쇠 문이 기 매 문이 다. 반전 대칭성을 가지는 oh 군의 입방체 결정 가 청 N aCl 건 정 에서는 1 차 라만 산란이 금지되어 라만 스펙트럼이 나타나지 않는다. 그러나 반 전 대칭성을 가지는 자리에 불순물 원자를 집어 넣 으면 결국 불순물과 ::::z. 주위원자들 사이의 전동운동에 의해서 전자 편국 윤 이 변조됨으로써 even pa rit y 를가지 는 AIg, Ec, T“ 대 칭 성 의 전동 모드의 라만 천 이 가 가 능하게 됨을 볼 수 있다. 즉, 양자역학적으로 볼 때에 가상 천이에 의한 3 차 섭동 과정으로 기술되는 전자 편극물의 계산에서 가장 간단한 경우, E < 0,A 1lf lI 'D li, Au> i, i /(E-E,,A,,)(E-E;,r) 를 보면, 한 예 로서 전자-포는 상호작용 g ep 가 AIg 표현식 에 속할 때, 위의 식이 0 이 아닌 유한한 값을 가지기 위해선 I' D® I' D 드I', 즉 반전 대칭성을 가지는 입방체 결정에서 보면 쌍극자 모멘트가 T I u 에 속 하므로 T1u®T1u=A,6E8E 흡 T1&T 가 되고 점 결함에 의해서 바로 위의 대칭성을 가지는 포논둔만이 전자 천이에 교합되어 타만 천이 활성을 보이게 됨을 예상할 수 있나. V-3. 4 색소 중심자 (Color Cente r s) 반도체 의 donor 또는 accep tor 불순물에 서 는 donor 전자의 궤 도반경 이 10~100A 정도가 되어 거시적 유전체 연속물질의 가정을 쓸 수가 있고 천이금속과 희토류 이온의 상자성 중심자에서는 광활성 전자의 궤도반경이 격자상수 a 보다 훨씬 적어서 고립된 원자로 취급할 수 있 었다.
이들 두 극단적인 경우와 달리 불순물 원자의 궤도전자의 반경이 격 자상수 a 와 비 등한 값을 가지 는 경 우로써 alkali halid e 의 F-cente r 를 들수있다. F-cente r 는 전도대 의 전자가 양이 온 빈자리 주위 에 포획 된 상태 를 가리키며 이 때 전자의 궤도는 양이온 빈 자 리의 최근접 이 웃인 6 개의 음이온 자리에까지 퍼져 있다. 원래 alkali hali de 결정들은 흡수 시작단 이 u.v. 영역에 속하여 투명하게 브이지만 F-cen t er 를 포함하게 되면 가시광 영역에서 전자 천이에 기인하는 종 (bell) 모양의 흡수 벤드를 가 지며 이 F-cen t e r 의 흡수에 의하여 색이 들 어 보인 다 . 이 전자 천 이 는 완전 대칭성의 s- 형 기처 상태로부터 3 중 축되를 가전 P - 형 상태 사이 의 천이에 해당된다. 아듣 입방체 대칭성을 가전 alkali halid e 단결정들은 1 차 라만 산란 이 금지되 어 있 지 만 F-cente r 등 정 결함울 프함 시 키 면 1 차 라만 스젝 트럼을 볼 수 있다 . 즉, 이들 결함이 반전 대칭성을유지하는자리에 들 어 가면 격 자 전동 중에 even pa rit y 의 포논들은 결함의 진동 및 전자상 태 즉, 전자 천이와 교합됨 으 로써 타만 산란에 의해서 포논 여기가 가
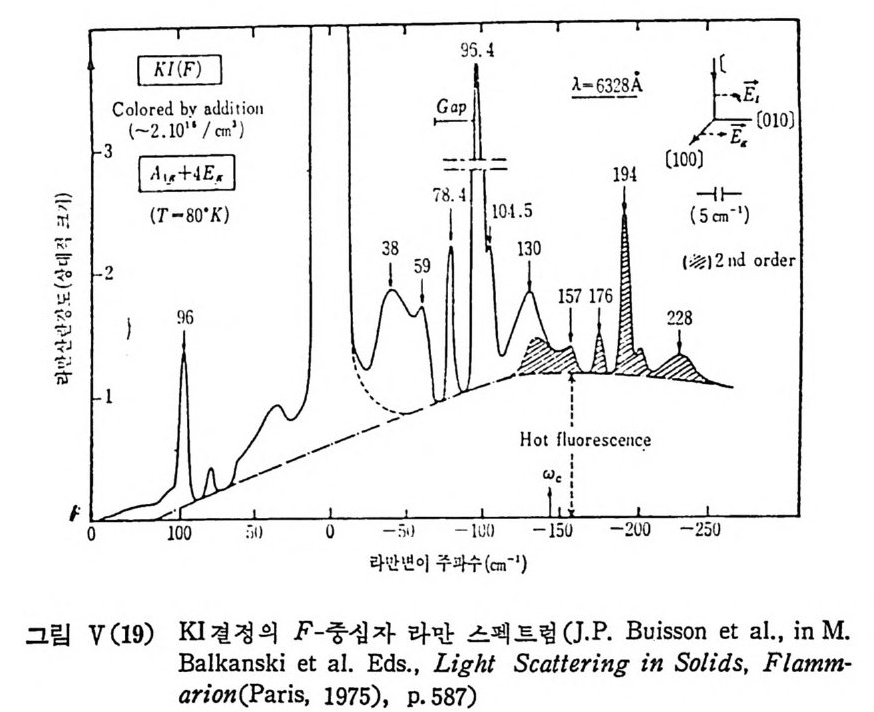-己숫,처~,o. j l32 ’( ~曰I 2(AT ., 1 '-0+ 8 40 /'E K 蠶cm ) 1' ) 3I8 59 가『lI 95. 4 11.53I 0 .t-6 321894A• (10(0*昆( 5). ) a 2n 11 'd) ord eO r J
능하게 된다. 라만 천이가 F- 벤드 흡수에 가까워지면 공명에 의한 증대로 ~10 피 cm3 정 도의 상당히 낮은 농도의 F-cente r 를 포함하는 경 우에 도 이 에 기인하는 라만 산란 스펙트럼을 충분히 관측할 수 있게 된다. 단결정 KI 를 보면 포논 벤드 갭 이 70 cm-1 와 96 cm-1 사이 에 있으며 F-cen t er 에 기인하는 E., 대칭성의 갭 모드가 78cm-1 에서, 또 A1., 대 칭성에 속하는 공명형 모드가 96.4cm-1 에서 라만 스펙트럼에 나타나 고있다. 결합 자체는 이러한 even p ar ity의 격자 전동에서는 node 에 정지해 있으므로 결함의 질량은 이 경우에 벌로 중요한 영향을 미치지 않으며 오히려 스펙트럼을 결정하는 중요한 양온 F-cen t er 의 최근접 이웃 이온 들의 변위에 대한 KI 단결정의 A1.,,E.,, 및 T2 g 대칭성을 갖는 포논듣 의 상태밀도 사영 성분, 따라서 포논 분산곡선에서의 위의 각 대칭성에 부합하는 임계점들이다. 보통 F-cen t er 의 경우 결함과 최근접 이웃 사이의 힘 상수가 원래의 힘 상수보다 70% 나 적은 값으로 나타나지만 F-cente r 불순물에 기 인하는 라만 산란이 가령 SrF2 의 Eu2+ 불순물에 의한 라만 산란보다 ~104 배까지 더 강하게 관측됨을 분 수 있으며 이것은 F-cen t er 의 과 동함수가 격자 포논과 더 강하게 교합되어 있음을 뜻하고 있다. 참고문현 1. J.A . Reis s land, The Phy si c s of Phonons, Joh n-Wi ley and Sons(London, 1973). 2. B. Di Barto l o and R.C . Powell, Phonons and Resonances in Soli ds, Jo hn-Wi ley & Sons(New York, 1976), Chap. 12(1nfr ar ed Absorpt ion and Raman Scatt er in g ). 3. W. Hay es and R. Loudon, Scatt er in g of Lig h t by Crys ta l s, Joh n-W ile y & Sons(New York, 1978), Chap s. 3 & 4 (Phonons-2nd order, defe c ts , pola rito n s, etc . ), Chap. 6 (mag n eti c scatt er in g ) and ~hap . 7 (electr o nic Raman scatt er in g ). 4. P.M. Platz m an and P.A. Wolf f, Waves and Inte r acti on s in Soli d Sta t e Plasmas, in Sol. St. Phys . Supp l. 13, Academi c Press(New York, 1973), Chap. V( ligh t scatt er i ng exp er im ents ) . 5. H. Raeth e r, Exc itat i on of Plasmons and lnte r band Transit ion s by
Electr o ns, in Sp r in g e r Tracts in Modern Phys i c s , 88, Sp ri n g e r-Verlag (Berlin , 1980). 6. R. Claus, L. Merte n and J. Brandmi ille r, Lig h t Scatt er i ng by Phonon-Polarit on s, in Sp ri n g e r Tracts in Modern Phys i c s , 75, Sp ri n g e r-Verlag (Berlin , 1975). 7. M. Balkanski, R.C. Leit e and S.P. Porto , Eds., Proceedin g s of the 3 rd Int' I Con/. on Ligh t Scatt er in g in Solid s , Flammari on (Paris , 1976), Chap. IV (mag n ons and mag n eti c excit at i on s), chap. IX(defe c ts and im p - uri ties ). 8. P.Y. Yu, Stu d y of Excit on s and Excit on -Phonon Inte r acti on s by Resonan t Raman and Brill o uin Sp ec tr o scop ies , in Exc iton s: Top /ics in Current Phys i c s , Vol. 14 , ed. by K. Cho, Sp ri n g e r-Verlag (B erlin , 1979), pp. 211~ 253. 9. D. Bauerle, Vi br ati on al Sp ec tr a of Electr o n and Hy d rog e n Cente r s in Ionic Crys t a l s, in Sol. St. Phys i c s : Sp r in g e r Tracts in Modern Phys i c s, Vol. 68, Sp r in g e r-Verlag (B erlin , 1973), pp. 76~160. 10. J.L . Bir m an, in Ex c iton s, eds. E. Rashba and M. Stu r ge , North - Holland (1982), chap . 2. add it ion al boundary cond iti on(abc) 에 대한 최근 revie w 논문.
제 VI 장 특수 논제 앞에서 라만 산란이 분광학적 도구로서 고체에서의 여러가지 가능한 기본 여기파들의 분광학적 연구에 어떻게 기여하고 있는지를 살펴브았 다. 이제 라만 산란은 단순한 분광학적 의의를 넘어서 반도체, 표면 현 상, 상전이 문제, 비선형 현상, 생화학적 현상 등에 이미 많은 기여를 하고 있다. 이 중에서 특히 물성론에 관련되는 옆 가지 문제들에 대한 연구 현황을 소개하고자 한다. VI-1 공명 성 라만 산란 vI-1.1 가변주파수 염료레이저 가변 단일 주파수 염료레이처의 출현은 공명성 라만 산란의 급속한 발전을 가져왔다. 염색에 쓰이는 많은 염료 분자의 에너지 준위가 레이처를 만드는 페 에 적합한 조건을 갖추고 있다. 가령 Rhodami ne 6 G 로 불리 는 염 료분자를 예 로 들면 sin g l e t 기 저 상태 So 에서 sin g le t 여기상태인 S1 으로 질소 레이처의 자의선 영역에서 부터 Ar+ 이온 레이처의 가시광 영역에 걸쳐 쉽게 펌평시킬 수가 있다. 이들 S1 상태의 분자들온 So 다중쌍 내의 한 전동준위로 자발복사 천 이를 하거나 또는 3 중쌍 상태 T1 으로 비복사천이를하게 된다. 이 TJ 상태 의 분자들은 S1->S 。 사이 의 례 이 저 천이 에 방해 가 되 는 덫집 (t ra p)을
형성하므로 연속 발전 영로레이저를 얻으려면 T 근강태에 있는 분자들을 s 。 상태로 급속히 천이시키거나 또는 제거시키는 방법이 제공되어야 한 다. 다라서 대부분의 경우 연속 발전 염료레이처의 dye cell 은 계속 광펌 핑 아 가능한 요 상태 의 새 로운 분자들울 공급해 주는 ‘jet flow ' 를 이용하고 있다. 영로의 S1-+S 。 천이에 의한 형광 스펙트럼은 매우 넓은 폭의 벤드를 형성하고 있기 대문에 (Rh 6G 의 경우 5.X 1 0-3M 의 농도로 e t hanol 에 녹였을 때 5950A 에서 정봉, 500A 정도의 벤드 폭을 보인다) 한 가지 영로를 사용하여 300A 정도의 너른 법위에서 레이저 진등수 선택울 할 수 있다. 제일 간단한 방법으로는 우선 프리즘아나 희철 격자를 써서 레이저 전등수를 선택할 수 있으며 이때의 레이처 선폭은 회철 한계의 값을 갖 게 되므로 망원경 광속 확대기를 쓰면 선폭을 줄일 수 있다. 여기에 다시 Fabry -P erot 에탈론을 결합시키면 단일 모드 작동이 가능하게 된다. 사실 전혀 동조 소자를 쓰지 않고 레아처 공전기 거울만 두어도 레이 처 출력의 선폭은 소위 이득 좁힘 및 모드 경합에 의해서 ~20A 정도 로 줄어들게 된다. 여 기 에 free spe ctr a l rang e (FSR) 가 105 GHz 정 도 되 는 tun in g wedg e 을 쓰면 4)).:::::250 GHz (.:::::3 A) 가 되 고 FSR 가 900 GHz 인 에 탈론을 쓰면 4)) :::::4 0 GHz 로 줄어 든다. 위 의 4)):::: :4 0 GHz 안에 는 사실 100 여 개 정 도의 종축 모드가 공전하 고 있으며 여기에 또 FSR 가 좁은 (~60,20,10GHz) 에탈론을 공전기 안에 추가시켜야 단일 모드 작동이 이루어지게 되는 것이다. 이와 같 이 여러 개의 광학 소자들을 쓰기 때문에 가령 1W 의 5145A 알곤 레 이처로 펌평시킬 때에 20~50MHz 의 선폭을 가지는 단일 모드 레이 처의 출력은 겨우 lOmW 정도로 줄어들게 되는 것이다. 이러한 출력 문제를 극복한 레이처가 바로 ][장에서 설명한 환상형 염료레이저이다. 염료레이처의 염료 용액에 따라 레이처의 과장을 4000A 에서부터 1 µm 에 이르기까지 연속해서 공조시킬 수 있으며 이 모든 영역에서 단 일 모드 작동을 할 수 있는 것이다. 여기에 제 2 조화과 발생, 주파수 합성의 소자를 조합시키면 ~2500 A 에서 lµm 에 이르기까지 임의의 파장을 선택할 수 있는 단일 주과수
공조 가능 염료레이처를 얻게 된다. 찰 알려 진 염 료로서 자의 선 쪽에 Sti lb e n 3, 가시 광 영 역 에 Coumarin 7, Fluo re s c ei n e , Rhodami ne 6 G, 적 색 영 역 에 cres y l- vio l et, Ni le Blue, 적의선 쪽에 HITC-P, Dat Te tr a C 로 불리는 영료가 시판되고 있으며 펌핑 에는 각각 자의선의 A r2 + 레이저, Ar+ 가시광 레아저, K 균 레이처 의 6--17 1 A, 7993 A 을 쓰고 있다. \1-1. 2 공명성 라만 산란 격 자 전동에 의한 1 차 라만 산란에 가장 큰 기여를 하는 섭동 항은 아래 의 표 현 그림으로 표시된다.
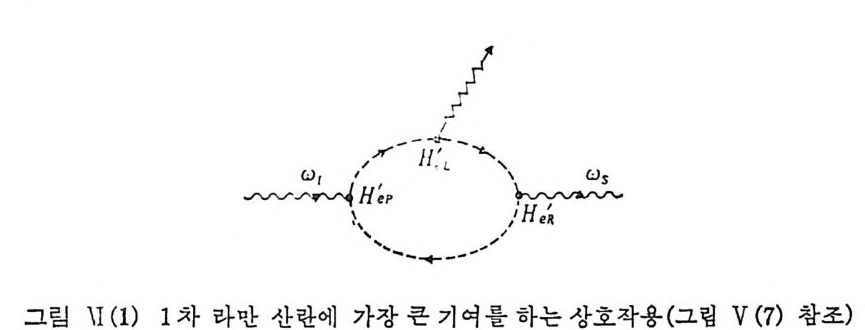Q, I / / 一 一I I/- 각.'L - ` \ \ \ Q s
위의 표현그림에 해당하는 산란덴서를 계산해 보면 전자-포논 상호작 용 玩 ’ c p ' 애 기 인하는 행 렬 요소가 만일 입 사광 또논 산란광의 전동수 와 전자의 중간상태를 포함한 가상 천아의 전동수 사이에 공명조건이 만족될 때에 매우 큰 값으로 증가됨을 볼 수 있다. 이러한 사실은 라만 산란이 매우 약하게 나타나는 불두명체, 특히 반 도체의 타만 산란 실험을 가능하게 해주는 매우 유익한 현상아다. 제일 간단한 경우로 만일 입사파 (JJ。 또는 산란과 (JJ s 가 벤드 간격 (JJ: 에 접 근하는 경 우를 보면 중간상태 (a, p) 가 모두 다음과 같이 전자-정 공쌍 여기상태를 나타낼 때에, 즉 (J)a =( J)~=(J)g12t+,2mk — 2* (VI; 1) 가 되면 타만 산란 단면적의 a, (3에 대한 합산, Xa,P 를 파수 벡터 k 에 대한 적분으로 대치할 수 있고 Oo
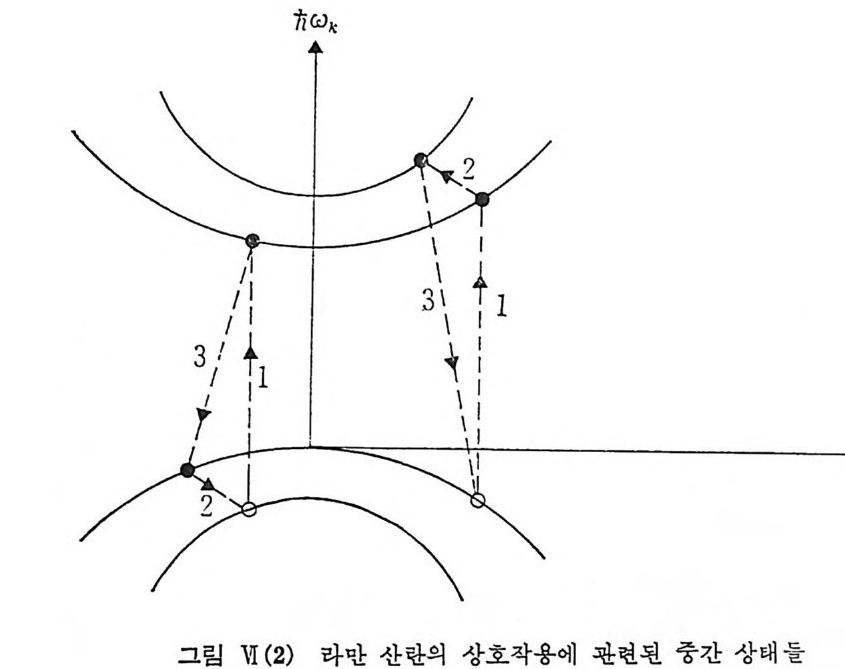方 ok
(듦) oc { ((I)g+(I)_(I)。) 1/2_ ((I)g_(I)。) 1/2} 2 (W. 2) res 이것은 (I)。=(I)g에서 유한한 값을 나타내고 있지만 그 기울기가 발산 하게 됨을 주목할 수 있다. 산란 단면적 이 0 이 되 는 (I)。 가 촌재함을 볼 수 있 는데 이 것 온 타만덴 서에 기여하는 공명성 항들과 비공명성 항들 사이에 소멀적인 간섭효과 에 기인하고 있다. 위의 이론 결과는 횡과 편극의 포논에 대한 실험 결과와 찰 맞고 있 음이 밝혀졌지만 종파 포논에 대해서는 찰 맞지 않고 있다. 공명성 라만 산란과 관련하여 위의 자유 전자-양공쌍의 연속상태보 다도 더욱 홍미 있는 전자 상태는 산재성 엑씨돈 상태의 기여가 된다. 엑씨론 천이는 실제로 매우 복잡다양하게 나타나지만 (I) cx 의 단일 엑씨돈 천이만을 고려할 때에도 ~d
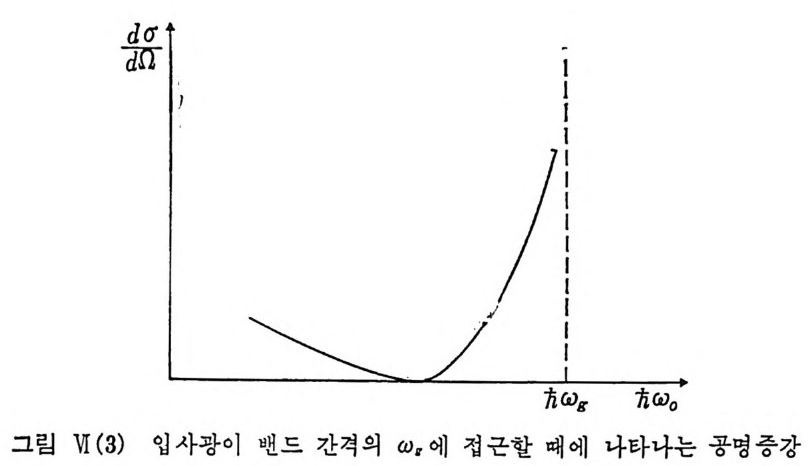蘇
와 같은 결과 를 얻는다. 여기서 r 는 엑씨 튼 의 감쇠상수를 나타내고 위의 결과를 Wo 의 함수 로 그립을 그려 보면 아태에서 보는 바와 같이 2 중쌍 정봉을 나타내게 된다. 2 중쌍 정봉은 각각 입사광 Wo, 산란광 Ws 가 엑씨돈 천이 Wex 에 접근하는 경우에 대웅하고 있다. 또한 공명 산란의 조건에 서 는 전자-격 자 상호작용 念 'e p’의 원거 리 성 분 즉, Froh li ch 상호작용 항이 q =O 산란에 대해서는 0 이 되어 기여가 없지만, 포논 방출과 관련하여 완전하게 q =O 를 만족시키지는 않게 됨 울 고려하면, 죽 q에 대해서 1 차 이상의 고차 섭동에 속하는 항들을
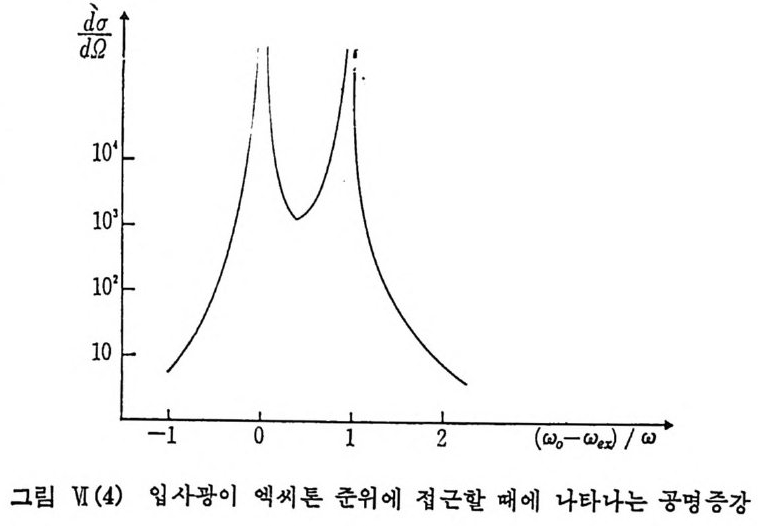劃
고려하게 되면, 바로 이러한 원거리 상호작용 항 에 의해서 , 단거리 상 호작용만 고려할 때 대칭성 선택물에 다타 금 지 되 었던 포논밴드가 새로 나타나게 되는 경우가 있다. \I-2 표면-증강 라만 산란 (SERS) ,1-2.1 실험적 관측 사실 피 리 던 (C5H5N) 분자를 온 (Ag ) 표면에 단일 분자충 (monolay er ) 으로 흡착시켜 라만 산란 실험을 하면 분자당 라만 산란 단면적이 ~10 배 까지 증강되어 표면의 단일 분자층에 의한 란탄 산탄 스팩트럼을 쉽게 관측할 수 있음이 확인되었다. Jea nmair e 와 Van Duy n e 에 의 하여 이 러 한 현상은 단지 표면적 의 기 하학적 증가에 기인하는 것이 아니고 금속 표면과 흡착된 분자와 빛 사 이의 새로운 상호작용에 기인하는 독수한 효과임을 주목하게 되었다. 이러한 SERS 와 관련되어 나타나는 실험적 목성을 종합해 보면 1 분자가 금속표면에 흡착되면 그 분자가 어떤 체적 상태 (액체 또는 고체 ) 또는 용액 상태 에 서 가지 는 타만 산란 단면적 보다 10;~10 6 배 의 훨씬 큰 단면적을 가진다. 2 증강된 분자 고유의 라만 스펙트럼과 등시에 넓게 퍼진 연속적 바 닥 신호가 그 밑에 겹쳐 등시에 나타나고 있다. 3 체적 또는 용액상태에서 얻는 스펙트럼에 나타나지 않는, 즉 타 만-금지되었던 모드들이 나타나고 있어 라만 산란의 선댁 뮬 일부가 깨어지고 있다. 4 SERS 가 찰 나타나는 금속표면과 흡착 분자들이 한정되어 있다. 가령 Ag ( ~106), Cu 및 Au(~10 합, Pt ,P d,Hg ,T i 등의 금속표면 과 피리던, CN-, CO 등의 흡착 분자들이 가장 대표적인 SERS 현 상을 나타내 보이고 있으며 CHaOH, CC14 등은 SERS 효과를 전혀 보이지 않는 것으로 브고되어 있다. 5 흡착된 분자가 나타내는 SERS 의 라만 스팩트럼 선들이 체적 또 는 용액상태의 스팩트럼 선들에 비해서 ~10cm-1 정도의 전동수 변이 (freq u ency sh ift)를 보이고 있으며 또 이것은 흡착충 두꺼1 에 따라 큰 변화를 보이고 있다. 6 SERS 스팩트럽의 강도가 입사광 레이처의 과장에 복잡한 함수관
계를 가지며 더우기 기판 금 속의 종류에 따라 그 함수관계가 달라 전다. 7 SE R S 를 나타내는 모든 거치른 금속 표면 자체에서 ~lOc m -1 정 도의 전동수 를 갖는 비 탄성 Mi e 산란이 매 우 강하개 나타나며 여 기에 0.05M 정도의 괴리단을첨가하면 이 M i e 산란이 휠 싼 증강되 어 나타남이 알려져 있다 . 다음 철 에서 이러한 SERS 현상을 설명하기 위한 여러가지 이론적 모 델들을 검토해 보겠다. \I- 2 . 2 이론적 고찰 앞 철에서 열거한 SERS 의 많은 목성 중에서도 ~106 배의 증강이 어 렇 게 주어질 수 있는지가 많은 사람들의 제일 큰 관십거리였다. 한편, 실험적으로 〈 반들반들 〉 한 금속표면에 있어서는 ~102 배 정도 의 산란 증강이 나타나고 그 이 상 ~104 배 에 해 당하논 증강은 반드시 흡착표면 에 거칠기 (rou g hen i n g)가 주어져야 됨이 확인되고 있다. 따라서 첫째 매끄러운 금속 표면에 분자가 홉착되면 왜 자유 분자의 상태보다 라만 산란 단면적이 증가할 수 있는지를 살펴본다. 라만 산란의 강도에 기 여 하는 인자들을 분자적 효과와 전자기 학적 효 과의 두 가지로 크게 나눌 수 있고 전자에는 주로 분자의 편국물 a, 후 자에는 주로 국소 전장의 세기와 산란광 방출에서 공전성 공명을 통한 증강이 문제되고 있다 . 매끄러운 금속 표면에서 고전 전자기학적 현상에 의한 증강을 생각해 보면 우선 표면 전장이 입사파 전장의 2 배에 달하고 쌍극자 복사에서 도 그 전장이 2 배로 증가됨을 모두 고려하면 결국 라만 산탄광의 세기 가 16 배 정도까지 증강될 수 있는 것이다 . 금속에서의 표면 풀라스몬 여기과는 국소 표면 전장을 형성하고 이때 국소 전장은 거 칠기 (또는 gra ti ng ) 의 전폭 f (단, i; w/c
고 이에 따라 푼라스몬과를 여기시킬 수 있게 된다. 사실 표면이 완전 평면인 경우에도 전동 쌍국자의 근접 장 분포가 불 군일 (inh omog en eous) 하기 대 문에 표면 풀라스몬이 여 기 될 수는 있 지 만 이 러 한 평 면 금속의 표면 플라스몬은 광자 방출이 불가능하고 이 플라 스몬에 의한 전자과 복사는 오칙 회철격자 또는 ATR 프리즘 구조를 가 지는 표면에서 가능한 것이 되어 이론적으로는 이상적으로 평평한 금속 표면과 회절격자 구조의 금속 표면 사이에 ~500 배 정도의 라만 산란 강도의 차이가 주어지게 된다. 이러한 표면 풀라스몬의 국소 전장 이의에 금속 표면이 가령 반경 a 의 아주 미소한 구형 입자를 포함하고 있다면 레이처 전기장에 의해서 아래와 같은 쌍극자 모멘트가 유도됨을 알 수 있다. 죽, 구형 입 자의 유전상수를 E1 (w) , 주위 매 질의 유전상수를 €2 라 하면 p= a3 E따1 (a,) )+-2€E22 E 타 (w)E 。 (\'I. 4) 또 이 입자 표면에 바로 라만 산란의 전동 쌍극자가 되는 흡착 분자 µ 를 생각하면 이 쌍극자 µ가 위에서와 마찬가지로 다음과 같은 쌍극자 모멘트 p'를 유도하계 된다. p'={3(c v')Eµ, cv'=cv— Wu C\'I• 5) 죽, 분자 자체의 타만 산란과 동시에 미소 입자도 같은 라만 전동수 o_Ou 의 쌍극자 전동에 의한 복사를 하게 되는 것이다. 따라서 전체 라만 산란의 강도는 |{3( o-Ou) (3( cv) I2 에 비 례하게 되고 여기서 {3 (cv) 는 ReE1( 야 )+2@=O 를 만족시키는 야에서 극대값을 갖는 공명 현상올 보이고, 이때 분자의 전동 주과수 Wu 가 공명 선폭보다 작 온 값이 되면 {3 (o-Ou) 도 WR 에서 동시에 공명 증가를 나타내게 된다. 이때의 공명에 의한 중강 인자가 {ImE1(wR)}-4 를 포함케 되어 유전 손실이 작은 구형 미립자 은 (A g)에 대해서 ~106 까지 될 수 있다. 만일 흡착 분자가 구형 입자의 표면에서 d 의 거리에 떨어져 있으면 표면에 흡착된 경 우에 비 해 서 {a/ (a+d) } 12 만큼 증강 인자가 감소하게 되고 따라서 a}}d 일 때에 그리 민감하지 않음울 보여주고 있다. 구형 입자 대신에 타원체 미립자를 생각하면 이 미립자에 유도되는 쌍극자의 전동에 기인하는 라만 산란의 증강 인자가 타원체의 a,b 축에
관계된 공명 주파수불 가지게 되며 은 (A g) 입자의 경우 a=b 일 때에는 (J)n =3. 5 eV, a=7 b 일 대에 는 wR=l . 6 eV 가 되 는 큰 차이를 보이게 된다. 이러한 거칠기에 관련된 전자기학적 공명의 증강이 SERS 의 전부 또 는 한 부분에 지나지 않는지는 아칙 실험적으로 명확히 판가름되어 있 지 못한 상태 에 있 다. 액 체 수은의 전국판 또는 초고전공 (ultr a hig h vacuum) 의 SERS 실험결과에서 보면 반들반들한 매끄러운 됴면에서도 SERS 가 관측되고 있으며 이러한 사실은 분자화학적 특성에 기인하는 효과도 같은 정도로 SERS 에 기여하고 있음을 시사하고 있다. 첫째, 분자의 한 전자 에너지 준위가 금속표면에 기인한 영상 쌍극자 전장에 의해서 쌍극자-유도 쌍극자 상호작용 즉 자유전자 금속표면의 편국에 의하여 변이 및 선폭 확장을 겪게 되고 이에 따라 금속의 Fermi 준위와 홉착 분자의 한 에너지 준위 사이에 입사광 레이저의 진동수에 대한 공명성 라만 산란의 조건을 만족시킬 수가 있다. 둘째, 흡착 분자의 전동운동에 따른 금속표면에서의 변위 4r 을 생각 할 때 전하 이동 상호작용에 의해서 금속표면의 전자들이 아래와 같이 라만 산란에 기여할 수 있다. +（글 )2( 옹 )2(4r) 2 rn. 6) 여기서 d q /dr 은 바로 분자의 변위에 따른 전하 이동의 크기이고, 대 표적인 경우에서 보통 2 원자 분자의 라만 산란 단면적의 20 배값을 갖 는다. 또 위의 결과는 보동 타만 산란에서 보는 (I)법칙에 따르지 않으며, or =iaj o Qj 에 서 aj - 4= 0 에 대 응하는, 즉 or 에 칙 접 기 여 하는 정 격 모드 들만이 이러한 증강에 기여하게 됨을 알수 있다. 죽, SERS 의 모드의 존성에 대한 가능성을 시사하고 있다. 표면의 거칠기를 목별히 요구하지 않는 도 하나의 이론으로써 광자가 금속의 전자-양공쌍을 생성하고 이 전자가 흡착 분자의 이온 핵심과 상 호작용, 전동준위 여기를 시키고 양공과 재결합, (I)＿아의 광자를 방출 하는 과정으로 볼 때 금속의 전자-양공쌍 여기에너지가 흡착 분자에 전 달되는 여러가지 가능한 과정이 따르고 이들을 포함한 편국물을 계산하 떤 ~104 배의 증강이 가능하며 연속체 바닥신호를 주는 형광복사가 예 상된다.
마지막으로 금속표면의 표면전하 밀도 p는 레이처 전장에 의한 표면 플라스몬의 여기와 흡착 분자에 의한 쌍극자 전장, 따라서 흡착 분자 의 위치 R, 및 전하량에 관계되고 있다. 이것은 표면 플라스몬이 분자 들 핵의 전동운동에 따라 변조되고 있다고 볼 수 있으며 이때 금속 표 면전하 밀도에 의한 쌍극자 모멘트 µ는, µ(R;, w) =d2r rp ( r, R;, w) (II. 7) 에 의해서 (옮기 ·6R i에 비례하는 라만 산란이 예상된다. 따라서 표면 풀라 스몬이 여기되는 레이저 전동수에서 공명효과가 예측되고 도 표면 쌍 극자 모멘트는 정전기장의 영향을 받게 되므로 전기 화학적 c e ll 에서의 SERS 강도가 전극의 전압에 의촌할 것이 예측된다. vI-3 soft -m ode 라만 분광학 '\'I-3. 1 sof t-m ode 이 론 1959 년 Cochran 에 의 해 서 구조적 상전 이 를 동반하는 강유전체 에 서 의 상전이 문제가 격자 진동학의 포는 불안정성 문제와 직결되어 있음이 밝혀졌다. 즉, 격 자의 광과성 횡 모드 중의 한 특별한 모드의 전동수 아 가 T-- Tc 에서 0 에 접근하게 되는, 따라서 이 야 포논의 모드 변위에 대한 복원력이 0 이 되어 이 모드에 대한 불안정성 죽 자발 변형에 의해서 강유전성 상전이의 자발 분극이 나타나게 됨을 설명할 수 있었다. 우리는 이미 격자 운동학과 관련하여 다음 사실들을 알고 있다. 첫째, 광과성 횡 모드 WTO 는 유전체 반응함수 E(W) 의 p ole 로 주어 전다. 言1 =0, (W=Wr0) (\I.8) 또 강유전체 결정에 대하여서 정전 유전 상수 E(O) 은 다음의 Curie - We i ss 법칙을 만족시키고 있다. E(O) =C/(T— To ) (VI . 9)
따라서 식 (\i .8) 을 만족시키는 o 를 (J)＝(J) TO= 아’ + i(J)T II (W. 10) 라 놓으면 T=To 에서 (J) ro=O 가 되어야 합을 알 수 있다. 이때에 1 (J) T'1 미 (J)r' ' I 의 경우를 보통 공명형 so ft -mode 라 하고 1(J)T 'I 더 (J)T ’' I의 경 우를 이 완형 soft -m ode 라고 부른다• 광과성 종 모드와 횡 모드 사이에 LST 관계식이 성립하는 결정체를 생각하면 c€( (0O0 ) ) =- 0= L/ ,'2 / (l )T , 2 rn.11) 가 되므로, 유전상수의 고주파수 극한 E( oo ) 와 광과성 종 모드의 진동 수 (L) LI 이 온도에 거의 무관한 사실이 알려져 있으므로 (L) T1 의 온도 의존 성이 0 건 =A(T ― To) (W.12) 가 또됨 s을of t -알m o수de 있가다 .D eby e 이 완형 의 모드 ((J)' = O, (J)” * O) 일 때 에 는 유전 체 반웅함수 €((J)）가 E(w) =E(oo ) + E (Ol)+ -Ei w ( o 1o: ) (V1.13) 로 주어 지 고 이 E ((J)) 의 po le 을 (J)pI I' 근 (root) 을 (J) L” 이 라 할 때 다음 관 계식이 얻어진다. cc( (0O0)) =(JJ下L II (W. 14) 따라서 t= (JJp11 1 =- EE ((cOo)) (J)L1 ’ ' =-T-A_' T 。 (VI. 15) 즉 Deby e 이완성의 so ft -mode 는 T ..... To 로 접근할 때에 임계성 완속 의 양상을 보이고 있다. 이제 so ft -mode 에 대한 격자 운동론 이론을 살펴보면 아주 간단한 예 로서 전하량 +z, 질량 m, 전자 편국룰 a 를 가전 이온들로 구성된 입
방체 단순 격자 구조를 갖는 단결정에서 mX=-,.x+ZE10• P=ZX/V+aE10•/V 로 주어지는 운동 방정식을 생각할 수 있다. 이제 횡파 편국을 갖는 격자 전동과가 여기된 경우를 생각하면 E_Tl oc=Eo+ 도3 P ( \I. 16) 종과가 여기된 경우에는 E_Ll oc=Eo+ 으3 ~ P-4 김p (W. 17) 로 주어지므로 횡과 격자진동에 대해서 군 x~(-•/m+~二 )X+~E 。 (\1. 18) 3 3 V 종파 편극의 격자 전동에 대해서는 _(I)2 X=(-; :71+: z:v:)x+ 1+ITE 。 (VI.1 9) 의 결과를 얻게 된다. 여기서 우변의 첫째 항에서 X 의 계수는 유효 힘상수에 해당하고둘 째 항에서 Eo 의 계수는 유효 전하에 해당한다고 볼 수 있다. 횡과에 대한 식 (\I.18) 의 경우 유효 험상수를 정하는 두 항이 서로 반대의 부호를 갖게 되어 令-두읊 -/(1- 두令 )=O (VI. 20) 가 되면 공명 전동수가 0 이 될 수 있음을 알 수 있다. 한편 단거리 힘상수 K 는 비조화 항들을 고려하면 ,;=aT+b 의 온도 에 대한 함수관계를 나타내고 있으므로
z 2 ( 두 /vm ) 갑=―m - 1- 上3 프_V =a'T-b' oc w 。 2(T-To) (W .2 1) 의 결과를 얻게 됨을 알 수 있다. 이러한 so ft -mode 의 온도에 대한 함수관계를 찰 나타내고 있는 한 설 험결과를 아래 그립에서 볼 수 있다.
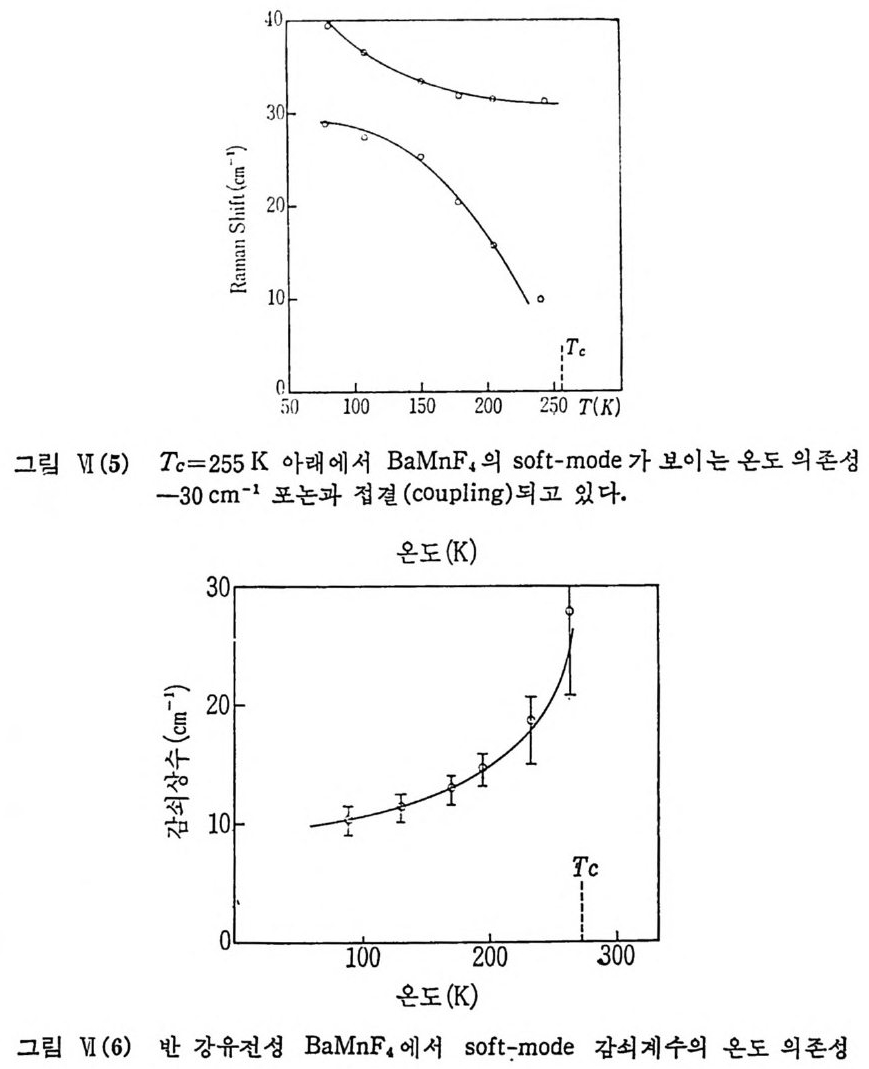·l0
이러한 격자 운동론의 입장에서 분 때에 so ft -mode 는 k=O 광과성 횡 모드에 국한되지 않고 zone 경계벽 포논, 음파성 모드, 또는 집체성 Jah n-Teller 효과를 유발하는 전자상태 여 기 에 서 나타날 수도 있 다. 또 이들 so ft -mode 는 반드시 변위형의 구조적 상전이 분만 아니라 질 서-무질서형의 구조적 상전이에도 관계하지만 이 질서-무질서계에서는 보통 포텐셜의 비조화성이 매우 커서 2 중쌍 극소골을 가지게 되고 이 경 우 굴작용 (tun nelin g ) 갈라침 이 충분히 커 야지 만 soft -m ode 전동수의 실수 부분이 0 이 아닌 값을 가지 며 따라서 공명 형 에 속하는 sof t ~m ode 가된다. \1-3. 2 centr a l mode 구조적 상전이를 가지는 많은 결정들이 Tc 에 접근할 때 그의 광산란 또는 중성자 산란 스팩트럼에 매우 좁온 선폭의 (!)：：：：：： 0 의 성분을 나타내 보이며 그 산란 강도가 Tc 에서 발산, 극대치를 갖게 된다. 이 들 준탄성 산란의 새 로운 벤드를 centr a l mode 또는 centr a l pe ak 라고 부르고 있다. 아칙 도 이 centr a l pe ak 의 강도에 동적 요동, 정 적 결함, 또는 불순 물 입자 등이 각각 어떻게 기여하고 있는지 논란이 계속되고 있다. 또 실험 결과에서 알려진 사실들로서 centr a l peak 의 관측이 임계 영 역보다 훨씬 넓은 온도 영역에 걸쳐 나타나고 있으며 그 제기가 또 so ft -mode 의 q값에 따라 크게 변하고 있음이 알려져 있다. 따라서 T 一 Tc 에 서 soft -m ode 요동의 spe ctr a l densit y 가 centr a l mode 로 전 달되 는 가능성이 있으며 이러한 근거에서 soft -m ode 운동방정식에 비조화성 상 호작용에 기인하는 감쇠효과를 고려할 때에 갈=-(.V。 2X+Fex p(i야)-t。 M( t-t'） X (t') dt' (\I. 22) 로 표시할 수 있다. 여기서 X=f t-x, Wo=A(T-To/'2, 기여함수 M 울 포함하는 멘 끝항의 적분은 포논-포논 상호작용에 기인하는 감쇠효 과를 나타내고 있다. 이 때 soft -m ode 전동수는 다음과 같이 재 규격 화되 어 학=(.()。 2+ -1+c.(v.2 I() '2r 군 (W. 23)
다타서 OJ! 2 ) 1 의 경 우 o 。 2=w 。 2 + I' /r cc ( T— Tc ) (\T. 24) 의 결과를 얻게 된다. 한편 이러한 전동자의 반응함수로부터 얻어지는 광산란 강도 l(w ）는 l(w) cc (합－硏)r 도 (t(I))2 『=I' /(l+w 단) C\i. 25) 로 주어 지 므로 (J)t > 1 의 경 우 여 기 서 centr a l pe ak 가 생 기 고 Ic/ Is cc (o 。 ;;) -2 (W. 26) 가 됨을 알 수 있다. 따라서 centr a l p e ak 는 Tc 에 아주 근접하지 않고 서 는 항상 soft -m ode pe ak 보다 매 우 약하게 나타날 것 으로 예 상할 수 있 다. 또 이 때 에 미 조화성 효과 가 cen tr a l mode 족으로 상당히 흡수되 면 soft -m ode 자체 는 완전히 0 의 전등수까지 내 려 가지 않게 될 수 있 음을 알수있다 • 많은 결정체에서 soft -m ode 전동수 Ws 가 0 으로접근하는온도 따와 상변화가 실제 일어나는온도 箕 사이에 Tc_T 。-=t- 0 죽 온도간격이 관 축되었고 이러한 T- g a p은 3 차 비조화성에 의한 so ft -mode 와 음파성 포논 밀도 요동 사이 의 상호작용에 기 인한다는 Cowley 의 이 론을 보면 이 때 soft -m ode 의 반웅함수 G (w) 가 G (l( I)) =(I)。드(I) 2 + i. (I) 7 。_ 1 +a iT(I) To (vI. 27) 로 주어 지 고 이 경 우 광산란 스펙 트럼 에 centr a l pe ak 를 포함하게 된다 는 것이 알려졌다. 그러나 이러한 포논밀도 요동등 바조화성에 기인한다는 이론밖에도 앞에서 언급한 바와 같이 열확산 모드, 모드-모드 결합의 비선형 효과, 정적 결함 등에 기인한다는 이론도 주장되고 있다. ,lf-3 . 3 coup le 된 모드의 라만 스펙트럼 KDP 결정에서의 soft -m ode 스펙트럼은 soft -m ode 자체가 과도 감쇠되
어 있고 이에 따라서 그 띠 선폭 안에 들어오는 다론 격자 전동 모드 와 상호 결합되어 실제 나타나는 스펙트럼은 매우 복잡해지고 우리는 이들 스펙트럼을 분석하여 그 결과로부터 상호 결합에 참여하는 모드들 각각에 대 한 정 보, 가령 soft -m ode 자체 의 온도에 의 한 변화 양상 둥 울 알아낼 수 있는 것이다. 상호 결합된 (cou p led) mode 에 의한 산란 스펙트럼을 구하기 전에 우 선 광산란 스펙트럼을 포논 전파인자(p ro p a g a t or), 즉 그린 함수 (Green's fu nc ti on) 를 써서 어떻게 표시할 수 있논지 알아본다. 편극물 (po lariz a bil ity) a (r, t) 를 기 준 전동 (normal mode) Q. 로 전개 하면 • a=a 묘(훑)。Qi (r, t) ( \If. 28) 로 쓸 수 있 고, 비 너 -킨찬 (Wi en er-Khin c hin e ) 정 리 로부터 ls (ws) = 上211 : 5J _ .... ei.,s T
마찬가지로, !2 ((J)) =S OO e i이 T dr: - OO = 통 Ebe - 5c, 〈 a l Q.J b>< b IQ i | a> O(cb-ca+(J )) =e Pw /1 (w) (YI. 32) 의 결과를 얻으며 이로부터 지연성 (reta r ded) 그린함수 Gu(•) 가 아래와 같이 주어침을 볼 수 있다. Gu (.) = -i( } (z-) <[ Q i(T ) , Qj (O) ] > = -i fJ (.) 같 )_:dw' U2 (w') -], (w') } e-;., = - i0 ( .) 吉t :d (J)’ (ePw'-1 )]1 ((J)’) e-i. ,” (W. 33) 이의 푸리에 변환을 보면 Cu (王) = 테 -러 °°d ( J),1_ (e’aI _ 1) A ((J)’) e-i 'f ei( a-n) r 。 -OO 2 元 = t-O :O dcv 나2-T (e’oI _ 1) 0A_( (Vo 1 I+)1 .7 에서 lni m내 _亢! _ --X--.2-!+?-#-. -= o( x) CVI. 34) 에 주목하면 Im Gu((JJ ) =-습 L:d (JJ' (eP ''-1 ) 11 ((JJI ) 6 ((JJ-(JJ') 국 (1- e'') / 1 ((JJ) (\I. 35) 의 관계식을 얻을 수 있다. 보우즈-아인슈틴 (Bose-E i ns t e i n) 동계 인자 (fl= 1) n( (JJ）e'=.,―-1느 (\I. 36) 를 쓰면, 마침내
J, (w) =2 n(w) biz G u(w) (\1, 37) 의 결과를 얻는다. 따라서 ls (ws) = E 승 (왕 웃 E 。 )22n (ws-Wo) x (훑)。 (훌-)。 Im Gu(ws-Wo) =C iI, :j P,P; n(ws-w0) Im Gu(ws-Wo) (\I. 38) 로 쑬 수 있다. 여기서, C=¼-( 왕끊 E 。)\ P=( 홀)。 를 나타내 며 , (J) s- (J)。=(J)＞ 0 인 anti -S to k es 와 (J) s- (J)。= -(J) <0 인 Sto k es 성분을 모두 (J)로 표시하던 n (-(J)) = -{ n ((J)) + 1}, @(-(J)) =-Cu((J)) (\]. 39) 가 성립하므로 ls ((J)) = C {n刀 ((((JJ)))) + l } Im 5'·J P;P; Ga ((J)) (\L 40) 로 쑬 수 있음을 알 수 있다. 하모닉 (harmonic ) 근사에서 격자 전등계의 해밀토니언은 念=판詞+당 ?n w 。2 러낸” '명 Duu,uJ (W. 41) 로주어지고 그린함수 G;;(l-t') =-i
G;;(t ) =G0(t) o ,;+ m L- :o,0o d t' G 0 ( t-t') ~L Di !G i ; (l') (VI . 43) Cu ((1)) == \장 - oO Oo( d(1)t) &G사u- ( mf) e정… ((1)) El Di l Cu ((1)) rn . 44) 로 주어 지 고, 위 에 서 GO ( t) 는 자유상태 , 즉 섭 동항 (coup li n g ter m) 이 없을 때의 그린함수로서 아래와 같이 주어지게 된다. G°(t) =-t· 2m 1 w o e-iO o1l 1 장 (o) = m (w2 -1w o 2 + ir;) (VI. 45) 이제 일반해 공식 rn. 44 ) 로부터 서로 독립적 인, 즉 단일 포논 (one p honon) 의 근사에 대한 그린함수를 구해 보면 G11° 三강= C0((JJ ) 1-m C0((JJ )D u = 1 1 m (w2-w 。 2 -Du+ ir;) = m1 ((J) 2_ (J)1。 ' 2+ iTJ) (VI. 46) 몰 얻게 된다. 한편 요동-소산 (fluc tu a ti on -dis s ip a ti on ) 정 리 에 의 해 서 유전 감수율 x 의 허수 부분 x(cv) 와 산란광 강도 Is 사이에 ls (w) =C{:~:; +I }x(w) nl[. 4 7) 의 관계가 주어지므로 식 (W.40) 에서 z (w) =Im L P;P; G;1 ( w) ( \If. 48) i,J 임을 알 수 있다. 따라서 단일 포논 전동자에 의한 광산란 스펙트럽은 식 (W.46,48) 로 부터
x (w) oc l (J) 2_ (J) 。 麟尸 (\1.49) 즉, 단순 감쇠 조화 진동자 (sim p le damp ed harmonic oscil la to r ) 의 스 펙트럼이 됨을 알 수 있다. 이제 두 개의 전동자가 가장 중요한 역할을 하게 되는 한 물리계에 대해서, 즉 2 개 합성 진동자(t wo coup le d osc i lla t or) 에 대한 그탄 함수 를 구해 보던 역시 식 ('1 .44) 로부터 , i,j, l=l,2 에 해당하므로 C11=G0+m G° CD11G11+D12G12) G12=G21=m G0 (D11G12+D12G22) =m G0 (D21G11+D22G21) G22=G0+111 G° CD21G12+D22G22) ( \T. 50) 를 얻고, 이들로부터 cII 1— G~1 °합 G~2 ° 2122 c22 1-C1 。c 2G°2 ° 2 군, C12= _ 1 _s1c21 °c 1C°8 C 22°1 22 (W. 51) 를 얻을 수 있다. 여기서 G1°,G2° 는식('1 .46) 으르 주어지고상호 결합작용의 항 D1 2 는 Z12= -mD12=A2+i( J)[' ( \If. 52) 실수 부분 (4) 과 허수 부분(I')으로 분리할 수 있다. 따라서 두 개의 결합된 전등자에 의해서 주어지는 산란광 스팩트럼은 x ((J)) = fm i,2j2= I PiP Ja , =lm{ -1:.i학 -2PI p 2 2'l2 학 C20+P 函 1-C1° C2° 2'122 } =Im{ ~ (야 -Q2 -im I '2) + P22 (따 (w12- 硏-i w I' 1) (w/-w2 --wi2따- i)w- I ('14) 2- 2-P i1 mP I'2 )(2L 12-iw I ') } (W. 53)
로 결정됨을 알 수 있다. 이것온 두 진동자에 관계된 변수 PI,P2, (J) h (J)I'i,I' 2,L1, I'의 8 개 변 수가 서로 어떻게 주어지느냐에 따라 실제 설협에서 관측되는 스팩트럼 율 얼마나 찰 맞추어갈 수 있는지 콤퓨터 계산에 의한 곡선 맞춤 (curve fitting ) 에 의 존하고 있 다. VI-4 비 선형 산란문제 챕 -4.1 비선형 광학 감응계수 매우 강한 레이저 전기장에 대해서 물체가 비선형적 반웅울 보이는 경우 물체에 유기되는 편국 P 는 P=Pm+P( 2)+pm + …… =xCI)E+xC2) : EE+x(3) : EEE+… ··· nL 54) 와 같이 표시할 수 있다. 여기서 광산란과 관련된 비선형 항은 바로 세번째의 3 차 비선형 항 으로서 이제 W1, 야 ,W3 의 입사광에 대해서 W4=W1-w2+wa 에 해당하는 출력 산란광파가 생성되는 예를 들면 PI(3)(o4)= 2 쩌i l(-0 나 0I, _%03)Ej@ ) Ek*(o2) EI( 어 i, k, l (\11. 55) 짜i l =xfJ ~i +x~; k t =x 臨+ 야- N((1)a1 _ii (1@ )2 ) ...::iI'R (vI. 56) 의 형태로 주어진다. 위에서 따온 비선형 산란 과정에서 여기되는 에너지 준위에 해당하 는 공명전동수로서 (J)4 _(I )3 죽 (J) 1_ (I) 2 에 대웅되는 값이다. 위식에서 보면 x(3) 가 바공명 (NR) 항과 공명 (R) 항으로 구성되어 있으며, XNR 에 기인하는 기처선 (back g round) 과의 간섭에 의한 선폭 모 양의 변형을 극복하는 것이 실제 실험에서 부딪치는 난관이 되며, 균에 의 한 공명 조건을 이 용하기 위 하여 동조가변 (tun able) 영 료레 이 저 ((J)h (J)2 ) 의 이 용이 필수적 이 다. 결국, 비선형 현상은 물질 자체의 성질에 기인하고 있는 것이며 아제
간단히 Drude 또는 Lorentz 모형 (model) 을 확장시켜 다음과 같이 전동 수 士(J) 1 과 土(J) 2 의 푸리에 성분을 지니는 의부 전장에 의해서 원자 또 는 분자의 운동이 비 조화성 (anharmonic ity) 을 고려 할 때 어 떻 게 되 는 지 알아보기로 한다. x +rx+ (J)。 2X+ DX 두二2m― {E1exp [i (k1z-(J) 1 l) J +E2 exp [i(k 2z-(J )zf)J +C.C.} ( llf. 57) 찰 알고 있는 바와 같이 D=O 의 선형 근사에서는 X((J)1 ) m (아。 2 -we , 2-iw,I ' ) L\ exp (ikl z-0l t) (\i. 58) 의 푸리에 성분을 가지는 해가 얻어지고 X(-w,) =X* (ai1) , l=l, 2 (W. 59) 가 성립한다. X( t)의 일반해는 X( t) = I: ReX( 이 i =.{2- It : {X(wz) +x*(*w z)} 로 주어지며 이에 대한 선형 감수울은 단위체적당 No 개의 분자를 고려 할때 P 鈴 @) =.{2- {P x (w) + P 균 (w) } =갑 (w)Ex(w) =N。 eX(w) 따라서, XL (a,) m ((/)。 2N_(o/ )e22 _ i(/)I') (\T. 60) 를 얻는다. 그러 나, D*O 의 비 선형 항을 고려 하면 (I)=2 (.()1, 2(I) 2 , O, W1+W2, W1- (I) 2 에 대웅하는 항들이 생기며, 가령 (I) 1+ (I) 2 항을 보면 X( (IJ급(IJ 2) #2DmE2I (E(.(2)。 2e_x(p.( [)i1(2k- li r+(.k()21))Z X
-@i2(_wW1 + 2w22_)i lI ]' o 2) 〔 Oo 드 (0l+02)2_iI '[(J)I— + (J)2 )] (vI. 61) 가 얻어침을 알 수 있다. 따라서, 3 차원의 한 특벌한 예를 들면 P 간(Q) 1 + c2) =N。 eX(w1+ 야) =z1i x ( — Wi , -w2; Wi , w2) Ex(W1)Ex(w2) (W. 62) 의 관계식에서 溫 x(_ (I) I, _(I)i (I) l 濁) = 2Nm。 2D e 3 x&((I)1 ) X X~x((J) 2 ) X~x(-(J) I, -(J)2) nL 63) 의 결과를 얻을 수 있으며 여기서 X 3< x 는 식 (\If .60) 으로 주어진다. 식 (\If. 60) 과 (\I. 63) 및 (\I. 62) 로부터 1-; 仁 1 ：：：：： 忍 2e\ I 간 |2|E 。 1 (\I. 64) 를 얻는다. 실제 (I)。 » w 인 경우 CVI.60) 식에서 #：：：：：： N0e2/ 沼(I)。 2 가 됨 에 주목하고, 원자 반경을 ao 라 할 때 X： ：：：：： ao 에 이르면 선형 항과 비선 형 항의 힘이 서로 같은 크기가 된다고 보면, 죽 ?n Oo2a 。 :::::mDa 。 2 ( \if. 65) 를 가정하면 D ：：：：：(J)집％ 또 원자 반겅에시의 쿨롱 전기장을 rff (ao) 라 하 떤 m (J)。%。：：：：： e rff (a 。)에서, 결국 lDW me 3 l # 12 = g (1a 。) (VI. 66) 의 결과를 얻는다. 따라서, IP 표 /PLI'.::'.IEol/ Jiff (a 。) | ('1. 67) 가됨을알수있다. 즉, 비선형 효과가 크게 나타나기 위해서는 원자에 미치는 입사광의 전장의 제기 Eo 가 원자 내의 쿨롱 전기장
야 항을 알 수 있고 상당히 강한 출력의 레이저를 렌즈로 집속시켜 얻 는 경우의 ~106V/cm 에서도 I E 。庫 (a 。) ' :::::::1 0-3, 즉 비선 형 문재는 섭동 효과로 취급할 수 있음을 볼 수 있다. 비선형 효과에서도 대칭성이 중요하게 작용하며, 한 예를 들면 3 차 원의 경우 제 2 차 비선형 효과, 가령 주파수 혼합(fr e q uenc y mi xi n g ) 또는 2 차 고조파 발생 (second harmonic ge nerati on ) 의 경 우 P,NL(W1+ 야) = 료 (-w1-w2; w 硏%) E; (w 1) Ek (w 2 ) ( \T. 68) 를 보면, 반전 대칭 (inv ersio n s y mme t r y)의 연산자 를 작용시 킬 때 (P;NL) '= -P,NL , E/= -E;, Ek '= -Ek 가 되고 만일 물질계가 반전 대칭성을 가지고 있다면 (x 麟 )'=x ?k , 즉 부호가 바뀌지 않으므로 이때에는 xfk= O, 따라서 반전 대칭 연산자에 대하여 불변인 계에서는 2 차 고조파 발생 등 2 차 비선형 현상이 나 타날 수 없음을 알 수 있다. VI-4.2 하이퍼-라만 산란 및 유도 라만 산란 입사 레이저광의 제 2 고조파 주파수를 중십으로 조사해 보면 이 고조 파로부터 분자의 전동모드 전동수 만큼 차이 가 나는 곳에 산란광의 스 팩트럼 선들이 관측될 수 있다. 이들 스펙트럼 선들은 또 하나의 3 광 과(th ree ph oto n ) 상호작용의 하이 퍼 -라만 효과에 기 인하고 있으며 하 이퍼-편극물 (h yp e rp olar i zab ilit y )의 변조 (modula ti on) 에 의한 타만 산란 현상이다. 이들 하이퍼-편극물의 크기와 부호를 하이퍼-라만 스펙트럼으로부터 결정할 수 있고 이것은 비선형 광학 감수율 (nonl i near op tica l suscept i- b ility)의 분산곡선율 구할 수 있는 중요한 방법이 되고 있다. 이 비선형 편국물과 관계되는 하이퍼-타만 효과에 적용되는 선택률은 보통의 선형 편극률과 관계된 라만 효과에 적용되는 선택물과 다르기 때문에 적의선 흡수 및 1 차 라만 산란의 스펙트럼에 전혀 나타나지 않 고 있는 소위 불활성 (sil en t) 모드에 속하는 분자운동도 하이퍼-라만 산 란에서는 관측될 수도 있다. 가령 NH4Cl 단결정 의 질서 -무질서 (order-dis o rder) 상전이 와 관련된
임 계 점 혼탁광 (criti ca l op a lescence) 이 선형 광산란 (line ar ligh t scatt e- rin g ) 으로는 관측이 안 되 고 있 는데 이 것 은 NH4+ 이 온의 선형 편극물텐 서 가 가지논 회전축 대칭성 (rota t i on al s y mme t r y)에 기 인하고 있다. 그 러나 비선형 편극물은 무질서상태에서는 0 이 되지만 질서상태에서는 유한한 값을 가지게 되어 입계접 온도 근처에서 온도의 함수로 하이퍼 타만 산탄강도를 정 밀 측정 하면 이 로부터 NH4+ 이 온의 질서 배 열 (ord- er i n g)에 의 한 상관관계 거 리 (correlati on len gth) 의 증가 양상을 알아넬 수 있고 또 NH4+ 이온들이 서로 다른 각도로 배열된 구역의 구조 및 성 장에 대해서도 정량적인 정보를 얻을 수 있다. 또 다론 한 예로 BaTi0 3 결정체의 상유전성一강유전성 (pa raelectr i c - fer roelect ri c ) 상전이 ( E ：：：：： 403°K) 와 관련된 정 입 방체 상 (cub i c ph ase) 의 Fu 대칭성을 갖는 연성-모드 (so ft -mode) 는 본래 라만 활성이 없지 만 (Raman ina cti ve ) 3- 광과 과정 인 하이 퍼 -라만 산란에 서 는 쉽 게 관측 할수 있다. 더우기 정입방체 상의 BaTi0 3 결정은 반전대칭 중십울 가 지고 있어 (centr o sym metr i c ) 하이퍼-레일레이 산란 (2w 。）이 금지되어 매 우 약하게 나타나므로 연성 -모드의 연성 과정 (soft en in g ) 을 2 Wo 에 매우 가까이 접근할 때까지 관측할 수 있는 장접이 있다. 광산란 이론에서 산란광의 모드당 광자(p ho t on) 갯수를 Ns 라 하고 입사광 래이처의 광자 갯수를 NL 이라고 할 때에 Ns 의 단위 길이당 증 가울은 쁘dx =A(Ns+ l) NL (W. 69) 로 주어진다. 따라서 Ns:}>l 이 되는 경우에는 Ns (X) =Ns (O) exp (gh x) (VI. 70) 와 같이 지수함수적인 증폭을 수반하는 유도 광산란 (s ti mula t ed lig h t scatt er in g ) 을 관측할 수 있 게 된다. 보통 유도 광산란의 관측에 필요한 입사광의 강도 L 은 106 W/cm2 < h <109 W/cm2 (VI. 71) 로 제약이 되고 있지만, 소위 자체집속 (se lf-fo cus i n g) 현상에 의하여 ~lOµm 정도의 례이처 필라멘트(fil amen t)가 형성되는 일부 물질에 있
어서는 위의 하한치가 훨씬 더 낮아질 수 있으며 또 이러한 자체집속 이 되지 않는 경우에도, 주로 반도체에서, 공명 증강의 효과를 이용 Ns~ I 의 조건 죽 유도 (sti m ulate d ) 산란이 , 아주 낮은 강도의 레 이 처 에 의해서도 관측될 수 있음이 알려쳐 있다. 라만 레이저 (Raman laser) 는 바로 이러한 유도 타만 산란 효과를 실용화한 것이다. 한편 상한치는 너무 강한 레이저 광속에 의해서 유도 산란 이의의 다른 바선형 효과 들 이 더 크게 나타날 수 있고 이러한 현상온 레이처 광속 자 체 에 많은 변 형을 가져와 유도 산란에 대한 정량적 연구가 불가능하게 되는 것이다. 또 레이처의 제기가 ~1012 W/cm2 이상이 되면 모든 물질이 풀 라스마 를 생성하게 되어 물질 자체가 변하게 된다. 보통의 자발성 (spo nta n eous) 광산란은 입 사광의 루과 (tra nsmi ss io n ) 에 아무런 영향을 주지 않지만 유도성 (sti m ulate d ) 광산란에서는 산란 자 체에 의하여 입사광에 대하여 본래 두명한 물체의 실제적인 두과울이 대폭 줄어들 수가 있다. W-4. 3 카스 간섭성 라만 산란 (CARS, Coherent Anti -S to k es Raman Scatt er in g ) 3 차 비선형 광학 감수울 X ij kl 에 의한 비선형 산란광의 크기 를 결정 짓는 3 차 비선형 편극 밀도(p olar i za ti on dens ity)가 한 예로 아래와 같 이 주어침을 이미 지적한 바 있다. P; (W4) =fxm1 (-w4, W1 , -w2, W3) E; (w,) E1 * (w2) E, (w3) (\T. 72) 카스 (CARS) 는 위의 일반적 비선형 라만 산란 중의 한 특벌한 경우 로서 다음과 같이 주어 진다 . P 玉)=웁 Zuu(_% (J) I, _(J)a (J )1 ) Ex(w1) Ex* (w 2) Ex(w1) (\I. 73) 즉, 카스에 실제 사용되는 레이처는 W i, W2(W1>W2) 의 두 개의 레이 처로서 x(8) 의 성질에 의하여 oI_ Ct) 2 가 어떤 라만 천이의 공명 주파수 Ct)R 에 접 근할 때 Px(wa) 죽 카스의 강도가 공명 조건에 의 하여 증가하 게 ’ 된다.
E((I)/ , z, t) =2i {E((I) /, z) e-i( 't-k ,z) +C.C.} , P(wn, z, t) =上2 {P((I) n )e-i( .,.1-1.z>+C.C.} 몰
i k 출 E( (J) n) ＝지을 P(3) ((J)' z, t)} ex p규 (kz- (J) n t) (W. 74) 에 대입하면 아태와 같은 결과를 얻을 수 있다. Ex@)= 울i w 집元福 X1111(-w 군 1, -w2,W4) X E 顯 )E,\. * （어 L~2) (W. 75) 를 얻을 수 있다. 여기서 Llk= I (2k1 -k2-k3) ·키 , X1111 =x~f1 1 + X1111 + i X1111 르 쓸 수 있고, 따라서 /(a,3) = 움硏 o l Ex (ws) 12 =奇 “12 0n3: n3 (운 )2 /2(w1) l(w2)U ~겁 ;1 감십2 2) X{lxff 11 l2+lx[1ul2+lx[[11l2+2xff 11 X[fu } (\1.7 6) 즉, 카스 스펙트럽에서 관측되는 라만 스펙트럽에는 네 가지 서로 다 론 성격의 항목들이 기여하게 됨을 볼 수 있다. 이로 인하여 카스의 라 만벤드 (Raman band) 는 매우 복잡한 벤드 형상 (band shap e) 을 가지게 되며 아래 그림에서와 같이 간섭 효과를 보이고 있다. 위 상 접 합(p hase ma t ch i n g)의 조건으로부터 최 대 강도의 라만 산란 광을 주는 광산란 길 이 (int e r acti on leng th) Le 는 Lc=1r/L1k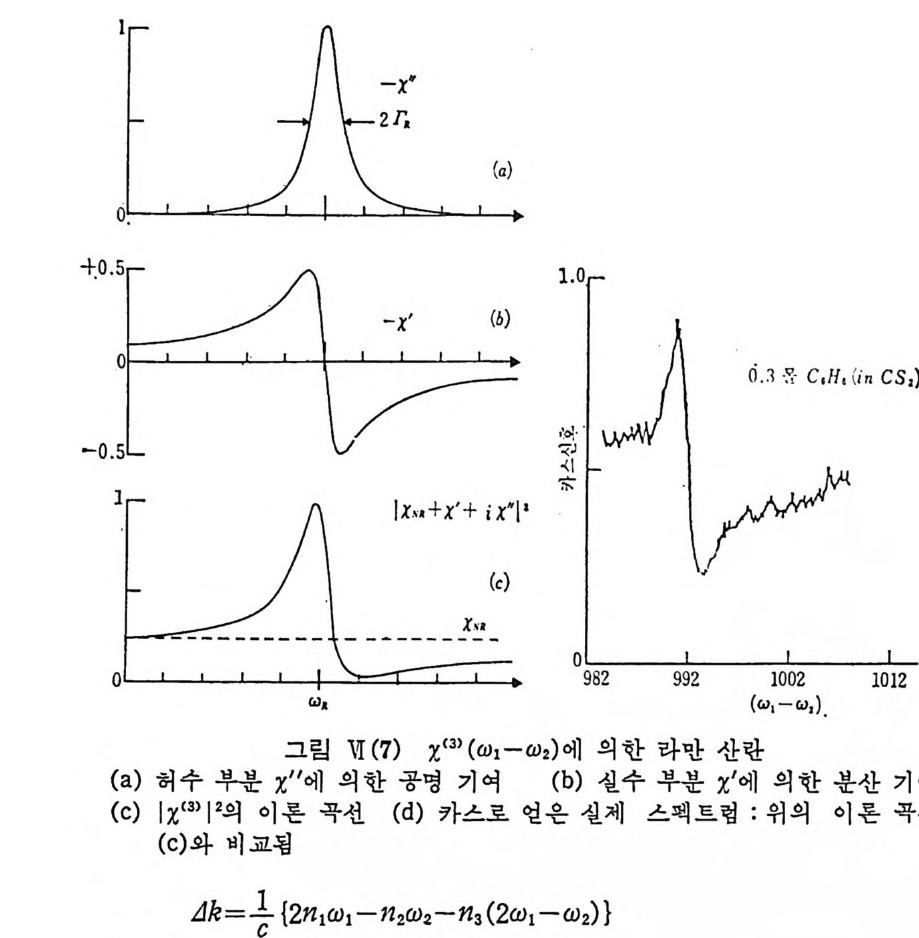
(a)
를택하면 도 ((I)1 _(I) 2) 2(2?i +(I)틀-) (젠. 77) 로 근사시킬 수 있다. 기체에 대해서는 Lc 가 보통 수 cm 에 이르고, 이것온 카스 실험에 서 레이저들이 서로 교차해 가는 길이로 결정되는 유효 산란작용 길이 (effec ti ve int e r acti on len gth) 보다 훨씬 길어 서 위상 접 합에 (Ak=O) 크 게 신경을 쑬 필요가 없으며 두((J) h (J) 2) 입사 광속 사이의 위상접합 각 (ph ase matc h i ng ang le ) fJ 는 f)= 0 가 된다. 카스의 대표적인 실험장치는 아래 그림에서 보는 바와 같다.
Tunable
위의 그립에서 o1 레이처는 보통 라만 산란의 실험에서와 같이 입의 르 정해진 레이처 진동수에 해당하고 02 레이저를 보통 라만 산란의 스 토욱스 (S t okes) 변이된 라만 산탄광 전동수에 동조(t un i n g)시키면 카스 출력 신호로서 W4=W1+w1-Wz 죽 상반-스토욱스 (an ti -S t okes) 라만 산 란에 해당하는 산란광이 나오게 되는 것이다. W-4. 4 라이크스 스펙트럼 (RIKES, Raman Induced Kerr Ef fec t Sp ec tr o scop y) 위의 카스 (CARS) 에서 실제 실험적으로 제일 문제가 되는 것은 XNR 에 기인하는 기처선 잡음 (back g round) 울 어떻게 제거시키느냐는 문제 이다. 라이크스 (RII
만 서 로 수칙 이 되 는 비 선형 펀극원체 (po liz a ti on source) 를 생 성 시 키 는 것이다. 따라서, P:L(W2) =웁i [x1212C-w2, W2, -w 군 1) E,Cw2)Ex * (w1)E,( 이 -:r.122 1 (-w2, W2, -wi , 。 1)E, . Cw2)E,*(w1)Ex@) 〕 =웁i[r. 1212-x1221 J E, （이 |E(wi ) 12 (\if. 78)
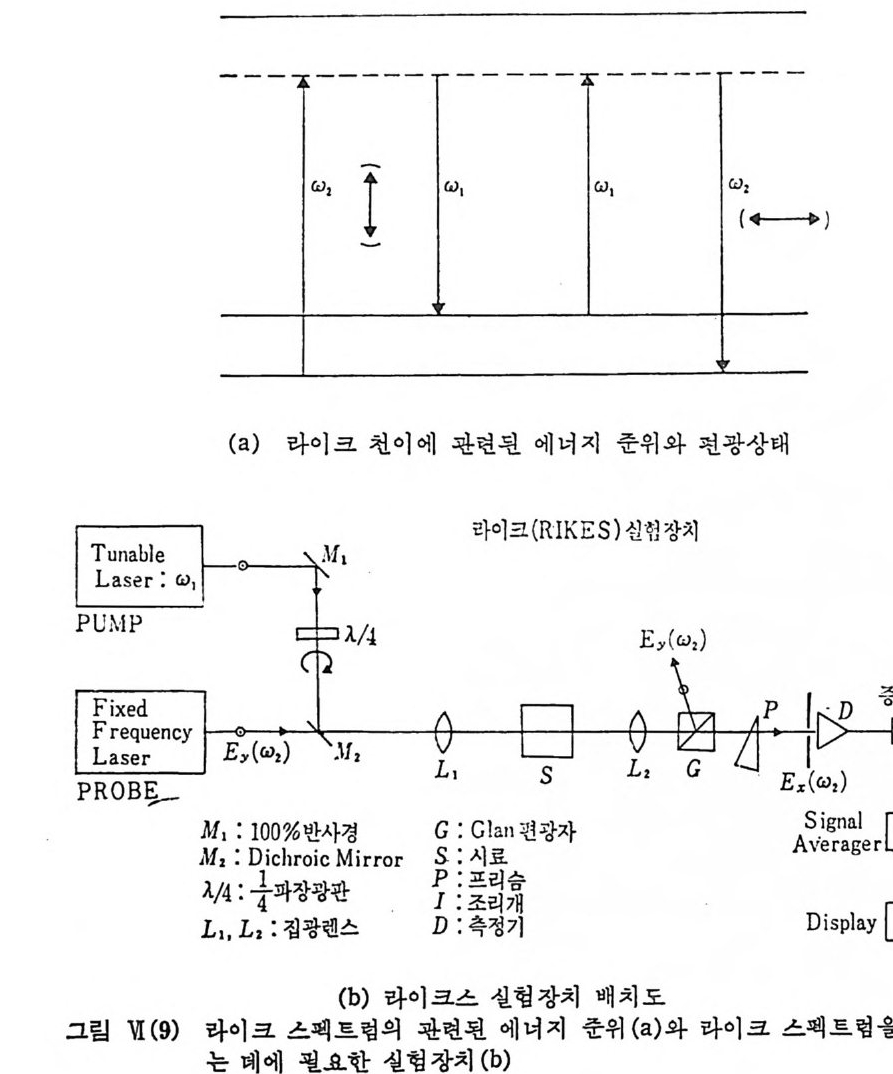___ 工 ____ -T _____ r-----__ _ _
를 만족하고, 여기서 Xii A1 = y갭 ?A i + x:m + i x;;J,,I 로 쓰면, 라이크스 (RIKES) 에서는 x ff 12~ t'tf2 1 의 조건이 만족되는 법위 안에서 XNR 에 기인하는 기저선 잡음 (back g round no i se) 이 없어침을 알 수 있다. 또한 탐색 레이처와 펌프 레이처 사이의 겹침각 (overla p ang le) 에 관 계없이 입방체 대칭성 즉 등방성 물체에 대해서는 항상 Llk=k2-k1 +k1 —k2 =0 ( \i[. 79) 가 만족되므로 카스에서와 당 리 위상접합 인자 s i n(L1kl/2)IL1kl/2 가 개입되지 않는 이접이 있다. 카스에서는 도 (JJI _(JJ 2 =(J JR ->0 즉 아주 낮 은 전동수를 갖는 모드의 경우, 파동 벡터 접합조건에 의해서 입사광과 카스 산탄광이 동선평행 (coll i near) 으로 전과되어 나가므로 카스 산란광 율 따로 분리시키는 데에 큰 어려움아 따르지만 타이크스에서는 그러한 어려움이 없다는 것도 하나의 잇접이 된다. 타이크스에 관련된 에너지 준위 설명도와 실험장치를 그림 \'1 (9) 에 표 시하였다. 참고문현 I. W. Ric h te r , Resonant Raman Scatt er in g in Semi co nducto rs, in Sol. St. Phys . , Sp ri n g e r Tracts in Modern Phy si c s vol. 78, Sp ing e r-Verlag (Berlin , 1976), pp. 121~2.72 . 2. 제 V 장의 참고문헌 ~7, Chap. I (Resonant Raman Scatt er in g ). 3. R. K. Chang and T. E. Furta k , Eds. , Surfa c e Enhanced Raman Scatt er - ing , Plenum Press (New York, 1982). 4. J. Lascombe and P. Huong , Eds., Proceedin g s of the VIII~th Inte r - nati on al Conf er ence on Raman Sp ec tr o scopy , Joh n Wi le y & Sons (Chic h - este r , 1982) , chap. 2 (Sur fac e Enhanced Raman Scatt er i ng ) . 5. R. Bli nc and B. Zeks, Soft Modes in Ferroelectr i c s and Ant iferr oelec- tri c s , North -Holland (Amste r dam, 1974). 6. V. Gin z burg, A. Levany u k and A Soby an in , Lig h t Scatt er in g near
Phase Transit ion Poin t s in Solid s , in Phys . Rep o rts (Phy s . Lett . C) 57, 7. NAo.. 3B (r1u9c 8e0 )a npdp .R 1. 51C~o2w4l0e.y , Str u ctu r al ph ase tra nsit ion s ]I[ . Crit ica l dy - nami cs and qu asi- e lasti c scatt er in g , in Adv. in Phys . 29, No. 1 (19 80) pp. 219~321. 8. A.S. Barker, Jr. , Far Infr ar ed Disp e rsio n and the Raman Sp e ctr a of Ferroelectr ic Crys ta l s, in Far-Inf ra red Prope rti es of Solid s , ed. by S. S. Mi tra and S. Nudelman, Plenum Press (New York, 1970) , pp, 247~ 296. 9. W. Kais e r and M. Maie r , Sti m ulate d Ray le ig h , Brill o uin and Raman Sp e ctr o scop y, in Laser Handbook, edit ed by F.T. Arecchi and E.0. Schulz-DuBois , North - Holland (Amste r dam, 1972), pp. 1078~1150. 10. M.D. Levenson, Coherent Raman Sp e ctr o scop y, in Phys ic s Today, 30 (5), 44(1 9 77) ; Intr o ducti on to Nonlin e ar Laser Sp e ctr o scop y, Academi c Press (New York, 1982). 11. G.L. Eesley, Coherent Raman Sp e ctq o copy , Perga mon Press (Oxfo r d, 1981). 12. Sp r in g e r-Verlag Top ics in Ap pli e d Phys ic s vol. 8 (1975), vol. 50 & 51 (1982) : Lig h t Scatt er in g in Soli ds I , Il & ]I[ , edit ed by M. Cardona and G. Griin t h e rodt. 13. 최 병 구, “Imp u rit y Ef fec ts on Phase Transit ion Anomalie s in KH2 PO , Crys t a l , Ph.D. the sis (KAIST, 1983). 14. 김 건기 , Raman Scatt er in g from Coup le d Modes in Soli ds , M. Sc th• esis (KAIST, 1984) .
A..H.,OLI
7 갭 모드. 209 결정 전장 205 결합손 길이측정 Io8 계수울 상한선 86 공명성 라만산란 217 공명 형광산란 36 공명형 모드 208 공명 형 soft -m ode 225 광신호 측정 한계 80, 82 광자 속밀도 40 광자수 연요동 42 광전관 이득 97 광전판 펄스 목성 98 광전 전류 스펙트럼 60 광전 증배판 96 광과 상관성 함수 43 구조파악 인자 193 국재형 모드 208 굴러 넘 기 (tum blin g ) 성분 146 굴작용(t unnel i n g) 갈라침 228 그린함수 230 극성 포논 182 금속-철 연체 상전이 208 기 여 함수 128, 228 L 난반사 산광 76 내재 좌표 121 내향 구면과 31 N- 인자 분포합수 l3’ Navie r -Sto k es 방정 식 15 2 Ni co l 프리즘 89 Ni el s Bohr 13
E: 단일모드 선폭 94 단과장 근사 27 대칭성과 라만댄서 177 도체 입자의 회절산란 26 도풀러 변이 167 도플러 퍼침 93 Deby e 차되 1 과수벡 터 I92 DID 상호작용 136 2 라만 레이처 240 라만 분광학 국제회의 20 라만산란 53, 73 라만산란 ,:.J:연적 I8o 라만산란 효울 I82 라만 스펙트럼 제 2 차_- 186 라만 편국을텐서 I75 라이 크스 (RIKES) 243 레이처 92 레이처 선의 선덱 75 레이저 선폭 56 레아처용 염료 2I7 레 일레 이 산란 38, 53, 56, 144 레일레이 선폭 155 레일레이 스펙트럼 58 레일레이 편극물텐서 I75 로렌츠 단전자 모델 33 로렌츠형 선모양 34 Lamb 변이 I4 Landau-Placzek 비 I 55 Lande g-인자 48 Lang e vin 방정 식 125 Li ou vil le 연산자 단일입자- 144
단체협동- I 수 4 Lib r ati on 105 Ri ng Dy e Laser 95 Russell-Saunders 결 합 46 口 마이크로과 흡수 106 매 그논 196 맥스웰 파동방정식 22 모드 경합 215 문분자의 대칭요소 115 미분 산란 단면적 25 미이 산란 17 밀도 요동 19, 194 Max Planck 13 mode-mode coup ling 155 Morse 포텐셜 109 닌 반도체 라만산란 206 방향각 회전확을밀도 I35 방향회전 요동 I44 변형포텐셜 182 복굴절 단결정 89 복사 감쇠상수 35 본성 제 2 차 스펙트럼 [87 부분과 위상변이 32 분자력 장 I96 분자의 전자준위 49 분자 편국물 17 분해능 69 볼가분 표현식 206 불완성 내부 전자각 46 브릴루엥 대 역 (zone) 161 브릴루엥 산란 56, 65, 72, l65, I68 브릴루엥 선폭 155 비너꾹 l 찬 정리 171,230
바등방성 상관함수 146 미선형 갑웅계수 235 비 선형 편극장제 기 237 비선형 효과 제 2 차·―- 238 제 3 차 __ 235 비조화 진동자 에너지 준위 209 미편광 산란 134 비편광 스팩트럼 142 빛의 간섭성 44 빛의 강도요동 44 Bloch 운동방정 식 199 Bloch 정 리 164 Brag g 반사면 73 Erag g 반사조건 I 59, I 66 van Hove 시 공간 상관함수 152 Yan Hove 독이 점 187 人 산란각 곡선 190 삼중겁 I48 상관함수 축정기 6l 상자성 중심자 205 상호결합된 모드 230 색 소 중심자 2[0 수소원자 스팩트럼 14 수소원자 평균수명 15 스켈라 파동방정식 30 스펙트럼 분포밀도 171 스펙트럼 분해기 56 스핀세도 상호작용 47 스핀 밀도 요동 196 쌍극자 근사 25,51 centr al mode 228 s 과 위상변이 32 scalin g counts 63 scannin g 속도 79
SERS 220 sin g le ph oto n counti ng 85 soft -m ode 224 공명형―― 225 이완형- 225 。 암 전유 100 에너지F—r en밀Pk도oell a요—r i동to n 2I90 2160 1 엑씨돈 Wannie r-20 1 엑씨돈-공명라만산란 204 영로 레이처 2I5 의향 구면과 3I 요동-소산정 리 194, 200 제 2— — l28 요동확을 129 위상접합 ―각 242 ―길이 24l 一인자 245 위상지연판 91 유도 광산란 239 유도 라만산란 238 유전 상수 요동 150 유전체 입 자의 희철산란 25 유체역학적 극한 154 유체역학적 모드 l34 유효굳철물 87 유효전하 187, 226 유효편국물 136 유효힘상수 226 이득 좁힘 2I5 이방성 에너지 I98 이상광선 9I
이중쌍 국소골 228 이중 회전발 분광기 76 임계성 완속 225 입계접 산란백광 I5I,239 입계검 온도 I48 입자쌍 분포함수 I32 입자쌍 상관함수 I32 abc 문계 205 Abraham-Lorentz 방정 식 35 ATR 프리즘 22I I2 흡수선 선폭 92 Iodin e 핀터 9I op tica l mi xi n g 58 Ornste i n - Zernik e 이 론 I 49, I 5 I 六 자리 군 206 자발 복사 51 자성체의 유전울 198 자체 집속 239 재복사 산란원 18 전방산란 29 전자의 고전반경 53 건자과 산란 21 전체 표현식 119 정상 광선 91 종과 모드 산란 단면적 183 중십력장 근사 46 증폭기의 S/N 79 지구의 전자과 산란 33 지연성 그란합수 231 jet flow 216 天 초미세구조 49
구 카스 (CARS) 간섭 성 타만산란 240 clip ping 63 CO 2 형 분자 II2 Comp ton 산란 2I Curie - Weis s 법 칙 224 Ki rc hhof f 적 분식 27 Kramers 이 중쌍 208 E 틴달 산란 17, 19 Thomas-Fermi 차페 파수벡 터 192 Thomson 산란 21 TO-LO 편극의 혼합 185 立 과수단위 45 펄스 누적현상 99 펄스 증폭기 84 편광 혼합 소자 91 편광 회전 소자 9I 편극률 이방성 138 편극물 자체상관 함수 138, 177 편국물 타원체 107, 177 편극 요동 19 편극 요동 상관함수 172 포논 밀도요동 229 포논 합성전동수 186 폴라리돈 187, 189
표면 푼라스몬 221 표현 행 렬 식 II8 푸른하 늘 과 광산란 36 플라스마 산란만먼저 193 플라스몬 191, 192 푼라스몬-포논 결합모드 I95 Fabry -P erot 간섭 계 66 Fermi 황금 물 50 FET source foll ower 85 fine sse 70, 93 Frohli ch 상호작용 2I9 FSR 68 눙 하이퍼 라만산란 238 하이퍼 레일레이 산란 239 합성 진동자 그린함수 234 허깨비 위성선 77 흉로 그래퍼 형 회철발 77 회전각 확산 146 회전운동 에너지준위 103 회전좌표 표현식 121 희철산란 27 횡과모드 산란단견적 184 흑체 복사 41 흡수 계수 34 hete r ody ne 측정 법 56 hig h Ry d berg sta t e s 14 homody n e 측정 법 56 Hund 법칙 46
金鍾銅 서울대학교 문리과대학 물리학과 졸업 미국 캘리포니아(싼타 바바라)대학교 물리학 박사 영 국 슈트라쓰 클라이 드대 학교 물리 화학연구실 연구원 미국 라이스대학교 전기공학과 연구원 미국 가돌릭대학교 물리학과 객원교수 영국 런던대학교(킹스대학) 물리학과 객원교수 현재 한국과학기술원 물리 학과 교수 논문 0-H .. ,O Raman Bands in KDP Melt s , Comments on Surfa c e Carbon Peaks in SERS 등 58 편 대우학술총서 자연과학 39 레이저 광산란 분광학 찍은날 1986 년 8 월 15 일 퍼낸날 1986 년 8 월 31 일 지온이 金鍾鎭 퍼낸이 *卜孟浩 퍼낸곳 民音社 출판둥목 1966. ,. 19 계 1-142 호 우편대체계좌번호 010041-31-523282 110 서 울 종로구 관철동 44-1 734-2000, 73,-8, 다(영 업 부) 734-4234, 734-6110 (편집 부) *파본온 교환해 드립 니 다. 값 5, 000 원
대우학술총서 •자연과 학 1 소립자와게이지상로삭용 金鎭 쥰 꽁 / 값 3.6 00 원 2 動力學特論 李炳 롯 /값 5,400 원 3 질소고정 宋承 達 콥 / 값 2,800 원 4 相轉移와區界現象 김 두절 픕 / 값 2,800 원 ＂媒作用 陳 宗植 픕 / 값 2,800 원 6 뫼스ttf-!f어分光學 玉 恒南 봅 / 젊 2 ,800 원 7 국기량원소의영양 昇 正子 큽 /값 6, 500 원 8 *慕 1 t틀嘉와 有劃顧it심 罪民 콥 / 값 5,000 원 9 抗生物質의全合成 姜 錫久 콥 / 값 9 , 000 원 10 국소적 형태의 A tiy ah-S inge r 지표이론 지동표 픕 / 값 2 ,800 원 11 Muco po l y sacchar i des 의 生it릎 및 生物理릎 박준 우 름 / 값 3 ,8 00 원 12 ASTROPHYSICS ( 天”物理學 ) 洪짜서 품 /값 4, 700 원 13 프로스타맑띤합성 숲 촬 표 폼 /;l3,600 원 14 천연물화학연구법 禹 源植 콥 /값 7 , 000 원 15 脂訪營警 숲淑 룡 著 /값 6 , 300 원 16 結昌化유리 金炳扇 著 / 값 4, 5 00 원 17 高分子의化學反應 趙 픕 煥 픕 /값 4 , 000 원 18 과학혁명 金永 植 름 / ~; 4 ,200 원 19 轉國地質論 뮬基弘著 /값 4, 000 원 2 0 정보이 촌은땅열술 갈点 500 원 21 原子核反應諭 鄭雲赫 흄 /값 8. 500 원 22 續壇力學 金相哲 름/값 4.700 원 23 분자궤도이른 이익준 흡/값 3 , 300 원 24 반응속도른 정경훈 름 / 값 4.000 원 25 미분위상수학 李鉉求 롭/값 2 . 500 원 26 자기공명방법 조 성호 흄 /값 4,700 원 27 1i라스마를리힉과 빠웅합 죄 덕인 불 危 4' O OO 원 28 천문관측과 분석 李詩雨 흩?..I 4, 000 원 29 석탠專七 변환 기술 金相數 룔 / 값 6, 500 원 30 海洋畵古生物學 白光浩 룔 값 6, 400 원 31 편미분방정식론 김종식 틀 /값 4,000 원 32 大續-理諭 소광 섭 휼 /값 5. 000 원 3 3 金 屬電 子系의 多體理論 金億洲 흡/값 6 , 600 원 3 4 액정중합체 陳政 -/ 값 6, 200 원 35 복합재료 信肅仁 / 값 5 , 200 원 36 단백짙 생합성 朴 仁源 / 값 9,000 원 37 한국의 鑛物種 金洙鎭 38 일반상대론 李哲勳/ 값 5,000 원 39 레이저광산란분광학 金鍾鎭 I '1 5. 00Y.린