 ’
’  ’
’
저자는 서울대학교 전자공학과를 졸업하고 미국 미 주 리대학교에서 공학석사 • 박사 학위를 취득했다. 독일 지멘스희 사 연구원 , 미 국 미주리대학 연구원, 과학기술원 연구원을지냈으며, 현재 한양대학교 공과대학 전자통신과 부교수로재직중이다 .
 정보이론
정보이론
머리말 情報理論 은 Shannon 의 논문 「동신의 수학적 이 론」에 기 반을 둔 아 문으로 많은 분야에 영 향울 주었다. 공학적 인 면에 서 도 송신된 AJ . 효 를 충 실히 재생시킨다는 것은 중요한 의미를 내포하고 있다. 정보 이 론 은 정 보의 전송에 관하여 정량적으로취급하고, 신뢰성 있는 몽 신 이 가능 케 하는 符號 理 論 울 탄생시켰다. 본서에서는 정보의 전송 과 부 호 이론을 초 동적으로 해설하였다. I948 년 Shannon 의 논문이 말표 된 이 래 세계적으로 많은 연구가 진행되었으나 우리나타에서는 저 서 및 번 역서가 거의 없는 실정이므로 본서가 조금이나마 학문발 전 에 보 탬 이 되기를 바라는 마음문이다. 정보이론의 중심적 테마인 . 채 널符號 化 定理 ( channel codin g t heorem) 를 중십으로 4 장으로 분류 하 여 엮 었다. 제 I 장은 정보이론의 개념과 확률론의 기초를 기술하 · 고 제 2 장 에 서 정보량의 정의로부터 파생되는 諸定理와· 情 報 源 에 대하 여 해설 하였다. 제 3 장은 정보이론에서 가장 큰 영향을 끼찬 채 널부호 화정 리 를 정 진적 으로 접 근하여 指數部 (ex p onen t)를 사용한 에러확률 의 상한을구하는과정을기술하였다. 끝으로제 4 장은정 보이론의 주된 응용이라 볼 수 있는 부호화, 복호화의 방법을 기초 적 으로 해설하였다. 렌돔부호화 ( random cod i n g)를적용시켜 에러확 · 률 의 상한을 구하고 이 로부터 부호화정 리 를 증명 하는 방법 을 중십 으로 기술하였기에 방대한 양의 정보이론에 관한 토픽은 참고문헌 . 및 참 고서란에 기재하였다. 끝으로. 본서를 집팔하게 하여준 대우재 만 제위와~ 출판과정에서 여러 면에서 도움을 준 민음사 여러분에게 감사드리며 원고를 읽고 수정을 하여주신 교수분들에게도 사의를 표 한다. 부록 B 에 설 런 한글의 일차 마코브정 보원으로서 의 遷移確率 과 엔트로피를 전자계산기로 산출하여 준 朴鍾元君에게 감사한다. 1985 년 저자-
정보이론 • 차례
머리말 5제 1 장 서론 1.1 정보이론의 개념 111. 1. 1 통신 계통 111. 1. 2 符號化와 情報址의 개념 141. 1. 3 情 報 傳送의 신뢰성 151. 2 확률론의 기초 181. 2. 1 確率空間 181. 2. 2 조건부확률, 독립성 201. 2. 3 확률변수, 분포함수, 기대 함수 211. 2. 4 다차원분포함수, 변환 241. 2. 5 정규분포함수 271. 2. 6 확률변수에 관한 부등식 301. 2. 7 대수의 법 칙 • 중심 극한정 리 32제 2 장 정보량과 정보원2.1 諸情報量 372. 1. 1 자기 정 보량과 엔트로피 372. 1. 2 情報傳送 의 모델 442. 1. 3 부호의 構成例 482. 1. 4 크라프트부동식 502. 1. 5 부호화의 제일기본정리 532. 1. 6 最適符號化 562. 1. 7 상호정보량 592. 1. 8 볼록함수, 오목함수 672. 1 .9 기타 정보량에 관한 정리 702.2 연속신호의 정보량 73
2. 2. 1 연속신호의 엔트로피 와 상호정 보량 732. 2. 2 엔트로피가 최대가 되는 분포함수 812. 2. 3 정규신호의 정보량 872. 3 情報源 872. 3. 1 마코브정 보원 872. 3. 2 단순한 마코브연쇄 의 엔트로피 912. 4 채널용량 942. 4. 1 상호정 보량과 채 널용량 942. 4. 2 채널용량계산법 98제 3 장 부호화정리3. 1 正規雜音채널 1073. 1. 1 신호의 直交展開 에 의 한 두 符號語의 誤率 1073. 1. 2 직교신호와 誤率의 上界 1133. 2 채널符號化 정리 1223. 2. 1 서론 1223. 2. 2 랜돔符號化 1283. 2. 3 채널符號化 정리 1323. 2. 4 이원대칭채널과 고잡음채널의 誤率 1363. 2. 5 誤率의 下界 1393.3 源符號化 정리 1463. 3. 1 歪曲測度, 源符號化 정 리 146제 4 장 부호화와 복호화의 기법4. 1 線形符號, 巡回符號 1554. 1. 1 線形블록부호의 구조 1554. 1. 2 線形부호의 에러 訂正能力 1624. 1. 3 해밍부호 1644. 1. 4 多數決論理復號 166
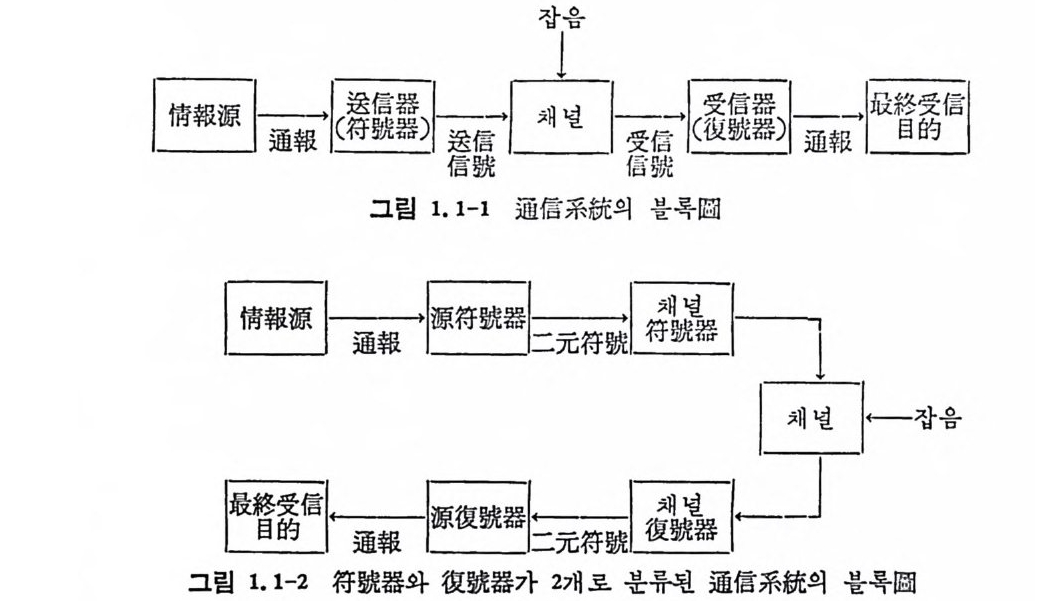
4. 1. 5 Reed-Muller 부호 1704. 1. 6 巡回부호 1744. 1. 7 BCH 부호 1844. 1. 8 무게 분포 1984. 2 콘볼루숀부호 2034. 2. 1 콘볼루숀부호의 표현 2034. 2. 2 쓰레 쉬 홀드復號 2114. 2. 3 메트릭 2144. 2. 4 나무부호, 트레리스圖 2154. 2. 5 M.L . 復號法 2184. 2. 6 콘볼루숀부호의 거리 특성 2204. 2. 7 逐次復號法 2234. 2. 8 버 스트에 러 訂正 콘볼루숀부호 232부록 A 群, 環 237B 한글의 일차마코브情報源으로서의 遷移確率과엔트로피 240색인 291제 1 장 서론 1.1 정보이론의 개념 1.1 .1 통신 계통 Shannon 이 1948 년 A Math m ati cal Theory of Communic a ti on 논문에서 〈 동신의 근본적인 문제는 다른 곳에서 선댁된 通報를 한 곳에서 정확히 또는 대 략적으로 재생시키는 것아다 (The fun damen- tal pro blem of communic a ti on is tha t of rep ro ducin g at one po in t eit he r exactl y or app r oxim ate l y a messag e selecte d at anoth e r po i n t ) 〉라고 말하였 다. 모르스신호의 경 우 채 널의 잡음에 의 한 영 향으로 보낸 축의 신호와 받는 측의 신호가 다를 수 있다. Shannon 은 이 러 한 통신계 통을 5 개 주요 부분으로 분류하고 그림 1. 1-1 에 보 여주고 있다. 여기서는 동산계통 및 정보이론의 槪略울 간단히 설 명한다. ® 情報源 (info r mati on source) 情報源은 동보 (messa g e) 또는 통보계 열 (seq u ence of messa g e) 을 발생시킨다. 통보의 집합을 {sI,s2, … ,s }이라 할 때 각 동보에는通 報의 발생확률 P(s;) 가 주어진다. ® 送信器 (tra nsmi tter ) 정보원에서 발생한 통보를 전송에 팔요한 형태의 신호로 변환시 키 는 장치 를 送信器라 부른다. 그러 나 많은 경우 동보를 符號化하 여 전송하므로 이 런 경 우 符號器 (encoder) 란 단어 를 사용하는 것 이
좋다. 符號器를 통하여 통보가 符易[化 (encod i n g)되고 이 렇 게 부호 화된 符號 (code) 를 채널 (channel ) 을 동하여 전송된다고 가정한다. 만일 채널의 잡음 (no i se ) 의 영향으로 부호 에 에러 ( error) 가 발생하 면 受信側에서는 原通報를 정확히 재생시키지 못한다. 그러므로 에 러를 訂正시킬 수 있는 부호로 만들어 傳送하면 受信i {Il 에서 는 原通 報를 보다 충실히 재생시킬 가능성이 더 많다• 편의상 符號유유문 源 符號器 (source encoder) 와 채 널符 號器 ( channel encoder ) 로 분류한 다. 알파벳 집 합이 {o, 1} 이 고, 부호의 문자(l e tt er) 가 O 또는 1 인 二 元符號 (b i nar y code) 를 생 각하면 源符號器 는 각 통보를 二元符號化 하는 데 문자의 수에 관계되며, 채널符號器는受信 0ll 에서 보 다 충실 히 재생시킬 수 있는 부호를 만들어 보내는 데 목적이 있다.
 三口圈」잡\음 i 로 I 급『|萱 I
三口圈」잡\음 i 로 I 급『|萱 I
® 채 널 (channel) 신호를 送信器에서 受信器로 전송하는 매 개 체 이 다. 실제 로 線路, 同軸케이불둥이며, 無線電波의 경우大氣등이다. 채널울체계적으로 분석 하기 위 하여 채 널모델의 정 립 이 필요하다. 無雜音채 널 (nois e less -c hannel) 이 란 送信側에서 보낸 신호가 채 널을 동하여 그대 로 수신되
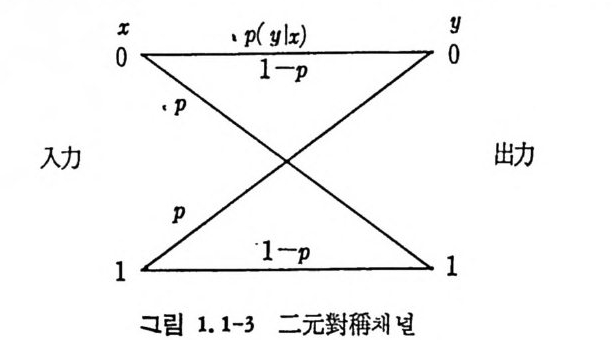
는 채널을 말한다. 그러나 無雜音채널은 실제 통신채널에서 거의 존재 치 않는다. 보통 통보를 전송하는 도중 채 널에 서 의 잡음등에 의하여 가산된 신호는 송신된 신호와 같지 않다. 그러므로 채널모 델의 정립을 위해서는 잡음의 특성을 규명할 팔요가 있다. 잡음은 렌돔 ( random ) 현상으로 확물론으로 기술되고 이론상으르나 실제면 에서 가장 중요한 잡음채널은 加 算 的白色正規雜 音채 널 (add iti ve whit e Gaussia n nois e channel) 이 다 . 加算的白色正規雜音이 란 잡음 이 신호에 가산되고 乘算 ( mul ti ca ti ve ) 되지 않으며, 잡음선호를 주 파수영역면에서 볼 때 모든 주파수를 균일하게 포함하고 있으며 잡 음선호 의 진폭의 확률분포가 정규분포인 잡음을 말하고 있다. 정규 잡음은 해석적 으로 분석이 용이하며, 실제 잡음채널과 유사하다. 송신기에서 송신된 신호는 채널에서 정규잡음과 합하여 수신선호가 된다. 동보를 二元符 號 化하여 符號系列을 송신할 경우 0 과 1 의 계 열 이 된다. 여기에 잡음이 가하여전 신호를 수신축에서는 받아 가 지 고 송신된 신호가 0 인지 1 인지 를 판단한다. 송신선호가 O ( 또는 1) 일 때 잡음 이 가산된 수신선호로부터 0( 또는 l) 로 판단되 는 확률을 l— p, 1( 또는 0) 로 판단되는 확물을 P 라 하면 이 확률은 조건부확 물 이다. 즉 0 을 보냈을 때 0 을 받는 조건부확물 P ( olo ) 은 1- p이 고 l 을 받는 조건부확룹 P ( l j o ) 은 P 이다. 이러한 채널을 二元對稱 채 널 (bi n a ry sym metr i c channel) 이 라 부른다. 다음은 좀더 광법 위 한 채 널로 離散無記憶채 널 (di s c rete memoryl e ss channel) 이 있 다. 離散無記憶 채 널은 유한개 의 알파벳으로부터 入力文字系列 a1, a2, …, an 이 촌재하고, 동일한 또는 상이한 알과벳으로부터 出力系列이 bi,
 。z ' p(1yl-:rp ) 。g
。z ' p(1yl-:rp ) 。g
b2, …, bm 일 때 出力系列의 각 문자의 해 당하는 위 치 의 入力 文字 에 만 통계적으로 의존하여 고정된 조전부 확률 F ( b J a i ) 로 결 정되는 채 널을 말한다. 二元對稱채널은 離 散 無記 憶채 널이 다 . ® 受 信器 (re ceiv e r) 수신기는 송신기의 역동작을 행하며, 수신선호로부터 통보를 재 생시킨다. 만일 수선신호가 부흐화된 신호일 때 부호로부터 동보를 재생시키는 장치를 復號 器 (decoder ) 라 한다. 符易隸유 에서 와 마 찬가 지 로 復號 器도 源 復 號器 (source decoder ) 와 채 널 復易땝읍 ( channel de- coder) 로 분류한다. ® 最終 受 信 目 的 (des ti na ti on ) 정보원의 반대로 최종적으로 통보를 받는 사 람 , 계산기와 계산기 사이의 데이타동신에서는 기계 장 치가 最終 受 信 目的이 된다. 1. 1. 2 符號化와 情報 量 의 개 념 정보이론의 중요한 개념은 〈 情 報傳送의 효율 〉 , 〈 情報傳送 의 신뢰 성〉 등의 문제이다• 電信 에 사용하는 모르스부호는 신호의 단위로 전류의 두 종류의 단속 죽 ·과 ―로 구성된다. 二元 符號 의 경우 신 호의 단위가 일반적으로 많이 표기되는 {o, 1} 로 이루어진다. 채널의 잡음이 없는 경 우 부호화는 비 교적 간단하다• 4 개 의 통보 S1, Sz, S3, S4. 가 있을 때 二元符號化하여 S1 에는 00, s2 에는 01, S3 에는 10, S 4 에는 11 을 배당할 수 있다. 일반적으로 M개 의 통보를 二元 符號 化할 때 각 동보당 이원부호의 길이를 같게 하면 二元符 號 의 길이는 K 이다. 즉 lo g 2M=K의 식이 성립한다. 영어의 알파벳이나 한글의 子 母 의 경우
다음 부호가 잡음채널을 동과하는 경우의 부호화는 좀더 복잡하 다. {O, 1} 이 K 개로 구성된 부호에 1 개를 더 첨가한 (K+1,K) 부호 를 고찰한다. K 길이 의 부호에 0 의 수가 偶數(또는 奇數)가 되 도록 1 개를 더 첨가하여 K+1 길이의 부호를 만든다. 1 개를 더 첨가한 비 트를 패리티검사비트 ( p ar ity check b it)라 부른다. 만일 K+1 개의 성분 중 하나의 성분에 에러가 발생하면 부호의 0 의 수가 우수에서 기수가 되므로 에러가 발생한 것을 검출할 수 있다. 그러나 어느 위치에 에러가 발생하였는지는 알 수 없다. 죽 에러를 검출할 수는 있지만 정정할 수는 없다. 이 개념을 더 확장하여 여러 개의 패리 티검사비트를 첨가하면 에러가 발생한 우1 치를 알 수 있게 부호화할 수 있다. 채널부호기에서는 부호길이 K의 이원부호를 K 보다 큰 수 N의 이원부호로 寫像시켜, 잡음채널을 동하여 충실한 통신이 가능 케 한다. 정보원의 출력을 이원부호로 부호화하는 데 객관적인 척 도로 정보량을 정의한 것은 바교적 근년의 일이다. 만일 정보원의 알파벳 중 볜문자 a i의 발생 확률이 P(a,) 이 면 이 때 自 己情報 華 은 I(a;) = —log P ( a; ) (1. 1-1) 로 정의된다. 여기서 대수는 단조증가함수이므로 어떤 대수의 밀수 를 취해도 대부분의 정보이론의 정리가 성립한다• 이 정의논 문자의 의미와는 무관하며, 발생확률에만 의존한다. 발생확률이 적으면 자기정보량은 커지며, 확물이 1 인 확실한 사상 의 정보량은 0 이다. 사상이 여러 개 존재하면 자기정보량의 평군을 취한 -In ; P(a. . ) Iog P (a;) , ~n P(a;) = l (1. 1-2) i= I - - i= l 정보량을 얻는다. 이 개념을 더 확장하면 여러 정보량을 정의할 수 있고, 또한 많은 정리가 성립한다. 1. 1. 3 情報傳送의 신뢰성 송신기에서 이원대칭채널을 동하여 0 과 1 의 이원부호를 송신할 때, 채널에는 가산적 잡음이 가해져 수신축에서 수신된 부호는 송
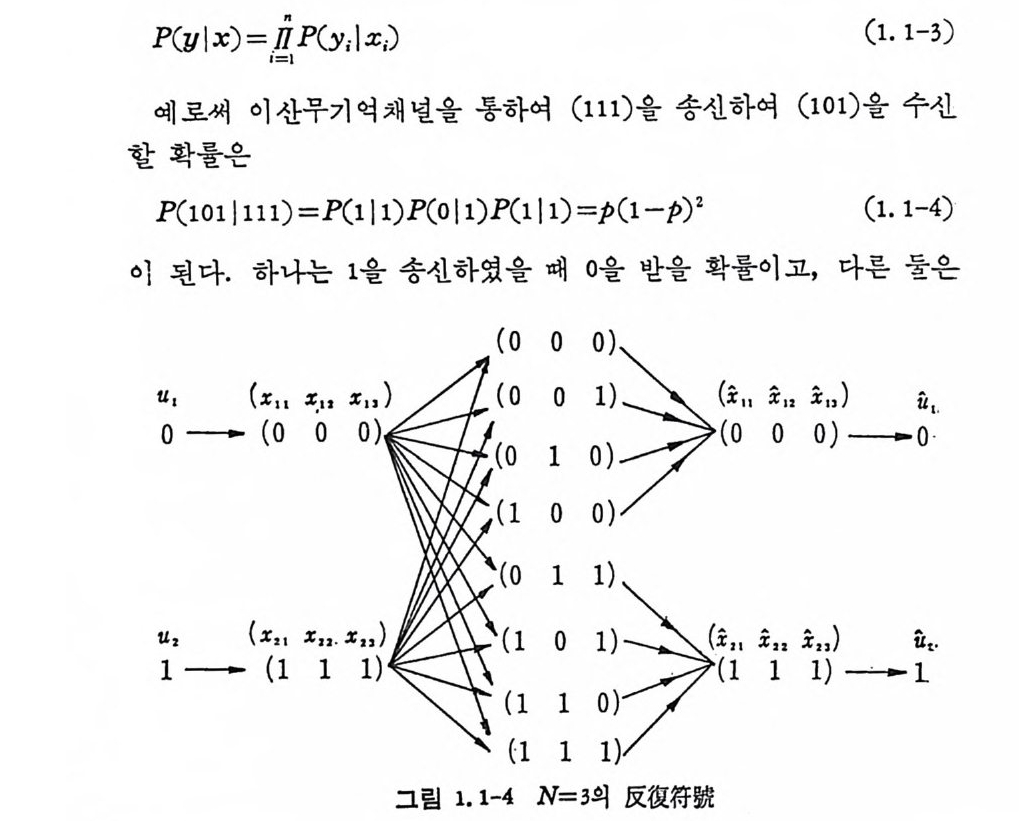
신측에서 보낸 이원부호와 동열하지 않을 수 있 다 . 죽 P 라는 에 라 확률 ( error p robab ility)이 있어, 송신축에서 0 을 송신 할 때 l 을 받 을 확률을 P 라면, 송신축에서 0 을 송신할 때 수신 축 에서 0 을 받 을 확울은 ( 1- p)이냐 앞으로는 에러확률을 誤率 로 부르기로 한다. 지금 0 하나를 송신할 때 0 을 N 번 반복하여 송신하고 l 을 보 낼 때 1 을 N 번 반복하여 송신한다 가정한다. 그러면 수신 축 에서는 잡 음 채널을 동하여 2N 개의 가능한 부호를 수신 할 것이다. 예로써 N=3 - 인 경우를 생각해 보면 그립 l. 1-4 와 같이 도시 할 수 있다. 二元 對 稱채 널을 동하여 特 定 符 號語 X; = (X; i, X; z, X ; 3) 을 송신 할 매 독정 부 호벡 터 y= (y1, Y2, Ys) 을 수신할 확률은 천이 확 률( t rans iti on pro ba· bil ity) p와 (1- p)로 결정된다. 천이확률을 P ( xl y ) 라 하면 이산무 기억채널은 다음으로 정의된다.
 P(y l x) = _l”l P (y; l x;) (1. 1-3)
P(y l x) = _l”l P (y; l x;) (1. 1-3)
1 을 보냈을 때 1 을 수신할 확률이다. 오i=(소 ,1 소i 2 소 ,3 ) 는 x i의 推定符 號語로 복호기 에 서 는 (y 1Y2% )을 받아 송신된 벡 터 (x,1x,2X i 3) 을 추 정하는 장치이다. 이상의 경우는 정보비트수 K=l 로 부호수 M= 2K=2 인 경우였으나, 일반적으로 K 비트의 U=(u,,Uz, … ,UK )의 벡터 가 채널부호기에 들어와 출력에는 N 비트를 갖는 M=2K 개의 부호 어로 변환한다. N 과 lo g M 의 比
 R= ―lo gN M一 (1. 1_5>
R= ―lo gN M一 (1. 1_5>
을 전송 윤 ( t ransm i ss i on ra t e ) 이라 부르며, R 이 크면 통신의 효율이 높고, R 이 적으면 동신 의 효율이 떨어진다. 먼처 예로 돌아가 복 · 호기가수신부호계열로부터 오 ,을 추정하는데 다음 법칙을 사용한다 고 가정 한다. ( 000 ) 을 송신할 때 수신부호가 송신부호와 1 개 가 상이 할 때는 ( 000 ) 으로 추정하고 2 개 이상 상이할 때는 (111) 로 추정한 다. 마찬가지로 송신부호가 ( 111 ) 일 대 수신부호가 송신부호와 1 개가 상이하면 ( 111 ) 로 추정하고 두개 이상 상이할때는 (000) 로추정한 다. 여기에는 천이확률 P 가 o< p<一12 -이1라 는 가정이 있다. p= _12_ 일나 타때나는는 동부신호 이계 불열 가의능 각한 상비태트이의며 보,수 E를> 취一2-함 으일로 때써는 p <채스널2- 의의 출이력원에대 칭채널로 변환시킬 수 있다• 이러한 복호법칙은 복호에러 (decod i n g error ) 의 확률 을 최소로 하는 것을 알 수 있다. X 로오월. 때 복호에 러의 사상을 E 라 하면 (ooo) 을 송신하였을 때 오울은
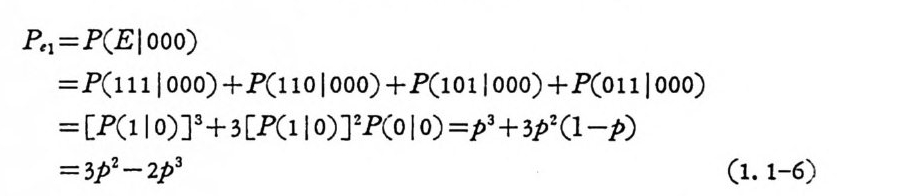 P,1=P(EIooo)
P,1=P(EIooo)
이 된다. 마찬가지로 (111) 을 송신하였을 때 오울도 P,2=3p 2 -2p:; . 이며, 부호어 (ooo) 와 (111) 이 발생할 확률을 각기 P1,P2 라 하연 평 군복호에러확률은
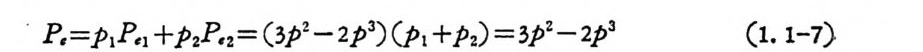 P, =P1P,1 +P2P,2 = (3P2 -2p 3) (p1+ P2) = 3P2 -2p 3 (1. 1-7)
P, =P1P,1 +P2P,2 = (3P2 -2p 3) (p1+ P2) = 3P2 -2p 3 (1. 1-7)
으로 부호어의 발생확률과 무관하다. 일반적으로 동일한 이원부흐 비트수를 (2N+1) 번 반복 송신함으로써 다 수결법칙을 사용하여 復 號한다면 平均復號誤率은 다음과 같다.
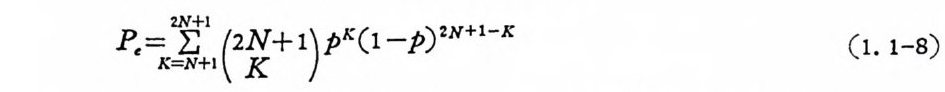 p축접; 1 (망+ l) pK (l-p) 2N+ l-K (1. 1-8)
p축접; 1 (망+ l) pK (l-p) 2N+ l-K (1. 1-8)
N은 정 수로서 동일한 비 트를 기 수번 반복 송신하기 위 하여 (2 N+ 1) 번 송신한 것아다. 만일 N>1 이면 P 가 0 에 접근함으로 써 R 을 0 으 로 접근시킬 수 있다. 또한p<―21- 가 고정되었을 때 N 을 무한 대로 접근시킴으로써 P, 를 0 으로 접근시킬 수 있다. 통 신에서는 정보 전 송의 신뢰 성 과 정 보전송의 효율이 매 우 중요한 문제 이 다. Shannon 은 잡음이 있는 채널에 대하여 신뢰성과 효율이 상호 대럽되는 문 제를 검토하여 다음과 같은 정리를 발견하였다. Shannon 의 符號化定理 무기억잡음채널에 대하여 어떤 定數 C 가 존재하여 전송률 R 이 C 보다 척으면 N을 충분히 크게 함으로써 오울을 임의로 작게 할 수 있논 동산이 가능하다. 죽 임의로 오울을 작게 하는 부호화법이 존 재한다. 1.2 확률론의 기초 1.2.1 確率空間 과학의 목적 중 하나는 우리가 사는 세계의 사건들 을 기술하고 예측하는 일이다. 이 목적을 달성하는 한 방법은 실세계를 적철히 기술할 수 있는 확몰모델이 필요하다. 그러므로 확률론에서는 어떤 공리를 만족하는 확물공간(p robab i l ity s p ace) 이라 부르는 수학적 모 델을 가지고 표현하는 것이 보통이다. 우선 두 개의 개념을 정의한 다. 표본공간 (sam p le s p ace) 이 란 실험의 모든 가능한 결과의 전체 또는 총체를 의미하고 9 로 표기한다. 사상 (even t)은 표본공간의 부 분집 합으로 모든 부분집 합의 큘라스 (class) 를 사상공간 (even t spa ce) 이라 말하고 교로 표기한다. 환언해서 교는 9 의 모든부분집합을포 함한다. 1,2,3,4,5,6 의 숫자가씌어 있는 6 면의 입방체를 던졌을때
표본공간은 il = {1,2,3,4,5,6} 이고, 사상은 군 =64 개의 사상이 있 고 이 64 개의 사 상 중에는 空事象 ¢고} 9 도 포함되어 있다. 다시 말 하c- 면 , u事, 象n )空 에間 닫.혀Jt l에있는다 .64 개즉의 忍사의 상임이의 의있다 .요 소교 (는el em3 e개n 의t ) B集 의合 演補算集 合 도 .Jtl에 속 하며 , .Jt/의 임 의 의 두 개 요소 B1 과 B2 의 공통부분 B1 UB z 도 .Jt/ 에 속한 다 . 다음과 같이 쓸 수 있 다. ® 9E . Jtl ® 만일 B E .JI이 면 BE.J tl ® 만 일 B1, B 2E sl 이 면 B1 UB2 E . Jtl ® ¢E . Jtl ®® 만만일일 BB11 ,, BB 22 ,E …꼬 B 어 투 .떤J t/B이1 면n BUzi=E lB .J.- ,t / ni= Bl ,Ed c1. 2 -1) 여기서 BUB = D 으 로 확실한 사상이며 BnB= rp으로 空事象 이라 한 다. 확률을 정 의하는 데 중요한 것은 事 象 공간이다. 확률함수 P ( · ) 는 영 역 .Jt/와 함 수의 법우] [O, 1 ] 의 집합함수로 다음 공리를 만 족한 다. CD P( B ) 2. 0, BE.J tl @ P( Q ) = l ® 만일 B1, Bz, …가 교내 相互排反 事象 系列, 죽 Bi n Bj= ¢, 꿉:j; 00 00 00 i,j =l , 2, …이고 B1UBz U … = iU= l B ,-Ed 이- 면- P(·i=U l B;-- ) =i=~ l P ( B ;) 이다. @ P( rp) = O ® 만일 BE .Jtl이 면 P( B ) = l 一 P ( B ) ® 만일 B, CE .51이 면 P( B )=P(B C )+ P(BC), P( B -C) =P(B C) =P(B ) -P(B C ) ® 만일 B, CE .51이 면 P( B U C) =P(B) +P(C )- P(B C) 이 다. (1 . 2-2) 사실 공리 CD, ® ,@ 으로부터 ®,®,®《 B 울 증명할 수 있다. 다음 확물공간을 정 의 한다. 9 가 표본공간이 고 忍가 사상의 집 합 체 , P ( . ) 가 영역 g를 가진 확률함수일 때 공리 ® & 》, ® 을 만족하 는 ( Q ,d,P(· ) )을 확률공간이라 말한다. 확률공간 개념은 확률의 기본적 요건을 갖추고 있기 때문에 확률론에서 정의 및 정리를 증
명하는 데 팔요한 도구로 사용된다• 1. 2. 2 조건부확률, 독립성 확률공간(Q,.RI ,P(.) )상에 B,CE .91이고, 사상 C 가 주어졌을 때 I 사상 C 의 조건부확률은 다음과 갇이 정 의 한다.
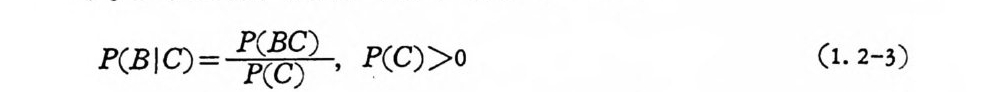 P(BI C)=1;晶? , P(C)>o (1. 2-3)
P(BI C)=1;晶? , P(C)>o (1. 2-3)
만일 P(C)=O 이면 조건부확률은 정의되지 않는다 . 물론조건부확 률의 정의에 의하여 P(B), P(C)>o 이면 P(BC)=PC B IC)P(C) =P(CIB)P(B) 이다. 조건부확률은 다음 3 공리를 만족한다. CD P(B I C) =P(BC)/P(C) 2:: 0, BE.R I @® P만( 일Q I CB1) =,BPz,( …QC 7l )- /Pg (내C ) =相P互(排C)反/P 事(C 象 )이 =고 l, iUo=o IB i E 교이면
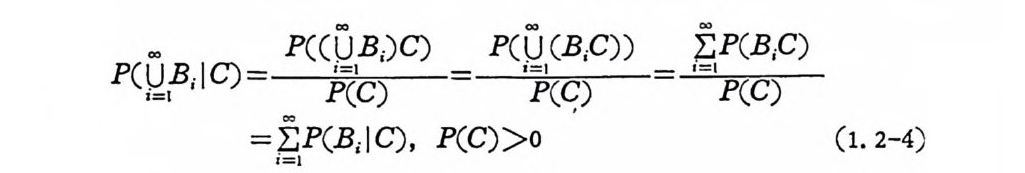 P(Ui.=. Bl ;I. C . )=P((~PUoo( BC ;)) C ) P(UIo 詞o (B, C)) •E=oo I P P((CB)iC )
P(Ui.=. Bl ;I. C . )=P((~PUoo( BC ;)) C ) P(UIo 詞o (B, C)) •E=oo I P P((CB)iC )
상기 3 공리로부터 다음을 구할 수 있다. @ P(
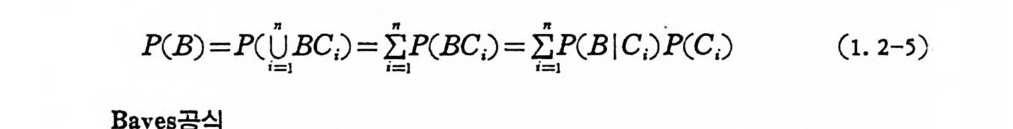 P(B)=P(l.) B C;)='i :,P (BC;)=i: ,P( BIC;)P(C;) (1. 2-5)
P(B)=P(l.) B C;)='i :,P (BC;)=i: ,P( BIC;)P(C;) (1. 2-5)
확물공간 (0, .fll, P(·) )상에 C1, C2, …, en 이 교내 상호배 반사상이 고, BE JIi일 때
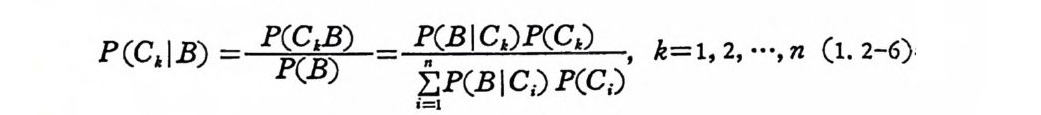 P(C,IB) =~닳옅 ~i~=” IP (B I C;) P.(C;) k=1,2,… ,n (1.2 -6)
P(C,IB) =~닳옅 ~i~=” IP (B I C;) P.(C;) k=1,2,… ,n (1.2 -6)
의 Ba y es 공석 이 성 립 한다 . Ba y es 공석 은 정 보이 론에 서 중요한 역 할을 한다. P ( C1 ) 을 사전확률 (a pr io r i p robab il ity ) 이 라 말하고 P(C1IB) 을 사 후 확률 ( a po ste r io r i p robab ility)이 라 칭한다. 獨立事象 확물공간(Q,.91 ,P(•) )상에 B,CE .91일 때 다음 3 조건 중 하나를 만 족할 때 사상 B 와 C 는 상호독립 이 다 라고 말한다.
 CD P( B C) = P( B ) P (C )
CD P( B C) = P( B ) P (C )
이 성립할 때 상호독립이다. 1. 2. 3 확률변수, 분포함수, 기대함수 다 음은 확률변수 (random var i able) 와 분포함수 (d ist r i bu ti on fun c- ti on ) 를 정 의 한다. 확불변수는 사상을 기 술하는 데 팔요하며 , 분포 함수는 확률변수로 사상의 확률을 규정 한다. 確李 꽂數 확률공간(Q,.J.1 ,P(.) )상에 X 또는 X(·) 로 표기되는 확물변수는 영 역 9 와 범 위 가 실선으로 된 함수이 다. 확물변수는 함수이 므로 X(· ) 가 정확한 기호이나 간단히 X 로 표기한다. 동전을 던졌을 때 Q= { 앞 면, 뒷면}이고, 만일 w= 앞면이떤 X(w)=l 이고, 만일 w= 뒷면이면 X(w)=O 를 취할 수 있고, 확률변수 X 는 각 실험의 결과에 대하여 실수를 취한다. 累積分布函數 누적 분포함수 (cumula ti ve dis t r i b u ti on fu nc ti on) 는 Fx(. )로 표가 되고, 모든 실수 x 에 대하여 Fx(x)=P(X$x)=P({wlX(w) 드:r;}) 을 만족하는 영역이 실선이고 범위가구간 [o,1] 인함수로정의된다. 누적분포함수의 특성은 다음과 같다.
 CD Fx(-oo)=lim Fx(x)=O, Fx(+oo) =lim Fx( x ) = 1
CD Fx(-oo)=lim Fx(x)=O, Fx(+oo) =lim Fx( x ) = 1
 E[X 니- COO 3 감 (x)dx (1. 2 一 13 〉
E[X 니- COO 3 감 (x)dx (1. 2 一 13 〉
로 표시 된다. E[ ·]을 기 대 함수 (ex p ec t a ti on fu nc ti on) 라 하며 기 대 치가 촌재하기 위해서는 식(1. 2-12) 의 급수가 수령하여야 하며, 식 (1. 2-13 ) 의 걱 분이 촌재 하여 야 한다. 식 (1. 2-14 )의 E[ X ] 가 존재 하 기 위해서 2 개의 적분이 유한하여야 한다. 연속확률변수 X 의 함수 g ( · ) 의 기대치는
 釋 X .) 〕 =J~.,g (x)f ( x )dx (1. 2-15)
釋 X .) 〕 =J~.,g (x)f ( x )dx (1. 2-15)
 이고, 다음 특성을 갖고 있다. 정수 c 에 대하여
이고, 다음 특성을 갖고 있다. 정수 c 에 대하여
 -m(t) =E[e' 전 (1. 2-20)
-m(t) =E[e' 전 (1. 2-20)
이 성립한다. 2 개 의 확률변수 X 와 Y 가 동일확 률 공간에 서 정 의 될 때 공분산 ( covar i ance ) 은 COV [X, YJ 또는 q XY 로 표기 되 고
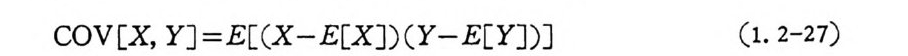 COV[X, Y] =旦 ( X-E[X]) ( Y-E[Y]) 〕 (1. 2-27)
COV[X, Y] =旦 ( X-E[X]) ( Y-E[Y]) 〕 (1. 2-27)
로 정의된다. 이 때 확률변수 X1, X2, ···X. 의 합의 평 균치 및 분산은
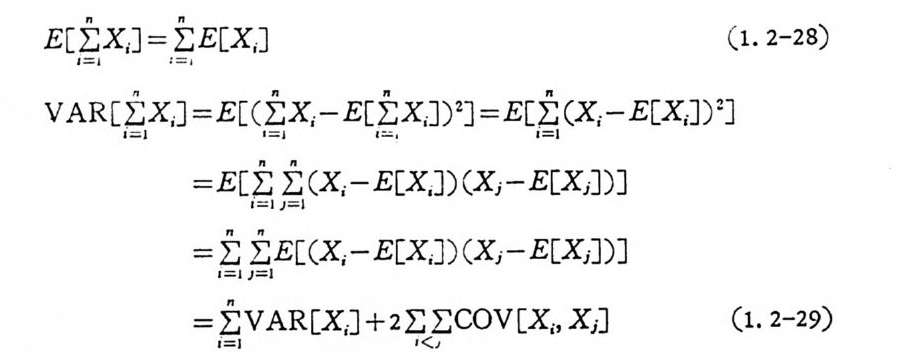 麻I;n X 』=I;n E 꼬,J (1. 2-28)
麻I;n X 』=I;n E 꼬,J (1. 2-28)
이 다. 목 히 a11 a2, ···, a. 이 정 수일 때
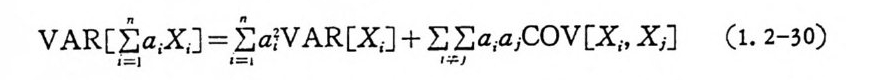 VAR[ ~ a.XJ = I; a;VAR[X 』 + I;I ;a;a jC OV[X., XJ (1. 2-30)
VAR[ ~ a.XJ = I; a;VAR[X 』 + I;I ;a;a jC OV[X., XJ (1. 2-30)
이고, X 와 Y 가 독립이면 COV[ X ,} 견= O 이냐 ”R 의 조건부확 물속 확밀불도변함수수이도 고마, 찬X가i지 I, x로,2 , 정…의, 된X;다r 과. XC XJ I1, ,XXj2 2, , ……, , xX. j), 가이 X1n, 차X2원, …의, x연. 의 排反部分집 합일 때 XJ I , XJ2 , …, X J,가 주어 진 Xu, X;2, ••• , x,r 의 조건부확물분포는
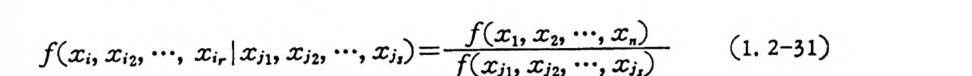 f(X j , Xi 2 , …, Xi r IXi) , Xj z , •··, Xi ,) ff(X( 따j l,’ Xxj2 2, , ……,, xX.j ,)) (1. 2-31)
f(X j , Xi 2 , …, Xi r IXi) , Xj z , •··, Xi ,) ff(X( 따j l,’ Xxj2 2, , ……,, xX.j ,)) (1. 2-31)
이 다. 만일 X1, X2, …, X. 이 상호독립 이 면
 f(x 1' % …, xn)=iJ=” lI f(x; ) (1. 2-32)
f(x 1' % …, xn)=iJ=” lI f(x; ) (1. 2-32)
이 성립한다.
X 가 연속확률변수이고, 밀도함수f(·)일 때 집합 X 와 Y 를 다음 과 같이 정의한다.
 X= {x\f( x )>o}, Y= {yly > o} (1. 2-33>
X= {x\f( x )>o}, Y= {yly > o} (1. 2-33>
 g -l( y)는 g (x) 의 역함수로 g -1 (y)는 g (x)= y에 대한 X 이다. g( x)
g -l( y)는 g (x) 의 역함수로 g -1 (y)는 g (x)= y에 대한 X 이다. g( x)
 이 된다.
이 된다.
 이 다. 이 러 한 변환을 확물적 분변환(p robab ility integral tra nsfo rm a·
이 다. 이 러 한 변환을 확물적 분변환(p robab ility integral tra nsfo rm a·
 …, Yn 의 확률밀도함수를 구할 수 있다. xl=g 5 '(yI , y 2 , ••• ,y).
…, Yn 의 확률밀도함수를 구할 수 있다. xl=g 5 '(yI , y 2 , ••• ,y).
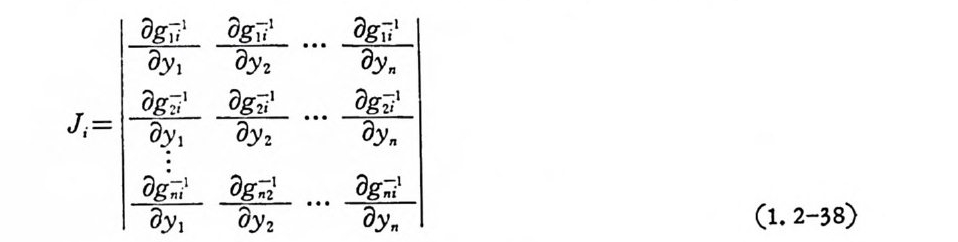 무aYI 무ay 2 … 투Oy, ,
무aYI 무ay 2 … 투Oy, ,
 행렬식 J;,i =l,2. … ,m 은 0 이 아니며, J계 모든 편미분은 연속
행렬식 J;,i =l,2. … ,m 은 0 이 아니며, J계 모든 편미분은 연속
1. 2. 5 정규분포함수 정규확률분포함수는 정보이론, 응용동계학, 통신공학 등에 많이 사용되는 확률분포함수로서 확률밀도함수가 다음과 같을 때 확률변 수 X 는 정규적으로 분포되었다고 말한다.
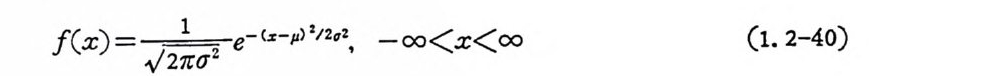 f(x ) = 一,./211r (J 2 e-(z-µ f I2c2, - 00
f(x ) = 一,./211r (J 2 e-(z-µ f I2c2, - 00
 변수 µ논 평군치이며 구간 _oo<µ
변수 µ논 평군치이며 구간 _oo<µ
 이고, y=(도가 L)/ q로 놓으면, dx=ady 이므로
이고, y=(도가 L)/ q로 놓으면, dx=ady 이므로
이 된다. 그러므로 평균치와 분산은 다음과 같다.
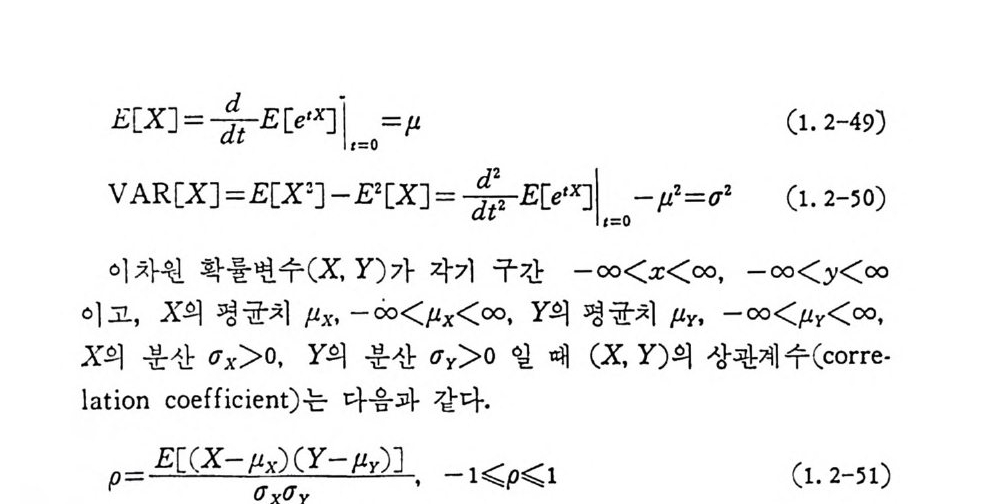 玩 X] = 훑 E[e 지 =µ (1. 2-49)
玩 X] = 훑 E[e 지 =µ (1. 2-49)
이때 이차원 정규확률밀도함수는
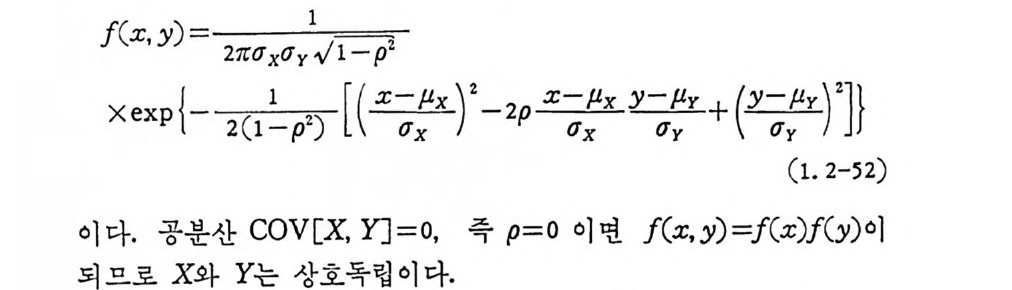 f(x , y )2=1 '(Jx~ (J y l, ./,~ l _ p2
f(x , y )2=1 '(Jx~ (J y l, ./,~ l _ p2
조건부 확률분포함수는 다음 식으로 표시되며
 JC xl y)=릅 (1. 2-53)
JC xl y)=릅 (1. 2-53)
이다. n 차원 정규확률밀도함수는 다음과 같이 표시 할 수 있 다 .
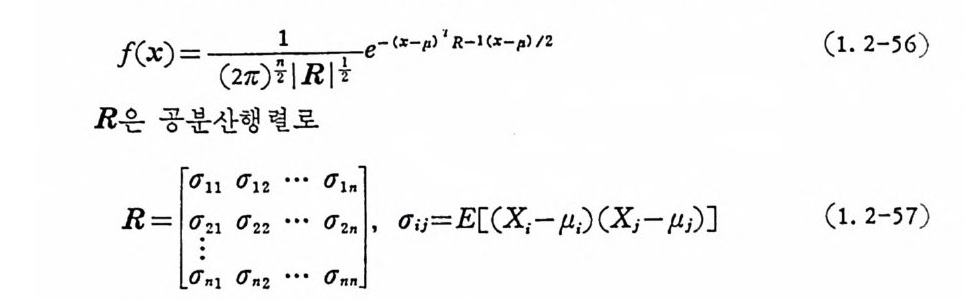 f(X ) = ~e-(X-p) .,R - 1(:<-p) /2 (1. 2-56)
f(X ) = ~e-(X-p) .,R - 1(:<-p) /2 (1. 2-56)
이다. 또한
 µT= [µi, µ2, … , µn] (1. 2- 5 8)
µT= [µi, µ2, … , µn] (1. 2- 5 8)
1. 2. 6 확률변수에 관한 부등식 Cheb y shev 의 부등식
 〈정 리 1. 2-1> X 가 유한분산을 갖은 확률변수일 때 다음 부등식 이
〈정 리 1. 2-1> X 가 유한분산을 갖은 확률변수일 때 다음 부등식 이
 P[IX-E[X 미 ~T<7 x ]
P[IX-E[X 미 ~T<7 x ]
이므로
 깍g》 X ) 〕 正g ( X ) ;>K 〕 (1. 2-62)
깍g》 X ) 〕 正g ( X ) ;>K 〕 (1. 2-62)
울 얻는 다. 또한
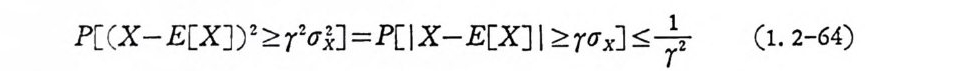 p 〔 e x 캘認 ])2 2.군(J } ]=P 目 X 캘 [X 미 츠 x J:::;r- 녹 (1. 2- 6 4)
p 〔 e x 캘認 ])2 2.군(J } ]=P 目 X 캘 [X 미 츠 x J:::;r- 녹 (1. 2- 6 4)
이 므 로
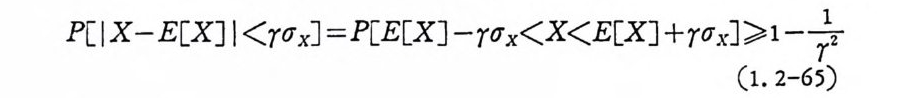 P[ I X 그:〔幻 l
P[ I X 그:〔幻 l
이 된다. J ensen 의 부등식
 〈 정 리 1. 2-2> g( X ) 가 볼 록함수 (convex fun cti on ) 이 고 평 군치
〈 정 리 1. 2-2> g( X ) 가 볼 록함수 (convex fun cti on ) 이 고 평 군치
이다. 멘 나중의 부동식은 기대함수의 목성®룰 이용하였다.
제 1 장서론 31
Schwarz 의 부등식
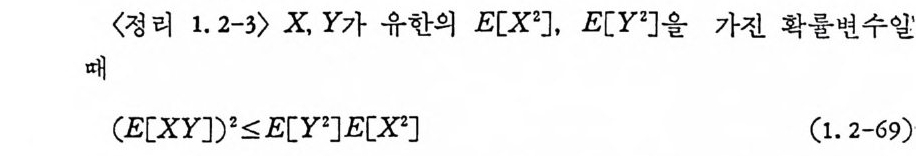 〈정 리 1. 2-3> X, Y 가 유한의 腐 X2], E[Y 汀울 가진 확률변수알
〈정 리 1. 2-3> X, Y 가 유한의 腐 X2], E[Y 汀울 가진 확률변수알
 이 성립한다. 등식은 정수 c 에 대하여 P[Y=cX 〕 =l 일 대 성립한냐
이 성립한다. 등식은 정수 c 에 대하여 P[Y=cX 〕 =l 일 대 성립한냐
1.2.7 대수의 법칙, 중심극한정리 大數의 弱法則
 독립 인 확률변수의 무한계 열 {xn} 의 부분합울
독립 인 확률변수의 무한계 열 {xn} 의 부분합울
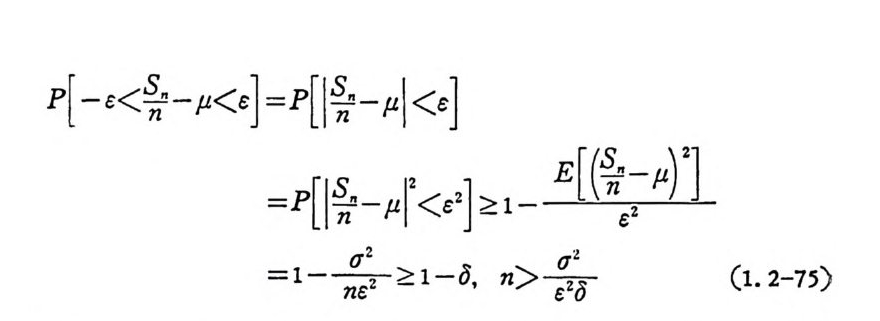 P[-e< 춥― µ
P[-e< 춥― µ
 이 된다. 그러 므로 대 수의 약 법 칙 (The weak law of large numbers)
이 된다. 그러 므로 대 수의 약 법 칙 (The weak law of large numbers)
 P[ I 분기
P[ I 분기
大數의 强法則 좀더 강한 대 수의 법 칙 이 Kolmo g orov 에 의 하여 증명 되 었다. {x.} 이 유한한 분산을 갖고 독립확률변수계열이 동일한 분포함수를 가 질 때, 만일
 2(J}
2(J}
이떤
 P(~ _ :〔S 』 --o) = 1 (1. 2-78)
P(~ _ :〔S 』 --o) = 1 (1. 2-78)
이 된다• cs "一 E 〔오 ])/n 이 0 이 될 확률이 1 이다. 다시 말해서 움이 평군치 E 〔 x 』캬에 수림한댜 中心極限定理 {다이 독립확률변수이고 E[X 』=µ., VAR[XJ =(J?이 유한하다.
 x一 n=n-1 E;.=;. lz . (1.2-79)
x一 n=n-1 E;.=;. lz . (1.2-79)
로 놓으떤 확률변수
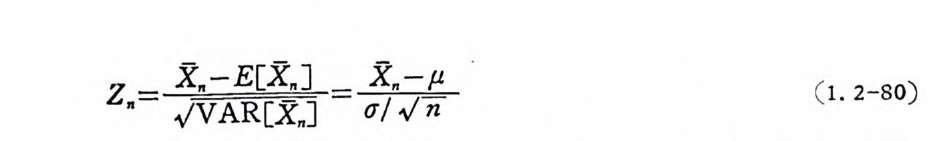 z.= 討x.-球E[茂X』 = Cx/ . .-.µ j下 (1 . 2-80)
z.= 討x.-球E[茂X』 = Cx/ . .-.µ j下 (1 . 2-80)
은 n 이 무한대 로 접 근함에 따라 표준정 규분 포 로 접 근 한 다. x n 을 표준화한 Z n 은 평군치 0, 분산 1 인 정규분포가 된다는 의미이다. 중심 극한정 리 (centr a l lim i t t heorem) 는 확률론에 서 가장 중요 한 정 리의 하나로 X 위 분포를 알려 주고 있다. 환 언 해 서 X n 은 평 군치 µ와 분산 (j 2/n 인 정 규분포가 된다. 확률변수 X;, i= l, 2, …, n 이 어 떤 분포함수를 가지고 있든 이 정리는 성립한다. 이 정리의 실 제적 인응용은평군또는합으로기술되논어떤사 상의 대략적 인 확률 값을 구하는 데 있다. 죽 xI,X2 , ••• ,x n 이 평군치 µ, 분 산 6 국 인 독립 확 률 변수이고 동일한 확률 분포 를 가지고 있으면 P[r
* 참고문헌 Abramson, N., Info r ma tion Theory and Codin g , McGraw-Hi ll , N ew York, 1963. Ash, R.B ., Info r mati on Theory, Inte r scie n ce Publi sh ers, New York, 1965. Bril lou in , L. , Sc ien ce of Info r m ation Theory, Academi c Press Inc. , New York 1956. Cram~r, H., Ma the matica l Me tho ds of Sta tistics , Prin c eto n Univ e rsit y Press, 1946. Davenp o rt, W.B. and Root, W.L., Random Sig na ls and Nois e , McGraw-Hi ll, New York, 1958.
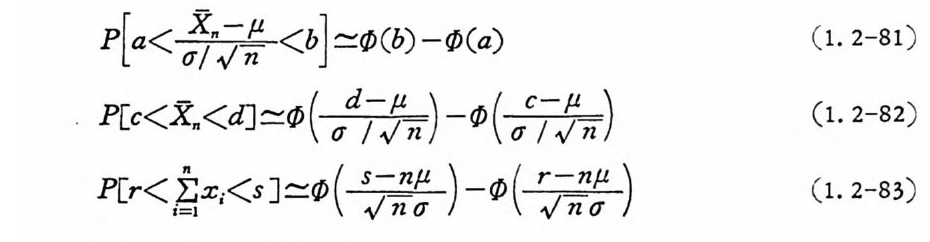 P[a< (j?言
P[a< (j?言
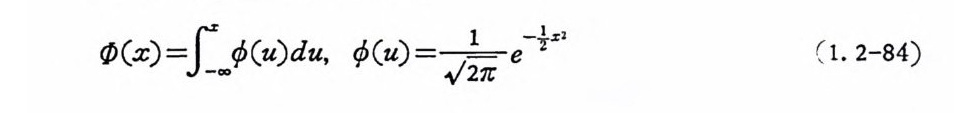 ( u)du, (u) =../2스7C 건 =2 (1 . 2-84)
( u)du, (u) =../2스7C 건 =2 (1 . 2-84)
여기서
Doob, J.L., Sto c hasti c Processes, W ile y , New York, 1953, Fano, R. , Transmi ss io n of Info r ma tion , W ile y , New York, 1961. Fein s te i n , A. , Foundati on s of Inf or mati on Theory, McGraw-Hi ll, New York, 1958. Feller, W. , An Intr o ducti on to Probabil i ty Theory and its A p pli c a ti on , vol. I, W ile y, New York, 1950. Feller, W . , An Intr o ducti on to Probabil it y Theory and its Ap pli c ation , Vol. II, W ile y, New York, 1966. ·Ga llag e r, R.G ., Info r mati on Theory and Relia b le Communic a ti on , W ile y, New York, 1968. Jel in e k, F. , Probabil i s t i c Inf or mati on Theory, McGraw-Hi ll , New York, 196 8 . Khin c hin , A. I. , Math emati ca l Foundati on of Inf or mati on Th~ory, Dover Public a ti on , Inc., New York, 1957. Mood, Gray b il l and Boes, Intr o ducti on to the Theory of Sta t i stics, 3rd Ed. McGraw-Hi ll, New York, 1963. :Sh annon, C.E . , A Math e mati ca l Theory of Communic a ti on , Bell Sy s t. Tech J. , Vol. 27, pp. 379-42 3 and 623-56, 1948, W ien er, N. , Extr a p ol ati on , Inte r po l ati on , and Smooth i n g of Sta t i on ary Ti m e Serie s , MIT Press, Cambrid g e, 1949.
제 2 장 정보량과 정보원 2.1 諸情報量 2.1 .1 자기정보량과 엔트로피 정보 ( i n fo rma ti on) 라는 단어는 일상생활에 많이 사용하고 있다. 그러나 정보이론에 있어서 정보의 뜻하는 바를 좀더 확실히 규명할 팔요가 있다. 정보이론에서 중요한 개념은 정보량 (measure of in· fo rma ti on ) 으로 이에 대하여 고찰하려 한다. 일기예보를 동고하는 관상대를 생각해 본다. 관상대에서 내일 일기예보를 〈맑음〉, 〈구 름 이 낌 〉 , 〈비가 옴〉이라는 3 개의 구분(사상) 중 하나를 택하여 일 기예보를 한다고 가정할 때 내일 비가 온다는 말에는 내일 비가 올· 확 률 이 많다라고 생 각할 수 있다. 〈내 일은 맑음〉, 〈내 일은 구름이 낌〉, 〈내일은· 비가 음〉이 상호배반사상이고, 〈내일은 맑음〉이라는 통보 (messa g e) 를 S1, 〈내일은 구름이 낌〉이라는 통보를 %, 〈내일은 비가 음〉이라는 통보를 S3 로 표기한다고 하자. 그리고 내일 밝을 확 률이 p1, 내일 구름이 껄 확률이 P2, 내일 비가 올 확률이 p 3 일 때 동보 s1, s2, S 제 각기 정 보량을 규정 하려 한다. 각기 동보를 표시 하 는 기 호 S1, S2, S3 의 발생 확률 Pi, P2, P3 을 알고 sl, s2, S3 의 뜻하는 바 를 모른다 하더라도 정보이론에서는 S1,S2,S3 의 각기 정보량을 규정할· 수 있으므로 정보량은 동보가 갖고 있는 말의 뜻에 대한 정의가 아 니고 발생확률에 기반올 둔 수학적인 정의라 말할 수 있다. 하나 의 예를 더 들어 본다. 우체국에서 4 가지의 電文울 구비하여 그때
그메 요구하는 사람에게 이용하게 하고 있다. 전문 A 를 S1, 전문 B 를 S2, 전문 C 를 S3, 전문 D 를 S4 로 표기 하고 장기 간 동안에 4 개 의 전문의 이용도를 조사해 본 질과 A 가 50%, B 가 30%, C 가 20% 그리고 D 가 10% 를 차지하고 있다고 가정한다. 우체국은 통보 S1 , Sz, S3, S4 를 발생 하는 정 보원 (inf o r mati on source) 이 라 부를 수 있 다. 일반적으로 정보원은 통보 또는 정보원알파벳 (source alph abet) s’ 를 확물 P 를 가지고 발생하는 장치이다• 다음 정보이론의 중요한 관 심 사가 되 는 자기 정 보량 (se lf-i n fo rma ti on) 을 규정 하여 본다. Shan· non 은 통보 s i의 자기정보량을 다음과 같이 정의하였다.
 I (s;) = log -pi1-i - (2 . 1-1)
I (s;) = log -pi1-i - (2 . 1-1)
죽 통보 s i가 발생할 확률의 역수에 대수를 취한 것이다. 정보량을 규정하는 데는 정보의 양으로 가질 수 있는 특성을 설정하여 놓고 이 목성에 맞도록 정보량을 규정하는 식을 유도하는 방법이 있으나 우리는 먼처 정보량을 정의하여 놓고 이에 대한 유용도를 정당화하 려 한다. 예로 내일 아침 해가 동쪽에서 뜬다라는 동보는 해는 항상 동쪽에서 드므로 정보를 가지고 있지 않다. 그러나 동쪽이 아니고 다른 방향에서 해가 뜬다면 이 통보는 많은 정보를 가지고 있다타 고 말할 수 있다. 확률적으로 말하면 확실한 사상, 즉 확률이 1 인 사상의 정보량은 0 이며, 발생확률이 0 인 사상의 정보량은 무한대 가 된다. 죽 발생확률이 적을수록 정보량이 많다는 것을 알 수 있 다. 다음 정보량의 정의에서 대수를 사용함으로써 정보량의 加法性 (add iti v ity)을 합리화하였다. 예로서 트럼프카드 52 개 중 하나를 택 하였을 때 그 카드가
자 3 의 발생 확률은 ―1느3 이 므로 통 보
 I=logn =log 7 p1 (2. 1-2>
I=logn =log 7 p1 (2. 1-2>
이 다. 자기 정 보량을 다음과 같이 요약한다. 동보의 집 합 {sI, s2, …, sJ 이 고 각 동보의 발생 확률이 P;=P(s;), i= 1, 2, …, n 되 는 정 보원을 생각할때
 1r”=;I p ;= l (2. 1-3)
1r”=;I p ;= l (2. 1-3)
이 되며, 자기정보량을 다음과 같이 정의한다.
I(s;)=Iog P—11 =-logp i (2 . 1-4>
이 정의논 확률에 기반을 둔 정의이지 동보의 의미에 기반 을 둔 정 의는 아니다. 정보량의 개념은 기술적 정의이며, 정보의 일반적 견 해를 보편적으로 대변한다고는 볼 수 없다. 정보량은 목정 s‘ 물 취 하는 사상에 의하여 제공된 정보의 양이라 해석 할 수 있다. 이 해 석 에 의하여 사상의 발생확률이 적을수록 많은 정보량을 나타내며 확 룰이 1 인 확실한 사상의 자기정보량은 0 이다. 죽 자기 정보량은 불 확실성 (unce rt a i n ty)의 측도라 볼 수 있 다. 정 보원에 서 발 생 하는 통 보와 각 통보의 발생확률을 알면 우리는 그 정보원의 평군자기 정 보 량을 구할 수 있다. 먼저 말한 우체국에서 취급하는 전문의 예를 들어 본다. 롱보 확률 S1 o. 5 s2 o. 3 S3 0.2 S4 o. 1 통보 S1 의 자기정보량은 정보량 정의에 의하여 구하여 보면 다음과 같다.
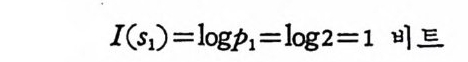 I(s1) = log p1= log 2 = 1 비 트
I(s1) = log p1= log 2 = 1 비 트
마찬가지 로 통보 %, S3, S4 에 대 한 정 보량을 구하여 보면
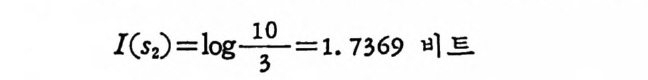 I(s2)=log —13—0 =1. 7369 비트
I(s2)=log —13—0 =1. 7369 비트
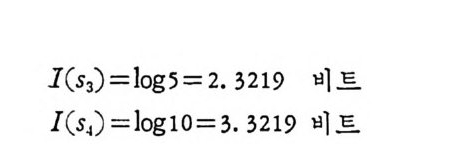 J( s3 )=log 5 =2. 3219 비트
J( s3 )=log 5 =2. 3219 비트
이 다. 이 대 정 보원 S 에 대 한 엔트로피 (en t ro py)는 통보당 평 군자기 정보량으로 각 통보에 대한 자기정보량의 평군을 취한 것이다. 평 군을 취하려면 각 통보의 정보량에 발생확률을 곱하여 더하면 얻을 수 있다. 이렇게 계산한 평군정보량을 확률벡터가 (P i, P2, …,p n) 일 매 발생확률의 함수로서 H ( p)로 표기한다.
 H( p ) = -1I= ” ; 1 p )o gp , (2. 1-5)
H( p ) = -1I= ” ; 1 p )o gp , (2. 1-5)
전문의 경우 엔트로피를 구하여 보면
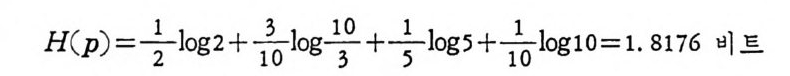 H ( p ) =―21 ,l o g 2_ +. -13f0n ,l o g13一0 +. ―15 ,l o g 5_ +. —110 log lO= l. 8176 비 트
H ( p ) =―21 ,l o g 2_ +. -13f0n ,l o g13一0 +. ―15 ,l o g 5_ +. —110 log lO= l. 8176 비 트
이다. 엔트로피란 용어는 통계열역학에서 나오는 용어로 비례정수 를 제 의하고는 식 ( 2.1-5 ) 와 동일하다. 엔트로피는 통보당 평균불확 실성을 나타내고 있다. 엔트로피의 실제적 응용은 뒤에 기술할 잡 음이 없는 채널에서의 부호화정리에 이용되고 있다. 일례로 한 개 의 동전을 던져 앞면이 나올 확물이 P 이고 뒷면이 나울 확룹이 ( 1- p ) 일 때 엔트로피는 다음과 같다•
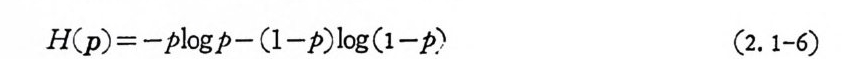 H( p) = -plo g p-( l-p) log (1-p) (2. 1-6)
H( p) = -plo g p-( l-p) log (1-p) (2. 1-6)
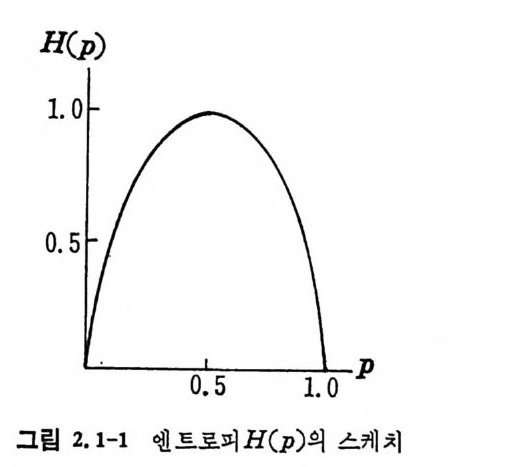
p를 변수로 하여 H ( p)을 도 시 하면 그림 2. 1-1 과 같다. 앞 연과 뒷떤이 나올 확률이 같을 때 죽 p= 上2- 일 때 엔트로피 는 최대가 된다. 엔트로피는 다음과 같은 수 학적 성질을 가지고 있다. ® H(pI , p2 , …, p)은 항상 負의 값이 아니며 P;=O 인 겅 우를 제의하고 正의 값이다.
 H( p)
H( p)
® H( p I, p 2, … ,P.) 은 변수 P, 의 순서를 변경하여도 불변이다. ® H( p I, p 2, ···,p n) 은 pi=-¼, i= l, 2, …, n 일 때 최 대치 H(P1, P 2,- … ,P. ) =I og n 이 된다. @ H( P i, P 2. … ,P., o)=H(pi ,P 2. …,p n) 이다. ®과 ®항 은 자명하냐 ®항이 성립되는 것을 보이기 위하여 p n 을 다른 확률에 의존하는 종속변수로 보면
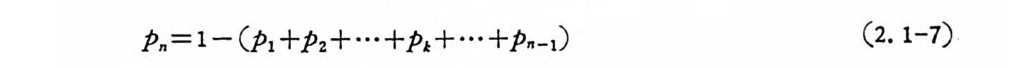 P.= 1-(P 1 +P2+ …+ P1+ …+ P--1) (2. 1-7)
P.= 1-(P 1 +P2+ …+ P1+ …+ P--1) (2. 1-7)
되고, 이때 엔트로피는 다음과 같다.
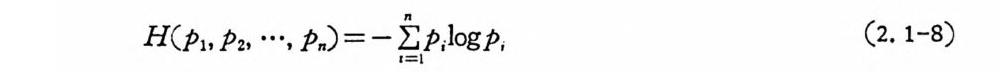 H( P i, P2, …, Pn) = -I1 =;l Ip )o gp , (2. 1-8)
H( P i, P2, …, Pn) = -I1 =;l Ip )o gp , (2. 1-8)
엔트로피의 최대치를 구하기 위하여 p k 와 p n 율 제의하고 다른 확률 · 은 상수로 보고 p k 에 대하여 미분하면
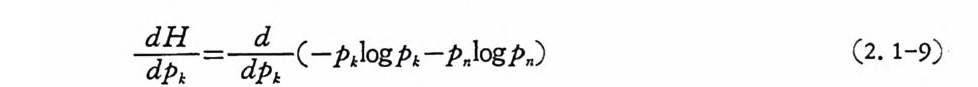 言dH= 따d (-P1lo gp 1-P .l o gp .) (2. 1-9)
言dH= 따d (-P1lo gp 1-P .l o gp .) (2. 1-9)
 되고, 식 (2.1-9) 와 다음 식을
되고, 식 (2.1-9) 와 다음 식을
사용하여 구하면 다음과 같다.
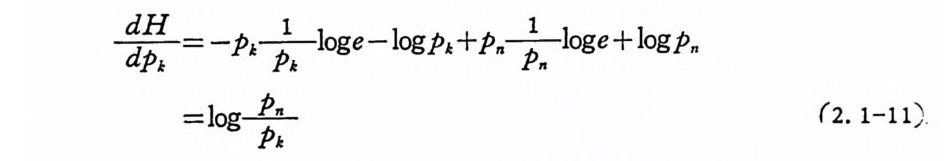 따d~H = -P.J :-j1; ;-,l o g e -l,o gP J. : +. P. .--j 1; :-log e + log p.
따d~H = -P.J :-j1; ;-,l o g e -l,o gP J. : +. P. .--j 1; :-log e + log p.
이것은 p .=Pn 일 때 0 이 되고 p.는 임의로 선택하였으므로
P1=Pz= .. ·=Pn 국 (2. 1-12);
이다. 또한 H(l, O, …, O)=O 로 엔트로피는 최소가 된다. P=O 일 때는 olo g O=O 로 해석하기로 한다.
앞으로 유용하게 사용될 대수함수의 부등식에 대하여 알아본다. 정수 x 에 대하여 lnx 의 x=l 의 기울기는
 쁩 1%=!=1 (2. 1-12)
쁩 1%=!=1 (2. 1-12)
이 의부각등기 식p 을I, p 2얻. …는다, p.“ 일 이때 부다동음식 부을등 사식용 이하 성여 립s 함I, s을2, ••보• ,인 s 은다의. 발생 확률
 H(p) ,
H(p) ,
죽
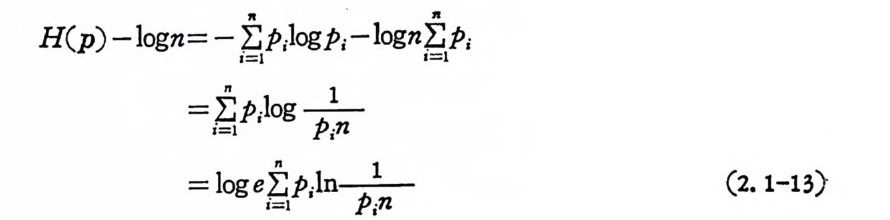
부등식 lnx
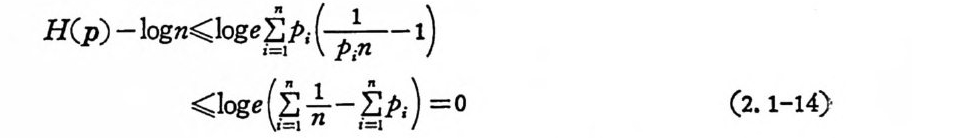 H(p) -lo g n
H(p) -lo g n
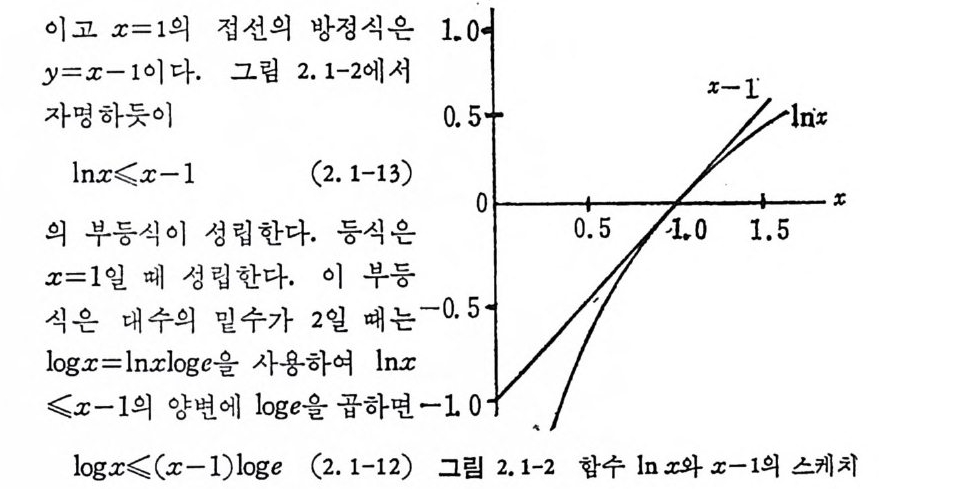 이고 x=l 의 접선의 방정식은 1.0
이고 x=l 의 접선의 방정식은 1.0
m 일 때 통신채널은 다음과 같이 조건부확률로 규정된다. 이 조건 부확률을 채 널의 천이 확률(t rans iti on pro babil it y ) 이 라고도 부른다. z 를 입력 Y 를 출력이라 할때 z 는 a1,a2,… , an 중하냐롤 취하고 Y 는 b1, b2, …, bm 중 하나를 취 한다고 가정 한다. 집 합 {a1, a2. …, a.} 온 X의 표본공간이 되 고, 집 합 {b1, b2. …, bm} 은 Y 의 표본공간이 된 다. ZEX이 면 2 는 특정한 a 를 취한다. 이원부호를 사용하는 몽 신계통에서는 X=Y={o, 1} 이 되고, 주로 이 경우가 관십의 대상이 된다. {a;, b;} , 1
 P(ai) =. Ei=' IP (ai, bj) (2. 1-15)
P(ai) =. Ei=' IP (ai, bj) (2. 1-15)
된다. 동석은 P 른숭일 때 성립하며, 동일한 발생확률이 아닐 때의 엔트로피 는 항상 l og n 보다 적 다. 2. 1. 2 情報傳送의 모델 송선기로부터 송신된 정보는 정보채널을 동하여 수신기에 도착한 다. 이렇게 송신된 정보는 채널에서 잡음이 가하여져 수선된다. 물 몬 채널에 잡음이 없으면 송신된 정보가 그대로 수신되나 잡음이 있을 경우 송신된 정보와 수신된 정보가 같지 않을 수 있다. 잡음 울 랜돔 (random) 현상으로 기술할 수 있듯이 정보가 유동하는 정보
 x채!널:도: 수동 1 계P(적bJ i 모a ,)델 \을:: l사Y용 할円 수〔 曰있다:.\ \송i신:기t에)서; 기로호] (: s y: mb:ol:)
x채!널:도: 수동 1 계P(적bJ i 모a ,)델 \을:: l사Y용 할円 수〔 曰있다:.\ \송i신:기t에)서; 기로호] (: s y: mb:ol:)
한다. x, y는 확률변수로서 작용하나 x, y의 표본공간이 동일할때는 혼동의 우려 가 있다. 만일 P(a J >o 이 면 입 력 z 가 a;, 출력 Y 가 b j인 조건부확 률
P( bi l a;) = ~ (2. 1-17)
로 정의한다. a, 와 b j가 상호독립이면
 P( a ;, b D =P( a; ) P ( bi ) (2. 1-18)
P( a ;, b D =P( a; ) P ( bi ) (2. 1-18)
이고 마찬가지로
 P( bi l a;) = P( bD (2. 1-19)
P( bi l a;) = P( bD (2. 1-19)
가 된다. 사 후 확률 P( a ;lbJ , 즉 b)를 수신할 때 a; 를 송신 했 을 확 물 을 말하며 채 널에 잡음이 없을 때는 P(a,lb J =l 이다. 또한
 P( a; , b;) = P( a; ) P ( b; l a;) (2. 1-20)
P( a; , b;) = P( a; ) P ( b; l a;) (2. 1-20)
이므로 두 식으로부터
 P( a ;lb;)P(=b;) ~ (2. 1-22)
P( a ;lb;)P(=b;) ~ (2. 1-22)
이고
 P( bD = iI=” :I P( a;)P(bi Ia ;) (2. 1-23)
P( bD = iI=” :I P( a;)P(bi Ia ;) (2. 1-23)
이므로
 P(a;lbJ .E= P(a;) P~(bi l a;) (2. 1-24)
P(a;lbJ .E= P(a;) P~(bi l a;) (2. 1-24)
이 다. 이 석 은 베 이 어 스공식 (Ba ye s' fo rmula). 으로 서 론에 서 말하였 다. N개 성분을 가전 입력계열 x=(xI,x2, … ,XN) 이고 출력계열 y= (Y1 ,Y 2, ···,YN) 일 때 벤출력기호가 i번입력기호에만 의존하는채 널을 이 산무기 억 채 널 (d i scre t e memoryl e ss channel) 이 라 하고 다음
수식으로 정의된다.
 P(y l x) =i.=l N ll P (y; l x;) (2. 1-25)
P(y l x) =i.=l N ll P (y; l x;) (2. 1-25)
득히 X= Y= {O, 나 일 때 조건부확률 P(I I O) =P( 이 I) =P P( 이 O)=P(l j 1)=1-p 인 무기억채널을 이원대칭채널 (b i nary sym metr i c channel ) 이라 하 고 그림 1. 1-3 에 도시하였다. 이원대칭채널에서는 2 개의 기호 0 이 나 또는 1 을 채널을 통하여 송신할 때 채널에서 잡음이 가해져 송 신된 0 을 수신축에서 1 로 판별할 확률이나 1 을 송신하여 수신축에 서 0 으로 판별할 확률이 같다. 마찬가지로 1 을 송신하였을 때 수신 측에서 옳게 1 을 받을 확률과 0 을 송신하였을 때 옳게 0 을 수신할 확률이 동일하다. 〈예 2.1-1> 이원대칭채널에 관한 각종 확률을 구해본다.
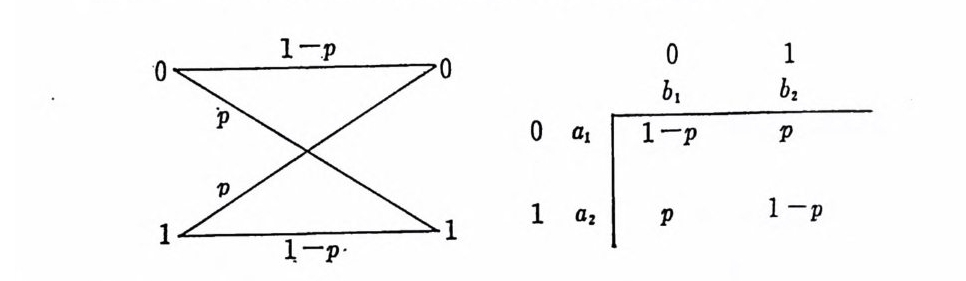 0b 12
0b 12
이원대칭채널로부터 P(o I o) =P(b1 I a1) =P(1 I 1) =P(bz I az) = 1-p P(o I 1) = P(b1 I a2) = P(1 I o) =P(bz I a1) =P 이다. 또한
 .~i=PI (b;la•; )=l, i~=2 I j.=E2 I P(b;la;)P(a;)=l
.~i=PI (b;la•; )=l, i~=2 I j.=E2 I P(b;la;)P(a;)=l
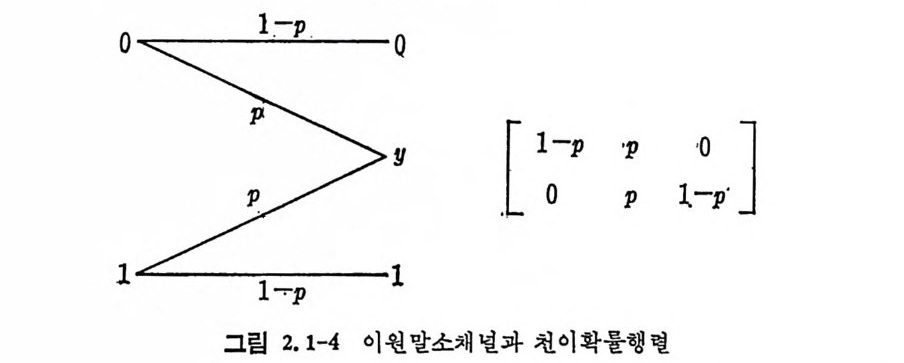
이원대칭채널은 실제채널을 가장 적철히 표현하고 있는 수학적인 채 널모델 이 라 볼 수 있 다. 그 외 이 원 말소채 널 (bin a ry erasure chan- nel) 로 입력기호 0, 1 에 대하여 출력은 O,y , 1 로 0 도 아니고 1 도 아 닌 알 수 없는 y상태가 존재한다. 수학적 해석을 위해서는 천이확 물행렬의 입력, 출력기호수와 행렬의 요소인 조건부확물을 적철히 변화시킵으 로써 많은 채널모델을 만들 수 있다.
 。 Q
。 Q
 P( a i, bi) = P(a z , b2) = P(b 1 Ja 1)P ( a1) =~2 (1-p)
P( a i, bi) = P(a z , b2) = P(b 1 Ja 1)P ( a1) =~2 (1-p)
2, 1. 3 부호의 構成例 M개 의 통보 sJ, s2' …, SM 과 그의 발생 확률이 P(s.) =P, 인 정 보원 X를 생각한다. 지금 정해진 알파벳집합 A= {ai, a2, …, a.} (2. 1-26) 이 면 알파벳의 요소 C:lemen t)를 문자(l e tt er) 또는 기 호 (s y mbol ) 라 부른다. 각 통보 s i가 알파벳 집 합 A 에 서 택 한 문자의 계 연 (seq u ence) 로구성될 때 xi= (xiI, Xi 2, …, X; N ), xuEA, j= l, 2. …, N (2. 1-27) x 를· 부호어 (code word) 라 한다. N은 부호어 의 길이 이 다. 각 동보 는 부호어 로 변환되 었으며 부호어 의 전체 의 집 합 C= {xi, x2. … , X 마 을 부호 (code) 라 부른다. 통보나 단어 (word) 는 유한한 문자의 계 열 로 변환될 수 있으며 동보를 부호어로 바꾸는 장치는 부호기 (enco· der) 이다. 부호화 (encod ing)란 하나의 언어로 구성된 유한한 문자 · 의 단어를 다른 언어의 문자로 구성된 단어로 1 대 1 로 사상하는 것 이다. 복호화 (decod ing)는 부호화의 반대동작으로 주어전 언어로부 터 본래 언어로 변환시키는 동작이다. 독립정보원이란 이미 규정된 확률을 가진 불연속통보 중에서 임의 의 동보를 추출하는 장치 이 다. 이 동보는 각기 발생 확률 P를· 가지 고 독립적으로 발생한다. 죽 정보원이 기억울 갖고 있지 않다. 그 국 림 2.1-5 에서 M개 의 통보가 있는 정보원에서 동보를 발생하고 부 호기를 통하여 각 동보가 n 개의 알파벳으로 구성된 문자의 계열로 이루어침을 보이고 있다.
 {:s1, Sz, …, Sy子} A= {三ai, az, ..., an급} 三
{:s1, Sz, …, Sy子} A= {三ai, az, ..., an급} 三
이원부호의 알파벳은문자 0 과 1 로구성되고 알파벳집합 A={o,1}
이다. 다음 이원부호로 부호화된 예를 본다. 4 개의 동보가 부호야 로 바뀌었다. 동보 부호어 S1 0 Sz 10 S3 110 S4 1110 이 부호를 관찰하면 모든 부호는 0 으로 끝난다. 부호가 연속적으 로 수신 될 때 0 이 나타나면 하나의 부호어 가 끝난 신호로 생 각할 수 있다. 4 개의 부호어를 사용함을 사전에 알면 유일 (un iq uel y)하 게 해독이 가능하다. 연속적으로 부호를 수신하였을 때 0 0 110 10 0 01 10 S1 S1 S3 S2 S1 S1 S3 으로 해독할 수 있다. 그러나 다론 부호의 경우는 통보 부호어 S1 。 S2 1 S3 00 S4 11 유일하게 해 독이 안 된다. 0011 계 열은 S1S1SzS2, S1S1S,, S3SzS2, S3S4 로. 해독할 수 있다. 다음 부호를 본다. 동보 부호어 s1 0 Sz 01 s3 011 S4 111 수신계열이 0 1 1 0 1 1 1 1 0 Ss S2 S4 S1
일 때 이 부호는 유일하게 해독이 가능하지만 처음부터 해 독 하려면 처음이 s1 인지 S2 또는 S3 인지 구별할 수 없다. 부호계 열 전 체를 수 신한 다음 역으로 해독하면 해독이 가능하다. 멘 먼처 예와 같 이 즉시 유일하게 해독되는 부호를 즉시부호 ( i ns t an t aneous code ) 라 부 르며 죽시부호가 되기 위해서는 한 부호어가 다론 부호어의 語頭部 分(p re fix)이 되지 않아야 즉시부호를 구성할 수 있다. 하나의 부 호어가 다론 부호어의 앞 부분을 이루지 말아야 한다. 다 음 두 부 호어는 즉시부호이다. 통보 부호어 1 부호어 2 S1 。 00 s2 10 01 s3 110 10 s~ 1110 110 Ss 1111 111 부호어 2 의 경우 s1=00, s2=01, s3=10 일 대 s4=11 을 사용하면 s5=110 의 앞 부분을 이루므로 즉시부호가 될 수 없다. 2. 1. 4 크라프트부등식 Kra ft부등식은 죽시부호의 촌재에 대한 필요충분조건으로 즉시부 호를 구성하는 부호길이의 조건을 말한다. 그러나 부호 자 체를 구 성하는 방법은 말하지 않고 있다. 〈정리 2.1-1> M 개 부호어의 부호길이가 li, l2 , … lA[ 일 때 즉 시부 호가 촌재하기 위 한 필요충분조건은 다음과 같다.
 i_=ME I D -1•<1 (2. 1-28)
i_=ME I D -1•<1 (2. 1-28)
D 는 부호를 구성하는 알파벳수이다. 〈증명〉 부호어의 길이 1 인 부호어의 수를 W 려라 하면 W1 은 알 파벳수 D 보다 클 수 없다.
 W1
W1
길이 2 를 가진 부호어의 수는 다음보다는 큘 수 없다.
 W2 <( D-W1)D=D 드 W1D (2. 1-30)
W2 <( D-W1)D=D 드 W1D (2. 1-30)
Kra ft부등식 은 유일해 독부호의 특별한 경우인 즉시 부호에 적 용하 였으나, McM i llan 은 동일한 부등식이 유일해독부호에도 적용되는 것을 증명하였다. 충분조건은 유일해독부호의 특별한 경우인 즉시 부호에서 층명할 수 있다는 것으로 충족하며 필요조건은 다음과 같 이 증명할수 있다. 〈정 리 2. 1-2> 유한개 의 알파벳 (a1, a2, ···, a )에 서 부호길이 Cl1t lz, · 짜리 인 유일해 독부호계 열 (Xi , X2, …, XM) 일 때
 ~MD -u<;1 (2. 1-35)
~MD -u<;1 (2. 1-35)
 C f D 처 =K• (2. 1-36)'
C f D 처 =K• (2. 1-36)'
〈예 2. 1-2> 다음 두 개 의 부호 중 McM i llan 의 부등식울사용하어 유일해독부호를 구별하라. 틍보 부호어 1 부호어 2 S1 。 。 S2 10 1 s3 110 00 s. 1110 11 부호어 1,2 의 경우
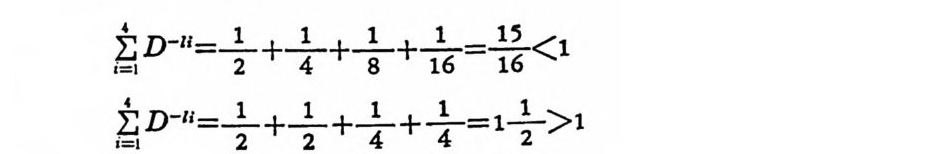 iI=~: l D,...-.1_,1, =— 12 .+ 14- +. -18+ . —116 =11-56< l
iI=~: l D,...-.1_,1, =— 12 .+ 14- +. -18+ . —116 =11-56< l
로 부호어 1 이 유일해독부호이다. 2. 1. 5 부호화의 제일기본정리 여기서는 엔트로피 H(X) 가 어떻게 실지로유용히 쓰이는가를 보 인다. 먼처 부호어의 평군길이를 설명한다. 4 개의 동보가 다음과 같이 부호어로 변환되었고 통보의 각기 발생확률이 통보 부호어 발생확률 SI 00 o. 5 s2 01 o. 25 S3 10 o. 125 S4 11 0. 125 일 때 부호의 평군길이는 각 부호어의 길이에 발생확률을 곱하여 더하면 얻을 수 있다.
 L-= 1I.=; I P( s, )l , =2 (2. 1-40)
L-= 1I.=; I P( s, )l , =2 (2. 1-40)
 P ( s,) 는 동보의 발생 확률이 며 , l i는 부호어 의 기 호수이 다. 가의 로
P ( s,) 는 동보의 발생 확률이 며 , l i는 부호어 의 기 호수이 다. 가의 로
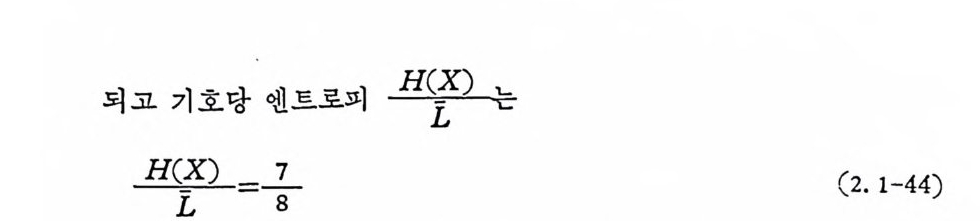 되고 기호당 엔트로피 H(L-X ) 亡..__
되고 기호당 엔트로피 H(L-X ) 亡..__
이다. 발생확률이 많은 동보에는 짧은 부호로 형성하고, 발생확률 이 적은 통보에는 건 부호로 만들면 평군부호건이 를 적 게 할 수 있 으므로 다음과 같이 부호화해 본다. 통보 부호어 S1 1 S2 10 S3 llO s4 lll 이때 평군부호길이 L 과 P ( o),P(1) 을 구해 본다.
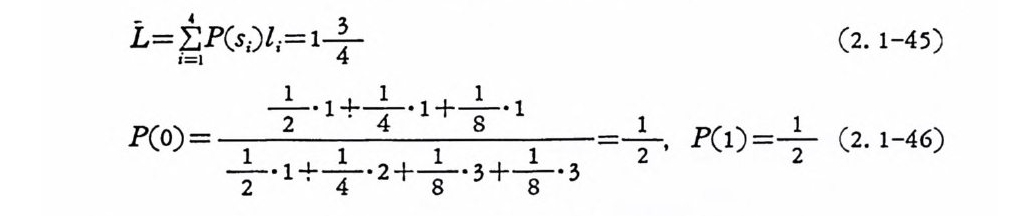 L= ij=:4 . l P( s;)l1= 14+ (2. 1-45)
L= ij=:4 . l P( s;)l1= 14+ (2. 1-45)
 평군부호길이는 먼처보다 작어졌으나 기호당 엔트로피는
평군부호길이는 먼처보다 작어졌으나 기호당 엔트로피는
로 먼처보다 많아졌음을 알 수 있다. 다음은 부호의 평균길이의 상 계와 하계를 정한다. 이 정리는 채널에 잡음이 없을 때 정보원에 대한 부호화정리로 부호화 제일기본정리라 부론다. 〈정리 2.1-3> D 개의 알파벳과 M개 의 통보로 구성된 정보원 X 에 각 동보에 대응하는 부호어의 평균길이는
 Hlo(gX D )
Hlo(gX D )
울 만족하는 부호화가 가능하다.
 〈증명 > 먼저 H(X)-Llo g D,,;;;o 가 성 립 함을 보인다. P(s1).
〈증명 > 먼저 H(X)-Llo g D,,;;;o 가 성 립 함을 보인다. P(s1).
로 유일해독부호의 평군부호길이의 하계를 설정해 준다. 통보가 각 기 sI, S2, …, s 'I I 이 고 각기 발생 확률이 P(s1), P(s2), …, P(sM) 일 때 s, 의 자기정보량은 I(s,)= 一 I og P(s,) 이고 알파벳기호에 관련된 최대 엔트로피는 lo g D 이다. 동보 s i에 대한 부호어의 최소 기호수는 l',= 꿉읊이나 일반적으로 l' i는 정수가 아니다. P(s,)=D- 일 때 만 정수이므로 다음 부등식이 성립하는 정수 l i를 선택할 수 있다.
 l;'
l;'
이고, 이 식을만족하는유일하게 해독할수있는부호가존재한다. 양변에 P(s;) 을 곱하여 더하면
 Hlo(g XD )
Hlo(g XD )
된다. 이 식은 유일해독부호의 평군길이와 엔트로피와의 관계를 기 술하고 있으며 평군부호길이의 상계와 하계를 정하여 주고 있다. 식 (2. 1-54) 를 잡음이 없는 채 널의 부호화의 제 일기 본정 리 라 부 른 다. 2. 1. 6 最適符號化法 Hu ff man 은 최소평군길이를 갖는 최적부호를 부호화하는 방 법 을 계시하였다. 동보 s i 의 발생확률을 P(s i)라 하고 부호어의 길 이 를 l, 라 하면 부호의 평군길이 L 은
 L=Ei=M IP (si) l i (2. 1-55)
L=Ei=M IP (si) l i (2. 1-55)
 가 된다. 편의상 부호알파벳 수 D=2 이고 동 보의 발생확 률이 감 소
가 된다. 편의상 부호알파벳 수 D=2 이고 동 보의 발생확 률이 감 소
되고, 각 동보에 해당하는 부호어의 길이는 다음 순서로 된다 .
 ll
ll
즉 발생할 확률이 큰 동보는 짧은 길이를 택하고 발생할 확 률 이 적 온 통보는 큰 길이를 택하였다. 만일 k>j일 때 P(s1)>P(s;) 이고 . h>l i이면 두 부호어의 평균길이는
 P(s.)l.+P(si) l; (2. 1-58)
P(s.)l.+P(si) l; (2. 1-58)
된다. 동보 s_. 와 s J에 해 당하는 부호어 를 상호교환하여 두 부호어 의 평균길이를계산하면
P(s1)l1 +P(s1)l, (2. 1-59)
이 다. 식 (2. 1-59) 에 서 식 (2. 1-58) 올 빼 면
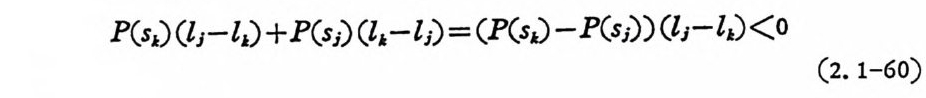 P(s1) (l1-l1) +P(s1) (l,-l 1) = (P(sJ -P(s;)) (l1-l1) <0
P(s1) (l1-l1) +P(s1) (l,-l 1) = (P(sJ -P(s;)) (l1-l1) <0
이므로 s. 오} s}의 부호어를 교환함으로써 평군부호길이를 감소시킬 수 있다. 그러므로 L1
 L1L = (P ( s; ) -P(s M ) ) (lM -l;)
L1L = (P ( s; ) -P(s M ) ) (lM -l;)
이다. L 은 증가하지 않고 lM 을 최대길이로 할수 있다. 최적부호에 서 lM 이 최장길이이면 타부호가 부호길이는 동일하고 최종기호가 다론 부호가 있다. 만일 그런 부호가 존재치 않으면 어두조전율 위 배치 않고 lA 려 최종기호를 제거할 수 있다. 만일 s i에 대한 부호어 가 sAl 에 대한 부호어와 최종기호만 들란다면, l;>LM -1 이 되어야 하 고, s,에 대한 부호어와 SM-I 에 대한 부호어를 평군부호길이를 증가 시 키 지 않고 교환할 수 있으므로 SM 와 SM-I 의 부호어 의 최 종기 호만 다른 부호가 존재한다. 부호알파벳 D 개를 가지고 최소부호길이의 최적부호를 작성하는 방법을 설명한다. ® 발생확률이 감소하는 순서로 통보믈 배열한다. ® 최소발생확률의 순서로부터 다음 작은 확률의 순서로 D 개를 합산하여 M 一 (D-1) 개의 확률을 다시 감소하는 순서로 배열한다. 만일 합산한 확률이 기존확률과 동일할 때는 두 동일한 확률을 임 의로 배열한다. 이와 동일한 과정을 반복하면 최후에 D 개의 확룰 만 남는다. 전체 통보의 수가 M 일 때 M=D+n(D-1) 이 성립한다. 여기서 n 은 정의 정수이다• 동식이 성립하지 않을때는 0 의 확률을 가진 B 개의 임의의 동보를 추가배열하면 B+M=D+n(D-1 ) 의 식이 성립한다. 이 식을 다시 쓰면 M-2=n(D-1)+(D-2+B) 이 고 최장부호에 대한 부호어는 동일한 부호길이에 최종기호만 다르 으로 o,<;B:<;D-2 의 부등식이 성립한다. 그러므로 o,<;D-2-B,<;
D-2 이다. M-2=n(D-1)+(D-2-B) 식으로부터 (D-2-B) 는 (M 군)를 (D 리)로 나눈 나머지이다. 이 나머지를 R 로 표시하 떤, 추가배열될 통보의 수는 B=D-2 一 R 이다. 추가배열된 통보의 발생확률은 0 이다. ® 부호알파벳 이 aI, a2. …, aD 일 때 처 음 합산한 D 개 의 확률에 각 71 aI, a2. … aD 를 부가하고 다음 합산한 D 개 에 ai , a2. …. %를 부가 한다. 이렇게 1+n(D-1) 번 과정을 거쳐 부호어를 만든다. 〈예 2.1-3> 6 개의 동보의 발생확률은 아래와 같다. 이때 최적부 호를 만들어 본다. P(s1)=0. 25, P(s2)=0. 25, P( s3 ) = 0. 20, P( s4 ) =O. 15, P(s5)=0. 10, P(s6)=0. 05 이고 부호알파벳은 {o. 1} 로 D= 2 이다. 먼처 추가통보의 유무를 식 M-2=n ( D 디 )+(D-2-B ) 로 부터 알아본다. 죽 M-2/D-1=4 로 나머지가 없으므로 B=D-2 _R=0 으로 추가통보는 없다.
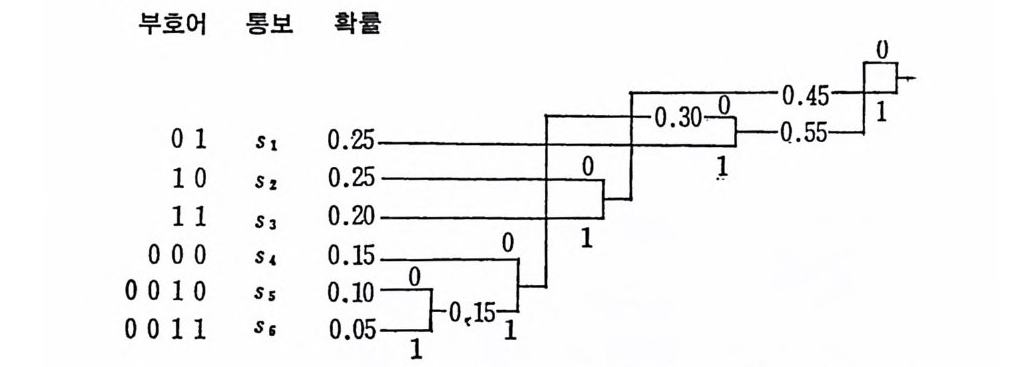 부호어 통보 확률
부호어 통보 확률
〈예 2. 1-4> 다 음과 같은 정 보원에 대 한 최 적 부호를 구한다. P(s1) =O. 25, P(s2)=0. 25, P(s3)=0. 20, P(s4)=0. 15, P(s5)=0. 10.
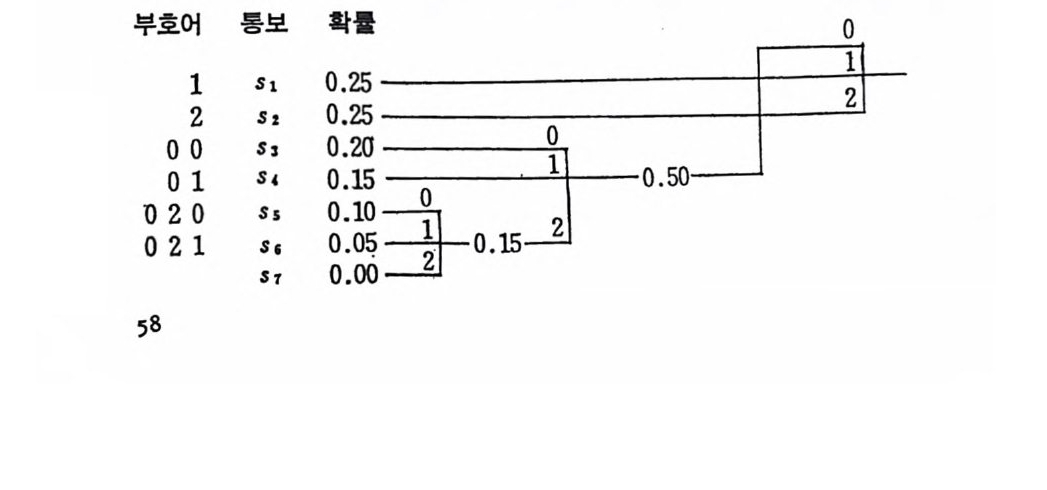 부5008호 022어 101 통sSsS보,1‘s 鬪盆 。〔 0.50 二
부5008호 022어 101 통sSsS보,1‘s 鬪盆 。〔 0.50 二
 된다. 이 식은 x, y쌍의 상호정보량을 정의한다. 이것은사전확률과
된다. 이 식은 x, y쌍의 상호정보량을 정의한다. 이것은사전확률과
가 된다• 만일 확률 P(x) 와 P(xl y)가 동일하면 P(xl y )=P(x) 이므 로 X 와 Y 는 상호독립적이 되어 상호정보량은 0 이 된다. 또한 P(xl y)가 0 으로 접근할 경우 l og (xl y)는 _OO 로 정근하므로 y= b;,
P( s6 ) = 0. 05 이고 부호알파벳은 {o, 1, 2} 로 D=3 이다. M-2/D 크에 서 나머지는 없으므로 R=O 이고 추가통보수는 B=D 一 2_R 에서· D=l 이다. 2.1 . 7 상호정보량 집 합 {a1 , az. … , an} 이 X의 표본공간이 고, 집 합 {bi, b2, ···, bm} 이 Y의 표본공간일 때 입 력 기 호 a;, 출력 기 호 b; 인 통신계 통은· 조건부확률 P ( a J b J ) 로 규정되었다. 이제 a,와 b j쌍의 상호정보량 (mu t ual inf o r- ma ti on ) 을 엔 트로피를 정의할 때와 마찬가지로 정의하여 이를정당
 화하I(려a, ; b한J다 = .l og ¥i (2. 1-62).
화하I(려a, ; b한J다 = .l og ¥i (2. 1-62).
 를 수신할 때 b; 와 완전히 무관한 a; 를 택한 겅우로 이 러한 겅 우는
를 수신할 때 b; 와 완전히 무관한 a; 를 택한 겅우로 이 러한 겅 우는
 이 므로 a 가 나타나므로 b 제 의 하여 제 공된 정 보량이 나, b ; 가 나타
이 므로 a 가 나타나므로 b 제 의 하여 제 공된 정 보량이 나, b ; 가 나타
되고 x, y,를 변수로 한 약식기호물 사용하였다. 상 호 정 보량 에 대한 엔트로피라 할 수 있는 평군상호정보량 I(X;Y) 는 채 널 을 동 하여 전송된 정보량이다. 좀더 수식울 전개하기 위하여 이제까지 전개한 수식을 확장하려 한다. 사상 x=a;,y = bi 쌍의 자기정보량은
 I(x, y) = -logP (x, y) (2. 1-68)
I(x, y) = -logP (x, y) (2. 1-68)
 되고 조건부 자기정보량에 평군을 취하면
되고 조건부 자기정보량에 평군을 취하면
이다. 이차원엔트로피(j o i n t ent ro p y) H(X, Y) 는 통신계동 전체의 평군 불확실성을 나타내며 H(XIY) 는 기호를 수신한 다음 송신된 기호의 평군 불확실성량이며 H(YIX) 는 기호를 송신하였을 대 수 산된 기호의 불확실성을 나타낸다. 〈 예 2. 1-5> 송신축에 서 5 개 의 문자로 구성 된 알파벳 {a1, a2, aa, a4, as} 을 가지고 있고 수신축에서 4 개의 문자로 구성된 알파벳 {bh b2, b3, b 4} 을 가지 고 있을 때 채 널과 이 차원확률은 다음과 같다. 이 때 각종 엔트로피를 구하라.
 aI b1b2b3 bb1 b2 b3 b4
aI b1b2b3 bb1 b2 b3 b4
 P(azlb1)=— oO. .3150= —72 P(b1laz)= ―OO. .一4100 =—41
P(azlb1)=— oO. .3150= —72 P(b1laz)= ―OO. .一4100 =—41
〈정 리 2. 1-4> X와 Y의 복합사상의 평군상호정 보량은 0 보다 크며
 .x와 Y 가 상호독립적일 때 등식이 성립한다.
.x와 Y 가 상호독립적일 때 등식이 성립한다.
 I(X; Y) =I(Y;X) 이 드로
I(X; Y) =I(Y;X) 이 드로
이다 . 채널에 잡음이 없을 경우
 H( X . Y) = H( X ) =H(Y ) (2. 1-90)
H( X . Y) = H( X ) =H(Y ) (2. 1-90)
P=O 인 잡음이 없는 채널에서는 I(a1;b1) 은 1 비트이다. b1 을 수신하 였을때 송신축에서 송신된것을확실히 알수있다. 그러나 P 가증 가하면 상호정보량은 감소되어 al 이 송신되었다는 확신을 감소시킨 다. p=끔-이면 통신이 이루어지지 않는 경우로 입력과 출력이 독 립된 상태이다 . 일반적으로 P 는 검_보다 적으며 a2 을 송신하여 bl 을 수신할 때 p<+이면 상호정보량은 부의 값을 갖게 되어 a3 보
 다 al 이 송신되었다는 것을 암시하고 있다. P 가 0 에 접근 하면
다 al 이 송신되었다는 것을 암시하고 있다. P 가 0 에 접근 하면
J(X ;Y) = H( X ) + H( Y )- H(X, Y) = 1 + 1-1 + [(1 -p) l o g (1 -p) +plo g p] = 1+ [(1 -p) l o g (1 -p) + plo g p] H(XIY) 는 잡음이 없는 상태, P=O 일 때 H(XI Y) =O 로 Y 가 주 어지면 X 를 알 수 있음을 표시하고 있다. 반대로 P=l 인 경우에도 H (X I Y) =O 이 다.
록함수가 되 기 위 한 필요충분조건은 모든 구간내 에 서 d2f / dx2<0 이 어야한다• 벡터 X의 볼록함수는 다음 2 개의 중요한 독성을 가지고 있다• ® 만일 f1 (X),fz (X ), …,fiX) 가 볼록함수이고 A;, i= l, 2, …, k 가 정수이면 Ek A ifi (X) 는 볼록함수이다. 이것은 볼록함수의 정의에 i= I 대입하면곧알수있다. ® X 가 n 차원 렌돔벡 터 (random vec t or) 이 고 f(X)가 볼록함수
2. 1. 8 볼록함수, 오목함수 정보이론의 많은 정리가 볼록함수를 이용하여 증명되므로 이에 대해 좀더 자세히 기술한다. 〈 정의 〉 실수함수 J C · ) 는 구간 I 에 대하여 다음 식이 성립하면 볼 록함수라 한다
 庫 ) + ( 1 국 ) / C x2 )< f [Ax1+(1- J )x2], x1,x2El, o
庫 ) + ( 1 국 ) / C x2 )< f [Ax1+(1- J )x2], x1,x2El, o
이면 다음 부등식이 성립한다. E[ f(X) ] 갑 (E[X J) (2. 1-95) 이 부등식 을 J ensen 의 부등식 이 라 부르며 제 1 장에 서 증명 하였 다. E[·] 는 기대함수이다. 다음 볼록함수의 정의를 사용하여 이산유한 표본공간에 대하여 귀납적으로 생각해 본다. 우선 두 개의 확률 iE=t p ,=1 에 대하여 보면 f(·)가 볼록함수이므로
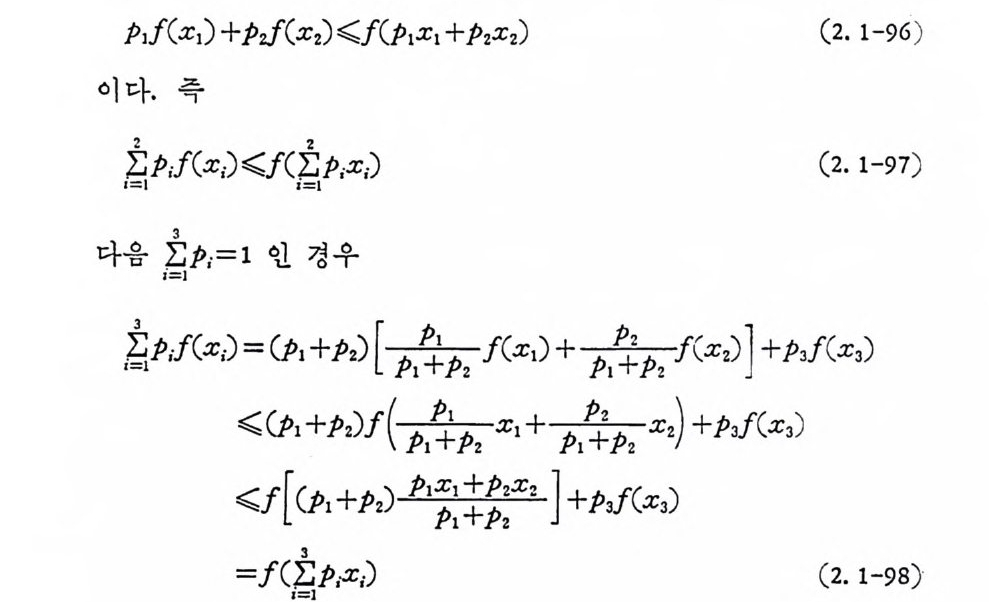 Pi f(xi ) +PJ (x 2)
Pi f(xi ) +PJ (x 2)
 되고, 귀납적으로 n 차까지 전개하면
되고, 귀납적으로 n 차까지 전개하면
의 경우 목성 1 에 의하여 J,(p)=-p.J o gp,가 볼록함수이으로 H(p} 도 볼록함수이다. 〈 정 리 2. 1-6> 평 군상호정 보량 I(X; Y) 는 입 력 확을 P(x) 에 대하 여 볼록함수이다. 〈 증명 〉 천이확률 P ( y lx) 를 고정하고 P( x )=AP1(x)+(1-).)Plx) 인 경우 다음 식이 성립됨을 증명하여야 한다.
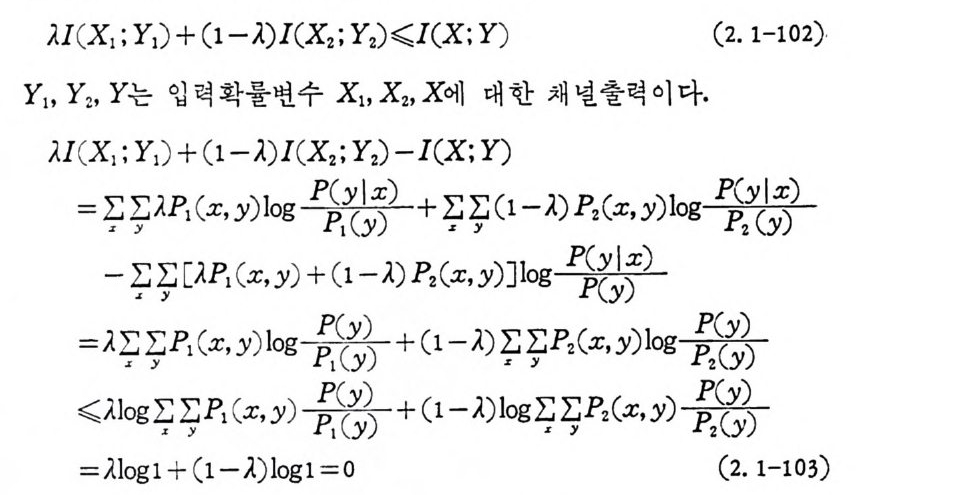 U (X1 ; Y1) + (1-}.)I(X2; Y2)~I(X ; Y) (2. 1-102).
U (X1 ; Y1) + (1-}.)I(X2; Y2)~I(X ; Y) (2. 1-102).
〈 정 리 2. 1-7> I(X ; Y ) 는 천이확률 P ( y lx ) 에 대하여 볼록함수이 다. 〈 증명 〉 입력확률 P ( 다 울 고정하고 두 개의 천이확률 P1CYIX) 과 Pz C y lx) 일 경우 P( y Ix)=AP1 ( y I x)+(1-A ) Pz(YIx) 일 때 다음을 증명하여야 한다.
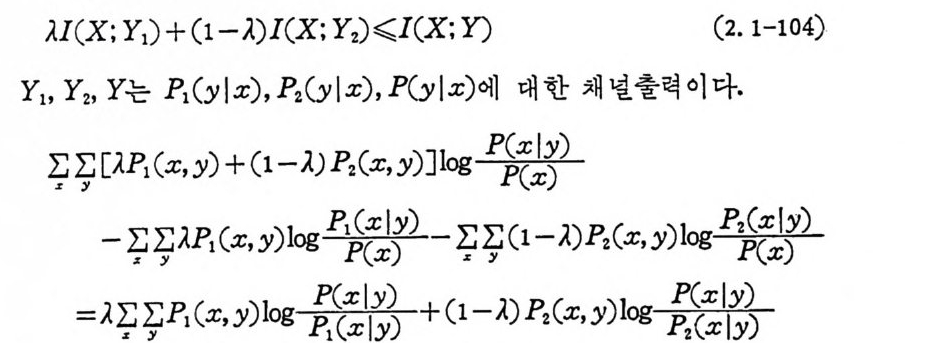 U (X ; Y1) + (1-A)J( X : Y2) ~J(X : Y) (2. 1-104)
U (X ; Y1) + (1-A)J( X : Y2) ~J(X : Y) (2. 1-104)

2.1-9 기타 정보량에 관한 정리 X,Y,Z 의 3 개의 확률변수를 생각할 때 한 쌍의 채널이라 볼 수 있다. X 는 1 번채널의 입력이고, Y 는 1 번채널의 출력인 동시에 2 번 채널의 입력이다. Z 는 2 번채널의 출력이라 볼 수 있다. 1 번채널의 천이확률 P( y lx) 이면 2 번채널의 천이확률 P(zl y )=P(zlx, y)이다. 2 번채널의 출력은 2 번채널의 입력에만 의존한다는 의미이다• 이것 은 일반적인 경우는 아니지만 통신계통의 기본적인 가정을 이루고 있다.
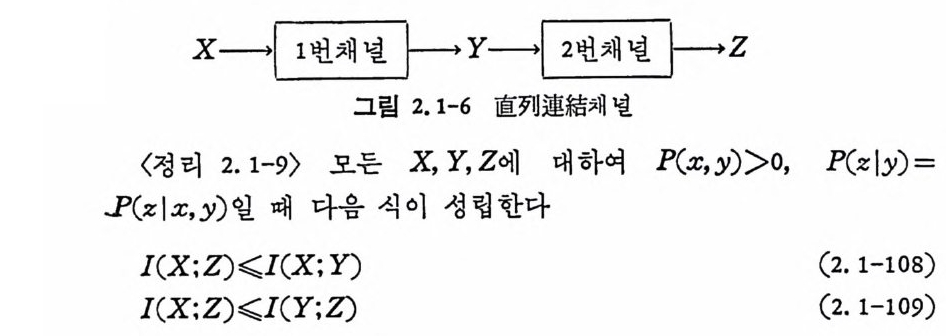 X 一曰…다一 Y 一尸프已一 Z
X 一曰…다一 Y 一尸프已一 Z
〈 증명 〉 정리 2.1-8 에 의하여 I(X, Y;Z)~I(X;Z) 이고, P( zl y) , =P ( zlx, y ) 이므로 I( X , Y;Z)=I(Y;Z) 이다. 그러므로 I(X;Z)< I ( Y;Z ) 이고, 마찬가지로 I( X ;Z) < I(X ; Y) 이다. 다음은 통신계통에 실제 적용하여 보면 정보원에서 k 차원 랜돔벡 터 U를 발생하고, 이것을 채널부호기를 통하여 n 차원 X벡 터로사 상된다. 채널을 동하여 수신된 벡터 Y 는 채널부호기를 통하여 벡 터 V로 부호된 다. 벡터 V 가 벡터 U와 동일하면 채널에서 에러가 발생치 않은 것이고 벡터 V 가 벡터 U와 상이하면 에러가 발생한 빠 것이다. 이러한 통신계통에서는 P(y l x,u)=P(yl x), P(vly , x)=. P ( v l y ) 로 특정지 어지므로 먼저 정리에 의하여 I(U;V )< I(X;V ) 이고 또한 I ( X; V) 만일 XN= (Xi, X2, …, XN), YN= (Y1, Yi, …, YN) 이 렌돔벡터이고 체널이 무기억 채널이면 다음 부등식이 성립한 다.
 I(X N ; YN) < IN: I(X; ; Y;) (2. 1-110).
I(X N ; YN) < IN: I(X; ; Y;) (2. 1-110).
 I(X 짝 Y勞 -£1=Il (X;; Yi) = Ey log P ( y I ) P (P 파( y) - :__f_( y N )
I(X 짝 Y勞 -£1=Il (X;; Yi) = Ey log P ( y I ) P (P 파( y) - :__f_( y N )
마찬가지 로 H(X1, X2, …, X) =H(X | X-1, …, X1) +H(X._ i , …, X1) 으로 표시할 수 있고 H(X. _1 , X. -2 , ···, X1)=H(X._1 IX._2, …, X1) +H(Xn-2, … ,X1) 이 된다. 계속 반복하면 다음 식을 얻는다.
 H(X1, X2, …, X. ) = H(X1) + i幻=” 2 H (X i | Xi - I , …, X1) (2. 1-119)
H(X1, X2, …, X. ) = H(X1) + i幻=” 2 H (X i | Xi - I , …, X1) (2. 1-119)
된다. 석 (2. 1-123) 과 (2. 1-124) 를 식 (2. 1-122) 에 대 입 하면 식 (2. 1- . l20 ) 을 얻는다. 2. 2 연속신호의 정 보량 2. 2. 1 연속신호의 엔트로피와 상호정보량 지금까지는 신호가 이산적안 값을 갖는 경우를 고려하였다. 그러 나 많은 경 우 신호는 시 간 t의 연속함수로 연속적 인 값을 갖는다. 이 산부호에서와 마찬가지로 연속신호에 대하여 제정보량을 정의할 수 있으나 그 의미는 다소 불분명할 경우가 있다. 모돈 정보이론의 근
 원이 Shannon 의 논문에 기원하듯이 연속선호에 대한 정보량의 개
원이 Shannon 의 논문에 기원하듯이 연속선호에 대한 정보량의 개
로 정의하였다. 연속신호의 경우도 마찬가지로고찰해 본다. 연속선 호가 시간의 함수 x( t)이면 x( t)는 일반적으로 신호의 전폭을 나다 낸다. 신호의 진폭 x 의 연속확률밀도함수를 f ( x ) 라 하면
 fJ(x )dx=l (2. 2-3)
fJ(x )dx=l (2. 2-3)
이다. 실수축 x 를 4x 크기로 양자화할 때 신호가 구간 X,+4x 에 있을 확률은f( x i )4x 이다. 이때 엔트로피는
 H(X) = -i=합- .o. o (x,)L1x1o g(J (x i )4x ) (2. 2-4> ,
H(X) = -i=합- .o. o (x,)L1x1o g(J (x i )4x ) (2. 2-4> ,
 로피도 무한대가 된다. 그리하여 자기정보량은 이산신호에만 국한
로피도 무한대가 된다. 그리하여 자기정보량은 이산신호에만 국한
로 정 의 한다. X 는 신호 x( t)의 전폭으로 연속확률밀도함수 f( x) 의 확률변수이다. 이 정의논 자기정보량의 평군이 아니므로 자연히 이산신호의 엔트로피와 다론 특성을 갖는다. 연속신호의 엔트로피 의 특성을 이산신호의 엔트로피와 비교하여 열거한다. ® 연속확률밀도함수의 확률변수 X 의 엔트로피는 부의 값을 가 질 수 있다. 일례로 X 가 군일분포함수일 때 엔트로피는
 fH(x( X) = ) =7 i-' so:
fH(x( X) = ) =7 i-' so:
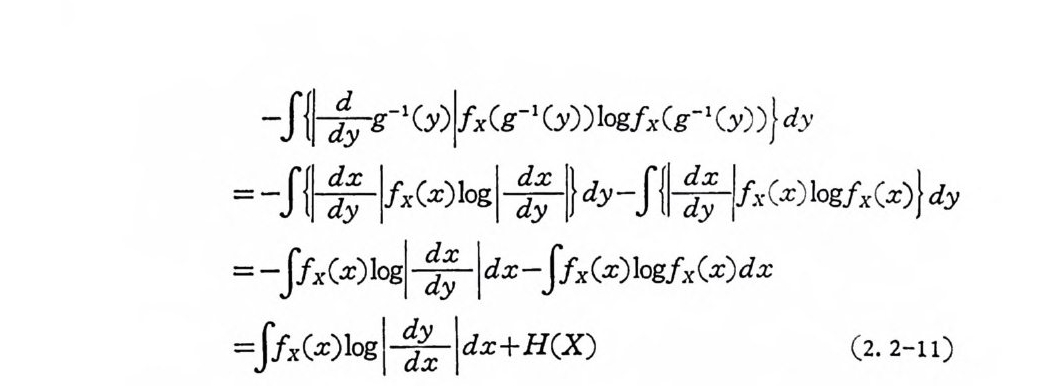 -J{|끓g -1 (y)l fx (g -1 (y)) log fx(g -1 (y ) )} dy
-J{|끓g -1 (y)l fx (g -1 (y)) log fx(g -1 (y ) )} dy
이 다. 식 (2. 2-11) 의 1 번항을 보면 확률변수 X 가 나타나나 이 산신 호의 경 우는 발생 확률에 만 관계 되 고, 확률변수는 나타나지 않는다. 동전을 던져 앞면과 뒷면이 나올 확률이 각기 검-이면 엔트로피는 H(X)=l 비트이다. 확률변수를 변환하여 Y=X2 일 메도 발생확률은 변치 않고d 上2 이므로 H(Y)=l 비트이다. 그러나선형변환 Y=CX 일 때 겅~g -l( y )=C 이므로
 H(Y) =H(X) +log I C I (2.2-12)
H(Y) =H(X) +log I C I (2.2-12)
이다. 일반적으로 선형변환 Y=CX+D 에서 Y의 엔트로피 H(Y) 는 D 와는 무관하며 C=l 일 때는 H(Y)=H(X) 가 된다. 다음 n 차원신호의 변환에 대하여 생각해 본다 . n 차원신호 x= (:x :x2, …, :x n) 의 n 차원확물밀도함수fx (x) =fxi, x2, …, Xn(:x h :x2, …, .x) 일 때 변환 y=g (x) 는 Y1=g 1 (zh z2, …, zn) Y2=g 2 (z Z2, …, z) Yn=g n (X1, 따, …, x.) (2. 2-13) 에 의하여 변환한다. 1 대 1 의 변환에 의하여 떠=gj I (y 1,Y2, …,y.) X2=g -; 1(Yi ,Y2 , …,y.) zn=g ?(y1, Y2, …,y.) (2.2-14)
되 며 Y의 확률밀도함수는 다음과 같이 된다• fr1 , Y2, …, Yn(y I, y 2, …, Y.)= IJ lf xi , x2, …, x.(g7 1 ( y,,Y 2, …,y), gzI CY1,Y2, …, Yn), …,g;1 (Yi ,Y2 , …, Y.)) (2. 2-15) 이때 Y 의 엔트로피는 H (Y ) =H( X ) +JJ-·Jfx1, xz, …, x.(x 1 , x2, …, xn) log JJ J dx1dx2• • ·dx. (2. 2-16) 이 며 J는 J acob i an 이 다.
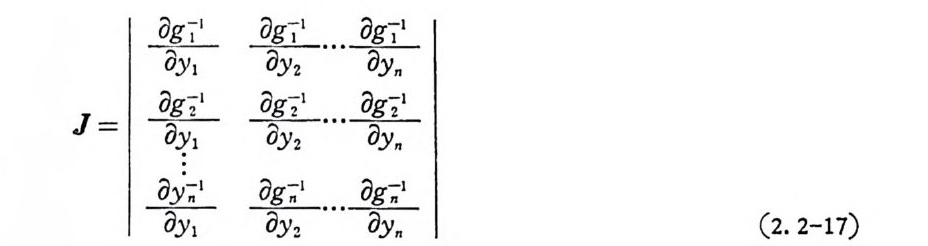 o8gY jI 1 aOg y1 2 1. . . o8g y1n 1
o8gY jI 1 aOg y1 2 1. . . o8g y1n 1
〈 예 2.2-1> X1,X2,X 가 상호독립적인 표준정규확률변수이고 변 환 y1 =x1, y2 =(x1+x2) /2 , y3=(x1+x2+x3)/3 에 의한 Y의 엔트 로피를 구하려 한다. X1=Y1, Xz=2y z -Yi, Xa=3 y 3-2Y2 이므로 1 대 1 의 변환이 성립되고J acob i an 은
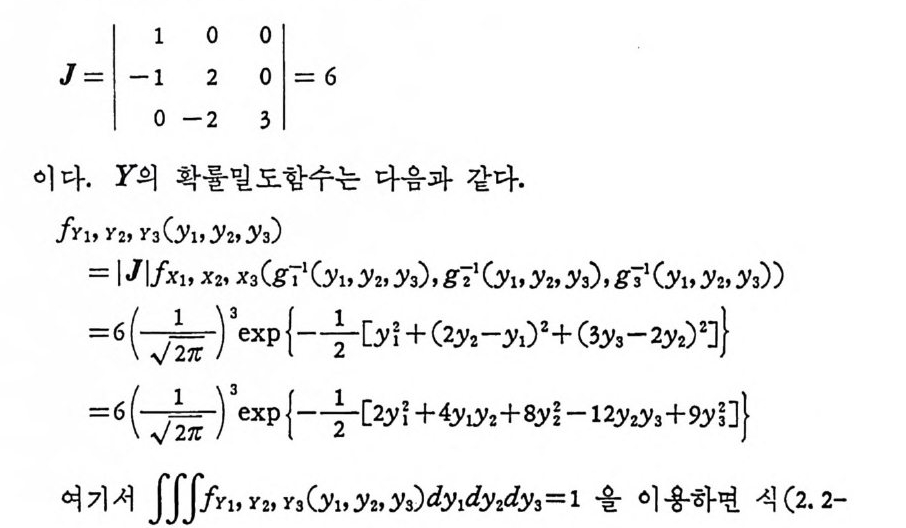 1 0 003
1 0 003
16) 에 의하여 쉽게 엔트로피를 구할수있고 다음과 같은 관계가성 립한다. H(Y)=H(X )+ log 6 ® 2 개의 엔트로피 차를 정의한 정보량은 불변이다. 확률밀도함수 f (x)= 습, o
H(X, Y) = -fft(x, y ) log f(x , y) dxdy (2. 2-18) 이다. 먼저 말한 바와 같이 f (x)= ff (x, y )dy 이므로 X의 엔트로피 는 H(X) = -ff(x)l og f(x )dx (2. 2-19). 이고 f(y)=fJ (x, y )dx 이므로 Y의 엔트로피는 H(Y) = -ff(y)lo g f(y)d y (2. 2-20) 이다. X 조건부 Y 의 확물밀도함수는
 J(y jx) = 信? (2. 2-21)
J(y jx) = 信? (2. 2-21)
이산신호의 경우와 마찬가지로 연속선호의 경우도 다음 독성이 성립한다. CD H( X , Y)
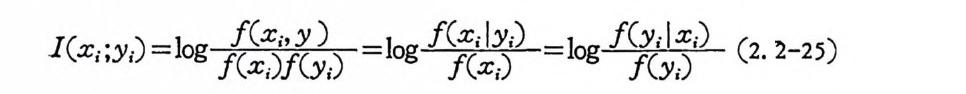 I(x, ;y,) =log f信麟 =log f(김:,) =log f(김~ (2. 2-25)
I(x, ;y,) =log f信麟 =log f(김:,) =log f(김~ (2. 2-25)
 로 표기된다. 이 표기는 이산신호의 경우와 동일하나 좀더 명확히
로 표기된다. 이 표기는 이산신호의 경우와 동일하나 좀더 명확히
 4x 와 4y 를 0 으로 접 근시 키 면 각 확률은 0 으로 접 근하나 분자,
4x 와 4y 를 0 으로 접 근시 키 면 각 확률은 0 으로 접 근하나 분자,
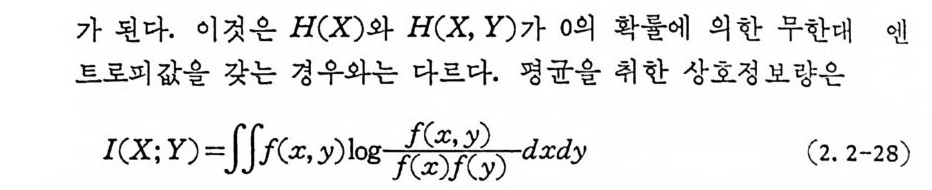 가 된다. 이것은 H(X) 와 H(X, Y) 가 O 의 확률에 의한 무한대 엔
가 된다. 이것은 H(X) 와 H(X, Y) 가 O 의 확률에 의한 무한대 엔
이 고, 이 산신호의 경 우와 마찬가지 로 부의 값을 갖지 않으므로 정 보량으로서 의미를 지니고 있다. 연속신호의 상호정보량도 이산신 호의 경우와 마찬가지로 다음 목성을 갖는다. CD I(X; Y) =l(Y;X) ® I(X;Y) 각 O @ I(X;Y )= H(X)-H(XIY)=H(Y)-H(YIX) =H(X ) +H(Y) - H(X, Y) (2.2-29) 제®항과 ®항은 쉽게 증명할 수 있고 제®항은 대수의 볼록함수 의 성질을 이용하여 보일 수 있다. 죽
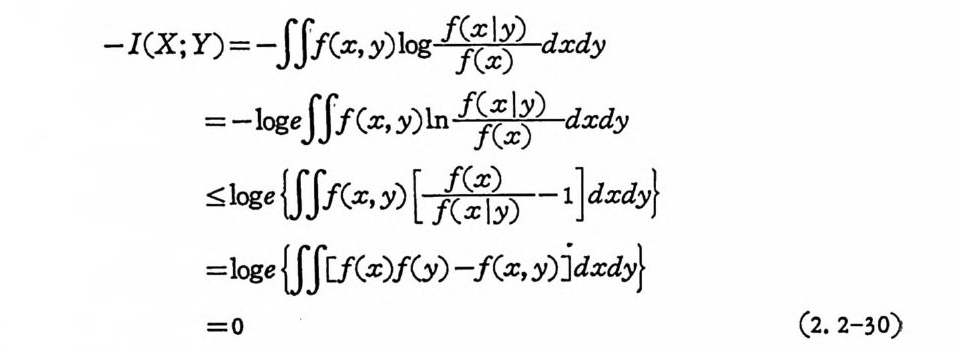 -I(X; Y) = -fJJ(x , y )I og~』:) d:c d y
-I(X; Y) = -fJJ(x , y )I og~』:) d:c d y
f(y lx)=f (y)이면 등식이 성립한다. 마지막으로 상호정보량이 선 형변환하에서도 변치 않음을 보인다. 지금 W=g 1 (X)=BX+D (2. 2- 3 1)
 Z=g z (Y ) = CY+E (2. 2-32)
Z=g z (Y ) = CY+E (2. 2-32)
이다. 각 엔트로피는 선형변환에 의하여 변하지만 상호정보량은 불 변이다. 2. 2. 2 엔트로피가 최대가 되는 분포함수 이산신 호에서 엔트로피가 최대가 되기 위해서는 모든 事象 의 발 · 생확률이 동일할 때 최대가 되었다. 그러나 연속신호에서는 엔트로 피가 최대가 되는 확률밀도함수f( x) 를 구하여야 한다. f (x) 가 일 . 차원 확률밀도함수이고 확률변수 X 가 분산 (J 2 올 가지고 있을때 엔 트로피 H(X) 를 최 대 로 하는 J (x) 를 구해 본다. 어 떤 구속이 가해 질 때 최 대 로 하는 문제 는 La g ran g e 승수방법 이 있다. 다음과 같은 구속I=이J : g가(해x ,질f ( x 때) )dx b C:1 =f‘’ gab i(x,J (x ))dx C.=ra g. ( x,f (x) )dx • (2. 2-39)
 f( x) 를 최대로 하기 위하여 다음식을푼다. 여기서 C;,i = l,2,… ,n
f( x) 를 최대로 하기 위하여 다음식을푼다. 여기서 C;,i = l,2,… ,n
 H(X) 는 f (x) 의 범함수(fu nc ti onal) 이며 H 의 국대화도 J ( x ) 에
H(X) 는 f (x) 의 범함수(fu nc ti onal) 이며 H 의 국대화도 J ( x ) 에
 되고 A 과 A 2 을 식 ( 2.2-46 ) 에 내입하면 엔 트 로피를 최 대로하는f를
되고 A 과 A 2 을 식 ( 2.2-46 ) 에 내입하면 엔 트 로피를 최 대로하는f를
 · 이고 엔트로피의 단위는 내트 (na t)이다. n 차원신호의 경우도 마
· 이고 엔트로피의 단위는 내트 (na t)이다. n 차원신호의 경우도 마
 이 된다.
이 된다.
로 표시할 수 있고, |RI 온 공분산행렬 R 의 행렬식이고, R-1 은 R 의 역행렬, X 는 종벡터, XT 는 X 의 轉置이다. X 의 평군치를 X
로표기하면 X=o (2.2-53} 이고 공분산행렬 R 은 XXT=R (2. 2-S4) 로 표시할 수 있다. 엔트로피는 -ln f (x) 의 평군치이므로
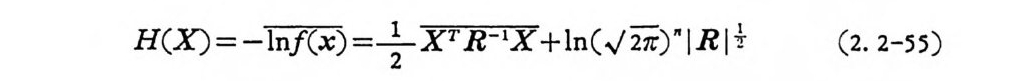 H(X ) = -同向 =上2 xTR-lx+1n( 亭) lR I + (2. 2-55)
H(X ) = -同向 =上2 xTR-lx+1n( 亭) lR I + (2. 2-55)
 되고, t r 을 행렬의 트레스(t race), I를 단위행렬로 표기하면
되고, t r 을 행렬의 트레스(t race), I를 단위행렬로 표기하면
이 된다. 다차원정규분포의 엔트로피는 공분산행렬의 행렬식에 와 하여 정해진다. 2. 2. 3 정규신호의 정보량 만일 송선신호 X 와 수선신호 Y 가 이차원 정규분포이면
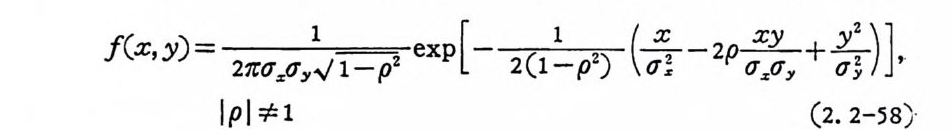 J(x ,y) =~exp [-~ (국 2 p:곱)], .
J(x ,y) =~exp [-~ (국 2 p:곱)], .
 되고 랴와 야는 x, y의 분산이며 p는 상관계수이다. 이때 확률변수
되고 랴와 야는 x, y의 분산이며 p는 상관계수이다. 이때 확률변수
천다. 이때 각 엔트로피를 구하여 보면 다음과 같다.
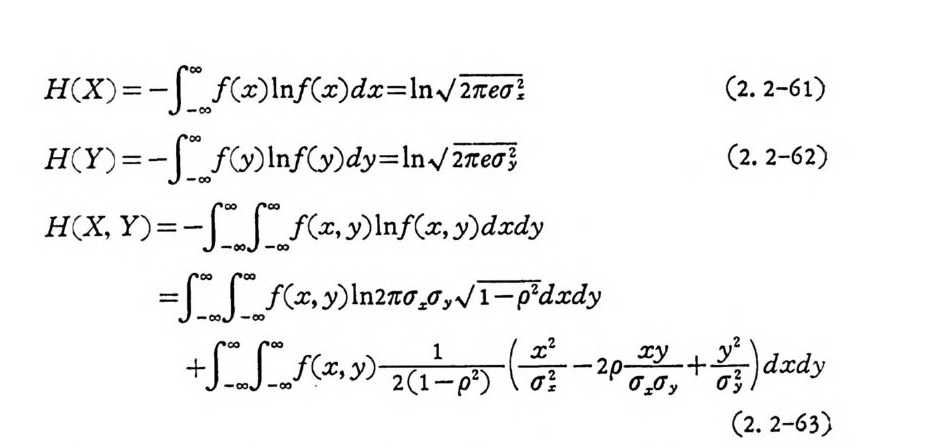 H (X ) = -J~_ 0.0,c ,o f ( x ) ln f ( x)dx=ln../2 호 (2. 2-61)
H (X ) = -J~_ 0.0,c ,o f ( x ) ln f ( x)dx=ln../2 호 (2. 2-61)
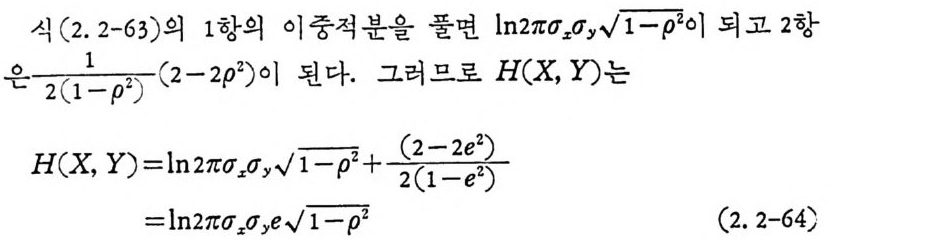 석 (2. 2 - 63 ) 의 1 항의 이 중 적 분을 풀면 ln21r <1 z <1선 T 二 7 이 되 고 2 항
석 (2. 2 - 63 ) 의 1 항의 이 중 적 분을 풀면 ln21r <1 z <1선 T 二 7 이 되 고 2 항
이 다. 상호정 보 량 I(X ; Y ) 는 H (X ), H(Y), H(X, Y) 를 사용하여 구 할 수 있다.
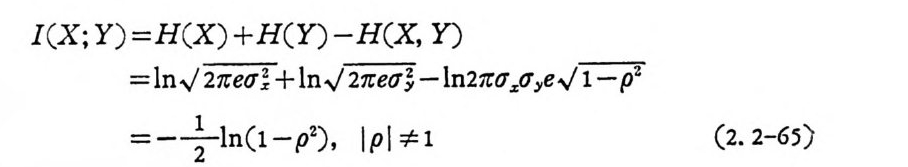 I(X ; Y) =H( X ) +H( Y )- H(X , Y)
I(X ; Y) =H( X ) +H( Y )- H(X , Y)
 상 호 정보량은 상관계수 p의 함수임을 알 수 있다. 조건부엔트로
상 호 정보량은 상관계수 p의 함수임을 알 수 있다. 조건부엔트로
송신신호 X 에 평군치 0, 잡음전력 u!0J. Gauss 잡음 n 아 가해져 수신되면, 수신신호 Y 는 y= x+n (2. 2-67)
으로 표시할 수 있고 이 때 변환 을 사용 하여 조건 부 확률밀도함수 f ( y lx) 울 구하면
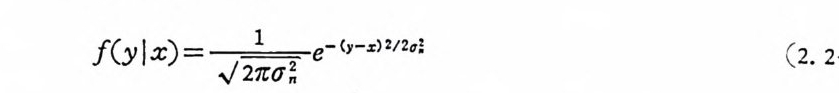 f(y J x) =― ,J 2m느가 e-( y-,c )2 / 2a! (2. 2-68)
f(y J x) =― ,J 2m느가 e-( y-,c )2 / 2a! (2. 2-68)
으로 평군치 x, 분산 아인 정규확 률 분포가 된다. 조건 부엔트 로 퍼 H(YIX) 를 구하여 보면 다음과 같다.
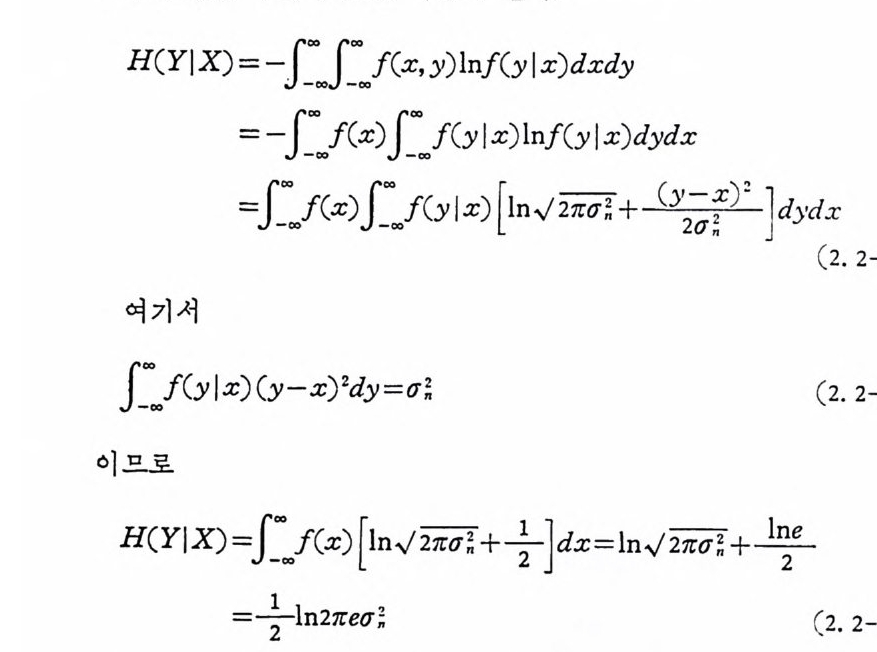 H(YI X) === J--:ff0• ~~0 --oOO/o..O O C.. J f x ~-() oOo .xfO . f)~ J0(0x f- O: ,. O( . y fy ) ( l I yxn )fl x [(1) y n I nl루 xf) ( d y 루x l xdy) d y ~ d x ]d y d x
H(YI X) === J--:ff0• ~~0 --oOO/o..O O C.. J f x ~-() oOo .xfO . f)~ J0(0x f- O: ,. O( . y fy ) ( l I yxn )fl x [(1) y n I nl루 xf) ( d y 루x l xdy) d y ~ d x ]d y d x
이다. 、 Y 는 2 개의 독립적인 정규확률변수 X 와 n 의 합이드로 Y 의 분산은 6 ; +6: 이며 f(y)는 정규분포이다.
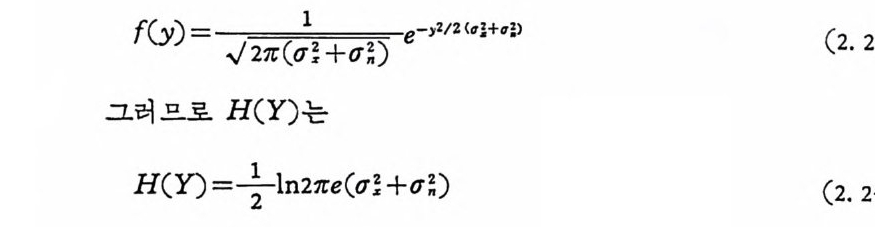 f(y)=...—; 27. (=( j !_ + (j:) 'e 구 /2 《 4+4) (2. 2-7 2 )
f(y)=...—; 27. (=( j !_ + (j:) 'e 구 /2 《 4+4) (2. 2-7 2 )
이 고 J(X ; Y) 는 다음과 같다.
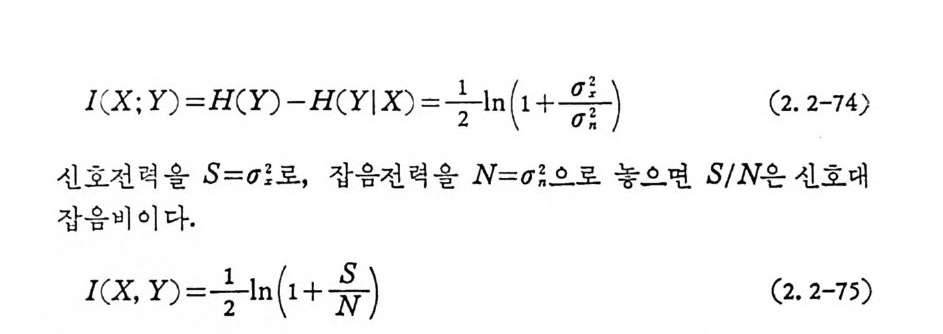 l(X ; Y) =H(Y) -H(YI X) = +ln (1 +뭉_) (2.2-74)
l(X ; Y) =H(Y) -H(YI X) = +ln (1 +뭉_) (2.2-74)
N 이 0 에 접근하면 출력 Y 는 입력 X 에 접근하므로 상호정보량 l ( X;Y ) 는 무한대로 접근한다. 2.3 情報源 2. 3. 1 마코브정 보원 전에는 정보원이 정보를 발생할 때 과거에 발생한 정보에 의촌치 않 고 독립적으로 발생하였다. 영어의 알파벳의 집합 A={a,b,… ,z} 이 고 age , book, fri end 는 알파벳 의 계 열로 단어 를 구성 한다. 단어 는 각기 3,4,6 개 文字로 되어 있다. 상기 예는독립적인 정보원이라 볼 수 없나 영어에서는 q가 나오면 반드시 U 가 따라나오기 때문에 먼처 나온 문자는 나중 나온 문자에 영향을 미치고 있다. 정보원이 n 개의 알파벳을 가지고 있고 알파벳의 집합 A={a i, a2, … ,an} 이면 다음과 같은 문자의 계 열 이 나타난다.
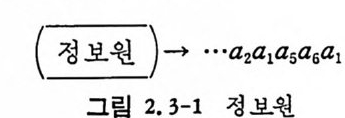 ( 정보원 )-+ … a2 로로
( 정보원 )-+ … a2 로로
시 각 t(t= l, 2, …)에 발생한 문자를 X‘ 라 하면 다음과 같이 표기 할수있다. X1=a; 정보원에서 발생한 문자는 이미 정하여진 발생확률을· 가지고 발 생한다. 그러나 각 문자가 독립적으로 발생치 않고, 시각 t에 발생 한 문자 xt7 } a i인 확률은 그 이 전 발생 한 문자의 계 열 …X 1-2X1-1
에 영향을 받는다. 이전의 m 개 (m=I,2, …) 문자의 계열이 X,-m ...: r:,- 2:r :1- ] 일 대 시각 t에 문자 x, 의 발생확률은
 P(x, lx,-m, ... , X,-2, X1-1) (2. 3-1)
P(x, lx,-m, ... , X,-2, X1-1) (2. 3-1)
 이다. 시각 t -m 에서 t사이의 문자계열 X t -m, … ,X1-1,X, 가 나타날
이다. 시각 t -m 에서 t사이의 문자계열 X t -m, … ,X1-1,X, 가 나타날
 P(x,-', …, X1-1, x,) =P(x, I X1-m, …, x,_1)P(x,_,., …, X1-1) (2. 3 크 )
P(x,-', …, X1-1, x,) =P(x, I X1-m, …, x,_1)P(x,_,., …, X1-1) (2. 3 크 )
올 의미한다. 앞으로는 정상적 정보원만취급한다. 문자의 발생확률 이 과거 m 개의 문자에 의존하고 그 이전 문자에는 의존하지 않는 다고 가정한다. 과거에 a;1,a;2, … ,a i m 의 문자계열을 발생하였다는 것은 정보원이 현재 상태 (s t a t e) Sa=a; i, a ; 2, … ,a i m 에 있다고 말한 다. 다음 문자 a 율· 발생할 확불은
 P(a;j a;1 , a;2… , a;m), i= l, 2, …, n;ip = l, 2, •··, n (2. 3-5)
P(a;j a;1 , a;2… , a;m), i= l, 2, …, n;ip = l, 2, •··, n (2. 3-5)
이 러 한 정 보원을 m 차마코브정 보원 (mt h order Markov source) 이 라 한다. n 개의 문자가 있으므로 m 차 마코브정보원은 n' 개의 가 능한 상태가 존재한다. 정보원으로부터 문자가 1 개 발생하면 상태 는 변한다. 마코브정 보원은 狀態圖 (s t a t e d i a gram) 를 통하여 설명 하는 것이 용이하다. 상태도에서는 정보원의 n' 개의 가능한 상태를 원으로 표시하고 한 상태에서 다음 상태로의 가능한 천이를 화살표
로 표시한다. 그립 2. 3-2 는 A= {O, 마인 경우로 이차마코브정보원의 4 개의 상 태 00,01, 10, 11 을 원으로 표시하고 있다. 천이확률인 조건부확률은 상태간의 선상에 기입되어 있으며 다음과 같다. P ( 이 01) =P(o 110 ) =P(1 I 01) =P(1 J 10) =O. 5 P ( 이 oo ) =P ( 1 J 11) = 0. 7, P( 11 oo) = P(o l11)=0. 3 상태 11 에서는 상태 11 이나 10 으로 갈 수 있으나 00 이나 01 로는 갈 수 없다.
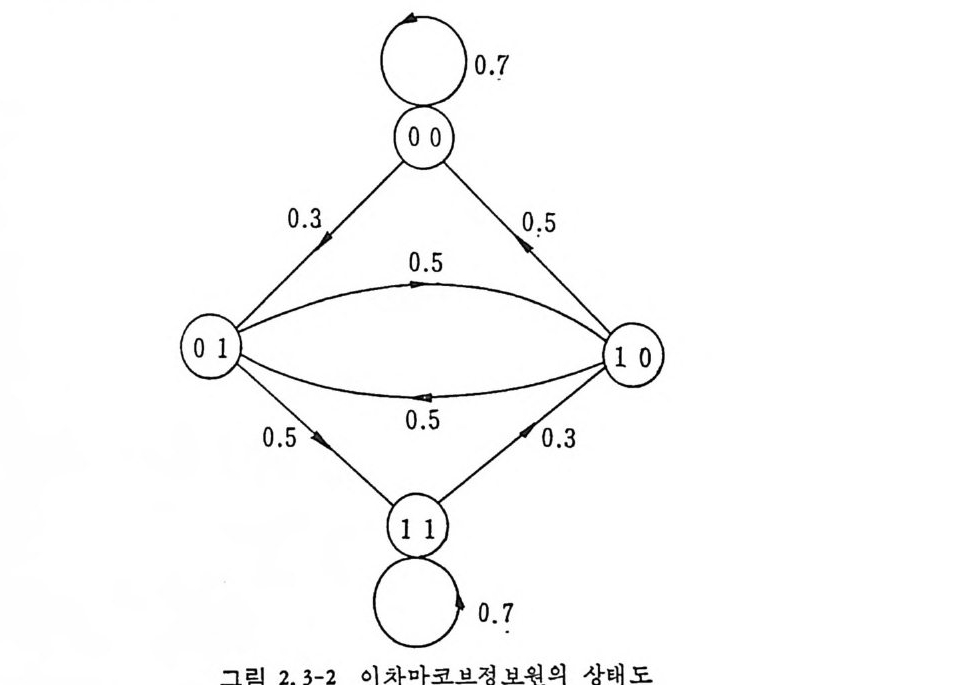 그립 2.3-2 이차마코브정보원의 상태도
그립 2.3-2 이차마코브정보원의 상태도
상태 요에서 상태 S2 로 천이하는 확뮬 P12=P(S2IS1) 을 사용하여 다음[P과J =같 [P은i.:1 천~이P.2 확> •률••}( tP: •r]•a ns iti on p robab ility)행 렬을 정 의 한다(•2 .3-7)
천이확률행렬의 행의 요소의 합은 1 이 된다. 현재의 상태에 의존 하여 확률적 으로 상태 가 천이 하는 과정 을 마코브連 鎖 ( Markov chain ) 라 한다. 현재상태j에서 t번 천이하여 상태 k 가되는 확률을 PJ i1= P(SdS j)(t)라 표기하면 이는 용이하게 구할 수 있다. t =l 이면
P(S1 IS i) m =P (Si) P(S, IS J (2. 3-8) 이다. t =2 일 때 다음 그림을 생각해 본다.
그립 2. 3-3 t =2 의 유한연쇄
 상태 J·에서 두 번 천이하여 상태 k 가 되는 확률은
상태 J·에서 두 번 천이하여 상태 k 가 되는 확률은
이고, 이것을 확장하여 상태 j에서 t번 천이하여 상태 k 가 되는 확 률 P(Sd Sj) (t) 을 행 렬식으로 표시 하면 P(SdSj) (t)=[%][P ]' (2. 3-10> 이다[P.D ]행 ~렬 [ T[%)]P는( :다 ,) 음…으로 0규] 정된다. P(S1) o … 0 0 0 …P (Sff) (2. 3-11)
P(S;), i =l,2, … ,n 은 상태의 초기확률이며 [%]는 대각선행렬아
 다. 다음 조기상태를 알지 못하고, 환언해서 초기상태가 S;, i= l,2.
다. 다음 조기상태를 알지 못하고, 환언해서 초기상태가 S;, i= l,2.
이다. [P < 0 > ]=[P ( S1)P(S2) … P(S) ]인 행의 행렬이다. 천이행렬을 t승한 [P]' 의 요소가 전부 0 보다 크면, 이러한 마코브연쇄를 정규 (re g ular ) 마코브연쇄라 부른다. P(S ji SD=l 은 자기상태에서 이탈 하지 못하는 경우로 정규연쇄가 아니다. 다론 상태로 0 이상의 정 수의 확 률 로 천이 하는 연쇄 를 에 르고딕 連鎖 (er god i c cha i n) 라 부론 다. 정규연쇄논 에르고덕연쇄이나 그 역은 진실이 아니다. 2.3.2 단순한 마코브연쇄의 엔트로피 알파벳집합 A= {ai, a 2, … ,an} 울 가진 정보원 X에서 시각 t -m 에 서 t- 1 까지 문자계 열 Xt- m, …, X1-1 이 발생 할 확률은 P(X1-m, …, x,-1) 이 고 다음 문자 x, 가 발생 할 조건부확률은 P(x, lx,_m, …, X t -1) 이 다. 정상적 정보원에서는 시간 t와 무관하므로 다음과 같이 조건부확률― 울 표기한다.
 P(xj | Xj l , Xj 2 , …, Xjm )
P(xj | Xj l , Xj 2 , …, Xjm )
 이 고, m 차마코브정 보원은 n' 개 의 가능한 상태 가 존재 하고 n' 개 의
이 고, m 차마코브정 보원은 n' 개 의 가능한 상태 가 존재 하고 n' 개 의
이 된다. H(X) 는 과거의 문자계열의 출현을조건으로 한 일 문자 한 한개 문자의 엔트로피의 평균값이다. 과거의 무한의 문자계열이 나타난상태에서 L 개 문자계열 xI,X2, … ,XL 을 생각할 때 정보량 I 는
 I= -IogP (xi, x2, …, xL l x..,)
I= -IogP (xi, x2, …, xL l x..,)
천이행렬의 열의 요소의 합은 1 이고, H1 가 상태 S 제서 한 번 천 이할때 엔트로피라하면
 n
n
일반적으로 상태 S,에 서 t번 천이하여 상태 s j가되는 엔트로피는 마찬가지로
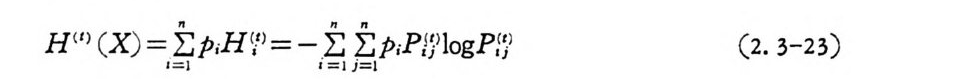 H U) (X ) = •파=”I P i H \t )= - •E= l iE= Ip iPi ?lo g P;;) (2. 3-23)
H U) (X ) = •파=”I P i H \t )= - •E= l iE= Ip iPi ?lo g P;;) (2. 3-23)
이다. 상태 S 제서 상태 s J로 (t +l) 번 천이하여 도달할 경우 한 번 천이하고 다음 t번 천이한다고 가정할 때 엔트로피는
 n
n
이다. 기츠
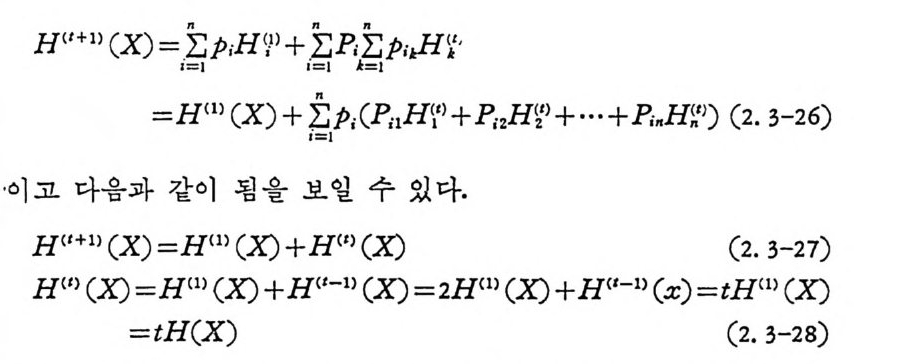 H(t+ 1) (X) =i2 =n IP iH 9) +i2=n IR El=n JP iE t’
H(t+ 1) (X) =i2 =n IP iH 9) +i2=n IR El=n JP iE t’
t번 천이한 마코브연쇄의 엔트로피는 한 번 천이한 엔트로피의 t배 이다. 임의의 초기확률로 시작하는 정규마코브연쇄에서 엔트로피는 다음과 같이 정의할 수 있다.
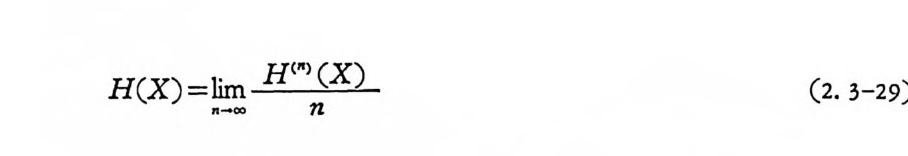 H(X)=ln- OiO mn~ (2. 3-29)
H(X)=ln- OiO mn~ (2. 3-29)
2.4 채널용량 2. 4. 1 상호정보량과 채널용량 평군상호정보량은 I(X; Y) =H(X)-H(XI 約 (2.4-1) 로 표현되며, 정보원의 불확실성 H(X) 와 Y 를 수신한 후 X 에 대 한 불확실성의 차가 정보의 변화라 볼 수 있다. 다시 말해서 채널 을 통해 전송된 정보량이다. 잡음이 없는 채널에서는 J( X; Y)=H(X) (2.4-2) 이며 이때 최대정보량은 n 개의 기호가 동일 확률로 발생할 경우 lo gn 이다. 만일 입력기호와 출력기호가 상호독립적일 경우 상호정 보량은 0 이 된다. 또한 상호정보량은
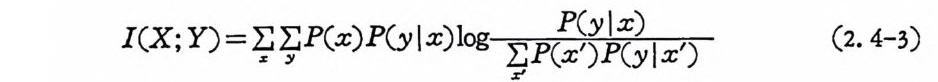 I(X; Y) = 꾸 꾸 P(x)P (y | x)lo g~;匡 ) (2. 4-3)
I(X; Y) = 꾸 꾸 P(x)P (y | x)lo g~;匡 ) (2. 4-3)
로 발생확률 P(x) 와 천이확물 P (y lx) 의 함수로 천이확률은 채널이 정하여지면 고정된 常數다. 따라서 채널을 통해 전송된 최대정보량 울 구하려면 발생확물 P(x) 를 변화시켜 얻을 수 있다. 채널용량 (channel ca p ac ity)은 다음과 같이 정 의 한다.
 C=m/>(:a::) xl(X; Y) (2.4-4)
C=m/>(:a::) xl(X; Y) (2.4-4)
 일반적으로 채널용량을 구하는 것은 용이한 일이 아니며 다음은 채
일반적으로 채널용량을 구하는 것은 용이한 일이 아니며 다음은 채
 충분조건은 어떤 실수 A 가 촌재하여
충분조건은 어떤 실수 A 가 촌재하여
〈 증명 > 충분조건 : 석 (2. 4-5) 와 (2. 4-6) 이 어 떤 실수 A 와 확률벡 ];,1 p에 대하여 만족한다고 가정한다. p 이의의 확률벡터 q가 존재 하여 f ( q ) -f ( p )
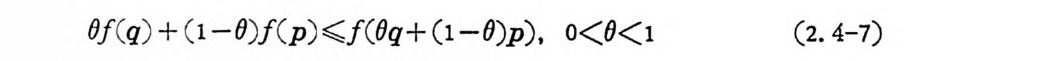 OJ( q) + ( 1 -0)f ( p )
OJ( q) + ( 1 -0)f ( p )
되고 정리하면
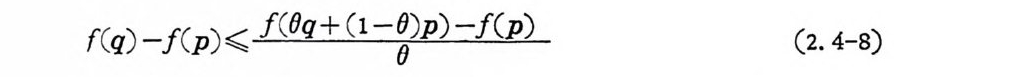 f(q ) - f(p ) < ~ (2.4-8)
f(q ) - f(p ) < ~ (2.4-8)
된다. 이것은 모든 0,o<0<1 에 대하여 성립하므로 국한을 취하면 f( q) 一f(p)< d[ f ( O q갈 ;1-O ) p] I 8=O 걸 afa>E > ( q; -p;) (2. 4-9) 된다• 여 기 서 하 ( p ) /op j가 석 (2. 4-5) 와 (2. 4-6) 을 만족하는 데 주 의하고, P 와 q가 확률벡터이므로 f( q ) -f(p ) ¾ I; A( q;-p;) = O i; I f(q ) -f(p)
된다. 이로써 충분조건을 증명하였다. 필요조겁 : p가 f(p)를 최대화하고 편미분이 p접에서 연속이라 가 정한다. 그러면 임의의 확률벡터 q와 실수 0 에 대하여
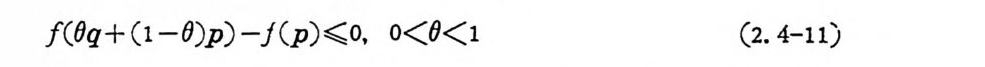 f(O q + (1 -0)p) -J(p)< ;o, o<0<1 (2. 4-11)
f(O q + (1 -0)p) -J(p)< ;o, o<0<1 (2. 4-11)
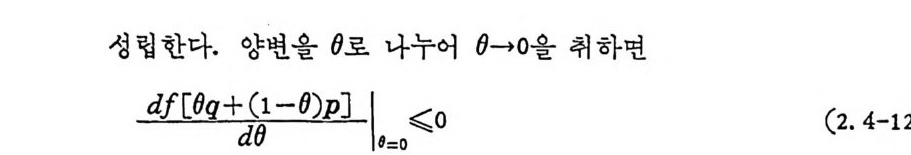 성 립 한다. 양변을 (}로 나누어 (}-+O 을 취 하면
성 립 한다. 양변을 (}로 나누어 (}-+O 을 취 하면
되고, 이것은
 효 쁠흔(q i 一 P;)<;o (2. 4- 1 3)
효 쁠흔(q i 一 P;)<;o (2. 4- 1 3)
로 표시된다. 적어도p의 1 개 성분은 엄밀히 正이므로 기 호를 간단 히 하기 위하여 P1>0 이라 가정한다. eK 를 K 성분이 1 이고 타성분 은 0 이 되는 n 차원 단위벡터로 표기한다. o< t
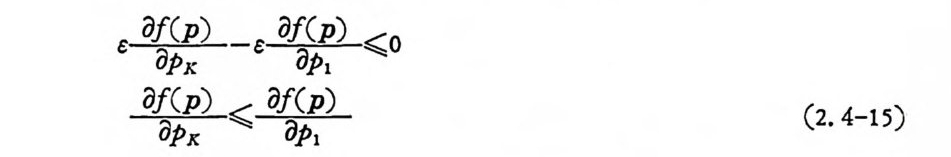 C 보8pA . -c 무apI ,
C 보8pA . -c 무apI ,
되고, 만일 Px>o 이면 려t 負값으로 택할수 있고 이 경우식 (2.4-15} 의 부등식은 반대가 되어 결국 등식
 뵤O@P_x =-뵤 @op_l , pK >0 (2. 4-16)
뵤O@P_x =-뵤 @op_l , pK >0 (2. 4-16)
 가 성 립 한다. A=8f (p )/8p i로 놓으면 식 (2. 4-15) 와 (2. 4-16) 에 서
가 성 립 한다. A=8f (p )/8p i로 놓으면 식 (2. 4-15) 와 (2. 4-16) 에 서
되고, e--- tO 일 때 우변 제 1 항은 of (p )/0P1 의 연속성 때문에 유한
 하고, 제 2 항은 +00 로 발산한다. 그러므로매우적은 e>o 에 대하여
하고, 제 2 항은 +00 로 발산한다. 그러므로매우적은 e>o 에 대하여
된다. 이것은f ( p)가 최대가 아님을 의미한다. 〈 정리 2.4-2> 기여이 없는 채널에서 채널행렬이
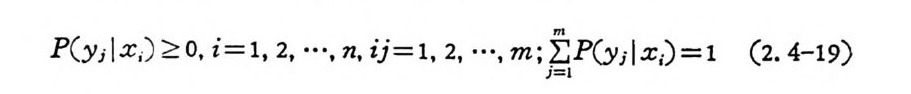 P( yi jx; ) ~ O, i= l, 2, ···, n, ij=1 , 2, …. m; jI=m ; I P( y ;Jx ;)=l (2. 4-19)
P( yi jx; ) ~ O, i= l, 2, ···, n, ij=1 , 2, …. m; jI=m ; I P( y ;Jx ;)=l (2. 4-19)
의하여 독 칭지어질 때 입력확률벡터 p가 상호정보량 I(X;Y) 를 최 대로 하기 위한 팔요충분조건은 어떤 수 C 가 존재하여
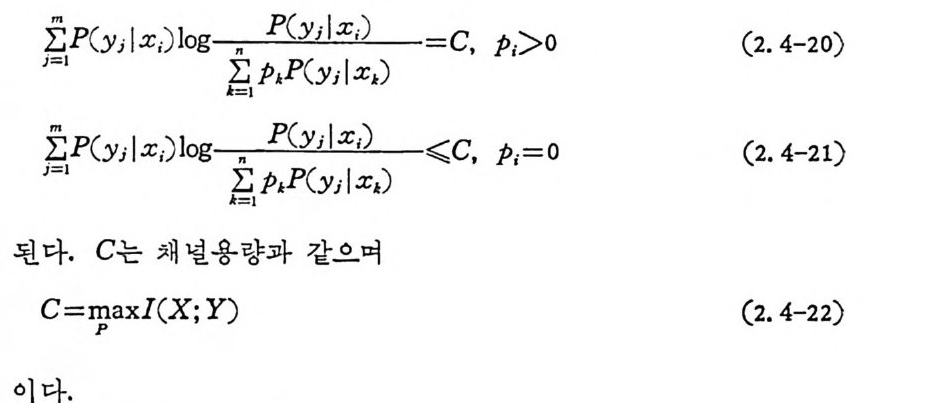 j합= I ( y기:x ; ) lo gI~: p:.P ( xy; I : ,x) .) =C, P;>o (2.4-20)
j합= I ( y기:x ; ) lo gI~: p:.P ( xy; I : ,x) .) =C, P;>o (2.4-20)
〈증명 〉 어떤 입력확률벡터 p에 대하여 I(X;Y) 가 최대가 된다고 가정한다. 죽
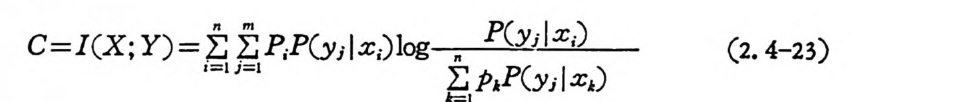 C=I(X ;Y)=it= l if=; I P; P(y ilx ;)lo k~=gI p .P(~ y기 x. ) (2. 4-23)
C=I(X ;Y)=it= l if=; I P; P(y ilx ;)lo k~=gI p .P(~ y기 x. ) (2. 4-23)
 I(X;Y) 를 p의 함수 l( p)로 놓고, p에 대하여 최대가 되기 위
I(X;Y) 를 p의 함수 l( p)로 놓고, p에 대하여 최대가 되기 위
 이다. I (p)를 pi에 대하여 편미분하면
이다. I (p)를 pi에 대하여 편미분하면
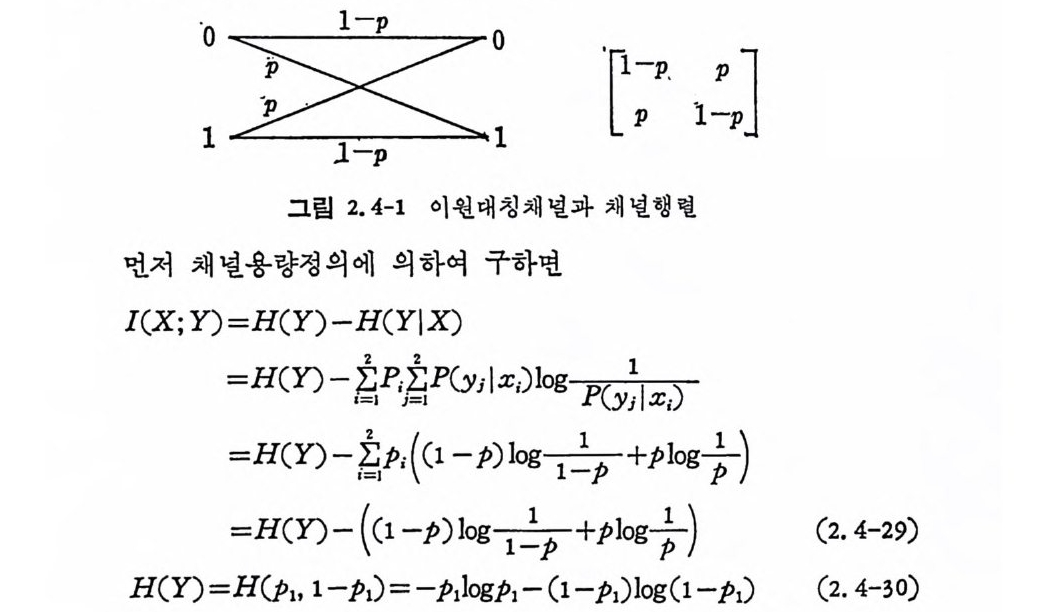
되고 C= ..:l +1 로 놓으면 식 (2. 4-20) 과 (2. 4-21) 을 얻는다. 정리 2.4-2 를 이용하여 채널용량을 구하기는 어렵다. 하나의 중 요한 이용가치는 상호정보량을 최대로 하는 입력확률에 대해 정리 2. 4-2 를 사용하여 채 널용량을 검 토할 수 있다. 2.4.2 채널용량계산법 채널용량계산울 예를 들어가며 계산해 본다. 이원대칭채널은그립 2. 4-1 과 같고 채 널행 렬은 다음과 같다.
 :三二: · -_l-ppi p l
:三二: · -_l-ppi p l
 되고 p 1=P ( o ) 이다. P1= 쉽-일 때 I(X;Y) 는 최대가 되고 H(Y)=
되고 p 1=P ( o ) 이다. P1= 쉽-일 때 I(X;Y) 는 최대가 되고 H(Y)=
된다. 정 리 2. 4-2 를 이 용하여 식 (2. 4-31) 을 만족하는가 본다. i= l, 2 의 경우
 접 P ( y기갑 ]og 2 P ( y기다
접 P ( y기갑 ]og 2 P ( y기다
 p=(검-'+)일 대 상호정보량은 최대가 되고, 채널용량은 다음
p=(검-'+)일 대 상호정보량은 최대가 되고, 채널용량은 다음
 =(1-p) l og 2 (2. 4-34):
=(1-p) l og 2 (2. 4-34):
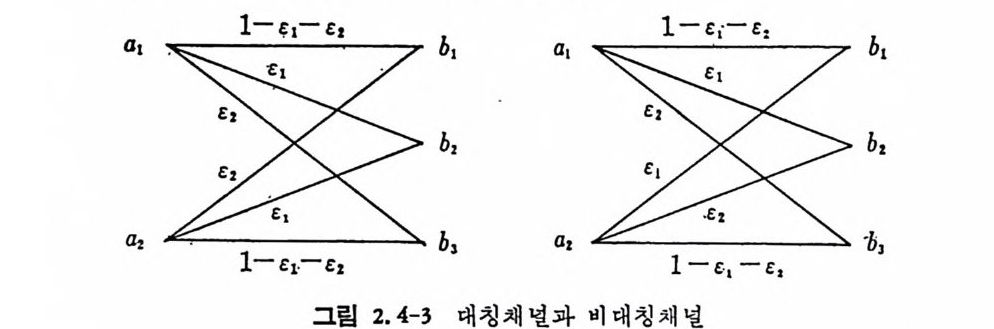
이 다. 다음과 같은 2 개 의 채 널을 고찰한다.
 aI 1-~1-£1 b1 aI 1-ei- e, b1
aI 1-~1-£1 b1 aI 1-ei- e, b1
그림 2.4-3 에서 a 固는 출력 b1,b3 에 대하여 보면 대칭이나 b 岡 는 그렇지 않다. 다음은 넓은 의미에서의 대칭채널을 정의한다. 출력집합 B={bi, b2, … , bm} 을 부분집 합으로 분할하여 부분집 합에 대 웅하는 채 널행 렬 울 형성한다. 이때 임의의 부분행렬의 행벡터가 다론 한 행벡터의 성분을 치환하여도 일치하고, 열벡터도 다론 한 연벡터의 성분율 ~ 치환하여도 일치할 때 광범위의 대칭행렬이라 부른다 . 그림 2.4-3- 에서의 예를 다음과 갈이 부분집합으로 분할하고 순열을 이루면 일 치하므로 광범위의 대칭행렬이다.
 ~:(1 -:b:1- Ez 1-e~b32 -e2)( b!z: ) (2. 4-37)
~:(1 -:b:1- Ez 1-e~b32 -e2)( b!z: ) (2. 4-37)
이다. 상 기 식은 임의의 i에 대하여 성립한다. 〈 증 명〉 식 (2. 4-20 ) 에 p,=i울 대 입하면 식 (2. 4-38) 을 얻는다. 그런데 한 열벡터와 다른 열벡터의 순열이 일치하므로 출력확물
r2='. :,I T1 P(y j |z ,) (2.4-39)
 은 일정하다. 마찬가지로 한 행벡터가 다른 행벡터의 순열과 일치
은 일정하다. 마찬가지로 한 행벡터가 다른 행벡터의 순열과 일치
 는 일정하다. 그러으로 부분집합의 합
는 일정하다. 그러으로 부분집합의 합
는 i에 관계없이 일정하다. (mXm) 비대칭채널행렬일 때 다음과 같은 해석적 방법을이용할 수 있다. 다음 등식 을 만족시 키 는 보조변수 0l, 0z, ···, 0m 을 사용한다.
 iI=m; l P( y;l x;)(};=iE =m IP (yj lx i) I og P ( yA xi) , j= 1, 2, ••• , m (2.4-4 2 )
iI=m; l P( y;l x;)(};=iE =m IP (yj lx i) I og P ( yA xi) , j= 1, 2, ••• , m (2.4-4 2 )
여기서 P~=P (y/)로 출력확률이다. I(X;Y) 를 최대로 하기 위하
여 La g ran g e 승수방법 을 사용하여 다음 함수를 최 대 화한다.
 L=-Im: P U og p1 + Im:p 1 0;+A(lm: P D (2. 4 -44 )
L=-Im: P U og p1 + Im:p 1 0;+A(lm: P D (2. 4 -44 )
되고 이 연립방정석은 다음을 만족시키고 있다.
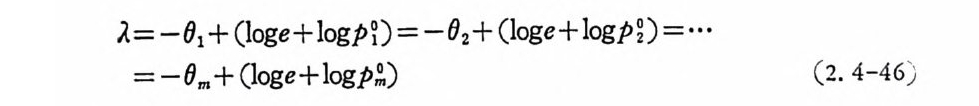 A= -()급 (log e +log pD = -()급 (log e +log pD = …
A= -()급 (log e +log pD = -()급 (log e +log pD = …
 채널용량은
채널용량은
그러나 이렇게 구한 C 의 값은 입력확물 P i의 本來條件 P;> o. 고 P i =1 을 만족시키지 않아도 성립한다. 이때 C 의 값은 채널용량이 아니다. 기억이 없는 이산채널에서 천이확률은
 p(y;I x;), i= l, 2, …, n;j= l, 2. …. m;Im: P( y; lx;)=l (2.4-49)
p(y;I x;), i= l, 2, …, n;j= l, 2. …. m;Im: P( y; lx;)=l (2.4-49)
으로 표시하고, n 개의 입력 m 개의 출력의 채널의 Ar i mo t o 의 채널 용량계산법을 설명한다. 입력정보원 X 일 때 입력과 출력간의 상호 정보량은
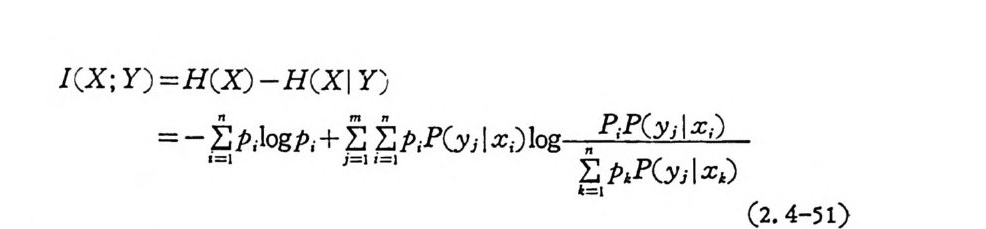 I(X ; Y) =H(X) - H(XI Y)
I(X ; Y) =H(X) - H(XI Y)
로 표시된다. p를 사전확률벡터로 보고 사후확률분포는 베이어스공 식에 의하여
 P( x, lyj )= n p,P (y; |xi) (2. 4-52)
P( x, lyj )= n p,P (y; |xi) (2. 4-52)
로 표시할 수 있냐 상호정보량을 입력확률벡터 p의 함수로 놓았 다 . 다음과 같은 집합을 가지고
 (/)=¢= { (
(/)=¢= { (
로 되고 C 를 축차적으로 구하는 방법을 Ar i mo t o 는고안하였다. 야 축차적 방법을 다음에 열거한다.
® 초기입력확률분포p낼~ p에서 임의로 선택한다. 실제로 等確 率分布p l=( 今,습,…,令)을 택하는 것이 좋다. ® 다음을계산한다.
 C11 = moeao xl(p1 ; rp) (2. 4-57)
C11 = moeao xl(p1 ; rp) (2. 4-57)
 실제로 Cl1 계산은 다음과 같다.
실제로 Cl1 계산은 다음과 같다.
 · 이때 p 2 은 다음과 같이 구한다.
· 이때 p 2 은 다음과 같이 구한다.
 일반적으로
일반적으로
 브 IP i =P i극, i= 1,2,, .. ,n (2.4~65)
브 IP i =P i극, i= 1,2,, .. ,n (2.4~65)
* 참고문헌 Abramson, N. , Info r mati on Theory and Codin g , McGraw-Hi ll, New York, 1963. Arim oto , S., An Algo rit hm for Comp u ti ng The Capa c it y of Arbit ra ry Di sc rete Memoryl e ss Channels, IEEE Trans. Info r m. Theory, Vol. IT-18 pp. 14-20, 1972. Arim oto , 『 情報理 論』 , 共立出版株式 會 社, 1976. Blackwell, D., Breim an L. and Thomasia n , A.J., The Capa c it y of a Class of Channels, Ann. Math . Sta tist., Vol.3 0 , pp. 1229-41, Dec. 1959. Davis s on, L.D . , Univ e rsal Nois e less Codin g , IEEE Trans. Inf or m. The- ory, Vol. IT-9, pp. 783-95, 1973. Fano, R.M ., Transmi ss io n of Info r mati on , MIT Press, Cambrid g e, 1961. Fein s te i n , A. , Foundati on s of Info r mati on Theory, McGraw- H i ll, New York, 1958. Gallag er , R.G . , Info r ma tion Theory and Relia b le Communic a t io n , W ile y, New York, 1968. Golomb, S., A New Deriv a ti on of The Entr op y Exp re ssio n , IRE Trans. Info r m. Theory, Vol. IT-7, no.3 . pp. 166-7, Jul y, 1961. Hammi ng , R.E ., Error Dete c ti ng and Error Correcti ng Codes, Be ll Sy st .
Tech. J., Vol. 29 pp. 147-50, 1950, Hammi ng , R.W ., Codin g and Inf or mati on Theory, Prenti ce -Hall, Inc., 1980_ Huff m an, D.A., A Meth o d for the Constr a cti on of M ini m um Redundancy Codes, Proc. IRE, Vol. 40 , pp. 1098-101, 1952, Karush, J., A Sim p le Proof of an Ineq u ali ty of McM ill an, IRE Trans. Info r m. Theory, Vol. IT-7, pp. 118-118, 1961. Kolmog o roff , A.N . , On the Shannon Theory of Info r mati on in the Case of Conti nu ous Sig n als, IRE Trans. Info r m. Theory, Vol. IT-2, pp. 102-8, 1956. Kraft , L.G ., A Devic e for Qu anti zi n g , Group ing and Codin g Amp li tu d e Modulate d Pulses, M.S. Thesis Dep t. Elec. Eng ., MIT, 1969. McGi ll, W .J. , Multi va ria t e Info r mati on Transmi ss io n , IRE Trans. Inf or m. Theory, Vol. 4, pp. 93-111. Sep t., 1954. McMi lla n, B., The Basic Theorems of Info r mati on Theory , Ann. Math . Stat i st. , Vol. 24 , pp. 196-219, 1953. McMi lla n, B., Two Ineq u ali ties Imp li e d by Uniq u e Decip h erabil i ty , IRE Trans. Info r m. Theory, Vol. IT-2, pp. 115-6, Dec., 1956. Murog a, S. , On the Capa c it y of a Di sc rete Channel I, J. Phy s . Soc. Jap a n, Vol. 8, pp. 484-94, 1953. Reza, F.M ., An Intr o duc tion to Inf or mati on Theory, McGraw-Hi ll, New York, 1961, Shannon, C.E., A Math e mati ca l Theory of Communic a ti on , Bell Sy s t. Tech. J. , vol. 27 , pp. 379-423 and 623-56, 1948. Shannon, C.E . , Pred ict i on and Entr op y of Prin t e d Eng li sh , Bell. Sy s t. Tech. J., 30, pp. 50-64, 1951. Sil v erman, R.A., On Bi na ry Channels and Their Cascades, IRE Trans. Info r m. Theory, Vol. IT-1, pp. 19-27, Dec., 1955, Slep ian , D. , Key Pap e rs in the Develop m ent of Info r mati on Theory, IEEE . Press, 1974, Van Trees, H.L. , De tec t ion , Esti ma ti on and Modulati on Theory, Part, I W ile y, New York, 1968, Vi terb i, A.J. and Omura, J.K., Pr inci p le s of Di gital Communic a ti on and' Codin g , McGraw-Hi ll, 1979. Zie m er, R.E . and Trante r , W.H ., Princ ip le of Communic a ti on s, Houg h to n . M ifflin Co., 1976.
제 3 장 부호화정리 3.1 正規雜音채널 3. 1. 1 신호의 直交展開에 의한 두 符號語의 誤率 g,n ( t ) 와 g. ( t ) 를 구간 a
 (gm . gn) =Jbg m (t) gn (t) d t= {01,, mm= -:f:nn ., mn== 1l,, 2 2, . …… (3. 1-1)
(gm . gn) =Jbg m (t) gn (t) d t= {01,, mm= -:f:nn ., mn== 1l,, 2 2, . …… (3. 1-1)
상기 식에 의하여 g n 의 항으로 표시할 수 있다. 상수 Cn 은 直交性 때문에 용이하게 구할 수 있다.
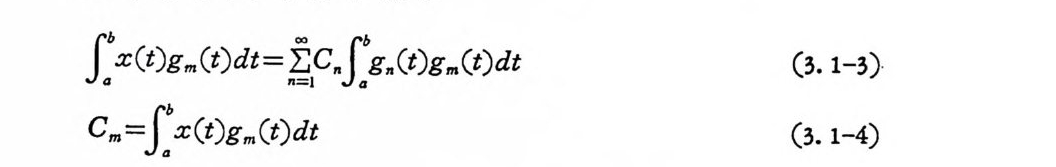 S:x( t)g m (t)d t = fp.J:g. (t)gm (t)d t (3. 1-3)
S:x( t)g m (t)d t = fp.J:g. (t)gm (t)d t (3. 1-3)
두 개 의 신호 x( t)와 y(t) 일 때 , x( t)와 y(t)를 정 규칙 교함수를 사용하여 표시할 수 있다.
 ..
..
內積으로 표시하면 계수 xm, y은
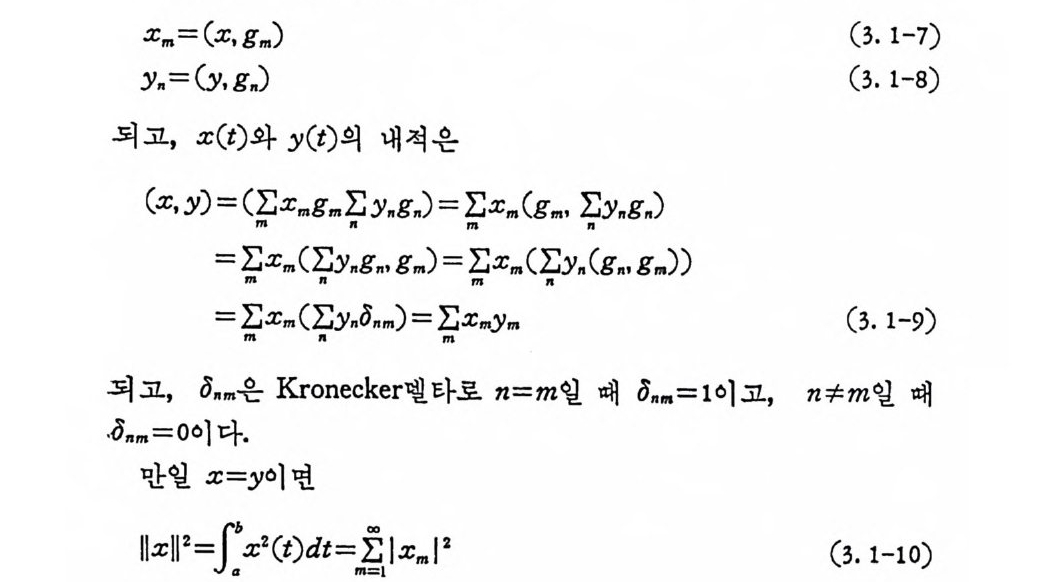 꾸 m=(x, g m) (3. 1-7)
꾸 m=(x, g m) (3. 1-7)
으로 Parseval 정 리 가 성 립 한다. x,..,( t)를 x( t)를 k 항만 사용한 나머 지 이 면
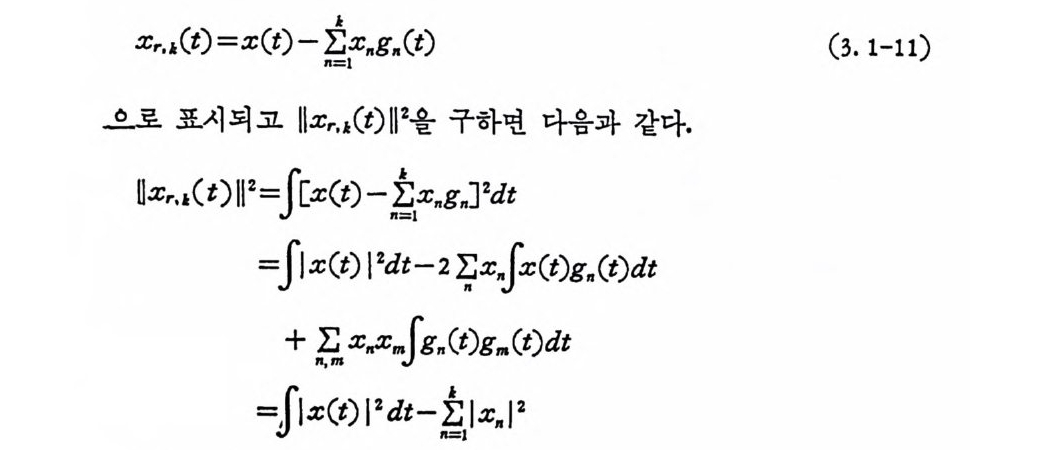 Xr, 1 (t) = x(t) -l:&; x. g. (t) (3. 1-11)
Xr, 1 (t) = x(t) -l:&; x. g. (t) (3. 1-11)
 = II.x Ct)l l2- •l =k: I l .x』 2 (;. 1-12)
= II.x Ct)l l2- •l =k: I l .x』 2 (;. 1-12)
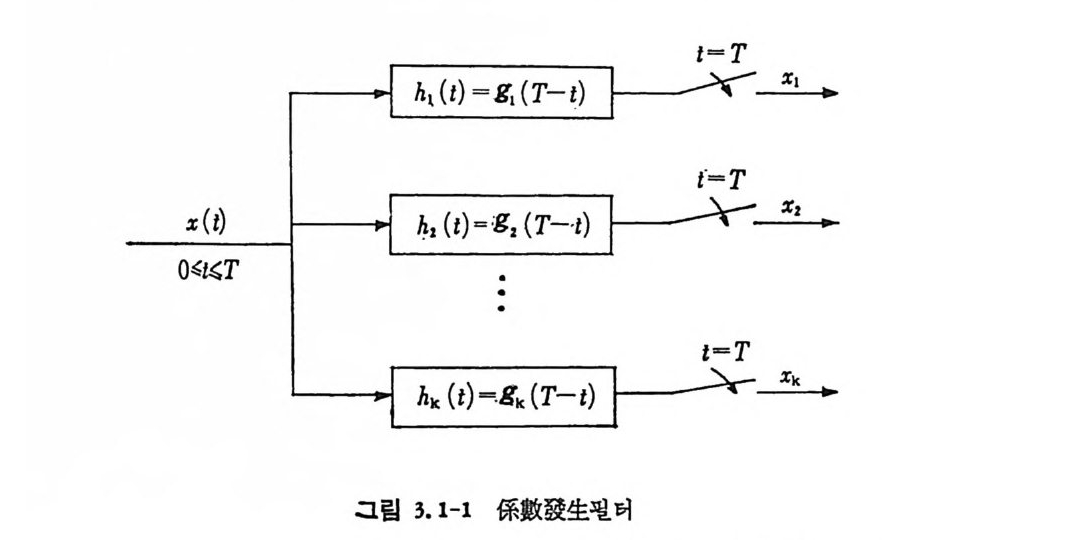
으로 표시하면, 이대 계수 X ij는 다음 그림 3.1-1 에서 구할수 있다.
 t= T
t= T
여기서 적분구간은 [o, T] 이고, 계수 x. J 는 다 음 과 같 다.
 X ij=『。 X;( t)g l t )d t (3. 1-17)
X ij=『。 X;( t)g l t )d t (3. 1-17)
git)에 정합된 線形팔터를 동과한 후 t= T 대 출력을 취항으로 써 구할 수 있다. i번선호 X;( t)가 채 널을 동할 때 加 算 的白色가우 스잡음 (add iti ve whit e Gaussia n no i se) 이 가하여 진다고 가정 한다. 가우스잡음은 수학적으로 해석하기가 용이하고 실제 通 信 系統에 많 이 적용되므로 앞으로 기술할 모든 잡음은 목벌한 경우를 제의하고 평 균치 가 0 이 고 自 己相關函數 (au t ocorrela ti on fun cti on ) R (-.) = 푹 o(-.)o, l 가산적 백색가우스잡음만 취급한다. 입력 x i ( t ) 에 대하 여 채 널을 동한 출력 y(t)는
 y(t) =x,(t) +n(t), o
y(t) =x,(t) +n(t), o
이다. 여기서 n( t)는 잡음이다. 또한
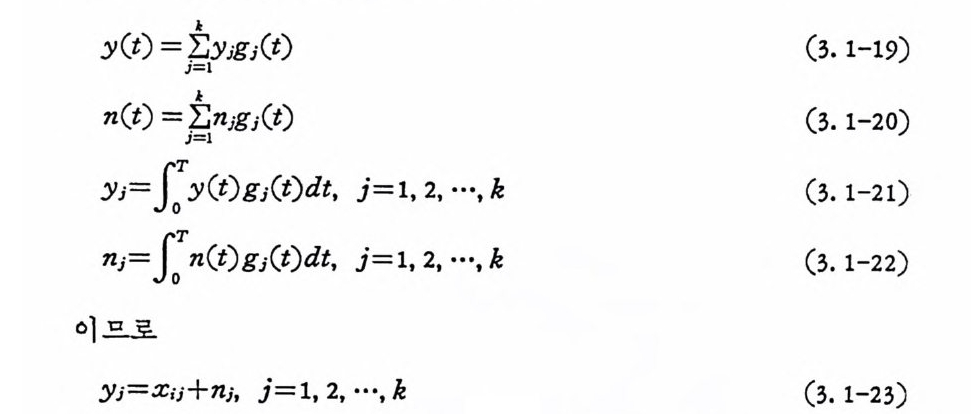 y(t) =j I=k; Iy jgj(t) (3. 1-19)
y(t) =j I=k; Iy jgj(t) (3. 1-19)
로 표시할 수 있다. Y j의 평균치와 분산은 각기 다음과 같다.
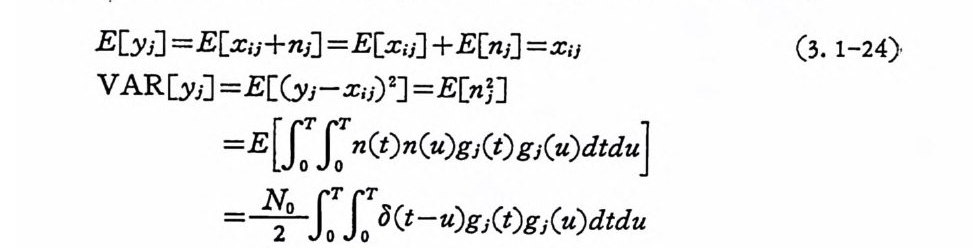 E[yi ] =E[X;j+ ni] =E[x;;] +E[ni] =x;1 (3. 1-24)
E[yi ] =E[X;j+ ni] =E[x;;] +E[ni] =x;1 (3. 1-24)
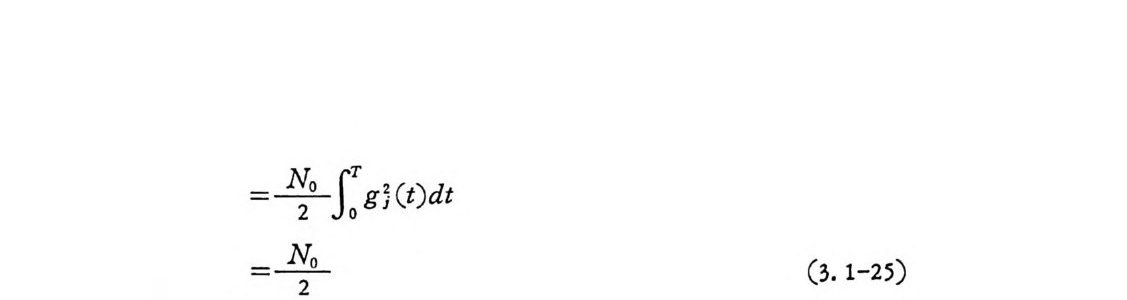 =푸-J。~g; (t)d t
=푸-J。~g; (t)d t
마찬가지 로 공분산은 j *l 일 때 0 이 된다.
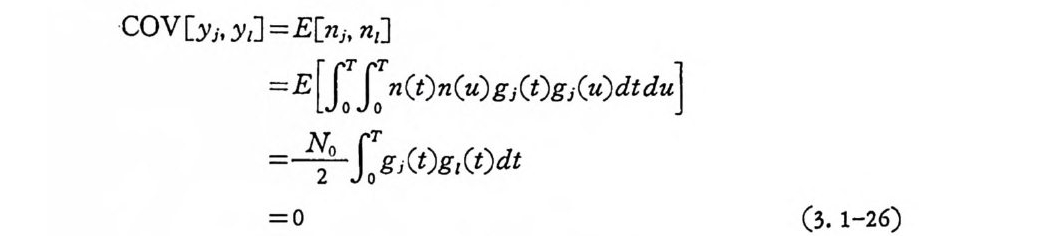 COV 屈y ,]=E 屈띠
COV 屈y ,]=E 屈띠
즉 k 개의 계수를 벡터로 표시하여 y=(y1, y 2· ···,y K) 일 때 각 성 묘 독립 적 인 가우스 확률변수로서 평 균치 Xi j, 분산 」문 을 갖는 다. 신호벡터 X,=(xil, x,2, … .X i K) 일 대 조건부 X i의 확물분포함수 P(y lx;) 는
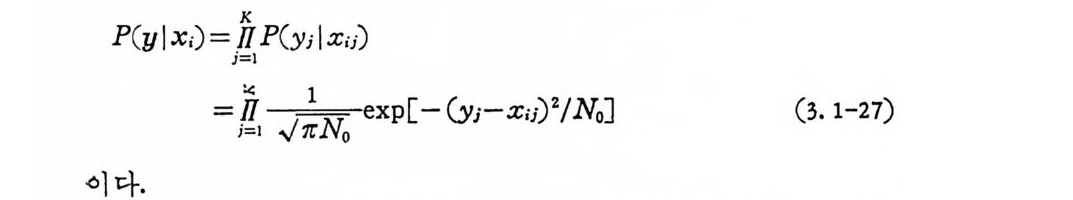 P( y l x.) == i!iK= l~=I lI I P (J y— T i1 l N xu。 )e xp [-(y j -X i합 /No] (3. 1-27)
P( y l x.) == i!iK= l~=I lI I P (J y— T i1 l N xu。 )e xp [-(y j -X i합 /No] (3. 1-27)
떠(t)와 x2( t)가 정규직교함수의 N 개를 사용한 선형걷합이라 하 자.
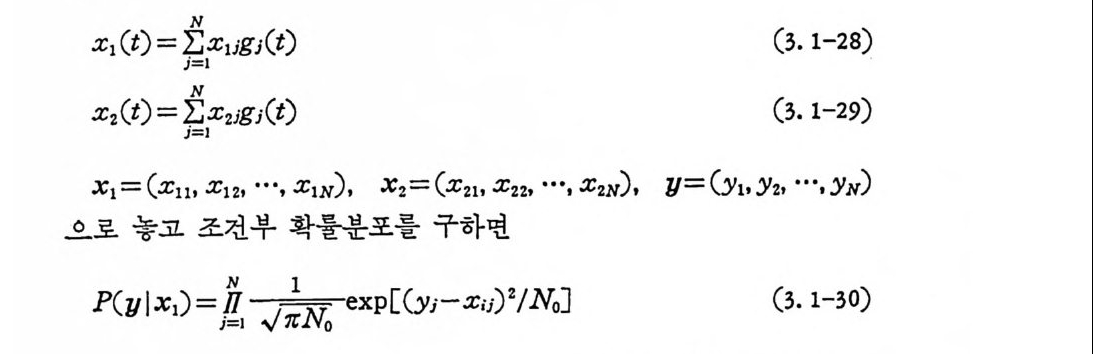 X1 (t) = IjN=: Ix 1 ;g; (t) (3. 1-28)
X1 (t) = IjN=: Ix 1 ;g; (t) (3. 1-28)
 P(y l x2)=jNl=l I J— r1 N。 ex p [(y ;-x2;)2/N 』 (3. 1-31)
P(y l x2)=jNl=l I J— r1 N。 ex p [(y ;-x2;)2/N 』 (3. 1-31)
 된다. 이것은 신호검출에서 사용하는 식과 동일하다. 동보 i= l,2
된다. 이것은 신호검출에서 사용하는 식과 동일하다. 동보 i= l,2
이고, y =ax 일 때 Y 의 분산은 VAR[ y] =a2VAR[x] 를 이용하여 A( y)의 분산율 계산하면
 VAR[A(y) ] = j.NE= I (X1 j -X 값 (3. 1 一 34)
VAR[A(y) ] = j.NE= I (X1 j -X 값 (3. 1 一 34)
된다. X1 을 송신할 때 A(y )
P.,= ✓갈 (:l J국 )2 f:ex p [ -+:도 :1~)2 ]dA j= I (3. 1-35)
 A __1 2N (xu_x2j)
A __1 2N (xu_x2j)
으로 놓고 정리하면
 P,1=
P,1=
된다 . .x 2 ( t ) 를 송신할 때 誤率 P,2 도 동일하므로 전체평군오울은
 P,=
P,=
이 고, 다시 Parseval 공식 을 사용하여 표시 하면 에 너 지 차에 의 촌함 울 알 수 있다.
 E= 이순사@(t)국(t ))2d t] (3. 1-40)
E= 이순사@(t)국(t ))2d t] (3. 1-40)
두 선호의 에너지가 동일하고, 두 신호의 상관계수 k 를 아태와 같이 정의하면 이대 오울은 잡음전력 검노을감안하여 다음과같다.
 s:x; (t )d t =5: 따 (t)d t= E (3. 1-41)
s:x; (t )d t =5: 따 (t)d t= E (3. 1-41)
최소오울 P. 는 X1( t )=-x it)로 상관계수 l=-1 일 때 값이다. 3. 1. 2 직교신호와 誤率의 上界 가설 H 를 다음과 같이 표기 하고
 H; : y(t)= x;(t)+ n(t), i= l, 2, ···, M (3. 1-- 44)
H; : y(t)= x;(t)+ n(t), i= l, 2, ···, M (3. 1-- 44)
신호 y(t)를 수신하여 송신선호 x.(t) , i= I, 2. …. M 중 어 느 신호 를 송신하였나를 알아내는 것은 신호겁출의 문제이다. 신호를 검 출 하기 위해서는 일정한 판정기준이 있어야 한다. 신 호검 출 에서 는 보 편적으로 베이어스判定 基準 ( Ba y es' cr it er i on ) 을 사용하 여 판정 오 울 을 최소화시킨다. 베이어스판정기준은 2 개의 가정하에 기반 을 두고 있다. 첫째 가정은 송신신호 X i ( t)가 각기 P,의 확 률 로 발생 하고, 둘째 가정은 損 失 (cos t ) C;) 을 규정하여 가설 Hj 가 진실일 때 가 설 H올 택하는 손실을 C,i 로 표기하였다. P(D,IH;) 을 다음과 같이 정 의 한다.
 P(D; IH J =JRRi /(y l xJ d y (3. 1-45)
P(D; IH J =JRRi /(y l xJ d y (3. 1-45)
즉 가설 Hj 가 진실일 때 가설 H i을 덱하는 확률로 P ( D i lHj ) 는 검출확률이고, P(D;IHi )는 일종의 오울이다. R 을 관측공간이라 할 때 수신된 관측이 R 평역에 존재하면 가설 H i를 택한다. M개 의 가 설에 대한 평군손실은
 C= iE=M I MEi= CI ij P( Dj | Hj )pJ (3. 1-46)
C= iE=M I MEi= CI ij P( Dj | Hj )pJ (3. 1-46)
이고, 베이어스판정기준은 평군손실을 최소화한다. 가설 H제 대한 손실온
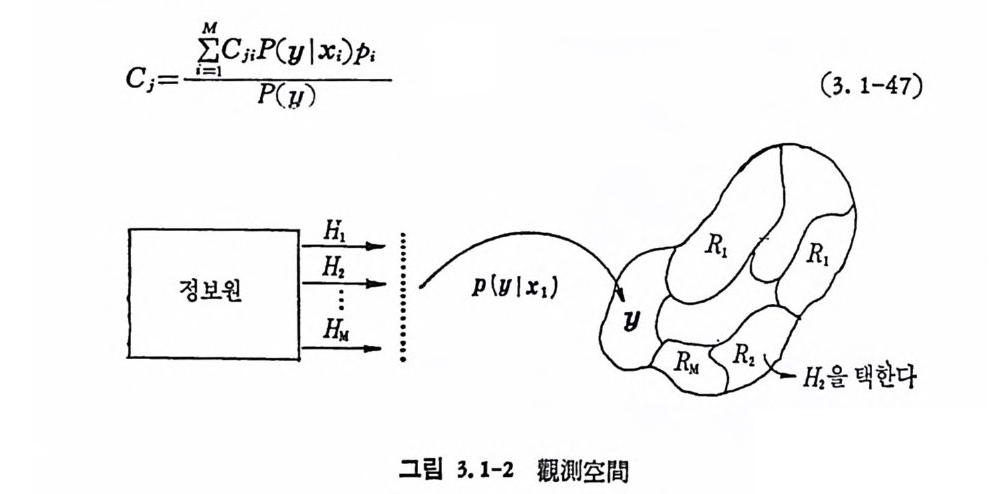 cj= iEM= \ IC ji PP (( yy ) I x HzIHi.)H一 一 . p I Ii- .................. (3. 1-47)
cj= iEM= \ IC ji PP (( yy ) I x HzIHi.)H一 一 . p I Ii- .................. (3. 1-47)
이 고, P ( y ) 는 가 설 에 무관하브로 판정 방법 은 가설 H제 대 하여
 Aj = ;EM= I Cj iP( y | X;)p , (3. 1-48)
Aj = ;EM= I Cj iP( y | X;)p , (3. 1-48)
 이고, A 가 최소인 H웁 택한다. A 가 최소일 때
이고, A 가 최소인 H웁 택한다. A 가 최소일 때
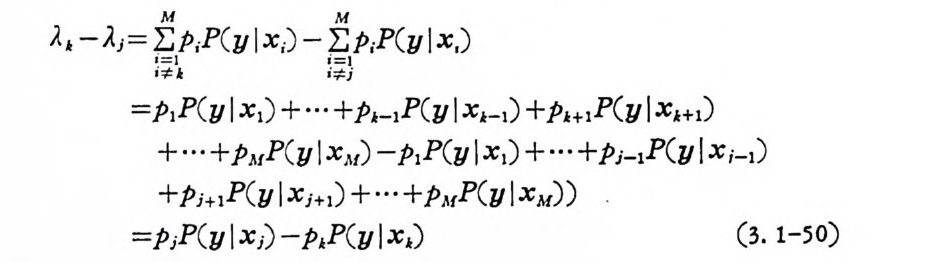 Ak -Aj = EM piP( y l x,) - E M piP( y | x,)
Ak -Aj = EM piP( y l x,) - E M piP( y | x,)
되고, 또한 Ak_A j >0 이므로
 PiP ( y l xJ >p.P ( y lx A) (3. 1-51)
PiP ( y l xJ >p.P ( y lx A) (3. 1-51)
된다. 즉 A 가 최소일 때 반대로 P i P( y lx 』)는 최대가된다. 그러므로 판정법칙은 P i P( y lx j)가 최대이면 가설 H J올택한다. 만일 ' pj=」{ 이면 판정법칙은
 P(y l xJ > P(y l x,), j-=t=k (3. 1-52)
P(y l xJ > P(y l x,), j-=t=k (3. 1-52)
이다. 정보원이 동보 i를 발생시키고 채널부호기를 통하여 x i울 송신할 때, 수신계열 y로부터 통보 i’을 추정한다. 만일 i*i'이면 에러 ,( error) 가 발생하고, 정보원이 동보 i를 발생하였을 때 復 號 誤率 l
 E,,= :E P(y l x,) (3. 1-53)
E,,= :E P(y l x,) (3. 1-53)
Y; 는 통보 i로 복호되는 계열의 집합이다. 벡터 y와 X i가 유한한
알파벳의 요소일 때 P, i 는 식 (3. 1-53) 으로 표시되 나, x , 가 가우스잡 음이 가해지는 연속채널을 통할 때에는 y의 각 성분도 연속함수가 되 므로 식 (3. 1-53) 에 서 2 는 적 분이 되 므로 주의 를 요한다. 동 보 i의 발생확물을 P i로 표기하면 평군복호오울은 다음과 같다 .
 P,=:'=M EI pjP ,. (3. 1-54)
P,=:'=M EI pjP ,. (3. 1-54)
P올 계산하기는 득벌한 경우를 제외하고 매우 복잡하므로 P, 의 상계식을· 구하려 한다. 두 부호어 XI,X2 일 때 P ( y lx i )> P ( y lx : ) 이 떤 통보 1 로 추정하고 통보 1 을 송신하였을 때 복호오울을 다시 쓰 면 다음과 같다.
 P,1 = µr도; Y I P(y I Xi) (3. 1-5 5)
P,1 = µr도; Y I P(y I Xi) (3. 1-5 5)
이 식은 s>1 일 때도 성립하나 이용가치가 없음을 알게 된다. 죽
 P,1< 11Ie:~Y1 P(y l x1)1-•P(y l x2)' (3. 1-58)
P,1< 11Ie:~Y1 P(y l x1)1-•P(y l x2)' (3. 1-58)
모돈 y에 대하여 합을 취하면 우변은 더 커지므로
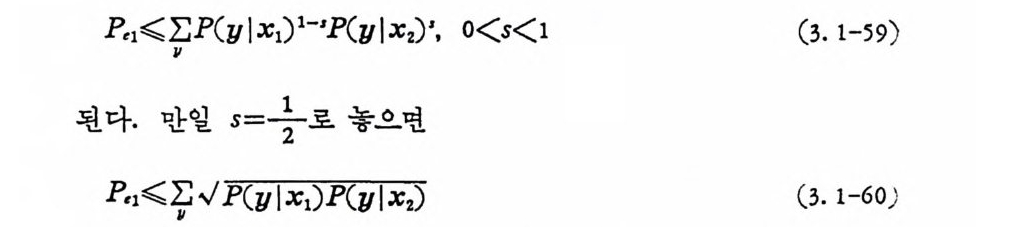 P,1<.E P (y l x1)1-•P(y l xz)', o
P,1<.E P (y l x1)1-•P(y l xz)', o
된다. M개 의 부호어 x1,X2. … ,XM 이 존재할 때 p,i는 i타인 모든 경우를 생각하여야 되므로 다음과 같은 上界式이 성립한다.
P조 ,곱,꾸J (u|x i )P(ulx1,), i*iI (3. 1-61)
가우스채 널의 경 우 석 (3. 1-61) 을 사용하여 오울의 상계를 구하여 본다. 신호 X;( t)을
 x;(t ) = J1N= : ;I x ug i(t) (3. 1-62)
x;(t ) = J1N= : ;I x ug i(t) (3. 1-62)
로 표시 할 때 석 (3. 1-62) 는 유일하므로 Xi j, j= 1, 2. …, N을 아는 것 은 X; ( t ) 를 아는 것과 동일하다. 신호 x i(t)에 평군치 0, 분산 」운 인 가우스잡음이 가하여 진 경 우, 수신선호 y(t)도 역 시 가우스프로 세스이다. 더우기 yJ =X ij +n 칠 때 y】 =s:。 y (t)g;(t)이며, yJ는 선형 변환에 의하여 평군치 X ij, 분산 흡드인 정규분포를 갖는다. 그러 므로 무기억채널의 경우
 P( y l x,) == j j nn=A= ’lI P J( y— r ; Nl x。 u )e - (y j -m ,WNo (3. 1-63)
P( y l x,) == j j nn=A= ’lI P J( y— r ; Nl x。 u )e - (y j -m ,WNo (3. 1-63)
이다. 또한
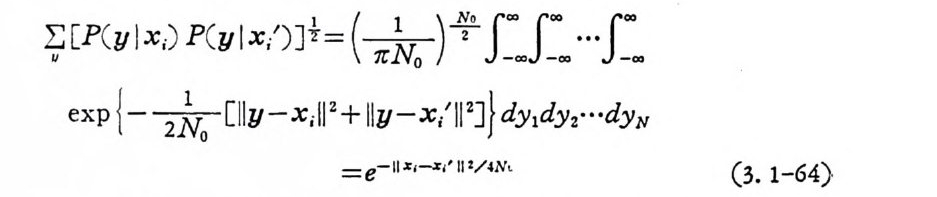 꾸 [P ( y l x; ) P( y l x,’)]½ =( *)門「O O 』OO OO …』OO OO
꾸 [P ( y l x; ) P( y l x,’)]½ =( *)門「O O 』OO OO …』OO OO
이다. M 개의 신호가동일한에너지 E 를가지고직교신호이면
J: x;( t)국 )d t= {운 閃; i,j=l , 2, …. M (2. 1-65}
이 고, 만일 직 교함수로 간단한 다음 함수를 취하면
g;= -,-J-1=E X;(t), i= l, 2, …, M (3. 1-66) Z ij={론 .1수·J. .J (3. 1-67) t =
이고 N=M 이면
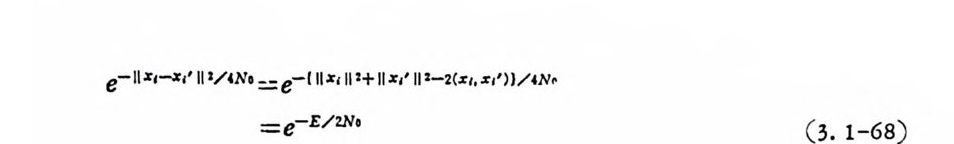 e-IIx ,-. ,r‘' ll ’/ 4N· =e-I IIX‘ '+1lx,’ l P-2(x, 마)J /4N 톤
e-IIx ,-. ,r‘' ll ’/ 4N· =e-I IIX‘ '+1lx,’ l P-2(x, 마)J /4N 톤
이다. 그러므로 P‘ 논 다음과 같다.
 P, ; <(M-l)e-u 'l.N。 (3. 1-69)
P, ; <(M-l)e-u 'l.N。 (3. 1-69)
만일 M 이 크면 P,;
 P(y lx ;') ~ P(y l x;) (3. 1-70)
P(y lx ;') ~ P(y l x;) (3. 1-70)
부등식 양면에 A 승을 취 하면, J >o 일 때 부등석 은 변치 않는다.
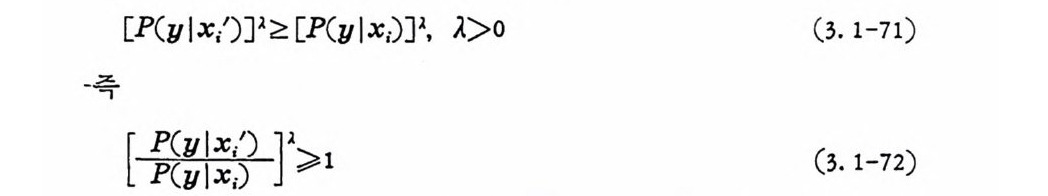 [P (y l x.')]l2: [P(y l x.)Jl, J> o (3. 1-71)
[P (y l x.')]l2: [P(y l x.)Jl, J> o (3. 1-71)
직 (3. 1-72) 에서 P( y lx;’) 을 P( y lx t:)로 놓고 모든 i'i*i에 대 하여 · 합하면 각 항은 負가 아니므로 다음과 같다.
 i'~ [ 잡臣? ]\ J> o (3. 1-73)
i'~ [ 잡臣? ]\ J> o (3. 1-73)
합에 는 P(y l x{' )도 포함된다. 식 (3. 1-73) 을 만족시 키 는 y의 집 합 울 Yi 라 할 때 P,ri= -
 P,;,< llE~f , P(y I X;) (3. 1-74)
P,;,< llE~f , P(y I X;) (3. 1-74)
이다. Y 가 동보 i를 발생하여 부호 따를 송신할 때 통보 i로 복호 되지 않는 수신계열의 집합이라 하면 식 (3.1-74) 는 모든 y EY i에 대하여 만족하므로
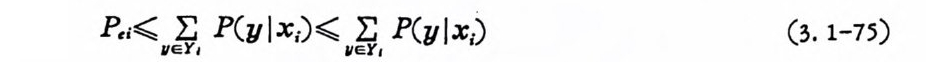 P,i¾ 11~eY , P(y- l x;) ¾ 11le;Y; , P(y l x;) (3. 1-75)
P,i¾ 11~eY , P(y- l x;) ¾ 11le;Y; , P(y l x;) (3. 1-75)
됨 을 알 수 있다. 조한 식 (3. 1-73) 에 p승을 취하여도 부등식은 성 립되므로
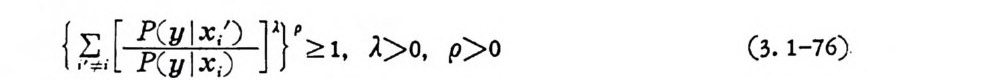 {g,[ : : :訂 ]『칙, -l> o, p> o (3. 1-76)
{g,[ : : :訂 ]『칙, -l> o, p> o (3. 1-76)
식 (3. 1-76 ) 을 석 (3. 1-75) 에 곱하여 정 리 하면
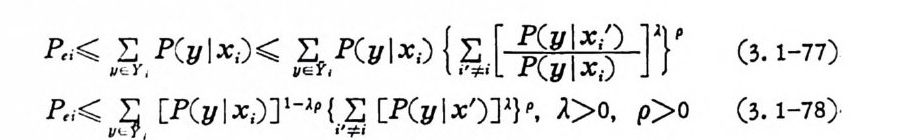 P ? 풀 , P ( y lx,) 나 , P( y lx;) {~,[ :::訂 ]T (3. 1-77)
P ? 풀 , P ( y lx,) 나 , P( y lx;) {~,[ :::訂 ]T (3. 1-77)
이다. 모 든 y에 대하여 合울 취하여도 우번은 더 커지므로
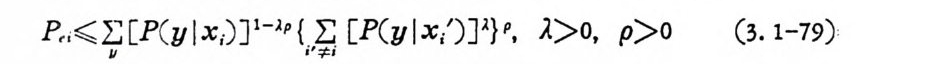 p쵸 고 고 [P(y l xi) ] ! -•P {_E [P(y l x/)Jl } P, .il> o, p> o (3. 1-79)
p쵸 고 고 [P(y l xi) ] ! -•P {_E [P(y l x/)Jl } P, .il> o, p> o (3. 1-79)
된얻다는.다 .A , p는 임의의 정수이므로 A= 一1 L+_p 로 놓으면 다음 상계식을
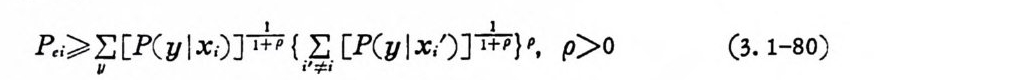 P,;> Iu: [.. P ( y- IX,). 〕- 눕{ ;I,:수 [P( y lx,')] 늙 }P, p>O (3. 1-80)
P,;> Iu: [.. P ( y- IX,). 〕- 눕{ ;I,:수 [P( y lx,')] 늙 }P, p>O (3. 1-80)
이 석 은 Galla g er 에 의 하여 유도되 었다. 만일 p =I 일 때는 식 @ 1-61) 과 같게 된다. 먼처와 같이 M 차 M ' 개 직교신호가 동일한 에너지를 가지고 있으면
 X ij={군 ~i. =:?j. ; i,j=l , 2, •••. M (3. 1-81),
X ij={군 ~i. =:?j. ; i,j=l , 2, •••. M (3. 1-81),
되고, P ( y lx;) 는 다음과 같다.
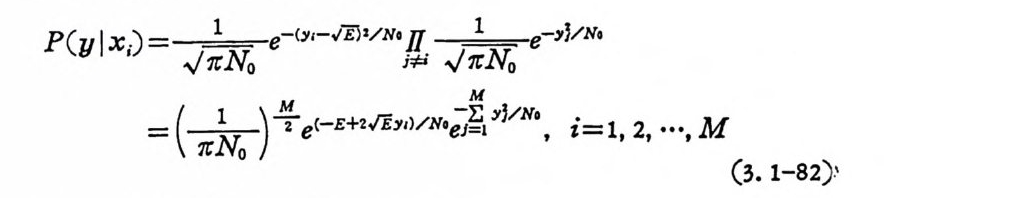 P(y l x;) =_느국- ( y ‘-V回 '/N‘H _e-yl/ N·
P(y l x;) =_느국- ( y ‘-V回 '/N‘H _e-yl/ N·
식 (3. 1-82) 를 식 (3. 1-80) 에 대 입 하면
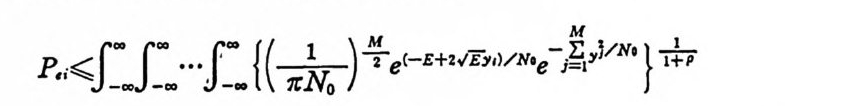 p길.. .. J_.. .... f .. {(志-) 우 e(-E+2V 百m )/NIe-EMl y ’/N’ } 늙
p길.. .. J_.. .... f .. {(志-) 우 e(-E+2V 百m )/NIe-EMl y ’/N’ } 늙
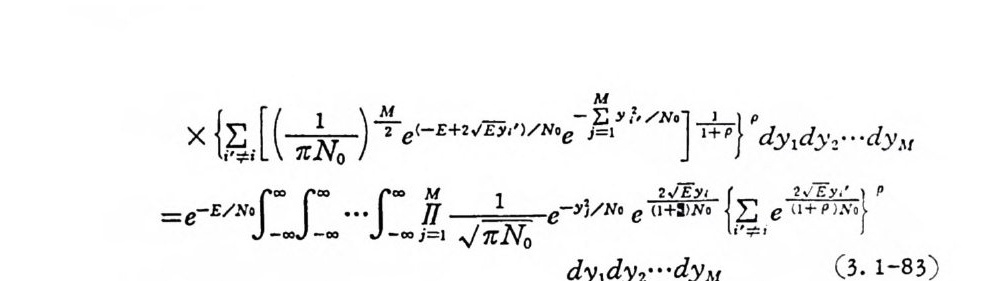 x {~』 (志) 문 e(-E+2 高 )/Noe- J홈 l“ 기 러 Pdy 1 dY2 … dy 4\(
x {~』 (志) 문 e(-E+2 高 )/Noe- J홈 l“ 기 러 Pdy 1 dY2 … dy 4\(
된다. 평균치 0, 분산 1 인 정규분포의 기대함수의 형석을 취하기 위 하여 z j=yJ.;J건 Y 万 5 로 놓으면 p,i
되고, 각 독립적인 정규분포 확률변수 zI,z2, ••• ,zM 에 대한 기대치는 다음과 같다.
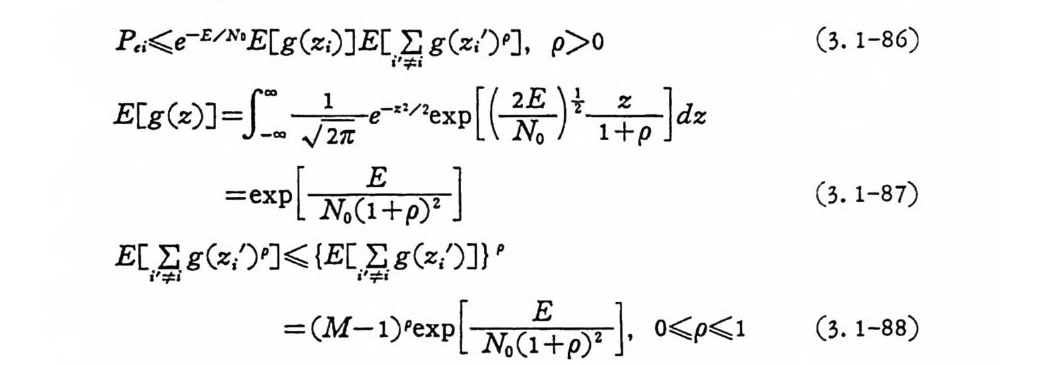 p‘i
p‘i
의 이부것동은석 을iE’수 ’g 이 (z용 i하')여가 구구간하 였o<다;. p < :;p1 에志 ] 대상하계여식 볼은록 함수이므로 Jen sen
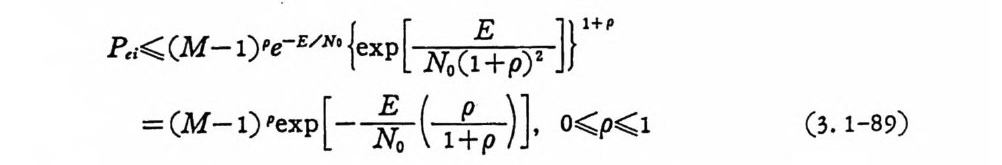 P,;¾(M-1)Pe- E/ N•{ex p[Ni。(~]}l+ P
P,;¾(M-1)Pe- E/ N•{ex p[Ni。(~]}l+ P
이다. 만일 p =l 이면
P,;<( M -1)e -um, (3. 1-90)
로 석 (3. 1-69 ) 와 같다. pc 는 모든 i에 대 하여 동일하므로 평 군오울 .P,도 같다.
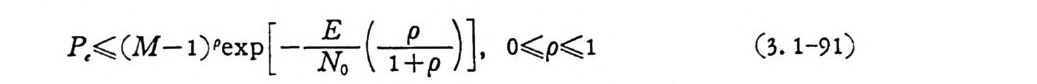 P‘< ( M-l )P ex p[-長(곱급], o
P‘< ( M-l )P ex p[-長(곱급], o
신 호대 잡음비 CT 와 전송물 RT 을 다음과 같이 정 의 한다.
 cT= 言E =TS (3. 1-92)
cT= 言E =TS (3. 1-92)
.s는 초당 신호전력이거나 에너지이다 . M 이 크면 (M-1)::::::M 으로 놓을 수 있고 식 (3. 1-92 ) 에 식 (3.1-91) 을 대 입하면
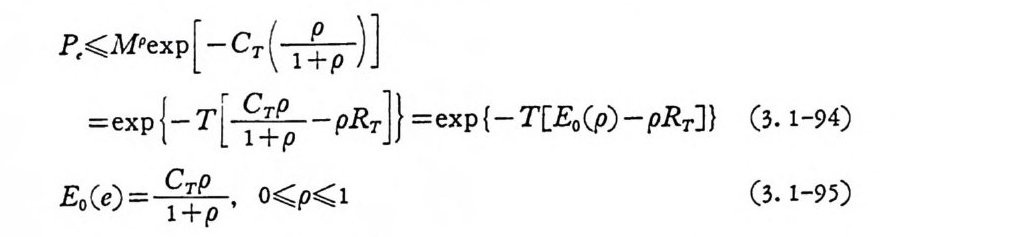 麟M Pex p [-cT ( 급)]
麟M Pex p [-cT ( 급)]
된다. R 을 최 소로 하기 위하여 E 。(p)-p RT 을 p에 대하여 마분을 취 하여 최대로 하면 된다.
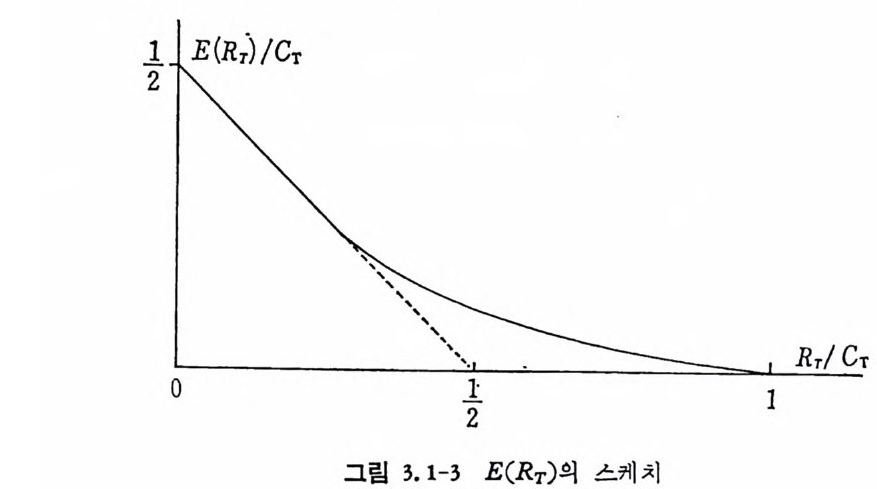
草。(pd)p- p RT 〕 -= (_l+ 느p ) 궁 T-RT (3. 1-96) RT< 국C느 이면 d[E 。(p)-p RT J /d p >o 이므로 최대치는 p= l 이고, , CT/4¾RT 이 면 d 〔 E 。(p)-p R 리 !d p =O 올 만족하는 P 논 .p= .JC T/RT-1 이다. 즉 E
이상의 결과를 그림 3.1-3 에 표시하였다. p =l 일 때 E(Rr)/Cr는 칙선이 되며 겁선으로 표시하였다. 결과적으로 CT>RT 일 때 T 즉 M을 무한대로 접근시키면 P, 는 0 으로 접근한다.
 니 E(R;)/Cr
니 E(R;)/Cr
3.2 채널符號化 정리 3.2.1 서론 q개의 알파벳으로 구성된 알파벳의 집합 A={a i, a2. … ,a q}에서 N 개의 성분으로 구성된 계열 (se q uence) 의 전체의 집합을
AN= {x=x11 X2, …, x 피 x,EA, i= 1, 2, …. N} (3. 2-1)
으로 표시한다. A={o,1} 일 때 X;, i =l,2, … ,n, 은 0 이거나 1 이다. 앞으로는 A={O, 마인 이원부호의 경우만 취급한다. x 가 M 개인 집 . 합을
 C= {X1, X2, …, X 떠 (3. 2-2),
C= {X1, X2, …, X 떠 (3. 2-2),
符號 (code) 라 하고 Xj, i= 1, 2, …, M을 符號語 (code word) 라 한다. 일반적으로 n 개의 성분으로 구성된 계열의 전체의 수는 2 이나, 부호어 의 수는 M개 이 다. 통보 (messa g e) 의 수를 M 이 라 하면 1 부터 ( M 까지의 整數로 구성된 집합 l={ i ,2,··•,M} 에서 집합 A 로 寫像
하는 것을 符 也[ 化 ( encod i n g)라 한다. M 개의 부호어를 X1=Cx11, X12 . … , X1N) , X2 = (X2 i, X 22. …, XzN), …, XM= (xMl, xM2. …, XMN) 으로 표시 하기 로 한다. 전송률을 다음과 같이 정 의 한다.
 R=lNn~M .' M=eNR ’ (3.2-3)
R=lNn~M .' M=eNR ’ (3.2-3)
채널에 잡음이 있을 경우 수신계열은 송신계열과 동일할 팔요는 없다. 수신계열의 집합을
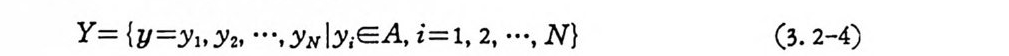 Y= {y= Y1 tY 2. …, YNIY; E A, i= l, 2, …, N} (3. 2-4)
Y= {y= Y1 tY 2. …, YNIY; E A, i= l, 2, …, N} (3. 2-4)
로 표 시하고 Y로 부터 C 로의 寫 像울 復號化 (decod i n g)라 한다. x 를 송신 할 때 y를 수신하는 조건부확률이
P( y l x) =i n=N lP (y; l x;) (3. 2-5)
일 때 채널을 무기억채널 (memor y less channel) 이라 한다. 동보 i가 x i 로 부호화되고 x i를 송신하여 y를 수신하였을 경우 y로부터 추정 한 i'가 i와 상이하면 에러 ( error) 가 발생한다. 동보의 사전확률을· p , 로 표시하고, y를 수신할 때 사후확률을 P (i l y)로 표시하면 베이 어스 공식에 의하여 사후확률은 다음과 같이 쑬 수 있다.
 P( il y )=P( y~ ) (3.2-6)
P( il y )=P( y~ ) (3.2-6)
復號器 (decorder) 는 y를 수신하여 통보 i로 복호할 때 復號誤率 (decordin g error) 은 1-P( i l y)이므로 P( i l y)를 최대화하면 오울은 최소화된다. 사전확률이 동일하고, P( y)는 동보 i와 무관하므로 복 호방법은 모든 i'-:P.i에 대하여
 P(y l x;') ;?: P(y l x;) , i' * i (3. 2-7)
P(y l x;') ;?: P(y l x;) , i' * i (3. 2-7)
가장 확률이 큰 것을 택한다. 이 復號法울 M.L. 복호 (m axim um like lih o od decod i n g)라 부른다. 예로서 동보 i가 두 개 있을 때 P( y lx1) 과 P( y lX2) 을 비교하여 P( y lx1) 이 P( y lx2) 보다 수치가 더 크면 동보 1 로 추정하고, P( y lX2) 가 P( y lx1) 보다 더 크면 통보
2 로 추정한다. M . L . 복호법은 사전확물이 동일하지 않거나 사전확뮬 운 모를 때도 적용시킬 수 있다. 즉 M.L. 복호법은 사전확물과 무관 하게 사용한다. 지금 정보원이 통보 i를 발생시키고 부호기를 동하 여 부호어 x i로 부호화하여 송신축에 서 X i울 송신하여 수신된 수신 계열이 y이고, y로부터 추정한 동보가 i'이면 i'*i일 때 復號誤率 (decodin g error p robab i l ity)은
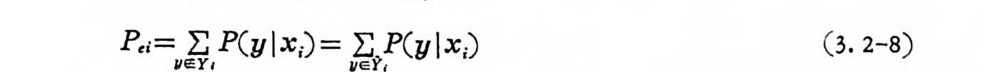 pei = v eEY, P(·y- l• xi•)• = i2ie 'i,P (y l xi) (3. 2-8)
pei = v eEY, P(·y- l• xi•)• = i2ie 'i,P (y l xi) (3. 2-8)
된다. Y; 는 동보 i로 복호되는 계연의 집합이고 Y i는 Y; 의 보집합 이다.
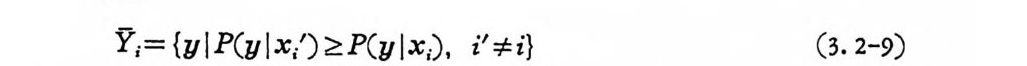 Y;= {yl P(y l x/)~P(y l x;), i'=l=i} (3. 2-9)
Y;= {yl P(y l x/)~P(y l x;), i'=l=i} (3. 2-9)
P; 가 통보의 사전확물이 면 평군복호오울은 다음과 같다.
P. = iI=M;J p ,P . ; (3. 2-10)
일례로 두 符號語 X1=(000), X2=(lll) 일 때, 복호법칙을 수신 계 열 y가 (000), (001), (010), (100) 이 면 통보 1 로 추정 하고, y가 (110), (101): (011), (111) 이면 동보 2 로 복호한다. 집합 Y1=Y2= {(ooo), (001), (010), (100)} 이 고, Y2= Y1 = {(011), (101), (110), (111) }이다. 이원대칭채널에서 천이확률 P( 이 1)=P(1Io)=P 이고 P(lll) =P( 이 0) = 1- p이 면, 동보 1 을 송신하였을 때 , 복호오울 PeI 는 다음과같다.
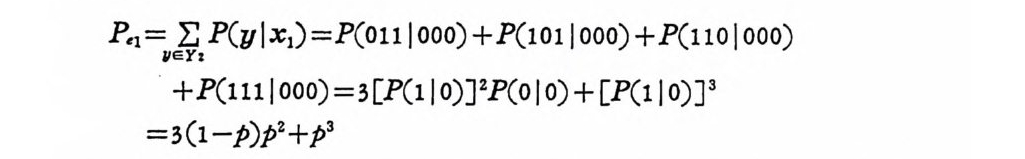 P.,=I Ie~y , P(y l x,)=P(ou j ooo)+P(1011ooo)+P(11 이 000)
P.,=I Ie~y , P(y l x,)=P(ou j ooo)+P(1011ooo)+P(11 이 000)
두 개의 부호어 x1 과 꾸가 존재할 때 P.1 의 상계식은 식 (3.1-58) 에 入1
 P,1< lII: P( y lx 1) 1-•P(y l x2)' (3. 2-10)
P,1< lII: P( y lx 1) 1-•P(y l x2)' (3. 2-10)
이고, 마찬가지로 P,2 에 적용시키면
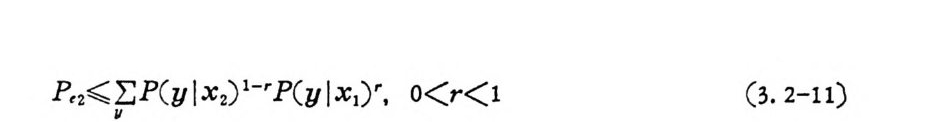 P,2< .uE P ( y l x2) 1-'P(y l x1Y, o
P,2< .uE P ( y l x2) 1-'P(y l x1Y, o
이 된다. r=l-s 로 놓으면 P,1 과 P,2 의 상계식은 동일하게 되므로 다음과 같이 쓸 수 있다.
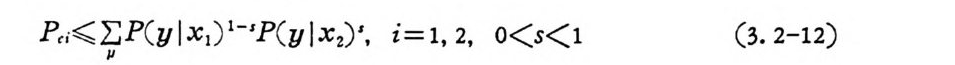 p쵸;;;Iµ; P ( y lx1 ) 1-'P ( y lx2)', i= l, 2, o
p쵸;;;Iµ; P ( y lx1 ) 1-'P ( y lx2)', i= l, 2, o
만일 채널이 무기억채널이떤
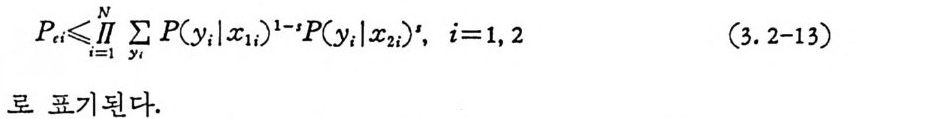 P,;:
P,;:
이원대칭채널에서 x1 이 N 개의 0 계열이고, 포가 N 개의 1 계열이면
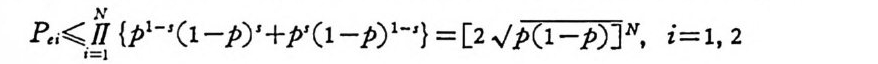 P,;
P,;
이고 기하평군은 산술평군보다 작으므로 P-= to . 5 일 때
 2. ,/p( 1 -p)
2. ,/p( 1 -p)
 P,,
P,,
E 는 보통 오울의 指數部 (exp onen t)라 부른다. N이 무한대로 접 근함에 따라 오울은 0 에 접근한다. 사전확률이 동일할 경우 평균 오울 P,=P1P,1+P2P,2=P,1 도 마찬가지로
![]() P,
P,
이다. 좀더 정확히 분석하기 위하여 수신계열 y의 0 의 수가 K 일 때 1 의 수는 N 一 K 이다. 그러므로 o< p
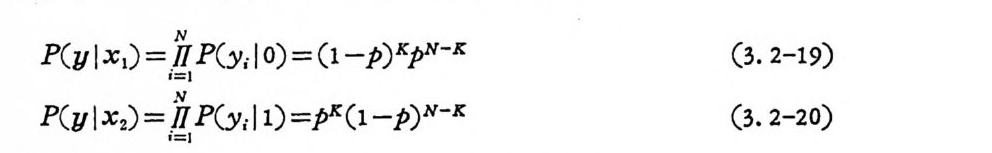 P(y l x1) = lNl P(y; J O) = C1-p) K p N- K (3. 2-19)
P(y l x1) = lNl P(y; J O) = C1-p) K p N- K (3. 2-19)
이다. P( y lx2)>P( y lx! )이면 N/2>K 인 경우이고 P, i, P,2· 는
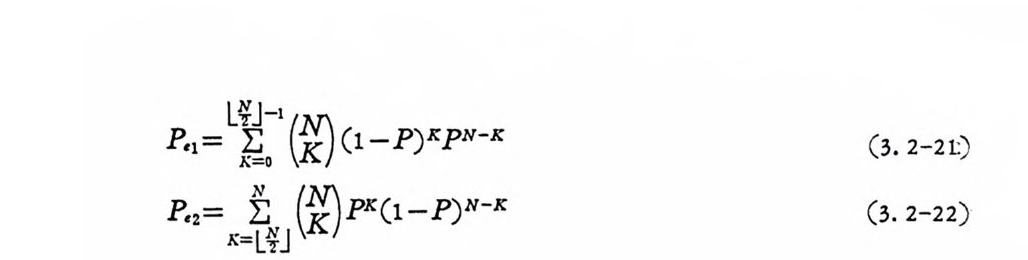 P,1 = \ (낍 (1-P)K P N-K (3. 2-2t )
P,1 = \ (낍 (1-P)K P N-K (3. 2-2t )
 이다. 71 호 망]는 흥보다 작지 않은 최소 정수이다. 이메 평균
이다. 71 호 망]는 흥보다 작지 않은 최소 정수이다. 이메 평균
된다. 상기 식도 N이 증가함에 따라 P. 도 0 에 접근하나 용이하게 알 수가 없다. 그러므로 指數部를 포함한 상계식을 구한다. 〈정 리 3. 2-1> 두 개 의 부호어 x1 이 N개 의 0 으로 구성 되 고, x2 7 l- N개 의 1 로 구성되었을 때 수신계열 y를 구성하는 0 의 수를 K, 1 의 수를 N-K 라 하면 오울에 대한 다음 상계식이 성립한다.
 P.\ 옳 e ~ NE, a= 훑효.
P.\ 옳 e ~ NE, a= 훑효.
 < N-m m 言p =- 言p 言p (3. 2-26)
< N-m m 言p =- 言p 言p (3. 2-26)
이 다. S ti r li n g공석
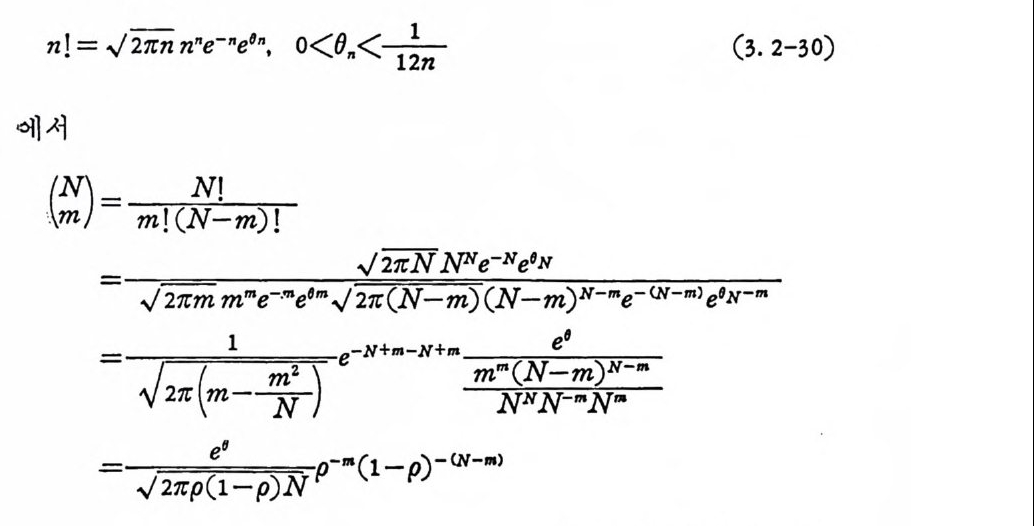 n! = ✓ 一21rn n•e-•e~•. o<()n1<21n - (3. 2-30)
n! = ✓ 一21rn n•e-•e~•. o<()n1<21n - (3. 2-30)
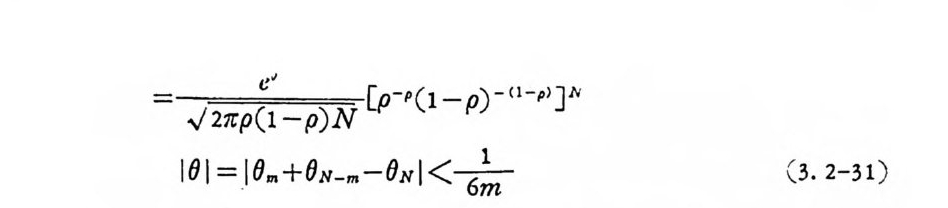 = ,./211 :p(¢ l-p) N [p-p( 1-p) - (1-p) ] N
= ,./211 :p(¢ l-p) N [p-p( 1-p) - (1-p) ] N
구할 수 있 다. 식 (3. 2-29) 와 식 (3. 2-31) 을 식 (3. 2-23) 에 대 입 하면 오울의 상계식을 얻는다.
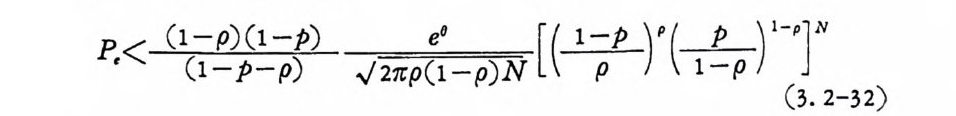 R< (l_p) ( 1_p ) e° [(上『(그 _)1- p ]N
R< (l_p) ( 1_p ) e° [(上『(그 _)1- p ]N
이 식을 좀더 정리하여 지수부를 사용한 식을 얻기 위하여, N>,2, m;;?,1 일 때 —21> ,p>,13— 이 되므로
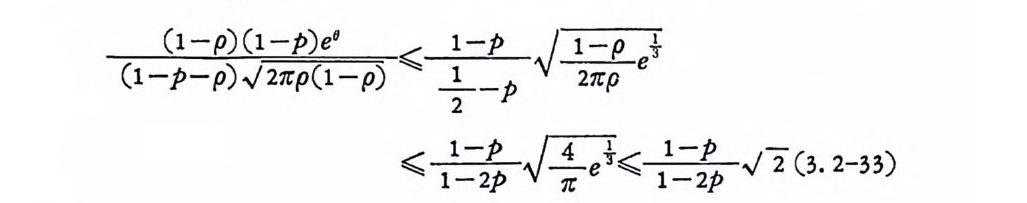 (l_ p )(1 군 )e° < 1 一 P J上二 Le+
(l_ p )(1 군 )e° < 1 一 P J上二 Le+
부등식이 성립된다. 그러므로 E 는 다음과 같이 표시할 수 있다.
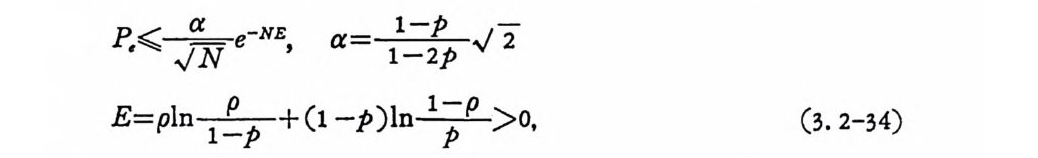 P. <크JN느 e-NE, a= 무1_2Jp 5
P. <크JN느 e-NE, a= 무1_2Jp 5
N이 偶數이면 p =O.5 이고 N이 奇數이떤 p =O.5- 下\지다. 만 일 p=승-이면 指數部 E=-ln[2 ,J灰 F구汀 이 되고 식 (3. 2-17) 과 동일한 지수부가 된다. 오울은 N 이 증가함에 따라 지수함수적으로 o 에 접근한다. 3.2.2 랜둠符號化 오울의 정확한 계산은 부호어의 수 M과 부호의 길이 N 이 커지 면 계 산이 복잡해 진다. 입 력 알파벳집 합 A= {ai, a2… , aq } 과 출력 알파벳의 집합 B={bi, b 2. … ,b, }울 가진 이산채널을 고찰한다. A의
알파벳 N개로 구성된 계열의 전체의 집합을 AN= {x=x! 다 ··x 짜 X;EA, i= l, 2, …. N} 로 하고 B 의 알파벳 N 개로 구성된 계열의 전체의 집합을 BN= {y =y i,y2· .. YNIY;EB, i= l, 2, …, N} 이면 AN 중 M 개의 부호어의 집합은 C= {Xi , X2, …, Xu} 이다. 우리가 주로 취급하는 알파벳은 A=B={o,1} 으로 이때 x,y · 는 이원부호이다. 집합 AN 에는 q N 개의 계열이 있으.나 M개 의 계열 울 선덱 하는 순열의 수는 q MN 이 다. (oo), (10), (10), (11) 중 반복 을 허용하여 2 개를 택할 수 있는 순열의 수는 22 x2 =l6 이다. 두 7}' 의 선덱된 계열이 X1=X2= ( 00 ) 일 경우도 발생할 수 있는 모순이 있다. AN 중에서 임의의 계열 x=(xI,X … ,XN) 을 취할 확률은. , 알파 벳이 독립적으로 선택될 때
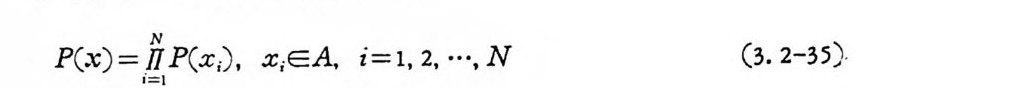 P( x ) = lNl P(x ,), x,EA, i= l, 2, …, N C3. 2-35) ,
P( x ) = lNl P(x ,), x,EA, i= l, 2, …, N C3. 2-35) ,
이 며 임 의 의 부호 C= {Xi, X2. …, XM} 을 취 할 확률을
 P(C) = •n=MIP (x .) (3. 2-36)
P(C) = •n=MIP (x .) (3. 2-36)
로 정 의 하여 오울을 부호전체 에 평 군시 킨다. 이 방법 은 Shannon 이 처음 고찰한 것으로 이렇게 부호화하는 방법을 렌동부호화 (random cod i n g)라 부른다 . 먼처 구한 오울의 상계 식 (3. 1-79) 를 다시 써 보 떤
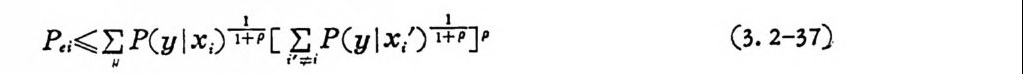 P,i¾ I: P(y I X,) 눕I [i.’ E=i P (y l x1’) iI+ P]P (3.2-37)
P,i¾ I: P(y I X,) 눕I [i.’ E=i P (y l x1’) iI+ P]P (3.2-37)
이 고 기 대 함수를 사용하여 평 군을 구하면 다음과 같다.
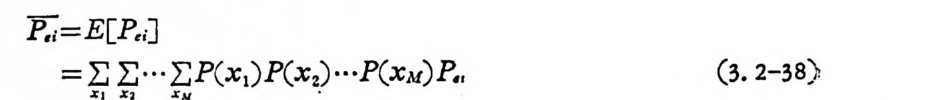 F.;=E [P,;]
F.;=E [P,;]
xl, X2, … , x~ 각기 x=(a., a1. …, a1) 에서 X=( a9 , a9, … a q)까 지 qN 번 합산하여야 하고 M 개가 있으므로 전체 합산은 q MN 계열 에 대한 것으로 P(x1)P(x2)•··P(xM) 을 곱하므로 평균을 취하였다. 즉 다음 과 같이 표시할 수 있다.
 F.:= ~C P(C) P ,i (3. 2-39)
F.:= ~C P(C) P ,i (3. 2-39)
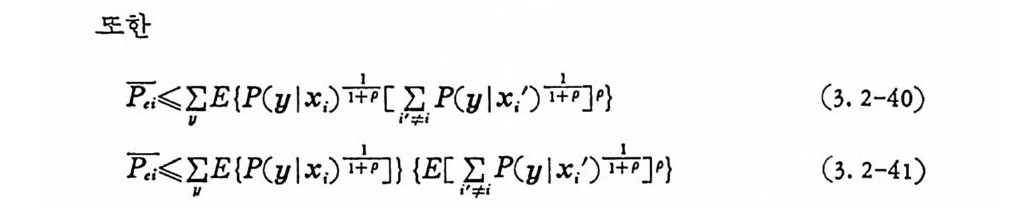 또한
또한
이다. 기대함수를 분리시킨 것은 M 개의 부호어가 상호독립적으로 택하여졌기 때문이다.
 g( x) = [ ~i’ 수 i.P ( y l x/)• 뉴 (3 .2-42)
g( x) = [ ~i’ 수 i.P ( y l x/)• 뉴 (3 .2-42)
놓으면 g (x) 는 볼록함수이브로 Jen sen 부등식을 사용하여 다음과 같이 표기할 수 있다.
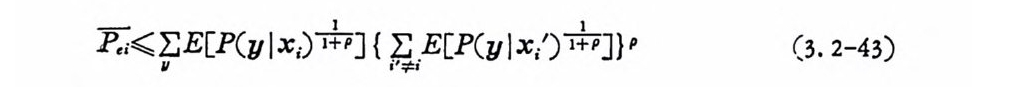 P.i<.E E[P( y lx ; ) 눕] { .E E 〔灰y Ix i')눕 ]}P (3. 2 -43)
P.i<.E E[P( y lx ; ) 눕] { .E E 〔灰y Ix i')눕 ]}P (3. 2 -43)
여기에 기대치의 정의를 사용하여
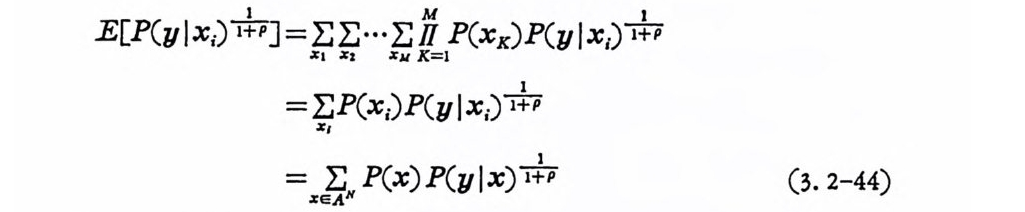 E[P(y l x;)T+ PJ = XEI EX2 ··• XEM K)M=/ I P (xx)P(y l x i)下I 7
E[P(y l x;)T+ PJ = XEI EX2 ··• XEM K)M=/ I P (xx)P(y l x i)下I 7
되고, 이것을 식 (3.2-43) 에 대입하면
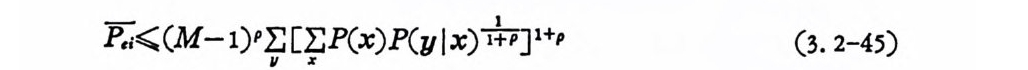 瓦< (M-l)P2II 따X (x)P( y l x) 눈 l+ p (3.2-45)
瓦< (M-l)P2II 따X (x)P( y l x) 눈 l+ p (3.2-45)
얻는다. 각 알파벳이 독립적으로 선택되고 채널이 무기여채널이면
 P( x ) = ni^= ’I P ( x ;) . X;EA (3.2-46)
P( x ) = ni^= ’I P ( x ;) . X;EA (3.2-46)
으로 표시 할 수 있 고 식 (3. 2-45) 는 다음과 같이 된다.
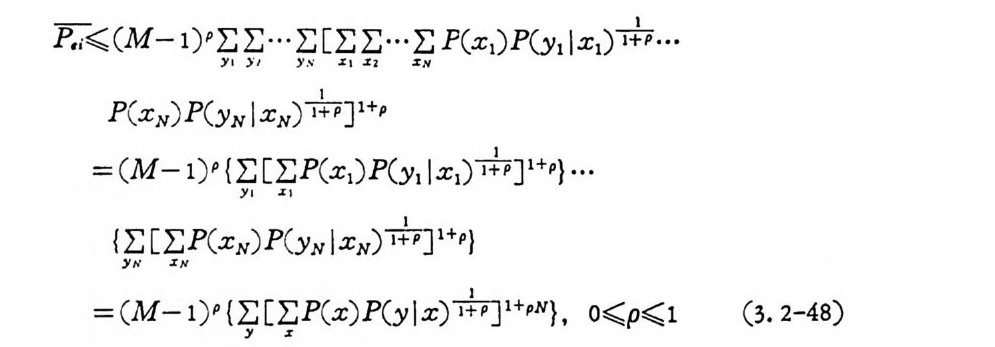 P.:< ( M-l ) P 효y, 고>., … y江N 효츠’ 고도 2 …IZ;N P(x,)P(y1 l x1)m •••
P.:< ( M-l ) P 효y, 고>., … y江N 효츠’ 고도 2 …IZ;N P(x,)P(y1 l x1)m •••
M 이 클 때에는 ( M-1 ) :::: M으 로 놓고, M=eNR 이므로
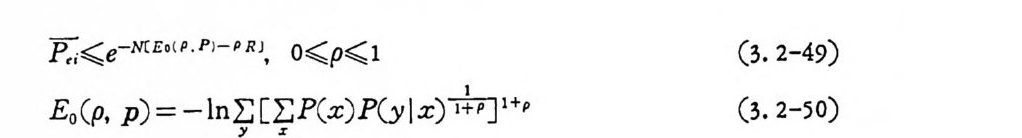 P,.< e-NC Eo CP. P J -P R!, O
P,.< e-NC Eo CP. P J -P R!, O
된다. Eo(P,P ) 의 p는 E 。(p,p)가 입 력확률 P(x) 의 함수임을 뜻한 다. 이 식 을 Galla g er 의 상계 식 이 라 부른다. E 는 Pe i의 평 군치 이 므 로 E 보다 크지 않은 부호가 존재 한다. 평균오울을 최소화하기 위해서 지수부를 최대로 하고, p는 구간 [0, 1 ] 에서 임의이며, P(x) 역시 ~P(x)=l, P(x)>o 을 만족시키 는 조건하에서 임의이다. 죽
 P,;<; e-NECR) (3. 2-51)
P,;<; e-NECR) (3. 2-51)
E 。(p,p)-p R 을 입력확률분포 P 와 Pl 대하여 최대화함으로써 万의 상계식을 얻는다.
 3. 2. 3 채널符號化 정리
3. 2. 3 채널符號化 정리
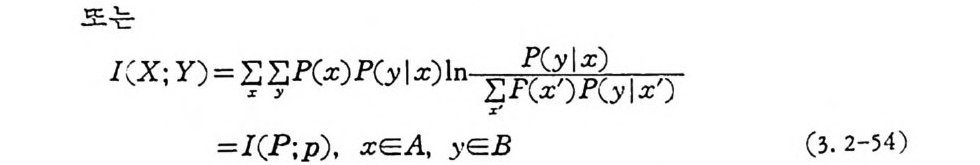 또는
또는
로 표기되기도 한다. 상호정보량을 입력확률분포벡터 p와채널천이 행렬 P의 함수로 표시하였다. 다음 정리에서 보듯이 I ( P; p)는 E 。(p,p ) 해석에 중요한 역할을 한다. 〈정리 3.2-2> p가 입력확률분:포이고 이산무기억채널에 대하여 I(P; p )>o 일 때 Eo (p,p)는 다음 목성 을 갖는다.
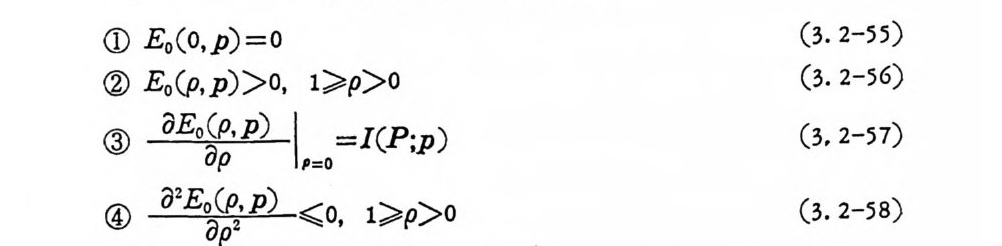 ® E。 (O, p) =O (3. 2 一 55)
® E。 (O, p) =O (3. 2 一 55)
식 (3. 2-58) 의 등식은 P;P (y기 x, ) *o 일 때 모든 i와 j에 대하여
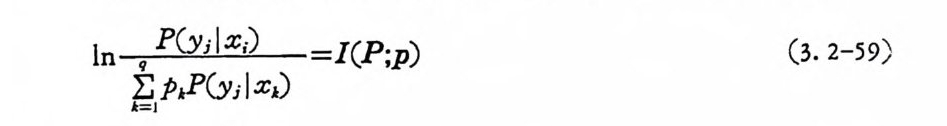 ln q p(y기 ~=l(P; p) (3. 2-59)
ln q p(y기 ~=l(P; p) (3. 2-59)
일 때 성립한다. 〈증명〉 식 (3.2-55) 는 p =O 로 놓으면 확인이 되며, 식 (3.2-57) 은 칙위해접서미 분입하의여의 p수 = Ob; 로>O 놓, c으;>면o . 알i= 수l, 2있, …다.. q일식 때 ( 3.H2o-l5d6e)r 울 의 증부등명식하은기·
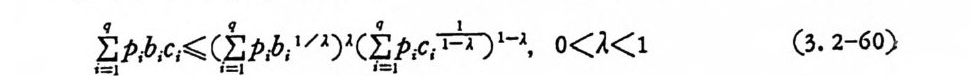 i=q[J: .-P ;-b ; C;¾ (,i=Iq: :l P, .b; I /A)A(iq~= lp .-C;눅 멱 o
i=q[J: .-P ;-b ; C;¾ (,i=Iq: :l P, .b; I /A)A(iq~= lp .-C;눅 멱 o
이고 둥석은 모든 i에 대하여 상수 d 가 존재하여
 p ‘b;1T =P,c i급1 d (3. 2-61)
p ‘b;1T =P,c i급1 d (3. 2-61)
로 각 j에 대하여 p가 증가함에 따라 비중가함수다. 따라서 E 。(p,p) 는 p에 관해 비감소함수이다. p =O 일 때 E 。 (o, p )=O 이며 p가 O 근 처에서 E 。 ( p,p)는 正値이므로 석 (3.2-56) 이 성립한다. 다음 식 3. 2-58 ) 을 증명하기 위해서 E 。(p, p)가 볼록함수임을 보인다 Holder 의 부등식 에 서
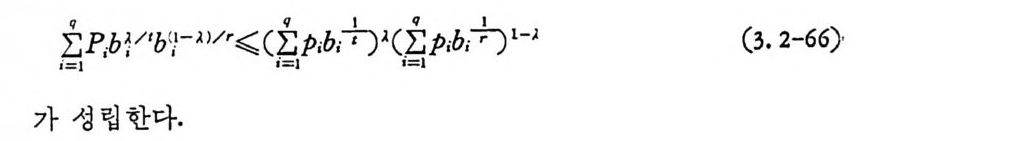 i2=q P l ,b} / Ib ( !-A)/r<(i=qE I P i b iT I) A(i=EO l pi b i수I )l-A (3. 2-66),
i2=q P l ,b} / Ib ( !-A)/r<(i=qE I P i b iT I) A(i=EO l pi b i수I )l-A (3. 2-66),
 一a1 =-tJ +.• 1r- J , a- l=tO (3. 2-67)
一a1 =-tJ +.• 1r- J , a- l=tO (3. 2-67)
로 놓으면 a(l-A)=r(l-8) 가 되고 석 (3. 2-66) 양변에 a 를 곱하어
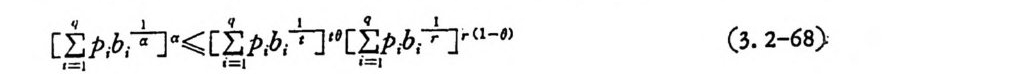 〔11:q= ;l P; b,.a l ] a<[ Iiq=; l p;b;I可 ',[Iiq=: I P ;b;I 可 r(I-6) (3.2-68)
〔11:q= ;l P; b,.a l ] a<[ Iiq=; l p;b;I可 ',[Iiq=: I P ;b;I 可 r(I-6) (3.2-68)
올 얻는다. 임의의 P1>0, P2>0, 1>0>o 에 대하여 Ps=P18+p ~( 1 -0) 로 정의한다. 그러면 t= I+P1t r=I+p 2, b =P (yj |x . ) 로 놓으면 ,1+ p 3 =1+0p 1 + (1-0)p2 =1 +O(t- 1) + (1-0) (r-1) =la+a( l- A) =a 이다. 그러므로 다음 식이 성립한다.
 E•'= I[ I;=u; Ip ;P (yj !X; ) 급門 1+ p 1 효:i= I [f;:=.I p;P (y jIX .) 志] U+P1) 0
E•'= I[ I;=u; Ip ;P (yj !X; ) 급門 1+ p 1 효:i= I [f;:=.I p;P (y jIX .) 志] U+P1) 0
가 된다• 이것은 Eo (p ,P) 가 볼록함수임을 증명하고 있다. 식 (3.2- 58) 의 동식이 성립하는 경우는 어떤 정수 d>o 가 존재하여 모든 j 에 대하여
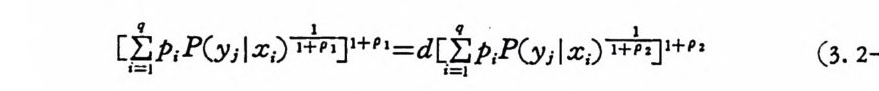 말?(yj lX;) 눕 l+ p 1=d[•=EqI pi. P( yj lx 注司 1+ p, (3. 2-73)
말?(yj lX;) 눕 l+ p 1=d[•=EqI pi. P( yj lx 注司 1+ p, (3. 2-73)
될 때 이 다. 식 (3. 2-71) 의 둥석 은 모든 j에 대 하여 P;P( y기 x;)>0 되는 경우이고 i에 대하여서는 P( y ;lx;) 가 X 제 독립적인 경우이다. 그러한 P (y ;Ix;) 을 식 (3.2-73) 양변에서 모든 j에 대하여 제거하면
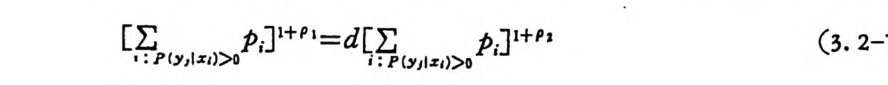 [2 pi]l+ p ' =d[2 PJ 1+ p , (3. 2-74)
[2 pi]l+ p ' =d[2 PJ 1+ p , (3. 2-74)
 된다. [ ]내는 일정상수이므로 a 라 놓고
된다. [ ]내는 일정상수이므로 a 라 놓고
로 표시할 수 있다. 그러므로 정리 3.2-2 를 증명하였다. 이 정리 중에서 중요한 사항은 E 。(p ,P) 을 p에 대하여 미분한 후 p =O 로 놓 으면 채 널의 入出力 X, Y에 대한 상호정보량과 일치된다 는 점이다 . 이를 그립 3.2-1 에 표시하였다• 채널용량은 다음과 감 이 정의하였 다.
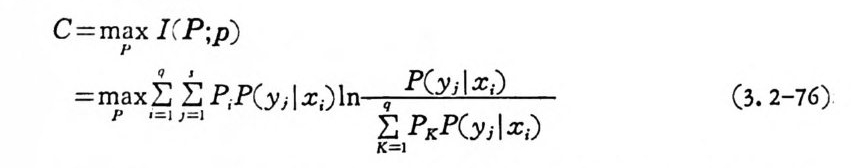 C=m~x I(P ;p)
C=m~x I(P ;p)
죽 이산무기억채널의 용량은 입력확률분포에 대하여 최대를 취한 _ 최대평군상호정보량이다. 용량 C 는 채널행렬 P의 함수이다. 상호 . 정보 량 이 최대 가 되는 입력확률분포를 p*로 놓고 p의 변화에 대한 : 指數部 E 。 ( p,p*)=rp묻 그립 3. 2-2 에 표지하였다.
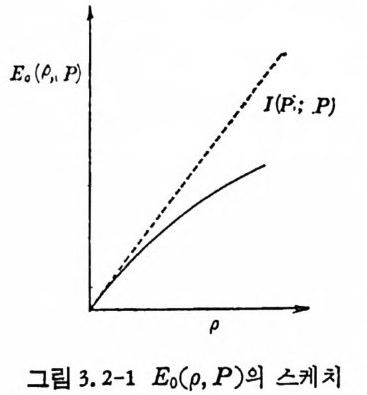 E,(P ,,P ) ’,, ,r
E,(P ,,P ) ’,, ,r
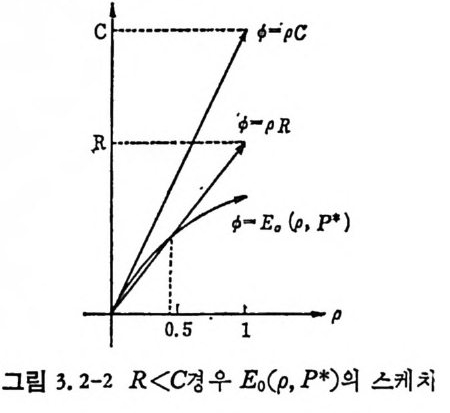 p
p
E 。(p,p*)는 볼록함수이고 E0 (p,p*)의 p =O 인 미분계수가 채널용 량이 다. R
 E(R) =mp~P x[E0( p,p)-pR ] > 0 (3. 2-77)
E(R) =mp~P x[E0( p,p)-pR ] > 0 (3. 2-77)
가 된다. 오울 E 는 N 이 증가함에 따라 지수함수적으로 감소 한 다. 그래서 다음 정리가 증명되었다. 〈정리 3.2-3> 채널이 무기여채널이고, C>o 일 때 오 울 이 다 음 식 에 상계되는 전송룰 R 의 N성 분으로 구성된 부호가 촌재한다.
 P,
P,
이것은 채널에 잡음이 있을 때 부호화정리로 Shannon 에 의해 처음 으로 다루어 전 것으로 채 널부호화정 리 (channel codin g t heorem ) 라 부른다. 부호화의 계일기본정리에 비하여 부호화의 제이기본 정 리라 고도부른다. 3. 2. 4 이원대칭채널과 고잡음채널의 誤率 일반적으로 상계식을 계산하기란 매우 복잡하다. 이원대칭 채널 에 서 p<승-일 때 오울의 指數部를 계 산해 본다.
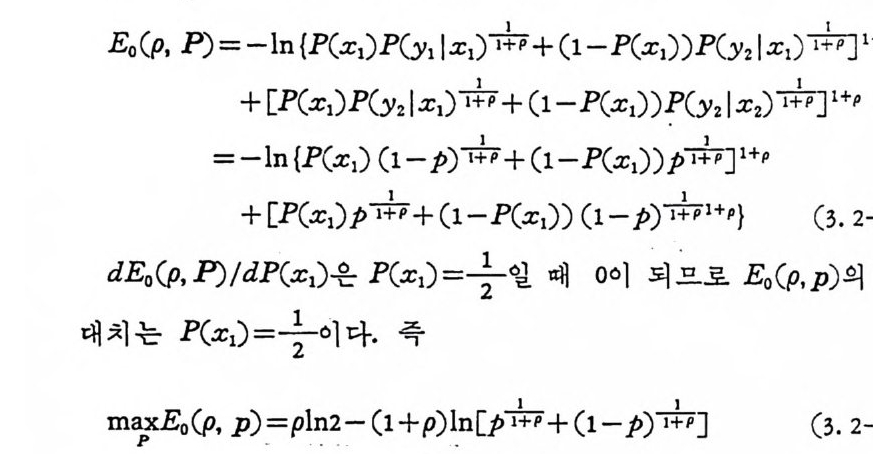 E 。(p, P) = -ln {P(x1)P(y I I 떠 곱짜 (1-P(x1))P(Y2 I따 눕〕 l+p
E 。(p, P) = -ln {P(x1)P(y I I 떠 곱짜 (1-P(x1))P(Y2 I따 눕〕 l+p
 0 과 1 의 발생확률이 동일할 때 Eo(P,P) 는 최대가 된다. 지금
0 과 1 의 발생확률이 동일할 때 Eo(P,P) 는 최대가 된다. 지금
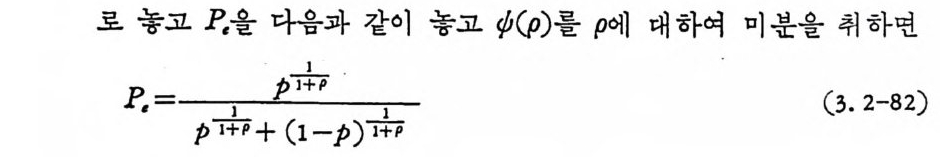 로 놓고 R 을 다음과 같이 놓고 ¢(p)를 p에 대하여 미분을 취하면
로 놓고 R 을 다음과 같이 놓고 ¢(p)를 p에 대하여 미분을 취하면
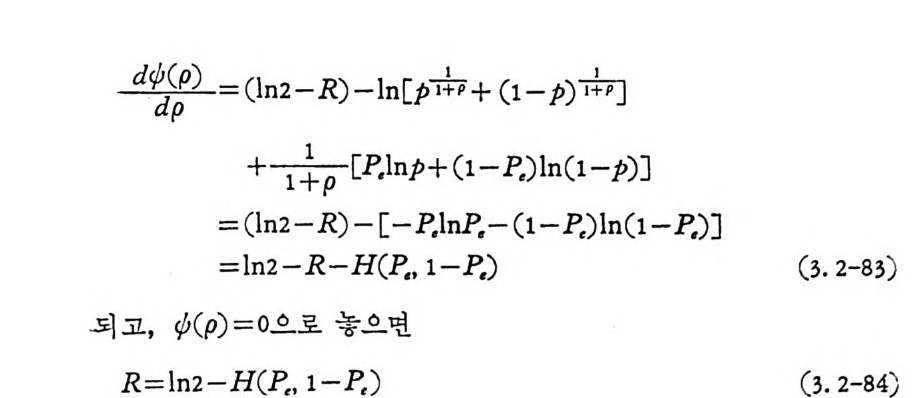 ~d=p (l n2-R)-ln[ p늙+ (1- p)눕
~d=p (l n2-R)-ln[ p늙+ (1- p)눕
된다. 이 둥석을 만족하는 p의 값이 cp(p)을 최대화한다. 다음과 감 이 각각의 구간에 대 하여 E(R) 값을 써 본다.
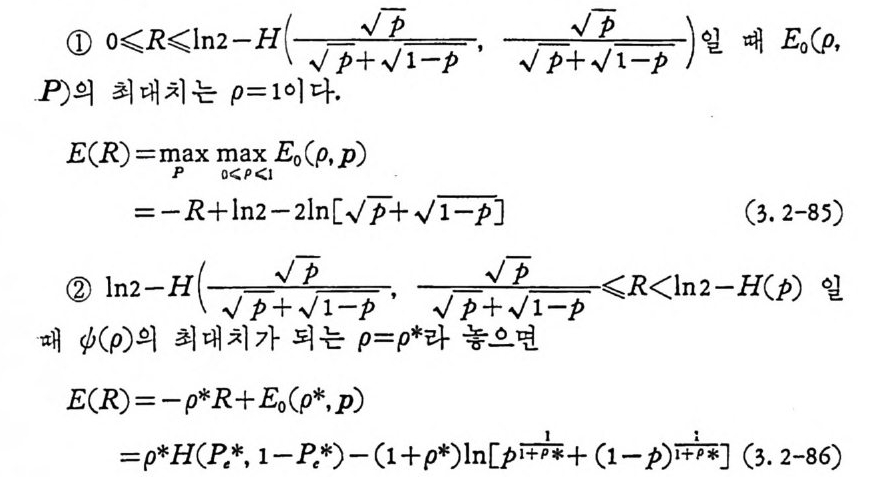 ® 。
® 。
이다. 위에서 보는 바와 같이 간단한 채널에 대하여서도 지수부를 구하는 것이 용이치 않다. 아원대칭채널의 용량은
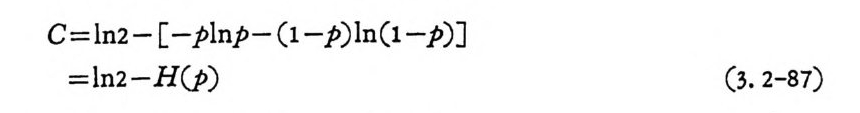 C=ln2-[- p ln p一 (1- p )ln(1- p)J
C=ln2-[- p ln p一 (1- p )ln(1- p)J
이 므로 C>R 일 때 ®과 ®로 구분하여 오울을 구하였 다. 다음은 채널이 高雜音인 경우를 고려한다. 여기서 고잡음채널이 란 Y j를 수신하는 조건부확률 P( y기 x; )가 입력 꾸와 거의 독립적인 상태를 말한다. 이를 수학적으로 표현하면
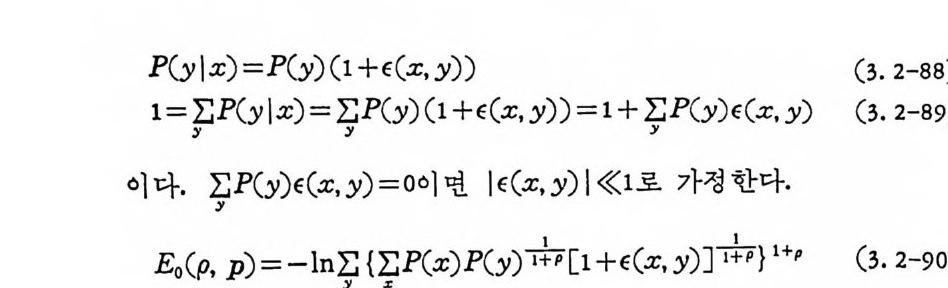 p(yl x)=P(y )( l+E(x,y )) (3. 2-88)'
p(yl x)=P(y )( l+E(x,y )) (3. 2-88)'
이고 IEI«1 이므로 E=O 인 Ta y lor 급수로 전개하여 이차승 이상온 제거하면
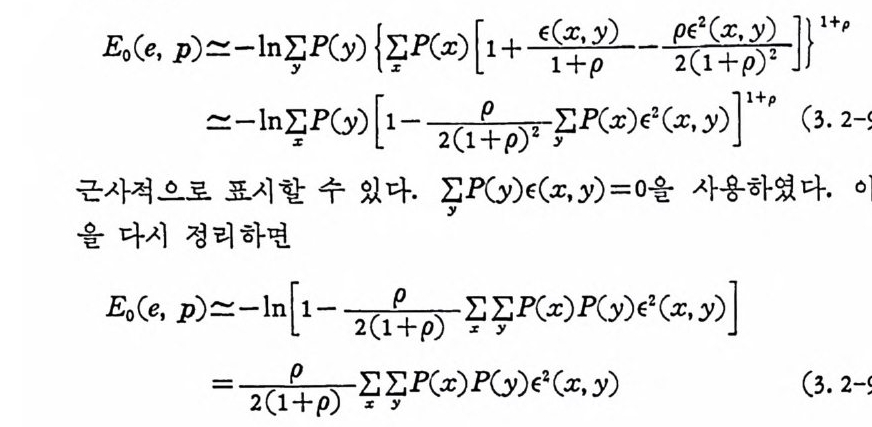 E 。 (e, p )=::-ln 꾸 P( y) {꾸 P(x) [1+ 靈-뭉隱]} 1+p
E 。 (e, p )=::-ln 꾸 P( y) {꾸 P(x) [1+ 靈-뭉隱]} 1+p
된다. 고잡음채널의 용량은
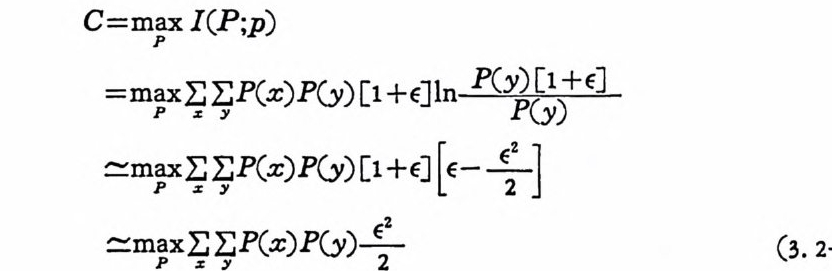 C=mp ~I(P;p)
C=mp ~I(P;p)
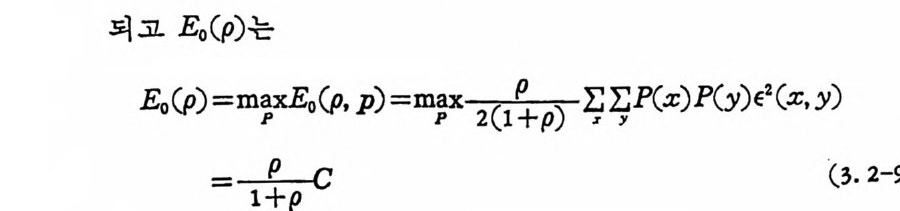 되고 E。 (p)는
되고 E。 (p)는
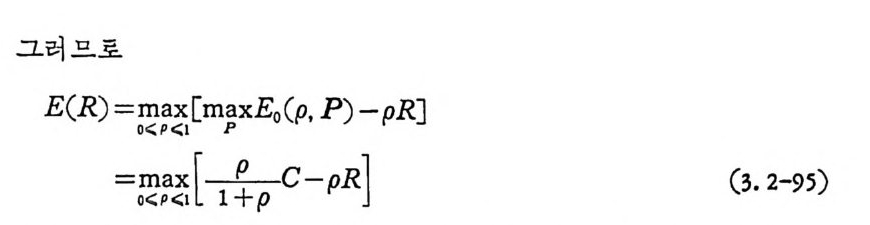 그러므로
그러므로
된다. 이 식은 가우스잡음이 있는채널에서의 식 (3.1-94) 의 지수부 와 동일하다. 즉 E(R) 가 최대가 되는 p는 운
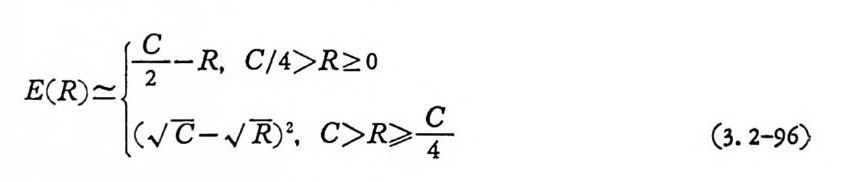 E(R) :::: l 운 -R, C/4>R 츠 0 c
E(R) :::: l 운 -R, C/4>R 츠 0 c
이 결과는 그림 3.1-3 에 표시되었다. 3.2.5 誤率의 下界 지금까지의 오울의 상계를 구하였다. 다음 오울의 하계를 구하고 이원대칭채널의 경우 오울의 하계를 계산해 본다. Cheno ff에 의한 이 결과는 Shannon 에 의 하여 확장되 고 여 러 사람들에 의 해 응용되 었다. 〈정리 3.2-4> P .( y)와 Pb( y)가 임의의 확률분포함수이다. YN 이 N차 원의 관측공간이고, YA 와 따가 부분공간일 때 YA 는 %의 보 집합이다. 만일 P.( y )Pb( y)-=l= O 이고 저어도 y EYN 이 촌재하면 각 s, o
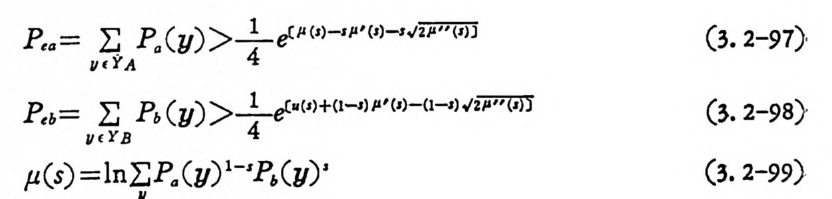 P,.= U.(EY A P.( y)>4」 g µ(3)- 마)--J로戶 (3. 2-97}
P,.= U.(EY A P.( y)>4」 g µ(3)- 마)--J로戶 (3. 2-97}
만일
 YA= {yll n(P0(y) /Pa(y) )<µ'(s)} =Ys (3. 2-100)
YA= {yll n(P0(y) /Pa(y) )<µ'(s)} =Ys (3. 2-100)
일 때 Pa(Y) 의 모멘트생 성 함수는 다음과 같다.
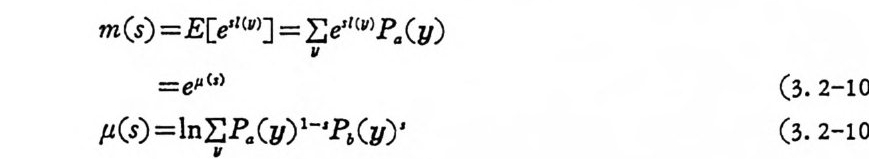 m(s) =E[e•1<11>] = :Ee •1<11> P0 (y)
m(s) =E[e•1<11>] = :Ee •1<11> P0 (y)
 s 에 대 하여 µ(s) 를 2 번 마 분하면
s 에 대 하여 µ(s) 를 2 번 마 분하면
 만일 s=O 이면 P,( y )=Pa(Y) 되고, s=l 이면 P,( y )=Pb( y)이다. 또
만일 s=O 이면 P,( y )=Pa(Y) 되고, s=l 이면 P,( y )=Pb( y)이다. 또
이다. P,( y)에 대한 尤度函數比 l( y)의 평균치 및 분산을 구하면
다음과 같다.
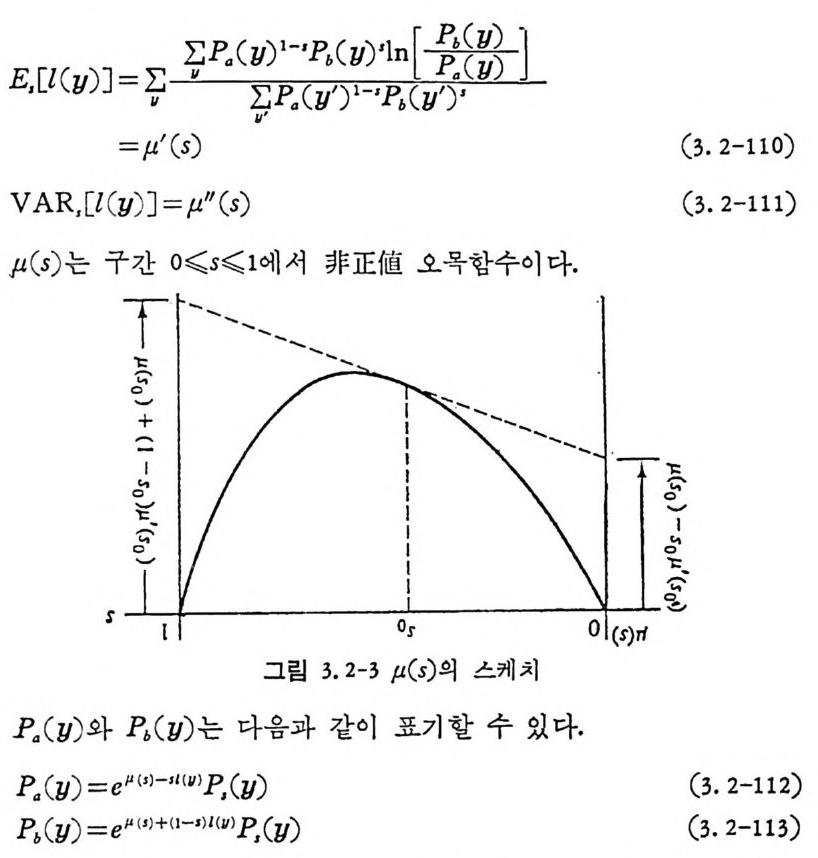 E,[l(y ) ]= I; 꾸 P.( y )EIR( y )'ln 濁응]
E,[l(y ) ]= I; 꾸 P.( y )EIR( y )'ln 濁응]
尤度 比 l ( y)가 쓰레쉬홀드(t hreshold) µ'(s) 로 판정할 때 판정영 역 YA 는 다음과 같은 집합으로 구성된다.
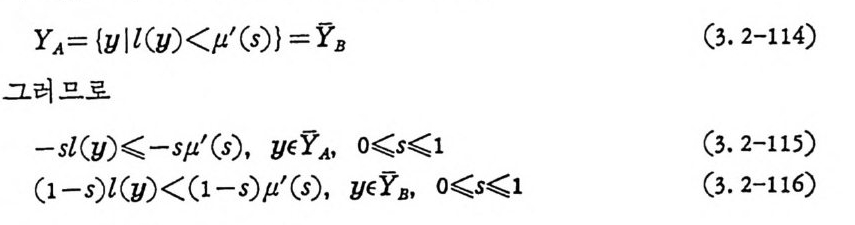 YA= {yll (y) < µ'(s)} =Y8 (3. 2-114)
YA= {yll (y) < µ'(s)} =Y8 (3. 2-114)
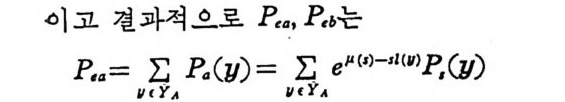 이고 결과적으로 R.,P‘b 는
이고 결과적으로 R.,P‘b 는
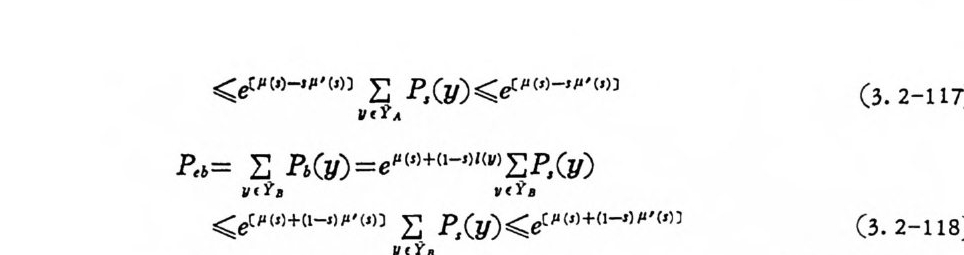
이 다. Cheb yshev 의 부동식 을 사용하여 부분공간 Y를 7 정 의 한다 . Cheb y shev 의 부등식 은
 P[ I X 규 lx l >,r (J x]< 국r1 (3. 2-119)
P[ I X 규 lx l >,r (J x]< 국r1 (3. 2-119)
이고 µx 와 6x 는 X의 평군치 및 분산이고 r 은 임의의 수이다. r=.../2 로 놓고 집합 Y, 를 정의한다.
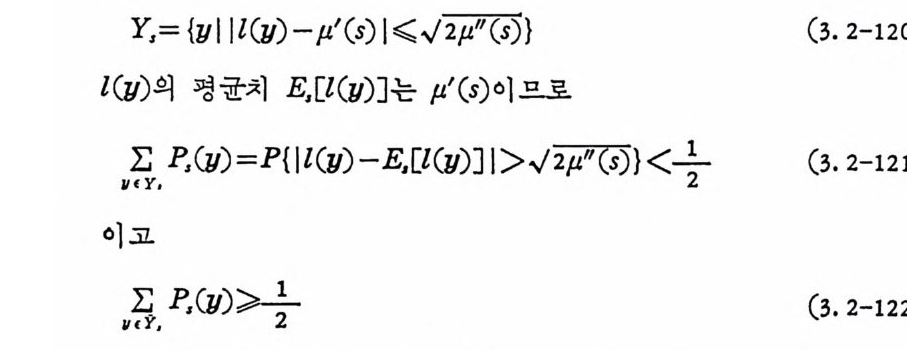 Y,= {yl ll(y) - µ'(s) I <.J2j}'(s)} (3. 2-120}
Y,= {yl ll(y) - µ'(s) I <.J2j}'(s)} (3. 2-120}
된다. P,. 와 P,b 의 하계 는 부분공간을 합한 경 우
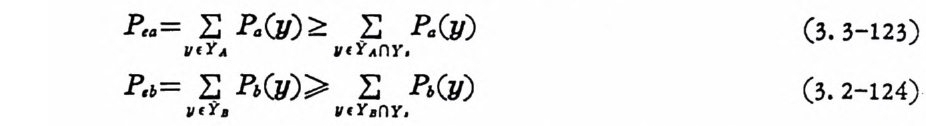 P,. = UI,;” P. (JJ) ;;;:: 'tIm; y . P. (JJ) (3.3-123)
P,. = UI,;” P. (JJ) ;;;:: 'tIm; y . P. (JJ) (3.3-123)
의 식이 성립한다. 그러나 |l( y )-µ'(s)l>../ 2µ강 5 는 모든 y €Y, 에. 대하여 다음 식과 동일하므로
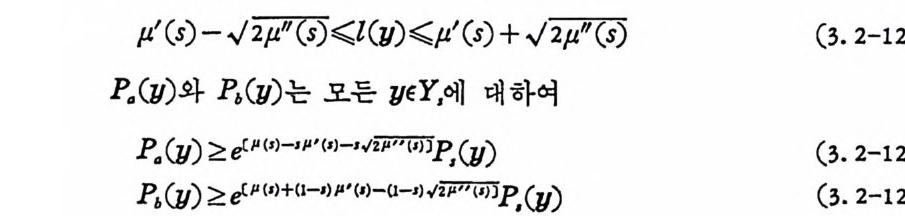 µ'(s)- ✓ 2µ쩡
µ'(s)- ✓ 2µ쩡
 -성 립한다. 그러므로
-성 립한다. 그러므로
석 (3. 2 - 101 ) 과 (3. 2-102) 를 Cheno ff한계 (Chenoff bound ) 라 부론 다. 만일 %이 두 통보의 수신벡 터 의 집 합이 고 R (y)와 Pl y)는 尤度함수비를 구성하는 확률밀도함수이면 YA 와 따는 각기의 판정 영역이 된다. Pca 와 P,b 는 두 통보에 대한 오울이다. 만일 µ'(s)=O 이 면 Pca 와 P,b 에 대 한 Cheno ff한계 는 같다. 정리 3.2-4 를 이원대칭채널에 응용하여 하계를 계산해 본다. 송 신벡 터 Xj = (xiI, Xi 2. …, X i N) 이 고 수신벡 터 y= (Yi , Y2. …, YN) 일 때 Y j수 X iJ이면 조건부천이확률은 P 이고 Y j =X ij이면 천이확률은 (1-p) 이다. 송신벡터와 수신백터 사이에 dm 개의 위치가 서로 다르면 P( y lx;) 는
 P(y I x ;) =pdm (l-Py -d m (3. 2-135)
P(y I x ;) =pdm (l-Py -d m (3. 2-135)
이다. dm 은 입력벡터와 출력벡터 사이의 해밍거리이다. P (]J)를 군 일확률분포로 하면
 .P(JJ) =i-N, yE YN (3. 2-136)
.P(JJ) =i-N, yE YN (3. 2-136)
이 고 정 리 3. 2-4 에 서 P.(Y) 를 P( y)로 Pb(Y ) 를 P( y l x; ) 로 놓으면 YA 는 Yj, YB 는 Y제 해 당된다. 동보 i에 다음 두 부둥식 중 적 어 도 하나는 성립한다.
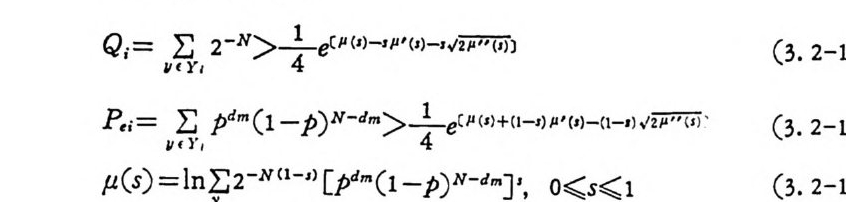 Qi= ll'E; y , -군 >~~ e4 - µ(1)-1µ'(1)-1 范元) (3. 2-137)
Qi= ll'E; y , -군 >~~ e4 - µ(1)-1µ'(1)-1 范元) (3. 2-137)
그러나 X 논· N차 원 이원벡터이고 y는 모든 벡터의 집합에 대해 합을 취하므로 dm=K, o
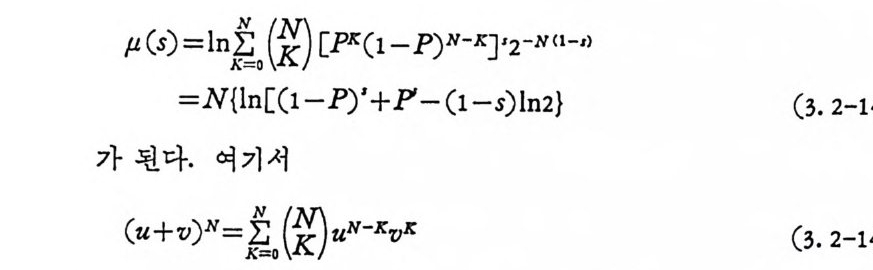 µ (s) =ln 요(衍 [PK . (1-P )H-사 '2-N(I-I)
µ (s) =ln 요(衍 [PK . (1-P )H-사 '2-N(I-I)
을 사용하였다. YI 는 상호배 반 판정 영 역 이 .31. YN 에 는 2N 개 의 y가 존재하므로
 iE=M I Q 1 =iEM= I VE< Y ,r N=1 (3. 2-142)
iE=M I Q 1 =iEM= I VE< Y ,r N=1 (3. 2-142)
 이고, 임의의 i'에 대하여
이고, 임의의 i'에 대하여
로 쓸 수 있 다. µ ( s ) 을 s 에 관하여 미분하면
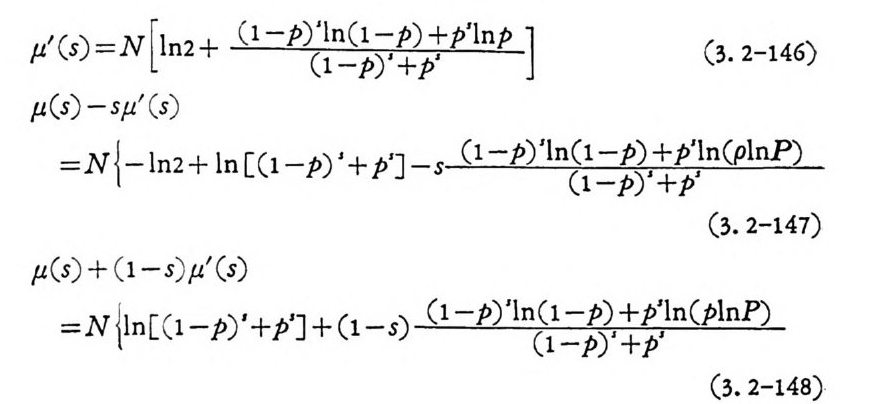 µ'( s) = N [ln 2 + ~ )』 폰 ;Y?『 'ln p ] (3. 2-146)
µ'( s) = N [ln 2 + ~ )』 폰 ;Y?『 'ln p ] (3. 2-146)
이 것 을 식 (3. 2 -144) 와 (3. 2-145) 에 대 입 하여 정 리 하면
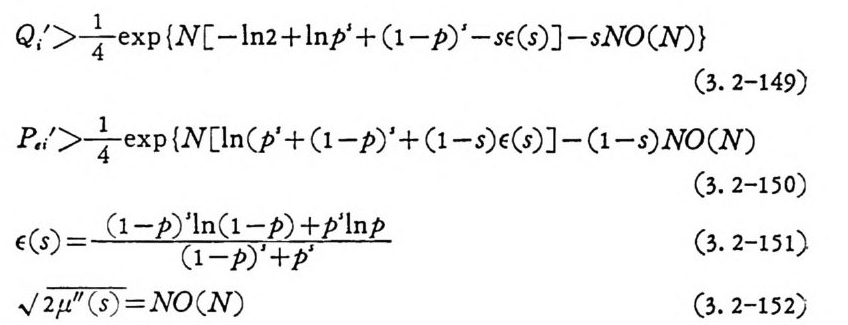 Qi' > --1t -ex p {N[-ln2+lnp '+ (1 -p) ' -sE(s)]- s NO(N )}
Qi' > --1t -ex p {N[-ln2+lnp '+ (1 -p) ' -sE(s)]- s NO(N )}
되 며 , NO ( N ) 은· N 이 무한대 로 접 근할 때 NO(N) 은 0 으로 접 근하 며 근사적으로 NO ( N) :::: 1/,.;N 이다• S 대신 1/l+ p울 대입하여 정 리 하여 하 계 를 구하여 보면 다음과 같다.
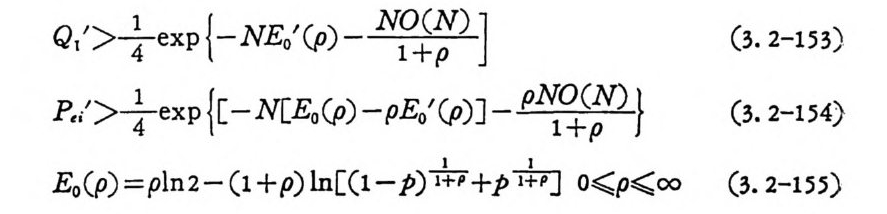 Qi' >+ex p {-NE 。 I (p)_ ~] (3. 2-153)
Qi' >+ex p {-NE 。 I (p)_ ~] (3. 2-153)
3.3 源符號化 정리 3. 3. 1 蓋曲洞]度, 源符號化 정 리 지금 정보원알파벳을 A= {a1 , a2. …, aq }. 사용자알파벳 을 B= {b., .IJ2 . .. , 이 일 때 정 보원과 사용자간의 至曲測度 (d i s t or ti on measure) 를 정의하려 한다. 정보원의 문자계열 x=(x1, x 2. …, xN) , X;EA, i= 1. 2, ... ,N 과사용자의 문자계열 y=(y l, y 2. … YN ) 일 때 왜곡축 도를 다음과 같이 정의한다.
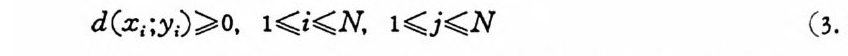 d(x 따,J;:;;;i: o, 1<;i< ;N, 1<;j< ;N (3. 3-1)
d(x 따,J;:;;;i: o, 1<;i< ;N, 1<;j< ;N (3. 3-1)
源使用者雙 (source - user p a i r) 이 동일한 알파벳을 사용할 때 xi= y, 이면 d(xi;Y j ) =O, x i *yi이면 d(x 따 ';)=l 로 놓을 수 있다. 또한 예 로써 d(x;;y; ) = (x;- y;)2으로 놓으면 문자를 전폭으로 표시 할 때 원 · 사용자쌍의 전폭이 동일하면 d(x;; y ;)=O 이고 전폭의 差가 크면 .d(x;; y;)는 진폭차의 자승에 비례한다. 죽 양자간의 거리에 관해서 무게를 부여함울 말한다. 일반적으로 유한수 do 가 다음과 같이 촌 재한다고 가정한다.
 o
o
정 보원의 알파벳 집 합 A= {ai, a2. …, aq } 이 고 각 문자의 발생 확률 이 P(a;) =P;, i= l, 2, …, N 일 때 정 보원의 문자계 열 x= (떠고 :2, ••• , .:X N) 의 확물이
 P(x) = ilN=l IP (x;) (3. 3-3)
P(x) = ilN=l IP (x;) (3. 3-3)
로. 표시될 때 정보원은 기억이 없다라고 말한다. 정보원계열 X= (다다 · · ··'N) 과 사용자계열 u=0l, y 2. … ,YN) 간의 왜곡측도의 평 균은
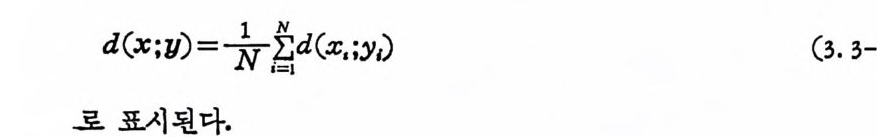 d(x; y)=1下 검N d(x 찌 (3. 3-4)
d(x; y)=1下 검N d(x 찌 (3. 3-4)
C={ yi, Y2, …,y . 'f}이 N7 사 문자로 구성된 M 개 계열의 집합일 때 , c 를 부 호, y,e c, i =1,2. … ,M 을부호어라부른다. q N 개의 정 보원 계열 중 평균 왜 곡측도가 최소가되도록 M 개의 부호어 Y;EC 로 부호 화한 다. 다시 말해서 임의의 x 에 C 의 부호어 중 평군 왜 곡측도가 가 장 작 은 y올 대응하여 q N 개의 계열이 M' 개의 계열로 압 축된다. 레 이 트 디 스 토숀 이 론 ( ra t e dis t o r tio n t heor y)에 서 는 이 것 을 원부호화 라 하며 C 를 源符號 ( source code ) 라 부른다. 최 소왜곡측도를 다음 과 같 이 표기한다 .
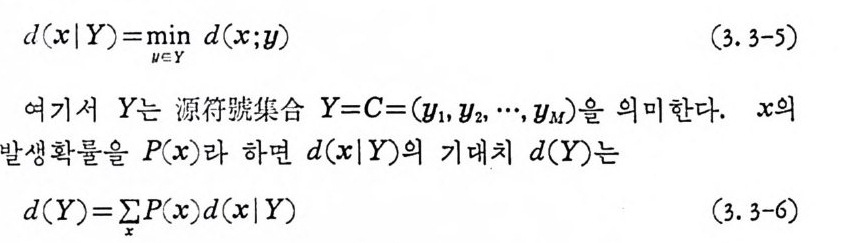 d( x l Y) = mi n d( x ;y) (3. 3-5)
d( x l Y) = mi n d( x ;y) (3. 3-5)
이고, 2 은 q N 번 행한다. 전송물 R 은 R=lnM/N으 로 정의되고, 데 이 타압축의 경 우 전송률 R 이 작으면 좋다. d(Y ) 를 계 산하는 것 온 정 보전송의 경우 오울 R 을 계산하는 것과 유사하고 일반적으로 용이치 않다. 어떤 허용치 D 가 주어졌을 때 d(Y )< Do.J. 조건하에 R을 작게 하는 문제가 발생한다. 정보원계열과 사용자계열간의 임의의 조건부확물
 P( x l y)= ;nN= IP (y ;l x ;) (3. 3-7)
P( x l y)= ;nN= IP (y ;l x ;) (3. 3-7)
를 도입한다. 이 확률은 천이확률의 형태와 동일하며 상호독립적이 다 이 조건부확률에 물리적 의미를 부여치 않고 단지 평군왜곡의 한계를 유도하는 데 사용한다. 사용자부호 Y 일 때 평군왜곡은
 d(Y)=I ;P( x)d(xl Y)
d(Y)=I ;P( x)d(xl Y)
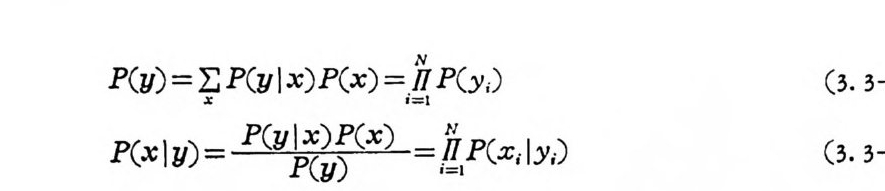 P(y) = I: P(y I x)P(x) = lNl P(y; ) (3. 3-10)
P(y) = I: P(y I x)P(x) = lNl P(y; ) (3. 3-10)
로 정한다. x 와 y에 대한 합을 두 개의 상호배반영역으로 분리하 여 다음과 같은 함수를 정의한다.
 rp (x, y ;Y)= 『' d(x;y) < d(XIY)
rp (x, y ;Y)= 『' d(x;y) < d(XIY)
d(Y) 의 상계식에 대하여 렌돔부호화를 행한다. Y= {y1, y2, …. u 퍼
 의 확물을
의 확물을
가 된다. 그런데 IY; IU; P( Y ) P( y) rp (x, y ; Y) = UII; 파UZ •U IM: IU : 대kM=I P(] J.) P(y) rp( x, y ; Y) =P[d(x, y)< mi n( d(x, Y1)d(x, Y2) …d ( x, YM))] <꼬1 <下1 (3.3-23) 이다. 그러므로 d(Y) <;d(P) +d0MP-1I ; [I;P( u)Q( x ly)1 1PJ P x u =d(P) +d0MP-1 {江I; P (y)Q (x ly) l'P]P } N (3. 3-24) x u 으로 표현된다. d(Y)
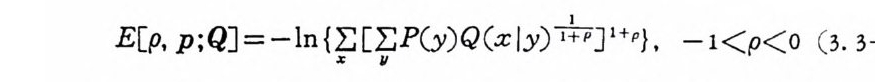 E 秘 p;Q〕=크 n{ Ix ;[Iu; P (y ) Q (xl y ) 尹]때. -1
E 秘 p;Q〕=크 n{ Ix ;[Iu; P (y ) Q (xl y ) 尹]때. -1
된다. E( p,p;Q)는 부호화정리에서 렌돔부호지수부와 동일한 표 현 이고, 다른 점은 부호화정리에서 p는 0 부터 1 까지 변하 였으 나 지 금 온 0 부터 _1 까지 변한다. 부호화정리에서는 P ( y j x ) 는 고정 되고 P ( x) 을 변하였으나, 지금은 {P ( y j x ) }을 변함으로써 P ( y ) 와 Q ( 미y ) 에 영향을 준다. Q= {Q ( :x l y ) }을 후행채 널 ( backward channel ) 이 라 부른다. 상호정보량은 I(X;Y ) =l ( Y;X) 이므로 P ( x ;) P ( y』 X, ) = P(yi )Q( x; IY;) 을 이 용하면 다음과 같이 표현할 수 있 다.
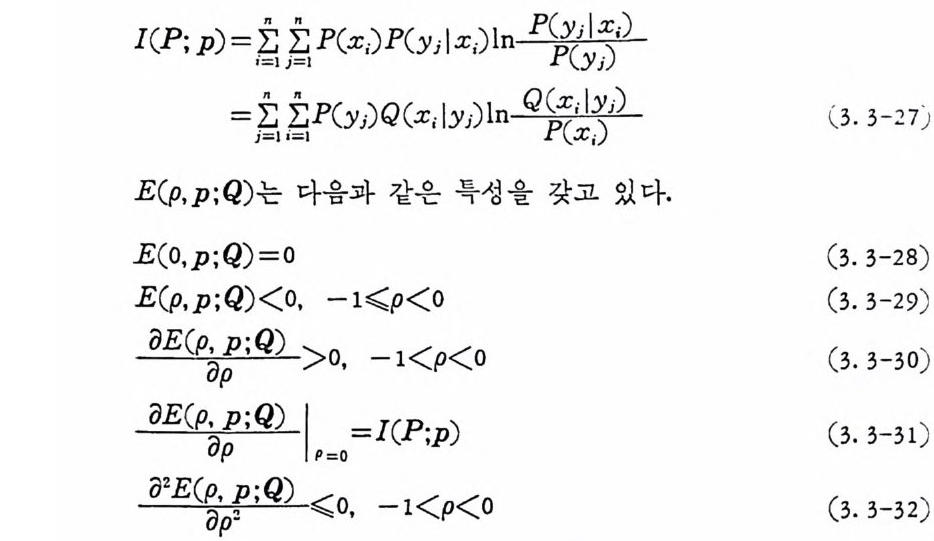 I(P; p) = .;=tl ij =t I P(x;)P(y i 巳 )ln4 룬
I(P; p) = .;=tl ij =t I P(x;)P(y i 巳 )ln4 룬
이 증명 은 정 리 3. 2-2 와 동일하므로 생 략한다. 식 (3. 3-25 ) 에 서 보는 바와 같이 E( p,p;Q)는 크면 좋다. 다음과 같은 조건부확률의 집합을 정의한다.
 PD= {P( y|x ) ID(P)<.;D} (3. 3-33>
PD= {P( y|x ) ID(P)<.;D} (3. 3-33>
 으로 놓으면 상호정보량은 P 의 연속함수이고 집합 PD 내에 최대차
으로 놓으면 상호정보량은 P 의 연속함수이고 집합 PD 내에 최대차
가 된다. 그러므로 다음 정리가 성립한다. 〈 정리 3. 3-1> (源符號化定理) 기억이 없는 정보원에서 임의의 수 o>o 가 존재하고 R>R(D)+o 이면, 임의의 e>o 에 대하여 부호길 이 N을 충 분히 크게 하면 平均至曲 d(Y) 가 다음을 만족하는 부호 Y 가 존재한다.
 d( Y ),< D +e, R>R(D) (3.3-39)
d( Y ),< D +e, R>R(D) (3.3-39)
* 참고문헌 Arim oto , S. , Comp u ta tion of Random Codin g Exp o nent Functi on s, IEEE Trans. Info r m. Theory, Vol. IT-22, pp. 665-71, 1976. Arim oto , S. , On the Converse to the Codin g Theorem for Di sc rete Me·
mory le ss Channel, IEEE Trans. Info r m. The or y. , Vo l. IT-19, pp. 357-9, 1973. iBe rge r, T., Ra te Di st o r tio n Theo r y, Prenti ce -H all, 1971. Blahut, R.E ., Hy po th e sis Testi n g and Info r mati on Theory , IEEE Trans Info r m. T_h eory, Vol. IT-20, pp. 405-17, 1974 . Chernoff , H., A Measure of Asym p tot i c Ef ficien cy for Test s of a Hy p o t· hesis Based on a Sum of Observati on , Ann. Math . Sta t i st. , 23, pp. 493-507, 1952. ·Co urant, R and Hi lb ert , D. , Meth o d of Math e mati ca l Phy s ic s , Vol. 1, Inte r scie n ce, New York, 1959. Fein s te i n , A., Foundati on of Info r ma tion Theo r y, McGraw- H i ll , New York, 1958. Fein s te i n A., A New Basic Theorem of Info r mati on Theory , IRE Trans. Info r m. Theory, Vol. PGIT- 4, pp. 2-22, 1954. ·Gallage r, R.G ., Info r m ation Theory and Relia b le Communic a tio n , W ile y , New York, 1968. {ialla ge r, R. G. , A sim p le Deriv a ti on of the Codin g Theorem and Some Ap plica ti on , IEEE Trans. Info r m. Theory, Vol. IT-11, pp. 3-18, 1965. Jel in e k, F., Evaluati on of Exp u rga te d Bound Exp o nents , IEEE Trans. Info r m. Theory, Vol. IT-14, pp. 501-5, 1968, Jel in e k, F., Probabil is tic Info r mati on Theory, McGraw-Hi ll, New York, 1968. •Om ura, J.K., A Source Codin g Theorem for Di sc rete - ti me Source, IEEE Trans. Info r m. Theory, Vol. IT-19, pp. 490-8, 1973. -Om ura, J.K., A Lower Boundin g Meth o d for Channel and Source Codin g Probabil ities , Info r m. Cont. , Vol. 27, pp. 148-77, 1975. Shannon, C.E., Cert ain Results in Codin g Theory for Nois y Channels, Info r m ation and Contr o l, Vol. 1, pp. 6-25, 1957. :Sh annon, C.E . , Codin g Theor~m for a Disc rete Source wi th a Fid e li ty Crite r io n , IRE Na tion al Conv. Rec. Part 4, pp. 142-63, 1959. Shannon, RE., Gallage r , RG., and B'e r lekamp , E.R., Lower Bounds to Error Probabil ity for Codin g on Disc rete Memoryl e ss Channels, Info r m ation and Contr o l, Vol. lo p p. 65-103 and pp. 522-52, 1967. St iglitz, I.G , Codin g for a Class of Unknown Channels, IEEE Trans. Info r m. Theory, Vol. IT-12, pp. 189-95, 1966.
Van Trees, H. L. , De te c t i on , Esti ma ti on and Modulati on Theory, Part 1, W ile y, New York, 1968. Vi ter bi, A.J., Perfo r mance of an M-ary Orth o g o nal Communic a ti on Sy st e m Usin g Sta t i on ary Sto c hasti c Sig n als, IEEE Trans. Info r m. Theory, vol. IT-13, pp. 414-22, 1967. Vi ter bi, A.J. and Omura, J.K., Prin c ip le of Di gital Communic a ti on and Codin g , McGraw-Hi ll , New York, 1979. Wozencraft , J.M . and Jac obs, I.M ., Prin c i ple s of Communic a ti on Eng ine e- rin g , W ile y, New York, 1965.
제 4 장 부호화와 복호화의 기법 4. 1 線形符號, 巡回符號 4. 1. 1 線形블록符號의 구조 전장에서 우리는 전송물 R 이 채널용량 C 보다 적을 때 임의로 적 은 부호오울을 갖는 부호의 존재에 대한 정리를 고찰하였다. 부호 이 론도 Shannon 의 부호화정 리 에 근원을 두고 있으며 Slep ian , Ham-mi ng , Muller, Reed, Pete r son 둥에 의 하여 체 계 화되 었 다. 부호이 론 의 목적의 하나는 정보전송을 충실히 이행하기 위한 符號化 (enco d i n g)와 復號 化 ( decod i n g)의 방법을 연구하는 데 있다. 먼저 線形 블록符號(li near block code) 를 취 급하고, 나중에 巡回符號 (c y cl i c · code) 에 대하여 설명한다. 앞으로 설명하는 모든 부호는 0 과 1 로 구성된 二元符號 (b in ar y· code) 만을 취급한다. k 개의 0 아니면 1 로 구성된 通報볼록 (mes sag e block) 이 符號器 (encoder) 를 통하여 n 개의 0 아니면 1 로 구 성 된 부호어 (code word) 로 변환된다. 부호기 에 서 n-k 의 패 리 티 검 사비 트(p ar ity check b it)가 k 의 정 보비 트(i n fo rma ti on b it)에 추가 · 된다. 추가된 패리티검사비트는 정보를 갖고 있지 아니하며 에러가 1 발생하였을 때 에러를 검출 또는 정정할 수 있는 능력을 가진다. u=(u1, u 2, … ,ak) 를 통보블록이라 하면 간의 통보가 촌재하며, . (ul,u2. … ,Uk) 의 정보비트에 n-k, n>k 의 패리티검사비트를 일정 한 법칙에 따라 추가되며 간의 부호어 x=( .x h .x z, …,.x 3 을 발생
시킨다. 이렇게 발생한 강의 부호어를 블록부호 라 하며 @ k ) 부호 로다. 표n시 을한 다부.호 길물이론 ( cUod;e= Ol,e n1g, thi)= , l,R 2=, … 下k, 율k, x符, =號O , 率1, ( cio=d el , r2a. t …e ) ,이 n 라이 부른다. 線形블록符號 (n, k) 는 간의 부호어 로 구성 된 볼록 부호로 k 정 보비트의 1 차결합으로 구성된다. 그래서 (n,k) 부호의 부호화방정식 은 다음과 같이 표기할 수 있으며, 이렇게 하여 구한 불록 부호를 線 形블록符號라 부른다 .
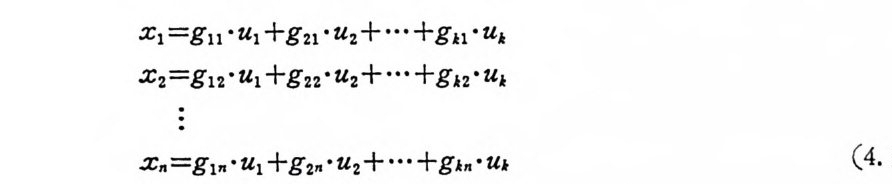 ..xxl2 = = gg1112 •• UU11 ++gg2212 •• UU2z ++ ……++ gguu •• U Uii
..xxl2 = = gg1112 •• UU11 ++gg2212 •• UU2z ++ ……++ gguu •• U Uii
係數, gjj는 0 이거나 1 이며 연립방정식에서 加 算과 乘算은 法울 2(modulo 2) 로 하여 행한다. 죽 l+l=O, 1+0=0+l=l, O+O=O, 0·1=1•0=0, O•O=O, 1·1=1 이다. 가산과 승산은 EB, X 을 사용하 기도 하나 편의에 의하여, +, ·울 사용한다. 위의 연립방정식을 행 렬식으로 표기하면
 x=uG (4. 1-2)
x=uG (4. 1-2)
강의 부호어가 서로 상이한 부호어를 형성하려면 G 행렬의 k 행이 일차독럽이어야 한다. 자동적으로 이 조건을 충족시키기 위하여 G 행렬을 다음 형태로 만든다.
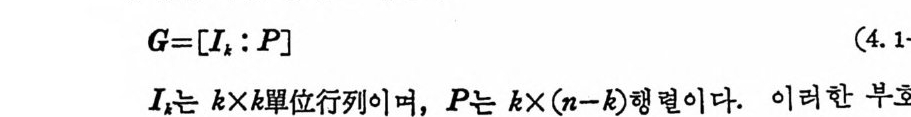 G= [l, : P] (4. 1-4)
G= [l, : P] (4. 1-4)
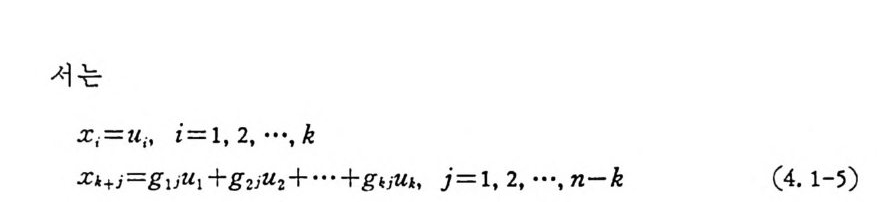 서는
서는
 G〈 예= 4[.:1 -: 1>: 生[ 成\ 行] 列이 다음과 같다.
G〈 예= 4[.:1 -: 1>: 生[ 成\ 行] 列이 다음과 같다.
이다. 이 부호는 (6, 3 ) 組織符號 이고, 23=8 개의 부호어는 다음과 같 다.
 통 보 부호어
통 보 부호어
모든 線 形符 號語 는 U1=U2=•• • =u1=0 일 때 X1= :X 2= …=:x n=O 인 零 符 號 語를 포함하고 기 타 21- 1 개의 부호어는 영 부호어 가 아니 다. (n, k) 組織 符 號 를 x=[x1 : X p]의 부호어로 표시하면 Xr=[:xi , :Xz , 빽 ·•,:X 1] 는 정보벡터이고 X p=[:x사1t X1+2, •••, X ]은 패리 티 겁사벡터이
이냐 부호어의 처음 k 비 트는 정보비트와 같고, 나머지 n-k 바트는 패 리티 검 사비트이다. 이 러한 특 성을 가진 (n , k) 부호를 組織 符 號 (sy s t e m ati c code) 라 부른다.
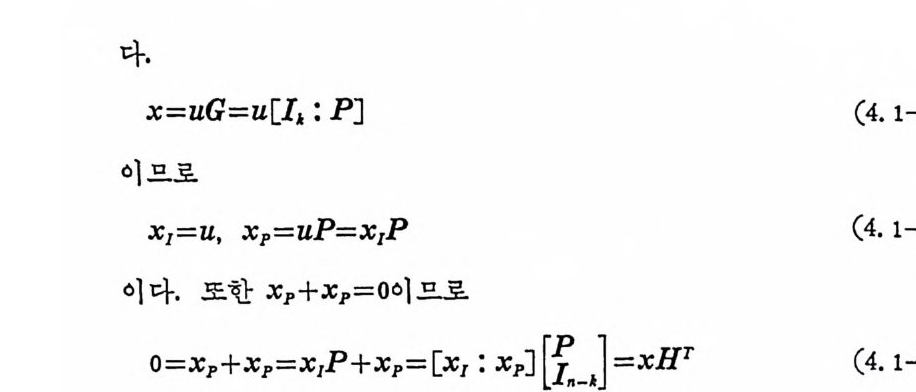 다.
다.
이다. 다시 말해서 X 가 부호어가 되기 위해서는 xHT=o 이어야 된 다. 행렬 HT 는 H 행렬의 傳置行列이고, H 행렬은 (n-k)Xn 행렬로 패 리 티 檢査行列 (pa rit y check matr i x ) 이 라 부르면 다음과 같다.
 H= [PT : I.-1] (4. 1-9)
H= [PT : I.-1] (4. 1-9)
된다. 이 예에서는 P=PT 이나 일반적으로 진실이 아니다. xHT=o 이므로 다음과 같은 3 개의 연립방정식이 성립한다.
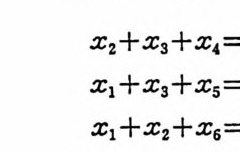 x2+x3+x,=O
x2+x3+x,=O
이 연립방정식은 미지수가 6 개이고, 방정식은. 3 개분이다. 이 방장 식 을 만족시 키 는 Xi, Xz, X3, X4, 따고 :6 을 구하면 8 개 의 부호어 를 구할
 수있다. 죽
수있다. 죽
은 3 개의 연립방정석을 만족시킨다. 만일 송신기로부터 x 를 잡음이 있는 채널을 통하여 송신할 때 수 신벡터 y는 일반적으로 x -:t:-y이다. 만일 잡음이 없는 채널을 통과 할 때에는 송신벡터 X 와 수신벡터 y는 동일하다. 부호이론의 목적 은 잡음이 있는 채널을 통하여 수신된 수신벡터 y로부터 x 를 찾아 내 는 일이 다. e= [ei , e 2, ... , e 』을 채 널에 러 벡 터 (channel error vecto r ) 라 정의하면 다음 관계석이 성립한다.
 y= x+e (4. 1-10)
y= x+e (4. 1-10)
울 만족한다. 즉 e 의 추정치 e 을 알면 오울 구할 수 있다. y가부호 어가 되려면 y HT=0 을 만족하여야 한다. 따라서 y HT 논어떤 의미 를 지니고 있다. 다음 신드롬 (s y ndrome) s 를 다음과 같이 정의한 다.
 s=y H 7 (4. 1-13)
s=y H 7 (4. 1-13)
이고 y I 는 수신정보벡터 yl =[ Y I,y 2 .… ,l] 이고 YP 는 수신패리 티 맥 터 yp= [YH1 tY H2. …,y n] 이다• 신드롬을 구하기 위해서는 수신정보 벡터 y 1 에다 P를 곱하여 수신패리티벡터 YP 를 가산하면 된다• 채 널에러벡터를 e=[e1 : e p]로 표시하면
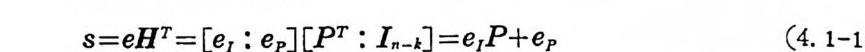 s=eHT= [e1 : e 가 [PT : I.-1] =e1P+ep (4. 1-16)
s=eHT= [e1 : e 가 [PT : I.-1] =e1P+ep (4. 1-16)
이다. s=eH 정서 e 의 강의 추정을 s 의 코셀 (cose t)이라부른다. 먼 처 예 4.1-2 의 (6. 3) 부호의 경우 s=Oll 일 때 8 개의 에러유형 (e rror pa tt er n) (000011), (100000), (010110), (001101), (1 10101) , (1 01110) , (011000), (111011) 은 식 s=eHT 을 만족하며, s=Oll 의 코 셀이 라 부른다. 8 개의 코셀 중 에러의 수가 가장 적은, 다시 말해서 1 의 수가 가장 적 은 코셀을 코셀 리 더 (coset leader) 라 부른다. (6. 3) 符號에서 에러유형의 총수는 상 =64 이며, 신드롬의 총수는 23=8 이다. 하나의 신드롬에 8 개의 에러유형이 있고, 또한 8 개의 신드롬이 있으므로 모든 에 러 유형 수는 64 개 가 된다. 만일 64 개 의 에러유형이 나타날 수 있는 표를 만들면 우리는 이 표를 사용하여 에러를 정정할 수 있다. 그림 4.1-1 은 (n,k) 부호의 復號表믈 만드 는 방법을 계시하고 있다. u1,u2. … ,U21 는 부호어이고 U1 은 零符號 語를 표시 하며 , e1, es, …, e2,,_k 는 코셀 리 터 , sI, s2. …, s2-k 는 신드롬을 말한다.
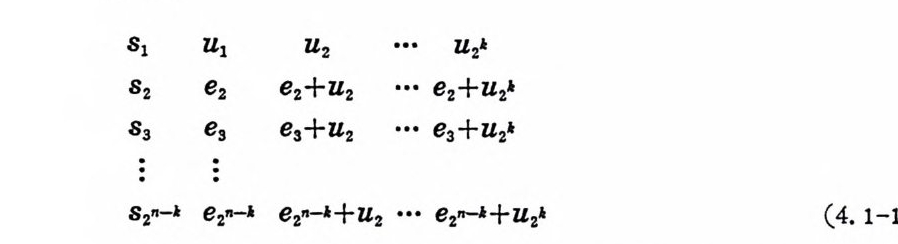 81 U1 U2 … u 산
81 U1 U2 … u 산
〈예 4. 1-3> 다 음은 (6. 3) 부호의 각 신드롬에 해 당하는 코셀, 코셀 리더를 보여준다.
 신드롬 코셀리더
신드롬 코셀리더
 010 000010 001100 010111 100001 011001 101111 110100 111010
010 000010 001100 010111 100001 011001 101111 110100 111010
으로 단일에러를 정정하였다. 이와 같이 에러를 정정하는 부호를 에 러 정 정 부호 ( error correcti ng code) 라 한다. (6. 3) 부호의 경 우 S=lll 를 제의하고 모든 코셀리더는 유일하다. S=lll 의 경우 (010010 ) 이나 (0 01001) 중 하나를 코셀리더로 선택할 수 있다. 이 부호표로는 단일에러를 정정할 수 있고, 2 개의 에러 중 하나의 에 러유형을 정정할 수 있다. 신드롬 復號器 (s y ndrome decoder) 는 s 을 계산하여 그 코셀 중 코
AX’ u jp U. ^e p 그립 4. 1-1 신드몽復號器
센리더를 e 로 선덱하는 부호기이다• 일반적으로 신드롬부호기는 판 정 함수 F를 e=F(s) 라 놓으면 e=F(s) 는 s 를 계 산하여 코 셀 리 더 인 에러유형을 선덱한다. 4. 1. 2 線形부호의 에러訂正能力 이 원부호의 경 우 해 밍 무게 (Hammi ng we ig h t)는 부호어 에 포함되 어 있는 1 의 수를 말하고, w(x) 로 표기한다. 2 개의 부호어 X 와 y 7. J-의 해 밍 거 리 (Hammi ng dis t a n ce) d(x, y)를 다음과 같이 정 의 한 다.
 d(x, y)=:E” lx;-y, I (4. 1-18)
d(x, y)=:E” lx;-y, I (4. 1-18)
x 와. Y; 가 상이할 때는 1 이며, 동일할 매는 0 이다. 해밍거리는 다 음 독성을 가지고 있다.
 CD d(x,y) 2'::0, 만일 x=y 이면 d(x,y )= O
CD d(x,y) 2'::0, 만일 x=y 이면 d(x,y )= O
또한 여러 부호어가 있으면 이중 가장 작은 해밍거리를 최소해밍 거 리 (mi ni m um Hammi ng d i s t ance) 라 부르며 , 부호의 에 러 를 검 출 또는 정정하는 데 중요한 역할을 한다. 간의 부호어 중 최소해밍거 리를 찾는 방법은 영부호어를 제외한 1 의 수가 가장 적은 부호어 의 해밍무게가 그 부호의 최소해밍거리이다. 두 개의 부호어 x=(101101) 과 y =(001100) 이 있을 때 w(x)=4, w(y) =2, d(x, y) =w(x+y ) =w((101101) + (001100)) =w(100001) =2 이 다. 해 밍 거 리를 사용하면 다음 설명할 세력권을 이해하는 데 도움이 된다. 세 력권은 부호 x 를 중십으로 반경 t의 원이다. 부호간 세력권이 중첩 되지 않으려면 부호간의 해밍거리가 2t + 1 이상 되어야 한다. t 7 사 의 에러를 정정하는 부호를 형성하는 것은 부호간의 해밍거리가
2 t +1 보다 크도록 부호어를 선정하는 일이다. 만일 두 부호어간의 해밍거리가 2 t이면 t 이하의 에러는 정정할 수 있지만 t개의 에러는 정정하지 못하고 에러가 발생하였다는 것만 감지할 수 있다. 이러 한 에러가 발생하였다는 것을 감지할 수 있는 부호를 에러검 출 부호 (er ror dete c ti ng code ) 라 부른다.
 그림 4. 1-2 符 號 의 勢 力圈
그림 4. 1-2 符 號 의 勢 力圈
X i, X2,X 3 ,X4 의 4 개 의 부호간의 해밍거리가 2 t +l=5 인 경우를 그 림 4.1-3 에 도시하였다. 4 개의 부호어와 96 개의 X 는 수신가능한 부 호 들이며 xl 울 중심으로 4 개의 ®는 xl 과 해밍거리가 1 이 되는 부호들이다. 線 은 각 부호어의 제력권을 표시하고 있다. 만일 수신된 부호를 부호어로부터 해밍거리가 가장 가까운 부호어를 택하여 復號 한다면 이 부호는 2 개 또는 이하의 에러를 정정할 수 있다. 부호간의 최소
해밍거리가 dm 일 겅우, 더 + ( dm 크)]개의 에 러 물정정할수있다. 여기 서 L J는 정수부분만을 취 하는 것을 의미한다. -X1 = (0111101), .x2 = (1 001101), .x3= (0110110), . X4=(1111011) 일 대 따를 송신하여 y= (1101011) 을 수신하면 w(x1 +y) =4, .w(x2+y )= 3, w(X3+y )
 X X X X X X X X X X
X X X X X X X X X X
=5, w( x ~+y ) =l 이드로 復號 된 부호어는 x4 로 하나의 에러 문 정 ' 정하였다. 4.1.3 해밍부호 해 밍 부호 (Hamm i n g code) 는 해 밍 거 리 3 이 상의 단일에 러 정 정 부호 이다. 부호길이 n=2m-l, 정보비트수 k=n-m=2 ,.. -1-m 이며, m 은 整 數 이다. (2-'-1)X(n-k) 의 패리티겁사행 렬 은 구성하기가 독 히 용이하다. 패리티검사행렬 H 의 i번列은 i의 십진수 를 이진수로
 표시H 하~고; 있r다 ;. ~ 예i 로 J m=3 의 (7. 4) 해 밍 부호의 H 행 렬 은 다 음( 과4. H같 다l) .
표시H 하~고; 있r다 ;. ~ 예i 로 J m=3 의 (7. 4) 해 밍 부호의 H 행 렬 은 다 음( 과4. H같 다l) .
위의 H 행렬로부터 組 織符號 를 구성하는 패 리티검사 행렬 을 만들 - 기 위하여 행렬의 초등연산을 행한다. 행 렬의 초등연산은 다음과 같다. ® 두 행의 교환 ® 행 에 0 이 아닌 상수의 곱셈 ® 한 행에 상수를 곱하여 다른 행에 더함 예를 들어 먼저 H 행령.로부터 조칙부호를 구성하는 패리티검사 행 렬을 만들기 위하여 먼저 H 행렬의 1 번행과 2 번행을 더하고, 다음 - 1 번행 과 3 번행 올 더 하고, 끝으로 1, 2, 3 번행 을 모두 더 함으로써 조 직부호의 패리티검사행렬의 1,2,3 번행을 구할 수 있다.
 0 1 1 1 1 0 0
0 1 1 1 1 0 0
패리티검사행렬 H 로부터 생성행렬 G 를 구할 수 있으며, x=u(l : 로부터 2'=16 개의 부호어를 구할 수 있다. 또한 xHT=O 로부터 다 음 식을 구할수 있다.
![]() 따+:.c 3+ :.c,+따 =O
따+:.c 3+ :.c,+따 =O
 .'.t.1 -: -X 3 -- rX 4 +Xs=O
.'.t.1 -: -X 3 -- rX 4 +Xs=O
이 므로 부호어 X 는 x= (xi, x2, x3, x,, x2+x3+x4, x1+x3+x,, x1+x:+x 4 ) 이다. 해밍부호의 신드롬은. H 행렬의 열의 위치와 같은 위치에 에러가 발생하고 있다. 〈 예 4.1-4> 부호가 다음과 같은 패리티검사행렬을 가지고 있다.
 H= [: : : : : : :l
H= [: : : : : : :l
이다. 신드롬은 H 행렬의 7 번위치이고, 에러가 7 번위치에 발생하였 으므로 부호된 부호어는 (1110000) 이다. 이것을 다음과 같이 수석 으로 표현하면 좀더 명확히 알 수 있다.
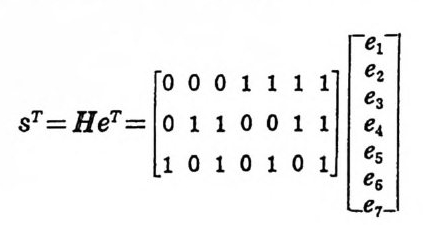 el
el
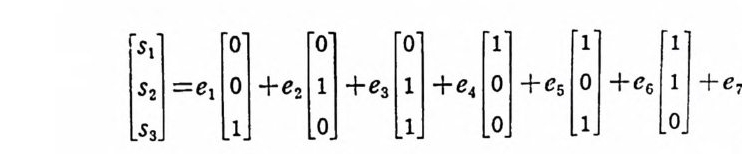 [::l = eI [[]+ e2 [:l + e3 [:l + e4 [:l + c5 [:l + c6 [:l + e7 [1:l
[::l = eI [[]+ e2 [:l + e3 [:l + e4 [:l + c5 [:l + c6 [:l + e7 [1:l
이므로 만일 Y1 에 에러가 발생하면 e1=1, e,-=0, 2¾i ¾ 7 이다. 入1 1 드롬 s=(OOl) 이고 1 번 위치에 에러가 발생함을 알 수 있다. 다음 摘張해 밍 符號 (ex t ended Hammi ng code) 를 설명 한다. 부호길 이 n=2m 이고, k=2m-1-m 이고, m 은 정수이다• 이 부호는 2 개의 에러가 발생하였을 때 이를 보호하기 위하여 해밍부호의 패리티 검 사행렬에 부가적으로 패리티검사를 가함으로써 摘張 해밍 符! 虎땝 순 형 성할 수 있다. (15.11) 해밍부호의 패리티검사행렬은 다음과 같다.
 -oo0-o001100 0110 1010 0010 111 l 0011 01010 001 1101 0111 1011 0011 -111 -01 1-
-oo0-o001100 0110 1010 0010 111 l 0011 01010 001 1101 0111 1011 0011 -111 -01 1-
이 패리티검사행렬은 모두 다른 열을 가지고 있어 단일에러는 정 정할 수 있으며 2 개의 에러가 발생하면 신드롬은 H 행렬의 열과 상 이하다. 그러므로 이 부호는 2 개의 에러를 겁출할 수 있고, 단일에 러를 정정할 수 있다. 4. 1. 4 多數決論理復號
 다음 (n, k) 부호의 패 리 티 검 사행 렬에 서 신드l몸 을 구해 본다.
다음 (n, k) 부호의 패 리 티 검 사행 렬에 서 신드l몸 을 구해 본다.
 s=[ e1 e2, .. e 』 | -hhh...I0l1 u2 I hhh2?2.01.1k 2 …………... h h h단Ok..0.u 2 )k-
s=[ e1 e2, .. e 』 | -hhh...I0l1 u2 I hhh2?2.01.1k 2 …………... h h h단Ok..0.u 2 )k-
이고 a ; =O,1; i =l,2,···,n-k 아다. 만일 a1=1 이고 a2=a3= --•· =a . _ , =O 이면 A j =S 를 의미한다. 일반적으로 J =2 t이며, t는 에러 수 이다. 이 렇 게 하여 구한 A1, A2 . … . A J을 패 리 티 檢 査 合(P ar ity check s um ) 이라 부르며, 패리티검사합 을 구하는 방법은 다음과 같다. 패 리 터검사 합의 집합 {A1,A2, … ,AJ}은 모든 패리터검사합이 에러비 트 el 을 포함하고, 나머지 에러비트에 대해서는 Ai ,A 2 , · ··,A1 에 한 번 이상 나타나지 않도록 J개의 패리티검사합을 구성한다. 이때 괘 리터검사 합 {A i, Az, ... ,AA 는 el 에 直交 (o rt ho g onal ) 한다라고 말한 다. J=2t개의 패리티검사합의 집합이 el 에 直交하고, t 또는 이굴l 의 에러가 이 집합에 의하여 겁사될 때 el 은 다음 부호법칙에 의하 여 에러를 정정할 수 있다• J개의 패리티검사합 중 t+ l 또는 이상 의 패리티검사합이 1 일 때 e1 에 에러가 발생함을 나타낸다. 죽 el 의 推 定 値 g 1 이 e1=1 이다. 만일 t개의 에러가 발생하였을때 e1=1 이면 나머지 t -1 개의 에러비트가 1 이다. e1 이 각 패리티검사합에 의하여 겁사되므로 적어도 2 t-(t -l)= t +l 개의 패리티겁사합은 1 이 된다.
만일 e1=0 이면 최고 데의 에러비트가 1 이 되고 많아야 데 의 패 리 티겁사합이 1 이 된다 . 그러므로 이 復號 法則은 t 또는 이하의 에러 를 訂正한다. 이러한 부호방법을 直交패리티 檢査 合의 多敷決論理復 號法 (majo r it y log ic decodin g ) 이 라 부른다. 〈예 4. 1-5> (6. 3) 부호의 패 리 티 검 사행 렬 이 다음과 같다.
 H=[: \ ; :l
H=[: \ ; :l
이다. 만일 el 에 에러가 발생하면 e1=1 이므로, A2=A3=l 이므로 eI 에 에러가 발생하였음을 알 수 있다. 그러나 el 에 에러가 발생치 않고 다론 비트에 에러가 하나 발생하였다면, 2 개의 패리티 검 사합 A2,As 중 하나가 1 이거나 A2=A3=0 이다. 즉 e4 에 에러가 발생하 였으면 A2=A3=0 이다. 이렇게 하여 el 에 에러가 발생하였을 때 에 러를 정정할 수 있다. 마찬가지로 %에 直交하는 2 개의 패리티검사 합은
 A1=s1=e2 꿉 +e,
A1=s1=e2 꿉 +e,
이다. 만일 A2=A3=l 이면 el 에, A1=A3=1 이연 e2 에, A1=A2=l 이 면 %에 에러가 발생하였음을 알 수 있다. 여기에 설명하는 부호는 조직부호이므로 정보비트의 에러를 訂 正하면 되나, 만일 c4 에 에러 가 하나 발생하였을 때는 3 개의 패리티검사합 A i,A 2,A3 중 A1=l, A2=A3=0 이면 e4 의 에러를 정정할 수 있다.
 〈예 4._ 11-160>01 _1 1(10801.0 012001 )00 0 부010010호 00000의0 0001-0 0 00패00 0 1리0- 0 0티 1 검 사행 렬 이 다음 과 같다.
〈예 4._ 11-160>01 _1 1(10801.0 012001 )00 0 부010010호 00000의0 0001-0 0 00패00 0 1리0- 0 0티 1 검 사행 렬 이 다음 과 같다.
이다. 4 개의 패리티 검사합이 모두 e1 을 포함하고 있고기타 에러비 트는 한 번씩만 포함되어 있음에 주의를 요한다. 4 개의 패리티검사 합 중 적어도 3 개 이상의 패리티검사합이 1 이면 e1=I 이고, 그렇지 않으면 e1=0 이다. e2 에 칙교하는 패리티검사합은 다음과 같다.
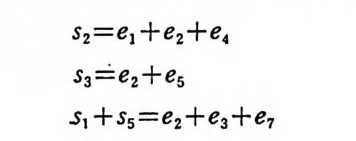 s2=e1 +e2+e,
s2=e1 +e2+e,
s6=e2+e8 4. 1. 5 Reed-Muller 부호 Reed-Muller 부호는 多數決論理復號法울 처 음으로 사용한 부호로 자세히 설명한다. L i n t는 이 부호를 해석적 방법으로 분석하였으며, n그=의2 m 접정근보방비법트으수로 k기=술l한+다(?.) +正(의?) +정…수 +m(,;r)', r패
 - V 。 - -1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1-
- V 。 - -1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1-
 로 표현된다. 다음 j번위치가 1 인 벡터 e i = ( OO … 010 … 0 ) 은
로 표현된다. 다음 j번위치가 1 인 벡터 e i = ( OO … 010 … 0 ) 은
로 표시한다. C;,1, p =l,2, … ,l 은 0 이거나 1 이다. m=4, n=2m=16, 일 때 g (l,2)= {jjj =C1 j 21-1+C2 j 22-1}={0,1,2,3} 로 식의 기저벡터 V1V2 를 곱한 항의 係數 (x 。 +X1+x2+X3) 의 x i 의 i의 수와 같다. 그러 므로 부호 x 는
 X=( jeI g; ( 0 l X1)V 。+ ( jeI g; ( I l Xj ) V1+… + ( jeE g ( m) x J ) vm
X=( jeI g; ( 0 l X1)V 。+ ( jeI g; ( I l Xj ) V1+… + ( jeE g ( m) x J ) vm
 로 표시할 수 있다.
로 표시할 수 있다.
되어 2m- 『식이 성립한다. 이형게 반복함으로써 정보비트에 대한 둥 석이 성립한다 . 만일 단일에러가 발생하면 2 -『개의 합 중 1 개의 합
이 상이하게 되고, 수신벡터 중 에러발생수가 감 -2m-r 이면 多數決 法則에 의하여 정보비트를 결정할 수 있다. 〈예 4. 1-7> m=4, r=2 인 r 차 Reed-Muller 부호에서 k=ll, n=16 이다. 정보벡터 u=(u i, u2 … u10)=(111111111l) 일 때 x=uG 에 의 하여 부호어 x=(x 。 X1 ... X15)=(10000001000101ll) 이 된다. 채 널을 통하여 수신벡터 중 1 번비트에 에러가 발생하였다고 가정하면 y=(y<1Y1 . ..y 15)=(0000000100010111) 이 다. 2 개의 기 저 벡 터 8'i 에 해 당 하는 정 보비 트 u,, s=6, 7, 8, 9, 10, 11 의 식 을 구한다. u6 의 경 우
 u6=J e Io~,1 , 2 3) Xj =J e u~.& 6 ,7 ) X j = Je 1&.~ 9, 1 0,IIl. xi= Je {-I 2~ 1 3 ,1. ‘., 1 5)_ Xj
u6=J e Io~,1 , 2 3) Xj =J e u~.& 6 ,7 ) X j = Je 1&.~ 9, 1 0,IIl. xi= Je {-I 2~ 1 3 ,1. ‘., 1 5)_ Xj
그러므로 多數決論理에 의하여 정보비트는 U=(lllllllllll) 로 단일에러를 정정하였다. 4.1.6 巡回부호 부호이론 특히 巡回符號 (c y cl i c code) 에서는 有限體(fi n it e fiel d) 의 이론을 도입하여 설명하고 있다. 여기서는 순회부호를 기술하는 데 최소한의 기초적 지식을 설명한다. (부록 A 참조) 최소 2 개의 元 (elemen t)을 갖는 집합 F의 임의의 2 元 a,b 에 대하 여 內部演算 +와 ·올 정의할 때 다음 3 조건을 만족시키는 代數系
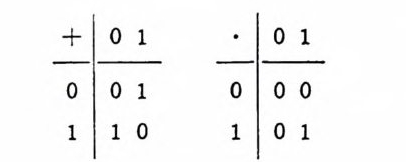 + I o 1 • I O 1
+ I o 1 • I O 1
이대 加 算 은 보동 ® 로 표기하나 앞으로는 +와 같이 혼용한다. 만일 郡 G의 1 개 元 a 에 대하여 승법은 지수표현을 사용하여 a•a=a2. a·a•a=a3 으로, 加 算 도 a+a=2a, a+a+a=3a 로 표기한 다. 일반적으로 a,a2 , a3, …이 계열이 유한할때 a;=a i(i
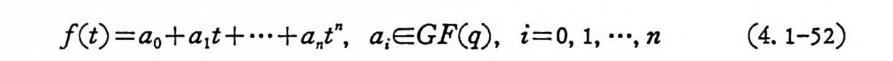 f(t )=a 。 +a1 t+… +a _t, a;EGF(q) , i= O, 1, …, n (4. 1-52)
f(t )=a 。 +a1 t+… +a _t, a;EGF(q) , i= O, 1, …, n (4. 1-52)
의 집합을 F[ t]로 쓰고, 다항석 f(t)의 次數를 de gf(t)로 쓰기로 한다. f( t ) 에서 t 0=1 이 되고, a;=O, i=O , 1. … ,n 일 때 다항식은 0 이 되며 a 군 : 0 일 때 n 차 다항식이 된다. 예로 f(t)=t 3+ t 2+ t와 g(t)=t을 GF(2) 上의 2 개의 다항식 일 때 f( O)=g ( O)=O, /(1) =g (l)=l 이므로 2 개 다항식은 서로 다르지만 GF(2) 상에서는 동일
하다. 일반적으로 位數 q의 體上에서 n 차 이하의 상이한 다항식은 q •+I 개이다. 다항식의 加法 및 승법은 다음과 같이 정의한다.
 f(t)=i;.Ji. g(t)=~g;ti에 대하여
f(t)=i;.Ji. g(t)=~g;ti에 대하여
〈정리 4.1-1> 임의의f(t), g(t)E F[t], g(t)1:- o 일 때 f(t)= a(t)g g(t)+ r(t), de gg(t )>de g r( t)되는 a(t), r( t )EF[ t]가 유일하게 존 재한다. 〈증명〉 주어전 f(t)와 g(t)에 대하여 몫(q uo ti en t) a( t)와 나머지 r( t)을 구하는 방법 은 deg f(t) =n 이 고, deg g(t) =m 일 때 , n
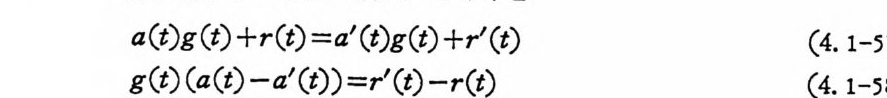 a (t)g (t) + r (t) =a ' (t)g(t) + r' (t) (4. 1-57)
a (t)g (t) + r (t) =a ' (t)g(t) + r' (t) (4. 1-57)
가 되며 r'( t )-r( t)의 次數는g(t)의 차수보다 낮으므로 a(t) - a'(t)- =O 이 된다. 이것은 r'(t )-r( t )=O 을 의미하며 a( t)와 r( t)가 유일
하게 존재한다. 〈 정 리 4. 1-2> n 차다항식 f( t) =O 이 면 F上 에 根이 존재하고, f(t ) 의 차수는 f ( t ) 의 根의 수보다 적 어 도 크다. 〈 증명 〉 f ( t ) = ( t -a) g ( t ) +r ( t ) ,r( t)드 F에 서 r( t)의 차수는 1 보다 적어야 하며 양변에 a 를 대입하면 J(a ) = O· g( a ) +r(a ) =r(a ) (4. 1-59) 가 된다. 그 러 나 f ( a)=r(a ) =O 이므로 a 는 f(t)의 根이고 f(t)= (t -a ) g ( t ) 에 서 g ( t ) 의 차수는 n-1 이다. 또한 aI,a2, … ,akEF 가 f ( t ) =O 의 k 개 의 근이면 f(t)= (t- a 1)(t- a 2) .. ·(t一 ak ) g(t)가 되며 g ( t ) 의 차 수는 n-k 이 다. 그러 므로 f ( t)의 차수는 f(t)의 근의 수보 다 적어도 크다. 부호벡 터 x= (.x o, .xI, …, .x n-I ) 을 생 각해 본다. 이 부호를 다항식 으로 표기한 것 을 符 號 多項式 ( code p ol y nom i al) 이타 부론다 . .x(t ) =.x 。+ .x 1 t+.X선 2+ …+.x • -1 t .-1 (4. 1-60) 다음 한 번 巡 回한 부호벡터 X(ll=( .x n -I,.x o, …,.x n-2) 에 대한 다항 식 .x (I)( t ) =.x n~1+ .x。t+…+.x •-2 t ·-1 이고, 일반적으로 i번 순회한 부 호다항석 x( I) ( t) =.xn -i+ .xn_ ,+1t + … +.x ~-l tn- 1 이 다• (n, k) 선형 부호 어의 집합을 C 라 할 때 각 부호어를 순회한 부호가 집합 C 내에 포함되어 있을 때 이 부호를 순회부호라 부른다.
 〈예 4.1-8> (7, 3) 부호의 생성행 렬이 다음과 같다.
〈예 4.1-8> (7, 3) 부호의 생성행 렬이 다음과 같다.
이다. 8 호어는 (0000000) 를 제의하고 이전 부호어를 1 번 우편으로 순회시킨 것이다. 이 부호의 해밍무게가 4 임을 주시하타. 부호벡터 (0011101) 를 부호다항식으로 표기하고, 이 다항식에 ti울 곱하여 t 7+1 로 나누어 본다.
 x(t) =t 2+ t 3+ 검+t 6
x(t) =t 2+ t 3+ 검+t 6
(n,k) 순회부호에는 (n-k) 차의 부호다항식이 하나 존재하는데 이 다항식을 生成多項式(g enera t or p ol y nom i al) 이라 부르며 g(t)로 쓴 다. 단
 g(t) =g。+g 1 t+ ••• +gn- At n- *
g(t) =g。+g 1 t+ ••• +gn- At n- *
 u(t) = u0+u1t+ … +UA-1t H (4. 1-64)
u(t) = u0+u1t+ … +UA-1t H (4. 1-64)
이 된다. h ( t)을 패 리 티 檢査多項式( p ar ity check p ol y nom i al) 이 라 부른다. h ( t )를 생성다항석으로 하여 생성된 부호를 g (t) 의 雙對符 號 ( dual code ) 라 한다. h ( t) 는 k 차 다항식이며 생성다항석으로 사 용할 수 있으므로 h0=hk=l 이다. @l 4. 1-9> f (t) = 1 +t+t 3 을 생 각해 본다• (7. 3) 순회 부호를 만들 기 위하여 f(t)가 t 1+1 로 나누어지는가 확인한다.
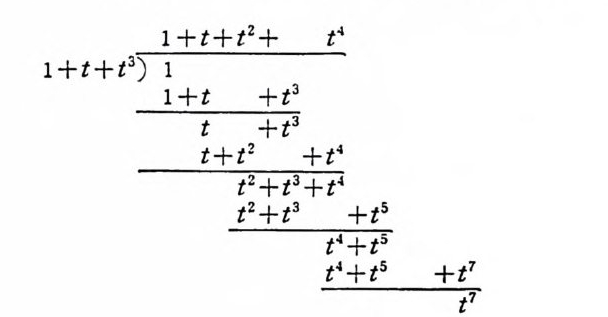 1 +t+t2+ t•
1 +t+t2+ t•
나머지가 t 1 이므로 1+ t+t 3 은 1+ t 1 으로 나누어진다. 생성다항식은 (n-k) 차이므로 g(t )=1+ t+t 2+ t•이고, g(t)는 t 1+1 로 나누어진 다. 다음 부호벡 터 를 x( t) =u( t)g(t)을 사용하여 만들어 보면 다음
 과같다.
과같다.
이것은 조직부호가 아니다. 다음 쌍대부호를 만들기 위하여 g(t )=l+ t+t 3 으로 놓으면 다음 부호벡터를 얻는다.
 (o o o o o o o) (1 1 o 1 o o o) (o 1 1 o 1 o o) (1 o 1 1 1 o o)
(o o o o o o o) (1 1 o 1 o o o) (o 1 1 o 1 o o) (1 o 1 1 1 o o)
g(t )=1+ t+t2+t'에 의하여 생성된 부호의 해밍무게는 모든 부호 어가 4 이었으나 여기서는 그렇지 않다. 그러나 각 부호어를 순회시 킨 것이 부호 내에 있으므로노 이 부호도 역시 순회부호이다. 組織符號를 만들기 위 하여 u( t)에 t다울 곱하여 g(t)로 나눈 나 머 지 를 p(t)라 하면 p(t)는 n-k-1 차이 다. 죽
 t•- lu (t) =q ( t)g(t) +p (t) (4. 1-70)
t•- lu (t) =q ( t)g(t) +p (t) (4. 1-70)
 는 패리티검사비트이고 나머지 k 바트는 정보비트로 조직부호가 된
는 패리티검사비트이고 나머지 k 바트는 정보비트로 조직부호가 된
조적 순회 부호에 서 t.- •u( t) +p(t)는 g(t)로 나누어 지 므로 부호어 이다. 정보비트에는 변경이 없고, 단지 패리티검사비트만 결정하여 주면 된다. 생성다항식이 g(t )=1+ g 1 t+g 2 t 2+ …+t •-k 일 때 (n -k) 段 쉬프트 레지스터 (shif t re gi s t er) 를 사용한 符號器 (encoder ) 는 다 음과같다 .
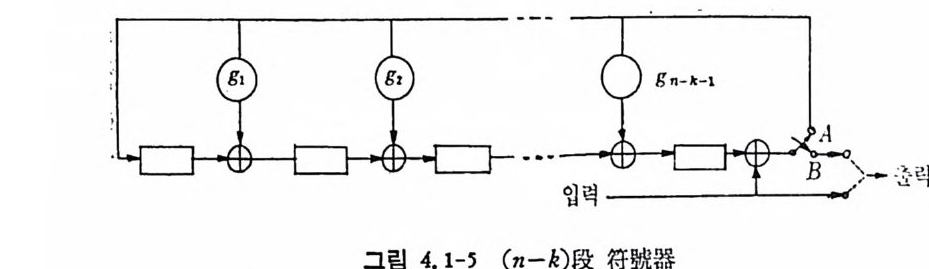 ’.. gl g:
’.. gl g:
. g ;=l 일 때 회로가 연결된 상태이고 g ;=O 일 때 회로가 개방된 상태 이다. ®는 modulo 2 加算器이다. 스위치가 A 의 위기에 연결되어 정보비트가 입력된 다음, 스위치를 B 의 위치로 전환하여 쉬프트 레 지스터 내용인 패리티검사비트가 출력으로 나온다. 〈예 4. 1-10> g (t) =l+ t+t 2+ t 4 일 때 4 단 符號器는 다음과 같다.
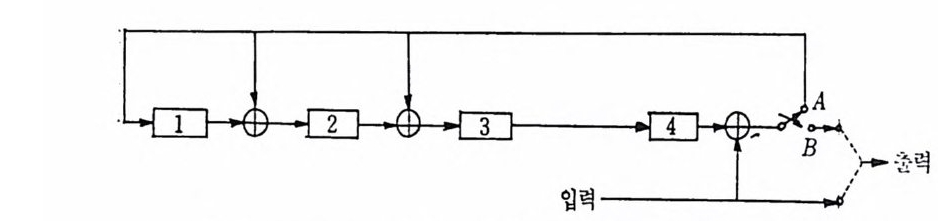 £ 슨 ’`` _ 출력
£ 슨 ’`` _ 출력
u=(lll) 일 때 3 번 이동한 후 쉬프트 레지스터의 내용은 다음과 같다.
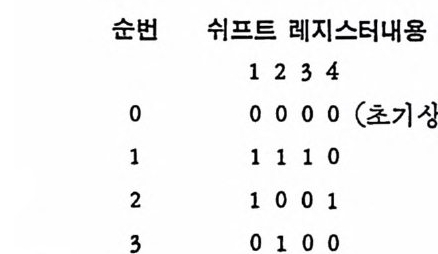 순번 쉬프트 폐지스터내용
순번 쉬프트 폐지스터내용
그러으로 부호어는 ( 0100111 ) 이다. 다음 되 1 리티검사다항식 h ( t )=1+h1 t +h 산나 ···+hk 강을 사용한 ki;. J: 쉬프트 레지스터 符號器는 다음과 같다.
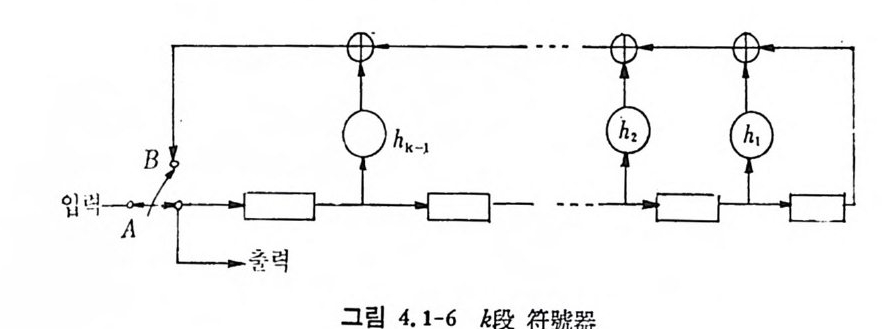 Olu리
Olu리
먼저 스위치가 A 에 연 걷 되어 k 개의 정보비트를 쉬프트 레지스터 에 입 력 시 킨 다음 스위치 를 B 로 이동하여 계산된 패리티검사비트를 볘 낸다. 〈 예 4.1-11> g ( t ) =1+ t+t 2 + t 4 에 대한 패리티검사다항식은 h(t) =l+ t+t 3 이다. 3 단 쉬프트 레지스터를 사용한 부호기는 다음과 같 다.
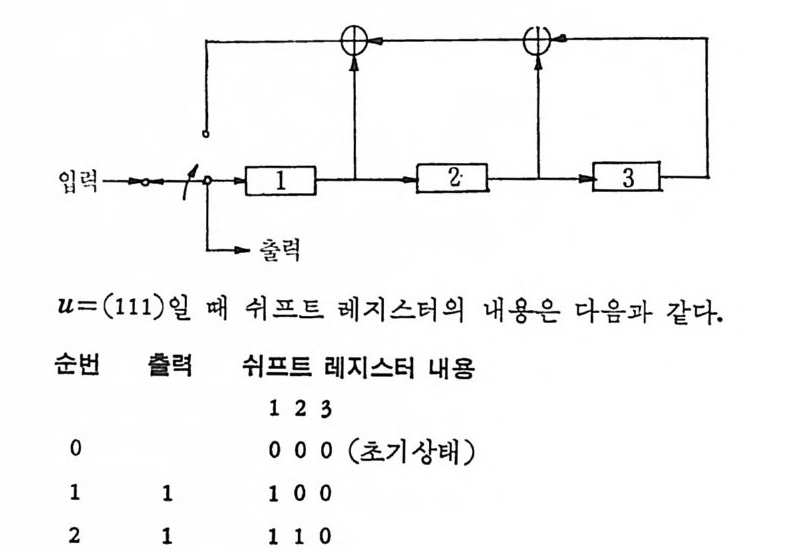 입 력
입 력
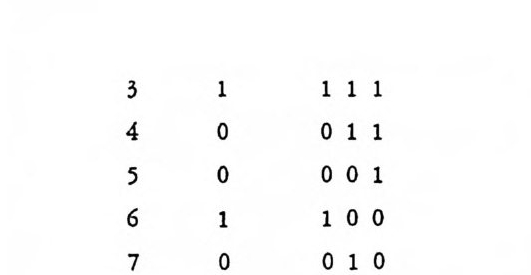 345l6070 1l00101 111010001 0
345l6070 1l00101 111010001 0
부호벡터는 (0100111) 이다. 신드롬 s= y 1P+ yp는 (n, k) 조칙 부호에 서 용이 하게 발생 시 킬 수 있다. 수신벡터 y=〔 Y1:YP] 에서 정보비트 Y1 을 부호기 에 입력시키 발생한 페리티검사비트에다 수신패리티검사비트 YP 를 가 산하면 신 드롬울 얻는다. 신드롬발생기는 다음과 같다.
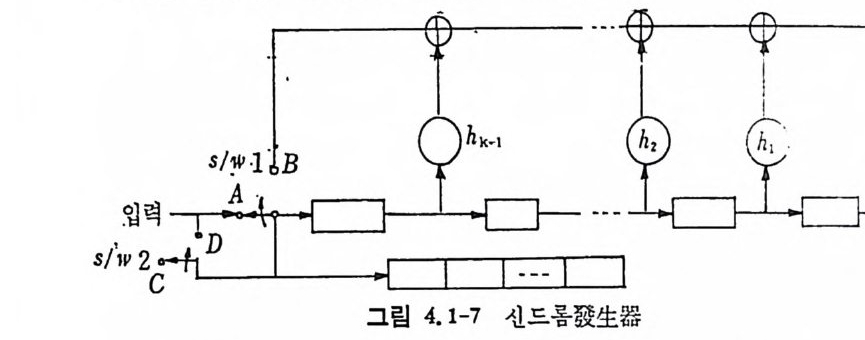 그립 4. 1-7 신드롬發生 器
그립 4. 1-7 신드롬發生 器
처음 스위치 1 이 A 에, 스위치 2 가 C 에 연결되어 있다. 수신정브 비트 Y1t Y 2, … ,Y i로 상단 k 개의 쉬프트 레지스터에서 패리 티 검사비 트를 계산한다. 그런 다음 상단 쉬프트 레지스터에서 계산된 패리 티 검 사비 트와 수신된 패 리 티 검 사비 트 yk+ 1, yk+ 2. …, y 올 가산하여 하 단 (n-k) 쉬프트 레지스터에 보낸다. 하단 쉬프트 레지스터에는 (n-k) 신드롬비 트가 남게 된다. 4.1.7 BCH 부호 여러 에러를 정정할 수 있는 부호에는 Bose-Chaudhur i와 Ho. cq uen g hem 이 각기 독립적으로 발견한 BCH 부호가 있다. t개의 랜 돔에러를 訂正할 수 있는 BCH 부호로 略記되는 Bose-Chaudhuri- Hocq u eng h em 부호는 구성법이 명료하고 復號法도 상세히 연구되 어 있다. BCH 부호를 이해하기 위해 최소한의 용어를 설명한 다음
BCH 부호의 구성 법 과 復號法울 Pe t erson 의 방법 에 따라 기 술한다. 다항석 중 匠約多項式(i rreduc i ble p ol y nom i al) 이 란 자기 자신과 1 이의는 나누어지지 않는 다항식을 말한다. 體 F 의 元 a 는, f( a )=O 이 면 a 는 f ( t ) 의 根이 되 고, f( t) =O 는 根이 있음을 의 미 한다. 다음 5 차다항석 f ( t ) =t 5+ t 2+1 을 고찰해 본다. 이 다항석은 1 차 다항석 t, t +I 로 나누어지지 않는다. 2 차다항석 t2, t2+ t =t(t + l), t 2+1= t 2+ 2t +I= ( t +l) 라 t2+ t + l 중 t 2+ t +l 을 제의하고 t와 t+ l 로 나누어지므로 t 2+ t +l 만 시험한다.
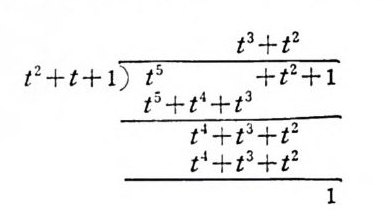 t3+ t 2
t3+ t 2
t 5+ t 2+1 은 t 2+ t +1 로 나누어지지 않는다. 3 차다항식으로 나누려 면 2 차다항석으로 나누어져야 하므로 f ( t)=t 5+ t2 +1 은 旺約多項式 이다. 그러므로 t, t+ l, t 2+ t +1 도 段約多項式이다. 득히 t의 最高 次敷의 係數가 1 인 다항식을 單位多項式 (man i c p ol y nom i al ) 이라칭 한다 . F[ t]에 m 차 기 약다항식 이 존재 하면 위 수 2m 의 體가 촌재 한다. 位 敷 2m 의 盟를 GF ( 2m ) 로 표기 한다. 다항석 f(t)=t나-t +l 에서 t =a 로 놓고 f (a)=a4+a+ t =O 이면 a 의 2‘-2 乘은 0 과 1 을 포함해서 2m 개의 元이 존재한다. 즉 GF(2) 상의 다항식 f(t)=t 4+ t +l 을 법으로 한 體 GF(24) 에는 16 개의 元 이 촌재한다.
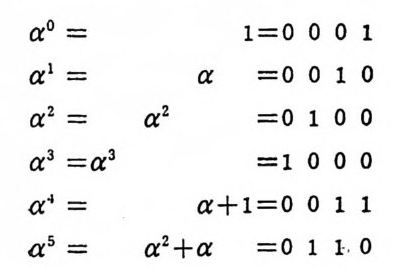 a0 = l=O O O 1
a0 = l=O O O 1
 a6 =a3+ a2 =l 1 o o
a6 =a3+ a2 =l 1 o o
일례로 al0 은 a10=aa9=a ( a3+a)=a•+a2= ( a+1)+a2 로 a4=a : +1 을 대입하여 얻었다. 이진수와 f( t)의 차수와 동일함에 주의를 0 요한다. 2m 개 元을 가진 體의 原始元(p r i m iti ve elemen t)이라 함은 한 원 의 2m-l 까지의 乘 울 한 元이 零 元이 아니고 GF ( 2m ) 의 元일 때를 말한다• a 가 原始元이 며 a, a2 . … , azm-1 이 零 元이 아니 고 GF( 2 ') 의 元이다. 다항식 f(t)=t 4+ t +1 에서는 a 와 a4 는 原始元이다. 0 과 1 을 포함하여 2m 개의 다른 원을 발생하는 m 차다항식을 원시 다항식 이 타 한다• 원시 다항식 은 紙約多項式이 다. /3 가 GF ( 2 m) 의 原始元이 고 槪約單位多項式 f(t)에 {3 를 대 입 하여 f((3) =0 이 면 f( t) 는원시다항식이다. GF(2) 上에 {3 가 GF(2m) 의 임 의 의 元이 고 다항식 m ( t)의 最小次 數가 되는 m( /3 )=0 인 다항식을 最小多項式 (m i n i mal p ol y nom i al) 이 라 부른다 . m( t)가 기 약다항식 임을 보이기 위하여 m(t) = m1(t) m z (t) 이면 m( /3 )=m1 (/3 )m2 (/3)는 0 이 되어야 하므로 m,( /3)나 mz(/3 ) 중 하나가 0 이 되어야 한다. 이것은 m( t)가 최소다항식이타는 가정에 위 배되 므로 최 소다항식은 기 약다항식 이 다. 또한 f(t)가 GF(2) 上에 다항식이고f(/3 )=0 이고 식 f(t )=m( t)q(t )+r( t)가 성립한다고 가 정한다. 여기서 m( t)는 최소다항식이고 r( t)의 차수는 m( t)의 차 수보다 적다. 그러 나 f(/3) =o, m(8)=0 이므로 r (/3 )=O 이 되어 야
한다. r ( t ) 의 차수는 m( t)의 차수보다 적으므로 r( t )=O 일 때 r ( /3 ) =0 이 된다. 이것은 /3에 대하여 m ( t ) 가유일하게존재함을의 미 하고, 기 약단위 다항석 f( t) 가 f( /3) =0 이 면 f( t) 가 최 소다항석 임 을· 말한다. GF ( 2 ) 上의 다항석 f ( t ) 가 다음과 같고
 f( t) = f,.t +fn-1 t •- I+ …+j.'’ (4. 1-75)
f( t) = f,.t +fn-1 t •- I+ …+j.'’ (4. 1-75)
 a9 t4+ t 3+ t 2+t+ l
a9 t4+ t 3+ t 2+t+ l
최소다항식의 次 數 와 根의 數 가 동일함에 유의할 팔요가 있다. GF(2 ,,. )의 모든 元에 대한 최소다항식이 존재하며 a 의 乘 이 m( t) 의 次數와 동일하거나 적음을 증명할 수 있다. 다항식 f ( t ) 의 계수 는 0 고} 1 이고, [f(t)〕 2'= f ( t 2') 이므로 m ; ( t )=m2; ( t ) 이다. m 과 t가 正의 整數이고 부호길이 n=2'-1, 패티티검사비트수 n-k
 g(t) =LCM(m1(t) , m2(t) , …, m2,Ct )) (4. 1-79)
g(t) =LCM(m1(t) , m2(t) , …, m2,Ct )) (4. 1-79)
 부호길이 n oJ_ 부호가g ( t ) 에 의해 생성된 부호다항식 x( t )=x 。 +X1 t
부호길이 n oJ_ 부호가g ( t ) 에 의해 생성된 부호다항식 x( t )=x 。 +X1 t
 이 된다. 죽 (n, k) 선형 부호의 최 소무게 do 가 되 기 위 한 조건으로
이 된다. 죽 (n, k) 선형 부호의 최 소무게 do 가 되 기 위 한 조건으로
이다. BCH 부호의 최소거리는 d 。>2t +1 이고, GF(2) 上에서 l=l, d0=2 t +l 일 때 x( t)가 부호다항식이 되기 위해서는 a,a3, …,a z,-1 이 根이 된다. u( t)가 通報多項式이면 符號多項式 x( t)는다음 식으로 생성된다.
 x(t) =u(t)g (t) (4. 1-84)
x(t) =u(t)g (t) (4. 1-84)
이며 二元符號의 경우 Y; 는 항상 1 이다. 그러므로 에러위치만 알면 된다. 그러 나 식 (4. 1-87) 은 유한하지 만 많은 解물 가지 고 있 다 . 지 금 r(r< t)의 에러가 발생할 때 (Jh (Jz, …,(J r 을 규정하는 식을 다음 과 같이 쓴다.
 (X+X1)(X+Xz) … (X+Xr)=X 나(Ji Xr-1+ …+(J r-1X+ (Jr
(X+X1)(X+Xz) … (X+Xr)=X 나(Ji Xr-1+ …+(J r-1X+ (Jr
이 된다. 이 식의 解는 r 에러가 발생하면 존재한다. 〈정리 4.1-3> 행 렬 M 은 s j가 X펴 - y,가 서로 다론 값을 갖고 X jyi *O 이면 正則이다.
 M= [三\ ::r+-rll (4. 1-91)
M= [三\ ::r+-rll (4. 1-91)
C〈 증=명 [ x〉;1 ~ -1 X」;2 키 尤,X I -D-= [\1xl °O2x2 •• Y\] (4. 1-92) .....1
행 렬 M은 CDCT 로 표시할 수 있다. 행 렬 C는 식 (4. 1-83 ) 과 같 이 요소 X, 가 서로 다르면 正則이다. D 행렬은 대각선행렬로 X,Y; -:;;0, 1 < i < r 이면 正則이므로 M행 렬도 정칙으로 解를 갖는다. 다 음은 예를 들어 먼저 기술한 방법을 설명한다. 二元符號에서 t =3 인 부호다항석 x ( t ) 는 a,a 라… ,a6 의 根이 되어야 하며 a 가 GF ( 2 4 ) 의 原始元일 때 생성다항석은 다음과 같다.
 g( t) L CM (m 1 ( t) m i t )m 5 ( t) ) (4. 1-93)
g( t) L CM (m 1 ( t) m i t )m 5 ( t) ) (4. 1-93)
(J 1 의 係數를 1 로 만들어 (J 1 을 소거 한다. 식 (4. 1-96) 에 a8=a-7 을 꼽 하고 식 (4. 1-97) 에 a12=a-s 을 석 (4. 1-98) 에 a5=a-” 을 곱하면 다
 음과같다.
음과같다.
1, a, a 라 …, a” 을 식 (4. 1-108) 에 대 입 하여 보면 a3, al0 의 두 근을 얻 는다. 지금 값에서 a1 의 에러크기를 갖고, a1° 위치에 all 의 에러크기를 가진 2 개의 에러가 발생하였을 때 에러위치분만 아니라 그 크기도 알아야한다.
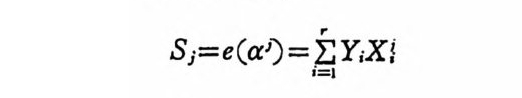 sj= e(aJ) =E, YiX i
sj= e(aJ) =E, YiX i
에 서 X 는 a 3 와 a IV 에 해 당하고 Y i는 a 1 과 all 에 해 당하므로 다음과 같은 신드음식을 얻는다.
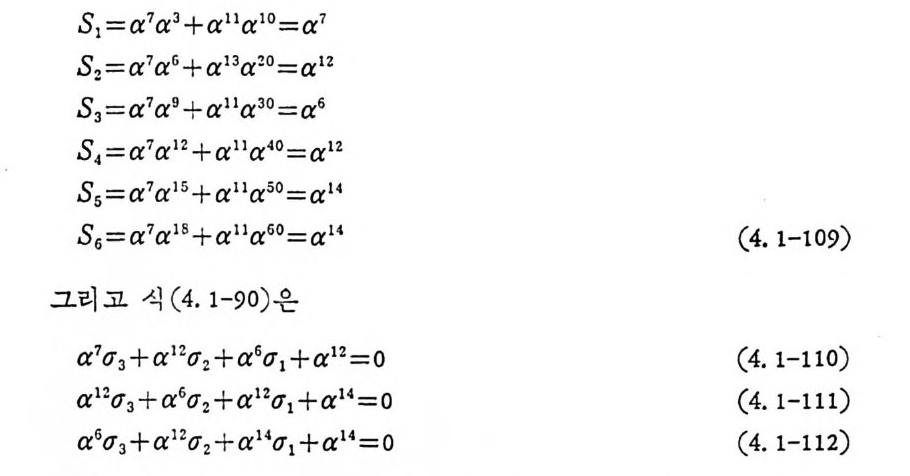 S1=a1aJ+ a11a1o=a1
S1=a1aJ+ a11a1o=a1
되 고, 먼저 와 마찬가지 로 61 을 소거 하기 위 하여 식 (4. 1-110), 식 (4. 1-111) , 석 (4. 1-112 ) 에 각기 a9=a 잡, a3=a-1z, a=a-” 을 곱 하여 정리 하면 다음과 같다.
 a0 3 + a '10 2 + 0 1 + a4 = 0 (4. 1-113)
a0 3 + a '10 2 + 0 1 + a4 = 0 (4. 1-113)
이 식의 두 근은 a3 와 alO 이다. 에러크기 Yi 는 S j =2'= IY i X i 에서 구할 수 있다.
 S1 = Y1X1 + Y2Xz (4. 1-119)
S1 = Y1X1 + Y2Xz (4. 1-119)
이 된다. 에러위치와 에러크기를 구하는 일반적 방법은 다음과 같다• ® 신드롬 Si, j= l, 2, …, 3 t를 계 산하고 @ s j로부터 (J;, i= l, 2, …, t를 구한다. ® c i로부터 X 를 계 산하고 ® Xi , S j로부터 Y; 를 구한다. 구하다는음 n방 一법 l 은방 정C 를식을 구 제하우는는 逐일次이다方.法 으죽로 iE=,. o S nj -번 i6의,r l= ln0 개, L6\+l1 의< j <값 n을, 퍄n ) 은 n 번 (Ji의 값이다. 이 방정식의 解를 구하기가 불가능할때는 n=ln 으로 놓고 ln 개의 6 을 생각한다. 에러위치방정식을 다음과 같 이 정의한다.
 6()(z)=6 언 +6 뿐 r+u~• 냥+… +c i %:1. (4. 1-125)
6()(z)=6 언 +6 뿐 r+u~• 냥+… +c i %:1. (4. 1-125)
 을 만족시 키 는 (1( n+1 ) (x) 의 최 소다항식 을 찾아낸다. 즉
을 만족시 키 는 (1( n+1 ) (x) 의 최 소다항식 을 찾아낸다. 즉
 다음과 같이 가정한다•
다음과 같이 가정한다•
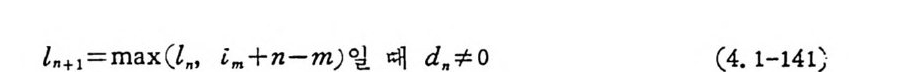 l.+1=max( l. , i m+n-m ) 일 대 dn*O (4. 1-141)
l.+1=max( l. , i m+n-m ) 일 대 dn*O (4. 1-141)
이다. 〈 증명 > 만일 d.=o 이 면 (J(n ) (x) 이 최 소해 이 므로 (J( n+I) (x) =(J(n ) (x) 이다. d“ -:t:- 0 일 경우 (J (m)(x) 와 (J (n)(x) 이 親知이면 (J(마 1) (다울 구할 수 있다. m-l,.>n-l. 이면 l.;>lm+n-m 이므로 l.+1=max(l., ! '+1l-m ) 에 의 하여 l. +1 =l” 이 고, 만일 m-lm
 (J( -l ) c x ) = l, L1=0, d_,=l (4. 1-142)
(J( -l ) c x ) = l, L1=0, d_,=l (4. 1-142)
로 이 조건은 6( g )(x) 로써는 타당성이 있다. 다음은 에러위치방정식과 에러위치를 구하는 순서를 다음에 가열 하였다. ®처음
 (Jc -1>(x)=l, L1=0, d_1=1
(Jc -1>(x)=l, L1=0, d_1=1
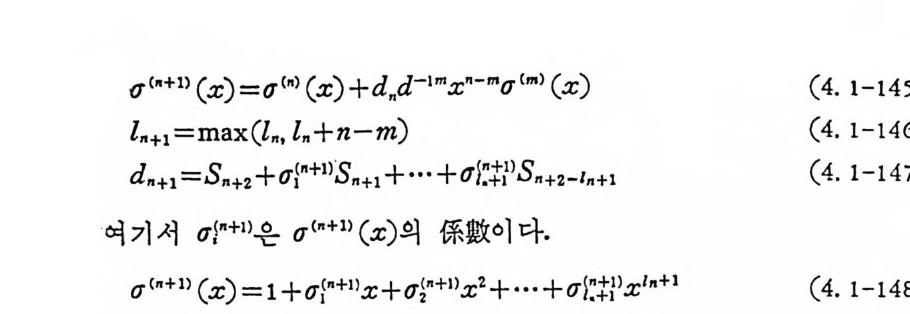 6( 마 ll (x)=(J () (x) +dnd-1mxn-'6(m) (x) (4. 1-145)
6( 마 ll (x)=(J () (x) +dnd-1mxn-'6(m) (x) (4. 1-145)
® 에러위치방정식에서 a를· 대입하여
 n 6(n)(x) d” o l n-l 비 고
n 6(n)(x) d” o l n-l 비 고
4.1.8 무게분포 q元 線形 (n,k) 부호 C 에서 해밍무게 i가 되는 부호벡터수를 A 이
 AI, ••• , An 이 라 하면 다항식
AI, ••• , An 이 라 하면 다항식
문 무게分布多項式 (we ig h t enumera t or) 이라 한다. 이원대칭채널에 있어서 채널에러유형이 부호길이 n 인 부호어에서 해밍무게 i와 같 을 확률은 P' ( 1-P ) ~ '이다• P 와 (1_ p)는 채널의 遷移確 2투 이다. 만 일 부호가 A0 = 1, 해밍무게 1 인 부호어수를 AI, 해밍무게 2 인 부 호어수를 A2, 해밍무게 i인 부호어수를 A; 라 할 때 채널에러유형아 부호어와 같을 확률은
 i2=n oA ;P'( l _ p)n - , (4. 1-150>
i2=n oA ;P'( l _ p)n - , (4. 1-150>
이다. 무거 1 분포다항석은 ( n,k ) 부호에서 특정한 n 에 대하여 k 가 클 때에는 모돈 부호어의 무게를 계산하기는 용이치 않다. 그러나 쌍 대부호의 무게를 계산하는 것이 더 용이할 때가 있다 . 만일 雙對符 號의 무게 를 알 때 MacW i ll i ams 의 둥식 을 이 용하여 본래 부호의 무 게 를 계 산할 수 있 다. MacW i ll i ams 의 등식 울 증명 하기 위 하여 먼 처 線形代數 에 나오는 팔요한 용어를 정의한다. 어떤 體 F上 의 벡터공산 V 를 다음 6 개 조건을 만족하는 代數系 로 정의한다. ® V는 加群 (add iti ve g rou p)이 다. @ xEV, aEF에 대 하여 axEV @ x, yE V, aEF 에 대 하여 a(x+y ) =ax+ay @) xE V, a, {3 EF에 대 하여 (a +{3 ) x=ax+{3 x @ xEV, a, {3 EF에 대하여 (a{ 3 ) x=a(/3 x ) @ l ·x=x (1 은 F의 單位元) 벡터공간 V의 부분집합 W ( 국)가 다음 두 조건을 만족하면 W 를 V의 部分空間 (subs p ace) 이라 한다• ¢는 공집합이다. ® wI,w2EW에 대하여 w1+w2EW ® aEF, wEW에 대하여 awEW F上 의 n 차원 벡터공간의 기저 vh 입 2. … u“ 일 때 V의 두 개의 벡타
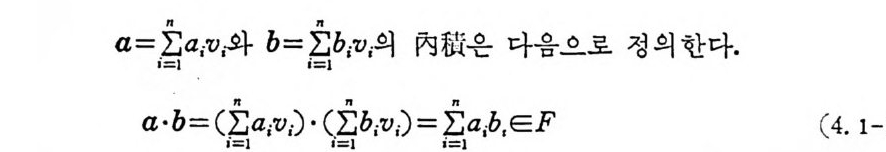
벡 터 a, bEV 는 a•b=O 일 때 直交한다. V의 부분공간 W의 斐對空 ra~ (dual spa ce) W 톨 다음과 같이 정 의 한다. 모든 y EW 에 대하여 x• y =O 이면 xEW .l이다. V 의 2 개의 부분공간 V1 과 V2 의 집합 (d i rec t sum ) 을 V1 EB Vz 로 표 시할 때 모든 yE VI, ZEV2 에 대하여 x= y +z이 면 XEVl ® V 호. 정 의한다. 〈정 리 4. 1-5> V 의 부분공간 u, w에 대 하여 u .L ® IV두 cu n w) .L 이다. 〈증명〉 (U. l ®W. l) ~cunw) .l와 (U .l ®W. l)그 cunw ) 정을 들어 증명한다.
 unw덕 u,w (4. 1-152)
unw덕 u,w (4. 1-152)
〈정리 4.1-6> V 를 位數 q의 體上의 n 차원 벡터공간이고 U 를 V의 j次元 부분공간일 때 W= U. l. 또한 A 를 V의 k 次元부분공간 일 때 B=A .l이다. 이때 IWnAI= t-j lunBI 이 된다. |S i는 S 의 元의 수이다. 〈증명 > d i mV울 V 의 차원으로 표시 한다.
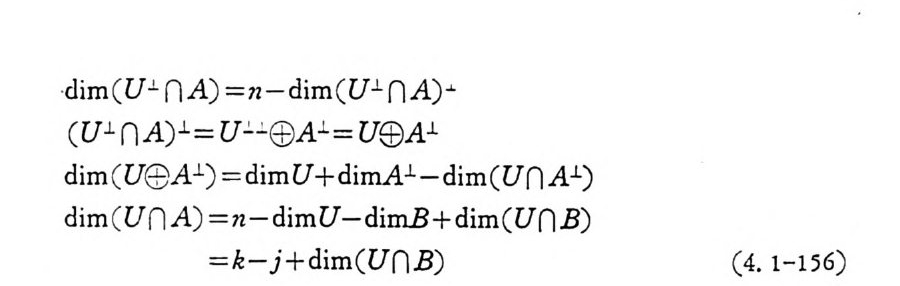 dim ( U .!. nA) =n-dim ( U .L n A) ....
dim ( U .!. nA) =n-dim ( U .L n A) ....
이 러 한 예 비 지 석 을 가지 고 MacW illi ams 의 둥석 울 증명 한다• 〈 정 리 4. 1-7> C 를 q元 (n, k) 선형 부호, D 를 C 의 雙對符號 라 하 고, A( z) , B ( z ) 를 각기 C, D 의 무거 1 분포다항식 이 타 하면 다음 둥 식이 성립한다.
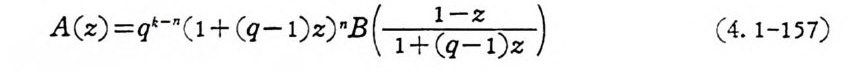 A( z) =q•- •(1 + ( q크 ) z)•B (~) (4. 1-157)
A( z) =q•- •(1 + ( q크 ) z)•B (~) (4. 1-157)
〈 증명〉 Fm을, 1
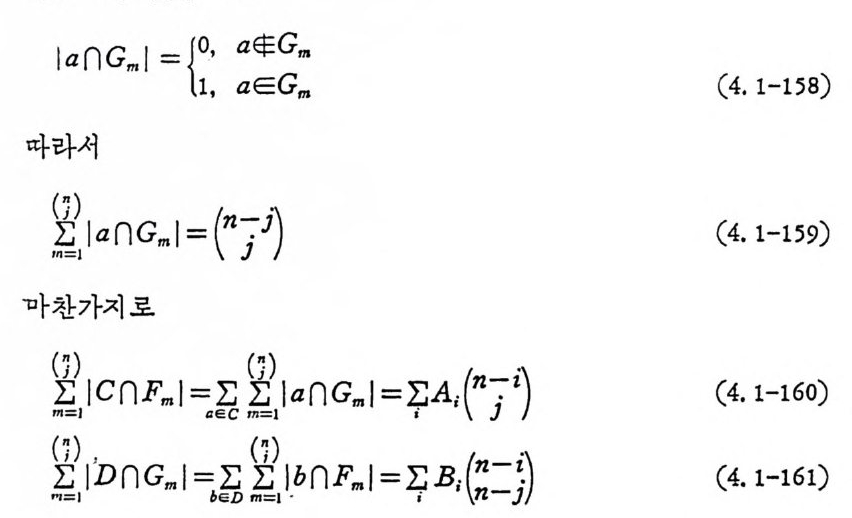 lanG 』 = {°, a 中 Gm
lanG 』 = {°, a 中 Gm
 정리 4.1-6 에서 1cnF 』 =q•-ilD nGml 이므로 식 (4. 1-160) 과 -
정리 4.1-6 에서 1cnF 』 =q•-ilD nGml 이므로 식 (4. 1-160) 과 -
(n. n-k) 부호 D 가 H행 렬에 의 하여 생 성 된 부호일 대 G 행 렬에 ; 의하여 생성된 (n,k) 부호 C 에 대하여 쌍대부호라 한다. 이때 H 행
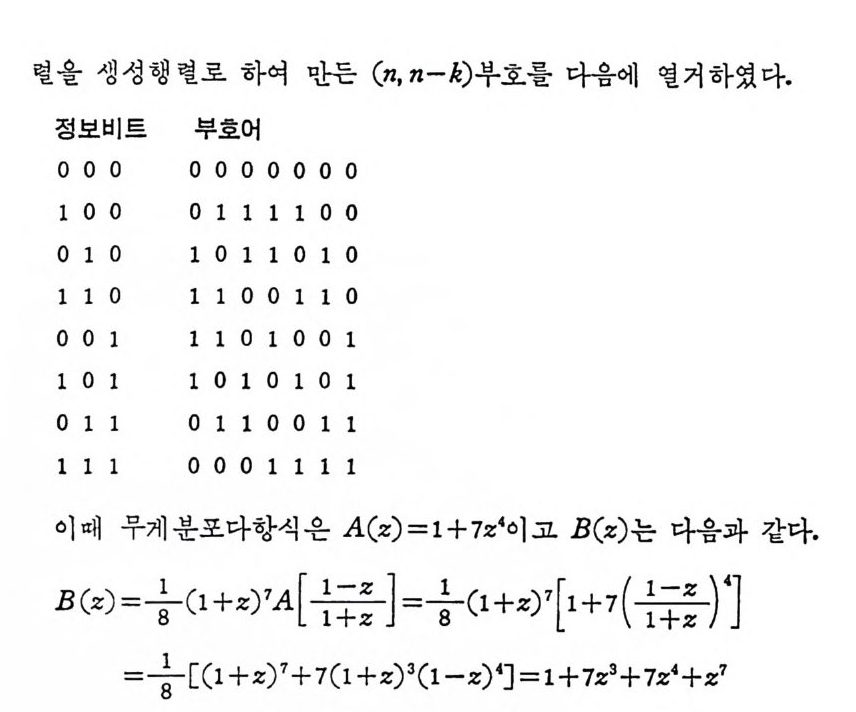 렬을 생성행렬로 하여 만든 (n,n-k) 부호를 다음에 열거하였다.
렬을 생성행렬로 하여 만든 (n,n-k) 부호를 다음에 열거하였다.
즉 G행 렬 에 의하여 생성된 부호 C 내에는 무게 0 인 부호가 1,3 개인 부호 7, 4 개인 부호 7, 무게 7 개인 부호가 1 개 있음을 알 수 있다. 4.2 콘볼루숀부호 4. 2. 1 콘볼루숀부호의 표현 지금까지 우리논 여러 형태의 에러를 訂正할 수 있는 블록부호에 대 하여 설 명 하였 다. 또 다른 중요한 형 태 의 부호는 1954 년 E li as 에 의하여 처음으로 소개된 콘볼루숀부호 (convolu ti onal code) 이다. 콘 볼 루숀부호는 블록부호가 아니며, 이 부호도 역시 여러 형태의 에 러 를 訂 正할 수 있는 능력을 가지고 있다. 부호는 k 정보비트를 받 아서 (n-k ) 의 패 리 티 검 사비 트를 발생 하고, k 와 ( n-k) 성 분을 합하 여 하나의 블록의 부호를 생성한다. 그러나 (n-k) 패리티비트는 현 재 通 報 블록 (messa g e block) 에 의하여 결정되는 것이 아니고, 이
전 N-1 동보블록에도 관계된다. 이 점은 다음어 설명 할 생 성행 렬 울 보면 알 수 있다. 通報系列 (messa g e se q uence ) 을 u= ( u 。 ( l ) u 。 ( 2 ) … u0(k)u1(1)u1(2) .. ·u1(k) …)라 하고 G .. 올 無 限生 成行列 이 라 하면 부호화된 계 열은 다음과 같다.
 x=uG. . (4. 2-1)
x=uG. . (4. 2-1)
 D•g. ,(i) = (-o._:… l드n 一 O g .,(i)) (4. 2-6)
D•g. ,(i) = (-o._:… l드n 一 O g .,(i)) (4. 2-6)
k 생성식 g .. (i ) 에서 처음 0. … 1• … O` 는 k 개의 성분 중 i번 위치에 1 이 됨을 의미하고 나머지는 0 이다. 또한 Dl g.,(i)는 g .. (i)가 오른쪽으 로 An 성분만큼 이동하였음을 의미하고 g.,(i) 이전은 0 이다. k 개의 생성식은 부분생성식으로 구성되어 있으며, 또한 (n,k) 부호의 k 개 의 생성식이 주어지면 생성식을 분해함으로써 k(n-k) 개의 부분생 성식을 구할 수 있다. 이로써 우리는 無限行列인 생성행렬 G. . 을 만들 수 있다.
 一 gg .. .. ((12)) -
一 gg .. .. ((12)) -
x, 이 l 번블록일 때 (n, k) 부호를 구속길이 (constr a in t leng th) N불 록 또는 구속길이 nN성 분의 콘볼루숀부호라 한다. 식 (4.2-8) 으로 부터 우리가 형성한 부호가 조직부호임을 알 수 있다. 또한 생성행 렬 G. . 로부터 패리티검사행렬 H .. 을 구할 수 있고 다음 등식이 성립 한다. G 고; .,=o (4.2-10)
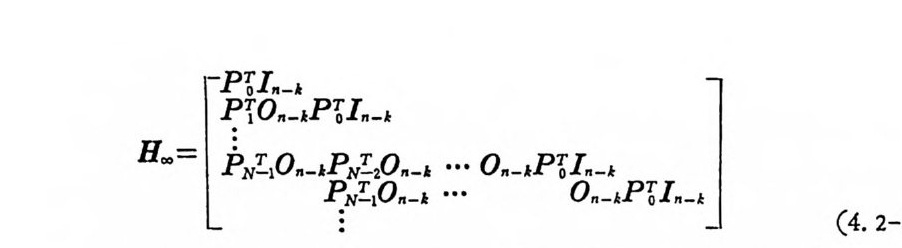 H = -pTpIo:n.0lTi1p0 INP T T -oI-knP TiTN -P-TN4&-- :k· . . 。 ” kPT OI nn okk PT oI n k __
H = -pTpIo:n.0lTi1p0 INP T T -oI-knP TiTN -P-TN4&-- :k· . . 。 ” kPT OI nn okk PT oI n k __
Pt l=O, 1, …, N 크, 은 kX (n-k) 행 렬이 고 PI 은 P 행 렬의 轉四 行 列이다. On-k 는 (n- · k)X(n-k) 零 行列이며, ln-k 는 (n -k)X (11 -k) 單 位行列이다. 부호화된 부호계열 x 를 송신하여 에러벡터 e 가가산 되어 수신된 벡터를 y라 하며
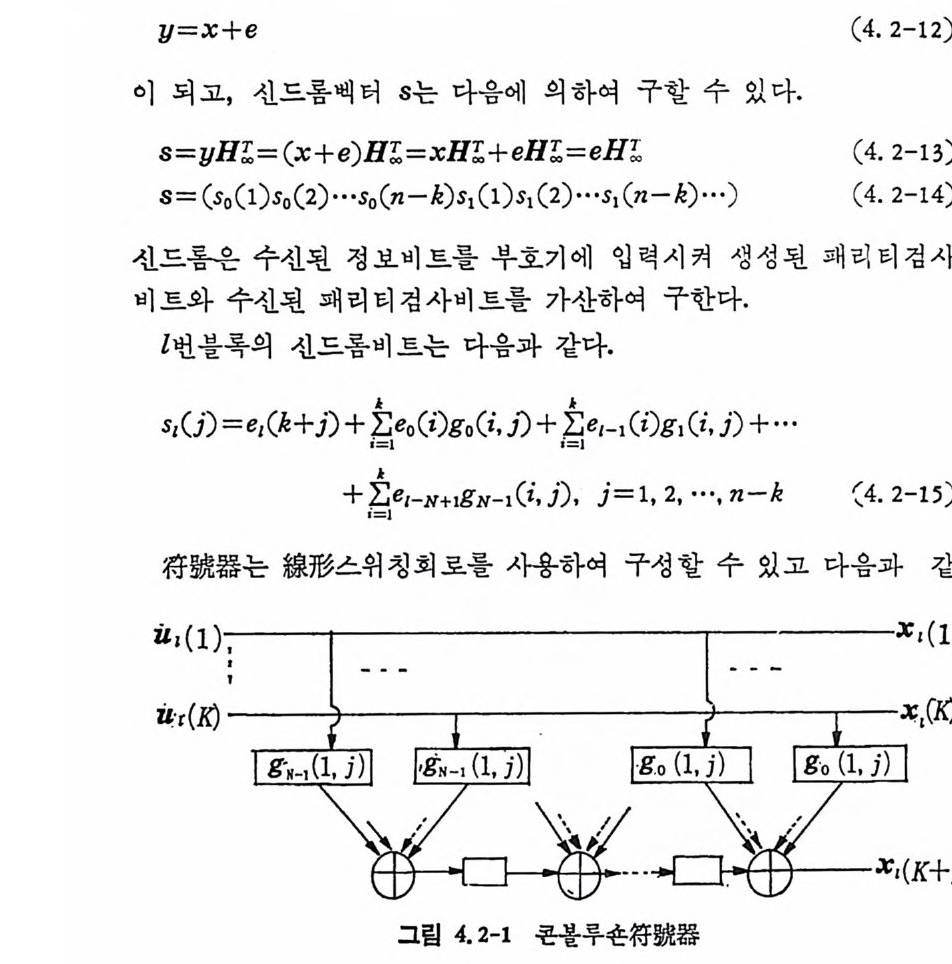 y= x+e (4. 2-12)
y= x+e (4. 2-12)
댜 gi(i,j ) =l 일 때는 線의 연결을 의미하고, gi(i, )) = O 은 斷線울 의미한다• 〈 예 4. 2-1> 拘束길이 N=2 인 (2, 1) 콘볼루숀부호가 다음 部分生 成式에 의하여 생성된다.
 g( l, 1) = (1, 1)
g( l, 1) = (1, 1)
만일 U=(100010001 …)이 면 x=(100101o q oo11 …)이 된다. 1 번바 트에 에러가 발생하여 수신된 계열이 y = ( 000101000011 … ) 이연 신 드롬비트 (s 。 (1)s1(1)s2(1))=(110) 이 된다. 2 번비트에 에러가 발 생하여 수신된 계열이 y= (010101000011… ) 되면 신드롬바트 는 (s 。 (1)s1(1)s2(1)) = (101) 이 된다. 마찬가지로 3 번비트에 에러가 발생하면 신드롬비트는 (s 。 (1)s1(1 ) sz( 1) )=(111) 되어 다음과 같이 나연할 수 있다. (s 。 (1)s1(1)s2(1))=(110) ; 1 번비트에러 (s 。 (1)s1(1)s2(1))=(101) ; 2 번바트에 러 (s 。 (~)s1(1)s z( 1))=(111) ; 3 번비트에러 죽 3 개의 신드롬 중 s 。 (1) 은 에러有無를 표시하여 So(l ) =l 일 때 에러가 발생하였음을 나타내고 있다. 다음 S i ( l ) s 2 (l) 는 에러위치를 이진수를 사용하여 알려 주고 있다. 수신된 12 개 비트 중 1 번블록의 1,2,3 비트.안에 에러가 하나 발생하면 에러를 정정할 수 있다. 먼저 예의 부호를 일반화하여 기술한다. 이 부호는 블록부호의 해 밍부호와 마찬가지로 신드롬에 나타난 숫자로 에러의 위치를 표시 하는 콘볼루숀부호이 다. m 이 正數일 때 n=2', k=2'-1, N=m+1 인 콘볼루숀부호를 단 일에러訂正 (2', 2'-1) W yn er-Ash 부호라 한다. 그러 면 2'-1 개 의 g(i, 1) = (1, i0, i1. …, i .. -1), i= l, 2, …, 2. . -1 이 존재 하고, 이 = O, 1. o
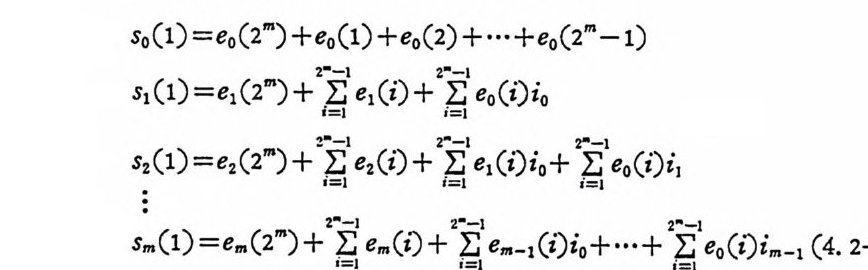 s 。 (l) =e 。 (2 .. ) +e 。 (l) +e 。 (2) + ••• +e 。 (2 .. -1)
s 。 (l) =e 。 (2 .. ) +e 。 (l) +e 。 (2) + ••• +e 。 (2 .. -1)
受信된 Nx2m 개 비트안에 처음 n=2m 비트內 에러가 없으면
e 。 (l ) = e 。 ( 2 ) = … =e 。 (2m)=O 이고, 따라서 s 。 (1)=0 이 된다. 물론 · NX2m7 n 비트.안에 에러가 없으면 s1(1)=s z( l)= … =%(1)=0 이다. W y ner - Ash 부호는 전체 Nx 2m 개 비 트 안에 1 개 의 에 러 가 발생 하였 을 때의 에러訂正符號이다. 만일 2m 개 비트 안에 i위치에 에러가 발 · 생하였다면 s 。 ( l ) = e 。 ( 1 ) = 1 죽 ( s1 ( 1 ) s 2 ( 1 ) … S m( l))=( i。i 1' i m- J)으로 에러위치를 나타낸다. 신J_ 드 몽 중 s 。 ( 1 ) 은 에 러 의 有 無 를 표시 하고, 나머 지 신드롬 S1(l), s2( l) , …, S m( l ) 은 처 음 2m 비 트의 에 러 위 치 를 알려 준다. 만일 2m 비 트 안에 에러가 없고 다음 2m 비트 안에 에러가 있으모면 신드롬은 다 음과 같이 s 。 (1 ) 을 0 으로 놓고, 다음 m 개 의 신드롬을 사용한다.
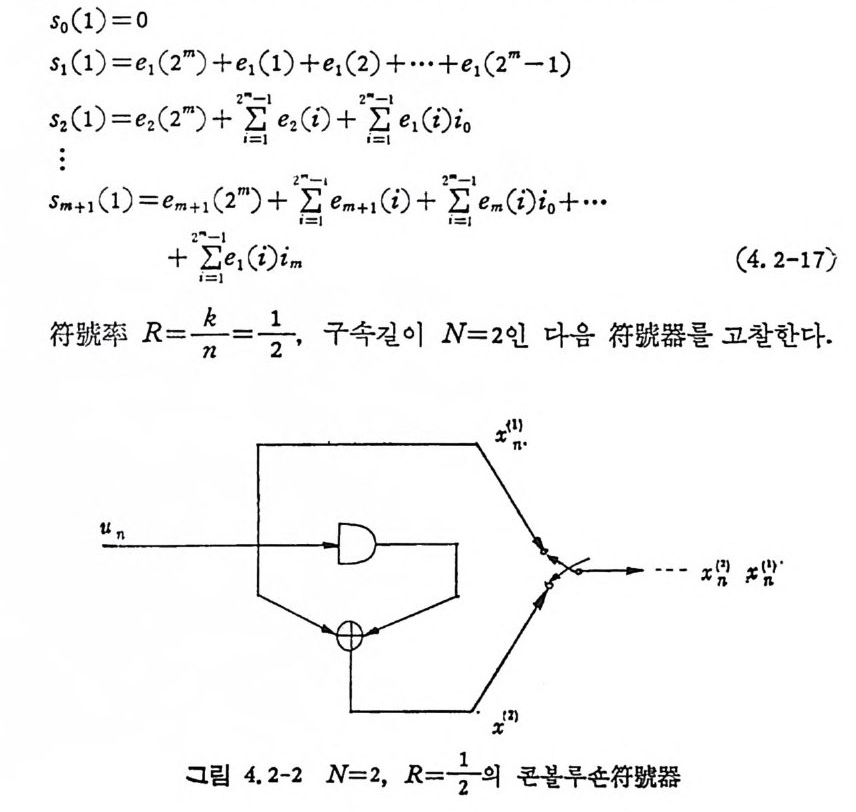 s 。 (1 ) =0
s 。 (1 ) =0
 이 符號器의 部分生成式과 生成式은 다음과 같다.
이 符號器의 部分生成式과 生成式은 다음과 같다.
x 인은 정보비트를 표시하고, x 언는 패리티검사바트를 표시한다. 일반적으로 u1,u2. … ,UL 의 정보비트를 N-1 개의 쉬프트 레지스터 를 가진 符號器에 입력시키면, uI,u2. …,U L 다음에 N-1 개의 0 이 첨 가된 u1, u2… , uLOO … 0 을 入力시 켜 야 (L+N-l)n 개 의 부호화된 비트가 出力에 나오며, 모든 쉬프트 레지스터의 내용이 0 이 되어 새로이 다음 정보비트를 받을 수 있다. 만일 L=3 이면 다음과 같 이 無限生成行列에서 有限生成行列울 구할 수 있다.
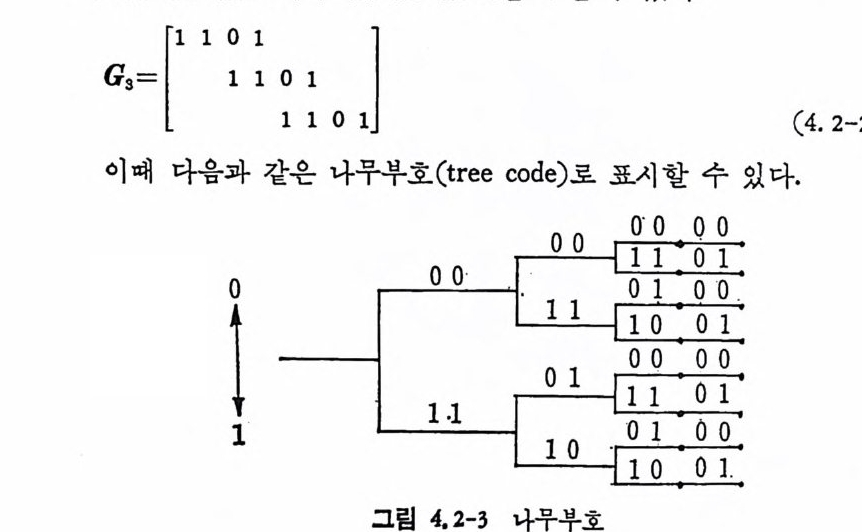 Gs= [1 1 \ 』 (4. 2-22)
Gs= [1 1 \ 』 (4. 2-22)
나무부호에 서 각 정 을 마디 (node) 라 부르며 마더 와 마디 를 연결 한 線 올 가지 ( branch ) 라 부론냐 모든 通路( p a t h ) 는 간개 가 존재 하 며, 말단의 긴 가지에는 N게 의 비트가 있다. 일반적으로 出力은 다음과 같이 표시할 수 있다. x = x \ 1 ) X ( f ) x T x \2 ) x} ) 과 ) 과 ) x \21 (4. 2-23) 入力이 U= ( U1 tl z U3 ) = ( 101 ) 이면 出力은 x= ( 11011101 ) 이 된다. 물 론 이러한 방법은 R= 스n- 인 경우에도 적용시킬 수 있다. 4.2.2 쓰레쉬홀드復號 콘볼루 숀符號 의 쓰레 쉬 홀드 復號 法 ( t hreshold decod i n g ) 은 블록부 호의 경우와 동일하며, 간단한 예를 들어 그 개념을 설명한다. 그 림 4. 2-2 에서 하나의 入力바트에 대하여 부호화된 2 개의 비트가 생 성되며, 실 제 채 널을 동 하여 송신할 때는 스위치를 통하여 부호화 된 비트가 직 렬 로 송신된다. 지금 예는 1 개의 입력비트에 2 개의 부 트호가화된 n 개비의트 가부 호발화생된하 는비 트R=로 」 2 러발생 1 할경 우경이나우, R =일 ―반kn- 적가으 로된 다k. 개 의하 나비 의 정보비트가 나온 다음 패리티검사비트가 전송되므로 일종의 조 직 부호이 다. 그림 4. 2-4 는 완전한 콘볼루숀 부호계 통을 보여 주고 있다. 이때 산드롬은 채널에서 잡음이 가해전 정보비트 x ~) -을 符號 器 를 다시 통과하여 나온 성분과 채널에서 잡음이 가하여진 패리티 비트 x 인과 합하여 구할 수 있다.
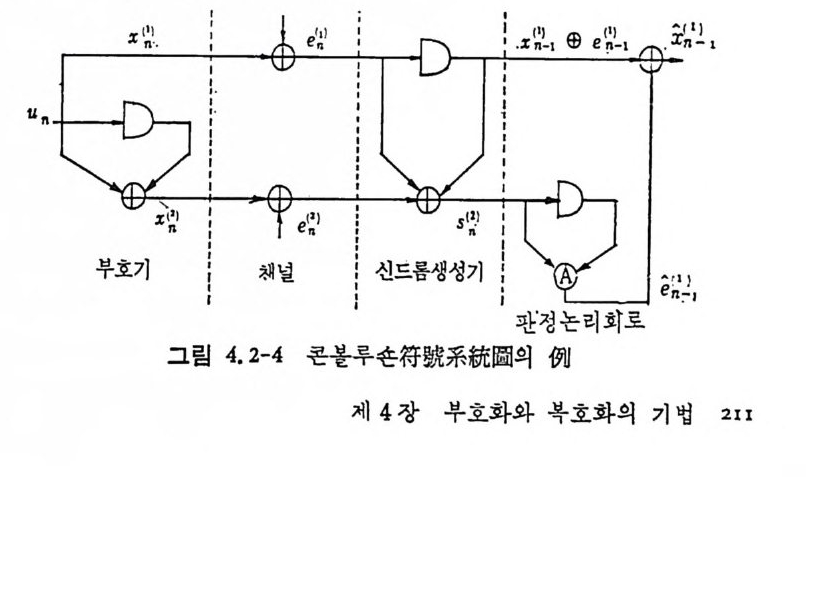 un x'~'- . III1IIIIIIIIIII 〔.Z^ ( nl l- 1
un x'~'- . III1IIIIIIIIIII 〔.Z^ ( nl l- 1
®는 AND 회 로이 며 , 소”는 x” 의 추정 치 이 다. s ~22 . 1 와 s~ ) 는 그립 I 4. 2-4 의 右邊下段에 나타나는 신드롬이 다. S~~I 과 s 언을 수식 으로 표 시하면 다음과 같다.
 sl~1 = (x.-2EBe l 밀 )EB(x.-1EBel~1)EB(x.-2EBXn-1EBe1 임)
sl~1 = (x.-2EBe l 밀 )EB(x.-1EBel~1)EB(x.-2EBXn-1EBe1 임)
이 된다. 이 2 개의 신드롬식은 채널잡음에만 의존하고, 신드롬식 • 으로부터 e ;1 .>. 1 을 추정할 수 있다. 만일 라밉 =1 이고, e! ) =e 언 =e ~ 밀 =e ; 잃 =0 인 경우 sl~,=s 언 =1 이 되며 판정논리회로의 AND 회로물 통하여 e; 씩을 올바르게 추정한다. 마찬가지로 e 1 밀 =0 이고 4 개의 에 러비트 중 하나가 1 이면 두 신드롬식 중 하나는 1 이 되어 AND 회 로를 동하여 e l 밉울 올바르게 추정 한다. 그래 서 라밀, e; 밀, e! \ e ;입 , e 만 중 하나의 에러가 발생하면, 다시 말해서 5 개의 受 信 成分중 하나 의 에러가 발생하면 이 復號器는 올바르게 추정할 수 있다. 이때
 에러P(가E ) 발=P생[할草 확 *률 e 訂은 =다 t음 (과i) P같 ; 다(1.- p )S 기
에러P(가E ) 발=P생[할草 확 *률 e 訂은 =다 t음 (과i) P같 ; 다(1.- p )S 기
이 식은 e ;쌉 이 정확히 추정되었다고 가정할 때 성립한다• 이와 같 온 復號器 롤 歸還 復號器(fe edback decoder) 라 하며 , 과거 의 判定울 사용치 않은 처음 부호기를 確定復號器 (de fi n it e decoder ) 라 한다 .
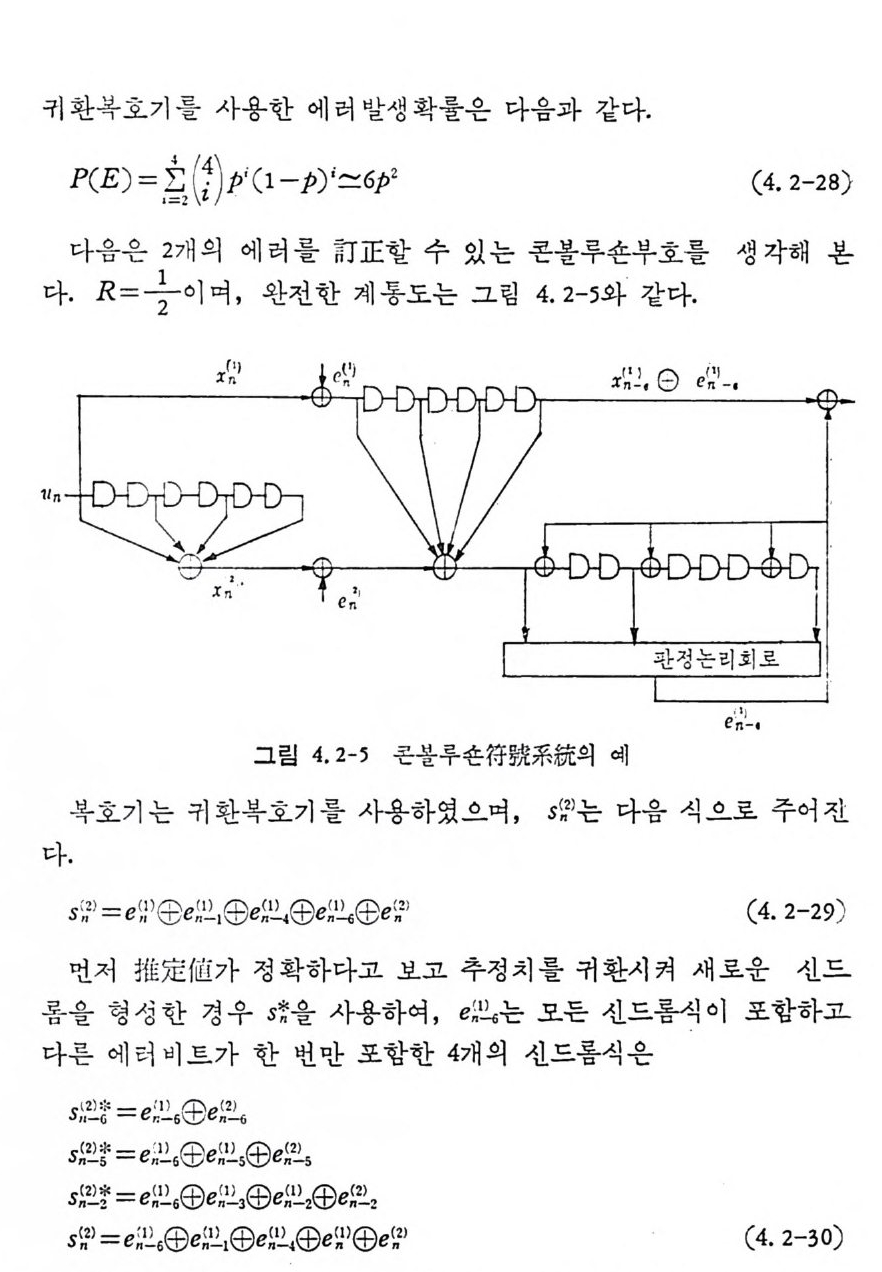 귀 환복호기 를 사용한 에 러 발생 확률은 다음과 같다.
귀 환복호기 를 사용한 에 러 발생 확률은 다음과 같다.
이 된다. 11 개의 수신비트 중 2 개 또는 이하의 에러가 발생하면 4 개의 신드롬식으로부터 에러를 訂正할 수 있다. 判定論理는 블록부호의 多數決論理의 경 우와 같다. 신드롬 또는-
산드롬의 합을 패리티검사합이라 부르며, 패리티검사합의 집합 {A i, A2. … ,A J}는 잡음성분 e 가 각 패리티검사합에 포함되어 있고. 기타 잡음성분은 한 번씩만 포함되어 있으면 잡음성분 c 에 {A1, A2, …, AJ } 가 直交한다라고 말한다. 만일 J= 2 t개 의 대 티 티 검 사합이 e 에 直交하면 t 또는 이하의 에러를 정정할 수 있다. 이 러한 復號法 울 다수결논리복호법 또는 쓰레쉬홀드복호법이타 부른다. 먼저 2 예 는 각기 t= l, t =2 인 경우이다. 4. 2. 3 메트릭 메트릭 (me t r i c) 은 콘볼루숀부호를 逐次復號法 ( se q uen ti al deco· d i n g)으로 복호하는 데 중요한 개 념 이 므로 선명 한다 . M 개 의 부호 집 합이 {Xo, X1. …, XM-I} 이 고 각 부호길 이 가 {110 , 111. …, 11.\/-1 } 아 타 가 정한다. 그러면 특정부호 Xi = (xil· x ,2. … ,x, m) 는 부호길이 n,이 다. M 개의 부호 중 최대부호길이를 가전 부호의 부호길이를 n 이타 하 면 n=max(n0, n1. …, nM-1) 이 다. 모든 부호가 부호길이 n 을 갖기 위해서는 길이 n 이 되지 않는 부호에 부가비트를 첨가한다. 즉 X,=(X,1Xi2 … x ,‘Xi n,. , • • • X i)이고 부가비트는 X i와 독립적으로 선택 한다고 가정 한다. 채 널을 동하여 수신된 부호. y= (3' I, y 2 . …, yn ) 를 복호하기 위하여 P(x;IY) 가 최대로 되는 복호법을 취하면
 P(x;IY)=P(x;, y)/ P(y) (4. 2-31)
P(x;IY)=P(x;, y)/ P(y) (4. 2-31)
 이다. P(x,., y)를 JU= Pl ( y;)로 나누어 대수를 취하면 다음과 같다.
이다. P(x,., y)를 JU= Pl ( y;)로 나누어 대수를 취하면 다음과 같다.
률석로 (4나. 2타-3난4 다) 는고 정가보정비하트면가 P독,=립2-R적n으’ 로죽 R발=생 _하nk; 고 울 대0 과입 하1 이여 같구은한 확식 이다. V ( x :) 를 메트락이라 부르며, 목히 +.lo g*울 R 로 대치한 메 트럭 을 Fano 메 트럭 이 라 한다. Fano 알고리 즘 (Fano al g or it hm) 은 콘볼루숀부호를 복호하는 데 메트럭이 최대가 되는 동로를 택하는 방법이다. 4. 2. 4 나무부호, 트레 리스圖 다 음 符號器 에 의 하여 생 성 된 콘볼루숀부호를 생 각한다.
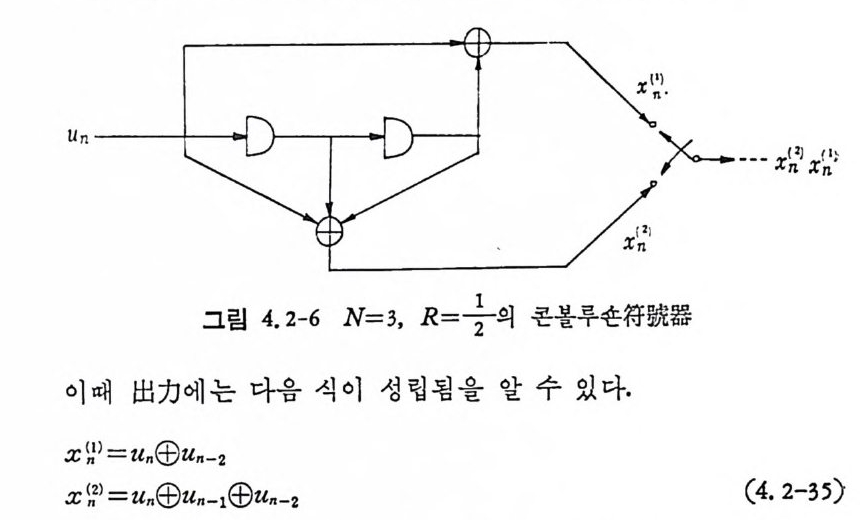 \;\
\;\
부호화된 비트를 계산하기 위해서는 부호기의 쉬프트 레지스터의 내용을 알면 되고, 쉬프트 레지스터의 내용을 부호기의 狀態 (s t a t e) 타 부른다. 그립 4. 2-6 의 경 우 상태 를 q로 표기 하면 다음과 같다.
 q= (u-I, u-2) (4. 2-36)
q= (u-I, u-2) (4. 2-36)
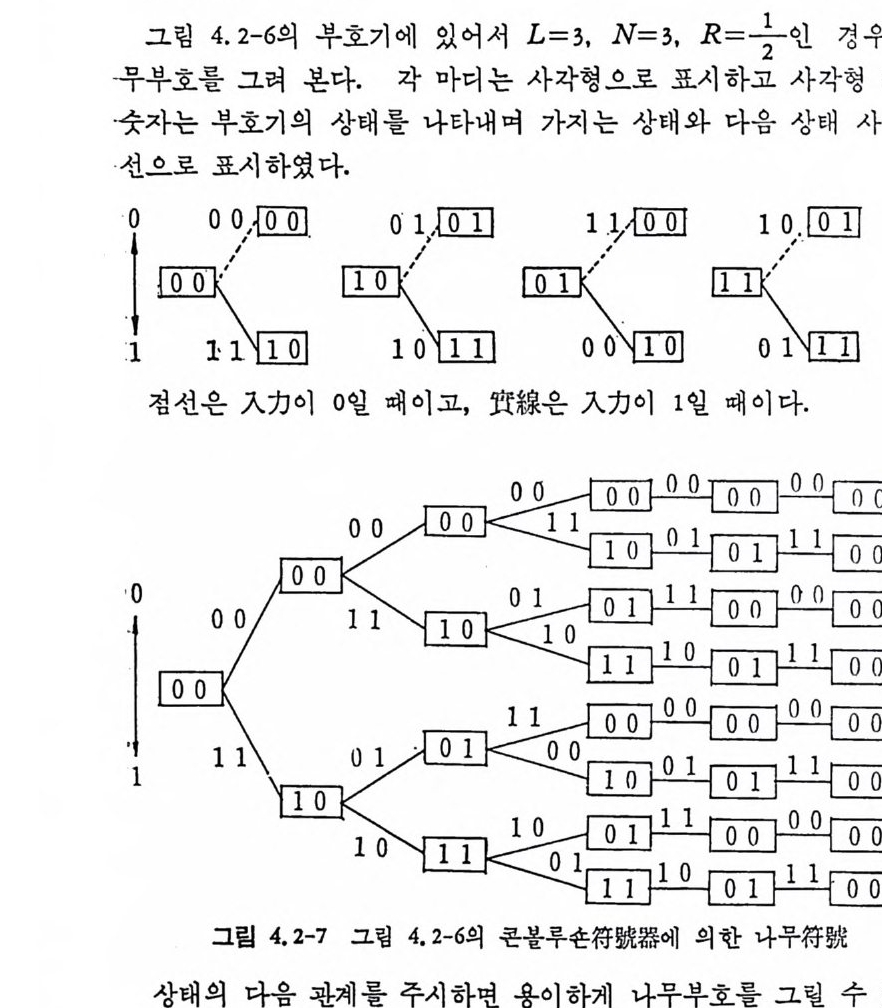 그림 4.2-6 의 부호기에 있어서 L=3, N=3, R=721 oJ_ 경우 나
그림 4.2-6 의 부호기에 있어서 L=3, N=3, R=721 oJ_ 경우 나
그림 4. 2-7 에 서 하나의 상태 에 서 다음 상태로 가는 가지가 하 나일 때는 입력이 0 이므로 주의 를 要한다. 이 상태들을 한데 묶 어 표시 하면 狀態圓 (st a t e dia · g ram ) 가 된다. 점선은 입 력 이 0 인 경우이고, 껏[線인 경우는 입 럭이 1 인 경우이다 . 일례로서 (1 10) 인 경 우 출력 은 ( 111010 ) 이 됨을 알 수 있다. 나무부호에서 마디 가 세로로 나 열된 것을 깊이 ( de pt h ) 라 부르며, 동일한 깊이 에 같은 상태 의 마디 가 둘 이 상 있으면 하나의 마디로 통합할 수 있다. 이 렇게 하여 만돈 구조를 트레 리 스 圖 (tr e llis dia g r am) 라 한 다. 깊이 2 를 보면 모든 상태를 다
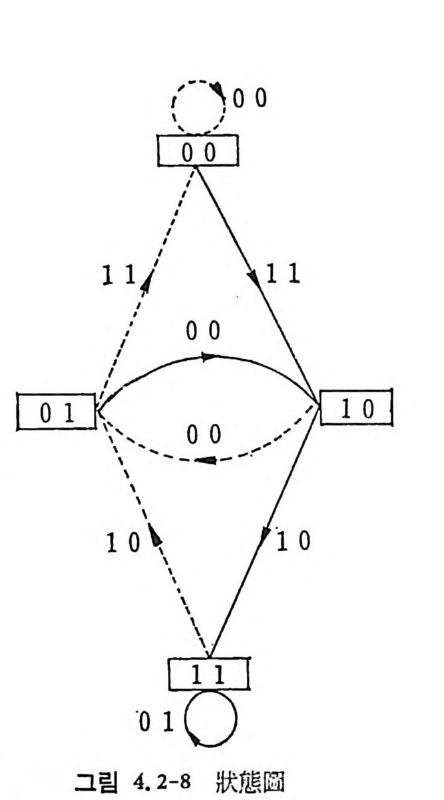 ’,~00
’,~00
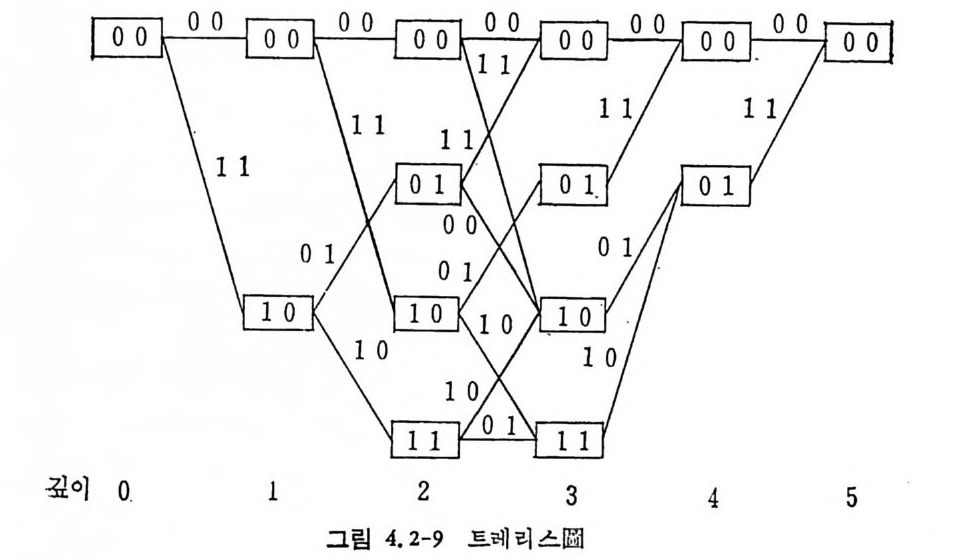 깊이 < l 2 3 4 5
깊이 < l 2 3 4 5
포항하고있다. 일반적으로 L 이 크면깊이 2 와같은형태가반복한 다. L=~ 일 때 트레리스도는 다음과 같다.
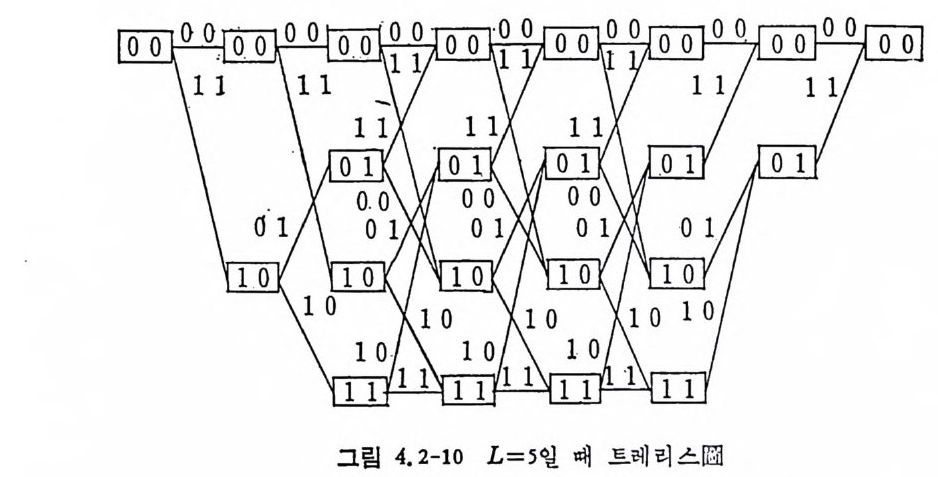 그립 4. 2-10 L=5 일 때 트레 리 스回
그립 4. 2-10 L=5 일 때 트레 리 스回
입력이 U=(10111(00)) 일 때 트레리스도로부터 쉽게 출력이 X=(11010010111011) 됨을 알 수 있다. u 벡터의 ( )내의 2 개의 O 은 쉬프트 레지스터를 0 으로 만들기 위한 것이다. 4. 2. 5 M.L 復號法 二元符號를 입 력 으로 한 離散無記憶채 널에서 最適復號法 ( o pti mum decod i n g)을 생각해 본다. 정보비트가 통계적으로 서로 독립적이고, 0 과 1 의 발생 확률이 동일하고, 트레 리 스도를 통하여 모든 동로에 0 과 1 이 동일확률로 나타난다고 가정한다. 그러 면 M.L. 부호법 (maxim um like lih o od decod i n g)은 다음 석 이 최대가 되는 통로를 찾는 방법이다.
 P(yl x;)=I fP( yi lx u) (4. 2-39)
P(yl x;)=I fP( yi lx u) (4. 2-39)
yJ는 無記憶채 널을 통하여 잡음이 가하여 진 수신벡 터 중 j번성 분 이며, X ij는 i번 부호어의 송신된 부호벡터 중 j번 성분이다. 다음 조건을 만족시 키 는 L 〔 x(u 汀을 通路尤度函數(p a t h lik e lih o od fun c- ti on) 라 부른다. n 은 부호벡 터 의 차원이 다.
 ® 互 x] = I;=n;I L [ x;]
® 互 x] = I;=n;I L [ x;]
그러 면 L[x(u) ]는 송신된 부호벡 터 xn 과 수신된 부호벡 터 y 사 이의 해밍거리로 負 의 수이다. 이 復號法은 수신된 벡터와 모든 송 신가능한 부호벡터와 비교하여 가장 해밍거리가 작은 동로를 찾는 最小距離復號法 (m i ni m um dis t a n ce decodin g ) 이 다 . P ( y \x, ) 을 최대로 하는 것은 送信벡터와 受信벡터 사이의 해밍거 리를 최소로 하는 것이므로 最 小距 離復號法 은 곧 M.L. 부호법이다. 트레리스도로부터 생각하여 보연 같은 상태를 가전 마디를 통합하 여 트레리스도를 형성하였으므로 가지를 통합할 때 尤度函數가 작 온 것은 버티고, 높은 尤度함수를 가진 가지만 택하는 방법을 사용 하면 수신된 랙터를 송산가능한 전체 수신벡터와 미교할 팔요가 없 다. 그림 4. 2-10 에서 깊이 3 인 곳에서는 4 개의 마디에 각기 2 개의 入力가지가 있으며, 2 가지 중 낮은 尤度函數를 가전 가지는 철단한 다. 그러면 4 개의 마디에 들어오는 가지는 각기 하나만 남을 것이 다. 다음 깊이 4 에서도 각 마디에 들어오는 두 가지 중 낮은 尤度 函數률 가진 가지는 절단하여 나아간다. 깊이 5,6,7 에서도 같은 방 법으로 가지 하나만 남게 하면 결국 트레리스도에는 하나의 통로만 남게 되고 이 동로가 최적통로이다. 그림의 예는 송신벡터 x= (11010010111011) 이고 수신벡터 y =(11110011111011) 일 때 최적통 로를 찾는 방법을 도시하였다. X 는 절단된 가지를 표시한다. 괄호 안에 숫자는 에러수이고, 괄호 앞에 숫자는 전체 에러합인 尤度函 數이다.
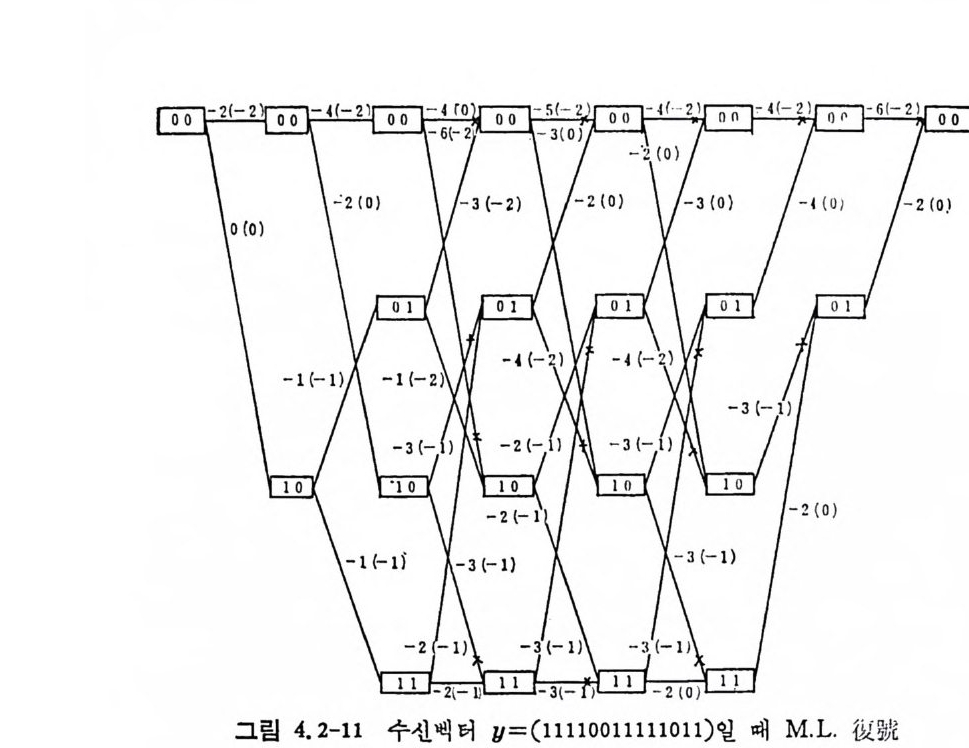 그림 4. 2-11 수신벡 터 y =(ll110011111011) 일 때 M.L . W:號
그림 4. 2-11 수신벡 터 y =(ll110011111011) 일 때 M.L . W:號
通路尤度函數의 값이 같을 때에는 임의로 下端가지를 철단하였으 며 최종마디로부터 逆으로 철단되지 않온 통로만 찾아 가면 X= (11010010111011) 이 된다. 이 방법을 사용한 復號法은 2 개의 에러 를 訂正하였다. 이러한 復號方法을 V it erb i알고리즘이라 한다. 4.2.6 콘볼루숀부호의 거리특성 다음과 같은 符號器률 생 각해 본다. 그립 4. 2-6 의 符號器의 스위 치작용이 반대로 된 부호기이다. L=3 일 때 이 부호기에 해당하 는 나무부호, 상태도, 트레리스도는 그림 4.2-12 와 같다. 지금 송신된 부호벡터가 X=(00000000) 일 때 수신된 부호 y에 에 러가 발생치 않았다면 복호하는 데 통로는 그립 4.2-12 ( c) 에서 가 장 위의 동로를 택할 것이다. 만일 다른 동로를 택하였을 때 零 벡 터와 해밍거리가 어떻게 변하는가를 알아보기 위하여 다음과 같이 〈 00) 상태의 마디를 벌려 본다.
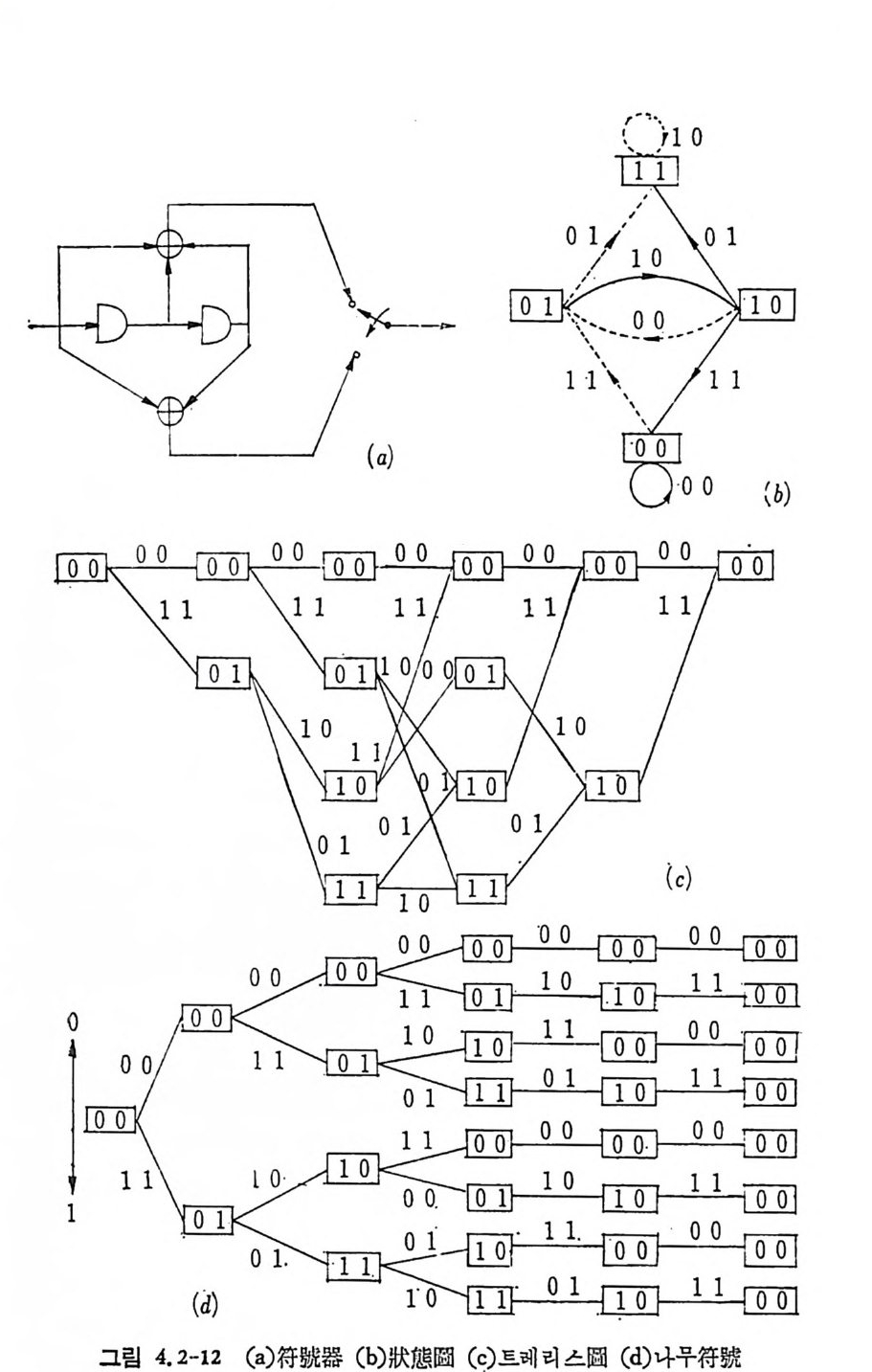 , --- 1`` 1`` - -\- _ _ 一 / 1 1
, --- 1`` 1`` - -\- _ _ 一 / 1 1
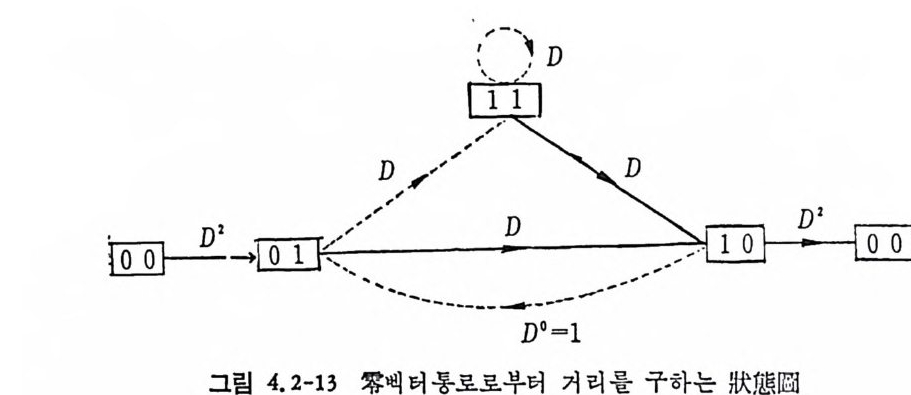 :·, .-` ~ D
:·, .-` ~ D
D0,D 1, D2 과 같은 D 의 指數는 한 마디에서 다음 마디로 갈 때 零벡터와의 해밍거리를 나타내고 있다. (oo) 상태에서 다시 ( oo) 상 태로 되돌아오기 위한 최소거리는 상태 (oo) 一 (01)-(10) ― (oo) 를 동과한 해밍거리 5 인 동로이다. 해밍거리 5 인 통로는 1 개 존재하 고, 해밍거리 6 인 동로는 2 개 촌재한다. 이와 같이 검토하면 모든 통로에 대한 거리를 구할 수 있다. (00) 상태에서 입력을 1 로 하여 신호흐름도의 개 념 을 이 용하여 轉達函數를 구하여 보면 다음과 같 다.
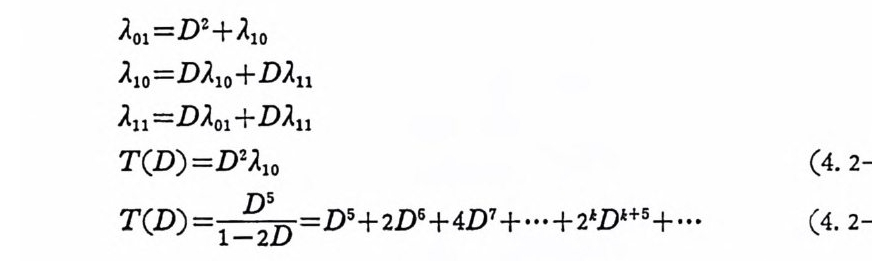 Ao1=D 나 A10
Ao1=D 나 A10
거리 5 인 동로는 1 개이고, 거리 6 인 통로는 2 개, 거리 7 인 통로 는 4 개임을 식으로부터 알 수 있다. 이 식을 生成函數(g enera ti ng f unc ti on) 라 부르며 D 의 함수이 다. 지 금 거 리 D 분만 아니 라 몽과 한 가지수 L 과 復號하였을 때 에러비트수 I의 함수로 하기 위하 여 그림 4. 2-14 에 L 과 I를 첨 가한다. 生成函數를 구하면 다음과 같다.
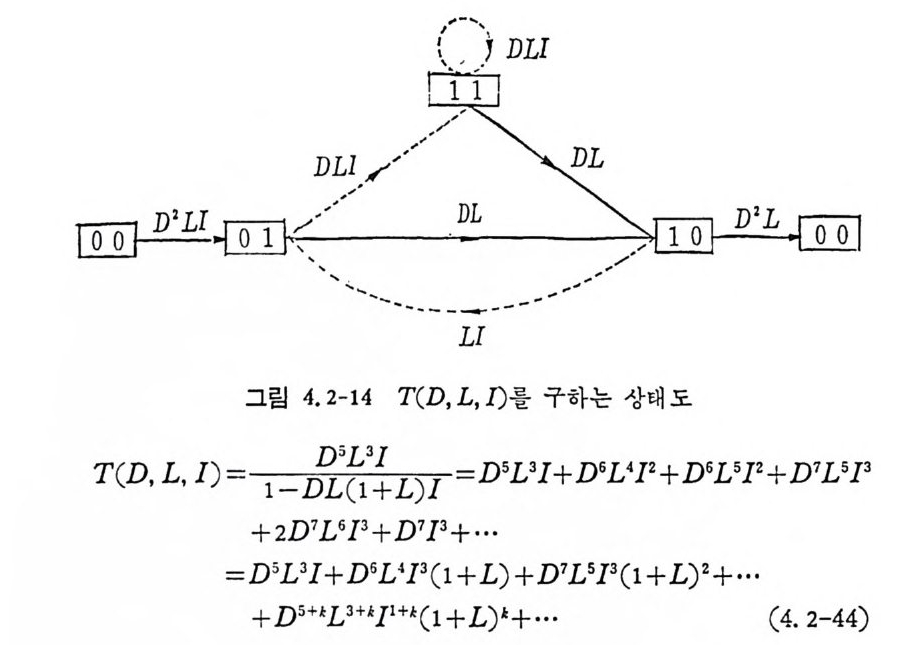 三 ’/` D.. `-- L`-/ I ' - / ✓ -‘. ’ DL
三 ’/` D.. `-- L`-/ I ' - / ✓ -‘. ’ DL
즉 거리 7 인 동 로는 모두 4 개 있으며, 하나는 가지를 3 번 통과하 고 에러바트수는 3 개이며, 2 개는 가지를 6 개 통과하고, 역시 에러 비트수는 3 개이며, 나머지 한 개는 7 개의 가지를 통과하고 에러비 트수는 3 개이다. 4.2.7 逐次復號法 나무부호의 길이가 길어 많은 마디를 가지고 있으면 모든 마디의 메 트릭 값을 계 산하기 탄 불가능하다. 스택 알고리 즘 (s t ack algo r it hm ) 은 逐 次 復號 法의 일종으로 계산을 가능한 한 작게 하고 메트릭값이 최대가 되는 최종마디를 구하는 한가지 방법이다. L 개의 정보비트 에 해당하는 마디와 L+N 一 1 개의 가지를 가전 나무부호를 생각한 다. 受 信 系列이 y=(yI, y 2. … ,YCL+N-1)) 일 때 각 가지 위에 그에 해 당하는 총 Fano 메트릭값울 기입하고, 각 마디에는 시발접으로부터 각 마디에 이르는 가지 위에 기입된 메트릭값의 합율 표시하여 최 종마디의 메트릭값이 가장 높은 통로를 택한다. 예로써 N=2,
(n,k) = ( 2, 1), L=3 인 다음과 같은 나무부호 를 고찰한다. 0 0 0'l
二元 對稱채 널을 통하여 O( 또는 1) 을 송신할 때 1 ( 또는 0 ) 을 수신 할 확률 P=O.057 이면 下記와 같은 메트 럭표를 얻는다. 메트릭값 에다 一定 數를 곱하여도 무관하므로 표에서는 메트릭값을 사사오입 하여 正 敷를 취 한 후 二( g· 하였다. 죽
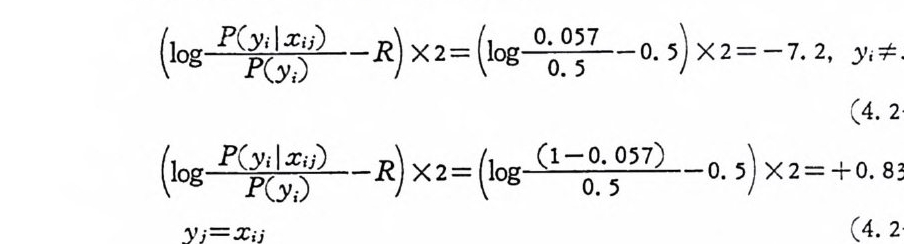 (log P (葛 ? ) 一 R) X 2 = (lo g윽뿐- o. 5) X 2 = -7 . 2, y, 주 X, J
(log P (葛 ? ) 一 R) X 2 = (lo g윽뿐- o. 5) X 2 = -7 . 2, y, 주 X, J
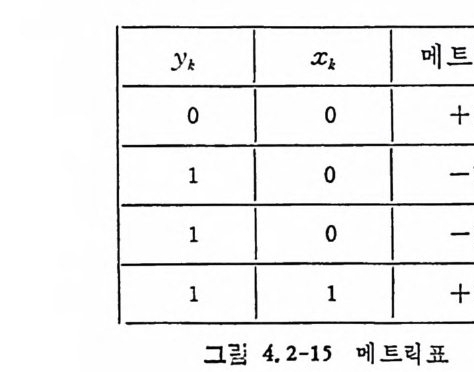 yk II xk |I 메트럭
yk II xk |I 메트럭
Yk 는 受信系列이고, X k 는 나무부호가지 위에 표시된 送信系列 이 다. 만일 수선계 열 y =(llOl … ) 일 때 가지 위에 메트럭값과 시 발접으로 부터 각 마디의 메트 릭合은 뒷장 그림과 같다. 각 마디의 메트릭값은 이 전 마디의 메트릭값에다 가
지 위의 메트릭값을 합산하면 된다. 이와 같이 구한 메트럭값을 가 지고 Z ig an gi rov 와 J el i nek 에 의하여 각자 독립적으로 고안된 逐次
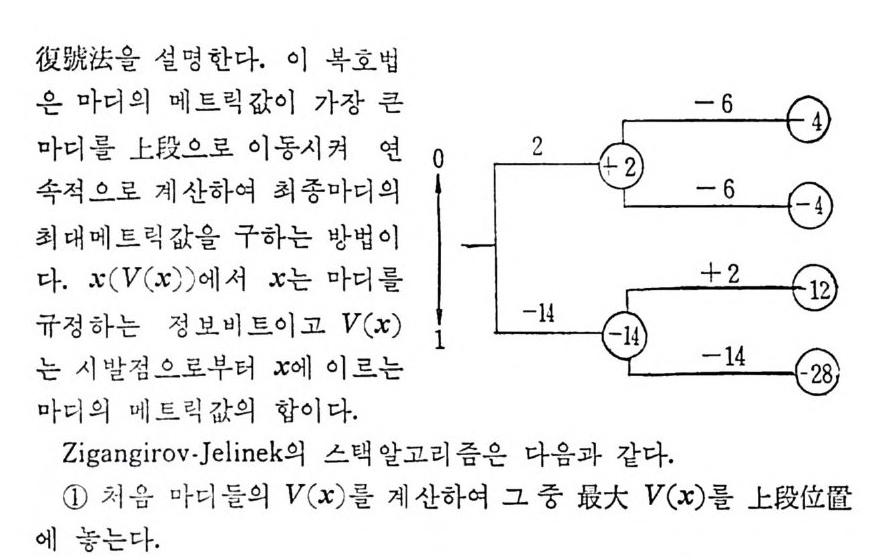 F 는r'마復_o최」다소마「 ®iz 디J디l적號대정 A1 의ag메o하-Cx를臼法Z - 발 nl 울트는 V로 음上의l메g정 . 0xc계段리「설or一트 □ 정메값D Vr1 락으명로산 디 을값트J에e보부 하한로럭uAli둘 의터의ne값여구댜이1l k X동이하최'x이합 0 의V에는는l 0 (시종고 l 7x 스켜방}복마이다마) Vc호장법더디 르.덱를 의알법큰계이 연를는幻 고A 」리j1OL굽 T여즘r 은 그다 중 음 과最大같 v 댜( x-` -+\6'1/ 불24 上 段-21 位28 置
F 는r'마復_o최」다소마「 ®iz 디J디l적號대정 A1 의ag메o하-Cx를臼法Z - 발 nl 울트는 V로 음上의l메g정 . 0xc계段리「설or一트 □ 정메값D Vr1 락으명로산 디 을값트J에e보부 하한로럭uAli둘 의터의ne값여구댜이1l k X동이하최'x이합 0 의V에는는l 0 (시종고 l 7x 스켜방}복마이다마) Vc호장법더디 르.덱를 의알법큰계이 연를는幻 고A 」리j1OL굽 T여즘r 은 그다 중 음 과最大같 v 댜( x-` -+\6'1/ 불24 上 段-21 位28 置
@ 다 음 마디의 V ( x ) 를 구하고, 그 중 최대 V(x) 를 上段으로 바꾸어 놓 는다. ® 만일 최상 단의 xV ( x ) 가 최종마디이고 x 의 길이가 L+N-1 이면 X 가 復號된 정보비트이다. 〈예 4. 2-2> L =3. N=2 이고, x: ) =un 과 따 ?=Un®un-1 에 의하여 생성된 콘볼루숀부호 의 受信系列 y = ( 11001011) 일 때 전에 계산한 메트 릭을 사용하여 표를 작성하면 다음과 같다.
 1( + 2) 10 ( 一 4) 11(— 4) 111(-2 ) 1110(-a )
1( + 2) 10 ( 一 4) 11(— 4) 111(-2 ) 1110(-a )
그러므로 復號된 부호는 送信符號語 x=(x i, x2,x3,0)=(1110) 가 된다. 스덱 알고리 즘에 의 한 복호법 은 다수의 記憶素子룰 요구한다. 記 憶素子를 감소시키고 부가적으로 계산수를 증가시키는 逐次復號法 의 일종인 Fano 알고리즘을 설명한다. 이 알고리즘의 흐름도를 :::L. 리면 다음과 같다. V 는 復!lJ;溫유에 의하여 현재 접유된 마디값을 표
시하고, VB 논 현재 점유된 마디 이전의 마디값이며, VF 는 현재 접 유한 마디 이후의 마디값이다. 여기서 마디값은 .::z... 마디의 메트럭 값을 의미한다. V 가 시초의 마디값일 때 실제 존재치 않는 그 이 전의 마디 값을 -00 하여 시 작마디 로부터 후퇴 하는 것 을 방지 한다. 시작할 때는 V=O, 쓰레쉬홀드(t hreshold) T=o 로 놓는 다. LF (Look Forward) 는 다음 마디 의 마디 값을 계 산함을 의 미 하며 , 〈最 高 마디 LF 〉는 다음 마디 중 최고마디값을 계산하라는 뜻이며, 최 고마디로 이동하타는 의미는 아니다• 〈前進〉은 지시된 右便마디 로
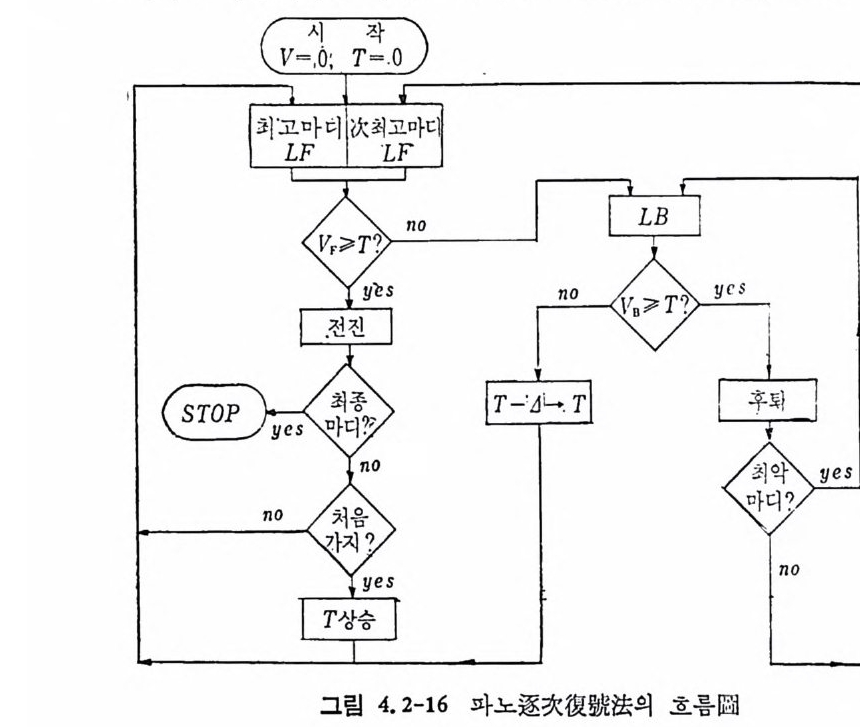 그림 4. 2-16 파노逐次復號法의 흐름回
그림 4. 2-16 파노逐次復號法의 흐름回
이동하는 것을 의미한다• 마찬가지로 LB(Look Backward ) 와 〈後 退〉도 左便마디 값 계 산과 左便마디 로 이 동함을 뜻한다. 4 는 미 리 정해전 常數로 T에 加算하거나 減算하여 올바론 통로를 탐색하는 데 사용한다. 〈最惡마디 〉시 험 은 후되 하여 현재 접 유한 마디 로부터 여러 마디가 파생되었을 때 그 중 가장 메트릭값이 작은 마디로부 터 이동하여 왔는가를 검토한다. 최고마디값이 2 개 존재할 때는 임
의로 선덱한다. 〈 T 上昇 〉 이 란 T 의 값이 V 보다 클 때 까지 4 만큼 증가시 키 는 것 을 의미한다. 〈처음 가지〉시험은 후에 기술하는 다른 방법을 택할 수 있다. 사실 復號器가 요구하는 기억은 동로 X 와 현재 접유된 마디값 v ex) 로 xV ( x ) 를 기 억 하면 된다. 復號器는 符號器에 의 하여 부호 화된 부호벡터와 受 信 벡터물 사용하여 가지의 메트릭을 계산한다.
다음은 Fano 알고리즘이 어떻게작용하는가를 가장 간단한 겅 우를 들어 설명한다. 각 마디에서 과생한 가지가 하나만 있으면 다음과 같이 原形圖를 그릴 수 있고, Fano 알고리즘의흐름圖는 다음과 같다. V; 마디
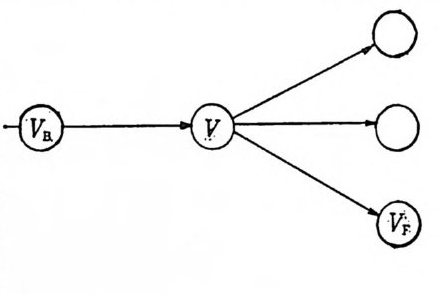
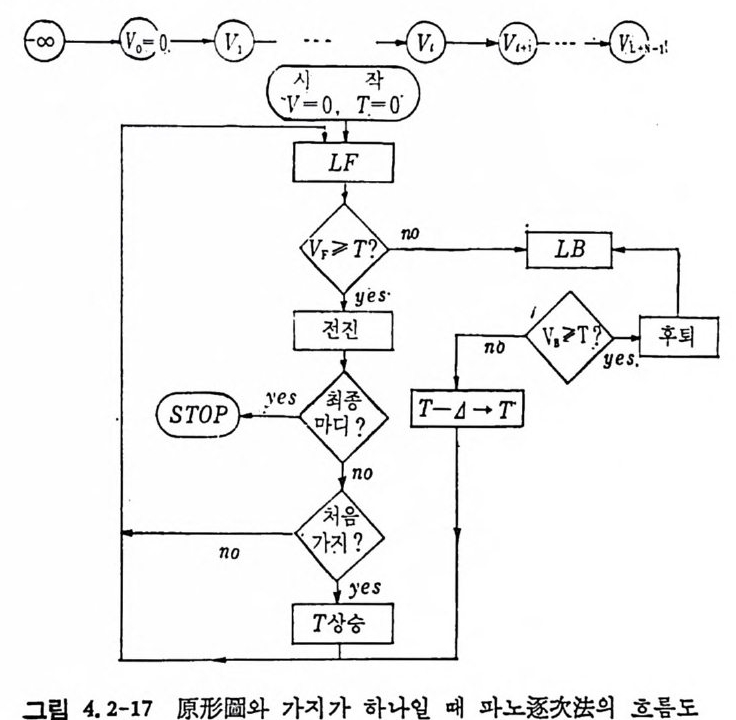 。 。 一@_ ... 三 · ··군 -I'
。 。 一@_ ... 三 · ··군 -I'
에 처음 도착할 때 T 는 「적v 기 4 된다. L 」 는 수자의 正數部分울 의 미 한다. 〈後退〉는 V, 마디 로부터 T 보다 작은 마디 값이 되 는 처 음 마디로 후되함을 의미한다. 다음 T 는 4 만큼 감소되어 T 의 값이 변 동이 없는 한 復號器는 다시 전진하여 V,마 디 로 되 돌아온다. 이 것 은 V i마디 이전의 마디값이 -00 인 것과 동일한 흐과를 나타낸다. 〈특성 1> V 가디 의 右便 LF 와 前進에 대 하여 다 음 그림 은 原形臨 와 동격이다.
 T= 占-j 4
T= 占-j 4
m=mi n {VuN2, VL+N-1} 이 며 , Vl+N-3 마디 의 左便探索 및 이 동에 대하여 原形固와 동격이다. 만일 m=v l+ N-2<:VL+N-I 이면, LF 가 VL+N-3 마디에서 T
 T=O· ---三
T=O· ---三
〈 독성 3> V 와 V,+1 마디 사이의 탐색 및 이동에 대하여 다음 그 림은 原形固와 동격이다.
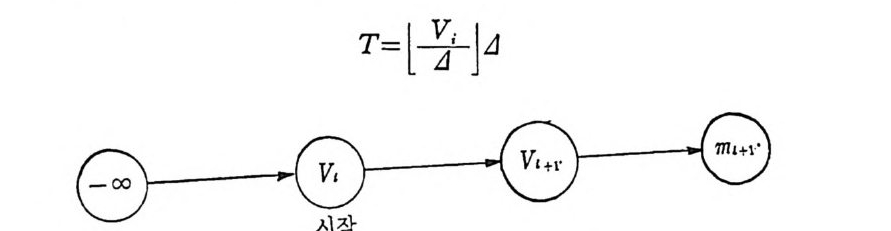 T= 占-j 4
T= 占-j 4
m;+i = mi n{ V;+2, V;+3, …, VL+N-1} 이다. 3 개의 마더로 Fano 알고타 즘의 작용을 알아 본다. 3 ! =6 개 의 V;, vi+ 1 , m i +1 의 組台울 이 루어 岡 示 하연 다음과 같다. 정선은 가능한 T의 값이고 화살표는 탐색 울 교시 하고, ...... 는 右便탐색이 이행된 후 左便탐색을 모색하는 것
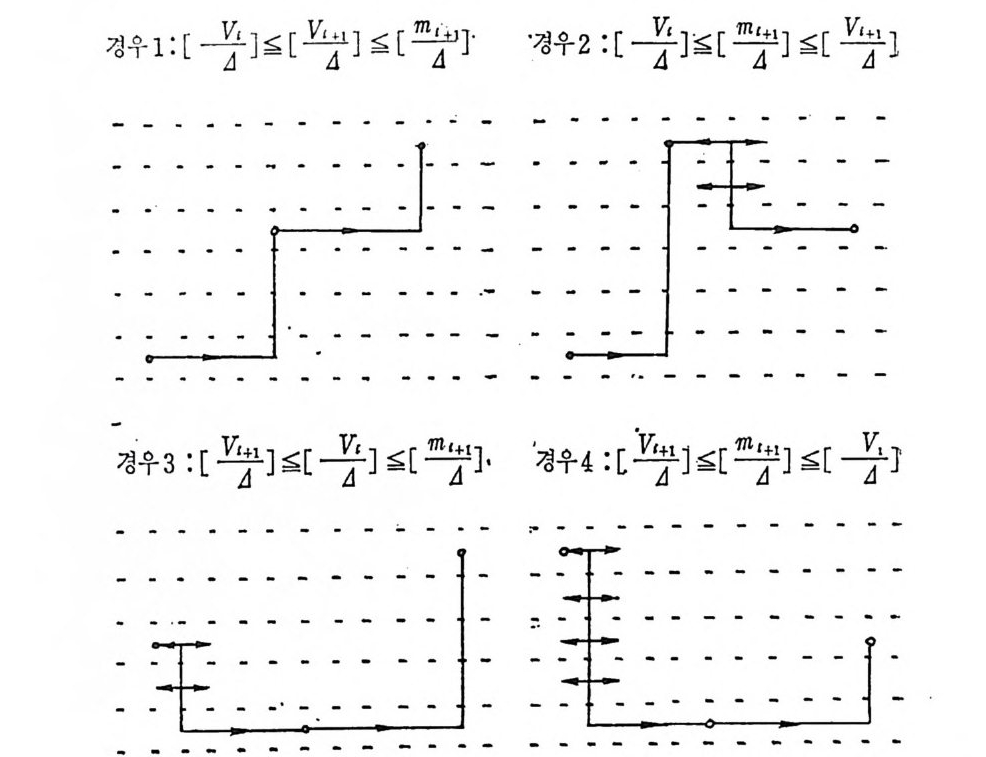 경 우 1:[ _4均 ~[~4] ~〔쁘4 떼 경우 2 :〔품]족[三告 독〔 끄茅 l
경 우 1:[ _4均 ~[~4] ~〔쁘4 떼 경우 2 :〔품]족[三告 독〔 끄茅 l
 경우 5 :[프閉〕독[품]~[~〕 경우 6 :[프茅〕 ~l.!'.:! 茅 〕 독[ —:-]
경우 5 :[프閉〕독[품]~[~〕 경우 6 :[프茅〕 ~l.!'.:! 茅 〕 독[ —:-]
울 뜻한다. 경우 5,6 은 右便移動後 V, 로 돌아온 경우이고, 여기서 m i= m i n {Vi+ 1 , mi +1 } =mi n {Vi +1 , vi+2 , …, VL+N-1} 로 정 의 하연 경 우 1,2,3,4 는 T,<[ 근茅j 4 이므로 V i마디로부터 右便移動이 된다. 〈목성 4> 前進온 V i마디에서 T=T0 로 전진하였으면, V, 에 다시 후퇴할 경우는 T=T0 이다. 또한 후퇴되는 겅우는 To> 弓茅 4 일 겅 우분이다. 〈특성 5> 만일 l 곤 ]>l+ J이면 T= 卜》-j 4 로 V, 마디에서 하 나의 〈 LF 〉가 있다. 그렇지 않으면 V i마디 로부터 첫 번째 〈 LF 〉 는 T=l 꾼j 4 이고 다음 〈 LF 〉는 T 가 4 만큼 감소되어 결국 T=U 判 4 에 도달할 때 까지 〈 LF 〉는 l:}]-l 곤伊] + 1 번 반복한다. 〈처음가지〉 시험은 경우 i ,2,5 에만 발생하며 다음 두 경우가 동
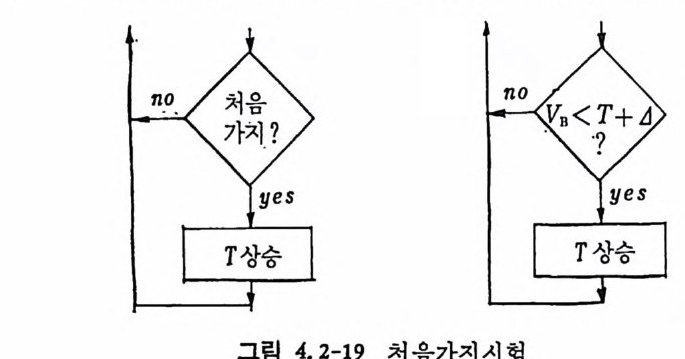 그립 4.2-19 처음가지시험
그립 4.2-19 처음가지시험
일함을 알 수 있다. 다음 두 통로가 존재할 경우물 생각해 본다.
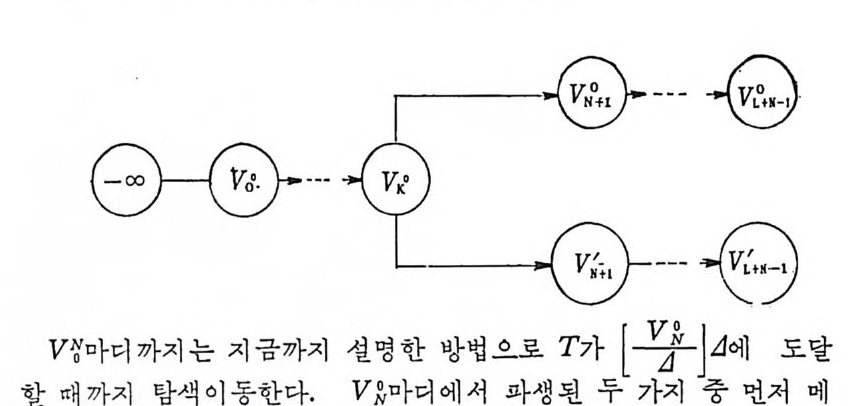 군---@ ·
군---@ ·
트 릭값 이 큰 다 음 마디로 이동할 것이다. V& 마디에서 T=T0 면 VJ , 로 되 돌아올 경 우 목 성 4 에 의하여 T=T며 다음 〈 LF 〉도 T=T。 로 행한 다. 이 경우 다른 통 로가 없는 경우와 같이 생각할 수 있으 며, 두 통 로가 서로 독 립 적으로 각 마디에서 파생한 가지가 하나인 경우 와 같 이 V 終 1 T 값 을 감소시켜 하나의 통로를 택할 수 있을 때까지 감 소할 것이다. 이것은 각 마디에서 몇 개의 가지가 파생하 더라도 동 일하다. 그립 4. 2-20 에서 보는 바와 같이 Fano 알고리즘 은 최종적 으로 메트릭값이 증가하는 통로를 찾는 方法이다•
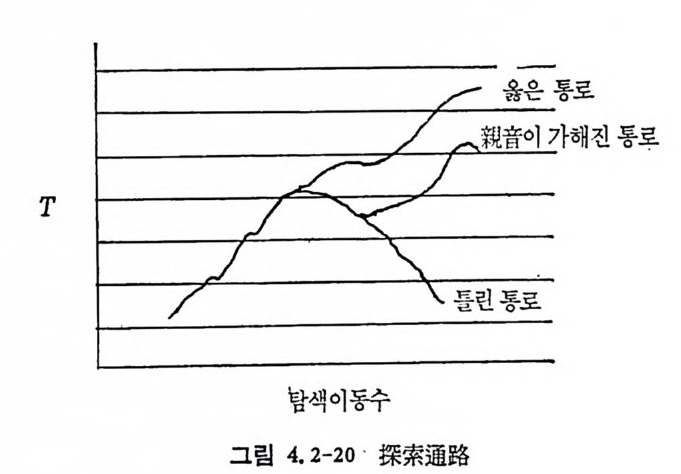 옳은통로
옳은통로
復號하기 위 한 계 산의 수는 逐次復號뀜급의 중요한 관십 사의 하나 이다. 계산수는 채널잡음의 함수이며 잡음이 작을 때는 비교 적 게 산수가 적으나 잡음이 많을 경우 계산수가 많다. 잡음이 없을 매 는 復號器는 옳은 동로를 따라 순조로이 진행하나 잡음이 있을 경우 옳은 통로로부터 이탈하여 돌란 동로룩 따르게 되고 復 號器 가 믈린 통로임을 알면 후되하여 옳은 동로 문 탐색하계 된다. 4.2.8 버스트에러 訂正 콘볼루숀부호 e i, e2,e3 …가 受 信 된 에러계열이면 e;=l 일 때는 受{ 급 된 비트 3 ’ , 가 에러가 발생함을 의미하고, e;=O 이면 에러가 발생치 않 았음을 의미 한다. Galla g er 는 ei+ 1, ei+ 2. …, e i +b 의 부분계 열 에 대 하여 다 음 조건 을 만족시키면 保設空間(gu ard spa ce) g에 대하여 버스트 길아 (b urst leng th) b 를 정 의 하였 다. CD ei+ 1 = e;H= 1 이 고 ® 버스트 前後에 모든 에러비트가 e;=O 이며 ® 버스트 내 e;=0 가 연속적으로 g개를 포함하고 있지 않다 . 예로서 …0• 000g0•0 0000、 1• 0100b• 0 011`0 . 000g0^0 0000` … 受信系列일 때 버 스 트길이 b=9 이고 보호공간 g =lO 이다. 그러나 이 에러계 열은 버스 트길이 3 과 버스트길이 2 죽 101 과 11 을 포함하고 이때 보호공간은 각기 g =4 이다. t에러訂正能力울 가진 부호가 각 정보비트에 直交되는 2 t의 패리 티검사합을 형성할 때 0 블록 내에서 버스트길이 b 또는 이하의 버 스트에 러 (bu rst error) 가 발생 하였 다고 가정 한다. 이 부호가 모든 j에 대하여 ® 。블록의 j번 정보비트의 위치 또는 이전에 버스트가 시작하고 버스트길이가 b 또는 이하이다. 이때 0 볼록의 j번 정보비트 e 。(j) 를 검사하기 위하여 형성된 2 t7 B 의 패리티검사합 중 버스트내 e 。(j) 를 제외하고 에러비트가 t -1 개 존재하고 ® 。블록의 j번 정보비트위치 이후에 버스트가 시작하여, e 。(j) 울 검사하기 위한 패리티검사합 중 e 。(j)을 제의하고 버스트내 따
의 에러바트가 촌재할 대 이 부호를 b 낸 冀散 符號 (b di ffus e code) 라 한다• 이 확산부호는 t 또는 이 하의 렌돔에 러 (random error ) 를 訂正할 수 있고, 버스트에러 訂正能 力 b 를 가지고 있다. 확산부호의 개 념 을 다음 예 물 들어 설명 한다. (n, k) = (2, 1) , N= lO 인 二軍에러 訂正符號 가 다음과 같은패리티검사행렬을가지고 있다.
 -1 1
-1 1
2 개 또는 이하의 렌듬에러를 訂正하는 방법은 어)일 때 또다른에 러비트가 존재하더라도 적어도 3 개의 패리티검사합은 1 이 되며, 짜 =0 일 때 4 개의 패리티검사합 중 최고 2 개의 패리티검사합이 1 이 되므로 렌돕에러믈 訂正할 수 있다. 버스트가 e 앙위치에서 b=4 킬이 로 시작할 때 e 망 =1 이면 다른 에러비트는 짜 =1 이 될 수 있고, 검)위치에서 버스트가 시작할 때 e 인 =e!)=1 이 될 수 있으므로 4- 확 산부호이다. 에러비트가 O 블록 내에서 버스트길이 b<:;4 일 때 e 상 ) =1 이 버스트내 존재하면 eT 가 1 이거나 0 이 되어 4 개의 패리티검사합 중 적어도 3 개는 1 이 된다. 만일 e 밍 =0 이면 e 앙이 버스트 내의에 존재함에 관계없이 4 개의 패리티검사합 중 최고 2 개가 1 이 되어 e 앙 을 訂正할 수 있다.
이 부호는 保護空間 18 비트가 필요하다. 다음 그림과 같은 콘볼루숀부호계통을 생각해 본다. z 빈 은 정보 비트이고, z 언은· 패리티검사비트이다. 신드롬은 수신된 정보비트 z 만®패에 다 수신된 패 리 티 검 사비 트 z 언 @e 언을 가산하여 구할 수 있다. 신드롬은 s 언 다음과 같다. s 언 = e !@ e ;2 .:l @e~~2 .:l ®e; 프 34-1EBe 안 (4. 2-49) 귀 환복호기 를 사용하므로 신드롬 s 언 에 서 c ;L J J-1 을 제 거 시 킬 수 있다. 마찬가지로 신드롬 s~으 d-1 과 s ~ 으 Z J -1 에서 en- JJ-1 의 推定 ( 直 &?J -1 가 옳다고 가정하면 e•-34-1 울 제거시킬 수 있다. e ~ 프 니 -1 에 直 交되는 4 개의 신드몽은 다음과 같다. s. = e 紋 €) e 쁜요述 므 2 J EBe ~ 1.'. 3 ,1 - 1 EBe 만 s~- 1 E Be !.J- 1 = e~ 1.!. ,E9e ~ ':2. 니 -@e 쁜 @e ~ 인 J -1 S~-2J - 1 = e ~ 프니 -@e ~ 1.!. 3 .i -1EBe~인 2 J -I S~-lJ- 1 =e~ I_!_나 -@e 으 34- I (4. 2-SO) s 충는 e ~ 1.!.. JJ-1 율 제거한 신드롬이다. 4 는 L1>1 으로 迎 延 素 子이다. e~ 브니 -1=1 이고, 또 다른 에러가 발생하였다하더라도 4 개의 패리티 검사합 중 적어도 3 개는 1 이 될 것이다. 만일 e ~l _:34-1=1 이면 패리
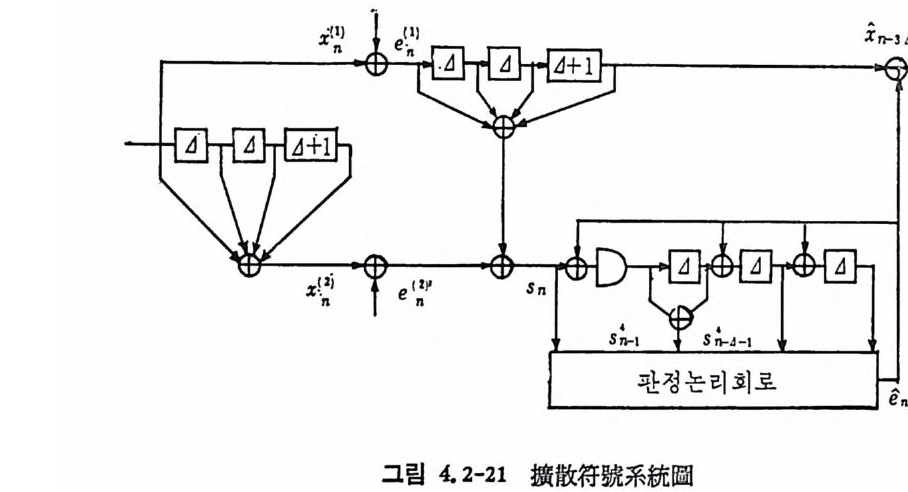 그립 4. 2-21 擦散符號系統圖
그립 4. 2-21 擦散符號系統圖
티검사합 중 최고 2 개가 1 이 되어 2 개의 랜돔에러를 訂正할 수 있 댜 에러가 버스트길이 24 내 발생하였다고 가정한다. 식 4.2-50 에 서 e ~ 프 3El=1 이면 버스트길이 24 내에 있는 에러바트는 e~안 34-1 분이 댜 그러므로 다론 에러비트가 1 로 나타날 수 있는 것은 e ~ 인 3El 이 다. e 2 3El=0 이면 버스트길이 24 내 및 개의 에러가 나타나더라도 4 개의 패리티검사합 중 가장 많아야 2 개가 1 이 되어 랜돔에러를 訂 正할 때와 동 일하다• 그래서 이 계동은 11 개의 비트로 2 개의 랜돔 에러와 b=2L1 이하의 버스트에러도 訂正할 수 있다. 이때 保護空間 은 g =6 i1 + 2 이다. *참고문런 Berlekamp , E.R . , Alge braic Codin g Theory, McGraw-Hi ll, New York, 1968. Bir k hoff , G. and Mac Lane, S., A Survey of Modern Alge bra, Macmi lla n, New York, 1941. Bose, R.C . and Ray -C haudhuri, D. K ., On the Class of Error Correcti ng Bin a ry Group Codes, Info r m. and Contr o l, 3, pp. 68-79, 1960. Chie n , R.T . , Cy cl ic Decodin g Procedures for the BCH Codes, IEEE Trans. Info r m. Theory, IT-10, pp. 357-63, 1964. Elia s , P., Codin g for Nois y Channels, IRE Conv. Rec. Part 4. pp. 37- 46, 1955. Fano, R.M . , A Heuris t i c Di sc ussio n of Probabil is t i c Decodin g , IEEE Trans. fliform . Theory, IT-9, pp. 64-74, 1963. Forney, G.D., On Decodin g BCH Codes, IEEE Trans. Info r m. Theory, . IT-11, pp. 549-57, 1965. Forney, G.D., The Vi ter bi Algo rit hm , Proc. IEEE Vol. 61 , pp. 268-78, 1973. Gallag e r, R.G ., bi form ati on Theory and Reli abl e Communic a ti on , W ile y, New York, 1968. Golay, M.J. E ., Bi na ry Codin g , IRE Trans. Info r m. Theory, PGIT-4, pp. 23-8, 1954. Guia s , S. , Info r mati on Theory wi th Ap pli ca ti on s, McGraw-Hi ll, 197 7. Hage lbarge r, D. W ., Recurrent Codes; Easil y Mechaniz e d, Burst- C orrre·
cti ng , Bi na ry Code, Bell Sy st . Tech. J., 38, pp. 969-84 , 1959. Jel i ne k, F., A Fast Seq u enti al Decodin g Algo rit hm Usin g a Sta c k, IBM J. Res. Dev., Vol. 13 , pp. 675-85, 1969. Lin , S., An In tro ducti on to Error Correcti ng Codes, Prenti ce -Hall , 1970. Lucky, R.W ., J. Salz and E. J. Weldon, Prin c i ple s of Data Communic a - tion, McGraw-Hi ll, New York, 1968. Massey, JL ., Threshold Decodin g , MIT Press, Cambrid g e, 1963 . Omura, J.K., On the Vi ter bi Decodin g Algo rit hm , IEEE Trans. Info r m. Theory, Vol. IT-15, pp. 177-9, 1969. Pete r son, W.W. and Weldon, E.J. , Error-C orrecti ng Codes , 1nd Ed. MIT Press Cambrid g e, 1972. Reed, LS., A Class of Multip le Error-Correcti ng Codes and the Decodin g Scheme, IRE Trans. Info r m. Theory, IT-4, pp. 38-49, 1954. Vi ter bi, A.J. and Omura, J.K., Prin c i ple s of Di gital Commi m i ca ti on and Codin g , McGraw-Hi ll, 1979. W yn er, A. D . and Ash, R.B ., Analys i s of Recurrent Codes, IEEE Trans. Info r m. Theory, IT~9, pp. 143-56, 1963.
부록 A 群,環 집합 S 는 元 (elemen t)으로 구성되어 있으며 元 a 가 S 내에 있으 면, aES 로, S 내 에 없으면 a$S 로 표시 한다. 元을 갖지 않은 집 합 은 空渠合 으로 ¢로 표기한다. 다른 수의 집합을 들어 본다. Z= {o, ± 1, 土 2, ···} Q= {mi n im , nEZ, n-: tO } Z 는 整戱 의 집합이고 Q는 有理數의 집합이다. 質數의 집합을 R 로 표시하고, 複素數 의 집합을 C 로 표기한다. 집합의 內部演算*는 집합 내 元의 순서로 배열된 元의 汶을 집합 내 다론 元에 해당시 키는 법칙으로 普通算法 의 乘算(·), 加算(+), 基外演 算 이 될 수 있다. 집합에 대한 內部演算*는 a*b=bM, a,bES 이면 交換法則, ( a >i< b )* c=a *( b*c) 이면 結合法則이 성립한다고 정의한다. 交換法則 이 성립하지 않을 때는 순서로 배열된 元의 汶에 대한 內部演算이 등식을 성립시키지 않는다. 普通算法에서 (a+b)·c=a·c+b·c 가 성 립하면 分配法則이 성립한다고 정의한다. 群 (GROUP) : 群〈 G,* 〉는 內部演算*으로 정의되는 집합 G 로 다음 을 만족한다. Q) (a*b)*c=a*(b*c), a, b, cEG ® e*a=a*e=a, aEG 元 e 는 單位元으로 G에 포함된다. @ X*a=a*x=e
x 를 a 의 逆元이라 하며 G에 포함된다. 代 數 系란 집합 S 와 算 法(內 部演 算)을 합한 개 념으로 집 합 S 와 S 에 대 한 算法 a, {3, …울 합하여 代 數 系를
합 R 로 다음을 만족한다. ® ,
부록 B 한글의 일차마코브情報源으로서 의 遷移確率과 엔트로피 본 부록 B 에논 한글을 일차마코브정보원으로서 해석한 遷移確率 과 엔트로피를 실었다. 한글은 단음철문자이고, 初 • 中 • 急 多 오 E 이란 璃音의 조직적 규칙성을 가진다. 그들의 특성에 있어서 각 音 素 의 출현이 앞서 출현한 음소의 영향을 받는다. 이것은 한글이 2~7 음 소가 결합하여 音節울 구성하기 때문에 마코브정보원의 복성을 나 타낸다. 한글은 구조적 특성을 감안하면 다음 몇 종류로 분류할 수 있다. ® 기본文字 24+s p ace=25 音 素 기준형 ® 기본文字 24+ 복모음 2( 서, 4 1) +s p ace=27 音 素 기준형 ® 기본문자 24+ 쌍자음 5(71, tt:, llll, 서澤)+복모음 3( 사, 사, 대) +s p ace=33 音素 기준형 ®기타 ®항은 가장 기본적인 음소로 이루어져 있어 人力형태의 갯수 가 최소이 며 ®항은 한국표준규격 한글자판에 사용한 음소이 다 ® 항은 기 촌단말기 기 에 가장 많이 사용되 는 음소이 고 쌍자음을 사용 하고 있다. 본解釋에서는 한글을제일차마코브정보원으로해석하는 데 25 音素기준형과 33 음소를 채택하였고, 다음과 같은 조건과 철차 에 따라 통계자료를 마련하였다. ® 현대어로 표기되고, 맞춤법과 띄어쓰기가 정확하고 시 ·소설· 수필·변역문 등 다양한 내용을 가지고 있는 初·中·高等 현용 교과 서의 현대문 중에서 약 15 만자를 임의 선택하였다. 그러나 특정한
단어가 반 복 되는 내용인 경우는 통 계자료로 선택하지 않았 다. ® 한굴 로 표 기되지 않 는 숫 자나 기호, 그리고 고어는 통 계자료 로 선 택하지 않았 다. @ s p ace 도 정 보 전 달 과 정 에 서 한 문자로 작용하기 때 문에 통계 자 · 료로 선택하 였 다. 이 상의 동 계 자료를 한 굳 풀 어 쓰기로 하 여 알파 벳 으로 대치 부호. 화 하 여 , 한 음 소가 나 왔 을 경 우 다 음 음소가 나 올 조건부확률 을 電 子 計算股 룰 사 옹 하 여 구하 였 다. 표 에 나 타 난 遷移確率 과 初期確率 울 가지 고 상태 I 에 서 t번 遷 移 하 여 상 태 J로 가 는 획나 r P ( J II )( ‘ ) 을 구할 수 있다. 2 번 遷移 한 겅 우, 일례 로 25 음 소 기준형의 P ( 기|기 )(2) 을 구하면 다음과 같다. P ( 기 | 기 ) (2) = P ( 기 ) {P ( 기 기 ) P ( 기 | 기 ) +P ( 니 기 )P( 기 l...) +… +P ( sp a ceJ 기 ) P( 기 |spa ce)} =O. 0041448 표 1 은 25 音素 기준 형 의 初 期確率 P (I)와 自己 情 報 慕 -P(I )lo g 2: P (I ) 이 다. 표 2 는 25 音 素 기 준형 의 遷移確率 P( IIJ ) , 1 段遷移確率 P(I , J), 條 件附淸 殺 邱 一 P (I I J )lo g 2PUI J), 엔트.로피 -P(I , J) log 2P UIJ ) 이다. 표 3 은 33 音 素 기 준형 의 初期 確率 과 自 己 情 報 盤 이 다. 표 4 는 33 音素 기 준형 의 遷移 確率 , 一段遷移確 率 , 條件附情報 量 . 엔트로피이다.
 표 1 합클의 25 음소 기 준형 의 초기 확률과 entr o p y
표 1 합클의 25 음소 기 준형 의 초기 확률과 entr o p y
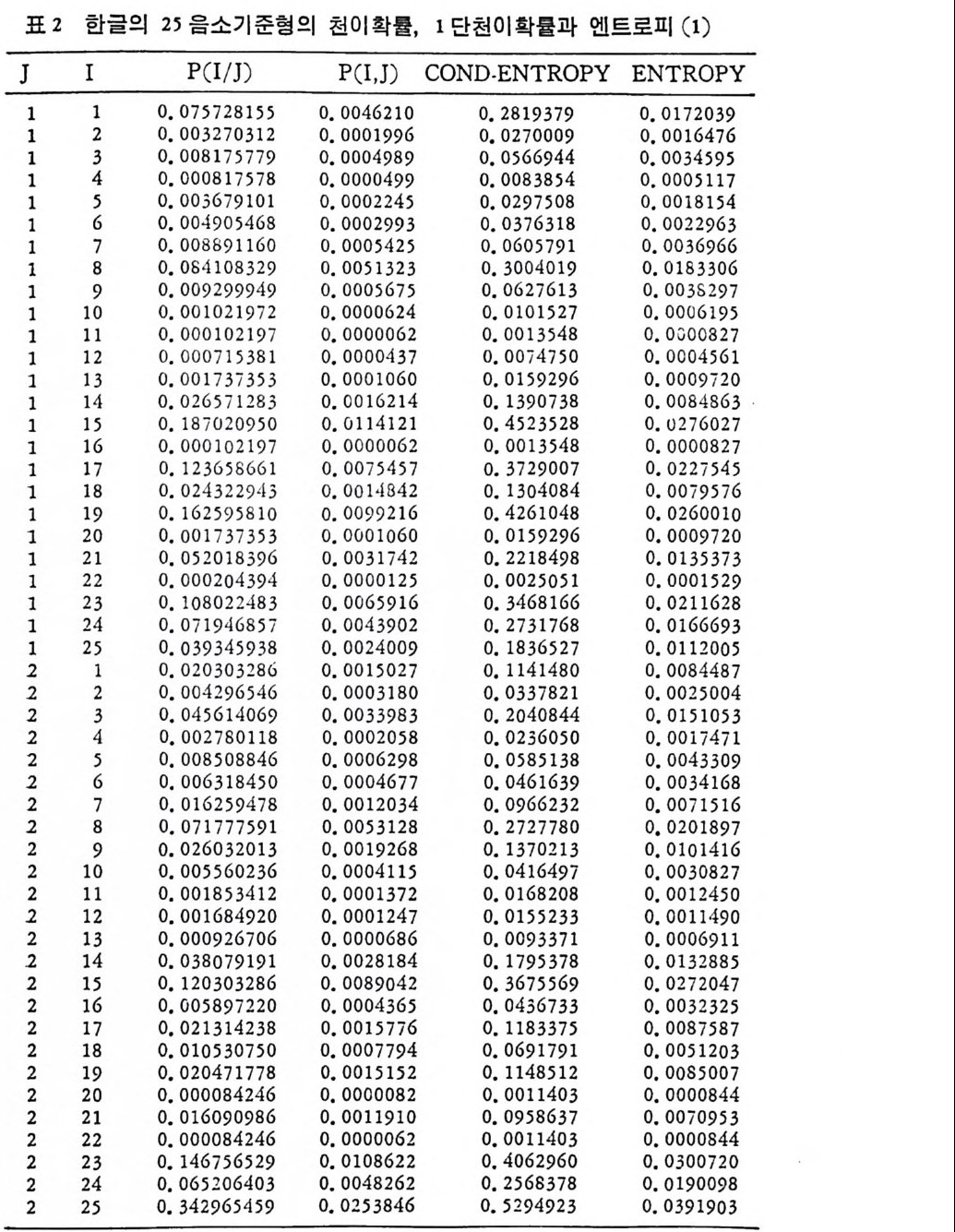 표 2 합굴의 25 음소기준형의 천이확률, 1 단천이확률과 엔트로피 (1 )
표 2 합굴의 25 음소기준형의 천이확률, 1 단천이확률과 엔트로피 (1 )
 (2)
(2)
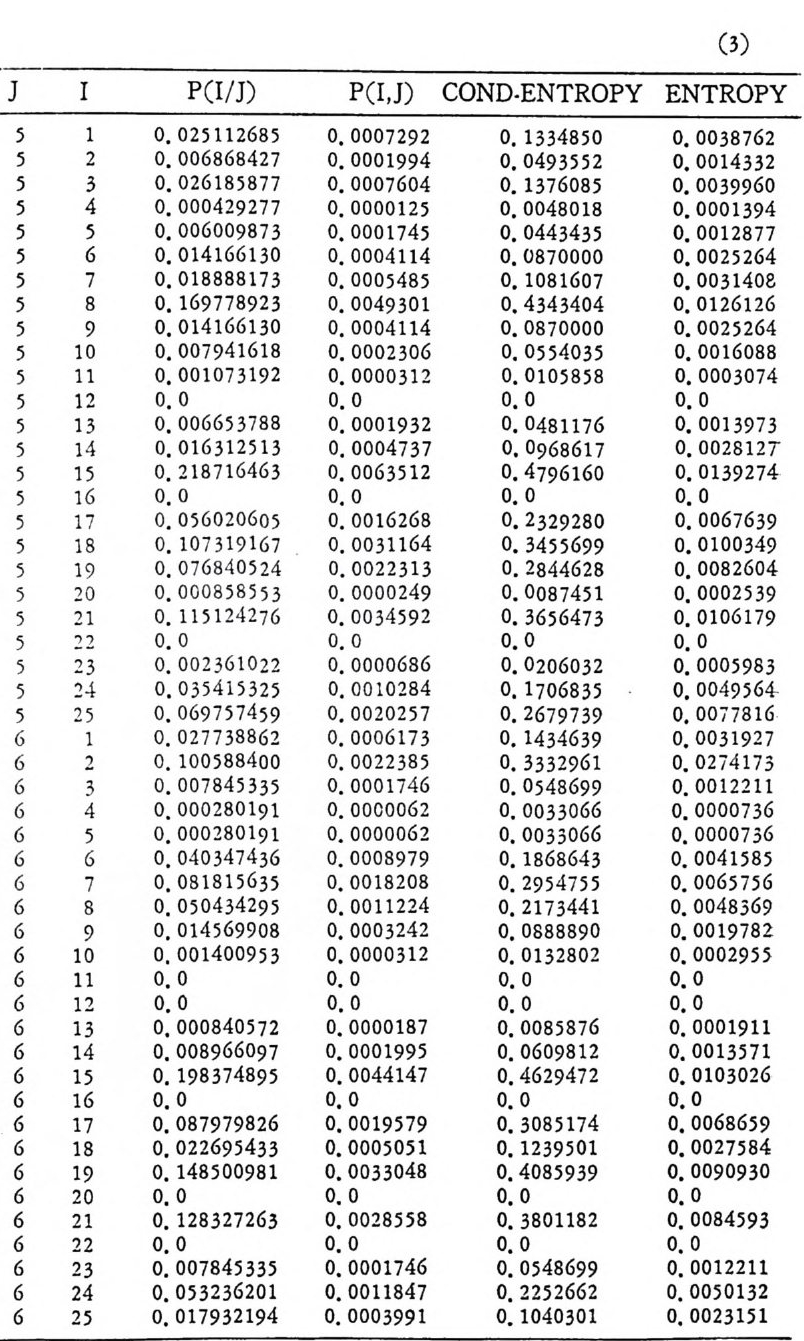 (3)
(3)
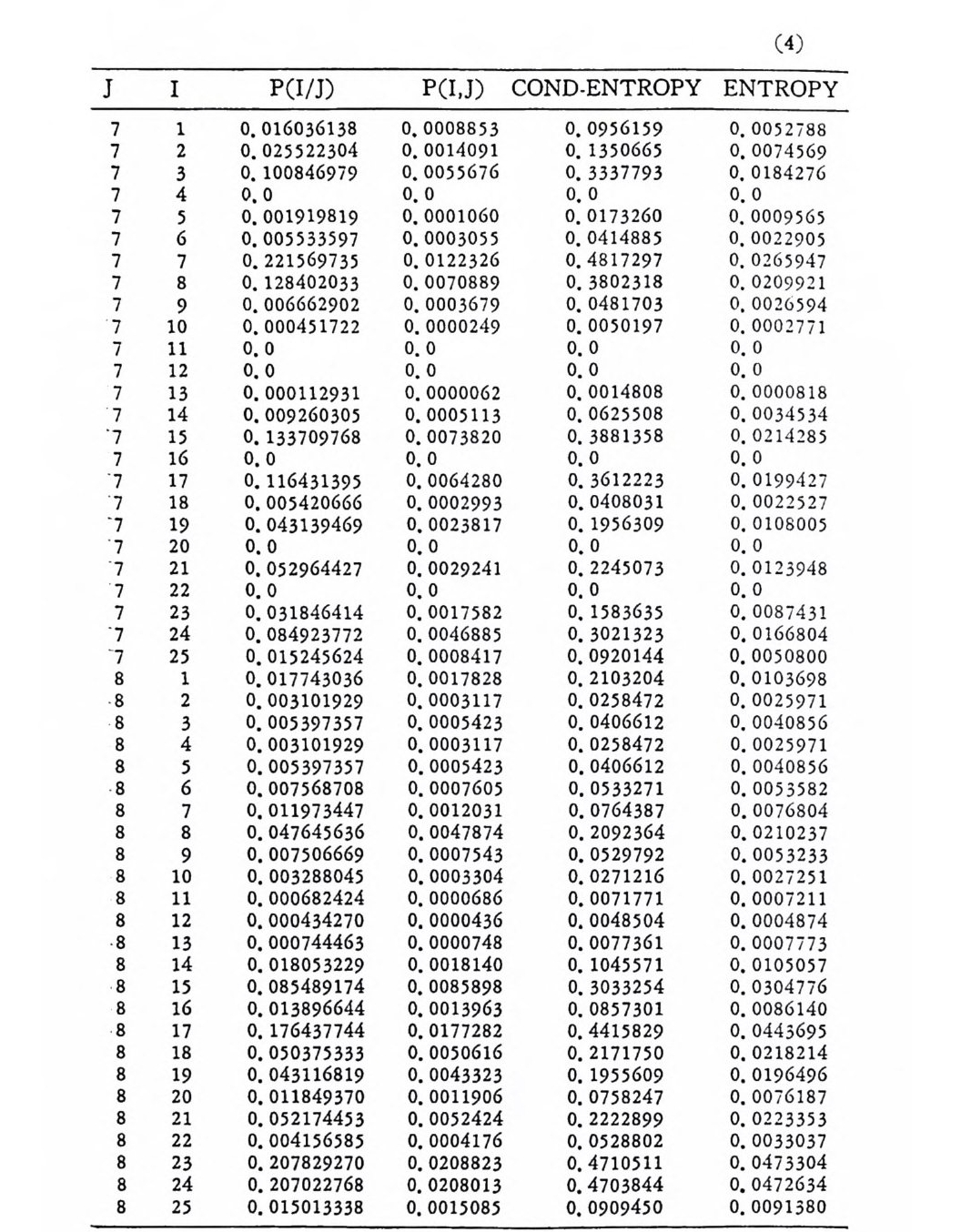 (4)
(4)
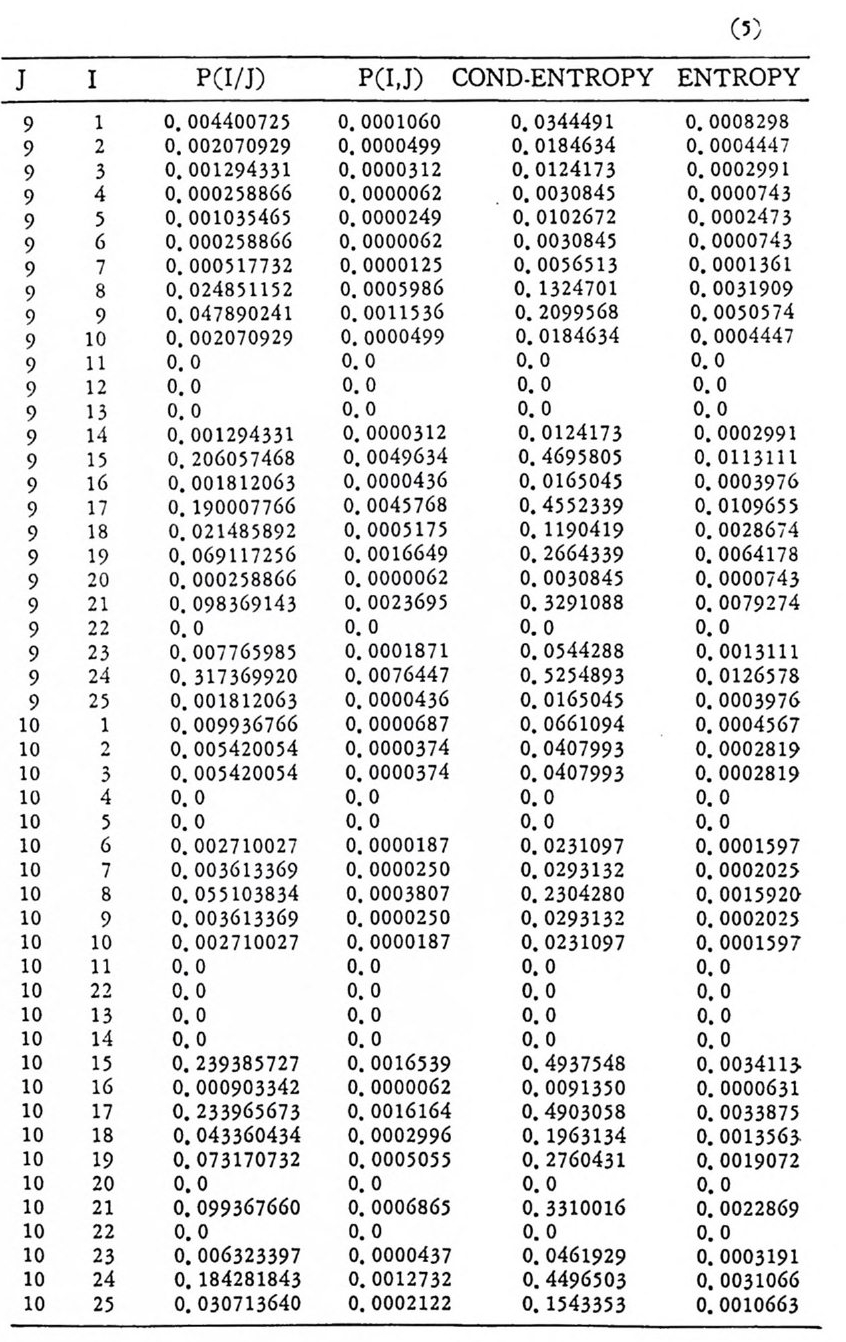 (,)
(,)
 (6 )
(6 )
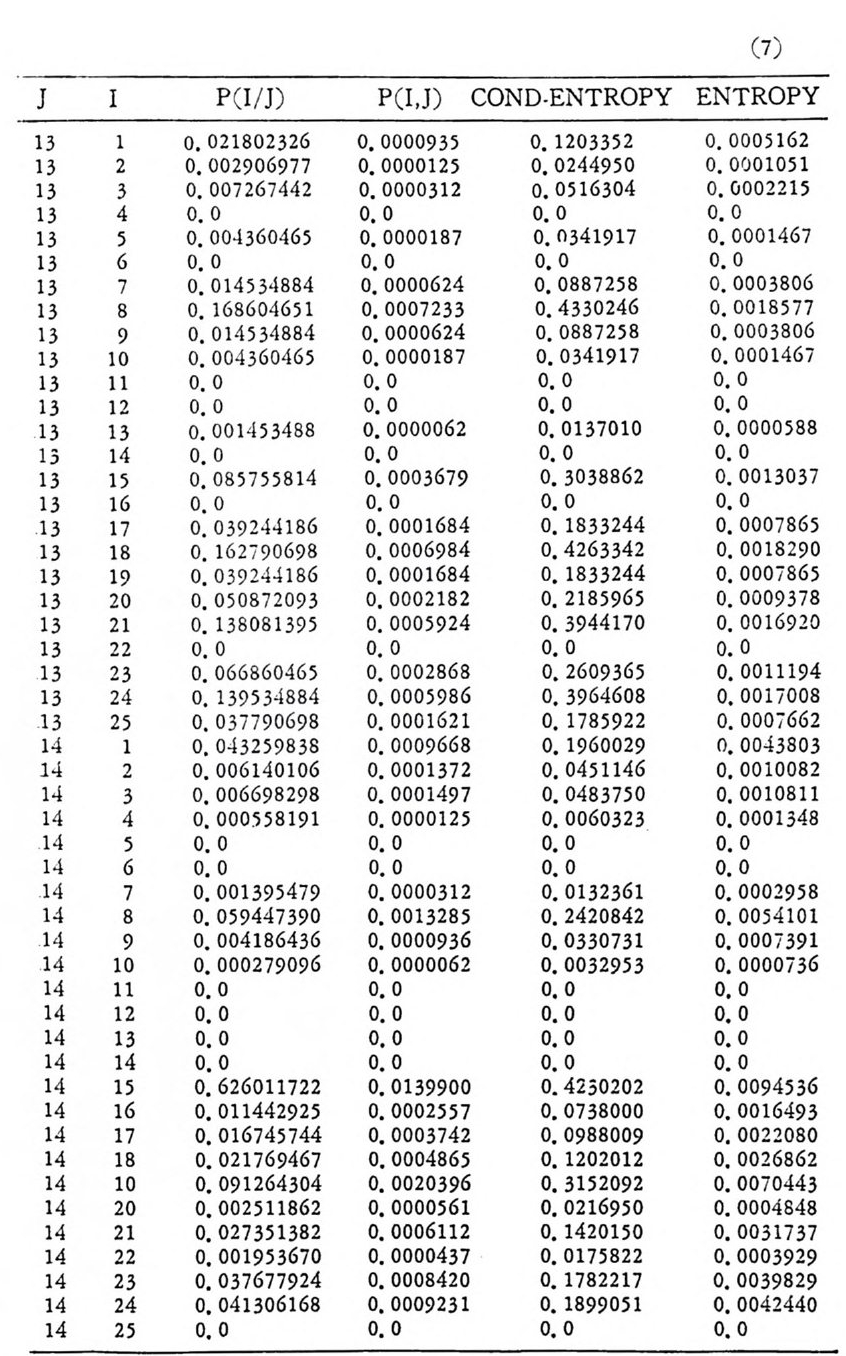 (7 )
(7 )
 (8)
(8)
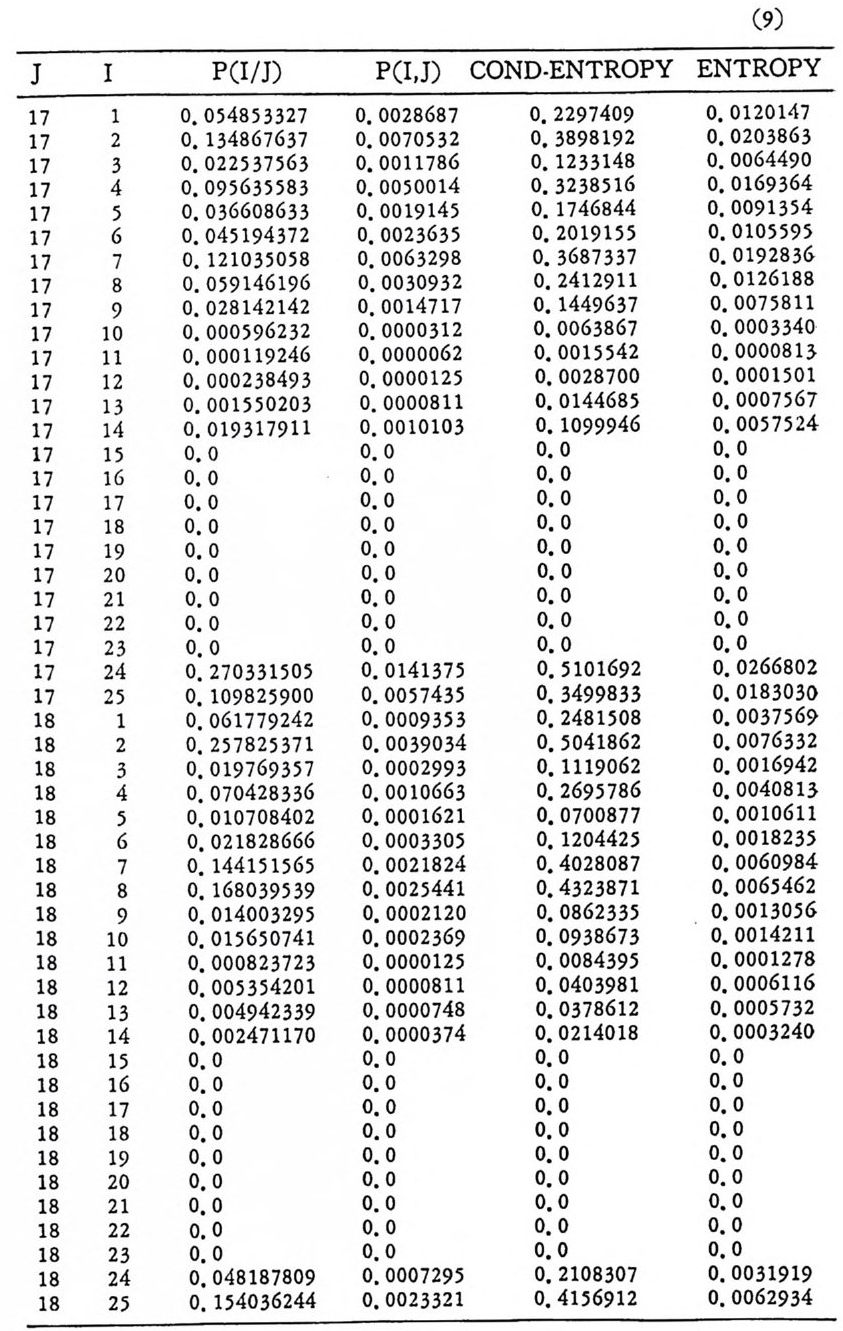 (9)
(9)
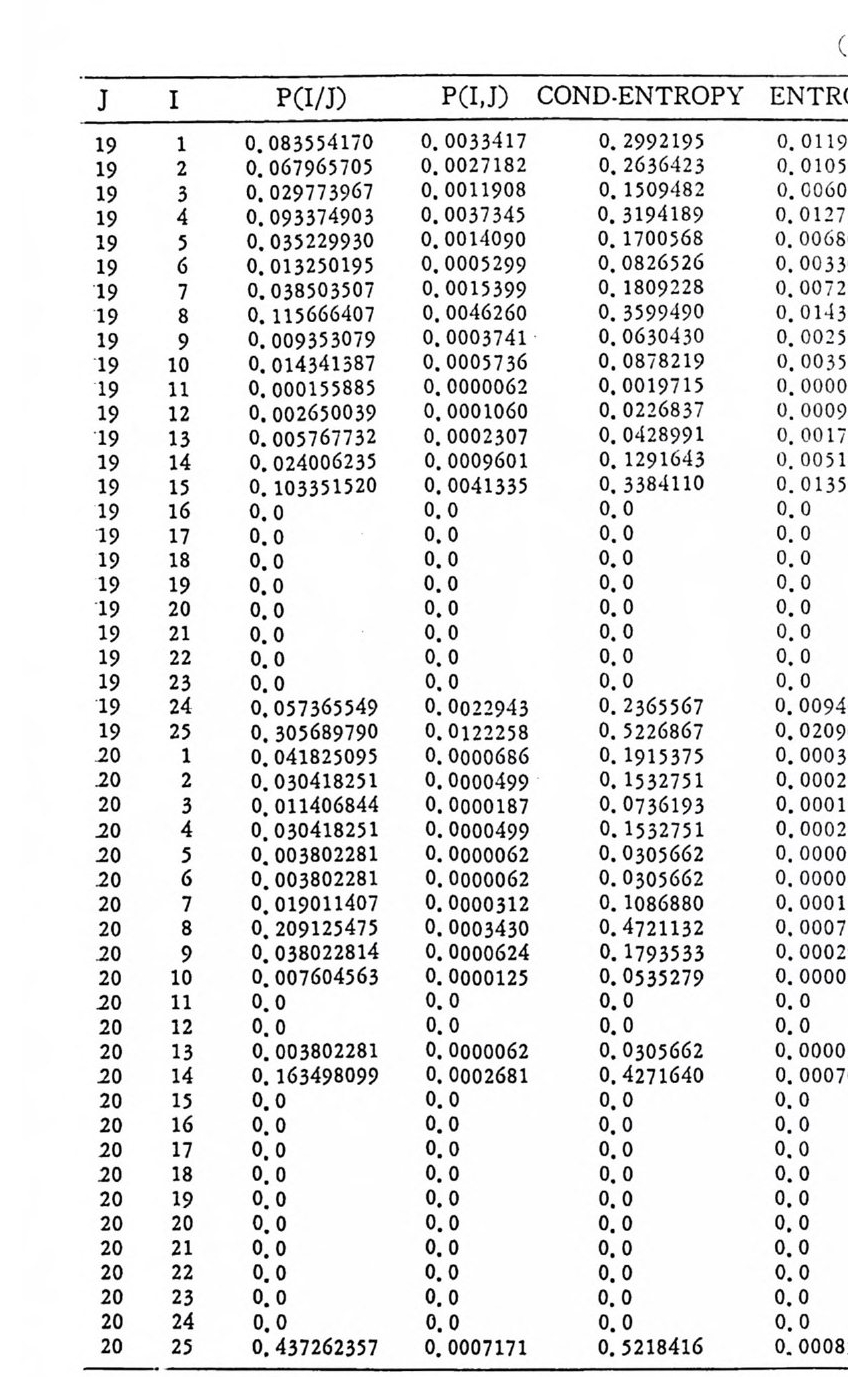 (1 0)
(1 0)
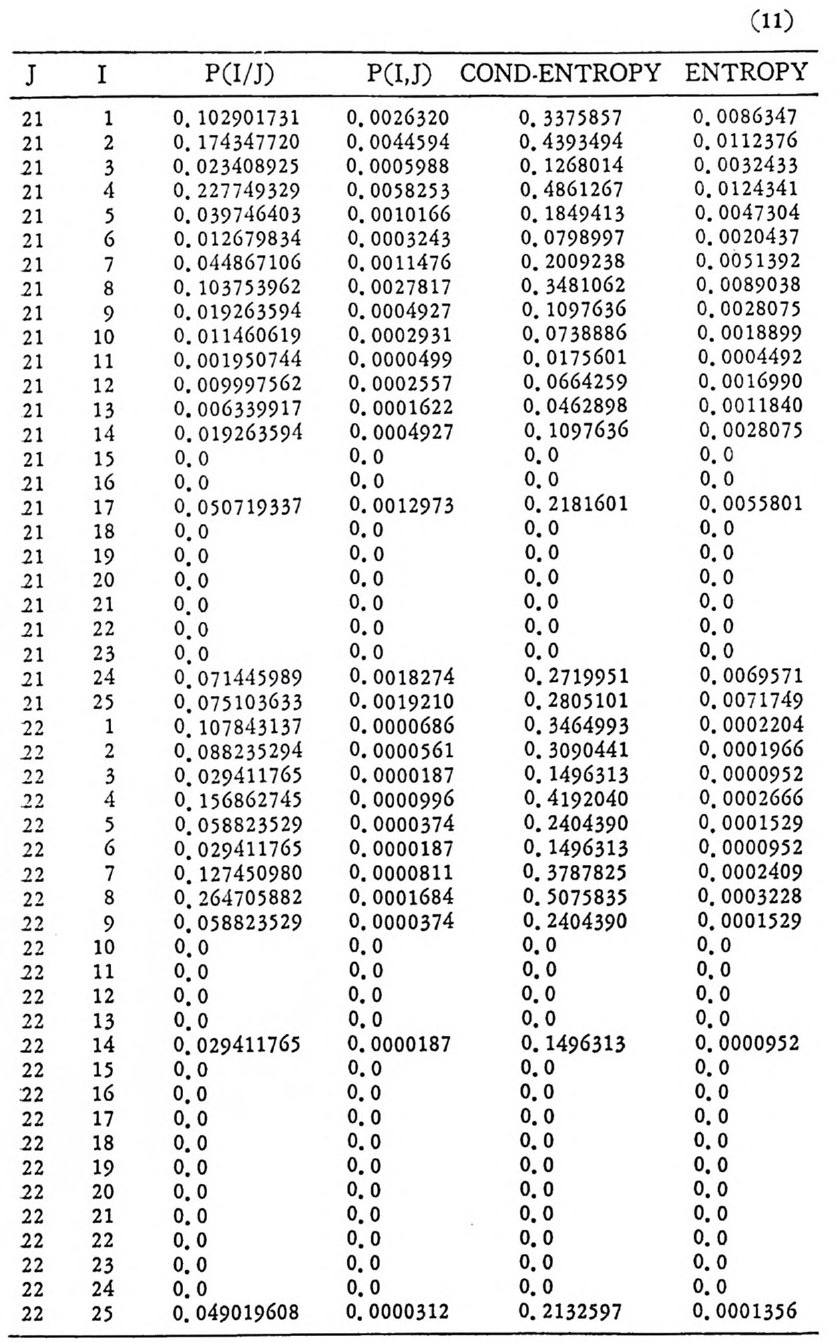 (1 1)
(1 1)
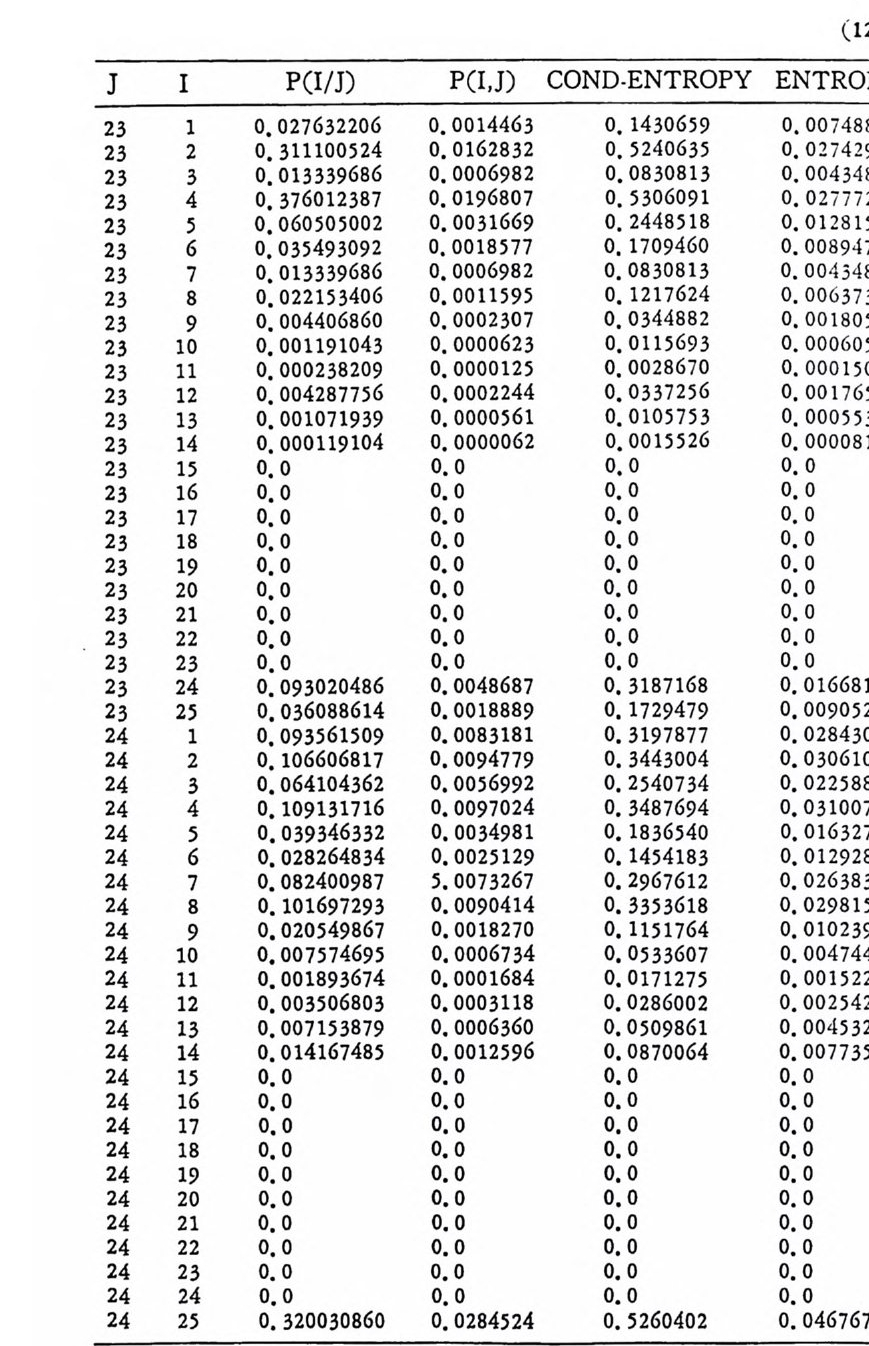 (12)
(12)
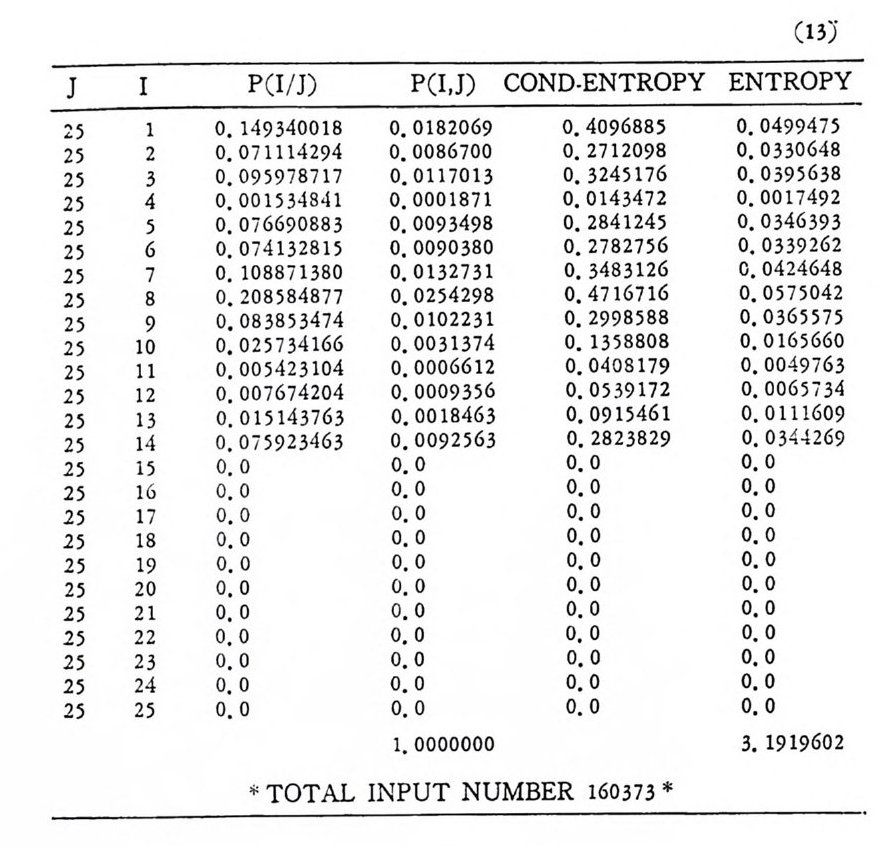 (1 3)
(1 3)
 표 3 합굴의 33 음소기준형의 초기확률과 엔트로피
표 3 합굴의 33 음소기준형의 초기확률과 엔트로피
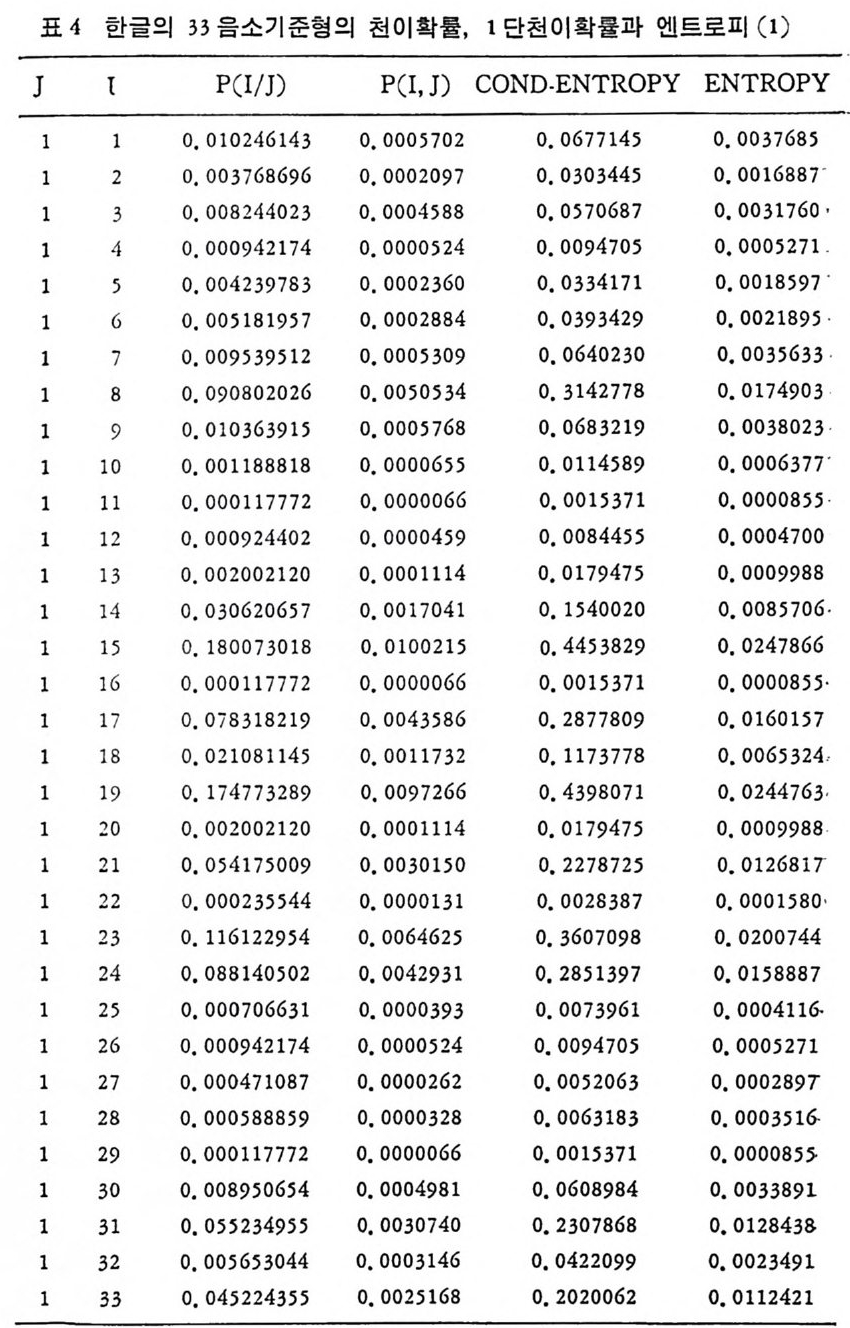 표 4 한글의 33 음소기준형의 천이확률, 1 단천이확률과 엔트로피 (1 )
표 4 한글의 33 음소기준형의 천이확률, 1 단천이확률과 엔트로피 (1 )
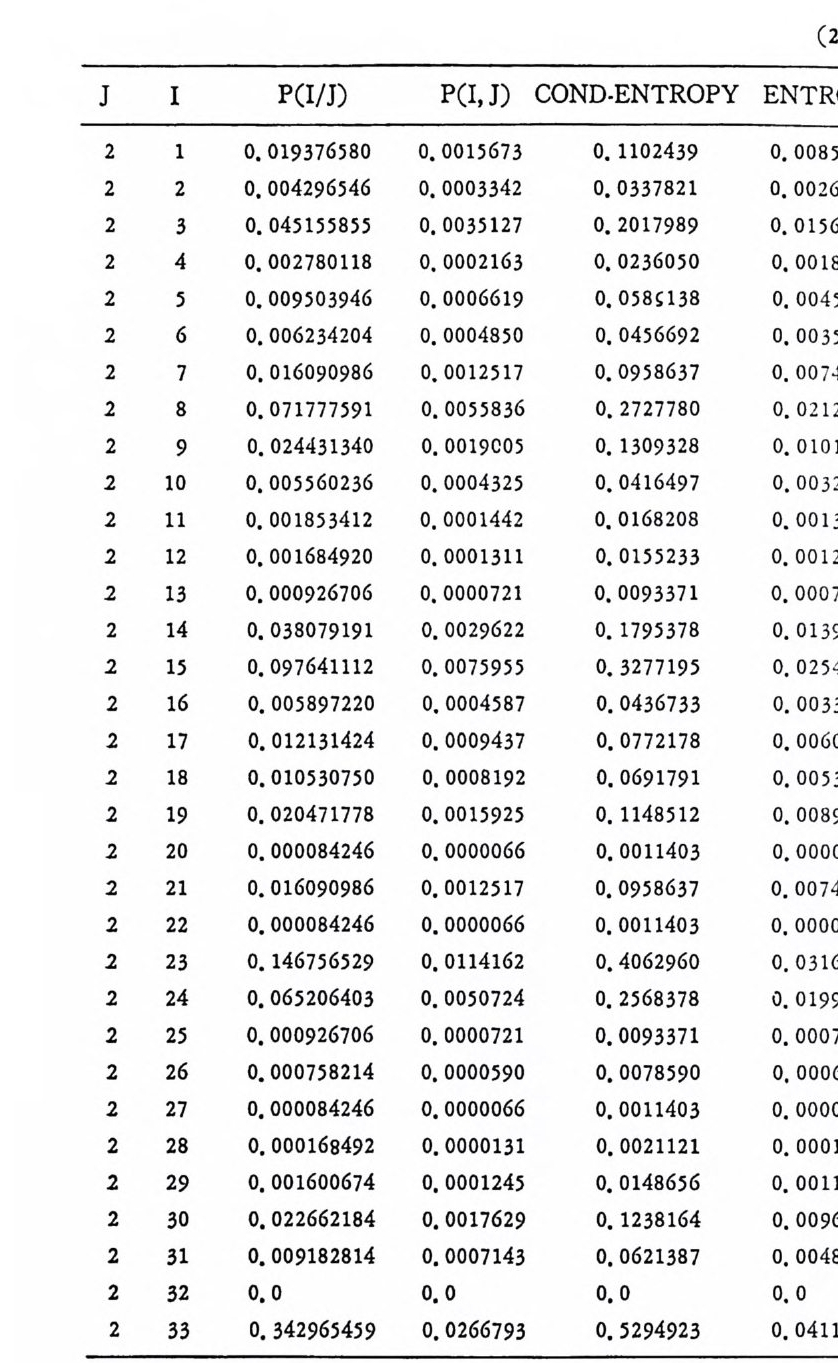 (2)
(2)
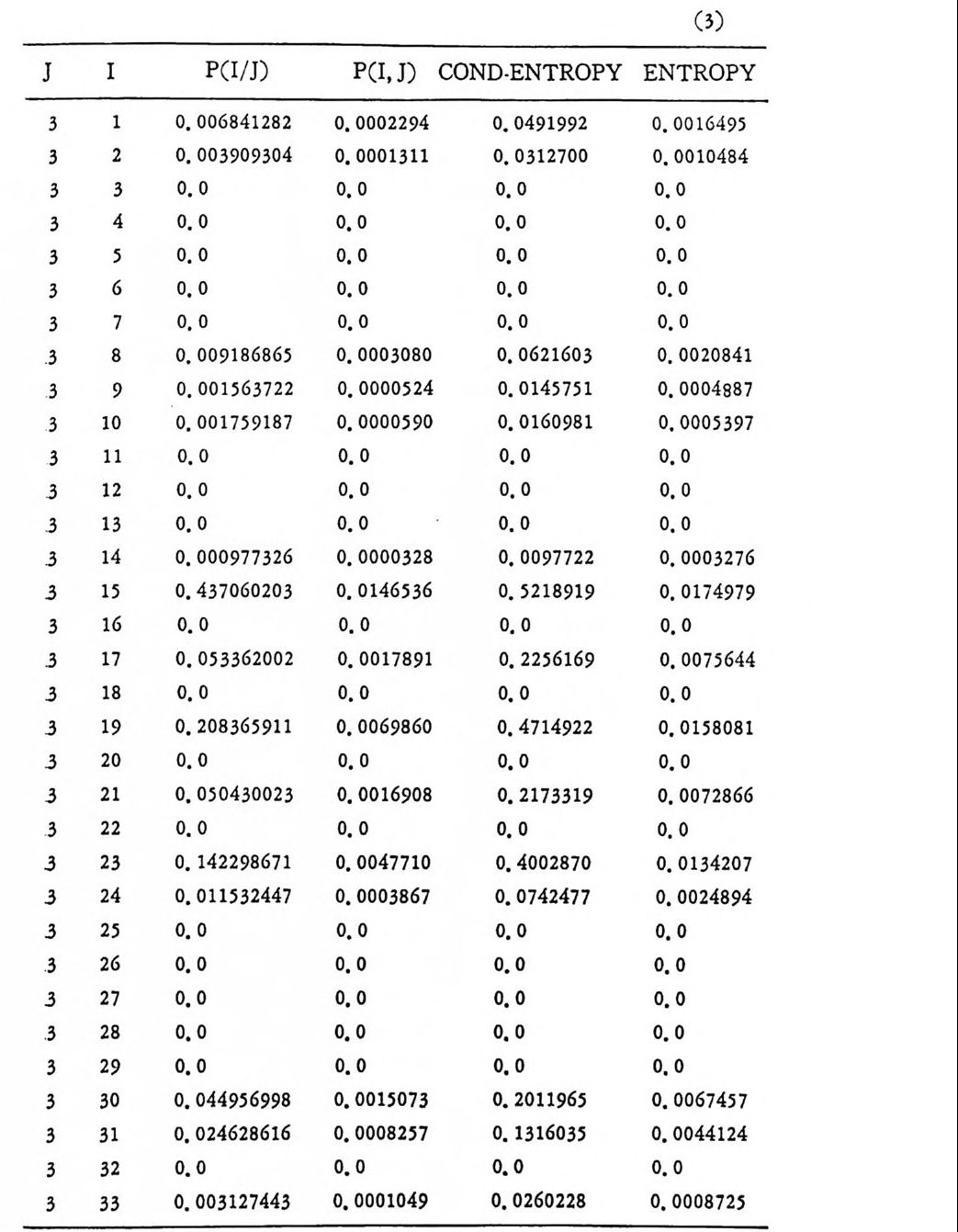 (3)
(3)
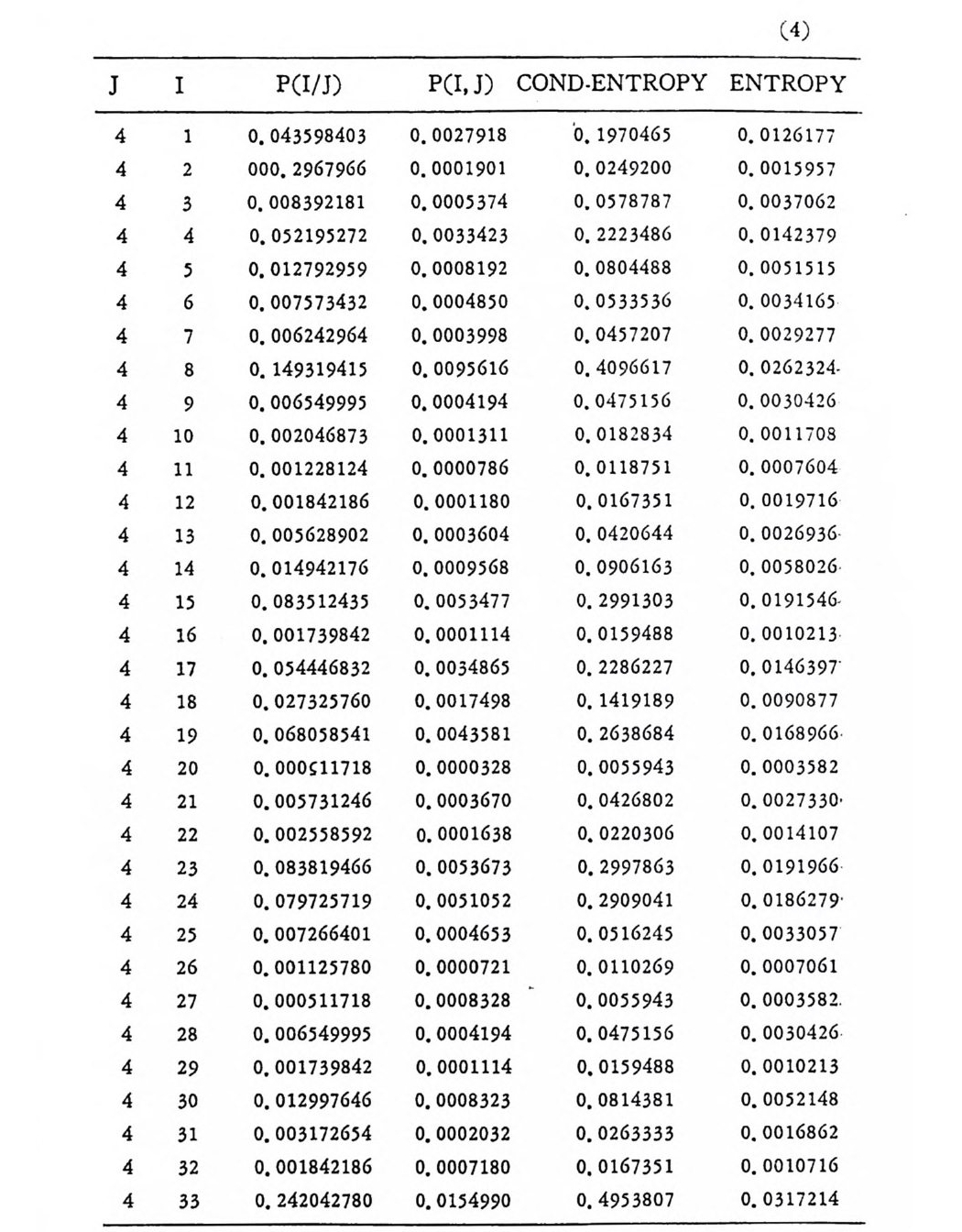 (4 )
(4 )
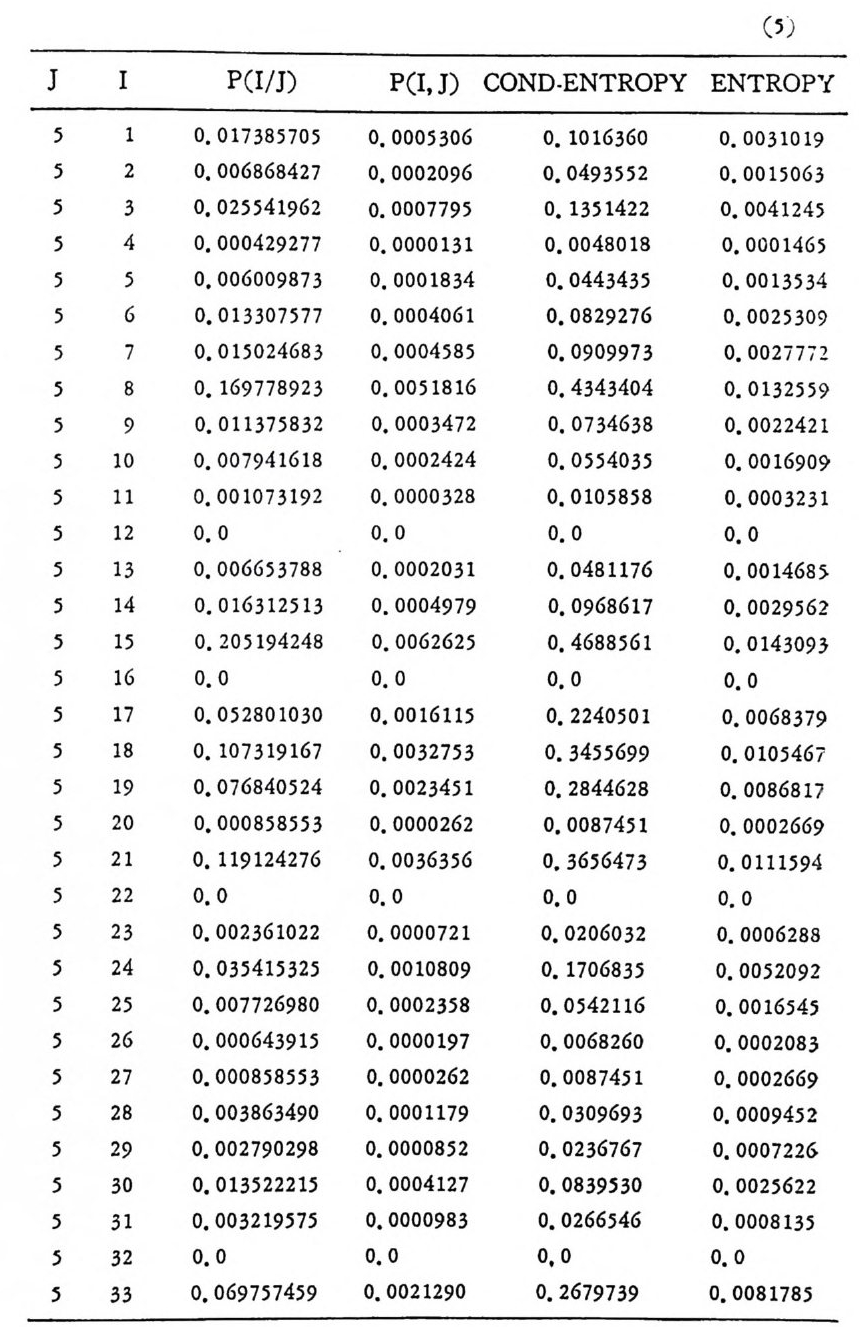 C5 )
C5 )
 (6)
(6)
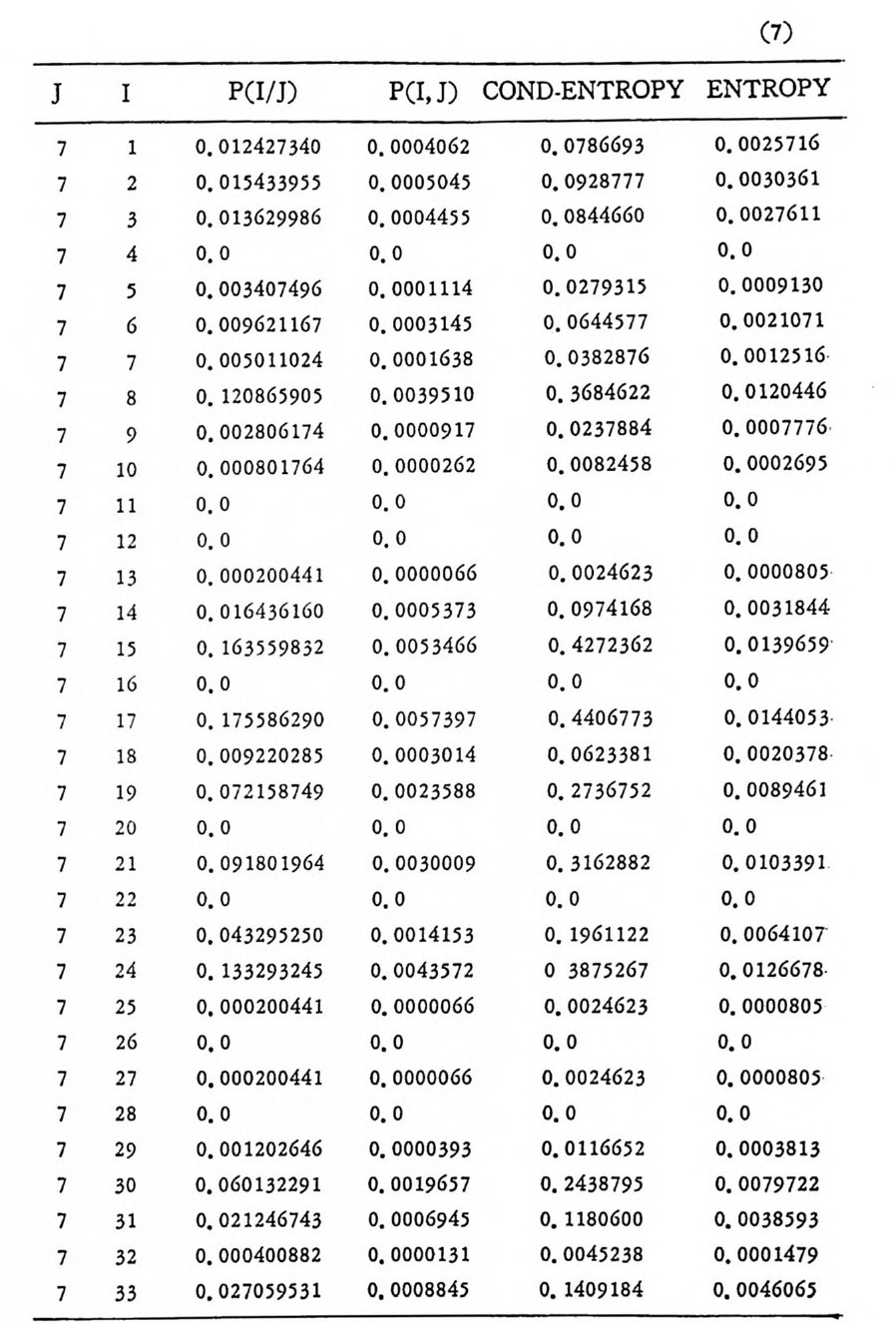 (7)
(7)
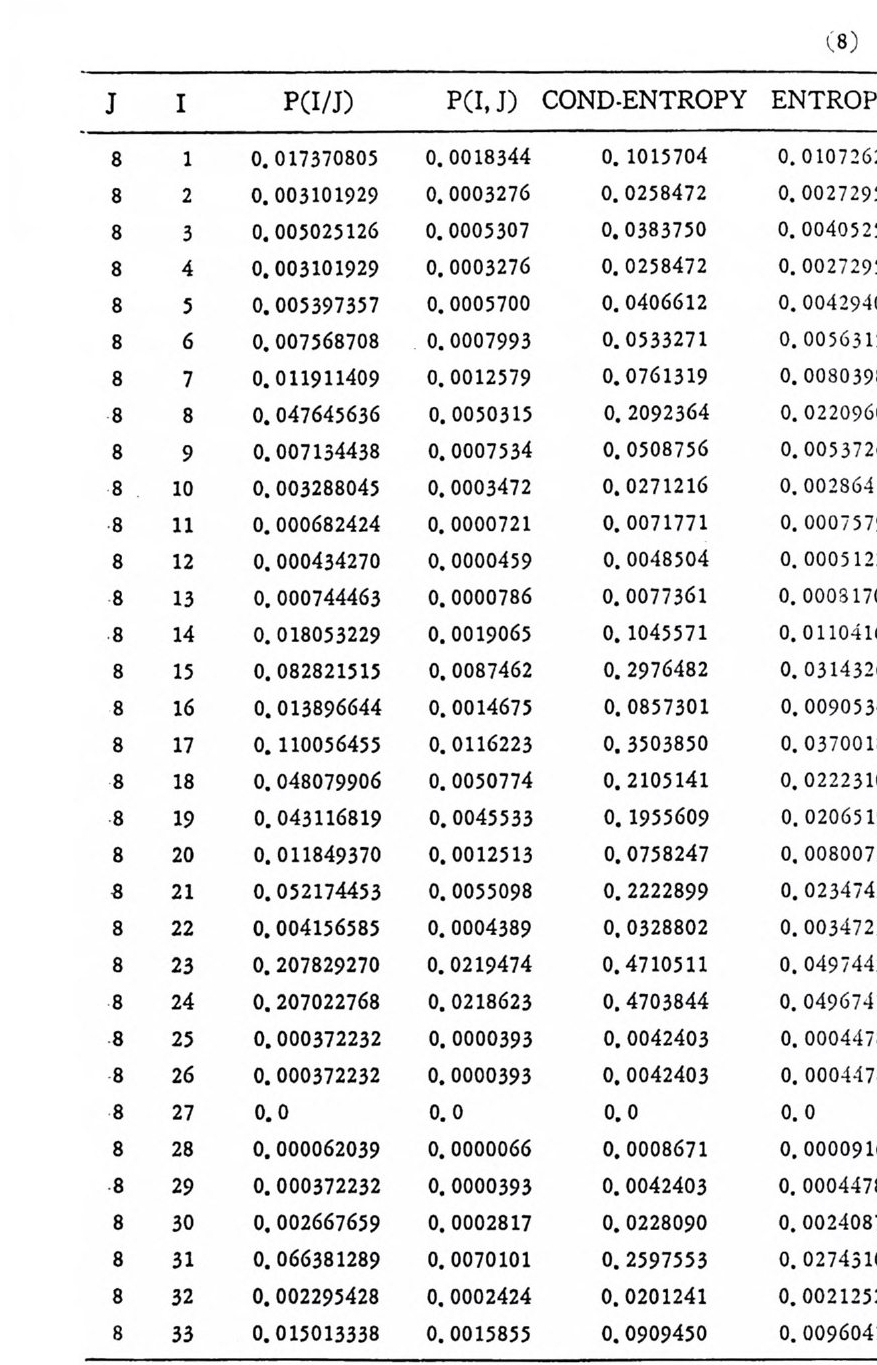 (8 )
(8 )
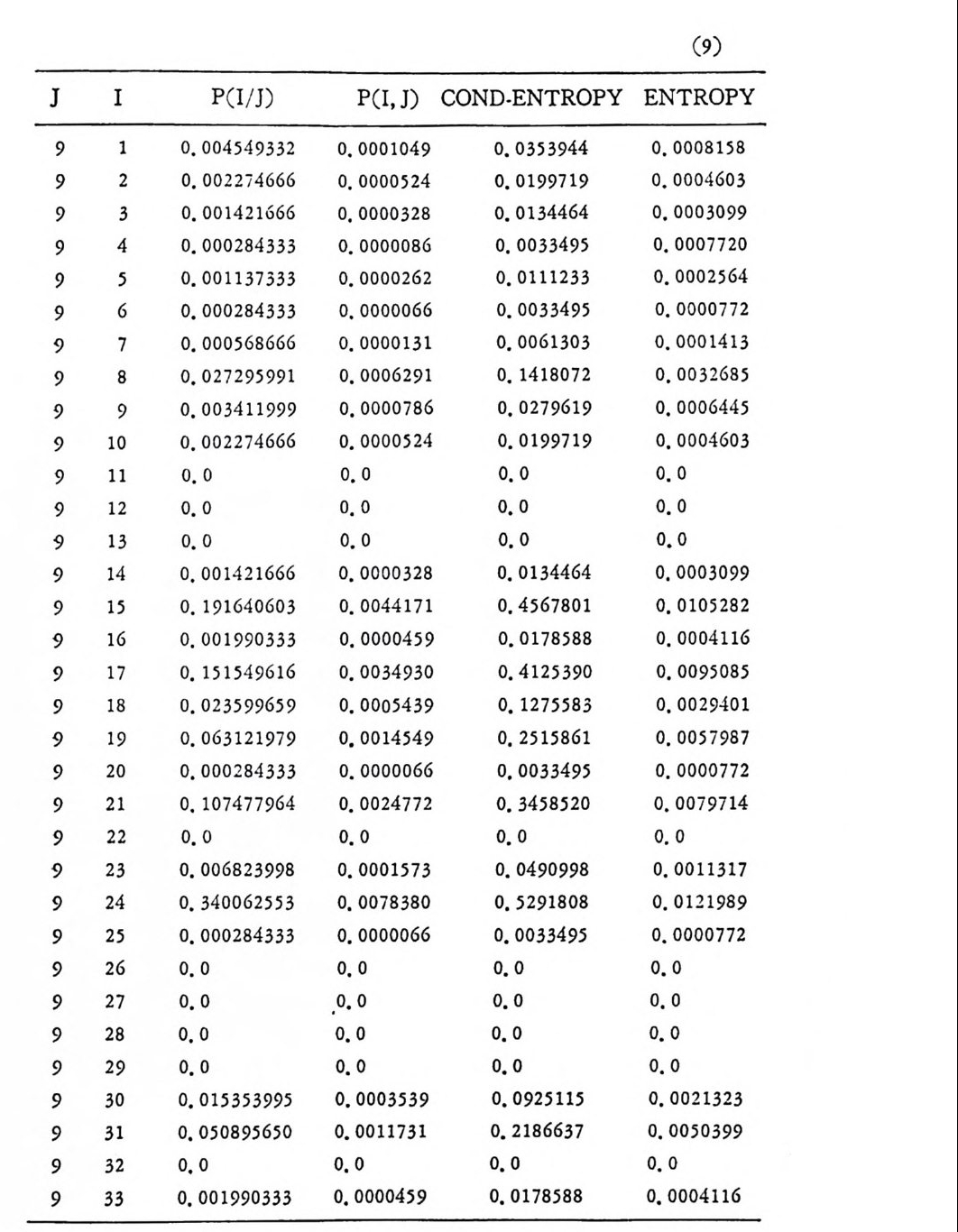 (9)
(9)
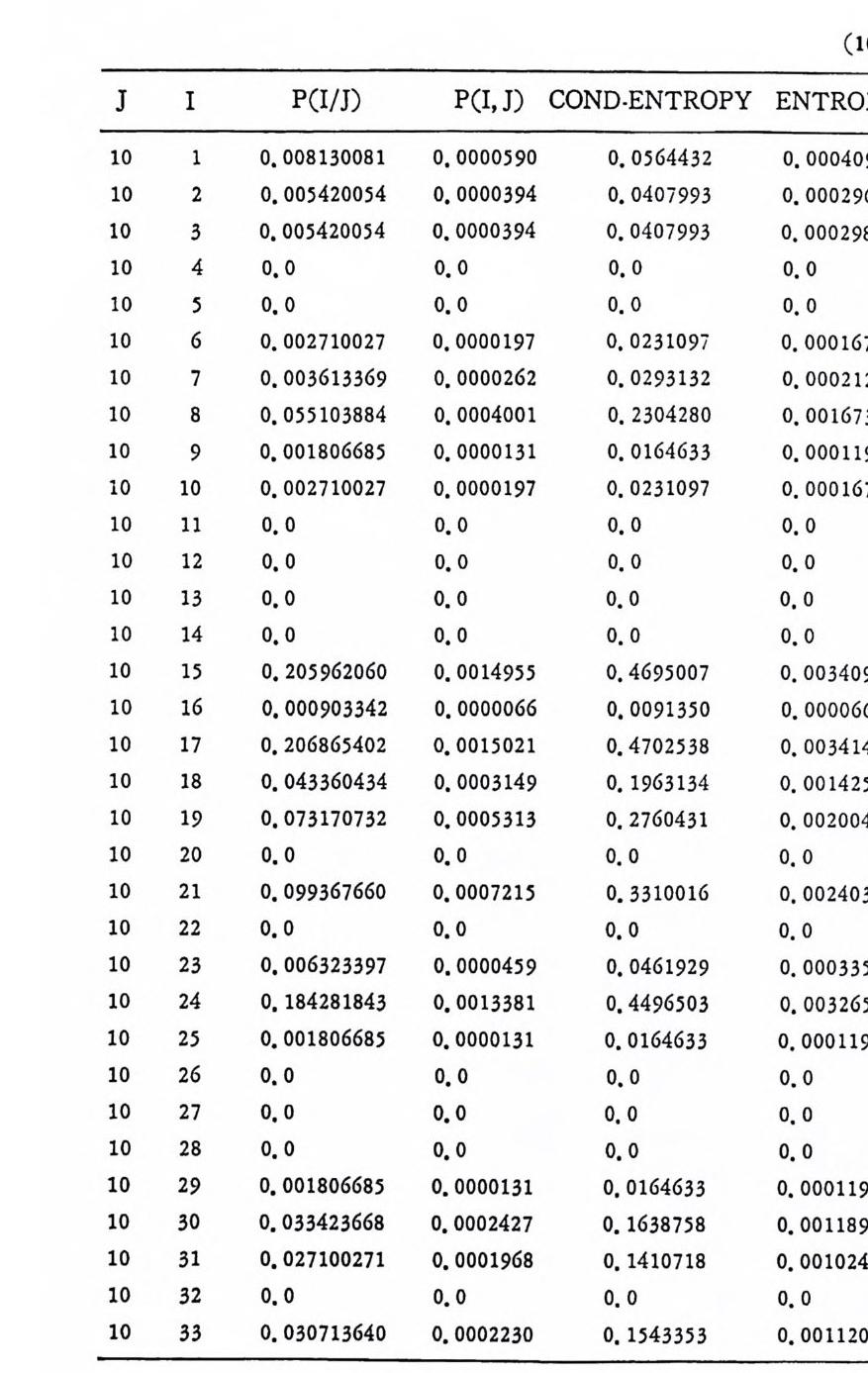 (10)
(10)
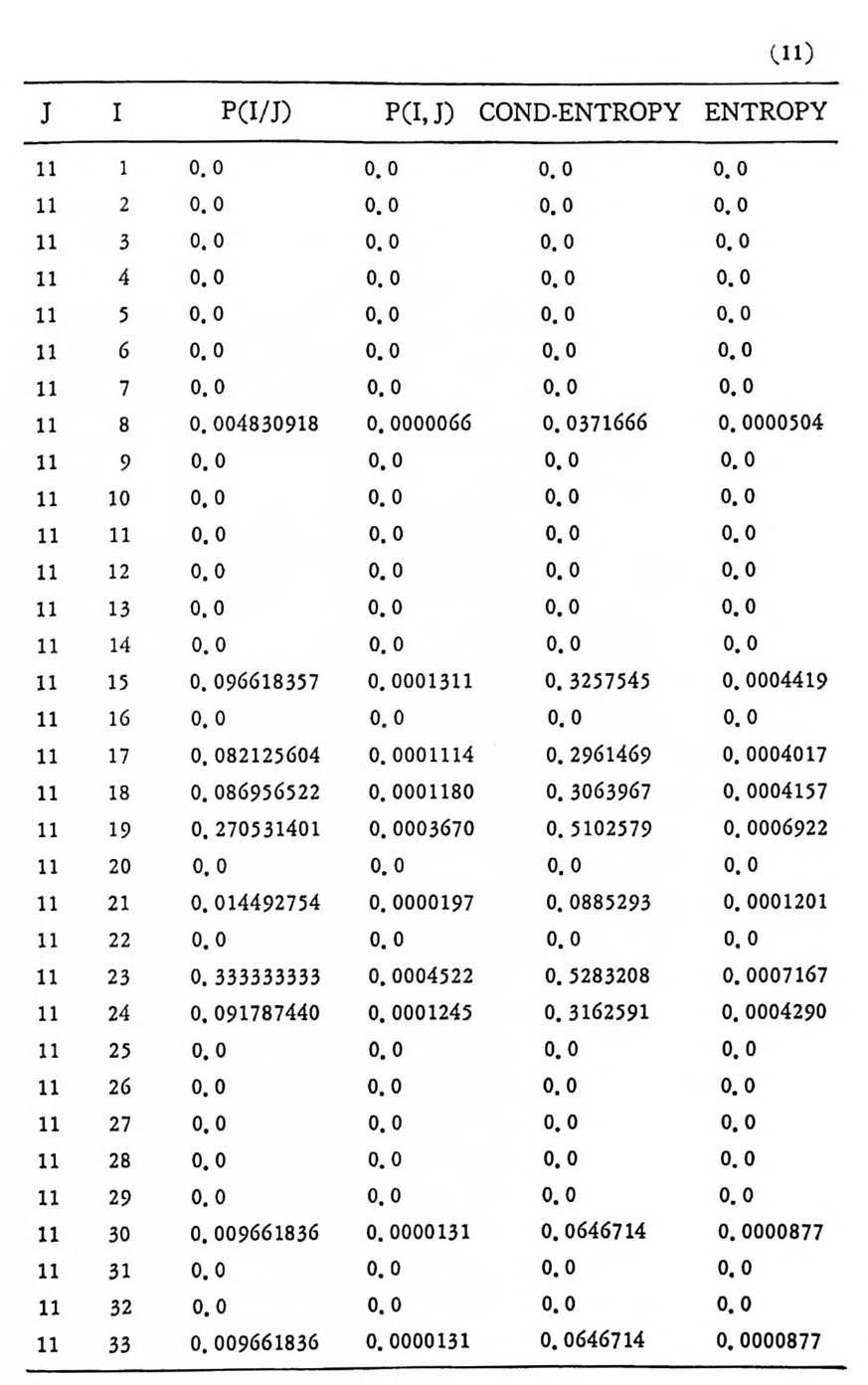 (1 1)
(1 1)
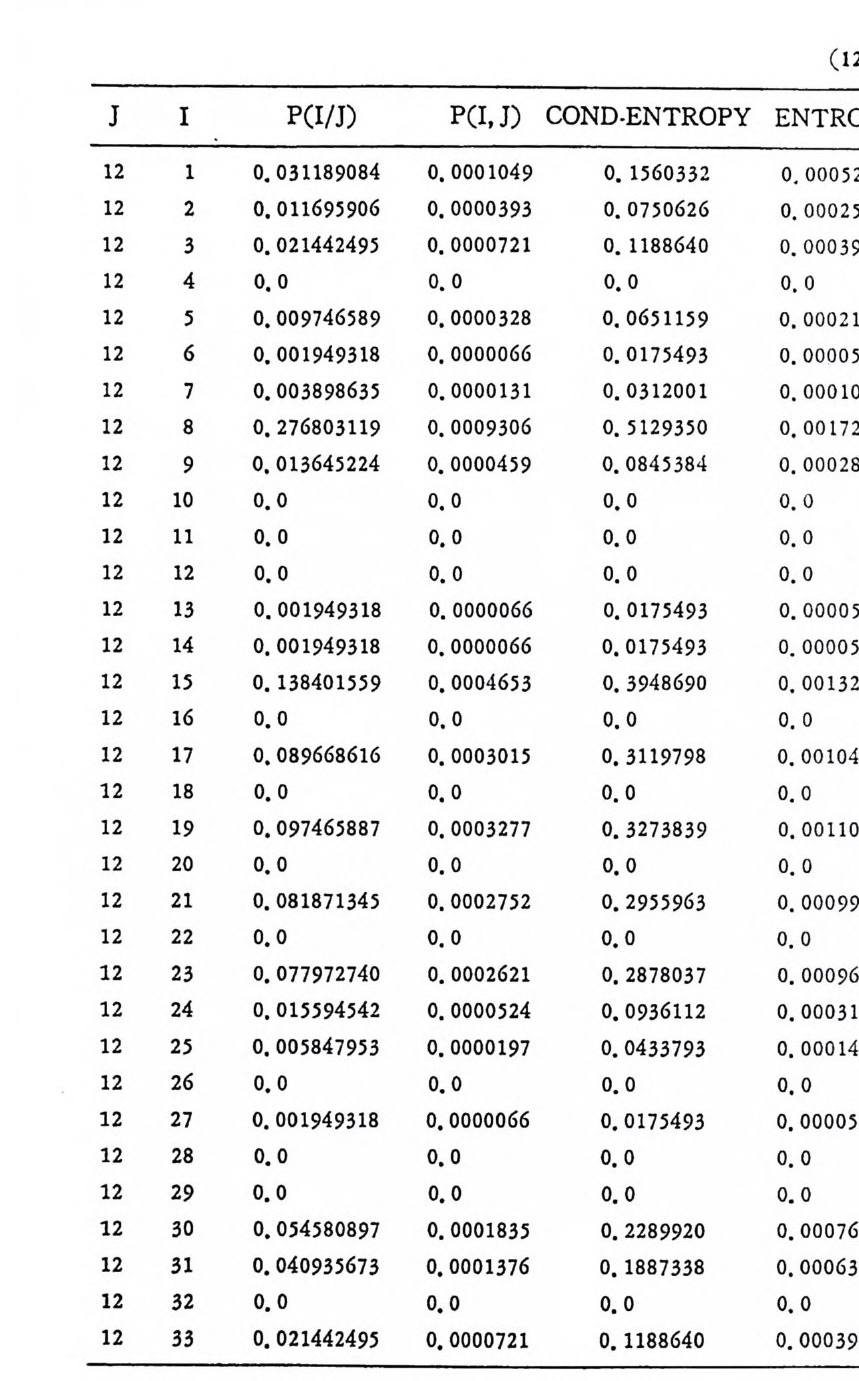 (1 2)
(1 2)
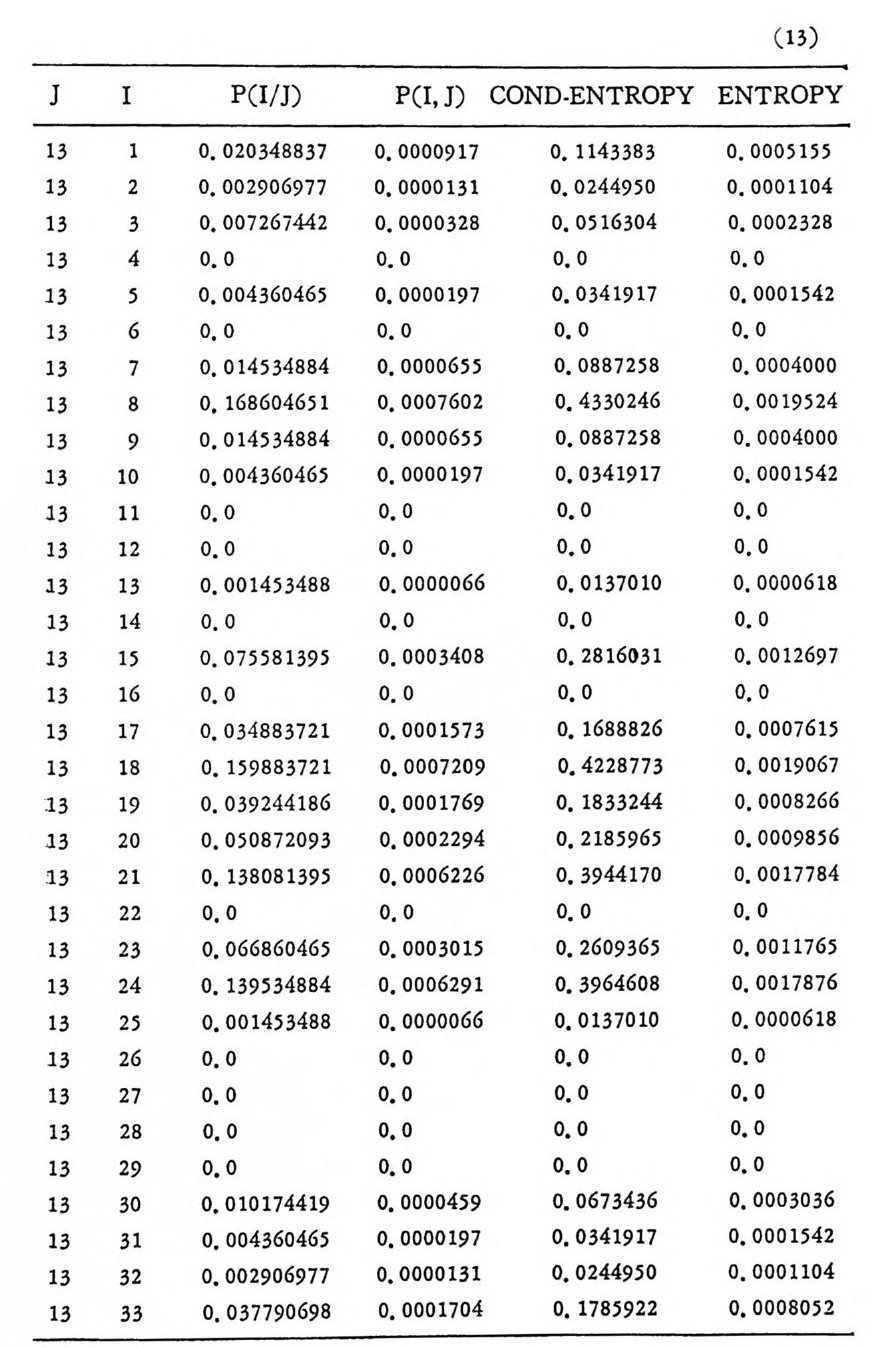 (1 3)
(1 3)
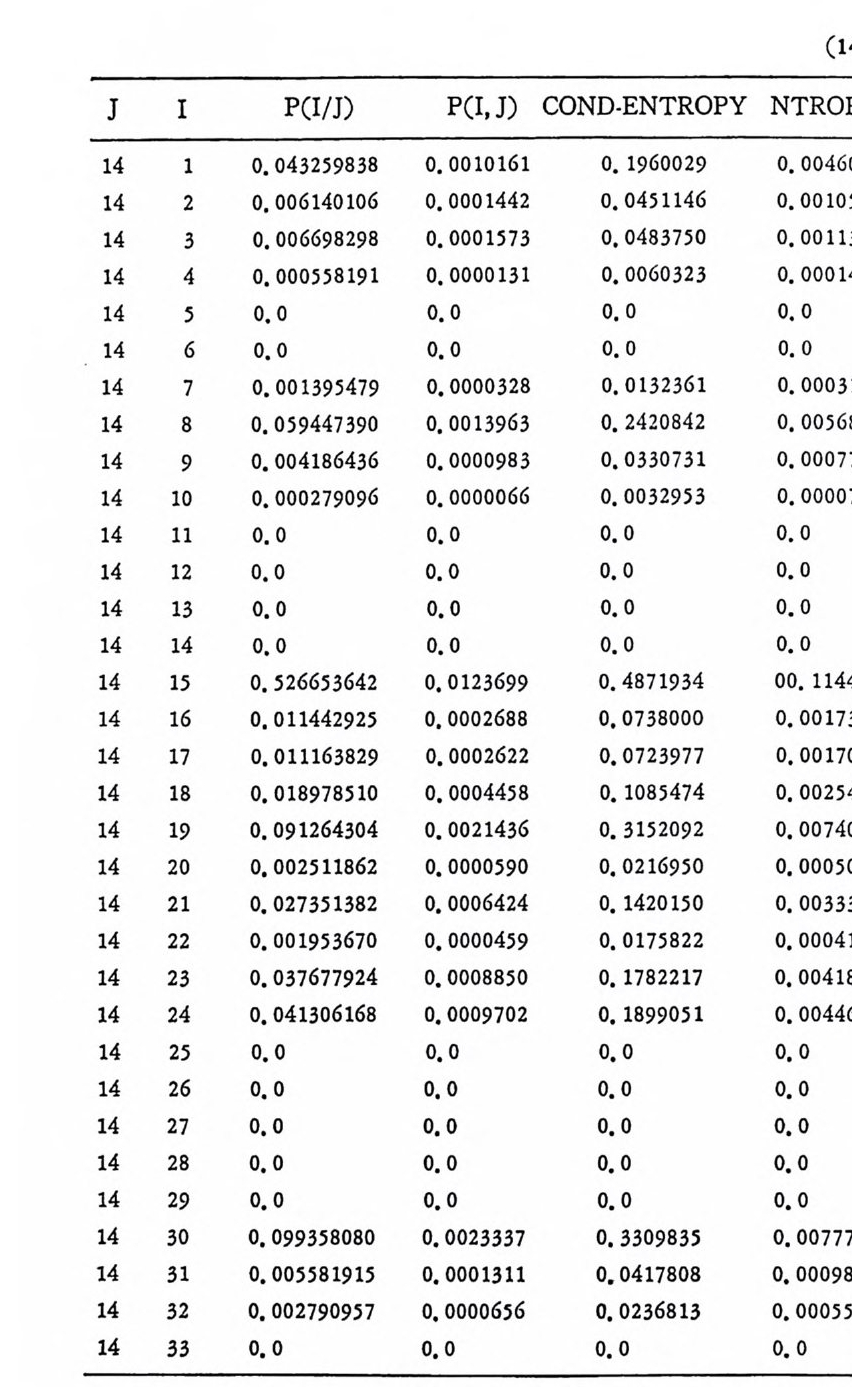 (14)
(14)
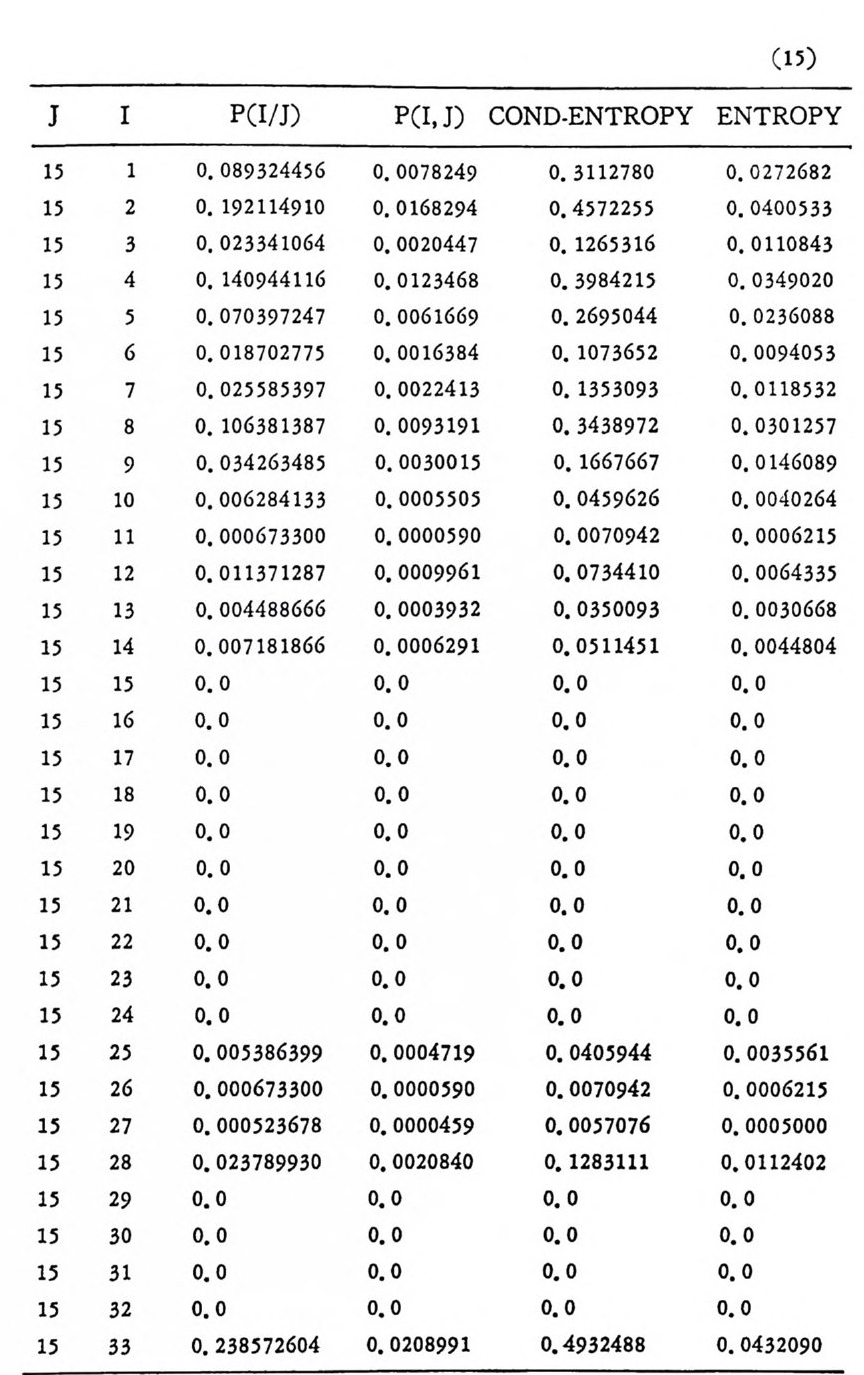 (1 5)
(1 5)
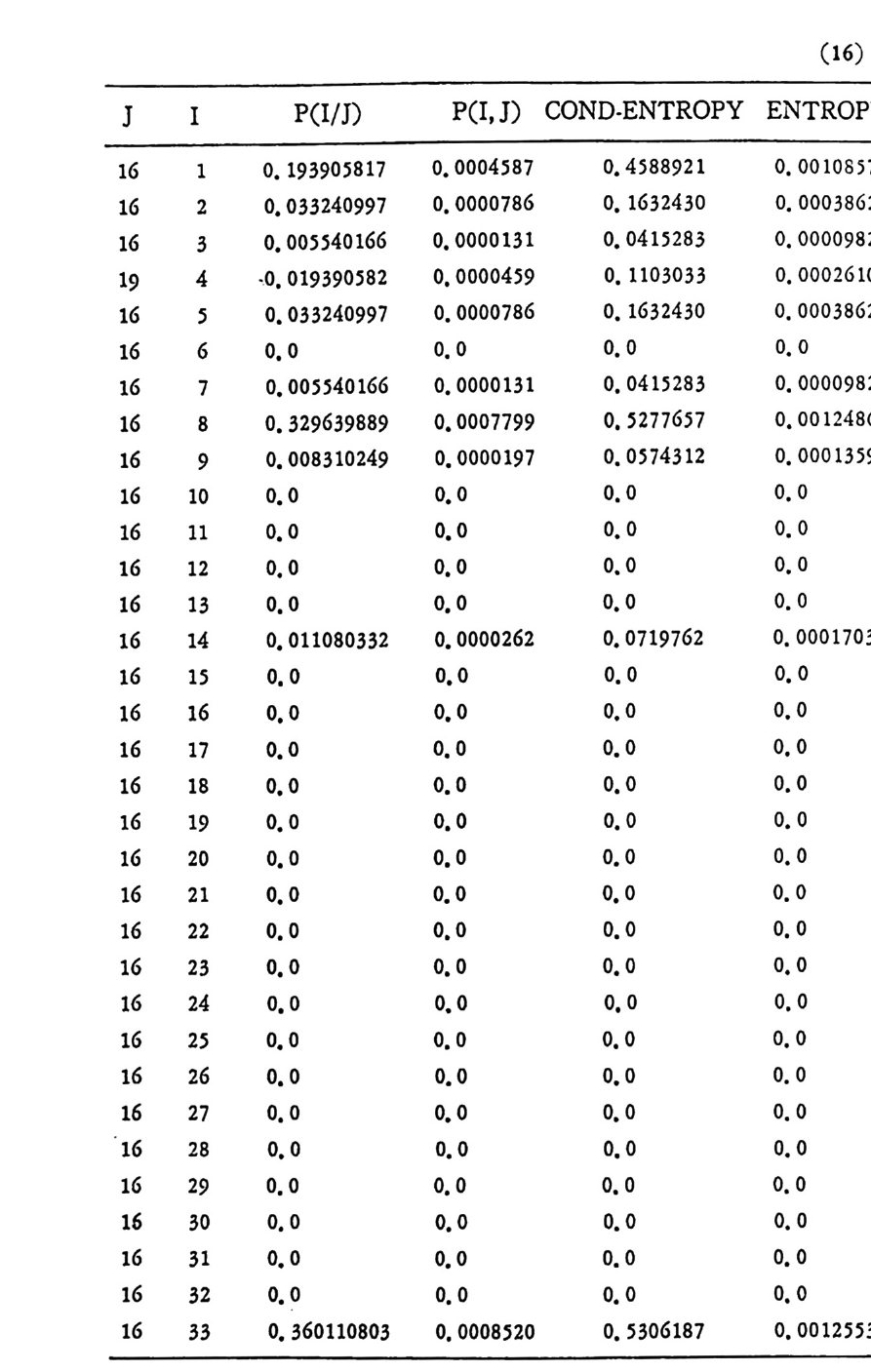 (16)
(16)
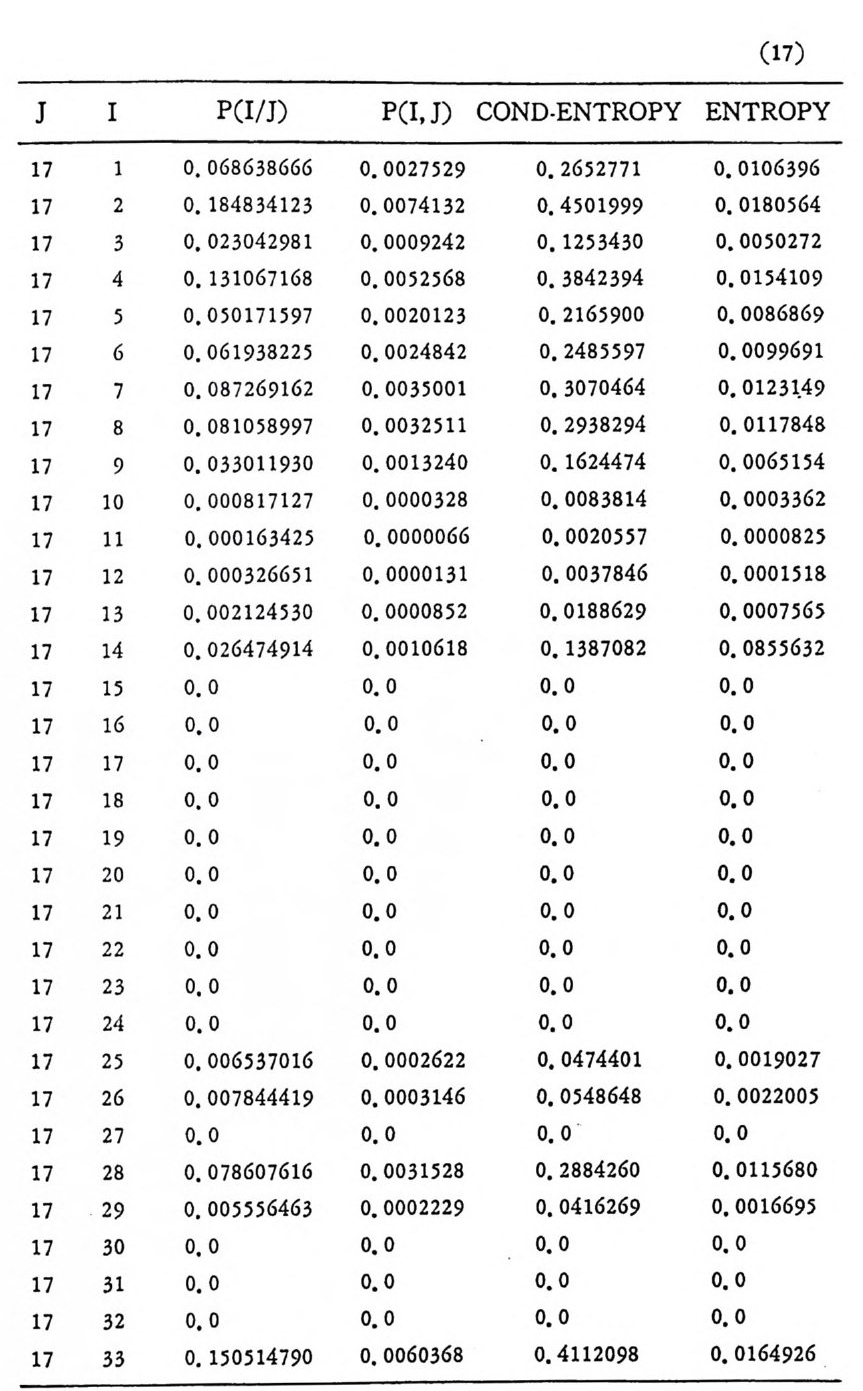 (17)
(17)
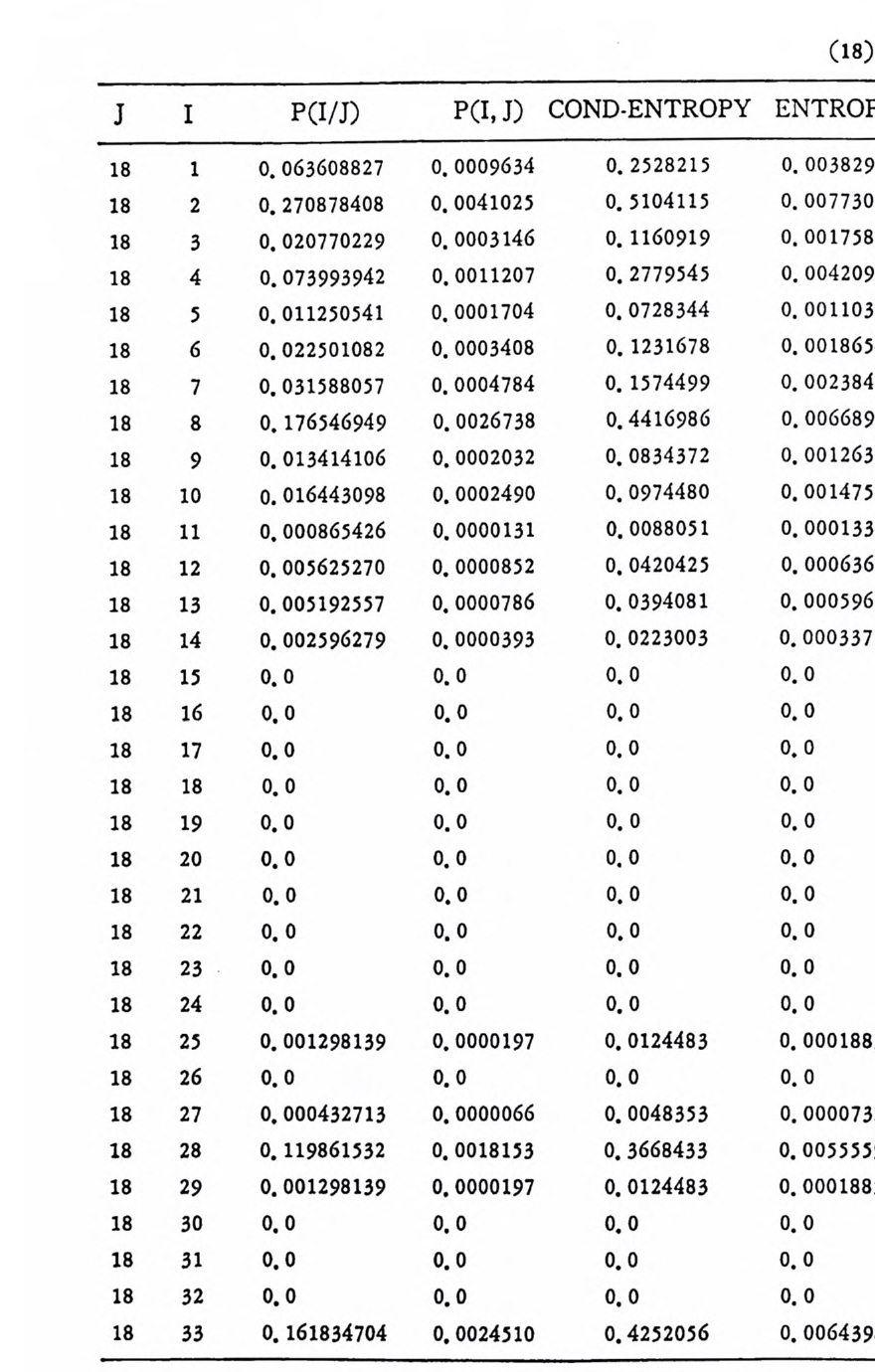 (18)
(18)
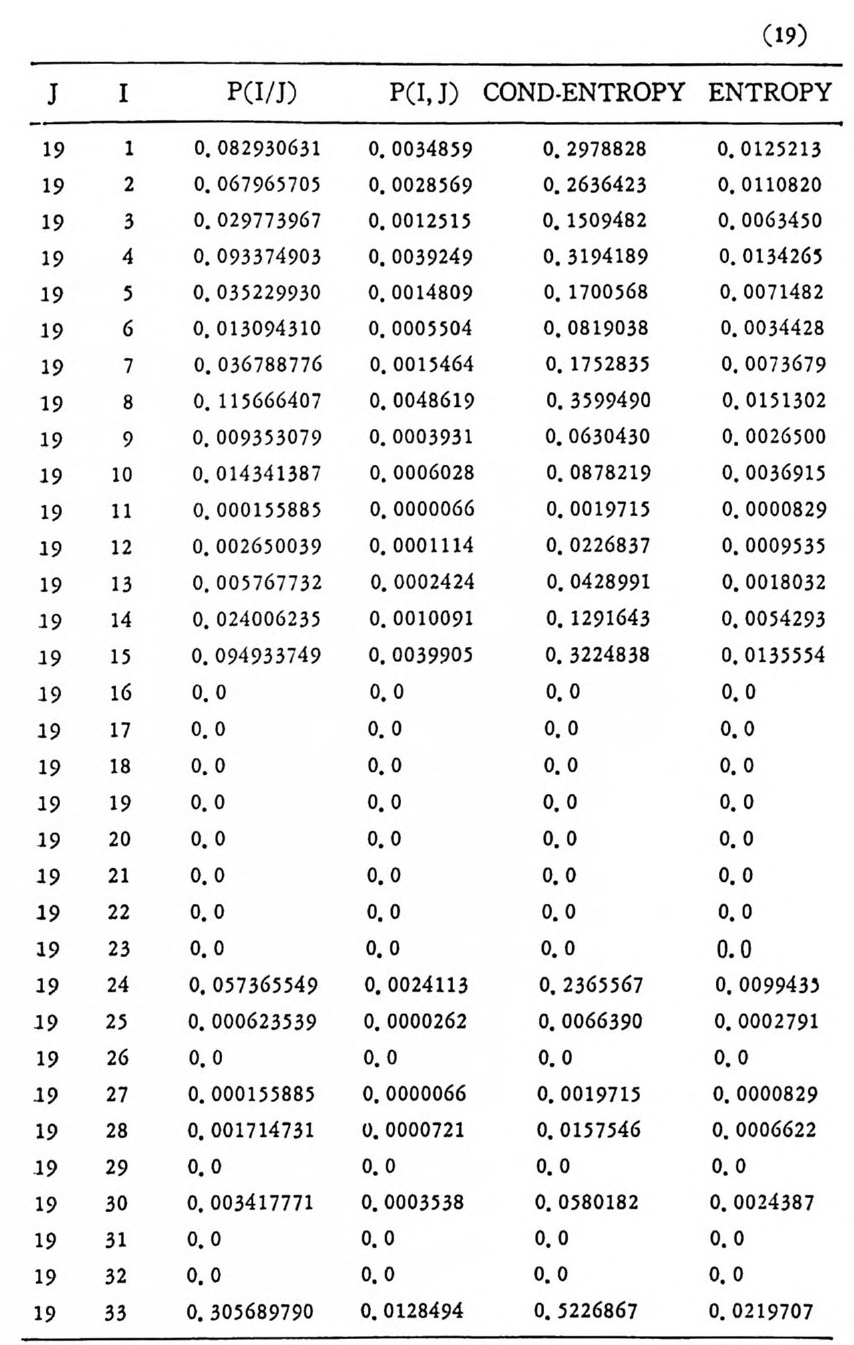 (19)
(19)
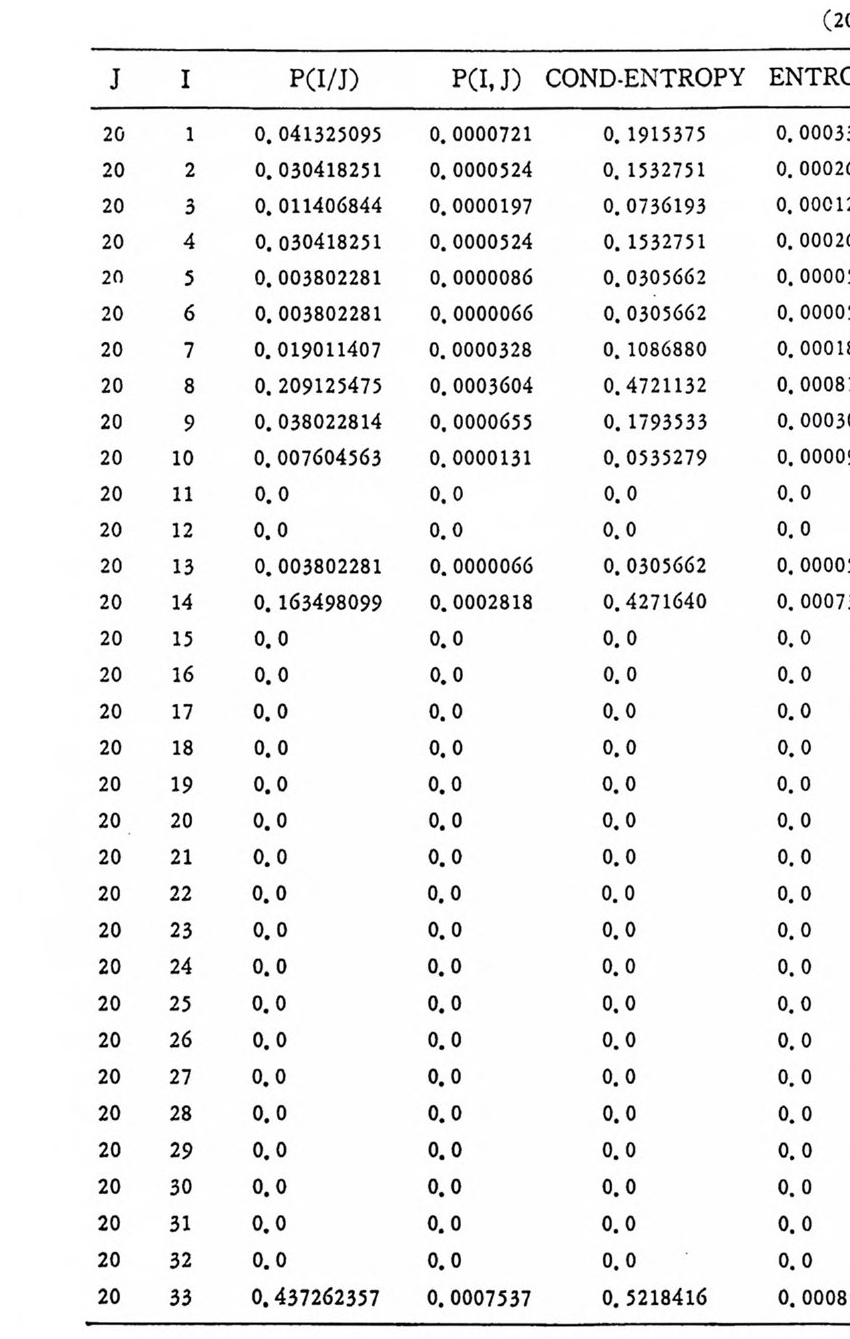 (2 0)
(2 0)
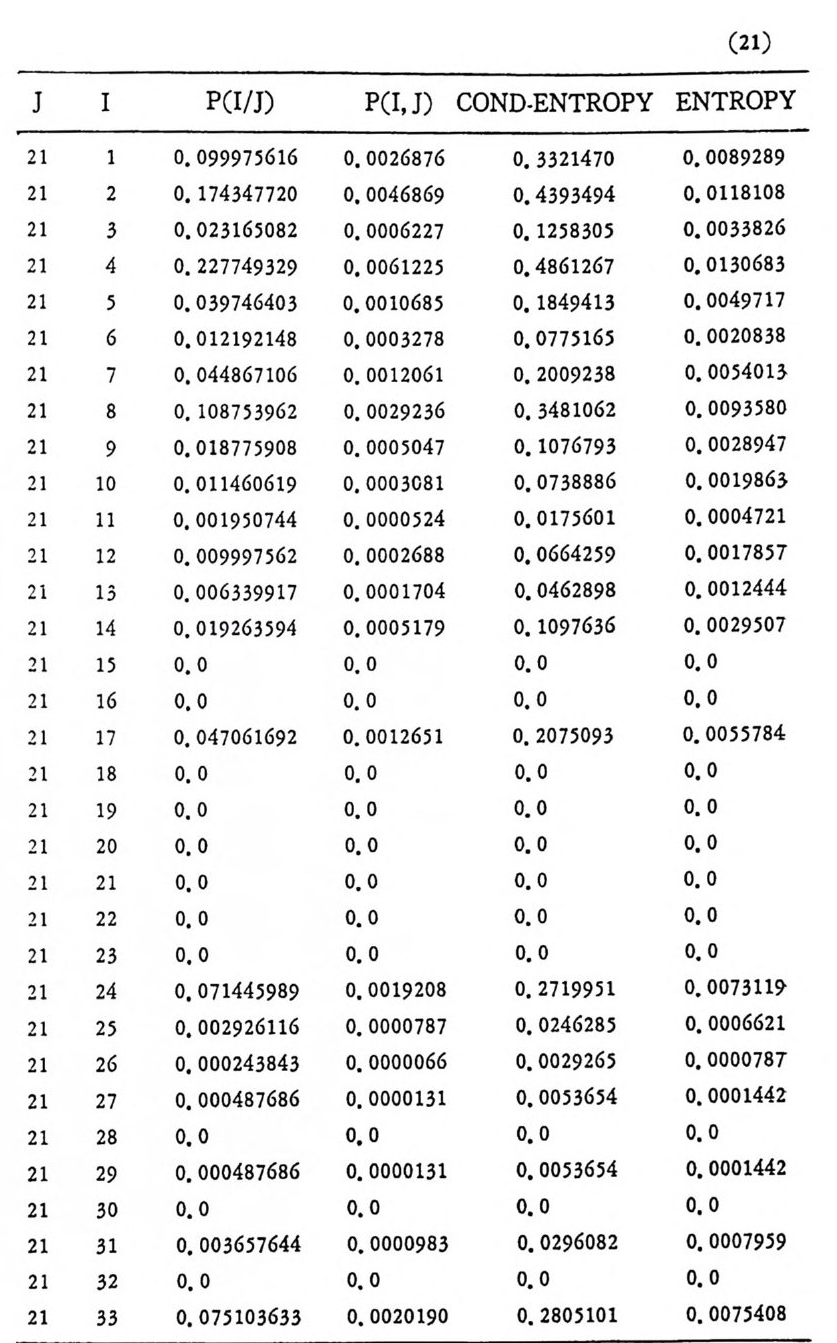 (21)
(21)
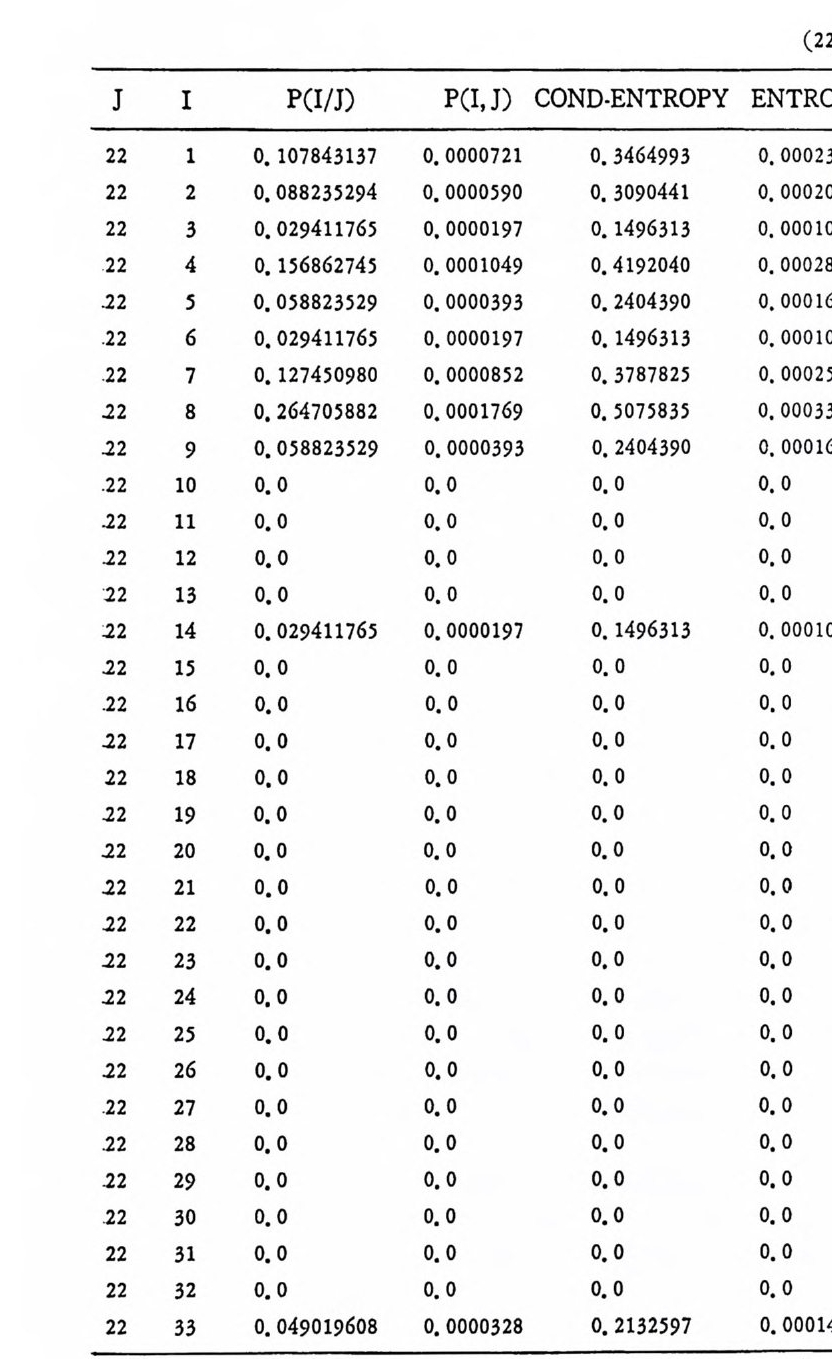 (2 2)
(2 2)
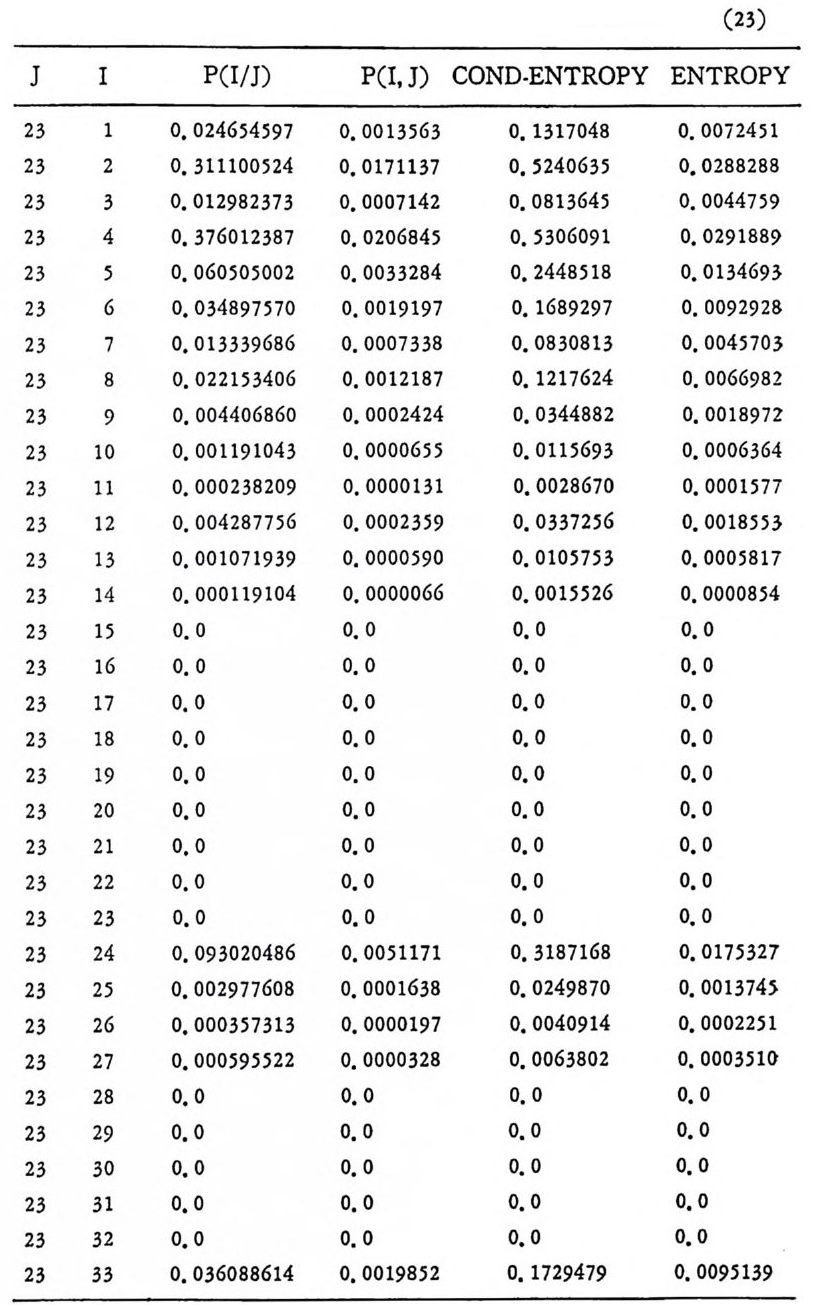 (23)
(23)
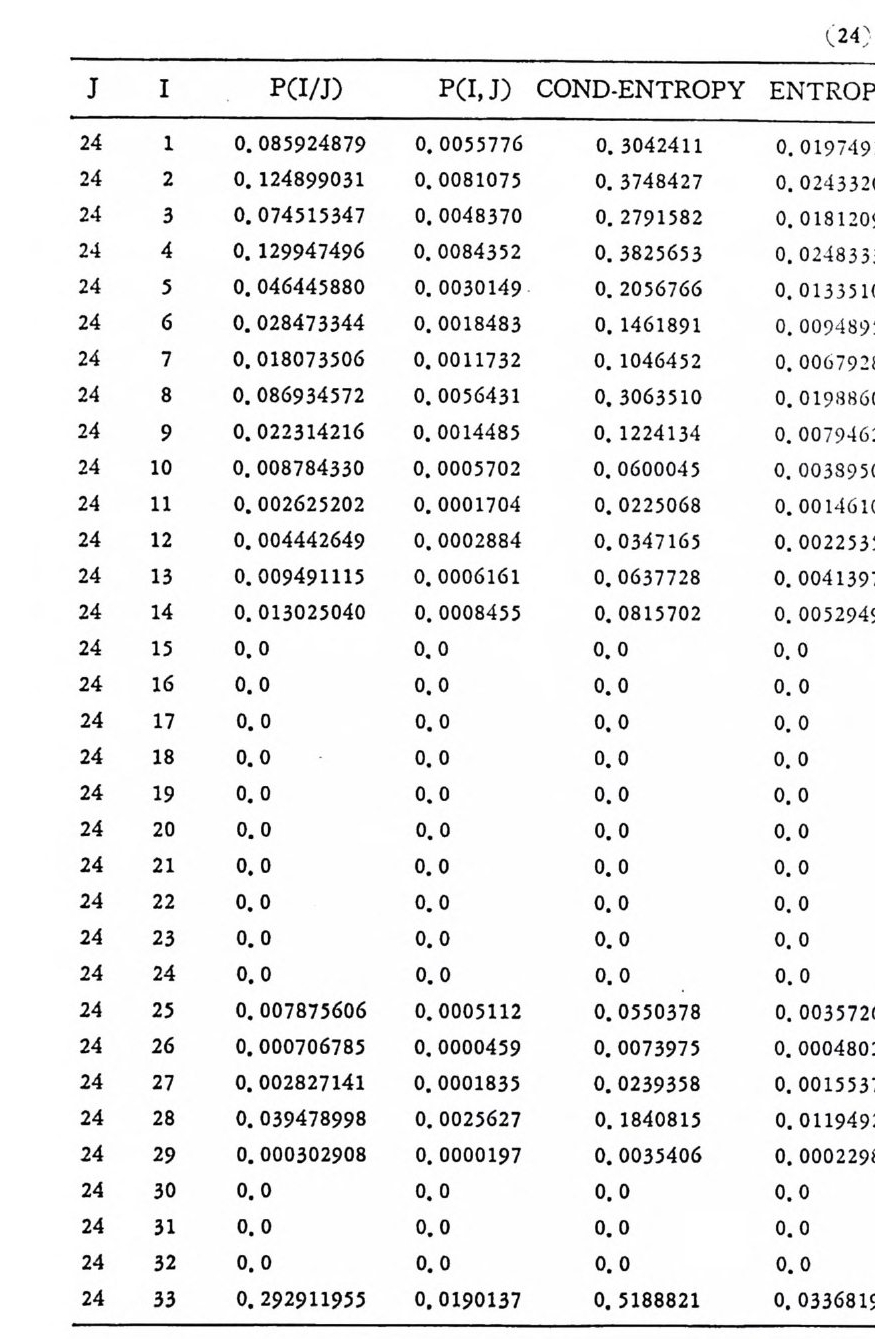 (2 4>
(2 4>
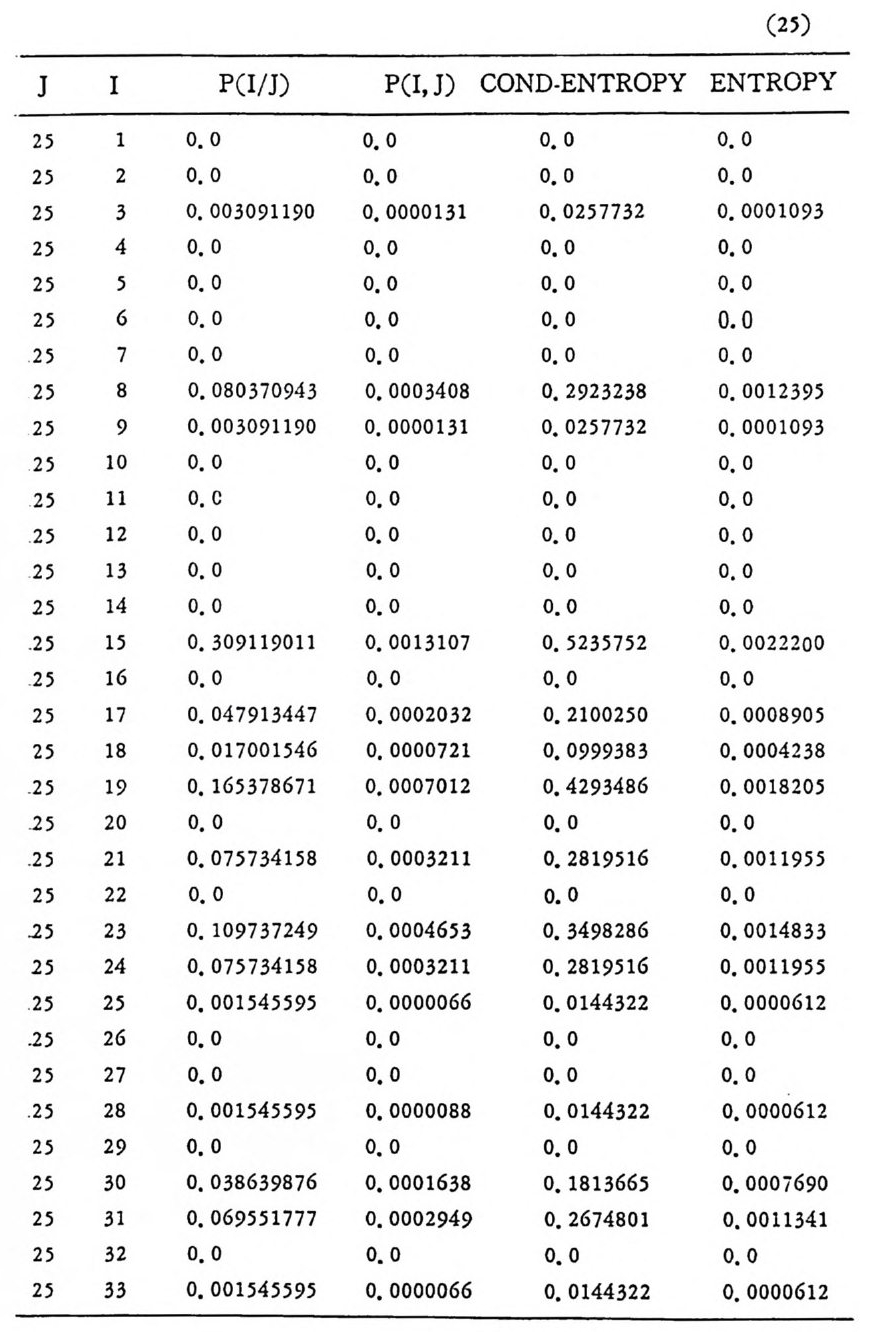 (25)
(25)
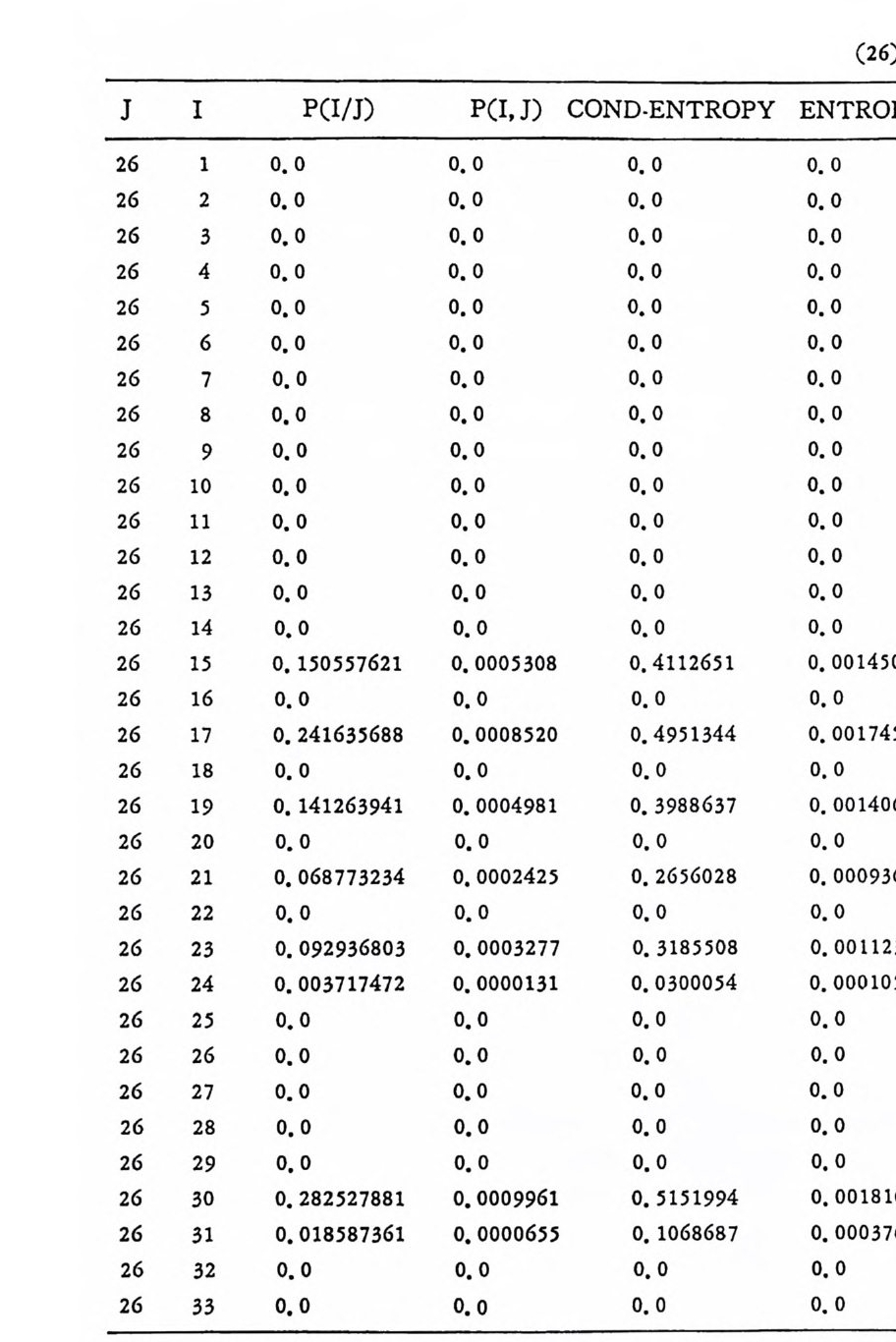 (26)
(26)
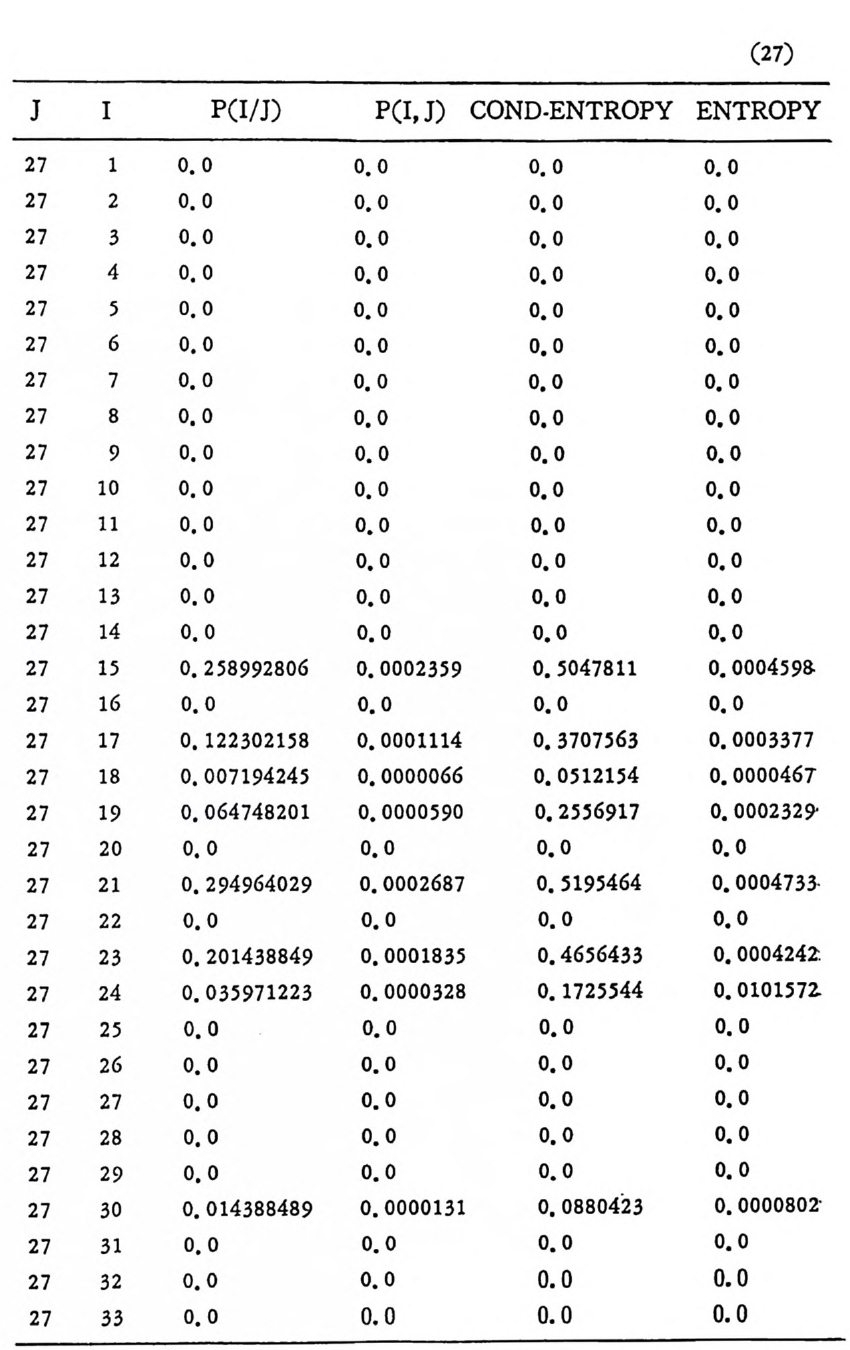 (27)
(27)
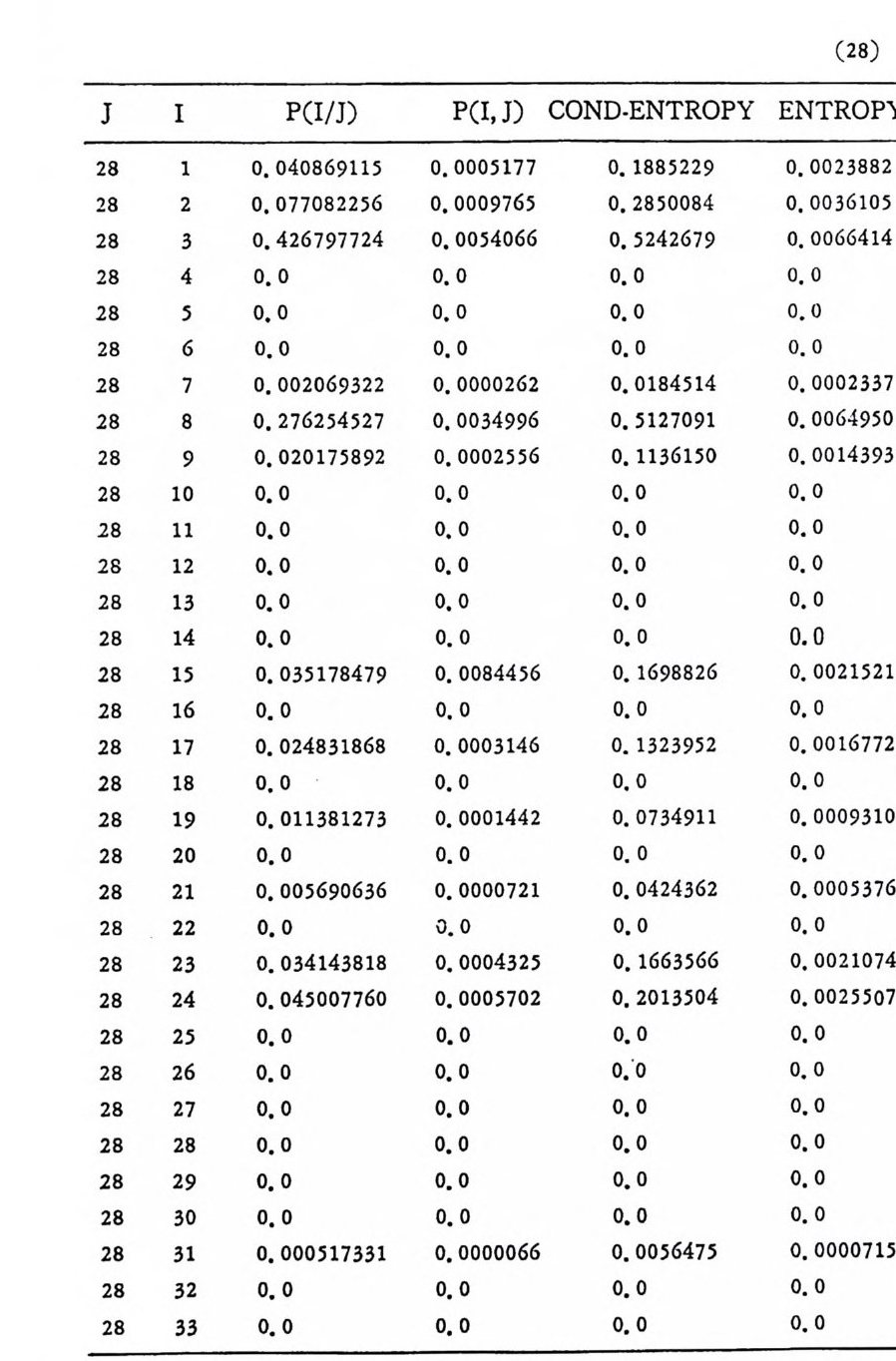 (2 8)
(2 8)
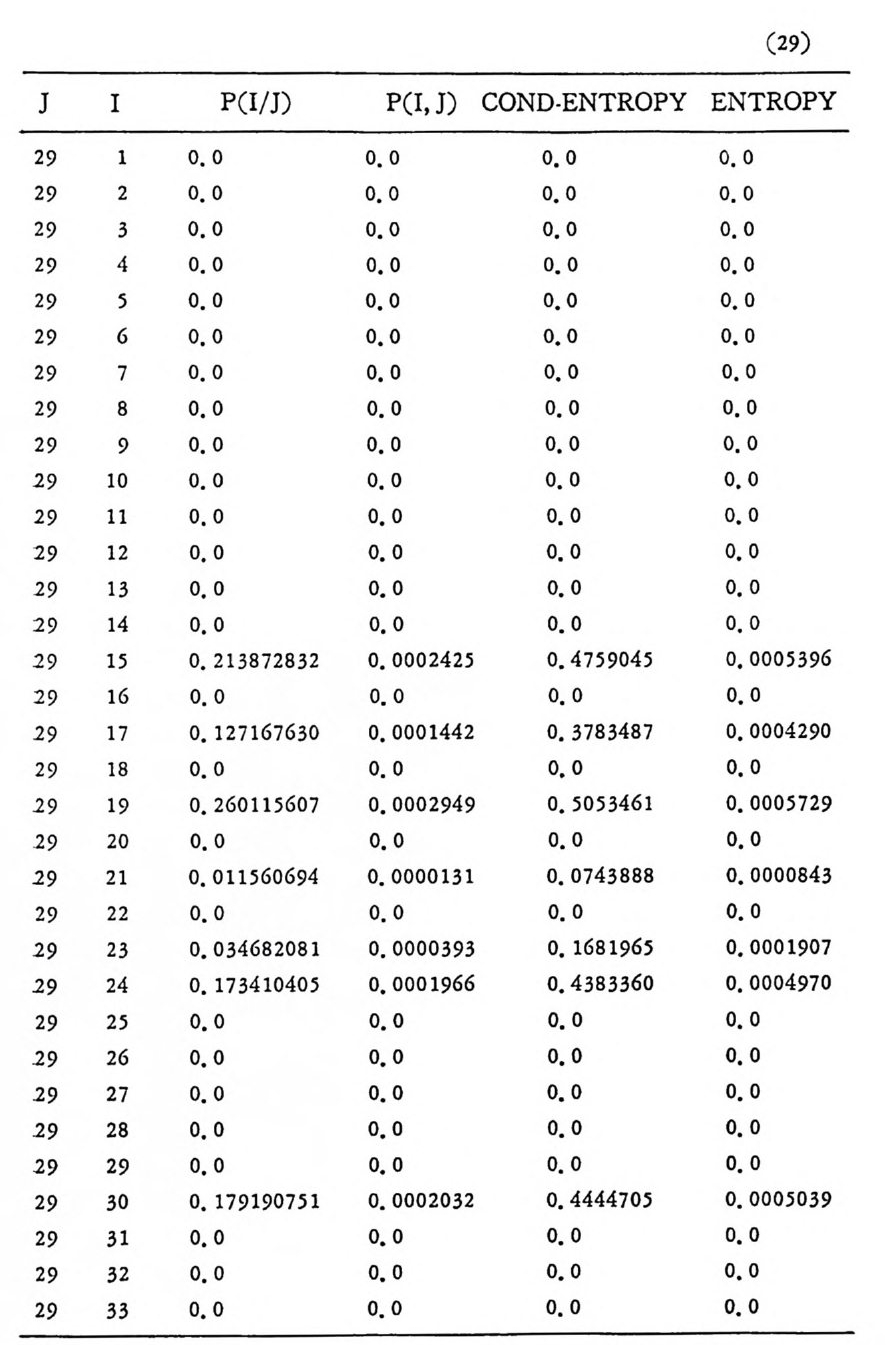 (29)
(29)
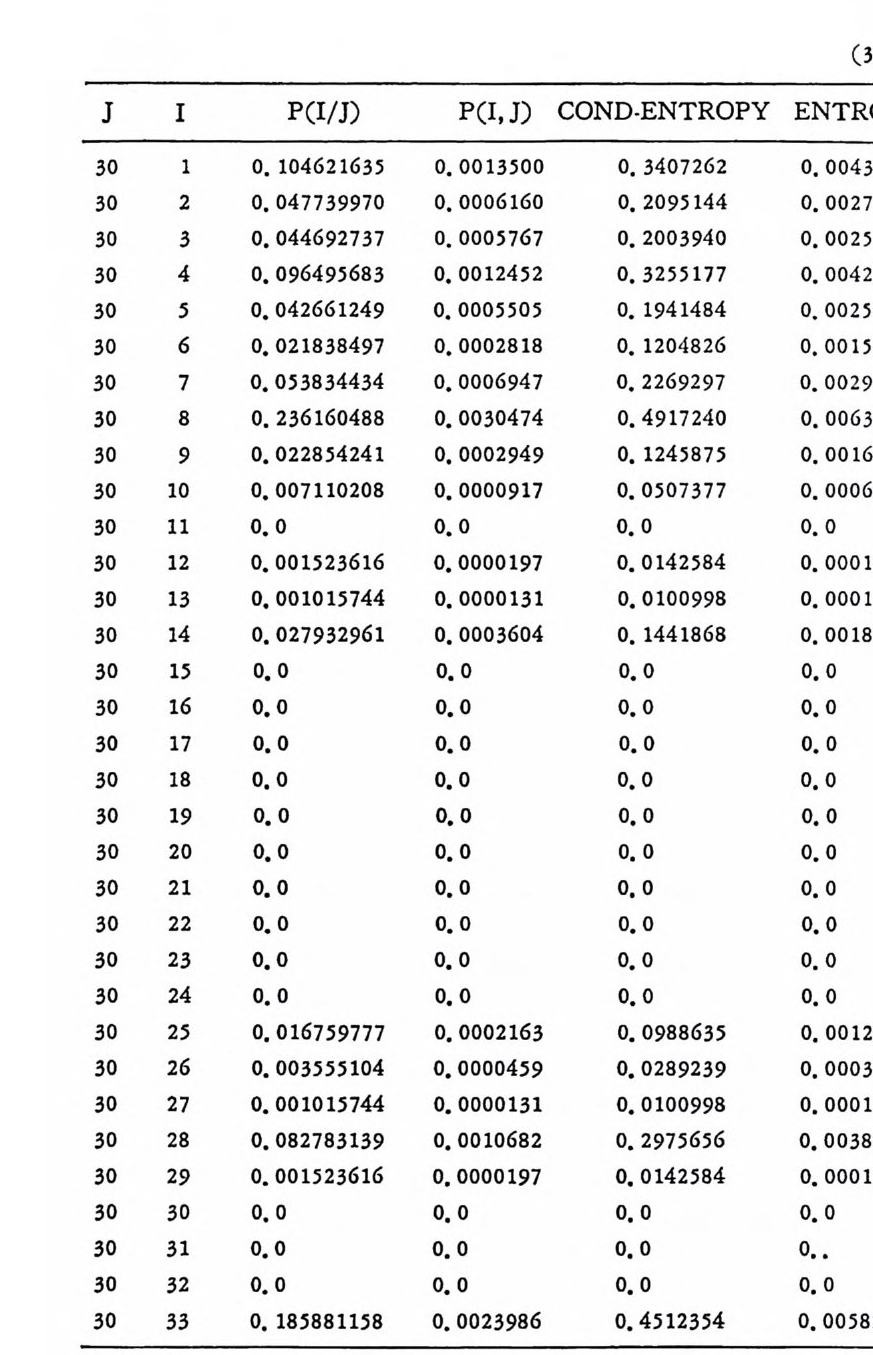 (30)
(30)
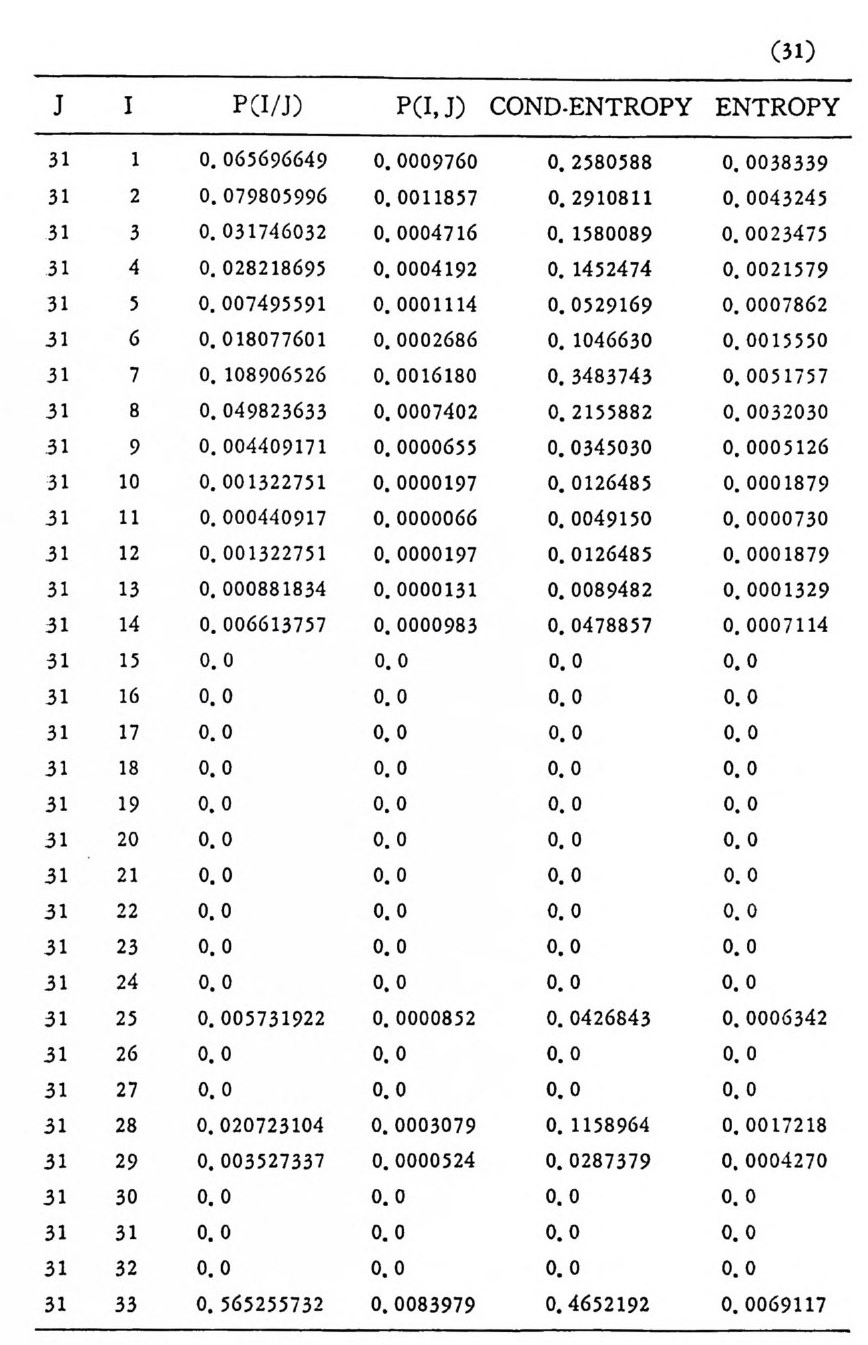 01)
01)
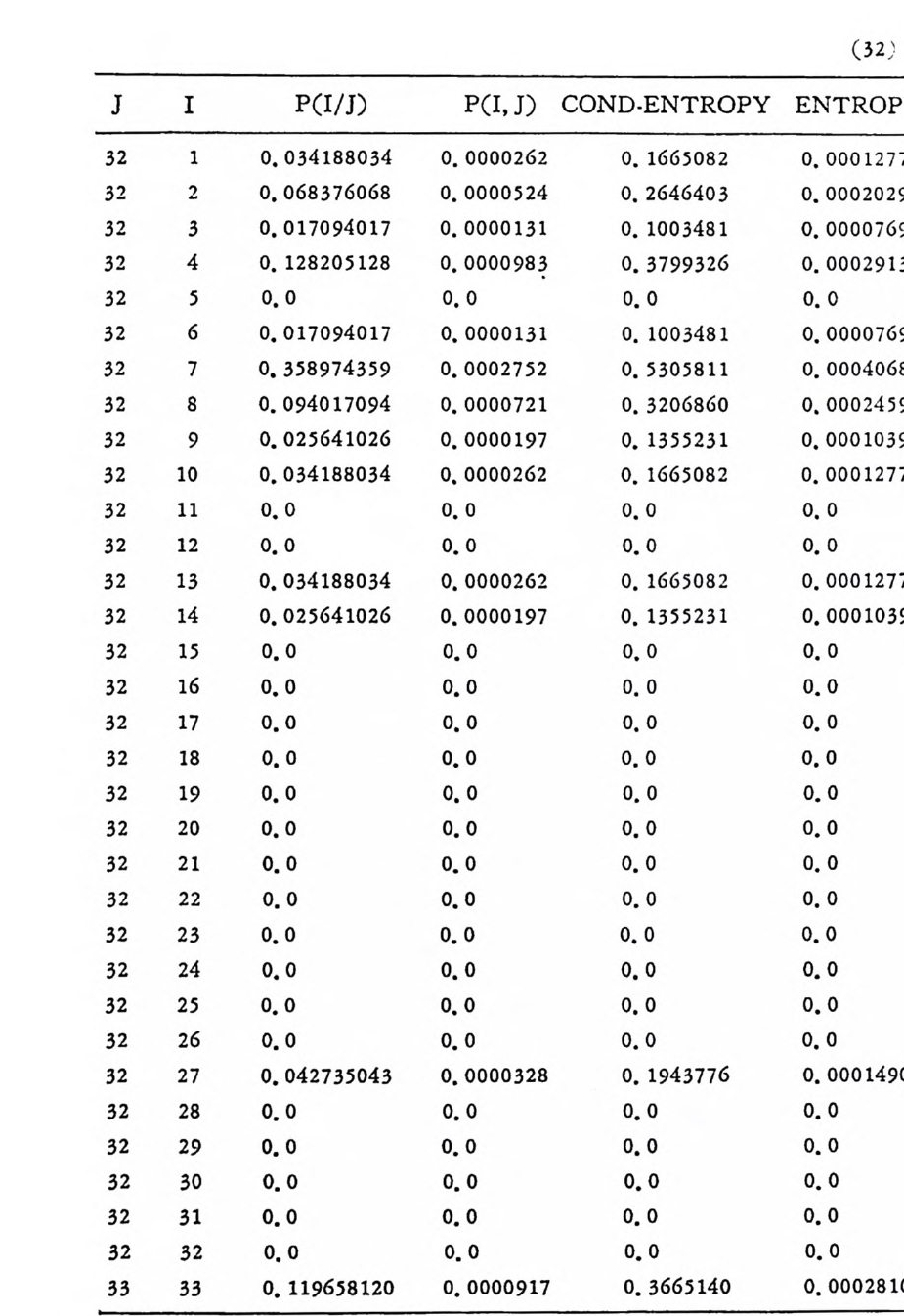 (3 2)
(3 2)
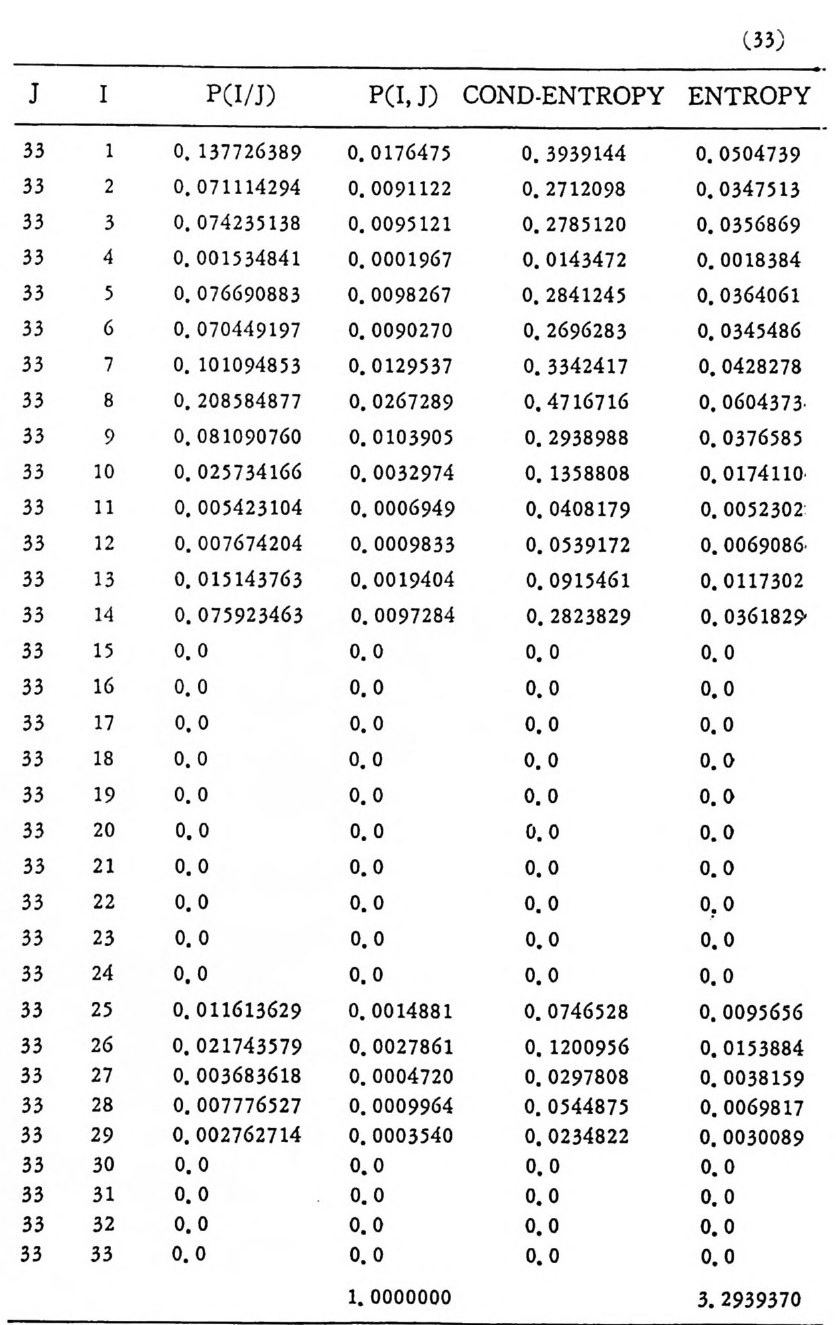 (33 )
(33 )
-l 가로 와체 Galois fiel d 175 加法性 add it ivi t y 38 加算的白色正規雜音채 널 addit ive whit e G a us sia n nois e channel 13 가 우스分;f[i Gaus si a n dis t r i b u ti on 27 가 지 bra nc h 21 1 계 연 seq u e nc e 48, 122 고 잡음계 .l very nois y channel 136 共;t/l ll cov a r ia n ce 25, 29 ~: l~! ; ! null even t 19 拘束길이 con st r a in t leng th 205 귀 환 복 궁t fee dback decoder 212 期 待値 exp ec ta t i on 23 기 대 함수 exp e cta t i on fun cti on 22 기 약다항식 irr ed ucib l e po lyn omi al 18 5 기 호 sym bol 44 , 48 L 나 무부호 tre e code 21 0, 215 내 트 nat 39 누 적 분포함 수 cumulati ve dis t r i b u ti on fun cti on 21 E: 다수 결 논리 복 호 majo r it y log ic deco- din g 166 단위 다항 식 monic po lyn omi al 185 대수의 법칙 law of the large number 32 大 數 의 약법칙 weak law of the large number 33 독립 ind ep e ndence 21
E2 렌돔부호 화 random codin g 128-9, 148 렌돔 數: random number 26 렌동에 러 random error 233 레 일 디 스토숀함수 rate dis t o rti on fun cti on 151 로그.우도비 log lik e lih o od rati o 112 리 드물러 부 호 Reed-Muller code 17 0 口 마디 node 211 마코브연쇄 Markov chain 90 마코브정 보 원 Mark o v source 87 맥 밀 란부등식 Mcmi lla n ine q u ali ty 52 메트릭 metr i c 214 모멘트생 성 함수 momen t ge nerati ng fun cti on 23, 28 무거 1 분포다항식 weig h t enumerato r 199 무기 여 채 널 memoryl e ss channel 123 무잡음채 널 nois e less channel 12 文字 lett er 12, 48 1:1 버 스트길이 burst leng th 232 버스트에러 burst error 23 2 베 이 어 스公式 Bay es ' for mula 20 변환 tra nsfo r mati on 24 보호공 7J gua rd spa c e 232 복호기 decoder 12, 14 복호에 러 decodin g error 17 복호오울 decodin g error pro babil ity
u5, 123 볼록함수 convex fun cti on 31, 67 부분생 성 식 subg e nerato r 204 符밟t code I2, 48, I22 부호기 encoder u, 481 1551 182 부호길이 code leng th 156 부호다항식 code po lyn omi al 177 부호어 code word 48, 107, 122, 1 5 5 부호울 code rate 156 부호화의 제 일기 본정 리 the firs t co- din g th eorem 53 분산 varia n ce 23, 28 분포함수 d i s t r i bu ti on fun cti on 21 불연속확물변수 dis c rete random va- ria b le 22 불확실성 uncerta i n ty 40 블록부호 block code 155 BCH 부호 BCH code 184 비 트. bit 39 人 寫像 map ping 15, 26 事象 event 18 사상공간 event spa ce 18 사전확물 a pr io ri p r obabil i ty 21, 123 사후확률 a po ste r io r i pr obabil i ty 21, 123 상계식 up pe r bound 116, 148 상관계 수 correlati on coeff icien t 29 상태 sta t e 88 상 태 도 sta t e dia g r am 88, 217 상호독립 mutu a lly ind ep e ndent 21 상호배 반사상 mutu a lly exclusiv e event 19 상호정 보량 mutu a l in fo r mati on 59,
65, 73, 94 생 성 다항식 ge nerato r po lyn omi al 178 생 성 식 ge nerato r 204 생 성 함수 ge nerati ng fun cti on 222 생 성 행 렬 ge nerati ng matr i x 156 선형 변환 lin e ar tra nsfo r mati o n 76 , 1 17 선형부호 line ar code 155 세 바 쉬巨노부등식 Cheby s hev ine q u alit y 30, 142 송신기 tra nsmi tter 11, 14 수신기 receiv e r 12 수신선호 receiv e d sig n al 순회 부호 cyc l ic code 155, 174 신드롬 syn drome 159 신드롬발생 기 syn drome ge nerato r 184 신드롬복호기 syn drome decoder 161 스택 알고리 즘 sta c k algo rit hm 223 쌍대 공간 dual spa ce 200 쌍대부호 dual code 179, 199 쓰레쉬홀드t hreshold 141 쓰레쉬 홀드복호 thr eshold decodin g 211 0 語頭부분p re fi x 50 에 러 error 12 에 러 검 출부호 error dete c ti ng code 163 에 러 정 정 부호 error correcti ng code 161 에 르고딕 연쇄 ergo dic chain 91 엔트로피 entr o p y 37, 41, 65
왜 곡 측 도 dis t o rti on measure 146 요소 element 19, 48 우도함수비 )ike lih o od fun cti on ra- tion 140 元 element 174 源복 호기 source decoder 12 源 부 호 sourc e code 147 源 부호기 sou rce encoder 12 源 부호화 정 리 source codin g the orem 146, 15 1 源 -사용자쌍 source-user pa ir 146
전송 뮬 tra nsmi ss io n rate 17 정 규분포함수 normal dis t r i b u ti on fun - cti on 27 정 보 in fo r mati o n 37 정 보 량 measure of in fo r mati on 14, :,7 정 보비트 inf o r mati on bit 17, 155 정 보원 in fo r mati on source 11, 38, 87 정 보원알파벨 source alph abet 38 정 보전송 in fo r mati on tra nsmi ss io n
原始 元 pr im i tive element 186 離散無記憶채 널 dis c rete memoryl e s:, channel 12, 16, 45 二元 對 稱 채 널 bin a ry sym metr i c cha- nnel 12, 16, 46, 65 二元妹 消 채 널 bin a ry erasure channel 47, 99 二元符 號 bin ary code 12, 14, 39 二次元엔트로피 joi n t entr o p y 61 :i;: 자기 정 보량 self -inf o r mati on 15, 38 자기 상관함수 auto correlati on 110 잡음 nois e 12
직 교 orth o g o nal 167 칙 교신호 orth o g o nal sig n al 113 * 채 널 channel 12 채 널복호기 channel decoder 12, 14 채 널부호기 channel encoder 12 채 널부호화정 리 channel codin g the o, rem 131, 136 채 널에 러 벡 터 channel error vecto r 159 채 널용량 channel cap ac it y 94 천이 확물 tra nsit ion pro babil i ty 16, 44, 89
M . L . 복호법 maxim um lik e lih o od de- codin g 118 연쇄 신호 conti nu ous sig n al 73 연쇄 확 물密度函數 conti nu ous pr oba- bil i ty densit y fun cti on 22 엔 센의 부등식 Jen sen's ine q u ality 31, 68, 149 오 목 함수 conca ve fun cti on 67 오 윤 error pro babil i ty 16, 107, 112 와이 너 애 쉬 부호 W yn er-Ash code 208
15 정 상적 정 보원 sta t i on ary source 88 조건부 자기 정 보량 condit ion al self - in fo r mati on 61 조건부확몰 condit ion al pr obabil it y 20 조직 부호 sys te m ati c code 157, 180 중심 국한정 리 centr a l lim i t the orem 32-3 즉 시 부호 ins ta nte n eous code 50 지 수부 exp o nent 125, 136
초기 확률 in it ial pr obabil i ty 90 최 소거 리 복호기 mi ni m um dis t a n ce decoder 219 최 소다항식 mi n im al po lyn omi al 186 최 소오울검 출기 mi ni m um error pro -babil it y dete c to r 112 최적복호 o pti mum decodin g 218 최 적 부호 op tim um code 56 최 종수신목적 desti na ti on 12, 14 추정 치 esti m ate i-5 9 축차복호법 seq u enti al decodin g 223 출력 계 열 outp u t seq u ence 13 더 코셀 coset 160 코셀 리 더 coset leader 1 60 콘볼루숀부호 convoluti on al code 203 크라프트부등식 Kraft ine q u ality 50 E 통로p a th 218 동로우도함수 pa th lik e lih o od fun c· tion 218 통보 messag e 11, 37, 122 통보계 열 seq u ence of messag e 11 트레 리 스固 tre llis dia g r am 215 포 파노메트릭 Fano metr i c 215
파노알고리 즘 Fano algo rit hm 215 패 리 티 검 사다항석 pa rit y check po ly- nomi al 179 패 리 티 검 사비 트 pa rit y check bit 1 5, 155 패 리 티 검 사합 pa rit y check sum 167 패 리 티 검 사행 렬 pa rit y check matr i x 158 평 군복호오울 averag e decodin g error pr obabil i ty 18 평 군상호정 보량 averag e mutu a l in- for mati on 60, 65 평 균치 mean 22, 28 표본공간 samp le spa ce 18 표준편차 sta n dard devia t i on 23 굴 하트리 Hartle y 39 해 밍 부호 Hammi ng code 164 해 밍 거 리 Hammi ng dis t a n ce 162 해 밍 무거] Hammi ng weig h t 162 확물공간 pro babil i ty spa ce 18 확물변수 random varia b le 19, 21 확물적 분변환 pr obabil i ty in te g r al tra nsfo r mati on 260 확산부호 dif fus e code 233 확장해 밍 부호 exte n ded Hammi ng code 166 후향채 널 backward channel 150
한영열 서 울대 학교 전자공학과 졸업 미국 미주리대학교 공학석사, 박사 독일 지멘스회사 연구원, 미국 미주리대학 연구원, 과학기 술원 연구원 논문 전자몽신 관계에 대한 논문 다수 현재 한양대학교 공과대학 부교수 Sig m a X i정회원 정보이론 인쇄 1985 년 2 월 25 일 발행 I985 년 3 월 10 , 일 처자 한영열 발행인 . *卜孟 浩 발행처 民音 社우편대체계좌번호 010041-31-5232 82 구 110 종로구 관 철 동 44 의 1 734-2000 • 735-85 나 • 734 국 234 출판등록 1966. 5. 16. 제 1-142 호 값 4,500 원 * 파본은 바구어 드립니다 .
대—우金학 著술 •총값 3, 6서00 원 ·자연과학 1 소립자와 게이지상호작용 2 動力學特論 3 질첨소昊고 정著 •값 5,400 윈 宋承達 著 • 값 2,切 0 원 4 相轉移와臨界現象 5 鵬김菓두철作 著用 • 값 2, !00-?:! 6 뫼陳宗스植바 著우 어• 分값 光2, 0學0 떼 7 극玉恒미南량 著원 소• 의값 2,영 80양 떼 昇正子 著 •값 6, 印어! 8 水素化覇素와 有機覇素化合物 9 麟荊物民質 著 의• 全값 合5,00成M ! 姜錫久 著 • 값 9, 0 00 원 10 국소저 형태의 A tiyah- S ing er 지표이론 지 동표 著 • 값 2, !00-?:! 11 Muco po l y sacchar i des 의 生化學 및 生麟學 박준우 著 • 값 3, !00-?:! 12 ASTROPH_YSICS (天體物理學) 13 프洪金承聲뚜樹표타 著著 글 • •값란 값 3 딘,46. 07합00 원0 원 성 14 천연물화학연구법 禹源植 著 • 값 5, 300 원 15 脂防營養 16 陶金淑池喜 유著 리• 값 6,300 원 17 高鉛分邑子 著의 化.값學 4反,50應0 원 趙著·값 4,000 원 18 科學革命 金永植 著 값 3, 200 원 19 章韓著國地·質값論 4, 000 원