이재형 서울대학교 공과대학 응용물리학과 졸업 미국로체스터 대학교에서 Ph.D. 받음 현재 연세대학교 물리학과 교수 논문 Abelia n Hig gs mechanis m in the Schrodin g e r pict u r e 외 30 여 편 발표
양자장이론
양자장이론
책 머리에 게이지 이론의 발전과 이를 기초로 한 표준모형 (sta n dard model) 의 성공 으로 인하여, 양자 장이론은 미시세계를 기술하는 입자물리학의 기본 이론 으로서 확고한 자리를 차지하게 되었다. 이제 중력의 양자 장이론을 구성하 려 하고 입자물리학이 아닌 다른 분야에까지 이용될 정도로, 양자 장이론의 개념과 계산 방법에 대한 필요성이 늘어나고 있다. 이에 따라 지금까지 양 자 장이론에 대한 많은 강의록과 교과서들이 출판되었다. 특히 ltz yk son & Zuber (Qu antw n Fie ld Theory , McGrow-Hi ll) , Ramond (Fie l d Theory : A Modem Prim er, 2nd ed., Addson-Wesley) 와 Ryd er (Qu antw n Fie ld Theory , Cambri dg e Un iv. Press) 등은 양자 장이론의 개념과 계산 방법들 을 체계적으로 잘 설명한 책들이다. 그러나 양자 장이론이 여러 분야에서 성공적으로 이용될 수 있다는 것은 그 이론체계가 복잡하다는 것을 의미하며, 좋은 책이 많디는 것은 그만큼 이해하기 어렵다는 것을 의미한다. 이 논저의 목적은 양자 장이론의 여러 가지 계산 방법들을 새로운 방법으로 더 쉽게 설명하려는 것이 아니라, 양 자적인 작용원리를 이용하여 현재 사용되고 있는 양자 장이론의 여러 가지 개념과 계산 방법들의 근거를 설명하고, 간단한 모형 장이론들을 이용하여 양자 장이론의 이론적인 구조를 쉽게 보여 줌으로써, 양자 장이론의 전체적 인 이론체계를 이해하는 데 도움을 주려는 데 있다. 현재 사용되고 있는 모든 양자 장이론의 개념과 계산 방법들은 세 가지 양자적인 작용원리에 그 근거를 두고 있다. 이들은 슈빙거 (Sch wing er) 의 작용원리와 화인만 (Fe ynma n) 의 경로적분 양자화 방법과 디락 (D ir ac) 의 작 용원리이다. 슈빙거의 작용원리는, 고전역학과 양자역학의 차이는 물리계
의 상태를 기술하는 방법에 있다는 점에 유의하여, 작용원리를 양자역학적 으로 표현한 것이다. 이 작용원리는 물리계의 확률진폭에 대한 함수미분방 정식 (func ti on al dif fere nti al e q ua ti on) 으로 표현되는데, 계의 운동방정식과 양자적인 연산지물 정의하는 동시 (반)교환관계뿐만 아니라, 운동방정식의 풀이 방법도 이 미분방정식으로부터 얻을 수 있다. 슈빙거의 함수미분방정 식을 적분하여 형식적인 해를 구하면, 그 결과가 바로 경로적분으로 표현한 화인만의 작용원리이다. 따라서 슈빙거의 작용원리와 화인만의 경로적분방 법은 서로 독립적인 것이 아니라, 같은 내용을 각각 미분방정식과 그 적분 으로 표현한 것이며, 서로 상보적인 관계에 있다는 것을 알 수 있다` 슈빙 거와 화인만의 작용원리는 하이젠버그 표현 (Heis e nberg picture ) 방법으로 나타낸 것인데 , 이들을 슈뢰딩거 표현 (Schrodin g e r picture ) 방법으로 나타 내면 디락의 작용원리를 얻는다. 디락의 작용원리는 최소유효작용 (e f fec ti ve ac ti on) 의 원리로 표현되기 때문에, 물리적인 정보를 변분법 (va riat i on al me th od) 적으로 계산하는 데 특히 편리하다. 이 책에서는 이러한 세 가지 양자적인 작용원리들을 설명하고, 이들 작용 원리로부터 얻을 수 있는 양자 장이론의 개념과 계산 방법들의 근거를 보여 주려고 한다. 그리고 풀 수 있는 2- 처원 장이론들과 비교적 간단한 4- 차원 장이론들을 이용하여, 이들 개념과 계산방법들을 쉽게 보여 중으로써 양자 장이론의 전체적인 이론체계를 짧은 시간내에 이해할 수 있도록 도와 주려 는데 목적이 있다. 이 책은 양자 장이론의 여러 가지 계산 방법들에 대한 자세한 설명보다는 양자 장이론의 전체적인 이해를 목적으로 쓴 것이기 때문에, 실제 계산에는 중요한 몇 가지 과제들(특히 재규격화 이론과 아벨리안이 아닌 게이지 이론 에 관한 자세한 설명)을 생략할 수밖에 없었다. 이 책의 또 한 가지 목적은 현재 사용되는 양자 장이론이 가지고 있는 한계를 제시하려는 것인데 (제 10 장), 이러한 목적을 위하여 가장 좋은 방법은 휘어전 시공간에서의 양자 장 이론과 중력의 양자 칭이론을 이용하는 것으로 보인다. 그러나 이들 이론에 대한 설명은 이 논저의 수준을 넘는 것이기 때문에, 민코프스키 공간에서의
양자화 방법의 변형과 유한온도 양자 장이론을 다루는 것으로 만족할 수밖 에 없었다. 끝으로 지금까지 물리학을 이해하는 데 많은 도움을 주신 은사 및 동료교. 수들께 감사드리며, 이 책을 쓰도록 지원해 주신 대우재단 여러분들께도 감 사드린다. 그리고 이 책의 원고로 공부했던 학생들도 이 책을 더 낫게 만드 는데 큰도움을주었다. 1991 년 1 월 이재형
[일러두기] 기호와 우리말 용어에 대하여 (가) 기호 (1) 자연단위계 (natu ral unit) : 특별히 필요한 경우를 제의하고는 c=l=n 인 자연단위계를 서용하였다. (2) 합의 약속과 적분 약속 : 한 항에서 반복되는 첨자와 반복되는 독립변수는, 다른 설명이 없으면 , 첨자에 대한 합과 독립변수에 대한 적분을 의미한다. [예] x 따 =~3X µXµ µ=O AiB i = 2N A,·Bi f(x )M(ix=, ly ) =fr1x t (x ) M(x,Y ) (3) 행렬표현 : 행렬방정식 a=b 는 그 성분방정식 a i =b i로 나타내기도 한다. 행렬 M 의 전치 (tr ans p ose) 행렬은 M 로 표현하지만, 혼동될 염려가 없을 때에는 ~표시를 생략하기도 한다. [예〕 xx=~xaxa= 泣 xBx = ~a,/xJ aBa/JX /J = iB x (4) 거 리 텐서 (metr ic ten sor) : 이 책에서 사용하는 4- 차원 시공간의 거리 텐서는
:』의; (ddx)x2=) d서x: 났 4µ -u 벡 dx터u는, x g도µ( v균=( , x-'1):O = ( 0;二 , X 二:0 0:서 고, 이들의 X • P=xµp µ= x0Po+xip ;= -x0p0 + x-p m 로Bi표o r현 ke된n-다Dr.el l 기호와의 관계 Bjo r ken-Drell 기호에서는 거리 텐서를 (1—000\10 00 0001 \0—0 0 l g EuD = l/ 로 택한다. 따라서 이 책의 모든 텐서 관계식은 다음과 같은 방법으로 Bjo r ken-Drell 기호를 사용한 관계식으로 바꿀 수 있다. 즉, 모든 텐서 성분을 첨자가 위에 붙은 반대로 변하는 (con tr ava ri an t) 성분으로 표현 하고〔단, 미분연산자 8µ 는 갔에 대한 미분이므로 같이 변하는 (covari an t) • 성분으로 나타내야 한다〕， 이들 관계식에 나타나는 gµv 를 -gµt D로 바꾸어 주면, Bjo r ken-Drell 기호를 사용한 관계식이 된 다.
*여기서 〈걷이 변한다났근 것은 벡터를 성분으로 표현하기 위해서 사용하는 기준 (basis ) 벡터와 갇이 변한다는 뜻이다.
[예] (i ) 4 펙터의 스宇가곱: x-p= xµg µv PV-- xµg µtDp v =-x • p (B-D) 認=훑 ·A,. 검巨=認 (B-D)
(ii ) 디락 행렬의 정의식 : -r'rv + rvrµ=-2g µ v-+ rµrv+ rvrµ=2l? G~ o (iii) 스칼라 장이론의 운동학적인 항 : 綴¢=릅g흙-+ -aµ 縱따 =-8µ¢ 탸 (B-D) 디락 장이론의 운동학적인 항 : 硏µ¢= E운 규셜급= 꿉떠 (B-D) (iv) 스칼라 장의 전파인자 : i< T((x)(o)) >=f高 e i X•P~ i< T((x)(o)) >s-v= f高 e- ix • Pf 노 디락 장의 전파인자: i< T(¢,(x) f(o )) >=}i끔 ce i x• P.훑 i< T(¢,(x) 祈 (o)) >B-D= f끔 ce- 따릅 (나) 우리말용어 이 책에서 몇 가지 새로운 우리말 용어를 시도하였다. 지금까지 사용된 우리 말 용어 중에는 그것이 어떤 의미를 갖는지 이해하기 어려운 용어들이 있었다. 이 중 몇 가지를, 우리말 용어로부터 물리학적인 의미를 짐작할 수 있는 용어로 바꾸거 사용하였다. 특히 cano ni cal 과 dege neracy? t 이에 해당한다. 물리학에 서 사용될 때, cano ni cal 이라는 용어는 GL준 이 되는〉 〈기준이 되는〉 혹은 〈좋 은〉의 뜻으로 쓰인다. 이 책에서는 cano ni cal 에 해당하는 우리말 용어를 GL 준〉으로 하였다. 예를 들면, canon ica l tran sfo r mati on ¾ GE준 변환〉으로, canon ica l va riab le& -( Il준변수〉로 썼다. de g enerac y는 여러 개의 상태가 한 준위에 겹쳐 있다는 뜻으로 쓰인다. 그래서 de ge nerac y에 해당하는 우리말 용
어로 〈 상태의 겹침 〉 혹은 〈 겹친 정도녔! 사용하였다. 그리고 ide nti ty tr ans fo rma ti o 峰 〈 제자리변환 〉 으로, unit ar y t rans fo rma ti o 머끌 〈 하나로운 변환 〉 으로 썼다. 〈 하나로운 〉 이라는 말은 생소하지만, 이것이 순수한 우리말이라 는 사실을 알고 나면 뜻이 통하는 용어이기에 사용하기로 하였다. 이의의 대부 분의 용어는 『물리학 용어집 』 에 나오는 것을 사용하였다.
양자 장이론■차례
책 머리에 5 일러두기 8 제 1 장 고전적인 작용원리 15 1.1 물리계의 기술 1.2 최소작용의 원리 18 1.3 라그란지안의 결정 20 1.4 하밀본 방정식 21 1.5 포아송 괄호 23 1.6 작용의 변화와 작용원리 25 1.7 표준변환 28 1.8 행렬표현 31 1.9 미세 표준변환 34 참고문헌 및 문제 • 40 제 2 장 양자적인 작용원리 1 : 자유도가 유한한 경우 41 2.1 양자역학적인 계의 기술 43 2.2 변환함수의 변화 44 2.3 양자적인 작용원리 48 2.4 작용의 변화 53 2.5 양자역학의 표현방법들 56 참고문헌 및 문제 • 62 제 3 장 양자적인 작용원리 2 : 자유도가 무한한 경우 63 3.1 양자 장이론의 작용원리 643.2 로렌츠 변환 68
3.3 작용의 변화 71 3.4 양자 장이론의 입자적 성질 76 3.5 로렌츠 불변성을 위한 디락-슈빙거 조건 79 참고문헌 및 문제 •86 제 4 장 기본적인 양자 장이론들 89 4.1 양자 장이론의 분류 91 4.2 스칼라 장이론 95 4.3 벡터 장이론 100 4.4 전자기 장이론 102 4.5 디락 장이론 106 4.6 양자 전기역학 110 참고문헌 및 문제 • 115 제 5 장 그린 함수와 그린 발생원에 대한 함수미분방정식 119 5.1 그림 함수와 그린 발생원 121 5.2 전파인자 (2-점합수) 130 5.3 그린 발생원에 대한 함수미분방정식 134 참고문헌 및 문제 • 137 제 6 장 풀 수 있는 모형들 139 6.1 티링 모형 140 6.2 페르미 장의 그린 함수 150 6.3 2-차원 벡터 메존 모형 153 6.4 게이지 이상현상 159 참고문헌 및 문제 • 161 제 7 장 함수미분방정식의 형식적인 해 : 경로적분 양자화 방법 -163 7.1 함수적분 1647.2 적분변수의 변환 169
7.3 스피너 장에 대한 함수적분 172 7.4 그린 발생원 175 7.5 화인만의 작용원리 178 7.6 슈빙거 모형 182 참고문헌 및 문제 • 190 제 8 장 그린 함수의 근사적인 계산 193 8.1 자유 장이론의 그린 함수 195 8.2 그린 함수의 섭동적인 계산 198 8.3 연결된 그린 함수 203 8.4 유효작용과 유효 포텐셜 207 8.5 고리전개 215 8.6 말안장 근사법 219 참고문헌 및 문제 • 228 제 9 장 양자 장이론의 슈뢰딩거 표현 방법 231 9.1 보즈 장이론의 슈뢰딩거 표현 233 9.2 페르미 장이론의 슈뢰 딩거 표현 240 9.3 게이지 이론의 슈뢰딩거 표현과 게이지 동등성 253 9.4 유효작용의 슈뢰딩거 표현과 디락의 작용원리 274 9.5 가우스 근사법 280 참고문헌 및 문제 • 292 제 10 장 양자 장이론의 확장 297 10.1 양자화 방법의 변형 299 10.2 유한온도에서의 양자 장이론 310 참고문헌 및 문제 • 333 찾아보기 337제 1장 고전적인 작용원리 고전역학의 이론체계를 이해하기 위해서 작용원리를 이용하는 것이 편리 하다. 작용원리는 물리계의 시간에 따른 진행을 결정하는 운동방정식을 줄 뿐만 아니라, 물리계의 운동을 기술하는 동등하지만 서로 다른 표현 방법들 사이의 관계 이것을 표준변환 (canon ica l tr ans fo rma ti on) 이라고 한다〕도 결 정한다. 이것은 물리계를 기술하기 위해서 사용하는 운동변수 (d ynami cal va ri able) 들은 작용윈리가 결정하는 조건들〔이들은 표준변수 (cano ni cal va ri able) 가 되어야 한다는 조건〕울 만족해야 한다는 것을 의미한다. (1,2,3) 양자역학도 이러한 이론체계를 가지고 있다. 양자적인 물리계를 기술하 기 위해서 사용하는 운동변수들은 동시 (반)교환관계를 만족하는 연산자로 표현되어야 하며, 이들 운동변수들은 운동방정식을 만족한다. 또 같은 물 리계를 기술하는 동등하지만 서로 다른 표현 방법들이 존재하며, 이들은 서 로 하나로운 변환(unit a ry tr ans fo nna ti on) 의 관계에 있다. 이러한 이론체 계는 모두 작용윈리로 나타낼 수 있다. 작용원리라는 관점에서는 고전역학과 양자역학은 같은 이론체계를 가지
고 있다. 이 장에서는 이러한 작용원리의 체계를, 자유도가 유한한 고전역 학의 경우를 이용하여 보여 주겠다. 다음 장에서는 이러한 이론체계를 그대 로 유지하면서 양자역학적인 가설을 만족하는 양자적인 작용원리를 구성하 겠다.
1.l 물리계의 기술 역학적인 물리계의 위치를 완전히 기술할 수 있는 변수, q; (i=l ,2,. . ·N) 를 이 계의 일반화 좌표(g eneral i zedcoor din a t e) 라고 한다. 물리계의 한 순간의 상태를 완전히 기술하는 변수로서, 계의 위치 q 2를 생각할 수 있다. 그러나 계의 일반화 좌표 qi가 결정되었다고 해서, 다음 순간의 위치를 유 일하게 결정할 수 있을 정도로, 계의 상태가 완전히 결정되는 것은 아니다. 왜냐하면, 이러한 계의 일반화 속도(g enera li zed veloc ity) q;의 값은 아직 결정되지 않았으며, 시간 dt 후의 계의 위치는 이들 일반화 속도에 의해서 달라질 수 있기 때문이다. 한 순간의 계의 위치와 속도를 준다고 해도, 다음 순간의 위치와 속도가 완전히 결정되는 것은 아니다. 다음 순간의 계의 속도는 가속도에 따라서 달라지기 때문이다. 그러나 지금까지 자연현상의 관찰 결과에 의하면, 한 순간의 계의 가속도는 그 순간의 위치와 속도에 의해서 완전히 결정된다. 이것은 한 순간의 물리계의 상태는 위치와 속도에 의해서 완전히 결정된다 는 것을 의미한다. 한 순간의 물리계의 상태를 완전히 기술하는 데 필요한 변수들을 그 계의 운동변수 (d ynami calva ri able) 라고 하며, 계의 상태를 기 술하는 데 필요한 독립된 운동변수의 수를 계의 자유도 (de gree of free dom) 라고 한다. 따라서 위치 qi와 속도 d i로 기술되는 계의 자유도는 2N 이다. 물리계의 가속도와 운동변수들 사이의 관계식을 운동방정식 (equ ati on of mo ti on) 이라고 한다. 따라서 역학적인 계의 운동방정식은 위치 qi(t)에 대 한 2- 계 미분방정식으로 나타낼 수 있다. 한 순간의 계의 운동변수들의 값 기 주어지면, 이 운동방정식을 적분하여 모든 다른 시각에서의 운동변수들 울 유일하게 결정할 수 있고, 이 결과로부터 계에 관한 모든 물리적인 정보 를얻을수있다. 한 순간의 계의 상태가 주어지면 다른 모든 시각에서의 상태는 운동방정
식에 의해서 유일하게 결정된다는 사실은, 고전역학적인 물리계뿐만 아니 라, 전자기학이나 양자역학과 양자 장이론에서도 마찬가지로 적용된다. 이 렇게 한 순간의 계의 상태가 결정되면 다른 모든 시간에서의 계의 상태는 운동방정식이 결정한다는 사실을 〈물 리계가 시간 방향으로 전행한다 〉 고 말 한다. 물리계가 시간 방향으로 진행한다는 사실은, 관습에 의한 한 가지 사 고방식에 불과한 것이 아니라, 자연에서 일어나는 물리현상을 기초로 하여 얻은 상대론적인 인과율의 필연적인 결과라는 점에 유의해야 한다. 이러한 사실은 상대론적인 양자론인 양자 장이론에서 분명하게 나타난다. 이 점에 대해서는 10.1 절에서 자세히 설명하겠다 . 1.2 최소작용의 원리 이 절에서는 작용원리의 가장 간단한 형태인 최소작용의 원리에 대하여 이야기하겠다. 시각 t 1 과 t2 일 때의 계의 위치가 각각 q (l) 과 q (2) 인 경우, 이 계의 작용 (ac ti on) 을 S=f .12L (q; , q;, t) d t (1- 1 ) t1 로 정의한다. 여기서 함수 L(q,
q,(t= h)=q {1 ), qi( t =t2) =q i(2) 를 만족하기 때문에 , 조전 8q; (t1) =0= 8q; (t2) (1-3) 이 성립한다. 따라서, 작용의 변화량은 8S=j 12L (q + 8q, q + 8q , t)d t- £ 12L(q, q, t)d t h t1 =jl (姜 硏費魏 )dt 로 쓸 수 있다. 여기서 같은 항에 반복되는 첨자 i에 대해서는, 모든 가능 한 i에 대하여 합해야 한다는 점에 유의해야 한다. 시간에 대한 미분과 함 수형태의 변화는 독립된 연산이므로 8 qi=d굶 -8 qi 이다. 따라서 8S=[蘇 8q i] ::+[I t 2(姜 곱 舊) 8q i dt (1-4) 로 쓸 수 있다. (1-3) 식을 이용하면, 최소작용의 원리, 8S=O 는 —oaqLi -—ddt —oaiL/i =0, i= l, 2,… , N (1-5) 로 표현되는 오일러-라그란지 (Euler-Lag ran g e) 방정식을 의미한다. 이것이 이 계의 시간에 따른 진행을 결정하는 운동방정식이며, 뉴턴의 법칙과 일치 한다. 이 방정식은 함수 qi(t)에 대한 2- 계 미분방정식이다. 따라서 이 방 정식의 풀이룰 유일하게 결정하려면, 2N 개의 경계조건이 필요하며, 이 숫자는 계의 자유도의 수와 같다. 두 라그란지안이 시간에 대한 전마분의 차이가 있을 때, 이들이 주는 운
동방정식에는 차이가 없다. 죽, L'(q, ri , t)= L(q, ri , t)곱 F( q, t) ( 1-6) 이면,작용은 S'=ft 2L (q, rj ,t )dt +f dt 훑 F( q,t) =S+F(q(2 > ,t2 ) -F(q< l l,t1 ) 이다. 따라서 끝점 t 1 과 t2 에서의 위치를 고정하면 8S'=8S 이며, 이들이 주는 운동방정식은 같다. 그러나 S 와 S'의 값은 서로 다르 며, 이들의 차이에 대해서는 뒤에 자세히 다루겠다. 1.3 라그란지안의 결정 라그란지안이 주어지면 물리계의 운동은 최소작용의 원리에 의하여 결정 된다. 그러면 물리계의 라그란지안은 어떻게 결정하는가? 우선 라그란지 안은 물리계가 가지고 있는 대칭성 원리를 만족해야 한다. 고전역학적인 계 의 경우, 라그란지안은 갈릴레오 변환 (Ga lil eo tr ans fo nna ti on) 에 대하여 불변이어야 한다. 상대론적인 계의 경우 라그란지안은 로렌츠 변환 (Lorentz tr ans fo nna ti on) 에 대하여 불변이다. 또한 게이지 대칭성 (ga ug e s ymm e try)과 같은 내부 대칭성을 가지는 계의 경우에는, 라그란지안은 또 그에 해당하는 불변성을 가져야 한다. 이러한 대칭성을 요구하더라도 라그 란지안은 유일하게 결정되지는 않고, 동등하지 않은 여러 가지 가능한 라그 란지안이 존재하는 것이 보통이다. 이렇게 대칭성 원리만으로 라그란지안 이 유일하게 결정되지 않을 때에는, 결국 실제 자연현상과 비교하여 라그란
지안을 결정해야 한다 . 대칭성을 이용하여 라그란지안을 결정하는 방법은 Landa 따 Lif s hit z0) 의 책에 자세히 다루어져 있다. 라그란지안이 일반화 좌표 qi 또는 다른 매개변수의 변화에 대하여 불변 일 때에는 각 불변성에 대웅되는 보존되는 양이 존재한다. 예를 들어서 위 치 q를 8 qi만큼 변화시킬 때, 라그란지안의 변화분은 8L= 急 8q i (i에 대한 宁] 아님) 이다. 라그란지안이 q의 변화에 대하여 불변이라는 것은 8L=O 임을 뜻한 다. 따라서 이 경우 —aaqLi = O 이며, 오일러-라그란지 방정식에 의하여 —ddt — aa—Lqi - =aa—Lqi = O 임을의미한다. 이 식은 p', .= 費 (1-7) 로 정의되는 양이 시간에 대하여 불변임을 뜻한다. 식 (1-7) 로 정의되는 양을 일반화 운동량 (ge neraliz e d momentu m) 이라고 한다. l·4 하밀론방정식 앞에서 이야기한 라그란지안은 qi, q{과 t만의 함수이므로, 그 변화량은 dL= 急如 ¾,d
로 쓸 수 있다. 이것은 라그란지안의 모든 가능한 변화는 q l와 Qi과 t의 변 화를 통해서만 생길 수 있다는 것을 의미하며, 또 물리계의 상태가 qi와 Qi 에 의해서 기술된다는 것을 의미한다. 그러나 q’와 d 을- 사용하여 물리계 를 기술하는 것이 계를 기술하는 유일한 방법은 아니며, 경우에 따라서는 中 변수들을 사용하는 것이 더 편리할 때도 있다. 르장드르 변환 (Leg en dre tr ans fo rma ti on) 을 사용하면, 라그란지안 방법으로부터 다른 기 술 방법들을 얻을 수 있다. (1-5) 식과 (1-7) 식을 이용하면, (1-8) 식은 dL= 隨i+pi d 如寄8L - d t 로쓸수있다. 이식의두번째항은 Pid r j i= d(pi rji)-rj idP i 로 쓸 수 있으므로, (1-8) 식은 다시 d(pi qi-L )= -P~ id ,q i+, q. id,P. i_ 잡oL - dt 로 된다. 이 식의 괄호 속에 있는 양을 하밀토니안 (Ha mi l t o ni an) H=p iqi-L (1-9) 로정의하면, 이 식은 dH= 뿔dq 1 릅틀 1 릅L dt (1-10) 로 쓸 수 있다. 이 식은 H가 qi와 P i와 t만의 힘수라는 것을 뜻한다. 즉, 하밀토니안 H( q,p,t)를 사용하여 계의 운동을 기술하면, 계의 상태는 qi와 P 를 사용하여 기술하게 된다는 것을 의미한다. 이 경우 운동방정식은, (1 -9) 와 (1-10) 식에 의하여
q. i=_ i8JpH_ i bi= -—88Hqi (1-11) 8H 8L 8t 8t 로 된다. 이 식들을 하밀돈 방정식이라고 한다. 하밀토니안의 시간에 대한 도함수는 뿜=뿔 d 弓告내! 이다. {1 - 11) 식에 의하여 이 식의 처음 두 항은 상쇄되므로 ddHt =-aa- Ht = -aaLt (1-12) 의 식을 얻는다. 이것은, 하밀토니안이나 라그란지안이 시간에 직접적으로 관계하지 않으면, 하밀토니안 H(q, p}E-보 존되는 양이라는 것을 의미한 다. 1.5 포아송괄호 독립된 운동변수들의 함수로 표현되는 물리량 f(q,p,t).9l 시간에 대한 도 함수는 뿔=훌훑硏尉 으로 쓸 수 있다. 이 식에 하밀돈 방정식을 대입하면 뿜=룹{f ,H}PB (1-13)
로 된다. 여기서 {A,B}Pri= - {A,B}PB= aaAqi 8apBi —— aaqB—i aa—pAi (1-14) 로 정의되며, A 와 B 의 포아송 괄호 (Po i ssonbracke t)라고 한다. 식 (1 -13) 은 물리량동기 시간에 따라 어떻게 변하는가 하는 것이 그 물리량과 하 밀토니안과의 포아송 괄호에 의하여 결정된다는 것을 의미한다. 운동변수들 사이의 포아송 괄호는 {q;,Q;} PB =0= {p;,p;} PB (1-15) {qi,pj}P B= 8ij 이며, 물리계의 상태를기술하는데 사용되는운동변수들을바꿀때, 이 관 계식들이 중요한 의미를 갖게 된다. 또 운동변수와 물리량, f(q,p,t) 사이 의포아송괄호는 {qi,f }PB 훑 {p;, /}PB= —_ a8qf_ i (1-16} 이 된다는 것을 쉽게 보일 수 있다. (1-16) 식은, 운동변수 qi와 p를· 변화 시킬 때, 이들의 함수인 물리량이 어떻게 변하는가를 보여 주는 관계식이 다. 이러한 변수변환에 대해서는 뒤에 자세히 설명하겠다. 물리계가 시간 에 따라 어떻게 진행하는가를 결정하는 운동방정식과, 변수변환에 대하여 물리계가 어떻게 반응하는가를 결정하는 관계식들을 모두 포아송 괄호를 사 용하여 표현할 수 있다는 것은 역학이론의 구조에 관계되는 중요한 사실이 다. 디락(Dir ac) 의 양자화 방법은 이러한 사실에 기초를 둔 것이다. 포아 송 괄호를 교환관계 (commuta tion rela ti on) 로 바꿈으로써 , 고전역학의 구 조를 그대로 유지하는 양자역학의 체계를 구성한 것이다.
1 . 6 작용의 변화와 작용원리 지금까지 주어전 경계조건(시각 t 1 과 E 에서의 위치가 각각 q (1) 과 q(Z ) 인)을 만족하면서 운동하는 물리계의 실제 운동경로가 어떻게 결정되는지 에 대해서 생각하였다. 이러한 운동경로는 작용을 최소로 만드는 경로이 며, 뉴턴의 법칙을 만족하는 경로이다.이제 경계조건을 고정하지 않고, 물 리적으로 가능한 모든 경계조건을 포함하는 운동을 생각해 보기로 한다. 그 러기 위해서는 끝점 t 1 과 t2 에서의 위치를 고정하지 않고 일어날 수 있는 작용의 가능한 변화를 생각해야 한다. 이렇게 하면 어떤 경계조건이 물리적 으로 가능한 것인지에 대해서도 알게 될 것이다. 다시 말하면, 작용원리가 물리적으로 가능한 경계조건까지도 결정하게 된다. 이제 작용의 일반적인 성질을 알아내기 위해서 끝점을 고정하지 않은 일 반적인 변화를 생각해 보자. {1-4) 식에 의하면, 작용의 변화는 as=[蘇 8q ,]::+jl (蒙 곱 蘇) 8q , dt {1-17) =p l.(2)8 qi(2)- pi (1)8q i(I)+ j1 틀- 젊 副 8q ,.dt 로 나타낼 수 있다. 물리계가 고전적인 실제 운동경로를 따라서 운동할 때 에는, 이 식의 마지막 항이 영이 된다. 따라서 물리계가 실제 운동경로를 따르면, 작용의 변화 8S 는 끝접 t 1 과 t2 에서의 위치의 변화 8q i에 의해서 만 일어날 수 있다. 다시 말하면, 계가 실제 운동경로를 따라서 운동하면, 작용 S는 끝점 t 1 과 t2 에서의 위치 q,i}만의 함수이다. 이 사실을 이용하 여 최소작용의 원리를 다음과 같이 더 편리한 형태로 표현할 수 있다. 작용원리 : · 작용의 변화량은 변수들의 끝점에서의 변화량만의 함수이다. 이 작용원리는 끝점에서의 운동변수들의 값을 정할 필요가 없기 때문에
더 일반적인 원리이며, 물리계에 대한 더 많은 정보를 포함한다. 계가 실제 운동경로를 따르는 경우, 작용 S의 함수형태를 알아보자. 이 경우, (1-17) 식은 8S= [pi8q j ]g (1-18) 로 쓸 수 있으며, 이 식은 S7} q l. (I) 과 qi (2) 의 어떤 함수인가를 결정한다• {1-17) 식에서는 끝점 t 1 과 t 2 를 고정하고 계산한 것이므로, S 의 h 과 t 2 에 대한 함수형태는 알 수 없다. 작용의 시간에 대한 함수형태를 알기 위하여 다음과 같은 경우를 생각하자. 즉, 정해진 시각 t 1 일 때 정해전 위치 q(I)에 서 출발하여, 임의의 시각 t2 = t일 때 정해전 위치 q (2) 에 이르는 경우를 생 각하자. 작용의 정의식 S=Jt I t 2 L dt 로부터, S 의 시간에 대한 전미분은 ~dt= L (1-19) 임을 알 수 있다. 이 경우 작용 S는 시간과 위치의 함수이므로 춥=홉틀-Qi=홉+p I q I 으로쓸수있다. 따라서 훌=홉_p;q ;=L ―p 1.d 른 -H (1-20) 이다. 따라서 t2 에서 시간과 위치를 변화시킬 때, 작용의 시간에 대한 전미 분은 dS=p ;dq ; - Hdt (1-21)
로 된다. 일반적으로, t1 과 t 2 에서 시간과 위치를 모두 변화시키면 dS= [p;dq;]/f-[H dt]g (1-22) 가된다는것을쉽게 알수있다. 이 결과는 끝점에서의 위치 (죽, 경계조건)는 마음대로 정할 수 있는 것 이 아니라 {1-22) 식의 오른쪽이 시간에 대한 전미분이 되도록 정해야 한다 는 것을 의미한다. 따라서 작용원리는 물리계가 가질 수 있는 운동상태에 대한 강한 조건을 부과한다. 특히 계에 작용하는 힘의 종류에 관계없이 이 들 조건이 성립되어야 한다. 이 결과를 이용하면, 위치와 운동량을 운동변수로 하여 작용원리를 표현 할수있다. 죽, 작용은 S=f t2(p i dq i _ Hdt) (1- 2 3) t1 로 쓸 수 있고, 이 작용의 변화량이 끝점에서의 변화량만의 함수가 되도록, 계의 운동이 결정된다. 이 경우 작용의 변화량은 8S=f 8 p; { dq ;-뿔 dt }+ [pi8q i -H 8t]g (1-24) -f8 q 障+뿔 dt }+f8 t {dH- 뿔 d t} 로 된다. 작용의 변화가 끝점에서의 변화에 의해서만 생긴다면, 이 식의 첫 째 항과 세번째와 마지막 항이 각각 영이 되어야 한다. 따라서 dq i=뿔 dt dp ;=-뿡 dt (1-25} dH= 뿔 dt 의 하밀톤 방정식이 성립해야 한다. 작용을 (1-23) 식으로 표현하는 것은,
위치와 운동량을 운동변수로 하는 것이기 때문에, 양자역학에 적용하는 데 특히 편리하다. 작용원리의 이러한 표현 방법을 하밀돈 방식의 작용원리라 고한다. ].7 표준변환 라그란지안이나 하밀토니안을 위치와 속도, 또는 위치와 운동량의 함수 로 기술하였는데, 여기서 사용한 일반화 좌표 qi나 일반화 운동량 P i의 선 택에도 여러 가지 가능성이 있다. 즉, 위치와 운동량 (qi,pi遷 ” RQi== P Q,(i(qqi,ip,p{,).) (1-26) 로 정의된 새로운 변수 (Q ;,P;) 로 변환할 수 있는 가능성이 있다. 그러나 이러한 변환에 대하여 하밀돈 방정식이 항상 불변인 것은 아니다. 이 변환 에 대하여 새로운 하밀토니안 H'( Qi ,R) 가 존재하고 Qi=뿔 Pi= -8—aHQIj (1-27) 의 하밀돈 방정식이 성립할 때, 이러한 변환 (1-26) 을 표준변환 (cano ni cal tran sfo rm ati on ) 이라고 한다. 표준변환의 형태는 작용원리 섀p,如 Hd t ]=O (1-28) 올 사용하여 구할 수 있다. 새로운 변수 (Q; ,P,)ol ] 대하여 하밀톤 방정식 (1-27) 이 성립하려면, 작용원리
8fi P;dQ ; -H'dt] = O (1-29) 가 성립되어야 한다. (1-28) 식과 (1-29) 식이 동등한 운동을 기술하려면, 적분기호 안에 있는 함수들의 차이가 어떤 함수의 시간에 대한 전미분으로 표시될 수 있어야 한다. 죽, p;dq; -Hdt= P;dQ ; -H'dt+ dF (1-30) 의 관계가 성립해야 한다. 이 경우 표준변환은 함수 F에 의하여 결정된다. 이 함수 F를 모함수(g enera ti n g fun c ti on) 라고 한다. (1-30) 식을 dF=p ;d q ;- P;dQ ; +(H'-H)dt (1-31) 로 표시하면, 이 식은 F 가 변수 qi와 Qi, 그리고 시간 t만의 함수라는 것 을의미한댜 따라서 p론:, Pi =-훑 , H'=H+ 풀 (1-32) 의 관계가 성립한다. 모함수 F 를 알면, (1-32) 식으로부터 변수 (qi,pi펴· (Q; ,P ;) -l-° 1 의 관계를 얻을 수 있다. 모함수가 qi와 Qi의 함수가 아닌 다른 변수들의 함수로 표현되는 표준변 환은, (1-31) 식을 르장드르 변환 (Le g endre tr a nsf orma ti on) 하여 얻을 수 있다. 표준변환을 할 때, 하밀토니안들 사이의 관계는 항상 같은 모양으로 표현 된다.죽, H'-H= 一aaFt 로 주어진다. 따라서 모함수 F 가 시간에 직접 관계하지 않을 때에는, H'( Q ;,P; )=H( q; , p;펴 관계가 성립한다. 포아송괄호를
{I, g}야aq, 근 8p싹I . _a뾰qi 8 弘pi {/,g}QP = 范8/겅 8阿g _ 겅8 og: 겅8百/ 로 정의하면, 변수 (q , p)와 (Q, P) 사이의 관계가 표준변환일 때, {f,g}qp= {f,g}QP (1-33) 의 관계가 성립한다는 것을 쉽게 보일 수 있다 . 특히, {{QQ;;, ,QPjJ}qq pp== 0ou= {P;, P Jq p (1-34) 를 만족한다. (1 - 34) 식은 변환 (q,p)---+(Q ,P) 가 표준변환이 되기 위한 조 건이라는 것을 뒤에 알게 될 것이다. 따라서 같은 물리계를 기술하는 방법에는 여러 가지가 있으며, 같은 계를 기술하는 동등하지만 서로 다른 방법들 사이를 연결하는 관계가 표준변환이 다. 뒤에 양자역학적인 경우를 다룰 때에도 중요하게 이용될 표준변환의 특 성 중 하나는, 물리계가 실제 운동경로를 따르기 때문에 일어나는 변수 (q, p)의 시간에 대한 변화를 표준변환으로 볼 수 있다는 것이다. 변수 (qt,P t) 를 시각 t 일 때의 계의 표준변수 (canon ica l va ri able) 라 하고, (qt+r ,Pt +r) 롤 시각 t+ r 일 때의 변수라고 하자. 그러면 Qt+r= q(qt,P t ,r) Pt+ r = p(qt,P t, r) 로 쓸 수 있으며, 이들을 표준변환식으로 볼 수 있다. 앞에서, (q,p)가 실 제 운동경로를 따를 때, 작용의 변화는 dS=Pt+ , dqt +r-P td q 1 가 된다는 것을 보았다. 이 식을 (1 - 31) 식과 비교하면, 이 표준변환을 발 생하는 모함수는 -호밖즌 것을 알 수 있다. 따라서, 실제 운동에 의해서
생기는 운동변수들의 변화는 작용이 발생하는 표준변환으로 불 수 있다. 1.8 행렬표현 디음 장에서 양자역학적인 작용윈리를 다루기 위해서는 운동변수들을 행 렬로 표현하는 것이 편리하다. 그리고 앞에서 이야기한 표준변환이 만족해 야 할 조건들을 구하기 위해서도 행렬표현을 사용하는 것이 편리하다. (2) 행 렬표현이란행렬 껴t ql 1)= | pqNI (1-35) PN 로 정의하는 것이다. 그러면 하밀톤 방정식은 8 i=J v뿔 , i,j=l , 2,… , 2N (1-36) 로쓸수 있다. 여기서 행렬 J는 !=(__~l O~) , 0, l:NxN 행렬 로 표시되는 반대칭행렬이다. 성분 형태로 쓴 (1-36) 식은 행렬방정식 ~=]aaH~TJ 로 쓸 수 있어서, 방정식들이 간단하게 표현된다. 새로운 운동변수 (Qi ,Pi 潘· 행렬 g로 표현하면, 시간에 무관한 표준변환
Qi= Q,·(q , p) P;=P;(q, p) 는
t= t(TJ) (1-37) 로 쓸 수 있다. 변수 t,S1 시간에 대한 도함수는 &=8~TJj ~ j 로 쓸 수 있고, 자코비안(J acob i an) 행 렬을 Mi j=훑 (1-38) 로 정의하면, t의 도함수는 t=M ~ (1-39) 로 된다. n 에 대한 운동방정식을 사용하면 ~=MJ뿔- (1-40) 를 얻는다. 하밀토니안을 t의 함수로 생각하면 쁘a1J=i 짚ag끄i a요1Ji , 또는 lfaf1-J = M· 원a'tg- (1-41) 의 관계를 가지므로, g에 대한 운동방정식은 t=MJM 뿔 (1-42) 로 된다. 따라서 변환 (1-37) 에 대하여 하밀돈 방정식이 불변일 조건은f=J뿔 =MJ M 뿔 이다. 따라서 변환 (1-37) 이 표준변환이 될 조건은 MJM =J 혹은 MJM =J (1-43) 이다. 여기서는 시간에 무관한 변환에 대해서만 다루었는데, 시간에 관계 하는 변환의 경우에도 같은 조건을 가진다는 것을 보일 수 있다. (2) 포아송 괄호의 행렬표현은 {f,g }n 훌롱 (1-44) 로 된다는 것을 쉽게 보일 수 있다. 특히 q와 p 사이의 포아송 괄호인 (1 -15) 식은 {TJ, TJ}~=J (1-45) 로된다. 새로운 변수 g들 사이의 포아송 괄호는 어떻게 되는가를 알아보자. 포아 송 괄호의 정의식 (1-44) 로부터 {g,t }n 툴~層 로표시되며, 낌81J뚝 자코비안행렬 M 이므로 {g,g}?=MJM (1-46) 로 쓸 수 있다. (1-43) 식을 사용하면, 변환 T' t가 표준변환일 조건은 {t,t}q=J (1-47)
가 된다는 것을 알 수 있다. 또, n 와 t는 표준변환의 관계에 있으므로 {t,th= J 도 성립한다. 같은 방법으로, 모든 포아송 괄호는 표준변환에 대하여 불변 이라는 것을 보일 수 있다. 따라서 식 (1-34) 또는 (1-47) 은 표준변환이 만족해야 할 조건이다. 이러한 조건을 만족하는 운동변수를 표준변수 (canonic al vari ab le) 라고 한다. 1.9 미세 표준변환 미세 표준변환이란 변수들을 영에 가까운 작은 양만큼 변화시키는 표준변 환이며, Qi=qi+ 8 q,. R=p i+ 8pi 혹은 g= n+81J (1-48) 로 표시한다. 이 변환은 제자리변환(i den tic altr ans fo rma ti on) 에 미세변환 울 더한 것으로 표현된다. 우선 제자리변환부터 생각하자. 모함수 o=q 1.P i (1-49) 에 의해서 발생되는 표준변환은 pi= aa-~q=j Pj Qj=접a~t =qi H'=H
이다. 따라서 모함수 (1-49) 로 기술되는 변환은 제자리변환이다. 미세 표 준변환은모함수 ~= q;P ;+ EG(q ,P , t) (1-50) 로 나타낼 수 있다. 여기서 e 은 아주 작은 양을 표시하는 연속 매개변수이 며, G 는 변수 (q ,P, t)들에 대하여 미분가능한 함수이다. 모함수 (1-50) 에 의하여 발생하는변환은 pi= —aaq0i = R+€—8a qG—i (1-51) Qi= a apo; = q辻 €장aG T (1-52) 로 표현된다. (1 - 52) 식의 두번째 항은 €에 비례하므로, '용와 룹》 1 차 이가 (1 - 52) 식에 주는 영향은 궁에 바례한다. 따라서 미세변환인 경우 (1 -52) 식은 Q;=q沖명8G祈 (1-53) 로 쓸 수 있다. (1-51) 식과 (1-53) 식을 8p,. = P i- pi= -e88- Gq-i 藍Q i -qi=출 로 쓸 수 있으며, 행렬표현을 사용하면 0 7J=€]8겅G; (1-54) 로 된다. 이 식은 미세변환 81J를 함수 G 로부터 유도할 수 있다는 것을 나
타내며, 함수 G 를 이 미세변환의 발생원(g enera t or) 이라고 부른다. 포아송 괄호의 정의식에 의하여 {r;J}=J훑 의 관계가 성립한다. 이 식의 f를 발생원 G로 택하면 8n={n,eG} (1-55) 로 된다. 이 식은 미세변환에 의해서 생기는 운동변수의 변화량 8n 는 운동 변수와 그 변환의 발생원과의 포아송 괄호로 주어진다는 것을 의미한다. 앞 에서 보았듯이, 물리계의 운동방정식은 물론 미세 표준변환과 모든 매개변 수에 대한 대칭변환도 포아송 괄호를 사용하여 표현할 수 있다. 한 가지 예로 하밀토니안이 발생원인 경우를 생각해 보자. 이 경우 n 의 변화는 8TJ = {TJ, EH}= dTJ, H}= E~ 이 된다. 이 식은 작은 매개변수 €이 시간 dt 라는 것을 뜻한다. 따라서 하밀토니안은 시각 t 일 때의 운동변수 (q,p潘? 시각 t+ dt 일 때의 변수로 변환시키는 미세 표준변환의 발생원임을 알 수 있다. 죽, 하밀토니안은 물 리계의 시간에 따른 변화를 기술하는 발생원이다. 마찬가지 방법으로 선운동량과 각운동량은 각각 물리계의 평행이동과 회 전변환을 기술하는 발생원이라는 것을 보일 수 있다. (2) 이제 작용의 변화와 미세 표준변환의 발생원 사이의 관계를 알아보자. (1-22) 식의 작용의 변화를 8S=[pi 8q i -H 8t] I~ = G(t2 ) -G(t1 ) (1~56) 으로 쓰면, 함수 G(t ~ 미세 표준변환의 발생원이 된다. 여기서 발생원 어근 앞에서 정의한 발생원에 작은 매개변수를 곱한 양이다. (1-56) 식에 의하여
G=p ,a q, - Hat (1-57) 이므로, q,의 변화예 의해서 유도되는 변환은 Gq =p;8 q ;, 시간 t의 변화에 의해서 유도되는 변환은 Gt= -H 8 t에 의하여 발생된다. (1-55) 식에 의 눙回 競= k,Gq }= {q;,qj}8 q j 8p; ={p;, Gq }={p;, pJ8 qF 0 이 성립해야 한다. 따라서 {q;,pj}= 8u, {p;,pj}= O 의 관계가 성립해야 한다. 이것은 표준변수가 만족해야 할 조건으로서 앞에 서 유도했던 결과이다. 따라서 작용의 변화량으로 정의한 발생원은, 물리 량들의 표준변환에 대한 반응을 결정할 뿐만 아니라, 운동변수들이 만족해 야 할 조건까지도 결정한다. 이것은 양자역학적인 경우에 아주 유용하게 이 용되는 작용의 성질이다. 위의 식에는 표준변수들이 만족해야 할 조건 (1-15) 식 중에서 {q;,qj}의 관계가 빠져 있다. 이것은 작용을 S=j[ p;d q; - Hdt] 로 표현하여, 변수 q와 p에 대하여 대칭이 아니기 때문에, 작용의 변화가 운동량의 변화 8p 에 무관하게 표현되었기 때문이다. 앞에서 보았듯이 라그 란지안에 시간에 대한 전미분을 더해 주어도 계의 운동에는 영향을 주지 않 는다. 꾸서 라그란지
로 정의하면, 운동변수들이 만족해야 할 모든 조건을 발생원으로부터 유도 할 수 있다. (1-6) 식에서 지적하였듯이, 이렇게 라그란지안을 변화시키 면, 끝접에서의 작용의 함수 형태가 달라진다. 죽, 8S= [p요 -H8 t ]8+ 8FIg = [}(pi8q i-qi 8p z. ) — H 8t] : (1-59) 로 되어서, 미세 표준변환의 발생원들은 Gqp=1궁 P i 8 q z- qi8p , ) (1-60) Gt= — H8t 로 된다. 변수 (q,p)의 변화를 유도하는 발생원의 형태가 달라졌으므로, 이 발생원에 의해서 생기는 물리량의 변화는 (1-55) 식 대신에 靜(q,p)= {/, Gqp } (1-61) 에 의해서 결정된다. 시간의 변화에 의해서 유도되는 변환은 여전히 (1 -55) 식으로 결정된다. (1-61) 식을 이용하면 운동변수가 만족해야 할 모든 조건을유도할수있다. 미세 표준변환을 이용하여 물리량들의 운동방정식을 얻을 때에는 주의를 요한다. 여기서 이야기한 변환은 변수변환이다. 그런데 운동방정식은 좌표 룰고정하고물리량의 변화를보려는것이다. 앞에서, 시각 t일 때의 상태 에서 시각 t +dt 일 때의 상태로 바뀌는 운동상태의 변화를 표준변환으로 해석할 때, 그 변환의 모함수는 _S 가 되어야 한다는 점을 지적하였다. 따 라서 계의 운동에 의해서 생기는 물리량의 시간에 따른 변화는 값(q,p)=-{/, Gt} ={/,H}8t (1-62) 로 된다. 발생원을 이용하여 운동방정식을 유도할 때에는 이 점에 유의해야 한다.
이들 결과물 종합하면, 작용원리의 내용을 다음과 같이 나타낼 수 있다. 위치 q와 운동량 p에 대하여 대칭이 되도록 작용을 표현하면, 작용은 S=J 1l+ Pid q i-qi dP i) - H(q,p ) dt] (1-63) 로 된다. 작용원리는, 모든 가능한 변화에 대하여 작용의 변화량이 8S= G(t2 ) -G(t1 ) (1-64) 로 되어야 한디는 것이다. 죽, 작용의 변화량은 끝점 t 1 과 k 에서의 변화 량만의 함수인 G( ti)로 표현되어야 하는데, 이 함수 G(t) i= 미세 표준변환 §하(q , p )={/,G}PB (1-65) 의 발생원이 된다. 표준변환에 대하여 물리량들이 만족해야 할 조건들은 이 (1-6 기석에 의해서 결정된다. 물리계의 운동방정식은 작용원리 (1-64) 식 에 의한 하밀돈 방정식이나, 혹은 (1-62) 식으로 표현되는 표준변환에 의해 서 결정된다. 지금까지 작용원리를 이용하여 고전역학의 이론적인 구조에 대하여 알아 보았다. 이러한 고전역학의 이론적인 구조에는 양자역학과 양자 장이론에 도 공통적인 것들이 많이 있다. 실제로 양자역학은 위에서 설명한 작용원리 의 체계를 양자역학적인 가청에 맞도록 다시 표현한 양자적인 작용원리로 나타낼 수 있다. 또 이러한 양자적인 작용원리를, 상대론적인 대칭성을 유 지하도록, 자유도가 무한히 많은 경우로 연장하면 양자 장이론의 이론체계 를 기술하는 작용원리를 얻을 수 있다. 다음 두 장에서는 이러한 방법으로 양자적인 작용원리를 구성하겠다.
[참고문헌〕 이 장의 내용은 Landau & L ifshitz 0 )와 Golds t e i n <2) 의 내용을 요약한 것이며 , 제깡과 제終》E 의 양자적인 작용원리와 쉽게 비교할 수 있도록 표현하였다. ( 1) L.D. Landau and E.M . Lif sh i tz, Mechanic s, 3 rded ., P erga m on Press (Oxfo r d) , 1976. (2) H. Goldste i n , Classic a l Me ch anic s , 2 nd e d., Addis o n-Wesley (Readin g , Mass.) , 19so. (3) E.C.G. Sudarshan and N. Mukunda, Cla ssi.ca l Dyna mi cs ; A Modern Pers pe c- five , Wi ley (New York) , 1974. [문제] l 한 순간의 계의 상태가 위치 qi, 속도 d i과 가속도 佑으로 기술된다면, 라그란 지안은 어떤 변수들의 함수이어야 하는가? 이 경우 오일러-라그란지 방정식을 유도하라. 2 (1-23) 식으로부터 (1-24) 식을 유도하라. 3 (1-28) 식과 (1-29) 식에서 유도한 모힘수 F는 가장 일반적인 표준변환의 모함 수인 것같이 보인다. 그러나 다른 가능성 , 예를 들면 G(q; , P ;) 등 에 의한 변환 도 가능한 이유는 무엇인가? 4 (1-33) 식과 (1-34) 식울 증명하라. 5 시간에 직접 관계하는 표준변환이 만족해야 할 조건을 유도하라. 6 선운동량과 각운동량이 물리계의 평행이동과 회전변환을 기술하는 발생원이라 는것을보이라. 7 (1-61) 식을 이용하여 표준변수들이 만족해야 할 조건들을 유도하라. 8 (1-62) 식을 이용하여 변수 (q, p, t)의 함수인 물리량 f(q, p, t )의 운동방정 식을유도하라.
제 2 장 양자적인 작용원리 1 : 자유도가 유한한 경우 제 1 장에서는 작용원리를 이용하여 고전역학의 이론적인 구조를 공부하였 다. 작용원리는 물리계의 시간에 따른 진행 (운동방정식 )을 결정할 뿐만 아 니라, 고전역학적인 계를 기술하는 동등하지만 서로 다른 여러 가지 기술 방법들 사이의 관계를 주는 표준변환 (cano ni cal tr ans fo nna ti on) 도 결정한 다. 작용의 끝점변화는 (1-64) 식에서와 같이 이들 미세 표준변환의 발생원 울 결정한다. 이들 발생원은 운동변수들이 만족해야 할 조건뿐만 아니라 물 리량들의 시간에 따른 진행도 결정한다는 것을 보았다. 이 장에서는 양자역학적인 물리계의 시간에 따른 진행과, 동등하지만 서 로 다른 표현 방법들 사이의 관계를 결정하는 양자적인 작용원리를 구성하 려고 한다. 이 양자적인 작용윈리는 앞 장에서 설명한 고전적인 작용원리의 체계를 양자역학적인 가정들에 맞도록 다시 표현한 것이다. 이러한 양자적 인 작용원리는 물리계의 성질을 결정하는 물리량이나 상태들이 만족해야 할 방정식들을 결정할 뿐만 아니라, 이러한 방정식들의 풀이 (solu ti on) 를 얻는 데에도 이용된다. 이 작용원리를, 이룰 개발한 사람의 이름을 따라 슈빙거
의 양자적 인 작용원리 (qu antu m acti on princ ip le of S chw ing e r ) 라고 부른 다. 이 작용원리의 결과는 보통 표준양자화 (canon ica l qu anti za ti on ) 또는 디락 양자화(Di rac q uan ti za ti on) 라고 알려진 양자화 방법과 동등하다는 것 울알게 될 것이다.
2.1 양자역학적인 계의 기술 양자역학이 고전역학과 다른 점은 물리량들을 나타내는 방법과, 한 순간 의 물리계의 상태를 기술하는 방법에 있다. 양자역학에서는 측정할 수 있는 것만이 우리가 자연에 관해서 알 수 있는 모든 것이라는 입장에서 출발한 다. 주어진 물리계에서 동시에 정확하게 측정할 수 있는 물리량들 중 독립 된 양들을 a',b',c',··· 로 표시하면, 측정값 a',b',c',··· 울 주는 계의 상태는 la',b',c',… >로 나타낸다. 이렇게 물리계의 상태를 기술하는 ld,b',c',··· > 울 계의 상태 벡터 (sta t e v ecto r ) 혹은상태함수 (s tat e fun c ti on) 라고 부르 고, 이를 줄여서 상태 (s t a t e) 라고 부르기도 한다. 물리량의 측정값 a’은 선 형 헤르미샨 연산자 (line ar Herm itian ope r ato r ) , a 의 고유값 (eig e nvalue) 으로 나타낼 수 있다. 그리고 계의 상태를 나타내는 상태 la',b',c', …>은 연산자 a,b,c, .. 들의 공통 고유상태 (e ig ens t a t e) 들이며, 이들의 집합은 힐 버트 공간 (H il be rt s p ace) 을 이룬다. 따라서 양자역학에서는 모든 물리량을 선형 헤르미샨 연산자로 나타낸다. 이러한 연산자들을 기호 a,b,c,… 등으 로 표시하겠다. 이들의 고유값은 각각 a',b',c',··· 이라 하고, 각 고유값에 해당하는 고유상태를 각각 |a'>,lb'>,lc'>,… 등으로 나타내겠다. 앞으로 한 물리계에서 서로 교환 가능한(따라서 동시에 측정 가능한) 헤 르미샨 연산자들의 완전집합을 한 개의 기호 a 혹은 b로 나타내겠다. 그러 면 변환함수 (tran sfo r mati on func ti on ) < a'l b' ＞은 상태 | b' ＞으로 기술되 는 물리계에서 물리량 a 를 측정할 때, 그 결과로 고유값 a’ 이 나올 확률진 폭(p robab ility am plitu de) 이다. 이 변환함수의 다른 해석도 가능하다. 즉,
있다는 것을 앞 장에서 보았다. 양자역학을 표현하는 방법에도 동등하지만 서로 다른 여러 가지가 있는데, 이들 사이에는 하나로운 변환의 관계가 있 다. 따라서 함수
8
(Hermi tian conju g at e ) 연산자이다. 이 결과와 (2 - 6) 식을 이용하면, 미세 연산자 oW가 헤르미샨 연산자라는 것을 알 수 있다. 즉, 8Wab= 8Wabt . (2-7) 따라서 상태함수 |a'>, 혹은 변환함수
=-i< a'l[x,G]la> 로쓸수있다. 이식은 8x= 규 [x,G] (2-11) 로 표현되는 연산자 관계식으로 기술할 수 있다. (2-11) 식은 표현 방법을 변화시킬 때 유도되는 고정된 연산자 x 의 행렬 요소의 변화를 나타낸다는 점에 유의해야 한다. 반면에 연산자 었문 하나로 운 변화시킬 때, 변환된 연산자를 f라고 하면 x=u-1xu (2-12) 로 표시된다. 따라서 연산자 자체를 변환시킬 때 생기는 변화는 f_ x=_8x (2-13) 로 된다. 여기서 8x 는 (2-10) 식으로 정의되는 연산자이다. (2-11) 식과 (2 ~12) 식을 종합하면, 하나로운 변환하에서 연산자의 행렬요소는 변하지 않 는다는 찰 알려진 결과를 얻게 된다. 지금까지, 정해전 한 시각에 물리계를 기술하는 방법을 바꿀 때 상태함수 나 연산자의 행렬요소가 어떻게 바뀌는가를 보았다. 물리계를 기술하는 방 법을 고정하고 계의 시간에 따른 진행을 보기 위해서는, 시각 t 1 일 때 상태 la{ ＞에 있던 계가 시각 t2 에 상태 |a2> 으로 전이할 확률전폭인, 변환함 수 < ai , t2la i' , ti >의 변화를 생각해야 한다. 이 함수의 변화량은 8< ai ,t2la i' ,t1> = i< ai ,t2l8 Wz1la1',t1 > (2-14) 로 정의되는 연산자 하 ½1 으로 기술할 수 있다. 무한히 작은 연산자 8W 는, 앞에서의 경우와 마찬가지로 88WW ii22t+ = 8 8WW2 3i2= 8W ia (2-15}
의 성질을 갖는다. 이것은 연산자 8W 가 물리계의 표현 방법의 변화뿐만 아니라 계의 시간에 따른 진행도 기술할 수 있다는 것을 의미한다. 다음 절 에서 8W가 양자역학적인 작용연산자의 변화라는 것을 알게 될 것이다. 그 리고 앞에서 도입한 발생원 G 는 작용의 끝점변화를 나타내는 연산자가 된 다. 다시 말하면, 양자역학의 경우에도, 물리계의 시간에 따른 진행과 표 현 방법의 변화를 결정하는 작용연산자를 정의할 수 있다는 것이다. 2.3 양자적인 작용원리 앞 절에서는 변환함수의 일반적인 성질에 대하여 이야기하였다. 물리계 의 운동을 기술할 수 있는 작용윈리를 구성하기 위하여, 여기서는 여러 가 지 가능한 변화를 나타내는 하 El 중에서 하나의 유한한 연산자 昭려 변화 량으로 표현할 수 있는 것만을 생각하겠다. 즉, 하 ½1= 8[腐] 이렇게 변환함수의 변화를 유도하는 연산자 Wi 1 을 작용연산자 (ac ti on o p era t or) 라고 한다. 미세연산자 aw가 식 (2-15) 를 만족하므로, 작용연 산자閉춘- W鬪it2+ = W腐23= ffi3 (2~16) 의 성질을 갖는다. 여기서 ¾'2 1 의 첨자는 서로 다른 시각 t2 와 t 1 을 뜻한다. t 1 과 & 사이의 시간간격을 무한히 작은 시간간격들 d t로 나누면, 작용 연산자는 Wi1= ~t Wt + dt, t 로쓸수 있다. 식 (2-5) 에 의해서 Wt t= O 이므로, 윗식의 각항은
lim Wt +d t, t=O dt- 0 의 성질을 갖는다. 따라서 Wt +d t,t는 dt 에 비례해야 한다. 죽, W1+d1,1= Ldt 로 쓸 수 있다. 작용원리로부터 운동방정식을 얻을 수 있다는 것은, 한 순 간의 계의 상태로부터 다음 순간의 상태가 결정된다는 것을 뜻한다. 이것은 윗식의 함수 L 이 한 순간의 변수 값만의 함수라는 것을 의미한다. 즉, Wt+ d1,1= L(t) d t 로 쓸 수 있다. 따라서 연산자 L은 시각 t 일 때의 연산지들만의 함수로 되 어야 한다. 만일 그렇지 않으면, 이 작용연산자가 기술하는 이론은 시간에 대한 비국소적인 (non-local) 이론이 된다. 그래서 작용연산자는 腐 =[2L( t )d t (2-17} t1 로 쓸 수 있고, 연산자 L( t潭- 라그란지안 연산자라고 한다. 한 순간의 물리계의 상태를 완전히 기술할 수 있는 물리량들에 해당하는 연산지롤 Xa 라 하면, 라그란지안 연산자는*
*여기서는 (1-63) 식에 해당하는 하밀튼 방식의 작용원리를 이야기하는 것이 므로, Xa 는 위치연산자와 운동량연산자를 모두 포함한다.
L(t) = L(xa (t)) 로 쓸 수 있다. 여기서 a=l,2, … ,n 이며, n 은 이 계의 자유도이다. 이제 작용연산자 硏 1= ft 2L(Xa( t ))dt tI 의 가능한 여러 가지 변화를 생각할 수 있다. Xa 에 대한 L(xa 펴 함수형태 의 변화와, 시간 t에 대한 x~] 함수형태의 변화, 또는 적분의
상하한인 시각 t 1 과 t2 의 변화 등을 생각할 수 있다. 이 모든 변화에 의해서 생기는 작용의 변화 하 ½1 은, 끝점 t 1 과 t2 에서의 변화량만으 로 기술되어야 한다는 것이 작용원리이다. 앞에서 지적한 바와 같이, 시각 t일 때의 물리계의 상태가 다음 시 각에서의 계의 상태를(운동방정식에 의해서) 완전히 결정할 수 있어 야 한다. 따라서 시각 t일 때의 변화는 그 시각에서의 변수들만의 함 수로 주어져야 한다. 이것은 운동방정식이 유한계 미분방정식이 된다 는 것을 의미한다. 그래서 상태함수의 변화는, (2-9) 식에 의해서, ool t2 l == -i
방정식에는 영향을 주지 않고, 계의 경계조건을 바꾸는 역할을 한다. 라그란지안을 T=L 」d뿐t 로 변화시키면, 작용은 W21= 鬪 -F( t 2)+F( t 1) 으로 변한다. 따라서 8 W21 = G( t2) — G( ti)-8F ( t2) + 8F( t1) =G( t2 ) ―言(t 1) (2-20) 로 쓸 수 있으며, 여기서 건 =G_8F (2-21) 로 정의한 연산자이다. 이렇게 라그란지안을 바꾸더라도 양자적인 작 용원리 (2-19) 는 여전히 성립한다. 이제 작용원리를 이용하여, 물리 계의 운동을 어떻게 기술할 수 있는지를 알아 보자. 물리계의 시간에 따른 진행을 기술하는 운동방정식은 유한계 미분 방정식이 되어야 한다는 점을 앞에서 지적하였다. 변수의 수를 증가 시키면, 유한계 미분방정식은 항상 l- 계 미분방정식들의 모임으로 표 현할 수 있다. 따라서 가장 일반적인 라그란지안의 형태를 L= 沿t1( xaAa, 갔 aAa,x,)-H(x, t) (2-22) 로 쓸 수 있고, 이렇게 하면, 운동방정식은 1- 계 미분방정식으로 표 현된다• 여기서 i=뿔이며, Aa’ 는 그 요소들이 상수인 상수행렬이 다. 이 라그란지안의 첫 항은 변수 x 와 그 도함수 i에 대하여 대칭 이 되도록 만들었다. 앞으로는 변수들의 행렬표현을 자유로이 사용하
겠다 . 따라서 첨자가 없는 변수 x 는 변수들 Xa 의 행렬표현이다. 라 그란지안 (2-22) 의 첫 항은 오일러-라그란지 방정식이 x 에 대한 미 분방정 식 이 되 기 위 하여 필요한 운동학적 인 (kin e mati ca l) 항이고, 두번 째 항은 계에 작용하는 힘을 기술하는 동역학적인 (dy na m ica l) 항이다. 위에서 운동변수로 택한 연산자 았즌 반드시 헤르미샨 연산자일 필요는 없다. 그러나 일반적인 연산자는 헤르미샨 연산자들의 합으로 표현할 수 있 다. 그래서 연산자 었룹 헤르미샨으로 택하겠다 ; Xat =xa. (2-23) 작용연산자는 헤르미샨이어야 하므로, 라그란지안 역시 헤르미샨이어야 한댜 따라서 행렬표현을 사용하여 라그란지안을 쓰면, L= 永 xA i_ iA x)_ H 이며, 그 헤르미샨 공액은 E =i{iAt x - x At 갔 -H t 로 된다*． 라그란지안이 헤르미샨이 되기 위해서는
*여기서 L4 i는 i A i올 의미한다 .
Ht = H, At = -A (2-24} 의 관계가 성립해야 한다. 죽, 상수행렬 A는 반헤르미샨 (an tih e rmiti an) 행렬이어야한다. 상수행렬 A 를 대칭행렬 s 와 반대칭행렬 a 의 합으로 표시할 수 있다. 그러면, A=s+a=-At At = st+ at= s•-a•
의 관계를 가지므로, s 는 순허수 대칭행렬이고, a 는 실수 반대칭 행렬이 되어야 한다. 따라서 행렬 A 는 A=(; °a) 의 형태로 쓸 수 있으며, 라그란지안의 운동학적인 항은 두 가지 독 립적인 경우로 완전히 분리된다. 행렬 A 가 대칭인 경우에 해당하는 연산자 x 는 반교환관계 (anti co mmuta tion rela ti on) 로 정의된다는 것을 뒤 에 알게 될 것이다. 죽, 상수행렬 s 로 기술되는 물리계는 페르미 입자 (fermi on) 들로 이루어진 물리계이다. 반대로 반대칭행렬 a 로 기술되는 경 우에는, 교환관계 (commuta t i on rela ti on) 로 정의되는 연산자로 기술되며 보즈 입자(b oson) 들로 이루어진 물리계이다. 여기서는 자유도가 유한한 양 자역학적인 계만을 다루기 때문에, 반대칭행렬 a 로 기술되는 계에 대해서 만 이야기하겠다. 이 경우 라그란지안 연산자는 고전적인 라그란지안과 갇 은 형태를 갖는다. 그리고 앞에서 지적한 바와 갇이, 운동방정식이 1- 계 미분방정식으로 표현되도록 라그란지안을 택하였으므로, 라그란지안은 연 산자 x 의 시간에 대한 1- 차도함수의 1- 차항들만을 포함한다. 따라서 여기 서 이야기하는 슈빙거의 양자적인 작용원리는 (1-63) 식에 해당하는 하밀돈 방식 (Ha milto n ian fo rma li sm) 의 작용원리이다. 2·4 작용의 변화 양자적인작용원리 8 < a2, t2la i' , t1> = i< at, t2l8 W i1l a i' ,t1> = i< az ,t2l8 J. taL (x,t) d tla i' ,t1> (2-25) tI = i< az ,t2I G (t2 ) -G (t1 ) lai' ,t >
의 내용을 이해하기 위해서 작용의 변화 開= 8J 1'[i{ xAd x— dx Ax)-Hdt] 를 생각해 보자. 작용원리에 의하면, 변화량 하 E1 은 끝점 t 1 과 t 2 에서의 변수들의 변화량만의 함수이어야 한다. 이 끝점변화에는 변수 t 1 과 t2 자 체 의 변화도 포함되는데, 이 변수의 변화를 운동변수 x 의 변화와 다르게 취 급하는 것은 편리하지 않다. 그래서 매개변수 r 를 도입하여, 변수 t를 t= t(r ) 와 같이 r 의 함수로 보는 것이 편리하다. 이렇게 하면, t의 변화량 8 t를 t의 r 에 대한 함수형태의 변화에 의해서 생긴다고 볼 수 있다. 변수 t의 변화를 이러한 방법으로 표현하면, t와 x 의 변화를 동등하게 취급할 수 있다. 따라서 작용의 변화는 卯= 8J .t'[i{xA dx— dx Ax)— Hd t] (2-26) =[기j{ xAdx-dxAx)-Hdt ] 로 표현할 수 있다. 여기서는 매개변수 r 의 끝점 n 과 r2 를 고정하기 때문 에, 8 는 x 와 t의 함수형태의 변화만을 의미한다. 함수형태의 변화를 의미하는 8 와 미분을 의미하는 d 사이에는 8dx= 8[x( r+ dr)-x( r)]= d8x 의 관계가 있다. 이 관계를 이용하면, 다음과 같은 등식을 얻을 수 있다 : 8[步 Adx- dxAx)-Hdt] = d[:½
이 등식을 {2-26) 식에 대입하고 작용원리를 적용하면, 물리계의 운동방 정식과 하나로운 변환하에서 계가 어떻게 반응하는가를 알 수 있다. {2 -27) 식의 첫 항은 전미분 항이므로 끝점에서의 변화량만의 함수아고, 따라 서 미세 하나로운 변환의 발생원울 결정하는 항이다. 나머지 항들은 끝점이 아닌 중간점에도 관계하는 항들이므로, 이들은 영이 되어야 한다. 즉, 8H= 8xAi —i A 8x 군뿐 8 t (2-28} 의 관계가 성립한다. 이 식은 연산자 H가 변수 x 와 t의 함수라는 사실과 ooHt -dd Ht (2-29) oxH= oxAi -iA ox 의 관계를 의미한다. 여기서 &는 변수 짜t 변화시키는 변화 (va ri a ti on) 를 의미한다. (2-29) 식은 하밀토니안 연산자 H의 변수 x 와 t 에 대한 함수형 태를 결정하는 관계식이다. 고전적으로는 이 식이 하밀돈의 운동방정식에 해당한다. 그러나 하나로운 변환이 시간에 따른 물리계의 진행도 기술할 수 있으므로, 발생원 G 를 이용해서 운동방정식을 유도할 수도 있다. (2-27) 식의 첫 항은 하나로운 변환의 발생원이 G=+xA8x— 8x Ax)-H8t {2-30) 으로 표현된다는 것을 의미한다. 연산자 x 의 변화로부터 유도되는 하나로 운변환은발생원 Gx=i: {xA ax-ax Ax) (2-31) 에 의해서 발생되고, 시간의 변화에 의해서 유도되는 하나로운 변환은 발생 원
Gt = -H8t (2-32) 에 의해서 발생된다. 이제 이러한 작용원리의 결과가 어떻게 구체적인 양자 역학으로 표현되는가를 알아 보자. 2.5 양자역학의 표현방법들 앞에서 지적한 바와 길이, 라그란지안의 운동학적인 항은 상수행렬 A 가 대칭인 경우와 반대칭인 경우로 분리된다. 보통 알려진 양자역학은, A 가 반대칭이고, 따라서 운동변수들이 교환관계에 있는 경우에 해당한다. 여기 서는 이 경우만을 생각하겠다. 이 경우 운동변수를 x=(: ）로 표현하고 A=-½(~-~) 로 표현하면, 라그란지안은 L=t1 { P;q• ;-q; p• ; )-H(q, p) (2-33) 의 형태로 된다. 이 라그란지안은 앞에서 지적한 바와 감이 변수 q와 p에 대해서 대칭으로 되어 있다. 이 경우 발생원 (2-30) 은 G=1 :
이 상태 벡터에 연산될 때에는 ½Oq < I=i < IGq , 伊 ,,
*제 1 장에서 설명한 바와 갇이, L= p,q ,-H 로 시작하면 발생원은 G=Gq + G t로 되며, 8q< l=i < IGq , 8 t
서로 교환가능한 물리량들의 완전집합을 a 라 하면, 물리계의 상태는 la' ＞으로 기술된다. 상태 la' ＞은 추상적인 힐버트 공간의 한 요소이기 때 문에 , 실제 계산을 위해서는 이 상태를 구체적으로 표현할 필요가 있다. 이 러한 구체적인 표현을 위해서 힐버트 공간을 완전히 기술하는 기준 벡터 (basis v ec t or) 를 집아서, 상태함수를 이들의 선형결합(li near combin a ti on ) 으로 전개하여 그 성분으로 표현한다. 위치연산자 q의 고유상태를 기준으 로 잡는 표현 방법을 q궁 L 간표현이라 하고, 운동량연산자 p의 고유상태를 기준으로 잡는 표현 방법을 p국執｝표현 또는 운동량 공간표현이라고 한다. 예를들면, q궁 L간 표현에서는상태 |a' ＞울기준벡터 l q'>에 나란한성분 인 둘로 기술한다. 이 상태함수
에 연산하면
< q',tlP i l 1 fl> = -£a—aq균~ ~ q',tl w > 가 되며, * 연산자 q의 고유값 방정식을 이용하면
* (2-36) 과 이 식을 유도하기 위해서 (2-29) 식의 두번째 식이, 상수 행렬 A 가 반대칭인 경우, [X, 8x] =O 을 의미한다는 사실을 이용하였다.
< q', tlq ;l 1 f l > = q;-< q', t| 1fl > 의 관계를 얻는다. 이 결과는 q - 공간표현에서 위치연산자 q는 그 고 유값 q'을 곱해 주는 연산자로, 그리고 운동량연산자 床근 q'에 대한 미분연산자로 표현된다는 것을 의미한다. 시간에 따른 변화를 기술하는 발생원 G t는 시각 t에서의 q-공간 표현에서 시각 t+ ot 에서의 q-공간표현으로의 변환을 유도한다. 이 변환은 01 < q',tl = -i< q', tlH o t 로 기술되며, 이 식을 미분방정식으로 표현하면 땅
붉p
점이 양자적인 작용원리의 장점이다. 발생원 G 를 이용하여 물리량들의 운동방정식 (시간에 대한 미분방정식) 을 유도할 때에는, 고전적인 경우와 마찬가지로 주의를 요한다. 이 때에는 표현 방법을 바꾸는 것이 아니라, 한 표현 방법에서 연산자의 시간에 따른 변화를 생각하는 것이며, 발생원이 기술하는 변화는 하나로운 변환에 의해 서 나타나는 고정된 연산자의 행렬요소의 변화이기 때문이다. 어떤 연산자 f가 q, /ft} 시간 t 의 함수이면, 변화된 연산자 T 는 시각 t+ ot 일 때의 연산자 f에 해당한다. 따라서 1=/-of= f(q(t+ ot), P (t+ ot), t) 로 쓸 수 있다. 여기서 -8f 는 식 (2-13) 에서와 같은 뜻으로 정의된 연산 자의 변화량이다. 이 식의 오른쪽에서 f가 (t +8t )의 직접함수가 아니라 변수 t만의 칙집함수인 이유는, 운동변수의 변화에 대하여 매개변수 t는 무관하기 때문이다. 윗식의 -하는 독립변수 q와 袋 1 변화를 통해서 나타 나는변화분이므로 -s1=(H)st (2-41) 로쓸수있다. 여기서 하는 싸=-i [/,G t]= i[f,H ]8t 로 표현되므로, (2-41) 식은 깝룰-i [/,H] (2-42) 로 된다. 이 식은 연산자의 시간에 따른 변화를 결정히는 하이젠버그 운동 방정식 (He isenberg equ a ti on of m oti on ) 이다. 위에서 양자적인 물리계의 여러 가지 표현 방법들을 작용원리를 이용하여 어떻게 유도하는지를 보았다. 이러한 여러 가지 표현 방법들은 서로 동등하
며, 이들 사이에는 하나로운 변환(unit a rytr ans fo rma ti on) 의 관계가 있다 는 것을 쉽게 보일 수 있다. 위에서 이야기한 표현 방법들은 물리계의 시간 에 따른 진행 (evolu ti on) 을 어떻게 기술하는가에 따라서 두 가지로 구분할 수 있다. (2-36) , (2-37) 과 (2-38) 식들은, 물리량들은 시간에 무관한 연 산자들로 표현되며, 물리계의 시간에 관한 모든 정보는 상태함수에 포함되 어 있다는 것을 의미한다. 따라서 물리계의 시간에 따른 진행은 상태함수의 슈뢰딩거 방정식 (2-37) 이 결정한다. 양자적인 물리계의 이러한 기술 방법 을 슈뢰딩거 표현 (Schro ding er pi c tur e) 이라고 한다. 반면에 (2-42) 식은 물 리계의 시간에 관한 정보가 연산자에 있으며, 따라서 물리계의 시간에 따른 진행은 연산자의 하이젠버그 방정식이 결정한다는 것을 의미한다. 이러한 기술방법을 하이젠버그 표현 (Heis e nberg picture) 이라고 한다. 보통 양자역학적인 물리계를 기술하는 방법으로는 표준 양자화 (cano ni cal qua nti za ti on ) 또는 디락 양자화(Di rac q uan ti za ti on) 라고 불리는 방법을 주 로 사용한다. 이 방법에서는, 그 계에 해당하는 고전적인 계를 포아송 괄호 를 사용하여 기술하고, 모든 포아송 괄호를 { , }PB 국~[ ' ] 의 교환관계로 바꾸는 방법이다. 앞에서 설명한 양자적인 작용원리의 유도 과정을 보면, 그 결과가 디락 양자화 방법과 일치한다는 것을 쉽게 알 수 있다. 따라서 양자적인 작용원리를 이용하면, 양자역학의 여러 가지 표현들을 통일된 한 가지 원리로부터 유도할 수 있다. 이 방법은 디락의 양자화 방법 과 동등한 방법이기는 하지만, 복잡한 물리계를 다루는 데는 더 합리적인 방법이다. 왜냐하면 이 방법에서는 운동방정식과 교환관계가 같은 원리로 부터 유도되고, 페르미 입자들로 이루어전 계에 해당하는 고전적인 물리계 는 존재하지 않기 때문이다. 또 한 가지 양자화 방법인 화인만 (Fe ynm an) 의 경로적분(p a thintegr al) 방법과 슈빙거의 작용원리와의 관계는 제 7 장에
서 자세히 설명하겠다. [참고문헌〕 이 장의 내용은 주로 Sch wi n g er의 MI T:강의록 (3) 의 설명 방법을 따른 것이다. 이 밖에 op }역학적인 계에 대한 작용원리의 설명은 Sch wi n g er의 출판된 책과 강 의록 (1 , 2)에 자세히 나와 있고, 제 3 장에서 인용한 논문들에도 자세히 설명되어 있 다. ( 1 ) J. Schw ing er , Quan tu m Ki ne mati cs and Dynam i cs, Benja m i n ( New York) , 1970. (2) J. Schw inger , In Pa 泊. cles and Fie ld Theory , Brandeis Lectu re Note s , Vol. n, ed. by S. D eser and K.W . Ford, Prenti ce- Hall, 1964. (3) J. S chw ing er , Differe ntia l Eq ua tio n of Quan tu m Fie ld Theory , MIT Lectu re Note (1960) 〔문제] 1 헤르미샨 연산자의 행렬요소는 하나로운 변환에 대하여 불변이라는 것을 보이 라. 2 제 1 장개서 디룬 고전적인 라그란지안은 (2-22) 식에서 x=7 J, A=_ 당1 로 놓 은 경우에 해당한다는 것을 보이라. 이 경우의 라그란지안은 q와 Jf>ll 대하여 대 칭이다. 3 등식 (2-27) 울 증명하라. 4 양자역학의 q굳撲간표현과 #공간표현 사이에 하나로운 변환의 관계가 있다는 것 울보이라. 5 작용원리의 라그란지 방식 (Lag ran g ian fo rma li sm) 에서는 작용의 운동학적인 향기 운동변수의 1-차 도함수의 2- 차항으로 구성된다. 이러한 라그란지 방식에 해당하는 oJ :;자적인 작용원리를 구성하라.
제 3 장 양자적인 작용원리 2 : 자유도가 무한한 경우 장(fi eld) 은 모든 시공간에서 정의된 함수로 표현된다. 특수 상대성이론 에 의하면, 공간-같은 (s p ace-l i ke) 간격으로 떨어진 두 점 사이에는 어떤 물리적인 정보도 서로 교환될 수 없다. 즉, 이들 두 점에서 정의된 물리량 둘은 서로 독립적으로 행동하며, 따라서 서로 다른 지유도에 해당한다. 그 래서 공간내의 위치를 나타내는 변수 쇼근 단지 서로 다른 자유도를 나타내 는 기호에 불과하다. 이러한 관점에서 보면, 장연산자 x( t ,x )i;근 양자역학 적인 연산자 x( t)에 무한히 많은 자유도를 나타내는 기호 되춘 도입한 것으 로 볼 수 있다. 다시 말하면, 양자 장이론에서 공간차원이 영인 국한울 취 하면 양자역학을 얻게 된다. 이 장에서는 이러한 관점에서 상대론적인 양자 장이론을 구성하겠다. 이 렇게 하면, 앞 장에서 이야기한 양자적인 작용원리로부터 양자 장이론에 대 한 작용원리를 쉽게 얻을 수 있고, 양자 장이론의 이론적인 구조를 양자역 학의 연장선에서 이해할 수 있다. 이러한 작용원리를 이용하여 양자 장이론 의 구조를 이해하고, 양자 장이론이 기술하는 물리계의 성질을 설명하겠다.
3.1 양자 장이론의 작용원리(1) 일반적으로 물리계의 상태는, 동시에 측정할 수 있는 모든 독립된 물리량 둘의 값을 중으로써 완전히 결정된다. 특수 상대성이론에 의하면, 공간-갇 은 (sp ac e-lik e ) 간격 (Ax)2_ (A t)2 >O 으로 떨어진 두 점 사이에는 물리적인 정보가 전달될 수 없고, 따라서 공간 같은 간격으로 떨어전 두 점에서 정의된 물리량 사이에는 간섭이 일어날 수 없다. 상대론적인 물리계의 운동변수를 x( t ,x) 라 하면, 이것은 x(t, x ~ x( t ,x') 가 서로 다른 자유도를 기술하는 양이라는 것을 의미한다. 따라서 공간 같은 곡면 6 에서 정의된 서로 교환 가능한 헤르미샨 연산자들의 완전 집합을 a 라 하면, 이들의 고유함수들로 물리계의 상태를 기술할 수 있다. t=상수로 표현되는 표면은 이들 공간 같은 곡면의 특별한 경우이다. 공간 같은 곡면 6 에서 연산자들 a 의 고유상태를 la',a> 라 하면, 상대론적인 물 리계의 물리적 정보는 변환함수 (3-1) 로부터 얻어낼 수 있다. 이들 물리계의 성질은, 제 2 장의 경우와 마찬가지 로 이 변환함수의 변화를 생각함으로써 이해할 수 있다. 변환함수 (3-1) 의 변화를 연산자 Wi 1 의 변화량의 행렬요소로 표현할 수 있다고가정하면 8< a2,(J2 lai', (Jl > = i< a2, (J시 8[ Wiilla1 ',(JI > (3-2) 로 쓸 수 있고, 헤르미샨 연산자 昭 1은 이 계의 작용연산자이다. 서로 무 한히 가까운 두 공간 갑은 곡면 (J와 (J+d (J 들을 생각하면, 작용연산자는
Wi1= ~ W11+dt1 ,t1 6 로 쓸 수 있다. 그립과 같이, 무한히 인접한 두 공간 같은 곡면 서이의 체적을 생각하자. 그림에서 X1 으로 표시된 작은 체적과 x 료. 표시된 체적 은 서로 공간 같은 간격으로 떨어져 있다. 그래서 이들 체적내에서 측정된 물리량들은 서로 독립이므로, 이들에 의한 작용에의 공헌은 W<1 + d< 1,<1= L((J) d,(J=fds !. l (xµ) d(J
틀 蠶 a6+ d
로 쓸 수 있다. 여기서 ds 는 좌표 6 에 수직인 곡면에 대한 적분을 나타낸 다. 따라서 변수 (J는 시간 방향을 나타내고, s 는 공간 방향을 나타낸다. 즉, dads= d4x= dx0dx1dx2dx3 는 4- 차원 시공간에서의 체적요소 (volume elemen t)를 나타낸다• 이 물리계 의 상태를 기술할 수 있는 연산자를 Xa( 갔)라 하면, 작용연산자는 腐=f/ 'd4x !l (xa( 갔)) (3-3) 6l 로 쓸 수 있다. 여기서 오은 라그란지안 밀도 (La gr an gi an dens ity)이다. 최근의 문헌에서는 이 라그란지안 밀도를 라그란지안이라 부르기도 한다. 연산자 Xa( t ,X, y ,z 治· 이 물리계의 독립변수이며 , 시공간의 모든 점에서 정 의된 장(fi eld) 함수이다. 위의 사실은 상대론적인 조건을 만족시키기 위해 서는, 장의 개념이 자연스럽게 도입된다는 것을 뜻한다. 여기서 사용할 단 위계는 n=c=l 인 자연단위계 (na tur al unit)이며, 다음과같은기호를사용
하겠다: x 도 (x0,x',x 라 x3)= (t,x ) (dx)'= dx'g,, d x, g,,= 1-1 01000O`01O 0•O l 。 aµ= 훑 3- 차원 공간의 서로 다른 점에서의 장함수 Xa 는 서로 독립된 자유도를 갖는 변수처럼 행동한다. 따라서 공간을 표시하는 변수 요근 물리계의 상태 를 기술하는 양이 아니라, 서로 다른 자유도를 표시하는 매개변수에 불과하 다. 물리계의 상태를 기술할 수 있는 기본 변수 Xa는 시공간의 함수이며, 상대론적인 조건을 만족해야 한다. 죽, 4- 처원 시공간의 좌표변환인 로렌 츠 변환 (Loren tztr ans fo rma ti on) 에 대하여, 장함수 Xa 는 정당한 텐서 (ten sor) 혹은 스피너 (sp ino r) 함수가 되어야 한다. (2,3 ) Xa 에서 첨자 a 는 3 -차원 공간에 의한 자유도를 제의한 다른 자유도를 표시하는 매개변수이다. 장이론의 경우에도 작용원리는 8 腐= G( 야)- G(
방정식으로 표현할 수 있으므로, 라그란지안 밀도는 일반적으로 g =-½
* 이와 같이 운동방정식이 시간에 대한 1- 계 미분방정식으로 표현되도록 기술 하면, 하밀톤 방식의 작용원리를 얻는다.
:A 껑µ x= Xa沿 , aµXp 를 뜻한다. 또 (3- 기식의 첫 항에 나타난 공간에 대한 미분은 상대론적인 불변성을 쉽게 보일 수 있게 하기 위하여 도입한 것이다. 앞 장에서의 경우와 마찬가지로, 식 (3-5) 의 라그란지안 g과 豆=g _aµ fµ (3-6) 는 같은 물리계를 기술한다. 여기서 8µF 는 제 2 장의 팡［의 상대론적인 연 장이다. 식 (3- 6) 에 의한 작용은 W21= 鬪』 ~ 2 d4xaµr= 臨-j 2d6µF+ i IdaJ µ 로 쓸 수 있다. 윗식의 마지막 부분은 4- 차원에서의 가우스 (Gauss) 정리를 사용하여 유도된 것이다. 여기서 da ,A근 시간-같은(ti me - li ke) 벡터 아에 수 직인 곡면(이 곡면은 공간 같은 곡면이다)에 대한 적분을 나타낸다. 예를 들면 d
G(a)= G(a)-8ldaµr d 로 되어서, aµr 항은 작용의 끝점변화에만 영향을 주게 되고, 따라서 계의 운동방정식에는 영향을 주지 않는다. 장연산자를 헤르미샨으로 택하면 라그란지안이 헤르미샨이므로 AVµt t= =V一 Aµ (3-7) 의 성질을 갖게 된다. 여기서 상수행렬 Aµ 의 계수 (rank) 는 독립된 장 함수 x 려수와같다. 라그란지안 오은 로렌츠 변환에 대하여 불변량 (Loren t zscalar) 이어야 하 고, 따라서 변화량 o 은 좌표계에 무관한 양이 되어야 한 다. 이 조건은 장이론이 로렌츠 불변성을 갖기 위한 필요 조건이다. 이제 이 로렌츠 불변성에 대해서 자세히 조사하겠다. 3.2 로렌츠 변환 시공간 좌표계를 로렌츠 (Loren tz) 변환할 때, 이에 의해서 생기는 라그 란지안의 변화를 생각하자. 좌표변환 굿µ= fµ1 1X11-f µ (3-8) 가 두 사건 (event) 사이의 거리를 그대로 유지하기 위해서는 d탔 d 굿µ= dxµdxµ 의 조건을 만족해야 한다. (3-8) 식이 위의 조건을 만족하기 위해서는 로렌 츠 변환을 나타내는 £%는 gµ11 f &f11p = gtfp, f/.fPp = 8p (3-9)
의 관계를 만족해야 한다. (3-9) 의 첫째 식에서 a=O= p인 경우를 보면 -go o=l= （셉 )2_ 23 (fo) 2 i= l 의 관계식을 얻는다. 따라서 짦는 3 (l舒 =1+ i:=E I (lo)2 칙 1 의 성질을 갖는다. 젊=::-이므로, 이것은 시간변화를 나타내는 성분이 며, 윗식에 의해서 갭는 1 보다 크거나 -냐 L다 작아야 한다. 따라서 시간 의 부호를 바꾸는 변환은 제자리변환 (ide nti ty tr ans fo rma ti on) 으로부터 매 개변수를 연속적으로 변화시킴으로 해서 얻을 수는 없다. 따라서 로렌츠 변 환을 짦가 영보다 큰 경우와 영보다 작은 경우의 두 가지로 구분할 수 있 다. 또한 좌표변환 ft는 그 행렬식이 영보다 큰 경우와 작은 경우로 구분 할 수 있는데, 여기서는 짦가 영보다 크고 tt의 행렬식도 영보다 큰 변환 (pro p er ort ho chronous Lorentz tr ans fo rma ti on) 만을 고려하겠다. 로렌츠 변환에 대한 자세한 설명은 라몬드 (Ramond)12) 와 라이더 (Ry der)13) 의 교과 서에 잘설명되어 있다. (3-8) 식으로 표현되는 좌표변환에 대해서 장함수는 Xa( 굿 )=La g x p (x) (3-10) 로 변환된다. 여기서 행 렬 L 은 로렌츠 변환의 한 표현 (re p resen t a ti on) 이 다. (2,3) 장이론이 로렌츠 변환에 대하여 불변이기 위해서는 변환 (3-8) 과 (3-10) 에 대해서 라그란지안이 불변이어야 한다. (3-8) 식의 변환에 대해서 미분연산자는 5µ=£%8I/ 로 변환한다. 따라서 로렌츠 변환하에서 변환된 라그란지안은
豆 =+xA 정µf― aµxAµx)-v(x) =卓 x(LA 뎃 u4)8ux_ 8ux( 乙 LAµL)x]_ V(Lx) 로 쓸 수 있다. 로렌츠 변환하에서 라그란지안이 불변이기 위해서는, 이 식 이 (3-5) 식과 같아야 한다. 따라서 LAµL= fµ1 1A11, V(Lx)= V(x) (3-11) 의 조건이 만족되어야 한다. (I) 포텐셜 연산자 V가 V=xBx, B= 싱수행렬 로 표현되는 간단한 경우에는 V(Lx)= xlBLx 이므로, (3-11) 의 두번째 조건은 l=BL-1B-1 로 쓸 수 있다. 여기서 행렬 B는 헤르미샨이며, 그 역행렬이 존재해야 한 다. 이 결과와 (3-11) 식의 첫번째 식을 종합하면 L-l(B-lAµ)L= £µu(B 古산) (3-12) 의 결과를 얻는다. 이 식은, 로렌츠 변환하에서 장이론이 불변이기 위해서 는, 행렬 B-1A 까 4 차원 시공간에서 벡터처럼 변환되어야 한다는 것을 의미한다.
3 . 3 작용의 변화(I) 이제 로렌츠 변환에 따른 작용의 변화를 생각해 보자. 갤가 영보다 크고 tµ겨 행렬식이 영보다 큰 로렌츠 변환은 제자리변환과 연속적으로 연결되 기 때문에, 여기서는 미세 로렌츠 변환만을 생각해도 충분하다. 좌표계의 평행이동을 포함한 미세 로렌츠 변환은 탔=갔―강+강 UX j/ 로 나타낼 수 있다. * 여기서 닫는 평행이동을 나타내는 무한히 작은 매개 변수이며, 강 U는 4- 차원 시공간에서의 회전을 나타내는 작은 매개변수이 다. 회전을 나타내는 변수는 강도一 €uµ 의 반대칭성을 갖는다. 이러한 미 세변환하에서 장함수 x 의 변환 L은
*평 행 이동변환과 로렌츠 변환을 포함하는 변환을 포인카레 (Poin c ar~) 변환 이라고 부른다.
L= l+½€µvSµ11 (3-13) 로 나타낼 수 있다. 여기서 평행이동을 나타내는 매개변수 강가 식 (3-13) 에 없는 이유는, 강가 미분연산자 aµ 에 영향을 주지 않고, 따라서 라그란 지안을 불변으로 만들기 위해서 o 에 의한 x 의 변환을 고려할 필요가 없기 때문이다 .(2) 행렬 SµII 는 장함수 x 에 연산되며, 그 장의 스핀 (s pi n) 을 결정 한다. 작용의 변화 햐 %1 은 시공간의 각 점에서 장함수 성분의 변화 8x 에 의해 서 유도될 수도 있고, 적분상한과 하한인 (J 1 과 (J2 의 변화에 의해서 유도될 수도 있다. 제 2 장에서 끝점의 변화를 t (r) 의 함수형태의 변화로 나타냈듯 이, 여기서도 끝점 (J 1 과 (J2 의 변화를 그들의 r 에 대한 함수형태의 변화로 나타내겠다. 그렇게 하면 작용연산자의 변화는
8 齡=iI r2 d4x8 오+irrI 2 요 8d4x (3-14) 로 쓸 수 있다. 체적요소의 변화량은 8d'x = d4xaµ8Xµ (3-15) 로 쓸 수 있다(문제 1). 이 식을 이용하면, (3-14) 식을 血 = f C2 죠 [8xµaµ fl + 80 미 + /@ 編 )d'x 111 .I111 = f: 2d4x8 。오 + f6 l62d4 짜( g 8갔 ) 로 쓸 수 있다. 여기서 80 는 f(굿 )-/(x)= J(x +8x)-/(x) = 『 (x)-/(x)+ 8xµaµf + 0( 紀) =8o/+8x 껑J 로 정의되며, 함수형태의 변화를 나타낸다. 4- 차원 시공간에서의 가 우스 (Gauss) 정리를 이용하면, 작용의 변화량은 血=f d4x[永 8 。 xA 껑 µx- aµxAµ8ox)-8 0 V(x) <11 +i Id2d4x[永 xAµ8oaµx-(&aµx)Aµx]+ i I( f 2d아 8xµ g 로 표현할 수 있다. oo 는 x 의 함수형태의 변화에 의해서 유도되는 변화량 을 뜻하므로, oo2 l- a;.: 근 교환 가능하다. 윗식의 두번째 항을 부분적분하 면, 血=J O2 죠 [ooxA 껑µ x- aµxAµoox]-o o V] <11 +1<~11 2d
=f d4x[8oxA 껑 ,,x-aµxAµBox- 80 V]+ G(<12 )-G (<11 ) 6l 으로 된다. 여기서 발생원 G(a»=- G(6)= f6 d아 [8x 뎅난 xAµ8 。 x-BoxAµx)] (3-17) 로 정의된다 . (3-16) 식의 첫 항은 작용원리에 의하여 영이 되어야 한다. 따 라서 방정식 8oxA 껑 ,,x-aµxAµBox= 80 V(x) (3-18) 이 성립해야 하며 , 이것이 장방정식 (field eq ua ti on) 을 주는 식이다. 이 장 방정식에 대해서는 뒤에 자세히 다루겠다. 여기서는 먼저 발생원 G(6) 가 의미하는 것이 무엇인가에 대해서 생각해 보자. 장함수의 전체 변화 8쌌 근 곡면 6 위의 한 점에서 함수형태의 변화에 의 해서 생기는 8 。변화와, 좌표의 미세 로렌츠 변환 굿 µ=xµ_8xµ 에 의해서 유도되는 변화의 합으로 이루어진다. 로렌츠 변환에 의해서 유도 되는변환은 祖)= Lx(x)= x(x)+f €µ11 Sµ11x(x) (3-19) = x(x) 一 8xµaµx(x) 로 나타낼 수 있다 . 이 식의 마지막 관계는 f(치의 테일러 전개 (Tay lo r ex p ans i on) 로 얻은 것이다. 따라서 좌표의 로렌츠 변환에 의해서 생기는 장함수의 변화는 굿 (x)- x(x)= 8.갔 aµx+ 숭 @uSµ11x(x) (3- 2 0)
로 쓸 수 있다. 장함수의 전체 변화는 8x= 8ox+ 麟µ x(x)+ 숭 €,,11S11x(x) 로 쓸 수 있으며, 이 식을 (3-17) 식에 대입하면 발생원은 G(6)=E4卓 xAµ8x - 8xAµx)+ 8x 자 -½
Tµv = g µv fl-卓 xA{µa u }x- 8{u x Aµ}x ] (3-23) -+ aA[xA
는 에너지급녓윙: 연산자이며, J µU는 4- 차원 각 운동량 연산자이다. 이들 연산자 사이의 교환관계는 포인카레 군 (Po i ncar~ gr ou p)의 성질에 의해서 결정되는데, 이에 대해서는 3 . 5 절에서 다루겠다. 3.4 양자 장이론의 입자적 성질(1) 로렌츠변환 탔 =xµ-oxµ, 0.갔= 강_ 강 11X11 에 대한 발생원은 (3-26) 식에 의하여 G 는다타｝나 로 쓸 수 있다는 것을 보았다. 이러한 좌표변환에 의해서 유도되는 장연산 자의 겉보기 변화는, (3-20) 식에 의해서 x(x)-x(x)= —8x = 터러 @11Sµx =[휴낙＠”（ xµ 장 -x 정+ iSµ )]x (3-28) 로 표현된다. 이 변화는 시공간의 한 점에서 장연산자의 함수형태의 변화를 나타낸다. 이러한 변화도 발생원에 의해서 교환관계 8x= -i [x , Gx] 로 결정된다. 이 식과 (3-28) 식을 비교하면, 로렌츠 변환에 의한 칭연산자 의 변화를 결정하는 교환관계 [x,Pµ]= -i aµ x (3-29) [x, r11] ＝규 (xµ 강― XII8µ+ i Sµ”)x (3-30)
울 얻는다. 이 식은 로렌츠 변환에 따른 양자 장이론의 반응을 결정하는 식 이다. (3-30) 식은 연산자 SµII가 칭연산자 x 의 스핀 (s pi n) 을 나타내는 연산 자라는것을의미한다. 장연산자 x( 따를 후리에 (Four ier ) 전개하면 x(x)=f d4p e i P •xx(P)=f d4Pe i( p,r-p• nx(P) (3-31) 로 쓸 수 있다. 여기서 에너지운동링: 연산자 Pµ 의 고유값 방정식을 PµIP'>=Pµ,IP'> 로 표현하고, (3-31) 식의 x(P~ 에너지운동량 고유값 f의 함수로 표현 된 장연산자이다. (3-31) 식을 (3-29) 식에 대입하면, x(P) 에 대한 교환관 겨] [x(P),Pµ]=t lx(P ) 를 얻는다. 이 식을 운동량 고유상태 IP' ＞에 연산하면 Pµx(P)IP' > = x(P)( p w-P 에p'>=(p P'- tl )x(P)IP' > (3-32) 의 식을 얻는다. 이 식은 x(P)IP' > 역시 연산자 pµ의 고유상태라는 것을 뜻하며 , 그 상태에 해당하는 고유값은 (p'-p)이다. 다시 말하면, 연산자 x(P) 가 상태 |P'> 에 연산되면 그 고유값이 다 (―p)만큼 바뀐 다른 고유상태 로 변환시킨다는 것을 의미한다. 이것은 장연산자가 에너지운동·량 /를 흡수하거나 방출할 수 있다는 것을 의미한다. 연산자 (3-31) 은 그 p o 의 값이 영보다 크거나 작은 두 가지 경우로 나눌 수 있다. 죽, 헤르미샨 연산자 었문 x=x(+)+x(-) 로 쓸 수 있으며, 여기서 x(+ ）는 그 진동수 p° 가 영보다 큰 경우이고, x(-) 는 진동수가 영보다 작은 경우에 해당하는 장연산자 부분이다. 4- 차원 시
공간에서 벡터의 영번째 성분의 부호는 로렌츠 변환에 대해서 불변이므로, 연산자를 위와 같이 나누는 과정은 로렌츠 불변인 과정이다. x(+ ）가 상태 IP'> 에 연산되면 그 에너지 값을 감소시키고, x(- ）가 연산되면 그 에너지 값 증가시킨다. 따라서 x(+ ）는 에너지를 파괴하는 파괴연산자 (ann i h i la tion ope rato r ) 이고, x( - ） 는 에너지를 생성하는 생성연산자 (creati on ope rato r ) 이다. 주어진 물리계의 상태 중에서 그 에너지가 제일 낮은 상태를 전공상태 (vacuum sta t e ) 로 정의한다. 진공상태의 공간성분 운동량 p'은 영이 되어 야 한다. 그렇지 않으면 진공상태가 유일하게 정의되지 않기 때문이다. 전 공상태의 에너지 값은 그 물리계에서 가능한 값 중에서 최소값이므로 그 값 울 영으로 택할 수 있고, 그래서 진공상태를 |0> 으로 나타낸다. 전공상태 의 에너지 값은 최소값이므로 x(+)|0>=O (3-33) 의 조건을 만족해야 한다. 이러한 진공상태에 연산자 x(- ）를 연산함으로써 다른 가능한 모든 상태들을 만둘 수 있다. (3-31) 식으로 표현되는 장연산자가 상대론적인 운동방정식을 만족하면, 운동량 고유값 P Jli.근 pµpµ = -m 2, pO= 土J굽汀구? (3-34) 의 조건을 만족한다. 이 식은 상대론적으로 운동하는 입자의 에너지와 운동 량 사이의 관계식과 같다. 장연산자가 상대론적인 운동방정식을 만족하도 록 하면, 연산자 x(+ ）와 x( -) 는 (3-34) 식을 만족하는 에너지급녓굉울 파괴 하거나 생성하는 연산자로 되며, 따라서 x(+ ）와 x(-) 를 상대론적인 입자의 파괴연산자와 생성연산자로 해석할 수 있다. 연산자 x(- ）가 전공상태에 한 번 연산되어 만들어전 상태는 상대론적인 단일입자의 운동을 기술하는 상태 함수가 된다. 양자 장이론을 사용하여 입자의 운동을 기술할 수 있는 것은 장이론의 이러한 성질 때문이다.
3,5 로렌츠 불변성을 위한 디락구f빙거 조건 장이론이 로렌츠 불변이기 위해서는 라그란지안이나 작용이 로렌츠 불변 이어야 한다. 그러나 라그란지안이 로렌츠 변환에 대하여 불변이라고 해 서, 그 장이론이 반드시 로렌츠 불변인 것은 아니다. 왜냐하면 물리량들의 계산 과정이나 양자화 과정에서 로렌츠 불변이 아닌 조건을 사용할 수가 있 기 때문이다. 예를 들면 게이지 이론에서 쿨롱 (Coulomb) 게이지를 사용할 경우, 게이지 조건은 로렌츠 불변이 아니다. 양자화 과정에서 사용하는 이 러한 조건들의 영향은 에너지-운동량 텐서 Tµ11 에 나타나게 되며, 에너지 운동량 텐서로 정의되는 발생원 pµ와 J µ11 에도 이들 조건의 영향이 나타나 게 된다. 따라서 양자 장이론이 로렌츠 불변일 조건은 이들 발생원이 포인 카레 군 (Poin c arl! gr ou p)의 정당한 발생원이 되는가를 검토함으로써 찾아 낼수있다. 미세 (infinites im al) 로렌츠 변환 8갔 =강― €µ ux u (3-35) 의 발생원이 G 尸같다 ½€µ11r11 (3-36) 로 표현된다는 것을 앞에서 보았다. 여기서 pµ와 J µII는 Pµ=1da11Tµ11 6 (3-37) J µ11= f d야 (갔 TIIA_ 갔 TP•) d' 로 정의되는 에너지운동량 연산자와 4- 차원 각운동량 연산자이다. 에너지
운동량텐서 Tµ”는 Tµu= T uµ aUTµu=O (3-38) 로 표현되는 대칭성과 보존법칙을 만족하기 때문에, pµ와 r11는 공간 같은 곡면 쩌 무관한 양이 되어야 한다. 다시 말하면, 발생원 pµ와 J µII는 보존 되는 물리량을 나타낸다. (3-3 기식으로 표현되는 변환들은 포인카레 군이 라고 부르는 군(gr ou p)을 형성한다. 따라서 이 군의 발생원인 pµ와 J µII는 다음과 같은 교환관계를 만족해야 한다. (1, 2,3) [Pµ,r]=O uµv. A] = igµA P11-ig fpµ (3-39) [F IJ,J이= igIJAJ µ 6-ig µA J IJ6 _ igIJ 6尸 + igµ6 JI JA. 즉, F 와 J µU 는 교환관계로 정의되는 곱셈에 대하여 포인카레 군대수 (grou p alge b ra) (3-39) 를 이루어야 한다. 3 . 3 절에서 본 바와 같이 연산자 P 따 J µU는 에너지급땅윙: 밀도 Toµ 로부터 계산할 수 있고, T 옛짜는 장 연산자 x(x) 로 이루어져 있다. 양자 장이론이 로렌츠 불변이기 위해서는, 장연산자들 사이의 동시 교환관계로부터 계산한 발생원 pµ와 J µU들 사이의 교환관계가 (3-39) 식의 교환관계와 일치해야 한다. 다시 말하면, 장이론이 로렌츠 불변일 조건 (3-39) 식은 그 양자 칭이론의 체계에 어떤 조건을 부 과하게 되는데, 이러한 구속 조건을 에너지급녓굉: 밀도인 T°µ 들 사이에 만족되어야 할 조건으로 표현할 수 있다. 이렇게 표현한 양자 장이론의 로 렌츠 불변 조건을 디락수「빙거 조건 (Dira c-Schw ing e r con diti on) 이라고 한 다 .(1,4) 이러한 디락수「빙거 조건을 유도하기 위해서 교환관계 (3-39) 중에서 두 개의 시간성분을 포함하는 식들을 생각해 보자. 이들은 [JO \p o ]= - iP, . U 짝 JO l]= - ijkl (3-40)
의 두 가지이며 , 순수한 로렌츠 변환 (pu re Lorentz tran sfo n nati on ) 에 관계 되는 조건들이다. (3-40) 식을 에너지국탄용량 밀도 T 어로 표현하면 [fd3xx k TOO(x), f강 x' T00(x')]= -i fd3xT 0k (3-41) [jd3x 갑 oo(x) ,jd ax'x'1 Too(x')]= —t . f강 x[xk TOl _xlTOk] 로 된다. 이 조건은 양자 장이론이 순수한 로렌츠 변환에 대하여 불변이기 위해서 만족되어야 할 필요조건이다. (3-41) 식은 연산자 T 叫를 적분한 양들 사이의 관계식이다. 이것을 국소 연산자(l ocal ope r ato r ) y oµ 들 사이의 관계로 표현하는 것이 실제 문제에 적용하는 데 편리하다. 그러기 위해서 로렌츠 변환을 유도하는 발생원 Gx=ldaµ Tµ118x11 (3-42) 6' 를 생각하자. 이 발생원은 한 공간 같은 곡면 6 에서 8x11 만큼 차이가 나는 다른 곡면 6+ 86 로의 변환을 유도하는 발생원이다. 곡면 6 에서 정의된 양 자적인물리계의 상태는 8< al=i < a1Gx (3-43) 만큼 변하게 된다. 변화량 8갔 는 시공간 좌표 갔의 함수이기 때문에 (3 -43) 식의 오른쪽은 함수 a(x) 의 범함수(fun c ti onal) 이다. 8a 가 작을 때에 는 그에 비례하는 항만이 중요하므로, 양변을 aa(x)로 나누면 (3-43) 식의 왼쪽은 a(x) 에 대한 함수적인 도함수(fun c ti onal de ri va ti ve) 로 되며, 이 방 정식은 a(x) 에 대한 함수미분방정식 (func tio n al differe nti al eq ua ti on) 이 된 다.＊ 이 함수미분방정식이 의미가 있기 위해서는 적분 가능 조건 *함수미분방정식에 대해서는 제 5 장에서 자세히 다루겠다. 여기서는 매개변수 에 대한 미분방정식의 연장이라고 이해하면 된다.
(int eg ra bil it y cond iti on) 을 만족해야 하는데, 이 적분 가능 조건이 국소연 산자인 Toµ 들 사이의 교환관계로 표현된다. 공간 같은 곡면 6 가 무한히 작은 부분에서만 휘어져 있고, 나머지 부분 에서는 평면인 경우를 생각하자. 그러면 곡면 6 를 기술하는 방정식은
T(O)(O):::: nµy µv nv (3-48) :::: nµT/l -0+ nµTµk(-aka) 로 쓸 수 있다. 곡면 6 가 평면에 무한히 가까우면, (8k6) 의 2- 차항 이상은 무시할 수 있다. 따라서 y (o)(o) 는 T(o)(o)= nµ T° 다 T0k(-o k6) 로 쓸 수 있다. 이 식을 (3-47) 식에 대입하면 발생원은 Gx=f d3x[ — 8<1 ( x)][ y
[결 T{ T(o)(o)+ TOka 아 (x)] < a!=O (3- 5 2) 로 쓸 수 있다. 여기서 두번째 항을 { }(x) 로 쓴 것은 연산자 T°µ 를 공간 의 함수로 표현했다는 것을 의미한다. (3-52) 식으로 표현된 함수미분방정 식이 적분 가능하기 위해서는 다음과 같은 조건이 만족되어야 한다. 죽, 곡 면 6 내에서 서로 다른 두 점 x와 X’에 서의 변화 8a(x) 와 8a(x 껴춘 연속적 으로 시킬 때, 물리계에 유도되는 결과는 이들 두 변화의 순서에 무관해야 한다. 이 조건을 식으로 나타내면 [급 -{y
질에는 무관한 국소적인 (loc al) 물리량이라는 것을 의미한다. 아러한 경우 (3-54) 식의 오른쪽의 마지막 두 항은 영이 된다. 따라서 적분 가능 조건 (3-54) 식은 [ T00(x), T00(x')]x•=Xo= 규[ T0k(x) + T0k(x')] ak8(x-x ') (3-5 5) 으로 된다. (3-5 기식은 양자 장이론이 순수한 로렌츠 변환에 대하여 불변 이기 위한 필요 조건이다. (3-55) 식의 양변에 잤롤 곱하여 적분하고, 또 이 식의 양변에 갔와 X'l 울 곱하여 양변을 적분하면, 교환관계 (3-40) 식을 얻는다는 것을 쉽게 보 일 수 있다(문제 7). 이것은 조건 (3-55) 가 순수한 로렌츠 변환에 대한 양 자 장이론의 불변성을 위한 필요충분 조건이라는 것을 의미한다. 이 필요충 분 조건을 디락국뿐拉거 조건이라고 한다. 포인카레 군대수를 이루는 교환관계 (3-39) 식 중에서 (3-40) 식을 제의 한 나머지 교환관계들은 3- 차원 공간내에서의 평행이동과 회전변환에 대한 불변성을 보장하는 조건들이다. 이들 교환관계에 대해서도 순수한 로렌츠 변환의 경우에 사용하였던 위의 과정들을 적용하면, 3- 차원 공간에서의 평 행이동과 회전변환에 대하여 양자 장이론이 불변일 필요충분 조건 [[ TTOOkk((xx)),, rroool((xx''))]]::,,ccO0 ==:,:c,0c·0 == -—- iii TTT0 ko 0l1(((xxx)) 정' )정a 8 18((8xx(-x-xx-'x')')) (3-56) -i T0k(x') 장 8(x-x') 울 얻을 수 있다 (문제 8) . (1,4) 앞게서 지적한 바와 같이, 양자 장이론의 라그란지안이나 작용이 로렌츠 불변이라 하더라도, 양자적인 계산울 하는 과정에서 로렌츠 불변이 아닌 과 정들을 사용하는 경우가 있다. 이러한 계산과정에 의해서 장이론의 로렌츠 불변성이 영향을 받는지에 대해서는 디락수한J거 조건 (3-55) 식과 (3-56) 식을 이용하여 확인할 수 있다.
〔참고문헌〕 이 장의 내용은 주로 Sch wi n g er 의 MIT 강의록(I)과 Brandeis 강의록(I)을 따라 서 설명하였다. 이들 강의록 의에도, 양짜적인 작용원리에 대해서는 Schw ing e r 의 Phy s. Rev. 논문들에 자세한 설명이 되어 있고, 디락슈팡거 조건에 대해서는 Di ra 떠 강의록 U) 과 슈빙거의 책 U ) 에도 찰 설명되어 있다. 보통 양자 장이론에 관 한 교과서들에서 다룬 작용원리는 라그란지 방식 (그 운동방정식이 시간에 대한 2 께 미분방정식으로 표현되는)의 작용원리이다. 로렌츠 변환과 그 표현 (re- p resen tati on) 에 대한 설명과 라그란지 방식의 작용원리에 대한 설명은 Ramond 의 책 (2) 에 잘 되어 있다. (1) J. Schw ing e r, Phy s. Rev . 브, 914 (1951) ;Phy s. R ev. 브, 713 (1953) ;MITLectu r e Note (l960) ; in Part icle s and Fi el d Theory , Brandeis L ectu r e Note Vol. Il , ed. b y S. Deser and K.W . Ford, Prenti ce -Hall, 1 964 ; Quan tu m Ki ne mati cs and Dynam ic s, Benja m i n (New York) , 1970. (2) P. Ramond, Fie ld Theory ; A Modern Pr ime r, 2nded., A dd iso n-W esley, 1989. (3) L.H . Ry d er, Quan tu m Fie l d Theory , Cambrid g e Un ive rsit y Press (London) , 1985. (4) P.A . M . Dira c, Rev. M od. P hy s. 프 , 592 (1962) ; Lectu re s on Quan tu m Mechanic s , Ye shiva Un ive rsity , 1964. J. S chw inge r, Phy s. R ev. 프7._. 324 (l962) ; Partz c les, Sources, and Fie ld s, Vol. I, Add iso n-Wesley, 1970. [문저 1 〕 1 (3-5) 식과 같이 라그란지안을 표현하면 그 운동방정식 (3-18) 은 시간에 대한 1 께 미분방정식이 되고, 이로부터 얻는 작용원리는 하밀돈 방식의 작용원리이 다. 운동방정식이 시간에 대한 2- 계 미분방정식이 되도록 라그란지안을 표현하 고, 이에 해당하는 양자적인 작용원리를 구성하라. 이러한 라그란지 방식의 작 용원리가 하밀돈 방식의 작용원리와 다른 결과를 주는 경우가 있는가?
2 (3-15) 식을 증명하라. 3 (3-23) 식을 유도하라. 4 로렌츠 변환에 의한 장연산자의 변화를 결정하는 교환관계 (3-29) 와 (3-30) 을 이용하여, 발생원 pµ와 J µU 를 pµ=-iaµ ]µ= —i (x µo-xoµ) +s w 로 표현 (re p resen t a ti on) 할 수 있다는 것을 보이라. 이 결과를 이용하여 발생 원 pµ와 J µ U 가 만족하는 교환관계를 유도하라. 연산자 Sµ 는 어떤 교환관계로 정의해야하는가? 5 절에서 칭연산자를 x+(p) -2} x-(p) .£ 분리하는 과정을 구체적으로 보이고, 이 과정이 로렌츠 불변이라는 것을 보이라. 6 곡면의 방정식과 그 표면의 표면요소 사이의 관계가 (3-45) 식으로 된다는 것을 보 °l 라. 7 (3-55) 식의 양변에 갔와 xkxll 을 곱하고 적분하면, 포인카레 대수를 정의하는 교환관계 중에서 시간성분이 둘인 (3~40) 식을 얻는다는 것을 보이라. 8 (3-56) 식을 유도하고, 이들이 3- 차원 공간에서의 좌표이동과 회전변환에 대한 op } 장이론의 불변성을 위한 충분 조건도 된다는 것을 보이라.
제 4 장 기본적인 양자 장이론들 제 3 칭에서 설명한 양자 장이론의 작용원리는 8 < ai'' ,
기술된다는 것을 의미한다. 이 작용원리는 양자 장이론으로 기술되는 물리 계의 물리적인 성질을 결정하는 물리량이나 상태 벡터들이 만족해야 할 방 정식을 결정한다. 또 아 작용원리를 이용하면, 이러한 물리계에 관한 물리 적인 정보를 얻는방법을찾을수도 있다(제 5~9 장). 이 장에서는 이러한 양자적인 작용원리로 기술되는 몇 가지 기본적인 상 대론적 양자 장이론들의 이론적인 체계를 설명하겠다. 이러한 양자 장이론 으로 기술되는 물리계의 물리적인 정보를 얻는 방법에 대해서는 다음 장들 에서 다루겠다.
4.1 양자 장이론의 분류(1) 작용원리 (4 ~ 1) 에 의해서 장연산자 x( 차는 방정식 8oxA 껑µ x 국 %xAµSax= So V(x) (4-3) 를 만족해야 한다는 것을 앞 장에서 보았다. 장연산자 x와 그 변화량 8ox 사이의 (반)교환관계가 결정되면, 방정식 (4-3) 은 미분방정식으로 나타낼 수 있다. 장연산자들 사이의 (반)교환관계는 3·3 절에서 설명한 바와 같이, 장연산자의 일반적인 변화를 유도하는 발생원 Gx=½J d(Jµ (x Aµ8x— ax Aµx) (4-4) 에 의해서 결정된다. 앞에서 보인 바와 같이, 상수행렬 Aµ 는 반헤르미샨 행렬이며, 이 행렬은 실수 반대칭행렬 aµ 와 허수 대칭행렬 sµ 의 모임인 A 니 。a µ :µ) (4-5) 로 나타낼 수 있다. 이렇게 상수행렬 Aµ 를 분리해서 표현하면, 장연산자들 도 두 가지 독립된 성분들로 분리된다. 행렬 aµ 와 sµ 에 해당하는 장성분들 울 각각 ¢(x) 와 ¢(x) 라고 하겠다 : x=( : ) . (4-6) (4-5) 식과 (4-6) 식을 (4-2) 식에 대입하면, 일반적인 양자 장이론의 라 그란지안은 요=卓 ¢a 일 -8µ¢a% ）담(
로 표현된다. (4-7) 식은 장연산자 ¢와 仇가 운동학적으로 (k i nema tic all y) 독립된 장연산자라는 것을 의미한다. 따라서 이들 각각에 대해서 작용원리 를 독립적으로 적용할 수 있다 . 장방정식 (4-3) 을 미분방정식으로 표현하려면, 장연산자들 사이의 (반) 교환관계가 결정되지 않았기 때문에, 왼쪽 미분 강과 오른쪽 미분 장롤 구 별하여 표현해야 한다. 라그란지안에 4- 벡터의 발산 [aµF 撲· 더해 주어도 장방정식에는 변화가 없다는 사실을 이용하면, (4-3) 식은 2A 껑 µx= 一8장x V (4-Sa) 혹은 _2A /J a/ J x= 一88xr V (4_8b) 로 쓸 수 있다. 장연산자 ¢의 경우 (4-8) 식은 2a /J a/ J¢=강海 v= _2 a- /J a / J¢=a海r· V (4-9) 로 된다. 이 식은 ¢장의 경우, 왼쪽 미분 :〉과 오른쪽 미분 :；가 같다는 것을 의미한다. 이것은 장연산자 ¢와 그 변화량 싸가 교환관계 [a¢, ¢J= o (4~10) 울 만족한다는 것을 뜻한다. 이 결과를 이용하면 장연산자 #1 변화를 유 도하는 발생원 (4-4) 는 G,=Hd(J,, (¢aµ8¢-寧 ¢) =fd(J ,, ¢ aµ8¢ (4-11) 로 쓸 수 있다. 따라서 칭연산자 ¢의 변화는 발생원 (4-11) 에 의해서
뇽¢= -i [ ¢, G9] (4-12) 로 결정되며, 이 식은 장연산자 ¢의 성분들 사이의 동시 교환관계를 결정 한다. 이들 교환관계에 대해서는 다음 절들에서 자세히 디루겠다. (4-10) 식에 의해서 연산자 ¢는 교환관계 (commuta t io n rela ti on) 로 정의되는 장연 산자라는 것을 알 수 있으며, 이러한 장이론은 보즈. － 아인슈타인 통계 (Bose-Ein s te i n s tati s ti cs) 를 만족하는 입자들의 운동을 기술한다. (2) 그래서 이러한 장연산자를 보즈. 장 (Bose fi eld) 이라고 부른다. 이들 보즈 장이 만 족하는 장방정식과 동시 교환관계의 구체적인 형태는 싱수행렬 aµ 의 성질 에 따라달라진다. 허수 대칭행렬 sµ 에 해당하는 장연산자 #가 만족하는 장방정식은 2sµ 磁=a¢장i v= 경장굽 V (4-13) 로표현된다. 따라서 장연산자 ¢와그변화량 싸는반교환관계 {8¢,¢}=0 (4-14) 룰 만족한다. 이 결과를 이용하면, 발생원 (4-4) 는 G¢ 댜k ( J사'S µ8
구체적인 형태는 각 양자 징이론울 다를 때 설명하겠다. 동시 반교환관계로 정의되는 양자 장이론은 페르미-디락 통계 (Ferm i-D i ra c s t a ti s ti es) 를 만족 하는 입자들의 운동을 기술하기 때문에, 이러한 장연산자를 페르미 장 (Ferm i fi eld) 이라고 부른다. (2 ) (4-13) 과 (4-14) 식은 포텐셜 V(x) 가 장연 산자 ¢의 짝함수가 되어야 한다는 것을 의미한다. 장연산자 ¢와 #는 서로 독립된 자유도를 기술하는 연산자이기 때문에 [0¢,r/J] =O=[orp ,¢] (4-17) 의 교환관계가 성립해야 한다. 장방정식 (4-3) 에서 시간에 대한 도함수 부분을 따로 쓰면, 2A0aox=—창 a—xV -2Aia a (4-18) 로 된다. 일반적으로 (4-18) 식에 나타나는 모든 장연산자의 성분들이 독립 된 운동변수 (d yn a mi cal va ri able) 인 것은 아니다. 제 1 장에서 설명한 바와 같이 , 독립된 운동변수들은 한 순간의 물리계의 상태를 완전히 결정하며 (양자 장이론의 경우에는 독립된 장연산자들의 고유값이 그 순간의 계의 상 태를 결정한다)， 이들 운동변수들의 다음 순간의 값들은 시간에 대한 미분 방정식인 운동방정식에 의해서 결정된다. 따라서 물리계의 독립된 운동변 수의 수(자유도)는 그 계의 운동방정식의 수와 같다 . 장방정식 (4 - 18) 의 성분 중에서 시간에 대한 미분방정식이 운동방정식이며, 그 수가 계의 독립 된 운동변수의 수와 같다. 이들 운동방정식을 제의한 나머지 방정식들을 구 속방정식 (cons tr a i n t e q ua ti on) 이라고 부르며, 이들은 시간에 대한 도함수 를 포함하지 않는 방정식이다. 이 사실을 이용하면 여러 가지 가능한 장이 론들을, 행렬 Ao 의 성질에 따라 다음과 같은 세 가지 유형으로 분류할 수 있다. (I ) 상수행렬 Ao 의 역이 존재하는 경우 : 모든 장함수의 성분들이 독립
된 운동변수이다. 스핀 - 1 / 2 인 디락 장 (D i rac fi eld) 이론이 이 경우에 속 한다. (Il ) 상수행렬 Ao 의 역이 존재하지 않지만, 변수들 사이에 충분한 관계 식이 존재하는 경우 : 장방정식 중에서 시간에 대한 도함수를 포함하는 방 정식들이 운동방정식이며, 시간에 대하여 미분되는 장성분들이 독립된 운동변수이다. 그러나 구속방정식의 수가 충분하여 장성분들을 유일하게 결정할 수 있는 경우이다. 스핀 -0 인 스칼라 장이론 (scalar fi eld th eo ry) 과 질량이 영이 아닌 스핀 -1 인 벡터 장이론 (vec t or field th eo ry)이 이 경 우에 속한다. (III) A0 의 역이 존재하지 않으며, 변수들 사이의 관계식이 충분하지 않 은 경우 : 이 경우에는 장방정식이 장성분들을 유일하게 결정하지 못하 여, 자유도가 남아 있게 된다. 질량이 영이고 스핀 4 인 게이지 장이론 (g au g e fi eld th eo ry)이 이 경우에 속한다. 게이지 이론에서는 변수들이 완전히 결정되지 않기 때문에 게이지 지유도(g au g e fr eedom) 가 있는 경 우 0] 다. 이들 각 경우에 제 3 장의 결과를 적용하면, 가능한 여러 가지 장방정식들 과 각 경우의 스핀과 통계 사이의 관계를 얻을 수 있다 . 이에 대한 자세한 논의는 슈빙거의 논문들(I)과 버그만과 위그너의 논문 (3) 에 다루어져 있다. 여기서는 자주 사용되는 기본적인 몇 가지 양자 장이론들을 소개하겠다. 4.2 스칼라장이론 양자 장이론이 로렌츠 불변이기 위해서 장함수는, 미세 로렌츠 변환에 대 굴回 祖)= Lx(x)=[ 거 -€µ11Sµ11]x(x) (4-19)
로 변환되어야 한다는 것을 제 3 장에서 보았다. 장함수들의 로렌츠 변환에 대한 성질은 이 변환식에 의해서 결정된다. 3- 차원 공간좌표의 회전변환에 대하여 1- 가함수 (sin gle -valued fun c ti on) 로 변환하는 함수를 텐서 (ten sor) 함수라고 하고, 2-가 함수 (double-valued f unc ti on) 로 변환하는 함수를 스피 너 (s pi nor) 함수斗고 한다 .(4) 장함수의 이러한 성질도 연산자 sµ” 에 의해서 결정된다. 텐서 함수로 기술되는 텐서 장이론 중에서 가장 간단한 경우가 Sµ=O 에 해당하는 스킬라 장이론이다. 로렌츠 스칼라인 헤르미샨 장연산자를 (x) 라 하면, (x~ Sµ11=0 인 경우의 (4-19) 석을 만족한다. 이 스칼라 장연산자를 (4-2) 식의 x(x) 로 생 각할 경우, 반대칭 싱수행렬 aµ 롤 만들 수 없다. 따라서 (4-2) 식에 나타나 게 될 8% 와 결합하여 스칼라 항을 만들 수 있는 벡터 장함수 µ(x* 도 입해야한다. 죽, 스칼라 장이론의 라그란지안을 (4-2) 식의 형태로 표현하기 위해서 장연산자로 x=(
상호작용이 없는 자유 장이론의 경우 포텐셜 항은 V( cp)=강짜 ¢2 랑釋 (4-22) 로 쓸 수 있다. 자유 스칼라 장이론의 장방정식은, (4~8) 식에 의해서 o8µµ< /¢Jµ= =¢mµ 2¢ (4-23) 로 표현된다. 이 식의 다섯 개의 성분들은 운동방정식과 구속방정식으로 나 눌 수 있다. 운동방정식은 시간에 대한 도함수를 포함하는 8 。¢=¢。 (4-24) a。 o= m2¢-a; 섬 이며 , 나머지 세 개의 방정식은 공간 같은 곡면 (J내에서 장함수들을 연결 하는 구속 조건이다. 따라서 이 계의 독립된 운동변수는 ¢(x). 2} ¢。 (x) 이 며, 나머지 세 개의 성분은, 구속방정식 섬=참¢ (4-25) 에 의하여 유일하게 결정된다. (4-23) 식의 다섯 개의 방정식을 조합하면 자유 스칼라 장이 만족하는 클레인-고든 방정식 (Klein - Gordon equ a ti on ) (-a 껑µ +m2)¢(x)=O (4-26) 으로 된다. 이 식은 시간에 대한 2 계 미분방정식이며, 라그란지 방식의 작 용원리로부터 얻는 오일러-라그란지 방정식이다. (4) 스칼라 장연산자의 일반적인 변화를 유도하는 발생원은 G 규fd 야 (寧- 霞¢) 단fd 3x( 寧-釋) (4-27}
로 쓸 수 있다. 이 식은 이 계의 독립된 운동변수는 ¢(xW ¢0(x) 이며 , 이 둘은 서로 표준공액 (canon ica l con j u g a t e) 의 관계에 있다는 것을 의미한다. 서로 공액관계에 있는 변수들에 대하여 Gi7 ~ 대칭되게 표현하였으므로, 장 연산자의 변화는 군 ¢(x)=[¢(x), G9] (4— 2 8) 끌f강 x'[ ¢(x),¢ (x') 綴 (x ' ) ― 0(x ') 8 ¢(x')] 로 결정된다. 이 식이 성립하기 위해서는 장연산자들 사이에 동시 교환관계 [[ ¢¢0( x(x),') , ((xx'))]]xx••== xxo o'= ' = 0 i o( x-x' ) (4-29) 이 만족되어야 한다는 것을 쉽게 보일 수 있다. 여기서 싸 (x) 가 다른 장연 산자와 교환 가능하다는 (4 - 10) 식을 이용하였다. ¢o( x ) 의 변화를 생각하 면, 나머지 동시 교환관계 [ ¢0(x), ¢0(x')]xo=xo '= 0 (4-30) 를 얻는다. 운동변수가 아닌 장성분들 사이의 교환관계는 위의 결과와 구속 방정식 (4-25) 를 이용하여 유도할 수 있다. 예를 들면 [¢°(x), ¢i( x' )]x0=x0'= —ia; a(x— x') 이 된다는 것을 쉽게 보일 수 있다. 교환관계 (4-29) 와 (4 - 30) 은 양자장 x가 어떤 양자적인 연산자인가를 결정하는 관계식이다〔양자 역학적인 계의 경우, 교환관계 (2-40) 이 물리량들이 어떤 양자적인 연산자로 표현되는가 를 결정한다〕． 장연산자의 이러한 성질을 이용하면, 교환관계 (4-29) 와 (4 -30) 으로 정의되는 장이론은 보즈-아인슈타인 통계를 만족하는 입자들의 운동을 기술한다는 것을 보일 수 있다. (2) 자유 스칼라 장이론의 에너지급녓펑: 텐서 TµU는 sµv=o 라는 사실과
(4-20) 식의 싱수행렬 aµ 를 사용하여 계산할 수 있다. 이들을 (3 - 23) 식에 대입하면, 에너지준둠링: 텐서는 yµv = g µ v !R-i{ xa 때 u)X- 8{uxaµ}x] (4-31) 로 표현된다. 이 결과를 이용하여 에너지웁돔-량 연산자와 각 운동량 연산 자, p o= 紅f강 x[(¢°)2_ ¢v2¢+ m 방] Pk= f강 X ,P 0ak ,P (4-32) ]k t=fd 3 浮(국-파)¢ 와 같은 물리량에 해당하는 연산자들을 계산할 수 있다. (4-32) 식을 이용 하여, 로렌츠 변환의 발생원과 칭연산자 사이의 교환관계를 계산하면 [[ <¢/>,AJki ] ]== —- iiO (kx < k P al-Xlak)
4.3 벡터 장이론 로렌츠 변환에 따른 장함수들의 변환식 (4-19) 에서 장함수의 성분들이 4 -차원 시공간에서의 벡터처럼 변환하는 경우, 이 장함수를 벡터 장 (vec t or fi eld) 이라고 한다. 헤르미샨 연산자인 4- 벡터 장을 ¢µ(x) 라고 하자. 벡터 장이론의 라그란지안에는 계수 (rank) 가 2 인 텐서처럼 변환하는 연산자 탸가 나타나기 때문에, 이들과 결합하여 스칼라 양을 만들 수 있는 텐서 함 Gµu( 짜를 도입해야 한다. 벡터 장이론 중에서 가장 간단한 경우는 반 대칭 텐서인 GµU 를 사용하는 경우이다. 반대칭 텐서 장함수 GµU 를 사용한 자유 벡터 장이론의 라그란지안은 IP=½(¢11aµcµ11-G µ11 祐)그f¢µ
서 운동변수 ¢h 와 GkO 의 함수로 완전히 결정된다는 것을 의미한다• 장방정식 (4-35) 중에서 운동방정식은 aa 。。' cP kko= =G -o,m. + 밖ak-¢ 。 8IGkI (4-37) 의 여섯 개이며, 네 개의 종속변수들은 구속방정식 mGk21¢=o =絲akG l-k O絲 k (4-38) 에 의해서 유일하게 결정된다. 따라서 10 개의 장성분들은 같은 수의 장방 정식에 의해서 완전히 결정된다. 발생원 (4-36) 에 나타니는 독립변수들은 스핀 -1 인 계의 스핀의 세 성분 울 기술한다. 앞에서와 같은 방법으로, 장연산자들 사이의 동시 교환관계 는
[[4.4 전자기 장이론 전자기 장이론은 질량이 영인 벡터 장이론이다. 앞 절에서 설명한 벡터 장이론의 라그란지안에서 질량을 영으로 놓으면, 전자기 장 Aµ(x) 로 이루 어진 자유 장이론의 라그란지안 g =慕 AV8Eµ-Fµua4) 나 -FµFµv (4-4oa) 를 얻는다. 최근의 문헌에서는 이 라그란지안과 물리적으로 동등한 요 = -½Fµ(aµ ,4-a Aµ) 나 FµFµv (4-4ob) 를 전자기 장이론의 라그란지안으로 택하는 것이 보통이다• 라그란지안 (4-40) 을 이용하면, 자유 전자기장의 장방정식 Fa1µ1vF=µ1 1a갑= 0 L- avAµ (4-41} 과 장함수의 변화를 발생하는 발생원 GA= 남d 6o(Ak8F0k ― F°k8Ak) (4-42) 롤 얻을 수 있다. 발생원 (4-42) 는 장연산자 Aµ 와 Fµ )I에 대해서 대칭이 되도록 표현한 라그란지안 (4-4oa) 로부터 얻은 발생원이다. 자유 전자기 칭이론의 장방정식 (4-41) 은 운동방정식 aa값 。 F hok== a - 갑a。i F+ 1 Fk ok (4-43) 팍급방성여
Fk1= a:갑 11_ 8 싸 k (4-44) akF0k=O 으로 나눌 수 있다. 운동방정식 (4-43) 은 변수 Fkl 과 Ao 가 종속변수라는 것을 의미하는데, 구속방정식 (4-44) 는 이들 중에서 Fkl 은 유일하게 결정 하지만 Ao는 결정하지 못한다. 이것은, 질량이 영이 아닌 경우의
(4-44) 식의 두번째 식은 변수 FOk 의 세로성분(l on gitu d i nal comp o nent) 이 영이라는 것을 의미한다. 따라서 운동변수 FOk 는 세 개의 성분으로 이 루어전 것으로 보이지만, 실제로는 두 개의 가로성분 (tran severse comp o- nen t)만으로 이루어져 있다. 전자기 장이론의 순수한 독립변수를 가려내기 위해서 장함수 Ak 를 세로성분과 가로성분의 합으로 분리하는 것이 편리하 다. 일반적인 벡터의 세로성분은 스칼라 함수의 기울기 (gr ad i en t)로 표현할 수 있고, 가로성분은 벡터 함수의 컬 (curl) 로 나타낼 수 있다. 따라서 (4 -45) 식의 게이지 변환은 장함수 A 려 세로성분만을 변화시킨다는 것을 알 수있다. 전자기 칭이론의 운동방정식을 가로성분과 세로성분으로 나누면, Ak 에 대한운동방정식은 aoA f; =a마 。 (4-46) a 값 lI=Ff 로 쓸 수 있다. 여기서 첨자 L 은 세로성분을, 그리고 T 는 가로성분을 나 타낸다. 이 식의 첫번째 식은 게이지 변환으로 흡수할 수 있다. 다시 말하 면, 게이지 자유도를 나타내는 매개변수 A 를 Af =a ,.A, A 。 =8 。 A 의 조건이 만족하도록 택하면, (4-46) 식의 첫번째 석은 저절로 만족된다. 따라서 전자기 장이론의 독립된 운동변수는 AI(x) 와 F0(x) 의 네 개이다. 장 연산자 Ak 를 가로성분과 세로성분으로 분리하여 A,.= AI+ Af = AI+ a,. /\ 와 같이 나타내고, (4-42) 식에 대입하면, 전자기장의 변화를 유도하는 발 생원은 GA=½f d a 。 (A!8FOk_ F0k8Af) (4-47)
로 되어서 가로성분들만으로 표현된다는 것을 알 수 있다. 이 발생원을 이 용하여 운동변수들 사이의 동시 교환관계를 계산하면 [[AF0I(,x.()x,A),T (AxT')](xx'o)]=xxoo=·x=o ·0 = = i [[8F1 01t, . (8x(),x F-0x1( 'x)'F)]x o=xo· (4-48} 의 결과를 얻는다. 여기서 [8%5(x- x' )F는 8k18(x- x')의 가로성분을 나 타낸다. 임의의 벡터의 가로성분은 AI=(8kl _j福) A1 로 나타낼 수 있으므로, (4-48) 식의 마지막 교환관계는 [F0(x), AT(x')]xo=xo·= i.[감 福] 8(x_ x') (4-49) = t.[8 f8 ( x_x ')- 忍禪] 로 나타낼 수 있다. (4-49) 식의 오른쪽의 두번째 항은 장함수 A,.(x) 의 세 로성분에 의한 영향을 나타내며, 이것은 장함수 A1r(x 펴 세로성분은 쿨롱 포텐셜 (Coulomb po t en ti al) 과 밀접한 관계가 있다는 것을 의미한다. 라그란지안 (4-40) 이나 장방정식 (4-41) 에는 전자기 장이론의 독립된 운동변수가 A,.(x) 와 F0(x 펴 여섯 개인 것처럼 나타나 있다. 그러나 위 에서 본 바와 갇이, 전자기 장이론에 존재하는 게이지 자유도 때문에 실제 운동변수는 AI와 F뿐 의 네 개뿐이다. 그래서 전자기 칭이론을 양자화할 때에는 이를 독립된 운동변수만이 양자화되도록 해야 한다. 그렇지 않으면 실제보다 더 많은 자유도가 있는 것 같은 잘못된 결과를 주게 된다. 전자기 장이론과 같은 게이지 이론의 양자적인 계산을 할 때에는, 게이지 자유도가 양자화되지 않도록 이들을 제거하는 조건을 부과해야 한다. 이렇게 게이지 자유도를 제거하는 조건을 게이지 고정조건(g au g e fixing con diti on) 또는 게이지 조건 (ga ug e con diti on) 이라고 한다. 이러한 게이지 조건을 부과하는
방법과 게이지 장이론의 양자적인 계산을 하는 방법에 대해서는 9.3 절에서 자세히 설명하겠다. 4 . 5 디락 장이론 (D ir ac field the ory )0 > 라그란지안 (4-2) 에서 상수행렬 Aµ 가 허수 대칭행렬인 경우의 장함수 ¢ 는 반교환관계 (4-14) 로 정의되는 스피너 장함수이다. 이 경우 Aµ 국2g 로 정의되는 실수 대칭행렬 /를 사용하면, 라그란지안 밀도는 요=구묘絲 -8µ¢랴 )- V(tf; ) (4-50) 로 쓸 수 있다. 반교환관계 (4-14) 를 사용하면, 장연산자의 변화를 유도하 는발생원은 G -1국/ d6 。 ¢a°8¢ (4-51) 로 표현된다. 이 발생원을 이용하여 장연산자 ¢의 변화량을 계산하면 靜上 )=[¢a(x), f죠당 ¢b(x'){a°8#(x')}b] =>fd3x' {
아 만족되어야 한다. 장함수 #(차는 헤르미샨 연산자이므로, (4-53) 식의 왼쪽은 영보다 크거나 같은 양이 되어야 한다. 따라서 상수행렬 ao 의 모든 행렬요소는 영보다 크거나 같은 값을 가져야 한다. ao는 실수 대칭행렬이 므로, 장성분 'P a 를 선형벼화하며 . ao 누 항상 단위행렬로 만들 수 있다. 그 래서 상수행렬 ao 를 a0=l (4-54) 로 태하면, 장연산자들 사이의 동시 반교환관계는 {
론은 질량 m 인 상대론적인 자유입자의 운동을 기술해야 한다. 그러기 위해 서 디락 방정식 (4-57) 은 p2= —( p o )2+p탸 짜= O (4-59) 의 관계를 만족하는 평면파 풀이를 가져야 한다. 이러한 조건을 만족하기 위해서는 —: #= (+aia ;+ m/ 3)2
의 반교환관계를 만족한다. 반교환관계 (4-63) 을 행렬 rµ 의 정의식으로 랙 할 수 있으며, 이 상수행렬도 디락 행렬이라고 부른다. 이 행렬을 사용하 딴 자유 디락 장이론의 라그란지안은 £ =망 ¢r% 일링 m
생원과 디락 칭연산자 #와의 교환관계를 계산하면 [[<싸/J ,,Pr 기1]== -- ii a [µX
g =}¢(1a 껑µ- m/ 3) 三 -Fµ u (84- 84) 나 -Fµ11Fµv+ Aµjµ (4-72) 로 쓸 수 있다. 이 식의 처음 세 항은 자유 헤르미샨 디락 장과 자유 전자 기장의 라그란지안이며, 마지막 항은 디락 장과 전자기장 사이의 상호작용 을 나타내는 항이다. 이 상호작용 항은 로렌츠 불변성을 만족하는 상호작용 중에서 가장 간단한 형태이며, 그래서 이 상호작용을· 최소결합(mini mal cou pli n g)이라고 부른다. 여기서 jP( x}i :-디 락 장으로 이루어진 벡터 함수 이다. 디락 장으로 만들 수 있는 벡터 장함수 중에서 가장 간단한 것은 jµ=
고 있으므로, 가장 간단한 경우의 디락 장
G = fd3xj° (x ) 8 /\ (x) (4-80) 로 표현된다. 디락 장의 게이지 변환 (4-76) 은 발생원 G^ 에 의해서 8
전하는 측정 가능한 물리량이기 때문에, 디락 장연산자를 전하연산자 Q 의 고유상태가 되도록 표현하는 것이 편리한 경우가 많이 있다. 8 개의 성분 을 갖는 디락 장 #（짜를 2- 차원 내부공간의 성분을 구체적으로 나타내어
로 표현된다. (4-88) 식의 공액 디락 장 efi (x )i근 #(x) 가 헤르미샨이 아니기 때문에, 디락 장 #와는 독립된 장연산자라는 점에 유의해야 한다. 라그란 지안 (4-87) 또는 (4-88) 에서 디락 장의 변화를 유도하는 발생원은 G~:::: ifd 宣 (x) 神 (x) (4_Ro\ 로 표현되며, 이를 이용하여 디락 장연산자들 사이의 동시 반교환관계를 계 산궁}면 {{< r/pJ(a x(x) ,) ,
변환의 표현 (re p resen t a ti on) 을 수행하는 수행자 (carr i er) 로서 장함수들을 도입 하는데 , 이 방법은 특히 여러 가지 스피너 장함수들의 성질을 이해하는 데 편리하 다. (l) 제 3 장위 참고문헌 l. (2) C. ltz yk son and J. -B. Zuber, Quan tu m Fie l d Theory , McGraw-Hi ll (New York) , 19so. (3) V. Bergm a nn and E.P . W igne r, P roceed ing s of Nat. Acad, Sci. 브 , 211 (1946) (4) P. Ramond, F神 ld Theory ; A Moder n Pri me r, 2nd ed., A ddis o n-W esley , 1 989 ; L.H. Ry d er, Q uan tu m Fie ld s Theory , Cambrid ge Univ e rsit y Press(London), 1985. (5) C.R . Hag en and L.P.S. Sin g h, Phy s. Rev. 혼 , 3378 (1973) . [문 X 1 포텐셜 항이 V=xBx 안 경우를 생각하여, 장방정식 (4-9) 와 (4-13) 이 각각 교 환관계 (4~10) 과 반교환관계 (4-14) 를 의미한다는 것을 보이라. 2 자유 스칼라 장이론의 동시 교환관계 (4-29), (4-30) 과 장방정식 (4 - 23) 을 만 족하도록 칭연산자 ¢(따와
에 대하여 불변이라는 것을 보이라. 7 (4-49) 식을 유도하라. 8 디락 행렬 (4-61) 의 고유값은 士 1 이며, 이들은 짝수 계수 (rank) 행렬이라는 것 울증명하라. 9. 디락 장이론의 라그란지안이 로렌츠 불변이기 위해서, 장연산자는 (4-68) 과 갇 이 변환해야 한다는 것을 보이라. 10 (4-69) 식의 SµU가 각운동량이 만족하는 교환관계 (3-39) 식을 만족한다는 것을 보 0] 라. 11 (4-69) 식과 (3-23) 식을 이용하여 자유 디락 장이론의 에너지쉼녓링연산자 P 따 각 운동량연산자 J µV를 계산하고, 이들이 교환관계 (4-70) 식을 만족한다 는것을보이라.
제 5 장 그린 함수와 그린 발생원에 대한 함수미분방정식 입자들의 성질이나 그들 사이의 상호작용은 주로 충돌현상을 통해서 실험 적으로 결정된다. 양자역학적으로는 충돌 전의 입자들의 상태 벡터와 충돌 후의 상태 벡터 사이의 스칼라 곱 (scalar p roduc t)으로 표현되는 변환함수 를 이용하여 충돌현상을 기술할 수 있다. 양자장이 입자를 생성하거나 파괴 하는 연산자로 작용함으로써 입자의 운동을 기술한다는 것을 제 3 장에서 보 았다. 따라서 여러 개의 입자들로 이루어전 계의 상태는 각 입자에 해당하 는 장연산자를 전공상태 10 >에 연산하여 구성할 수 있고, 충돌현상을 기술 하는 변환함수는 여러 가지 장연산자들의 곱의 전공기대값 (vacuum exp ec ta tion value) 으로 나타낼 수 있다. 이러한 장연산자들의 곱의 진공기 대값을 그린 함수 (Green's fun c ti on) 라고 한다. 따라서 물리계의 성질이나 그들의 시간에 따른 변화는 그린 함수를 이용하여 기술할 수 있다. 이 장에 서는 이들 그린 함수들을 양자적인 작용원리를 이용하여 정의하고, 또 그들 울 계산하는 방법을 찾고자 한다. 여러 가지 그린 함수들 중에서 충돌현상 을 기술하는 데 편리한 함수는 장연산자들의 시간군커곱(tim e-ordered p roduc t)의 전공기대값인데 , 이러한 그린 함수를 인과적인 (causal) 그린 함 수라고 한다. 주어진 계에서 가능한 모든 그린 함수들을 얻어낼 수 있는 범
함수 (fun c ti onal) 를 그 린 발 생 원 (ge neratin g func ti on al for Green's func - ti ons) 이라고 한다. 여기서는 이러한 그린 발생원이 만족하는 함수미분방정 식을 양자적인 작용원리를 이용하여 유도하고액 이 방정식의 해를 구하는 방법에 대해서는 다음 장들에서 다루겠다. 이러한 그린 발생원을 구성하기 위하여, 앞 장에서 언급한 바 있는 함수 미분 <2>( fun c ti onal diff eren ti a ti on) 을 자세히 정의할 필요가 있다. 범함수 F[ rp (x) ］의 함수미분은 함수 rp (x) 의 무한히 작은 변화 rp( x~ rp( x)+ 8rp( x) 에 의해서 생기는 F[ rp]의 변화로 정의한다 : 8F[rp] =F[rp + 8rp] -F[rp] =!~뭉rp (x). 이 식의 오른쪽개 있는 \잘경물 범함수 F[ rp]의 rp (x) 에 대한 함수적인 도함수(fun c ti onalde ri va ti ve) 라고 한다. 이 정의식을 이용하면, 함수미분 이 보통 매개변수에 대한 함수의 미분이 만족하는 여러 가지 성질을 모두 만족한다는 것울 보일 수 있다. 죽, a, b, c 가 함수 rp (x) 에 독립인 임의의 함수이면, 함수미분은 8rp8( x ) a=O, 誌 aF[ rp ]+bG[ rp]}=훌붉붕당, 誌 F[ rp ]G[ rp]}＝훑텁 G[ rp ]+F[ 아櫓惡 誌 F[G[ rp]]=f
5.1 그린 함수와 그린 발생원 양자 장이론으로 기술되는 물리계의 상태는 공간 갇은 곡면 6 에서 주어 지는 장연산자 x 의 고유값들로 나타낼 수 있고, 따라서 이러한 물리계의 상태를 상태 벡터 |x',a> 로 기술할 수 있다는 것을 앞에서 보았다. 양자적 인 작용원리에 의하면, 이러한 상태들 사이의 전이전폭(tr ans iti on amp li- tud e)
8<0, o:』 0,
鬪認' 8陶g 8g 로 나타낼 수 있는데, 장방정식에 의해서 福8!.l =O 이므로, 이 변화량은 영이다. 따라서 매개변수 g의 변화에 의해서 생기는 전공전이진폭의 변화는 Og < 0, 6. .. J0 ,6-m > = i < 0, (J. .. ,fd4x¢ (x)J( x ) I0, 6-.. > og 로 쓸 수 있다. 이 식의 양변을 8g 로 나누면, 전이진폭의 舒 ]l 대한 일차 도함수는 읊
을 의미하는 합의 약속을 사용하였다. (5-5) 식의 오른쪽에서 공간 같은 곡 면 6xo 에서의 행렬요소 < rp'' (Jx olF(x)Irp , ax•> 의 변화량은 영이다. 왜 냐하면 임의의 연산자 0 에 대하여 < (J,。| o l(Jo > = < a 。| ug- 1 ug a ug- 1 ug1 (Jo > 의 관계가성립하여, 8g < rp', (Jx olF(x)lrp ,ax• >=O 으로 되기 때문이다. 따라서 (5-5) 식의 오른쪽에 작용원리를 다시 한번 적 용하면몰, 이 0,식 (J;,을. IO다, a-음.. >과 =같 i이2f d쓸4x수 < 있0, 다(JO :O1 ;::d4x'F(x')l rp', ax• > + i2f X d <4x r p< ', aO,x(J• ;,I. FI rp('x, a)xlorp > ,a
--정/in < O,a. . l0,<1 -.. > = ifd4x 1d4x2·· ·d4xn x < O,a. . l T(F(x1)F(x2)… F (xn))I0,<1- oo > 로 된다는 것울 보일 수 있다. 위의 결과를 이용하여 전공 전이전폭
해석하겠다. 그러기 위하여 (5-7) 식에서 g= l 로 놓으면 진공 전이전폭은
*이 식과 (Hl) 식으로 정의되는 그린함수는, 정확하게 이야기하면, ¢들의 시간-순서곱의 서로 다른 상태 |0,(J -.. >와 |0,(J+ .. >에 대한 행렬요소이다. 그러나 이것을 전공기대값으로 부르는 것이 관례이다.
며, 관례대로 진공기대값에 허수 i들을 곱하여 그린 함수를 정의하였 다. 또 (5-10) 식으로 정의한 그린 함수 Dn(xI, … Xn) 은 의부근원이 없 는 경우 (J (x)=O) 의 그린 함수라는 점에 유의해야 한다. (5-10) 식으 로 정의되는 그린 함수는 Dn(xI,… , Xn) = i [n/2I~정 ;:.::::)0) |0,6-OO >l=O =i [nt 2 I < T((xi) < />(x2)… < />(xn)) >J=O (5-11) 로 쓸 수 있으며, 이들 그린 함수는 규격화된 (normal i zed) 진공기대값 으로 정의된다. 이 정의식에서 계수 i [n/2} 은 관례에 따라 포함한 것이며, 저자에 따라서는 이 계수를 다르게 정의하는 수도 있다. 이 그린 함수 D n( x1,X2 , … ,Xn 冷 n 점 함수 (n- po i ntfun c ti on) 라고 부르기도 한다. (5-10) 식과 (5-11) 식은, 자체 상호작용하는 스칼라 장이론의 모든 가능 한 인과적인 그린 함수를 전공 전이진폭
*그린 함수 중에는 장연산자의 시간-순서곱의 진공기대값이 아닌 다른 방법 으로 정의되는(예를 들면 와이트만 함수 (W ig h tm an fun c ti on) 는 <¢ (xl)¢(x2) … 로 정의된다) 것도 있다. 그러나 이러한 그린 함수들은 인과적인 그린 함수의 해석적인 연결 (anal yti c con ti nua ti on) 로 나타낼 수 있다.
< O,6OOIO,6-OO >)J= A< O,6OOI Te if d4 자 (X)/(x)IO' (J_ .. 건 로나타내고
로 표시하겠다. 또 기호롤 간략하게 하기 위해서 , 혼동할 우려가 없는 경우 에는 진공상태를 단순히 |0> 로 표시하겠다. 죽, 전공 전이진폭을
8,W=f d4x< &P >=fd 4x 아 (x)> 8f (x) (5-14) 로 쓸 수 있다• (5-14) 식을 J (x' ）에 대해서 다시 한번 변화시키면 81,<8,P>=8, 겔 = ifd4x' [< T(&P(x)81,P(x'))>_ < 認 > <8l'P >] (5-15) 로 된다는 것을 쉽게 보일 수 있다. 이 결과로부터 o,, < ¢(x) > = ifd4x'[ < T( ¢(x) ¢(x')) > oJ(x ') —< ¢(x) > < ¢(x') > oJ(x ')] (5-16) 의 관계를 얻는다. 장연산자 ¢(따는 에너지운동링울 생성하거나 파괴하는 연산자이기 때문에 의부근원을 없애면 기대값 < ¢(x) ＞는 영이 된다는 사 실을 이용하면, (5-16) 식은 &갑 (x) > l1=0= f바 'D i( x-x')8J (x') (5-17) 의 관계를 의미한다. 여기서 D2 는 2- 점함수 D2(x,x' ）이며 , 의부근원이 없 울 때에는 로렌츠 불변성에 의해서 시공간 4- 벡터의 차이만의 함수가 되어 야 한다는 사실을 이용하여 표시하였다. 이 2- 점함수를 전파인자 (p ro p a g a t or) 라고 부르는데, 스칼라 장이 기술하는 입자의 운동을 결정하 는 중요한 함수이다. 이제 이 전파인자의 성질에 대해서 자세히 알아 보자.
5 . 2 전파인자 (2- 점함수) 앞에서 정의한 인과적인 그린 함수의 성질을 이해하기 위해서, 자유 스칼 라 칭이론의 2 정함수를 생각해 보자. 라그란지안 (5-9) 에 의해서 유도되 는장방정식은
에 의해서 D2(x-x')= ~미 雲1 )0？ ~IO,cr1 > 으로 쓸 수 있다 . 이 함수의 경계조건은 시각이 XO~61 과 XO~62 인 접에 서 주어질 것이므로, 이러한 점 근방에서의 전파인자의 형태를 생각하면 D2(X ― x ' 퍼 경계조건을 얻을 수 있다. 그러기 위해서 시간좌표의 이동을 유도하는 변환 U를 생각하자. 좌표이동을 나타내는 변환은 U= l+ iGx , Gx= c,,P µ 로 표시되므로, 유한한 시간 x °PJ-큼 이동시키는 변환은 U= e-i:x o P • 로 쓸 수 있다. 따라서 (2-12) 식을 이용하면, 장연산자 (x~ ¢(x)= eiP O (:, cO-%(t)e -iP O(:, cO-t) 로 나타낼 수 있다. 여기서 t는 임의의 고정된 시각이며, F는 에너지 연 산자이다. 전파인자의 정의식을 생각하면, 시긱이 XO~62 인 근방에서는 x~ 62 ; D2 (x-x')= i< (t)e -i(P -P•vac)(Xo-t) (x') > 로 쓸 수 있다. 여기서 P0vac는 진공상태의 에너지 고유값이며, 따라서 (P0-P0vac~ 영보다 작은 고유값을 가질 수 없다. 따라서 야 근방에서 XO 의 함수로 본 전파인자 D2 는 영보다 큰 전동수를 갖는 파동들의 모임으 로 구성되어야 한다. (I) 마찬가지 방법으로, 곡면 61 근방에서는 x~ 61 ; D2(x-x')= i< (x')ei (P •-P•vac)(Xo-t) (t) > 로 쓸 수 있으며, 이 함수는 영보다 작은 진동수를 갖는 파동들만의 모임으 로 구성되어야 한다는 것을 의미한다. 따라서 그린 함수 Di (x-x'~ 본
{Xx°o-_xx0o'-'-->->+ - CcO o ::영영보보다다작큰은진진동동수수 (5-22) 의 파동들로 구성된다. 이것이 미분방정식 (5-21) 에 대한 경계조건이다. 이 경계조건은 시간군곤서곱으로 정의한 인과적인 그린 함수의 정의식 D2(x-x')={ii<< ¢¢((xx'))¢¢((xx')) >>,, xxoo<>xxoo'' (5-23) 과도 일치하는 결과이다. 이 결과는 칭연산지를 후리에 전개하여 양자화하 는 보통 교과서둘의 방법을 사용해서도 쉽게 확인할 수 있다. 이것을 보기 위하여 자유장의 전파인자를 D정 (x-x')= fd 4 p e i P•
(－강+짜 )G(x-x')=O 의 관계를 만족하기 때문에, 서로 다른 경계조건을 만족하는 (5-21) 의 해 가 된다. 경계조건 (5-22) 에 해당하는 적분은, 적분되는 함수에서 p o 를 po2_ _.p o2 + iE, E >O 로 대치하여, 분모에 허수 부분을 도입하면 얻을 수 있다. 따라서 자유 스 칼라 장이론의 전파인자는 D 섬 (x) ＝志fd 3 p e i P•xf d p °-굶은-i下PO亡x 0玉 . 으로 쓸 수 있다. 여기서 p·에 대한 적분을 계산하면 D 훈(x) ＝급f#운[ 0(x0)e 기 wXo+ 0(-xo)eiw Xo] 로 된다. 이 식은 x0 >0 일 때에는 D 정가 영보다 큰 진동수의 파동만으로, 그리고 x0<0 일 때에는 영보다 작은 진동수의 파동만으로 구성되어 있다는 것을 의미한다. 이 식에서 0(x0) 의 계수는 와이트만 함수 <¢(x)¢(o)> 이 며 0(-x0) 의 계수는 <¢(o)¢(x) ＞라는 것을 쉽게 보일 수 있다(문제 2). 이러한 경계조건을 포함히여, 전파안자를 후리에 전개식으로 표현하면 D 접 (x)=*f d 4 p e i P•x p2+」 2_ ic 로 된다. 여기서 적분되는 함수의 허수 부분은 인과적인 그린 함수의 경계 조건을 뜻한다. 이 그린 함수는 특이점을 갖는데, x 궁執간에서의 특이점은 (5-21) 식에서 알 수 있는 바와 같이 이 함수를 생기게 하는 근원 (source) 의 위치를 나타내고, p -공 간에서의 특이점의 위치는 장연산자가 기술하 는 입자의 에너지 고유값을 나타낸다. 일반적으로 그린 함수는 특이점을 갖 는데, 이들이 포함하는 물리적인 정보는 주로 그 특이점에 있다. 또 2- 점 함수의 특이점에서의 잉여수 (res i due) 는 장연산자가 기술하는 입자의 파동
함수와관계가있다. 5 . 3 그린 발생원에 대한 함수미분방정식 장이론으로 기술되는 물리계에 관한 물리적인 정보는 그린 함수로부터 얻 울 수 있고, 이들 그린 함수들은 전공-진공 전이전폭 <010> 서=
詞노 [(－꾼 +m 까志J +A{\ 志)}1 <010>Al= f (x) (5-27) 의 함수미분방정식을 얻는다. 이것이 그린 발생원 <010> 쩌룹 결정하는 함 수미분방정식이다. 이 결과와 (5-24) 식을 이용하면, n- 정함수가 만족하는 함수미분방정식도 유도할 수 있다. 이 결과는 장연산자가 만족하는 편미분 방정식을, 연산자가 아닌 범함수가 만족하는 함수 미분방정식으로 바꾸어 놓은 것이다. 따라서 이 결과를 이용하면 연산자방정식이 갖는 여러 가지 어려움을 피할 수 있어서 편리하다. 일반적인 장이론의 경우에도, 위와 같 은 과정을 이용하여 그 그린 발생원이 만족하는 함수미분방정식을 유도할 수 있다.(1 ,2) 함수미분방정식 (5-27) 을 풀면, 그 결과로부터 (5-24) 식을 이용하여 필 요한 모든 그린 함수들을 계산할 수 있다. 일반적인 경우에 방정식 (5-27) 울 푸는 방법에 대해서는 디음 장들에서 다루겠다. 여기서는 우선 자유 스 칼라 장이론의 경우 이 함수미분방정식을 푸는 방법을 생각해 보자. 방정식 (5-27) 에서 자체 상호작용항을 영 (A=O~ 로 놓으면 (-a2 + m 가 祐< OIO >,=J(x ) < OIO >, (5-28) 로 된다. 이 방정식은 (5-19) 식과 같은 형태의 미분방정식이다. 5.2 절의 과정을 이용하면, (5-28) 식의 해는 } 志 <010> 시=fd 4x'D정 (x-x') J (x')
없을때 전이진폭을
의 결과를 얻는다. 여기서 <01 0>,= <01 0>i , li~ o 이다. 따라서 자체 상호작용하는 스칼라 칭이론의 그린 발생원은 < OIO >) .J= e-f A J d•x fh綜 •et f d• x d•x' J (x)D i (x - x')J(지 (5-35) 로 표현된다. 자체 상호작용하는 스칼라 장이론의 경우 그린 발생원을 J ( x ) 에 대한 닫힌 형태의 범함수를 계산할 수는 없다. 즉, 이 식을 이용하 여 계산한 임의의 그린 힘수는 J ( x ) 에 대한 무한번의 미분을 포함하기 때 문에 , 이 이론은 완전히 풀 수 있는 경우가 아니다. 그러나 그린 발생원 (5 -35) 를 결합상수 A 에 대하여 전개하여, 그린 함수들을 근사적으로 계산할 수는 있다. 이 방법에 대해서는 제 8 장에서 자세히 이야기하겠다. 다른 장이론의 경우에도 갇은 방법으로 계산할 수 있다. 슈빙거의 강의 록 (I )에는 양자 전기역학의 경우가 자세히 다루어져 있고, 루리에 (L uri e) 의 책 (2 ) 에는 스칼라 장과 디락 장이 상호작용하는 경우가 다루어져 있다. 이들 책에는 (5-35) 식에 해당하는 결과로부터, 결합상수에 대하여 전개하여 각 차수에 해당하는 항들을 계산하는 방법도 자세히 설명되어 있다. 다음 장에 서는 완전히 풀 수 있는 모형 장이론을 이용하여, 그린 발생원을 계산하는 방법을 자세히 설명하겠다. 그리고 닫힌 형태로 그 해를 얻을 수 없는 장이 론들의 근사적인 계산 방법에 대해서는 제1PJ-과 제 9 장에서 설명하겠다. 〔참고문헌〕 (1) J. Schwi ng e r Proc. Nat. Acad. Sci. 프, 452 & 455 (1951) J. S chwi ng e r , H arvard Lectu r e Note ( l954) B. Zumi no , J. Math . Phy s, .!_, 1 ( 1960) K. Joh nson, in Part icle s and Fie ld Theory , Brandeis L ectu re Note s , Vol. ll ,
ed. by S. Deser and K.W . Ford, Prenti ce -Hall, 1964 (2) D. Lu ri~. Part icle s and Fie ld s, W ile y and Sons (New York) 1968 C. Nash, Relati vis tic Quan tu m Fie ld s, Academi c Press, 1978 〔문제〕 1 5-2 절에서 D 정의 유도과정을 완성하여 D 웃( x) 를 계산하라. 2 장방정식을 만족하는 자유 스칼러장을 후리에 전개하면 ¢(x) ＝志fd 3 꼴 a( p) eiP •x-iw t + at ( p) e-iP •x+i w t ] 로 쓸 수 있다는 것을 보이라. 또, 스칼라 장의 교환관계 [ ¢0(x), ¢(x')]x = x0·= io( x-x' ) 울 이용하여 연산자 a 와 a t사이의 교환관계를 유도하고, 이 결과를 이용하여 와이트만 함수 D+(x)= < ¢(x)¢(o) ＞와 인과적인 그린 함수 D 응 (x-x')= i< T(¢(x)¢(x')) > 를계산하라 3 질량기 없는(rd- =0) 자유 스칼라 장의 전파인자 D f (x) 를 계산하라. 4 라그란지안 (4 - 88) 으로 기술되는 계의 그린 발생원이 만족하는 함수미분방정식 을유도하라. 5 위 4 번 문제의 해를 (5-35) 식과 비슷한 수준까지 계산하라. 6 디락 장과 스칼라 장이 상호작용-라그란지안 !l1= g ¢ (x)rs
제 6 장 풀수 있는모형들 그린 발생원
6 . 1 티 링 모형 (Thir ring Model) 티링 모형은 2- 차원 시공간에서 자체 상호작용하는 디락 장이론이다. 헤 르미샨 디락 장을 사용하면, 티링 모형의 라그란지안은 (4) g =높팥婦弓-jµjµ+j µAµ (6-1) 로쓸수 있다. 여기서 디락 행렬은 a0= 1, a1=
곱해져 있다는 점에 유의해야 한다. 라그란지안 (6-1) 로 기술되는 물리계의 모든 텐서량에 관한 물리적인 정 보는 이 계의 전공 전이진폭
전류밀도 j µ(x) 의 진공기대값은, 형식적으로는 다음과 같이 그린 함수의 극한으로 나타낼 수 있다 :
다. 라그란지안 (6-1) 은 게이지 변환 ip( x)-+(1 + iqS. 1) ip( x) 에 대해서 불변이며, 따라서 전류밀도는 oµj µ( x)=O 의 보존법칙을 만족해야 한다. 그러나 그린 함수 G(x,x' ）은 게이지변 환에 따라 변하는 양이며, 이를 통해서 정의한 전류밀도 (6-9) 는 위 의 보존법칙을 만족하지 않는다. 이 문제는 슈빙거를 따라서 (3,4) 전류 밀도를
G 。 (x 一 x') = iii껑,JJ (x-x') (6-13) 으로 정의하면*， 새로운 그린 함수 D(x) 는 방정식
*같와 iiµ는 aii v+av ii또 _-2 g u 의 관계를 만족한다.
—a2 D(x-x') = J(x —x') 울 만족하며, 따라서 질량이 없는 자유 스칼라 장의 그린 함수라는 것을 알 수 있다. 여기서, 간논 fio= ao, 참 =-al 로 정의한 행렬둘이다. 후리에 변환 (Fou ri er tr ans fo rma ti on) 을 이용하 면, 이 그린 함수는 D(x)=¼t n( x2+ iE) (6-14) 로 된다는 것을 쉽게 보일 수 있다. 또, (6-11) 식의 그린 함수를 G(x,x')= G 。 (x-x')e iq [F(x)-F(X ')) (6-15) 로 놓으면, 함수 F( 자는 aa ,,F ( x)= aA µ(X) (6-16) 의 방정식을 만족한다. 방정식 (6-12) 를 사용하면, (6-16) 식의 해는 F(x)= 급. f d 2x'G 。 (x?' ）rt' Aµ(x') (6-17) 으로 된다는 것을 알 수 있다 . (6-13) 식과 (6-14) 식을 이용하면, xo=xo' 일 때 디락 장의 그린 함수는 G 。 (x-x') = - ―211r ― x―a-1x_ xo=xo' 로쓸수있다.
위의 결과들을 (6-10) 식에 대입하고 (6-16) 식을 이용하여 TT 와 극 한을 취하면, 게이지 불변인 전류밀도는
< jµ( x) > A= fd2 x' DP (x 一 x')Av (x ') (6-19) 로 쓸 수 있다. 이 결과를 (6-7) 식에 대입하면, 함수미분방정식 값訂 OIO >A = iflP( x-x')Av (x ') < OIO >A 울 얻는다. 이 식을 Aµ(X) 에 대 하여 적분하면 < OIO > A= e 당 A,(x)D (x-x, )A,( x') (6-20) 의 결과를 얻는다. 이 진공 전이전폭을 Aµ 에 대하여 두 번 함수미분 하면 겹1 1i 鬪 ~<성O !O>AIA=o=Dµ(x-x') 이 되는데, 이 식은 작용원리에 의하여 Dµ(x 국’)= i< T( jµ(x )j ( x')) > + <툴邑> (6~21) 로 쓸 수 있다. 이 식의 두번째 항은, 전류밀도 j P(X) 가 독립변수가 아니어서 의부근원 Aµ(x) 의 칙집함수일 가능성이 있기 때문에 나타 나는 항이다. 이 모형 장이론에서는, 전류의 게이지 불변성을 위하여 (6-10) 식에서 도입한 슈빙거의 인자 때문에, 두번째 항이 생길 수 있 다. 이 장이론은 국소적 인 (loc al) 장이론이기 때문에 (6 ~ 21) 식의 두번째 항은 8(x0-x0’) 에 비례하며, 그래서 이 항을 접촉항 (con t actt erm) 이라고 부른다. * 이 사실을 이용하면 그린 함수 Dµ” 를 이들 두 가지 항으로 분리 할 수 있다. Dµ(x) 의 함수형태를 보면, µ= v= l 일 때 접촉항이 나타나며 <8효Au冥(x>') =_ 上T 8 f 8 f 8(x-x') *이 접촉항은 (6-10) 식에서 도입한 슈빙거 인자에 의해서 생기며, 슈빙거 인 자는 xo=xo ' 일 때 공헌한다는 접에 유의하라.
이 된다는 것을 알 수 있다. 또, 그린 함수 (6-21) 의 시간에 대한 도 함수를 시간에 대하여 적분하면, 전하밀도 사이의 교환관계 [j0(x ),j1 ( x')]x•=x•·= ―上r 귬 o(x ― x') 를 얻는다. 이제 (6-6) 식을 이용하여, 자체 상호작용하는 경우의 진공 전이진 폭을 계산하자. (6-20) 식을 (6-6) 식에 대입하면 < OIO > u = e-•. 칸Af r d.2•x..8 Am8( X) 8AP8 (x) e균 i ,(x)D•1(x- x' )A,( x') (6-22) 로 된다. 자체 상호작용하는 디락 장의 그린 함수를 닫힌 형태로 계산하기 위하여 , (6-22) 식을 < OIO >;A= e냥 A,(X) t> (X- x' )A,(x') (6-23) 의 형태나 혹은 무한번의 미분을 포함하지 않는 형태로 계산해야 한다. 이 렇게 할 수 없는 경우에는 (6-22) 식을 A 에 대한 데일러 급수 (Tay lor ser i es) 로 전개하든가 혹은 다론 근사 방법을 이용해야 한다. (6-22) 식을 (6-23) 식의 형태로 계산하기 위하여, 일반적인 범함수 I= e 令 -k M/ 공 R e숭 &BunKm 울 생각하자. 여기서 첨자 i,j,k 등은 불연속적인 변수 (µ,11 등)와 연속적인 변수 (x,x' 등海올 모두 포함하며, 반복되는 첨자에 대해서는 합이나 적분 울 한다는 것을 의미한다. 범함수 I를 K1. oll 대하여 함수미분하면, 읊= e숭 土 M J~ iB i J(l e fK mB mnKn =i B uKil + [e나 *M j*, iB , . J(J e당 KmBmnKn (6-24) = iB uKi l- tl BuMi li志 I
로 된다. 이 식을 정리하면 훑 =[(l+ t1 BM) 기 u Bj K J 로 쓸 수 있다. 이 식을 K에 대해서 함수적분하면 I= Ce당 KI(1+ABM) ;.J B J ' 로 된다. 연속변수 x,x' 등을 구체적으로 표현하여 이 결과를 쓰면 e 布굶'xf Mo(X, x') ~efK1 (Y )B1m(Y, Y) Km(Y1) = Ce7K‘(X)
< 010 >AA= cefA , (XW'(X-x ')A , (X ') (6-27) 이 되며 , 여기서 C 는 A 계 무관한 상수이다. 연산자 jµ(짜에 대한 모든 그린 함수들은 발생원 (6-27) 을 의부근원 A 거 대하여 미분함으로써 얻어 낼수있다. 자유 디락 장의 경우 (
이 경우 보존되는 양은 유사 벡터처럼 변환하는 유사전류 (ax i al curren t)밀 도 jt=강 %(x) 이며*
* €µv 는 €0'=1 로 정의된 반대칭 Lev i-C i vita 기호이다.
aµj (= O 의 관계를 만족한다. 따라서 티링 모형을 푸는 과정에서 전류밀도 jµ만 보 존되도록 요구해야 할 이유가 없다• 가장 일반적인 해는 j µ(x) 와 jt(x) ½ 동등하게 취급하면서 계산해야 한다. 이와 갇이 jµ와 jt를 동등하게 취급하 는 계산 방법은 해겐 (Ha g en) 의 논문에 자세히 다루어져 있다. (4) 여기서는 슈빙거의 함수미분방정식을 푸는 방법을 쉽게 보이기 위해서, 전류밀도만 보존되도록 요구하는 방법을 보인 것이다. 6.2 페르미 장의 그린 함수 앞 절에서 계산한 <010> 샤는 전류밀도 연산자 F( 지들에 대한 그린 함 수를 발생하는 발생원이며, 디락 장 AA (6-2 8) 로 정의되는 함수를 생각하자. 이 함수를 이용하면, 디락 장에 대한 그린 함수는 GA (x 1,X2,… , X2n)= GAA(X1,X2,… ,X 2n)IA=O 로 나타낼 수 있다. 따라서 (6-28) 로 정의되는 함수 GM 를 계산할
수 있으면, 디락 장에 대한 그린 함수를 얻을 수 있다. 앞 철에서 사 용한 방법을 이용하면, G” 는 GM(X1,X2,… ,X 2n) =之而1 文다__j_ A, fr ,d, 2• - .....;..f..,..;§_j__詞 詞xf< OIO >AGA (x1 ,… , X2 n) (6-29} 으로 쓸 수 있다. 여기서 GA 는 GA (x1 ,… ,X 2n)= GM(X1,… ,X 2n)IA=O 로 정의되는 의부근원과 상호작용하는 자유 디락 장의 그린 함수이며, 앞 절에서 이야기한 2- 점함수의 경우와 마찬가지로 GA (x1 ,… ,X 2n)= G 。 (x1, … ,X2n)e i ;2;n1 qiF( Xt) (6-30) 로 쓸 수 있다. 여기서 q는 각 장함수 #(x i)에만 연산되는 전하행렬이고, 자유디락장의 그린 함수 Q는 다助 G 。(x1,· •· ,x 2n)= 첩 l)i8 (xl?i) (6-31) x c 。 (x2,X3, … ,X i -l,X i +l, … ,X2n) 의 방정식을 만족한다. 이것은 2- 점함수가 만족하는 방정식 (6-12) 식을 2n 정함수의 경우로 일반화시킨 방정식이다. (6-30) 식을 G A( x1, … ,X2n) 이 만족하는 방정식〔（ 6 － 11) 식을 2n_ 점함수의 경우로 연장한 방정식〕에 대입하 고 (6-31) 식을 사용하면 F(x;)= -i fd2x' G 。 (x i- x')cl 'Aµ {x') 의 결과를 얻는다. 이 결과를 이용하면, 함수 GM 믈 GAA(X1,X2, … ,X2n)1= ~G 。 (x1, … ,X2n)e- 占i 祠8 四8可
X e군 i . ,.(.Y. ,)- D ·- ·(· Y.. - Y·' ) A.,.(Y’..) , 강. 1.2.=:,!1 I q ,Go(x,- x' )a 야(x') 로 쓸 수 있다. 또, (6-13) 식을 사용하면, 함수 F(x 써근 F(xJ = (-g따 記 )!#x'o, JJ (x i -x')A v( x') 으로 쓸 수 있다. 이 결과를 윗식에 대입하면, G .u는 G. u(X 1,… , X2n)= G 。(x1, … ,X2n~ 面1 ~ e 군i 年8 尹詞8 X eti A, (y) D'(y- y')A,(yr) ei ;2 :n1 q ,(g -rsE'')iJ, D (x,-xrr)A,(xrr) (6-32) 로 된다. 이 식의 오른쪽은 (6-25) 식의 왼쪽과 같은 형태로 바꿀 수 있다. 따라서 (6-25) 식을 이용하면, (6-32) 식은 GAA(X1 ,… ,X2n) = e \2프n l q,A ,(x)N '(x -x,) GA (x 1,… ,X 2n) (6~ 3 3 ) 으로 쓸 수 있으며, 여기서 GA 와 N, )c근 Glx1,… , Xzn)= G 씨 A=o= G 。 (x1, … ,X2n)e丸 양'q 1D(x1-X J )(I- 繼 (6-34) Nµ(x-x i )=(aµ-1+\ 阮 @v'Y s all)D(x-X;) (6-35) 로 정의되는 함수이다(문제 5 참조)． 이 결과를 이용하면, 전류밀도 jµ와 디락 장 #들에 대한 그린 함수들을 모두 계산할 수 있다. 특히 자체 상호 작용하는 경우의 디락 장의 전파인자는 GA (x -x')= G 。 (x-x')e 국 괄 7rr[D(x- X' )-D(o) J (6-36) 으로 표시된다. (6-14) 식을 이용하면, x2-.oo 일 때 전파인자 (6-36) 이 특 이성 (s ingul a rity)을 갖는다는 것을 알 수 있다. 이러한 특이성을 적의선적 인 특이성 (infrar ed s ingul a rity)이라고 한다. 이것은 디락 장의 질량이 영
이기 때문에 나타나는 현상이다. 4- 차원 시공간에서의 양자 전기역학에서 도 이와 비슷한 적의선적인 특이성이 나타나는 데, 그래서 티링 모형은 적 의선적인 특이성 현상을 이해하는 데 편리하게 이용되는 모형이다. 요를 Aµ(x) 에 대하거 함수미분하면, 그린 함수 < T( jµ(x ) rp( x1) rp( x2)… rp ( X2n)) > 울 얻는다. 이 그린 함수를 이용하여 j µ(x 浮 #(x) 사이의 동시 교환관계 [j0(x ), rp( x')]x•=x•·= -qrp ( x)8(x-x ') [P(x), rp( x')]x•=x•·= - ~간 (x)8(x- x') (6-37) 등을계산할수있다. 6.3 2-차 원 벡터 메존 모형 풀 수 있는 모형 중에서 자주 논의되는 모형에 2- 차원 양자 전자기학인 슈빙거 모형 (Schw ing er model) 이 있다. 이 모형은 실제 자연현상울 기술하 는 현실적인 이론에서 나타날 수 있는 여러 가지 홍미있는 성질들을 보여주 기 때문에 많은 관심을 끄는 모형 장이론이다. 이러한 현상 중에 상호작용 에 의해서 동역학적 (d ynami cal) 인 방법으로 게이지 장이 질량을 얻게 되는 질량발생현상과 고전적인 경우에 존재하던 대칭성이 양자적인 상호작용에 의해서 깨어지는 이상 (anomal y)현상이 있다. 슈빙거 모형은풀수 있는모 형이면서 이러한 현상을 보여 주기 때문에, 이러한 현상들을 이해하는 데 편리하게 아용되는 모형이다. 이 절에서는 질량이 없는 디락 장과 질량이 있는 벡터 장이 상호작용하는 모형 장이론의 그린 발생원을 계산하겠다. 이 결과에서 벡터장의 원래 질량 이 영인 국한을 취하면 슈빙거 모형의 그린 발생원을 얻는다. 슈빙거 모형
을 직접 푸는 데는 게이지 자유도를 처리하는 문제가 복잡하기 때문에 이러 한 방법으로 푸는 것이 편리하다. 다음 장에서는 슈빙거 모형을 직접 계산 하는 한 가지 방법을 보여 주겠다. 2- 차원 벡터 메존 모형은 라그란지안 !l=-》 Gµu( 캘 u _ 誌)나 -GµUGµu 一운 BµBµ 담¢f 8尹 ej µBµ 打먀 +Bµ Jµ (6-38) 로 기술된다. 여기서 ¢(자는 티링 모형의 경우와 마찬가지로 헤르미샨 장 함수로 표현한 디락 장이며 µo는 벡터 장의 질량이다. 그리고 그린 함수를 계산하기 위하여 의부군원 Aµ(X 펴 Jµ (x) 와의 상호작용을 도입하였다. 전 류밀도 연산자 j µ(x) 와 디락 행렬은 앞 절의 경우와 마찬가지로 정의하였 다. 작용원리가 의미하는 장방정식은 < (+aµ-e qB µ-q 나 (x)=O Gµ11= 0 ,,B 11 一 011Bµ 011Gµ11= er+r-µ~B µ 이며, 독립된 운동변수들 사이의 동시 교환관계는 {ip( x),
폭 <010> eAJ로부터 얻을 수 있다. 라그란지안 (6-38) 에 작용원리를 적용 굴}면 ¾
의 함수미분방정식을 만족한다. (6-41) 식의 전공기대값을 취하면 (정 8u_ gµ念+gµ1/島 )
G 。µJJ (x)=( g P JJ_~전 µa )J)ff.끊 e i P•X~ =(gµJJ_ ¼장 a )J )A 。 (x) 로 쓸 수 있다. 여기서 A 。 (x~ 방정식 (— 꾼+ Jio )A 。 (x)= 8(x) 와 인과적인 경계조건을 만족하는, 질량이 µo 인 스칼라 장에 대한 인과적 인 그린 함수이며, 따라서 벡터 장의 그린 함수는 스칼라 장의 그린 함수를 이용하여 표현할 수 있다는 것을 뜻한다. 발생원
Aµu(x) ＝늙급二信훈 효 )D(x) + ;;; 1+e}/ 파(g µ 11 장一효 )A(x) Mµ11(x)= ~다 1+ e 됴/7[µ; [8 껑 11D(x)+ (µ2g µ 11 _ 효)b. (x)] 로 표현되며, 재규격화된 질량 µ는 µ2=µ~+eT-2 (6-48) 으로 정의되고, 그린 함수 A( 지는 방정식 (一 꾼 +µ2) b. (x)= 8(x) (6-49) 와 인과적인 경계조건을 만족한다. 식 (6-48) 은 양자적인 상호작용에 의해 서 벡터 메존의 질량이 µ로 달라전다는 것을 의미한다. µ웅 ➔ o 인 극한을 취하여 얻는 슈빙거 모형의 경우에도 이 성질은 그대로 유지된다. 슈빙거 모형은 원래 질량이 없는 장들로 이루어져 있다. 따라서 위의 현상은 양자 적인 상호작용에 의하여 질량이 없던 장이 질량을 얻게 된다는 것을 의미한 다. 이러한 현상을 동역학적인 질량발생 (dy na m ica l gen erati on of mass) 현 상이라고 부른다. 질량이 없는 벡터 장이론은 게이지 대칭성이라는 내부대 칭성을 갖고 있다. 이러한 질량발생 현상을 이용하면, 질량이 있는 실제 벡 터 입자들을 게이지 대칭성이 있는 게이지 이론으로 기술할 수 있기 때문에 편리하다. 특히 질량이 있는 경우 재규격화가 불가능하던 이론이 질량이 없 는 게이지 이론으로 되면 게이지 대칭성 때문에 재규격화가 가~춥}게 되는 경우가 있기 때문에, 이러한 질량발생 현상은 아주 중요하게 이용될 수 있 다. 티링 모형의 경우에서와 마찬가지로, 의부근원이 영인 국한에서 그린 함 수는
fiPv( x - x')= i < T( r(x W(x')) > + < -/!z2麟 > 의 관계를 가지며, 이로부터 F 에 대한 그린 함수와 f의 의부근원에 대한 의존도를 계산할 수 있다. 또, 이러한 그린 함수들로부터 연산자 j P(x) 와 합(짜들 사이의 동시 교환관계도 계산할 수 있다. 디락 장에 대한 그린 함수들도 티링 모형에서와 마찬가지 방법으로- 계산 할 수 있다. 이러한 계산에서 새로운 기술이 필요한 것은 아니므로 여기서 는 생략하겠다. 자세한 내용은 참고문헌 2 와 4 에 다루어져 있다. 6 . 4 게이지 이상(g au g e anomal y)현상 고전적인 이론의 경우에 존재하던 보존법칙이나 대칭성이 양자적인 효과 때문에 깨어지는 현상을 이상 (anomal y)현상이라고 한다. 특히 양자적인 효과에 의하여 게이지 대칭성이 깨어지는 현상을 게이지 이상현상이라고 부 른다. 티링 모형이나 슈빙거 모형은 질량이 영인 디락 장으로 이루어진 계 이다. 이들 모형의 라그란지안은 rp( x~(l+ iq8, 1) rp( x) (6-50) 로 표현되는 게이지 변환과 rp (x) ➔ (1+ iqrs 8t1 )rp( x) (6-51) 로 표현되는 카이랄 (c hi ra l) 변환에 대하여 불변이다. 이들 대칭성 때문에 유도되는 보존법칙은 각각 8µ]’(x)=O (6-52) 의 전하보존법칙과 aµ jt =aµ 강 11j 11=0 (6-~3)
의 유사 (ax i al) 전류 보존법칙이다. 그런데 이들 보존법칙 중 일부가 양자적 인 상호작용에 의해서 깨어지는 경우가 있다. 티링 모형의 경우에는 양자적 인 경우에도 여전히 두 가지 보존법칙이 성립하는 데 (의부군원이 영인 경 우) , 슈빙거 모형의 경우에는 (6~53) 식에 해딩하는 보존법칙이 성립하지 않는다.( ◄) 이러한 현상을 쉽게 이해하기 위하여 자유 디락 장이 의부근원 Aµ(x) 와 상호작용하는 경우를 생각해 보자. 이 경우 라그란지안은 오 =숭A=...2!.. e xli-mX Trqr l'GA (x ,x')e-;qf; A ,CY>dY' (6-54) 로 정의해야 한다. 이 함수를 계산하면 < jµ( X) > A= 룹{g µ11 a2-- 효 )D(x-x')A.,(x') (6-5 5) 이 된다. 이 전류밀도는 (6-52) 식은 만족하지만, (6-53) 식은 만족하지 않 는다. 이 경우 (6-53) 식에 해당하는 식은 oµ
이, 카이랄 변환이나 혹은 게이지 변환과 카이랄 변환의 조합에 대하여 불 변이 되도록 전류밀도의 행렬요소를 정의할 수도 있다 .(4) 그러나
〔문저|〕 l (6-10) 식으로 정의된 전류밀도가 게이지 변환에 대하여 불변임을 증명하라. 2 운동량 공간에서의 전파인자를 古= —if/ bleO( P2+ m2+i <) 으로 표현할 수 있다는 사실을 이용하여 (6-14) 식을 유도하라. 3 (6 - 10) 식으로부터 (6-18) 식을 얻는 유도과정을 보이라. 4 교환관계 [겁[i• Km]=81m 을 이용하여, (6-24) 식을 유도하라. 5 (6-25) 식에서 C 가 K 에 무관하다는 사실을 이용하여 C= e-AM11(x,x1)B11(X, 지 이 된다는 것을 증명하라. 6 (6-25) 식에서 x=K+B - 'N으로 표현되는 변수변환을 이용하여 (6-33) 식을 유 도하라. 7 (6-37) 식의 동시 교환관계를 유도하라. 8 (6-25) 식을 이용하여 (6-46) 식으로부터 (6-47) 식을 유도하라. 9 2- 차원 벡터 메존 모형에서 디락 장에 대한 그린 함수를 계산하라. 10 2- 차원 벡터 메존 모형의 그린 발생원에서 µ~-o 인 극한을 취하여 슈빙거 모형 의 그린 발생원을 구하라• 11 (6-54) 식에서 게이지 변환이 아니라 (6-51) 식의 카이랄 변환에 대하여 불변이 되도록
제 7 장 함수미분방정식의 형식적인 해 : 경로적분양자화방법 지금까지 그린 함수와 그린 발생원, 그리고 이들이 만족하는 함수미분방 정식에 대하여 이야기하였다. 그린 함수를 닫힌 형태로 풀 수 있는 2- 차원 모형들에서, 함수미분방정식을 푸는 방법에 대해서도 자세히 이야기하였 다. 이제 그린 발생원에 대한 함수미분방정식의 일반적인 해에 대해서 생각 해 보겠다. 현실적인 장이론의 대부분은 그 해를 닫힌 형태로 풀 수는 없기 때문에, 여기서 이야기할 함수미분방정식의 해는 형식적인 해 (for mal solu ti on) 이다. 이 형식적인 해로부터 물리계에 관한 많은 정보를 얻어낼 수 있다는 것을 알게 될 것이다. 보통의 매개변수에 대한 미분방정식의 해를 구하기 위해서는 미분방정식 을 적분해야 한다. 함수미분방정식의 경우에서도 마찬가지로, 그 해를 구 하기 위해서는 함수적인 적분(fun c ti onal i n t egr al) 을 해야 한다. (“ 이 함수 적분을 사용하여 함수적인 후리에 변환을 정의하고, 이를 이용하여 함수미 분방정식의 해를 구하겠다. 이렇게 얻은 해가 바로 화인만의 경로적분 양자 화 방법이 된다는 것을 알게 될 것이다. (1)
7 . l 함수적분(fu nc ti onal integ r a l) 힐버트 공간(Hi lbe rt s p ace) 에 속하는 실수함수 q; (x) 의 범힘수 F[ q;]를 함수 q; (x) 에 대하여 적분하는 경우를 생각해 보자. 다시 밀하면, 함수적분 f@rpF [rp] (7-1) 에 의미를 부여하려고 한다. (1) 여기서 적분이란 rp (x) 가 속한 힐버트 공간 전체에 대한 합을 의미한다. 이 적분에 의미를 줄 수 있는 한 가지 방법은 rp (x) 가 정의된 공간 x=(x1,X2, …）을 불연속적인 작은 구간들로 나누는 방 법이다. 죽, i번째 구간의 체적을 AVi 라 하고, 이 구간에서의 rp (x) 의 평 균값을 P i라하면 ¢i=jt福t1:1 v,
며, (7-1) 식의 힘수적분은 fq;rp F[rp( x)] =｝타F (a1,a2, … aN)da1,da2, … daN, (7-4) 로 표현되는 다중적분의 극한으로 정의할 수 있다. (7-4) 식으로 정의한 극한이 일반적으로 존재하는가에 대한 문제는 수학 적으로 아직도 열린 문제이다. 여기서는 (7-4) 식의 국한이 존재하는 가우 스 범함수 (Gauss i an fun cti on al) e 랑,.,= e 令f dx ,P (X) ,P (X) (7-5) 의 경우를 생각하겠다. 여기서 힐버트 공간에서의 스칼라 곱 (scalar p roduc t)을 ¢l • p2 =f dx¢l (x)p 2( x) (7-6) 로 표현하였다. 함수 ¢(차를 서로 직교하는 기준함수 Un(X) 로 전개하면, 가우스 범함수의 함수적분은 f씁 e 감'P·내터나 n 선혼 d홉 色急 ·d훔 =v 모nN j다저훔 =1 (7-7} 로 된다는 것을 쉽게 알 수 있다. 여기서 함수적분의 적분척도 (int e g rat i on measure) 롤 탸 =Inl d무 @ 로 정했다는 점에 유의해야 한다. 만일 이 적분척도를 다르게 택하면, 함수 적분 (7 구)은 유한한 값을 갖지 않는다. 함수적분에 대한 기본 가정들을 이용하면, 가우스 범함수의 함수적분으
로부터 양자 장이론에 관한 여러 가지 유용한 관계들을 얻어낼 수 있다. 특 히 함수적분에 대한 다음과 같은 가정을 하겠다 : (I) 함수적분은 변수함수의 평행이동 변환에 대하여 불변이다. 죽, j@rpF [rp ]=j@rpF [rp +p]. (7-8) (II) 軒적분 ！탸 F[ 아는 적분되는 범함수 F 에 대하여 선형관계에 있 다.죽, f@¢ {F[ 아] + G[ rp]} =j@ rpF [ 아] +j@rp G[ rp]. (7-9) 이들 가정을 사용하면, 매개변수에 대한 적분이 만족하는 여러 가지 관계 들을 함수적분도 만족한다는 것을 쉽게 보일 수 있다. 예를 돌면, 적분 (7 -7) 에 (7-8) 식을 적용하면 J(j/) ?e-½('I'+ p) 2=1 또는 f® ¢e 令9'•9'-'P •P=e 송 P•P 의 관계를 얻는다. 이 식은 함수 p에 대한 항등식이므로, p대신 -U를 대입하면 J@ rp e 쉽안+i'l' •l = e 뇽 (7-10) 의 관계를얻는다. 이제 함수적분 f
롤 생긱해 보자. 가정 ( n )를 이용하면, 이 함수적분은 F[ :· 訂 ]!@ q; e 감'I'나·f 로 쓸 수 있다. 이 결과에 (7-10) 식을 대입하면 f타[rp ]e 쉽'나 ·1=F[~]e 산J2 (7-11) 로 된다. 이 관계는 그린 발생원을 계산하는 데 편리하게 이용되는 관계이 다. 실수함수를 이용하여 얻은 위의 결과들을 복소수함수의 경우로 쉽게 연장 할 수 있다. (7 - 7) 식의 결과를 이용하면, 두 개의 실수함수 (fl 1 과 ¢2 에 대 한함수적분은 f® ¢l@ 京 2e---½PI· 나'/1 2• '/1 2=1 로 쓸 수 있다. 복소수함수 ¢(자를 ¢=1言 (({)1+ 學), ¢*=1전 (({)1- 후) 로 정의하면, 위의 함수적분은 f탸驛 e 구 .,=l (7-12) 로 쓸 수 있다. 이 식에서 적분변수함수를 p--+ ¢-tX 로평행이동하면, J~ 훑 갑v,*-v,+iv, *•x+ i x*·,=e-x•·x (7-13)
의 관계를 얻는다. 또, (7-11) 식에 해당하는 관계는 f'lJJ 浮 갑[q;*,q; ]e- 군•vi+ivi *·x+ i x*· vi (7-14) =F[불 ’ 틀 ]e-x* • x 로 된다는 것을 쉽게 보일 수 있다. 위에서 이야기한 함수적분의 성질들을 이용하면, 범함수의 힘수적인 후 리에 변환(fun c ti onal Fou rier t rans fo rma ti on) 을 정의할 수 있다. 실수함수 rp (x) 의 범함수 F[ rp］의 함수적인 후리에 변환은 F[ rp] =j@J F[J] ei'P •J (7-15) 로 정의한다. 이 변환의 역변환은 F[J] =j@ rp F[ rp] e-i'P •J (7-16) 이다. 매개변수의 힘수의 후리에변환을 이용하여 델타 함수를 정의히~준이, 함수적인 후리에 변환을 이용하여 델타 범함수를 정의할 수 있다 : 8[rp ! _ 症 2]= f@j ei( PI-P2)·I (7-17) 이렇게 정의한 델타 범힘수는 f(jj)
7.2 적분변수의 변환 적분변수함수인 짜짜를 변환할 때 생기는 함수적분의 변화를 생각해 보 자. 함수 q; (x) 의 변환 으로 표현된다. 따라서 함수적분의 적분변수를 (7-22) 의 관계가 있다는 것을 쉽게 보일 수 있다. 행렬의 행렬식은 표현방법에 무 관궁}므로 detK u = detK (x,x') (7-23) 의 관계가 있다. 따라서 (7-22) 식은 @( Krp ) = (detK )@ rp (7-24) 로쓸수있다. 복소수함수의 경우 ¢=r1z ( rp1 + 函) rp* =r1z ( rp1 —函) 로 정의하면, 적분변수의 변환은 rp'a(x )=j K(x ,x')rp a(x ')dx', a=l,2, (7-25) 로 나타낼 수 있다. 따라서 적분척도의 변화는 (j/J (Krp )(j/J (Krp *) = (detK 2)(jJJ p(jJJ rp* (7-26) 로 표현된다는 것을 알 수 있다. 적분변수의 변환을 이용하는 한 가지 예로, 함수적분 f{jJ)
cp'( x) = K½(x,x') • cp( x') 三frtx 'K삼 (x,x') cp( x') 울 생각하면, 범함수 cp• K. 針근 cp( x) • K(x,x') • cp( x') = cp' (x) • cp' (x) 로 쓸 수 있다. 따라서 위의 함수적분은 J@ rpe -½'•K•'=j @(K -½r p' )e-½~ =f
7.3 스피너 장에 대한 함수적분 지금까지는 교환 가능한 함수, 죽, [ rp; (x), rpix') ] =O 의 관계를 만족하는 함수들에 대한 함수적분을 이야기하였다. 교환관계로 정의되는 보즈 (Bose) 칭이론의 그린 발생원은 이러한 함수에 대한 함수미 분방정식을 만족하며, 그 해는 이들 함수에 대한 함수적분으로 표현된다. 그러나 반교환관계로 정의되는 페르미 (Ferm i) 장의 그린 함수나 그린 발생 원은,반교환관계 { 1Ji(x ) , 1Jj(x ')} = O 을 만족하는, 그러스만 변수 (Grassmannva ri able) 에 대한 함수미분방정식 울 만족하며, 또 그 해는 이들 그라스만 변수에 대한 함수적분으로 표현된 다. 예를 들면 자유 디락 장이 의부근원 TJ (X) 와 결합할 때, 그 라그란지안 은
g =뉴 (x) 죠rp (x)- 뿐의 성질을 갖는다. 따라서 함수 f (n) 를 전개하면 유한한 항만을 갖는 다 (n 이 유한할 때)． 예를 들면 n=2 인 경우, 가장 일반적인 함수 j(r;)는 f(r;) = a 。十 a11 /1 + a2r ;2 + a12T J1 1 /2 로 쓸 수 있다. 여기서 ao,a1,a2,a12 는 실수이다. 그라스만 변수에 대한 미분은, 그 반교환성 때문에 왼쪽 미분과 오 른쪽 미분을 구분해야 한다; 福1섬J t1Jj)= 8,.k1 J j - 8jh 1 Ji (7-31) : 창 1Ji1Jj) = 8jk 1 Ji - 8ih 1 Jj. (7-32) 기호를 간단하게 하기 위해서 앞으로는 왼쪽 미분만을 사용하고 첨자 l 을 생략하겠다. 미분연산자의 이러한 성질 때문에 {¾, 7Ji} =8u (7-33) 의 관계가 성립한다는 것을 쉽게 알 수 있다. 또, 미분연산자들 사이 에도 반교환관계 맡 읊 }=O (7-34) 가 성립한다. 이 식은 미분연산자의 역이, 보통의 의미로는 존재하지 않는다는 것을 의미한다. 이것이 그라스만 변수에 대한 적분연산의 정의를 어렵게 하는 이유이다. 그래서 그라스만 변수에 대한 적분을 정의하기 위해서는, 적분의 정의들을 만족하는 연산 (o p era ti on) 을 찾아내야 한다. 베레전 (Berez i n)<2> 이 제안한연산
fdTJ ; = O, fdT J; 7J;=l, (i에 대한 硏] 아님) (7-35) 이 적분연산의 모든 성질을 만족한다는 것을 알 수 있다. 이것은 〈마치 미 분하듯이 적분하라走· 것이며, 이러한 연산이 적분으로 성립하는 것은 변수 둘 사이의 반교환관계 때문이다. 그라스만 변수들의 반교환성을 이용하면, 지수함수 e½q K q= e½q ,K 1 Jq1 , Ki j= -K 는, n 이 유한하면 변수 n: 에 대한 다항식이 된디는 것을 알 수 있다. 이 둘은 (7-35) 식의 적분의 정의식을 사용하여 적분하면 fdTJ n d TJ n -1· • •d 1J 1 e 송q K q =de t K강 (7-36) 이 된디는것을보일수있다. 이 결과를 무한차원 공간의 경우로 연칭하면, 반교환성 함수에 대한 함수 적분을정의할수있다; f'!lJ 1J( x)e½~,Cx>Ko(x,x'>~1
f[ nd 7Ji d 7Jit ]e E 硏 Kun) = detK (7-39) I 의 관계를 쉽게 얻을수 있다. 복소수 그라스만 변수의 성분이 연속적으로 무한한 경우로 연장하면, 복 소수 그라스만 함수에 대한 함수적분 f(j/) n(x) 터 (x)e~' t (x)K l} (X , X ' )~ J (X ' )=de t K (7-40) 를얻는다. 이들 결과를 이용하면 페르미 (Ferm i) 장의 그린 힘수와 그린 발생원이 만족하는 함수미분방정석 (그러스만 변수에 대한 미분방정식)을 쓸 수 있 고, 이들의 해를 함수적분으로 표현할 수 있다. 그린 발생원이 만족하는 함수미분방정식의 해(형식적인 해)를 일반적으 로구하는방법을보이기 위하여, 여기서는자체 상호작용하는스칼라장이 론의 경우를 생긱하고, 그에 해당하는 미분방정식을 함수적인 후리에 변환 울이용하여 풀겠다. 7.4 그린 발생원 이제 그린 발생원이 만족하는 함수미분방정식의 해를 생각해 보자. 함수 미분방정식의 해를 구하는 방법을 쉽게 보이기 위하여, 라그란지안 (5-3) 으로 기술되는, 자체 상호작용하는 스칼라 장이론의 경우를 생각하겠다. 그린 발생원을 계산하는 데는 라그란지안을 (5-3) 식과 동등한 형태인 重])=½術)（장- m2)¢(x)--¾ 섬 (x)+ ¢(x)J (x ) (7-41) 로 표현하는 것이 편리하다. 이 계의 그린 발생원을
Z [J ]= < OIO > 시 라고 하면, 발생원 Z[ J~ 함수미분방정식 [(-a2 + m2 댑汀 —델 ] Z [J]= if(x) Z[J] (7-42) 룰만족한다. 함수미분방정식 (7-42) 를 풀기 위하여, Z [J]의 함수적 후리에 변환을 생각하는 것이 편리하다. Z [J]의 함수적 후리에 변환을 범함수 Z[ rp( x )] 라 하면, * 함수적 후리에 변환은
*¢(x) 는 스칼라 장연산자를 나타내며,
Z[J]= f
의 결과를 얻는다. 여기서 C 는 함수 q; (x) 에 무관한 적분상수이다. 따라서 라그란지안 (7-41) 로 기술되는 물리계의 그린 발생원은 Z[J] = Nf (j/) rp e if d•x 답,p (x)(a2-m') ,p (x)-¾ ,p •(x) +,p (x)/(x)I (7-48) 로 표현된다는 것을 알 수 있다. * 여기서 N은 적분상수 C 와 함수적분의 적분척도에 나타나는 상수를 합한 전체 규격화 상수 (norma li za ti on cons t an t)이다. 이 함수미분방정식의 해는 J (x) 의 범함수로 닫힌 형태로 쓸 수 있는 것이 아니기 때문에 형식적인 해이다.
*지수함수내의 x 에 대한 적분을 4- 차원 시공간의 경우로 표현하였다. 그러 나 시공간의 모든 차원의 경우에도 갇은 형태의 해를 갖는다.
발생원 (7-48) 은 함수 cp (x) 의 범함수를 후리에 변환한 형태로 표현된 것 이다. 이것을 제 5 장의 결과와 비교하기 위하여 J (x) 의 범함수로 표현해 보 자. (7-48) 식은 Z[J] = e- 눈J d 따눕늙 l'N j@
½
로 된다. 여기서 K-1 는 K- 1 1=[ 강노 ]( x,x' ) J (x ' )= ―ifd 'xD 정 ( x 玉)J (x ' ) (7-53) 으로 정의되는 연산자이다. 따라서 위의 결과는 제 5 장에서 얻은 결과 와 동일하다는 것울 알 수 있다. 위에서 그린 함수 D 옹 (x) 가 만족하 는 경계조건에 대해서는 언급하지 않았다. 함수적분 (7-49) 식이나 (7 -52) 식이 존재하기 위해서는, 이 그린 함수가 인과적인 경계조건을 만족해야 한다는 것을 보일 수 있다 (8 . 1 절 참조). 7 , 5 화인만의 작용원리 그린 발생원이 만족하는 함수미분방정식을 함수적분하여, 그 해인 그린 발생원 (7 - 48) 을 얻었다. 그리고 이 결과가 제 5 장에서 다른 방 법으로 계산한 결과와 일치한다는 것도 보았다. (7-48) 식과 같이 표 현된 해에서, 그 함수적분을 일반적으로 계산할 수는 없다. 이러한 뜻에서 이 해를 형 식 적 인 해 (form al solu ti on) 라고 부른다. 그러나 이 식 의 왼쪽은 양자 장이론의 성질을 나타내는 양인데, 그 오른쪽은 고전적인 함수인 cp (x) 만으로 표현되어 있다는 점이 중요하다. 즉, 양자 장이론의 물 리적인 정보를 연산자가 아닌 고전적인 함수만으로 표현할 수 있다는 것을 의미한다. 이것은 고전적인 이론을 양자화하는 데 이 해를 사용할 수 있다 는 것을 뜻한다. 이러한 양자화 방법을 화인만 (Fe ynm an) 의 경로적분 양자 화(p a th integ r al qu anti za ti on ) 방법이라고 부른다. (I) 이 사실을 좀더 쉽게 보기 위해서 (7-48) 식을 다음과 같이 쓰는 것이 편 리하다; Z[J] =
여기서 상수 N은 적분상수와 적분척도에 나타나는 상수들을 포함하는 규격 화 상수이며, gc (p ; ]注· gc (¢ ; ])=flr p (/ x)\ （I -장.? ― m2?)\ rp I( x)\ 二A균 (x)+ rp (x)J (x) (7-55) 이다. 이 라그란지안 ffc 는 양자적인 라그란지안 (7-41) 에서 연산자 ¢(x) 대신 고전적인 장함수 rp (x) 로 대치한 고전적인 라그란지안이다. 따라서 (7 -54) 식은, 고전적인 작용을 이용하여 양자적인 계의 그린 발생원을 표현 한, 양자화 방법의 한 가지라는 것을 의미한다. 양자적인 라그란지안을 1- 차도함수만으로 표현한 따 ,
로 쓸 수 있다. 이 결과는 양자적인 계의 진공-진공 전이전폭이 e i S 를 무게 인자로 하는 모든 가능한 경로 q; (x) 와 ¢µ(x) 에 대한 경로적분으로 주어진 다는 것을 의미한다. 이것이 화인만의 작용원리이다.(＂ 여기서는 h=l=c 인 단위계를 사용하기 때문에 위의 식들에서 싱수 柏} 나타나지 않는다. 이들 상수들을 복원하면, (7 - 59) 식의 무게인자는 e i S / ，，로 된다. 양자론의 고전적인 극한은 tz -o 인 극한으로 이야기하는데, 경로적분 양자화 방법에 서는 이러한 사실을 확실하게 볼 수 있다. tz -o 인 극한을 취하면, (7-59) 식에서 적분에 공헌하는 경우는 작용 S 가 최소값을 갖는 경우밖에 없다. 이것이 바로 고전적인 최소작용의 원리이다. 위의 결과는 일반적인 장이론의 경우로 쉽게 연장할 수 있다. 라그란지안 !l (x ;J )=+xA 껑 ,,x- aµxAµx)-V(x)+ xJ (7-60) 로 기술되는 양자 장이론에서, 공간 같은 곡면 아에서의 진공에서 6저 ]서 의 전공으로 전이할 전이전폭은
장의 기호와 맞추기 위해서 V(x 遷· H(x) 로 바꾸어 썼다. 이 경우, 시각 t 1 일 때 x' 인 상태에서 시각 t2 일 때 x '’으 로 전이할 확률밀도는 < x,t2 lx ',t1 > =Nf@ t e jnfd1 Lcet :J) (7-64) 로 표현된다. * 여기서도 고전적인 라그란지안 g c는 양자적인 라그란지안 (7-63) 에서 었춘 고전적인 함수 t(t)로 대치한 것이다. 제 따k 1] 서 설명한 관계들을 이용하면, (7-64) 식을 좀더 낯익은 변수인 P 와 q의 함수로 표현 할 수 있다 . 즉, 시각 t 1 일 때 위치 q 1 에 있던 계가 시각 t2 에 위치 q 2 에서 발견될확률진폭은
*여기서 x' 와 x 은 연산자 x 의 고유값들이다.
< Q2 ,t2 IQ 1 ,!1 >=j@q@p eil :ldt [ pq- H(q, p)J (7- 65 ) 로 된다. 양자역학적인 계의 경우 의부근원이 없는 경우를 주로 디루기 때 문에 (7 - 65) 식에서는 의부근원 J를 영으로 놓았다. (7-65) 의 함수적분을 계산하는 방법에는, 앞에서 이야기한 바와 같이 매개변수 t의 공간을 작은 구간으로 나누어 계산하는 방법과, 함수 q(t浮} p(t潘- 서로 직교하는 함수 들로 전개하여 계산하는 방법이 있다. 보통 교과서나 논문들에서는 매개변 수의 공간을 나누는 방법이 주로 사용된다. 지금까지 주로 사용되어 온 양자화 방법은 표준양자화 (cano ni cal qua nti za ti on ) , 슈빙거의 작용원리와 화인만의 작용원리의 세 가지이다. 제 2 장에서는 이들 방법 중 처음 두 가지가 동등하다는 것을 보았고, 이 장에 서는 화인만의 경로적분이 슈빙거의 함수적 미분방정식의 해로 주어진다는 것을 보았다. 따라서 이들 세 가지 방법은 서로 동등한 방법이며, 경우에 따라서 어떤 것이 다른 방법보다 편리한 경우가 있다. 칭연산자들 사이의 교환관계 또는 반교환관계와 장방정식들이 서로 모순이 없도록 유도하는 데 는 슈빙거의 작용원리가 편리하며, 장이론의 해를 닫힌 형태로 구할 수 없
는 경우에 여러 가지 근사적인 방법을 개발하는 데에는 화인만의 경 로적분이 편리하다. 양자 장이론의 섭동론적인 근사 방법에 대해서는 다음 장에서 자세히 이야기하겠다. 7.6 슈빙거 모형 함수미분방정식을 이용하여 풀 수 있는 모형들의 해를 구했던 것과 같이, 그 형식적인 해인 경로적분 방법을 이용하여서도 이들을 풀 수 있다. 여기서는 슈빙거 모형 (3) 의 해를 경로적분 방법을 이용하여 구 하겠다. 슈빙거 모형은 라그란지안 fl = ―귄l FP(a ,A v-avAµ)+ fl FµFµv+ 薄 rµ(aµ- i eA 泊 (7-66) 로 기술되는 2~ 차원 시공간에서의 양자 전기역학이다. 여기서는 디락 장연산자를 전하의 고유상태로 표현하였다. 이 모형은 게이지 대칭성 울 유지하면서 광자가 질량을 갖게 되는 현상을 보여 주는 모형이라 는 것을 앞 장에서 설명하였다. 이제 경로적분을 이용하여 광자가 질 량을 갖게 되는 현상을 살펴보자. 아 계의 그린 발생원은 Z= f
안 (7-66) 에 해당하는 고전적인 라그란지안이다. 전자기장이 질량을 갖게 되는 현상을 보기 위해서는, (7-67) 식에서 디락 장 幹와 짜에 대한 함수적 분을 계산하여, 그 결과가 전자기장에 어떤 영향을 주는가를 보면 된다. 이 러한 계산을 위해서는 외부근원과의 결합(상호작용)을 생각할 필요가 없으 며, 그래서 (7-67) 식에서 의부근원울도입하지 않았다. 디락 징이 전자기장과 게이지 결합을 할 때, 고전적으로 존재하던 대칭성 의 일부가 양자적인 영향에 의하여 깨어지게 되는 게이지 이상 (anomal y) 현상이 나타난다는 사실을 6 . 꾹길에서 보았다. 이러한 이상현싱이 경로적분 양자화 방법에서는 어떻게 나타나는지롤 보기 위하여, 무한히 작은 국소적 인 카이 랄 변환 (loc al chir a l tran sfo rm ati on ) ip (x) 규 '(x)= e-i1s E
그러나 국소적인 카이랄 변환에 대해서 고전적인 작용은 (7-69) 식과 갇 이 변하므로, 이 식이 성립하기 위해서는 적분척도 @帖 D 記가 카이랄 변환 에 대해서 불변이 아니라는 것을 의미한다 .(4) 이 식과 (7-69) 식은 또 유사 전류밀도의 보존법칙 aµj (=O 이 깨어진다는것을의미한다. 디락 장의 적분척도가 카이랄 변환에 대해서 불변이 아니라는 사실을 이 용하면, 여러 가지 2- 차원 모형들을 함수미분방정식의 형식적인 해인 경로 적분을 사용하여 풀 수 있다 .(5) 이들을 푸는 방법은, 디락 장을 적딩히 카 이랄 변환하여, 전자기장과의 상호작용이 없어지도록 하는 것이다. 이렇게 하면, 디락 장에 대한 적분을 계산한 것과 같은 효과를 주게 되는 것이다. 이러한 유한한 카이랄 변환을 할 때, 같은 시공간에서의 연산자들의 곱을 만나게 되고 이들은 발산하는 항을 주게 된다. 그래서 이러한 발산하는 항 울 규제 (re gu la t e) 해야 하고, 그러기 위해서는 계산을 유클리드 공간에서 하는 것이 편리하다. 유클리드 공간이란 x°--+_i x4, r°--+i r4 , A 。--+iA 4 로 해석적인 연장을 하는 것이다. 카이랄 변환의 효과를 계산하기 위해서 디락 연산자의 고유방정식을 생각 하자: flTJn (X) = rµDµTJ n = rµ(aµ-ie A µ) TJn (X)= '1n T/n (X). 이 고유방정식의 해 T/ n(X) 가 서로 직교하며 규격화되었다고 가정하겠다 ; fd2x71 J (x ) 7/n (X)= 8nm (7-70) 2nn(x) 까 (x')= 성 (x-x'). n 이제 디락 장함수를 이들 직교하는 함수들로 전개하여 함수적분할 수 있 다:
여기서 a~ bn은 그라스만 변수이며, 적분척도는
캘만.fd 2x 꾸 €(x) 까 (x) r5e-d2lM 2 7Jn (x) = lim t.fd2x c(x) Tr y 5¢ lJ2 lM2 정 (x-x1) MX2’-O-xO 후리에 변환으로 델타 함수를 표현하면 이 식은 ifd2xn f , €(Xhn t (x) rs TJn (X) (7~78) 겔뿔 if d 2x f떨屈 x) Trrse-./fl /M Z e-ik • Y 로된다. %昞 ,/Jl=— 蠶곱닫 %Fµ IJ (7-79) 를 이용하여 (7-78) 식을 계산하면 ifd2xn~ E(x) TJJ (x) rs TJn (x) =l i m t.f# x f룹 €(X) TrrseJ h< a• 븀퍄야 ,,) e- i k•Y (7-80) My--O OO = 같fd 2xE(x) 간 11Fµ11 로 된다. 따라서 적분척도는
@ ifi= e-若 f d2XE(X)EF,_(X) qf} 굽’. (7-82) 따라서 무한히 작은 카이랄 변환하에서 디락 장에 대한 적분척도는 이
다. 따라서 전자기장은 Aµ= Eµvaj) <1( x) (7-87) 로 쓸 수 있다. 또, 2- 차원 r- 행렬들은 €µuru=r5Yµ 의 관계를 만족한다. (7-87) 식과 이 식을 이용하면 슈빙거 모형의 라그란 지안은 요 = -½Fµ(a,A — avAµ) 나 -Fµ11Fµ11 + 薄y µ(aµ + iey s a µ6)
라면, 무한히 작은 카이랄 변환하에서 적분척도는 이타= (jJ) ¢ ' 타 '[1 을 /#x8E( x )€µ11(Fµ 11 + Fµt) ] (7-90) 로 변화된다. *여기서 Fµ t=―i (dµ€11 p -dv € µp)At이다.
*원래의 슈빙거 모형에서 카이랄 변환하면, 이러한 항이 유도되기 때문에 이 가능성을 무시하지 말아야 한다.
파)만큼 카이랄 변환시킬 때 나타니는 적분척도의 변화량은 8( 이(jJ) ¢)=(jJ)¢'( jJ) 祈'-(jJ)頓(jj) ¢ (7-91) = (jj) 韓 呼f#造 (x) 같 11 (Fµ11+ 麟)] 로 된다. 무한히 작은 r5- 변환을 8€만 큼 한 번 행하면, 작용에는 fd %祐%cp aµ8E(x) 의 항이 유도되어, A i=e上 aµ8€(x) 에 해당하는 유사전류 결합이 생기게 된 다. 따라서 Fµ 얹는 €(x) 에 따라 변하며 8Fµ t =-~aeµ €11 p -a11€µ p)장 8€(x) (7-92) 의 관계를 갖게 되고, €=0 이면 Fµ t =O 이다. 이 조건을 만족하는 (7-92) 식의해는 Fµ~= 갑 @cv p-표 )8Pc(x) (7-93) 로쓸수있다. 따라서 강 11(Fµ11+Fµ t)= €µ11Fµ11+ 썹e a2€(x) (7-94)
로 쓸 수 있다. 이 결과를 이용하면 (7-91) 식의 해는 이'@¢'= 이@ ¢ e 若f d'X(!(X)EF,' 남 c(x) 파 (X)] (7-95) 로된다는것을알수있다. 이제 전자기장과 결합하는 항이 없어지는, (7-89) 식의 디락장으로 변환 하기 위해서 E(x)=e <1 (x) 로 택하면 된다. 이 결과를 대입하여 유한한 r5- 변환하에서의 적분척도의 변화를 계산하면 이@ f=@ x@ x e怪 f d2xA•(x)A,(X) (7-96) 가 된다. 아것은 카이랄 변환 후 슈빙거 모형의 유효 라그란지안 (e ff ec ti ve La gr an gi an) 은 요 =-½Fµ11(a~11- 誌)+-t Fµ11Fµ11~A 따 冠泣 (7-97) 로 된다는 것을 의미한다. 이것은 또 슈빙거 모형은 질량이 &巧 7 인 광자 를 기술하는 이론이라는 것을 의미한다. 페르미 장의 적분척도가 카이랄 변환에 대하여 불변이 아니라는 사실을 이용하여 다른 모형들의 해도 구할 수 있다. 그리고 앞에서 지적한 바와 같 이 전류만이 보존되도록 양자화하는 것이 아니라, 전류와 유사전류의 임의 의 선형결합이 보존되도록 이들 모형의 해를 구할 수도 있다. 2- 차원 모형 칭이론들의 이러한 풀이 방법에 대해서는 참고문헌 5 의 두번째 논문에 자세 히 설명되어 있다. 〔참고문헌〕 이 장에서 설명한 함수적분과 화인만의 작용원리의 유도 방법은 Lur i~의 책(I)에
서 사용한 방법을, 그리고 슈빙거 모형의 풀이 방법은 Barcelos-Ni et o & Das(5> 의 방법을 따른 것이다. 일반적인 2- 차원 모형 장이론들의 해를 경로적분 방법으 로 계산하는 방법은 Das & Ma th u r< 5) 에 자세히 설명되어 있다 . ( 1) R.P . Feyn ma n and A.R. Hi bb s, Quan tu m Mechanic s and Path Inte gr als, McGraw-Hi ll, 1965 ; L.D . Faddeev, in Meth o ds in Fie ld Theory , Les Houches Lectu r e Nate s , ed. by R. Balian and J. Zin n -Ju s ti n, 1976 ; D. Luri(! , Part icle s and Fie ld s, Wi le y, 1968 ; C. Nash, Relati vis tic Q uan tu m Fie ld s, Academi c Press, 1978. (2) F.A . Berezin , Meth o d of the Second Qua nti za tio n , Academi c Press, N.Y . 1966; L.H . Ry d er, Q uan tu m Fie l d Theory , Cambrid g e Un ive rsity Press, 1985. T.D . Lee, P art icle Phys ics and Intr o ductio n to Fie l d Theory , Harwood Aca- demi c Publi sh ers, 1981. (3) J. S chwin g e r , P hys . Rev. 프 혼, 2425 (1962} . (4) K. Fuji ka wa, Phys , R ev. Lett . _42,, 1195 (1979) ; Phys . R ev. D 21, 2848 (1980} ;D22, 1499 (E) ( 1980) . (5) R. Roskie s and F.A . Schapo snik , Phys . R ev 쁘 8(1981}. A. Das and V.S . Math u r, Phy s. Rev. 쁘 ~. 489(1986} J. B arcelos-Neto and A. Das, P hys . Rev. 쁘 , 2262 (1986} . 〔문제〕 1 {7-22) 식과 {7-23) 식을 유도하라. 2 지수함수를 급수전개하고 각 항을 적분하여 (7-36) 식을 증명하라. 3 그리스만변수의 변환 따)=fd x' ij, Gu(x,x')TJ ;(x ') 에 대하여, 함수적분 (7-37) 식이 어떻게 변화하는지를보아라.
4 (7-38) 식과 (7-39) 식을 유도하라. 5 (7 - 42) 식을 함수적인 후리에 변환하여 (7-45) 식이 된다는 것을 보이라. 6 (7-57) 식에서 ¢µ(x)o ll 대한 적분을 계산하여 그 결과가 (7-48) 식이 된다는 것 을보이라. 7 (7-60) 식으로 기술되는 장이론의 그린 발생원이 만족하는 함수미분방정식을 구 하고, 그 해가 (7-61) 식으로 된다는 것을 보이라• 8 자유도가 유한한 양자역학적인 계의 경우 확률전폭
제 8 장 그린 함수의 근사적인 계산 라그란지안 IP (x;J) =-½
그러나 (8-2) 식은 장이론의 여러 가지 성질을 알아내거나 근사적인 계산 방법을 개발하는 데 편리하게 이용될 수 있다. 이 장에서는 (8-2) 식과 갇 은 함수적분을 이용하여 그린 함수나 그린 발생원을 근사적으로 계산하는 방법들을 소개하겠다. (1,2 ,3)
8.l 자유 장이론의 그린 함수 제 5 장에서와 마찬가지로, 장이론의 그린 함수들은 전공-진공 전이진폭 (8-2) 의 의부근원 J (x) 에 대한 함수미분으로 나타낼 수 있다. 작용원리를 이용하면, 전공-진공 전이전폭의 1- 차도함수는 志 <0,a,l0,a;> =if
=Nj@
J =Ne-½J (x )K-l(x,x')](X') (@ rp'e -½,p '( x)K(X,X'),P ' (x') 8-8) 로 쓸 수 있다. 이 식의
연산자 K(x, 지울 K(x,x') =I} 떳 i( 훗 + m2 -i E)o(x-x') (8-9) 로 정의하면, (8-6) 과 (8-8) 식의 함수적분이 존재한다는 것을 쉽게 보일 수 있다. 따라서 자유 장이론의 전공 전이진폭은
인 그린 함수가 되는 것도 이러한 조건 때문이다. 이 결과는 제 7 장에서 형 식적으로 정의한 함수적분에 정확한 의미를 부여한 것이기도 하다. 8.2 그린 함수의 섭동적인 계산 그린 함수나 그린 발생원을 근사적으로 계산하는 방법 중에서 가장 흔히 사용하는 것이 결합상수에 대해서 전개하는 섭동론(p e rtu rba ti on th eo ry)이 다. (1,2) 이러한 섭동적인 계산방법의 체계를 세우는 가장 확실한 방법이 경 로적분을 이용하는 것이다. 섭동적 계산의 체계를 세우는 방법을 쉽게 보이 기 위해서, 제 7 장에서 이야기한 스칼라 장이론을 생각하겠다. 이 계의 라 그란지안은 요=＿露莊}四µ_宇 2_ ｝섬+심 (8-13) 이며, 이 계의 그린 발생원은 Z[J ] =
Z [J]=홀꿉子 )n[( ;· 編 )4]ne 방 (Y)Do( y-y')/(y') (8-15) 로 된다. 여기서 (} 8]?x))4은 x 에 대하여 적분한다는 의미를 포함한다. (8-15) 식은 발생원을 결합상수 A 에 대한 급수로 전개한 것이며, 이 식을 이용하면 그린 함수들을 A 의 원하는 차수까지 계산할 수 있다. 이러한 계산을 하는 한 가지 예로 2 점함수를 생각하자. 이 그린 함수는 i
하다• 이 목적을 위해서 고안된 것이 화인만 도표 (Fe ynm an grap h ) 또는 화인만 그립 (Feyn ma n d i a gr am) 이다. 이 방법은 (8-17) 식을 다음과 같은 약속을 하여 그림으로 나타내는 것이다. 죽, 화인만 도표의 내부선 (int e r nal li ne) 과 꼭지점 (ve rt ex) 을 내묘 : x ―—x '=Do(x-x')= 꼈~fd 4% 구~ (8-18} 꼭지점: ><다 의 그림으로 약속하고, 그린 함수의 반복되는 변수 (x 나 x' 등)들에 대해서 는 적분하기로 약속하면, (8-16) 식은 i< 0| T(¢(x)¢(x'))|0 > =X― x '+ 오x '+ OO+… (8-19) 로 나타낼 수 있다. 이 경우 대칭인자 S, 는 꼭지접 하나 (A 의 l- 차항의 경 우)로부터 (B-19) 식의 그림들을 만들 수 있는 경우의 수에 十을 곱한 값이 다. 요의 경우, 꼭지점 하나에서 변수 x 를 택할 수 있는 경우의 수가 4 이 며, 그런 다음 x' 울 택할 수 있는 경우의 수가 3 이다. 따라서 S1=4X3X ¾=3 이다. s 눅 꼭지접의 네 선 중에서 두 개를 골라 고리 (l oo p)를 만들 수 있는 가짓수이므로, &=.c2x¾=¾ 이다. (8-18) 식과 같은 약속을 화 인만 공식 (Fe ynm anrule) 이라고 하고, (8-19) 식과 같은 도표를 화인만 도 표라고 부른다. 화인만 공식에서 반복되는 변수며 (8-17) 식이나 (8-19) 식에서 변수 y〕에 대해서는 적분해야 한다는 점에 유의해야 한다. (8-16) 식에서 沿에 비례하는 항은 다섯 개의 전파인자 Do(x-x' ）과 두 개의 꼭지 접으로 만들 수 있는 모든 가능한 도표들을 모은 것이다. 따라서 이렇게 도 표를 사용해서 그린 함수를 계산하는 것이 그린 발생원을 직접 미분하는 것 보다쉽고편리하다. 그린 함수를 화인만 도표를 사용하여 계산하는 데에는, 위에서와 갇이 시
공간 좌표계에서 계산하는 것보다 운동량 공간에서 계산하는 것이 편리한 경우가 많이 있다. 운동량 공간에서 그린 함수를 도표로 나타내기 위해서는 운동량공간화인만공식을구성해야한다. 이것을보이기 위해서, (8~16} 식의 A2 에 비례하는항중에서 다음과같은도표를생각해 보자; 식3 추=키 2SDo(x-Y1)Do(Y1-Y2) x x x D o(y1 — y2) Do(y I — Y2) Do(y 2 -x') (8-20} 이 경우 대칭인자는 S=~=6 이다. 운동량 공간 화인만 공식을 유 도하기 위해서 , (8-12) 식의 후리에 변환식을 사용하여 (8-20) 식을 다음과 같이 쓰는 것이 편리하다 ; 玉1;,= -A2S fd 4Y1d4Y2f 융堯·습 re i P1•(X-Y1) X eiP 2•(Y1-Y2l +iPo •(Y1-Y2)+i P ,•(Y1-Y2l+ iP5 •(Y2-x') 갭I P} ＋노니 = -A2 這닌~i P1•X- i P&• x' 8(P2+Pa+P 라) X 8( 硏 Pa+P.-Ps)ll1(下 노이 검Jd 4 p e i P•(x-x ' >(-A2S) fjl+걸亡五 xf ~ 걸》2 4 ql2 +;2_i e q8 +;2_ic x (p-q l_ q』~ (8-21) 이 식은 운동량 p만의 함수를 후리에 변환한 함수로 볼 수 있다. 따라서 (8-21) 식을
X 군x ' =Ttiffd 4 p e i P•(X 一x')-;B-;- 로 쓰면, (8-20) 식의 운동량 공간에서의 표현인 -;0; =(p나니 2高 fd 4 q 1d4 q 2~ x q杓+ m1 2_ i€ (p_ ql _ q1갑 + m2-i€ (8-22) 을 얻게 된다. 이 화인만 도표의 (8-22) 식에 해당하는 결과를 직접 얻기 위해서는 다음과 같은 약속을 하면 된다 ; 내부선: p) :三 p2+ m12 _i € (운동량 공간 전파인자) 꼭지접: X =zil, (각 꼭지점에서 운동량이 보존됨) *
*에너지-운동량이 꼭지접에서 보존되는 것은 (8-21) 식의 델타 함수 때문이 다.
고리적분: 庫Y · (8-23) 이것이 운동량 공간에서의 화인만 공식이다. (8-22) 식에 해당하는 도표를 q1 p크도 p-q1 -q2 로 표현하고, 이 그립에는 독립된 두 개의 고리가 있다는 점을 고려하여 (8 -23) 식의 공식을 적용하면 (8-22) 식의 오른쪽을 쉽게 얻을 수 있다. 임의의 장이론을 기술하는 라그란지안이 주어지면, 위와 갇은 방법을 이 용하여, 그린 함수들을 원하는 차수까지 체계적으로 계산할 수 있다. 일반 적인 정이론의 그린 함수를 결합상수의 급수로 계산하는 과정은 다음과 갇 은순서로한다: (1) 그린 발생원 Z[ J] =
부터 화인만 공식을 유도한다. (2) 결합상수의 각 차수에 해당하는 가능한 모든 독립된 화인만 도 표를 그린다. (3) 화인만 공식을 사용하여 각 그린 함수를 식으로 쓰고 계산한 다. 화인만 공식은 경로적분 표현을 사용하지 않고도 유도할 수 있으 나, 아벨리안이 아닌 게이지 이론의 경우와 갇이 복잡한 장이론의 경 우에는 경로적분 방법을 사용하는 것이 거의 필수적이다. 일반적인 장이론에서 화인만 공식과 그를 이용한 계산방법은 't H oo ft와 Vel t man<2) 에 자세히 설명되어 있다. 8 . 3 연결된 그린 함수 (3) 그린 함수를 화인만 도표로 나타낼 때, 앞 절에서 이야기한 2- 점함 수 < OIT(¢(x)¢(x ' ))IO > 이나 일반적인 n- 정함수
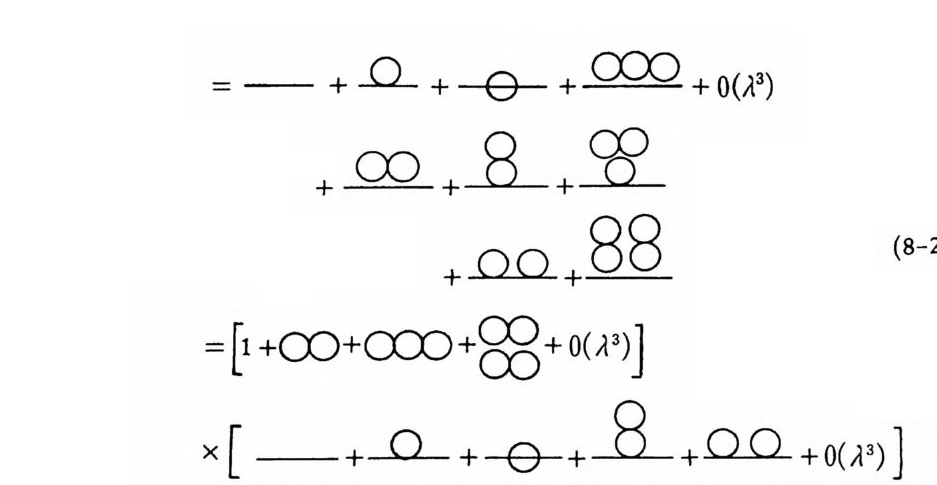= —— + __Q_ + -e--+ 오 죠~ + 0(1t3 )
와 감이 진공 전이진폭 <010> 와 연결된 그린 함수의 곱으로 표현된다. 따 라서 규격화된 (norma li zed) 2- 점함수 D(x?')= 广0 | T(5 집: x')) 距= — +요 +e +… (8-25) 는 연결된 도표만으로 이루어져 있으며, 연결된 2- 점함수이다. 따라서 제 5 장에서 정의한 n- 점함수 D(n)(xI, ... Xn)= 눅:(n/2<) OI T(¢(x1 파)… 는 전공도표 (vacuum di agr am) 를 제거한 도표들만으로 이루어져 있다. 그 러나 이렇게 규격화된 n- 정함수도 일반적으로는 연결되지 않은 그린 함수 이다. 예를 들면 4 점함수 D(4) (xI, x2, X3, x4) 는
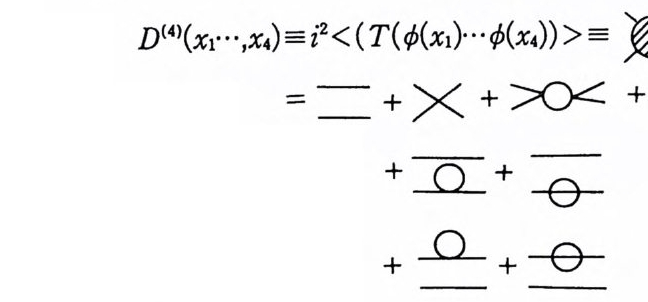DU)(xr · ·지 국 < ( T(¢(x,)… ¢ (x4)) > 三 擊
와 같이 연결되지 않은 구 분 결 을 포함하고 있다. 그런데 이 4- 점함수의 연 결되지 않은 부분을 모두 합하면, 이들은 연결된 2- 점함수의 곱으로 표현 된다. 죽, 규격화된 4- 점함수는 f < T( (x1)… < />(x 이) > =? < T((x1)… ¢ (x4)) > C (8-26) +?~< T( 幹)>< T()> 으로 쓸 수 있다. 여기서 < T( … )>c 는 연결된 도표만으로 된 4- 점함수를 의미하며, 두번째 항의 고는 x 돌을 교환한 항들에 대한 합을 의미한다. 이 것은 연결되지 않은 그린 함수를 연결된 그린 함수의 함수로 표현할 수 있 다는 것을 뜻한다. 이것은 일반적인 n- 점함수의 경우에도 성립한다. (8-26) 식의 연결된 그린 함수는 발생원 W[J ]=+1 tnZ [ J]=+1 tn< O,~. . |0,6-.. >1 (8-27) 로부터 얻을 수 있다. 이 발생원을 연결된 그린 발생원이라고 한다. (8 -27) 식을 의부근원 J (x) 에 대하여 네 번 미분하면 ! 晶) 히『찌 ~W[J]l1= 0 =T1 i히(마J·4 · 히(교 ln Z[J] 11 =0 . . (8_28) 국
다음과 같이 그 합을 간단하게 나타낼 수 있는 도표들이 있다 ; 「 , +푸 , +~ , +~ , + ··· =\)x y y三 ' = 广y ((—-\~t~ ,(8 29) 이 식에서 1 은 o( x - y遷- 나타내며, 반복되는 변수에 대한 적분약속을 사 용하였다. {8-29) 식은 운동량 공간에서 표현하면 더욱 편리하다 : --r + -0-+ -ee-+ ---0 0-0-+ • • • =#+m21_ 1.€ g+ m12 _e(p) p 2+m1 드 i e (8-30) (8-29) 식의 분모에 나타나는 도표를 A22(x _y )= Xe y (8- 3 1) 로 표시하면, ~(x— y~ 스칼라 장의 자체 에너지 (self -ener gy)를 나타내 는 함수이다. (8-29) 식은 무한히 많은 연결된 도표들의 합을 자유 전파인 자와 자체 에너지 고만의 함수로 표현할 수 있다는 것을 의미한다. 따라서 이것은 연결된 그린 함수들도 모두 계산할 필요는 없다는 것을 의미한다. (8-29) 식의 왼쪽의 각 항에 나타나는 도표를 lPR 도표 (one - p a rti cle redu ci ble di a gr am) 라고 부른다. lPR 도표란 그 내부선 중 하니률 자르면 두 개의 떨어진 도표로 분리되는 도표이다. 이에 반하여 (8 - 31) 식과 같은 도표는, 그 내부선 중 하나를 잘라서 두 개의 분리된 도표로 만들 수 없는 도표이며, 이러한 도표를 lPI 도표 (one- p a rti cle irr educib l e di a gr am) 라고 부른다. 모든 lPR 도표들은 그 급수를 합하여 * lPI 도표들의 함수로 쓸 수 있다. 이것은 그린 함수를 계산하기 위하여, 연결된 그린 함수 모두를 계산할 필요는 없고, 그 중에서 lPI 도표에 해당하는 것들만 계산하여도 충분하다는 것을 의미한다. *그린 함수를 결합상수에 대하여 전개하면 lPR 도표들의 무한급수를 포함하 게 된다.
따라서 lPl 도표에 해당하는 그린 함수만을 발생하는 발생원을 구성 할 수 있다면, 물리적인 정보를 얻는 데 훨씬 편리할 것이다. 이렇게 내부선 하나를 잘라서 둘로 분해할 수 없는 그린 함수인 1PI 그린 함수를 발생하는 발생원을 유효작용 (e ff ec ti veac ti on) 이라고 한다. 이 유효작용은 양자적인 효과를 모두 포함하면서 고전적인 작용의 성 질을 갖는 범함수이기 때문에 , 계의 물리적인 성질을 알아내는 데 아~느 편 리한양이다. 8 . 4 유효작용과 유효 포텐셜 (3) 연결된 그린 함수의 발생원 W[ J}E 진공 전이전폭과 Z[J] = < OIO >,= e i wrn= j@
관한상수이어야한다. 이제 발생원 WU] 의 르장드르 변환 (Le g endre tr ans fo rma ti on) 을 생각하 자; 따]= W[ J]-fd4x ](x)¢(x) (8~36) 이 르장드르 변환은 J의 범함수인 W[ 刀룰 硏의 범함수인 I'[싸로 바꾸어 주는 변환이다. {8-36) 식을 #(x) 에 대해서 미분하면 晶= 8f 『') :;(길 J (x)- ft』 rp( x')= -J(x ) (8-37) 로 된다. 따라서 {8-34) 식과 (8-3 기석을 이용하면 編 ~=V=O (8-38) 의 결과를 얻는다. 여기서 v=O 인 경우가 자발적인 대칭성 깨어짐이 없는 경우이다. 이 식은
이러한 범함수를 유효 포텐셜 (e ff ec ti vep o t en ti al) 이라고 한다. 운동량이 영 이 아닌 경우에는 ¢ = v 가 범함수 I'의 극점에 해당하며, r는 작용의 성질 울 갖기 때문에 유효작용 (e ff ec ti veac ti on) 이라고 부른다. 이제 범함수 I'[¢]가 발생하는 그린 함수에 대해서 알아 보자. 기호를 간단하게 하기 위하여 ¢(x) 를 ¢i로 표시하겠다. 따라서 첨자 i 는 ¢(x) 의 내부공간에서의 성분을 나타낼 뿐만 아니라 시공간 좌표 갔도 포함하는 기호이다. 이렇게 하면 (8-33) 식은 뿔=亨쁜츠=
의 관계를이용하면 (x-1)ul/=O = 〈거 /=0= —忍 開 1=0= - Du (s-46) 으로 나타낼 수 있다. 여기서 Dv는 전파인자이다. 따라서 극점에서의 2 점함수 X』 ¢=V= 〈幻 ¢=v= I'J 2> 는 전파인자 D ii의 역함수라는 것을 알 수 있다 . 따라서 1PI 2- 점함수는 전파인자의 역함수이다. 1PI 3 정함수를 얻기 위하여 (8-4 기식을 Jl 에 대해서 미분하면 8]訂i8 LW8 ]l 88#]kj 1 8정fA WIj 8#紅m8# k 쉔8f쁘l = O 울 얻는다. (8-44) 식을 사용하면 이 식은 - ~~ wx TTj k-xT;T;- 1i~ 83I x' 겉 =O 로된다. 이 식은다시 - ~~= wX 1T1T -1X TTj ；；-；1 l Txr갑 -1 ~~I' (8-47) 로 쓸 수 있다. ]=0,
든 그린 함수는 이와 같이 외부선을 잘라낸 그린 함수인데, 이런 뜻에서 r(n) 을 다리를 자른 그린 함수 (amp ut a t e d 혹은 trunk ate d Green's func - tion ) , 혹은 순수한 꼭지점함수 (pro p e r ver tex fun c ti on) 라고 부른다. 일반적으로
京o =_8 o]
으로 쓸 수 있다. 이 식의 오른쪽에서 i m 은 장함수의 내부공간에서의 성분 울 뜻하며, X i는 시공간 좌표이다. 좌표 이동에 대한 장이론의 불변성으로 인하여, 그린 함수 I' (n) 은 좌표들 사이의 거리 (x i _Xj )들만의 함수이어야 한다. 독립된 이들 변수의 수는 (n ― 1) 개이며, 따라서 I' (n) 의 후리에 변환 인 f (n) 은 R, 露 (=P1J. /nk,~· \·n ·(,PXn1),(X212r,)·4··,8x(nP)1 ＋f ]拓/-+ix·,. p· ,· d +4Xp;n ) (8-55) i= l 로 된다. 이것은 좌표이동에 대한 불변성 때문에 전체 운동량이 보존된다는 것을 의미한다. 순수한 꼭지점함수를 그립으로 표시할 때에는 댕p3 t 三 r%, ....P n ) :의平J에 전파 인자가 없음. Pn 와 같이 나타내며, 이 그립에서는 각 의부선은 전파인자를 뜻하지 않는다. 이 그립에서와 갇이 각 운동량의 방향을 안으로 들어가는 방향으로 잡으면, 운동량보존법칙은 2pi =O 로된다. 앞에서 간단하게 이야기하였던, 방정식 開 I=0=v i’ 뿔겔 ¢=u=O (8-56) 의 의미에 대해서 생각해 보자. 이를 위하여 ¢가 상수인 경우를 생각하자. 유효 포텐셜 V( t/J遷 정의하기 위하여 발생원 r(¢ 潟· 운동량 공간에서 운 동량 p,에 대하여 전개하자. 운동량 공간에서 표현한 발생원 f[t/J~ p,.oJ] 대한 급수에서 그 첫번째 항을 유효 포텐셜로 정의한다. 죽,
I'[
는 경우가 계의 바닥상태를 나타낸다. 유효 포텐셜 V를 h 에 대해서 급수 전개하면, 그 첫번째 항이 고전적인 포텐셜 U 가 된다는 것을 다음 절에서 알게 될 것이다. (B-32) 식의 오른쪽을 tz -o 인 극한에서 계산하면*, W[ J)7} 고전적인 작용(의부근원과의 상호작용항을 포함하는)이 된다는 것을 알 수 있다. 따 라서 발생원 W는 양자적인 효과를 포함하는 작용의 성질을 갖는다는 것을 알 수 있다. 또한 (8-36) 식의 르장드르 변환은 발생원 W 에서 의부근원과 의 상호작용항을 뺀 부분을 발생원 r[ 싸로 정의한다. 따라서 발생원 r[¢] 는 순수한 양자적인 계의 작용의 성질을 가지며 , 장함수 rp( x~ 진공기대 값°J
*이 계산은 8.6 철의 말안장 근사법 부분에 되어 있다.
¢i(x )= < 0| ¢i(x )|0 > 의 범함수로 표현된다. 이러한 의미에서 발생원 r 를 유효작용 (e ff ec ti ve ac ti on) 이라고 부른다 .(4) 유효 포텐셜의 경우와 마찬가지로, r[ 싸를 h 의 급수로 전개하면 그 첫 항은 고전적인 작용 S[ rp]이다. 8 , 5 고리전개 (loo p exp an sio n ) 지금까지 그린 발생원 W [J]와 I'[#]가 갖는 의미와 이들을 섭동적으로 계산하는 방법에 대해서 이야기하였다. 그린 함수를 결합상수의 급수로 전 개하여 계산하는 이 방법은 물리적인 정보에서 자유입자와 다른 부분을- 근 사적으로 계산하는 것이다. 죽, 전개하는 매개변수(결합상수)가 영일 때의 결과는 자유입자의 경우로 되는 것이다. 자유입자의 경우는 장이론을 정확 하게 닫힌 형태로 풀 수 있고, 따라서 우리가 잘 알고 있는 경우이기 때문 에 이 근사 방법이 편리한 경우가 있다.
자유입자의 경우 의에 우리가 쉽게 알 수 있는 경우가 고전적인 경 우이다. 따라서 물리적인 정보에서 고전적인 경우와 차이가 나는 부 분을 근사적으로 계산하는 방법이 편리하게 이용될 수 있는 경우가 있을 것이다. 이러한 전개 방법은 물리량을 플랑크 상수 h 에 대하여 전개하면 얻을 수 있다. 이러한 근사 방법을 고리전개 (loo p exp a n- s i on) 라 한다. (1, 3) 여기서 고리란 화인만 그림에서의 고리를 뜻한다. 화인만 그림의 독립된 고리의 숫자가, 그린 함수를 紀의 급수로 전개할 때 나타나 는 h 의 차수에 해당한다는 것을 곧 알게 될 것이다. 이러한 그린 함수의 전개식에서 그 첫 항(fz O 에 비례하는 항)은 고전적인 값을 주는 항이다 . 그린 함수의 고리전개법을 쉽게 보이기 위해서 스칼라 ¢4 이론의 그린 발 생원을 생각하자. 이 계의 그린 발생원은, 가상적인 매개변수 a 를 도입하 여 Z[J] = eiw u1=f (jJ) rp e il d 따묘안')당'P (X)](X)) 로 쓸 수 있다. 이렇게 도입한 a 는 전파인자를 D;(x— y) =[-¼K(x-y ) r1= aK-1(x-y )= aD 。 (x- y) 로 변화시킨다. 따라서 그린 발생원은 Z[J] = e ild’ 당[e 1 ~J efa J ( y)D o(Y- Y t )J(yt) (8- 61 ) 로 쓸 수 있다. 여기서 오志곤 라그란지안 중에서 상호작용을 기술하는 항이 다. 이 식은 새로 도입한 매개변수 a 때문에 전파인자 Do 와 꼭지점의 화 인만 공식에 변화를 준다는 것을 의미한다. 앞 절에서 이야기한 화인만 공 식에서 전파인자를 Do 에서 aDo 로, 그리고 꼭지점을 a 에서 iA /a 로 바꾸 면, 앞 절의 방법을 그대로 사용하여 (8-61) 식에 의한 그린 힘수들을 계산 할 수 있다. 이러한 방법을 사용하여 그린 함수들을 매개변수 a 의 멱급수 로 계산할 수 있다. 여기서 a 는 가상적인 매개변수이지만, 플랑크 상수 h
룰 구체적으로 나타내는 단위계를 사용하여 그린 발생원을 나타내면, 이 플 랑크 상수 h 가 바로 매개변수 a 에 해당한다. 이것은 h 가 작용의 단위를 갖는 싱수이며, 지수함수의 지수 (ex ponen t)는 단위가 없는 값이 되어야 한 다는 사실로부터 쉽게 이해할 수 있다. 따라서 (8-61) 식을 a 에 대해서 전 개하는 것은 h 에 대한 급수전개와 같다. 이제 의부선이 E 개, 내부선이 1 개이며 꼭지접이 V개 인 화인만 그립을 생각하자, 앞에서 이야기한 화인만 공식의 변화에 의해서, 이 그립이 그린 함수의 a 에 대한 전개식에 공헌하는 것은 a 1-V+E 의 처수에 해당하는 항이다. 이 화인만 그립에 해당하는 1PI 그린 함수 r(E) 는, 위에서 이야기한 그린 함수에서 각 의부선에 해당하는 전파인자를 나누어 준 것에 해당한다. 따라서 이 그림은 1PI 그린 함수 r(E) 에서는 a l-V 의 차수에 해당하는 항에 공헌한다. 위에서 이야기한 화인만 그립이 ER 의 독립된 내부고리를 갖고 있으면, 운동량 공간 화인만 공식에 의해서, 이 항은 L 개의 운동량변수에 대해서 적분해야 한다. 이 그립의 내부선은 각각 운동량변수를 갖는데 (죽, 이 그 립에는 I 개의 운동량변수가 있다), 각 꼭지점에서는 운동량이 보존되므로, 이들 운동량변수들은 V개 의 구속방정식을 만족한다. 그런데 이 그립 전체 의 운동량 보존법칙은 남아 있어야 하므로, 실제 구속방정식의 개수는 (V-1) 개이다. 따라서 적분해 주어야 하는 운동량변수의 개수는 1-(V- l)= (J -V+l) 개이다. 이것이 독립된 고리의 수이다. 따라서 L=I— v+ 1 이다. 이 식을 이용하면 I' (E) 에 공헌하는 화인만 그림의 처수는
al-V=al-1= 上a l a 로 쓸 수 있다. 따라서 위의 그린 함수 I' (E)는 a 에 대한 전개식에서 al-1 에 해딩하는 항에 공헌한다. 그린 발생원 W [J]와 I'[싸는 작용의 단위를 갖는다. 따라서 lPI 그린 발생원 I'는 *I'[#]=*홀。 flL I 'L[cp ] (8-62) 로 쓸 수 있다. 죽, r[ 싸룰 플랑크 상수 h 에 대하여 전개할 때, h 의 차 수는화인만그림의 고리의 수에 해당한다. 다시 말하면, I'[¢]에 공헌하는 항 중에서 K 에 무관한 항은 그 화인만 그림이 내부고리를 포함하지 않는 나무 모양 그림(tr ee di a gr am) 이며, E 에 비례하는 항은 그 그림이 내부고 리 하니를 포함하는 항들이다. EH 의 독립된 고리를 갖는 화인만그림은 발생원 W나 I'에서 fi L 에 비례하는 공헌을 한다. 이러한 이유때문에 h 에 대한 급수전개를 고리전개라고 한다. 그린 함수나 발생원을 플랑크 상수에 대한 멱급수로 전개하는 것이 편리 한 것은 h 가 양자적인 효과의 크기를 나타내는 매개변수이기 때문이다. 고 리전개가 결합상수에 대한 전개보다 더 편리한 또 한가지 이유는 고리전개 가 계의 라그란지안이 갖는 대칭성을 유지하는 근사 방법이기 때문이다. 예 를 들면, 게이지 이론에서 결합상수를 영으로 놓으면, 그 라그란지안은 게 이지 대칭성을 갖지 않게 된다. 그래서 결합상수에 대한 근사 방법은 게이 지 불변성을깨뜨리게 되며, 따라서 이 근사방법은게이지 이론의 경우좋 은 근사 방법이 못 된다. 이에 비하여, a(n) 의 어떤 값에 대해서도 원래 라그란지안이 갖는 대칭성은 그대로 유지된다. 따라서 고리전개법은 게이 지 이론과 같이 대칭성이 중요한 역할을 하는 장이론을 다루는 데 특히 편 리하다.
8 • 6 말안장 근사법 (saddle po in t meth o d) 그린 발생원을 플랑크 상수 h 의 멱급수로 전개하면, 각 항의 h 의 차수 는 화인만 그림의 독립된 고리의 수와 같다는 것을 보았다. 이러한 사실을 이용하면 고리전개의 각 항을 계산할 수 있다. 특히 말안장 근사법 (saddle poi n t meth o d) 또는 최급하강법 (ste e pe s t descent me th od) 이라고 불리는 계 산 방법을 사용하면 고리전개의 각항을 계산하는 데 편리하다. 여기서는 스 칼라 ¢4 이론의 예를 들어서 고리전개의 각 항을 계산하는 방법을 보이겠 다. (1, 3) 스칼라 ¢4 이론의 라그란지안은 ft=-뷰 ¢8% ―구 ¢2_4 섬 (8-63) 으로 쓸 수 있다. 이 계의 연결된 그린 함수들을 발생하는 발생원 W[ J~ eiW [J] /h =NJ @rp eff d•x[ !l /'Pl+ 'P ( X) J( X)] (8-64) 로 표현된다. 여기서는 발생원을 h 의 급수로 전개하기 위하여 플랑크 상수 롤 구체적으로 표시하였다. 말안장 근사법이란 적분되는 함수를 지수함수로 쓰고, 그 지수를 어떤 근 사점울 중심으로 한 데일러 급수 (Ta y lorse ri es) 로 전개하여 계산하는 것이 다. {8-64) 식의 적분되는 범함수는 이미 지수함수로 표현되어 있고, 그 지 수는 고전적인 작용이다. 따라서 {8-64) 식을 말안장 근사법으로 계산하기 위해서, 고전적인 작용 S[rp ]+ rp (x) J (x)= j죠[파)+ rp( x)J( x )] {8-65) 를 고전적인 해 rp( x)=< po (x) 근방에서 테일러 전개하면 된다. 이렇게 하 면, 작용 {8-65) 는
S[
였다. 그린 발생원 W룰 W[ J]= Wo[J ]+ n Wi[J]+ n2 Wi[J] +… (8-71) 로 전개하면, (8-70) 식은 W제 공헌하지 않는다는 것을 알 수 있다. 따라 서 (8-69) 식에 의하면 W。 [J눗 w。 [J]= S[
Do]=D 。 (x- y)J(y)=fd 4 yD 。 (x —y)J(y) 로 정의되며, (8-73) 식의 마지막 결과는 이 식의 첫 줄에 있는 관계를 되 풀이하여 대입함으로써 얻은 것이다. (8-73) 식을 (8-72) 식에 대입하면 Wo [J]=숭JD ol 卓 D 。 (x-x') J (x')] 나·· (8-74) 의 결과를 얻는다. 이 식은 Wo[ 기가 내부고리가 없는 나무 모양의 화인만 그림들만의 모임이라는 것을 의미한다. 고리전개의 no 에 해당하는 항에서 , 양자장의 전공기대값인
x N f탸 e당 瓦닫梅詞 ,(X)- 'P o(X)I[,;,( y)-'P o(Y )i 로부터 계산할 수 있다. 함수적분의 성질을 이용하면 eiW l[J 1 =Nf( j/)
=X D 그 。 2(럽x ;; i- '-1x -2)~n ~ (xf2)d D4 。X (1x2' -죠X3) 걸 (x 야 .. D 。뇨 —XI) p祐 ((x8I-)7 9) 로 쓸 수 있다. 따라서 柏에 비례하는 항까지의 연결된 그린 발생원은 W[ J]= Wo[J ] 국tz Tr i o~ 白: . = W。 [J]-it2z— ;2~;-'1 (-3n, -l) n D 。 (x1-x2 潟 (x2) …D 。 (xn- X l 潟 (xl) (8-80) 으로표현된다. 이 식에 나타나는 ({Jo (X~ 의부근원 J (x) 의 범함수이므로, (8-73) 식을 이 식에 대입하면, W [J遷 함수 J (x) 만의 범함수로 나타낼 수있다. 이제 순수한 꼭지점함수를 발생하는 발생원 r[ 싸를 拍에 비례하는 항까 지 계산하자. r[ 싸는 I'[
=S[¢]+J (x )¢(x)+ 0( 리 (8-83) 로 된다. 즉, w。 [J住 h 에 비례하는 항까지도 (8-83) 식으로 주어진다. 왜냐하면 이 식의 두번째 줄에서 중괄호 안의 함수는 장방정식에 의해서 영 이 되기 때문이다. 따라서 h 에 비례하는 항까지 계산한 연결된 그린 발생 원을 (8-82) 식의 rp (x) 의 함수로 표시하면 W[J ]= Wo+1 iWi = S[rft ] +J(x )rp ( x) 부 Tr i o~ 로 된다. 따라서 이 차수까지의 유효작용은 I'[ rp] = I'o +n n = W-J( x ) rp( x) =S[ 小]溫2 T., r,l iov 5g 8
V( ip)=구맡나-ip ◄ 극 Trlo 占햏 (8-86) =무 ¢2 국戶隋f潟鬪#+:〈』 n 이 된다는 것을 쉽게 알 수 있다. 그런데 이 식의 n=l 인 항과 n=2 인 항 은 그 적분값이 무한대이다. 이 발산항들은 운동량값(또는 전동수)이 클 때 생기는 발산항이므로 자의발산 (ultr a v iole t s i n gu lar ity)항이라고 부른다. 이러한 자의발산항을 포함하는 이론 중에는 그 이론에 존재하는 매개변수들 울 다시 정의함으로써〔이것을 재규격화 (renormal i za ti on) 라고 한다〕 발산하 는 항들기 측정 가능한 물리량에는 나타나지 않게 만들 수 있는 장이론이 있다. 이러한 장이론을 재규격화 가능한 (renorrnal i zable) 이론이라고 부론 다. {8-86) 식에서 발산하는 항인 n=l 과 n=2 인 항들은 각각 ¢2 과 ¢4 에 비례하며, 이러한 항들은 고전적인 포텐셜에 이미 존재하는 항들이다. 따 라서 {8-86) 식의 발산항들은 ¢2 항과 ¢4 의 계수인 m2 과 A 를 다시 정의함 으로써 유효 포텐셜을 유한하게 만들 수 있다. 그래서 재규격화된 질량 mR 과 재규격화된 결합상수 AR 을 mR2=m2_i 3A hf (g #+」 2_ i€ (8-87) AR= tl +9 tl 2 미 :4 (p2 + ;2 玉 )2 로 정의하면, 유효 포텐셜은 V( 莊)=강血얕며넘 4 弓ff읊끊흡辻p 2;;AR:: i c 『 (8-88) 로 되어 유한하게 만들 수 있다. 유효 포텐셜은 운동량이 영일 때의 lPI 발생원으로~ 정의된 발생원이므로, 위에서 한 재규격화를 lPI 발생원 I'에 대해서 표현하면
rr<(42)l((Pp1I ,,Pp 2 2,)/I> PJ ,, = Po4)= 1 P-,=mo=i —3 !A R (8-89) 의 조건을 요구하는 것에 해당한다. * (8-89) 식과 같은 조건을 재규격화 조 건이라고 한다. (8-89) 식의 조건들은 물리량 mR 과 A~ 의미를 주는 식이 기도 하다. 다시 말하면, 라그란지안 (8-63) 에 나타나는 매개변수 m 과 A 를 입자의 질량과 결합상수라고 부르는 것은 잘못이며 \ 물리적인 질량은 2 정함수의 발산점 (pole) 의 위치로 정의해야 하고 물리적인 결합상수는 순 수한 4- 점꼭지점의 크기로 정의해야 한다는 것을 (8-89) 식은 뜻한다. (8 -88) 식의 형태를 보면, 스칼라 섬이론에서 양자적인 효과는 #의 값이 클 때 크게 나타난다는 것을 알 수 있다.
*이 조건은 고전적인 작용 I'o [#] 에 나타나는 질량과 결합항의 형태가, 재규 격화점 (renormal i za ti on p o i n t)인 p ;=O 에서의, 양자적인 작용 r[¢] 에서도 유지되도록 요구한 것이다. t이것은 양자적인 상호작용에 의해서 매개변수 m 과 A 의 의미가 달라지기 때 문이다.
지금까지 스칼라 섬이론을 이용하여 발생원 W [J]와 r[#] 의 fi O 에 비례 하는 항과 1i에 비례하는 항을 계산하는 방법을 설명하였다. 그보다 높은 치수의 항들(fi L 의 계수, L느 2) 은, (8-70) 식에서 지금까지 무시했던 항들 울 계산하면 얻을 수 있다. 즉, L 뇨 2 인 항들은 고전적인 작용에서 양자적 인 변동 (fluc tu ati on ) 항인 S' = fd 4x[뉴 (x)( 장 -m 2 -3A< :p/) cp( x)-1i1 '2 A< :po <:p3 (x) 거감 (x)] (8-90) 에 의해서 결정된다. 앞에서는 (8_90) 식에서 1i에 무관한 부분만을 택해서 계산하였고, 고리전개식에서 L 느 2 인 항<:p 3( 떠들은 이 식의 마지막 두 항에 의해서 결정된다. 그런데 이들 두 항은 rp 3(x) 과 <:p 4(x) 에 비례하기 때문에 (8-70) 식의 함수적분을 닫힌 형태로 계산할 수는 없다. 그래서 이 부분을
h 의 멱급수로 전개하여 각 항을 적분해야 한다. 예를 들면 (8-90) 식 의 마지막 두 항이 (8-70) 식에 공헌하는 부분은 e-iA Ih II2Po 한 (X) 나 },;,•(x)] 인데, 이 함수를 h 에 대해서 전개하면, 始에 비례하는 항은 F[rp ]= —따 A섭 (x)-n tAr2 po( x) rp 3(x) ,P o(Y)
〔문제〕 1 유클리드 공간에서 함수적분을 정의하면, (8-8) 식의 함수적분이 존재한다는 것 울보이라. 2 자유 디락 장의 경우 함수적분표현이 의미가 있기 위해서, 2- 정함수에 주어야 하는조건을기술하라. 3 (8-24) 식에 나터나는 화인만 그립에 해당하는 그린 함수들을 계산하고, 각 그림 에 해당하는 대칭인자를 확인하라• 4 발생원 W[ J)7} 발생하는 그린 함수가 연결된 그린 함수리는 것을 보이라. 5 라그란지안 (6-1) 과 (6-38) 로 기술되는 티링 모형과 벡터 메존 모형의 그린 발생 원을 경로적분으로 표현하고, 이로부터 이들 장이론의 화인만 공식을 유도하라. 6 (8-36) 식으로 정의된 I'가
제 9 장 양자 장이론의 슈뢰딩거 표현 방법 지금까지 양자 장이론의 물리적인 정보를 알아내기 위해서, 하이젠버그 표현 (He i senber gpi c tur e) 에서 장연산자가 만족하는 운동방정식을 푸는 방 법에 대하여 주로 이야기하였다. 이 연산자 방정식은 다루기 어렵기 때문 에, 이들을 그린 함수가 만족하는 함수미분방정식으로 바꾸어서 풀거나, 혹은 이 함수미분방정식의 형식적인 해인 경로적분을 이용하여 물리적인 정 보를 얻어내려고 하였다. 이러한 기술 방법에서 모든 물리적인 정보는 인과 적인 그린 함수 (causal Green's f unc ti on) 들이나 혹은 이들을 발생하는 그린 발생원을 통하여 표현되었다. 양자 장이론의 이러한 기술 방법은 입자들의 산란이나 정상상태 문제들을 다루는 데는 편리하지만, 우주의 전화과정이 나 평형상태에 있지 않은 다체계 (many bod y s y s t em) 의 문제와 같이 물리 계의 시간에 따른 변화가 중요하게 작용하는 문제의 경우에는 그리 좋은 방 법이 아니다. 이러한 문제들의 경우에는 물리계의 시간에 관한 정보를 상태 함수가 결정하는 슈뢰딩거 표현 (Schr~ ding er pict ure) 을 사용하는 기술 방 법이 더 편리하다.
양자 칭이론의 슈뢰딩거 표현 방법은, 섭동적인 계산을 하는 데 불편하다 는 점과 재규격화의 어려움 때문에, 주로 참고문헌 1 에서와 같은 형식적인 (form al) 계산을 하는 데에만 사용되었었다. 그러나 슈뢰딩거 표현에서의 재규격화 문제가 이해되고, 특히 비섭동적인 계산에 편리하다는 사실이 알 려지면서부터 슈뢰딩거 표현 방법이 많이 연구되기 시작하였다. (2) 이 장에 서는 양자 장이론의 슈뢰딩거 표현 방법을 설명하고, 양자적인 작용원리의 슈뢰딩거 표현인 디 락의 작용원리 (acti on pri n c ip le of D i rac) 를 유도하겠 다. (3) 그리고 이 작용원리를 이용한 양자 칭이론의 변분적인 (varia t i on al) 근사 방법을 소개하겠다.
9.1 보즈 장이론의 슈뢰딩거 표현 슈뢰딩거 표현이란 양자적인 연산지들은 시간에 무관한 행렬요소로 표현 되고 , 모든 시간에 관한 정보는 상태함수가 포함하는 표현 방법이다. 따라 서 물리계의 시간에 따른 변화는 상태함수가 만족하는 미분방정식 (슈뢰딩 거 방정식)이 결정하게 된다. 보즈 장이론 (Boson fi eld th eo ry)의 슈뢰딩거 표현 방법은 2 . 5 절에서 설명한 양자역학적인 계의 경우와 같은 방법으로 얻 울수있다. 일반적인 보즈 장이론은 라그란지안 밀도 g =-½
Gx=½f d 바 (x)o(x) 국 (x)o1r(x)] (9-3) 이다. (9-3) 을 (2-39) 식에 대입하면, 장연산자 必斗 T가 만족해야 할 동시 교환관겨] [[ ¢¢((xx)), , 77 ff((xx '))]]x:xoo ==:x:ox o· =·= i08=( [x 7-f(xx )' ), 7f(x ')]:xo =:xo· (9-4) 울 얻는다. 또, 시공간 좌표 갔의 변화를 유도하는 발생원은, (3-26) 식에 의해서 Gx= fd < 三 Tµu (9-5) 로 표현된다. 여기서 Tµv는 이 계의 에너지쉼녓굉: 텐서이다. 특히 시간 의 변화에 따른 하나로운 변환을 유도하는 발생원은 G t=fd < J o8xoT00=- fd 3x 8t~(虹) (9-6) =-H[¢,1e]8t 로쓸수있다. 여기서 H[¢, 처=f강 x#(¢,7C)= fd 3xTOO 는 라그란지안 (9-2) 로 기술되는 물리계의 하밀토니안 연산자이다. 라그란지안 밀도 (9-2) 로 기술되는 보즈 장이론의 ¢궁只간 슈뢰딩거 표현 울 얻기 위해서, 장연산자 ¢의 고유값방정식 ¢(x)I rp( x), t > = rp( x)I rp( x),t > (9-7) 울 생각하자. 기호를 간편하게 하기 위해서 (9-7) 식을 'Pa l(p a ,t> =(pal (p a ,f> (9-8}
로 쓰겠다. 여기서 첨자 a 는
로 된다. 죽, 연산자 ¢의 고유상태를 기준으로 하는 표현에서 운동량 공액 点는 (9-14) 로 표현되는 행렬로 나타내진다. 따라서 연산자 r가 임의의 상 태 |伊>에 연산될 때에는그성분이 < = O(rp, _ 떨) a[ rp-rp'] (9-16) 로 표시되는 행렬로 표현된다. 위의 결과를 이용하면, 양자 장이론에서 모 든 연산자들의 슈뢰딩거 표현을 얻을 수 있다. 장이론의 슈뢰딩거 표현에서 물리계의 시간에 따른 변화가 어떻게 기술되 는지롤 보기 위해서, 발생원 (9-6) 이 기준 벡터 |rp,t>에 주는 변화를 생 각해 보자. 발생원 G t는 시각 t에서의 ¢꽁·간 표현에서 시각 t +o t에서의 ¢공간 표현으로의 미세 하나로운 변환을 유도한다. 따라서 이 변환은 Bt< 'P,tl = — i< ,p,tlH [,1e]8t (9-17) 로나타낼수있으며, 이 식은 뎨d < ,p,tl= <_, p, tlH [,7C] (9-18) 로 표현되는 운동방정식을 의미한다. (9-18) 식울 임의의 상태 |汀>에 연 산하면, 땅< rp,tl W >= < rp,tlH [¢,1r]lrp ',t > < ,p',tl W >
= H[ cp三같] < cp,tl 1 Jf > (9-19) 로 표현되는 함수적인 슈뢰딩거 방정식 (fun cti on al Schrod ing er e qua ti on) 이 된다. 라그란지안 (9-2) 로 기술되는 양자 장이론에서, 한 순간의 계의 물 리적인 상태는 상태 범함수
에 의해서 결정된다. 여기서는 상태 범함수를
표현된다는 것을 알 수 있다. 이 상태에 해당하는 에너지 고유값은, (9 -27) 식에 의해서 E= f강 x f릅내티互[高 t悼 2+m2 (9-28) 로 된다. 이것은 자유 스칼라 장이론의 영점 에너지와 일치하며, 따라서 가 우스 범함수 (9-24) 와 (9-27) 로 기술되는 상태가 이 계의 옳은 전공상태라 는 것을 알 수 있다. 자유 스칼라 장이론의 둘뜬· 상태에 해당하는 해도 양 자역학에서와 같은 방법으로 얻을 수 있다. 위에서 얻은 보즈 장이론의 슈뢰딩거 표현은 양자역학적인 계의 슈뢰딩거 표현과 아주 유사한 구조를 가지고 있다. 이 서실을 이용하면 양자역학에서 와 같은 방법으로 양자 장이론으로 기술되는 계의 물리적인 정보를 얻을 수 있다. 그러나 이러한 양자 장이론의 슈뢰딩거 표현 방법이 그 동안 관심을 끌지 못했던 것은 양자 장이론에 나타나는 발산항들을 처리하는 방법이 최 근에 와서야 이해되었기 때문이다 .(2) 자유 스칼라 장이론의 경우에는 특히 바닥상태 (전공상태)를 쉽게 계산할 수 있다는 것을 보았다. 제 5 장에서 본 바와 같이 물리계의 모든 그린 함수를 발생하는 그린 발생원은 전공-진공 전이진폭으로 결정된다. 따라서 물리계의 진공상태로부터 계의 모든 정상 상태에 관한 정보를 얻을 수 있기 때문에 , 전공상태를 결정할 수 있다는 것 은 중요한 의미를 갖는다. 양자적인 상호작용이 있는 경우에는 일반적으로 전공상태를 정확하게 결정할 수는 없다. 그러나 이러한 문제는 하이젠버그 표현을 사용한 경우에도 마찬가지이므로, 슈뢰딩거 표현에서만의 특별한 문제는 아니다. 슈뢰딩거 표현 방법이 특히 유리한 점은 상호작용이 있는 경우에도 함수적인 변분법 (func tio n al varia t i on al me th od) 을 사용하여 진공 상태의 비섭동적인 근사를 얻을 수 있다는 점이다. (2,3 , 4) 슈뢰딩거 표현 방법 에서 그린 발생원과 전공상태의 근사적인 계산 방법에 대한 설명은 9. 꾹i과 9.5 절에서 자세히 하겠다. 슈뢰딩거 표현 방법이 특히 유리한 점은, 시간의 직접함수인 하밀토니안의 경우에도, 운동방정식 (9-19) 를 디를 수 있다는
점이다. 이 점은 우주의 진화과정이나 평형상태에 있지 않은 다체계 문제를 다루는 데 특히 편리하게 이용될 수 있다. (4) 9.2 페르미 장이론의 슈뢰딩거 표현 제 4 장에서 본 바와 같이 스핀 -1/2 인 입자들로 이루어진 물리계를 기술 하는 페르미 장이론은 헤르미샨 (He rmiti an) 장연산자를 사용하여 기술할 수도 있고, 헤르미샨이 아닌 (non-Herm itian ) 장연산자를 사용하여 기술할 수도 있다. 헤르미샨 장연산자를 사용하는 경우 일반적인 스핀 -1/2 칭이론 의 라그란지안밀도는 요=숭 #aµaµrp- V(
G1=-H[¢]8 t=-}강 x~(¢)8 t (9-33) 로 표현되며, 여기서 H는 이 계의 하밀토니안 연산자이다. (9 - 29) 식의 장연산자 ¢(차는 헤르미샨 연산자이기 때문에 전하연산자의 고유상태가 아니다. 따라서 전하를 띤 디락 입자로 이루어전 계를 기술하는 데는, 전하연산자의 고유상태인 헤르미샨이 아닌 디락 장을 서용-하는 것이 편리하다. 제 4 장에서 설명한 바와 같이 이러한 장연산자물 사용하면, 라그 란지안밀도는 오 =꿍 祐껑µ¢ —a沿 µ¢)- V(¢,¢) =京¢t g— 낀t#）갑(¢,¢) (9-34) 로쓸수있다. 여기서 굽=
는발생원은 G t =-H[
범함수의 공액범함수 (duals t a t e fun c ti onal) 를 찾는 것이 쉽지 않다는 것이 다. 이러한 문제만 해결하면 페르미 장이론의 슈뢰딩거 표현은 보~ 장이론 의 경우에서와 같은 방법으로 얻을 수 있다. 그러면 장연산자를 슈뢰딩거 표현하는 방법부터 생각해 보자. 위에서 지 적한 바와 같이, 장연산자 ¢'=¢는 자기 자신의 운동량공액이기 때문에 그 고유값으로 표현할 수는 없다. 실수 그라스만 변수 0a(x)*= 0a(x), {0a(x), 0b(x')}=O 울 사용하여 장연산자 競t 표현할 때, ¢가 자기 자신의 운동량공액이라는 사실은
¢a? 日파 )7 志] (9-42)이다 .(5) 전하연산자의 고유싱-태인 디락 장연산자의 슈뢰딩거 표현은, 앞에서 지 적한 바와 같이, (9-41) 식이나 (9-42) 식을 두 번 반복하여 적용하면 얻을 수 있다. 전하를 띤 페르미 장을 두 개의 헤르미샨 장
¢2= 土 (o 블), 0*= 0 (9-47} 로 나타내면, (9-43) 식의 장연산자는
혹은 (9-40) 식을 이용하여 표현할 수 있다. 따라서 이 계의 슈뢰딩거 방정 식은 곱< 0,t| 伊> =끼古 (o 당)]< e,tl 1 Jf> (9-50) 로 표현된다. 헤르미샨이 아닌 장연산자를 사용하여 기술하는 계의 경우에 도 같은 방법으로 슈뢰딩거 방정식을 얻을 수 있다. 앞 절에서의 경우와 마 찬가지로, 이러한 물리계의 한 순간의 상태는 상태 범함수
로 정의된다. 이 계의 힐버트 공간은 전공상태 |0 >와 한입자상태 (one pa rt icle sta te) II >로 구성되며 alO>=O, at l O>=ll> (9-53) all>=IO>,a 기 l>=O 의 관계를 갖는다. 이 힐버트 공간을 실수 그라스만 변수 0= 0* 로 표현하 려고 한다. 그런데 그라스만 변수는 00=O 의 관계를 가지기 때문에, 일반적인 0 의 함수 1/1( 0~ 1/f(0 )=a+/3 0 , a, /3=상수 (9-54) 로 쓸 수 있다. 이것은 이 힐버트 공간의 0-표 현이 (1,0) 의 두 개의 성분 을 갖는 기준 (bas i s) 으로 기술된다는 것을 의미한다. 따라서 힐버트 공간의 요소인 |0> 와 |1> 을표현하는한가지 방법은 IO>=l (9-55) 11>=0 로 표현하는 것이다. 이것은 각 상태 벡터의 0- 표현을 <010>=1, <011>=0 (9-56) 로 정한다는 것을 의미한다. 이 식은 기준 벡터 (basis v ecto r ) I0 >들 사이 의 변환함수가 < 0'10> = < 0'10> <010> + < 0'11> <110> = l+ 0'0= e0'8 (9-57) 로 되어서, 보즈 장이론의 경우와는 달리 대각선화되지 않는다는 것을 의미 한다. 이 변환함수를 사용하면 (9-51) 식의 0- 표현을 쉽게 얻을 수 있다. 죽, 두 상태 벡터의 스칼라 곱은
< 福 > =J@ o@0 ' ＜ 福 '> < 8'1 8 > < 8| lJJ;.> =f@0 W1[8] 1fl?.[8 ] (9-58} 로 쓸 수 있다. 여기서 상태 범함수를 짜 0]=<81 1fl> (9-59). 로 나타냈으며, 1Jl [O) 의 공액파동 범함수 (dualwave fu nc ti onal) 는 iiJ[ eJ= f@ e' < 1J!l0 ' > < 0'l e > (9-60) :::::f@ e' < 1JJl 8 ' > e6'8 로 정의된다. (9-60) 식에서 < 1Jf l0> 는 < 01 1/f>의 복소공액의 전치행렬 로 정의되는 헤르미샨 공액 < 1Jfl 0>=[< 0l1 Jf>Jt =< 籠>* (9-61) 이다. 따라서 페르미 장이론의 슈뢰딩거 표현에서 상태 범함수의 공액 범함 수는 (9-60) 식으로 정의된다. 만일 변환함수 < 0'| 0 >가 대각선화되었더 라면, 공액상태의 0- 표현은 보즈 장의 경우에서와 마찬가지로, 단순한 헤 르미샨 공액 (9-61) 식으로 정의되었을 것이다. 이 결과는 자유도가 많은 경우로 쉽게 연장할 수 있다. 일반적인 페르미 장이론의 슈뢰딩거 표현에서 공액상태 범함수는 ifi[ 0(x)]=J @ 0' < 1Jfl 0 '(x) > e8'( x 'Je < r> (9-62) 로 정의된다. 이 식에서 0(x~ 행렬표현을 사용한 기호이기 때문에, 내부 공간에서의 성분을 가질 수 있고, 이 식의 오른쪽의 지수에서 반복되는 공 간변수에 대한 적분약속을 사용하였다. 예를들면가운스범함수
If![ 0]= e½8a(X)Gab(X,Y )8o(Y) (9- 6 3) 의 공액은가우스범함수 iJf[ 0]= ce½8a(x)Cao(X. Y) 8o(Y) (9-64) 로 된다는 것을 쉽게 보일 수 있다. 여기서 C 는 0 에 무관한 상수이며 (문 제 6)` C 는 G=[Gt ]- 1 (9-65) 로 정의되는 G 의 헤르미샨 공액의 역행렬이다. 위의 결과를 이용하면 헤르미샨이 아닌 장연산자를 사용하는 경우의 상태 범함수와 그 공액 사이의 관계도 얻을 수 있다. 풀로리아니니-제키브 표현 (9-46) 을 사용하는 경우, 상태 범함수 1/![0 ,0t ]= < 0,0 기 1/!>의 공액은 ijf[ O, 0 기=J@ 0'@ 0't < 1JJ'I0 ',0't > eB' t(x )B(x)-Bt (x)B'( x ) (9-66) 로 결정되며, 이 식에서 < 1JJ' l0,0 t>는 (9-61) 식과 같이 정의한 <8, 0 기1[f>의 헤르미샨공액이며` °t는 0 의 복소공액의 전치행렬이다` 이 경 우에도가는스범함수 1Jf[ 8, 8 t ]= e1J.t G1J . (9-67) 의 공액은 여전히 가우스` 범함수인 iJf [0,0 기= Ceet Ce (9-68 ) 로 되며, C=G t -1 의 관계를유지한다. 실수그라스만 변수를사용하여 해 르미샨이 아닌 디락 장을 표현하는 (9-48) 식을 이용하는 경우에도 마찬가 지 방법으로 공액상태를 얻을 수 있다(문제 7) . 페르미 장연산자의 슈뢰딩거 표현과 상태 범함수의 공액 범함수를 결정하 는 방법을 알았기 때문에, 이러한 장이론의 물리적인 정보를 양자역학에서
와 비슷한 방법으로 얻어낼 수 있다. 보즈. 장이론의 경우에서와 마찬가지 로, 이 슈뢰딩거 표현을 사용하면 물리계에 관한 비섭동론적인 정보를 체계 적으로 얻을 수 있다는 장점이 있다. (5,6 ) 여기서는 자유 디락 칭이론의 진공 상태를 계산하는 방법을 구체적으로 보이겠다. 전하를 띤 자유 디락 입자들을 기술하는 장이론의 라그란지안 밀도는 !l = i
한구조를가지기 때문에, 자유스칼라장이론의 경우와마찬가지로, 그바 닥상태 (진공상태) 범함수가 가우스 범함수로 될 것이라는 것을 알 수 있 다.그래서 가우스 범함수 1jf= e8c t CcD8D (9-74) 를 생각하자. 이 범함수를 (9-73) 식에 대입하면 [伊 As(l+ G)s A + 01(1-G )Ashsc(l+ G)cD0D] 1/f= E1 /f (9-75) 의 결과를 얻는다. 따라서 (9-74) 식이 고유값방정식 (9-73) 의 해가 되기 위해서는 (E1=-—G2 )Thr(hl (+l +G )G=)O= -¼2 TrhG ((99--7767)) l l 의 두 가지 조건이 만족되어야 한다. 여기서 Tr 는 내부공간과 공간변수 모두에 대한 흔적 (trac e) TrhG =h AaGaA =fd3xd 3y h a,(X,Y ) G,a( y,x ) 를 의미하며, a 와 沿는 디락 첨자(Di rac i ndex) 와 다른 내부공간의 성분을 나타낸다. 방정식 (9-76) 은 내부공간 (a, /3)와 공간 (x, y)에서의 행렬방정식이다. 그런데 공간변수 (x, y)에 해당하는 행렬 부분은 단위행렬 8(x- y)라는 것 을 쉽게 알 수 있다. 따라서 이 방정식의 내부공간에서의 행렬방정식 부분 만 풀면 된다. (9-76) 식의 가장 간단한 해는 Ga,(x,y) = 土 8a118(x— y ) 이다. 그러나 이 해에 해당하는 에너지 고유값 (9-77) 은 영이며, 이 값은
가능한 에너지 고유값의 최소값이 아니기 때문에 이 해는 바닥상태에 해당 하는 해가 아니다. 방정식 (9-76) 의 간단하지 않은 해는 G= 土―范1— h (9-78) 라는 것을 쉽게 보일 수 있다. 여기서 h2 은 Ira /J(x-y)=(－守+짜 )8a /J 8(x- y) (9-79} 로 정의된 행렬이다. (9-78) 식을 (9-77) 식에 대입하면 에너지 고유값은 E= 土 ½Tr范 = 土差f# x f겅뀝깊굽二규 (9- 8 0) 이 된다. 여기서 N은 디락 장연산자의 성분의 수이다. 따라서 자유 디락 장이론의 바닥상태(전공상태) 에너지는 E=- 舒이때도 (9-81) 이며, 바닥상태 범함수는 행렬 G=g~ h (9-82) 로 주어지는 가우스 범함수 (9 - 74) 이다. 행렬 (9 - 82) 의 행렬요소를 구체 적으로나타내면 Ga p (x, y)=f걸끊 e i P•
앞에서 본 바와 같이, 자유 스칼라 장이론이나 자유 디락 장이론의 전공 상태는 모두 가누스 범함수로 표현되며, 이들 가우스 범함수들은 규격화할 수 있는 범함수이다. 이러한 사실을 이용하면 가우스 범함수를 시도파동 범 함수(tri al wave fun c ti onal) 로 하는 변분법을 개발할 수 있다. (2 ,4, 6 ) 이러한 비섭동론적인 근사 방법에 대해서는 9.5 철에서 자세히 설명하겠다. 9.3 게이지 이론의 슈뢰딩거 표현과 게이지 동등성 9 . 1 절에서 얻은 슈뢰딩거 표현 방법은 일반적인 보즈. 장이론들에 적용할 수 있다. 따라서 게이지 장이론의 슈뢰딩거 표현도 9.1 절의 결과를 이용하 여 얻을 수 있다. 그러나 4 . ~길 에서 설명한 바와 같이, 게이지 이론의 라그 란지안에 나타나는 칭연산자들이 모두 독립변수인 것은 아니기 때문에, 양 자적인 계산을 하는 데 복잡한 문제가 발생한다. 게이지 이론의 양자적인 계산을 할 때에는, 게 이지 고정조건 (ga ug e fixing con diti on) 을 부과하여 , 독립변수가 아닌 변수들은 양자화되지 않도록 해야 한다. 여기서 변수들이 양자화된다는 말은 디음과 같은 의미를 갖는다. 경로적분으로 표현한 그린 발생원을 계산하기 위해서 힘수적분하는 장함수는 그 계의 독립변수들이 다. 게이지 이론에서와 같이 독립변수가 아닌 변수들이 있을 때에는 이들에 대해서는 적분하지 말아야 한다. 즉, 전자기 칭이론의 경우에는 AW Fr° i 의 네 가지 함수에 대해서만 함수적분해서 그린 발생원을 계산해야 한다. 만일 이들의 세로성분에 대해서도 적분하여 그린 발생원을 계산한다면, 그 결과는 전자기 장이론보다 자유도가 더 많은 물리계의 결과가 될 것이다. 이렇게 독립변수가 아닌 변수들에 대해서 함수적분되지 않도록 하기 위해 서, 게이지 변환과 모순이 없도록 게이지 고정조건을 부과해야 한다. 이 절 에서는 슈뢰딩거 표현 방법에서 이러한 게이지 조건을 어떻게 부과하는지에 대해서 알아 보고, 여러 가지 게이지 조건하에서 양자화한 결과들 사이에 어떤 관계가 있는지에 대해서 생각해 보겠다. 슈뢰딩거 표현 방법에서 게이
지 조건을 부과하는 방법을 쉽게 보이기 위해서 아벨리안 힉스 모형 (Abeli an Higgs model) 을 생각하겠다. 아벨리안 힉스 모형이란 전하를 띤 스칼라 정이 자체 상호작용과 전자기적인 상호작용을 하는 장이론이다. 전 하를 띤 스칼라 장을 두 개의 성분을 갖는 헤르미샨 장연산자로 기술하면, 이 모형의 라그란지안 밀도는 fl =今 Fµu(84-84) 나 -FµUFµU 국표 -eAµ ¢2)2 宁硏 eAµ
독립변수인 것처럼 보이지만, 이 계에 촌재하는 게이지 자유도 때문에 이들 의 가로성분인 (Ah E f )의 네 성분만이 진정한 독립된 운동변수이다. 따라 서 양자적인 계산울 할 때 이들 게이지 자유도를 제거하는 게이지 조건을 부과해야 한다 . 이러한 게이지 조건에는 여러 가지가 있는데, 여기서는 자 주 사용되는 몇 가지 게이지의 부과 방법을 생각하겠다. (가) 쿨롱 게이지 (Coulomb ga ug e) 전자기 장의 벡터 포텐셜 A i와 전기장 E i 의 가로성분만이 전정한 운동 변수이기 때문에, 물리적으로 가장 분명한 게이지 조건은 세로성분을 제거 하는 것이다 . 임의의 포텐셜 Aµ 룰 게이지 변환하면 v • A=O (9-85) 의 조건을 만족하도록 만둘 수 있다. 따라서 이 조건 (9-85) 를 게이지 조 건으로 부과하면, A 의 세로성분이 없어지고 하밀토니안은 A i의 가로성분 만으로 표현된다. 그리고 전기장의 세로성분은 가우~: 법칙 구속조건 V • E_e1°=O (9-86) 에 의해서 결정된다. 이러한 게이지를 쿨롱 게이지라고 한다. 가우스 법칙 (9-86) 을 사용하면, 쿨롱 게이지에서 아벨리안 힉스 모형의 하밀토니안연산자는 He= fd 3x[½7ra7ra 담年 a i硏〈隨子(ef> a r/> a)2 (9-87) + i eA/ r/> a Q aba i ¢b 며 Ar1 . Ar i ¢半나 -E i E i난 -B i B i] 로 쓸 수 있다. 여기서 이 하밀토니안이 쿨롱 게이지에서의 하밀토니안이라 는 것을 나타내기 위해서 H쵸 」 나타내었으며, 첨자 T는 벡터 A 를 A i =(o 드福) A j근幅A j =A}+AL
와 갇이 가로성분과 세로성분으로 분해하여 표현한 가로성분을 나타낸다. (9-87) 식에서 전자기장의 운동 에너지 항은, (9-86) 식을 이용하면 E' . E=E 辻감 +EL i EL i =E T'ET1 을/ d3 yF (x:F( y) 로 쓸 수 있다. 4. 炫i의 결과를 이용하면, 독립된 전자기장의 운동변수들 사 01 에는 [EKx), AKx')]xa=xa·= i (8 iJ~隣) 8(x-x') (9-88) 의 동시 교환관계가 성립해야 한다는 것을 알 수 있다. 이제 9.1 철의 결과를 이용하면, (9-4) 식과 (9-88) 식을 만족하는 장연산 자들의 슈뢰딩거 표현은 'Pa -
의할때 < 1Jf1| 타 > =f(j/) (/Ja (j /JA i 8 ['v • A] 1Jf1* 1J!2 켕떳!(j/) (/J a (j/) A i e 습J d3X(V•A)Z 1/fi* 1/fi (9-90) 와 같이 세로성분을 제거하는 것이 편리하다. 이렇게 하면 쿨롱 게이지에서 의 슈뢰딩거 방정식은 떨 l/f[
이지를 시간축방향 게이지 (tim e-lik e axia l g au g e) 라고 부르기도 한다. 보통 축방향 게이지라고 할 때에는 硏가 공간-같은 벡터인 경우를 이른다. 이 바일 게이지에서는 A’의 세로성분을 제거하지 않았기 때문에, 게이지 조건 (9-92) 가 게이지 자유도를 완전히 제거하지는 못한다는 것을 알 수 있다. 그러나 바일 게이지에서 연산자 관계식 단계에서는 (9-92) 식이 게이 지 고정 조건으로 충분하다고 가정한다. (9-92) 식을 라그란지안 밀도 (9 -83) 에 대입하면, 바일 게이지에서의 전자기장의 변화를 유도하는 발생원 은
GA=U西 (A i 8E i -El . 8A i) 로 표현된다는 것을 알 수 있다. 이것은 표준공액의 관계가 있는 연산자들 사이의 동시 교환관계는 [[ ¢Ea i ((xx)), ,AT ib ((xx')'])x]o “국 국 ' = ' = 硏 i8a 8 b(8x(-x x-x')' ) (9-94) 이며, 칭연산자들 사이의 다른 동시 교환관계는 영이라는 것을 의미한다. 바일 게이지에서의 하밀토니안 연산자는 Hw= fd 3x[강 7fa 'ff.건 a i<1> aa i<1> a +1f半난 -E i E 답 B i B J 로 표현된다. 하밀토니안 (9-95) 로 기술되는 계가 모순이 없는 정당한 양 자 장이론이 되기 위해서는 전자기 장들의 운동방정식이 (3-29) 식에 의해 入1 Ai= -i[A i ,H w] Ei= - i[E i, Hw] (9-96) 와 같이 결정되어야 한다. 동시 교환관계 (9-94) 식을 이용하면, (9-96) 식이 아벨리안 힉스 모형의 옳은 운동방정식이 된다는 것을 보일 수 있다. 이 것은 바일 게이지 조건 (9-92) 를 사용하여 게이지 이론의 양자적인 계산을 모순 없이 할 수 있디는 것을 의미한다. 바일 게이지롤 사용하면 위에서 본 바와 같이, 계의 모든 운동방정식을 하밀토니안과의 동시 교환관계 (9-94) 로부터 얻을 수 있지만, 가우스 법칙 (9~86) 은 얻울 수 없다. 앞에서 지적한 바와 같이, 바일 게이지에서는 전 자기 장의 여섯 개의 성분인 (Ai , Ei ) 모두를 운동변수로 취급하기 때문 에 게이지 자유도가 아직은 완전히 제거되지 않았다. 이렇게 남아 있는 게 이지 지유도를 가우스 법칙 (9-86) 이 제거하게 된다. 그런데 가우스 법칙 은 동시 교환관계 (9-94) 와 모순이 되기 때문에 , 이 구속조건을 연산자 관 계식으로 부과할 수는 없었다. 바일 게아지에서 가우스 법칙이 하는 일울 알아내기 위해서, (9-86) 식의 왼쪽을적분하여 G A = f강 x /\ (x)['v • E-e] °(x)] (9-97) 로 정의되는 연산자를 생각하자. 장연산자 A i와 G 의 교환관계를 계산하면 [A1,G ^ ]= f강y/\(y )[A i (x) , 'v • E( y)]=-i장/\（ x) 를 얻는다. (2-11) 식을 이용하면, 이 식은 8Ai = - i[A i , G]=-장 /\ (x) (9-98) 로 쓸 수 있으며, 연산자 (9-97) 은 하밀토니안과 교환관계 [Hw,G]=O (9-99) 롤 만족한다는 것을 쉽게 보일 수 있다. (9-98) 과 (9-99) 식은 연산자 G^ 가 이 계의 대칭변환을 유도하는 발생원이라는 것을 의미한다. (9-98) 식을 4 .4철의 결과와 비교하면, 이 대칭변환이 바로 3- 차원 공간내에서의 게이지
변환이라는 것을 알 수 있다. 따라서 가우스 법칙 구속 조건을 연산자 관계 식으로 부과할 수는 없지만, 물리계의 상태 범함수가 게이지 불변이어야 한 다는조건인 Gl1J f'> =0 (9-100) 혹은 (v • E-ef° )I lfl > = O (9-101) 울 부과하면, 바일 게이지의 님아 있는 게이지 자유도를 제거할 수 있다. 그래서 바일 게이지에서는, 연산자 관계식 단계에서는 조건 (9-92) 를 부과 하고, 남아 있는 게이지 자유도를 제거하기 위해서 상태 벡터가 (9-100) 혹은 (9-101) 식의 조건을 만족하도록 함으로써 물리적인 상태 벡터를 골라 내도록한다. 바일 게이지에서는 게이지 지유-도를 제거하는 조건이 상태 벡터에 부과되 기 때문에, 바일 게이지에서의 양자적인 계산은 슈뢰딩거 표현 방법을 서용 하여 하는 것이 특히 편리하다. 이 게이지에서 슈뢰딩거 방정식은 떨7Jl[
qq;;21= = pp cs oins 00 (9-104) 를 사용하여 표현하는 것이 편리하다. 이 극좌표계를 사용하여 구속 조건 (9-103) 을 나타내면 [a i--b ;r —골 ] lJf[ (f)a ,A i ] =0 (9-105) 로 된다. (9-105) 식의 첫 항은 A‘ 의 세로성분에 대한 미분이므로, 이 식 은 A i의 세로성분과 0 사이의 관계를 결정하는 구속 조건이다. 이 구속 조 건을 만족하는 파동 범함수의 성질을 이해하기 위해서, 변수변환 su==av •v A• A— -vb2 (8v 2/ e()0 /e) (9-106) 을 생각하는 것이 편리하다. 여기서 a 와 妹즌 서로 같지 않은 상수이다. 새 로운 변수 s 와 u 를 시용하여 (9-105) 식을 표현하면 ~1/f[rpa, Ai ]=¾1/f[p,A },s,u]=O (9-107) 로 된다. 이 식은 1/f가 변수 u 에 무관하면 가우스 법칙 구속 조건을 만족 한다는것을의미한다. (9 - 106) 과 (9-107) 식을 이용하면, 바일 게이지롤 사용한 게이지 이론의 슈뢰딩거 표현 방법을 구체화하는 여러 가지 방법을 얻을 수 있다. 그 한 가지는 구속 조건 (9-105) 를 만족하는 파동 범함수 1/fw = 1/fw[ p ,A h v • A~e v2 0, t] (9-1os) 만을 생각하여 , 이 범함수가 슈뢰딩거 방정식 (9-102) 를 만족하도록 하는 것이다. 또 한 가지 방법은, 슈뢰딩거 방정식 (9-102) 를 만족하는 일반적 인 해롤 먼저 구하고, 그 해 중에서 구속 조건 (9-107) 을 만족하는 부분만
물리적인 정보를 계산할 때 공헌하도록 하는 방법이다. 이 방법에서는 파동 범함수 1/f는 스칼라 장 =J@
=f탸 @A8[a 'v • A -1e 파] 1Jf1[pa ,A']* x~ 깁 ~+a~) 福 ,A i] 로 쓸 수 있다. 이 식의 두번째 줄을 얻는 데는 l[f w 가 (9-107) 식의 조건을 만족한다는 사실을 사용하였으며, 네번째 줄과 마지막 줄에서는 괄호 안의 미분연산자가 변수 u 에 연산되면 영이 된다는 사실을 서용하였다. 윗식에 서 (a,b)=(l,O) 인 경우를 생각하면, 바일 게이지 하밀토니안의 전기장의 세로성분 항이 쿨롱 게이지 하밀토니안의 쿨롱 상호작용항을 준다는 것을 쉽게 보일 수 있다. 따라서 가우스 법칙 구속 조건 (9-107) 을 구체화하는 방법 중에서 (a,b)=(l,O) 인 경우는 쿨롱 게이지의 결과와 일치하며, 이것 은 이들 두 게이지의 동등성을 의미한다. (10) 게이지 이론의 물리적인 성질을 이해하기 위해서 사용하는 게이지들 중에 하나로운 게이지 (unit ar y g au g e) 가 있다. 이 게이지는 변수변환 Aµ=Bµ-~e1a µe
매개변수를 택할 수 있다. 이와 같이 슈뢰딩거 표현방법은, 게이지 이론에 서 게이지 조건을 부과하는 문제를 이해하거나, 게이지 이론의 양지적인 계 산을 하는 데 특히 편리하게 이용될 수 있다 . (7,10) (다) 로렌츠 공변 게이지 (Lorentz covari an t ga ug e) 앞에서 이야기한 쿨롱 게이지와 바일 게이지는 게이지 고정 조건이 로렌 츠 불변이 아닌 식으로 표현된다. 그래서 이들 게이지에서의 계산 과정은 로렌츠 불변성을 뚜렷하게 보여 주지 못하는 약점이 있다. 계산 과정의 로 렌츠 불변성은 특히 섭동론적인 계산이나 재규격화 과정을 간단하게 해준 다. 그런데 쿨롱 게아지나 바일 게이지에서는 계산 과정의 로렌츠 불변성을 요구할 수 없기 때문에 이러한 계산들이 복잡해전다. 그래서 하이젠버그 표 현이나 상호작용 표현* (inter act ion pi c tu re) 을 사용하는 경우에는, 게이지 고정 조건이 로렌츠 불변인 식으로 표현되는 로렌츠 공변 게이지 (Loren t z covari an t g au g e) 를 주로 사용한다. 이 게이지는 벡터 포텐셜 Aµ 를 적당히 게이지 변환하여 로렌츠 불변인 조건
* 상호작용 표현은 하밀토니안을 자유 하밀토니안 항과 상호작용항으로 나누 고, 시간에 따른 연산자의 변화는 자유 하밀토니안이 , 그리고 상태함수의 변화는 상호작용 하밀토니안이 결정하도록 하는 표현 방법이다.
J[A ]= aiAµ — a(x)=O (9-111) 을 만족하도록 만들 수 있다는 사실을 이용한 것이다. 여기서 a( 따는 임의 의 스칼라 함수이다. 조건 (9-111) 을 게이지 이론의 게이지 자유도를 제거 하는 데 사용하는 게이지를 로렌츠 공변 게이지라고 한다. 특히 a=O 인 경 우를 로렌츠 게이지 (Lorentz g aug e) 라고 부른다. 로렌츠 공변 게이지를 사용하여 양자적인 계산을 하는 과정을 설명하는 데는 경로적분 방법을 이용하는 것이 편리하다. (8,11) 이롤 위하여 전자기장 이 전류밀도 ]µ(X) 와 상호작용하는 경우를 생각하자. 단순하게 생각하면, 이 경우의 진공-전공 전이진폭은
< OIO > = j @Fµ 엘 Aµe if d•x( 랑 F’*(a 규 .-a .,A ,)+F,.F,. +A’J, 1 =j@ APe if d•x 탄A' (u,.a2-a 舊 a,)A•+A'},] (9-112) =j@ APe if d 당 A 鼻 K,'A.+A 鼻J ,l 로 쓸 것이다. 만일 A 적 모든 성분이 독립된 운동변수라면, (9-112) 식을 제 7 장에서와 같은 방법으로 적분할 수 있고, 그 결과는 옳은 진공 전이전 폭을 줄 것이다. 스칼라 장의 경우와 비교하면, (9-112) 식의 적분 결과는 전자기 장의 전파인자(p ro p a g a t or) 가 Kµv-1 로 된다는 것을 의미할 것이다. 그러나 A 적 성분들이 모두 독립변수인 것은 아니며, 그래서 (9-112) 는 잘못된 결과를 주게 된다. 이 경로적분 방법에서는 이것이, 연산자 K가 Kµv {x ,x')= —( gµ 11 강― 8品 ) o(x— x ') 으로 표현되는 두영연산자(p ro j ec ti ono p era t or) 여서, 그 역이 존재하지 않 는다는 사실로 나타난다. 연산자 Kµ.f a] 역이 존재하지 않고, 그래서 (9-112) 의 적분이 발산하는 이유는 적분하지 않아야 할 종속변수에 대해서도 적분을 했기 때문이다. 포 텐셜 A 떨게이지 변환한포텐셜을 A 것 =A 나정 /\(x) (9-113) 로 나타내면, A 적- A~ 는 동일한 물리계의 상태를 기술한다. (9-112) 식에 서는 (9-113) 식으로 연결되는 모든 Aµ들 에 대한 적분을 한 것이며, 그래 서 적분해서는 안 되는 게이지 매개변수 A 에 대한 적분까지 포함되었기 때 문에 발산하는 결괴를 준 것이다. (9-112) 식으로 표현된 양이 옳은 진공 전이전폭이 되도록 만드는 방법은, 게이지 매개변수 A 에 대한 적분이 인 수분해되도록 하여서, (9-112) 식을 독립된 운동변수들만의 경로적분으로 표현되도록 하는 것이다. 이를 위해서 (9-111) 로 정의한 함수 f [A] 에 대 한함수적분
j@f[A ] o[/[A ]] = 1 (9-114) 롤여 게생각이하지자 .변 환여한기 서함수 f이[다A .^} E -(9- (191~41)1 1식) 에식서에 서f 에A µ대 를,한 적(9분-11을3) 매식개을변 사수용 하^ (x) 에 대한 적분으로 바꾸면 j@ /\tiAA ]a[/[A]]= I (9-115) 로 된다. 여기서 A 志 변수변환 f一 A 에 따른 자코바안(J acob i an) l:iA A]=de1판 ) =de t [o28(x ―y)] (9-116) 이다. 자코비안 A 六근 게이지 변환에 대하여 불변이라는 것을 쉽게 보일 수 있다(문제 14). 따라서 (9-115) 식은 AAA] (@ ^ 8[ f[A 』]= l (9-117) 로쓸수있디 (9-112) 식에 (9-117) 식을 곱해 주면, 진공 전이전폭은
된 운동변수인 것처럼 취급하여 계산하면 된다는 것을 의미한다. (9 -120) 식에서 a 는 로렌츠 공변 게이지의 종류를 결정하는 매개변수인 데, a=O 인 경우를 렌다우 게이지 (Landaug au g e), a=l 인 경우를 화인 만 게이지 (Feyn ma n g au g e) 라고 부른다. 위에서 설명한 로렌츠 공변 게이지롤 부과하여 양자적인 계산을 하는 방 법은 아벨리안이 아닌 (non-Abeli an ) 게이지 이론에도 적용할 수 있다. 이 경우에는 벡터 포텐셜 A 떡 내부공간에서의 성분이 여럿이고 게이지 변환 이 복잡해지기 때문에, 자코비안 (9-116) 이 A 떡 함수로 되며, 유령장 (g hos tfi eld) 과 게이지 장이 결합하여 상호작용하게 된다. 아벨리안 게이지 이론의 경우에는, (9-120) 식에서 보는 바와 같이, 유령장이 다른 물질 장 이나 게이지 장과 결합하지 않기 때문에 유령힝 ~7 무시하는 경우가 많다. 그러나 슈뢰딩거 표현에서 게이지 이론의 성질을 이해하는 데는 중요한 역 할을 하기 때문에, 여기서는 이 유령항을 포함하는 전체 라그란지안을 생각 하겠다. 앞에서 설명한 바와 갇이, 아벨리안 힉스 모형을 로렌츠 공변 게이지에서 양자화하기 위해서는, 라그란지안 밀도 (9-83) 대신, 게이지 고정항과 유 령항을합한 fl! =f l! AH_ 」2a국 8 갑 lµ)2+ i8µ 詞7J (9-121) 룰 사용하고, 이 라그란지안에 나타나는 모든 변수를 독립변수로 취급하여 계산하면 된다. * 여기서 IRA 쩌근 (9-83) 식으로 표현되는 아벨리안 힉스 모 형의 원래 라그란지안이다. 라그란지안 (9-121) 에 나타나는 모든 칭연산자 * (9-121) 식의 마지막 두 항은 일반화 좌표만의 함수로 표현되었다는 점에 유 의해야 한다. 지금까지 설명한 하밀돈 방식의 작용원리를 적용하기 위해서 는 이들 두 항을 일반화 좌표와 그 운동량 공액의 함수로 표현해야 한다. 예를 들면, 게이지 고정항은 7rAoa, Aµ+운 7rAo' 으로 표현해야, 하밀돈 방식의 작용원리를 적용할 수 있다.
가 독립변수라는 점에 유의하면, 스칼라 장과 게이지 장은 9.1 절에서 설명한 일반적인 보즈 장에 해당하는 동시 교환관계를 만족한다는 것 을 알 수 있다. 그리고 유령장 n 와 7 는 그 운동량공액인 r? ＝荷와 Tr= 규iJ들과 페르미 장에 해당하는 동시 반교환관계를 만족한다는 것을 보일 수 있다(문제 16). 로렌츠 공변 게이지를 사용한 게이지 이론의 슈뢰딩거 표현 방법을 얻기 위해서는, 라그란지안 밀도 (9 - 121) 로부터 하밀토니안 연산자를 계산하고, 9.1 절과 9.2 절의 결과를 이용하여 슈뢰딩거 방정식 망重 ,A,,, TJ, ff;t]= Hl/ ![({Ja ,A,,,TJ, ff;t], (9- 1 22} H= f강 X [ ;/t' AH- 웅1fA • 7fA 0- 7fA o 'v • A- i7fq7ff-i(합) • V1 J] 룰 유도하고 그 해를 구하면 된다(문제 17). 여기서 ;/{AH 는 (9-84) 식 으로 주어진 아벨리안 힉스 모형의 원래 하밀토니안 밀도이며, TAO 는 장연산자 Ao 의 운동량 공액연산자이다. 그러나 로렌츠 공변 게이지를 사용한 게이지 이론의 슈뢰딩거 표현 방법을 얻기 위하여 이러한 과정을 수행하는 데에는 몇 가지 문제가 있다. 그 하나는 라그란지안 (9-121) 로부터 얻는 장방정식 중에 구속 조건으로 나타나는 방정식 강 (a i.A ,,)=O 를 구체화하는 과정에서 나타난다. 이 식은 연산자 (a 갑iµ)가 질량이 영인 스칼라 장이라는 것을 뜻하며, 이 조건이 바로 게이지 구속 조 건 (9-111) 에 해당한다. 그런데 이 게이지 조건은, 게이지 장들 사이 의 동시 교환관계와 모순이 되기 때문에, 연산자 관계식으로 부과할 수가 없다. 이러한 문제가 생기는 근본적인 이유는 독립된 운동변수 가 아닌 변수들을 독립된 변수인 것처럼 계산하기 때문에 일어난다. 따라서 이 구속 조건은, 연산자들 사이의 방정식이 아니라, 상태 범
함수에 요구하는 조건으로 구체화해야 한다. 로렌츠 공변 게이지를 사용할 때 나타나는 또 한 가지 문제는 (9-121) 식에 나타나는 유령장 에 의한 것이다. 이들은 서로 반교환하는 장이면서 스칼라 장에 해당 하는 운동방정식을 만족하기 때문에 옳은 스핀-통계 관계를 갖지 못 한다. 따라서 이러한 장에 해당하는· 입자들은 물리적인 상태 벡터에 나타나서는 안 되며 양자화 과정에서 이것을 보장할 수 있는 방법을 찾아야 한다. (11 ,12) 이러한 문제들을 해결하는 확실한 방법은 라그란지안 (9-121) 이 갖 는 BRS 불변성 (BRS i nvar i ance) 을 이용하는 것이다. (12) 라그란지안 (9 -121) 은 게이지를 이미 고정했기 때문에, 국소적인 (loc al) 게이지 변환에 대해서는 불변이 아니다. 그러나 이 라그란지안은 BRS 변환이라고 부르는 변환 8Aµ=(aµ7J k 8¢a= ieq ab < Pb 7/€ 訪=석a 8 』%, 8n=O (9-123) 에 대해서 불변이다. 여기서 点픈 유령장 n 나 平와 반교환하는 상수이다. 이 변환식에서 TJ (x)E=A(x) 로 놓으면, 스칼라 장과 게이지 장의 변환은 국소적인 게이지 변환과 일치한다. 따라서 라그란지안 (9-121) 의 BRS 대 칭성은, 이 게이지 이론의 원래 라그란지안 fl AH 의 게이지 대칭성에 따른 것이며, 아벨리안 힉스 모형으로 기술되는 계의 물리적인 정보의 게이지 대 칭성을 보정해 주는 대칭성이다.(1 2) 라그란지안 (9-121) 이 BRS 변환 (9-123) 에 대해서 불변아라는 사실로 부터,보존법칙 8,J Bµ =O 울 만족하는 BRS 전류밀도 JB µ 를 얻을 수 있다. 따라서 BRS 대칭성 때둡 에 나타나는 보존되는 양은 BRS 전하
Q B= fd 3X]B°= f강 X[ T} a p o i-i e 7}qJQ 7r+ i7rij 7 r Ao] (9-124) 이며, 이 연산자가 하밀토니안과 교환 가능하디는 것을 쉽게 보일 수 있다 (문제 19}. 이 BRS 전하는 BRS 변환을 발생하는 발생원이다. 죽, GBRS =€Q B 라 하면, GBRs 는 (2-11) 식에 의해서 변환식 (9-123) 을 준다는 것을 쉽게 보일수있다. 물리계의 물리적인 정보가 게이지 불변이라는 사실은 BRS 대칭성으로 표현된다. 앞에서 본 바와 갇이, 아벨리안 힉스 모형의 라그란지안과 하밀 토니안은 BR 없당변이다. 이제 물리계의 상태를 기술하는 상태 벡터가 BRS 불변이면, 죽, 상태 벡터가 BRS 불변 조건 Q괴 1Jl> =O (9-125) 울 만족하면, 계에 관한 모든 물리적인 정보가 게이지 불변이라는 것을 보 장하게 되며, 앞에서 지적한 게이지 조건의 부과 문제와 유령장에 의한 문 제를 동시에 해결해 준다. (12 ) 조건 (9-125) 를 만족하는 상태를 물리적인 상 태라고 한다. 9.1 철과 9.2 절의 결과를 이용하면, (9-125) 식의 슈뢰딩거 표 현은 if강 x[ TJ (x){a i~) ？읊집-결汀誤늪-] X lJ![cpa ,Aµ,T/ , rj;t]= O (9-126) 로 된다는 것을 알 수 있다. 여기서 8(x}i= -스 칼라 장을 극좌표계 (9-104) 로 표현할 때 나타나는 장연산자의 슈뢰딩거 표현이다. 따라서 로렌츠 공변 게이지를 사용한 아벨리안 힉스 모형의 슈뢰딩거 표현 방법은 슈뢰딩거 방 정식 (9-122) 를 BRS 불변 조건 (9-126) 에 맞도록 푸는 문제로 된다. (9-126) 식을 다루기 편리하게 만들기 위해서 상태 범함수를 lJl[fPa ,Aµ, TJ, 7f;t] = eii< x )D(x-y ,t)q(y)~[rpa ,Aµ;t] (9-127) 로 놓는 것이 편리하다. (9-127) 을 (9-126) 식에 대입하면, BRS 불변 조
건은 [福늪-영戶― D(x- x'信志]이 %,Aµ; t ]=o (9-128) 로 된다. 여기서 D(x— x', t) = D(x'x,t ) 이다. 바일 게이지의 경우에서와 마찬가지로변수변환 r = 'v • A(x)-fJ -1 (x:._ x',t)'v망 (x') s='v · A(x)-—e1 'v2 0(x) (9-129) u=a 'v ·A(x) 一.f?e. 'v 28(x)-cf J -1(x-x ' , t)현4. o(x ' ) 울 하면, BRS 불변 조건 (9-128) 은 ~(8! )[({Ja,A µ;t] = O (9-130) 으로 된다. (9-129) 식에서 매개변수 a,b 와 섬근 a-b-c*O 인 임의의 상 수값을 가질 수 있다. 이 사실을 이용하면, 바일 게이지의 경우에서와 비슷 한 방법으로, 게이지 이론의 양자적인 계산이나 로렌츠 공변 게이지와 디른 게이지와의 관계를 쉽게 이해할 수 있다. 슈뢰딩거 표현 방법을 사용하여 로렌츠 공변 게이지에서의 게이지 이론을 푼다는 것은, 구속 조건 (9 - 130) 을 만족하는 슈뢰딩거 방정식 (9-122) 의 해를 구하는 것이다. 바일 게이지의 경우에서와 마찬가지로, 이 경우에도 구속 조건에 관계없이 슈뢰딩거 방정식 (9-122) 를 풀고, 물리적인 정보를 계산할 때 BRS 불변 조건 (9-130) 을 만족하는 상태만 공헌하도록 할 수 있다. 슈뢰딩거 표현 방법에서 물리적인 정보는 상태 벡터들 사이의 스칼라 곱에 의해서 확률적으로 결정된다. BRS 불변조건 (9-130) 은 물리적인 상 태벡터는 변수 u(x) 에 무관해야 한다는 것을 의미한다. 따라서 물리적인 확률진폭은
< 福 > =fq/)
< 福 > =fq/)
ow< 1JJI H(Q , P)l1J f> =0 (9-133) 와 같이 최소로 만들면서, 구속 조건 << 11JJffll Q1 Jf l> 1 J =f>l =q(t), < 1JflP l1 Jf>=p(t) (9-134) 을 만족하는 상태 | 깐 >를 찾는 것이다. 여기서 q와 §르 고전적인 시간의 함수이다. 이렇게 하여 얻은 하밀토니안의 기대값은 에너지 고유값이 아니 라 q와院] 함수인 Heff = < 1Jlo( q ,p)I H(Q , P)l1J lo( q ,p) > {9-135) 이다. 여기서 I Wo> 는 (9-133) 과 (9-134) 식을 만족하는 상태 벡터이다. (9-135) 식으로 정의되는 양을 유효 하밀토니안 (e ff ec ti ve Ha mi l t o ni an) 이라 고 한다. 이 유효 하밀토니안은 계에 관한 많은 정보를 포함한다. 우선 Hef f가 q와 #1 함수이므로, 이들에 대해서 H 따울 최소화하면 그 결과는 계의 바닥상태의 에너지 고유값이며 , 이 경우의 상태 벡터 I 1Jl0 > 는 바닥상 태 벡터이다. 또 유효 하밀토니안은 고전적인 함수인 q와 Poll 대한 고전적 인 함수이므로, 이를 고전적인 좌표 q와 운동량 院] 함수로 표현된 고전적 인 하밀토니안으로 볼 수 있다. 그래서 유효 하밀토니안 H eff로부터 하밀 톤 방정식 (1 - 11) 을 사용하여, q(t)와 p(t潭- 결정할 수 있다. 이렇게 결 정한 함수 (q,p)i:-( 9-134) 식에 의해서 위치연산자 Q와 운동량연산자 P의 기대값이다. 따라서 H 미를 알면, 고전역학적인 계산을 하여, 양자적인 정 보인 < WI Q I 1Jl>와 < 1J! IPI 1Jl>를 시간의 함수로 얻을 수 있다 .. 닫힌 형 태로 풀 수 없는 물리계의 경우에는, (9-133) 과 (9-134) 식의 I w> 를 시 도파동함수 (trial wave fun c ti on) 로 하여 이들 변분방정식을 풀어서 , 포텐셜 언덕을 굴러내리는(q uan t umroll) 문제나 양자적인 터널 효과(tunn el eff ec t) 등에 관한 많은 정보를 쉽게 얻을 수 있다. (13) (9-135) 식에서 p =O 인 경우를 계산하면, 그 결과는 유효 하밀토니안에 서 운동 에너지 부분을 영으로 한
Vg (q)= < lJfo( q )I H(Q , P)I lfl.。(q) > (9-136) 이 된다. 이 양을 유효 포텐셜 (e ffe c ti vep o t en ti al) 이라고 부른다. 유효 포 텐셜은 고전적인 힘수이기 때문에 고전적인 포텐셜의 경우와 같은 방법으로 그것이 주는 물리적인 정보를 계산할 수 있는데, 그 결과는 양자적인 물리 계에 관한 것이기 때문에 편리하게 사용되는 양이다. 이러한 양자역학적인 계산 방법들은 양자 장이론에 적용할 수 있도록 연 장하여 사용할 수 있다 .(2~ 변분원리를 이용하여 정의한 유효 하밀토니안 과 유효 포텐셜은 제昭) 1 서 정의한 양들과 같다는 것을 보일 수 있다. 이 사실은 제 5 칭이나 제8-Ao버]서 하이젠버그 표현을 사용하여 정의한 그린 발 생원들을 슈뢰딩거 표현으로 바꾸어 나타내면 쉽게 보일 수 있다. 한 걸음 더 나아가서 함수미분방정식으로 표현한 슈빙거의 작용윈리나 경로적분을 사용하여 표현한 화인만의 작용원리를 슈뢰딩거 표현으로 바꾸어 놓을 수 있다. 이렇게 슈뢰딩거 표현에서 표현한 작용원리를 디락의 작용원리 (acti on princ i ple of Dirac ) 라고 부른다. (3) 슈빙거의 작용윈리는 8 灰 0,+oolO,-oo >Y= i 8 < O, +ool8f d4x[ 9? ( x)+x(x)J( x )]I0,-00 >Y = i 8 < O,+ ooiG (+ oo) —G (-oo )I0,- 0 0 >8 (9~ 1 37) 로 쓸 수 있다 . 여기서 J(차는 의부근원이며, 상태 벡터 위에 붙인 첨자 H는 이들이 하이젠버그 표현에서의 상태 벡터라는 것을 강조하기 위하여 붙인 것이다. (9 - 137) 식은 J (x) 에 대한 함수미분방정식으로 나타낼 수 있 고, 제 7 장에서 보인 바와 같이, 이들을 형식적으로 풀면 H
의 결과를 얻는다. 여기서 ¢(x 注· 양자장 x(x) 에 해당하는 고전적인 장함 수이다. 이것이 양자적인 계의 그린 발생원을 고전적인 함수에 대한 경로적 분으로 표현한 화인만의 작용원리이다. (9-138) 식의 W[ J~ 의부근원과의 상호작용항울 포함한 유효작용이다. 이 발생원 W를 르장드르 변환한 발생원 I'[q;]= W[ J]—fd4 x
f (9-140) 로 표현되는 양자장 x( 지의 진공기대값(정확하게 부르려면 행렬요소라고 해야 함)이다. 발생원 I'[아는 순수한 꼭지점함수(p ro pe rve rt ex functi on) 들을 발생하는 발생원이며, 이 발생원울 고리전개하면 그 첫 항이 고전적인 작용이 된다는 것을 제 했버]서 보았다. 하이젠버그 표현 방법으로 나타낸 이러한 작용원리를 슈뢰딩거 표현 방법 으로 나타내려면, 변환함수(확률전폭)의 슈뢰딩거 표현과 하이젠버그 표현 사이의 변환식 < a2,t2 la 1,t1 > H 국< a2 J2 le- i H1C t다 )|a1,t 1>5 국< a2,t2 l e-i 1 lt2 -t) -iH1C t -t,>l a1,t1 > s (9-141) =5< a2,tl a 1,t >5
을 이용하면 된다. 여기서 HA :-의 부군원과의 상호작용항을 포함한 계의 하밀토니안이며, 상태 벡터 위에 붙인 첨자 S 는 슈뢰딩거 표현에서의 상태 임을 나타낸다. 이 변환식을 사용하면 (9-138) 식은 e;w1n=s<-,ti +,t> s (9-142) 로 쓸 수 있다. 여기서 상태 벡터 1 土,t >s 는 슈뢰딩거 표현에서, 들어가는 전공상태 (in vacuum sta te) I + , -oo >와 나가는 전공상태 (out vacuumsta te) 1-,+oo> 를 시각 t까지 진행시킨 상태 벡터들을 나타낸다. 따라서 이들상태는 臘匡,t >5=IO,+ (X)＞ 의 성질을 가지며, 슈뢰딩거 방정식 땅 l±, t >5=[H-fd 3xx (x)J( x )]| 다 >s (9-143) 울 만족한다. (3) 여기서 하밀토니안 H는 의부근원과의 상호작용항을 제의한 순수한 양자적인 계의 하밀토니안이다• (3 - 142) 식의 발생원 W [J擇 (9-139) 식을 이용하여 르장드르 변환하면, 유효작용의 슈뢰딩거 표현을 얻는다. 이를 위해서 (3-143) 식의 상태를 I+ ,t >s= e;f~- d t 'w (t '> I 1fl+,t > |—,t >s=eil ;dt 'w (t' ) I 뿐,t> (9- 1 44) 로변환하는것이 편리하다. 상태 벡터 I 깐土,t>는운동방정식 區 —H +fd3x x(x)J( x )] l7J J+, t > = w( t) I四 t > (9-145) 璃一 H+ fd 3xx(x) J (x)]I 뿐,t >= w*(t) I 뿐,t > 를 만족한다. 상태 벡터 | 7Jl±,t >둘 사이의 스칼라 곱울 < 뿐,ti 7Jl+,t > =1 (9-146) 로 규격화하면, 발생원 (9-142) 는 s< _,ti+,t>s =e;wu1 W[J] = [-.... d t w (t) (9-147) 로 된다는 것을 쉽게 보일 수 있다. 이제 (9-145) 식을 이용하여 (9-147)
식의 W [.T擇 계산하고, (9 ~ 139) 식을 사용하여 르장드르 변환하면, 유효 작용은 슈뢰딩거 표현에서 r[
가 슈뢰딩거 방정식 (9-145) 를 만족하는 상태이며, 따라서 그 때의 I'[rp] 가 바로 유효작용이 된다. 이것은 고전적인 작용원리를 양자적으로 연장한 것이며, 이를디락의 작용원리라고부른다 .(3) op 回인 작용원리 (9-151) 과 (9 ~ 150) 에서 시간에 무관한 경우의 극한 울 취하면, (9-133) 과 (9-134) 식으로 표현된 유효 하밀토니안에 대한 변 분원리로 된다. 이 디락의 작용원리는, 앞에서 설명한 양자역학에서의 변 분원리와 같이, 양자 장이론의 슈뢰딩거 표현 방법에서 함수적인 변분 방법 (func ti on al vari at i on al me th od) 을 사용하는 근사 방법의 근거가 된다. (9 -151) 식에서 상태 I W土 ,t >를 시도파동 범함수(tri al wave fun c ti onal) 로 택 하여 계산하면, 양자 장이론의 전공상태와 유효작용의 비섭동적인 근사를 얻게된다. 9 . 5 가우스 근사법 (Gaussia n ap pro x ima ti on meth o d) 디락의 작용원리에 의하면, 유효작용은 칭연산자의 기대값을 < 뿐,t lx(x)| 1/T+,t >= rp( x) (9-152) 로 하는 규격화된 상태 博길,t >의 변화에 대한, 범함수 I'=fdt< 뿐,t l i a t -HI 1/T+,t> (9-153) 의 극값으로 주어진다. 이 식의 상태 IW土 ,t>를 몇 가지 변분 매개변수를 포함하는 시도파동 범함수로 대치하고, (9-153) 식의 오른쪽이 극값이 되는 r[ 아를 계산하면, 이 I'[이는 유효작용의 변분법적인 근사이다. 시도 파동 범함수로 가유스 범함수 (Gaussia n fun c ti onal) 를 택하여 계산한 유효작용과 유효 포텐셜의 근사를 가우스 유효작용 (Gaussia n eff ec ti ve ac ti on) 과 가우 스 유효 포텐셜 (Gaussia n eff ec ti ve p o t en ti al) 이라고 부른다. 이 절에서는 몇 가지 간단한 모형들을 예로 들어서 가우스. 근사의 계산 방법을 설명하겠
다. 먼저 하밀토니안 H=~P2+V(Q) (9-154) 로 기술되는 양자역학적인 계의 경우를 생각하자. (3,13) 구속 조건 (9-134) 룰 만족하는 가우스. 파동함수는 lJf( Q,t)= (2TCnG)-¾e--fi j(Q-q)B (t) (Q-q)+i-P< Q -q) (9-155) 라는 것을 쉽게 보일 수 있다. 여기서 B( t)=강 c-l( t)― Z il l( t) (9-156) 이며, 실수함수 q(t), p(t), G( t)와 Il(t) i= 변분 매개변수이다. 그리고 가우스 근사와 고리전개의 결과를 비교하기 위해서 플랑크 상수 h 를 구체 적으로 나타내었다. 시도파동함수 (9 - 155) 는 규격화되었으며 << l깐fT II PQI I l깐fT>>==qp(t(t)) (9-157) 의 구속 조건을 만족한다. 파동함수 (9-155) 를 사용하여 G 와 ll의 · 변화에 대한 (9-153) 식의 극값을 계산하면 가우스 유효작용이 되고, G 와 H의 변 화에 대한 (9-135) 식의 최소값을 계산하면 가우쓰二 유효 하밀토니안이 된 다. (9-155) 식을 사용하여 계산하면, < WI Q기 1Jl>=q2 +f iG (t) < Wl i.당 I 1Jl>=pq +fillG (9-158) < 쩌 V( Q )l 1fl >=(2TC 1i G)-½ fd Q V( q+Q-q )e 값-(Q - q )G-l( Q-q) = V( q)＋吉 V(2)( q)< 1fl|(Q-q)기 1fl>
나 v(4)( q)＜ 1jJ I( Q-q)기 1Jl> +… = V( q)弓 v(2)(q) G 」『 v(4)(q) G 도 .. 의 관계들을 쉽게 얻을 수 있다. 여기서 V(n)은 V( q)의 n - 차 도함수를 나 타낸다. 이들 결과를 이용하면 (9-153) 식은 I'[q,p,G ,II]=Ldt[ P < i -H(q,p )+ n{II G 검 -V(2)( q) G -03 (9-159) _\G-I-2n2G} 千 G2 V(4l(q )+ … ] 로 된다. 여기서 H(q ,p~ (9-154) 식에서 (Q, P) 대신 (q , p遷- 대입한 고 전적인 하밀토니안이며, V( q펴 6- 차도함수 이상은 무시하였다. 유효작용 울 얻기 위해서 (9-159) 식을 G 와 II 에 대해서 변분 (va ri a ti on) 하면, G=4GII iI=강 G-2_2II 간 v(2)( q)구 v(4)( q )G (9- 1 60) 의 결과를 얻는다. (9-160) 식을 (9-159) 에 대입하면 유효작용의 가우쓰: 근사인 I'[q,싸룰 얻는다. (9-159) 와 (9-160) 식에 나타나는 E 의 차수를 보면 가우스 근사가 비록 일부이기는 하지만, 2 '.고 리 (2- lo op ) 이상의 공헌 울 포함한다는 것을 알 수 있다. (9-159) 식에 나타나는 변수들이 시간에 무관한 경우를 계산하면 유효 포 텐셜의 가우스 근사를 얻는다. 이 경우, (9-159) 식의 p에 대한 변분식 (va riat i on al eq ua ti on) 은 .q = 꿉
으로 표현되므로, p(t)= O=II(t~ . 된다. 이 결과를 (9-159) 와 (9-160) 식에 대입하면, 유효 포텐셜의 가우스 근사인ve /f(q)= V( q )+h[½GV(2)( q)나이같 c2 v<4>(q ) (9-161) 와, 변분 매개변수 G 를 결정하는 관계식 높 2= V(2)( q)나 GV(4)( q) (9-162) 를 얻는다. 위치 에너지가 V( Q)카(I) 2 Q 2 인 경우, (9-162) 식은 c-2=4(I )2 으로 된다. 이 식을 (9-161) 에 대입하면 유효 포텐셜은 Ve ft(q)= V( q)十건1( I) ,9-163) 가 된다. 이 경우에는 위치 에너지가 2- 차함수로 주어진 경우이기 때문에, (9-163) 식은 양자적인 효과를 포함하는 정확한 유효 포텐셜이다. (9-163) 식의, q의 변화에 대한, 최소값을 계산하면 이 계의 바닥상태 에너지 E 。= ½臼蟲 얻는다. 위치 에너지가 복잡하거 닫힌 형태로 풀 수 없는 경우에도 (9-162) 식을 계산하여 가우스 유효 포텐셜을 얻을 수 있다. 참고문헌 13 에 는 여러 가지 양자역학적인 계의 가우스 근사들이 계산되어 있다. 양자 장이론의 경우에도 같은 방법으로 가우스 근사를 계산할 수 있다. (2) 칭이론에서는 상태가 파동 범함수로 표현되기 때문에, 변분 매개변수가 시 공간의 함수이며, 변분이 함수적인 변분(fun c ti onalva ri a ti on) 으로 된다는 점에서만 양자역학의 경우와 다르다. 라그란지안 밀도가 요=卓짜-¢*)―다(¢,리 (9-164)
이며, 하밀토니안 밀도가 뚜靜+起파)국꿉子섭 (9-165) 인 스칼라 장이론의 가우스 유효 포텐셜을 생각해 보자. 9.1 절의 슈뢰딩거 표현방법을 사용하면, 연산자들은
을 보이기 위해서 플랑크 상수 h 를 구체적으로 나타내었다. 이 기대값을 최소로 만들기 위해서 변분조건 oc< lJflH I lJf> =O 을 요구하면, G를 결정하는 방정식 +c-2(x,y) = [-'i/ 2 나 -V(2)( ip)+ n v<4>( ip) G(x,x)]o(x-y ) (9-169) 를 얻는다. 이제 (9-169) 식을 G 에 대하여 풀어서 (9-168) 식에 대입하고, 장연산자의 기대값 §가 상수인 경우를 계산하면 유효 포텐셜을 얻게 된다. 방정식 (9-169) 식을 풀기 위해서 G(x- y遷· 후리에 변환 G(x- y)=f꿉꿉 e i P•(X-Y) g(p) (9-170) 로 표현하면, (9-169) 식은 g-2 (p )= 4(p2 + m2) (9-171) 으로 된다. 여기서 유효질량 m 은 짜= V(2) （硏)난 -V(4)( g )G(x,x) (9-172) 로 정의된 양이다. 이 결과를 (9-168) 식에 대입하면, 가우스노유효 포텐셜 vdf (莊)=룬참니묘」규짜―/링젊 )2 며 11- 무 I2(M) 님戶(야「당) (9-173) 울 얻는다. 이 식에서 유효질량은 m2 군국I 국 참-강 m2I2 멸놉김룹 (9-174)
으로쓸수 있고, I1 과 I2 는 k= f高 디高占孛-~) 로 정의되는 발산하는 양이며, M은 질량의 단위를 갖는 임의의 상수이다. (9-173) 에서는 硏에 무관하게 발산하는 양은 무시하였다. 유효 포텐셜 (9-173) 은 L 과 I료 . 표현되는 두 가지 발산항을 포함하기 때문에 재규격화해야 한다. 따라서 이들 발산하는 항들을, 물리량들을 다 시 정의하여 없애기 위해서는 두 가지 재규격화 조건이 필요하다. 그런데 (9-165) 식의 포텐셜 연산자에는 질량과 결합싱수의 두 가지 물리량이 나타 나고, 이돌은 각각 포텐셜의 장함수 ¢에 대한 2- 차도함수와 4 - 차도함수로 정의된다. 이들 물리량들은 양자적인 상호작용에 의해서 그 의미가 달라지 기 때문에, 이에 맞도록 물리적인 질량과 결합상수를 다시 정의해야 한다. 제昭싸서 설명한 바와 같이, 물리적인 질량(재규격화된 질량) µR 은 유효 포텐셜의 2- 차도함수로, 그리고 물리적인 결합상수(재규격화된 결합상수) A 표 유효 포텐셜의 4- 차도함수로 정의해야 한다. 따라서 이들 물리적인 질량과결합상수는 急 mo 룻 (9-175} 와 같 mo= 古 (9-176) 로정의할수있다. (9-173) 식을 (9-175) 와 (9-176) 에 대하면,
座AR =브A +' 냐2 I (9-177) 과
t=+- ½12(M) (9-178) 의 재규격화 조건을 얻는다. 이들을 (9-173) 식에 대입하면, 재규격화된 유 효포텐셜 ve Jf(g)=국主근 $2 롱 m2 님럴석t-½] (9-179) 을 얻는다. (2) 여기서 유효질량 m 은 m2=µ~4$2 궁 m2 틀 (9-180) 으로 표현된다. 이 계산에서도 §에 무관하게 유효 포텐셜에 나타나는 발산 競 무시하였다. 이 가우스 유효 포텐셜은 点 전개 방법 (여기서 N은 내 부공간에서 스칼라 장 ¢의 성분의 수이다)을 사용하여 계산한 결과와 일치 한다 .(14) 이 결과로부터 대칭성 깨어짐과 같은 양자적인 스칼라 ¢4 이론의 여러 가지 성질들을 알아낼 수 있다. (2,4) 페르미 장이론의 가우스 유효 포텐셜을 계산하는 방법을 (6) 보이기 위해서 그로스대뷰 모형 (Gross-Neveu model) c i s) 을 생각하겠다. 이 모형은 2- 차원 시공간에서 자체 상호작용하는 디락 장이론이며, 라그란지안 밀도 2= i¢,忍硏紅(표)2, a=l,2,… , N (9-181) 로 기술된다. 여기서 rµ는 (9-36) 식을 만족하는 2X2 디락 행렬이며, 첨자 cl=-N - 차원 내부공간에서의 성분을 나타낸다. 이 계의 하밀토니안 밀도는:lt= - i ¢ar1a i ¢a- 높( 표 )2 (9-182) 이다. 디락 장 ¢(xp } ¢t (x 펴 슈뢰딩거 표현으로. (9 -4 6) 식을 사용하고 시도파동 범함수로는 가우스 범함수 I G >= eo}c ,.s.
ho 는 h 。= Yo( 一 iy10 1) (9-187) 로 정의된 연산자이다. (9-186) 식에서 흔적계산을 하면, 이 식의 마지막 굴岭 彈 %떨에 비해서 §인자만큼 작은 항이라는 것을 알 수 있다. 여 기서는 간단한 계산을 통해서 근사 방법을 설명하는 것이 목적이므로, 이 마지막 항을 무시하고 계산하겠다. 이렇게 계산한 결과는 N 이 큰 근사법의 결과와 같아진다. (9-186) 식의 마지막 항을 무시하면, 하밀토니안 밀도의 기대값은 <3t(x ) > =숭t r h 。Q (x,x)- ft r '{0Q tr '{O 요 (9-188) 로된다. 변분 매개변수 G(x, y펴 변화에 대한 하밀토니안 밀도의 기대값 (9 -188) 의 최소값을 계산하면, 그 결과는 이 계의 바닥상태 (전공상태)의 에 너지 밀도값이 된다. 왜냐하면 여기서는 상태 범함수를 (9-152) 식의 오른 쪽이 영이 되도록 택했기 때문이다. 스피너 장이론의 경우에는 유효 포텐셜 울 계산하기 위해서 (9-152) 식의 오른쪽이 영이 아닌 상수가 되도록 택할 수 없다. 로렌츠 변환하에서 스피너처럼 변환하는 상수는 존재하지 않기 때 문이다. 따라서 스피너 장이론의 경우에도 유효 포텐셜은 스칼라 장(의 기 대값)의 함수로 계산해야 한다. 그로스-네뷰 모형에서 쉽게 생각할 수 있 는 스칼라 장은 祝#이다. 그래서 이 모형의 유효 포텐셜을 스칼라 함수 a(x)=g < 麟 )¢a(x)>= 꿍t r -y0 Q ( x,x) (9-189) 의 범함수로 계산하는 것이 편리하다. 그러기 위해서는 하밀토니안 밀도 (9-188) 을, G(x, y)의 모든 성분의 변환에 대해서 최소로 해서는 안 된다. G(x, 파의 성분 중에서 (9-189) 에 해당하는 부분은 고정하고, 그 나머지
성분의 변화에 대한
a= 6 (9-195) 가 된다는 것을 쉽게 알 수 있다. 이 결과를 (9-194) 식에 대입하고 적분 계산을 하면, 그로스대뷰 모형의 유효 포텐셜 vef f=<」 ?[#I2(M) 검皇征信 —1)] (9-196) 울 얻는다. 여기서 I2 는 I2(M)= f뽑g눕 7 로 정의되는 발산하는 적분이다. 이 결과는 N 이 큰 근사법의 결과와 일치 한다. (15) N 이 큰 근사법에서와 같이 재규격화 조건 텔 do=l (9-197) 울 요구하면, 재규격화된 유효 포텐셜은 vej j (6)= 靜나른군[阮릅니 (9- 1 98) 로 된다. 이 유효 포텐셜은 6의 값이 영이 아닌 곳에서 최소값을 갖는다. 앞에서 보인 바와 같이, 유효 포텐셜을 최소로 하는 6 의 값은 이 계의 바닥 상태 (전공상태)에 해당한다. 따라서 이것은, 이 계가 가지고 있던 6一 _6 의 변환에 대한 대칭성이 전공상태에 의해서 깨어진다는 것을 의미한다. 이 모형에서는 운동변수인 #(x) 와 ¢t (x 펴 합성연산자 (com p os it e ope r ato r ) 의 진공기대값에 의해서 대칭성이 깨어진다. 이러한 대칭성 깨어짐을 동역 학적인 대칭성 깨어짐 (dyn a m ica l sym me tr y break i n g)이라고 한다. 지금까지 몇 가지 간단한 모형들을 이용하여 가우스: 근사 방법을 설명하 였다. 이러한 계산 방법은 휘어전 공간에서의 양자 장이론이나 열평형상태 에 있지 않은 다체계의 문제들에도 연장하여 적용할 수 있고액 처원이 높
은 시공간에서의 페르미 장이론에도 적용할 수 있다. (6) [참고문헌〕 (1) R. Jac kiw , Rev. Mod. Phys . ~. 681 (1977) (2) K. Syr na nzik , N ucl. Phys . B 쁘, 1 (1981) M. Liis ch er, Nucl. Phys . B 브 52 (1985) F. C oope r and E. Mott ol a, Phys . R ev. D 프, 3114 (1987) S.- Y . Pi and M. Sam iul lah, Phy s. Rev. D 프, 3128 (1987) (3) R. Jac kiw and A. Kerman, Phys . L ett . 프 ~. 158 (1979) (4) 0. Eboli, R. Jac kiw , and S.- Y . Pi, Phys . R ev. 만 !..., 3557 (19881 S.K . Kim , W. Namg ung, K.S. Soh, and J.H . Yee, Phys . R ev. D 프 , 1853 (1988) J. G uven, B. L ieb erman, a nd C.T . Hil l, P hys . Rev. 으 프, 438 ( 1989) . 0. Eboli, S .- Y . Pi, and M. Sami ul lah, A nn. Phys . 쁘 , 102 ( 1989) . (5) A. Duncan, H. Mey e r-Ortm a ns and R. Roskie s , Phys . R ev. 펙, 3788 ( 1987) R. Floreani ni and R. Jac kiw , Phys . R ev. Q프, 2206(1988) (6) S.K . Kim, J. Yang , K.S. Soh and J.H . Yee, Phys . Rev. 브으 , 2647 ( 1989) S.K . Kim , K.S. Soh and J.H . Yee, Phys . Rev. 브~. 1345 (1990) (7) S.K . Kim , W. Namg u ng , K.S. Soh and J.H . Yee. Phy s. Rev. ~. 1209 (1990) . (8) L.D. Faddeev and A.A. Slavnov, Gau ge Fie l ds ; Intr o ductio n to Quan tu m Theory , Benja m i n/ Cummi ng s , 1 980. G. Leib b randt, R ev. Mod. P hys . 프 , 1067 (1987) . (9) R. Jac kiw , Analys i s on Infinite- D i m e nsio n al Manif old s ; Schrod ing e r Re- pre senta t io n for Qu anti ze d Fie l ds, Semi na re de Math e mati qu es Sup e rie u res, Montr ea l, Canada, 1988. (10) S.K. Kim , W. Namg ung, K.S. Soh, and J.H . Yee, Phy s. R ev. 쁘.!., 3792 (1990) S.K . Kim, W. Namg ung, K.S. Soh, and J.H . Yee, Prep rint ( 1 990)
(11) E.S.A bers and B.W. Lee, Phy s. R ep. ?_f, 1 (1973) C. ltz yk son and J.-B. Zuber, Quan tu m Fie ld Theory , McGraw-Hi ll, 1980. (12) C. Becch i, A. Rouet and R. Sto r a, Phys . Lett . 堅 344 (1974) ;Co mm. Math . Phys . 므 , 127 (1975) T. Kug o and I. Oji ma , Prog. Theor. Phys . Sup pl. 쁘, 1 (1979) ( 13) F. Coop er , S.- Y . Pi and P.N Sta n doff , P hys . Rev. 만 !, 3831 ( 1988) (14) S. C oleman, R. Jac kiw , and D. Poli tze r, Phys . Rev. 만으, 2491 (1974). (15) D.J . G ross and A. Neveu, Phy s. R ev. 만 으 , 3235 (1974) . [문제〕 1 자유 스칼라 장이론의 7(궁땅 표현을 구하고, 그 바닥상태 에너지 고유 범함수 를계산하라. 2 (9-27) 식이, 제 5 장과 제 7 장에서 설명한 자유 스칼라 장의 전파인자의 역함수에 서 시각이 같은 경우에 해당한다는 것을 보이라. 3 발생원 (9-33) 을 이용하여 페르미 장이론의 슈뢰딩거 방정식을 유도하라. 4 (9-62) 와 (9~64) 식을 증명하라. 5 (9 - 66) 식을 유도하고 이를 이용하여 (9-68) 식울 증명하라. 6 (9-64) 와 (9-68) 식의 상수 범함수 C를 계산하라. 보즈 장이론의 경우와는 달 리, 페르미 계의 상태 범함수의 공액관계가 성립하기 위해서는 특별한 계수 C 가 필요하다는 점에 유의해야 한다. 7 던칸, 마이어-오트만스와 로스키스의 표현 (9-68) 을 사용하는 경우, 공액상태의 정의식을 유도하고, 가우스 범함수의 공액을 계산하라. 8 (9-73) 과 (9-74) 로부터 (9-75) 식을 유도하고, (9-78) 식이 (9-76) 식의 해가 된다는것을보이라. 9 (9 - 82) 식의 G(x- y)가 갇은 시각에서 디락 장의 전파인자에 비례한다는 것을 보 °l 라. 10 (9-83) 식으로부터 하밀토니안 밀도 (9 ~ 84) 를 유도하라. 11 자유 전자기장의 진공상태를 쿨롱 게이지에서 계산하라.
12 (9-96) 식이 아벨리안 힉스 모형의 운동방정식이 된디는 것을 보이라. 13 (9-99) 식을 증명하고, 연산자 G 와 칭연산자 ,Pa , lia, E' 와의 교환관계를 계 산하여, G가 게이지 변환의 발생원이라는 것을 보이라. 14 (9-116) 식으로 정의된 자코비안 AAA 屈 게이지 불변임을 증명하라• 15 (9-118) 식으로부터 진공 전이진폭 (9 - 120) 을 유도하라. 16 라그란지안밀도 E= 썼荊찌 로기술되는유령 장이론의 슈뢰딩거 표현을유도하라. 또, 유령 장이론의 상태 범함수와 그 공액 사이의 관계를 찾아라. 17 라그란지안 밀도 (9-121) 로부터 하밀토니안 연산자와 장연산자들 사이의 동시 (반)교환관계를 구하고, 슈뢰딩거 방정식을 유도하라. 18 게이지 고정조건 (9-111) 이 문제 17 에서 얻은 동시 교환관계와 모순이 된다는 것을증명하라. 19 BRS 변환 (9-123) 에 대하여 라그란지안 (9-121) 이 불변이라는 사실로부터 보존되는 BRS 전류 JB µ를 유도하고, BRS 전하 QB E (2-11) 식에 의해서 변환 식 (9-123) 을 준다는 것을 보이라. 20 BRS 불변조건 (9-126) 이 Gup ta- Bleuler 조건 < 1[f 18g 1 서1Jf >=O 과 동등하 다는것을보이라. 21 (9-122) 와 (9-131) 식이, a=O=b 일 때, 바일 게이지의 경우와 동등하게 된다 는 것울 보이라. 이 경우 가우쓰? 법칙 구속 조건은 어떻게 얻어지는가? 22 (9-142) 식의 상태 벡터 |土,t >s 가 (9-143) 식을 만족한다는 것을 증명하라. 23 (9-139) 와 (9-147) 식으로부터 (9-148) 식을 유도하라. 24 위치 에너지가 V( Q)국(J) 2 Q 2 국Q 4 인 경우, (9-162) 식을 풀어서 가우스 유효 포텐셜을 구하라. 25 스칼라 섬이론의 가우스 유효 포텐셜 (9-179) 에서 자발적인 대칭성 깨어짐이 일어나는 경우가 있는가? 또, 이 유효 포텐셜이 의미가 있는 것은 어떤 영역에 서인가?
26 (9-184) 와 (9-186) 식을 유도하라. 27 (9-186) 식의 마지막 항을 무시하지 않는 경우, 가우스 유효 포텐셜을 계산하 라. 28 재규격화 조건 (9-197) 은 어떤 근거에서 요구한 것인가? 이 모형을 디론 방법 으로 재규격화하여도 (9-198) 과 같은 결과를 얻는가?
제 10 장 양자 장이론의 확장 지금까지 전통적인 양자장이론의 개념과그이론적인구조에 대하여, 그 리고 이들을 이용하여 어떻게 물리계를 기술하고 미래의 물리계에 관한 예 측을 하는가에 대하여 설명하였다. 이러한 양자 칭이론의 체계는 슈빙거의 작용원리 8< x,a2lx',a, > = i< x,a2l81~•d4x!l (x) lx',a, > 151 = i< x,a2IG( 야)_ G(6I)|x',6I > (10-1) 로 요약할 수 있다. 여기서 61 과 야는 서로 다른 공간 같은 곡면 (sp ac e-li ke s urface) 을 나타내는 매개변수(이것을 시간이라고 불렀다)이며, 이 식은 한 곡면 (한 순간)에서의 계의 상태는 그 순간의 독립된 물리량들의 값(또는 독립된 장연산지들의 고유값 x' 과 x ）에 의해서 완전히 결정된다 는 것을 뜻한다. * 따라서 한순간의 계의 상태가주어지면 다른순간에서의 계 *제 2 장과 제 3 장에서 설명한 바와 같이 연산자 x 는 장연산자와 그 표준공액 모두를 포함하며, 이 작용원리는 하밀톤 방식을 사용한 것이기 때문에 운동 방정식은 시간에 대한 1- 계 미분방정식으로 표현된다.
의 상태는 작용원리나 운동방정식에 의해서 결정된다. 이것은 물리계의 물리적인 정보가 한 공간-같은 곡면에서 다음 공 간같은 곡면으로 그에 수직인 방향 (6 방향)인 시간-같은 방향(ti me -like di rec ti on) 으로 진행 (evolu ti on) 한디는 것을 뜻하며 , 이 시간에 따른 진행을 결정하는 것이 작용원리나 운동방정식이다. 물리계의 물리적인 정 보가 시간 방향으로 진행한디는 것은, 제 1 칭에서 설명한 바와 같이, 양자 장이론뿐만 아니라 모든 물리학에서 받아들이는 자연현상의 기술 방법이 다. 이 장에서는 자연현상을 기술하는 이러한 방법이 바꿀 수 있는 여러 가지 가능한 사고방식 중 하나인지, 아니면 바꿀 수 없는 자연현상의 근본적인 성질인지에 대해서 생각해 보겠다. 그리고 양자 칭이론의 개념과 계산 방법 울 이용하여 지금까지 다루지 않았던 물리계를 기술할 수 있는지에 대해서 도 생각해 보겠다. 이 중에서 특히 양자 장이론을 이용하여 통계역학적인 다체계를 기술하는 방법을 자세히 설명하겠다. 이렇게 양자 장이론의 개념 과 계산 방법을 확장하려고 하는 것은, 보다 넓은 범위의 자연현상들을 합 리적이고 논리적인 방법으로 기술하려는 목적과 함께, 양자 장이론의 확장 과정에서 생기는 문제들을 조사함으로써 양자 징이론과 지금까지 가지고 있 었던 물리적인 개념들에 대한 안목을 넓히려는 데 의미가 있다. 양자 장이론의 개념과 방법을 확장하려는 시도 중에 휘어진 공간 (curved s p ace) 에서의 양자 장이론과 중력의 양자론(q uan t um the ory of g r avity)이 있다. 이러한 시도가 아직 완성되지 않았고, 또 완전히 체계적인 계산 방법 을 얻어내지는 못했지만, 자연현상을 이해하기 위해서 지금까지 도입한 여 러 가지 물리적인 개념들에 대한 안목을 넓혀 준다는 점에서 특히 중요하 다. 그러나 이러한 과제를 설명하는 데는 수학적인 언어를 도입하는 데 많 은 지면을 필요로 하기 때문에 여기서는 다루지 않겠다.
l0. l 양자화방법의변형 지금까지 설명한 양자 장이론의 기술 방법에서는 공간 갇은 곡면
표면이 x 도 (x1) 나 (x2 )2 +(x3)2+(x4 )2 =R2 (10-3) 으로 표현되는 4- 차원 유클리드 공간에서의 공의 표면이 되며, 이 표 면에 수직인 xµ- 방향은 이 공의 반경 방향이 된다. 따라서 이 양자 화 표면의 각 점에서의 시간 방향이 서로 다르다는 점에 유의해야 한다. 양자화 표면을 이렇게 택하면, 양자적인 작용원리를 나타내는 (10-1) 식은 8
로 기술된다. 따라서 x2=R2 을 양자화 표면으로 택하는 양자화 방법 에서 시간’’의 변화를 유도하는 발생원은 GR = —fd 6µ X ,. ,Tµ110R {10-7) =-DoR 로 쓸 수 있다• 여기서 연산자 D 는 D= f도 Tµv (10-8) 로 정의되는 팽창연산자 (d il a t a ti ono p era t or) 이다. 이것은 (10-6) 식으로 표현되는 변환이 4 차원 시공간의 척도 (scale) 를 바꾸는 변환이기 때문에 붙인 이름이다. (10-7) 과 (2-9) 식을 이용하면, 상태 벡터의 ‘‘시간”에 따른 변화는미분방정식 8<1=-i< ID8R 혹은 훑
에서 R 의 크기를 바꾸는 방향으로 진행한다는 것을 의미하며 , 이러한 변환 은 4- 차원 시공간의 척도 (scale) 를 바꾸는 변환과 일치한디는 것을 보았다. 따라서 운동방정식 (10-10) 은 시공간의 척도를 바꿀 때 물리계의 상태가 어떻게 반응하는가를 결정하는 방정식이다. 그래서 물리계가 척도의 변환 (scale tr ans fo rma ti on) 에 대해서 불변이 아니면 팽창연산자 D 는 보존되지 않으며, 이것은 시간 방향으로 양자화하는 경우 하밀토니안이 보존되지 않 는 경우와 비슷한 경우이다. 라그란지안에 물리적인 차원을 갖는 질량과 같 은 매개변수들이 나타나는 경우 팽창연산자는 보존(“시간’’ R 에 대해서)되 지 않는다. 또, 이러한 매개변수가 없는 장이론에서도 척도변환에 대한 불 변성이 양자적인 효과에 의해서 깨어지는 것이 보통이다. 따라서 갔 =R2 울 양자화 표면으로 택하여 양자화하는 방법은 일반적으로 편리한 방법은 아니며, 척도 변환에 따른 물리계의 반응이나 이를 이용하여 양자 장이론의 이론적인 구조를 이해하는 데는 편리하게 이용될 수 있다 .(I) 양자화 표면 갔 =R 저 공간 같은 표면이기 때문에, 이 양자화 방법은 앞에서 설명한 작 용원리를 모순이 없이 적용할 수 있을 뿐만 아니라 상대론적인 인과율과도 모순이 없다. 양자 장이론의 문제를 푼다는 것은 가능한 모든 그린 함수를 완전히 결정 하는 것이다. 따라서 그린 함수들을 완전히 결정할 수 있다면, 초기 조건을 부과하는 표면을 임의로 택할 수 있다고 주장할 수도 있다. 국단적인 예로 시간―같은 표면 (tim e-lik e s urf ace) 을 양자화 표면으로 택하고, 물리계의 전행 방향은 그에 수직인 공간 같은 방향으로 정해서, 운동방정식’’이 공간 변수에 대한 미분방정식으로 표현되는 경우를 생각해 보자. 그러나 이러한 기술 방법은 상대론적인 인과율과 모순이 된다. 왜냐하면 시간 같은 간격으 로 떨어진 두 점 사이에는 물리적인 정보의 교환이 가능하고, 따라서 이들 두 접에서 정의된 장함수는 서로 독립된 자유도를 뜻하지 않기 때문에 초기 조건을 시간 같은 곡면의 모든 점에 부과한다는 것은 무의미하기 때문이다. 반면에 공간 갇은 간격으로 떨어전 두 점 사이에는 물리적인 정보의 교환이
불가능하기 때문에 (빛보다 빠른 입자가 존재하지 않으면), 이들 사이의 관계를 운동방정식 ’ ’이 결정한다고 생각하는 것은 잘못이다. 상대론적인 인 과율은 지금까지 알려진 실험결과와 모순이 없기 때문에, 시간 같은 곡면을 양자화 표면으로 택하는 것은 옳지 않은 일이다. 따라서 양자화 표면을 랙 하는 일이 자유로운 것은 아니라는 것을 알 수 있다. 이런 점에서 문제가 될 수 있는 경우가 빛 같은 표면 (ligh t- like s urf ace) 을 양자화 표면으로 택 하는 경우이다 .(2) 4- 차원 시공간에서의 위치를 좌표 갔= (x+, x1 , x2, x-) 균=吉 (x 난 xo) {10-11) 롤 사용하여 기술하는 방법을 광원뿔 좌표계 (ligh t- c one coor di na t es) 라고 한다. 이 좌표계에서의 거 리 텐서 (metr i c t ensor) 는 (0|00\01O1 01O\ 00,l_ 00 0) 距 = (10-12) 이며, 따라서 두 벡터 사이의 스칼라 곱은 x2= x 따= 갔gµ vXv= zx+x-+ (x1) 사 (갔 )2 으로 정의된다. 이 좌표계에서 E= 상수인 표면을 양자화 표면으로 택하 여, 변수 x+ 를 ‘‘시간으로 취급하는 양자화 방법을 광원뿔 양자화 (ligh t- c one qu anti za ti on ) 라고 한다. 광원뿔 양자화 방법의 문제를 쉽게 이해하기 위해서 2- 차원 시공간에서 의 자유 스칼라 장이론을 생각하겠다. 2- 차원 광원뿔 좌표계는 x±= 士났士 xo) (10-13)
로 정의할 수 있다• 이 좌표계에서 거리 텐서는 gµIJ=< 。1 ) (10-14) 이며, 두 벡터 사이의 스칼라 곱은 x2=2x+x- 로 정의된다. 2- 차원 자유 스칼라 장이론의 라그란지안은 fl= 一 ¢µ탸+송¢µ¢µ_뿔후 (10-15) 으로 쓸 수 있다. 이 계의 장방정식은 ¢µ=aµ¢ (10-16) —a µ¢µ+m2 ¢ =0 이라는 것을 쉽게 보일 수 있다. 변수 i를 “시간으로 택했기 때문에, (10-16) 의 장방정식 중에서 운동방정식은 ¢-=a-¢= 나=훑¢ (10- 1 7) —a +¢+-i}_
_#¢+m2¢= 一 2o+a-¢+m2¢=0 (10-19) 에서 더욱 확실히 나타난다. (10-19) 식은 “시간’’ 갑에 대한 1- 계 미분방정 식이기 때문에, 보통 양자화 방법 (conventi on al q uan ti za ti onme th od) 에서 시간 t 에 대한 2- 계 미분방정식으로 기술되는 경우에 바해서 자유도가 반 으로 줄어든다는 것을 의미한다. 광원뿔 양자화 방법을 사용하여 계산한 물리계의 자유도가 보통 양자화 방법으로 기술한 경우의 반이 된다는 사실은 장연산자의 변화를 유도하는 발생원에서도 나타난다. 죽, 장연산자의 변화를 기술하는 발생원은 (10 -15) 식으로부터 G= 士Jd x-( ― ¢畜>+ 써+¢) 라는 것을 알 수 있다. 그런데 장연산자 ¢와 ¢+는 (10-18) 식으로 구속되 어 있으므로, 이 발생원은 G=- fd x-( 나)써 (10- 2 0) 로 쓸 수 있다. 이 발생원과 (2-11) 식을 이용하면, 장연산자 사이의 동일 갔교환관계 [ r/> (x), r/> (x')] x+=x+ ' ＝뉴 (x- -x-') ( 10-21) 울 얻는다. 여기서 e( 자는 x 의 부호를 나타내는 계단함수 (st e pfun c ti on) 이 다. t=싱수 인 표면을 양자화 표면으로 택하는 보통 양자화 방법에서는, 동시 교환관계 [r/>, r/> ]xo = xa· 과 [7C, r/> ]xa=xa · 은 서로 독립된 조건이었다. 그러 나 광원뿔 양자화의 경우에는 연산자 ¢의 운동량공액이 7[~ =-¢+=-a-rt> (10-22} 이기 때문에, 이들두교환관계가
[;r/x ),¢(x')]x+ = x•· = — a _[¢(x),¢(x')]x+ = x+' 으로 구속되어 있다. 이 결과 역시 광원뿔 양자화한 물리계의 자유도가 보 동 경우의 반이라는 사실을 의미한다. 따라서 광원뿔 양자화를 상대론적인 인과율과 모순 없이 수행할 수 있다 하더라도, 그 결과는 t=상수인 표면 울 양자화 표면으로 택한 결과와 일치할 수 없다는 것을 알 수 있다. 이 사 실은 제@。닝]서 풀었던 벡터 메존 모형을 광원뿔 양자화하여 그 결과를 비 교하면 확인할 수 있다. (2) 광원뿔 양자화 방법에서 이러한 문제가 생기는 근본적인 이유를- 이해하기 위해서, 빛-같은·표면을 양자화 표면으로 택할 때 그린 함수들을 모순 없 이 결정할 수 있는지에 대해서 생각해 보자. 앞 장들에서 설명한 바와 같 이, 인과적인 그린 함수들을 모두 알면 그 계의 물리적인 정보를 완전히 알 수가 있다. 그런데 지유 장이론의 경우에는 모든 인과적인 그린 함수들은 2 정함수의 곱으로 표현할 수 있다. 따라서 자유 장이론의 경우, 2- 점함수 만 결정하면 계에 관한 모든 물리적인 정보가 결정된다. 그런데 인과적인 그린 함수는 교환관계로 정의한 그린 함수 G(x-x')= < Ol [ ¢(x), ¢(x')] IO > = < Ol ¢(x) ¢(x')— ¢ (x') ¢(x) IO > (10-23) 와 해석적으로 연결되어 (analyt ica lly conti nu ed) 있기 때문에 , 그린 함수 G(x) 만 결정되면 계에 관한 모든 것이 결정된다. 그래서 이 교환관계로 정 의한 그린 함수 G( 짜를 결정하는 방법에 대해서 생각하겠다. 장방정식 (10-19) 를 이용하면 그린 함수 G(xR 운동방정식 ( —짱 + m2) G(x)= O {10- 2 4) 울 만족한다는 것을 쉽게 보일 수 있다. t=상수인 표면을 양자화 표면으 로 택하는 경우, 그린 함수 G 는 동시 교환관계에 의해서 초기 조건 G(x)lxa=o=
훑 G(x)l x•= o= < OI[ ¢(x) , ¢(0)]xa= ol 0 > = —io( x) (10- 2 5) 를 만족한다. 따라서 양자 칭이론에서 그린 함수를 결정한다는 것은 표준 교환관계를 초기 조건으로 하여 운동방정식 (10-24) 의 해를 구하는 것과 같다. 만일 이 계를 광원뿔 양자화 방법을 사용하여 계산한다면, 그 초기 조건은 (10 - 21) 식에 의해서 G(x)lr = o 국紅) (10-26) 가 된다. 앞에서 지적한 바와 같이, 운동량공액 T 와 장연산자 ¢ 사이의 동일-갔 교환관계는 (10 - 26) 식과 같은 조건을 준다. 따라서 보통 양자화 방법에서는 두 개의 초기 조건 (10-25) 를 만족하는 t에 대한 2- 계 미분방 정식 (10 - 24) 를 푸는 것이고, 광원뿔 양자화 방법에서는 하나의 초기 조건 (10-26) 을 만족하는 x + 에 대한 1 - 계 미분방정식 (10-24) 를 푸는 것으로 된다 . 계산울 간단히 하기 위해서 질량이 없는 경우를 생각하겠다. 질량이 영인 경우 방정식 (10-24) 는 (-爵 +o;)G( t ,x)=O (10-27) 혹은 2o+o-G(x+ ,x -)=0 (10-28) 로 쓸 수 있다. 이들 방정식의 가장 일반적인 해는 G(x)=f (x + )+ g ( x-) (10-29) =信 ={x+ t})+丑 ={x- t}) 로 쓸 수 있으며 , 여기서 I 와 g는 임의의 함수이다. (10-27) 식과 (10 -28) 식은 단순한 변수변환의 관계에 있기 때문에, 이 단계에서는 양자화
방법의 차이는 구별되지 않는다. 앞에서 지적한 바와 같이 , 그린 함수를 결 정하는 과정에서 나타나는 양자화 방법의 차이는 초기 조건을 어떤 표면에 서 부과하느냐의 차이로 나타나기 때문이다. 파동방정식 (10-27) 혹은 (10-28) 은 소위 쌍곡형방정식 (hy pe rboli c eq ua ti on) 이라고 불리는 편미분방정식에 속한다. 쌍곡형방정식의 해를 유일 하게 결정하기 위해서는, 이 방정식의 모든 가능한 특성곡선 (characte r i s- ti cs) 을 자르는 열린 표면 (op en su rf ace) 에 서 코쉬 경 계 조건 (Cauchy boundary cond iti on)정 부과해야 한다. (3) 이 파동방정식의 특성곡선은
*코쉬 경계조건이란 경계면에서 파동함수의 값과, 그 기울기의 면에 수직인 성분값을 주는 조건이다.
x 도상수 (10-30) x- ＝상수 의 두 가지이다. 2- 차원 시공간에서 x0= t =O 인 직선은 (10-30) 식으로 표 현되는 모든 가능한 특성곡선을 자르는 열린 직선이다. 따라서 x0=0 인 표 면에서 그린 함수 G 의 값과 룹戶의 값울 주는 경계조건은 파동방정식 (10 -27) 혹은 (10-28) 의 해를 유일하게 결정한다. 죽, 경계조건 (10-25) 는 (10-29) 식의 I 와 g를 유일하게 결정하여 그린 함수 G( t ,x 潘· 완전히 결 정한다. 이것은, 따라서 t=상수 인 표면을 양자화 표면으로 택하는 경우 에는 ' 교환관계로 정의되는 그린 함수 G(x 遷- 유일하게 결정할 수 있디는 것을의미한다. 그러나 경계조건 (10-26) 과 같이 갔 =0 인 직선 위에서 경계조건을 부과 하면, 이 경계면은 (10-30) 식으로 표현되는 특성곡선 중에서 x- ＝상수인 곡선들만 자르기 때문에, 파동방정식의 해롤 유일하게 결정할 수 없다. 경 계조건 (10-26) 은 (10 - 29) 식의 g는 유일하게 결정하지만, f는 결정할 수 없어서 f는 임의의 함수로 남게 된다. 따라서 광원뿔 양자화 방법에서는 그린 함수 (10-29) 를 유일하게 결정
하는 데 문제가 있다는 것을 알 수 있다. 양자 장이론들 중에는 경계조건 (10-26) 이 결정할 수 없는 부분을, 무한대인 접에서의 장연산자의 성질이나 에너지국문동량이 유한해야 한다는 성질, 혹은 양자 장이론이 국소적인 장이론(l ocal fi eld th eo ry) 이 되어야 한다는 등의 조건을 사용하여, 결정할 수 있는 경우가 있다. 2 -차원 시공간에서 질량이 영인 스칼라 장이론이나 디락 장이론의 경우에는, 이러한 조건들을 사용하여 그린 함수를 유일하게 결정할 수 있고, 따라서 광원뿔 양자화 과정울 모순 없이 수행할 수 있다는 것을 보일 수 있다. (2) 이러한 경우에는 위에서 설명한 조건들을 사용하여 (10-29) 식의 f를 영으 로 만들 수 있는 경우이다. 따라서 이러한 장이론을 광원뿔 양자화하여 계 산한 결과는, t=O 인 면을 양자화 표면으로 덱하여 계산한 결과에 비하 여, 그 지유도가 반으로 줄어든 경우에 해당한다는 사실을 이해할 수 있다. 질량이 영이 아닌 2- 차원 모형이나 3- 차원 이상에서의 장이론의 경우에 도, 운동방정식 (10-24) 의 유일한 해를 결정하기 위한 경계조건의 성질 (모 든 특성곡선을 끊는 경계면에서 코쉬 경계조건을 부과해야 한다)에는 변함 이 없다. 그러나 이 경우에는 (10-29) 식의 f와 g에 해당하는 함수들 사이 에 구속 조건이 존재해서, 그 중 하나를 영으로 만들 수 없게 된다. 그래서 방정식 (10-24) 의 해를 유일하게 결정할 수 없게 되는 문제에 부딛치게 된 다. 실제로 에너지웁븀링: 텐서 TµU 가 그 흔적이 영아 되는 조건, Tµµ=O 울 만족하여 척도변환에 대하여 불변인 경우를 제의하고는, 그렇지 않은 모 든 장이론을 광원뿔 양자화하면 로렌츠 불변성을 깨뜨리게 된다는 것을 증 명할 수 있다. (2) 질량이 없는 2- 차원 스칼라 장이론이나 질량이 없는 디락 장이론은 척도변환에 대하여 불변이기 때문에, 위에서 설명한 바와 같이, 광원뿔 양자화 방법을 모순 없이 적용할 수 있었다. 그러나 그렇지 않은 장 이론을 광원뿔 양자화하면, 상대론적인 불변성과 모순이 되는 문제를 가지 게 된다. 이것이 바로 앞에서 지적한, 양자화 표면을 공간一같은 표면으로
택하지 않을 때 생기는, 상대론적인 인과율과의 모순으로 인한 문제의 다른 표현이다. 따라서 양자화 표면을 택하는 일이 완전히 자유로운 것은 아니라는 것을 알 수 있다. 공간-감은 곡면 a= 상수인 표면에 초기 조건을 부과하고 그 에 수칙인 방향으로의 물리계의 진행은 운동방정식이 결정한다고 기술하는 것이, 관습에 의한 우리들의 한 가지 사고방식에 불과한 것처럼 보일 수도 있지만, 이것은 실제로 자연에서 일어나는 물리현상을 기초로 하여 얻은 상 대론적인 인과율의 필연적인 결과라는 것을 알 수 있다. 게이지 이론을 양자화할 때 게아지 자유도를 제거하기 위하여 사용하는 게이지 고정 조건 중에 광원뿔 게이지 (lig h t -cone g au g e) 라는 것이 있다. 이것은 게이지 포텐셜 A 적 성분에 A+(x)=A-(x)= 숭因 Ao)=O (10-31) 의 조건을 부과하여 게이지 자유도를 제거하려는 방법이다. t=상수인 표 면을 양자화 표면으로 택하여 양자화하면서 이 게이지 조건을 사용하면, 앞 에서 이야기한 광원뿔 양자화 방법 때문에 생기는 문제는 일어나지 않는다. 그러나 이 게이지는 축방향 게이지 (ax i al g au g e) 의 일종이기 때문에, 축방 향 게이지가 갖는 어려운 문제를 가지게 될 가능성이 있어서 주의를 요하는 게이지이다 .(4) 10.2 유한온도에서의 양자 장이론 이 절에서는 양자 장이론의 계산 방법을 이용하여 열역학적인 평형상태에 있는 다체계의 물리량이나 그린 함수 또는 그린 발생원을 계산하는 방법들 울 소개하겠다. 이러한 계산 방법들을 유한온도에서의 양자 장이론이라고 부른다. 열평형상태에 있는 다체계에 관해서 우리가 관심을 갖는 양은
Z= Tre-PH (10- 32 ) 로 정의되는 분배함수(p a rtiti on fun c ti on) 나 연산자들의 시간국포 1 곱의 앙 상블 평균 (ensenbleavera g e) 값으로 정의되는 통계역학적인 그린 함수 또는 열역학적인 그린 함수 Gi x1 ,X2,… X n)= z-1 Tr[e-/JH T(¢(x1)¢(x2)… ¢ ,(xn))] (10-33) 이다. 여기서 /3= 1/kT, 岭근 볼츠만 상수 (Bol tz mann consta n t) , T 는 절 대온도이며, H는 이 계의 전체 하밀토니안 연산자이다. 이러한 통계역학 적인 양을 계산하는 방법들은 크게 두 가지로 나눌 수 있다. 이들을 각각 허수시간 방법 (im ag ina ry time fo rmal i sm) 과 실수시간 방법 (real time for- mal i sm) 이라고 부른다. 여기서는 역사적인 순서를 따라서 허수시간 방법을 먼저 이야기하고, 실수시간 방법을 소개한 다음, 열역학적인 평형상태에 있지 않은 다체계를 양자 장이론의 방법을 사용하여 기술하려는 시도에 대 해서 언급하겠다. (가) 허수시간방법 양자 장이론의 계산 방법을 사용하여 열역학적인 평형상태에 있는 다체계 의 문제를 다룰 수 있는 것은, 통계역학에서의 볼츠만 인자 (Bol tz mann fac to r ) e-PH 와 양자적인 계의 시간진행연산자(tim e evoluti on ope r ato r ) e- i H t가 비슷한 형태를 가지며, 이들 두 연산자 사이를 매개변수의 변환으 로 연결할 수 있기 때문이다• 시각 t=O 에서의 양자적인 상태를 시각 t 에 서의 양자적인 상태로 변환하는 시간전행연산자 I lJJ(t) >= e-iH t l 阿 (O) > 는, 시간 t를허수시간 t=一t.g (10-34) 로 변환하면, 볼츠만 인자와 같은 모양을 갖게 된다. 이러한 변환 관계를
이용하면, 양자 장이론의 계산 방법을 사용하여 물리량들의 통계역학적인 평균값을 계산할 수 있다. (5) 이러한 계산울 체계적으로 수행하기 위해서, 제 7 장에서 설명한 양자 장이론의 경로적분 표현을 사용하는 것이 편리하 다 .(6) 열역학적인 물리량들의 체계적인 계산 방법을 찾기 위해서 하밀토니안 밀 도 :K=:K(¢,찌 (10-35) 로 기술되는 물리계를 생각하자. 여기서 T( (x, t)는 장연산자 ¢(x ,t)의 운동 량광객이다. 상태 |
와 l 을 시각 t =O 에서 장연산자 ¢(x, t펴 고유 AJ 태 ¢(x,O)lrpo >=
룰 생각하고, 변수 r 에 대한 미분기호를 仁弦8r 로 정하겠다. 이러한 변환하에서 (10-37) 식은 < p I|e-'H1
=N j釋'iJ} 7C eft dr f d3 x[in :;-미 (10-39) 로 된다. (10-39) 식의 왼쪽은 볼츠만 인자의 행렬요소이므로, 이 행렬의 흔적 (tr ace) 을 계산하면 분배함수를 얻는다 ; Z= Tre-/JH =2< p|e -/JH l< p> ¢’ =N/ 미軒 e ft dr J d•x[ in:; - 미 (10-40) 주기적, 여기서 함수적분 표현을 사용하여 흔적을 계산한다는 것은 구간 Osrsf] 에서 모든 가능한 주기함수 ¢에 대하여 함수적분한다는 것을 의미한다. 보 통 양자 장이론에서는 하밀토니안 밀도 #는 운동량공액 7[의 2- 차함수이 다. 따라서 r 에 대한 함수적분을 계산하면, 분배함수는 Z= Tre 대 =Nf , ;,.7] :,j?
원은 Zp [J]=싸 탸 e fg dr f d3x(' 다 )+,(x)/ (X )] (10-42) 주 기져. 로 쓸 수 있다. 이 발생원이 결정하는 그린 함수에서 시간담근서 곱은 변수 r 에 대한 순서곱으로 된다 . 따라서 라그란지안 오로 기술되며 온도 T 에서 열역학적인 평형상태에 있는 물리계에 관한 모든 열역학적인 정보는 발생원 (10 - 42) 로부터 얻어낼 수 있다. 그린 발생원이나 그린 함수를 닫힌 형태로 풀 수 없는 경우에는, 제昞}의 방법들을 사용하여, (10 - 42) 식으로부터 근 사적인 계산을 할 수 있다. (10-42) 식으로부터 열역학적인 그린함수의 근사적인 계산 방법을 얻어내 기 위해서는, 이 그린 발생원과 온도가 영인 경우의 발생원 z。 [J] =NJ @¢ e if d 안 (어봅 ) +jl (X ) /(X ) ) (10- 4 3) 와의 몇 가지 차이점에 유의해야 한다. 발생원 {10-42) 는 변수변환 (10 -38) 에 의해서 유클리드 공간에서 표현한 발생원으로 되었으며 , 시간변수 r 의 영역이 유한하다. 또 한 가지 차이점은 (10 - 42) 식의 함수적분이 r 의 영역 O~r~ /3에서 주기함수인 모든 가능한 ¢(x) 에 대한 적분이러는 점이 다. 이러한 조건은 발생원이 발생하는 그린 함수에 반영되어 , 그린 함수의 경계조건이 달라지게 된다. 열역학적인 전파인자가 만족하는 경계조건을 얻기 위해서, 스칼라 장의 열역학적인 와이트만 함수 (W ig h tm an func tio n ) Dl （짜를 먼저 생각하겠 다. 이 그린 함수는, {10-33) 식에 의해서 Dt (x -y)= z-1 Tre-PH¢(x) ¢(y) Di ( x-y) = z-1 Tre-PH¢(y) ¢ (x) (10-44) 로 정의된다. 민코프스키 (Mi nk owski) 공간에서 양자 장연산자
(x,t) = eiH
* 이 절에서는 유클리드 공간에서의 기호를 간단하게 하기 위해서, 전파인자 D 와 S 를 제 5 장에서 정의한 전파인자에 (-i)인자를 곱해준 것으로 정의했 다.
D p (x 一y )=z-1 Tre-PHT¢(x)¢(y) ={m(x_y ) rx>ry (10-49) Dp - (x-y) Tx
Sp( x ,y) =z-1 Tre-/JH T¢(x) f(y) (10-51) 는 디락 장의 반교환관계에 의해서, 반주기적인 경계조건 s/J( x )l,=o= —S/J( x)I,=/J (10-52} 를 만족한다는 것을 보일 수 있다. 이제 시간변수 r 의 영역이 유한하다는 사실에 유의하면, 통계역학 적인 그린 함수들을 계산하기 위한 화인만 공식을 발생원 (10-42) 로 부터 유도할 수 있다. 제 8 장에서와 같은 방법을 사용하면, 온도가 영 인 경우의 화인만 공식에서 변수들을 庫点一》호 .. f高 po - i(.I)n, (.I)n =27Cn//3 (10 -53) (27r)• 성 (P1 +拓+ …)-41< z7 C)3Bw1+w2+ ... a3(p 1 +P2+ …) 로 바꾸어 주면 통계역학적인 계에 관한 화인만 공식이 된다는 것을 알 수 있다. (10-53) 석에 나타나는 허수인자 i는 유클리드 공간으로 변환할 때 나타나는 인자이다. 예를 들면, 스칼라 장이론의 통계역학 적인 화인만 전파인자 D, 는 D,(x,r) 멜f릅 e i P•x+ i wnrD,(p) Dp (p)= (J)n 2+p1 2 +m2 (10-54) 로 표현된다. 이 화인만 공식을 이용하면, 제 8 장에서와 같은 방법으로, 통계역학 적인 그린 함수들을 계산할 수 있다. 그런데 발생원 (10-42) 이나 이 로부터 얻은 화인만 공식을 사용하여 계산한 그린 함수들은 유클리드 공간에서의 그린 함수들이다. 그린 함수들로부터 물리량을 계산하기
위해서는 이들을 민코프스키 공간으로 해석적인 연장을 해야 하는데, 이 과정이 일반적으로 상당히 복잡하다. 그래서 민코프스키 그린 함 수를 계산하는 데는 이 허수시간 방법을 이용하는 것보다는 뒤에서 설명할 실수시간 방법을 사용하여 직접 계산하는 것이 더 편리하다. 그러나 유효 포텐셜은 시간에 무관한 양이기 때문에 허수시간 방법을 사용하여 계산할 수 있다. 여기서는 게이지 대칭성이 자발적으로 깨 어지는 모형을 이용하여, 통계역학적인 유효 포텐셜을 계산하는 방법 울 설명하겠다. 온도가 영인 경우와 마찬가지로, 통계역학적인 연결된 그린 발생원 은
WP[J ] =+1 tnZ p [f] (10-55) 로 정의하며, 통계역학적인 유효작용은 르장드르 변환 I'p[g]= WP[ J]-f따 (x) J (x) (10-56) 로 정의한다. 여기서 시공간에 대한 적분은 fd 4x= —t .f/Jd rf d 3x 。 를 뜻하며 , fp (x) 와 J (x) 는 온도가 영 인 경우에서와 마찬가지로 rp (x)= 뿔빈, J(x )= －醫칭 (10-57) 로 표현할 수 있다. 의부근원이 영일 때 함수 針는 휘 ,=o =Z -1 Tre-/J% (x) 三 v (10-:58 ) 로 되며, 이 양은 양자 장연산자 ¢(x) 의 앙상블 평균값이다. 대칭성 이 깨어지지 않는 장이론에서는 v=O 이며, 자발적으로 대칭성이 깨어지는 장이론에서는 v 가 영이 아닌 상수값을 갖는다. 열역학적인 유효 포텐셜은, 제 8 장에서와 같이 운동량 공간의 원점에서의 유효작 용 I'p(p; :::: 0) :::: i/3(2 7r)38(0) Vi( ~) (10-59) 로 정의한다. (10-57) 식에 의하면 革8q|) l 'l'= V ::::O (10-60) 이 된다는 것을 알 수 있고, 따라서 이 식은 i= v 인 접은 통계역학 적인 유효 포텐셜의 극점이라는 것을 의미한다. 유효작용 rP 가 발생 하는 2- 점함수는 전파인자의 역함수이므로, 유효 포텐셜의 2- 차도함 수는 뿔 l
O (10-61) 이 된다 . 이것은 ip =v 인 점이 통계역학적인 유효 포텐셜의 최소점이 라는 것을 의미한다. 제 8 장에서 설명한 바와 같이 유효작용의 고리전개 (loo p exp an sio n ) 에서 고리가 하나인 항까지의 유효작용은 I'p[ip ]=S[ ;p]+f Tr i~넓~ (10-62) 로 쓸 수 있다. 여기서 S[ 한는 고전적인 작용이며 , S 의 2- 차도함수는 전 파인자의 역함수이다. 통계역학적인 유효 포텐셜의 고리전개도 Vi= Ve+ Vii+ Vi2+ … (10-63) 로쓸수 있다. 이 식의 첫번째 항은고전적인 포텐셜이며, 고리-하나 항인 Vin?:- (10-62) 식으로부터
Vp 1= 志힌舊끊f nde t D 값 (v, p) (10-64) 로 된다는 것을 알 수 있다. 여기서 a 와 b 는 장연산자의 내부공·간 성분을 나타내는 첨자이며, de t는 이 내부공간에서의 행렬식을 의미한다. (10 -64) 식의 D-I는 고전적인 작용의 衍에 대한 2- 차도함수인데, 다음과 같이 계산할 수 있다. 즉, 장연산자 ¢(짜를 rp( x)= v+
포텐셜은 다 mv2 며 -v4 같입건틀 [~+EM2] (10-70) 으로쓸수있다. 여기서 E 갑=p z+M2 이다. 이 식에서 n 에 대한 급수는 발산한다. 그러나 f (E)=~ fn(부 미 훑 =~n~= 2/3 [½+-eJ=r] 의 관계를 이용하여 계산하면 f (E)=2 /3[운 +½tn(l — e -'E)]+Aokr (10-71) 로 되어서, 발산하는 항은 E 에 무관한 상수로 된다는 것울 알 수 있다. 이 러한 상수항은 (10-70) 식의 유효 포텐셜에도 상수로 공헌하기 때문에 무시 할 수 있다. 이 결과를 이용하여 계산하면, 유효 포텐셜의 R 에 비례하는 %達 Wl= f潟層내f n(l- e-11E )] (10-72) 으로 된다. 이 식의 첫 항은 온도가 영인 경우의 유효 포텐셜의 고리-하나 항이며, 두번째 항은 순수한 온도의 영향을 나타내는 항이다. (10-72) 식의 적분을 계산하면, 순수하게 고리-하나인 경우에만 나타날 수 있는 항과 고리가 둘 이상인 항에서도 나타날 수 있는 항〔유효 포텐셜 (10-70) 을 온도 매개변수 8 의 전개식으로 불 때〕들을 얻는다. 높은 온도 [/3-+ 0] 근사를 위한 고리-하니까지의 계산에서는 이렇게 둘 이상의 고리항
에서도 나타날 수 있는 항들은 믿을 수 없으며, 따라서 이런 항들은 버려야 한다. 높은 온도 극한에서 고리-하나인 항에서만 나타날 수 있는 항들만 택 하면, 열역학적인 유효 포텐셜은 w= -훑 -+ 2?;2 맹짜남 )v 」 v4+ 0(1//3) (10-73) 로 된다. 여기서 무시한 항들은 높은 온도 극한에서 온도에 비례하거나 그 보다 작은 항들이다. 유효 포텐셜 (10~73) 이 극값을 갖는 경우는 v=O, 혹은 #=-잇값門志) =vc2 (10-74) 아다. 열역학적인 유효 포텐셜의 2- 차 도함수를 조사하면, 온도가 쨩1 <✓尹 1= _一 ―24 Tm ―2 (10-75) 인 경우에는, 유효포텐셜은 v=O 에서 극대값을 갖고 v=vc 에서 최소값을 갖는다. 반대로 온도가 임계온도 (c ritic. al tem p er atu re ) 1/ /J c 보다 큰 경우 에는, 유효 포텐셜은 v=O 에서 최소값을 갖는다. 이것은 온도가 영일 때 깨어졌던 (m2<0 인 경우) 대칭성이 임계온도보다 높은 온도에서는, 열역학 적인 영향에 의해서 회복된다는 것을 의미한다. 계의 온도기· 영에서 임계온 도 1/ /J c 까지 증가함에 따라서, 열역학적인 유효 포텐셜 (10-73) 의 최소점 Ve= ✓永 - m2 24A/J 2 ) 는 연속적으로 영에 접근한다. 이러한 모양으로 일어나는 상전이(p hase tr ans iti on) 를 2- 차상전이 (second order ph ase tr ans iti on) 라고 한다. 지금까지 간단한 스칼라 장이론을 이용하여 통계역학적인 유효 포텐셜을 계산하는 방법을 설명하였다. 게이지 장과의 결합을 도입하여도 계산과정 이 복잡해지기는 하지만, 같은 방법으로 열역학적인 유효 포텐셜울 계산할 수 있다. 그러나 상호작용항의 모양에 따라서 상전이의 형태가 달라질 수
있다는 점에 유의해야 한다. 예를 들면 게이지 군(g aug e gr ou p)이 커지면 스킬라 장의 자체 상호작용항에 ¢3 항을 도입할 수 있다. 이러한 경우에는 상전이의 형태가 1- 차상전이 (firs t o rder pha se tr ans iti on) 로 되며, 상전이 과정에서 숨은 열 (lat e n t hea t)이 나타나게 된다 . (7) 위에서 설명한 허수시간 방법은, 시공간에 무관한 양을 계산하는 데는 편 리하지만, 그린 함수를 실제 시간의 함수로 계산하는 데는 불편하다. 시공 간의 함수인 그린 함수들을 계산하기 위해서는 실수시간 방법을 사용하는 것이 편리하다. 실수시간 방법의 이해를 위해서 먼저 연산자들의 앙상블 평 균값 (10-33) 을 직접 계산하려는 시도에 대한 설명부터 시작하겠다. (나) 실수시간방법 실수시간 방법에서 서용하는 개념들을 쉽게 이해하기 위해서 자유 스칼라 장이론의 경우를 먼저 생각하겠다. 자유 장이론의 경우에는 (10-33) 식의 앙상블 평균을 직접 계산할 수 있다 .(8) 스칼라 장연산자를 후리에 전개 (Fouri er exp an sio n ) 하면 ¢(x)= 구元닌 A(k)e i k•x+A t (k)e- i k 기 (10-76) 로 쓸 수 있으며, 이렇게 전개하면 자유 스칼라 장이론의 하밀토니안은 H= 2k ! (J)cA t ( k)A( k) 로 표현된다. 여기서는 체적이 V인 상자 안에서 양자화하였으며 k=赫 n, n=(nx,ny, nz) ; 정수 ko=( JJ=a 이며, 연산자 A t와 A는 교환관계 [A(k),At ( k')]= 8,.,,.,
[A(k),A(k')]=O= [At ( k), At (k' )] 를 만족하는 생성연산자와 파괴연산자이다. 고정된 k 의 값에 대한 자유 장 이론의 에너지 고유값은 nw 이다. 이 사실들을 이용하면, 자유 스칼라 장 이론의 모든 연산자의 앙상블 평균값을 계산할 수 있다. 예를 들면 < A t (k)A( k') >p=~ 홈 e-PE· < alA t (k)A(k')l a > a =8k,k 乞1 三 8k,k 'f( ( J}) (10-77) < A( k)A+( k) > p:::: 8k,k'[ l+! ( (J}) ]
= -t f(잡 4 e1 기 店 」 2_ 1€ + 2m8(k 사 짜)f((J))] (10-79) 로 된다는 것을 알 수 있다. 이 식은 열역학적인 전파인자가 온도가 영인 경우의 전파인자와 온도의 영향으로 나타나는 부분의 합으로 이루어져 있으 며, 온도의 영향은 순전히 전파인자의 허수 부분에만 공헌한다는 것을 보여 준다. 자유 디락 장이론의 경우에도 같은 방법으로 연산자들의 앙상블 평균값을 계산할 수 있다. 자유 디락 장의 열역학적인 전파인자는 Sp (p)= < T( 紅굽) >p(p) =— i (—,Jf+ m)[ #+ 」白€ — 2m·8 (p 2 + m2片 날司 (10-80) 로표현된다. 단순하게 생각하면, 위에서 얻은 자유장의 전파인자는 열역학적인 계를 기술하는 화인만 공식의 일부라고 생각할 수 있다. 왜냐하면 보통 화인만 공식에서 전파인자는 자유 장이론의 인과적인 2 - 점 그린 함수이기 때문이 다 . 또, 열역학적인 나무 모양 꼭지점함수(tr eeve rt ex f unc ti on) 는 온도가 영인 경우와 같다. 그래서 온도가 영인 경우의 화인만 공식에서 전파인자만 {10-79) 와 (10-80) 식으로 대치하면, 열역학적인 그린 함수를 계산하기 위 한 화인만 공식이 얻어졌다고 생각할 수 있다. 그러나 이러한 단순한 방법 으로 계산한 그린 함수는 고리가 하나인 경우까지는 옳은 결과를 주지만, 그 이상에서는 잘못된 결과를 준다*． 고리가 둘 이상인 그린 함수에는, 위 에서 얻는 단순한 화인만 공식에 의하면 f읍 [D /J (k)]n *경이우러에한 도단 있순었한다 생 (9각.3이 철 잘참조못) .되 었던 예는 온도가 영일. 때의 게아지 이론의
과 같은 항이 공헌하는데, 이 항은 [o(k2+m2)]n 모양의 항울 포함 하기 때문에, 수학적으로 정의되지 않는 양이 된다. 이러한 문제가 생기는 근본적인 이유는 볼츠만 인자 e-PH 에서 상호작용항(여기서 H 는 전체 하밀토니안이다)의 영향을 무시하고 화인만 공식을 유도했기 때문이다. 이러한 문제를 해결하는 방법에 여러 가지가 있는데, 여기 서는 경로적분 방법을 이용하여 실수시간 그린 발생원을 계산하는 방 법을 이용하여 설명하겠다. (9) 하밀토니안 H( (x,t ') = eiH
J@rp jrp,t > < rp,t l=l= f@미 1r, t > < 1r,t l 열역학적인 그린 함수 (10-33) 의 계산울 쉽게 하기 위해서 시간 t 의 영역을 복소수평면 전체로 확장하겠다. 그러면 (10-82) 와 (10-84) 식의 시간이동식은 =eiH zjr p( x), [> (10-85)
_To C1 Imt C3 T o Ret
면서 허수 부분이 감소하는 방향으로)를 주겠다. 그리고 시간순곤서 곱의 개념을 확장한 Tc 는 경로에 따른 순서곱임을 뜻한다. 이 적분경로에 따른 델타함수와계단함수를 fC dr& (r— r')f ( r )=f (r ') (10-89} &(r-f) =frdr ’'& (t - f) C 으로 정의하면, 함수미분은 罰= &(r-i ) a3(x-x') (10-90) 와 갇이 확장할 수 있다. (10-88) 식을 경로 C 에서 Tc- 순서 곱으로 정의 한 열역학적인 그린 힘수의 발생원으로 생각할 수 있다. 이 식에서 적분경 로 C를 시간의 실수축 부분으로만 한정하면 (10-87) 식으로 된다. (10-88) 식을 경로적분으로 나터내기 위해서, 시각 t =O 에서의 연산자 rp (x) 의 고유상태를 이용하여 흔적을 계산하면 Zp [f]=J@
(10-91) 로 쓸 수 있다. (10-85) 식을 이용하여 이 식의 상태 벡터를 경로 C의 끝 점으로이동하면 Zp [f] =J@
=f@
쩌 l 대하여 적분하면, 발생원은 z/ J[J]=f巧 eif cd 4 x[I f('l')+'PJI (10-97} C 로 된다. 여기서 라그란지안 밀도는 먀)=½rp (a/- m2) rp-V ( rp) 이며, 첨자 C는 시간변수의 영역을경로 C 로택했다는것을의미한다. 열 역학적인 그린 함수의 섭동론적인 계산 방법을 알아내기 위해서 {10-97) 식 을 제 5 장에서와 같은 방법으로 계산하면, z/J[J ]= e-I.Je d 4X V 出晶] e-상fc d4 y dV J(y )D/ J(y - y')/(y') (10-98} 로 된다. 여기서 열역학적인 전파인자 D lf_근 미분방정식 (ac2_ 짜 )D p( x- y)= i8c(x -y) (10-99) 룰 만족하는 경로 C 에서의 그린 함수이다. 이 전파인자는 열역학적인 와이 트만 함수 D' 별一 이용하여 Dp( x)= 0c(r)D/(x)+ 0c(-r)Df ( x) 로 쓸 수 있으며, 앞에서와 같은 방법을 사용하여 이들 와이트만 함수는 경 계조건 D/(x, r-i/3 )= D11-(x, r) (10-100) 를 만족한다는 것을 보일 수 있다 . 이들 결과를 이용하면, (10-99) 식의 해는 D,(w, r) ＝志 나 -'o [ 0c(T){e-iw r+ e-l w +iw r} 겔(- r){eiw r+ e-lw-iw r}] (10-101)
로 쓸 수 있다. 여기서 (1)＝J E 下굶히며, 이 식은 (10-99) 식의 전파인자 롤 3- 차원 공간에 대해서 후리에 변환한 것이다. 이제 T。 -oo 인 극한을 취하면 경로 C~ C.2 무한히 멀리 가게 되며 , 리만의 예비정리 (Riem ann's lemma) 에 의해서 Dp (r I,2— [3, 4)-0 으로 된다. 여기서 fi ,2 와 r3,4 는 각 구간 C;,(i =l , 2, 3, 4 ) 에서의 r 값을 나 타낸다. 따라서 발생원 ZP 는 C1 과 C2 에서의 발생원과 C 퍼- c4 에서의 발 생원의 곱으로 인수분해된다 ; Zp [J] =ZpU ; C,,C2] Zp [J ; Ca,C4) (10-102) 이 식의 오른쪽의 각 인자는 Zp (J ; C1,C2]= e-ifc ,, c ,d •x vft b1e -½1c,.cz d'Yd'y'J D p f (10-103) 와
Zp [f ; Ca,C4]= e-ifc ,,c , d •xvf¾ -'11 e-½lc,,c, d'yd• y f Dp / 로 표현된다. (10-86) 식을 사용하여 실수시간의 함수인 그린 함수를 계산 할 때, Z,[J ; C3,C4] 부분은 전혀 공헌하지 않기 때문에 규격화 상수에 포 함시킬 수 있다. 따라서 실수시간의 함수인 열역학적인 그린 함수는 발생원 Zp [J] =Zp [f; C1, C2] (10-104) 로부터 , (10-86) 식을 사용하여 계산할 수 있다. 열역학적인 그린 함수 (10-33) 을 계산하는 데는 (10-103) 식의 오른쪽 인자의 지수 부분을 새로운 기호 L. c , d4y d4 y 'J(y)D / J(y-yg)j(y’) CI , C2=LdtL dt'd 3 xd3x'Ja (x, t)D t (x -x' , t— t')Jix', t') (10-105) _OO -OO 으로 나타내는 것이 편리하다. 여기서 a,b=l,2 이며, 의부근원 Ja( x). 2} 전파인자 D ff b( 짜는 각각 ]1 (x) = J(x ) , Jz(x) = J( x, t —i( J/2 ) (10-106) 와 DD}}12((xx))==D-pD (xp )-, ( x,t+ D i/ 『3/ (2 x),) =D pD( -/x1)(,x )=-Dp + (x,t- if]/2) (10-107) 로 정의된 함수들이다. 이들 새로운 기호를 사용하여 열역학적인 그린 발생 원을나타내면 Zp [f1J 2] = e- il d•x1v~1-v 晶li e- 송f d4 y d4 Y'J aD:• Jo (10-108) =f@ rp ae ;f d 단'l' a(D;' )Db,p o -V (
(10-79) 는 이 식의 D}1 에 해당한다. 이제 열역학적인 그린 발생원 (10-108) 을 사용하여, 제昞》 ]서와 같은 방법으로 유효작용을 계산하여 물리적인 정보를 얻거나, 화인만 공식을 유 도하여 열역학적인 그린 함수들을 계산할 수 있다. 발생원 (10-108) 의 오 른쪽은 r/> 1 과 ¢2 두 개의 성분을 갖는 스칼라 장에 대한 경로적분으로 되어 있다. 그러나 (10-109) 식은 이들 두 가지 형태의 장힘수 중에서 첫번째 성 분인 r/> 1 만 그린 함수의 의부선에 나타날 수 있고, 두번째 형태의 장인 ¢2 는 내부선에서만 나타나는 유령장과 비슷한 역할을 한다는 것을 의미한다. 발생원 (10-108) 로부터 유도한 화인만 공식에는 두 가지 형태의 꼭지점함 수가 있는데, 첫번째 꼭지점은 r/> 1 장들만을 연결하며 두번째 꼭지점은 ¢2 장만을 연결한다. 그러나 전파인자에는, (10-110) 식에서 보는 바와 같이 두 가지 서로 다른 형태의 장을 연결하는 부분이 있다. 따라서 두번째 형태 의 장 ¢2 가 물리적인 그린 함수에 공헌하는 것은 고리가 둘 이상인 경우뿐 이라는 것을 알 수 있다. 앞에서, 자유 장이론의 결과를 이용하여 화인만 공식을 구성하려고 했던 단순한 방법에 문제가 있다는 접을 지적하였다. 델 타 함수의 곱을 적분해야 하기 때문에 생겼던 이러한 문제는, (10-110) 식 의 대각선이 아닌 성분들에 의해서 상쇄되기 때문에 여기서는 일어나지 않 는다 .(9) 위에서 설명한 통계역학적인 그린 발생원의 실수시간 경로적분 표현은 디 락 장이나 게이지 칭이론의 경우로 쉽게 연장할 수 있다. (9) 유한온도에서의 양자 장이론들을 재규격화하는 문제나, 이들을 이용하여 상대론적인 물리 계의 온도 영향을 계산하는 방법에 대해서는 참고문헌 11 에 자세히 다루어 져있다. 지금까지 열역학적인 평형상태에 있는 다체계의 문제를, 양자 장이론의 개념과 계산 방법을 이용하여 표현하고 계산하는 방법들을 설명하였다. 그 러나 실제 우리가 관심을 가지는 문제들에는, 우주의 전화과정에서와 같 이, 열역학적인 평형상태에 있지 않은 경우가 많이 있다. 이러한 문제를 이 해하기 위해서는 평형상태에 있지 않은 다체계를 다룰 수 있는 방법이 필요
하다. 이러한 물리계를 다루기 위해서는 루이빌 방정식 (Liou vil le e qu a ti on ) 뿔=i[p ,H] (10-111) 를 풀 수 있는 방법을 찾아야 한다. 여기서 成근, 슈뢰딩거 표현에서 파동 범함수의 완전집합을 { 1/fn } 이라 하고 계가 상태 1/fn 에 존재할 확률을 Pn 이 라할때 p [({)1 , %]=~Pn Wi晶] 합[집 (10-112) 로 정의되는 밀도행렬 (dens ity ma tri x) 이다. 그리고 H 는 이 계의 전체 하 밀토니안인데, 일반적으로 시간의 직접함수일 수도 있다. 최근 이 루이빌 방정식을, 양자적인 작용원리가 슈뢰딩거 방정식을 결정하듯이, 변분법으 로 유도할 수 있는 방법이 제안되었다. (12) 이 사실을 이용하면, 9.5 절의 방 법을 사용하여 루이빌 방정식의 변분법적인 근사해를 구할 수 있다. 〔참고문헌〕 유한온도 양자 장이론은, 그 웅용 범위가 넓다는 사실 때문에, 최근에 활발히 연구되는 분야이다. 이러한 연구 결과를 가장 폭 넓고 깊이있게 설명한 논문은 Landsman & van Wee rt <9) 로 보인다. 이 책의 허수시간 방법은 주로 Bemard(6) 와 Dol~n & J ack i w<6) 의 논문을, 그리고 실수시간 방법은 Nie mi & Semenoff< 9> 의 논문을 따라서 설명하였다. (I) S. Fubin i, A .J . Hanson, a nd R. Jac kiw , Phy s. Rev. 프 , 1732 (1973) A. diSe ssa, Jou r. M ath . Phys . 프 , 1892 (1974) C.M . Sommerf ield , Ann. Phys . (N.Y.) 쁘, 285 (1974) D. Gromes, H.J. R oth e , and B. Ste c h, Nucl. Phys . 쁘 ~ 313 (1974) (2) C.R. Hage n and J.H . Yee, Phys . Rev. 만 2 , 2789 (1976) C.R . Hage n and J.H . Yee, Phys . Rev. 만으, 1206 (1977)
C.R. Hage n , Phys . Rev. Q.브, 2605 (1981) (3) J. M ath e ws and R.L. Walker, Math e mati ca l Metl w ds of Phys i·cs , 2nded., Ben- jam i n, 1973. P.M. Morse and H. Feshbach, Metl w ds of Theoretic a l Phys ics , McGraw- Hill, 1953. (4) J. S chwin g e r , Phys . Rev. 브으, 402 (1963) Y.P . Yao, ]. Math . Phys . ~. 1319 & 1322 (1964) J.H . Yee, in Monop ole s, Soliti on s and Non-l in e ar Phenomena, ed. by H.S. Song, Mi n Eum Sa (Seoul) , 1984. (5) T. Mats u bara, Prog . T heor. Phys . ( K y o t o) 브, 351 (1955) P.C . Mart in and J. Schw ing e r , Phys . Rev 墨 1342 (1959) L.P. Kadanoff and G. Baym , Quan tu m Sta tistica l Phys i·cs , Benja m i n, 1962 (6) L. Dolan and R. Jac kiw , Phys . Rev. 쁘 , 3320 (1974) S. Wein b erg, Phys . Rev. 쁘. 3357(1974) C.W. Bernard, Phys . Rev. 쁘, 3312 (1974) (7) K.S. Vis w anath an and J.H . Yee, Phys . Rev. D 프, 1906 (1979) (8) C. lt z yk son and J.-B.Zu ber, Quan tu m Fie ld Theory , McGraw-Hi ll, 1980. (9) I. O jim a, Ann, Phy s. (N.Y), 브~. 1(1981) A.J. Nie m i and G.W . Semenoff , Ann. Phys . ( N. Y. ) , 므~. 105 (1984) N.P. Landsman and Ch. G. van Weert , Phys . R ep. C 브~ 141 (1987) (10) E.S. Abers and B.W. Lee, Phys . R ep. 안, 1 (1973). (11) J.H . Yee. Phys . Lett 141B, 411 (1984) H. Mats u moto , I. Oji ma and H. Umezawa, Ann. Phy s. (N.Y. ) , 152, 348 (1984) J.H . Yee, in Selecte d Ta pics in Theoreti ca l Phys i c s , ed. by H.S. Song, Ky o- hak, Seoul, 1987. ].I. Kapu sta , Fin i t e-T emp er tu re Fie l d Theory , Cambri dg e Univ e rsity Press, 1989 N.P. Landsman and Ch .G . van Weert , 참고문헌 9 와 이에 인용된 논문들 (12) 0. f:bo li , R. Jac kiw and S.-Y. Pi, Phys . Rev. 쁘!. .. 3557 (1988)
〔문저 1 〕 1 스칼라 장이론의 경우 작용원리 (10-4) 로부터 장연산자의 변화를 유도하는 발생 원 G’ 와 G 를 계산하라. 또, 이 결과를 이용하여 동일구퓸! 교환관계를 구하 라. 2 라그란지안 (10-15) 로부터 발생원 (10-20) 을 유도하고, 이로부터 (10-21) 식이 성립한다는 것을 보이라. 3 동계역학적인 그린 함수의 경계조건 (10-48) , (10-50) 과 (10-52) 를 증명하라. 4 (10-72) 식의 적분을 계산하여, 고리 하나까지의 유효 포텐셜이 (10-73) 으로 된 다는것을보이라. 5 자유 장이론의 열역학적인 전파인자 (i 0-79) 와 (10~80) 을 구체적으로 계산하여 보 0] 라. 6 (10-93) 식으로부터 (10-94) 식을 유도하라. 7 방정식 (10-99) 의 해가 전파인자 (10-101) 이라는 것을 보이라. 8 디락 장이론의 경우 실수시간 그린 함수를 발생하는 열역학적인 그린 발생원을 구하고, 디락 장의 열역학적인 전파인자를 (10-110) 식의 모양으로 나타내라. 9 (9.3) 절에서 설명한 유령장(g hos t fi eld) 의 열역학적인 전파인자를 구하라.
찾아보기
-l 가우스 근사법 280 가우 스 유효 포텐셜 Gaussia n eff ec - tive po te n ti al 280 각 운동량 연산자 76 게 이 지 고정 조건 ga ug e fixi n g cond i- tion 105, 253, 264 게 이 지 고정 항 ga ug e fixi n g ter m 267, 313 게 이 지 변환 ga ug e tran sfo r mati on 103, II2 게 이 지 분별성 gau g e inv ari an ce 142, 271 게이지 이상현상 159, 183 게 이 지 자유도 ga uge free dom 95, I03 게 이 지 장이 론 ga ug e field the ory 95, 253 경로적분--+ 함수적분 경로적분 양자화 163 고리전개 loop exp a nsio n 215 광원뿔 게이지 ligh t- c o ne gau g e 310 광원뿔 양자화 ligh t- c one qu anti za ti on 3°3 교환관계 24, 53, 59, 76, 93 구속방정 식 constr an int equ ati on 94, 97, 101, 103 그라스만 변수 Grassmann vari ab le 172, 242 그로스-내뷰 모형 Gross-Neveu model 287 그린 발생 원 gen er、a會 ti ng func ti on al for Green's func ti on s 120, 121, 127,
I98 그린 함수 Green's f un cti on 119, 121, I26 꼭지 접 verte x 200 L 내부 공간 int e r nal spa ce 111, 287 내부선 int e r nal line 200 E: 동시 교환관계 93, 98, IOI, 105, 234, 255, 258 동시 반교환관계 93, 106, u5, 240, 241 동역학적인 대칭성 깨어짐 dyn amica l sym me tr y breakin g 291 동역학적인 질량발생 dy namica l gen - erati on of mass 158 디 락 방정식 Dira c equ ati on 107 디 락-슈빙 거 조건 Dir ac -Schw inge r cond ition 79, 80, 85 디락 양자화 42, 61 디 락의 작용원 리 acti on principle of Dira c 232, 274, 276, 280 디 락 장이론 Dira c-fi el d the ory 95, 106, 107 디 락 행 렬 Dir ac matr ix 108, 109, 240, 241 2 라그란지 방식의 작용원리 62, 86 라그란지 안 밀도 Lag rangian densit y
65, 67 라그란지안 연산자 49, 5I 렌다우 게 이 지 Londau gau g e 268 로렌츠 게이지 Lorentz ga ug e 187, 264 로렌츠 공변 게 이 지 Lorentz covar- ian t ga ug e 264 로 렌 츠 변 환 Lorentz tran sfo r mati on 66, 68, 76, 79 로렌츠 불변성 68, 79 루이 빌 방정 식 Lio u v ille equ ati on 333 르장드르 변환 Lege ndre tran sfo r ma- tion 22, 29, 208, 277, 317 口 말안장 근사법 saddle poi n t moth o d 2I9 모함수 ge nerati ng func ti on 29 닌 바일 게이지 Wey] gau g e 257 반교환관계 53, 93, 172, 246 벡 터 메 존 모형 vecto r meson model I39, I53 벡터 장이론 vecto r field the ory 95, 100 변분법 vari at io n al meth o d 239, 274 변분원 리 va riat io n al pri n ciple 274 변환함수 43 서 4, 64 보즈-아인슈타안 동계 Bose-Ein s te i n sta t is t ie s 93 보즈 입자 53
보즈 장 Bose fiel d 93, 233 분배 함수 pa rtit ion fun cti on 3 r r BRS 불변성 BRS inv aria n ce 274 人 상호작용 표현 int e r acti on pict u r e 264 생성연산자 creati on ope r ato r 78, 246, 323 섭동론 pe rt ur bati on the ory 198 순수한 꼭지점 함수 pro p er vert ex func ti on 211, 277 슈뢰딩거 방정식 58, 83, 237, 246, 260, 269, 278, 301 슈뢰 딩 거 표현 schrodin g e r pictur e 61, 231 슈빙거 모형 schwi ng e r model 139, 182 슈빙거의 작용원리 41, 181, 276 스칼라 장이론 scalar fiel d the ory 95, 96 스피너 함수 66, 96 스핀 spi n 71, 77 시 간-순서 곱 tim e-ordered pro duct I 19, 124, 125 시간축 게이지 tem p o ral gau g e 257 실수시 간 방법 real time for malis m 311 。 아벨리안이 아닌 게이지 이론 non- Abelia n ga ug e the ory 100, 268 아벨리안 힉스 모형 Abelia n Higg's
model 254 앙상블 평균 311, 322 양자 장이론의 작용원리 64 양자적 인 작용원리 39, 41 , 50, 53 양자 전기 역 학 Qu antw n Elect rody na m ics 110, 112 에너지-운동량 보존법칙 75 에너지 - 운동량 연산자 76 n 정 함수 n-po in t func tio n 127, 203 연결된 그린발생원 205 연결된 그린함수 connecte d Green's func ti on 128, 203 오일러-라그란지 방정식 19 와이트만함수 Wi gh tm a n func tio n 127 운동방정식 17, 94, 237, 298 운동변수 dyn a mi ca l varia b le 17, 52, 94, 95 유사전류 axia l current 150, 183 유효작용 eff ec ti ve acti on 207, 209, 215, 225, 274 유효 포텐셜 eff ec ti ve po te n ti al 209, 214, 226, 276, 317 이상 anomaly 현상 153, 159 2- 차 상전 이 second-order ph ase tran - siti on 321 인과적인 그린함수 I19, 197 1- 차 상전이 firs t- o rder pha se tran si- tion 322 lP 무 one-pa rtic le irr educi bl e dia- gram 206 1PR도 표 one-pa rt icle reduc ibl e dia- gram 206
': 자발적인 대칭성 깨어짐 207 자의 발산 ultr a vi ol et sin g u la rity 226 자유도 17, 94 자체 에 너 지 self-e nergy 206 작용연산자 48, 64 장방정 식 fiel d equ ati on 73 재규격화 renomaliz a ti on 226, 286 재규격화 조건 227, 286 전이전폭 tran sit ion amp litud e 121 전자기 장이론 102 전파인자 pro p a ga t o r 129, 130, 210 진공상태 vacuum sta te 78 진공 전이전폭 121, 125 진공 지 속전폭 vacuum per sis t e n ce amp litud e 126 -K 최 급하강법 ste e pe s t descent meth o d 2I9 최 소결 합 minim al coup ling 1 n 최소 작용의 원리 I8, I8o 축방향 게 이 지 axia l gau g e 257 =J 카이 랄변환 chir al tran sfo r mati on 149, I59, 183 쿨롱 게이지 coulomb ga ug e 255 q-공간표현 57 클레인-고든 방정식 klein -G o rdon equ ati on 97
E 텐서함수 66, 96 동계역학적인 그린함수 3II 티 링 모형 Th irring model 139, 140 고: 파괴 연산자 an nihila ti on op er ato r 78, 246, 323 파디 에 프-포포프 유령 항 Faddeer- pop ov gh ost ter m 267 팽 창 연산자 dila ta t i on ope r ato r 301 페 르미 ~ 디 락 동계 Ferm i-D i ra c sta t i s- tics 94 페르미 입자 5.3 , 242 페르미 장 Ferm i fiel d 94, 172, 240 포아송 괄호 23, 6I 포인카레 군 Poin c are grou p 76, 79 포인카레 변환 7I 표준변수 canon ica l varia b le 30, 34 표준변환 canon ica l tran sfo r mati on ”' 28, 3I, 74 표준 양자화 conon ica l qua nti za ti on 42, 6I, I8I p-공간표현 57 궁 하나로운 게 이 지 unitary ga ug e 263
하나로운 변환 unit ar y tra nsfo rm a- tion 15, 43, 46, 61 하밀돈 방식의 작용원리 28, 53, 67, 268 하밀돈 방정식 23, 49 하이젠버그 운동방정식 60, 325 하이 젠 버 그 표현 Heis e nberg pictur e 61, 231, 264, 276 함수미분 func ti on al differ enti at i on 120, 236 함수미분방정식 8I, I34 함수적 도함수 fun cti on al deriv a ti ve 8I, I20 함수적 인 슈뢰 딩거 방정 식 func ti on al schrodin g e r eq u ati on 237 함수적 인 적 분 fun cti on al int e g ral I63, I72 함수적인 `후 리에 변환 fun cti on al Fourie r tran sfo r mati on 168, 176 허수시간 방법 im ag ina ry tim e for- mahsm 3II 화인만 게이지 Feyn ma n gau g e 257, 268 화인만 공식 Feyn ma n rule 200 화인만 도표 Feyn ma n diag ram 125, 200 화인만의 경로적분 양자화 pa th int e - gral qua nti za ti on of Feyn ma n 163, 178 화인만의 작용원리 178, 181, 277
01 재형 서울대학교 공과대학 응용물리학과 졸업 미국 로체스터 대학교에서 Ph.D . 받음 현재 연세대학교 물리학과 교수 논문 Abelia n Hig gs mechan ism in the Schrodin g e r pict u r e” 의 30 여 편 발표 양자 장이론 대우학술총서 • 자연과학 69 찍은날一 1991 년 4 월 5 일 펴• 낸날― 1991 년 4 월 15 일 지은이―이재형 펴낸이―朴孟浩 펴• 낸곳―民音社 출판등록 1966. 5.1 9 제1. -142 호 우편대체번호 010041-31-05232892 은행지로번호 3007783 135-120 서울 강남구 신사동 506 번지 515~2003~5( 편집부) 515~2000~2( 영업부) ©5•1 5~이2재00형7,, 211091 9(1팩 시밀리) 자연과학 • 물리학 KDC/420. 1 Print e d in Seoul, Korea 값 10,500 원
대우학술총서 자연과학 l 소립자와 계이지 상호작용 김진의 2 동력학특론 이병호 3 질소고정 송승달 4 相轉移와 임계현상 김두칠 5 촉매작용 진종식 6 외스바우어 분광학 옥항납 7 국미량원소의 영양 승정자 8 수소화붕소와 유기붕소화합물 윤능민 9 항생물질의 전합성 강석구 10 국소적형대의 Aliy a h- Si n g er 지표이론 지동표 11 Muco po l y sacchar i de 핵 생화학 및 생물리학 박준우 12 천체물리학 홍승수 13 프로스타굴라딘 합성 김성각 14 천연물화학 연구법 우원식 15 脂訪營養 김숙희 16 결정화유리 김병호 17 고분자의 화학반응 조의환 18 과학혁명 김영식 19 한국지질론장기홍 20 정보이론 한영열 21 원자핵반응론 정운혁 22 파괴역학 김상철 23 분자궤도이론 이익춘 24 반응속도론 정경훈 25 미분위상수학 이현구 26 磁器共鳴방법 조성호 27 풀라스마울리학과 핵융합 최덕인 28 천문관측과 분석 이시우 29 석탄에너지 변환기술 김상돈 30 해양微 古生物學 백광호 31 편 이분 방정식론 김종식 32 대통일이론 소광섭
